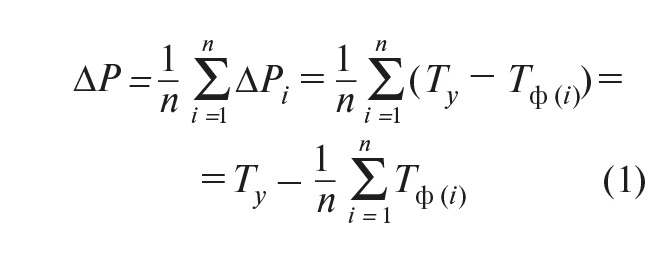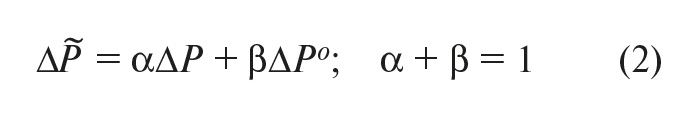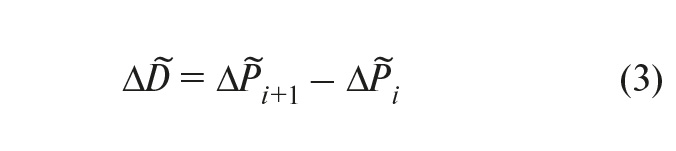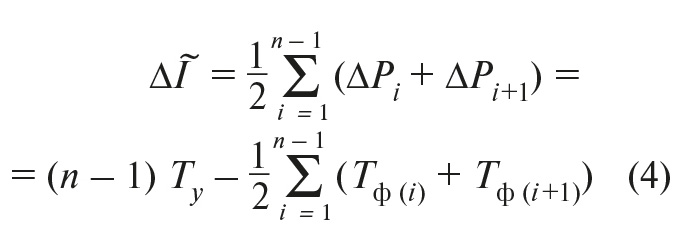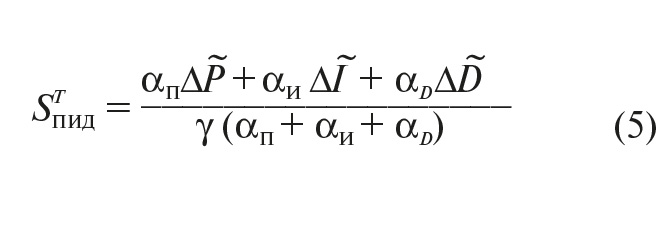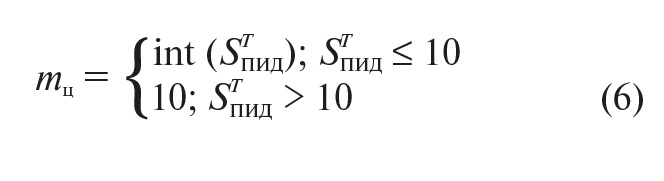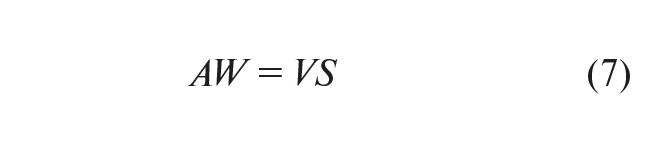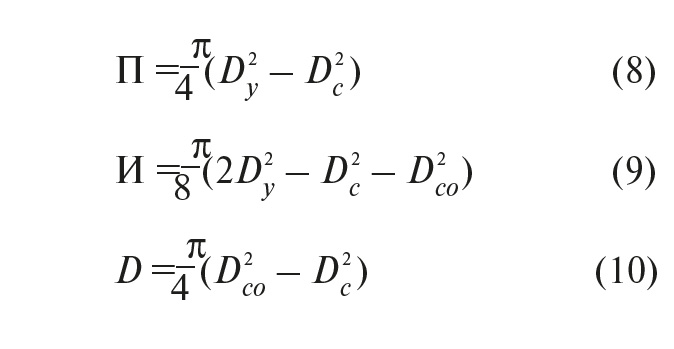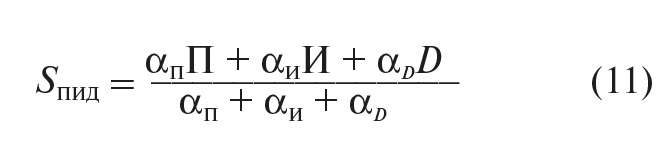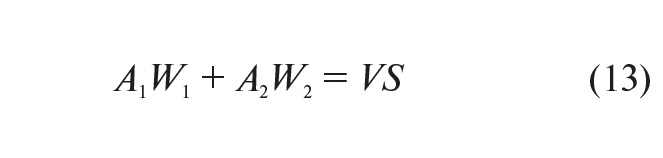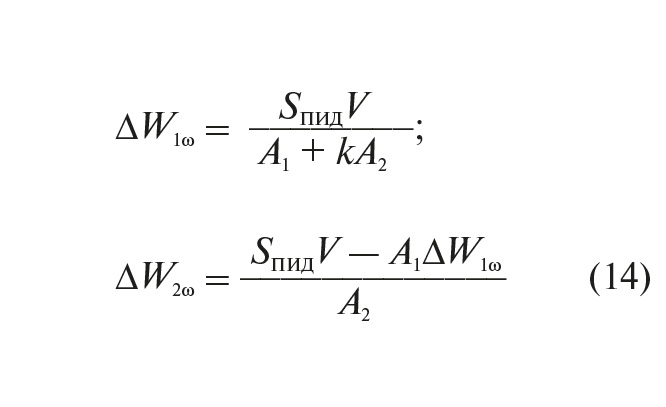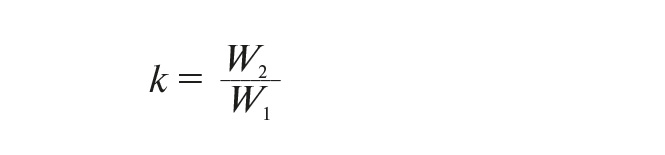Your integral $$\int_{\mathbb{R}}(\hat{f}(x,h)-f(x))^2dx$$ is a random variable because your density estimate $$\hat{f}(x,h)$$ depends on your sample. The integral above measures the quality of your estimate by integrating the square of the difference over the reals. The result is still a random number whose expectation can be calculated given that you know the common distribution of your sample.
Further Information
Let’s consider a specific example. Let $X(i), i=1,2,…n$ be a sequence of independent random variables of a common known pdf. Let the common distribution be uniform over the interval $[0,1]$. Say, $n=10$ and the actual sample is 0.2, 0.3, 0.22223, 0.89, 0.565, 0.11, 0.1222, 0.3454, 0.12, 0.0001. Now, you can calculate the density estimate based on the formula given at your reference if $h$ is given. Then you can calculate the integral in question because you know the common distribution of your samples. Then perform another experiment resulting in another $10$ sample points. You can calculate the integral again; you will get another result. If you repeat this experiment ($10$ samples each time) then the average of the results will tend to the expectation:
$$\mathbb E\left [\int_{\mathbb{R}}(\hat{f}(x,h)-f(x))^2dx \right].$$
Now, you may ask why we estimate the density if we already know it. Please, go back to your reading and see why the author does all this.
Введение
Современный рынок предъявляет высокие требования к качеству изолирования изготавливаемых кабелей. Поддержание таких параметров кабеля, как точность внешнего диаметра изоляции, овальность, эксцентриситет, электрическая и механическая прочность изоляции и другие, требует применения новаторских решений на основе передовых технологий автоматизации.
Поставляемые на российский рынок зарубежными фирмами экструзионные линии часто являются недоступными по цене для большинства отечественных производителей кабельной продукции. На предприятии ООО «Псковгеокабель» реализован ряд проектов по созданию автоматизированных систем управления экструзионными линиями собственного производства.
Назначение и функциональные возможности системы управления
Экструзионная линия предназначена для наложения на токопроводящую жилу одно- или двухслойной изоляции. Технологическая схема типовой экструзионной линии показана на рис. 1.
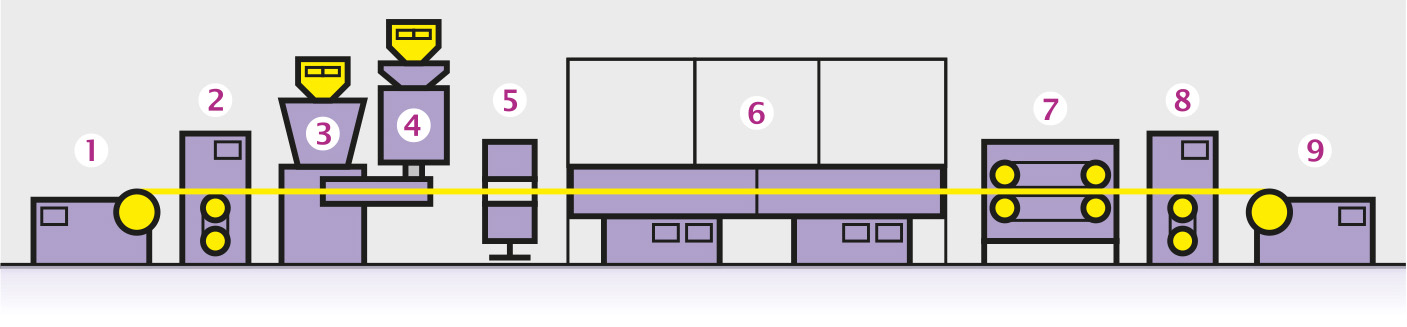
Условные обозначения:
1 — отдающее устройство; 2 — компенсатор отдающего устройства; 3 и 4 — экструдеры; 5 — измеритель диаметра; 6 — ванны охлаждения; 7 — тяговое устройство; 8 — компенсатор приёмного устройства; 9 — приёмное устройство.
К процессу изолирования предъявляются жёсткие требования по надёжности, вытекающие из того обстоятельства, что запущенная линия может быть остановлена только после завершения всей рабочей длины изготавливаемого кабеля. Остановка на промежуточной длине недопустима по причине невозможности прерывистого управления расходом пластиката, поступающего из шнека.
Система управления линией должна решать следующие основные задачи:
-
оперативный сбор информации о состоянии технологического процесса в виде цифровых и аналоговых сигналов (цифровыми, или дискретными сигналами в данном случае являются сигналы с кнопок и переключателей, индуктивных датчиков, а также сигналы готовности частотных регуляторов – рис. 2; аналоговые входные сигналы для экструзионных линий – это, как правило, сигналы термопар);
-
выдача управляющих воздействий функциональным узлам линии в цифровом и аналоговом виде (цифровые выходы системы служат для вывода дискретных сигналов управления реле, контакторами, частотными регуляторами, сигнальными приборами; через аналоговые выходы осуществляется управление заданиями частотных регуляторов исполнительных двигателей линии);
-
отображение на рабочем месте изолировщика (рис. 3) информации, позволяющей ему не только вести слежение за технологическим процессом, но и оперативно вмешиваться в него (при этом система должна обеспечивать иерархию прав доступа к изменению параметров технологического процесса);
-
обеспечение безопасности и надёжности процесса изготовления кабеля посредством блокировки недопустимых ситуаций и выдачи аварийных сообщений (тревог);
-
протоколирование в реальном времени параметров технологического процесса с последующей их обработкой и преобразованием в удобную для восприятия форму.
Кроме того, для всех экструзионных линий существуют общие технологические задачи, решение которых не обходится без систем управления:
-
поддержание в заданных технологических пределах температур зон нагрева шнеков, жилы и ванн охлаждения;
-
обеспечение целостности изготавливаемого кабеля, а также точности внешнего диаметра изоляции, его эксцентриситета и овальности в заданных пределах;
-
контроль диэлектрической прочности изоляции;
-
измерение длины изготавливаемого кабеля.
Эти задачи во многом взаимосвязаны, поэтому более подробно рассмотрим только отдельные из них.
Регулирование температуры зон нагрева шнеков
Поддержание на заданном технологическом уровне температур зон нагрева шнеков является важнейшей задачей, так как от этого зависит вязкость выдавливаемого пластиката. Если вязкость расплавленного пластиката выходит за требуемый технологический диапазон, то меняется производительность шнека и возможно возникновение разрыва наносимой изоляции. Температура зон должна находиться строго в допуске, который для отдельных материалов не превышает 2…3°С.
В реализованных нашей фирмой проектах систем управления экструзионными линиями применяются два варианта подсистем регулирования температуры зон нагрева.
В первом варианте подсистема предполагает использование терморегуляторов типа «Термодат-22» фирмы «Системы контроля». В данных приборах реализован пропорционально-интегральный (ПИ) алгоритм регулирования температур. Коэффициенты ПИ-регулирования задаются с панели прибора. Терморегуляторы имеют последовательный интерфейс RS-485 с протоколом обмена ASCII, что позволило включить их в обмен с центральным компьютером, задавать уставки и выводить значения температуры на экран монитора.
Во втором варианте подсистема регулирования температур построена с применением многофункциональной платы PCL-812PG фирмы Advantech. В этом варианте нами реализован пропорционально-интегрально-дифференциальный (ПИД) алгоритм регулирования температуры.
Если рассматривать выборку из n измерений, то средняя пропорциональная ошибка ∆P может быть найдена из выражения:
Здесь Ty – уставка температуры в зоне нагрева;
Tф (i) – вектор последовательной выборки n фактических температур.
С учётом сглаживания помехи окончательная формула для вычисления средней пропорциональной ошибки ∆P~ может быть предложена в виде:
Здесь ∆P – пропорциональная ошибка, вычисленная по формуле (1) на текущем временном интервале;
∆Po – пропорциональная ошибка, вычисленная по формуле (1) на предыдущем временном интервале;
α, β – весовые сглаживающие коэффициенты.
Средняя дифференциальная ошибка ∆D~ регулирования температуры может быть найдена по формуле:
Здесь значения ∆P~i+1, ∆P~i вычисляются по формуле (2).
Средняя интегральная ошибка ∆I~ регулирования для n измерений может быть определена по формуле:
Суммарная ошибка STПИД ПИД-регулирования температуры вычисляется как взвешенная сумма ошибок:
Здесь αП , αИ , αD – весовые коэффициенты ПИД-регулирования;
γ – масштабный коэффициент.
Весовые и масштабный коэффициенты выбираются экспериментально при отладке системы регулирования температуры зон нагрева и являются для системы задаваемыми параметрами.
Мощность регулирования температуры пропорциональна длительности импульса цифрового выхода управления нагревом данной зоны (рис. 4).
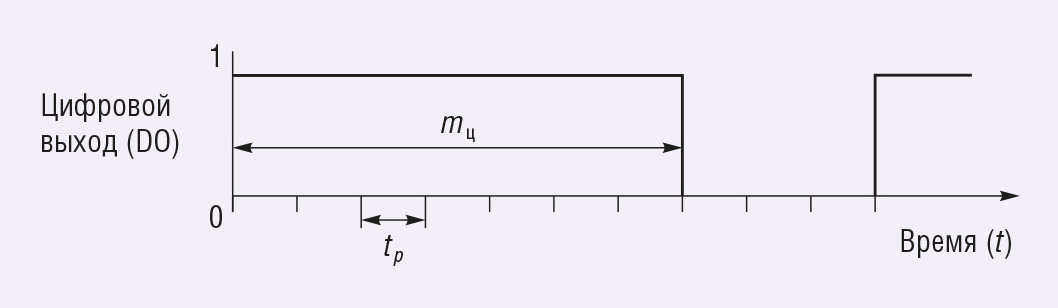
Дискретность этого импульса определяется длительностью программного цикла tp ≤ 0,5 с, а его длительность (mц) находится из следующего выражения:
Регулирование диаметра изоляции кабеля
Для управления диаметром наносимой на жилу изоляции нашей фирмой была разработана замкнутая подсистема измеритель диаметра – исполнительные электродвигатели шнеков (или тяги), в основе которой также лежит алгоритм ПИД-регулирования. Компьютерная программа по ряду измеренных значений диаметра вычисляет пропорциональную, интегральную и дифференциальную ошибки. Управляющий аналоговый сигнал на частотный регулятор шнеков (или тяги) вычисляется пропорционально суммарной ошибке ПИД-регулирования с заданными весовыми коэффициентами.
Предлагаемый алгоритм ПИД-регулирования реализован для двух типов экструзионных систем: одношнековой экструзионной системы (один шнек и одна экструзионная головка) и двухшнековой экструзионной системы (два шнека совместно работают на одну экструзионную головку).
ПИД-регулирование диаметра кабеля в одношнековой системе
Основное уравнение процесса экструзии расплава на токопроводящую жилу связывает объёмную производительность и угловую скорость шнека:
Здесь A – постоянная шнека;
W – угловая скорость шнека (обороты в минуту);
V – линейная скорость кабеля;
S – площадь поперечного сечения изоляции кабеля.
Ошибки регулирования представляют собой пропорциональную, интегральную и дифференциальную составляющие отклонения площади сечения изоляции от установленного значения:
Здесь Dy – установленное значение диаметра;
Dco – среднее значение диаметра в предыдущем цикле регулирования.
Суммарная ошибка ПИД-регулирования находится по формуле:
Здесь αП, αИ, αD – весовые коэффициенты ПИД-регулирования, являющиеся задаваемыми параметрами.
Корректирующее значение угловой скорости шнека в этом случае находится из выражения:
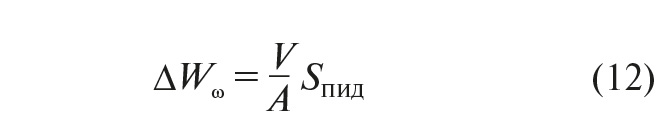
ПИД-регулирование диаметра кабеля в двухшнековой системе
Уравнение экструзии для двухшнековой системы может быть записано в виде:
Здесь A1, A2 – постоянные шнеков при совместной работе; W1, W2 – угловые скорости шнеков.
Корректировки угловых скоростей шнеков по суммарной ошибке ПИД-регулирования в двухшнековой системе находятся из следующих выражений:
Здесь k – технологическое соотношение угловых скоростей шнеков, определяемое по формуле:
Аппаратная часть системы управления экструзионной линией
В качестве основы аппаратной части разработанных и внедрённых предприятием ООО «Псковгеокабель» систем управления экструзионными линиями выбраны промышленный компьютер и многофункциональные платы ввода-вывода фирмы Advantech, а также частотные регуляторы фирмы ControlTechnique. На рис. 5 показан шкаф управления экструзионной линии, в котором наряду с прочей аппаратурой размещены монитор изолировщика и промышленный компьютер Advantech с процессорной платой PCA-6770 (Pentium III) в отказоустойчивом шасси IPC-6908.
В реализованных системах управления используются и отечественные устройства, такие как измеритель диаметра «Цикада» (фирма ЭРМИС) и уже упомянутые терморегуляторы «Термодат-22».
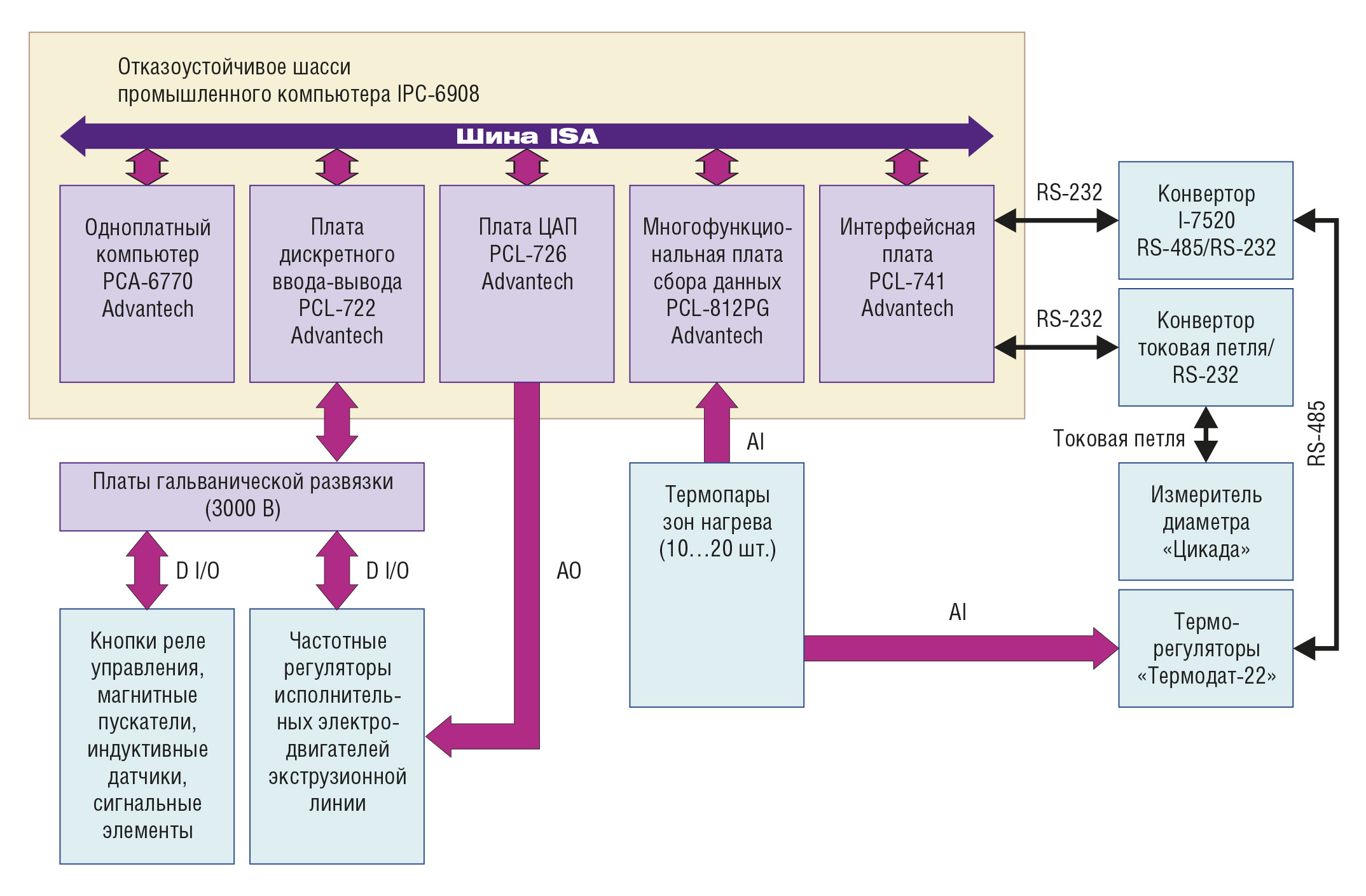
Структурная схема системы управления приведена на рис. 6. Схема отражает случай совместного применения обоих вариантов построения подсистемы регулирования температур для двухшнековой системы: один шнек регулируется с помощью платы PLC-812PG, другой — посредством терморегуляторов.
Программная часть системы управления
Программная часть системы управления экструзионной линией реализована в среде SCADA-системы VisiDAQ v3.11 (Advantech). Выбор в качестве среды разработки данной SCADA-системы объясняется преимущественным комплектованием аппаратной части системы управления платами фирмы Advantech. Типичные экраны среды разработки программного проекта и исполнительной среды программы управления экструзионной линией показаны соответственно на рис. 7 и 8.
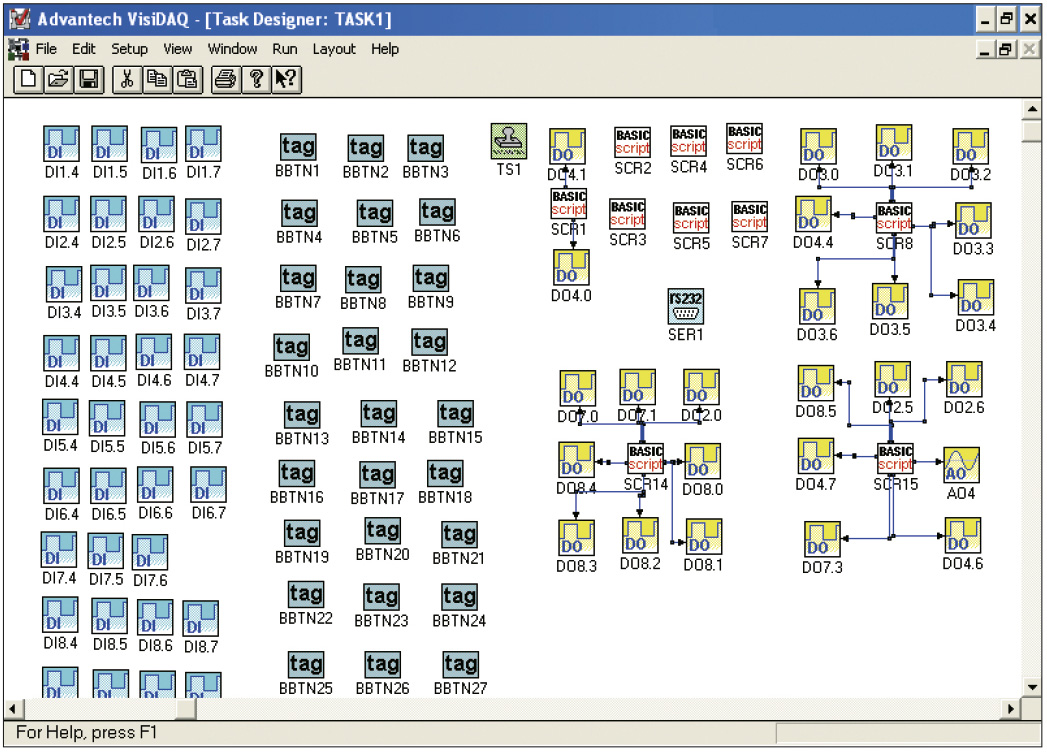
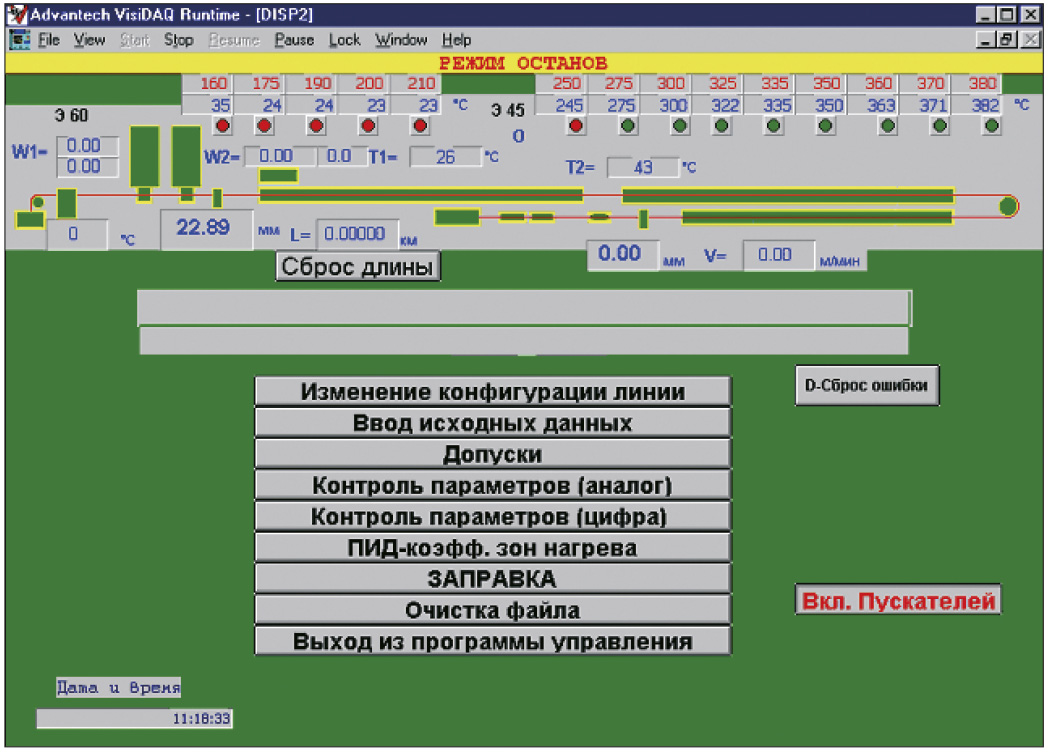
Помимо стандартных функциональных блоков среды разработки использованы скрипты, с помощью которых реализованы алгоритмы ПИД-регулирования диаметра кабеля и температуры зон нагрева. Использование дополнительных динамических библиотек, стандартно не поставляемых вместе c дистрибутивом VisiDAQ, позволило организовать более гибкий, по сравнению с организованным стандартным блоком последовательного интерфейса, обмен по RS-485/RS-232. Хотя исполнительную среду VisiDAQ в общем случае нельзя назвать системой реального времени, тем не менее проведённые многочисленные тесты по сканированию времени программного цикла показали, что в ОС Windows 98 задаваемый параметр scan time выдерживается с точностью, необходимой для управления.
Заключение
Разработанные и внедрённые ООО «Псковгеокабель» системы управления экструзионными линиями намного дешевле зарубежных аналогов. В них реализованы оригинальные аппаратные и программные решения. В то же время данные системы являются открытыми для дальнейшего усовершенствования и развития.
Опыт эксплуатации экструзионных линий показал, что аппаратная и программная части внедрённых систем управления обеспечивают требуемые показатели надёжности и качества изготавливаемых кабелей при использовании практически любых изоляционных материалов, включая фторполимеры.
Разработанные алгоритмы могут быть легко адаптированы к любому измерительному оборудованию (измерители диаметра, длины, эксцентриситета и т.п.) как зарубежных, так и отечественных производителей, имеющему интерфейс последовательной связи. ●
Авторы — сотрудники ООО «Псковгеокабель»
Телефоны: (8112) 7919-41/53
В статистике , то средняя интегральная ошибка (режиссура) используется в оценке плотности . MISE оценки неизвестной плотности вероятности определяется выражением
где ƒ — неизвестная плотность, ƒ n — ее оценка, основанная на выборке из n независимых и одинаково распределенных случайных величин. Здесь E обозначает ожидаемое значение по отношению к этому образцу.
MISE также известен как функция риска L 2 .
Смотрите также
- Оценка минимального расстояния
- Среднеквадратичная ошибка
Среднеквадратичная ошибка (Mean Squared Error) – Среднее арифметическое (Mean) квадратов разностей между предсказанными и реальными значениями Модели (Model) Машинного обучения (ML):
Рассчитывается с помощью формулы, которая будет пояснена в примере ниже:
$$MSE = \frac{1}{n} × \sum_{i=1}^n (y_i — \widetilde{y}_i)^2$$
$$MSE\space{}{–}\space{Среднеквадратическая}\space{ошибка,}$$
$$n\space{}{–}\space{количество}\space{наблюдений,}$$
$$y_i\space{}{–}\space{фактическая}\space{координата}\space{наблюдения,}$$
$$\widetilde{y}_i\space{}{–}\space{предсказанная}\space{координата}\space{наблюдения,}$$
MSE практически никогда не равен нулю, и происходит это из-за элемента случайности в данных или неучитывания Оценочной функцией (Estimator) всех факторов, которые могли бы улучшить предсказательную способность.
Пример. Исследуем линейную регрессию, изображенную на графике выше, и установим величину среднеквадратической Ошибки (Error). Фактические координаты точек-Наблюдений (Observation) выглядят следующим образом:
Мы имеем дело с Линейной регрессией (Linear Regression), потому уравнение, предсказывающее положение записей, можно представить с помощью формулы:
$$y = M * x + b$$
$$y\space{–}\space{значение}\space{координаты}\space{оси}\space{y,}$$
$$M\space{–}\space{уклон}\space{прямой}$$
$$x\space{–}\space{значение}\space{координаты}\space{оси}\space{x,}$$
$$b\space{–}\space{смещение}\space{прямой}\space{относительно}\space{начала}\space{координат}$$
Параметры M и b уравнения нам, к счастью, известны в данном обучающем примере, и потому уравнение выглядит следующим образом:
$$y = 0,5252 * x + 17,306$$
Зная координаты реальных записей и уравнение линейной регрессии, мы можем восстановить полные координаты предсказанных наблюдений, обозначенных серыми точками на графике выше. Простой подстановкой значения координаты x в уравнение мы рассчитаем значение координаты ỹ:
Рассчитаем квадрат разницы между Y и Ỹ:
Сумма таких квадратов равна 4 445. Осталось только разделить это число на количество наблюдений (9):
$$MSE = \frac{1}{9} × 4445 = 493$$
Само по себе число в такой ситуации становится показательным, когда Дата-сайентист (Data Scientist) предпринимает попытки улучшить предсказательную способность модели и сравнивает MSE каждой итерации, выбирая такое уравнение, что сгенерирует наименьшую погрешность в предсказаниях.
MSE и Scikit-learn
Среднеквадратическую ошибку можно вычислить с помощью SkLearn. Для начала импортируем функцию:
import sklearn
from sklearn.metrics import mean_squared_errorИнициализируем крошечные списки, содержащие реальные и предсказанные координаты y:
y_true = [5, 41, 70, 77, 134, 68, 138, 101, 131]
y_pred = [23, 35, 55, 90, 93, 103, 118, 121, 129]Инициируем функцию mean_squared_error(), которая рассчитает MSE тем же способом, что и формула выше:
mean_squared_error(y_true, y_pred)
Интересно, что конечный результат на 3 отличается от расчетов с помощью Apple Numbers:
496.0Ноутбук, не требующий дополнительной настройки на момент написания статьи, можно скачать здесь.
Автор оригинальной статьи: @mmoshikoo
Фото: @tobyelliott
Основываясь на теореме Парсеваля, можно сформулировать задачу о выборе параметров из условия минимума интегральной квадратичной ошибки для произвольных входных сигналов. Задача минимизации распадается на четыре последовательных шага. Первый шаг состоит в определении изображения Фурье ошибки как функции комплексной переменной 
Эта функция будет зависеть от параметров системы, которыми мы можем распоряжаться. Второй шаг состоит в выражении интегральной квадратичной ошибки 
в функции изображения ошибки 
на основании теоремы Парсеваля
При этом если 
— дробно-рациональная функция, то 
может быть представлена в виде
где 
— полиномы от 
Третий шаг заключается в вычислении интеграла. К счастью, определенный интеграл (2.3-2) был вычислен как функция коэффициентов полиномов. Таблица этих интегралов вместе с описанием помещена в приложении V. После вычисления интеграла мы получаем интегральную квадратичную ошибку как функцию параметров 
а именно
Четвертый шаг состоит в выборе значений параметров из условия минимума интегральной квадратичной ошибки. Формально это может быть сделано обычным методом, если приравнять частные производные 
по параметрам нулю и решить полученную систему уравнений относительно значений параметров. Эта система из К уравнений имеет вид
К сожалению, во многих практических задачах формальная процедура определения значений параметров, минимизирующих интегральную квадратичную ошибку, приводит к системе нелинейных уравнений, для которых не существует простых методов решения.
Если уравнения (2.3-3) достаточно сложны для решения аналитическими методами, то можно использовать численные методы или методы последовательных приближений. Однако когда для решения уравнений относительно параметров необходимы такие методы, то, вероятно, удобнее обратиться непосредственно к выражению интегральной квадратичной ошибки, изобразив ее как функцию одного параметра и считая остальные значения параметров фиксированными. Используя несколько совокупностей значений параметров и соответственно достаточное число кривых, можно определить значения всех параметров, обеспечивающих интегральную квадратичную ошибку, достаточно близкую, для практических целей, к ее минимальному значению. Непосредственное использование интегральной квадратичной ошибки позволяет избежать вычисления ее частных производных относительно параметров, которое может быть достаточно сложной и трудоемкой задачей. Процедуру отыскания минимума интегральной квадратичной ошибки можно пояснить на примере. Для иллюстрации рассмотрим расчет следящей системы по положению. В качестве входного сигнала возьмем ступенчатую функцию с высотой М. Задача
следящей системы состоит в том, чтобы сделать сигнал на выходе равным сигналу на входе. Следовательно, в этом случае желаемый сигнал на выходе совпадает с входным. В качестве заданного элемента системы выбран сервомотор, которому соответствует интегрирующее звено, соединенное последовательно с апериодическим. Физически это соответствует двигателю постоянного тока с регулированием в цепи якоря.
Если предположить, что напряжение на якоре пропорционально сигналу управления и пренебречь индуктивностью якоря, то постоянная времени 
будет равна моменту инерции всей системы, приведенному к валу двигателя и деленному на коэффициент электрического демпфирования двигателя. Момент нагрузки и вязкое трение считаются достаточно малыми и не учитываются. Поскольку рассматривается следящая система по положению, то нужно считать передаточную функцию в цепи обратной связи равной единице.
В качестве корректирующего элемента используем самый простой усилитель. Тогда единственным регулируемым параметром будет коэффициент усиления.
Для выбранной следящей системы необходимо определить интегральную квадратичную ошибку в функции коэффициента усиления и такое значение коэффициента, при котором эта ошибка минимальна. Если воспользоваться принятыми обозначениями, то задачу можно сформулировать следующим образом.
Дано. Сигнал на входе
Для желаемого выходного сигнала имеем
Передаточная функция неизменяемой части системы
Передаточная функция элемента в обратной связи
Передаточная функция корректирующего элемента
где 
— коэффициент усиления системы по скорости. Этот коэффициент включает в себя коэффициент усиления неизменной части системы и коэффициент усиления звена коррекции.
Необходимо определить. Вначале необходимо определить интегральную квадратичную ошибку как функцию 
то есть 
Затем необходимо определить такое значение 
при котором ошибка минимальна.
Решение. На основании рис. 2.1-2 можно записать следующее выражение для изображения ошибки:
На основании данных задачи для передаточной функции всей системы имеем
Изображение Фурье входного сигнала имеет вид
Соответственно изображение желаемого сигнала на выходе
Следовательно, можно записать изображение ошибки в виде
Согласно теореме Парсеваля, для интегральной квадратичной ошибки получим
где
и
Формула для 
имеется в приложении V:
Подставляя значения коэффициентов из (2.3-15) и (2.3-16) в это выражение, получаем
или после деления на 
имеем
Это дает первый искомый результат — величину интегральной квадратичной ошибки как функцию 
При определении значения 
при котором интегральная квадратичная ошибка минимальна, необходимо вначале определить
область значений 
обеспечивающих устойчивость системы. Из (2.3-10) видно, что система устойчива для любых положительных значений и неустойчива для отрицательных значений 
Согласно (2.3-18), можно заключить, что значение 
минимизирующее интегральную квадратичную ошибку, равно 
Это дает ответ на второй поставленный вопрос. Отметим, что если не принимать во внимание условия устойчивости, то можно получить нулевое значение интегральной квадратичной ошибки, положив 
Это необходимо учитывать при определении значений параметров, минимизирующих интегральную квадратичную ошибку. Очевидно, приемлемыми значениями будут только те, при которых система устойчива. Из физических соображений ясно, что если значение параметра соответствует неустойчивой системе, то интегральная квадратичная ошибка обращается в бесконечность. Тот факт, что значение интегральной квадратичной ошибки (которая вычисляется на основании таблицы интегралов V.2-1 приложения V) конечно для значений параметров, соответствующих неустойчивости, можно объяснить условиями, использованными при выводе этих определенных интегралов. Эти условия сводятся к тому, что 
должна иметь все нули в левой полуплоскости. Для неустойчивой системы они, очевидно, не удовлетворяются и значение интегральной квадратичной ошибки, формально полученное при помощи таблицы интегралов, недействительно.
Рассмотрение этого примера подтвердит наше заключение о том, что коэффициент усиления системы для минимальной интегральной ошибки должен быть бесконечным. Коэффициент демпфирования системы второго порядка, определяемый (2.3-10), равен
а собственная частота
Если подставить эти параметры в (2.3-10), получим
Для ошибки, когда на входе действует единичная функция и желаемый сигнал совпадает с входным, имеем
Согласно (2.3-19), коэффициент демпфирования убывает при увеличении коэффициента усиления и поэтому является несколько неожиданным, что интегральная квадратичная ошибка убывает с увеличением коэффициента усиления. Однако если записать выражение для ошибки как функцию параметров 
то получим
Это выражение показывает, что «огибающая» ошибки имеет затухание, определяемое только постоянной времени двигателя 
и не зависящее от усиления 
Следовательно, при увеличении усиления 
функция 
носит все более колебательный характер, при этом ее огибающая в первом приближении не изменяется, как показано на рис. 2.3-1. Это объясняет тот факт, что интегральная квадратичная ошибка остается всегда конечной, независимо от того, насколько велик коэффициент усиления.
Для малых коэффициентов усиления значения огибающей будут несколько больше, чем для больших из-за наличия квадратного, корня в знаменателе (2.3-23). В связи с этим следует ожидать увеличения интегральной квадратичной ошибки при уменьшении коэффициента усиления.
С другой стороны, для очень больших значений усиления огибающая в (2.3-23) практически не зависит от 
однако число колебаний, заключенных в этой огибающей, становится настолько большим, что на любом малом интервале времени колебания имеют практически синусоидальную форму. Среднее квадратичное значение синусоидального сигнала равно половине квадрата амплитуды. Это означает, что можно вычислять интегральное квадратичное значение ошибки для больших 
как половину интегральной квадратичной, ошибки от огибающей, т. е.
или
После вычисления определенного интеграла получаем
Это значение можно также получить из (2.3-18) при 
В большинстве практических задач увеличение коэффициента усиления до бесконечности делает систему неустойчивой, при этом интегральная квадратичная ошибка обращается в бесконечность. Таким образом, результат рассмотренного примера является скорее необычным и его можно объяснить простотой элементов (см. (2.3-6)), составляющих неизменную часть системы.
Рис. 2.3-1. Ошибка в системе второго порядка при единичном ступенчатом воздействии: а) вход; б) ошибка при 
ошибка при 
Такая идеализация в отношении заданных элементов в общем случае неприемлема при больших коэффициентах усиления. Один из путей ограничения диапазона изменения параметров так, чтобы идеализация заданных элементов системы была приемлемой, заключается в том, что задается собственная частота системы и после этого решается задача о выборе параметров из условия минимума интегральной квадратичной ошибки. Здесь следует считать, что постоянная времени двигателя и усиление по скорости 
выбираются произвольно. Значение 
можно переписать как функцию коэффициента демпфирования и собственной частоты
Легко видеть, что 
достигает минимума при 
Этот результат был впервые получен Холлом [21]. Значение коэффициента демпфирования, равное половине, является наиболее разумным для системы второго порядка.
Процедура минимизации интегральной квадратичной ошибки, рассмотренная выше и иллюстрированная примером, может применяться лишь в случае, когда изображение ошибки 
является дробно-рациональной функцией. В противном случае этот метод приводит к серьезным затруднениям в расчете, в частности, если изображение ошибки является иррациональной функцией. Одним из возможных путей преодоления этих затруднений является аппроксимация функции времени так, чтобы изображение было дробно-рациональной функцией. Другой путь состоит в том, чтобы аппроксимировать изображение ошибки дробно-рациональной функцией. Наконец, третий путь заключается в том, чтобы производить все вычисления в области времени. Первые два пути очевидны, так как задача представляется в форме, рассмотренной выше. Третий путь будет кратко рассмотрен в следующем параграфе.