Среднеквадратичная ошибка (Mean Squared Error) – Среднее арифметическое (Mean) квадратов разностей между предсказанными и реальными значениями Модели (Model) Машинного обучения (ML):
Рассчитывается с помощью формулы, которая будет пояснена в примере ниже:
$$MSE = \frac{1}{n} × \sum_{i=1}^n (y_i — \widetilde{y}_i)^2$$
$$MSE\space{}{–}\space{Среднеквадратическая}\space{ошибка,}$$
$$n\space{}{–}\space{количество}\space{наблюдений,}$$
$$y_i\space{}{–}\space{фактическая}\space{координата}\space{наблюдения,}$$
$$\widetilde{y}_i\space{}{–}\space{предсказанная}\space{координата}\space{наблюдения,}$$
MSE практически никогда не равен нулю, и происходит это из-за элемента случайности в данных или неучитывания Оценочной функцией (Estimator) всех факторов, которые могли бы улучшить предсказательную способность.
Пример. Исследуем линейную регрессию, изображенную на графике выше, и установим величину среднеквадратической Ошибки (Error). Фактические координаты точек-Наблюдений (Observation) выглядят следующим образом:
Мы имеем дело с Линейной регрессией (Linear Regression), потому уравнение, предсказывающее положение записей, можно представить с помощью формулы:
$$y = M * x + b$$
$$y\space{–}\space{значение}\space{координаты}\space{оси}\space{y,}$$
$$M\space{–}\space{уклон}\space{прямой}$$
$$x\space{–}\space{значение}\space{координаты}\space{оси}\space{x,}$$
$$b\space{–}\space{смещение}\space{прямой}\space{относительно}\space{начала}\space{координат}$$
Параметры M и b уравнения нам, к счастью, известны в данном обучающем примере, и потому уравнение выглядит следующим образом:
$$y = 0,5252 * x + 17,306$$
Зная координаты реальных записей и уравнение линейной регрессии, мы можем восстановить полные координаты предсказанных наблюдений, обозначенных серыми точками на графике выше. Простой подстановкой значения координаты x в уравнение мы рассчитаем значение координаты ỹ:
Рассчитаем квадрат разницы между Y и Ỹ:
Сумма таких квадратов равна 4 445. Осталось только разделить это число на количество наблюдений (9):
$$MSE = \frac{1}{9} × 4445 = 493$$
Само по себе число в такой ситуации становится показательным, когда Дата-сайентист (Data Scientist) предпринимает попытки улучшить предсказательную способность модели и сравнивает MSE каждой итерации, выбирая такое уравнение, что сгенерирует наименьшую погрешность в предсказаниях.
MSE и Scikit-learn
Среднеквадратическую ошибку можно вычислить с помощью SkLearn. Для начала импортируем функцию:
import sklearn
from sklearn.metrics import mean_squared_errorИнициализируем крошечные списки, содержащие реальные и предсказанные координаты y:
y_true = [5, 41, 70, 77, 134, 68, 138, 101, 131]
y_pred = [23, 35, 55, 90, 93, 103, 118, 121, 129]Инициируем функцию mean_squared_error(), которая рассчитает MSE тем же способом, что и формула выше:
mean_squared_error(y_true, y_pred)
Интересно, что конечный результат на 3 отличается от расчетов с помощью Apple Numbers:
496.0Ноутбук, не требующий дополнительной настройки на момент написания статьи, можно скачать здесь.
Автор оригинальной статьи: @mmoshikoo
Фото: @tobyelliott
Время на прочтение
6 мин
Количество просмотров 23K
Заранее хочу отметить, что тот кто знает как обучается персептрон — в этой статье вряд ли найдет что-то новое. Вы можете смело пропускать ее. Почему я решил это написать — я хотел бы написать цикл статей, связанных с нейронными сетями и применением TensorFlow.js, ввиду этого я не мог опустить общие теоретические выдержки. Поэтому прошу отнестись с большим терпением и пониманием к конечной задумке.
При классическом программировании разработчик описывает на конкретном языке программирования определённый жестко заданный набор правил, который был определен на основании его знаний в конкретной предметной области и который в первом приближении описывает процессы, происходящие в человеческом мозге при решении аналогичной задачи.
Например, может быть запрограммирована стратегия игры в крестики-нолики, шахмат и другое (рисунок 1).
Рисунок 1 – Классический подход решения задач
В то время как алгоритмы машинного обучения могут определять набор правил для решения задач без участия разработчика, а только на базе наличия тренировочного набора данных.
Тренировочный набор — это какой-то набор входных данных ассоциированный с набором ожидаемых результатов (ответами, выходными данными). На каждом шаге обучения, модель за счет изменения внутреннего состояния, будет оптимизировать и уменьшать ошибку между фактическим выходным результатом модели и ожидаемым результатом (рисунок 2).
Рисунок 2 – Машинное обучение
Нейронные сети
Долгое время учёные, вдохновляясь процессами происходящими в нашем мозге, пытались сделать реверс-инжиниринг центральной нервной системы и попробовать сымитировать работу человеческого мозга. Благодаря этому родилось целое направление в машинном обучении — нейронные сети.
На рисунке 3 вы можете увидеть сходство между устройством биологического нейрона и математическим представлением нейрона, используемого в машинном обучении.
Рисунок 3 – Математическое представление нейрона
В биологическом нейроне, нейрон получает электрические сигналы от дендритов, модулирующих электрические сигналы с разной силой, которые могут возбуждать нейрон при достижении некоторого порогового значения, что в свою очередь приведёт к передаче электрического сигнала другим нейронам через синапсы.
Персептрон
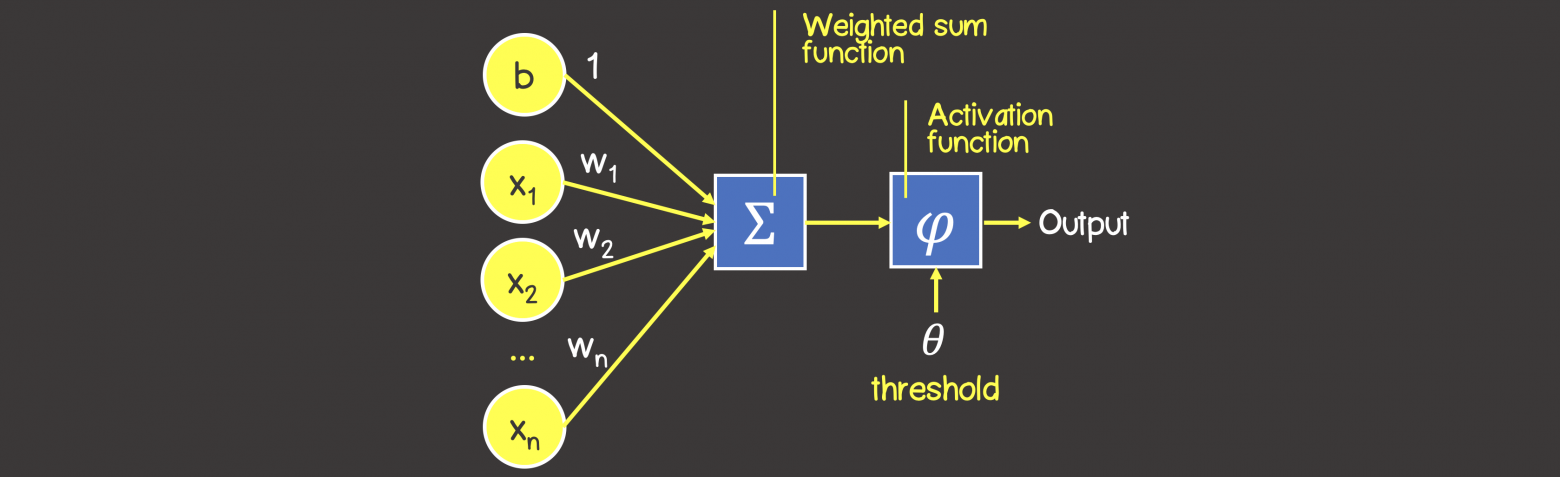
Математическая модель нейронной сети, состоящего из одного нейрона, который выполняет две последовательные операции (рисунок 4):
- вычисляет сумму входных сигналов с учетом их весов (проводимости или сопротивления) связи
- применяет активационную функцию к общей сумме воздействия входных сигналов.
Рисунок 4 – Математическая модель персептрона
В качестве активационной функции может использоваться любая дифференцируемая функция, наиболее часто используемые приведены в таблице 1. Выбор активационной функции ложиться на плечи инженера, и обычно этот выбор основан или на уже имеющемся опыте решения похожих задач, ну или просто методом подбора.
Заметка
Однако есть рекомендация – что если нужна нелинейность в нейронной сети, то в качестве активационной функции лучше всего подходит ReLU функция, которая имеет лучшие показатели сходимости модели во время процесса обучения.
Таблица 1 — Распространенные активационные функции
Процесс обучения персептрона
Процесс обучения состоит из несколько шагов. Для большей наглядности, рассмотрим некую вымышленную задачу, которую мы будем решать нейронной сетью, состоящей из одного нейрона с линейной активационной функции (это по сути персептрон без активационной функции вовсе), также для упрощения задачи – исключим в нейроне узел смещения b (рисунок 5).
Рисунок 5 – Обучающий набор данных и состояние нейронной сети на предыдущем шаге обучения
На данном этапе мы имеем нейронную сеть в некотором состоянии с определенными весами соединений, которые были вычислены на предыдущем этапе обучения модели или если это первая итерация обучения – то значения весов соединений выбраны в произвольном порядке.
Итак, представим, что мы имеем некоторый набор тренировочных данных, значения каждого элемента из набора представлены вектором входных данных (input data), содержащих 2 параметра (feature) 
. Под в модели в зависимости от рассматриваемой предметной области может подразумеваться все что угодно: количество комнат в доме, расстояние дома от моря, ну или мы просто пытаемся обучить нейронную сеть логической операции И, или ИЛИ.
Каждый вектор входных данных в тренировочном наборе сопоставлен с вектором ожидаемого результата (expected output). В данном случае вектор выходных данных содержит только один параметр, которые опять же в зависимости от выбранной предметной области может означать все что угодно – цена дома, результат выполнения логической операции И или ИЛИ.
ШАГ 1 — Прямое распространение ошибки (feedforward process)
На данном шаге мы вычисляем сумму входных сигналов с учетом веса каждой связи и применяем активационную функцию (в нашем случае активационной функции нет). Сделаем вычисления для первого элемента в обучающем наборе:
Рисунок 6 – Прямое распространение ошибки
Обратите внимание, что написанная формула выше – это упрощенное математическое уравнение для частного случая операций над тензорами.
Тензор – это по сути контейнер данных, который может иметь N осей и произвольное число элементов вдоль каждой из осей. Большинство с тензорами знакомы с математики – векторы (тензор с одной осью), матрицы (тензор с двумя осями – строки, колонки).
Формулу можно написать в следующем виде, где вы увидите знакомые матрицы (тензоры) и их перемножение, а также поймете о каком упрощении шла речь выше:
![${\vec{Y}}_{predicted}=\ {\vec{X}}^T\vec{W}=\left[\begin{matrix}x_1\\x_2\\\end{matrix}\right]^T\cdot \left [ \begin{matrix} w_1\\ w_2 \end{matrix} \right ]=\left [ \begin{matrix} x_1 & x_2 \end{matrix} \right ] \cdot \left [ \begin{matrix} w_1\\ w_2 \end{matrix} \right ] =\left [ x_1w_1+x_2w_2 \right ]$](https://habrastorage.org/getpro/habr/formulas/a36/9d4/929/a369d49299583d08cbd19bea1e116daf.svg)
ШАГ 2 — Расчет функции ошибки
Функция ошибка – это метрика, отражающая расхождение между ожидаемыми и полученными выходными данными. Обычно используют следующие функции ошибки:
— среднеквадратичная ошибка (Mean Squared Error, MSE) – данная функция ошибки особенно чувствительна к выбросам в тренировочном наборе, так как используется квадрат от разности фактического и ожидаемого значений (выброс — значение, которое сильно удалено от других значений в наборе данных, которые могут иногда появляться в следствии ошибок данных, таких как смешивание данных с разными единицами измерения или плохие показания датчиков):
— среднеквадратичное отклонение (Root MSE) – по сути это тоже самое что, среднеквадратичная ошибка в контексте нейронных сетей, но может отражать реальную физическую единицу измерения, например, если в нейронной сети выходным параметров нейронной сети является цена дома выраженной в долларах, то единица измерения среднеквадратичной ошибки будет доллар квадратный (
), а для среднеквадратичного отклонения это доллар ($), что естественно немного упрощает задачу анализа человеком:
— среднее отклонение (Mean Absolute Error, MAE) -в отличии от двух выше указанных значений, является не столь чувствительной к выбросам:
— перекрестная энтропия (Cross entropy) – использует для задач классификации:
где
– число экземпляров в тренировочном наборе
– число классов при решении задач классификации
— ожидаемое выходное значение
– фактическое выходное значение обучаемой модели
Для нашего конкретного случая воспользуемся MSE:
ШАГ 3 — Обратное распространение ошибки (backpropagation)
Цель обучения нейронной сети проста – это минимизация функции ошибки:
Одним способом найти минимум функции – это на каждом очередном шаге обучения модифицировать веса соединений в направлении противоположным вектору-градиенту – метод градиентного спуска, и это математически выглядит так:
где 
– k -ая итерация обучения нейронной сети;
– шаг обучения (learning rate) и задается инженером, обычно это может быть 0.1; 0.01 (о том как шаг обучения влияет на процесс сходимости обучения отметить чуть позже)
– градиент функции-ошибки
Для нахождения градиента, используем частные производные по настраиваемым аргументам 
:
![$\nabla L\left(\vec{w}\right)=\left[\begin{matrix}\frac{\partial L}{\partial w_1}\\\vdots\\\frac{\partial L}{\partial w_N}\\\end{matrix}\right]$](https://habrastorage.org/getpro/habr/formulas/d25/bb0/a13/d25bb0a13bb5593a7c26f98f0ed48352.svg)
В нашем конкретном случае с учетом всех упрощений, функция ошибки принимает вид:
Памятка формул производных
Напомним некоторые формулы производных, которые пригодятся для вычисления частных производных
Найдем следующие частные производные:
Тогда процесс обратного распространения ошибки – движение по модели от выхода по направлению к входу с модификацией весов модели в направлении обратном вектору градиента. Задавая обучающий шаг 0.1 (learning rate) имеем (рисунок 7):
Рисунок 7 – Обратное распространение ошибки
Таким образом мы завершили k+1 шаг обучения, чтобы убедиться, что ошибка снизилась, а выход от модели с новыми весами стал ближе к ожидаемому выполним процесс прямого распространения ошибки по модели с новыми весами (см. ШАГ 1):
Как видим, выходное значение увеличилось на 0.2 единица в верном направлении к ожидаемому результату – единице (1). Ошибка тогда составит:
Как видим, на предыдущем шаге обучения ошибка составила 0.64, а с новыми весами – 0.36, следовательно мы настроили модель в верном направлении.
Следующая часть статьи:
Машинное обучение. Нейронные сети (часть 2): Моделирование OR; XOR с помощью TensorFlow.js
Машинное обучение. Нейронные сети (часть 3) — Convolutional Network под микроскопом. Изучение АПИ Tensorflow.js
Среднеквадратичная ошибка (Mean Squared Error, MSE) является одной из самых распространенных метрик для измерения точности работы нейронной сети. Она позволяет оценить разницу между предсказанными значениями и истинными значениями на основе средней квадратичной разности между ними.
Эта метрика особенно полезна в задачах регрессии, где требуется предсказать непрерывные значения. Она позволяет определить, насколько хорошо модель соответствует реальным данным и в какой степени модель ошибается. Чем меньше значение среднеквадратичной ошибки, тем лучше модель.
Влияние среднеквадратичной ошибки на результаты обучения состоит в том, что она является основным критерием, используемым во время обучения нейронной сети. Она служит для определения оптимальных значений весов и смещений модели с целью минимизации ошибки. В процессе обучения модель пытается найти такие веса и смещения, которые минимизируют среднеквадратичную ошибку.
Важно отметить, что среднеквадратичная ошибка не является единственной метрикой для измерения точности нейронной сети. В некоторых случаях она может не являться оптимальной или непригодной для конкретной задачи. В таких случаях может потребоваться использование других метрик, например, средней абсолютной ошибки или коэффициента детерминации.
Содержание
- Среднеквадратичная ошибка нейронной сети
- Что это такое
- Влияние на результаты обучения
Среднеквадратичная ошибка нейронной сети
Среднеквадратичная ошибка (MSE) является одним из самых популярных критериев оценки точности работы нейронной сети. Она измеряет разницу между предсказанными значениями нейронной сети и фактическими значениями.
MSE вычисляется путем усреднения квадратов разностей между каждым предсказанным значением и соответствующим фактическим значением.
Математическая формула MSE выглядит следующим образом:
MSE = (1 / n) * Σi=1n (yi — ŷi)2
где n — количество примеров в выборке, yi — фактическое значение, ŷi — предсказанное значение.
Высокая среднеквадратичная ошибка указывает на большую разницу между предсказанными и фактическими значениями. На самом деле, меньшее значение MSE соответствует более точной нейронной сети.
Среднеквадратичная ошибка имеет несколько преимуществ:
- Простота вычисления: MSE является простой и легко вычислимой метрикой.
- Чувствительность к большим ошибкам: очень великая ошибка будет иметь большое влияние на общую оценку MSE.
- Гладкость: MSE является гладкой функцией, что облегчает оптимизацию и применение стохастического градиентного спуска.
Однако MSE также имеет некоторые недостатки:
- Чувствительность к выбросам: из-за возведения в квадрат разницы между предсказанными и фактическими значениями выбросы могут иметь слишком большое влияние на результат.
- Непонятность: MSE не всегда имеет наглядную интерпретацию, что затрудняет понимание, насколько хорошо нейронная сеть выполняет задачу.
В целом, среднеквадратичная ошибка — это полезная метрика для оценки точности работы нейронной сети. Она позволяет обнаружить, насколько хорошо нейронная сеть предсказывает фактические значения и служит важным инструментом при оптимизации и обучении сети.
Что это такое
Среднеквадратичная ошибка (Mean Squared Error, MSE) является одним из наиболее распространенных критериев оценки качества работы нейронных сетей. Она используется для измерения разницы между предсказанными и фактическими значениями выходов модели.
Среднеквадратичная ошибка определяется как средняя арифметическая разница между квадратами ошибок для каждого примера в наборе данных. Ошибка для каждого примера рассчитывается путем вычитания фактического значения из предсказанного значения и возведения разности в квадрат.
Полученная сумма ошибок делится на количество примеров в наборе данных, чтобы получить среднеквадратичную ошибку.
Среднеквадратичная ошибка является положительным числом и может принимать значения от 0 до бесконечности. Чем меньше значение MSE, тем лучше работает нейронная сеть, так как она предсказывает значения, более близкие к фактическим.
Среднеквадратичная ошибка может быть использована для оптимизации модели путем изменения параметров нейронной сети таким образом, чтобы минимизировать значение MSE. Часто используется градиентный спуск для этой цели, который позволяет находить оптимальные значения параметров модели.
Влияние на результаты обучения
Среднеквадратичная ошибка (MSE) играет важную роль в процессе обучения нейронной сети. Она определяет качество работы модели и может влиять на ее результаты.
Основной целью обучения нейронной сети является минимизация среднеквадратичной ошибки. Именно с помощью этой метрики происходит оценка разницы между предсказанной и правильной целевой переменной.
Чем меньше значение MSE, тем лучше модель способна предсказывать правильные значения выходных данных. Однако низкое значение MSE не всегда безусловно является индикатором хорошей обученности нейронной сети. В некоторых случаях модель может переобучиться на тренировочных данных и показывать плохие результаты на новых, незнакомых данных.
С другой стороны, высокое значение MSE может указывать на плохую обученность модели или на то, что данные содержат большой уровень шума. Поэтому при выборе модели и оптимизации гиперпараметров необходимо учитывать баланс величины среднеквадратичной ошибки и общей производительности модели.
Важно отметить, что среднеквадратичная ошибка не единственная метрика, используемая для оценки моделей машинного обучения. В зависимости от задачи и специфики данных могут быть выбраны и другие метрики, такие как средняя абсолютная ошибка (MAE) или коэффициент детерминации (R-квадрат).
В целом, среднеквадратичная ошибка имеет существенное влияние на результаты обучения нейронной сети. Правильный выбор модели, алгоритма обучения и гиперпараметров позволяет достичь наилучших результатов и повысить точность предсказаний.
Среднеквадратичная ошибка в PyTorch рассчитывается почти так же, как и общее уравнение потерь, приведенное ранее. Мы также рассмотрим значение смещения, поскольку это также параметр, который необходимо обновлять в процессе обучения.
(y-Ax+b)2
Среднеквадратичная ошибка лучше всего поясняется иллюстрацией.
Предположим, у нас есть набор значений, и мы начинаем с рисования некоторого параметра линии регрессии, размер которого определяется случайным набором веса и значения смещения, как и раньше.
Ошибка соответствует тому, как далеко фактическое значение от прогнозируемого значения – фактическое расстояние между ними.
Для каждой точки ошибка рассчитывается путем сравнения прогнозируемых значений, сделанных нашей линейной моделью, с фактическим значением по следующей формуле.
Каждая точка связана с ошибкой, что означает, что мы должны выполнить суммирование ошибки для каждой точки. Мы знаем, что прогноз можно переписать как:
Поскольку мы вычисляем среднеквадратичную ошибку, мы должны взять среднее значение, разделив его на количество точек данных. Упомянутый ранее градиент функции ошибки должен вести нас в направлении наибольшего увеличения ошибки.
Двигаясь к отрицательному градиенту нашей функции стоимости, мы движемся в направлении наименьшей ошибки. Мы будем использовать этот градиент как компас, который всегда ведет нас вниз. В градиентном спуске мы игнорируем наличие смещения, но для ошибки требуется определить оба параметра A и b.
Теперь мы вычисляем частные производные для каждого, и, как и раньше, мы начинаем с любой пары значений A и b.
Мы используем алгоритм градиентного спуска для обновления A и b в направлении наименьшей ошибки на основе двух частных производных, упомянутых выше. Для каждой отдельной итерации новый вес равен:
A1=A0-∝ f'(A).
И новое значение смещения равно
b1=b0-∝ f'(b).
Основная идея написания кода в том, что мы начинаем с некоторой случайной модели со случайным набором параметров веса и значения смещения. Эта случайная модель будет иметь большую функцию ошибки, большую функцию стоимости, и затем мы используем градиентный спуск, чтобы обновить вес нашей модели в направлении наименьшей ошибки. Минимизация этой ошибки возвращает оптимизированный результат.
Изучаю Python вместе с вами, читаю, собираю и записываю информацию опытных программистов.
y question is about Neural Network Training. I already searched about this but, there is no good explanation about it.
There are dozens of good explanations on the web, and in the literature, one such example may be the book by Haykin: Neural Networks and Learning machines
So for the first one, how to calculate mean square error? (I know this is silly, but I really don’t get it)
In the most simple terms, mean squared error is defined as
sum_i 1/n (desired_output(i) - model_output(i))^2
So you simply calculate the mean of the squares of the errors (differences between your output, and the desired one).
Now when should we calculate the mean square error? does it when we already take all pairs? or does we calculate it for each pair?
Both methods are used, one is called batch learning, and one is online learning. So all next questions have the answer «both are correct, depending whether you are using batch or online learning». Which one to choose? Obviously — it depends, but for a sake of simplicity I would suggest starting with batch learning (so you compute the error over all training samples and then update).