Среднеквадратичная ошибка нейронной сети

Время на прочтение
6 мин

Количество просмотров 23K

Заранее хочу отметить, что тот кто знает как обучается персептрон — в этой статье вряд ли найдет что-то новое. Вы можете смело пропускать ее. Почему я решил это написать — я хотел бы написать цикл статей, связанных с нейронными сетями и применением TensorFlow.js, ввиду этого я не мог опустить общие теоретические выдержки. Поэтому прошу отнестись с большим терпением и пониманием к конечной задумке.

При классическом программировании разработчик описывает на конкретном языке программирования определённый жестко заданный набор правил, который был определен на основании его знаний в конкретной предметной области и который в первом приближении описывает процессы, происходящие в человеческом мозге при решении аналогичной задачи.

Например, может быть запрограммирована стратегия игры в крестики-нолики, шахмат и другое (рисунок 1).


Рисунок 1 – Классический подход решения задач

В то время как алгоритмы машинного обучения могут определять набор правил для решения задач без участия разработчика, а только на базе наличия тренировочного набора данных.
Тренировочный набор — это какой-то набор входных данных ассоциированный с набором ожидаемых результатов (ответами, выходными данными). На каждом шаге обучения, модель за счет изменения внутреннего состояния, будет оптимизировать и уменьшать ошибку между фактическим выходным результатом модели и ожидаемым результатом (рисунок 2).


Рисунок 2 – Машинное обучение

Нейронные сети

Долгое время учёные, вдохновляясь процессами происходящими в нашем мозге, пытались сделать реверс-инжиниринг центральной нервной системы и попробовать сымитировать работу человеческого мозга. Благодаря этому родилось целое направление в машинном обучении — нейронные сети.

На рисунке 3 вы можете увидеть сходство между устройством биологического нейрона и математическим представлением нейрона, используемого в машинном обучении.


Рисунок 3 – Математическое представление нейрона

В биологическом нейроне, нейрон получает электрические сигналы от дендритов, модулирующих электрические сигналы с разной силой, которые могут возбуждать нейрон при достижении некоторого порогового значения, что в свою очередь приведёт к передаче электрического сигнала другим нейронам через синапсы.

Персептрон

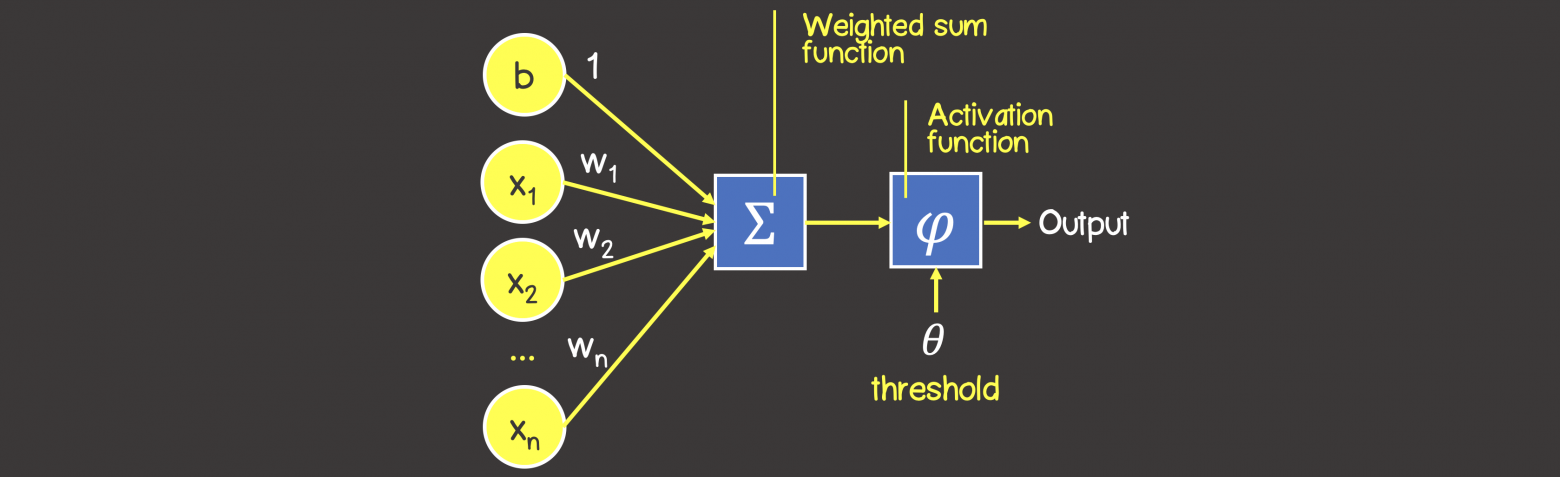
Математическая модель нейронной сети, состоящего из одного нейрона, который выполняет две последовательные операции (рисунок 4):

  • вычисляет сумму входных сигналов с учетом их весов (проводимости или сопротивления) связи

    ${sum=\ \vec{X}}^T\vec{W}+\vec{B}=\sum_{i=1}^{n}{x_iw_i}+b$

  • применяет активационную функцию к общей сумме воздействия входных сигналов.

    $out=\varphi(sum)$

Рисунок 4 – Математическая модель персептрона

В качестве активационной функции может использоваться любая дифференцируемая функция, наиболее часто используемые приведены в таблице 1. Выбор активационной функции ложиться на плечи инженера, и обычно этот выбор основан или на уже имеющемся опыте решения похожих задач, ну или просто методом подбора.

Заметка

Однако есть рекомендация – что если нужна нелинейность в нейронной сети, то в качестве активационной функции лучше всего подходит ReLU функция, которая имеет лучшие показатели сходимости модели во время процесса обучения.

Таблица 1 — Распространенные активационные функции

Процесс обучения персептрона

Процесс обучения состоит из несколько шагов. Для большей наглядности, рассмотрим некую вымышленную задачу, которую мы будем решать нейронной сетью, состоящей из одного нейрона с линейной активационной функции (это по сути персептрон без активационной функции вовсе), также для упрощения задачи – исключим в нейроне узел смещения b (рисунок 5).


Рисунок 5 – Обучающий набор данных и состояние нейронной сети на предыдущем шаге обучения

На данном этапе мы имеем нейронную сеть в некотором состоянии с определенными весами соединений, которые были вычислены на предыдущем этапе обучения модели или если это первая итерация обучения – то значения весов соединений выбраны в произвольном порядке.

Итак, представим, что мы имеем некоторый набор тренировочных данных, значения каждого элемента из набора представлены вектором входных данных (input data), содержащих 2 параметра (feature) $x_1,x_2$. Под $x_1,x_2$ в модели в зависимости от рассматриваемой предметной области может подразумеваться все что угодно: количество комнат в доме, расстояние дома от моря, ну или мы просто пытаемся обучить нейронную сеть логической операции И, или ИЛИ.

Каждый вектор входных данных в тренировочном наборе сопоставлен с вектором ожидаемого результата (expected output). В данном случае вектор выходных данных содержит только один параметр, которые опять же в зависимости от выбранной предметной области может означать все что угодно – цена дома, результат выполнения логической операции И или ИЛИ.

ШАГ 1 — Прямое распространение ошибки (feedforward process)
На данном шаге мы вычисляем сумму входных сигналов с учетом веса каждой связи и применяем активационную функцию (в нашем случае активационной функции нет). Сделаем вычисления для первого элемента в обучающем наборе:

$y_{predicted}=\sum_{i=1}^{n}{x_iw_i}=1\cdot0.1+0.5\cdot0.2=0.2$


Рисунок 6 – Прямое распространение ошибки

Обратите внимание, что написанная формула выше – это упрощенное математическое уравнение для частного случая операций над тензорами.

Тензор – это по сути контейнер данных, который может иметь N осей и произвольное число элементов вдоль каждой из осей. Большинство с тензорами знакомы с математики – векторы (тензор с одной осью), матрицы (тензор с двумя осями – строки, колонки).
Формулу можно написать в следующем виде, где вы увидите знакомые матрицы (тензоры) и их перемножение, а также поймете о каком упрощении шла речь выше:

${\vec{Y}}_{predicted}=\ {\vec{X}}^T\vec{W}=\left[\begin{matrix}x_1\\x_2\\\end{matrix}\right]^T\cdot \left [ \begin{matrix} w_1\\ w_2 \end{matrix} \right ]=\left [ \begin{matrix} x_1 & x_2 \end{matrix} \right ] \cdot \left [ \begin{matrix} w_1\\ w_2 \end{matrix} \right ] =\left [ x_1w_1+x_2w_2 \right ]$

ШАГ 2 — Расчет функции ошибки
Функция ошибка – это метрика, отражающая расхождение между ожидаемыми и полученными выходными данными. Обычно используют следующие функции ошибки:
— среднеквадратичная ошибка (Mean Squared Error, MSE) – данная функция ошибки особенно чувствительна к выбросам в тренировочном наборе, так как используется квадрат от разности фактического и ожидаемого значений (выброс — значение, которое сильно удалено от других значений в наборе данных, которые могут иногда появляться в следствии ошибок данных, таких как смешивание данных с разными единицами измерения или плохие показания датчиков):

$L=\frac{1}{N}\sum_{i=1}^{N}\left(y_{predicted(i)}-y_{expected(i)}\right)^2$

— среднеквадратичное отклонение (Root MSE) – по сути это тоже самое что, среднеквадратичная ошибка в контексте нейронных сетей, но может отражать реальную физическую единицу измерения, например, если в нейронной сети выходным параметров нейронной сети является цена дома выраженной в долларах, то единица измерения среднеквадратичной ошибки будет доллар квадратный ($$^2$), а для среднеквадратичного отклонения это доллар ($), что естественно немного упрощает задачу анализа человеком:

$L=\sqrt{\frac{1}{N}\sum_{i=1}^{N}\left(y_{predicted(i)}-y_{expected(i)}\right)^2}$

— среднее отклонение (Mean Absolute Error, MAE) -в отличии от двух выше указанных значений, является не столь чувствительной к выбросам:

$L=\frac{1}{N}\sum_{i=1}^{N}\left|y_{predicted(i)}-y_{expected(i)}\right|$

— перекрестная энтропия (Cross entropy) – использует для задач классификации:

$L=-\sum_{i=1}^{N}\sum_{j=1}^{M}{y_{expected(ij)}\log(y_{predicted(ij)})}$

где
$N$ – число экземпляров в тренировочном наборе
$M$ – число классов при решении задач классификации
$y_{expected}$ — ожидаемое выходное значение
$y_{predicted}$ – фактическое выходное значение обучаемой модели

Для нашего конкретного случая воспользуемся MSE:

$L=\frac{1}{N}\sum_{i=1}^{N}\left(y_{predicted(i)}-y_{expected(i)}\right)^2={(0.2-1)}^2=0.64$

ШАГ 3 — Обратное распространение ошибки (backpropagation)
Цель обучения нейронной сети проста – это минимизация функции ошибки:

$L\rightarrow min$

Одним способом найти минимум функции – это на каждом очередном шаге обучения модифицировать веса соединений в направлении противоположным вектору-градиенту – метод градиентного спуска, и это математически выглядит так:

${\vec{w}}^{(k+1)}={\vec{w}}^k-\mu\nabla L({\vec{w}}^k)$

где $k$ – k -ая итерация обучения нейронной сети;
$\mu$ – шаг обучения (learning rate) и задается инженером, обычно это может быть 0.1; 0.01 (о том как шаг обучения влияет на процесс сходимости обучения отметить чуть позже)
$\nabla L$ – градиент функции-ошибки
Для нахождения градиента, используем частные производные по настраиваемым аргументам $w_1,w_2$:

$\nabla L\left(\vec{w}\right)=\left[\begin{matrix}\frac{\partial L}{\partial w_1}\\\vdots\\\frac{\partial L}{\partial w_N}\\\end{matrix}\right]$

В нашем конкретном случае с учетом всех упрощений, функция ошибки принимает вид:

$L\left(w_1,w_2\right)={(y_{predicted}-y_{expected})}^2={(x_1w_1+x_2w_2-y_{expected})}^2=$

$={(1\cdot w_1+0.5\cdot w_2-1)}^2$

Памятка формул производных

Напомним некоторые формулы производных, которые пригодятся для вычисления частных производных

Найдем следующие частные производные:

$\frac{\partial}{\partial w_1}{(w_1+0.5w_2-1)}^2=2\cdot\left(w_1+0.5w_2-1\right)\frac{\partial}{\partial w_1}\left(w_1+0.5w_2-1\right)=$

$=2\cdot\left(w_1+0.5w_2-1\right)\cdot1=2\left(0.1+0.5\cdot0.2-1\right)=-1.6$

$\frac{\partial}{\partial w_2}{(w_1+0.5w_2-1)}^2=2\cdot\left(w_1+0.5w_2-1\right)\frac{\partial}{\partial w_2}\left(w_1+0.5w_2-1\right)=$

$=2\cdot\left(w_1+0.5w_2-1\right)\cdot0.5=2\left(0.1+0.5\cdot0.2-1\right)\cdot0.5=-0.8$

Тогда процесс обратного распространения ошибки – движение по модели от выхода по направлению к входу с модификацией весов модели в направлении обратном вектору градиента. Задавая обучающий шаг 0.1 (learning rate) имеем (рисунок 7):

$w_1^{(k+1)}=w_1^{(k)}-\mu\frac{\partial L\left(w_1,w_2\right)}{\partial w_1}=0.1-0.1\cdot\left(-1.6\right)=0.26$

$w_2^{(k+1)}=w_2^{(k)}-\mu\frac{\partial L\left(w_1,w_2\right)}{\partial w_2}=0.2-0.1\cdot\left(-0.8\right)=0.28$


Рисунок 7 – Обратное распространение ошибки
Таким образом мы завершили k+1 шаг обучения, чтобы убедиться, что ошибка снизилась, а выход от модели с новыми весами стал ближе к ожидаемому выполним процесс прямого распространения ошибки по модели с новыми весами (см. ШАГ 1):

$y_{predicted}=x_1w_1+x_2w_2=1\cdot0.26+0.5\cdot0.28=0.4$

Как видим, выходное значение увеличилось на 0.2 единица в верном направлении к ожидаемому результату – единице (1). Ошибка тогда составит:

$L={(0.4-1)}^2=0.36$

Как видим, на предыдущем шаге обучения ошибка составила 0.64, а с новыми весами – 0.36, следовательно мы настроили модель в верном направлении.

Следующая часть статьи:
Машинное обучение. Нейронные сети (часть 2): Моделирование OR; XOR с помощью TensorFlow.js
Машинное обучение. Нейронные сети (часть 3) — Convolutional Network под микроскопом. Изучение АПИ Tensorflow.js

Источник

Выбор функции потерь для задач построения нейронных сетей

Время прочтения: 4 мин.

При построении нейронных сетей перед нами часто встаёт вопрос правильного выбора функции потерь, используемой для формирования соответствий между входными и выходными параметрами. Функция потерь отвечает за оценку того, насколько хорошо модель предсказывает реальное значение, и построение модели сводится к решению задачи минимизации значения этой функции на каждом этапе. И в зависимости от того, как выглядят наши данные, требуется использовать разные подходы.

В рамках данной статьи мы рассмотрим три функции потерь для нейронных сетей, решающих регрессионные задачи.  

Mean Squared Error

 Среднеквадратичная ошибка (MSE) — одна из основных функций расчёта отклонения. Для каждой точки вычисляется квадрат отклонения, после чего полученные значения суммируются и делятся на общее количество точек. Чем ближе полученное значение к нулю, тем точнее наша модель. Данный метод расчёта в значительной мере чувствителен к выбросам в выборке, или к выборкам где разброс значений очень большой. В основном, данная функция применяется для переменных, распределение которых близко к распределению Гаусса.

Mean Absolute Error

Средняя абсолютная ошибка (MAE) – это усреднённая сумма модулей разницы между реальным и предсказанным значениями. MAE во многом похожа на MSE, но она отличается меньшей чувствительностью к выбросам значений (так как не берётся квадрат отклонения).

Mean Squared Logarithmic Error

Среднеквадратичная логарифмическая ошибка (MSLE) – усреднённая сумма квадратов разностей между логарифмами значений. Благодаря большому гасящему эффекту логарифма она более применима к моделям, строящимся на данных, которые имеют большой разброс значений на несколько порядков.

 Продемонстрируем как выбор функции потерь влияет на процесс построения нейронной сети. Для генерации данных будем использовать встроенную в scikit-learn функцию make_regression, а в качестве нейронной сети будет выступать многослойный перцептрон.

Код используемый для демонстрации:

from sklearn.datasets import make_regression
from sklearn.preprocessing import StandardScaler
from keras.models import Sequential
from keras.layers import Dense
from keras.optimizers import SGD
from matplotlib import pyplot
# формирование датасета
X, y = make_regression(n_samples=1000, n_features=20, noise=0.1, random_state=1)
# нормализация
X = StandardScaler().fit_transform(X)
y = StandardScaler().fit_transform(y.reshape(len(y),1))[:,0]
# разделение
n_train = 500
trainX, testX = X[:n_train, :], X[n_train:, :]
trainy, testy = y[:n_train], y[n_train:]
# определение для модели
model = Sequential()
model.add(Dense(25, input_dim=20, activation='relu', kernel_initializer='he_uniform'))
model.add(Dense(1, activation='linear'))
opt = SGD(lr=0.01, momentum=0.9)
model.compile(loss=вид функции потерь, optimizer=opt)
# расчёт
history = model.fit(trainX, trainy, validation_data=(testX, testy), epochs=100, verbose=0)
# Оценка качества
train_mse = model.evaluate(trainX, trainy, verbose=0)
test_mse = model.evaluate(testX, testy, verbose=0)
print('Train: %.3f, Test: %.3f' % (train_mse, test_mse))
# plot Демонстрация результата
pyplot.title('Loss / Mean Squared Error')
pyplot.plot(history.history['loss'], label='train')
pyplot.plot(history.history['val_loss'], label='test')
pyplot.legend()
pyplot.show()

В данном коде мы будем заменять только указанный вид функции потерь.
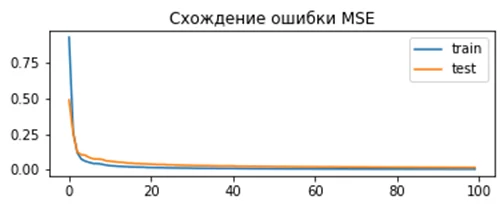
Результат для MSE:

model.compile(loss='mean_squared_error', optimizer=opt)

Полученное отклонение для модели:

Train: 0.000, Test: 0.001

Как видно из графика, модель показывает хорошую сходимость и низкое отклонение.

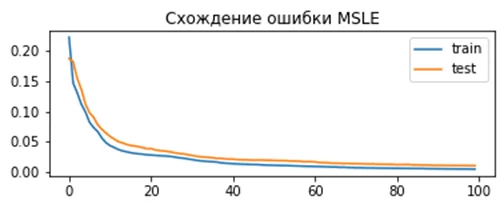
Результат для MSLE:

model.compile(loss=' mean_squared_logarithmic_error', optimizer=opt)

Полученное отклонение для модели:

Train: 0.165, Test: 0.184

По графику видно, что для данного набора данных MSLE сходится медленней чем MSE. С одной стороны, это может привести к тому что модель будет строиться медленней и получится хуже, с другой – использование MSE может привести к переобучению. Результат для MAE:

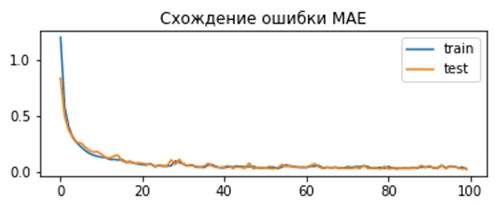
model.compile(loss='mean_absolute_error', optimizer=opt)

Полученное отклонение для модели:

Train: 0.002, Test: 0.002

Здесь мы можем увидеть, что результат сходится очень эффективно, но ошибка имеет нерегулярный характер. Так как используемый нами генератор строит гауссово распределение без выбросов, использование MAE не даёт значительных преимуществ.

Очевидно, что от выбора правильной функции потерь сильно зависит точность, качество и скорость построения модели, поэтому следует внимательно подходить к выбору опираясь как на используемую модель, так и на характеристики входных данных.

Источник

y question is about Neural Network Training. I already searched about this but, there is no good explanation about it.

There are dozens of good explanations on the web, and in the literature, one such example may be the book by Haykin: Neural Networks and Learning machines

So for the first one, how to calculate mean square error? (I know this is silly, but I really don’t get it)

In the most simple terms, mean squared error is defined as

sum_i 1/n (desired_output(i) - model_output(i))^2

So you simply calculate the mean of the squares of the errors (differences between your output, and the desired one).

Now when should we calculate the mean square error? does it when we already take all pairs? or does we calculate it for each pair?

Both methods are used, one is called batch learning, and one is online learning. So all next questions have the answer «both are correct, depending whether you are using batch or online learning». Which one to choose? Obviously — it depends, but for a sake of simplicity I would suggest starting with batch learning (so you compute the error over all training samples and then update).

Источник

Среднеквадратичная ошибка в PyTorch рассчитывается почти так же, как и общее уравнение потерь, приведенное ранее. Мы также рассмотрим значение смещения, поскольку это также параметр, который необходимо обновлять в процессе обучения.
(y-Ax+b)2
Среднеквадратичная ошибка лучше всего поясняется иллюстрацией.

Предположим, у нас есть набор значений, и мы начинаем с рисования некоторого параметра линии регрессии, размер которого определяется случайным набором веса и значения смещения, как и раньше.

Среднеквадратичная ошибка

Ошибка соответствует тому, как далеко фактическое значение от прогнозируемого значения – фактическое расстояние между ними.

Фактическое и прогнозируемое значение

Для каждой точки ошибка рассчитывается путем сравнения прогнозируемых значений, сделанных нашей линейной моделью, с фактическим значением по следующей формуле.

Формула сравнения значений

Каждая точка связана с ошибкой, что означает, что мы должны выполнить суммирование ошибки для каждой точки. Мы знаем, что прогноз можно переписать как:

Прогноз

Поскольку мы вычисляем среднеквадратичную ошибку, мы должны взять среднее значение, разделив его на количество точек данных. Упомянутый ранее градиент функции ошибки должен вести нас в направлении наибольшего увеличения ошибки.

Двигаясь к отрицательному градиенту нашей функции стоимости, мы движемся в направлении наименьшей ошибки. Мы будем использовать этот градиент как компас, который всегда ведет нас вниз. В градиентном спуске мы игнорируем наличие смещения, но для ошибки требуется определить оба параметра A и b.

Теперь мы вычисляем частные производные для каждого, и, как и раньше, мы начинаем с любой пары значений A и b.

Вычисление частных производных

Мы используем алгоритм градиентного спуска для обновления A и b в направлении наименьшей ошибки на основе двух частных производных, упомянутых выше. Для каждой отдельной итерации новый вес равен:

A1=A0-∝ f'(A).

И новое значение смещения равно

b1=b0-∝ f'(b).

Основная идея написания кода в том, что мы начинаем с некоторой случайной модели со случайным набором параметров веса и значения смещения. Эта случайная модель будет иметь большую функцию ошибки, большую функцию стоимости, и затем мы используем градиентный спуск, чтобы обновить вес нашей модели в направлении наименьшей ошибки. Минимизация этой ошибки возвращает оптимизированный результат.

Изучаю Python вместе с вами, читаю, собираю и записываю информацию опытных программистов.

Источник

Лабораторная
работа №4
Нелинейные ИНС в задачах
прогнозирования.

Цель работы: Изучить обучение и
функционирование нелинейной ИНС при
решении задач прогнозирования.

1. Математические
основы алгоритма обратного распространения
ошибки

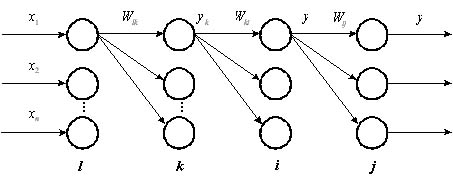
Рис. 1.
Четырехслойная нейронная сеть.

Алгоритм обратного распространения
ошибки был предложен в и является
эффективным средством для обучения
многослойных нейронных сетей.

Рассмотрим нейронную сеть, состоящую
из четырех слоев (рис 1). Обозначим слои
нейронных элементов от входа к выходу
соответственно через
.
Тогда выходное значение j-го нейрона
последнего слоя равняется:

(1)

,
(2)

где
—
взвешенная сумма j-го нейрона
выходного слоя;
—
выходное
значение i-го нейрона
предпоследнего слоя;
и
—
соответственно весовой коэффициент и
порог j-го нейрона выходного слоя.

Аналогичным образом выходное значение
i-го нейрона предпоследнего слоя
определяется, как:

(3)

.
(4)

Соответственно для k-го слоя:

(5)

.
(6)

Алгоритм обратного распространения
ошибки минимизирует среднеквадратичную
ошибку нейронной сети. Для этого с целью
настройки синаптических связей
используется метод градиентного спуска
в пространстве весовых коэффициентов
и порогов нейронной сети. Согласно
методу градиентного спуска изменение
весовых коэффициентов и порогов нейронной
сети происходит по следующему правилу:

,
(7)

,
(8)

где
—
среднеквадратичная ошибка нейронной
сети для одного образа.

Она определяется, как

,
(9)

где
—
эталонное выходное значение j-го
нейрона.

Ошибка j-го нейрона выходного слоя
равняется:

.
(10)

Теорема 2.2. Для любого скрытого слоя
ошибка
-го
нейронного элемента определяется
рекурсивным образом через ошибки
нейронов следующего слоя
:

(11)

где
—
количество нейронов следующего слоя
по отношению к слою
;
—
синаптическая связь между
-м
и
-м
нейроном различных слоев;
—
взвешенная сумма
-го
нейрона.

Теорема 2.3. Производные среднеквадратичной
ошибки по весовым коэффициентам и
порогам нейронных элементов для любых
двух слоев
и
многослойной
сети определяются следующим образом:

(12)

(13)

Следствие 2.1: Для минимизации
среднеквадратичной ошибки сети весовые
коэффициенты и пороги нейронных элементов
должны изменяться с течением времени
следующим образом:

(14)

(15)

где—
скорость обучения.

Данное следствие является очевидным.
Оно определяет правило обучения
многослойных нейронных сетей в общем
виде, которое называется обобщенным
дельта правилом .

2. Обобщенное дельта
правило для различных функций активации
нейронных элементов

Определим выражения (14) и (15) для различных
функций активации нейронных элементов.

2.1. Сигмоидная функция

Выходное значение j-го нейронного
элемента определяется следующим

образом:

,
(16)

.
(17)

Тогда

(18)

В результате обобщенное дельта правило
для сигмоидной функции активации можно
представить в следующем виде:

(19)

(20)

Ошибка для j-го нейрона выходного
слоя определяется, как

.
(21)

Для j-го нейронного элемента скрытого
слоя:

(22)

где m— количество нейронных
элементов следующего слоя по отношению
к слою i(рис. 2).

Рис.
2. Определение ошибки j-го
нейронного элемента.

2.2. Биполярная сигмоидная
функция

Выходное значение j-го нейрона
определяется, как

(23)

Тогда

(24)

Отсюда получаем следующие выражения
для обучения нейронной сети с биполярной
сигмоидной функцией активации:

(25)

(26)

Ошибка для j-го нейрона выходного и
скрытого слоев определяется соответственно,
как:

(27)

.
(28)

2.3. Гиперболический
тангенс

Для данной функции активации выходное
значение j-го нейрона определяется
следующим образом:

.
(29)

Определим производную функции
гиперболический тангенс:

.
(30)

Тогда правило обучения можно представить
в виде следующих выражений:

(31)

(32)

Ошибка для j-го нейрона выходного и
скрытого слоев соответственно равняется:

,
(33)

.
(34)

Используя полученные в данном разделе
выражения можно определить алгоритм
обратного распространения ошибки для
различных функций активации нейронных
элементов.

3. Алгоритм обратного
распространения ошибки

Как уже отмечалось, алгоритм обратного
распространения ошибки был предложен
в 1986 г. рядом авторов независимо друг
от друга. Он является эффективным
средством обучения нейронных сетей и
представляет собой следующую
последовательность шагов:

1. Задается шаг обучения
и
желаемая среднеквадратичная ошибка
нейронной сети
.

2. Случайным образом инициализируются
весовые коэффициенты и пороговые
значения нейронной сети.

3. Последовательно подаются образы из
обучающей выборки на вход нейронной
сети. При этом для каждого входного
образа выполняются следующие действия:

a) производится фаза прямого распространения
входного образа по нейронной сети. При
этом вычисляется выходная активность
всех нейронных элементов сети:

,

где индекс j характеризует нейроны
следующего слоя по отношению к слою i.

b) производится фаза обратного
распространения сигнала, в результате
которой определяется ошибка
нейронных
элементов для всех слоев сети. При этом
соответственно для выходного и скрытого
слоев:

,

.

В последнем выражении индекс i
характеризует нейронные элементы
следующего слоя по отношению к слою
.

c) для каждого слоя нейронной сети
происходит изменение весовых коэффициентов
и порогов нейронных элементов:

.

4. Вычисляется суммарная среднеквадратичная
ошибка нейронной сети:

где
—
размерность обучающей выборки.

5. Если
то
происходит переход к шагу 3 алгоритма.
В противном случае алгоритм обратного
распространения ошибки заканчивается.

Таким образом, данный алгоритм
функционирует до тех пор, пока суммарная
среднеквадратичная ошибка сети не
станет меньше заданной, т. е.
.

Задание.

1. Написать на любом ЯВУ программу
моделирования прогнозирующей нелинейной
ИНС. Для тестирования использовать
функцию


.

Варианты заданий приведены в следующей
таблице:

№ варианта

a

b

с

d

Кол-во входов
ИНС

Кол-во НЭ в
скрытом слое

1

0.1

0.1

0.05

0.1

6

2

2

0.2

0.2

0.06

0.2

8

3

3

0.3

0.3

0.07

0.3

10

4

4

0.4

0.4

0.08

0.4

6

2

5

0.1

0.5

0.09

0.5

8

3

6

0.2

0.6

0.05

0.6

10

4

7

0.3

0.1

0.06

0.1

6

2

8

0.4

0.2

0.07

0.2

8

3

9

0.1

0.3

0.08

0.3

10

4

10

0.2

0.4

0.09

0.4

6

2

11

0.3

0.5

0.05

0.5

8

3

Для прогнозирования использовать
многослойную ИНС с одним скрытым слоем.
В качестве функций активации для скрытого
слоя использовать сигмоидную функцию,
для выходного — линейную.

2. Результаты представить в виде отчета
содержащего:

  1. Титульный лист,

  2. Цель работы,

  3. Задание,

  4. График прогнозируемой функции на
    участке обучения,

  5. Результаты обучения: таблицу со
    столбцами: эталонное значение, полученное
    значение, отклонение; график изменения
    ошибки в зависимости от итерации.

  6. Результаты прогнозирования: таблицу
    со столбцами: эталонное значение,
    полученное значение, отклонение.

  7. Выводы по лабораторной работе.

Результаты для пунктов 3 и 4 приводятся
для значения , при
котором достигается минимальная ошибка.
В выводах анализируются все полученные
результаты.

Контрольные вопросы.

  1. ИНС какой архитектуры Вы использовали
    в данной работе? Опишите принцип
    построения этой ИНС.

  2. Как функционирует используема Вами
    ИНС?

  3. Опишите (в общих чертах) алгоритм
    обучения Вашей ИНС.

  4. Как формируется обучающая выборка для
    решения задачи прогнозирования?

  5. Как выполняется многошаговое
    прогнозирование временного ряда?

  6. Предложите критерий оценки качества
    результатов прогноза.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
Источник

Понравилась статья? Поделить с друзьями:
  • Среднеквадратичная ошибка на английском
  • Среди грамматических ошибок распространены
  • Спускаясь к реке мальчик остановился грамматическая ошибка
  • Среднеарифметическая ошибка формула
  • Справочник ошибок бмв