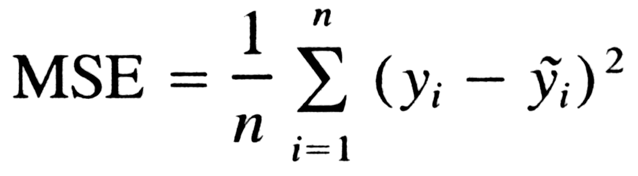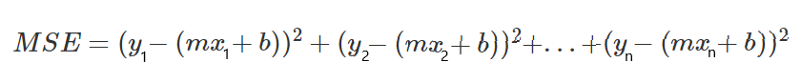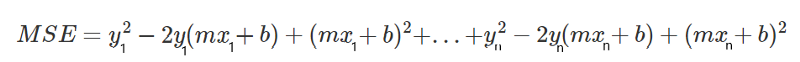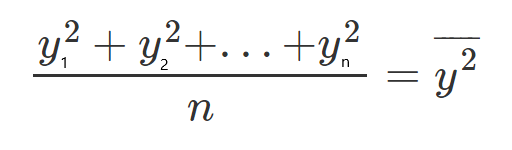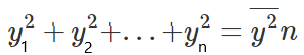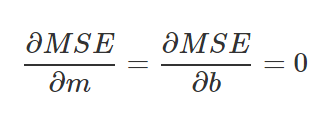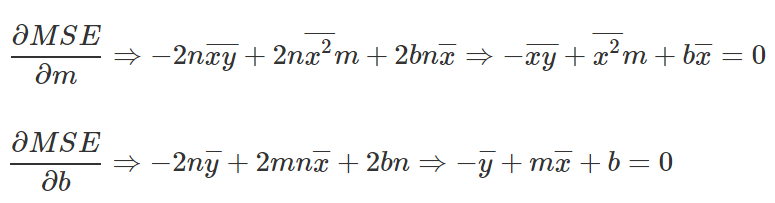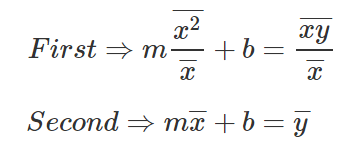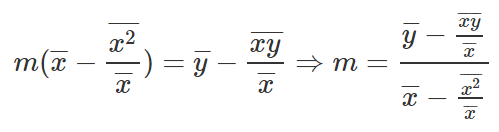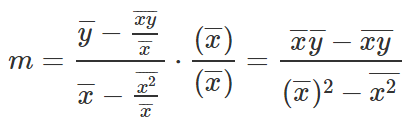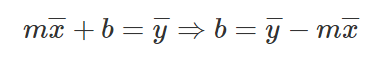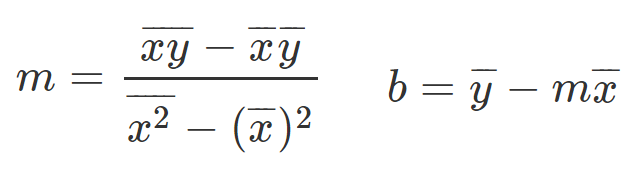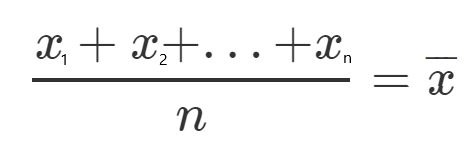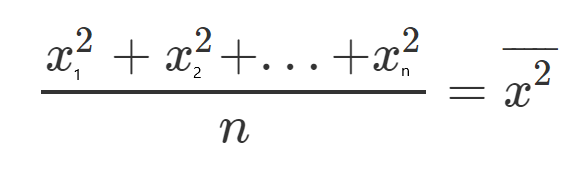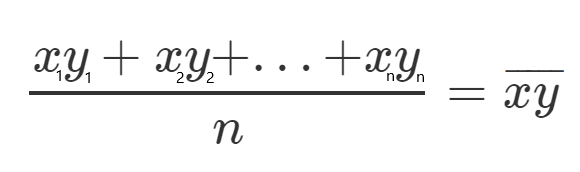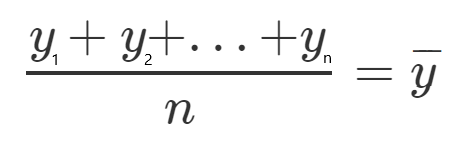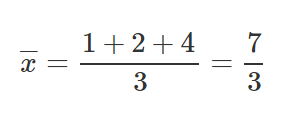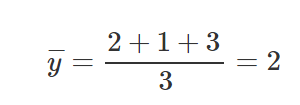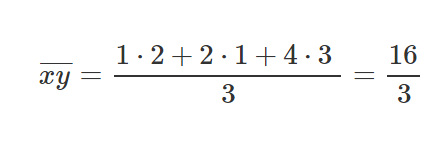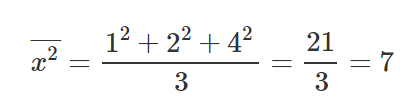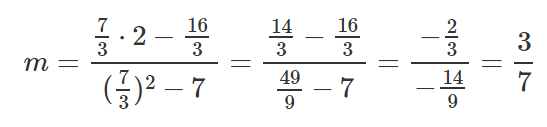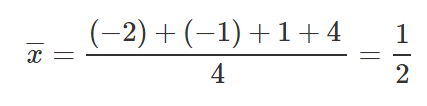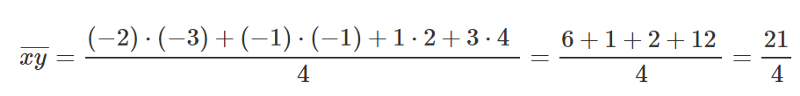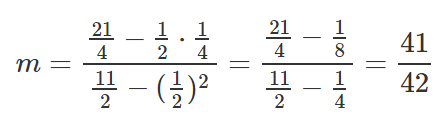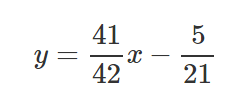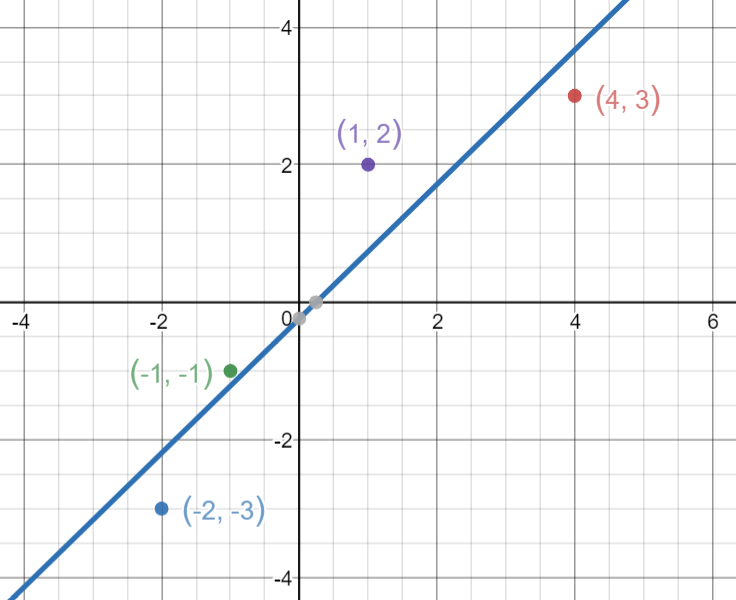Среднеквадратичная ошибка (Mean Squared Error) – Среднее арифметическое (Mean) квадратов разностей между предсказанными и реальными значениями Модели (Model) Машинного обучения (ML):
Рассчитывается с помощью формулы, которая будет пояснена в примере ниже:
$$MSE = \frac{1}{n} × \sum_{i=1}^n (y_i — \widetilde{y}_i)^2$$
$$MSE\space{}{–}\space{Среднеквадратическая}\space{ошибка,}$$
$$n\space{}{–}\space{количество}\space{наблюдений,}$$
$$y_i\space{}{–}\space{фактическая}\space{координата}\space{наблюдения,}$$
$$\widetilde{y}_i\space{}{–}\space{предсказанная}\space{координата}\space{наблюдения,}$$
MSE практически никогда не равен нулю, и происходит это из-за элемента случайности в данных или неучитывания Оценочной функцией (Estimator) всех факторов, которые могли бы улучшить предсказательную способность.
Пример. Исследуем линейную регрессию, изображенную на графике выше, и установим величину среднеквадратической Ошибки (Error). Фактические координаты точек-Наблюдений (Observation) выглядят следующим образом:
Мы имеем дело с Линейной регрессией (Linear Regression), потому уравнение, предсказывающее положение записей, можно представить с помощью формулы:
$$y = M * x + b$$
$$y\space{–}\space{значение}\space{координаты}\space{оси}\space{y,}$$
$$M\space{–}\space{уклон}\space{прямой}$$
$$x\space{–}\space{значение}\space{координаты}\space{оси}\space{x,}$$
$$b\space{–}\space{смещение}\space{прямой}\space{относительно}\space{начала}\space{координат}$$
Параметры M и b уравнения нам, к счастью, известны в данном обучающем примере, и потому уравнение выглядит следующим образом:
$$y = 0,5252 * x + 17,306$$
Зная координаты реальных записей и уравнение линейной регрессии, мы можем восстановить полные координаты предсказанных наблюдений, обозначенных серыми точками на графике выше. Простой подстановкой значения координаты x в уравнение мы рассчитаем значение координаты ỹ:
Рассчитаем квадрат разницы между Y и Ỹ:
Сумма таких квадратов равна 4 445. Осталось только разделить это число на количество наблюдений (9):
$$MSE = \frac{1}{9} × 4445 = 493$$
Само по себе число в такой ситуации становится показательным, когда Дата-сайентист (Data Scientist) предпринимает попытки улучшить предсказательную способность модели и сравнивает MSE каждой итерации, выбирая такое уравнение, что сгенерирует наименьшую погрешность в предсказаниях.
MSE и Scikit-learn
Среднеквадратическую ошибку можно вычислить с помощью SkLearn. Для начала импортируем функцию:
import sklearn
from sklearn.metrics import mean_squared_errorИнициализируем крошечные списки, содержащие реальные и предсказанные координаты y:
y_true = [5, 41, 70, 77, 134, 68, 138, 101, 131]
y_pred = [23, 35, 55, 90, 93, 103, 118, 121, 129]Инициируем функцию mean_squared_error(), которая рассчитает MSE тем же способом, что и формула выше:
mean_squared_error(y_true, y_pred)
Интересно, что конечный результат на 3 отличается от расчетов с помощью Apple Numbers:
496.0Ноутбук, не требующий дополнительной настройки на момент написания статьи, можно скачать здесь.
Автор оригинальной статьи: @mmoshikoo
Фото: @tobyelliott
Время на прочтение
4 мин
Количество просмотров 5.7K

Функции потерь Python являются важной частью моделей машинного обучения. Эти функции показывают, насколько сильно предсказанный моделью результат отличается от фактического.
Существует несколько способов вычислить эту разницу. В этом материале мы рассмотрим некоторые из наиболее распространенных функций потерь.
Ниже будут рассмотрены следующие четыре функции потерь.
-
Среднеквадратическая ошибка
-
Среднеквадратическая ошибка
-
Средняя абсолютная ошибка
-
Кросс-энтропийные потери
Из этих четырех функций потерь первые три применяются к модели классификации.
1. Среднеквадратическая ошибка (MSE)
Среднеквадратичная ошибка (MSE) рассчитывается как среднее значение квадратов разностей между прогнозируемыми и фактически наблюдаемыми значениями. Математически это можно выразить следующим образом:
Реализация MSE на языке Python выглядит следующим образом:
import numpy as np # импортируем библиотеку numpy
def mean_squared_error(act, pred): # функция
diff = pred - act # находим разницу между прогнозируемыми и наблюдаемыми значениями
differences_squared = diff ** 2 # возводим в квадрат (чтобы избавиться от отрицательных значений)
mean_diff = differences_squared.mean() # находим среднее значение
return mean_diff
act = np.array([1.1,2,1.7]) # создаем список актуальных значений
pred = np.array([1,1.7,1.5]) # список прогнозируемых значений
print(mean_squared_error(act,pred))
Выход :
0.04666666666666667Вы также можете использовать mean_squared_error из sklearn для расчета MSE. Вот как работает функция:
from sklearn.metrics import mean_squared_error
act = np.array([1.1,2,1.7])
pred = np.array([1,1.7,1.5])
mean_squared_error(act, pred)
Выход :
0.04666666666666667
2. Корень среднеквадратической ошибки (RMSE)
Итак, ранее, для того, чтобы найти действительную ошибку среди между прогнозируемыми и фактически наблюдаемыми значениями (там могли быть положительные и отрицательные значения), мы возводили их в квадрат (для того чтобы отрицательные значения участвовали в расчетах в полной мере). Это была среднеквадратичная ошибка (MSE).
Корень среднеквадратической ошибки (RMSE) мы используем для того чтобы избавиться от квадратной степени, в которую мы ранее возвели действительную ошибку среди между прогнозируемыми и фактически наблюдаемыми значениями. Математически мы можем представить это следующим образом:
Реализация Python для RMSE выглядит следующим образом:
import numpy as np
def root_mean_squared_error(act, pred):
diff = pred - act # находим разницу между прогнозируемыми и наблюдаемыми значениями
differences_squared = diff ** 2 # возводим в квадрат
mean_diff = differences_squared.mean() # находим среднее значение
rmse_val = np.sqrt(mean_diff) # извлекаем квадратный корень
return rmse_val
act = np.array([1.1,2,1.7])
pred = np.array([1,1.7,1.5])
print(root_mean_squared_error(act,pred))
Выход :
0.21602468994692867
Вы также можете использовать mean_squared_error из sklearn для расчета RMSE. Давайте посмотрим, как реализовать RMSE, используя ту же функцию:
from sklearn.metrics import mean_squared_error
act = np.array([1.1,2,1.7])
pred = np.array([1,1.7,1.5])
mean_squared_error(act, pred, squared = False) #Если установлено значение False, функция возвращает значение RMSE.
Выход :
0.21602468994692867
Если для параметра squared установлено значение True, функция возвращает значение MSE. Если установлено значение False, функция возвращает значение RMSE.
3. Средняя абсолютная ошибка (MAE)
Средняя абсолютная ошибка (MAE) рассчитывается как среднее значение абсолютной разницы между прогнозами и фактическими наблюдениями. Математически мы можем представить это следующим образом:
Реализация Python для MAE выглядит следующим образом:
import numpy as np
def mean_absolute_error(act, pred): #
diff = pred - act # находим разницу между прогнозируемыми и наблюдаемыми значениями
abs_diff = np.absolute(diff) # находим абсолютную разность между прогнозами и фактическими наблюдениями.
mean_diff = abs_diff.mean() # находим среднее значение
return mean_diff
act = np.array([1.1,2,1.7])
pred = np.array([1,1.7,1.5])
mean_absolute_error(act,pred)
Выход :
0.20000000000000004
Вы также можете использовать mean_absolute_error из sklearn для расчета MAE.
from sklearn.metrics import mean_absolute_error
act = np.array([1.1,2,1.7])
pred = np.array([1,1.7,1.5])
mean_absolute_error(act, pred)
Выход :
0.20000000000000004
4. Функция потерь перекрестной энтропии в Python
Функция потерь перекрестной энтропии также известна как отрицательная логарифмическая вероятность. Это чаще всего используется для задач классификации. Проблема классификации — это проблема, в которой вы классифицируете пример как принадлежащий к одному из более чем двух классов.
Давайте посмотрим, как вычислить ошибку в случае проблемы бинарной классификации.
Давайте рассмотрим проблему классификации, когда модель пытается провести классификацию между собакой и кошкой.
Код Python для поиска ошибки приведен ниже.
from sklearn.metrics import log_loss
log_loss(["Dog", "Cat", "Cat", "Dog"],[[.1, .9], [.9, .1], [.8, .2], [.35, .65]])
Выход :
0.21616187468057912
Мы используем метод log_loss из sklearn.
Первый аргумент в вызове функции — это список правильных меток классов для каждого входа. Второй аргумент — это список вероятностей, предсказанных моделью.
Вероятности представлены в следующем формате:
[P(dog), P(cat)]
Заключение
Это руководство было посвящено функциям потерь в Python. Мы рассмотрели различные функции потерь как для задач регрессии, так и для задач классификации. Надеюсь, вам понравился материал, ведь все было достаточно легко и понятно!
Кстати, для тех, кто хотел бы пойти дальше в изучении функций потерь, мы предлагаем разобрать одну вот такую — это очень интересная функция потерь Triplet Loss в Python (функцию тройных потерь), которую для вас любезно подготовил автор.
В машинном обучении различают оценки качества для задачи классификации и регрессии. Причем оценка задачи классификации часто значительно сложнее, чем оценка регрессии.
Содержание
- 1 Оценки качества классификации
- 1.1 Матрица ошибок (англ. Сonfusion matrix)
- 1.2 Аккуратность (англ. Accuracy)
- 1.3 Точность (англ. Precision)
- 1.4 Полнота (англ. Recall)
- 1.5 F-мера (англ. F-score)
- 1.6 ROC-кривая
- 1.7 Precison-recall кривая
- 2 Оценки качества регрессии
- 2.1 Средняя квадратичная ошибка (англ. Mean Squared Error, MSE)
- 2.2 Cредняя абсолютная ошибка (англ. Mean Absolute Error, MAE)
- 2.3 Коэффициент детерминации
- 2.4 Средняя абсолютная процентная ошибка (англ. Mean Absolute Percentage Error, MAPE)
- 2.5 Корень из средней квадратичной ошибки (англ. Root Mean Squared Error, RMSE)
- 2.6 Cимметричная MAPE (англ. Symmetric MAPE, SMAPE)
- 2.7 Средняя абсолютная масштабированная ошибка (англ. Mean absolute scaled error, MASE)
- 3 Кросс-валидация
- 4 Примечания
- 5 См. также
- 6 Источники информации
Оценки качества классификации
Матрица ошибок (англ. Сonfusion matrix)
Перед переходом к самим метрикам необходимо ввести важную концепцию для описания этих метрик в терминах ошибок классификации — confusion matrix (матрица ошибок).
Допустим, что у нас есть два класса и алгоритм, предсказывающий принадлежность каждого объекта одному из классов.
Рассмотрим пример. Пусть банк использует систему классификации заёмщиков на кредитоспособных и некредитоспособных. При этом первым кредит выдаётся, а вторые получат отказ. Таким образом, обнаружение некредитоспособного заёмщика () можно рассматривать как «сигнал тревоги», сообщающий о возможных рисках.
Любой реальный классификатор совершает ошибки. В нашем случае таких ошибок может быть две:
- Кредитоспособный заёмщик распознается моделью как некредитоспособный и ему отказывается в кредите. Данный случай можно трактовать как «ложную тревогу».
- Некредитоспособный заёмщик распознаётся как кредитоспособный и ему ошибочно выдаётся кредит. Данный случай можно рассматривать как «пропуск цели».
Несложно увидеть, что эти ошибки неравноценны по связанным с ними проблемам. В случае «ложной тревоги» потери банка составят только проценты по невыданному кредиту (только упущенная выгода). В случае «пропуска цели» можно потерять всю сумму выданного кредита. Поэтому системе важнее не допустить «пропуск цели», чем «ложную тревогу».
Поскольку с точки зрения логики задачи нам важнее правильно распознать некредитоспособного заёмщика с меткой , чем ошибиться в распознавании кредитоспособного, будем называть соответствующий исход классификации положительным (заёмщик некредитоспособен), а противоположный — отрицательным (заемщик кредитоспособен ). Тогда возможны следующие исходы классификации:
- Некредитоспособный заёмщик классифицирован как некредитоспособный, т.е. положительный класс распознан как положительный. Наблюдения, для которых это имеет место называются истинно-положительными (True Positive — TP).
- Кредитоспособный заёмщик классифицирован как кредитоспособный, т.е. отрицательный класс распознан как отрицательный. Наблюдения, которых это имеет место, называются истинно отрицательными (True Negative — TN).
- Кредитоспособный заёмщик классифицирован как некредитоспособный, т.е. имела место ошибка, в результате которой отрицательный класс был распознан как положительный. Наблюдения, для которых был получен такой исход классификации, называются ложно-положительными (False Positive — FP), а ошибка классификации называется ошибкой I рода.
- Некредитоспособный заёмщик распознан как кредитоспособный, т.е. имела место ошибка, в результате которой положительный класс был распознан как отрицательный. Наблюдения, для которых был получен такой исход классификации, называются ложно-отрицательными (False Negative — FN), а ошибка классификации называется ошибкой II рода.
Таким образом, ошибка I рода, или ложно-положительный исход классификации, имеет место, когда отрицательное наблюдение распознано моделью как положительное. Ошибкой II рода, или ложно-отрицательным исходом классификации, называют случай, когда положительное наблюдение распознано как отрицательное. Поясним это с помощью матрицы ошибок классификации:
-
Истинно-положительный (True Positive — TP) Ложно-положительный (False Positive — FP) Ложно-отрицательный (False Negative — FN) Истинно-отрицательный (True Negative — TN)
Здесь — это ответ алгоритма на объекте, а — истинная метка класса на этом объекте.
Таким образом, ошибки классификации бывают двух видов: False Negative (FN) и False Positive (FP).
P означает что классификатор определяет класс объекта как положительный (N — отрицательный). T значит что класс предсказан правильно (соответственно F — неправильно). Каждая строка в матрице ошибок представляет спрогнозированный класс, а каждый столбец — фактический класс.
# код для матрицы ошибок # Пример классификатора, способного проводить различие между всего лишь двумя # классами, "пятерка" и "не пятерка" из набора рукописных цифр MNIST import numpy as np from sklearn.datasets import fetch_openml from sklearn.model_selection import cross_val_predict from sklearn.metrics import confusion_matrix from sklearn.linear_model import SGDClassifier mnist = fetch_openml('mnist_784', version=1) X, y = mnist["data"], mnist["target"] y = y.astype(np.uint8) X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:] y_train_5 = (y_train == 5) # True для всех пятерок, False для в сех остальных цифр. Задача опознать пятерки y_test_5 = (y_test == 5) sgd_clf = SGDClassifier(random_state=42) # классификатор на основе метода стохастического градиентного спуска (англ. Stochastic Gradient Descent SGD) sgd_clf.fit(X_train, y_train_5) # обучаем классификатор распозновать пятерки на целом обучающем наборе # Для расчета матрицы ошибок сначала понадобится иметь набор прогнозов, чтобы их можно было сравнивать с фактическими целями y_train_pred = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3) print(confusion_matrix(y_train_5, y_train_pred)) # array([[53892, 687], # [ 1891, 3530]])
Безупречный классификатор имел бы только истинно-положительные и истинно отрицательные классификации, так что его матрица ошибок содержала бы ненулевые значения только на своей главной диагонали (от левого верхнего до правого нижнего угла):
import numpy as np
from sklearn.datasets import fetch_openml
from sklearn.metrics import confusion_matrix
mnist = fetch_openml('mnist_784', version=1)
X, y = mnist["data"], mnist["target"]
y = y.astype(np.uint8)
X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:]
y_train_5 = (y_train == 5) # True для всех пятерок, False для в сех остальных цифр. Задача опознать пятерки
y_test_5 = (y_test == 5)
y_train_perfect_predictions = y_train_5 # притворись, что мы достигли совершенства
print(confusion_matrix(y_train_5, y_train_perfect_predictions))
# array([[54579, 0],
# [ 0, 5421]])
Аккуратность (англ. Accuracy)
Интуитивно понятной, очевидной и почти неиспользуемой метрикой является accuracy — доля правильных ответов алгоритма:
Эта метрика бесполезна в задачах с неравными классами, что как вариант можно исправить с помощью алгоритмов сэмплирования и это легко показать на примере.
Допустим, мы хотим оценить работу спам-фильтра почты. У нас есть 100 не-спам писем, 90 из которых наш классификатор определил верно (True Negative = 90, False Positive = 10), и 10 спам-писем, 5 из которых классификатор также определил верно (True Positive = 5, False Negative = 5).
Тогда accuracy:
Однако если мы просто будем предсказывать все письма как не-спам, то получим более высокую аккуратность:
При этом, наша модель совершенно не обладает никакой предсказательной силой, так как изначально мы хотели определять письма со спамом. Преодолеть это нам поможет переход с общей для всех классов метрики к отдельным показателям качества классов.
# код для для подсчета аккуратности: # Пример классификатора, способного проводить различие между всего лишь двумя # классами, "пятерка" и "не пятерка" из набора рукописных цифр MNIST import numpy as np from sklearn.datasets import fetch_openml from sklearn.model_selection import cross_val_predict from sklearn.metrics import accuracy_score from sklearn.linear_model import SGDClassifier mnist = fetch_openml('mnist_784', version=1) X, y = mnist["data"], mnist["target"] y = y.astype(np.uint8) X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:] y_train_5 = (y_train == 5) # True для всех пятерок, False для в сех остальных цифр. Задача опознать пятерки y_test_5 = (y_test == 5) sgd_clf = SGDClassifier(random_state=42) # классификатор на основе метода стохастического градиентного спуска (Stochastic Gradient Descent SGD) sgd_clf.fit(X_train, y_train_5) # обучаем классификатор распозновать пятерки на целом обучающем наборе y_train_pred = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3) # print(confusion_matrix(y_train_5, y_train_pred)) # array([[53892, 687] # [ 1891, 3530]]) print(accuracy_score(y_train_5, y_train_pred)) # == (53892 + 3530) / (53892 + 3530 + 1891 +687) # 0.9570333333333333
Точность (англ. Precision)
Точностью (precision) называется доля правильных ответов модели в пределах класса — это доля объектов действительно принадлежащих данному классу относительно всех объектов которые система отнесла к этому классу.
Именно введение precision не позволяет нам записывать все объекты в один класс, так как в этом случае мы получаем рост уровня False Positive.
Полнота (англ. Recall)
Полнота — это доля истинно положительных классификаций. Полнота показывает, какую долю объектов, реально относящихся к положительному классу, мы предсказали верно.
Полнота (recall) демонстрирует способность алгоритма обнаруживать данный класс вообще.
Имея матрицу ошибок, очень просто можно вычислить точность и полноту для каждого класса. Точность (precision) равняется отношению соответствующего диагонального элемента матрицы и суммы всей строки класса. Полнота (recall) — отношению диагонального элемента матрицы и суммы всего столбца класса. Формально:
Результирующая точность классификатора рассчитывается как арифметическое среднее его точности по всем классам. То же самое с полнотой. Технически этот подход называется macro-averaging.
# код для для подсчета точности и полноты: # Пример классификатора, способного проводить различие между всего лишь двумя # классами, "пятерка" и "не пятерка" из набора рукописных цифр MNIST import numpy as np from sklearn.datasets import fetch_openml from sklearn.model_selection import cross_val_predict from sklearn.metrics import precision_score, recall_score from sklearn.linear_model import SGDClassifier mnist = fetch_openml('mnist_784', version=1) X, y = mnist["data"], mnist["target"] y = y.astype(np.uint8) X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:] y_train_5 = (y_train == 5) # True для всех пятерок, False для в сех остальных цифр. Задача опознать пятерки y_test_5 = (y_test == 5) sgd_clf = SGDClassifier(random_state=42) # классификатор на основе метода стохастического градиентного спуска (Stochastic Gradient Descent SGD) sgd_clf.fit(X_train, y_train_5) # обучаем классификатор распозновать пятерки на целом обучающем наборе y_train_pred = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3) # print(confusion_matrix(y_train_5, y_train_pred)) # array([[53892, 687] # [ 1891, 3530]]) print(precision_score(y_train_5, y_train_pred)) # == 3530 / (3530 + 687) print(recall_score(y_train_5, y_train_pred)) # == 3530 / (3530 + 1891) # 0.8370879772350012 # 0.6511713705958311
F-мера (англ. F-score)
Precision и recall не зависят, в отличие от accuracy, от соотношения классов и потому применимы в условиях несбалансированных выборок.
Часто в реальной практике стоит задача найти оптимальный (для заказчика) баланс между этими двумя метриками. Понятно что чем выше точность и полнота, тем лучше. Но в реальной жизни максимальная точность и полнота не достижимы одновременно и приходится искать некий баланс. Поэтому, хотелось бы иметь некую метрику которая объединяла бы в себе информацию о точности и полноте нашего алгоритма. В этом случае нам будет проще принимать решение о том какую реализацию запускать в производство (у кого больше тот и круче). Именно такой метрикой является F-мера.
F-мера представляет собой гармоническое среднее между точностью и полнотой. Она стремится к нулю, если точность или полнота стремится к нулю.
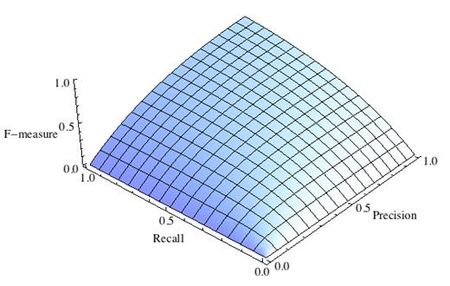
Данная формула придает одинаковый вес точности и полноте, поэтому F-мера будет падать одинаково при уменьшении и точности и полноты. Возможно рассчитать F-меру придав различный вес точности и полноте, если вы осознанно отдаете приоритет одной из этих метрик при разработке алгоритма:
где принимает значения в диапазоне если вы хотите отдать приоритет точности, а при приоритет отдается полноте. При формула сводится к предыдущей и вы получаете сбалансированную F-меру (также ее называют ).
-
Рис.1 Сбалансированная F-мера,
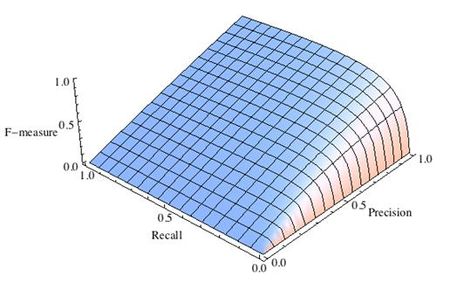
-
Рис.2 F-мера c приоритетом точности,
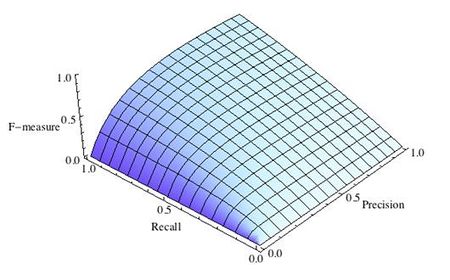
-
Рис.3 F-мера c приоритетом полноты,
F-мера достигает максимума при максимальной полноте и точности, и близка к нулю, если один из аргументов близок к нулю.
F-мера является хорошим кандидатом на формальную метрику оценки качества классификатора. Она сводит к одному числу две других основополагающих метрики: точность и полноту. Имея «F-меру» гораздо проще ответить на вопрос: «поменялся алгоритм в лучшую сторону или нет?»
# код для подсчета метрики F-mera: # Пример классификатора, способного проводить различие между всего лишь двумя # классами, "пятерка" и "не пятерка" из набора рукописных цифр MNIST import numpy as np from sklearn.datasets import fetch_openml from sklearn.model_selection import cross_val_predict from sklearn.linear_model import SGDClassifier from sklearn.metrics import f1_score mnist = fetch_openml('mnist_784', version=1) X, y = mnist["data"], mnist["target"] y = y.astype(np.uint8) X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:] y_train_5 = (y_train == 5) # True для всех пятерок, False для в сех остальных цифр. Задача опознать пятерки y_test_5 = (y_test == 5) sgd_clf = SGDClassifier(random_state=42) # классификатор на основе метода стохастического градиентного спуска (Stochastic Gradient Descent SGD) sgd_clf.fit(X_train, y_train_5) # обучаем классификатор распознавать пятерки на целом обучающем наборе y_train_pred = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3) print(f1_score(y_train_5, y_train_pred)) # 0.7325171197343846
ROC-кривая
Кривая рабочих характеристик (англ. Receiver Operating Characteristics curve).
Используется для анализа поведения классификаторов при различных пороговых значениях.
Позволяет рассмотреть все пороговые значения для данного классификатора.
Показывает долю ложно положительных примеров (англ. false positive rate, FPR) в сравнении с долей истинно положительных примеров (англ. true positive rate, TPR).
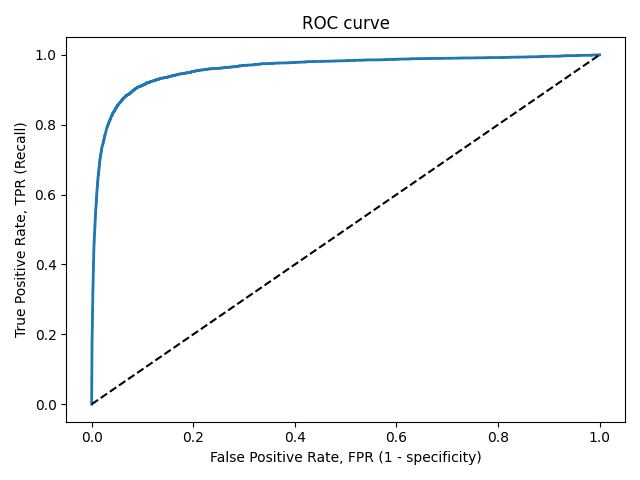
Доля FPR — это пропорция отрицательных образцов, которые были некорректно классифицированы как положительные.
- ,
где TNR — доля истинно отрицательных классификаций (англ. Тrие Negative Rate), представляющая собой пропорцию отрицательных образцов, которые были корректно классифицированы как отрицательные.
Доля TNR также называется специфичностью (англ. specificity). Следовательно, ROC-кривая изображает чувствительность (англ. seпsitivity), т.е. полноту, в сравнении с разностью 1 — specificity.
Прямая линия по диагонали представляет ROC-кривую чисто случайного классификатора. Хороший классификатор держится от указанной линии настолько далеко, насколько это
возможно (стремясь к левому верхнему углу).
Один из способов сравнения классификаторов предусматривает измерение площади под кривой (англ. Area Under the Curve — AUC). Безупречный классификатор будет иметь площадь под ROC-кривой (ROC-AUC), равную 1, тогда как чисто случайный классификатор — площадь 0.5.
# Код отрисовки ROC-кривой # На примере классификатора, способного проводить различие между всего лишь двумя классами # "пятерка" и "не пятерка" из набора рукописных цифр MNIST from sklearn.metrics import roc_curve import matplotlib.pyplot as plt import numpy as np from sklearn.datasets import fetch_openml from sklearn.model_selection import cross_val_predict from sklearn.linear_model import SGDClassifier mnist = fetch_openml('mnist_784', version=1) X, y = mnist["data"], mnist["target"] y = y.astype(np.uint8) X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:] y_train_5 = (y_train == 5) # True для всех пятерок, False для в сех остальных цифр. Задача опознать пятерки y_test_5 = (y_test == 5) sgd_clf = SGDClassifier(random_state=42) # классификатор на основе метода стохастического градиентного спуска (Stochastic Gradient Descent SGD) sgd_clf.fit(X_train, y_train_5) # обучаем классификатор распозновать пятерки на целом обучающем наборе y_train_pred = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3) y_scores = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3, method="decision_function") fpr, tpr, thresholds = roc_curve(y_train_5, y_scores) def plot_roc_curve(fpr, tpr, label=None): plt.plot(fpr, tpr, linewidth=2, label=label) plt.plot([0, 1], [0, 1], 'k--') # dashed diagonal plt.xlabel('False Positive Rate, FPR (1 - specificity)') plt.ylabel('True Positive Rate, TPR (Recall)') plt.title('ROC curve') plt.savefig("ROC.png") plot_roc_curve(fpr, tpr) plt.show()
Precison-recall кривая
Чувствительность к соотношению классов.
Рассмотрим задачу выделения математических статей из множества научных статей. Допустим, что всего имеется 1.000.100 статей, из которых лишь 100 относятся к математике. Если нам удастся построить алгоритм , идеально решающий задачу, то его TPR будет равен единице, а FPR — нулю. Рассмотрим теперь плохой алгоритм, дающий положительный ответ на 95 математических и 50.000 нематематических статьях. Такой алгоритм совершенно бесполезен, но при этом имеет TPR = 0.95 и FPR = 0.05, что крайне близко к показателям идеального алгоритма.
Таким образом, если положительный класс существенно меньше по размеру, то AUC-ROC может давать неадекватную оценку качества работы алгоритма, поскольку измеряет долю неверно принятых объектов относительно общего числа отрицательных. Так, алгоритм , помещающий 100 релевантных документов на позиции с 50.001-й по 50.101-ю, будет иметь AUC-ROC 0.95.
Precison-recall (PR) кривая. Избавиться от указанной проблемы с несбалансированными классами можно, перейдя от ROC-кривой к PR-кривой. Она определяется аналогично ROC-кривой, только по осям откладываются не FPR и TPR, а полнота (по оси абсцисс) и точность (по оси ординат). Критерием качества семейства алгоритмов выступает площадь под PR-кривой (англ. Area Under the Curve — AUC-PR)
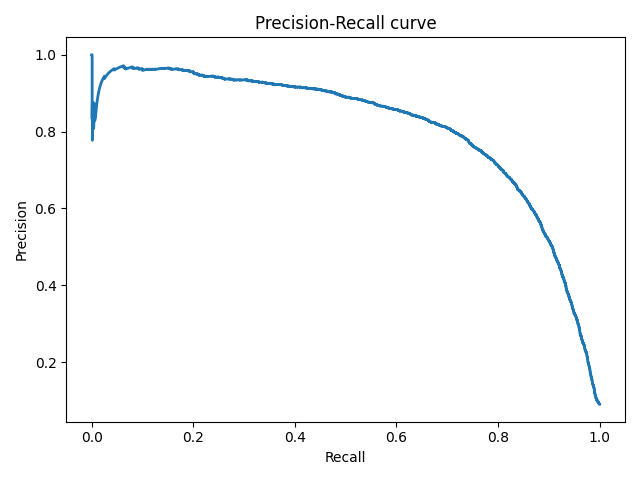
# Код отрисовки Precison-recall кривой # На примере классификатора, способного проводить различие между всего лишь двумя классами # "пятерка" и "не пятерка" из набора рукописных цифр MNIST from sklearn.metrics import precision_recall_curve import matplotlib.pyplot as plt import numpy as np from sklearn.datasets import fetch_openml from sklearn.model_selection import cross_val_predict from sklearn.linear_model import SGDClassifier mnist = fetch_openml('mnist_784', version=1) X, y = mnist["data"], mnist["target"] y = y.astype(np.uint8) X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:] y_train_5 = (y_train == 5) # True для всех пятерок, False для в сех остальных цифр. Задача опознать пятерки y_test_5 = (y_test == 5) sgd_clf = SGDClassifier(random_state=42) # классификатор на основе метода стохастического градиентного спуска (Stochastic Gradient Descent SGD) sgd_clf.fit(X_train, y_train_5) # обучаем классификатор распозновать пятерки на целом обучающем наборе y_train_pred = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3) y_scores = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3, method="decision_function") precisions, recalls, thresholds = precision_recall_curve(y_train_5, y_scores) def plot_precision_recall_vs_threshold(precisions, recalls, thresholds): plt.plot(recalls, precisions, linewidth=2) plt.xlabel('Recall') plt.ylabel('Precision') plt.title('Precision-Recall curve') plt.savefig("Precision_Recall_curve.png") plot_precision_recall_vs_threshold(precisions, recalls, thresholds) plt.show()
Оценки качества регрессии
Наиболее типичными мерами качества в задачах регрессии являются
Средняя квадратичная ошибка (англ. Mean Squared Error, MSE)
MSE применяется в ситуациях, когда нам надо подчеркнуть большие ошибки и выбрать модель, которая дает меньше больших ошибок прогноза. Грубые ошибки становятся заметнее за счет того, что ошибку прогноза мы возводим в квадрат. И модель, которая дает нам меньшее значение среднеквадратической ошибки, можно сказать, что что у этой модели меньше грубых ошибок.
- и
Cредняя абсолютная ошибка (англ. Mean Absolute Error, MAE)
Среднеквадратичный функционал сильнее штрафует за большие отклонения по сравнению со среднеабсолютным, и поэтому более чувствителен к выбросам. При использовании любого из этих двух функционалов может быть полезно проанализировать, какие объекты вносят наибольший вклад в общую ошибку — не исключено, что на этих объектах была допущена ошибка при вычислении признаков или целевой величины.
Среднеквадратичная ошибка подходит для сравнения двух моделей или для контроля качества во время обучения, но не позволяет сделать выводов о том, на сколько хорошо данная модель решает задачу. Например, MSE = 10 является очень плохим показателем, если целевая переменная принимает значения от 0 до 1, и очень хорошим, если целевая переменная лежит в интервале (10000, 100000). В таких ситуациях вместо среднеквадратичной ошибки полезно использовать коэффициент детерминации —
Коэффициент детерминации
Коэффициент детерминации измеряет долю дисперсии, объясненную моделью, в общей дисперсии целевой переменной. Фактически, данная мера качества — это нормированная среднеквадратичная ошибка. Если она близка к единице, то модель хорошо объясняет данные, если же она близка к нулю, то прогнозы сопоставимы по качеству с константным предсказанием.
Средняя абсолютная процентная ошибка (англ. Mean Absolute Percentage Error, MAPE)
Это коэффициент, не имеющий размерности, с очень простой интерпретацией. Его можно измерять в долях или процентах. Если у вас получилось, например, что MAPE=11.4%, то это говорит о том, что ошибка составила 11,4% от фактических значений.
Основная проблема данной ошибки — нестабильность.
Корень из средней квадратичной ошибки (англ. Root Mean Squared Error, RMSE)
Примерно такая же проблема, как и в MAPE: так как каждое отклонение возводится в квадрат, любое небольшое отклонение может значительно повлиять на показатель ошибки. Стоит отметить, что существует также ошибка MSE, из которой RMSE как раз и получается путем извлечения корня.
Cимметричная MAPE (англ. Symmetric MAPE, SMAPE)
Средняя абсолютная масштабированная ошибка (англ. Mean absolute scaled error, MASE)
MASE является очень хорошим вариантом для расчета точности, так как сама ошибка не зависит от масштабов данных и является симметричной: то есть положительные и отрицательные отклонения от факта рассматриваются в равной степени.
Обратите внимание, что в MASE мы имеем дело с двумя суммами: та, что в числителе, соответствует тестовой выборке, та, что в знаменателе — обучающей. Вторая фактически представляет собой среднюю абсолютную ошибку прогноза. Она же соответствует среднему абсолютному отклонению ряда в первых разностях. Эта величина, по сути, показывает, насколько обучающая выборка предсказуема. Она может быть равна нулю только в том случае, когда все значения в обучающей выборке равны друг другу, что соответствует отсутствию каких-либо изменений в ряде данных, ситуации на практике почти невозможной. Кроме того, если ряд имеет тенденцию к росту либо снижению, его первые разности будут колебаться около некоторого фиксированного уровня. В результате этого по разным рядам с разной структурой, знаменатели будут более-менее сопоставимыми. Всё это, конечно же, является очевидными плюсами MASE, так как позволяет складывать разные значения по разным рядам и получать несмещённые оценки.
Недостаток MASE в том, что её тяжело интерпретировать. Например, MASE=1.21 ни о чём, по сути, не говорит. Это просто означает, что ошибка прогноза оказалась в 1.21 раза выше среднего абсолютного отклонения ряда в первых разностях, и ничего более.
Кросс-валидация
Хороший способ оценки модели предусматривает применение кросс-валидации (cкользящего контроля или перекрестной проверки).
В этом случае фиксируется некоторое множество разбиений исходной выборки на две подвыборки: обучающую и контрольную. Для каждого разбиения выполняется настройка алгоритма по обучающей подвыборке, затем оценивается его средняя ошибка на объектах контрольной подвыборки. Оценкой скользящего контроля называется средняя по всем разбиениям величина ошибки на контрольных подвыборках.
Примечания
- [1] Лекция «Оценивание качества» на www.coursera.org
- [2] Лекция на www.stepik.org о кросвалидации
- [3] Лекция на www.stepik.org о метриках качества, Precison и Recall
- [4] Лекция на www.stepik.org о метриках качества, F-мера
- [5] Лекция на www.stepik.org о метриках качества, примеры
См. также
- Оценка качества в задаче кластеризации
- Кросс-валидация
Источники информации
- [6] Соколов Е.А. Лекция линейная регрессия
- [7] — Дьяконов А. Функции ошибки / функционалы качества
- [8] — Оценка качества прогнозных моделей
- [9] — HeinzBr Ошибка прогнозирования: виды, формулы, примеры
- [10] — egor_labintcev Метрики в задачах машинного обучения
- [11] — grossu Методы оценки качества прогноза
- [12] — К.В.Воронцов, Классификация
- [13] — К.В.Воронцов, Скользящий контроль
by Moshe Binieli
Introduction
This article will deal with the statistical method mean squared error, and I’ll describe the relationship of this method to the regression line.
The example consists of points on the Cartesian axis. We will define a mathematical function that will give us the straight line that passes best between all points on the Cartesian axis.
And in this way, we will learn the connection between these two methods, and how the result of their connection looks together.
General explanation
This is the definition from Wikipedia:
In statistics, the mean squared error (MSE) of an estimator (of a procedure for estimating an unobserved quantity) measures the average of the squares of the errors — that is, the average squared difference between the estimated values and what is estimated. MSE is a risk function, corresponding to the expected value of the squared error loss. The fact that MSE is almost always strictly positive (and not zero) is because of randomness or because the estimator does not account for information that could produce a more accurate estimate.
The structure of the article
- Get a feel for the idea, graph visualization, mean squared error equation.
- The mathematical part which contains algebraic manipulations and a derivative of two-variable functions for finding a minimum. This section is for those who want to understand how we get the mathematical formulas later, you can skip it if that doesn’t interest you.
- An explanation of the mathematical formulae we received and the role of each variable in the formula.
- Examples
Get a feel for the idea
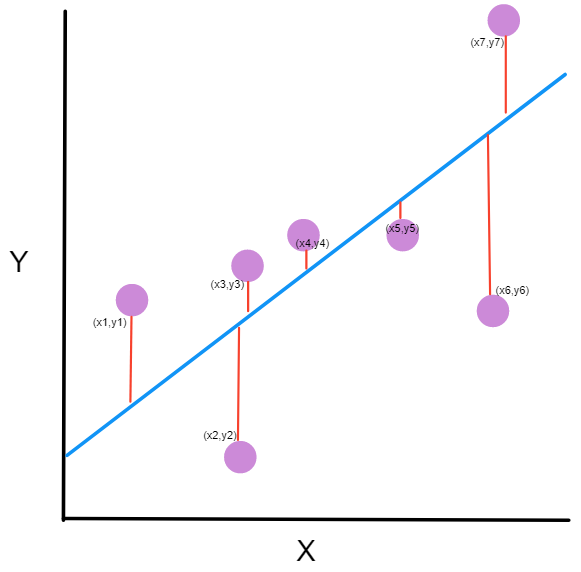
Let’s say we have seven points, and our goal is to find a line that minimizes the squared distances to these different points.
Let’s try to understand that.
I will take an example and I will draw a line between the points. Of course, my drawing isn’t the best, but it’s just for demonstration purposes.
You might be asking yourself, what is this graph?
- the purple dots are the points on the graph. Each point has an x-coordinate and a y-coordinate.
- The blue line is our prediction line. This is a line that passes through all the points and fits them in the best way. This line contains the predicted points.
- The red line between each purple point and the prediction line are the errors. Each error is the distance from the point to its predicted point.
You should remember this equation from your school days, y=Mx+B, where M is the slope of the line and B is y-intercept of the line.
We want to find M (slope) and B (y-intercept) that minimizes the squared error!
Let’s define a mathematical equation that will give us the mean squared error for all our points.
Let’s analyze what this equation actually means.
- In mathematics, the character that looks like weird E is called summation (Greek sigma). It is the sum of a sequence of numbers, from i=1 to n. Let’s imagine this like an array of points, where we go through all the points, from the first (i=1) to the last (i=n).
- For each point, we take the y-coordinate of the point, and the y’-coordinate. The y-coordinate is our purple dot. The y’ point sits on the line we created. We subtract the y-coordinate value from the y’-coordinate value, and calculate the square of the result.
- The third part is to take the sum of all the (y-y’)² values, and divide it by n, which will give the mean.
Our goal is to minimize this mean, which will provide us with the best line that goes through all the points.
From concept to mathematical equations
This part is for people who want to understand how we got to the mathematical equations. You can skip to the next part if you want.
As you know, the line equation is y=mx+b, where m is the slope and b is the y-intercept.
Let’s take each point on the graph, and we’ll do our calculation (y-y’)².
But what is y’, and how do we calculate it? We do not have it as part of the data.
But we do know that, in order to calculate y’, we need to use our line equation, y=mx+b, and put the x in the equation.
From here we get the following equation:
Let’s rewrite this expression to simplify it.
Let’s begin by opening all the brackets in the equation. I colored the difference between the equations to make it easier to understand.
Now, let’s apply another manipulation. We will take each part and put it together. We will take all the y, and (-2ymx) and etc, and we will put them all side-by-side.
At this point we’re starting to be messy, so let’s take the mean of all squared values for y, xy, x, x².
Let’s define, for each one, a new character which will represent the mean of all the squared values.
Let’s see an example, let’s take all the y values, and divide them by n since it’s the mean, and call it y(HeadLine).
If we multiply both sides of the equation by n we get:
Which will lead us to the following equation:
If we look at what we got, we can see that we have a 3D surface. It looks like a glass, which rises sharply upwards.
We want to find M and B that minimize the function. We will make a partial derivative with respect to M and a partial derivative with respect to B.
Since we are looking for a minimum point, we will take the partial derivatives and compare to 0.
Let’s take the two equations we received, isolating the variable b from both, and then subtracting the upper equation from the bottom equation.
Let’s subtract the first equation from the second equation
Let’s get rid of the denominators from the equation.
And there we go, this is the equation to find M, let’s take this and write down B equation.
Equations for slope and y-intercept
Let’s provide the mathematical equations that will help us find the required slope and y-intercept.
So you probably thinking to yourself, what the heck are those weird equations?
They are actually simple to understand, so let’s talk about them a little bit.
Now that we understand our equations it’s time to get all things together and show some examples.
Examples
A big thank you to Khan Academy for the examples.
Example #1
Let’s take 3 points, (1,2), (2,1), (4,3).
Let’s find M and B for the equation y=mx+b.
After we’ve calculated the relevant parts for our M equation and B equation, let’s put those values inside the equations and get the slope and y-intercept.
Let’s take those results and set them inside the line equation y=mx+b.
Now let’s draw the line and see how the line passes through the lines in such a way that it minimizes the squared distances.
Example #2
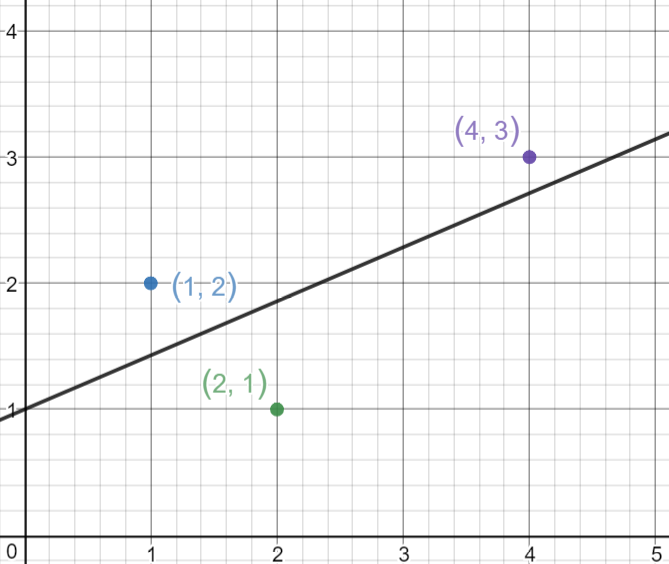
Let’s take 4 points, (-2,-3), (-1,-1), (1,2), (4,3).
Let’s find M and B for the equation y=mx+b.
Same as before, let’s put those values inside our equations to find M and B.
Let’s take those results and set them inside line equation y=mx+b.
Now let’s draw the line and see how the line passes through the lines in such a way that it minimizes the squared distances.
In conclusion
As you can see, the whole idea is simple. We just need to understand the main parts and how we work with them.
You can work with the formulas to find the line on another graph, and perform a simple calculation and get the results for the slope and y-intercept.
That’s all, simple eh? ?
Every comment and all feedback is welcome — if it’s necessary, I will fix the article.
Feel free to contact me directly at LinkedIn — Click Here.
Learn to code for free. freeCodeCamp’s open source curriculum has helped more than 40,000 people get jobs as developers. Get started
В машинном обучении функция потерь — это математическая функция, которая измеряет, насколько хорошо модель машинного обучения способна делать прогнозы. Функция потерь сравнивает прогнозируемый результат модели с истинным выходом и выдает оценку, которая показывает, насколько они различаются. Цель модели машинного обучения — свести к минимуму эту разницу или «потерю», чтобы делать точные прогнозы.
Выбор функции потерь зависит от рассматриваемой проблемы и типа используемой модели машинного обучения. Например, в задачах классификации функция кросс-энтропийных потерь часто используется для измерения разницы между предсказанным распределением вероятностей и истинными метками. В задачах регрессии функция потерь среднеквадратичной ошибки (MSE) часто используется для измерения разницы между прогнозируемыми значениями и истинными значениями.
Как только функция потерь определена, модель можно обучить, чтобы минимизировать ее, используя такие методы оптимизации, как градиентный спуск. Во время обучения параметры модели корректируются итеративно, чтобы минимизировать функцию потерь и повысить точность прогнозов модели.
Введение
В машинном обучении цель модели — делать точные прогнозы на основе набора входных данных. Для этого модель должна быть обучена на наборе помеченных примеров, где известен правильный вывод для каждого входа. Во время обучения модель корректируется для минимизации функции потерь, которая измеряет разницу между прогнозируемым выходом модели и истинным выходом.
Существует множество различных типов функций потерь, каждый из которых имеет свои сильные и слабые стороны. Вот несколько примеров:
- Среднеквадратичная ошибка (MSE) — это часто используемая функция потерь в задачах регрессии. Он измеряет среднеквадратичную разницу между прогнозируемым выходом и истинным выходом. Эта функция потерь чувствительна к выбросам и имеет тенденцию наказывать за большие ошибки сильнее, чем за меньшие.
- Кросс-энтропия — это часто используемая функция потерь в задачах классификации. Он измеряет разницу между предсказанным распределением вероятностей и истинными метками. Эта функция потерь обычно используется с моделями, которые выводят вероятности для каждого класса, такими как нейронные сети.
- Двоичная кросс-энтропия — это вариант функции потери кросс-энтропии, которая используется для задач бинарной классификации. Он измеряет разницу между предсказанной вероятностью положительного класса и истинной меткой. Эта функция потерь обычно используется с моделями логистической регрессии.
- Потери шарнира — это функция потерь, которая используется с машинами опорных векторов (SVM) в задачах классификации. Он измеряет разницу между прогнозируемым выходом и истинным выходом и наказывает только те ошибки, которые превышают определенный порог.
- Расхождение Кульбака-Лейблера. Это функция потерь, которая измеряет разницу между двумя распределениями вероятностей. Он часто используется в генеративных моделях, таких как вариационные автоэнкодеры (VAE) и генеративно-состязательные сети (GAN).
Это всего лишь несколько примеров множества различных типов функций потерь, которые используются в машинном обучении. Выбор функции потерь зависит от рассматриваемой проблемы и типа используемой модели. Важно выбрать функцию потерь, подходящую для задачи, и тщательно настроить ее гиперпараметры во время обучения, чтобы добиться наилучшей производительности.
Среднеквадратическая ошибка (MSE)
MSE — это обычная функция потерь, используемая в задачах регрессии, где цель состоит в том, чтобы предсказать непрерывное значение. MSE измеряет среднеквадратичную разницу между прогнозируемым выходом и истинным выходом. Это дается следующим уравнением:
MSE = 1/n * Σ(i=1 to n) (yi — ŷi)²
где:
n— количество точек данныхyi— это истинный результат для i-й точки данных.- ŷi — прогнозируемый результат для i-й точки данных
MSE вычисляется путем взятия квадрата разницы между каждым прогнозируемым выходом и соответствующим ему истинным выходом, суммирования этих различий и последующего деления на общее количество точек данных. Результатом является одно число, которое измеряет среднеквадратичную разницу между прогнозируемым и истинным выходными данными.
Вот пример, иллюстрирующий, как работает MSE. Допустим, у нас есть набор данных о ценах на жилье, и мы хотим предсказать цену нового дома на основе его квадратных метров. Имеем следующие данные:
Square Footage (x) Price (y) 1000 $100,000 1500 $150,000 2000 $200,000 2500 $250,000 3000 $300,000
Мы можем использовать линейную регрессию, чтобы предсказать цену дома на основе его квадратных метров. Допустим, наша модель линейной регрессии предсказывает следующие цены:
Square Footage (x) Predicted Price (ŷ) 1000 $110,000 1500 $160,000 2000 $210,000 2500 $260,000 3000 $310,000
Мы можем вычислить MSE наших прогнозов, подставив эти значения в уравнение:
MSE = 1/5 * [(100,000–110,000)² + (150,000–160,000)² + (200,000–210,000)² + (250,000–260,000)² + (300,000–310,000)²]
= 1/5 * [100,000 + 100,000 + 100,000 + 100,000 + 100,000] = 100,000
MSE в этом случае равен 100,000, что является мерой среднего квадрата разницы между нашими прогнозируемыми ценами и истинными ценами. Более низкий MSE указывает на то, что модель делает более точные прогнозы.
Функция перекрестной энтропийной потери
Перекрестная энтропия — это обычно используемая функция потерь в задачах классификации, где цель состоит в том, чтобы предсказать вероятность принадлежности выборки к определенному классу. Перекрестная энтропия измеряет разницу между предсказанным распределением вероятностей и истинными метками. Это дается следующим уравнением:
CE = - Σ(i=1 to n) yi * log(ŷi)
где:
nколичество классовyiявляется бинарным индикатором(0 or 1)того, является ли истинная метка i-м классом- ŷi — прогнозируемая вероятность принадлежности выборки к i-му классу
Перекрестная энтропия вычисляется путем произведения истинной метки и логарифма предсказанной вероятности для каждого класса, суммирования этих произведений и последующего отрицания результата. Результатом является одно число, которое измеряет разницу между предсказанным распределением вероятностей и истинными метками.
Вот пример, иллюстрирующий, как работает кросс-энтропия. Допустим, у нас есть проблема бинарной классификации, где мы хотим предсказать, является ли образец кошкой или собакой на основе изображения. Имеем следующие данные:
Image True Label Cat 1 Dog 0 Cat 1 Dog 0 Cat 1
Мы можем использовать логистическую регрессию, чтобы предсказать вероятность того, что каждая выборка является кошкой. Допустим, наша модель логистической регрессии предсказывает следующие вероятности:
Image Predicted Probability of Cat (ŷ) Cat 0.9 Dog 0.1 Cat 0.8 Dog 0.2 Cat 0.95
Мы можем вычислить кросс-энтропию наших прогнозов, подставив эти значения в уравнение:
CE = -(1 * log(0.9) + 0 * log(0.1) + 1 * log(0.8) + 0 * log(0.2) + 1 * log(0.95)) = -(-0.105 + 0 + -0.223 + 0 + -0.051) = 0.38
Перекрестная энтропия в этом случае равна 0.38, что является мерой разницы между нашим предсказанным распределением вероятностей и истинными метками. Более низкая перекрестная энтропия указывает на то, что модель делает более точные прогнозы.
Функция потери шарнира
Потеря шарнира — это функция потерь, обычно используемая в задачах бинарной классификации. Это особенно полезно при работе с машинами опорных векторов (SVM) и предназначено для поощрения SVM к правильной классификации. Потери шарнира определяются следующим уравнением:
HL = max(0, 1 - y * ŷ)
где:
yэто истинная метка (-1 или 1)ŷэто прогнозируемый результат SVM
Потери шарнира вычисляются путем получения разницы между прогнозируемым выходом и истинной меткой, а затем взятия максимума из 0 и этой разницы. Это означает, что потери шарнира равны 0, когда прогнозируемый результат правильный, и положительный, когда прогнозируемый результат неверен.
Вот пример, иллюстрирующий, как работает потеря шарнира. Допустим, у нас есть проблема с бинарной классификацией, когда мы хотим предсказать, является ли электронное письмо спамом или нет, основываясь на его содержании. Имеем следующие данные:
Приложения
некоторые из ключевых применений функций потерь в машинном обучении:
- Обучение модели. Функции потерь используются для обучения моделей машинного обучения путем оптимизации параметров модели для минимизации потерь. Во время обучения функция потерь вычисляет разницу между прогнозируемым выходом модели и истинным выходом, и оптимизатор пытается минимизировать эту разницу.
- Оценка. Функции потерь также используются для оценки производительности модели в тестовом или проверочном наборе. Потери вычисляются для каждого входа в тестовом наборе, а средние потери указываются как мера производительности модели.
- Регуляризация. В некоторых случаях регуляризация используется для предотвращения переобучения. Функции потерь можно изменить, включив в них член регуляризации, который штрафует большие веса в модели.
- Обнаружение выбросов. Функции потерь можно использовать для выявления выбросов в наборе данных. Выбросы можно выявить путем вычисления потерь для каждой точки данных и выявления точек с высокими значениями потерь.
- Обнаружение аномалий. Функции потерь можно использовать для выявления аномалий в данных. Аномалии можно выявить путем вычисления потерь для каждой точки данных и выявления точек с высокими значениями потерь.
В целом, функции потерь играют решающую роль в оптимизации и оценке моделей машинного обучения. Они позволяют модели учиться на данных и улучшать свою производительность с течением времени, что в конечном итоге приводит к более точным прогнозам и лучшим возможностям принятия решений.
Заключение
В заключение, функция потерь — это функция, которая измеряет разницу между прогнозируемым результатом модели машинного обучения и истинным результатом. Это важнейший компонент многих алгоритмов машинного обучения, включая глубокое обучение, и играет центральную роль в обучении, оценке и оптимизации моделей.
Различные типы функций потерь используются для разных задач машинного обучения, и каждый из них имеет свои сильные и слабые стороны. Среднеквадратическая ошибка (MSE) — это популярная функция потерь для задач регрессии, кросс-энтропийная потеря обычно используется для задач классификации, а потеря шарнира полезна для обучения машин опорных векторов (SVM).
Используя функцию потерь для оптимизации параметров модели, алгоритмы машинного обучения могут учиться на данных и со временем улучшать свою производительность. В свою очередь, это обеспечивает лучшие возможности для принятия решений и более точные прогнозы.