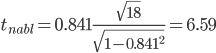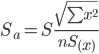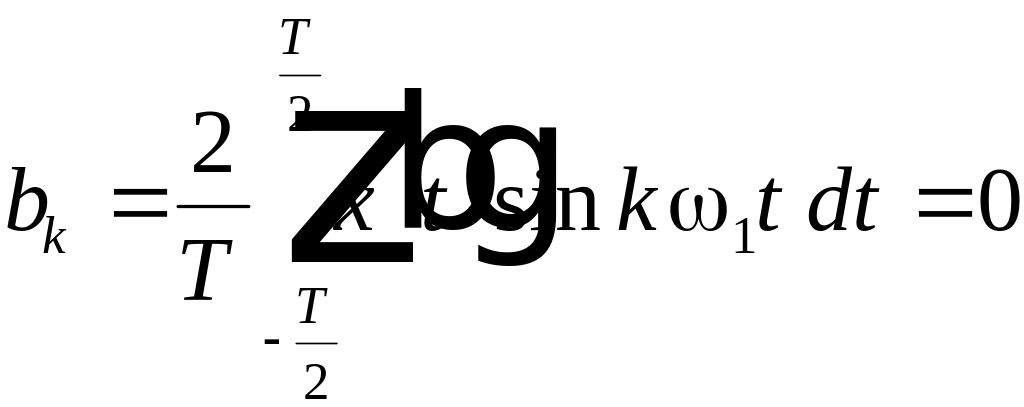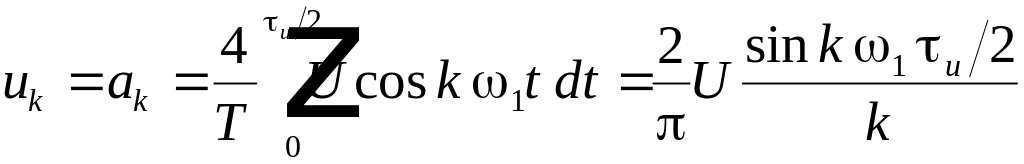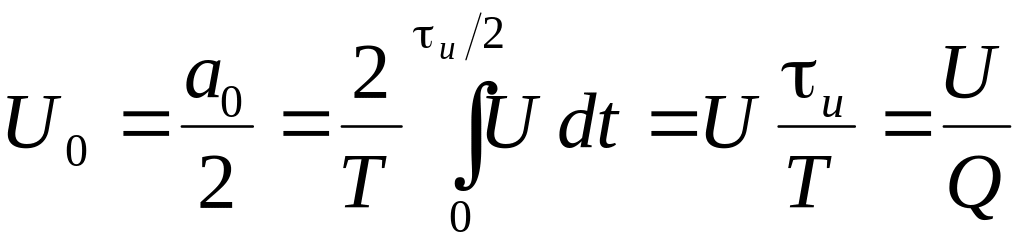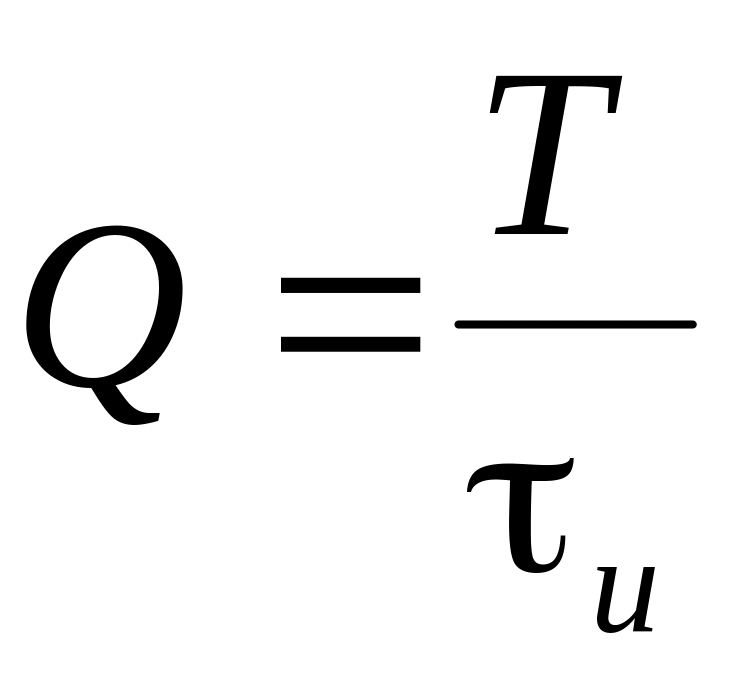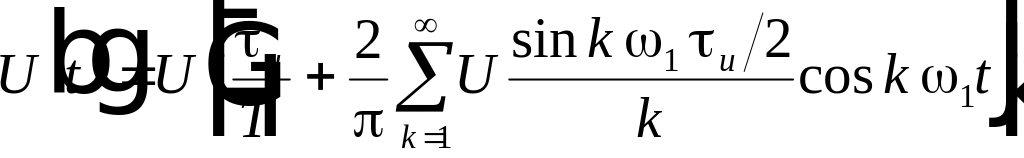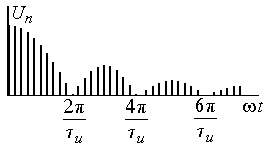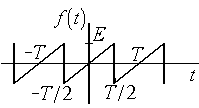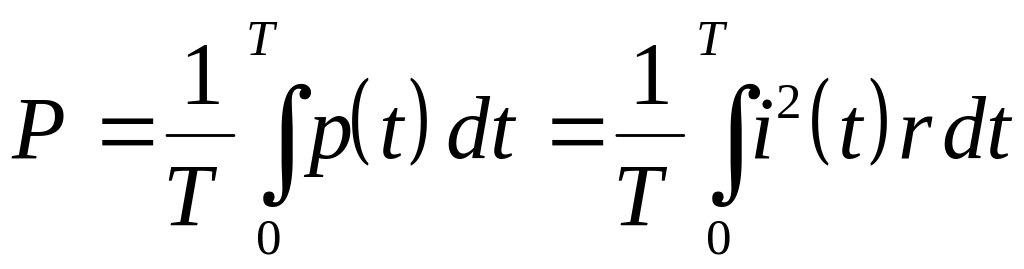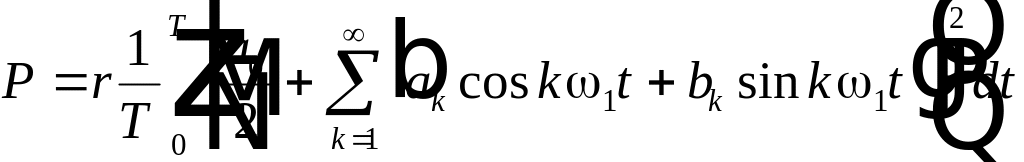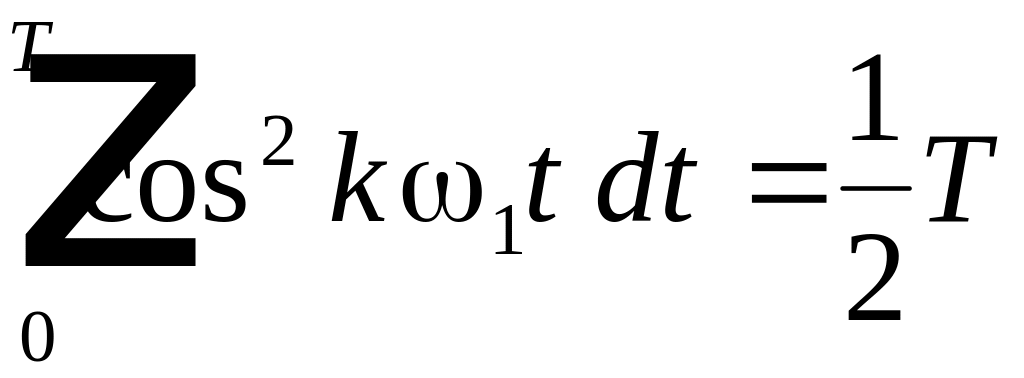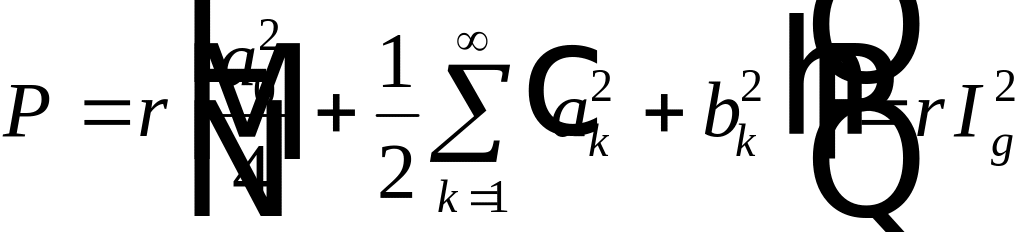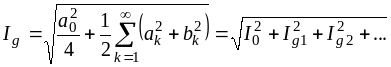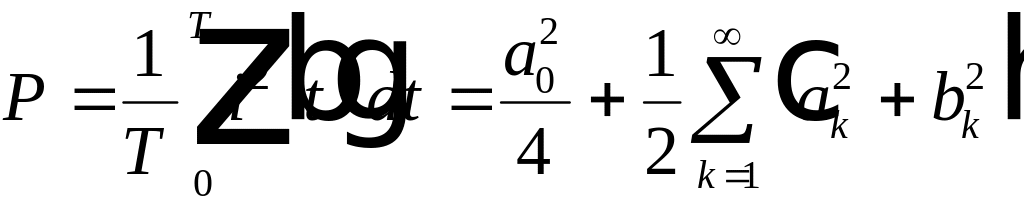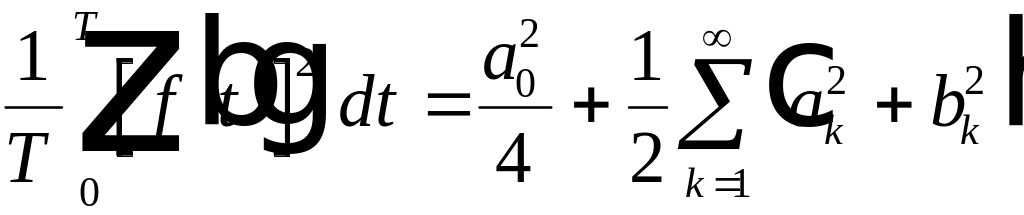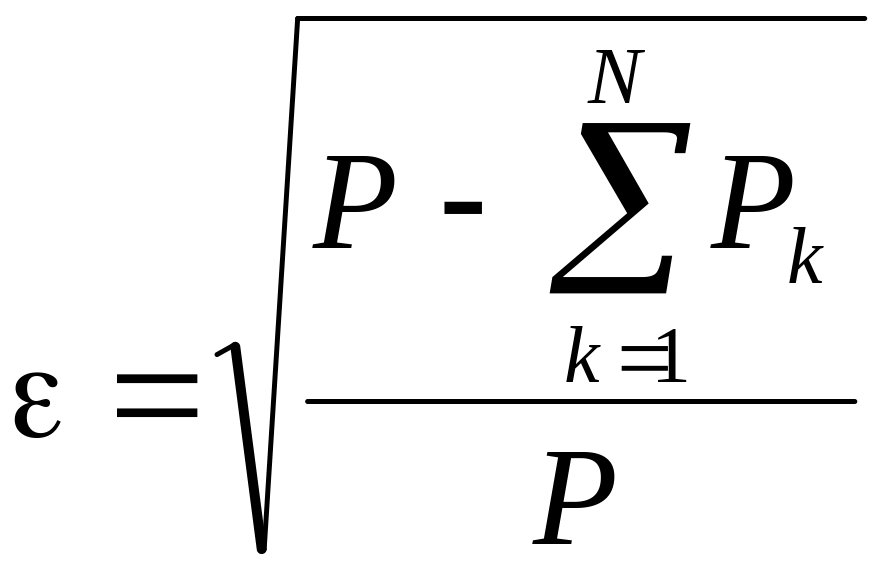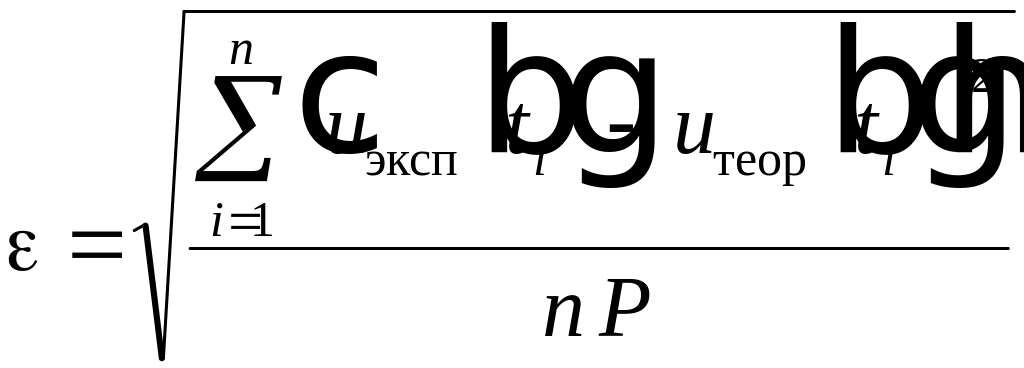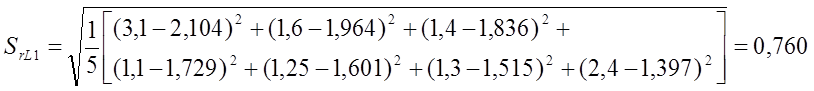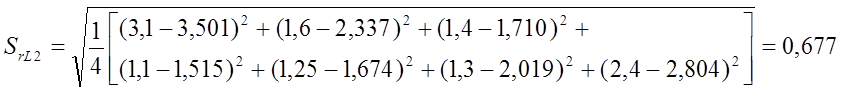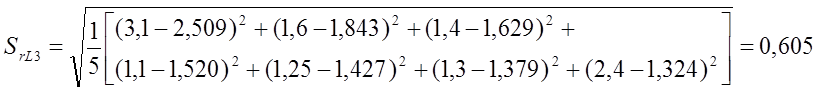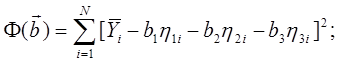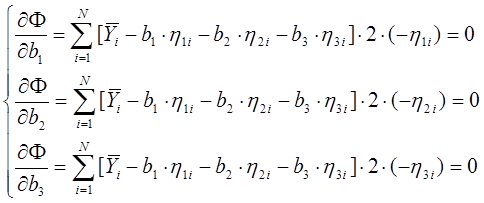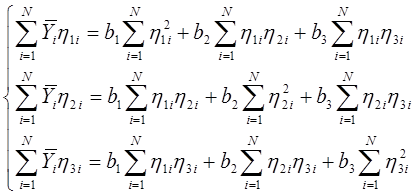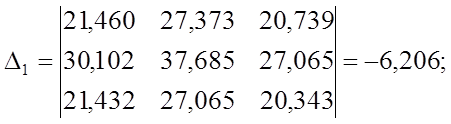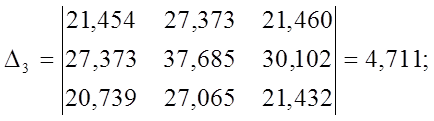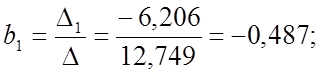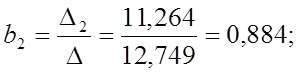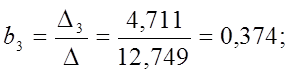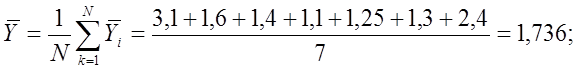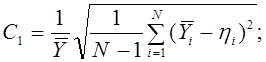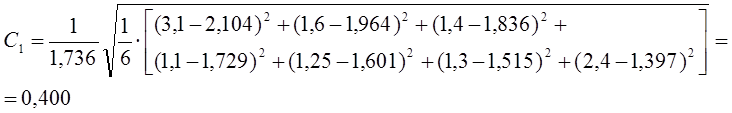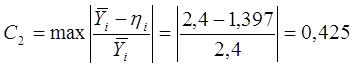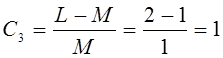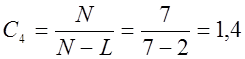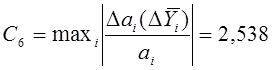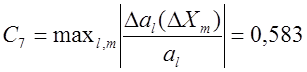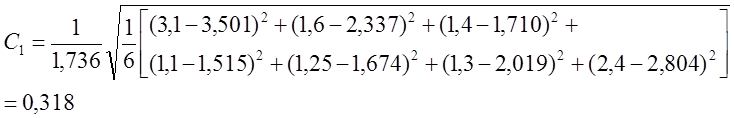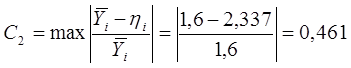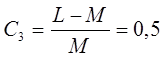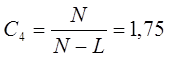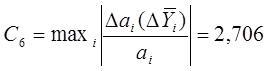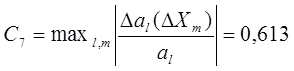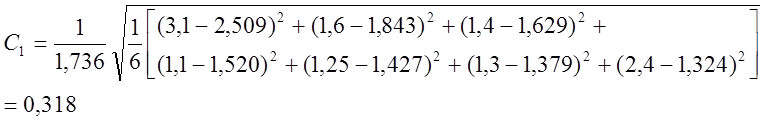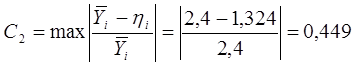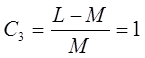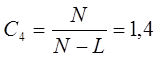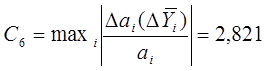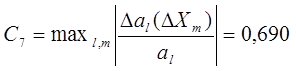Среднеквадратичная ошибка (Mean Squared Error) – Среднее арифметическое (Mean) квадратов разностей между предсказанными и реальными значениями Модели (Model) Машинного обучения (ML):
Рассчитывается с помощью формулы, которая будет пояснена в примере ниже:
$$MSE = \frac{1}{n} × \sum_{i=1}^n (y_i — \widetilde{y}_i)^2$$
$$MSE\space{}{–}\space{Среднеквадратическая}\space{ошибка,}$$
$$n\space{}{–}\space{количество}\space{наблюдений,}$$
$$y_i\space{}{–}\space{фактическая}\space{координата}\space{наблюдения,}$$
$$\widetilde{y}_i\space{}{–}\space{предсказанная}\space{координата}\space{наблюдения,}$$
MSE практически никогда не равен нулю, и происходит это из-за элемента случайности в данных или неучитывания Оценочной функцией (Estimator) всех факторов, которые могли бы улучшить предсказательную способность.
Пример. Исследуем линейную регрессию, изображенную на графике выше, и установим величину среднеквадратической Ошибки (Error). Фактические координаты точек-Наблюдений (Observation) выглядят следующим образом:
Мы имеем дело с Линейной регрессией (Linear Regression), потому уравнение, предсказывающее положение записей, можно представить с помощью формулы:
$$y = M * x + b$$
$$y\space{–}\space{значение}\space{координаты}\space{оси}\space{y,}$$
$$M\space{–}\space{уклон}\space{прямой}$$
$$x\space{–}\space{значение}\space{координаты}\space{оси}\space{x,}$$
$$b\space{–}\space{смещение}\space{прямой}\space{относительно}\space{начала}\space{координат}$$
Параметры M и b уравнения нам, к счастью, известны в данном обучающем примере, и потому уравнение выглядит следующим образом:
$$y = 0,5252 * x + 17,306$$
Зная координаты реальных записей и уравнение линейной регрессии, мы можем восстановить полные координаты предсказанных наблюдений, обозначенных серыми точками на графике выше. Простой подстановкой значения координаты x в уравнение мы рассчитаем значение координаты ỹ:
Рассчитаем квадрат разницы между Y и Ỹ:
Сумма таких квадратов равна 4 445. Осталось только разделить это число на количество наблюдений (9):
$$MSE = \frac{1}{9} × 4445 = 493$$
Само по себе число в такой ситуации становится показательным, когда Дата-сайентист (Data Scientist) предпринимает попытки улучшить предсказательную способность модели и сравнивает MSE каждой итерации, выбирая такое уравнение, что сгенерирует наименьшую погрешность в предсказаниях.
MSE и Scikit-learn
Среднеквадратическую ошибку можно вычислить с помощью SkLearn. Для начала импортируем функцию:
import sklearn
from sklearn.metrics import mean_squared_errorИнициализируем крошечные списки, содержащие реальные и предсказанные координаты y:
y_true = [5, 41, 70, 77, 134, 68, 138, 101, 131]
y_pred = [23, 35, 55, 90, 93, 103, 118, 121, 129]Инициируем функцию mean_squared_error(), которая рассчитает MSE тем же способом, что и формула выше:
mean_squared_error(y_true, y_pred)
Интересно, что конечный результат на 3 отличается от расчетов с помощью Apple Numbers:
496.0Ноутбук, не требующий дополнительной настройки на момент написания статьи, можно скачать здесь.
Автор оригинальной статьи: @mmoshikoo
Фото: @tobyelliott
Выборочные
средние.
Выборочные
дисперсии:
Среднеквадратическое
отклонение
Коэффициент
корреляции b можно находить по формуле,
не решая систему непосредственно:
Коэффициент корреляции
Рассчитываем
показатель тесноты связи. Таким
показателем является выборочный линейный
коэффициент корреляции, который
рассчитывается по формуле:

коэффициент корреляции принимает
значения от –1 до +1.
Связи между
признаками могут быть слабыми и сильными
(тесными). Их критерии оцениваются по
шкале Чеддока:
0.1 < rxy <
0.3: слабая;
0.3 < rxy <
0.5: умеренная;
0.5 < rxy <
0.7: заметная;
0.7 < rxy <
0.9: высокая;
0.9 < rxy <
1: весьма высокая;
В нашем примере связь
между признаком Y фактором X высокая и
прямая.
Кроме того, коэффициент линейной
парной корреляции может быть определен
через коэффициент регрессии b:
Уравнение регрессии (оценка
уравнения регрессии).
Линейное
уравнение регрессии имеет вид y = 0.54 x +
75.82
Коэффициентам уравнения линейной
регрессии можно придать экономический
смысл.
Коэффициент регрессии b = 0.54
показывает среднее изменение
результативного показателя (в единицах
измерения у) с повышением или понижением
величины фактора х на единицу его
измерения. В данном примере с увеличением
на 1 единицу y повышается в среднем на
0.54.
Коэффициент a = 75.82 формально
показывает прогнозируемый уровень у,
но только в том случае, если х=0 находится
близко с выборочными значениями.
Но
если х=0 находится далеко от выборочных
значений х, то буквальная интерпретация
может привести к неверным результатам,
и даже если линия регрессии довольно
точно описывает значения наблюдаемой
выборки, нет гарантий, что также будет
при экстраполяции влево или вправо.
Подставив
в уравнение регрессии соответствующие
значения х, можно определить выровненные
(предсказанные) значения результативного
показателя y(x) для каждого наблюдения.
Связь
между у и х определяет знак коэффициента
регрессии b (если > 0 – прямая связь,
иначе — обратная). В нашем примере связь
прямая.
Коэффициент
эластичности.
Коэффициенты
регрессии (в примере b) нежелательно
использовать для непосредственной
оценки влияния факторов на результативный
признак в том случае, если существует
различие единиц измерения результативного
показателя у и факторного признака
х.
Для этих целей вычисляются коэффициенты
эластичности и бета — коэффициенты.
Средний
коэффициент эластичности E показывает,
на сколько процентов в среднем по
совокупности изменится результат у от
своей средней величины при изменении
фактора x на
1% от своего среднего значения.
Коэффициент
эластичности находится по
формуле:
Коэффициент
эластичности меньше 1. Следовательно,
при изменении Х на 1%, Y изменится менее
чем на 1%. Другими словами — влияние Х на
Y не существенно.
Ошибка аппроксимации.
Оценим
качество уравнения регрессии с помощью
ошибки абсолютной аппроксимации. Средняя
ошибка аппроксимации — среднее отклонение
расчетных значений от фактических:
Ошибка
аппроксимации в пределах 5%-7% свидетельствует
о хорошем подборе уравнения регрессии
к исходным данным.
Поскольку
ошибка больше 7%, то данное уравнение не
желательно использовать в качестве
регрессии.
Коэффициент
детерминации.
Квадрат
(множественного) коэффициента корреляции
называется коэффициентом детерминации,
который показывает долю вариации
результативного признака, объясненную
вариацией факторного признака.
Чаще
всего, давая интерпретацию коэффициента
детерминации, его выражают в процентах.
R2=
0.8412 =
0.7072
т.е. в 70.72 % случаев изменения х
приводят к изменению y. Другими словами
— точность подбора уравнения регрессии
— высокая. Остальные 29.28 % изменения Y
объясняются факторами, не учтенными в
модели (а также ошибками спецификации).
Для
оценки качества параметров регрессии
построим расчетную таблицу (табл. 2)
|
x |
y |
y(x) |
(yi-ycp)2 |
(y-y(x))2 |
(xi-xcp)2 |
|y |
|
913 |
596 |
566.54 |
22425.06 |
868.11 |
50086.44 |
0.0494 |
|
1095 |
417 |
664.36 |
855.56 |
61185.18 |
164673.64 |
0.59 |
|
606 |
354 |
401.53 |
8510.06 |
2259.32 |
6922.24 |
0.13 |
|
876 |
526 |
546.65 |
6360.06 |
426.42 |
34894.24 |
0.0393 |
|
1314 |
934 |
782.06 |
237900.06 |
23084.89 |
390375.04 |
0.16 |
|
593 |
412 |
394.55 |
1173.06 |
304.67 |
9254.44 |
0.0424 |
|
754 |
525 |
481.08 |
6201.56 |
1929.12 |
4199.04 |
0.0837 |
|
528 |
367 |
359.61 |
6280.56 |
54.62 |
25985.44 |
0.0201 |
|
520 |
364 |
355.31 |
6765.06 |
75.52 |
28628.64 |
0.0239 |
|
539 |
336 |
365.52 |
12155.06 |
871.53 |
22560.04 |
0.0879 |
|
540 |
409 |
366.06 |
1387.56 |
1843.92 |
22260.64 |
0.1 |
|
682 |
452 |
442.38 |
33.06 |
92.54 |
51.84 |
0.0213 |
|
537 |
367 |
364.45 |
6280.56 |
6.52 |
23164.84 |
0.00696 |
|
589 |
328 |
392.4 |
13983.06 |
4146.75 |
10040.04 |
0.2 |
|
626 |
460 |
412.28 |
189.06 |
2277.03 |
3994.24 |
0.1 |
|
521 |
380 |
355.85 |
4389.06 |
583.36 |
28291.24 |
0.0636 |
|
626 |
439 |
412.28 |
52.56 |
713.87 |
3994.24 |
0.0609 |
|
521 |
344 |
355.85 |
10455.06 |
140.35 |
28291.24 |
0.0344 |
|
658 |
401 |
429.48 |
2047.56 |
811.16 |
973.44 |
0.071 |
|
746 |
514 |
476.78 |
4590.06 |
1385.44 |
3226.24 |
0.0724 |
|
13784 |
8925 |
8925 |
352033.75 |
103060.32 |
861867.2 |
1.97 |
2.
Оценка параметров уравнения
регрессии.
Значимость
коэффициента корреляции.
Выдвигаем
гипотезы:
H0:
rxy =
0, нет линейной взаимосвязи между
переменными;
H1:
rxy ≠
0, есть линейная взаимосвязь между
переменными;
Для того чтобы при уровне
значимости α проверить нулевую гипотезу
о равенстве нулю генерального коэффициента
корреляции нормальной двумерной
случайной величины при конкурирующей
гипотезе H1 ≠
0, надо вычислить наблюдаемое значение
критерия (величина случайной ошибки)
и
по таблице критических точек распределения
Стьюдента, по заданному уровню значимости
α и числу степеней свободы k = n — 2 найти
критическую точку tкрит двусторонней
критической области. Если tнабл <
tкрит оснований
отвергнуть нулевую гипотезу. Если
|tнабл|
> tкрит —
нулевую гипотезу отвергают.
По
таблице Стьюдента с уровнем значимости
α=0.05 и степенями свободы k=18 находим
tкрит:
tкрит (n-m-1;α/2)
= (18;0.025) = 2.101
где m = 1 — количество
объясняющих переменных.
Если |tнабл|
> tкритич,
то полученное значение коэффициента
корреляции признается значимым (нулевая
гипотеза, утверждающая равенство нулю
коэффициента корреляции,
отвергается).
Поскольку |tнабл|
> tкрит,
то отклоняем гипотезу о равенстве 0
коэффициента корреляции. Другими
словами, коэффициент корреляции
статистически значим
В
парной линейной регрессии t2r =
t2b и
тогда проверка гипотез о значимости
коэффициентов регрессии и корреляции
равносильна проверке гипотезы о
существенности линейного уравнения
регрессии.
2.2.
Интервальная оценка для коэффициента
корреляции (доверительный
интервал).
Доверительный
интервал для коэффициента корреляции.
r(0.573;1)
2.3.
Анализ точности определения оценок
коэффициентов регрессии.
Несмещенной
оценкой дисперсии возмущений является
величина:
S2 =
5725.573 — необъясненная дисперсия (мера
разброса зависимой переменной вокруг
линии регрессии).
S
= 75.67 — стандартная ошибка оценки
(стандартная ошибка регрессии).
Sa —
стандартное отклонение случайной
величины a.
Sb —
стандартное отклонение случайной
величины b.
2.4.
Доверительные интервалы для зависимой
переменной.
Экономическое
прогнозирование на основе построенной
модели предполагает, что сохраняются
ранее существовавшие взаимосвязи
переменных и на период упреждения. Для
прогнозирования зависимой переменной
результативного признака необходимо
знать прогнозные значения всех входящих
в модель факторов.
Прогнозные значения
факторов подставляют в модель и получают
точечные прогнозные оценки изучаемого
показателя.
(a + bxp ±
ε)
где
tкрит (n-m-1;α/2)
= (18;0.025) = 2.101
Рассчитаем границы
интервала, в котором будет сосредоточено
95% возможных значений Y при неограниченно
большом числе наблюдений и Xp =
104
Вычислим ошибку прогноза для
уравнения y = bx + a
y(104)
= 0.537*104 + 75.824 = 131.721
131.721 ± 106.33
(25.39;238.05)
С
вероятностью 95% можно гарантировать,
что значения Y при неограниченно большом
числе наблюдений не выйдет за пределы
найденных интервалов.
Вычислим ошибку
прогноза для уравнения y = bx + a +
ε
(-59.54;322.98)
Доверительный
интервал для коэффициентов уравнения
регрессии.
Определим
доверительные интервалы коэффициентов
регрессии, которые с надежность 95% будут
следующими:
(b — tкрит Sb;
b + tкрит Sb)
(0.54
— 2.101 • 0.0815; 0.54 + 2.101 • 0.0815)
(0.366;0.709)
С
вероятностью 95% можно утверждать, что
значение данного параметра будут лежать
в найденном интервале.
(a — tкрит Sa;
a + tкрит Sa)
(75.824
— 2.101 • 58.67; 75.824 + 2.101 • 58.67)
(-47.435;199.083)
С
вероятностью 95% можно утверждать, что
значение данного параметра будут лежать
в найденном интервале.
Так как точка
0 (ноль) лежит внутри доверительного
интервала, то интервальная оценка
коэффициента a
статистически
незначима.
2) F-статистика. Критерий
Фишера.
Коэффициент детерминации
R2 используется
для проверки существенности уравнения
линейной регрессии в целом.
Проверка
значимости модели регрессии проводится
с использованием F-критерия Фишера,
расчетное значение которого находится
как отношение дисперсии исходного ряда
наблюдений изучаемого показателя и
несмещенной оценки дисперсии остаточной
последовательности для данной модели.
Если
расчетное значение с k1=(m)
и k2=(n-m-1)
степенями свободы больше табличного
при заданном уровне значимости, то
модель считается значимой.
где m –
число факторов в модели.
Оценка
статистической значимости парной
линейной регрессии производится по
следующему алгоритму:
1. Выдвигается
нулевая гипотеза о том, что уравнение
в целом статистически незначимо: H0:
R2=0
на уровне значимости α.
2. Далее
определяют фактическое значение
F-критерия:
где
m=1 для парной регрессии.
3. Табличное
значение определяется по таблицам
распределения Фишера для заданного
уровня значимости, принимая во внимание,
что число степеней свободы для общей
суммы квадратов (большей дисперсии)
равно 1 и число степеней свободы остаточной
суммы квадратов (меньшей дисперсии) при
линейной регрессии равно n-2.
Fтабл —
это максимально возможное значение
критерия под влиянием случайных факторов
при данных степенях свободы и уровне
значимости α. Уровень значимости α —
вероятность отвергнуть правильную
гипотезу при условии, что она верна.
Обычно α принимается равной 0,05 или
0,01.
4. Если фактическое значение
F-критерия меньше табличного, то говорят,
что нет основания отклонять нулевую
гипотезу.
В противном случае, нулевая
гипотеза отклоняется и с вероятностью
(1-α) принимается альтернативная гипотеза
о статистической значимости уравнения
в целом.
Табличное значение критерия
со степенями свободы k1=1
и k2=18,
Fтабл =
4.41
Поскольку фактическое значение
F > Fтабл,
то коэффициент детерминации статистически
значим (найденная оценка уравнения
регрессии статистически надежна).
Связь
между F-критерием Фишера и t-статистикой
Стьюдента выражается равенством:
Дисперсионный
анализ.
При
анализе качества модели регрессии
используется теорема о разложении
дисперсии, согласно которой общая
дисперсия результативного признака
может быть разложена на две составляющие
– объясненную и необъясненную уравнением
регрессии дисперсии.
Задача дисперсионного
анализа состоит в анализе дисперсии
зависимой переменной:
∑(yi —
ycp)2 =
∑(y(x) — ycp)2 +
∑(y — y(x))2
где
∑(yi —
ycp)2 —
общая сумма квадратов отклонений;
∑(y(x)
— ycp)2 —
сумма квадратов отклонений, обусловленная
регрессией («объясненная» или
«факторная»);
∑(y — y(x))2 —
остаточная сумма квадратов отклонений.
|
Источник |
Сумма |
Число |
Дисперсия |
F-критерий |
|
Модель |
0 |
1 |
0 |
43.48 |
|
Остаточная |
103060.32 |
18 |
5725.57 |
1 |
|
Общая |
352033.75 |
20-1 |
Показатели
качества уравнения регрессии.
|
Показатель |
Значение |
|
Коэффициент |
0.71 |
|
Средний |
0.83 |
|
Средняя |
9.86 |
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Цель
работы. Изучить возможности синтеза
сигналов с помощью ряда Фурье по
ортогональной системе тригонометрических
функций. Синтезировать периодические
сигналы различной формы и исследовать
влияние числа ортогональных составляющих
на погрешность аппроксимации.
4.1. Разложение сигналов в обобщенный ряд фурье
4.1.1. Спектры простейших периодических функций
Если
функция
четная (симметричная относительно оси
ординат), т.е.
,
то в этом случае
;
(4.1)
.
(4.2)
Разложение
функции будет следующим
. (4.3)
Аналогично
для нечетной функции можно найти, что
. (4.4)
На
рис. 4.1 показана последовательность
прямоугольных импульсов которую можно
рассматривать как четную функцию.
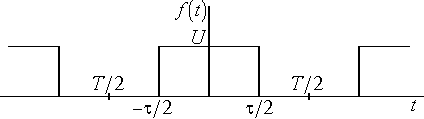
Рис.
4.1. Последовательность прямоугольных
импульсов
По
формуле (4.1) находим амплитуду
-й
гармоники:
. (4.5)
Постоянная
составляющая будет равна
;
. (4.6)
где
–
скважность импульсов. Разложение функции
запишется в виде:
. (4.7)
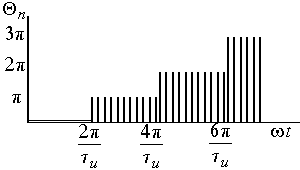
Графически
амплитудный и фазовый спектры прямоугольных
импульсов показаны на рис. 4.2.
Расстояния
между отдельными спектральными
составляющими обратно пропорциональны
периоду следования импульсов —
,
а положение нулей кратно
.
а) б)
Рис.
4.2. Амплитудный и фазовый спектры
прямоугольных импульсов
Можно
показать, что для импульсов, представленных
на рис. 4.3, разложения в ряд Фуре будут
иметь следующий вид:
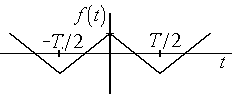
а) б)
Рис.
4.3. Пилообразное колебание и треугольные
импульсы
для
периодического пилообразного колебания
(рис 4.3,а);
; (4.8)
для
периодической последовательности
треугольных импульсов (рис.4.3,б):
. (4.9)
4.1.2. Мощность и действующее значение периодического сигнала
Пусть
несинусоидальный периодический ток
течет через активное сопротивление
.
Средняя за период мощность будет равна
. (4.10)
здесь
мгновенная мощность. Представим функцию
в виде ряда Фурье (4.6), тогда
.
Возводя
в квадрат и интегрируя каждое из слагаемых
можно убедиться, что только интегралы
вида:
, 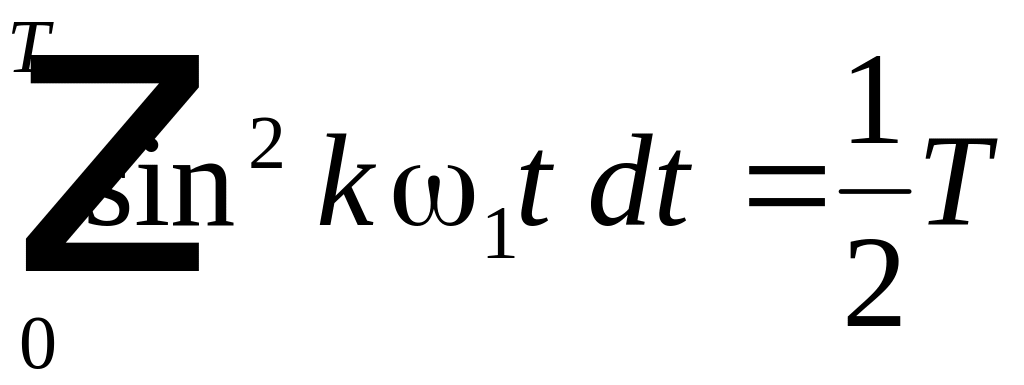
имеют
значения, не равные 0. Все остальные
интегралы равны нулю Поэтому после
интегрирования получим
,
где
. (4.11)
;
;
. (4.12)
Величины
,
,
,
,
… называют действующими значениями
тока. Аналогично вычисляются и
действующие значения напряжения. Если
сопротивление
Ом, то мощность равна
. (4.13)
Последнее
выражение справедливо для любой
периодической функции, т.е.
. (4.14)
В
таком виде последнее соотношение носит
название равенства Парсеваля.
4.1.3. Среднеквадратическая погрешность аппроксимации
Представим
приближенно функцию
разложением в усеченный ряд по
ортонормированным базисным функциям
(см. п. 2.1)
(4.15)
и
определим коэффициенты
так, чтобы минимизировать среднеквадратическую
погрешность:
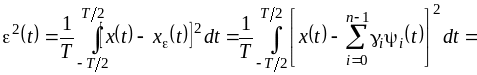
.
С
учетом (2.4) можно записать
. (4.16)
Погрешность
принимает минимальное значение, если
,
т.е. если коэффициенты разложения в
усеченном представлении (4.15) являются
коэффициентами обобщенного ряда Фурье.
Исходя из (4.16) можно записать
или
. (4.17)
Неравенство
(4.17) называют неравенством Бесселя.
С ростом
величина среднеквадратической погрешности
уменьшается. Если при
среднеквадратическая погрешность
стремится к нулю, то систему базисных
функций
называют полной. Эта система функций
является также замкнутой, т.к. для
любой функции
неравенство (4.17) переходит при
в равенство.
Точность
аппроксимации периодических сигналов
зависит от числа членов ряда при конечном
числе членов ряда. Относительную
среднеквадратическую погрешность
аппроксимации периодической функции
конечным числом членов ряда Фурье можно
определить по формуле :
. (4.18)
где
— средняя мощность сигнала;
— средняя мощность
-й
ортогональной составляющей сигнала.
Экспериментальное
значение погрешности аппроксимации
может быть найдено следующим образом.
Пусть имеется
экспериментально полученных точек
сигнала. Известен также теоретический
вид зависимости. Тогда погрешность
аппроксимации может быть вычислена
следующим образом
, (4.19)
где
— теоретическое значение отсчета сигнала
в момент времени
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Остаточный член ряда Фурье. Погрешности приближения функций. Численное дифференцирование
Страницы работы
Содержание работы
12.Остаточный член ряда Фурье.
Для функции f(x) Î L2[a,b]
обобщенный ряд Фурье сходится к ней в среднеквадратичном смысле и методическая
погрешность аппроксимации может быть определена выражением (1.48)
Представим
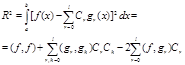 |
Имея ввиду, что функции gr(x), rÎ[0,l] ортогональны, а коэфиценты Фурье вычисляются по
соотношению (1.51) получим
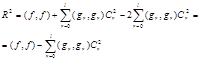 |
oткуда
(1.54)
а если gr(x), rÎ[0,l] ортонормированные, то
(1.55)
Если на приближаемую функцию
наложить дополнительные ограничения, то обобщенный ряд Фурье может сходиться к ней
и в равномерном смысле. Например, необходимым и достаточным условием
равномерной сходимости обобщенного ряда Фурье по полиномам Лежандра или
Чебышева к f(x) на [a,b]. Независимо от типа сходимости, иногда оказывается
необходимо оценить погрешность аппроксимации на [a,b] в
виде максимального отклонения ряда Фурье от приближаемой f(x), что
можно осущесвить дав оценку остаточного члена ряда Фурье
(1.56)
Однако в общнм случае
аппроксимации таких оценок не существует. В частности, же, например, для (l+1) раз
дифферинцируемых функций f(x), xÎ[a,b]
(1.57)
где a(x) –
значение частичной суммы ряда Фурье на [a,b].Если
более конкретизировать
задачу аппроксимации, положив
в качестве базисных функций ряда Фурье полиномы Чебышева, то
(1.58)
Оценка остаточного члена ряда
Фурье для непрерывной, преиодической, периода 2p функции f(x)
(1.59)
где K – некоторая
константа, определение которой, вообще говоря, проблематично, l
— максимальное значение скорости изменения f(x) на
интервале аппроксимации. Оценки (1.57) ¸(1.59) являются
неконструктивными, поскольку содержат в себе параметры, определение которых
практически невозможны или вызывают существенные трудности. Представляется
целесообразным в случае неоходимости оценку остаточного члена (1.56) давать по
некоторой модели аппроксимируемой функции, которая принадлежит к тому же
классу, что и f(x), но в то же время является наиболее неблагоприятной в
отношении точности аппроксимации. Учитывая наиболее вероятную с практической
точки зрения априорную информацию об аппроксимируемой функции, за такую модель
может быть принята функция вида
(1.60)
где fmin и
fmax – минимальное и максимальное значение f(x) на [a,b], WМ –
максимальное значение круговой частоты спектра аппроксимируемой функции, если
таковая информация может быть получена, или
WМ = VМ / AМ
где VМ – максимальная скорость изменения f(x) на [a,b]. При
аппроксимации модели (1.60) обобщенными рядами Фурье по полиномам Лежандра и
Чебышева первого рода были получены экспериментальные номограммы
которые позволили дать оценки остаточных членов в
следующем аналитическом виде
(1.61)
где K≈0,212(5,3125 + l) для полиномов
Лежандра и Kl =4
для полиномов Чебышевва. Следует отметить, что модельная оценка (1.61)
совпадает с оценкой (1.58), если модели положить AМ = 1,
a
имея в виду, что
13.Погрншности приближения функций.
Результирующая погрешноси
приближения функции f(x), xÎ[a,b] в виде некоторой F(x), xÎ[a,b]
вобщем случае складывается составляющих .
1. Методическая погрешность
используемого способа приближения, возникающая из-за отбрасывания остаточного
члена при опрнделении F(x). Данная погрешность уменьшается с увеличением числа
слагаемых в F(x), и в ряде случаев её удаётся оценить.
2. Погрешность приближенных
вычислений ЭВМ, которые, в свою очередь, можно подразделить на две группы:
Методическая погрешность,
возникающая в результате использования численных методовпри реализации
алгоритмов вычислений требуемых параметров. Данная погрешность имеет место,
например, при исппользовании квадратурных формул численного интегрирования для
определения коэфициентов Фурье. Эта погрешность может быть уменьшена за счет
использования более точного вычислительного алгоритма и оценена в виде
методической погрешности данного алгоритма.
Вычислительная погрешность,
порождаемая конечностью разрядной сетки памяти ЭВМ и зависящая (при выбранном
алгоритме) от возможностей используемой вычислительной техники.
3. Погрешность от неточного
задания исходных данных, которая носит случайный характер и может быть оценена
вероятностными характеристиками. На пример, при аппроксимации некоторой
функции f*(x)=f(x)+ sf(x), где
sf(x) –
погрешности, искажающие истинную f(x) и
характеризуемые математическим ожиданием М{sf(x)}=0
и дисперсией D{sf(x)}=s2, увеличение числа учитываемых членов ряда Фурье
приводит к тому, что математическое ожидание случайной погрешности определения
коэффициентов Фурье остаётся нулевым, а вот дисперсия возрастает.
Анализируя поведение
приведённых погрешностей в зависимости от числа слагаемых в приближающей F(x),
можно сделать вывод, что увеличение количества учитываемых членов в F(x)
приводит к тому, чтометодическая погрешность приближения уменьшается, в то
время как все остальные, связанные, как правило, свычислением коэфициентов
приближающей функции, возрастает. Таким образом, существует некое оптимальное
значение числа учитываемых членов функции F(x),
превышение которого приведёт к увеличению результирующей погрешности, поскольку
скорость нарастания вычислительной погрешности становится больше, чем скорость
уменьшения методической.
Похожие материалы
- Аппроксимация кубическим сплайном (моделирование сплайн-интерполяции)
- Вычисление корней многочлена p(x) = x6 + 5×5 – 7×4 + 3×3 – 6×2 + x +12 различными методами. Решение обыкновенных дифференциальных уравнений
- Использование методов вычислительной математики для решения задач с использованием доступных средств компьютерной поддержки
Информация о работе
Тип:
Ответы на экзаменационные билеты
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание — внизу страницы.
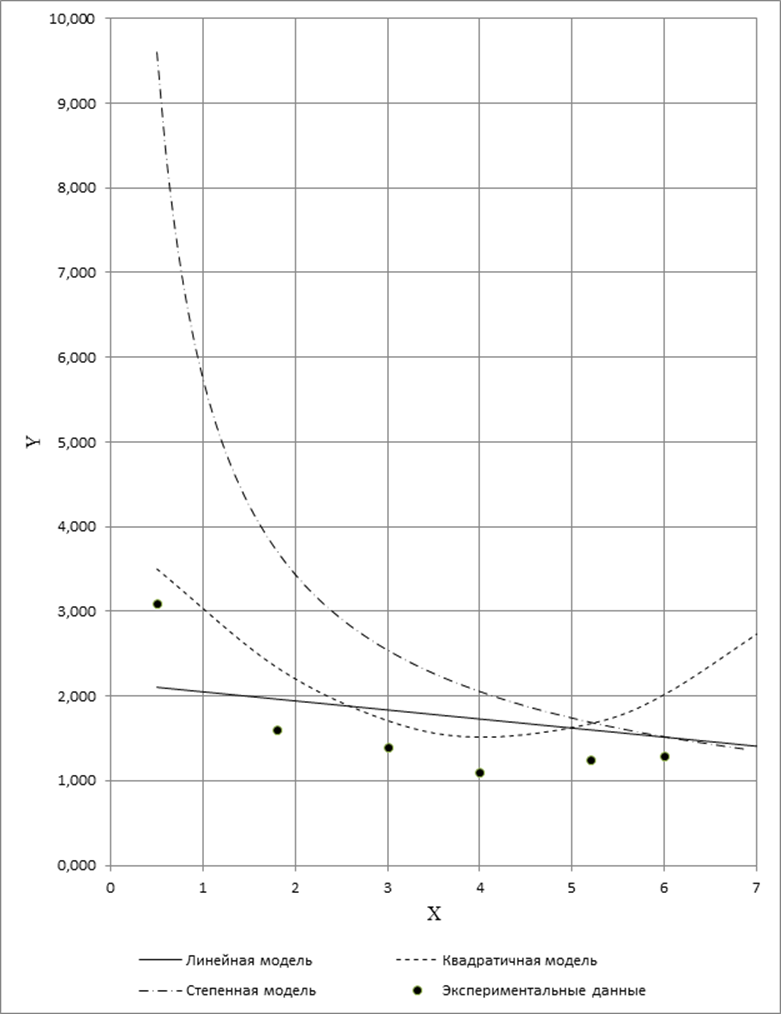
Рис.
1. Графики моделей
Выбор
лучшей модели
;
.
Таблица 5
|
№ |
X |
Y |
η1i |
η2i |
η3i |
|
1 |
0,5 |
3,1 |
2,104 |
3,501 |
2,509 |
|
2 |
1,8 |
1,6 |
1,964 |
2,337 |
1,843 |
|
3 |
3,0 |
1,4 |
1,836 |
1,710 |
1,629 |
|
4 |
4,0 |
1,1 |
1,729 |
1,515 |
1,520 |
|
5 |
5,2 |
1,25 |
1,601 |
1,674 |
1,427 |
|
6 |
6,0 |
1,3 |
1,515 |
2,019 |
1,379 |
|
7 |
7,1 |
2,4 |
1,397 |
2,804 |
1,324 |
Выбор
лучшей модели по среднеквадратичной ошибке аппроксимации
Среднеквадратичная ошибка аппроксимации функции
отклика SrL1:
Среднеквадратичная ошибка аппроксимации функции
отклика SrL2:
Среднеквадратичная ошибка аппроксимации функции
отклика SrL3:
Статистическая
модель предпочтительна, если ее среднеквадратичная ошибка аппроксимации имеет
наименьшую величину по сравнению с другими рассматриваемыми моделями. В
рассматриваемом случаеследовательно,
наилучшей моделью с позиции выбора лучшей модели по среднеквадратичной ошибке
аппроксимации является степенная модель η3.
Выбор лучшей модели по критерию Уилкса
Линейная
комбинация моделей:
Функционал ошибок:
Вычислим
частные производные:
Раскрываем скобки и получаем систему уравнений:
Таблица 6
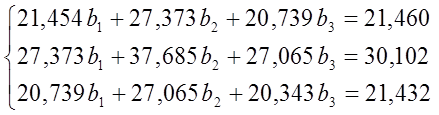
Решение СЛАУ методом Крамера:
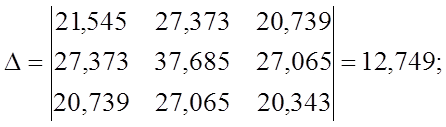
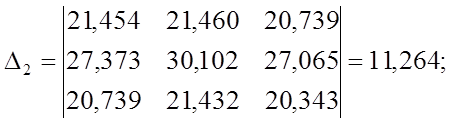
Чем
больше величина коэффициента bQ,
тем лучше работает модель. Так как то
квадратичная модель η2
является наилучшей с точки зрения критерия Уилкса.
Выбор лучшей модели по
комплексной функции качества
Комплексная
функция качества
Линейная
модель
Среднее значение отклика по всем
точкам плана:
– выборочное среднее отклика в i-й
точке.
Относительная среднеквадратичная
ошибка:
Относительная
максимальная ошибка:
Коэффициент,
характеризующий громоздкость модели:
L
– количество коэффициентов ai
в модели,
M
– количество независимых переменных xm.
Коэффициент
насыщенности модели:
Коэффициент,
характеризующий монотонность модели:
C5
= 1 – для модели полиномного типа.
Коэффициент,
характеризующий устойчивость модели к ошибке воспроизведения функции отклика:
– вариация отклика,
взятая в пределах погрешности воспроизведения
Коэффициент,
характеризующий устойчивость коэффициентов al
к
изменению независимых переменных:
ΔXm
– вариация m–й независимой
переменной, определяемая условно
ΔXm
= 10% |Xm|.
Квадратичная
модель
Среднее
значение отклика по всем точкам плана:
Относительная среднеквадратичная ошибка:
Относительная
максимальная ошибка:
Коэффициент,
характеризующий громоздкость модели:
Коэффициент
насыщенности модели:
Коэффициент,
характеризующий монотонность модели:
C5
= 0,5 – для модели степенного типа.
Коэффициент,
характеризующий устойчивость модели к ошибке воспроизведения функции отклика:
Коэффициент,
характеризующий устойчивость коэффициентов al
к
изменению независимых переменных:
Степенная
модель
Среднее
значение отклика по всем точкам плана:
Относительная среднеквадратичная ошибка:
Относительная
максимальная ошибка:
Коэффициент,
характеризующий громоздкость модели:
Коэффициент
насыщенности модели:
Коэффициент,
характеризующий монотонность модели:
C5
= 0,5 – для модели степенного типа.
Коэффициент,
характеризующий устойчивость модели к ошибке воспроизведения функции отклика:
Коэффициент,
характеризующий устойчивость коэффициентов al
к
изменению независимых переменных:
Лучшей
считается модель, у которой величина функции качества С наименьшая,
следовательно, по критерию комплексной функции качества лучшей является
квадратичная модель.
Вывод
На первом этапе
выполнения данного расчетного задания был выполнен корреляционный анализ,
который показал, что случайные величины слабо коррелируют между собой, при этом
наблюдается обратная зависимость. Далее были построены линейная, квадратичная и
степенная модели, а также сформированы их графики. Затем был выполнен выбор
наилучшей модели. Для этого использовались критерии: по среднеквадратичной
ошибке аппроксимации, критерий Уилкса и критерий комплексной функции качества.
Метод по среднеквадратичной ошибке аппроксимации указал на степенную модель.
Критерий Уилкса указал на квадратичную модель. Критерий комплексной функции
качества указал на квадратичную модель. На основании этих трёх критериев, в
качестве лучшей принимаем квадратичную модель.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание — внизу страницы.
Пусть – система ортогональных многочленов на
с весом
– заданная функция.
Представим функцию в виде
Где –ошибка аппроксимации в точке
,
– отрезок ряда Фурье по системе
,
Согласно постановке задачи среднеквадратичного приближения необходимо найти коэффициенты , минимизирующие среднеквадратичную ошибку, т. е.
В силу ортогональности полиномов Лежандра, решение системы (30) дается формулой (33).
.
При этих значениях коэффициентов многочлен
–
– наилучший в среднеквадратичном многочлен -го порядка, т. е.
=
Вычислим квадрат нормы среднеквадратичной ошибки:
|
|
(11) (38) |
Распишем скалярное произведение в (38):
|
|
(12) (39) |
Распишем последнее слагаемое в (38):
|
|
(13) (40) |
Подставляя (39) и (40) в формулу (38) для ошибки, получим:
|
|
(14) (41) |
Из неравенства (41) следует так называемое Неравенство Бесселя для среднеквадратичного приближения:
.
Т. к. система многочленов полна, то в пределе получаем
,
Причем стремление к нулю монотонное: .
Пример 17. Пусть , найти наилучший в среднеквадратичном многочлен 2-ой степени, приближающий
на отрезке
. Вычислить среднеквадратичную ошибку аппроксимации.
В данном случае весовая функция
, поэтому используем ортогональную систему полиномов Лежандра. Для
три первых полинома найдены в примере 1:
По формуле (33), учитывая, что
В результате получаем: , и среднеквадратичная погрешность данного приближения
| < Предыдущая | Следующая > |
|---|