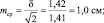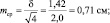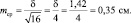Представление результатов исследования
В научных публикациях важно представление результатов исследования. Очень часто окончательный результат приводится в следующем виде: M±m, где M – среднее арифметическое, m –ошибка среднего арифметического. Например, 163,7±0,9 см.
Прежде чем разбираться в правилах представления результатов исследования, давайте точно усвоим, что же такое ошибка среднего арифметического.
Ошибка среднего арифметического
Среднее арифметическое, вычисленное на основе выборочных данных (выборочное среднее), как правило, не совпадает с генеральным средним (средним арифметическим генеральной совокупности). Экспериментально проверить это утверждение невозможно, потому что нам неизвестно генеральное среднее. Но если из одной и той же генеральной совокупности брать повторные выборки и вычислять среднее арифметическое, то окажется, что для разных выборок среднее арифметическое будет разным.
Чтобы оценить, насколько выборочное среднее арифметическое отличается от генерального среднего, вычисляется ошибка среднего арифметического или ошибка репрезентативности.
Ошибка среднего арифметического обозначается как m или
Ошибка среднего арифметического рассчитывается по формуле:
где: S — стандартное отклонение, n – объем выборки; Например, если стандартное отклонение равно S=5 см, объем выборки n=36 человек, то ошибка среднего арифметического равна: m=5/6 = 0,833.
Ошибка среднего арифметического показывает, какая ошибка в среднем допускается, если использовать вместо генерального среднего выборочное среднее.
Так как при небольшом объеме выборки истинное значение генерального среднего не может быть определено сколь угодно точно, поэтому при вычислении выборочного среднего арифметического нет смысла оставлять большое число значащих цифр.
Правила записи результатов исследования
- В записи ошибки среднего арифметического оставляем две значащие цифры, если первые цифры в ошибке «1» или «2».
- В остальных случаях в записи ошибки среднего арифметического оставляем одну значащую цифру.
- В записи среднего арифметического положение последней значащей цифры должно соответствовать положению первой значащей цифры в записи ошибки среднего арифметического.
Представление результатов научных исследований
В своей статье «Осторожно, статистика!», опубликованной в 1989 году В.М. Зациорский указал, какие числовые характеристики должны быть представлены в публикации, чтобы она имела научную ценность. Он писал, что исследователь «…должен назвать: 1) среднюю величину (или другой так называемый показатель положения); 2) среднее квадратическое отклонение (или другой показатель рассеяния) и 3) число испытуемых. Без них его публикация научной ценности иметь не будет “с. 52
В научных публикациях в области физической культуры и спорта очень часто окончательный результат приводится в виде: (М±m) (табл.1).
Таблица 1 — Изменение механических свойств латеральной широкой мышцы бедра под воздействием физической нагрузки (n=34)
| Эффективный модуль
упругости (Е), кПа |
Эффективный модуль
вязкости (V), Па с |
|||
| Этап
эксперимента |
Рассл. | Напряж. | Рассл. | Напряж. |
| До ФН | 7,0±0,3 | 17,1±1,4 | 29,7±1,7 | 46±4 |
| После ФН | 7,7±0,3 | 18,7±1,4 | 30,9±2,0 | 53±6 |
Литература
- Высшая математика и математическая статистика: учебное пособие для вузов / Под общ. ред. Г. И. Попова. – М. Физическая культура, 2007.– 368 с.
- Гласс Дж., Стэнли Дж. Статистические методы в педагогике и психологии. М.: Прогресс. 1976.- 495 с.
- Зациорский В.М. Осторожно — статистика! // Теория и практика физической культуры, 1989.- №2.
- Катранов А.Г. Компьютерная обработка данных экспериментальных исследований: Учебное пособие/ А. Г. Катранов, А. В. Самсонова; СПб ГУФК им. П.Ф. Лесгафта. – СПб.: изд-во СПб ГУФК им. П.Ф. Лесгафта, 2005. – 131 с.
- Основы математической статистики: Учебное пособие для ин-тов физ. культ / Под ред. В.С. Иванова.– М.: Физкультура и спорт, 1990. 176 с.
Условное
обозначение средней арифметической
величины через М (от латинского слова
Media) чаще применяется в медицинских и
педагогических исследованиях. В
математической статистике предпочитают
обозначение через .
Средняя арифметическая величина является
производной, обобщающей количественные
признаки ряда однородных показателей
(совокупности). Выражая одним числом
определенную совокупность, она как бы
ослабляет влияние случайных индивидуальных
отклонений, и акцентирует некую обобщенную
количественную характеристику, наиболее
типичное свойство изучаемого ряда
показателей.
Определяя
значение средней арифметической
величины, следует придерживаться
некоторых правил.
1.
Средняя арифметическая величина может
характеризовать только те признаки
изучаемого объекта, которые присущи
всей совокупности, но в разной
количественной мере (например, уровень
развития быстроты движений характерен
для каждого человека, хотя и в разной
количественной мере). Средняя арифметическая
величина не может характеризовать
количественную меру тех признаков,
которые одной части совокупности
присущи, а другой нет, т. е. она не может
отражать присутствие или отсутствие
того или иного признака (например, умение
или неумение выполнять то или иное
двигательное действие).
2.
Средняя арифметическая величина должна
включать все показатели, полученные в
данном исследовании. Произвольное
исключение даже некоторых из них
неизбежно приведет к искажению конечного
результата.
3.
Средняя арифметическая величина обязана
отражать только однородную совокупность.
Нельзя, например, определять средний
уровень физического развития школьников,
не разделив их предварительно по возрасту
и полу.
4.
Средняя арифметическая величина должна
вычисляться на достаточно большой
совокупности, размеры которой определяются
в каждом конкретном случае отдельно
(см. «Подбор исследуемых»).
5.
Необходимо стремиться к тому, чтобы
средняя арифметическая величина имела
четкие и простые свойства, позволяющие
легко и быстро ее вычислять.
6.
Средняя арифметическая величина должна
обладать достаточной устойчивостью к
действию случайных факторов. Только в
этом случае она будет отражать
действительное состояние изучаемого
явления, а не его случайные изменения.
7.
Точность вычисления средней арифметической
величины должна соответствовать
содержанию изучаемого педагогического
явления. В некоторых случаях нет
необходимости в расчетах с большой
точностью, в других — большая точность
нужна при вычислениях, но совершенно
не нужна в выводах. Например, при расчете
средних величин числа подтягиваний на
перекладине можно пользоваться и сотыми
долями целого, но представлять и выводах,
что исследуемые в среднем подтянулись
7,83 раза, было бы неграмотна, так как
невозможно измерение с подобной
точностью. В этом случае необходимо в
выводах представлять числа, округленные
до целых единиц.
В
простейшем случае этот показатель
вычисляется путем сложения всех
полученных значений (которые называются
вариантами) и деления суммы на число
вариант:
где
S — знак суммирования;
V
— полученные в исследовании значения
(варианты);
п
— число вариант.
По
этой формуле вычисляется так называемая
простая средняя арифметическая величина.
Применяется она в тех случаях, когда
имеется небольшое число вариант.
При
большом числе вариант прибегают к
вычислению так называемой взвешенной
средней арифметической величины. С этой
целью строят ряд распределения, или
вариационный ряд, который представляет
собой ряд вариант и их частот,
характеризующих какой-нибудь признак
в убывающем или возрастающем порядке.
Например, в нашем случае измерение
точности попадания мячом в цель дало
125 вариант, т. е. в группе I, где применялась
методика обучения «А», одноразово
исследовалось 125 детей с числовым
выражением от 0 (точное попадание в цель)
до 21,5 см (максимальное отклонение от
цели). Каждое числовое выражение
встречалось в исследовании один и более
раз, например «0» встретился 28 раз.
Другими словами, 28 участников эксперимента
точно попали в цель. Этот показатель
называется числом наблюдений или
частотой вариант и условно обозначается
буквой «Р» (число наблюдений составляет
часть числа вариант).
Для
упрощения числовых операций все 125
вариант разбиваются на классы с величиной
интервала 1,9 см. Число классов зависит
от величины колебаний вариант (разности
между максимальной и минимальной
вариантами), наличия вариант для каждого
класса (если, например, для первого
класса — «0 — 1,9» — нет соответствующих
вариант, т.е. ни один исследуемый не имел
точных попаданий или отклонений от цели
в пределах от 0 до 1,9 см, то подобный класс
не вносится в вариационный ряд) и,
наконец, требуемой точности вычисления,
(чем больше классов, тем точность
вычисления выше). Вполне понятно, что
чем больше величина интервала, тем
меньше число классов при одной и той же
величине колебаний вариант.
После
разбивки вариант по классам в каждом
классе определяется срединная варианта
«Vc»,
и для каждой срединной варианты
проставляется число наблюдений. Пример
этих операций, и дальнейший ход вычислений
приведены в следующей таблице:
|
Классы |
Серединные |
Число |
VCP |
VC-M=d |
d2 |
d2P |
|
0 |
1 |
28 |
28 |
-4.6 |
21.16 |
592.48 |
|
2 |
3 |
29 |
87 |
-2.6 |
6.76 |
196.04 |
|
4 |
5 |
22 |
110 |
-0.6 |
0.36 |
7.92 |
|
6 |
7 |
13 |
91 |
1.4 |
1.96 |
25.48 |
|
8 |
9 |
11 |
99 |
3.4 |
11.56 |
127.16 |
|
10 |
11 |
13 |
143 |
5.4 |
29.16 |
379.08 |
|
12 |
13 |
4 |
52 |
7.4 |
54.76 |
219.04 |
|
14 |
15 |
2 |
30 |
9.4 |
88.36 |
176.72 |
|
16 |
17 |
1 |
17 |
11.4 |
130.00 |
130.00 |
|
18 |
19 |
1 |
19 |
13.4 |
179.60 |
179.60 |
|
20 |
21 |
1 |
21 |
15.4 |
237.20 |
237.20 |
|
125 |
697 |
2270.72 |
Очередность
числовых операций:
1)
вычислить сумму числа наблюдений (в
нашем примере она равна 125);
2)
вычислить произведение каждой срединной
варианты на ее частоту (например, 1*28 =
28);
3)
вычислить сумму произведений срединных
вариант на их частоты (в нашем примере
она равна 697);
4)
вычислить взвешенную среднюю арифметическую
величину по формуле:
Средняя
арифметическая величина позволяет
сравнивать и оценивать группы изучаемых
явлений в целом. Однако для характеристики
группы явлений только этой величины
явно недостаточно, так как размер
колебаний вариант, из которых она
складывается, может быть различным.
Поэтому в характеристику группы явлений
необходимо ввести такой показатель,
который давал бы представление о величине
колебаний вариант около их средней
величины.
Вычисление
средней ошибки среднего арифметического.
Условное обозначение средней ошибки
среднего арифметического — т. Следует
помнить, что под «ошибкой» в статистике
понимается не ошибка исследования, а
мера представительства данной величины,
т. е. мера, которой средняя арифметическая
величина, полученная на выборочной
совокупности (в нашем примере — на 125
детях), отличается от истинной средней
арифметической величины, которая была
бы получена на генеральной совокупности
(в нашем примере это были бы все дети
аналогичного возраста, уровня
подготовленности и т. д.). Например, в
приведенном ранее примере определялась
точность попадания малым мячом в цель
у 125 детей и была получена средняя
арифметическая величина примерно равная
5,6 см. Теперь надо установить, в какой
мере эта величина будет характерна,
если взять для исследования 200, 300, 500 и
больше аналогичных детей. Ответ на этот
вопрос и даст вычисление средней ошибки
среднего арифметического, которое
производится по формуле:
Для
приведенного примера величина средней
ошибки среднего арифметического будет
равна:
Следовательно,
M±m = 5,6±0,38. Это означает, что полученная
средняя арифметическая величина (M =
5,6) может иметь в других аналогичных
исследованиях значения от 5,22 (5,6 — 0,38 =
5,22) до 5,98 (5,6+0,38 = 5,98).
Соседние файлы в предмете Ветеринарная генетика
- #
- #
- #
2.1. Стандартное отклонение среднего выборочного значения (ошибка среднего) и доверительный интервал
Результаты измерений обычно показывают с так называемой «средней статистической ошибкой средней величины» и для нашего случая (см. табл. 1.1) это будет запись: «высота сеянцев в опыте составила 5,0 ± 0,28 см». Словосочетание «средняя статистическая ошибка» обычно сокращают до названия «ошибка среднего» или просто «ошибка», обозначают буквой m и определяют по очень простой формуле. Для итогов упомянутой таблицы, где расчеты по 25 высотам дали значение δ = 1,42 см, эта ошибка составит:
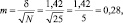
|
где δ – |
стандартное отклонение; |
|
N – |
число наблюдений или объем выборки, шт. |
Если объем выборки взять 100 шт., то ошибка снизится в 2 раза: 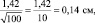
Рассмотрим эту «среднюю статистическую ошибку» (далее просто ошибка) подробно, так как именно в ней скрыто понимание того, что называют статистическим мышлением. Интуитивно мы понимаем, что малая выборка дает большую ошибку, т.е. неточное определение среднего значения. Последний термин настолько привычен, что мы даже не задумываемся о том, что его правильное и полное название «среднее выборочное значение», т.е. среднее, определяемое в некоторой выборке. И выборки могут быть очень разные по численности. Начнем с самых малых. Например, что произойдет с ошибкой, если объем выборки сократить до 2 измерений? Такие выборки бывают, например, в почвенных исследованиях, когда каждое измерение достается дорогой ценой. Для этого вернемся к рис. 1.1. На нем стандартное отклонение ±δ, которое отражает разброс значений вокруг среднего в левую и правую сторону в виде холма, наблюдается при объеме выборки 1 шт. В этом случае ошибка среднего выборочного значения будет равна стандартному отклонению: m = δ = 1,42. С увеличением N ошибка уменьшается:
при объеме выборки N = 2 ошибка будет
при объеме выборки N = 4 ошибка будет
при объеме выборки N = 16 ошибка будет
Важно понять, что ряд распределения частот этих выборочных средних будет постепенно как бы съеживаться и приближаться к центру, где находится так называемое «генеральное» среднее. Поясним, что в математике генеральное среднее значение называется математическим ожиданием и его обозначают буквой «М». Например, это может быть средняя высота, рассчитанная по всем измеренным в теплице сеянцам, или среднее число семян в 1 шишке у дерева после подсчета семян во всех собранных с дерева шишках (50, 100, 500 и т.д., т.е. весьма небольшая генеральная совокупность). Распределение частот значений выборочных средних, которых может быть множество, будет иметь форму такого же холма, как и распределение единичных значений на рис. 1.1. При этом, если выборка будет из 1 шт., то холм будет в точности таким же, но при выборках из 2 шт. его форма съежится в 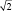
в 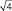
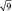
Для этих сокращающихся рядов распределения выборочных средних можно рассчитать свое, особое стандартное отклонение. Вероятно, чтобы не путать его со СТАНДОТКЛ, его стали называть по-другому, т.е. «средней статистической ошибкой средней величины». Чем больше по объему выборки, тем короче ряд распределения средних значений этих выборок с его «хвостами» в левую и правую сторону, и тем меньше величина этого особого стандартного отклонения. Закон распределения частот выборочных средних точно такой же, и имеет те же свойства: в пределах ±2m находится 95 % всех значений выборочных средних, в пределах ±3m – 99,5 %, а в пределах ±4m находится 100 % всех значений xср. Форма этого распределения меняется от пологой при малых выборках до очень крутой, вплоть до «схлопывания» в центре при выборках большого объема, когда ошибка среднего стремится к нулю.
Здесь следует пояснить, что, на наш взгляд, словосочетание «средняя статистическая ошибка средней величины», сокращаемое до «ошибки среднего значения» или просто до «ошибки», вводит нас в некоторое заблуждение, так как мы привыкли со школы, что ошибки надобно исправлять. Более правильным, вместо слов «ошибка среднего значения», будет использование слов «стандартное отклонение выборочных средних значений от генерального среднего». Не случайно математики выбрали для обозначения величины этого отклонения букву «m», а для обозначения генерального среднего (математического ожидания) – букву «М». Слова для объяснения этих сложных явлений могут быть разными, но и у математиков, и у биологов есть единодушие в понимании статистического смысла, лежащего за этими буквенными символами. Вообще, лучше было бы ввести некий иной термин вместо слов «ошибка» или «отклонение», так как они изначально имеют в нашем сознании иной смысл; на наш взгляд, более всего подходит слово «скачок» (чем сильнее отскакивает выборочное среднее от генерального среднего, тем реже оно встречается). Но так уж получилось, что не нашлось нейтрального (иностранного) слова, и слово «ошибка» традиционно используют, и мы также будем его использовать; важно понимать его иной, чем в обыденном употреблении, математический и статистический смысл.
Для самого точного определения средней высоты сеянцев нужно измерять все растения в питомнике, и тогда мы получим «генеральное среднее значение». Но так не делают, а измеряют несколько сотен растений в разных местах и этого бывает достаточно для определения среднего выборочного значения с приемлемой точностью. В нашем примере при 100 растениях ошибка его определения составит 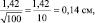
Вообще, точность опыта не самоцель; гораздо важнее сократить численность (объем) выборки до минимума. Представим себе, что средняя высота сеянцев xср = 5,0 см, а ее ±δ = 1,42 см, рассмотренные выше, получены при измерении 1000 растений потомства сосны, например, из Кунгура. Поделив ±δ на корень из 1000 получаем ошибку опыта m = ±0,045 см. Далее получаем точность опыта
Р = m/xср×100 = 0,045/5,0×100 = 0,9 %.
Точность получилась очень высокой. Но в питомнике есть потомства и из других мест и такой уровень точности совершенно не нужен, так как нужно узнать еще высоты сеянцев, например, из Очера, Осы, Добрянки и других районов. Если выборку из 1 тыс. растений снижать, то будет увеличиваться ошибка в определении средней высоты. И нужно найти приемлемую величину такой ошибки, которая позволит нам, тем не менее, уверенно утверждать, что это потомство растет быстрее, либо медленнее других. Причем происхождений может быть несколько сотен и минимизация выборок крайне важна, так как масштабы работ ограничены физическими возможностями бригады селекционеров. Следовательно, надо сокращать объем выборки. Как это сделать правильно?
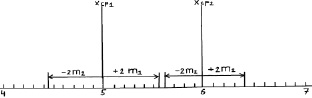
Рассмотрим два потомства. Первое – это упомянутые сеянцы происхождением из Кунгура (хср1), второе – сеянцы из Кизела с хср2 = 6,0 см и δ2 = ± 1,0 см (превышение высоты на 20 %). Надо это превышение доказать. При выборках из 100 растений ранее определенная ошибка m1 была равна 0,14 см, вторая ошибка m2 после расчетов по формуле (2.1) составит 0,1 см. По закону нормального распределения 99,5 % всех возможных значений этих средних хср1 и хср2 будут в пределах «плюс-минус три ошибки», что можно показать графически (рис. 2.1) или в виде формул:
хср1 ± 3m1 = 5,0 ± 3×0,14 = 5,0 ± 0,4 см
и
хср2 ± 3m2 = 6,0 ± 3×0,1 = 6,0 ± 0,3 см.
Возможные теоретические значения средних в генеральной совокупности не перекрывают друг друга, значит, различие достоверно. А если сократить выборки до 50 сеянцев? Тогда 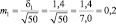
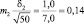
хср1 ± 3m1 = 5,0 ± 3×0,20 = 5,0 ± 0,6 см;
хср2 ± 3m2 = 6,0 ± 3×0,14 = 6,0 ± 0,3 см.
Рис. 2.1. Средние значения по выборкам из 100 растений и их тройные ошибки (пределы возможных значений выборочных средних в 99,5 % случаев)
Снова вынесем эти пределы на график (рис. 2.2).
Рис. 2.2. Средние значения при N = 50 растений и их тройные ошибки
Как видим, пределы сблизились и если еще сократить выборки, то они перекроются. Можно ли далее снижать объем выборки?
Можно, но здесь вступает в силу так называемое условие безошибочного прогноза. Мы это условие задали на уровне 99,5 % и для этого взяли ±3m для распределения ошибок. Но можно взять уровень пониже, с пределами ±2δ (уровень 95 %) и даже с пределами ±1,7δ (уровень 90 %).
При выборках из 25 штук сеянцев, получаем две ошибки: 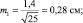
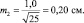
хср1 ± 2m1 = 5,0 ± 2×0,28 = 5,0 ± 0,56 см;
хср2 ± 2m2 = 6,0 ± 2×0,20 = 6,0 ± 0,40 см.
Выносим эти пределы опять на график (рис. 2.3).
Рис. 2.3. Средние значения при N = 25 растений и их двойные ошибки (пределы возможных значений средних в 95 % случаев)
Как видим, просвет все еще есть, и поэтому между возможными значениями средних высот сеянцев в других выборках из происхождений Кунгур и Кизел различия будут опять доказаны. Но уровень доказательства понизился до 95 %, и для 5 % оставшихся случаев нет гарантии, что различия будут иметь место при выборке из 25 растений. Их может и не быть, но эту вероятность в 5 % мы допускаем.
Итак, мы загрузили данные, посмотрели на них, почистили — пора приступить к внимательному изучению, чего мы там насобирали. Частично мы уже сталкивались с описательными статистиками в предыдущих главах — теперь же будем разбираться подробно.
Описательные статистики (descriptive statistics1) — обобщенные статистики, количественно описывающие особенности имеющихся данных.
Описательная статистика (descriptive statistics2) — области статистики, занимающаяся обработкой статистических данных, их наглядным представлением, и собственно описанием через описательные статистики3.
Зачем нам описательные статиски? Чтобы ёмко описать имеющиеся данные и составить на основе этих описаний общее представление о них, а также обнаружить особенности, которые могут повлиять на дальнейший анализ.
Слишком много описаний, поехали к делу уже!
Меры центральной тенденции
Насколько ёмко мы хотим описать наши даннные? Ну, попробуем для начала максимально ёмко и максимально просто — одним числом. Например, самым часто встречающимся наблюдением. Как мы будем это наблюдение искать, зависит от шкалы конкретной переменной.
| Шкала | Мера центральная тенденции |
|---|---|
| Номинальная | Мода |
| Порядковая | Медиана |
| Интервальная | Среднее арифметическое |
| Абсолютная | Среднее геометрическое и др. |
Мода
Мода (mode) — наиболее часто встречающееся значение данной переменной.
Тут все достаточно просто и интуитивно понятно. Пусть у нас есть следующий вектор наблюдений:
x <- c(1,3,4,6,4,2,4,3,2,4,1)Если мы составим таблицу частот по этому вектору, то получим следующее:
## x
## 1 2 3 4 6
## 2 2 2 4 1Очевидно, что \(4\) всречается в векторе чаще других значений — это и есть мода.
Также очевидно, что моду невозможно посчитать на непрерывной шкале.
Почему?
Формально моду можно определить как значение переменной, при котором функция вероятности (probability mass function) принимает максимальное значение:
\[
\mathrm{mode}(X) = \max(\mathrm{PMF}(X))
\]
К сожалению, в R нет встроенной функции для расчёта моды.
Напишите функцию, которая принимает на вход вектор значений дискретной переменной, и вычисляет моду данной переменной4. Если мод у данной переменной несколько, необходимо вернуть все.
## [1] 4mode(c(1, 2, 2, 3, 4, 4))## [1] 2 4Медиана
Если мы уже гуляем на просторах порядковой шкалы, то можем посчитать медиану.
Медиана (median) — это значение, которые располягается на середине сортированного5 вектора значений переменной. То есть, она делит все наблюдения переменной ровно пополам и 50% наблюдений оказывается по одну сторону от медианы, а 50% — по другую. По этой причине медиана также называется вторым квартилем распределения.
Почему нельзя посчитать медиану на номинальной шкале?
Формальное определение медианы зависит от количества значений в векторе: если есть нечётное количество значений — то это ровно середина сортированного вектора, если есть чётное количество наблюдение — то медиана определяется как (арифметическое) среднее между двумя срединными наблюдениями.
\[
\mathrm{median} = \begin{cases}
X(\frac{n+1}{2}), & \text{ if } n \text{ is odd},\\
\dfrac{X(\frac{n}{2}) + X(\frac{n}{2}+1)}{2}, & \text{ otherwise},
\end{cases}
\]
где \(X\) — вектор налюдений данной переменной, \(n\) — число наблюдений, \(X(a)\) — наблюдение с индексом \(a\) в сортированном векторе \(X\).
Для вектора x, который был создан выше, расчёт медианы выглядит так:
## [1] 3Изи.
Среднее
А ежели мы уже на уровне интервальной шкалы, что не грех и среднее посчитать. Вот только какое?
Арифметическое
Как правило, считается среднее арифметическое (поэтому если не указано иного, мы понимает под термином «среднее» именно «арифметическое среднее»), и далее люди не заморачиваются, что в целом разумно. По сему, мы уделим основное внимание ему, а другие посмотрим лишь обзорно.
С арифметическим средним (arithmetic mean, mean, average) все знакомы ещё со школы, и считается оно предельно просто — суммируем все наблюдения и полученную сумму делим на количество наблюдений.
\[
\bar x = \dfrac{\sum_{i=1}^{n}x_i}{n},
\]
где \(\bar X\) — среднее арифметическое, \(x_i\) — наблюдение в векторе \(X\), \(n\) — количество наблюдений.
В R оно считается абсолютно элементарно:
## [1] 3.090909Кстати, оценка генерального среднего через выборочное среднее — это один из примеров точечной оценки параметра методом моментов.
Давайте сравним для рассмотреные статистики (используем все тот же вектор x):
## [1] 4## [1] 3## [1] 3.090909
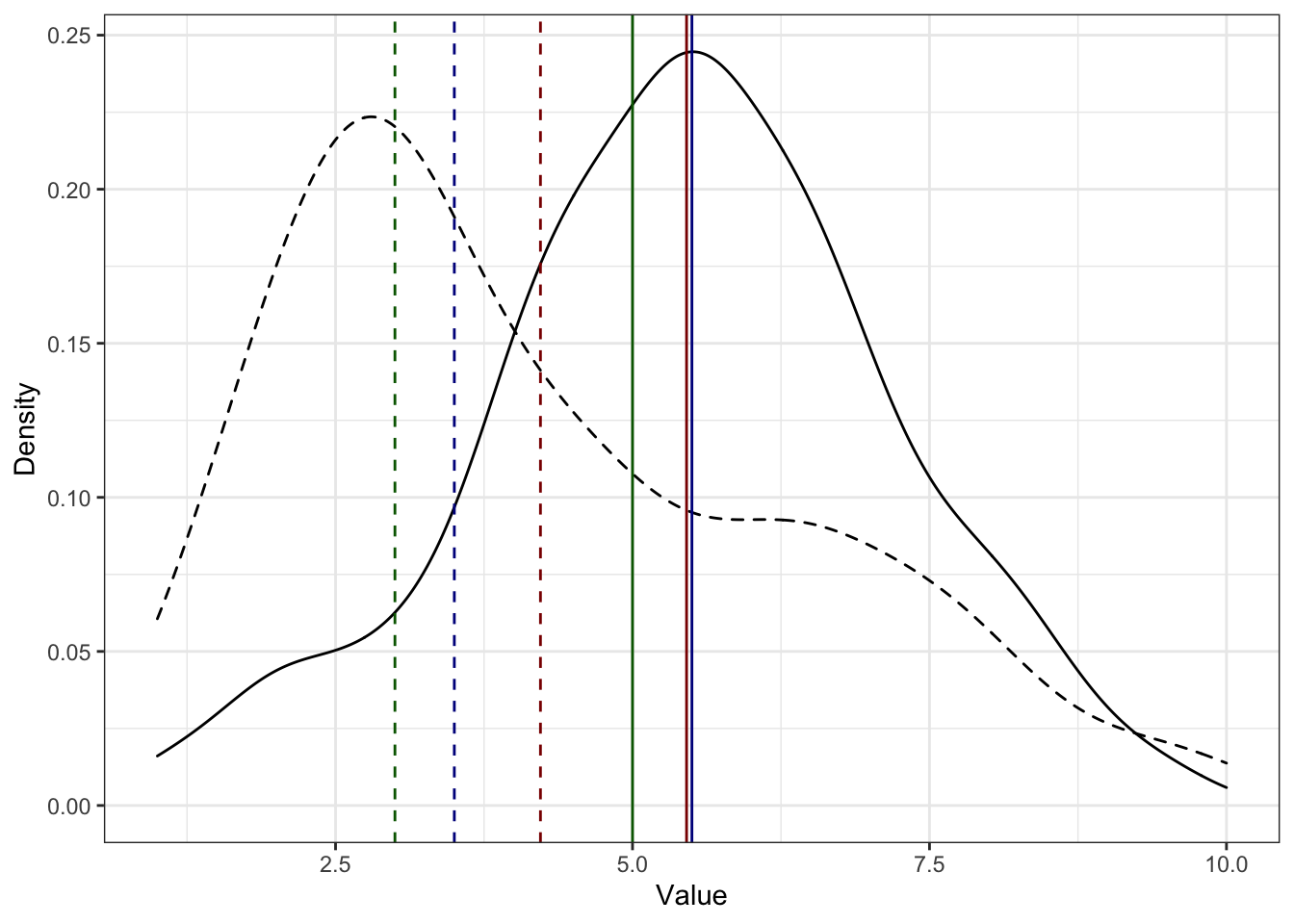
Как мы видим, хотя все три статистики описывают цкентральную тенденцию, тем не менее они всё же дают разные результаты. Посмотрим их взаимное положение на графике:
mean
median
mode
Что тут можно пронаблюдать?
- Есть два распределения — более симметричное (сплошная чёрная линия) и сильно скошенное (прерывистая чёрная линия).
- Медианы (синие линии) делят площади под графиками пополам, как и ожидалось.
- Кроме того, у симметричного распределения медиана и среднее оченю близки, а у скошенного распределения среднее смещается в сторону массивного правого хвоста.
- Мода же у скошенного распредления очень близка к пику распределения.
Что из этого можно заключить?
- Близкие значения медианы и среднего — один из показателей симметричности распределения6
- Медиана более устойчива к выбросам
Почему?
- Если у нас квазинепрерывная7 шкала и мы можем посчитать моду, она будет близка к пику распределения
Геометрическое
Редко встречается в научных работах, но заради общего представления пусть будет.
Геометрическое среднее (geometric mean) идейно похоже на арифметическое, только наблюдения не складываются, а перемножаются. Отсюда появляется ключевое ограничение на его использование — оно может быть рассчитано только на абсолютной шкале. В психологии абсолютных шкал прям скажем небагато, поэтому, скорее всего, вы его никогда и не встретите в практике.
И всё же есть в психологии одна абсолютная шкала, широко используемая, например, в когнитивных исследованиях. Какая?
Вычисляется она следующим образом:
\[
G_{X} = \sqrt[n]{\prod_{i=1}^n x_i} = \Big(\prod_{i=1}^n x_i\Big)^{\tfrac{1}{n}}
\]
Встроенной функции для вычисления геометрического среднего в R нет, но можно поупражняться. 😊
Напишите функцию, которая принимает на вход вектор значений переменной и вычисляет геометрическое среднее. Функция должна возвращать одно число.
## [1] 2.698696Геометрическое среднее используется при работе с экспоненциально растущими величинами (например, численность населения).
Гармоническое
Суперэкзотичный покемон.
Тут даже говорить не буду ничего говорить, просто насладитесь формулой, а если хотите больше, то можно покопаться, например, здесь.
\[
H_X = \frac{n \prod_{i=1}^n x_i}{\sum_{i=1}^n (\tfrac{1}{x} \prod_{j=1}^n x_j)} = \frac{n}{\sum_{i=1}^n \tfrac{1}{x_i}}
\]
Квадратичное
А вот это уже более полезная история. Мы с ним столкнёмся далее, правда под разными масками.
Квадратичное среднее (quadratic mean, root mean square, RMS) — это квадратный корень из среднего квадрата наблюдений. Ничего не понятно, поэтому по порядку.
- есть наблюдение \(x_i\)
- значит есть и его квадрат \(x_i^2\)
- мы умеем считать обычно среднее арифметическое, но ведь \(x_i^2\) — это тоже наблюдение, просто в квадрате, так?
- значит можем посчитать среднее арифметическое квадратов наблюдений — средний квадрат
\[
\frac{\sum_{i=1}^n x_i^2}{n}
\]
- норм, а теперь извлечём из этого дела корень — получим то, что там надо
\[
X_{\mathrm{RMS}} = \sqrt{\frac{\sum_{i=1}^n x_i^2}{n}}
\]
Что-то оно напоминает, да?
Per se мы его вряд ли ещё когда-то увидим, но вот когда будем идеть дело с estimation theory…
Напишите функцию, которая вычисляет квадратичное среднее по данному вектору наблюдений. Функция должна принимать на вход числовой вектор и возвращать одно число.
## [1] 1.028519Усеченное
Так, ну, тут уже попроще.
Усеченное среднее (truncated mean, trimmed mean) — это младшая сестра среднего арифметического с той только разницей, что вычисляется не по всем наблюдениям, а по усеченной с обеих сторон выборке. То есть, из всей выборке, которая у нас есть, мы выбрасываем сколько-то низких значений и сколько-то высоких. Сколько? Ну, от 5% до 25%. По умолчанию отбрасывается по 2.5% с обеих сторон.
Зачем? Чтобы сравнить с обычным средним. Если они близки, то можно ожидать, что распределение симметрично и/или в нём нет выбросов. Если они значительно различаются, то, скорее всего, требуется почистить данные или обратить внимание на форму распределения.
Межквартильное
То же самое, что и в предыдущем пункте. Почти.
Межквартильное среднее (interquartile mean, midmean, IQM) — то же, что и усеченное среднее, только считаем мы по выборке, попавшей в пределы межквартильного размаха.
Как посчитать? Вот так:
\[
X_{\mathrm{IQM}} = \frac{2}{n} \sum_{i=\frac{n}{4}+1}^{\frac{3n}{4}} x_i
\]
Напишите функцию, которая вычисляет усеченное среднее и межквартильное среднее по данному вектору наблюдений. Функция должна принимать на вход вектор наблюдений и долю наблюдений, которую необходимо отсечь от выборки, и возвращать именованный вектор, содержащий две требуемые статистики.
Взвешенное
Полезная вещь.
Часто бывает такая ситуация, что нас нужно посчитать среднее по каким-либо имеющимся параметрам, но одни параметры для нас важнее, чем другие. Например, мы хотим вычислить суммарный балл обучающегося за курс на основе ряда работ, выполненных в течение курса, однако мы понимаем, что тест из десяти вопросов с множественном выбором явно менее показателен, чем, например, аналитическое эссе или экзаментационная оценка. Что делать? Взвесить параметры!
Что значит взвесить? Умножить на некоторое число. На самом деле, любое. Пусть мы посчитали, что написать эссе в три абстрактных раза тяжелее, чем написать тест, а сдать экзамен в два раза тяжелее, чем написать эссе. Тогда мы можем присвоить баллу за тест вес \(1\), баллу за аналитическое эссе вес \(3\), а экзамену — вес \(6\). Тогда итоговая оценка за курс будет рассчитываться следующим образом:
\[
\text{final score } = 1 \cdot \text{test} + 3 \cdot \text{essay} + 6 \cdot \text{exam}
\]
Суперкласс. Однако! Весьма вероятно, что в учебном заведении принята единая система оценки для всех видов работ (ну, скажем, некая абстрактная десятибалльная система в сферическом вакууме). Получается, если и за тест, и за эссе, и за экзамен у студента по 10 баллов, то суммарный балл 100, что, кажется, больше, чем 10. Чтобы вернуться к изначальным границам баллов, нужно моделить суммарный балл на сумму весов параметров:
\[
\text{final score } = \frac{1 \cdot \text{test} + 3 \cdot \text{essay} + 6 \cdot \text{exam}}{1 + 3 + 6}
\]
Кайф! Собственно, это и есть взвешенное среднее. Коэффициенты, на которые мы умножаем значение парамернов, называются весами параметров. И в общем виде формула принимает следующий вид.
\[
\bar x = \frac{\sum_{i=1}^n w_i x_i}{\sum_{i=1}^n w_i} = \sum_{i=1}^n w_i’ x_i,
\]
где \(x_i\) — значения конкретных параметров, \(w_i\) — веса конкретных параметров, \(w_i’\) — нормированные веса параметров.
Вторая часть формулы показывается нам, что можно облегчить себе вычислительную жизнь, если заранее нормировать веса, то есть разделить каждый коэффициент на сумму коэффициентов:
\[
w_i’ = \frac{w_i}{\sum_{i=1}^n w_i}
\]
Тогда сумма коэффициентов будет равна единице. Так чаще всего и поступают, так как тогда коэффициент будет представлять долю, которую весит данный параметр в суммарной оценке. Удобно, практично, красиво.
Взвещенное среднее часто применяется именно во всякого рода ассессментах, и не только образовательных. Например, вы HR-аналитик и оцениваете персонал. Вы аналитически вычисляете веса коэффициентов (допусти, с помощью линейной регрессии), а далее на их основе высчитаете интегральный балл, по которому будете оценивать сотрудников. Это как один из индустриальных примеров.
Есть специально обученная функция, которая вычисляет взвешенное среднее:
weighted.mean(x = c(10, 8, 8), # вектор значений параметров (например, баллы за тест, эссе и экзамен)
w = c(0.1, 0.3, 0.6)) # веса в итоговой оценке## [1] 8.2На этом список средних не заканчивается, но нам обозначенных выше будет более чем достаточно.
Меры разброса
Несмотря на удобство и высокую степень приятности описания всей выборки только мерой центральной тенденции, этого маловато.
Простенький пример для наглядности. Пусть у нас есть два следующих вектора:
## [1] 5 50 12 4 4 6 24## [1] 20 30 6 8 2 11 1 13 28 31## [1] 15## [1] 15Средние по выборкам одинаковы, однако мы явно наблдаем, что вектора различны. Более того, если пристально посмотреть, то мы обнаружим, что у них разный разброс значений. Вообще-то помня о том, что неопределенность и вариация — главные характеристики статистических данных, было бы крайне неразумно пренебречь описанием этой самой вариативности. Что ж, займемся этим вопросом.
Минимум и максимум
Как можно описать разброс? Указать минимум и максимум!
Это, во-первых, справедливо, во-вторых, просто, что даже останавливаться на этом не будем. Вот соответствующие функции:
min(x1); min(x2) # да, точка с запятой в R тоже работает## [1] 4## [1] 1max(x1); max(x2) # но заклинаю вас использовать её не в ущерб удобочитаемости## [1] 50## [1] 31Минимум и максимум по переменных всегда полезно смотреть при исследовании данных — так можно обнаружить ошибки записи. Например, если вы психометрик и используете в вопросах опросника семибальную шкалу его высочества Ликерта (Лайкерта), а при исследовании собранных данных обнаруживаете минимум по какому-либо вопросу 0, а максимум 9 — явно что-то пошло не так. Или, допустим, вы анализируете заработную плату сотрудников организации и обнаруживаете минимум по переменной «фонд оплаты труда» ниже МРОТ — повод задуматься. Конечно, сразу выкидывать наблюдения не надо, но точно надо обратить на них внимание и изучить возможные причины появления таких значений — может сотрудник устроен на 0.1 ставки?
Очевидно, что минимум — это первый элемент отсортированного (по возрастанию) массива, а максимум — последний. А как найти минимум (или максимум) без сортировки?
Напишите функцию, которая принимает на вход массив (вектор) и возвращает минимальный (максимальный) элемент массива. Внутри функции нельзя использовать сортировку и встроенные в R функции.
min_custom(x1); min_custom(x2)## [1] 4## [1] 1max_custom(x1); max_custom(x2)## [1] 50## [1] 31P.S. Функции для поиска минимума и максимума будут практически идентичны, поэтому если вы напишите одну из них, тут же поймете, как её модифицировать, чтобы получить вторую.
P.P.S. Да, это задание на алгоритмы, но это единственное задание на алгоритмы в этой книге. Вот подсказка. 🙄
Размах
А если у нас есть минимум и максимум — значит можно посчитать разницу между ими. И получить такую статистику как размах (range). Добрые люди написали одноименную функцию, правда считает она не сам размах, а выводит минимум и максимум по массиву:
## [1] 4 50## [1] 1 31Но это не беда, потому что другие добрые люди написали более серьезные функции, чтобы облегчить нам статистическую жизнь. С ними познакомимся далее.
Дисперсия
Ну, хорошо, range() нам указал, что действительно разброс в наших векторах различный, несмотря на то, что средние в точности равны. Что нам еще надо?
Вот другой пример. Есть два таких вектора.
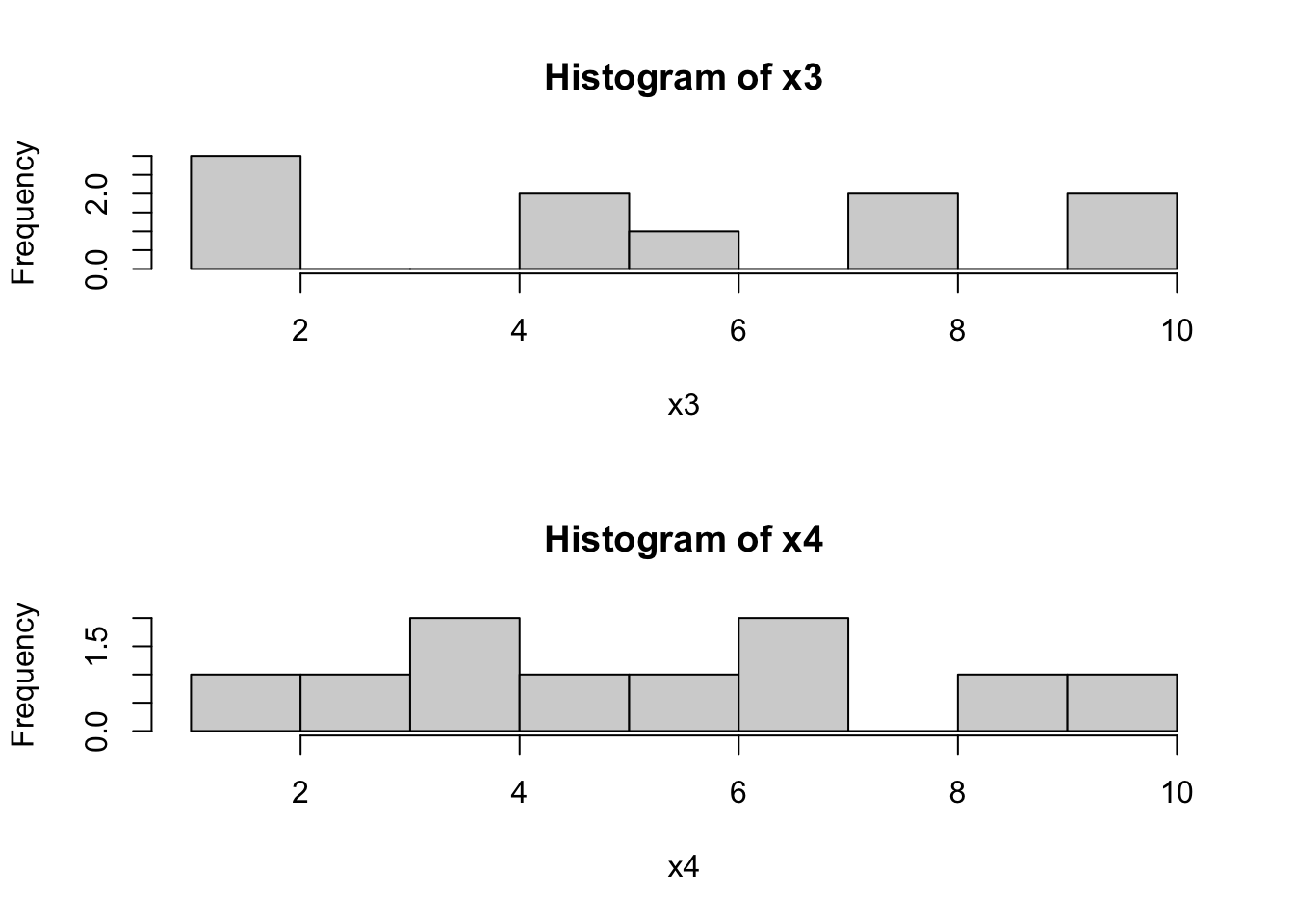
## [1] 1 1 2 5 5 6 8 8 10 10## [1] 1 3 4 4 5 6 7 7 9 10## [1] 5.6## [1] 5.6## [1] 1 10## [1] 1 10Вроде и средние одинаковы, и размах одинаковый. Но вектора явно различаются. Можно даже посмотреть на картинку:
par(mfrow=c(2,1)) # размещаем два графика друг по другом
hist(x3, breaks = 10)
hist(x4, breaks = 10)par(mfrow=c(1,1)) # откатываем настройки обратноВсё это безобразие приводит нас к мысли о том, что нам недостаточно описания «общей», «внешней» вариативности, нам надо ещё постараться как-то ухватить вариативность «внутри» ряда наблюдений. И желательно тоже в какой-нибудь одной чиселке.
Будем действовать аккуратно и пошагово. Что у нас есть сейчас? Мы умеем считать средне, которое отражает центральную тенденцию. Ок, давайте зацепимся за него и — раз это «центр» — будем считать вариативность относительного него. Каждое наблюдение в ту или иную сторону отклоняется от среднего. Ок, мы в состоянии посчитать отклонение (deviation) каждого наблюдения:
\[
d = \bar x — x_i
\]
Топчик! А что, если… посмотреть, как в среднем все наблюдения отклоняются от среднего значения? Отличная же идея! Считаем среднее отклонение!
\[
\frac{\sum_{i=1}^n(\bar x — x_i)}{n},
\]
\(n\) — количество наблюдений в выборке.
План хорош — но не без изъяна… Так как отклонения у нас происходят в обе стороны от среднего — в положительную и отрицательную — то и в сумме они дадут нам что-то около нуля. Соответственно, и среднее отклонение у нас будет где-то около нуля. Известно, что есть два путя, как победить минус — взять модуль или возвести в квадрат.
- Модуль. Преимущество первого в том, что размерность величины разброса остается той же, что и у измеряемой переменной8.
- Квадрат. Преимущество второго в том, что сильные отклонения будут оказывать более сильное влияние на окончательное значение статистики, в то время как для первого малые и большие отклонения равноценны.
Второй пункт на практике нам оказывается важнее, посему, мы избирем путь Мандалора, то есть возведения в квадрат.
Итак, возводим отклонения в квадрат и — о, боги — мы получили формулу дисперсии, или вариации (dispersion, variance)!
\[
\sigma^2 = \frac{\sum_{i=1}^n (\bar x — x_i)^2}{n}
\]
Так, а что мы в итоге получили? Формулу дисперсии. Какой?
Если со средними всё было легко и непринужденно, то с дисперсией нам придётся ещё поскрипеть мозгами над тем, что такое…
Степени свободы
Википедия предлагает нам следующее определение: «количество наблюдений в финальном вычислении статистики, которые могут свободно варьироваться». Лаконично, красиво, непонятно.
В собственных заплывах на просторы статистики я нашёл два подхода к тому, как можно приблизиться к пониманию концепта степеней свободы, коими здесь с вами поделюсь. Возможно, они не столько математически точны, как хотелось бы, но позволяют уловить идею. И, в прицнипе, этого достаточно, по крайней мере, до определенного момента вашего статистического бытования.
Прежде всего, необходимо вспомнить, что мы рассчитываем наши статистики на выборке, а не на всей генеральной совокупности. Этот факт и требует внесения коррективов в формулу.
Подход номер раз
Обратим внимание, что для расчёта дисперсии мы первоначально рассчитали выборочное среднее, и далее, основываясь на рассчитанном значении, рассчитываем собственно выборочную дисперсию. То есть, чтобы рассчитать требуемую статистику, мы заранее рассчитали ещё одну как бы зафиксировав нашу выборку, чтобы нам было от чего считать отклонения. И нам надо учесть этот факт в формуле дисперсии — вычесть из числа наблюдений единицу (ту самую «одну статистику», которую мы рассчитали). Таким образом, число степеней свободы будет \(n-1\).
Аналогичная идея будет при вычислении степеней свободы в дисперсионном анализе, например.
Подход номер два
Это рассуждение ближе к математическому. Мы помним, что наш вектор наблюдений — это значения некоторой случайной величины, которые в общем-то могут быть и совсем другими при последующих измерениях. А если представить, что мы знаем только среднее по выборке? Солько измерений нам надо произвести, чтобы восстановить весь ряд наших наблюдений? Если знаем среднее, значит знаем и сумму по выборке. Чтобы восстановить все наблюдения нам надо провести \(n-1\) измерение, ведь если мы знаем сумму \(n-1\) значений, то последнее мы высчитаем следующим образом: \(x_n = \bar x — \sum_{i=1}^{n-1} x_i\). Получается, что если мы знаем среднее, то можем восстановить все \(n\) наблюдений по \(n-1\). Это и есть потерянная степень свободы.
Если таки концепт степеней свободы даётся пока что сложно — не беда. Самая главная общая идея в том, что когда мы рассчитываем выборочные статистики, нам необходимо сделать некоторые дополнительные манипуляции, чтобы избежать смещения оценок. Поэтому вводится понятие степеней свободы, которые позволяют эти манипуляции осуществить.
Итак, возвращаемся к дисперсии и разбираемся, что к чему. Формула, которую мы получили, справедлива для генеральной совокупности. В числителе дроби находится сумма квадратов отклонений (сумму квадратов, sum of squares, SS). В знаменателе находится количество наблюдений. На выборке такая формула будет давать смещённую оценку дисперсии, поэтому она также называется смещённая дисперсия.
Дисперсия генеральной совокупности (смещённая дисперсия)
\[
\sigma^2_X = \mathrm{var}(X) = \frac{\sum_{i=1}^n (\bar x — x_i)^2}{n}
\]
Для того, чтобы скорректировать оценку дисперсии, необходимо разделить сумму квадратов не на количество наблюдений, а на количество степенйе свободы, которое как мы выяснили равно \(n-1\). Выборочная дисперсия имеет собственное обозначение \(s^2\).
Выборочная дисперсия (несмещённая дисперсия, исправленная дисперсия)
\[
s^2 = \frac{\sum_{i=1}^n (\bar x — x_i)^2}{n-1}
\]
Функция, которая занимается вычислением дисперсии, называется var(), так как «вариация» (variance) — это полный синоним дисперсии.
var(x3); var(x4) # вычисляется несмещённая дисперсия## [1] 11.82222## [1] 7.6И — voila! — дисперсии у наших векторов действительно различны.
Функция для расчёта дисперсии у нас есть, а вот для суммы квадратов — нет. 😞
Напишите функцию, которая вычисляет сумму квадратов отклонений от среднего значения по данному вектору. Функция принимает числовой вектор и возвращает одно число.
## [1] 68.4Векторное представление дисперсии
— А скажи мені, автор, заради чого ми так довго топталися на цій дисперсії?
— Заради майбутнього…
Вообще концепт дисперсии — ключевой во всем статистическом анализе, поэтому дисперсия будет встречаться нам так или иначе в каждой теме.
Стандартное отклонение
Есть существует \(\sigma^2\), то где-то должна быть и \(\sigma\). И согласно здравому смыслу, вычисляться она должна извлечением квадратного корня из дисперсии.
Действительно, \(\sigma\) существует и обозначает стандартное отклонение (среднее квадратичное отклонение, standart deviation) — ещё одну меру разброса. А она нам зачем?
Дисперсия прекрасна и замечательна как статистический показатель, но вот её значение достаточно трудно интерпретировать, так как её размерность — это единицы измерения переменной в квадрате. Например, ПРИМЕР. Стандартное отклонение возвращает размерность обратно.
Так как существует две дисперсии — генеральная и выборочная — то и стандартных отклонения будет существовать два:
- стандартное отклонение генеральной совокупности
\[
\sigma_X = \sqrt{\sigma^2_X} = \sqrt{\frac{\sum_{i=1}^n (\bar x — x_i)^2}{n}} = \sqrt{\frac{\sum_{i=1}^n d_i^2}{n}},
\]
где \(d_i = \bar x — x_i\) — отклонение. Узнали? Согласны?
- стандартное отклонение выборки
\[
s = \mathrm{sd}(X) = \sqrt{s^2} = \sqrt{\frac{\sum_{i=1}^n (\bar x — x_i)}{n-1}}
\]
Раскопайте из недр R доказательство, что стандартное отклонение вычисляется согласно представленной выше формуле.
Помните, что R — это программное обеспечение с открытым исходным кодом?
Стандартная ошибка среднего
Набираем много выборок из генеральной совокупности. Получаем распределение средних значений. Стандартное оклонение данного распределение называется стандартной ошибкой среднего (standard error of mean).
- стандартная ошибка среднего в генеральной совокупности
\[
\sigma_X^- = \frac{\sigma_X}{\sqrt{n}}
\]
- стандартная ошибка среднего по выборке
\[
s_X^- = \mathrm{se}(X) = \frac{s_X}{\sqrt{n}}
\]
Стандартная ошибка, во-первых, сама по себе является интервальной оценкой среднего, а кроме того, используется при вычислении доверительного интервала. ОБЪЯСНЕНИЕ
Квантили
Мы уже обсуждали квантили в теме распределений. Теперь попробуем переложить имеющиеся знания на работу с эмпирическими данными.
Как мы знаем, квантиль — это точка на шкале признака, которая не превышается с опредлённой вероятностью по данному распределению. То есть ниже квантиля 0,02 (\(x_{0,02}\)) лежит 2% наблюдений, а ниже квантиля 0,98 (\(x_{0,98}\)) лежит практически все распределение (98%).
С произвольными квантилями в практике мы практически не работаем. Рассмотрим «особенные» квантили.
Квартили
Квартили (quartiles) — это квантили, которые делят нашу выборку на четыре части (по 25%).
- нулевой квартиль (\(Q_0\)), он же минимум, так как ниже него лежит 0% наблюдений,
- первый квартиль (\(Q_1\)), ниже которого лежит 25% наблюдений,
- второй квартиль (\(Q_2\)), ниже которого лежит 50% наблюдений — это есть медиана нашего распределения,
- третий квартиль (\(Q_3\)), ниже которого лежит 75% наблюдений,
- четвертый квартиль (\(Q_4\)), он же максимум, так как ниже него лежит 100% наблюдений.
Квартили хорошо визуализируются графиком «ящик с усами» (boxplot). По этому графику можно увидеть симметричность распределения, разброс значений переменной, сравнить вариативность нескольких переменных.
Квартили в R можно рассчитать следующим образом:
x5 <- rnorm(100, mean = 3.5, sd = 0.45)
quantile(x5) # обратите внимание на название функции :)## 0% 25% 50% 75% 100%
## 2.184432 3.162326 3.507951 3.804915 4.436762С первым и третьим квартилями связана следующая полезная метрика — межквартильный размах (interquartile range). Это разность между третьим и первым квартилем:
\[
\text{IQR}(X) = Q_3(X) — Q_1(X) = x_{0,75} — x_{0,25}
\]
Есть ли в R встроенная функция, вычисляющая межквартильный размах?
Эта метрика помогает нам определить…
Нехарактерные значения (выбросы)
Вообще нехарактерные значения — это такие значения в нашем распределении, которые сильно отклоняются от среднего. Но что значит «сильно»? Глобально — что определите, то и значит. Однако есть несколько общепринятых подходов к вопросу о том, что считать сильными отклонениями.
Нехарактерными значениями можно считать те, что отклоняются
- от первого квартиля вниз и от третьего квартиля вверх более, чем на полтора межквартильных размаха;
- от выборочного среднего более, чем на два (или три) стандартных отклонения.
Какой подход использовать? Зависит от вас, вашей области, требуемой строгости определения выбросов, … Стандартным считается первый подход.
На графике boxplot выбросы отображаются точками.
Что делать с обнаруженными выбросами? Желательно — анализировать. Если нехарактерные значения представляют собой артефакты записи данных, то можно от них избавиться, а если, несмотря на свою «нехарактерность», они все-таки несут в себе важное содержание, придется учитывать их в анализе, хотя они и доставляют часто множество неудобств.
Напишите функцию, которая находит выбросы. Функция должна принимать на вход числовой вектор и возвращать логический вектор такой же длины, как и исходный. Каждое значение логического вектора будет ответом на вопрос, является ли выбросом соответствующее ему значение исходного вектора. Для определения выбросов воспользуйтесь первым из упомянутых подходов.
## [1] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
## [13] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
## [25] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
## [37] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
## [49] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
## [61] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE TRUE FALSE FALSE FALSE
## [73] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
## [85] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
## [97] FALSE FALSE FALSE FALSE TRUEАсимметрия
Коэффициент асимметрии (skewness) характеризует симметричность распределение относительно среднего значения. Как мы говорили ранее, коэффициент асимметрии связан c третьим центральным моментом распределения, поэтому выборочный коэффициент асимметрии также рассчитывается на его основе.
\[
\text{skew}(X) = \frac{m_3}{s^3} = \frac{\frac{1}{n} \sum_{i=1}^n (\bar x — x_i)^3}{\big(\frac{1}{n-1} \sum_{i=1}^n (\bar x — x_i)^2\big)^{3/2}},
\]
где \(\bar x\) — выборочное среднее, \(s\) — выборочное стандартное отклонение, \(m_3\) — выборочный третий центральный момент.
Коэффициент асимметрии может принимать положительные и отрицательные значения, а также быть равным нулю.
- положительный коэффициент асимметрии (positive skew) указывает на наличие длинного правого хвоста распределения, соответственно всё распределение будет скошено влево (то есть преобладают низкие значения)
- отрицательный коэфффициент асимметрии (negative skew) указывает на наличие длинного левого хвоста распределения, соответственно всё распределения будет скошено вправо (то есть преобладают высокие значения)
- значения коэффициента асимметрии, близкие к нулю, говорят о симметричности распределения
Эксцесс
Коэффиент эксцесса (excess kurtosis) показывает отсроту пика распределения. Как мы говорили ранее, коэффициент эксцесса связан с четвертым центральным моментом распределения, поэтому выборочный коэффициент эксцесса также рассчитывается на его основе.
\[
\text{kurt}(X) = \frac{m_4}{s^4} — 3 = \frac{\frac{1}{n} \sum_{i=1}^n (\bar x — x_i)^4}{\big(\frac{1}{n-1} \sum_{i=1}^n (\bar x — x_i)^2\big)^2} — 3
\]
Что в формуле коэффициента эксцесса делает \(-3\)?
Коэффициент эксцесса, как и коэффициент асимметрии, может принимать положительные, отрицательные или нулевые значения.
- нулевой коэффициент эксцесса обозначает такой же эксцесс, как у стандартного нормального распределения (то есть, «нормальный»)
- положительный коэффициент эксцесса обозначает, что распределение имеет более острую вершину (то есть у нас очень много средних значений, но тонкие «хвосты» — мало низких и высоких значений)
- отрицательный коэффициент эксцесса обозначает, что распределение имеет более пологую вершину (то есть у нас меньше средних значений и толстые «хвосты» — много низких и высоких значений)
Описательные статистики в R
Ну, хорошо. А считать-то как?
Можно по отдельности:
## ── Attaching packages ─────────────────────────────────────── tidyverse 1.3.0 ──## ✓ tibble 3.0.4 ✓ dplyr 1.0.2
## ✓ tidyr 1.1.2 ✓ stringr 1.4.0
## ✓ readr 1.4.0 ✓ forcats 0.5.0
## ✓ purrr 0.3.4## ── Conflicts ────────────────────────────────────────── tidyverse_conflicts() ──
## x dplyr::filter() masks stats::filter()
## x dplyr::lag() masks stats::lag()# воспользуемся данными, которые уже видели
share <- read_csv('https://raw.githubusercontent.com/angelgardt/mk_ggplot2/master/sharexp_data.csv')##
## ── Column specification ────────────────────────────────────────────────────────
## cols(
## .default = col_double(),
## trialtype = col_character(),
## platform = col_character()
## )
## ℹ Use `spec()` for the full column specifications.## [1] 1.599066## [1] 1.346363## [1] 0.7451164## [1] 0.8632012## [1] 0.5392201## [1] 12.23256Но можно и все сразу:
psych::describe(share$time1)## vars n mean sd median trimmed mad min max range skew kurtosis se
## X1 1 16200 1.6 0.86 1.35 1.45 0.5 0.54 12.23 11.69 3.03 16.88 0.01Но это мы посчитали по всей переменной времени реакции сразу. А обычно нас интересуют описательные статистики по экспериментальным группам. Это можно сделать так:
psych::describeBy(share$time1, group = share$trialtype)##
## Descriptive statistics by group
## group: both
## vars n mean sd median trimmed mad min max range skew kurtosis se
## X1 1 5400 1.38 0.6 1.23 1.29 0.39 0.54 10.89 10.35 3.35 26.63 0.01
## ------------------------------------------------------------
## group: dots
## vars n mean sd median trimmed mad min max range skew kurtosis se
## X1 1 5400 1.68 0.93 1.4 1.52 0.55 0.58 12.23 11.66 2.92 15.97 0.01
## ------------------------------------------------------------
## group: tray
## vars n mean sd median trimmed mad min max range skew kurtosis se
## X1 1 5400 1.74 0.97 1.45 1.57 0.59 0.58 11.88 11.3 2.68 12.25 0.01psych::describeBy(share$time1, group = interaction(share$trialtype, share$setsize))##
## Descriptive statistics by group
## group: both.8
## vars n mean sd median trimmed mad min max range skew kurtosis se
## X1 1 1800 1.24 0.44 1.13 1.18 0.32 0.54 4.86 4.32 2.11 7.45 0.01
## ------------------------------------------------------------
## group: dots.8
## vars n mean sd median trimmed mad min max range skew kurtosis se
## X1 1 1800 1.43 0.68 1.26 1.33 0.41 0.58 7.65 7.07 3.21 17.73 0.02
## ------------------------------------------------------------
## group: tray.8
## vars n mean sd median trimmed mad min max range skew kurtosis se
## X1 1 1800 1.44 0.62 1.28 1.34 0.42 0.63 6.56 5.93 2.68 12.46 0.01
## ------------------------------------------------------------
## group: both.12
## vars n mean sd median trimmed mad min max range skew kurtosis se
## X1 1 1800 1.37 0.61 1.22 1.28 0.37 0.6 10.89 10.29 4.37 43.73 0.01
## ------------------------------------------------------------
## group: dots.12
## vars n mean sd median trimmed mad min max range skew kurtosis se
## X1 1 1800 1.68 0.86 1.43 1.54 0.56 0.59 11.66 11.07 2.64 14.76 0.02
## ------------------------------------------------------------
## group: tray.12
## vars n mean sd median trimmed mad min max range skew kurtosis se
## X1 1 1800 1.73 0.86 1.5 1.6 0.6 0.6 10.03 9.43 2.19 8.78 0.02
## ------------------------------------------------------------
## group: both.16
## vars n mean sd median trimmed mad min max range skew kurtosis se
## X1 1 1800 1.53 0.69 1.35 1.43 0.49 0.55 9.25 8.7 2.72 16.06 0.02
## ------------------------------------------------------------
## group: dots.16
## vars n mean sd median trimmed mad min max range skew kurtosis se
## X1 1 1800 1.92 1.13 1.59 1.74 0.71 0.6 12.23 11.64 2.62 12.49 0.03
## ------------------------------------------------------------
## group: tray.16
## vars n mean sd median trimmed mad min max range skew kurtosis se
## X1 1 1800 2.05 1.22 1.68 1.85 0.81 0.58 11.88 11.3 2.31 8.61 0.03Но мы же с вами осваивали tidyverse не просто так, поэтому воспользуемся его мощностями:
share %>%
filter(trialtype != 'both') %>%
group_by(trialtype, setsize, platform, id) %>%
summarise(mean = mean(time1),
median = median(time1),
var = var(time1),
sd = sd(time1),
min = min(time1),
max = max(time1),
se = sd/sqrt(length(time1)),
skew = moments::skewness(time1),
kurt = moments::kurtosis(time1))## `summarise()` regrouping output by 'trialtype', 'setsize', 'platform' (override with `.groups` argument)## # A tibble: 216 x 13
## # Groups: trialtype, setsize, platform [12]
## trialtype setsize platform id mean median var sd min max se
## <chr> <dbl> <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 dots 8 android 4 1.37 1.16 0.342 0.585 0.750 3.40 0.0827
## 2 dots 8 android 6 1.20 0.945 0.669 0.818 0.667 5.92 0.116
## 3 dots 8 android 7 1.86 1.77 0.325 0.570 0.809 3.15 0.0807
## 4 dots 8 android 8 1.85 1.59 0.578 0.760 1.03 4.53 0.108
## 5 dots 8 android 10 1.04 0.964 0.0997 0.316 0.614 2.01 0.0447
## 6 dots 8 android 11 1.20 1.11 0.145 0.380 0.766 2.45 0.0538
## 7 dots 8 android 12 1.21 1.06 0.199 0.447 0.666 2.62 0.0632
## 8 dots 8 android 15 1.48 1.29 0.445 0.667 0.807 4.55 0.0943
## 9 dots 8 android 16 1.16 1.05 0.233 0.483 0.648 2.65 0.0683
## 10 dots 8 android 18 1.42 1.20 0.287 0.536 0.813 2.96 0.0758
## # … with 206 more rows, and 2 more variables: skew <dbl>, kurt <dbl>Кода побольше, зато всё кастомное, а значит всем этим можно управлять! Обратите внимание, что для расчёта коэффициента асимметрии и коэффициента эксцесса потребуются функции из дополнительного пакета moments, который нужно установить через команду install.packages("moments").
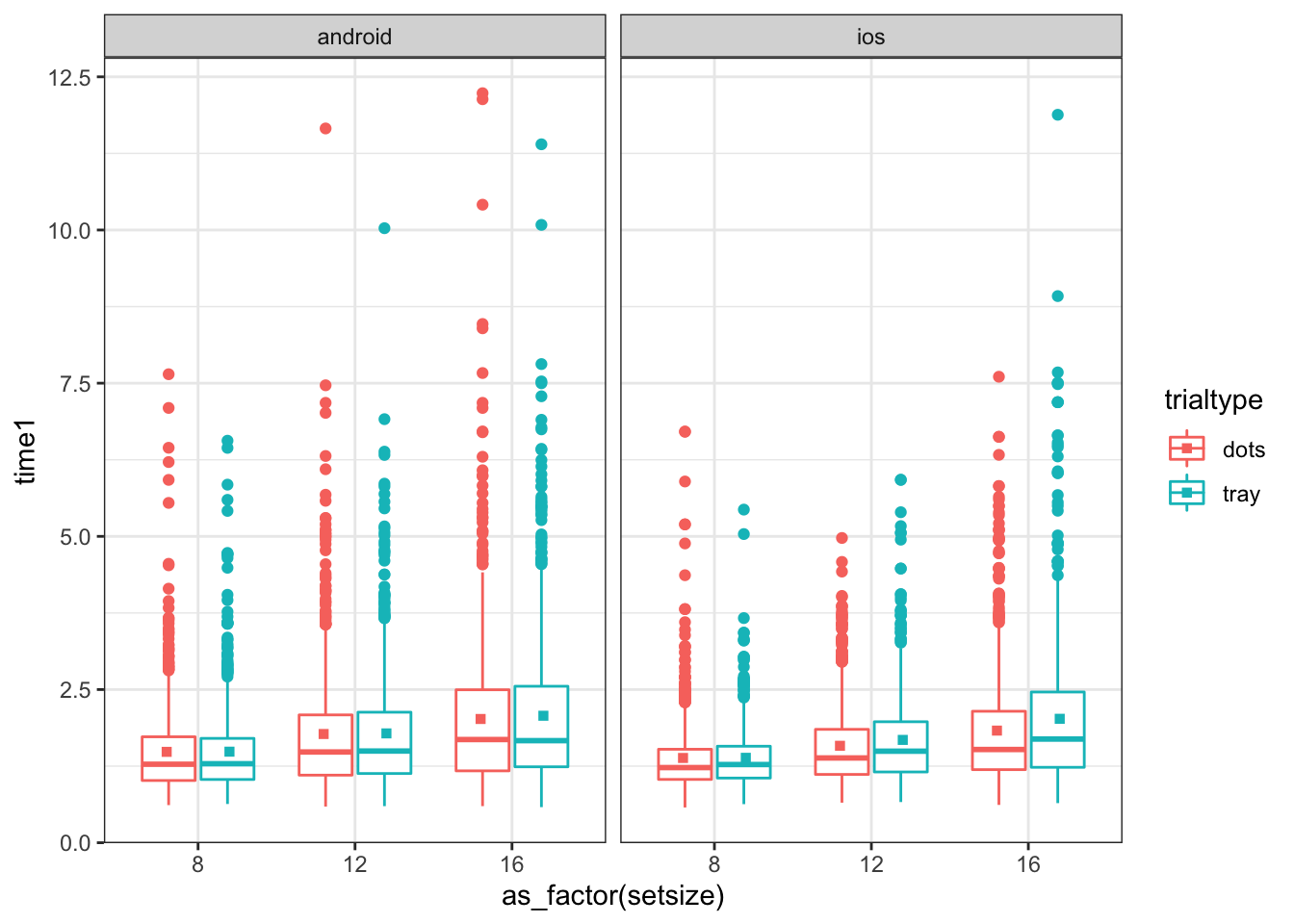
Кучу описательных статистик мы насчитали. Теперь разберёмся в квартилями и выбросами (нехарактерными значениями). Когда мы с вами говорили о визуализации, мы упоминали, что график «ящик с усами» (boxplot) отображает выбросы. Посмотрим:
theme_set(theme_bw())
share %>%
filter(trialtype != 'both') %>%
ggplot(aes(as_factor(setsize), time1, color = trialtype)) +
geom_boxplot() +
stat_summary(fun = mean, geom = 'point', shape = 15, position = position_dodge(0.8)) +
facet_wrap(~ platform)Видим много-много точек над ящиками — это и есть выбросы. Это данные поведенческого эксперимента, поэтому для последующего анализа мы желаем, чтобы таких значений в данных не было. Почистим!
share %>%
filter(trialtype != 'both') %>%
group_by(trialtype, setsize, platform, id) %>%
summarise(lower = quantile(time1)[2] - 1.5 * IQR(time1),
upper = quantile(time1)[4] + 1.5 * IQR(time1)) %>%
right_join(share) %>%
filter(time1 > lower & time1 < upper) %>%
select(-lower, -upper) -> share_clear## `summarise()` regrouping output by 'trialtype', 'setsize', 'platform' (override with `.groups` argument)## Joining, by = c("trialtype", "setsize", "platform", "id")Вот так мы удалили все выбросы. Можно было также воспользоваться функцией is_outlier(), которую мы написали в одном из заданий:
share %>%
filter(trialtype != 'both') %>%
group_by(trialtype, setsize, platform, id) %>%
mutate(outlier = is_outlier(time1)) %>%
filter(!outlier)## # A tibble: 10,213 x 23
## # Groups: trialtype, setsize, platform, id [216]
## trialtype setsize time1 click1x click1y time2 click2x click2y id platform
## <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <chr>
## 1 tray 8 1.67 -227 202 1.28 14 -351 1 ios
## 2 tray 8 1.13 -69 231 1.06 -44 -392 1 ios
## 3 tray 8 1.59 -241 43 0.931 -25 -397 1 ios
## 4 tray 8 1.14 -51 59 0.896 10 -383 1 ios
## 5 tray 8 2.14 99 62 0.879 -29 -372 1 ios
## 6 tray 8 1.63 213 46 0.947 -27 -353 1 ios
## 7 tray 8 2.02 -70 -82 0.970 -19 -394 1 ios
## 8 tray 8 1.08 72 -95 1.33 30 -399 1 ios
## 9 tray 8 1.50 222 -55 0.879 46 -344 1 ios
## 10 tray 8 1.36 -231 -229 0.880 -8 -388 1 ios
## # … with 10,203 more rows, and 13 more variables: posx1 <dbl>, posy1 <dbl>,
## # posxmin1 <dbl>, posxmax1 <dbl>, posymin1 <dbl>, posymax1 <dbl>,
## # posx2 <dbl>, posy2 <dbl>, posxmin2 <dbl>, posxmax2 <dbl>, posymin2 <dbl>,
## # posymax2 <dbl>, outlier <lgl>Ну, вот теперь у нас мало того, что опрятные, так они еще и чистые!
Download Article
Download Article
After collecting data, oftentimes the first thing you need to do is analyze it. This usually entails finding the mean, the standard deviation, and the standard error of the data. This article will show you how it’s done.
Cheat Sheets
-
1
Obtain a set of numbers you wish to analyze. This information is referred to as a sample.
- For example, a test was given to a class of 5 students, and the test results are 12, 55, 74, 79 and 90.
Advertisement
-
1
Calculate the mean. Add up all the numbers and divide by the population size:[1]
- Mean (μ) = ΣX/N, where Σ is the summation (addition) sign, xi is each individual number, and N is the population size.
- In the case above, the mean μ is simply (12+55+74+79+90)/5 = 62.
-
1
Calculate the standard deviation. This represents the spread of the population.
Standard deviation = σ = sq rt [(Σ((X-μ)^2))/(N)].[2]
- For the example given, the standard deviation is sqrt[((12-62)^2 + (55-62)^2 + (74-62)^2 + (79-62)^2 + (90-62)^2)/(5)] = 27.4. (Note that if this was the sample standard deviation, you would divide by n-1, the sample size minus 1.)
Advertisement
-
1
Calculate the standard error (of the mean). This represents how well the sample mean approximates the population mean. The larger the sample, the smaller the standard error, and the closer the sample mean approximates the population mean. Do this by dividing the standard deviation by the square root of N, the sample size.[3]
Standard error = σ/sqrt(n)[4]
- So for the example above, if this were a sampling of 5 students from a class of 50 and the 50 students had a standard deviation of 17 (σ = 21), the standard error = 17/sqrt(5) = 7.6.
Add New Question
-
Question
How do you find the mean given number of observations?
To find the mean, add all the numbers together and divide by how many numbers there are. e.g to find the mean of 1,7,8,4,2: 1+7+8+4+2 = 22/5 = 4.4.
-
Question
The standard error is calculated as 0.2 and the standard deviation of a sample is 5kg. Can it be said to be smaller or larger than the standard deviation?
The standard error (SE) must be smaller than the standard deviation (SD), because the SE is calculating by dividing the SD by something — i.e. making it smaller.
-
Question
How can I find out the standard deviation of 50 samples?
The results of all your figures (number plus number plus number etc.) divided by quantity of samples 50 =SD.
See more answers
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
Video
-
Calculations of the mean, standard deviation, and standard error are most useful for analysis of normally distributed data. One standard deviation about the central tendency covers approximately 68 percent of the data, 2 standard deviation 95 percent of the data, and 3 standard deviation 99.7 percent of the data. The standard error gets smaller (narrower spread) as the sample size increases.
Thanks for submitting a tip for review!
Advertisement
-
Check your math carefully. It is very easy to make mistakes or enter numbers incorrectly.
Advertisement
References
About This Article
Article SummaryX
The mean is simply the average of a set of numbers. You can work it out by adding up all the numbers and dividing the total by the amount of numbers. For example, if you wanted to find the average test score of 3 students who scored 74, 79, and 90, you’d add the 3 numbers together to get 243, then divide it by 3 to get 81. The standard error represents how well the sample mean approximates the population mean. All you need to do is divide the standard deviation by the square root of the sample size. For instance, if you were sampling 5 students from a class of 50 and the 50 students had a standard deviation of 17, you’d divide 17 by the square root of 5 to get 7.6. For more tips, including how to calculate the standard deviation, read on!
Did this summary help you?
Thanks to all authors for creating a page that has been read 1,007,216 times.