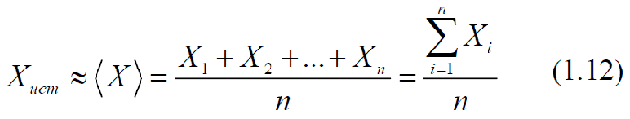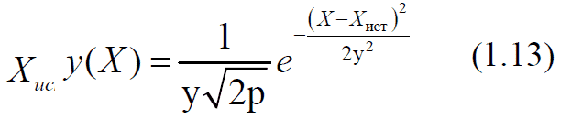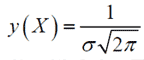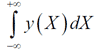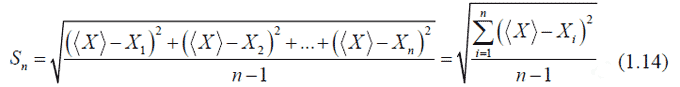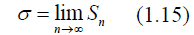Среднеарифметическая ошибка измерения

Среднее арифметическое значение, средняя квадратичная и средняя арифметическая погрешности измеряемой величины

Первой величиной,
которую приходится вычислять при
обработке результатов опытов, является
среднее арифметическое из результатов
ряда измерений, которое определяется
по формуле (6).

Практически число
измерений всегда ограничено, поэтому
среднее арифметическое
не равно
истинному значению измеряемой величины
,
но будет
тем ближе к нему, чем больше число
выполненных измерений .
В теории
вероятностей доказывается, что среднее
арифметическое из результатов отдель­ных
измерений является наиболее вероятным
значением измеряемой величины. Это
утверждение справедливо при условии,
когда все
измерения равноточные, а распределение
погрешности измерений подчиняется
вышеупомянутому закону распределения—
закону Гаусса.

Если вместо
истинного значения неизвестной величины
использовать среднее арифметическое
,
тогда на
основании равенства (1) имеем:

(11)

В (11) погрешность
несколько
отличается от истинной и называется
абсолютной погрешностью единичного
измерения

(12)

Лучшим из критериев
для оценки погрешностей результатов
измерений является средняя квадратичная
погрешность, которая характеризует
степень (меру) рассеяния результатов
отдельных измерений
около среднего
их значения. Для определения
среднеквадратической погрешности
единичных изме­рений при ограниченном
числе опытов используется формула (7),
которая с учетом (12) записывается в виде:

. (13)

Средняя квадратическая
погрешность, вычисляемая по формуле
(13), характеризует погрешность единичного
результата из всего ряда n
измерений.

Как уже отмечалось,
при увеличении числа n
измерений наблюдается взаимная
компенсация случайных ошибок. Поэтому
усредненная средняя квадратичная
погрешность,
определяемая по формуле (9) и характеризующая
окончательный результат измерений,
уменьшается при увеличении числаn
повторных
измерений искомой величины. Поскольку
вычисления величины
достаточно громоздки, то в ряде случаев
(если не оговорено в условиях решаемой
задачи) для оценки ошибки, допущенной
при определении средней величины,
пользуются средней арифметической
погрешностью, которая вычисляется как
средняя величина всех величин абсолютных
погрешностей единичных измерений (12),
взятых по модулю:

.
(14)

Так как суммирование
в (14) выполняется без учета знака ,
то формула (14) даёт среднее значение
максимальной возможной погрешности.

Вопрос о том, какой
формулой пользоваться при оценке
измерений, решается при планировании
эксперимента. Считается, что при числе
измерений меньше пяти можно ограничиться
вычислением средней абсолютной
погрешности по формуле (14).

Средняя абсолютная
погрешность даёт возможность указать
пределы (интервал), внутри которых
заключено истинное значение измеряемой
величины.

Сама по себе
абсолютная погрешность не даёт достаточно
наглядного представления о степени
точности измерения, поэтому для оценки
точности результата применяется
относительная погрешность. Относительная
погрешность величины x
при ограниченном числе опытов вычисляется
по формуле:

.
(15)

Источник

Среднее арифметическое значение серии измерений <X> определяется как частное от деления арифметической суммы всех результатов измерений в серии Xi на общее число измерений в серии n:

При увеличении n среднее значение <X> стремится к истинному значению измеряемой величины Xист. Поэтому, за наиболее вероятное значение измеряемой величины следует принять ее среднее арифметическое значение, если ошибки подчиняются нормальному закону распределения ошибок —закону Гаусса.

Формула Гаусса может быть выведена из следующих предположений:

  • ошибки измерений могут принимать непрерывный ряд значений;
  • при большом числе наблюдений ошибки одинаковой величины, но разного знака встречаются одинаково часто;
  • вероятность, то есть относительная частота появления ошибок, уменьшается с увеличением величины ошибки. Иначе говоря, большие ошибки встречаются реже, чем малые.

Нормальный закон распределения описывается следующей функцией:

где σ – средняя квадратичная ошибка; σ2 – дисперсия измерения; Хист – истинное значение измеряемой величины.

Анализ формулы (1.13) показывает, что функция нормального распределения симметрична относительно прямой X = Xист и имеет максимум при X = Xист. Значение ординаты этого максимума найдем, поставив в правую часть уравнения (1.13) Xист вместо X. Получим

,

откуда следует, что с уменьшением σ возрастает y(X). Площадь под кривой

должна оставаться постоянной и равной 1, так как вероятность того, что измеренное значение величины Х будет заключено в интервале от -∞ до +∞ равно 1 (это свойство называется условием нормировки вероятности).

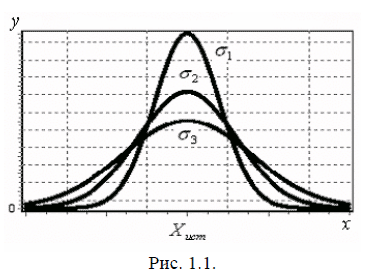
На рис. 1.1 приведены графики трех функций нормального распределения для трех значений σ (σ3 > σ2 > σ1) и одном Хист. Нормальное распределение характеризуется двумя параметрами: средним значением случайной величины, которая при бесконечно большом количестве измерений (n → ∞) совпадает с ее истинным значением, и дисперсией σ. Величина σ характеризует разброс погрешностей относительно среднего значения принимаемого за истинное. При малых значениях σ кривые идут более круто и большие значения ΔХ менее вероятны, то есть отклонение результатов измерений от истинного значения величины в этом случае меньше.

Для оценки величины случайной ошибки измерения существует несколько способов. Наиболее распространена оценка с помощью стандартной или среднеквадратичной ошибки. Иногда применяется средняя арифметическая ошибка.

Стандартная ошибка (среднеквадратическая) среднего в серии из n измерений определяется по формуле:

.

Если число наблюдений очень велико, то подверженная случайным случайным колебаниям величина Sn стремится к некоторому постоянному значению σ, которое называется статистическим пределом Sn:

Именно этот предел и называется средней квадратичной ошибкой. Как уже было отмечено выше, квадрат этой величины называется дисперсией измерения, которая входит в формулу Гаусса (1.13).

Величина σ имеет большое практическое значение. Пусть в результате измерений некоторой физической величины нашли среднее арифметическое <Х> и некоторую ошибку ΔX. Если измеряемая величина подвержена случайной ошибке, то нельзя безоговорочно считать, что истинное значение измеряемой величины лежит в интервале (<Х> – ΔХ, <Х> + ΔХ) или (<Х> – ΔХ) < Х < (<Х> + ΔХ)). Всегда существует некоторая вероятность того, что истинное значение лежит за пределами этого интервала.

Доверительным интервалом называется интервал значений (<Х> – ΔХ, <Х> + ΔХ) величины X, в который по определению попадает ee истинное значение Хист с заданной вероятностью.

Надежностью результата серии измерений называют вероятность того, что истинное значение измеряемой величины попадает в данный доверительный интервал. Надежность результата измерения или доверительная вероятность выражается в долях единицы или процентах.

Пусть α означает вероятность того, что результат измерений отличается от истинного значения на величину, не большую, чем ΔХ. Это принято записывать в виде:

Р((<Х> – ΔХ) < Х < (<Х> + ΔХ)) = α

(1.16).

Выражение (1.16) означает, что с вероятностью, равной α, результат измерений не выходит за пределы доверительного интервала от <Х> – ΔХ до <Х> + ΔХ. Чем больше доверительный интервал, то есть чем больше задаваемая погрешность результата измерений ΔХ, тем с большей надежностью искомая величина Х попадает в этот интервал. Естественно, что величина α зависит от числа n произведенных измерений. а также от задаваемой погрешности ΔХ.

Таким образом, для характеристики величины случайной ошибки, необходимо задать два числа, а именно:

  • величину самой ошибки (или доверительный интервал);
  • величину доверительной вероятности (надежности).

Указание одной только величины ошибки без указания соответствующей ей доверительной вероятности в значительной мере лишено смысла, так как при этом мы не знаем, сколь надежны наши данные. Знание доверительной вероятности позволяет оценить степень надежности полученного результата.

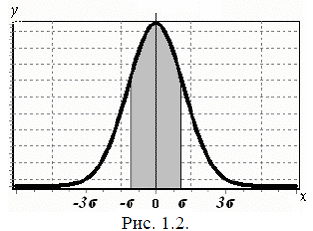
Необходимая степень надежности задается характером проводимых изменений. Средней квадратичной ошибке Sn соответствует доверительная вероятность 0.68, удвоенной средней квадратичной ошибке (2σ) – доверительная вероятность 0.95, утроенной (3σ) – 0.997.

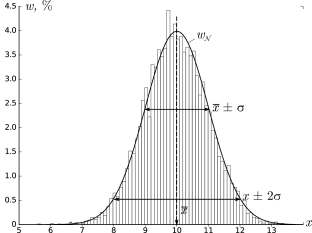
Если в качестве доверительного интервала выбран интервал (X – σ, X + σ), то мы можем сказать, что из ста результатов измерений 68 будут обязательно находиться внутри этого интервала (рис. 1.2). Если при измерении абсолютная погрешность ∆Х > 3σ, то это измерение стоит отнести к грубым погрешностям или промаху. Величину 3σ обычно принимают за предельную абсолютную погрешность отдельного измерения (иногда вместо 3σ берут абсолютную погрешность измерительного прибора).

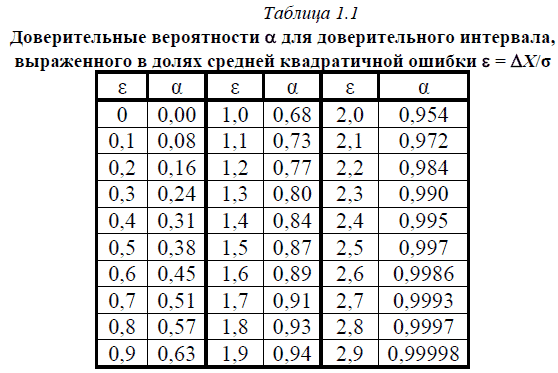
Для любой величины доверительного интервала по формуле Гаусса может быть рассчитана соответствующая доверительная вероятность. Эти вычисления проведены и их результаты сведены в табл. 1.1.

Доверительные вероятности α для доверительного интервала, выраженного а долях средней квадратичной ошибки ε = ΔX/σ:

Источник

Измеряя линей­ные размеры предметов измерительными инстру­ментами : линейкой, штангенциркулем, микрометром, проводя измерения времени секундомером или силы электрического тока или величины напряжения соответствующими электроизмерительными приборами Вы проводите прямые измерения.

Погрешность измерений

Любое измерение проводится с определенной точностью, при этом измеренное значение всегда отличается от истинного, так как инструменты измерения, методики и органы чувств человека несовершенны. Поэтому важную роль играет оценка погрешности измерений, результат измерений с учетом погрешности записывается в виде: X ± ΔX, где ΔX — абсолютная погрешность измерений.

Случайные и систематичес­кие погрешности

Погрешности подразделяются на случайные и систематичес­кие.
Систематические погрешности остаются постоянными или закономерно меняются в процессе измерения. Например неточность прибора, неправильная его регулировка ведет к систематической погрешности. Если причина систематической погрешности известна, то чаще всего такую погрешность можно исключить.
Случайные погрешности вызваны различными случайными факторами, влияющими на точность измерений. Например, при измерении секундомером отрезков времени, случайные погрешности связаны с различным (случайным) временем реакции экспериментатора на события запускающие и останавливающие секундомер. Чтобы уменьшить влияние случайной погрешности необходимо проводить многократное измерение физической величины.
Калькулятор ниже вычисляет случайную погрешность выборки прямых измерений для заданного доверительного интервала. Немного теории можно найти сразу за калькулятором.

PLANETCALC, Расчет погрешностей непосредственных измерений.

Расчет погрешностей непосредственных измерений.

Доверительная вероятность

Точность вычисления

Знаков после запятой: 3

Относительная погрешность в %

В большинстве случаев результат измерения подчиняется нормальному закону распределения, поэтому истинное значение измерения будет равно пределу:
x_0=\lim_{n \to \infty} \frac{1}{n}\sum_{i=1}^{n} x_i
В случае ограниченного количества измерений, наиболее близким к истинному будет среднее арифметическое:
\bar{x}=\frac{1}{n}\sum_{i=1}^{n} x_i

Согласно элементарной теории ошибок Гаусса случайную погрешность отдельного измерения характеризует так называемое среднеквадратическое отклонение:
S_n=\left. \sqrt{\frac{\sum_{i=1}^{n}{(x_i-\bar{x})^2}}{n-1}} \right, квадрат этой величины называется дисперсией. При увеличении этой величины возрастает разброс результатов измерений, т. е. увеличивается погрешность.

Для оценки погрешности всей серии измерений, вместо отдельного измерения надо найти среднюю квадратичную погрешность среднего арифметического, характеризующую отклонение \bar{x} от истинного значения искомой величины x_0.
По закону сложения ошибок среднее арифметическое имеет меньшую ошибку, чем результат каждого отдельного измерения. Cред­няя квадратичная погрешность среднего арифметического равна:
S_{\bar{x}}=\frac{S_n}{\sqrt{n}} = \left. \sqrt{\frac{\sum_{i=1}^{n}{(x_i-\bar{x})^2}}{{n}({n-1})}} \right
Стандартная случайная погрешность Δх равна:
\Delta_{x}=t_{\alpha,k}S_{\bar{x}},, где t_{\alpha,k} — коэффициент Стьюдента для заданной доверительной вероятности \alpha и числа степеней свободы k = n-1.
Коэффициент Стьюдента можно получить по таблице или воспользоваться нашим калькулятором для вычисления квантилей распределения Стьюдента: Квантильная функция распределения Стьюдента. Следует иметь в виду, что квантильная функция выдает значения одностороннего критерия Стьюдента. Значение двустороннего квантиля для заданной доверительно вероятности \alpha соответствует значению одностороннего квантиля для вероятности: 1-\frac{1-\alpha}{2}

Источник
По результатам измерений величин d и Л установлено среднее значение диаметра цилиндра (i p 9.12 мм, среднее значение высоты цилиндра Лдо = 16,22 мм, средние квадратические значения ошибок единичных измерений диаметра и высоты цилиндра = 0,008 мм, a i — 0,012 мм. Средние квадратические ошибки определения средних арифметических значений диаметра d и высоты h цилиндра  [c.314]

Иногда неверно трактуется понятие п параллельных определений . Так, рН-метрическое измерение активной кислотности продукта включает несколько стадий размол, растворение в воде, настаивание и определение рН-раствора. Принимая за результат измерения, среднее арифметическое значение результатов двух параллельных определений, разработчики допускают ошибку, так как дважды повторяют только последнюю стадию — определение кислотности раствора на pH метре.  [c.86]

При определении е и tg б возможны случайные ошибки. С целью их исключения измерения производят несколько раз. Число измерений указывается в стандартах на материалы и изделия. При испытаниях жидких материалов расхождения между результатами отдельных измерений не должны превышать 15% при измерении Ц б и 5% при измерении С . Для твердых материалов допускаемые расхождения указываются в стандартах на материал. По результатам нескольких измерений находят средние арифметические значения тангенса угла диэлектрических потерь и диэлектрической проницаемости  [c.59]

Средняя квадратическая погрешность (ошибка) результата при гг. измерениях Среднеквадратическая погрешность среднего арифметического, из п. измерений а  [c.95]

Простым следствием из теоремы Чебышева является принятие среднего арифметического значения из большого ряда наблюдений одной случайной величины за среднее значение (математическое ожидание) этой величины. Если случайной величиной являются ошибки измерений, наблюдений и т. д.. то среднее арифметическое значение многократно измеренной величины принимается за её истинное значение.  [c.290]

А. Определение вероятностных характеристик. При малом числе наблюдений п (обычно имеющих одинаковые веса) вычисление среднего арифметического значения J , средней квадратической ошибки а и вероятной ошибки г производится теми же приёмами, что указаны в отношении равноточных измерений (пример 1), или приёмами, указанными в примерах 4 и 5 Сведений из теории вероятностей» (стр. 283, 284). В последнем случае вероятности р (j ,) заменяются частостями, полученными при проведении опыта, результаты которого обрабатываются.  [c.304]

Если имеют место только одиночные измерен,1я каждого из значений, то подобное же сопоставление можно сделать, пользуясь вместо ошибки среднего арифметического значения а- ошибкой измерения  [c.314]

Пример 1. По миллиметровой шкале тензометра получены при измерении значения 10,3 10,4 10.3 10,5 10,3. Среднее арифметическое равно 10,36 при кажущихся ошибках —0,06 — -0,04 —0.06 4-0,14 —0,06. Средняя кажущаяся ошибка равна 0,07. Результат записывается так 10,36 0,07 (верхний предел измеренной величины равен 10.4, нижний —10,3). При пересчёте на удлинения (при т = 1200 . )=20 мм)  [c.248]

Случайная ошибка среднего арифметического ряда наблюдений в 1 /I/» п, раз меньше ошибки единичного наблюдения (измерения). Если принять ошибку единичного наблюдения за 1,0, то при четырех наблюдениях она снизится в 2 раза, при девяти — в 3 раза, при 16— в 4 раза и т. д. Таким образом, при очень большом числе наблюдений случайная ошибка среднего арифметического стремится к нулю. Само собой разумеется, что никакое увеличение числа наблюдений не спасает нас от систематических ошибок. Негативная сторона большого числа наблюдений состоит в том, что они вызывают удорожание опыта и рост его продолжительности.  [c.73]

В числителе выражения для ошибки среднего арифметического стоит стандарт распределения наблюдаемой (измеряемой) величины Ох, который включает в себя как случайную ошибку измерений, так и рассеяние объекта. При этом в подавляющем большинстве промышленных экспериментов рассеяние объекта, т. е. его нестабильность во время опыта, намного превышает случайную ошибку измерений. Отсюда следует, что мощным средством повышения точности, по своей природе совершенно равноценным числу замеров, является уменьшение рассеяния объекта, достигаемое путем стабилизации режима собственно парогенератора и защиты его от внешних возмущений.  [c.73]

В предыдущих разделах, оценивая ошибки отдельного наблюдения или среднего арифметического, мы исходили из того, что дисперсия известна. Напомним, что по определению дисперсия должна вычисляться по весьма большому количеству наблюдений (измерений). Естественно возникает вопрос какие числа считать большими, какие малыми и каково то минимальное число измерений, которое необходимо произвести на исследуемом объекте Возможна и другая постановка вопроса. Число наблюдений, которыми мы располагаем, задано и увеличить его или невозможно, или это связано с большими дополнительными затратами. Подобное положение имеет место, если какая-то серия измерений проводилась попутно с решением иной задачи и интерес к этой группе возник уже в процессе обработки экспериментальных данных.  [c.74]

Пользуясь распределением Стьюдента, оценим ошибку измерений давления по первым четырем наблюдениям примера, приведенного в 4-2, а именно 102, 98, 99 и 100. Среднее арифметическое из четырех наблюдений = 99,75. Выборочные дисперсия и стандарт будут равны  [c.76]

При малом числе наблюдший (обычно имеющих одинаковые веса) вычисление значений х — среднего арифметического значения, а — средней квадратической ошибки и — вероятной ошибки производится теми же приемами, что указаны для равноточных измерений.  [c.216]

Непосредственно получаемые из опыта результаты измерений содержат здесь двойное рассеивание самой величины и ошибок измерения. В части определения среднего значения (центра группирования отклонений) самой величины это не вносит добавочных затруднений, так как ошибки измерений обычно подчиняются закону Гаусса. Поэтому если систематической ошибки измерения не было, то среднее значение их равно нулю, и получаемое в результате обработки опытных данных среднее арифметическое значение X может быть, как и в условиях третьей задачи, принято за истинное значение центра группирования величины X. Если  [c.225]

Исходную технологическую информацию задают в виде ряда значений 2(г). При этом можно 1) исключить резко выделяющиеся результаты измерений, представляющие собой грубые ошибки 2) вычислить статистические характеристики выборочное среднее значение (среднее арифметическое) Z, определяющее центр группировки погрешностей выборочное среднее квадратическое отклонение S, характеризующее рассеяние опытных значений Zf, 3) сгруппировать опытные данные, вычислить частоты и интервалы группировки для построения гистограммы распределения, число интервалов no=[L + 3,32 Ig Л ] при этом для большинства задач L=1 6 4) произвести выравнивание эмпирического распределения по принятому гипотетическому закону 5) сопоставить заданное эмпирическое распределение «с гипотетическим законом по критерию Пирсона 6) для исключения влияния интервала группирования на гистограмму распределения построить несколько вариантов гистограмм в зависимости от числа интервалов группирования.  [c.16]

Затем находятся дисперсия и стандартная ошибка единичного наблюдения. Из числа наблюдений исключаются единичные наблюдения, у которых отклонение от среднего значения больше За. После этого проводится второе приближение, для чего определяется среднее арифметическое значение от оставшихся измерений и определяется новое значение стандартной ошибки единичного измерения и снова определяется величина предельной ошибки Зст.  [c.31]

Допустим, что в результате измерений температуры металла трубы в нижней радиационной части котла сверхкритического давления с помощью температурной вставки получено 26 ее значений, которые приведены во втором столбце табл. 1-2. Обработку экспериментальных данных следует начать с определения среднего арифметического X. При этом получается значение j 514° . Затем подсчитывается отклонение каждой наблюдаемой величины от среднего арифметического (х —I). Остаток алгебраической суммы этих отклонений, как видно из таблицы, не равен нулю, что указывает на недостаточно точный подсчет (более точное значение х не 514, а 513,6538). Однако для первого приближения в данном случае ошибка порядка 0,35, связанная с разрешающей способностью логарифмической линейки, вполне допустима. В столбце пятом табл. 1-2 подсчитаны квадраты каждого отклонения, которые входят в расчетную формулу дисперсии  [c.31]

Таким образом, в данном примере оказалось, что ошибка среднего арифметического в 5 раз меньше, чем ошибка единичных измерений, из которых складывается среднее арифметическое.  [c.33]

Среднее арифметическое напряжений, т. е. средние арифметические ошибки измерения составляют  [c.25]

Средняя арифметическая ошибка недостаточна для оценки точности измерений, так как при ее вычислении значительные по величине ошибки разных знаков мало влияют на результат. Этот недостаток в тех случаях, когда ошибки обоих знаков равнозначны, можно устранить дополнительным вычислением средней квадратической погрешности  [c.26]

Таким образом, можно утверждать, что принятый метод обработки столбиков для измерения остаточных напряжений дает удовлетворительную точность, характеризуемую средней арифметической погрешностью = —0,3 кгс/мм и средней квадратической ошибкой о ,р = 2 кгс/мм.  [c.26]

Средняя арифметическая и средняя квадратичная ошибки. При проведении экспериментов каждый единичный опыт следует повторить достаточное число раз, чтобы случайные ошибки результата были незначительными по сравнению с систематическими. При проведении п измерений единичного результата среднее арифметическое величин 1, 2, из,. .., 71 составит  [c.247]

При измерении среднего диаметра на микроскопах или проекторе за действительный средний диаметр принимают среднее арифметическое из результатов измерения по правым и левым сторонам профиля (рис. 2.19, а) для компенсации ошибки, вызываемой перекосом от резьбового изделия относительно направления продольного перемещения стола прибора.  [c.100]

При статистической обработке остальных результатов вычислялись средние арифметические значения измеряемых величин Жср, средние квадратичные ошибки отдельных измерений Ох, квадратичные ошибки средних арифметических tq, коэффициент вариации V. Окончательный результат измерений полагали А = = (Та + Хер, а предельные отклонения — равными 3Wx- В табл. 6.1 приведены результаты обработки при определении коэффициента к , модуля El и коэффициента Ui.  [c.239]

Результаты статистической обработки числа Fo/Fo p при Кр = = 0,5 и числе измерений п = 10 таковы среднее арифметическое значение = 0,444 средняя квадратичная ошибка отдельного измерения = 0,058, квадратичная ошибка среднего арифметического tq = 0,0184 коэффициент вариации V = 13%.  [c.247]

Значения средней квадратичной ошибки одного измерения диагонали отпечатка и ошибка среднего арифметического из результатов 70 измерений отпечатков приведены в табл. 2.  [c.27]

Температура измерения микротвердости Прибор Средняя квадратичная ошибка одного измерения Средняя квадратичная ошибка среднего арифметического из 70 отпечатков  [c.27]

При измерении размеров в машиностроении редко прибегают к неудобному в производственных условиях исключению систематических ошибок с помощью поправочных таблиц или формул. Зато всюду, где это возможно, стремятся устранить систематические ошибки в самом процессе измерения, вызванные, например, несовпадением оси измеряемых объектов с линией измерения, эксцентриситетами и другими причинами, путем определения среднего арифметического из двух отсчетов в противолежащих положениях (например, при измерении шага и половины угла профиля резьбы, при измерении угла угловой плитки на гониометре и т. д.).  [c.68]

Среднее арифметическое рассматривается как наиболее достоверное значение, которое мы можем приписать измеряемой величине и которое стремится при неограниченном увеличении числа измерений к истинному значению этой величины. Вместе с тем остаточные погрешности стремятся к равенству с соответствующими случайными ошибками.  [c.69]

При измерении шага колонка микроскопа устанавливается с наклоном, соответствующим углу подъема винтовой линии измеряемой резьбы. Для компенсации ошибки, вызываемой перекосом оси резьбового изделия в горизонтальной плоскости,, измерение на микроскопе производится по правым и левым сторонам (рис. 96, в). За действительный размер 5 принимается среднее арифметическое из четырех измерений. Погрешность такого измерения зависит от глазомерного визирования по краю профиля рисками окулярной сетки микроскопа и не превышает 2—4 мкм.  [c.203]

Величина представляет собой приближенное значение дисперсии среднего арифметического суммы независимых величин л ,, определяет нормированную ошибку измерения и при имеет распределение, которое обозначается 5 ( )  [c.23]

Если при подсчете среднего арифметического систематические ошибки, обусловленные, например, изменением условий испытаний, личными ошибками наблюдателя или неточностью действия прибора, не исключены, это следует учитывать, определяя для этих случаев погрешность результата прямого измерения по формуле  [c.200]

Отметим, что при N = 7/271 правая часть (4.67) совпадает с известным выражением для средней квадратичной ошибки среднего арифметического N независимых измерений случайной величины. Таким образом, осреднение стационарной функции с временем корреляции Тх по периоду 2МТ эквивалентно осреднению по N независимым измерениям этой функции (т.е. по N реализациям).  [c.204]

Систематическая погрешность может быть исключена из результатов измерений, если ее природа известна и величина может быть определена, путем внесения поправок в результаты измерений. В технических измерениях метод внесения поправок используется редко. Для устранения систематических погрешностей в процессе измерения чаще прибегают к их переводу в случайные. Например, систематическая ошибка может возникнуть при измерении диаметра цилиндрической детали из-за ее овальности. Она будет зависеть от величины овальности детали и направления измерения. Эту систематическую погрешность можно перевести в случайную, измерив диаметр детали в разных направлениях и определив среднее арифметическое измерений.  [c.130]

При этом мы считаем, что все отдельные погрешности отличаются только знаком и имеют по абсолютной величине максимально возможное значение 0.05. Такое допущение только завысит общую погрешность результата, что для нас сейчас несущественно. Пусть при измерении первого образца мы допустили погрешность, равную +0.05, вероятность чего, как уже говорилось, равна 1/2. Вероятность того, что и при измерении второго образца мы сделаем снова положительную погрешность, будет в соответствии с известным нам правилом умножения вероятностей равна (1/2) , т.е. 1/4. Наконец, вероятность при всех 100 измерениях сделать ошибку одного и того же знака будет (0.5) , или примерно 2-10 . Такая вероятность (в соответствии со сказанным выше) с любой практической точки зрения равна нулю. Таким образом, мы пришли к заклк>-чению, что невозможно сделать погрешность в общей массе образцов в 5 г (0.05 100), ибо вероятность такой погрешности незначимо мало превышает нуль. Иначе говоря, действительная погрешность при таком способе взвешивания будет всегда меньше 5 г. Мы выбрали наиболее неблагоприятный случай — погрешность каждого взвешивания имеет наибольшее значение, и все погрешности оказались одного знака. Теория вероятностей дает возможность оценить,какова будет вероятность появления погрешностей других численных значений. Для этого введем сперва понятие средней квадратической, а также средней арифметической погрешностей.  [c.32]

В условиях эксплуатации автотолераторы работают в динамическом режиме. Поэтому наряду с проверкой метрологических характеристик в статических условиях для автотолераторов обязательна проверка их динамических характеристик. При этом главными динамическими характеристиками автотолератора следует считать амплитудно-частотную характеристику точности и время срабатывания. При проверке следует установить не только математическое ожидание погрешности, но и их случайные составляющие. Средняя арифметическая величина погрешности, ее математическое ожидание важны как для определения возможной ошибки измерения, так и для внесения динамической поправки, а случайная составляющая будет оказывать влияние па рассеи-  [c.117]

Если имеют место только одиночные измерения каждого из значений, то подобное же сопоставление можно сделать, пользуясь вместо ошибки среднего арифметического значения ст-ошибкой измерения а . Другим приемом, использующим в обоих рассматриваемых случаях способ наименьших квадратов, является установление параметров линейных зависимостей не только для того сочетания значений величины, которое получено из опыта, но и для нескольких других разнообразных сочетаний, отличающихся от первых на а , 2а- или соответственно на огц, 2стц. Если для всех таких сочетаний будут получаться линейные зависимости одного типа (например, все возрастающие или все убывающие), то вывод об истинности соответственного изменения исследуемого свойства можно считать надежным. В противном случае следует увеличить число наблюдений, до получения установленных в указанном выше смысле результатов.  [c.231]

По результатам опыта могут быть рассчитаны три значения теплоемкости Ср перегретого водяного пара, полученные при одинаковой начальной температуре (температура пара на входе в калориметр), одинаковом повышении температуры пара при калориметрирован ии (одинаковой мощности калориметрического нагревателя), одинаковом расходе пара и одинаковой температуре оболочки калориметра. Расхождения полученных значений теплоемкости обусловливаются только некоторыми отклонениями этих величин от среднего значения во время опыта (колебаниями режима), т. е. случайными ошибками. Окончательная величина Ср должна быть взята как среднее арифметическое значение трех ее измерений.  [c.235]

Предельную ошибку среднего арифметического УНцт следует поршмать как предельную погрешность аттестации размера, которому приписано значение среднего арифметического . Иначе говоря, при повторной аттестации размера в тех же условиях и теми же средствами измерений значение среднего арифметического будет практически находиться в пределах  [c.70]

Анализ возм ожных ошибок измерения и оценку их влияния на точность результатов испытаний произв10Дят известными способами [29], [49], [54]. При этом, в зависимости от требований к оценке точности произведенных измерений, определяют среднюю квадратическую ошибку отдельного измерения о, характеризующую среднее отклонение измеренной величины от найденного среднего арифметического, или величину погрешности среднего арифметического О, характеризующую возможную разность между средним арифметическим и действительным значением измеренной величины  [c.200]

Из табл. 1 видим, что 13-е измерение дало значение (263,8), сильно отличающееся от всех остальных значений ряда. Пови-димому, здесь имеется промах вследствие какой-то крупной ошибки наблюдателя. Это измерение следует исключить из ряда. Найдем по формуле (I, 3) среднее арифметическое из остальных 15 значений ряда. Оно оказывается равным ср= 277,6°. Определим теперь разность У,- между каждым измеренным знч-чснгем и /ср. Эти разности приведены в третьем столбце таблицы.  [c.13]

Подведем итоги. Было установлено, что при проведении серии измерений в качестве наилучшего результата следует брать средний арифметический х и показано, как определять его доверительный интервал (будем обозначать его Дмакс). По определению х отличается от [1 не больше, чем на Амакс- В свою очередь, л может отличаться от истинного значения измеряемой величины х на величину систематической ошибки А  [c.397]

Для приборов, находившихся долгое время в эксплуатации, угол этот больше он может достигать 5—6° и более Очевидно, что при измерении интенсивности окраски весьма разбавленных растворов, т. е. обладаю щих слабой окраской, влияние мертвого угла на ре з ультаты определения может оказаться существенным При очень разбавленных растворах результаты измере ния будут соизмеримы с величиной мертвого угла Уменьшить роль этого фактора можно, применяя дву кратное измерение, т. е. приведение стрелки гальвано метра к нулю вращением барабана сначала только в одну сторону, а затем повторением этой операции, но уже при вращении барабана только в другую сторону. Полученные отсчеты будут различны, беря их среднее арифметическое значение, можно уменьшить ошибку от мертвого угла . Следует заметить, что при этом встречаются случаи, когда положение барабана соответствует как бы отрицательным значениям, т. е. окраска раствора сравнения оказывается как бы интенсивнее окраски колори-метрируемого раствора. С такими казусами приходится сталкиваться при попытке колориметрировать растворы, в которых или совсем не содержится определяемое вещество или его концентрация ий лючительно мала. В этом случае также надо проводить двукратное измерение, оценивая величину отрицательного отклонения или на глаз или используя условный нуль, т. е. Подводя стрелку гальванометра не к нулю, а к какому-либо делению, дающему возможность получать только положительные отсчеты по барабану, а затем вводить поправку. Конечно, все эти ухищрения не дают права считать получаемые при этом результаты достоверными. Однако к ним в некоторых случаях приходится прибегать, например, чтобы разрушить иллюзию о присутствии определяемого вещества в тех растворах, где оно быть не может.  [c.228]

Источник

Результат любого измерения не определён однозначно и имеет случайную составляющую.
Поэтому адекватным языком для описания погрешностей является язык вероятностей.
Тот факт, что значение некоторой величины «случайно», не означает, что
она может принимать совершенно произвольные значения. Ясно, что частоты, с которыми
возникает те или иные значения, различны. Вероятностные законы, которым
подчиняются случайные величины, называют распределениями.

2.1 Случайная величина

Случайной будем называть величину, значение которой не может быть достоверно определено экспериментатором. Чаще всего подразумевается, что случайная величина будет изменяться при многократном повторении одного и того же эксперимента. При интерпретации результатов измерений в физических экспериментах, обычно случайными также считаются величины, значение которых является фиксированным, но не известно экспериментатору. Например смещение нуля шкалы прибора. Для формализации работы со случайными величинами используют понятие вероятности. Численное значение вероятности того, что какая-то величина примет то или иное значение определяется либо как относительная частота наблюдения того или иного значения при повторении опыта большое количество раз, либо как оценка на основе данных других экспериментов.

Замечание. 
Хотя понятия вероятности и случайной величины являются основополагающими, в литературе нет единства в их определении. Обсуждение формальных тонкостей или построение строгой теории лежит за пределами данного пособия. Поэтому на начальном этапе лучше использовать «интуитивное» понимание этих сущностей. Заинтересованным читателям рекомендуем обратиться к специальной литературе: [5].

Рассмотрим случайную физическую величину x, которая при измерениях может
принимать непрерывный набор значений. Пусть
P[x0,x0+δ⁢x] — вероятность того, что результат окажется вблизи
некоторой точки x0 в пределах интервала δ⁢x: x∈[x0,x0+δ⁢x].
Устремим интервал
δ⁢x к нулю. Нетрудно понять, что вероятность попасть в этот интервал
также будет стремиться к нулю. Однако отношение
w⁢(x0)=P[x0,x0+δ⁢x]δ⁢x будет оставаться конечным.
Функцию w⁢(x) называют плотностью распределения вероятности или кратко
распределением непрерывной случайной величины x.

Замечание. В математической литературе распределением часто называют не функцию
w⁢(x), а её интеграл W⁢(x)=∫w⁢(x)⁢𝑑x. Такую функцию в физике принято
называть интегральным или кумулятивным распределением. В англоязычной литературе
для этих функций принято использовать сокращения:
pdf (probability distribution function) и
cdf (cumulative distribution function)
соответственно.

Гистограммы.

Проиллюстрируем наглядно понятие плотности распределения. Результат
большого числа измерений случайной величины удобно представить с помощью
специального типа графика — гистограммы.
Для этого область значений x, размещённую на оси абсцисс, разобьём на
равные малые интервалы — «корзины» или «бины» (англ. bins)
некоторого размера h. По оси ординат будем откладывать долю измерений w,
результаты которых попадают в соответствующую корзину. А именно,
пусть k — номер корзины; nk — число измерений, попавших
в диапазон x∈[k⁢h,(k+1)⁢h]. Тогда на графике изобразим «столбик»
шириной h и высотой wk=nk/n.
В результате получим картину, подобную изображённой на рис. 2.1.

Рис. 2.1: Пример гистограммы для нормального распределения (x¯=10,
σ=1,0, h=0,1, n=104)

Высоты построенных столбиков будут приближённо соответствовать значению
плотности распределения w⁢(x) вблизи соответствующей точки x.
Если устремить число измерений к бесконечности (n→∞), а ширину корзин
к нулю (h→0), то огибающая гистограммы будет стремиться к некоторой
непрерывной функции w⁢(x).

Самые высокие столбики гистограммы будут группироваться вблизи максимума
функции w⁢(x) — это наиболее вероятное значение случайной величины.
Если отклонения в положительную и отрицательную стороны равновероятны,
то гистограмма будет симметрична — в таком случае среднее значение ⟨x⟩
также будет лежать вблизи этого максимума. Ширина гистограммы будет характеризовать разброс
значений случайной величины — по порядку величины
она, как правило, близка к среднеквадратичному отклонению sx.

Свойства распределений.

Из определения функции w⁢(x) следует, что вероятность получить в результате
эксперимента величину x в диапазоне от a до b
можно найти, вычислив интеграл:

Px∈[a,b]=∫abw⁢(x)⁢𝑑x. (2.1)

Согласно определению вероятности, сумма вероятностей для всех возможных случаев
всегда равна единице. Поэтому интеграл распределения w⁢(x) по всей области
значений x (то есть суммарная площадь под графиком w⁢(x)) равен единице:

Это соотношение называют условием нормировки.

Среднее и дисперсия.

Вычислим среднее по построенной гистограмме. Если размер корзин
h достаточно мал, все измерения в пределах одной корзины можно считать примерно
одинаковыми. Тогда среднее арифметическое всех результатов можно вычислить как

Переходя к пределу, получим следующее определение среднего значения
случайной величины:

где интегрирование ведётся по всей области значений x.
В теории вероятностей x¯ также называют математическим ожиданием
распределения.
Величину

σ2=(x-x¯)2¯=∫(x-x¯)2⁢w⁢𝑑x (2.3)

называют дисперсией распределения. Значение σ есть
срекднеквадратичное отклонение в пределе n→∞. Оно имеет ту
же размерность, что и сама величина x и характеризует разброс распределения.
Именно эту величину, как правило, приводят как характеристику погрешности
измерения x.

Доверительный интервал.

Обозначим как P|Δ⁢x|<δ вероятность
того, что отклонение от среднего Δ⁢x=x-x¯ составит величину,
не превосходящую по модулю значение δ:

P|Δ⁢x|<δ=∫x¯-δx¯+δw⁢(x)⁢𝑑x. (2.4)

Эту величину называют доверительной вероятностью для
доверительного интервала |x-x¯|≤δ.

2.2 Нормальное распределение

Одним из наиболее примечательных результатов теории вероятностей является
так называемая центральная предельная теорема. Она утверждает,
что сумма большого количества независимых случайных слагаемых, каждое
из которых вносит в эту сумму относительно малый вклад, подчиняется
универсальному закону, не зависимо от того, каким вероятностным законам
подчиняются её составляющие, — так называемому нормальному
распределению (или распределению Гаусса).

Доказательство теоремы довольно громоздко и мы его не приводим (его можно найти
в любом учебнике по теории вероятностей). Остановимся
кратко на том, что такое нормальное распределение и его основных свойствах.

Плотность нормального распределения выражается следующей формулой:

w𝒩⁢(x)=12⁢π⁢σ⁢e-(x-x¯)22⁢σ2. (2.5)

Здесь x¯ и σ
— параметры нормального распределения: x¯ равно
среднему значению x, a σ —
среднеквадратичному отклонению, вычисленным в пределе n→∞.

Как видно из рис. 2.1, распределение представляет собой
симметричный
«колокол», положение вершины которого
соответствует x¯ (ввиду симметрии оно же
совпадает с наиболее вероятным значением — максимумом
функции w𝒩⁢(x)).

При значительном отклонении x от среднего величина
w𝒩⁢(x)
очень быстро убывает. Это означает, что вероятность встретить отклонения,
существенно большие, чем σ, оказывается пренебрежимо
мала. Ширина «колокола» по порядку величины
равна σ — она характеризует «разброс»
экспериментальных данных относительно среднего значения.

Замечание. Точки x=x¯±σ являются точками
перегиба графика w⁢(x) (в них вторая производная по x
обращается в нуль, w′′=0), а их положение по высоте составляет
w⁢(x¯±σ)/w⁢(x¯)=e-1/2≈0,61
от высоты вершины.

Универсальный характер центральной предельной теоремы позволяет широко
применять на практике нормальное (гауссово) распределение для обработки
результатов измерений, поскольку часто случайные погрешности складываются из
множества случайных независимых факторов. Заметим, что на практике
для приближённой оценки параметров нормального распределения
случайной величины используются выборочные значения среднего
и дисперсии: x¯≈⟨x⟩, sx≈σx.

x-x0σ2=2w⁢(x)σ1=1

Рис. 2.2: Плотность нормального распределения

Доверительные вероятности.

Вычислим некоторые доверительные вероятности (2.4) для нормально
распределённых случайных величин.

Замечание. Значение интеграла вида ∫e-x2/2⁢𝑑x
(его называют интегралом ошибок) в элементарных функциях не выражается,
но легко находится численно.

Вероятность того, что результат отдельного измерения x окажется
в пределах x¯±σ оказывается равна

P|Δ⁢x|<σ=∫x¯-σx¯+σw𝒩⁢𝑑x≈0,68.

Вероятность отклонения в пределах x¯±2⁢σ:

а в пределах x¯±3⁢σ:

Иными словами, при большом числе измерений нормально распределённой
величины можно ожидать, что лишь треть измерений выпадут за пределы интервала
[x¯-σ,x¯+σ]. При этом около 5%
измерений выпадут за пределы [x¯-2⁢σ;x¯+2⁢σ],
и лишь 0,27% окажутся за пределами
[x¯-3⁢σ;x¯+3⁢σ].

Пример. В сообщениях об открытии бозона Хиггса на Большом адронном коллайдере
говорилось о том, что исследователи ждали подтверждение результатов
с точностью «5 сигма». Используя нормальное распределение (2.5)
нетрудно посчитать, что они использовали доверительную вероятность
P≈1-5,7⋅10-7=0,99999943. Такую точность можно назвать фантастической.

Полученные значения доверительных вероятностей используются при
стандартной записи результатов измерений. В физических измерениях
(в частности, в учебной лаборатории), как правило, используется P=0,68,
то есть, запись

означает, что измеренное значение лежит в диапазоне (доверительном
интервале) x∈[x¯-δ⁢x;x¯+δ⁢x] с
вероятностью 68%. Таким образом погрешность ±δ⁢x считается
равной одному среднеквадратичному отклонению: δ⁢x=σ.
В технических измерениях чаще используется P=0,95, то есть под
абсолютной погрешностью имеется в виду удвоенное среднеквадратичное
отклонение, δ⁢x=2⁢σ. Во избежание разночтений доверительную
вероятность следует указывать отдельно.

Замечание. Хотя нормальный закон распределения встречается на практике довольно
часто, стоит помнить, что он реализуется далеко не всегда.
Полученные выше соотношения для вероятностей попадания значений в
доверительные интервалы можно использовать в качестве простейшего
признака нормальности распределения: в частности, если количество попадающих
в интервал ±σ результатов существенно отличается от 2/3 — это повод
для более детального исследования закона распределения ошибок.

Сравнение результатов измерений.

Теперь мы можем дать количественный критерий для сравнения двух измеренных
величин или двух результатов измерения одной и той же величины.

Пусть x1 и x2 (x1≠x2) измерены с
погрешностями σ1 и σ2 соответственно.
Ясно, что если различие результатов |x2-x1| невелико,
его можно объяснить просто случайными отклонениями.
Если же теория предсказывает, что вероятность обнаружить такое отклонение
слишком мала, различие результатов следует признать значимым.
Предварительно необходимо договориться о соответствующем граничном значении
вероятности. Универсального значения здесь быть не может,
поэтому приходится полагаться на субъективный выбор исследователя. Часто
в качестве «разумной» границы выбирают вероятность 5%,
что, как видно из изложенного выше, для нормального распределения
соответствует отклонению более, чем на 2⁢σ.

Допустим, одна из величин известна с существенно большей точностью:
σ2≪σ1 (например, x1 — результат, полученный
студентом в лаборатории, x2 — справочное значение).
Поскольку σ2 мало, x2 можно принять за «истинное»:
x2≈x¯. Предполагая, что погрешность измерения
x1 подчиняется нормальному закону с и дисперсией σ12,
можно утверждать, что
различие считают будет значимы, если

Пусть погрешности измерений сравнимы по порядку величины:
σ1∼σ2. В теории вероятностей показывается, что
линейная комбинация нормально распределённых величин также имеет нормальное
распределение с дисперсией σ2=σ12+σ22
(см. также правила сложения погрешностей (2.7)). Тогда
для проверки гипотезы о том, что x1 и x2 являются измерениями
одной и той же величины, нужно вычислить, является ли значимым отклонение
|x1-x2| от нуля при σ=σ12+σ22.


Пример. Два студента получили следующие значения для теплоты испарения
некоторой жидкости: x1=40,3±0,2 кДж/моль и
x2=41,0±0,3 кДж/моль, где погрешность соответствует
одному стандартному отклонению. Можно ли утверждать, что они исследовали
одну и ту же жидкость?
Имеем наблюдаемую разность |x1-x2|=0,7 кДж/моль,
среднеквадратичное отклонение для разности
σ=0,22+0,32=0,36 кДж/моль.
Их отношение |x2-x1|σ≈2. Из
свойств нормального распределения находим вероятность того, что измерялась
одна и та же величина, а различия в ответах возникли из-за случайных
ошибок: P≈5%. Ответ на вопрос, «достаточно»
ли мала или велика эта вероятность, остаётся на усмотрение исследователя.

Замечание. Изложенные здесь соображения применимы, только если x¯ и
его стандартное отклонение σ получены на основании достаточно
большой выборки n≫1 (или заданы точно). При небольшом числе измерений
(n≲10) выборочные средние ⟨x⟩ и среднеквадратичное отклонение
sx сами имеют довольно большую ошибку, а
их распределение будет описываться не нормальным законом, а так
называемым t-распределением Стъюдента. В частности, в зависимости от
значения n интервал ⟨x⟩±sx будет соответствовать несколько
меньшей доверительной вероятности, чем P=0,68. Особенно резко различия
проявляются при высоких уровнях доверительных вероятностей P→1.

2.3 Независимые величины

Величины x и y называют независимыми если результат измерения одной
из них никак не влияет на результат измерения другой. Для таких величин вероятность того, что x окажется в некоторой области X, и одновременно y — в области Y,
равна произведению соответствующих вероятностей:

Обозначим отклонения величин от их средних как Δ⁢x=x-x¯ и
Δ⁢y=y-y¯.
Средние значения этих отклонений равны, очевидно, нулю: Δ⁢x¯=x¯-x¯=0,
Δ⁢y¯=0. Из независимости величин x и y следует,
что среднее значение от произведения Δ⁢x⋅Δ⁢y¯
равно произведению средних Δ⁢x¯⋅Δ⁢y¯
и, следовательно, равно нулю:

Δ⁢x⋅Δ⁢y¯=Δ⁢x¯⋅Δ⁢y¯=0. (2.6)

Пусть измеряемая величина z=x+y складывается из двух независимых
случайных слагаемых x и y, для которых известны средние
x¯ и y¯, и их среднеквадратичные погрешности
σx и σy. Непосредственно из определения (1.1)
следует, что среднее суммы равно сумме средних:

Найдём дисперсию σz2. В силу независимости имеем

Δ⁢z2¯=Δ⁢x2¯+Δ⁢y2¯+2⁢Δ⁢x⋅Δ⁢y¯≈Δ⁢x2¯+Δ⁢y2¯,

то есть:

Таким образом, при сложении независимых величин их погрешности
складываются среднеквадратичным образом.

Подчеркнём, что для справедливости соотношения (2.7)
величины x и y не обязаны быть нормально распределёнными —
достаточно существования конечных значений их дисперсий. Однако можно
показать, что если x и y распределены нормально, нормальным
будет и распределение их суммы.

Замечание. Требование независимости
слагаемых является принципиальным. Например, положим y=x. Тогда
z=2⁢x. Здесь y и x, очевидно, зависят друг от друга. Используя
(2.7), находим σ2⁢x=2⁢σx,
что, конечно, неверно — непосредственно из определения
следует, что σ2⁢x=2⁢σx.

Отдельно стоит обсудить математическую структуру формулы (2.7).
Если одна из погрешностей много больше другой, например,
σx≫σy,
то меньшей погрешностью можно пренебречь, σx+y≈σx.
С другой стороны, если два источника погрешностей имеют один порядок
σx∼σy, то и σx+y∼σx∼σy.

Эти обстоятельства важны при планирования эксперимента: как правило,
величина, измеренная наименее точно, вносит наибольший вклад в погрешность
конечного результата. При этом, пока не устранены наиболее существенные
ошибки, бессмысленно гнаться за повышением точности измерения остальных
величин.

Пример. Пусть σy=σx/3,
тогда σz=σx⁢1+19≈1,05⁢σx,
то есть при различии двух погрешностей более, чем в 3 раза, поправка
к погрешности составляет менее 5%, и уже нет особого смысла в учёте
меньшей погрешности: σz≈σx. Это утверждение
касается сложения любых независимых источников погрешностей в эксперименте.

2.4 Погрешность среднего

Выборочное среднее арифметическое значение ⟨x⟩, найденное
по результатам n измерений, само является случайной величиной.
Действительно, если поставить серию одинаковых опытов по n измерений,
то в каждом опыте получится своё среднее значение, отличающееся от
предельного среднего x¯.

Вычислим среднеквадратичную погрешность среднего арифметического
σ⟨x⟩.
Рассмотрим вспомогательную сумму n слагаемых

Если {xi} есть набор независимых измерений
одной и той же физической величины, то мы можем, применяя результат
(2.7) предыдущего параграфа, записать

σZ=σx12+σx22+…+σxn2=n⁢σx,

поскольку под корнем находится n одинаковых слагаемых. Отсюда с
учётом ⟨x⟩=Z/n получаем

Таким образом, погрешность среднего значения x по результатам
n независимых измерений оказывается в n раз меньше погрешности
отдельного измерения. Это один из важнейших результатов, позволяющий
уменьшать случайные погрешности эксперимента за счёт многократного
повторения измерений.

Подчеркнём отличия между σx и σ⟨x⟩:

величина σx — погрешность отдельного
измерения — является характеристикой разброса значений
в совокупности измерений {xi}, i=1..n. При
нормальном законе распределения примерно 68% измерений попадают в
интервал ⟨x⟩±σx;

величина σ⟨x⟩ — погрешность
среднего — характеризует точность, с которой определено
среднее значение измеряемой физической величины ⟨x⟩ относительно
предельного («истинного») среднего x¯;
при этом с доверительной вероятностью P=68% искомая величина x¯
лежит в интервале
⟨x⟩-σ⟨x⟩<x¯<⟨x⟩+σ⟨x⟩.

2.5 Результирующая погрешность опыта

Пусть для некоторого результата измерения известна оценка его максимальной
систематической погрешности Δсист и случайная
среднеквадратичная
погрешность σслуч. Какова «полная»
погрешность измерения?

Предположим для простоты, что измеряемая величина в принципе
может быть определена сколь угодно точно, так что можно говорить о
некотором её «истинном» значении xист
(иными словами, погрешность результата связана в основном именно с
процессом измерения). Назовём полной погрешностью измерения
среднеквадратичное значения отклонения от результата измерения от
«истинного»:

Отклонение x-xист можно представить как сумму случайного
отклонения от среднего δ⁢xслуч=x-x¯
и постоянной (но, вообще говоря, неизвестной) систематической составляющей
δ⁢xсист=x¯-xист=const:

Причём случайную составляющую можно считать независимой от систематической.
В таком случае из (2.7) находим:

σполн2=⟨δ⁢xсист2⟩+⟨δ⁢xслуч2⟩≤Δсист2+σслуч2. (2.9)

Таким образом, для получения максимального значения полной
погрешности некоторого измерения нужно квадратично сложить максимальную
систематическую и случайную погрешности.

Если измерения проводятся многократно, то согласно (2.8)
случайная составляющая погрешности может быть уменьшена, а систематическая
составляющая при этом остаётся неизменной:

Отсюда следует важное практическое правило
(см. также обсуждение в п. 2.3): если случайная погрешность измерений
в 2–3 раза меньше предполагаемой систематической, то
нет смысла проводить многократные измерения в попытке уменьшить погрешность
всего эксперимента. В такой ситуации измерения достаточно повторить
2–3 раза — чтобы убедиться в повторяемости результата, исключить промахи
и проверить, что случайная ошибка действительно мала.
В противном случае повторение измерений может иметь смысл до
тех пор, пока погрешность среднего
σ⟨x⟩=σxn
не станет меньше систематической.


Замечание. Поскольку конкретная
величина систематической погрешности, как правило, не известна, её
можно в некотором смысле рассматривать наравне со случайной —
предположить, что её величина была определена по некоторому случайному
закону перед началом измерений (например, при изготовлении линейки
на заводе произошло некоторое случайное искажение шкалы). При такой
трактовке формулу (2.9) можно рассматривать просто
как частный случай формулы сложения погрешностей независимых величин
(2.7).
Подчеркнем, что вероятностный закон, которому подчиняется
систематическая ошибка, зачастую неизвестен. Поэтому неизвестно и
распределение итогового результата. Из этого, в частности, следует,
что мы не можем приписать интервалу x±Δсист какую-либо
определённую доверительную вероятность — она равна 0,68
только если систематическая ошибка имеет нормальное распределение.
Можно, конечно, предположить,
— и так часто делают — что, к примеру, ошибки
при изготовлении линеек на заводе имеют гауссов характер. Также часто
предполагают, что систематическая ошибка имеет равномерное
распределение (то есть «истинное» значение может с равной вероятностью
принять любое значение в пределах интервала ±Δсист).
Строго говоря, для этих предположений нет достаточных оснований.


Пример. В результате измерения диаметра проволоки микрометрическим винтом,
имеющим цену деления h=0,01 мм, получен следующий набор из n=8 значений:

Вычисляем среднее значение: ⟨d⟩≈386,3 мкм.
Среднеквадратичное отклонение:
σd≈9,2 мкм. Случайная погрешность среднего согласно
(2.8):
σ⟨d⟩=σd8≈3,2
мкм. Все результаты лежат в пределах ±2⁢σd, поэтому нет
причин сомневаться в нормальности распределения. Максимальную погрешность
микрометра оценим как половину цены деления, Δ=h2=5 мкм.
Результирующая полная погрешность
σ≤Δ2+σd28≈6,0 мкм.
Видно, что σслуч≈Δсист и проводить дополнительные измерения
особого смысла нет. Окончательно результат измерений может быть представлен
в виде (см. также правила округления
результатов измерений в п. 4.3.2)



d=386±6⁢мкм,εd=1,5%.


Заметим, что поскольку случайная погрешность и погрешность
прибора здесь имеют один порядок величины, наблюдаемый случайный разброс
данных может быть связан как с неоднородностью сечения проволоки,
так и с дефектами микрометра (например, с неровностями зажимов, люфтом
винта, сухим трением, деформацией проволоки под действием микрометра
и т. п.). Для ответа на вопрос, что именно вызвало разброс, требуются
дополнительные исследования, желательно с использованием более точных
приборов.


Пример. Измерение скорости
полёта пули было осуществлено с погрешностью δ⁢v=±1 м/c.
Результаты измерений для n=6 выстрелов представлены в таблице:

Усреднённый результат ⟨v⟩=162,0⁢м/с,
среднеквадратичное отклонение σv=13,8⁢м/c, случайная
ошибка для средней скорости
σv¯=σv/6=5,6⁢м/с.
Поскольку разброс экспериментальных данных существенно превышает погрешность
каждого измерения, σv≫δ⁢v, он почти наверняка связан
с реальным различием скоростей пули в разных выстрелах, а не с ошибками
измерений. В качестве результата эксперимента представляют интерес
как среднее значение скоростей ⟨v⟩=162±6⁢м/с
(ε≈4%), так и значение σv≈14⁢м/с,
характеризующее разброс значений скоростей от выстрела к выстрелу.
Малая инструментальная погрешность в принципе позволяет более точно
измерить среднее и дисперсию, и исследовать закон распределения выстрелов
по скоростям более детально — для этого требуется набрать
бо́льшую статистику по выстрелам.


Пример. Измерение скорости
полёта пули было осуществлено с погрешностью δ⁢v=10 м/c. Результаты
измерений для n=6 выстрелов представлены в таблице:

Усреднённый результат ⟨v⟩=163,3⁢м/с,
σv=12,1⁢м/c, σ⟨v⟩=5⁢м/с,
σполн≈11,2⁢м/с. Инструментальная
погрешность каждого измерения превышает разброс данных, поэтому в
этом опыте затруднительно сделать вывод о различии скоростей от выстрела
к выстрелу. Результат измерений скорости пули:
⟨v⟩=163±11⁢м/с,
ε≈7%. Проводить дополнительные выстрелы при такой
большой инструментальной погрешности особого смысла нет —
лучше поработать над точностью приборов и методикой измерений.

2.6 Обработка косвенных измерений

Косвенными называют измерения, полученные в результате расчётов,
использующих результаты прямых (то есть «непосредственных»)
измерений физических величин. Сформулируем основные правила пересчёта
погрешностей при косвенных измерениях.

2.6.1 Случай одной переменной

Пусть в эксперименте измеряется величина x, а её «наилучшее»
(в некотором смысле) значение равно x⋆ и оно известно с
погрешностью σx. После чего с помощью известной функции
вычисляется величина y=f⁢(x).

В качестве «наилучшего» приближения для y используем значение функции
при «наилучшем» x:

Найдём величину погрешности σy. Обозначая отклонение измеряемой
величины как Δ⁢x=x-x⋆, и пользуясь определением производной,
при условии, что функция y⁢(x) — гладкая
вблизи x≈x⋆, запишем

где f′≡d⁢yd⁢x — производная фукнции f⁢(x), взятая в точке
x⋆. Возведём полученное в квадрат, проведём усреднение
(σy2=⟨Δ⁢y2⟩,
σx2=⟨Δ⁢x2⟩), и затем снова извлечём
корень. В результате получим


Пример. Для степенной функции
y=A⁢xn имеем σy=n⁢A⁢xn-1⁢σx, откуда



σyy=n⁢σxx,или  εy=n⁢εx,


то есть относительная погрешность степенной функции возрастает пропорционально
показателю степени n.

Пример. Для y=1/x имеем ε1/x=εx
— при обращении величины сохраняется её относительная
погрешность.

Упражнение. Найдите погрешность логарифма y=ln⁡x, если известны x
и σx.

Упражнение. Найдите погрешность показательной функции y=ax,
если известны x и σx. Коэффициент a задан точно.

2.6.2 Случай многих переменных

Пусть величина u вычисляется по измеренным значениям нескольких
различных независимых физических величин x, y, …
на основе известного закона u=f⁢(x,y,…). В качестве
наилучшего значения можно по-прежнему взять значение функции f
при наилучших значениях измеряемых параметров:

Для нахождения погрешности σu воспользуемся свойством,
известным из математического анализа, — малые приращения гладких
функции многих переменных складываются линейно, то есть справедлив
принцип суперпозиции малых приращений:

где символом fx′≡∂⁡f∂⁡x обозначена
частная производная функции f по переменной x —
то есть обычная производная f по x, взятая при условии, что
все остальные аргументы (кроме x) считаются постоянными параметрами.
Тогда пользуясь формулой для нахождения дисперсии суммы независимых
величин (2.7), получим соотношение, позволяющее вычислять
погрешности косвенных измерений для произвольной функции
u=f⁢(x,y,…):

σu2=fx′⁣2⁢σx2+fy′⁣2⁢σy2+… (2.11)

Это и есть искомая общая формула пересчёта погрешностей при косвенных
измерениях.

Отметим, что формулы (2.10) и (2.11) применимы
только если относительные отклонения всех величин малы
(εx,εy,…≪1),
а измерения проводятся вдали от особых точек функции f (производные
fx′, fy′ … не должны обращаться в бесконечность).
Также подчеркнём, что все полученные здесь формулы справедливы только
для независимых переменных x, y, …

Остановимся на некоторых важных частных случаях формулы
(2.11).


Пример. Для суммы (или разности) u=∑i=1nai⁢xi имеем



σu2=∑i=1nai2⁢σxi2.

(2.12)


Пример. Найдём погрешность степенной функции:
u=xα⋅yβ⋅…. Тогда нетрудно получить,
что



σu2u2=α2⁢σx2x2+β2⁢σy2y2+…


или через относительные погрешности



εu2=α2⁢εx2+β2⁢εy2+…

(2.13)


Пример. Вычислим погрешность произведения и частного: u=x⁢y или u=x/y.
Тогда в обоих случаях имеем



εu2=εx2+εy2,

(2.14)

то есть при умножении или делении относительные погрешности складываются
квадратично.


Пример. Рассмотрим несколько более сложный случай: нахождение угла по его тангенсу



u=arctgyx.


В таком случае, пользуясь тем, что (arctgz)′=11+z2,
где z=y/x, и используя производную сложной функции, находим
ux′=uz′⁢zx′=-yx2+y2,
uy′=uz′⁢zy′=xx2+y2, и наконец



σu2=y2⁢σx2+x2⁢σy2(x2+y2)2.


Упражнение. Найти погрешность вычисления гипотенузы z=x2+y2
прямоугольного треугольника по измеренным катетам x и y.

По итогам данного раздела можно дать следующие практические рекомендации.

  • •

    Как правило, нет смысла увеличивать точность измерения какой-то одной
    величины, если другие величины, используемые в расчётах, остаются
    измеренными относительно грубо — всё равно итоговая погрешность
    скорее всего будет определяться самым неточным измерением. Поэтому
    все измерения имеет смысл проводить примерно с одной и той же
    относительной погрешностью    .

  • •

    При этом, как следует из (2.13), особое внимание
    следует уделять измерению величин, возводимых при расчётах в степени
    с большими показателями. А при сложных функциональных зависимостях
    имеет смысл детально проанализировать структуру формулы
    (2.11):
    если вклад от некоторой величины в общую погрешность мал, нет смысла
    гнаться за высокой точностью её измерения, и наоборот, точность некоторых
    измерений может оказаться критически важной.

  • •

    Следует избегать измерения малых величин как разности двух близких
    значений (например, толщины стенки цилиндра как разности внутреннего
    и внешнего радиусов): если u=x-y, то абсолютная погрешность
    σu=σx2+σy2
    меняется мало, однако относительная погрешность
    εu=σux-y
    может оказаться неприемлемо большой, если x≈y.

Источник

Понравилась статья? Поделить с друзьями:
  • Справки бк ошибка открытия файла
  • Спросить вопрос тип ошибки
  • Сработают ли подушки безопасности если горит ошибка
  • Срединная ошибка формула
  • Справочник не многоуровневый 1с ошибка