Софизм 1 2 где ошибка

Математические софизмы

• Авторы
• Руководители
• Файлы работы
• Наградные документы

Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF

1. Введение

Математика — один из наших любимых школьных предметов. Он нам нравится не только потому, что это основной школьный предмет, но и потому, что без математических знаний в жизни не обойтись. Занятие математикой развивает логическое мышление, сосредоточенность, находчивость, устойчивое внимание, хорошую память, смекалку.

Тема нашей работы «Софизмы в нашей жизни». Мы выбрали эту тему для своего проекта не случайно. Как-то вечером папа задал мне вопрос: «Саша, а ты знаешь, что 6 = 7? Мне стало интересно. Папа с легкостью доказал это равенство.

Вот как это было: 6=7.

Запишем верное равенство: 42 +12 — 54 = 49 +14 – 63.

Вынесем общий множитель за скобки: 6(7 + 2 – 9) = 7(7 + 2 – 9)

Разделим обе части на общий множитель (7 + 2 – 9).

Получим, что 6 = 7 , что и требовалось доказать. Где ошибка? Ведь этого быть не может. Папа сказал, что есть такое понятия, как софизм. Так я определился с темой проекта. Катя сама выбрала тему из списка, который был предложен учителем математики. Для нее понятие софизм тоже было неизвестно, поэтому она решила узнать, что означает это незнакомое и интересное слово.

В процессе работы мы выяснили, что существует великое множество софизмов, и с их помощью можно доказать практически что угодно: как равенство всех чисел между собой (например, 34 =7), так и то, что прямой угол равен тупому.
Эта тема сейчас актуальна, потому что софизм — это обман, а так как не каждый может его распознать, то с помощью софизмов люди обманывают друг друга в наше время, как и тысячелетия назад.

Цель: узнать, что такое софизмы и научиться находить ошибку в софизмах.

Задачи:

1. Познакомиться с историей софизмов.

2. Узнать, какие бывают софизмы. Классификация софизмов.

3. Понять, как найти ошибку в софизмах?

4. Разбор софизмов.

5. Составить анкету для обучающихся, познакомить одноклассников с результатами работы.

6. Составить рекомендации для нахождения ошибок в софизмах.

Гипотеза: софизмы — тренировка для ума.

Объект и предмет исследования: софизмы

Методы исследования:

1. Анализ литературы и информации, полученной из Интернет источников

2. Обсуждение темы с учителем, родными и одноклассниками

3. Анкетирование одноклассников

4. Анализ и обобщение полученных данных.

2. Теоретическая часть

Что такое софизмы?

Софизм (от греч. — мастерство, умение, хитрая выдумка, уловка, мудрость) — ложное умозаключение, которое, тем не менее, при поверхностном рассмотрении кажется правильным. Софизм основан на преднамеренном, сознательном нарушении правил логики.

Что же такое математический софизм? Математический софизм — удивительное утверждение, в доказательстве которого кроются незаметные, а подчас и довольно тонкие ошибки. История математики полна неожиданных и интересных софизмов, разрешение которых порой служило толчком к новым открытиям. Очень часто понимание ошибок в софизме ведет к пониманию математики в целом, помогает развивать логику и навыки правильного мышления. Если нашел ошибку в софизме, значит, ты ее осознал, а осознание ошибки предупреждает от ее повторения в дальнейших математических рассуждениях. Софизмы не приносят пользы, если их не понимать. Что касается типичных ошибок в софизмах, то они таковы: запрещенные действия, пренебрежение условиями теорем, формул и правил, ошибочный чертеж, опора на ошибочные умозаключения. Нередко, ошибки, допущенные в софизме, настолько умело скрыты, что даже опытный математик не сразу их выявит. Именно в этом и проявляется связь математики и философии в софизмах. На самом деле, софизм — гибрид не только математики и философии, но и логики с риторикой. Основные создатели софизмов – древнегреческие ученые-философы, но тем не менее, они создавали математические софизмы, основываясь на элементарных аксиомах, что еще раз подтверждает связь математики и философии в софизмах. Кроме того, очень важно правильно преподнести софизм, так, чтобы докладчику поверили, а значит, необходимо владеть даром красноречия и убеждения. Группа древнегреческих ученых, начавшая заниматься софизмами как отдельным математическим явлением, назвала себя софистами.

2.2. История возникновения софизмов

Мы изучили историю возникновения софизмов. Софистика – это искусство ведения спора. Она вошла в моду в Греции в V веке до нашей эры. Имея в этом выгоду или просто интерес, многие умные и хитрые люди строго логически доказывали, что черное – это белое, истина – это ложь, добро – это зло и т.д. Так появились софизмы – формально кажущиеся правильными, но по существу ложными умозаключениями. Эти рассуждения могут быть истинны в каждой отдельной части, но неверные в целом.

Софизм – слово греческого происхождения, в переводе означающее хитроумную выдумку, ухищрение или головоломку. Речь идет о «доказательстве», направленном на формально – логическое установление абсурдного положения. В основном математические софизмы строятся на неверном словоупотреблении, на неточности формулировок, на скрытом выполнении невозможных действий, на незаконных обобщениях.

Систематический анализ софизмов был дан впервые Аристотелем   (384-322 до н. э.) в особом трактате, в котором все ошибки разделяются на два класса: «неправильности речи» и ошибки «вне речи», т.е. в мышлении. Каков бы ни был софизм, он обязательно содержит замаскированные ошибки. Часто в математических софизмах скрыто выполняются запрещенные действия или не учитываются условия применения теорем, формул и правил.

Одна из основных задач софистов заключалась в том, чтобы научить человека доказывать (подтверждать или опровергать) все, что угодно, выходить победителем из любого интеллектуального состязания. Для этого они разрабатывали разнообразные логические, риторические и психологические приемы. К логическим приемам нечестного, но удачного ведения дискуссии и относятся софизмы. Однако, одних только софизмов для победы в любом споре недостаточно. Ведь если объективная истина окажется не на стороне спорящего, то он, в любом случае, проиграет полемику, несмотря на все свое софистическое искусство. Это хорошо понимали и сами софисты. Поэтому помимо различных логических, риторических и психологических уловок в их арсенале была важная философская идея (особенно дорогая для них), состоявшая в том, что никакой объективной истины не существует: сколько людей, столько и истин. Софисты утверждали, что все в мире субъективно и относительно. Если признать эту идею справедливой, то тогда софистического искусства будет вполне достаточно для победы в любой дискуссии: побеждает не тот, кто находится на стороне истины, а тот, кто лучше владеет приемами полемики.

Софист – это:

1. Человек, прибегающий к софизмам для доказательства заведомо неверных мыслей, положений.

2. В древней Греции первоначальный мудрец, знаток, потом платный учитель философии, красноречия, искусства спора, а также — философ, расходившийся с общепринятыми взглядами в вопросах религии и морали и обвинявшийся противниками в пользовании софизмами.

Наиболее серьезную роль сыграли математические софизмы, придуманные в V веке до нашей эры мудрецом Зеноном из южно-итальянского города Элеи. Например, одна из них: «В каждый момент времени летящая стрела неподвижна. Значит, она неподвижна во все моменты времени, и ее движение никогда не сможет начаться».

В истории развития математики софизмы способствовали повышению строгости в рассуждениях и более глубокому пониманию понятий и методов математики.

2.3. Классификация ошибок в софизмах

Первую систематизацию софизмов дал еще Аристотель в IV веке до нашей эры. Он разделил все ошибки на 2 класса «ошибки речи» и ошибки «вне речи», то есть в мышлении.

Софисты в своих рассуждениях использовали разные ошибки, такие как:

Логические и ошибки в рассуждениях. Например: «Закон Моисеев запрещал воровство. Но закон Моисеев потерял свою силу, следовательно, воровство не запрещено»,   или «Все люди разумные существа, жители планет не люди, следовательно, они не разумные существа;

Терминологические ошибки – неправильное употребление слов или построение предложения. Например, «Все углы треугольника равны 180 градусам» в смысле «Сумма углов треугольника равна 180 градусам».  

Ошибки в применении формул. Например : Чётное и нечётное. 5 есть 2 + 3 («два и три»). Два — число чётное, три — нечётное, выходит, что пять — число и чётное и нечётное. Пять не делится на два, также, как и 2 + 3, значит, оба числа не чётные! 

Практическая часть

3.1. Разбор математических софизмов

Рассмотрим некоторые софизмы, помогающие нам развить логическое мышление и проверить, насколько глубоко мы понимаем некоторые моменты курса математики. Как было сказано ранее, в математических софизмах чаще всего используются «запрещенные действия» либо не учитываются условия применимости теорем, формул или правил. Часто понимание людьми ошибок в софизме ведет к пониманию математики в целом, развивает логику и навыки правильного мышления. Математические софизмы делятся на 4 вида: арифметические, алгебраические, геометрические, логические. Мы рассмотрим некоторые из них.

Арифметические софизмы– это числовые выражения, имеющие неточность или ошибку, не заметную с первого взгляда. 
Дважды два – пять (2 * 2 = 5)
Доказательство:
Пусть исходное соотношение — очевидное равенство:
4:4= 5:5 (1) .
Вынесем за скобки общий множитель каждой части (1) равенства, и мы получим:
4*(1:1)=5*(1:1) (2)
Разложим число 4 на произведение 2 *2
(2*2)* (1:1)=5*(1:1) (3)
Наконец, зная, что 1:1=1, мы из соотношения (2) устанавливаем: 2*2=5.
Ошибка заключается в том, что нельзя было выносить множитель за скобки в в частном, множитель можно выносить либо из суммы, либо из разности.

Один рубль не равен ста копейкам
Доказательство:
Известно, что любые два неравенства можно перемножать почленно, не нарушая при этом равенства, т.е. Если a=b, c=d, то ac=bd.
Применим это положение к двум очевидным равенствам
1 р.=100 коп, (1)
10р.=10*100коп.(2)
Перемножая эти равенства почленно, получим 10 р.=100000 коп.
Наконец, разделив последнее равенство на 10 получим, что 1 р.=10 000 коп., таким образом, один рубль не равен ста копейкам.
Ошибка, допущенная в этом софизме, состоит в нарушении правил действия с именованными величинами: необходимо переходить к единым единицам измерения.

Софизм «5 = 6»

Докажем, что 5 =6. С этой целью возьмем числовое равенство 35 + 10- 45 = 42 + 12 — 54. Вынесем общий множитель левой и правой части за скобки. Получим 5(7 + 2 — 9) = 6 (7 + 2 — 9). Разделим обе части этого равенства на общий множитель (7 + 2 — 9). Получаем 5=6. В чем ошибка?

Ошибка: нельзя делить на равенство (7 + 2 — 9), т. к. (7 + 2 — 9)= 0. Ма знаем еще из начальной школы, что на 0 делить нельзя.

Таки образом, можно доказать равенство любых разных двух чисел.

Софизм «Пропавший рубль»

Три подруги зашли в кафе выпить по чашке кофе7 Выпили. Официант принес им счет на 30 рублей. Подруги заплатили по 10 рублей и вышли. Однако хозяин кафе решил сделать скидку посетительницам, сказав что кофе стоит 25 рублей. Официант взял деньги и побежал доганять подруг, но пока он бежал, подумал, что им будет трудно делить 5 рублей, ведь их трое, поэтому решил отдать им по 1 рублю, а 2 рубля оставить себе. Так и сделал.

Что же получилось? Подруги заплатили по 9 рублей. 9 . 3 = 27 рублей, да 2 рубля осталось у официанта. А где же еще 1 рубль?

Ошибка. Задача сформулирована так, чтобы запутать читателя. Подруги заплатили 27 рублей, из этой суммы 25 рублей осталось у хозяина кафе, а 2 рубля у официанта. И никакого пропавшего рубля!

Логические софизмы

Софизмы выглядят как лишенная смысла и цели игра с языком; игра, опирающаяся на многозначность языковых выражений, их неполноту, недосказанность, зависимость их значений от контекста и т.д. Эти софизмы кажутся особенно наивными и несерьезными. Приведем некоторые примеры:

Полный стакан равен пустому

Рассмотрим стакан, наполненный водой до половины. Тогда можно сказать, что стакан, наполовину полный равен стакану наполовину пустому.

Увеличивая обе части равенства вдвое, получим, что стакан полный равен

стакану пустому. Где ошибка?

Ясно, что приведенное рассуждение неверно, так как в нем применяется неправомерное действие: увеличение вдвое. В данной ситуации его применение бессмысленно, т.к. пустое увеличить вдвое не возможно.

Софизм учебы

Данным софизмом является песенка, сочиненная английскими студентами:

The more you study, the more you know

The more you know, the more you forget

The more you forget, the less you know

The less you know, the less you forget

The less you forget, the more you know

So why study?

Перевод:

Чем больше учишься, тем больше знаешь.

Чем больше знаешь, тем больше забываешь.

Чем больше забываешь, тем меньше знаешь.

Чем меньше знаешь, тем меньше забываешь.

Но чем меньше забываешь, тем больше знаешь.

Так для чего учиться?

Это стихотворение можно смело назвать логическим софизмом!

Геометрические софизмы

Геометрические софизмы – это умозаключения или рассуждения, обосновывающие какую-нибудь заведомую нелепость, абсурд или парадоксальное утверждение, связанное с геометрическими фигурами и действиями над ними.

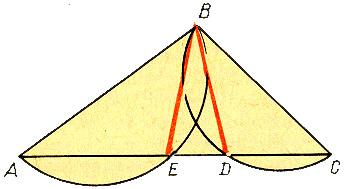
Софизм «Загадочное исчезновение» (Приложение 1). У нас есть произвольный прямоугольник на котором начерчено 13 одинаковых линий на равном расстоянии друг от друга. Теперь «разрежем» прямоугольник прямой MN, проходящей через верхний конец первой и нижний конец последней линии. Сдвигаем обе половины вдоль по этой линии и замечаем, что линий вместо 13 стало 12. Одна линия исчезла бесследно. Куда исчезла 13-я линия?

Разбор софизма. 13-я линия удлинила каждую из оставшихся на 1/12 своей длины.

Примеры софизмов приведены в Приложении 2.

Работая над проектом, мы составили рекомендации по нахождению ошибок в софизмах (Приложение 3).

3.2. Анкетирование

Мы провели анкетирование среди обучающихся 7 классов на знание софизмов. В анкетировании приняло участие 40 человек. Были заданы следующие вопросы:

1. Доводилось ли вам слышать подобную фразу: «Дважды два равно пяти» или хотя бы «Два равно трём»?

«Да» – 24 человека, 60 %

2. Знакомо ли вам понятие «софизм»?

«Да» — 10 человек, 25 %

3. Хотелось ли вам познакомиться с софизмами?

«Да» — 36 человек, 90 %.

Анкетирование показало, что немногим ребятам известно понятие «софизм». 90 % обучающихся хотели бы больше узнать о софизмах. Мы выступим перед ребятами с нашим проектом.

Заключение

Из года в год появляются новые софизмы, некоторые из них могут остаться в истории, о многих быстро забудут. Ведь софизмы — это смесь математики и логики, поэтому они помогают не только развивать логику, но и лучше понимать математику в целом. В современном мире есть много людей, так или иначе употребляющих софизмы в обычной жизни, даже не зная, что это такое. Есть же и такие люди, которые целенаправленно изучают софизмы, например политики или СМИ, чтобы вводить людей в заблуждение, или просто развить свои навыки логики и правильности рассуждений.
Поначалу может показаться, что существует мало софизмов, или что они не используются в жизни, то есть бесполезны. Но это не так. За свою жизнь человек слышит десятки софизмов, не умея отличить их от правдивых утверждений, и даже не зная, что вообще означает слово софизм.
Понять софизм, то есть решить его, получается не сразу. Поначалу, чтобы решить некоторые софизмы, приходилось по многу раз их внимательно перечитывать, вдумываться. К концу работы над проектом ошибки стали находиться быстрее. Благодаря софизмам можно научиться искать ошибки в рассуждениях других, научится грамотно строить свою речь.

Вообще, решение софизмов – интересное и познавательное занятие. Поиск заключенных в софизме ошибок, ясное понимание их причин ведут к осмысленному постижению математики. Работая над проектом, мы составили рекомендации по разбору софизмов (Приложение 3). Наш проект будет полезен людям, которые начинают работать с софизмами с целью развития свих интеллектуальных способностей.

Мы считаем, наш проект актуален и имеет практическое применение. Задачи выполнены, цель достигнута.
Решение софизмов тренируют наш мозг, то есть наша гипотеза верна.

Действительно, софизмы являются тренировкой для ума.

Информационные источники

«Математические софизмы». Книга для учащихся 7-11 классов. Авторы: А.Г. Мадера, Д.А. Мадера. Издательство Москва «Просвещение» 2003.

«Математическая шкатулка». Автор: Ф.Ф. Нагибин. Государственное учебно-педагогическое издательство министерства просвещения РСФСР 1961.

Т.Н. Михеева. Софизмы

«Математика после уроков». Пособие для учителей. Авторы: М.Б.Балк, Г.Д.Балк. Издательство Москва «Просвещение», 1971.

«Парадоксы науки». Автор: А.К.Сухотин. Издательство «Молодая гвардия», 1978 г.

Приложение 1

«Загадочное исчезновение»

Приложение 2

Лекарства

«Лекарство, принимаемое больным, есть добро. Чем больше делать добра, тем лучше. Значит, лекарств нужно принимать как можно больше».

Девушка — не человек

Доказательство от противного. Допустим, девушка – человек. Девушка – молодая, значит девушка – молодой человек. Молодой человек – это парень. Противоречие. Значит девушка — не человек.

Вор
Вор не желает приобрести ничего дурного. Приобретение хорошего есть дело хорошее. Следовательно, вор желает хорошего.

Разговор софиста и любителя спорить

Софист: “Может ли мёд быть сладким и несладким одновременно?”

Любитель: “нет”

Софист: “ А мёд сладкий?”

Любитель: “Да”

Софист: “А мёд желтый?”

Любитель: “Да”

Софист: “А жёлтый — значит сладкий?”

Любитель: “Нет”

Софист: “Значит мёд сладкий и несладкий одновременно!”

Не знаешь то, что знаешь

— Знаешь ли ты то, о чём я хочу тебя спросить?
— Нет.
— Знаешь ли ты, что добродетель есть добро?
— Знаю.
— Об этом я и хотел тебя спросить. А ты, выходит, не знаешь то, что знаешь.

Примеры геометрических софизмов, которые можно услышать на уроке геометрии:

— Смежные углы равны 180 градусам;

— Накрест лежащие углы равны.

Приложение 3

Рекомендации по нахождению ошибок в софизмах

Внимательно прочитать условие предложенной вам задачи.
Начинать поиск ошибки лучше с условия предложенного софизма. В некоторых софизмах абсурдный результат получается из-за противоречивых или неполных данных в условии, неправильного чертежа, ложного первоначального предположения, а далее все рассуждения проводятся верно. Это и вызывает затруднения при поиске ошибки.
 

Установить темы, которые отражены в софизме. Обучающиеся, учителя привыкли, что задания, предлагаемые в учебнике, не содержат ошибок в условии, поэтому, если получается неверный результат, то ошибку они ищут непременно по ходу решения.
 

Воспроизвести вслух точные формулировки утверждений. Установить темы, которые отражены в софизме, предложенных преобразованиях. Софизм может делиться на несколько тем, которые потребуют детального анализа каждой из них. И если вы увидели эти темы, попытайтесь зрительно разбить «большой софизм» на маленькие. 
 

Выяснить, соблюдены ли все условия применимости теорем, правил, формул, логичности. Воспроизвести вслух точные формулировки утверждений, используемых в софизме. Например: 2 * 2 =5. Если произнести эту фразу вслух, то мы можем услышать ошибку, услышав самого себя, или более подробно разобраться в смысле софизма.
 

Проверять преобразования. После каждого перехода проверить полученный результат обратным действием. Выяснить, соблюдены ли все условия применимости теорем, правил, формул, соблюдена ли логичность. Действительно, некоторые софизмы построены на неверном использовании определений, законов, на «забывании» условий применимости некоторых теорем. Очень часто в формулировках, правилах запоминаются основные, главные фразы и предложения, всё остальное упускаются. И тогда второй признак равенства треугольников превращается в признак «по стороне и двум углам».

Просмотров работы: 13198

Администрация города   Нижнего Новгорода

Департамент образования

Муниципальное бюджетное общеобразовательное учреждение

«Школа №181»

—————————————————————————————————

603124, город Нижний Новгород, улица Лесной городок, дом 6-а тел.
2218983

Исследовательская работа

Математические софизмы

Выполнил: Мокрушенко Георгий

                  ученик 6 «А» класса

                  МБОУ «Школа №181»

Научный руководитель: Грязева

                   Наталья Викторовна

                   учитель математики

Нижний Новгород

2017

СОДЕРЖАНИЕ.

1.  Введение…. . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . 3

2.  Что такое софизмы . . . . . . …. . . . . . . . . . . . . . . . . .
. . . .  4

3.  Экскурс в историю. . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . 5

4.  Арифметические софизмы. . . . . . . . . . . . . . . . . . . . . . .
. . 6

5.  Алгебраические софизмы. . . . . . . . . . . . . . . . . . . . . . .
. . . 8

6.  Геометрические софизмы . . . . . . . . . . . . . . . . . . . . . .
. . . 10

7.  Прочие софизмы.  . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . .  12

8.  Исследовательская часть . . . . . . . . . . . . . . . . . . . . . .
. . . . 15

9.  Заключение . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . 16

10.  Список литературы. . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . 17

11. Приложение 1. . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . 18

Введение

«История ошибок человеческого ума,
   возможно, так же важна,
 как исто­рия его движения вперед к истине».

П. Теннери

Наверняка, каждый человек хоть раз в жизни слышал
подобную фразу: «Дважды два равно пяти» или хотя бы: «Два равно трем». На самом
деле, таких примеров можно привести  много, но что все они обозначают? Кто их
выдумал? Имеют ли они какое-нибудь логическое объяснение или же это лишь
вымысел?

Именно эти вопросы я хочу рассмотреть в своей работе,
название которой – «Математические софизмы: обман или путь к открытию?». Речь в
ней пойдет о софизмах.  

Неслучайно я выбрал именно софизмы. Во-первых, я очень
люблю решать задачи и разгадывать математические ребусы, а математические
софизмы — это «задачи-ловушки», которые помогают развивать логическое мышление.
Во-вторых, мне было интересно узнать, что некоторые заведомо ложные
утверждения, оказывается, можно доказать.

В процессе работы  я выяснил, что существует великое
множество софизмов, и с их помощью можно доказать практически что угодно: как
равенство всех чисел между собой, так и то, что прямой угол равен тупому.

Теме софизмов посвящено много публикаций и книг, таких
как, книга для учащихся 7-11 классов Мадера А.Г и Мадера Д.А. «Математические
софизмы: Правдоподобные рассуждения, приводящие к ошибочным утверждениям»,
книга Литцмана В. «Где ошибка?» и множество других замечательных авторов, среди
которых не могу не упомянуть нашего земляка Михаила Андреевича Давыдова,
который в своей книге «Красота математики» посвятил одну из глав математическим
софизмам.

Эта тема сейчас актуальна, потому что софизм — это ложь, обряженная в одежды истины
(как остроумно заметил писатель Даниил Гранин), а так как не каждый может это распознать, то с
помощью софизмов люди обманывают друг друга в наше время, как и тысячелетия
назад.

Цель моего исследования – понять, что такое
математические софизмы, научиться их разгадывать. Для достижения данной цели
передо мной стояли следующие задачи:

·       
узнать, как и откуда появились
софизмы

·       
привести примеры софизмов

·       
разобрать несколько
примеров

·       
понять, как найти ошибку в
них

• проведя разбор софизмов, сделать вывод

Что такое софизмы

Определение софизма в различных
толковых словарях и энциклопедиях подобны. Рассмотрим самые известные из них.

Софизм — логически порочное
умозаключение, в котором ложные посылки выдаются за истинные или делается вывод
с нарушением законов логики (Большая советская энциклопедия, том 40, стр.136).

Софизм — формально кажущееся
правильным, но по существу ложное умозаключение, основанное на преднамеренно
неправильном подборе исходных положений (Толковый словарь русского языка С. И.
Ожегова).

 Софизм — мудрствованье, ложный
вывод, заключенье, сужденье, которому придан внешний вид истины. Софистическое
рассуждение — ложное, ошибочное, под видом истинного (Толковый словарь В. И.
Даля).

Софизм — формально правильное, но
ложное по существу умозаключение, основанное на натяжке, на преднамеренно
неправильном подборе исходных положений в цепи рассуждений (Толковый словарь
русского языка Д. Н. Ушакова).

Таким образом, анализируя
определения софизма из различных энциклопедий и толковых словарей, можно
выделить основные существенные признаки:

ü это утверждение (умозаключение)

ü формально — правильное

ü по существу — ложное

ü ошибка допущена и замаскирована намеренно.

 Софизмы встречаются в различных
областях знаний, но выделенные критерии всегда присутствуют. Поэтому
определение математического софизма не будет существенно отличаться от всех
вышеперечисленных. В математическом софизме замаскированная ошибка, в процессе
вывода приводит к абсурдному результату, нарушающему все законы математики.

Каков бы ни был софизм, он
обязательно содержит одну или несколько замаскированных ошибок. Особенно часто
в математических софизмах скры­то выполняются запрещенные действия или не
учитываются условия применимости теорем, формул и правил. Иногда рассуждения
ведутся с использованием ошибочного чертежа или опираются на приводящие к
ошибочным заключениям, «очевидности». Встречаются софизмы, содержащие и другие
ошибки.

В истории развития математики
софизмы играли существенную роль. Они способствовали повышению строгости в
математических рассуждениях и содействовали более глубокому уяснению понятий и
методов математики. Роль софизмов в развитии математики сходна с той ролью,
какую играли непреднамеренные ошибки в математических доказательствах,
допускаемые даже выдающимися математиками. И.П. Павлов говорил, что «правильно
понятая ошибка — это путь к открытию». Действительно, уяснение ошибок, в математических
рассуждениях часто содействовало развитию математики.

Экскурс в историю

Софистика – направление философии, которое возникло в
V-IV вв. до н.э. в Греции и стало очень популярным а Афинах. Софистами называли
платных «учителей мудрости», которые учили граждан риторике, искусству слова,
приемам ведения спора, красноречию. Одним из представителей софистов был
философ Протагор, который говорил: «Я обучаю людей риторике, а это и есть
гражданское искусство».

         Софисты считали, что истина субъективна, то есть у каждого
человека своя истина, человек сам создает себе истину и сам же её оценивает,
поэтому в суждениях об истине очень много личного. Справедливость, как и
истина, у каждого человека тоже своя, а значит, о каждой вещи можно судить
двояко, то есть о каждой вещи есть два противоположных мнения. Софисты учили
людей оценивать одно и то же событие, как положительное и как отрицательное
одновременно, таким образом,  они приучали людей к широте взглядов.

Первую систематизацию софизмов дал еще Аристотель в IV веке до нашей
эры. Он разделил все ошибки на 2 класса «ошибки речи» и ошибки «вне речи», то
есть в мышлении.

Софисты в своих рассуждениях использовали разные ошибки, такие как:

·       
логические и ошибки в
рассуждениях. Например: «Закон Моисеев запрещал воровство, закон Моисеев
потерял свою силу, следовательно, воровство не запрещено»,  «Все люди разумные
существа, жители планет не люди, следовательно, они не разумные существа».

·       
терминологические –
неправильное употребление слов или построение предложения. Например, «Все углы
треугольника = π» в смысле «Сумма углов треугольника = π»,  «Сколько будет:
пять плюс два умножить на два?» Здесь трудно решить имеется ли в виду 9 (т.е. 5
+ (2*2)) или 14 (т.е. (5 + 2) * 2).

• ошибки в применении
  формул. Например, «Чётное и нечётное»: 5 есть 2 + 3 («два и три»). Два —
  число чётное, три — нечётное, выходит, что пять — число и чётное и
  нечётное. Пять не делится на два, так же, как и 2 + 3, значит, оба числа
  нечётные.

Примеры софизмов

Разбор и решение любого рода
математических задач, а в особенности нестандартных, помогает  развивать
смекалку и логику. Математические софизмы относятся именно к таким задачам. В
этом разделе работы я рассмотрю три типа математических софизмов:
арифметические, алгебраические  и геометрические.

Арифметические
софизмы

Арифметика — (греч. arithmetika, от arithmys — число), наука о числах,
в первую очередь о натуральных (целых положительных) числах  и (рациональных)
дробях, и действиях над ними.

Так что же такое
арифметические софизмы? Арифметические софизмы – это числовые выражения,
имеющие неточность или ошибку, незаметную с первого взгляда.

1. 4 руб. = 40000 коп

Возьмем
верное равенство 2руб. = 200 коп. и возведем его по частям в квадрат. Получится
4 руб. = 40000коп.

Вопрос: В чем ошибка?

Ответ: Возведение в квадрат величин не имеет смысла.
В квадрат возводятся только числа.

Точно
так же можно показать, к примеру, что1 руб. = 10 коп.

Так
как ¼ руб. = 25 коп., то √ ¼ руб. = √ 25 коп.,
следовательно: ½ руб. = 5 коп. или 1 руб. = 10 коп.

В
данных математических софизмах нарушены правила действий с именованными
величинами.

2. Два умножить на два будет пять
                         2 · 2 = 5

Имеем числовое
равенство (верное):  4 : 4 = 5 : 5.

Вынесем за скобки в
каждой части его общий множитель.

Получим: 4 ·
(1 : 1) = 5 · (1 : 1).

Числа в скобках
равны, поэтому 4 = 5, или 2 · 2 = 5.

Вопрос: Где здесь ошибка?

Ответ: Ошибка допущена в вынесении общего множителя
за скобки в левой и правой частях тождества 4 : 4 = 5 : 5.

3. Два равно трем
                2 = 3

Возьмем
два верных равенства:
10 — 10 = 0

15 — 15 = 0

Так
как правые части равны, то приравняем левые: 10 — 10 = 15 — 15

                                                                                       
2· (5 — 5) = 3· (5 — 5)

                                                                                       
2 = 3

Вопрос: В чем ошибка?

Ответ: Ошибка в том, что на ноль (5 — 5)
делить нельзя.

4. Единица равна двум
                   1 = 2

Простым
вычитанием легко убедиться в справедливости ра­венства

1 — 3 = 4 — 6.

Добавив
к обеим частям этого равенства число , получим новое равенство

1 – 3  +  = 4 – 6 + ,

в
котором, как нетрудно заметить, правая и левая части представляют собой полные
квадраты, т. е.

(1 — ) = (2 — )

Извлекая
из правой и левой частей предыдущего равенства квадратный корень, получаем
равенство:

1 —  = 2 —  

откуда
следует, что 1 = 2.

5. Пять равно одному
                  5 = 1

Для
доказательства, что 5 = 1, будем рассуждать так. Из чисел 5 и 1 по
отдельности вычтем одно и то же число 3:

5 – 3 = 2 и 1 – 3 = — 2.

При
возведении в квадрат этих чисел получаются равные числа:
 2² = 4 и (- 2)² = 4.
Значит, должны быть равны и исходные числа 5 и 1.

Вопрос: Где ошибка?

Ответ: Из равенства квадратов двух чисел не следует,
что сами эти числа равны.

6. Четыре равно пяти
               4 = 5

Рассмотрим верное
числовое равенство:

16 – 36 = 25 – 45

16 – 36 + 20,25 =
25 – 45 + 20,25

(4 – 4,5)2 = (5 –
4,5)2;    4 – 4,5 = 5 – 4,5;

4 = 5.

Вопрос: В чём ошибка?

Ответ: (4 – 4,5) · 2 = (5 – 4,5) · 2 , только тогда, когда  |4 – 4,5| = |5 – 4,5|.

Алгебраические
софизмы

Алгебра — один из больших разделов математики, принадлежащий наряду с
арифметикой и геометрией к числу старейших ветвей этой науки. Задачи, а также
методы алгебры, отличающие её от других отраслей математики, создавались
постепенно, начиная с древности. Алгебра возникла под влиянием нужд
общественной практики, в результате поисков общих приёмов для решения
однотипных арифметических задач. Приёмы эти заключаются обычно в составлении и
решении уравнений. Т.е. алгебраические софизмы – намеренно скрытые ошибки в
уравнениях и числовых выражениях.

Все, мною рассмотренные до этого софизмы о
равенстве чисел, можно рассмотреть в общем случае:

1. Все числа равны между собой

Возьмем два
произвольных неравных между собой числа а и b и запишем для них очевидное
тождество:

а²— 2ab + b =  b — 2ab +  а²

Слева и справа стоят
полные квадраты, т. е. можем записать

(а — b)²
= (b — а)²   

Извлекая из обеих
частей последнего равенства квадратный корень, получим:

а — b = b — a

или 2а = 2b,
или окончательно

a = b.

Или, 2. Неравные числа равны

Возьмем два неравных
между собой произвольных числа а и b. Пусть их разность равна с, т. е. а — b
= с. Умножив обе части этого равенства на а — b, получим

(а — b)²
= c(a — b),

a раскрыв скобки,
придем к равенству

a² —
2ab + b² = ca — cb,

из которого следует
равенство

а² — аb
— ас = аb –b ² — bc.

Вынося общий
множитель а слева, и общий множитель b справа за скобки, получим

а(а – b — с) = b(а
– b — с)

Разделив последнее
равенство на (а – b — с), получаем, что

а = b,

другими словами, два неравных между собой
произвольных числа а и b равны.
В данных софизмах рассмотрены наиболее популярные ошибки: неправильное
извлечение квадратного корня из квадрата выражения и деление на 0.

Приведу еще несколько примеров алгебраических
софизмов, решение которых мне пока сложно постичь до конца в силу малого багажа
 знаний.

3. Всякое число равно своему удвоенному значению.
Запишем очевидное для любого числа а тождество

а² — а²
= а² — а².

Вынесем
а в левой части за скобку, а правую часть разло­жим на множители по
формуле разности квадратов, получив

а(а
— а) = (а + а)(а — а).                                                                                                                                                                                                                                                        
                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                

Разделив
обе части на а — а, получим а = а + а, или

а =2а.

 Итак, всякое число равно своему
удвоенному значению.

4. Из двух неравных чисел
первое всегда больше второго.

Пусть a и b – произвольные числа и a ≠ b.
Имеем:

(a – b)²  >  0,
т.е. a²  – 2ab – b² > 0,
или a²  +
b²  > 2ab.

К обеим частям этого
неравенства прибавим  – 2b².
Получим:

а² –
b²  > 2ab – 2b², или  (a + b) (a – b) > 2b (a – b).

После деления обеих
частей на (a – b) имеем:

a + b > 2b, откуда следует, что a > b.

Геометрические софизмы

       Геометрические софизмы – это умозаключения или
рассуждения, обосновывающие какую-нибудь заведомую нелепость, абсурд или
парадоксальное утверждение, связанное с геометрическими фигурами и действиями
над ними.

1. Софизм об исчезающем квадрате.

  Большой квадрат составлен из четырёх одинаковых
четырёхугольников и маленького квадрата (рис. 1).

 Если четырёхугольники
развернуть (рис. 2), то они заполнят площадь, занимаемую маленьким квадратом,
хотя площадь большого квадрата визуально не изменится.

В чём же тут ошибка?                                                                

Посмотрим внимательно на ход действий.

Одинаковая ли площадь у обоих квадратов?  Нет, так как
сторона и площадь нового квадрата меньше стороны и площади того, который был
вначале. При решении данного софизма я воспользовался разрезанием этого
квадрата, сложив части, и сравнив с исходным квадратом, получил, что он
действительно становится меньше.

2. Задача о треугольнике.

Дан прямоугольный треугольник 13×5 клеток, составленный из 4
частей (Рис.1)

После перестановки частей при визуальном сохранении
изначальных пропорций появляется дополнительная, не занятая ни одной частью,
клетка (Рис. 2).

Однако же, если посмотрим внимательно на чертежи, то заметим,
что гипотенузы больших треугольников не совпадают.

Ошибка станет хорошо видна, если провести точное построение.
На самом деле новая фигура не будет треугольником. Это будет ломаный
четырехугольник (Рис.3)

Прочие софизмы

Кроме математических софизмов, существует множество других, например:
логические, терминологические, психологические и т.д. Понять абсурдность таких
утверждений проще, но от этого они не становятся менее интересными. Очень
многие софизмы выглядят как лишенная смысла и цели игра с языком; игра,
опирающаяся на многозначность языковых выражений, их неполноту, недосказанность,
зависимость их значений от контекста и т.д. Эти софизмы кажутся особенно
наивными и несерьезными.

Логические софизмы

Логические софизмы – это софизмы, ошибки которых заключаются в неправильных
рассуждениях.

1. Нет
правил без исключений

Это предложение, очевидно, само является
правилом, сле­довательно, и из этого утверждения имеются исключения. Тем самым
мы приходим к противоречию.

2. Не знаешь то, что знаешь
Знаешь ли ты, о чём я хочу
тебя спросить?» — «Нет». — «Знаешь ли ты, что добродетель есть добро?» —
«Знаю». — «Об этом я и хотел тебя спросить. А ты, выходит, не знаешь то, что
знаешь».  

3. Может ли всемогущий маг создать камень,
который не сможет поднять?

Если не может — значит, он не всемогущий. Если
может — значит, всё равно не всемогущий, т.к. он не может поднять это камень.

4. Полупустое и полуполное

«Полупустое есть то же, что и полуполное. Если
равны половины, значит равны и целые. Следовательно, пустое есть то же, что и
полное».

5. Равен ли полный стакан пустому?

Пусть имеется стакан, наполненный водой до
половины. Тогда можно сказать, что стакан, наполовину полный равен стакану,
наполовину пустому. Увеличивая обе части равенства вдвое, получим, что стакан
полный равен стакану пустому.

6. Лекарства

«Лекарство, принимаемое больным, есть добро.
Чем больше делать добра, тем лучше. Значит, лекарств нужно принимать как можно
больше».

7. Некто
А говорит В: «Я солгал в своей жизни только три раза».

На это В отвечает: «Тогда ты лжешь теперь в чет­вертый раз».

Это заключение противоречиво: либо А дей­ствительно до сих пор солгал
только три раза и тогда он, сейчас говорит правду, либо он лгал больше, чем три
раза, и тогда в данный момент он солгал более, чем в четвертый раз.

8.  Крокодил

У одной египтянки крокодил похитил ребенка. Египтянка просила вернуть
ребенка, и крокодил обещал ей это, если она правильно укажет, как поступит
крокодил.

Мать ребенка сказала: «Ты не возвратишь мне
моего ребенка»

На это крокодил ответил: «Если ты
действительно права,  то ты, как сама говоришь, не получишь назад ребенка; если
же твое высказывание неверно, то, согласно нашему уговору, ты  не получишь
ребенка. В любом случае ребенок должен остаться у меня»

 «Наоборот, — возразила женщина,- если мое
высказывание, верно, то я получу ребенка в силу нашего условия; если же я
ошиблась, то это означает, что ты сам вернешь мне ребенка. В каждом из случаев
я должна полу­чить ребенка назад»

Кто из них прав?

9.    Кто виноват?

Некто купил шапку, которая оказалась для него негодной, она была
слишком мала.

Кто виноват, шапка или голова?

Шапка во всяком случае не виновата, так как если бы голова была меньше,
она бы подошла.

Следовательно, вино­вата голова!

Но это также неверно. Если бы шапка была больше, то она была бы годна.

Следовательно, ни шапка, ни голова не виноваты.

10. Хитрый хозяин

В приведенных ниже стишках, взятых из одного
английского журнала, выходившего в прошлом веке, рассказывается о хитром
хозяине гостиницы, сумевшем разместить в девяти номерах десять гостей так, что
каждому из них досталось по отдельной комнате.

Другой же софизм гласит, что «Единица равна двум»

Простым
вычитанием легко убедиться в справедливости
равенства

1-3
= 4-6.

Добавив
к обеим частям этого равенства число ,
получим новое равенство

1-3
+ =
4-6+,

в
котором, как нетрудно заметить, правая
и левая части представляют собой полные
квадраты, т. е.

(1-)=(2-)

Извлекая
из правой и левой частей предыдущего
равенства квадратный корень, получаем
равенство:

1-=2-

откуда
следует, что

1=2.

Где
ошибка?

Разбор
софизма:

По
определению представляет
собой некоторое неотрицательное число,
которое, будучи возведено в квадрат,
дастх. Ясно,
что этому определению удовлетворяют
два числа, а именно х и -х. Итак,
если число х неотрицательно (х>0), то=х; если
же число х отрицательно, то есть
число -х положительно, то=
— x. Отсюда заключаем, что(свойство
арифметического квадратного корня),
что не учитывается в содержании этих
софизмов и приводит к ложным выводам.

«Всякое число равно своей половине.»

Запишем
очевидное для любого числа a тождествоa² —
a² =
a² —
a²,где
а-любое число.

Вынесем a в
левой части за скобку, а правую часть
разложим на множители по формуле разности
квадратов, получим a(a
– a) = (a + a)(a — a).

Разделив
обе части на a
— a,
получим a
= a + a,
или a=2a.

Разделим
на 2 и получим
а= а/2

Где
ошибка?

Мы
делим обе части на ноль, а деление на
ноль запрещено.

«Меньшее число больше,чем большее.»

Очевидно,что7>5
и что -8=-8

Тогда:7-8>5-8
или -1>-3

Это
не противоречит основному понятию об
отрицательных величина, на основании
которого мы считаем меньшей ту
отрицательную величину,численное
значение которой больше,и наоборот.

Умножим
обе части последнего неравенства на
(-4).

Получим
(-1)∙ (-4)>(-3)∙(-4) или 4>12

Где
ошибка?

Разбор
софизма:

При
умножении неравенства на отрицательное
число, знак неравенства изменяется на
противоположный.

«Через точку на прямую можно опустить два перпендикуляра»

Попытаемся
«доказать», что через точку, лежащую
вне прямой, к этой прямой можно провести
два перпендикуляра. С этой целью возьмем
треугольник АВС. На сторонах АВ и ВС
этого треугольника, как на диаметрах,
построим полуокружности. Пусть эти
полуокружности пересекаются со стороной
АС в точках Е и D.
Соединим точки  Е и D
прямыми с точкой В. Угол АЕВ прямой, как
вписанный, опирающийся на диаметр; угол
ВДС также прямой. Следовательно, ВЕ 
перпендикулярна АС и ВD
перпендикулярна АС. Через точку В
проходят два перпендикуляра к прямой
АС.

Где
ошибка?

Разбор
софизма:

Рассуждения,
о том, что из точки на прямой можно
опустить два перпендикуляра, опирались
на ошибочный чертеж. В действительности
полуокружности пересекаются со стороной
АС в одной точке, т.е. ВЕ совпадает с ВD.
Значит, из одной точки на прямой нельзя
опустить два перпендикуляра.

Всякое
положительное число является отрицательным.

Пусть
n-положительное число.

Очевидно,
2n-1<2n.

Возьмём
другое произвольное положительное
число a и умножим обе части неравенства
на (-а): -2an+a<-2an.

Вычитая
из обеих частей этого неравенства
величину (-2an), получим неравенство a<0,
доказывающее, что всякое положительное
число является отрицательным.

Где
ошибка?

Разбор
софизма:

При
умножении на отрицательное число знак
неравенства меняется.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

МАТЕМАТИЧЕСКИЙ СОФИЗМ – удивительное
утверждение, в доказательстве которого кроются
незаметные, а подчас и довольно тонкие ошибки.

Мартин ГАРДНЕР

Трудно, изучая математику, не заинтересоваться
математическими софизмами. В 2003 году в
издательстве “Просвещение” вышла книга А.Г.
Мадеры и Д.А.Мадеры “Математические софизмы”, в
которой более восьмидесяти математических
софизмов, по крупицам собранным из различных
источников. Цитата из книги: “Математический
софизм представляет собой, по существу,
правдоподобное рассуждение, приводящее к
неправдоподобному результату. Причем полученный
результат может противоречить всем нашим
представлениям, но найти ошибку в рассуждении
зачастую не так-то просто; иной раз она может быть
и довольно тонкой и глубокой. Поиск заключенных в
софизме ошибок, ясное понимание их причин ведут к
осмысленному постижению математики. Обнаружение
и анализ ошибки, заключенной в софизме, зачастую
оказываются более поучительными, чем просто
разбор решений “безошибочных” задач. Эффектная
демонстрация “доказательства” явно неверного
результата, в чем и состоит смысл софизма,
демонстрация того, к какой нелепице приводит
пренебрежение тем или иным математическим
правилом, и последующий поиск и разбор ошибки,
приведшей к нелепице, позволяют на эмоциональном
уровне понять и “закрепить” то или иное
математическое правило или утверждение. Такой
подход при обучении математике способствует
более глубокому ее пониманию и осмыслению.”

Для развития познавательной деятельности
математические софизмы можно применять при
изучении математики в школе:

1. на уроках, чтобы сделать их более интересными,
   для создания проблемных ситуаций;
2. в домашних задачах, для более осмысленного
   понимания материала, пройденного на уроках
   (найти ошибку в МС, придумать свои МС);
3. при проведении различных математических
   соревнований, для разнообразия;
4. на занятиях факультативов, для более глубокого
   изучения тем математики;
5. при написании реферативных и исследовательских
   работ.

Математические софизмы в зависимости от
содержания и “прячущейся” в них ошибке можно
применять с различными целями на уроках
математики при изучении различных тем.

При разборе МС выделяются основные ошибки,
“прячущиеся” в МС:

1. деление на 0;
2. неправильные выводы из равенства дробей;
3. неправильное извлечение квадратного корня из
   квадрата выражения;
4. нарушения правил действия с именованными
   величинами;
5. путаница с понятиями “равенства” и
   “эквивалентность” в отношении множеств;
6. проведение преобразований над математическими
   объектами, не имеющими смысла;
7. неравносильный переход от одного неравенства к
   другому;
8. выводы и вычисления по неверно построенным
   чертежам;
9. ошибки, возникающие при операциях с
   бесконечными рядами и предельным переходом.

Самыми популярными являются 1-3.

Цели применения МС на уроках математики могут
быть самыми разнообразными:

• изучение исторического аспекта темы;
• создание проблемной ситуации при объяснении
  нового материала;
• проверка уровня усвоения изученного материала;
• для занимательного повторения и закрепления
  изученного материала.

Часто применяя на уроках МС, я составила с
помощью учеников на факультативных занятиях
таблицу применения МС на уроках алгебры в7-8-[
классах (Приложение1). Это
была интересная и познавательная для ребят
работа, которая завершилась важным практическим
результатом, которым можно воспользоваться при
проведении урока.

В книге[1] представлена большая группа софизмов,
которые можно применять при изучении темы
“Свойства арифметического квадратного корня”,
повторяя при этом темы “Преобразование
многочленов”, “Формулы сокращённого
умножения”.

Например:

“Все числа равны между собой”

Возьмем два произвольных неравных между собой
числа а и b и запишем для них очевидное тождество:

а-2ab+b= b-2ab+ а

Слева и справа стоят полные квадраты, т. е. можем
записать

(а-b)² = (b-а)². (1)

Извлекая из обеих частей последнего равенства
квадратный корень, получим:

a-b = b-a (2)

или 2а = 2b, или окончательно

a=b.

“Единица равна двум”

Простым вычитанием легко убедиться в
справедливости равенства

1-3 = 4-6.

Добавив к обеим частям этого равенства число ,
получим новое равенство

1-3 +
= 4-6+,

в котором, как нетрудно заметить, правая и левая
части представляют собой полные квадраты, т. е.

(1-)=(2-)

Извлекая из правой и левой частей предыдущего
равенства квадратный корень, получаем равенство:

1-=2-

откуда следует, что

1=2.

Комментарий.

По определению представляет собой некоторое
неотрицательное число, которое, будучи возведено
в квадрат, даст х². Ясно, что этому
определению удовлетворяют два числа, а именно х
и -х. Итак, если число х неотрицательно (х>0),
то =х;
если же число х отрицательно, т. е. число -х
положительно, то = — x. Отсюда заключаем, что (свойство
арифметического квадратного корня), что не
учитывается в содержании этих софизмов и
приводит к ложным выводам.

Но все же самой популярной ошибкой в софизмах
является “Деление на 0”. “Деление на нуль
является одним из наиболее распространенных
источников ошибок при проведении преобразований
различных выражений и при решении уравнений.
“Сокращение” уравнений на общий множитель
зачастую приводит либо к потере корней
уравнения, либо к приобретению посторонних
корней, либо вообще к бессмыслице.” [1]

Предупредить ошибки подобного рода поможет
рассмотрение софизмов. Например при изучении
темы “Преобразования многочленов” в 7кл.

“Неравные числа равны.”

Возьмем два неравных между собой произвольных
числа а и b. Пусть их разность равна с, т. е. а-b = с.
Умножив обе части этого равенства на а-b, получим

(а-b)² = = c(a-b),

a раскрыв скобки, придем к равенству

a²-2ab + b² = = ca-cb,

из которого следует равенство

а²— аb — ас = аb -b² -bc.

Вынося общий множитель а слева, и общий
множитель b справа за скобки, получим

а(а-b-с) = b(а-b-с). (1)

Разделив последнее равенство на (а-b-с),
получаем, что

а=b,

другими словами, два неравных между собой
произвольных числа а и b равны.

Разбор софизма: Здесь ошибка совершена при
переходе от равенства (1) к равенству а = b. Действительно,
согласно условию разность двух произвольных
чисел а и b равна с, т. е. а-b = с, откуда
а-b-с = 0. Можно записать равенство (1) в виде а-0=
b-0. Переход от равенства (1) к равенству а = b осуществляется
путем деления обеих частей (1) на равное нулю
число а-b-с = 0. Следовательно, здесь мы имеем
деление нуля на нуль, которое не имеет смысла,
поскольку равенство а0 = b0 выполняется при любых а и b. Поэтому
вывод, сделанный в софизме, что числа а и b равны,
неверен.

Неоценимую помощь оказывают МС для более
глубокого осмысления материала на уроках
геометрии. Например, софизм, который можно
использовать на уроке по теме “Окружность”,
повторяя при этом тему “Признаки равенства
треугольников”:

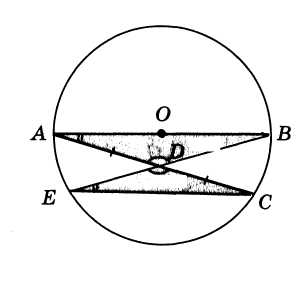
“В любой окружности хорда, не проходящая через
её центр, равна её диаметру”

В произвольной окружности проводим
диаметр АВ и хорду АС. Через середину D этой
хорды и точку В проводим хорду BE. Соединив
точки С и Е, получаем два треугольника ABD и
CDE. Углы ВАС и СЕВ равны как вписанные в
одну и ту же окружность, опирающиеся на одну и ту
же дугу; углы ADB и CDE равны как
вертикальные; стороны AD и CD равны по
построению.

Отсюда заключаем, что треугольники ABD и CDE равны
(по стороне и двум углам). Но стороны равных
треугольников, лежащие против равных углов, сами
равны, а потому

АВ=СЕ

т. е. диаметр окружности оказывается равным
некоторой (не проходящей через центр окружности)
хорде, что противоречит утверждению о том, что
диаметр больше всякой не проходящей через центр
окружности хорды.

Разбор софизма.

В софизме доказывается, что два треугольника ABD
и CDE равны, ссылаясь при этом на признак
равенства треугольников по стороне и двум углам.
Однако такого признака нет. Правильно
сформулированный признак равенства
треугольников гласит:

Если сторона и прилежащие к ней углы одного
треугольника равны соответственно стороне и
прилежащим к ней углам другого треугольника, то
такие треугольники равны.

Рассматривая МС на уроках геометрии можно в
ненавязчивой форме подчеркнуть важность
соответствия условия задачи и правильно
построенного к ней чертежа или схемы.

Например, один из самых интересных софизмов:

“Окружность имеет два центра”

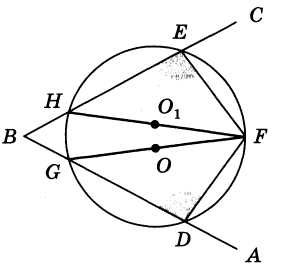
Построим произвольный угол ABC и, взяв на его
сторонах две произвольные точки D и Е,
восстановим из них перпендикуляры к сторонам
угла . Перпендикуляры эти должны пересечься (если
бы они были параллельны, параллельны были бы и
стороны АВ и СВ). Обозначим их точку
пересечения буквой F.

Через три точки D, E, F проводим окружность,
что всегда возможно, так как эти три точки не
лежат на одной прямой. Соединив точки Н и G (точки
пересечения сторон угла ABC с окружностью) с
точкой F, получим два вписанных в окружность
прямых угла GDF и HEF.

Итак, мы получили две хорды GF и HF, на
которые опираются вписанные в окружность прямые
углы GDF и HEF. Но в окружности вписанный
прямой угол всегда опирается на ее диаметр,
следовательно, хорды GF и HF представляют
собой два диаметра, имеющие общую точку F, лежащую
на окружности.

Поскольку эти две хорды, являющиеся, как мы
установили, диаметрами, не совпадают, то,
следовательно, точки О и О₁₉ делящие
отрезки GF и HF пополам, представляют собой
не что иное, как два центра одной окружности.

Разбор софизма.

Ошибка здесь кроется в неправильно построенном
чертеже. На самом деле окружность, проведенная
через точки Е, F и, обязательно пройдет через
вершину В угла ABC, т. е. точки В, Е, F и D обязательно
должны лежать на одной окружности. Тогда,
конечно, никакого софизма не возникает.

Действительно, восстановив перпендикуляры в
точках Е и D к прямым ВС и ВА соответственно
и продолжив их до взаимного пересечения в точке F,
получаем четырехугольник BEFD. У этого
четырехугольника сумма двух его противоположных
углов BEF и BDF равна 180°. Но согласно
известному в геометрии утверждению вокруг
четырехугольника можно описать окружность тогда
и только тогда, когда сумма двух его
противоположных углов равна 180°.

Отсюда следует, что все вершины
четырехугольника BEFD должны принадлежать
одной окружности. Поэтому точки G и Н совпадут
с точкой В и у окружности окажется, как и должно
быть, один центр.

Очевидна и важность геометрических фактов,
повторяемых во время разбора этого МС.

С большим интересом воспринимают МС ребята 5-6-х
классов. Например МС, где нарушены правила
действий с именованными величинами.

Один рубль не равен 100 копеек.

1 р=100 коп

10 р=1000 коп

Умножим обе части этих верных равенств,
получим:

10 р=100000 коп, откуда следует:

1 р=10000 коп.

Применение этого софизма является также
пропедевтикой использования именованных
величин при решении физических задач.

И, конечно, я всегда начинаю знакомить ребят с
математическими софизмами, утверждая, что:

“Два умножить на два будет пять”

2*2=4

44=55,

вынесем за скобки слева 4, справа5

4(11)=5(11),

разделим левую и правую часть на (11),
получим

4=5, откуда следует

2*2=5.

Начиная с этого урока, ребята с нетерпением
ждут новых МС.

Очень интересны МС древнегреческих
философов-математиков Зенона, Прокла, Перрона.
Они открывают обширное поле деятельности для
исследовательских работ учащихся. В книге [1]
представлены следующие “авторские” МС:
парадокс Зенона “Ахиллес никогда не догонит
черепаху”, софизм Прокла “Две непараллельные на
плоскости прямые не пересекаются”, софизм
Перрона “Единица есть наибольшее натуральное
число”.

Хотелось бы рекомендовать коллегам
использовать математические софизмы более
разнообразно в своей практике. Это сделает
изучение математики более увлекательным.
Огромную помощь окажет им замечательная книга
А.Г. Мадеры и Д.А.Мадеры “Математические
софизмы”.

(В Приложении 2
содержаться тексты математических софизмов из
таблицы Приложение1.)

Литература.

1. А.Г. Мадера и Д.А.Мадера, “Математические
   софизмы”, М., “Просвещение”, 2003г.
2. Обреимов В.И., , “Математические
   софизмы”,СПб,1989г.

Филиал Муниципального казенного общеобразовательного учреждения

 «Основная общеобразовательная школа села Благословенное имени

 Героя Советского Союза Георгия Дорофеевича Лопатина»  в с. Нагибово

Исследовательская работа

 «Математические софизмы»

Выполнил:

Декина София,

Ученица 5 класса

Руководитель:

Логунова О.Н.

учитель математики

I категория

с. Нагибово  

2020год

Введение……………………………………………………….……..2

1. Гипотеза ………………………………………….…………………3

2. Софизмы в математике…………………………………..……..…4

3. Анализ софизмов………………………………………………..…5

Заключение………………………………………………………..……6

Список литературы…..………………………………………………..7

Здравствуйте. Меня зовут Декина София. Я учусь в 5 классе. Мне очень нравится математика. Однажды мы пожаловались учителю, что очень много задают. А учительница сказала нам, что сейчас докажет, что вообще не учимся. Предлагаю и вам это доказательство.

Как доказать, что ученики ничего не делают?

Доказательство:

1. По ночам занятий нет, значит, половина суток свободна. Остается

365 -182 = 183 дня.

2. В школе ученики занимаются половину дня, значит, другая половина (или четвертая часть суток) может быть свободна. Остается

183 — 183:4 = 137 дней.

3. В году 52 воскресенья. Из них на каникулы приходится =15 дней, таким образом выходных в учебном году

52 -15 = 37 дней.

Итого остается

137 — 37 = 100 дней.

4. Но есть еще каникулы: осенние (= 5 дней), зимние (=10 дней), весенние (= 7 дней), летние (= 78 дней).

Всего 5 + 10+ 7+ 78 = 100 дней.

5. Итак, школьники заняты в году

100 — 100 = 0 дней.

Когда же учиться?! Где ошибка в рассуждениях?

Мне стало интересно, и наша учительница предложила мне рассмотреть другие математические софизмы.

 Я считаю эту тему очень увлекательной, развивающей познавательный интерес к урокам математики. История математики полна неожиданных и интересных софизмов.

Гипотеза. Разобрать софизм — значит найти эту ошибку.

Актуальность . Разбор софизмов прежде всего развивает логическое мышление, т.е. прививает навыки правильного мышления. Обнаружить ошибку в софизме — это значит осознать ее, а осознание ошибки предупреждает от повторения ее в других математических рассуждениях

Цель: изучить данную тему, а именно, узнать что такое софизмы

Задачи: 

1. Познакомиться с софизмами;

2. Понять, как найти ошибку во внешне безошибочных рассуждениях?

Темы для исследования:

— Что такое софизм?

— Математические софизмы

Методы исследования.

• Изучение литературных источников.
• Наблюдение и сопоставление материала.
• Просмотр сайтов в Интернете

Практическая значимость: понимание математики пригодится в жизни и в первую очередь для успешной учебы в школе, надо не только точно знать правила и формулы, но уметь находить свои ошибки и ошибочные рассуждения

Софизм – слово греческого происхождения, в переводе означающее хитроумную выдумку или головоломку.

Математический софизм представляет собой  тот частный случай, когда при разительной неверности результата ошибка, приводящая к нему, более или менее хорошо замаскирована. Раскрыть софизм — это значит указать ошибку в рассуждении.

 Предлагаю вашему вниманию несколько простейших софизмов. А вы попытайтесь найти ошибку.

1. Размещение по одному тринадцати человек в двенадцати комнатах.

Администратор одной гостиницы не отказался от решения следующей, казалось бы, неразрешимой задачи: разместить в двенадцати одноместных комнатах тринадцать человек, не допуская поселения в одной комнате двух человек.

Предупредив тринадцатого (под этим номером занесенного в список приехавших), что он временно помещается в первой комнате, предприимчивый администратор принялся за размещение остальных по одному и каждой комнате, начиная с первой.

  В итоге расселения в первой комнате оказалось два человека; третий человек был помещен во второй комнате, четвертый — в третьей, пятый — в четвертой и так до двенадцатого, который, очевидно, был вселен в одиннадцатую комнату.

  Двенадцатую комнату, которая, как видим, осталась свободной, администратор предоставил временному жильцу первой комнаты — тринадцатому клиенту гостиницы.

Выходит, что задача разрешима: 12=13

2. На двух нормальных руках одиннадцать пальцев.

В наличии десяти элементов в некоторой группе можно с одинаковым успехом убедиться как с помощью счета от одного до десяти, так и с помощью обратного счёта. присвоим пальцам числительные (номера) как на рисунке, и сложим их.

5+6=11. И так, на двух нормальных руках, одиннадцать пальцев.

3. Квадратные рубли.

Как известно, всякие два равенства можно перемножать почленно.

Применяя эту правило к следующим двум равенствам:

                1 рубль= 100 копеек , 2 рублей=200 копеек,

       Возведём левую и правую часть в квадрат;

(22 )рубля =(2002 )копеек,   или  4 рубля = 40000 копеек,
                                         что явно неверно

4.    40:8=41

Маленький Петя очень не любил считать устно. Решая задачу о дележе 40 орехов между 8 мальчиками поровну, он и в этом случае обратился к схеме письменного

деления. Выполнение действия деления у него выглядело так:

Полученный ответ, естественно, смутил Петю. Он хорошо понимал, что не может каждый из мальчиков получить больше орехов, чем их было у всех вместе, но своей ошибки в делении все-таки обнаружить не мог.

Помогите маленькому Пете понять свою ошибку.

5. Дважды два — пять!

Возьмем в качестве исходного соотношения следующее

очевидное равенство: 4:4=5:5

  После вынесения за скобки общего множителя из каждой части равенства будем иметь:

 4 (1: 1)=5 (1: 1)

Или (2*2)(1:1)=5(1:1)

Зная, что 1:1=1, получаем 2*2=5

Анализ софизмов.

1. В рассуждении допущена ошибка: второй клиент гостиницы остался без комнаты, так как об его существовании просто «забыли» при распределении номеров гостиницы.

Число может быть и количественным и порядковым. Путем сознательного смешения понятий количественного и порядкового чисел и достигается иллюзия правдоподобности приведенного рассуждения. В самом деле, мы рассуждали так.. «в итоге расселения в первой комнате оказалось два человека»— число количественное; «третий человек был помещён во второй комнате» — число порядковое. Подобная структура рассуждения и дала возможность отвлечь внимание от факта пропуска второго клиента.

2.В рассуждении допущено намеренное отождествление понятий порядкового и количественного чисел. Ошибка возникает потому, что для пальцев левой руки имеет место совпадение порядкового и количественного чисел, а для правой руки такого совпадения нет.

3. Когда мы имеем дело с деньгами возводить в квадрат рубли нельзя, так как никаких «квадратных рублей» и «квадратных копеек» не существует.

4. Из курса математики известно. Что остаток не может быть равен делителю.

5. В рассуждении создана иллюзия правдоподобия на основе ложной аналогии с распределительным свойством умножения относительно сложения. Такие ошибки невозможны, если в качестве знака деления использовать дробную черту.

4:4== 4 =4*(1:4)      и     5:5== 5 =5*(1:5)

И напоследок. В самом первом рассуждении мы установили, что ученики вообще не учатся ни одного дня. Как так получилось.  А очень просто, выходные и каникулы были посчитаны дважды.

Заключение.

О математических софизмах можно говорить бесконечно много, как и о математике в целом. Софизмы это смесь философии и математики, которая не только помогает развивать логику и искать ошибку в рассуждениях. Исследовать софизмы действительно очень интересно и необычно. Порой сам попадаешься на уловки софиста, на столь безукоризненность его рассуждений. Перед тобой открывается какой-то особый мир рассуждений, которые поистине кажутся верными. Благодаря софизмам можно научиться искать ошибки в рассуждениях других людей, научиться  грамотно строить свои рассуждения и логические объяснения. Практика обучения математике показывает, что поиск заключенных в софизме ошибок, ясное понимание их причин ведут к осмысленному постижению математики. Осознание ошибки достигается противопоставлением ложному доказательству истинного. Такой подход способствует более глубокому пониманию  и осмыслению математики.