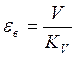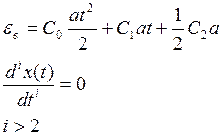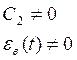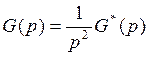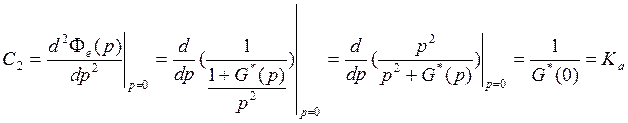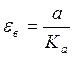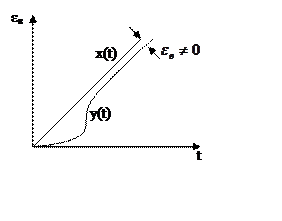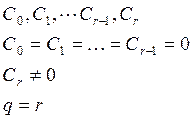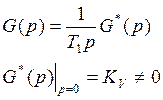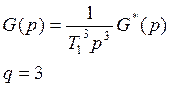Скоростная ошибка тау это - TopOshibok.ru - решение и исправление самых разных ошибок

1. Понятие об
управлении. Управлением
называется любое действие, вносящее
желаемые изменения в процесс, подлежащий
управлению. Под процессом
понимается нечто, изменяющееся качественно
или количественно во времени. Процессы
протекают в объектах различного вида.
Объекты бывают технические, экономические,
биологические, человеческие коллективы
и т.д. Нас интересуют технические объекты
и технологические процессы, протекающие
в этих объектах.

Желаемое
изменение процесса, имеющего место в
объекте, определяется целью
управления.
Цели управления весьма разнообразны.

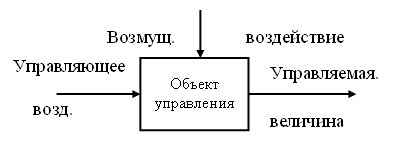
Объектом
управления
или управляемой
системой
называется техническое устройство,
выходные параметры которого необходимо
изменять по желаемому закону. Выходные
параметры объекта управления называются
выходными
величинами или управляемыми величинами.

Все внешние
воздействия, оказывающие влияние на
ход управляемого процесса, другими
словами, на объект управления, можно
разделить на полезные и «вредные».

Полезные внешние
воздействия, которые дают возможность
обеспечить протекание процесса в нужном
русле, называются управляющими
воздействиями.
Это контролируемые воздействия,
приложенные к объекту управления,
позволяет изменять ход процесса в
желаемом направлении. За их счет
реализуется цель управления.

Обычно другие
«вредные» внешние как контролируемые,
так и неконтролируемые воздействия,
изменяющие состояние объекта нежелательным
образом, называются возмущающими
воздействиями.
Почему происходят нежелательные
отклонения, причем неопределенные?

В случае корабля
положение руля и мощность сигналов,
поступающих на двигатели, являются
управляющими воздействиями. Их изменение
приводит к желаемым значениям некоторых
выходных сигналов, например курса и
скорости движения. Ветер, волны и течение
являются возмущающими воздействиями,
т.к. они стремятся нежелательным образом
повлиять на управляемые величины:
местоположение, курс и скорость корабля.
Кроме того, возмущения вызывают усиление
таких движений корабля как бортовая и
килевая качки, вертикальное перемещение.

В общем случае
связь между управляющими воздействиями,
возмущающими воздействиями, объектом
управления и управляемыми величинами
показана на рисунке ниже.

зависимости от способа формирования
управляющего воздействия различают:

1. Ручное
управление.
Осуществляется оператором, недостатки:
низкая точность, малое быстродействие.

2. Автоматизированное
управление.
Осуществляется оператором с помощью
ЦВМ. При этом оператор принимает решения,
анализируя результаты, получаемые от
ЦВМ, ЦВМ выступает как советник. Другое
название — супервизорное управление.

3. Автоматическое
управление.
Осуществляется техническими средствами
без непосредственного участия человека.
Самодействующее управление.

Техническое
устройство, с помощью которого
осуществляется автоматическое управление,
т.е. вырабатывается управляющее
воздействие, называется управляющим
устройством.
(УУ) или регулятором.

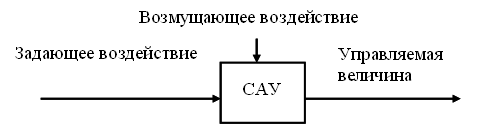
При автоматическом
управлении УУ соединяется с объектом
управления. Совокупность взаимосвязанных
между собой объекта управления (ОУ) и
управляющего устройства (УУ) называется
системой
автоматического управления (САУ).

Информация о цели
управления вводится в САУ с помощью
задающего
воздействия.

В общем случае все
эти воздействия и САУ связаны между
собой, как показано на рис. выше, и
являются векторными сигналами.

Пример.

Пусть объект
управления: помещение. Управляемая
величина: температура.

Нужно обеспечить
стабилизацию температуры, чтобы она
была постоянной. Возмущающие воздействия
– окружающая среда оказывает влияние
через окна и стены (температура горячей
воды, температура окружающего воздуха,
направление и скорость ветра).

Ручное управление.

Управляющее
воздействие – изменение расхода горячей
воды с помощью вентиля (управляющего
органа), степень открытия вентиля.

2. Автоматическое
управление.
Первое требование для управления
(регулирования) температурой в помещении
иметь устройство (датчик), которое
определяет или «чувствет» изменения
температуры. Второе требование – надо
иметь устройство (управляющее устройство),
которое изменяет подводимую в помещение
теплоту (тепловую энергию).

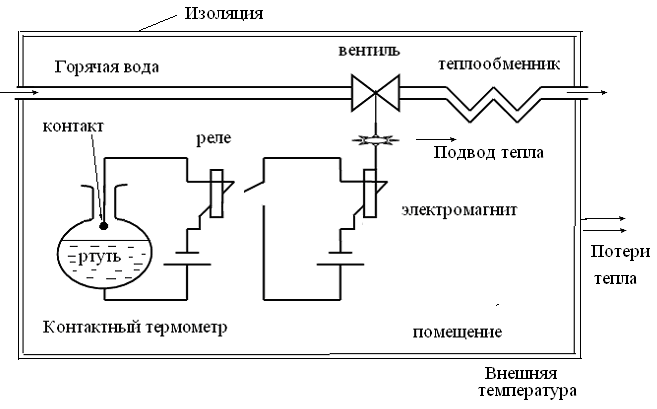
П
рерывистое
управление. Физическая реализация
системы автоматического регулирования
температуры показана на рис. ниже.

Система работает
следующим образом. Если температура в
помещении повысилась относительно
желаемого значения, столбик ртути в
термометре (датчике) поднимается,
достигает контакта, замыкается токовая
цепь, включается реле, затем срабатывает
электромагнит, вентиль закрывается,
отопление отключается. Через некоторое
время температура в помещении падает,
столбик ртути опускается, отключается
реле, вентиль открывается. Такая система
работает только на охлаждение температуры.

Вопрос №2.
Определение порядка астатизма по
передаточной функции разомкнутой
системы.

Рассмотрим замкнутую систему с единичной
обратной связью и с порядком астатизма,
равным ν, которая в разомкнутом
состоянии имеет передаточную функцию

Действительно, передаточная функция
по ошибке

где

Следовательно, коэффициент статической
ошибки согласно

будет равен:

Полагая ν≥1, разложим

в ряд Маклорена в окрестности точки
р=0:

Так как

,
то

Приравнивая коэффициенты при одинаковых
степенях р у двух последних выражений,
получаем

Следовательно, для системы с единичной
обратной связью, содержащей ν
интегрирующих звеньев, первые ν
коэффициентов ошибок обращаются в нуль,
т.е. такая система имеет ν-ый порядок
астатизма.

Определение астатической системы
порядка ν как системы, у которой
первые ν коэффициентов ошибок равны
нулю, является более общим, чем ее
определение как системы, имеющей ν
интегрирующих звеньев.

Ненулевые коэффициенты ошибок С_i
обязательно включают в себя в качестве
делителя коэффициент усиления системы.
Поэтому с увеличением коэффициента
усиления величина ненулевых коэффициентов
ошибок уменьшается.

Нужно отметить, что для системы с
единичной обратной связью основное
значение в вопросе обеспечения заданной
точности имеют коэффициент усиления и
порядок астатизма. Однако, стремление
увеличить коэффициент усиления и (или)
порядок астатизма может повлечь за
собой дестабилизацию системы.

Вопрос №3 Основные принципы управления.

Применяют два основных принципа
управления: один из них приводит к
разомкнутой системе, второй – к замкнутой
системе.

2. Замкнутые системы (системы с обратной
связью (ОС))

Остановимся на двух законах управления,
используемых в замкнутых системах.

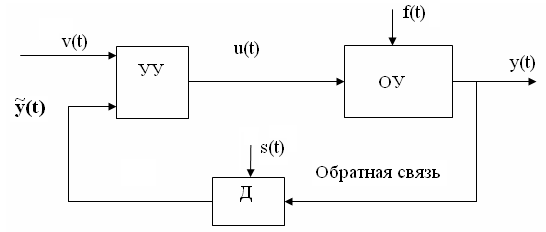
а) Управление с прямой и обратной
связью.

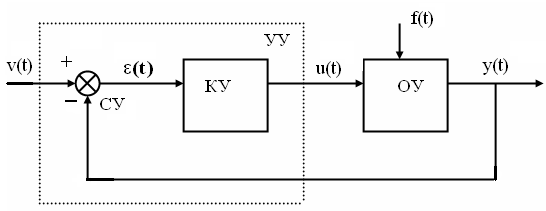
Функциональная схема замкнутой системы:

В данной системе используется
информация о результатах управления.
Она заключена в ОС. Информацию содержит

.

Закон управления с прямой и обратной
связью:

Используется только информация прошлая
и текущая (в настоящий момент времени).
Замкнутые системы обладают более высоким
качеством и большей точностью, чем
разомкнутые, т.к.:

Уменьшает влияние неопределенности и
изменчивости свойств ОУ на управляемую
величину (обеспечивают робастность).
Снижают эффект, обусловленный возмущающим
воздействием.
Позволяют изменять реакцию системы на
задающее воздействие.
Дают возможность управлять неустойчивыми
ОУ.

К недостаткам замкнутых систем следует
отнести проблемы, порождаемые обратной
связью, а именно, обеспечение устойчивости
(обратная связь может дестабилизировать
систему) и помехоустойчивости (возникает
проблема уменьшения влияния шума
измерения).

Управляющее устройство проектируется
так, чтобы обеспечить компромисс между
требованиями, предъявляемыми к
робастности, точности воспроизведения
задающего воздействия, виду реакции на
внешние воздействия, и устойчивостью
системы.

б) Принцип управления по ошибке (по
отклонению)

Этот принцип называют принципом
Ползунова-Уатта.

Пусть

и ошибка

.

Тогда закон управления по ошибке
имеет вид:

Функциональная схема системы, в которой
используется закон управления по ошибке:

Управляющее устройство (УУ) состоит из
сравнивающего устройства (СУ), определяющего
ошибку управления, и корректирующего
устройства (КУ), вырабатывающего
управляющее воздействие.

Философия таких систем весьма прозрачна:

Независимо от причины возникновения
ошибки УУ система стремится свести эту
ошибку к нулю. В сущности управляющее
устройство работает, используя
лингвистические правила:

Если ошибка больше нуля, то управление
положительное, Если ошибка меньше нуля,
то управление отрицательное, Если ошибка
равна нулю, то управление равно нулю.

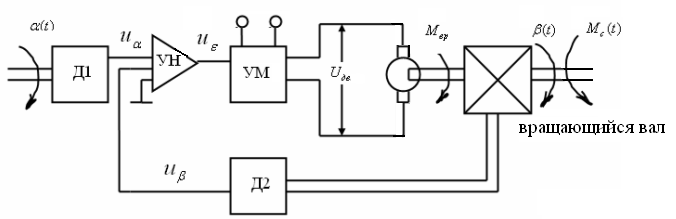
Пример. Электромеханическая следящая
система.

Здесь

(t)
— момент сопротивления,

(t)
— момент вращения.

Двигатель с вращающим валом является
ОУ. Цель управления состоит в обеспечении
примерного равенства углов поворота
задающей оси и следящего (вращающегося)
вала, т.е.

,
причем угол

изменяется случайным образом. С помощью
датчика Д1 в систему вводится информация
о цели управления. Задающий сигнал

,
где

— коэффициент пропорциональности. За
счет датчика Д2 система получает
информацию о результатах управления.
Его выходная величина

пропорциональна управляемой величине

и является сигналом ОС.

Дифференциальный усилитель напряжения
(УН) служит для вычисления разности
напряжений

и

,
и ее последующего усиления, так что его
выход

.

С учетом выражений для

сигнал рассогласования

оказывается пропорциональным отклонению
(ошибке, рассогласованию)
.

К двигателю подводится управляющее
воздействие

,представляющее
собой преобразованный усилителем
мощности (УМ) сигнал рассогласования.
Как видим, управляющее воздействие
пропорционально ошибке. Следовательно,
в системе используется принцип управления
по ошибке.

Система работает следующим образом.

Если

>0,
то

>
,
при этом сигнал рассогласования

>0,
усиленный УН и УМ, поступает на двигатель,
как

>0,
создается момент, ускоряющий вращение
вала в необходимую сторону, и вал начинает
«догонять» задающую ось; если ошибка
отрицательна

<0,

>
,
при этом

<0,
то

<0,
то к валу двигателя прикладывается
момент противоположного знака, и следящий
вал тормозится.

Для данной системы возмущающим
воздействием является момент сопротивления
(нагрузки) на валу двигателя.

В описанной простейшей системе
функции управляющего устройства сводятся
к вычитанию сигналов двух датчиков и
умножению разности (сигнала ошибки) на
постоянный коэффициент, равный
произведению коэффициентов усиления
усилителей напряжения и мощности. Как
мы убедимся в дальнейшем, для высокого
качества управления (малости ошибки)
приходится усложнять эти функции, вводя
в закон управления производные и
интегралы от ошибки.

Установившееся
значение ошибки воспроизведения в ряде
случаев определяется с помощью известной
в операционном исчислении теоремы о
конечном значении, которая применительно
к данному случаю может быть записана в
видеε_уст=
(8)

Преобразование
Лапласа ε(р) ошибки легко найти, если
известны преобразование Лапласа v(р)
входного сигнала и передаточная функция
для ошибки Ф_ε(р),
связанная с передаточной функцией Ф(р)
замкнутой системы соотношением

Ф_ε(р)=1-Ф(р) (9)Действительно,
согласно (4)ε(р)=Ф_ε(р)v(p)(10)

Принимая
во внимание существующую связь между
передаточными функциями замкнутой Ф(р)
и разомкнутой W(р)
системФ(р)=W(p)/(1+W(p)),а
также, что_,на
основании (9) имеемФ_ε(р)=

Передаточная
функция по ошибке называется также
функцией чувствительности.

Следовательно,
(11)

Учитывая,
что W₀(p)
обладает свойством W₀(0)=1
получаем
(12)

Выражение
(12) имеет смысл, если ε(t)
стремится к определенному пределу при
t→∞.
В противном случае выражение (8)
неприменимо. Рассмотрим от каких факторов
зависит ошибка ε_уст
при типовых входных сигналах, для которых
вышеуказанное требование соблюдается.

Входной
сигнал – ступенчатая функция v(t)=a₀1(t).

Операторное
выражение такой функции v(p)=a₀/p.
При этом

(13)

Если
ν=0 (система не содержит интегрирующих
звеньев), то

(14)

Следовательно,
в такой системе, даже при постоянном
входном сигнале, имеет место ошибка,
называемая ошибкой по положению или
статической ошибкой. Ошибка

при известном а₀
определяется статизмом системы
(15)

и
она тем меньше, чем больше коэффициент
усиления k.

Системы,
обладающие статической ошибкой,
называются статическими системами.
Коэффициент усиления k
статических систем является безразмерной
величиной, так как величины а₀
и ε_уст
имеют одинаковую размерность.

Отметим,
что статическая ошибка, определяемая
выражением (14), является принципиальной
(методической) ошибкой и обусловлена
принципом действия системы.

Если
ν>1 (система содержит одно или несколько
интегрирующих звеньев), то, как это видно
из выражения (13), статическая ошибка
равна нулю. Системы, обладающие нулевой
статической ошибкой, называются
астатическими системами. При этом
величина ν, как говорят, определяет
порядок астатизма системы.

Астатическую
систему можно рассматривать как
статическую систему с бесконечно большим
коэффициентом усиления k.
Действительно, наличие интегрирующих
звеньев приводит к тому, что при постоянном
входе сигнал на выходе разомкнутой
системы с течением времени растет до
бесконечности.

Входной
сигнал v(t)=a₁t,
изменяющийся с постоянной скоростью
a₁.

В
этом случае v(p)=a₁/p²,
а установившаяся ошибка

(16)

Если
ν=0 (статическая система), то ε_уст=∞.
Полученному результату легко дать
объяснение, если учесть, что в установившемся
режиме, т.е. при t→∞,
на входе системы имеется бесконечно
большой сигнал и поэтому при конечном
коэффициенте усиления k,
согласно (14), ошибка ε_уст
равна бесконечности. Другими словами,
данный случай можно рассматривать как
предыдущий при v(t)=a₀,
если положить a₀=∞.

Если
ν=1 (система с астатизмом первого порядка),
то

(17)

При
этом ошибка ε_уст
обратно пропорциональна коэффициенту
усиления и носит название скоростной
ошибки. Так как входной сигнал v
и ошибка ε имеют одинаковую размерность,
то коэффициент усиления системы с
астатизмом первого порядка имеет
размерность [сек^-1]
и характеризует установившуюся скорость
изменения выходной величины разомкнутой
системы при постоянном входном сигнале.

Физический
смысл полученного результата виден на
примере простейшей следящей системы
(рис. 1). Если на входе имеем сигнал v,
изменяющийся с постоянной линейной
скоростью a₁,
то установившийся режим будет иметь
место лишь в случае, когда выходная
величина у будет изменяться с той же
скоростью а₁.

Р
ис.
1

Но
для этого необходимо подвести к двигателю
определенное напряжение U=a₁/K_дв,
зависящее от коэффициента усиления
двигателя К_дв.
Это напряжение может появиться только
при наличии сигнала ошибки ε_уст.
Чем больше коэффициент усиления усилителя
К_ус,
а следовательно, и всей системы –
К=К_усК_дв,
тем меньшее значение ε_уст=а₁/К_ус
требуется для вращения двигателя со
скоростью, равной скорости изменения
входного сигнала.

Используя
выражение (17), по заданным значениям
скорости а₁₀
и скоростной ошибки (ε_ск)_доп
можно найти величину коэффициента
усиления

(18)обеспечивающую
требуемую точность воспроизведения
сигнала v(t)=a₁₀t.

Если
ν≥2 (система с порядком астатизма выше
первого), то скоростная ошибка равна
нулю.

Входной
сигнал

,
изменяющийся с постоянным ускорением
а₂.

Так
как

,
то ошибка с учетом (12)

(19)

Если
ν=0, 1, то установившаяся ошибка равна
бесконечности. Если ν=2 (система с
астатизмом второго порядка), то ошибка
определяется выражением

(20)

и
носит название ошибки по ускорению. Как
видно их этого выражения, коэффициент
усиления системы с астатизмом второго
порядка имеет размерность [сек^-2].

Если
ν≥3, то установившаяся ошибка равна
нулю.

Таким
образом, точность работы САУ при входных
сигналах вида степенной функции

(20а)
зависит только от порядка астатизма ν
и коэффициента усиления k
системы, причем, чем больше значения ν
и k,
тем меньше величина ошибки воспроизведения.

Формулу
(12) для определения ошибки ε_уст
удобно использовать, если входное
воздействие представляет собой степенную
функцию вида (20а). Однако на практике
часто встречаются входные сигналы,
которые меняются достаточно медленно
по известному, а порой и неизвестному,
законам. Обычно такие сигналы на некотором
текущем интервале времени можно
представить в виде ряда Тейлора. В этом
случае удобно ввести понятие о
коэффициентах ошибок, с помощью которых
нетрудно найти установившуюся ошибку
воспроизведения.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
#
#
#
#
#
#
15.04.2015104.96 Кб27ТБ.doc
#
#
#
#

Источник

Уровень сложности
Средний

Время на прочтение
6 мин

Количество просмотров 3.5K

7.1 Общие понятия о точности процесса управления

Как отмечалось в разделе 6, интегральная оценка управления складывается из 3-х основных понятий:

устойчивость САР;
точность САР;
качество переходного процесса.

Очевидно, что главным является устойчивость САР (или запас устойчивости). Если САР не устойчива или очень мал запас устойчивости, то говорить о точности (неустойчивая САР) или о качестве переходного процесса (малые запасы устойчивости) не имеет смысла.

Если САР устойчива и запасы устойчивости достаточны по величине, то понятие точность САР является весьма важным показателем.

Точность определяют по отработке САР следующих видов воздействий:

ступенчатое внешнее воздействие (управляющее или возмущающее) часто называется постоянным внешним воздействием;
линейное внешнее воздействие т.е. линейно изменяющееся внешнее воздействие (управляющее или возмущающее);
гармоническое воздействие, т.е. ;
медленно меняющееся произвольное внешнее (управляющее или возмущающее) воздействие;
другие воздействия (параболическое, импульсное и т.д.).

Наиболее часто для оценки точности САР используются постоянное (ступенчатое) и линейное воздействия.

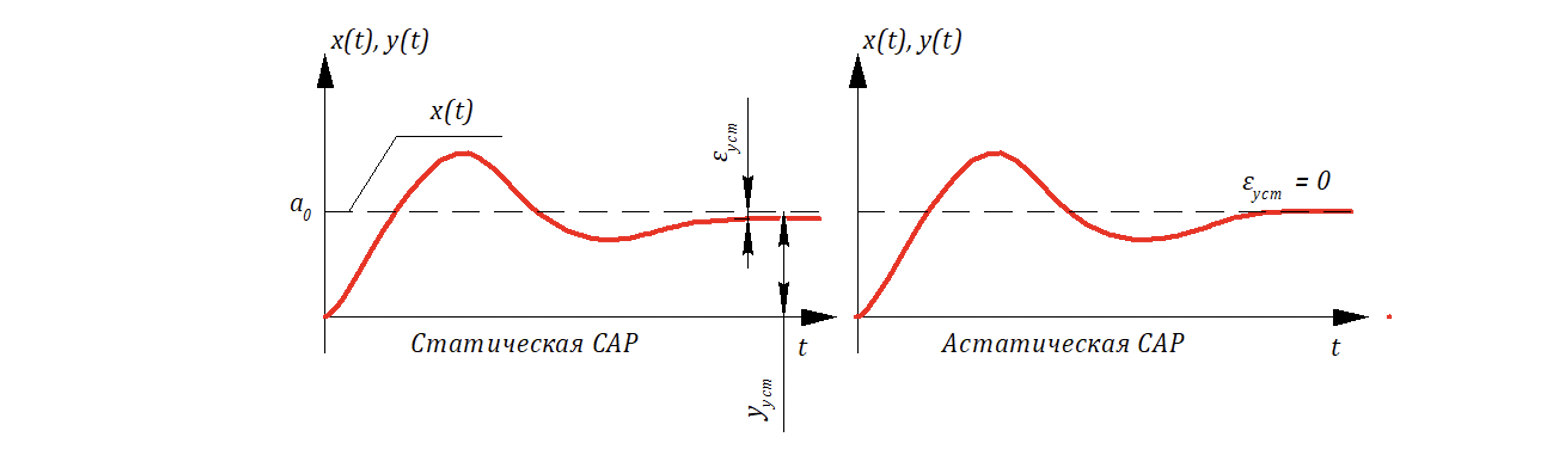
Различают статические и астатические САР:

Рисунок 7.1.1 Переходные процессы статической и астатической САР

Данные графики будем относить к следующей структуре САР:

Рисунок 7.1.2 Струкутурная схема САР для анализа устойчивости

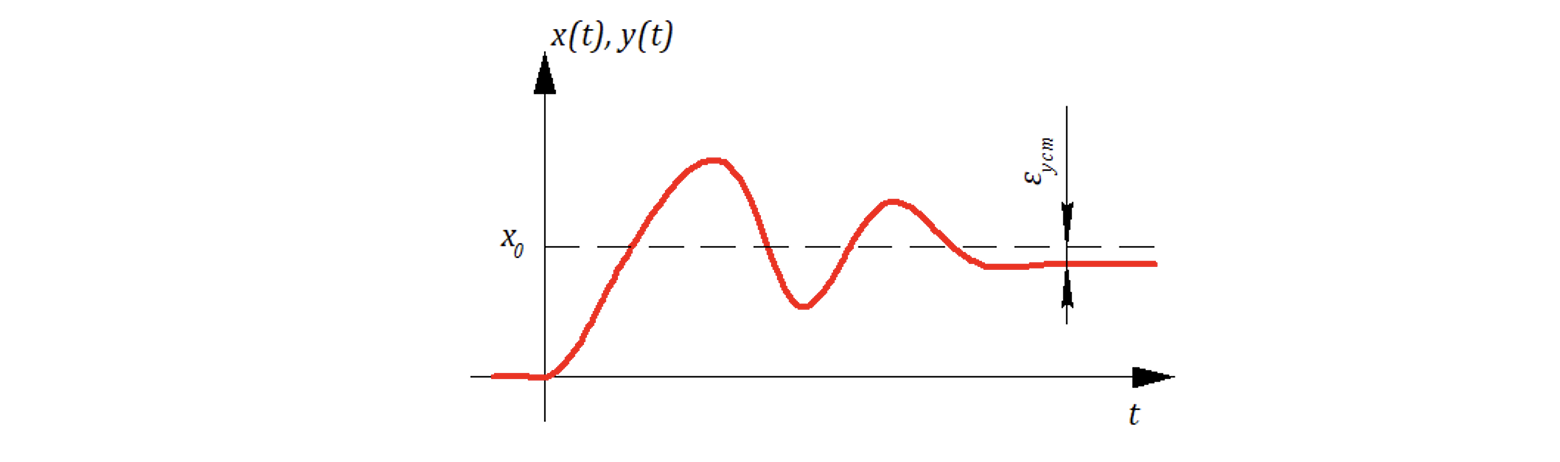
По установившейся ошибкой понимают:

$\varepsilon _{уст.}=\lim_{t\rightarrow\infty}\varepsilon(t)$

Если входное воздействие — ступенчатое, to $\varepsilon_{уст.}$ — «постоянная» ошибка.

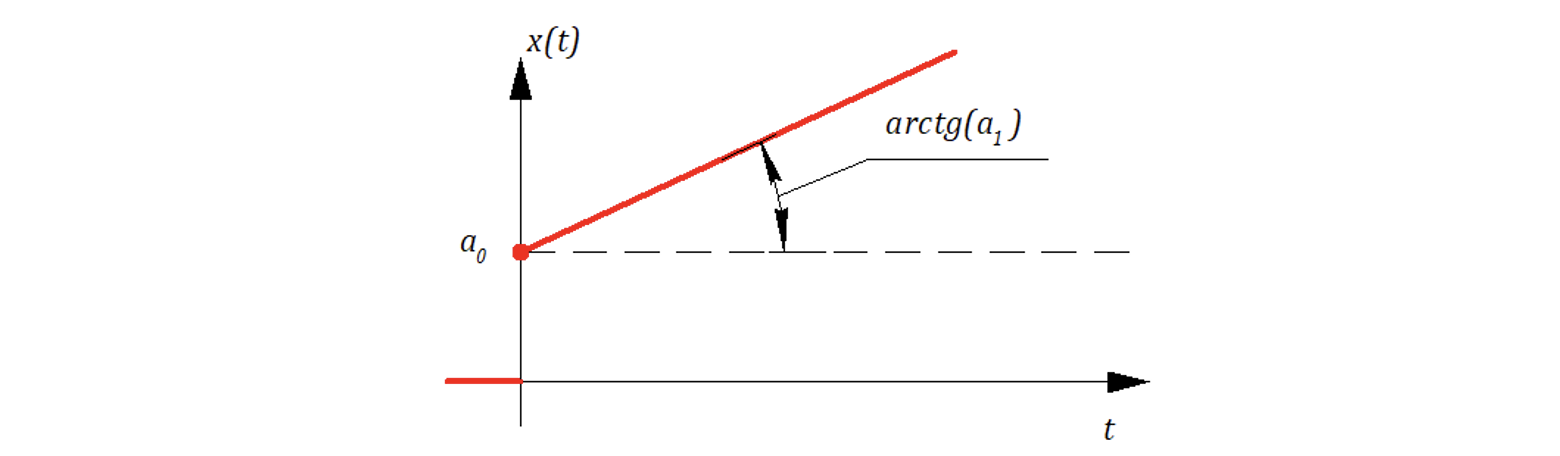
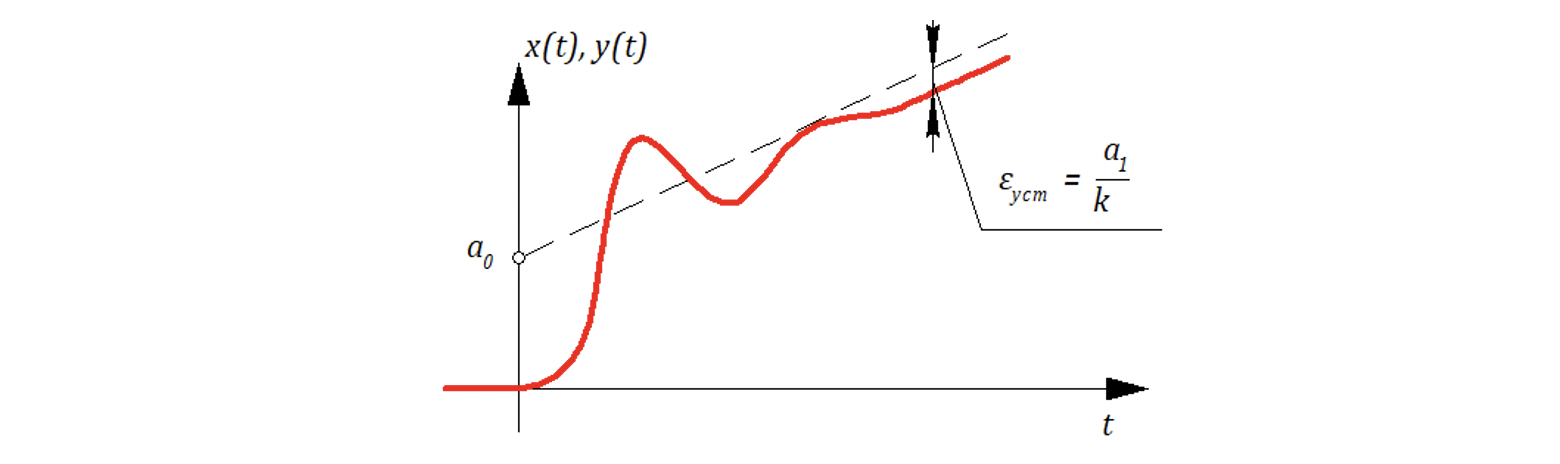
Если входное воздействие — линейное, to $\varepsilon_{уст.}$ — «скоростная» ошибка.

Различают астатизм по управляющему воздействию, а также астатизм по возмущающему воздействию, причем наличие того или иного астатизма определяется по-разному (см. следующие подразделы).

Главной задачей системы автоматического регулирования является точная и быстрая (но плавная) отработка управляющих воздействий, причем учитывая требования качества САР – точность очень важная «характеристика».

Наиболее часто точность САР оценивают по отработке управляющих воздействий. Рассмотрим последовательно различные виды управляющих (задающих) воздействий.

7.2 Точность при постоянном задающем воздействии. Постоянные ошибки

Для упрощения дальнейших преобразований будем считать, что структура САР приведена к стандартному виду (см. п.5 Передаточные функции и уравнения динамики система автоматического регулирования):

Рисунок 7.2.1 САР общего вида

Примем, что отсутствует возмущающее воздействие

Рассмотрим единичное ступенчатое воздействие $x(t)=x_0\cdot1(t);$

Считая, что замкнутая САР устойчива, найдем $\varepsilon_{уст}=\lim_{t\rightarrow\infty}\varepsilon(t)$

Примем, что свободные коэффициенты в полиномах и передаточной функции разомкнутой САР равны 1.

$W(s)=\frac{k\cdot N(s)}{L(s)}$ — передаточная функция замкнутой САР.

Используя передаточную функцию замкнутой САР (см. раздел 5) для ошибки можно записать выражение:

$\Phi_\varepsilon(s)=\frac{E(s)}{X(s)} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(7.2.1)}$

где: $\Phi(s)= \frac{k\cdot N(s)}{L(s)+k\cdot N(s)}$ — главная передаточная функция (см. раздел 5).

согласно 1-й предельной теореме (см. раздел 2)

$\lim_{t\rightarrow\infty}\varepsilon(t)= \lim_{s\rightarrow 0}s\cdot E(s) \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(7.2.2)}$

Учитывая, что единичное ступенчатое воздействие в отображениях: $x(t)=x_0\cdot1(t)\rightarrow X(s)=\frac{x_0}{s}$ :

$\lim_{t\rightarrow\infty}\varepsilon(t)=\lim_{s\rightarrow0}s\cdot \Phi_\varepsilon(s)\cdot X(s)=\lim_{s\rightarrow 0}\cdot s\cdot\frac{L(s)}{L(s)+k\cdot N(s)}\cdot\frac{x_0}{s}\Rightarrow$ $\varepsilon_{уст}=\lim_{t\rightarrow\infty}\varepsilon(t)=\frac{x_0}{k+1} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(7.2.3)}$

Т.е. если полином имеет свободный член, равный единице, то САР не может точно «отработать» постоянное воздействие, т.е. она статична.

Величина $\varepsilon_{уст}=\frac{x_0}{1+k}$ — называют постоянной или статической ошибкой.

Рисунок 7.2.2 Переходной процесс после ступенчатого воздействия для статичной САР

В случае если полином не имеет свободных членов, то его можно представить как $L(s)=s\cdot L_1(s)$ где — полином который имеет свободный член равный единицы. В этом случае установившаяся погрешность:

$\varepsilon_{уст}=\lim_{s\rightarrow0}s\cdot\frac{s\cdot L_1(s)}{s\cdot L_1+k\cdot N(s)}\cdot\frac{x_0}{s}=0 \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(7.2.4)}$

Если $L(s)=s^{v} \cdot L_1(s)$ , где — порядок астатизьма, то при постоянном (ступенчатом) воздействии установившаяся ошибка равна нулю.

$\Rightarrow \varepsilon_{уст}=\lim_{t\rightarrow\infty}\varepsilon(t)=\left\{ \begin{align} &\frac{x_0}{k+1}, если \ \ САР - статическая \\ &0, если \ \ САР - астатическая \end{align} \right.$

Из соотношения 7.2.3 очевидно, чем выше k — коэффициент усиления, тем меньше ошибка (для статических САР). Выводы: необходимо повышать общий коэффициент усиления разомкнутой САР, для сокращения ошибки.

Однако увеличение может привести к резкому уменьшению запасов устойчивости (что ухудшит качество переходного процесса) вплоть до потери устойчивости (см. раздел 6).

Цитата:

«Необходимо отметить, что для разомкнутой САР, имеющей $W(i\cdot\omega)$ годограф похожий на рис. 6.5.5 левый вариант, устойчивость системы (замкнутой) нарушится только с увеличением общего коэффициента усиления К. (Дейстивительно при увеличении коэффициента K увеличится длинна вектора и он может охватить точку -1). «

Поэтому при проектировании САР необходимо «решать» «оптимальную» задачу, т.е. выбрать оптимальное значение , обеспечивающее удовлетворительную точность и неплохое качество переходного процесса.

В последнее время практически все САР проектируются как астатические, что легко достигается за счет использования астатических регуляторов (например ПИ-регуляторов (пропорционально-интегрирующих).

В этом случае говорить о постоянной ошибке нет смысла, т.к. $\varepsilon_{уст}=0$

Пример 1:

Определить установившуюся ошибку, если входное воздействие $x(t)=0.2\cdot1(t)$ , а структура САР имеет вид:

Рисунок 7.2.3 Структура САР для анализа

Необходимо заметить, что прямое использование формулы (7.2.3) в данном случае не проходит, т.к. статическая ошибка $\varepsilon_{уст}$ в исходной САР не соответствует статической ошибке в эквивалентной САР:

Рисунок 7.2.4 Эквивалентная струкутура

Прежде чем определять статическую ошибку $\varepsilon_{уст}$ необходимо удостовериться в том, что исходная замкнутая САР устойчива. Выполеним преобразование:

$\Rightarrow \Phi(s)=\frac{W_1(s)}{1+W_1(s)\cdot W_{oc}(s)}=\frac{200\cdot(s+1)\cdot(3\cdot s+1)}{(s+s+1)\cdot(3\cdot s+1)+400\cdot(s+1)}\Rightarrow$

Характерестический полином эквивалентной передаточной функции: $D(s)=3\cdot s^3+4\cdot s^2+404\cdot s+401$

Для определение устойчивости критерий Гурвица (см. раздел 6):

$Г =\left | \begin{matrix}4 \ \ 401 \ \ 0\\ 3 \ \ 404 \ \ 0 \\ 0 \ \ 4 \ \ 401 \end{matrix} \right |=\left\{ \begin{align} &\Delta_1=4>0;\\ &\Delta_2 =\left | \begin{matrix} 4 \ \ 401\\ 3 \ \ 404 \end{matrix} \right |=4\cdot 404-3\cdot401>0; \\ &\Delta_3 =\Delta_2\cdot 401>0; \end{align} \right.$

Все главные определители матрицы Гурвица больше нуля $\Rightarrow$ САР устойчива.

Перейдя к изображению $x(t)=0.2\cdot 1(t)\rightarrow X(s)= \frac{0.2}{s}$ Найдем выражения для отклонение в изображениях:

$E(s)=X(s)-Y_1(s)=X(s)-W_{ос}(s)\cdot Y(s)=X(s)-W_{ос}(s)\cdot W_1(s)\cdot E(s)\Rightarrow$ $E(s)=\frac{X(s)}{1+W_{oc}(s)\cdot W_1(s)}$

Подставляем значения и $W_{oc}$ , имеем:

$E(s)=\frac{0.2}{s\cdot [1+\frac{200(s+1)}{s^2+s+1}\cdot\frac{2}{3\cdot s+1}]}=\frac{0.2\cdot(s^2+s+1)\cdot(3\cdot s+1)}{s\cdot[(s^2+s+1)\cdot(3\cdot s+1)+400\cdot(s+1)]}$ $\varepsilon_{уст}=\lim_{s\rightarrow 0} s\cdot E(s) = \lim_{s\rightarrow0}s\cdot\frac{0.2\cdot(s^2+s+1)\cdot(3\cdot s+1)}{s\cdot[(s^2+s+1)\cdot(3\cdot s+1)+400\cdot(s+1)]}=\frac{0.2}{401}$ $\varepsilon_{уст}\approx5\cdot10^{-4}$

7.3 Точность при линейном воздействии. Скоростные ошибки

В данном подразделе рассмотрим САР замкнутую единичной обратной связью (если обратная связь не единична, то с помощью структурных преобразований ее можно привести к единичной, подробнее об этом смотри раздел 4 Структурные преобразования систем автоматического регулирования)

Рисунок 7.3.1 САР с единичной обратной связи

где $x(t)=a_0\cdot1(t)+a_1\cdot t$ — входное воздействие.

Рисунок 7.3.2 Линейное входное воздействие

В соответствии со своим назначением устойчивая САР обязана «отслеживать» (с какой-то степенью точности) управляющее воздействие.

Воспользуемся первой предельной теоремой:

$\varepsilon_{уст}=\lim_{t\rightarrow\infty}\varepsilon(t)=\lim_{s\rightarrow0}s\cdot E (s)\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(7.3.1)}$

Рассмотрим различные варианты САР: статическую и астатическую (1-го и 2-го порядка)

Статическая САР

Передаточная функция соответствует статической САР:

$W(s)=\frac{k\cdot N(s)}{L(s)}$

где полниномы и имеют свободный член равный 1.

Отклонение в отображениях:

$E(s)=X(s)\cdot\Phi(s)$

Где — изображение входного воздействия; $\Phi_\varepsilon(s)$ — передаточная функция по возмущению:

$\Phi_\varepsilon(s)=\frac{L(s)}{(L(s)+k\cdot N(s))}$

Изображение входного воздействия $x(t)\rightarrow X(s)$ :

$X(s)=\frac{a_0}{s}+\frac{a_1}{s^2}=\frac{a_0\cdot s+a_1}{s^2}$ $\varepsilon_{уст}=\lim_{s\rightarrow 0}s\cdot E(s)=\lim_{s\rightarrow0}s\cdot\Phi_\varepsilon \cdot X(s)=\frac{L(s)}{L(s)+k\cdot N(s)}\cdot\frac{a_0\cdot s+a_1}{s^2}=\infty$ $\varepsilon_{уст}=\infty \ \ \ \ \ \ \ \ \ \ \ \mathbf{(7.3.2)}$

Вывод: Cтатическая САР не способна «отслеживать» линейное воздействие.

Астатическая САР со степенью астатизма 1

Для САР со степенью астатизма 1 полином не содержит совбодного члена равного 1, но его можно представит в виде произведения $s\cdot L_1(s)$ где — полином содержащий свободный член равный 1.

Примечание: Степень астатизма равна количеству нулевых полюсов полинома (см. раздел 5)

В этом случае установившиеся статистическая ошибка:

$\varepsilon_{уст}=\lim_{s\rightarrow 0}s\cdot E(s)=\lim_{s\rightarrow0}s\cdot\frac{s\cdot L_1(s)}{s\cdot L_1(s)+k\cdot N(s)}\cdot\frac{a_0\cdot s+a_1}{s^2}=\frac{a_1}{k}$ $\varepsilon_{уст}=\frac{a_1}{k} \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(7.3.3)}$

Вывод: Если разомкнутая САР имеет астатизм первого порядка (имеет один нулевой полюс), то установившияся ошибка для замкнутой САР $\varepsilon_{уст}={a_1}/{k}$

Рисунок 7.3.3 Реакция на линейное воздействие САР с астатизьмом 1-го порядка

Ошибка в астатической САР (1^-го порядка) называется скоростной ошибкой, а общий коэффициент часто называют коэффициентом добротности или просто добротностью.

Анализ формулы (7.3.3) показывает, что чем выше тем меньше $\varepsilon_{уст}$ . Однако необходимо помнить, что повышение может привести к потери устойчивости САР (или уменьшению запасов устойчивости с соответствующим ухудшением качества переходного процесса).(см. раздел 6).

Астатическая САР со степенью астатизма 2

Для САР со степенью астатизма 2 полином не содержит не только совбодного члена равного 1, и члена у которого степень равна 1. Такой полином можно представит в виде произведения $s^2\cdot L_1(s)$ где — полином содержащий свободный член равный 1.

В этом случае установившиеся статистическая ошибка:

$\varepsilon_{уст}=\lim_{s\rightarrow0}s\cdot\frac{s^2\cdot L(s)}{s^2\cdot L_1(s)+k\cdot N(s)}\cdot\frac{a_0\cdot s+a_1}{s^2}=0$ $\varepsilon_{уст}=0 \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(7.3.6)}$

Рисунок 7.3.4 Реакция на линейное воздействие системы с астатизьмом 2-го порядка

Очевидно, что если степень астатизма >2, то установившаяся статическая ошибка, тем более будет равна 0. Т.е. чем выше астатизм САР, тем лучше точность. Хотя повышение астатизма ухудшает устойчивость (запас устойчивости).

Модели из статьи можно взять здесь…

В предыдущих сериях:

1. Введение в теорию автоматического управления.2. Математическое описание систем автоматического управления 2.1 — 2.3, 2.3 — 2.8, 2.9 — 2.13.

3. Частотные характеристики звеньев и систем автоматического управления регулирования. 3.1. Амплитудно-фазовая частотная характеристика: годограф, АФЧХ, ЛАХ, ФЧХ. 3.2. Типовые звенья систем автоматического управления регулирования. Классификация типовых звеньев. Простейшие типовые звенья. 3.3. Апериодическое звено 1–го порядка инерционное звено. На примере входной камеры ядерного реактора. 3.4. Апериодическое звено 2-го порядка. 3.5. Колебательное звено. 3.6. Инерционно-дифференцирующее звено. 3.7. Форсирующее звено. 3.8. Инерционно-интегрирующее звено (интегрирующее звено с замедлением). 3.9. Изодромное звено (изодром). 3.10 Минимально-фазовые и не минимально-фазовые звенья. 3.11 Математическая модель кинетики нейтронов в «точечном» реакторе «нулевой» мощности.

4. Структурные преобразования систем автоматического регулирования.

5. Передаточные функции и уравнения динамики замкнутых систем автоматического регулирования (САР).

6. Устойчивость систем автоматического регулирования. 6.1 Понятие об устойчивости САР. Теорема Ляпунова. 6.2 Необходимые условия устойчивости линейных и линеаризованных САР. 6.3 Алгебраический критерий устойчивости Гурвица. 6.4 Частотный критерий устойчивости Михайлова. 6.5 Критерий Найквиста.

Источник

C₁V –
скоростная ошибка, ошибка от скорости.

С₁
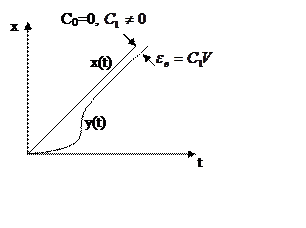
– коэффициент скоростной ошибки.

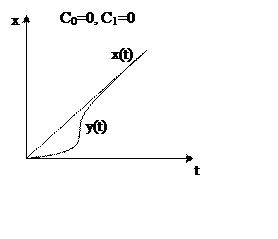q=1, I
порядок астатизма Данная система называется системой
с астатизмом второго порядка и она содержит в разомкнутой системе 2 и более
интеграторов.

Определим коэффициент С₁ для системы с
первым порядком астатизма

K_V – Добротность
системы по скорости.

— статический
коэффициент усиления позиционной части

разомкнутой системы.

Можно сказать, что общее значение

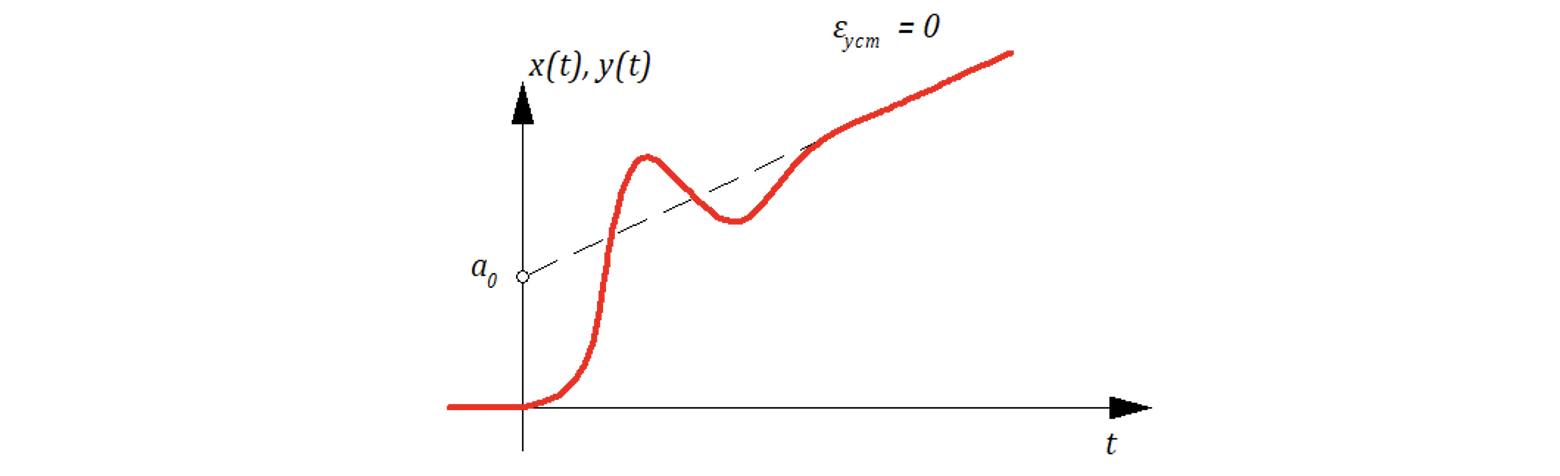
5.2.3 Режим изменения задающей величины с постоянным
ускорением.

Пусть

— ускорение

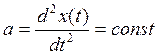
Чтобы система имела необходимо,
чтоб С₀, С₁=0, иначе ошибка будет неограниченно расти.

Установившееся значение ошибки

С₂ – коэффициент ошибки от ускорения

Система с ошибкой от ускорения

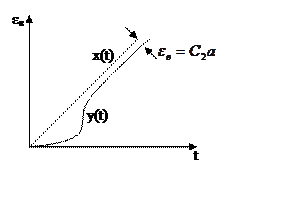Система
с астатизмом второго порядка (q=2), содержит в разомкнутом виде два интегрирующих
звена.

— позиционная часть разомкнутой
системы.

Система без ошибки от ускорения

Если в системе С₂=0, ε_в=0, то
это система без ошибки от ускорения.

Система
с астатизмом выше второго порядка

q>2

Свяжем С₂ с передаточной функцией
разомкнутой системы

— коэффициент
усиления позиционной части разомкнутой системы, добротность системы по
ускорению.

5.2.4 Связь астатизма системы с ЛАЧХ разомкнутой
системы.

Порядок астатизма – целое число q, которое равно
порядку в описании входного сигнала , при котором
установившаяся ошибка постоянна и отлична от нуля.

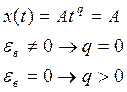
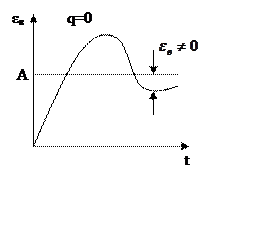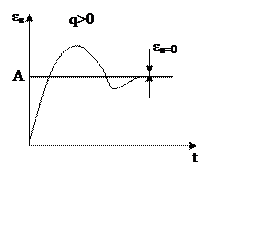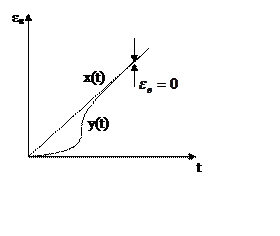
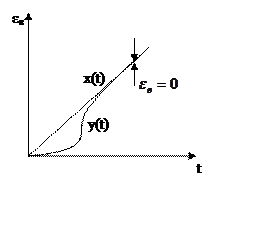
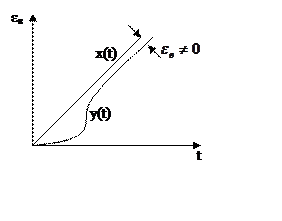q=2
q>2

На практике астатизм выше второго порядка (q>2)
не применяется, поэтому мы их не рассматриваем.

5.2.5 Способы определения порядка астатизма

1. По коэффициентам ошибок

2. По количеству интегрирующих звеньев в передаточной
функции разомкнутой системы.

— позиционная
часть системы

Система имеет r интеграторов и q=r

3.По наклону ЛАЧХ в низкочастотной области.

Предположим, что передаточная функция разомкнутой
системы имеет вид

Тогда
ЛАЧХ будет иметь следующий вид.

Пусть , где

— позиционная
часть

Этот случай в жизни практически не встречается

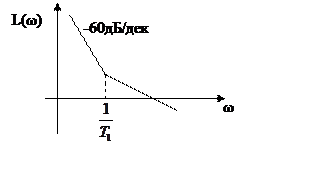
В итоге, астатизм системы определяется по ЛАЧХ
следующим образом

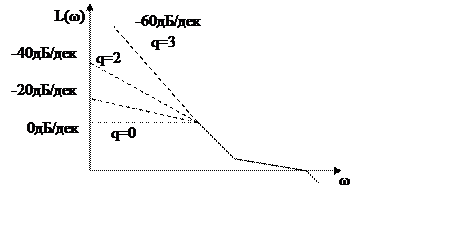5.2.6 Исследование точности в условиях действия
управляющих и возмущающих сигналов

В общем случае на систему действуют как управляющие
(задающие), так и возмущающие сигналы.

Источник

§ 19.1. Статические и скоростные ошибки автоколебательных систем

В предыдущих главах исследовались симметричные автоколебания как результат свободного движения системы (т. е. без внешнего воздействия) при симметричных нелинейностях. Однако, как будет показано, важное практическое значение имеет также рассмотрение несимметричных автоколебаний.

Несимметрия автоколебаний может вызываться различными причинами;

1) несимметричностью нелинейной характеристики как при наличии, так и при отсутствии внешних воздействий;

2) наличием постоянного или медленно меняющегося внешнего воздействия при симметричных нелинейностях;

3) наличием постоянной или медленно меняющейся скорости изменения внешнего воздействия при симметричных нелинейностях (для тех случаев, когда постоянное воздействие не вызывает смещения центра колебаний; обычно это имеет место в следящих системах и вообще в астатических системах).

В самом деле, если имеется несимметричная нелинейная характеристика (например, рис. 19.1, а, б), то даже при симметричных колебаниях переменной возникают несимметричные по амплитуде колебания переменной (рис. 19.1, б).

Рис. 19.1.

Если же нелинейность симметрична (например, рис. 19.2, а, б), то при наличии постоянного внешнего воздействия (или в астатических системах при наличии постоянной скорости изменения внешнего

воздействия) смещается центр колебаний переменной вследствие чего колебания переменной становятся несимметричными по амплитуде и по времени (рис. 19.2, а) или только по времени (рис. 19.2, б).

Рис. 19.2.

Пусть задана автоматическая система, динамика которой описывается уравнением

В данном параграфе будем считать для статических систем или же для астатических систем. Астатической системой называется такая, в которой многочлен имеет общий множитель , т. е. .

Поэтому запишем уравнение (19.1) в виде

где соответственно

При этом решение нелинейного уравнения (19.1), в отличие от прежнего (§ 18.2), ищется в форме

причем а, являются неизвестными постоянными.

С учетом величины смещения первые члены разложения в ряд Фурье вместо (18.6) и (18.7) следует записать в виде

где при обозначении

Отсюда видно, что в общем случае все три коэффициента являются функциями трех неизвестных:

В частных случаях эти зависимости могут быть более простыми.

Подстановка выражений (19.4) и (19.5) в заданное дифференциальное уравнение (19.1) с учетом свойства фильтра (см. § 18.2) дает

Это уравнение разбивается на два:

При таком разделении сохраняются существенно нелинейные свойства и отсутствие суперпозиции решений, так как остается нелинейная взаимосвязь обоих уравнений через соотношения (19.7).

Можно предложить два метода решения задачи.

Первый метод состоит в следующем. Уравнение (19.9) совпадает с прежним уравнением (18.33); отличие состоит лишь в том, что теперь коэффициенты q и согласно (19.7) зависят не только от а и , но и от смещения Поэтому, написав как прежде, характеристическое уравнение

заменив на ивыделив вещественную и мнимую части, в отличие от (18.36), получим здесь два алгебраических уравнения с тремя неизвестными:

Эти уравнения дают возможность определить амплитуду и частоту автоколебаний как функции постоянной составляющей

Для решения этой задачи можно применять любой из способов, описанных в § 18.2, в зависимости от того, какой из них лучше подходит к условиям заданной конкретной задачи. Таким же способом можно определить зависимость а и не только от но и от параметров системы с целью выбора последних. Что касается тех способов § 18.2, где используются графики и , то здесь их необходимо строить в виде серии кривых при разных постоянных значениях (рис. 19.3).

После того как из уравнений (19.11) определены зависимости (19.12), можно, воспользовавшись первым из выражений (19.7), найти функцию смещения

Подставив ее в (19.8), получим алгебраическое уравнение

с одной неизвестной которая отсюда и определяется. Чаще всего это уравнение относительно является трансцендентным и решается графически. Затем согласно (19.12) определяются также амплитуда и частота

Указанную зависимость (19.12) амплитуды и частоты автоколебаний от величины смещения центра колебаний, характерную именно для нелинейных систем (в линейных системах смещение центра колебаний не играет роли), надо всегда иметь в виду.

Рис. 19.3.

При одних нелинейностях она может быть весьма существенной, при других — менее существенной.

Второй метод решения той же задачи состоит, наоборот, в том, что сначала решается уравнение (19.8), где согласно (19.7) будет или часто . Решение получает вид

Это решение подставляется затем в уравнения (19.11), которые, таким образом, буду! содержать только две неизвестные: Определив последние (по любому из способов § 18.2), вычисляем потом по (19.15) и величину которая будет в результате зависеть от формы нелинейности, от параметров системы и от внешнего воздействия

Величина и является искомой статической или скоростной ошибкои соответственно для статической и астатической систем.

В тех случаях, когда передаточная функция линейной части системы имеет нулевой корень в знаменателе (что часто бывает), т. е. когда вместо (19.14) получаем уравнение

откуда определяется статическое отклонение или скоростная ошибка

В случае, когда при отсутствии внешнего воздействия определяются автоколебания в системе с несимметричной нелинейностью, т. е. нелинейностью или же для которой

вместо уравнения (19.8) получаем

Оно решается любым из тех же двух методов, описанных выше для уравнения (19.8). Одновременно согласно (19.11) определяются

Если в этом случае знаменатель передаточной функции линейной части системы имеет нулевой корень, то и, следовательно, уравнение (19.18) с учетом (19.13) принимает вид

откуда определяется Это означает, что в указанных системах возникает такое смещение колебаний переменной х, которое ликвидирует свойственную данной нелинейности несимметрию колебаний переменной F (т. е. обеспечивается ), как показано, например, на рис. 19.4 в отличие от рис. 19.1, б.

Приведем пример исследования совместного влияния двух внешних воздействий, причем из дальнейшего будет видно, что, в отличие от линейных систем, здесь нельзя просто складывать статические ошибки от отдельно взятых в ействий.

Уравнения автоматической системы (рис. 19.5) заданы в виде

где — простейшая симметричная релейная характеристика, показанная на рис. 19.5:

Чтобы воспользоваться выведенными выше общими формулами, надо сначала привести заданную систему уравнений (19.20) — (19.22) к одному уравнению типа (19.1).

Рис. 19.4.

Рис. 19.5.

В результате получаем

Пусть является задающим воздействием, изменяющимся с постоянной скоростью:

которое требуется воспроизвести на выходе системы в виде Допустим также, что второе внешнее воздействие является возмущающим и имеет постоянную величину (например, постоянная нагрузка на выходном валу системы):

Его влияние требуется свести к минимуму. Найдем установившуюся ошибку на выходе системы. Правая часть уравнения (19.24) будет при этом постоянной, и установившееся решение для х с учетом автоколебаний следует искать

в виде

Гармоническая линеаризация нелинейности (19.23) при этом согласно (19.6) дает

В данной задаче согласно (19.24) уравнение (19.9) для периодических составляющих получит вид

а уравнение (19.8) для постоянных составляющих будет

где согласно (19 24)-(19.26)

Выше были указаны два метода решения задачи. Для иллюстрации обоих методов решим данную задачу каждым из них.

Согласно первому методу сначала решается уравнение (19.29) для определения зависимостей

Характеристическое уравнение здесь будет

и уравнения (19.11) поэтому примут вид

Исключая отсюда находим частоту автоколебаний

Частота в данной задаче оказалась не зависящей от смещения , а следовательно, и от величины внешнего воздействия. Затем, подставляя в первое из уравнений (19.33) выражение q из (19.28) и из (19.34), получаем биквадратное уравнение для отыскания зависимости амплитуды автоколебаний от смещения

где величина

представляет собой амплитуду автоколебаний в данной системе при отсутствии смещения (при ). Отсюда

Полученное выражение мояшо записать также в виде

если обозначить

Результат (19.37) или (19.38) и представляет собой искомую зависимость

Далее, согласно первому методу решения задачи подставим полученное значение амплитуды из (19.38) в выражение (19.28) для откуда с использованием (19.39) найдем функцию смещения

где А определяется через параметры системы формулой (19.36).

Подставив величину (19.40) в уравнение (19.30) для постоянных составляющих, с учетом (19.31) и (19.36) получим

Сравнивая это с формулой (19.39), видим, что для искусственно введенной ранее величины а можно записать следующее выражение:

Эта величина характеризует совокупность приложенных к системе внешних воздействий. Учитывая это, из формулы (19.38) находим амплитуду автоколебаний

Существенно то, что амплитуда автоколебаний зависит не только от параметров системы (см. (19.36)), но еще и от величины внешних воздействий. Эта зависимость нелинейная. В данном случае при увеличении внешних воздействий амплитуда уменьшается по закону косинуса, в то время как частота не зависит от внешних воздействий.

Из формулы (19.43) видно, что автоколебания существуют до тех пор, пока величины внешних воздействий удовлетворяют условию

При этом амплитуда автоколебаний изменяется в пределах

Таков первый метод определения установившихся величин смещения амплитуды и частоты автоколебаний при наличии внешних воздействий.

Проиллюстрируем также и второй метод. Согласно второму методу сначала решается уравнение (19.30). По (19.30) и первой из формул (19.28) находим

или, с учетом (19.31),

Для отыскания входящей сюда амплитуды а воспользуемся уравнением (19.29). Характеристическое уравнение для него будет (19.32), и уравнения (19.11) поэтому примут вид:

где согласно (19.28) и (19.45)

Исключая из уравнений (19.46) величину находим частоту автоколебаний

Подставив найденные выражения q в первое из уравнений (19.46), найдем амплитуду автоколебаний

где величина

является амплитудой автоколебаний при отсутствии внешних воздействий (при

Подставив найденное выражение амплитуды (19.49) в формулу (19.45) получим окончательно величину смещения

Как видно, второй метод в данной задаче приводит к тем же самым результатам значительно более коротким путем, чем первый, что очень важно для практических расчетов (принципиально же оба метода эквивалентны друг другу). По-видимому, большая простота второго метода будет иметь место и в большинстве других задач.

В этом втором методе, в отличие от первого, функция смещения не определяется. Однако последняя может понадобиться в дальнейшем для других целей. Но ее тоже легко можно определить при использовании второго метода. Здесь величины и их отношение выражены через величины внешних воздействий. Функция же смещения не должна содержать ни величин внешних воздействий, ни амплитуды зависящей от них. Подставив значение квадратной скобки из (19.51) в (19.45), получим

а подставив это в первую из формул (19.28), сразу получим искомую функцию смещения

где А выражается только через параметры системы согласно (19.50).

Важно отметить, что функция смещения не зависит ни от числа внешних воздействий, ни от характера их изменения (если они постоянные или медленно меняющиеся), что наиболее наглядно было видно из первого метода решения задачи.

Итак, двумя разными методами определена величина смещения автоколебаний на входе реле. Найдем теперь установившуюся ошибку на выходе системы Поскольку на выходе должно воспроизводиться внешнее воздействие то согласно рис. 19.5 и второму уравнению (19.20) ошибка данной системы выражается величиной установившееся решение для которой, следовательно, и надо искать. Выразив переменную через х, которая уже известна, из заданных уравнений системы (19.20) и (19.21) получаем

Учитывая (19.25) и (19.27), перепишем данное уравнение в виде

В соответствии с видом правой части установившееся решение этого линейного уравнения следует искать в виде

где — постоянные, а — периодическая составляющая.

Подставив это в (19.54), получим три уравнения для отыскания указанных величин:

Второе из них дает

Тогда из (19.56) находим

где определяется формулой (19.51) через внешние воздействия. Наконец, из уравнения (19.58) получаем амплитуду автоколебаний переменной

где определяется формулой (19.49) через внешнее воздействие, а — формулой (19.48).

Итак, в данной системе имеются все три составляющие ошибки (19.55), зависящие от величины внешних воздействий и от параметров системы. Наиболее нежелательной из них является составляющая возрастающая пропорционально времени. Поэтому систему необходимо видоизменить в первую очередь так, чтобы уничтожить эту составляющую ошибки, т. е. сделать Для этого можно было бы вовсе изъять дополнительную обратную связь (рис. 19.5), так как при кос согласно (19.59) будет Однако при этом существенно возрастает амплитуда автоколебаний (19.61), т. е. периодическая составляющая ошибки. Поэтому более целесообразной мерой будет замена жесткой обратной связи на гибкую . Тогда в уравнении (19.54) величина заменится на :

Как видим, составляющая, пропорциональная времени, в правой части уравнения исчезла, вследствие чего установившееся решение для ошибки х в отличие от (19.55), будет

При этом из (19.62) находимз

причем изменяются, конечно, и формулы для (их можно получить таким же способом). Подбором параметров системы амплитуду автоколебаний ошибки можно сделать весьма малой.

Источник

1. Точность САУ

2. План

1 Общие положения
2 Понятие о типовых режимах САУ
3 Теорема о предельном значении оригинала и
методика определения установившихся
ошибок
4 Ошибки статических и астатических САУ в
типовых режимах
5 Ошибки САУ при произвольных входных
сигналах (коэффициенты ошибок)
6 Методы повышения точности САУ

3. 1 Общие положения

Точность является важнейшим критерием
качества систем. В настоящее время
практически все многочисленные
элементы любых технических систем
изготавливаются автоматически т.е. с
помощью САУ. Таким образом точность
САУ определяет качество продукции,
товаров, их надежность,
энергопотребление, долговечность и т.д.
и т.п.

4. 2 Понятие о типовых режимах САУ

Точность САУ принято оценивать по величине
ошибок в типовых режимах. Типовыми
называются режимы просто описываемые
математически и имеющие четкий
физический смысл. К ним относятся:
— режим покоя, когда х(t)=const;
— режим линейно-нарастающих сигналов, когда
х(t)=a*t, где а=const;
— режим гармонических входных сигналов,
когда х(t)=A*sinωt.

5.

ε
Итак, нам необходимо вычислить
установившуюся ошибку ε(t) при t→∞,
при типовых режимах и по ней можно
будет судить о точности САУ.

6. 3 Теорема о предельном значении оригинала и методика определения установившихся ошибок

Сформулируем для этого теорему о
предельном значении оригинала:
limX(t)=limX(s),
t→ ∞
s→ 0
т.е. предел оригинала при t→∞ равен
пределу изображения по Лапласу при
s→0.

7.

Передаточная функция САУ по ошибке:
( s)
1
F (s)
x( s ) 1 w p ( s )
Итак, чтобы определить установившуюся (при t→ ∞)
ошибку САУ нужно:
— Найти x(s) зная x(t)
— Определить Fε(s)
— Найти ε(s)= X(s) * Fε (s)
— Определить εуст= lim ε(s)
S→0

8. 4 Ошибки статических и астатических САУ в типовых режимах

Рассмотрим ошибки САУ в типовых режимах:
1. Ошибка САУ в покое (статическая ошибка)
X(t)=X0=const X(s)=X0
K
Пусть W p ( s )
— статическая
(T1S 1)(T2 S 1)
САУ, поскольку в знаменателе нет
множителя S, т.е. интегрирующего элемента
в системе

9.

По теореме о предельном значении аргумента
1
ст lim (t ) lim (s) (s) * F (s) (s) *
t
s 0
1 Wp ( s)
Подставляя Wp(s) в (1) получим:
X 0 (T1S 1)(T2 S 1)
X0
ст lim
s 0 (T S 1)(T S 1) K
1 K
1
2
(1)

10.

Статическая ошибка в
статической САУ в
(1+К) раз меньше
входной величины.
y(t)
X0
εст
t

11.

Пусть теперь
— астатическая САУ (есть
интегратор, т.е.
множитель S в знаменателе передаточной
функции)
K
W p ( s)
S (T1S 1)
ст
X 0 *1
X 0 S (TS 1)
lim (s) lim
lim
0
s 0
s 0 1 W ( s )
s 0 K S (TS 1)
p

12.

Таким образом,
статическая ошибка
в астатической САУ
равна 0
y(t)
X0
εст=0
t

13.

2. Второй типовой режим — движение с постоянной
скоростью (скоростная ошибка)
x(t)=at
a=cost
x( s)
a
s
Пусть:
K
W p ( s)
— статическая САУ
(T1S 1)(T2 S 1)
Тогда:
a (T1S 1)(T2 S 1)
(
t
)
lim
t a s 0 s K (T1S 1)(T2 S 1)

14.

x(t)=at
εα→∞
y(t)
α
t
tgα=a
Ошибка в статической
САУ при линейнонарастающем входном
сигнале x(t)=at
возрастает до ∞.
Т.о. статические САУ в
таком режиме не
работоспособны.

15.

Пусть теперь
K
Wp ( s)
S (TS 1)
— астатическая САУ
Тогда
S ( ST 1)
a
a
*
t a ( t ) lims 0(s) lim
s 0 s
K S (TS 1) K

16.

a
a
K
x(t)
y(t)
t
Т.о. в астатических
САУ при x(t)=at
a=const
устанавливается
ошибка в “К” раз
меньше чем “a”, т.е.
они работоспособны
в таких режимах.

17. 3. Третий режим — гармонических входных сигналов.

Пусть x(t)=xmsinωkt
xm,ωk – амплитуда и
частота “качки”.
x(s)
ε(s)
Wp(S)
y(s)

18. Определим амплитуду εm ошибки САУ в этом режиме.

Для этого найдем:
1
( s)
F ( s)
1 W p ( s ) x( s )
— ПФ САУ по ошибке
Подставим S=jωk
X ( j k )
( j k )
1 Wp ( j k )
(1)

19. Выражение (1) справедливо и для амплитуд, т.е.

m
xm
Xm
1 W p ( j k ) W p ( j k )
Откуда следует:
W p ( j k )
Ак
20 lg
xm
xm
(2)
m
Прологарифмируем (2):
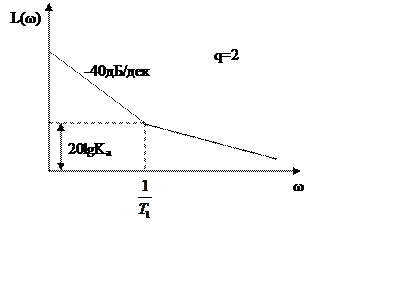
L(ω)
m
ω
ω=ωk
Ак – контрольная точка
20 lg W p ( j k ) 20 lg
xm
m
(3)

20.

Из (3) следует, что САУ будет иметь амплитуду
ошибки не более допустимой εдоп, если
20 lg W p ( j k ) L( k ) 20 lg
xm
доп

21. Т.о. чтобы ошибка САУ в гармоническом режиме не превышала допустимой εдоп необходимо:

1. Определить положение контрольной точки
Ак с координатами:
xm
ω=ωк и 20 lg
доп
2. Обеспечить прохождение L(ω) выше
контрольной точки Ак

22. 5 Ошибки САУ при произвольных входных сигналах (коэффициенты ошибок)

Пусть на вход САУ действует сигнал x(t)
произвольной формы. Чтобы определить
ошибку ε(t) в этом случае найдем вначале ее
изображение.
x(s)
ε(s)
Wp(S)
y(s)

23.

( s)
Поскольку:
1
F ( s)
x( s ) 1 W p ( s )
(1)
То:
x( s )
( s)
1 Wp ( s)
(2)
Разложим далее Fε(s) по возрастающим
степеням S в ряд, тогда (2) можно записать в
виде:
C2 2 C3 3
( s ) C0 C1S S S x( s )
2!
3!
(3)

24.

При нулевых начальных условиях
S p
d
dt
и переходя в (3) к оригиналам можно записать
2
dx(t ) C2 d x(t )
(t ) C0 x(t ) C1 *
*
2
dt 2! dt
Величины С0, С1, С2 … называются
коэффициентами ошибок САУ.
(4)

25. Чтобы определить ошибку САУ при произвольной форме входного сигнала x(t) необходимо:

1. Определить передаточную функцию
САУ по ошибке Fε(s);
2. Разложить в ряд Fε(s) путем деления
ее числителя на знаменатель и найти
коэффициенты С0, С1, С2 …;
3. Подставить коэффициенты ошибок в
(4) и найти установившуюся ошибку
ε(t).

26. Пример

Найти ошибку в САУ при:
Если:
bt 2
x(t ) x0 at
2
K
W p (s)
S (T1S 1)(T2 S 1)

27. Решение:

1.Найдем
1
F (s)
1 Wp ( s)
1
S (T1S 1)(T2 S 1)
T1T2 S 3 (T1 T2 ) S 2 S
F ( s)
1 W p ( s) K S (T1S 1)(T2 S 1) T1T2 S 3 (T1 T2 ) S 2 S K

28. 2. Разложим (1) в степенной ряд путем деления числителя на знаменатель

S (T1 T2 ) S T1T2 S
2
—
—
3
1
1
S S 2 * (T1 T2 ) S 3 …
K
K
1 2
T T 3
T1 T2 S T1T2 1 2 S …
K
K
1 2
T1 T2 S …
K
K S (T1 T2 )S 2 T1T2 S 3
1 2
1 1
S * T1 T2 S
K
K K

29.

Ограничимся первыми тремя членами
ряда, т.к. входной сигнал X(t) имеет
лишь три не нулевых первых
производных.

30.

3. Итак:
1
1 2
T1T2
F ( s ) S
2 S
K
K
K
(5)
Сопоставляя (5) и (4) имеем коэффициенты
ошибок:
T1T2
1
1
С0=0
C2 2
2 (6)
C1
K
K
K

31.

4. Определим далее производные от X(t):
bt 2
x(t ) x0 at
2
dx(t )
a bt
dt
d 2 x(t )
b
dt
(7)

32.

5. Подставляя коэффициенты С0, С1, С2… и
производные (7) в (4) получим:
1
1
T1T2
(t ) * (a bt )
2 *b
K
K
K
Т.е. ошибка с течением времени будет
нарастать до ∞ из-за члена “bt”.

33. 6 Методы повышения точности САУ

Анализируя выражения для
коэффициентов ошибок отметим, что:
1. Все коэффициенты обратнопропорциональны коэффициенту К –
усиления системы;
2. Чем выше порядок астатизма “v” тем
большее количество первых
коэффициентов ошибок равны 0

34. ВНИМАНИЕ

Порядок астатизма “v” определяется числом
интегрирующих звеньев в контуре системы.
Формально “v” равно показателю степени
множителя S в знаменателе передаточной
функции wp.
N ( s)
wp v
S M ( s)

35. 1. Первый способ повышения точности САУ – увеличение К

Т.о. самым универсальным способом
повышения точности САУ являются
увеличение коэффициента К усиления
системы. При этом все коэффициенты
ошибок уменьшаются, а это означает, что
система во всех режимах работы будет иметь
меньшие ошибки. Однако этот способ
снижает запасы устойчивости системы и рано
или поздно приводит к полной потере
устойчивости. Это можно показать на
примере критерия Найквиста.

36.

Im
K2>K1
К1
К2
-1;j0
wp(jω)
Re

37. 2. Способ повышения точности САУ – путем увеличения астатизма “v”

Этот способ исключает первые коэффициенты в
ряду ошибок. Действительно:
v=0 (статическая САУ)
Все коэффициенты не
равны 0, т.е. с0≠0 с1≠0
с2≠0 …, т.е. статическая
система в любых
режимах работы, в т.ч. и
в покое будет иметь
ошибки

38.

v=1 (астатическая САУ
с астатизмом
первого порядка)
с0=0 с1≠0 с2≠0 …, т.е.
такая система не
будет иметь ошибки
в режиме покоя.
v=2 (астатическая САУ
с астатизмом
второго порядка)
с0=0 с1=0 с2≠0 с3≠0 …,
такая система не
будет иметь ошибок
не только в режиме
покоя, но и при
линейнонарастающем
сигнале

39.

К сожалению, этот способ также снижает
запасы устойчивости САУ. Действительно:
Im
v=2
Re
-1;j0
v=0
v=1
По критерию Найквиста системы при v=0, v=1
могут быть как устойчивыми так и не
устойчивыми, но при v=2 они становятся не
устойчивыми при любых коэффициентах К.

40. 3. Повышение точности САУ с использованием принципов комбинированного управления.

Принцип комбинированного управления
состоит в том, что в дополнение к принципу
обратной связи реализуется принцип
управления по возмущению. V(t)
Измеритель
x(t)
y(t)
Регулятор
Объект

41.

Здесь сочетается (комбинируются) оба
названных принципа:
— Управление по возмущению (за счет
измерения возмущения v(t) и выработки
дополнительного управляющего сигнала
компенсирующего действия возмущения);
— Управление по отклонению или принцип
обратной связи реализуется за счет главной
отрицательной обратной связи и сигнала
рассогласования и регулятора.

42.

Рассмотрим следящую систему с
комбинированным управлением и найдем
передаточную функцию обычной системы
эквивалентной по точности.
W3(S)
y(s)
x(s)
W1(s)
W2(S)
≡
Wэ(S)

43.

Для этого приравняем их передаточные функции.
wэ (s)
y(s) w1 (s)w2 (s)
w2 (s)
F (s)
w3 (s)
x(s) 1 w1 (s)w2 (s)
1 w1 (s)w2 (s) 1 wэ (s)
(1)

44.

Из (1) после некоторых преобразований можно
получить:
w1 ( s) w3 ( s)
wэ ( s) w2 ( s) *
1 w3 ( s) w2 ( s)
(2)
Как видно из последнего выражения, при:
1
w3 ( s )
w2 ( s )
wэ(s)=∞
Условие (3) называется условием полной
инвариантности.
(3)

45.

Это означает, что ошибка рассматриваемой
комбинированной следящей системы будет
равна 0 в любых режимах работы поскольку:
( s)
1
F ( s )
0
x( s ) 1 wэ ( s )

46.

Достоинство принципа комбинированного
управления в том, что он не изменяет
(не ухудшает) устойчивости и качества
переходных процессов. Однако,
реализовать точно условие полной
инвариантности практически
невозможно.

47. ПРИМЕР

Пусть:
K
w2 ( s)
S (T1S 1)(T2 S 1)
Найдем:
1
S (T1S 1)(T2 S 1) 1
T1 T2 2 T1T2 3
w3 ( s)
S
S
S
w2 ( s)
K
K
K
K

48.

Структурная схема такой комбинированной
следящей системы имеет вид:
III
II
I
T1T2
S3
K
T1 T2 2
S
K
1
S
K
x(s)
w1(s)
K
S (T1S 1)(T2 S 1)
y(s)

49.

Итак, чтобы точно реализовать условие полной
инвариантности в нашем примере необходимо:
• реализовать канал I (тахогенератор)
• реализовать канал II (это 2-ая производная от угла)
• реализовать канал III (это 3-ая производная от угла)
Точно это сделать практически нельзя. Кроме того, в
реальных САУ имеется множество нелинейностей,
которые мы не учитывали при выводе условия
полной инвариантности.
Поэтому часто используют частично-инвариантные
САУ, т.е. САУ не имеющие ошибок лишь в некоторых
режимах.

Источник

7.1 Общие понятия о точности процесса управления

7.2 Точность при постоянном задающем воздействии. Постоянные ошибки

7.3 Точность при линейном воздействии. Скоростные ошибки

Статическая САР

Астатическая САР со степенью астатизма 1

Астатическая САР со степенью астатизма 2

§ 19.1. Статические и скоростные ошибки автоколебательных систем

1. Точность САУ

2. План

3. 1 Общие положения

4. 2 Понятие о типовых режимах САУ

5.

6. 3 Теорема о предельном значении оригинала и методика определения установившихся ошибок

7.

8. 4 Ошибки статических и астатических САУ в типовых режимах

9.

10.

11.

12.

13.

14.

15.

16.

17. 3. Третий режим — гармонических входных сигналов.

18. Определим амплитуду εm ошибки САУ в этом режиме.

19. Выражение (1) справедливо и для амплитуд, т.е.

20.

21. Т.о. чтобы ошибка САУ в гармоническом режиме не превышала допустимой εдоп необходимо:

22. 5 Ошибки САУ при произвольных входных сигналах (коэффициенты ошибок)

23.

24.

25. Чтобы определить ошибку САУ при произвольной форме входного сигнала x(t) необходимо:

26. Пример

27. Решение:

28. 2. Разложим (1) в степенной ряд путем деления числителя на знаменатель

29.

30.

31.

32.

33. 6 Методы повышения точности САУ

34. ВНИМАНИЕ

35. 1. Первый способ повышения точности САУ – увеличение К

36.

37. 2. Способ повышения точности САУ – путем увеличения астатизма “v”

38.

39.

40. 3. Повышение точности САУ с использованием принципов комбинированного управления.

41.

42.

43.

44.

45.

46.

47. ПРИМЕР

48.

49.

Интересное по теме: