| Binary Hamming codes | |
|---|---|

The Hamming(7,4) code (with r = 3) |
|
| Named after | Richard W. Hamming |
| Classification | |
| Type | Linear block code |
| Block length | 2r − 1 where r ≥ 2 |
| Message length | 2r − r − 1 |
| Rate | 1 − r/(2r − 1) |
| Distance | 3 |
| Alphabet size | 2 |
| Notation | [2r − 1, 2r − r − 1, 3]2-code |
| Properties | |
| perfect code | |
|
In computer science and telecommunication, Hamming codes are a family of linear error-correcting codes. Hamming codes can detect one-bit and two-bit errors, or correct one-bit errors without detection of uncorrected errors. By contrast, the simple parity code cannot correct errors, and can detect only an odd number of bits in error. Hamming codes are perfect codes, that is, they achieve the highest possible rate for codes with their block length and minimum distance of three.[1]
Richard W. Hamming invented Hamming codes in 1950 as a way of automatically correcting errors introduced by punched card readers. In his original paper, Hamming elaborated his general idea, but specifically focused on the Hamming(7,4) code which adds three parity bits to four bits of data.[2]
In mathematical terms, Hamming codes are a class of binary linear code. For each integer r ≥ 2 there is a code-word with block length n = 2r − 1 and message length k = 2r − r − 1. Hence the rate of Hamming codes is R = k / n = 1 − r / (2r − 1), which is the highest possible for codes with minimum distance of three (i.e., the minimal number of bit changes needed to go from any code word to any other code word is three) and block length 2r − 1. The parity-check matrix of a Hamming code is constructed by listing all columns of length r that are non-zero, which means that the dual code of the Hamming code is the shortened Hadamard code, also known as a Simplex code. The parity-check matrix has the property that any two columns are pairwise linearly independent.
Due to the limited redundancy that Hamming codes add to the data, they can only detect and correct errors when the error rate is low. This is the case in computer memory (usually RAM), where bit errors are extremely rare and Hamming codes are widely used, and a RAM with this correction system is a ECC RAM (ECC memory). In this context, an extended Hamming code having one extra parity bit is often used. Extended Hamming codes achieve a Hamming distance of four, which allows the decoder to distinguish between when at most one one-bit error occurs and when any two-bit errors occur. In this sense, extended Hamming codes are single-error correcting and double-error detecting, abbreviated as SECDED.
History[edit]
Richard Hamming, the inventor of Hamming codes, worked at Bell Labs in the late 1940s on the Bell Model V computer, an electromechanical relay-based machine with cycle times in seconds. Input was fed in on punched paper tape, seven-eighths of an inch wide, which had up to six holes per row. During weekdays, when errors in the relays were detected, the machine would stop and flash lights so that the operators could correct the problem. During after-hours periods and on weekends, when there were no operators, the machine simply moved on to the next job.
Hamming worked on weekends, and grew increasingly frustrated with having to restart his programs from scratch due to detected errors. In a taped interview, Hamming said, «And so I said, ‘Damn it, if the machine can detect an error, why can’t it locate the position of the error and correct it?'».[3] Over the next few years, he worked on the problem of error-correction, developing an increasingly powerful array of algorithms. In 1950, he published what is now known as Hamming code, which remains in use today in applications such as ECC memory.
Codes predating Hamming[edit]
A number of simple error-detecting codes were used before Hamming codes, but none were as effective as Hamming codes in the same overhead of space.
Parity[edit]
Parity adds a single bit that indicates whether the number of ones (bit-positions with values of one) in the preceding data was even or odd. If an odd number of bits is changed in transmission, the message will change parity and the error can be detected at this point; however, the bit that changed may have been the parity bit itself. The most common convention is that a parity value of one indicates that there is an odd number of ones in the data, and a parity value of zero indicates that there is an even number of ones. If the number of bits changed is even, the check bit will be valid and the error will not be detected.
Moreover, parity does not indicate which bit contained the error, even when it can detect it. The data must be discarded entirely and re-transmitted from scratch. On a noisy transmission medium, a successful transmission could take a long time or may never occur. However, while the quality of parity checking is poor, since it uses only a single bit, this method results in the least overhead.
Two-out-of-five code[edit]
A two-out-of-five code is an encoding scheme which uses five bits consisting of exactly three 0s and two 1s. This provides ten possible combinations, enough to represent the digits 0–9. This scheme can detect all single bit-errors, all odd numbered bit-errors and some even numbered bit-errors (for example the flipping of both 1-bits). However it still cannot correct any of these errors.
Repetition[edit]
Another code in use at the time repeated every data bit multiple times in order to ensure that it was sent correctly. For instance, if the data bit to be sent is a 1, an n = 3 repetition code will send 111. If the three bits received are not identical, an error occurred during transmission. If the channel is clean enough, most of the time only one bit will change in each triple. Therefore, 001, 010, and 100 each correspond to a 0 bit, while 110, 101, and 011 correspond to a 1 bit, with the greater quantity of digits that are the same (‘0’ or a ‘1’) indicating what the data bit should be. A code with this ability to reconstruct the original message in the presence of errors is known as an error-correcting code. This triple repetition code is a Hamming code with m = 2, since there are two parity bits, and 22 − 2 − 1 = 1 data bit.
Such codes cannot correctly repair all errors, however. In our example, if the channel flips two bits and the receiver gets 001, the system will detect the error, but conclude that the original bit is 0, which is incorrect. If we increase the size of the bit string to four, we can detect all two-bit errors but cannot correct them (the quantity of parity bits is even); at five bits, we can both detect and correct all two-bit errors, but not all three-bit errors.
Moreover, increasing the size of the parity bit string is inefficient, reducing throughput by three times in our original case, and the efficiency drops drastically as we increase the number of times each bit is duplicated in order to detect and correct more errors.
Description[edit]
If more error-correcting bits are included with a message, and if those bits can be arranged such that different incorrect bits produce different error results, then bad bits could be identified. In a seven-bit message, there are seven possible single bit errors, so three error control bits could potentially specify not only that an error occurred but also which bit caused the error.
Hamming studied the existing coding schemes, including two-of-five, and generalized their concepts. To start with, he developed a nomenclature to describe the system, including the number of data bits and error-correction bits in a block. For instance, parity includes a single bit for any data word, so assuming ASCII words with seven bits, Hamming described this as an (8,7) code, with eight bits in total, of which seven are data. The repetition example would be (3,1), following the same logic. The code rate is the second number divided by the first, for our repetition example, 1/3.
Hamming also noticed the problems with flipping two or more bits, and described this as the «distance» (it is now called the Hamming distance, after him). Parity has a distance of 2, so one bit flip can be detected but not corrected, and any two bit flips will be invisible. The (3,1) repetition has a distance of 3, as three bits need to be flipped in the same triple to obtain another code word with no visible errors. It can correct one-bit errors or it can detect — but not correct — two-bit errors. A (4,1) repetition (each bit is repeated four times) has a distance of 4, so flipping three bits can be detected, but not corrected. When three bits flip in the same group there can be situations where attempting to correct will produce the wrong code word. In general, a code with distance k can detect but not correct k − 1 errors.
Hamming was interested in two problems at once: increasing the distance as much as possible, while at the same time increasing the code rate as much as possible. During the 1940s he developed several encoding schemes that were dramatic improvements on existing codes. The key to all of his systems was to have the parity bits overlap, such that they managed to check each other as well as the data.
General algorithm[edit]
The following general algorithm generates a single-error correcting (SEC) code for any number of bits. The main idea is to choose the error-correcting bits such that the index-XOR (the XOR of all the bit positions containing a 1) is 0. We use positions 1, 10, 100, etc. (in binary) as the error-correcting bits, which guarantees it is possible to set the error-correcting bits so that the index-XOR of the whole message is 0. If the receiver receives a string with index-XOR 0, they can conclude there were no corruptions, and otherwise, the index-XOR indicates the index of the corrupted bit.
An algorithm can be deduced from the following description:
- Number the bits starting from 1: bit 1, 2, 3, 4, 5, 6, 7, etc.
- Write the bit numbers in binary: 1, 10, 11, 100, 101, 110, 111, etc.
- All bit positions that are powers of two (have a single 1 bit in the binary form of their position) are parity bits: 1, 2, 4, 8, etc. (1, 10, 100, 1000)
- All other bit positions, with two or more 1 bits in the binary form of their position, are data bits.
- Each data bit is included in a unique set of 2 or more parity bits, as determined by the binary form of its bit position.
- Parity bit 1 covers all bit positions which have the least significant bit set: bit 1 (the parity bit itself), 3, 5, 7, 9, etc.
- Parity bit 2 covers all bit positions which have the second least significant bit set: bits 2-3, 6-7, 10-11, etc.
- Parity bit 4 covers all bit positions which have the third least significant bit set: bits 4–7, 12–15, 20–23, etc.
- Parity bit 8 covers all bit positions which have the fourth least significant bit set: bits 8–15, 24–31, 40–47, etc.
- In general each parity bit covers all bits where the bitwise AND of the parity position and the bit position is non-zero.
If a byte of data to be encoded is 10011010, then the data word (using _ to represent the parity bits) would be __1_001_1010, and the code word is 011100101010.
The choice of the parity, even or odd, is irrelevant but the same choice must be used for both encoding and decoding.
This general rule can be shown visually:
-
Bit position 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 … Encoded data bits p1 p2 d1 p4 d2 d3 d4 p8 d5 d6 d7 d8 d9 d10 d11 p16 d12 d13 d14 d15 Parity
bit
coveragep1 p2 p4 p8 p16
Shown are only 20 encoded bits (5 parity, 15 data) but the pattern continues indefinitely. The key thing about Hamming Codes that can be seen from visual inspection is that any given bit is included in a unique set of parity bits. To check for errors, check all of the parity bits. The pattern of errors, called the error syndrome, identifies the bit in error. If all parity bits are correct, there is no error. Otherwise, the sum of the positions of the erroneous parity bits identifies the erroneous bit. For example, if the parity bits in positions 1, 2 and 8 indicate an error, then bit 1+2+8=11 is in error. If only one parity bit indicates an error, the parity bit itself is in error.
With m parity bits, bits from 1 up to 

| Parity bits | Total bits | Data bits | Name | Rate |
|---|---|---|---|---|
| 2 | 3 | 1 | Hamming(3,1) (Triple repetition code) |
1/3 ≈ 0.333 |
| 3 | 7 | 4 | Hamming(7,4) | 4/7 ≈ 0.571 |
| 4 | 15 | 11 | Hamming(15,11) | 11/15 ≈ 0.733 |
| 5 | 31 | 26 | Hamming(31,26) | 26/31 ≈ 0.839 |
| 6 | 63 | 57 | Hamming(63,57) | 57/63 ≈ 0.905 |
| 7 | 127 | 120 | Hamming(127,120) | 120/127 ≈ 0.945 |
| 8 | 255 | 247 | Hamming(255,247) | 247/255 ≈ 0.969 |
| 9 | 511 | 502 | Hamming(511,502) | 502/511 ≈ 0.982 |
| … | ||||
| m | 
|

|
Hamming
|

|
Hamming codes with additional parity (SECDED)[edit]
Hamming codes have a minimum distance of 3, which means that the decoder can detect and correct a single error, but it cannot distinguish a double bit error of some codeword from a single bit error of a different codeword. Thus, some double-bit errors will be incorrectly decoded as if they were single bit errors and therefore go undetected, unless no correction is attempted.
To remedy this shortcoming, Hamming codes can be extended by an extra parity bit. This way, it is possible to increase the minimum distance of the Hamming code to 4, which allows the decoder to distinguish between single bit errors and two-bit errors. Thus the decoder can detect and correct a single error and at the same time detect (but not correct) a double error.
If the decoder does not attempt to correct errors, it can reliably detect triple bit errors. If the decoder does correct errors, some triple errors will be mistaken for single errors and «corrected» to the wrong value. Error correction is therefore a trade-off between certainty (the ability to reliably detect triple bit errors) and resiliency (the ability to keep functioning in the face of single bit errors).
This extended Hamming code was popular in computer memory systems, starting with IBM 7030 Stretch in 1961,[4] where it is known as SECDED (or SEC-DED, abbreviated from single error correction, double error detection).[5] Server computers in 21st century, while typically keeping the SECDED level of protection, no longer use the Hamming’s method, relying instead on the designs with longer codewords (128 to 256 bits of data) and modified balanced parity-check trees.[4] The (72,64) Hamming code is still popular in some hardware designs, including Xilinx FPGA families.[4]
[7,4] Hamming code[edit]
In 1950, Hamming introduced the [7,4] Hamming code. It encodes four data bits into seven bits by adding three parity bits. As explained earlier, it can either detect and correct single-bit errors or it can detect (but not correct) both single and double-bit errors.
With the addition of an overall parity bit, it becomes the [8,4] extended Hamming code which is SECDED and can both detect and correct single-bit errors and detect (but not correct) double-bit errors.
Construction of G and H[edit]
The matrix

and 
This is the construction of G and H in standard (or systematic) form. Regardless of form, G and H for linear block codes must satisfy

Since [7, 4, 3] = [n, k, d] = [2m − 1, 2m − 1 − m, 3]. The parity-check matrix H of a Hamming code is constructed by listing all columns of length m that are pair-wise independent.
Thus H is a matrix whose left side is all of the nonzero n-tuples where order of the n-tuples in the columns of matrix does not matter. The right hand side is just the (n − k)-identity matrix.
So G can be obtained from H by taking the transpose of the left hand side of H with the identity k-identity matrix on the left hand side of G.
The code generator matrix 


and

Finally, these matrices can be mutated into equivalent non-systematic codes by the following operations:[6]
- Column permutations (swapping columns)
- Elementary row operations (replacing a row with a linear combination of rows)
Encoding[edit]
- Example
From the above matrix we have 2k = 24 = 16 codewords.
Let 
![{\displaystyle {\vec {a}}=[a_{1},a_{2},a_{3},a_{4}],\quad a_{i}\in \{0,1\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/898ddf319567d4af0acecf5c7fd450f5f466e28b)



For example, let ![{\displaystyle {\vec {a}}=[1,0,1,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e838e2ec81e9fe6223596b61f747b195d3d338fb)


[8,4] Hamming code with an additional parity bit[edit]
The [7,4] Hamming code can easily be extended to an [8,4] code by adding an extra parity bit on top of the (7,4) encoded word (see Hamming(7,4)).
This can be summed up with the revised matrices:
and
Note that H is not in standard form. To obtain G, elementary row operations can be used to obtain an equivalent matrix to H in systematic form:
For example, the first row in this matrix is the sum of the second and third rows of H in non-systematic form. Using the systematic construction for Hamming codes from above, the matrix A is apparent and the systematic form of G is written as
The non-systematic form of G can be row reduced (using elementary row operations) to match this matrix.
The addition of the fourth row effectively computes the sum of all the codeword bits (data and parity) as the fourth parity bit.
For example, 1011 is encoded (using the non-systematic form of G at the start of this section) into 01100110 where blue digits are data; red digits are parity bits from the [7,4] Hamming code; and the green digit is the parity bit added by the [8,4] code.
The green digit makes the parity of the [7,4] codewords even.
Finally, it can be shown that the minimum distance has increased from 3, in the [7,4] code, to 4 in the [8,4] code. Therefore, the code can be defined as [8,4] Hamming code.
To decode the [8,4] Hamming code, first check the parity bit. If the parity bit indicates an error, single error correction (the [7,4] Hamming code) will indicate the error location, with «no error» indicating the parity bit. If the parity bit is correct, then single error correction will indicate the (bitwise) exclusive-or of two error locations. If the locations are equal («no error») then a double bit error either has not occurred, or has cancelled itself out. Otherwise, a double bit error has occurred.
See also[edit]
- Coding theory
- Golay code
- Reed–Muller code
- Reed–Solomon error correction
- Turbo code
- Low-density parity-check code
- Hamming bound
- Hamming distance
Notes[edit]
- ^ See Lemma 12 of
- ^ Hamming (1950), pp. 153–154.
- ^ Thompson, Thomas M. (1983), From Error-Correcting Codes through Sphere Packings to Simple Groups, The Carus Mathematical Monographs (#21), Mathematical Association of America, pp. 16–17, ISBN 0-88385-023-0
- ^ a b c Kythe & Kythe 2017, p. 115.
- ^ Kythe & Kythe 2017, p. 95.
- ^ a b Moon T. Error correction coding: Mathematical Methods and
Algorithms. John Wiley and Sons, 2005.(Cap. 3) ISBN 978-0-471-64800-0
References[edit]
- Hamming, Richard Wesley (1950). «Error detecting and error correcting codes» (PDF). Bell System Technical Journal. 29 (2): 147–160. doi:10.1002/j.1538-7305.1950.tb00463.x. S2CID 61141773. Archived (PDF) from the original on 2022-10-09.
- Moon, Todd K. (2005). Error Correction Coding. New Jersey: John Wiley & Sons. ISBN 978-0-471-64800-0.
- MacKay, David J.C. (September 2003). Information Theory, Inference and Learning Algorithms. Cambridge: Cambridge University Press. ISBN 0-521-64298-1.
- D.K. Bhattacharryya, S. Nandi. «An efficient class of SEC-DED-AUED codes». 1997 International Symposium on Parallel Architectures, Algorithms and Networks (ISPAN ’97). pp. 410–415. doi:10.1109/ISPAN.1997.645128.
- «Mathematical Challenge April 2013 Error-correcting codes» (PDF). swissQuant Group Leadership Team. April 2013. Archived (PDF) from the original on 2017-09-12.
- Kythe, Dave K.; Kythe, Prem K. (28 July 2017). «Extended Hamming Codes». Algebraic and Stochastic Coding Theory. CRC Press. pp. 95–116. ISBN 978-1-351-83245-8.
External links[edit]
- Visual Explanation of Hamming Codes
- CGI script for calculating Hamming distances (from R. Tervo, UNB, Canada)
- Tool for calculating Hamming code
Время на прочтение
6 мин
Количество просмотров 62K
Код Хэмминга – не цель этой статьи. Я лишь хочу на его примере познакомить вас с самими принципами кодирования. Но здесь не будет строгих определений, математических формулировок и т.д. Эта просто неплохой трамплин для понимания более сложных блочных кодов.
Самый, пожалуй, известный код Хэмминга (7,4). Что значат эти цифры? Вторая – число бит информационного слова — то, что мы хотим передать в целости и сохранности. А первое – размер кодового слова: информация удобренная избыточностью. Кстати термины «информационное слово» и «кодовое слово», употребляются во всех 7-ми книгах по теории помехоустойчивого кодирования, которые мне довелось бегло пролистать.
Такой код исправляет 1 ошибку. И не важно где она возникла. Избыточность несёт в себе 3 бита информации, этого достаточно, чтобы указать на одно из 7 положений ошибки или показать, что её нет. То есть ровно 8 вариантов ответов мы ждём. А 8 = 2^3, вот как всё совпало.
Чтобы получить кодовое слово, нужно информационное слово представить в виде полинома и умножить его на порождающий полином g(x). Любое число, переведя в двоичный вид, можно представить в виде полинома. Это может показаться странным и у не подготовленного читателя сразу встаёт только один вопрос «да зачем же так усложнять?». Уверяю вас, он отпадёт сам собой, когда мы получим первые результаты.
К примеру информационное слово 1010, значение каждого его разряда это коэффициент в полиноме:
Во многих книгах пишут наоборот x+x^3. Не поддавайтесь на провокацию, это вносит только путаницу, ведь в записи числа 2-ичного, 16-ричного, младшие разряды идут справа, и сдвиги мы делаем влево/вправо ориентируясь на это. А теперь давайте умножим этот полином на порождающий полином. Порождающий полином специально для Хэмминга (7,4), встречайте: g(x)=x^3+x+1. Откуда он взялся? Ну пока считайте что он дан человечеству свыше, богами (объясню позже).
Если нужно складывать коэффициенты, то делаем по модулю 2: операция сложения заменяется на логическое исключающее или (XOR), то есть x^4+x^4=0. И в конечном итоге результат перемножения как видите из 4х членов. В двоичном виде это 1001110. Итак, получили кодовое слово, которое будем передавать на сторону по зашумлённому каналу. Замете, что перемножив информационное слово (1010) на порождающий полином (1011) как обычные числа – получим другой результат 1101110. Этого нам не надо, требуется именно «полиномиальное» перемножение. Программная реализация такого умножения очень простая. Нам потребуется 2 операции XOR и 2 сдвига влево (1й из которых на один разряд, второй на два, в соответствии с g(x)=1011):
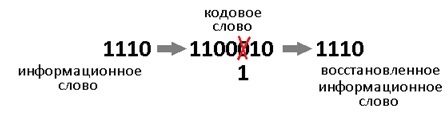
Давайте теперь специально внесём ошибку в полученное кодовое слово. Например в 3-й разряд. Получиться повреждённое слово: 1000110.
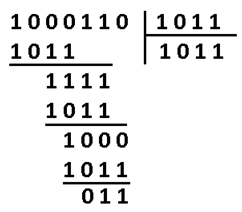
Как расшифровать сообщение и исправить ошибку? Разумеется надо «полиномиально» разделить кодовое слово на g(x). Тут я уже не буду писать иксы. Помните что вычитание по модулю 2 — это то же самое что сложение, что в свою очередь, тоже самое что исключающее или. Поехали:
В программной реализации опять же ничего сверх сложного. Делитель (1011) сдвигаем влево до самого конца на 3 разряда. И начинаем удалять (не без помощи XOR) самые левые единицы в делимом (100110), на его младшие разряды даже не смотрим. Делимое поэтапно уменьшается 100110 -> 0011110 -> 0001000 -> 0000011, когда в 4м и левее разрядах не остаётся единиц, мы останавливаемся.
Нацело разделить не получилось, значит у нас есть ошибка (ну конечно же). Результат деления в таком случае нам без надобности. Остаток от деления является синдром, его размер равен размеру избыточности, поэтому мы дописали там ноль. В данном случае содержание синдрома нам никак не помогает найти местоположение повреждения. А жаль. Но если мы возьмём любое другое информационное слово, к примеру 1100. Точно так же перемножим его на g(x), получим 1110100, внесём ошибку в тот же самый разряд 1111100. Разделим на g(x) и получим в остатке тот же самый синдром 011. И я гарантирую вам, что к такому синдрому мы придём в обще для всех кодовых слов с ошибкой в 3-м разряде. Вывод напрашивается сам собой: можно составить таблицу синдромов для всех 7 ошибок, делая каждую из них специально и считая синдром.
В результате собираем список синдромов, и то на какую болезнь он указывает:
Теперь у нас всё есть. Нашли синдром, исправили ошибку, ещё раз поделили в данном случае 1001110 на 1011 и получили в частном наше долгожданное информационное слово 1010. В остатке после исправления уже будет 000. Таблица синдромов имеет право на жизнь в случае маленьких кодов. Но для кодов, исправляющих несколько ошибок – там список синдромов разрастается как чума. Поэтому рассмотрим метод «вылавливания ошибок» не имея на руках таблицы.
Внимательный читатель заметит, что первые 3 синдрома вполне однозначно указывают на положение ошибки. Это касается только тех синдромов, где одна единица. Кол-во единиц в синдроме называют его «весом». Опять вернёмся к злосчастной ошибке в 3м разряде. Там, как вы помните был синдром 011, его вес 2, нам не повезло. Сделаем финт ушами — циклический сдвиг кодового слова вправо. Остаток от деления 0100011 / 1011 будет равен 100, это «хороший синдром», указывает что ошибка во втором разряде. Но поскольку мы сделали один сдвиг, значит и ошибка сдвинулась на 1. Вот собственно и вся хитрость. Даже в случае жуткого невезения, когда ошибка в 6м разряде, вы, обливаясь потом, после 3 мучительных делений, но всё таки находите ошибку – это победа, лишь потому, что вы не использовали таблицу синдромов.
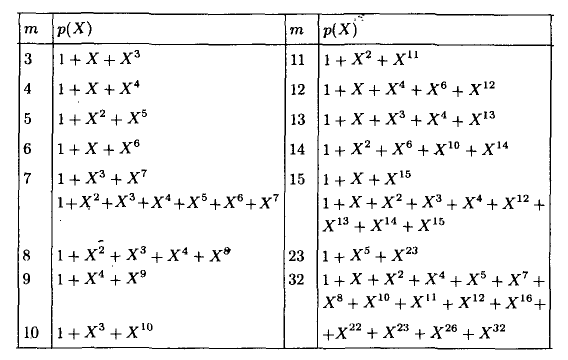
А как насчёт других кодов Хэмминга? Я бы сказал кодов Хэмминга бесконечное множество: (7,4), (15,11), (31,26),… (2^m-1, 2^m-1-m). Размер избыточности – m. Все они исправляют 1 ошибку, с ростом информационного слова растёт избыточность. Помехоустойчивость слабеет, но в случае слабых помех код весьма экономный. Ну ладно, а как мне найти порождающую функцию например для (15,11)? Резонный вопрос. Есть теорема, гласящая: порождающий многочлен циклического кода g(x) делит (x^n+1) без остатка. Где n – нашем случае размер кодового слова. Кроме того порождающий полином должен быть простым (делиться только на 1 и на самого себя без остатка), а его степень равна размеру избыточности. Можно показать, что для Хэмминга (7,4):
Этот код имеет целых 2 порождающих полинома. Не будет ошибкой использовать любой из них. Для остальных «хэммингов» используйте вот эту таблицу примитивных полиномов:
Соответственно для (15,11) порождающий многочлен g(x)=x^4+x+1. Ну а теперь переходим к десерту – к матрицам. С этого обычно начинают, но мы этим закончим. Для начала преобразую g(x) в матрицу, на которую можно умножить информационное слово, получив кодовое слово. Если g = 1011, то:
Называют её «порождающей матрицей». Дадим обозначение информационному слову d = 1010, а кодовое обозначим k, тогда:
Это довольно изящная формулировка. По быстродействию ещё быстрее, чем перемножение полиномов. Там нужно было делать сдвиги, а тут уже всё сдвинуто. Вектор d указывает нам: какие строки брать в расчёт. Самая нижняя строка матрицы – нулевая, строки нумеруются снизу вверх. Да, да, всё потому что младшие разряды располагаются справа и от этого никуда не деться. Так как d=1010, то я беру 1ю и 3ю строки, произвожу над ними операцию XOR и вуаля. Но это ещё не всё, приготовьтесь удивляться, существует ещё проверочная матрица H. Теперь перемножением вектора на матрицу мы можем получить синдром и никаких делений полиномов делать не надо.
Посмотрите на проверочную матрицу и на список синдромов, который получили выше. Это ответ на вопрос откуда берётся эта матрица. Здесь я как обычно подпортил кодовое слово в 3м разряде, и получил тот самый синдром. Поскольку сама матрица – это и есть список синдромов, то мы тут же находим положение ошибки. Но в кодах, исправляющие несколько ошибок, такой метод не прокатит. Придётся вылавливать ошибки по методу, описанному выше.
Чтобы лучше понять саму природу исправления ошибок, сгенерируем в обще все 16 кодовых слов, ведь информационное слово состоит всего из 4х бит:
Посмотрите внимательно на кодовые слова, все они, отличаются друг от друга хотя бы на 3 бита. К примеру возьмёте слово 1011000, измените в нём любой бит, скажем первый, получиться 1011010. Вы не найдёте более на него похожего слова, чем 1011000. Как видите для формирования кодового слова не обязательно производить вычисления, достаточно иметь эту таблицу в памяти, если она мала. Показанное различие в 3 бита — называется минимальное «хэммингово расстояние», оно является характеристикой блокового кода, по нему судят сколько ошибок можно исправить, а именно (d-1)/2. В более общем виде код Хэмминга можно записать так (7,4,3). Отмечу только, что Хэммингово расстояние не является разностью между размерами кодового и информационного слов. Код Голея (23,12,7) исправляет 3 ошибки. Код (48, 36, 5) использовался в сотовой связи с временным разделением каналов (стандарт IS-54). Для кодов Рида-Соломона применима та же запись, но это уже недвоичные коды.
Список используемой литературы:
1. М. Вернер. Основы кодирования (Мир программирования) — 2004
2. Р. Морелос-Сарагоса. Искусство помехоустойчивого кодирования (Мир связи) — 2006
3. Р. Блейхут. Теория и практика кодов, контролирующих ошибки — 1986
Число обнаруживаемых или исправляемых ошибок.
При применении двоичных кодов учитывают
только дискретные искажения, при которых
единица переходит в нуль (1 → 0) или нуль
переходит в единицу (0 → 1). Переход 1 →
0 или 0 → 1 только в одном элементе кодовой
комбинации называют единичной ошибкой
(единичным искажением). В общем случае
под кратностью ошибки подразумевают
число позиций кодовой комбинации, на
которых под действием помехи одни
символы оказались заменёнными на другие.
Возможны двукратные (t= 2) и многократные (t> 2) искажения элементов в кодовой
комбинации в пределах 0 <t<n.
Минимальное кодовое расстояние является
основным параметром, характеризующим
корректирующие способности данного
кода. Если код используется только для
обнаружения ошибок кратностью t0,
то необходимо и достаточно, чтобы
минимальное кодовое расстояние было
равно
dmin
> t0
+ 1. (13.10)
В этом случае никакая комбинация из t0ошибок не может перевести одну разрешённую
кодовую комбинацию в другую разрешённую.
Таким образом, условие обнаружения всех
ошибок кратностьюt0можно записать в виде:
t0≤ dmin — 1. (13.11)
Чтобы можно было исправить все ошибки
кратностью tии менее, необходимо иметь минимальное
расстояние, удовлетворяющее условию:
. (13.12)
В этом случае любая кодовая комбинация
с числом ошибок tиотличается от каждой разрешённой
комбинации не менее чем вtи+ 1 позициях. Если условие (13.12) не выполнено,
возможен случай, когда ошибки кратностиtисказят переданную
комбинацию так, что она станет ближе к
одной из разрешённых комбинаций, чем к
переданной или даже перейдёт в другую
разрешённую комбинацию. В соответствии
с этим, условие исправления всех ошибок
кратностью не болееtиможно записать в виде:
tи
≤(dmin
— 1) / 2 . (13.13)
Из (13.10) и (13.12) следует, что если код
исправляет все ошибки кратностью tи,
то число ошибок, которые он может
обнаружить, равноt0= 2∙tи. Следует
отметить, что соотношения (13.10) и (13.12)
устанавливают лишь гарантированное
минимальное число обнаруживаемых или
исправляемых ошибок при заданномdminи не ограничивают возможность обнаружения
ошибок большей кратности. Например,
простейший код с проверкой на чётность
сdmin= 2 позволяет обнаруживать не только
одиночные ошибки, но и любое нечётное
число ошибок в пределахt0<n.
Корректирующие возможности кодов.
Вопрос о минимально необходимой
избыточности, при которой код обладает
нужными корректирующими свойствами,
является одним из важнейших в теории
кодирования. Этот вопрос до сих пор не
получил полного решения. В настоящее
время получен лишь ряд верхних и нижних
оценок (границ), которые устанавливают
связь между максимально возможным
минимальным расстоянием корректирующего
кода и его избыточностью.
Так, граница Плоткинадаёт верхнюю
границу кодового расстоянияdminпри заданном числе разрядовnв
кодовой комбинации и числе информационных
разрядовm, и для
двоичных кодов:
(13.14)
или
при
. (13.15)
Верхняя граница Хеммингаустанавливает
максимально возможное число разрешённых
кодовых комбинаций (2m)
любого помехоустойчивого кода при
заданных значенияхnиdmin:

где
—
число сочетаний изnэлементов поiэлементам.
Отсюда можно получить выражение для
оценки числа проверочных символов:

Для значений (dmin/n)
≤ 0,3 разница между границей Хемминга и
границей Плоткина сравнительно невелика.
Граница Варшамова-Гильбертадля
больших значенийnопределяет нижнюю
границу для числа проверочных разрядов,
необходимого для обеспечения заданного
кодового расстояния:

Отметим, что для некоторых частных
случаев Хемминг получил простые
соотношения, позволяющие определить
необходимое число проверочных символов:
дляdmin= 3,
дляdmin= 4.
Блочные коды с dmin= 3 и 4 в литературе обычно называют кодами
Хемминга.
Все приведенные выше оценки дают
представление о верхней границе числаdminпри фиксированных значенияхnиmили оценку снизу числа проверочных
символовkпри заданныхmиdmin.
Существующие методы построения избыточных
кодов решают в основном задачу нахождения
такого алгоритма кодирования и
декодирования, который позволял бы
наиболее просто построить и реализовать
код с заданным значением dmin.
Поэтому различные корректирующие коды
при одинаковыхdminсравниваются по сложности кодирующего
и декодирующего устройств. Этот критерий
является в ряде случаев определяющим
при выборе того или иного кода.
Соседние файлы в папке ЛБ_3
- #
- #
14.04.2015937 б75KodHemmig.m
- #
14.04.20150 б67ЛБ_3.exe
Содержание
Раздел разработан в 2010 г. при поддержке компании RAIDIX
Для понимания материалов настоящего раздела крайне желательно ознакомиться с разделом КОДИРОВАНИЕ
.
Код Хэмминга
Будем рассматривать двоичные коды, т.е. упорядоченные наборы (строки) $ (x_1,\dots,x_{n}) $ из $ n_{} $ чисел $ \{x_1,\dots,x_n\}\subset \{0,1\} $. Множество таких наборов, рассматриваемое вместе с операцией умножения на константы $ 0_{} $ или $ 1_{} $ и операцией поразрядного сложения по модулю $ 2_{} $:
$$ (x_1,\dots,x_n)\oplus (y_1,\dots,y_n)=(x_1\oplus y_1 ,\dots,x_n\oplus y_n ) =
$$
$$ = (x_1+y_1 \pmod{2},\dots,x_n+y_n \pmod{2}) $$
образует линейное пространство, которое мы будем обозначать $ \mathbb V^n $, а собственно составляющие его наборы будем называть векторами; причем, для определенности, именно векторами-строками. Это пространство состоит из конечного числа векторов: $ \operatorname{Card} (\mathbb V^n)=2^n $.
Расстояние Хэмминга
Расстоянием Хэмминга между двумя векторами $ B=(b_1,\dots,b_n) $ и $ C=(c_1,\dots,c_n) $ из $ \mathbb V^n $ называется число разрядов, в которых эти слова отличаются друг от друга; будем обозначать его $ \rho(B,C) $.
?
Доказать, что
$$ \rho(B,C)= \displaystyle \sum_{j=1}^n \left[ (1-b_j)c_j+ (1-c_j)b_j \right] \, .$$
Весом Хэмминга вектора $ B=(b_1,\dots,b_n) $ называется число его отличных от нуля координат, будем обозначать его $ w(B) $. Таким образом1)
$$ w(B)= b_1+\dots+b_n, \qquad \rho(B,C)=|b_1-c_1|+\dots+ |b_n-c_n|=w(B-C) \ . $$
Расстояние Хэмминга является метрикой в пространстве $ \mathbb V^n $, т.е. для любых векторов $ \{X_1,X_2,X_3\} \subset \mathbb V^n $ выполняются свойства
1.
$ \rho(X_1,X_2) \ge 0 $, и $ \rho(X_1,X_2) = 0 $ тогда и только тогда, когда $ X_1=X_2 $;
2.
$ \rho(X_1,X_2) = \rho(X_2,X_1) $;
3.
$ \rho(X_1,X_3)\le \rho(X_1,X_2)+ \rho(X_2,X_3) $ («неравенство треугольника»).
Пусть теперь во множестве $ \mathbb V^n $ выбирается произвольное подмножество $ \mathbb U $, содержащее $ s_{} $ векторов: $ \mathbb U=\{ U_1,\dots,U_s \} $. Будем считать эти векторы кодовыми словами, т.е. на вход канала связи будем подавать исключительно только эти векторы; само множество $ \mathbb U $ будем называть кодом. По прохождении канала связи эти векторы могут зашумляться ошибками. Каждый полученный на выходе вектор будем декодировать в ближайшее (в смысле расстояния Хэмминга) кодовое слово множества $ \mathbb U $. Таким образом, «хорошим» кодом — в смысле исправления максимального числа ошибок — может считаться код $ \mathbb U $, для которого кодовые слова далеко отстоят друг от друга. С другой стороны, количество кодовых слов $ s_{} $ должно быть достаточно велико, чтобы делать использование кода осмысленным; во всяком случае, будем всегда считать $ s>1 $.
Минимальное расстояние между различными кодовыми словами кода $ \mathbb U $, т.е.
$$ d=\min_{\{j,k\}\subset \{1,\dots,s \} \atop j\ne k} \rho (U_j,U_k) $$
называется кодовым расстоянием кода $ \mathbb U $; будем иногда также писать $ d(\mathbb U) $.
Т
Теорема. Код $ \mathbb U $ с кодовым расстоянием $ d_{} $
a) способен обнаружить от $ 1_{} $ до $ d-1 $ (но не более) ошибок;
б) способен исправить от $ 1_{} $ до $ \left\lfloor \displaystyle \frac{d-1}{2} \right\rfloor $ (но не более) ошибок. Здесь $ \lfloor \ \ \ \rfloor $ — целая часть числа.
Доказательство. Если $ U_1 $ — переданное кодовое слово, а $ V_{} $ — полученный на выходе с канала вектор с $ \tau_{} $ ошибками, то $ \rho(U_1,V)=\tau $. Мы не сможем обнаружить ошибку если $ V_{1} $ совпадет с каким-то другим кодовым словом $ U_2 $, т.е. при условии $ \rho(U_2,V)=0 $. Оценим
$ \rho(U_2,V) $ при условии, что $ \tau \le d-1 $. По неравенству треугольника
3
получаем
$$ \rho(U_2,V) \ge \rho(U_1,U_2)-\rho(U_1,V) \ge d-\tau \ge 1>0 \ . $$
Для доказательства части б) предположим, что $ 2\,\tau \le d-1 $. Тогда те же рассуждения приведут к заключению
$$ \rho(U_2,V) \ge d-\tau \ge (2\,\tau+1)-t > \tau = \rho(U_1,V) \ , $$
т.е. вектор $ V_{} $ ближе к $ U_1 $, чем к любому другому кодовому слову.
♦
П
Пример. Код Адамара строится на основании матрицы Адамара — квадратной матрицы, элементами которой являются только числа $ \{+1,-1\} $; при этом ее строки (как, впрочем, и столбцы) попарно ортогональны. Так, матрица Адамара порядка $ 8_{} $ —
$$
H=\left(
\begin{array}{rrrrrrrr}
1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 \\
-1 & 1 &-1 & 1 & -1 & 1 &-1 & 1\\
1 & 1 & -1 & -1 & 1 & 1 & -1 & -1 \\
-1 & 1 & 1 & -1 & -1 & 1 & 1 & -1 \\
1 & 1 & 1 & 1 & -1 & -1 & -1 & -1 \\
-1 & 1 &-1 & 1 & 1 & -1 &1 & -1\\
1 & 1 & -1 & -1 & -1 & -1 & 1 & 1 \\
-1 & 1 & 1 & -1 & 1 & -1 & -1 & 1
\end{array}
\right) \ .
$$
Код строится следующим образом. Берутся строки матрицы $ H_{} $ и умножаются на $ +1 $ и на $ -1 $; в каждой строке множества
$$ H^{[1]},H^{[2]},\dots,H^{[8]},-H^{[1]},-H^{[2]},\dots,-H^{[8]} $$
производится замена $ +1 \to 0, -1 \to 1 $. Получаются $ 16 $ векторов
$$
(00000000),\ (10101010),\ (00110011),\ (10011001),\ (00001111),\ (10100101),\ (00111100),\
(10010110),
$$
$$
(11111111),\ (01010101), (11001100),\ (01100110),\ (11110000),\ (01011010),\ (11000011),\
(01101001),
$$
которые обозначим $ U_1,\dots,U_8,U_{-1},\dots,U_{-8} $.
Поскольку строки $ \pm H^{[j]} $ и $ \pm H^{[k]} $ ортогональны при $ j\ne k_{} $ и состоят только из чисел $ \pm 1 $, то ровно в половине своих элементов они должны совпадать, а в половине — быть противоположными. Соответствующие им векторы $ U_{} $ будут совпадать в половине своих компонент и различаться в оставшихся. Таким образом
$$ \rho( U_{\pm j}, U_{\pm k}) = 4 \quad npu \quad j\ne k, \ \rho( U_{j}, U_{-j}) = 8 , $$
и кодовое расстояние равно $ 4_{} $. В соответствии с теоремой, этот код способен обнаружить до трех ошибок, но исправить только одну. Так, к примеру, если при передаче по каналу связи слова $ U_8=(00111100) $ возникает только одна ошибка и на выходе получаем $ V_8= (00111101) $, то $ \rho(U_8,V_8)=1 $, в то время как $ \rho(U_j,V_8)\ge 3 $ для других кодовых слов. Если же количество ошибок возрастет до двух —
$ \tilde V_8= (00111111) $, — то $ \rho(U_8,\tilde V_8)=2 $, но при этом также $ \rho(U_9,\tilde V_8)=2 $. Ошибка обнаружена, но однозначное декодирование невозможно.
♦
Т
Теорема. Если существует матрица Адамара порядка $ n_{}>2 $, то
а) $ n_{} $ кратно $ 4_{} $, и
б) существует код $ \mathbb U \subset \mathbb V^n $, состоящий из $ 2\,n $ кодовых слов, для которого кодовое расстояние $ d=n/2 $.
Проблема построения кодов Адамара заключается в том, что существование матриц Адамара произвольного порядка $ n_{} $ кратного $ 4_{} $ составляет содержание не доказанной2) гипотезы Адамара. Хотя для многих частных случаев $ n_{} $ (например, для $ n=2^m, m \in \mathbb N $, см.
☞
ЗДЕСЬ ) матрицы Адамара построены.
Т
Теорема. Если код $ \mathbb U \subset \mathbb V^n $ может исправлять самое большее $ m_{} $ ошибок, то количество $ s_{} $ его слов должно удовлетворять следующему неравенству
$$ s \le \frac{2^n}{C_n^0+C_n^1+\dots+C_n^m} \ , $$
где $ C_n^{j} $ означает биномиальный коэффициент.
Число в правой части неравенства называется верхней границей Хэмминга для числа кодовых слов.
Доказательство. Для простоты предположим, что одно из кодовых слов кода $ \mathbb U $ совпадает с нулевым вектором: $ U_1=\mathbb O_{1\times n} $. Все векторы пространства $ \mathbb V_n $, отстоящие от $ U_1 $ на расстояние $ 1_{} $ заключаются во множестве
$$ (100\dots 0),\ (010 \dots 0),\ \dots,\ (000 \dots 1) ; $$
их как раз $ n=C_n^1 $ штук. Векторы из $ \mathbb V^n $, отстоящие от $ \mathbb O_{} $ на расстояние $ 2_{} $ получаются в ходе расстановки двух цифр $ 1_{} $ в произвольных местах нулевого вектора. Нахождение количества способов такой расстановки относится к задачам комбинаторики, и решение этой задачи можно найти
☞
ЗДЕСЬ. Оно равно как раз $ C_n^{2}=n(n-1)/2 $. Аналогичная задача расстановки $ j_{} $ единиц в $ n_{} $-векторе имеет решением число $ C_n^j $.
Таким образом общее количество векторов, отстоящих от $ \mathbb O_{} $ на расстояние $ \le m_{} $
равно $ C_n^1+\dots+C_n^m $.
Вместе в самим $ \mathbb O_{} $-вектором получаем как раз число из знаменателя границы Хэмминга.
Предыдущие рассуждения будут справедливы и для любого другого кодового слова из $ \mathbb U $ — каждое из них можно «окружить $ m_{} $-окрестностью» и каждая из этих окрестностей будет содержать
$$ 1+C_n^1+\dots+C_n^m $$
векторов из $ \mathbb V^n $. По предположению теоремы, эти окрестности не должны пересекаться. Но тогда общее количество векторов $ \mathbb V^n $, попавших в эти окрестности (для всех $ s_{} $ кодовых слов) не должно превышать количества векторов в $ \mathbb V^n $, т.е. $ 2^{n} $.
♦
?
Доказать, что если $ n_{} $ — нечетно, а $ m=\lfloor n/2 \rfloor=(n-1)/2 $ то верхняя граница Хэмминга равна в точности $ 2_{} $.
П
Пример. Для $ n=10 $ имеем
| $ m_{} $ | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| $ s\le $ | 93 | 18 | 5 | 2 | 1 |
Чем больше ошибок хотим скорректировать (при фиксированном числе $ n_{} $ разрядов кодовых слов) — тем меньше множество кодовых слов.
Коды, для которых верхняя граница Хэмминга достигается, называются совершенными.
Линейные коды
Идея, лежащая в основе этих кодов достаточно проста: это — обобщение понятия контрольной суммы. Если вектор $ (x_1,\dots,x_k) \in \mathbb V^k $ содержит информационные биты, которые требуется передать, то для контроля целостности при передаче их по каналу присоединим к этому вектору еще один «служебный» бит с вычисленным значением
$$ x_{k+1}=x_1+\dots+x_k \pmod{2} \ . $$
Очевидно, $ x_{k+1}=1 $ если среди информационных битов содержится нечетное число единиц, и $ x_{k+1}=0 $ в противном случае. Поэтому этот бит называют битом четности. Кодовым словом становится вектор
$$ X=(x_1,\dots,x_k,x_{k+1}) \in \mathbb V^{k+1} \ . $$
По прохождении его по каналу, для полученного вектора $ Y=(y_1,\dots,y_k,y_{k+1}) $ производится проверка условия
$$ y_{k+1} = y_1+\dots+y_k \pmod{2} \ . $$
Если оно не выполнено, то при передаче произошла ошибка. Если же сравнение оказывается справедливым, то это еще не значит, что ошибки при передаче нет — поскольку комбинация из двух (или любого четного числа) ошибок не изменит бита четности.
Для более вероятного обнаружения ошибки вычислим несколько контрольных сумм — выбирая различные разряды информационного вектора $ (x_1,\dots,x_k) $:
$$
\begin{array}{lclcll}
x_{k+1}&=&x_{i_1}+&\dots&+x_{i_s} \pmod{2}, \\
x_{k+2}&=&x_{j_1}+&\dots&+x_{j_t} \pmod{2}, \\
\vdots & & \vdots \\
x_n &=&x_{\ell_1}+& \dots & +x_{\ell_w} \pmod{2}.
\end{array}
$$
Полученные биты присоединим к информационному блоку. Кодовым словом будет вектор
$$ X=(x_1,\dots,x_k,x_{k+1},\dots,x_n) \in \mathbb V^n \ , $$
который и поступает в канал связи. По прохождении его по каналу, для соответствующих разрядов полученного вектора $ Y_{} $ проверяется выполнимость контрольных сравнений. Если все они выполняются, то ошибка передачи считается невыявленной.
На первый взгляд кажется, что при увеличении количества контрольных сумм увеличивается и вероятность обнаружения ошибки передачи. Однако с увеличением количества разрядов кодового слова увеличивается и вероятность появления этой ошибки.
П
Пример. Если вероятность ошибочной передачи одного бита по каналу равна $ P_1=0.1 $, то вероятность появления хотя бы одной ошибки при передаче $ k_{} $ битов равна $ P_k= 1-(0.9)^k $, т.е.
| $ k $ | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| $ P_k $ | 0.1 | 0.19 | 0.271 | 0.344 | 0.410 | 0.469 | 0.522 | 0.570 | 0.613 | 0.651 |
♦
Обычно, количество проверочных соотношений берется меньшим (и даже много меньшим) количества информационных битов3). Осталось только понять как составлять эти проверочные соотношения так, чтобы они смогли реагировать на ошибки передачи по каналу связи.
Сначала формализуем предложенную выше идею. В пространстве $ \mathbb V^n $ выделим некоторое подпространство $ \mathbb V^n_{[k]} $, состоящее из векторов
$$ (x_1,\dots,x_k,x_{k+1},\dots,x_n) \ , $$
первые $ k_{} $ компонентов которых считаются произвольными, а оставшиеся $ n-k_{} $ полностью определяются первыми посредством заданных линейных соотношений:
$$ \begin{array}{lclcll}
x_{k+1}&=&h_{k+1,1}x_1+&\dots&+h_{k+1,k}x_k \pmod{2} \\
\vdots & & \vdots \\
x_n &=&h_{n1}x_1+& \dots & +h_{nk}x_k \pmod{2}
\end{array} \qquad npu \qquad \{h_{j\ell}\} \subset \{0,1\} \ .
$$
Кодовые слова выбираются именно из подпространства $ \mathbb V^n_{[k]} $, их количество равно $ \operatorname{Card} (\mathbb V^n_{[k]} )=2^k $. При этом начальная часть каждого кодового слова, т.е. вектор $ (x_1,\dots,x_k) $, заключает информацию, которую нужно передать — эти разряды называются информационными. Остальные разряды кодового слова, т.е. биты вектора $ (x_{k+1},\dots,x_n) $, которые вычисляются с помощью выписанных линейных соотношений, являются служебными — они называются проверочными и предназначены для контроля целостности передачи информационных разрядов по каналу связи (и/или коррекции ошибок). Код такого типа называется линейным (n,k)-кодом.
В дальнейшем будем экономить на обозначениях: знак операции $ +_{} $ будет означать суммирование по модулю $ 2_{} $.
П
Пример. Пусть $ n=5, k=3 $. Пусть проверочные биты связаны с информационными соотношениями
$$ x_4=x_1 + x_2,\ x_5=x_1 + x_3 \ . $$
Тогда $ \mathbb V^5_{[3]} $ состоит из векторов
$$ (00000),\ (10011),\ (01010),\ (00101),\ (11001),\ (10110),\ (01111),\ (11100) \ . $$
♦
Для описания пространства $ \mathbb V^n_{[k]} $ привлечем аппарат теории матриц. С одной стороны, в этом подпространстве можно выбрать базис — систему из $ k_{} $ линейно независимых векторов: обозначим их $ \{X_1,\dots,X_k\} $. Матрица, составленная из этих векторов-строк,
$$
\mathbf G=\left( \begin{array}{c} X_1 \\ \vdots \\ X_k \end{array} \right)_{k\times n}
$$
называется порождающей матрицей кода. Так, в только что приведенном примере в качестве порождающей матрицы может быть выбрана
$$
\mathbf G=
\left( \begin{array}{ccccc}
1 & 0 & 0 & 1 & 1 \\
0 & 1 & 0 & 1 & 0 \\
0 & 0 & 1 & 0 &1
\end{array}
\right) \qquad \mbox{ или } \qquad
\mathbf G=
\left( \begin{array}{ccccc}
1 & 0 & 0 & 1 & 1 \\
1 & 1 & 0 & 0 & 1 \\
1 & 1 & 1 & 0 & 0
\end{array}
\right) \ .
$$
Любая строка $ X_{} $ кода может быть получена как линейная комбинация строк порождающей матрицы:
$$ X=\alpha_1 X_1+\alpha_2X_2+\dots+\alpha_k X_k \quad npu \quad \{\alpha_1,\dots,\alpha_k\} \subset \{0,1\} . $$
Можно переписать это равенство с использованием операции матричного умножения:
$$ X=(\alpha_1,\dots,\alpha_k) \mathbf G \ . $$
Так, продолжая рассмотрение предыдущего примера:
$$
(x_1,x_2,x_3,x_4,x_5)=(x_1,x_2,x_3)
\left( \begin{array}{ccccc}
1 & 0 & 0 & 1 & 1 \\
0 & 1 & 0 & 1 & 0 \\
0 & 0 & 1 & 0 &1
\end{array}
\right)=
$$
$$
=(x_1+x_2,x_2+x_3,x_3)
\left( \begin{array}{ccccc}
1 & 0 & 0 & 1 & 1 \\
1 & 1 & 0 & 0 & 1 \\
1 & 1 & 1 & 0 & 0
\end{array}
\right) \pmod{2} \ .
$$
С другой стороны, для описания $ \mathbb V^n_{[k]} $ имеются проверочные соотношения. Объединяя их в систему линейных уравнений, перепишем их с использованием матричного формализма:
$$
(x_1,\dots,x_k,x_{k+1},\dots,x_n) \cdot
\left(\begin{array}{cccc}
h_{k+1,1} & h_{k+2,1} & \dots &h_{n1} \\
h_{k+1,2} & h_{k+2,2} & \dots & h_{n2} \\
\vdots & & & \vdots \\
h_{k+1,k} & h_{k+2,k} & \dots & h_{nk} \\
-1 & 0 & \dots & 0 \\
0 & -1 & \dots & 0 \\
\vdots & & \ddots & \vdots \\
0 & 0 & \dots & -1
\end{array}
\right)= (0,0,\dots,0)_{1\times (n-k)}
$$
или, в альтернативном виде, с использованием транспонирования4):
$$
\underbrace{\left(\begin{array}{llclcccc}
h_{k+1,1} & h_{k+1,2} & \dots &h_{k+1,k} & 1 & 0 & \dots & 0 \\
h_{k+2,1} & h_{k+2,2} & \dots & h_{k+2,k}& 0 & 1 & \dots & 0 \\
\vdots & & & \vdots & \dots & & \ddots & \vdots \\
h_{n1} & h_{n2} & \dots & h_{nk} & 0 & 0 & \dots & 1 \\
\end{array}
\right)}_{\mathbf H}\left( \begin{array}{c} x_1 \\ x_2 \\ \vdots \\ x_n \end{array} \right)
=\left( \begin{array}{c} 0 \\ 0 \\ \vdots \\ 0 \end{array} \right)_{(n-k)\times 1}
$$
Матрица $ \mathbf H_{} $ порядка $ (n-k)\times n $ называется проверочной матрицей кода5). Хотя вторая форма записи (когда вектор-столбец неизвестных стоит справа от матрицы) более привычна для линейной алгебры, в теории кодирования чаще используется именно первая — с вектором-строкой $ X_{} $ слева от матрицы:
$$ X\cdot \mathbf H^{\top} = \mathbb O_{1\times k} \ . $$
Для приведенного выше примера проверочные соотношения переписываются в виде
$$ x_1 + x_2 +x_4=0,\ x_1 + x_3 + x_5=0 \ $$
и, следовательно, проверочная матрица:
$$ \mathbf H=
\left( \begin{array}{ccccc}
1 & 1 & 0 & 1 & 0 \\
1 & 0 & 1 & 0 & 1
\end{array}
\right) \ .
$$
Т
Теорема 1. Имеет место матричное равенство
$$ \mathbf G \cdot \mathbf H^{\top} = \mathbb O_{k\times (n-k)} \ .$$
Доказательство. Каждая строка матрицы $ \mathbf G $ — это кодовое слово $ X_{j} $ , которое, по предположению, должно удовлетворять проверочным соотношениям $ X_j \cdot \mathbf H^{\top} = \mathbb O_{1\times k} $. Равенство из теоремы — это объединение всех таких соотношений в матричной форме. Фактически, порождающая матрица $ \mathbf G $ состоит из строк, составляющих фундаментальную систему решений системы уравнений $ X \mathbf H^{\top}= \mathbb O $.
♦
=>
Если проверочная матрица имеет вид $ \mathbf H=\left[ P^{\top} \mid E_{n-k} \right] $,
где $ E_{n-k} $ — единичная матрица порядка $ n — k_{} $, $ P_{} $ — некоторая матрица порядка $ k \times (n-k) $, а $ \mid_{} $ означает операцию конкатенации, то порождающая матрица может быть выбрана в виде $ \mathbf G = \left[ E_k \mid P \right] $.
Доказательство следует из предыдущей теоремы, правила умножения блочных матриц —
$$ \mathbf G \cdot \mathbf H^{\top} = E_k \cdot P + P \cdot E_{n-k} = 2P \equiv \mathbb O_{k\times (n-k)} \pmod{2} \ , $$
и того факта, что строки матрицы $ \mathbf G $ линейно независимы. Последнее обстоятельство обеспечивается структурой этой матрицы: первые $ k_{} $ ее столбцов являются столбцами единичной матрицы. Любая комбинация
$$ \alpha_1 \mathbf G^{[1]}+\dots+\alpha_k \mathbf G^{[k]} $$
строк матрицы дает строку $ (\alpha_1,\dots,\alpha_k,\dots ) $ и для обращения ее в нулевую необходимо, чтобы $ \alpha_1=0,\dots,\alpha_k=0 $.
♦
Видим, что по структуре матрицы $ \mathbf G $ и $ \mathbf H $ очень похожи друг на друга. Задав одну из них, однозначно определяем другую. В одном из следующих пунктов, мы воспользуемся этим обстоятельством — для целей исправления ошибок оказывается выгоднее сначала задавать $ \mathbf H $.
Т
Теорема 2. Кодовое расстояние линейного подпространства $ \mathbb V^{n}_{[k]} $ равно минимальному весу его ненулевых кодовых слов:
$$ d( \mathbb V^{n}_{[k]})= \min_{ U \in \mathbb V^{n}_{[k]} \atop U \ne \mathbb O } w(U) \ . $$
Доказательство. Линейное подпространство замкнуто относительно операции сложения (вычитания) векторов. Поэтому если $ \{U_1,U_2\}\subset \mathbb V^{n}_{[k]} $, то и $ U_1-U_2 \in \mathbb V^{n}_{[k]} $, а также $ \mathbb O \in V^{n}_{[k]} $. Тогда
$$ \rho(U_1,U_2)=\rho(U_1-U_2, \mathbb O)= w(U_1-U_2) \ . $$
♦
Кодовое расстояние дает третью характеристику линейного кода — теперь он описывается набором чисел $ (n,k,d) $.
Т
Теорема 3. Пусть $ d_{} $ означает кодовое расстояние кода $ \mathbb V^{n}_{[k]} $ с проверочной матрицей $ \mathbf H $. Тогда любое подмножество из $ \ell_{} $ столбцов этой матрицы будет линейно независимо при $ \ell < d $. Обратно, если любое подмножество из $ \ell_{} $ столбцов матрицы $ \mathbf H $ линейно независимо, то $ d > \ell $.
Доказательство. Если $ d_{} $ — кодовое расстояние, то, в соответствии с теоремой 2, ни одно ненулевое кодовое слово $ X\in \mathbb V^{n}_{[k]} $ не должно иметь вес, меньший $ d_{} $. Если предположить,
что столбцы $ \{\mathbf H_{[i_1]},\dots,\mathbf H_{[i_{\ell}]}\} $ линейно зависимы при $ \ell< d $, то
существуют числа $ x_{i_1},\dots,x_{i_{\ell}} $ не все равные нулю, такие что
$$ x_{i_1}\mathbf H_{[i_1]}+\dots+x_{i_{\ell}} H_{[i_{\ell}]} = \mathbb O \ . $$
Придавая всем остальным переменным $ \{x_1,\dots,x_n\} \setminus \{ x_{i_1},\dots,x_{i_{\ell}} \} $ нулевые значения, получаем вектор $ X_{} \in \mathbb V^n $, удовлетворяющий равенству
$$ x_1 \mathbf H_{[1]}+\dots + x_n \mathbf H_{[n]} = \mathbb O \ , $$
и вес этого вектора $ \le \ell< d $. Но тогда этот вектор принадлежит и $ \mathbb V^{n}_{[k]} $ поскольку $ \mathbf H X^{\top} = \mathbb O $.
Это противоречит предположению о весе кодовых слов. Следовательно любые $ \ell_{} $ столбцов матрицы $ \mathbf H $ линейно независимы если $ \ell < d $.
Обратно, пусть любые $ \ell_{} $ столбцов матрицы $ \mathbf H $ линейно независимы, но существует кодовое слово $ X_{}=(x_1,\dots,x_n) \ne \mathbb O $ веса $ \le \ell $. Пусть, для определенности, $ x_{\ell+1}=0,\dots, x_{n}=0 $. Тогда
$$ x_1 \mathbf H_{[1]}+\dots + x_{\ell} \mathbf H_{[\ell]}= \mathbb O $$
при хотя бы одном из чисел $ \{x_j\}_{j=1}^{\ell} $ равном $ 1_{} $. Но это означает, что столбцы
$ \mathbf H_{[1]},\dots, \mathbf H_{[\ell]} $ линейно зависимы, что противоречит предположению.
♦
Испровление ашибок
До сих пор мы не накладывали ни каких дополнительных ограничений ни на порождающую ни на проверочную матрицы кода: любая из них могла быть выбрана почти произвольной.
Теперь обратимся собственно к задаче обнаружения (а также возможной коррекции) ошибок при передаче кодового слова по зашумленному каналу связи.
Если $ X\in \mathbb V^{n}_{[k]} $ — кодовое слово, а $ Y\in \mathbb V^n $ — вектор, получившийся по прохождении этого слова по каналу, то $ Y-X $ называется вектором ошибок. Понятно, что при $ w(Y-X)=0 $ ошибки при передаче нет.
Предположим, что $ w(Y-X)=1 $, т.е. что при передаче произошла ошибка ровно в одном разряде кодового слова $ X_{} $. Попробуем ее обнаружить исходя из предположения, что кодовое слово выбиралось во множестве $ \mathbb V^{n}_{[k]} $ линейного $ (n,k) $-кода, определенного в предыдущем пункте при какой-то проверочной матрице $ \mathbf H $. Если для полученного вектора $ Y_{} $ выполняются все проверочные условия:
$$ Y \cdot \mathbf H^{\top} = \mathbb O_{1\times k} \ , $$
(или, что то же $ Y \in \mathbb V^{n}_{[k]} $), то ошибка передачи считается не выявленной.
Для произвольного вектора $ Y \in \mathbb V^{n} $ вектор-строка
$$ S=Y \cdot \mathbf H^{\top} \in \mathbb V^{k} $$
называется синдромом вектора Y. C точки зрения линейной алгебры его можно интерпретировать как показатель отхода вектора $ Y_{} $ от гиперплоскости, заданной системой однородных уравнений $ X\cdot \mathbf H^{\top}=\mathbb O $.

Если синдром $ S_{} $ ненулевой: $ Y \cdot \mathbf H^{\top} \ne \mathbb O_{1\times k} $,
то полученный вектор $ Y_{} $ не принадлежит множеству $ \mathbb V^{n}_{[k]} $ допустимых кодовых слов. Факт ошибки подтвержден. Изначально мы предположили, что произошла только одна ошибка, т.е.
$$ Y-X= {\mathfrak e}_j = \big(\underbrace{0,\dots,0,1}_{j},0,\dots,0\big) $$
при некотором $ j\in \{1,\dots n\} $. Тогда
$$ S= Y \cdot \mathbf H^{\top} = (X+{\mathfrak e}_j) \cdot \mathbf H^{\top}=X\cdot \mathbf H^{\top}+
{\mathfrak e}_j \cdot \mathbf H^{\top}=
$$
$$
=\mathbb O_{1\times k} + \mathbf H_{[j]}^{\top} = \mathbf H_{[j]}^{\top}
$$
при $ \mathbf H_{[j]} $ означающем $ j_{} $-й столбец проверочной матрицы $ \mathbf H $. Таким образом получили соответствие
$$ {}_{} \mathbf{HOMEP} \mbox{ поврежденного бита} \mathbf{=HOMEP} \mbox{ столбца проверочной матрицы.} $$
И, следовательно, мы получили возможность обнаружить место повреждения — по факту совпадения синдрома со столбцом проверочной матрицы. К сожалению, реальность оказывается более сложной…
П
Пример. В примере предыдущего пункта проверочная матрица была выбрана в виде
$$ \mathbf H=
\left( \begin{array}{ccccc}
1 & 1 & 0 & 1 & 0 \\
1 & 0 & 1 & 0 & 1
\end{array}
\right) \ .
$$
Если при передаче кодового слова $ (10011) $ произошла ошибка в первом бите, т.е. $ Y=(00011) $, то синдром
$$ S=Y \cdot \mathbf H^{\top} = (11) $$
однозначно укажет на номер столбца матрицы $ \mathbf H $. Если же ошибка произошла в четвертом бите, т.е. $ Y=(10001) $, то
$$ S=(10) \ , $$
но таких6) столбцов в матрице $ \mathbf H $ два!
♦
Вывод. Для однозначного обнаружения места ошибки7) достаточно, чтобы все столбцы матрицы $ \mathbf H $ были различными.
Столбцами этой матрицы являются транспонированные строки пространства $ \mathbb V^{n-k} $.
Построение кода
Итак, исходя из соображений, завершающих предыдущий пункт, будем строить код, исправляющий одну ошибку, беря за стартовую точку именно матрицу $ \mathbf H $. Выбираем ее произвольного порядка $ M\times N $ при $ \{M,N\} \in \mathbb N, M<N $ и вида
$$ \mathbf H_{M\times N} = \left[ \tilde P \mid E_M \right] \ , $$
где матрица $ E_M $ — единичная порядка $ M_{} $, а матрица $ \tilde P $ имеет порядок $ M\times (N-M) $, и столбцы ее должны быть различными, ненулевыми и отличаться от столбцов матрицы $ E_M $. По этой проверочной матрице — в соответствии со следствием к теореме $ 1 $ из
☞
ПУНКТА — строим порождающую матрицу:
$$ \mathbf G_{(N-M)\times N} = \left[ E_{N-M} \mid \tilde P^{\top} \right] \ . $$
Строки матрицы $ \mathbf G $ могут быть взяты в качестве базисных векторов подпространства кодовых слов.
П
Пример. Пусть $ M=2 $. Здесь имеем единственный вариант:
$$ \mathbf H_{2\times 3} = \left( \begin{array}{c|cc} 1 & 1 & 0 \\ 1 & 0 & 1 \end{array} \right) \ , $$
поскольку в $ \mathbb V^2 $ имеется лишь одна ненулевая строка, отличная от $ (10) $ и $ (01) $. Таким образом $ N=3 $ и
$$ \mathbf G_{1\times 3}=( 1\, 1\, 1 ) \ . $$
Следовательно, подпространство кодовых слов в $ \mathbb V^3 $ является одномерным, и имеем всего два возможных кодовых слова: $ (000) $ и $ (111) $.
Пусть $ M=3 $. В $ \mathbb V^3 $ имеется уже большой выбор строк, отличных от $ (100), (010), (001) $. Так, можно взять
$$
\mathbf H_{3\times 4} = \left( \begin{array}{c|ccc} 1 & 1 & 0 & 0 \\ 1 & 0 & 1 & 0 \\ 1 & 0 & 0 & 1 \end{array} \right) \quad \mbox{ или } \quad
\mathbf H_{3\times 5} = \left( \begin{array}{cc|ccc} 1 & 0 & 1 & 0 & 0 \\ 1 & 1 & 0 & 1 & 0 \\ 0 & 1 & 0 & 0 & 1 \end{array} \right)
$$
$$
\mbox{ или } \quad
\mathbf H_{3\times 6} =
\left( \begin{array}{ccc|ccc} 1 & 0 & 1 & 1 & 0 & 0 \\ 1 & 1 & 0 & 0 & 1 & 0 \\ 0 & 1 & 1 & 0 & 0 & 1 \end{array} \right) \quad \mbox{ или } \quad
\mathbf H_{3\times 7} =
\left( \begin{array}{cccc|ccc} 1 & 1 & 0 & 1 & 1 & 0 & 0 \\ 1 & 1 & 1 & 0 & 0 & 1 & 0 \\ 1 & 0 & 1 & 1 & 0 & 0 & 1 \end{array} \right) \ .
$$
Соответственно,
$$ \mathbf G= (1\, 1\, 1\, 1) \quad \quad \mbox{ или } \quad
\mathbf G=
\left( \begin{array}{cc|ccc} 1 & 0 & 1 & 1 & 0 \\ 0 & 1 & 0 & 1 & 1 \end{array} \right)
\quad
$$
$$
\mbox{ или } \quad
\mathbf G=
\left( \begin{array}{ccc|ccc} 1 & 0 & 0 & 1 & 1 & 0 \\ 0 & 1 & 0 & 0 & 1 & 1 \\ 0 & 0 & 1 & 1 & 0 & 1 \end{array} \right)
\quad \quad \mbox{ или } \quad
\mathbf G=
\left( \begin{array}{cccc|ccc} 1 & 0 & 0 & 0 & 1 & 1 & 1 \\ 0 & 1 & 0 & 0 & 1 & 1 & 0 \\ 0 & 0 & 1 & 0 & 0 & 1 & 1 \\ 0 & 0 & 0 & 1 & 1 & 0 & 1
\end{array} \right) \ .
$$
Кодовых векторов в соответствующих кодах будет $ 2^1,2^2,2^3,2^4 $. Любой из них способен исправить одну ошибку, полученную в ходе передачи.
♦
Если поставить задачу максимизации числа кодовых слов, то матрицу $ \mathbf H $ следует выбирать самой широкой, т.е. делать $ N_{} $ максимально возможным. При фиксированном $ M_{} $ это достигается при выборе $ N=2^M-1 $. Тогда соответствующий линейный $ (n,k) $-код имеет значения параметров $ n=2^M-1,k=2^M-M-1 $, и именно он обычно и выбирается в качестве кода Хэмминга.
Найдем величину его кодового расстояния $ d_{} $. В соответствии с теоремой $ 3 $ из
☞
ПУНКТА, $ d>\ell $, если любое подмножество из $ \ell_{} $ столбцов матрицы $ \mathbf H $ линейно независимо. Поскольку столбцы проверочной матрицы кода Хэмминга все различны, то любая пара из них линейно независима (свойство
3
☞
ЗДЕСЬ ). Следовательно, $ d>2 $. По теореме из
☞
ПУНКТА, получаем —
Если при передаче произошла ровно одна ошибка, то код Хэмминга способен ее исправить; если при передаче произошло ровно две ошибки, то код Хэмминга достоверно устанавливает лишь факт наличия ошибки.
Если попробовать исправить заглавие предыдущего пункта, исходя только из информации о структуре набора составляющих текст букв, то этой информации оказывается недостаточно: набор букв в правильном тексте будет таким же
П
Пример. Для проверочной матрицы $ (7,4) $-кода Хэмминга
$$
\mathbf H_{3\times 7} =
\left( \begin{array}{ccccccc} 1 & 1 & 0 & 1 & 1 & 0 & 0 \\ 1 & 1 & 1 & 0 & 0 & 1 & 0 \\ 1 & 0 & 1 & 1 & 0 & 0 & 1 \end{array} \right)
$$
вектор $ X=(0011110) $ является кодовым. Если при передаче произошла лишь одна ошибка и на выходе канала получили вектор $ Y=(1011110) $, то синдром этого вектора $ S=Y \mathbf H^{\top}=(111) $. Поскольку $ S^{\top} $ совпадает с первым столбцом матрицы $ \mathbf H $, то заключаем, что ошибка произошла в первом разряде. Тут же исправляем его на противоположный: $ X=Y+\mathfrak e_1 $.
Если при передаче произошло две ошибки и на выходе канала получили вектор $ \tilde Y=(1011010) $, то синдром этого вектора $ S=\tilde Y \mathbf H^{\top}=(011) $. Поскольку синдром ненулевой, то факт наличия ошибки подтвержден. Однако корректно исправить ее — по аналогии с предыдущим — не удается. $ S^{\top} $ совпадает с третьим столбцом матрицы $ \mathbf H $, но в третьем разряде полученного вектора ошибки нет.
Наконец, если при передаче произошли три ошибки и на выходе канала получили вектор $ \widehat Y=(1011011) $, то синдром этого вектора $ S=\widehat Y \mathbf H^{\top}=(010) $. Наличие ошибки подтверждено, исправление невозможно. Если же — при передаче того же вектора $ X=(0011110) $ — получаем вектор
$ \widehat Y_1=(1111111) $ (также с тремя ошибками), то его синдром оказывается нулевым: $ \widehat Y_1 \mathbf H^{\top}=(000) $ и ошибка не обнаруживается.
♦
Проблема сравнения синдрома полученного вектора $ Y_{} $ со столбцами проверочной матрицы $ \mathbf H $ с целью определения места ошибки — не такая тривиальная, особенно для больших $ n_{} $. Для упрощения этой процедуры воспользуемся следующим простым соображением. Размещение проверочных разрядов в конце кодового слова обусловлено лишь соображениями удобства изложения учебного материала. С точки зрения практической реализации, $ n-k $ проверочных разрядов можно разместить в любых местах кодового слова $ X_{} $ и даже «вразбивку», т.е. не подряд. Перестановке разрядов в кодовом слове будет соответствовать перестановка столбцов в матрице $ \mathbf H $, при этом само множество столбцов остается неизменным — это транспонированные строки пространства $ \mathbb V^{n-k} $ (ненулевые и различные). Рассмотрим $ (n,k) $-код Хэмминга при $ n=2^M-1,k=2^M-M-1, M \ge 2 $. Тогда каждую ненулевую строку пространства $ \mathbb V^{n-k}= \mathbb V^M $ можно интерпретировать как двоичное представление числа из множества
$ \{1,2,3,\dots,2^M-1\} $. Пусть
$$ j=\underline{{\mathfrak b}_1{\mathfrak b}_2 \dots {\mathfrak b}_{M-1} {\mathfrak b}_{M}}=
{\mathfrak b}_1 \times 2^{M-1}+{\mathfrak b}_2 \times 2^{M-2}+\dots+{\mathfrak b}_{M-1} \times 2+ {\mathfrak b}_{M} \quad npu \quad \{ {\mathfrak b}_j\}_{j=1}^M\subset \{0,1\} \quad — $$
— двоичное представление числа $ j_{} $. Переупорядочим столбцы проверочной матрицы $ \mathbf H $ так, чтобы
$$ \mathbf H_{[j]}=\left[ {\mathfrak b}_1{\mathfrak b}_2 \dots {\mathfrak b}_{M-1} {\mathfrak b}_{M}\right]^{\top} \ , $$
т.е. чтобы $ j_{} $-й столбец содержал двоичное представление числа $ j_{} $. При таком упорядочении,
синдром произвольного вектора $ Y_{} $, отличающегося от кодового слова $ X_{} $ в единственном разряде, является двоичным представлением номера этого разряда:
$$ {\bf \mbox{СИНДРОМ }} \ (Y)=\mathbf{HOMEP} \ (\mbox{ошибочный разряд}) \ . $$
Осталось теперь выяснить какие разряды кодового слова содержат проверочные биты.
П
Пример. Для $ (7,4) $-кода Хэмминга матрицу $ \mathbf H $, построенную в предыдущем примере, переупорядочим по столбцам; будем рассматривать ее в виде
$$
\begin{array}{c}
\left( \begin{array}{ccccccc}
0 & 0 & 0 & 1 & 1 & 1 & 1 \\
0 & 1 & 1 & 0 & 0 & 1 & 1 \\
1 & 0 & 1 & 0 & 1 & 0 & 1
\end{array} \right) \\
\begin{array}{ccccccc}
\uparrow & \uparrow & \uparrow & \uparrow & \uparrow & \uparrow & \uparrow \\
\scriptstyle 1 & \scriptstyle 2 & \scriptstyle 3 & \scriptstyle 4 & \scriptstyle 5 & \scriptstyle 6 & \scriptstyle 7
\end{array}
\end{array}
$$
Распишем проверочные соотношения $ X\mathbf H^{\top}=\mathbb O $ покомпонентно:
$$
\left\{
\begin{array}{ccccccc}
& & & x_4&+x_5&+x_6&+x_7=0 \\
&x_2&+x_3& & & +x_6&+x_7=0 \\
x_1& & +x_3& & +x_5 & & +x_7=0
\end{array} \right. \quad \iff
$$
$$
\iff \quad
\left\{
\begin{array}{ccccccc}
x_1& & +x_3& & +x_5 & & +x_7=0 \\
&x_2&+x_3& & & +x_6&+x_7=0 \\
& & & x_4&+x_5&+x_6&+x_7=0
\end{array} \right.
$$
Переписанные в последнем виде, эти уравнения представляют конечный пункт прямого хода метода Гаусса решения системы линейных уравнений, а именно — трапециевидную форму этой системы. Если бы мы поставили задачу поиска общего решения этой (однородной) системы и нахождения фундаментальной системы решений, то в качестве зависимых переменных однозначно бы выбрали $ x_1, x_2, x_4 $. Выпишем это общее решение 
$$
x_1=x_3+x_5+x_7,\ x_2=x_3+x_6+x_7,\ x_4=x_5+x_6+x_7 \ .
$$
Это и есть проверочные соотношения, а проверочными разрядами кодового вектора являются $ 1_{} $-й, $ 2_{} $-й и $ 4_{} $-й.
Проверим правильность этих рассуждений. Придадим оставшимся разрядам произвольные значения, например:
$ x_3=1,x_5=1,x_6=0,x_7=1 $. Тогда $ x_1=1, x_2=0,x_4=0 $ и кодовый вектор $ X=(1010101) $. Пусть на выходе из канала он превратился в $ Y=(1000101) $. Синдром этого вектора $ Y\mathbf H^{\top}=(011) $ — это двоичное представление числа $ 3_{} $. И ведь действительно: ошибка — в третьем разряде!
♦
Алгоритм построения (n,k)-кода Хэмминга
для $ n=2^M-1,k=2^M-M-1, M \ge 2 $.
1.
Строится матрица $ \mathbf H $ порядка $ M \times (2^M-1) $ из столбцов, представляющих двоичные представления чисел $ \{1,2,3,\dots,2^M-1\} $ (младшие разряды — внизу).
2.
Проверочные разряды имеют номера, равные степеням двойки: $ 1,2,2^2,\dots,2^{M-1} $.
3.
Проверочные соотношения получаются из матричного представления $ X\mathbf H^{\top}=\mathbb O $ выражением проверочных разрядов через информационные.
Можно немного улучшить код Хэмминга, увеличив кодовое расстояние до $ 4_{} $.
?
Является ли $ 8_{} $-мибитный код Адамара из примера
☞
ПУНКТА линейным кодом?
.
Источники
[1]. Питерсон У., Уэлдон Э. Коды, исправляющие ошибки. М.Мир. 1976.
[2]. Марков А.А. Введение в теорию кодирования. М.Наука. 1982
Корректирующие коды на пальцах
12 Jul 2019
Корректирующие (или помехоустойчивые) коды — это коды, которые могут обнаружить и, если повезёт, исправить ошибки, возникшие при передаче данных. Даже если вы ничего не слышали о них, то наверняка встречали аббревиатуру CRC в списке файлов в ZIP-архиве или даже надпись ECC на планке памяти. А кто-то, может быть, задумывался, как так получается, что если поцарапать DVD-диск, то данные всё равно считываются без ошибок. Конечно, если царапина не в сантиметр толщиной и не разрезала диск пополам. Как нетрудно догадаться, ко всему этому причастны корректирующие коды. Собственно, ECC так и расшифровывается — «error-correcting code», то есть «код, исправляющий ошибки». А CRC — это один из алгоритмов, обнаруживающих ошибки в данных. Исправить он их не может, но часто это и не требуется. Давайте выясним, что это такое. Первую версию этой статьи я написал для «Хабра». Привожу её здесь с минимальными изменениями.
Для понимания статьи не нужны никакие специальные знания. Достаточно лишь понимать, что такое вектор и матрица, как они перемножаются и как с их помощью записать систему линейных уравнений. Я постарался всё объяснить, но без карандаша и бумаги текст может показаться немного запутанным.
Каналы с ошибкой
Разберёмся сперва, откуда вообще берутся ошибки, которые мы собираемся исправлять. Перед нами стоит следующая задача. Нужно передать несколько блоков данных, каждый из которых кодируется цепочкой двоичных цифр. Получившаяся последовательность нулей и единиц передаётся через канал связи. Но так сложилось, что реальные каналы связи часто подвержены ошибкам. Вообще говоря, ошибки могут быть разных видов — может появиться лишняя цифра или какая-то пропасть. Но мы будем рассматривать только ситуации, когда в канале возможны лишь замены нуля на единицу и наоборот. Причём опять же для простоты будем считать такие замены равновероятными.
Ошибка — это маловероятное событие (а иначе зачем нам такой канал вообще, где одни ошибки?), а значит, вероятность двух ошибок меньше, а трёх уже совсем мала. Мы можем выбрать для себя некоторую приемлемую величину вероятности, очертив границу «это уж точно невозможно». Это позволит нам сказать, что в канале возможно не более, чем \(k\) ошибок. Это будет характеристикой канала связи.
Для простоты введём следующие обозначения. Пусть данные, которые мы хотим передавать, — это двоичные последовательности фиксированной длины. Чтобы не запутаться в нулях и единицах, будем иногда обозначать их заглавными латинскими буквами (\(A\), \(B\), \(C\), …). Что именно передавать, в общем-то неважно, просто с буквами в первое время будет проще работать.
Кодирование и декодирование будем обозначать прямой стрелкой (\(\rightarrow\)), а передачу по каналу связи — волнистой стрелкой (\(\rightsquigarrow\)). Ошибки при передаче будем подчёркивать.
Например, пусть мы хотим передавать только сообщения \(A=0\) и \(B=1\). В простейшем случае их можно закодировать нулём и единицей (сюрприз!):
\[\begin{aligned}
A &\to 0,\\
B &\to 1.
\end{aligned}\]
Передача по каналу, в котором возникла ошибка будет записана так:
\[A \to 0 \rightsquigarrow \underline{1} \to B.\]
Цепочки нулей и единиц, которыми мы кодируем буквы, будем называть кодовыми словами. В данном простом случае кодовые слова — это \(0\) и \(1\).
Код с утроением
Давайте попробуем построить какой-то корректирующий код. Что мы обычно делаем, когда кто-то нас не расслышал? Повторяем дважды:
\[\begin{aligned}
A &\to 00,\\
B &\to 11.
\end{aligned}\]
Правда, это нам не очень поможет. В самом деле, рассмотрим канал с одной возможной ошибкой:
\[A \to 00 \rightsquigarrow 0\underline{1} \to ?.\]
Какие выводы мы можем сделать, когда получили \(01\)? Понятно, что раз у нас не две одинаковые цифры, то была ошибка, но вот в каком разряде? Может, в первом, и была передана буква \(B\). А может, во втором, и была передана \(A\).
То есть, получившийся код обнаруживает, но не исправляет ошибки. Ну, тоже неплохо, в общем-то. Но мы пойдём дальше и будем теперь утраивать цифры.
\[\begin{aligned}
A &\to 000,\\
B &\to 111.
\end{aligned}\]
Проверим в деле:
\[A \to 000 \rightsquigarrow 0\underline{1}0 \to A?.\]
Получили \(010\). Тут у нас есть две возможности: либо это \(B\) и было две ошибки (в крайних цифрах), либо это \(A\) и была одна ошибка. Вообще, вероятность одной ошибки выше вероятности двух ошибок, так что самым правдоподобным будет предположение о том, что передавалась именно буква \(A\). Хотя правдоподобное — не значит истинное, поэтому рядом и стоит вопросительный знак.
Если в канале связи возможна максимум одна ошибка, то первое предположение о двух ошибках становится невозможным и остаётся только один вариант — передавалась буква \(A\).
Про такой код говорят, что он исправляет одну ошибку. Две он тоже обнаружит, но исправит уже неверно.
Это, конечно, самый простой код. Кодировать легко, да и декодировать тоже. Ноликов больше — значит передавался ноль, единичек — значит единица.
Если немного подумать, то можно предложить код исправляющий две ошибки. Это будет код, в котором мы повторяем одиночный бит 5 раз.
Расстояния между кодами
Рассмотрим поподробнее код с утроением. Итак, мы получили работающий код, который исправляет одиночную ошибку. Но за всё хорошее надо платить: он кодирует один бит тремя. Не очень-то и эффективно.
И вообще, почему этот код работает? Почему нужно именно утраивать для устранения одной ошибки? Наверняка это всё неспроста.
Давайте подумаем, как этот код работает. Интуитивно всё понятно. Нолики и единички — это две непохожие последовательности. Так как они достаточно длинные, то одиночная ошибка не сильно портит их вид.
Пусть мы передавали \(000\), а получили \(001\). Видно, что эта цепочка больше похожа на исходные \(000\), чем на \(111\). А так как других кодовых слов у нас нет, то и выбор очевиден.
Но что значит «больше похоже»? А всё просто! Чем больше символов у двух цепочек совпадает, тем больше их схожесть. Если почти все символы отличаются, то цепочки «далеки» друг от друга.
Можно ввести некоторую величину \(d(\alpha, \beta)\), равную количеству различающихся цифр в соответствующих разрядах цепочек \(\alpha\) и \(\beta\). Эту величину называют расстоянием Хэмминга. Чем больше это расстояние, тем меньше похожи две цепочки.
Например, \(d(010, 010) = 0\), так как все цифры в соответствующих позициях равны, а вот \(d(010101, 011011) = 3\).
Расстояние Хэмминга называют расстоянием неспроста. Ведь в самом деле, что такое расстояние? Это какая-то характеристика, указывающая на близость двух точек, и для которой верны утверждения:
- Расстояние между точками неотрицательно и равно нулю только, если точки совпадают.
- Расстояние в обе стороны одинаково.
- Путь через третью точку не короче, чем прямой путь.
Достаточно разумные требования.
Математически это можно записать так (нам это не пригодится, просто ради интереса посмотрим):
- \[d(x, y) \geqslant 0,\quad d(x, y) = 0 \Leftrightarrow x = y;\]
- \[d(x, y) = d(y, x);\]
- \(d(x, z) + d(z, y) \geqslant d(x, y)\).
Предлагаю читателю самому убедиться, что для расстояния Хэмминга эти свойства выполняются.
Окрестности
Таким образом, разные цепочки мы считаем точками в каком-то воображаемом пространстве, и теперь мы умеем находить расстояния между ними. Правда, если попытаться сколько нибудь длинные цепочки расставить на листе бумаги так, чтобы расстояния Хэмминга совпадали с расстояниями на плоскости, мы можем потерпеть неудачу. Но не нужно переживать. Всё же это особое пространство со своими законами. А слова вроде «расстояния» лишь помогают нам рассуждать.
Пойдём дальше. Раз мы заговорили о расстоянии, то можно ввести такое понятие как окрестность. Как известно, окрестность какой-то точки — это шар определённого радиуса с центром в ней. Шар? Какие ещё шары! Мы же о кодах говорим.
Но всё просто. Ведь что такое шар? Это множество всех точек, которые находятся от данной не дальше, чем некоторое расстояние, называемое радиусом. Точки у нас есть, расстояние у нас есть, теперь есть и шары.
Так, скажем, окрестность кодового слова \(000\) радиуса 1 — это все коды, находящиеся на расстоянии не больше, чем 1 от него, то есть отличающиеся не больше, чем в одном разряде. То есть это коды:
\[\{000, 100, 010, 001\}.\]
Да, вот так странно выглядят шары в пространстве кодов.
А теперь посмотрите. Это же все возможные коды, которые мы получим в канале в одной ошибкой, если отправим \(000\)! Это следует прямо из определения окрестности. Ведь каждая ошибка заставляет цепочку измениться только в одном разряде, а значит удаляет её на расстояние 1 от исходного сообщения.
Аналогично, если в канале возможны две ошибки, то отправив некоторое сообщение \(x\), мы получим один из кодов, который принадлежит окрестности \(x\) радиусом 2.
Тогда всю нашу систему декодирования можно построить так. Мы получаем какую-то цепочку нулей и единиц (точку в нашей новой терминологии) и смотрим, в окрестность какого кодового слова она попадает.
Сколько ошибок может исправить код?
Чтобы код мог исправлять больше ошибок, окрестности должны быть как можно шире. С другой стороны, они не должны пересекаться. Иначе если точка попадёт в область пересечения, непонятно будет, к какой окрестности её отнести.
В коде с удвоением между кодовыми словами \(00\) и \(11\) расстояние равно 2 (оба разряда различаются). А значит, если мы построим вокруг них шары радиуса 1, то они будут касаться. Это значит, точка касания будет принадлежать обоим шарам и непонятно будет, к какому из них её отнести.
Именно это мы и получали. Мы видели, что есть ошибка, но не могли её исправить.
Что интересно, точек касания в нашем странном пространстве у шаров две — это коды \(01\) и \(10\). Расстояния от них до центров равны единице. Конечно же, в обычно геометрии такое невозможно, поэтому рисунки — это просто условность для более удобного рассуждения.
В случае кода с утроением, между шарами будет зазор.
Минимальный зазор между шарами равен 1, так как у нас расстояния всегда целые (ну не могут же две цепочки отличаться в полутора разрядах).
В общем случае получаем следующее.
Этот очевидный результат на самом деле очень важен. Он означает, что код с минимальным кодовым расстоянием \(d_{\min}\) будет успешно работать в канале с \(k\) ошибками, если выполняется соотношение
\[d_{\min} \geqslant 2k+1.\]
Полученное равенство позволяет легко определить, сколько ошибок будет исправлять тот или иной код. А сколько код ошибок может обнаружить? Рассуждения такие же. Код обнаруживает \(k\) ошибок, если в результате не получится другое кодовое слово. То есть, кодовые слова не должны находиться в окрестностях радиуса \(k\) других кодовых слов. Математически это записывается так:
\(d_{\min}\geqslant k + 1.\)
Рассмотрим пример. Пусть мы кодируем 4 буквы следующим образом.
\[\begin{aligned}
A \to 10100,\\
B \to 01000,\\
C \to 00111,\\
D \to 11011.\\
\end{aligned}\]
Чтобы найти минимальное расстояние между различными кодовыми словами, построим таблицу попарных расстояний.
| A | B | C | D | |
|---|---|---|---|---|
| A | — | 3 | 3 | 4 |
| B | 3 | — | 4 | 3 |
| C | 3 | 4 | — | 3 |
| D | 4 | 3 | 3 | — |
Минимальное расстояние \(d_{\min}=3\), а значит \(3\geqslant2k+1\), откуда получаем, что такой код может исправить до \(k=1\) ошибок. Обнаруживает же он две ошибки.
Рассмотрим пример:
\[A \to 10100 \rightsquigarrow 101\underline{1}0.\]
Чтобы декодировать полученное сообщение, посмотрим, к какому символу оно ближе всего.
\[\begin{aligned}
A:\, d(10110, 10100) &= 1,\\
B:\, d(10110, 01000) &= 4,\\
C:\, d(10110, 00111) &= 2,\\
D:\, d(10110, 11011) &= 3.
\end{aligned}\]
Минимальное расстояние получилось для символа \(A\), значит вероятнее всего передавался именно он:
\[A \to 10100 \rightsquigarrow 101\underline{1}0 \to A?.\]
Итак, этот код исправляет одну ошибку, как и код с утроением. Но он более эффективен, так как в отличие от кода с утроением здесь кодируется уже 4 символа.
Таким образом, основная проблема при построении такого рода кодов — так расположить кодовые слова, чтобы они были как можно дальше друг от друга, и их было побольше.
Для декодирования можно было бы использовать таблицу, в которой указывались бы все возможные принимаемые сообщения, и кодовые слова, которым они соответствуют. Но такая таблица получилась бы очень большой. Даже для нашего маленького кода, который выдаёт 5 двоичных цифр, получилось бы \(2^5 = 32\) варианта возможных принимаемых сообщений. Для более сложных кодов таблица будет значительно больше.
Попробуем придумать способ коррекции сообщения без таблиц. Мы всегда сможем найти полезное применение освободившейся памяти.
Интерлюдия: поле GF(2)
Для изложения дальнейшего материала нам потребуются матрицы. А при умножении матриц, как известно мы складываем и перемножаем числа. И тут есть проблема. Если с умножением всё более-менее хорошо, то как быть со сложением? Из-за того, что мы работаем только с одиночными двоичными цифрами, непонятно, как сложить 1 и 1, чтобы снова получилась одна двоичная цифра. Значит вместо классического сложения нужно использовать какое-то другое.
Введём операцию сложения как сложение по модулю 2 (хорошо известный программистам XOR):
\[\begin{aligned}
0 + 0 &= 0,\\
0 + 1 &= 1,\\
1 + 0 &= 1,\\
1 + 1 &= 0.
\end{aligned}\]
Умножение будем выполнять как обычно. Эти операции на самом деле введены не абы как, а чтобы получилась система, которая в математике называется полем. Поле — это просто множество (в нашем случае из 0 и 1), на котором так определены сложение и умножение, чтобы основные алгебраические законы сохранялись. Например, чтобы основные идеи, касающиеся матриц и систем уравнений по-прежнему были верны. А вычитание и деление мы можем ввести как обратные операции.
Множество из двух элементов \(\{0, 1\}\) с операциями, введёнными так, как мы это сделали, называется полем Галуа GF(2). GF — это Galois field, а 2 — количество элементов.
У сложения есть несколько очень полезных свойств, которыми мы будем пользоваться в дальнейшем.
\[x + x = 0.\]
Это свойство прямо следует из определения.
\[x + y = x — y.\]
А в этом можно убедиться, прибавив \(y\) к обеим частям равенства. Это свойство, в частности означает, что мы можем переносить в уравнении слагаемые в другую сторону без смены знака.
Проверяем корректность
Вернёмся к коду с утроением.
\[\begin{aligned}
A &\to 000,\\
B &\to 111.
\end{aligned}\]
Для начала просто решим задачу проверки, были ли вообще ошибки при передаче. Как видно, из самого кода, принятое сообщение будет кодовым словом только тогда, когда все три цифры равны между собой.
Пусть мы приняли вектор-строку \(x\) из трёх цифр. (Стрелочки над векторами рисовать не будем, так как у нас почти всё — это вектора или матрицы.)
\[\dots \rightsquigarrow x = (x_1, x_2, x_3).\]
Математически равенство всех трёх цифр можно записать как систему:
\[\left\{
\begin{aligned}
x_1 &= x_2,\\
x_2 &= x_3.
\end{aligned}
\right.\]
Или, если воспользоваться свойствами сложения в GF(2), получаем
\[\left\{
\begin{aligned}
x_1 + x_2 &= 0,\\
x_2 + x_3 &= 0.
\end{aligned}
\right.\]
Или
\[\left\{
\begin{aligned}
1\cdot x_1 + 1\cdot x_2 + 0\cdot x_3 &= 0,\\
0\cdot x_1 + 1\cdot x_2 + 1\cdot x_3 &= 0.
\end{aligned}
\right.\]
В матричном виде эта система будет иметь вид
\[Hx^T = 0,\]
где
\[H =
\begin{pmatrix}
1 & 1 & 0\\
0 & 1 & 1
\end{pmatrix}.\]
Транспонирование здесь нужно потому, что \(x\) — это вектор-строка, а не вектор-столбец. Иначе мы не могли бы умножать его справа на матрицу.
Будем называть матрицу \(H\) проверочной матрицей. Если полученное сообщение — это корректное кодовое слово (то есть, ошибки при передаче не было), то произведение проверочной матрицы на это сообщение будет равно нулевому вектору.
Умножение на матрицу — это гораздо более эффективно, чем поиск в таблице, но у нас на самом деле есть ещё одна таблица — это таблица кодирования. Попробуем от неё избавиться.
Кодирование
Итак, у нас есть система для проверки
\[\left\{
\begin{aligned}
x_1 + x_2 &= 0,\\
x_2 + x_3 &= 0.
\end{aligned}
\right.\]
Её решения — это кодовые слова. Собственно, мы систему и строили на основе кодовых слов. Попробуем теперь решить обратную задачу. По системе (или, что то же самое, по матрице \(H\)) найдём кодовые слова.
Правда, для нашей системы мы уже знаем ответ, поэтому, чтобы было интересно, возьмём другую матрицу:
\[H =
\begin{pmatrix}
1 & 0 & 1 & 0 & 0 \\
0 & 1 & 1 & 0 & 1\\
0 & 0 & 0 & 1 & 1
\end{pmatrix}.\]
Соответствующая система имеет вид:
\[\left\{
\begin{aligned}
x_1 + x_3 &= 0,\\
x_2 + x_3 + x_5 &= 0,\\
x_4 + x_5 &= 0.
\end{aligned}
\right.\]
Чтобы найти кодовые слова соответствующего кода нужно её решить.
В силу линейности сумма двух решений системы тоже будет решением системы. Это легко доказать. Если \(a\) и \(b\) — решения системы, то для их суммы верно
\[H(a+b)^T=Ha^T+Hb^T=0+0=0,\]
что означает, что она тоже — решение.
Поэтому если мы найдём все линейно независимые решения, то с их помощью можно получить вообще все решения системы. Для этого просто нужно найти их всевозможные суммы.
Выразим сперва все зависимые слагаемые. Их столько же, сколько и уравнений. Выражать надо так, чтобы справа были только независимые. Проще всего выразить \(x_1, x_2, x_4\).
Если бы нам не так повезло с системой, то нужно было бы складывая уравнения между собой получить такую систему, чтобы какие-то три переменные встречались по одному разу. Ну, или воспользоваться методом Гаусса. Для GF(2) он тоже работает.
Итак, получаем:
\[\left\{
\begin{aligned}
x_1 &= x_3,\\
x_2 &= x_3 + x_5,\\
x_4 &= x_5.
\end{aligned}
\right.\]
Чтобы получить все линейно независимые решения, приравниваем каждую из зависимых переменных к единице по очереди.
\[\begin{aligned}
x_3=1, x_5=0:\quad x_1=1, x_2=1, x_4=0 \Rightarrow x^{(1)} = (1, 1, 1, 0, 0),\\
x_3=0, x_5=1:\quad x_1=0, x_2=1, x_4=1 \Rightarrow x^{(2)} = (0, 1, 0, 1, 1).
\end{aligned}\]
Всевозможные суммы этих независимых решений (а именно они и будут кодовыми векторами) можно получить так:
\[a_1 x^{(1)}+a_2 x^{(2)},\]
где \(a_1, a_2\) равны либо нулю или единице. Так как таких коэффициентов два, то всего возможно \(2^2=4\) сочетания.
Но посмотрите! Формула, которую мы только что получили — это же снова умножение матрицы на вектор.
\[(a_1, a_2)\cdot
\begin{pmatrix}
1 & 1 & 1 & 0 & 0 \\
0 & 1 & 0 & 1 & 1
\end{pmatrix}
= aG.\]
Строчки здесь — линейно независимые решения, которые мы получили. Матрица \(G\) называется порождающей. Теперь вместо того, чтобы сами составлять таблицу кодирования, мы можем получать кодовые слова простым умножением на матрицу:
\[a \to aG.\]
Найдём кодовые слова для этого кода. (Не забываем, что длина исходных сообщений должна быть равна 2 — это количество найденных решений.)
\[\begin{aligned}
00 &\to 00000,\\
01 &\to 01011,\\
10 &\to 11100,\\
11 &\to 10111.
\end{aligned}\]
Итак, у нас есть готовый код, обнаруживающий ошибки. Проверим его в деле. Пусть мы хотим отправить 01 и у нас произошла ошибка при передаче. Обнаружит ли её код?
\[a=01 \to aG=01011 \rightsquigarrow x=01\underline{1}11 \to Hx^T = (110)^T \neq 0.\]
А раз в результате не нулевой вектор, значит код заподозрил неладное. Провести его не удалось. Ура, код работает!
Для кода с утроением, кстати, порождающая матрица выглядит очень просто:
\[G=\begin{pmatrix}1&1&1\end{pmatrix}.\]
Подобные коды, которые можно порождать и проверять матрицей, называются линейными (бывают и нелинейные), и они очень широко применяются на практике. Реализовать их довольно легко, так как тут требуется только умножение на константную матрицу.
Ошибка по синдрому
Ну хорошо, мы построили код обнаруживающий ошибки. Но мы же хотим их исправлять!
Для начала введём такое понятие, как вектор ошибки. Это вектор, на который отличается принятое сообщение от кодового слова. Пусть мы получили сообщение \(x\), а было отправлено кодовое слово \(v\). Тогда вектор ошибки по определению
\[e = x — v.\]
Но в странном мире GF(2), где сложение и вычитание одинаковы, будут верны и соотношения:
\[\begin{aligned}
v &= x + e,\\
x &= v + e.
\end{aligned}\]
В силу особенностей сложения, как читатель сам может легко убедиться, в векторе ошибки на позициях, где произошла ошибка будет единица, а на остальных ноль.
Как мы уже говорили раньше, если мы получили сообщение \(x\) с ошибкой, то \(Hx^T\neq 0\). Но ведь векторов, не равных нулю много! Быть может то, какой именно ненулевой вектор мы получили, подскажет нам характер ошибки?
Назовём результат умножения на проверочную матрицу синдромом:
\[s(x)=Hx^T.\]
И заметим следующее
\[s(x) = Hx^T = H(v+e)^T = He^T = s(e).\]
Это означает, что для ошибки синдром будет таким же, как и для полученного сообщения.
Разложим все возможные сообщения, которые мы можем получить из канала связи, по кучкам в зависимости от синдрома. Тогда из последнего соотношения следует, что в каждой кучке будут вектора с одной и той же ошибкой. Причём вектор этой ошибки тоже будет в кучке. Вот только как его узнать?
А очень просто! Помните, мы говорили, что у нескольких ошибок вероятность ниже, чем у одной ошибки? Руководствуясь этим соображением, наиболее правдоподобным будет считать вектором ошибки тот вектор, у которого меньше всего единиц. Будем называть его лидером.
Давайте посмотрим, какие синдромы дают всевозможные 5-элементные векторы. Сразу сгруппируем их и подчеркнём лидеров — векторы с наименьшим числом единиц.
| \(s(x)\) | \(x\) |
|---|---|
| \(000\) | \(\underline{00000}, 11100, 01011, 10111\) |
| \(001\) | \(\underline{00010}, 11110, 01001, 10101\) |
| \(010\) | \(\underline{01000}, 10100, 00011, 11111\) |
| \(011\) | \(01010, 10110, \underline{00001}, 11101\) |
| \(100\) | \(\underline{10000}, 01100, 11011, 00111\) |
| \(101\) | \(\underline{10010}, 01110, 11001, \underline{00101}\) |
| \(110\) | \(11000, \underline{00100}, 10011, 01111\) |
| \(111\) | \(11010, \underline{00110}, \underline{10001}, 01101\) |
В принципе, для корректирования ошибки достаточно было бы хранить таблицу соответствия синдрома лидеру.
Обратите внимание, что в некоторых строчках два лидера. Это значит для для данного синдрома два паттерна ошибки равновероятны. Иными словами, код обнаружил две ошибки, но исправить их не может.
Лидеры для всех возможных одиночных ошибок находятся в отдельных строках, а значит код может исправить любую одиночную ошибку. Ну, что же… Попробуем в этом убедиться.
\[a=01 \to aG=01011 \rightsquigarrow x=01\underline{1}11 \to s(x)=Hx^T = (110)^T \to e=(00100).\]
Вектор ошибки равен \((00100)\), а значит ошибка в третьем разряде. Как мы и загадали.
Ура, всё работает!
Что же дальше?
Чтобы попрактиковаться, попробуйте повторить рассуждения для разных проверочных матриц. Например, для кода с утроением.
Логическим продолжением изложенного был бы рассказ о циклических кодах — чрезвычайно интересном подклассе линейных кодов, обладающим замечательными свойствами. Но тогда, боюсь, статья уж очень бы разрослась.
Если вас заинтересовали подробности, то можете почитать замечательную книжку Аршинова и Садовского «Коды и математика». Там изложено гораздо больше, чем представлено в этой статье. Если интересует математика кодирования — то поищите «Теория и практика кодов, контролирующих ошибки» Блейхута. А вообще, материалов по этой теме довольно много.
Также у Александра Шеня есть замечательные видеолекции о помехоустойчивом кодировании.
Всячески рекомендую!