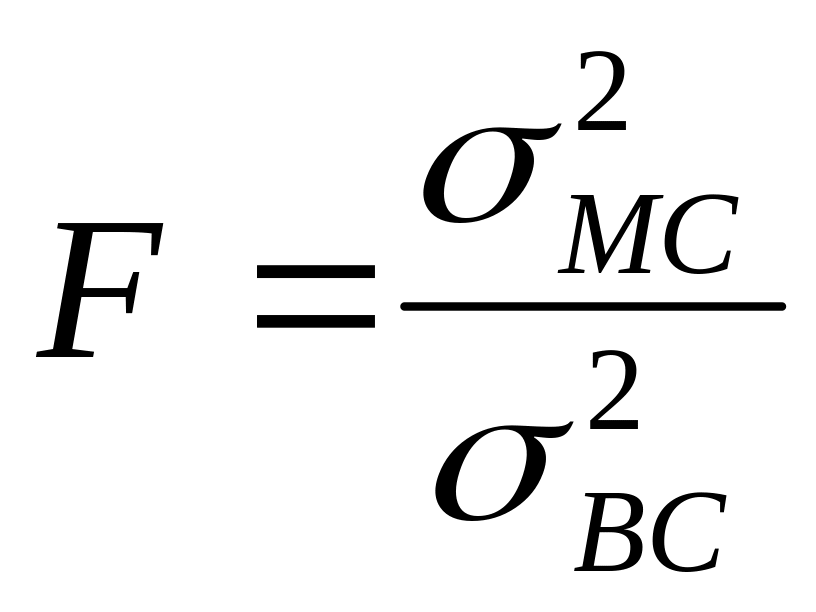Систематические ошибки измерений способы обнаружения и учета

Результаты наблюдений,
полученные при наличии системати­ческой
погрешности, называются неисправленными.
При проведении
измерений стараются в максимальной
степени исключить или учесть влияние
систематических погрешностей. Это может
быть дос­тигнуто следующими путями:

• устранением источников погрешностей
до начала измерений. В большинстве
областей измерений известны главные
источники систематических погрешностей
и разработаны методы, исключаю­щие
их возникновение или устраняющие их
влияние на результат измерения. В связи
с этим в практике измерений стараются
устра­нить систематические погрешности
не путем обработки экспери­ментальных
данных, а применением СИ, реализующих
соответст­вующие методы измерений;

• определением
поправок и внесением их в результат
измерения;

• оценкой границ неисключенных
систематических погрешностей.

Постоянная систематическая
погрешность не может быть най­дена
методами совместной обработки результатов
измерений. Од­нако она не искажает ни
показатели точности измерений,
характе­ризующие случайную погрешность,
ни результат нахождения переменной
составляющей систематической погрешности.

Дейст­вительно, результат одного
измерения

где х_и
– истинное значение измеряемой величины;
Δ_i
– i-я
случай­ная погрешность; θ_i
– i-я
систематическая погрешность. После
ус­реднения результатов многократных
измерений получаем среднее арифметическое
значение измеряемой величины

Если систематическая
погрешность постоянна во всех измере­ниях,
т.е. θ_i=θ
, то

Таким образом, постоянная систематическая
погрешность не уст­раняется при
многократных измерениях.

Постоянные систематические
погрешности могут быть обнару­жены
лишь путем сравнения
результатов измерений с другими,
по­лученными с помощью более высокоточных
методов и средств. Ино­гда эти
погрешности могут быть устранены
специальными приемами проведения
процесса измерений. Эти методы рассмотрены
ниже.

Наличие существенной переменной
систематической погрешно­сти искажает
оценки характеристик случайной
погрешности и ап­проксимацию ее
распределения. Поэтому она должна
обязательно выявляться и исключаться
из результатов измерений.

Для устранения постоянных систематических
погрешностей при­меняют следующие
методы:

• Метод
замещения,
представляющий собой
разновидность ме­тода сравнения,
когда сравнение осуществляется заменой
измеряе­мой величины известной
величиной, причем так, что при этом в
состоянии и действии всех используемых
средств измерений не про­исходит
никаких изменений. Этот метод дает
наиболее полное ре­шение задачи. Для
его реализации необходимо иметь
регулируе­мую меру, величина которой
однородна измеряемой.

• Метод
противопоставления,
являющийся разновидностью
метода сравнения, при котором измерение
выполняется дважды и проводится так,
чтобы в обоих случаях причина постоянной
по­грешности оказывала разные, но
известные по закономерности воздействия
на результаты наблюдений. Например,
способ взве­шивания Гаусса [3].

Пример 7.1. Измерить
сопротивление с помощью одинарного
моста ме­тодом противопоставления.

Сначала измеряемое
сопротивление R_x
уравновешивают известным со­противлением
R₁
включенным в плечо сравнения моста. При
этом R_х
= R₁·R₃
/R₄,
где R₃,
R₄
– сопротивления плеч моста. Затем
резисторы R_x
и R₁
меняют местами и вновь уравновешивают
мост, регулируя сопро­тивление
резистора R₁.
В этом случае R_x
= R΄₁·R₃/R₄.

Из двух последних уравнений
исключается отношение R₃/R₄.
Тогда

• Метод
компенсации погрешности по знаку
(метод изменения знака
систематической погрешности),
предусматривающий измерение с двумя
наблюдениями, выполняемыми так, чтобы
постоян­ная систематическая погрешность
входила в результат каждого из них с
разными знаками.

Пример 7.2. Измерить ЭДС
потенциометром постоянного тока,
имею­щим паразитную термо–ЭДС.

При выполнении одного
измерения получаем ЭДС Е₁
Затем меняем полярность измеряемой ЭДС
и направление тока в потенциометре.
Вновь проводим его уравновешивание –
получаем значение Е₂.
Если термо–ЭДС дает погрешность ΔЕ
и Е₁=Е_x+ΔЕ,
то Е₂=Е_x–ΔЕ.
Отсюда Е_x
= (Е
₁+
Е₂)/2.
Сле­довательно, систематическая
погрешность, обусловленная действием
термо–ЭДС, устранена.

• Метод
рандомизации –
наиболее универсальный способ ис­ключения
неизвестных постоянных систематических
погрешностей. Суть его состоит в том,
что одна и та же величина измеряется
раз­личными методами (приборами).
Систематические погрешности ка­ждого
из них для всей совокупности являются
разными случайны­ми величинами.
Вследствие этого при увеличении
числа используемых методов (приборов)
систематические погрешности вза­имно
компенсируются.

Для устранения переменных и монотонно
изменяющихся сис­тематических
погрешностей применяют следующие приемы
и ме­тоды.

• Анализ
знаков неисправленных случайных
погрешностей.
Ес­ли знаки
неисправленных случайных погрешностей
чередуются с какой-либо закономерностью,
то наблюдается переменная система­тическая
погрешность. Если последовательность
знаков «+» у слу­чайных погрешностей
сменяется последовательностью знаков
«–» или наоборот, то присутствует
монотонно изменяющаяся система­тическая
погрешность. Если группы знаков «»+ и
«–» у случайных погрешностей чередуются,
то присутствует периодическая
система­тическая погрешность.

• Графический
метод. Он
является одним из наиболее простых
способов обнаружения переменной
систематической погрешности в ряду
результатов наблюдений и заключается
в построении графика последовательности
неисправленных значений результатов
наблю­дений. На графике через построенные
точки проводят плавную кри­вую, которая
выражает тенденцию результата измерения,
если она существует. Если тенденция не
прослеживается, то переменную
сис­тематическую погрешность считают
практически отсутствующей.

• Метод
симметричных наблюдений.
Рассмотрим сущность
этого метода на примере измерительного
преобразователя, передаточная функция
которого имеет вид у = kх
+ у₀,
где х, у – входная и выходная величины
преобразователя; k
– коэффициент, погреш­ность которого
изменяется во времени по линейному
закону; у₀
– постоянная.

Для устранения систематической
погрешности трижды измеря­ется
выходная величина у через равные
промежутки времени Δt.
При первом и третьем измерениях на вход
преобразователя подает­ся сигнал х₀
от образцовой меры. В результате измерений
получа­ется система уравнений:

;

;

Ее решение позволяет получить
значение х, свободное от пере­менной
систематической погрешности, обусловленной
изменением коэффициента k:

Специальные статистические
методы. К
ним относятся спо­соб последовательных
разностей, дисперсионный анализ, и др.
Рас­смотрим подробнее некоторые из
них.

Способ последовательных
разностей (критерий Аббе).
При­меняется для обнаружения
изменяющейся во времени системати­ческой
погрешности и состоит в следующем.
Дисперсию результа­тов наблюдений
можно оценить двумя способами: обычным

и вычислением суммы квадратов
последовательных (в порядке
про­ведения измерений) разностей
(х_i–1
– х_i)²

Если в процессе измерений
происходило смещение центра груп­пирования
результатов наблюдений, т.е. имела место
переменная систематическая погрешность,
то σ²[x]
дает преувеличенную оцен­ку дисперсии
результатов наблюдений. Это объясняется
тем, что на σ²[x]
влияют вариации

.
В то же время изменения центра
груп­пирования

весьма мало сказываются на значениях
последова­тельных разностей d_i
= х_i+1
– х_i
поэтому смещения

почти не отра­зятся на значении Q²[x].

Отношение

является критерием для обнаруже­ния
систематических смещений центра
группирования результа­тов наблюдений.
Критическая область для этого критерия
(крите­рия Аббе) определяется как
Р(v<v_q)=q,
где q=1–Р
– уровень значимости, Р
– доверительная вероятность. Значения
v_ч
для раз­личных
уровней значимости q
и числа наблюдений n
приведены в табл. 7.1. Если полученное
значение критерия Аббе меньше v
при заданных q
и n,
то гипотеза о постоянстве центра
группирования результатов наблюдений
отвергается, т.е. обнаруживается
перемен­ная систематическая погрешность
результатов измерений.

Таблица 7.1

Значения критерия Аббе V_q.

n	Vq при q, равном	n	Vq при q, равном
0,001	0,01	0,05	0,001	0,01	0,05
4 5 6 7 8 9 10 11 12	0,295 0,208 0,182 0,185 0,202 0,221 0,241 0,260 0,278	0,313 0,269 0,281 0,307 0,331 0,354 0,376 0,396 0,414	0,390 0,410 0,445 0,468 0,491 0,512 0,531 0,548 0,564	13 14 15 16 17 18 19 20	0,295 0,311 0,327 0,341 0,355 0,368 0,381 0,393	0,431 0,447 0,461 0,474 0,487 0,499 0,510 0,520	0,578 0,591 0,603 0,614 0,624 0,633 0,642 0,650

Пример 7.3. Используя
способ после до нательных разностей,
определить, присутствует ли систематическая
погрешность в ряду результатов
наблю­дений, приведенных во втором
столбце табл. 7.2.

Таблица 7.2

Результаты наблюдений

n	xi	d1=xi+1–xi	di2		vi2
1	13,4	–	–	–0,6	0,36
2	13,3	–0,1	0,01	–0,7	0,49
3	14,5	+1,2	1,44	+0,5	0,25
4	13,8	–0,7	0,49	–0,2	0,04
5	14,5	+0,7	0,49	+0,5	0,25
6	14,6	+0,1	0,01	+0,6	0,36
7	14,1	–0,5	0,25	+0,1	0,01
8	14,3	+0,2	0,04	+0,3	0,09
9	14,0	+0,3	0,09	0,0	0,0
10	14,3	+0,3	0,09	+0,3	0,09
11	14,2	–1,1	1,21	–0,8	0,64
Σ154,0	–0,2	4,12	0,0	2,58

Для приведенного ряда
результатов вычисляем: среднее
арифмети­ческое

= 154,0/11 = 14; оценку дисперсии σ²[х]
= 2,58/10 = 0,258; зна­чение Q²[х]
= 4,12/(2·10)
= 0,206; критерий Аббе v
= 0,206/0,258 = 0,8.

Как видно из табл. 7.1, для
всех уровней значимости (q
= 0,001; 0,01 и 0,05) при n
= 11 имеем v
>v_q,
т.е. подтверждается
нулевая гипотеза о постоянстве центра
группирования. Следовательно, условия
измерений для приведенного ряда
оставались неизменными и систематических
расхожде­ний между результатами
наблюдений нет.

Дисперсионный анализ
(критерий Фишера). В
практике из­мерений часто бывает
необходимо выяснить наличие систематиче­ской
погрешности результатов наблюдений,
обусловленной влияни­ем какого-либо
постоянно действующего фактора, или
определить, вызывают ли изменения этого
фактора систематическое смещение
результатов измерений. В данном случае
проводят многократные измерения,
состоящие из достаточного числа серий,
каждая из кото­рых соответствует
определенным (пусть неизвестным, но
различным) значениям влияющего фактора.
Влияющими факторами, по кото­рым
производится объединение результатов
наблюдений по сериям, могут быть внешние
условия (температура, давление и т.д.),
временная последовательность проведения
измерений и т.п.

После проведения N
измерений их разбивают на s
серий (s>3)
по n_j
результатов наблюдений (sn_j
= N)
в каждой серии и затем уста­навливают,
имеется или отсутствует систематическое
расхождение между результатами наблюдений
в различных сериях. При этом долж­но
быть установлено, что результаты в
сериях распределены нор­мально.
Рассеяние результатов наблюдений в
пределах каждой се­рии отражает только
случайные влияния, характеризует лишь
случайные погрешности измерений в
пределах этой серии.

Характеристикой совокупности случайных
внутрисерийных по­грешностей будет
средняя сумма дисперсий результатов
наблюде­ний, вычисленных раздельно
для каждой серии, т.е.

,

где

,
x
_ji
– результат i-го
измерения в j-й
серии.

Внутрисерийная дисперсия

,
характеризует случайные по­грешности
измерений, так как только случайные
влияния обуслов­ливают те различия
(отклонения результатов наблюдений),
на ко­торых она основана. В то же время
рассеяние

различных серий обусловливается не
только случайными погрешностями
измерений, но и систематическими
различиями (если они существуют) между
результатами наблюдений, сгруппированными
по сериям. Следова­тельно, усредненная
межсерийная дисперсия

где

–
выражает силу действия фактора,
вызывающего систематические различия
между сериями.

Таким образом,

характеризует долю дисперсии всех
результатов наблюдений, обусловленную
наличием случайных погрешностей
измерений, а

– долю дисперсии, обу­словленную
межсерийными различиями результатов
наблюдений.

Первую из них называют
коэффициентом ошибки,
вторую – пока­зателем
дифференциации.
Чем больше отношение
показателя диф­ференциации к
коэффициенту ошибки, тем сильнее действие
фак­тора, по которому группировались
серии, и тем больше систематическое
различие между ними.

Критерием оценки наличия
систематических погрешностей в данном
случае является дисперсионный критерий
Фишера

.
Критическая область для
критерия Фишера соответ­ствует Р(F>
F_q)
= q.

Значения F_q
для различных уровней значимости q,
числа изме­рений N
и числа серий s
приведены в таблице в конце лекции, где
k₂=
N – s,
k₁
= s
– 1. Если полученное
значение критерия Фишера больше F_q
(при заданных q,
N и s),
то гипотеза об отсутствии систематических
смещения результатов наблюдений по
сериям отвергается, т.е. обна­руживается
систематическая погрешность, вызываемая
тем факто­ром, по которому группировались
результаты наблюдений,

Пример 7.4. Было сделано
38 измерений диаметра детали восемью
различ­ными штангенциркулями. Каждым
из них проводились
по пять измерений. Внутрисерийная
дисперсия равна 0,054 мм²,
межсерийная — 0,2052 мм².
Оп­ределить наличие систематической
погрешности измерения диаметра детали.

Расчетное значение критерия
Фишера F
= 0,2052/0,054 = 3,8. Для s
–1 = 7, N
– s
= 30 по табл. П1.3 приложения 1 имеем при q
= 0,05 F_0,05
= 2,3 и при q
= 0,01 F_0,01
= 3,3. Полученное значение F
больше, чем 2,2 и 2,9. Следовательно, в
результатах наблюдений обнаруживается
наличие систе­матических погрешностей.

Из всех рассмотренных способов обнаружения
систематических погрешностей дисперсионный
анализ является наиболее эффектив­ным
и достоверным, так как позволяет не
только установить факт наличия
погрешности, но и дает возможность
проанализировать источники ее
возникновения.

Критерий Вилкоксона.
Если закон распределения результатов
измерений неизвестен, то для обнаружения
систематической по­грешности применяют
статистический критерий Вилкоксона.

Из двух групп результатов
измерений x₁,
х₂,…,
х_n
и у₁,
у₂,…,
у_m,
где n
m
5
составляется
вариационный ряд, в котором все n+m
значений х₁,
х₂,…,
х_n;
у₁,
у₂,…,
у_m
располагают в порядке их возрастания
и приписывают им ранги – порядковые
номера членов вариационного ряда.
Различие средних значений каждого из
рядов можно считать допустимым, если
выполняется неравенство

где R_i
– ранг (номер) члена x_i
равный его номеру в вариационном ряду;

и

– нижнее и верхнее критические значения
для вы­бранного уровня значимости q.
При m
< 15 эти критические значе­ния
определяются по табл. 7.3. При m>15
они рассчитываются по формулам:

где z_р
– квантиль нор­мированной функции
Лапласа.

Более полная табли­ца
значений критиче­ских значений

и

приведена в реко­мендации МИ 2091-90
«ГСИ. Измерения физи­ческих величин.
Общие требования».

Таблица №7.3

Критические
значения

и

при q
= 0,05 и 0,01

n	m	q = 0,05	q = 0,01
8	8 10 15	49 53 65	87 99 127	43 47 56	93 105 136
9	9 15	62 79	109 146	56 69	115 156
10	10 15	78 94	132 166	71 84	139 176
12	12 15	115 127	185 209	105 115	195 221
14	14 15	160 164	246 256	147 151	259 268
15	15	184	282	171	294

Результаты измерений, полученные при наличии систематической погрешности, называются неисправленными.

В процессе измерений оценить или исключить систематические погрешности можно следующими мерами:

а)  устранение  или  учет  возможных  систематических  погрешностей с помощью специальных методов и средств измерений.

Пример.

Учесть влияние температуры на напряженное состояние строительных конструкций можно путем установки дополнительного (компенсационного) тензометра по направлению, перпендикулярному направлению измеряемых напряжений (рис.3.1). Это дает возможность измерить чисто температурные деформации и вычленить их из суммарных, отделив их от деформаций, вызванных силовым воздействием.

Рис. 3.1 Установка тензометров с учетом температурных деформаций

б) определение поправок, компенсирующих систематическую погрешность, и учет их в результатах измерений.

Пример.

При измерениях прочности бетона склерометром его тарировочная кривая уточняется для данного конкретного бетона. Это выполняется  путем проведения нескольких измерений более точным, хотя и более трудоемким способом «вырыва» ( после определения прочности бетона в каком-либо месте склерометром в этом же месте в тело бетона забуривается и распирается в нем специальное анкерное устройство, которое затем вытаскивается, вырывая кусок бетона. По усилию вырыва определяется прочность бетона в этом месте). Другим способом уточнения тарировочной кривой является выбуривание кернов с последующим испытанием их на прессе.

Следует отметить, что систематическую погрешность нельзя устранить многократными измерениями.

Существует, однако, ряд приемов при измерениях, которые помогают бороться с систематическими погрешностями.

При измерениях применяются следующие методы.

Метод замещения, когда прямое измерение какого-либо параметра «Х» заменяется более точным измерением другой величины – «Y», функционально связанной с «Х», т.е. Y = f(X).

Пример.

При лабораторных испытаниях экспериментального образца величину прилагаемого усилия можно измерять не по манометру на гидравлическом прессе (в большом количестве случаев в показаниях манометров есть систематические ошибки, связанные с системой подачи масла), а по показаниям контрольных тензометров на образце.

Метод противопоставления, при котором измерение выполняется дважды таким образом, чтобы результаты измерений разнились между собой.

Пример.

Для выявления и учета негоризонтального положения трубы нивелира можно снять отсчеты по двум реперам, отстоящим от нивелира на разные расстояния (рис.3.2).

Репер 1 (отсчет Н1)

L1

нивелир          L2

Репер 2 (отсчет Н2)

Рис. 3.2. Учет негоризонтального положения трубы нивелира

Пусть ϕ угол наклона оси трубы нивелира.

Имеем отметки:

Отсюда получаем:

Н1=Н1ист+ϕ⋅L1;

Н2=Н2ист+ϕ⋅L2.

ϕ  (H 2 − H1) − (H 2ист − H1ист ) .           (3.1)

L2 − L1

Метод компенсации погрешности, когда в двух наблюдениях погрешность входит в результат с разными знаками.

Пример.

Погрешность уровня нивелира выявляется его установкой «так и наоборот». Тогда измеряемый наклон определится как среднее по

этим двум измерениям:

ϕ1=ϕизм.+Δ,

ϕ2=ϕизм.-Δ,

где Δ угол отклонения оси нивелира от горизонтали.

Отсюда

ϕизм=  1

 ϕ 2

2

.           (3.2)

Метод рандомизации, предусматривающий измерения различными приборами. При этом систематические погрешности в совокупности представляют случайную величину, распределенную по нормальному закону.

Материал взят из книги Основные понятия метрологии, стандартизации и сертификации (А.И. Васильев)