Систематические ошибки эксперимента возникают

Статьи
Главная страница

 

Из графика
видно, что существует вероятность, пусть и очень маленькая, что наше единичное
измерение покажет результат, сколь угодно далеко отстоящий от истинного
значения. Выходом из положения является проведение серии измерений. Если на
разброс данных действительно влияет случай, то в результате нескольких
измерений мы скорее всего получим следующее (рис 2):

Будет ли
рассчитанное среднее значение нескольких измерений совпадать с истинным? Как
правило – нет. Но по теории вероятности, чем больше сделано измерений, тем
ближе найденное среднее значение к истинному. На языке математики это можно
записать так:

Но с бесконечностью у всех дело обстоит неважно. Поэтому на практике мы имеем дело
не со всеми возможными результатами измерений, а с некоторой выборкой из этого
бесконечного множества. Сколько же реально следует делать измерений? Наверное,
до тех пор, пока полученное среднее значение не будет отличаться от истинного
меньше чем точность отдельного измерения.

Следовательно,
когда наше среднее значение (рис. 2) отличается от истинного меньше чем
погрешность измерений, дальнейшее увеличение числа опытов бессмысленно. Однако
на практике мы не знаем истинного значения! Значит, получив среднее по
результатам серии опытов, мы должны определить, какова вероятность того, что
истинное значение находится внутри заданного интервала ошибки. Или каков тот
доверительный интервал, в который с заданной надежностью попадет истинное
значение (рис 3).

Рассмотрим
некоторый условный эксперимент, где в серии измерений получены некоторые
значения величины Х (см. табл. 1).  Рассчитаем среднее значение и, чтобы  оценить
разброс данных найдем величины DХ = Х –
Х_ср

Ясно, что
величины DХ  как-то характеризуют
разброс данных. На практике для усредненной характеристики разброса серии измерений используется
дисперсия выборки:

и среднеквадратичное или стандартное отклонение выборки:

Последнее
показывает, что каждое измерение в данной серии (в данной выборке) отличается
от другого в среднем на ± s.

Понятно, что каждое отдельное
значение оказывает влияние на средний результат. Но это влияние тем меньше, чем
больше измерений в нашей выборке. Поэтому дисперсия и стандартное отклонение
среднего значения, будет определяться по формулам:

Можем ли мы теперь определить вероятность того, что
истинное значение попадет в указанный интервал среднего? Или наоборот,
рассчитать тот доверительный интервал в который истинное значение
попадет с заданной вероятностью (95%)? Поскольку кривая на наших графиках это
распределение вероятностей, то площадь под кривой, попадающая в указанный
интервал и будет равна этой вероятности (доля площади, в процентах). А площади
математики научились рассчитывать хорошо, знать бы только уравнение этой
кривой.

И здесь мы сталкиваемся еще с одной сложностью. Кривая, которая описывает распределение
вероятности для выборки, для ограниченного числа измерений, уже не будет кривой нормального
распределения. Ее форма будет зависеть
не только от дисперсии (разброса данных) но и от степени свободы для выборки
(от числа независимых измерений) (рис 4):

Уравнения этих кривых впервые были предложены в 1908
году английским математиком и химиком Госсетом, который опубликовал их под
псевдонимом Student (студент), откуда пошло хорошо известные термины
«коэффициент Стьюдента» и аналогичные. Коэффициенты Стьюдента получены на
основе обсчета этих кривых для разных степеней свободы (f = n-1) и уровней
надежности (Р) и сведены в специальные таблицы. Для получения доверительного интервала необходимо
умножить уже найденное стандартное отклонение среднего на соответствующий
коэффициент Стьюдента. ДИ = s_ср*t_{f, P}

Проанализируем, как меняется доверительный интервал
при изменении требований к надежности результата и числа измерений в серии.
Данные в таблице 2 показывают, что чем больше требование к надежности, тем
больше будет коэффициент Стьюдента и, следовательно, доверительный интервал. В большинстве случаев, приемлемым считают значение Р=95%

Из таблицы 3 и графика
видно, что чем больше число измерений, тем меньше коэффициент и доверительный
интервал для данного уровня надежности. Особенно значительное падение
происходит при переходе от степени свободы 1 (два измерения) к 2 (три
измерения). Отсюда следует, что имеет смысл ставить не менее трех параллельных
опытов, проводить не менее трех измерений.

Окончательно
для измеряемой величины Х получаем значение Х_сред±s_ср*t_f,P. В
нашем случае получаем: f=3; t=3,18;
ДИ = 3,18*10,2 = 32,6; X = 143,5 ±32,6

Как правило,
значение доверительного интервала округляется до одной значащей цифры, а
значение измеряемой величины – в соответствии с округлением доверительного
интервала. Поэтому для нашей серии окончательно имеем: X = 140 ±30

Найденная
нами погрешность является абсолютной погрешностью и ничего не говорит еще о
точности измерений. Она свидетельствует о точности измерений только в сравнении
с измеряемой величиной. Отсюда представление об относительной ошибке:

           

Косвенные определения.

Исследуемая величина рассчитывается в этом случае с помощью
математических формул по другим величинам, которые были измерены
непосредственно. В этом случае для расчета ошибок можно использовать
соотношения, приведенные в таблице 4.

Таблица 4. Формулы для расчета абсолютных и относительных ошибок.
Формула	Абсолютная	Относительная
x = a ± b	Dx = Da+Db	e = (Da+Db) /(a±b )
x = a* b; x = a* k	Dx = bDa+aDb; Dx = kDa	e = Da/a+Db/b = ea + e b
x = a / b	Dx = (bDa+aDb) / b2	e = Da/a+Db/b = ea + e b
x = a*k; (x = a / k)	Dx = Da*k; (Dx = Da/k )	e = ea
x = a2	Dx = 2aDa	e = 2Da/a = 2ea
x = Öa	Dx = Da/(2Öa)	e = Da/2a = ea/2

Из таблицы видно, что относительная ошибка и точность определения не изменяются при умножении (делении) на некоторый постоянный коэффициент. Особенно сильно относительная ошибка может возрасти при вычитании
близких величин, так как при этом абсолютные ошибки суммируются, а значение Х
может уменьшиться на порядки.

Пусть например, нам необходимо определить
объем проволочки.
Если диаметр проволочки измерен с погрешностью 0,01 мм (микрометром) и равен 4 мм, то относительная погрешность составит 0,25% (приборная). Если
длину проволочки (200 мм) мы измерим линейкой с погрешностью 0,5 мм, то относительная погрешность также составит 0,25%. Объем можно рассчитать по формуле: V=(pd²/4)*L. Посмотрим, как будут меняться ошибки
по мере проведения расчетов (табл. 5):

Таблица 5. Расчет абсолютных и относительных ошибок.
Величина	Значение	Абсолютная	Относительная
d2	16	Dx = 2*4*0,01=0,08	e = 0,5%
pd2 *)	50,27	Dx = 0,08*3,14+0,0016*16 =0,28	e = 0,55%
pd2/4	12,57	Dx = 0,28/4 = 0,07	e = 0,55%
(pd2/4)*L	2513	Dx = 12,57*0,5+200*0,07=20	e = 0,8%
*) Если мы возьмем привычное p=3,14, то Dp=0,0016 то ep = 0,05%, но если используем более точное значение, то Dp и ep можно будет пренебречь

Окончательный
результат V=2510±20 (мм³) e
=0,8%. Чтобы повысить точность косвенного определения, нужно в первую очередь
повышать точность измерения той величины, которая вносит больший вклад в ошибку
(в данном случае – точность измерения диаметра проволочки).

План проведения измерений:

[1]

1.   Знакомство
с методикой, подготовка прибора, оценка приборной погрешности d. Оценка возможных причин
систематических ошибок, их исключение.

2.   
Проведение серии измерений. Если получены совпадающие результаты, можно
считать что случайная ошибка равна 0, DХ
= d. Переходим к пункту 7.

3.   
Исключение промахов – результатов значительно отличающихся по своей
величине от остальных.

4.   
Расчет
среднего значения Х_ср, и стандартного отклонение среднего
значения s_cp

5.   
Задание значения уровня надежности P,
определение коэффициента Стьюдента t и
нахождение доверительного интервала ДИ= t*s_cp

6.   
Сравнение случайной и приборной погрешности, при этом возможны варианты:

—    
ДИ << d, можно
считать, что DХ = d, повысить точность измерения
можно, применив более точный прибор

—    
ДИ >> d, можно
считать, что DХ = ДИ,
повысить точность можно, уменьшая случайную ошибку, повышая число измерений в
серии, снижая требования к надежности.

—    
ДИ » d, в этом
случае расчитываем ошибку по формуле DХ
=

7.   
Записывается окончательный результат Х = Х_ср ± DХ.
Оценивается относительная ошибка
измерения e = DХ/Х_ср

Если
проводится несколько однотипных измерений (один прибор, исследователь, порядок
измеряемой величины, условия) то подобную работу можно проводить один раз. В
дальнейшем можно считать DХ
постоянной и ограничиться минимальным числом измерений (два-три измерения
должны отличаться не более, чем на DХ)

Для косвенных
измерений необходимо провести обработку данных измерения каждой величины. При
этом желательно использовать приборы, имеющие близкие относительные погрешности
и задавать одинаковую надежность для расчета доверительного интервала. На
основании полученных значений Da, Db, определяется DХ
для результирующей величины (см табл. 4). Для повышения точности надо
совершенствовать  измерение той величины, вклад ошибки которой в DХ наиболее существенен.

Изучение зависимостей.

Частым вариантом экспериментальной работы является
измерение различных величин с целью установления зависимостей. Характер этих
зависимостей может быть различен: линейный, квадратичный, экспоненциальный,
логарифмический, гиперболический. Для выявления зависимостей широко
используется построение графиков.

При построении графиков вручную важно правильно
выбрать оси, величины, масштаб, шкалы. Следует предупредить школьников, что
шкалы должны иметь равномерный характер, нежелательна как слишком детальная,
так и слишком грубая их разметка. Точки должны заполнять всю площадь графика,
их расположение в одном углу, или «прижатыми» к одной из осей, говорит о
неправильно выбранном масштабе и затрудняет определение характера зависимости.
При проведении линии по точкам надо использовать теоретические представление о
характере зависимости: является она непрерывной или прерывистой, возможно ли ее
прохождение через начало координат, отрицательные значения, максимумы и
минимумы.

Наиболее легко проводится и анализируется прямая
линия. Поэтому часто при изучении более сложных зависимостей часто используется
линеаризация зависимостей, которая достигается подходящей заменой переменных.
Например:

Зависимость . Вводя новую переменную
, получаем уравнение
a = bx, которое
будет изображаться на графике прямой линией. Наклон этой прямой позволяет
рассчитать константу диссоциации.

Разумеется и в этом случае полученные в эксперименте данные включают в себя различные ошибки, и точки редко лежат строго на прямой. Возникает
вопрос, как с наибольшей точностью провести прямую по экспериментальным точкам, каковы ошибки в определении
параметров.

Математическая статистика показывает, что наилучшим
приближением будет такая линия, для которой дисперсия (разброс) точек
относительно ее будет минимальным. А дисперсия определяется как средний квадрат
отклонений наблюдаемого положения точки от расчитанного:

Отсюда название этого метода – метод наименьших
квадратов. Задавая условие, чтобы величина s²
принимала минимальное значение, получают формулы для коэффициентов а и b в уравнении прямой у = а + bx:

и формулы для расчета соответствующих ошибок
^[2].

Если
делать расчеты, используя калькулятор, то лучше оформлять их в виде таблицы:

x	x2	y	y2	xy
…	…	…	…	…
…	…	…	…	…
Sx =	Sx2 =	Sy =	Sy2 =	Sxy =

Подводя
итог, следует сказать, что обработка данных эксперимента достаточно сложный
этап работы ученого. Необходимость проведения большого числа измерений требует
большой затраты времени и материальных ресурсов. Громоздкость формул,  необходимость
использования большого числа значащих цифр затрудняют вычисления. Поэтому, возможно,
не все рекомендации этой статьи применимы в рамках школьного исследования. Но
понимать их сущность, значимость, необходимость, и в соответствии с этим
адекватно оценивать свои результаты, должен любой исследователь.

В настоящее время обработку экспериментальных данных
существенно облегчают современные компьютерные технологии, современное
программное обеспечение. Об том, как их можно использовать –  в следующей
статье.

Литература:

---

[1]
Кассандрова О.Н., Лебедев В.В. Обработка результатов наблюдений, М., «Наука»,
1970, 194 с.

[2]
Петерс Д., Хайес Дж., Хифтье Г. Химическое разделение и измерение – М.,: Химия,
1978, 816 с.

---

Изучение
всех влияющих на исследуемый объект
факторов одновременно провести
невозможно, поэтому в эксперименте
рассматривается их ограниченное число.
Остальные активные факторы стабилизируются,
т.е. устанавливаются на каких-то одинаковых
для всех опытов уровнях.

Некоторые
факторы не могут быть обеспечены
системами стабилизации (например,
погодные условия, самочувствие оператора
и т.д.), другие же стабилизируются с
какой-то погрешностью (например,
содержание какого-либо компонента в
среде зависит от ошибки при взятии
навески и приготовления раствора).
Учитывая также, что измерение
параметра у осуществляется
прибором, обладающим какой-то погрешностью,
зависящей от класса точности прибора,
можно прийти к выводу, что результаты
повторностей одного и того же опыта у_к будут
приближенными и должны отличаться один
от другого и от истинного значения
выхода процесса. Неконтролируемое,
случайное изменение и множества других
влияющих на процесс факторов
вызывает случайныеотклонения
измеряемой величины у_к от
ее истинного значения — ошибку опыта.

Каждый
эксперимент содержит элемент
неопределенности вследствие ограниченности
экспериментального материала. Постановка
повторных (или параллельных) опытов не
дает полностью совпадающих результатов,
потому что всегда существует ошибка
опыта (ошибка воспроизводимости). Эту
ошибку и нужно оценить по параллельным
опытам. Для этого опыт воспроизводится
по возможности в одинаковых условиях
несколько раз и затем берется среднее
арифметическое всех результатов. Среднее
арифметическое у равно сумме всех n
отдельных результатов, деленной на
количество параллельных опытов n:

Отклонение
результата любого опыта от среднего
арифметического можно представить как
разность y₂— ,
где y₂ —
результат отдельного опыта. Наличие
отклонения свидетельствует об
изменчивости, вариации значений повторных
опытов. Для измерения этой изменчивости
чаще всего используют дисперсию.

Дисперсией
называется среднее значение квадрата
отклонений величины от ее среднего
значения. Дисперсия обозначается s² и
выражается формулой:

где
(n-1) — число степеней свободы, равное
количеству опытов минус единица. Одна
степень свободы использована для
вычисления среднего.

Корень
квадратный из дисперсии, взятый с
положительным знаком, называется средним
квадратическим отклонением, стандартом
или квадратичной ошибкой:

Ошибка
опыта является суммарной величиной,
результатом многих ошибок: ошибок
измерений факторов, ошибок измерений
параметра оптимизации и др. Каждую из
этих ошибок можно, в свою очередь,
разделить на составляющие.

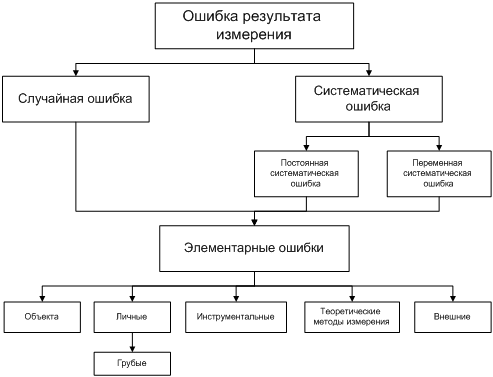
Все
ошибки принято разделять на два класса:
систематические и случайные (рисунок
1).

Систематические
ошибки порождаются причинами, действующими
регулярно, в определенном направлении.
Чаще всего эти ошибки можно изучить и
определить количественно. Систематическая
ошибка —
это ошибка, которая остаётся постоянно
или закономерно изменяется при повторных
измерениях одной и той же величины. Эти
ошибки появляются вследствие неисправности
приборов, неточности метода измерения,
какого либо упущения экспериментатора,
либо использования для вычисления
неточных данных. Обнаружить систематические
ошибки, а также устранить их во многих
случаях нелегко. Требуется тщательный
разбор методов анализа, строгая проверка
всех измерительных приборов и безусловное
выполнение выработанных практикой
правил экспериментальных работ. Если
систематические ошибки вызваны известными
причинами, то их можно определить.
Подобные погрешности можно устранить
введением поправок.

Систематические
ошибки находят, калибруя измерительные
приборы и сопоставляя опытные данные
с изменяющимися внешними условиями
(например, при градуировке термопары
по реперным точкам, при сравнении с
эталонным прибором). Если систематические
ошибки вызываются внешними условиями
(переменной температуры, сырья и т.д.),
следует компенсировать их влияние.

Случайными ошибками
называются те, которые появляются
нерегулярно, причины, возникновения
которых неизвестны и которые невозможно
учесть заранее. Случайные ошибки
вызываются и объективными причинами и
субъективными. Например, несовершенством
приборов, их освещением, расположением,
изменением температуры в процессе
измерений, загрязнением реактивов,
изменением электрического тока в цепи.
Когда случайная ошибка больше величины
погрешности прибора, необходимо
многократно повторить одно и тоже
измерение. Это позволяет сделать
случайную ошибку сравнимой с погрешностью
вносимой прибором. Если же она меньше
погрешности прибора, то уменьшать её
нет смысла. Такие ошибки имеют значение,
которое отличается в отдельных измерениях.
Т.е. их значения могут быть неодинаковыми
для измерений сделанных даже в одинаковых
условиях. Поскольку причины, приводящие
к случайным ошибкам неодинаковы в каждом
эксперименте, и не могут быть учтены,
поэтому исключить случайные ошибки
нельзя, можно лишь оценить их значения.
При многократном определении какого-либо
показателя могут встречаться результаты,
которые значительно отличаются от
других результатов той же серии. Они
могут быть следствием грубой ошибки,
которая вызвана невнимательностью
экспериментатора.

Систематические
и случайные ошибки состоят из множества
элементарных ошибок. Для того чтобы
исключать инструментальные ошибки,
следует проверять приборы перед опытом,
иногда в течение опыта и обязательно
после опыта. Ошибки при проведении
самого опыта возникают вследствие
неравномерного нагрева реакционной
среды, разного способа перемешивания
и т.п.

При
повторении опытов такие ошибки могут
вызвать большой разброс экспериментальных
результатов.

Очень
важно исключить из экспериментальных
данных грубые ошибки, так называемый
брак при повторных опытах. Грубые
ошибки легко
обнаружить. Для выявления ошибок
необходимо произвести измерения в
других условиях или повторить измерения
через некоторое время. Для предотвращения
грубых ошибок нужно соблюдать аккуратность
в записях, тщательность в работе и записи
результатов эксперимента. Грубая ошибка
должна быть исключена из экспериментальных
данных. Для отброса ошибочных данных
существуют определённые правила.

Например,
используют критерий Стьюдента t (Р; f):
Опыт считается бракованным, если
экспериментальное значение критерия
t по модулю больше табличного значения
t (Р; f).

Если
в распоряжении исследователя имеется
экспериментальная оценка дисперсии
S²(y_k)
с небольшим конечным числом степеней
свободы, то доверительные ошибки
рассчитываются с помощью критерий
Стьюдента t (Р; f):

?()
= t (Р; f)* S(y_k)/=
t (Р; f)* S()

?(y_k)
= t (Р; f)* S(y_k)

6.
Результат прямого измерения — случайная
величина, подчиняющаяся нормальному
закону распределения

Результаты,
которые получаются при экспериментальном
исследовании какого-либо технологического
процесса, зависят от целого ряда факторов.
Поэтому результат исследования является
случайной величиной, распределённой
по нормальному закону распределения.
Оно названо нормальным, т. к. именно
это распределение для случайной величины
является обычным и
называется гаусовским или лапласским. Под распределением
случайной величиныпонимают
совокупность всех возможных значений
случайной величины и соответствующих
им вероятностей.

Законом
распределения случайной величины называется
всякое соотношение, устанавливающее
связь между возможными значениями
случайной величины и соответствующим
им вероятностям.

При
экспериментальном исследовании
какого-либо технологического процесса
измеряемый результат последнего является
случайной величиной, на которую оказывает
влияние огромное число факторов
(изменение погодных условий, самочувствие
оператора, неоднородность сырья, влияние
износа измерительной и стабилизирующей
аппаратуры и т.д. и т.п.). Именно поэтому
результат исследования является
случайной величиной, распределенной
по нормальному закону. Однако если
исследователь какой-либо активный
фактор не заметил или отнес его к
неактивным, а неконтролируемое изменение
этого фактора может вызвать несоразмерно
большое изменение эффективности процесса
и параметра, характеризующего эту
эффективность, то распределение
вероятности последнего может нормальному
закону не подчиниться.

Точно
так же приведет к нарушению нормальности
закона распределения наличие в массиве
экспериментальных данных грубых ошибок.
Именно поэтому в первую очередь проводят
анализ на наличие в экспериментальных
данных грубых ошибок с принятой
доверительной вероятностью.

Случайная
величина будет распределена по нормальному
закону, если она представляет собой
сумму очень большого числа взаимно
зависимых случайных величин, влияния
каждой из которых ничтожно мало. Если
измерения искомой величины y проведены
много раз, то результат можно наглядно
представить, построив диаграмму, которая
показывала бы, как часто получались те
или иные значения. Такая диаграмма
называется гистограммой. Что
бы построить гистограмму нужно разбить
весь диапазон измеренных значений на
равные интервалы. И посчитать сколько
раз каждая величина попадает в каждый
интервал.

Если
измерения продолжать до тех пор, пока
число измеренных значений n не станет
очень большим, то ширину интервала можно
сделать очень малой. Гистограмма перейдёт
в непрерывную прямую, которая
называется кривой
распределения.

В
основе теории случайных ошибок лежат
два предположения:

1.
при большом числе измерений случайные
погрешности одинаково велики, но с
разными знаками встречаются одинаково
часто;

2.
большие (по абсолютной величине)
погрешности встречаются реже, чем малые.
Т. е. вероятность появления погрешности
уменьшается с ростом её величины.

Согласно
закону больших чисел при бесконечно
большом числе измерений n, истинное
значение измеряемой величины y равно
среднеарифметическому значению всех
результатов измерений ?

Для
всех m-повторностей можно записать:

Разделив
это уравнение на число повторностей m,
получим после подстановки:

За
экспериментальную оценку истинного
значения (математического ожидания)
критерия оптимальности у принимается среднеарифметическая
оценкарезультатов
всех т повторностей:

Если
число m велико (m>?), то будет справедливо
равенство:

Таким
образом, при бесконечно большом числе
измерений истинное значение измеряемой
величины y равно среднеарифметическому
значению ? всех результатов произведённых
измерений: y=?, при m>?.

При
ограниченном числе измерений (m??)
среднеарифметическое значение y будет
отличаться от истинного значения, т.е.
равенство y=? будет неточным, а приближённым:
y?? и величину этого расхождения необходимо
оценить.

Если
в распоряжении исследователя имеется
только единичный результат измерения
y_k,
то оценка истинного значения измеряемой
величины будет менее точной. чем
среднеарифметическая оценка при любом
числе повторностей: |y-?|<|y-yk|.

Появление
того или иного значения yk в процессе
измерения является случайным событием.
Функция плотности нормального
распределения случайной величины
характеризуется двумя параметрами:

·
истинным значением y;

·
среднеквадратичным отклонением ?.

а)
б)

Рисунок
— 1а — кривая плотности нормального
распределения; 1б — кривая плотности
вероятности нормально распределенной
случайной величины при различных
дисперсиях

Плотность
нормального распределения (рис. 1а)
симметрична относительно y и достигает
максимального значения при yk= y, стремится
к 0 при увеличении.

Квадрат
среднеквадратичного отклонения
называется дисперсией случайной величины
и является количественной характеристикой
разброса результатов вокруг истинного
значения y. Мера рассеяния результатов
отдельных измерений yk от среднего
значения ? должна выражаться в тех же
единицах, то и значения измеряемой
величины. В связи с этим в качестве
показателя разброса гораздо чаще
используют величину ?:

Значения
этой величины определяют форму кривой
распределения py. Площади под тремя
кривыми одинаковы, но при малых значения
? кривые идут более круто и имеют большее
значение py. С увеличением ? значение py
уменьшается и кривая распределения
растягивается вдоль оси y. Т.о. кривая 1
характеризует плотность распределения
случайной величины, воспроизводимость
которой в повторных измерениях лучше,
чем воспроизводимость случайных величин
имеющих плотность распределения 2, 4. На
практике не возможно произвести слишком
много замеров. Поэтому нельзя построить
нормальное распределение, чтобы точно
определить истинное значение y. В этом
случае хорошим приближением к истинному
значению можно считать ?, а достаточно
точной оценкой ошибки выборочную
дисперсию ??n, вытекающую из закона
распределения, но относящуюся к конечному
числу измерения. Такое название величины
??n объясняется тем, что из всего множества
возможных значений yk, т.е. из генеральной
совокупности выбирают лишь конечное
число значений равное m, называемых
выборкой, которая характеризуется
выборочным средним значением и выборочной
дисперсией.

Соседние файлы в папке planirovanie

• #
• #
• #
• #
• #
• #

Проведение
эксперимента

Познакомимся с
вычислением ошибки опыта, или, как ее часто называют, ошибки воспроизводимости.

Ошибки параллельных
опытов

Каждый
эксперимент содержит элемент неопределен­ности вследствие ограниченности
экспериментального ма­териала. Постановка повторных (или параллельных) опытов
не дает полностью совпадающих результатов, потому что всегда существует ошибка
опыта (ошибка воспроиз­водимости). Эту ошибку и нужно оценить по параллель­ным
опытам. Для этого опыт воспроизводится по возмож­ности в одинаковых условиях
несколько раз и затем бе­рется среднее арифметическое всех результатов. Среднее
арифметическое  равно сумме всех п отдельных резуль­татов, деленной на количество
параллельных опытов п

.

Отклонение
результата любого опыта от среднего арифметического можно представить как
разность  где  – результат отдельного опыта. Наличие
откло­нения свидетельствует об изменчивости, вариации значе­ний повторных
опытов. Для измерения этой изменчи­вости чаще всего используют дисперсию.
Диспер­сией называется среднее значение квадрата отклонений величины от ее
среднего значения. Дисперсия обозна­чается s² и
выражается формулой

.

где (n – 1) – число
степеней свободы, равное количе­ству опытов минус единица. Одна степень свободы
исполь­зована для вычисления среднего.

Корень квадратный из
дисперсии, взятый с положи­тельным знаком, называется средним квадратическим от­клонением,
стандартом или квадратичной ошибкой

Стандарт имеет
размерность той величины, для кото­рой он вычислен. Дисперсия и стандарт – это
меры рассеяния, изменчивости. Чем больше дисперсия и стан­дарт, тем больше
рассеяны значения параллельных опы­тов около среднего значения.

Ошибка опыта являемся
суммарной величиной, результатом многих ошибок: ошибок измерений факторов,
ошибок измерений параметра оптимизации и др. Каждую из этих ошибок можно, в свою
очередь, разделить на состав­ляющие.

Вопрос о классификации ошибок
довольно сложный и вызывает много дискуссий. В качестве примера одной из
возможных схем классификации мы приведем схему из книги Ю. В. Кельница «Теория
ошибок измере­ний» (М., изд-во «Недра», 1967).

Все ошибки принято разделять
на два класса: система­тические и случайные.

Систематические ошибки
порождаются причинами, действующими регулярно, в определенном направлении. Чаще
всего эти ошибки можно изучить и определить количественно.

Систематические ошибки
находят, калибруя измери­тельные приборы и сопоставляя опытные данные с изме­няющимися
внешними условиями (например, при градуи­ровке термопары по реперным точкам,
при сравнении с эта­лонным прибором).

Если систематические ошибки
вызываются внешними условиями (переменной температуры, сырья и т. д.), следу­ет
компенсировать их влияние. Как это делать, будет показано ниже.

Случайными ошибками называются
те, которые появ­ляются нерегулярно, причины возникновения которых неизвестны и
которые невозможно учесть заранее.

Систематические и случайные
ошибки состоят из мно­жества элементарных ошибок. Для того, чтобы исключать инструментальные
ошибки, следует проверять приборы перед опытом, иногда в течение опыта и обязательно
после опыта. Ошибки при проведении самого опыта возникают вследствие неравномерного
нагрева реакционной среды, раз­ного способа перемешивания и т.п. При повторении
опытов такие ошибки могут вызвать большой разброс эксперимен­тальных
результатов.

Очень важно исключить из экспе­риментальных
данных грубые ошибки, так называемый брак при повторных опытах. Для отброса оши­бочных
опытов существуют правила. Для определения брака используют, например, кри­терий
Стьюдента

.

Значение t берут из таблицы t-распределения Стьюдента. Опыт считается
бракованным, если эксперименталь­ное значение критерия t по модулю больше табличного значения.

Дисперсия параметра
оптимизации

Дисперсия всего эксперимента
получается в результате усреднения дисперсий всех опытов. По терми­нологии,
принятой в планировании эксперимента, речь идет о подсчете дисперсии параметра
оптимизации  или, что то же самое, дисперсии воспроизводимости эксперимента

При подсчете дисперсии
параметра оптимизации квад­рат разности между значением y_q в каждом опыте и средним значением из n повторных наблюдений y нужно просумми­ровать по числу опытов в
матрице N, а затем разделить на N(n — 1):

,

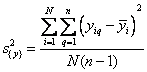
Где i = 1, 2, …, N;      q = 1, 2, …, n.

Такой формулой можно
пользоваться в случаях, когда число повторных опытов одинаково во всей матрице.

Дисперсию воспроизводимости
проще всего рассчиты­вать, когда соблюдается равенство числа повторных опы­тов
во всех экспериментальных точках. На практике весь­ма часто приходится
сталкиваться со случаями, когда число повторных опытов различно. Это происходит
вследствие отброса грубых наблюдений, неуверенности экспе­риментатора в
правильности некоторых результатов (в таких случаях возникает желание еще и еще
раз повторить опыт) и т.п.

Тогда при усреднении
дисперсий приходится пользо­ваться средним взвешенным значением дисперсий,
взятым с учетом числа степеней свободы

,

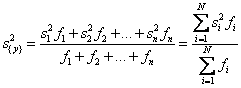
где

– дисперсия i-го опыта;

 – число степеней свободы i-м опыте, равное числу параллельных опытов
n_i минус 1.

Число степеней
свободы средней дисперсии принима­ется равным сумме чисел степеней свободы
дисперсий, из которых она вычислена.

Случай с неравным числом
наблюдений, который мы рассмотрели выше, связан с нарушением ортогональности
матрицы. Поэтому здесь нельзя использовать расчетные формулы для коэффициентов,
приведенные ранее. Этот вопрос будет рассмотрен ниже.

Экспериментатору не следует
забывать о про­верке однородности дисперсий, неоднородные дисперсии усреднять
нельзя. Прежде чем пользоваться приведёнными выше формулами, нужно убедиться в
однородности суммируемых дисперсий.

Проверка
однородности дисперсий

Проверка однородности
дисперсий производится с помощью различных статистических критериев. Простей­шим
из них является критерий Фишера, предназначенный для сравнения двух дисперсий.
Критерий Фишера (F—критерий)
представляет собою отношение большей дисперсии к меньшей. Полученная величина
сравнивается с таблич­ной величиной F-критерия.

Если полученное значение
дисперсионного отно­шения больше приведенного в таблице для соответствую­щих
степеней свободы и выбранного уровня значимости, это означает, что дисперсии
значимо отличаются друг от друга, т. е. что они неоднородны.

Если сравниваемое количество
дисперсий больше двух и одна дисперсия значительно превышает остальные, можно воспользоваться
критерием Кохрена. Этот критерий пригоден для случаев, когда во всех точках
имеется одина­ковое число повторных опытов. При этом подсчитывается дисперсия в
каждой горизонтальной строке матрицы

,

а затем из
всех дисперсий находится наибольшая  ко­торая делится на сумму всех дисперсий. Критерий Кохрена – это
отношение максимальной дисперсии к сумме всех дисперсий

.

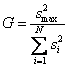
Гипотеза
об однородности дисперсий подтверждается, если экспериментальное значение
критерия Кохрена не превы­шает табличного значения. Тогда можно усреднять дис­персии
и пользоваться формулой

.

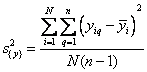
Если возникает предположение
о наличии неодно­родности дисперсий для случая, когда число повторных опытов неодина­ково
во всех точках, можно воспользоваться критерием Бартлета. По уже знакомой
формуле подсчитывается дисперсия воспроизводимости

.

Далее
находится величина

,

где

.

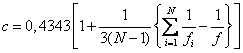
Здесь число
степеней свободы равно N–1, где N – число сравниваемых дисперсий. При планировании экспе­римента типа
2^k это число равно числу опытов в матрице.

Бартлет показал, что величина
 приближенно подчиняется  – распределению с (N–1) степенями свободы. Значимость критерия
Бартлета проверяется обычным способом.

Критерий Бартлета базируется
на нормальном распре­делении. Если имеются отклонения от нормального распре­деления,
то проверка неоднородности дисперсий может привести к ошибочным результатам.

Можно предложить
использование F-критерия даже в тех случаях, когда число
дисперсий больше двух. Делается это следующим образом. Из всех дисперсий
выделяются наибольшая и наименьшая. По F-критерию производится проверка, значимо ли они различаются между
собой. Ясно, что если наибольшая и наименьшая дисперсии не отличаются значимо,
то диспер­сии, имеющие промежуточные значения, также не могут значимо
отличаться друг от друга. Тогда всю группу дис­персий можно считать
принадлежащей к единой совокуп­ности. В таких случаях нет надобности применять
кри­терий Бартлета.

Рандомизация

Чтобы исключить влияние
систематических ошибок, вызванных внешними условиями (переменой температуры,
сырья, лаборанта и т. д.), рекомендуется случайная пос­ледовательность при
постановке опытов, запланированных матрицей. Опыты необходимо рандомизировать
во времени. Термин «рандомизация» происходит от английского слова random – случайный.

Если экспериментатор
располагает сведениями о пред­стоящих изменениях внешней среды, сырья,
аппаратуры и т. п., то целесообразно планировать эксперимент таким образом,
чтобы эффект влияния внешних условий был сме­шан с определенным
взаимодействием, которое не жалко потерять. Так, при наличии двух партий сырья
матрицу 2³ можно разбить на два блока таким образом, чтобы эффект
сырья сказался на величине трехфакторного взаимодейст­вия. Тогда все линейные
коэффициенты и парные взаимо­действия будут освобождены от влияния
неоднородности сырья.

В этой матрице при
составлении блока 1 отобраны все строки, для которых , а при составления бло­ка 2 – все строки,
для которых . Различие в сырье можно рассматривать как
новый фактор . Тогда матрица 2³, разбитая на
два блока, представляет собой полуреплику 2^4-1 с определяющим
контрастом .

,                 ;

,                ;

,               ;

,                  ;

,                 ;

,              ;

,              ;

,                ;

Эффект сырья
отразился на подсчете свободного члена b₀ и
эффекта взаимодействия второго порядка b₁₂₃.

Аналогично можно разбить на
два блока любой экспе­римент типа 2³. Главное – правильно выбрать
взаимодей­ствие, которым можно безболезненно пожертвовать. При отсутствии
априорных сведений выбирают взаимодействие самого высокого порядка: x₁x₂x₃ для 2³, x₁x₂x₃х₄ для 2⁴, x₁x₂x₃x₄x₅ 2⁵ и т. д. Но если
экспериментатору известно, что одно из парных взаимодействий лишено, например,
физико-химического смысла, то можно пожертвовать парным взаимодействием.

Матрицу типа 2^k можно разбить на количество блоков 2ⁿ (n – степень
двойки) при . Так, матрица 2³
разбивается на два блока по четыре опыта в каждом и на четыре блока по
два опыта в каждом. Матрица 2⁴ – на два блока по 8 опытов в каждом,
на четыре блока по четыре опыта и на восемь блоков по два опыта и т.д.