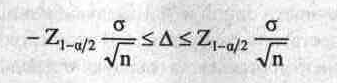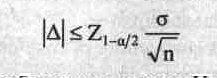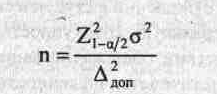Систематическая ошибка социология

3. Случайные и систематические ошибки

Уменьшение случайных ошибок при возрастании объема выборки и независимость систематических ошибок от величины массива. Сколько человек нужно опросить для получения репрезентативных данных? Примеры из практики исследовании. Почему предвыборный прогноз «Literary Digest» 1936 г. оказался ошибочным?

Ошибки выборки подразделяются на два типа. Случайные ошибки уменьшаются при возрастании объема выборочной совокупности. Так кубик при достаточно большом числе бросаний будет падать примерно равное количество раз на каждую грань. При нескольких бросаниях он может показать преимущественное выпадение, например «шестерки». Тогда мы говорим, что число наблюдений слишком мало, чтобы судить о неслучайности выпадения «шестерок». Но если «шестерки» выпадают постоянно при сотнях и тысячах бросаний, мы говорим: крайне маловероятно, чтобы это происходило случайно. Таким образом, случайная ошибка — это вероятность того, что выборочная средняя выйдет (или не выйдет) за пределы заданного интервала. При случайном отборе следует неукоснительно соблюдать следующую заповедь: критерии доступа к единицам исследования должны быть независимы от изучаемых переменных.

Чудесное свойство случайных ошибок уменьшаться при возрастании объема выборочной совокупности делает бессмысленными обследования огромных массивов, которые предпринимаются чаще всего с целью произвести впечатление на профессионально неподготовленного заказчика.

154

Даже национальные выборки достаточно малы. Первая национальная выборка в США, спроектированная в 1935 г. тогда только начинавшим карьеру «поллстера» Джорджем Гэллапом старшим, насчитывала 1327 человек и пропорционально отражала основные группы населения. Одной из наиболее важных тем общественного мнения тогда, в 1930-е гг., было возобновление запрета на производство и продажу спиртных напитков. Чтобы установить вариацию выборочной средней, обусловленную величиной массива, выборка была случайным образом разбита на три примерно равных по численности группы⁷. Посмотрим на распределение опрошенных в первой подвыборке (табл. 5.3).

Таблица 5.3

Отношение американцев к возобновлению запрета на спиртные напитки, опрос Дж. Гэллапа, 1935 г., первая подвыборка: 442 человека

Аналогичные результаты Гэллап получил во второй и третьей подвыборках примерно такой же величины. Каждая из них показывала некоторое отклонение от общей выборочной средней, и, если проанализировать подвыборки накопленным итогом, можно установить степень приближения результатов малых выборок к результатам большой. Мысленная экстраполяция совершенно точно указывает предел точности выборочной средней — это генеральная средняя. Но и на промежуточных стадиях видно, что подвыборочные средние отклоняются от параметров большой национальной выборки незначительно (табл. 5.4).

⁷ Gallup G. A guide to public opinion polls. 2nd ed. Princеton: Princeton University Press, 1948. P. 14.

155

Таблица 5.4

Отношение американцев к возобновлению запрета на спиртные напитки, опрос Дж. Гэллапа, 1935 г., три подвыборки накопленным итогом, %

Третья строка таблицы показывает значения, полученные в проектной выборочной совокупности, — они ненамного отличаются от средней и малой подвыборок. А изменятся ли выборочные параметры при увеличении объема? Чтобы узнать это, Гэллап провел дополнительные обследования той же генеральной совокупности выборками нарастающего объема таким образом, что величина максимальной из них составила 12 494 человека. Каковы же результаты расширения выборки почти в десять раз (табл. 5.5)?

Таблица 5.5

Отношение американцев к запрету спиртных напитков в дополнительных выборках большего объема, опрос Дж. Гэллапа, 1935 г., %

156

Мы видим, что самое большое расхождение между данными по двенадцатитысячной выборке и другим выборкам меньшего объема составляет два процентных пункта (по признаку несогласия с запретом спиртного). Отсюда следует, что в обследовании отношения американцев к запрету спиртного выборка может состоять из 442, равно как и из 12 494 человек, а результаты будут практически одинаковыми.

В практике массовых опросов относительная несущественность количества обследованных для получения точных результатов демонстрировалась неоднократно. Надо заметить, что предвыборные опросы — вероятно, единственная область социологических обследований, в которых выборочные параметры получают незамедлительное подтверждение либо опровержение: параметры генеральной совокупности обнаруживают себя сразу же после подсчета голосов. В остальных обследованиях такой возможности нет, генеральная совокупность ничем себя не показывает. В получении точных данных при минимальной выборке и проявляется мастерство «поллстера».

В лаборатории по исследованию общественного мнения Принстонского университета, которой руководил Хэрви Кентрил, изучались предпочтения избирателей штата Нью-Йорк. Шел 1942 г. За неделю до выборов один интервьюер, разъезжая по штату, опросил 200 человек. Они распределились в соответствии с плотностью населения в различных зонах территории штата (табл. 5.6).

Таблица 5.6

Распределение выборочной совокупности в обследовании избирателей штата Нью-Йорк, опрос X. Кентрила, 1942 г., абс.

157

Продолжение

Респонденты были распределены также по расовой принадлежности, экономическому положению, возрасту. Эти переменные и определили структуру выборки. Избирательные предпочтения ньюйоркцев оказались следующими: за Дьюи собирались проголосовать 115 человек, за Беннета — 72, за Альфанжа — 12 и за Амстера — 1. Ошибка предсказания победы Дьюи составила 5%, средняя ошибка трех лидирующих кандидатов — 3,3% (табл. 5.7).

Таблица 5.7

Данные опроса выборочной совокупности численностью 200 человек и результаты выборов в штате Нью-Йорк, опрос X. Кентрила, 1942 г., %

Выборка Кентрила минимальна, зато точность его данных была всего на один процентный пункт меньше, чем в опросе «Нью-Йорк дейли ньюс», где численность опрошенных составила48 тыс. человек. Американский институт общественного мнения (Дж. Гэллап) основы

158

вал тогда свой прогноз на обследовании 2500 человек, и ошибка составила 1,3 процентных пункта⁸. Результаты неплохие.

Итак, даже очень маленькая выборка при условии, что она хорошо распределена в генеральной совокупности, может быть вполне репрезентативной. Чем больше объем выборки, тем выше точность ее результатов, однако очевидно, что огромная выборка не гарантирует стопроцентного попадания. Плохо распределенная выборка в десять миллионов человек хуже, чем хорошо распределенная выборка в сто человек.

Со времени своего создания в 1935 г. Американский институт общественного мнения провел сотни предвыборных опросов. Средняя ошибка репрезентативности в 1936—1940гг. составляла 5,6 процентных пункта, в 1940—1944 гг. — 3,4, в 1944—1947 гг. — 2,6. В 1944 г. прогноз Гэллапа на президентских выборах был выполнен с точностью до 1,8 процентных пункта, а средняя ошибка по 48 штатам составила 2,5. В 1950—1958 гг. ошибка прогноза была 1,7 процентных пункта, в 1960—1968 гг. — 1,5, в 1970—1978 гг. — 1,1⁹.

Второй тип ошибок выборки — систематические ошибки. Это неконтролируемые перекосы в распределении выборочных наблюдений, которые приводят к «утере» проектируемого объекта исследования. В отличие от случайных систематические ошибки распределяются вокруг средней неравномерно, при возрастании объема выборки не уменьшаются. Число опрошенных здесь уже не имеет значения, потому что фактическая генеральная совокупность — та, что соответствует выборке, уже «уехала» от проектируемой, а исследователь продолжает надеяться на репрезентативность. Систематические ошибки в отличие от случайных не поддаются предварительному контролю.

Осенью 1936 г. в истории социологических исследований произошло событие, радикально изменившее представления о построении выборки для массовых опросов. В первые десятилетия XX в. американские газеты и журналы соревновались за то, чтобы стать выразителями общественного мнения. Журнал «Литерэри Дайджест» проводил «соломенные опросы» перед выборами с 1925 г. и никогда не ошибался. Рассылались миллионы почтовых бюллетеней — тем, кто числился в телефонных справочниках и списках автовладельцев. Система работала хорошо до тех пор, пока избиратели со средними и высокими доходами голосовали в равной степени и за демократов, и

⁸ Gallup G. A guide to public opinion polls. Princeton: Princeton University Press, 1948. P. 20-22.

⁹ Gallup G. The Gallup poll: Public opinion 1978. Wilmington, Delaware: Scholarly Resources, 1979. P. XLIV.

159

за республиканцев. И наоборот: избиратели с низкими доходами были склонны голосовать за любого кандидата.

С началом «Нового курса» американский электорат стал резко стратифицироваться: люди с доходами выше среднего, придерживавшиеся демократических взглядов, переменили их на республиканские, а те, кто принадлежал к малодоходным группам, стали симпатизировать демократической партии.

В 1936 г. на пост президента США претендовали Франклин Рузвельт — демократ и Альфред Лэндон — республиканец. Журнал «Литерэри Дайджест» разослал по почте десять миллионов бюллетеней — была охвачена примерно треть американских семей. Вернули бюллетени 2 376 523 человека. Очевидно, выборка «Литерэри Дайджест», состоящая из владельцев телефонов и автомобилей, была обречена на смещение в пользу республиканцев. Так и получилось. Предвыборный опрос показал, что за Лэндона собираются проголосовать 57% избирателей, а за Рузвельта — 43%. На выборах же победил Рузвельт с результатом 62,5%, а за Лэндона было подано 37,5% голосов.

К этому времени службы Дж. Гэллапа, Э. Роупера и А. Кроссли уже давно вели эксперименты с выборочными опросами. В частности, Гэллап в 1935 г. установил сдвиг политических ориентации состоятельных избирателей вправо, а бедных — влево. В 1936 г. он обнаружил, что большинство владельцев телефонов предпочитают Лэндона Рузвельту, в то время как только 18% получающих пособие собираются голосовать за Лэндона. 12 июля 1936 г., когда началась предвыборная кампания, Гэллап опубликовал статью с предупреждением об ошибке «Литерэри Дайджест», который, как считал автор, по всей вероятности, предскажет победу Лэндона над Рузвельтом со счетом 56: 44. Гэллап получил этот прогноз, разослав по почте всего 3 тыс. бюллетеней. Он подробно проанализировал причины возможной ошибки. В ответ в «Литерэри Дайджест» была опубликована сердитая статья, где редактор писал: «Никогда и никто еще не предсказывал результаты наших опросов еще до того, как они начались… Нашему доброму статистическому другу (имелся в виду Гэллап. — Г. Б.) можно было бы напомнить, что эти старомодные методы обеспечивают «Дайджесту» правильные прогнозы с точностью до одной сотой процента» ¹⁰.

Основной источник систематической ошибки вопросе «Литерэри Дайджест» — использование для определения адресов респондентов телефонных справочников и регистрационных книг владельцев ав

¹⁰ GallupG. Op. cit. P. XV.

160

томобилей. Естественно, выборка сместилась в сторону «верхних» слоев социальной структуры. Владельцы телефонов и автомобилей — группы, в значительной степени пересекающиеся, — и составили реальный объект исследования, в то время как проектируемый объект отождествлялся с электоратом США. В итоге сформировалась выборка из респондентов, избирательные предпочтения которых отличались от предпочтений среднего американца. Средневыборочные значения оказались смещенными в сторону более состоятельных и образованных слоев населения.

Эти социально-структурные параметры имели определяющее влияние на распределение доверия к Рузвельту среди электората. Проводимый президентом с 1932 г. «Новый курс» был основан на вмешательстве государства в сферу свободного предпринимательства, антимонопольной политике и защите интересов низших слоев населения, в том числе расширение избирательных прав для иммигрантов. Немаловажным фактором, обусловившим размежевание позиций избирателей, был и процесс крупных корпораций против Рузвельта в Верховном суде, который был выигран «капиталистами» в 1936 г. Это способствовало его популярности среди низших классов. Да и сам облик Рузвельта — человека, с молодых лет прикованного к инвалидной коляске, но сумевшего стать выдающимся политиком, импонировал демократическому большинству. Оптимальное размещение выборки в таких условиях было несовместимо с «уклоном» в сторону богатых. Этот «уклон» значительно усилился по причине пренебрежения со стороны аналитиков «Литерэри Дайджест» к динамике электоральных предпочтений в различных социальных стратах.

В лекции «Лекция 10» также много полезной информации.

В предыдущих опросах «Литерэри Дайджест» анкеты рассылались тем же группам и прогнозы оправдывались, но в 1936г. не были учтены два исключительно важных обстоятельства: во-первых, дифференциация избирательных установок в зависимости от уровня доходов — эта тенденция усилилось с приходом в 1932 г. в Белый дом президента Рузвельта; во-вторых, значительное расширение избирательного ценза. Новые контингента электората в основном принадлежали к беднейшим классам — они и предпочитали видеть Рузвельта на посту президента.

Метод исследования — почтовый опрос — также усугубил ошибку. Вероятность возврата вопросника по почте была и остается намного выше у людей с высоким образованием и доходами выше среднего, а те, кто не возвратил заполненный вопросник, как правило, принадлежали к низшим классам. Поэтому, если бы даже поллстеры из «Литерэри Дайджест» использовали списки избирателей, а не телефонные справочники, выборка все равно оказалась бы смещенной в сторону богатых и образованных.

161

11-365

Против «Литерэри Дайджест» работал и фактор времени. Состоятельные и более образованные люди обычно определяют «своего» кандидата на президентских выборах еще летом и, вообще, заранее имеют по этому поводу обоснованную позицию, а «простые» люди ничего заранее не умышляют. «Литерэри Дайджест» опрашивал миллионы преуспевающих американцев как раз в начале сентября, когда богатые уже определились в своем выборе, а бедные еще нет. Ошибочно предполагалось, что полученная картина сохранится до ноября, в том числе сохранится и доля тех, кто не мог сказать ничего определенного. К осени ситуация стала меняться. Количество определившихся в своем «нет» Рузвельту осталось относительно стабильным, зато подгруппа не имеющих мнения начала резко сокращаться и перетекать в «да» Рузвельту. Так величайшая по объему выборка в истории массовых опросов оказалась ошибочной, и инцидент показал, что главное для репрезентативности — не объем, а хорошее размещение единиц отбора.

«Каждая единица имеет равный шанс попасть в выборку» — первый принцип выборочной процедуры. Тогда же, в июле 1936 г., молодые и еще неизвестные поллстеры (так стали называть тех, кто проводит массовые опросы, в отличие от социологов), опросив несколько тысяч человек, точно предсказали победу Рузвельту. С этого времени начался институциональный период в истории обследований общественного мнения. Институты Гэллапа, Роупера и Харриса к началу 1960-х гг. уже были международными корпорациями.

Как мы уже знаем, репрезентативность — свойство выборочной совокупности представлять характеристику генеральной. Если совпадения нет, говорят об ошибке репрезентативности — мере отклонения статистической структуры выборки от структуры соответствующей генеральной совокупности. Предположим, что средний ежемесячный семейный доход пенсионеров в генеральной совокупности составляет 2 тыс. руб., а в выборочной — 6 тыс. руб. Это означает, что социолог опрашивал только зажиточную часть пенсионеров, а в его исследование вкралась ошибка репрезентативности. Иными словами, ошибкой репрезентативности называется расхождение между двумя совокупностями — генеральной, на которую направлен теоретический интерес социолога и представление о свойствах которой он хочет получить в конечном итоге, и выборочной, на которую направлен практический интерес социолога, которая выступает одновременно как объект обследования и средство получения информации о генеральной совокупности.

Наряду с термином «ошибка репрезентативности» в отечественной литературе можно встретить другой — «ошибка выборки». Иногда они употребляются как синонимы, а иногда «ошибка выборки» используется вместо «ошибки репрезентативности» как количественно более точное понятие.

Ошибка выборки — отклонение средних характеристик выборочной совокупности от средних характеристик генеральной совокупности.

На практике ошибка выборки определяется путем сравнения известных характеристик генеральной совокупности с выборочными средними. В социологии при обследованиях взрослого населения чаще всего используют данные переписей населения, текущего статистического учета, результаты предшествующих опросов. В качестве контрольных параметров обычно применяются социально-демографические признаки. Сравнение средних генеральной и выборочной совокупностей, на основе этого определение ошибки выборки и ее уменьшение называется контролированием репрезентативности. Поскольку сравнение своих и чужих данных можно сделать по завершении исследования, такой способ контроля называется апостериорным, т.е. осуществляемым после опыта.

В опросах Института Дж. Гэллапа репрезентативность контролируется по имеющимся в национальных переписях данным о распределении населения по полу, возрасту, образованию, доходу, профессии, расовой принадлежности, месту проживания, величине населенного пункта. Всероссийский центр изучения общественного мнения (ВЦИОМ) использует для подобных целей такие показатели, как пол, возраст, образование, тип поселения, семейное положение, сфера занятости, должностной статус респондента, которые заимствуются в Государственном комитете по статистике РФ. В том и другом случае генеральная совокупность известна. Ошибку выборки невозможно установить, если неизвестны значения переменной в выборочной и генеральной совокупностях.

Специалисты ВЦИОМ обеспечивают при анализе данных тщательный ремонт выборки, чтобы минимизировать отклонения, возникшие на этапе полевых работ. Особенно сильные смещения наблюдаются по параметрам пола и возраста. Объясняется это тем, что женщины и люди с высшим образованием больше времени проводят дома и легче идут на контакт с интервьюером, т.е. являются легко достижимой группой по сравнению с мужчинами и людьми «необразованными»35.

Ошибка выборки обусловливается двумя факторами: методом формирования выборки и размером выборки.

Ошибки выборки подразделяются на два типа — случайные и систематические. Случайная ошибка — это вероятность того, что выборочная средняя выйдет (или не выйдет) за пределы заданного интервала. К случайным ошибкам относят статистические погрешности, присущие самому выборочному методу. Они уменьшаются при возрастании объема выборочной совокупности.

Второй тип ошибок выборки — систематические ошибки. Если социолог решил узнать мнение всех жителей города о проводимой местными органами власти социальной политике, а опросил только тех, у кого есть телефон, то возникает предумышленное смещение выборки в пользу зажиточных слоев, т.е. систематическая ошибка.

Таким образом, систематические ошибки — результат деятельности самого исследователя. Они наиболее опасны, поскольку приводят к довольно значительным смещениям результатов исследования. Систематические ошибки считаются страшнее случайных еще и потому, что они не поддаются контролю и измерению.

Они возникают, когда, например:

1. выборка не соответствует задачам исследования (социолог решил изучить только работающих пенсионеров, а опросил всех подряд);
2. налицо незнание характера генеральной совокупности (социолог думал, что 70% всех пенсионеров не работает, а оказалось, что не работает только 10%);
3. отбираются только «выигрышные» элементы генеральной совокупности (например, только обеспеченные пенсионеры).

Внимание! В отличие от случайных ошибок систематические ошибки при возрастании объема выборки не уменьшаются.

Обобщив все случаи, когда происходят систематические ошибки, методисты составили их реестр. Они полагают, что источником неконтролируемых перекосов в распределении выборочных наблюдений могут быть следующие факторы:

• нарушены методические и методологические правила проведения социологического исследования;
• выбраны неадекватные способы формирования выборочной совокупности, методы сбора и расчета данных;
• произошла замена требуемых единиц наблюдения другими, более доступными;
• отмечен неполный охват выборочной совокупности (недополучение анкет, неполное их заполнение, труднодоступность единиц наблюдения).

Намеренные ошибки социолог допускает редко. Чаще ошибки возникают из-за того, что социологу плохо известна структура генеральной совокупности: распределение людей по возрасту, профессии, доходам и т.д.

Систематические ошибки легче предупредить (по сравнению со случайными), но их очень трудно устранить. Предупреждать систематические ошибки, точно предвидя их источники, лучше всего заранее — в самом начале исследования.

Вот некоторые способы избежать ошибок выборки:

• каждая единица генеральной совокупности должна иметь равную вероятность попасть в выборку;
• отбор желательно производить из однородных совокупностей;
• надо знать характеристики генеральной совокупности;
• при составлении выборочной совокупности надо учитывать случайные и систематические ошибки.

Если выборочная совокупность (или просто выборка) составлена правильно, то социолог получает надежные результаты, харастеризующие всю генеральную совокупность. Если она составлена неправильно, то ошибка, возникшая на этапе составления выборки, на каждом следующем этапе проведения социологического исследования приумножается и достигает в конечном счете такой величины, которая перевешивает ценность проведенного исследования. Говорят, что от такого исследования больше вреда, нежели пользы.

Подобные ошибки могут произойти только с выборочной совокупностыо. Чтобы избежать или уменьшить вероятность ошибки, самый простой способ — увеличивать размеры выборки (в идеале до объема генеральной: когда обе совокупности совпадут, ошибка выборки вообще исчезнет). Экономически такой метод невозможен. Остается другой путь — совершенствовать математические методы составления выборки. Они то и применяются на практике. Таков первый канал проникновения в социологию математики. Второй канал — математическая обработка данных.

Особенно важной проблема ошибок становится в маркетинговых исследованиях, где используются не очень большие выборки. Обычно они составляют несколько сотен, реже — тысячу респондентов. Здесь исходным пунктом расчета выборки выступает вопрос об определении размеров выборочной совокупности. Численность выборочной совокупности зависит от двух факторов:

1. стоимости сбора информации,
2. стремления к определенной степени статистической достоверности результатов, которую надеется получить исследователь.

Конечно, даже не искушенные в статистике и социологии люди интуитивно понимают, что чем больше размеры выборки, т.е. чем ближе они к размерам генеральной совокупности в целом, тем более надежны и достоверны полученные данные. Однако выше мы уже говорили о практической невозможности сплошных опросов в тех случаях, когда они проводятся на объектах, численность которых превышает десятки, сотни тысяч и даже миллионы. Понятно, что стоимость сбора информации (включающая оплату тиражирования инструментария, труда анкетеров, полевых менеджеров и операторов по компьютерному вводу) зависит от той суммы, которую готов выделить заказчик, и слабо зависит от исследователей. Что же касается второго фактора, то мы остановимся на нем чуть подробнее.

Итак, чем больше величина выборки, тем меньше возможная ошибка. Хотя необходимо отметить, что при желании увеличить точность вдвое вам придется увеличить выборку не в два, а в четыре раза. Например, чтобы сделать в два раза более точной оценку данных, полученных путем опроса 400 человек, вам потребуется опросить не 800, а 1600 человек. Впрочем, вряд ли маркетинговое исследование испытывает нужду в стопроцентной точности. Если пивовару необходимо узнать, какая часть потребителей пива предпочитает именно его марку, а не сорт его конкурента, — 60% или 40%, то на его планы никак не повлияет разница между 57%, 60 или 63%.

Ошибка выборки может зависеть не только от ее величины, но и от степени различий между отдельными единицами внутри генеральной совокупности, которую мы исследуем. Например, если нам нужно узнать, какое количество пива потребляется, то мы обнаружим, что внутри нашей генеральной совокупности нормы потребления у различных людей существенно различаются (гетерогенная генеральная совокупность). В другом случае мы будем изучать потребление хлеба и установим, что у разных людей оно различается гораздо менее существенно {гомогенная генеральная совокупность). Чем больше различия (или гетерогенность) внутри генеральной совокупности, тем больше величина возможной ошибки выборки. Указанная закономерность лишь подтверждает то, что нам подсказывает простой здравый смысл. Таким образом, как справедливо утверждает В. Ядов, «численность (объем) выборки зависит от уровня однородности или разнородности изучаемых объектов. Чем более они однородны, тем меньшая численность может обеспечить статистически достоверные выводы».

Определение объема выборки зависит также от уровня доверительного интервала допустимой статистической ошибки. Здесь имеются в виду так называемые случайные ошибки, которые связаны с природой любых статистических погрешностей. В.И. Паниотто приводит следующие расчеты репрезентативной выборки с допущением 5%-ной ошибки:
Это означает,что если вы, опросив, предположим, 400 человек в районном городе, где численность взрослого платежеспособного населения составляет 100 тыс. человек, выявили, что 33% опрошенных покупателей предпочитают продукцию местного мясокомбината, то с 95%-ной вероятностью можете утверждать, что постоянными покупателями этой продукции являются 33+5% (т.е. от 28 до 38%) жителей этого города.

Можно также воспользоваться расчетами института Гэллапа для оценки соотношения размеров выборки и ошибки выборки.

вызванные различн. причинами отклонения выбороч. оценок при­знаков от их значений по генеральной совокуп­ности. По происхождению В.о. можно подразде­лить на теоретические, возникающие до процес­са отбора на стадии формирования концептуаль­ного представления об объекте исследования и выработки стратегии отбора; процедурные ошиб­ки, связанные с построением выборочн. модели; и ошибки на этапе реализации вплоть до непосред­ственного контакта с единицей наблюдения. По характеру воздействия на выборочную оценку различают случайную и систематич. компонен­ту В.о. Случайная компонента ошибки имеет ве­роятностную природу, она органически присуща выборочн. наблюдению, если отбор организован по строго случайному принципу. В вероятностных выборках неизбежность случайной ошибки вы­звана тем, что обследованию подлежит часть, а не все множество объектов генеральной совокуп­ности. Величина случайной ошибки зависит от плана построения выборки (см. Выборка много­ступенчатая, Выборка гнездовая, Выборка рай­онированная), объема выборочной совокупности, степени вариации признаков и может быть оце­нена по данным выборки с помощью аппарата математич. статистики. Основание для вычисления случайной ошиб­ки по любой случайно составленной выборке дает центральная предельная теорема. Из этой тео­ремы следует, что каков бы ни был закон рас­пределения исходной совокупности, при много­кратном извлечении выборок объема п распре­деление выбороч. средних близко к нормально­му со средним, равным среднему генеральной совокупности, и дисперсией, равной о2/п, где О2 – дисперсия признака в генеральной совокуп­ности. Имея в распоряжении одну-единственную выборку, исследователь может определить ту степень, с к-рой оценки, полученные из различн. выборок, будут отличаться друг от друга, т. е. оценить меру разброса выборочн. распределения средних. Т.обр., случайная ошибка является ха­рактеристикой не единичной выборки, а сово­купности всех возможных выборок того же объ­ема из данной генеральной совокупности и определяется в терминах выборочн. распределения средних. Поэтому случайная ошибка также носит название стандартной, или средней, ошибки вы­борки. Отметим, что дисперсия признака в гене­ральной совокупности, необходимая для расчета случайной ошибки выборки, часто бывает неиз­вестна и на практике пользуются ее выбороч. оцен­кой с поправкой на смещение:

Для районированной выборки стандартная ошиб­ка вычисляется как сумма взвешенных квадра­тов в каждом слое. Зная величину случайной ошибки, можно рассчитать доверительный интервал, в к-ром с заданной вероятностью будет находиться ис­тинное значение признака. С этой целью выби­рают нек-рую вероятность и по таблице распре­деления нормальной случайной величины находят значение параметра z-аргумента функции рас­пределения. Систематич. компонента ошибки (смещение) носит неслучайный характер и представляет собой нек-рую постоянную или закономерно из­меняющуюся величину. Смещение имеет различн. источники, каждый их к-рых искажает рез-ты, либо увеличивая, либо уменьшая значение вы­борочн. оценки, поэтому общее смещение явля­ется алгебраич. суммой всех смещений. Смеще­ния, вызываемые различн. источниками, могут частично погашать друг друга, так что устране­ние одного из них способно привести к увеличе­нию общего смещения. За редким исключением, систематич. ошибки не уменьшаются с увеличе­нием размера выборочной совокупности. Природа выборочн. смещений различна. На предпроектной стадии они могут быть обуслов­лены несоответствием выборочн. модели систе­ме представлений об объекте, теоретически не­верным определением генеральной совокупности, выбором признакового пространства, неадекватного объекту исследования или не отражащего в выборочн. совокупности многомерности этого пространства, непродуманной с реализации выборки. В процессе построения выборки источником смещения может стать сам процедура извлечения представительной выбор! ки при неслучайных способах формирования вы борочной совокупности или применение неадек­ватных процедур отбора, нарушающих пропор­циональное представительство элементов гене­ральной совокупности или принцип равной ве­роятности включения в выборку единиц наблю­дения при проектировании вероятностных вы­борок: неполнота выбороч. основы (см. Выборки основа), а также пропуски и дублирование-при ее подготовке. К категории выборочных относят и смещения, появляющиеся в рез-те использо­вания заведомо смещенных, но состоятельных оценок, т. е. оценок, смещение к-рых при увели­чении объема выборки уменьшается и исчезает при сплошном обследовании (напр., оценка по от­ношению). Однако в социологич. исследованиях и опросах населения особенно величины таких смещений, если они и присутствуют, настолько незначительны по сравнению с др. ошибками, что для оценки качества выборки они представляют чисто теоретич. интерес. При реализации выбор­ки источник смещения составляют т.н. труднодос­тупные единицы – элементы выборочной сово­купности, по к-рым трудно или практически не­возможно получить необходимую информацию. Обычно к ним относят лиц, отсутствующих дома в момент визита интервьюера, отказавшихся от­вечать на вопросы, больных, временно отсутст­вующих дома (командировка, отпуск и т. п.). Оценка величины систематич. ошибки час­то оказывается для исследователя непростой задачей, т. к. наиболее очевидный способ внеш­него контроля – сравнение с генеральными дан­ными – не всегда представляется возможным и целесообразным. Для одних источников, таких, напр., как труднодоступные единицы, оценка смещений и степени их влияния на выборочн. рез-ты осуществляется с помощью специальных приемов анализа полученных данных, дополни­тельно разработанных полевых документов. Для др. источников факт смещенности выбороч. рез-тов может быть в лучшем случае зафиксирован и не поддается числовой оценке. В отличие от случайной компоненты ошиб­ки отдельные источники смещений имеют место и при организации неслучайного отбора. Лит.: Волович В.И. Надежность информации в со­циологическом исследовании. Киев, 1974; Докторов Б.З. и надежности измерения в социологическом исследовании. Л.. 1979; Саганенко Г.И. Надежность результатов социологи­ческого исследования. Л., 1983; Kish L. Survey sampling-N-»-L., Sydney, 1967; Total survey error. San Francisco, Wash., i. 1979; How nonresponse in Detroit area study surveys a ten year analysis. North Carolina, 1979. Г.Н. Сотником.

Социологи изучают
поведение (мнения, оценки, мотивы) не
отдельно взятых людей, но некоторых
человеческих «совокупно­стей»
— социальных групп, классов, сообществ.
Информация о мас­совых социальных
явлениях и процессах может быть получена
как из объективных, так и из субъективных
источников. К объективным источникам
относятся официальная государственная
статистика, статистика министерств и
ведомств, служб социальной защиты,
профессиональных союзов, общественных
партий и движений и т.п. Такие данные,
как правило, касаются обобщенных
количественных характеристик социальных
общностей, явлений, процессов, напри­мер,
численность населения, уровень
безработицы, средняя зарпла­та,
национальный валовой продукт, численность
и состав партий и общественных объединений,
реализуемый тираж печатных изданий.
Объективное и даже официальное
происхождение таких данных не всегда
гарантирует их точность и однозначность.
Так, существенно расходятся оценки
уровня безработицы службами занятости
и профсоюзами, которые используют для
определения этого уровня разные методики.
Средний уровень доходов, определяемый
министерством статистики, является
заведомо заниженным, так как в нем не
учиты­ваются (или учитываются не в
полном объеме) заработки в теневом
секторе экономики и доходы от индивидуальной
трудовой деятель­ности. Заведомо
занижены данные о распространенности
наркома­нии или пьянства за рулем
из-за того, что регистрируются далеко
не все случаи этих явлений. А данные о
читателях библиотек, напро­тив,
завышены, так как библиотека считает
своим читателем каждого, кто был в нее
записан, даже если человек посетил ее
лишь однажды.

Субъективными
источниками данных являются сами люди.
Только от них можно узнать о настроениях
населения или отдель­ных социальных
групп, к ним обращаются службы общественного
мнения, по их ответам прогнозируют
результаты выборов и опреде­ляют
рейтинги телепередач. При работе с
такими источниками воз­никают, как
минимум, две методологические проблемы.
Во-первых, данные, полученные от отдельных
людей, должны характеризовать изучаемое
явление или процесс в целом. Следовательно,
они долж­ны быть некоторым образом
обобщены. Во-вторых, наиболее точ­ные
результаты могут быть получены при
исследовании полной со­вокупности
объектов, имеющих отношение к изучаемой
проблеме, — генеральной
совокупности. Лучшим
примером подобного исследо­вания
является перепись населения. Однако
подобные проекты чрезвычайно трудоемки
и дорогостоящи, а в информации от
субъек­тивных источников общество
нуждается постоянно. Поэтому
социо­логические исследования в
большинстве случаев бывают выбороч­ными.
Главной проблемой выборочного исследования
является от­бор из генеральной
совокупности объектов такой подсовокупности
(выборки),
которая
сделала бы исследование одновременно
и пред­ставительным, и экономичным.

Представительностью
или репрезентативностью
выборки
называется ее способность правильно
отражать состояние дел в ге­неральной
совокупности, из которой она извлечена
и для изучения которой предназначена.
Понятие эффективности
(экономичности)
выборки связано со стоимостью исследования.
Эффективной называ­ется выборка,
которая позволяет получить наиболее
точные результа­ты при заданной
стоимости исследования либо обеспечить
заданную точность результатов при
минимальных затратах. Репрезентативность
и эффективность зависят от дизайна
выборки —
стратегии и конкретных процедур ее
формирования.

Дизайн
исследования определяется
его целями, задачами и ги­потезами, а
также характеристиками генеральной
совокупности. В зависимости от целей и
задач различают дескриптивные
(описатель­ные), аналитические, полевые
исследования и исследования отдель­ных
случаев.

Дескриптивные
(описательные) исследования, называемые
также просто обследованиями,
предназначены
для получения обоб­щенных характеристик
генеральной совокупности. Они бывают
сплошными и выборочными, а также разовыми
и лонгитюдными. Основным методом сбора
информации является интервьюирование
(анкетирование).

Сплошное дескриптивное
исследование предполагает обсле­дование
всей генеральной совокупности, как,
например, при пере­писи населения.
Собранная информация может быть
использована для классификации объектов,
получения обобщенных характери­стик
генеральной совокупности, измерения
связей между показате­лями. Полное
обследование позволяет получить
абсолютно надеж­ную информацию, но
требует значительных усилий и материальных
средств.

Выборочное
обследование имеет дело не со всей
генеральной совокупностью, но только
с некоторой ее частью. Для того, чтобы
выборка была репрезентативной (позволяла
воспроизвести основ­ные характеристики
генеральной совокупности), необходимо
со­блюдать специальные процедуры.
Данные выборочного обследова­ния
позволяют оценивать неизвестные
характеристики генеральной совокупности,
проверять гипотезы, анализировать
парные и множе­ственные связи между
переменными. Выборочное обследование
яв­ляется самым распространенным
дизайном в социальных исследо­ваниях,
ниже мы рассмотрим его более подробно.

Как
сплошные, так и выборочные обследования
бывают разо­выми и лонгитюдными.
Разовые исследования позволяют получить
«срез» информации о состоянии
генеральной совокупности в опре­деленный
момент времени. При изучении социальных
процессов в динамике возможна организация
мониторингового исследования как
последовательности разовых обследований,
проводимых по об­щей программе и
инструментарию, для каждого из которых
строит­ся новая выборка. Обязательное
требование к мониторинговым исследованиям
— применение на всех этапах одних и тех
же процедур
формирования выборки.

Исследование
случаев (case
study)
обычно направлено на ин­тенсивный
анализ единичных случаев изучаемого
феномена. Иссле­дователь интервьюирует
индивидуумов или изучает документы
ис­тории их жизни, чтобы глубже понять
их поведение; пытается опре­делить
как уникальные, так и общие черты,
свойственные всем людям из данного
класса (социальной группы). Для исследования
общих тенденций случаи могут быть
сгруппированы по типам. Ме­тод
эффективен для исследований личности
и процессов социализа­ции, разработки
новых понятий либо проверки существующих.
Данные об отдельных случаях могут быть
закодированы для после­дующей
статистической обработки.

Сплошное или
выборочное обследование генеральной
сово­купности может применяться в
комбинации с исследованием от­дельных
случаев для более глубокого освещения
происходящих процессов и наблюдаемых
феноменов. Случаи отбираются после
обследования таким образом, чтобы
продемонстрировать поведение объектов
с типичными либо, наоборот, резко
выделяющимися ха­рактеристиками.
Таким образом, найденные статистические
законо­мерности иллюстрируются
данными об отдельных судьбах, что
по­зволяет изучать и описывать процессы
социализации личности с большей глубиной.

Остановимся более
подробно на методах выборочного
обсле­дования — дизайна, наиболее
распространенного в социологических
исследованиях. Построение репрезентативной
(представительной) выборки невозможно
без корректного определения генеральной
со­вокупности (ГС), которое далеко не
всегда очевидно. Оно включает ответы
на следующие вопросы:

— какие именно
объекты (элементы) составляют ГС —
отдель­ные люди, семьи, академические
группы, предприятия, населенные пункты
или целые государства;

— какими признаками
обладают элементы ГС, насколько они
доступны для определения;

— какова численность
ГС;

— как ГС размещена
территориально;

— как ГС ограничена
во времени.

В
большинстве социальных исследований
в качестве элементов генеральной
совокупности выступают обычные люди.
Однако это не
является общим правилом. В демографических
исследовани­ях элементом наблюдения
часто является домохозяйство или семья;
в микроэкономических исследованиях —
домохозяйство, фирма, предприятие; в
сравнительных международных исследованиях
— го­сударство или регион. Ошибки в
определении элементов генераль­ной
совокупности приводят к систематическим
ошибкам в получен­ных результатах.

По характеру
элементов генеральные совокупности
(ГС) де­лятся на конкретные и
гипотетические. Конкретные ГС состоят
из элементов, которые могут быть выделены
относительно легко. На­пример, учителя
составляют достаточно большую, но
конкретную ГС, так как их можно найти и
обследовать через министерство
обра­зования и школы. Элементы
гипотетической ГС обладают характе­ристиками,
которые трудно или даже невозможно
определить до на­чала исследования.
Например, нельзя определить, принадлежит
ли человек к зрителям телевизионного
шоу, до тех пор, пока он сам не ответит
на этот вопрос, или к генеральной
совокупности избирате­лей — до того,
как он пришел на избирательный участок.
К гипоте­тическим генеральным
совокупностям относятся аудитория СМИ,
сторонники различных учений, потребители
некоторых товаров, коллекционеры и т.п.

Численность
конкретных генеральных совокупностей
в боль­шинстве случаев известна или
может быть относительно легко уточнена.
Численность некоторых гипотетических
ГС, например, национальных меньшинств,
тоже может быть определена без боль­ших
усилий (например, по данным официальной
статистики). До­вольно часто приходится
довольствоваться заведомо завышенными
или заниженными оценками, основанными
на реальных данных. Например, численность
читателей библиотеки можно оценить по
картотеке, но такая оценка будет
завышенной. Оценка численности безработных
по картотеке биржи труда или наркоманов
по данным наркологической службы будут
заведомо заниженными. Наконец, численность
таких генеральных совокупностей, как
аудитория СМИ может быть оценена только
с помощью специального исследования.
Иногда бывает полезно различать конечные
и «бесконечные» генеральные
совокупности. На практике к бесконечным
относят ге­неральные совокупности
численностью более ста тысяч элементов.
Так, вполне конкретную ГС учителей
Беларуси можно считать прак­тически
бесконечной; а весьма гипотетичная ГС
узбеков, проживающих в Минске, является
конечной, так как ее численность
опре­деленно не превышает нескольких
десятков человек.

В соответствии с
территориальным размещением генеральные
совокупности бывают национальными,
региональными, городскими, и т.п. Они
могут также ограничиваться принадлежностью
к опреде­ленным ведомствам, организациям,
сообществам, социальным группам.

Временные рамки
генеральной совокупности в большинстве
случаев ограничиваются моментом
обследования. Однако в некото­рых
исследованиях время играет весьма
значительную роль. Так, при изучении
демографических или миграционных
процессов учи­тываются все случаи
рождений, смертей, эмиграции, иммиграций
на определенной территории за год или
за пять лет. В лонгитюдных ис­следованиях
время фигурирует как условие выделения
генеральной совокупности по принципу
образовательной или возрастной когор­ты.
Например, в республиканском лонгитюдном
исследовании «Пу­ти поколения»
ГС была определена как «лица, получившие
среднее образование в 1983 году».

Большинство
выборочных процедур предполагает, что
из­вестны не только общие характеристики,
но и списочный состав ге­неральной
совокупности. На практике так бывает
далеко не всегда, поэтому следующим
этапом построения выборки является
опреде­ление ее представительной
основы —
совокупности,
из которой вы­борка будет непосредственно
формироваться. При опросах взросло­го
населения в качестве основы выборки
используют картотеку ад­ресного
стола, списки избирателей, или списки
адресов, которыми располагают коммунальные
службы (хотя все эти источники, как
правило, не вполне точны); при исследовании
читателей прессы -списки подписчиков
в почтовых отделениях (хотя газеты
читают не только они); при телефонных
опросах населения — номера телефо­нов,
включенные в городской справочник (хотя
значительная часть населения не охвачена
этим видом услуг) и т.п.

Поскольку выборка
является средством изучения генеральной
совокупности, основное требование к
ней — возможность обобщения результатов
выборочного исследования на генеральную
совокуп­ность. Соответствие выборки
этому требованию определяет ее
ре­презентативность. Выбор конкретных
методов формирования вы­борки зависит
от характеристик генеральной совокупности,
а также имеющихся материальных и
временных ресурсов.

Существует два
основных подхода к обоснованию
репрезен­тативности выборки:
статистический и внестатистический.
При ста­тистическом подходе
репрезентативность обеспечивается
специаль­ными вероятностными методами
извлечения выборки. Для обобще­ния
результатов исследования на генеральную
совокупность применяются строгие
индуктивные процедуры статистического
вы­вода, оценивается ошибка выборки
с заданной доверительной ве­роятностью.
Внестатистическое обоснование
репрезентативности предполагает
теоретическое доказательство того, что
выборка дос­таточно хорошо представляет
генеральную совокупность. При
ис­пользовании этого подхода
статистическое оценивание ошибок
вы­борки не производится.

Поскольку
абсолютное большинство методов
статистического анализа разработаны
для статистически обоснованных
(вероятност­ных) выборок, мы будем
говорить, главным образом, о них.
Разли­чают три основных вида случайного
отбора: простой, стратифици­рованный
и кластерный. Простой
случайный отбор из
генеральной совокупности предполагает,
что (1) генеральная совокупность
одно­родна; (2) все ее элементы доступны
для исследования в одинаковой степени;
(3) имеется полный список элементов,
составляющих гене­ральную совокупность
(или хотя бы репрезентативная основа
вы­борки); (4) к этому списку применяются
процедуры случайного от­бора, с
использованием таблиц или компьютерных
генераторов слу­чайных чисел. При
правильной организации простого
случайного отбора все элементы генеральной
совокупности имеют одинаковую вероятность
попасть в выборку, что значительно
упрощает ее стати­стическое обоснование.

Основными проблемами
простого случайного отбора являют­ся
сложность и неоднозначность понятия
однородности генеральной совокупности;
невозможность получения представительной
основы выборки; разная степень доступности
элементов генеральной сово­купности
и их готовности участвовать в исследовании.

Однородность
генеральной совокупности является
одним из наиболее сложных для определения
понятий. Она означает не столько
одинаковое поведение ее элементов,
сколько однородность условий, в которых
эти элементы находятся. Условия, по
которым контролируется однородность
ГС, должны быть тесно связанными с
задачами и гипотезами исследования.
Так, при экологических ис­следованиях,
всю территорию Беларуси делят на две
относительно однородные части —
загрязненную радиоактивными элементами
и «чистую». При исследованиях
общественного мнения неодинаково ведут
себя городское и сельское население.
При предсказании ре­зультатов выборов
необходимо принимать во внимание
различия в политических симпатиях
населения западных и восточных районов
страны. В некоторых исследованиях
критериями неоднородности могут быть
возраст, образование, принадлежность
к религиозным конфессиям, даже пол
респондента.

Для получения
основы выборки применяются два главных
подхода, выбор которых зависит от
определения генеральной сово­купности.
Если она определена по территориальному
принципу (как население, проживающее
на определенной территории), формиро­вание
основы выборки также производится по
территориальному принципу — через
адресные или справочные столы, по спискам
из­бирателей или подписчиков газет,
домовым книгам, спискам адре­сов,
планам населенных пунктов и т.п. Если
генеральная совокуп­ность определяется
по производственному принципу, основа
выбор­ки формируется по спискам
работников предприятий, учащихся учебных
заведений, списков членов партий или
других сообществ, библиотечных картотек,
и так далее. Термин «производственный»
здесь трактуется широко, как
зарегистрированное членство в любой
организации. Возможность получения
основы выборки зависит от степени
конкретности/гипотетичности генеральной
совокупности, ее объема, особенностей
организации.

Наконец, необходимо
учитывать, что социальные объекты мо­гут
проявлять разную степень готовности
участвовать в исследовании (вплоть до
полного отказа), а также могут иметь
разную степень дос­тупности. Например,
менее доступными часто оказываются
молодые респонденты, особенно мужчины,
ведущие мобильный образ жизни; в зимнее
время в некоторых районах могут оказаться
практически недос­тупными для опроса
жители сельской глубинки и т.п.

Таким образом,
соблюдение условий простого случайного
от­бора возможно не всегда, а если и
возможно теоретически, то не всегда
приемлемо с экономической точки зрения,
так как опрос рес­пондентов, равномерно
«рассеянных» на большой территории,
и особенно в сельской местности, требует
значительных материаль­ных средств.
Лучшим, с точки зрения теории выборки,
решением этой проблемы является
применение других методов случайного
от­бора — стратифицированного или
гнездового (кластерного).

Стратифицированный
случайный отбор заключается
в том, что генеральную совокупность
разделяют на относительно однород­ные
части или слои (страты), для каждой страты
определяют собст­венную основу
выборки, из которой производят простой
случайный отбор. Предполагаемый объем
выборки при этом делится между стратами
пропорционально их численности, что
позволяет обеспе­чить для всех
элементов генеральной совокупности
одинаковую ве­роятность быть отобранным.
Стратифицированный случайный от­бор
применяется, когда генеральная
совокупность не является одно­родной,
а также в тех случаях, когда она слишком
велика или имеет сложную структуру, так
что основу выборки значительно проще
по­лучить для отдельных ее частей,
чем для генеральной совокупности в
целом. В тех случаях, когда стратификация
производится по тер­риториальному
принципу, отбор иногда называют
районированным.
Например,
при национальных опросах в Беларуси
часто применяют районирование по
областям.

Если
генеральная совокупность может быть
представлена как совокупность относительно
мелких групп элементов (кластеров,
гнезд), к ней могут применяться процедуры
кластерного
(гнездово­го) отбора. Основа
выборки представляет собой список
кластеров, к которому применяется
процедура простого случайного отбора.
За­тем отобранные кластеры обследуются
полностью или выборочно.

Сплошное
(серийное)
обследование
кластеров применяется, если численность
групп примерно одинакова, и различия
между группами меньше, чем различия
между отдельными элементами внутри
группы. Примерами серийного отбора
являются опросы старшеклассников целыми
классами, студентов — академическими
группами, рабочих — бригадами и т.п.

Если кластеры не
удовлетворяют требованиям серийного
от­бора, их рассматривают как некие
промежуточные ступени в много­ступенчатом
отборе. Например, на территории отбираются
в качест­ве кластеров отдельные
населенные пункты, в которых затем
произ­водится выборочное обследование
населения.

Метод случайного
кластерного отбора применяется в тех
слу­чаях, когда трудно получить
репрезентативную основу выборки
(по­лучить список кластеров, в любом
случае, значительно проще), а также при
ограниченных материальных и временных
ресурсах, так как групповой опрос по
месту учебы или работы или проведение
обследования только в некоторых
населенных пунктах весьма эконо­мичны.

Наряду
с методами случайного отбора на практике
использу­ется также ряд квазислучайных
методов, не использующих таблицы и
генераторы случайных чисел, но позволяющих
получить результа­ты, аналогичные
результатам случайного отбора. Наиболее
попу­лярным из них является
систематический отбор. При систематиче­ском
отборе основа
выборки упорядочивается по какому-либо
кри­терию, а затем из упорядоченного
списка, с заданным шагом, извлекаются
элементы. Критерий упорядочивания
должен исклю­чать возникновение в
списке каких-либо циклических
закономерно­стей. Лучшим критерием
для списков людей считается алфавитный
порядок. Более крупные объекты (населенные
пункты, организации, фирмы) могут быть
упорядочены по размеру, объему
товарооборота, и т.п. Систематический
отбор, как и случайный, может быть
про­стым, стратифицированным и
кластерным.

Популярным
вариантом систематического отбора
является «маршрутная» выборка, при
которой адреса домохозяйств извлека­ются
из списка, упорядоченного по улицам
населенного пункта. Вместе с маршрутной
выборкой часто применяют рандомизирующие
процедуры,
призванные обеспечить «случайность»
отбора элемента генеральной совокупности
в выборку. К ним относятся, например,
случайный выбор первого адреса из
списка, запрет на обследование подряд
однотипных квартир, процедуры случайного
отбора респон­дента в семье.

В
рамках теории выборки разработаны также
разнообразные стратегии и методы, к
которым можно обратиться, если случайный
отбор невозможен или требует недопустимо
высоких затрат. Основ­ным нестатистическим
методом извлечения выборок является
квотный
отбор. Его
применяют, если распределение генеральной
сово­купности по основным
социально-демографическим или другим
су­щественным для исследования
признакам известно, но ее списки получить
невозможно, или если для осуществления
случайного от­бора недостаточно
времени и средств. В этом случае
интервьюерам поручают опросить
определенное число лиц с заданными
характе­ристиками, отбирая их по
своему усмотрению. Квотный отбор
кри­тикуется специалистами по теории
выборки, главным образом, за то, что
точность результатов, полученных по
квотным выборкам, не может быть оценена
статистически. Тем не менее, он достаточно
популярен благодаря своей простоте,
относительно низкой стоимости и
анонимности. При исследовании общественного
мнения, цен­ностей, установок, мотивов
квотный отбор обычно дает удовлетво­рительные
результаты. Однако его категорически
не рекомендуется использовать в
исследованиях социальной структуры,
стратифика­ции, мобильности.

Метод
основного массива применяется
на небольших гене­ральных совокупностях,
для которых нет смысла проводить
выбо­рочное исследование. Обоснование
репрезентативности в этом случае носит
внестатистический характер, оно
осуществляется посредством сравнения
исследованной и неисследованной частей
генеральной со­вокупности.

Наиболее
уязвим, с точки зрения соответствия
полученных результатов реальному
положению дел, метод
доступной выборки, который
применяется при исследовании генеральных
совокупно­стей, слишком сложных для
исследования другими методами. Обычно
это гипотетические генеральные
совокупности — аудитория СМИ (опрашиваемая
непосредственно через СМИ), потребители
определенных товаров (опрашиваемые в
магазинах), национальные меньшинства,
представителей которых опрашивают в
культурных обществах или в местах
компактного проживания и т.п.

Метод
«снежного кома» представляет
собой нечто среднее между методами
доступной выборкой и основного массива.
Он применяется к малочисленным
гипотетическим генеральным сово­купностям,
например, к коллекционерам или экспертам
по узкой проблеме. Каждого найденного
члена такой совокупности спраши­вают,
кого из своих коллег он мог бы назвать.
Полученный список принимается за основу
выборки; опрос продолжается до тех пор,
пока имена в списке не начнут повторяться.

К
большим генеральным совокупностям со
сложной структу­рой часто применяют
многоступенчатый
отбор. Для
этого гене­ральную совокупность
структурируют, разбивая ее на конечное
чис­ло подсовокупностей. Образуется
новая, конкретная и конечная, ге­неральная
совокупность, элементами (единицами
отбора) которой являются выделенные
подсовокупности. Часть из них отбирается
для продолжения исследования. Эта
операция может повторяться несколько
раз, пока не будут получены подсовокупности,
доступные для непосредственного
изучения, причем на разных ступенях
могут использоваться разные методы
отбора и репрезентации.

При многоступенчатом
отборе основой выборки на каждой ступени
является список выделенных структурных
единиц отбора. На последней ступени
единицы отбора совпадают с единицами
на­блюдения — объектами из генеральной
совокупности, включенными в выборку и
подлежащими непосредственному
исследованию.

Результаты
выборочных исследований всегда являются
отчас­ти неопределенными. Это происходит
потому, что изучается только часть
генеральной совокупности, и измерения
производятся с ошиб­ками. Однако при
отсутствии грубых просчетов в планировании
и реализации выборки эти ошибки можно
контролировать, то есть с высокой
вероятностью полагать, что они находятся
в некоторых пределах, которые представляются
исследователю допустимыми.

Обычно
выделяют две составляющие ошибки
выборки, одну из которых называют
систематической, а другую случайной
ошиб­кой. Систематическая
ошибка представляет
собой некоторое сме­щение выборочного
среднего значения признака по отношению
к генеральному среднему, не уменьшающееся
с увеличением объема выборки.
Систематические ошибки обычно связывают
с ошибками проектирования выборки и
ошибками инструментария исследова­ния.
Их часто трудно обнаружить и еще труднее
измерить; для этого проводятся специальные
методологические исследования и
приме­няются специальные процедуры
тестирования выборки и измери­тельных
шкал. Иногда систематические ошибки
могут быть опреде­лены, если со временем
становится известным распределение
при­знака в генеральной совокупности
(например, результаты выборов), или в
результате скрупулезного анализа
артефактов, обнаруженных при анализе
данных.

Случайные
ошибки связаны
с вероятностным характером про­цедур
извлечения выборки из генеральной
совокупности и ошибка­ми измерения,
не имеющими систематического характера.
Ошибки такого рода неустранимы, но
подчиняются статистическим законам и,
соответственно, поддаются контролю.
Важнейшее свойство слу­чайных ошибок
состоит в том, что они уменьшаются с
увеличением объема выборки. Следовательно,
увеличивая объем выборки, их можно
свести к допустимому пределу, и, тем
самым, обеспечить же­лательную степень
точности результатов исследования.

Степень точности
для каждого показателя, измеряемого в
процессе обследования, задается (и
измеряется) двумя количествен­ными
характеристиками: предельно допустимой
величиной ошибки и вероятностью того,
что эта величина не будет превышена
(довери­тельной вероятностью). Оба
эти значения существенным образом
зависят от объема выборки и способа ее
извлечения. Стремление повысить точность
приводит к быстрому росту необходимого
объе­ма выборки и, соответственно,
стоимости исследования. Таким об­разом,
каждая реализованная выборка является
компромиссом меж­ду желательной
степенью точности и имеющимися в
распоряжении исследователя временными
и материальными ресурсами.

Итак,
ошибкой
выборки (А)
называется разность между сред­ними
арифметическими значениями признака
по выборке и по гене­ральной совокупности:

где х — среднее
арифметическое значение признака по
выборке; μ — среднее арифметическое
значение признака по генеральной
совокупности.

Таким образом,
ошибка выборки измеряется в тех же
едини­цах, что и измеряемый показатель.
Поскольку в реальном исследо­вании
среднее значение признака по генеральной
совокупности (μ) обычно неизвестно
(напротив, исследование проводится с
целью его оценить), ошибка выборки не
может быть вычислена точно, а только
оценена статистическими методами. Сразу
оговоримся, что стати­стическое
оценивание ошибок возможно только для
вероятностных выборок, на всех ступенях
которых применяются случайные методы
отбора, и при этом оценивается только
случайная составляющая ошибки, а ее
систематическая составляющая полагается
равной ну­лю. Мы рассмотрим наиболее
простой случай оценивания ошибки и
объема выборки — при простом случайном
отборе.

Случайные
ошибки простой случайной выборки из
бесконеч­ной генеральной совокупности
имеют распределение, близкое к нормальному
(Гауссовому), с нулевым средним и
дисперсией, рав­ной σ²/n,
где σ ²
— дисперсия признака по выборке, n
— ее объем.

Величина
Δ_ст
=σ/√n
называется стандартной ошибкой выборки.

Из свойств
нормального распределения следуют два
важных обстоятельства. Во-первых,
значения таких ошибок обычно невели­ки.
С вероятностью (1-а) они не выходят за
пределы так называе­мого доверительного
интервала, который имеет вид:

(1)

или

(2)

Вероятность
а выбирается заранее. Наиболее часто
использу­ются значения а = 0.01, 0.05 или
0.1. Соответствующие уровни до­верительной
вероятности (1-а) составляют 0.99, 0.95 и 0.9.
Дове­рительный коэффициент Z_{1-
α /2}
соответствующий доверительной вероятности
(1 — α), определяется по таблице стандартного
нормаль­ного распределения. Перечисленным
уровням вероятности соответст­вуют
значения доверительного коэффициента,
равные 2.58; 1.96; 1.65. Во-вторых, стандартная
ошибка выборки Δ_ст
и диапазон изменения
случайной
ошибки выборки Δ
обратно пропорциональны √n
, сле­довательно, их можно контролировать,
увеличивая объем выборки.

Формулы
(1) и (2) применяются для оценивания ошибки
вы­борки после завершения исследования.
Однако во многих случаях необходимо до
его начала определить, какой объем
выборки при выбранном дизайне может
обеспечить необходимую точность
ре­зультатов. Желательная точность
результатов (для конкретного при­знака)
задается двумя численными величинами:
предельно допусти­мым значением
ошибки Δ_доп
и вероятностью превысить эту ошибку а.
Для простой случайной выборки из
бесконечной генеральной со­вокупности
эти две величины связаны с дисперсией
признака по ге­неральной совокупности
а²
и объемом выборки п выражением

(3)

откуда

(4)

В
этой формуле предельная ошибка выборки
Δ_доп
и вероят­ность а задаются исследователем
произвольно, а дисперсия гене­ральной
совокупности, если она неизвестна,
должна быть предварительно оценена,
например, с помощью пилотажного
исследования.

Степень точности
одной и той же выборки для разных
показа­телей может существенно
различаться. В этой сложной ситуации
мы рекомендуем ориентироваться, в первую
очередь, на достижение удовлетворительной
точности для признаков, наиболее важных
с точки зрения целей исследования.

Если генеральная
совокупность конечна, и ее объем сравним
с объемом выборки, дисперсию ошибки
выборки следует вычислять с поправкой
на объем генеральной совокупности. Она
будет равна:

где N — объем
генеральной совокупности. Следовательно,
формула для оценивания ошибки выборки
примет вид:

(2а)

а формула для
вычисления необходимого объема выборки:

(4a)

Приведенные выше
формулы справедливы для простой
слу­чайной выборки. При более сложном
дизайне применяются более сложные
оценки дисперсии выборочной ошибки и
необходимого объема выборки. С этими
вопросами можно познакомиться в
специ­альной статистической литературе.

Вопросы для
самоконтроля и повторения

1. Выберете
подходящий дизайн для исследования:

а) самочувствия
национальных меньшинств;

б) проблем наркоманов;

в) рейтинга
телевизионных программ;

г) межличностных
отношений в студенческой группе.

2. а) Определите
генеральную совокупность для изучения
бытовых проблем в студенческом общежитии
вашего университета: состав,
конкретность/гипотетичность, численность,
структуру, б) Разработайте выборку для
такого исследования.

1. 3.           
   В каких единицах
   будет определяться ошибка выборки при
   иссле­довании:

а) доходов;

б)
коэффициента интеллекта IQ;

в) возраста;

г) при предсказании
результатов выборов?

4. а) Определите
ошибку выборки, если по прогнозу
ожидалось, что за кандидата в депутаты
проголосует 49 % избирателей, в то время
как реально проголосовали 51 %.

б) Можно ли с
вероятностью 0.99 утверждать, что эта
ошибка явля­ется случайной, то есть
может быть объяснена последствиями
слу­чайного отбора, если объем простой
случайной выборки составил 1600 человек,
а дисперсия равна 0.25?

в) С какой максимальной
вероятностью можно утверждать, что
ошибка выборки является случайной?

г) Какой объем
выборки понадобился бы, чтобы при той
же диспер­сии ошибка выборки с
вероятностью 0.99 не превысила 1 %?

Литература

1.
Кокрен У.
Методы выборочного исследования. М.,
1976.

2. Методы сбора
информации в социологическом исследовании:
В 2-х кн. М., 1990.

3. Ноэль Э. Массовые
опросы: введение в методику демоскопии.
М., 1978.

4. Оперативные
социологические исследования. Мн., 1997.

5. Паниотто В.И.
Качество социологической информации.
Киев, 1986.

6. Территориальная
выборка в социологических исследованиях.
М., 1980.

7. Чурилов Н.Н.
Проектирование выборочного социологического
ис­следования. Киев, 1986.

8. Шляпентох В.Э.
Проблемы репрезентативности социологической
информации (случайные и неслучайные
выборки в социологии). М., 1976.

1. 9.           
   Шэреги Ф.Э.,
   Гуцу В.Г., Папоян Г.Р. Выборка в опросах
   общест­венного мнения: учебное
   пособие. Кишинев, 1989.

Систематическая ошибка результата

компонент ошибки результата, который остается постоянным или закономерно изменяется в ходе получения результатов проверки для одного признака.

Повышай знания с онлайн-тренажером от Автор24!

1. Напиши термин
2. Выбери определение из предложенных или загрузи свое
3. Тренажер от Автор24 поможет тебе выучить термины с помощью удобных и приятных
   карточек