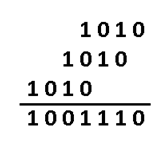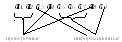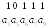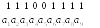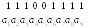Время на прочтение
6 мин
Количество просмотров 62K
Код Хэмминга – не цель этой статьи. Я лишь хочу на его примере познакомить вас с самими принципами кодирования. Но здесь не будет строгих определений, математических формулировок и т.д. Эта просто неплохой трамплин для понимания более сложных блочных кодов.
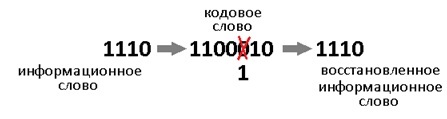
Самый, пожалуй, известный код Хэмминга (7,4). Что значат эти цифры? Вторая – число бит информационного слова — то, что мы хотим передать в целости и сохранности. А первое – размер кодового слова: информация удобренная избыточностью. Кстати термины «информационное слово» и «кодовое слово», употребляются во всех 7-ми книгах по теории помехоустойчивого кодирования, которые мне довелось бегло пролистать.
Такой код исправляет 1 ошибку. И не важно где она возникла. Избыточность несёт в себе 3 бита информации, этого достаточно, чтобы указать на одно из 7 положений ошибки или показать, что её нет. То есть ровно 8 вариантов ответов мы ждём. А 8 = 2^3, вот как всё совпало.
Чтобы получить кодовое слово, нужно информационное слово представить в виде полинома и умножить его на порождающий полином g(x). Любое число, переведя в двоичный вид, можно представить в виде полинома. Это может показаться странным и у не подготовленного читателя сразу встаёт только один вопрос «да зачем же так усложнять?». Уверяю вас, он отпадёт сам собой, когда мы получим первые результаты.
К примеру информационное слово 1010, значение каждого его разряда это коэффициент в полиноме:
Во многих книгах пишут наоборот x+x^3. Не поддавайтесь на провокацию, это вносит только путаницу, ведь в записи числа 2-ичного, 16-ричного, младшие разряды идут справа, и сдвиги мы делаем влево/вправо ориентируясь на это. А теперь давайте умножим этот полином на порождающий полином. Порождающий полином специально для Хэмминга (7,4), встречайте: g(x)=x^3+x+1. Откуда он взялся? Ну пока считайте что он дан человечеству свыше, богами (объясню позже).
Если нужно складывать коэффициенты, то делаем по модулю 2: операция сложения заменяется на логическое исключающее или (XOR), то есть x^4+x^4=0. И в конечном итоге результат перемножения как видите из 4х членов. В двоичном виде это 1001110. Итак, получили кодовое слово, которое будем передавать на сторону по зашумлённому каналу. Замете, что перемножив информационное слово (1010) на порождающий полином (1011) как обычные числа – получим другой результат 1101110. Этого нам не надо, требуется именно «полиномиальное» перемножение. Программная реализация такого умножения очень простая. Нам потребуется 2 операции XOR и 2 сдвига влево (1й из которых на один разряд, второй на два, в соответствии с g(x)=1011):
Давайте теперь специально внесём ошибку в полученное кодовое слово. Например в 3-й разряд. Получиться повреждённое слово: 1000110.
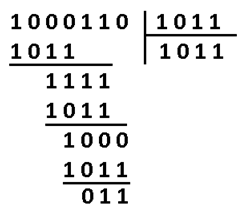
Как расшифровать сообщение и исправить ошибку? Разумеется надо «полиномиально» разделить кодовое слово на g(x). Тут я уже не буду писать иксы. Помните что вычитание по модулю 2 — это то же самое что сложение, что в свою очередь, тоже самое что исключающее или. Поехали:
В программной реализации опять же ничего сверх сложного. Делитель (1011) сдвигаем влево до самого конца на 3 разряда. И начинаем удалять (не без помощи XOR) самые левые единицы в делимом (100110), на его младшие разряды даже не смотрим. Делимое поэтапно уменьшается 100110 -> 0011110 -> 0001000 -> 0000011, когда в 4м и левее разрядах не остаётся единиц, мы останавливаемся.
Нацело разделить не получилось, значит у нас есть ошибка (ну конечно же). Результат деления в таком случае нам без надобности. Остаток от деления является синдром, его размер равен размеру избыточности, поэтому мы дописали там ноль. В данном случае содержание синдрома нам никак не помогает найти местоположение повреждения. А жаль. Но если мы возьмём любое другое информационное слово, к примеру 1100. Точно так же перемножим его на g(x), получим 1110100, внесём ошибку в тот же самый разряд 1111100. Разделим на g(x) и получим в остатке тот же самый синдром 011. И я гарантирую вам, что к такому синдрому мы придём в обще для всех кодовых слов с ошибкой в 3-м разряде. Вывод напрашивается сам собой: можно составить таблицу синдромов для всех 7 ошибок, делая каждую из них специально и считая синдром.
В результате собираем список синдромов, и то на какую болезнь он указывает:
Теперь у нас всё есть. Нашли синдром, исправили ошибку, ещё раз поделили в данном случае 1001110 на 1011 и получили в частном наше долгожданное информационное слово 1010. В остатке после исправления уже будет 000. Таблица синдромов имеет право на жизнь в случае маленьких кодов. Но для кодов, исправляющих несколько ошибок – там список синдромов разрастается как чума. Поэтому рассмотрим метод «вылавливания ошибок» не имея на руках таблицы.
Внимательный читатель заметит, что первые 3 синдрома вполне однозначно указывают на положение ошибки. Это касается только тех синдромов, где одна единица. Кол-во единиц в синдроме называют его «весом». Опять вернёмся к злосчастной ошибке в 3м разряде. Там, как вы помните был синдром 011, его вес 2, нам не повезло. Сделаем финт ушами — циклический сдвиг кодового слова вправо. Остаток от деления 0100011 / 1011 будет равен 100, это «хороший синдром», указывает что ошибка во втором разряде. Но поскольку мы сделали один сдвиг, значит и ошибка сдвинулась на 1. Вот собственно и вся хитрость. Даже в случае жуткого невезения, когда ошибка в 6м разряде, вы, обливаясь потом, после 3 мучительных делений, но всё таки находите ошибку – это победа, лишь потому, что вы не использовали таблицу синдромов.
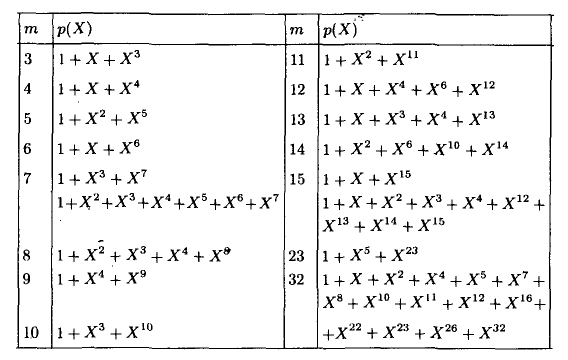
А как насчёт других кодов Хэмминга? Я бы сказал кодов Хэмминга бесконечное множество: (7,4), (15,11), (31,26),… (2^m-1, 2^m-1-m). Размер избыточности – m. Все они исправляют 1 ошибку, с ростом информационного слова растёт избыточность. Помехоустойчивость слабеет, но в случае слабых помех код весьма экономный. Ну ладно, а как мне найти порождающую функцию например для (15,11)? Резонный вопрос. Есть теорема, гласящая: порождающий многочлен циклического кода g(x) делит (x^n+1) без остатка. Где n – нашем случае размер кодового слова. Кроме того порождающий полином должен быть простым (делиться только на 1 и на самого себя без остатка), а его степень равна размеру избыточности. Можно показать, что для Хэмминга (7,4):
Этот код имеет целых 2 порождающих полинома. Не будет ошибкой использовать любой из них. Для остальных «хэммингов» используйте вот эту таблицу примитивных полиномов:
Соответственно для (15,11) порождающий многочлен g(x)=x^4+x+1. Ну а теперь переходим к десерту – к матрицам. С этого обычно начинают, но мы этим закончим. Для начала преобразую g(x) в матрицу, на которую можно умножить информационное слово, получив кодовое слово. Если g = 1011, то:
Называют её «порождающей матрицей». Дадим обозначение информационному слову d = 1010, а кодовое обозначим k, тогда:
Это довольно изящная формулировка. По быстродействию ещё быстрее, чем перемножение полиномов. Там нужно было делать сдвиги, а тут уже всё сдвинуто. Вектор d указывает нам: какие строки брать в расчёт. Самая нижняя строка матрицы – нулевая, строки нумеруются снизу вверх. Да, да, всё потому что младшие разряды располагаются справа и от этого никуда не деться. Так как d=1010, то я беру 1ю и 3ю строки, произвожу над ними операцию XOR и вуаля. Но это ещё не всё, приготовьтесь удивляться, существует ещё проверочная матрица H. Теперь перемножением вектора на матрицу мы можем получить синдром и никаких делений полиномов делать не надо.
Посмотрите на проверочную матрицу и на список синдромов, который получили выше. Это ответ на вопрос откуда берётся эта матрица. Здесь я как обычно подпортил кодовое слово в 3м разряде, и получил тот самый синдром. Поскольку сама матрица – это и есть список синдромов, то мы тут же находим положение ошибки. Но в кодах, исправляющие несколько ошибок, такой метод не прокатит. Придётся вылавливать ошибки по методу, описанному выше.
Чтобы лучше понять саму природу исправления ошибок, сгенерируем в обще все 16 кодовых слов, ведь информационное слово состоит всего из 4х бит:
Посмотрите внимательно на кодовые слова, все они, отличаются друг от друга хотя бы на 3 бита. К примеру возьмёте слово 1011000, измените в нём любой бит, скажем первый, получиться 1011010. Вы не найдёте более на него похожего слова, чем 1011000. Как видите для формирования кодового слова не обязательно производить вычисления, достаточно иметь эту таблицу в памяти, если она мала. Показанное различие в 3 бита — называется минимальное «хэммингово расстояние», оно является характеристикой блокового кода, по нему судят сколько ошибок можно исправить, а именно (d-1)/2. В более общем виде код Хэмминга можно записать так (7,4,3). Отмечу только, что Хэммингово расстояние не является разностью между размерами кодового и информационного слов. Код Голея (23,12,7) исправляет 3 ошибки. Код (48, 36, 5) использовался в сотовой связи с временным разделением каналов (стандарт IS-54). Для кодов Рида-Соломона применима та же запись, но это уже недвоичные коды.
Список используемой литературы:
1. М. Вернер. Основы кодирования (Мир программирования) — 2004
2. Р. Морелос-Сарагоса. Искусство помехоустойчивого кодирования (Мир связи) — 2006
3. Р. Блейхут. Теория и практика кодов, контролирующих ошибки — 1986
Назначение помехоустойчивого кодирования – защита информации от помех и ошибок при передаче и хранении информации. Помехоустойчивое кодирование необходимо для устранения ошибок, которые возникают в процессе передачи, хранения информации. При передачи информации по каналу связи возникают помехи, ошибки и небольшая часть информации теряется.
Без использования помехоустойчивого кодирования было бы невозможно передавать большие объемы информации (файлы), т.к. в любой системе передачи и хранении информации неизбежно возникают ошибки.
Рассмотрим пример CD диска. Там информация хранится прямо на поверхности диска, в углублениях, из-за того, что все дорожки на поверхности, часто диск хватаем пальцами, елозим по столу и из-за этого без помехоустойчивого кодирования, информацию извлечь не получится.
Использование кодирования позволяет извлекать информацию без потерь даже с поврежденного CD/DVD диска, когда какая либо область становится недоступной для считывания.
В зависимости от того, используется в системе обнаружение или исправление ошибок с помощью помехоустойчивого кода, различают следующие варианты:
- запрос повторной передачи (Automatic Repeat reQuest, ARQ): с помощью помехоустойчивого кода выполняется только обнаружение ошибок, при их наличии производится запрос на повторную передачу пакета данных;
- прямое исправление ошибок (Forward Error Correction, FEC): производится декодирование помехоустойчивого кода, т. е. исправление ошибок с его помощью.
Возможен также гибридный вариант, чтобы лишний раз не гонять информацию по каналу связи, например получили пакет информации, попробовали его исправить, и если не смогли исправить, тогда отправляется запрос на повторную передачу.
Исправление ошибок в помехоустойчивом кодировании
Любое помехоустойчивое кодирование добавляет избыточность, за счет чего и появляется возможность восстановить информацию при частичной потере данных в канале связи (носителе информации при хранении). В случае эффективного кодирования убирали избыточность, а в помехоустойчивом кодировании добавляется контролируемая избыточность.
Простейший пример – мажоритарный метод, он же многократная передача, в котором один символ передается многократно, а на приемной стороне принимается решение о том символе, количество которых больше.
Допустим есть 4 символа информации, А, B, С,D, и эту информацию повторяем несколько раз. В процессе передачи информации по каналу связи, где-то возникла ошибка. Есть три пакета (A1B1C1D1|A2B2C2D2|A3B3C3D3), которые должны нести одну и ту же информацию.
Но из картинки справа, видно, что второй символ (B1 и C1) они отличаются друг от друга, хотя должны были быть одинаковыми. То что они отличаются, говорит о том, что есть ошибка.
Необходимо найти ошибку с помощью голосования, каких символов больше, символов В или символов С? Явно символов В больше, чем символов С, соответственно принимаем решение, что передавался символ В, а символ С ошибочный.
Для исправления ошибок нужно, как минимум 3 пакета информации, для обнаружения, как минимум 2 пакета информации.
Параметры помехоустойчивого кодирования
Первый параметр, скорость кода R характеризует долю информационных («полезных») данных в сообщении и определяется выражением: R=k/n=k/m+k
- где n – количество символов закодированного сообщения (результата кодирования);
- m – количество проверочных символов, добавляемых при кодировании;
- k – количество информационных символов.
Параметры n и k часто приводят вместе с наименованием кода для его однозначной идентификации. Например, код Хэмминга (7,4) значит, что на вход кодера приходит 4 символа, на выходе 7 символов, Рида-Соломона (15, 11) и т.д.
Второй параметр, кратность обнаруживаемых ошибок – количество ошибочных символов, которые код может обнаружить.
Третий параметр, кратность исправляемых ошибок – количество ошибочных символов, которые код может исправить (обозначается буквой t).
Контроль чётности
Самый простой метод помехоустойчивого кодирования это добавление одного бита четности. Есть некое информационное сообщение, состоящее из 8 бит, добавим девятый бит.
Если нечетное количество единиц, добавляем 0.
1 0 1 0 0 1 0 0 | 0
Если четное количество единиц, добавляем 1.
1 1 0 1 0 1 0 0 | 1
Если принятый бит чётности не совпадает с рассчитанным битом чётности, то считается, что произошла ошибка.
1 1 0 0 0 1 0 0 | 1
Под кратностью понимается, всевозможные ошибки, которые можно обнаружить. В этом случае, кратность исправляемых ошибок 0, так как мы не можем исправить ошибки, а кратность обнаруживаемых 1.
Есть последовательность 0 и 1, и из этой последовательности составим прямоугольную матрицу размера 4 на 4. Затем для каждой строки и столбца посчитаем бит четности.
Прямоугольный код – код с контролем четности, позволяющий исправить одну ошибку:
И если в процессе передачи информации допустим ошибку (ошибка нолик вместо единицы, желтым цветом), начинаем делать проверку. Нашли ошибку во втором столбце, третьей строке по координатам. Чтобы исправить ошибку, просто инвертируем 1 в 0, тем самым ошибка исправляется.
Этот прямоугольный код исправляет все одно-битные ошибки, но не все двух-битные и трех-битные.
Рассчитаем скорость кода для:
- 1 1 0 0 0 1 0 0 | 1
Здесь R=8/9=0,88
- И для прямоугольного кода:
Здесь R=16/24=0,66 (картинка выше, двадцать пятую единичку (бит четности) не учитываем)
Более эффективный с точки зрения скорости является первый вариант, но зато мы не можем с помощью него исправлять ошибки, а с помощью прямоугольного кода можно. Сейчас на практике прямоугольный код не используется, но логика работы многих помехоустойчивых кодов основана именно на прямоугольном коде.
Классификация помехоустойчивых кодов
- Непрерывные — процесс кодирования и декодирования носит непрерывный характер. Сверточный код является частным случаем непрерывного кода. На вход кодера поступил один символ, соответственно, появилось несколько на выходе, т.е. на каждый входной символ формируется несколько выходных, так как добавляется избыточность.
- Блочные (Блоковые) — процесс кодирования и декодирования осуществляется по блокам. С точки зрения понимания работы, блочный код проще, разбиваем код на блоки и каждый блок кодируется в отдельности.
По используемому алфавиту:
- Двоичные. Оперируют битами.
- Не двоичные (код Рида-Соломона). Оперируют более размерными символами. Если изначально информация двоичная, нужно эти биты превратить в символы. Например, есть последовательность 110 110 010 100 и нужно их преобразовать из двоичных символов в не двоичные, берем группы по 3 бита — это будет один символ, 6, 6, 2, 4 — с этими не двоичными символами работают не двоичные помехоустойчивые коды.
Блочные коды делятся на
- Систематические — отдельно не измененные информационные символы, отдельно проверочные символы. Если на входе кодера присутствует блок из k символов, и в процессе кодирования сформировали еще какое-то количество проверочных символов и проверочные символы ставим рядом к информационным в конец или в начало. Выходной блок на выходе кодера будет состоять из информационных символов и проверочных.
- Несистематические — символы исходного сообщения в явном виде не присутствуют. На вход пришел блок k, на выходе получили блок размером n, блок на выходе кодера не будет содержать в себе исходных данных.
В случае систематических кодов, выходной блок в явном виде содержит в себе, то что пришло на вход, а в случае несистематического кода, глядя на выходной блок нельзя понять что было на входе.
Смотря на картинку выше, код 1 1 0 0 0 1 0 0 | 1 является систематическим, на вход поступило 8 бит, а на выходе кодера 9 бит, которые в явном виде содержат в себе 8 бит информационных и один проверочный.
Код Хэмминга
Код Хэмминга — наиболее известный из первых самоконтролирующихся и самокорректирующихся кодов. Позволяет устранить одну ошибку и находить двойную.
Код Хэмминга (7,4) — 4 бита на входе кодера и 7 на выходе, следовательно 3 проверочных бита. С 1 по 4 информационные биты, с 6 по 7 проверочные (см. табл. выше). Пятый проверочный бит y5, это сумма по модулю два 1-3 информационных бит. Сумма по модулю 2 это вычисление бита чётности.
Декодирование кода Хэмминга
Декодирование происходит через вычисление синдрома по выражениям:
Синдром это сложение бит по модулю два. Если синдром не нулевой, то исправление ошибки происходит по таблице декодирования:
Расстояние Хэмминга
Расстояние Хэмминга — число позиций, в которых соответствующие символы двух кодовых слов одинаковой длины различны. Если рассматривать два кодовых слова, (пример на картинке ниже, 1 0 1 1 0 0 1 и 1 0 0 1 1 0 1) видно что они отличаются друг от друга на два символа, соответственно расстояние Хэмминга равно 2.
Кратность исправляемых ошибок и обнаруживаемых, связано минимальным расстоянием Хэмминга. Любой помехоустойчивый код добавляет избыточность с целью увеличить минимальное расстояние Хэмминга. Именно минимальное расстояние Хэмминга определяет помехоустойчивость.
Помехоустойчивые коды
Современные коды более эффективны по сравнению с рассматриваемыми примерами. В таблице ниже приведены Коды Боуза-Чоудхури-Хоквингема (БЧХ)
Из таблицы видим, что там один класс кода БЧХ, но разные параметры n и k.
- n — количество символов на входе.
- k — количество символов на выходе.
- t — кратность исправляемых ошибок.
- Отношение k/n — скорость кода.
- G (энергетический выигрыш) — величина, показывающая на сколько можно уменьшить отношение сигнал/шум (Eb/No) для обеспечения заданной вероятности ошибки.
Несмотря на то, что скорость кода близка, количество исправляемых ошибок может быть разное. Количество исправляемых ошибок зависит от той избыточности, которую добавим и от размера блока. Чем больше блок, тем больше ошибок он исправляет, даже при той же самой избыточности.
Пример: помехоустойчивые коды и двоичная фазовая манипуляция (2-ФМн). На графике зависимость отношения сигнал шум (Eb/No) от вероятности ошибки. За счет применения помехоустойчивых кодов улучшается помехоустойчивость.
Из графика видим, код Хэмминга (7,4) на сколько увеличилась помехоустойчивость? Всего на пол Дб это мало, если применить код БЧХ (127, 64) выиграем порядка 4 дБ, это хороший показатель.
Компромиссы при использовании помехоустойчивых кодов
Чем расплачиваемся за помехоустойчивые коды? Добавили избыточность, соответственно эту избыточность тоже нужно передавать. Нужно: увеличивать пропускную способность канала связи, либо увеличивать длительность передачи.
Компромисс:
- Достоверность vs полоса пропускания.
- Мощность vs полоса пропускания.
- Скорость передачи данных vs полоса пропускания
Необходимость чередования (перемежения)
Все помехоустойчивые коды могут исправлять только ограниченное количество ошибок t. Однако в реальных системах связи часто возникают ситуации сгруппированных ошибок, когда в течение непродолжительного времени количество ошибок превышает t.
Например, в канале связи шумов мало, все передается хорошо, ошибки возникают редко, но вдруг возникла импульсная помеха или замирания, которые повредили на некоторое время процесс передачи, и потерялся большой кусок информации. В среднем на блок приходится одна, две ошибки, а в нашем примере потерялся целый блок, включая информационные и проверочные биты. Сможет ли помехоустойчивый код исправить такую ошибку? Эта проблема решаема за счет перемежения.
Пример блочного перемежения:
На картинке, всего 5 блоков (с 1 по 25). Код работает исправляя ошибки в рамках одного блока (если в одном блоке 1 ошибка, код его исправит, а если две то нет). В канал связи отдается информация не последовательно, а в перемешку. На выходе кодера сформировались 5 блоков и эти 5 блоков будем отдавать не по очереди а в перемешку. Записали всё по строкам, но считывать будем, чтобы отправлять в канал связи, по столбцам. Информация в блоках перемешалась. В канале связи возникла ошибка и мы потеряли большой кусок. В процессе приема, мы опять составляем таблицу, записываем по столбцам, но считываем по строкам. За счет того, что мы перемешали большое количество блоков между собой, групповая ошибка равномерно распределится по блокам.
| Binary Hamming codes | |
|---|---|

The Hamming(7,4) code (with r = 3) |
|
| Named after | Richard W. Hamming |
| Classification | |
| Type | Linear block code |
| Block length | 2r − 1 where r ≥ 2 |
| Message length | 2r − r − 1 |
| Rate | 1 − r/(2r − 1) |
| Distance | 3 |
| Alphabet size | 2 |
| Notation | [2r − 1, 2r − r − 1, 3]2-code |
| Properties | |
| perfect code | |
|
In computer science and telecommunication, Hamming codes are a family of linear error-correcting codes. Hamming codes can detect one-bit and two-bit errors, or correct one-bit errors without detection of uncorrected errors. By contrast, the simple parity code cannot correct errors, and can detect only an odd number of bits in error. Hamming codes are perfect codes, that is, they achieve the highest possible rate for codes with their block length and minimum distance of three.[1]
Richard W. Hamming invented Hamming codes in 1950 as a way of automatically correcting errors introduced by punched card readers. In his original paper, Hamming elaborated his general idea, but specifically focused on the Hamming(7,4) code which adds three parity bits to four bits of data.[2]
In mathematical terms, Hamming codes are a class of binary linear code. For each integer r ≥ 2 there is a code-word with block length n = 2r − 1 and message length k = 2r − r − 1. Hence the rate of Hamming codes is R = k / n = 1 − r / (2r − 1), which is the highest possible for codes with minimum distance of three (i.e., the minimal number of bit changes needed to go from any code word to any other code word is three) and block length 2r − 1. The parity-check matrix of a Hamming code is constructed by listing all columns of length r that are non-zero, which means that the dual code of the Hamming code is the shortened Hadamard code, also known as a Simplex code. The parity-check matrix has the property that any two columns are pairwise linearly independent.
Due to the limited redundancy that Hamming codes add to the data, they can only detect and correct errors when the error rate is low. This is the case in computer memory (usually RAM), where bit errors are extremely rare and Hamming codes are widely used, and a RAM with this correction system is a ECC RAM (ECC memory). In this context, an extended Hamming code having one extra parity bit is often used. Extended Hamming codes achieve a Hamming distance of four, which allows the decoder to distinguish between when at most one one-bit error occurs and when any two-bit errors occur. In this sense, extended Hamming codes are single-error correcting and double-error detecting, abbreviated as SECDED.
History[edit]
Richard Hamming, the inventor of Hamming codes, worked at Bell Labs in the late 1940s on the Bell Model V computer, an electromechanical relay-based machine with cycle times in seconds. Input was fed in on punched paper tape, seven-eighths of an inch wide, which had up to six holes per row. During weekdays, when errors in the relays were detected, the machine would stop and flash lights so that the operators could correct the problem. During after-hours periods and on weekends, when there were no operators, the machine simply moved on to the next job.
Hamming worked on weekends, and grew increasingly frustrated with having to restart his programs from scratch due to detected errors. In a taped interview, Hamming said, «And so I said, ‘Damn it, if the machine can detect an error, why can’t it locate the position of the error and correct it?'».[3] Over the next few years, he worked on the problem of error-correction, developing an increasingly powerful array of algorithms. In 1950, he published what is now known as Hamming code, which remains in use today in applications such as ECC memory.
Codes predating Hamming[edit]
A number of simple error-detecting codes were used before Hamming codes, but none were as effective as Hamming codes in the same overhead of space.
Parity[edit]
Parity adds a single bit that indicates whether the number of ones (bit-positions with values of one) in the preceding data was even or odd. If an odd number of bits is changed in transmission, the message will change parity and the error can be detected at this point; however, the bit that changed may have been the parity bit itself. The most common convention is that a parity value of one indicates that there is an odd number of ones in the data, and a parity value of zero indicates that there is an even number of ones. If the number of bits changed is even, the check bit will be valid and the error will not be detected.
Moreover, parity does not indicate which bit contained the error, even when it can detect it. The data must be discarded entirely and re-transmitted from scratch. On a noisy transmission medium, a successful transmission could take a long time or may never occur. However, while the quality of parity checking is poor, since it uses only a single bit, this method results in the least overhead.
Two-out-of-five code[edit]
A two-out-of-five code is an encoding scheme which uses five bits consisting of exactly three 0s and two 1s. This provides ten possible combinations, enough to represent the digits 0–9. This scheme can detect all single bit-errors, all odd numbered bit-errors and some even numbered bit-errors (for example the flipping of both 1-bits). However it still cannot correct any of these errors.
Repetition[edit]
Another code in use at the time repeated every data bit multiple times in order to ensure that it was sent correctly. For instance, if the data bit to be sent is a 1, an n = 3 repetition code will send 111. If the three bits received are not identical, an error occurred during transmission. If the channel is clean enough, most of the time only one bit will change in each triple. Therefore, 001, 010, and 100 each correspond to a 0 bit, while 110, 101, and 011 correspond to a 1 bit, with the greater quantity of digits that are the same (‘0’ or a ‘1’) indicating what the data bit should be. A code with this ability to reconstruct the original message in the presence of errors is known as an error-correcting code. This triple repetition code is a Hamming code with m = 2, since there are two parity bits, and 22 − 2 − 1 = 1 data bit.
Such codes cannot correctly repair all errors, however. In our example, if the channel flips two bits and the receiver gets 001, the system will detect the error, but conclude that the original bit is 0, which is incorrect. If we increase the size of the bit string to four, we can detect all two-bit errors but cannot correct them (the quantity of parity bits is even); at five bits, we can both detect and correct all two-bit errors, but not all three-bit errors.
Moreover, increasing the size of the parity bit string is inefficient, reducing throughput by three times in our original case, and the efficiency drops drastically as we increase the number of times each bit is duplicated in order to detect and correct more errors.
Description[edit]
If more error-correcting bits are included with a message, and if those bits can be arranged such that different incorrect bits produce different error results, then bad bits could be identified. In a seven-bit message, there are seven possible single bit errors, so three error control bits could potentially specify not only that an error occurred but also which bit caused the error.
Hamming studied the existing coding schemes, including two-of-five, and generalized their concepts. To start with, he developed a nomenclature to describe the system, including the number of data bits and error-correction bits in a block. For instance, parity includes a single bit for any data word, so assuming ASCII words with seven bits, Hamming described this as an (8,7) code, with eight bits in total, of which seven are data. The repetition example would be (3,1), following the same logic. The code rate is the second number divided by the first, for our repetition example, 1/3.
Hamming also noticed the problems with flipping two or more bits, and described this as the «distance» (it is now called the Hamming distance, after him). Parity has a distance of 2, so one bit flip can be detected but not corrected, and any two bit flips will be invisible. The (3,1) repetition has a distance of 3, as three bits need to be flipped in the same triple to obtain another code word with no visible errors. It can correct one-bit errors or it can detect — but not correct — two-bit errors. A (4,1) repetition (each bit is repeated four times) has a distance of 4, so flipping three bits can be detected, but not corrected. When three bits flip in the same group there can be situations where attempting to correct will produce the wrong code word. In general, a code with distance k can detect but not correct k − 1 errors.
Hamming was interested in two problems at once: increasing the distance as much as possible, while at the same time increasing the code rate as much as possible. During the 1940s he developed several encoding schemes that were dramatic improvements on existing codes. The key to all of his systems was to have the parity bits overlap, such that they managed to check each other as well as the data.
General algorithm[edit]
The following general algorithm generates a single-error correcting (SEC) code for any number of bits. The main idea is to choose the error-correcting bits such that the index-XOR (the XOR of all the bit positions containing a 1) is 0. We use positions 1, 10, 100, etc. (in binary) as the error-correcting bits, which guarantees it is possible to set the error-correcting bits so that the index-XOR of the whole message is 0. If the receiver receives a string with index-XOR 0, they can conclude there were no corruptions, and otherwise, the index-XOR indicates the index of the corrupted bit.
An algorithm can be deduced from the following description:
- Number the bits starting from 1: bit 1, 2, 3, 4, 5, 6, 7, etc.
- Write the bit numbers in binary: 1, 10, 11, 100, 101, 110, 111, etc.
- All bit positions that are powers of two (have a single 1 bit in the binary form of their position) are parity bits: 1, 2, 4, 8, etc. (1, 10, 100, 1000)
- All other bit positions, with two or more 1 bits in the binary form of their position, are data bits.
- Each data bit is included in a unique set of 2 or more parity bits, as determined by the binary form of its bit position.
- Parity bit 1 covers all bit positions which have the least significant bit set: bit 1 (the parity bit itself), 3, 5, 7, 9, etc.
- Parity bit 2 covers all bit positions which have the second least significant bit set: bits 2-3, 6-7, 10-11, etc.
- Parity bit 4 covers all bit positions which have the third least significant bit set: bits 4–7, 12–15, 20–23, etc.
- Parity bit 8 covers all bit positions which have the fourth least significant bit set: bits 8–15, 24–31, 40–47, etc.
- In general each parity bit covers all bits where the bitwise AND of the parity position and the bit position is non-zero.
If a byte of data to be encoded is 10011010, then the data word (using _ to represent the parity bits) would be __1_001_1010, and the code word is 011100101010.
The choice of the parity, even or odd, is irrelevant but the same choice must be used for both encoding and decoding.
This general rule can be shown visually:
-
Bit position 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 … Encoded data bits p1 p2 d1 p4 d2 d3 d4 p8 d5 d6 d7 d8 d9 d10 d11 p16 d12 d13 d14 d15 Parity
bit
coveragep1 p2 p4 p8 p16
Shown are only 20 encoded bits (5 parity, 15 data) but the pattern continues indefinitely. The key thing about Hamming Codes that can be seen from visual inspection is that any given bit is included in a unique set of parity bits. To check for errors, check all of the parity bits. The pattern of errors, called the error syndrome, identifies the bit in error. If all parity bits are correct, there is no error. Otherwise, the sum of the positions of the erroneous parity bits identifies the erroneous bit. For example, if the parity bits in positions 1, 2 and 8 indicate an error, then bit 1+2+8=11 is in error. If only one parity bit indicates an error, the parity bit itself is in error.
With m parity bits, bits from 1 up to 

| Parity bits | Total bits | Data bits | Name | Rate |
|---|---|---|---|---|
| 2 | 3 | 1 | Hamming(3,1) (Triple repetition code) |
1/3 ≈ 0.333 |
| 3 | 7 | 4 | Hamming(7,4) | 4/7 ≈ 0.571 |
| 4 | 15 | 11 | Hamming(15,11) | 11/15 ≈ 0.733 |
| 5 | 31 | 26 | Hamming(31,26) | 26/31 ≈ 0.839 |
| 6 | 63 | 57 | Hamming(63,57) | 57/63 ≈ 0.905 |
| 7 | 127 | 120 | Hamming(127,120) | 120/127 ≈ 0.945 |
| 8 | 255 | 247 | Hamming(255,247) | 247/255 ≈ 0.969 |
| 9 | 511 | 502 | Hamming(511,502) | 502/511 ≈ 0.982 |
| … | ||||
| m | 
|

|
Hamming
|

|
Hamming codes with additional parity (SECDED)[edit]
Hamming codes have a minimum distance of 3, which means that the decoder can detect and correct a single error, but it cannot distinguish a double bit error of some codeword from a single bit error of a different codeword. Thus, some double-bit errors will be incorrectly decoded as if they were single bit errors and therefore go undetected, unless no correction is attempted.
To remedy this shortcoming, Hamming codes can be extended by an extra parity bit. This way, it is possible to increase the minimum distance of the Hamming code to 4, which allows the decoder to distinguish between single bit errors and two-bit errors. Thus the decoder can detect and correct a single error and at the same time detect (but not correct) a double error.
If the decoder does not attempt to correct errors, it can reliably detect triple bit errors. If the decoder does correct errors, some triple errors will be mistaken for single errors and «corrected» to the wrong value. Error correction is therefore a trade-off between certainty (the ability to reliably detect triple bit errors) and resiliency (the ability to keep functioning in the face of single bit errors).
This extended Hamming code was popular in computer memory systems, starting with IBM 7030 Stretch in 1961,[4] where it is known as SECDED (or SEC-DED, abbreviated from single error correction, double error detection).[5] Server computers in 21st century, while typically keeping the SECDED level of protection, no longer use the Hamming’s method, relying instead on the designs with longer codewords (128 to 256 bits of data) and modified balanced parity-check trees.[4] The (72,64) Hamming code is still popular in some hardware designs, including Xilinx FPGA families.[4]
[7,4] Hamming code[edit]
In 1950, Hamming introduced the [7,4] Hamming code. It encodes four data bits into seven bits by adding three parity bits. As explained earlier, it can either detect and correct single-bit errors or it can detect (but not correct) both single and double-bit errors.
With the addition of an overall parity bit, it becomes the [8,4] extended Hamming code which is SECDED and can both detect and correct single-bit errors and detect (but not correct) double-bit errors.
Construction of G and H[edit]
The matrix

and 
This is the construction of G and H in standard (or systematic) form. Regardless of form, G and H for linear block codes must satisfy

Since [7, 4, 3] = [n, k, d] = [2m − 1, 2m − 1 − m, 3]. The parity-check matrix H of a Hamming code is constructed by listing all columns of length m that are pair-wise independent.
Thus H is a matrix whose left side is all of the nonzero n-tuples where order of the n-tuples in the columns of matrix does not matter. The right hand side is just the (n − k)-identity matrix.
So G can be obtained from H by taking the transpose of the left hand side of H with the identity k-identity matrix on the left hand side of G.
The code generator matrix 


and

Finally, these matrices can be mutated into equivalent non-systematic codes by the following operations:[6]
- Column permutations (swapping columns)
- Elementary row operations (replacing a row with a linear combination of rows)
Encoding[edit]
- Example
From the above matrix we have 2k = 24 = 16 codewords.
Let 
![{\displaystyle {\vec {a}}=[a_{1},a_{2},a_{3},a_{4}],\quad a_{i}\in \{0,1\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/898ddf319567d4af0acecf5c7fd450f5f466e28b)



For example, let ![{\displaystyle {\vec {a}}=[1,0,1,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e838e2ec81e9fe6223596b61f747b195d3d338fb)


[8,4] Hamming code with an additional parity bit[edit]
The [7,4] Hamming code can easily be extended to an [8,4] code by adding an extra parity bit on top of the (7,4) encoded word (see Hamming(7,4)).
This can be summed up with the revised matrices:
and
Note that H is not in standard form. To obtain G, elementary row operations can be used to obtain an equivalent matrix to H in systematic form:
For example, the first row in this matrix is the sum of the second and third rows of H in non-systematic form. Using the systematic construction for Hamming codes from above, the matrix A is apparent and the systematic form of G is written as
The non-systematic form of G can be row reduced (using elementary row operations) to match this matrix.
The addition of the fourth row effectively computes the sum of all the codeword bits (data and parity) as the fourth parity bit.
For example, 1011 is encoded (using the non-systematic form of G at the start of this section) into 01100110 where blue digits are data; red digits are parity bits from the [7,4] Hamming code; and the green digit is the parity bit added by the [8,4] code.
The green digit makes the parity of the [7,4] codewords even.
Finally, it can be shown that the minimum distance has increased from 3, in the [7,4] code, to 4 in the [8,4] code. Therefore, the code can be defined as [8,4] Hamming code.
To decode the [8,4] Hamming code, first check the parity bit. If the parity bit indicates an error, single error correction (the [7,4] Hamming code) will indicate the error location, with «no error» indicating the parity bit. If the parity bit is correct, then single error correction will indicate the (bitwise) exclusive-or of two error locations. If the locations are equal («no error») then a double bit error either has not occurred, or has cancelled itself out. Otherwise, a double bit error has occurred.
See also[edit]
- Coding theory
- Golay code
- Reed–Muller code
- Reed–Solomon error correction
- Turbo code
- Low-density parity-check code
- Hamming bound
- Hamming distance
Notes[edit]
- ^ See Lemma 12 of
- ^ Hamming (1950), pp. 153–154.
- ^ Thompson, Thomas M. (1983), From Error-Correcting Codes through Sphere Packings to Simple Groups, The Carus Mathematical Monographs (#21), Mathematical Association of America, pp. 16–17, ISBN 0-88385-023-0
- ^ a b c Kythe & Kythe 2017, p. 115.
- ^ Kythe & Kythe 2017, p. 95.
- ^ a b Moon T. Error correction coding: Mathematical Methods and
Algorithms. John Wiley and Sons, 2005.(Cap. 3) ISBN 978-0-471-64800-0
References[edit]
- Hamming, Richard Wesley (1950). «Error detecting and error correcting codes» (PDF). Bell System Technical Journal. 29 (2): 147–160. doi:10.1002/j.1538-7305.1950.tb00463.x. S2CID 61141773. Archived (PDF) from the original on 2022-10-09.
- Moon, Todd K. (2005). Error Correction Coding. New Jersey: John Wiley & Sons. ISBN 978-0-471-64800-0.
- MacKay, David J.C. (September 2003). Information Theory, Inference and Learning Algorithms. Cambridge: Cambridge University Press. ISBN 0-521-64298-1.
- D.K. Bhattacharryya, S. Nandi. «An efficient class of SEC-DED-AUED codes». 1997 International Symposium on Parallel Architectures, Algorithms and Networks (ISPAN ’97). pp. 410–415. doi:10.1109/ISPAN.1997.645128.
- «Mathematical Challenge April 2013 Error-correcting codes» (PDF). swissQuant Group Leadership Team. April 2013. Archived (PDF) from the original on 2017-09-12.
- Kythe, Dave K.; Kythe, Prem K. (28 July 2017). «Extended Hamming Codes». Algebraic and Stochastic Coding Theory. CRC Press. pp. 95–116. ISBN 978-1-351-83245-8.
External links[edit]
- Visual Explanation of Hamming Codes
- CGI script for calculating Hamming distances (from R. Tervo, UNB, Canada)
- Tool for calculating Hamming code
Код Хэмминга
является разновидностью линейных кодов
и позволяет не только обнаруживать, но
и исправлять ошибки. В коде Хэмминга
вводится понятие кодового расстояния–
это степень различия кодовых комбинаций
. Кодовое расстояние для двух любых
кодовых комбинаций определяется числом
несовпадающих в них разрядов. Наименьшее
кодовое расстояние называется минимальным
кодовым расстоянием
(
расстояние Хэмминга ).
К кодам Хэмминга
обычно относятся коды с
=3,
исправляющие все одиночные ошибки и
коды с=4,
исправляющие все одиночные и обнаруживающие
все двойные ошибки. Для исправления
всех одиночных ошибок число синдромов
должно бытьn+1
( n
– число разрядов ). Из них n
синдромов используются для указания
местоположения ошибки, а один – нулевой,
соответствует их отсутствию. Следовательно,
.n=m+k,
где m
–информационные разряды, к –проверочные.
Д
проверочных разрядов выбираются
комбинации, где присутствует одна «1»,
остальные будут информационными.
Сгруппируем в
первую сумму все элементы, номера которых
имеют значение «1» в 1-м младшем разряде
двоичного числа. Во вторую сумму
сгруппируем элементы, номера которых
имеют значение «1» во втором разряде
двоичного числа и т.д. для третьей и
четвертой сумм.
Проверочные биты
входят
только в одну сумму. Такой выбор позволяет
находить ошибочно принятые информационные
элементы и исправлять одиночные ошибки.
Полная кодовая
комбинация передаваемая в линию будет
иметь вид:
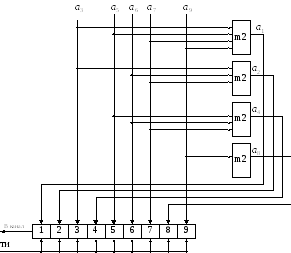
Порядок кодирования
кодом Хэмминга в устройстве защиты от
ошибок передатчика:
1. от источника
принимается 5-ти элементная кодовая
комбинация и ее разряды записываются
в отведенных для них местах 3,5,6,7 и 9.
2. Суммированием
по модулю 2 определяются проверочные
разряды. Их значения должны быть такими,
чтобы сумма, в которую входит данный
проверочный разряд, равнялась «0».
Другими словами, каждый проверочный
разряд должен дополнить свою сумму до
четного количества единиц.
3. Полученные
проверочные элементы размещаются на
отведенных для них местах 1,2,4 и 8 в полной
кодовой комбинации.
4. Сформированная
таким образом кодовая комбинация
передается в канал.
Рассмотрим пример:
Источник выдает информационные элементы
Тогда полная
кодовая комбинация, которая будет
передаваться в канал, имеет вид:
Порядок декодирования
на приеме в устройстве защиты от ошибок.
1. Подсчитываем 4
суммы
в
каждую из которых входят информационные
разряды и по одному проверочному.
2. Производится
анализ полученных сумм, при этом возможны
три случая:
а) проверочное
число, состоящее из результатов
суммирований равно 0000, что свидетельствует
об отсутствии ошибок.
б) проверочное
число отличается от значения 0000, причем
по его значению можно определить номер
ошибочного разряда.
в) проверочное
число отличается от значения 0000, но
определить место ошибки невозможно.
3. В зависимости
от результатов анализа:
а) информация
выдается потребителю;
б) ошибки исправляются
и информация выдается потребителю;
в) принятая
комбинация стирается и в устройстве
защиты от ошибок вырабатывается сигнал
«ошибка».
Принята комбинация:
Все «0», значит
комбинация принята верно.
Д
что произошло искажение в третьем
элементе и вместо 1 принят 0. Тогда
принятая комбинация имеет вид:
В данном случае
синдром равен 0011, что соответствует
ошибке в 3 элементе кодовой комбинации.
Для устранения данной ошибки необходимо
изменить находящийся в этом элементе
символ на обратный.
Схема кодера.
Схема декодера.
Декодер путем
сложения по модулю 2 от схемы «И» и от
информационного разряда позволяет
исправить ошибку, возникшую в процессе
передачи.
Код Хэмминга имеет
существенный недостаток: при
обнаружении любого числа ошибок он
исправляет лишь одиночные ошибки.
Избыточность семиэлементного кода
Хэмминга равна 0,43. При
увеличении значности кодовых
комбинаций увеличивается число
проверок, но уменьшается избыточность
кода. К тому же код Хэмминга не
позволяет обнаружить групповые ошибки, сконцентрированные
в пакетах. Длина пакета ошибок представляет
собой увеличенную на единицу разность
между именами старшего и младшего
ошибочных элементов.
Соседние файлы в папке Будылдина2
- #
11.04.20152.54 Mб24ДКР рисунок Mumarev.vsd
- #
11.04.20152.49 Mб30ДКР рисунок.vsd
- #
- #
- #
- #
Содержание
Раздел разработан в 2010 г. при поддержке компании RAIDIX
Для понимания материалов настоящего раздела крайне желательно ознакомиться с разделом КОДИРОВАНИЕ
.
Код Хэмминга
Будем рассматривать двоичные коды, т.е. упорядоченные наборы (строки) $ (x_1,\dots,x_{n}) $ из $ n_{} $ чисел $ \{x_1,\dots,x_n\}\subset \{0,1\} $. Множество таких наборов, рассматриваемое вместе с операцией умножения на константы $ 0_{} $ или $ 1_{} $ и операцией поразрядного сложения по модулю $ 2_{} $:
$$ (x_1,\dots,x_n)\oplus (y_1,\dots,y_n)=(x_1\oplus y_1 ,\dots,x_n\oplus y_n ) =
$$
$$ = (x_1+y_1 \pmod{2},\dots,x_n+y_n \pmod{2}) $$
образует линейное пространство, которое мы будем обозначать $ \mathbb V^n $, а собственно составляющие его наборы будем называть векторами; причем, для определенности, именно векторами-строками. Это пространство состоит из конечного числа векторов: $ \operatorname{Card} (\mathbb V^n)=2^n $.
Расстояние Хэмминга
Расстоянием Хэмминга между двумя векторами $ B=(b_1,\dots,b_n) $ и $ C=(c_1,\dots,c_n) $ из $ \mathbb V^n $ называется число разрядов, в которых эти слова отличаются друг от друга; будем обозначать его $ \rho(B,C) $.
?
Доказать, что
$$ \rho(B,C)= \displaystyle \sum_{j=1}^n \left[ (1-b_j)c_j+ (1-c_j)b_j \right] \, .$$
Весом Хэмминга вектора $ B=(b_1,\dots,b_n) $ называется число его отличных от нуля координат, будем обозначать его $ w(B) $. Таким образом1)
$$ w(B)= b_1+\dots+b_n, \qquad \rho(B,C)=|b_1-c_1|+\dots+ |b_n-c_n|=w(B-C) \ . $$
Расстояние Хэмминга является метрикой в пространстве $ \mathbb V^n $, т.е. для любых векторов $ \{X_1,X_2,X_3\} \subset \mathbb V^n $ выполняются свойства
1.
$ \rho(X_1,X_2) \ge 0 $, и $ \rho(X_1,X_2) = 0 $ тогда и только тогда, когда $ X_1=X_2 $;
2.
$ \rho(X_1,X_2) = \rho(X_2,X_1) $;
3.
$ \rho(X_1,X_3)\le \rho(X_1,X_2)+ \rho(X_2,X_3) $ («неравенство треугольника»).
Пусть теперь во множестве $ \mathbb V^n $ выбирается произвольное подмножество $ \mathbb U $, содержащее $ s_{} $ векторов: $ \mathbb U=\{ U_1,\dots,U_s \} $. Будем считать эти векторы кодовыми словами, т.е. на вход канала связи будем подавать исключительно только эти векторы; само множество $ \mathbb U $ будем называть кодом. По прохождении канала связи эти векторы могут зашумляться ошибками. Каждый полученный на выходе вектор будем декодировать в ближайшее (в смысле расстояния Хэмминга) кодовое слово множества $ \mathbb U $. Таким образом, «хорошим» кодом — в смысле исправления максимального числа ошибок — может считаться код $ \mathbb U $, для которого кодовые слова далеко отстоят друг от друга. С другой стороны, количество кодовых слов $ s_{} $ должно быть достаточно велико, чтобы делать использование кода осмысленным; во всяком случае, будем всегда считать $ s>1 $.
Минимальное расстояние между различными кодовыми словами кода $ \mathbb U $, т.е.
$$ d=\min_{\{j,k\}\subset \{1,\dots,s \} \atop j\ne k} \rho (U_j,U_k) $$
называется кодовым расстоянием кода $ \mathbb U $; будем иногда также писать $ d(\mathbb U) $.
Т
Теорема. Код $ \mathbb U $ с кодовым расстоянием $ d_{} $
a) способен обнаружить от $ 1_{} $ до $ d-1 $ (но не более) ошибок;
б) способен исправить от $ 1_{} $ до $ \left\lfloor \displaystyle \frac{d-1}{2} \right\rfloor $ (но не более) ошибок. Здесь $ \lfloor \ \ \ \rfloor $ — целая часть числа.
Доказательство. Если $ U_1 $ — переданное кодовое слово, а $ V_{} $ — полученный на выходе с канала вектор с $ \tau_{} $ ошибками, то $ \rho(U_1,V)=\tau $. Мы не сможем обнаружить ошибку если $ V_{1} $ совпадет с каким-то другим кодовым словом $ U_2 $, т.е. при условии $ \rho(U_2,V)=0 $. Оценим
$ \rho(U_2,V) $ при условии, что $ \tau \le d-1 $. По неравенству треугольника
3
получаем
$$ \rho(U_2,V) \ge \rho(U_1,U_2)-\rho(U_1,V) \ge d-\tau \ge 1>0 \ . $$
Для доказательства части б) предположим, что $ 2\,\tau \le d-1 $. Тогда те же рассуждения приведут к заключению
$$ \rho(U_2,V) \ge d-\tau \ge (2\,\tau+1)-t > \tau = \rho(U_1,V) \ , $$
т.е. вектор $ V_{} $ ближе к $ U_1 $, чем к любому другому кодовому слову.
♦
П
Пример. Код Адамара строится на основании матрицы Адамара — квадратной матрицы, элементами которой являются только числа $ \{+1,-1\} $; при этом ее строки (как, впрочем, и столбцы) попарно ортогональны. Так, матрица Адамара порядка $ 8_{} $ —
$$
H=\left(
\begin{array}{rrrrrrrr}
1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 \\
-1 & 1 &-1 & 1 & -1 & 1 &-1 & 1\\
1 & 1 & -1 & -1 & 1 & 1 & -1 & -1 \\
-1 & 1 & 1 & -1 & -1 & 1 & 1 & -1 \\
1 & 1 & 1 & 1 & -1 & -1 & -1 & -1 \\
-1 & 1 &-1 & 1 & 1 & -1 &1 & -1\\
1 & 1 & -1 & -1 & -1 & -1 & 1 & 1 \\
-1 & 1 & 1 & -1 & 1 & -1 & -1 & 1
\end{array}
\right) \ .
$$
Код строится следующим образом. Берутся строки матрицы $ H_{} $ и умножаются на $ +1 $ и на $ -1 $; в каждой строке множества
$$ H^{[1]},H^{[2]},\dots,H^{[8]},-H^{[1]},-H^{[2]},\dots,-H^{[8]} $$
производится замена $ +1 \to 0, -1 \to 1 $. Получаются $ 16 $ векторов
$$
(00000000),\ (10101010),\ (00110011),\ (10011001),\ (00001111),\ (10100101),\ (00111100),\
(10010110),
$$
$$
(11111111),\ (01010101), (11001100),\ (01100110),\ (11110000),\ (01011010),\ (11000011),\
(01101001),
$$
которые обозначим $ U_1,\dots,U_8,U_{-1},\dots,U_{-8} $.
Поскольку строки $ \pm H^{[j]} $ и $ \pm H^{[k]} $ ортогональны при $ j\ne k_{} $ и состоят только из чисел $ \pm 1 $, то ровно в половине своих элементов они должны совпадать, а в половине — быть противоположными. Соответствующие им векторы $ U_{} $ будут совпадать в половине своих компонент и различаться в оставшихся. Таким образом
$$ \rho( U_{\pm j}, U_{\pm k}) = 4 \quad npu \quad j\ne k, \ \rho( U_{j}, U_{-j}) = 8 , $$
и кодовое расстояние равно $ 4_{} $. В соответствии с теоремой, этот код способен обнаружить до трех ошибок, но исправить только одну. Так, к примеру, если при передаче по каналу связи слова $ U_8=(00111100) $ возникает только одна ошибка и на выходе получаем $ V_8= (00111101) $, то $ \rho(U_8,V_8)=1 $, в то время как $ \rho(U_j,V_8)\ge 3 $ для других кодовых слов. Если же количество ошибок возрастет до двух —
$ \tilde V_8= (00111111) $, — то $ \rho(U_8,\tilde V_8)=2 $, но при этом также $ \rho(U_9,\tilde V_8)=2 $. Ошибка обнаружена, но однозначное декодирование невозможно.
♦
Т
Теорема. Если существует матрица Адамара порядка $ n_{}>2 $, то
а) $ n_{} $ кратно $ 4_{} $, и
б) существует код $ \mathbb U \subset \mathbb V^n $, состоящий из $ 2\,n $ кодовых слов, для которого кодовое расстояние $ d=n/2 $.
Проблема построения кодов Адамара заключается в том, что существование матриц Адамара произвольного порядка $ n_{} $ кратного $ 4_{} $ составляет содержание не доказанной2) гипотезы Адамара. Хотя для многих частных случаев $ n_{} $ (например, для $ n=2^m, m \in \mathbb N $, см.
☞
ЗДЕСЬ ) матрицы Адамара построены.
Т
Теорема. Если код $ \mathbb U \subset \mathbb V^n $ может исправлять самое большее $ m_{} $ ошибок, то количество $ s_{} $ его слов должно удовлетворять следующему неравенству
$$ s \le \frac{2^n}{C_n^0+C_n^1+\dots+C_n^m} \ , $$
где $ C_n^{j} $ означает биномиальный коэффициент.
Число в правой части неравенства называется верхней границей Хэмминга для числа кодовых слов.
Доказательство. Для простоты предположим, что одно из кодовых слов кода $ \mathbb U $ совпадает с нулевым вектором: $ U_1=\mathbb O_{1\times n} $. Все векторы пространства $ \mathbb V_n $, отстоящие от $ U_1 $ на расстояние $ 1_{} $ заключаются во множестве
$$ (100\dots 0),\ (010 \dots 0),\ \dots,\ (000 \dots 1) ; $$
их как раз $ n=C_n^1 $ штук. Векторы из $ \mathbb V^n $, отстоящие от $ \mathbb O_{} $ на расстояние $ 2_{} $ получаются в ходе расстановки двух цифр $ 1_{} $ в произвольных местах нулевого вектора. Нахождение количества способов такой расстановки относится к задачам комбинаторики, и решение этой задачи можно найти
☞
ЗДЕСЬ. Оно равно как раз $ C_n^{2}=n(n-1)/2 $. Аналогичная задача расстановки $ j_{} $ единиц в $ n_{} $-векторе имеет решением число $ C_n^j $.
Таким образом общее количество векторов, отстоящих от $ \mathbb O_{} $ на расстояние $ \le m_{} $
равно $ C_n^1+\dots+C_n^m $.
Вместе в самим $ \mathbb O_{} $-вектором получаем как раз число из знаменателя границы Хэмминга.
Предыдущие рассуждения будут справедливы и для любого другого кодового слова из $ \mathbb U $ — каждое из них можно «окружить $ m_{} $-окрестностью» и каждая из этих окрестностей будет содержать
$$ 1+C_n^1+\dots+C_n^m $$
векторов из $ \mathbb V^n $. По предположению теоремы, эти окрестности не должны пересекаться. Но тогда общее количество векторов $ \mathbb V^n $, попавших в эти окрестности (для всех $ s_{} $ кодовых слов) не должно превышать количества векторов в $ \mathbb V^n $, т.е. $ 2^{n} $.
♦
?
Доказать, что если $ n_{} $ — нечетно, а $ m=\lfloor n/2 \rfloor=(n-1)/2 $ то верхняя граница Хэмминга равна в точности $ 2_{} $.
П
Пример. Для $ n=10 $ имеем
| $ m_{} $ | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| $ s\le $ | 93 | 18 | 5 | 2 | 1 |
Чем больше ошибок хотим скорректировать (при фиксированном числе $ n_{} $ разрядов кодовых слов) — тем меньше множество кодовых слов.
Коды, для которых верхняя граница Хэмминга достигается, называются совершенными.
Линейные коды
Идея, лежащая в основе этих кодов достаточно проста: это — обобщение понятия контрольной суммы. Если вектор $ (x_1,\dots,x_k) \in \mathbb V^k $ содержит информационные биты, которые требуется передать, то для контроля целостности при передаче их по каналу присоединим к этому вектору еще один «служебный» бит с вычисленным значением
$$ x_{k+1}=x_1+\dots+x_k \pmod{2} \ . $$
Очевидно, $ x_{k+1}=1 $ если среди информационных битов содержится нечетное число единиц, и $ x_{k+1}=0 $ в противном случае. Поэтому этот бит называют битом четности. Кодовым словом становится вектор
$$ X=(x_1,\dots,x_k,x_{k+1}) \in \mathbb V^{k+1} \ . $$
По прохождении его по каналу, для полученного вектора $ Y=(y_1,\dots,y_k,y_{k+1}) $ производится проверка условия
$$ y_{k+1} = y_1+\dots+y_k \pmod{2} \ . $$
Если оно не выполнено, то при передаче произошла ошибка. Если же сравнение оказывается справедливым, то это еще не значит, что ошибки при передаче нет — поскольку комбинация из двух (или любого четного числа) ошибок не изменит бита четности.
Для более вероятного обнаружения ошибки вычислим несколько контрольных сумм — выбирая различные разряды информационного вектора $ (x_1,\dots,x_k) $:
$$
\begin{array}{lclcll}
x_{k+1}&=&x_{i_1}+&\dots&+x_{i_s} \pmod{2}, \\
x_{k+2}&=&x_{j_1}+&\dots&+x_{j_t} \pmod{2}, \\
\vdots & & \vdots \\
x_n &=&x_{\ell_1}+& \dots & +x_{\ell_w} \pmod{2}.
\end{array}
$$
Полученные биты присоединим к информационному блоку. Кодовым словом будет вектор
$$ X=(x_1,\dots,x_k,x_{k+1},\dots,x_n) \in \mathbb V^n \ , $$
который и поступает в канал связи. По прохождении его по каналу, для соответствующих разрядов полученного вектора $ Y_{} $ проверяется выполнимость контрольных сравнений. Если все они выполняются, то ошибка передачи считается невыявленной.
На первый взгляд кажется, что при увеличении количества контрольных сумм увеличивается и вероятность обнаружения ошибки передачи. Однако с увеличением количества разрядов кодового слова увеличивается и вероятность появления этой ошибки.
П
Пример. Если вероятность ошибочной передачи одного бита по каналу равна $ P_1=0.1 $, то вероятность появления хотя бы одной ошибки при передаче $ k_{} $ битов равна $ P_k= 1-(0.9)^k $, т.е.
| $ k $ | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| $ P_k $ | 0.1 | 0.19 | 0.271 | 0.344 | 0.410 | 0.469 | 0.522 | 0.570 | 0.613 | 0.651 |
♦
Обычно, количество проверочных соотношений берется меньшим (и даже много меньшим) количества информационных битов3). Осталось только понять как составлять эти проверочные соотношения так, чтобы они смогли реагировать на ошибки передачи по каналу связи.
Сначала формализуем предложенную выше идею. В пространстве $ \mathbb V^n $ выделим некоторое подпространство $ \mathbb V^n_{[k]} $, состоящее из векторов
$$ (x_1,\dots,x_k,x_{k+1},\dots,x_n) \ , $$
первые $ k_{} $ компонентов которых считаются произвольными, а оставшиеся $ n-k_{} $ полностью определяются первыми посредством заданных линейных соотношений:
$$ \begin{array}{lclcll}
x_{k+1}&=&h_{k+1,1}x_1+&\dots&+h_{k+1,k}x_k \pmod{2} \\
\vdots & & \vdots \\
x_n &=&h_{n1}x_1+& \dots & +h_{nk}x_k \pmod{2}
\end{array} \qquad npu \qquad \{h_{j\ell}\} \subset \{0,1\} \ .
$$
Кодовые слова выбираются именно из подпространства $ \mathbb V^n_{[k]} $, их количество равно $ \operatorname{Card} (\mathbb V^n_{[k]} )=2^k $. При этом начальная часть каждого кодового слова, т.е. вектор $ (x_1,\dots,x_k) $, заключает информацию, которую нужно передать — эти разряды называются информационными. Остальные разряды кодового слова, т.е. биты вектора $ (x_{k+1},\dots,x_n) $, которые вычисляются с помощью выписанных линейных соотношений, являются служебными — они называются проверочными и предназначены для контроля целостности передачи информационных разрядов по каналу связи (и/или коррекции ошибок). Код такого типа называется линейным (n,k)-кодом.
В дальнейшем будем экономить на обозначениях: знак операции $ +_{} $ будет означать суммирование по модулю $ 2_{} $.
П
Пример. Пусть $ n=5, k=3 $. Пусть проверочные биты связаны с информационными соотношениями
$$ x_4=x_1 + x_2,\ x_5=x_1 + x_3 \ . $$
Тогда $ \mathbb V^5_{[3]} $ состоит из векторов
$$ (00000),\ (10011),\ (01010),\ (00101),\ (11001),\ (10110),\ (01111),\ (11100) \ . $$
♦
Для описания пространства $ \mathbb V^n_{[k]} $ привлечем аппарат теории матриц. С одной стороны, в этом подпространстве можно выбрать базис — систему из $ k_{} $ линейно независимых векторов: обозначим их $ \{X_1,\dots,X_k\} $. Матрица, составленная из этих векторов-строк,
$$
\mathbf G=\left( \begin{array}{c} X_1 \\ \vdots \\ X_k \end{array} \right)_{k\times n}
$$
называется порождающей матрицей кода. Так, в только что приведенном примере в качестве порождающей матрицы может быть выбрана
$$
\mathbf G=
\left( \begin{array}{ccccc}
1 & 0 & 0 & 1 & 1 \\
0 & 1 & 0 & 1 & 0 \\
0 & 0 & 1 & 0 &1
\end{array}
\right) \qquad \mbox{ или } \qquad
\mathbf G=
\left( \begin{array}{ccccc}
1 & 0 & 0 & 1 & 1 \\
1 & 1 & 0 & 0 & 1 \\
1 & 1 & 1 & 0 & 0
\end{array}
\right) \ .
$$
Любая строка $ X_{} $ кода может быть получена как линейная комбинация строк порождающей матрицы:
$$ X=\alpha_1 X_1+\alpha_2X_2+\dots+\alpha_k X_k \quad npu \quad \{\alpha_1,\dots,\alpha_k\} \subset \{0,1\} . $$
Можно переписать это равенство с использованием операции матричного умножения:
$$ X=(\alpha_1,\dots,\alpha_k) \mathbf G \ . $$
Так, продолжая рассмотрение предыдущего примера:
$$
(x_1,x_2,x_3,x_4,x_5)=(x_1,x_2,x_3)
\left( \begin{array}{ccccc}
1 & 0 & 0 & 1 & 1 \\
0 & 1 & 0 & 1 & 0 \\
0 & 0 & 1 & 0 &1
\end{array}
\right)=
$$
$$
=(x_1+x_2,x_2+x_3,x_3)
\left( \begin{array}{ccccc}
1 & 0 & 0 & 1 & 1 \\
1 & 1 & 0 & 0 & 1 \\
1 & 1 & 1 & 0 & 0
\end{array}
\right) \pmod{2} \ .
$$
С другой стороны, для описания $ \mathbb V^n_{[k]} $ имеются проверочные соотношения. Объединяя их в систему линейных уравнений, перепишем их с использованием матричного формализма:
$$
(x_1,\dots,x_k,x_{k+1},\dots,x_n) \cdot
\left(\begin{array}{cccc}
h_{k+1,1} & h_{k+2,1} & \dots &h_{n1} \\
h_{k+1,2} & h_{k+2,2} & \dots & h_{n2} \\
\vdots & & & \vdots \\
h_{k+1,k} & h_{k+2,k} & \dots & h_{nk} \\
-1 & 0 & \dots & 0 \\
0 & -1 & \dots & 0 \\
\vdots & & \ddots & \vdots \\
0 & 0 & \dots & -1
\end{array}
\right)= (0,0,\dots,0)_{1\times (n-k)}
$$
или, в альтернативном виде, с использованием транспонирования4):
$$
\underbrace{\left(\begin{array}{llclcccc}
h_{k+1,1} & h_{k+1,2} & \dots &h_{k+1,k} & 1 & 0 & \dots & 0 \\
h_{k+2,1} & h_{k+2,2} & \dots & h_{k+2,k}& 0 & 1 & \dots & 0 \\
\vdots & & & \vdots & \dots & & \ddots & \vdots \\
h_{n1} & h_{n2} & \dots & h_{nk} & 0 & 0 & \dots & 1 \\
\end{array}
\right)}_{\mathbf H}\left( \begin{array}{c} x_1 \\ x_2 \\ \vdots \\ x_n \end{array} \right)
=\left( \begin{array}{c} 0 \\ 0 \\ \vdots \\ 0 \end{array} \right)_{(n-k)\times 1}
$$
Матрица $ \mathbf H_{} $ порядка $ (n-k)\times n $ называется проверочной матрицей кода5). Хотя вторая форма записи (когда вектор-столбец неизвестных стоит справа от матрицы) более привычна для линейной алгебры, в теории кодирования чаще используется именно первая — с вектором-строкой $ X_{} $ слева от матрицы:
$$ X\cdot \mathbf H^{\top} = \mathbb O_{1\times k} \ . $$
Для приведенного выше примера проверочные соотношения переписываются в виде
$$ x_1 + x_2 +x_4=0,\ x_1 + x_3 + x_5=0 \ $$
и, следовательно, проверочная матрица:
$$ \mathbf H=
\left( \begin{array}{ccccc}
1 & 1 & 0 & 1 & 0 \\
1 & 0 & 1 & 0 & 1
\end{array}
\right) \ .
$$
Т
Теорема 1. Имеет место матричное равенство
$$ \mathbf G \cdot \mathbf H^{\top} = \mathbb O_{k\times (n-k)} \ .$$
Доказательство. Каждая строка матрицы $ \mathbf G $ — это кодовое слово $ X_{j} $ , которое, по предположению, должно удовлетворять проверочным соотношениям $ X_j \cdot \mathbf H^{\top} = \mathbb O_{1\times k} $. Равенство из теоремы — это объединение всех таких соотношений в матричной форме. Фактически, порождающая матрица $ \mathbf G $ состоит из строк, составляющих фундаментальную систему решений системы уравнений $ X \mathbf H^{\top}= \mathbb O $.
♦
=>
Если проверочная матрица имеет вид $ \mathbf H=\left[ P^{\top} \mid E_{n-k} \right] $,
где $ E_{n-k} $ — единичная матрица порядка $ n — k_{} $, $ P_{} $ — некоторая матрица порядка $ k \times (n-k) $, а $ \mid_{} $ означает операцию конкатенации, то порождающая матрица может быть выбрана в виде $ \mathbf G = \left[ E_k \mid P \right] $.
Доказательство следует из предыдущей теоремы, правила умножения блочных матриц —
$$ \mathbf G \cdot \mathbf H^{\top} = E_k \cdot P + P \cdot E_{n-k} = 2P \equiv \mathbb O_{k\times (n-k)} \pmod{2} \ , $$
и того факта, что строки матрицы $ \mathbf G $ линейно независимы. Последнее обстоятельство обеспечивается структурой этой матрицы: первые $ k_{} $ ее столбцов являются столбцами единичной матрицы. Любая комбинация
$$ \alpha_1 \mathbf G^{[1]}+\dots+\alpha_k \mathbf G^{[k]} $$
строк матрицы дает строку $ (\alpha_1,\dots,\alpha_k,\dots ) $ и для обращения ее в нулевую необходимо, чтобы $ \alpha_1=0,\dots,\alpha_k=0 $.
♦
Видим, что по структуре матрицы $ \mathbf G $ и $ \mathbf H $ очень похожи друг на друга. Задав одну из них, однозначно определяем другую. В одном из следующих пунктов, мы воспользуемся этим обстоятельством — для целей исправления ошибок оказывается выгоднее сначала задавать $ \mathbf H $.
Т
Теорема 2. Кодовое расстояние линейного подпространства $ \mathbb V^{n}_{[k]} $ равно минимальному весу его ненулевых кодовых слов:
$$ d( \mathbb V^{n}_{[k]})= \min_{ U \in \mathbb V^{n}_{[k]} \atop U \ne \mathbb O } w(U) \ . $$
Доказательство. Линейное подпространство замкнуто относительно операции сложения (вычитания) векторов. Поэтому если $ \{U_1,U_2\}\subset \mathbb V^{n}_{[k]} $, то и $ U_1-U_2 \in \mathbb V^{n}_{[k]} $, а также $ \mathbb O \in V^{n}_{[k]} $. Тогда
$$ \rho(U_1,U_2)=\rho(U_1-U_2, \mathbb O)= w(U_1-U_2) \ . $$
♦
Кодовое расстояние дает третью характеристику линейного кода — теперь он описывается набором чисел $ (n,k,d) $.
Т
Теорема 3. Пусть $ d_{} $ означает кодовое расстояние кода $ \mathbb V^{n}_{[k]} $ с проверочной матрицей $ \mathbf H $. Тогда любое подмножество из $ \ell_{} $ столбцов этой матрицы будет линейно независимо при $ \ell < d $. Обратно, если любое подмножество из $ \ell_{} $ столбцов матрицы $ \mathbf H $ линейно независимо, то $ d > \ell $.
Доказательство. Если $ d_{} $ — кодовое расстояние, то, в соответствии с теоремой 2, ни одно ненулевое кодовое слово $ X\in \mathbb V^{n}_{[k]} $ не должно иметь вес, меньший $ d_{} $. Если предположить,
что столбцы $ \{\mathbf H_{[i_1]},\dots,\mathbf H_{[i_{\ell}]}\} $ линейно зависимы при $ \ell< d $, то
существуют числа $ x_{i_1},\dots,x_{i_{\ell}} $ не все равные нулю, такие что
$$ x_{i_1}\mathbf H_{[i_1]}+\dots+x_{i_{\ell}} H_{[i_{\ell}]} = \mathbb O \ . $$
Придавая всем остальным переменным $ \{x_1,\dots,x_n\} \setminus \{ x_{i_1},\dots,x_{i_{\ell}} \} $ нулевые значения, получаем вектор $ X_{} \in \mathbb V^n $, удовлетворяющий равенству
$$ x_1 \mathbf H_{[1]}+\dots + x_n \mathbf H_{[n]} = \mathbb O \ , $$
и вес этого вектора $ \le \ell< d $. Но тогда этот вектор принадлежит и $ \mathbb V^{n}_{[k]} $ поскольку $ \mathbf H X^{\top} = \mathbb O $.
Это противоречит предположению о весе кодовых слов. Следовательно любые $ \ell_{} $ столбцов матрицы $ \mathbf H $ линейно независимы если $ \ell < d $.
Обратно, пусть любые $ \ell_{} $ столбцов матрицы $ \mathbf H $ линейно независимы, но существует кодовое слово $ X_{}=(x_1,\dots,x_n) \ne \mathbb O $ веса $ \le \ell $. Пусть, для определенности, $ x_{\ell+1}=0,\dots, x_{n}=0 $. Тогда
$$ x_1 \mathbf H_{[1]}+\dots + x_{\ell} \mathbf H_{[\ell]}= \mathbb O $$
при хотя бы одном из чисел $ \{x_j\}_{j=1}^{\ell} $ равном $ 1_{} $. Но это означает, что столбцы
$ \mathbf H_{[1]},\dots, \mathbf H_{[\ell]} $ линейно зависимы, что противоречит предположению.
♦
Испровление ашибок
До сих пор мы не накладывали ни каких дополнительных ограничений ни на порождающую ни на проверочную матрицы кода: любая из них могла быть выбрана почти произвольной.
Теперь обратимся собственно к задаче обнаружения (а также возможной коррекции) ошибок при передаче кодового слова по зашумленному каналу связи.
Если $ X\in \mathbb V^{n}_{[k]} $ — кодовое слово, а $ Y\in \mathbb V^n $ — вектор, получившийся по прохождении этого слова по каналу, то $ Y-X $ называется вектором ошибок. Понятно, что при $ w(Y-X)=0 $ ошибки при передаче нет.
Предположим, что $ w(Y-X)=1 $, т.е. что при передаче произошла ошибка ровно в одном разряде кодового слова $ X_{} $. Попробуем ее обнаружить исходя из предположения, что кодовое слово выбиралось во множестве $ \mathbb V^{n}_{[k]} $ линейного $ (n,k) $-кода, определенного в предыдущем пункте при какой-то проверочной матрице $ \mathbf H $. Если для полученного вектора $ Y_{} $ выполняются все проверочные условия:
$$ Y \cdot \mathbf H^{\top} = \mathbb O_{1\times k} \ , $$
(или, что то же $ Y \in \mathbb V^{n}_{[k]} $), то ошибка передачи считается не выявленной.
Для произвольного вектора $ Y \in \mathbb V^{n} $ вектор-строка
$$ S=Y \cdot \mathbf H^{\top} \in \mathbb V^{k} $$
называется синдромом вектора Y. C точки зрения линейной алгебры его можно интерпретировать как показатель отхода вектора $ Y_{} $ от гиперплоскости, заданной системой однородных уравнений $ X\cdot \mathbf H^{\top}=\mathbb O $.
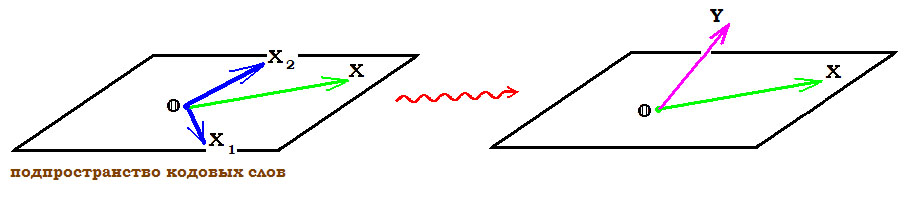
Если синдром $ S_{} $ ненулевой: $ Y \cdot \mathbf H^{\top} \ne \mathbb O_{1\times k} $,
то полученный вектор $ Y_{} $ не принадлежит множеству $ \mathbb V^{n}_{[k]} $ допустимых кодовых слов. Факт ошибки подтвержден. Изначально мы предположили, что произошла только одна ошибка, т.е.
$$ Y-X= {\mathfrak e}_j = \big(\underbrace{0,\dots,0,1}_{j},0,\dots,0\big) $$
при некотором $ j\in \{1,\dots n\} $. Тогда
$$ S= Y \cdot \mathbf H^{\top} = (X+{\mathfrak e}_j) \cdot \mathbf H^{\top}=X\cdot \mathbf H^{\top}+
{\mathfrak e}_j \cdot \mathbf H^{\top}=
$$
$$
=\mathbb O_{1\times k} + \mathbf H_{[j]}^{\top} = \mathbf H_{[j]}^{\top}
$$
при $ \mathbf H_{[j]} $ означающем $ j_{} $-й столбец проверочной матрицы $ \mathbf H $. Таким образом получили соответствие
$$ {}_{} \mathbf{HOMEP} \mbox{ поврежденного бита} \mathbf{=HOMEP} \mbox{ столбца проверочной матрицы.} $$
И, следовательно, мы получили возможность обнаружить место повреждения — по факту совпадения синдрома со столбцом проверочной матрицы. К сожалению, реальность оказывается более сложной…
П
Пример. В примере предыдущего пункта проверочная матрица была выбрана в виде
$$ \mathbf H=
\left( \begin{array}{ccccc}
1 & 1 & 0 & 1 & 0 \\
1 & 0 & 1 & 0 & 1
\end{array}
\right) \ .
$$
Если при передаче кодового слова $ (10011) $ произошла ошибка в первом бите, т.е. $ Y=(00011) $, то синдром
$$ S=Y \cdot \mathbf H^{\top} = (11) $$
однозначно укажет на номер столбца матрицы $ \mathbf H $. Если же ошибка произошла в четвертом бите, т.е. $ Y=(10001) $, то
$$ S=(10) \ , $$
но таких6) столбцов в матрице $ \mathbf H $ два!
♦
Вывод. Для однозначного обнаружения места ошибки7) достаточно, чтобы все столбцы матрицы $ \mathbf H $ были различными.
Столбцами этой матрицы являются транспонированные строки пространства $ \mathbb V^{n-k} $.
Построение кода
Итак, исходя из соображений, завершающих предыдущий пункт, будем строить код, исправляющий одну ошибку, беря за стартовую точку именно матрицу $ \mathbf H $. Выбираем ее произвольного порядка $ M\times N $ при $ \{M,N\} \in \mathbb N, M<N $ и вида
$$ \mathbf H_{M\times N} = \left[ \tilde P \mid E_M \right] \ , $$
где матрица $ E_M $ — единичная порядка $ M_{} $, а матрица $ \tilde P $ имеет порядок $ M\times (N-M) $, и столбцы ее должны быть различными, ненулевыми и отличаться от столбцов матрицы $ E_M $. По этой проверочной матрице — в соответствии со следствием к теореме $ 1 $ из
☞
ПУНКТА — строим порождающую матрицу:
$$ \mathbf G_{(N-M)\times N} = \left[ E_{N-M} \mid \tilde P^{\top} \right] \ . $$
Строки матрицы $ \mathbf G $ могут быть взяты в качестве базисных векторов подпространства кодовых слов.
П
Пример. Пусть $ M=2 $. Здесь имеем единственный вариант:
$$ \mathbf H_{2\times 3} = \left( \begin{array}{c|cc} 1 & 1 & 0 \\ 1 & 0 & 1 \end{array} \right) \ , $$
поскольку в $ \mathbb V^2 $ имеется лишь одна ненулевая строка, отличная от $ (10) $ и $ (01) $. Таким образом $ N=3 $ и
$$ \mathbf G_{1\times 3}=( 1\, 1\, 1 ) \ . $$
Следовательно, подпространство кодовых слов в $ \mathbb V^3 $ является одномерным, и имеем всего два возможных кодовых слова: $ (000) $ и $ (111) $.
Пусть $ M=3 $. В $ \mathbb V^3 $ имеется уже большой выбор строк, отличных от $ (100), (010), (001) $. Так, можно взять
$$
\mathbf H_{3\times 4} = \left( \begin{array}{c|ccc} 1 & 1 & 0 & 0 \\ 1 & 0 & 1 & 0 \\ 1 & 0 & 0 & 1 \end{array} \right) \quad \mbox{ или } \quad
\mathbf H_{3\times 5} = \left( \begin{array}{cc|ccc} 1 & 0 & 1 & 0 & 0 \\ 1 & 1 & 0 & 1 & 0 \\ 0 & 1 & 0 & 0 & 1 \end{array} \right)
$$
$$
\mbox{ или } \quad
\mathbf H_{3\times 6} =
\left( \begin{array}{ccc|ccc} 1 & 0 & 1 & 1 & 0 & 0 \\ 1 & 1 & 0 & 0 & 1 & 0 \\ 0 & 1 & 1 & 0 & 0 & 1 \end{array} \right) \quad \mbox{ или } \quad
\mathbf H_{3\times 7} =
\left( \begin{array}{cccc|ccc} 1 & 1 & 0 & 1 & 1 & 0 & 0 \\ 1 & 1 & 1 & 0 & 0 & 1 & 0 \\ 1 & 0 & 1 & 1 & 0 & 0 & 1 \end{array} \right) \ .
$$
Соответственно,
$$ \mathbf G= (1\, 1\, 1\, 1) \quad \quad \mbox{ или } \quad
\mathbf G=
\left( \begin{array}{cc|ccc} 1 & 0 & 1 & 1 & 0 \\ 0 & 1 & 0 & 1 & 1 \end{array} \right)
\quad
$$
$$
\mbox{ или } \quad
\mathbf G=
\left( \begin{array}{ccc|ccc} 1 & 0 & 0 & 1 & 1 & 0 \\ 0 & 1 & 0 & 0 & 1 & 1 \\ 0 & 0 & 1 & 1 & 0 & 1 \end{array} \right)
\quad \quad \mbox{ или } \quad
\mathbf G=
\left( \begin{array}{cccc|ccc} 1 & 0 & 0 & 0 & 1 & 1 & 1 \\ 0 & 1 & 0 & 0 & 1 & 1 & 0 \\ 0 & 0 & 1 & 0 & 0 & 1 & 1 \\ 0 & 0 & 0 & 1 & 1 & 0 & 1
\end{array} \right) \ .
$$
Кодовых векторов в соответствующих кодах будет $ 2^1,2^2,2^3,2^4 $. Любой из них способен исправить одну ошибку, полученную в ходе передачи.
♦
Если поставить задачу максимизации числа кодовых слов, то матрицу $ \mathbf H $ следует выбирать самой широкой, т.е. делать $ N_{} $ максимально возможным. При фиксированном $ M_{} $ это достигается при выборе $ N=2^M-1 $. Тогда соответствующий линейный $ (n,k) $-код имеет значения параметров $ n=2^M-1,k=2^M-M-1 $, и именно он обычно и выбирается в качестве кода Хэмминга.
Найдем величину его кодового расстояния $ d_{} $. В соответствии с теоремой $ 3 $ из
☞
ПУНКТА, $ d>\ell $, если любое подмножество из $ \ell_{} $ столбцов матрицы $ \mathbf H $ линейно независимо. Поскольку столбцы проверочной матрицы кода Хэмминга все различны, то любая пара из них линейно независима (свойство
3
☞
ЗДЕСЬ ). Следовательно, $ d>2 $. По теореме из
☞
ПУНКТА, получаем —
Если при передаче произошла ровно одна ошибка, то код Хэмминга способен ее исправить; если при передаче произошло ровно две ошибки, то код Хэмминга достоверно устанавливает лишь факт наличия ошибки.
Если попробовать исправить заглавие предыдущего пункта, исходя только из информации о структуре набора составляющих текст букв, то этой информации оказывается недостаточно: набор букв в правильном тексте будет таким же
П
Пример. Для проверочной матрицы $ (7,4) $-кода Хэмминга
$$
\mathbf H_{3\times 7} =
\left( \begin{array}{ccccccc} 1 & 1 & 0 & 1 & 1 & 0 & 0 \\ 1 & 1 & 1 & 0 & 0 & 1 & 0 \\ 1 & 0 & 1 & 1 & 0 & 0 & 1 \end{array} \right)
$$
вектор $ X=(0011110) $ является кодовым. Если при передаче произошла лишь одна ошибка и на выходе канала получили вектор $ Y=(1011110) $, то синдром этого вектора $ S=Y \mathbf H^{\top}=(111) $. Поскольку $ S^{\top} $ совпадает с первым столбцом матрицы $ \mathbf H $, то заключаем, что ошибка произошла в первом разряде. Тут же исправляем его на противоположный: $ X=Y+\mathfrak e_1 $.
Если при передаче произошло две ошибки и на выходе канала получили вектор $ \tilde Y=(1011010) $, то синдром этого вектора $ S=\tilde Y \mathbf H^{\top}=(011) $. Поскольку синдром ненулевой, то факт наличия ошибки подтвержден. Однако корректно исправить ее — по аналогии с предыдущим — не удается. $ S^{\top} $ совпадает с третьим столбцом матрицы $ \mathbf H $, но в третьем разряде полученного вектора ошибки нет.
Наконец, если при передаче произошли три ошибки и на выходе канала получили вектор $ \widehat Y=(1011011) $, то синдром этого вектора $ S=\widehat Y \mathbf H^{\top}=(010) $. Наличие ошибки подтверждено, исправление невозможно. Если же — при передаче того же вектора $ X=(0011110) $ — получаем вектор
$ \widehat Y_1=(1111111) $ (также с тремя ошибками), то его синдром оказывается нулевым: $ \widehat Y_1 \mathbf H^{\top}=(000) $ и ошибка не обнаруживается.
♦
Проблема сравнения синдрома полученного вектора $ Y_{} $ со столбцами проверочной матрицы $ \mathbf H $ с целью определения места ошибки — не такая тривиальная, особенно для больших $ n_{} $. Для упрощения этой процедуры воспользуемся следующим простым соображением. Размещение проверочных разрядов в конце кодового слова обусловлено лишь соображениями удобства изложения учебного материала. С точки зрения практической реализации, $ n-k $ проверочных разрядов можно разместить в любых местах кодового слова $ X_{} $ и даже «вразбивку», т.е. не подряд. Перестановке разрядов в кодовом слове будет соответствовать перестановка столбцов в матрице $ \mathbf H $, при этом само множество столбцов остается неизменным — это транспонированные строки пространства $ \mathbb V^{n-k} $ (ненулевые и различные). Рассмотрим $ (n,k) $-код Хэмминга при $ n=2^M-1,k=2^M-M-1, M \ge 2 $. Тогда каждую ненулевую строку пространства $ \mathbb V^{n-k}= \mathbb V^M $ можно интерпретировать как двоичное представление числа из множества
$ \{1,2,3,\dots,2^M-1\} $. Пусть
$$ j=\underline{{\mathfrak b}_1{\mathfrak b}_2 \dots {\mathfrak b}_{M-1} {\mathfrak b}_{M}}=
{\mathfrak b}_1 \times 2^{M-1}+{\mathfrak b}_2 \times 2^{M-2}+\dots+{\mathfrak b}_{M-1} \times 2+ {\mathfrak b}_{M} \quad npu \quad \{ {\mathfrak b}_j\}_{j=1}^M\subset \{0,1\} \quad — $$
— двоичное представление числа $ j_{} $. Переупорядочим столбцы проверочной матрицы $ \mathbf H $ так, чтобы
$$ \mathbf H_{[j]}=\left[ {\mathfrak b}_1{\mathfrak b}_2 \dots {\mathfrak b}_{M-1} {\mathfrak b}_{M}\right]^{\top} \ , $$
т.е. чтобы $ j_{} $-й столбец содержал двоичное представление числа $ j_{} $. При таком упорядочении,
синдром произвольного вектора $ Y_{} $, отличающегося от кодового слова $ X_{} $ в единственном разряде, является двоичным представлением номера этого разряда:
$$ {\bf \mbox{СИНДРОМ }} \ (Y)=\mathbf{HOMEP} \ (\mbox{ошибочный разряд}) \ . $$
Осталось теперь выяснить какие разряды кодового слова содержат проверочные биты.
П
Пример. Для $ (7,4) $-кода Хэмминга матрицу $ \mathbf H $, построенную в предыдущем примере, переупорядочим по столбцам; будем рассматривать ее в виде
$$
\begin{array}{c}
\left( \begin{array}{ccccccc}
0 & 0 & 0 & 1 & 1 & 1 & 1 \\
0 & 1 & 1 & 0 & 0 & 1 & 1 \\
1 & 0 & 1 & 0 & 1 & 0 & 1
\end{array} \right) \\
\begin{array}{ccccccc}
\uparrow & \uparrow & \uparrow & \uparrow & \uparrow & \uparrow & \uparrow \\
\scriptstyle 1 & \scriptstyle 2 & \scriptstyle 3 & \scriptstyle 4 & \scriptstyle 5 & \scriptstyle 6 & \scriptstyle 7
\end{array}
\end{array}
$$
Распишем проверочные соотношения $ X\mathbf H^{\top}=\mathbb O $ покомпонентно:
$$
\left\{
\begin{array}{ccccccc}
& & & x_4&+x_5&+x_6&+x_7=0 \\
&x_2&+x_3& & & +x_6&+x_7=0 \\
x_1& & +x_3& & +x_5 & & +x_7=0
\end{array} \right. \quad \iff
$$
$$
\iff \quad
\left\{
\begin{array}{ccccccc}
x_1& & +x_3& & +x_5 & & +x_7=0 \\
&x_2&+x_3& & & +x_6&+x_7=0 \\
& & & x_4&+x_5&+x_6&+x_7=0
\end{array} \right.
$$
Переписанные в последнем виде, эти уравнения представляют конечный пункт прямого хода метода Гаусса решения системы линейных уравнений, а именно — трапециевидную форму этой системы. Если бы мы поставили задачу поиска общего решения этой (однородной) системы и нахождения фундаментальной системы решений, то в качестве зависимых переменных однозначно бы выбрали $ x_1, x_2, x_4 $. Выпишем это общее решение 
$$
x_1=x_3+x_5+x_7,\ x_2=x_3+x_6+x_7,\ x_4=x_5+x_6+x_7 \ .
$$
Это и есть проверочные соотношения, а проверочными разрядами кодового вектора являются $ 1_{} $-й, $ 2_{} $-й и $ 4_{} $-й.
Проверим правильность этих рассуждений. Придадим оставшимся разрядам произвольные значения, например:
$ x_3=1,x_5=1,x_6=0,x_7=1 $. Тогда $ x_1=1, x_2=0,x_4=0 $ и кодовый вектор $ X=(1010101) $. Пусть на выходе из канала он превратился в $ Y=(1000101) $. Синдром этого вектора $ Y\mathbf H^{\top}=(011) $ — это двоичное представление числа $ 3_{} $. И ведь действительно: ошибка — в третьем разряде!
♦
Алгоритм построения (n,k)-кода Хэмминга
для $ n=2^M-1,k=2^M-M-1, M \ge 2 $.
1.
Строится матрица $ \mathbf H $ порядка $ M \times (2^M-1) $ из столбцов, представляющих двоичные представления чисел $ \{1,2,3,\dots,2^M-1\} $ (младшие разряды — внизу).
2.
Проверочные разряды имеют номера, равные степеням двойки: $ 1,2,2^2,\dots,2^{M-1} $.
3.
Проверочные соотношения получаются из матричного представления $ X\mathbf H^{\top}=\mathbb O $ выражением проверочных разрядов через информационные.
Можно немного улучшить код Хэмминга, увеличив кодовое расстояние до $ 4_{} $.
?
Является ли $ 8_{} $-мибитный код Адамара из примера
☞
ПУНКТА линейным кодом?
.
Источники
[1]. Питерсон У., Уэлдон Э. Коды, исправляющие ошибки. М.Мир. 1976.
[2]. Марков А.А. Введение в теорию кодирования. М.Наука. 1982