Циклический
код
является разновидностью помехоустойчивых
кодов, применяется в технике передачи
дискретных сообщений. Особенности
циклических кодов заключены в двух
свойствах разрешенных кодовых комбинаций:
1. любая
из разрешенных кодовых комбинаций
циклического кода делится по модулю
два без остатка на некоторое, так
называемое «образующее двоичное число»,
определяющее помехоустойчивые свойства
кода, т.е. расстояние d;
2.
циклический сдвиг разрядов разрешенной
кодовой комбинации на один элемент
влево порождает другую разрешенную
кодовую комбинацию.
Например:
01011 и 10110 – две разрешенные кодовые
комбинации некоторого циклического
кода с образующим числом 1011 (d=3).
Поэтому они делятся по модулю два без
остатка на образующее число:
0
1011 10110 1011
0000
01
1011
10
1011
0000
1011
0000
000
000
При
этом d=4
>d=3.
Кроме
того циклический сдвиг на один разряд
влево элементов первой комбинации
порождают вторую комбинацию.
01011 => 10110
Делимость
без остатка разрешенных кодовых
комбинаций на известное образующее
число лежит в основе операций обнаружения
и исправления ошибок при использовании
циклических кодов.
Структурная
схема СПДС, содержит кодер и декодер
циклического кода. Структура разрешенных
кодовых комбинаций циклического кода
состоит из двух частей. В начале комбинации
располагается n-проверочных
разрядов, структура которых определяется
кодерами циклического кода из условия
обеспечения делимости без остатка
формируемой разрешенной кодовой
комбинации на образующее число.
Идея
построения циклического кода (n,k)
сводится к тому, что информационную
часть кодовой комбинации G(x)
нужно преобразовать в комбинацию F(x),
которая без остатка делится на порождающий
полином Р(х) степени r=n-k.
Рассмотрим последовательность операций
построения циклического кода:
1.
Представляем информационную часть
кодовой комбинации в виде полинома
G(x).
Например информационная часть 110101.
Тогда
.
2.
Умножаем G(x)
на одночлен
( старшую степень порождающего полинома
Р(х) ) и получаем.
Пусть
у нас порождающий полином 1011,
тогда
.
3. Делим
на
порождающий полином Р(х), при этом
получаем остаток от деленияR(x).
Добавим
полученный остаток R
(x)
к комбинации
и
получим комбинацию,
которая будет передана в линию. Данная
комбинацияF(x)
делится без остатка на образующий
полином и представляет собой разрешенную
кодовую комбинацию циклического (n,k)
кода. На приеме производится деление
полученной кодовой комбинации на
образующий полином. Если ошибок нет, то
деление пройдет без остатка. Если при
делении получен остаток, то комбинация
принята с ошибками.
При
использовании в циклических кодах
декодирования с исправлением ошибок
остаток от деления может играть роль
синдрома. Нулевой синдром указывает на
то, что принятая комбинация является
разрешенной. Всякому ненулевому синдрому
соответствует определенная конфигурация
ошибок, которая и исправляется.
Построение
кодеров, декодеров.
Пример:
Кодер
строится на основе полинома P(x).
=> 1011
–
веса
При
построении устройства число ячеек
регистров сдвига берется по высшей
степени образующего полинома
=>
3 регистра сдвига; число регистров
задержки берется также по высшей степени
образующего полинома; число сумматоров
по модулю два берется по весовой части
образующего полинома минус единица =>
3-1=2m.
Состояния
регистров (1,2,3
– регистры; m
– сумматоры)
На
вход подается
110101000
Декодер
–
правила построения такие же, как у
кодера, но количество регистров задержки
определяется по высшей степени
информационной комбинации плюс 1
5+1=6
Деление
на образующий полином происходит за 9
тактов. Пока идет деление на образующий
полином К2 разомкнут, а К1 замкнут в
течении 6 тактов пока идет запись
информационных импульсов. После 6 такта
К1 размыкается. После 10 такта К2 замыкается
и формируется сигнал:
1. Если хотя бы в
одной ячейке регистра будет «1», то
значит произошла ошибка. Формируется
сигнал «1» и информация из регистров
сдвигов будет удаляться.
2. Если во всех
ячейках регистров сдвига будут «0», то
формируется сигнал «0» и информация
будет выдана потребителю.
Состояния
регистров
Если хотя бы в одной
ячейке регистра будет «1», то значит
произошла ошибка.
Информация из
регистров сдвигов будет удаляться. Если
во всех ячейках регистров сдвига будут
«0», то формируется сигнал «0» и информация
будет выдана потребителю.
Выбор образующего
полинома.
В
теории циклических кодов показано, что
образующий полином представляет собой
произведение так называемых минимальных
многочленов (),
являющихся простыми сомножителями,
(т.е. делящимися без остатка лишь на себя
и на 1).
Кроме
образующего полинома необходимо найти
и количество проверочных разрядов
r.
=1
если n=7,
то
tи.ош
– число ошибок, исправляемых циклическим
кодом.
После
определения количества проверочных
разрядов
r
вычисление образующего полинома удобно
осуществить, пользуясь таблицей
минимальных многочленов.
Ниже приведена часть такой таблицы.
|
r |
Pr(x) |
Двоичная |
|
2 |
|
111 |
|
3 |
|
1011 1101 |
В частности, если
r=3,
tи.ош=1,
j=2*1-1=1,
образующий полином будет представлять
собой единственный минимальный многочлен
P(x)= x3+x+1
(первая строка, второй столбец таблицы
). Соответственно образующее число равно
1011.
Синдром циклического
кода.
Синдром циклического
кода определяется суммой по модулю 2
принятых проверочных элементов и
элементов проверочной группы,
сформированных из принятых элементов
информационной группы. В циклическом
коде для определения синдрома следует
разделить принятую кодовую комбинацию
на кодовую комбинацию порождающего
полинома. Если все элементы приняты без
ошибок, то остаток от деления R(х)
равен нулю. Если есть ошибки, то остаток
не будет равен нулю. Следовательно,
синдромом циклического кода является
многочлен R(x).
Обнаружение и исправление ошибок
производится только на основе анализа
синдрома. В зависимости от остатка
определяется элемент в котором произошла
ошибка. Для исправления ошибок необходимо
чтобы количество ненулевых остатков
равнялось количеству элементов n
( при исправлении одной ошибки ) или
числу комбинаций из n.
Соседние файлы в папке Будылдина2
- #
11.04.20152.54 Mб24ДКР рисунок Mumarev.vsd
- #
11.04.20152.49 Mб30ДКР рисунок.vsd
- #
- #
- #
- #
Вычисление синдрома и исправление ошибок в циклических кодах
Вычисление синдрома для циклических кодов является довольно простой процедурой, совершенно аналогичной процедуре кодирования. Рассмотрим ее.
Пусть и(х) и и(х) — полиномы, соответствующие переданному кодовому слову и принятой последовательности. Они могут совпадать, если передача сообщения была осуществлена безошибочно, или не совпадать в противном случае.
Разделив й(х) на порождающий полином g(x), получим
где q(х) — частное от деления; s(x) — остаток от деления.
Если й(х) является допустимым кодовым полиномом, то он делится на g(x) без остатка, т.е. s(x) = 0.
Следовательно, результат s(x) ф 0 является условием наличия ошибки в принятой последовательности, а полином s(x) имеет смысл синдрома ошибки в последовательности и(х).
Синдром s(x) имеет в общем случае вид
Поскольку синдром вычисляется как остаток от деления некоего полинома на порождающий полином, то очевидно, что схема вычисления синдрома подобна схемам кодирования, рассмотренным выше, с той лишь разницей, что в качестве входной последовательности в нее подается вектор й (см. рис. 4.8).
При наличии в принятой последовательности й хотя бы одной ошибки вектор синдрома s будет иметь по крайней мере один ненулевой элемент, при этом факт наличия ошибки легко обнаружить, объединив по элементу ИЛИ выходы всех ячеек регистра синдрома.
Покажем, что синдромный многочлен s(x) однозначно связан с многочленом ошибки е(х), а значит, с его помощью можно не только обнаруживать, но и локализовать ошибку в принятой последовательности.
Рис. 4.8. Схема получения синдрома для порождающего полинома д(х) =х 3 +х+1
Пусть е(х) — полином вектора ошибки. Тогда полином принятой последовательности
Учтем, что п(х) — допустимый кодовый полином, нацело делящийся на порождающий полином g(x), и запишем два выражения:
По определению вектора (полинома) ошибки:
То есть синдромный полином s(x) есть остаток от деления полинома ошибки е(х) на порождающий полином д(х).
Отсюда следует, что по синдрому s(x) можно однозначно определить вектор ошибки е(х), а следовательно, и исправить эту ошибку.
Декодирование линейных кодов
1. Пусть с = (ci, С2. сп) — передаваемый вектор кодового слова линейного кода С над GF(q), av = (vi, Vi. vn) — соответствующий принятый вектор. Векторы с и v могут различаться по причине возникновения ошибок в процессе передачи кодового слова. Это различие может быть записано следующим образом:
где е = (©1, ©2,еп) — вектор, символы которого принимают ненулевые значения в ошибочных разрядах и нулевые — в разрядах, переданных без ошибки.
Вектор е из соотношения (2.13) называется вектором ошибок.
Собственно, задача декодирования линейного кода состоит в том, чтобы отыскать вектор ошибок и по известному вектору ошибок восстановить исходное кодовое слово.
Далее для определения одного из алгоритмов декодирования нам понадобятся дополнительные сведения из алгебры.
2. Непустое подмножество Н группы (G, *) называется подгруппой группы (G, *), если Н является группой относительно той же групповой операции *.
Очевидно, что подгруппа как самостоятельная группа должна удовлетворять всем аксиомам группы. При этом очевидно, что ассоциативность наследуется из исходной группы G (как и коммутативность в случае, если G — абелева группа, см. параграф 1.1).
В качестве примера подгруппы можно привести множество всех четных чисел в группе % всех целых чисел относительно операции арифметического сложения.
Подгруппа, содержащая конечное число элементов, называется конечной подгруппой.
Пример 2.1.5. Пусть G = <0,1,2,3>— аддитивная абелева группа с групповой операцией, задаваемой следующей таблицей:
Легко проверить, что элементы 0 и 2 образуют множество, замкнутое относительно групповой операции группы G:
Остальные аксиомы групп также имеют место для указанных элементов. Таким образом, элементы 0 и 2 группы 6 образуют подгруппу Н = <0, 2 > относительно групповой операции исходной группы G.
Пусть Н — произвольная подгруппа произвольной группы G.
Предположим, что для любых а и b из Н а*Ь и а -1 также принадлежат Н. Тогда для Ь = а -1 элемент а*Ь = а*а -1 также принадлежит Н. Таким образом, в Н для любого элемента а найдется элемент а*а
что означает выполнение аксиомы групп о существовании единичного элемента. Выполнение аксиомы замкнутости в этом случае очевидно. Предположим теперь, что, помимо предыдущего предположения, для каждого а и b из Н а*Ь -1 также принадлежат Н. Пусть с = = а*Ь
В силу первого предположения, а -1 принадлежит Н и а _1 *а = е. Тогда а- 1 *а*Ь -1 = а _1 *с или Ь -1 = а _1 *с, что означает существование обратного элемента любого элемента Н.
Таким образом, необходимым и достаточным условием того, что непустое подмножество Н элементов группы G образует подгруппу, является выполнение для любых двух элементов а и Ь из Н следующих условий:
- — если а и Ь принадлежат Н, то а*Ь и а- 1 также принадлежат Н
- — если а и Ь принадлежат Н, то а*Ь -1 также принадлежит Н.
Кроме того, следует отметить, что единичный элемент подгруппы всегда совпадает с единичным элементом исходной группы [8].
Очевидно, что подмножество <е>любой группы G, состоящее только из единичного элемента, а также сама группа G удовлетворяют условиям образования подгруппы. Такие подгруппы называются тривиальными подгруппами.
Пусть Н — подгруппа группы G, a g — произвольный фиксированный элемент G. Множество
называется правым смежным классом группы G по подгруппе Н, порождаемым элементом g. Аналогично множество
называется левым смежным классом группы G по подгруппе Н, порождаемым элементом g.
В случае некоммутативной группы G число левых смежных классов группы G по подгруппе Н совпадает с числом правых смежных классов. При этом в общем случае никакой левый смежный класс не совпадает ни с каким правым смежным классом. Исключение составляют так называемые нормальные делители — подгруппы, для любого элемента которых H*g = g*H [10].
Очевидно, что если G — абелева группа, то ее левые смежные классы по подгруппе Н совпадают с правыми. Условимся в случае абелевой группы обозначать смежные классы группы G по подгруппе Н в форме соотношения (2.14).
Пусть Н — подгруппа некоторой конечной группы G.
Предположим, что два элемента одного и того же смежного класса группы G
по подгруппе Н равны: gi*hj = gi*hk. Тогда умножение слева на g;
1 дает равенство hj = hk. Но это противоречит определению подгруппы.
Предположим теперь, что два элемента двух смежных классов g;*H и gk*H
равны: gi*hj = gk*hs. Умножение справа на hj— 1 дает равенство g; = gk*hs*hj
Рассмотрим теперь смежный класс:
В силу замкнутости Н относительно операции *, элемент hs*hj-‘ l *h также принадлежит Н. Обозначив hs*hj-‘*h = h‘, получим:
Итак, рассматриваемые элементы g/ и g* порождают один и тот же смежный класс группы G по подгруппе Н.
Таким образом, смежные классы группы G по подгруппе Н, содержащие хотя бы один общий элемент, совпадают.
Из двух последних соотношений также следует, что число повторяющихся смежных классов группы G по подгруппе Н для каждого элемента g группы G соответствует порядку подгруппы Н.
Для получения смежного класса, совпадающего с некоторым исходным смежным классом g/c* Н и порождаемого отличным от gk элементом G, в качестве порождающего элемента можно взять любой элемент gj-g к* hj данного смежного класса g/c* Н, где е.
Иными словами, если выбрать в качестве элемента, порождающего смежный класс, любой отличный от порождающего элемент уже определенного смежного класса, то получим исходный смежный класс.
Пусть Н = hn> — подгруппа конечной группы G. Пусть g n ) как векторном пространстве GF n (q).
Таким образом, векторное подпространство GF k (q) кода С разбивает исходное векторное пространство GF n (q) на непересекающиеся смежные классы, определяемые следующим образом:
где а — элемент GF n (q), порождающий смежный класс.
Как было показано в предыдущем пункте этого подпараграфа, число элементов каждого смежного класса совпадает с числом кодовых слов кода С. Иными словами, каждый смежный класс а + С содержит q k элементов. Число всех непересекающихся смежных классов определяется соотношением (2.15) и имеет значение q n
Таким образом, векторное пространство GF n (q) можно представить как объединение множеств:

k — 1 — элементы GF n (q), образующие все различные
(не пересекающиеся) смежные классы.
Будем считать, что в соотношении (2.16) а(°) = 0. Тогда смежный класс а(°) + + С совпадает с кодом С.
Как было показано в предыдущем пункте этого подпараграфа, каждый смежный класс вида (2.16) может быть порожден q k различными элементами (векторами) векторного пространства GF n (q).
Пример 2.1.7. Рассмотрим построение отличных от исходного кода смежных классов двоичного линейного (6, 3)-кода С из примера 2.1.4.
Множество всех кодовых слов в данном случае содержит восемь элементов (векторов) векторного пространства GF 6 (2), которые можно представить в виде двоичных последовательностей длиной не более шести двоичных символов:
Число элементов (векторов) каждого смежного класса соответствует числу q k = 8 кодовых слов кода С.
Пусть, например, а = 000001. Тогда смежный класс а + С будет состоять из следующих элементов (векторов):
Нетрудно проверить, что то же множество векторов может быть получено при а = 001100, 010010, 011111, 100111,101010,110100,111001. То есть при любом другом отличном от исходного порождающего элемента а значении, принадлежащем указанному смежному классу.
Согласно соотношению (2.16), число не пересекающихся смежных классов в этом случае: q n
k = 8 (в следующем примере мы укажем их все). Все остальные (отличные от самого кода С) смежные классы могут быть получены, например, при следующих значениях порождающего элемента а:
При этом каждый смежный класс может быть образован, помимо указанных, семью другими значениями вектора а из GF 6 (2), принадлежащими тому же смежному классу.
Любой элемент (вектор) каждого смежного класса, как и сам смежный класс, может быть получен восемью различными способами как а + с для восьми различных значений порождающего элемента а и всех восьми кодовых слов с кода С. Например, элемент 111001 рассмотренного выше в этом примере смежного класса, порожденного элементом а = 000001, может быть получен как а + с для значений а = 000001, 001100, 010010, 011111, 100111, 101010, 110100, 111001 и с = 111000, 110101, 101011, 100110, 011110, 010011, 001101, 000000 соответственно.
4. Пусть С — линейный (л, к)-код над GF(q) и v = с + е — вектор принятого сообщения.
Как было показано выше в этом подпараграфе, вектор v всегда принадлежит одному из q n
k не пересекающихся смежных классов вида (2.16). При отсутствии ошибок вектор v принадлежит смежному классу, совпадающему с кодом С. При ненулевом векторе ошибок вектор i/оказывается в другом смежном классе а + С (пока будем считать, что вес вектора ошибок не превосходит максимального числа t исправляемых кодом ошибок).
Принимая вектор е за порождающий элемент смежного класса е + С, по известному вектору v мы можем определить q k возможных значений вектора е. Очевидно, наиболее вероятным является значение е наименьшего веса.
Элемент (вектор) минимального веса в смежном классе а + С называется лидером смежного класса а + С.
Если в смежном классе а + С несколько векторов имеют минимальный вес, то в качестве лидера смежного класса выбирается любой из них. Таким образом, вектор ошибок принимается равным лидеру смежного класса, которому принадлежит принятый вектор v.
В этом случае аппаратная реализация декодера основана на так называемом табличном методе и требует хранения в памяти устройства всех смежных классов и их лидеров. Подобного рода декодер даже при небольшой длине кода требует значительных аппаратных затрат. Например, для рассмотренного в примерах 2.1.4 и 2.1.7 двоичного линейного (6, 3)-кода требуется хранить в памяти декодера q n
k = 8 смежных классов по q k = 8 двоичных векторов длины п = 6 символов.
Однако табличный декодер может быть несколько упрощен.
Пусть Н — проверочная матрица линейного (л, /с)-кода С. Тогда матрица-строка s(y) = у-Н т размера 1 х к называется синдромом вектора у.
Пусть у = v = с + е — вектор принятого сообщения. Тогда, в силу соотношения (2.10), s(y) = s(e) и, стало быть, равенство нулю s(v) означает принадлежность вектора v коду С. Это в свою очередь означает отсутствие ошибок вектора v. Пока будем считать, что вес вектора ошибок не превосходит максимального числа t исправляемых кодом ошибок. К этому вопросу мы еще вернемся ниже, в конце этого подпараграфа.
Пусть С — линейный (л, к)-код над GF(q), а у и z — два вектора векторного пространства GF n (q).
Очевидно, что s(y) = s(z) тогда и только тогда, когда у-Н т = z-H T или (у — z) х х Н т = 0. Это означает, что вектор у — z принадлежит С. Тогда y-z = Ck- некоторое кодовое слово кода С. Последнее равенство выполняется и в том случае,
если у = а + CiVz = а + Cj, где с,- — су = с*, а — некоторый вектор GF n (q). Равенство синдромов векторов у и z означает принадлежность обоих векторов одному смежному классу.
Таким образом, в силу равенства синдромов s(v) и s(e), вектор v принятого сообщения и вектор ошибок е всегда принадлежат одному смежному классу и по известному синдрому s(v) можно однозначно определить лидер соответствующего смежного класса.
Теперь мы можем описать один из возможных алгоритмов декодирования линейных кодов.
- 1. Определить синдром s(v) принятого сообщения v.
- 2. По известному синдрому s[v) определить соответствующий лидер смежного класса, синдром которого совпадает с s(v).
- 3. Определить исходное кодовое слово с согласно соотношению (2.13) как c-v-e.
Аппаратная реализация декодера в этом случае требует хранения q k синдромов длины п — к (/-ичных символов и q k соответствующих им лидеров смежных классов длины п q-ичных символов в памяти устройства.
Такой метод декодирования называется декодированием линейных кодов по лидерам смежных классов.
Пример 2.1.8. Рассмотрим снова двоичный линейный (6, 3)-код из примеров 2.1.4 и 2.1.7.
В таблице 2.1 показаны смежные классы, лидеры смежных классов и соответствующие им синдромы рассматриваемого кода. Во избежание громоздкости элементы смежных классов представлены соответствующими десятичными значениями. Жирным шрифтом выделены значения лидеров смежных классов.
Лидер смежного класса
< 1, 12, 18,31,39, 42, 52, 57 >
< 2, 15, 17, 28, 36,41,55, 58 >
< 4, 9, 23, 26, 34,47, 49, 60 >
- 001010
- 010100
- 100001
Нетрудно убедиться в том, что синдром любого элемента каждого смежного класса совпадает с синдромом лидера этого смежного класса.
Как видно из таблицы 2.1, в данном случае лидеры смежных классов представлены всеми возможными двоичными векторами веса 1. Эти векторы определены однозначно (в каждом смежном классе только один такой вектор). Таким образом, в случае одиночной ошибки существует единственным образом определяемый синдром, позволяющий однозначно определить вектор ошибки. Поэтому рассмотренный линейный (6,3)-код позволяет гарантированно исправлять одиночную ошибку.
Кроме того, в одном (последнем) смежном классе три лидера веса 2. Это позволяет с небольшой (1/3) вероятностью декодировать двойную ошибку (при условии, что вероятности всех векторов принимаемых сообщений с двойной ошибкой равны).
Очевидно, избыточность рассмотренного в примерах 2.1.4, 2.1.7 и 2.1.8 двоичного линейного (6, 3)-кода немного превышает накладываемые на него корректирующие свойства, так как помимо достаточных для декодирования лидеров смежных классов веса 1 в одном из смежных классов имеют место лидеры веса 2.
Если в качестве лидеров q n
k смежных классов кода удается взять векторы веса t и менее и только их, то код называется совершенным кодом. Если же в качестве лидеров q n
k смежных классов кода удается взять все необходимые для исправления не менее t ошибок векторы веса t и менее, а также несколько векторов веса t + 1, то код называется квазисовершенным кодом.
Проще говоря, у совершенных кодов избыточности «ровно столько, сколько нужно» для исправления не менее чем t ошибок кодового слова.
Возвращаясь к примеру 2.1.4, отметим, что в случае двоичного линейного
- (5,3)-кода вообще нельзя определить однозначно лидеры смежных классов веса
- 1. Пусть, например, проверочная матрица (5,3)-кода имеет вид:
Тогда порождающая матрица:
В этом случае лидер смежного класса веса 1 будет однозначно определен только в одном смежном классе, отличном от смежного класса самого кода. В двух других смежных классах будет по два лидера веса 1. В смежном классе, совпадающем с кодом, также будут два лидера веса 2. Таким образом, данный код не может исправлять одиночную ошибку кодового слова.
Этот вывод подтверждается неравенством (2.5), так как минимальное расстояние (5, 3)-кода равно двум и, следовательно, ни одно целое положительное значение t исправляемых кодом ошибок данному неравенству не удовлетворяет.
Таким образом, при длине информационного сообщения к = 3 двоичных символа и длине проверочной последовательности г=п-к = 2 символа код вообще не позволяет исправлять одиночную ошибку кодового слова, а при длине г — 3 символа уже оказывается не совершенным (хотя и квазисовершенным).
Следует отметить, что совершенные коды, равно как и квазисовершенные, для некоторых значений п и к вообще могут не существовать [10]. Далее мы рассмотрим несколько видов кодов из класса линейных кодов, конструкция которых часто позволяет получить квазисовершенный или даже совершенный код.
Выше мы считали, что вес вектора ошибок не превосходит значение t исправляемых кодом ошибок, так как восстановление исходного кодового слова возможно только в этом случае. В противном случае исходное кодовое слово и принятый вектор могут попасть в один смежный класс, и восстановление кодового слова будет невозможно. Таким образом, число ошибок, превышающее корректирующую способность кода, приводит к ошибочному декодированию.
Если же число ошибок превосходит t и принятый вектор попадает в смежный класс, отличный от смежного класса кода, то декодирование возможно лишь с некоторой (обычно небольшой) вероятностью. При этом возможны два способа декодирования:
- — декодирование любого полученного кодового слова в ближайшее кодовое слово;
- — декодирование только кодовых слов, число ошибок которых не превосходит максимально возможное для данного кода число ошибок t, если число ошибок превышает t, происходит отказ от декодирования.
В первом случае декодер называется полным декодером, а во втором — неполным декодером.
Очевидно, что по сравнению с неполным декодером полный декодер чаще декодирует неправильно. Поэтому полный декодер используется обычно только в тех случаях, когда лучше «угадывать» сообщение, чем вообще не иметь никакой оценки.
В силу указанных особенностей мы будем рассматривать только неполные декодеры.
Метод декодирования линейных кодов по лидерам смежных классов является общим для всех линейных кодов. При этом вполне очевидно, что этот метод связан с трудоемким процессом определения лидеров смежных классов.
Например, для линейного (31, 26)-кода над GF(2) требуется определить 32 смежных класса по 67108864 вектора длины 31 в каждом и найти лидеры каждого смежного класса.
Таким образом, метод декодирования линейных кодов по лидерам смежных классов в общем случае не является приемлемым.
Однако мы можем заранее определить некоторый удобный метод декодирования и на его основе построить линейный код специального вида.
Корректирующие коды «на пальцах»

Как нетрудно догадаться, ко всему этому причастны корректирующие коды. Собственно, ECC так и расшифровывается — «error-correcting code», то есть «код, исправляющий ошибки». А CRC — это один из алгоритмов, обнаруживающих ошибки в данных. Исправить он их не может, но часто это и не требуется.
Давайте же разберёмся, что это такое.
Для понимания статьи не нужны никакие специальные знания. Достаточно лишь понимать, что такое вектор и матрица, как они перемножаются и как с их помощью записать систему линейных уравнений.
Внимание! Много текста и мало картинок. Я постарался всё объяснить, но без карандаша и бумаги текст может показаться немного запутанным.
Каналы с ошибкой
Разберёмся сперва, откуда вообще берутся ошибки, которые мы собираемся исправлять. Перед нами стоит следующая задача. Нужно передать несколько блоков данных, каждый из которых кодируется цепочкой двоичных цифр. Получившаяся последовательность нулей и единиц передаётся через канал связи. Но так сложилось, что реальные каналы связи часто подвержены ошибкам. Вообще говоря, ошибки могут быть разных видов — может появиться лишняя цифра или какая-то пропасть. Но мы будем рассматривать только ситуации, когда в канале возможны лишь замены нуля на единицу и наоборот. Причём опять же для простоты будем считать такие замены равновероятными.
Ошибка — это маловероятное событие (а иначе зачем нам такой канал вообще, где одни ошибки?), а значит, вероятность двух ошибок меньше, а трёх уже совсем мала. Мы можем выбрать для себя некоторую приемлемую величину вероятности, очертив границу «это уж точно невозможно». Это позволит нам сказать, что в канале возможно не более, чем ошибок. Это будет характеристикой канала связи.
Для простоты введём следующие обозначения. Пусть данные, которые мы хотим передавать, — это двоичные последовательности фиксированной длины. Чтобы не запутаться в нулях и единицах, будем иногда обозначать их заглавными латинскими буквами (,
,
, …). Что именно передавать, в общем-то неважно, просто с буквами в первое время будет проще работать.
Кодирование и декодирование будем обозначать прямой стрелкой (), а передачу по каналу связи — волнистой стрелкой (
). Ошибки при передаче будем подчёркивать.
Например, пусть мы хотим передавать только сообщения и
. В простейшем случае их можно закодировать нулём и единицей (сюрприз!):
Передача по каналу, в котором возникла ошибка будет записана так:
Цепочки нулей и единиц, которыми мы кодируем буквы, будем называть кодовыми словами. В данном простом случае кодовые слова — это и
.
Код с утроением
Давайте попробуем построить какой-то корректирующий код. Что мы обычно делаем, когда кто-то нас не расслышал? Повторяем дважды:
Правда, это нам не очень поможет. В самом деле, рассмотрим канал с одной возможной ошибкой:
Какие выводы мы можем сделать, когда получили ? Понятно, что раз у нас не две одинаковые цифры, то была ошибка, но вот в каком разряде? Может, в первом, и была передана буква
. А может, во втором, и была передана
.
То есть, получившийся код обнаруживает, но не исправляет ошибки. Ну, тоже неплохо, в общем-то. Но мы пойдём дальше и будем теперь утраивать цифры.
Проверим в деле:
Получили . Тут у нас есть две возможности: либо это
и было две ошибки (в крайних цифрах), либо это
и была одна ошибка. Вообще, вероятность одной ошибки выше вероятности двух ошибок, так что самым правдоподобным будет предположение о том, что передавалась именно буква
. Хотя правдоподобное — не значит истинное, поэтому рядом и стоит вопросительный знак.
Если в канале связи возможна максимум одна ошибка, то первое предположение о двух ошибках становится невозможным и остаётся только один вариант — передавалась буква .
Про такой код говорят, что он исправляет одну ошибку. Две он тоже обнаружит, но исправит уже неверно.
Это, конечно, самый простой код. Кодировать легко, да и декодировать тоже. Ноликов больше — значит передавался ноль, единичек — значит единица.
Если немного подумать, то можно предложить код исправляющий две ошибки. Это будет код, в котором мы повторяем одиночный бит 5 раз.
Расстояния между кодами
Рассмотрим поподробнее код с утроением. Итак, мы получили работающий код, который исправляет одиночную ошибку. Но за всё хорошее надо платить: он кодирует один бит тремя. Не очень-то и эффективно.
И вообще, почему этот код работает? Почему нужно именно утраивать для устранения одной ошибки? Наверняка это всё неспроста.
Давайте подумаем, как этот код работает. Интуитивно всё понятно. Нолики и единички — это две непохожие последовательности. Так как они достаточно длинные, то одиночная ошибка не сильно портит их вид.
Пусть мы передавали , а получили
. Видно, что эта цепочка больше похожа на исходные
, чем на
. А так как других кодовых слов у нас нет, то и выбор очевиден.
Но что значит «больше похоже»? А всё просто! Чем больше символов у двух цепочек совпадает, тем больше их схожесть. Если почти все символы отличаются, то цепочки «далеки» друг от друга.
Можно ввести некоторую величину , равную количеству различающихся цифр в соответствующих разрядах цепочек
и
. Эту величину называют расстоянием Хэмминга. Чем больше это расстояние, тем меньше похожи две цепочки.
Например, , так как все цифры в соответствующих позициях равны, а вот
.
Расстояние Хэмминга называют расстоянием неспроста. Ведь в самом деле, что такое расстояние? Это какая-то характеристика, указывающая на близость двух точек, и для которой верны утверждения:
- Расстояние между точками неотрицательно и равно нулю только, если точки совпадают.
- Расстояние в обе стороны одинаково.
- Путь через третью точку не короче, чем прямой путь.
Достаточно разумные требования.
Математически это можно записать так (нам это не пригодится, просто ради интереса посмотрим):
.
Предлагаю читателю самому убедиться, что для расстояния Хэмминга эти свойства выполняются.
Окрестности
Таким образом, разные цепочки мы считаем точками в каком-то воображаемом пространстве, и теперь мы умеем находить расстояния между ними. Правда, если попытаться сколько нибудь длинные цепочки расставить на листе бумаги так, чтобы расстояния Хэмминга совпадали с расстояниями на плоскости, мы можем потерпеть неудачу. Но не нужно переживать. Всё же это особое пространство со своими законами. А слова вроде «расстояния» лишь помогают нам рассуждать.
Пойдём дальше. Раз мы заговорили о расстоянии, то можно ввести такое понятие как окрестность. Как известно, окрестность какой-то точки — это шар определённого радиуса с центром в ней. Шар? Какие ещё шары! Мы же о кодах говорим.
Но всё просто. Ведь что такое шар? Это множество всех точек, которые находятся от данной не дальше, чем некоторое расстояние, называемое радиусом. Точки у нас есть, расстояние у нас есть, теперь есть и шары.
Так, скажем, окрестность кодового слова радиуса 1 — это все коды, находящиеся на расстоянии не больше, чем 1 от него, то есть отличающиеся не больше, чем в одном разряде. То есть это коды:
Да, вот так странно выглядят шары в пространстве кодов.
А теперь посмотрите. Это же все возможные коды, которые мы получим в канале в одной ошибкой, если отправим ! Это следует прямо из определения окрестности. Ведь каждая ошибка заставляет цепочку измениться только в одном разряде, а значит удаляет её на расстояние 1 от исходного сообщения.
Аналогично, если в канале возможны две ошибки, то отправив некоторое сообщение , мы получим один из кодов, который принадлежит окрестности
радиусом 2.
Тогда всю нашу систему декодирования можно построить так. Мы получаем какую-то цепочку нулей и единиц (точку в нашей новой терминологии) и смотрим, в окрестность какого кодового слова она попадает.
Сколько ошибок может исправить код?
Чтобы код мог исправлять больше ошибок, окрестности должны быть как можно шире. С другой стороны, они не должны пересекаться. Иначе если точка попадёт в область пересечения, непонятно будет, к какой окрестности её отнести.
В коде с удвоением между кодовыми словами и
расстояние равно 2 (оба разряда различаются). А значит, если мы построим вокруг них шары радиуса 1, то они будут касаться. Это значит, точка касания будет принадлежать обоим шарам и непонятно будет, к какому из них её отнести.
Именно это мы и получали. Мы видели, что есть ошибка, но не могли её исправить.
Что интересно, точек касания в нашем странном пространстве у шаров две — это коды и
. Расстояния от них до центров равны единице. Конечно же, в обычно геометрии такое невозможно, поэтому рисунки — это просто условность для более удобного рассуждения.
В случае кода с утроением, между шарами будет зазор.
Минимальный зазор между шарами равен 1, так как у нас расстояния всегда целые (ну не могут же две цепочки отличаться в полутора разрядах).
В общем случае получаем следующее.
Этот очевидный результат на самом деле очень важен. Он означает, что код с минимальным кодовым расстоянием будет успешно работать в канале с
ошибками, если выполняется соотношение
Полученное равенство позволяет легко определить, сколько ошибок будет исправлять тот или иной код. А сколько код ошибок может обнаружить? Рассуждения такие же. Код обнаруживает ошибок, если в результате не получится другое кодовое слово. То есть, кодовые слова не должны находиться в окрестностях радиуса
других кодовых слов. Математически это записывается так:
Рассмотрим пример. Пусть мы кодируем 4 буквы следующим образом.
Чтобы найти минимальное расстояние между различными кодовыми словами, построим таблицу попарных расстояний.
| A | B | C | D | |
|---|---|---|---|---|
| A | — | 3 | 3 | 4 |
| B | 3 | — | 4 | 3 |
| C | 3 | 4 | — | 3 |
| D | 4 | 3 | 3 | — |
Минимальное расстояние , а значит
, откуда получаем, что такой код может исправить до
ошибок. Обнаруживает же он две ошибки.
Чтобы декодировать полученное сообщение, посмотрим, к какому символу оно ближе всего.
Минимальное расстояние получилось для символа , значит вероятнее всего передавался именно он:
Итак, этот код исправляет одну ошибку, как и код с утроением. Но он более эффективен, так как в отличие от кода с утроением здесь кодируется уже 4 символа.
Таким образом, основная проблема при построении такого рода кодов — так расположить кодовые слова, чтобы они были как можно дальше друг от друга, и их было побольше.
Для декодирования можно было бы использовать таблицу, в которой указывались бы все возможные принимаемые сообщения, и кодовые слова, которым они соответствуют. Но такая таблица получилась бы очень большой. Даже для нашего маленького кода, который выдаёт 5 двоичных цифр, получилось бы варианта возможных принимаемых сообщений. Для более сложных кодов таблица будет значительно больше.
Попробуем придумать способ коррекции сообщения без таблиц. Мы всегда сможем найти полезное применение освободившейся памяти.
Интерлюдия: поле GF(2)
Для изложения дальнейшего материала нам потребуются матрицы. А при умножении матриц, как известно мы складываем и перемножаем числа. И тут есть проблема. Если с умножением всё более-менее хорошо, то как быть со сложением? Из-за того, что мы работаем только с одиночными двоичными цифрами, непонятно, как сложить 1 и 1, чтобы снова получилась одна двоичная цифра. Значит вместо классического сложения нужно использовать какое-то другое.
Введём операцию сложения как сложение по модулю 2 (хорошо известный программистам XOR):
Умножение будем выполнять как обычно. Эти операции на самом деле введены не абы как, а чтобы получилась система, которая в математике называется полем. Поле — это просто множество (в нашем случае из 0 и 1), на котором так определены сложение и умножение, чтобы основные алгебраические законы сохранялись. Например, чтобы основные идеи, касающиеся матриц и систем уравнений по-прежнему были верны. А вычитание и деление мы можем ввести как обратные операции.
Множество из двух элементов с операциями, введёнными так, как мы это сделали, называется полем Галуа GF(2). GF — это Galois field, а 2 — количество элементов.
У сложения есть несколько очень полезных свойств, которыми мы будем пользоваться в дальнейшем.
Это свойство прямо следует из определения.
А в этом можно убедиться, прибавив к обеим частям равенства. Это свойство, в частности означает, что мы можем переносить в уравнении слагаемые в другую сторону без смены знака.
Проверяем корректность
Вернёмся к коду с утроением.
Для начала просто решим задачу проверки, были ли вообще ошибки при передаче. Как видно, из самого кода, принятое сообщение будет кодовым словом только тогда, когда все три цифры равны между собой.
Пусть мы приняли вектор-строку из трёх цифр. (Стрелочки над векторами рисовать не будем, так как у нас почти всё — это вектора или матрицы.)
Математически равенство всех трёх цифр можно записать как систему:
Или, если воспользоваться свойствами сложения в GF(2), получаем
В матричном виде эта система будет иметь вид
Транспонирование здесь нужно потому, что — это вектор-строка, а не вектор-столбец. Иначе мы не могли бы умножать его справа на матрицу.
Будем называть матрицу проверочной матрицей. Если полученное сообщение — это корректное кодовое слово (то есть, ошибки при передаче не было), то произведение проверочной матрицы на это сообщение будет равно нулевому вектору.
Умножение на матрицу — это гораздо более эффективно, чем поиск в таблице, но у нас на самом деле есть ещё одна таблица — это таблица кодирования. Попробуем от неё избавиться.
Кодирование
Итак, у нас есть система для проверки
Её решения — это кодовые слова. Собственно, мы систему и строили на основе кодовых слов. Попробуем теперь решить обратную задачу. По системе (или, что то же самое, по матрице ) найдём кодовые слова.
Правда, для нашей системы мы уже знаем ответ, поэтому, чтобы было интересно, возьмём другую матрицу:
Соответствующая система имеет вид:
Чтобы найти кодовые слова соответствующего кода нужно её решить.
В силу линейности сумма двух решений системы тоже будет решением системы. Это легко доказать. Если и
— решения системы, то для их суммы верно
что означает, что она тоже — решение.
Поэтому если мы найдём все линейно независимые решения, то с их помощью можно получить вообще все решения системы. Для этого просто нужно найти их всевозможные суммы.
Выразим сперва все зависимые слагаемые. Их столько же, сколько и уравнений. Выражать надо так, чтобы справа были только независимые. Проще всего выразить .
Если бы нам не так повезло с системой, то нужно было бы складывая уравнения между собой получить такую систему, чтобы какие-то три переменные встречались по одному разу. Ну, или воспользоваться методом Гаусса. Для GF(2) он тоже работает.
Чтобы получить все линейно независимые решения, приравниваем каждую из зависимых переменных к единице по очереди.
Всевозможные суммы этих независимых решений (а именно они и будут кодовыми векторами) можно получить так:
где равны либо нулю или единице. Так как таких коэффициентов два, то всего возможно
сочетания.
Но посмотрите! Формула, которую мы только что получили — это же снова умножение матрицы на вектор.
Строчки здесь — линейно независимые решения, которые мы получили. Матрица называется порождающей. Теперь вместо того, чтобы сами составлять таблицу кодирования, мы можем получать кодовые слова простым умножением на матрицу:
Найдём кодовые слова для этого кода. (Не забываем, что длина исходных сообщений должна быть равна 2 — это количество найденных решений.)
Итак, у нас есть готовый код, обнаруживающий ошибки. Проверим его в деле. Пусть мы хотим отправить 01 и у нас произошла ошибка при передаче. Обнаружит ли её код?
А раз в результате не нулевой вектор, значит код заподозрил неладное. Провести его не удалось. Ура, код работает!
Для кода с утроением, кстати, порождающая матрица выглядит очень просто:
Подобные коды, которые можно порождать и проверять матрицей называются линейными (бывают и нелинейные), и они очень широко применяются на практике. Реализовать их довольно легко, так как тут требуется только умножение на константную матрицу.
Ошибка по синдрому
Ну хорошо, мы построили код обнаруживающий ошибки. Но мы же хотим их исправлять!
Для начала введём такое понятие, как вектор ошибки. Это вектор, на который отличается принятое сообщение от кодового слова. Пусть мы получили сообщение , а было отправлено кодовое слово
. Тогда вектор ошибки по определению
Но в странном мире GF(2), где сложение и вычитание одинаковы, будут верны и соотношения:
В силу особенностей сложения, как читатель сам может легко убедиться, в векторе ошибки на позициях, где произошла ошибка будет единица, а на остальных ноль.
Как мы уже говорили раньше, если мы получили сообщение с ошибкой, то
. Но ведь векторов, не равных нулю много! Быть может то, какой именно ненулевой вектор мы получили, подскажет нам характер ошибки?
Назовём результат умножения на проверочную матрицу синдромом:
И заметим следующее
Это означает, что для ошибки синдром будет таким же, как и для полученного сообщения.
Разложим все возможные сообщения, которые мы можем получить из канала связи, по кучкам в зависимости от синдрома. Тогда из последнего соотношения следует, что в каждой кучке будут вектора с одной и той же ошибкой. Причём вектор этой ошибки тоже будет в кучке. Вот только как его узнать?
А очень просто! Помните, мы говорили, что у нескольких ошибок вероятность ниже, чем у одной ошибки? Руководствуясь этим соображением, наиболее правдоподобным будет считать вектором ошибки тот вектор, у которого меньше всего единиц. Будем называть его лидером.
Давайте посмотрим, какие синдромы дают всевозможные 5-элементные векторы. Сразу сгруппируем их и подчеркнём лидеров — векторы с наименьшим числом единиц.
В принципе, для корректирования ошибки достаточно было бы хранить таблицу соответствия синдрома лидеру.
Обратите внимание, что в некоторых строчках два лидера. Это значит для для данного синдрома два паттерна ошибки равновероятны. Иными словами, код обнаружил две ошибки, но исправить их не может.
Лидеры для всех возможных одиночных ошибок находятся в отдельных строках, а значит код может исправить любую одиночную ошибку. Ну, что же… Попробуем в этом убедиться.
Вектор ошибки равен , а значит ошибка в третьем разряде. Как мы и загадали.
Ура, всё работает!
Что же дальше?
Чтобы попрактиковаться, попробуйте повторить рассуждения для разных проверочных матриц. Например, для кода с утроением.
Логическим продолжением изложенного был бы рассказ о циклических кодах — чрезвычайно интересном подклассе линейных кодов, обладающим замечательными свойствами. Но тогда, боюсь, статья уж очень бы разрослась.
Если вас заинтересовали подробности, то можете почитать замечательную книжку Аршинова и Садовского «Коды и математика». Там изложено гораздо больше, чем представлено в этой статье. Если интересует математика кодирования — то поищите «Теория и практика кодов, контролирующих ошибки» Блейхута. А вообще, материалов по этой теме довольно много.
Надеюсь, когда снова будет свободное время, напишу продолжение, в котором расскажу про циклические коды и покажу пример программы для кодирования и декодирования. Если, конечно, почтенной публике это интересно.
источники:
http://studref.com/365851/tehnika/dekodirovanie_lineynyh_kodov
http://habr.com/ru/post/328202/
Реферат Отчет 38 с., 3 главы, 22 рис., 2 табл., 16 источников, 4 прил видео стеганография, стеганография mpeg, сокрытие информации в видео, встраивание и извлечение информации, дискретное косинусное преобразование, помехоустойчивое кодирование, циклические
Построение таблицы синдромов ошибок
|
Скачать 318,6 Kb.
|
- Навигация по данной странице:
- Декодирование и исправление ошибок
Построение таблицы синдромов ошибок
Перед тем как начать декодирование, необходимо построить таблицу синдромов ошибок, с помощью которой будет происходить исправление ошибок. Для этого нужно знать количество ошибок, которое двоичный циклический 


где 

Минимальное кодовое расстояние 



Таблица 1.1
Кодовые слова двоичного циклического (7,4)-кода (
|
0000000 |
0100111 |
1000101 |
1100010 |
|
0001011 |
0101100 |
1001110 |
1101001 |
|
0010110 |
0110001 |
1010011 |
1110100 |
|
0011101 |
0111010 |
1011000 |
1111111 |
Так как двоичный циклический (7,4)-код исправляет всего одну ошибку, то общее количество многочленов ошибок равно длине кодового слова 

Таблица 1.2
Синдромы однократных ошибок двоичного циклического (7,4)-кода с порождающим многочленом 
|
Ошибка |
Синдром |
|
0000001 |
001 |
|
0000010 |
010 |
|
0000100 |
100 |
|
0001000 |
011 |
|
0010000 |
110 |
|
0100000 |
111 |
|
1000000 |
101 |
Декодирование и исправление ошибок
Декодирование двоичного циклического 

-
Вычисляется синдром ошибки с помощью алгоритма деления Евклида, описанном в 1.2.1.1.
-
Если синдром нулевой, то кодовое слово не содержит ошибок. Если синдром ненулевой, то определятся ошибочный бит с помощью таблицы синдромов и исправляется.
-
Так как кодирование систематическое, то можно просто отсечь проверочную часть длиныи получить декодированное информационное слово.
Ниже представлен пример декодирования кодового слова (0010011) с помощью двоичного циклического (7,4)-кода с порождающим многочленом 
-
Находим остаток от деления (синдром ошибки) с помощью алгоритма деления Евклида
0
0
1
0
0
1
1
=
0
0
1
0
1
1
0
=
1
0
1
=
-
Синдром не равен нулю, поэтому находим синдром в таблице синдромов (табл. 1.2) и соответствующий ему ошибочный бит (1000000).
-
Исправляем ошибочный бит и получаем правильное кодовое слово (1010011). Отсекаем проверочную часть и получаем информационное слово (1010).
-
Каталог: data -> 2014
2014 -> Программа дисциплины для направления/ специальности подготовки бакалавра/ магистра/ специалиста
2014 -> «Особенности реализации личностно-ориентированного подхода в профессиональной подготовке студентов высших учебных заведений»
2014 -> Программа «Управление образованием»
2014 -> Кадровая политика вуза
2014 -> Баврина Анна Петровна профессиональная мотивация преподавателей вуза (на примере нгма) Выпускная квалификационная работа по направлению 080200. 68 «Менеджмент» магистранта группы №12учр
2014 -> «Российское общество эпохи реформ Александра ii»
2014 -> «Корпоративная культура средств массовой информации на примере телеканала рен тв»
2014 -> Начиная с восьмидесятых годов двадцатого века тема корпоративной или организационной культуры стала одной из центральных в управленческой литературе. Все больше исследователей посвящают этому феномену свои научные труды
2014 -> Система методического сопровождения педагогов по формированию метапредметных результатов в условиях подготовки и введения Федеральных государственных образовательных стандартовСкачать 318,6 Kb.
Поделитесь с Вашими друзьями:
В силу первого предположения, а -1 принадлежит Н и а _1 *а = е. Тогда а- 1 *а*Ь -1 = а _1 *с или Ь -1 = а _1 *с, что означает существование обратного элемента любого элемента Н.
Таким образом, необходимым и достаточным условием того, что непустое подмножество Н элементов группы G образует подгруппу, является выполнение для любых двух элементов а и Ь из Н следующих условий:
Кроме того, следует отметить, что единичный элемент подгруппы всегда совпадает с единичным элементом исходной группы [8].
Очевидно, что подмножество <е>любой группы G, состоящее только из единичного элемента, а также сама группа G удовлетворяют условиям образования подгруппы. Такие подгруппы называются тривиальными подгруппами.
Пусть Н — подгруппа группы G, a g — произвольный фиксированный элемент G. Множество
называется правым смежным классом группы G по подгруппе Н, порождаемым элементом g. Аналогично множество
называется левым смежным классом группы G по подгруппе Н, порождаемым элементом g.
В случае некоммутативной группы G число левых смежных классов группы G по подгруппе Н совпадает с числом правых смежных классов. При этом в общем случае никакой левый смежный класс не совпадает ни с каким правым смежным классом. Исключение составляют так называемые нормальные делители — подгруппы, для любого элемента которых H*g = g*H [10].
Очевидно, что если G — абелева группа, то ее левые смежные классы по подгруппе Н совпадают с правыми. Условимся в случае абелевой группы обозначать смежные классы группы G по подгруппе Н в форме соотношения (2.14).
Пусть Н — подгруппа некоторой конечной группы G.
по подгруппе Н равны: gi*hj = gi*hk. Тогда умножение слева на g;
1 дает равенство hj = hk. Но это противоречит определению подгруппы.
равны: gi*hj = gk*hs. Умножение справа на hj— 1 дает равенство g; = gk*hs*hj
Пусть Н = hn> — подгруппа конечной группы G. Пусть g n ) как векторном пространстве GF n (q).
Таким образом, векторное подпространство GF k (q) кода С разбивает исходное векторное пространство GF n (q) на непересекающиеся смежные классы, определяемые следующим образом:
где а — элемент GF n (q), порождающий смежный класс.
Как было показано в предыдущем пункте этого подпараграфа, число элементов каждого смежного класса совпадает с числом кодовых слов кода С. Иными словами, каждый смежный класс а + С содержит q k элементов. Число всех непересекающихся смежных классов определяется соотношением (2.15) и имеет значение q n
Таким образом, векторное пространство GF n (q) можно представить как объединение множеств:
где a s ), s = 0,1. q n
k — 1 — элементы GF n (q), образующие все различные
(не пересекающиеся) смежные классы.
Будем считать, что в соотношении (2.16) а(°) = 0. Тогда смежный класс а(°) + + С совпадает с кодом С.
Как было показано в предыдущем пункте этого подпараграфа, каждый смежный класс вида (2.16) может быть порожден q k различными элементами (векторами) векторного пространства GF n (q).
Пример 2.1.7. Рассмотрим построение отличных от исходного кода смежных классов двоичного линейного (6, 3)-кода С из примера 2.1.4.
Множество всех кодовых слов в данном случае содержит восемь элементов (векторов) векторного пространства GF 6 (2), которые можно представить в виде двоичных последовательностей длиной не более шести двоичных символов:
Число элементов (векторов) каждого смежного класса соответствует числу q k = 8 кодовых слов кода С.
Пусть, например, а = 000001. Тогда смежный класс а + С будет состоять из следующих элементов (векторов):
Нетрудно проверить, что то же множество векторов может быть получено при а = 001100, 010010, 011111, 100111,101010,110100,111001. То есть при любом другом отличном от исходного порождающего элемента а значении, принадлежащем указанному смежному классу.
Согласно соотношению (2.16), число не пересекающихся смежных классов в этом случае: q n
k = 8 (в следующем примере мы укажем их все). Все остальные (отличные от самого кода С) смежные классы могут быть получены, например, при следующих значениях порождающего элемента а:
При этом каждый смежный класс может быть образован, помимо указанных, семью другими значениями вектора а из GF 6 (2), принадлежащими тому же смежному классу.
Любой элемент (вектор) каждого смежного класса, как и сам смежный класс, может быть получен восемью различными способами как а + с для восьми различных значений порождающего элемента а и всех восьми кодовых слов с кода С. Например, элемент 111001 рассмотренного выше в этом примере смежного класса, порожденного элементом а = 000001, может быть получен как а + с для значений а = 000001, 001100, 010010, 011111, 100111, 101010, 110100, 111001 и с = 111000, 110101, 101011, 100110, 011110, 010011, 001101, 000000 соответственно.
4. Пусть С — линейный (л, к)-код над GF(q) и v = с + е — вектор принятого сообщения.
Как было показано выше в этом подпараграфе, вектор v всегда принадлежит одному из q n
k не пересекающихся смежных классов вида (2.16). При отсутствии ошибок вектор v принадлежит смежному классу, совпадающему с кодом С. При ненулевом векторе ошибок вектор i/оказывается в другом смежном классе а + С (пока будем считать, что вес вектора ошибок не превосходит максимального числа t исправляемых кодом ошибок).
Принимая вектор е за порождающий элемент смежного класса е + С, по известному вектору v мы можем определить q k возможных значений вектора е. Очевидно, наиболее вероятным является значение е наименьшего веса.
Элемент (вектор) минимального веса в смежном классе а + С называется лидером смежного класса а + С.
Если в смежном классе а + С несколько векторов имеют минимальный вес, то в качестве лидера смежного класса выбирается любой из них. Таким образом, вектор ошибок принимается равным лидеру смежного класса, которому принадлежит принятый вектор v.
В этом случае аппаратная реализация декодера основана на так называемом табличном методе и требует хранения в памяти устройства всех смежных классов и их лидеров. Подобного рода декодер даже при небольшой длине кода требует значительных аппаратных затрат. Например, для рассмотренного в примерах 2.1.4 и 2.1.7 двоичного линейного (6, 3)-кода требуется хранить в памяти декодера q n
k = 8 смежных классов по q k = 8 двоичных векторов длины п = 6 символов.
Однако табличный декодер может быть несколько упрощен.
Пусть Н — проверочная матрица линейного (л, /с)-кода С. Тогда матрица-строка s(y) = у-Н т размера 1 х к называется синдромом вектора у.
Пусть у = v = с + е — вектор принятого сообщения. Тогда, в силу соотношения (2.10), s(y) = s(e) и, стало быть, равенство нулю s(v) означает принадлежность вектора v коду С. Это в свою очередь означает отсутствие ошибок вектора v. Пока будем считать, что вес вектора ошибок не превосходит максимального числа t исправляемых кодом ошибок. К этому вопросу мы еще вернемся ниже, в конце этого подпараграфа.
Пусть С — линейный (л, к)-код над GF(q), а у и z — два вектора векторного пространства GF n (q).
Очевидно, что s(y) = s(z) тогда и только тогда, когда у-Н т = z-H T или (у — z) х х Н т = 0. Это означает, что вектор у — z принадлежит С. Тогда y-z = Ck- некоторое кодовое слово кода С. Последнее равенство выполняется и в том случае,
если у = а + CiVz = а + Cj, где с,- — су = с*, а — некоторый вектор GF n (q). Равенство синдромов векторов у и z означает принадлежность обоих векторов одному смежному классу.
Таким образом, в силу равенства синдромов s(v) и s(e), вектор v принятого сообщения и вектор ошибок е всегда принадлежат одному смежному классу и по известному синдрому s(v) можно однозначно определить лидер соответствующего смежного класса.
Теперь мы можем описать один из возможных алгоритмов декодирования линейных кодов.
- 1. Определить синдром s(v) принятого сообщения v.
- 2. По известному синдрому s[v) определить соответствующий лидер смежного класса, синдром которого совпадает с s(v).
- 3. Определить исходное кодовое слово с согласно соотношению (2.13) как c-v-e.
Аппаратная реализация декодера в этом случае требует хранения q k синдромов длины п — к (/-ичных символов и q k соответствующих им лидеров смежных классов длины п q-ичных символов в памяти устройства.
Такой метод декодирования называется декодированием линейных кодов по лидерам смежных классов.
Пример 2.1.8. Рассмотрим снова двоичный линейный (6, 3)-код из примеров 2.1.4 и 2.1.7.
В таблице 2.1 показаны смежные классы, лидеры смежных классов и соответствующие им синдромы рассматриваемого кода. Во избежание громоздкости элементы смежных классов представлены соответствующими десятичными значениями. Жирным шрифтом выделены значения лидеров смежных классов.
Лидер смежного класса
< 1, 12, 18,31,39, 42, 52, 57 >
< 2, 15, 17, 28, 36,41,55, 58 >
< 4, 9, 23, 26, 34,47, 49, 60 >
- 001010
- 010100
- 100001
Нетрудно убедиться в том, что синдром любого элемента каждого смежного класса совпадает с синдромом лидера этого смежного класса.
Как видно из таблицы 2.1, в данном случае лидеры смежных классов представлены всеми возможными двоичными векторами веса 1. Эти векторы определены однозначно (в каждом смежном классе только один такой вектор). Таким образом, в случае одиночной ошибки существует единственным образом определяемый синдром, позволяющий однозначно определить вектор ошибки. Поэтому рассмотренный линейный (6,3)-код позволяет гарантированно исправлять одиночную ошибку.
Кроме того, в одном (последнем) смежном классе три лидера веса 2. Это позволяет с небольшой (1/3) вероятностью декодировать двойную ошибку (при условии, что вероятности всех векторов принимаемых сообщений с двойной ошибкой равны).
Очевидно, избыточность рассмотренного в примерах 2.1.4, 2.1.7 и 2.1.8 двоичного линейного (6, 3)-кода немного превышает накладываемые на него корректирующие свойства, так как помимо достаточных для декодирования лидеров смежных классов веса 1 в одном из смежных классов имеют место лидеры веса 2.
Если в качестве лидеров q n
k смежных классов кода удается взять векторы веса t и менее и только их, то код называется совершенным кодом. Если же в качестве лидеров q n
k смежных классов кода удается взять все необходимые для исправления не менее t ошибок векторы веса t и менее, а также несколько векторов веса t + 1, то код называется квазисовершенным кодом.
Проще говоря, у совершенных кодов избыточности «ровно столько, сколько нужно» для исправления не менее чем t ошибок кодового слова.
Возвращаясь к примеру 2.1.4, отметим, что в случае двоичного линейного
- (5,3)-кода вообще нельзя определить однозначно лидеры смежных классов веса
- 1. Пусть, например, проверочная матрица (5,3)-кода имеет вид:
Тогда порождающая матрица:
В этом случае лидер смежного класса веса 1 будет однозначно определен только в одном смежном классе, отличном от смежного класса самого кода. В двух других смежных классах будет по два лидера веса 1. В смежном классе, совпадающем с кодом, также будут два лидера веса 2. Таким образом, данный код не может исправлять одиночную ошибку кодового слова.
Этот вывод подтверждается неравенством (2.5), так как минимальное расстояние (5, 3)-кода равно двум и, следовательно, ни одно целое положительное значение t исправляемых кодом ошибок данному неравенству не удовлетворяет.
Таким образом, при длине информационного сообщения к = 3 двоичных символа и длине проверочной последовательности г=п-к = 2 символа код вообще не позволяет исправлять одиночную ошибку кодового слова, а при длине г — 3 символа уже оказывается не совершенным (хотя и квазисовершенным).
Следует отметить, что совершенные коды, равно как и квазисовершенные, для некоторых значений п и к вообще могут не существовать [10]. Далее мы рассмотрим несколько видов кодов из класса линейных кодов, конструкция которых часто позволяет получить квазисовершенный или даже совершенный код.
Выше мы считали, что вес вектора ошибок не превосходит значение t исправляемых кодом ошибок, так как восстановление исходного кодового слова возможно только в этом случае. В противном случае исходное кодовое слово и принятый вектор могут попасть в один смежный класс, и восстановление кодового слова будет невозможно. Таким образом, число ошибок, превышающее корректирующую способность кода, приводит к ошибочному декодированию.
Если же число ошибок превосходит t и принятый вектор попадает в смежный класс, отличный от смежного класса кода, то декодирование возможно лишь с некоторой (обычно небольшой) вероятностью. При этом возможны два способа декодирования:
- — декодирование любого полученного кодового слова в ближайшее кодовое слово;
- — декодирование только кодовых слов, число ошибок которых не превосходит максимально возможное для данного кода число ошибок t, если число ошибок превышает t, происходит отказ от декодирования.
В первом случае декодер называется полным декодером, а во втором — неполным декодером.
Очевидно, что по сравнению с неполным декодером полный декодер чаще декодирует неправильно. Поэтому полный декодер используется обычно только в тех случаях, когда лучше «угадывать» сообщение, чем вообще не иметь никакой оценки.
В силу указанных особенностей мы будем рассматривать только неполные декодеры.
Метод декодирования линейных кодов по лидерам смежных классов является общим для всех линейных кодов. При этом вполне очевидно, что этот метод связан с трудоемким процессом определения лидеров смежных классов.
Например, для линейного (31, 26)-кода над GF(2) требуется определить 32 смежных класса по 67108864 вектора длины 31 в каждом и найти лидеры каждого смежного класса.
Таким образом, метод декодирования линейных кодов по лидерам смежных классов в общем случае не является приемлемым.
Однако мы можем заранее определить некоторый удобный метод декодирования и на его основе построить линейный код специального вида.
Корректирующие коды «на пальцах»
Корректирующие (или помехоустойчивые) коды — это коды, которые могут обнаружить и, если повезёт, исправить ошибки, возникшие при передаче данных. Даже если вы ничего не слышали о них, то наверняка встречали аббревиатуру CRC в списке файлов в ZIP-архиве или даже надпись ECC на планке памяти. А кто-то, может быть, задумывался, как так получается, что если поцарапать DVD-диск, то данные всё равно считываются без ошибок. Конечно, если царапина не в сантиметр толщиной и не разрезала диск пополам.
Как нетрудно догадаться, ко всему этому причастны корректирующие коды. Собственно, ECC так и расшифровывается — «error-correcting code», то есть «код, исправляющий ошибки». А CRC — это один из алгоритмов, обнаруживающих ошибки в данных. Исправить он их не может, но часто это и не требуется.
Давайте же разберёмся, что это такое.
Для понимания статьи не нужны никакие специальные знания. Достаточно лишь понимать, что такое вектор и матрица, как они перемножаются и как с их помощью записать систему линейных уравнений.
Внимание! Много текста и мало картинок. Я постарался всё объяснить, но без карандаша и бумаги текст может показаться немного запутанным.
Каналы с ошибкой
Разберёмся сперва, откуда вообще берутся ошибки, которые мы собираемся исправлять. Перед нами стоит следующая задача. Нужно передать несколько блоков данных, каждый из которых кодируется цепочкой двоичных цифр. Получившаяся последовательность нулей и единиц передаётся через канал связи. Но так сложилось, что реальные каналы связи часто подвержены ошибкам. Вообще говоря, ошибки могут быть разных видов — может появиться лишняя цифра или какая-то пропасть. Но мы будем рассматривать только ситуации, когда в канале возможны лишь замены нуля на единицу и наоборот. Причём опять же для простоты будем считать такие замены равновероятными.
Ошибка — это маловероятное событие (а иначе зачем нам такой канал вообще, где одни ошибки?), а значит, вероятность двух ошибок меньше, а трёх уже совсем мала. Мы можем выбрать для себя некоторую приемлемую величину вероятности, очертив границу «это уж точно невозможно». Это позволит нам сказать, что в канале возможно не более, чем ошибок. Это будет характеристикой канала связи.
Для простоты введём следующие обозначения. Пусть данные, которые мы хотим передавать, — это двоичные последовательности фиксированной длины. Чтобы не запутаться в нулях и единицах, будем иногда обозначать их заглавными латинскими буквами (, , , …). Что именно передавать, в общем-то неважно, просто с буквами в первое время будет проще работать.
Кодирование и декодирование будем обозначать прямой стрелкой (), а передачу по каналу связи — волнистой стрелкой (). Ошибки при передаче будем подчёркивать.
Например, пусть мы хотим передавать только сообщения и . В простейшем случае их можно закодировать нулём и единицей (сюрприз!):
Передача по каналу, в котором возникла ошибка будет записана так:
Цепочки нулей и единиц, которыми мы кодируем буквы, будем называть кодовыми словами. В данном простом случае кодовые слова — это и .
Код с утроением
Давайте попробуем построить какой-то корректирующий код. Что мы обычно делаем, когда кто-то нас не расслышал? Повторяем дважды:
Правда, это нам не очень поможет. В самом деле, рассмотрим канал с одной возможной ошибкой:
Какие выводы мы можем сделать, когда получили ? Понятно, что раз у нас не две одинаковые цифры, то была ошибка, но вот в каком разряде? Может, в первом, и была передана буква . А может, во втором, и была передана .
То есть, получившийся код обнаруживает, но не исправляет ошибки. Ну, тоже неплохо, в общем-то. Но мы пойдём дальше и будем теперь утраивать цифры.
Проверим в деле:
Получили . Тут у нас есть две возможности: либо это и было две ошибки (в крайних цифрах), либо это и была одна ошибка. Вообще, вероятность одной ошибки выше вероятности двух ошибок, так что самым правдоподобным будет предположение о том, что передавалась именно буква . Хотя правдоподобное — не значит истинное, поэтому рядом и стоит вопросительный знак.
Если в канале связи возможна максимум одна ошибка, то первое предположение о двух ошибках становится невозможным и остаётся только один вариант — передавалась буква .
Про такой код говорят, что он исправляет одну ошибку. Две он тоже обнаружит, но исправит уже неверно.
Это, конечно, самый простой код. Кодировать легко, да и декодировать тоже. Ноликов больше — значит передавался ноль, единичек — значит единица.
Если немного подумать, то можно предложить код исправляющий две ошибки. Это будет код, в котором мы повторяем одиночный бит 5 раз.
Расстояния между кодами
Рассмотрим поподробнее код с утроением. Итак, мы получили работающий код, который исправляет одиночную ошибку. Но за всё хорошее надо платить: он кодирует один бит тремя. Не очень-то и эффективно.
И вообще, почему этот код работает? Почему нужно именно утраивать для устранения одной ошибки? Наверняка это всё неспроста.
Давайте подумаем, как этот код работает. Интуитивно всё понятно. Нолики и единички — это две непохожие последовательности. Так как они достаточно длинные, то одиночная ошибка не сильно портит их вид.
Пусть мы передавали , а получили . Видно, что эта цепочка больше похожа на исходные , чем на . А так как других кодовых слов у нас нет, то и выбор очевиден.
Но что значит «больше похоже»? А всё просто! Чем больше символов у двух цепочек совпадает, тем больше их схожесть. Если почти все символы отличаются, то цепочки «далеки» друг от друга.
Можно ввести некоторую величину , равную количеству различающихся цифр в соответствующих разрядах цепочек и . Эту величину называют расстоянием Хэмминга. Чем больше это расстояние, тем меньше похожи две цепочки.
Например, , так как все цифры в соответствующих позициях равны, а вот .
Расстояние Хэмминга называют расстоянием неспроста. Ведь в самом деле, что такое расстояние? Это какая-то характеристика, указывающая на близость двух точек, и для которой верны утверждения:
- Расстояние между точками неотрицательно и равно нулю только, если точки совпадают.
- Расстояние в обе стороны одинаково.
- Путь через третью точку не короче, чем прямой путь.
Достаточно разумные требования.
Математически это можно записать так (нам это не пригодится, просто ради интереса посмотрим):
- .
Предлагаю читателю самому убедиться, что для расстояния Хэмминга эти свойства выполняются.
Окрестности
Таким образом, разные цепочки мы считаем точками в каком-то воображаемом пространстве, и теперь мы умеем находить расстояния между ними. Правда, если попытаться сколько нибудь длинные цепочки расставить на листе бумаги так, чтобы расстояния Хэмминга совпадали с расстояниями на плоскости, мы можем потерпеть неудачу. Но не нужно переживать. Всё же это особое пространство со своими законами. А слова вроде «расстояния» лишь помогают нам рассуждать.
Пойдём дальше. Раз мы заговорили о расстоянии, то можно ввести такое понятие как окрестность. Как известно, окрестность какой-то точки — это шар определённого радиуса с центром в ней. Шар? Какие ещё шары! Мы же о кодах говорим.
Но всё просто. Ведь что такое шар? Это множество всех точек, которые находятся от данной не дальше, чем некоторое расстояние, называемое радиусом. Точки у нас есть, расстояние у нас есть, теперь есть и шары.
Так, скажем, окрестность кодового слова радиуса 1 — это все коды, находящиеся на расстоянии не больше, чем 1 от него, то есть отличающиеся не больше, чем в одном разряде. То есть это коды:
Да, вот так странно выглядят шары в пространстве кодов.
А теперь посмотрите. Это же все возможные коды, которые мы получим в канале в одной ошибкой, если отправим ! Это следует прямо из определения окрестности. Ведь каждая ошибка заставляет цепочку измениться только в одном разряде, а значит удаляет её на расстояние 1 от исходного сообщения.
Аналогично, если в канале возможны две ошибки, то отправив некоторое сообщение , мы получим один из кодов, который принадлежит окрестности радиусом 2.
Тогда всю нашу систему декодирования можно построить так. Мы получаем какую-то цепочку нулей и единиц (точку в нашей новой терминологии) и смотрим, в окрестность какого кодового слова она попадает.
Сколько ошибок может исправить код?
Чтобы код мог исправлять больше ошибок, окрестности должны быть как можно шире. С другой стороны, они не должны пересекаться. Иначе если точка попадёт в область пересечения, непонятно будет, к какой окрестности её отнести.
В коде с удвоением между кодовыми словами и расстояние равно 2 (оба разряда различаются). А значит, если мы построим вокруг них шары радиуса 1, то они будут касаться. Это значит, точка касания будет принадлежать обоим шарам и непонятно будет, к какому из них её отнести.
Именно это мы и получали. Мы видели, что есть ошибка, но не могли её исправить.
Что интересно, точек касания в нашем странном пространстве у шаров две — это коды и . Расстояния от них до центров равны единице. Конечно же, в обычно геометрии такое невозможно, поэтому рисунки — это просто условность для более удобного рассуждения.
В случае кода с утроением, между шарами будет зазор.
Минимальный зазор между шарами равен 1, так как у нас расстояния всегда целые (ну не могут же две цепочки отличаться в полутора разрядах).
В общем случае получаем следующее.
Этот очевидный результат на самом деле очень важен. Он означает, что код с минимальным кодовым расстоянием будет успешно работать в канале с ошибками, если выполняется соотношение
Полученное равенство позволяет легко определить, сколько ошибок будет исправлять тот или иной код. А сколько код ошибок может обнаружить? Рассуждения такие же. Код обнаруживает ошибок, если в результате не получится другое кодовое слово. То есть, кодовые слова не должны находиться в окрестностях радиуса других кодовых слов. Математически это записывается так:
Рассмотрим пример. Пусть мы кодируем 4 буквы следующим образом.
Чтобы найти минимальное расстояние между различными кодовыми словами, построим таблицу попарных расстояний.
| A | B | C | D | |
|---|---|---|---|---|
| A | — | 3 | 3 | 4 |
| B | 3 | — | 4 | 3 |
| C | 3 | 4 | — | 3 |
| D | 4 | 3 | 3 | — |
Минимальное расстояние , а значит , откуда получаем, что такой код может исправить до ошибок. Обнаруживает же он две ошибки.
Чтобы декодировать полученное сообщение, посмотрим, к какому символу оно ближе всего.
Минимальное расстояние получилось для символа , значит вероятнее всего передавался именно он:
Итак, этот код исправляет одну ошибку, как и код с утроением. Но он более эффективен, так как в отличие от кода с утроением здесь кодируется уже 4 символа.
Таким образом, основная проблема при построении такого рода кодов — так расположить кодовые слова, чтобы они были как можно дальше друг от друга, и их было побольше.
Для декодирования можно было бы использовать таблицу, в которой указывались бы все возможные принимаемые сообщения, и кодовые слова, которым они соответствуют. Но такая таблица получилась бы очень большой. Даже для нашего маленького кода, который выдаёт 5 двоичных цифр, получилось бы варианта возможных принимаемых сообщений. Для более сложных кодов таблица будет значительно больше.
Попробуем придумать способ коррекции сообщения без таблиц. Мы всегда сможем найти полезное применение освободившейся памяти.
Интерлюдия: поле GF(2)
Для изложения дальнейшего материала нам потребуются матрицы. А при умножении матриц, как известно мы складываем и перемножаем числа. И тут есть проблема. Если с умножением всё более-менее хорошо, то как быть со сложением? Из-за того, что мы работаем только с одиночными двоичными цифрами, непонятно, как сложить 1 и 1, чтобы снова получилась одна двоичная цифра. Значит вместо классического сложения нужно использовать какое-то другое.
Введём операцию сложения как сложение по модулю 2 (хорошо известный программистам XOR):
Умножение будем выполнять как обычно. Эти операции на самом деле введены не абы как, а чтобы получилась система, которая в математике называется полем. Поле — это просто множество (в нашем случае из 0 и 1), на котором так определены сложение и умножение, чтобы основные алгебраические законы сохранялись. Например, чтобы основные идеи, касающиеся матриц и систем уравнений по-прежнему были верны. А вычитание и деление мы можем ввести как обратные операции.
Множество из двух элементов с операциями, введёнными так, как мы это сделали, называется полем Галуа GF(2). GF — это Galois field, а 2 — количество элементов.
У сложения есть несколько очень полезных свойств, которыми мы будем пользоваться в дальнейшем.
Это свойство прямо следует из определения.
А в этом можно убедиться, прибавив к обеим частям равенства. Это свойство, в частности означает, что мы можем переносить в уравнении слагаемые в другую сторону без смены знака.
Проверяем корректность
Вернёмся к коду с утроением.
Для начала просто решим задачу проверки, были ли вообще ошибки при передаче. Как видно, из самого кода, принятое сообщение будет кодовым словом только тогда, когда все три цифры равны между собой.
Пусть мы приняли вектор-строку из трёх цифр. (Стрелочки над векторами рисовать не будем, так как у нас почти всё — это вектора или матрицы.)
Математически равенство всех трёх цифр можно записать как систему:
Или, если воспользоваться свойствами сложения в GF(2), получаем
В матричном виде эта система будет иметь вид
Транспонирование здесь нужно потому, что — это вектор-строка, а не вектор-столбец. Иначе мы не могли бы умножать его справа на матрицу.
Будем называть матрицу проверочной матрицей. Если полученное сообщение — это корректное кодовое слово (то есть, ошибки при передаче не было), то произведение проверочной матрицы на это сообщение будет равно нулевому вектору.
Умножение на матрицу — это гораздо более эффективно, чем поиск в таблице, но у нас на самом деле есть ещё одна таблица — это таблица кодирования. Попробуем от неё избавиться.
Кодирование
Итак, у нас есть система для проверки
Её решения — это кодовые слова. Собственно, мы систему и строили на основе кодовых слов. Попробуем теперь решить обратную задачу. По системе (или, что то же самое, по матрице ) найдём кодовые слова.
Правда, для нашей системы мы уже знаем ответ, поэтому, чтобы было интересно, возьмём другую матрицу:
Соответствующая система имеет вид:
Чтобы найти кодовые слова соответствующего кода нужно её решить.
В силу линейности сумма двух решений системы тоже будет решением системы. Это легко доказать. Если и — решения системы, то для их суммы верно
что означает, что она тоже — решение.
Поэтому если мы найдём все линейно независимые решения, то с их помощью можно получить вообще все решения системы. Для этого просто нужно найти их всевозможные суммы.
Выразим сперва все зависимые слагаемые. Их столько же, сколько и уравнений. Выражать надо так, чтобы справа были только независимые. Проще всего выразить .
Если бы нам не так повезло с системой, то нужно было бы складывая уравнения между собой получить такую систему, чтобы какие-то три переменные встречались по одному разу. Ну, или воспользоваться методом Гаусса. Для GF(2) он тоже работает.
Чтобы получить все линейно независимые решения, приравниваем каждую из зависимых переменных к единице по очереди.
Всевозможные суммы этих независимых решений (а именно они и будут кодовыми векторами) можно получить так:
где равны либо нулю или единице. Так как таких коэффициентов два, то всего возможно сочетания.
Но посмотрите! Формула, которую мы только что получили — это же снова умножение матрицы на вектор.
Строчки здесь — линейно независимые решения, которые мы получили. Матрица называется порождающей. Теперь вместо того, чтобы сами составлять таблицу кодирования, мы можем получать кодовые слова простым умножением на матрицу:
Найдём кодовые слова для этого кода. (Не забываем, что длина исходных сообщений должна быть равна 2 — это количество найденных решений.)
Итак, у нас есть готовый код, обнаруживающий ошибки. Проверим его в деле. Пусть мы хотим отправить 01 и у нас произошла ошибка при передаче. Обнаружит ли её код?
А раз в результате не нулевой вектор, значит код заподозрил неладное. Провести его не удалось. Ура, код работает!
Для кода с утроением, кстати, порождающая матрица выглядит очень просто:
Подобные коды, которые можно порождать и проверять матрицей называются линейными (бывают и нелинейные), и они очень широко применяются на практике. Реализовать их довольно легко, так как тут требуется только умножение на константную матрицу.
Ошибка по синдрому
Ну хорошо, мы построили код обнаруживающий ошибки. Но мы же хотим их исправлять!
Для начала введём такое понятие, как вектор ошибки. Это вектор, на который отличается принятое сообщение от кодового слова. Пусть мы получили сообщение , а было отправлено кодовое слово . Тогда вектор ошибки по определению
Но в странном мире GF(2), где сложение и вычитание одинаковы, будут верны и соотношения:
В силу особенностей сложения, как читатель сам может легко убедиться, в векторе ошибки на позициях, где произошла ошибка будет единица, а на остальных ноль.
Как мы уже говорили раньше, если мы получили сообщение с ошибкой, то . Но ведь векторов, не равных нулю много! Быть может то, какой именно ненулевой вектор мы получили, подскажет нам характер ошибки?
Назовём результат умножения на проверочную матрицу синдромом:
И заметим следующее
Это означает, что для ошибки синдром будет таким же, как и для полученного сообщения.
Разложим все возможные сообщения, которые мы можем получить из канала связи, по кучкам в зависимости от синдрома. Тогда из последнего соотношения следует, что в каждой кучке будут вектора с одной и той же ошибкой. Причём вектор этой ошибки тоже будет в кучке. Вот только как его узнать?
А очень просто! Помните, мы говорили, что у нескольких ошибок вероятность ниже, чем у одной ошибки? Руководствуясь этим соображением, наиболее правдоподобным будет считать вектором ошибки тот вектор, у которого меньше всего единиц. Будем называть его лидером.
Давайте посмотрим, какие синдромы дают всевозможные 5-элементные векторы. Сразу сгруппируем их и подчеркнём лидеров — векторы с наименьшим числом единиц.
В принципе, для корректирования ошибки достаточно было бы хранить таблицу соответствия синдрома лидеру.
Обратите внимание, что в некоторых строчках два лидера. Это значит для для данного синдрома два паттерна ошибки равновероятны. Иными словами, код обнаружил две ошибки, но исправить их не может.
Лидеры для всех возможных одиночных ошибок находятся в отдельных строках, а значит код может исправить любую одиночную ошибку. Ну, что же… Попробуем в этом убедиться.
Вектор ошибки равен , а значит ошибка в третьем разряде. Как мы и загадали.
Ура, всё работает!
Что же дальше?
Чтобы попрактиковаться, попробуйте повторить рассуждения для разных проверочных матриц. Например, для кода с утроением.
Логическим продолжением изложенного был бы рассказ о циклических кодах — чрезвычайно интересном подклассе линейных кодов, обладающим замечательными свойствами. Но тогда, боюсь, статья уж очень бы разрослась.
Если вас заинтересовали подробности, то можете почитать замечательную книжку Аршинова и Садовского «Коды и математика». Там изложено гораздо больше, чем представлено в этой статье. Если интересует математика кодирования — то поищите «Теория и практика кодов, контролирующих ошибки» Блейхута. А вообще, материалов по этой теме довольно много.
Надеюсь, когда снова будет свободное время, напишу продолжение, в котором расскажу про циклические коды и покажу пример программы для кодирования и декодирования. Если, конечно, почтенной публике это интересно.
http://studref.com/365851/tehnika/dekodirovanie_lineynyh_kodov
http://habr.com/ru/post/328202/





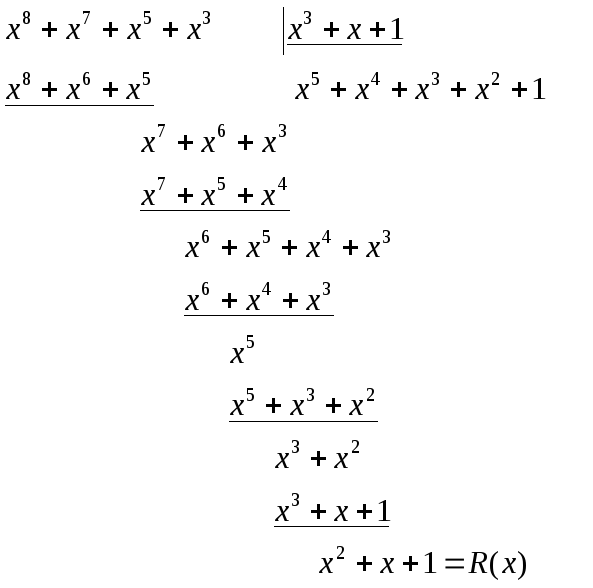
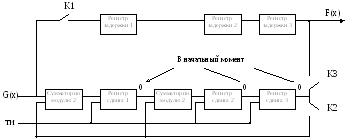



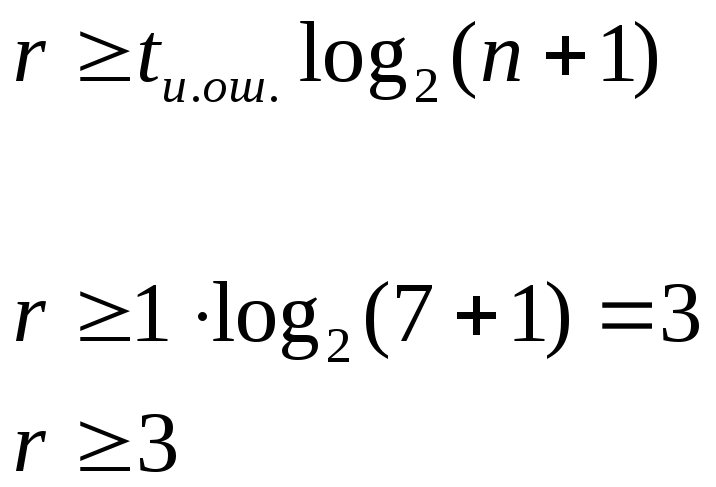




















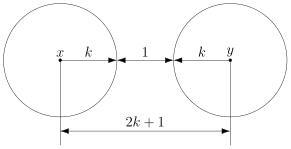

 и получить декодированное информационное слово.
и получить декодированное информационное слово.








