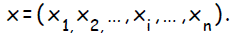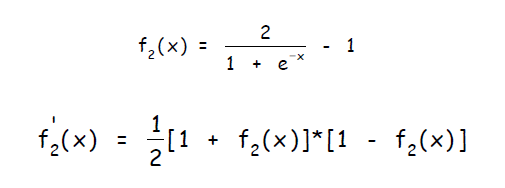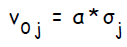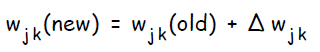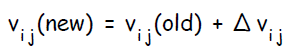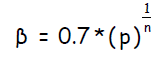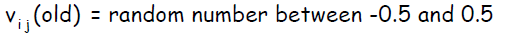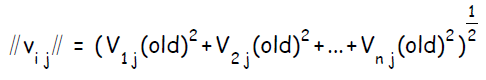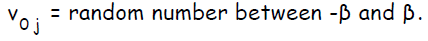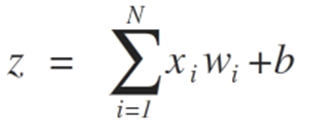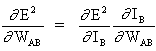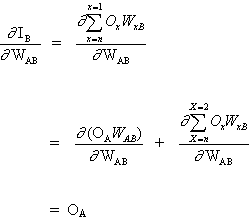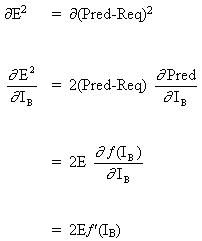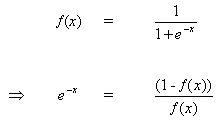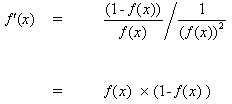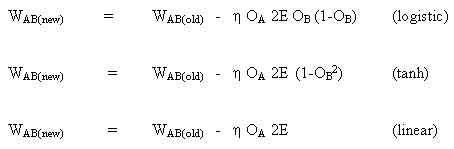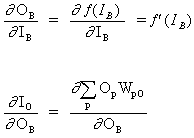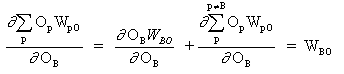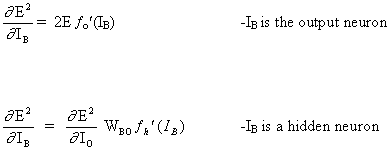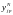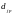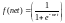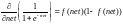Время на прочтение
19 мин
Количество просмотров 287K
Тема нейронных сетей была уже ни раз освещена на хабре, однако сегодня я бы хотел познакомить читателей с алгоритмом обучения многослойной нейронной сети методом обратного распространения ошибки и привести реализацию данного метода.
Сразу хочу оговориться, что не являюсь экспертом в области нейронных сетей, поэтому жду от читателей конструктивной критики, замечаний и дополнений.
Теоретическая часть
Данный материал предполагает знакомство с основами нейронных сетей, однако я считаю возможным ввести читателя в курс темы без излишних мытарств по теории нейронных сетей. Итак, для тех, кто впервые слышит словосочетание «нейронная сеть», предлагаю воспринимать нейронную сеть в качестве взвешенного направленного графа, узлы ( нейроны ) которого расположены слоями. Кроме того, узел одного слоя имеет связи со всеми узлами предыдущего слоя. В нашем случае у такого графа будут иметься входной и выходной слои, узлы которых выполняют роль входов и
выходов соответственно. Каждый узел ( нейрон ) обладает активационной функцией — функцией, ответственной за вычисление сигнала на выходе узла ( нейрона ). Также существует понятие смещения, представляющего из себя узел, на выходе которого всегда появляется единица. В данной статье мы будем рассматривать процесс обучения нейронной сети, предполагающий наличие «учителя», то есть процесс обучения, при котором обучение происходит путем предоставления сети последовательности обучающих примеров с правильными откликами.
Как и в случае с большинством нейронных сетей, наша цель состоит в обучении сети таким образом, чтобы достичь баланса между способностью сети давать верный отклик на входные данные, использовавшиеся в процессе обучения ( запоминания ), и способностью выдавать правильные результаты в ответ на входные данные, схожие, но неидентичные тем, что были использованы при обучении ( принцип обобщения). Обучение сети методом обратного распространения ошибки включает в себя три этапа: подачу на вход данных, с последующим распространением данных в направлении выходов, вычисление и обратное распространение соответствующей ошибки и корректировку весов. После обучения предполагается лишь подача на вход сети данных и распространение их в направлении выходов. При этом, если обучение сети может являться довольно длительным процессом, то непосредственное вычисление результатов обученной сетью происходит очень быстро. Кроме того, существуют многочисленные вариации метода обратного распространения ошибки, разработанные с целью увеличения скорости протекания
процесса обучения.
Также стоит отметить, что однослойная нейронная сеть существенно ограничена в том, обучению каким шаблонам входных данных она подлежит, в то время, как многослойная сеть ( с одним или более скрытым слоем ) не имеет такого недостатка. Далее будет дано описание стандартной нейронной сети с обратным распространением ошибки.
Архитектура
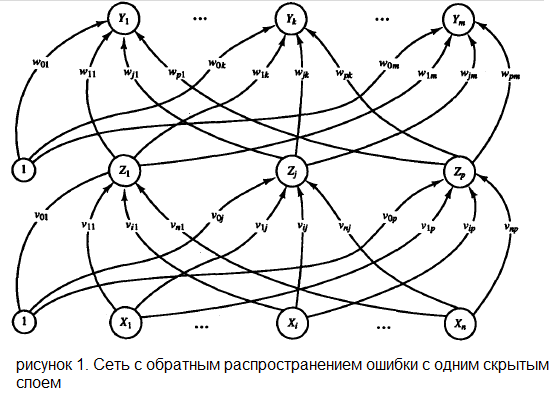
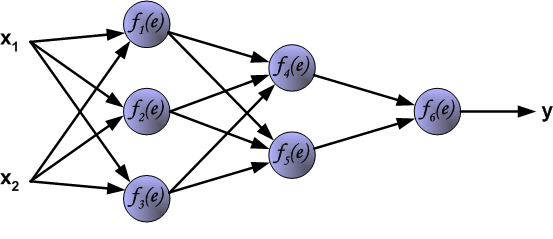
На рисунке 1 показана многослойная нейронная сеть с одним слоем скрытых нейронов ( элементы Z ).
Нейроны, представляющие собой выходы сети ( обозначены 



Описание алгоритма
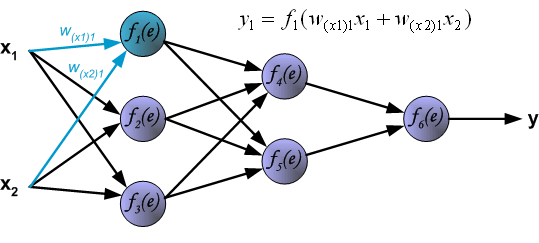
Алгоритм, представленный далее, применим к нейронной сети с одним скрытым слоем, что является допустимой и адекватной ситуацией для большинства приложений. Как уже было сказано ранее, обучение сети включает в себя три стадии: подача на входы сети обучающих данных, обратное распространение ошибки и корректировка весов. В ходе первого этапа каждый входной нейрон 










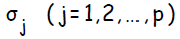

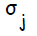
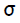
Обозначения:
В алгоритме обучения сети используются следующие обозначения:



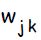



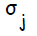
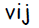




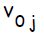


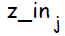
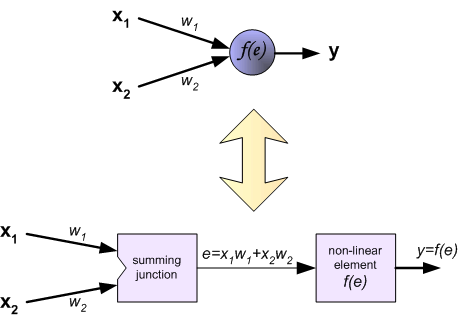
Сигнал на выходе
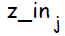




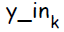


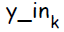

Функция активации
Функция активация в алгоритме обратного распространения ошибки должна обладать несколькими важными характеристиками: непрерывностью, дифференцируемостью и являться монотонно неубывающей. Более того, ради эффективности вычислений, желательно, чтобы ее производная легко находилась. Зачастую, активационная функция также является функцией с насыщением. Одной из наиболее часто используемых активационных функций является бинарная сигмоидальная функция с областью значений в ( 0, 1 ) и определенная как:
Другой широко распространенной активационной функцией является биполярный сигмоид с областью значений ( -1, 1 ) и определенный как:
Алгоритм обучения
Алгоритм обучения выглядит следующим образом:
Шаг 0.
Инициализация весов ( веса всех связей инициализируются случайными небольшими значениями ).
Шаг 1.
До тех пор пока условие прекращения работы алгоритма неверно, выполняются шаги 2 — 9.
Шаг 2.
Для каждой пары { данные, целевое значение } выполняются шаги 3 — 8.
Распространение данных от входов к выходам:
Шаг 3.
Каждый входной нейрон 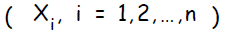

Шаг 4.
Каждый скрытый нейрон 
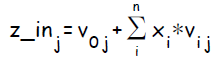
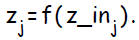
Шаг 5.
Каждый выходной нейрон 

Обратное распространение ошибки:
Шаг 6.
Каждый выходной нейрон 

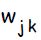



Шаг 7.
Каждый скрытый нейрон 

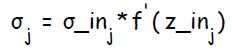
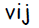

Шаг 8. Изменение весов.
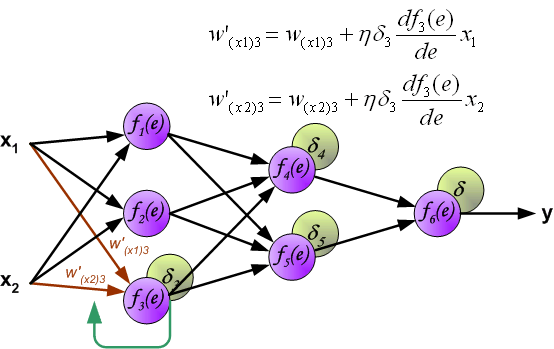
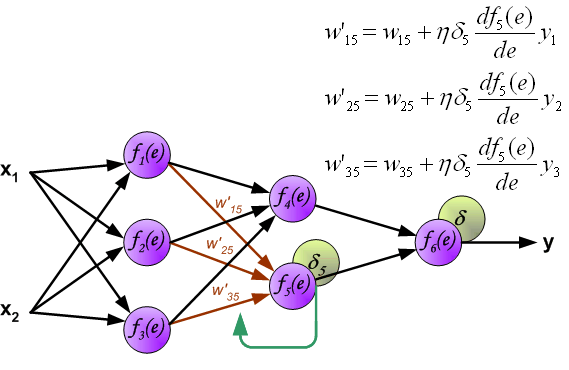
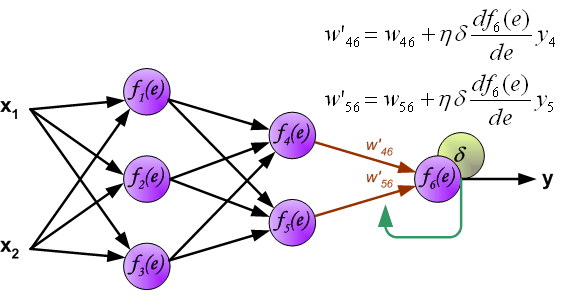
Каждый выходной нейрон 
Каждый скрытый нейрон 
Шаг 9.
Проверка условия прекращения работы алгоритма.
Условием прекращения работы алгоритма может быть как достижение суммарной квадратичной ошибкой результата на выходе сети предустановленного заранее минимума в ходе процесса обучения, так и выполнения определенного количества итераций алгоритма. В основе алгоритма лежит метод под названием градиентный спуск. В зависимости от знака, градиент функции ( в данном случае значение функции — это ошибка, а параметры — это веса связей в сети ) дает направление, в котором значения функции возрастают (или убывают) наиболее стремительно.
Выбор первоначальных весов и смещения
Случайная инициализация. Выбор начальных весов окажет влияние на то, сумеет ли сеть достичь глобального ( или только локального) минимума ошибки, и насколько быстро этот процесс будет происходить. Изменение весов между двумя нейронами связано с производной активационной функции нейрона из последующего слоя и активационной функции нейрона слоя предыдущего. В связи с этим, важно избегать выбора таких начальных весов, которые обнулят активационную функцию или ее производную. Также начальные веса не должны быть слишком большими ( или входные сигнал для каждого скрытого или выходного нейрона скорее всего попадут в регион очень малых значений сигмоида ( регион насыщения ) ). С другой стороны, если начальные веса будут слишком маленькими, то входной сигнал на скрытые или выходные нейроны будет близок к нулю, что также приведет к очень низкой скорости обучения. Стандартная процедура инициализации весов состоит в присвоении им случайных значений в интервале ( -0,5; 0,5). Значения могут быть как положительными, так и отрицательными, так как конечные веса, получающиеся после обучения сети, могут быть обоих знаков. Инициализация Nguyen – Widrow. Представленная далее простая модификация стандартной процедуру инициализации способствует более быстрому обучению: Веса связей скрытых и выходных нейронов, а также смещение выходного слоя инициализируются также, как и в стандартной процедуре — случайными значениями из интервала ( -0,5; 0,5).
Введем обозначения:

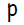
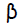
Процедура состоит из следующих простых шагов:
Для каждого скрытого нейрона 
инициализировать его вектор весов ( связей с входными нейронами ):
вычислить
переинициализировать веса:
задать значение смещения:
Практическая часть
Начну с реализации концепции нейрона. Было решено представить нейроны входного слоя базовым классом, а скрытые и выходные как декораторы базового класса. Кроме того, нейрон хранит в себе информацию об исходящих и входящих связях, а также каждый нейрон композиционно имеет в своем составе активационную функцию.
Интерфейс нейрона
/**
* Neuron base class.
* Represents a basic element of neural network, node in the net's graph.
* There are several possibilities for creation an object of type Neuron, different constructors suites for
* different situations.
*/
template <typename T>
class Neuron
{
public:
/**
* A default Neuron constructor.
* - Description: Creates a Neuron; general purposes.
* - Purpose: Creates a Neuron, linked to nothing, with a Linear network function.
* - Prerequisites: None.
*/
Neuron( ) : mNetFunc( new Linear ), mSumOfCharges( 0.0 ) { };
/**
* A Neuron constructor based on NetworkFunction.
* - Description: Creates a Neuron; mostly designed to create an output kind of neurons.
* @param inNetFunc - a network function which is producing neuron's output signal;
* - Purpose: Creates a Neuron, linked to nothing, with a specific network function.
* - Prerequisites: The existence of NetworkFunction object.
*/
Neuron( NetworkFunction * inNetFunc ) : mNetFunc( inNetFunc ), mSumOfCharges( 0.0 ){ };
Neuron( std::vector<NeuralLink<T > *>& inLinksToNeurons, NetworkFunction * inNetFunc ) :
mNetFunc( inNetFunc ),
mLinksToNeurons(inLinksToNeurons),
mSumOfCharges(0.0){ };
/**
* A Neuron constructor based on layer of Neurons.
* - Description: Creates a Neuron; mostly designed to create an input and hidden kinds of neurons.
* @param inNeuronsLinkTo - a vector of pointers to Neurons which is representing a layer;
* @param inNetFunc - a network function which is producing neuron's output signal;
* - Purpose: Creates a Neuron, linked to every Neuron in provided layer.
* - Prerequisites: The existence of std::vector<Neuron *> and NetworkFunction.
*/
Neuron( std::vector<Neuron *>& inNeuronsLinkTo, NetworkFunction * inNetFunc );
virtual ~Neuron( );
virtual std::vector<NeuralLink<T > *>& GetLinksToNeurons( ){ return mLinksToNeurons; };
virtual NeuralLink<T> * at( const int& inIndexOfNeuralLink ) { return mLinksToNeurons[ inIndexOfNeuralLink ]; };
virtual void SetLinkToNeuron( NeuralLink<T> * inNeuralLink ){ mLinksToNeurons.push_back( inNeuralLink ); };
virtual void Input( double inInputData ){ mSumOfCharges += inInputData; };
virtual double Fire( );
virtual int GetNumOfLinks( ) { return mLinksToNeurons.size( ); };
virtual double GetSumOfCharges( );
virtual void ResetSumOfCharges( ){ mSumOfCharges = 0.0; };
virtual double Process( ) { return mNetFunc->Process( mSumOfCharges ); };
virtual double Process( double inArg ){ return mNetFunc->Process( inArg ); };
virtual double Derivative( ){ return mNetFunc->Derivative( mSumOfCharges ); };
virtual void SetInputLink( NeuralLink<T> * inLink ){ mInputLinks.push_back( inLink ); };
virtual std::vector<NeuralLink<T > *>& GetInputLink( ){ return mInputLinks; };
virtual double PerformTrainingProcess( double inTarget );
virtual void PerformWeightsUpdating( );
virtual void ShowNeuronState( );
protected:
NetworkFunction * mNetFunc;
std::vector<NeuralLink<T > *> mInputLinks;
std::vector<NeuralLink<T > *> mLinksToNeurons;
double mSumOfCharges;
};
template <typename T>
class OutputLayerNeuronDecorator : public Neuron<T>
{
public:
OutputLayerNeuronDecorator( Neuron<T> * inNeuron ){ mOutputCharge = 0; mNeuron = inNeuron; };
virtual ~OutputLayerNeuronDecorator( );
virtual std::vector<NeuralLink<T > *>& GetLinksToNeurons( ){ return mNeuron->GetLinksToNeurons( ) ;};
virtual NeuralLink<T> * at( const int& inIndexOfNeuralLink ){ return ( mNeuron->at( inIndexOfNeuralLink ) ) ;};
virtual void SetLinkToNeuron( NeuralLink<T> * inNeuralLink ){ mNeuron->SetLinkToNeuron( inNeuralLink ); };
virtual double GetSumOfCharges( ) { return mNeuron->GetSumOfCharges( ); };
virtual void ResetSumOfCharges( ){ mNeuron->ResetSumOfCharges( ); };
virtual void Input( double inInputData ){ mNeuron->Input( inInputData ); };
virtual double Fire( );
virtual int GetNumOfLinks( ) { return mNeuron->GetNumOfLinks( ); };
virtual double Process( ) { return mNeuron->Process( ); };
virtual double Process( double inArg ){ return mNeuron->Process( inArg ); };
virtual double Derivative( ) { return mNeuron->Derivative( ); };
virtual void SetInputLink( NeuralLink<T> * inLink ){ mNeuron->SetInputLink( inLink ); };
virtual std::vector<NeuralLink<T > *>& GetInputLink( ) { return mNeuron->GetInputLink( ); };
virtual double PerformTrainingProcess( double inTarget );
virtual void PerformWeightsUpdating( );
virtual void ShowNeuronState( ) { mNeuron->ShowNeuronState( ); };
protected:
double mOutputCharge;
Neuron<T> * mNeuron;
};
template <typename T>
class HiddenLayerNeuronDecorator : public Neuron<T>
{
public:
HiddenLayerNeuronDecorator( Neuron<T> * inNeuron ) { mNeuron = inNeuron; };
virtual ~HiddenLayerNeuronDecorator( );
virtual std::vector<NeuralLink<T > *>& GetLinksToNeurons( ){ return mNeuron->GetLinksToNeurons( ); };
virtual void SetLinkToNeuron( NeuralLink<T> * inNeuralLink ){ mNeuron->SetLinkToNeuron( inNeuralLink ); };
virtual double GetSumOfCharges( ){ return mNeuron->GetSumOfCharges( ) ;};
virtual void ResetSumOfCharges( ){mNeuron->ResetSumOfCharges( ); };
virtual void Input( double inInputData ){ mNeuron->Input( inInputData ); };
virtual double Fire( );
virtual int GetNumOfLinks( ){ return mNeuron->GetNumOfLinks( ); };
virtual NeuralLink<T> * ( const int& inIndexOfNeuralLink ){ return ( mNeuron->at( inIndexOfNeuralLink) ); };
virtual double Process( ){ return mNeuron->Process( ); };
virtual double Process( double inArg ){ return mNeuron->Process( inArg ); };
virtual double Derivative( ){ return mNeuron->Derivative( ); };
virtual void SetInputLink( NeuralLink<T> * inLink ){ mNeuron->SetInputLink( inLink ); };
virtual std::vector<NeuralLink<T > *>& GetInputLink( ){ return mNeuron->GetInputLink( ); };
virtual double PerformTrainingProcess( double inTarget );
virtual void PerformWeightsUpdating( );
virtual void ShowNeuronState( ){ mNeuron->ShowNeuronState( ); };
protected:
Neuron<T> * mNeuron;
};
Интерфейс нейронных связей представлен ниже, каждая связь хранит вес и указатель на нейрон:
Интерфейс нейронной связи
template <typename T>
class Neuron;
template <typename T>
class NeuralLink
{
public:
NeuralLink( ) : mWeightToNeuron( 0.0 ),
mNeuronLinkedTo( 0 ),
mWeightCorrectionTerm( 0 ),
mErrorInformationTerm( 0 ),
mLastTranslatedSignal( 0 ){ };
NeuralLink( Neuron<T> * inNeuronLinkedTo, double inWeightToNeuron = 0.0 ) :
mWeightToNeuron( inWeightToNeuron ),
mNeuronLinkedTo( inNeuronLinkedTo ),
mWeightCorrectionTerm( 0 ),
mErrorInformationTerm( 0 ),
mLastTranslatedSignal( 0 ){ };
void SetWeight( const double& inWeight ){ mWeightToNeuron = inWeight; };
const double& GetWeight( ){ return mWeightToNeuron; };
void SetNeuronLinkedTo( Neuron<T> * inNeuronLinkedTo ){ mNeuronLinkedTo = inNeuronLinkedTo; };
Neuron<T> * GetNeuronLinkedTo( ){ return mNeuronLinkedTo; };
void SetWeightCorrectionTerm( double inWeightCorrectionTerm ){ mWeightCorrectionTerm = inWeightCorrectionTerm; };
double GetWeightCorrectionTerm( ){ return mWeightCorrectionTerm; };
void UpdateWeight( ){ mWeightToNeuron = mWeightToNeuron + mWeightCorrectionTerm; };
double GetErrorInFormationTerm( ){ return mErrorInformationTerm; };
void SetErrorInFormationTerm( double inEITerm ){ mErrorInformationTerm = inEITerm; };
void SetLastTranslatedSignal( double inLastTranslatedSignal ){ mLastTranslatedSignal = inLastTranslatedSignal; };
double GetLastTranslatedSignal( ){ return mLastTranslatedSignal; };
protected:
double mWeightToNeuron;
Neuron<T> * mNeuronLinkedTo;
double mWeightCorrectionTerm;
double mErrorInformationTerm;
double mLastTranslatedSignal;
};
Каждая активационная функция наследует от абстрактного класса, реализуя саму функцию и производную:
Интерфейс активационной функции
class NetworkFunction {
public:
NetworkFunction(){};
virtual ~NetworkFunction(){};
virtual double Process( double inParam ) = 0;
virtual double Derivative( double inParam ) = 0;
};
class Linear : public NetworkFunction {
public:
Linear(){};
virtual ~Linear(){};
virtual double Process( double inParam ){ return inParam; };
virtual double Derivative( double inParam ){ return 0; };
};
class Sigmoid : public NetworkFunction {
public:
Sigmoid(){};
virtual ~Sigmoid(){};
virtual double Process( double inParam ){ return ( 1 / ( 1 + exp( -inParam ) ) ); };
virtual double Derivative( double inParam ){ return ( this->Process(inParam)*(1 - this->Process(inParam)) );};
};
class BipolarSigmoid : public NetworkFunction {
public:
BipolarSigmoid(){};
virtual ~BipolarSigmoid(){};
virtual double Process( double inParam ){ return ( 2 / ( 1 + exp( -inParam ) ) - 1 ) ;};
virtual double Derivative( double inParam ){ return ( 0.5 * ( 1 + this->Process( inParam ) ) * ( 1 - this->Process( inParam ) ) ); };
};
За производство нейронов ответственна нейронная фабрика:
Интерфейс нейронной фабрики
template <typename T>
class NeuronFactory
{
public:
NeuronFactory(){};
virtual ~NeuronFactory(){};
virtual Neuron<T> * CreateInputNeuron( std::vector<Neuron<T > *>& inNeuronsLinkTo, NetworkFunction * inNetFunc ) = 0;
virtual Neuron<T> * CreateOutputNeuron( NetworkFunction * inNetFunc ) = 0;
virtual Neuron<T> * CreateHiddenNeuron( std::vector<Neuron<T > *>& inNeuronsLinkTo, NetworkFunction * inNetFunc ) = 0;
};
template <typename T>
class PerceptronNeuronFactory : public NeuronFactory<T>
{
public:
PerceptronNeuronFactory(){};
virtual ~PerceptronNeuronFactory(){};
virtual Neuron<T> * CreateInputNeuron( std::vector<Neuron<T > *>& inNeuronsLinkTo, NetworkFunction * inNetFunc ){ return new Neuron<T>( inNeuronsLinkTo, inNetFunc ); };
virtual Neuron<T> * CreateOutputNeuron( NetworkFunction * inNetFunc ){ return new OutputLayerNeuronDecorator<T>( new Neuron<T>( inNetFunc ) ); };
virtual Neuron<T> * CreateHiddenNeuron( std::vector<Neuron<T > *>& inNeuronsLinkTo, NetworkFunction * inNetFunc ){ return new HiddenLayerNeuronDecorator<T>( new Neuron<T>( inNeuronsLinkTo, inNetFunc ) ); };
};
Сама нейронная сеть хранит указатели на нейроны, организованные
слоями ( вообще, указатели на нейроны хранятся в векторах, которые
нужно заменить на объекты-слои ), включает в себя абстрактную
фабрику нейронов, а также алгоритм обучения сети.
Интерфейс нейронной сети
template <typename T>
class TrainAlgorithm;
/**
* Neural network class.
* An object of that type represents a neural network of several types:
* - Single layer perceptron;
* - Multiple layers perceptron.
*
* There are several training algorithms available as well:
* - Perceptron;
* - Backpropagation.
*
* How to use this class:
* To be able to use neural network , you have to create an instance of that class, specifying
* a number of input neurons, output neurons, number of hidden layers and amount of neurons in hidden layers.
* You can also specify a type of neural network, by passing a string with a name of neural network, otherwise
* MultiLayerPerceptron will be used. ( A training algorithm can be changed via public calls);
*
* Once the neural network was created, all u have to do is to set the biggest MSE required to achieve during
* the training phase ( or u can skip this step, then mMinMSE will be set to 0.01 ),
* train the network by providing a training data with target results.
* Afterwards u can obtain the net response by feeding the net with data;
*
*/
template <typename T>
class NeuralNetwork
{
public:
/**
* A Neural Network constructor.
* - Description: A template constructor. T is a data type, all the nodes will operate with. Create a neural network by providing it with:
* @param inInputs - an integer argument - number of input neurons of newly created neural network;
* @param inOutputs- an integer argument - number of output neurons of newly created neural network;
* @param inNumOfHiddenLayers - an integer argument - number of hidden layers of newly created neural network, default is 0;
* @param inNumOfNeuronsInHiddenLayers - an integer argument - number of neurons in hidden layers of newly created neural network ( note that every hidden layer has the same amount of neurons), default is 0;
* @param inTypeOfNeuralNetwork - a const char * argument - a type of neural network, we are going to create. The values may be:
* <UL>
* <LI>MultiLayerPerceptron;</LI>
* <LI>Default is MultiLayerPerceptron.</LI>
* </UL>
* - Purpose: Creates a neural network for solving some interesting problems.
* - Prerequisites: The template parameter has to be picked based on your input data.
*
*/
NeuralNetwork( const int& inInputs,
const int& inOutputs,
const int& inNumOfHiddenLayers = 0,
const int& inNumOfNeuronsInHiddenLayers = 0,
const char * inTypeOfNeuralNetwork = "MultiLayerPerceptron"
);
~NeuralNetwork( );
/**
* Public method Train.
* - Description: Method for training the network.
* - Purpose: Trains a network, so the weights on the links adjusted in the way to be able to solve problem.
* - Prerequisites:
* @param inData - a vector of vectors with data to train with;
* @param inTarget - a vector of vectors with target data;
* - the number of data samples and target samples has to be equal;
* - the data and targets has to be in the appropriate order u want the network to learn.
*/
bool Train( const std::vector<std::vector<T > >& inData,
const std::vector<std::vector<T > >& inTarget );
/**
* Public method GetNetResponse.
* - Description: Method for actually get response from net by feeding it with data.
* - Purpose: By calling this method u make the network evaluate the response for u.
* - Prerequisites:
* @param inData - a vector data to feed with.
*/
std::vector<int> GetNetResponse( const std::vector<T>& inData );
/**
* Public method SetAlgorithm.
* - Description: Setter for algorithm of training the net.
* - Purpose: Can be used for dynamic change of training algorithm.
* - Prerequisites:
* @param inTrainingAlgorithm - an existence of already created object of type TrainAlgorithm.
*/
void SetAlgorithm( TrainAlgorithm<T> * inTrainingAlgorithm ) { mTrainingAlgoritm = inTrainingAlgorithm; };
/**
* Public method SetNeuronFactory.
* - Description: Setter for the factory, which is making neurons for the net.
* - Purpose: Can be used for dynamic change of neuron factory.
* - Prerequisites:
* @param inNeuronFactory - an existence of already created object of type NeuronFactory.
*/
void SetNeuronFactory( NeuronFactory<T> * inNeuronFactory ) { mNeuronFactory = inNeuronFactory; };
/**
* Public method ShowNetworkState.
* - Description: Prints current state to the standard output: weight of every link.
* - Purpose: Can be used for monitoring the weights change during training of the net.
* - Prerequisites: None.
*/
void ShowNetworkState( );
/**
* Public method GetMinMSE.
* - Description: Returns the biggest MSE required to achieve during the training phase.
* - Purpose: Can be used for getting the biggest MSE required to achieve during the training phase.
* - Prerequisites: None.
*/
const double& GetMinMSE( ){ return mMinMSE; };
/**
* Public method SetMinMSE.
* - Description: Setter for the biggest MSE required to achieve during the training phase.
* - Purpose: Can be used for setting the biggest MSE required to achieve during the training phase.
* - Prerequisites:
* @param inMinMse - double value, the biggest MSE required to achieve during the training phase.
*/
void SetMinMSE( const double& inMinMse ){ mMinMSE = inMinMse; };
/**
* Friend class.
*/
friend class Hebb<T>;
/**
* Friend class.
*/
friend class Backpropagation<T>;
protected:
/**
* Protected method GetLayer.
* - Description: Getter for the layer by index of that layer.
* - Purpose: Can be used by inner implementation for getting access to neural network's layers.
* - Prerequisites:
* @param inInd - an integer index of layer.
*/
std::vector<Neuron<T > *>& GetLayer( const int& inInd ){ return mLayers[inInd]; };
/**
* Protected method size.
* - Description: Returns the number of layers in the network.
* - Purpose: Can be used by inner implementation for getting number of layers in the network.
* - Prerequisites: None.
*/
unsigned int size( ){ return mLayers.size( ); };
/**
* Protected method GetNumOfOutputs.
* - Description: Returns the number of units in the output layer.
* - Purpose: Can be used by inner implementation for getting number of units in the output layer.
* - Prerequisites: None.
*/
std::vector<Neuron<T > *>& GetOutputLayer( ){ return mLayers[mLayers.size( )-1]; };
/**
* Protected method GetInputLayer.
* - Description: Returns the input layer.
* - Purpose: Can be used by inner implementation for getting the input layer.
* - Prerequisites: None.
*/
std::vector<Neuron<T > *>& GetInputLayer( ){ return mLayers[0]; };
/**
* Protected method GetBiasLayer.
* - Description: Returns the vector of Biases.
* - Purpose: Can be used by inner implementation for getting vector of Biases.
* - Prerequisites: None.
*/
std::vector<Neuron<T > *>& GetBiasLayer( ) { return mBiasLayer; };
/**
* Protected method UpdateWeights.
* - Description: Updates the weights of every link between the neurons.
* - Purpose: Can be used by inner implementation for updating the weights of links between the neurons.
* - Prerequisites: None, but only makes sense, when its called during the training phase.
*/
void UpdateWeights( );
/**
* Protected method ResetCharges.
* - Description: Resets the neuron's data received during iteration of net training.
* - Purpose: Can be used by inner implementation for reset the neuron's data between iterations.
* - Prerequisites: None, but only makes sense, when its called during the training phase.
*/
void ResetCharges( );
/**
* Protected method AddMSE.
* - Description: Changes MSE during the training phase.
* - Purpose: Can be used by inner implementation for changing MSE during the training phase.
* - Prerequisites:
* @param inInd - a double amount of MSE to be add.
*/
void AddMSE( double inPortion ){ mMeanSquaredError += inPortion; };
/**
* Protected method GetMSE.
* - Description: Getter for MSE value.
* - Purpose: Can be used by inner implementation for getting access to the MSE value.
* - Prerequisites: None.
*/
double GetMSE( ){ return mMeanSquaredError; };
/**
* Protected method ResetMSE.
* - Description: Resets MSE value.
* - Purpose: Can be used by inner implementation for resetting MSE value.
* - Prerequisites: None.
*/
void ResetMSE( ) { mMeanSquaredError = 0; };
NeuronFactory<T> * mNeuronFactory; /*!< Member, which is responsible for creating neurons @see SetNeuronFactory */
TrainAlgorithm<T> * mTrainingAlgoritm; /*!< Member, which is responsible for the way the network will trained @see SetAlgorithm */
std::vector<std::vector<Neuron<T > *> > mLayers; /*!< Inner representation of neural networks */
std::vector<Neuron<T > *> mBiasLayer; /*!< Container for biases */
unsigned int mInputs, mOutputs, mHidden; /*!< Number of inputs, outputs and hidden units */
double mMeanSquaredError; /*!< Mean Squared Error which is changing every iteration of the training*/
double mMinMSE; /*!< The biggest Mean Squared Error required for training to stop*/
};
И, наконец, сам интерфейс класса, ответственного за обучение сети:
Интерфейс алгоритма обучения
template <typename T>
class NeuralNetwork;
template <typename T>
class TrainAlgorithm
{
public:
virtual ~TrainAlgorithm(){};
virtual double Train(const std::vector<T>& inData, const std::vector<T>& inTarget) = 0;
virtual void WeightsInitialization() = 0;
protected:
};
template <typename T>
class Hebb : public TrainAlgorithm<T>
{
public:
Hebb(NeuralNetwork<T> * inNeuralNetwork) : mNeuralNetwork(inNeuralNetwork){};
virtual ~Hebb(){};
virtual double Train(const std::vector<T>& inData, const std::vector<T>& inTarget);
virtual void WeightsInitialization();
protected:
NeuralNetwork<T> * mNeuralNetwork;
};
template <typename T>
class Backpropagation : public TrainAlgorithm<T>
{
public:
Backpropagation(NeuralNetwork<T> * inNeuralNetwork);
virtual ~Backpropagation(){};
virtual double Train(const std::vector<T>& inData, const std::vector<T>& inTarget);
virtual void WeightsInitialization();
protected:
void NguyenWidrowWeightsInitialization();
void CommonInitialization();
NeuralNetwork<T> * mNeuralNetwork;
};
Весь код доступен на github: Sovietmade/NeuralNetworks
В качестве заключения, хотелось бы отметить, что тема нейронных сетей на данный момент не разработана полностью, вновь и вновь мы видим на страницах хабра упоминания о новых достижениях ученых в области нейронных сетей, новых удивительных разработках. С моей стороны,
эта статья была первым шагом освоения интереснейшей технологии, и я надеюсь для кого — то она окажется небесполезной.
Использованная литература:
Алгоритм обучения нейронной сети был взят из изумительной книги:
Laurene V. Fausett “Fundamentals of Neural Networks: Architectures, Algorithms And Applications”.
Рад снова всех приветствовать, и сегодня продолжим планомерно двигаться в выбранном направлении. Речь, конечно, о масштабном разборе искусственных нейронных сетей для решения широкого спектра задач. Продолжим ровно с того момента, на котором остановились в предыдущей части, и это означает, что героем данного поста будет ключевой процесс — обучение нейронных сетей.
- Градиентный спуск
- Функция ошибки
- Метод обратного распространения ошибки
- Пример расчета
Тема эта крайне важна, поскольку именно процесс обучения позволяет сети начать выполнять задачу, для которой она, собственно, и предназначена. То есть нейронная сеть функционирует не по какому-либо жестко заданному на этапе проектирования алгоритму, она совершенствуется в процессе анализа имеющихся данных. Этот процесс и называется обучением нейронной сети. Математически суть процесса обучения заключается в корректировке значений весов синапсов (связей между имеющимися нейронами). Изначально значения весов задаются случайно, затем производится обучение, результатом которого будут новые значения синаптических весов. Это все мы максимально подробно разберем как раз в этой статье.
На своем сайте я всегда придерживаюсь концепции, при которой теоретические выкладки по максимуму сопровождаются практическими примерами для максимальной наглядности. Так мы поступим и сейчас 👍
Итак, суть заключается в следующем. Пусть у нас есть простейшая нейронная сеть, которую мы хотим обучить (продолжаем рассматривать сети прямого распространения):

То есть на входы нейронов I1 и I2 мы подаем какие-либо числа, а на выходе сети получаем соответственно новое значение. При этом нам необходима некая выборка данных, включающая в себя значения входов и соответствующее им, правильное, значение на выходе:
| \bold{I_1} | \bold{I_2} | \bold{O_{net}} |
|---|---|---|
| x_{11} | x_{12} | y_{1} |
| x_{21} | x_{22} | y_{2} |
| x_{31} | x_{32} | y_{3} |
| … | … | … |
| x_{N1} | x_{N2} | y_{N} |
Допустим, сеть выполняет суммирование значений на входе, тогда данный набор данных может быть таким:
| \bold{I_1} | \bold{I_2} | \bold{O_{net}} |
|---|---|---|
| 1 | 4 | 5 |
| 2 | 7 | 9 |
| 3 | 5 | 8 |
| … | … | … |
| 1000 | 1500 | 2500 |
Эти значения и используются для обучения сети. Как именно — рассмотрим чуть ниже, пока сконцентрируемся на идее процесса в целом. Для того, чтобы иметь возможность тестировать работу сети в процессе обучения, исходную выборку данных делят на две части — обучающую и тестовую. Пусть имеется 1000 образцов, тогда можно 900 использовать для обучения, а оставшиеся 100 — для тестирования. Эти величины взяты исключительно ради наглядности и демонстрации логики выполнения операций, на практике все зависит от задачи, размер обучающей выборки может спокойно достигать и сотен тысяч образцов.
Итак, итог имеем следующий — обучающая выборка прогоняется через сеть, в результате чего происходит настройка значений синаптических весов. Один полный проход по всей выборке называется эпохой. И опять же, обучение нейронной сети — это процесс, требующий многократных экспериментов, анализа результатов и творческого подхода. Все перечисленные параметры (размер выборки, количество эпох обучения) могут иметь абсолютно разные значения для разных задач и сетей. Четкого правила тут просто нет, в этом и кроется дополнительный шарм и изящность )
Возвращаемся к разбору, и в результате прохода обучающей выборки через сеть мы получаем сеть с новыми значениями весов синапсов.
Далее мы через эту, уже обученную в той или иной степени, сеть прогоняем тестовую выборку, которая не участвовала в обучении. При этом сеть выдает нам выходные значения для каждого образца, которые мы сравниваем с теми верными значениями, которые имеем.
Анализируем нашу гипотетическую выборку:

Таким образом, для тестирования подаем на вход сети значения x_{(M+1)1}, x_{(M+1)2} и проверяем, чему равен выход, ожидаем очевидно значение y_{(M+1)}. Аналогично поступаем и для оставшихся тестовых образцов. После чего мы можем сделать вывод, успешно или нет работает сеть. Например, сеть дает правильный ответ для 90% тестовых данных, дальше уже встает вопрос — устраивает ли нас данная точность или процесс обучения необходимо повторить, либо провести заново, изменив какие-либо параметры сети.
В этом и заключается суть обучения нейронных сетей, теперь перейдем к деталям и конкретным действиям, которые необходимо осуществить для выполнения данного процесса. Двигаться снова будем поэтапно, чтобы сформировать максимально четкую и полную картину. Поэтому начнем с понятия градиентного спуска, который используется при обучении по методу обратного распространения ошибки. Обо всем этом далее…
Обучение нейронных сетей. Градиентный спуск.
Рассмотрев идею процесса обучения в целом, на данном этапе мы можем однозначно сформулировать текущую цель — необходимо определить математический алгоритм, который позволит рассчитать значения весовых коэффициентов таким образом, чтобы ошибка сети была минимальна. То есть грубо говоря нам необходима конкретная формула для вычисления:
Здесь \Delta w_{ij} — величина, на которую необходимо изменить вес синапса, связывающего нейроны i и j нашей сети. Соответственно, зная это, необходимо на каждом этапе обучения производить корректировку весов связей между всеми элементами нейронной сети. Задача ясна, переходим к делу.
Пусть функция ошибки от веса имеет следующий вид:
Для удобства рассмотрим зависимость функции ошибки от одного конкретного веса:

В начальный момент мы находимся в некоторой точке кривой, а для минимизации ошибки попасть мы хотим в точку глобального минимума функции:
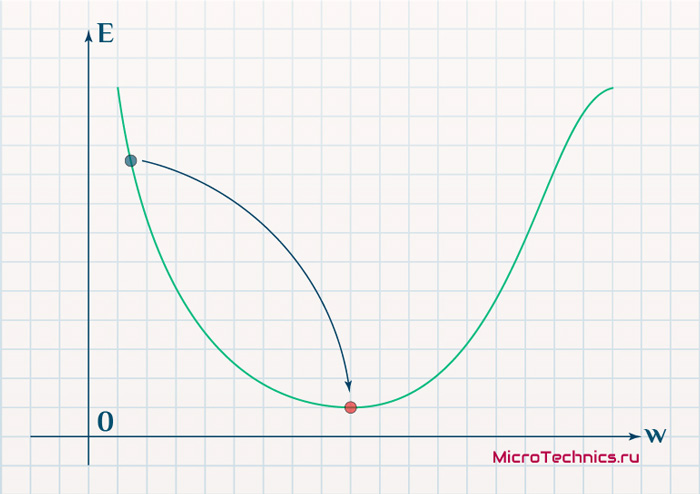
Нанесем на график вектора градиентов в разных точках. Длина векторов численно равна скорости роста функции в данной точке, что в свою очередь соответствует значению производной функции по данной точке. Исходя из этого, делаем вывод, что длина вектора градиента определяется крутизной функции в данной точке:
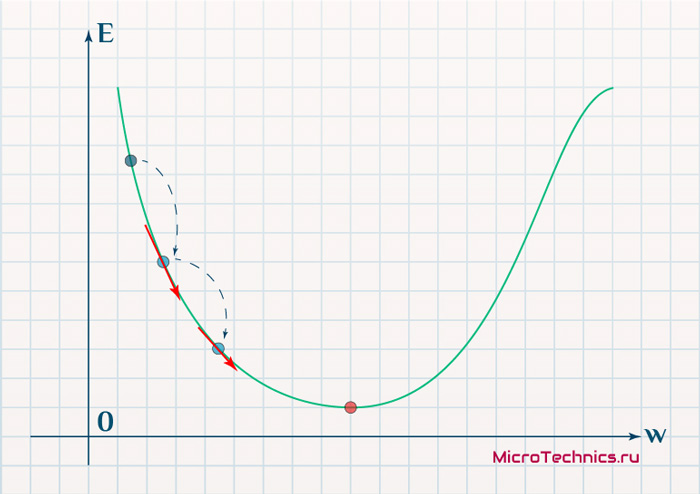
Вывод прост — величина градиента будет уменьшаться по мере приближения к минимуму функции. Это важный вывод, к которому мы еще вернемся. А тем временем разберемся с направлением вектора, для чего рассмотрим еще несколько возможных точек:
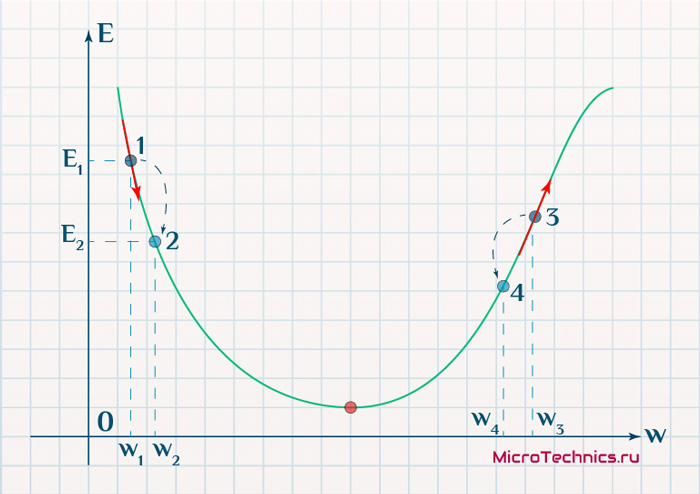
Находясь в точке 1, целью является перейти в точку 2, поскольку в ней значение ошибки меньше (E_2 < E_1), а глобальная задача по-прежнему заключается в ее минимизации. Для этого необходимо изменить величину w на некое значение \Delta w (\Delta w = w_2 — w_1 > 0). При всем при этом в точке 1 градиент отрицательный. Фиксируем данные факты и переходим к точке 3, предположим, что мы находимся именно в ней.
Тогда для уменьшения ошибки наш путь лежит в точку 4, а необходимое изменение значения: \Delta w = w_4 — w_3 < 0. Градиент же в точке 3 положителен. Этот факт также фиксируем.
А теперь соберем воедино эту информацию в виде следующей иллюстрации:
| Переход | \bold{\Delta w} | Знак \bold{\Delta w} | Градиент |
|---|---|---|---|
| 1 \rArr 2 | w_2 — w_1 | + | — |
| 3 \rArr 4 | w_4 — w_3 | — | + |
Вывод напрашивается сам собой — величина, на которую необходимо изменить значение w, в любой точке противоположна по знаку градиенту. И, таким образом, представим эту самую величину в виде:
\Delta w = -\alpha \cdot \frac{dE}{dw}
Имеем в наличии:
- \Delta w — величина, на которую необходимо изменить значение w.
- \frac{dE}{dw} — градиент в этой точке.
- \alpha — скорость обучения.
Собственно, логика метода градиентного спуска и заключается в данном математическом выражении, а именно в том, что для минимизации ошибки необходимо изменять w в направлении противоположном градиенту. В контексте нейронных сетей имеем искомый закон для корректировки весов синаптических связей (для синапса между нейронами i и j):
\Delta w_{ij} = -\alpha \cdot \frac{dE}{dw_{ij}}
Более того, вспомним о важном свойстве, которое мы отдельно пометили. И заключается оно в том, что величина градиента будет уменьшаться по мере приближения к минимуму функции. Что это нам дает? А то, что в том случае, если наша текущая дислокация далека от места назначения, то величина, корректирующая вес связи, будет больше. А это обеспечит скорейшее приближение к цели. При приближении к целевому пункту, величина \frac{dE}{dw_{ij}} будет уменьшаться, что поможет нам точнее попасть в нужную точку, а кроме того, не позволит нам ее проскочить. Визуализируем вышеописанное:
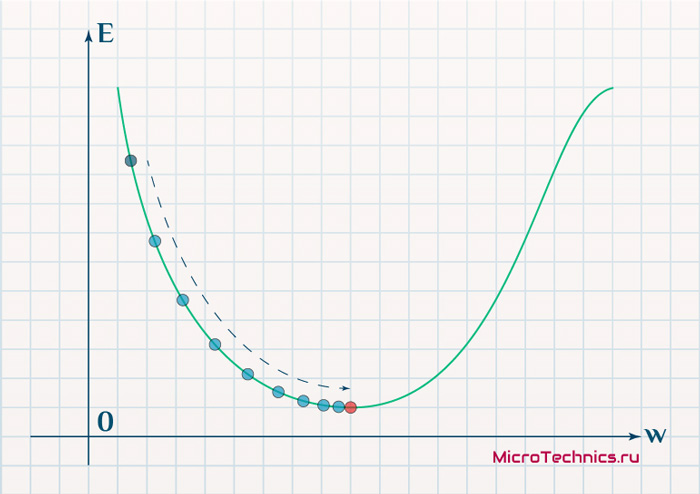
Скорость же обучения несет в себе следующий смысл. Она определяет величину каждого шага при поиске минимума ошибки. Слишком большое значение приводит к тому, что точка может «перепрыгнуть» через нужное значение и оказаться по другую сторону от цели:
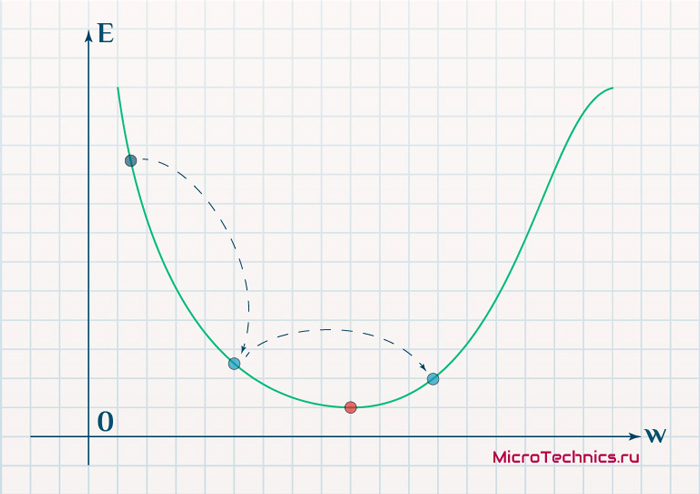
Если же величина будет мала, то это приведет к тому, что спуск будет осуществляться очень медленно, что также является нежелательным эффектом. Поэтому скорость обучения, как и многие другие параметры нейронной сети, является очень важной величиной, для которой нет единственно верного значения. Все снова зависит от конкретного случая и оптимальная величина определяется исключительно исходя из текущих условий.
И даже на этом еще не все, здесь присутствует один важный нюанс, который в большинстве статей опускается, либо вовсе не упоминается. Реальная зависимость может иметь совсем другой вид:
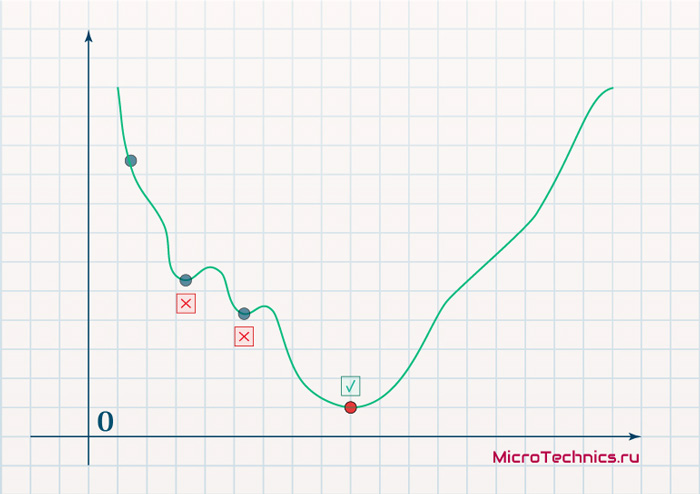
Из чего вытекает потенциальная возможность попадания в локальный минимум, вместо глобального, что является большой проблемой. Для предотвращения данного эффекта вводится понятие момента обучения и формула принимает следующий вид:
\Delta w_{ij} = -\alpha \cdot \frac{dE}{dw_{ij}} + \gamma \cdot \Delta w_{ij}^{t - 1}
То есть добавляется второе слагаемое, которое представляет из себя произведение момента на величину корректировки веса на предыдущем шаге.
Итого, резюмируем продвижение к цели:
- Нашей задачей было найти закон, по которому необходимо изменять величину весов связей между нейронами.
- Наш результат — \Delta w_{ij} = -\alpha \cdot \frac{dE}{dw_{ij}} + \gamma \cdot \Delta w_{ij}^{t — 1} — именно то, что и требовалось 👍
И опять же, полученный результат логичным образом перенаправляет нас на следующий этап, ставя вопросы — что из себя представляет функция ошибки, и как определить ее градиент.
Обучение нейронных сетей. Функция ошибки.
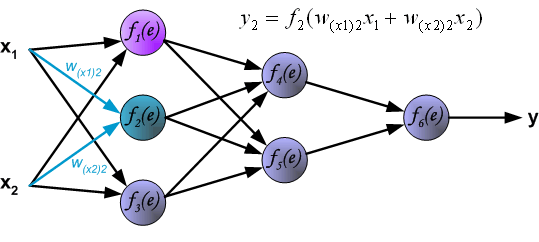
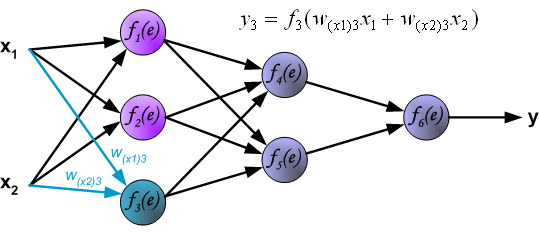
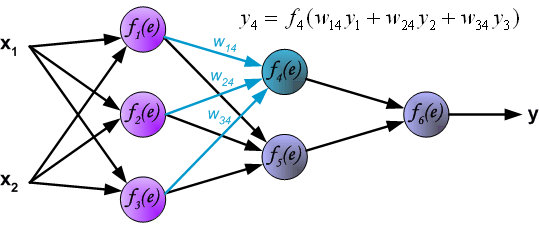
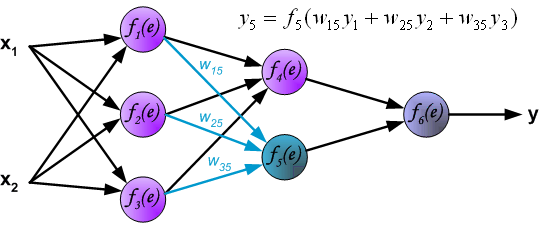
Начнем с того, что определимся с тем, что у нас в наличии, для этого вернемся к конкретной нейронной сети. Пусть вид ее таков:
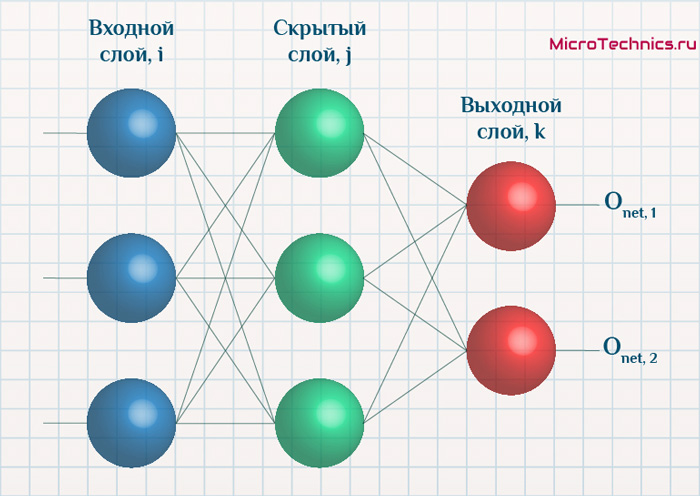
Интересует нас, в первую очередь, часть, относящаяся к нейронам выходного слоя. Подав на вход определенные значения, получаем значения на выходе сети: O_{net, 1} и O_{net, 2}. Кроме того, поскольку мы ведем речь о процессе обучения нейронной сети, то нам известны целевые значения: O_{correct, 1} и O_{correct, 2}. И именно этот набор данных на этом этапе является для нас исходным:
- Известно: O_{net, 1}, O_{net, 2}, O_{correct, 1} и O_{correct, 2}.
- Необходимо определить величины \Delta w_{ij} для корректировки весов, для этого нужно вычислить градиенты (\frac{dE}{dw_{ij}}) для каждого из синапсов.
Полдела сделано — задача четко сформулирована, начинаем деятельность по поиску решения.
В плане того, как определять ошибку, первым и самым очевидным вариантом кажется простая алгебраическая разность. Для каждого из выходных нейронов:
E_k = O_{correct, k} - O_{net, k}
Дополним пример числовыми значениями:
| Нейрон | \bold{O_{net}} | \bold{O_{correct}} | \bold{E} |
|---|---|---|---|
| 1 | 0.9 | 0.5 | -0.4 |
| 2 | 0.2 | 0.6 | 0.4 |
Недостатком данного варианта является то, что в том случае, если мы попытаемся просуммировать ошибки нейронов, то получим:
E_{sum} = e_1 + e_2 = -0.4 + 0.4 = 0
Что не соответствует действительности (нулевая ошибка, говорит об идеальной работе нейронной сети, по факту оба нейрона дали неверный результат). Так что вариант с разностью откидываем за несостоятельностью.
Вторым, традиционно упоминаемым, методом вычисления ошибки является использование модуля разности:
E_k = | O_{correct, k} - O_{net, k} |
Тут в действие вступает уже проблема иного рода:
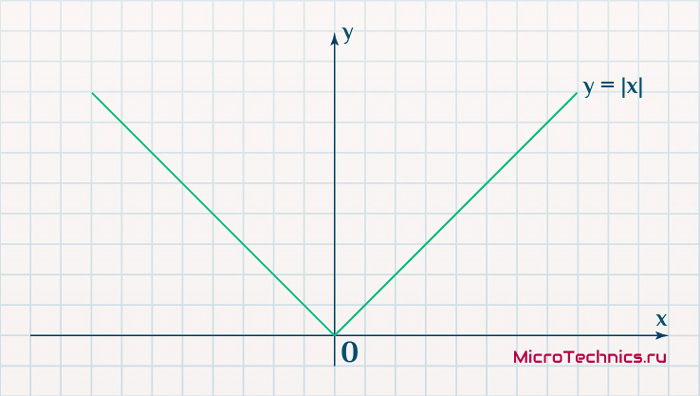
Функция, бесспорно, симпатична, но при приближении к минимуму ее градиент является постоянной величиной, скачкообразно меняясь при переходе через точку минимума. Это нас также не устраивает, поскольку, как мы обсуждали, концепция заключалась в том числе в том, чтобы по мере приближения к минимуму значение градиента уменьшалось.
В итоге хороший результат дает зависимость (для выходного нейрона под номером k):
E_k = (O_{correct, k} - O_{net, k})^2
Функция по многим своим свойствам идеально удовлетворяет нуждам обучения нейронной сети, так что выбор сделан, остановимся на ней. Хотя, как и во многих аспектах, качающихся нейронных сетей, данное решение не является единственно и неоспоримо верным. В каких-то случаях лучше себя могут проявить другие зависимости, возможно, что какой-то вариант даст большую точность, но неоправданно высокие затраты производительности при обучении. В общем, непаханное поле для экспериментов и исследований, это и привлекательно.
Краткий вывод промежуточного шага, на который мы вышли:
- Имеющееся: \frac{dE}{dw_{jk}} = \frac{d}{d w_{jk}}(O_{correct, k} — O_{net, k})^2.
- Искомое по-прежнему: \Delta w_{jk}.
Несложные диффернциально-математические изыскания выводят на следующий результат:
\frac{dE}{d w_{jk}} = -(O_{correct, k} - O_{net, k}) \cdot f{\Large{\prime}}(\sum_{j}w_{jk}O_j) \cdot O_j
Здесь эти самые изыскания я все-таки решил не вставлять, дабы не перегружать статью, которая и так выходит объемной. Но в случае необходимости и интереса, отпишите в комментарии, я добавлю вычисления и закину их под спойлер, как вариант.
Освежим в памяти структуру сети:
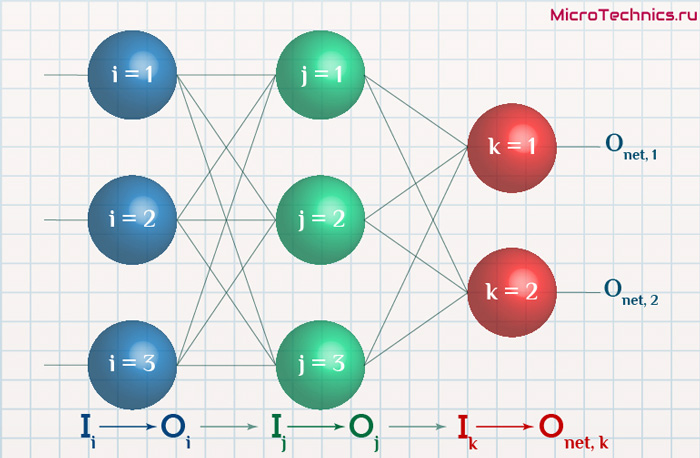
Формулу можно упростить, сгруппировав отдельные ее части:
- (O_{correct, k} — O_{net, k}) \cdot f{\Large{\prime}}(\sum_{j}w_{jk}O_j) — ошибка нейрона k.
- O_j — тут все понятно, выходной сигнал нейрона j.
f{\Large{\prime}}(\sum_{j}w_{jk}O_j) — значение производной функции активации. Причем, обратите внимание, что \sum_{j}w_{jk}O_j — это не что иное, как сигнал на входе нейрона k (I_{k}). Тогда для расчета ошибки выходного нейрона: \delta_k = (O_{correct, k} — O_{net, k}) \cdot f{\Large{\prime}}(I_k).
Итог: \frac{dE}{d w_{jk}} = -\delta_k \cdot O_j.
Одной из причин популярности сигмоидальной функции активности является то, что ее производная очень просто выражается через саму функцию:
f{'}(x) = f(x)\medspace (1\medspace-\medspace f(x))
Данные алгебраические вычисления справедливы для корректировки весов между скрытым и выходным слоем, поскольку для расчета ошибки мы используем просто разность между целевым и полученным результатом, умноженную на производную.
Для других слоев будут незначительные изменения, касающиеся исключительно первого множителя в формуле:
\frac{dE}{d w_{ij}} = -\delta_j \cdot O_i
Который примет следующий вид:
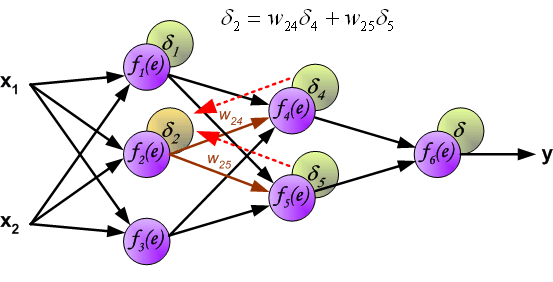
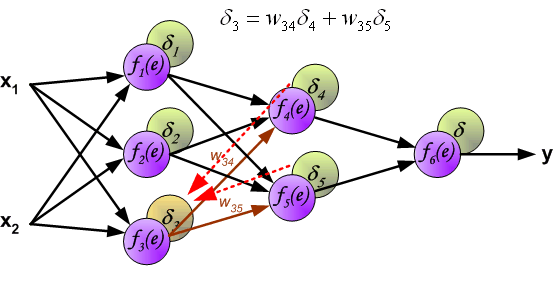
\delta_j = (\sum_{k}{}{\delta_k\medspace w_{jk}}) \cdot f{\Large{\prime}}(I_j)
То есть ошибка для элемента слоя j получается путем взвешенного суммирования ошибок, «приходящих» к нему от нейронов следующего слоя и умножения на производную функции активации. В результате:
\frac{dE}{d w_{ij}} = -(\sum_{k}{}{\delta_k\medspace w_{jk}}) \cdot f{\Large{\prime}}(I_j) \cdot O_i
Снова подводим промежуточный итог, чтобы иметь максимально полную и структурированную картину происходящего. Вот результаты, полученные нами на двух этапах, которые мы успешно миновали:
- Ошибка:
- выходной слой: \delta_k = (O_{correct, k} — O_{net, k}) \cdot f{\Large{\prime}}(I_k)
- скрытые слои: \delta_j = (\sum_{k}{}{\delta_k\medspace w_{jk}}) \cdot f{\Large{\prime}}(I_j)
- Градиент: \frac{dE}{d w_{ij}} = -\delta_j \cdot O_i
- Корректировка весовых коэффициентов: \Delta w_{ij} = -\alpha \cdot \frac{dE}{dw_{ij}} + \gamma \cdot \Delta w_{ij}^{t — 1}
Преобразуем последнюю формулу:
\Delta w_{ij} = \alpha \cdot \delta_j \cdot O_i + \gamma \cdot \Delta w_{ij}^{t - 1}
Из этого мы делаем вывод, что на данный момент у нас есть все, что необходимо для того, чтобы произвести обучение нейронной сети. И героем следующего подраздела будет алгоритм обратного распространения ошибки.
Метод обратного распространения ошибки.
Данный метод является одним из наиболее распространенных и популярных, чем и продиктован его выбор для анализа и разбора. Алгоритм обратного распространения ошибки относится к методам обучение с учителем, что на деле означает необходимость наличия целевых значений в обучающих сетах.
Суть же метода подразумевает наличие двух этапов:
- Прямой проход — входные сигналы двигаются в прямом направлении, в результате чего мы получаем выходной сигнал, из которого в дальнейшем рассчитываем значение ошибки.
- Обратный проход — обратное распространение ошибки — величина ошибки двигается в обратном направлении, в результате происходит корректировка весовых коэффициентов связей сети.
Начальные значения весов (перед обучением) задаются случайными, есть ряд методик для выбора этих значений, я опишу в отдельном материале максимально подробно. Пока вот можно полистать — ссылка.
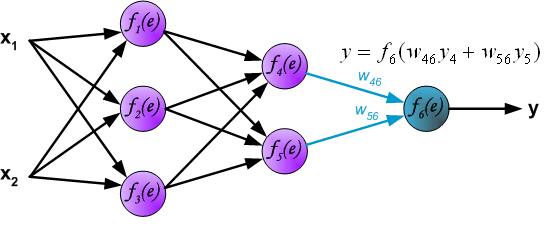
Вернемся к конкретному примеру для явной демонстрации этих принципов:
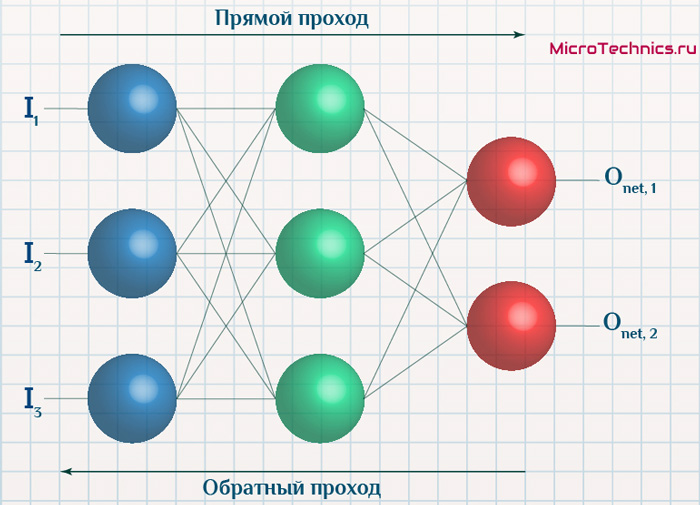
Итак, имеется нейронная сеть, также имеется набор данных обучающей выборки. Как уже обсудили в начале статьи — обучающая выборка представляет из себя набор образцов (сетов), каждый из которых состоит из значений входных сигналов и соответствующих им «правильных» значений выходных величин.
Процесс обучения нейронной сети для алгоритма обратного распространения ошибки будет таким:
- Прямой проход. Подаем на вход значения I_1, I_2, I_3 из обучающей выборки. В результате работы сети получаем выходные значения O_{net, 1}, O_{net, 2}. Этому целиком и полностью был посвящен предыдущий манускрипт.
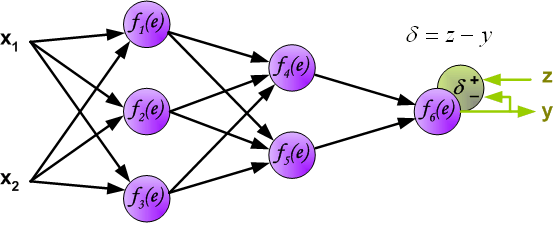
- Рассчитываем величины ошибок для всех слоев:
- для выходного: \delta_k = (O_{correct, k} — O_{net, k}) \cdot f{\Large{\prime}}(I_k)
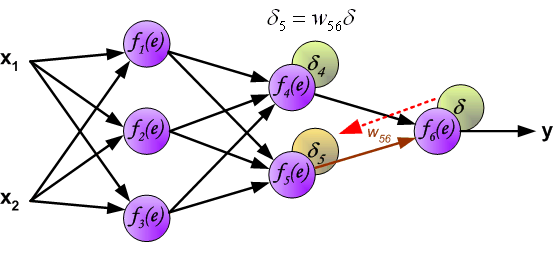
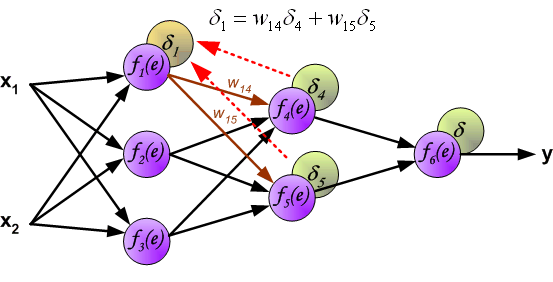
- для скрытых: \delta_j = (\sum_{k}{}{\delta_k\medspace w_{jk}}) \cdot f{\Large{\prime}}(I_j)
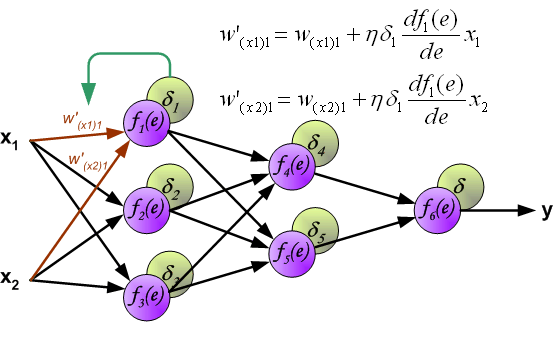
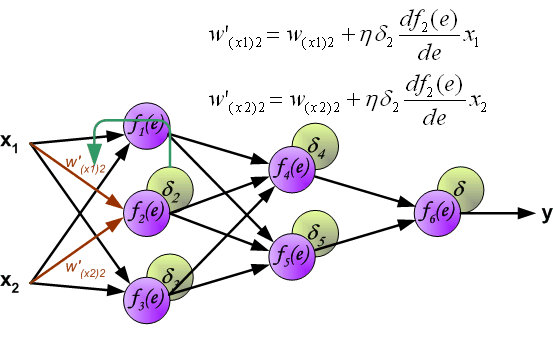
- Далее используем полученные значения для расчета \Delta w_{ij} = \alpha \cdot \delta_j \cdot O_i + \gamma \cdot \Delta w_{ij}^{t — 1}
- И финишируем, рассчитывая новые значения весов: w_{ij \medspace new} = w_{ij} + \Delta w_{ij}
- На этом один цикл обучения закончен, данные шаги 1 — 4 повторяются для других образцов из обучающей выборки.
Обратный проход завершен, а вместе с ним и одна итерация процесса обучения нейронной сети по данному методу. Собственно, обучение в целом заключается в многократном повторении этих шагов для разных образцов из обучающей выборки. Логику мы полностью разобрали, при повторном проведении операций она остается в точности такой же.
Таким образом, максимально подробно концентрируясь именно на сути и логике процессов, мы в деталях разобрали метод обратного распространения ошибки. Поэтому переходим к завершающей части статьи, в которой разберем практический пример, произведя полностью все вычисления для конкретных числовых величин. Все в рамках продвигаемой мной концепции, что любая теоретическая информация на порядок лучше может быть осознана при применении ее на практике.
Пример расчетов для метода обратного распространения ошибки.
Возьмем нейронную сеть и зададим начальные значения весов:
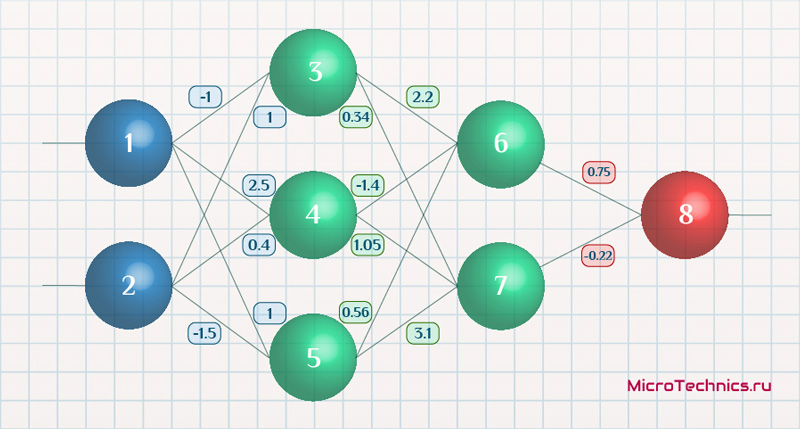
Здесь я задал значения не в соответствии с существующими на сегодняшний день методами, а просто случайным образом для наглядности примера.
В качестве функции активации используем сигмоиду:
f(x) = \frac{1}{1 + e^{-x}}
И ее производная:
f{\Large{\prime}}(x) = f(x)\medspace (1\medspace-\medspace f(x))
Берем один образец из обучающей выборки, пусть будут такие значения:
- Входные: I_1 = 0.6, I_1 = 0.7.
- Выходное: O_{correct} = 0.9.
Скорость обучения \alpha пусть будет равна 0.3, момент — \gamma = 0.1. Все готово, теперь проведем полный цикл для метода обратного распространения ошибки, то есть прямой проход и обратный.
Прямой проход.
Начинаем с выходных значений нейронов 1 и 2, поскольку они являются входными, то:
O_1 = I_1 = 0.6 \\ O_2 = I_2 = 0.7
Значения на входе нейронов 3, 4 и 5:
I_3 = O_1 \cdot w_{13} + O_2 \cdot w_{23} = 0.6 \cdot (-1\medspace) + 0.7 \cdot 1 = 0.1 \\
I_4 = 0.6 \cdot 2.5 + 0.7 \cdot 0.4 = 1.78 \\
I_5 = 0.6 \cdot 1 + 0.7 \cdot (-1.5\medspace) = -0.45
На выходе этих же нейронов первого скрытого слоя:
O_3 = f(I3\medspace) = 0.52 \\ O_4 = 0.86\\ O_5 = 0.39
Продолжаем аналогично для следующего скрытого слоя:
I_6 = O_3 \cdot w_{36} + O_4 \cdot w_{46} + O_5 \cdot w_{56} = 0.52 \cdot 2.2 + 0.86 \cdot (-1.4\medspace) + 0.39 \cdot 0.56 = 0.158 \\
I_7 = 0.52 \cdot 0.34 + 0.86 \cdot 1.05 + 0.39 \cdot 3.1 = 2.288 \\
O_6 = f(I_6) = 0.54 \\
O_7 = 0.908
Добрались до выходного нейрона:
I_8 = O_6 \cdot w_{68} + O_7 \cdot w_{78} = 0.54 \cdot 0.75 + 0.908 \cdot (-0.22\medspace) = 0.205 \\
O_8 = O_{net} = f(I_8) = 0.551
Получили значение на выходе сети, кроме того, у нас есть целевое значение O_{correct} = 0.9. То есть все, что необходимо для обратного прохода, имеется.
Обратный проход.
Как мы и обсуждали, первым этапом будет вычисление ошибок всех нейронов, действуем:
\delta_8 = (O_{correct} - O_{net}) \cdot f{\Large{\prime}}(I_8) = (O_{correct} - O_{net}) \cdot f(I_8) \cdot (1-f(I_8)) = (0.9 - 0.551\medspace) \cdot 0.551 \cdot (1-0.551\medspace) = 0.0863 \\
\delta_7 = (\sum_{k}{}{\delta_k\medspace w_{jk}}) \cdot f{\Large{\prime}}(I_7) = (\delta_8 \cdot w_{78}) \cdot f{\Large{\prime}}(I_7) = 0.0863 \cdot (-0.22\medspace) \cdot 0.908 \cdot (1 - 0.908\medspace) = -0.0016 \\
\delta_6 = 0.086 \cdot 0.75 \cdot 0.54 \cdot (1 - 0.54\medspace) = 0.016 \\
\delta_5 = (\sum_{k}{}{\delta_k\medspace w_{jk}}) \cdot f{\Large{\prime}}(I_5) = (\delta_7 \cdot w_{57} + \delta_6 \cdot w_{56}) \cdot f{\Large{\prime}}(I_7) = (-0.0016 \cdot 3.1 + 0.016 \cdot 0.56) \cdot 0.39 \cdot (1 - 0.39\medspace) = 0.001 \\
\delta_4 = (-0.0016 \cdot 1.05 + 0.016 \cdot (-1.4)) \cdot 0.86 \cdot (1 - 0.86\medspace) = -0.003 \\
\delta_3 = (-0.0016 \cdot 0.34 + 0.016 \cdot 2.2) \cdot 0.52 \cdot (1 - 0.52\medspace) = -0.0087
С расчетом ошибок закончили, следующий этап — расчет корректировочных величин для весов всех связей. Для этого мы вывели формулу:
\Delta w_{ij} = \alpha \cdot \delta_j \cdot O_i + \gamma \cdot \Delta w_{ij}^{t - 1}
Как вы помните, \Delta w_{ij}^{t — 1} — это величина поправки для данного веса на предыдущей итерации. Но поскольку у нас это первый проход, то данное значение будет нулевым, соответственно, в данном случае второе слагаемое отпадает. Но забывать о нем нельзя. Продолжаем калькулировать:
\Delta w_{78} = \alpha \cdot \delta_8 \cdot O_7 = 0.3 \cdot 0.0863 \cdot 0.908 = 0.0235 \\
\Delta w_{68} = 0.3 \cdot 0.0863 \cdot 0.54= 0.014 \\
\Delta w_{57} = \alpha \cdot \delta_7 \cdot O_5 = 0.3 \cdot (−0.0016\medspace) \cdot 0.39= -0.00019 \\
\Delta w_{47} = 0.3 \cdot (−0.0016\medspace) \cdot 0.86= -0.0004 \\
\Delta w_{37} = 0.3 \cdot (−0.0016\medspace) \cdot 0.52= -0.00025 \\
\Delta w_{56} = \alpha \cdot \delta_6 \cdot O_5 = 0.3 \cdot 0.016 \cdot 0.39= 0.0019 \\
\Delta w_{46} = 0.3 \cdot 0.016 \cdot 0.86= 0.0041 \\
\Delta w_{36} = 0.3 \cdot 0.016 \cdot 0.52= 0.0025 \\
\Delta w_{25} = \alpha \cdot \delta_5 \cdot O_2 = 0.3 \cdot 0.001 \cdot 0.7= 0.00021 \\
\Delta w_{15} = 0.3 \cdot 0.001 \cdot 0.6= 0.00018 \\
\Delta w_{24} = \alpha \cdot \delta_4 \cdot O_2 = 0.3 \cdot (-0.003\medspace) \cdot 0.7= -0.00063 \\
\Delta w_{14} = 0.3 \cdot (-0.003\medspace) \cdot 0.6= -0.00054 \\
\Delta w_{23} = \alpha \cdot \delta_3 \cdot O_2 = 0.3 \cdot (−0.0087\medspace) \cdot 0.7= -0.00183 \\
\Delta w_{13} = 0.3 \cdot (−0.0087\medspace) \cdot 0.6= -0.00157
И самый что ни на есть заключительный этап — непосредственно изменение значений весовых коэффициентов:
w_{78 \medspace new} = w_{78} + \Delta w_{78} = -0.22 + 0.0235 = -0.1965 \\
w_{68 \medspace new} = 0.75+ 0.014 = 0.764 \\
w_{57 \medspace new} = 3.1 + (−0.00019\medspace) = 3.0998\\
w_{47 \medspace new} = 1.05 + (−0.0004\medspace) = 1.0496\\
w_{37 \medspace new} = 0.34 + (−0.00025\medspace) = 0.3398\\
w_{56 \medspace new} = 0.56 + 0.0019 = 0.5619 \\
w_{46 \medspace new} = -1.4 + 0.0041 = -1.3959 \\
w_{36 \medspace new} = 2.2 + 0.0025 = 2.2025 \\
w_{25 \medspace new} = -1.5 + 0.00021 = -1.4998 \\
w_{15 \medspace new} = 1 + 0.00018 = 1.00018 \\
w_{24 \medspace new} = 0.4 + (−0.00063\medspace) = 0.39937 \\
w_{14 \medspace new} = 2.5 + (−0.00054\medspace) = 2.49946 \\
w_{23 \medspace new} = 1 + (−0.00183\medspace) = 0.99817 \\
w_{13 \medspace new} = -1 + (−0.00157\medspace) = -1.00157\\
И на этом данную масштабную статью завершаем, конечно же, не завершая на этом деятельность по использованию нейронных сетей. Так что всем спасибо за прочтение, любые вопросы пишите в комментариях и на форуме, ну и обязательно следите за обновлениями и новыми материалами, до встречи!
Введение
- В последнее время, с ростом популярности этих двух методов появилось много библиотек на Matlab, R, Python, C ++ и т.д., которые получают на вход обучающий набор и автоматически создают соответствующую нейронную сеть для вашей задачи.
- Однако при использовании готовых библиотек бывает сложно понять, что именно происходит и как мы получаем оптимизированную сеть. А ведь знание основ решения важно для дальнейшего развития этих методов. Итак, в данной статье мы создадим очень простую структуру для алгоритма нейронной сети.
- Мы постараемся понять, как работает базовый тип нейронной сети — перцептрон с одним нейроном и многослойный перцептрон — замечательный алгоритм, который отвечает за обучение сети (градиентный спуск и обратное распространение). Эти сетевые модели будут основой для более сложных моделей, существующих на сегодняшний день.
Краткий обзор истории
- Первая нейронная сеть была задумана Уорренном Маккалоком и Уолтером Питтсом в 1943 году. Они написали великолепную статью о том, как должны работать нейроны, а затем построили модель на основе своих идей — создали простую нейронную сеть с электрическими цепями.
- Исследования в области искусственного интеллекта быстро развивались, и в 1980 году Кунихико Фукусима разработал первую настоящую многослойную нейронную сеть.
- Первоначальной целью нейронной сети было создание компьютерной системы, способной решать проблемы подобно тому, как это делает человеческий мозг. Однако, со временем исследователи сменили фокус и начали использовать нейронные сети для решения особенных задач. С тех пор нейронные сети выполняют самые разнообразные задачи, включая компьютерное зрение, распознавание голоса, машинный перевод, фильтрацию социальных сетей, настольные игры или видеоигры, медицинскую диагностику, прогноз погоды, прогнозирование временных рядов, распознавание (изображения, текста, голоса) и др.
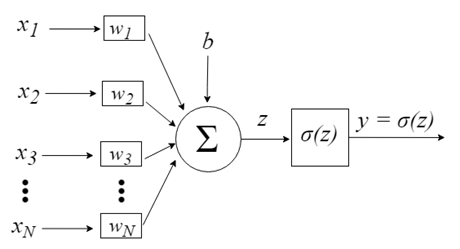
Компьютерная модель нейрона: перцептрон
Перцептрон
Перцептрон вдохновлен идеей обработки информации единственной нервной клетки, называемой нейроном. Нейрон принимает на вход сигналы через свои дендриты, которые передают электрический сигнал телу клетки. Точно так же перцептрон получает входные сигналы из примеров обучающих данных, которые предварительно взвесили и объединили в линейное уравнение, называемое активацией.
- z = sum(weight_i * x_i) + bias
Где weight — это вес сети, X — это входное значение, i — индекс веса или входные данные, а смещение — это специальный вес, который не имеет множитель в виде входного значения (можем считать, что входные данные всегда равны 1.0).
Затем активация преобразуется в выходное (прогнозируемое) значение с помощью передаточной функции (функция активации).
- y = 1.0 если z >= 0.0, иначе 0.0
Таким образом, перцептрон представляет собой алгоритм классификации проблем с двумя классами (двоичный классификатор), где для разделения двух классов может использоваться линейное уравнение.
Это тесно связано с линейной регрессией и логистической регрессией, которые осуществляют прогнозы аналогичным образом (например, взвешенная сумма входов).
Алгоритм перцептрона — простейший вид искусственной нейронной сети. Это модель одного нейрона, которая может использоваться в задачах классификации двух классов и обеспечивает основу для дальнейшего развития гораздо более крупных сетей.
Входы нейронов представлены вектором x = [x1, x2, x3,…, xN], который может соответствовать, к примеру, ряду торговых цен актива, значениям технических индикаторов, числовой последовательности в пикселях изображения. Когда они попадают к нейрону, они умножаются на соответствующие синаптические веса, которые являются элементами вектора w = [w1, w2, w3, …, wN], и таким образом генерируют значение z, обычно называемое потенциалом активации, согласно выражению:
b обеспечивает более высокую степень свободы и не зависит от входа в это выражение, что обычно соответствует нейрону смещения (склонности). Затем z-значение проходит через функцию активации σ, которая отвечает за ограничение этого значения определенным интервалом (например, 0 — 1), что дает окончательное выходное значение и значение нейрона. Некоторые используемые триггерные функции: шаг, сигмоид, гиперболический тангенс, softmax и ReLU («rectified linear unit»).
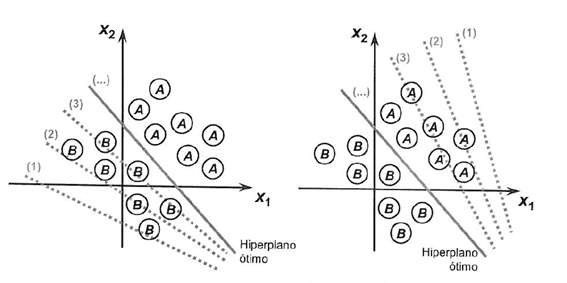
Чтобы проиллюстрировать процесс, направленный на достижение предела разделимости классов, ниже мы показываем две ситуации, которые демонстрируют их сближение к стабилизации с учетом только двух входов {x1 и x2}
Веса алгоритма перцептрона следует оценивать на основе данных обучения с использованием стохастического градиентного спуска.
Стохастический градиент
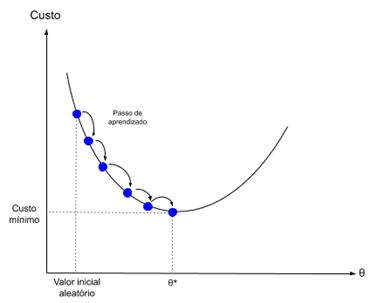
Градиентный спуск — это процесс минимизации функции в направлении градиента функции стоимости.
Это подразумевает знание формулы стоимости, а также производной, чтобы с определенной точки мы могли узнать наклон и могли двигаться в этом направлении, например, вниз по направлению к минимальному значению.
В машинном обучении мы можем использовать метод, который оценивает и обновляет веса для каждой итерации, называемый стохастическим градиентным спуском, чтобы минимизировать ошибку модели в наших обучающих данных.
Принцип работы этого алгоритма оптимизации заключается в том, что каждый обучающий экземпляр показывается модели по одному. Модель делает прогноз для обучающего экземпляра, вычисляет ошибку и обновляет модель, чтобы уменьшить ошибку для следующего прогноза.
Эту процедуру можно использовать для поиска набора весов в модели, который дает наименьшую ошибку для модели в обучающих данных.
Для алгоритма перцептрона на каждой итерации веса w обновляются с использованием уравнения:
- w = w + learning_rate * (expected — predicted) * x
Где w оптимизируется, learning_rate — это скорость обучения, которую мы должны установить (например, 0.1), (expected — predicted) — ошибка прогнозирования для модели в обучающих данных, относящихся к весу, а x — входное значение.
Для стохастического градиентного спуска требуются два параметра:
- Коэффициент обучения: используется для ограничения размера корректировки веса при каждом его обновлении.
- Эпохи — сколько раз обучающие данные должны выполняться при обновлении веса.
Они вместе с обучающими данными будут аргументами для функции.
Нам нужно выполнить 3 цикла в функции:
1. Цикл для каждой эпохи.
2. Цикл для каждой строки в обучающих данных для эпохи.
3. Цикл для каждого веса, который обновляется для одной строке в одной эпохи.
Веса обновляются в зависимости от ошибки, допущенной моделью. Ошибка рассчитывается как разница между фактическим значением и прогнозом, сделанным с помощью весов.
Для каждого входного атрибута есть свой вес, и они постоянно обновляются, например:
- w(t+1)= w(t) + learning_rate * (expected(t) — predicted(t)) * x(t)
Смещение обновляется аналогичным образом, только без входа, поскольку оно не связано с конкретным входным значением:
- bias(t+1) = bias(t) + learning_rate * (expected(t) — predicted(t)).
Применение модели нейрона:
Теперь перейдем к практическому применению.
Этот урок разделен на 2 части:
1. Делаем прогнозы
2. Оптимизация веса сети
Эти шаги обеспечат основу для реализации и применения алгоритма перцептрона к другим задачам классификации.
Нам нужно определить количество столбцов в нашем наборе X, для этого мы определяем константу
#define nINPUT 3
В MQL5 многомерный массив может быть статическим или динамическим только для первого измерения, а поскольку все остальные измерения будут статическими, при объявлении массива необходимо указать размер.
1. Делаем прогнозы
Первый шаг — разработать функцию, которая может делать прогнозы.
Это будет необходимо как при оценке значений весов кандидатов при стохастическом градиентном спуске, так и после завершения модели. Прогнозы надо делать и на тестовых данных, и на новых.
Ниже приведена функция predict, которая прогнозирует выходное значение для строки исходя от определенного набора весов.
Первый вес всегда является смещением, поскольку он автономен и не работает с конкретным входным значением.
template <typename Array> double predict(const Array &X[][nINPUT], const Array &weights[], const int row=0) { double z = weights[0]; for(int i=0; i<ArrayRange(X, 1)-1; i++) { z+=weights[i+1]*X[row][i]; } return activation(z); }
Перенос нейронов:
Как только нейрон активирован, нам нужно передать активацию, чтобы увидеть, каковы на самом деле выходные данные нейрона.
double activation(const double activation) { return activation>=0.0?1.0:0.0; }
Мы получаем в качестве аргумента в функции прогнозирования входной набор X, массив с весами (W) и строку, для которой прогнозируется входной набор X.
Мы можем придумать небольшой набор данных, чтобы проверить нашу функцию прогнозирования.
Мы также можем использовать заранее подготовленные веса, чтобы делать прогнозы для этого набора данных.
double weights[] = {-0.1, 0.20653640140000007, -0.23418117710000003};
После того, как мы собрали все это вместе, мы можем протестировать нашу функцию прогнозирования ниже.
#define nINPUT 3 void OnStart() { random.seed(42); double dataset[][nINPUT] = { {2.7810836,2.550537003,0}, {1.465489372,2.362125076,0}, {3.396561688,4.400293529,0}, {1.38807019,1.850220317,0}, {3.06407232,3.005305973,0}, {7.627531214,2.759262235,1}, {5.332441248,2.088626775,1}, {6.922596716,1.77106367,1}, {8.675418651,-0.242068655,1}, {7.673756466,3.508563011,1} }; double weights[] = {-0.1, 0.20653640140000007, -0.23418117710000003}; for(int row=0; row<ArrayRange(dataset, 0); row++) { double predict = predict(dataset, weights, row); printf("Expected=%.1f, Predicted=%.1f", dataset[row][nINPUT-1], predict); } } template <typename Array> double predict(const Array &X[][nINPUT], const Array &weights[], const int row=0) { double z = weights[0]; for(int i=0; i<ArrayRange(X, 1)-1; i++) { z+=weights[i+1]*X[row][i]; } return activation(z); } double activation(const double activation) { return activation>=0.0?1.0:0.0; }
Есть два входных значения (X1 и X2) и три коэффициента веса (bias, w1 и w2). Уравнение активации, которое мы моделируем для данной проблемы, выглядит так:
activation = (w1 * X1) + (w2 * X2) + b
Или с конкретными значениями веса, мы вручную выбираем как:
activation = (0.206 * X1) + (-0.234 * X2) + -0.1
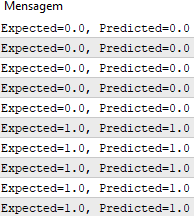
После завершения работы функции мы получаем прогнозы, которые соответствуют ожидаемым выходным значениям y.
Теперь можем реализовать стохастический градиентный спуск для оптимизации значений веса.
2. Оптимизируем веса сети
Веса для наших обучающих данных можно оценить, используя стохастический градиентный спуск, как было сказано ранее.
Ниже приведена функция train_weights(), которая вычисляет значения веса для набора обучающих данных с использованием стохастического градиентного спуска.
В MQL5 мы не можем получить возврат из этого массива с данными обученных весов, потому что, в отличие от переменных, массивы могут быть переданы в функцию только по ссылке. Это означает, что функция не создает собственный экземпляр массива, а вместо этого работает напрямую с переданным ей массивом. Таким образом, все изменения, осуществляемые в этом массиве внутри функции влияют на исходный массив.
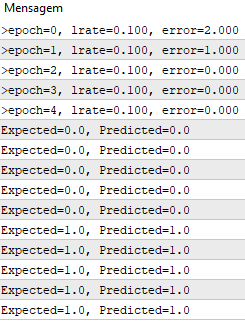
template <typename Array> void train_weights(Array &weights[], const Array &X[][nINPUT], double l_rate=0.1, int n_epoch=5) { ArrayResize(weights, ArrayRange(X, 1)); for(int i=0; i<ArrayRange(X, 1); i++) { weights[i]=random.random(); } for(int epoch=0; epoch<n_epoch; epoch++) { double sum_error = 0.0; for(int row=0; row<ArrayRange(X, 0); row++) { double y = predict(X, weights, row); double error = X[row][nINPUT-1] - y; sum_error += pow(error, 2); weights[0] = weights[0] + l_rate * error; for(int i=0; i<ArrayRange(X, 1)-1; i++) { weights[i+1] = weights[i+1] + l_rate * error * X[row][i]; } } printf(">epoch=%d, lrate=%.3f, error=%.3f",epoch, l_rate, sum_error); } }
На каждой эпохе мы отслеживаем сумму квадратичной ошибки (положительное значение), чтобы отслеживать уменьшение ошибки. Это позволяет наблюдать как алгоритм минимизирует ошибку на каждой эпохе.
Давайте протестируем нашу функцию с одним и тем же набором данных, представленным выше.
#define nINPUT 3 void OnStart() { random.seed(42); double dataset[][nINPUT] = { {2.7810836,2.550537003,0}, {1.465489372,2.362125076,0}, {3.396561688,4.400293529,0}, {1.38807019,1.850220317,0}, {3.06407232,3.005305973,0}, {7.627531214,2.759262235,1}, {5.332441248,2.088626775,1}, {6.922596716,1.77106367,1}, {8.675418651,-0.242068655,1}, {7.673756466,3.508563011,1} }; double weights[]; train_weights(weights, dataset); ArrayPrint(weights, 20); for(int row=0; row<ArrayRange(dataset, 0); row++) { double predict = predict(dataset, weights, row); printf("Expected=%.1f, Predicted=%.1f", dataset[row][nINPUT-1], predict); } } template <typename Array> double predict(const Array &X[][nINPUT], const Array &weights[], const int row=0) { double z = weights[0]; for(int i=0; i<ArrayRange(X, 1)-1; i++) { z+=weights[i+1]*X[row][i]; } return activation(z); } double activation(const double activation) { return activation>=0.0?1.0:0.0; } template <typename Array> void train_weights(Array &weights[], const Array &X[][nINPUT], double l_rate=0.1, int n_epoch=5) { ArrayResize(weights, ArrayRange(X, 1)); ArrayInitialize(weights, 0); for(int epoch=0; epoch<n_epoch; epoch++) { double sum_error = 0.0; for(int row=0; row<ArrayRange(X, 0); row++) { double y = predict(X, weights, row); double error = X[row][nINPUT-1] - y; sum_error += pow(error, 2); weights[0] = weights[0] + l_rate * error; for(int i=0; i<ArrayRange(X, 1)-1; i++) { weights[i+1] = weights[i+1] + l_rate * error * X[row][i]; } } printf(">epoch=%d, lrate=%.3f, error=%.3f",epoch, l_rate, sum_error); } }
Мы используем скорость обучения 0,1 и обучаем модель только для 5 эпох или 5 показов весов для всего набора обучающих данных.
При выполнении примера для каждой эпохи печатается сообщение с суммой квадратичной ошибки для этой эпохи и окончательным набором весов.
Мы видим, как быстро алгоритм выучивает проблему.
Этот тест можно найти в файле PerceptronScript.mq5.
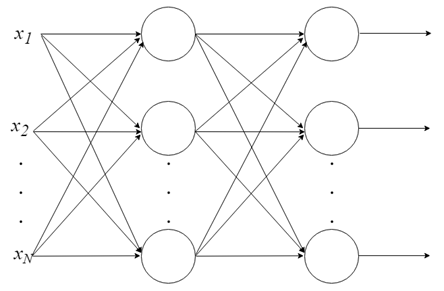
Многослойный перцептрон
- Объединеняем нейроны в слои
С одним нейроном мало что можно сделать, но мы можем объединить их в многоуровневую структуру, каждый с разным количеством нейронов, и сформировать нейронную сеть, называемую многослойным перцептроном («multi layer perceptron, MLP»). Вектор входных значений X проходит через начальный слой, выходные значения которого связаны со входами следующего уровня, и так далее, пока сеть не предоставит выходные значения последнего слоя в качестве результата. Сеть может быть организована в несколько слоев, что делает ее глубокой и способной выучить все более сложные отношения.
Обучение MLP
Для того, чтобы такая сеть работала, ее нужно обучать. Это как учить ребенка читать. Обучение MLP происходит в контексте машинного обучения с учителем, но как это работает?
Обучение с учителем:
- Нам дается набор отмеченных данных, для которых мы уже знаем какой именно является нашим правильным выходом, и он должен быть аналогичен набору, имея представление о том, что существует связь между входом и выходом.
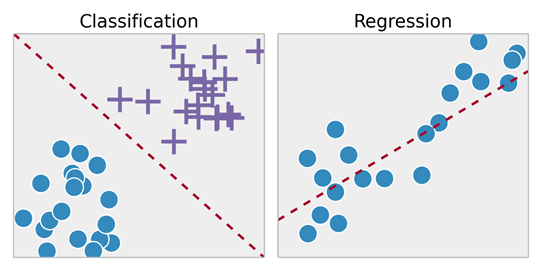
- Задачи обучения с учителем подразделяются на задачи «регрессии» и «классификации». В задачах регрессии мы пытаемся предсказать результаты на непрерывном выходе, что означает, что мы пытаемся сопоставить входные переменные с некоторой непрерывной функцией. В задачах классификации мы стараемся предсказать результаты на дискретном выходе. Другими словами, мы пытаемся сопоставить входные переменные по разным категориям.
Пример 1:
- Учитывая набор данных о размерах домов на рынке недвижимости, попробуйте спрогнозировать их цену. Цена в зависимости от размера — это непрерывный результат, так что это проблема регрессии.
- Мы могли бы также превратить этот пример в задачу классификации, чтобы прогнозировать о том, «продастся ли дом дороже или дешевле, чем запрашиваемая цена». Здесь мы рассортируем дома по цене на две разные категории.
Обратное распространение
Обратное распространение, без сомнений, является самым важным алгоритмом в истории нейронных сетей — без (эффективного) обратного распространения, было бы невозможно обучить сети глубокого обучения так, как мы это делаем сегодня. Обратное распространение можно считать краеугольным камнем современных нейронных сетей и глубокого обучения.
Разве мы не учимся на ошибках?
Идея алгоритма обратного распространения ошибки состоит в том, чтобы на основе расчетной ошибки, полученной на выходном слое нейронной сети, пересчитать значение весов вектора W последнего слоя нейронов. Затем мы переходим к предыдущему слою и так далее, от конца к началу, то есть, он состоит из обновления всех весов W слоев, от последнего до достижения входного слоя сети путем обратного распространения ошибки, полученной сетью. Другими словами, ошибка вычисляется между тем, что предсказала сеть, и тем, что она была на самом деле (фактический 1, предсказанный 0; у нас есть ошибка!), поэтому мы пересчитываем значения всех весов, начиная с последнего слоя и переходя к первому, всегда обращая внимание на уменьшение этой ошибки.
Алгоритм обратного распространения ошибки состоит из двух этапов:
1. Прямой проход («forward pass»), при котором наши входы проходят через сеть и получают прогнозы выхода (этот шаг также известен как фаза распространения).
2. Обратный проход («backward pass»), при котором мы вычисляем градиент функции потерь на последнем слое (то есть слое прогнозирования) сети и используем этот градиент для рекурсивного применения цепного правила («chain rule») для обновления весов в нашей сети (также известного как стадия обновления веса или обратное распространение)
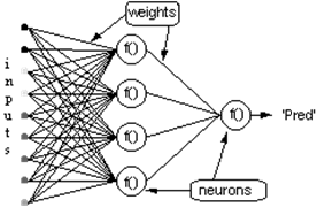
Рассмотрим сеть выше со слоем скрытых нейронов и выходным нейроном. Когда входной вектор распространяется по сети, для текущего набора весов существует выходной Pred(y). Цель обучения с учителем — настроить веса так, чтобы уменьшить разницу между Pred(y) сети и требуемым выходным Req(y). Для этого требуется алгоритм, который уменьшает абсолютную ошибку, что аналогично уменьшению квадратичной ошибки, где:
(1)
Сетевая ошибка = Pred — Req
= E
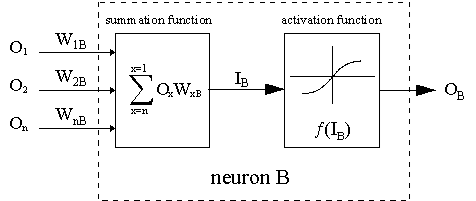
Алгоритм должен регулировать веса, чтобы минимизировать E². Обратное распространение — это алгоритм, который выполняет минимизацию градиентного спуска E². Чтобы минимизировать E², необходимо рассчитать его чувствительность к каждому весу. Другими словами, нам нужно знать, какое влияние будет иметь изменение каждого веса на E². Если нам будет известно, веса можно будет отрегулировать в направлении, уменьшающем абсолютную ошибку. Последующее описание правила обратного распространения основано на такой диаграмме:
Пунктирная линия представляет нейрон B, который может быть скрытым или выходным нейроном. Выходы n нейронов (O 1 … O n) на предыдущем слое являются взодами для нейрона B. Если нейрон B находится в скрытом слое, он просто является входным вектором. Эти выходы умножаются на соответствующие веса (W1B … WnB), где WnB — вес, соединяющий нейрон n и нейрону B. Функция суммы складывает все эти произведения для получения входных данных, IB, который обрабатывается функцией триггера f(.) нейрона B. f (IB) это выход OB нейрона B. Рассмотрим пример. Назовем нейрон 1 нейроном A и рассмотрим вес WAB между двумя нейронами. Подход, используемый для изменения веса, определяется правилом дельты:
(2)
где — параметр скорости обучения, который определяет скорость обучения, а
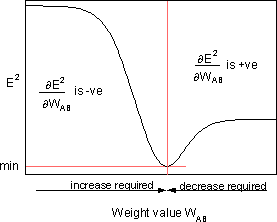
является чувствительностью ошибки E² к весу WAB и определяет направление поиска в пространстве весов для нового веса WAB (новый), как изображено на рисунке ниже.
Чтобы минимизировать E², правило дельты обеспечивает необходимое направление изменения веса.
Ключевой концепцией приведенного выше уравнения является вычисление выражения ∂E² /∂WAB, которое состоит в вычислении частных производных функции ошибок E² по отношению к каждому весу вектора W.
Дифференцирование сложной функции:
(3)
и
(4)
поскольку остальные входы нейрона B не зависят от веса WAB. Таким образом, исходя из уравнений (3) и (4), уравнение (2) становится
(5)
и изменение веса WAB зависит от чувствительности квадрата ошибки E² на входе IB, единицы B и входного сигнала OА.
Возможны две ситуации:
1. B — выходной нейрон;
2. B — скрытый нейрон.
Рассмотриваем первый случай:
Поскольку B является выходным нейроном, изменение квадрата ошибки из-за настроки WAB просто является изменением квадрата ошибки выходного сигнала B.
(6)
объединяя уравнение (5) и уравнение (6), получаем
(7)
Правило изменения весов, когда нейрон B является выходным нейроном, если выходная функция активации, f (.), является логистической функцией:
(8)
Дифференцируем уравнение (8) по аргументу x:
(9)
Но,
(10)
при вставке (10) в (9) получаем:
(11)
таким же образом для функции tanh
или для линейной функции (identity)
Так мы получаем:
Рассматривая второй случай:
B это скрытый нейрон
(12)
где O представляет выходной нейрон
(13)
где p это индекс, который охватывает все нейроны, включая нейрон B, который обеспечивает входные сигналы для выходного нейрона. Расширяем правую часть уравнения (13),
(14)
поскольку веса других нейронов WpO (p! = B) не имеют зависимости от OB.
При вставке (13) и (13) в (12):
(15)
Следовательно, теперь это выражается как функция от
, вычисляемая, как описано в уравнении (6).
Полное правило изменения веса WAB между нейроном A, который посылает сигнал нейрону B, является таким:
(16)
где
где fo (.) и fh (.) это скрытые функции активации и выхода соответственно.
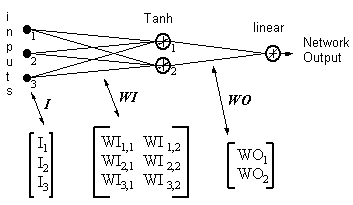
Пример
Выход из сети = [tanh(I T .WI)] . WO
HID = [Tanh(I T.WI)] T— выходы скрытых нейронов
ERROR = (выход из сети — нужный выход)
LR = коеффициент обучения
Обновления веса становятся
нейроном с линейным выходом
(17)
WO = WO — ( LR x ERROR x HID )
скрытым нейроном
(18)
WI = WI — { LR x [ERROR x WO x (1- HID 2)] . I T } T
Уравнения 17 и 18 показывают, что изменение веса — это входной сигнал, умноженный на локальный градиент. Это обеспечивает направление, величина которого также зависит от величины ошибки. Если берем направление без величины, все изменения будут одинакового размера, и это будет зависеть от темпа обучения. Вышеуказанный алгоритм является упрощенной версией, так как имеется только один выходной нейрон. В исходном алгоритме допускается более одного выхода, а уменьшение градиента минимизирует общую квадратную ошибку всех выходов. Есть много алгоритмов, которые произошли от исходного алгоритма для увеличения скорости обучения. Они кратко изложены в:
« Back Propagation family album» — Technical report C/TR96-05, Department of Computing, Macquarie University, NSW, Australia».
Обратное распространение — это элегантный и умелый алгоритм. Современные модели глубокого обучения, такие как сверточные нейронные сети, хотя и более совершенные, чем MLP, показали себя намного лучше в таких задачах, как классификация изображений и используют обратное распространение в качестве метода обучения, а также так называемые рекуррентные нейронные сети в условиях естественной языковой обработки, которые также используют этот алгоритм. Самое невероятное, что таким моделям удается находить ненаблюдаемые и непонятные закономерности для нас, людей, что удивляет и позволяет нам считать, что скоро мы получим помощь глубокого обучения для решения многих основных проблем, с которыми сталкивается человечество.
Применение модели MLP
Этот урок разделен на 5 частей:
1. Инициализация сети.
2. Прямое распространение (FeedForward).
3. Обратное распространение.
4. Обучение сети.
5. Прогноз.
Для нашей разработки мы реализуем применение на чистом MQL. Нам уже известно, что существуют библиотеки на других языках, которые уже являются гораздо более сложными, и настоятельно рекомендуется использовать их из практических соображений и соображений производительности, но, как уже было сказано в начале, важно понимать внутреннее устройство таких библиотек, чтобы иметь больший контроль над всем процессом. Мы также не использовали ООП в нашем тесте, поскольку это всего лишь алгоритм для иллюстрации предыдущих уравнений, в нем нет необходимости. Однако в реальных случаях гораздо практичнее использовать ООП, поскольку оно обеспечивает масштабируемость проекта.
1. Инициализация сети
У каждого нейрона есть набор весов, которые необходимо поддерживать. Вес для каждого входного соединения и дополнительный вес для смещения.
Рекомендуем инициализировать веса сети для небольших случайных чисел. В этом случае мы будем использовать случайные числа в диапазоне от 0 до 1. Для этого мы создали функцию для генерации случайных чисел.
double random(void) { return ((double)rand())/(double)SHORT_MAX; }
Ниже представлена функция под названием initialize_network(), которая создает веса нашей нейронной сети.
void forward_propagate(void) { int i = 0; for(i = 0; i<numHidden; i++) { hiddenVal[i] = 0.0; for(int j = 0; j<numInputs; j++) { hiddenVal[i] += (X[patNum][j] * weightsIH[j][i]); } hiddenVal[i] = tanh(hiddenVal[i]); } outPred = 0.0; for(i = 0; i<numHidden; i++) { outPred += hiddenVal[i] * weightsHO[i]; } errThisPat = outPred - y[patNum]; }
3. Обратное распространение
Алгоритм обратного распространения назван в честь способа обучения весов
Ошибка вычисляется между ожидаемыми выходами и выходными сигналами сети прямого распространения. Затем эти ошибки передаются обратно по сети от выходного слоя к скрытому слою, перекладывая ответственность за ошибку и обновляя веса по мере их поступления.
Математика ошибки обратного распространения была объяснена выше.
void backward_propagate_error(void) { for(int k = 0; k<numHidden; k++) { double weightChange = LR_HO * errThisPat * hiddenVal[k]; weightsHO[k] -= weightChange; regularisationWeights(weightsHO[k]); } for(int i = 0; i<numHidden; i++) { for(int k = 0; k<numInputs; k++) { double x = 1 - pow(hiddenVal[i],2); x = x * weightsHO[i] * errThisPat * LR_IH; x = x * X[patNum][k]; double weightChange = x; weightsIH[k][i] -= weightChange; } } }
метод regularizationWeights был создан только для регуляризации весов в диапазоне от -5 до 5.
void regularisationWeights(double &weight) { weight<-5?weight=-5:weight>5?weight=5:weight=weight; }
4. Обучение сети
Сеть обучается методом стохастического градиентного спуска.
Это включает в себя несколько итераций, раскрывающих набор обучающих данных в сети, и для каждой строки данных прямое распространение входных данных, обратное распространение ошибки и обновление весов сети.
//# Train a network for a fixed number of epochs void train(void) { for(int j = 0; j <= numEpochs; j++) { for(int i = 0; i<numPatterns; i++) { patNum = rand()%numPatterns; forward_propagate(); backward_propagate_error(); } calcOverallError(); printf("epoch = %d RMS Error = %f",j,RMSerror); } }
5. Прогноз
Делать прогнозы с помощью обученной нейронной сети довольно просто.
Мы уже видели, как распространить паттерн входа для получения выходных данных. Это все, что нам нужно сделать, чтобы осуществить прогноз. Мы можем использовать выходные значения напрямую как вероятность принадлежности паттерна к каждому выходному классу.
void predict(void) { for(int i = 0; i<numPatterns; i++) { patNum = i; forward_propagate(); printf("real = %d predict = %f",y[patNum],outPred); } }
Полный пример можно найти в файле MLP_Script.mq5.
Заключение
Мы занимались вычислениями, задействованными в процессе развития нейрона перцептрона, а также сети нейронов перцептрона, называемой «multi layer perceptron, MLP». В данном процессе мы поняли, как осуществляется обучение этого типа сетей с использованием обратного распространения ошибки и градиентного спуска.
Алгоритм обратного распространения ошибки
В начале обучения весам
сети присваиваются некоторые случайные
малые (чтобы предотвратить выход многих
нейронов сети в области «насыщения»
при использовании сигмоидной функции
активации) значения из диапазона
[-0.3,0.3]. При обучении сети на ее входы и
выходы поступают обучающие сигналы из
обучающей последовательности. Выходной
сигнал сети сравнивается с обучающим
выходным сигналом и определяется сигнал
ошибки. Целью обучения является
минимизация ошибки распознавания
образов, соответствующих тем классам,
из образцов которых была построена
обучающая последовательность. Обучающие
образцы подаются на вход сети в случайном
порядке, чтобы сеть не запоминала порядок
поступления обучающих сигналов, а
формировала признаки распознаваемых
классов. Существует два способа обучения
персептрона:
Коррекция всех весов
производится после предъявления сети
каждого обучающего примера.
Коррекция всех весов
производится после предъявления сети
всей обучающей последовательности или
заранее определенной ее части – пакетное
(batch) обучение. Просуммированные по всем
предъявленным образцам ошибки используются
для одновременной коррекции всех весовых
коэффициентов.
Процедура минимизации
ошибки при этом может быть описана в
известных терминах нахождения экстремума
функции в предположении, что функционал
ошибки на выходе сети имеет минимум.
Одним из часто используемых
методов нахождения экстремума является
метод градиента. Чтобы применить его к
конкретной задаче, необходимо потребовать,
чтобы рассматриваемая функция была
дифференцируема на всем пространстве
поиска, т.е. во всей области допустимых
значений аргументов, по которым
производится дифференцирование. Для
нахождения производной от функционала
на выходе сети можно использовать цепное
правило дифференцирования. Далее
необходимо приравнять полученные
производные по всем аргументам к нулю
и решить систему нелинейных уравнений
для нахождения оптимальных значений.
В случае многослойных сетей такой подход
сопряжен с большим объемом вычислений
и требует затраты больших объемов памяти
и машинного времени. Поэтому для настройки
сети применяют приближенный метод
вычисления минимума, называемый методом
наискорейшего спуска. В этом методе
поиск решения состоит из ряда итераций,
в каждой из которых оптимизируемый
параметр изменяет свое значение в
соответствии с правилом
вычисленное
значение ошибки на выходе сети в момент
времени t, -коэффициент
скорости обучения, принимающий значения
0<<1. Как видим,
метод наискорейшего спуска дает правило
обучения, имеющее ту же структуру, что
и -правило.
Основная идея обратного
распространения состоит в том, как
получить оценку ошибки для нейронов
скрытых слоев. Заметим, что известные
ошибки, делаемые нейронами выходного
слоя, возникают вследствие неизвестных
пока ошибок нейронов скрытых слоев. Чем
больше вес синаптической связи между
нейроном скрытого слоя и выходным
нейроном, тем сильнее ошибка первого
влияет на ошибку второго. Следовательно,
оценку вклада каждого весового
коэффициента скрытых слоев можно
получить, как функцию от взвешенной
суммы ошибок последующих слоев. При
обучении информация распространяется
от низших слоев иерархии к высшим, а
оценки ошибок на выходах нейронов
скрытых слоев определяются как функции
от суммы ошибок последующих слоев. Т.е
рассматривается распространение ошибки
в обратном направлении по сравнению с
направлением распространения сигнала.
Поэтому метод получил название «Метода
обратного распространения ошибки» (EBP
– Error Back Propagation).
В качестве ошибки
обучения можно применять любую существенно
положительную функцию разности обучающего
сигнала и выхода нейрона. Она называется
целевой функцией. Согласно методу
наименьших квадратов минимизируемой
целевой функцией ошибки на выходе сети
является величина

где
— реальный выходной сигнал нейрона j
выходного слоя N нейронной сети при
подаче на ее входы р-го образца,
— идеальное (желаемое) выходное состояние
этого нейрона. В этом случае суммируются
ошибки, вычисленные для всех нейронов
выходного слоя при предъявлении всех
обучающих образов. Такой вид функции
ошибки соответствует пакетному (batch)
правилу обучения, при котором коррекция
весов производится по значению ошибки,
накопленной в сети после предъявления
всех или заданного числа обучающих
примеров. Функция ошибки является в
этом случае квадратичной, а поверхность
ошибки в пространстве весовых коэффициентов
(в области поиска) при использовании
сигмоидальной активационной функции
имеет сложный рельеф, характеризующийся
множеством локальных минимумов.
Целью решения задачи
оптимизации является отыскании экстремума
функции ошибки. Для этого можно
использовать метод градиента, который
сводится к вычислению производных от
функции ошибки по всем свободным
параметрам сети с последующим
приравниванием к 0 полученных выражений
и решения системы уравнений относительно
множества свободных параметров. Для
вычисления градиента используется
цепное правило дифференцирования.
Реальные сети имеют большое число
параметров, и такого рода задача
становится NP неразрешимой.
Для получения приемлемого
решения за разумное время используется
метод градиентного спуска, при котором
вычисление производных выходного
сигнала для каждого нейрона каждого
слоя происходит одновременно с вычислением
значения выходного сигнала этого слоя.
Это возможно благодаря выбору активационной
функции, всюду дифференцируемой во всем
пространстве свободных параметров
сети. Настройка всех весов сети
производится одновременно после
завершения обратного прохода сигнала
ошибки через всю сеть к ее входу.
Производная сигмоидальной
функции
по аргументу net легко вычисляется и
равна
,
и может быть реализована аппаратными
средствами одновременно с вычислением
f(net).
Производная от функции
ошибки по весовому коэффициенту
произвольного слоя определяется как
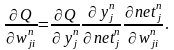
Здесь
-выход
j-го нейрона n-го слоя. Последний сомножитель
в этом выражении равен
,
второй сомножитель – это производная
от активационной функции. Первый
сомножитель вычисляется по измеренному
значению ошибки в выходном слое с
использованием цепного правила
дифференцирования для скрытых слоев.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Нейронная сеть — введение
Принцип обучения многослойной нейронной сети с помощью алгоритма обратного распространения
Рассмотрим процесс обучения нейронной сети с использованием алгоритма обратного распространения ошибки (backpropagation).
Для иллюстрации этого процесса используем нейронную сеть состоящую из трёх слоёв и имеющую два входа и один выход:
здесь, автор считает слои по-другому и не учитывает «2 нейрона» входного слоя
Каждый нейрон состоит из двух элементов.
Первый элемент – дендриты — добавляют весовые коэффициенты ко входным сигналам.
Второй элемент – тело — реализует нелинейную функцию, т.н. функцию активации нейрона.
Сигнал е – это взвешенная сумма входных сигналов
у = f (е)
— выходной сигнал нейрона.
Чтобы обучить нейронную сеть мы должны подготовить обучающие данные(примеры).
В нашем случае, тренировочные данные состоят из входных сигналов (х1 и х2) и желаемого результата z.
Обучение – это последовательность итераций (повторений).
В каждой итерации весовые коэффициенты нейронов подгоняются с использованием новых данных из тренировочных примеров.
Изменение весовых коэффициентов и составляют суть алгоритма, описанного ниже.
Каждый шаг обучения начинается с воздействия входных сигналов из тренировочных примеров. После этого мы можем определить значения выходных сигналов для всех нейронов в каждом слое сети.
Иллюстрации ниже показывают, как сигнал распространяется по сети.
Символы W(Xm)n представляют вес связи между сетевым входом Xm и нейрона n во входном слое.
Символы y(n) представляют выходной сигнал нейрона n.
Распространение сигнала через скрытый слой.
Символы Wmn представляют весовые множители связей между выходом нейрона m и входом нейрона n в следующем слое.
Распространение сигнала через выходной слой
На следующем шаге алгоритма, выходной сигнала сети y сравнивается с желаемым выходным сигналом z, который хранится в тренировочных данных.
Разница между этими двумя сигналами называется ошибкой d выходного слоя сети.
Невозможно непосредственно вычислить сигнал ошибки для внутренних нейронов, потому что выходные значения этих нейронов, неизвестны.
На протяжении многих лет был неизвестен эффективный метод для обучения многослойной сети.
Только в середине восьмидесятых годов был разработан алгоритм обратного распространения ошибки.
Идея заключается в распространении сигнала ошибки d (вычисленного в шаге обучения) обратно на все нейроны, чьи выходные сигналы были входящими для последнего нейрона.
Весовые коэффициенты Wmn, используемые для обратного распространения ошибки, равны тем же коэффициентам, что использовались во время вычисления выходного сигнала. Только изменяется направление потока данных (сигналы передаются от выхода ко входу).
Этот процесс повторяется для всех слоёв сети. Если ошибка пришла от нескольких нейронов — она суммируются:
Когда вычисляется величина ошибки сигнала для каждого нейрона – можно скорректировать весовые коэффициенты каждого узла ввода(дендрита) нейрона.
В формулах ниже df(e)/de — является производной от функции активации нейрона (чьи весовые коэффициенты корректируются).
как помним, для активационной функции типа сигмоид
1 S(x) = ----------- 1 + exp(-x)производная выражается через саму функцию:
S'(x) = S(x)*(1 - S(x)), что позволяет существенно сократить вычислительную сложность метода обратного распространения ошибки.
Вычисление производной необходимо, потому что для корректировки весовых коэффициентов при обучении ИНС с помощью алгоритма обратного распространения, используется метод градиентного спуска.
Коэффициент h влияет на скорость обучения сети.
Есть несколько методов для выбора этого параметра.
Первый способ — начать учебный процесс с большим значением параметра h. Во время коррекции весовых коэффициентов, параметр постепенно уменьшают.
Второй — более сложный метод обучения, начинается с малым значением параметра h. В процессе обучения параметр увеличивается, а затем вновь уменьшается на завершающей стадии обучения.
Начало учебного процесса с низким значением параметра h позволяет определить знак весовых коэффициентов.
продолжение следует…
Ссылки
Оригинал статьи (на английском)
http://ru.wikipedia.org/wiki/Метод_обратного_распространения_ошибки
http://en.wikipedia.org/wiki/Backpropagation
Нейросеть в 11 строчек на Python
An overview of gradient descent optimization algorithms
По теме
Нейронная сеть — введение
Пример работы самоорганизующейся инкрементной нейронной сети SOINN