Sem стандартная ошибка среднего - Решение и исправление самых разных ошибок на TopOshibok.ru

From Wikipedia, the free encyclopedia

For a value that is sampled with an unbiased normally distributed error, the above depicts the proportion of samples that would fall between 0, 1, 2, and 3 standard deviations above and below the actual value.

The standard error (SE)^[1] of a statistic (usually an estimate of a parameter) is the standard deviation of its sampling distribution^[2] or an estimate of that standard deviation. If the statistic is the sample mean, it is called the standard error of the mean (SEM).^[1]

The sampling distribution of a mean is generated by repeated sampling from the same population and recording of the sample means obtained. This forms a distribution of different means, and this distribution has its own mean and variance. Mathematically, the variance of the sampling mean distribution obtained is equal to the variance of the population divided by the sample size. This is because as the sample size increases, sample means cluster more closely around the population mean.

Therefore, the relationship between the standard error of the mean and the standard deviation is such that, for a given sample size, the standard error of the mean equals the standard deviation divided by the square root of the sample size.^[1] In other words, the standard error of the mean is a measure of the dispersion of sample means around the population mean.

In regression analysis, the term «standard error» refers either to the square root of the reduced chi-squared statistic or the standard error for a particular regression coefficient (as used in, say, confidence intervals).

Standard error of the sample mean[edit]

Exact value[edit]

Suppose a statistically independent sample of observations $x_{1},x_{2},\ldots ,x_{n}$ is taken from a statistical population with a standard deviation of $\sigma$ . The mean value calculated from the sample, ${\bar {x}}$ , will have an associated standard error on the mean, ${\sigma }_{\bar {x}}$ , given by:^[1]

${\sigma }_{\bar {x}}={\frac {\sigma }{\sqrt {n}}}.$

Practically this tells us that when trying to estimate the value of a population mean, due to the factor $1/{\sqrt {n}}$ , reducing the error on the estimate by a factor of two requires acquiring four times as many observations in the sample; reducing it by a factor of ten requires a hundred times as many observations.

Estimate[edit]

The standard deviation $\sigma$ of the population being sampled is seldom known. Therefore, the standard error of the mean is usually estimated by replacing $\sigma$ with the sample standard deviation $\sigma _{x}$ instead:

${\sigma }_{\bar {x}}\ \approx {\frac {\sigma _{x}}{\sqrt {n}}}.$

As this is only an estimator for the true «standard error», it is common to see other notations here such as:

${\widehat {\sigma }}_{\bar {x}}:={\frac {\sigma _{x}}{\sqrt {n}}}\qquad {\text{ or }}\qquad {s}_{\bar {x}}\ :={\frac {s}{\sqrt {n}}}.$

A common source of confusion occurs when failing to distinguish clearly between:

Accuracy of the estimator[edit]

When the sample size is small, using the standard deviation of the sample instead of the true standard deviation of the population will tend to systematically underestimate the population standard deviation, and therefore also the standard error. With n = 2, the underestimate is about 25%, but for n = 6, the underestimate is only 5%. Gurland and Tripathi (1971) provide a correction and equation for this effect.^[3] Sokal and Rohlf (1981) give an equation of the correction factor for small samples of n < 20.^[4] See unbiased estimation of standard deviation for further discussion.

Derivation[edit]

The standard error on the mean may be derived from the variance of a sum of independent random variables,^[5] given the definition of variance and some simple properties thereof. If $x_{1},x_{2},\ldots ,x_{n}$ is a sample of independent observations from a population with mean ${\bar {x}}$ and standard deviation $\sigma$ , then we can define the total

$T=(x_{1}+x_{2}+\cdots +x_{n})$

which due to the Bienaymé formula, will have variance

$\operatorname {Var} (T)={\big (}\operatorname {Var} (x_{1})+\operatorname {Var} (x_{2})+\cdots +\operatorname {Var} (x_{n}){\big )}=n\sigma ^{2}.$

where we’ve approximated the standard deviations, i.e., the uncertainties, of the measurements themselves with the best value for the standard deviation of the population. The mean of these measurements ${\bar {x}}$ is simply given by

${\bar {x}}=T/n.$

The variance of the mean is then

$\operatorname {Var} ({\bar {x}})=\operatorname {Var} \left({\frac {T}{n}}\right)={\frac {1}{n^{2}}}\operatorname {Var} (T)={\frac {1}{n^{2}}}n\sigma ^{2}={\frac {\sigma ^{2}}{n}}.$

The standard error is, by definition, the standard deviation of ${\bar {x}}$ which is simply the square root of the variance:

$\sigma _{\bar {x}}={\sqrt {\frac {\sigma ^{2}}{n}}}={\frac {\sigma }{\sqrt {n}}}.$

For correlated random variables the sample variance needs to be computed according to the Markov chain central limit theorem.

Independent and identically distributed random variables with random sample size[edit]

There are cases when a sample is taken without knowing, in advance, how many observations will be acceptable according to some criterion. In such cases, the sample size is a random variable whose variation adds to the variation of such that,

$\operatorname {Var} (T)=\operatorname {E} (N)\operatorname {Var} (X)+\operatorname {Var} (N){\big (}\operatorname {E} (X){\big )}^{2}$

^[6]
which follows from the law of total variance.

If has a Poisson distribution, then $\operatorname {E} (N)=\operatorname {Var} (N)$ with estimator $n=N$ . Hence the estimator of $\operatorname {Var} (T)$ becomes $nS_{X}^{2}+n{\bar {X}}^{2}$ , leading the following formula for standard error:

$\operatorname {Standard~Error} ({\bar {X}})={\sqrt {\frac {S_{X}^{2}+{\bar {X}}^{2}}{n}}}$

(since the standard deviation is the square root of the variance).

Student approximation when σ value is unknown[edit]

In many practical applications, the true value of σ is unknown. As a result, we need to use a distribution that takes into account that spread of possible σ’s.
When the true underlying distribution is known to be Gaussian, although with unknown σ, then the resulting estimated distribution follows the Student t-distribution. The standard error is the standard deviation of the Student t-distribution. T-distributions are slightly different from Gaussian, and vary depending on the size of the sample. Small samples are somewhat more likely to underestimate the population standard deviation and have a mean that differs from the true population mean, and the Student t-distribution accounts for the probability of these events with somewhat heavier tails compared to a Gaussian. To estimate the standard error of a Student t-distribution it is sufficient to use the sample standard deviation «s» instead of σ, and we could use this value to calculate confidence intervals.

Note: The Student’s probability distribution is approximated well by the Gaussian distribution when the sample size is over 100. For such samples one can use the latter distribution, which is much simpler.

Assumptions and usage[edit]

An example of how $\operatorname {SE}$ is used is to make confidence intervals of the unknown population mean. If the sampling distribution is normally distributed, the sample mean, the standard error, and the quantiles of the normal distribution can be used to calculate confidence intervals for the true population mean. The following expressions can be used to calculate the upper and lower 95% confidence limits, where ${\bar {x}}$ is equal to the sample mean, $\operatorname {SE}$ is equal to the standard error for the sample mean, and 1.96 is the approximate value of the 97.5 percentile point of the normal distribution:

In particular, the standard error of a sample statistic (such as sample mean) is the actual or estimated standard deviation of the sample mean in the process by which it was generated. In other words, it is the actual or estimated standard deviation of the sampling distribution of the sample statistic. The notation for standard error can be any one of SE, SEM (for standard error of measurement or mean), or S_E.

Standard errors provide simple measures of uncertainty in a value and are often used because:

in many cases, if the standard error of several individual quantities is known then the standard error of some function of the quantities can be easily calculated;
when the probability distribution of the value is known, it can be used to calculate an exact confidence interval;
when the probability distribution is unknown, Chebyshev’s or the Vysochanskiï–Petunin inequalities can be used to calculate a conservative confidence interval; and
as the sample size tends to infinity the central limit theorem guarantees that the sampling distribution of the mean is asymptotically normal.

Standard error of mean versus standard deviation[edit]

In scientific and technical literature, experimental data are often summarized either using the mean and standard deviation of the sample data or the mean with the standard error. This often leads to confusion about their interchangeability. However, the mean and standard deviation are descriptive statistics, whereas the standard error of the mean is descriptive of the random sampling process. The standard deviation of the sample data is a description of the variation in measurements, while the standard error of the mean is a probabilistic statement about how the sample size will provide a better bound on estimates of the population mean, in light of the central limit theorem.^[7]

Put simply, the standard error of the sample mean is an estimate of how far the sample mean is likely to be from the population mean, whereas the standard deviation of the sample is the degree to which individuals within the sample differ from the sample mean.^[8] If the population standard deviation is finite, the standard error of the mean of the sample will tend to zero with increasing sample size, because the estimate of the population mean will improve, while the standard deviation of the sample will tend to approximate the population standard deviation as the sample size increases.

Extensions[edit]

Finite population correction (FPC)[edit]

The formula given above for the standard error assumes that the population is infinite. Nonetheless, it is often used for finite populations when people are interested in measuring the process that created the existing finite population (this is called an analytic study). Though the above formula is not exactly correct when the population is finite, the difference between the finite- and infinite-population versions will be small when sampling fraction is small (e.g. a small proportion of a finite population is studied). In this case people often do not correct for the finite population, essentially treating it as an «approximately infinite» population.

If one is interested in measuring an existing finite population that will not change over time, then it is necessary to adjust for the population size (called an enumerative study). When the sampling fraction (often termed f) is large (approximately at 5% or more) in an enumerative study, the estimate of the standard error must be corrected by multiplying by a »finite population correction» (a.k.a.: FPC):^[9]
^[10]

$\operatorname {FPC} ={\sqrt {\frac {N-n}{N-1}}}$

which, for large N:

$\operatorname {FPC} \approx {\sqrt {1-{\frac {n}{N}}}}={\sqrt {1-f}}$

to account for the added precision gained by sampling close to a larger percentage of the population. The effect of the FPC is that the error becomes zero when the sample size n is equal to the population size N.

This happens in survey methodology when sampling without replacement. If sampling with replacement, then FPC does not come into play.

Correction for correlation in the sample[edit]

Expected error in the mean of A for a sample of n data points with sample bias coefficient ρ. The unbiased standard error plots as the ρ = 0 diagonal line with log-log slope −1⁄2.

If values of the measured quantity A are not statistically independent but have been obtained from known locations in parameter space x, an unbiased estimate of the true standard error of the mean (actually a correction on the standard deviation part) may be obtained by multiplying the calculated standard error of the sample by the factor f:

$f={\sqrt {\frac {1+\rho }{1-\rho }}},$

where the sample bias coefficient ρ is the widely used Prais–Winsten estimate of the autocorrelation-coefficient (a quantity between −1 and +1) for all sample point pairs. This approximate formula is for moderate to large sample sizes; the reference gives the exact formulas for any sample size, and can be applied to heavily autocorrelated time series like Wall Street stock quotes. Moreover, this formula works for positive and negative ρ alike.^[11] See also unbiased estimation of standard deviation for more discussion.

References[edit]

^ ^a ^b ^c ^d Altman, Douglas G; Bland, J Martin (2005-10-15). «Standard deviations and standard errors». BMJ: British Medical Journal. 331 (7521): 903. doi:10.1136/bmj.331.7521.903. ISSN 0959-8138. PMC 1255808. PMID 16223828.
^ Everitt, B. S. (2003). The Cambridge Dictionary of Statistics. Cambridge University Press. ISBN 978-0-521-81099-9.
^ Gurland, J; Tripathi RC (1971). «A simple approximation for unbiased estimation of the standard deviation». American Statistician. 25 (4): 30–32. doi:10.2307/2682923. JSTOR 2682923.
^ Sokal; Rohlf (1981). Biometry: Principles and Practice of Statistics in Biological Research (2nd ed.). p. 53. ISBN 978-0-7167-1254-1.
^ Hutchinson, T. P. (1993). Essentials of Statistical Methods, in 41 pages. Adelaide: Rumsby. ISBN 978-0-646-12621-0.
^ Cornell, J R; Benjamin, C A (1970). Probability, Statistics, and Decisions for Civil Engineers. NY: McGraw-Hill. pp. 178–179. ISBN 0486796094.
^ Barde, M. (2012). «What to use to express the variability of data: Standard deviation or standard error of mean?». Perspect. Clin. Res. 3 (3): 113–116. doi:10.4103/2229-3485.100662. PMC 3487226. PMID 23125963.
^ Wassertheil-Smoller, Sylvia (1995). Biostatistics and Epidemiology : A Primer for Health Professionals (Second ed.). New York: Springer. pp. 40–43. ISBN 0-387-94388-9.
^ Isserlis, L. (1918). «On the value of a mean as calculated from a sample». Journal of the Royal Statistical Society. 81 (1): 75–81. doi:10.2307/2340569. JSTOR 2340569. (Equation 1)
^ Bondy, Warren; Zlot, William (1976). «The Standard Error of the Mean and the Difference Between Means for Finite Populations». The American Statistician. 30 (2): 96–97. doi:10.1080/00031305.1976.10479149. JSTOR 2683803. (Equation 2)
^ Bence, James R. (1995). «Analysis of Short Time Series: Correcting for Autocorrelation». Ecology. 76 (2): 628–639. doi:10.2307/1941218. JSTOR 1941218.

Источник

Стандартное отклонение (SD), измеряет количество изменчивости или дисперсии, из отдельных значений данных, к среднему значению, в то время как стандартная ошибка среднего (SEM) мер, как далеко образец среднее (среднее) данных, вероятно, будет от истинного среднего значения населения. SEM всегда меньше SD.

Ключевые выводы

Стандартное отклонение (SD) измеряет разброс набора данных относительно его среднего значения.
Стандартная ошибка среднего (SEM) измеряет, насколько вероятно расхождение между средним значением выборки по сравнению со средним значением генеральной совокупности.
SEM берет SD и делит его на квадратный корень из размера выборки.

SEM против SD

Стандартное отклонение и стандартная ошибка используются во всех типах статистических исследований, включая исследования в области финансов, медицины, биологии, инженерии, психологии и т. Д. В этих исследованиях стандартное отклонение (SD) и расчетная стандартная ошибка среднего (SEM) ) используются для представления характеристик данных выборки и объяснения результатов статистического анализа. Однако некоторые исследователи иногда путают SD и SEM. Таким исследователям следует помнить, что расчеты SD и SEM включают разные статистические выводы, каждый из которых имеет свое значение. SD – это разброс отдельных значений данных.

Другими словами, SD указывает, насколько точно среднее значение представляет данные выборки. Однако значение SEM включает статистический вывод, основанный на распределении выборки. SEM – это стандартное отклонение теоретического распределения выборочных средних (выборочное распределение).

Расчет стандартного отклонения

Формула SD требует нескольких шагов:

Во-первых, возьмите квадрат разницы между каждой точкой данных и средним значением выборки, найдя сумму этих значений.
Затем разделите эту сумму на размер выборки минус один, который представляет собой дисперсию.
Наконец, извлеките квадратный корень из дисперсии, чтобы получить стандартное отклонение.

Стандартная ошибка среднего

SEM рассчитывается путем деления стандартного отклонения на квадратный корень из размера выборки.

Стандартная ошибка дает точность выборочного среднего путем измерения изменчивости выборочного среднего от образца к образцу. SEM описывает, насколько точное среднее значение выборки является оценкой истинного среднего значения совокупности. По мере увеличения размера выборки данных SEM уменьшается по сравнению с SD; следовательно, по мере увеличения размера выборки среднее значение выборки оценивает истинное среднее значение генеральной совокупности с большей точностью. Напротив, увеличение размера выборки не обязательно делает SD больше или меньше, это просто становится более точной оценкой SD населения.

Стандартная ошибка и стандартное отклонение в финансах

В финансах стандартная ошибка средней дневной доходности актива измеряет точность выборочного среднего как оценки долгосрочной (постоянной) средней дневной доходности актива.

С другой стороны, стандартное отклонение доходности измеряет отклонения индивидуальных доходов от среднего значения. Таким образом, SD является мерой волатильности и может использоваться в качестве меры риска для инвестиций. Активы с более высокими ежедневными движениями цен имеют более высокое SD, чем активы с меньшими ежедневными движениями. Предполагая нормальное распределение, около 68% дневных изменений цен находятся в пределах одного стандартного отклонения от среднего, при этом около 95% дневных изменений цен находятся в пределах двух стандартных значений среднего.

Standard Error of the Mean vs. Standard Deviation: An Overview

Standard deviation (SD) measures the amount of variability, or dispersion, from the individual data values to the mean. SD is a frequently-cited statistic in many applications from math and statistics to finance and investing.

Standard error of the mean (SEM) measures how far the sample mean (average) of the data is likely to be from the true population mean. The SEM is always smaller than the SD.

Standard deviation and standard error are both used in statistical studies, including those in finance, medicine, biology, engineering, and psychology. In these studies, the SD and the estimated SEM are used to present the characteristics of sample data and explain statistical analysis results.

However, even some researchers occasionally confuse the SD and the SEM. Such researchers should remember that the calculations for SD and SEM include different statistical inferences, each of them with its own meaning. SD is the dispersion of individual data values. In other words, SD indicates how accurately the mean represents sample data.

However, the meaning of SEM includes statistical inference based on the sampling distribution. SEM is the SD of the theoretical distribution of the sample means (the sampling distribution).

Key Takeaways

Standard deviation (SD) measures the dispersion of a dataset relative to its mean.
SD is used frequently in statistics, and in finance is often used as a proxy for the volatility or riskiness of an investment.
The standard error of the mean (SEM) measures how much discrepancy is likely in a sample’s mean compared with the population mean.
The SEM takes the SD and divides it by the square root of the sample size.
The SEM will always be smaller than the SD.

Click Play to Learn the Difference Between Standard Error and Standard Deviation

Standard error estimates the likely accuracy of a number based on the sample size.

Standard error of the mean, or SEM, indicates the size of the likely discrepancy compared to that of the larger population.

Calculating SD and SEM

standard deviation

∑

(

−

)

−

variance

standard error

(

)

where:

the sample’s mean

the sample size

begin{aligned} &text{standard deviation } sigma = sqrt{ frac{ sum_{i=1}^n{left(x_i — bar{x}right)^2} }{n-1} } \ &text{variance} = {sigma ^2 } \ &text{standard error }left( sigma_{bar x} right) = frac{{sigma }}{sqrt{n}} \ &textbf{where:}\ &bar{x}=text{the sample’s mean}\ &n=text{the sample size}\ end{aligned}

standard deviation σ=n−1∑i=1n(xi−xˉ)2variance=σ2standard error (σxˉ)=nσwhere:xˉ=the sample’s meann=the sample size

Standard Deviation

The formula for the SD requires a few steps:

First, take the square of the difference between each data point and the sample mean, finding the sum of those values.
Next, divide that sum by the sample size minus one, which is the variance.
Finally, take the square root of the variance to get the SD.

Standard Error of the Mean

SEM is calculated simply by taking the standard deviation and dividing it by the square root of the sample size.

Standard error gives the accuracy of a sample mean by measuring the sample-to-sample variability of the sample means. The SEM describes how precise the mean of the sample is as an estimate of the true mean of the population.

As the size of the sample data grows larger, the SEM decreases vs. the SD. As the sample size increases, the sample mean estimates the true mean of the population with greater precision.

Increasing the sample size does not make the SD necessarily larger or smaller; it just becomes a more accurate estimate of the population SD.

A sampling distribution is a probability distribution of a sample statistic taken from a greater population. Researchers typically use sample data to estimate the population data, and the sampling distribution explains how the sample mean will vary from sample to sample. The standard error of the mean is the standard deviation of the sampling distribution of the mean.

Standard Error and Standard Deviation in Finance

In finance, the SEM daily return of an asset measures the accuracy of the sample mean as an estimate of the long-run (persistent) mean daily return of the asset.

On the other hand, the SD of the return measures deviations of individual returns from the mean. Thus, SD is a measure of volatility and can be used as a risk measure for an investment.

Assets with greater day-to-day price movements have a higher SD than assets with lesser day-to-day movements. Assuming a normal distribution, around 68% of daily price changes are within one SD of the mean, with around 95% of daily price changes within two SDs of the mean.

How Are Standard Deviation and Standard Error of the Mean Different?

Standard deviation measures the variability from specific data points to the mean. Standard error of the mean measures the precision of the sample mean to the population mean that it is meant to estimate.

Is the Standard Error Equal to the Standard Deviation?

No, the standard deviation (SD) will always be larger than the standard error (SE). This is because the standard error divides the standard deviation by the square root of the sample size.

If the sample size is one, they will be the same, but a sample size of one is rarely useful.

How Can You Compute the SE From the SD?

If you have the standard error (SE) and want to compute the standard deviation (SD) from it, simply multiply it by the square root of the sample size.

Why Do We Use Standard Error Instead of Standard Deviation?

What Is the Empirical Rule, and How Does It Relate to Standard Deviation?

A normal distribution is also known as a standard bell curve, since it looks like a bell in graph form. According to the empirical rule, or the 68-95-99.7 rule, 68% of all data observed under a normal distribution will fall within one standard deviation of the mean. Similarly, 95% falls within two standard deviations and 99.7% within three.

The Bottom Line

Investors and analysts measure standard deviation as a way to estimate the potential volatility of a stock or other investment. It helps determine the level of risk to the investor that is involved. When reading an analyst’s report, the level of riskiness of an investment may be labeled «standard deviation.»

Standard error of the mean is an indication of the likely accuracy of a number. The larger the sample size, the more accurate the number should be.

Standard Error of the Mean vs. Standard Deviation: An Overview

Standard error of the mean (SEM) measures how far the sample mean (average) of the data is likely to be from the true population mean. The SEM is always smaller than the SD.

However, the meaning of SEM includes statistical inference based on the sampling distribution. SEM is the SD of the theoretical distribution of the sample means (the sampling distribution).

Key Takeaways

Standard deviation (SD) measures the dispersion of a dataset relative to its mean.
SD is used frequently in statistics, and in finance is often used as a proxy for the volatility or riskiness of an investment.
The standard error of the mean (SEM) measures how much discrepancy is likely in a sample’s mean compared with the population mean.
The SEM takes the SD and divides it by the square root of the sample size.
The SEM will always be smaller than the SD.

Click Play to Learn the Difference Between Standard Error and Standard Deviation

Standard error estimates the likely accuracy of a number based on the sample size.

Standard error of the mean, or SEM, indicates the size of the likely discrepancy compared to that of the larger population.

Calculating SD and SEM

standard deviation

∑

(

−

)

−

variance

standard error

(

)

where:

the sample’s mean

the sample size

standard deviation σ=n−1∑i=1n(xi−xˉ)2variance=σ2standard error (σxˉ)=nσwhere:xˉ=the sample’s meann=the sample size

Standard Deviation

The formula for the SD requires a few steps:

First, take the square of the difference between each data point and the sample mean, finding the sum of those values.
Next, divide that sum by the sample size minus one, which is the variance.
Finally, take the square root of the variance to get the SD.

Standard Error of the Mean

SEM is calculated simply by taking the standard deviation and dividing it by the square root of the sample size.

As the size of the sample data grows larger, the SEM decreases vs. the SD. As the sample size increases, the sample mean estimates the true mean of the population with greater precision.

Increasing the sample size does not make the SD necessarily larger or smaller; it just becomes a more accurate estimate of the population SD.

Standard Error and Standard Deviation in Finance

In finance, the SEM daily return of an asset measures the accuracy of the sample mean as an estimate of the long-run (persistent) mean daily return of the asset.

On the other hand, the SD of the return measures deviations of individual returns from the mean. Thus, SD is a measure of volatility and can be used as a risk measure for an investment.

How Are Standard Deviation and Standard Error of the Mean Different?

Is the Standard Error Equal to the Standard Deviation?

No, the standard deviation (SD) will always be larger than the standard error (SE). This is because the standard error divides the standard deviation by the square root of the sample size.

If the sample size is one, they will be the same, but a sample size of one is rarely useful.

How Can You Compute the SE From the SD?

If you have the standard error (SE) and want to compute the standard deviation (SD) from it, simply multiply it by the square root of the sample size.

Why Do We Use Standard Error Instead of Standard Deviation?

What Is the Empirical Rule, and How Does It Relate to Standard Deviation?

The Bottom Line

Standard error of the mean is an indication of the likely accuracy of a number. The larger the sample size, the more accurate the number should be.

Стандартная ошибка среднего — это способ измерить, насколько разбросаны значения в наборе данных. Он рассчитывается как:

Стандартная ошибка среднего = s / √n

куда:

s : стандартное отклонение выборки
n : размер выборки

В этом руководстве объясняются два метода, которые вы можете использовать для вычисления стандартной ошибки среднего значения для набора данных в Python. Обратите внимание, что оба метода дают одинаковые результаты.

Способ 1: используйте SciPy

Первый способ вычислить стандартную ошибку среднего — использовать функцию sem() из библиотеки SciPy Stats.

Следующий код показывает, как использовать эту функцию:

from scipy. stats import sem

#define dataset 
data = [3, 4, 4, 5, 7, 8, 12, 14, 14, 15, 17, 19, 22, 24, 24, 24, 25, 28, 28, 29]

#calculate standard error of the mean 
sem(data)

2.001447

Стандартная ошибка среднего оказывается равной 2,001447 .

Способ 2: использовать NumPy

Другой способ вычислить стандартную ошибку среднего для набора данных — использовать функцию std() из NumPy.

Обратите внимание, что мы должны указать ddof=1 в аргументе этой функции, чтобы вычислить стандартное отклонение выборки, а не стандартное отклонение генеральной совокупности.

Следующий код показывает, как это сделать:

import numpy as np

#define dataset
data = np.array([3, 4, 4, 5, 7, 8, 12, 14, 14, 15, 17, 19, 22, 24, 24, 24, 25, 28, 28, 29])

#calculate standard error of the mean 
np.std(data, ddof= 1 ) / np.sqrt (np.size (data))

2.001447

И снова стандартная ошибка среднего оказывается равной 2,001447 .

Как интерпретировать стандартную ошибку среднего

Стандартная ошибка среднего — это просто мера того, насколько разбросаны значения вокруг среднего. При интерпретации стандартной ошибки среднего следует помнить о двух вещах:

1. Чем больше стандартная ошибка среднего, тем более разбросаны значения вокруг среднего в наборе данных.

Чтобы проиллюстрировать это, рассмотрим, изменим ли мы последнее значение в предыдущем наборе данных на гораздо большее число:

from scipy. stats import sem

#define dataset 
data = [3, 4, 4, 5, 7, 8, 12, 14, 14, 15, 17, 19, 22, 24, 24, 24, 25, 28, 28, 150 ]

#calculate standard error of the mean 
sem(data)

6.978265

Обратите внимание на скачок стандартной ошибки с 2,001447 до 6,978265.Это указывает на то, что значения в этом наборе данных более разбросаны вокруг среднего значения по сравнению с предыдущим набором данных.

2. По мере увеличения размера выборки стандартная ошибка среднего имеет тенденцию к уменьшению.

Чтобы проиллюстрировать это, рассмотрим стандартную ошибку среднего для следующих двух наборов данных:

from scipy.stats import sem 

#define first dataset and find SEM
data1 = [1, 2, 3, 4, 5]
sem(data1)

0.7071068

#define second dataset and find SEM
data2 = [1, 2, 3, 4, 5, 1, 2, 3, 4, 5]
sem(data2)

0.4714045

Второй набор данных — это просто первый набор данных, повторенный дважды. Таким образом, два набора данных имеют одинаковое среднее значение, но второй набор данных имеет больший размер выборки, поэтому стандартная ошибка меньше.

Дополнительные ресурсы

Как рассчитать стандартную ошибку среднего в R
Как рассчитать стандартную ошибку среднего в Excel
Как рассчитать стандартную ошибку среднего в Google Sheets

Содержание

Расчет ошибки средней арифметической
- Способ 1: расчет с помощью комбинации функций
- Способ 2: применение инструмента «Описательная статистика»
Вопросы и ответы

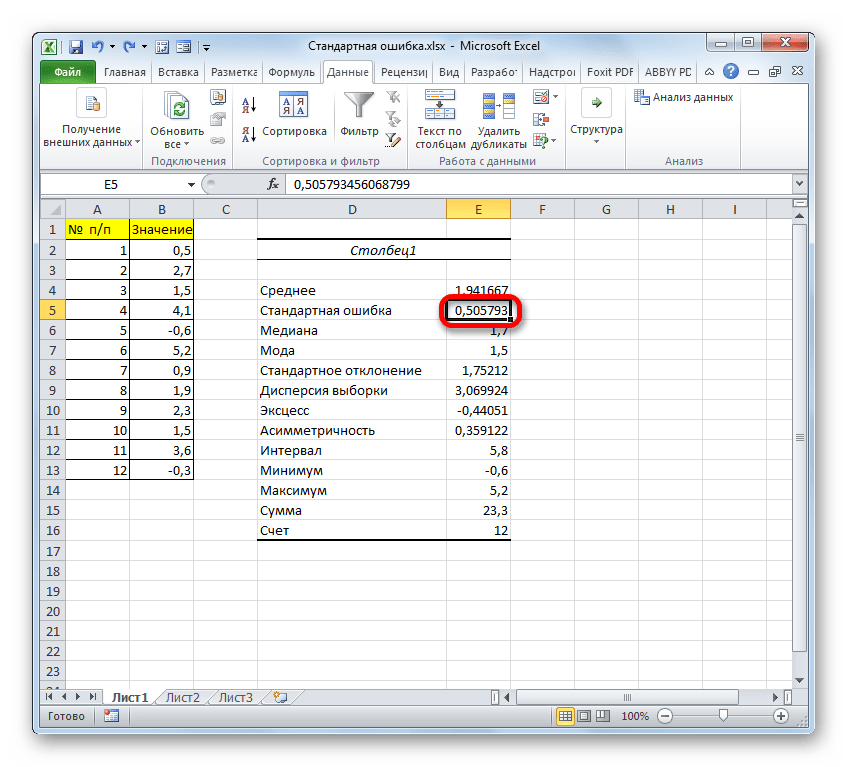
Стандартная ошибка или, как часто называют, ошибка средней арифметической, является одним из важных статистических показателей. С помощью данного показателя можно определить неоднородность выборки. Он также довольно важен при прогнозировании. Давайте узнаем, какими способами можно рассчитать величину стандартной ошибки с помощью инструментов Microsoft Excel.

Расчет ошибки средней арифметической

Одним из показателей, которые характеризуют цельность и однородность выборки, является стандартная ошибка. Эта величина представляет собой корень квадратный из дисперсии. Сама дисперсия является средним квадратном от средней арифметической. Средняя арифметическая вычисляется делением суммарной величины объектов выборки на их общее количество.

В Экселе существуют два способа вычисления стандартной ошибки: используя набор функций и при помощи инструментов Пакета анализа. Давайте подробно рассмотрим каждый из этих вариантов.

Способ 1: расчет с помощью комбинации функций

Прежде всего, давайте составим алгоритм действий на конкретном примере по расчету ошибки средней арифметической, используя для этих целей комбинацию функций. Для выполнения задачи нам понадобятся операторы СТАНДОТКЛОН.В, КОРЕНЬ и СЧЁТ.

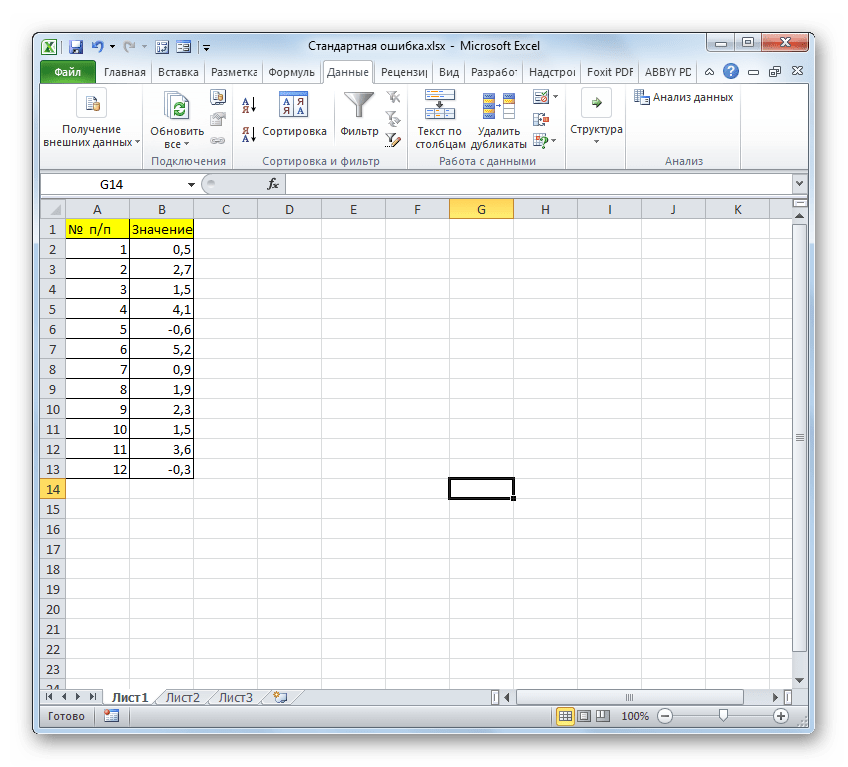
Для примера нами будет использована выборка из двенадцати чисел, представленных в таблице.

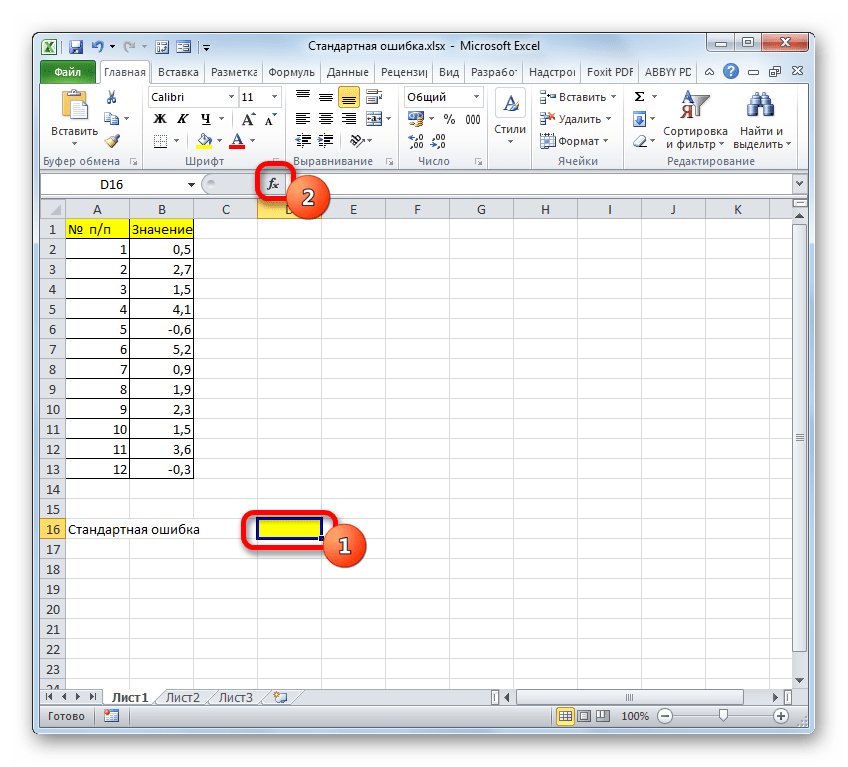
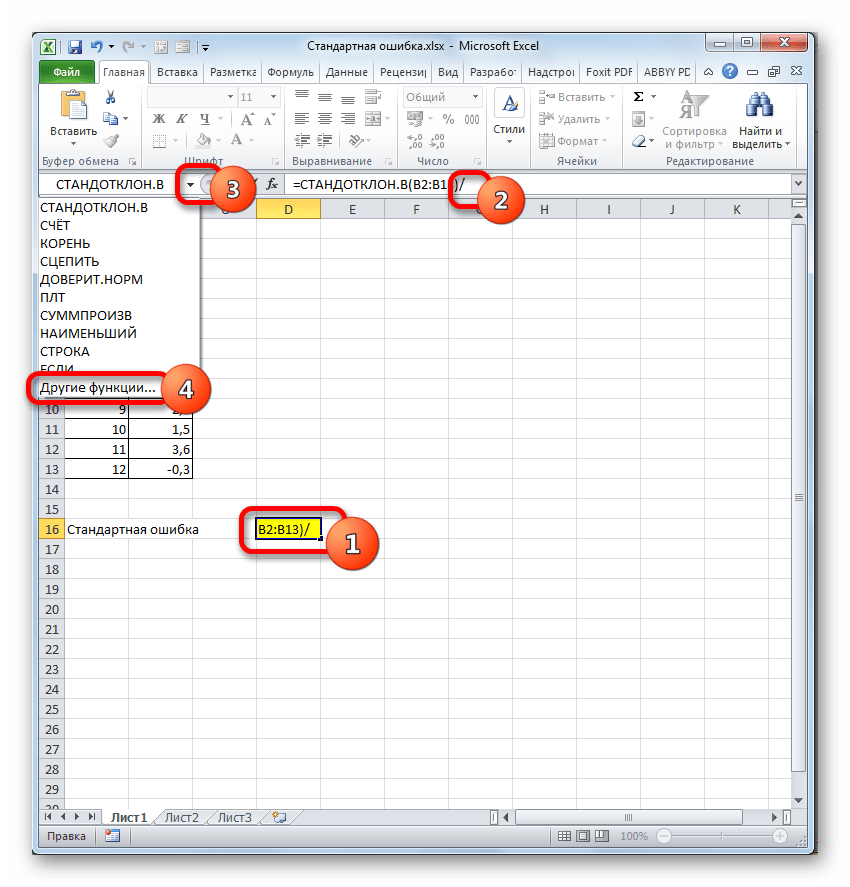
Выделяем ячейку, в которой будет выводиться итоговое значение стандартной ошибки, и клацаем по иконке «Вставить функцию».

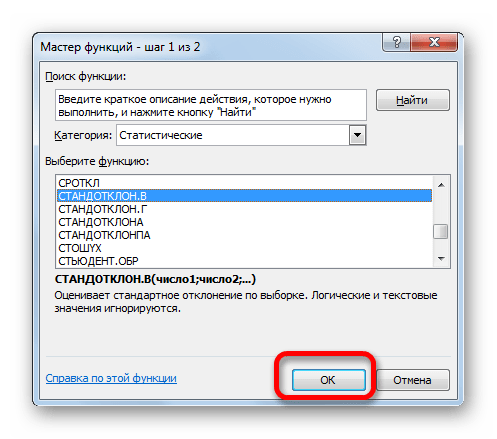
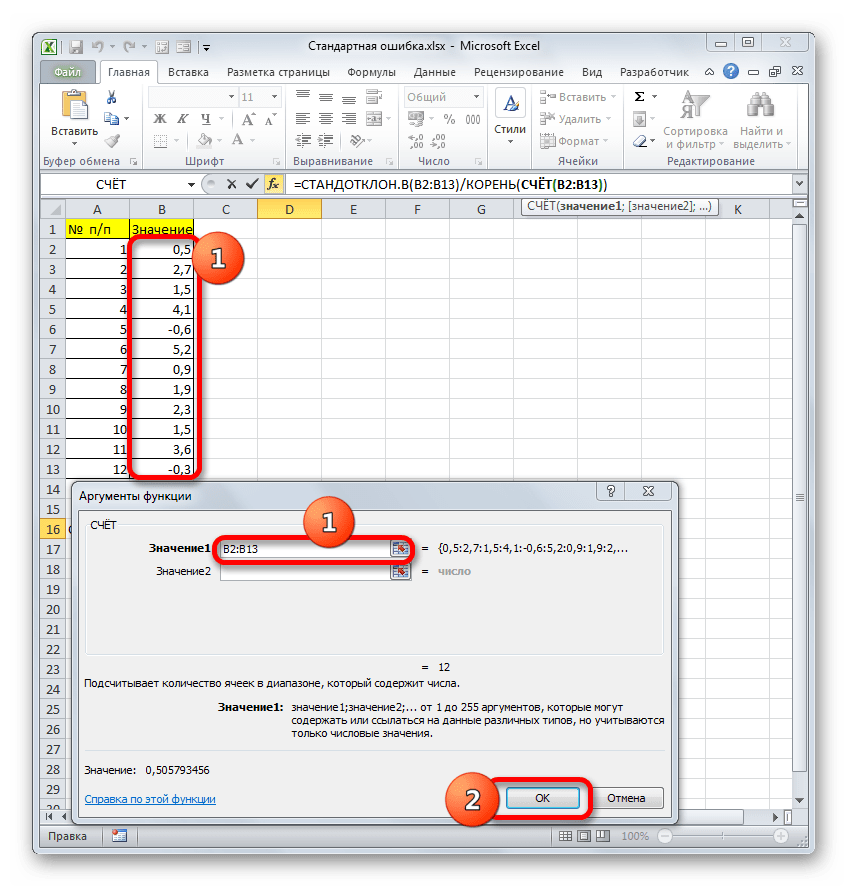
Открывается Мастер функций. Производим перемещение в блок «Статистические». В представленном перечне наименований выбираем название «СТАНДОТКЛОН.В».

Запускается окно аргументов вышеуказанного оператора. СТАНДОТКЛОН.В предназначен для оценивания стандартного отклонения при выборке. Данный оператор имеет следующий синтаксис:
=СТАНДОТКЛОН.В(число1;число2;…)

«Число1» и последующие аргументы являются числовыми значениями или ссылками на ячейки и диапазоны листа, в которых они расположены. Всего может насчитываться до 255 аргументов этого типа. Обязательным является только первый аргумент.

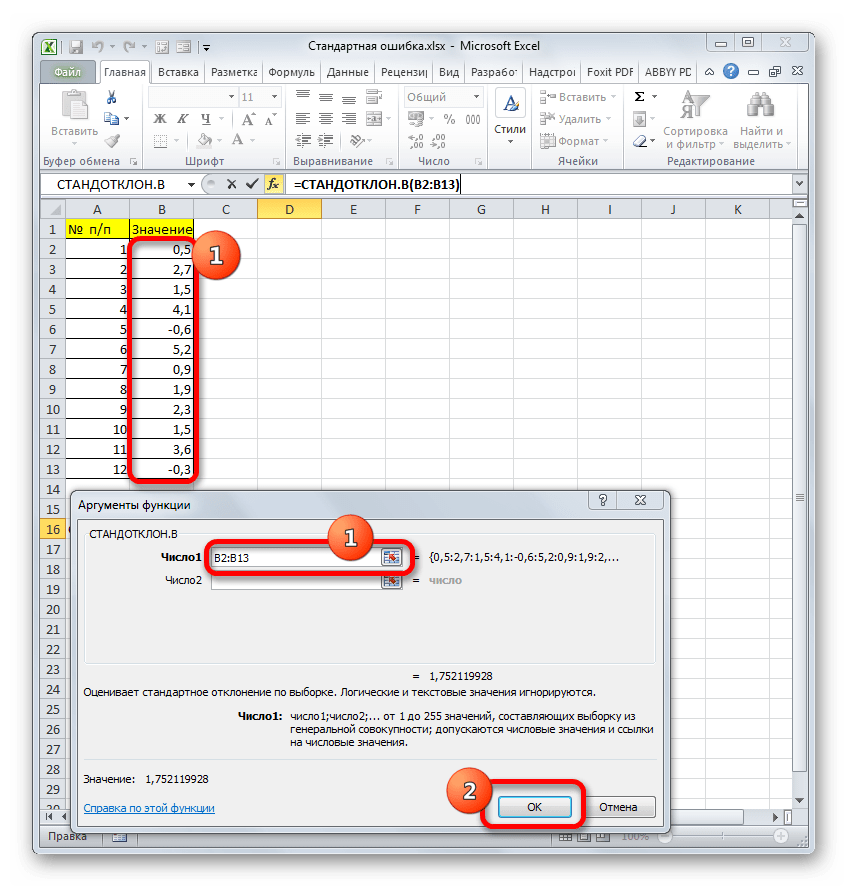
Итак, устанавливаем курсор в поле «Число1». Далее, обязательно произведя зажим левой кнопки мыши, выделяем курсором весь диапазон выборки на листе. Координаты данного массива тут же отображаются в поле окна. После этого клацаем по кнопке «OK».

В ячейку на листе выводится результат расчета оператора СТАНДОТКЛОН.В. Но это ещё не ошибка средней арифметической. Для того, чтобы получить искомое значение, нужно стандартное отклонение разделить на квадратный корень от количества элементов выборки. Для того, чтобы продолжить вычисления, выделяем ячейку, содержащую функцию СТАНДОТКЛОН.В. После этого устанавливаем курсор в строку формул и дописываем после уже существующего выражения знак деления (/). Вслед за этим клацаем по пиктограмме перевернутого вниз углом треугольника, которая располагается слева от строки формул. Открывается список недавно использованных функций. Если вы в нем найдете наименование оператора «КОРЕНЬ», то переходите по данному наименованию. В обратном случае жмите по пункту «Другие функции…».

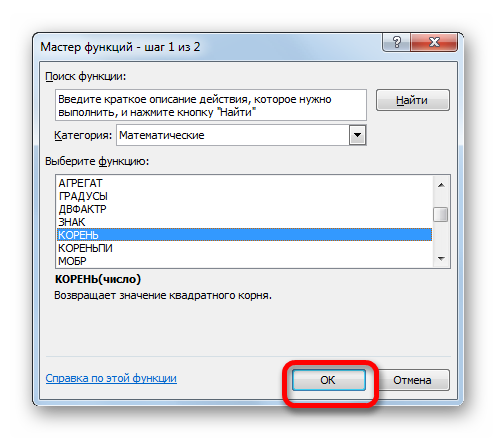
Снова происходит запуск Мастера функций. На этот раз нам следует посетить категорию «Математические». В представленном перечне выделяем название «КОРЕНЬ» и жмем на кнопку «OK».

Открывается окно аргументов функции КОРЕНЬ. Единственной задачей данного оператора является вычисление квадратного корня из заданного числа. Его синтаксис предельно простой:
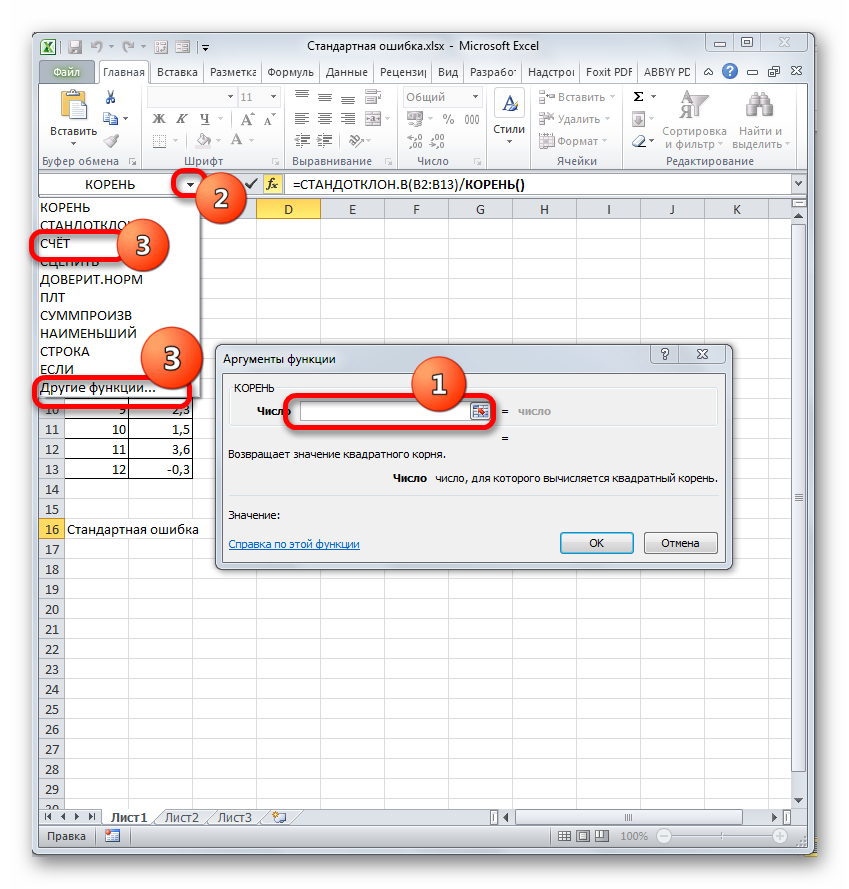
=КОРЕНЬ(число)

Как видим, функция имеет всего один аргумент «Число». Он может быть представлен числовым значением, ссылкой на ячейку, в которой оно содержится или другой функцией, вычисляющей это число. Последний вариант как раз и будет представлен в нашем примере.

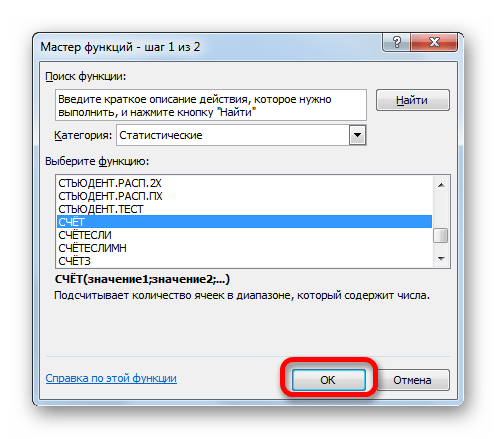
Устанавливаем курсор в поле «Число» и кликаем по знакомому нам треугольнику, который вызывает список последних использованных функций. Ищем в нем наименование «СЧЁТ». Если находим, то кликаем по нему. В обратном случае, опять же, переходим по наименованию «Другие функции…».

В раскрывшемся окне Мастера функций производим перемещение в группу «Статистические». Там выделяем наименование «СЧЁТ» и выполняем клик по кнопке «OK».

Запускается окно аргументов функции СЧЁТ. Указанный оператор предназначен для вычисления количества ячеек, которые заполнены числовыми значениями. В нашем случае он будет подсчитывать количество элементов выборки и сообщать результат «материнскому» оператору КОРЕНЬ. Синтаксис функции следующий:
=СЧЁТ(значение1;значение2;…)

В качестве аргументов «Значение», которых может насчитываться до 255 штук, выступают ссылки на диапазоны ячеек. Ставим курсор в поле «Значение1», зажимаем левую кнопку мыши и выделяем весь диапазон выборки. После того, как его координаты отобразились в поле, жмем на кнопку «OK».

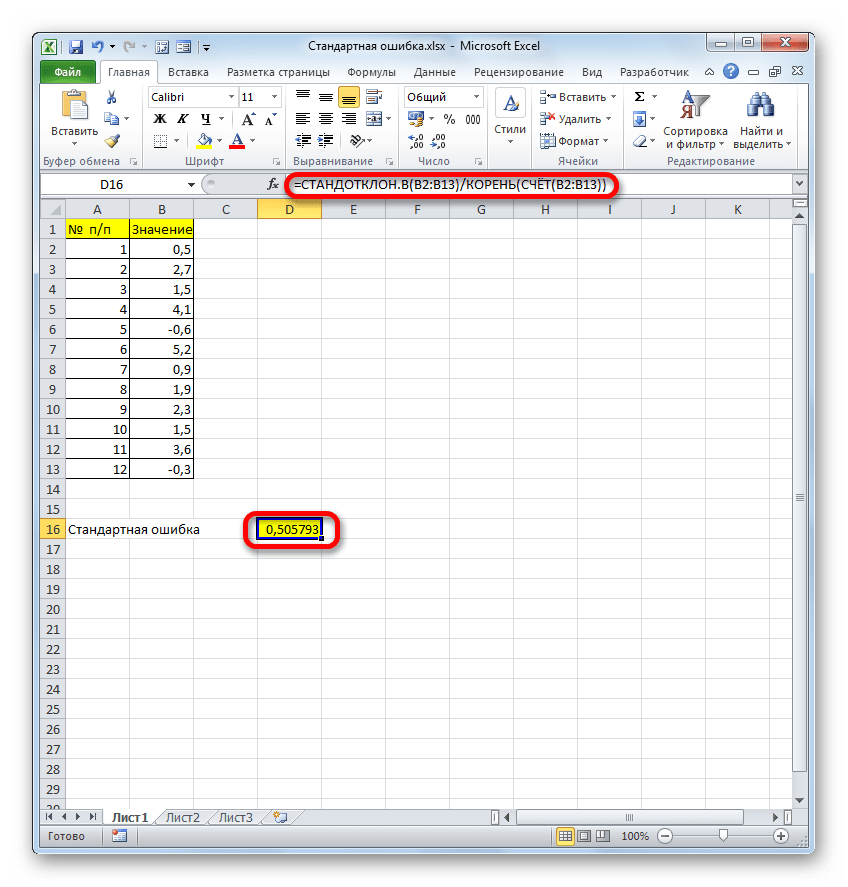
После выполнения последнего действия будет не только рассчитано количество ячеек заполненных числами, но и вычислена ошибка средней арифметической, так как это был последний штрих в работе над данной формулой. Величина стандартной ошибки выведена в ту ячейку, где размещена сложная формула, общий вид которой в нашем случае следующий:
=СТАНДОТКЛОН.В(B2:B13)/КОРЕНЬ(СЧЁТ(B2:B13))

Результат вычисления ошибки средней арифметической составил 0,505793. Запомним это число и сравним с тем, которое получим при решении поставленной задачи следующим способом.

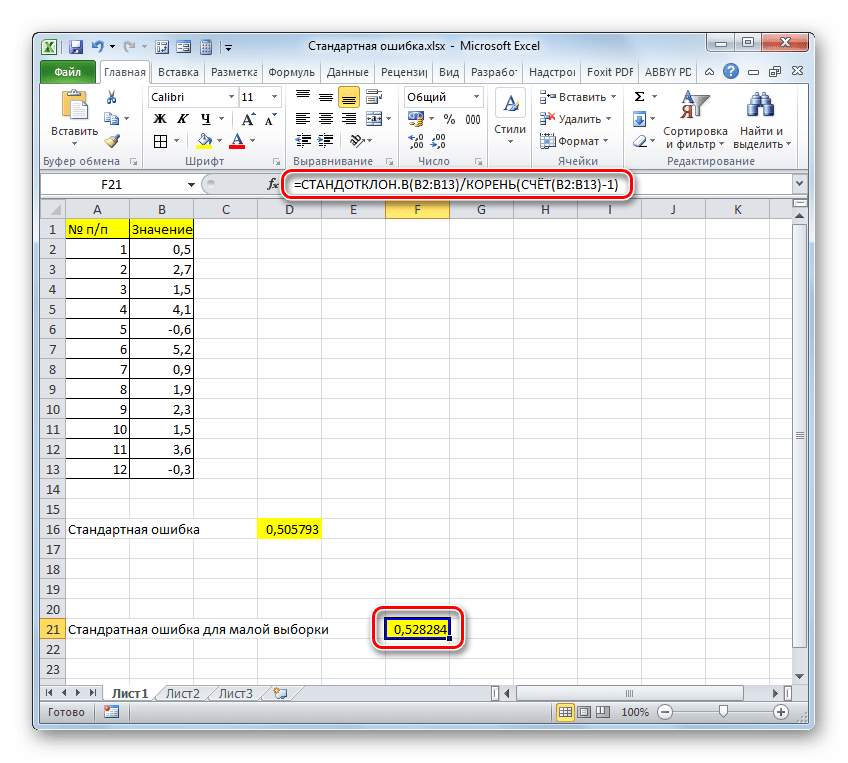
Но дело в том, что для малых выборок (до 30 единиц) для большей точности лучше применять немного измененную формулу. В ней величина стандартного отклонения делится не на квадратный корень от количества элементов выборки, а на квадратный корень от количества элементов выборки минус один. Таким образом, с учетом нюансов малой выборки наша формула приобретет следующий вид:

=СТАНДОТКЛОН.В(B2:B13)/КОРЕНЬ(СЧЁТ(B2:B13)-1)

Урок: Статистические функции в Экселе

Способ 2: применение инструмента «Описательная статистика»

Вторым вариантом, с помощью которого можно вычислить стандартную ошибку в Экселе, является применение инструмента «Описательная статистика», входящего в набор инструментов «Анализ данных» («Пакет анализа»). «Описательная статистика» проводит комплексный анализ выборки по различным критериям. Одним из них как раз и является нахождение ошибки средней арифметической.

Но чтобы воспользоваться данной возможностью, нужно сразу активировать «Пакет анализа», так как по умолчанию в Экселе он отключен.

После того, как открыт документ с выборкой, переходим во вкладку «Файл».

Далее, воспользовавшись левым вертикальным меню, перемещаемся через его пункт в раздел «Параметры».

Запускается окно параметров Эксель. В левой части данного окна размещено меню, через которое перемещаемся в подраздел «Надстройки».

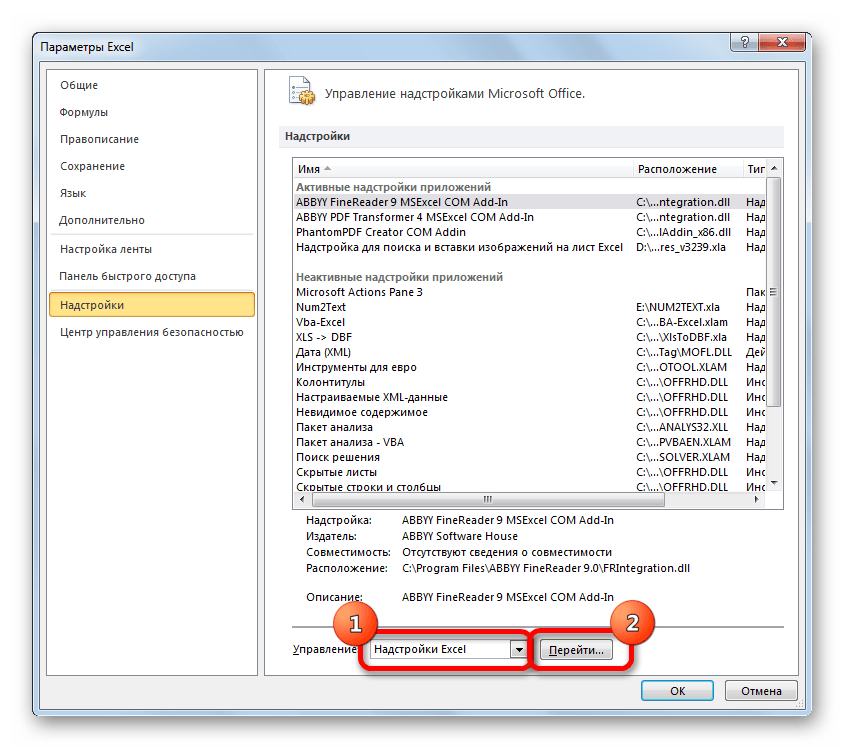
В самой нижней части появившегося окна расположено поле «Управление». Выставляем в нем параметр «Надстройки Excel» и жмем на кнопку «Перейти…» справа от него.

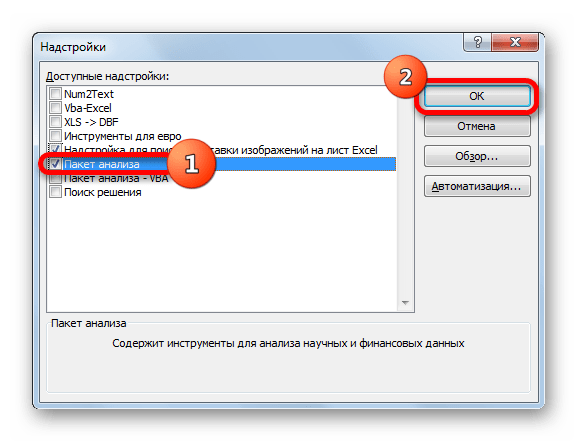
Запускается окно надстроек с перечнем доступных скриптов. Отмечаем галочкой наименование «Пакет анализа» и щелкаем по кнопке «OK» в правой части окошка.

После выполнения последнего действия на ленте появится новая группа инструментов, которая имеет наименование «Анализ». Чтобы перейти к ней, щелкаем по названию вкладки «Данные».

После перехода жмем на кнопку «Анализ данных» в блоке инструментов «Анализ», который расположен в самом конце ленты.

Запускается окошко выбора инструмента анализа. Выделяем наименование «Описательная статистика» и жмем на кнопку «OK» справа.

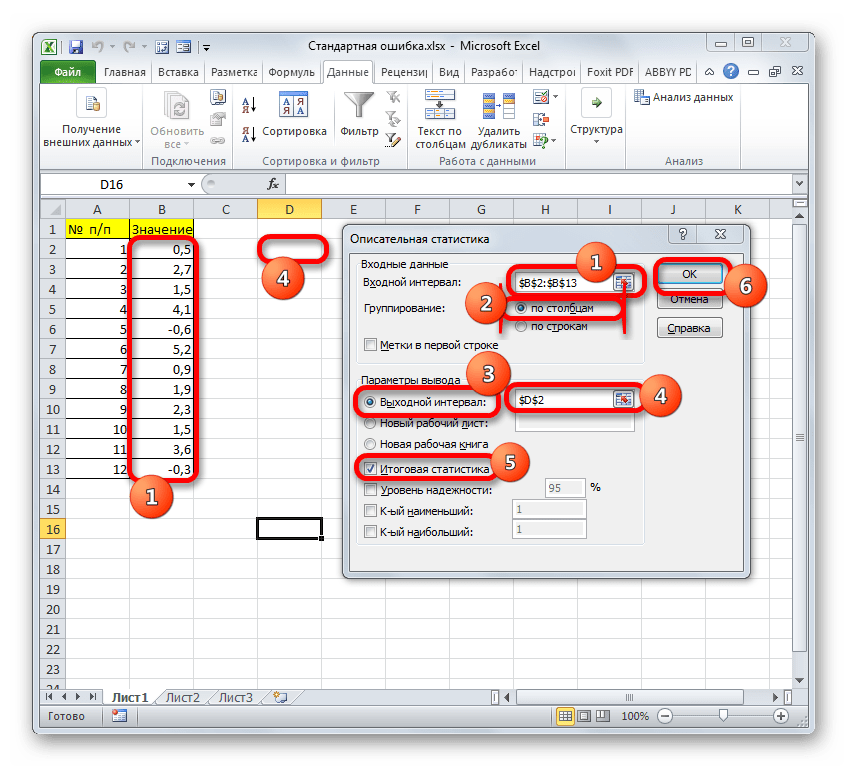
Запускается окно настроек инструмента комплексного статистического анализа «Описательная статистика».
В поле «Входной интервал» необходимо указать диапазон ячеек таблицы, в которых находится анализируемая выборка. Вручную это делать неудобно, хотя и можно, поэтому ставим курсор в указанное поле и при зажатой левой кнопке мыши выделяем соответствующий массив данных на листе. Его координаты тут же отобразятся в поле окна.

В блоке «Группирование» оставляем настройки по умолчанию. То есть, переключатель должен стоять около пункта «По столбцам». Если это не так, то его следует переставить.

Галочку «Метки в первой строке» можно не устанавливать. Для решения нашего вопроса это не важно.

Далее переходим к блоку настроек «Параметры вывода». Здесь следует указать, куда именно будет выводиться результат расчета инструмента «Описательная статистика»:
- На новый лист;
- В новую книгу (другой файл);
- В указанный диапазон текущего листа.
Давайте выберем последний из этих вариантов. Для этого переставляем переключатель в позицию «Выходной интервал» и устанавливаем курсор в поле напротив данного параметра. После этого клацаем на листе по ячейке, которая станет верхним левым элементом массива вывода данных. Её координаты должны отобразиться в поле, в котором мы до этого устанавливали курсор.

Далее следует блок настроек определяющий, какие именно данные нужно вводить:
- Итоговая статистика;
- К-ый наибольший;
- К-ый наименьший;
- Уровень надежности.
Для определения стандартной ошибки обязательно нужно установить галочку около параметра «Итоговая статистика». Напротив остальных пунктов выставляем галочки на свое усмотрение. На решение нашей основной задачи это никак не повлияет.

После того, как все настройки в окне «Описательная статистика» установлены, щелкаем по кнопке «OK» в его правой части.

После этого инструмент «Описательная статистика» выводит результаты обработки выборки на текущий лист. Как видим, это довольно много разноплановых статистических показателей, но среди них есть и нужный нам – «Стандартная ошибка». Он равен числу 0,505793. Это в точности тот же результат, который мы достигли путем применения сложной формулы при описании предыдущего способа.

Урок: Описательная статистика в Экселе

Как видим, в Экселе можно произвести расчет стандартной ошибки двумя способами: применив набор функций и воспользовавшись инструментом пакета анализа «Описательная статистика». Итоговый результат будет абсолютно одинаковый. Поэтому выбор метода зависит от удобства пользователя и поставленной конкретной задачи. Например, если ошибка средней арифметической является только одним из многих статистических показателей выборки, которые нужно рассчитать, то удобнее воспользоваться инструментом «Описательная статистика». Но если вам нужно вычислить исключительно этот показатель, то во избежание нагромождения лишних данных лучше прибегнуть к сложной формуле. В этом случае результат расчета уместится в одной ячейке листа.

Чтобы
судить о том, насколько точно проведенные
измерения отражают состав генеральной
совокупности, необходимо вычислить
стандартную ошибку средней арифметической
выборочной совокупности.

Стандартная
ошибка средней арифметической
характеризует степень отклонения
выборочной средней арифметической от
средней арифметической генеральной
совокупности.

Стандартная
ошибка средней арифметической вычисляется
по формуле:

где 
– стандартное отклонение результатов
измерений, n
– объем выборки.

Зачастую
мы имеем дело с одной случайной выборкой
и с одной полученной при ее обработке
выборочной средней. Задача заключается
в суждении о величине неизвестной
генеральной средней по полученной
неточной величине случайной выборочной
средней.

Вычислим
среднюю ошибку найденного выборочного
среднего значения роста:

195
см; σ = 8,8 см;
см.

2,8 см
составляют не максимальную, а среднюю
возможную ошибку среднего. Отдельные
выборочные средние могут отклоняться
от генеральной как больше, так и меньше,
чем на 2,8 см.

Каковы
же пределы возможных ошибок случайной
выборки, какова ее максимальная ошибка?
Величина максимальной ошибки зависит
от величины средней ошибки и вычисляется
по формуле

При
объеме выборки n
= 10:

Все
случайные выборочные средние, которые
могут быть получены в подобных опытах
(в том числе и фактически полученная
выборочная средняя
= 195 см), при своем варьировании около
неизвестного генерального среднего в
подавляющем количестве группируются
около него так, что лишь ничтожный
процент их отклоняется от генеральной
средней более, чем на величину максимальной
ошибки.

Другими
словами, генеральная средняя определяется
как

Эти пределы
колебаний значительно сужаются, если
средняя ошибка уменьшается благодаря
увеличению численности выборки.

Искомая
генеральная средняя лежит между
и.
Таким образом, при высокой точности
выполнения эксперимента и достаточно
большом числе измерений можно определить
среднюю арифметическую бесконечно
большого числа экспериментов.

До сих
пор мы определяли максимальную ошибку
выборочной средней, исходя из того, что
все остальные показатели известны. Если
же мы хотим достичь определенной
точности, определенного приближения к
генеральной средней, в этом случае
встает вопрос о численности выборки (о
том, сколько измерений, опытов необходимо
провести).

Допустим, что
максимальная ошибка должна быть равна
5 см. Сколько человек надо обследовать
(измерить) в нашем случае?

Следовательно,
мы должны провести измерения роста у
36 баскетболистов высокого класса.

10. Достоверность различий

Следующим
важным вопросом практически для каждого
экспериментатора является умение
доказать достоверность различий между
двумя рядами признаков.

Проверку
достоверности различия двух рядов
измерений производят путем вычисления
критерия достоверности различия – t:

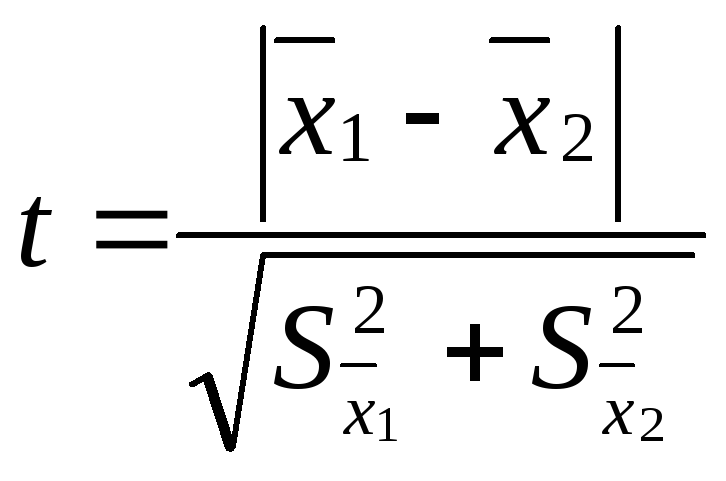
где
– средняя одной выборки;– средняя другой выборки;– средняя ошибка первой выборки;– второй выборки. Если t < 2, то различие
между двумя выборками считается
недостоверным, если t
2, то различие между двумя выборками
достоверно на 95%.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Понимание центральной предельной теоремы, стандартной ошибки и доверительных интервалов

Перевод

Ссылка на автора

В этом посте мы создадим интуитивное понимание описательной статистики, включая среднее и стандартное отклонение, а также выводной статистики, включая стандартную ошибку среднего и доверительные интервалы. Мы также разработаем понимание центральной предельной теоремы в этом процессе. Код R, используемый для генерации примеров в этом посте, доступен Вот,

Давайте начнем наше путешествие, предположив, что у нас есть N = 10 000 учеников в стране, которые изучали физику в своем первом классе. Мы отметили оценки, которые они получили, из 100, после их финального экзамена, и гистограмма (с интервалами 10) этих отметок показана на рисунке 1. Эта гистограмма отражает распределение населения.

Рисунок 1Гистограмма оценок, полученных всеми учащимися 10-х классов по физике по всей стране (распределение населения).

Теперь мы можем рассчитать среднее значение по населению (μ) и стандартное отклонение (σ), используя следующие формулы:

где xᵢ представляет оценки, набранные iᵗʰ учеником, а N — общее количество студентов по всей стране. Для распределения населения, показанного на рисунке 1, μ = 71,52 и σ = 16,15. Они оба являются описательной статистикой, потому что они описывают некоторые особенности данных в руке. Среднее значение представляет центральность данных (центр — это медиана), а стандартное отклонение показывает, насколько каждая точка отличается от среднего значения в среднем смысле. Маленькое σ означает, что значения в наборе данных в среднем близки к среднему значению данных, а большое σ означает, что значения в наборе данных находятся в среднем дальше от среднего значения. Мы можем видеть, что у нашего распределения населения более длинный хвост слева по сравнению с правым, и такие распределения известны как левый перекос.

Следует отметить, что наше распределение населения требует данных от всех студентов по всей стране. Это требование практически очень трудно выполнить, и мы обычно не имеем доступа к распределению населения (и соответствующей описательной статистике: μ и σ). В таких ситуациях мы прибегаем к случайной выборкеделать выводописательная статистика основного распределения населения из описательной статистики выборочного распределения — давайте поймем это!

Случайная выборка означает, что вместо сбора данных от всех учащихся, то есть всего населения, мы случайным образом выбираем несколько репрезентативных студентов по всей стране для проведения нашего анализа. Давайте предположим, что в нашей первой попытке случайной выборки s1 мы отобрали не более 50 репрезентативных студентов по всей стране и записали их оценки. Давайте обозначим описательную статистику для s₁ как µ₁ и σ₁, а также обозначим наше первое событие случайной выборки как s₁: n₁, µ₁, σ₁. Следуя этой записи и процедуре случайной выборки, мы можем случайным образом выбрать несколько групп репрезентативных студентов из нашего распределения населения. Помните, что распределение населения включает всех учащихся по всей стране, а выборочное распределение содержит только 50 случайно выбранных студентов — каждое выборочное распределение является подмножеством распределения населения.

Как описательная статистика наших выборочных распределений соотносится с описательной статистикой нашего распределения населения? Ответ даетсяЦентральная предельная теоремакоторый простыми словами утверждает, что —

Для независимые случайные величины распределение средних выборочных распределений стремится к нормальному распределению (неофициальнокривая колокола»), Независимо от формы распределения населения.

Теперь давайте применим эту теорему к нашему примеру и посмотрим, что мы можем понять с помощью этого упражнения. Случайные переменные в нашем случае — это оценки, полученные каждым учеником, и они действительно являются независимыми случайными переменными, потому что оценки, набранные одним студентом, не зависят от оценок, выставленных другим. Далее, скажем, мы получаем r = 20 случайных выборок, каждая с n = 50 студентами, из нашего распределения населения, и эти распределения выборок можно записать как:

здесь n₁ = n₂ =… nᵣ = 50 и r = 20. Среднее из 20 выборочных средних можно вычислить следующим образом:

Давайте теперь наметим средства из наших 20 примеров дистрибутивов и посмотрим, как выглядит их распределение. Из рисунка 2 видно, что распределение действительно выглядит как кривая колокола, независимо от формы нашего распределения населения (которое фактически является бета-распределением, см. Код для деталей).

фигура 2Распределение средних по 20 случайным выборкам (μ₁, μ₂,…, μ₂₀). Средние значения выборки (μ₂₀means = 72,26) желтой пунктирной вертикальной линии и фактического среднего населения (μ = 71,52), зеленой вертикальной линии, также нанесены для сравнения.

Нормальность распределения средних значений для образца намного выше, если мы получим (r =) 80 случайных выборок (каждая размером n = 50) вместо (r =) 20, как показано на рисунке 3. Среднее значение 80 выборочных средних можно рассчитать следующим образом:

Рисунок 3Распределение средних 80 случайных выборок (μ₁, μ₂,…, μ₈₀). Средние значения выборки (μ₈₀means = 71,66) желтой пунктирной вертикальной линии и фактического среднего населения (μ = 71,52), зеленой вертикальной линии, также нанесены для сравнения.

Из рисунка 2 и рисунка 3 также видно, что среднее значение выборки означает приближение к среднему значению населенности, когда мы рисуем больше случайных выборок. Обратите внимание, что только при r * n = 80 * 50 = 4000 баллов по студентам мы можем получить достаточно точную оценку (μ₈₀means = 71,66) среднего значения по совокупности (μ = 71,52) N = 10000 баллов по студентам. Это означает, что если у нас есть достаточное количество случайных выборок, тогда нам фактически не нужно полное распределение населения для нашего анализа.

В. Должны ли мы использовать несколько случайных выборок, каждая с меньшим числом наблюдений, или одну случайную выборку с большим количеством наблюдений для реальной задачи анализа данных?

Мы только что увидели, что, используя 80 случайных выборок, каждая из которых имеет 50 наблюдений (баллов по студентам), мы можем приблизить среднее значение основного распределения населения. Однако на практике мы обычно работаем с одной случайной выборкой, содержащей достаточно большое количество (n) точек данных (баллов студентов), так что n ≪ N, здесь n представляет количество студентов в нашей случайной выборке, а N представляет всю совокупность студентов по всей стране.

Теперь мы будем работать с одной случайной выборкой, содержащей n студентов, и обозначим стандартное отклонение и среднее значение этой случайной выборки как s и μₑ (e как в оценке), соответственно. На рисунке 4 показано, что принципы центральной предельной теоремы все еще остаются в силе — для n = 4000 распределение нашей случайной выборки имеет форму колокола, и его среднее значение µₑ = 71,58 является хорошей оценкой среднего числа населения (µ = 71,52).

Рисунок 4Распределение случайной выборки, содержащей n = 4000 наблюдений. Среднее значение выборки (μₑ = 71,58), желтая пунктирная вертикальная линия и среднее значение фактической популяции (μ = 71,52), зеленая вертикальная линия, также показаны для сравнения.

Важно отметить, что оба, µₑ и s, сами являются случайными переменными, потому что их значения зависят от стратегии, используемой для случайной выборки.

Выведенный статистика

Вышеупомянутые наблюдения имеют большое значение для анализа данных, потому что мы обычно не имеем доступа ко всему населению, и поэтому описательная статистика распределения населения обычно неизвестна. В таких ситуациях центральная предельная теорема дает нам возможность проводить анализ данных со случайно выбранными точками данных иточность такого анализаможет быть определен количественно с помощьювыведенный статистикавключая стандартную ошибку среднего и доверительных интервалов, которые обсуждаются далее. Эти статистические данные являются выводными, потому что мы используем распределения случайной выборки, чтобы вывести характеристики основного распределения населения.

Стандартная ошибка среднего (SEM): Из центральной предельной теоремы мы знаем, что наше выборочное распределение нормально со средним значением = μₑ. Но μₑ сама по себе является случайной величиной, поскольку она зависит от выбора наших случайных выборок. Другими словами, любое изменение в нашем распределении выборок изменяет наш μₑ. Стандартная ошибка среднего просто количественно определяет это изменение, вычисляя стандартное отклонение нашей оценки, µₑ, среднего значения популяции (µ). Формально это можно вычислить следующим образом:

Взяв квадратный корень с обеих сторон вышеприведенного уравнения, мы получим требуемую стандартную ошибку среднего:

Обратите внимание, что мы можем использовать одну случайную выборку с достаточным размером выборки (n), чтобы вычислить стандартную оценку ошибки среднего значения по совокупности. Если у нас достаточно большое n, мы можем получить почти нулевую стандартную ошибку. Это означает, что если мы имеем большую случайную выборку точек данных, то среднее распределение нашей выборки точно приближает среднее значение лежащего в основе неизвестного распределения населения. Таким образом, более высокое n часто желательно в различных задачах машинного обучения и статистических данных для лучшей обобщения.

Доверительные интервалы:Доверительный интервал — это интервал вокруг расчетного среднего значения (μₑ), который может включать неизвестное среднее значение по совокупности (μ). Давайте разберемся в этом — мы хотим оценить среднее значение µ основного распределения населения, и у нас есть доступ к случайной выборке, содержащей n наблюдений со стандартным отклонением s и средним значением µ understand. Доверительные интервалы построены науровень доверия, например, 95%, выбранный пользователем. Уровень достоверности описывает неопределенность, связанную сметод отбора проб, Предположим, что мы использовали один и тот же метод выборки, чтобы выбрать несколько случайных выборок и рассчитать доверительные интервалы, используя μₑ каждой случайной выборки. Естественно, у нас будет несколько доверительных интервалов (один вокруг каждого μₑ). Некоторые из этих интервальных оценок будут включать среднее значение, μ, а некоторые не будут Уровень достоверности 95% означает, что мы ожидаем, что 95% интервальных оценок будут включать среднее значение по населению. Обычно мы работаем только с одной случайной выборкой, содержащей большое количество точек данных, и в этом случае у нас есть только одна оценка доверительного интервала, которая может быть рассчитана следующим образом для уровня достоверности 95%:

Обратите внимание, что член после знака плюс-минус в правой части вышеприведенного уравнения количественно определяет неопределенность в оценке среднего значения для населения (μ) в терминах среднего значения для выборки (μₑ). 1.96 умножается на стандартную ошибку среднего, потому что для стандартного нормального распределения N (0,1) 95% данных находятся в пределах 1,96 стандартных отклонений от среднего значения, как показано на рисунке 5.

Рисунок 5Стандартное нормальное распределение со средним 0 и стандартным отклонением 1, N (0,1) [Изображение из Википедия ]

Иногда 1,96 округляется до 2 для целей расчета. Наконец, более высокая стандартная ошибка приводит к более широкому доверительному интервалу, который указывает на то, что среднее значение μₑ нашей случайной выборки не является хорошим приближением к среднему значению μ основного распределения населения.

Среднее арифметическое, как известно, используется для получения обобщающей характеристики некоторого набора данных. Если данные более-менее однородны и в них нет аномальных наблюдений (выбросов), то среднее хорошо обобщает данные, сведя к минимуму влияние случайных факторов (они взаимопогашаются при сложении).

Когда анализируемые данные представляют собой выборку (которая состоит из случайных значений), то среднее арифметическое часто (но не всегда) выступает в роли приближенной оценки математического ожидания. Почему приближенной? Потому что среднее арифметическое – это величина, которая зависит от набора случайных чисел, и, следовательно, сама является случайной величиной. При повторных экспериментах (даже в одних и тех же условиях) средние будут отличаться друг от друга.

Для того, чтобы на основе статистического анализа данных делать корректные выводы, необходимо оценить возможный разброс полученного результата. Для этого рассчитываются различные показатели вариации. Но то исходные данные. И как мы только что установили, среднее арифметическое также обладает разбросом, который необходимо оценить и учитывать в дальнейшем (в выводах, в выборе метода анализа и т.д.).

Интуитивно понятно, что разброс средней должен быть как-то связан с разбросом исходных данных. Основной характеристикой разброса средней выступает та же дисперсия.

Дисперсия выборочных данных – это средний квадрат отклонения от средней, и рассчитать ее по исходным данным не составляет труда, например, в Excel предусмотрены специальные функции. Однако, как же рассчитать дисперсию средней, если в распоряжении есть только одна выборка и одно среднее арифметическое?

Расчет дисперсии и стандартной ошибки средней арифметической

Чтобы получить дисперсию средней арифметической нет необходимости проводить множество экспериментов, достаточно иметь только одну выборку. Это легко доказать. Для начала вспомним, что средняя арифметическая (простая) рассчитывается по формуле:

где x_i – значения переменной,
n – количество значений.

Теперь учтем два свойства дисперсии, согласно которым, 1) — постоянный множитель можно вынести за знак дисперсии, возведя его в квадрат и 2) — дисперсия суммы независимых случайных величин равняется сумме соответствующих дисперсий. Предполагается, что каждое случайное значение x_i обладает одинаковым разбросом, поэтому несложно вывести формулу дисперсии средней арифметической:

Используя более привычные обозначения, формулу записывают как:

где σ² – это дисперсия, случайной величины, причем генеральная.

На практике же, генеральная дисперсия известна далеко не всегда, точнее совсем редко, поэтому в качестве оной используют выборочную дисперсию:

Стандартное отклонение средней арифметической называется стандартной ошибкой средней и рассчитывается, как квадратный корень из дисперсии.

Формула стандартной ошибки средней при использовании генеральной дисперсии

Формула стандартной ошибки средней при использовании выборочной дисперсии

Последняя формула на практике используется чаще всего, т.к. генеральная дисперсия обычно не известна. Чтобы не вводить новые обозначения, стандартную ошибку средней обычно записывают в виде соотношения стандартного отклонения выборки и корня объема выборки.

Назначение и свойство стандартной ошибки средней арифметической

Стандартная ошибка средней много, где используется. И очень полезно понимать ее свойства. Посмотрим еще раз на формулу стандартной ошибки средней:

Числитель – это стандартное отклонение выборки и здесь все понятно. Чем больше разброс данных, тем больше стандартная ошибка средней – прямо пропорциональная зависимость.

Посмотрим на знаменатель. Здесь находится квадратный корень из объема выборки. Соответственно, чем больше объем выборки, тем меньше стандартная ошибка средней. Для наглядности изобразим на одной диаграмме график нормально распределенной переменной со средней равной 10, сигмой – 3, и второй график – распределение средней арифметической этой же переменной, полученной по 16-ти наблюдениям (которое также будет нормальным).

Судя по формуле, разброс стандартной ошибки средней должен быть в 4 раза (корень из 16) меньше, чем разброс исходных данных, что и видно на рисунке выше. Чем больше наблюдений, тем меньше разброс средней.

Казалось бы, что для получения наиболее точной средней достаточно использовать максимально большую выборку и тогда стандартная ошибка средней будет стремиться к нулю, а сама средняя, соответственно, к математическому ожиданию. Однако квадратный корень объема выборки в знаменателе говорит о том, что связь между точностью выборочной средней и размером выборки не является линейной. Например, увеличение выборки с 20-ти до 50-ти наблюдений, то есть на 30 значений или в 2,5 раза, уменьшает стандартную ошибку средней только на 36%, а со 100-а до 130-ти наблюдений (на те же 30 значений), снижает разброс данных лишь на 12%.

Лучше всего изобразить эту мысль в виде графика зависимости стандартной ошибки средней от размера выборки. Пусть стандартное отклонение равно 10 (на форму графика это не влияет).

Видно, что примерно после 50-ти значений, уменьшение стандартной ошибки средней резко замедляется, после 100-а – наклон постепенно становится почти нулевым.

Таким образом, при достижении некоторого размера выборки ее дальнейшее увеличение уже почти не сказывается на точности средней. Этот факт имеет далеко идущие последствия. Например, при проведении выборочного обследования населения (опроса) чрезмерное увеличение выборки ведет к неоправданным затратам, т.к. точность почти не меняется. Именно поэтому количество опрошенных редко превышает 1,5 тысячи человек. Точность при таком размере выборки часто является достаточной, а дальнейшее увеличение выборки – нецелесообразным.

Подведем итог. Расчет дисперсии и стандартной ошибки средней имеет довольно простую формулу и обладает полезным свойством, связанным с тем, что относительно хорошая точность средней достигается уже при 100 наблюдениях (в этом случае стандартная ошибка средней становится в 10 раз меньше, чем стандартное отклонение выборки). Больше, конечно, лучше, но бесконечно увеличивать объем выборки не имеет практического смысла. Хотя, все зависит от поставленных задач и цены ошибки. В некоторых опросах участие принимают десятки тысяч людей.

Дисперсия и стандартная ошибка средней имеют большое практическое значение. Они используются в проверке гипотез и расчете доверительных интервалов.

Поделиться в социальных сетях:

Источник

Стандартная ошибка среднего

Стандартная ошибка среднего (SEM) — теоретическое стандартное отклонение всех средних выборки размера , извлекаемое из совокупности.

Стандартная ошибка среднего подсчитывается следующим образом:

где s — стандартное отклонение, подсчитанное по выборке,

– число наблюдений в выборке.

Связанные определения:
Выборочное среднее, среднее значение выборки
Выброс
Дисперсия (рассеяние, разброс)
Дисперсия выборки (выборочная дисперсия)
Коэффициент вариации
Максимум
Математическое ожидание дискретной случайной величины
Математическое ожидание непрерывной случайной величины
Медиана
Меры дисперсии, меры разброса
Минимум
Мода
Описательные статистики
Описательный анализ
Параметры рассеяния
Параметры центральной тенденции
Среднее значение
Среднеквадратичное отклонение популяции
Стандартное отклонение

Связанные статьи:
Описательные статистики
Основные статистики и t-критерий Стьюдента

Примеры:
Исследование гемограмм пациентов

Источник

ЧАСТЬ 1. Характеризуем данные

Интуитивно

Например, анализируя каждое значение в выборке по мере поступления.

Через связки описательных статистик

Statistics of location / Центральные тенденции

Statistics of dispersion / Меры разброса

ЧАСТЬ 2. Cвязка медиана + квантили; 5-number summary.

Медиана

Предположим, мы занимаемся селекцией яблонь и хотим охарактеризовать урожай нашей любимой яблони, на которую мы возлагаем большие надежды. Симулируем данные измерения диаметров яблок.

set.seed(14)
apples <- rnorm(8, 8, 1) #Возьмем восемь случайных
                          #значений из нормального распределения
apples <- round(apples,1) #Перезапишем вектор, округлив измерения
                          #до первого знака после запятой
apples

## [1]  7.3  9.7 10.1  9.5  8.0  9.2  7.9  9.1

Медиана

Наши данные в исходном виде выглядят примерно так:

Чтобы увидеть медиану, мы должны ранжировать, или отсортировать, наш вектор по возрастанию:

sort(apples)

## [1]  7.3  7.9  8.0  9.1  9.2  9.5  9.7 10.1

Медиана

В ранжированном ряду медиана расположена так, что слева и справа от нее находится равное число измерений.

Если n нечетное, то медиана = значение с индексом $\frac{n+1}{2}$.
Если n четное, то медиана посередине между $\frac{n}{2}$ и $\frac{n+1}{2}$ значениями.

sort(apples)

## [1]  7.3  7.9  8.0  9.1  9.2  9.5  9.7 10.1

Медиана находится в промежутке между значениями 9.1 и 9.2, т.е. 9.15

Проверим себя:

median(apples)

## [1] 9.15

Медиана: устойчивость к выбросам

Медиана обладает чрезвычайно приятным свойством – устойчивостью к выбросам.

Представим, что наше распределение пострадало от неаккуратности. Допустим сотрудник, которому мы поручили измерять яблоки, измерил также диаметр арбуза и записал этот результат вместе со всеми остальными.

apples2 <- c(apples, 68) #Создадим вектор с новым значением
sort(apples2)

## [1]  7.3  7.9  8.0  9.1  9.2  9.5  9.7 10.1 68.0

Медиана теперь равна 9.2

median(apples2)

## [1] 9.2

Медиана: устойчивость к выбросам

Давайте для сравнения посмотрим на среднюю.

mean(apples)

## [1] 8.85

mean(apples2)

## [1] 15.4

Как видим, она не так благополучно пережила это вторжение. Единственное неверное измерение сбило ее из разряда довольно крупных яблок в область гигантских грейпфрутов.

Квантили

Квантили делят распределение на четыре равные части, каждая из которых включает по 25% значений.

I квантиль отсекает как раз 25%. II — 50%. Это ни что иное, как медиана. III квантиль отсекает 75% значений.

Определим их с помощью команды quantile

quantile(apples)

##    0%   25%   50%   75%  100% 
##  7.30  7.97  9.15  9.55 10.10

Нам показали так же минимальную и максимальную величины.

5-number summary

Аналогичные значения, только со средней в качестве бесплатного приложения, возвращает и функция summary:

summary(apples)

##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##    7.30    7.97    9.15    8.85    9.55   10.10

summary(apples2)

##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##     7.3     8.0     9.2    15.4     9.7    68.0

Персентили

Так же как медиана это частный случай квантиля, так и сам квантиль — частный случай персентиля.

Ничто не помешает нам узнать, например, какие значения отсекают 10% или 99% значений выборки. Подставим соответствующие аргументы:

quantile(apples, probs = c(0.1, 0.99))

##   10%   99% 
##  7.72 10.07

Боксплот: 5-number summary на графике

boxplot(apples)

Отложим числа, характеризующие выборку, по оси Y:

жирная линия в центре это медиана,
нижняя и верхняя границы «коробочки» это I и III квантили,
усы достигают минимального и максимального значений.

Расстояние между I и III квантилями (высота «коробочки») называется интерквартильное расстояние

Если в выборке присутствуют выбросы (значения, отстоящие от границ «коробочки» больше чем на 1.5 интерквартильных расстояния), то они будут изображены отдельными точками.

Case study: диатомовые водоросли в желудках фильтраторов. Самостоятельная работа.

В морских сообществах встречаются два вида фильтраторов, один из которых любит селиться прямо на поверхности тела другого.

Tegella armifera это вид-хозяин. Он может жить как сам по себе, так и вместе с симбионтом.

Loxosomella nordgardi — вид-симбионт. Он практически никогда не встречается в одиночестве.

fig:

Case study: диатомовые водоросли в желудках фильтраторов.

В файле data\2.1_diatome_count.csv даны количества диатомовых водорослей в желудках этих животных. Прочитаем эти данные и посмотрим на их структуру:

diatoms <- read.table("data/2.1_diatome_count.csv", 
                      header = T, sep = "")
head(diatoms)

##          sp count
## 1 host_free    10
## 2 host_free     0
## 3 host_free     1
## 4 host_free     0
## 5 host_free     2
## 6 host_free     0

В таблице 2 переменные: вид (sp) и число водорослей в желудке (count). В переменной sp есть три варианта значений: «host_free» «host_symbiont» и «symbiont»

Ваша задача рассчитать 5-number summary для количества диатомовых в желудках хозяев и симбионтов.

Решение

summary(diatoms$count[diatoms$sp == "host_free"])

##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max.    NA's 
##     0.0     1.0     4.0     4.7     8.0    12.0       1

summary(diatoms$count [diatoms$sp == "host_symbiont"])

##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##    0.00    0.25    4.50    5.35    8.00   20.00

summary(diatoms$count [diatoms$sp == "symbiont"])

##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max.    NA's 
##     0.0     0.0     1.0     1.5     2.0     7.0       4

Боксплоты в ggplot2

Формат данных несколько сложен для человеческого глаза, зато очень подходит для ggplot.

library("ggplot2")
ggplot(data = diatoms, aes(y = count, x = sp)) + geom_boxplot()

Квантили и боксплот: непараметрические характеристики выборки

Главный плюс, но так же и минус связки медиана + квантили это ее независимость от формы распределения.

Будь оно симметричным или с хвостом, 5-number summary опишет, а боксплот нарисует его без искажений. Однако, далеко на этих характеристиках не уедешь.

Бывают случаи, когда можно применять более специальные, но и более информативные характеристики.

ЧАСТЬ 3. Нормальное распределение

Все распределения равны, но некоторые равнее

Это непрерывное распределение, получаемое из мерных данных. Однако, многие распределения других типов тоже могут приближаться к нормальному.

Относительная частота и плотность вероятности

На оси Y может быть отложена относительная частота значений Х в эмпирическом распределении, или вероятность получить такие значения из теоретического распределения.

На оси Х отложены значения Х в интервале от 0 до 20, в действительности же кривая простирается от $-\infty$ до $+\infty$

Площадь под кривой = 1. Интегрируя кривую на промежутке $(k,..,l)$, можно узнать вероятность встречи значений $(x_k,…x_l)$.

НО! Нельзя рассчитать вероятность одного значения $X = x_k$, так как это точка, и под ней нет площади.

Условия появления нормально распределенных признаков

Множество факторов
Наличие/отсутствие каждого фактора не зависит от остальных
Эффекты факторов аддитивны и независимы
Вклад каждого фактора в итоговую изменчивость одинаков

Что-то напоминает, не правда ли?

Приятные особенности

Нормальных кривых бесконечно много, и их описывает заковыристая формула с двумя параметрами. Достаточно знать эти два значения чтобы восстановить или смоделировать любое нормальное распределение.

Если:

данные в выборке распределены нормально
мы можем узнать или оценить параметры этого распределения

можно считать что выборка у нас в кармане! Нам больше не нужно знать результаты измерений, чтобы строить предположения о природе данных.

Так что же это за чудодейственные параметры? Средняя и стандартное отклонение конечно!

ЧАСТЬ 4. Связка среднее + стандартное отклонение

Центральная тенденция

Арифметическое среднее

Формула

\[\bar{x}=\frac{\sum{x_i}}{n}\]

Рассчитаем вручную и проверим:

mean_apple_diam <- sum(apples) / length(apples)
mean_apple_diam

## [1] 8.85

round(mean_apple_diam,3) == round(mean(apples),3)

## [1] TRUE

Меры разброса

Девиата (отклонение)

Первым кирпичиком в построении параметрических мер разброса будет разность между значением вариаты (измерения) и средней:

\[x_i — \bar{x}\]

raw.deviates <- c(apples - mean(apples))
raw.deviates

## [1] -1.55  0.85  1.25  0.65 -0.85  0.35 -0.95  0.25

Как теперь из этого вектора значений получить одну числовую характеристику?

Меры разброса

К сожалению мы не можем просто сложить все значения девиат и поделить их на объем выборки. Сумма девиат всегда будет равна нулю.

round(sum(raw.deviates))

## [1] 0

Путь 1: среднее отклонение = Average Deviation

Первый выход, который бросается в глаза, это использовать абсолютные значения

\[AD = \frac{\sum{\lvert x_i — \bar{x} \rvert}}{n}\]

sum(abs(raw.deviates)) / length(apples)

Меры разброса

Путь 2: сумма квадратов = SS, Sum of Squares

Избавиться от знака девиаты можно не только с помощью модуля, но и возведя значение в квадрат.

\[SS = \sum{{(x_i — \bar{x})}^2}\]

sum((raw.deviates)^2)

Меры разброса

Дисперсия = MS, Mean Square, Variance

Если мы теперь поделим сумму квадратов на объем выборки, то получим дисперсию.

\[variance=\frac{\sum{(x_i — \bar{x})^2}}{n}= \frac{SS}{n}\]

sum((raw.deviates)^2) / length(apples)

Среднеквадратичное/стандартное отклонение = Standard Deviation

Квадратный корень из дисперсии позволит вернуться к исходным единицам измерения

\[SD=\sqrt{\frac{\sum{(x_i — \bar{x})^2}}{n}} = \sqrt{variance}\]

sqrt(sum((raw.deviates)^2) / length(apples))

Особенности применения связки

только вместе,
чувствительны к выбросам,
плохо работают с несимметричными распределениями.

Сравните разброс в выборках

Проверим себя

Задание

Из пяти положительных чисел создайте выборку со средней = 10 и медианой = 7

Решение 1

В выборке с медианой = 7 и n = 5, мы точно знаем: (а) одно из значений должно быть равно 7, (б) два значения должны быть меньше, и два — больше 7.

Создадим вектор, в котором одно значение задано, а три других просто придумаем:

example <- c(2, 5, 7, 10)

Среднее это сумма всех значений выборки, поделенная на ее объем. Умножив среднюю на 5 получим сумму всех значений.

Определим недостающее и проверим себя:

10 * 5 - sum(example)

## [1] 26

example <- c(2, 5, 7, 10, 26) #перезапишем вектор
mean(example)

## [1] 10

ЧАСТЬ 5. От статистик к параметрам.

Выборка и генеральная совокупность

Статистики

описывают выборки
их обозначают латинскими буквами: $М$, $s^2$.

Параметры

описывают генеральную совокупность
их обозначают греческими буквами: $\mu$, $\sigma^2$

С помощью выборочных статистик мы стремимся описать популяционные параметры.

Степени свободы в стандартном отклонении

Среднеквадратичное отклонение, которое мы только что сконструировали, верно описывает выборку, но не годится для генеральной совокупности, так как недооценивает ее истинное разнообразие. Чтобы это исправить, в знаменатель нужно внести поправку, из объема выборки превратить его в степень свободы.

Сумма «сырых» девиат всегда равна нулю, поэтому зная n-1 значений, мы без труда рассчитаем каким должно быть последнее. А значит, оно не может варьировать «свободно».

Дисперсия (выборочная оценка параметра)

\[\sigma^2=\frac{\sum{(x_i — \bar{x})^2}}{n-1}\]

Стандартное отклонение (выборочная оценка параметра)

\[\sigma=\sqrt{\frac{\sum{(x_i — \bar{x})^2}}{n-1}}\]

Степени свободы в стандартном отклонении

Давайте проверим как работают степени свободы на примере.

Создадим простейшую выборку со следующими признаками:

sim.mean <- 100
sim.sd <- 2
sim.n <- 11

Сначала рассчитаем дисперсию и сумму квадратов

sim.var <- sim.sd^2
sim.ss <- sim.var * (sim.n - 1)

SD = 2 это маленький разброс, так что надо выбирать значения недалеко от среднего. Например, 101 — очень удобное число. Заполним ими нашу выборку почти до конца:

sim.sample <- rep(101,10)

Степени свободы в стандартном отклонении

Итак, 10 значений мы взяли практически с потолка. Последнее, одиннадцатое, должно быть предсказано, иначе наша затея не сработает, и выборка с желаемыми признаками не получится.

Рассчитаем значение суммы квадратов для уже созданных нами «свободных» вариат:

free.ss <- (10) * ((101-100)^2)
free.ss

## [1] 10

Из общей суммы квадратов вычтем уже имеющуюся:

determined.ss <- sim.ss - free.ss

Определим значение одиннадцатой девиаты, т.е. расстояние от среднего до последнего значения в выборке.

sqrt(determined.ss)

## [1] 5.48

Степени свободы в стандартном отклонении

10 предыдущих значений были больше среднего, значит последнее должно быть меньше, иначе выборка не уравновесится

last.value <- 100 - sqrt(determined.ss)
last.value

## [1] 94.5

Добавим последнее, «детерминированное», значение к остальным:

sim.sample <- c(rep(101,10), last.value)
sim.sample

##  [1] 101.0 101.0 101.0 101.0 101.0 101.0 101.0 101.0 101.0 101.0  94.5

Можем теперь проверить себя:

round(mean(sim.sample))

## [1] 100

round(sd(sim.sample))

## [1] 2

Ошибка среднего, SEM

Имея дело с выборками и стремясь распространить то, что мы узнали, на всю генеральную совокупность, исследователю к лицу некоторая скромность.

Наша выборка — лишь одна из множества возможных выборок, берущих начало из одной генеральной совокупности. Значения попадают в выборки случайно, а потому не одинаковыми будут и итоговые выборочные статистики.

Каждая из них, хотя и будет описывать популяционный параметр, имеет шанс быть неверной.

Модель генеральной совокупности

Давайте для наших экспериментов создадим генеральную совокупность с параметрами $\mu = 50$ и $\sigma = 7$.

Вот график ее частотного распределения.

Возьмем выборку из этой генеральной совокупности

В разных выборках средние значения будут отличаться.

Что будет со средними, если взять много выборок?

Давайте возьмем много-много выборок, вычислим для каждой выборочное среднее и построим распределение этих выборочных средних.

Выборочные средние нормально распределены с параметрами $\mu$ и $SD _\bar{x}$

Среднее значение выборочных средних стремится к среднему в генеральной совокупности

Чем больше объем выборок, тем точнее оценка среднего в генеральной совокупности

\[SE _\bar{x} = \sigma / \sqrt{N}\]

SEM, Стандартная ошибка среднего (= стандартное отклонение выборочного распределения среднего) будет в N раз меньше, чем дисперсия в генеральной совокупности

То есть, чем больше будет объем выборок, тем меньше будет эта стандартная ошибка, и тем точнее мы оценим (параметрическое) среднее в генеральной совокупности.

SD vs SE

Выборку должны характеризовать центральная тенденция (средняя) и мера разброса.

Стандартное отклонение, описывающее непосредственно выборку, т.е. отличия значений от выборочного среднего, характеризует разброс в выборке напрямую, а значит является более хорошей описательной статистикой, чем стандартное отклонение (=стандартная ошибка) среднего.

Поэтому лучше характеризовать данные в формате

\[Mean \pm SD (N)\]

а не

\[Mean \pm SE (N)\]

Take home messages

Описательные статистики ходят только в связке.
Выбирая между медианой и средней, учитывайте природу данных.

Источник

Ключевые выводы

Стандартное отклонение (SD) измеряет разброс набора данных относительно его среднего значения.
Стандартная ошибка среднего (SEM) измеряет, насколько вероятно расхождение между средним значением выборки по сравнению со средним значением генеральной совокупности.
SEM берет SD и делит его на квадратный корень из размера выборки.

SEM против SD

Стандартное отклонение и стандартная ошибка используются во всех типах статистических исследований, включая исследования в области финансов, медицины, биологии, инженерии, психологии и т. Д. В этих исследованиях стандартное отклонение (SD) и расчетная стандартная ошибка среднего (SEM) ) используются для представления характеристик данных выборки и объяснения результатов статистического анализа. Однако некоторые исследователи иногда путают SD и SEM. Таким исследователям следует помнить, что расчеты SD и SEM включают разные статистические выводы, каждый из которых имеет свое значение. SD — это разброс отдельных значений данных.

Другими словами, SD указывает, насколько точно среднее значение представляет данные выборки. Однако значение SEM включает статистический вывод, основанный на распределении выборки. SEM — это стандартное отклонение теоретического распределения выборочных средних (выборочное распределение).

Расчет стандартного отклонения

Формула SD требует нескольких шагов:

Во-первых, возьмите квадрат разницы между каждой точкой данных и средним значением выборки, найдя сумму этих значений.
Затем разделите эту сумму на размер выборки минус один, который представляет собой дисперсию.
Наконец, извлеките квадратный корень из дисперсии, чтобы получить стандартное отклонение.

Стандартная ошибка среднего

SEM рассчитывается путем деления стандартного отклонения на квадратный корень из размера выборки.

Стандартная ошибка и стандартное отклонение в финансах

Источник

Standard error of the sample mean[edit]

Exact value[edit]

Estimate[edit]

Accuracy of the estimator[edit]

Derivation[edit]

Independent and identically distributed random variables with random sample size[edit]

Student approximation when σ value is unknown[edit]

Assumptions and usage[edit]

Standard error of mean versus standard deviation[edit]

Extensions[edit]

Finite population correction (FPC)[edit]

Correction for correlation in the sample[edit]

See also[edit]

References[edit]

Ключевые выводы

SEM против SD

Расчет стандартного отклонения

Стандартная ошибка среднего

Стандартная ошибка и стандартное отклонение в финансах

Standard Error of the Mean vs. Standard Deviation: An Overview

Key Takeaways

Click Play to Learn the Difference Between Standard Error and Standard Deviation

Calculating SD and SEM

Standard Deviation

Standard Error of the Mean

Standard Error and Standard Deviation in Finance

How Are Standard Deviation and Standard Error of the Mean Different?

Is the Standard Error Equal to the Standard Deviation?

How Can You Compute the SE From the SD?

Why Do We Use Standard Error Instead of Standard Deviation?

What Is the Empirical Rule, and How Does It Relate to Standard Deviation?

The Bottom Line

Standard Error of the Mean vs. Standard Deviation: An Overview

Key Takeaways

Click Play to Learn the Difference Between Standard Error and Standard Deviation

Calculating SD and SEM

Standard Deviation

Standard Error of the Mean

Standard Error and Standard Deviation in Finance

How Are Standard Deviation and Standard Error of the Mean Different?

Is the Standard Error Equal to the Standard Deviation?

How Can You Compute the SE From the SD?

Why Do We Use Standard Error Instead of Standard Deviation?

What Is the Empirical Rule, and How Does It Relate to Standard Deviation?

The Bottom Line

Способ 1: используйте SciPy

Способ 2: использовать NumPy

Как интерпретировать стандартную ошибку среднего

Дополнительные ресурсы

Расчет ошибки средней арифметической

Способ 1: расчет с помощью комбинации функций

Способ 2: применение инструмента «Описательная статистика»

10. Достоверность различий

Понимание центральной предельной теоремы, стандартной ошибки и доверительных интервалов

Расчет дисперсии и стандартной ошибки средней арифметической

Назначение и свойство стандартной ошибки средней арифметической

Стандартная ошибка среднего

ЧАСТЬ 1. Характеризуем данные

Интуитивно

Через связки описательных статистик

Statistics of location / Центральные тенденции

Statistics of dispersion / Меры разброса

ЧАСТЬ 2. Cвязка медиана + квантили; 5-number summary.

Медиана

Медиана

Медиана

Медиана: устойчивость к выбросам

Медиана: устойчивость к выбросам

Квантили

5-number summary

Персентили

Боксплот: 5-number summary на графике

Case study: диатомовые водоросли в желудках фильтраторов. Самостоятельная работа.

Case study: диатомовые водоросли в желудках фильтраторов.

Решение

Боксплоты в ggplot2

Квантили и боксплот: непараметрические характеристики выборки

ЧАСТЬ 3. Нормальное распределение

Все распределения равны, но некоторые равнее

Относительная частота и плотность вероятности