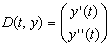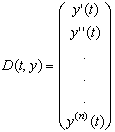Сообщение от Symon
1. Пишете I1*(t) вместо I(t)1. Получается элемент вектора I умножается на t. Тогда как t является аргументом вектор-функции I.
2. Далее появляется I22. Получается I является вектором по крайней мере из 22-х элементов? Или вы хотели использовать двойной индекс и определить матрицу?
3. При использовании rkfixed лучше использовать вектор (матрицу из одного столбца)
4. Пока все.
1. Внес исправления — не заметил, что для этого есть отдельная функция на панели.
2. I22 не является вектором из 22 элементов, также как и I11 вектором из 11 элементов. Я просто не совсем понимаю, как правильно его нужно записать. Они являются просто заменой I1 и I2. Если я обозначу I11 и I22 это же будет неверно?
3 Вы имеете ввиду, что будет лучше, если результатом rfixed будет вектор?
Сейчас упростил задачу, повыбрасывал лишние вещи, упростил уравнения и задал другие данные — уравнения решаются.
Но стоит мне подставить данные, хоть подобные моим — сразу же появлется ошибка «Эту функцию здесь использовать нельзя».
Мои данные расположены перед таблицей в следующем файле. Они имеют гораздо меньшее значение.
Как правильно задать начальные условия, чтобы решение происходило с моими данными?
Вот полученный результат.
Я промоделировал схему в программе-симуляторе Протеус — токи выше 0,03 А и 0,01 А не повышаются. Ставлю в качетстве начальных значений токи ниже этих значений — Расчет не идет.
Может ли кто-нибудь найти ошибку в выложенном мною файле?
Рискну предположить, что проблема в исходных данных — их сочетание вызывает расчетные трудности.
1. Судя по е(t)=37sin(11t) период колебаний, навязываемых источником — 0,57 секунды.
2. С другой стороны, величины L и C Такие, что резонансная частота должна быть 0,3 МГц при периоде 3*10е-6 секунды.
3. Однако сопротивление R1 = 6,25 кОм — процесс для собственных колебаний явно апериодический.
То есть для расчета хотя бы трех колебаний на частоте е(t) надо брать интервал времени 1,5…2 секунды.
Но из-за переходного процесса в LC цепи вроде бы надо брать интервал 10е-7 секунды.
Формулы посмотрел на бегу — похоже на правду. И второй вариант — не с контурными токами, а с общим током и напряжением на C.
Прикрепляю свои версии файлов с результатими расчета для предложенных данных и еще дополнительно со своими L, C, R1.
Calculation3_modified.zip
Calculation3_modified_2.zip
RTF.zip
Изменено пользователем fider
Сообщение от Symon
1. Пишете I1*(t) вместо I(t)1. Получается элемент вектора I умножается на t. Тогда как t является аргументом вектор-функции I.
2. Далее появляется I22. Получается I является вектором по крайней мере из 22-х элементов? Или вы хотели использовать двойной индекс и определить матрицу?
3. При использовании rkfixed лучше использовать вектор (матрицу из одного столбца)
4. Пока все.
1. Внес исправления — не заметил, что для этого есть отдельная функция на панели.
2. I22 не является вектором из 22 элементов, также как и I11 вектором из 11 элементов. Я просто не совсем понимаю, как правильно его нужно записать. Они являются просто заменой I1 и I2. Если я обозначу I11 и I22 это же будет неверно?
3 Вы имеете ввиду, что будет лучше, если результатом rfixed будет вектор?
Сейчас упростил задачу, повыбрасывал лишние вещи, упростил уравнения и задал другие данные — уравнения решаются.
Но стоит мне подставить данные, хоть подобные моим — сразу же появлется ошибка «Эту функцию здесь использовать нельзя».
Мои данные расположены перед таблицей в следующем файле. Они имеют гораздо меньшее значение.
Как правильно задать начальные условия, чтобы решение происходило с моими данными?
Вот полученный результат.
Я промоделировал схему в программе-симуляторе Протеус — токи выше 0,03 А и 0,01 А не повышаются. Ставлю в качетстве начальных значений токи ниже этих значений — Расчет не идет.
Может ли кто-нибудь найти ошибку в выложенном мною файле?
Рискну предположить, что проблема в исходных данных — их сочетание вызывает расчетные трудности.
1. Судя по е(t)=37sin(11t) период колебаний, навязываемых источником — 0,57 секунды.
2. С другой стороны, величины L и C Такие, что резонансная частота должна быть 0,3 МГц при периоде 3*10е-6 секунды.
3. Однако сопротивление R1 = 6,25 кОм — процесс для собственных колебаний явно апериодический.
То есть для расчета хотя бы трех колебаний на частоте е(t) надо брать интервал времени 1,5…2 секунды.
Но из-за переходного процесса в LC цепи вроде бы надо брать интервал 10е-7 секунды.
Формулы посмотрел на бегу — похоже на правду. И второй вариант — не с контурными токами, а с общим током и напряжением на C.
Прикрепляю свои версии файлов с результатими расчета для предложенных данных и еще дополнительно со своими L, C, R1.
Calculation3_modified.zip
Calculation3_modified_2.zip
RTF.zip
Изменено 25 ноября, 2014 пользователем fider
Дело в том, что когда b1 и b2 — обнулены, функция работает, как только стоит задать ей отличные от нуля значения, она ругается на то, что эту функцию здесь использовать нельзя.
Кто разбирается в mathCAD — можете подсказать, в чем проблема?
Your problem has nothing to do with MC14 — you get exactly the same failure in MC13 and MC11.
I recommend posting files in MC11 format whenever possible. You attract a larger audience and are likely to get a quicker response. Also, MC11 files are much smaller. XMCD files are extremely bloated, and really bad for the bandwidth. If something cannot be posted in MC11 format, at least use the XMCDZ format, without the pictures.
Your problem is just the way you have set up the problem. You get complex numbers. The reason is that you are taking fraction powers of negative numbers. And that happens when your state variables go negative. Which happens immediately, as your initial conditions are zero, and one of the derivatives is negative at that point.
� � � � Tom Gutman
You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
-
Forums
-
Homework Help
-
Engineering and Comp Sci Homework Help
Help with Mathcad Rkadapt function
-
Thread starter
Natty727 -
Start date
Jul 16, 2007 -
-
Tags -
Function
Mathcad
-
- Jul 16, 2007
-
- #1
Homework Statement
I’m trying to use the rkadapt function in mathcad 13 but it’s coming up in red and telling me ‘This function cannot be used here’. Not really sure why because all the constants used have been defined above it and take sensible values. The values of x1 and x2 have been defined in the matrix x. If anyone can help me with this that would be great!
Homework Equations
[PLAIN]http://server3.uploadit.org/files/nattyuk-Rkadapt3.JPG [Broken]
The Attempt at a Solution
[PLAIN]http://server3.uploadit.org/files/nattyuk-Rkadapt3.JPG [Broken]
Last edited by a moderator: May 3, 2017
Answers and Replies
- Aug 6, 2007
-
- #2
Hello!
I have the same problem… Natty, did you find an answer to the problem?
(I have used the Rkadapt function in Mathcad 2000 and it worked just fine, but in Mathcad 13 i don;t know what the problem is 
Thx!
- Aug 6, 2007
-
- #3
Hey johnny, I’ve got mine working now but I still don’t know what was wrong with it originally! I started a new worksheet and re-wrote it which seemed to do the trick, not sure why because all the positioning and declarations were exactly the same… Sorry I can’t provide a more helpful answer!
Suggested for: Help with Mathcad Rkadapt function
- Jan 5, 2023
- Nov 10, 2022
- Nov 29, 2022
- Sep 29, 2022
- May 25, 2023
- May 15, 2023
- Sep 12, 2022
- Sep 25, 2022
- Aug 13, 2022
- Aug 19, 2021
-
Forums
-
Homework Help
-
Engineering and Comp Sci Homework Help
Может ли кто-нибудь найти ошибку в выложенном мною файле?
Рискну предположить, что проблема в исходных данных — их сочетание вызывает расчетные трудности.
1. Судя по е(t)=37sin(11t) период колебаний, навязываемых источником — 0,57 секунды.
2. С другой стороны, величины L и C Такие, что резонансная частота должна быть 0,3 МГц при периоде 3*10е-6 секунды.
3. Однако сопротивление R1 = 6,25 кОм — процесс для собственных колебаний явно апериодический.
То есть для расчета хотя бы трех колебаний на частоте е(t) надо брать интервал времени 1,5…2 секунды.
Но из-за переходного процесса в LC цепи вроде бы надо брать интервал 10е-7 секунды.
Формулы посмотрел на бегу — похоже на правду. И второй вариант — не с контурными токами, а с общим током и напряжением на C.
Прикрепляю свои версии файлов с результатими расчета для предложенных данных и еще дополнительно со своими L, C, R1.
Calculation3_modified.zip
Calculation3_modified_2.zip
RTF.zip
Изменено 25 ноября, 2014 пользователем fider
Альтернативным методом
решения ОДУ является использование
встроенных функций rkfixed(
), Rkadapt( ) или Bulstoer(
). Этот метод несколько
проигрывает первому и в простоте, и в
наглядности, однако иногда приходится
решать ОДУ с помощью альтернативного
метода, например, при следующих
обстоятельствах:
— ОДУ решается в контексте с более
сложными задачами, в которые входят
системы дифференциальных уравнений
(для которых вычислительный блок
неприменим) — в этом случае может
потребоваться единый стиль программирования;
— ответ предпочтительнее получить в
виде матрицы, а не функции;
— в старых версиях Mathcad’a
не было вычислительного блока, а у
пользователя имеется много документов,
созданных с помощью альтернативного
метода.
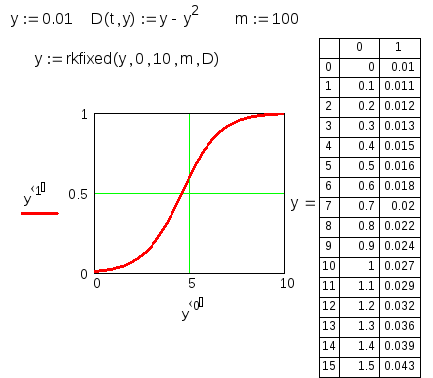
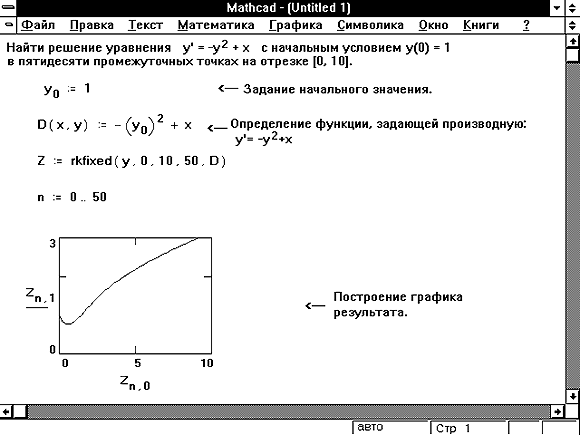
Приведем пример использования
функции rkfixed( ) для решения той же самой
задачи Коши для ОДУ первого порядка у’
=у-у2.
Здесь необходимо явно задать начальное
значение y:=0.01,
описать первую производную D(t,y):=y-y2
и указать количество точек интегрирования
m=100.
Результат получаем
в виде матрицы
y
размерностью (m+1)
x
2.
В первом столбце содержатся значения
аргумента t
в интервале от 0
до 10,
во втором столбце — значения искомой
функции y(t),
рис. 5.2.
Рис. 5.2. Решение задачи Коши
для ОДУ первого порядка вторым способом
Это не лучший стиль решения
задачи Коши. В самом деле, сначала
переменной у
присвоено значение скаляра у=0.01,
а затем этой же переменной присвоено
матричное значение (результат решения
ОДУ). Нужно избегать такого стиля, когда
один и тот же идентификатор используется
при разных типах данных. Неплохим
решением было бы назвать результат
по-другому, например u.
Рассмотренный пример взят
из области математической экологии и
описывает динамику популяций с
внутривидовой конкуренцией. Сначала
происходит рост численности популяции,
близкий к экспоненциальному, а затем
осуществляется выход на стационарное
состояние.
Оду высшего порядка
Обыкновенное дифференциальное
уравнение с неизвестной функцией y(t),
в которое входят производные этой
функции вплоть до y(n)(t),
называется ОДУ n-го
порядка. Если имеется такое уравнение,
то для корректной постановки задачи
Коши кроме самого уравнения требуется
задать n
начальных условий на саму функцию y(t)
и ее производные от первого до (n
-1) го порядка включительно. В Mathcad’e
можно решать ОДУ высших порядков как с
помощью вычислительного блока
Given-Odesolve(
), так и альтернативным
методом с использованием функций типа
rkfixed().
Внутри вычислительного
блока
Given-Odesolve(
):
— ОДУ должно быть линейно относительно
старшей производной;
— начальные условия должны
иметь форму y(t0)=b
или y(n)(t0)=b;
В остальном, решение ОДУ
высших порядков ничем не отличается от
решения уравнений первого порядка.
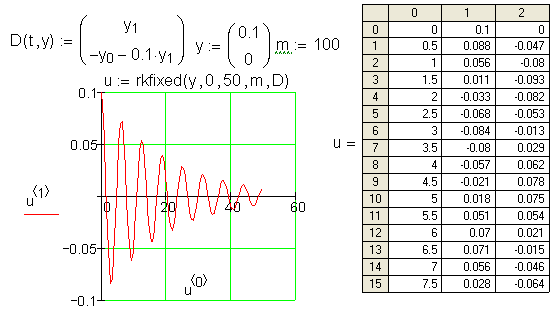
На рис. 5.3 показано решение
дифференциального
уравнения второго порядка
затухающего гармонического осциллятора,
которое описывает, например, колебания
маятника. Для модели маятника функция
y(t)
описывает изменения угла его отклонения
от вертикали, y'(t)
— угловую скорость маятника, y»(t)
— ускорение, а начальные условия,
соответственно, начальное отклонение
маятника у
(0) =0.1 (в радианах) и
начальную скорость у'(0)=
0.
Рис. 5.3. Решение дифференциального
уравнения второго порядка
Альтернативный метод решения
ОДУ высшего порядка реализуется с
помощью трех встроенных функций, которые
позволяют решать поставленную задачу
в форме Коши различными численными
методами:
— rkfixed(y,
t0, t1, m,
D) — метод Рунге-Кутта
с фиксированным шагом;
— Rkadapt(y,
t0, t1, m,
D) — метод Рунге-Кутта
с переменным шагом;
— Bulstoer(y,
t0, t1, m, D)
— метод
Bulirsch-Stoer;
— у
— вектор начальных значений в точке t0
размерностью n
x1;
— t0
— начальная точка интервала;
— t1
— конечная точка интервала;
— m
— число шагов, на которых численный метод
находит решение;
— D
— векторная функция
дифференциальных уравнений размером
n
x1
от двух аргументов — скалярного t,
по которому
взяты производные
и векторного у,
элементы которого являются младшими
производными искомой функции.
Покажем на примере дифференциального
уравнения третьего порядка
методику формирования
векторной функции D(t,y).
Для этой цели нужно разрешить уравнение
относительно старшей производной
З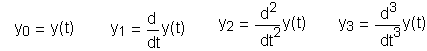
следует в этом уравнении выполнить
замену производных компонентами вектораy:
Врезультате замены получим:
После этого можно записать
векторную функцию D(t,y):
В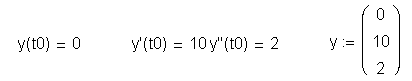
функцияD(t,y)
имеет количество компонентов, равное
порядку дифференциального уравнения.
Поскольку младших производных нет, то
вместо уравнений записываются их
обозначения (y1
и y2).
Вместо старшей производной записывается
правая часть y3.
Начальные условия должны задаваться
для искомой функции и каждой младшей
производной, например:
Каждая из приведенных
функций выдает решение в виде матрицы
размером (m+1)
х
(n+1).
В ее левом столбце находятся значения
аргумента t,
делящие интервал на равномерные шаги,
а в остальных n
столбцах — значения искомых функций
y0(t)
,y1(t),
y2(t)…,
рассчитанные для этих значений аргумента.
Поскольку всего точек (помимо начальной)
m,
то строк в матрице решения будет всего
m+1.
В подавляющем большинстве
случаев достаточно использовать функцию
rkfixed(
), как это показано
на рис. 5.4 на примере решения системы
ОДУ модели осциллятора с затуханием:
Рис. 4.4. Решение системы ОДУ
второго порядка
Система ОДУ на рис. 5.4
задается с помощью векторной функции
D(t,y),
составленной по описанной выше методике.
Такой же размер имеет вектор начальных
значений у.
Число шагов, на которых определяется
решение, задано параметром m=100.
Решение системы ОДУ осуществляется на
интервале (0,
50). Просмотреть все
компоненты матрицы можно с помощью
вертикальной полосы прокрутки.
Решения обыкновенных
дифференциальных уравнений часто
удобнее изображать не в функции от
аргумента t,
а в фазовом пространстве. Фазовый портрет
системы — это кривая на фазовой плоскости,
построенная в координатах y’(t)
и y(t),
рис. 5.5.
Фазовый портрет, как правило,
имеет одну стационарную точку (аттрактор),
на которую «накручивается» решение.
В теории динамических систем аттрактор
такого типа называется фокусом.
В общем случае, если система
состоит из n
ОДУ, то фазовое пространство является
n-мерным.
При n>3
наглядность теряется, и для визуализации
фазового портрета приходится строить
различные его проекции.
Метод Рунге-Кутта четвертого
порядка обеспечивает малую погрешность
для широкого класса систем ОДУ за
исключением жестких систем. Поэтому в
большинстве случаев стоит применять
функцию rkfixed(
). Если по различным причинам время
расчетов становится критичным или
точность неудовлетворительна, стоит
попробовать вместо rkfixed(
) другие функции.
Рис. 5.5. Фазовый портрет
решения системы ОДУ
Функция Rkadapt(
) может быть полезна
в случае, когда известно, что решение
на рассматриваемом интервале меняется
слабо, либо существуют участки медленных
и быстрых его изменений. Метод Рунге-Кутта
с переменным шагом разбивает интервал
не на равномерные шаги, а более оптимальным
способом. Там, где решение меняется
слабо, шаги выбираются более редкими,
а в областях его сильных изменений —
частыми. В результате, для достижения
одинаковой точности требуется меньшее
число шагов, чем для rkfixed(
). Метод Bulirsch-Stoer
часто оказывается более эффективным
для поиска гладких решений.
Соседние файлы в папке Пособие_MathCAD
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Электронный курс по MathCAD



5.2 Решение дифференциальных уравнений и систем.(Задача Коши и граничные задачи).
Решение одиночного дифференциального уравнения.
Для численного решения одиночного дифференциального уравнения в MathCAD имеется функция Odesolve, с помощью которой может быть решена как задача Коши для обыкновенного дифференциального уравнения, так и граничная задача. Эта функция входит в состав блока решения и сявляется его заключительным ключевым словом.
Odesolve(x,b,[step]) — Возвращает функцию, которая является решением дифференциального уравнения. Используется в блоке с оператором Given.
x — переменная интегрирования, действительное число
b — конечная точка отрезка интегрирования
step — величина шага по переменной интегрирования (необязательный аргумент)
Замечания:
- Уравнение должно быть линейным относительно старшей производной.
- Число заданных начальных или граничных условий внутри блока должно быть равно порядку уравнения.
- При записи уравнения для обозначения производных функции используйте специальные кнопки с панели Math или ‘ (штрих) — [Ctrl+F7], для знака равенства = [Ctrl+=] (в том числе и для дополнительных условий).
- Конечная точка должна быть больше начальной.
- Не допускаются начальные и граничные условия смешанного типа (f ‘(a)+f(a)=5).
- Искомая функция в блоке дложна быть обязательно с аргументом ( f(x))
Численное решение задачи Коши для дифференциальных уравнений и систем.
Для численного решения задачи Коши для дифференциальных уравнений и систем могут быть использованы функции:
rkfixed(y,x1,x2,n,F) — возвращает матрицу решений системы уравнений методом Рунге-Кутта 4-го порядка при фиксированном шаге по x
rkadapt(y,x1,x2,n,F) — ищет решение с переменным шагом ( там, где решение меняется медленнее, шаг увеличивается, а в области быстрого изменения решения шаг функции уменьшается). Возвращается решение с равным шагом. Функция работает быстрее, чем rkfixed
Bulstoer(y,x1,x2,n,F) — дает более точное решение (методом Bulirsch-Stoer)
Агрумкнты вышеуказанных функций:
y — вектор начальных условий
x1,x2 — границы интервала для поиска решения
n — количество точек на интервале
F(x,y) — вектор-функция первых производных
При решении дифференциальных уравнений порядка выше первого (или систем уравнений, выше первого порядка) исходное уравнение (систему) необходимо преобразовать к системе дифференциальных уравнений первого порядка.
В результате работы укзанных функций рассчитывается матрица, количество стобцов которой равно порядку уравнения +1(или сумме порядков уравнений в системе +1), а количество строк равно параметру n. Первый столбец содержит значения независимой переменной, второй — значение функции, третий — для диф. уравнений 2-го порядка — значение производной искомой функции (если решается система двух уравнений 1-го порядка, то третий столбец будет содержать значения второй функции). Для выделения решений (функций или их производных) можно воспользоваться стандартным оператором вывода столбцов матрицы M < >
Если матрица правых частей дифференциальных уравнений почти вырождена, то такие системы называются жесткими. В этом случае решения, возвращаемые функцией rkfixed будет неустойчивым и для решения таких систем необходимо применять функции Stiffb , Stiffr
Stiffb(y,x1,x2,n,F,J) — ищет решение диф. уравнения или системы дифференциальных уравнений методом Bulirsch-Stoer
Stiffr(y,x1,x2,n,F,J) — ищет решение диф. уравнения или системы дифференциальных уравнений методом Rosenbrock
Первые пять аргументов такие же,как и при решении хорошо обусловленных систем дифференциальных уравнений . Дополнительный аргумент — матрица J размером nx(n+1), первый столбец которой содержит частные производные dF/dx, остальные столбцы и строки представляют собой матрицу Якоби dF/dy
Пример решения жесткой системы дифференциальных уравнений.
Для отыскания решения системы диф. уравнений только в конечной точке используются функции bulstoer,rkadapt, stiffb, stiffr (начинаются с прописной буквы).
Набор парамтров для этих функций :
bulstoer(y,x1,x2,acc,F,kmax,save)
rkadapt(y,x1,x2,acc,F,kmax,save)
stiffb(y,x1,x2,acc,F,J,kmax,save)
stiffr(y,x1,x2,acc,F,J,kmax,save)
Первые три параметра и пятый (F) этих функций те же, что идля функции Rkadapt. Дополнительные параметры:
acc — параметр, контролирующий точность решения (реком. асс=0.001)
kmax — максимальное число промежуточных точек в которых ищется решение
save — минимально допустимый интервал между точками, в которых ищется решение
Решение граничных задач для обыкновенных дифференциальных уравнений.
Если для дифференциального уравнения n-го порядка k граничных условий заданы в начальной точке х1, а (n-k) граничных условий — в конечной точке х2, то такая задача называется краевой. В MathCAD реализованы две функции, позволяющие численно найти недостающие условия в точках х1 и х2.
Двухточечная краевая задача
Задача решается в два этапа. Сначала с помощью функции sbval находятся недостающие начальные значения, а затем применяется одна из выше описанных функций для решения стандартной задачи Коши на отрезке.
sbval(v,x1,x2,F,load,score) — ищет недостающие начальные условия в точке х1
v — вектор началных приближений для искомых начальных значений в точке х1,
х1,х2 — граничные точки интервала
F(x,y) — вектор-столбец из n элементов, содержит правые части дифференциальных уравнений
load(x1,v) — вектор-столбец из n элементов, содержит начальные значения в точке х1; некоторые из значений- константы, другие неизвестны и будут найдены в процессе решения.
score(x2,y) — вектор-столбец размерности вектора v, содержащий разность между начальным условием в точке х2 и значеием искомого решения в этой точке.
Краевая задача с условиями внутри интервала.
На первом этапе используется функция
balfit(V1,V2,x1,x2,xf,F,load1,load2,score) — ищет недостающие начальные условия в точках х1 и х2, сшивая решения, выходящие из этих точек, в точке xf
V1,V2 — вектора началных приближений для искомых начальных значений в точках х1 и х2
х1,х2 — граничные точки интервала
load1(x1,V1) — вектор-столбец из n элементов, содержит начальные значения в точке х1; некоторые из значений- константы, другие неизвестны и будут найдены в процессе решения
load2(x2,V2) — вектор-столбец из n элементов, содержит начальные значения в точке х2; некоторые из значений- константы, другие неизвестны и будут найдены в процессе решения.
score(xf,y) — вектор-столбец размерности n, содержащий разность между решениями, начинающимися в точках х1 и х2, в точке xf
При решении дифференциального уравнения искомой величиной является функция. Для ОДУ неизвестная функция — функция одной переменной. Дифференциальные уравнения в частных производных — это дифференциальные уравнения, в которых неизвестной является функция двух или большего числа переменных. Mathcad имеет ряд встроенных функций, предназначенных для решения ОДУ. Каждая из этих функций предназначена для численного решения дифференциального уравнения. В результате решения получается матрица, содержащая значения функции, вычисленные на некотором множестве точек (на некоторой сетке значений). Для каждого алгоритма, который используется при решении дифференциальных уравнений, Mathcad имеет различные встроенные функции. Несмотря на различные методы поиска решения, каждая из этих функций требует, чтобы были заданы по крайней мере следующие величины, необходимые для поиска решения:
- Начальные условия.
- Набор точек, в которых нужно найти решение.
- Само дифференциальное уравнение, записанное в некотором специальном виде, который будет детально описан в этой главе.
В этом разделе описано, как решить ОДУ, используя функцию rkfixed. Раздел начинается с примера того, как решить простейшее дифференциальное уравнение первого порядка. Затем будет показано, как можно решать дифференциальные уравнения более высокого порядка.
Дифференциальные уравнения первого порядка
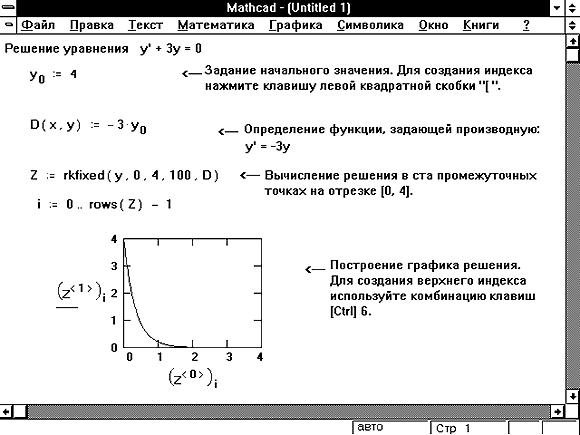
Дифференциальное уравнение первого порядка — это уравнение, которое не содержит производных выше первого порядка от неизвестной функции. На Рисунке 1 показан пример того, как решить относительно простое дифференциальное уравнение:
с начальными условиями: y(0) = 4
Функция rkfixed на Рисунке 1 использует для поиска решения метод Рунге-Кутты четвертого порядка. В результате решения получается матрица, имеющая два следующих столбца:
- Первый столбец содержит точки, в которых ищется решение дифференциального уравнения.
- Второй столбец содержит значения найденного решения в соответствующих точках.
Рисунок 1: Решение дифференциального уравнения первого порядка.
Функция rkfixed имеет следующие аргументы:
| y = | Вектор начальных условий размерности n, где n — порядок дифференциального уравнения или число уравнений в системе (если решается система уравнений). Для дифференциального уравнения первого порядка, как, например, для уравнения, приведенного на Рисунке 1, вектор начальных значений вырождается в одну точку y0 = y(x1). |
| x1, x2 = | Граничные точки интервала, на котором ищется решение дифференциальных уравнений. Начальные условия, заданные в векторе y, — это значение решения в точке x1. |
| npoints = | Число точек (не считая начальной точки), в которых ищется приближенное решение. При помощи этого аргумента определяется число строк (1 + npoints) в матрице, возвращаемой функцией rkfixed. |
| D (x, y) = | Функция, возвращающая значение в виде вектора из n элементов, содержащих первые производные неизвестных функций. |
Наиболее трудная часть решения дифференциального уравнения состоит в определении функции D(x, y), которая содержит вектор первых производных от неизвестных функций. В примере, приведенном на Рисунке 1, было достаточно просто разрешить уравнение относительно первой производной , и определить функцию D(x, y). Иногда, особенно в случае нелинейных дифференциальных уравнений, это может быть трудно. В таких случаях иногда удаётся разрешить уравнение относительно в символьном виде и подставить это решение в определение для функции D(x, y). Используйте для этого команду Решить относительно переменной из меню Символика.
Рисунок 2: Более сложный пример, содержащий нелинейное дифференциальное уравнение.
Дифференциальные уравнения второго порядка
Как только Вы научились решать дифференциальное уравнение первого порядка, можно приступать к решению дифференциальных уравнений более высокого порядка. Мы начнем с дифференциального уравнения второго порядка. Основные отличия от уравнения первого порядка состоят в следующем:
- Вектор начальных условий y теперь состоит из двух элементов: значений функции и её первой производной в начальной точке интервала x1.
- Функция D(t, y) является теперь вектором с двумя элементами:
Пример, приведенный на Рисунке 3, показывает, как решить следующее дифференциальное уравнение второго порядка:
Рисунок 3: Решение дифференциального уравнения второго порядка.
Уравнения более высокого порядка
Методика решения дифференциальных уравнений более высокого порядка является развитием методики, которая применялась для решения дифференциальных уравнений второго порядка. Основное различие состоит в следующем:
- Вектор начальных значений y теперь состоит из n элементов, определяющих начальные условия для искомой функции и ее производных y, y’ , y». y (n-1)
- Функция D является теперь вектором, содержащим n элементов:
Пример, приведенный на Рисунке 4, показывает, как решить следующее дифференциальное уравнение четвертого порядка:
с начальными условиями:
Рисунок 4: Решение дифференциального уравнения более высокого порядка.
Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter
28. Тема 7. Решение дифференциальных уравнений и систем в MathCad. Краткие теоретические сведения
Для решения дифференциальных уравнений с начальными условиями система Mathcad имеет ряд встроенных функций:
Rkfixed – функция для решения ОДУ и систем ОДУ методом Рунге–Кутта четвертого порядка с постоянным шагом;
Rkadapt – функция решения ОДУ и систем ОДУ методом Рунге–Кутта с переменным шагом;
Odesolve – функция, решающая ОДУ блочным методом.
Ниже приведено описание стандартной функции Rkfixed с указанием параметров функции.
Y – вектор начальных условий из K элементов (k – количество уравнений в системе);
X1 и X2 – левая и правая границы интервала, на котором ищется решение ОДУ или системы ОДУ;
P – число точек внутри интервала (x1, x2), в которых ищется решение;
D – вектор, состоящий из K-Элементов, который содержит первую производную искомой функции или первые производные искомых функций, если речь идет о решении системы.
Результатом работы функции является матрица из p+1 строк, первый столбец которой содержит точки, в которых получено решение, а остальные столбцы – сами решения.
На рисунке 2.7.1 приведены конкретные примеры решения различных дифференциальных уравнений и систем ОДУ в MathCAD.
При решении дифференциального уравнения первого порядка нужно создать вектор начальных условий из одного элемента Y1, который затем используется при формировании вектора-функции правой части дифференциального уравнения. При обращении к функции Rkfixed Указывается имя вектора Y, границы интервала, на котором ищется решение уравнения, например, (0 ; 2), количество точек, в которых ищется решение – 100, вектор-функция, описывающая правую часть дифференциального уравнения – D. В результате получается матрица Z, в первом столбце которой содержатся значения аргумента искомой функции, во втором – значения самой результирующей функции. При построении графика функции первый столбец полученной матрицы указывается как аргумент, второй столбец – как функция.
При решении системы дифференциальных уравнений нужно создать вектор начальных условий из двух элементов, например, вектор V, который затем используется при формировании вектора-функции правой части дифференциального уравнения. При обращении к функции Rkfixed Указывается имя вектора V, и границы интервала, на котором ищется решение уравнения, например, (0 ; 5), количество точек, в которых ищется решение – 100, вектор-функция, описывающая правую часть дифференциального уравнения – D. В результате получается матрица S, в первом столбце которой содержатся значения аргумента искомых функций, во втором и третьем столбцах – значения самих функций при соответствующем значении аргумента. При построении графика можно воспользоваться первым столбцом полученной матрицы как аргументом, а вторым и третьим столбцами – как функциями.
На рисунке 2.7.2 приведен пример решения дифференциального уравнения второго порядка с использованием функции Rkfixed. Необходимо решить дифференциальное уравнение второго порядка с заданными начальными условиями вида:
Рисунок 2.7.2 – Пример решения дифференциальных уравнений второго порядка с помощью Rkfixed
Для решения уравнения с помощью функции Rkfixed нужно выполнить замену переменных и привести дифференциальное уравнение второго порядка к двум дифференциальным уравнениям первого порядка. Вид этих уравнений приведен ниже.
Документ формируется точно так же, как и при решении системы ОДУ.
На рисунке 2.7.2 показана возможность вычисления вектора второй производной найденной функции – вектора А, построены графики исходной функции, функций первой и второй производных.
источники:
http://old.exponenta.ru/soft/MathCAD/usersguide/chapter16/16_1.asp
http://matica.org.ua/metodichki-i-knigi-po-matematike/reshenie-zadach-v-srede-mathcad/28-tema-7-reshenie-differentcialnykh-uravnenii-i-sistem-v-mathcad-kratkie-teoreticheskie-svedeniia
Для решения дифференциальных уравнений с начальными условиями система Mathcad имеет ряд встроенных функций:
Rkfixed – функция для решения ОДУ и систем ОДУ методом Рунге–Кутта четвертого порядка с постоянным шагом;
Rkadapt – функция решения ОДУ и систем ОДУ методом Рунге–Кутта с переменным шагом;
Odesolve – функция, решающая ОДУ блочным методом.
Ниже приведено описание стандартной функции Rkfixed с указанием параметров функции.
Rkfixed(y, x1, x2, p, D)
Аргументы функции:
Y – вектор начальных условий из K элементов (k – количество уравнений в системе);
X1 и X2 – левая и правая границы интервала, на котором ищется решение ОДУ или системы ОДУ;
P – число точек внутри интервала (x1, x2), в которых ищется решение;
D – вектор, состоящий из K-Элементов, который содержит первую производную искомой функции или первые производные искомых функций, если речь идет о решении системы.
Результатом работы функции является матрица из p+1 строк, первый столбец которой содержит точки, в которых получено решение, а остальные столбцы – сами решения.
На рисунке 2.7.1 приведены конкретные примеры решения различных дифференциальных уравнений и систем ОДУ в MathCAD.
При решении дифференциального уравнения первого порядка нужно создать вектор начальных условий из одного элемента Y1, который затем используется при формировании вектора-функции правой части дифференциального уравнения. При обращении к функции Rkfixed Указывается имя вектора Y, границы интервала, на котором ищется решение уравнения, например, (0 ; 2), количество точек, в которых ищется решение – 100, вектор-функция, описывающая правую часть дифференциального уравнения – D. В результате получается матрица Z, в первом столбце которой содержатся значения аргумента искомой функции, во втором – значения самой результирующей функции. При построении графика функции первый столбец полученной матрицы указывается как аргумент, второй столбец – как функция.
При решении системы дифференциальных уравнений нужно создать вектор начальных условий из двух элементов, например, вектор V, который затем используется при формировании вектора-функции правой части дифференциального уравнения. При обращении к функции Rkfixed Указывается имя вектора V, и границы интервала, на котором ищется решение уравнения, например, (0 ; 5), количество точек, в которых ищется решение – 100, вектор-функция, описывающая правую часть дифференциального уравнения – D. В результате получается матрица S, в первом столбце которой содержатся значения аргумента искомых функций, во втором и третьем столбцах – значения самих функций при соответствующем значении аргумента. При построении графика можно воспользоваться первым столбцом полученной матрицы как аргументом, а вторым и третьим столбцами – как функциями.
На рисунке 2.7.2 приведен пример решения дифференциального уравнения второго порядка с использованием функции Rkfixed. Необходимо решить дифференциальное уравнение второго порядка с заданными начальными условиями вида:
Рисунок 2.7.2 – Пример решения дифференциальных уравнений второго порядка с помощью Rkfixed
Для решения уравнения с помощью функции Rkfixed нужно выполнить замену переменных и привести дифференциальное уравнение второго порядка к двум дифференциальным уравнениям первого порядка. Вид этих уравнений приведен ниже.
Документ формируется точно так же, как и при решении системы ОДУ.
На рисунке 2.7.2 показана возможность вычисления вектора второй производной найденной функции – вектора А, построены графики исходной функции, функций первой и второй производных.
| < Предыдущая | Следующая > |
|---|
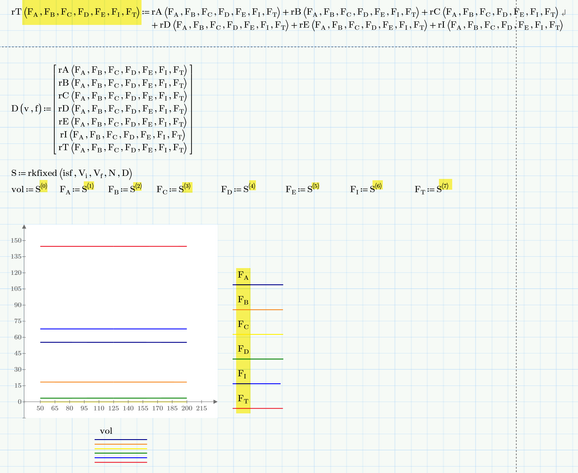
The first error is that you forgot the function arguments when you defined rt. That way you defined a simple variable, not a function (thats what the error message tries to tell us).
The second error is that you tried to access the columns of S by typing S^(0), etc. You have to use the column selector (either from the menu or by typing Ctrl-Shift-C).
A third problem occurred due to Prime infamous auto labelling. I had to manually label the highlighted variables in the plot to be «variable».