Рассчитать ошибку прямого измерения - TopOshibok.ru - решение и исправление самых разных ошибок

Если проведение
неоднократных измерений физической
величины даёт повторяющиеся результаты,
то это означает, что в данных условиях
преобладают приборные погрешности. В
этих случаях погрешность прямых измерений
определяется приборной погрешностью.

Если неоднократные
измерения дают некоторый разброс
результатов, то это означает присутствие
случайных ошибок. Если число измерений
неограниченно возрастает, то для
определения среднего значения и дисперсии
можно воспользоваться формулами (3) …
(7). На практике число измерений всегда
ограничено, поэтому существует
конечная вероятность того, что истинное
значение среднеквадратичного
отклонения отличается от вычисленного
по формуле (6). Поэтому при небольшом
числе измерений для оценки величины 

пользуются
соотношениями, вытекающими из так
называемого распределения Стьюдента,
которое при неограниченном увеличении
числа измерений стремится к нормальному
распределению (5).

В соответствии с
этой методикой сначала находится
среднеарифметическое значение измеряемой
величины по формуле (3).

Следующим шагом
для оценки точности найденного
среднеарифметического значения будет
вычисление вспомогательной величины
S:

(9)

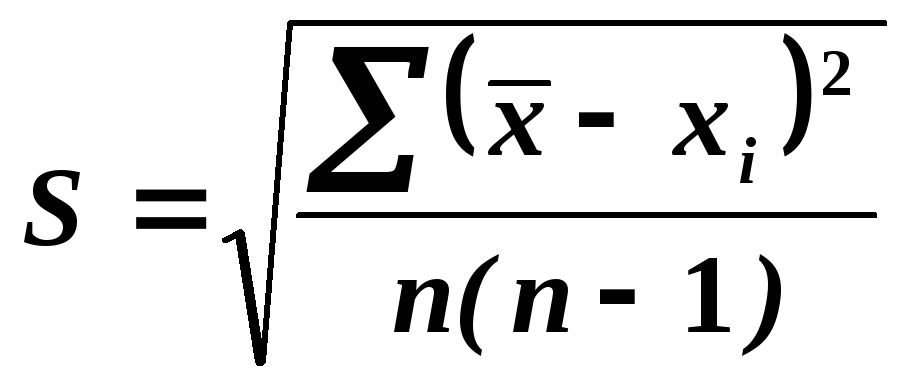
Из Таблицы 1
коэффициентов Стьюдента находим
вспомогательный коэффициент ,
зависящий от числа измерений n и
доверительной вероятности Р. Этот
коэффициент совместно с величиной S
позволяет рассчитать доверительный
интервал x.

Абсолютная
погрешность значения искомой величины
«а», найденной как среднеарифметическое
из n измерений составит:

(10)

Искомая величина
«а» представляется в виде:

(11)

Дисперсия всей
совокупности измерений случайной
величины «х»
будет равна S².

7. Расчёт ошибок косвенных измерений

Пусть искомая
величина А
при выбранном
методе косвенных измерений рассчитывается
по формуле:

A
= f(x₁
,x₂
,x₃
,…,x_n
) (12)

где x₁,x₂,…,x_n
— величины, найденные в результате прямых
измерений, с учётом ошибок о которых
шла речь выше. Из-за этих ошибок величина
«А»
так же будет определяться с ошибками.

Пусть X₁,X₂,…,X_N
— значения f(x₁
,x₂
,x₃
,…,x_n
), вычисленные
для разных серий измерений (x₁,x₂,…,x_n).

Таблица 1

Таблица коэффициентов
Стьюдента

Число измерений	Доверительная вероятность
0.7	0.8	0.9	0.95	0.99	0.999
2	2.0	3.1	6.3	12.7	63.7	636.6
3	1.3	1.9	2.9	4.3	9.9	31.6
4	1.3	1.6	2.4	3.2	5.8	12.9
5	1.2	1.5	2.1	2.8	4.6	8.6
10	1.1	1.4	1.8	2.3	3.3	4.8
15	1.1	1.3	1.8	2.1	3.0	4.1
20	1.1	1.3	1.7	2.1	2.9	3.9

Абсолютной ошибкой
косвенных измерений, по аналогии с
абсолютной ошибкой прямых измерений,
называют разность между истинным
значением «А» и её значениями,
полученными в результате измерений:

(13)

Размерность
абсолютной ошибки совпадает с размерностью
определяемой величины. Относительной
ошибкой косвенных измерений называют
отвлечённое число:

(14)

Иногда относительную
ошибку выражают в процентах:

(15)

Для определения
величины «А» в формулах (12)…(15) по
теории

вероятностей
следует брать величину Х, которую можно
определить двумя способами:

1) А
= Х
= (Х₁
+ Х₂
+…+Х_n)/n
(16)

2) A
= X
= f(x₁
+ x₂
+…+x_n)
(17)

где x₁,
x₂
,…, x_n
определяют по формуле (3). Если ошибки
измерений малы, то оба способа дают
практически тождественные результаты.

Рассмотрим способы
нахождения ошибки величины А,
определённой из косвенных измерений,
по найденным значениям оши

бок прямых измерений.
Выше отмечалось, что возможны различные
соотношения между приборной систематической
и случайными ошибками.

1-й случай. Преобладают
приборные ошибки. В этом случае можно
дать только оценку максимальной ошибки.
Формулы для нахождения предельной
ошибки косвенных измерений по внешнему
виду совпадают с формулами дифференциального
исчисления. В связи с этим для предельной
абсолютной ошибки используется формула:

(18)

а для расчёта
предельной относительной ошибки пригодна
фор

— 19 —

мула:

(19)

Формулы для расчёта
предельных ошибок некоторых часто
встречающихся функций, когда приборные
ошибки превышают случайные, приведены
в Таблице 2. Эти выражения легко
рассчитываются по формулам (18) и (19).

2-й случай. Преобладают
случайные ошибки. Для определения
среднеквадратичной ошибки теория
вероятностей даёт следующую формулу:

(20)

Относительная
ошибка вычисляется по формуле:

(21)

При выполнении
промежуточных расчётов необходимо
помнить, что число точных цифр в результате
расчётов не может увеличиваться. Поэтому
промежуточные результаты округляют,
сохраняя

1…2 избыточных
знака. При этом последующие цифры,
меньшие

5,отбрасываются;если
первая из отбрасываемых цифр больше 5,

то последняя из
оставшихся цифр увеличивается на
единицу. Ес

ли первая
отбрасываемая цифра 5, то предыдущая
цифра остаётся

без изменений,
если она чётная, и увеличивается на
единицу, если

она нечётная.
Выражения для среднеквадратичной ошибки
некоторых часто встречающихся функций
приведены в Таблице 3. Для определения
ошибок косвенных измерений используют
большую из инструментальной или случайной
ошибок прямого измерения.

Соседние файлы в папке TIU-11

Источник

Измеряя линейные размеры предметов измерительными инструментами : линейкой, штангенциркулем, микрометром, проводя измерения времени секундомером или силы электрического тока или величины напряжения соответствующими электроизмерительными приборами Вы проводите прямые измерения.

Погрешность измерений

Любое измерение проводится с определенной точностью, при этом измеренное значение всегда отличается от истинного, так как инструменты измерения, методики и органы чувств человека несовершенны. Поэтому важную роль играет оценка погрешности измерений, результат измерений с учетом погрешности записывается в виде: X ± ΔX, где ΔX — абсолютная погрешность измерений.

Случайные и систематические погрешности

Погрешности подразделяются на случайные и систематические.
Систематические погрешности остаются постоянными или закономерно меняются в процессе измерения. Например неточность прибора, неправильная его регулировка ведет к систематической погрешности. Если причина систематической погрешности известна, то чаще всего такую погрешность можно исключить.
Случайные погрешности вызваны различными случайными факторами, влияющими на точность измерений. Например, при измерении секундомером отрезков времени, случайные погрешности связаны с различным (случайным) временем реакции экспериментатора на события запускающие и останавливающие секундомер. Чтобы уменьшить влияние случайной погрешности необходимо проводить многократное измерение физической величины.
Калькулятор ниже вычисляет случайную погрешность выборки прямых измерений для заданного доверительного интервала. Немного теории можно найти сразу за калькулятором.

Расчет погрешностей непосредственных измерений.

Доверительная вероятность

Точность вычисления

Знаков после запятой: 3

Относительная погрешность в %

В большинстве случаев результат измерения подчиняется нормальному закону распределения, поэтому истинное значение измерения будет равно пределу:
$x_0=\lim_{n \to \infty} \frac{1}{n}\sum_{i=1}^{n} x_i$
В случае ограниченного количества измерений, наиболее близким к истинному будет среднее арифметическое:
$\bar{x}=\frac{1}{n}\sum_{i=1}^{n} x_i$

Согласно элементарной теории ошибок Гаусса случайную погрешность отдельного измерения характеризует так называемое среднеквадратическое отклонение:
$S_n=\left. \sqrt{\frac{\sum_{i=1}^{n}{(x_i-\bar{x})^2}}{n-1}} \right$ , квадрат этой величины называется дисперсией. При увеличении этой величины возрастает разброс результатов измерений, т. е. увеличивается погрешность.

Для оценки погрешности всей серии измерений, вместо отдельного измерения надо найти среднюю квадратичную погрешность среднего арифметического, характеризующую отклонение $\bar{x}$ от истинного значения искомой величины x_0 .
По закону сложения ошибок среднее арифметическое имеет меньшую ошибку, чем результат каждого отдельного измерения. Cредняя квадратичная погрешность среднего арифметического равна:
$S_{\bar{x}}=\frac{S_n}{\sqrt{n}} = \left. \sqrt{\frac{\sum_{i=1}^{n}{(x_i-\bar{x})^2}}{{n}({n-1})}} \right$
Стандартная случайная погрешность Δх равна:
$\Delta_{x}=t_{\alpha,k}S_{\bar{x}},$ , где $t_{\alpha,k}$ — коэффициент Стьюдента для заданной доверительной вероятности $\alpha$ и числа степеней свободы k = n-1.
Коэффициент Стьюдента можно получить по таблице или воспользоваться нашим калькулятором для вычисления квантилей распределения Стьюдента: Квантильная функция распределения Стьюдента. Следует иметь в виду, что квантильная функция выдает значения одностороннего критерия Стьюдента. Значение двустороннего квантиля для заданной доверительно вероятности $\alpha$ соответствует значению одностороннего квантиля для вероятности: $1-\frac{1-\alpha}{2}$

Источник

Оценка погрешности прямых измерений

Следующий калькулятор может вычислить погрешность прямых измерений для заданной вами выборки и доверительного интервала.

Нас часто окружают прямые измерения: мы меряем линейкой, метром, микрометром, штангенциркулем, бывает измеряем силу электрического тока, напряжение и так далее.

Погрешность измерений

Все измерения делаются с определенной точностью, но часто значение, которое мы получаем при измерении, отличается от эталонного, мы полагаемся на свои чувства, а также на измерительные приборы, но ни те ни другие не совершенны. Именно по этому вычисление погрешности измерений несет особую роль в измерениях.

Результат измерений + учет погрешности можно записать как:

X ± ΔX,

где ΔX — абсолютная погрешность измерений.

Погрешности есть 2-х типов: случайные и постоянные (систематические).

К систематическим погрешностям можно отнести: неточность самого измерительного прибора.

К случайным погрешностям можно отнести: человеческий фактор при нажатии на секундомер например (можно нажать чуть раньше или позже). Чтобы уменьшить процент влияния такого рода фактора нужно испытание проводить много раз и считать среднее значение.

Следующий калькулятор может вычислить случайную погрешность выборки прямых измерений для заданного вами интервала.

Расчет погрешностей непосредственных измерений.

Доверительная вероятность:

Относительная погрешность в %:

15 декабря 2015
Статистика

Источник

Прямыми измерениями называются непосредственные измерения какой-либо физической величины с использованием прибора. Например, прямыми являются измерения
длины, массы, температуры. Измерение плотности, т.е. вычисление плотности по измеренным массе и объему тела, являются косвенными измерениями.

Абсолютная погрешность физической величины ΔА — это разница между точным
значением физической величины и ее приближенным значением и измеряется в тех же единицах, что и сама величина:

ΔА = А — А_пр .

Так как мы никогда не знаем точного значения величины А, а лишь определяем
из опыта ее приближенное значение, то и величину абсолютной погрешности мы можем определить лишь приблизительно. Наиболее просто находится максимальная величина абсолютной погрешности,
которая и используется нами в лабораторных работах.

Погрешность измерений может иметь различную природу. Рассмотрим два вида погрешностей, с которыми мы встречаемся в ходе лабораторных работ.

1. Инструментальная погрешность(Δ_и) – погрешность прибора, задаваемая при его изготовлении.

Рассмотрите таблицу инструментальных погрешностей приборов, с которыми вы встречаетесь на лабораторных работах.

2. Погрешность отсчета (Δо) – погрешность, возникающая при снятии
показаний прибора, равна половине интервала округления.

Интервал округления (ИО) – интервал, задающий точность снятия показаний. При измерениях за интервал округления обычно принимают цену деления шкалы. Тогда погрешность отсчета
равна половине цены деления шкалы. При получении результата прямых измерений инструментальная погрешность и погрешность отсчета складываются:

Δℓ = Δиℓ +Δоℓ

«Правило ничтожных погрешностей»

при суммировании погрешностей любым из слагаемых можно пренебречь, если оно не превосходит ⅓ – ⅟4 от другого.

Поэтому при достаточно точном снятии показаний прибора (малом Δоℓ) погрешностью отсчета можно пренебречь. И наоборот, если условия измерения таковы, что точно снять показания затруднительно
(например, указатель имеет большую толщину), инструментальной погрешностью пренебрегают по сравнению с погрешностью отсчета.

3. Запись результата с указанием погрешности.

Абсолютная погрешность измерений обычно округляется до 1 значащей цифры, а, если эта цифра 1, то до двух.

Пример:

Результат записывается в виде:

А = А_изм ± ΔА, например: ℓ = (13 ± 2) мм.

При этом в измеренном значении следует оставлять столько десятичных знаков, сколько их в значении
погрешности (последняя цифра погрешности «поправляет» последнюю цифру измеренного значения). Значение величины и погрешность следует
выражать в одних и тех же единицах!

Пример:

Если единственная цифра в значении погрешности 1, но следует оставить две значащие цифры.

Пример:

Источник

7. Расчёт ошибок косвенных измерений

Погрешность измерений

Случайные и систематичес­кие погрешности

Расчет погрешностей непосредственных измерений.

Оценка погрешности прямых измерений

Интересное по теме:

Случайные и систематические погрешности