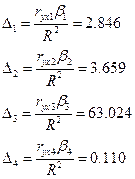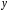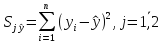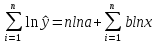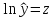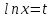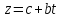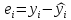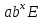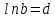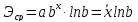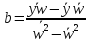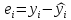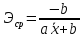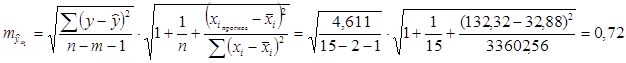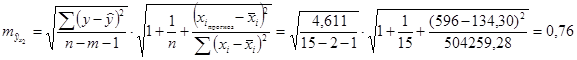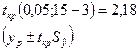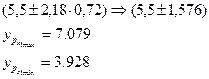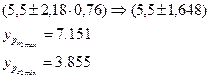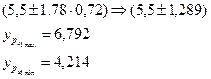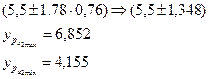Имеются данные о деятельности
крупнейших компаний США в 1996
г. (табл. 1).
Таблица 1
|
п/n |
Чистый |
Оборот капитала, млрд. долл. США |
Использованный |
Численность служащих, тыс. чел. |
Рыночная капитализация компании, млрд. долл. США |
|
Y |
X1 |
X2 |
X3 |
X4 |
|
|
1 |
0,9 |
31,3 |
18,9 |
43,0 |
40,9 |
|
2 |
1,7 |
13,4 |
13,7 |
64,7 |
40,5 |
…………………………………………………………………..
|
25 |
0,7 |
15,5 |
5,8 |
80,8 |
27,2 |
Задание
1.
Рассчитайте
матрицу парных коэффициентов корреляции; оцените статистическую значимость коэффициентов
корреляции.
2.
Рассчитайте
параметры линейного уравнения множественной регрессии с полным перечнем
факторов.
3.
Оцените
статистическую значимость параметров регрессионной модели с помощью t-критерия; нулевую гипотезу о
значимости уравнения проверьте с помощью F-критерия; оцените качество
уравнения регрессии с помощью
коэффициента детерминации .
4.
Дайте
сравнительную оценку силы связи факторов с результатом с помощью коэффициентов
эластичности, и
коэффициентов.
5.
Оцените
точность уравнения через среднюю относительную ошибку аппроксимации.
6.
Отберите
информативные факторы в модель по t-критерию для коэффициентов
регрессии. Постройте модель только с
информативными факторами и оцените ее параметры.
7.
Рассчитайте
прогнозное значение результата, если прогнозные значения факторов составляют
80% от их максимальных значений.
8.
Рассчитайте
ошибки и доверительный интервал прогноза для уровня значимости 5 или 10% (а =
0,05; а = 0,10).
1.Использование
инструмента Корреляция (Анализ
данных в EXCEL).
Для проведения корреляционного анализа выполните
следующие действия:
·
Данные для корреляционного анализа должны
располагаться в смежных диапазонах ячеек.
·
Выберите команду СервисÞАнализ данных.
·
В диалоговом окне Анализ данных выберите
инструмент Корреляция, а затем
щелкните на кнопке ОК.
·
В диалоговом окне Корреляця в поле Входной интервал необходимо ввести диапазон ячеек,
содержащих исходные данные (выбираем $B$7:$F$32). Если выделены и заголовки
столбцов, то установить флажок Метки в первой строке.
·
Выберите параметры вывода.
·
ОК.
Рис.1 Диалоговое окно Корреляция
Таблица 1.
Результат корреляционного анализа.
|
Чистый доход, Y |
Оборот капитала, X1 |
Использо-ванный капитал, X2 |
Числен-ность служа-щих, X3 |
Рыночная капитализация компании, X4 |
|
|
Чистый до-ход, Y |
1 |
||||
|
Оборот капитала, X1 |
0,848 |
1 |
|||
|
Использованный капитал, X2 |
0,763 |
0,898 |
1 |
||
|
Численность служащих, X3 |
0,830 |
0,912 |
0,713 |
1 |
|
|
Рыночная капитализация компании, |
0,269 |
0,249 |
0,348 |
0,115 |
1 |
Анализ матрицы
коэффициентов парной корреляции показывает, что зависимая переменная У имеет
тесную связь с Х1 (ryx1=0,848), с Х2 (ryx2=0.763), X3 (ryx3=0.830). Однако факторы X3 и X1 тесно связаны между собой (rx1x3=0.912), что
свидетельствует о наличие мультиколлинеарности.
ryxi>rxixk r yx1>r x1x3
r yx1>r x1x2
ryxk>rxixk 0,848>0,912 не верно 0,848>0,898 не верно
rxixk<0,8 r yx3> r x1x3
r yx2>r x1x2
0,830>0,912 не верно 0,763>0,898 не верно
r x1x3<0,8 r x1x2 <0,8
0,912<0,8 не верно 0,898<0,8 не верно
Если приведенные неравенства (или хотя бы одно из них) не
выполняются, то в модель включают тот фактор, который наиболее тесно связан с
У.
Оценим
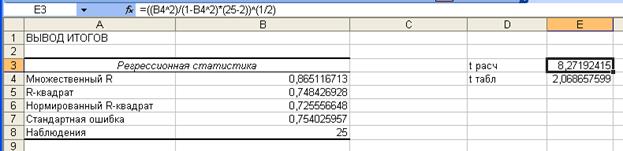
значимость коэффициента корреляции. Для этого рассчитаем значение t-статистики по формуле
t расч = (r2/(1-r2)(n-2))/^(1/2)
Рис.2 Фрагмент рабочего листа Excel
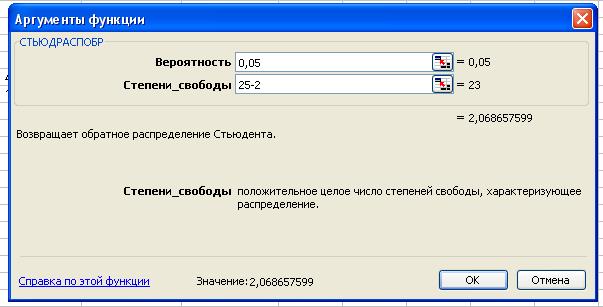
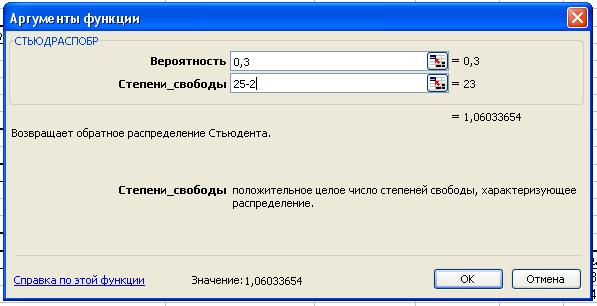
Табличное значение критерия Стьюдента можно найти с
помощью функции СТЬЮДРАСПОБР: t табл(уровень
значимости равен 0,05; число степеней свободы k=25-2) = 2,068.
Рис.3 Фрагмент рабочего листа Excel
Сравнивая числовые значения критериев, видно, что
t расч> t табл , т.е. полученное значение коэффициента
корреляции значимо.
2.
Для проведения регрессионного анализа выполните
следующие действия:
·
Выберите команду СервисÞАнализ данных.
·
В диалоговом окне Анализ данных выберите
инструмент Регрессия, а затем
щелкните на кнопке ОК
·
В диалоговом окне Регрессия в поле Входной интервал Y введите адрес
одного диапазона ячеек, который
представляет зависимую переменную ($B$7:$B$32). В поле Входной
интервал Х введите адреса одного или нескольких диапазонов, которые
содержат значения независимых переменных ($C$7:$F$32) (Рисунок 1.).
·
Если выделены и заголовки столбцов, то установить
флажок Метки
в первой строке.
·
Выберите параметры вывода. В данном примере Новая
рабочая книга
·
В поле Остатки поставьте необходимые
флажки.
·
ОК.
Рисунок
4. Диалоговое окно Регрессия подготовлено
к выполнению анализа данных.
Результат регрессионного анализа содержится в таблицах 1
–3. Рассмотрим содержание этих таблиц.
|
Регрессионная |
|
|
Множественный |
0,869743924 |
|
R-квадрат |
0,756454493 |
|
Нормированный |
0,707745392 |
|
Стандартная |
0,77810933 |
|
Наблюдения |
25 |
|
Дисперсионный |
|||||
|
df |
SS |
MS |
F |
Значимость F |
|
|
Регрессия |
4 |
37,6109174 |
9,402729351 |
15,53004412 |
6,2879E-06 |
|
Остаток |
20 |
12,1090826 |
0,60545413 |
||
|
Итого |
24 |
49,72 |
|
Коэффициенты |
Стандартная |
t-статистика |
|
|
Y-пересечение |
-0,362521945 |
1,191933731 |
-0,304146057 |
|
Оборот |
0,003502997 |
0,019577778 |
0,178927183 |
|
Использо-ванный |
0,017414898 |
0,021687383 |
0,802996741 |
|
Числен-ность |
0,005335038 |
0,003215755 |
1,659031404 |
|
Рыночная |
0,02862124 |
0,036582896 |
0,782366704 |
|
ВЫВОД |
||
|
Наблюдение |
Предсказанное |
Остатки |
|
1 |
1,476278764 |
-0,576278764 |
|
2 |
1,427339482 |
0,272660518 |
|
3 |
1,216824293 |
-0,516824293 |
|
4 |
1,125836172 |
0,574163828 |
|
5 |
1,720269033 |
0,879730967 |
|
6 |
1,064856936 |
0,235143064 |
|
7 |
4,752057832 |
-0,652057832 |
|
8 |
1,560162019 |
0,039837981 |
|
9 |
6,285770796 |
0,614229204 |
|
10 |
0,701068329 |
-0,301068329 |
|
11 |
0,953926401 |
0,346073599 |
|
12 |
1,291100351 |
0,608899649 |
|
13 |
0,993876693 |
0,906123307 |
|
14 |
1,969626222 |
-0,569626222 |
|
15 |
1,414341773 |
-1,014341773 |
|
16 |
0,814491677 |
-0,014491677 |
|
17 |
1,588975843 |
0,211024157 |
|
18 |
1,166154601 |
-0,266154601 |
|
19 |
1,43458937 |
-0,33458937 |
|
20 |
1,044173477 |
0,855826523 |
|
21 |
1,274936197 |
-2,174936197 |
|
22 |
1,04746402 |
0,25253598 |
|
23 |
1,066479099 |
0,933520901 |
|
24 |
0,607050917 |
-0,007050917 |
|
25 |
1,002349703 |
-0,302349703 |
Уравнение
регрессии можно записать в следующем
виде:
y = -0,362 + 0,003х1 + 0.017x2 +0.005х3
+ 0,028х4
3. Оценим статистическую значимость
параметров регрессионной модели с помощью t-критерия:
Значимость
коэффициентов уравнения регрессии оценим с использованием t-критерия Стьюдента.
ta0 = -0,304
ta1 = 0,1789
ta2 = 0,8029
ta3 = 1,659
ta4 = 0,7823
Расчетные значения
t-критерия Стьюдента для коэффициентов уравнения регрессии приведены в
четвертом столбце таблицы 7 протокола EXCEL.
Табличное значение t-критерия Стьюдента можно найти с помощью функции СТЬЮДРАСПОБР
Табличное значение
t-критерия при 5% уровне значимости и степенях свободы (25-4-1=20) составляет 2.08
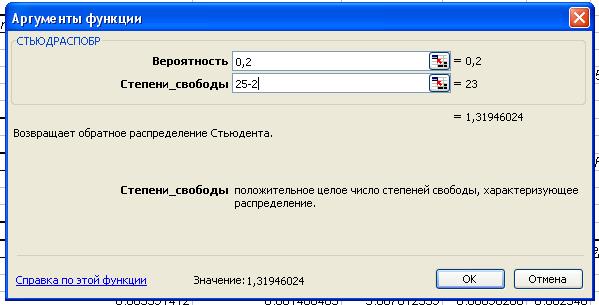
При α=0,2
табличное значение t-критерия составляет 1,32.
При α=0,3 табличное
значение t-критерия составляет 1,06.
Значим только Х3.
Рис.5
Рис.6
Проверим нулевую гипотезу о значимости
уравнения проверим с помощью F-критерия:
Значение
F-критерия Фишера можно найти в таблице 6
протокола EXCEL.
Табличное значение
F-критерия при доверительной вероятности 0,95 при = k =4 и
=n – k -1= 25 – 4 — 1=20 составляет 2.86. Табличное значение
F-критерия можно найти с помощью функции FРАСПОБР
Поскольку F=
15,53004412>F, уравнение регрессии следует признать адекватным.
Оценим качество уравнения регрессии с помощью коэффициента детерминации
Значение коэффициентов детерминации и множественной
корреляции можно найти в таблице Регрессионная
статистика.
Коэффициент детерминации:
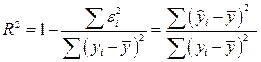
0,756454493
Он показывает долю
вариации результативного признака под воздействием изучаемых факторов.
Следовательно, около 75% вариации зависимой переменной учтено в модели и обусловлено
влиянием включенных факторов.
Чем ближе R2 к 1, тем выше качество
модели.
Коэффициент множественной корреляции R:
= 0,869743924.
Он показывает тесноту
связи (связь тесная) зависимой переменной Y с включенными в модель
объясняющими факторами.
4.
Дайте сравнительную оценку силы связи факторов с
результатом с помощью коэффициентов эластичности, и
коэффициентов.
Проанализируем влияние факторов на зависимую
переменную по модели.
Учитывая, что
коэффициент регрессии невозможно использовать для непосредственной оценки
влияния факторов на зависимую переменную из-за различия единиц измерения,
используем коэффициент эластичности
(Э):
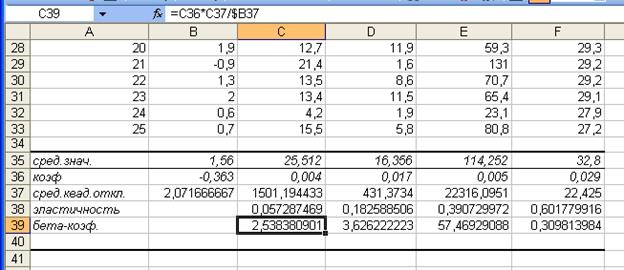
Рис.7 Лист Excel
0.004´25.512/1.56=0.057
0,017´16.356/1.56=0.183
0.005´114.252/1.56=0,391
0.029´32.8/1.56=0,602
Коэффициент
эластичности показывает, на сколько процентов изменяется зависимая переменная
при изменении фактора на один процент. Видим, что при изменении фактора рыночная
капитализация на 1 процент чистый доход
измениться на 60,2%.
Рассчитаем
бета-коэффициенты:
Рис.8 Расчет в Excel β
2,538
3,626
57,469
0,310
При неизменном уровне
остальных признаков увеличение оборотов капитала на величину
среднеквадратического отклонения увеличим чистый доход на на 2,538 ее
среднеквадратического отклонения.
При неизменном уровне остальных
признаков увеличение использ. капитала на величину среднеквадратического
отклонения увеличим чистый доход на 3,626 ее среднеквадратического отклонения.
При неизменном уровне
остальных признаков увеличение числен служащих на величину среднеквадратического
отклонения увеличим чистый доход на на 57,469 ее среднеквадратического
отклонения.
При неизменном уровне
остальных признаков увеличение рыночной капитализации компании на величину
среднеквадратического отклонения увеличим чистый доход на 0,310 ее среднеквадратического
отклонения.
Вычислим -коэффициенты:
Доля влияния
оборотного капитала в суммарном
влиянии всех факторов составляет
2,846%, а доля влияния использ капитала -3,659%, числ служащих -63,024%, рыночн
капитализация компании – 0,11%.
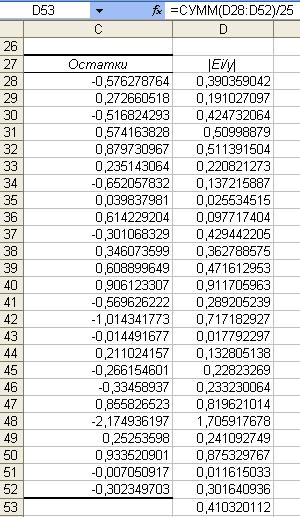
5. Оцените точность уравнения через
среднюю относительную ошибку аппроксимации.
Определим среднюю относительную ошибку:
|
|Ei/y| |
|
0,390359042 |
|
0,191027097 |
|
0,424732064 |
|
0,50998879 |
|
0,511391504 |
|
0,220821273 |
|
0,137215887 |
|
0,025534515 |
|
0,097717404 |
|
0,429442205 |
|
0,362788575 |
|
0,471612953 |
|
0,911705963 |
|
0,289205239 |
|
0,717182927 |
|
0,017792297 |
|
0,132805138 |
|
0,22823269 |
|
0,233230064 |
|
0,819621014 |
|
1,705917678 |
|
0,241092749 |
|
0,875329767 |
|
0,011615033 |
|
0,301640936 |
|
0,410320112 |
Рис.9 Рабочий лист Excel
Рис.10 Расчет в Excel
Еотн =1/n*∑|
yi – ŷi / yi |*100% = 1/n∑ | εi
/ yi |*100% = 41%
Ошибка
аппроксимации меньше 7% свидетельствует о хорошем качестве модели.
В среднем расчетные значения у для линейной модели отличаются
от фактических значений на 41%
6. Отберите информативные факторы в
модель по t-критерию для коэффициентов
регрессии. Постройте модель только с
информативными факторами и оцените ее параметры.
В модель отбираем X3
Рис.11 Диалоговое окно Регрессия
|
Регрессионная |
|||
|
Множественный |
0,82956794 |
||
|
R-квадрат |
0,688182968 |
||
|
Нормированный |
0,674625705 |
||
|
Стандартная |
0,821015883 |
||
|
Наблюдения |
25 |
||
|
Дисперсионный |
|||
|
df |
SS |
MS |
|
|
Регрессия |
1 |
34,21645715 |
34,21645715 |
|
Остаток |
23 |
15,50354285 |
0,674067081 |
|
Итого |
24 |
49,72 |
|
|
Коэффициенты |
Стандартная |
t-статистика |
|
|
Y-пересечение |
0,646798516 |
0,208305812 |
3,105043066 |
|
X3 |
0,007992871 |
0,001121855 |
7,124689806 |
|
ВЫВОД |
|||
|
Наблюдение |
Предсказанное Y |
Остатки |
|
|
1 |
0,990491964 |
-0,090491964 |
|
|
2 |
1,163937262 |
0,536062738 |
|
|
3 |
0,838627417 |
-0,138627417 |
|
|
4 |
1,048040634 |
0,651959366 |
|
|
5 |
1,49404283 |
1,10595717 |
|
|
6 |
1,418909843 |
-0,118909843 |
|
|
7 |
3,420324711 |
0,679675289 |
|
|
8 |
1,330988264 |
0,269011736 |
|
|
9 |
6,601487321 |
0,298512679 |
|
|
10 |
0,679569287 |
-0,279569287 |
|
|
11 |
0,861007456 |
0,438992544 |
|
|
12 |
0,988094103 |
0,911905897 |
|
|
13 |
1,140757937 |
0,759242063 |
|
|
14 |
2,341287143 |
-0,941287143 |
|
|
15 |
1,486049959 |
-1,086049959 |
|
|
16 |
0,914559691 |
-0,114559691 |
|
|
17 |
1,781786181 |
0,018213819 |
|
|
18 |
1,414114121 |
-0,514114121 |
|
|
19 |
1,765800439 |
-0,665800439 |
|
|
20 |
1,120775759 |
0,779224241 |
|
|
21 |
1,693864601 |
-2,593864601 |
|
|
22 |
1,211894487 |
0,088105513 |
|
|
23 |
1,169532272 |
0,830467728 |
|
|
24 |
0,831433834 |
-0,231433834 |
|
|
25 |
1,292622483 |
-0,592622483 |
7. Рассчитайте прогнозное значение
результата, если прогнозные значения факторов составляют 80% от их максимальных
значений.
x3=596
Y= y=0,6467+0,0079*596= 5,3551
8. Рассчитайте ошибки и доверительный
интервал прогноза для уровня значимости 5 или 10% (а = 0,05; а = 0,10).
Доверительный интервал
прогноза будет иметь следующие границы:
Верхняя граница прогноза: Yпр+U(1)
Нижняя граница прогноза Yпр— U(1)
Se= 0,754
Рис.12 Лист Excel
нижняя граница 5,719-1,126=4,594
верхняя граница 5,719+1,126=6,845
Выполнить
прогноз заработной платы
при прогнозном значении среднедушевого
прожиточного минимума

составляющем 107% от среднего уровня.
,
где
— это 107%
от среднего уровня значения среднедушевого
прожиточного минимума
|
xp |
94,33833333 |
|
ytxp |
151,8603984 |
|
mytxp |
1,042112077 |
|
интервал |
149,538428 |
154,1823688 |
12. Найти доверительный интервал для индивидуальных значений зависимой переменной.
—
индивидуальное значение среднедневной
заработной платы, руб.
(у)
|
my* |
10,04971 |
|
дов |
129,4682388 |
129,4682388 |
13. Найти коэффициент эластичности.
Коэффициент
эластичности показывает на сколько
процентов в среднем по совокупности
изменится среднедневная
заработная плата, руб.
(у) от своей средней величины при изменении
среднедушевого
прожиточного минимума в день одного
трудоспособного, руб. (
В
общем случае:
Для
линейной регрессии:
|
Эср |
0,556481356 |
0,556481356 |
При
изменении среднедушевого
прожиточного минимума в день одного
трудоспособного, руб. (
на 1% среднедневная
заработная плата, руб.
(у) изменится на 0,556%.
14. Вычислить остатки; найти остаточную сумму квадратов; оценить дисперсию остатков ; построить график остатков.
e
= y-yt
|
y |
yt |
у-yt |
|
124 |
128,4843 |
-4,48427 |
|
145 |
133,0971 |
11,90293 |
|
152 |
137,7099 |
14,29013 |
|
133 |
141,4001 |
-8,40011 |
|
127 |
143,2452 |
-16,2452 |
|
138 |
146,0129 |
-8,01291 |
|
146 |
149,7031 |
-3,70315 |
|
159 |
150,6257 |
8,374294 |
|
155 |
151,5483 |
3,451734 |
|
153 |
154,3159 |
-1,31595 |
|
154 |
156,1611 |
-2,16106 |
|
168 |
161,6964 |
6,303576 |
Дисперсия
|
остаточная |
90,65657435 |
15. Проверить выполнение предпосылок мнк.
15.1.
Математическое ожидание остатков равно
нулю.
|
сумма |
8,53E-14 |
15.2.
Дисперсия остатков постоянна
Для
оценки на гомо- гетероскедастичность
остаточной дисперсии воспользуемся
методом Голдфельда-Квандта:
15.2.1.
Упорядочим n
наблюдений по мере возрастания
среднедушевого
прожиточного минимума в день одного
трудоспособного, руб. (
|
x |
y |
|
69 |
124 |
|
74 |
145 |
|
79 |
152 |
|
83 |
133 |
|
85 |
127 |
|
88 |
138 |
|
92 |
146 |
|
93 |
159 |
|
94 |
155 |
|
97 |
153 |
|
99 |
154 |
|
105 |
168 |
15.2.2.
Разделим совокупность на две группы.
|
x |
y |
|
69 |
124 |
|
74 |
145 |
|
79 |
152 |
|
83 |
133 |
|
85 |
127 |
|
88 |
138 |
|
x |
y |
|
92 |
146 |
|
93 |
159 |
|
94 |
155 |
|
97 |
153 |
|
99 |
154 |
|
105 |
168 |
15.2.3.
Определение остаточной суммы квадратов
для первой регрессии и для второй по
формуле:
|
S1yt |
764,6721944 |
|
S2yt |
141,893549 |
15.2.4.Вычисляем
соотношение
|
Fнабл |
5,389055384 |
15.2.5.
Рассчет критического значения F
|
Fкритич |
5,050329058 |
Так
как
, то имеет место гетероскедастичность
дисперсии, что приводит к ненадежности
линейной модели данной регрессии.
15.3.
В ряду остатков отсутствует существенная
автокорреляция.
Ряд
случайных величин называется
автокоррелированным, если имеется
корреляционная связь между последовательными
значениями переменной в этом ряду.
Для
проверки автокорреляции воспользуемся
критерием Дарвина-Уотсона.
Рассчитаем
d-статистику:
|
d-stat |
1,326068615 |
Воспользуемся
«схемой критерия». Так, как 1,32<
1,326068615<2,
то уровень ряда остатков признается
независимым.
15.4.
Распределение остатков подчинено
нормальному закону.
ННГУ
им. Лобачевского
Отчет по лабораторной
работе №2
по предмету
эконометрика
«Нелинейная
регрессия».
Работу
выполнила
студентка
725гр.
Зотагина
Анастасия
2011г
Модели
разделяют на два класса нелинейности:
—
регрессии, нелинейные относительно
включенных в анализ объясняемых
переменных, но линейные по оцениваемому
параметру
—
нелинейные по оцениваемому параметру
-
Степенная
модель
-
Параметры
уравнения степенной регрессии
y
=
Необходимо
линеаризовать модель (привести к
линейному виду):
Произведем
замену:
|
z=ln(y) |
t=ln(x) |
|
2,093422 |
1,838849 |
|
2,161368 |
1,869232 |
|
2,181844 |
1,897627 |
|
2,123852 |
1,919078 |
|
2,103804 |
1,929419 |
|
2,139879 |
1,944483 |
|
2,164353 |
1,963788 |
|
2,201397 |
1,968483 |
|
2,190332 |
1,973128 |
|
2,184691 |
1,986772 |
|
2,187521 |
1,995635 |
|
2,225309 |
2,021189 |
|
b |
0,538144 |
|
c |
1,117906 |
1.2.
Степенная модель регрессии
Найдя
параметры b
и c,
составим уравнение в линейном виде,
выполнив его потенцирование, получим
степенную модель.
|
y_тер |
|
128,0773595 |
|
132,991107 |
|
137,7537421 |
|
141,464392 |
|
143,2887179 |
|
145,9884389 |
|
149,5228002 |
|
150,3952341 |
|
151,2633459 |
|
153,8424112 |
|
155,5413621 |
|
160,5453351 |
1.3.
Коэффициент детерминации
Коэффициент
детерминации используется для оценки
качества подбора уравнения степенной
регрессии.
Коэффициент
детерминации характеризует долю
дисперсии среднедневной
заработной платы, руб.
(у), объясняемую регрессией в общей
дисперсии среднедневной
заработной платы, руб.
(у).

|
R^2 |
|
0,52915 |
Воспользуемся
шкалой оценки силы связи между переменными
в зависимости от

Так как
, то сила связи между
среднедушевым
прожиточным минимумом в день одного
трудоспособного, руб. (
и среднедневной
заработной платы, руб.
(у) является заметной.
Значит
уравнение регрессии объясняется 53%
дисперсии среднедневной
заработной платы, руб.
(у) на долю прочих факторов, приходящихся
на 47%.
1.4.
Адекватность модели по F-критерию
Фишера (α=0,05).
Оценка
статистической значимости уравнения
регрессии в целом осуществляется с
помощью F-критерия
Фишера, которая заключается в проверке
гипотезы

статистической незначимости уравнения
регрессии.
|
Fрассч |
|
11,23821 |
1.5.
Оценка точности модели.
А
– ошибка аппроксимации.
|
Аппроксимация |
|
5,178802 |
Ошибка
, что свидетельствует об удовлетворительной
подборке модели к исходным данным.
1.6.
Коэффициент эластичности.
Коэффициент
эластичности показывает на сколько
процентов в среднем по совокупности
изменится среднедневная
заработная плата, руб.
(у) от своей средней величины при изменении
среднедушевого
прожиточного минимума в день одного
трудоспособного, руб. (
В
общем случае:
Для
степенной регрессии:
|
Э |
|
0,538144 |
При
изменении среднедушевого
прожиточного минимума в день одного
трудоспособного, руб. (
на 1% среднедневная
заработная плата, руб.
(у) изменится на 0,538144%.
1.7.
Построим точечный график по исходным
данным.
-
Показательная
модель-
Параметры
уравнения показательной регрессии
-
y
=
Необходимо
линеаризовать модель (привести к
линейному виду):
Произведем
замену:
|
z=ln(y) |
|
4,820282 |
|
4,976734 |
|
5,023881 |
|
4,890349 |
|
4,844187 |
|
4,927254 |
|
4,983607 |
|
5,068904 |
|
5,043425 |
|
5,030438 |
|
5,036953 |
|
5,123964 |
|
d |
0,006378 |
|
c |
4,41849 |
2.2.
Показательная модель регрессии
Найдя
параметры d
и c,
составим уравнение в линейном виде,
выполнив его потенцирование, получим
степенную модель.
|
yтеор |
|
128,8415 |
|
133,0166 |
|
137,327 |
|
140,8756 |
|
142,6842 |
|
145,4407 |
|
149,199 |
|
150,1537 |
|
151,1144 |
|
154,0338 |
|
156,0112 |
|
162,0973 |
2.3.
Коэффициент детерминации
Коэффициент
детерминации используется для оценки
качества подбора уравнения степенной
регрессии.
Коэффициент
детерминации характеризует долю
дисперсии среднедневной
заработной платы, руб.
(у), объясняемую регрессией в общей
дисперсии среднедневной
заработной платы, руб.
(у).

|
R^2 |
|
0,546678 |
Воспользуемся
шкалой оценки силы связи между переменными
в зависимости от

Так как
, то сила связи между
среднедушевым
прожиточным минимумом в день одного
трудоспособного, руб. (
и среднедневной
заработной платы, руб.
(у) является заметной.
Значит
уравнение регрессии объясняется 55%
дисперсии среднедневной
заработной платы, руб.
(у) на долю прочих факторов, приходящихся
на 45%.
2.4.
Адекватность модели по F-критерию
Фишера (α=0,05).
Оценка
статистической значимости уравнения
регрессии в целом осуществляется с
помощью F-критерия
Фишера, которая заключается в проверке
гипотезы

статистической незначимости уравнения
регрессии.
|
Fрассч |
|
12,05936 |
2.5.
Оценка точности модели.
А
– ошибка аппроксимации.
|
аппроксимация |
|
6,124207 |
Ошибка
, что свидетельствует об удовлетворительной
подборке модели к исходным данным.
2.6.
Коэффициент эластичности.
Коэффициент
эластичности показывает на сколько
процентов в среднем по совокупности
изменится среднедневная
заработная плата, руб.
(у) от своей средней величины при изменении
среднедушевого
прожиточного минимума в день одного
трудоспособного, руб. (
В
общем случае:
Для
показательной регрессии:
|
эластичность |
|
0,562341 |
При
изменении среднедушевого
прожиточного минимума в день одного
трудоспособного, руб. (
на 1% среднедневная
заработная плата, руб.
(у) изменится на 0,562341%.
2.7.
Построим точечный график по исходным
данным.
3.
Равносторонняя гипербола
3.1.Параметры
уравнения показательной регрессии
Необходимо
линеаризовать модель (привести к
линейному виду):
Произведем
замену:
Тогда:
|
w=1/x |
|
0,014493 |
|
0,013514 |
|
0,012658 |
|
0,012048 |
|
0,011765 |
|
0,011364 |
|
0,01087 |
|
0,010753 |
|
0,010638 |
|
0,010309 |
|
0,010101 |
|
0,009524 |
|
b |
-6426,99 |
|
a |
220,0962 |
-
Равносторонняя
гипербола
Найдя
параметры a
и b,
составим уравнение в линейном виде.
|
yтеор |
|
126,9514 |
|
133,2449 |
|
138,7419 |
|
142,6625 |
|
144,4845 |
|
147,0622 |
|
150,2376 |
|
150,9887 |
|
151,7239 |
|
153,8385 |
|
155,1771 |
|
158,8867 |
3.3.
Коэффициент детерминации
Коэффициент
детерминации используется для оценки
качества подбора уравнения степенной
регрессии.
Коэффициент
детерминации характеризует долю
дисперсии среднедневной
заработной платы, руб.
(у), объясняемую регрессией в общей
дисперсии среднедневной
заработной платы, руб.
(у).
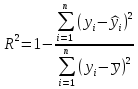
|
R^2 |
|
0,499468 |
Воспользуемся
шкалой оценки силы связи между переменными
в зависимости от

Так как
, то сила связи между
среднедушевым
прожиточным минимумом в день одного
трудоспособного, руб. (
и среднедневной
заработной платы, руб.
(у) является заметной.
Значит
уравнение регрессии объясняется 50%
дисперсии среднедневной
заработной платы, руб.
(у) на долю прочих факторов, приходящихся
на 50%.
3.4.
Адекватность модели по F-критерию
Фишера (α=0,05).
Оценка
статистической значимости уравнения
регрессии в целом осуществляется с
помощью F-критерия
Фишера, которая заключается в проверке
гипотезы

статистической незначимости уравнения
регрессии.
|
Fрассч |
|
9,978747 |
3.5.
Оценка точности модели.
А
– ошибка аппроксимации.
|
аппроксимация |
|
6,360027 |
Ошибка
, что свидетельствует об удовлетворительной
подборке модели к исходным данным.
3.6.
Коэффициент эластичности.
Коэффициент
эластичности показывает на сколько
процентов в среднем по совокупности
изменится среднедневная
заработная плата, руб.
(у) от своей средней величины при изменении
среднедушевого
прожиточного минимума в день одного
трудоспособного, руб. (
В
общем случае:
Для
равносторонней гиперболы:
|
эластичность |
|
0,495216 |
При
изменении среднедушевого
прожиточного минимума в день одного
трудоспособного, руб. (
на 1% среднедневная
заработная плата, руб.
(у) изменится на 0,495216%.
Вывод.
Общая таблица.
|
Fрассч |
Апроксимация |
R |
|
|
линейная |
11,63844 |
6,218619987 |
0,733389 |
|
степенная |
11,23821 |
5,178801772 |
0,727427 |
|
показательная |
12,05936 |
6,1242074 |
0,739377 |
|
равносторонняя |
9,978747 |
6,360027106 |
0,706731 |
В
равной степени хорошо нашу задачу
описывает показательная модель регрессии,
так как в ней максимален коэффициент
детерминации и максимальна Fрассч.
Соседние файлы в папке Эконометрика польза
- #
27.03.201540.67 Кб49лр1,лр2 зад.1 вар.8.xlsx
- #
27.03.201564.88 Кб44лр1,лр2 росстат.xlsx
- #
27.03.201531.26 Кб42лр3 росстат.xlsx
- #
27.03.201530.67 Кб62лр3,вар4.xlsx
- #
27.03.201529.4 Кб50лр4.xlsx
- #
- #
- #
- #
Доверительный интервал при уровне значимости 5 %
Доверительный интервал при уровне значимости 10 %
Аналитическая записка.
Рассматриваем линейную зависимость чистого дохода по совокупности 15 компаний от двух факторов – оборота капитала и численности служащих.
Получено уравнение регрессии:
Внимание!
Если вам нужна помощь в написании работы, то рекомендуем обратиться к
профессионалам. Более 70 000 авторов готовы помочь вам прямо сейчас. Бесплатные
корректировки и доработки. Узнайте стоимость своей работы.
При увеличении оборота капитала, на один млрд. долл. чистый доход увеличивается на 14,2 млн. долл., а при увлечении численность служащих на одну тыс. чел. чистый доход вырастет на 4,7 млн. долл.
В данной ситуации большее влияние на чистый доход оказывает второй фактор – численность служащих, чем первый – оборот капитала. Об этом говорят частные коэффициенты эластичности и стандартизованные коэффициенты регрессии:
= 0,42
; = 0,539
=0,243;
=0,329
Парные коэффициенты показывают следующие:
¾ Связь между оборотом капитала и чистым доходом прямая и весьма высокая.
¾ Связь между численностью служащих и чистым доходом прямая и весьма высокая.
¾ Связь между численностью служащих и оборотом капитала прямая и весьма высокая.
Множественный коэффициент корреляции показывает, что чистый доход очень сильно зависит от численности служащих и оборота капитала.
Коэффициент детерминации равен 0,88, что говорит о влиянии вышеперечисленных 2-х факторов на чистый доход на 88%, остальные 12% — влияние случайных факторов.
Поскольку фактическое значение Fфакт > Fтабл, то уравнение регрессии статистически надежно.
Значение прогноза в точке =(132,32;596) равняется 5,5.
Доверительный интервал для прогноза является:
Для уровня значимости 5%:
Для уровня значимости 10%:
Получить выполненную работу или консультацию специалиста по вашему
учебному проекту
Узнать стоимость
Эконометрика
Вариант 1
Задание 1. Модель парной линейной регрессии.
Имеются данные о размере среднемесячных доходов в разных группах семей
|
Номер группы |
Среднедушевой денежный доход в месяц, руб., X |
Доля оплаты труда в структуре доходов семьи, %, Y |
|
1 |
79,8 |
64,2 |
|
2 |
152,1 |
66,1 |
|
3 |
199,3 |
69,0 |
|
4 |
240,8 |
70,6 |
|
5 |
282,4 |
72,4 |
|
6 |
301,8 |
74,3 |
|
7 |
385,3 |
76,0 |
|
8 |
457,8 |
77,1 |
|
9 |
577,4 |
78,4 |
Задания:
1. Рассчитать линейный коэффициент парной корреляции, оценить его статистическую значимость и построить для него доверительный интервал с уровнем значимости a =0,05. Сделать выводы
2. Построить линейное уравнение парной регрессии Y на X и оценить статистическую значимость параметров регрессии. Сделать рисунок.
3. Оценить качество уравнения регрессии при помощи коэффициента детерминации. Сделать выводы. Проверить качество уравнения регрессии при помощи F-критерия Фишера.
4. Выполнить прогноз доли оплаты труда структуре доходов семьи Y при прогнозном значении среднедушевого денежного дохода X, составляющем 111% от среднего уровня. Оценить точность прогноза, рассчитав ошибку прогноза и его доверительный интервал для уровня значимости a =0,05. Сделать выводы.
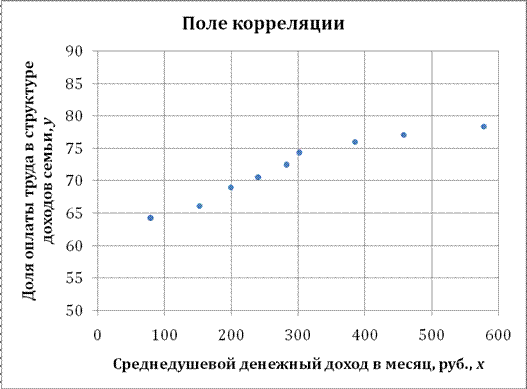
Решение: Построим поле корреляции зависимости доли оплаты труда в структуре доходов семьи от среднедушевого денежного дохода в месяц.
Точки на построенном графике размещаются вблизи кривой, напоминающей по форме Прямую, поэтому можно предположить, что между указанными величинами существует Линейная зависимость вида .
Для расчета линейного коэффициента парной корреляции и параметров линейной регрессии составим вспомогательную таблицу.
|
№ п/п |
X |
Y |
X×Y |
X2 |
Y2 |
|
1 |
79,8 |
64,2 |
5123,16 |
6368,04 |
4121,64 |
|
2 |
152,1 |
66,1 |
10053,81 |
23134,41 |
4369,21 |
|
3 |
199,3 |
69,0 |
13751,70 |
39720,49 |
4761,00 |
|
4 |
240,8 |
70,6 |
17000,48 |
57984,64 |
4984,36 |
|
5 |
282,4 |
72,4 |
20445,76 |
79749,76 |
5241,76 |
|
6 |
301,8 |
74,3 |
22423,74 |
91083,24 |
5520,49 |
|
7 |
385,3 |
76,0 |
29282,80 |
148456,09 |
5776,00 |
|
8 |
457,8 |
77,1 |
35296,38 |
209580,84 |
5944,41 |
|
9 |
577,4 |
78,4 |
45268,16 |
333390,76 |
6146,56 |
|
S |
2676,7 |
648,1 |
198645,99 |
989468,27 |
46865,43 |
|
Среднее |
297,41 |
72,01 |
22071,78 |
109940,92 |
5207,27 |
Вычислим коэффициент корреляции. Используем следующую формулу:
= 0,9568.
Можно сказать, что между рассматриваемыми признаками существует Прямая тесная Корреляционная связь.
Среднюю ошибку коэффициента корреляции определим по формуле:
= 0,032.
Найдем табличное значение TТабл по таблице распределения Стьюдента для
a = 0,05 и числе степеней свободы K = N – M – 1 = 9 – 1 – 1 = 7.
TТабл(0,05; 7) = 2,36.
Запишем доверительный интервал для коэффициента корреляции.
Доверительный интервал не включает число 0, поэтому при заданном уровне значимости коэффициент корреляции является статистически значимым.
Вычислим параметры уравнения регрессии.
= 0,03.
= 72,01 – 0,03×297,41 = 63,09.
Получим следующее уравнение: .
Для проверки статистической значимости (существенности) линейного коэффициента парной корреляции рассчитаем T-критерий Стьюдента по формуле:

Фактическое значение по абсолютной величине больше табличного, что свидетельствует о значимости линейного коэффициента корреляции и существенности связи между рассматриваемыми признаками.
Проверим значимость оценок теоретических коэффициентов регрессии с помощью t-статистики Стьюдента и сделаем соответствующие выводы о значимости этих оценок.
Для определения статистической значимости коэффициентов A и B найдем T-статистики Стьюдента:
Рассчитаем по полученному уравнению теоретические значения. Составим вспомогательную таблицу.
|
№ п/п |
X |
Y |
|
|
|
|
1 |
79,8 |
64,2 |
65,48 |
1,6384 |
47354,1 |
|
2 |
152,1 |
66,1 |
67,65 |
2,4025 |
21115,0 |
|
3 |
199,3 |
69,0 |
69,07 |
0,0049 |
9625,6 |
|
4 |
240,8 |
70,6 |
70,31 |
0,0841 |
3204,7 |
|
5 |
282,4 |
72,4 |
71,56 |
0,7056 |
225,3 |
|
6 |
301,8 |
74,3 |
72,14 |
4,6656 |
19,3 |
|
7 |
385,3 |
76,0 |
74,65 |
1,8225 |
7724,7 |
|
8 |
457,8 |
77,1 |
76,82 |
0,0784 |
25725,0 |
|
9 |
577,4 |
78,4 |
80,41 |
4,0401 |
78394,4 |
|
S |
2676,7 |
648,1 |
648,09 |
15,4421 |
193388,1 |
Вычислим стандартные ошибки коэффициентов уравнения.


Вычислим T-статистики.
Сравнение расчетных и табличных величин критерия Стьюдента показывает, что и
, т. е. оценки A и B теоретических коэффициентов регрессии статистически значимы.
Сделаем рисунок.
Рассчитаем коэффициент детерминации: = 0,95682= 0,915 = 91,5%.
Таким образом, вариация результата Y на 91,5% объясняется вариацией фактора X.
Оценку значимости уравнения регрессии проведем с помощью F-критерия Фишера:

Найдем табличное значение Fтабл по таблице критических точек Фишера для
a = 0,05; K1 = M = 1 (число факторов), K2 = N – M – 1 = 9 – 1 – 1 = 7.
Fтабл(0,05; 1; 7) = 5,59.
Поскольку F > FТабл, уравнение регрессии с вероятностью 0,95 в целом Является статистически значимым.
Выполним прогноз доли оплаты труда структуре доходов семьи y при прогнозном значении среднедушевого денежного дохода x, составляющем 111% от среднего уровня.
XP = 297,41 × 1,11 = 330,1.
Вычислим прогнозное значение Yp с помощью уравнения регрессии.
» 73%.
Доверительный интервал прогноза имеет вид
(УP – Tкр×My, УP + Tкр×My),
Где 

Запишем доверительный интервал прогноза:
Þ
Данный прогноз является надежным, поскольку доверительный интервал не включает число 0, точность прогноза составляет 4.
Задание 2. Модель парной нелинейной регрессии.
По территориям Центрального района известны данные за 1995 г.
|
Район |
Прожиточный минимум в среднем на одного пенсионера в месяц, тыс. руб., X |
Средний размер назначенных ежемесячных пенсий, тыс. руб., Y |
|
Брянская обл. |
178 |
240 |
|
Владимирская обл. |
202 |
226 |
|
Ивановская обл. |
197 |
221 |
|
Калужская обл. |
201 |
226 |
|
Костромская обл. |
189 |
220 |
|
Орловская обл. |
166 |
232 |
|
Рязанская обл. |
199 |
215 |
|
Смоленская обл. |
180 |
220 |
|
Тверская обл. |
181 |
222 |
|
Тульская обл. |
186 |
231 |
|
Ярославская обл. |
250 |
229 |
Задания:
1. Построить поле корреляции и сформулируйте гипотезу о форме связи. Рассчитать параметры уравнений полулогарифмической () и степенной (
) парной регрессии. Сделать рисунки.
2. Дать с помощью среднего коэффициента эластичности сравнительную оценку силы связи фактора с результатом для каждой модели. Сделать выводы. Оценить качество уравнений регрессии с помощью средней ошибки аппроксимации и коэффициента детерминации. Сделать выводы.
3. По значениям рассчитанных характеристик выбрать лучшее уравнение регрессии. Дать экономический смысл коэффициентов выбранного уравнения регрессии
4. Рассчитать прогнозное значение результата, если прогнозное значение фактора увеличится на 10% от его среднего уровня. Определите доверительный интервал прогноза для уровня значимости a =0,05. Сделать выводы.
Решение: Решение: Для предварительного определения вида связи между указанными признаками построим поле корреляции. Для этого построим в системе координат точки, у которых первая координата X, а вторая – Y.
Получим следующий рисунок.
По внешнему виду диаграммы рассеяния трудно предположить, какая зависимость существует между указанными показателями.
Построение полулогарифмической модели регрессии.
Уравнение логарифмической кривой: .
Обозначим:
Получим линейное уравнение регрессии:
Y = A + B×X.
Произведем линеаризацию модели путем замены . В результате получим линейное уравнение
.
Рассчитаем его параметры, используя данные таблицы.
|
№ п/п |
X |
Y |
X = ln(X) |
Xy |
X2 |
Y2 |
|
|
|
Ai |
|
1 |
178 |
240 |
5,1818 |
1243,63 |
26,85 |
57600 |
226,40 |
206,314 |
184,904 |
6,006 |
|
2 |
202 |
226 |
5,3083 |
1199,67 |
28,18 |
51076 |
225,17 |
0,132 |
0,694 |
0,370 |
|
3 |
197 |
221 |
5,2832 |
1167,59 |
27,91 |
48841 |
225,41 |
21,496 |
19,464 |
1,957 |
|
4 |
201 |
226 |
5,3033 |
1198,55 |
28,13 |
51076 |
225,22 |
0,132 |
0,615 |
0,348 |
|
5 |
189 |
220 |
5,2417 |
1153,18 |
27,48 |
48400 |
225,82 |
31,769 |
33,833 |
2,576 |
|
6 |
166 |
232 |
5,1120 |
1185,98 |
26,13 |
53824 |
227,08 |
40,496 |
24,172 |
2,165 |
|
7 |
199 |
215 |
5,2933 |
1138,06 |
28,02 |
46225 |
225,31 |
113,132 |
106,362 |
4,577 |
|
8 |
180 |
220 |
5,1930 |
1142,45 |
26,97 |
48400 |
226,29 |
31,769 |
39,601 |
2,781 |
|
9 |
181 |
222 |
5,1985 |
1154,07 |
27,02 |
49284 |
226,24 |
13,223 |
17,968 |
1,874 |
|
10 |
186 |
231 |
5,2257 |
1207,15 |
27,31 |
53361 |
225,97 |
28,769 |
25,273 |
2,225 |
|
11 |
250 |
229 |
5,5215 |
1264,41 |
30,49 |
52441 |
223,09 |
11,314 |
34,980 |
2,651 |
|
Итого |
2129 |
2482 |
57,862 |
13054,74 |
304,48 |
560528 |
2482,00 |
498,545 |
487,867 |
27,530 |
|
Среднее |
193,5 |
225,6 |
5,260 |
1186,79 |
27,68 |
50957,091 |
225,636 |
45,322 |
44,352 |
2,503 |
= -9,76.
= 225,6 – (-9,76)×5,26 = 276,99.
Уравнение модели имеет вид:
Определим индекс корреляции
Используя данные таблицы, получим:

Рассчитаем коэффициент детерминации: = 0,14642= 0,021 = 2,1%.
Вариация результата Y всего на 2,1% объясняется вариацией фактора X.
Сделаем рисунок.
Рассчитаем средний коэффициент эластичности по формуле:
= -0,04%.
Коэффициент эластичности показывает, что при среднем росте признака X на 1% признак Y снижается на 0,04%.
Вычислим среднюю ошибку аппроксимации. Используя данные расчетной таблицы, получаем:
= 2,5%.
Построение степенной модели парной регрессии.
Уравнение степенной модели имеет вид: .
Для построения этой модели необходимо произвести линеаризацию переменных. Для этого произведем логарифмирование обеих частей уравнения:
.
Произведем линеаризацию модели путем замены и
. В результате получим линейное уравнение
.
Рассчитаем его параметры, используя данные таблицы.
|
№ п/п |
X |
Y |
X = ln(X) |
Y = ln(Y) |
XY |
X2 |
Y2 |
|
|
|
|
Ai |
|
1 |
178 |
240 |
5,1818 |
5,4806 |
28,3995 |
26,851 |
30,037 |
226,3 |
206,3 |
188,391 |
241,661 |
6,07 |
|
2 |
202 |
226 |
5,3083 |
5,4205 |
28,7737 |
28,178 |
29,382 |
225,1 |
0,132 |
0,835 |
71,479 |
0,406 |
|
3 |
197 |
221 |
5,2832 |
5,3982 |
28,5196 |
27,912 |
29,140 |
225,3 |
21,496 |
18,671 |
11,934 |
1,918 |
|
4 |
201 |
226 |
5,3033 |
5,4205 |
28,7467 |
28,125 |
29,382 |
225,1 |
0,132 |
0,753 |
55,570 |
0,385 |
|
5 |
189 |
220 |
5,2417 |
5,3936 |
28,2720 |
27,476 |
29,091 |
225,7 |
31,769 |
32,607 |
20,661 |
2,530 |
|
6 |
166 |
232 |
5,1120 |
5,4467 |
27,8437 |
26,132 |
29,667 |
226,9 |
40,496 |
25,675 |
758,752 |
2,233 |
|
7 |
199 |
215 |
5,2933 |
5,3706 |
28,4284 |
28,019 |
28,844 |
225,2 |
113,132 |
104,576 |
29,752 |
4,540 |
|
8 |
180 |
220 |
5,1930 |
5,3936 |
28,0089 |
26,967 |
29,091 |
226,2 |
31,769 |
38,059 |
183,479 |
2,728 |
|
9 |
181 |
222 |
5,1985 |
5,4027 |
28,0858 |
27,024 |
29,189 |
226,1 |
13,223 |
16,950 |
157,388 |
1,821 |
|
10 |
186 |
231 |
5,2257 |
5,4424 |
28,4407 |
27,308 |
29,620 |
225,9 |
28,769 |
26,413 |
56,934 |
2,275 |
|
11 |
250 |
229 |
5,5215 |
5,4337 |
30,0021 |
30,487 |
29,525 |
223,1 |
11,314 |
34,846 |
3187,116 |
2,646 |
|
Итого |
2129 |
2482 |
57,862 |
59,603 |
313,521 |
304,479 |
322,969 |
2480,927 |
498,545 |
487,777 |
4774,727 |
27,548 |
|
Среднее |
193,5 |
225,6 |
5,260 |
5,418 |
28,502 |
27,680 |
29,361 |
225,539 |
45,322 |
44,343 |
434,066 |
2,504 |
С учетом введенных обозначений уравнение примет вид: Y = A + BX – линейное уравнение регрессии. Рассчитаем его параметры, используя данные таблицы.
= -0,042.
= 5,418 – 0,959×5,26 = 5,637.
Перейдем к исходным переменным X и Y, выполнив потенцирование данного уравнения.
A = eA = e5,637 = 280,76
Получим уравнение степенной модели регрессии: .
Определим индекс корреляции
Используя данные таблицы, получим:

Рассчитаем коэффициент детерминации: = 0,1472= 0,021 = 2,1%.
Вариация результата Y всего на 2,1% объясняется вариацией фактора X.
Сделаем рисунок.
Для степенной модели средний коэффициент эластичности равен коэффициенту B.
= -0,042%.
Коэффициент эластичности показывает, что при среднем росте признака X на 1% признак Y снижается на 0,042%.
Вычислим среднюю ошибку аппроксимации. Используя данные расчетной таблицы, получаем:
= 2,5%.
Сводная таблица вычислений
|
Параметры |
Модель |
|
|
Полулогарифмическая |
Степенная |
|
|
Уравнение связи |
|
|
|
Индекс корреляции |
0,1464 |
0,147 |
|
Коэффициент детерминации |
0,021 |
0,021 |
|
Средняя ошибка аппроксимации, % |
2,5 |
2,5 |
Для выявления формы связи между указанными признаками были построены полулогарифмическая и степенная модели регрессии. Анализ показателей корреляции, а также оценка качества моделей с использованием средней ошибки аппроксимации позволил предположить, что из перечисленных моделей более адекватной является степенная модель, поскольку для нее индекс корреляции принимает наибольшее значение R = 0,147, свидетельствующий о том, что между рассматриваемыми признаками наблюдается Слабая корреляционная связь.
Рассчитаем прогнозное значение результата по степенной модели регрессии, если прогнозируется увеличение значения фактора на 10% от среднего уровня.
Прогнозное значение составит:
= 193,5 × 1,1 = 212,9 тыс. р., тогда прогнозное значение Y составит:
= 224,6 тыс. р.
Определим доверительный интервал прогноза для уровня значимости a = 0,05.
Вычислим Среднюю стандартную ошибку прогноза По следующей формуле:

Получаем: 
Найдем предельную ошибку прогноза , где для доверительной вероятности 0,95 значение T составляет 1,96.
= 14,8.
Запишем доверительный интервал прогноза.
= 224,6 – 14,8 = 209,8 тыс. р.
= 224,6 + 14,8 = 239,4 тыс. р.
Таким образом, с вероятностью 0,95 можно утверждать, что прогнозное значение среднего размера назначенных ежемесячных пенсий будет находиться в пределах от 209,8 тыс. р. до 239,4 тыс. р.
Задание 3. Моделирование временных рядов
Имеются поквартальные данные по розничному товарообороту России в 1995-1999 гг.
|
Номер квартала |
Товарооборот % к предыдущему периоду |
Номер квартала |
Товарооборот % к предыдущему периоду |
|
1 |
100 |
11 |
98,8 |
|
2 |
93,9 |
12 |
101,9 |
|
3 |
96,5 |
13 |
113,1 |
|
4 |
101,8 |
14 |
98,4 |
|
5 |
107,8 |
15 |
97,3 |
|
6 |
96,3 |
16 |
112,1 |
|
7 |
95,7 |
17 |
97,6 |
|
8 |
98,2 |
18 |
93,7 |
|
9 |
104 |
19 |
114,3 |
|
10 |
99 |
20 |
108,4 |
Задания:
1. Построить график данного временного ряда. Охарактеризовать структуру этого ряда.
2. Рассчитать сезонную компоненты временного ряда и построить его Мультипликативную Модель.
3. Рассчитать трендовую компоненту временного ряда и построить его график
4. Оценить качество модели через показатели средней абсолютной ошибки и среднего относительного отклонения.
Решение: Пронумеруем указанные месяцы от 1 до 24 и построим график временного ряда.
Полученный график показывает, что а данном временном ряду присутствуют сезонные колебания.
Построим мультипликативную модель временного ряда.
Эта модель предполагает, что каждый уровень временного ряда может быть представлен как произведение трендовой (T), сезонной (S) и случайной (E) компонент.
Построение мультипликативной моделей сведем к расчету значений T, S и E для каждого уровня ряда.
Процесс построения модели включает в себя следующие шаги.
1) Выравнивание исходного ряда методом скользящей средней.
2) Расчет значений сезонной компоненты S.
3) Устранение сезонной компоненты из исходных уровней ряда и получение выровненных данных T×E.
4) Аналитическое выравнивание уровней T×E и расчет значений T с использованием полученного уравнения тренда.
5) Расчет полученных по модели значений T×E.
6) Расчет абсолютных и/или относительных ошибок.
Шаг 1. Проведем выравнивание исходных уровней ряда методом скользящей средней. Для этого:
1.1. Просуммируем уровни ряда последовательно за каждые четыре месяца со сдвигом на один момент времени и определим условные годовые уровни объема продаж (гр. 3 табл. 2.1).
1.2. Разделив полученные суммы на 4, найдем скользящие средние (гр. 4 табл. 2.1). Полученные таким образом выровненные значения уже не содержат сезонной компоненты.
1.3. Приведем эти значения в соответствие с фактическими моментами времени, для чего найдем средние значения из двух последовательных скользящих средних – центрированные скользящие средние (гр. 5 табл. 2.1).
Таблица 2.1
|
№ месяца, T |
Товарооборот, Yi |
Итого за четыре месяца |
Скользящая средняя за четыре месяца |
Центрированная скользящая средняя |
Оценка сезонной компоненты |
|
1 |
2 |
3 |
4 |
5 |
6 |
|
1 |
100,0 |
– |
– |
– |
– |
|
2 |
93,9 |
392 |
98 |
– |
– |
|
3 |
96,5 |
400 |
100 |
99 |
0,975 |
|
4 |
101,8 |
402 |
100,5 |
100,25 |
1,015 |
|
5 |
107,8 |
402 |
100,5 |
100,5 |
1,073 |
|
6 |
96,3 |
398 |
99,5 |
100 |
0,963 |
|
7 |
95,7 |
394 |
98,5 |
99 |
0,967 |
|
8 |
98,2 |
397 |
99,25 |
98,875 |
0,993 |
|
9 |
104,0 |
400 |
100 |
99,625 |
1,044 |
|
10 |
99,0 |
404 |
101 |
100,5 |
0,985 |
|
11 |
98,8 |
413 |
103,25 |
102,125 |
0,967 |
|
12 |
101,9 |
412 |
103 |
103,125 |
0,988 |
|
13 |
113,1 |
411 |
102,75 |
102,875 |
1,099 |
|
14 |
98,4 |
309 |
77,25 |
90 |
1,093 |
|
15 |
97,3 |
196 |
49 |
63,125 |
1,541 |
|
16 |
112,1 |
303 |
75,75 |
62,375 |
1,797 |
|
17 |
97,6 |
418 |
104,5 |
90,125 |
1,083 |
|
18 |
93,7 |
414 |
103,5 |
104 |
0,901 |
|
19 |
114,3 |
– |
– |
– |
– |
|
20 |
108,4 |
– |
– |
– |
– |
Шаг 2. Найдем оценки сезонной компоненты как частное от деления фактических уровней ряда на центрированные скользящие средние (гр. 6 табл. 2.1). Эти оценки используются для расчета сезонной компоненты S (табл. 2.2). Для этого найдем средние за каждый месяц оценки сезонной компоненты Si. Так же как и в аддитивной модели считается, что сезонные воздействия за период взаимопогашаются. В мультипликативной модели это выражается в том, что сумма значений сезонной компоненты по всем месяцам должна быть равна числу периодов в цикле. В нашем случае число периодов одного цикла равно 4.
Таблица 2.2
|
Показатели |
Год |
№ квартала, I |
|||
|
I |
II |
III |
IV |
||
|
1 |
– |
– |
0,975 |
1,015 |
|
|
2 |
1,073 |
0,963 |
0,967 |
0,993 |
|
|
3 |
1,044 |
0,985 |
0,967 |
0,988 |
|
|
4 |
1,099 |
1,093 |
1,541 |
1,797 |
|
|
5 |
1,083 |
0,901 |
– |
– |
|
|
Всего за I-й квартал |
4,299 |
3,942 |
4,45 |
4,793 |
|
|
Средняя оценка сезонной компоненты для I-го квартала, |
0,860 |
0,788 |
0,890 |
0,959 |
|
|
Скорректированная сезонная компонента, |
0,984 |
0,901 |
1,018 |
1,097 |
Имеем: 0,860 + 0,788 + 0,890 + 0,959 = 3,497.
Определяем корректирующий коэффициент: K = 4 : 3,497 = 1,144.
Скорректированные значения сезонной компоненты получаются при умножении ее средней оценки
на корректирующий коэффициент K.
Проверяем условие: равенство 4 суммы значений сезонной компоненты:
0,984 + 0,901 + 1,018 + 1,097 = 4.
Шаг 3. Разделим каждый уровень исходного ряда на соответствующие значения сезонной компоненты. В результате получим величины (гр. 4 табл. 2.3), которые содержат только тенденцию и случайную компоненту.
Таблица 2.3
|
T |
Yt |
St |
|
T |
T×S |
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
1 |
100,0 |
0,984 |
101,6 |
100,02 |
98,42 |
1,016 |
|
2 |
93,9 |
0,901 |
104,2 |
100,19 |
90,27 |
1,040 |
|
3 |
96,5 |
1,018 |
94,8 |
100,36 |
102,17 |
0,945 |
|
4 |
101,8 |
1,097 |
92,8 |
100,53 |
110,28 |
0,923 |
|
5 |
107,8 |
0,984 |
109,6 |
100,7 |
99,09 |
1,088 |
|
6 |
96,3 |
0,901 |
106,9 |
100,87 |
90,88 |
1,060 |
|
7 |
95,7 |
1,018 |
94,0 |
101,04 |
102,86 |
0,930 |
|
8 |
98,2 |
1,097 |
89,5 |
101,21 |
111,03 |
0,884 |
|
9 |
104,0 |
0,984 |
105,7 |
101,38 |
99,76 |
1,043 |
|
10 |
99,0 |
0,901 |
109,9 |
101,55 |
91,50 |
1,082 |
|
11 |
98,8 |
1,018 |
97,1 |
101,72 |
103,55 |
0,954 |
|
12 |
101,9 |
1,097 |
92,9 |
101,89 |
111,77 |
0,912 |
|
13 |
113,1 |
0,984 |
114,9 |
102,06 |
100,43 |
1,126 |
|
14 |
98,4 |
0,901 |
109,2 |
102,23 |
92,11 |
1,068 |
|
15 |
97,3 |
1,018 |
95,6 |
102,4 |
104,24 |
0,933 |
|
16 |
112,1 |
1,097 |
102,2 |
102,57 |
112,52 |
0,996 |
|
17 |
97,6 |
0,984 |
99,2 |
102,74 |
101,10 |
0,965 |
|
18 |
93,7 |
0,901 |
104,0 |
102,91 |
92,72 |
1,011 |
|
19 |
114,3 |
1,018 |
112,3 |
103,08 |
104,94 |
1,089 |
|
20 |
108,4 |
1,097 |
98,8 |
103,25 |
113,27 |
0,957 |
|
Среднее |
101,4 |
1,0011 |
Шаг 4. Определим компоненту T в мультипликативной модели. Для этого рассчитаем параметры линейного тренда, используя уровни T×E. Составим вспомогательную таблицу.
Таблица 2.4
|
T |
|
T2 |
|
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
|
1 |
101,6 |
1 |
101,6 |
2,5 |
1,58 |
2,0 |
|
|
2 |
104,2 |
4 |
208,4 |
13,2 |
3,87 |
56,3 |
|
|
3 |
94,8 |
9 |
284,4 |
32,1 |
5,88 |
24,0 |
|
|
4 |
92,8 |
16 |
371,2 |
71,9 |
8,33 |
0,2 |
|
|
5 |
109,6 |
25 |
548 |
75,9 |
8,08 |
41,0 |
|
|
6 |
106,9 |
36 |
641,4 |
29,4 |
5,63 |
26,0 |
|
|
7 |
94,0 |
49 |
658 |
51,3 |
7,48 |
32,5 |
|
|
8 |
89,5 |
64 |
716 |
164,6 |
13,07 |
10,2 |
|
|
9 |
105,7 |
81 |
951,3 |
18,0 |
4,08 |
6,8 |
|
|
10 |
109,9 |
100 |
1099 |
56,3 |
7,58 |
5,8 |
|
|
11 |
97,1 |
121 |
1068,1 |
22,6 |
4,81 |
6,8 |
|
|
12 |
92,9 |
144 |
1114,8 |
97,4 |
9,69 |
0,3 |
|
|
13 |
114,9 |
169 |
1493,7 |
160,5 |
11,20 |
136,9 |
|
|
14 |
109,2 |
196 |
1528,8 |
39,6 |
6,39 |
9,0 |
|
|
15 |
95,6 |
225 |
1434 |
48,2 |
7,13 |
16,8 |
|
|
20 |
102,2 |
400 |
2044 |
0,2 |
0,37 |
114,5 |
|
|
21 |
99,2 |
441 |
2083,2 |
12,3 |
3,59 |
14,4 |
|
|
22 |
104,0 |
484 |
2288 |
1,0 |
1,05 |
59,3 |
|
|
23 |
112,3 |
529 |
2582,9 |
87,6 |
8,19 |
166,4 |
|
|
24 |
98,8 |
576 |
2371,2 |
23,7 |
4,49 |
49,0 |
|
|
Сумма |
230 |
2035,2 |
3670 |
23588 |
1008,3 |
122,49 |
778,2 |
|
Среднее |
11,5 |
101,8 |
183,5 |
1179,4 |
50,4 |
6,12 |
38,91 |
Вычислим параметры уравнения тренда.

= 99,85.
В результате получим уравнение тренда:
T = 99,85 + 0,17×T.
Подставляя в это уравнение значения T = 1,2,…,16, найдем уровни T для каждого момента времени (гр. 5 табл. 2.3).
Шаг 5. Найдем уровни ряда, умножив значения T на соответствующие значения сезонной компоненты (гр. 6 табл. 2.3). На одном графике откладываем фактические значения уровней временного ряда и теоретические, полученные по мультипликативной модели.
Расчет ошибки в мультипликативной модели произведем по формуле:
Средняя абсолютная ошибка составила 1,0011 (см. гр. 7 табл. 2.3).
Рассчитаем сумму квадратов абсолютных ошибок .
Используя 5-й столбец таблицы 2.4, получим:

Рассчитаем среднюю относительную ошибку: .
Используя 6-й столбец таблицы 2.4, получим, что средняя относительная ошибка составила 6,12%, т. е. построенная модель достаточно точно описывает динамику данного явления.
| < Предыдущая | Следующая > |
|---|
Погрешность и доверительный интервал: в чем разница?
читать 2 мин
Часто в статистике мы используем доверительные интервалы для оценки значения параметра совокупности с определенным уровнем достоверности.
Каждый доверительный интервал принимает следующий вид:
Доверительный интервал = [нижняя граница, верхняя граница]
Погрешность равна половине ширины всего доверительного интервала.
Например, предположим, что у нас есть следующий доверительный интервал для среднего значения генеральной совокупности:
95% доверительный интервал = [12,5, 18,5]
Ширина доверительного интервала составляет 18,5 – 12,5 = 6. Допустимая погрешность равна половине ширины, которая будет равна 6/2 = 3 .
В следующих примерах показано, как рассчитать доверительный интервал вместе с погрешностью для нескольких различных сценариев.
Пример 1: Доверительный интервал и допустимая погрешность для среднего значения генеральной совокупности
Мы используем следующую формулу для расчета доверительного интервала для среднего значения генеральной совокупности:
Доверительный интервал = x +/- z*(s/ √n )
куда:
- x : выборочное среднее
- z: z-критическое значение
- s: стандартное отклонение выборки
- n: размер выборки
Пример: Предположим, мы собираем случайную выборку дельфинов со следующей информацией:
- Размер выборки n = 40
- Средний вес выборки x = 300
- Стандартное отклонение выборки s = 18,5
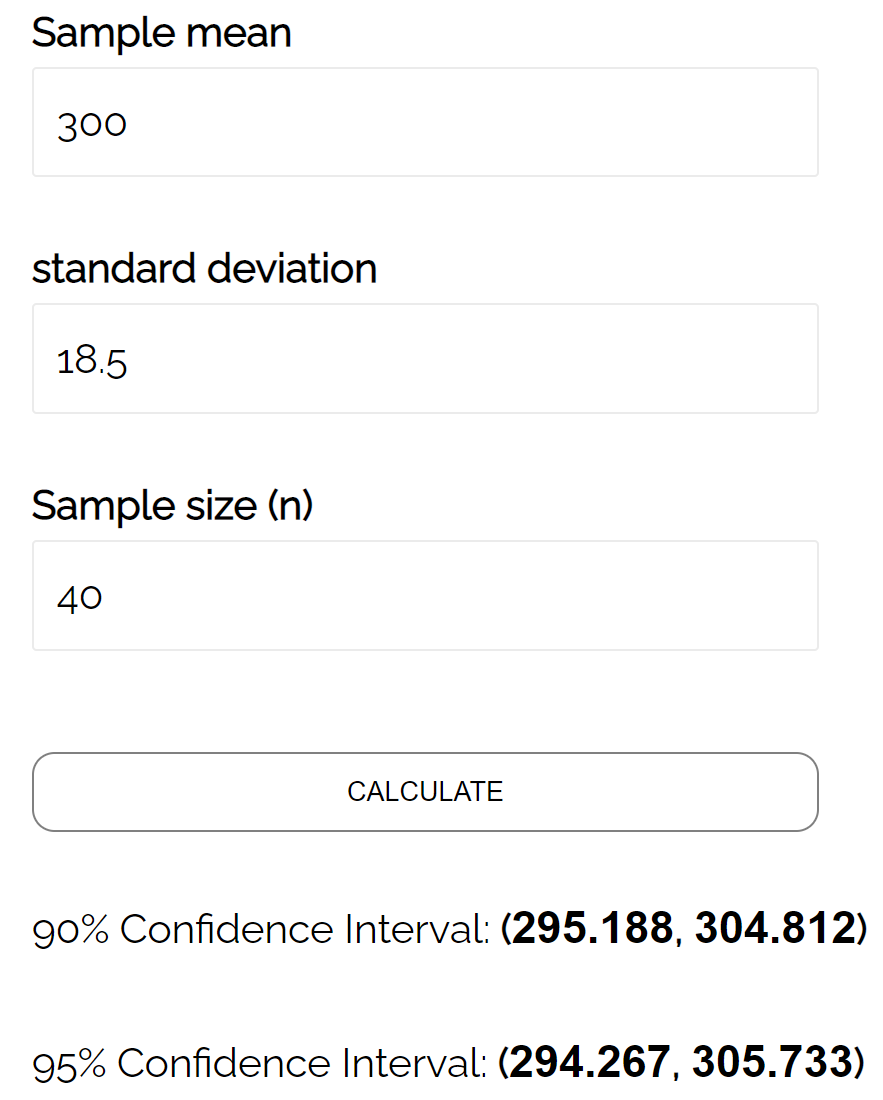
Мы можем подставить эти числа в калькулятор доверительного интервала , чтобы найти 95% доверительный интервал:
95% доверительный интервал для истинного среднего веса популяции черепах составляет [294,267, 305,733] .
Погрешность будет равна половине ширины доверительного интервала, который равен:
Погрешность: (305,733 – 294,267) / 2 = 5,733 .
Пример 2: Доверительный интервал и допустимая погрешность для доли населения
Мы используем следующую формулу для расчета доверительного интервала для доли населения:
Доверительный интервал = p +/- z * (√ p (1-p) / n )
куда:
- p: доля выборки
- z: выбранное значение z
- n: размер выборки
Пример: Предположим, мы хотим оценить долю жителей округа, поддерживающих определенный закон. Мы выбираем случайную выборку из 100 жителей и спрашиваем их об их отношении к закону. Вот результаты:
- Размер выборки n = 100
- Доля в пользу закона p = 0,56
Мы можем подставить эти числа в доверительный интервал для калькулятора пропорций , чтобы найти 95% доверительный интервал:
95% доверительный интервал для истинной доли населения составляет [0,4627, 0,6573] .
Погрешность будет равна половине ширины доверительного интервала, который равен:
Погрешность: (0,6573 – 0,4627) / 2 = 0,0973 .
Дополнительные ресурсы
Погрешность и стандартная ошибка: в чем разница?
Как найти погрешность в Excel
Как найти погрешность на калькуляторе TI-84