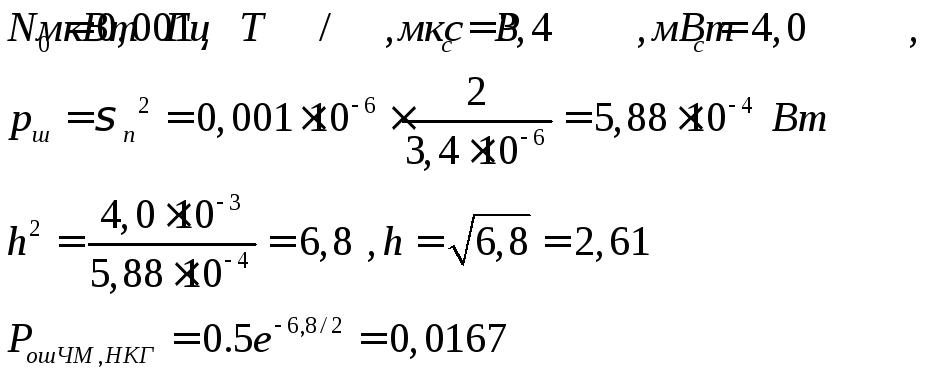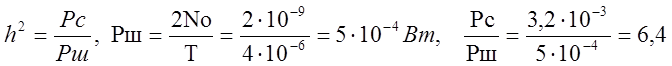,
где 
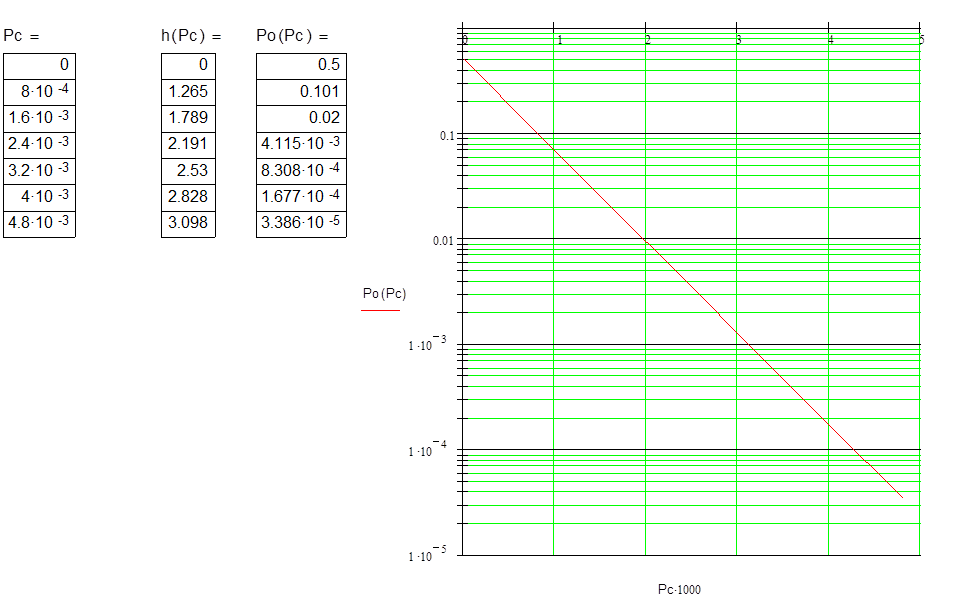
Зависимость
вероятности ошибки от мощности сигнала
Рассчитаем и
построим зависимость вероятности ошибки
от мощности сигнала. Мощность сигнала
будем изменять от 0 до такого значения,
при котором получается настолько малая
вероятность ошибки, что имеющихся таблиц
не хватает для ее нахождения.
Рис.6 График зависимости
вероятности ошибки от мощности сигнала
На графике
значения мощности сигнала откладываем
в линейном масштабе, а значения
вероятностей ошибок – в логарифмическом.
Самая верхняя
точка (начало координат) соответствует
вероятности, равной единице. Чем меньше
вероятность ошибки, тем ниже на оси
ординат располагается соответствующее
значение вероятности. На графике особо
указана точка, соответствующая заданной
мощности сигнала Pc.
В проведенных выше расчетах вероятность
ошибки вычислено без учета помехоустойчивого
или статистического кодирования.
4. Сравнение выбранной схемы приемника с оптимальным приемником
Оптимальный
приемник– это такой приемник, который
обеспечивает максимальную помехоустойчивость
при данном способе передачи (данном
виде сигнала) и данном виде помех.
Различают оптимальный приемник полностью
известных сигналов и оптимальный
приемник неполностью известных сигналов,
когда приемник использует не все
параметры сигнала, например, не учитывает
фазу несущего колебания. В первом случае
приемник обеспечивает максимально
возможную (потенциальную) помехоустойчивость.
Потенциальная
помехоустойчивость достигается благодаря
тому, что при приеме учитываются все
параметры сигнала, не несущие информации:
амплитуда, частота, фаза несущего
колебания, а также длительность сигнала
Т, т.к. интегрирование (фильтрация)
осуществляется в течение этого времени.
Решение о принятом сигнале обычно
осуществляется в конце каждого интервалаТ, для чего в приемнике должна иметься
специальная система синхронизации
элементов сигнала.
Алгоритм
идеального приемника Котельниковапри равной вероятности сигналов
и
имеет вид:
,
то
,
иначе
,
где y(t)– сигнал на входе приемника, содержащий,
кроме помехиn(t),
также ожидаемый сигнал
,
либо
.
Физический
смысл неравенства: если среднеквадратическое
отклонениеy(t)от возможного сигнала
меньше, чем среднеквадратическое
отклоненияy(t)от
,
тоy(t)ближе к
(содержит
)
и приемник выдает
;
иначе приемник выдает
.
Структурная
схема оптимального приемного устройства
приведена на рис. 7. На схеме “–“ –
вычитающие устройства; генераторы
опорных сигналов
и
;
«Кв» – квадраторы (устройства возведения
в квадрат);
–
интеграторы; РУ – решающее устройство
(схема сравнения), определяющее в моменты
времени, кратныеT(при замыкании ключей), номер ветви с
минимальным сигналом.
Рис.7 –
Структурная схема идеального приемника
Котельникова
Сравнительный
анализ помехоустойчивости ДАМ, ДЧМ, ДФМ
Помехоустойчивостьприемника определяется вероятностью
ошибки при заданном отношении
сигнал/помеха. Для разных видов модуляции
помехоустойчивость различна.
В общем виде
вероятность ошибкиопределяется
формулой:

где E– энергия элемента сигнала,N0– спектральная мощность помехи.
При оптимальной
фильтрации вводится величина:
.
При дискретной
амплитудной модуляции (ДАМ):
(Еравна энергии первого сигнала);
.
Подставив эту
величину в формулу, получим:
При дискретной
частотной модуляции(ДЧМ):
.
При частотной
модуляции сигналы
и
являются взаимноортогональными,
поэтому их функция взаимной корреляции
равна нулю. Кроме того, благодаря равной
амплитуде сигналовЕ1=Е2.
В результате
Е = 2Е1и
.
Подставив эту
величину в формулу , получим:
При дискретной
фазовой модуляции (ДФМ):
Подставив эту
величину в формулу, получим:
Сравнивая между
собой формулы, видно, что для достижения
заданной вероятности ошибки при ДЧМ
требуется величина h0в
больше, чем при ДФМ, а при ДАМ – в 2 раза
больше, чем при ДФМ. Отсюда следует, что
переход от ДАМ к ДЧМ дает двукратный
выигрыш по мощности, а к ДФМ –
четырехкратный. Причину этого можно
наглядно установить, рассматривая
векторные диаграммы сигналов для разных
видов модуляций.
Рисунок 8–
Векторные диаграммы сигналов для разных
видов модуляции
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Рассчитаем — вероятность ошибки цифрового сигнала на выходе приёмника, учитывая особенности передачи сигнала по каналу связи.
Вероятность ошибочного приема при относительной фазовой модуляции и некогерентном способе приема для известного отношения сигнала / шум определяется согласно следующему выражению:
(3.1)
где — соотношение сигнал/шум находится как:
(3.2)
где — мощность сигнала на входе приёмника;
— спектральная плотность.
(3.3)
Используя (3.1), (3.2) и (3.3) рассчитываем:
Длина кодового слова:
(3.4)
где — число уровней квантования.
n=log2 256=8
Рассчитаем длительность кодового слова для заданной системы связи:
Длительность между посылками кодовых слов ?t=125 мкс, длительности кодового слова = . Свободное же между посылками время . Это свободное время может быть использовано для применения помехоустойчивого кодирования, или для создания многоканальной системы связи, или же для улучшения соотношения сигнал/шум.
Полученная вероятность ошибки велика по сравнению с вероятностью ошибки в соответствии с ГОСТ’ом (). Чтобы уменьшить вероятности ошибки хотя бы на 2-3 порядка можно сузить полосу пропускания системы путём увеличения длительности элементарной посылки, поставить оптимальный фильтр, увеличить длительность кодового слова или же перейти к другому виду модуляции. В данном случае это не целесообразно, так как ОФМ является наилучшим видом модуляции.
Сравнение выбранной схемы с оптимальным приемником
Для уменьшения вероятности ошибки мы поставим в схему приемника оптимальный фильтр (Рис. 4.1). Оптимальный фильтр улучшает соотношения сигнал/шум, но при этом возникает межсимвольная интерференция, которую можно устранить путем установки в схему ключа, который будет разряжать интегрирующую цепочку после поступления каждого импульса. Схема приемника сигнала усложняется, что может сказаться на надежности, однако выигрыш в соотношении сигнал/шум существенен.
Теперь соотношение сигнал/шум находится как:
(4.1)
При помощи (4.1) и (3.1) найдем вероятность ошибки и соотношение сигнал/шум:
При установки в схему согласованного фильтра мы добились того, что наша вероятность ошибки стала оптимальной за счет уменьшения полосы пропускания. Оставшееся свободное время можно использовать для организации служебного канала, Интернета или помехоустойчивого кодирования.
Все дальнейшие расчёты будем производить с данными для оптимального приёмника, полученными в этом пункте:
мкс;
Передача аналоговых сигналов методом ИКМ
Прямое аналого-цифровое преобразование является высококачественным методом кодирования. Еще в 60-х годах был принят алгоритм оцифровки голоса под названием импульсно-кодовой модуляции (ИКМ). Оцифровка голосового сигнала включает измерение уровня аналогового сигнала через равные промежутки времени. В соответствии со стандартом принимается, что для узнаваемости голоса необходимо обеспечить передачу его частотных составляющих в диапазоне от 300 до 3400 Гц.
Для преобразования непрерывных сообщений в дискретную форму (сигналы импульсно-кодовой модуляции) используются операции дискретизации и квантования. Полученная таким образом последовательность квантовых отсчётов кодируется и передаётся по дискретному каналу, как всякое дискретное сообщение. На приёмной стороне после декодирования восстанавливается (с той или иной точностью) непрерывное сообщение.
Для передачи непрерывных сообщений методом ИКМ можно воспользоваться дискретным каналом. Для этого необходимо преобразовать непрерывное сообщение в дискретный сигнал, то есть в последовательность символов, сохранив содержащуюся в сообщении существенную часть информации. Типичными примерами цифровых систем передачи непрерывных сообщений являются системы с кодово-импульсной модуляцией и дельта-модуляцией (ДМ).
Кодово-импульсная модуляция складывается из трех операций: дискретизация по времени в соответствии с теоремой Котельникова , квантование отсчетов и кодирование квантованных отсчетов блочным равновесным двоичным кодом. При этом каждый отсчет кодируется в одну комбинацию представлением отображающей его m-ичной цифры в двоичной (m=2) системе счисления. Для полного использования кода, число квантованных значений m=N, обычно выбирают m=2n. Для речевых сообщений чаще всего m=32, 64, 128 и 256, что соответствует n= 5, 6, 7 и 8.
Цифровые методы передачи обладает рядом преимуществ перед аналоговыми. Из основных можно указать следующие:
малое влияние аппаратурных погрешностей на точность передачи сообщения;
высокая помехоустойчивость;
возможность регенерации сигналов (восстановление их формы) при ретрансляции;
высокие технико-экономические показатели — широкое использование элементов цифровой техники, низкие требования к линейности общего тракта и т.д.
При цифровой системе передачи непрерывных сообщений можно повысить верность применением помехоустойчивого кодирования. Высокая помехоустойчивость цифровых систем позволяет осуществить практически неограниченную по дальности связи при использовании каналов сравнительно на высокого качества.
Другим существенным преимуществом цифровых систем передачи информации является широкое использование в аппаратуре преобразования сигналов современной элементарной базы цифровой вычислительной техники и микроэлектроники. Более того, на цифровой основе могут быть объединены в единой системе сигналы передачи данных с сигналами передачи речи и телевидения.
Рассмотрим структурную схему цифрового канала связи. В отличие от аналогового канала передачи, в составе цифрового канала предусмотрены устройства для преобразования непрерывного сообщения в цифровую форму — АЦП на передающей стороне и устройства преобразования цифрового сигнала в непрерывный — АЦП на приемной стороне.
Полученный с выхода АЦП сигнал ИКМ поступает или непосредственно в линию связи или на вход передатчика (модулятора), где последовательность двоичных импульсов преобразуется в радиоимпульсы.
На приемной стороне лини связи последовательность импульсов после демодуляции и регенерации в приемнике поступает на ЦАП, назначение которого состоит обратном преобразовании (восстановлении) непрерывного сообщения по принятой последовательности кодовых комбинаций. В состав ЦАП входят декодирующее устройство, предназначенное для преобразования кодовых комбинаций в квантованную последовательность отсчетов, и сглаживающий фильтр, восстанавливающий непрерывные сообщения по квантованным значениям.
Преобразование непрерывных сообщений в цифровую форму в системах ИКМ округлением мгновенных значений до ближайших разрешенных уровней квантования. Возникающая при этом погрешность представления является неустранимой, но контролируемой (так как не превышает половины уровня квантования). Выбрав достаточно малый шаг квантования, можно обеспечить эквивалентность по заданному Е-критерию исходного и квантованного сообщений. Погрешность (ошибку) квантования, представляют собой разность между исходным сообщением и сообщением восстановленным по квантованным отчетам, называют «шумом квантования».
Одной из причин, приводящих к отличию принятого сообщения от переданного в системе с ИКМ, является шум квантования, другой — помехи в канале, которые накладываются на передаваемые символы кодовых комбинаций и могут вызывать ошибки. Ошибки в символах (при отсутствии избыточности) приводят к ошибочному декодированию всей кодовой комбинации.
Длина кода определяется из следующего неравенства:
, при этом , так как .
В данной курсовой работе было заданно число уровне квантования N=256=28, то есть n=8.
Большое значение, для оценки качества принимаемого сигнала, имеет понятие шумы квантования. Этот шум не связан с помехами в канале и целиком определяется выбором числа уровней квантования. Его можно сделать сколь угодно малым, увеличивая число уровней. Воздействие шума квантования можно заметно уменьшить, применяя неравномерное квантование, при котором большие уровни сообщения квантуются с большим шагом, а низкие уровни — с меньшим шагом. Шум квантования при этом коррелирован с сообщением и имеет тем меньшую мгновенную мощность, чем меньше уровень сообщения. Это позволяет лучше различать слабые отрезки сообщения.
Отношение мощности сигнала к мощности шума квантования определяется выражением
(5.1)
где n — число разрядов кода, П — пик-фактор сигнала.
Мощность шума квантования находится по следующей формуле:
В2 (5.2)
Данный способ передачи имеет очень важные положительные качества. Самое главное данный способ обеспечивает не накопление ошибок при передаче сигнала через ретрансляторы. В сравнении с аналоговыми способами передачи требует значительно меньшую мощность при той же вероятности ошибки. Пригоден для передачи цифровых данных. Аппаратура системы связи строится на дискретных элементах, которые не требуют настройки.
К недостаткам можно отнести необходимость в широкополосном канале связи.
В данном случае шумами квантования, В2, можно пренебречь и число уровней квантования, N=256, будет достаточно.
Содержание
Задание
1.
Структурная
схема системы
связи
2.
Выбор
схемы приемника
3.
Расчет
вероятности ошибки на выходе приемника
4.
Сравнение
выбранной схемы с оптимальным приемником
5.
Передача
аналоговых сигналов методом ИКМ
6.
Помехоустойчивое
кодирование
7.
Пропускная
способность канала связи
Заключение
Задание
Разработать структурную схему системы
связи, предназначенной для передачи данных и передачи аналоговых сигналов
методом ИКМ для заданного вида модуляции и способа приема сигналов. Рассчитать
основные параметры системы связи. Указать и обосновать пути совершенствования
разработанной системы связи.
Исходные данные
Вид модуляции — ОФМ;
Способ приема – способ сравнения фаз;
Мощность сигнала на входе приемника
Рс=3,2 мВт;
Длительность элементарной посылки Т=4
мкс;
Помеха-белый шум с гауссовским законом
распределения,
Спектральная плотность мощности помехи
No=0,001 мкВт/Гц;
Вероятность передачи сигнала
«1» Р(1)=0,9
Число уровней квантования N=128
Пик-фактор аналогового сигнала П=2,2
1.
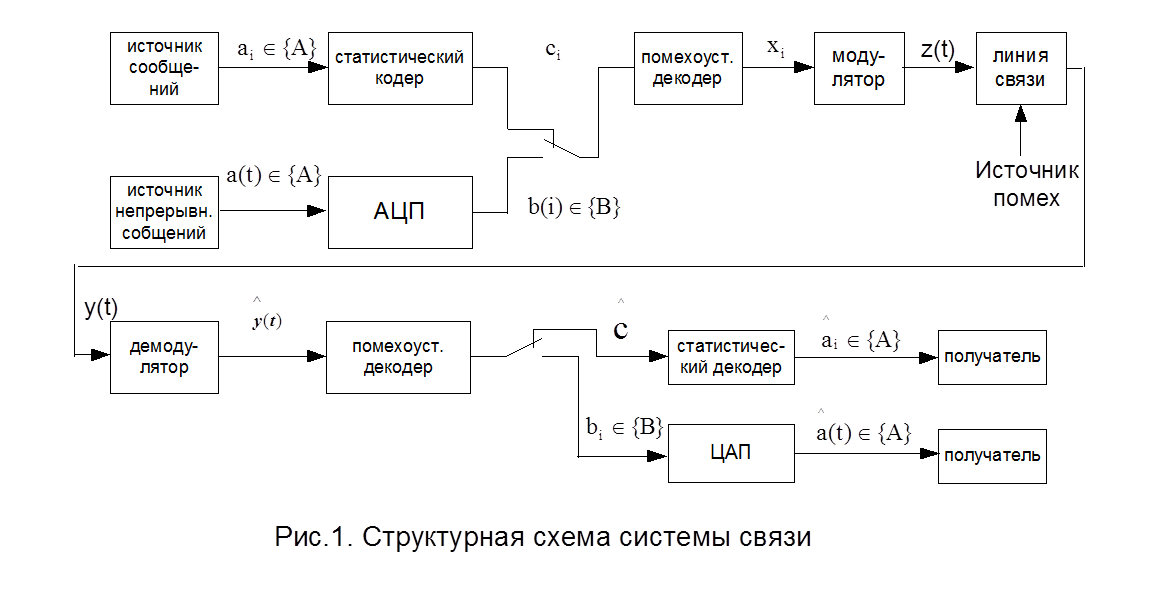
Структурная схема системы связи
Системой связи называется совокупность
технических средств, обеспечивающих передачу информации от источника (И) к
получателю (П). Этими средствами являются передающее устройство, линия связи и
приемное устройство.
Основное устройство системы — канал
связи – расположен между источником и получателем сообщения.
Передающее устройство преобразует
сообщение (речь, изображение, данные от различных датчиков) в электрический
сигнал. При передаче аналоговых сигналов по дискретному каналу необходимо
преобразовать непрерывное сообщение в цифровой сигнал. Обычно используют
системы с импульсно-кодовой модуляцией (ИКМ) и дельта-модуляцией (ДМ).
Передаваемое сообщение представляется в виде последовательности m-ичных кодовых
комбинаций. Полученный с выхода АЦП сигнал ИКМ поступает на вход модулятора,
где последовательность двоичных импульсов преобразуется в радиоимпульсы. На
приемной стороне линии связи последовательность импульсов после демодуляции и
регенерации в приемнике поступает на цифроаналоговый преобразователь ЦАП,
назначение которого состоит в восстановлении непрерывного сообщения по принятой
последовательности кодовых комбинаций.
Статистическое кодирование применяют для
повышения пропускной способности канала связи, помехоустойчивое – для повышения
помехоустойчивости.
2.
Выбор схемы приемника
На вход приемного устройства любой
системы связи обычно поступает смесь переданного сигнала S(t) и помехи п(t):
x(t)=S(t)+п(t), причем сигнал S(t) представляет
собой, как правило, сложное колебание, содержащее множество параметров: S(t)=f(a,b,c,…t). Основной
задачей приемника является определение параметров сигнала, несущего информацию
с помощью всех остальных параметров сигнала, не несущих информацию. Оптимальный
приемник выполняет это наилучшим образом, когда обеспечивается наибольшее
значение показателя качества.
Дискретная фазовая модуляция
обеспечивает наиболее высокую помехоустойчивость приема дискретных сигналов.
Однако при практической реализации под действием помех возможна «обратная
работа». Для устранения «обратной работы» применяется «относительная» фазовая
модуляция ОФМ.
При
приеме ОФМ осуществляется сравнение фазы каждой посылки с фазой предыдущей посылки.
Если фаза очередной посылки совпадает с фазой предыдущей, то приемник выдает
«1», если же фазы противоположны, то приемник выдаст «0». При некогерентном
приеме ОФМ сигналов в приемнике вместо опорного генератора используется линия задержки,
задерживающая входной высокочастотный сигнал на время, равное длительности
элементарной посылки:
Рис.2. Схема некогерентного ОФМ приемника
Так
как в этой схеме опорное напряжение содержит, кроме высокочастотного напряжения
предыдущей посылки, также составляющую помехи, то эта схема обеспечивает
меньшую помехоустойчивость, чем схема когерентного приемника.
3. Расчет вероятности ошибки на выходе
приемника
Для приемника ОФМ сигнала,
вероятность ошибки при некогерентном приеме, описывается выражением:
Рассчитаем вероятность ошибки на выходе
приемника при ОФМ, Рс=3,2 мВт, Т=4 мкс: :Здесь
Рош=8,308·10-4
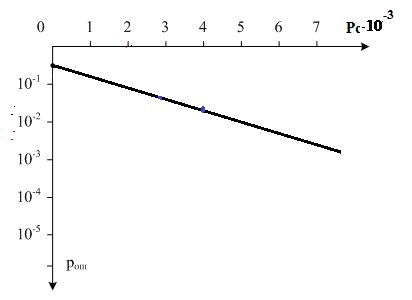
Рассчитаем зависимость вероятности
ошибки от мощности сигнала:
Рис.3 График
зависимости вероятности ошибки от мощности сигнала
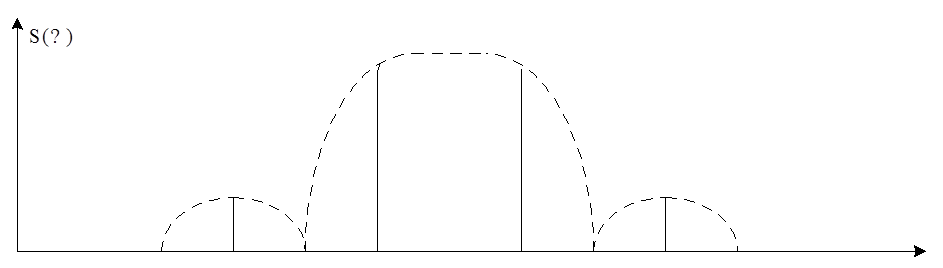
ω0-Ω3 ω1 ω0-Ω1 ω0 ω0+Ω1 ω0+Ω3 ω
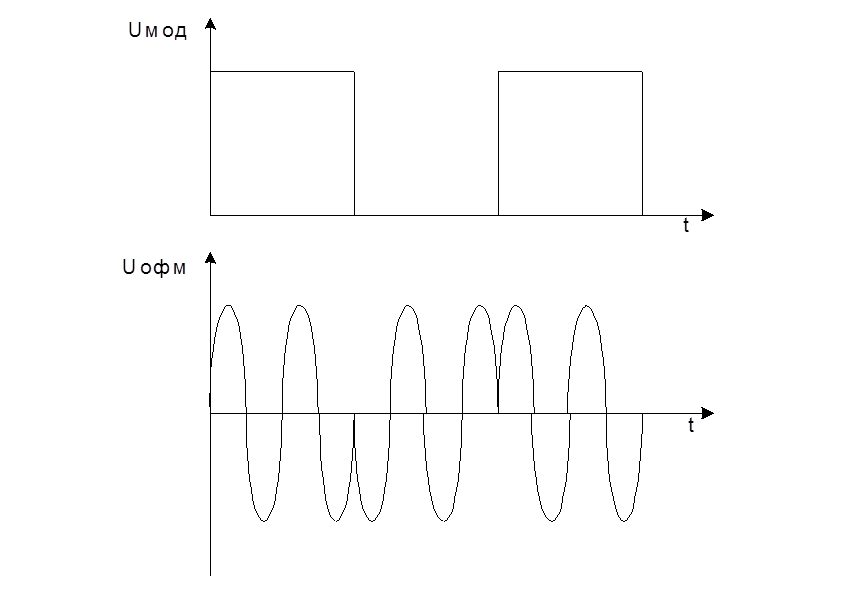
Рис.4.
Временная и спектральная диаграммы ОФМ сигнала.
4 Сравнение выбранной схемы приемника с
оптимальным приемником