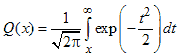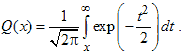From Wikipedia, the free encyclopedia
In digital transmission, the number of bit errors is the numbers of received bits of a data stream over a communication channel that have been altered due to noise, interference, distortion or bit synchronization errors.
The bit error rate (BER) is the number of bit errors per unit time. The bit error ratio (also BER) is the number of bit errors divided by the total number of transferred bits during a studied time interval. Bit error ratio is a unitless performance measure, often expressed as a percentage.[1]
The bit error probability pe is the expected value of the bit error ratio. The bit error ratio can be considered as an approximate estimate of the bit error probability. This estimate is accurate for a long time interval and a high number of bit errors.
Example[edit]
As an example, assume this transmitted bit sequence:
1 1 0 0 0 1 0 1 1
and the following received bit sequence:
0 1 0 1 0 1 0 0 1,
The number of bit errors (the underlined bits) is, in this case, 3. The BER is 3 incorrect bits divided by 9 transferred bits, resulting in a BER of 0.333 or 33.3%.
Packet error ratio[edit]
The packet error ratio (PER) is the number of incorrectly received data packets divided by the total number of received packets. A packet is declared incorrect if at least one bit is erroneous. The expectation value of the PER is denoted packet error probability pp, which for a data packet length of N bits can be expressed as
,
assuming that the bit errors are independent of each other. For small bit error probabilities and large data packets, this is approximately
Similar measurements can be carried out for the transmission of frames, blocks, or symbols.
The above expression can be rearranged to express the corresponding BER (pe) as a function of the PER (pp) and the data packet length N in bits:
Factors affecting the BER[edit]
In a communication system, the receiver side BER may be affected by transmission channel noise, interference, distortion, bit synchronization problems, attenuation, wireless multipath fading, etc.
The BER may be improved by choosing a strong signal strength (unless this causes cross-talk and more bit errors), by choosing a slow and robust modulation scheme or line coding scheme, and by applying channel coding schemes such as redundant forward error correction codes.
The transmission BER is the number of detected bits that are incorrect before error correction, divided by the total number of transferred bits (including redundant error codes). The information BER, approximately equal to the decoding error probability, is the number of decoded bits that remain incorrect after the error correction, divided by the total number of decoded bits (the useful information). Normally the transmission BER is larger than the information BER. The information BER is affected by the strength of the forward error correction code.
Analysis of the BER[edit]
The BER may be evaluated using stochastic (Monte Carlo) computer simulations. If a simple transmission channel model and data source model is assumed, the BER may also be calculated analytically. An example of such a data source model is the Bernoulli source.
Examples of simple channel models used in information theory are:
- Binary symmetric channel (used in analysis of decoding error probability in case of non-bursty bit errors on the transmission channel)
- Additive white Gaussian noise (AWGN) channel without fading.
A worst-case scenario is a completely random channel, where noise totally dominates over the useful signal. This results in a transmission BER of 50% (provided that a Bernoulli binary data source and a binary symmetrical channel are assumed, see below).
In a noisy channel, the BER is often expressed as a function of the normalized carrier-to-noise ratio measure denoted Eb/N0, (energy per bit to noise power spectral density ratio), or Es/N0 (energy per modulation symbol to noise spectral density).
For example, in the case of QPSK modulation and AWGN channel, the BER as function of the Eb/N0 is given by:

People usually plot the BER curves to describe the performance of a digital communication system. In optical communication, BER(dB) vs. Received Power(dBm) is usually used; while in wireless communication, BER(dB) vs. SNR(dB) is used.
Measuring the bit error ratio helps people choose the appropriate forward error correction codes. Since most such codes correct only bit-flips, but not bit-insertions or bit-deletions, the Hamming distance metric is the appropriate way to measure the number of bit errors. Many FEC coders also continuously measure the current BER.
A more general way of measuring the number of bit errors is the Levenshtein distance.
The Levenshtein distance measurement is more appropriate for measuring raw channel performance before frame synchronization, and when using error correction codes designed to correct bit-insertions and bit-deletions, such as Marker Codes and Watermark Codes.[3]
Mathematical draft[edit]
The BER is the likelihood of a bit misinterpretation due to electrical noise 





Knowing that the noise has a bilateral spectral density 


and 

Returning to BER, we have the likelihood of a bit misinterpretation 


where 

We can use the average energy of the signal 
±§
Bit error rate test[edit]
BERT or bit error rate test is a testing method for digital communication circuits that uses predetermined stress patterns consisting of a sequence of logical ones and zeros generated by a test pattern generator.
A BERT typically consists of a test pattern generator and a receiver that can be set to the same pattern. They can be used in pairs, with one at either end of a transmission link, or singularly at one end with a loopback at the remote end. BERTs are typically stand-alone specialised instruments, but can be personal computer–based. In use, the number of errors, if any, are counted and presented as a ratio such as 1 in 1,000,000, or 1 in 1e06.
Common types of BERT stress patterns[edit]
- PRBS (pseudorandom binary sequence) – A pseudorandom binary sequencer of N Bits. These pattern sequences are used to measure jitter and eye mask of TX-Data in electrical and optical data links.
- QRSS (quasi random signal source) – A pseudorandom binary sequencer which generates every combination of a 20-bit word, repeats every 1,048,575 words, and suppresses consecutive zeros to no more than 14. It contains high-density sequences, low-density sequences, and sequences that change from low to high and vice versa. This pattern is also the standard pattern used to measure jitter.
- 3 in 24 – Pattern contains the longest string of consecutive zeros (15) with the lowest ones density (12.5%). This pattern simultaneously stresses minimum ones density and the maximum number of consecutive zeros. The D4 frame format of 3 in 24 may cause a D4 yellow alarm for frame circuits depending on the alignment of one bits to a frame.
- 1:7 – Also referred to as 1 in 8. It has only a single one in an eight-bit repeating sequence. This pattern stresses the minimum ones density of 12.5% and should be used when testing facilities set for B8ZS coding as the 3 in 24 pattern increases to 29.5% when converted to B8ZS.
- Min/max – Pattern rapid sequence changes from low density to high density. Most useful when stressing the repeater’s ALBO feature.
- All ones (or mark) – A pattern composed of ones only. This pattern causes the repeater to consume the maximum amount of power. If DC to the repeater is regulated properly, the repeater will have no trouble transmitting the long ones sequence. This pattern should be used when measuring span power regulation. An unframed all ones pattern is used to indicate an AIS (also known as a blue alarm).
- All zeros – A pattern composed of zeros only. It is effective in finding equipment misoptioned for AMI, such as fiber/radio multiplex low-speed inputs.
- Alternating 0s and 1s — A pattern composed of alternating ones and zeroes.
- 2 in 8 – Pattern contains a maximum of four consecutive zeros. It will not invoke a B8ZS sequence because eight consecutive zeros are required to cause a B8ZS substitution. The pattern is effective in finding equipment misoptioned for B8ZS.
- Bridgetap — Bridge taps within a span can be detected by employing a number of test patterns with a variety of ones and zeros densities. This test generates 21 test patterns and runs for 15 minutes. If a signal error occurs, the span may have one or more bridge taps. This pattern is only effective for T1 spans that transmit the signal raw. Modulation used in HDSL spans negates the bridgetap patterns’ ability to uncover bridge taps.
- Multipat — This test generates five commonly used test patterns to allow DS1 span testing without having to select each test pattern individually. Patterns are: all ones, 1:7, 2 in 8, 3 in 24, and QRSS.
- T1-DALY and 55 OCTET — Each of these patterns contain fifty-five (55), eight bit octets of data in a sequence that changes rapidly between low and high density. These patterns are used primarily to stress the ALBO and equalizer circuitry but they will also stress timing recovery. 55 OCTET has fifteen (15) consecutive zeroes and can only be used unframed without violating one’s density requirements. For framed signals, the T1-DALY pattern should be used. Both patterns will force a B8ZS code in circuits optioned for B8ZS.
Bit error rate tester[edit]
A bit error rate tester (BERT), also known as a «bit error ratio tester»[4] or bit error rate test solution (BERTs) is electronic test equipment used to test the quality of signal transmission of single components or complete systems.
The main building blocks of a BERT are:
- Pattern generator, which transmits a defined test pattern to the DUT or test system
- Error detector connected to the DUT or test system, to count the errors generated by the DUT or test system
- Clock signal generator to synchronize the pattern generator and the error detector
- Digital communication analyser is optional to display the transmitted or received signal
- Electrical-optical converter and optical-electrical converter for testing optical communication signals
See also[edit]
- Burst error
- Error correction code
- Errored second
- Pseudo bit error ratio
- Viterbi Error Rate
References[edit]
- ^ Jit Lim (14 December 2010). «Is BER the bit error ratio or the bit error rate?». EDN. Retrieved 2015-02-16.
- ^
Digital Communications, John Proakis, Massoud Salehi, McGraw-Hill Education, Nov 6, 2007 - ^
«Keyboards and Covert Channels»
by Gaurav Shah, Andres Molina, and Matt Blaze (2006?) - ^ «Bit Error Rate Testing: BER Test BERT » Electronics Notes». www.electronics-notes.com. Retrieved 2020-04-11.
This article incorporates public domain material from Federal Standard 1037C. General Services Administration. (in support of MIL-STD-188).
External links[edit]
- QPSK BER for AWGN channel – online experiment

13
период выходной последовательности всегда8 в два раза больше периода входной!
Расчет вероятности битовой ошибки
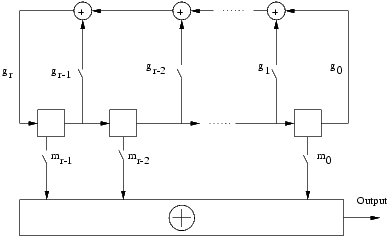
Перейдем теперь к расчету вероятности ошибки на выходе дифференциального декодера. Вероятность ошибки на входе декодера считается заданной, и определяется каналом передачи информации.
Пусть ошибки в канале независимые и происходят с вероятностью p . Тогда дифференциальный кодер, канал и декодер в эквиваленте дадут канал с памятью, т. е. такой канал, ошибки в котором — зависимые. Канал с памятью может быть описан с помощью следующей модели, рис. 2.
Рис. 2 Модель канала с памятью
Такой канал полностью вероятностей
Здесь буквой «П» обозначено событие «правильный прием», буквой «О» — «ошибочный прием». Обозначение PП/О означает «вероятность правильного приема при условии, что предыдущий прием был ошибочным». Эта вероятность является условной. Зависимость вероятности от условия является признаком наличия памяти в канале. определяется матрицей условных (переходных)
|
P= |
PП/П |
PП/О |
. |
(9) |
|
PО/О) |
||||
|
(PО/П |
Обратите внимание, что буквам «П» и «О» слева соответствует момент времени tn−1 , а таким же буквам справа — tn . Время — это неотъемлемая черта каналов с памятью. Говорят, «канал помнит несколько предыдущих состояний», и эти состояния влияют на вероятность текущего состояния.
Систему «дифференциальный кодер, канал и декодер» удобно рассматривать как некоторый цифровой автомат, на выходе которого в каждый момент времени либо правильный прием, либо — ошибочный; жизнь такого автомата описывается некоторой последовательностью букв
8 За исключением случая когда числитель Y (z) сокращает знаменатель K (z ) , — в этом случае период не меняется
(матрице переходных вероятностей)
(т. е. в канале с независимыми
14
… О П П П П П О О П П П …
Цель нашего повествования — вычислить вероятность ошибки на выходе дифференциального декодера, которая в рамках принятых обозначений
|
соответствует событию «О» и обозначается |
как PО |
. Эта вероятность будет |
|
зависеть от вероятностей перехода PX/X , |
которых, |
по сути, всего две, т. к. |
|
оставшиеся две являются дополнениями до единицы. |
Всякая вероятность есть предельная величина, определяемая по бесконечному количеству событий, поэтому чтобы определить PО требуется выписать всю «линию жизни» автомата и подсчитать долю букв «О» относительно общего количества букв; практически это сделать невозможно, а вот в уме — возможно, чем мы и займемся.
Предположим, что автомат начал жить, и его жизнь кратна дням, т. е. каждый день выпадает буква, «О» или «П». Какова вероятность того, что в первый день жизни произойдет ошибочный прием «О»? Эту вероятность логично приравнять к вероятности ошибки в канале без памяти
ошибками), PО 1 =p . Во второй день могут выпасть буквы либо «О», либо «П». Соответствующие вероятности вычисляются вполне однозначно по матрице канала
(PPПО)2 =(PPП/ПО/П PPП/ОО/О)(PPПО)1 ,
и так далее. Логика данного уравнения основана на формуле умножения и сложения вероятностей.
Упражнение: распишите матричное уравнение в виде системы линейных алгебраических уравнений, и поразмыслите над смыслом умножения и сложения вероятностей.
Пусть теперь уже прошло очень много дней жизни автомата… В этом случае вероятности PО n и PП n должны сходиться к искомым безусловным вероятностям PО и PП
|
PП n+1 ≈ PП n |
, |
lim |
PП n = PП |
. |
(10) |
|
|
(PО) |
(PО) |
n→∞ |
(PО) (PО) |
Тогда справедливо предельное равенство

15
(PPПО)=(PPП/ПО/П PPП/ОО/О)(PPПО) ,
из которого однозначно определяются искомые вероятности
|
PО= |
PО/П |
, |
PП=1−PО= |
PП/О |
. |
(11) |
|
|
PП/О +PО/П |
PО/П+PП/О |
||||||
|
Остается понять как |
переходные вероятности |
зависят |
от вероятности |
ошибки p в канале без памяти, и цель данного повествования будет достигнута.
Предположим для наглядности, что передаются одни нули, тогда единицы будут указывать на ошибки Рассмотрим все возможные комбинации канальных ошибок на входе дифференциального декодера. Разделим рассмотрение на четыре части, согласно матрице переходных вероятностей (9).
I. Правильный прием в предыдущем и текущем битах, PП/П :
1 1 1, декодируем как 0 0,
0 0 0, декодируем как 0 0,
(1 + 1 = 0, 1 + 1 = 0),
(0 + 0 = 0, 0 + 0 = 0).
Вероятность этого события равна PП/П=p2 +(1−p)2 .
Замечание: здесь и далее первый бит (вспомогательный), который не выделен жирным шрифтом, не влияет на вероятность, потому что перебираются все его возможные значения, 0 и 1; следующие два бита полностью определяются значением вспомогательного и поставленным ограничивающим условием.
II. Ошибочный прием в предыдущем бите и правильный — в текущем, PП/О : 0 1 1, декодируем как 1 0, (0 + 1 = 1, 1 + 1 = 0), 1 0 0, декодируем как 1 0, (1 + 0 = 1, 0 + 0 = 0).
Вероятность этого события равна PП/О=p2 +(1−p)2 . III.Ошибочный прием в предыдущем и текущем битах, PО/О :
0 1 0, декодируем как 1 1, (0 + 1 = 1, 1 + 0 = 1), 1 0 1, декодируем как 1 1, (1 + 0 = 1, 0 + 1 = 1).
Вероятность этого события равна PО/О= p(1−p)+(1−p) p=2 p(1− p) .
16
IV.Правильный прием в предыдущем и ошибочный — в текущем, PО/П : 0 0 1, декодируем как 0 1, (0 + 0 = 0, 0 + 1 = 1), 1 1 0, декодируем как 0 1, (1 + 1 = 0, 1 + 0 = 1).
|
Вероятность этого события равна |
PО/П=p(1−p)+(1− p) p=2 p(1−p) . |
||
|
Подставим найденные переходные вероятности в (11) и получим |
|||
|
окончательный результат |
|||
|
PО=2 p(1−p) , |
PП= p2 +(1−p)2 . |
(12) |
|
|
Таким образом, вероятность ошибки на выходе дифференциального |
|||
|
декодера почти в два раза превышает канальную вероятность ошибки p |
; этот |
||
|
результат тем точнее, чем лучше |
канал, |
т. е. чем меньше p . Данный |
факт |
объясняется достаточно просто: при малых p ошибки происходят изредка и, в основном, по одиночке, а из логики дифференциального декодирования следует, что одна одиночная ошибка после декодирования трансформируется в две.
Любопытно также отметить, что если в канале вероятность ошибки равна ½, то после дифференциального декодирования вероятность ошибки остается той же!
Введение
Моя сеть приёма сигналов со спутников r2cloud постепенно растёт. Однако уровень приёма оставляет желать лучшего. Несмотря на то, что на спектограмме виден сигнал, демодулятор не может восстановить его. В попытках найти проблему, я понял, что мне не хватает фундаментальных знаний по теории обработки сигналов и некоторой математики. Дело в том, что в интернете зачастую выкладываются демодуляторы без обоснования их работы. Меня это не устраивает, потому что нужны метрики по которым я буду понимать насколько один алгоритм эффективнее другого. И стал ли новый код лучше, если я добавлю какой-нибудь другой блок в обработку.
Всё это привело меня к \( E_b / N_0 \). Эта метрика показывает отношение энергии сигнала, приходящейся на 1 бит принимаемого сообщения (\( E_b \)), к энергетической спектральной плотности шума (\( N_0 \)). Почему она так важна? Дело в том, что она не зависит от способа модуляции сигнала и пропускной способности канала. Из-за этого её можно использовать, чтобы сравнивать различные модуляции между собой. Обычно строят график отношения \( E_b / N_0 \) к вероятности ошибки (BER). Вот пример графика сравнения BPSK/QPSK/8-PSK/16-PSK:
Что из этого графика можно понять?
- Если увеличивать энергию передаваемого бита, то уменьшается вероятность возникновения ошибки.
- В BPSK/QPSK ошибка возникает значительно реже, чем в 8-PSK и 16-PSK при одинаковых значениях энергии передаваемого бита.
- График, например, читается следующим образом: при \( E_b / N_0 \) равным 4 децибелла и BPSK модуляции можно получить 1 ошибочный бит на каждые 100 полученных.
Мне же график прежде всего нужен:
- Сравнивать теоретические значения с практической реализацией демодулятора. Прямо сейчас я точно знаю, что различия есть из-за ограниченной точности АЦП. Дело в том, что rtl-sdr имеет разрешающую способность 8 бит. А в теории числа могут быть бесконечной точности. Именно эта разница и должна давать ошибку.
- Анализировать улучшится ли демодулятор, если добавить какой-то определённый блок. Как минимум я хочу попробовать различные алгоритмы получения несущего сигнала и компенсации многолучевого распространения.
Ну и для того, чтобы понять математику, я решил проделать выводы сам. Ниже я буду рассчитывать вероятности ошибки для BPSK (см. синий график выше). Вдохновение я черпал у dsplog плюс добавлял свои мысли.
Дано
Прежде всего необходимо описать физику процесса. Схема процесса показана ниже:
- Изначальное сообщение кодируется в аналоговый сигнал. “1” кодируется в \(+\sqrt{E_b}\), “0” кодируется в \(-\sqrt{E_b}\). Почему именно как корень из \(E_b\)? Не знаю. Это единственное место, где я не разобрался.
- После этого сигнал складывается с аддитивным белым гауссовским шумом.
- Далее сигнал демодулируется.
Модулированный BPSK сигнал выглядит следующим образом:
Красными точками обозначается сигнал без шума. Синими — сигнал с добавлением белого гауссовского шума. Как демодулируется этот сигнал? Все точки, которые больше “0” становятся “1”, а те, что меньше “0” становятся “0”. На рисунке выше все синие точки достаточно далеко от “0”, поэтому информацию можно однозначно восстановить. Но что если шум будет сильнее?
Тут уже не всё так однозначно. Видно, что некоторые точки закодированные как “1” на самом деле оказались меньше “0”. И если бы я попытался их демодулировать, то получил бы неправильную информацию.
Решение
Теперь, когда стало понятно влияние шума на результат демодуляции, можно переходить к графику зависимости вероятности от энергии сигнала. Этот график поможет посчитать вероятность ошибок для различных входных значений. Для начала возьмём сигнал без шума. Вероятность получения “0” или “1” всегда 1.
Частота получения ошибочных битов (Bit error rate) будет 0. Т.е. 0 ошибочных битов на бесконечное количество принятых. В случае наличия гауссовского шума, вероятность получения определяется гауссовской функцией вероятности:
Гауссовский шум определяется следующей формулой:
$$
p(x) = \dfrac{1}{\sqrt{2\pi\sigma^2}}e^\dfrac{-(x-\mu)^2}{2\sigma^2}
$$
Где:
- \(\mu=0\),
- \(\sigma^2=N_0/2\)
При передаче “1” \(\mu=+\sqrt{E_b}\), при “0” \(\mu=-\sqrt{E_b}\). Подставляя это в формулу:
$$
\begin{align}
P(x|s_0)=\dfrac{1}{\sqrt{\pi N_0}}e^\dfrac{-(x+\sqrt{E_b})^2}{N_0} \newline
P(x|s_1)=\dfrac{1}{\sqrt{\pi N_0}}e^\dfrac{-(x-\sqrt{E_b})^2}{N_0}
\end{align}
$$
Теперь самое интересное.
На этом рисунке показаны области возникновения ошибки. Зелёная область — это место, где возникает ошибка при передаче “1”, красная — при передаче “0”. Общую вероятность ошибки можно записать с помощью формулы полной вероятности:
$$
P(error)=\dfrac{1}{2}P(error|s_0) + \dfrac{1}{2}P(error|s_1)
$$
После этого необходимо найти каждую из вероятностей:
$$
\begin{align}
P(error|s_0) = \int_{0}^{\infty}P(x|s_0)dx = \dfrac{1}{\sqrt{\pi N_0}}\int_{0}^{\infty}e^\dfrac{-(x+\sqrt{E_b})^2}{N_0}dx \newline
P(error|s_1) = \int_{-\infty}^{0}P(x|s_1)dx = \dfrac{1}{\sqrt{\pi N_0}}\int_{-\infty}^{0}e^\dfrac{-(x-\sqrt{E_b})^2}{N_0}dx
\end{align}
$$
Обычно вероятность ошибки записывают с помощью функции ошибок:
$$
erfc(x)=\dfrac{2}{\sqrt\pi}\int_{0}^{x}e^{-t^2}dt
$$
Для этого необходимо сделать следующее:
$$
z=\dfrac{y+\sqrt{E_b}}{\sqrt{N_0}} => z\sqrt{N_0} = y + \sqrt{E_b}
$$
Заменить пределы интегрирования:
$$
\begin{align}
y=0 => z = \dfrac{\sqrt{E_b}}{\sqrt{N_0}} \newline
y=\infty => z = \infty
\end{align}
$$
Получившаяся ошибка записывается как:
$$
\begin{align}
P(error|s_0)=\dfrac{1}{\sqrt{\pi N_0}}\int_\limits{\sqrt{\dfrac{E_b}{N_0}}}^{\infty}e^{-z^2}\sqrt{N_0}dz
=\dfrac{1}{\sqrt{\pi}}\int_\limits{\sqrt{\dfrac{E_b}{N_0}}}^{\infty}e^{-z^2}dz
=\dfrac{1}{2}erfc(\sqrt{\dfrac{E_b}{N_0}})
\end{align}
$$
Аналогично можно найти ошибку при передаче “1”:
$$
\begin{align}
P(error|s_1)=1-P(s_1)=1-\dfrac{1}{2}erfc(-\sqrt{\dfrac{E_b}{N_0}})
\end{align}
$$
Можно воспользоваться свойством функции ошибок:
$$
\begin{align}
erfc(-x)=2-erfc(x) => P(error|s_1) = \dfrac{1}{2}erfc(\sqrt{\dfrac{E_b}{N_0}})
\end{align}
$$
Если подставить в формулу полной вероятности:
$$
P(error)=\dfrac{1}{2}(\dfrac{1}{2}erfc(\sqrt{\dfrac{E_b}{N_0}})) + \dfrac{1}{2}(\dfrac{1}{2}erfc(\sqrt{\dfrac{E_b}{N_0}}))=\dfrac{1}{2}erfc(\sqrt{\dfrac{E_b}{N_0}})
$$
Ответ
Получившийся график:
4.7.1. Вероятность появления ошибочного бита при когерентном обнаружении сигнала BPSK
4.7.2. Вероятность появления ошибочного бита при когерентном обнаружении сигнала в дифференциальной модуляции BPSK
4.7.3. Вероятность появления ошибочного бита при когерентном обнаружении сигнала в бинарной ортогональной модуляции FSK
4.7.4. Вероятность появления ошибочного бита при некогерентном обнаружении сигнала в бинарной ортогональной модуляции FSK
4.7.5. Вероятность появления ошибочного бита для бинарной модуляции DPSK
4.7.6. Вероятность ошибки для различных модуляций
4.7.1. Вероятность появления ошибочного бита при когерентном обнаружении сигнала BPSK
Важной мерой производительности, используемой для сравнения цифровых схем модуляции, является вероятность ошибки, РЕ Для коррелятора или согласованного фильтра вычисление РЕ можно представить геометрически (см. рис. 4.6). Расчет РЕ включает нахождение вероятности того, что при данном векторе переданного сигнала, скажем si вектор шума n выведет сигнал из области 1. Вероятность принятия детектором неверного решения называется вероятностью символьной ошибки, рE. Несмотря на то что решения принимаются на символьном уровне, производительность системы часто удобнее задавать через вероятность битовой ошибки (Ps). Связь РВ и РЕ рассмотрена в разделе 4.9.3 для ортогональной передачи сигналов и в разделе 4.9.4 для многофазной передачи сигналов.
Для удобства изложения в данном разделе мы ограничимся когерентным обнаружением сигналов BPSK. В этом случае вероятность символьной ошибки — это то же самое, что и вероятность битовой ошибки. Предположим, что сигналы равновероятны. Допустим также, что при передаче сигнала принятый сигнал r(t) равен
, где n(t) — процесс AWGN; кроме того, мы пренебрегаем ухудшением качества вследствие введенной каналом или схемой межсимвольной интерференции. Как показывалось в разделе 4.4.1, антиподные сигналы
и
можно описать в одномерном сигнальном пространстве, где
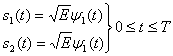
Детектор выбирает с наибольшим выходом коррелятора
; или, в нашем случае антиподных сигналов с равными энергиями, детектор, используя формулу (4.20), принимает решение следующего вида.
(4.74)
Как видно из рис. 4.9, возможны ошибки двух типов: шум так искажает переданный сигнал , что измерения в детекторе дают отрицательную величину z(T), и детектор выбирает гипотезу H2, что был послан сигнал s2(t). Возможна также обратная ситуация: шум искажает переданный сигнал
, измерения в детекторе дают положительную величину z(T), и детектор выбирает гипотезу Н1, соответствующую предположению о передаче сигнала
.
В разделе 3.2.1.1 была выведена формула (3.42), описывающая вероятность битовой ошибки РB для детектора, работающего по принципу минимальной вероятности ошибки.
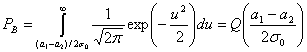
Здесь σ0 — среднеквадратическое отклонение шума вне коррелятора. Функция Q(x), называемая гауссовым интегралом ошибок, определяется следующим образом.
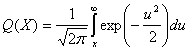
Эта функция подробно описывается в разделах 3.2 и Б.3.2.
Для передачи антиподных сигналов с равными энергиями, таких как сигналы в формате BPSK, приведенные в выражении (4.74), на выход приемника поступают следующие компоненты: , при переданном сигнале
, и
, при переданном сигнале s2(t), где Еь — энергия сигнала, приходящаяся на двоичный символ. Для процесса AWGN дисперсию шума
вне коррелятора можно заменить N0/2 (см. приложение В), так что формулу (4.76) можно переписать следующим образом.
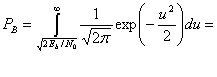
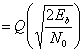
Данный результат для полосовой передачи антиподных сигналов BPSK совпадает с полученными ранее формулами для обнаружения антиподных сигналов с использованием согласованного фильтра (формула (3.70)) и обнаружения узкополосных антиподных сигналов с применением согласованного фильтра (формула (3.76)). Это является примером описанной ранее теоремы эквивалентности. Для линейных систем теорема эквивалентности утверждает, что на математическое описание процесса обнаружения не влияет сдвиг частоты. Как следствие, использование согласованных фильтров или корреляторов для обнаружения полосовых сигналов (рассмотренное в данной главе) дает те же соотношения, что были выведены ранее для сопоставимых узкополосных сигналов.
4.7.2. Вероятность появления ошибочного бита при когерентном обнаружении сигнала в дифференциальной модуляции BPSK
Сигналы в канале иногда инвертируются; например, при использовании когерентного опорного сигнала, генерируемого контуром ФАПЧ, фаза может быть неоднозначной. Если фаза несущей была инвертирована при использовании схемы DPSK, как это скажется на сообщении? Поскольку информация сообщения кодируется подобием или отличием соседних символов, единственным следствием может быть ошибка в бите, который инвертируется, или в бите, непосредственно следующим за инвертированным. Точность определения подобия или отличия символов не меняется при инвертировании несущей. Иногда сообщения (и кодирующие их сигналы) дифференциально кодируются и когерентно обнаруживаются, чтобы просто избежать неопределенности в определении фазы.
Вероятность появления ошибочного бита при когерентном обнаружении сигналов в дифференциальной модуляции PSK (DPSK) дается выражением [5].
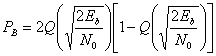
Это соотношение изображено на рис. 4.25. Отметим, что существует незначительное ухудшение достоверности обнаружения по сравнению с когерентным обнаружением сигналов в модуляции PSK. Это вызвано дифференциальным кодированием, поскольку любая отдельная ошибка обнаружения обычно приводит к принятию двух ошибочных решений. Подробно вероятность ошибки при использовании наиболее популярной схемы — когерентного обнаружения сигналов в модуляции DPSK — рассмотрена в разделе 4.7.5.
Рис. 4.25. Вероятность появления ошибочного бита для бинарных систем нескольких типов
4.7.3. Вероятность появления ошибочного бита при когерентном обнаружении сигнала в бинарной ортогональной модуляции FSK
Формулы (4.78) и (4.79) описывают вероятность появления ошибочного бита для когерентного обнаружения антиподных сигналов. Более общую трактовку для когерентного обнаружения бинарных сигналов (не ограничивающихся антиподными сигналами) дает следующее выражение для РВ [6].
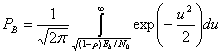
Из формулы (3.64,б) — временной коэффициент взаимной корреляций между
и
, где θ — угол между векторами сигналов
и s2 (см. рис. 4.6). Для антиподных сигналов, таких как сигналы BPSK, θ = π, поэтому ρ = -1.
Для ортогональных сигналов, таких как сигналы бинарной FSK (BFSK), θ = π/2, поскольку векторы и s2 перпендикулярны; следовательно, ρ = 0, что можно доказать с помощью формулы (3.64,а), поэтому выражение (4.81) можно переписать следующим образом.
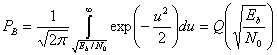
Здесь Q(x) — дополнительная функция ошибок, подробно описанная в разделах 3.2 и Б.3.2. Зависимость (4.82) для когерентного обнаружения ортогональных сигналов BFSK, показанная на рис. 4.25, аналогична зависимости, полученной для обнаружения ортогональных сигналов с помощью согласованного фильтра (формула (3.71)) и узкополосных ортогональных сигналов (униполярных импульсов) с использованием согласованного фильтра (формула (3.73)). В данной книге мы не рассматриваем амплитудную манипуляцию ООК (on-off keying), но соотношение (4.82 применимо к обнаружению с помощью согласованного фильтра сигналов ООК, так же как и к когерентному обнаружению любых ортогональных сигналов.
Справедливость соотношения (4.82) подтверждает и то, что разность энергий между ортогональными векторами сигналов и s2 с амплитудой
, как показано на рис. 3.10, б, равна квадрату расстояния между концами ортогональных векторов Ed = 2Eb. Подстановка этого результата в формулу (3.63) также дает формулу (4.82). Сравнивая формулы (4.82) и (4.79), видим, что, по сравнению со схемой BPSK, схема BFSK требует на 3 дБ большего отношения E/N0 для обеспечения аналогичной достоверности передачи. Этот результат не должен быть неожиданным, поскольку при данной мощности сигнала квадрат расстояния между ортогональными векторами вдвое (на 3 дБ) больше квадрата расстояния между антиподными векторами.
4.7.4. Вероятность появления ошибочного бита при некогерентном обнаружении сигнала в бинарной ортогональной модуляции FSK
Рассмотрим бинарное ортогональное множество равновероятных сигналов FSK , определенное формулой (4.8).
Фаза φ неизвестна и предполагается постоянной. Детектор описывается М = 2 каналами, состоящими, как показано на рис. 4.19, из полосовых фильтров и детекторов огибающей. На вход детектора поступает принятый сигнал r(t) = si(t) + n(t), где n(i) — гауссов шум с двусторонней спектральной плотностью мощности No/2. Предположим, что и
достаточно разнесены по частоте, чтобы их перекрытием можно было пренебречь. Вычисление вероятности появления ошибочного бита для равновероятных сигналов
и
начнем, как и в случае узкополосной передачи, с уравнения (3.38).
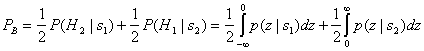
Для бинарного случая тестовая статистика z(T) определена как . Предположим, что полоса фильтра Wf равна 1/T, так что огибающая сигнала FSK (приблизительно) сохраняется на выходе фильтра. При отсутствии шума в приемнике значение z(T) равно
при передаче s1(t) и —
— при передаче s2(t). Вследствие такой симметрии оптимальный порог γ0=0. Плотность вероятности
подобна плотности вероятности
.
(4.84)
Таким образом, можем записать
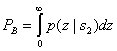
или
(4.86)
где z1 и z2 обозначают выходы z1(T) и z2(T) детекторов огибающей, показанных на рис.4.19. При передаче тона , т.е. когда r(t) = s2(t) + n(t), выход z1(T) состоит исключительно из случайной переменной гауссового шума; он не содержит сигнального компонента. Распределение Гаусса в нелинейном детекторе огибающей дает распределение Релея на выходе [6], так что
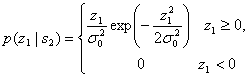
где — шум на выходе фильтра. С другой стороны, z2(T) имеет распределение Раиса, поскольку на вход нижнего детектора огибающей подается синусоида плюс шум [6]. Плотность вероятности p(z2\s2) записывается как
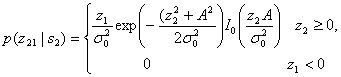
где и, как и ранее,
— шум на выходе фильтра. Функция 10(х), известная как модифицированная функция Бесселя первого рода нулевого порядка [7], определяется следующим образом.
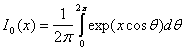
Ошибка при передаче s2(t) происходит, если выборка огибающей z1(T), полученная из верхнего канала (по которому проходит шум), больше выборки огибающей z2(T), полученной из нижнего канала (по которому проходит сигнал и шум). Таким образом, вероятность этой ошибки можно получить, проинтегрировав до бесконечности с последующим усреднением результата по всем возможным z2.
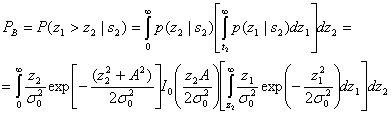
Здесь , внутренний интеграл — условная вероятность ошибки, при фиксированном значении z2, если был передан сигнал s2(1), а внешний интеграл усредняет условную вероятность по всем возможным значениям z2. Данный интеграл можно вычислить аналитически [8], и его значение равно следующему.
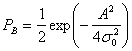
С помощью формулы (1.19) шум на выходе фильтра можно выразить как
(4.93)
где a Wf — ширина полосы фильтра. Таким образом, формула (4.92) приобретает следующий вид.
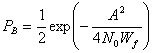
Выражение (4.94) показывает, что вероятность ошибки зависит от ширины полосы полосового фильтра и РB уменьшается при снижении Wf. Результат справедлив только при пренебрежении межсимвольной интерференцией (intersymbol interference — ISI). Минимальная разрешенная Wf (т.е. не дающая межсимвольной интерференции) получается из уравнения (3.81) при коэффициенте сглаживания г = 0. Следовательно, Wf= R бит/с =1/T, и выражение (4.94) можно переписать следующим образом.
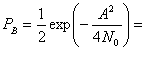
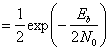
Здесь Еь= (1/2)А2Т — энергия одного бита. Если сравнить вероятность ошибки схем некогерентной и когерентной FSK (см. рис. 4.25), можно заметить, что при равных РB некогерентная FSK требует приблизительно на 1 дБ большего отношения Eb/N0, чем когерентная FSK (для РB < 10-4). При этом некогерентный приемник легче реализуется, поскольку не требуется генерировать когерентные опорные сигналы. По этой причине практически все приемники FSK используют некогерентное обнаружение. В следующем разделе будет показано, что при сравнении когерентной ортогональной схемы FSK с нёкогерентной схемой DPSK имеет место та же разница в 3 дБ, что и при сравнении когерентной ортогональной FSK и когерентной PSK. Как указывалось ранее, в данной книге не рассматривается амплитудная манипуляция ООК (on-off keying). Все же отметим, что вероятность появления ошибочного бита РB, выраженная в формуле (4.96), идентична РB для некогерентного обнаружения сигналов ООК.
4.7.5. Вероятность появления ошибочного бита для бинарной модуляции DPSK
Определим набор сигналов BPSK следующим образом.
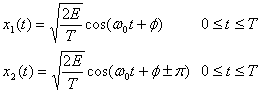
Особенностью схемы DPSK является отсутствие в сигнальном пространстве четко определенных областей решений. В данном случае решение основывается на разности фаз между принятыми сигналами. Таким образом, при передаче сигналов DPSK каждый бит в действительности передается парой двоичных сигналов.
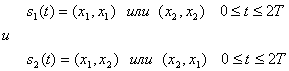
Здесь обозначает сигнал
, за которым следует сигнал
. Первые Т секунд каждого сигнала — это в действительности последние Т секунд предыдущего. Отметим, что оба сигнала s1(t) и s2(t) могут принимать любую из возможных форм и что
и
— это антиподные сигналы. Таким образом, корреляцию между
и s2(t) для любой комбинации сигналов можно записать следующим образом.
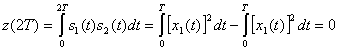
Следовательно, каждую пару сигналов DPSK можно представить как ортогональный сигнал длительностью 2Т секунд. Обнаружение может соответствовать некогерентному обнаружению огибающей с помощью четырех каналов, согласованных с каждым возможным выходом огибающей, как показано на рис. 4.26. Поскольку два детектора огибающей, представляющих каждый символ, обратны друг другу, выборки их огибающих будут совпадать. Значит, мы можем реализовать детектор как один канал для , согласовывающегося с
или
, и один канал для
, согласовывающегося с
или
, как показано на рис. 4.26. Следовательно, детектор DPSK сокращается до стандартного двухканального некогерентного детектора. В действительности фильтр может согласовываться с разностным сигналом; так что необходимым является всего один канал. На рис. 4.26 показаны фильтры, которые согласовываются с огибающими сигнала (в течение двух периодов передачи символа). Что это означает, если вспомнить, что DPSK — это схема передачи сигналов с постоянной огибающей? Это означает, что нам требуется реализовать детектор энергии, подобный квадратурному приемнику на рис. 4.18, где каждый сигнал в течение периода
представляется синфазным и квадратурным опорными сигналами.
синфазный опорный сигнал квадратурный опорный сигнал
синфазный опорный сигнал
квадратурный опорный сигнал
Поскольку пары сигналов DPSK ортогональны, вероятность ошибки при подобном некогерентном обнаружении дается выражением (4.96). Впрочем, поскольку сигналы DPSK длятся 2Т секунд, энергия сигналов , определенных в формуле (4.98), равна удвоенной энергии сигнала, определенного в течение одного периода передачи символа.
а)
б)
Рис. 4.26. Обнаружение в схеме DPSK: а) четырехканальное дифференциально-когерентное обнаружение сигналов в бинарной модуляции DPSK; б) эквивалентный двухканальный детектор сигналов в бинарной модуляции DPSK
Таким образом, РВможно записать в следующем виде.
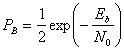
Зависимость (4.100), изображенная на рис. 4.25, представляет собой дифференциальное когерентное обнаружение сигналов в дифференциальной модуляции PSK, или просто DPSK. Выражение справедливо для оптимального детектора DPSK (рис. 4.17, в). Для детектора, показанного на рис. 4.17, б, вероятность ошибки будет несколько выше приведенной в выражении (4.100) [3]. Если сравнить вероятность ошибки, приведенную в формуле (4.100), с вероятностью ошибки когерентной схемы PSK (см. рис. 4.25), видно, что при равных РB схема DPSK требует приблизительно на 1 дБ большего отношения E^N0, чем схема BPSK (для ). Систему DPSK реализовать легче, чем систему PSK, поскольку приемник DPSK не требует фазовой синхронизации. По этой причине иногда предпочтительнее использовать менее эффективную схему DPSK, чем более сложную схему PSK.
4.7.6. Вероятность ошибки для различных модуляций
В табл. 4.1 и на рис. 4.25 приведены аналитические выражения и графики РB для наиболее распространенных схем модуляции, описанных выше. Для РB = 10-4 можно видеть, что разница между лучшей (когерентной PSK) и худшей (некогерентной ортогональной FSK) из рассмотренных схем равна приблизительно 4 дБ. В некоторых случаях 4 дБ — это небольшая цена за простоту реализации, увеличивающуюся от когерентной схемы PSK до некогерентной FSK (рис. 4.25); впрочем, в других случаях ценным является даже выигрыш в 1 дБ. Помимо сложности реализации и вероятности РB существуют и другие факторы, влияющие на выбор модуляции; например, в некоторых случаях (в каналах со случайным затуханием) желательными являются некогерентные системы, поскольку иногда когерентные опорные сигналы затруднительно определять и использовать. В военных и космических приложениях весьма желательны сигналы, которые могут противостоять значительному ухудшению качества, сохраняя возможность обнаружения.
Таблица 4.1. Вероятность ошибки для различных бинарных модуляций
|
Модуляция |
PB |
|
PSK (когерентное обнаружение) |
|
|
DPSK (дифференциальное когерентное обнаружение) |
|
|
Ортогональная FSK (когерентное обнаружение) |
|
|
Ортогональная FSK (некогерентное обнаружение) |
|
В публикации приведены основные функции Communications Toolbox.
Список функций Communications Toolbox (Список соответствует версии пакета 3.0 (R14)).
Источники сигналов
-
randerr — создание матрицы с заданным количеством случайно расположенных единиц
-
randint — создание матрицы случайных целых чисел, равномерно распределенных в заданном диапазоне
-
randsrc — создание матрицы случайных символов из заданного алфавита
-
wgn — генерация белого нормального шума
Функции оценки помехоустойчивости
-
berawgn — вероятность битовой ошибки для некодированной модуляции и канала с аддитивным белым гауссовым шумом
-
bercoding — вероятность битовой ошибки для кодированной модуляции и канала с аддитивным белым гауссовым шумом
-
berconfint — расчет оценки и доверительного интервала для вероятности битовой ошибки по результатам статистического моделирования
-
berfading — вероятность битовой ошибки для канала с рэлеевскими замираниями
-
berfit — подгонка аналитической функции к экспериментальным данным о вероятности битовой ошибки
-
bersync — вероятность битовой ошибки при неточной временной синхронизации
-
biterr — вычисление числа ошибочных бит и вероятности ошибки на бит (BER)
-
distspec — расчет спектра сверточного кода
-
eyediagram — вывод глазковой диаграммы
-
noisebw — расчет эквивалентной шумовой полосы дискретного фильтра нижних частот
-
scatterplot — вывод диаграммы рассеяния
-
semianalytic — расчет вероятности битовой ошибки полуаналитическим методом
-
symerr — вычисление числа ошибочных символов и вероятности ошибки на символ
Кодирование источника
-
arithdeco — декодирование двоичного арифметического кода
-
arithenco — арифметическое кодирование последовательности символов
-
compand — логарифмическое или экспоненциальное преобразование (законы A и m )
-
dpcmdeco — декодирование дифференциальной импульсно-кодовой модуляции
-
dpcmenco — кодирование сигнала с использованием дифференциальной импульсно-кодовой модуляции
-
dpcmopt — оптимизация параметров дифференциальной импульсно-кодовой модуляции
-
huffmandeco — декодер Хаффмана
-
huffmandict — генерирование словаря для кода Хаффмана при известном распределении вероятности источника
-
huffmanenco — кодер Хаффмана
-
lloyds — оптимизация параметров квантования с использованием алгоритма Ллойда
-
quantiz — квантование сигнала по заданному набору уровней
Помехоустойчивое кодирование и декодирование
-
bchdec — декодер для кодов БЧХ (устаревший аналог — bchdeco)
-
bchenc — кодер для кодов БЧХ (устаревший аналог — bchenco)
-
bchgenpoly — генерация порождающего полинома для кода БЧХ (устаревший аналог — bchpoly)
-
convenc — кодирование двоичных данных с использованием сверточного кода
-
cyclgen — генерация проверочной и порождающей матриц для циклического кода
-
cyclpoly — генерация порождающего полинома для циклического кода
-
decode — декодирование данных, закодированных с использованием блочного кода
-
encode — кодирование данных с использованием блочных кодов
-
gen2par — преобразование порождающей матрицы в проверочную и обратно
-
gfweight — расчет кодового расстояния для линейного блочного кода
-
hammgen — генерация проверочной и порождающей матриц для кода Хэмминга
-
rsdec — декодер для кодов Рида-Соломона
-
rsenc — кодер для кодов Рида-Соломона
-
rsdecof — декодирование текстового файла, закодированного с использованием кода Рида-Соломона
-
rsencof — кодирование текстового файла с использованием кода Рида-Соломона
-
rsgenpoly — генерация порождающего полинома для кода Рида-Соломона
-
syndtable — генерация таблицы зависимости векторов ошибок от синдрома (таблицы декодирования) для двоичных кодов
-
vitdec — декодирование сверточного кода с помощью алгоритма Витерби
Перемежение/Деперемежение
-
algdeintrlv — алгебраическое блоковое деперемежение
-
algintrlv — алгебраическое блоковое перемежение
-
convdeintrlv — сверточное деперемежение с линейным изменением задержки
-
convintrlv — сверточное перемежение с линейным изменением задержки
-
deintrlv — табличное блоковое деперемежение
-
intrlv — табличное блоковое перемежение
-
heldeintrlv — сверточное деперемежение со спиральным сканированием
-
helintrlv — сверточное перемежение со спиральным сканированием
-
helscandeintrlv — блоковое деперемежение со спиральным сканированием
-
helscanintrlv — блоковое перемежение со спиральным сканированием
-
matdeintrlv — матричное блоковое деперемежение
-
matintrlv — матричное блоковое перемежение
-
muxdeintrlv — табличное сверточное деперемежение
-
muxintrlv — табличное сверточное перемежение
-
randdeintrlv — случайное блоковое деперемежение
-
randintrlv — случайное блоковое перемежение
Аналоговая модуляция/демодуляция
-
ammod — амплитудная модуляция (AM)
-
amdemod — амплитудная демодуляция
-
fmmod — частотная модуляция (FM)
-
fmdemod — частотная демодуляция
-
pmmod — фазовая модуляция (PM)
-
pmdemod — фазовая демодуляция
-
ssbmod — однополосная амплитудная модуляция (SSB)
-
ssbdemod — однополосная амплитудная демодуляция
Цифровая модуляция/демодуляция
-
dpskmod — фазоразностная манипуляция (DPSK)
-
dpskdemod — демодуляция сигнала с фазоразностной манипуляцией
-
fskmod — частотная манипуляция (FSK)
-
fskdemod — демодуляция сигнала с частотной манипуляцией
-
genqammod — квадратурная манипуляция с произвольным созвездием (QASK)
-
genqamdemod — демодуляция сигнала с квадратурной манипуляцией с произвольным созвездием
-
modnorm — расчет коэффициента масштабирования для нормировки АИМ- или КАМ-сигнала по мощности
-
mskmod — частотная манипуляция с минимальным сдвигом (MSK)
-
mskdemod — демодуляция сигнала с частотной манипуляцией с минимальным сдвигом
-
oqpskmod — квадратурная фазовая манипуляция со сдвигом (Offset QPSK)
-
oqpskdemod — демодуляция сигнала с квадратурной фазовой манипуляцией со сдвигом (offset)
-
pammod — амплитудно-импульсная модуляция (PAM)
-
pamdemod — амплитудно-импульсная демодуляция
-
pskmod — фазовая манипуляция (PSK)
-
pskdemod — демодуляция сигнала с фазовой манипуляцией
-
qammod — квадратурная манипуляция с квадратным созвездием (QASK)
-
qamdemod — демодуляция сигнала с квадратурной манипуляцией с квадратным созвездием
Модуляция и демодуляция (устаревшие функции)
-
ademod — аналоговая демодуляция (вещественный входной сигнал)
-
ademodce — аналоговая демодуляция (вход — комплексная огибающая)
-
amod — аналоговая модуляция (вещественный выходной сигнал)
-
amodce — аналоговая модуляция (выход — комплексная огибающая)
-
apkconst — графическое изображение концентрического сигнального созвездия для квадратурной манипуляции
-
ddemod — цифровая демодуляция (вещественный входной сигнал)
-
ddemodce — цифровая демодуляция (вход — комплексная огибающая)
-
demodmap — преобразование аналогового демодулированного сигнала в цифровой сигнал
-
dmod — цифровая модуляция (вещественный выходной сигнал)
-
dmodce — цифровая модуляция (выход — комплексная огибающая)
-
modmap — преобразование цифрового сигнала в аналоговые параметры модуляции
-
qaskdeco — преобразование аналогового демодулированного сигнала в цифровое сообщение с использованием квадратного созвездия для квадратурной манипуляции
-
qaskenco — преобразование цифрового сообщения в аналоговый модулирующий сигнал с использованием квадратного созвездия для квадратурной манипуляции
Формирующие фильтры
-
intdump — интегратор со сбросом
-
rcosflt — интерполяция сигнала фильтром с косинусоидальным сглаживанием АЧХ
-
rectpulse — ступенчатая (кусочно-постоянная) интерполяция сигнала
Специальные фильтры
-
hank2sys — преобразование матрицы Ханкеля в описание линейной системы
-
hilbiir — расчет рекурсивного фильтра, аппроксимирующего преобразование Гильберта
-
rcosine — расчет фильтра с косинусоидальным сглаживанием АЧХ
Низкоуровневые функции для расчета специальных фильтров
-
rcosfir — расчет нерекурсивного фильтра с косинусоидальным сглаживанием АЧХ
-
rcosiir — расчет рекурсивного фильтра с косинусоидальным сглаживанием АЧХ
Модели каналов
-
awgn — канал с аддитивным белым нормальным шумом
-
bsc — двоичный симметричный канал
-
rayleighchan — конструктор объекта канала с рэлеевскими замираниями
-
ricianchan — конструктор объекта канала с райсовскими замираниями
-
filter — метод объектов каналов, осуществляющий фильтрацию сигнала
-
reset — метод объектов каналов, осуществляющий сброс объекта в исходное состояние
Эквалайзеры
-
lms — конструктор объекта адаптивного алгоритма LMS
-
signlms — конструктор объекта адаптивного алгоритма LMS, использующего один из вариантов знаковых преобразований
-
normlms — конструктор объекта нормированного варианта адаптивного алгоритма LMS
-
varlms — конструктор объекта адаптивного алгоритма LMS с переменным шагом
-
rls — конструктор объекта адаптивного алгоритма RLS
-
cma — конструктор объекта алгоритма слепого выравнивания для сигналов с постоянной амплитудой (constant modulus algorithm, CMA)
-
lineareq — конструктор объекта линейного эквалайзера
-
dfe — конструктор объекта эквалайзера с обратной связью по решению
-
equalize — компенсация искажений сигнала с помощью объекта эквалайзера
-
reset — метод объектов эквалайзеров, осуществляющий сброс объекта в исходное состояние
-
mlseeq — прием сигнала с межсимвольной интерференцией с помощью алгоритма Витерби
Вычисления в конечных полях (полях Галуа) с характеристикой 2
-
gf — создание объекта, представляющего массив элементов конечного поля
-
gfhelp — вывод списка операций, применимых к объектам конечных полей
-
convmtx — матрица свертки для вектора элементов конечного поля
-
cosets — генерация циклотомических классов для конечного поля
-
dftmtx — матрица дискретного преобразования Фурье в конечном поле
-
gftable — создание вспомогательного файла для ускорения вычислений в конечном поле
-
isprimitive — проверка полинома, заданного в конечном поле, на примитивность
-
minpol — поиск минимального полнома для элемента конечного поля
-
primpoly — поиск примитивных полиномов в конечном поле
Вычисления в недвоичных конечных полях (полях Галуа)
-
gfadd — сложение полиномов в конечном поле
-
gfconv — умножение полиномов в конечном поле
-
gfcosets — генерация циклотомических классов для конечного поля
-
gfdeconv — деление полиномов в конечном поле
-
gfdiv — деление элементов конечного поля
-
gffilter — фильтрация данных в простом конечном поле
-
gflineq — поиск частного решения системы линейных уравнений Ax = b в простом конечном поле
-
gfminpol — поиск минимального полнома для элемента конечного поля
-
gfmul — умножение элементов конечного поля
-
gfplus — сложение элементов расширенных конечных полей с характеристикой 2 (в версиях пакета начиная с 2.1 (R13) вместо данной функции используется оператор «+», поэтому функция числится устаревшей, хотя по-прежнему доступна для использования)
-
gfpretty — отображение полинома в традиционном формате
-
gfprimck — проверка полинома в конечном поле на примитивность
-
gfprimdf — генерация примитивных полиномов по умолчанию для конечного поля
-
gfprimfd — поиск примитивных полиномов в конечном поле
-
gfrank — вычисление ранга матрицы в конечном поле
-
gfrepcov — преобразование между двумя формами представления полиномов в конечном поле GF(2)
-
gfroots — поиск корней полинома в простом конечном поле
-
gfsub — вычитание полиномов в конечном поле
-
gftrunc — минимизация длины полиномиального представления
-
gftuple — упрощение или преобразование формата представления элементов конечного поля
Утилиты
-
bi2de — преобразование векторов, содержащих цифры, в числа
-
de2bi — преобразование чисел в векторы цифр
-
istrellis — проверка того, является ли объект таблицей переходов сверточного кода
-
marcumq — обобщенная Q-функция Маркума
-
mask2shift — расчет задержки псевдослучайной последовательности, вносимой путем применения маски к сдвиговому регистру
-
oct2dec — преобразование чисел из восьмеричной системы счисления в десятичную
-
poly2trellis — преобразование представления сверточного кода из полиномиальной формы в таблицу переходов
-
qfunc — Q-функция (дополнение гауссовой интегральной функции распределения до единицы)
-
qfuncinv — обратная Q-функция (обратная гауссова интегральная функция распределения с обратным знаком)
-
shift2mask — расчет маски сдвигового регистра, необходимой для формирования задержанной псевдослучайной последовательности
-
vec2mat — преобразование вектора в матрицу с заданным числом столбцов
Графический пользовательской интерфейс -
bertool — среда анализа вероятности ошибки на бит (Bit Error Rate Analysis Tool)
Демонстрационные программы -
basicsimdemo — демонстрация моделирования линии связи
-
gfdemo — демонстрация работы с полями Галуа
-
rcosdemo — демонстрация использования фильтра с косинусоидальным сглаживанием АЧХ
-
scattereyedemo — демонстрация использования глазковой диаграммы и диаграммы рассеяния
-
vitsimdemo — демонстрация использования сверточного кодера и декодера Витерби
Функции-примеры -
bertooltemplate — шаблон для создания функций моделирования, вызываемых из среды BERTool
-
simbasebandex — моделирование квадратурной манипуляции (комплексная огибающая)
-
viterbisim — функция приема сигнала с помощью декодера Витерби, предназначенная для вызова из среды BERTool
Примеры из главы «Getting Started» документации пакета -
commdoc_mod — модуляция/демодуляция
-
commdoc_const — отображение сигнального созвездия
-
commdoc_gray — модификация примера commdoc_mod: добавлено использование кода Грея
-
commdoc_rrc — модификация примера commdoc_gray: добавлено формирование спектра с помощью фильтра с косинусоидальным сглаживанием АЧХ
-
commdoc_code — модификация примера commdoc_rrc: добавлено использование сверточного кода
-
commdoc_bertool — модификация примера commdoc_gray: функция переработана для вызова из среды BERTool
-
commdoc_mcurves — модификация примера commdoc_mod: реализован многократный вызов процедуры моделирования с различными значениями параметров
Наверх
randerr — создание матрицы с заданным количеством случайно расположенных единиц
Синтаксис:
out = randerr(m);
out = randerr(m,n);
out = randerr(m,n,errors);
out = randerr(m,n,errors,state);
Описание:
При любом варианте синтаксиса все строки матрицы out создаются функцией randerr независимо.
out = randerr(m)
Возвращает двоичную матрицу размером m на m, в каждой строке которой имеется ровно один случайно расположенный ненулевой элемент. Все возможные положения этого элемента равновероятны.
out = randerr(m,n)
Возвращает двоичную матрицу размером m на n, в каждой строке которой имеется ровно один случайно расположенный ненулевой элемент. Все возможные положения этого элемента равновероятны.
out = randerr(m,n,errors)
Возвращает двоичную матрицу размером m на n, количество ненулевых элементов в каждой строке которой определяется параметром errors следующим образом:
-
если errors — скаляр, то он задает число ненулевых элементов для всех строк матрицы;
-
если errors — вектор-строка, то он задает несколько возможных равновероятных вариантов числа ненулевых элементов для всех строк матрицы;
-
если errors — матрица, содержащая две строки, то первая строка содержит возможные значения числа ненулевых элементов, а вторая — соответствующие вероятности (сумма элементов второй строки должна быть равна единице).
Сначала функция randerr определяет число ненулевых элементов для каждой строки создаваемой матрицы, а затем эти элементы случайным образом размещаются в строке, так что все возможные варианты их расположения равновероятны.
out = randerr(m,n,errors,state)
То же, что и предыдущий вариант синтаксиса, но в данном случае дополнительно можно задавать начальное состояние генератора случайных чисел MATLAB (функция rand) с помощью целочисленного параметра state.
Примеры.
Двоичную матрицу размером 8 на 7, в каждой строке которой с равной вероятностью содержится ни одного или два случайно расположенных ненулевых элемента, можно сгенерировать с помощью следующей команды:
out = randerr(8,7,[0 2])
out =
0 0 0 0 0 0 0
0 0 0 0 0 0 0
0 0 1 0 0 0 1
1 0 1 0 0 0 0
0 0 0 0 0 0 0
0 0 0 0 0 0 0
0 0 0 0 1 1 0
1 0 1 0 0 0 0
А теперь сделаем так, чтобы вероятность получить два ненулевых элемента в строке была в три раза больше, чем вероятность не получить ни одного. Для этого можно использовать команду, приведенную ниже (обратите внимание на то, что сумма элементов второй строки параметра errors равна единице):
out2 = randerr(8,7,[0 2; .25 .75])
out =
0 0 0 0 0 0 0
1 0 0 0 0 0 1
1 0 0 0 0 0 1
0 0 0 1 0 1 0
0 0 0 0 0 0 0
0 1 0 0 0 0 1
0 0 0 0 0 0 0
1 0 0 0 1 0 0
Наверх
randint — создание матрицы случайных целых чисел, равномерно распределенных в заданном диапазоне
Синтаксис:
out = randint;
out = randint(m);
out = randint(m,n);
out = randint(m,n,range);
out = randint(m,n,range,state);
Описание:
out = randint
Возвращает случайное число, с одинаковой вероятностью равное нулю или единице.
out = randint(m)
Возвращает матрицу размером m на m, элементы которой являются независимыми случайными числами, с равной вероятностью принимающими значения 0 и 1.
out = randint(m,n)
Возвращает матрицу размером m на n, элементы которой являются независимыми случайными числами, с равной вероятностью принимающими значения 0 и 1.
out = randint(m,n,range)
Возвращает матрицу размером m на n, элементы которой являются независимыми случайными целыми числами, равновероятно принимающими значения из диапазона, задаваемого параметром range. Если range=0, результатом является нулевая матрица. В остальных случаях диапазон распределения случайных целых чисел определяется следующим образом:
-
[0, range-1], если range — положительное целое число;
-
[range+1, 0], если range — отрицательное целое число;
-
[min(range), max(range)], если range — двухэлементный вектор, содержащий целые числа.
out = randint(m,n,range,state)
Этот вариант вызова эквивалентен предыдущему, но он дополнительно позволяет задавать начальное состояние генератора случайных чисел MATLAB (функция rand) с помощью целочисленного параметра state.
Примеры.
Матрицу размером 10 на 10, целочисленные элементы которой равномерно распределены в диапазоне от 0 до 7, можно сгенерировать с помощью любой из двух приведенных ниже команд:
out = randint(10,10,[0,7]);
out = randint(10,10,8);
Наверх
randsrc — создание матрицы случайных символов из заданного алфавита
Синтаксис:
out = randsrc;
out = randsrc(m);
out = randsrc(m,n);
out = randsrc(m,n,alphabet);
out = randsrc(m,n,[alphabet; prob]);
out = randsrc(m,n,…,state);
Описание:
out = randsrc
Возвращает случайное число, с одинаковой вероятностью равное 1 или –1.
out = randsrc(m)
Возвращает матрицу размером m на m, элементы которой являются независимыми случайными числами, с равной вероятностью принимающими значения 1 и –1.
out = randsrc(m,n)
Возвращает матрицу размером m на n, элементы которой являются независимыми случайными числами, с равной вероятностью принимающими значения 1 и –1.
out = randsrc(m,n,alphabet)
Возвращает матрицу размером m на n, элементы которой являются независимыми случайными числами, с равной вероятностью выбираемыми из вектора-строки alphabet. Если в векторе alphabet содержатся повторяющиеся значения, они учитываются только один раз и не приводят к увеличению вероятности появления соответствующих чисел в матрице out.
out = randsrc(m,n,[alphabet; prob])
Возвращает матрицу размером m на n, элементы которой являются независимыми случайными числами, выбираемыми из вектора-строки alphabet. Повторяющиеся значения в векторе alphabet игнорируются. Вектор-строка prob содержит вероятности появления символов, так что символу alphabet(k) соответствует вероятность prob(k), где k — целое число в диапазоне от единицы до размера вектора alphabet. Сумма элементов вектора prob должна быть равна единице.
out = randsrc(m,n,…,state);
То же, что и при двух предыдущих вариантах синтаксиса, но в данном случае дополнительно можно задавать начальное состояние генератора случайных чисел MATLAB (функция rand) с помощью целочисленного параметра state.
Примеры.
Матрицу размером 10 на 10, целочисленные элементы которой равновероятно выбраны из набора {-3,-1,1,3}, можно сгенерировать с помощью любой из двух приведенных ниже команд:
out = randsrc(10,10,[-3 -1 1 3]);
out = randsrc(10,10,[-3 -1 1 3; .25 .25 .25 .25]);
Чтобы внести перекос в распределение вероятностей, так, чтобы каждый из символов –1 и 1 встречался с вероятностью 0.3, а каждый из символов –3 и 3 — с вероятностью 0.2, можно использовать следующую команду:
out = randsrc(10,10,[-3 -1 1 3; .2 .3 .3 .2]);
Наверх
wgn — генерация белого нормального шума
Синтаксис:
y = wgn(m,n,p);
y = wgn(m,n,p,imp);
y = wgn(m,n,p,imp,state);
y = wgn(…,powertype);
y = wgn(…,outputtype);
Описание:
y = wgn(m,n,p)
Возвращает матрицу размером m на n, содержащую дискретный белый гауссовский (нормальный) шум (ДБГШ; White Gaussian Noise, WGN). Параметр p задает мощность шума в децибелах. По умолчанию используется импеданс нагрузки, равный 1 Ом.
y = wgn(m,n,p,imp)
То же, что и предыдущий вариант синтаксиса, но в данном случае параметр imp задает импеданс нагрузки в омах.
y = wgn(m,n,p,imp,state)
То же, что и предыдущий вариант синтаксиса, но в данном случае дополнительно можно задавать начальное состояние генератора гауссовских случайных чисел MATLAB (функция randn) с помощью целочисленного параметра state.
y = wgn(…,powertype)
То же, что и предыдущие варианты синтаксиса, но в данном случае строковый параметр powertype задает единицы измерения мощности, использованные при указании параметра p. Возможные значения параметра powertype следующие: ‘dB’, ‘dBm’ и ‘linear’.
y = wgn(…,outputtype)
То же, что и предыдущие варианты синтаксиса, но в данном случае строковый параметр outputtype позволяет задавать генерацию вещественного или комплексного шума. Возможные значения параметра outputtype следующие: ‘real’ и ‘complex’. Если генерируется комплексный шум, его вещественная и мнимая части имеют мощности p/2.
Примеры.
Вектор-столбец из 100 элементов, содержащий вещественный дискретный белый гауссовский шум с мощностью 0 дБ, можно сгенерировать с помощью следующей команды:
y1 = wgn(100,1,0);
Вектор-столбец из 100 элементов, содержащий комплексный дискретный белый гауссовский шум с мощностью 0 дБ, можно сгенерировать с помощью следующей команды:
y2 = wgn(100,1,0,’complex’);
Наверх
berawgn — вероятность битовой ошибки для некодированной модуляции и канала с аддитивным белым гауссовым шумом
Синтаксис:
ber = berawgn(EbNo, ‘pam’, M)
ber = berawgn(EbNo, ‘qam’, M)
ber = berawgn(EbNo, ‘psk’, M, dataenc)
ber = berawgn(EbNo, ‘dpsk’, M)
ber = berawgn(EbNo, ‘fsk’, M, coherence)
ber = berawgn(EbNo, ‘msk’, dataenc)
berlb = berawgn(EbNo, ‘cpfsk’, M, modindex, kmin)
Графический интерфейс:
Вместо использования функции berawgn можно запустить среду BERTool (функция bertool) и использовать для расчетов ее вкладку Theoretical.
Описание:
Общая информация о синтаксисе
Функция berawgn возвращает вероятность битовой ошибки (Bit Error Rate, BER) для различных видов модуляции в канале связи с аддитивным гауссовым шумом (АБГШ; английский термин — Additive White Gaussian Noise, AWGN). Первый входной параметр, EbNo, задает отношение (в децибелах) энергии одного бита к спектральной плотности мощности белого шума. Если параметр EbNo является вектором, результат работы ber будет вектором того же размера, элементы которого соответствуют различным значениям отношения Eb/N0. Поддерживаемые виды модуляции, задаваемые вторым входным параметром функции, перечислены в следующей таблице.
| Вид модуляции | Второй входной параметр |
| Частотная манипуляция с непрерывной фазой (ЧМНФ; Continuous phase frequency shift keying, CPFSK) | ‘cpfsk’ |
| Фазоразностная манипуляция (ФРМ; Differential phase shift keying, DPSK) | ‘dpsk’ |
| Частотная манипуляция (ЧМн; Frequency shift keying, FSK) | ‘fsk’ |
| Минимальная частотная манипуляция (МЧМ; Minimum shift keying, MSK) | ‘msk’ |
| Фазовая манипуляция (ФМн; Phase shift keying, PSK) | ‘psk’ |
| Амплитудно-импульсная модуляция (АИМ; Pulse amplitude modulation, PAM) | ‘pam’ |
| Квадратурная манипуляция (КАМ; Quadrature amplitude modulation, QAM) | ‘qam’ |
В большинстве вариантов синтаксиса вызова функции также имеется входной параметр M, задающий число позиций манипуляции. M должно быть равно 2k для некоторого положительного целого числа k. Конкретные варианты синтаксиса
ber = berawgn(EbNo, ‘pam’, M)
Возвращает BER для некодированной амплитудно-импульсной модуляции (PAM) в АБГШ-канале при когерентной демодуляции. Предполагается, что сигнальное созвездие сформировано с использованием кода Грея.
ber = berawgn(EbNo, ‘qam’, M)
Возвращает BER для некодированной квадратурной манипуляции (QAM) в АБГШ-канале при когерентной демодуляции. Предполагается, что сигнальное созвездие сформировано с использованием кода Грея. Размер алфавита M должен быть не меньше 4. Для крестообразных созвездий (когда M равно двойке в нечетной степени) результат ber дает верхнюю границу BER. (Замечание. Верхняя граница, используемая в данной функции, является менее плотной, чем верхняя граница, используемая для QAM с крестообразными созвездиями в функции semianalytic.)
ber = berawgn(EbNo, ‘psk’, M, dataenc)
Возвращает BER для некодированной фазовой манипуляции (PSK) в АБГШ-канале при когерентной демодуляции. Предполагается, что сигнальное созвездие сформировано с использованием кода Грея. Входной строковый параметр dataenc может быть равен ‘diff’ при дифференциальном кодировании данных или ‘nondiff’ при недифференциальном кодировании данных. Если параметр dataenc равен ‘diff’, то входной параметр M не должен превышать 4. Использованный здесь метод вычислений подробно изложен в [2].
ber = berawgn(EbNo, ‘dpsk’, M)
Возвращает BER для некодированной фазоразностной манипуляции (DPSK) в АБГШ-канале.
ber = berawgn(EbNo, ‘fsk’, M, coherence)
Возвращает BER для ортогональной некодированной частотной манипуляции (FSK) в АБГШ-канале. Входной строковый параметр coherence может быть равен ‘coherent’ при когерентной демодуляции или ‘noncoherent’ при некогерентной демодуляции. Размер алфавита M должен быть не больше 64.
ber = berawgn(EbNo, ‘msk’, dataenc)
Возвращает BER для некодированной минимальной частотной манипуляции (MSK) в АБГШ-канале при когерентной демодуляции. Входной строковый параметр dataenc может быть равен ‘diff’ при дифференциальном кодировании данных или ‘nondiff’ при недифференциальном кодировании данных. Использованный здесь метод вычислений подробно изложен в [2].
berlb = berawgn(EbNo, ‘cpfsk’, M, modindex, kmin)
Возвращает нижнюю границу BER для некодированной частотной манипуляции с непрерывной фазой (CPFSK) в АБГШ-канале. Входной параметр modindex задает индекс модуляции, он должен быть положительным вещественным числом. Входной параметр kmin задает число путей, имеющих минимальное расстояние друг от друга; если это число неизвестно, можно принять значение данного параметра равным 1.
Примеры:
Приведенный ниже код использует функцию berawgn для вычисления вероятности ошибки на символ в случае амплитудно-импульсной модуляции (Pulse Amplitude Modulation, PAM) при разных значениях отношения Eb/N0. Выполняется также моделирование прохождения 8-уровневого PAM-сигнала через АБГШ-канал, после чего оценивается та же самая вероятность символьной ошибки. Для сравнения результатов две зависимости помехоустойчивости от отношения Eb/N0, полученные теоретически и путем моделирования, отображаются в виде графиков в общих координатных осях.
% 1. Вычисляем вероятность ошибок с помощью функции BERAWGN
M = 8; % Число уровней PAM-сигнала
EbNo = [0:13]; % Ряд отношений Eb/No
ser = berawgn(EbNo,’pam’,M).*log2(M); % множитель log2(M) — пересчет битовых ошибок в символьные
% Отображаем теоретические результаты
figure; semilogy(EbNo,ser,’r’);
xlabel(‘E_b/N_0 (dB)’); ylabel(‘Symbol Error Rate’);
grid on; drawnow;
% 2. Оценка вероятности ошибки путем моделирования
% Инициализация
n = 10000; % Число обрабатываемых символов
k = log2(M); % Число бит на символ
% Пересчет отношения Eb/No в отношение сигнал/шум (SNR)
% Замечание: Поскольку No = 2*noiseVariance^2, при расчете SNR
% нужно добавить 3 дБ. Подробности см. в [3]
snr = EbNo+3+10*log10(k);
ynoisy=zeros(n,length(snr)); % Для ускорения расчета выделяем память заранее
% Главный цикл моделирования
x = randint(n,1,M); % Случайное сообщение
y = pammod(x,M); % Модуляция
% Пропускаем модулированный сигнал через АБГШ-канал
% в цикле по необходимым значениям SNR
for jj = 1:length(snr)
ynoisy(:,jj) = awgn(real(y),snr(jj),’measured’);
end
z = pamdemod(ynoisy,M); % Демодуляция
% Вычисляем эмпирическую вероятность символьной ошибки
[num,rt] = symerr(x,z);
% 3. Отображаем эмпирические результаты в тех же осях
hold on; semilogy(EbNo,rt,’b.’);
legend(‘Theoretical SER’,’Empirical SER’);
title(‘Comparing Theoretical and Empirical Error Rates’);
hold off;
В результате выполнения приведенного кода получается график, показанный на следующем рисунке. Полученные вами результаты могут отличаться, так как при модулировании используется генерация псевдослучайных чисел.
Ограничения:
Численная точность результатов, возвращаемых данной функцией, ограничена следующими факторами:
-
Приближенными соотношениями, использованными при выводе формул, по которым производится расчет.
-
Приближениями, производимыми при реализации численных расчетов.
Обычно можно считать надежными первые две значащие цифры возвращаемого результата. Однако для четырехпозиционной фазоразностной манипуляции (вид модуляции ‘dpsk’ при M=4) и дифференциально кодированной фазовой манипуляции (вид модуляции ‘psk’ при значении ‘diff’ для параметра dataenc) имеются дополнительные ограничения, так что функция возвращает 0 для больших значений входного параметра EbNo.
Сопутствующие функции: bercoding, berfading, bersync.
Литература:
-
Anderson, John B., Tor Aulin, and Carl-Erik Sundberg, Digital Phase Modulation, New York, Plenum Press, 1986.
-
Lindsey, William C. and Marvin K. Simon, Telecommunication Systems Engineering, Englewood Cliffs, N.J., Prentice-Hall, 1973.
-
Proakis, John G., Digital Communications, 4th ed., New York, McGraw-Hill, 2001. (Имеется русский перевод предыдущего издания: Прокис Дж. Цифровая связь. Пер. с англ. / Под ред. Д. Д. Кловского. — М.: Радио и связь, 2000.)
Наверх
bercoding — вероятность битовой ошибки для кодированной модуляции и канала с аддитивным белым гауссовым шумом
Синтаксис:
berub = bercoding(EbNo, ‘conv’, decision, coderate, dspec)
berub = bercoding(EbNo, ‘block’, ‘hard’, n, k, dmin)
berub = bercoding(EbNo, ‘block’, ‘soft’, n, k, dmin)
Графический интерфейс:
Вместо использования функции bercoding можно запустить среду BERTool (функция bertool) и использовать для расчетов ее вкладку Theoretical.
Описание:
berub = bercoding(EbNo, ‘conv’, decision, coderate, dspec)
Возвращает верхнюю границу BER для двоичного сверточного кода, используемого в сочетании с двух- или четырехпозиционной фазовой манипуляцией (PSK) в АБГШ-канале при когерентной демодуляции. Первый входной параметр, EbNo, задает отношение (в децибелах) энергии одного бита к спектральной плотности мощности белого шума. Если параметр EbNo является вектором, результат работы berub будет вектором того же размера, элементы которого соответствуют различным значениям отношения Eb/N0. Если предполагаются жесткие решения на входе декодера, строковый параметр decision должен иметь значение ‘hard’; чтобы задать декодирование с мягкими решениями на входе, параметр decision должен иметь значение ‘soft’. Входной параметр coderate задает скорость кодирования. Последний входной параметр dspec должен быть структурой, содержащей информацию о дистанционном спектре кода:
-
Поле dspec.dfree содержит значение минимального кодового расстояния.
-
Поле dspec.weight содержит дистанционный спектр кода.
Чтобы найти дистанционный спектр кода, используйте функцию distspec или обратитесь к методике, приведенной в [1] и [3].
Замечание. Результаты для двух- и четырехпозиционной фазовой манипуляции являются одинаковыми. Фазовую манипуляцию с другим числом позиций данная функция не поддерживает.
berub = bercoding(EbNo, ‘block’, ‘hard’, n, k, dmin)
Возвращает верхнюю границу BER для двоичного блокового кода с параметрами (n, k), используемого в сочетании с двух- или четырехпозиционной фазовой манипуляцией (PSK) в АБГШ-канале при когерентной демодуляции и жестких решениях на входе декодера. Входной параметр dmin задает минимальное кодовое расстояние используемого кода.
berub = bercoding(EbNo, ‘block’, ‘soft’, n, k, dmin)
Возвращает верхнюю границу BER для двоичного блокового кода с параметрами (n, k), используемого в сочетании с двух- или четырехпозиционной фазовой манипуляцией (PSK) в АБГШ-канале при когерентной демодуляции и мягких решениях на входе декодера. Входной параметр dmin задает минимальное кодовое расстояние используемого кода.
Примеры:
В приведенном ниже коде оценивается верхняя граница BER для блокового кода. Также в нем производится аппроксимация полученной зависимости с помощью функции berfit.
n = 23; % Длина кодового слова
k = 12; % Длина инфомрационного блока
dmin = 7; % Минимальное кодовое расстояние
EbNo = 1:10; % Ряд отношений Eb/No
ber_block = bercoding(EbNo,’block’,’hard’,n,k,dmin);
berfit(EbNo, ber_block) % функция berfit отображает исходные точки и аппроксимирующую кривую
ylabel(‘Bit Error Probability’);
title(‘BER Upper Bound vs. Eb/No, with Best Curve Fit’);
Ограничения:
Численная точность результатов, возвращаемых данной функцией, ограничена следующими факторами:
-
Приближенными соотношениями, использованными при выводе формул, по которым производится расчет.
-
Приближениями, производимыми при реализации численных расчетов.
Обычно можно считать надежными первые две значащие цифры возвращаемого результата.
Сопутствующие функции: berawgn, berfading, bersync, distspec.
Литература:
-
Cedervall, M., and R. Johannesson, «A Fast Algorithm for Computing Distance Spectrum of Convolutional Codes,» IEEE Transactions on Information Theory, Vol. IT-35, No. 6, Nov. 1989, pp. 1146-1159.
-
Frenger, Pal, Pal Orten, and Tony Ottosson, «Convolutional Codes with Optimum Distance Spectrum,» IEEE Communications Letters, Vol. 3, No. 11, Nov. 1999, pp. 317-319.
-
Odenwalder, J. P., Error Control Coding Handbook, Final Report, LINKABIT Corporation, San Diego, CA, 1976.
-
Proakis, John G., Digital Communications, 4th ed., New York, McGraw-Hill, 2001. (Имеется русский перевод предыдущего издания: Прокис Дж. Цифровая связь. Пер. с англ. / Под ред. Д. Д. Кловского. — М.: Радио и связь, 2000.)
Наверх
berconfint — расчет оценки и доверительного интервала для вероятности битовой ошибки по результатам статистического моделирования
Синтаксис:
[ber, interval] = berconfint(nerrs, ntrials)
[ber, interval] = berconfint(nerrs, ntrials, level)
Описание:
[ber, interval] = berconfint(nerrs, ntrials)
Возвращает оценку вероятности ошибки ber и доверительный интервал interval, соответствующий доверительной вероятности 95%, для статистического (Монте-Карло) моделирования, при котором производилось ntrials испытаний (то есть передавалось ntrials бит или символов) и произошло nerrs ошибок. Результат interval представляет собой двухэлементный вектор, содержащий края доверительного интервала. Если число ошибок и испытаний измеряется в битах, это соответствует оцениванию вероятности битовой ошибки (Bit Error Rate, BER); если число ошибок и испытаний измеряется в символах, это соответствует оцениванию вероятности символьной ошибки (Symbol Error Rate, SER).
[ber, interval] = berconfint(nerrs, ntrials, level)
То же, что предыдущий вариант синтаксиса, но дополнительный входной параметр level задает уровень доверительной вероятности. Этот параметр должен лежать в диапазоне от нуля до единицы.
Примеры:
Если моделирование системы связи дало 100 ошибочных бит на 106 испытаний, то оценка BER (вероятности битовой ошибки) для данного моделирования равна отношению этих чисел, то есть 10-4. Приведенная ниже команда позволяет определить доверительный интервал для BER при доверительной вероятности 95%.
nerrs = 100; % Число ошибочных бит при моделировании
ntrials = 10^6; % Число испытаний при моделировании
level = 0.95; % Уровень доверительной вероятности
[ber, interval] = berconfint(nerrs, ntrials, level)
Приведенный далее результат работы этого кода показывает, что при доверительной вероятности 95% BER для моделируемой системы лежит в диапазоне от 0.0000814 до 0.0001216.
ber =
1.0000e-004
interval =
1.0e-003 *
0.0814 0.1216
Сопутствующие функции: binofit (Statistics Toolbox), mle (Statistics Toolbox)
Литература:
-
Jeruchim, Michel C., Philip Balaban, and K. Sam Shanmugan, Simulation of Communication Systems, Second Edition, New York, Kluwer Academic/Plenum, 2000.
Наверх
berfading — вероятность битовой ошибки для канала с рэлеевскими замираниями
Синтаксис:
ber = berfading(EbNo, modtype, M, divorder)
ber = berfading(EbNo, ‘fsk’, 2, divorder, coherence)
Графический интерфейс:
Вместо использования функции berfading можно запустить среду BERTool (функция bertool) и использовать для расчетов ее вкладку Theoretical.
Описание:
ber = berfading(EbNo, modtype, M, divorder)
Возвращает вероятность битовой ошибки (Bit Error Rate, BER) для фазоразностной манипуляции (DPSK) или когерентной фазовой манипуляции (PSK) в канале связи с рэлеевскими неселективными замираниями (flat Rayleigh fading channel) при отсутствии кодирования. Первый входной параметр, EbNo, задает среднее отношение (в децибелах) энергии одного бита к спектральной плотности мощности белого шума для каждого канала разнесенного приема. Если параметр EbNo является вектором, результат работы ber будет вектором того же размера, элементы которого соответствуют различным значениям отношения Eb/N0. Строковый параметр modtype задает тип модуляции, он может принимать значение ‘dpsk’ или ‘psk’. Входной параметр M задает число позиций манипуляции, он должен быть равен двойке в положительной степени. Входной параметр divorder представляет собой положительное целое число, задающее число каналов разнесенного приема. Если divorder больше единицы, то M может быть равно только 2 или 4, поскольку для больших значений M не имеется широкоизвестных теоретических результатов.
ber = berfading(EbNo, ‘fsk’, 2, divorder, coherence)
Возвращает вероятность битовой ошибки (Bit Error Rate, BER) для некодированной частотной манипуляции (FSK) в канале связи с рэлеевскими неселективными замираниями. Строковый входной параметр coherence указывает, когерентная или некогерентная демодуляция подразумевается, он может принимать значение ‘coherent’ или ‘noncoherent’.
Примеры:
Приведенный ниже код вычисляет и отображает BER для некодированной DQPSK (четырехпозиционной фазоразностной манипуляции) в канале связи с рэлеевскими неселективными замираниями.
EbNo = 0:5:35;
M = 4; % Так как используется DQPSK, M = 4.
divorder = 1;
ber = berfading(EbNo,’dpsk’,M,divorder);
semilogy(EbNo,ber,’b.-‘);
Ограничения:
Численная точность результатов, возвращаемых данной функцией, ограничена следующими факторами:
-
Приближенными соотношениями, использованными при выводе формул, по которым производится расчет.
-
Приближениями, производимыми при реализации численных расчетов.
Обычно можно считать надежными первые две значащие цифры возвращаемого результата.
Сопутствующие функции: berawgn, bercoding, bersync
Литература:
-
Proakis, John G., Digital Communications, 4th ed., New York, McGraw-Hill, 2001. (Имеется русский перевод предыдущего издания: Прокис Дж. Цифровая связь. Пер. с англ. / Под ред. Д. Д. Кловского. — М.: Радио и связь, 2000.)
Наверх
berfit — подгонка аналитической функции к экспериментальным данным о вероятности битовой ошибки
Синтаксис:
fitber = berfit(empEbNo, empber)
fitber = berfit(empEbNo, empber, fitEbNo)
fitber = berfit(empEbNo, empber, fitEbNo, options)
fitber = berfit(empEbNo, empber, fitEbNo, options, fittype)
[fitber, fitprops] = berfit(…)
berfit(…)
berfit(empEbNo, empber, fitEbNo, options, ‘all’)
Описание:
fitber = berfit(empEbNo, empber)
Производит подгонку аналитической функции к экспериментальным данным о вероятности битовой ошибки (BER), содержащимся в векторе empber, и возвращает вектор подогнанных значений BER. Значения в векторах empber и fitber соответствуют отношениям Eb/N0, содержащимся (в децибелах) в векторе empEbNo. Величины в векторе empEbNo должны быть упорядочены по возрастанию, кроме того, этот вектор должен содержать по крайней мере четыре элемента.
Замечание. Функция berfit предназначена для подгонки аналитической функции или интерполяции, но не для экстраполяции. Попытка экстраполировать BER в сторону уменьшения более чем на порядок от минимального экспериментального значения в любом случае даст принципиально ненадежные результаты.
fitber = berfit(empEbNo, empber, fitEbNo)
Производит подгонку аналитической функции к экспериментальным данным о вероятности битовой ошибки (BER), содержащимся в векторе empber, соответствующих отношениям Eb/N0, содержащимся (в децибелах) в векторе empEbNo. После этого функция вычисляет значения подогнанной функции для отношений Eb/N0, содержащихся (в децибелах) в векторе fitEbNo и возвращает рассчитанные значения. Длина вектора fitEbNo должна равняться длине вектора empEbNo или превосходить ее.
fitber = berfit(empEbNo, empber, fitEbNo, options)
В данном варианте синтаксиса используется дополнительный параметр options, позволяющий управлять параметрами оптимизации. Параметр options представляет собой структуру, передаваемую оптимизирующей функции fminsearch. Создать структуру options можно с помощью функции optimset. Назначение основных полей данной структуры приведено в следующей таблице.
| Поле | Описание |
| options.Display | Уровень отображения: ‘off’ (данный вариант принят по умолчанию) — не отображается ничего; ‘iter’ — отображаются промежуточные результаты на каждой итерации; ‘final’ — отображаются только окончательные результаты; ‘notify’ — результаты отображаются только в том случае, если итерационный процесс не сошелся |
| options.MaxFunEvals | Максимально допустимое число вызовов целевой функции оптимизации. Значение по умолчанию равно 104. Уменьшение данного значения может ускорить работу функции, но привести при этом к ухудшению качества подгонки |
| options.MaxIter | Максимально допустимое число итераций. Значение по умолчанию равно 104. Уменьшение данного значения может ускорить работу функции, но привести при этом к ухудшению качества подгонки |
| options.TolFun | Критерий остановки оптимизации: если изменение значения целевой функции на очередной итерации оказывается ниже данного уровня, решение считается найденным. Значение по умолчанию равно 10-4. |
| options.TolX | Критерий остановки оптимизации: если изменение значений оптимизируемых коэффициентов на очередной итерации оказывается ниже данного уровня, решение считается найденным. Значение по умолчанию равно 10-4. |
fitber = berfit(empEbNo, empber, fitEbNo, options, fittype)
В данном варианте синтаксиса дополнительно задается, какая из возможных аппроксимирующих функций должна использоваться. Возможные варианты перечислены далее в разделе «Алгоритм». Дополнительный строковый параметр fittype может принимать значения ‘exp’, ‘exp+const’, ‘polyRatio’ или ‘doubleExp+const’. Чтобы использовать параметры оптимизации, принятые по умолчанию, задайте для них значение в виде пустой матрицы: options = [].
[fitber, fitprops] = berfit(…)
В данном варианте синтаксиса используется дополнительный выходной параметр fitprops, представляющий собой структуру, описывающую результаты подгонки. Поля структуры перечислены в следующей таблице.
| Поле | Описание |
| fitprops.fitType | Тип функции, использованной при подгонке: ‘exp’, ‘exp+const’, ‘polyRatio’, ‘doubleExp+const’ или ‘all’ (все). |
| fitprops.coeffs | Подобранные коэффициенты функции |
| fitprops.sumSqErr | Сумма квадратов разностей логарифмов экспериментальных и подогнанных значений BER |
| fitprops.exitState | Строка, описывающая результат численной оптимизации:
|
| fitprops.funcCount | Число вызовов минимизируемой функции в процессе численной оптимизации |
| fitprops.iterations | Число выполненных итераций оптимизационного процесса. Оно не обязательно равно числу вызовов минимизируемой функции |
berfit(…)
При вызове без выходных параметров функция графически отображает экспериментальные и подогнанные данные.
berfit(empEbNo, empber, fitEbNo, options, ‘all’)
В данном варианте синтаксиса графически отображаются результаты подгонки при использовании всех возможных аппроксимирующих функций (см. далее раздел «Алгоритм»). Чтобы использовать параметры оптимизации, принятые по умолчанию, задайте для них значение в виде пустой матрицы: options = [].
Примеры:
Приводимые ниже примеры иллюстрируют использование функции berfit, но для простоты в них вместо результатов моделирования используются таблично-заданные либо аналитически полученные данные.
Приведенный ниже код строит график подобранной функции для таблично-заданного набора данных.
EbNo = [0:13];
berdata = [.2 .15 .13 .12 .08 .09 .08 .07 .06 .04 .03 .02 .01 .004];
berfit(EbNo,berdata); % График подобранной функции
В данном случае построенная кривая соединяет прямыми линиями точки, соответствующие значениям подобранной функции, рассчитанным для значений аргумента из вектора EbNo. Чтобы построенная кривая выглядела более гладкой, используйте синтаксис berfit(EbNo,berdata,[0:0.2:13]). В этом случае подобранная функция останется прежней, но для построения ее графика будет использованы более часто расположенные точки.
В следующем примере строятся графики для всех возможных аппроксимирующих функций, при этом в качестве исходных данных используются искаженные результаты расчета, полученные с помощью функции berfading. Обратите внимание на то, что одна из функций оказывается не слишком подходящей для этого набора данных, в то время как остальные функции демонстрируют намного лучшее соответствие.
M = 4; EbNo = [3:10];
berdata = berfading(EbNo,’psk’,M,2); % Теоретический расчет BER
noisydata = berdata.*[.93 .92 .5 .89 .058 .35 .8 .01]; % Искаженные данные
figure; berfit(EbNo,noisydata,EbNo,[],’all’); % График всех подобранных вариантов функции
Приведенный ниже код показывает использование входной структуры options и выходной структуры fitprops. Значение ‘notify’ для уровня отображения заставляет функцию выводить сообщение, когда оптимизационный процесс для какого-либо варианта аппроксимирующей функции не сходится. Поле exitState выходной структуры тоже показывает, для каких функций оптимизация удалась, а для каких нет.
M = 4; EbNo = [3:10];
berdata = berfading(EbNo,’psk’,M,2); % Теоретический расчет BER
noisydata = berdata.*[.93 .92 .5 .89 .058 .35 .8 .01];
% Задаем вывод сообщений при неудаче оптимизации
options = optimset(‘display’,’notify’);
disp(‘*** Пробуем отношение полиномов’) % В этом случае оптимизация не сходится
[fitber1,fitprops1] = berfit(EbNo,noisydata,EbNo,…
options,’polyRatio’)
disp(‘*** Пробуем сумму двух экспонент с константой’) % В этом случае все хорошо
[fitber2,fitprops2] = berfit(EbNo,noisydata,EbNo,…
options,’doubleExp+const’)
Результат работы данного кода приведен ниже.
*** Пробуем отношение полиномов
Exiting: Maximum number of function evaluations has been exceeded
— increase MaxFunEvals option.
Current function value: 6.136681
fitber1 =
0.0472 0.0289 0.0187 0.0121 0.0077 0.0044 0.0019 0.0001
fitprops1 =
fitType: ‘polyRatio’
coeffs: [6×1 double]
sumSqErr: 6.1367
exitState: ‘The maximum number of function evaluations was exceeded.’
funcCount: 10001
iterations: 3333
*** Пробуем сумму двух экспонент с константой
fitber2 =
0.0338 0.0260 0.0192 0.0134 0.0087 0.0049 0.0021 0.0001
fitprops2 =
fitType: ‘doubleExp+const’
coeffs: [9×1 double]
sumSqErr: 6.7044
exitState: ‘The curve fit converged to a solution.’
funcCount: 1237
iterations: 822
Алгоритм:
Функция berfit ищет коэффициенты подгоняемой функции, используя процедуру нелинейной оптимизации без ограничений, реализованную в функции fminsearch. Используемые аппроксимирующие функции перечислены в следующей таблице. Здесь x — это линейное (не в децибелах!) отношение Eb/N0, а f — оценка BER. Было эмпирически найдено, что данные функции хорошо соответствуют кривым помехоустойчивости в разнообразных задачах, включая экспоненциально падающий BER, линейно падающий BER, а также кривые BER, стремящиеся к ненулевой константе.
Используемая для оптимизации функция fminsearch минимизирует квадратическую ошибку аппроксимации, рассчитываемую как
где экспериментальные значения BER — это величины из вектора empber и суммирование ведется по всем точкам Eb/N0из вектора empEbNo. Использование логарифма вероятности ошибки необходимо для того, чтобы области с высокими значениями BER не вносили слишком большой вклад в целевую функцию.
Сопутствующие функции: fminsearch, optimset
Литература:
В указанной книге приведены общие сведения о нелинейной оптимизации без ограничений.
-
Chapra, Steven C., and Raymond P. Canale, Numerical Methods for Engineers, Fourth Edition, New York, McGraw-Hill, 2002.
Наверх
biterr — вычисление числа ошибочных бит и вероятности ошибки на бит (BER)
Синтаксис:
[number,ratio] = biterr(x,y);
[number,ratio] = biterr(x,y,k);
[number,ratio] = biterr(…,flag);
[number,ratio,individual] = biterr(…)
Описание:
Для всех вариантов синтаксиса
Функция biterr сравнивает беззнаковые двоичные представления элементов массивов x и y. Схемы, приведенные ниже, показывают, как именно происходит сравнение при различной размерности x и y.
Все элементы x и y должны быть неотрицательными целыми числами; функция biterr конвертирует каждый элемент в его беззнаковое двоичное представление. Выходной параметр number представляет собой скаляр или вектор, содержащий число различающихся бит. Выходной параметр ratio — это вероятность ошибки на бит, то есть значение number, деленное на общее число сравниваемых бит. Общее число сравниваемых бит, размер вектора number и правила сравнения определяются размерностями массивов x и y, а также дополнительными параметрами.
Для конкретных вариантов синтаксиса
[number,ratio] = biterr(x,y)
Сравниваются элементы x и y. Если для представления самого большого числа, содержащегося в x и y требуется минимум k бит, то общее число сравниваемых бит равно k, умноженному на число элементов в меньшем по размеру входном параметре. Размеры массивов x и y определяют, как именно сравниваются элементы:
-
если x и y — матрицы одинакового размера, функция biterr сравнивает их поэлементно (см. схему а, приведенную выше);
-
если один из входных параметров является вектором-строкой (столбцом), а другой — матрицей, функция biterr поэлементно сравнивает вектор с каждой строкой (каждым столбцом) матрицы. Длина вектора должна быть равна числу столбцов (строк) матрицы. Выходной параметр number будет вектором-столбцом (строкой), m-й элемент которого показывает число различающихся бит, полученное при сравнении вектора с m-й строкой (столбцом) матрицы (см. схемы б и в, приведенные выше).
[number,ratio] = biterr(x,y,k)
То же, что и предыдущий вариант синтаксиса, но число бит, требующееся для представления элементов x и y, не определяется автоматически, а задается параметром k. Общее число сравниваемых бит равно k, умноженному на число элементов в меньшем по размеру входном параметре. Если для представления какого-либо элемента x или y необходимо больше чем k бит, выдается сообщение об ошибке.
[number,ratio] = biterr(x,y,k,flag)
То же, что и предыдущие варианты синтаксиса, но правила сравнения элементов и вычисления результатов определяются не по умолчанию, а задаются строковым параметром flag. Возможными значениями параметра flagявляются строки ‘row-wise’, ‘column-wise’ и ‘overall’. Приведенная ниже таблица показывает, как производится сравнение и как вычисляются результаты при различных комбинациях входных параметров. Как всегда, выходной параметр ratio вычисляется путем деления number на общее число сравниваемых бит. Если параметр k не задан, он определяется автоматически как число бит, минимально необходимое для представления самого большого из чисел, содержащихся в x и y.
Таблица: Сравнение двумерной матрицы x со вторым входным параметром y
| Размер y | Значение flag | Правила сравнения | Значение number | Общее число сравниваемых бит |
| Двумерная матрица | ‘overall’ (используется по умолчанию) | Поэлементное сравнение | Общее число несовпадающих бит | k, умноженное на число элементов в y |
| ‘row-wise’ | m-я строка x сравнивается с m-й строкой y | Вектор-столбец, элементы которого показывают число несовпадающих бит для разных строк сравниваемых матриц | k, умноженное на число элементов в y | |
| ‘column-wise’ | m-й столбец x сравнивается с m-м столбцом y | Вектор-строка, элементы которого показывают число несовпадающих бит для разных столбцов сравниваемых матриц | k, умноженное на число элементов в y | |
| Вектор-строка | ‘overall’ | y сравнивается с каждой строкой x | Общее (суммарное по всем строкам) число несовпадающих бит | k, умноженное на число элементов в x |
| ‘row-wise’ (используется по умолчанию) | y сравнивается с каждой строкой x | Вектор-столбец, элементы которого показывают число несовпадающих бит для разных строк матрицы x | k, умноженное на число элементов в y | |
| Вектор-столбец | ‘overall’ | y сравнивается с каждым столбцом x | Общее (суммарное по всем столбцам) число несовпадающих бит | k, умноженное на число элементов в x |
| ‘column-wise’ (используется по умолчанию) | y сравнивается с каждым столбцом x | Вектор-строка, элементы которого показывают число несовпадающих бит для разных столбцов матрицы x | k, умноженное на число элементов в y |
[number,ratio,individual] = biterr(…)
Дополнительно возвращает матрицу individual, размерность которой совпадает с размерностью большего из входных параметров x и y. Каждый элемент матрицы individual соответствует сравнению пары элементов из x и y; он показывает число несовпадающих бит, полученное при данном сравнении.
Примеры.
Пример 1.
Команда, приведенная ниже, выполняет сравнение вектора-столбца [0; 0; 0] с каждым столбцом случайной двоичной матрицы. Рассчитываются число единичных элементов в каждом столбце случайной матрицы, их доля и расположение. В данном случае выходной параметр individual совпадает с участвующей в сравнении случайной матрицей.
format rat;
[number,ratio,individual] = biterr([0;0;0],randint(3,5))
number =
2 0 0 3 1
ratio =
2/3 0 0 1 1/3
individual =
1 0 0 1 0
1 0 0 1 0
0 0 0 1 1
Пример 2.
Команды, приведенные ниже, иллюстрируют использование параметра flag для изменения правила построчного сравнения, принятого по умолчанию. Обратите внимание на то, что выходные параметры number и ratio в данном случае являются скалярами, а individual имеет те же размеры, как больший из входных параметров функции biterr.
format rat;
[number,ratio,individual] = biterr([1 2; 3 4],[1 3],3,’overall’)
number =
5
ratio =
5/12
individual =
0 1
1 3
Пример 3.
Приведенный ниже сценарий вносит ошибки в 10% элементов матрицы. Каждый элемент матрицы — это двухбитовое число в десятичной форме. Сценарий вычисляет вероятность ошибки на бит с помощью функции biterr и вероятность ошибки на символ с помощью функции symerr.
x = randint(100,100,4); % Исходный сигнал
% Вносим ошибки в 10 процентов элементов матрицы x.
% Ошибки могут быть равны 1, 2 или 3 (но не нулю).
errorplace = (rand(100,100) > .9); % Места введения ошибок
errorvalue = randint(100,100,[1,3]); % Величины ошибок
error = errorplace.*errorvalue;
% Добавляем ошибки и берем остаток от деления результата на 4
y = rem(x+error,4);
format short
[num_bit,ratio_bit] = biterr(x,y,2)
[num_sym,ratio_sym] = symerr(x,y)
Пример результатов работы сценария приводится ниже. Обратите внимание на то, что значение вероятности ошибки на символ (ratio_sym) близко к намеченной величине 0.10. Полученные вами результаты могут отличаться от приведенных, поскольку в примере используются случайные числа.
num_bit =
1304
ratio_bit =
0.0652
num_sym =
981
ratio_sym =
0.0981
Наверх
eyediagram — вывод глазковой диаграммы
Синтаксис:
eyediagram(x,n);
eyediagram(x,n,period);
eyediagram(x,n,period,offset);
eyediagram(x,n,period,offset,plotstring);
eyediagram(x,n,period,offset,plotstring,h);
h = eyediagram(…);
Описание:
eyediagram(x,n)
Вывод глазковой диаграммы для сигнала x с “длительностью горизонтальной развертки”, равной n отсчетам. Параметр n должен быть целым числом, большим единицы. Крайние значения горизонтальной оси считаются равными –1/2 и 1/2. Функция предполагает, что целочисленным значениям времени соответствуют первый отсчет сигнала и следующие за ним с шагом n. Интерпретация массива x и число выводимых диаграмм зависят от размера массива и наличия у него мнимой части:
-
если x — вещественная двухстолбцовая матрица, функция eyediagram интерпретирует первый столбец как синфазную, а второй — как квадратурную составляющую. Диаграммы для двух составляющих выводятся в отдельных осях в общем графическом окне;
-
если x — комплексный вектор, функция eyediagram интерпретирует его вещественную часть как синфазную, а мнимую — как квадратурную составляющую. Диаграммы для двух составляющих выводятся в отдельных осях в общем графическом окне;
-
если x — вещественный вектор, функция eyediagram интерпретирует его как вещественный сигнал. Графическое окно в данном случае содержит единственную диаграмму.
eyediagram(x,n,period)
То же, что и предыдущий вариант синтаксиса, но крайние значения горизонтальной оси считаются равными -period/2 и period/2.
eyediagram(x,n,period,offset)
То же, что и предыдущий вариант синтаксиса, но функция предполагает, что значениям времени, кратным длительности символьного такта period, соответствуют (offset+1)-й отсчет сигнала и следующие за ним с шагом n. Значение параметра offset должно быть неотрицательным целым числом, лежащим в диапазоне от 0 до n-1.
eyediagram(x,n,period,offset,plotstring)
То же, что и предыдущий вариант синтаксиса, но параметр plotstring задает символы точек, тип линии и цвет для графика. Параметр plotstring — это строка, формат и назначение элементов которой те же самые, что и в функции plot.
eyediagram(x,n,period,offset,plotstring,h)
То же, что и предыдущий вариант синтаксиса, но вместо создания нового графического окна график создается в существующем окне с дескриптором h. Параметр h должен быть дескриптором графического окна, ранее созданного функцией eyediagram.
Внимание! Для вывода нескольких сигналов в одном окне нельзя использовать команду hold on.
h = eyediagram(…)
То же, что предыдущие варианты синтаксиса, с возвратом дескриптора окна, содержащего график, в выходном параметре h.
Примеры.
Приведенный ниже код иллюстрирует использование глазковой диаграммы для поиска оптимальных точек взятия отсчетов. Случайный цифровой сигнал сначала преобразуется в точки 16-точечного квадратурного созвездия, затем в сигнал вносятся искажения с помощью фильтра с косинусоидальным сглаживанием АЧХ. Несколько команд выделяют из фильтрованного сигнала фрагмент, соответствующий установившемуся состоянию. Наконец, для результирующего сигнала выводится глазковая диаграмма.
% Задаем число точек созвездия, а также две частоты дискретизации
M = 16; Fd = 1; Fs = 10;
% Число отсчетов сигнала
Pd = 100;
% Случайные целые числа в диапазоне [0,M-1]
msg_d = randint(Pd,1,M);
% Преобразование целых чисел в параметры квадратурной модуляции
msg_a = modmap(msg_d,Fd,Fd,’qask’,M);
% Пусть канал связи описывается фильтром
% с косинусоидальным сглаживанием АЧХ
delay = 3; % вносимая фильтром задержка (в символах)
rcv = rcosflt(msg_a,Fd,Fs,’fir/normal’,.5,delay);
% Обрезаем переходные процессы (начало и конец
% выходного сигнала фильтра)
propdelay = delay .* Fs/Fd + 1; % задержка (в отсчетах)
rcv1 = rcv(propdelay:end-(propdelay-1),:); % усеченный сигнал
N = Fs/Fd;
% Выводим глазковую диаграмму, не сдвигая моменты взятия отсчетов
offset1 = 0;
h1 = eyediagram(rcv1,N,1/Fd,offset1);
set(h1,’Name’,’Eye Diagram Displayed with No Offset’);
Обратите внимание на то, что вертикальная линия, проведенная в центре диаграммы, пересечет “глаз” в месте его максимального “раскрытия” (левый рисунок).
На рисунке, приведенном справа, упомянутая вертикальная линия окажется в стороне от места максимального “раскрытия” “глаза”. Этот рисунок получен с помощью следующих команд:
offset2 = 2;
h2 = eyediagram(rcv1,N,1/Fd,offset2,’r-‘);
set(h2,’Name’,’Eye Diagram Displayed with Offset of Two’);
Продолжим пример, использовав информацию, полученную с помощью глазковой диаграммы, для сдвига точек взятия отсчетов в функции demodmap. (Обратите внимание на то, что в функцию demodmap передается значение сдвига, равное offset1+1, поскольку функции eyediagram и demodmap трактуют величину сдвига по-разному.)
% Продолжаем, используя информацию о сдвиге для декодирования
% цифрового квадратурного сигнала
newmsg1 = demodmap(rcv1,[Fd offset1+1],Fs,’qask’,16);
s1 = symerr(msg_d,newmsg1) % Число искаженных символов
s1 =
0
Как видите, ошибки приема отсутствуют. Если же использовать значение сдвига, равное offset2, это приведет к появлению искажений в декодированном цифровом сигнале. Полученное вами число ошибок в данном примере может несколько отличаться от приведенного, поскольку обрабатываемое сообщение msg_d состоит из случайных чисел.
newmsg2 = demodmap(rcv1,[Fd offset2+1],Fs,’qask’,16);
s2 = symerr(msg_d,newmsg2)
s2 =
8
Использование глазковых диаграмм иллюстрируется демонстрационной программой scattereyedemo.
Наверх
scatterplot — вывод диаграммы рассеяния
Синтаксис:
scatterplot(x);
scatterplot(x,n);
scatterplot(x,n,offset);
scatterplot(x,n,offset,plotstring);
scatterplot(x,n,offset,plotstring,h);
h = scatterplot(…);
Описание:
scatterplot(x)
Вывод диаграммы рассеяния для сигнала x. Интерпретация массива x зависит от его размера и наличия мнимой части:
-
если x — вещественная двухстолбцовая матрица, функция scatterplot интерпретирует первый столбец как синфазную, а второй — как квадратурную составляющую;
-
если x — комплексный вектор, функция scatterplot интерпретирует его вещественную часть как синфазную, а мнимую — как квадратурную составляющую;
-
если x — вещественный вектор, функция scatterplot интерпретирует его как вещественный сигнал (то есть в данном случае квадратурная составляющая равна нулю).
scatterplot(x,n)
То же, что и предыдущий вариант синтаксиса, но при построении графика используется только каждый n-й отсчет сигнала, начиная с первого (то есть перед формированием графика выполняется прореживание сигнала x с коэффициентом n).
scatterplot(x,n,offset)
То же, что и первый вариант синтаксиса, но при построении графика используется только каждый n-й отсчет сигнала x, начиная с отсчета с номером (offset+1).
scatterplot(x,n,offset,plotstring)
То же, что и предыдущий вариант синтаксиса, но параметр plotstring задает символы точек, тип линии и цвет для графика. Параметр plotstring — это строка, формат и назначение элементов которой те же самые, что и в функции plot.
scatterplot(x,n,offset,plotstring,h)
То же, что и предыдущий вариант синтаксиса, но вместо создания нового графического окна график создается в существующем окне с дескриптором h. Параметр h должен быть дескриптором графического окна, ранее созданного функцией scatterplot. Для вывода нескольких сигналов в одном окне используйте команду hold on.
h = scatterplot(…)
То же, что предыдущие варианты синтаксиса, с возвратом дескриптора окна, содержащего график, в выходном параметре h.
Примеры.
Приведенный ниже код отображает случайный цифровой сигнал в точки 16-точечного созвездия квадратурной манипуляции. Затем с помощью фильтра с косинусоидальным сглаживанием АЧХ имитируются искажения, вносимые каналом связи. Несколько команд выделяют из фильтрованного сигнала фрагмент, соответствующий установившемуся состоянию. Наконец, для результирующего сигнала выводится диаграмма рассеяния.
% Число точек созвездия и частоты дискретизации
M = 16; Fd = 1; Fs = 10;
% Число отсчетов сигнала
Pd = 200;
% Случайные целые числа в диапазоне [0,M-1]
msg_d = randint(Pd,1,M);
% Преобразование целых чисел в параметры квадратурной модуляции
msg_a = modmap(msg_d,Fd,Fs,’qask’,M);
% Пусть канал связи описывается фильтром
% с косинусоидальным сглаживанием АЧХ
rcv = rcosflt(msg_a,Fd,Fs);
% Создаем диаграмму рассеяния для принятого сигнала,
% игнорируя три первых и четыре последних символа
N = Fs/Fd;
rcv_a = rcv(3*N+1:end-4*N,:);
h = scatterplot(rcv_a,N,0,’bx’);
Третий параметр функции scatterplot определяет смещение точек взятия отсчетов при прореживании. Нулевое смещение дает оптимальные результаты (левая диаграмма).
Правая диаграмма построена с помощью команд, приведенных ниже. Крестики и плюсы на диаграмме показывают два неоптимальных варианта смещения (в одном случае отсчеты берутся слишком рано, в другом — слишком поздно). Обратите внимание на то, что отсчеты, взятые вовремя (на правой диаграмме они отображаются точками), совпадают с точками используемого созвездия, а крестики и плюсы разбросаны вблизи этих точек.
hold on;
scatterplot(rcv_a,N,N+1,’r+’,h); % Запаздывание (плюсы)
scatterplot(rcv_a,N,N-1,’mx’,h); % Опережение (крестики)
scatterplot(rcv_a,N,0,’b.’,h); % Отсчеты взяты вовремя (точки)
Еще один пример содержится на странице с описанием функции demodmap. Этот пример также иллюстрирует построение нескольких диаграмм рассеяния в одном графическом окне.
Использование диаграмм рассеяния иллюстрируется демонстрационной программой scattereyedemo.
Наверх
symerr — вычисление числа ошибочных символов и вероятности ошибки на символ
Синтаксис:
[number,ratio] = symerr(x,y);
[number,ratio] = symerr(x,y,flag);
[number,ratio,loc] = symerr(…)
Описание:
Для всех вариантов синтаксиса
Функция symerr подсчитывает число несовпадающих элементов массивов x и y. Схемы, приведенные ниже, показывают, как именно происходит сравнение при различной размерности x и y.
Выходной параметр number представляет собой скаляр или вектор, содержащий число различающихся элементов массивов. Размер результата number определяется необязательным параметром flag, а также размерностями массивов x и y. Выходной параметр ratio — это вероятность ошибки на символ, то есть значение number, деленное на число элементов в меньшем по размеру входном параметре.
Для конкретных вариантов синтаксиса
[number,ratio] = symerr(x,y)
Сравниваются элементы x и y. Размеры массивов x и y определяют, как именно сравниваются элементы:
-
если x и y — матрицы одинакового размера, функция symerr сравнивает их поэлементно. Результат number является скаляром (см. схему а, приведенную выше);
-
если один из входных параметров является вектором-строкой (столбцом), а другой — матрицей, функция symerr поэлементно сравнивает вектор с каждой строкой (каждым столбцом) матрицы. Длина вектора должна быть равна числу столбцов (строк) матрицы. Выходной параметр number будет вектором-столбцом (строкой), m-й элемент которого показывает число различающихся элементов, полученное при сравнении вектора с m-й строкой (столбцом) матрицы (см. схемы б и в, приведенные выше).
[number,ratio] = symerr(x,y,flag)
То же, что и предыдущий вариант синтаксиса, но правила сравнения элементов и вычисления результатов определяются не по умолчанию, а задаются строковым параметром flag. Возможными значениями параметра flagявляются строки ‘row-wise’, ‘column-wise’ и ‘overall’. Приведенная ниже таблица показывает, как производится сравнение и как вычисляются результаты при различных комбинациях входных параметров. Во всех случаях выходной параметр ratio вычисляется путем деления number на число элементов вектора y.
Таблица: Сравнение двумерной матрицы x со вторым входным параметром y
| Размер y | Значение flag | Правила сравнения | Значение number |
| Двумерная матрица | ‘overall’ (используется по умолчанию) | Поэлементное сравнение | Общее число несовпадающих символов (элементов) |
| ‘row-wise’ | m-я строка x сравнивается с m-йстрокой y | Вектор-столбец, элементы которого показывают число несовпадающих элементов для разных строк сравниваемых матриц | |
| ‘column-wise’ | m-й столбец x сравнивается с m-м столбцом y | Вектор-строка, элементы которого показывают число несовпадающих элементов для разных столбцов сравниваемых матриц | |
| Вектор-строка | ‘overall’ | y сравнивается с каждой строкой x | Общее (суммарное по всем строкам) число несовпадающих элементов |
| ‘row-wise’ (используется по умолчанию) | y сравнивается с каждой строкой x | Вектор-столбец, элементы которого показывают число несовпадающих элементов для разных строк матрицы x | |
| Вектор-столбец | ‘overall’ | y сравнивается с каждым столбцом x | Общее (суммарное по всем столбцам) число несовпадающих элементов |
| ‘column-wise’ (используется по умолчанию) | y сравнивается с каждым столбцом x | Вектор-строка, элементы которого показывают число несовпадающих элементов для разных столбцов матрицы x |
[number,ratio,loc] = symerr(…)
Дополнительно возвращает матрицу loc, которая показывает, какие именно элементы x и y различаются. Элемент матрицы loc равен нулю, если соответствующее сравнение дает совпадение элементов, и единице, если имеет место несовпадение.
Примеры.
Пример, использующий функцию symerr, имеется на странице с описанием функции biterr.
Команда, приведенная ниже, показывает, как работает функция symerr, если один входной параметр является вектором, а другой — матрицей. В данном случае сравниваются вектор-столбец [1,2,3]’ с матрицей
1 1 3 1
3 2 2 2
3 3 8 3
По умолчанию сравнение производится по столбцам:
num = symerr([1 2 3]’,[1 1 3 1;3 2 2 2; 3 3 8 3])
num =
1 0 2 0
В качестве следующего примера приведенная ниже команда иллюстрирует использование параметра flag для изменения правила построчного сравнения, принятого по умолчанию. Обратите внимание на то, что выходные параметры number и ratio в данном случае являются скалярами.
format rat; [number,ratio,loc] = symerr([1 2; 3 4],…
[1 3],’overall’)
number =
3
ratio =
3/4
loc =
0 1
1 1
Наверх
arithdeco — декодирование двоичного арифметического кода
Синтаксис:
dseq = arithdeco(code,counts,len)
Описание:
dseq = arithdeco(code,counts,len)
Декодирует двоичный арифметический код из вектора code, восстанавливая исходную последовательность из len символов. Вектор counts представляет статистические характеристики источника сообщения — в нем содержится число вхождений в тестовый набор данных каждого символа из алфавита сообщения. Данная функция рассчитана на декодирование данных, закодированных с помощью функции arithenco.
Примеры:
Данный пример аналогичен тому, что приведен на странице с описанием функции arithenco, за исключением того, что помимо кодирования здесь демонстрируется и восстановление исходной последовательности данных с помощью функции arithdeco.
counts = [99 1]; % Соотношение единиц и двоек – 99 к одному
len = 1000;
seq = randsrc(1,len,[1 2; .99 .01],19069); % Случайная последовательность
code = arithenco(seq,counts);
dseq = arithdeco(code,counts,length(seq)); % Декодирование
isequal(seq,dseq) % Проверка совпадения исходного и декодированного сообщений
Результат работы примера показывает, что результат декодирования совпадает с исходным сообщением:
ans =
1
Алгоритм:
Алгоритм, используемый данной функцией, описан в приведенной ниже ссылке на литературу.
Литература:
Sayood, Khalid, Introduction to Data Compression, San Francisco, Morgan Kaufmann, 2000.
Наверх
arithenco — арифметическое кодирование последовательности символов
Синтаксис:
code = arithenco(seq,counts)
Описание:
code = arithenco(seq,counts)
Генерирует двоичный арифметический код, соответствующий последовательности символов, содержащейся в векторе seq (символы сообщения должны представлять собой целые положительные числа). Вектор counts представляет статистические характеристики источника сообщения — в нем содержится число вхождений в тестовый набор данных каждого символа из алфавита сообщения.
Примеры:
Данный пример иллюстрирует сжатие данных, которое в некоторых случаях может быть обеспечено арифметическим кодом. Источник имеет алфавит, состоящий из символов “1” и “2”, причем единица встречается с вероятностью 99%. Кодирование 1000 символов, произведенных этим источником, дает кодовый вектор, имеющий намного меньшее число элементов. Точное число элементов в векторе code зависит от конкретной случайной последовательности символов, содержащейся в векторе seq.
counts = [99 1]; % Соотношение единиц и двоек – 99 к одному
len = 1000;
seq = randsrc(1,len,[1 2; .99 .01],19069); % Случайная последовательность
code = arithenco(seq,counts);
s = size(code) % Длина вектора code – всего лишь 8.3% от длины вектора seq
Результат работы примера показывает, что вектор code содержит всего лишь 83 элемента:
s =
1 83
Алгоритм:
Алгоритм, используемый данной функцией, описан в приведенной ниже ссылке на литературу.
Литература:
Sayood, Khalid, Introduction to Data Compression, San Francisco, Morgan Kaufmann, 2000.
Наверх
compand — логарифмическое или экспоненциальное преобразование (законы A и m )
Синтаксис:
out = compand(in,mu,maxim);
out = compand(in,mu,maxim,’mu/compressor’);
out = compand(in,mu,maxim,’mu/expander’);
out = compand(in,A,maxim,’A/compressor’);
out = compand(in,A,maxim,’A/expander’);
Описание:
-
out = compand(in,param,maxim)
Реализует компрессор — логарифмический преобразователь входного вектора in по закону m. Параметр mu задает m , а параметр maxim — максимально возможную амплитуду входного сигнала. Результат out имеет такие же размеры и максимальную амплитуду, как входной сигнал in.
-
out = compand(in,mu,maxim,’mu/compressor’)
То же, что предыдущий вариант синтаксиса.
-
out = compand(in,mu,maxim,’mu/expander’)
Реализует экспандер — экспоненциальный преобразователь входного вектора in по закону m. Параметр mu задает m, а параметр maxim — максимально возможную амплитуду входного сигнала. Результат out имеет такие же размеры и максимальную амплитуду, как входной сигнал in.
-
out = compand(in,A,maxim,’A/compressor’)
Реализует компрессор — логарифмический преобразователь входного вектора in по закону A. Скаляр A задает параметр A закона преобразования, а параметр maxim — максимально возможную амплитуду входного сигнала. Результат out имеет такие же размеры и максимальную амплитуду, как входной сигнал in.
-
out = compand(in,A,maxim,’A/expander’)
Реализует экспандер — экспоненциальный преобразователь входного вектора in по закону A. Скаляр A задает параметр A закона преобразования, а параметр maxim — максимально возможную амплитуду входного сигнала. Результат out имеет такие же размеры и максимальную амплитуду, как входной сигнал in.
Замечание. На практике чаще всего используются значения m = 255 и A = 87,6.
Примеры.
Приводимые ниже команды иллюстрируют тот факт, что компрессор и экспандер выполняют взаимно обратные действия — последовательно выполнив логарифмическое и экспоненциальное преобразования, мы получаем исходные значения.
compressed = compand(1:5,87.6,5,’a/compressor’)
compressed =
3.5296 4.1629 4.5333 4.7961 5.0000
expanded = compand(compressed,87.6,5,’a/expander’)
expanded =
1.0000 2.0000 3.0000 4.0000 5.0000
Алгоритм.
При использовании закона m действие компрессора на сигнал x описывается следующей формулой:
,
где V — максимальная амплитуда сигнала x, m — параметр закона преобразования, sgn — знаковая функция (sign в MATLAB).
При использовании закона A действие компрессора на сигнал x описывается следующей формулой:
где A — параметр закона преобразования, а остальные обозначения имеют тот же смысл, что и для закона m .
Наверх
dpcmdeco — декодирование дифференциальной импульсно-кодовой модуляции
Синтаксис:
sig = dpcmdeco(indx,codebook,predictor);
[sig,quanterror] = dpcmdeco(indx,codebook,predictor);
Описание:
-
sig = dpcmdeco(indx,codebook,predictor)
Реализует декодирование индексов ДИКМ, содержащихся в векторе indx. Параметр codebook представляет собой вектор, содержащий квантованные значения, соответствующие индексам квантования. Параметр predictor представляет собой вектор, задающий импульсную характеристику предсказывающего фильтра. Если порядок предсказывающего фильтра равен M, вектор predictor должен иметь длину M + 1 и значение первого элемента, равное нулю. Для правильного декодирования параметры codebook и predictor должны быть теми же, что использовались при кодировании сигнала с помощью функции dpcmenco.
Более подробная информация о формате параметров partition и codebook имеется на странице с описанием функции quantiz.
-
[sig,quanterror] = dpcmdeco(indx,codebook,predictor)
То же, что предыдущий вариант синтаксиса, но второй выходной параметр quanterror содержит квантованные значения ошибки предсказания, полученные в процессе восстановления сигнала. Вектор quanterror имеет такой же размер, что и вектор sig.
Замечание. Подобрать оптимальные значения входных параметров codebook, partition и predictor можно с помощью функции dpcmopt.
Наверх
dpcmenco — кодирование сигнала с использованием дифференциальной импульсно-кодовой модуляции
Синтаксис:
indx = dpcmenco(sig,codebook,partition,predictor)
[indx,quants] = dpcmenco(sig,codebook,partition,predictor)
Описание:
-
indx = dpcmenco(sig,codebook,partition,predictor)
Реализует кодирование вектора отсчетов сигнала sig с использованием ДИКМ. Параметр partition представляет собой вектор, элементы которого задают границы между зонами квантования ошибки предсказания. Параметр codebook представляет собой вектор, длина которого на единицу больше длины вектора partition, этот вектор задает квантованную величину для каждой зоны квантования. Параметр predictor задает импульсную характеристику предсказывающего фильтра. Если порядок предсказывающего фильтра равен M, вектор predictor должен иметь длину M + 1 и значение первого элемента, равное нулю. Выходной вектор indx представляет собой набор индексов квантованных величин.
Более подробная информация о формате параметров partition и codebook имеется на странице с описанием функции quantiz.
-
[indx,quants] = dpcmenco(sig,codebook,partition,predictor)
То же, что предыдущий вариант синтаксиса, но второй выходной параметр quants содержит квантованные значения сигнала sig, полученные в процессе квантования. Вектор quants имеет такой же размер, что и вектор sig.
Замечание. Если порядок предсказывающего фильтра равен единице, ДИКМ называется дельта-модуляцией.
Наверх
dpcmopt — оптимизация параметров дифференциальной импульсно-кодовой модуляции
Синтаксис:
predictor = dpcmopt(trainingset,ord);
[predictor,codebook,partition] = dpcmopt(trainingset,ord,length);
[predictor,codebook,partition] = dpcmopt(trainingset,ord,initcodebook);
Описание:
-
predictor = dpcmopt(trainingset,ord)
Возвращает вектор, содержащий отсчеты импульсной характеристики предсказывающего фильтра порядка ord, оптимального для обработки сигнала, содержащегося в векторе trainingset. Выходной результат predictor представляет собой вектор-строку длиной ord+1, первый элемент которого равен нулю.
Замечание. Функция dpcmopt подбирает оптимальные параметры, анализируя сигнал, содержащийся в векторе trainingset. Для получения наилучших результатов сигнал trainingset должен быть аналогичен тем данным, которые затем будут подвергаться ДИКМ с применением полученных оптимизированных параметров.
-
[predictor,codebook,partition] = dpcmopt(trainingset,ord,length)
То же, что предыдущий вариант синтаксиса, но дополнительно функция возвращает оптимизированные значения квантованных величин (codebook) и границ зон квантования (partition). Входной параметр length представляет собой целое число, задающее число зон квантования, то есть длину вектора codebook. Длина вектора partition равна length–1.
Более подробная информация о формате параметров partition и codebook имеется на странице с описанием функции quantiz.
-
[predictor,codebook,partition] = dpcmopt(trainingset,ord,initcodebook)
То же, что предыдущий вариант синтаксиса, но вместо числового параметра, задающего число зон квантования, указывается вектор initcodebook — начальное приближение для набора квантованных величин. Длина вектора initcodebook должна быть не меньше двух. Выходной параметр codebook представляет собой вектор той же длины, что и входной вектор initcodebook. Длина выходного вектора partition на единицу меньше, чем длина вектора codebook.
Примеры.
Приведенные ниже код MATLAB демонстрирует использование функций dpcmopt, dpcmenco и dpcmdeco. В качестве обрабатываемого сигнала используется запись произнесенного слова “MATLAB”, содержащаяся во входящем в поставку MATLAB файле mtlb.mat. Оптимизация параметров ДИКМ производится для предсказывающего фильтра второго параметра и 32 уровней квантования ошибки предсказания.
% загружаем обрабатываемый сигнал
load mtlb
% производим оптимизацию параметров ДИКМ
[predictor, codebook, partition] = dpcmopt(mtlb, 2, 32);
% кодируем сигнал, используЯ оптимизированные параметры
[index, quants] = dpcmenco(mtlb, codebook, partition, predictor);
% обратное декодирование
[sig, quanterror] = dpcmdeco(index, codebook, predictor);
% ошибка квантованиЯ
e_sig = mtlb(:)-sig(:);
% средний квадрат ошибки
dist1 = sum(e_sig.^2)/length(e_sig);
fprintf(‘Средний квадрат ошибки %.2e\n’, dist1)
В результате расчета будет выдан следующий результат:
Средний квадрат ошибки 6.49e-004
Теперь выполним обычное (не дифференциальное) квантование того же сигнала с помощью функции quantiz, использовав тоже 32 уровня и оптимизировав параметры квантования с помощью функции lloyds.
% оптимизируем параметры квантования
[partition2, codebook2] = lloyds(mtlb, 32);
% производим квантование и получаем средний квадрат ошибки
[index2, quant2, dist2] = quantiz(mtlb, partition2, codebook2);
fprintf(‘Средний квадрат ошибки %.2e\n’, dist2)
В результате расчета будет выдан следующий результат:
Средний квадрат ошибки 1.56e-003
Таким образом, дифференциальное квантование позволяет уменьшить средний квадрат ошибки воспроизведение сигнала почти в два с половиной раза.
Наверх
huffmandeco — декодер Хаффмана
Синтаксис:
dsig = huffmandeco(comp,dict)
Описание:
dsig = huffmandeco(comp,dict)
Декодирует закодированный по Хаффману числовой вектор comp с использованием кодового словаря dict. Входной параметр dict должен быть массивом ячеек размером N на 2, где N — объем алфавита источника. Первый столбец массива dict представляет символы источника, второй столбец — соответствующие кодовые слова. Каждое кодовое слово должно быть представлено числовым вектором-строкой, и ни одно кодовое слово в массиве dict не должно быть префиксом в другом кодовом слове. Создать массив dict можно с помощью функции huffmandict, а выполнить кодирование сигнала — с помощью функции huffmanenco. Если все символы алфавита источника из словаря dict являются числовыми, то результат dsig будет числовым вектором; если хотя бы один из элементов алфавита источника, перечисленных в dict, будет символьным, то dsig будет одномерным массивом ячеек.
Примеры:
Приведенный ниже код кодирует и затем декодирует вектор случайных данных, которые имеют заданное распределение вероятности.
symbols = [1:6]; % Алфавит источника
p = [.5 .125 .125 .125 .0625 .0625]; % Распределение вероятностей
[dict,avglen] = huffmandict(symbols,p); % Создание словаря
actualsig = randsrc(1,100,[symbols; p]); % Случайные данные с распределением p
comp = huffmanenco(actualsig,dict); % Кодирование данных
dsig = huffmandeco(comp,dict); % Декодирование кода Хаффмана
isequal(actualsig,dsig) % Проверка правильности декодирования
Приведенный далее результат работы данного кода показывает, что данные после процессов кодирования и декодирования восстановлены правильно.
ans =
1
Сопутствующие функции: huffmandict, huffmanenco.
Литература:
[1] Sayood, Khalid, Introduction to Data Compression, San Francisco, Morgan Kaufmann, 2000.
Наверх
huffmandict — генерирование словаря для кода Хаффмана при известном распределении вероятности источника
Синтаксис:
[dict,avglen] = huffmandict(symbols,p)
[dict,avglen] = huffmandict(symbols,p,N)
[dict,avglen] = huffmandict(symbols,p,N,variance)
Описание:
Для всех вариантов синтаксиса
Функция huffmandict генерирует словарь для кода Хаффмана, соответствующий источнику данных с известной вероятностной моделью. Обязательными являются два входных параметра:
-
symbols — алфавит источника данных. Данный параметр может быть задан в виде числового вектора, числового массива ячеек или массива ячеек, содержащего символьные данные. Если используется массив ячеек, он должен быть строкой или столбцом.
-
p — вектор значений вероятности, k-й элемент которого представляет собой вероятность появления k-го элемента параметра symbols на выходе источника данных. Длина вектора p должна совпадать с длиной параметра symbols. Выходные параметры, производимые функцией huffmandict, имеют следующий смысл:
-
dict — двухстолбцовый массив ячеек, в первом столбце которого перечислены элементы алфавита источника из входного параметра symbols, а во втором столбце — соответствующие кодовые слова кода Хаффмана. Кодовые слова во втором столбце представлены в виде числовых векторов-строк.
-
avglen — средняя длина кодового слова, вычисленная в соответствии с вероятностями из входного вектора p.
Для конкретных вариантов синтаксиса
[dict,avglen] = huffmandict(symbols,p)
Генерирует словарь для двоичного кода Хаффмана с использованием алгоритма максимальной дисперсии.
[dict,avglen] = huffmandict(symbols,p,N)
Генерирует словарь для N-ичного кода Хаффмана с использованием алгоритма максимальной дисперсии. Входной параметр N должен быть целым числом в диапазоне от 2 до 10, не превосходящим объем алфавита источника данных.
[dict,avglen] = huffmandict(symbols,p,N,variance)
Генерирует словарь для N-ичного кода Хаффмана с использованием алгоритма минимальной дисперсии, если входной строковый параметр variance имеет значение ‘min’, или с использованием алгоритма максимальной дисперсии, если variance имеет значение ‘max’. Входной параметр N должен быть целым числом в диапазоне от 2 до 10, не превосходящим объем алфавита источника данных.
Примеры:
Приведенный ниже код генерирует словарь для кода Хаффмана, соответствующий источнику, выдающему символы от 1 до 5 с неодинаковой вероятностью. После этого отображается кодовое слово, соответствующее последнему, пятому, символу.
symbols = [1:5];
p = [.3 .3 .2 .1 .1];
[dict,avglen] = huffmandict(symbols,p)
samplecode = dict{5,2} % Кодовое слово для пятого символа алфавита источника
Далее приводится результат работы кода, где в первом столбце массива ячеек dict перечислены символы алфавита symbols, а во втором содержатся соответствующие им кодовые слова.
dict =
[1] [1×2 double]
[2] [1×2 double]
[3] [1×2 double]
[4] [1×3 double]
[5] [1×3 double]
avglen =
2.2000
samplecode =
1 1 0
Сопутствующие функции: huffmanenco, huffmandeco.
Литература:
[1] Sayood, Khalid, Introduction to Data Compression, San Francisco, Morgan Kaufmann, 2000.
Наверх
huffmanenco — кодер Хаффмана
Синтаксис:
comp = huffmanenco(sig,dict)
Описание:
comp = huffmanenco(sig,dict)
Кодирует сигнал sig с использованием кода Хаффмана, описываемого словарем dict. Входной параметр sig может быть числовым вектором, числовым массивом ячеек или символьным массивом ячеек. Если sig — массив ячеек, он должен быть строкой или столбцом. Второй входной параметр dict должен быть массивом ячеек размером N на 2, где N — объем алфавита источника. Первый столбец массива dict представляет символы источника, второй столбец — соответствующие кодовые слова. Каждое кодовое слово должно быть представлено числовым вектором-строкой, и ни одно кодовое слово в массиве dict не должно быть префиксом в другом кодовом слове. Создать массив dict можно с помощью функции huffmandict.
Примеры:
Приведенный ниже код кодирует вектор случайных данных, которые имеют заданное распределение вероятности.
symbols = [1:6]; % Алфавит источника
p = [.5 .125 .125 .125 .0625 .0625]; % Распределение вероятностей
[dict,avglen] = huffmandict(symbols,p); % Создание словаря
actualsig = randsrc(100,1,[symbols; p]); % Случайные данные с распределением p
comp = huffmanenco(actualsig,dict); % Кодирование данных
Сопутствующие функции: huffmandict, huffmandeco.
Литература:
[1] Sayood, Khalid, Introduction to Data Compression, San Francisco, Morgan Kaufmann, 2000.
Наверх
lloyds — оптимизация параметров квантования с использованием алгоритма Ллойда
Синтаксис:
[partition,codebook] = lloyds(trainingset,initcodebook);
[partition,codebook] = lloyds(trainingset,length);
[partition,codebook] = lloyds(trainingset,…,tol);
[partition,codebook] = lloyds(trainingset,…,tol,plotflag);
[partition,codebook,distor] = lloyds(…);
[partition,codebook,distor,reldistor] = lloyds(…);
Описание:
-
[partition,codebook] = lloyds(trainingset,initcodebook)
Оптимизирует параметры нелинейного квантования partition и codebook по тестовому набору данных из вектора trainingset. Входной параметр initcodebook является вектором, содержащим хотя бы два элемента, и задает начальное приближение для набора уровней квантования (codebook). Результат codebook — оптимизированный набор уровней квантования, он является вектором той же длины, что и initcodebook. Результат partition — вектор, длина которого на единицу меньше, чем длина вектора codebook. Этот вектор задает границы зон квантования.
Подробное описание смысла параметров partition и codebook приведено на странице с описанием функции quantiz.
Замечание. Функция lloyds подбирает параметры квантования, минимизирующие среднеквадратическую ошибку квантования для набора данных из вектора trainingset. Поэтому вектор trainingset должен содержать выборку, типичную для данных, которые планируется квантовать с использованием оптимизированных параметров.
-
[partition,codebook] = lloyds(trainingset,length)
То же, что предыдущий вариант синтаксиса, но вторым входным параметром функции является не вектор, а скаляр length, который задает длину вектора codebook. Начальное приближение в данном случае выбирается автоматически.
-
[partition,codebook] = lloyds(trainingset,…,tol)
То же, что предыдущие варианты синтаксиса, но параметр tol задает пороговое значение для завершения работы итерационного алгоритма (см. далее). По умолчанию значение tol равно 10–7.
-
[partition,codebook] = lloyds(trainingset,…,tol,plotflag)
То же, что предыдущий вариант синтаксиса, но дополнительно выводится график тестового сигнала, на котором также показаны оптимизированные уровни квантования и границы зон квантования. Значение параметра plotflag может быть любым, важно лишь его наличие.
-
[partition,codebook,distor] = lloyds(…)
Дополнительно возвращает средний квадрат ошибки квантования — выходной параметр distor.
-
[partition,codebook,distor,reldistor] = lloyds(…)
Дополнительно возвращает параметр reldistor, связанный с завершением работы итерационного алгоритма. При первой причине завершения (см. далее) reldistor показывает относительное изменение среднего квадрата ошибки на последней итерации. При второй причине завершения значение reldistor равно значению distor.
Примеры.
Приведенный ниже код оптимизирует параметры квантования для передачи синусоидального сигнала по трехбитовому каналу. Поскольку типичным примером сигнала является синусоида, вектор trainingset представляет собой набор отсчетов синусоиды. Поскольку предполагаемый канал связи является трехбитовым, функция lloyds оптимизирует набор уровней и границ зон для восьмиуровневого квантования (23 = 8).
% Генерируем один период синусоидального сигнала
x = sin([0:1000]*pi/500);
% Оптимизируем параметры квантования
[partition,codebook] = lloyds(x,2^3)
partition =
-0.8540 -0.5973 -0.3017 0.0031 0.3077 0.6023 0.8572
codebook =
Columns 1 through 7
-0.9504 -0.7330 -0.4519 -0.1481 0.1558 0.4575 0.7372
Column 8
0.9515
Алгоритм.
Функция lloyds использует итерационный алгоритм для минимизации среднеквадратической ошибки квантования. Завершение работы алгоритма может происходить по одной из двух причин:
-
Относительное изменение среднего квадрата ошибки на очередной итерации стало меньше чем tol (по умолчанию значение параметра tol равно 10–7).
-
Средний квадрат ошибки стал меньше чем eps*max(trainingset), где eps — относительная точность вычислений с плавающей запятой в MATLAB.
Сопутствующие функции: compand, dpcmopt, quantiz.
Литература:
-
S. P. Lloyd. «Least Squares Quantization in PCM.» IEEE Transactions on Information Theory. Vol IT-28, March 1982, 129–137.
-
J. Max. «Quantizing for Minimum Distortion.» IRE Transactions on Information Theory. Vol. IT-6, March 1960, 7–12.
Наверх
quantiz — квантование сигнала по заданному набору уровней
Синтаксис:
index = quantiz(sig,partition);
[index,quants] = quantiz(sig,partition,codebook);
[index,quants,distor] = quantiz(sig,partition,codebook);
Описание:
-
index = quantiz(sig,partition)
Возвращает номера уровней квантования для вещественного вектора sig, используя границы зон квантования из параметра partition. Параметр partition — вещественный вектор, элементы которого расположены в строго возрастающем порядке. Если длина вектора partition равна n, то результат index — вектор-столбец, k-й элемент которого равен:
— 0, если sig(k) <= partition(1);
— m, если partition(m) < sig(k) <= partition(m+1);
— n, если sig(k) > partition(n).
-
[index,quants] = quantiz(sig,partition,codebook)
То же, что предыдущий вариант синтаксиса, но входной параметр codebook задает квантованные значения для каждой зоны квантования, а выходной параметр quants содержит квантованные значения отсчетов сигнала sig. Параметр codebook должен быть вектором, длина которого на единицу больше длины вектора partition. Результат quants — вектор-столбец, длина которого равна длине входного сигнала sig. Вектор quants связан с векторами codebook и index следующим образом: quants = codebook(index+1);
-
[index,quants,distor] = quantiz(sig,partition,codebook)
То же, что предыдущий вариант синтаксиса, но выходной параметр distor содержит величину среднего квадрата ошибки квантования.
Примеры.
Приведенная ниже команда округляет несколько чисел, расположенных в диапазоне между 1 и 100 до ближайших значений, кратных десяти. Результат quants содержит округленные числа, а результат index — номера соответствующих уровней квантования.
[index,quants] = quantiz([3 34 84 40 23],10:10:90,10:10:100)
index =
0
3
8
3
2
quants =
10 40 90 40 30
Наверх
convenc — кодирование двоичных данных с использованием сверточного кода
Синтаксис:
code = convenc(msg,trellis);
code = convenc(msg,trellis,initstate);
[code,finalstate] = convenc(…);
Описание:
-
code = convenc(msg,trellis)
Кодирует двоичный вектор msg с использованием сверточного кода, описание таблицы переходов которого содержится в MATLAB-структуре trellis. Подробная информация о назначении полей этой структуры приведена на странице с описанием функции istrellis. Каждый символ в сообщении msg содержит log2(trellis.numInputSymbols) бит. Вектор msg может содержать один или несколько символов. Выходной двоичный вектор code содержит столько же символов, сколько и входное сообщение, при этом каждый выходной символ состоит из log2(trellis.numOutputSymbols) бит.
-
code = convenc(msg,trellis,initstate)
То же, что и предыдущий вариант синтаксиса, но входной параметр initstate задает начальное внутреннее состояние кодера. Скалярный параметр initstate является целым числом в диапазоне от 0 до trellis.numStates-1. Если схема кодера предполагает наличие нескольких входных битовых потоков, то состояние сдвигового регистра, принимающего первыйвходной битовый поток, соответствует младшим битам параметра initstate, а состояние сдвигового регистра, принимающего последний поток, — старшим битам этого параметра. Чтобы использовать нулевое начальное состояние, принимаемое по умолчанию, задайте параметр initstate равным 0 или [].
-
[code,finalstate] = convenc(…)
Кодирует входное сообщение и, помимо этого, возвращает в скалярном выходном параметре finalstate заключительное внутреннее состояние кодера. Формат параметра finalstate такой же, как у входного параметра initstate.
Примеры.
Пример 1.
Приведенная ниже команда кодирует пять случайных двухбитовых символов с использованием сверточного кода, имеющего скорость кодирования 2/3. Структурная схема этого кодера приведена на странице с описанием функции poly2trellis.
code1 = convenc(randint(10,1,2,123), poly2trellis([5 4],[27 33 0; 0 5 13]));
Пример 2.
Приведенные ниже команды создают структуру таблицы переходов в явном виде, а затем с помощью функции convenc производят кодирование десяти однобитовых символов. Решетчатая диаграмма для используемого в данном примере кода (его скорость равна 1/2) показана на рисунке.
trel = struct(‘numInputSymbols’,2,’numOutputSymbols’,4,…
‘numStates’,4,’nextStates’,[0 2;0 2;1 3;1 3],…
‘outputs’,[0 3;1 2;3 0;2 1]);
code2 = convenc(randint(10,1),trel);
Пример 3.
Приведенные ниже команды демонстрируют использование дополнительных параметров initstate и finalstate для того, чтобы кодировать сообщение по частям, вызывая функцию convenc несколько раз. Объединенный выходной вектор [code3; code4] совпадает с результатами кодирования, полученными в Примере 1 (вектор code1).
trel = poly2trellis([5 4],[27 33 0; 0 5 13]);
msg = randint(10,1,2,123);
% Encode part of msg, recording final state for later use.
[code3,fstate] = convenc(msg(1:6),trel);
% Encode the rest of msg, using state as an input argument.
code4 = convenc(msg(7:10),trel,fstate);
Наверх
cyclgen — генерация проверочной и порождающей матриц для циклического кода
Синтаксис:
parmat = cyclgen(n,pol);
parmat = cyclgen(n,pol,opt);
[parmat,genmat] = cyclgen(…);
[parmat,genmat,k] = cyclgen(…);
Описание:
Для всех вариантов синтаксиса длина кодового слова обозначается как n, а размер блока исходного сообщения — как k. Полином может породить циклический код с длиной кодового слова n и размером блока исходного сообщения k тогда и только тогда, когда этот полином имеет степень (n – k) и является делителем полинома xn – 1. (В двоичном конечном поле GF(2) xn – 1 — это то же самое, что и xn + 1.) Отсюда следует, что k равняется n минус степень порождающего полинома.
-
parmat = cyclgen(n,pol)
Возвращает содержащую (n – k) строк и n столбцов проверочную матрицу для систематического двоичного циклического кода с длиной кодового слова n. Вектор-строка pol содержит двоичные коэффициенты порождающего полинома степени (n – k) в порядке возрастания степеней.
-
parmat = cyclgen(n,pol,opt)
То же, что предыдущий вариант синтаксиса, но входной параметр opt определяет, должна итоговая матрица соответствовать систематическому или несистематическому коду. Возможные значения для параметра opt — ‘system’ (систематический код) и ‘nonsys’ (несистематический код).
-
[parmat,genmat] = cyclgen(…)
То же, что parmat = cyclgen(…), но дополнительно возвращает порождающую матрицу genmat, содержащую k строк и n столбцов и соответствующую проверочной матрице parmat.
-
[parmat,genmat,k] = cyclgen(…)
То же, что [parmat,genmat] = cyclgen(…), но дополнительно возвращает размер блока исходного сообщения k.
Примеры.
Приведенный ниже код создает проверочную и порождающую матрицы для двоичного циклического кода с длиной кодового слова, равной 7, и размером блока исходного сообщения, равным 4.
pol = cyclpoly(7,4);
[parmat,genmat,k] = cyclgen(7,pol)
parmat =
1 0 0 1 1 1 0
0 1 0 0 1 1 1
0 0 1 1 1 0 1
genmat =
1 0 1 1 0 0 0
1 1 1 0 1 0 0
1 1 0 0 0 1 0
0 1 1 0 0 0 1
k = 4
Рассматривая результат работы приведенной ниже команды, обратите внимание на то, что полученная проверочная матрица отличается от рассчитанной ранее матрицы parmat, поскольку теперь она соответствует несистематическомуциклическому коду. Иными словами, новая матрица parmatn, в отличие от матрицы parmat, не содержит в своей левой части блока в виде единичной матрицы размером 3 на 3.
parmatn = cyclgen(7,cyclpoly(7,4),’nonsys’)
parmatn =
1 1 1 0 1 0 0
0 1 1 1 0 1 0
0 0 1 1 1 0 1
Наверх
cyclpoly — генерация порождающего полинома для циклического кода
Синтаксис:
pol = cyclpoly(n,k);
pol = cyclpoly(n,k,opt);
Описание:
Для всех вариантов синтаксиса полином представляется в виде строки, содержащей коэффициенты полинома в порядке возрастания степеней.
-
pol = cyclpoly(n,k)
Возвращает вектор-строку, представляющий один из нетривиальных порождающих полиномов для циклического кода с длиной кодового слова n и длиной блока исходного сообщения k.
-
pol = cyclpoly(n,k,opt)
Производит поиск одного или нескольких нетривиальных порождающих полиномов для циклических кодов с длиной кодового слова n и длиной блока исходного сообщения k. Результат pol зависит от входного параметра opt, как показано в следующей таблице.
| Opt | Смысл результата pol | Формат результата pol |
| ‘min’ | Один порождающий полином, имеющий минимально возможный вес | Вектор-строка, представляющий полином |
| ‘max’ | Один порождающий полином, имеющий максимально возможный вес | Вектор-строка, представляющий полином |
| ‘all’ | Все порождающие полиномы | Матрица, каждая строка которой представляет один из полиномов |
| Положительное целое число | Все порождающие полиномы, имеющие вес opt | Матрица, каждая строка которой представляет один из полиномов |
Вес полинома с двоичными коэффициентами — это число членов в нем (то есть число ненулевых коэффициентов). Если нет ни одного полинома, удовлетворяющего заданным при вызове функции условиям, то выводится сообщение об ошибке, а результат pol представляет собой пустую матрицу.
Примеры.
Первая из приведенных ниже команд дает представления для трех порождающих полиномов циклического кода (15, 4).
Вторая команда показывает, что порождающим полиномом с максимальным весом (числом ненулевых коэффициентов) является 1 + x + x2 + x3+ x5+ x7+ x8+ x11.
Третья команда демонстрирует, что для циклического кода (15, 4) не существует порождающих полиномов с весом (числом ненулевых коэффициентов), равным трем.
c1 = cyclpoly(15,4,’all’)
c1 =
1 1 0 0 0 1 1 0 0 0 1 1
1 0 0 1 1 0 1 0 1 1 1 1
1 1 1 1 0 1 0 1 1 0 0 1
c2 = cyclpoly(15,4,’max’)
c2 =
1 1 1 1 0 1 0 1 1 0 0 1
c3 = cyclpoly(15,4,3)
No generator polynomial satisfies the given constraints.
c3 = []
Алгоритм:
Порождающий полином циклического кода с длиной кодового слова n является делителем полинома xn – 1. Степень порождающего полинома для кода с длиной блока исходного сообщения k составляет n – k. Функция производит перебор всех возможных полиномов нужной степени и выбирает делители xn – 1, удовлетворяющие заданным условиям.
Наверх
decode — декодирование данных, закодированных с использованием блочного кода
Синтаксис:
msg = decode(code,n,k,’hamming/format’,primpoly);
msg = decode(code,n,k,’linear/format’,genmat,trt);
msg = decode(code,n,k,’cyclic/format’,genpoly,trt);
msg = decode(code,n,k,’bch/format’,errorcorr,primpoly);
msg = decode(code,n,k,’rs/format’,field);
msg = decode(code,n,k);
[msg,err] = decode(…);
[msg,err,ccode] = decode(…);
[msg,err,ccode,cerr] = decode(…);
Необязательные входные параметры:
| Параметр | Значение по умолчанию |
| format | Binary |
| primpoly | gfprimdf(m), где n = 2m – 1 |
| genpoly | cyclpoly(n,k) |
| trt | Таблица декодирования, создаваемая функцией syndtable на основе проверочной матрицы используемого кода |
Описание:
Функция decode предназначена для декодирования сообщений, закодированных с использованием помехоустойчивых кодов. Параметры функции должны соответствовать тем, что использовались при кодировании сообщения.
Общая информация о синтаксисе:
В разделе “Общая информация о синтаксисе” на странице с описанием функции encode объясняется смысл параметров n и k, возможные значения преобразования format, а также возможные форматы для параметров code и msg. Там же приводятся соглашения об обозначениях, которые необходимо знать для понимания оставшейся части описания. Использование функции decode для обработки кодированного сообщения code, которое было создано не с помощью функции encode, может привести к ошибкам.
Конкретные варианты синтаксиса:
-
msg = decode(code,n,k,’hamming/format’,primpoly)
Декодирование сообщения code с использованием кода Хэмминга. Параметр n должен быть равен 2m – 1, где m — целое число, большее или равное 3, при этом параметр k должен быть равен n – m. Параметр primpoly — вектор-строка, содержащий двоичные коэффициенты (в порядке возрастания степеней) примитивного полинома над полем GF(2m), который использовался при кодировании сообщения. По умолчанию значение параметра primpoly равно gfprimdf(m). Таблица декодирования, используемая функцией, генерируется как syndtable(hammgen(m)). Данный код позволяет исправлять только однократные ошибки.
-
msg = decode(code,n,k)
То же самое, что msg = decode(code,n,k,’hamming/binary’).
-
msg = decode(code,n,k,’linear/format’,genmat,trt)
Декодирование сообщения code с использованием линейного блочного кода, задаваемого порождающей матрицей genmat размером k на n. Исправление ошибок производится с помощью таблицы декодирования trt, которая представляет собой матрицу размером 2n–k на n.
-
msg = decode(code,n,k,’cyclic/format’,genpoly,trt)
Декодирование сообщения code с использованием циклического кода. Исправление ошибок производится с помощью таблицы декодирования trt, которая представляет собой матрицу размером 2n–k на n. Параметр genpoly — вектор-строка, содержащий коэффициенты (в порядке возрастания степеней) двоичного порождающего полинома циклического кода. По умолчанию значение параметра genpoly равно cyclpoly(n,k). Порождающий полином циклического кода (n, k) по определению имеет степень n – k и должен быть делителем полинома xn – 1.
-
msg = decode(code,n,k,’bch/format’,errorcorr,primpoly)
Декодирование сообщения code с использованием кода БЧХ. Параметр primpoly — вектор-строка, содержащий коэффициенты (в порядке возрастания степеней) примитивного полинома над полем GF(2m), который будет использоваться при декодировании. По умолчанию значение параметра primpoly равно gfprimdf(m). Параметр n должен быть равен 2m – 1, где m — целое число, большее или равное 3. Параметры k и errorcorr должны быть корректными длиной блока сообщения и корректирующей способностью соответственно; их значения можно получить из второго и третьего элементов строки params, рассчитываемой командой params = bchpoly(n).
-
msg = decode(code,n,k,’rs/format’,field)
Декодирование сообщения code с использованием кода Рида—Соломона. Параметр n должен быть равен 2m – 1, где m — целое число, большее или равное 3. Параметр field — матрица, перечисляющая все элементы поля GF(2m) в следующем формате: матрица имеет m столбцов и 2m строк, элементы матрицы равны 0 или 1, строки представляют собой различные комбинации нулей и единиц. По умолчанию значение для параметра field генерируется командой gftuple([-1:2^m-2]’,m).
-
[msg,err] = decode(…)
Дополнительно возвращает вектор-столбец err, который содержит информацию об исправлении ошибок. Неотрицательное число в r-й строке err (или в r-й строке матрицы vec2mat(err,k), если code — вектор-столбец) показывает число ошибок, исправленных в r-м блоке сообщения; отрицательное число показывает, что число ошибок в r-м слове превысило корректирующую способность кода.
-
[msg,err,ccode] = decode(…)
Дополнительно возвращает исправленное кодированное сообщение ccode.
-
[msg,err,ccode,cerr] = decode(…)
Дополнительно возвращает вектор-столбец cerr, содержимое которого зависит от формата кодированного сообщения code:
-
Если code — двоичный вектор, то неотрицательное целое число в r-й строке матрицы vec2mat(cerr,n) показывает число ошибок, исправленное в r-м кодовом слове; отрицательное число показывает, что число ошибок в r-м кодовом слове превысило корректирующую способность кода.
-
Если code — не двоичный вектор, то cerr = err.
Примеры.
Приведенный ниже пример иллюстрирует использование выходных параметров err и cerr в случае, когда сообщение имеет формат двоичного вектора. Программа кодирует два пятибитовых блока с помощью кода БЧХ. Каждое кодовое слово содержит 15 бит. Ошибки вносятся в первые два бита первого кодового слова и в первый бит второго кодового слова. Затем сообщение декодируется с помощью функции decode. Поскольку число ошибок на кодовое слово не превосходит корректирующей способности кода, все ошибки исправляются. Выходной параметр err имеет тот же размер, что и декодированное сообщение msg, а выходной параметр cerr — тот же размер, что и кодированное сообщение code. Параметр err отражает тот факт, что первый блок сообщения был восстановлен после исправления двух ошибок, а второй — после исправления одной ошибки. Параметр cerr отражает тот факт, что первое кодовое слово было декодировано после исправления двух ошибок, а второе — после исправления одной ошибки.
m = 4; n = 2^m-1; % Длина кодового слова — 15
k = 5; % Допустимая длина блока сообщения для кода БЧХ с n = 15
t = 3; % Соответствующая кратность исправляемых ошибок
msg = ones(10,1); % Два блока сообщения по пять бит
code = encode(msg,n,k,’bch’); % Кодирование
% Вводим две ошибки в первое кодовое слово и одну во второе.
% Ошибки создаются путем инверсии некоторых битов.
noisycode = code;
noisycode(1:2) = bitxor(noisycode(1:2),[1 1]’);
noisycode(16) = bitxor(noisycode(16),1);
% Декодирование с попыткой исправления ошибок
[newmsg,err,ccode,cerr] = decode(noisycode,n,k,’bch’,t);
disp(‘Transpose of err is’); disp(err’)
disp(‘Transpose of cerr is’); disp(cerr’)
Результат работы программы приведен ниже.
Transpose of err is
2 2 2 2 2 1 1 1 1 1
Transpose of cerr is
Columns 1 through 12
2 2 2 2 2 2 2 2 2 2 2 2
Columns 13 through 24
2 2 2 1 1 1 1 1 1 1 1 1
Columns 25 through 30
1 1 1 1 1 1
Кроме того, примеры использования функции decode имеются на странице с описанием функции encode.
Алгоритм.
В зависимости от используемого кода функция decode вызывает низкоуровневые функции hammgen, syndtable, cyclgen, bchdeco и rsdeco.
Наверх
encode — кодирование данных с использованием блочных кодов
Синтаксис:
code = encode(msg,n,k,’linear/format’,genmat);
code = encode(msg,n,k,’cyclic/format’,genpoly);
code = encode(msg,n,k,’bch/format’,genpoly);
code = encode(msg,n,k,’hamming/format’,primpoly);
code = encode(msg,n,k,’rs/format’,genpoly);
code = encode(msg,field,k,’rs/format’,genpoly);
code = encode(msg,n,k);
[code,added] = encode(…);
Необязательные входные параметры:
| Параметр | Значение по умолчанию |
| format | binary |
| genpoly | Для циклических кодов — cyclpoly(n,k); для кодов БЧХ — bchpoly(n,k); для кодов Рида—Соломона — rspoly(n,k) или rspoly(n,k,field) |
| primpoly | gfprimdf(n-k) |
Описание:
Функция encode кодирует сообщения, используя один из следующих помехоустойчивых (корректирующих) блочных кодов:
-
Линейные блочные коды общего вида
-
Циклические коды
-
Коды Боуза—Чоудхури—Хоквингема (БЧХ)
-
Коды Хэмминга
-
Коды Рида—Соломона
Общая информация о синтаксисе:
Для всех кодов параметр n — длина кодового слова (кодовой комбинации), а параметр k — длина блока сообщения (информационной комбинации).
Параметр msg, который представляет исходное сообщение, может иметь различные форматы. В приведенной ниже табл. 1, которая относится ко всем методам кодирования, кроме кодов Рида—Соломона, описаны возможные форматы для параметра msg, соответствующие значения параметра format и форматы кодированного сообщения code. Аналогичная информация для кодов Рида—Соломона сведена в табл. 2. Примеры в таблицах приведены для k = 4 и (для кодов Рида—Соломона) m = 3. Если параметр format при вызове функции не указан, по умолчанию он принимает значение binary.
Замечание. Если значение 2n или 2k велико, следует применять формат binary и избегать использования формата decimal. Дело в том, что внутри функции в любом случае используется двоичный формат, а при преобразовании больших чисел между двоичным и десятичным форматами могут возникать значительные ошибки округления.
Таблица 1. Форматы представления сообщений для всех кодов, кроме кодов Рида—Соломона
| Формат исходного сообщения msg | Значение параметра ‘format’ | Формат кодированного сообщения code |
| Двоичный (состоящий из нулей и единиц) вектор-столбец | binary | Двоичный (состоящий из нулей и единиц) вектор-столбец |
| Пример: msg = [0 1 1 0, 0 1 0 1, 1 0 0 1]’ | ||
| Двоичная (состоящая из нулей и единиц) матрица, имеющая k столбцов | binary | Двоичная (состоящая из нулей и единиц) матрица, имеющая n столбцов |
| Пример: msg = [0 1 1 0; 0 1 0 1; 1 0 0 1] | ||
| Вектор-столбец, содержащий целые числа в диапазоне [0, 2k – 1] | decimal | Вектор-столбец, содержащий целые числа в диапазоне [0, 2n – 1] |
| Пример: msg = [6, 10, 9]’ |
Таблица 2. Форматы представления сообщений для кодов Рида—Соломона
| Формат исходного сообщения msg (n = 2m – 1, где m — целое число, большее или равное 3) | Значение параметра ‘format’ | Формат кодированного сообщения code |
| Двоичная (состоящая из нулей и единиц) матрица, имеющая m столбцов | binary | Двоичная (состоящая из нулей и единиц) матрица, имеющая m столбцов |
| Пример: msg = [1 1 0; 1 0 1; 1 0 0; 0 1 1; 1 1 0; 1 0 1; 1 0 0; 0 1 1] | ||
| Двоичный (состоящий из нулей и единиц) вектор-столбец | binary | Двоичный (состоящий из нулей и единиц) вектор-столбец |
| Пример: msg = [1 1 0, 1 0 1, 1 0 0, 0 1 1, 1 1 0, 1 0 1, 1 0 0, 0 1 1]’ | ||
| Матрица, имеющая k столбцов и содержащая целые числа в диапазоне [0, 2m – 1] | decimal | Матрица, имеющая n столбцов и содержащая целые числа в диапазоне [0, 2m – 1] |
| Пример: msg = [3, 5, 1, 6; 3, 5, 1, 6] | ||
| Матрица, имеющая k столбцов и содержащая целые числа в диапазоне [–1, 2m – 2] | power | Матрица, имеющая n столбцов и содержащая целые числа в диапазоне [–1, 2m – 2] |
| Пример: msg = [2, 4, 0, 5; 2, 4, 0, 5] |
Конкретные варианты синтаксиса:
-
code = encode(msg,n,k,’linear/format’,genmat)
Кодирует msg с помощью линейного блочного кода, описываемого порождающей матрицей genmat. Параметр genmat должен быть матрицей размером k на n и является обязательным.
-
code = encode(msg,n,k,’cyclic/format’,genpoly)
Кодирует msg с помощью циклического кода, описываемого порождающим полиномом genpoly. Параметр genpoly является вектором-строкой, содержащим коэффициенты (в порядке возрастания степеней) двоичного порождающего полинома циклического кода. По умолчанию параметр genpoly имеет значение cyclpoly(n,k). Порождающий полином для циклического кода (n, k) по определению имеет степень n – k и является делителем полинома xn – 1.
-
code = encode(msg,n,k,’bch/format’,genpoly)
Кодирует msg с помощью кода БЧХ. Параметр genpoly является вектором-строкой, содержащим коэффициенты (в порядке возрастания степеней) двоичного порождающего полинома кода БЧХ (полином имеет степень n – k). По умолчанию параметр genpoly имеет значение bchpoly(n,k). В данном случае значение n должно быть равно 2m – 1 для некоторого целого m, большего или равного 3. Параметр k должен быть корректной длиной сообщения; его значение можно получить из второго элемента строки params, рассчитываемой командой params = bchpoly(n).
-
code = encode(msg,n,k,’hamming/format’,primpoly)
Кодирует msg с помощью кода Хэмминга. В данном случае значение n должно быть равно 2m – 1 для некоторого целого m, большего или равного 3, а значение k должно быть равно n – m. Параметр primpoly — вектор-строка, содержащий двоичные коэффициенты (в порядке возрастания степеней) примитивного полинома над полем GF(2m), используемого для кодирования. По умолчанию primpoly — это примитивный полином, рассчитываемый с помощью вызова функции gfprimdf(m).
-
code = encode(msg,n,k)
То же самое, что code = encode(msg,n,k,’hamming/binary’).
-
code = encode(msg,n,k,’rs/format’,genpoly)
Кодирует msg с помощью кода Рида—Соломона. В данном случае значение n должно быть равно 2m – 1 для некоторого целого m, большего или равного 3. Параметр genpoly — вектор-строка, содержащий коэффициенты (в порядке возрастания степеней), порождающего полинома кода. Коэффициенты полинома являются элементами конечного поля GF(2m), представленными в экспоненциальном формате (см. замечание ниже). По умолчанию значение параметра genpoly рассчитывается с помощью функции rspoly.
Замечание. Все ненулевые элементы конечного поля GF(pm) могут быть представлены в экспоненциальном виде a c, где a — примитивный элемент поля, а c — целые числа от 0 до pm – 2. В MATLAB для представления элементов конечных полей в экспоненциальном формате используются целые числа c, лежащие в указанном диапазоне, а нулевой элемент представляется значением –Inf. Представление элементов конечного поля в экспоненциальном формате не является однозначным, оно зависит от выбранного примитивного элемента.
-
code = encode(msg,field,k,’rs/format’,genpoly)
То же, что и предыдущий вариант синтаксиса, но параметр field является матрицей, перечисляющей все элементы поля GF(2m) в следующем формате: матрица имеет m столбцов и 2m строк, элементы матрицы равны 0 или 1, строки представляют собой различные комбинации нулей и единиц. Такую матрицу можно сгенерировать, например, командой gftuple([-1:2^m-2]’,m). Число столбцов матрицы (m) позволяет определить параметр n, равный 2m – 1. При данном способе вызова функция работает быстрее, чем при предыдущем.
-
[code,added] = encode(…)
Дополнительно возвращает параметр added, значение которого равно числу нулей, добавленных в конец параметра msg перед кодированием. Это может понадобиться, чтобы привести сообщение к “подходящему” размеру, который зависит от n, k, исходного размера матрицы msg и используемого кода.
Примеры.
Пример 1.
Приведенный ниже пример показывает использование трех различных форматов сообщения (двоичный вектор, двоичная матрица, целочисленный вектор) для кода Хэмминга. Три сообщения имеют одно и то же содержание, представленное в разных форматах; соответственно, то же самое можно сказать и про три созданных функцией encode кодированных сообщения.
m = 4; n = 2^m-1; % Длина кодового слова = 15
k = 11; % Длина блока сообщения
% Создаем 100 блоков сообщения по k бит каждый
msg1 = randint(100*k,1,[0,1]); % msg1 — Вектор-столбец
msg2 = vec2mat(msg1,k); % msg2 – матрица с k столбцами
msg3 = bi2de(msg2); % msg3 – столбец целых чисел
% Создаем 100 кодовых комбинаций по n бит каждая
code1 = encode(msg1,n,k,’hamming/binary’);
code2 = encode(msg2,n,k,’hamming/binary’);
code3 = encode(msg3,n,k,’hamming/decimal’);
if ( vec2mat(code1,n)==code2 & de2bi(code3,n)==code2 )
disp(‘All three formats produced the same content.’)
end
Пример 2.
В следующем примере сообщение кодируется циклическим кодом, затем добавляется шум и производится декодирование зашумленного сообщения с помощью функции decode. Полученная вами вероятность ошибок может отличаться от приведенной, поскольку в примере используются случайные числа.
n = 3; k = 2; % Используем циклический код (3,2)
msg = randint(100,k,[0,1]); % 100 блоков сообщения по k бит каждый
code = encode(msg,n,k,’cyclic/binary’);
% Добавляем шум
noisycode = rem(code + randerr(100,n,[0 1;.7 .3]), 2);
newmsg = decode(noisycode,n,k,’cyclic’); % Пытаемся декодировать
% Вычисляем вероятность ошибок после декодирования
% зашумленного сообщения
[number,ratio] = biterr(newmsg,msg);
disp([‘The bit error rate is ‘,num2str(ratio)])
The bit error rate is 0.08
Пример 3.
В следующем примере одно и то же сообщение кодируется с помощью кода Хэмминга, кода БЧХ и циклического кода. Перед кодированием с помощью кода БЧХ вызывается функция bchpoly, чтобы определить корректные значения размеров блока сообщения кодовой комбинации. В данном примере также создается еще один экземпляр того же кода Хэмминга, причем он задается как линейный код общего вида — с помощью порождающей матрицы и параметра ‘linear’. Затем все кодированные сообщения декодируются и результаты сравниваются с исходным сообщением.
n = 6; % Начальный размер кодовой комбинации — 6
% Находим корректные параметры для кода БЧХ
params = bchpoly(n);
n = params(1,1); % Переопределяем размер кодовой комбинации,
% если предыдущее значение было недопустимым
k = params(1,2); % Длина блока сообщения
m = log2(n+1); % Определяем m, зная, что n=2^m-1
msg = randint(100,1,[0,2^k-1]); % Столбец целых чисел
% Кодируем разными методами
codehamming = encode(msg,n,k,’hamming/decimal’);
[parmat,genmat] = hammgen(m);
codehamming2 = encode(msg,n,k,’linear/decimal’,genmat);
if codehamming==codehamming2
disp(‘The »linear» method can create Hamming code.’)
end
codebch = encode(msg,n,k,’bch/decimal’);
codecyclic = encode(msg,n,k,’cyclic/decimal’);
% Декодируем, воссоздавая исходное сообщение
decodedhamming = decode(codehamming,n,k,’hamming/decimal’);
decodedbch = decode(codebch,n,k,’bch/decimal’);
decodedcyclic = decode(codecyclic,n,k,’cyclic/decimal’);
if (decodedhamming==msg & decodedbch==msg & decodedcyclic==msg)
disp(‘All decoding worked flawlessly in this noiseless world.’)
end
Алгоритм.
В зависимости от используемого кода функция encode вызывает низкоуровневые функции hammgen, cyclgen, bchenco и rsenco.
Наверх
gen2par — преобразование порождающей матрицы в проверочную и обратно
Синтаксис:
parmat = gen2par(genmat);
genmat = gen2par(parmat);
Описание:
parmat = gen2par(genmat)
Преобразует двоичную порождающую матрицу genmat, представленную в стандартной форме, в соответствующую проверочную матрицу parmat.
genmat = gen2par(parmat)
Преобразует двоичную проверочную матрицу parmat, представленную в стандартной форме, в соответствующую порождающую матрицу genmat.
Стандартные формы для порождающей и проверочной матриц двоичного линейного кода (n, k) приведены в следующей таблице.
| Тип матрицы | Стандартная форма | Размерность |
| Порождающая | [Ik P] или [P Ik] | k строк, n столбцов |
| Проверочная | [–P’ In – k] или [In – k –P’] | (n – k) строк, n столбцов |
Здесь Ik — единичная матрица размером k, а апостроф ( ‘ ) обозначает транспонирование матрицы. Для каждой матрицы приведено два варианта стандартной формы, поскольку в различных литературных источниках используются разные соглашения. Для двоичных кодов знак “минус” в приведенных выше формулах для проверочной матрицы не имеет значения, поскольку в двоичном конечном поле –1 = 1.
Примеры:
Приведенные ниже команды преобразуют проверочную матрицу для кода Хэмминга в соответствующую порождающую матрицу и обратно.
parmat = hammgen(3)
parmat =
1 0 0 1 0 1 1
0 1 0 1 1 1 0
0 0 1 0 1 1 1
genmat = gen2par(parmat)
genmat =
1 1 0 1 0 0 0
0 1 1 0 1 0 0
1 1 1 0 0 1 0
1 0 1 0 0 0 1
parmat2 = gen2par(genmat) % Результат должен быть равен parmat
parmat2 =
1 0 0 1 0 1 1
0 1 0 1 1 1 0
0 0 1 0 1 1 1
Наверх
gfweight — расчет кодового расстояния для линейного блочного кода
Синтаксис:
wt = gfweight(genmat);
wt = gfweight(genmat,’gen’);
wt = gfweight(parmat,’par’);
wt = gfweight(genpoly,n);
Описание:
Кодовое расстояние для линейного блокового кода равно минимальному числу различающихся элементов в произвольной паре кодовых слов.
-
wt = gfweight(genmat)
Возвращает кодовое расстояние для линейного блокового кода с порождающей матрицей genmat.
-
wt = gfweight(genmat,’gen’)
Возвращает кодовое расстояние для линейного блокового кода с порождающей матрицей genmat.
-
wt = gfweight(parmat,’par’)
Возвращает кодовое расстояние для линейного блокового кода с проверочной матрицей parmat.
-
wt = gfweight(genpoly,n)
Возвращает кодовое расстояние для циклического кода с длиной кодового слова n и порождающим полиномом genpoly. Параметр genpoly должен быть вектором-строкой, содержащим коэффициенты порождающего полинома в порядке возрастания степеней.
Примеры:
Приведенные ниже команды показывают три способа вычисления кодового расстояния для циклического кода (7,4).
n = 7;
% Порождающий полином для циклического кода (7,4)
genpoly = cyclpoly(n,4);
[parmat, genmat] = cyclgen(n,genpoly);
wts = [gfweight(genmat,’gen’), gfweight(parmat,’par’), gfweight(genpoly,n)]
wts =
3 3 3
Наверх
hammgen — генерация проверочной и порождающей матриц для кода Хэмминга
Синтаксис:
h = hammgen(m);
h = hammgen(m,pol);
[h,g] = hammgen(…);
[h,g,n,k] = hammgen(…);
Описание:
Для всех вариантов синтаксиса длина кодового слова обозначается как n. Величина n равна 2m – 1 для некоторого целочисленного m, большего или равного трем. Длина блока исходного сообщения обозначается как k, она равна n – m.
-
h = hammgen(m)
Возвращает проверочную матрицу (m строк, n столбцов) для кода Хэмминга с длиной кодового слова n = 2m – 1. Входной параметр m должен быть целым числом, большим или равным трем. Длина блока исходного сообщения для получаемого кода равна n – m. Для получения кода Хэмминга применяется двоичный примитивный полином, используемый в MATLAB по умолчанию для конечного поля GF(2m). Этот полином рассчитывается с помощью функции gfprimdf(m).
-
h = hammgen(m,pol)
То же, что и предыдущий вариант синтаксиса, но второй входной параметр pol в явном виде задает примитивный полином над конечным полем GF(2m), используемый для получения кода Хэмминга. Этот параметр должен представлять собой вектор-строку и содержать коэффициенты полинома в порядке возрастания степеней. Если полином, представляемый параметром pol, не является примитивным, функция выдает сообщение об ошибке.
-
[h,g] = hammgen(…)
То же, что предыдущие варианты синтаксиса, но в данном случае наряду с проверочной функция возвращает и порождающую матрицу кода — выходной параметр g (k строк, n столбцов). Длина блока исходного сообщения, k, равна n – m, или, что то же самое, 2m – 1 – m.
-
[h,g,n,k] = hammgen(…)
То же, что предыдущий вариант синтаксиса, но наряду с проверочной и порождающей матрицами кода функция возвращает также длину кодового слова n и длину блока исходного сообщения k.
Замечание. Если значение m не превышает 25 и для генерации кода используется примитивный полином по умолчанию, синтаксис hammgen(m) скорее всего окажется более быстрым, чем hammgen(m,pol).
Примеры:
Приведенная ниже команда выводит на экран проверочную и порождающую матрицы для кода Хэмминга с длиной кодового слова 7 = 23 – 1 и длиной блока исходного сообщения 4 = 7 – 3.
[h,g,n,k] = hammgen(3)
h =
1 0 0 1 0 1 1
0 1 0 1 1 1 0
0 0 1 0 1 1 1
g =
1 1 0 1 0 0 0
0 1 1 0 1 0 0
1 1 1 0 0 1 0
1 0 1 0 0 0 1
n = 7
k = 4
Следующая команда использует явно заданный примитивный полином 1 + x2 + x3, показывая тем самым, что вид проверочной матрицы зависит от выбора примитивного полинома. Чтобы в этом убедиться, сравните выведенную ниже матрицу h1 с матрицей h из предыдущего примера.
h1 = hammgen(3,[1 0 1 1])
h1 =
1 0 0 1 1 1 0
0 1 0 0 1 1 1
0 0 1 1 1 0 1
Наверх
rsdecof — декодирование текстового файла, закодированного с использованием кода Рида-Соломона
Синтаксис:
rsdecof(file_in,file_out);
rsdecof(file_in,file_out,err_cor);
Описание:
Данная функция является обратной по отношению к функции rsencof — она осуществляет декодирование файла, закодированного с помощью функции rsencof.
-
rsdecof(file_in,file_out)
Декодирует текстовый (ASCII) файл file_in, созданный с помощью функции rsencof с использованием кода Рида— Соломона (117, 127), исправляющего 5-кратные ошибки. Декодированное сообщение записывается в файл file_out. Параметры file_in и file_out должны быть строками.
Замечание. Если число символов в файле file_in не делится на 127, то функция дополняет файл символами char(4). Если кодирование и декодирование файла выполнялись функциями rsencof и rsdecof соответственно, в конце декодированного файла может содержаться некоторое количество символов char(4), которых не было в исходном файле.
-
rsdecof(file_in,file_out,err_cor)
То же, что и предыдущий вариант синтаксиса, но параметр err_cor задает корректирующую способность кода (кратность исправляемых ошибок). Длина блока равна 127 символам. Длина сообщения в блоке составляет 127-2*err_cor. Значение параметра err_cor должно совпадать с тем, что использовалось функцией rsencof при создании файла file_in.
Наверх
rsencof — кодирование текстового файла с использованием кода Рида-Соломона
Синтаксис:
rsencof(file_in,file_out);
rsencof(file_in,file_out,err_cor);
Описание:
-
rsencof(file_in,file_out)
Кодирование текстового (ASCII) файла file_in с использованием кода Рида—Соломона (127, 117). Данный код позволяет исправлять 5-кратные ошибки. Закодированный текст записывается в файл file_out. Параметры file_in и file_out должны быть строками.
-
rsencof(file_in,file_out,err_cor)
То же, что и предыдущий вариант синтаксиса, но параметр err_cor задает корректирующую способность кода (кратность исправляемых ошибок). Длина блока равна 127 символам. Длина сообщения в блоке составляет 127-2*err_cor.
Замечание. Если число символов в файле file_in не делится на 127-2*err_cor, то функция дополняет файл символами char(4).
Примеры.
Файл matlabroot/toolbox/comm/comm/oct2dec.m содержит текст справки об использовании функции oct2dec пакета Communications. Приведенные ниже команды осуществляют кодирование этого файла с помощью функции rsencof и его декодирование с помощью функции rsdecof.
file_in = [matlabroot ‘/toolbox/comm/comm/oct2dec.m’];
file_out = ‘encodedfile’; % Имя кодированного файла
rsencof(file_in,file_out) % Кодирование
file_in = file_out;
file_out = ‘decodedfile’; % Имя декодированного файла
rsdecof(file_in,file_out) % Декодирование
Для просмотра текстов исходного и декодированного файла в среде MATLAB используйте приведенные ниже команды.
type oct2dec.m
type decodedfile
Наверх
rsgenpoly — генерация порождающего полинома для кода Рида-Соломона
Синтаксис:
genpoly = rspoly(n,k);
genpoly = rspoly(n,k,m);
genpoly = rspoly(n,k,field);
[genpoly,t] = rspoly(…);
Описание:
-
genpoly = rspoly(n,k)
Возвращает порождающий полином для кода Рида—Соломона с длиной кодового слова n и длиной блока исходного сообщения k. Результат genpoly представляет собой вектор-строку, этот вектор содержит коэффициенты полинома в порядке возрастания степеней. Каждый коэффициент является элементом конечного поля GF(2m), представленным в экспоненциальном формате.
-
genpoly = rspoly(n,k,m)
То же, что и genpoly = rspoly(2^m-1,k), но работает быстрее. Если n не равно 2m – 1, выводится сообщение об ошибке.
-
genpoly = rspoly(n,k,field)
То же, что первый вариант синтаксиса, но входной параметр field косвенно задает примитивный элемент конечного поля GF(2m), относительно которого будет формироваться экспоненциальный формат представления коэффициентов полинома в выходном преобразование genpoly. Параметр field должен представлять собой матрицу, перечисляющую все элементы поля GF(2m) в следующем формате: матрица имеет m столбцов и 2m строк, элементы матрицы равны 0 или 1, строки представляют собой различные комбинации нулей и единиц. Такую матрицу можно сгенерировать, например, командой gftuple([-1:2^m-2]’,m). Обе матрицы field и genpoly используют экспоненциальный формат, связанный с одним и тем же примитивным элементом. Данный вариант синтаксиса работает быстрее, чем первый из перечисленных.
-
[genpoly,t] = rspoly(…)
Дополнительно возвращает корректирующую способность полученного кода Рида—Соломона (выходной параметр t).
Примеры:
Приведенная ниже команда показывает, что порождающий полином для кода Рида—Соломона (15, 11) имеет вид .
genpoly = rspoly(15,11,4)
genpoly =
10 3 6 13 0
Следующий вариант синтаксиса использует третий входной параметр fieldи дает тот же результат, что и предыдущий пример.
m = 4;
field = gftuple([-1:2^m-2]’,m,2);
genpoly2 = rspoly(15,11,field)
genpoly2 =
10 3 6 13 0
Наверх
syndtable — генерация таблицы зависимости векторов ошибок от синдрома (таблицы декодирования) для двоичных кодов
Синтаксис:
t = syndtable(parmat);
Описание:
t = syndtable(parmat)
Возвращает таблицу декодирования для двоичного корректирующего кода с длиной кодового слова n и длиной сообщения k. Параметр parmat — проверочная матрица кода, имеющая (n – k) строк и n столбцов. Результат t — двоичная матрица, содержащая 2n – k строк и n столбцов. r-я строка матрицы t представляет собой вектор ошибок для принятого двоичного кодового слова, синдром декодирования которого имеет десятичное целочисленное значение r – 1. (Синдром декодирования равен произведению принятого кодового слова и транспонированной проверочной матрицы.) Иными словами, строки матрицы t представляют собой лидеры смежных классов (coset leaders) из стандартного расположения (standard array) для данного кода.
При преобразовании десятичных величин в двоичные и наоборот левый столбец двоичных матриц интерпретируется как двоичная цифра старшего разряда. Это отличается от соглашения, которое по умолчанию используется функциями bi2de и de2bi.
Примеры:
Приведенные ниже команды вычисляют таблицу декодирования для кода Хэмминга (7, 4). Данный код имеет кодовое расстояние 3 и, следовательно, позволяет обнаруживать двукратные и исправлять однократные ошибки.
m = 3; n = 2^m-1; k = n-m;
parmat = hammgen(m); % Проверочная матрица
trt = syndtable(parmat) % Таблица декодирования
trt =
0 0 0 0 0 0 0
0 0 1 0 0 0 0
0 1 0 0 0 0 0
0 0 0 0 1 0 0
1 0 0 0 0 0 0
0 0 0 0 0 0 1
0 0 0 1 0 0 0
0 0 0 0 0 1 0
Первая строка таблицы декодирования соответствует случаю отсутствия ошибок при приеме. Остальные строки содержат все семь возможных векторов однократных ошибок, исправляемых данным кодом.
Декодирование с использованием данной таблицы осуществляется следующим образом. Сначала путем умножения принятого кодового слова на транспонированную проверочную матрицу вычисляется синдром декодирования. Пусть он оказывается равным, например, [0 1 0]. Десятичное значение синдрома равно 2. Соответствующий вектор ошибок, таким образом, следует брать из третьей (2 + 1) строки таблицы декодирования:
trt(3,:)
ans =
0 1 0 0 0 0 0
Полученный вектор ошибок необходимо прибавить (по модулю два) к принятому кодовому слову. Итак, в данном примере для исправления однократной ошибки следует инвертировать второй разряд принятого кодового слова.
Наверх
vitdec — декодирование сверточного кода с помощью алгоритма Витерби
Синтаксис:
decoded = vitdec(code,trellis,tblen,opmode,dectype);
decoded = vitdec(code,trellis,tblen,opmode,’soft’,nsdec);
decoded = vitdec(…,’cont’,…,initmetric,initstates,initinputs);
[decoded, finalmetric, finalstates, finalinputs] = vitdec(…,’cont’,…);
Описание:
-
decoded = vitdec(code,trellis,tblen,opmode,dectype)
Производит декодирование вектора code с помощью алгоритма Витерби. MATLAB-структура trellis описывает таблицу переходов используемого сверточного кода. Подробная информация о назначении полей этой структуры приведена на странице с описанием функции istrellis. Входной вектор code может содержать один или несколько символов, каждый из которых состоит из log2(trellis.numOutputSymbols) бит. Результат декодирования — выходной двоичный вектор decoded — содержит столько же символов, сколько и входной вектор code, при этом каждый декодированный символ состоит из log2(trellis.numInputSymbols) бит. Скалярный входной параметр tblen — положительное целое число, задающее глубину просмотра решетки при декодировании.
Строковый параметр opmode задает режим работы декодера и используемые предположения относительно работы кодера, сгенерировавшего входной вектор code. Возможные значения данного параметра приведены в табл. 1.
Таблица 1. Возможные значения входного параметра opmode
| Значение | Смысл |
| ‘trunc’ | Начальное внутреннее состояние кодера считается нулевым. Декодер производит обратную трассировку от состояния с наилучшей метрикой |
| ‘term’ | Начальное и конечное внутренние состояния кодера считаются нулевыми. Декодер производит обратную трассировку от нулевого внутреннего состояния |
| ‘cont’ | Начальное внутреннее состояние кодера считается нулевым. Декодер производит обратную трассировку от состояния с наилучшей метрикой. Декодированные символы появляются в выходном векторе с задержкой на tblen символов |
Строковый параметр dectype задает тип декодирования, используемый декодером. От значения этого параметра зависит и вид требуемых входных данных в векторе code. Возможные значения данного параметра приведены в табл. 2.
Таблица 2. Возможные значения входного параметра dectype
| Значение | Смысл |
| ‘unquant’ | Вектор code содержит вещественные числа, при этом 1 соответствует логическому нулю, а –1 представляет логическую единицу (жесткое декодирование) |
| ‘hard’ | Вектор code содержит двоичные данные, то есть каждый из его элементов может быть равен нулю или единице (жесткое декодирование) |
| ‘soft’ | Мягкое декодирование, описание синтаксиса для данного режима приводится ниже. Наличие входного параметра nsdec в этом случае является обязательным |
Синтаксис для реализации мягкого декодирования
-
decoded = vitdec(code,trellis,tblen,opmode,’soft’,nsdec)
Производит мягкое декодирование вектора code. Входной вектор code должен содержать целые числа в диапазоне от 0 до 2nsdec – 1, при этом значение 0 представляет бит, с наибольшей достоверностью равный нулю, а значение 2nsdec – 1 означает бит, с наибольшей достоверностью равный единице. Промежуточные значения соответствуют промежуточным степеням достоверности принятой двоичной информации.
Дополнительные варианты синтаксиса для реализации блочного декодирования
-
decoded = vitdec(…,’cont’,…,initmetric,initstates,initinputs)
То же, что предыдущие варианты синтаксиса, но начальное состояние декодера (текущие метрики, трассы выживших путей и последовательности соответствующих им символов) задаются входными параметрами initmetric, initstates и initinputs соответственно. Вещественные числа в векторе initmetric, длина которого равна числу состояний кодера, задают начальные метрики для всех внутренних состояний. Каждая из матриц initstates и initinputs, совместно задающих начальное состояние памяти кодера, должна иметь trellis.numStates строк и tblen столбцов. Матрица initstates должна содержать целые числа в диапазоне от 0 до trellis.numStates-1. Если схема кодера предполагает наличие нескольких входных битовых потоков, то состояние сдвигового регистра, принимающего первый входной битовый поток, соответствует младшим битам элементов матрицы initstates, а состояние сдвигового регистра, принимающего последнийпоток, — старшим битам этих величин. Матрица initinputs должна содержать целые числа в диапазоне от 0 до trellis.numInputSymbols-1. Чтобы использовать значения по умолчанию для всех этих входных параметров, можно задать их в виде пустых матриц: [],[],[].
-
[decoded,finalmetric,finalstates,finalinputs] = vitdec(…,’cont’,…)
То же, что предыдущие варианты синтаксиса, но три дополнительных выходных параметра содержат конечные значения метрик (finalmetric), трассы выживших путей (finalstates) и последовательности соответствующих им символов (finalinputs). Выходной параметр finalmetric является вектором длиной trellis.numStates, содержащим конечные значения метрик для всех внутренних состояний. Выходные параметры finalstates и finalinputs являются матрицами, содержащими trellis.numStates строк и tblen столбцов. Их формат аналогичен формату матриц initstates и initinputs.
Примеры
Пример 1.
В данном примере производится сверточное кодирование случайных данных с последующим добавлением шума. Далее выполняется декодирование зашумленного сигнала, при этом иллюстрируются все три типа декодирования, поддерживаемых функцией vitdec. Обратите внимание на то, что при использовании неквантованных входных данных (dectype = ‘unquant’), а также в случае мягкого декодирования (dectype = ‘soft’) результат работы кодирующей функции convenc имеет не тот вид, который требуется для декодирования с помощью функции vitdec. В этих случаях кодированный вектор ncode перед подачей на вход функции vitdec необходимо подвергнуть дополнительным преобразованиям.
trel = poly2trellis(3,[6 7]); % Описание кода
msg = randint(100,1,2,123); % Случайные данные
code = convenc(msg,trel); % Кодирование
ncode = rem(code + randerr(200,1,[0 1;.95 .05]),2); % Добавляем шум
tblen = 3; % Глубина просмотра при декодировании
% Вариант 1 – жесткое декодирование
decoded1 = vitdec(ncode,trel,tblen,’cont’,’hard’);
% Вариант 2 — жесткое декодирование с неквантованным входом
ucode = 1-2*ncode; % преобразуем 0 в +1, а 1 в -1
decoded2 = vitdec(ucode,trel,tblen,’cont’,’unquant’);
% Вариант 3 – мягкое декодирование
% Производим восьмиуровневое квантование зашумленного сигнала
[x,qcode] = quantiz(1-2*ncode,[-.75 -.5 -.25 0 .25 .5 .75],…
[7 6 5 4 3 2 1 0]); % Значения в векторе qcode лежат в диапазоне от 0 до 2^3-1.
decoded3 = vitdec(qcode’,trel,tblen,’cont’,’soft’,3);
% Вычисляем вероятности ошибок с учетом того, что выходной сигнал
% декодера задержан на tblen символов
[n1,r1] = biterr(decoded1(tblen+1:end),msg(1:end-tblen));
[n2,r2] = biterr(decoded2(tblen+1:end),msg(1:end-tblen));
[n3,r3] = biterr(decoded3(tblen+1:end),msg(1:end-tblen));
disp([‘The bit error rates are: ‘,num2str([r1 r2 r3])])
The bit error rates are: 0.020619 0.020619 0.020619
Пример 2.
Данный пример демонстрирует использование дополнительных параметров функции vitdec для того, чтобы декодировать сообщение по частям, вызывая функцию vitdec несколько раз. Объединенный декодированный вектор [decoded4;decoded5] совпадает с результатами декодирования, полученными при обработке всего сообщения целиком (вектор decoded6).
trel = poly2trellis(3,[6 7]);
code = convenc(randint(100,1,2,123),trel);
% Декодируем первую половину сигнала и сохраняем текущее состояние декодера
[decoded4,f1,f2,f3] = vitdec(code(1:100),trel,3,’cont’,’hard’);
% Декодируем вторую половину сигнала, используя сохраненное состояние кодера
decoded5 = vitdec(code(101:200),trel,3,’cont’,’hard’,f1,f2,f3);
% Декодируем весь сигнал целиком
decoded6 = vitdec(code,trel,3,’cont’,’hard’);
isequal(decoded6,[decoded4; decoded5])
ans =
1
Наверх
algdeintrlv — алгебраическое блоковое деперемежение
Синтаксис:
deintrlvd = algdeintrlv(data,num,’takeshita-costello’,k,h)
deintrlvd = algdeintrlv(data,num,’welch-costas’,alph)
Описание:
deintrlvd = algdeintrlv(data,num,’takeshita-costello’,k,h)
Восстанавливает исходную последовательность элементов входного массива data, используя таблицу перестановки, полученную алгебраически согласно методу Такешиты-Костелло (Takeshita-Costello). Входной параметр num должен быть равен числу элементов data, если data — вектор, или числом строк в data, если data — матрица. При использовании метода Такешиты-Костелло параметр num должен быть степенью числа 2. Мультипликативный коэффициент k должен быть нечетным целым числом, меньшим чем num, а циклический сдвиг h должен быть неотрицательным целым числом, меньшим чем num. Если входной параметр data является матрицей, ее столбцы обрабатываются независимо.
deintrlvd = algdeintrlv(data,num,’welch-costas’,alph)
В данном варианте синтаксиса для восстановления исходной последовательности элементов используется метод Уэлча-Костаса (Welch-Costas). При использовании метода Уэлча-Костаса величина num+1 должна быть простым числом. Входной параметр alph должен быть целым числом, лежащим между 1 и num и представляющим примитивный элемент конечного поля GF(num+1). Это означает, что все ненулевые элементы поля GF(num+1) могут быть получены путем возведения числа alph в некоторую целочисленную степень.
Чтобы данная функция компенсировала результат действия функции algintrlv, используйте в обеих функциях одинаковые входные параметры num, k и h (или num и alph). В этом случае последовательное применение функций algintrlv и algdeintrlv сохранит массив data неизмененным.
Примеры
Приведенный ниже код использует метод Такешиты-Костелло при вызове функций перемежения (algintrlv) и деперемежения (algdeintrlv).
num = 16; % величина num должны быть степенью двойки
ncols = 3; % Число столбцов данных для перемежения
data = rand(num,ncols); % Случайные данные для перемежения
k = 3;
h = 4;
intdata = algintrlv(data,num,’takeshita-costello’,k,h);
deintdata = algdeintrlv(intdata,num,’takeshita-costello’,k,h);
Наверх
algintrlv — алгебраическое блоковое перемежение
Синтаксис:
intrlvd = algintrlv(data,num,’takeshita-costello’,k,h)
intrlvd = algintrlv(data,num,’welch-costas’,alph)
Описание:
intrlvd = algintrlv(data,num,’takeshita-costello’,k,h)
Переставляет элементы входного массива data, используя таблицу перестановки, полученную алгебраически согласно методу Такешиты-Костелло (Takeshita-Costello). Входной параметр num должен быть равен числу элементов data, если data — вектор, или числом строк в data, если data — матрица. При использовании метода Такешиты-Костелло параметр num должен быть степенью числа 2. Мультипликативный коэффициент k должен быть нечетным целым числом, меньшим чем num, а циклический сдвиг h должен быть неотрицательным целым числом, меньшим чем num. Если входной параметр data является матрицей, ее столбцы обрабатываются независимо.
intrlvd = algintrlv(data,num,’welch-costas’,alph)
В данном варианте синтаксиса для перестановки используется метод Уэлча-Костаса (Welch-Costas). При использовании метода Уэлча-Костаса величина num+1 должна быть простым числом. Входной параметр alph должен быть целым числом, лежащим между 1 и num и представляющим примитивный элемент конечного поля GF(num+1). Это означает, что все ненулевые элементы поля GF(num+1) могут быть получены путем возведения числа alph в некоторую целочисленную степень.
Примеры
Данный пример показывает, как использовать метод алгебраического перемежения Уэлча-Костаса.
1. Задаем величину num и исходные данные для перемежения.
num = 10; % Целое число, для которого num+1 — простое числоncols = 3; % Число столбцов данных для перемеженияdata = randint(num,ncols,num); % Случайные исходные данные
2. Находим примитивный элемент конечного поля GF(num+1). Функция gfprimfd представляет все примитивные полиномы в виде строк, каждая из которых содержит коэффициенты полинома в порядке возрастания степеней.
pr = gfprimfd(1,’all’,num+1) % Примитивные полиномы поля GF(num+1)pr = 3 1 4 1 5 1 9 1
3. Обратите внимание на то, что результат pr имеет два столбца, и второй столбец заполнен единицами. Другими словами, все примитивные полиномы являются монарными полиномами первой степени. Это следует из того, что num+1 является простым числом. В результате найти примитивный элемент, который является корнем примитивного полинома, можно, вычитая из num+1первый столбец матрицы pr.
primel = (num+1)-pr(:,1) % Примитивные элементы поля GF(num+1)primel = 8 7 6 2
4. Теперь задаем параметр alph равным одному из элементов вектора primel и вызываем функцию перемежения algintrlv.
alph = primel(1); % Выбираем примитивный элементintrlvd = algintrlv(data,num,’Welch-Costas’,alph); % Перемежение
Алгоритм
-
Перемежитель Такешиты-Костелло использует вектор цикла длины num, элементы которого равны mod(k*(n-1)*n/2, num) для всех целых n от 1 до num. Далее строится вектор перемежения: элементы вектора цикла перебираются в порядке возрастания значений и в вектор перемежения заносятся стоящие справа от них элементы вектора цикла. Окончательная таблица перемежения получается путем циклического сдвига вектора перемежения на h позиций влево. (Все операции с числами и индексами выполняются по модулю num.)
-
Перемежитель Уэлча-Костаса использует таблицу перемежения, которая отображает целое число K в число mod(AK,num+1)-1.
Сопутствующие функции: algdeintrlv
Литература
1. Heegard, Chris, and Stephen B. Wicker, Turbo Coding, Boston, Kluwer Academic Publishers, 1999.
2. Takeshita, O. Y., and D. J. Costello, Jr., «New Classes Of Algebraic Interleavers for Turbo-Codes,» Proc. 1998 IEEE International Symposium on Information Theory, Boston, Aug. 16-21, 1998. pp. 419.
Наверх
convdeintrlv — сверточное деперемежение с линейным изменением задержки
Синтаксис:
deintrlved = convdeintrlv(data,nrows,slope)
[deintrlved,state] = convdeintrlv(data,nrows,slope)
[deintrlved,state] = convdeintrlv(data,nrows,slope,init_state)
Описание:
deintrlved = convdeintrlv(data,nrows,slope)
Восстанавливает исходную последовательность элементов входного массива data, используя набор из nrows внутренних регистров сдвига. Задержка, вносимая k-м регистром, равна (k-1)*slope, где k = 1, 2, 3, …, nrows. Перед началом обработки данных все регистры сдвига заполняются нулями. Если входной параметр data является матрицей, ее столбцы обрабатываются независимо.
[deintrlved,state] = convdeintrlv(data,nrows,slope)
Дополнительно возвращает структуру state, которая содержит состояния регистров задержки на момент окончания обработки данных. Поле state.value содержит все еще не попавшие на выход символы. Поле state.index содержит номер регистра, в который должен попасть следующий входной символ.
[deintrlved,state] = convdeintrlv(data,nrows,slope,init_state)
В данном варианте синтаксиса дополнительный входной параметр init_state позволяет задать исходное состояние регистров сдвига. Регистры инициализируются значениями из поля init_state.value, а первый входной символ направляется в регистр с номером, определяемым содержимым поля init_state.index. Структура init_state, как правило, получается в качестве выходного параметра при обработке предыдущего блока данных. Она не имеет отношения к соответствующему перемежителю.
Использование пары «перемежитель-деперемежитель»
Чтобы использовать данную функцию для восстановления порядка символов, переставленных с помощью функции convintrlv, используйте в обеих функциях одинаковые входные параметры nrows и slope. В этом случае функции convintrlv и convdeintrlv будут взаимно обратными в том смысле, что их последовательное применение сохранит массив данных неизмененным, внося, однако, в него задержку, равную nrows*(nrows-1)*slope.
Примеры
Приведенный ниже пример показывает, что функция convdeintrlv восстанавливает исходные данные, лишь внося в них некоторую задержку.
x = randint(1000,1); % исходные данные
nrows = 5; % используем 5 регистров сдвига
slope = 3; % задержки будут равны 0, 3, 6, 9 и 12
y = convintrlv(x,nrows,slope); % перемежение
x1 = convdeintrlv(y,nrows,slope); % деперемежение
d = nrows*(nrows-1)*slope; % вносимая задержка
isequal(x(1:end-d),x1(d+1:end)) % сравниваем исходные и восстановленные данные
Результат работы этого кода, приведенный ниже, показывает, что вектор x1, полученный после выполнения операции деперемежения, после компенсации задержки совпадает с исходным вектором x:
ans =
1
Пример использования выходного параметра state и входного параметра init_state имеется на странице с описанием функции muxdeintrlv; для функции condevintrlv все делается аналогично.
Сопутствующие функции: convintrlv, muxdeintrlv.
Литература:
1. Heegard, Chris, and Stephen B. Wicker, Turbo Coding, Boston, Kluwer Academic Publishers, 1999.
Наверх
convintrlv — сверточное перемежение с линейным изменением задержки
Синтаксис:
intrlved = convintrlv(data,nrows,slope)
[intrlved,state] = convintrlv(data,nrows,slope)
[intrlved,state] = convintrlv(data,nrows,slope,init_state)
Описание:
intrlved = convintrlv(data,nrows,slope)
Переставляет элементы входного массива data, используя набор из nrows внутренних регистров сдвига. Задержка, вносимая k-м регистром, равна (k-1)*slope, где k = 1, 2, 3, …, nrows. Перед началом обработки данных все регистры сдвига заполняются нулями. Если входной параметр data является матрицей, ее столбцы обрабатываются независимо.
[intrlved,state] = convintrlv(data,nrows,slope)
Дополнительно возвращает структуру state, которая содержит состояния регистров задержки на момент окончания обработки данных. Поле state.value содержит все еще не попавшие на выход символы. Поле state.index содержит номер регистра, в который должен попасть следующий входной символ.
[intrlved,state] = convintrlv(data,nrows,slope,init_state)
В данном варианте синтаксиса дополнительный входной параметр init_state позволяет задать исходное состояние регистров сдвига. Регистры инициализируются значениями из поля init_state.value, а первый входной символ направляется в регистр с номером, определяемым содержимым поля init_state.index. Структура init_state, как правило, получается в качестве выходного параметра при обработке предыдущего блока данных. Она не имеет отношения к соответствующему деперемежителю.
Примеры
Приведенный ниже пример показывает, что функция convintrlv является частным случаем более общей функции muxintrlv. Обе функции дают одинаковые численные результаты:
x = randint(100,1); % исходные данные
nrows = 5; % используем 5 регистров сдвига
slope = 3; % задержки будут равны 0, 3, 6, 9 и 12
y = convintrlv(x,nrows,slope); % перемежение с помощью convintrlv
delay = [0:3:12]; % явно выражаем набор задережек
y1 = muxintrlv(x,delay); % перемежение с помощью muxintrlv
isequal(y,y1) % сравнение двух результатов
Результат работы этого кода, приведенный ниже, показывает, что вектор y, полученный с помощью функции convintrlv, совпадает с вектором y1, полученным с помощью функции muxintrlv:
ans =
1
Пример использования выходного параметра state и входного параметра init_state имеется на странице с описанием функции muxdeintrlv; для функции convintrlv все делается аналогично.
Сопутствующие функции: convdeintrlv, muxintrlv, helintrlv.
Литература:
1. Heegard, Chris, and Stephen B. Wicker, Turbo Coding, Boston, Kluwer Academic Publishers, 1999.
Наверх
deintrlv — табличное блоковое деперемежение
Синтаксис:
deintrlvd = deintrlv(data,elements)
Описание:
deintrlvd = deintrlv(data,elements)
Восстанавливает исходную последовательность элементов во входном массиве data, действуя обратным образом по отношению к функции intrlv. Если data — вектор длины N или матрица, содержащая N строк, то второй входной параметр elements должен быть вектором длины N, содержащим целые числа от 1 до N. Чтобы данная функция компенсировала результат действия функции intrlv, при вызове обеих функций должен использоваться один и тот же вектор elements. В этом случае последовательное применение функций intrlv и deintrlv сохранит массив data неизмененным.
Примеры
Приведенный ниже код иллюстрирует взаимно обратное соотношение между функциями intrlv и deintrlv.
p = randperm(10); % таблица перестановки
a = intrlv(10:10:100,p); % переставляем вектор [10 20 30 … 100].
b = deintrlv(a,p) % деперемежение восстанавливает последовательность элементов
Вот результат работы этого кода:
b =
10 20 30 40 50 60 70 80 90 100
Наверх
intrlv — табличное блоковое перемежение
Синтаксис:
intrlvd = intrlv(data,elements)
Описание:
intrlvd = intrlv(data,elements)
Переставляет элементы входного массива data без пропуска или дублирования. Если data — вектор длины N или матрица, содержащая N строк, то второй входной параметр elements должен быть вектором длины N, содержащим целые числа от 1 до N. Последовательность этих чисел определяет порядок, в котором элементы вектора data или каждого столбца матрицы data появятся в выходном результате intrlvd. Если входной параметр data является матрицей, ее столбцы обрабатываются независимо.
Примеры
Приведенная ниже команда переставляет элементы вектора. Полученные
вами результаты могут отличаться от приведенных, поскольку в данном
примере используется случайно задаваемая таблица перестановки.
p = randperm(10); % таблица перестановки
a = intrlv(10:10:100, p)
Ниже приведен результат работы этого кода.
a =
10 90 60 30 50 80 100 20 70 40
Следующая команда переставляет элементы каждого из двух столбцов матрицы.
b = intrlv([.1 .2 .3 .4 .5; .2 .4 .6 .8 1]’,[2 4 3 5 1])
b =
0.2000 0.4000
0.4000 0.8000
0.3000 0.6000
0.5000 1.0000
0.1000 0.2000
Наверх
heldeintrlv — сверточное деперемежение со спиральным сканированием
Синтаксис:
[deintrlved,state] = heldeintrlv(data,col,ngrp,stp)
[deintrlved,state] = heldeintrlv(data,col,ngrp,stp,init_state)
deintrlved = heldeintrlv(data,col,ngrp,stp,init_state)
Описание:
[deintrlved,state] = heldeintrlv(data,col,ngrp,stp)
Восстанавливает исходную последовательность элементов входного массива data, заполняя внутренний промежуточный массив по строкам и затем считывая группы элементов из его столбцов по спирали. Если входной параметр data является вектором, он должен содержать cols*ngrp элементов. Если входной параметр data является матрицей, она должна содержать cols*ngrp строк; ее столбцы обрабатываются независимо. Второй выходной параметр state — это структура, в которой хранится заключительное состояние внутреннего массива. В поле state.value хранятся входные символы, не использованные при формировании выходного сигнала.
Операции, производимые функцией, можно представить как заполнение внутреннего промежуточного массива. Этот массив имеет col столбцов и неограниченное число строк, нумеруемых как 1, 2, 3 и т. д. Прежде всего верхняя часть массива заполняется нулями. Затем функция построчно заполняет ngrp верхних строк массива, используя для этого col*ngrp входных символов. Далее функция формирует выходной сигнал deintrlved длиной col*ngrp символов, считывая элементы группами по ngrp символов; элементы k-й группы берутся из k-го столбца, начиная со строки 1 + (k — 1)*stp. При этом некоторые выходные символы имеют принятые по умолчанию нулевые значения, а часть входных символов так и не появляется на выходе.
[deintrlved,state] = heldeintrlv(data,col,ngrp,stp,init_state)
В данном варианте синтаксиса промежуточный массив инициализируется не нулями, а значениями из поля структуры init_state.value. Дополнительный входной параметр init_state должен быть структурой; как правило, здесь используется значение выходного параметра state, полученное при предыдущем вызове той же самой функции. К соответствующему перемежителю данный параметр не имеет отношения. В данном случае часть выходных символов имеет принятые по умолчанию нулевые значения, часть представляет собой входные символы из массива data и еще часть является начальными значениями из поля структуры init_state.value.
deintrlved = heldeintrlv(data,col,ngrp,stp,init_state)
То же, что предыдущий вариант синтаксиса, но в данном случае не сохраняется заключительное состояние внутреннего массива деперемежителя. Такой способ вызова можно использовать при последнем из серии последовательных вызовов функции heldeintrlv. Однако, если функция должна будет вызываться в дальнейшем для продолжения процесса деперемежения, следует использовать предыдущий вариант синтаксиса.
Использование пары «перемежитель-деперемежитель»
Чтобы использовать данную функцию для восстановления порядка символов, переставленных с помощью функции helintrlv, используйте в обеих функциях одинаковые входные параметры col, ngrp и stp. В этом случае функции helintrlv и heldeintrlv будут взаимно обратными в том смысле, что их последовательное применение сохранит массив данных неизмененным, внося, однако, в него задержку, равную col*ngrp*ceil(stp*(col-1)/ngrp).
Внимание! Поскольку вносимая задержка является кратной общему числу символов в массиве data, чтобы получить на выходе символы из входного сигнала (а не принятые по умолчанию нулевые значения), функцию heldeintrlv необходимо использовать как минимум дважды (а, может быть, и большее число раз — в зависимости от точной величины вносимой задержки).
Примеры
Приведенный ниже пример показывает, как восстановить данные после перемежения, учитывая вносимую парой «перемежитель-деперемежитель» задержку.
col = 4; ngrp = 3; stp = 2; % Параметры спирального перемежения
% Вычисляем задержку, вносимую парой «перемежитель-деперемежитель»
delayval = col * ngrp * ceil(stp * (col-1)/ngrp);
len = col*ngrp; % Длина блока символов для одной операции
data = randint(len,1,10); % Случайные данные
data_padded = [data; zeros(delayval,1)]; % Дополняем данные нулями
% Перемежаем данные, дополненные нулями
[i1,istate] = helintrlv(data_padded(1:len),col,ngrp,stp);
[i2,istate] = helintrlv(data_padded(len+1:2*len),col,ngrp,stp,istate);
i3 = helintrlv(data_padded(2*len+1:end),col,ngrp,stp,istate);
% Деперемежение
[d1,dstate] = heldeintrlv(i1,col,ngrp,stp);
[d2,dstate] = heldeintrlv(i2,col,ngrp,stp,dstate);
d3 = heldeintrlv(i3,col,ngrp,stp,dstate);
% Сравниваем результаты деперемежения с исходными данными
d0 = [d1; d2; d3]; % Полный результат деперемежения
d0_trunc = d0(delayval+1:end); % Компенсируем задержку
ser = symerr(data,d0_trunc)
Результат работы данного примера показывает, что исходный сигнал восстановлен без ошибок.
ser =
0
Наверх
helintrlv — сверточное перемежение со спиральным сканированием
Синтаксис:
intrlved = helintrlv(data,col,ngrp,stp)
[intrlved,state] = helintrlv(data,col,ngrp,stp)
[intrlved,state] = helintrlv(data,col,ngrp,stp,init_state)
Описание:
intrlved = helintrlv(data,col,ngrp,stp)
Переставляет элементы входного массива data, заполняя массив с бесконечным количеством строк по спирали и затем считывая его содержимое по строкам. Если входной параметр data является вектором, он должен содержать cols*ngrp элементов. Если входной параметр data является матрицей, она должна содержать cols*ngrp строк; ее столбцы обрабатываются независимо.
Операции, производимые функцией, можно представить как заполнение внутреннего промежуточного массива. Этот массив имеет col столбцов и неограниченное число строк, нумеруемых как 1, 2, 3 и т. д. Функция разделяет col*ngrp входных символов на col групп, в каждую из которых входит ngrp символов, следующих друг за другом. Затем символы k-й группы размещаются в промежуточном массиве вдоль столбца k, начиная со строки 1 + (k — 1)*stp. Элементы массива, не заполненные входными символами, по умолчанию имеют нулевые значения. Наконец, функция формирует выходной сигнал intrlved длиной col*ngrp символов, поочередно считывая из промежуточного массива ngrp первых строк. При этом некоторые выходные символы имеют принятые по умолчанию нулевые значения, а часть входных символов так и не появляется на выходе.
[intrlved,state] = helintrlv(data,col,ngrp,stp)
Дополнительно возвращает структуру state, в которой хранится заключительное состояние промежуточного массива. Точнее, в поле state.value хранятся символы, не использованные при формировании выходного сигнала.
[intrlved,state] = helintrlv(data,col,ngrp,stp,init_state)
В данном варианте синтаксиса промежуточный массив инициализируется значениями из поля структуры init_state.value. Дополнительный входной параметр init_state должен быть структурой; как правило, здесь используется значение выходного параметра state, полученное при предыдущем вызове той же самой функции. К соответствующему деперемежителю данный параметр не имеет отношения. В данном случае часть выходных символов имеет принятые по умолчанию нулевые значения, часть представляет собой входные символы из массива data и еще часть является начальными значениями из поля структуры init_state.value.
Примеры
В приведенном ниже примере производится перестановка чисел от 1 до 24.
% Производим перемежение, сохраняем состояние внутреннего массива
[i1,state] = helintrlv([1:12]’,3,4,1);
% Еще одна операция перемежения, при которой восстанавливается
% состояние перемежителя, полученное после предыдущей операции
i2 = helintrlv([13:24]’,3,4,1,state);
disp(‘Данные, подвергаемые перемежению:’)
disp([i1,i2]’)
disp(‘Символы, не попавшие на выход после первой операции перемежения:’)
state.value{:}
При двух вызовах функции helintrlv она создает промежуточные массивы, содержащие по три столбца. Массив при первом вызове:
[1 0 0;
2 5 0;
3 6 9;
4 7 10;
0 8 11;
0 0 12]
Массив при втором вызове:
[13 8 11;
14 17 12;
15 18 21;
16 19 22;
0 20 23;
0 0 24]
В массиве, созданном при втором вызове, элементы, равные 8, 11 и 12 — это символы, не попавшие на выход при первом вызове функции. Используя дополнительный входной параметр init_state при втором вызове функции, мы заставляем ее использовать эти значения вместо принятых по умолчанию нулевых величин.
Ниже показан результат работы данного примера. (Обрабатываемые данные представляли собой матрицу, вытянутую по вертикали; для удобства отображения она транспонирована.) Результат перемежения — это первые четыре строки промежуточных массивов, показанных выше. Обратите внимание на следующее:
-
часть символов в первой половине выходного сигнала имеет принятые по умолчанию нулевые значения;
-
часть символов во второй половине выходного сигнала при первом вызове функции helintrlv не попала на выход, оставшись в промежуточном массиве;
-
несколько входных символов (20, 23 и 24) так и не появились на выходе.
Данные, подвергаемые перемежению:
Columns 1 through 10
1 0 0 2 5 0 3 6 9 4
13 8 11 14 17 12 15 18 21 16
Columns 11 through 12
7 10
19 22
Символы, не попавшие на выход после первой операции перемежения:
ans =
[]
ans =
8
ans =
11 12
Наверх
helscandeintrlv — блоковое деперемежение со спиральным сканированием
Синтаксис:
deintrlvd = helscandeintrlv(data,Nrows,Ncols,hstep)
Описание:
deintrlvd = helscandeintrlv(data,Nrows,Ncols,hstep)
Переставляет элементы входного массива data, заполняя промежуточную матрицу по спирали и затем считывая ее содержимое по строкам. Входные параметры Nrows и Ncols задают размеры промежуточной матрицы. Входной параметр hstep задает наклон спирали, то есть величину, на которую увеличивается счетчик строк при увеличении счетчика столбцов на единицу. Параметр hstep должен быть неотрицательным целым числом, меньшим чем Nrows.
Спиральное сканирование означает, что функция размещает элементы вдоль диагоналей промежуточной матрицы. Число элементов в каждой диагонали в точности равно Ncols, при необходимости в процессе записи происходит переход от нижнего края матрицы к верхнему. Перемещение по диагонали происходит таким образом, что каждый раз изменяются номера и строки, и столбца. Каждая следующая диагональ начинается на одну строку ниже первого элемента предыдущей диагонали.
Если входной параметр data является вектором, он должен содержать Nrows*Ncols элементов. Если входной параметр data является матрицей, она должна содержать Nrows*Ncols строк; ее столбцы обрабатываются независимо.
Чтобы данная функция компенсировала результат действия функции helscanintrlv, при вызове обеих функций должны использоваться одни и те же значения параметров Nrows, Ncols и hstep. В этом случае последовательное применение функций helscanintrlv и helscandeintrlv сохранит массив data неизмененным.
Примеры
Приведенная ниже команда переставляет элементы вектора, используя промежуточную матрицу размером 3 на 4 и единичный наклон диагоналей.
d = helscandeintrlv(1:12,3,4,1)
d =
Columns 1 through 10
1 10 7 4 5 2 11 8 9 6
Columns 11 through 12
3 12
Функция создает промежуточную матрицу, содержащую 3 строки и 4 столбца, заполняя ее по диагоналям (каждая диагональ содержит 4 элемента):
[1 10 7 4;
5 2 11 8;
9 6 3 12]
Затем элементы матрицы считываются построчно, формируя результат d.
Наверх
helscanintrlv — блоковое перемежение со спиральным сканированием
Синтаксис:
intrlvd = helscanintrlv(data,Nrows,Ncols,hstep)
Описание:
Переставляет элементы входного массива data, заполняя промежуточную матрицу по строкам и затем считывая ее содержимое по спирали. Входные параметры Nrows и Ncols задают размеры промежуточной матрицы. Входной параметр hstep задает наклон спирали, то есть величину, на которую увеличивается счетчик строк при увеличении счетчика столбцов на единицу. Параметр hstep должен быть неотрицательным целым числом, меньшим чем Nrows.
Спиральное сканирование означает, что функция считывает элементы вдоль диагоналей промежуточной матрицы. Число элементов в каждой диагонали в точности равно Ncols, при необходимости в процессе считывания происходит переход от нижнего края матрицы к верхнему. Перемещение по диагонали происходит таким образом, что каждый раз изменяются номера и строки, и столбца. Каждая следующая диагональ начинается на одну строку ниже первого элемента предыдущей диагонали.
Если входной параметр data является вектором, он должен содержать Nrows*Ncols элементов. Если входной параметр data является матрицей, она должна содержать Nrows*Ncols строк; ее столбцы обрабатываются независимо.
Примеры
Пара приведенных ниже команд переставляет элементы вектора, используя спиральное сканирование с разными наклонами диагоналей.
i1 = helscanintrlv(1:12,3,4,1) % Наклон диагоналей равен 1
i2 = helscanintrlv(1:12,3,4,2) % Наклон диагоналей равен 2.
Вот результат работы этого примера:
i1 =
Columns 1 through 10
1 6 11 4 5 10 3 8 9 2
Columns 11 through 12
7 12
i2 =
Columns 1 through 10
1 10 7 4 5 2 11 8 9 6
Columns 11 through 12
3 12
В каждом случае функция создает промежуточную матрицу, содержащую 3 строки и 4 столбца, заполняя ее по строкам:
[1 2 3 4;
5 6 7 8;
9 10 11 12]
При формировании результата i1 функция перебирает элементы по диагоналям с единичным наклоном, каждый раз смещаясь на одну строку вниз и на один столбец вправо. Первая диагональ, таким образом, содержит элементы 1, 6, 11 и 4, а вторая диагональ начинается с элемента 5, находящегося в промежуточной матрице в точности под элементом 1.
При формировании результата i2 функция формирует диагонали с наклоном 2, каждый раз смещаясь на две строки вниз и на один столбец вправо. Первая диагональ, таким образом, содержит элементы 1, 10, 7 и 4, а вторая диагональ начинается с элемента 5, находящегося в промежуточной матрице в точности под элементом 1.
Наверх
matdeintrlv — матричное блоковое деперемежение
Синтаксис:
deintrlvd = matdeintrlv(data,Nrows,Ncols)
Описание:
deintrlvd = matdeintrlv(data,Nrows,Ncols)
Переставляет элементы входного массива data, заполняя промежуточную матрицу по столбцам и затем считывая ее содержимое по строкам. Входные параметры Nrows и Ncols задают размеры промежуточной матрицы. Если входной параметр data является вектором, он должен содержать Nrows*Ncols элементов. Если входной параметр data является матрицей, она должна содержать Nrows*Ncols строк; ее столбцы обрабатываются независимо.
Чтобы данная функция компенсировала результат действия функции matintrlv, при вызове обеих функций должны использоваться одни и те же значения параметров Nrows и Ncols. В этом случае последовательное применение функций matintrlv и matdeintrlv сохранит массив data неизмененным.
Примеры
Приведенный ниже код иллюстрирует взаимно обратное
соотношение между функциями matintrlv и matdeintrlv.
Nrows = 2; Ncols = 3;
data = [1 2 3 4 5 6; 2 4 6 8 10 12]’;
a = matintrlv(data,Nrows,Ncols); % перемежение
b = matdeintrlv(a,Nrows,Ncols) % деперемежение
Результат работы этого кода показывает, что матрица b совпадает с исходной матрицей data.
b =
1 2
2 4
3 6
4 8
5 10
6 12
Наверх
matintrlv — матричное блоковое перемежение
Синтаксис:
intrlvd = matintrlv(data,Nrows,Ncols)
Описание:
intrlvd = matintrlv(data,Nrows,Ncols)
Переставляет элементы входного массива data, заполняя промежуточную матрицу по строкам и затем считывая ее содержимое по столбцам. Входные параметры Nrows и Ncols задают размеры промежуточной матрицы. Если входной параметр data является вектором, он должен содержать Nrows*Ncols элементов. Если входной параметр data является матрицей, она должна содержать Nrows*Ncols строк; ее столбцы обрабатываются независимо.
Примеры
Приведенная ниже команда переставляет элементы каждого из двух столбцов матрицы.
b = matintrlv([1 2 3 4 5 6; 2 4 6 8 10 12]’, 2, 3)
b =
1 2
4 8
2 4
5 10
3 6
6 12
При формировании первого столбца результата функция создает промежуточную матрицу с двумя строками и тремя столбцами и заполняет ее по строкам: [1 2 3; 4 5 6]. Затем функция считывает эту матрицу по столбцам, получая последовательность [1 4 2 5 3 6]. Второй столбец результата формируется аналогично.
Наверх
muxdeintrlv — табличное сверточное деперемежение
Синтаксис:
deintrlved = muxdeintrlv(data,delay)
[deintrlved,state] = muxdeintrlv(data,delay)
[deintrlved,state] = muxdeintrlv(data,delay,init_state)
Описание:
deintrlved = muxdeintrlv(data,delay)
Восстанавливает исходную последовательность элементов входного массива data, используя набор внутренних регистров сдвига. Второй входной параметр delay должен быть вектором, содержащим величину задержки для каждого регистра. Задержка, вносимая k-м регистром, равна delay[k]; таким образом, общее число регистров сдвига равно length(delay). Перед началом обработки данных все регистры сдвига заполняются нулями. Если входной параметр data является матрицей, ее столбцы обрабатываются независимо.
[deintrlved,state] = muxdeintrlv(data,delay)
Дополнительно возвращает структуру state, которая содержит состояния регистров задержки на момент окончания обработки данных. Поле state.value содержит все еще не попавшие на выход символы. Поле state.index содержит номер регистра, в который должен попасть следующий входной символ.
[deintrlved,state] = muxdeintrlv(data,delay,init_state)
В данном варианте синтаксиса дополнительный входной параметр init_state позволяет задать исходное состояние регистров сдвига. Регистры инициализируются значениями из поля init_state.value, а первый входной символ направляется в регистр с номером, определяемым содержимым поля init_state.index. Структура init_state, как правило, получается в качестве выходного параметра при обработке предыдущего блока данных. Она не имеет отношения к соответствующему перемежителю.
Использование пары «перемежитель-деперемежитель»
Чтобы использовать данную функцию для восстановления порядка символов, переставленных с помощью функции muxintrlv, используйте в обеих функциях одинаковый входной параметр delay. В этом случае функции muxintrlv и muxdeintrlv будут взаимно обратными в том смысле, что их последовательное применение сохранит массив данных неизмененным, внося, однако, в него задержку, равную length(delay)*max(delay).
Примеры
Приведенный ниже пример показывает, как можно использовать дополнительные входной и выходной параметры для доступа к внутренним состояниям регистров сдвига и организации блоковой обработки данных.
delay = [0 4 8 12]; % задержки, вносимые регистрами сдвига
symbols = 100; % число обрабатываемых символов
% Производим перемежение случайных данных
intrlved = muxintrlv(randint(symbols,1,2,123),delay);
% Производим деперемежение первой половины массива, сохраняя внутреннее состояние деперемежителя
[deintrlved1,state] = muxdeintrlv(intrlved(1:symbols/2),delay);
% Производим деперемежение второй половины массива, используя сохраненное внутреннее состояние деперемежителя
deintrlved2 = muxdeintrlv(intrlved(symbols/2+1:symbols),delay,state);
% Производим деперемежение всего массмва сразу
deintrlved = muxdeintrlv(intrlved,delay);
isequal(deintrlved,[deintrlved1; deintrlved2]) % сравнение двух вариантов
Результат работы этого кода, приведенный ниже, показывает, что вектор [deintrlved1; deintrlved2], полученный после выполнения операции деперемежения двух половин массива по отдельности с сохранением промежуточного внутреннего состояния, совпадает с вектором deintrlved, полученным в результате выполнения операции деперемежения без разбиения массива на блоки:
ans =
1
Литература:
1. Heegard, Chris, and Stephen B. Wicker, Turbo Coding, Boston, Kluwer Academic Publishers, 1999.
Наверх
muxintrlv — табличное сверточное перемежение
Синтаксис:
intrlved = muxintrlv(data,delay)
[intrlved,state] = muxintrlv(data,delay)
[intrlved,state] = muxintrlv(data,delay,init_state)
Описание:
intrlved = muxintrlv(data,delay)
Переставляет элементы входного массива data, используя набор внутренних регистров сдвига, вносящих разные задержки. Второй входной параметр delay должен быть вектором, содержащим величину задержки для каждого регистра. Задержка, вносимая k-м регистром, равна delay[k]; таким образом, общее число регистров сдвига равно length(delay). Перед началом обработки данных все регистры сдвига заполняются нулями. Если входной параметр data является матрицей, ее столбцы обрабатываются независимо.
[intrlved,state] = muxintrlv(data,delay)
Дополнительно возвращает структуру state, которая содержит состояния регистров задержки на момент окончания обработки данных. Поле state.value содержит все еще не попавшие на выход символы. Поле state.index содержит номер регистра, в который должен попасть следующий входной символ.
[intrlved,state] = muxintrlv(data,delay,init_state)
В данном варианте синтаксиса дополнительный входной параметр init_state позволяет задать исходное состояние регистров сдвига. Регистры инициализируются значениями из поля init_state.value, а первый входной символ направляется в регистр с номером, определяемым содержимым поля init_state.index. Структура init_state, как правило, получается в качестве выходного параметра при обработке предыдущего блока данных. Она не имеет отношения к соответствующему деперемежителю.
Примеры
Пример использования функции muxintrlv имеется на странице с описанием функции convintrlv.
Пример использования выходного параметра state и входного параметра init_state имеется на странице с описанием функции muxdeintrlv; для функции muxintrlv все делается аналогично.
Сопутствующие функции: muxdeintrlv, convintrlv, helintrlv.
Литература:
1. Heegard, Chris, and Stephen B. Wicker, Turbo Coding, Boston, Kluwer Academic Publishers, 1999.
Наверх
randdeintrlv — случайное блоковое деперемежение
Синтаксис:
deintrlvd = randdeintrlv(data,state)
Описание:
deintrlvd = randdeintrlv(data,state)
Восстанавливает исходную последовательность элементов во входном массиве data, действуя обратным образом по отношению к функции randintrlv. Входной параметр state задает начальное состояние генератора случайных чисел, который используется при расчете порядка перестановки. Перестановки, генерируемые для любого фиксированного значения параметра state, являются повторяемыми и обратимыми, однако разные значения state дадут разные перестановки. Если входной параметр data является матрицей, ее столбцы обрабатываются независимо.
Чтобы данная функция компенсировала результат действия функции randintrlv, при вызове обеих функций должно использоваться одно и то же значение параметра state. В этом случае последовательное применение функций randintrlv и randdeintrlv сохранит массив data неизмененным.
Наверх
randintrlv — случайное блоковое перемежение
Синтаксис:
intrlvd = randintrlv(data,state)
Описание:
intrlvd = randintrlv(data,state)
Переставляет элементы входного массива data случайным образом. Входной параметр state задает начальное состояние генератора случайных чисел, который используется при расчете порядка перестановки. Перестановки, генерируемые для любого фиксированного значения параметра state, являются повторяемыми и обратимыми, однако разные значения state дадут разные перестановки. Если входной параметр data является матрицей, ее столбцы обрабатываются независимо.
Примеры
Следующий пример показывает, как перемежитель уменьшает вероятность ошибок в системе связи, где канал производит пакетные (следующие подряд) ошибки. Случайный перемежитель переставляет биты, захватывая при этом несколько кодовых слов одновременно. После этого в сигнал вносится пакетная ошибка, такая что на каждое из двух соседних кодовых слов приходится по три ошибки.
Эти три ошибки превосходят корректирующую способность используемого кода Хэмминга (7, 4). Однако данный пример показывает, что при использовании этого же кода Хэмминга в сочетании с перемежением система оказывается способна правильно восстановить исходное сообщение, несмотря на наличие пакета из шести ошибок. Улучшение помехоустойчивости происходит здесь благодаря тому, что перемежение перераспределяет ошибки во времени, превращая пакетные ошибки в одиночные, так что число ошибок в каждом кодовом слове не превосходит корректирующей способности используемого кода.
st1 = 27221; st2 = 4831; % Начальные состояния генератора случайных чисел
n = 7; k = 4; % Параметры кода Хэмминга
msg = randint(k*500,1,2,st1); % Кодируемые данные
code = encode(msg,n,k,’hamming/binary’); % Кодирование
% Создаем пакет ошибок, затрагивающий два соседних кодовых слова
errors = zeros(size(code)); errors(n-2:n+3) = [1 1 1 1 1 1];
% Вариант с перемежением
%————————
inter = randintrlv(code,st2); % Перемежение
inter_err = bitxor(inter,errors); % Добавляем пакет ошибок
deinter = randdeintrlv(inter_err,st2); % Деперемежение
decoded = decode(deinter,n,k,’hamming/binary’); % Декодирование
disp(‘Число и вероятность ошибок при использовании перемежения:’);
[number_with,rate_with] = biterr(msg,decoded) % Статистика ошибок
% Вариант без перемежения
%————————
code_err = bitxor(code,errors); % Добавляем пакет ошибок
decoded = decode(code_err,n,k,’hamming/binary’); % Декодирование
disp(‘Число и вероятность ошибок без использования перемежения:’);
[number_without,rate_without] = biterr(msg,decoded) % Статистика ошибок
Далее приведен результат работы данного примера.
Число и вероятность ошибок при использовании перемежения:
number_with =
0
rate_with =
0
Число и вероятность ошибок без использования перемежения:
number_without =
4
rate_without =
0.0020
Итак, пакет ошибок при отсутствии перемежения приводит к появлению четырех ошибочных битов в декодированном сообщении. Использование перемежения (в данном случае случайного) позволяет превратить пакет ошибок в набор одиночных ошибок и декодировать сообщение корректно.
Наверх
ammod — амплитудная модуляция (AM)
Синтаксис:
y = ammod(x,Fc,Fs)
y = ammod(x,Fc,Fs,ini_phase)
y = ammod(x,Fc,Fs,ini_phase,carramp)
Описание
y = ammod(x,Fc,Fs)
Использует информационный входной сигнал x для амплитудной модуляции несущего колебания с частотой Fc (Гц). Несущее колебание и модулирующий сигнал x имеют одинаковую частоту дискретизации Fs (Гц). Модулированный сигнал имеет нулевую начальную фазу и нулевую амплитуду несущего колебания, так что результатом является АМ с подавленной несущей.
Замечание. Входные параметры x, Fc и Fs должны удовлетворять условию Fs > 2(Fc + BW), где BW — ширина спектра модулирующего сигнала x.
y = ammod(x,Fc,Fs,ini_phase)
То же, что предыдущий вариант синтаксиса, но дополнительный входной параметр ini_phase задает начальную фазу несущего колебания в радианах.
y = ammod(x,Fc,Fs,ini_phase,carramp)
То же, что предыдущий вариант синтаксиса, но дополнительный входной параметр carramp задает амплитуду несущего колебания. Таким образом, в данном случае формируется классический вариант АМ с неподавленной несущей.
Примеры
В приведенном ниже коде производится сравнение обычной амплитудной модуляции и АМ с одной боковой полосой.
% Частота дискретизации 100 Гц, длительность сигнала 2 секунды
Fs = 100;
t = [0:2*Fs+1]’/Fs;
Fc = 10; % Несущая частота
x = sin(2*pi*t); % Синусоидальный модулирующий сигнал
% Реализуем двухполосную и однополосную АМ
ydouble = ammod(x,Fc,Fs);
ysingle = ssbmod(x,Fc,Fs);
% Вычисляем спектры обоих модулированных сигналов
zdouble = fft(ydouble);
zdouble = abs(zdouble(1:length(zdouble)/2+1));
frqdouble = [0:length(zdouble)-1]*Fs/length(zdouble)/2;
zsingle = fft(ysingle);
zsingle = abs(zsingle(1:length(zsingle)/2+1));
frqsingle = [0:length(zsingle)-1]*Fs/length(zsingle)/2;
% Выводим графики спектров обоих модулированных сигналов
figure;
subplot(2,1,1); plot(frqdouble,zdouble);
title(‘Spectrum of double-sideband signal’);
subplot(2,1,2); plot(frqsingle,zsingle);
title(‘Spectrum of single-sideband signal’);
Наверх
amdemod — амплитудная демодуляция
Синтаксис:
z = amdemod(y,Fc,Fs)
z = amdemod(y,Fc,Fs,ini_phase)
z = amdemod(y,Fc,Fs,ini_phase,carramp)
z = amdemod(y,Fc,Fs,ini_phase,carramp,num,den)
Описание
z = amdemod(y,Fc,Fs)
Демодулирует сигнал y, амплитудно-модулированный при частоте несущего колебания Fc (Гц). Несущее колебание и модулированный сигнал y имеют одинаковую частоту дискретизации Fs (Гц). Предполагается, что модулированный сигнал y имеет нулевую начальную фазу и нулевую амплитуду несущего колебания, так что он представляет собой АМ с подавленной несущей. В процессе демодуляции используется фильтр нижних частот Баттерворта, рассчитываемый как [num,den] = butter(5,Fc*2/Fs).
Замечание. Входные параметры Fc и Fs должны удовлетворять условию Fs > 2(Fc + BW), где BW — ширина спектра информационного (модулирующего) сигнала.
z = amdemod(y,Fc,Fs,ini_phase)
То же, что предыдущий вариант синтаксиса, но дополнительный входной параметр ini_phase задает начальную фазу несущего колебания в радианах.
z = amdemod(y,Fc,Fs,ini_phase,carramp)
То же, что предыдущий вариант синтаксиса, но дополнительный входной параметр carramp задает амплитуду несущего колебания, использованную при модуляции. Таким образом, в данном случае предполагается, что демодуляции подвергается классический АМ-сигнал с неподавленной несущей.
z = amdemod(y,Fc,Fs,ini_phase,carramp,num,den)
То же, что предыдущий вариант синтаксиса, но дополнительные входные параметры задают коэффициенты полиномов числителя (num) и знаменателя (den) функции передачи фильтра нижних частот, используемого в процессе демодуляции.
Примеры
Приведенный ниже код иллюстрирует реализацию демодуляции с использованием нестандартного фильтра нижних частот.
t = .01;
Fc = 10000; Fs = 80000;
t = [0:1/Fs:0.01]’;
s = sin(2*pi*300*t)+2*sin(2*pi*600*t); % Исходный сигнал
[num,den] = butter(10,Fc*2/Fs); % Фильтр нижних частот
y1 = ammod(s,Fc,Fs); % Модуляция
s1 = amdemod(y1,Fc,Fs,0,0,num,den); % Демодуляция
Наверх
fmmod — частотная модуляция (FM)
Синтаксис:
y = fmmod(x,Fc,Fs,freqdev)
y = fmmod(x,Fc,Fs,freqdev,ini_phase)
Описание
y = fmmod(x,Fc,Fs,freqdev)
Использует информационный входной сигнал x для частотной модуляции несущего колебания с частотой Fc (Гц). Несущее колебание и модулирующий сигнал x имеют одинаковую частоту дискретизации Fs (Гц), которая должна быть не меньше, чем 2*Fc. Входной параметр freqdev задает девиацию частоты модулированного сигнала в герцах (при значении модулирующего сигнала, равном единице, отклонение частоты будет равно freqdev Гц). Модулированный сигнал имеет нулевую начальную фазу.
y = fmmod(x,Fc,Fs,freqdev,ini_phase)
То же, что предыдущий вариант синтаксиса, но дополнительный входной параметр ini_phase задает начальную фазу несущего колебания в радианах.
Примеры
Приведенный ниже код выполняет модуляцию многоканального сигнала с использованием функции fmmod и его демодуляцию с использованием функции fmdemod.
Fs = 8000; % Частота дискретизации сигналов
Fc = 3000; % Несущая частота
t = [0:Fs]’/Fs; % Вектор моментов времени
s1 = sin(2*pi*300*t)+2*sin(2*pi*600*t); % Модулирующий сигнал первого канала
s2 = sin(2*pi*150*t)+2*sin(2*pi*900*t); % Модулирующий сигнал второго канала
x = [s1,s2]; % Двухканальный сигнал
dev = 50; % Девиация частоты при частотной модуляции
y = fmmod(x,Fc,Fs,dev); % Модуляция двухканального сигнала
z = fmdemod(y,Fc,Fs,dev); % Демодуляция обоих каналов
Наверх
fmdemod — частотная демодуляция
Синтаксис:
z = fmdemod(y,Fc,Fs,freqdev)
z = fmdemod(y,Fc,Fs,freqdev,ini_phase)
Описание
z = fmdemod(y,Fc,Fs,freqdev)
Демодулирует сигнал y, частотно-модулированный при частоте несущего колебания Fc (Гц). Несущее колебание и модулированный сигнал y имеют одинаковую частоту дискретизации Fs (Гц), которая должна быть не меньше, чем 2*Fc. Входной параметр freqdev задает девиацию частоты, использованную при модуляции (предполагается, что при значении модулирующего сигнала, равном единице, отклонение частоты равно freqdev Гц). Предполагается, что модулированный сигнал имеет нулевую начальную фазу.
z = fmdemod(y,Fc,Fs,freqdev,ini_phase)
То же, что предыдущий вариант синтаксиса, но дополнительный входной параметр ini_phase задает начальную фазу несущего колебания в радианах.
Наверх
pmmod — фазовая модуляция (PM)
Синтаксис:
y = pmmod(x,Fc,Fs,phasedev)
y = pmmod(x,Fc,Fs,phasedev,ini_phase)
Описание
y = pmmod(x,Fc,Fs,phasedev)
Использует информационный входной сигнал x для фазовой модуляции несущего колебания с частотой Fc (Гц). Несущее колебание и модулирующий сигнал x имеют одинаковую частоту дискретизации Fs (Гц), которая должна быть не меньше, чем 2*Fc. Входной параметр phasedev задает девиацию фазы модулированного сигнала в радианах (при значении модулирующего сигнала, равном единице, отклонение фазы будет равно phasedev радиан). Модулированный сигнал имеет нулевую начальную фазу.
y = pmmod(x,Fc,Fs,phasedev,ini_phase)
То же, что предыдущий вариант синтаксиса, но дополнительный входной параметр ini_phase задает начальную фазу несущего колебания в радианах.
Примеры
В приведенном ниже коде производится фазовая модуляция с использованием модулирующего сигнала в виде суммы двух синусоид. Затем моделируется канал связи с аддитивным белым гауссовым шумом, производится демодуляция зашумленного сигнала и выводятся графики исходного и демодулированного сигналов.
Fs = 100; % Частота дискретизации
t = [0:2*Fs+1]’/Fs; % Вектор моментов времени
% Создаем модулирующий сигнал в виде суммы двух синусоид
x = sin(2*pi*t) + sin(4*pi*t);
Fc = 10; % Несущая частота
phasedev = pi/2; % Девиация фазы для фазовой модуляции
y = pmmod(x,Fc,Fs,phasedev); % Фазовая модуляция
y = awgn(y,10,’measured’,103); % Добавление шума
z = pmdemod(y,Fc,Fs,phasedev); % Демодуляция
% Выводим графики исходного и демодулированного сигналов
figure; plot(t,x,’k-‘,t,z,’g-‘);
legend(‘Original signal’,’Recovered signal’);
Наверх
pmdemod — фазовая демодуляция
Синтаксис:
z = pmmod(y,Fc,Fs,phasedev)
z = pmmod(y,Fc,Fs,phasedev,ini_phase)
Описание
z = pmmod(y,Fc,Fs,phasedev)
Демодулирует сигнал y, модулированный по фазе при частоте несущего колебания Fc (Гц). Несущее колебание и модулированный сигнал y имеют одинаковую частоту дискретизации Fs (Гц), которая должна быть не меньше, чем 2*Fc. Входной параметр phasedev задает девиацию фазы, использованную при модуляции (предполагается, что при значении модулирующего сигнала, равном единице, отклонение фазы равно phasedev радиан). Предполагается, что модулированный сигнал имеет нулевую начальную фазу.
z = pmmod(y,Fc,Fs,phasedev,ini_phase)
То же, что предыдущий вариант синтаксиса, но дополнительный входной параметр ini_phase задает начальную фазу несущего колебания в радианах.
Наверх
ssbmod — однополосная амплитудная модуляция (SSB)
Синтаксис:
y = ssbmod(x,Fc,Fs)
y = ssbmod(x,Fc,Fs,ini_phase)
y = ssbmod(x,fc,fs,ini_phase,’upper’)
Описание
y = ssbmod(x,Fc,Fs)
Использует информационный входной сигнал x для однополосной амплитудной модуляции с нижней боковой полосой. Частота несущего колебания Fc (Гц). Несущее колебание и модулирующий сигнал x имеют одинаковую частоту дискретизации Fs (Гц). Модулированный сигнал имеет нулевую начальную фазу.
y = ssbmod(x,Fc,Fs,ini_phase)
То же, что предыдущий вариант синтаксиса, но дополнительный входной параметр ini_phase задает начальную фазу несущего колебания в радианах.
y = ssbmod(x,fc,fs,ini_phase,’upper’)
То же, что предыдущий вариант синтаксиса, но дополнительный строковый параметр со значением ‘upper’ задает формирование сигнала с верхней боковой полосой.
Наверх
ssbdemod — однополосная амплитудная демодуляция
Синтаксис:
z = ssbdemod(y,Fc,Fs)
z = ssbdemod(y,Fc,Fs,ini_phase)
z = ssbdemod(y,Fc,Fs,ini_phase,num,den)
Описание
z = ssbdemod(y,Fc,Fs)
Демодулирует сигнал y, модулированный с использованием однополосной АМ при частоте несущего колебания Fc (Гц). Несущее колебание и модулированный сигнал y имеют одинаковую частоту дискретизации Fs (Гц). Предполагается, что модулированный сигнал y имеет нулевую начальную фазу; использованная при модуляции боковая полоса не имеет значения. В процессе демодуляции используется фильтр нижних частот Баттерворта, рассчитываемый как [num,den] = butter(5,Fc*2/Fs).
Замечание. Входные параметры Fc и Fs должны удовлетворять условию Fs > 2(Fc + BW), где BW — ширина спектра информационного (модулирующего) сигнала.
z = ssbdemod(y,Fc,Fs,ini_phase)
То же, что предыдущий вариант синтаксиса, но дополнительный входной параметр ini_phase задает начальную фазу несущего колебания в радианах.
z = ssbdemod(y,Fc,Fs,ini_phase,num,den)
То же, что предыдущий вариант синтаксиса, но дополнительные входные параметры задают коэффициенты полиномов числителя (num) и знаменателя (den) функции передачи фильтра нижних частот, используемого в процессе демодуляции.
Примеры
Приведенный ниже код демонстрирует, что функция ssbdemod может демодулировать сигнал как с верхней, так и с нижней боковой полосой.
Fc = 12000; Fs = 270000;
t = [0:1/Fs:0.01]’;
s = sin(2*pi*300*t)+2*sin(2*pi*600*t);
y1 = ssbmod(s,Fc,Fs,0); % Сигнал с нижней боковой полосой
y2 = ssbmod(s,Fc,Fs,0,’upper’); % Сигнал с верхней боковой полосой
s1 = ssbdemod(y1,Fc,Fs); % Демодулируем сигнал с нижней боковой полосой
s2 = ssbdemod(y2,Fc,Fs); % Демодулируем сигнал с верхней боковой полосой
% Выводим графики результатов, чтобы показать их совпадение
figure; plot(t,s1,’r-‘,t,s2,’k—‘);
legend(‘Demodulation of upper sideband’,’Demodulation of lower sideband’)
Наверх
dpskmod — фазоразностная манипуляция (DPSK)
Синтаксис:
y = dpskmod(x,M)
y = dpskmod(x,M,phaserot)
Описание
Возвращает комплексную огибающую y, полученную в результате передачи информационной последовательности x с использованием фазоразностной манипуляции. Входной параметр M задает размер алфавита (число позиций манипуляции) и должен целым числом. Информационная последовательность x должна состоять из целых чисел, лежащих в диапазоне от 0 до M-1 включительно. Если x — матрица, то ее столбцы обрабатываются независимо.
y = dpskmod(x,M,phaserot)
То же, что предыдущий вариант синтаксиса, но третий входной параметр phaserot задает дополнительный фазовый сдвиг между символами (в радианах), добавляемый к величине, получаемой согласно закону фазоразностной манипуляции. В конечном счете это приводит к частотному сдвигу сгенерированного сигнала.
Примеры
Приведенный ниже код графически отображает результаты работы функции dpskmod. График показывает возможные переходы между соседними (по времени) символами в созвездии фазоразностной манипуляции.
M = 4; % четырехпозиционная манипуляция
x = randint(500,1,M,13); % случайные исходные данные
y = dpskmod(x,M,pi/8); % модуляция с дополниетльным сдвигом фазы
plot(y) % отображаем все точки, соединенные линиями
Наверх
dpskdemod — демодуляция сигнала с фазоразностной манипуляцией
Синтаксис:
z = dpskdemod(y,M)
z = dpskdemod(y,M,phaserot)
Описание
Выполняет демодуляцию комплексной огибающей сигнала с фазоразностной модуляцией y. Входной параметр M задает размер алфавита (число позиций манипуляции) и должен быть целым числом. Демодулированная информационная последовательность z состоит из целых чисел, лежащих в диапазоне от 0 до M-1 включительно. Если y — матрица, то ее столбцы обрабатываются независимо.
Замечание. Первый элемент результата z, или первая строка z, если z — матрица, представляет начальное состояние, поскольку при дифференциальной демодуляции текущее значение сигнала сравнивается с предыдущим.
z = dpskdemod(y,M,phaserot)
То же, что предыдущий вариант синтаксиса, но при демодуляции предполагается, что к фазовому сдвигу между соседними символами при формировании сигнала добавлялось значение дополнительного входного параметра phaserot.
Примеры
Приведенный ниже код иллюстрирует тот факт, что первый выходной символ фазоразностного демодулятора представляет начальное состояние, а не полезную информацию.
M = 4; % число позиций манипуляции
x = randint(1000,1,M); % случайное сообщение
y = dpskmod(x,M); % модуляция
z = dpskdemod(y,M); % демодуляция
% Проверяем, правильно ли демодулировано сообщение
s1 = symerr(x,z) % Один (первый) символ должен быть неверным
s2 = symerr(x(2:end),z(2:end)) % Если исключить первый символ, ошибок не должно быть
Результат работы кода приведен ниже.
s1 =
1
s2 =
0
Наверх
fskmod — частотная манипуляция (FSK)
Синтаксис:
y = fskmod(x,M,freq_sep,nsamp)
y = fskmod(x,M,freq_sep,nsamp,Fs)
y = fskmod(x,M,freq_sep,nsamp,Fs,phase_cont)
Описание
y = fskmod(x,M,freq_sep,nsamp)
Возвращает комплексную огибающую y, полученную в результате передачи информационной последовательности x с использованием частотной манипуляции. Входной параметр M задает размер алфавита (число позиций манипуляции) и должен быть степенью числа 2. Информационная последовательность x должна состоять из целых чисел, лежащих в диапазоне от 0 до M-1 включительно. Входной параметр freq_sep задает расстояние (в герцах) между соседними частотами манипуляции. Входной параметр nsamp должен быть положительным целым числом, большим единицы; он задет число отсчетов результирующего вектора y, приходящееся на один информационный символ из входного вектора x. Предполагается, что частота дискретизации выходного вектора y равна 1 Гц. Согласно теореме Котельникова, чтобы в дискретном виде могли быть представлены все частоты манипуляции, параметры M и freq_sep должны удовлетворять следующему неравенству: (M-1)*freq_sep < 1. Если x — матрица, то ее столбцы обрабатываются независимо.
y = fskmod(x,M,freq_sep,nsamp,Fs)
То же, что предыдущий вариант синтаксиса, но дополнительный входной параметр Fs задает частоту дискретизации выходного сигнала y (в герцах). Поскольку, согласно теореме Котельникова, максимальная частота манипуляции должна быть меньше чем Fs/2, входные параметры должны удовлетворять неравенству (M-1)*freq_sep < Fs.
y = fskmod(x,M,freq_sep,nsamp,Fs,phase_cont)
То же, что предыдущий вариант синтаксиса, но дополнительный входной параметр phase_cont позволяет управлять непрерывностью фазы сгенерированного сигнала: при значении ‘cont’ генерируется сигнал с непрерывной фазой, при значении ‘discont’ — нет. По умолчанию используется значение ‘cont’.
Примеры:
Приведенный ниже код иллюстрирует синтаксис вызова функции fskmod, реализуя передачу случайного сигнала.
M = 4; % число позиций манипуляции
freqsep = 8; % разнос частот манипуляции (в герцах)
nsamp = 8; % число отсчетов на символ
Fs = 32; % частота дискретизации (в герцах)
x = randint(1000,1,M); % случайная информационная последовательность
y = fskmod(x,M,freqsep,nsamp,Fs); % Модуляция
ly = length(y);
% Выводим график энергетического спектра модулированного сигнала
freq = [-Fs/2 : Fs/ly : Fs/2 — Fs/ly]; % вектор значений частот
Syy = 10*log10(fftshift(abs(fft(y)))); % энергетический спектр
plot(freq,Syy)
Наверх
fskdemod — демодуляция сигнала с частотной манипуляцией
Синтаксис:
z = fskdemod(y,M,freq_sep,nsamp)
z = fskdemod(y,M,freq_sep,nsamp,Fs)
Описание
z = fskdemod(y,M,freq_sep,nsamp)
Выполняет некогерентную демодуляцию комплексной огибающей сигнала с частотной манипуляцией y. Входной параметр M задает размер алфавита (число позиций манипуляции) и должен быть степенью числа 2. Демодулированная информационная последовательность z состоит из целых чисел, лежащих в диапазоне от 0 до M-1 включительно. Входной параметр freq_sep задает расстояние (в герцах) между соседними частотами манипуляции. Входной параметр nsamp должен быть положительным целым числом, большим единицы; он задет число отсчетов сигнала y, приходящееся на один информационный символ. Предполагается, что частота дискретизации сигнала y равна 1 Гц. Если y — матрица, то ее столбцы обрабатываются независимо.
z = fskdemod(y,M,freq_sep,nsamp,Fs)
То же, что предыдущий вариант синтаксиса, но дополнительный входной параметр Fs задает частоту дискретизации сигнала y (в герцах).
Примеры:
Приведенный ниже код иллюстрирует формирование сигнала с частотной манипуляцией, пропускание его через канал связи с аддитивным белым гауссовым шумом (АБГШ), демодуляцию зашумленного сигнала, оценку вероятности битовой ошибки (BER) и сравнение полученного значения с теоретическим.
M = 2; % число позиций манипуляции
k = log2(M); % число бит на символ
EbNo = 5; % отношение энергии бита к СПМ шума
Fs = 16; % частота дискретизации
N = Fs;
nsamp = 17; % число отсчетов на символ
freqsep = 8; % разнос частот манипуляции
msg = randint(5000,1,M); % случайный сигнал
txsig = fskmod(msg,M,freqsep,nsamp,Fs); % модуляция
msg_rx = awgn(txsig,EbNo+10*log10(k)-10*log10(N),…
‘measured’,[],’dB’); % АБГШ-канал
msg_rrx = fskdemod(msg_rx,M,freqsep,nsamp,Fs); % демодуляция
[num,SER] = symerr(msg,msg_rrx); % оценка вероятности символьной ошибки
BER = SER*(M/2)/(M-1) % пересчет в вероятность битовой ошибки
BER_theory = berawgn(EbNo,’fsk’,M,’noncoherent’) % теоретическое значение BER
Ниже приведен результат работы этого кода. Полученная вами экспериментальная оценка BER может отличаться от приведенной, так как в данном примере используется генератор случайных чисел.
BER =
0.1006
BER_theory =
0.1029
Наверх
genqammod — квадратурная манипуляция с произвольным созвездием (QASK)
Синтаксис:
y = genqammod(x,const)
Описание
y = genqammod(x,const)
Возвращает комплексную огибающую y, полученную в результате передачи информационной последовательности x с использованием квадратурной манипуляции. Информационная последовательность x должна состоять из целых чисел, лежащих в диапазоне от 0 до length(const)-1 включительно. Сигнальное созвездие задается вектором комплексных чисел const. Если x — матрица, то ее столбцы обрабатываются независимо.
Примеры:
Приведенный ниже код отображает сигнальное созвездие с шестиугольными ячейками. Также здесь использованы функции genqammod и genqamdemod, чтобы выполнить модуляцию и демодуляцию сообщения [3 8 5 10 7] с использованием данного созвездия.
% Создаем описание шестиугольного созвездия
inphase = [1/2 1 1 1/2 1/2 2 2 5/2];
quadr = [0 1 -1 2 -2 1 -1 0];
inphase = [inphase;-inphase]; inphase = inphase(:);
quadr = [quadr;quadr]; quadr = quadr(:);
const = inphase + j*quadr;
% Отображаем созвездие
h = scatterplot(const);
% Выполняем модуляцию с использованием данного созвездия
x = [3 8 5 10 7]; % Сообщение
y = genqammod(x,const);
z = genqamdemod(y,const); % Модуляция
% Отображаем модулированный сигнал на том же графике
hold on; scatterplot(y,1,0,’ro’,h);
legend(‘Constellation’,’Modulated signal’,’Location’,’NorthWest’); % Добавляем к графику легенду
hold off;
Наверх
genqamdemod — демодуляция сигнала с квадратурной манипуляцией с произвольным созвездием
Синтаксис:
z = genqamdemod(y,const)
Описание
z = genqamdemod(y,const)
Выполняет демодуляцию комплексной огибающей сигнала с квадратурной манипуляцией y. Сигнальное созвездие задается вектором комплексных чисел const. Демодулированная информационная последовательность z состоит из целых чисел, лежащих в диапазоне от 0 до length(const)-1 включительно. Если y — матрица, то ее столбцы обрабатываются независимо.
Наверх
modnorm — расчет коэффициента масштабирования для нормировки АИМ- или КАМ-сигнала по мощности
Синтаксис:
scale = modnorm(const, ‘avpow’, avpow)
scale = modnorm(const, ‘peakpow’, peakpow)
Описание
scale = modnorm(const, ‘avpow’, avpow)
Возвращает коэффициент масштабирования, на который необходимо умножить выходной сигнал PAM- или QAM-модулятора, чтобы его средняя мощность (равная среднему квадрату модуля) стала равна avpow. Вектор комплексных чисел const задает сигнальное созвездие, для которого рассчитывается нормировочный коэффициент.
scale = modnorm(const, ‘peakpow’, peakpow)
Возвращает коэффициент масштабирования, на который необходимо умножить выходной сигнал PAM- или QAM-модулятора, чтобы его пиковая мощность (равная максимальному квадрату модуля) стала равна peakpow.
Примеры:
Приведенный ниже код показывает, как можно использовать функцию modnorm, чтобы сформировать КАМ-сигнал с пиковой мощностью, равной единице.
M = 16; % Размер алфавита
const = qammod([0:M-1],M); % Генерируем созвездие
x = randint(1,100,M);
scale = modnorm(const,’peakpow’,1); % Вычисляем коэффициент масштабирования
y = scale * qammod(x,M); % Модуляция и нормировка
ynoisy = awgn(y,10); % Зашумляем сигнал
ynoisy_unscaled = ynoisy/scale; % Обратное масштабирование в приемнике
z = qamdemod(ynoisy_unscaled,M); % Демодуляция
% Смотрим, как масштабирование влияет на созвездие
h = scatterplot(const,1,0,’ro’); % Немасштабированное созвездие
hold on; % Следующий график будет выведен в то же окно
scatterplot(const*scale,1,0,’bx’,h); % Масштабированное созвездие
hold off;
На приведенном ниже графике символы «o» показывают точки исходного КАМ-созвездия, а символы «x» — точки масштабированного созвездия. В канале связи в данном примере предавались точки из масштабированного созвездия.
Наверх
mskmod — частотная манипуляция с минимальным сдвигом (MSK)
Синтаксис:
y = mskmod(x,nsamp)
y = mskmod(x,nsamp,dataenc)
y = mskmod(x,nsamp,dataenc,ini_phase)
[y,phaseout] = mskmod(…)
Описание
y = mskmod(x,nsamp)
Возвращает комплексную огибающую y, полученную в результате передачи информационной последовательности x с использованием дифференциальной минимальной частотной манипуляции. Элементы входной информационной последовательности x могут принимать значения 0 и 1. Входной параметр nsamp должен быть положительным целым числом, большим единицы; он задет число отсчетов результирующего вектора y, приходящееся на один информационный символ из входного вектора x. Начальная фаза комплексной огибающей равна нулю. Если x — матрица, то ее столбцы обрабатываются независимо.
y = mskmod(x,nsamp,dataenc)
То же, что предыдущий вариант синтаксиса, но дополнительный входной параметр dataenc задает метод кодирования входных данных: при значении ‘diff’ дифференциальное кодирование используется, при значении ‘nondiff’ — не используется.
y = mskmod(x,nsamp,dataenc,ini_phase)
То же, что предыдущий вариант синтаксиса, но дополнительный входной параметр ini_phase задает начальную фазу комплексной огибающей в радианах. Этот параметр должен быть вектором-строкой с размером, равным числу каналов (столбцов) в сигнале y, а значения элементов этого вектора должны быть кратны pi/2. Чтобы использовать значение по умолчанию для параметра dataenc, его следует задать в виде пустой матрицы: [].
[y,phaseout] = mskmod(…)
То же, что предыдущие варианты синтаксиса, но в данном случае функция возвращает дополнительный результат phaseout — конечное значение фазы сформированного колебания. Это значение может затем использоваться в качестве входного параметра ini_phase при реализации блоковой обработки сигнала с сохранением непрерывности фазовой функции. Вектор phaseout имеет такой же размер, как входной параметр ini_phase, и может содержать значения, равные 0, pi/2, pi или 3*pi/2.
Примеры:
Приведенный ниже код осуществляет построение глазковой диаграммы для МЧМ-сигнала.
x = randint(99,1); % случайный сигнал
y = mskmod(x,8,[],pi/2); % модуляция
y = awgn(y,30,’measured’); % добавление шума
eyediagram(y,16); % построение глазковой диаграммы
Функция mskmod также используется в примере, приведенном на странице с описанием функции mskdemod.
Литература
1. Pasupathy, Subbarayan, «Minimum Shift Keying: A Spectrally Efficient Modulation», IEEE Communications Magazine, July, 1979, pp. 14-22.
Наверх
mskdemod — демодуляция сигнала с частотной манипуляцией с минимальным сдвигом
Синтаксис:
z = mskdemod(y,nsamp)
z = mskdemod(y,nsamp,dataenc)
z = mskdemod(y,nsamp,dataenc,ini_phase)
z = mskdemod(y,nsamp,dataenc,ini_phase,ini_state)
[z,phaseout] = mskdemod(…)
[z,phaseout,stateout] = mskdemod(…)
Описание
z = mskdemod(y,nsamp)
Выполняет демодуляцию комплексной огибающей сигнала с дифференциальной минимальной частотной манипуляцией y. Элементы демодулированной информационной последовательности z могут принимать значения 0 и 1. Входной параметр nsamp должен быть положительным целым числом, большим единицы; он задет число отсчетов сигнала y, приходящееся на один информационный символ. Начальная фаза комплексной огибающей должна быть равна нулю. Если y — матрица, то ее столбцы обрабатываются независимо.
z = mskdemod(y,nsamp,dataenc)
То же, что предыдущий вариант синтаксиса, но дополнительный входной параметр dataenc задает метод кодирования принимаемых данных: при значении ‘diff’ предполагается, что дифференциальное кодирование использовалось, при значении ‘nondiff’ — что не использовалось.
z = mskdemod(y,nsamp,dataenc,ini_phase)
То же, что предыдущий вариант синтаксиса, но дополнительный входной параметр ini_phase задает начальную фазу комплексной огибающей в радианах. Этот параметр должен быть вектором-строкой с размером, равным числу каналов (столбцов) в сигнале y, а значения элементов этого вектора должны быть кратны pi/2. Чтобы использовать значение по умолчанию для параметра dataenc, его следует задать в виде пустой матрицы: [].
z = mskdemod(y,nsamp,dataenc,ini_phase,ini_state)
То же, что предыдущий вариант синтаксиса, но дополнительный входной параметр ini_state задает начальное состояние демодулятора. Этот параметр должен содержать последние полсимвола из принятого ранее фрагмента сигнала. Таким образом, параметр ini_state должен представлять собой матрицу с nsamp строками и C столбцами, где C — число каналов (столбцов) в сигнале y.
[z,phaseout] = mskdemod(…)
То же, что предыдущие варианты синтаксиса, но в данном случае функция возвращает дополнительный результат phaseout — конечное значение фазы принимаемого колебания. Это значение может затем использоваться в качестве входного параметра ini_phase при реализации блоковой демодуляции сигнала. Вектор phaseout имеет такой же размер, как входной параметр ini_phase, и может содержать значения, равные 0, pi/2, pi или 3*pi/2.
[z,phaseout,stateout] = mskdemod(…)
То же, что предыдущие варианты синтаксиса, но в данном случае функция, помимо параметра phase_out, возвращает дополнительный результат stateout — конечное состояние демодулятора, то есть последние nsamp отсчетов сигнала y. Это значение может затем использоваться в качестве входного параметра ini_state при реализации блоковой демодуляции сигнала. Матрица stateout имеет такие же размеры, как входной параметр ini_state.
Примеры:
Приведенный ниже код иллюстрирует блоковую обработку сигнала функциями mskmod и mskdemod. Для обеспечения непрерывности фазовой функции сигнала и правильности его демодуляции использован синтаксис вызова указанных функций с установкой начальных и сохранением конечных значений фазы сигнала и внутреннего состояния демодулятора.
% задание параметров
numbits = 99; % число бит на итерацию
numchans = 2; % число каналов (столбцов) сигнала
nsamp = 16; % число отсчетов на символ
% инициализация
numerrs = 0; % счетчик числа ошибок демодуляции
demod_ini_phase = zeros(1,numchans); % текущая фаза демодулятора
mod_ini_phase = zeros(1,numchans); % текущая фаза модулятора
ini_state = complex(zeros(nsamp,numchans)); % текущее состояние демодулятора
% основной цикл
for iRuns = 1 : 10
x = randint(numbits,numchans); % двоичный сигнал
[y,mod_ini_phase] = mskmod(x,nsamp,[],mod_ini_phase); % модуляция
[z,demod_ini_phase,ini_state] = mskdemod(y,nsamp,[],demod_ini_phase,ini_state); % демодуляция
numerrs = numerrs + biterr(x,z); % накопление числа ошибок
end
disp([‘Total number of bit errors = ‘ num2str(numerrs)])
Ниже приведен результат работы этого кода.
Total number of bit errors = 0
Литература
1. Pasupathy, Subbarayan, «Minimum Shift Keying: A Spectrally Efficient Modulation», IEEE Communications Magazine, July, 1979, pp. 14-22.
Наверх
oqpskmod — квадратурная фазовая манипуляция со сдвигом (Offset QPSK)
Синтаксис:
y = oqpskmod(x)
y = oqpskmod(x,ini_phase)
Описание
y = oqpskmod(x)
Возвращает комплексную огибающую y, полученную в результате передачи информационной последовательности x с использованием квадратурной фазовой манипуляции со сдвигом. Информационная последовательность x должна состоять из целых чисел, лежащих в диапазоне от 0 до 3 включительно. Поскольку данный вид модуляции требует наличия сдвига на полтакта между квадратурными составляющими сигнала, число отсчетов на один такт модулированного сигнала должно быть четным. Поэтому функция oqpskmod неявно повышает частоту дискретизации сигнала в два раза. Длина вектора y равна length(x)*2 + 1. Если x — матрица, то ее столбцы обрабатываются независимо.
y = oqpskmod(x,ini_phase)
То же, что предыдущий вариант синтаксиса, но дополнительный входной параметр ini_phase задает начальную фазу комплексной огибающей в радианах.
Примеры:
Приведенный ниже код формирует сигнал с квадратурной фазовой манипуляцией со сдвигом и выводит графики его вещественной и мнимой частей. Для большей наглядности графики слегка сдвинуты друг относительно друга по вертикали.
x = randint(20, 1, 4); % случайное сообщение
y = oqpskmod(x); % модуляция
stairs([real(y)+0.01 imag(y)-0.01])
Из графика хорошо видно, что моменты смены уровня вещественной и мнимой частей сформированного сигнала сдвинуты друг относительно друга по времени.
Наверх
oqpskdemod — демодуляция сигнала с квадратурной фазовой манипуляцией со сдвигом (offset)
Синтаксис:
z = oqpskdemod(y)
z = oqpskdemod(y,ini_phase)
Описание
z = oqpskdemod(y)
Выполняет демодуляцию комплексной огибающей сигнала с квадратурной фазовой манипуляцией со сдвигом y. Поскольку данный вид модуляции требует наличия сдвига на полтакта между квадратурными составляющими сигнала, число отсчетов на один такт модулированного сигнала должно быть четным. Поэтому функция oqpskdemod неявно понижает частоту дискретизации сигнала в два раза. Входной сигнал y должен содержать полуцелое число тактов, то есть нечетное количество отсчетов. Длина демодулированного вектора z равна (length(y) — 1)/2. Демодулированная информационная последовательность z состоит из целых чисел, лежащих в диапазоне от 0 до 3 включительно. Если y — матрица, то ее столбцы обрабатываются независимо.
z = oqpskdemod(y,ini_phase)
То же, что предыдущий вариант синтаксиса, но дополнительный входной параметр ini_phase задает начальную фазу комплексной огибающей в радианах.
Примеры:
Приведенный ниже код осуществляет построение кривой помехоустойчивости квадратурной фазовой манипуляции со сдвигом.
N = 10000; % размер сообщения
snr = -10:10; % вектор отношений сигнал/шум (в децибелах)
for k = 1:length(snr) % цикл по значениям SNR
x = randint(N, 1, 4); % случайное сообщение
y = oqpskmod(x); % модуляция
yn = awgn(y, snr(k), ‘measured’); % добавление шума
z = oqpskdemod(yn); % демодуляция
[tmp, ser(k)] = symerr(z, x); % вероятность ошибки на символ
[tmp, ber(k)] = biterr(z, x, 2); % вероятность ошибки на бит
end
semilogy(snr, [ber’ ser’])
xlabel(‘SNR, dB’)
ylabel(‘Error rate’)
legend(‘Bit error rate’, ‘Symbol error rate’)
Результат работы кода приведен ниже. Из графиков видно, что при отношении сигнал/шум более 8 дБ ошибок демодуляции не произошло.
Наверх
pammod — амплитудно-импульсная модуляция (PAM)
Синтаксис:
y = pammod(x,M)
y = pammod(x,M,ini_phase)
Описание
y = pammod(x,M)
Возвращает комплексную огибающую y, полученную в результате передачи информационной последовательности x с использованием амплитудно-импульсной модуляции. Входной параметр M задает размер алфавита (число позиций манипуляции). Информационная последовательность x должна состоять из целых чисел, лежащих в диапазоне от 0 до M-1 включительно. Евклидово расстояние между соседними точками сигнального созвездия равно 2 (то есть используются значения амплитуды от -(M — 1) до (M — 1) с шагом 2). Начальная фаза комплексной огибающей равна нулю. Если x — матрица, то ее столбцы обрабатываются независимо.
y = pammod(x,M,ini_phase)
То же, что предыдущий вариант синтаксиса, но дополнительный входной параметр ini_phase задает начальную фазу комплексной огибающей в радианах.
Примеры:
В приведенном ниже коде с помощью функции berawgn вычисляется вероятность ошибки на символ для амплитудно-импульсной модуляции (АИМ) при ряде значений отношения энергии одного бита к спектральной плотности мощности шума (Eb/N0). Кроме того, в данном коде моделируется передача 8-позиционного АИМ-сигнала по каналу с аддитивным белым гауссовым шумом для сравнения аналитических результатов и результатов моделирования. Также код выводит в общих осях координат графики зависимости теоретической и экспериментально полученной вероятности ошибки от отношения Eb/N0.
% 1. Вычисляем теоретическую вероятность ошибки с помощью функции BERAWGN.
M = 8; % Размер алфавита
EbNo = [0:13]; % Вектор отношений Eb/N0
ser = berawgn(EbNo,’pam’,M).*log2(M); % Теоретическая вероятность ошибки
% Выводим теоретические результаты
figure;
semilogy(EbNo,ser,’r’);
xlabel(‘E_b/N_0 (dB)’);
ylabel(‘Symbol Error Rate’);
grid on;
drawnow;
% 2. Оцениваем вероятность ошибки путем моделирования
n = 10000; % Число символов для моделирования
k = log2(M); % Число бит на символ
% Пересчитываем отношение Eb/N0 в отношение сигнал/шум (SNR)
snr = EbNo+3+10*log10(k);
ynoisy=zeros(n,length(snr)); % Выделение памяти для ускорения вычислений
% Главный цикл моделирования
x = randint(n,1,M); % Информационное сообщение
y = pammod(x,M); % Модуляция
% Пропускаем модулированный сигнал через канал связи
% при различных отношениях Eb/N0
for jj = 1:length(snr)
ynoisy(:,jj) = awgn(real(y),snr(jj),’measured’);
end
z = pamdemod(ynoisy,M); % Демодуляция
% Вычисляем эмпирическую вероятность ошибки на символ
[num,rt] = symerr(x,z);
% 3. Выводим эмпирические результаты в тех же осях координат
hold on;
semilogy(EbNo,rt,’b.’);
legend(‘Theoretical SER’,’Empirical SER’);
title(‘Comparing Theoretical and Empirical Error Rates’);
hold off;
Результатом работы примера является график, подобный приведенному ниже. Ваши результаты могут отличаться, поскольку в примере используется генератор случайных чисел.
Наверх
pamdemod — амплитудно-импульсная демодуляция
Синтаксис:
z = pamdemod(y,M)
z = pamdemod(y,M,ini_phase)
Описание
z = pamdemod(y,M)
Выполняет демодуляцию комплексной огибающей сигнала с амплитудно-импульсной модуляцией y. Входной параметр M задает размер алфавита (число позиций манипуляции). Демодулированная информационная последовательность z состоит из целых чисел, лежащих в диапазоне от 0 до M-1 включительно. Евклидово расстояние между соседними точками сигнального созвездия модулированного сигнала должно быть равно 2 (то есть при модуляции должны быть использованы значения амплитуды от -(M — 1) до (M — 1) с шагом 2). Предполагается, что начальная фаза комплексной огибающей равна нулю. Если y — матрица, то ее столбцы обрабатываются независимо.
z = pamdemod(y,M,ini_phase)
То же, что предыдущий вариант синтаксиса, но дополнительный входной параметр ini_phase задает начальную фазу комплексной огибающей в радианах.
Наверх
pskmod — фазовая манипуляция (PSK)
Синтаксис:
y = pskmod(x,M)y = pskmod(x,M,ini_phase)
Описание
y = pskmod(x,M)
Возвращает комплексную огибающую y, полученную в результате передачи информационной последовательности x с использованием фазовой манипуляции. Входной параметр M задает размер алфавита (число позиций манипуляции) и должен быть степенью числа 2. Информационная последовательность x должна состоять из целых чисел, лежащих в диапазоне от 0 до M-1 включительно. Начальная фаза комплексной огибающей равна нулю. Если x — матрица, то ее столбцы обрабатываются независимо.
y = pskmod(x,M,ini_phase)
То же, что предыдущий вариант синтаксиса, но дополнительный входной параметр ini_phase задает начальную фазу комплексной огибающей в радианах.
Наверх
pskdemod — демодуляция сигнала с фазовой манипуляцией
Синтаксис:
z = pskdemod(y,M)
z = pskdemod(y,M,ini_phase)
Описание
z = pskdemod(y,M)
Выполняет демодуляцию комплексной огибающей сигнала с фазовой манипуляцией y. Входной параметр M задает размер алфавита (число позиций манипуляции) и должен быть степенью числа 2. Демодулированная информационная последовательность z состоит из целых чисел, лежащих в диапазоне от 0 до M-1 включительно. Предполагается, что начальная фаза комплексной огибающей равна нулю. Если y — матрица, то ее столбцы обрабатываются независимо.
z = pskdemod(y,M,ini_phase)
То же, что предыдущий вариант синтаксиса, но дополнительный входной параметр ini_phase задает начальную фазу комплексной огибающей в радианах.
Примеры:
В приведенном ниже коде производится сравнение фазовой манипуляции (PSK) и амплитудно-импульсной модуляции (PAM) с целью показать, что фазовая манипуляция более чувствительна к фазовому шуму. Это ожидаемый результат, поскольку сигнальное созвездие PSK имеет вид окружности, а сигнальное созвездие PAM — вид прямой линии.
len = 10000; % Число символов
M = 16; % Размер алфавита
msg = randint(len,1,M); % Исходное сообщение
% Для сравнения двух методов модуляции генерируем сигналы
% с использованием PSK и PAM
txpsk = pskmod(msg,M); % PSK-сигнал
txpam = pammod(msg,M); % PAM-сигнал
% Вносим фазовый шум в сформированные комплексные огибающие
phasenoise = randn(len,1)*.015;
rxpsk = txpsk.*exp(j*2*pi*phasenoise);
rxpam = txpam.*exp(j*2*pi*phasenoise);
% Выводим диаграммы рассеяния для сигналов с фазовым шумом
scatterplot(rxpsk); title(‘Noisy PSK Scatter Plot’)
scatterplot(rxpam); title(‘Noisy PAM Scatter Plot’)
% Демодулируем сигналы с фазовым шумом
recovpsk = pskdemod(rxpsk,M);
recovpam = pamdemod(rxpam,M);
% Вычисляем число ошибочных символов для обоих случаев
numerrs_psk = symerr(msg,recovpsk)
numerrs_pam = symerr(msg,recovpam)
Далее приведены выводимые результаты и диаграммы рассеяния. Полученные вами результаты могут отличаться от приведенных, так как в данном примере используется генератор случайных чисел.
numerrs_psk =
374
numerrs_pam =
1
Наверх
qammod — квадратурная манипуляция с квадратным созвездием (QASK)
Синтаксис:
y = qammod(x,M)
y = qammod(x,M,ini_phase)
Описание
y = qammod(x,M) Возвращает комплексную огибающую y, полученную в результате передачи информационной последовательности x с использованием квадратурной манипуляции с квадратным созвездием. Входной параметр M задает размер алфавита (число точек созвездия) и должен быть степенью числа 2. Информационная последовательность x должна состоять из целых чисел, лежащих в диапазоне от 0 до M-1 включительно. Сигнальное созвездие имеет вид квадрата (если M равняется двойке в четной степени) или креста (если M равняется двойке в нечетной степени). Точки созвездия имеют целочисленные координаты, расстояние между ближайшими точками созвездия равно двум. Начальная фаза комплексной огибающей равна нулю. Если x — матрица, то ее столбцы обрабатываются независимо.
y = qammod(x,M,ini_phase)
То же, что предыдущий вариант синтаксиса, но дополнительный входной параметр ini_phase задает начальную фазу комплексной огибающей в радианах.
Примеры:
Приведенный ниже код генерирует случайный цифровой сигнал, выполняет модуляцию, добавление шума, построение диаграммы рассеяния, демодуляцию зашумленного сигнала и вычисление вероятности символьной ошибки.
% Создаем случайное сообщение
M = 16; % Размер алфавита
x = randint(5000, 1, M); % Случайное сообщение
% Используем 16-точечную КАМ
y = qammod(x, M);
% Передаем сигнал через канал с аддитивным белым гауссовым шумом
ynoisy = awgn(y, 15, ‘measured’);
% Строим диаграмму рассеяния для зашумленного сигнала
scatterplot(ynoisy);
% Производим демодуляцию
z = qamdemod(ynoisy,M);
% Оцениваем вероятность символьной ошибки
[num,rt]= symerr(x,z)
Рассчитанная вероятность ошибки и построенная диаграмма рассеяния приводятся ниже. Полученные вами результаты могут отличаться, так как в данном примере используется генератор случайных чисел.
num =
94
rt =
0.0188
Из-за добавления шума диаграмма рассеяния имеет вид пятен, расположенных в точках используемого сигнального созвездия.
Наверх
qamdemod — демодуляция сигнала с квадратурной манипуляцией с квадратным созвездием
Синтаксис:
z = qamdemod(y,M)
z = qamdemod(y,M,ini_phase)
Описание
z = qamdemod(y,M)
Выполняет демодуляцию комплексной огибающей сигнала с квадратурной манипуляцией y. Входной параметр M задает размер алфавита (число точек созвездия) и должен быть степенью числа 2. При демодуляции используется сигнальное созвездие в форме квадрата или креста (см. описание функции qammod). Демодулированная информационная последовательность z состоит из целых чисел, лежащих в диапазоне от 0 до M-1 включительно. Предполагается, что начальная фаза комплексной огибающей равна нулю. Если y — матрица, то ее столбцы обрабатываются независимо.
z = qamdemod(y,M,ini_phase)
То же, что предыдущий вариант синтаксиса, но дополнительный входной параметр ini_phase задает начальную фазу комплексной огибающей в радианах.
Примеры:
Приведенный ниже код показывает, какие области комплексной плоскости соответствуют разным символам при демодуляции. Программа демодулирует случайные комплексные числа, находит числа, которые при демодуляции дали символы 0 и 3, а затем отображает эти числа в виде точек на комплексной плоскости соответственно красным и синим цветом. Кроме того, при этом демонстрируется влияние поворота созвездия на pi/8.
% Создаем случайные точки на комплексной плоскости
y = 4*(rand(1000,1)-1/2)+j*4*(rand(1000,1)-1/2);
% Демодулируем, используя начальную фазу pi/8
z = qamdemod(y,4,pi/8);
% Находим индексы точек, которые при демодуляции дали символы 0 и 3
red = find(z==0);
blue = find(z==3);
% Отображаем входные точки, соответствующие символам 0 и 3
h = scatterplot(y(red,:),1,0,’r.’); hold on
scatterplot(y(blue,:),1,0,’b.’,h);
legend(‘Points corresponding to 0′,’Points corresponding to 3’);
hold off
Рассчитанная вероятность ошибки и построенная диаграмма рассеяния приводятся ниже. Полученные вами результаты могут отличаться, так как в данном примере используется генератор случайных чисел.
num =
94
rt =
0.0188
Из-за добавления шума диаграмма рассеяния имеет вид пятен, расположенных в точках используемого сигнального созвездия.
Наверх
ademod — аналоговая демодуляция (вещественный входной сигнал)
Синтаксис:
z = ademod(y,Fc,Fs,’amdsb-tc’,offset,num,den);
z = ademod(y,Fc,Fs,’amdsb-tc/costas’,offset,num,den);
z = ademod(y,Fc,Fs,’amdsb-sc’,num,den);
z = ademod(y,Fc,Fs,’amdsb-sc/costas’,num,den);
z = ademod(y,Fc,Fs,’amssb’,num,den);
z = ademod(y,Fc,Fs,’qam’,num,den);
z = ademod(y,Fc,Fs,’fm’,num,den,vcoconst);
z = ademod(y,Fc,Fs,’pm’,num,den,vcoconst);
z = ademod(y,Fc,[Fs phase],…);
Необязательные входные параметры:
|
Параметр |
Значение по умолчанию |
|
offset |
Выбирается так, чтобы каждый выходной сигнал имел нулевое среднее значение |
|
num, den |
[num,den] = butter(5,Fc*2/Fs); |
|
vcoconst |
1 |
Описание:
Функция ademod выполняет аналоговую демодуляцию, используя вещественный входной сигнал с заданной несущей частотой. Соответствующая функция модуляции — amod. В приведенной ниже таблице перечислены поддерживаемые функцией ademod виды модуляции.
|
Вид модуляции |
Четвертый входной параметр |
|
Амплитудная демодуляция |
‘amdsb-tc’ или ‘amdsb-tc/costas’ |
|
Амплитудная демодуляция, две боковых полосы с подавленной несущей |
‘amdsb-sc’ или ‘amdsb-sc/costas’ |
|
Амплитудная демодуляция, одна боковая полоса с подавленной несущей |
‘amssb’ |
|
Квадратурная амплитудная демодуляция |
‘qam’ |
|
Частотная демодуляция |
‘fm’ |
|
Фазовая демодуляция |
‘pm’ |
Общая информация о синтаксисе:
При всех вариантах вызова функции z = ademod(y,Fc,Fs,…) в качестве принятого модулированного сигнала используется массив y. Параметр Fc — это несущая частота в герцах, а Fs — частота дискретизации в герцах. Начальная фаза несущего колебания равна нулю.
Параметры y и z — вещественные матрицы, размеры которых зависят от вида модуляции:
-
Квадратурная амплитудная модуляция. Если y — вектор размера n, то z будет матрицей, содержащей n строк и 2 столбца. Если y — матрица с n строками и m столбцами, то каждый столбец y обрабатывается независимо и результат z содержит n строк и 2m столбцов. Столбцы z с нечетными номерами представляют синфазные компоненты демодулированного сигнала, а столбцы с четными номерами — его квадратурные компоненты.
-
Другие виды модуляции. Массивы y и z имеют одинаковые размеры. Если y — двумерная матрица, то ее столбцы обрабатываются независимо друг от друга.
Можно задать частоту дискретизации в виде двухэлементного вектора:
z = ademod(y,Fc,[Fs phase],…).
В данном случае первый элемент этого вектора (Fs) задает частоту дискретизации, как описано выше. Второй элемент (phase) — это начальная фаза несущего колебания в радианах.
Функция ademod использует фильтр нижних частот для отделения демодулированного низкочастотного сигнала от побочных продуктов демодуляции, имеющих частоты, равные частоте несущего колебания или превышающие ее. Чтобы задать параметры фильтра, включите в список входных параметров векторы num и den. Параметры num и den должны быть векторами-строками, содержащими коэффициенты полиномов числителя и знаменателя функции передачи фильтра в порядке убывания степеней. Если параметр num является пустой матрицей, равен нулю или отсутствует, по умолчанию используется фильтр Баттерворта 5-го порядка с частотой среза, равной несущей частоте. Фильтр рассчитывается с помощью функции butter, входящей в пакет Signal Processing:
[num,den] = butter(5,Fc*2/Fs);
Конкретные варианты синтаксиса:
-
z = ademod(y,Fc,Fs,’amdsb-tc’,offset,num,den)
Реализует амплитудную демодуляцию при наличии двух боковых полос. Параметр offset — это вектор, k-й элемент которого вычитается из k-го столбца матрицы демодулированных сигналов. Если offset — пустая матрица, то по умолчанию из каждого столбца z вычитается такая константа, чтобы среднее значение столбца стало нулевым (если z — вектор, то из него вычитается его среднее значение).
-
z = ademod(y,Fc,Fs,’amdsb-tc/costas’,offset,num,den)
То же, что и предыдущий вариант синтаксиса, но для демодуляции используется алгоритм Костаса (алгоритм с фазовой автоподстройкой частоты (ФАПЧ)).
-
z = ademod(y,Fc,Fs,’amdsb-sc’,num,den)
Реализует демодуляцию амплитудно-модулированного сигнала с двумя боковыми полосами и подавленной несущей.
-
z = ademod(y,Fc,Fs,’amdsb-sc/costas’,num,den)
То же, что и предыдущий вариант синтаксиса, но для демодуляции используется алгоритм Костаса (алгоритм с ФАПЧ).
-
z = ademod(y,Fc,Fs,’amssb’,num,den)
Реализует демодуляцию амплитудно-модулированного сигнала с одной боковой полосой и подавленной несущей.
-
z = ademod(y,Fc,Fs,’qam’,num,den)
Реализует демодуляцию сигнала с квадратурной амплитудной модуляцией.
-
z = ademod(y,Fc,Fs,’fm’,num,den,vcoconst)
Реализует частотную демодуляцию. Для демодуляции используется петля ФАПЧ, состоящая из перемножителя (используемого в качестве фазового детектора), фильтра нижних частот и генератора, управляемого напряжением (ГУН) (английский термин — voltage-controlled oscillator, VCO). Если Fs — двухэлементный вектор, то его второй элемент задает начальную фазу ГУН в радианах. Необязательный параметр vcoconst — число, задающее коэффициент преобразования ГУН в Гц/В.
-
z = ademod(y,Fc,Fs,’pm’,num,den,vcoconst)
Реализует фазовую демодуляцию. Для демодуляции используется петля ФАПЧ (которая реализует частотный демодулятор), на выходе которой включен интегратор. Петля ФАПЧ состоит из перемножителя (используемого в качестве фазового детектора), фильтра нижних частот и ГУН. Если Fs — двухэлементный вектор, то его второй элемент задает начальную фазу ГУН в радианах. Необязательный параметр vcoconst — число, задающее коэффициент преобразования ГУН в Гц/В и коэффициент усиления интегратора.
Примеры.
Данный пример иллюстрирует использование параметра offset. Поскольку первая команда ademod использует то же значение offset, равное 0.3, что и предшествующая команда amod, демодулированный сигнал z1 идентичен исходному модулирующему сигналу. При втором вызове функции ademod параметр offset опущен, поэтому демодулированный сигнал z2 имеет среднее значение, близкое к нулю (оно не в точности равно нулю из-за ошибок округления).
Fc = 25; % Несущая частота
Fs = 100; % Частота дискретизации
t = [0:1/Fs:5]’; % Моменты дискретизации сигнала
x = [cos(t), sin(t)]; % Два сигнала – косинус и синус
y = amod(x,Fc,Fs,’amdsb-tc’,.3); % Осуществляем модуляцию,
% добавляя постоянное смещение, равное 0.3
z1 = ademod(y,Fc,Fs,’amdsb-tc’,.3); % Демодуляция
z2 = ademod(y,Fc,Fs,’amdsb-tc’); % Демодуляция
plot(t,z1,’b’,t,z2,’r—‘) % Графики демодулированных сигналов
На рисунке график сигнала z1 выведен сплошной линией, а график сигнала z2 — пунктирной линией.
Еще один пример использования функции ademod можно найти на странице с описанием функции amod под заголовком “Пример использования гильбертовского фильтра”.
Наверх
ademodce — аналоговая демодуляция (вход — комплексная огибающая)
Синтаксис:
z = ademodce(y,Fs,’amdsb-tc’,offset,num,den);
z = ademodce(y,Fs,’amdsb-tc/costas’,offset,num,den);
z = ademodce(y,Fs,’amdsb-sc’,num,den);
z = ademodce(y,Fs,’amdsb-sc/costas’,num,den);
z = ademodce(y,Fs,’amssb’,num,den);
z = ademodce(y,Fs,’qam’,num,den);
z = ademodce(y,Fs,’fm’,num,den,vcoconst);
z = ademodce(y,Fs,’pm’,num,den,vcoconst);
z = ademodce(y,[Fs phase],…);
Необязательные входные параметры:
|
Параметр |
Значение по умолчанию или поведение функции, если параметр опущен |
|
offset |
Выбирается так, чтобы каждый выходной сигнал имел нулевое среднее значение |
|
num, den |
Если данные параметры опущены, то ademodce не использует фильтр |
|
vcoconst |
1 |
Описание.
Функция ademodce выполняет аналоговую демодуляцию, используя входной сигнал в виде комплексной огибающей модулированного сигнала. Соответствующая функция модуляции — amodce. В приведенной ниже таблице перечислены поддерживаемые функцией ademodce виды модуляции.
|
Вид модуляции |
Третий входной параметр |
|
Амплитудная демодуляция |
‘amdsb-tc’ |
|
Амплитудная демодуляция, две боковых полосы с подавленной несущей |
‘amdsb-sc’ или ‘amdsb-sc/costas’ |
|
Амплитудная демодуляция, одна боковая полоса с подавленной несущей |
‘amssb’ |
|
Квадратурная амплитудная демодуляция |
‘qam’ |
|
Частотная демодуляция |
‘fm’ |
|
Фазовая демодуляция |
‘pm’ |
Общая информация о синтаксисе:
При всех вариантах вызова функции z = ademodce(y,Fs,…) в качестве принятого модулированного сигнала используется массив y. Параметр Fs — частота дискретизации в герцах. Начальная фаза несущего колебания равна нулю. Параметр y — комплексная матрица, а результат z — вещественная матрица. Размеры этих матриц зависят от вида модуляции:
-
Квадратурная амплитудная модуляция. Если y — вектор размера n, то z будет матрицей, содержащей n строк и 2 столбца. Если y — матрица с n строками и m столбцами, то каждый столбец y обрабатывается независимо и результат z содержит n строк и 2m столбцов. Столбцы z с нечетными номерами представляют синфазные компоненты демодулированного сигнала, а столбцы с четными номерами — его квадратурные компоненты.
-
Другие виды модуляции. Массивы y и z имеют одинаковые размеры. Если y — двумерная матрица, то ее столбцы обрабатываются независимо друг от друга.
Можно задать частоту дискретизации в виде двухэлементного вектора:
z = ademodce(y,[Fs phase],…).
В данном случае первый элемент этого вектора (Fs) задает частоту дискретизации, как описано выше. Второй элемент (phase) — это начальная фаза несущего колебания в радианах.
Чтобы пропустить демодулированный сигнал через фильтр нижних частот, включите в список входных параметров векторы num и den. Параметры num и den должны быть векторами-строками, содержащими коэффициенты полиномов числителя и знаменателя функции передачи фильтра в порядке убывания степеней. Если параметр num является пустой матрицей, равен нулю или отсутствует, по умолчанию функция ademodce не производит фильтрации демодулированного сигнала.
Конкретные варианты синтаксиса:
-
z = ademodce(y,Fs,’amdsb-tc’,offset,num,den)
Реализует амплитудную демодуляцию при наличии двух боковых полос. Параметр offset — это вектор, k-й элемент которого вычитается из k-го столбца матрицы демодулированных сигналов. Если offset — пустая матрица или отсутствует, то по умолчанию из каждого столбца z вычитается такая константа, чтобы среднее значение столбца стало нулевым (если z — вектор, то из него вычитается его среднее значение).
-
z = ademodce(y,Fs,’amdsb-tc/costas’,offset,num,den)
То же, что и предыдущий вариант синтаксиса, но для демодуляции используется алгоритм Костаса (алгоритм с фазовой автоподстройкой частоты (ФАПЧ)).
-
z = ademodce(y,Fs,’amdsb-sc’,num,den)
Реализует демодуляцию амплитудно-модулированного сигнала с двумя боковыми полосами и подавленной несущей.
-
z = ademodce(y,Fs,’amdsb-sc/costas’,num,den)
То же, что и предыдущий вариант синтаксиса, но для демодуляции используется алгоритм Костаса (алгоритм с ФАПЧ).
-
z = ademodce(y,Fs,’amssb’,num,den)
Реализует демодуляцию амплитудно-модулированного сигнала с одной боковой полосой и подавленной несущей.
-
z = ademodce(y,Fs,’qam’,num,den)
Реализует демодуляцию сигнала с квадратурной амплитудной модуляцией.
-
z = ademodce(y,Fs,’fm’,num,den,vcoconst)
Реализует частотную демодуляцию. Для демодуляции используется петля ФАПЧ, состоящая из перемножителя (используемого в качестве фазового детектора), фильтра нижних частот (задаваемого с помощью параметров num и den; по умолчанию фильтр отсутствует) и генератора, управляемого напряжением (ГУН) (английский термин — voltage-controlled oscillator, VCO). Если Fs — двухэлементный вектор, то его второй элемент задает начальную фазу ГУН в радианах. Необязательный параметр vcoconst — число, задающее коэффициент преобразования ГУН в Гц/В.
-
z = ademodce(y,Fs,’pm’,num,den,vcoconst)
Реализует фазовую демодуляцию. Для демодуляции используется петля ФАПЧ (которая реализует частотный демодулятор), на выходе которой включен интегратор. Петля ФАПЧ состоит из перемножителя (используемого в качестве фазового детектора), фильтра нижних частот и ГУН. Если Fs — двухэлементный вектор, то его второй элемент задает начальную фазу ГУН в радианах. Необязательный параметр vcoconst — число, задающее коэффициент преобразования ГУН в Гц/В.
Примеры.
В приведенном ниже примере модуляции и демодуляции подвергаются три сигнала одновременно: синус, косинус и пилообразный сигнал. Все три сигнала имеют одинаковую частоту дискретизации и одинаковое число отсчетов. В качестве результата работы выводятся графики модулирующих и демодулированных сигналов.
Fs = 100; % Частота дискретизации сигнала
t = [0:1/Fs:5]’; % Моменты дискретизации сигнала
% Комбинируем три сигнала в трехстолбцовую матрицу
% Каждому сигналу соответствует столбец матрицы
x = [sin(2*pi*t), .5*cos(5*pi*t), sawtooth(4*t)];
y = amodce(x,Fs,’fm’); % Модуляция
z = ademodce(y,Fs,’fm’); % Демодуляция
plot(x); figure; plot(z); % Графики исходных и выходных сигналов
Наверх
amod — аналоговая модуляция (вещественный выходной сигнал)
Синтаксис:
y = amod(x,Fc,Fs,’amdsb-sc’);
y = amod(x,Fc,Fs,’amdsb-tc’,offset);
y = amod(x,Fc,Fs,’amssb/opt’);
y = amod(x,Fc,Fs,’amssb/opt’,num,den);
y = amod(x,Fc,Fs,’amssb/opt’,hilbertflag);
y = amod(x,Fc,Fs,’qam’);
y = amod(x,Fc,Fs,’fm’,deviation);
y = amod(x,Fc,Fs,’pm’,deviation);
y = amod(x,Fc,[Fs phase],…);
[y,t] = amod(…);
Необязательные входные параметры:
|
Параметр |
Значение по умолчанию или поведение функции, если параметр опущен |
|
offset |
-min(min(x)) |
|
opt |
Если данный параметр опущен, функция amod формирует однополосный сигнал с нижней боковой полосой |
|
deviation |
1 |
Описание:
Функция amod выполняет аналоговую модуляцию, генерируя вещественный выходной сигнал с заданной несущей частотой. Соответствующая функция демодуляции — ademod. В приведенной ниже таблице перечислены поддерживаемые функцией amod виды модуляции.
|
Вид модуляции |
Четвертый входной параметр |
|
Амплитудная модуляция, передаются две боковых полосы и несущее колебание |
‘amdsb-tc’ |
|
Амплитудная модуляция, две боковых полосы с подавленной несущей |
‘amdsb-sc’ |
|
Амплитудная модуляция, одна боковая полоса с подавленной несущей |
‘amssb’ или ‘amssb/up’ |
|
Квадратурная амплитудная модуляция |
‘qam’ |
|
Частотная модуляция |
‘fm’ |
|
Фазовая модуляция |
‘pm’ |
Общая информация о синтаксисе:
При всех вариантах вызова функции y = amod(x,Fc,Fs,…) в качестве модулирующего сигнала используется массив x. Параметр Fc — это несущая частота в герцах, а Fs — частота дискретизации в герцах. (Соответственно, период дискретизации для x и y составляет 1/Fs.) Начальная фаза несущего колебания равна нулю. Согласно теореме Найквиста, частота дискретизации должна быть как минимум в два раза больше несущей частоты. Параметры x и y — вещественные матрицы, размеры которых зависят от вида модуляции:
-
Квадратурная амплитудная модуляция. Массив x должен иметь четное число столбцов. Столбцы с нечетными номерами представляют синфазные компоненты модулирующего сигнала, а столбцы с четными номерами — квадратурные компоненты. Если массив x имеет n строк и 2m столбцов, то модулированный сигнал y будет иметь nстрок и m столбцов; все пары столбцов массива x обрабатываются независимо друг от друга.
-
Другие виды модуляции. Массивы x и y имеют одинаковые размеры. Если x — двумерная матрица, то ее столбцы обрабатываются независимо друг от друга.
Можно задать частоту дискретизации в виде двухэлементного вектора: y = amod(x,Fc,[Fs phase],…). В данном случае первый элемент этого вектора (Fs) задает частоту дискретизации, как описано выше. Второй элемент (phase) — это начальная фаза несущего колебания в радианах.
Конкретные варианты синтаксиса:
-
y = amod(x,Fc,Fs,’amdsb-tc’,offset)
Реализует двухполосную амплитудную модуляцию. Параметр offset — это постоянное смещение, добавляемое к x перед модуляцией. Если параметр offset опущен, его значение по умолчанию равно -min(min(x)). Это обеспечивает стопроцентную глубину модуляции.
-
y = amod(x,Fc,Fs,’amdsb-sc’)
Реализует двухполосную амплитудную модуляцию с подавленной несущей.
-
y = amod(x,Fc,Fs,’amssb/opt’)
Реализует однополосную амплитудную модуляцию с подавленной несущей. По умолчанию формируется сигнал с нижней боковой полосой; если ключ opt имеет значение up, формируется сигнал с верхней боковой полосой. При данном варианте вызова для формирования сигнала используется преобразование Гильберта в частотной области.
Внимание! Указанный в документации способ управления боковой полосой формируемого сигнала на самом деле не работает. Для устранения этой ошибки можно заменить в строке 79 файла amod.m имя вызываемой функции strcmp на findstr. Впрочем, можно добиться результата и не редактируя файлы MATLAB — достаточно при вызове указать отрицательное значение несущей частоты, и будет сформирован сигнал с верхней боковой полосой.
-
y = amod(x,Fc,Fs,’amssb/opt’,num,den)
То же, что и предыдущий вариант синтаксиса, но преобразование Гильберта выполняется во временной области. Параметры num и den — векторы-строки, задающие коэффициенты числителя и знаменателя функции передачи фильтра (в порядке убывания степеней переменной z). Для расчета фильтра Гильберта можно использовать функцию hilbiir.
-
y = amod(x,Fc,Fs,’amssb/opt’,hilbertflag)
То же, что и предыдущий вариант синтаксиса, но фильтр, выполняющий преобразование Гильберта во временной области, рассчитывается по умолчанию следующим образом: [num,den] = hilbiir(1/Fs) (параметры num и den были описаны выше). Входной параметр hilbertflag может иметь произвольное значение.
Внимание! При использовании преобразования Гильберта во временной области функция amod работает, мягко говоря, плохо. Причиной является то, что разработчики забыли компенсировать задержку квадратурной составляющей сигнала, неизбежно появляющуюся при фильтрации.
-
y = amod(x,Fc,Fs,’qam’)
Реализует квадратурную амплитудную модуляцию. Параметр x должен быть матрицей с четным числом столбцов, при этом столбцы с нечетными номерами служат синфазными модулирующими сигналами, а столбцы с четными номерами — квадратурными модулирующими сигналами. Выходной сигнал y будет матрицей с числом столбцов, в два раза меньшим, чем у x.
-
y = amod(x,Fc,Fs,’fm’,deviation)
Реализует частотную модуляцию. Спектр модулированного сигнала лежит в полосе частот от (min(x) + Fc) до (max(x) + Fc). Необязательный параметр deviation — число, задающее девиацию частоты. Модулирующий сигнал x перед модуляцией умножается на константу deviation, так что вызов y = amod(x,Fc,Fs,’fm’,deviation) эквивалентен вызову y = amod(x*deviation,Fc,Fs,’fm’).
-
y = amod(x,Fc,Fs,’pm’,deviation)
Реализует фазовую модуляцию. Необязательный параметр deviation — число, задающее девиацию фазы. Модулирующий сигнал x перед модуляцией умножается на константу deviation, так что вызов y = amod(x,Fc,Fs,’pm’,deviation) эквивалентен вызову y = amod(x*deviation,Fc,Fs,’pm’).
-
[y,t] = amod(…)
Дополнительно возвращает вектор значений времени t, использованных при вычислениях.
Примеры.
Сравнение двухполосной и однополосной модуляции.
В первом примере сравниваются спектры сигналов с двухполосной и однополосной модуляцией. Модулирующий сигнал — синусоида с частотой 1 Гц, несущая частота равна 10 Гц. Приведенный ниже сценарий использует при вызове функции amod параметры ‘amdsb-sc’ и ‘amssb’, чтобы создать модулированные сигналы ydouble (двухполосная модуляция) ysingle (однополосная модуляция). Затем строятся спектры обоих модулированных сигналов.
% Частота дискретизации 100 Гц, продолжительность сигнала 2 с
Fs = 100;
t = [0:2*Fs+1]’/Fs;
Fc = 10; % Несущая частота
x = sin(2*pi*t); % Синусоидальный модулирующий сигнал
% Производим двухполосную и однополосную амплитудную модуляцию.
ydouble = amod(x,Fc,Fs,’amdsb-sc’);
ysingle = amod(x,Fc,Fs,’amssb’);
% Выводим графики спектров обоих модулированных сигналов.
zdouble = fft(ydouble);
zdouble = abs(zdouble(1:length(zdouble)/2+1));
frqdouble = [0:length(zdouble)-1]*Fs/length(zdouble)/2;
plot(frqdouble,zdouble); % Левый график, приведенный ниже
figure;
zsingle = fft(ysingle);
zsingle = abs(zsingle(1:length(zsingle)/2+1));
frqsingle = [0:length(zsingle)-1]*Fs/length(zsingle)/2;
plot(frqsingle,zsingle); % Правый график, приведенный ниже
Обратите внимание на то, что спектр на левом графике имеет два пика, представляющие собой нижнюю и верхнюю боковые полосы модулированного сигнала. Эти две боковые полосы симметричны относительно несущей частоты Fc, равной 10 Гц. Ширина спектра сигнала с двухполосной АМ в два раза больше, чем максимальная частота, содержащаяся в спектре входного (модулирующего) сигнала. На правом графике есть только один пик, поскольку при однополосной модуляции передается только одна (в данном случае нижняя) боковая полоса.
Пример использования гильбертовского фильтра.
Следующий пример иллюстрирует выполнение преобразования Гильберта во временной области.
Fc = 25; % Несущая частота
Fs = 100; % Частота дискретизации сигнала
[numh,denh] = hilbiir(1/Fs,15/Fs,15); % Расчет фильтра Гильберта.
t = [0:1/Fs:5]’; % Моменты дискретизации сигнала
x = cos(t); % Синусоидальный сигнал.
y = amod(x,Fc,[Fs pi/4],’amssb’,numh,denh); % Модулируем,
% используя преобразование Гильберта во временной области.
z = ademod(y,Fc,[Fs pi/4],’amssb’); % Демодуляция.
plot(t,z) % График демодулированного сигнала.
Результирующий график показан ниже слева. Если заменить шестую строку приведенного кода на
y = amod(x,Fc,[Fs pi/4],’amssb’); % Модулируем,
то при однополосной модуляции будет используется преобразование Гильберта в частотной области. Результат демодуляции показан на рисунке ниже справа. Два приведенных графика незначительно различаются начальными переходными процессами.
Внимание! Данный пример приводится в документации пакета Communications и вроде бы работает, несмотря на сформулированные выше предупреждения. Однако качество сформированного однополосного сигнала в данном примере практически не влияет на результат демодуляции. Если же вывести график спектра однополосного сигнала, сформированного с помощью преобразования Гильберта, выполняемого во временной области, окажется, что подавление верхней боковой полосы составляет всего лишь около 20 дБ. Да и такое подавление достигнуто лишь благодаря тому, что период модулирующего сигнала (6,28 с) значительно превышает вносимую гильбертовским фильтром задержку, заданную в числе параметров функции hilbiir и равную 15/Fs = 0,15 с.
Наверх
amodce — аналоговая модуляция (выход — комплексная огибающая)
Синтаксис:
y = amodce(x,Fs,’amdsb-tc’,offset);
y = amodce(x,Fs,’amdsb-sc’);
y = amodce(x,Fs,’amssb’);
y = amodce(x,Fs,’amssb/time’,num,den);
y = amodce(x,Fs,’amssb/time’);
y = amodce(x,Fs,’qam’);
y = amodce(x,Fs,’fm’,deviation);
y = amodce(x,Fs,’pm’,deviation);
y = amodce(x,[Fs phase],…);
Необязательные входные параметры:
|
Параметр |
Значение по умолчанию или поведение функции, если параметр опущен |
|
offset |
-min(min(x)) |
|
deviation |
1 |
Описание:
Функция amodce выполняет аналоговую модуляцию, генерируя комплексную огибающую выходного модулированного сигнала. Соответствующая функция демодуляции — ademodce. В приведенной ниже таблице перечислены поддерживаемые функцией amodce виды модуляции.
|
Вид модуляции |
Третий входной параметр |
|
Амплитудная модуляция, две боковых полосы |
‘amdsb-tc’ |
|
Амплитудная модуляция, две боковых полосы с подавленной несущей |
‘amdsb-sc’ |
|
Амплитудная модуляция, одна боковая полоса с подавленной несущей |
‘amssb’ или ‘amssb/time’ |
|
Квадратурная амплитудная модуляция |
‘qam’ |
|
Частотная модуляция |
‘fm’ |
|
Фазовая модуляция |
‘pm’ |
Общая информация о синтаксисе:
При всех вариантах вызова функции y = amodce(x,Fs,…) в качестве модулирующего сигнала используется массив x, а возвращается комплексная огибающая модулированного сигнала. Параметр Fs — это частота дискретизации в герцах. (Соответственно, период дискретизации для x и y составляет 1/Fs.) Начальная фаза несущего колебания равна нулю. x — вещественная матрица, а y — комплексная матрица. Размеры x и y зависят от вида модуляции:
-
Квадратурная амплитудная модуляция. Массив x должен иметь четное число столбцов. Столбцы с нечетными номерами представляют синфазные компоненты модулирующего сигнала, а столбцы с четными номерами — квадратурные компоненты. Если массив x имеет n строк и 2m столбцов, то модулированный сигнал y будет иметь nстрок и m столбцов; все пары столбцов массива x обрабатываются независимо друг от друга.
-
Другие виды модуляции. Массивы x и y имеют одинаковые размеры. Если x — двумерная матрица, то ее столбцы обрабатываются независимо друг от друга.
Можно задать частоту дискретизации в виде двухэлементного вектора: y = amodce(x,[Fs phase],…). В данном случае первый элемент этого вектора (Fs) задает частоту дискретизации, как описано выше. Второй элемент (phase) — это начальная фаза несущего колебания в радианах.
Конкретные варианты синтаксиса:
-
y = amodce(x,Fs,’amdsb-tc’,offset)
Реализует двухполосную амплитудную модуляцию. Параметр offset — это постоянное смещение, добавляемое к x перед модуляцией. Если параметр offset опущен, его значение по умолчанию равно -min(min(x)). Это обеспечивает стопроцентную глубину модуляции.
-
y = amodce(x,Fs,’amdsb-sc’)
Реализует двухполосную амплитудную модуляцию с подавленной несущей.
-
y = amodce(x,Fs,’amssb’)
Реализует однополосную амплитудную модуляцию с подавленной несущей. По умолчанию формируется сигнал с нижней боковой полосой. При данном варианте вызова для формирования сигнала используется преобразование Гильберта в частотной области.
-
y = amodce(x,Fs,’amssb/time’,num,den)
То же, что и предыдущий вариант синтаксиса, но преобразование Гильберта выполняется во временной области. Параметры num и den — векторы-строки, задающие коэффициенты числителя и знаменателя функции передачи фильтра (в порядке убывания степеней переменной z). Для расчета фильтра Гильберта можно использовать функцию hilbiir.
-
y = amodce(x,Fs,’amssb/time’)
То же, что и предыдущий вариант синтаксиса, но фильтр, выполняющий преобразование Гильберта во временной области, рассчитывается по умолчанию следующим образом: [num,den] = hilbiir(1/Fs) (параметры num и den были описаны выше).
-
y = amodce(x,Fs,’qam’)
Реализует квадратурную амплитудную модуляцию. Параметр x должен быть матрицей с четным числом столбцов, при этом столбцы с нечетными номерами служат синфазными модулирующими сигналами, а столбцы с четными номерами — квадратурными модулирующими сигналами. Выходной сигнал y будет матрицей с числом столбцов, в два раза меньшим, чем у x.
-
y = amodce(x,Fs,’fm’,deviation)
Реализует частотную модуляцию. Ширина полосы частот модулированного сигнала равна max(x) – min(x). Необязательный параметр deviation — число, задающее девиацию частоты.
-
y = amodce(x,Fs,’pm’,deviation)
Реализует фазовую модуляцию. Необязательный параметр deviation — число, задающее девиацию фазы.
Примеры.
Данный пример аналогичен приведенному под заголовком “Пример использования гильбертовского фильтра” на странице с описанием функции amod, отличие состоит лишь в том, что в данном случае моделируется комплексная огибающая. Графики для случая вещественного сигнала (см. описание функции amod) показывают наличие значительно более заметных искажений в демодулированном сигнале. Результат работы данного примера демонстрирует, что средняя разница между модулирующим и демодулированным сигналами не превосходит 10-16.
Fs = 100; % Частота дискретизации сигнала
[numh,denh] = hilbiir(1/Fs,15/Fs,15); % Расчет фильтра Гильберта.
t = [0:1/Fs:5]’; % Моменты дискретизации сигнала
x = cos(t); % Синусоидальный сигнал.
y = amodce(x,[Fs pi/4],’amssb/time’,numh,denh); % Модулируем,
% используя преобразование Гильберта во временной области.
z = ademodce(y,[Fs pi/4],’amssb’); % Демодуляция.
d = ceil(log10(sum(abs(x-z))/length(x)))
d =
-16
Наверх
apkconst — графическое изображение концентрического сигнального созвездия для квадратурной манипуляции
Синтаксис:
apkconst(numsig);
apkconst(numsig,amp);
apkconst(numsig,amp,phs);
apkconst(numsig,amp,’n’);
apkconst(numsig,amp,phs,plotspec);
y = apkconst(…);
Описание:
Аббревиатура APK обозначает комбинированную амплитудно-фазовую манипуляцию (Amplitude- and Phase-Keying).
apkconst(numsig)
Отображает концентрическое сигнальное созвездие. Параметр numsig должен быть вектором положительных целых чисел. Формируемый график содержит length(numsig) окружностей. При этом k-я окружность имеет радиус k и содержит numsig(k) равномерно распределенных точек созвездия. Одна из точек на каждой окружности имеет нулевую фазу.
apkconst(numsig,amp)
То же, что предыдущий вариант синтаксиса, но amp(k) задает радиус k-й окружности. Параметр amp должен быть вектором положительных целых чисел. Длины векторов amp и numsig должны быть одинаковыми.
apkconst(numsig,amp,phs)
То же, что предыдущий вариант синтаксиса, но наличие точки с нулевой фазой на каждой окружности не является обязательным. Вместо этого одна из точек на k-й окружности имеет фазу, равную phs(k). Длины векторов phs, amp и numsig должны быть одинаковыми.
apkconst(numsig,amp,phs,’n’)
То же, что предыдущий вариант синтаксиса, но рядом с точками созвездия отображаются числа, показывающие, каким символам сообщения будут соответствовать эти точки при использовании параметров numsig, amp и phs в функциях модуляции и демодуляции, таких как dmodce/ddemodce или modmap/demodmap.
apkconst(numsig,amp,phs,plotspec)
То же, что apkconst(numsig,amp,phs), но строковый параметр plotspec задает вид выводимых на график точек таким же образом, как это делается в функции plot. Параметр plotspec должен быть двухсимвольной строкой, содержащей по одному символу из первого и третьего столбцов приведенной ниже таблицы.
|
Символ цвета |
Значение |
Символ маркера |
Значение |
|
y |
Желтый |
. |
Точка |
|
m |
Фиолетовый |
o |
Окружность |
|
C |
Голубой |
x |
Крестик |
|
r |
Красный |
+ |
Знак “плюс” |
|
g |
Зеленый |
* |
Звездочка |
|
b |
Синий |
s |
Квадрат |
|
w |
Белый |
d |
Ромб |
|
k |
Черный |
v |
Треугольник вершиной вниз |
|
^ |
Треугольник вершиной вверх |
||
|
< |
Треугольник вершиной влево |
||
|
> |
Треугольник вершиной вправо |
||
|
p |
Пятиконечная звезда |
||
|
h |
Шестиконечная звезда |
y = apkconst(…)
В данном случае график не выводится, вместо этого функция возвращает комплексный вектор y, который содержит координаты точек созвездия. Вещественная часть вектора y соответствует синфазным амплитудам, а мнимая — квадратурным амплитудам.
Примеры.
Приведенная ниже команда формирует график, имеющий три окружности. Первая (внутренняя) окружность имеет радиус 1 и содержит четыре точки, одна из которых имеет нулевую фазу. Вторая (средняя) окружность имеет радиус, равный 4, и содержит пять точек, одна из которых имеет фазу, равную p . Третья (внешняя) окружность имеет радиус, равный 5, и содержит две точки, одна из которых имеет фазу, равную p /4. Полученный график также приведен ниже.
apkconst([4 5 2],[1 4 5],[0 pi pi/4])
Приведенная ниже команда формирует вектор, содержащий координаты точек на комплексной плоскости, соответствующих приведенному выше графику.
y = apkconst([4 5 2],[1 4 5],[0 pi pi/4])
y =
Columns 1 through 4
1.0000 0.0000 + 1.0000i -1.0000 + 0.0000i -0.0000 — 1.0000i
Columns 5 through 8
-4.0000 + 0.0000i -1.2361 — 3.8042i 3.2361 — 2.3511i 3.2361 + 2.3511i
Columns 9 through 11
-1.2361 + 3.8042i 3.5355 + 3.5355i -3.5355 — 3.5355i
Литература
Thomas, C. Melvil, Michaeil Y. Weidner, and S. H. Durrani. «Digital Amplitude-Phase Keying with M-ary Alphabets.» IEEE Transactions on Communications. Vol Com-22, No. 2, Feb. 1974, 168-180.
Наверх
ddemod — цифровая демодуляция (вещественный входной сигнал)
Синтаксис:
z = ddemod(y,Fc,Fd,Fs,’ask/opt’,M,num,den);
z = ddemod(y,Fc,Fd,Fs,’fsk/opt’,M);
z = ddemod(y,Fc,Fd,Fs,’msk’);
z = ddemod(y,Fc,Fd,Fs,’psk/opt’,M,num,den);
z = ddemod(y,Fc,Fd,Fs,’qask/opt’,M,num,den);
z = ddemod(y,Fc,Fd,Fs,’qask/arb/opt’,inphase,quadr,num,den);
z = ddemod(y,Fc,Fd,Fs,’qask/cir/opt’,numsig,amp,phs,num,den);
z = ddemod(y,Fc,Fd,[Fs phase],…);
Необязательные входные параметры:
|
Параметр |
Значение по умолчанию или поведение функции, если параметр опущен |
|
opt |
После демодуляции функция ddemod производит преобразование аналогового сигнала в цифровое сообщение (demapping). Если вид манипуляции — АМн, при демодуляции не используетсяалгоритм Костаса. Если вид манипуляции — ЧМн, применяется когерентная демодуляция. |
|
num, den |
При отсутствии этих параметров функция ddemod не подвергает демодулированный сигнал фильтрации. |
|
amp |
[1:length(numsig)] |
|
phs |
numsig*0 |
Описание:
Функция ddemod выполняет цифровую демодуляцию, используя вещественный входной сигнал с заданной несущей частотой. Соответствующая функция модуляции — dmod. В приведенной ниже таблице перечислены поддерживаемые функцией ddemod виды манипуляции.
|
Вид манипуляции |
Пятый входной параметр |
Возможные значения флага /opt |
|
M-уровневая амплитудная манипуляция (АМн) |
‘ask/opt’ |
/nomap; /costas |
|
M-позиционная частотная манипуляция (ЧМн) |
‘fsk/opt’ |
/noncoherence |
|
Минимальная частотная манипуляция (МЧМ) |
‘msk’ |
|
|
M-позиционная фазовая манипуляция (ФМн) |
‘psk/opt’ |
/nomap |
|
Квадратурная амплитудная манипуляция (КАМн) |
‘qask/opt’, ‘qask/cir/opt’ или ‘qask/arb/opt’ |
/nomap |
Флаг /opt во втором столбце таблицы может быть опущен; остальная часть пятого входного параметра при вызове функции ddemod является обязательной. В третьем столбце перечислены возможные значения для флагов /opt. При использовании нескольких флагов одновременно они могут следовать в любом порядке.
Отключение первичного отображения (только АМн, ФМн и КАМн):
Обычно функция ddemod сначала выполняет аналоговую демодуляцию входного сигнала, а затем осуществляет преобразование аналогового демодулированного сигнала в цифровое сообщение (demapping). Необязательный флаг /nomap, добавляемый к пятому входному параметру (строке, задающей вид манипуляции), отключает указанное преобразование. В этом случае результатом работы функции являются отсчеты аналогового демодулированного сигнала с частотой дискретизации Fs. Для преобразования этого сигнала в цифровое сообщение можно использовать функцию ddemodmap. Флаг /nomap нельзя использовать для частотной (ЧМн) и минимальной частотной (МЧМ) манипуляции (‘fsk’ и ‘msk’).
Размер массива z при использовании флага /nomap зависит от вида манипуляции:
-
АМн. Размеры массивов y и z совпадают. Если y — матрица, каждый ее столбец обрабатывается независимо от других.
-
ФМн и КАМн. Массив z имеет вдвое больше столбцов, чем массив y, а число строк этих двух массивов совпадает. Каждый столбец y обрабатывается независимо. Столбцы z с нечетными номерами представляют синфазные компоненты демодулированного сигнала, а столбцы с четными номерами — его квадратурные компоненты.
Общая информация о синтаксисе:
При всех вариантах вызова функции z = ddemod(y,Fc,Fd,Fs,…) цифровое сообщение z восстанавливается из принятого аналогового сигнала y. После измерения расстояния от принятого сигнала до сигналов, соответствующих всем возможным символам (в соответствии с используемым видом манипуляции) функция выбирает ближайший вариант и возвращает соответствующий символ.
Если y — вектор длины n*Fs/Fd, то декодированное сообщение z будет вектором длины n. Если же y — матрица, имеющая n*Fs/Fd строк и m столбцов, то сообщение z будет матрицей, имеющей n строк и m столбцов; каждый столбец матрицы y в данном случае обрабатывается независимо от других.
Параметр Fc — это несущая частота в герцах. Частоты дискретизации (в герцах) для сигналов y и z равны, соответственно, Fs и Fd. (Таким образом, величина 1/Fd представляет собой период следования символов из сигнала z, а величина 1/Fs — период дискретизации сигнала y.) Отношение Fs/Fd должно быть целым положительным числом. Начальная фаза несущего колебания считается равной нулю.
Можно задать частоту дискретизации в виде двухэлементного вектора: z = ddemod(y,Fc,Fd,[Fs phase],…). В данном случае первый элемент этого вектора (Fs) задает частоту дискретизации, как описано выше. Второй элемент (phase) — это начальная фаза несущего колебания в радианах.
В случае АМн, ФМн и КАМн функция ddemod после выполнения аналоговой демодуляции может использовать фильтр нижних частот для устранения побочных продуктов демодуляции. Чтобы задать параметры фильтра, включите в список входных параметров векторы num и den. Параметры num и den должны быть векторами-строками, содержащими коэффициенты полиномов числителя и знаменателя функции передачи фильтра в порядке убывания степеней. Если параметр num является пустой матрицей, равен нулю или отсутствует, фильтрация не производится.
Конкретные варианты синтаксиса:
-
z = ddemod(y,Fc,Fd,Fs,’ask’,M)
Реализует демодуляцию M-уровневой амплитудной манипуляции (АМн). Элементы z будут лежать в диапазоне [0, M-1].
-
z = ddemod(y,Fc,Fd,Fs,’ask/costas’,M)
То же, что и предыдущий вариант синтаксиса, но для демодуляции используется алгоритм Костаса (алгоритм с фазовой автоподстройкой частоты (ФАПЧ)).
-
z = ddemod(y,Fc,Fd,Fs,’fsk’,M,tone)
Реализует когерентную демодуляцию M-позиционной частотной манипуляции (ЧМн). Необязательный параметр tone задает расстояние между соседними используемыми частотами в модулированном сигнале y. По умолчанию значение tone равно Fd. Элементы z будут лежать в диапазоне [0, M-1].
-
z = ddemod(y,Fc,Fd,Fs,’fsk/noncoherence’,M,tone)
То же, что и предыдущий вариант синтаксиса, но используется некогерентная демодуляция.
-
z = ddemod(y,Fc,Fd,Fs,’msk’)
Реализует демодуляцию минимальной частотной манипуляции (МЧМ). Элементы z будут равны 0 или 1. Расстояние между двумя используемыми для манипуляции частотами равно Fd/2.
-
z = ddemod(y,Fc,Fd,Fs,’psk’,M)
Реализует корреляционную демодуляцию M-позиционной фазовой манипуляции (ФМн). Элементы z будут лежать в диапазоне [0, M-1].
-
z = ddemod(y,Fc,Fd,Fs,’qask’,M)
Реализует демодуляцию M-позиционной квадратурной амплитудной манипуляции с использованием “квадратного” сигнального созвездия. Приведенная ниже таблица показывает максимальные значения синфазной и квадратурной амплитуд точек созвездия для нескольких небольших значений M.
|
M |
Максимальные значения координат точек созвездия |
M |
Максимальные значения координат точек созвездия |
|
2 |
1 |
32 |
5 |
|
4 |
1 |
64 |
7 |
|
8 |
3 (для квадратурной амплитуды — 1) |
128 |
11 |
|
16 |
3 |
256 |
15 |
Примечание. Чтобы узнать, как именно символы передаваемого дискретного сообщения отображаются в точки “квадратного” созвездия, можно вывести соответствующий рисунок с помощью функции qaskenco(M).
-
z = ddemod(y,Fc,Fd,Fs,’qask/arb’,inphase,quadr)
Реализует демодуляцию квадратурной амплитудной манипуляции с использованием произвольного сигнального созвездия, задаваемого с помощью векторов inphase и quadr. Точка созвездия, соответствующая символу сообщения, равному k, имеет синфазную амплитуду, равную inphase(k+1), и квадратурную амплитуду, равную quadr(k+1).
-
z = ddemod(y,Fc,Fd,Fs,’qask/cir’,numsig,amp,phs)
Реализует демодуляцию квадратурной амплитудной манипуляции с использованием “концентрического” сигнального созвездия. Параметры numsig, amp и phs должны быть векторами одинаковой длины. Элементы векторов numsig и amp должны быть положительными числами. Если k — целое число из диапазона [1, length(numsig)], то amp(k) — радиус k-й окружности, numsig(k) — число точек созвездия, лежащих на этой окружности, а phs(k) — фаза первой точки, лежащей на k-й окружности. Все точки, лежащие на одной окружности, распределены на ней равномерно. Если параметр phs не указан, его значение по умолчанию равно numsig*0. Если не указан и параметр amp, его значение по умолчанию равно [1:length(numsig)].
Примечание. Чтобы узнать, как именно символы передаваемого дискретного сообщения отображаются в точки “концентрического” созвездия, можно вывести соответствующий рисунок с помощью функции apkconst(numsig,amp,phs,’n’).
Примеры.
В данном примере генерируется случайное цифровое сообщение, выполняется амплитудная манипуляция с помощью функции dmod и к манипулированному сигналу добавляется шум. Затем зашумленный сигнал демодулируется и вычисляется вероятность ошибки на символ. Функция ddemod демодулирует аналоговый сигнал y и преобразует демодулированный сигнал в цифровое сообщение z.
M = 16; % Используем 16-уровневую манипуляцию
Fc = 10; % Несущая частота 10 Гц
Fd = 1; % Частоты дискретизации сообщения и модулированного
Fs = 50; % сигналов равны 1 Гц и 50 Гц соответственно
x = randint(100,1,M); % Случайное цифровое сообщение
% Сигнал y имеет M-уровневую амплитудную манипуляцию
y = dmod(x,Fc,Fd,Fs,’ask’,M);
% Добавляем нормальный шум
ynoisy = y + .01*randn(Fs/Fd*100,1);
% Демодулируем y, чтобы восстановить сообщение
z = ddemod(ynoisy,Fc,Fd,Fs,’ask’,M);
s = symerr(x,z) % Число ошибочно принятых символов
s =
0
Наверх
ddemodce — цифровая демодуляция (вход — комплексная огибающая)
Синтаксис:
z = ddemodce(y,Fd,Fs,’ask/opt’,M,num,den);
z = ddemodce(y,Fd,Fs,’fsk/opt’,M);
z = ddemodce(y,Fd,Fs,’msk’);
z = ddemodce(y,Fd,Fs,’psk/opt’,M,num,den);
z = ddemodce(y,Fd,Fs,’qask/opt’,M,num,den);
z = ddemodce(y,Fd,Fs,’qask/arb/opt’,inphase,quadr,num,den);
z = ddemodce(y,Fd,Fs,’qask/cir/opt’,numsig,amp,phs,num,den);
z = ddemodce(y,Fd,[Fs phase],…);
Необязательные входные параметры:
|
Параметр |
Значение по умолчанию или поведение функции, если параметр опущен |
|
opt |
После демодуляции функция ddemodce производит преобразование аналогового сигнала в цифровое сообщение (demapping). Если вид манипуляции — АМн, при демодуляции не используется алгоритм Костаса. Если вид манипуляции — ЧМн, применяется когерентнаядемодуляция. |
|
num, den |
При отсутствии этих параметров функция ddemodce не подвергает демодулированный сигнал фильтрации. |
|
amp |
[1:length(numsig)] |
|
phs |
numsig*0 |
Описание:
Функция ddemodce выполняет цифровую демодуляцию, используя входной сигнал в виде комплексной огибающей модулированного сигнала. Соответствующая функция модуляции — dmodce. В приведенной ниже таблице перечислены поддерживаемые функцией ddemodce виды манипуляции.
|
Вид манипуляции |
Четвертый входной параметр |
Возможные значения флага /opt |
|
M-уровневая амплитудная манипуляция (АМн) |
‘ask/opt’ |
/nomap; /costas |
|
M-позиционная частотная манипуляция (ЧМн) |
‘fsk/opt’ |
/noncoherence |
|
Минимальная частотная манипуляция (МЧМ) |
‘msk’ |
|
|
M-позиционная фазовая манипуляция (ФМн) |
‘psk/opt’ |
/nomap |
|
Квадратурная амплитудная манипуляция (КАМн) |
‘qask/opt’, ‘qask/cir/opt’ или ‘qask/arb/opt’ |
/nomap |
Флаг /opt во втором столбце таблицы может быть опущен; остальная часть четвертого входного параметра при вызове функции ddemodce является обязательной. В третьем столбце перечислены возможные значения для флагов /opt. При использовании нескольких флагов одновременно они могут следовать в любом порядке.
Отключение первичного отображения (только АМн, ФМн и КАМн):
Обычно функция ddemodce сначала выполняет аналоговую демодуляцию входного сигнала, а затем осуществляет преобразование аналогового демодулированного сигнала в цифровое сообщение (demapping). Необязательный флаг /nomap, добавляемый к четвертому входному параметру (строке, задающей вид манипуляции), отключает указанное преобразование. В этом случае результатом работы функции являются отсчеты аналогового демодулированного сигнала с частотой дискретизации Fs. Для преобразования этого сигнала в цифровое сообщение можно использовать функцию ddemodmap. Флаг /nomap нельзя использовать для частотной (ЧМн) и минимальной частотной (МЧМ) манипуляции (‘fsk’ и ‘msk’).
Размер массива z при использовании флага /nomap зависит от вида манипуляции:
-
АМн. Размеры массивов y и z совпадают. Если y — матрица, каждый ее столбец обрабатывается независимо от других.
-
ФМн и КАМн. Массив z имеет вдвое больше столбцов, чем массив y, а число строк этих двух массивов совпадает. Каждый столбец y обрабатывается независимо. Столбцы z с нечетными номерами представляют синфазные компоненты демодулированного сигнала, а столбцы с четными номерами — его квадратурные компоненты.
Общая информация о синтаксисе:
При всех вариантах вызова функции z = ddemodce(y,Fd,Fs,…) цифровое сообщение z восстанавливается из принятого аналогового сигнала y. После измерения расстояния от принятого сигнала до сигналов, соответствующих всем возможным символам (в соответствии с используемым видом манипуляции) функция выбирает ближайший вариант и возвращает соответствующий символ.
Параметр y — комплексный массив, а результат z — вещественный целочисленный массив. Если y — вектор длины n*Fs/Fd, то декодированное сообщение z будет вектором длины n. Если же y — матрица, имеющая n*Fs/Fd строк и mстолбцов, то сообщение z будет матрицей, имеющей n строк и m столбцов; каждый столбец матрицы y в данном случае обрабатывается независимо от других.
Частоты дискретизации (в герцах) для сигналов y и z равны, соответственно, Fs и Fd. (Таким образом, величина 1/Fd представляет собой период следования символов из сигнала z, а величина 1/Fs — период дискретизации сигнала y.) Отношение Fs/Fd должно быть целым положительным числом. Начальная фаза несущего колебания считается равной нулю.
Можно задать частоту дискретизации в виде двухэлементного вектора: z = ddemod(y,Fc,Fd,[Fs phase],…). В данном случае первый элемент этого вектора (Fs) задает частоту дискретизации, как описано выше. Второй элемент (phase) — это начальная фаза несущего колебания в радианах.
В случае АМн, ФМн и КАМн функция ddemod после выполнения аналоговой демодуляции может использовать фильтр нижних частот для устранения побочных продуктов демодуляции. Чтобы задать параметры фильтра, включите в список входных параметров векторы num и den. Параметры num и den должны быть векторами-строками, содержащими коэффициенты полиномов числителя и знаменателя функции передачи фильтра в порядке убывания степеней. Если параметр num является пустой матрицей, равен нулю или отсутствует, фильтрация не производится.
Конкретные варианты синтаксиса:
-
z = ddemodce(y,Fd,Fs,’ask’,M)
Реализует демодуляцию M-уровневой амплитудной манипуляции (АМн). Элементы z будут лежать в диапазоне [0, M-1].
-
z = ddemodce(y,Fd,Fs,’ask/costas’,M)
То же, что и предыдущий вариант синтаксиса, но для демодуляции используется алгоритм Костаса (алгоритм с фазовой автоподстройкой частоты (ФАПЧ)).
-
z = ddemodce(y,Fd,Fs,’fsk’,M,tone)
Реализует когерентную демодуляцию M-позиционной частотной манипуляции (ЧМн). Необязательный параметр tone задает расстояние между соседними используемыми частотами в модулированном сигнале y. По умолчанию значение tone равно Fd. Элементы z будут лежать в диапазоне [0, M-1].
-
z = ddemodce(y,Fd,Fs,’fsk/noncoherence’,M,tone)
То же, что и предыдущий вариант синтаксиса, но используется некогерентная демодуляция.
-
z = ddemodce(y,Fd,Fs,’msk’)
Реализует демодуляцию минимальной частотной манипуляции (МЧМ). Элементы z будут равны 0 или 1. Расстояние между двумя используемыми для манипуляции частотами равно Fd/2.
-
z = ddemodce(y,Fd,Fs,’psk’,M)
Реализует корреляционную демодуляцию M-позиционной фазовой манипуляции (ФМн). Элементы z будут лежать в диапазоне [0, M-1].
-
z = ddemodce(y,Fd,Fs,’qask’,M)
Реализует демодуляцию M-позиционной квадратурной амплитудной манипуляции с использованием “квадратного” сигнального созвездия. Приведенная ниже таблица показывает максимальные значения синфазной и квадратурной амплитуд точек созвездия для нескольких небольших значений M.
|
M |
Максимальные значения координат точек созвездия |
M |
Максимальные значения координат точек созвездия |
|
2 |
1 |
32 |
5 |
|
4 |
1 |
64 |
7 |
|
8 |
3 (для квадратурной амплитуды — 1) |
128 |
11 |
|
16 |
3 |
256 |
15 |
Примечание. Чтобы узнать, как именно символы передаваемого дискретного сообщения отображаются в точки “квадратного” созвездия, можно вывести соответствующий рисунок с помощью функции qaskenco(M).
-
z = ddemodce(y,Fd,Fs,’qask/arb’,inphase,quadr)
Реализует демодуляцию квадратурной амплитудной манипуляции с использованием произвольного сигнального созвездия, задаваемого с помощью векторов inphase и quadr. Точка созвездия, соответствующая символу сообщения, равному k, имеет синфазную амплитуду, равную inphase(k+1), и квадратурную амплитуду, равную quadr(k+1).
-
z = ddemodce(y,Fd,Fs,’qask/cir’,numsig,amp,phs)
Реализует демодуляцию квадратурной амплитудной манипуляции с использованием “концентрического” сигнального созвездия. Параметры numsig, amp и phs должны быть векторами одинаковой длины. Элементы векторов numsig и amp должны быть положительными числами. Если k — целое число из диапазона [1, length(numsig)], то amp(k) — радиус k-й окружности, numsig(k) — число точек созвездия, лежащих на этой окружности, а phs(k) — фаза первой точки, лежащей на k-й окружности. Все точки, лежащие на одной окружности, распределены на ней равномерно. Если параметр phs не указан, его значение по умолчанию равно numsig*0. Если не указан и параметр amp, его значение по умолчанию равно [1:length(numsig)].
Примечание. Чтобы узнать, как именно символы передаваемого дискретного сообщения отображаются в точки “концентрического” созвездия, можно вывести соответствующий рисунок с помощью функции apkconst(numsig,amp,phs,’n’).
Наверх
demodmap — преобразование аналогового демодулированного сигнала в цифровой сигнал
Синтаксис:
z = demodmap(x,Fd,Fs,’ask’,M);
z = demodmap(x,Fd,Fs,’fsk’,M,tone);
z = demodmap(x,Fd,Fs,’msk’);
z = demodmap(x,Fd,Fs,’psk’,M);
z = demodmap(x,Fd,Fs,’qask’,M);
z = demodmap(x,Fd,Fs,’qask/arb’,inphase,quadr);
z = demodmap(x,Fd,Fs,’qask/cir’,numsig,amp,phs);
z = demodmap(x,[Fd offset],Fs,…)
Необязательные входные параметры:
|
Параметр |
Значение по умолчанию |
|
tone |
Fd |
|
amp |
[1:length(numsig)] |
|
phs |
numsig*0 |
Описание:
Процесс цифровой демодуляции включает в себя два шага: демодуляцию аналогового сигнала и преобразование аналогового демодулированного сигнала в цифровое сообщение. Первый из перечисленных шагов можно реализовать с помощью функций ademod, ademodce, или «самодельной» функции модуляции. Функция demodmap выполняет второй шаг. В приведенной ниже таблице перечислены поддерживаемые функцией demodmap виды манипуляции.
|
Вид манипуляции |
Значение четвертого входного параметра |
|
M-уровневая амплитудная манипуляция (АМн) |
‘ask’ |
|
M-позиционная частотная манипуляция (ЧМн) |
‘fsk’ |
|
Минимальная частотная манипуляция (МЧМ) |
‘msk’ |
|
M-позиционная фазовая манипуляция (ФМн) |
‘psk’ |
|
Квадратурная амплитудная манипуляция (КАМн) |
‘qask’, ‘qask/cir’ или ‘qask/arb’ |
Преобразование аналогового сигнала в цифровой — общая информация:
Функция demodmap вызывается следующим образом:
z = demodmap(x,Fd,Fs,…)
При этом производится восстановление цифрового сообщения z из аналогового сигнала x. После измерения расстояния от значений входного сигнала до всех точек используемого созвездия функция выбирает символ, соответствующий ближайшей точке.
Размеры параметров x и z зависят от используемого метода манипуляции: АМн, ЧМн, МЧМ. Если x — вектор длины n*Fs/Fd, то z будет вектором-столбцом длины n. Если x — матрица, содержащая (n*Fs/Fd) строк и m столбцов, то каждый столбец x обрабатывается независимо от других и z будет матрицей, имеющей n строк и m столбцов. ФМн, КАМн. Матрица x должна иметь четное число столбцов. Столбцы x с нечетными номерами представляют амплитуды синфазных составляющих, а столбцы с четными номерами — амплитуды квадратурных составляющих. Каждая пара столбцов x обрабатывается независимо от других. Если x — матрица, содержащая (n*Fs/Fd) строк и 2m столбцов, то z будет матрицей, имеющей n строк и m столбцов.
Частоты дискретизации (в герцах) для сигналов x и z равны, соответственно, Fs и Fd. (Таким образом, величина 1/Fd представляет собой период следования символов из сигнала z, а величина 1/Fs — период дискретизации сигнала x.) Отношение Fs/Fd должно быть положительным целым числом. Расстояние между соседними точками принятия решения о переданных символах равно 1/Fd.
Чтобы сдвинуть точки принятия решения вперед на целое число отсчетов offset, вместо числа Fd задается двухэлементный вектор:
z = demodmap(x,[Fd offset],…)
Такая модификация может использоваться для всех перечисленных далее вариантов синтаксиса. По умолчанию offset = 0.
Преобразование аналогового сигнала в цифровой — конкретные варианты синтаксиса:
-
z = demodmap(x,Fd,Fs,’ask’,M)
Преобразует сигнал, используя созвездие M-уровневой амплитудной манипуляции (АМн). Элементы z будут лежать в диапазоне [0, M-1].
-
z = demodmap(x,Fd,Fs,’fsk’,M,tone)
Преобразует частотный сдвиг (относительно несущей), соответствующий M-позиционной частотной манипуляции (ЧМн), в символы цифрового сообщения. Необязательный параметр tone задает расстояние между соседними используемыми частотами манипуляции. По умолчанию значение tone равно Fd. Элементы z будут лежать в диапазоне [0, M-1].
-
z = demodmap(x,Fd,Fs,’msk’)
Преобразует частотный сдвиг (относительно несущей), соответствующий минимальной частотной манипуляции (МЧМ), в символы цифрового сообщения. Это частный случай ЧМн, когда расстояние между двумя используемыми частотами составляет Fd/2. Элементы z будут равны 0 или 1.
-
z = demodmap(x,Fd,Fs,’psk’,M)
Преобразует сигнал, используя созвездие M-позиционной фазовой манипуляции (ФМн). Элементы z будут лежать в диапазоне [0, M-1].
-
z = demodmap(x,Fd,Fs,’qask’,M)
Преобразует сигнал, используя «квадратное» созвездие M-позиционной квадратурной манипуляции (КАМн). Элементы z будут лежать в диапазоне [0, M-1]. Приведенная ниже таблица показывает максимальные значения координат точек созвездия для нескольких небольших значений M.
|
М |
Максимальное значение координат точек созвездия |
М |
Максимальное значение координат точек созвездия |
|
2 |
1 |
32 |
5 |
|
4 |
1 |
64 |
7 |
|
8 |
Синфазная амплитуда — 3, квадратурная амплитуда — 1 |
128 |
11 |
|
16 |
3 |
256 |
15 |
Примечание. Чтобы узнать, как именно символы передаваемого дискретного сообщения отображаются в точки «квадратного» созвездия, можно вывести соответствующий рисунок с помощью функции qaskenco(M) или modmap(‘qask’,M).
-
z = demodmap(x,Fd,Fs,’qask/arb’,inphase,quadr)
Преобразует сигнал, используя произвольное созвездие квадратурной манипуляции (КАМн), задаваемое с помощью векторов inphase и quadr. Точка созвездия, соответствующая символу сообщения, равному k, имеет синфазную амплитуду, равную inphase(k+1), и квадратурную амплитуду, равную quadr(k+1).
-
z = demodmap(x,Fd,Fs,’qask/cir’,numsig,amp,phs)
Преобразует сигнал, используя «концентрическое» созвездие квадратурной манипуляции (КАМн). Параметры numsig, amp и phs должны быть векторами одинаковой длины. Элементы векторов numsig и amp должны быть положительными числами. Если k — целое число из диапазона [1, length(numsig)], то amp(k) — радиус k-й окружности, numsig(k) — число точек созвездия, лежащих на этой окружности, а phs(k) — фаза первой точки, лежащей на k-й окружности. Все точки, лежащие на одной окружности, распределены на ней равномерно. Если параметр phs не указан, его значение по умолчанию равно numsig*0. Если не указан и параметр amp, его значение по умолчанию равно [1:length(numsig)].
Примечание. Чтобы узнать, как именно символы передаваемого дискретного сообщения отображаются в точки «концентрического» созвездия, можно вывести соответствующий рисунок с помощью функции apkconst(numsig,amp,phs,’n’).
Примеры.
Приведенный ниже сценарий показывает, какие области на плоскости в координатах (синфазная амплитуда — квадратурная амплитуда) соответствуют разным символам цифрового сообщения при использовании 4-позиционной ФМн. Для этого формируются случайно расположенные на плоскости точки, с помощью функции demodmap они преобразуются в символы сообщения. Далее точки, отображенные функцией в символ 0, выводятся на график красным цветом, а в символ 2 — синим. Горизонтальная ось соответствует синфазной амплитуде, вертикальная — квадратурной.
|
x = 4*(rand(1000,2)-1/2); |
% Создаем случайные координаты точек |
|
y = demodmap(x,1,1,’psk’,4); |
% Преобразуем в цифровое сообщение, используя ФМн-4 |
|
red = find(y==0); |
% Индексы точек, давших символ 0 |
|
h = scatterplot(x(red,:),1,0,’r.’); hold on |
% Выводим красным цветом |
|
blue = find(y==2); |
% Индексы точек, давших символ 2 |
|
scatterplot(x(blue,:),1,0,’b.’,h); hold off |
% Выводим синим цветом |
Наверх
dmod — цифровая модуляция (вещественный выходной сигнал)
Синтаксис:
y = dmod(x,Fc,Fd,Fs,’method/nomap’…);
y = dmod(x,Fc,Fd,Fs,’ask’,M);
y = dmod(x,Fc,Fd,Fs,’fsk’,M,tone);
y = dmod(x,Fc,Fd,Fs,’msk’);
y = dmod(x,Fc,Fd,Fs,’psk’,M);
y = dmod(x,Fc,Fd,Fs,’qask’,M);
y = dmod(x,Fc,Fd,Fs,’qask/arb’,inphase,quadr);
y = dmod(x,Fc,Fd,Fs,’qask/cir’,numsig,amp,phs);
y = dmod(x,Fc,Fd,[Fs phase],…);
[y,t] = dmod(…);
Необязательные входные параметры:
|
Параметр |
Значение по умолчанию |
|
tone |
Fd |
|
amp |
[1:length(numsig)] |
|
phs |
numsig*0 |
Описание:
Функция dmod выполняет цифровую модуляцию (манипуляцию), генерируя вещественный выходной сигнал с заданной несущей частотой. Соответствующая функция демодуляции — ddemod. В приведенной ниже таблице перечислены поддерживаемые функцией dmod виды манипуляции.
|
Вид манипуляции |
Пятый входной параметр |
|
M-уровневая амплитудная манипуляция (АМн) |
‘ask’ |
|
M-позиционная частотная манипуляция (ЧМн) |
‘fsk’ |
|
Минимальная частотная манипуляция (МЧМ) |
‘msk’ |
|
M-позиционная фазовая манипуляция (ФМн) |
‘psk’ |
|
Квадратурная амплитудная манипуляция (КАМн) |
‘qask’, ‘qask/cir’ или ‘qask/arb’ |
Отключение первичного отображения:
Обычно функция dmod сначала выполняет отображение (mapping) цифрового сигнала в аналоговый модулирующий сигнал, а затем осуществляет аналоговую модуляцию. Приведенный ниже обобщенный синтаксис
y = dmod(x,Fc,Fd,Fs,’method/nomap’…)
использует флаг /nomap, чтобы сообщить функции dmod о том, что цифровой сигнал уже преобразован в аналоговый сигнал x, имеющий частоту дискретизации Fs. При таком способе вызова функция dmod не будет выполнять указанное отображение. Для преобразования цифрового сигнала в аналоговый можно использовать функцию modmap. В этом обобщенном синтаксисе параметр method — одно из семи возможных строковых значений, перечисленных в приведенной выше таблице. Смысл остальных параметров объясняется в следующем разделе.
Общая информация о синтаксисе:
При всех вариантах вызова функции y = dmod(x,Fc,Fd,Fs,…) в качестве передаваемого цифрового сообщения используется массив x, который должен представлять собой матрицу, состоящую из неотрицательных целых чисел. Если x — вектор длины n, то модулированный сигнал y будет вектором длины n*Fs/Fd. Если же x — матрица, имеющая n строк и m столбцов, то y будет матрицей, имеющей (n*Fs/Fd) строк и m столбцов; каждый столбец матрицы x в данном случае обрабатывается независимо от других.
Параметр Fc — это несущая частота в герцах. Частоты дискретизации (в герцах) для сигналов x и y равны, соответственно, Fd и Fs. (Таким образом, величина 1/Fd представляет собой период следования символов из сигнала x, а величина 1/Fs — период дискретизации сигнала y.) Отношение Fs/Fd должно быть целым положительным числом. Для получения лучших результатов частотные параметры должны соотноситься друг с другом следующим образом: Fs > Fc > Fd. Начальная фаза несущего колебания считается равной нулю.
Можно задать частоту дискретизации в виде двухэлементного вектора: y = dmod(x,Fc,Fd,[Fs phase],…). В данном случае первый элемент этого вектора (Fs) задает частоту дискретизации, как описано выше. Второй элемент (phase) — это начальная фаза несущего колебания в радианах.
Конкретные варианты синтаксиса:
y = dmod(x,Fc,Fd,Fs,’ask’,M)
Реализует M-уровневую амплитудную манипуляцию (АМн). Элементы x должны лежать в диапазоне [0, M-1]. Максимальное значение модулированного сигнала равно 1.
y = dmod(x,Fc,Fd,Fs,’fsk’,M,tone)
Реализует M-позиционную частотную манипуляцию (ЧМн). Элементы x должны лежать в диапазоне [0, M-1]. Необязательный параметр tone задает расстояние между соседними используемыми частотами в модулированном сигнале y. По умолчанию значение tone равно Fd. Максимальное значение y равно 1.
y = dmod(x,Fc,Fd,Fs,’msk’)
Реализует минимальную частотную манипуляцию (МЧМ). Элементы x должны быть равны 0 или 1. Максимальное значение y равно 1. Расстояние между двумя используемыми частотами равно Fd/2.
y = dmod(x,Fc,Fd,Fs,’psk’,M)
Реализует M-позиционную фазовую манипуляцию (ФМн). Элементы x должны лежать в диапазоне [0, M-1]. Максимальное значение y равно 1.
y = dmod(x,Fc,Fd,Fs,’qask’,M)
Реализует M-позиционную квадратурную амплитудную манипуляцию с использованием “квадратного” сигнального созвездия. Приведенная ниже таблица показывает максимальные значения y для нескольких небольших значений M.
|
M |
Максимальное значение y |
M |
Максимальное значение y |
|
2 |
1 |
32 |
5 |
|
4 |
1 |
64 |
7 |
|
8 |
3 |
128 |
11 |
|
16 |
3 |
256 |
15 |
Примечание. Чтобы узнать, как именно символы передаваемого дискретного сообщения отображаются в точки “квадратного” созвездия, можно вывести соответствующий рисунок с помощью функции qaskenco(M).
y = dmod(x,Fc,Fd,Fs,’qask/arb’,inphase,quadr)
Реализует квадратурную амплитудную манипуляцию с использованием произвольного сигнального созвездия, задаваемого с помощью векторов inphase и quadr. Точка созвездия, соответствующая символу сообщения, равному k, имеет синфазную амплитуду, равную inphase(k+1), и квадратурную амплитуду, равную quadr(k+1).
y = dmod(x,Fc,Fd,Fs,’qask/cir’,numsig,amp,phs)
Реализует квадратурную амплитудную манипуляцию с использованием “концентрического” сигнального созвездия. Параметры numsig, amp и phs должны быть векторами одинаковой длины. Элементы векторов numsig и amp должны быть положительными числами. Если k — целое число из диапазона [1, length(numsig)], то amp(k) — радиус k-й окружности, numsig(k) — число точек созвездия, лежащих на этой окружности, а phs(k) — фаза первой точки, лежащей на k-й окружности. Все точки, лежащие на одной окружности, распределены на ней равномерно. Если параметр phs не указан, его значение по умолчанию равно numsig*0. Если не указан и параметр amp, его значение по умолчанию равно [1:length(numsig)].
Примечание. Чтобы узнать, как именно символы передаваемого дискретного сообщения отображаются в точки “концентрического” созвездия, можно вывести соответствующий рисунок с помощью функции apkconst(numsig,amp,phs,’n’).
[y,t] = dmod(…)
Дополнительно возвращает вектор значений времени t, использованных при вычислениях. Длина этого вектора равна числу строк в модулированном сигнале y.
Примеры.
Приведенный ниже код показывает график сигнала, реализующего передачу символов 0 и 1 с помощью 4-уровневой АМн. Обратите внимание на то, что при вызове функции dmod использованы два выходных параметра. Второй выходной параметр t используется для оцифровки горизонтальной оси графика в значениях времени.
Fc = 20; Fd = 10; Fs = 50;
M = 4; % 4-уровневая АМн
x = ones(Fd,1)*[0 1]; x=x(:);
% Модуляция с возвратом вектора значений времени
[y,t] = dmod(x,Fc,Fd,Fs,’ask’,M);
plot(t,y) % График зависимости сигнала от времени
Наверх
dmodce — цифровая модуляция (выход — комплексная огибающая)
Синтаксис:
y = dmodce(x,Fd,Fs,’method/nomap’…);
y = dmodce(x,Fd,Fs,’ask’,M);
y = dmodce(x,Fd,Fs,’fsk’,M,tone);
y = dmodce(x,Fd,Fs,’msk’);
y = dmodce(x,Fd,Fs,’psk’,M);
y = dmodce(x,Fd,Fs,’qask’,M);
y = dmodce(x,Fd,Fs,’qask/arb’,inphase,quadr);
y = dmodce(x,Fd,Fs,’qask/cir’,numsig,amp,phs);
y = dmodce(x,Fd,[Fs phase],…);
Необязательные входные параметры:
|
Параметр |
Значение по умолчанию |
|
tone |
Fd |
|
amp |
[1:length(numsig)] |
|
phs |
numsig*0 |
Описание:
Функция dmodce выполняет цифровую модуляцию (манипуляцию), генерируя комплексную огибающую выходного модулированного сигнала. Соответствующая функция демодуляции — ddemodce. В приведенной ниже таблице перечислены поддерживаемые функцией dmodce виды модуляции.
|
Вид манипуляции |
Четвертый входной параметр |
|
M-уровневая амплитудная манипуляция (АМн) |
‘ask’ |
|
M-позиционная частотная манипуляция (ЧМн) |
‘fsk’ |
|
Минимальная частотная манипуляция (МЧМ) |
‘msk’ |
|
M-позиционная фазовая манипуляция (ФМн) |
‘psk’ |
|
Квадратурная амплитудная манипуляция (КАМн) |
‘qask’, ‘qask/cir’ или ‘qask/arb’ |
Отключение первичного отображения:
Обычно функция dmodce сначала выполняет отображение (mapping) цифрового сигнала в аналоговый модулирующий сигнал, а затем осуществляет аналоговую модуляцию. Приведенный ниже обобщенный синтаксис
y = dmodce(x,Fd,Fs,’method/nomap’…)
использует флаг /nomap, чтобы сообщить функции dmodce о том, что цифровой сигнал уже преобразован в аналоговый сигнал x, имеющий частоту дискретизации Fs. При таком способе вызова функция dmodce не будет выполнять указанное отображение. Для преобразования цифрового сигнала в аналоговый можно использовать функцию modmap. В этом обобщенном синтаксисе параметр method — одно из семи возможных строковых значений, перечисленных в приведенной выше таблице. Смысл остальных параметров объясняется в следующем разделе.
Общая информация о синтаксисе:
При всех вариантах вызова функции y = dmodce(x,Fd,Fs,…) в качестве передаваемого цифрового сообщения используется массив x, который должен представлять собой матрицу, состоящую из неотрицательных целых чисел. Если x — вектор длины n, то модулированный сигнал y будет вектором длины n*Fs/Fd. Если же x — матрица, имеющая n строк и m столбцов, то y будет матрицей, имеющей (n*Fs/Fd) строк и m столбцов; каждый столбец матрицы x в данном случае обрабатывается независимо от других. Поскольку функция demodce генерирует комплексную огибающую модулированного сигнала, элементы массива y являются комплексными числами.
Частоты дискретизации (в герцах) для сигналов x и y равны, соответственно, Fd и Fs. (Таким образом, величина 1/Fd представляет собой период следования символов из сигнала x, а величина 1/Fs — период дискретизации сигнала y.) Отношение Fs/Fd должно быть целым положительным числом. Начальная фаза несущего колебания считается равной нулю.
Можно задать частоту дискретизации в виде двухэлементного вектора: y = dmodce(x,Fd,[Fs phase],…). В данном случае первый элемент этого вектора (Fs) задает частоту дискретизации, как описано выше. Второй элемент (phase) — это начальная фаза несущего колебания в радианах.
Конкретные варианты синтаксиса:
-
y = dmodce(x,Fd,Fs,’ask’,M)
Реализует M-уровневую амплитудную манипуляцию (АМн). Элементы x должны лежать в диапазоне [0, M-1]. Максимальное значение модулированного сигнала равно 1.
-
y = dmodce(x,Fd,Fs,’fsk’,M,tone)
Реализует M-позиционную частотную манипуляцию (ЧМн). Элементы x должны лежать в диапазоне [0, M-1]. Необязательный параметр tone задает расстояние между соседними используемыми частотами в модулированном сигнале y. По умолчанию значение tone равно Fd. Максимальное значение y равно 1.
-
y = dmodce(x,Fd,Fs,’msk’)
Реализует минимальную частотную манипуляцию (МЧМ). Элементы x должны быть равны 0 или 1. Максимальное значение y равно 1. Расстояние между двумя используемыми частотами равно Fd/2.
-
y = dmodce(x,Fd,Fs,’psk’,M)
Реализует M-позиционную фазовую манипуляцию (ФМн). Элементы x должны лежать в диапазоне [0, M-1]. Максимальное значение y равно 1.
-
y = dmodce(x,Fd,Fs,’qask’,M)
Реализует M-позиционную квадратурную амплитудную манипуляцию с использованием “квадратного” сигнального созвездия. Приведенная ниже таблица показывает максимальные значения y для нескольких небольших значений M.
|
M |
Максимальное значение y |
M |
Максимальное значение y |
|
2 |
1 |
32 |
5 |
|
4 |
1 |
64 |
7 |
|
8 |
3 |
128 |
11 |
|
16 |
3 |
256 |
15 |
Примечание. Чтобы узнать, как именно символы передаваемого дискретного сообщения отображаются в точки “квадратного” созвездия, можно вывести соответствующий рисунок с помощью функции qaskenco(M).
-
y = dmodce(x,Fd,Fs,’qask/arb’,inphase,quadr)
Реализует квадратурную амплитудную манипуляцию с использованием произвольного сигнального созвездия, задаваемого с помощью векторов inphase и quadr. Точка созвездия, соответствующая символу сообщения, равному k, имеет синфазную амплитуду, равную inphase(k+1), и квадратурную амплитуду, равную quadr(k+1).
-
y = dmodce(x,Fd,Fs,’qask/cir’,numsig,amp,phs)
Реализует квадратурную амплитудную манипуляцию с использованием “концентрического” сигнального созвездия. Параметры numsig, amp и phs должны быть векторами одинаковой длины. Элементы векторов numsig и amp должны быть положительными числами. Если k — целое число из диапазона [1, length(numsig)], то amp(k) — радиус k-й окружности, numsig(k) — число точек созвездия, лежащих на этой окружности, а phs(k) — фаза первой точки, лежащей на k-й окружности. Все точки, лежащие на одной окружности, распределены на ней равномерно. Если параметр phs не указан, его значение по умолчанию равно numsig*0. Если не указан и параметр amp, его значение по умолчанию равно [1:length(numsig)].
Примечание. Чтобы узнать, как именно символы передаваемого дискретного сообщения отображаются в точки “концентрического” созвездия, можно вывести соответствующий рисунок с помощью функции
apkconst(numsig,amp,phs,’n’).
Примеры.
В этом примере реализуется ЧМн с разным расстоянием между соседними частотами (параметр tone). Результаты показывают, что вероятность ошибки приема символов зависит от значения tone. Результаты, полученные вами, могут отличаться от приведенных, поскольку в примере используются случайные числа.
M = 4; Fd = 1; Fs = 32;
SNRperBit = 5;
adjSNR = SNRperBit-10*log10(Fs/Fd)+10*log10(log2(M));
x = randint(5000,1,M); % Исходное сообщение
% Реализуем ЧМн с ортогональными символами (МЧМ)
tone = .5;
% Начальное состояние генератора нормальных случайных чисел
randn(‘state’,1945724);
w1 = dmodce(x,Fd,Fs,’fsk’,M,tone);
y1 = awgn(w1, adjSNR, ‘measured’, [], ‘dB’);
z1 = ddemodce(y1,Fd,Fs,’fsk’,M,tone);
ser1 = symerr(x,z1)
ser1 =
67
% Реализуем ЧМн с неортогональными символами
tone = .25;
% Восстанавливаем прежнее состояние генератора случайных чисел
randn(‘state’,1945724);
w2 = dmodce(x,Fd,Fs,’fsk’,M,tone);
y2 = awgn(w2, adjSNR, ‘measured’, [], ‘dB’);
z2 = ddemodce(y2,Fd,Fs,’fsk’,M,tone);
ser2 = symerr(x,z2)
ser2 =
258
Наверх
modmap — преобразование цифрового сигнала в аналоговые параметры модуляции
Синтаксис:
modmap(‘method’,…);
y = modmap(x,Fd,Fs,’ask’,M);
y = modmap(x,Fd,Fs,’fsk’,M,tone);
y = modmap(x,Fd,Fs,’msk’);
y = modmap(x,Fd,Fs,’psk’,M);
y = modmap(x,Fd,Fs,’qask’,M);
y = modmap(x,Fd,Fs,’qask/arb’,inphase,quadr);
y = modmap(x,Fd,Fs,’qask/cir’,numsig,amp,phs);
Необязательные входные параметры:
|
Параметр |
Значение по умолчанию |
|
tone |
Fd |
|
amp |
[1:length(numsig)] |
|
phs |
numsig*0 |
Описание:
Процесс цифровой модуляции (манипуляции) включает в себя два шага: преобразование цифрового сигнала в аналоговые параметры модуляции и выполнение аналоговой модуляции с использованием этих параметров. Функция modmap выполняет первый из перечисленных шагов. Второй шаг можно реализовать с помощью функций amod, amodce, или «самодельной» функции модуляции. В приведенной ниже таблице перечислены поддерживаемые функцией modmap виды манипуляции.
|
Вид манипуляции |
Значение параметра ‘method’ |
|
M-уровневая амплитудная манипуляция (АМн) |
‘ask’ |
|
M-позиционная частотная манипуляция (ЧМн) |
‘fsk’ |
|
Минимальная частотная манипуляция (МЧМ) |
‘msk’ |
|
M-позиционная фазовая манипуляция (ФМн) |
‘psk’ |
|
Квадратурная амплитудная манипуляция (КАМн) |
‘qask’, ‘qask/cir’ или ‘qask/arb’ |
Отображение сигнального созвездия:
modmap( ‘method’ ,…)
Выводит график, характеризующий метод M-ичной манипуляции, указанный параметром ‘method’. Параметр ‘method’ — одна из строк, перечисленных в правом столбце приведенной выше таблицы. Если ‘method’ = ‘fsk’ или ‘msk’, выводится график спектра частотно-манипулированного сигнала; в остальных случаях демонстрируется сигнальное созвездие (амплитуды и фазы, соответствующие символам цифрового сигнала).
В большинстве случаев параметры, следующие после параметра ‘method’в этом варианте синтаксиса те же, что и при осуществлении преобразования цифрового сигнала в аналоговый. Подробно эти параметры описаны ниже, в разделе «Преобразование цифрового сигнала в аналоговый — конкретные варианты синтаксиса».
Исключение составляет случай минимальной частотной манипуляции (‘method’ = ‘msk’), при этом синтаксис для вывода графика должен быть следующим:
modmap(‘msk’,Fd)
Здесь Fd — тактовая частота (символьная скорость) входного цифрового сообщения.
Преобразование цифрового сигнала в аналоговый — общая информация:
Функция modmap вызывается следующим образом:
y = modmap(x,Fd,Fs,…)
При этом производится преобразование цифрового сообщения x в аналоговый сигнал. Параметр x — матрица неотрицательных целых чисел. Размеры матриц x и y зависят от метода манипуляции:
АМн, ЧМн, МЧМ. Если x — вектор длины n, то y будет вектором-столбцом длины n*Fs/Fd. Если x — матрица, содержащая n строк и m столбцов, то каждый столбец x обрабатывается независимо от других и y будет матрицей, имеющей (n*Fs/Fd) строк и m столбцов.
ФМн, КАМн. Если x — вектор длины n, то y будет матрицей, имеющей (n*Fs/Fd) строк и 2 столбца. Если x — матрица, содержащая n строк и mстолбцов, то каждый столбец x обрабатывается независимо от других и y будет матрицей, имеющей (n*Fs/Fd) строк и 2m столбцов. Столбцы y с нечетными номерами представляют амплитуды синфазных составляющих, а столбцы с четными номерами — амплитуды квадратурных составляющих.
Частоты дискретизации (в герцах) для сигналов x и y равны, соответственно, Fd и Fs. (Таким образом, величина 1/Fd представляет собой период следования символов из сигнала x, а величина 1/Fs — период дискретизации сигнала y.) Отношение Fs/Fd должно быть положительным целым числом.
Преобразование цифрового сигнала в аналоговый — конкретные варианты синтаксиса:
-
y = modmap(x,Fd,Fs,’ask’,M)
Преобразует сигнал, используя созвездие M-уровневой амплитудной манипуляции (АМн). Элементы x должны лежать в диапазоне [0, M-1]. Значения элементов y лежат в диапазоне [-1, 1].
-
y = modmap(x,Fd,Fs,’fsk’,M,tone)
Преобразует сигнал в набор частотных сдвигов (относительно несущей) для реализации M-позиционной частотной манипуляции (ЧМн). Элементы x должны лежать в диапазоне [0, M-1]. Необязательный параметр tone задает расстояние между соседними используемыми частотами манипуляции. По умолчанию значение tone равно Fd.
-
y = modmap(x,Fd,Fs,’msk’)
Преобразует сигнал в набор частотных сдвигов (относительно несущей) для реализации минимальной частотной манипуляции (МЧМ). Элементы x должны быть равны 0 или 1. Расстояние между двумя используемыми частотами в данном случае равно Fd/2.
-
y = modmap(x,Fd,Fs,’psk’,M)
Преобразует сигнал, используя созвездие M-позиционной фазовой манипуляции (ФМн). Элементы x должны лежать в диапазоне [0, M-1].
-
y = modmap(x,Fd,Fs,’qask’,M)
Преобразует сигнал, используя «квадратное» созвездие M-позиционной квадратурной манипуляции (КАМн). Элементы x должны лежать в диапазоне [0, M-1]. Приведенная ниже таблица показывает максимальные значения синфазной и квадратурной амплитуд для нескольких небольших значений M.
|
М |
Максимальное значение y |
М |
Максимальное значение y |
|
2 |
1 |
32 |
5 |
|
4 |
1 |
64 |
7 |
|
8 |
128 |
Синфазная амплитуда — 3, квадратурная амплитуда — 1 |
11 |
|
16 |
3 |
256 |
15 |
Примечание. Чтобы узнать, как именно символы передаваемого дискретного сообщения отображаются в точки «квадратного» созвездия, можно вывести соответствующий рисунок с помощью функции qaskenco(M) или modmap(‘qask’,M).
-
y = modmap(x,Fd,Fs,’qask/arb’,inphase,quadr)
Преобразует сигнал, используя произвольное созвездие квадратурной манипуляции (КАМн), задаваемое с помощью векторов inphase и quadr. Точка созвездия, соответствующая символу сообщения, равному k, имеет синфазную амплитуду, равную inphase(k+1), и квадратурную амплитуду, равную quadr(k+1).
-
y = modmap(x,Fd,Fs,’qask/cir’,numsig,amp,phs)
Преобразует сигнал, используя «концентрическое» созвездие квадратурной манипуляции (КАМн). Параметры numsig, amp и phs должны быть векторами одинаковой длины. Элементы векторов numsig и amp должны быть положительными числами. Если k — целое число из диапазона [1, length(numsig)], то amp(k) — радиус k-й окружности, numsig(k) — число точек созвездия, лежащих на этой окружности, а phs(k) — фаза первой точки, лежащей на k-й окружности. Все точки, лежащие на одной окружности, распределены на ней равномерно. Если параметр phs не указан, его значение по умолчанию равно numsig*0. Если не указан и параметр amp, его значение по умолчанию равно [1:length(numsig)].
Примечание. Чтобы узнать, как именно символы передаваемого дискретного сообщения отображаются в точки «концентрического» созвездия, можно вывести соответствующий рисунок с помощью функции apkconst(numsig,amp,phs,’n’).
Примеры.
Приведенная ниже команда выводит график сигнального созвездия 32-позиционной фазовой манипуляции (ФМн).
modmap(‘psk’,32);
Приведенный ниже сценарий преобразует цифровое сообщение в аналоговые параметры модуляции для случая 32-позиционной ФМн. Затем к аналоговому сигналу добавляется шум, производится обратное преобразование аналогового сигнала в цифровое сообщение и вычисляется число ошибок. В данном примере используются случайные числа, поэтому от запуска к запуску результаты могут меняться.
|
M = 32; Fd = 1; Fs = 3; |
|
|
x = randint(100,1,M); |
% Исходное сообщение |
|
y = modmap(x,Fd,Fs,’psk’,M); |
% Преобразование для ФМн-32 |
|
ynoisy = y+.1*rand(100*Fs,2); |
% Добавляем шум |
|
z = demodmap(ynoisy,Fd,Fs,’psk’,M); |
% Обратное преобразование |
|
s = symerr(x,z) |
% Число ошибок после обратного преобразования |
|
s = |
8 |
Наверх
qaskdeco — преобразование аналогового демодулированного сигнала в цифровое сообщение с использованием квадратного созвездия для квадратурной манипуляции
Синтаксис:
msg = qaskdeco(inphase,quadr,M);
msg = qaskdeco(inphase,quadr,M,minmax);
Описание:
msg = qaskdeco(inphase,quadr,M)
Получает сообщение msg из набора координат точек M-позиционной квадратурной манипуляции (QASK), представленных во входных векторах inphase и quadr. Вектор inphase должен содержать синфазные амплитуды, а вектор quadr — квадратурные амплитуды. Параметр M должен быть степенью числа 2. При данном варианте синтаксиса функция qaskdeco использует значения по умолчанию для максимальных и минимальных значений синфазных и квадратурных амплитуд. Эти величины для некоторых небольших значений M приведены на странице с описанием функции qaskenco.
Замечание. Вывести изображение квадратного созвездия квадратурной манипуляции можно с помощью команды qaskenco(M).
msg = qaskdeco(inphase,quadr,M,minmax)
То же, что предыдущий вариант синтаксиса, но параметр minmax задает минимальные и максимальные значения синфазных и квадратурных амплитуд. Параметр minmax представляет собой матрицу размера 2 на 2, элементы которой имеют следующий смысл:
Примеры.
Приведенные ниже команды демонстрируют, что функции qaskdeco и qaskenco выполняют взаимно обратные действия.
msg = [0 3 5 3 2 5]’; M = 8; % преобразование сообщения в координаты точек
[inphase,quadr] = qaskenco(msg,M); % обратное преобразование (восстановление сообщения)
newmsg = qaskdeco(inphase,quadr,M)
newmsg =
0
3
5
3
2
5
Наверх
qaskenco — преобразование цифрового сообщения в аналоговый модулирующий сигнал с использованием квадратного созвездия для квадратурной манипуляции
Синтаксис:
qaskenco(M)
qaskenco(msg,M)
[inphase,quadr] = qaskenco(M)
[inphase,quadr] = qaskenco(msg,M)
Описание:
qaskenco(M)
Отображает “квадратное” созвездие для M-позиционной квадратурной манипуляции (QASK), обозначая M точек созвездия числами в диапазоне [0, M-1]. Величина M должна быть степенью числа 2. Если квадратный корень из Mявляется целым числом, то qaskenco нумерует точки так, чтобы реализовать код Грея.
qaskenco(msg,M)
То же, что предыдущий вариант синтаксиса, но отображаются только точки, соответствующие сообщению msg. Элементы вектора msg должны быть целыми числами из диапазона [0, M-1].
[inphase,quadr] = qaskenco(M)
Возвращает векторы inphase и quadr, содержащие координаты точек сигнального созвездия M-позиционной квадратурной манипуляции. Вектор inphase содержит синфазные амплитуды точек, а quadr — квадратурные амплитуды. Параметр M должен быть степенью числа 2.
[inphase,quadr] = qaskenco(msg,M)
То же, что предыдущий вариант синтаксиса, но векторы inphase и quadr содержат координаты точек, соответствующих символам из вектора сообщения msg. (Это те же точки, что отображаются на графике при вызове функции qaskenco(msg,M) без выходных параметров.) Элементы вектора msg должны быть целыми числами из диапазона [0, M-1].
В следующей таблице приведены максимальные значения inphase и quadr для некоторых небольших значений M.
|
M |
Максимальное значение inphase и quadr |
M |
Максимальное значение inphase и quadr |
|
2 |
1 |
32 |
5 |
|
4 |
1 |
64 |
7 |
|
8 |
Для inphase — 3, для quadr — 1 |
128 |
11 |
|
16 |
3 |
256 |
15 |
Примеры.
Приведенная ниже команда отображает часть 8-точечного “квадратного” созвездия квадратурной манипуляции, соответствующую символам сообщения [0 3 4 3 2 5].
qaskenco([0 3 4 3 2 5],8)
Приведенная ниже команда вместо построения графика возвращает ту же информацию в виде векторов inphase и quadr.
[inphase,quadr] = qaskenco([0 3 5 3 2 5],8);
inphase’
ans =
1 -1 -3 -1 1 -3
quadr’
ans =
1 -1 1 -1 -1 1
Приведенная ниже команда возвращает в векторах inphase и quadr координаты всех восьми точек 8-позиционного “квадратного” созвездия квадратурной манипуляции.
[inphase2,quad2] = qaskenco(8);
Наверх
intdump — интегратор со сбросом
Синтаксис:
y = intdump(x,nsamp)
Описание:
y = intdump(x,nsamp)
Интегрирует (суммирует) сигнал x по каждому символьному интервалу и возвращает результаты накопления для всех символов. Длина каждого символа составляет nsamp отсчетов. Если x содержит несколько символов, они обрабатываются независимо. Если x — матрица, ее столбцы рассматриваются как разные каналы сигнала и обрабатываются независимо.
Примеры:
Приведенный ниже код использует функцию rectpulse для формирования сигнала на передающей стороне и функцию intdump для понижения частоты дискретизации на приемной стороне.
M = 16; % Объем алфавита
x = randint(5000,1,M); % Исходное сообщение
Nsamp = 4; % Коэффициент повышения частоты дискретизации
y = qammod(x,M); % Используем КАМ-16
ypulse = rectpulse(y,Nsamp); % Формирование прямоугольных сигнальных посылок
ynoisy = awgn(ypulse,15,’measured’); % АБГШ-канал
ydownsamp = intdump(ynoisy,Nsamp); % Понижение частоты дискретизации в приемнике
z = qamdemod(ydownsamp,M); % Демодуляция переданного сообщения
biterr(x,z) % Подсчет числа ошибок
Результат работы этого кода показывает, что ошибок не произошло:
ans =
0
Наверх
rcosflt — интерполяция сигнала фильтром с косинусоидальным сглаживанием АЧХ
Синтаксис:
y = rcosflt(x,Fd,Fs);
y = rcosflt(x,Fd,Fs,’filter_type’,r,delay,tol);
y = rcosflt(x,Fd,Fs,’filter_type/Fs’,r,delay,tol);
y = rcosflt(x,Fd,Fs,’filter_type/filter’,num,den);
y = rcosflt(x,Fd,Fs,’filter_type/filter’,num,den,delay);
y = rcosflt(x,Fd,Fs,’filter_type/filter/Fs’,num,den…);
[y,t] = rcosflt(…);
Необязательные входные параметры:
|
Параметр |
Значение по умолчанию |
|
filter_type |
fir/normal |
|
r |
0.5 |
|
delay |
3 |
|
tol |
0.01 |
|
den |
1 |
Описание:
Функция rcosflt выполняет интерполяцию входного цифрового сигнала, пропуская его через фильтр с косинусоидальным сглаживанием АЧХ. При этом можно дать функции rcosflt рассчитать фильтр автоматически либо задать его параметры в явном виде.
Автоматический расчет фильтра:
-
y = rcosflt(x,Fd,Fs)
Рассчитывает нерекурсивный фильтр с косинусоидальным сглаживанием АЧХ и интерполирует с его помощью входной сигнал x. Частота дискретизации входного цифрового сигнала x равна Fd, частота дискретизации выходного сигнала y равна Fs. Отношение Fs/Fd должно быть положительным целым числом. В процессе работы функция rcosflt повышает частоту дискретизации сигнала в Fs/Fd раз, вставляя между отсчетами соответствующее количество нулей. Полученный сигнал пропускается через интерполирующий фильтр, порядок которого равен 1+2*delay*Fs/Fd, где задержка delay по умолчанию равна 3. Если x — вектор, то размеры векторов x и y связаны следующим соотношением:
length(y) = (length(x) + 2 * delay)*Fs/Fd
Если же x — матрица, то y — тоже матрица, каждый из столбцов которой является результатом интерполяции соответствующего столбца x.
-
y = rcosflt(x,Fd,Fs,’filter_type’,r,delay,tol)
Рассчитывает рекурсивный или нерекурсивный фильтр с косинусоидальным сглаживанием АЧХ и выполняет с его помощью интерполяцию входного сигнала x. Отношение Fs/Fd должно быть положительным целым числом. Параметр r — коэффициент сглаживания АЧХ, который должен быть вещественным числом в диапазоне [0, 1]. Параметр delay — вносимая фильтром групповая задержка, измеряемая в символах входного цифрового сигнала. В единицах времени групповая задержка равна delay/Fd секунд. Параметр tol задает допуск, используемый при синтезе рекурсивных фильтров. При расчете нерекурсивных фильтров этот параметр игнорируется.
Параметры x, Fd, Fs и y имеют тот же смысл, что и ранее.
Четвертый входной параметр, ‘filter_type’, представляет собой строку, задающую тип рассчитываемого фильтра. Возможные значения перечислены в приводимой ниже таблице.
Таблица: Типы фильтров и соответствующие значения параметра filter_type:
|
Тип фильтра |
Значение параметра filter_type |
|
Нерекурсивный фильтр |
‘default’, ‘fir’ или ‘fir/normal’ |
|
Рекурсивный фильтр |
‘iir’ или ‘iir/normal’ |
|
Нерекурсивный фильтр, sqrt-вариант |
‘sqrt’ или ‘fir/sqrt’ |
|
Рекурсивный фильтр, sqrt-вариант |
‘iir/sqrt’ |
-
y = rcosflt(x,Fd,Fs,’filter_type/Fs’,r,delay,tol)
То же, что предыдущий вариант синтаксиса, но предполагается, что входной сигнал x имеет частоту дискретизации Fs. При этом производится простая фильтрация, без интерполяции. Параметр Fd используется только для расчета фильтра. Если x — вектор, то размеры векторов x и y связаны следующим соотношением:
length(y) = length(x) + (2 * delay * Fs/Fd)
Как обычно, если x — матрица, то y — тоже матрица, каждый столбец которой является результатом обработки соответствующего столбца матрицы x.
Задание фильтра в явном виде:
-
y = rcosflt(x,Fd,Fs,’filter_type/filter’,num,den)
Интерполирует входной сигнал x с использованием фильтра, числитель и знаменатель функции передачи которого заданы соответственно векторами num и den. Если строка filter_type содержит fir, подразумевается нерекурсивный фильтр и указывать параметр den не нужно. Смысл параметров x, Fd, Fs и filter_type тот же, что и раньше.
-
y = rcosflt(x,Fd,Fs,’filter_type/filter’,num,den,delay)
Использует параметр delay аналогично тому, как это делает функция rcosine. В этом варианте синтаксиса предполагается, что фильтр, описываемый параметрами num, den и delay, рассчитан с помощью функции rcosine.
Как обычно, если x — матрица, то y — тоже матрица, каждый столбец которой является результатом обработки соответствующего столбца матрицы x.
-
y = rcosflt(x,Fd,Fs,’filter_type/filter/Fs’,num,den…)
То же, что предыдущие варианты синтаксиса, но предполагается, что входной сигнал x имеет частоту дискретизации Fs. При этом производится простая фильтрация, без интерполяции. Если x — вектор, то размеры векторов x и y связаны следующим соотношением:
length(y) = length(x) + (2 * delay * Fs/Fd)
Дополнительный выходной параметр:
-
[y,t] = rcosflt(…)
Данный вариант вызова дополнительно возвращает вектор t, содержащий значения времени, соответствующие отсчетам сигнала y.
Наверх
rectpulse — ступенчатая (кусочно-постоянная) интерполяция сигнала
Синтаксис:
y = rectpulse(x,nsamp)
Описание:
y = rectpulse(x,nsamp)
Осуществляет формирование прямоугольных сигнальных посылок, повышая частоту дискретизации сигнала x в nsamp раз. Это означает, что каждый символ из x повторяется nsamp раз в выходном сигнале y. Если x — матрица, ее столбцы рассматриваются как разные каналы сигнала и обрабатываются независимо.
Замечание. Если при повышении частоты дискретизации вместо повторения символов необходимо вставить между ними нулевые значения, используйте функцию upsample.
Примеры:
Пример использования функции rectpulse имеется на странице с описанием функции intdump. Приведенный ниже код осуществляет ступенчатую интерполяцию двухканального сигнала, каждый канал которого содержит три символа данных. В сформированном выходном сигнале y на каждый символ приходится четыре отсчета.
nsamp = 4; % Число отсчетов на символ
nsymb = 3; % Число символов
ch1 = randint(nsymb,1,2,68521); % Случайные двоичные символы
ch2 = [1:nsymb]’;
x = [ch1 ch2] % Двухканальный сигнал
y = rectpulse(x,nsamp)
Далее приводится результат работы этого кода. В матрице y каждый столбец соответствует своему каналу, а каждая строка — одному отсчету. Первые четыре строки матрицы y соответствуют первому символу, следующие четыре строки — второму, а последние четыре строки матрицы y соответствуют последнему, третьему, символу.
x =
1 1
1 2
0 3
y =
1 1
1 1
1 1
1 1
1 2
1 2
1 2
1 2
0 3
0 3
0 3
0 3
Наверх
hank2sys — преобразование матрицы Ханкеля в описание линейной системы
Синтаксис:
[num,den] = hank2sys(h,ini,tol)
[num,den,sv] = hank2sys(h,ini,tol)
[a,b,c,d] = hank2sys(h,ini,tol)
[a,b,c,d,sv] = hank2sys(h,ini,tol)
Описание:
[num,den] = hank2sys(h,ini,tol)
Преобразует матрицу Ханкеля h в числитель num и знаменатель den функции передачи линейной системы. Векторы num и den содержат коэффициенты соответствующих полиномов в порядке убывания степеней переменной z. Параметр ini — значение импульсной характеристики системы в нулевой момент времени. Если tol > 1, то tol задает порядок рассчитываемой системы. Если tol < 1, то tol задает допуск, используемый при выборе порядка системы на основе сингулярных чисел матрицы h. Если параметр tol опущен, его значение по умолчанию равно 0.01. Преобразование осуществляется путем разложения по особым (сингулярным) числам.
[num,den,sv] = hank2sys(h,ini,tol)
То же, что предыдущий вариант синтаксиса, но дополнительно возвращается вектор sv, содержащий сингулярные числа матрицы h.
[a,b,c,d] = hank2sys(h,ini,tol)
Преобразует матрицу Ханкеля h в соответствующее описание линейной системы в пространстве состояний. Результаты a, b, c и d — матрицы, описывающие систему. Смысл входных параметров тот же, что и раньше.
[a,b,c,d,sv] = hank2sys(h,ini,tol)
То же, что предыдущий вариант синтаксиса, но дополнительно возвращается вектор sv, содержащий сингулярные числа матрицы h.
Примеры.
h = hankel([1 0 1]);
[num,den,sv] = hank2sys(h,0,.01)
num =
0 1.0000 -0.0000 1.0000
den =
1.0000 0.0000 0.0000 0.0000
sv =
1.6180
1.0000
0.6180
Наверх
hilbiir — расчет рекурсивного фильтра, аппроксимирующего преобразование Гильберта
Синтаксис:
hilbiir;
hilbiir(ts);
hilbiir(ts,dly);
hilbiir(ts,dly,bandwidth);
hilbiir(ts,dly,bandwidth,tol);
[num,den] = hilbiir(…);
[num,den,sv] = hilbiir(…);
[a,b,c,d] = hilbiir(…);
[a,b,c,d,sv] = hilbiir(…);
Описание.
Функция hilbiir рассчитывает рекурсивный фильтр, осуществляющий преобразование Гильберта. Результатом работы может являться:
-
График импульсной характеристики фильтра;
-
Описание фильтра в виде коэффициентов полиномов функции передачи либо параметров пространства состояния.
Теоретическая информация:
Идеальный фильтр, осуществляющий преобразование Гильберта, имеет комплексную частотную характеристику H(s) = –j sgn(s), где sgn(.) — знаковая функция (в MATLAB’е она имеет имя sign). Импульсная характеристика фильтра Гильберта имеет вид
Поскольку идеальный фильтр Гильберта является нереализуемым (он не удовлетворяет требованию причинности), функция hilbiir рассчитывает его аппроксимацию, внося групповую задержку dly. Идеальный фильтр Гильберта с такой задержкой имеет импульсную характеристику вида
Выбор значения групповой задержки:
Рассчитываемый фильтр является аппроксимацией. Если вы задаете значение вносимой групповой задержки в явном виде, воспользуйтесь следующими двумя советами:
-
Значение групповой задержки dly должно как минимум в несколько раз превышать величину периода дискретизации ts. Рекомендуется также выбирать соотношение между этими двумя параметрами так, чтобы dly было равно полуцелому числу интервалов ts (то есть rem(dly,ts) = ts/2). Например, можно взять ts равным 2*dly/N, где N — положительное нечетное целое число.
-
В точке t = dly, где импульсная характеристика фильтра Гильберта испытывает разрыв, ее значение может быть интерпретировано как 0, -Inf или Inf. Если один из отсчетов импульсной характеристики попадает в эту точку, функция hilbiir использует нулевое значение. Для улучшения точности результатов фильтрации следует избегать данной ситуации (приведенная выше рекомендация о выборе соотношения между dly и ts гарантирует, что данная точка окажется ровно посередине между отсчетами рассчитанной импульсной характеристики).
Варианты синтаксиса для вывода графика:
Каждый из приведенных в данном разделе вариантов синтаксиса обеспечивает вывод графика импульсной характеристики рассчитанного фильтра и соответствующего идеального фильтра Гильберта.
-
hilbiir
Выводит график импульсной характеристики фильтра Гильберта 4-го порядка с групповой задержкой, равной 1 с. Период дискретизации сигнала считается равным 2/7 с. При синтезе фильтра используется допуск, равный 0.05. Выводится также график импульсной характеристики идеального фильтра Гильберта, имеющего групповую задержку, равную 1 с.
-
hilbiir(ts)
Выводит график импульсной характеристики фильтра Гильберта 4-го порядка с интервалом дискретизации ts секунд и групповой задержкой, равной ts*7/2 секунд. При синтезе фильтра используется допуск, равный 0.05. Выводится также график импульсной характеристики идеального фильтра Гильберта, имеющего интервал дискретизации ts секунд и групповую задержку, равную ts*7/2 секунд.
-
hilbiir(ts,dly)
То же, что и предыдущий вариант синтаксиса, но групповая задержка для рассчитываемого и идеального фильтров равна dly. Рекомендации по поводу выбора значения параметра dly см. выше в разделе “Выбор значения групповой задержки”.
-
hilbiir(ts,dly,bandwidth)
То же, что и предыдущий вариант синтаксиса, но параметр bandwidth задает предполагаемую полосу частот входного сигнала, позволяя фильтру использовать компенсатор для входного сигнала. Если bandwidth = 0 или bandwidth > 1/(2*ts), то функция hilbiir не использует компенсатор.
-
hilbiir(ts,dly,bandwidth,tol)
То же, что и предыдущий вариант синтаксиса, но параметр tol задает допуск, используемый при расчете фильтра. Если tol < 1, значение этого параметра задает допуск, используемый при синтезе фильтра методом разложения по сингулярным числам. Если tol > 1, параметр рассчитываемого фильтра будет равен tol.
Варианты синтаксиса для расчета фильтра:
Каждый из приведенных в данном разделе вариантов синтаксиса дает количественное описание рассчитанного фильтра, но не выводит графиков. Смысл входных параметров тот же, что и раньше (см. выше раздел “Варианты синтаксиса для вывода графика”)
-
[num,den] = hilbiir(…)
Возвращает коэффициенты числителя и знаменателя функции передачи рекурсивного фильтра.
-
[num,den,sv] = hilbiir(…)
Возвращает коэффициенты числителя и знаменателя функции передачи рекурсивного фильтра, а также сингулярные числа матрицы Ханкеля, используемой при вычислениях.
-
[a,b,c,d] = hilbiir(…)
Возвращает описание рассчитанного фильтра в пространстве состояний. Результат a — матрица, b и c — векторы, d — скаляр.
-
[a,b,c,d,sv] = hilbiir(…)
Возвращает описание рассчитанного фильтра в пространстве состояний, а также сингулярные числа матрицы Ханкеля, используемой при вычислениях.
Алгоритм.
Функция hilbiir рассчитывает импульсную характеристику идеального фильтра Гильберта с заданной групповой задержкой. Затем выполняется аппроксимация этой импульсной характеристики методом разложения соответствующей матрицы Ханкеля по особым (сингулярным) числам (см. раздел “Литература”).
Примеры.
В командной строке MATLAB наберите hilbiir или [num,den] = hilbiir, чтобы вывести графики или рассчитать фильтр, используя параметры по умолчанию.
Наверх
rcosine — расчет фильтра с косинусоидальным сглаживанием АЧХ
Синтаксис:
num = rcosine(Fd,Fs);
[num,den] = rcosine(Fd,Fs,type_flag);
[num,den] = rcosine(Fd,Fs,type_flag,r);
[num,den] = rcosine(Fd,Fs,type_flag,r,delay);
[num,den] = rcosine(Fd,Fs,type_flag,r,delay,tol);
Описание:
-
num = rcosine(Fd,Fs)
Рассчитывает нерекурсивный фильтр с косинусоидальным сглаживанием АЧХ, возвращая отсчеты его импульсной характеристики. Входной цифровой сигнал имеет символьную скорость Fd. Частота дискретизации фильтруемого сигнала равна Fs. Отношение Fs/Fd должно быть положительным целым числом. По умолчанию используется коэффициент сглаживания АЧХ, равный 0.5. Вносимая фильтром групповая задержка равна трем символьным тактам входного сигнала, или, что то же самое, 3/Fd секундам.
-
[num,den] = rcosine(Fd,Fs,type_flag)
Рассчитывает фильтр с косинусоидальным сглаживанием АЧХ, тип фильтра задается строковым параметром type_flag. Возможные типы фильтров и соответствующие им значения параметра type_flag перечислены в следующей таблице.
Таблица: Типы фильтров и соответствующие значения параметра type_flag:
|
Тип фильтра |
Значение параметра type_flag |
|
Нерекурсивный фильтр |
‘default’, ‘fir’ или ‘fir/normal’ |
|
Рекурсивный фильтр |
‘iir’ или ‘iir/normal’ |
|
Нерекурсивный фильтр, sqrt-вариант |
‘sqrt’ или ‘fir/sqrt’ |
|
Рекурсивный фильтр, sqrt-вариант |
‘iir/sqrt’ |
Допуск, используемый при синтезе рекурсивного фильтра, по умолчанию равен 0.01.
-
[num,den] = rcosine(Fd,Fs,type_flag,r)
Дополнительно задается коэффициент сглаживания АЧХ r. Этот параметр должен быть вещественным числом, лежащим в диапазоне [0, 1].
-
[num,den] = rcosine(Fd,Fs,type_flag,r,delay)
Дополнительно задается вносимая фильтром групповая задержка delay, измеряемая в символах входного цифрового сигнала. Параметр delay должен быть положительным целым числом. В единицах времени групповая задержка равна delay/Fd секунд.
-
[num,den] = rcosine(Fd,Fs,type_flag,r,delay,tol)
Дополнительно задается допуск tol, используемый при синтезе рекурсивных фильтров. При расчете нерекурсивных фильтров параметр tol игнорируется.
Наверх
awgn — канал с аддитивным белым нормальным шумом
Синтаксис:
y = awgn(x,snr);
y = awgn(x,snr,sigpower);
y = awgn(x,snr,’measured’);
y = awgn(x,snr,sigpower,state);
y = awgn(x,snr,’measured’,state);
y = awgn(…,powertype);
Описание:
-
y = awgn(x,snr)
Добавляет белый гауссов шум к вектору сигнала x. Скаляр snr задает отношение сигнал/шум в децибелах. Если значения x являются комплексными, функция awgn добавляет комплексный шум. При этом предполагается, что мощность сигнала x равна 0 дБ.
-
y = awgn(x,snr,sigpower)
То же, что и предыдущий вариант синтаксиса, но в данном случае параметр sigpower указывает мощность сигнала x в децибелах.
-
y = awgn(x,snr,’measured’)
То же, что y = awgn(x,snr), но мощность сигнала не считается равной 0 дБ, а автоматически измеряется.
-
y = awgn(x,snr,sigpower,state)
То же, что y = awgn(x,snr,sigpower), но целочисленный параметр state позволяет задавать внутреннее состояние генератора гауссовых случайных чисел MATLAB (функция randn).
-
y = awgn(x,snr,’measured’,state)
То же, что y = awgn(x,snr,’measured’), но целочисленный параметр state позволяет задавать внутреннее состояние генератора гауссовых случайных чисел MATLAB (функция randn).
-
y = awgn(…,powertype)
То же, что предыдущие варианты синтаксиса, но в данном случае строковый параметр powertype задает единицы измерения, использованные при указании параметров snr и sigpower. Возможные значения параметра powertype — ‘dB’ и ‘linear’. При значении ‘linear’ мощность измеряется в ваттах.
Примеры.
Приведенные ниже команды добавляют нормальный белый шум к пилообразному сигналу. Затем выводятся графики исходного и зашумленного сигналов.
t = 0:.1:10;
x = sawtooth(t); % Создаем пилообразный сигнал
y = awgn(x,10,’measured’); % Добавляем белый гауссов шум
plot(t,x,t,y) % Выводим графики обоих сигналов
Наверх
gf — создание объекта, представляющего массив элементов конечного поля
(начиная с версии 2.1 пакета Communications Toolbox (Release 13))
Синтаксис:
x_gf = gf(x,m);
x_gf = gf(x,m,prim_poly);
x_gf = gf(x);
Описание:
x_gf = gf(x,m)
Создает массив элементов конечного поля из матрицы x. Конечное поле имеет 2^m элементов, при этом m должно быть целым числом в диапазоне от 1 до 16. Элементы x должны быть целыми числами в диапазоне от 0 до 2^m-1. Результат x_gf является переменной, которую MATLAB трактует не как массив целых чисел, а как массив элементов конечного поля. Вследствие этого при применении к переменной x_gf операторов или функций, таких как + или det, MATLAB будет производить вычисления в данном конечном поле.
x_gf = gf(x,m,prim_poly)
То же, что предыдущий вариант синтаксиса, но для задания поля используется примитивный полином, указанный параметром prim_poly. Параметр prim_poly должен быть целочисленным представлением примитивного полинома. Например, число 41 представляет полином D5 + D2 + 1, потому что в двоичном виде число 41 записывается как 1 0 0 1 0 1 (левая цифра здесь соответствует младшему разряду).
x_gf = gf(x)
Создает массив элементов простого двоичного конечного поля GF(2) из матрицы x. Элементы x может быть равны 0 или 1.
Примитивные полиномы по умолчанию
В приведенной ниже таблице перечислены примитивные полиномы, которые функция gf использует для всех возможных конечных полей GF(2^m). Чтобы использовать иной примитивный полином, следует задать его при вызове функции gf явно — в виде третьего входного параметра prim_poly.
|
m |
Примитивный полином по умолчанию |
Целочисленное представление |
|
1 |
D + 1 |
3 |
|
2 |
D2 + D + 1 |
7 |
|
3 |
D3 + D + 1 |
11 |
|
4 |
D4 + D + 1 |
19 |
|
5 |
D5 + D2 + 1 |
37 |
|
6 |
D6 + D + 1 |
67 |
|
7 |
D7 + D3 + 1 |
137 |
|
8 |
D8 + D4 + D3 + D2 + 1 |
285 |
|
9 |
D9 + D4 + 1 |
529 |
|
10 |
D10 + D3 + 1 |
1033 |
|
11 |
D11 + D2 + 1 |
2053 |
|
12 |
D12 + D6 + D4 + D + 1 |
4179 |
|
13 |
D13 + D4 + D3 + D + 1 |
8219 |
|
14 |
D14 + D10 + D6 + D + 1 |
17475 |
|
15 |
D15 + D + 1 |
32771 |
|
16 |
D16 + D12 + D3 + D + 1 |
69643 |
Примеры:
Приведенный ниже код создает вектор-строку, элементы которого принадлежат конечному полю GF(4), а затем складывает эту строку с самой собой.
x = 0:3; % Строка целых чисел
m = 2; % Будем работать в конечном поле GF(2^2), то есть GF(4)
a = gf(x,m) % Создаем массив элементов поля GF(2^m)
b = a + a % Складываем a с самим собой, создавая массив b
Результат работы примера выглядит так:
a = GF(2^2) array. Primitive polynomial = D^2+D+1 (7 decimal)
Array elements =
0 1 2 3
b = GF(2^2) array. Primitive polynomial = D^2+D+1 (7 decimal)
Array elements =
0 0 0 0
Результат показывает значения переменных a и b — массивов элементов конечного поля. Каждая секция вывода отображает следующую информацию:
-
Размерность поля — в данном случае она равна GF(2^2) = GF(4).
-
Примитивный полином, использованный для данного поля. В данном примере используется примитивный полином, принятый в пакете Communications Toolbox для поля GF(4) по умолчанию (см. приведенную ранее таблицу).
-
Собственно элементы массива. В нашем примере элементы массива a в точности совпадают с элементами вектора x, а все элементы массива b равны нулю.
Строка кода, создавшая массив b, показывает, что с массивами элементов конечных полей можно выполнять математические операции, используя операторную нотацию (в данном примере для сложения массивов использовался обычный оператор +). Проверив тип переменной, MATLAB узнает, что выполнять вычисления следует в поле GF(4). Анализ результата демонстрирует следующее:
-
Слагаемые a и сумма b определены в одном и том же конечном поле и используют один и тот же примитивный полином. При создании переменной b не нужно указывать размерность поля, поскольку MATLAB возьмет необходимую информацию из переменных-слагаемых (в данном случае — из переменной a).
-
Все элементы массива b равны нулю, поскольку сумма любого числа с самим собой в двоичном конечном поле, простом или расширенном, равна нулю. Этот результат отличается от результата сложения x + x, который представляет собой результат выполнения операции сложения в бесконечном поле целых чисел.
Наверх
gfadd — сложение полиномов в конечном поле
Внимание!
Приведенное ниже описание относится к версии 2.0 пакета Communications, (MATLAB 6.1). В версии 2.1 (MATLAB 6.5) сложение объектов двоичных конечных полей (в том числе расширенных) производится с помощью оператора «+», а данная функция применяется только к полям GF(pm), где p — простое число, большее двух.
Синтаксис:
c = gfadd(a,b);
c = gfadd(a,b,p);
c = gfadd(a,b,p,len);
c = gfadd(a,b,field);
Описание:
-
c = gfadd(a,b)
Выполняет сложение двух полиномов над полем GF(2). Входные параметры и результат работы представляют собой векторы-строки, содержащие коэффициенты соответствующих полиномов в порядке возрастания степеней. Каждый коэффициент может быть равен 0 или 1, поскольку вычисления производятся в поле GF(2). Если a и b — матрицы одинакового размера, они обрабатываются построчно.
-
c = gfadd(a,b,p)
Выполняет сложение двух полиномов над полем GF(p), где p — простое число. Параметры a, b и c представляют собой векторы-строки, содержащие коэффициенты соответствующих полиномов в порядке возрастания степеней. Возможные значения коэффициентов лежат в диапазоне от 0 до p — 1. Если a и b — матрицы одинакового размера, они обрабатываются построчно.
-
c = gfadd(a,b,p,len)
То же, что и предыдущий вариант синтаксиса, но длина возвращаемого вектора гарантированно равна len. Результат c обрезается или дополняется нулями, чтобы получить вектор нужной длины.
-
c = gfadd(a,b,field)
Выполняет сложение двух элементов поля GF(pm), где m — положительное целое число. Входные параметры a и b — слагаемые, представленные в экспоненциальном формате по отношению к некоторому примитивному элементу поля GF(pm). Третий входной параметр field представляет собой матрицу, в которой перечислены все элементы поля GF(pm), упорядоченные по степеням того же самого примитивного элемента. Получить такую матрицу можно с помощью функции gftuple. Результат c — сумма, представленная в экспоненциальном формате по отношению к тому же самому примитивному элементу. Если входные параметры a и b представляют собой матрицы одинакового размера, они суммируются поэлементно.
Примеры:
В приведенном ниже коде переменной sum5 присваивается значение суммы полиномов 2 + 3x + x2 and 4 + 2x + 3×2 в поле GF(5), а переменной linpart — значение той же суммы, но обрезанное так, чтобы максимальная степень результирующего полинома была равна единице.
sum5 = gfadd([2 3 1],[4 2 3],5)
sum5 =
1 0 4
linpart = gfadd([2 3 1],[4 2 3],5,2)
linpart =
1 0
Приведенный ниже код показывает, что в поле GF(9) выполняется равенство a2 + a4 = a1, где a — корень примитивного полинома 2 + 2x + x2.
p = 3; m = 2;
primpoly = [2 2 1];
field = gftuple([-1:p^m-2]’,primpoly,p);
g = gfadd(2,4,field)
g =
1
Наверх
gfconv — умножение полиномов в конечном поле
Внимание! Приведенное ниже описание относится к версии 2.0 пакета Communications, (MATLAB 6.1). В версии 2.1 (MATLAB 6.5) умножение объектов полиномов двоичных конечных полей (в том числе расширенных) производится с помощью функции conv, а данная функция применяется только к полям GF(pm), где p — простое число, большее двух.
Синтаксис:
c = gfconv(a,b);
c = gfconv(a,b,p);
c = gfconv(a,b,field);
Описание:
Функция gfconv производит умножение полиномов, заданных над конечным полем. Для перемножения элементовконечного поля используется функция gfmul. С алгебраической точки зрения умножение полиномов в конечном поле эквивалентно свертке векторов, содержащих коэффициенты полиномов. При вычислении свертки должна использоваться арифметика над тем же конечным полем.
-
c = gfconv(a,b)
Выполняет умножение двух полиномов над полем GF(2). Входные параметры и результат работы представляют собой векторы-строки, содержащие коэффициенты соответствующих полиномов в порядке возрастания степеней. Каждый коэффициент может быть равен 0 или 1, поскольку вычисления производятся в поле GF(2).
-
c = gfconv(a,b,p)
Выполняет умножение двух полиномов над полем GF(p), где p — простое число. Параметры a, b и c представляют собой векторы-строки, содержащие коэффициенты соответствующих полиномов в порядке возрастания степеней. Возможные значения коэффициентов лежат в диапазоне от 0 до p – 1.
-
c = gfconv(a,b,field)
Выполняет умножение двух элементов поля GF(pm), где m — положительное целое число. Входные параметры a и b — векторы-строки коэффициентов (в порядке возрастания степеней) перемножаемых полиномов, представленные в экспоненциальном формате по отношению к некоторому примитивному элементу поля GF(pm). Третий входной параметр field представляет собой матрицу, в которой перечислены все элементы поля GF(pm), упорядоченные по степеням того же самого примитивного элемента. Получить такую матрицу можно с помощью функции gftuple. Результат c — произведение полиномов, представленное в экспоненциальном формате по отношению к тому же самому примитивному элементу.
Примеры:
Приведенная ниже команда показывает, что в простом двоичном поле GF(2) выполняется равенство .
gfc = gfconv([1 1 0 0 1],[0 1 1])
gfc =
0 1 0 1 0 1 1
Приведенный ниже код иллюстрирует выполнение равенства в поле GF(p) для случая, когда p = 7, r = 5 и s = 3. (Разумеется, данное равенство остается справедливым для произвольного простого числа p и произвольных положительных целых чисел r и s.)
p = 7; r = 5; s = 3;
a = gfrepcov([r s]); % вычислили x^r + x^s
% ВычислЯем a^p в поле GF(p).
c = 1;
for ii = 1:p
c = gfconv(c,a,p);
end;
% ПроверЯем равенство c = x^(rp) + x^(sp).
powers = [];
for ii = 1:length(c)
if c(ii)~=0
powers = [powers, ii];
end;
end;
if (powers==[r*p+1 s*p+1] | powers==[s*p+1 r*p+1])
disp(‘Равенство проверено при заданных величинах r, s и p.’)
end
Наверх
gfcosets — генерация циклотомических классов для конечного поля
Внимание! Приведенное ниже описание относится к версии 2.0 пакета Communications, (MATLAB 6.1). В версии 2.1 (MATLAB 6.5) генерация циклотомических классов для двоичных конечных полей (в том числе расширенных) производится с помощью функции cosets, а данная функция применяется только к полям GF(pm), где p — простое число, большее двух.
Синтаксис:
c = gfcosets(m);
c = gfcosets(m,p);
Описание:
c = gfcosets(m)
Возвращает циклотомические классы для конечного поля GF(2m), где m — положительное целое число.
c = gfcosets(m,p)
Возвращает циклотомические классы для конечного поля GF(pm), где m — положительное целое число, а p — простое число.
В обоих случаях возвращаемая матрица c структурирована так, что каждая строка представляет один циклотомический класс. Представление формируется путем перечисления (в экспоненциальном формате) элементов, образующих класс. Экспоненциальное представление элементов формируется на базе примитивного полинома, используемого для данного поля по умолчанию.
В первом столбце матрицы c содержатся представители классов (coset leaders). Поскольку число элементов в разных классах неодинаково, более короткие строки дополняются значениями NaN.
Циклотомический класс (cyclotomic coset) — это множество элементов конечного поля, которым соответствует один и тот же минимальный полином. Более подробные сведения приведены в указанной ниже литературе.
Примеры:
Приведенная ниже команда находит циклотомические классы для поля GF(9).
c = gfcosets(2,3)
c =
0 NaN
1 3
2 6
4 NaN
5 7
С помощью функции gfminpol можно убедиться в том, что все элементы из, скажем, третьей строки матрицы c действительно принадлежат к одному циклотомическому классу (то есть имеют общий минимальный полином).
m = [gfminpol(2,2,3); gfminpol(6,2,3)] % Строки результата должны быть идентичны
m =
2 0 1
2 0 1
Наверх
gfdeconv — деление полиномов в конечном поле
Внимание! Приведенное ниже описание относится к версии 2.0 пакета Communications, (MATLAB 6.1). В версии 2.1 (MATLAB 6.5) деление объектов полиномов двоичных конечных полей (в том числе расширенных) производится с помощью функции deconv, а данная функция применяется только к полям GF(pm), где p — простое число, большее двух.
Синтаксис:
[quot,remd] = gfdeconv(b,a);
[quot,remd] = gfdeconv(b,a,p);
[quot,remd] = gfdeconv(b,a,field);
Описание:
Функция gfdeconv производит деление полиномов, заданных над конечным полем. Для деления элементов конечного поля используется функция gfdiv. С алгебраической точки зрения деление полиномов в конечном поле эквивалентно обращению свертки векторов, содержащих коэффициенты полиномов. При вычислении обращения свертки должна использоваться арифметика над тем же конечным полем.
-
[quot,remd] = gfdeconv(b,a)
Выполняет деление полинома b на полином a над полем GF(2), возвращая частное в выходном параметре quot и остаток от деления в выходном параметре remd. Входные параметры и результаты работы представляют собой векторы-строки, содержащие коэффициенты соответствующих полиномов в порядке возрастания степеней. Каждый коэффициент может быть равен 0 или 1, поскольку вычисления производятся в поле GF(2).
-
[quot,remd] = gfdeconv(b,a,p)
Выполняет деление полинома b на полином a над полем GF(p), возвращая частное в выходном параметре quot и остаток от деления в выходном параметре remd. Третий входной параметр p — простое число. Параметры b, a, quot и remd представляют собой векторы-строки, содержащие коэффициенты соответствующих полиномов в порядке возрастания степеней. Возможные значения коэффициентов лежат в диапазоне от 0 до p – 1.
-
[quot,remd] = gfdeconv(b,a,field)
Выполняет деление полинома b на полином a над полем GF(pm), возвращая частное в выходном параметре quot и остаток от деления в выходном параметре remd. Здесь p — простое число, а m — положительное целое число. Входные и выходные параметры представляют собой векторы-строки коэффициентов (в порядке возрастания степеней) соответствующих полиномов, представленные в экспоненциальном формате по отношению к некоторому примитивному элементу поля GF(pm). Третий входной параметр field представляет собой матрицу, в которой перечислены все элементы поля GF(pm), упорядоченные по степеням того же самого примитивного элемента. Получить такую матрицу можно с помощью функции gftuple.
Пример:
Приведенный ниже код показывает, что в простом двоичном поле GF(2) выполняется равенство с остатком 1. Код также проверяет корректность деления.
p = 2;
b = [0 1 0 1 1];
a = [1 1];
[quot, remd] = gfdeconv(b,a,p)
% Проверка результата
bnew = gfadd(gfconv(quot,a,p),remd,p);
if isequal(bnew,b)
disp(‘Правильно.’)
end;
Результат работы примера приведен ниже:
quot =
1 0 0 1
remd =
1
Правильно.
Приведенный ниже код выводит список тех полиномов вида (для k от 2 до 8), которые нацело делятся на полином
в поле GF(3).
p = 3; m = 2;
a = [1 0 1]; % делитель равен 1+x^2
for ii = 2:p^m-1
b = gfrepcov(ii); % вычислили x^ii
b(1) = p-1; % вычислили -1+x^ii
[quot, remd] = gfdeconv(b,a,p);
% выводим полином -1+x^ii, если он делитсЯ на a без остатка if remd==0
gfpretty(b)
end
end
Результат работы примера приведен ниже:
4
2 + X
8
2 + X
Как видите, на делятся без остатка полиномы
и
. Это, в частности, означает, что неприводимый в поле GF(3) полином
не является примитивным для поля GF(9) (см. раздел “Алгоритм” на странице с описанием функции gfprimck).
Алгоритм:
Функция gfdeconv использует тот же алгоритм, что и функция deconv базовой библиотеки MATLAB, вычисляя частное как импульсную характеристику дискретного фильтра с функцией передачи, описываемой полиномами b и a. Вычисления производятся с помощью функции gffilter. Для расширенных конечных полей в текущей версии пакета не поддерживается операция дискретной фильтрации, поэтому нахождение частного в данном случае сводится к вычитанию в цикле.
Наверх
gfdiv — деление элементов конечного поля
Внимание! Приведенное ниже описание относится к версии 2.0 пакета Communications, (MATLAB 6.1). В версии 2.1 (MATLAB 6.5) деление объектов двоичных конечных полей (в том числе расширенных) производится с помощью оператора “./”, а данная функция применяется только к полям GF(pm), где p — простое число, большее двух.
Синтаксис:
quot = gfdiv(b,a);
quot = gfdiv(b,a,p);
quot = gfdiv(b,a,field);
Описание:
Функция gfdiv производит деление элементов конечного поля. Для деления полиномов, заданных над конечным полем, используется функция gfdeconv.
-
quot = gfdiv(b,a)
Выполняет деление b на a в простом двоичном поле GF(2). Входные параметры и результат работы (частное quot) могут быть равны 0 или 1, поскольку вычисления производятся в поле GF(2). Если a и b — матрицы одинакового размера, они обрабатываются поэлементно.
-
quot = gfdiv(b,a,p)
Выполняет деление b на a в поле GF(p), где p — простое число. Входные параметры a и b должны лежать в диапазоне от 0 до p – 1, в том же диапазоне будет находиться и частное quot. Если a и b — матрицы одинакового размера, они обрабатываются поэлементно.
-
quot = gfdiv(b,a,field)
Выполняет деление b на a в поле GF(pm), где m — положительное целое число. Делимое b, делитель a и частное quot представлены в экспоненциальном формате по отношению к некоторому примитивному элементу поля GF(pm). Третий входной параметр field представляет собой матрицу, в которой перечислены все элементы поля GF(pm), упорядоченные по степеням того же самого примитивного элемента. Получить такую матрицу можно с помощью функции gftuple. Если входные параметры a и b представляют собой матрицы одинакового размера, они обрабатываются поэлементно.
Во всех вариантах синтаксиса попытка деления на ноль приводит к результату, равному NaN.
Примеры:
Приведенный ниже код выводит таблицу обратных значений для ненулевых элементов конечных полей GF(5) и GF(25). В качестве входных параметров функции gfdiv используются векторы-столбцы.
% Находим обратные значениЯ длЯ ненулевых элементов полЯ GF(5)
p = 5;
b = ones(p-1,1);
a = [1:p-1]’;
quot1 = gfdiv(b,a,p);
disp(‘Обратные величины в поле GF(5):’)
disp(‘Элемент Обратное значение’)
disp([a, quot1])
% Находим обратные значениЯ длЯ ненулевых элементов полЯ GF(25)
m = 2;
field = gftuple([-1:p^m-2]’,m,p);
b = zeros(p^m-1,1); % Числитель равен нулю, т.к. 1 = alpha^0
a = [0:p^m-2]’;
quot2 = gfdiv(b,a,field);
disp(‘Обратные величины в поле GF(25), представленные’)
disp(‘в экспоненциальном формате с использованием’)
disp(‘примитивного полинома по умолчанию:’)
disp(‘Элемент Обратное значение’)
disp([a, quot2])
Наверх
gffilter — фильтрация данных в простом конечном поле
Внимание! Приведенное ниже описание относится к версии 2.0 пакета Communications, (MATLAB 6.1). В версии 2.1 (MATLAB 6.5) фильтрация данных, представленных в виде объектов двоичных конечных полей (в том числе расширенных), производится с помощью функции filter, а данная функция применяется только к полям GF(p), где p — простое число, большее двух.
Синтаксис:
y = gffilter(b,a,x);
y = gffilter(b,a,x,p);
Описание:
-
y = gffilter(b,a,x)
Выполняет фильтрацию данных x фильтром, функция передачи которого описывается векторами b (коэффициенты числителя) и a (коэффициенты знаменателя). Вычисления выполняются над полем GF(2). Результат y представляет собой выходной сигнал фильтра. Элементы всех векторов могут принимать значения 0 или 1, поскольку вычисления производятся в поле GF(2).
-
y = gffilter(b,a,x,p)
То же, что и предыдущий вариант синтаксиса, но вычисления выполняются в поле GF(p), где p — простое число. Элементы всех векторов могут лежать в диапазоне от 0 до p – 1.
Примеры:
Приведенный ниже код рассчитывает и графически отображает импульсную характеристику конкретного дискретного фильтра, заданного в простом двоичном поле.
b = [1 0 0 1 0 1 0 1];
a = [1 0 1 1];
y = gffilter(b,a,[1,zeros(1,19)]);
stem(y);
axis([0 20 -.1 1.1])
Алгоритм:
Согласно принципу работы дискретного фильтра, результат y является решением разностного уравнения
где:
-
A + 1 — длина вектора a;
-
B + 1 — длина вектора b;
-
n принимает значения от 1 до длины вектора x.
Для реализации дискретной фильтрации в простом двоичном поле GF(2), в принципе, можно использовать функцию filter базовой библиотеки MATLAB, взяв даваемый ею результат по модулю два, например, так:
y = abs(rem(filter(b,a,x),2));
Однако если данный фильтр, рассматриваемый не в конечном поле, а в обычном поле комплексных чисел, является неустойчивым, его выходной сигнал может неограниченно возрастать. При этом результат вычисления остатка от деления на два будет правильным только до тех пор, пока выходной сигнал фильтра не превысит по абсолютной величине 252 (именно такие целые числа могут быть точно представлены в используемом MATLAB 8-байтовом формате double чисел с плавающей запятой). Функция же gffilter даст правильный результат во всех случаях.
Наверх
gflineq — поиск частного решения системы линейных уравнений Ax = b в простом конечном поле
Внимание! Приведенное ниже описание относится к версии 2.0 пакета Communications, (MATLAB 6.1). В версии 2.1 (MATLAB 6.5) фильтрация данных, представленных в виде объектов двоичных конечных полей (в том числе расширенных), производится с помощью функции filter, а данная функция применяется только к полям GF(p), где p — простое число, большее двух.
Синтаксис:
x = gflineq(A,b);
x = gflineq(A,b,p);
[x,vld] = gflineq(…);
Описание:
-
x = gflineq(A,b)
Возвращает частное решение системы линейных уравнений A x = b в конечном поле GF(2). Если A — матрица, имеющая kстрок и n столбцов, а b — вектор длины k, то решение x будет вектором длины n. Элементы массивов A, x и b могут быть равны 0 или 1. Если решения не существует, возвращаемый результат x представляет собой пустую матрицу.
-
x = gflineq(A,b,p)
Возвращает частное решение системы линейных уравнений A x = b в конечном поле GF(p), где p — простое число. Если A — матрица, имеющая k строк и n столбцов, а b — вектор длины k, то решение x будет вектором длины n. Элементы массивов A, x и b являются целыми числами, лежащими в диапазоне от 0 до p-1.
-
[x,vld] = gflineq(…)
Дополнительно возвращает флаг vld, который индицирует существование решения. Если vld = 1, то решение существует и возвращаемый результат x является корректным решением; если vld = 0, решения не существует.
Примеры:
Приведенный ниже код находит корректное решение системы линейных уравнений в поле GF(2).
A=[1 0 1;
1 1 0;
1 1 1];
%Пример, в котором имеется корректное решение
[x,vld] = gflineq(A,[1;0;0])
x =
1
1
0
vld =
1
В следующем случае система линейных уравнений не имеет решений.
[x2,vld2] = gflineq(zeros(3,3),[1;0;0])
This linear equation has no solution.
x2 =
[]
vld2 =
0
Алгоритм:
Функция gflineq использует гауссово исключение переменных.
Наверх
gfminpol — поиск минимального полнома для элемента конечного поля
Внимание! Приведенное ниже описание относится к версии 2.0 пакета Communications, (MATLAB 6.1). В версии 2.1 (MATLAB 6.5) фильтрация данных, представленных в виде объектов двоичных конечных полей (в том числе расширенных), производится с помощью функции filter, а данная функция применяется только к полям GF(p), где p — простое число, большее двух.
Синтаксис:
pol = gfminpol(k,m);
pol = gfminpol(k,primpoly);
pol = gfminpol(k,m,p);
pol = gfminpol(k,primpoly,p);
Описание:
pol = gfminpol(k,m)
Находит минимальный полином для элемента a k конечного поля GF(2), где a — корень примитивного полинома, используемого по умолчанию для поля GF(2m). Входной параметр m — целое число, большее единицы. Возвращаемый результат pol имеет следующий формат:
-
Если k — неотрицательное целое число, то pol — вектор-строка, содержащий коэффициенты минимального полинома в порядке возрастания степеней.
-
Если k — вектор длины len, все элементы которого являются неотрицательными целыми числами, то pol — матрица, имеющая len строк; ее r-я строка содержит коэффициенты минимального полинома для элемента a k(r) в порядке возрастания степеней.
pol = gfminpol(k,primpoly)
То же, что первый вариант синтаксиса, но a является корнем примитивного полинома для поля GF(2m), заданного вторым входным параметром primpoly. Параметр primpoly должен быть вектором-строкой, содержащим коэффициенты примитивного полинома степени m в порядке возрастания степеней.
pol = gfminpol(k,m,p)
То же, что первый вариант синтаксиса, но вместо 2 в качестве характеристики поля используется значение третьего входного параметра p (он должен быть простым числом).
pol = gfminpol(k,primpoly,p)
То же, что первый вариант синтаксиса, но вместо 2 в качестве характеристики поля используется значение третьего входного параметра p (он должен быть простым числом) и, кроме того, a является корнем примитивного полинома для поля GF(pm), заданного вторым входным параметром primpoly. Параметр primpoly должен быть вектором-строкой, содержащим коэффициенты примитивного полинома степени m в порядке возрастания степеней.
Примеры:
Приведенный ниже код определяет, какие элементы поля GF(24) принадлежат также и полю GF(22), проверяя степени их минимальных полиномов.
p = 2; m = 4; %Рассматриваем элементы поля GF(16)
primpoly = gfprimdf(4);
%Получаем минимальные полиномы для всех элементов, кроме 0 и 1
k = [1:p^m-2];
minpolys = gfminpol(k,primpoly);
%Ищем минимальные полиномы, степень которых равна 2
gf4=[];
for ii = 1:p^m-2
if length(gftrunc(minpolys(ii,:)))==3 %Полином степени 2
gf4=[gf4, ii];
end
end
disp([‘Элементами поля GF(4) являются 0, 1, alpha^’,…
int2str(gf4(1)),’ и alpha^’,int2str(gf4(2))])
disp(‘где alpha – корень примитивного полинома в поле GF(16)’)
gfpretty(primpoly)
Вот результат работы данного примера:
Элементами поля GF(4) являются 0, 1, alpha^5 и alpha^10
где alpha — корень примитивного полинома в поле GF(16)
1 + X + X4
Наверх
gfmul — умножение элементов конечного поля
Внимание!
Приведенное ниже описание относится к версии 2.0 пакета Communications, (MATLAB 6.1). В версии 2.1 (MATLAB 6.5) умножение объектов двоичных конечных полей (в том числе расширенных) производится с помощью оператора “.*”, а данная функция применяется только к полям GF(pm), где p — простое число, большее двух.
Синтаксис:
c = gfmul(a,b);
c = gfmul(a,b,p);
c = gfmul(a,b,field);
Описание:
Функция gfmul производит умножение элементов конечного поля. Для перемножения полиномов, заданных над конечным полем, используется функция gfconv.
c = gfmul(a,b)
Выполняет умножение двух элементов поля GF(2). Входные параметры и результат работы могут быть равны 0 или 1, поскольку вычисления производятся в поле GF(2). Если a и b — матрицы одинакового размера, они обрабатываются поэлементно.
c = gfmul(a,b,p)
Выполняет умножение двух элементов поля GF(p), где p — простое число. Входные параметры a и b должны лежать в диапазоне от 0 до p – 1, в том же диапазоне будет находиться и результат c. Если a и b — матрицы одинакового размера, они обрабатываются поэлементно.
c = gfmul(a,b,field)
Выполняет умножение двух элементов поля GF(pm), где m — положительное целое число. Входные параметры a и b — сомножители, представленные в экспоненциальном формате по отношению к некоторому примитивному элементу поля GF(pm). Третий входной параметр field представляет собой матрицу, в которой перечислены все элементы поля GF(pm), упорядоченные по степеням того же самого примитивного элемента. Получить такую матрицу можно с помощью функции gftuple. Результат c — произведение, представленное в экспоненциальном формате по отношению к тому же самому примитивному элементу. Если входные параметры a и b представляют собой матрицы одинакового размера, они перемножаются поэлементно.
Примеры:
Приведенный ниже код строит таблицу умножения для поля GF(5). Если a и b лежат в диапазоне от 0 до 4, то элемент матрицы gfp_mul(a+1,b+1) содержит значение произведения a*b, вычисленного в поле GF(5). Например, gfp_mul(3,5) = 3, поскольку ((2*4) mod 5) = 3.
p = 5;
row = 0:p-1;
table = ones(p,1)*row;
gfp_mul = gfmul(table,table’,p)
gfp_mul =
0 0 0 0 0
0 1 2 3 4
0 2 4 1 3
0 3 1 4 2
0 4 3 2 1
Приведенный ниже код показывает, что в поле GF(9) выполняется равенство a 2 ´ a 4 = a 6, где a — корень примитивного полинома 2 + 2x + x2.
p = 3; m = 2;
primpoly = [2 2 1];
field = gftuple([-1:p^m-2]’,primpoly,p);
a = gfmul(2,4,field)
a =
6
Наверх
gfplus — сложение элементов расширенных конечных полей с характеристикой 2 (в версиях пакета начиная с 2.1 (R13) вместо данной функции используется оператор «+», поэтому функция числится устаревшей, хотя по-прежнему доступна для использования)
Внимание!
Приведенное ниже описание относится к версии 2.0 пакета Communications, (MATLAB 6.1). В версии 2.1 (MATLAB 6.5) сложение объектов двоичных конечных полей (в том числе расширенных) производится с помощью оператора “+”, а данная функция объявлена устаревшей.
Синтаксис:
k = gfplus(a,b,fvec,ivec);
Описание:
k = gfplus(a,b,fvec,ivec)
Выполняет сложение элементов a и b в поле GF(2m), используя экспоненциальный формат для представления входных и выходных параметров. Если a и b являются матрицами, они должны иметь одинаковый размер; в этом случае они суммируются поэлементно.
Входные параметры fvec и ivec должны быть векторами длиной 2m. Элементы обоих векторов должны быть целыми числами, лежащими в диапазоне от 0 до 2m – 1. Вектор fvec содержит ту же информацию, что параметр field, используемый функцией gfadd, но не в виде матрицы двоичных цифр, а в виде числового вектора. Вектор ivec содержит таблицу обратного преобразования элементов поля. Чтобы вычислить значения fvec и ivec, задайте m и используйте следующие команды:
fvec = bi2de(gftuple([-1 : 2^m-2]’,m));
ivec(fvec + 1) = 0 : 2^m — 1;
В приведенном выше варианте для формирования экспоненциального представления элементов поля используется примитивный полином, определенный в пакете Communications по умолчанию. Можно использовать иной примитивный полином, получив вектор его коэффициентов pol с помощью функции gfprimfd и передав этот вектор функции gftuple:
fvec = bi2de(gftuple([-1 : 2^m-2]’,pol));
ivec(fvec + 1) = 0 : 2^m — 1;
Примеры:
В данном примере суммируются две матрицы, содержащие случайные ненулевые элементы поля GF(25).
m = 5; % Создаем две случайных матрицы размером 3 на 6 в поле GF(2^5)
a = randint(3,6,2^m-1,1234);
b = randint(3,6,2^m-1);
fvec = gftuple([-1 : 2^m — 2]’,m)*2.^[0 : m-1]’;
ivec(fvec + 1) = 0 : 2^m — 1;
aplusb = gfplus(a,b,fvec,ivec) % Суммируем матрицы
aplusb =
22 25 4 23 9 29
9 30 24 23 -Inf 19
15 17 10 12 25 30
Наверх
gfpretty — отображение полинома в традиционном формате
Синтаксис:
gfpretty(a)
gfpretty(a,st)
gfpretty(a,st,n)
Описание:
-
gfpretty(a)
Отображает полином в традиционном формате относительно переменной X. Коэффициенты полинома задаются вектором-строкой a в порядке возрастания степеней. Слагаемые полинома выводятся также в порядке возрастания степеней. Члены с нулевыми коэффициентами не отображаются.
-
gfpretty(a,st)
То же, что первый вариант синтаксиса, но формируется полином не от X, а от переменной, задаваемой строковым параметром st.
-
gfpretty(a,st,n)
То же, что первый вариант синтаксиса, но формируется полином не от X, а от переменной, задаваемой строковым параметром st, и каждая выводимая строка имеет длину n символов вместо принятого по умолчанию значения 79.
Замечание. Выводимый результат будет выглядеть корректно только при использовании шрифта фиксированной ширины. Это касается всех вариантов синтаксиса.
Примеры:
Приведенный ниже код выводит утверждение о свойствах элементов конечного поля GF(16).
p = 2; m = 4;
ii = randint(1,1,[1,p^m-2]); % Случайный показатель степени для примитивного элемента
primpolys = gfprimfd(m,’all’);
[rows, cols] = size(primpolys);
jj = randint(1,1,[1,rows]); % Случайный примитивный полином
disp(‘Если A является корнем примитивного полинома’)
gfpretty(primpolys(jj,:)) % Полином относительно X
disp(‘то элемент’)
gfpretty([zeros(1,ii),1],’A’) % Полином A^ii
disp(‘может также быть представлен в виде’)
gfpretty(gftuple(ii,m,p),’A’) % Полином относительно A
Вот результат работы данного примера:
Если A является корнем примитивного полинома
4
1 + X + X
то элемент
14
A
может также быть представлен в виде
3
1 + A
Наверх
gfprimck — проверка полинома в конечном поле на примитивность
Внимание! Приведенное ниже описание относится к версии 2.0 пакета Communications, (MATLAB 6.1). В версии 2.1 (MATLAB 6.5) поиск корней полинома в двоичных конечных полях (в том числе расширенных) производится с помощью функции roots, а данная функция применяется только к полям GF(pm), где p — простое число, большее двух.
Синтаксис:
ck = gfprimck(a);
ck = gfprimck(a,p);
Описание:
ck = gfprimck(a)
Возвращает флаг ck, индицирующий, является ли полином в конечном поле GF(2) неприводимым или примитивным. Входной параметр a — вектор-строка, содержащий коэффициенты полинома в порядке возрастания степеней. Каждый коэффициент может быть равен 0 или 1, поскольку рассматривается двоичное поле GF(2). Если степень полинома равна m, то результат работы ck равен:
-
–1, если a не является неприводимым полиномом.
-
0, если a является неприводимым, но не является примитивным в поле GF(2m).
-
1, если a — примитивный полином для поля GF(2m).
Полином с нулевыми коэффициентами трактуется как не являющийся неприводимым. Все полиномы нулевой и первой степени считаются примитивными.
ck = gfprimck(a,p)
То же, что предыдущий вариант синтаксиса, но в качестве характеристики поля вместо 2 используется значение параметра p, который должен быть простым числом.
Примеры:
Приведенный ниже код демонстрирует неприводимость всех минимальных полиномов. Однако минимальный полином для непримитивного элемента не является примитивным. В примере принято p = 3; m = 4, то есть рассматривается конечное поле GF(34).
p = 3; m = 4;
% Используем примитивный полином по умолчанию
prim_poly = gfminpol(1,m,p);
ckprim = gfprimck(prim_poly,p);
% ckprim = 1, так как prim_poly представляет примитивный полином
notprimpoly = gfminpol(5,m,p);
cknotprim = gfprimck(notprimpoly,p);
% cknotprim = 0 (неприводимый, но не примитивный),
% так как alpha^5 не является примитивным элементом для p = 3
ckreducible = gfprimck([0 1 1],p);
% ckreducible = -1, так как полином является приводимым
Алгоритм:
Неприводимый полином степени 2 и более, заданный в конечном поле GF(p), считается примитивным в том и только том случае, если он не является делителем полинома –1 + xk для всех положительных целых k, меньших чем pm – 1.
Наверх
gfprimdf — генерация примитивных полиномов по умолчанию для конечного поля
Внимание! Приведенное ниже описание относится к версии 2.0 пакета Communications, (MATLAB 6.1). В версии 2.1 (MATLAB 6.5) генерация примитивных полиномов для двоичных конечных полей (в том числе расширенных) производится с помощью функции primpoly, а данная функция применяется только к полям GF(pm), где p — простое число, большее двух.
Синтаксис:
pol = gfprimdf(m);
pol = gfprimdf(m,p);
Описание:
pol = gfprimdf(m)
Возвращает вектор-строку, содержащий коэффициенты (в порядке возрастания степеней) примитивного полинома, используемого пакетом Communications Toolbox по умолчанию для поля GF(2m). Входной параметр m — положительное целое число.
pol = gfprimdf(m,p)
Возвращает вектор-строку, содержащий коэффициенты (в порядке возрастания степеней) примитивного полинома, используемого пакетом Communications Toolbox по умолчанию для поля GF(pm). Входной параметр m — положительное целое число, входной параметр p — простое число.
< I>
Примеры:
Приведенная ниже команда показывает, что примитивным полиномом для поля GF(52) по умолчанию является полином 2 + x + x2.
pol = gfprimdf(2,5)
pol =
2 1 1
Приведенный ниже код отображает примитивные полиномы, используемые по умолчанию для полей GF(2m), где mменяется от 3 до 5.
for m = 3:5
gfpretty(gfprimdf(m))
end
3
1 + X + X
4
1 + X + X
2 5
1 + X + X
Наверх
gfprimfd — поиск примитивных полиномов в конечном поле
Внимание! Приведенное ниже описание относится к версии 2.0 пакета Communications, (MATLAB 6.1). В версии 2.1 (MATLAB 6.5) поиск примитивных полиномов для двоичных конечных полей (в том числе расширенных) производится с помощью функции primpoly, а данная функция применяется только к полям GF(pm), где p — простое число, большее двух.
Синтаксис:
pol = gfprimfd(m);
pol = gfprimfd(m,opt);
pol = gfprimfd(m,opt,p);
Описание:
Для всех вариантов синтаксиса, если m = 1, возвращается результат pol = [1 1].
Полином представляется в виде вектора-строки, содержащего коэффициенты в порядке возрастания степеней.
pol = gfprimfd(m)
Возвращает вектор, строку, содержащий один примитивный полином для поля GF(2m). Входной параметр m должен быть положительным целым числом.
pol = gfprimfd(m,opt)
Осуществляет поиск одного или нескольких примитивных полиномов для поля GF(2m), где m — положительное целое число. Если m > 1, то результат pol зависит от второго входного параметра opt согласно приведенной ниже таблице.
|
Значение opt |
Смысл результата pol |
Формат результата pol |
|
‘min’ |
Один примитивный полином для поля GF(2m), имеющий минимально возможное число ненулевых коэффициентов |
Вектор-строка, представляющий полином |
|
‘max’ |
Один примитивный полином для поля GF(2m), имеющий максимально возможное число ненулевых коэффициентов |
Вектор-строка, представляющий полином |
|
‘all’ |
Все примитивные полиномы для поля GF(2m) |
Матрица, каждая строка которой представляет один примитивный полином |
|
Положительное целое число |
Все примитивные полиномы для поля GF(2m), имеющие ровно opt ненулевых коэффициентов |
Матрица, каждая строка которой представляет один примитивный полином |
pol = gfprimfd(m,opt,p)
То же, что pol = gfprimfd(m,opt), однако в качестве характеристики поля вместо двойки используется значение параметра p, который должен быть простым числом. Таким образом, в данном случае вычисления производятся для поля GF(pm).
Примеры
Приведенный ниже код осуществляет поиск примитивных полиномов для поля GF(32), имеющих различные дополнительные свойства. Обратите внимание на то, что переменная fourterms оказывается пустой матрицей, поскольку для данного поля не существует примитивных полиномов, имеющих ровно четыре ненулевых коэффициента. Также отметьте, что переменная manyterms представляет один примитивный полином, имеющий ровно пять ненулевых коэффициентов, а переменная fiveterms представляет все примитивные полиномы, имеющие ровно пять ненулевых коэффициентов.
p = 2; m = 5; % Работаем в поле GF(32)
manyterms = gfprimfd(5,’max’)
fiveterms = gfprimfd(5,5)
fourterms = gfprimfd(5,4)
Ниже приводится результат работы примера.
manyterms =
1 1 1 1 0 1
fiveterms =
1 1 1 1 0 1
1 1 1 0 1 1
1 1 0 1 1 1
1 0 1 1 1 1
No primitive polynomial satisfies the given constraints.
fourterms =
[]
Алгоритм:
Функция gfprimfd тестирует полиномы на примитивность, используя для этого функцию gfprimck. Если параметр opt имеет значение ‘min’, ‘max’ или опущен, то полиномы конструируются путем формирования m-значных представлений целых чисел в системе счисления с основанием p. Последовательно перебирая целые числа в направлении увеличения или уменьшения, функция gfprimfd возвращает первый найденный полином, удовлетворяющий заданным условиям.
Наверх
gfrank — вычисление ранга матрицы в конечном поле
Внимание! Приведенное ниже описание относится к версии 2.0 пакета Communications, (MATLAB 6.1). В версии 2.1 (MATLAB 6.5) фильтрация данных, представленных в виде объектов двоичных конечных полей (в том числе расширенных), производится с помощью функции filter, а данная функция применяется только к полям GF(p), где p — простое число, большее двух.
Синтаксис:
rk = gfrank(A);
rk = gfrank(A,p);
Описание:
-
rk = gfrank(A)
Вычисляет ранг матрицы A в конечном поле GF(2).
-
rk = gfrank(A,p)
Вычисляет ранг матрицы A в конечном поле GF(p), где p — простое число.
Алгоритм:
Функция gfrank использует алгоритм, аналогичный гауссову исключению переменных.
Примеры:
В приведенном ниже коде функция gfrank показывает, что ранг матрицы A меньше максимального. Этот вывод соответствует действительности, поскольку определитель матрицы A, вычисленный с использованием обычной арифметики, является четным (то есть равным нулю по модулю два).
A=[1 0 1;
1 1 0;
0 1 1];
det_a = det(A); % Обычный определитель матрицы A
detmod2 = rem(det(A),2); % Определитель, взятый по модулю два
rank2 = gfrank(A); % Ранг в двоичном конечном поле
disp([‘Определитель = ‘,num2str(det_a)])
disp([‘Определитель mod 2 = ‘,num2str(detmod2)])
disp([‘Ранг в поле GF(2) = ‘,num2str(rank2)])
Ниже показан результат работы примера.
Определитель = 2
Определитель mod 2 = 0
Ранг в поле GF(2) = 2
Обратите внимание на то, что функция gflineq находит только тривиальное (нулевое) решение системы уравнений Ax = 0, хотя из немаксимального ранга матрицы A следует существование бесконечного множества решений.
sol = gflineq(A,[0;0;0])’
sol =
0 0 0
Наверх
gfrepcov — преобразование между двумя формами представления полиномов в конечном поле GF(2)
Внимание! Приведенное ниже описание относится к версии 2.0 пакета Communications, (MATLAB 6.1). В версии 2.1 (MATLAB 6.5) фильтрация данных, представленных в виде объектов двоичных конечных полей (в том числе расширенных), производится с помощью функции filter, а данная функция применяется только к полям GF(p), где p — простое число, большее двух.
Синтаксис:
polystandard = gfrepcov(poly2)
Описание:
В двоичном конечном поле GF(2) существует два логичных способа представления полиномов.
-
Вектор [A_0 A_1 A_2 … A_(m-1)] представляет полином
-
A_0 + A_1 x + A_2 x2 + … + A_(m–1) xm–1,
то есть элементы вектора представляют собой коэффициенты полинома, перечисленные в порядке возрастания степеней. Каждый элемент вектора, A_k, может быть равен нулю или единице. Вектор [A_0 A_1 A_2 … A_(m-1)] представляет полином
xA_0 + xA_1 + xA_2 + … + xA_(m–1),
то есть элементы вектора перечисляют показатели степени ненулевых слагаемых полинома. Элементы вектора, A_k, должны быть неотрицательными целыми числами. Все элементы вектора должны быть различными.
Формат 1 является стандартным для функций работы с конечными полями из пакета Communications, однако в некоторых случаях формат 2 оказывается более удобным.
polystandard = gfrepcov(poly2)
Преобразует формат 2 в формат 1. Степень полинома должна быть не меньше двух. Параметры poly2 и polystandard — векторы-строки. Элементы вектора poly2 должны быть различными целыми числами и хотя бы одно из них должно быть дольше единицы. Элементы результирующего вектора polystandard равны 0 или 1.
Замечание. Если вектор poly2 является двоичным (то есть его элементу равны 0 или 1), функция gfrepcov считает, что он уже представлен в формате 1, и возвращает вектор неизмененным.
Примеры:
Приведенная ниже команда преобразует формат представления полинома 1 + x2 + x5.
polystandard = gfrepcov([0 2 5])
polystandard =
1 0 1 0 0 1
Наверх
gfroots — поиск корней полинома в простом конечном поле
Внимание! Приведенное ниже описание относится к версии 2.0 пакета Communications, (MATLAB 6.1). В версии 2.1 (MATLAB 6.5) поиск корней полинома в двоичных конечных полях (в том числе расширенных) производится с помощью функции roots, а данная функция применяется только к полям GF(pm), где p — простое число, большее двух.
Синтаксис:
rt = gfroots(f);
rt = gfroots(f,m);
rt = gfroots(f,primpoly);
rt = gfroots(f,m,p);
rt = gfroots(f,primpoly,p);
[rt,rt_tuple] = gfroots(…);
[rt,rt_tuple,field] = gfroots(…);
Описание:
Для всех вариантов синтаксиса параметр f — это вектор-строка, содержащий коэффициенты полинома степени d в порядке возрастания степеней.
Замечание. Результат работы функции gfroots содержит каждый корень полинома ровно один раз, независимо от его кратности.
-
rt = gfroots(f)
Находит в конечном поле GF(2d) корни полинома, представленного вектором f. Результат rt — вектор-столбец, содержащий корни полинома в экспоненциальном формате. Экспоненциальный формат формируется по отношению к корню примитивного полинома, используемого для поля GF(2d) по умолчанию.
-
rt = gfroots(f,m)
Находит в конечном поле GF(2m) корни полинома, представленного вектором f. Параметр m должен быть целым числом, большим или равным степени полинома d. Результат rt — вектор-столбец, содержащий корни полинома в экспоненциальном формате. Экспоненциальный формат формируется по отношению к корню примитивного полинома, используемого для поля GF(2m) по умолчанию.
-
rt = gfroots(f,primpoly)
Находит в конечном поле GF(2m) корни полинома, представленного вектором f. Результат rt — вектор-столбец, содержащий корни полинома в экспоненциальном формате. Экспоненциальный формат формируется по отношению к корню примитивного полинома, представленного входным параметром primpoly. Этот параметр должен представлять полином степени m, являющийся примитивным для поля GF(2m). Здесь m — целое число, большее или равное степени полинома d.
-
rt = gfroots(f,m,p)
То же, что и rt = gfroots(f,m), но вычисления производятся в конечном поле GF(pm). Параметр p должен быть простым числом.
-
rt = gfroots(f,primpoly,p)
То же, что и rt = gfroots(f,primpoly), но вычисления производятся в конечном поле GF(pm). Параметр p должен быть простым числом.
-
[rt,rt_tuple] = gfroots(…)
Дополнительно возвращает матрицу rt_tuple, k-я строка которой представляет найденный корень rt(k) в полиномиальном формате. Полиномиальный (rt_tuple) и экспоненциальный (rt) форматы формируются по отношению к одному и тому же примитивному элементу.
-
[rt,rt_tuple,field] = gfroots(…)
Дополнительно возвращает матрицы rt_tuple и field. Описание матрицы rt_tuple приведено выше. Матрица field содержит список элементов расширенного поля. Этот список (field), а также полиномиальный (rt_tuple) и экспоненциальный (rt) форматы результата формируются по отношению к одному и тому же примитивному элементу.
Примеры:
Приведенный ниже код находит полиномиальный формат корней примитивного полинома в поле GF(16). Затем корни представляются в традиционной форме — как полиномы от переменной alpha. Поскольку primpoly одновременно является примитивным полиномом и анализируемым полиномом, переменная alpha сама является его корнем.
p = 2; m = 4;
primpoly = [1 0 0 1 1]; % Примитивный полином для поля GF(16)
f = primpoly; % Будем искать корни примитивного полинома
[rt,rt_tuple] = gfroots(f,primpoly,p);
% Отображаем корни в виде полиномов от alpha
for ii = 1:length(rt_tuple)
gfpretty(rt_tuple(ii,:),’alpha’)
end
Наверх
gfsub — вычитание полиномов в конечном поле
Внимание!
Приведенное ниже описание относится к версии 2.0 пакета Communications, (MATLAB 6.1). В версии 2.1 (MATLAB 6.5) вычитание объектов двоичных конечных полей (в том числе расширенных) производится с помощью оператора “–”, а данная функция применяется только к полям GF(pm), где p — простое число, большее двух.
Синтаксис:
c = gfsub(a,b);
c = gfsub(a,b,p);
c = gfsub(a,b,p,len);
c = gfsub(a,b,field);
Описание:
c = gfsub(a,b)
Выполняет вычитание (a – b) двух полиномов над полем GF(2). Входные параметры и результат работы представляют собой векторы-строки, содержащие коэффициенты соответствующих полиномов в порядке возрастания степеней. Каждый коэффициент может быть равен 0 или 1, поскольку вычисления производятся в поле GF(2). Если a и b — матрицы одинакового размера, они обрабатываются построчно.
c = gfsub(a,b,p)
Выполняет вычитание (a – b) двух полиномов над полем GF(p), где p — простое число. Параметры a, b и c представляют собой векторы-строки, содержащие коэффициенты соответствующих полиномов в порядке возрастания степеней. Возможные значения коэффициентов лежат в диапазоне от 0 до p – 1. Если a и b — матрицы одинакового размера, они обрабатываются построчно.
c = gfsub(a,b,p,len)
То же, что и предыдущий вариант синтаксиса, но длина возвращаемого вектора гарантированно равна len. Результат c обрезается или дополняется нулями, чтобы получить вектор нужной длины.
c = gfsub(a,b,field)
Выполняет вычитание (a – b) двух элементов поля GF(pm), где m — положительное целое число. Входные параметры a и b — соответственно уменьшаемое и вычитаемое, представленные в экспоненциальном формате по отношению к некоторому примитивному элементу поля GF(pm). Третий входной параметр field представляет собой матрицу, в которой перечислены все элементы поля GF(pm), упорядоченные по степеням того же самого примитивного элемента. Получить такую матрицу можно с помощью функции gftuple. Результат c — разность, представленная в экспоненциальном формате по отношению к тому же самому примитивному элементу. Если входные параметры a и b представляют собой матрицы одинакового размера, производится поэлементное вычитание.
Примеры:
В приведенном ниже коде переменной differ присваивается значение разности полиномов 2 + 3x + x2 and 4 + 2x + 3×2 в поле GF(5), а переменной linpart — значение той же разности, но обрезанное так, чтобы максимальная степень результирующего полинома была равна единице.
differ = gfsub([2 3 1],[4 2 3],5)
differ =
3 1 3
linpart = gfsub([2 3 1],[4 2 3],5,2)
linpart =
3 1
Приведенный ниже код показывает, что в поле GF(9) выполняется равенство a 2 – a 4 = a 7, где a — корень примитивного полинома 2 + 2x + x2.
p = 3; m = 2;
primpoly = [2 2 1];
field = gftuple([-1:p^m-2]’,primpoly,p);
d = gfsub(2,4,field)
d =
7
Наверх
gftrunc — минимизация длины полиномиального представления
Синтаксис:
c = gftrunc(a);
Описание:
-
c = gftrunc(a)
Укорачивает вектор-строку a, содержащий коэффициенты полинома в конечном поле GF(p) в порядке возрастания степеней. Если a(k) = 0 для всех k > d + 1, то степень полинома равна d. В результирующем векторе c эти последние нулевые элементы отбрасываются, так что длина вектора составит d + 1.
Примеры:
Приведенный ниже код показывает, что из вектора, представляющего полином x2 + 2×3 + 3×4 + 4×7 + 5×8, функция gftrunc удаляет только концевые нули, сохраняя нули, расположенные в начале и середине вектора.
c = gftrunc([0 0 1 2 3 0 0 4 5 0 0])
c =
0 0 1 2 3 0 0 4 5
Наверх
gftuple — упрощение или преобразование формата представления элементов конечного поля
Внимание! Приведенное ниже описание относится к версии 2.0 пакета Communications, (MATLAB 6.1). В версии 2.1 (MATLAB 6.5) соответствующие вычисления для двоичных конечных полей (в том числе расширенных) производятся с помощью оператора возведения в степень (.^) и функции log, а данная функция применяется только к полям GF(pm), где p — простое число, большее двух.
Синтаксис:
tp = gftuple(a,m);
tp = gftuple(a,primpoly);
tp = gftuple(a,m,p);
tp = gftuple(a,primpoly,p);
tp = gftuple(a,primpoly,p,prim_ck);
[tp,expform] = gftuple(…);
Описание:
Общая информация о синтаксисе
Функция gftuple служит для упрощения полиномиального или экспоненциального формата представления элементов конечных полей, а также для преобразования одного формата в другой.
В данном описании формат элемента конечного поля GF(pm) называется простейшим, если все экспоненты примитивного элемента удовлетворяют следующим условиям:
-
Лежат в пределах от 0 до m – 1 для полиномиального формата.
-
Равны -Inf или лежат в пределах от 0 до pm – 2 для экспоненциального формата.
Для всех вариантов синтаксиса входной параметр a является матрицей, каждая строка которой представляет один элемент конечного поля. Интерпретация матрицы a зависит от ее размера:
-
Если a представляет собой вектор-столбец целых чисел, то MATLAB интерпретирует элементы этого вектора как элементы конечного поля, представленные в экспоненциальном формате. Все отрицательные числа считаются эквивалентными -Inf и представляют нулевой элемент поля.
-
Если a содержит несколько столбцов, то MATLAB интерпретирует каждую строку как представление элемента конечного поля в полиномиальном формате. (Элементы матрицы a должны быть целыми числами, лежащими в диапазоне от 0 до p – 1, где p — характеристика конечного поля. Если параметр p при вызове функции не задан, по умолчанию он считается равным 2.)
Как экспоненциальный, так и полиномиальный форматы представления определяются по отношению к конкретному примитивному элементу поля. Способ выбора этого примитивного элемента описывается далее, при рассмотрении конкретных вариантов синтаксиса.
Конкретные варианты синтаксиса:
tp = gftuple(a,m)
Возвращает представление элементов из матрицы a в простейшем полиномиальном формате. При этом k-я строка результата tp соответствует k-й строке матрицы a. Форматы определяются по отношению к корню примитивного полинома, используемого по умолчанию для поля GF(2m).Входной параметр m — положительное целое число. Если возможно, производится упрощение полиномиальных форматов с помощью примитивного полинома по умолчанию.
Tp = gftuple(a,primpoly)
Возвращает представление элементов из матрицы a в простейшем полиномиальном формате. При этом k-я строка результата tp соответствует k-й строке матрицы a. Форматы определяются по отношению к корню примитивного полинома, коэффициенты которого содержатся, в порядке возрастания степеней, в векторе-строке primpoly. Если возможно, производится упрощение полиномиальных форматов с помощью данного примитивного полинома.
Tp = gftuple(a,m,p)
То же, что tp = gftuple(a,m), однако в качестве характеристики поля вместо двойки используется значение параметра p, который должен быть простым числом. Таким образом, в данном случае вычисления производятся для поля GF(pm).
Tp = gftuple(a,primpoly,p)
То же, что tp = gftuple(a,primpoly), однако в качестве характеристики поля вместо двойки используется значение параметра p, который должен быть простым числом. Таким образом, в данном случае вычисления производятся для поля GF(pm).
Tp = gftuple(a,primpoly,p,prim_ck)
То же, что tp = gftuple(a,primpoly,p), однако, функция gftuple проверяет, действительно ли полином, представляемый параметром primpoly, является примитивным. Если нет, функция gftuple генерирует сообщение об ошибке и результат tp не возвращается. Последний входной параметр prim_ck может быть произвольным силом или строкой; имеет значение только его наличие.
[tp,expform] = gftuple(…)
Дополнительно возвращает матрицу expform, k-я строка которой содержит представление элемента из k-й строки матрицы a в простейшем экспоненциальном формате.
Примеры:
Приведенный ниже вызов функции gftuple генерирует список элементов поля GF(pm), упорядоченный по отношению к корню примитивного полинома, используемого по умолчанию. Некоторые функции пакета Communications используют такой список в качестве входного параметра.
p = 5; % Произвольное простое число
m = 4; % Произвольное положительное целое число
field = gftuple([-1:p^m-2]’,m,p);
Две следующих команды иллюстрируют влияние формы входной матрицы на ее интерпретацию. В первом случае вектор-столбец трактуется как последовательность элементов, представленных в экспоненциальном формате. Во втором случае вектор-строка трактуется как единственный элемент, представленный в полиномиальном формате.
tp1 = gftuple([0; 1],3)
tp1 =
1 0 0
0 1 0
tp2 = gftuple([0, 0, 0, 1],3)
tp2 =
1 1 0
Полученные результаты показывают, что при использовании примитивного полинома, принятого для поля GF(8) по умолчанию, имеют место следующие равенства:
a0 = 1 + 0a+ 0a2,
a1 = 0 + 1a + 0a2,
0 + 0a + 0a2 + a3 = 1 + a + 0a2.
Наверх
bi2de — преобразование векторов, содержащих цифры, в числа
Синтаксис:
d = bi2de(b);
d = bi2de(b,flg);
d = bi2de(b,p);
d = bi2de(b,p,flg);
Описание:
d = bi2de(b)
Преобразует вектор-строку двоичных цифр b в неотрицательное целое число. Если b — матрица, каждая ее строка обрабатывается отдельно. В этом случае результат d является вектором-столбцом, каждый элемент которого представляет в целочисленном виде соответствующую строку матрицы b.
Замечание. По умолчанию функция bi2de интерпретирует первый столбец параметра b как цифры младшего разряда.
d = bi2de(b,flg)
То же, что предыдущий вариант синтаксиса, но строковый параметр flg определяет, является первый столбец параметра b цифрами младшего или старшего разряда. Возможные значения для flg — ‘right-msb’ (первый столбец — младший разряд) и ‘left-msb’ (первый столбец — старший разряд). По умолчанию используется вариант ‘right-msb’.
d = bi2de(b,p)
Преобразует вектор-строку b, состоящую из p-ичных цифр (p — основание использованной системы счисления), в неотрицательное целое число. Параметр p должен быть целым числом, не меньшим двух. Первый столбец параметра bинтерпретируется как цифра младшего разряда. Если b — матрица, результат d является вектором-столбцом, каждый элемент которого представляет в целочисленном виде соответствующую строку матрицы b.
d = bi2de(b,p,flg)
То же, что предыдущий вариант синтаксиса, но строковый параметр flg определяет, является первый столбец параметра b цифрами младшего или старшего разряда. Возможные значения для flg — ‘right-msb’ (первый столбец — младший разряд) и ‘left-msb’ (первый столбец — старший разряд). По умолчанию используется вариант ‘right-msb’.
Примеры.
Приведенный ниже код генерирует матрицу, содержащую двоичные представления пяти случайных целых чисел, лежащих в диапазоне от 0 до 15. Затем двоичные представления конвертируются в целые числа.
b = randint(5,4); % Создаем случайную двоичную матрицу размером 5 на 4
de = bi2de(b);
disp(‘ Dec Binary’)
disp(‘ —— ——————-‘)
disp([de, b])
Пример результатов работы этого фрагмента кода приведен ниже. Полученные вами результаты могут отличаться от приведенных, поскольку в примере используются случайные числа.
Dec Binary
—— ——————-
13 1 0 1 1
7 1 1 1 0
15 1 1 1 1
4 0 0 1 0
9 1 0 0 1
Приведенная ниже команда преобразует набор пятеричных цифр в целое число, считая, что левая цифра (в данном примере — 4) представляет старший разряд. Данный пример отражает тот факт, что 4(53) + 2(52) +50 = 551.
d = bi2de([4 2 0 1],5,’left-msb’)
d =
551
Наверх
de2bi — преобразование чисел в векторы цифр
Синтаксис:
b = de2bi(d);
b = de2bi(d,n);
b = de2bi(d,n,p);
b = de2bi(d,[],p);
b = de2bi(d,…,flg)
Описание:
b = de2bi(d)
Преобразует неотрицательное целое число d в вектор-строку двоичных цифр b. Если d — вектор, результат b представляет собой матрицу, каждая строка которой является двоичным представлением соответствующего элемента вектора d. Если d является матрицей, функция de2bi трактует этот параметр как вектор d(:).
Замечание. По умолчанию функция de2bi размещает в первом столбце результата b цифры младшего разряда.
b = de2bi(d,n)
То же что b = de2bi(d), но результат содержит n столбцов, где n — положительное целое число. Если двоичные представления элементов вектора d требуют более чем n цифр, выдается сообщение об ошибке. При необходимости двоичные представления элементов вектора d дополняются нулями в старших разрядах.
b = de2bi(d,n,p)
Преобразует неотрицательное число d в вектор-строку p-ичных цифр, где p — целое число, не меньшее двух (оно задает основание используемой системы счисления). Первый столбец результата b содержит цифры младшего разряда. При необходимости b дополняется нулями, так что результат содержит n столбцов, где n — положительное целое число. Если p-ичные представления элементов вектора d требуют более чем n цифр, выдается сообщение об ошибке. Если d — вектор неотрицательных целых чисел, результат b представляет собой матрицу, каждая строка которой является p-ичным представлением (при необходимости дополненным нулями до n разрядов) соответствующего элемента из вектора d. Если d является матрицей, функция de2bi трактует этот параметр как вектор d(:).
b = de2bi(d,[],p)
При данном варианте синтаксиса задается основание системы счисления p, но не указывается число разрядов цифрового представления (число столбцов результата).
b = de2bi(d,…,flg)
При данном варианте синтаксиса строковый параметр flg определяет, цифры младшего или старшего разряда размещаются в первом столбце результата b. Возможные значения для flg — ‘right-msb’ (первый столбец — младший разряд) и ‘left-msb’ (первый столбец — старший разряд). По умолчанию используется вариант ‘right-msb’.
Примеры.
Приведенный ниже код выводит числа от 1 до 10 в десятичной и двоичной системах счисления.
d = (1:10)’;
b = de2bi(d);
disp(‘ Dec Binary ‘)
disp(‘ —— ——————-‘)
disp([d, b])
Результат работы кода выглядит. следующим образом:
Dec Binary
—— ——————-
1 1 0 0 0
2 0 1 0 0
3 1 1 0 0
4 0 0 1 0
5 1 0 1 0
6 0 1 1 0
7 1 1 1 0
8 0 0 0 1
9 1 0 0 1
10 0 1 0 1
Приведенная ниже команда показывает, как функция de2bi дополняет результат нулями в старших разрядах.
bb = de2bi([3 9],5) % Дополнение нулями до пяти разрядов
bb =
1 1 0 0 0
1 0 0 1 0
Приведенная ниже команда показывает, как получить троичное представление числа, не задавая число разрядов результата.
t = de2bi(12,[],3) % Преобразуем число 12 в троичное представление
t =
0 1 1
Наверх
istrellis — проверка того, является ли объект таблицей переходов сверточного кода
Синтаксис
[isok,status] = istrellis(s);
Описание
[isok,status] = istrellis(s)
Функция проверяет, является ли входной параметр s структурой, описывающей таблицу переходов сверточного кода. Если проверка дает положительный результат, выходной параметр isok равен 1, а выходной параметр status представляет собой пустую строку. В противном случае результат isok равен 0, а в выходном параметре status возвращается строка, описывающая, почему входной параметр s не может служить описанием сверточного кода.
Корректное описание сверточного кода представляет собой MATLAB-структуру, поля которой описаны в следующей таблице.
Таблица. Поля структуры описания сверточного кода, имеющего скорость k/n
|
Имя поля структуры |
Размерность |
Назначение |
|
numInputSymbols |
Скаляр |
Число возможных входных символов: 2k |
|
numOutputsymbols |
Скаляр |
Число возможных выходных символов: 2n |
|
numStates |
Скаляр |
Число внутренних состояний кодера |
|
nextStates |
Матрица: numStates строк, 2kстолбцов |
Таблица переходов, указывающая состояния кодера, в которые осуществляется переход, для всех комбинаций текущего состояния и входного символа |
|
outputs |
Матрица: numStates строк, 2kстолбцов |
Таблица формирования выходного сигнала, содержащая значения выходных символов для всех комбинаций текущего состояния и входного символа |
Элементы матрицы nextStates должны представлять собой целые числа в диапазоне от 0 до numStates–1. Элемент в s-й строке и u-м столбце указывает следующее состояние кодера, в которое осуществляется переход, если текущее состояние равно s – 1, а входной символ имеет десятичное представление u – 1. При преобразовании входных битов в десятичное представление первый входной бит должен считаться старшим (MSB). Например, второй столбец матрицы nextStates содержит номера состояний, в которые осуществляется переход, если входной символ представляет собой последовательность бит {0, …, 0, 1}.
Для получения десятичных значений внутренних состояний кодера используется следующее правило. Если k больше 1, то тот элемент памяти кодера, который получает первый (по времени) бит входного символа, соответствует младшимдвоичным разрядам номера состояния, а тот элемент памяти кодера, который получает последний бит входного символа, соответствует старшим двоичным разрядам номера состояния.
Элемент матрицы outputs, расположенный в s-й строке и u-м столбце, указывает выходной символ, генерируемый кодером, когда текущее состояние равно s – 1, а входной символ имеет десятичное представление u – 1. При преобразовании выходных битов в десятичное представление первый выходной бит должен считаться старшим (MSB).
Примеры
Приведенные ниже команды задают значения полей для описания очень простого сверточного кода и производят проверку корректности созданной структуры.
trellis.numInputSymbols = 2;
trellis.numOutputSymbols = 2;
trellis.numStates = 2;
trellis.nextStates = [0 1;0 1];
trellis.outputs = [0 0;1 1];
[isok,status] = istrellis(trellis)
isok =
1
status =
‘ ‘
Наверх
marcumq — обобщенная Q-функция Маркума
Синтаксис
Q = marcumq(a,b);
Q = marcumq(a,b,m);
Описание
Q = marcumq(a,b)
Вычисляет Q-функцию Маркума от аргументов a и b. Функция определяется следующей формулой:
Входные параметры a и b должны быть неотрицательными вещественными числами. В приведенной формуле I0обозначает модифицированную функцию Бесселя первого рода и нулевого порядка.
Q = marcumq(a,b,m)
Вычисляет обобщенную Q-функцию Маркума от аргументов a, b и m. Функция определяется следующей формулой:
Входные параметры a и b должны быть неотрицательными вещественными числами, а m — неотрицательным целым числом. В приведенной формуле Im – 1 обозначает модифицированную функцию Бесселя первого рода порядка m – 1.
Наверх
mask2shift — расчет задержки псевдослучайной последовательности, вносимой путем применения маски к сдвиговому регистру
Синтаксис
shift = mask2shift(prpoly,mask)
Описание
shift = mask2shift(prpoly,mask)
Возвращает величину задержки псевдослучайной последовательности, получаемой путем применения заданной маски mask к регистру сдвига с обратной связью. Обратные связи задаются с помощью примитивного полинома prpoly. Входной параметр prpoly может быть задан в одном из двух форматов:
-
В виде двоичного вектора, содержащего коэффициенты примитивного полинома в порядке убывания степеней.
-
В виде целого числа, двоичное представление которого дает коэффициенты примитивного полинома, так что младший двоичный разряд соответствует свободному члену полинома.
Входной параметр mask должен быть двоичным вектором с длиной, равной степени примитивного полинома prpoly.
Замечание. Для ускорения вычислений функция mask2shift не проверяет полином prpoly на примитивность. Если он не является примитивным, выдаваемый функцией результат не имеет смысла. Для нахождения примитивных полиномов используйте функцию primpoly или алгоритмы из [2].
Более подробная информация о связи маски регистра и задержки генерируемой псевдослучайной последовательности приведена на странице с описанием функции shift2mask.
Определение эквивалентной задержки
Если A — корень примитивного полинома, а m(A) — значение полинома, описывающего маску и вычисленного в точке A, то эквивалентная задержка s является решением уравнения As = m(A). При полиномиальном представлении маски элементы вектора mask трактуются как коэффициенты полинома, следующие в порядке убывания степеней.
Примеры
Первая из приведенных ниже команд рассчитывает задержку, эквивалентную маске x3 + 1, примененной к регистру с обратными связями, описываемыми примитивным полиномом x4 + x3 + 1. Вторая приведенная ниже команда показывает, что маска, равная 1, эквивалентна нулевой задержке. В обоих случаях обратите внимание на то, что длина вектора mask на единицу меньше, чем длина вектора prpoly.
s = mask2shift([1 1 0 0 1],[1 0 0 1])s = 4s2 = mask2shift([1 1 0 0 1],[0 0 0 1])s2 = 0
Наверх
oct2dec — преобразование чисел из восьмеричной системы счисления в десятичную
Синтаксис:
d = oct2dec(c)
Описание:
d = oct2dec(c)
Поэлементно конвертирует восьмеричную матрицу c в десятичную матрицу d. Как в восьмеричном, так и в десятичном представлениях самая правая цифра является младшим разрядом числа.
Замечание. Под восьмеричными числами здесь подразумеваются числа, в десятичной записи которых цифрытрактуются как восьмеричные. Поэтому, например, число 10 будет преобразовано в 1*8 = 8, а число 25 — в 2*8+5 = 21.
Примеры.
Приведенная ниже команда конвертирует восьмеричную матрицу размером 2 на 2.
d = oct2dec([12 144;0 25])
d =
10 100
0 21
Например, восьмеричное число 144 эквивалентно десятичному числу 100, поскольку 144 (восьмеричное) = 1*82 + 4*81 + 4*80 = 64 + 32 + 4 = 100.
Наверх
poly2trellis — преобразование представления сверточного кода из полиномиальной формы в таблицу переходов
Синтаксис
trellis = poly2trellis(ConstraintLength,CodeGenerator);
trellis = poly2trellis(ConstraintLength,CodeGenerator,…
FeedbackConnection);
Описание
Функция poly2trellis принимает на входе полиномиальное описание сверточного кода и возвращает структуру, содержащую соответствующую таблицу переходов. Эта структура может использоваться для описания кода при вызове функций convenc и vitdec.
trellis = poly2trellis(ConstraintLength,CodeGenerator)
Выполняет преобразование для кода со скоростью k/n без обратных связей. Входной параметр ConstraintLength должен быть вектором-строкой длиной k, указывающим число элементов памяти, используемых для каждого из k входных битов. Входной параметр CodeGenerator должен быть матрицей, имеющей k строк и n столбцов и содержащей восьмеричные числа, описывающие полиномиальную связь между каждым из n бит выходного символа и каждым из k бит входного символа.
trellis = poly2trellis(ConstraintLength,CodeGenerator,…FeedbackConnection)
То же, что предыдущий вариант синтаксиса, но для случая кодера с обратной связью. Входной параметр FeedbackConnection должен быть вектором-строкой длиной k, содержащим восьмеричные числа, описывающие обратные связи для каждого из k бит входного символа.
Для обоих вариантов синтаксиса результатом работы функции является MATLAB-структура, поля которой описаны в следующей таблице.
Таблица. Поля структуры описания сверточного кода, имеющего скорость k/n
|
Имя поля структуры |
Размерность |
Назначение |
|
numInputSymbols |
Скаляр |
Число возможных входных символов: 2k |
|
numOutputsymbols |
Скаляр |
Число возможных выходных символов: 2n |
|
numStates |
Скаляр |
Число внутренних состояний кодера |
|
nextStates |
Матрица: numStates строк, 2kстолбцов |
Таблица переходов, указывающая состояния кодера, в которые осуществляется переход, для всех комбинаций текущего состояния и входного символа |
|
outputs |
Матрица: numStates строк, 2kстолбцов |
Таблица формирования выходного сигнала, содержащая значения выходных символов для всех комбинаций текущего состояния и входного символа |
Более подробные комментарии о заполнении полей структуры имеются на странице с описанием функции istrellis.
Примеры
Рассмотрим сверточный кодер со скоростью 2/3 без обратных связей, структурная схема которого приведена на рисунке. Пример использования этого кодера имеется на странице с описанием функции convenc.
Для данного кода вектор ConstraintLength имеет вид [5, 4], а матрица CodeGenerator равна [27,33,0; 0,5,13]. Ниже показано формирование таблицы переходов для данного кода.
trellis = poly2trellis([5 4],[27 33 0; 0 5 13])
trellis =
numInputSymbols: 4
numOutputSymbols: 8
numStates: 128
nextStates: [128×4 double]
outputs: [128×4 double]
Скалярное поле trellis.numInputSymbols равно 4, поскольку входные символы являются двухбитовыми, что дает 4 возможных значения. Аналогично, поле trellis.numOutputSymbols равно 8, поскольку три бита выходного символа дают 8 возможных комбинаций.
Скалярное поле trellis.numStates равно 128 (то есть 27), поскольку каждый из семи элементов памяти кодера может находиться в одном из двух состояний (0 или 1).
Чтобы получить информацию о содержимом матричных полей trellis.nextStates и trellis.outputs, необходимо запросить ее в явном виде. Например, выведем первые пять строк матрицы trellis.nextStates, имеющей 128 строк и 4 столбца.
trellis.nextStates(1:5,:)
ans =
0 64 8 72
0 64 8 72
1 65 9 73
1 65 9 73
2 66 10 74
Первая строка показывает, что если кодер находится в нулевом состоянии и получает входные символы 00, 01, 10 или 11, то будет осуществлен переход соответственно в состояние 0, 64, 8 или 72. Номер состояния 64 означает, что нижний левый элемент памяти на структурной схеме хранит значение 1, а остальные шесть элементов памяти находятся в нулевом состоянии.
Наверх
qfunc — Q-функция (дополнение гауссовой интегральной функции распределения до единицы)
Синтаксис:
y = qfunc(x)
Описание:
y = qfunc(x)
Результат равен дополнению гауссовой интегральной функции распределения до единицы, вычисленной для всех элементов входного вещественного массива x. Для скалярного значения x формула выглядит следующим образом:
Q-функция связана с дополнительной функцией ошибок erfc следующей формулой:
Примеры:
Приведенный ниже код вычисляет Q-функцию для матричного аргумента (поэлементно):
x = [0 1 2; 3 4 5];
format short e % Включаем экспоненциальный формат вывода чисел на экран
y = qfunc(x)
format % Возвращаем формат вывода чисел по умолчанию
Далее приводится результат работы этого кода:
y =
5.0000e-001 1.5866e-001 2.2750e-002
1.3499e-003 3.1671e-005 2.8665e-007
Наверх
qfuncinv — обратная Q-функция (обратная гауссова интегральная функция распределения с обратным знаком)
Синтаксис:
y = qfuncinv(x)
Описание:
y = qfuncinv(x)
Возвращает значение аргумента, при котором Q-функция равна x. Входной параметр x должен быть вещественным массивом, элементы которого лежат в интервале от 0 до 1 включительно. Q-функция представляет собой дополнение гауссовой интегральной функции распределения до единицы и вычисляется по следующей формуле:
Q-функция связана с дополнительной функцией ошибок erfc следующей формулой:
Примеры:
Приведенный ниже код иллюстрирует взаимно обратное соотношение между функциями qfunc и qfuncinv.
x1 = [0 1 2; 3 4 5];
y1 = qfuncinv(qfunc(x1)) % Обращаем qfunc и восстанавливаем x1
x2 = 0:.2:1;
y2 = qfunc(qfuncinv(x2)) % Обращаем qfuncinv и восстанавливаем x2
Далее приводится результат работы этого кода.
y1 =
0 1 2
3 4 5
y2 =
0 0.2000 0.4000 0.6000 0.8000 1.0000
Наверх
shift2mask — расчет маски сдвигового регистра, необходимой для формирования задержанной псевдослучайной последовательности
Синтаксис
mask = shift2mask(prpoly,shift)
Описание
mask = shift2mask(prpoly,shift)
Возвращает маску, которую необходимо применить к регистру сдвига с обратной связью для получения псевдослучайной последовательности, задержанной на shift тактов. Обратные связи в регистре задаются с помощью примитивного полинома prpoly. Входной параметр prpoly может быть задан в одном из двух форматов:
-
В виде двоичного вектора, содержащего коэффициенты примитивного полинома в порядке убывания степеней.
-
В виде целого числа, двоичное представление которого дает коэффициенты примитивного полинома, так что младший двоичный разряд соответствует свободному члену полинома.
Входной параметр shift должен быть целочисленным скаляром.
Замечание. Для ускорения вычислений функция shift2mask не проверяет полином prpoly на примитивность. Если он не является примитивным, выдаваемый функцией результат не имеет смысла. Для нахождения примитивных полиномов используйте функцию primpoly или алгоритмы из [2].
Определение эквивалентной маски
Эквивалентная маска, соответствующая задержке последовательности на s тактов, определяется как остаток от деления полинома xs на заданный примитивный полином. Результирующий вектор mask представляет полином остатка, перечисляя его коэффициенты в порядке убывания степеней.
Задержки и маски при генерации псевдослучайных последовательностей
Использование линейного сдвигового регистра с обратными связями — один из способов реализации генераторов псевдослучайных последовательностей. На приведенном ниже рисунке показана блок-схема такого генератора. Все сумматоры выполняют сложение по модулю 2.
Коэффициенты примитивного полинома определяют состояния ключей, обозначенных на рисунке как gk, а маска управляет состояниями ключей, обозначенных как mk. Нижняя половина схемы показывает реализацию задержки псевдослучайной последовательности В результате сложения по модулю 2 состояний некоторых ячеек регистра, определяемых маской, можно получить псевдослучайную последовательность, задержанную на произвольное число тактов. Точкой отсчета, то есть последовательностью с нулевой задержкой, считается сигнал, снимаемый с выхода крайней правой ячейки. Это соответствует замкнутому ключу m0 и разомкнутым всем остальным ключам mk. Приведенная ниже таблица показывает, как задержка влияет на выходной сигнал генератора.
|
Время (такты) |
T = 0 |
T = 1 |
T = 2 |
… |
T = s |
T = s+1 |
|
Shift = 0 |
x0 |
x1 |
x2 |
… |
xs |
xs+1 |
|
Shift = s>0 |
xs |
xs+1 |
xs+2 |
… |
x2s |
x2s+1 |
Параметры маски и задержки могут использоваться в Simulink при реализации генератора псевдослучайной последовательности с помощью блока PN Sequence Generator из набора Communications Blockset.
Примеры
Приведенная ниже команда конвертирует задержку, равную 5, в эквивалентную маску x3 +x + 1 для регистра, обратные связи в котором описываются примитивным полиномом x4 + x3 + 1.
mk = shift2mask([1 1 0 0 1],5)mk = 1 0 1 1
Наверх
vec2mat — преобразование вектора в матрицу с заданным числом столбцов
Синтаксис:
mat = vec2mat(vec,matcol);
mat = vec2mat(vec,matcol,padding);
[mat,padded] = vec2mat(…);
Описание:
mat = vec2mat(vec,matcol)
Преобразует вектор vec в матрицу, имеющую matcol столбцов, заполняя ее по строкам. Если длина вектора не кратна значению matcol, последняя строка формируемой матрицы mat дополняется нулями. Число строк в матрице mat будет равно ceil(length(vec)/matcol).
mat = vec2mat(vec,matcol,padding)
То же, что предыдущий вариант синтаксиса, но значения, которыми при необходимости дополняется последняя строка формируемой матрицы mat, последовательно берутся из матрицы padding. Если padding имеет меньше элементов, чем нужно, оставшееся место заполняется копиями последнего элемента.
[mat,padded] = vec2mat(…)
В этом варианте дополнительно возвращается целое число padded, показывающее, сколько дополнительных элементов было помещено в последнюю строку матрицы mat.
Замечание. Функция vec2mat аналогична встроенной функции MATLAB reshape. Однако при векторном входном параметре функция reshape заполняет формируемую матрицу по столбцам, а не по строкам. Кроме того, reshapeтребует, чтобы число элементов во входной и выходной матрицах было одинаковым, тогда как vec2mat при необходимости вставляет в формируемую матрицу дополнительные значения.
Примеры.
vec = [1 2 3 4 5];
[mat,padded] = vec2mat(vec,3)
mat =
1 2 3
4 5 0
padded =
1
[mat2,padded2] = vec2mat(vec,4)
mat2 =
1 2 3 4
5 0 0 0
padded2 =
3
mat3 = vec2mat(vec,4,[10 9 8; 7 6 5; 4 3 2])
mat3 =
1 2 3 4
5 10 7 4



![{\displaystyle p_{e}=1-{\sqrt[{N}]{(1-p_{p})}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f5d380e45b0451c45265e199221fae5bd5b84bf9)




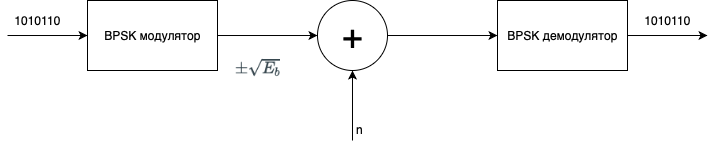
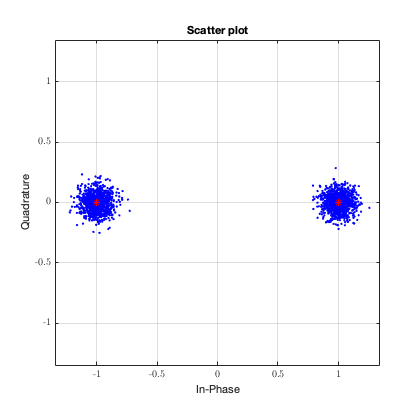
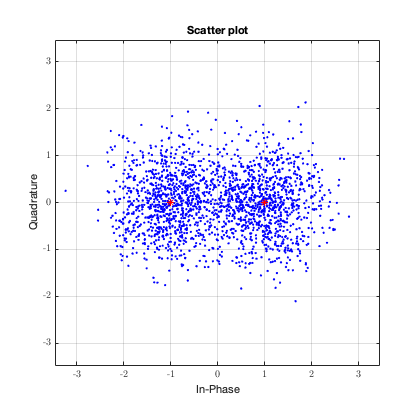
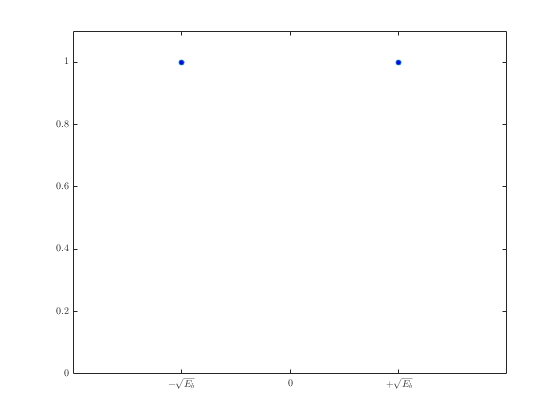
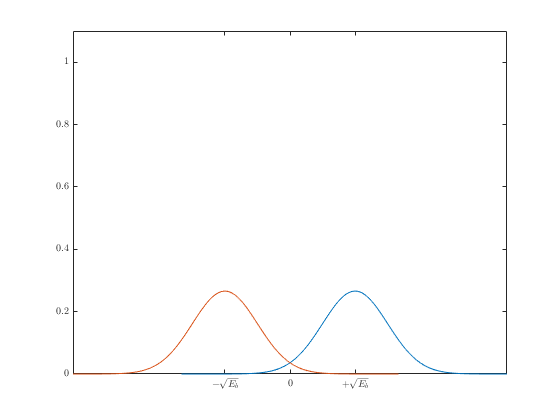
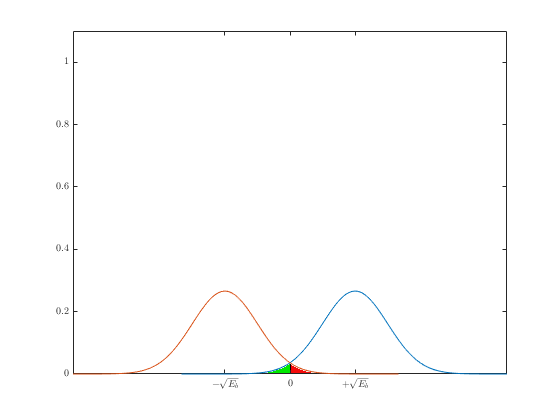
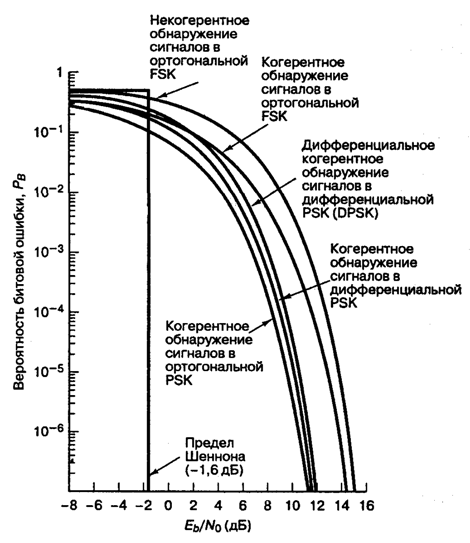
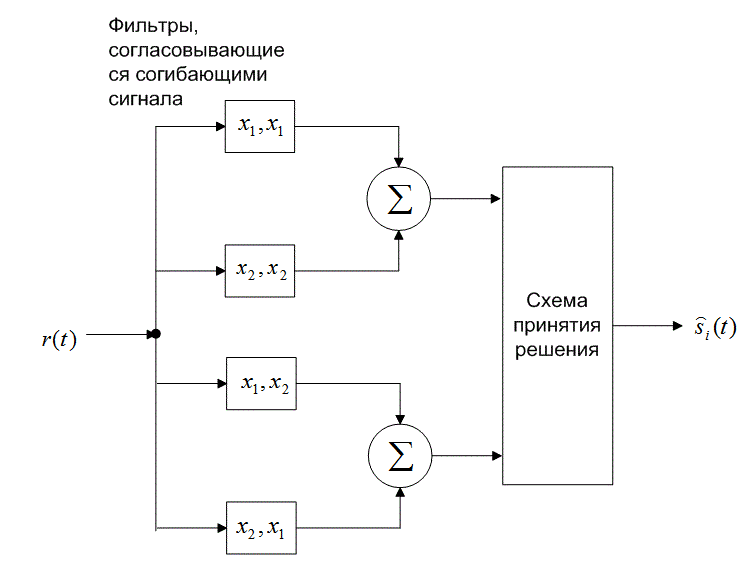
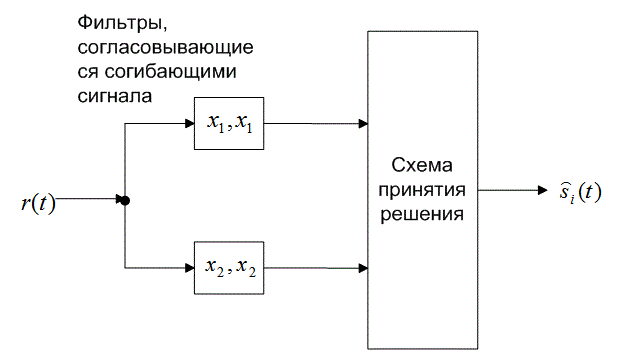
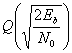
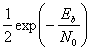
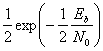
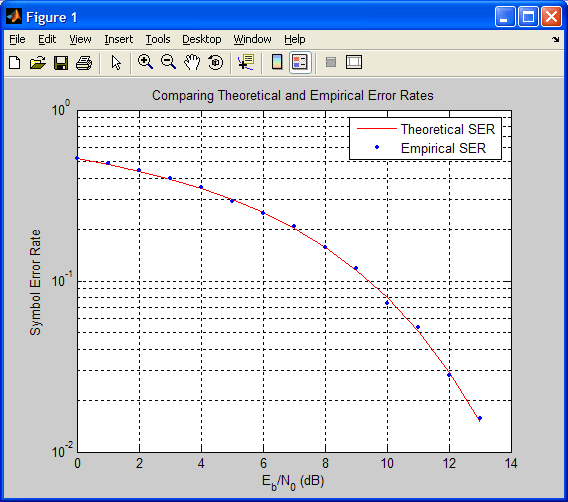
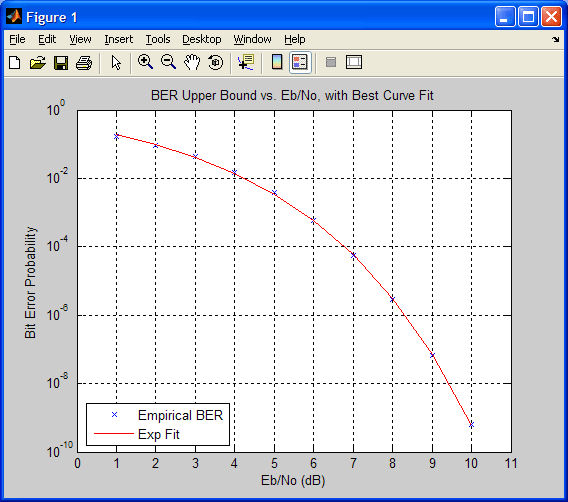
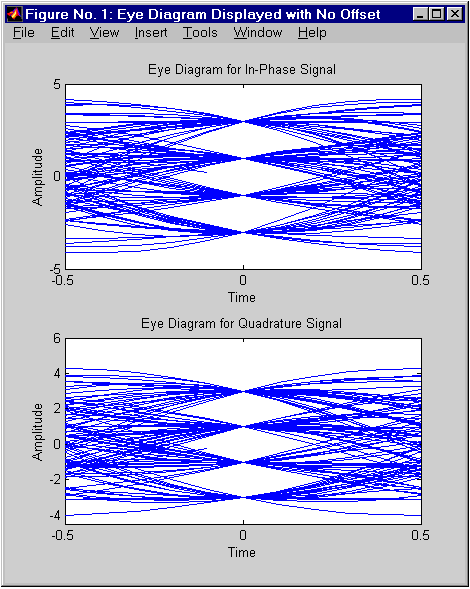
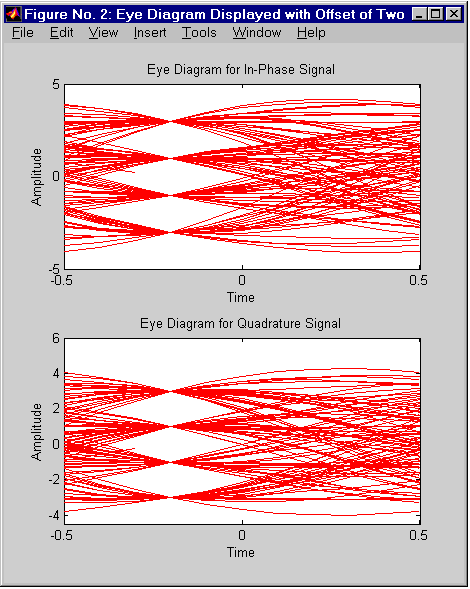
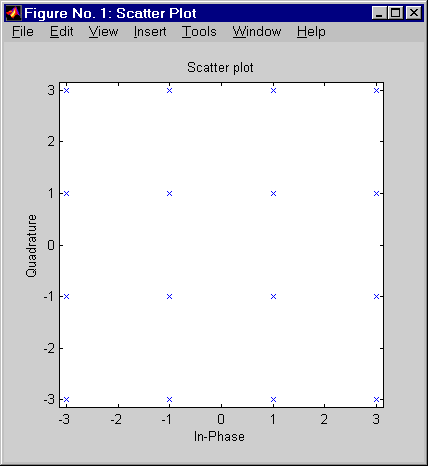
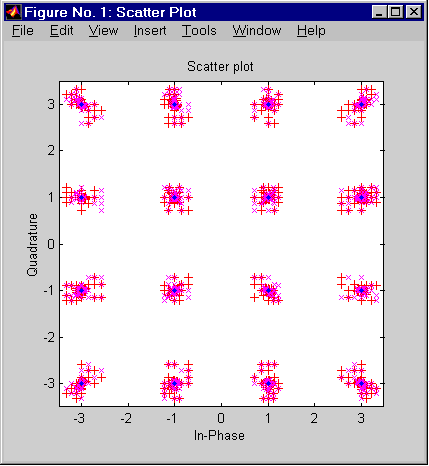
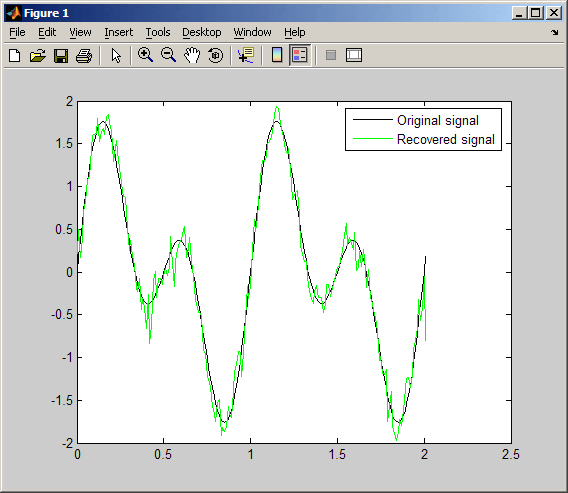
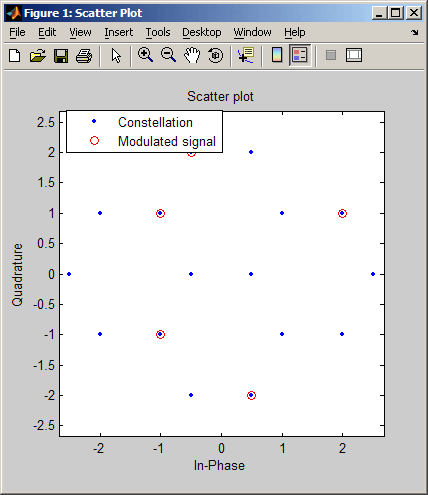
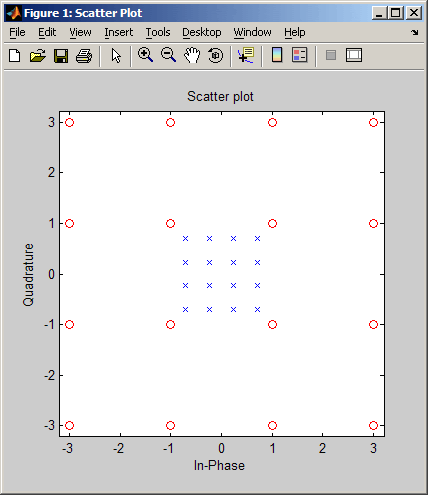
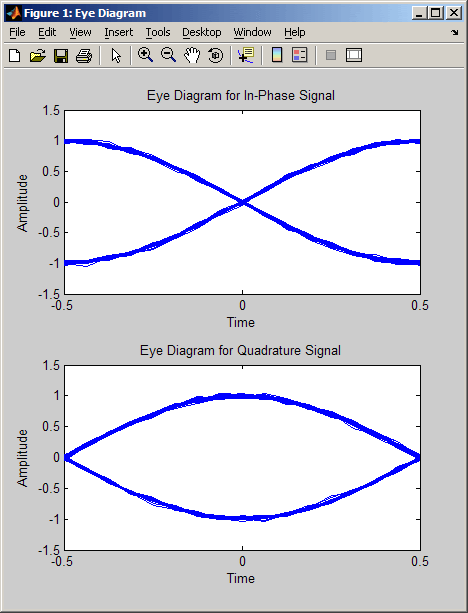
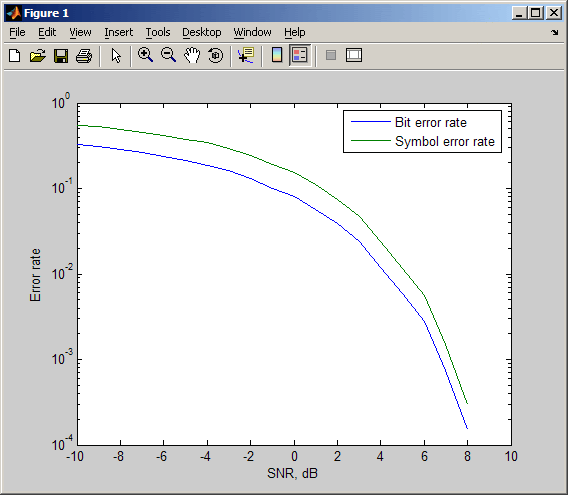
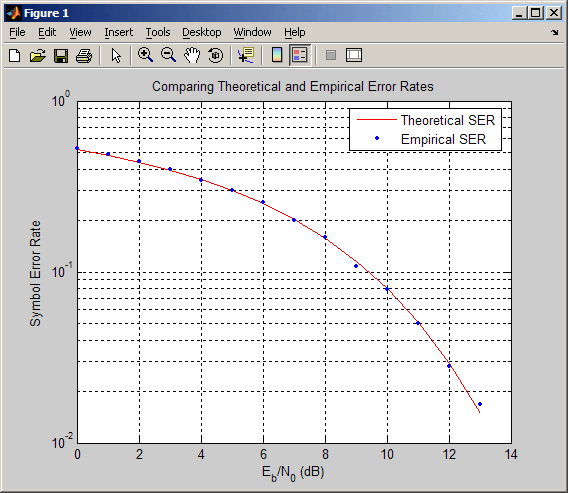
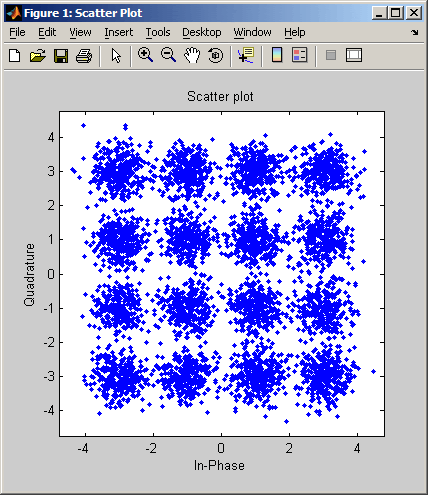
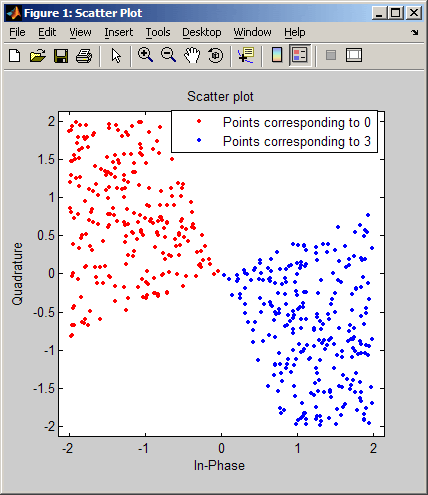
.gif)