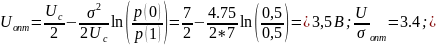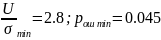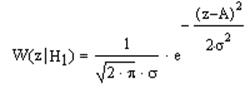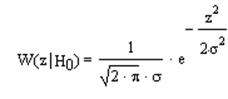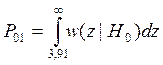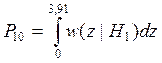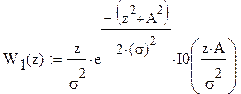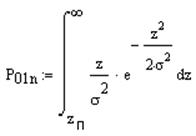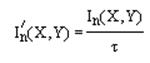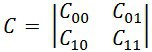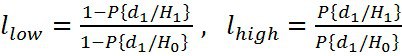Расчет вероятностей ошибок и оптимального порога

ФЕДЕРАЛЬНОЕ
АГЕНТСТВО СВЯЗИ

Ордена
Трудового Красного Знамени федеральное
государственное бюджетное образовательное
учреждение высшего образования

Московский
технический университет связи и
информатики

(МТУСИ)

Кафедра
общей теории связи

Лабораторная
работа № 16

по
дисциплине «Общая теория связи»:

«Обнаружение
импульсных сигналов в шуме»

Вариант
№8

Выполнил:
**********

Проверил(а):
Кудряшова А.Ю.

_________________________

Москва,
2020

1
Цель работы

Изучение
принципа порогового обнаружения двоичных
сигналов, механизма возникновения
ошибок обнаружения, метода анализа и
оптимизации процесса обнаружения.
Экспериментальное исследование
зависимости вероятностей ошибок условий
обнаружения.

Принципиальная
схема установки:

2
Домашнее задание

Исходные
данные:

• Вариант
  №8

• Напряжение
  сигнала,
  

• Мощность
  шума,
  

• Априорная
  вероятность сигнала, p(1)
  = 0,75

1. Рассчитать
   и построить графики зависимости
   вероятностей p(1/0)
   и p(0/1)
   ошибок обнаружения от порога U₀
   решающего устройства.

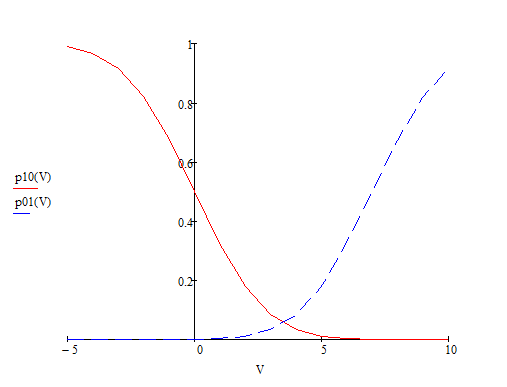
Рис.
1
График зависимости вероятностей ошибок
обнаружения от порога

решающего устройства

1. Рассчитать
   и построить на том же графике зависимость
   средней вероятности ошибки p_ОШ
   от порога U₀
   для двух других значений априорной
   вероятности сигнала: p(1)=0,5
   и p(1)
   –0.75 из исходных данных.

Средняя
вероятность ошибки

равна:

где

• 

  – априорная
  вероятность единицы;

• 

  – априорная
  вероятность нуля;

• 

  – условная
  вероятность нуля при передаче единицы;

• 

  – условная
  вероятность единицы при передаче нуля;

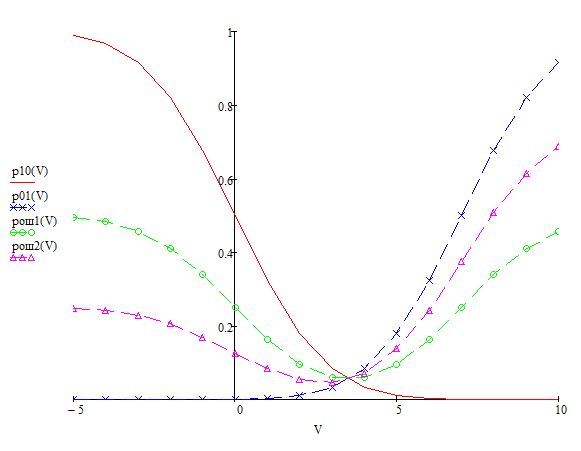
Рис.
2
Зависимость средней вероятности ошибки

от порога

для двух значений априорной вероятности
сигнала

и

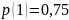
1. Для
   тех же двух значений априорной вероятности
   сигнала p(1)
   вычислить оптимальные пороги U_{0
   ОПТ}
   и соответствующие им значения p_{ОШ
   min}.
   Найденные точки U_{0
   ОПТ}
   и p_{ОШ
   min}
   отметить на построенных раннее
   зависимостях p_ОШ=
   p_ОШ(U₀).

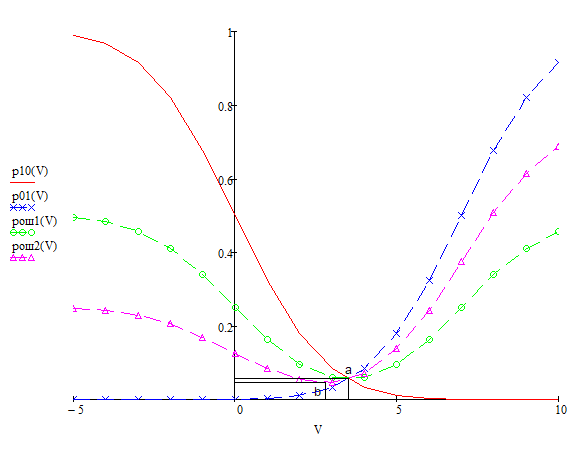
Рис.
3 Зависимости
с указанными значениями

3
Выполнение

Тестирование

1. Вопрос

Ответ:

1. Вопрос

Ответ:

1. Вопрос

Ответ:

1. Вопрос

Ответ:

1. Вопрос

Ответ:

1. Вопрос

Ответ:

1. Вопрос

Ответ:

1. Вопрос

Ответ:

1. Вопрос

Ответ:

1. Вопрос

Ответ:

1. Вопрос

Ответ:

1. Вопрос

Ответ:

1. Вопрос

Ответ:

1. Вопрос

Ответ:

1. Вопрос

Ответ:

1. Вопрос

Ответ:

1. Вопрос

Ответ:

1. Вопрос

Ответ:

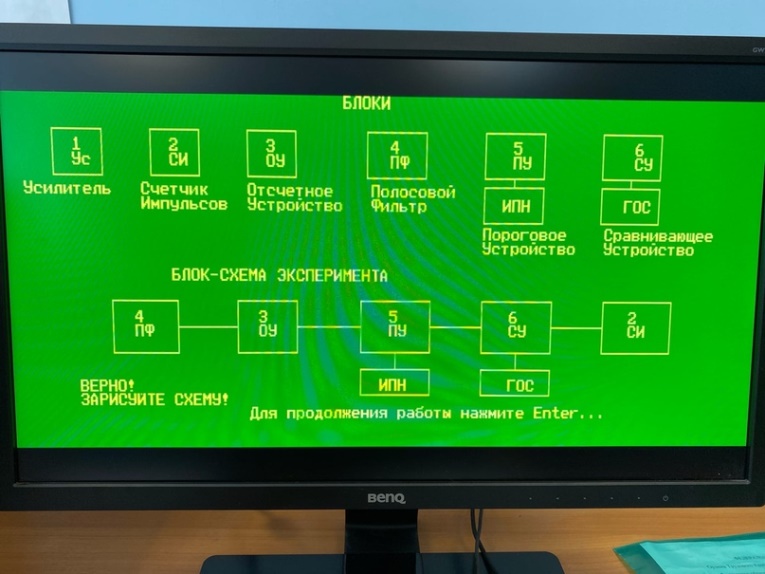
4
Компьютерный
эксперимент

1)
При
V=-3

2)
При
V=-2.5

3)
При
V=-2

4)
При
V=-1.5

5)
При
V=-1

6)
При
V=-0.5

7)
При
V=0

При
V=0.5

9)
При
V=1

10)
При
V=1.5

11)
При
V=2

12)
При
V=2.5

13)
При
V=3

14)
При
V=3.5

15)
При
V=4

16)
При
V=4.5

17)
При
V=5

18)
При
V=5.5

5
Результаты
тестирования

Соседние файлы в папке Лабы

• #
• #
• #
• #
• #
• #
• #

В
зависимости от того какая, гипотеза будет аксиомой, такой же будет плотность
распределения (отличаются сдвигом на величину амплитуды сигнала(А))

Рис № 6 График распределения
плотности вероятности шумовой реализации при отсутствии сигнала, при наличии
сигнала амплитудой A.

6.
Случаи когерентного и некогерентного приёма Определение оптимального по
критерию идеального наблюдателя порога, условные вероятности ошибок первого и
второго рода, средняя вероятность ошибки, скорость передачи информации при
наличии помех.

6.1.
Когерентный прием.

Когерентный
прием – прием сигнала, параметры которого полностью известны. Выясняем только
наличие сигнала.

Плотности
распределения вероятности (ПРВ):

Условная
ПРВ для сигнал+шум W(z êН₁):

Условная
ПРВ для шума W(z êН₀):

Вероятность ошибки
первого рода (ложной тревоги) описывается следующим выражением:

,

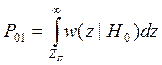
где z_п – пороговый
уровень.

В то же время вероятность ошибки
второго рода (пропуск сигнала) описывается формулой:

.

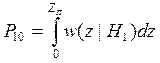
Далее задача состоит в вычислении
оптимального порога z_п.

Если
значение будет лежать слева от z_п, то приемник будет считать, что
передавался    символ 0, если справа, –  то 1.

Решением данного
уравнения будет z_п, расположенный на пересечении графиков
распределения p₀×w(z|H₀) и p₁×w(z|H₁).

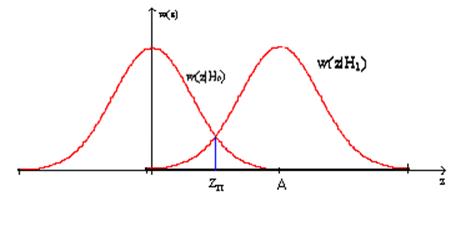
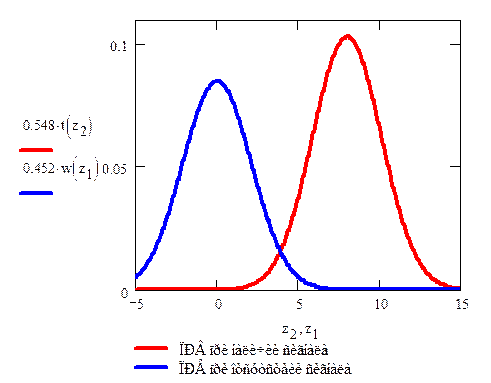
Рис.
№7 Графики функций гауссовских плотностей вероятности для мгновенных значений
сигнала  z.

Из графика
определяем значение порогового значения z_п

                                                          z_п
= 3,91  

В данной работе:

 w(z|H₀) = 1 / (2·3,14·4,5)^1/2·exp[-z²/4,5];

 w(z|H₁) = 1 /
(2·3,14·4,5)^1/2·exp[-(z-8)²/4,5]

Подставляя z_п в выражения
для ошибок 1 -го и 2 -го родов получаем:

P₀₁ = 0,047

P₁₀ = 0,039

Средняя
вероятность ошибки: Р_ош = Р₀×
Р₀₁ + Р₁×Р₁₀

Р_ош =
0,452·0,067+0,548·0,027 = 0,021

Скорость
передачи информации:

Взаимная
информация:

,

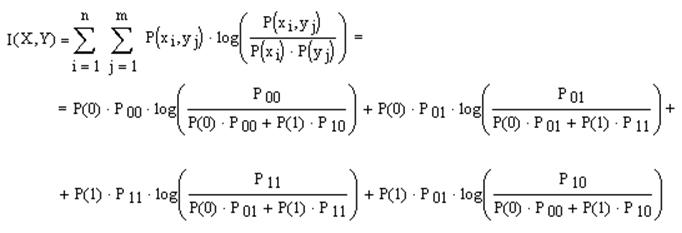
где
Р₀₀ и Р₁₁ найдем из соотношения:

,

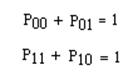
тогда

          
Р₀₀ = 1 – Р₀₁          Р₀₀ = 1 – 0,047 = 0,953

          
Р₁₁ = 1 – Р₁₀          Р₁₁ = 1 – 0,039 = 0,961

Следовательно:

I(X,Y) = 0,452·0,953·1,076+
0,452·0,047·(-3,543) + 0,548·0,961·0,811+0,548·0,047·   (-3,535)

I(X,Y)
= 0,724 [бит]

I^/(X,Y)
= 0,724/0,5·10^-6

Скорость передачи информации в канале с шумами:

I^/(X,Y) = 1,44·10⁶
[бит/c]

6.2.
Некогерентный прием.

Некогерентный
прием – прием сигнала, параметры которого известны не полностью.

Плотности
распределения вероятности (ПРВ):

Условная ПРВ для сигнал+шум W(z êН₁):

Условная ПРВ для шума W(z êН₀):

,

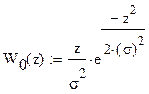
тогда

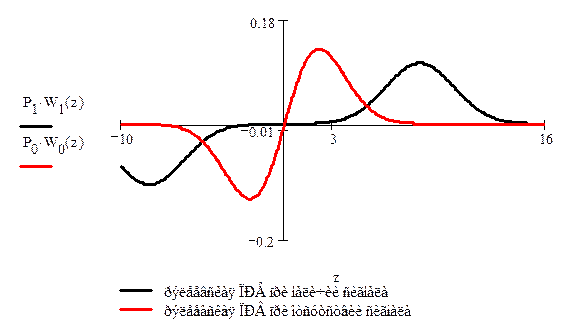
Рис. №8 Графики функций рэлеевских
плотностей вероятности для мгновенных значений сигнала  z.

Из
графика определяем оптимальный порог: z_п = 4,95.

Вероятность
ошибки первого рода:

Вероятность
ошибки второго рода:

,

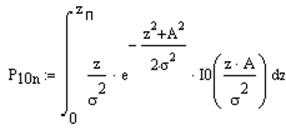
тогда

P_01n
= 0,066

P_10n
= 0,054

Средняя
вероятность ошибки:

Р_ош = Р(0)·Р_01n
+ Р(1)·Р_10n

Р_ош = 0,452·0,066+0,548·0,054

Р_ош =0,0595

Скорость
передачи информации:

Взаимная
информация:

,

где
Р_00n и Р_11n найдем из соотношения:

Р_00n
+ Р_01n = 1

Р_11n + Р_10n =
1,

тогда

Р_00n
= 1 – Р_01n                         Р_00n = 1 – 0,066 =
0,934

Р_11n
= 1 – Р_10n                         Р_11n = 1 – 0,054 =
0,946,

следовательно

I_n(X,Y)
= 0,452·0,934·1,048+ 0,452·0,066·(-3,054) + 0,548·0,946·0,787 +0,548·0,054·    
(-3,085)

I_n(X,Y) = 0,668 [бит],

I^/_n(X,Y)
= 0,668/0,5·10^-6

I^/_n(X,Y) = 1,34·10⁶[бит/с]

Сравнительный результат полученных
данных.

При
когерентном способе перед приема мы выигрываем по всем параметрам вероятностям ошибок первого и второго рода,
средней вероятности ошибки т.е. помехоустойчивость при когерентном приёме
увеличивается.

7. Описание принципа
корреляционной обработки и согласованной фильтрации; расчет фильтра.

7.1
Описание
принципа корреляционной обработки и согласованной фильтрации

Для принятия
пороговым устройством решения о пришедших из линии связи сигнале или паузе
нужно вычислить корреляционный интеграл, а затем проверить неравенство:

Применение статистических критериев при решении задач обнаружения в радиотехнике

Аннотация

В статье рассмотрены основы статистической обработки сигналов и методы их оптимальной обработки* на фоне шума.

Введение

Основной задачей радиотехники является приём, передача и обработка информации с использованием в качестве переносчика – радиосигнала. Главное требование, предъявляемое к радиотехническим системам – получение своевременной и достоверной информации от источника к потребителю. Однако этому мешает физика принципов работы приёмопередающих устройств и среды распространения сигнала, суть которой заключается во флюктуации физических параметров системы и случайным значением принимаемого сигнала, имеющего шумовую составляющую, также относящуюся к стохастическим процессам.

На текущий момент, самый эффективный способ различения полезных сигналов на фоне шумов и помех является оптимальная обработка, реализуемая, как правило, сравнением принимаемой входной реализации с априорно известной формой полезного сигнала. При этом шумы, которые по своей природе процесс слабокоррелированный, вносят меньший вклад в величину, показывающую степень этого сравнения и называющуюся коэффициентом корреляции. Таким образом, любая задача обнаружения сводится к проверке минимум двух гипотез. В общем случае задача обнаружения состоит из двух гипотез: H_0 – сигнал отсутствует на входе приёмного устройства, H_1 – сигнал присутствует на входе приёмного устройства. Различные алгоритмы обнаружения обеспечивают различную вероятность правильного обнаружения P{d_1/H_1} при различных прочих статистических параметрах. Для сравнения эффективности алгоритмов обнаружения существуют критерии, а так как обрабатываются вероятностные величины, то характер этих критериев статистический. Иными словами критерий можно определить как мерило сравнения.

Статистические критерии обнаружения

Большая часть алгоритмов обнаружения радиолокационных целей включают в себя следующие этапы:

1. Прием входной реализации
2. Формирование порога на основе априорной или апостериорной информации.
3. Оптимальная фильтрация входной реализации
4. Принятие решения о наличии сигнала/цели

При этом очередность приёма входной реализации и формирования порога зависит непосредственно от типа алгоритма. Алгоритмы, формирующие порог на основе апостериорной информации о принятой входной реализации называют адаптивными [1]. Критерий выбирается эмпирически исходя из типа задачи. Например: при выборе места работы обычно рассматривают два критерия:

• Максимума отношения заработанных денег к затраченной силе.
• Максимума удовольствия, получаемого от работы.

К сожалению, современные реалии ставят в приоритет такого специалиста, навыки которого позволяли бы как можно быстрее выпустить продукцию и максимизировать прибыль компании. И зачастую второй критерий либо отбрасывается, либо при анализе ситуации ему присваивается низкий приоритет. Показатель, в данном случае, определяющий приоритет критериев, называется его мощностью.

В математической статистике мощность критерия определяется, как вероятность не совершить ошибку второго рода при принятии решения. В нашем случае ошибка второго рода — это не устроится на оптимальную для себя работу, в общем же случае это ложное принятие за истину события соответствующего гипотезе H_0.

Разумеется, универсальных критериев не существует. Так, например, критерий, имеющий наибольшую мощность, в решении одной задачи, в решении другой может оказаться наихудшим по этому показателю.

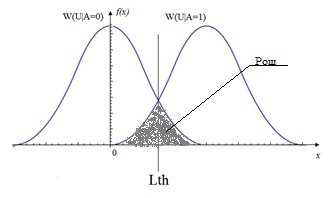
Критерий минимального среднего риска (критерий Байеса)

Рис.1 График распределения условной плотности вероятности наличия W(U|A=1) и отсутствия W(U|A=0) с вероятностями ошибок

Пусть A = 1 соответствует наличию сигнала s(t), а A = 0 – его отсутствию. Множество решений d вырождается в два: d_0 →A=1 and d_1→A=0.
При решении задачи бинарного обнаружения задача эквивалентна проверке гипотезы H_1 о том, что А = 1, при альтернативной гипотезе H_0 о том, что А = 0, а функция потерь переходит в квадратную матрицу:

Таким образом, условный риск при A = 0 равен r_0= C_00 P{d_0/H_0 }+ C_01 P{d_1/H_0 }=C_00 (1-P{d_1/H_0 })+ C_01 P{d_1/H_0 }, а при A = 1 равен r_1= C_10 P{d_0/H_1 }+ C_11 P{d_1/H_1}=C_10 (1-P{d_1/H_1} )+C_11 P{d_1/H_1}, где P{d_1/H_1} – вероятность правильного обнаружения, а P{d_1/H_0 } – вероятность ложной тревоги.

Средний риск определяется как r ̅=qr_0+pr_1, где q – априорная вероятность отсутствия сигнала, а p – априорная вероятность присутствия сигнала и определяет средние потери при ложной тревоге и пропуске цели [2]. Например: при использовании такого критерия для выставления порога срабатывания пожарной сигнализации, стоимость риска при ложной тревоге – вызов пожарной службы, а при пропуске – стоимость вещей в сгоревшей квартире или офисе.

На рис.1 проиллюстрированы графики распределения плотности вероятности при наличии и отсутствии сигнала, также выделены зоны, площадь которых численно равна вероятностям ошибок при принятии решения. Ввиду стохастической природы явлений рассматриваемых в данном примере, распределения имеют ненулевую дисперсию. Согласно критерию минимального среднего риска лучшим алгоритмом обнаружения сигнала будет тот, у которого величина r ̅ будет минимальна [2].

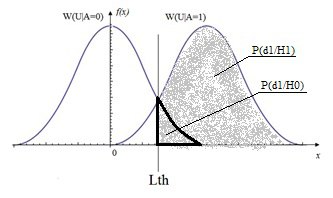
Критерий максимума апостериорной вероятности (максимального правдоподобия)

Этот критерий получается из критерия минимального среднего риска при условии, что потери при совершении ошибки обратно пропорциональны вероятности их совершения C_01=1/P{d_0}, C_10=1/P{d_1}. При этом порог оптимального обнаружителя выставляется таким образом, чтобы минимизировать сумму вероятностей ошибок P_ош=P{d_0/H_1 }+P{d_1/H_0 } (см рис.2).

Рис.2 График распределения условной плотности вероятности наличия W(U|A=1) и отсутствия W(U|A=0) с вероятностью ошибки

Двухпороговый критерий Вальда

В случаях, когда большую роль играет время наблюдения за процессом, например при наличии нескольких каналов и одного обнаружителя или круговом обзоре РЛС, применяют критерий последовательной проверки гипотез Вальда также известный под названием двухпороговый.

Рис.3 График распределения условной плотности вероятности наличия W(U|A=1) и отсутствия W(U|A=0) с вероятностью правильного обнаружения и вероятностью ложной тревоги

По этому критерию область определения вероятности делится на три подобласти, разделяемыми двумя порогами, определяемыми вероятностями правильного обнаружения и ложной тревоги (см.рис 3):
Критерий Вальда является оптимальным в смысле минимизации среднего времени наблюдения по большому количеству экспериментов [4]. Так как наиболее предпочтительным для радиолокации является сокращение длительности процедуры обнаружения, современные реалии ведут к всё более активному использованию этого критерия [5].

Критерий Неймана-Пирсона

Большим минусом критериев Байесовского класса является необходимость априорного знания элементов матрицы потерь. Например: при пропуске вражеского бомбардировщика на союзную территорию стоимость рисков не поддается исчислению.

В критерии Неймана-Пирсона фиксируется время обнаружения. Оптимальным будет алгоритм с максимальной вероятностью правильного обнаружения P{d_1/H_1 }, при условии, что вероятность ложной тревоги P{d_1/H_0 } не превышает заданной величины [6].

В виду того, что критерий Неймана-Пирсона не требует знания априорных вероятностей ситуаций A = 1 и A = 0, в радиолокации его используют одним из основных [5].

Заключение

При разработке обнаружителей очень важно осознанно выбирать критерий оптимальности, ведь, как уже упоминалось ранее, каждый критерий имеет максимальную мощность в какой-либо определенной ситуации и применение иных может привести к нежелательным последствиям.

Список использованных источников:

[1] Bulyakulov R.R. The adaptive threshold device // Processing of the 2014 IEEE North West Russia Section Young Researches in Electrical and Electronic Engineering Conference. P.165.
doi: 10.1109/EIConRusNW.2016.7448237
[2] Бакулев, П.А. Радиолокационные системы. Учебник для ВУЗов / П.А. Бакулев; М.: Радиотехника, 2004. – 46 с.
[3] Юревич, Е.И. Теория автоматического управления / Е.И. Юревич; М.: Энергия, 1969
[4] Богатырев, А.А. Стандартизация статистических методов управления качеством / А. А. Богатырев, Ю. Д. Филиппов; М.: Изд-во стандартов, 1989. – 42 с.
[5] Храменков, А.С. Сопоставительный анализ радиолокационных обнаружителей, основанных на критерии неймана-пирсона и последовательном критерии отношения вероятностей /А.С. Храменков, С.Н. Ярмолик // доклады БГУИР №6(76) Минск, 2013.
[6] Васильев, К.К. Методы обработки сигналов: Учебное пособие / К.К. Васильев; Ульяновск, 2001.