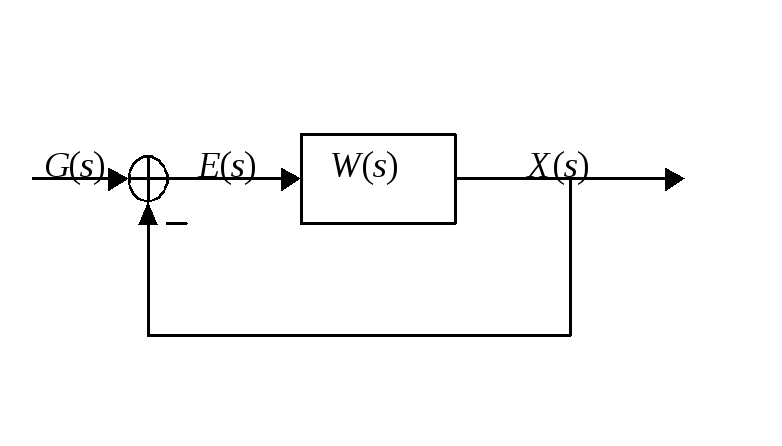
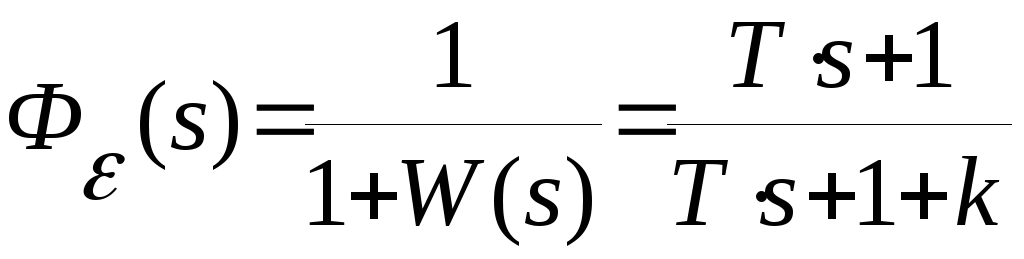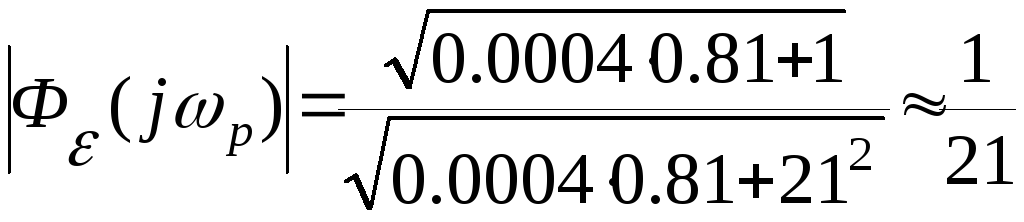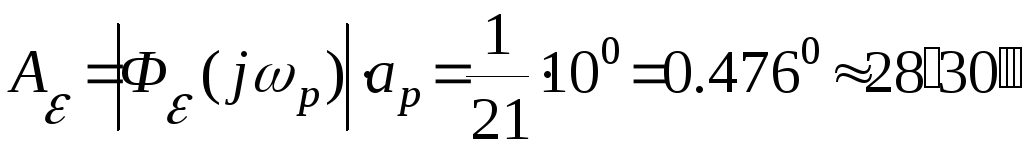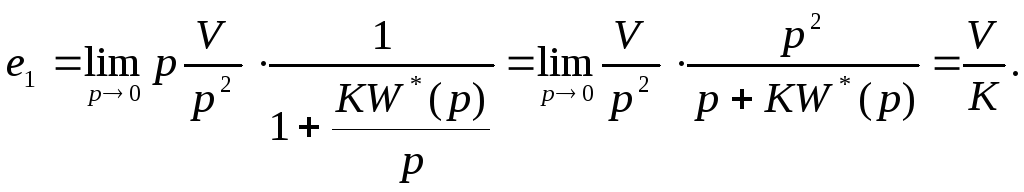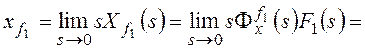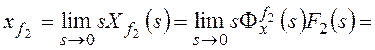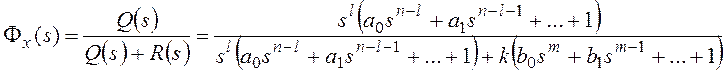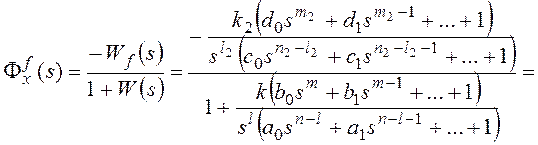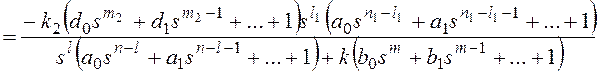Точность систем автоматического управления при гармоническом входном воздействии.
Пусть
на вход системы автоматического
управления поступает сигнал вида
(1)
К
такому виду сигналов могут быть приведены
различные виды входных воздействий.
Часто при проектировании систем
автоматического управления задаются
максимальные значения скорости и
ускорения, которые должна отрабатывать
автоматическая система.
В
этом случае по известным максимальным
скоростям и ускорениям входного
воздействия
и
строят эквивалентное гармоническое
воздействие.
Здесь
эквивалентность понимается в том смысле,
что обеспечивается равенство максимальных
значений скоростей и ускорений реального
входного воздействия и эквивалентного
синусоидального воздействия
.
(2)
Каким
должно быть
и
,
чтобыимела максимальную скорость
и максимальное ускорение, равное
.
Из
(2) имеем
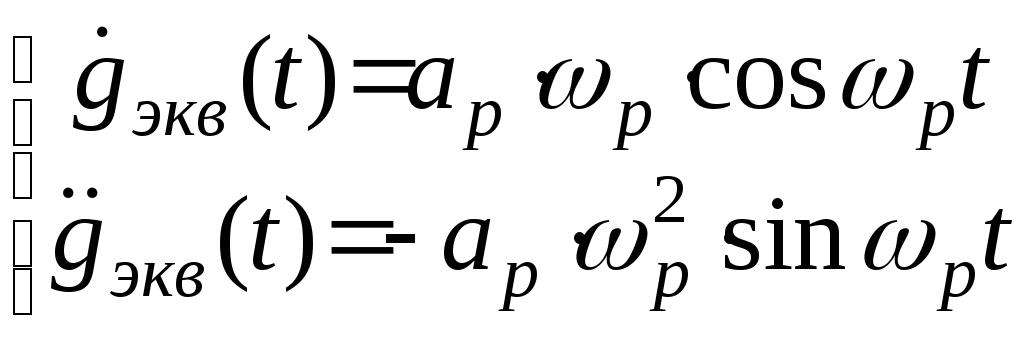
Откуда
получаем
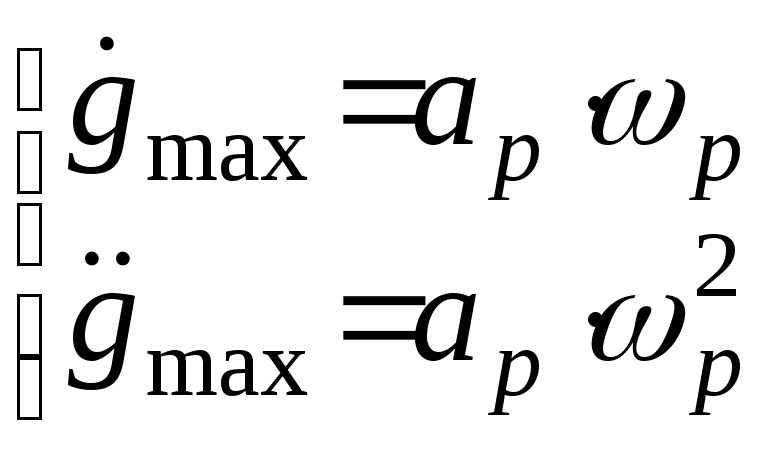
Из
последних уравнений окончательно
получаем


Итак,
будем считать, что структурная схема
системы приведена к расчетной
а
на вход системы подается входной сигнал
,
где
и
— рабочая амплитуда и частота входного
гармонического сигнала. В этом случае
амплитудасигнала ошибки системы будет определяться
по формуле,
или с учетом того, что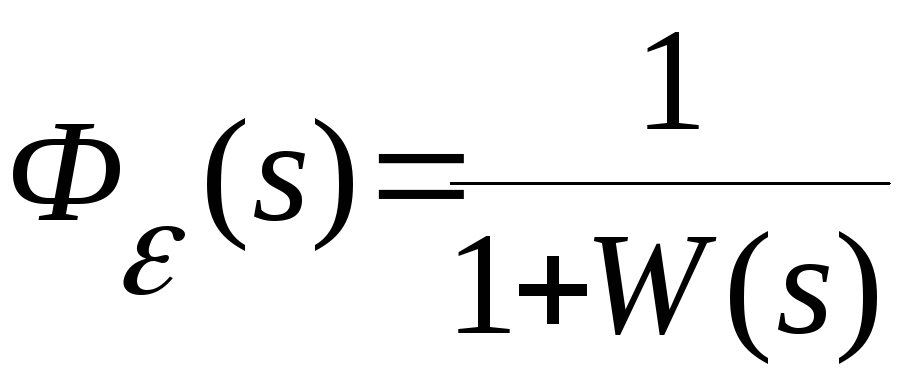
значениебудет равно
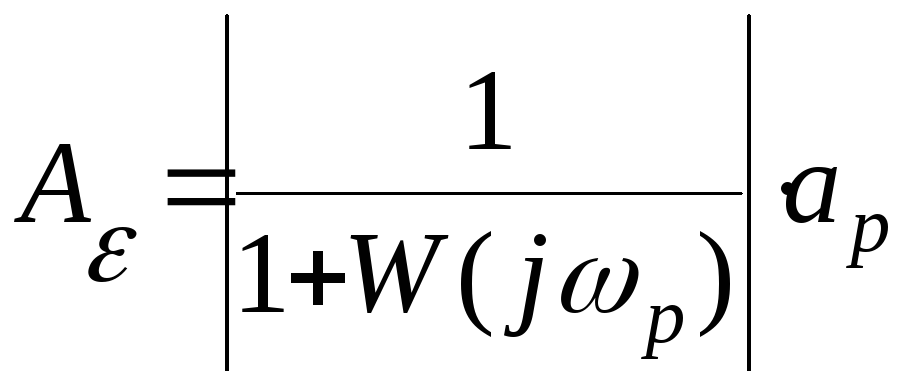
(4)
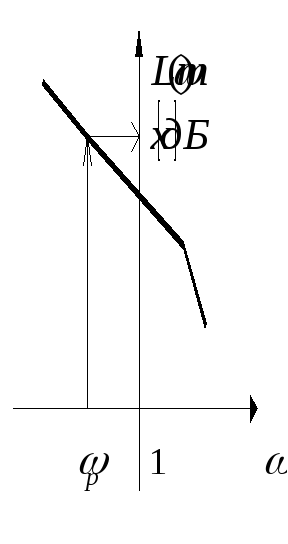
Если
рабочая частота
такова, что справедливо неравенство
,
то равенство (4) можно заменить приближением
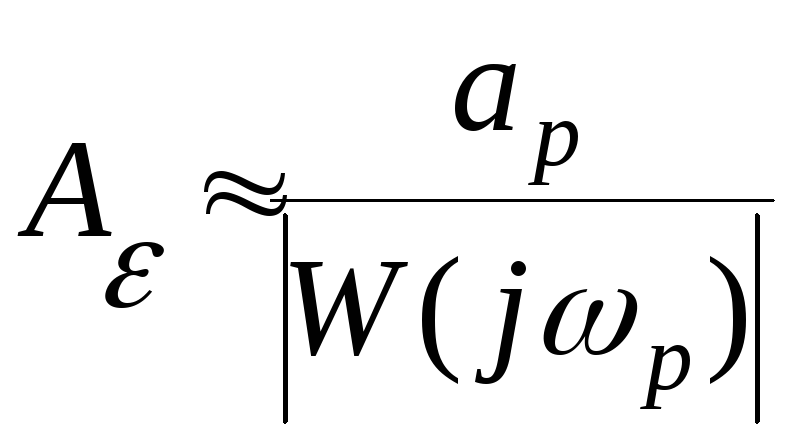
(5)
С
помощью соотношений (4) и (5) можно оценить
амплитуду ошибки отработки гармонического
сигнала (1). Практическое значение
приближенного равенства (5) состоит в
том, что с его помощью и используя
логарифмические амплитудно-частотные
характеристики исследуемой системы,
можно оценить максимальное значение
ошибки в системе при гармоническом
входном воздействии.
Пусть
даны:
—
амплитуда входного гармонического
сигнала;
—
рабочая частота входного гармонического
сигнала.
Логарифмическая
амплитудно-частотная характеристика
разомкнутой системы
.
Требуется
определить
максимальное значение амплитуды ошибки
в замкнутой системы
.
Для
решения этой задачи необходимо:
-
На
рабочей частоте
по графику логарифмической
амплитудно-частотной характеристики
определяет значениев дБ.
-
Так
как по определению логарифмической
амплитудно-частотной характеристики
,
то
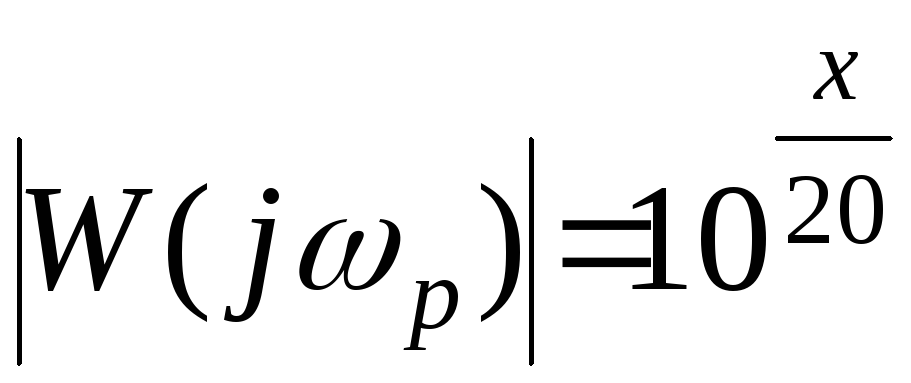
(6)
-
Подставив
(6) в приближенное равенство (5) получаем
то
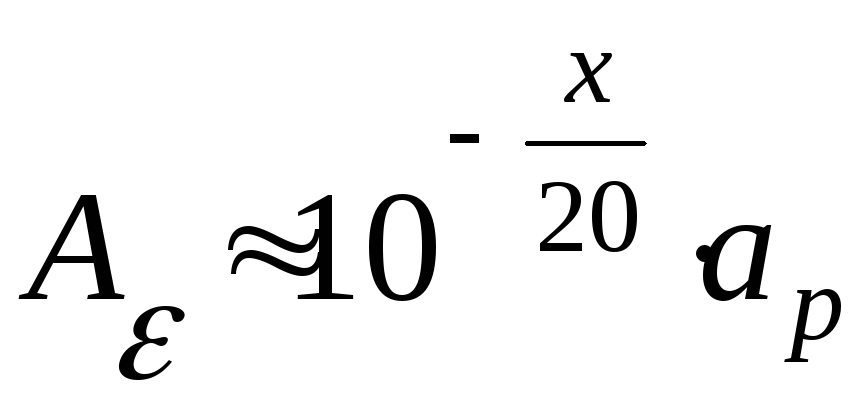
(7)
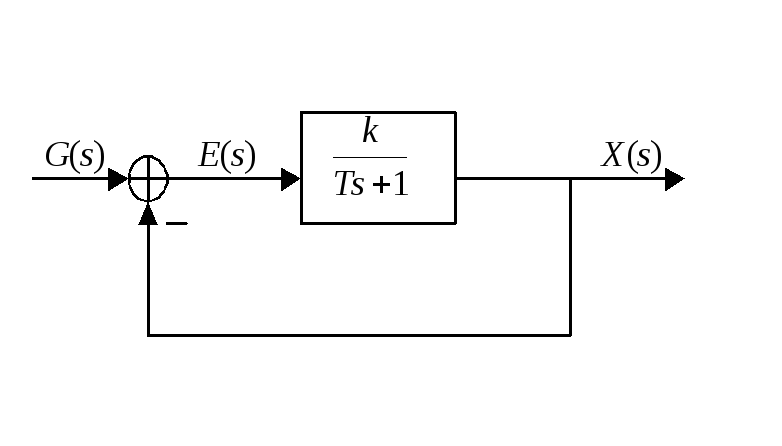
Пример.
Задана система автоматического
управления, структурная схема которой
имеет
где
;
.
На
вход системы поступает входной
гармонический сигнал
,
где— амплитуда;
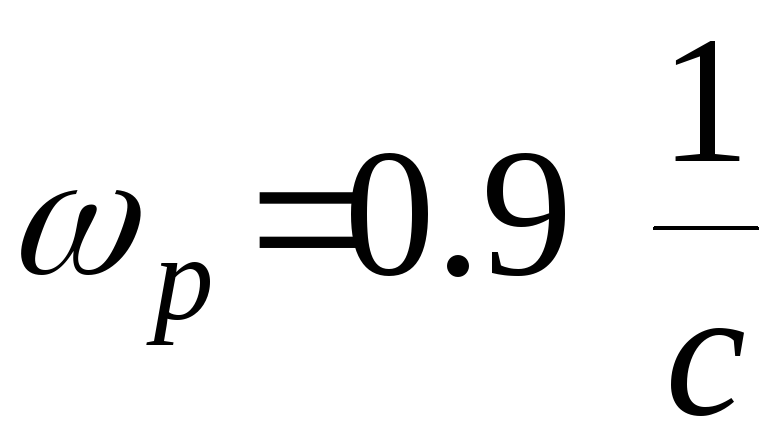
Найти
амплитуду ошибки в заданной системе
управления.
Решение.
Передаточная функция разомкнутой
системы
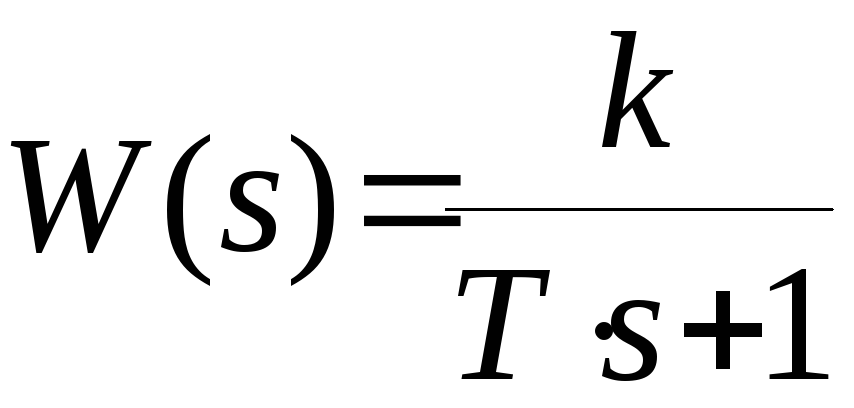
Передаточная
функция замкнутой системы по ошибке
Из
последнего равенства получаем
Для
заданных значений
,
и
получаем
Поэтому
искомое значение амплитуды ошибки
Вычислим
значение
по приближенной формуле (5)
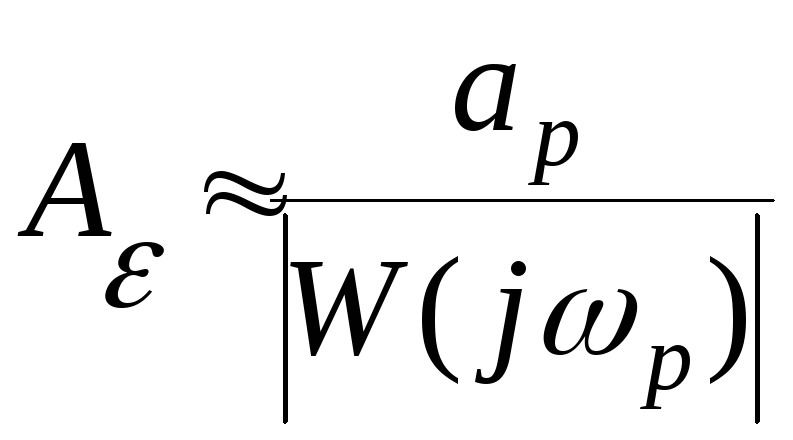
Из
передаточной функции разомкнутой
системы
последовательно получаем
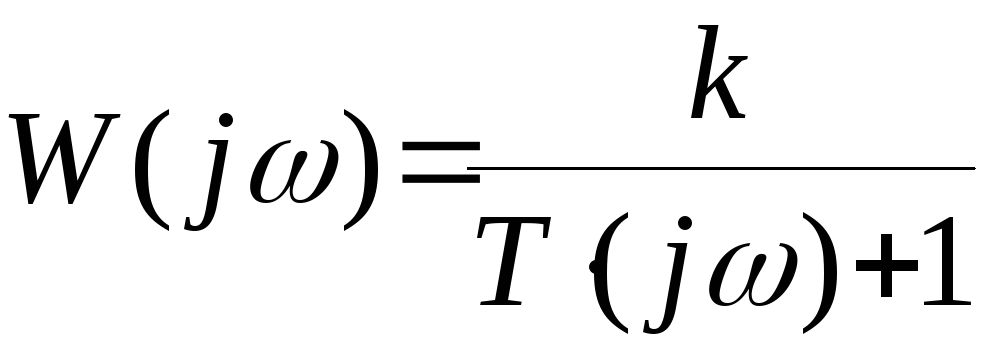

Для
заданных значений параметров имеем:
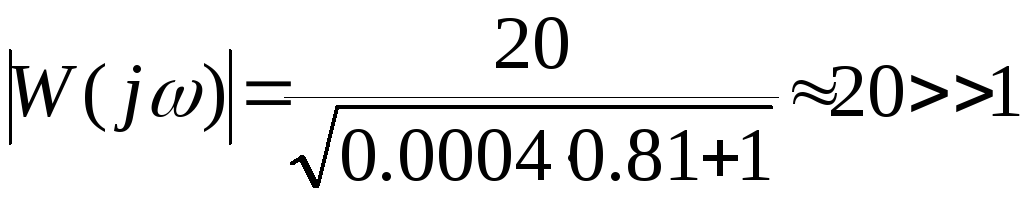
Поэтому,
на основании приближенного равенства
(5) получаем:
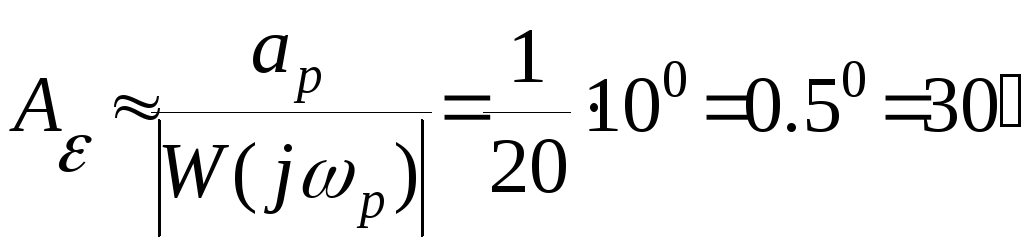
Соседние файлы в папке шпоргалка
- #
22.02.20141.17 Mб941.doc
- #
- #
- #
- #
- #
- #
- #
110
Лекция № 23
Тема: Ошибка
в САУ.
План лекции:
1. Ошибка при движении с постоянной
скоростью.
2. Ошибка при движении с постоянным
ускорением.
3. Ошибка при гармоническом задающем
воздействии.
Ошибка при
движении с постоянной скоростью.
Пусть задающее
воздействие изменяется с постоянной
скоростью
f=vt , v=const .
Возмущающее
воздействие постоянно . В этом случае
Относительно
составляющей е2 остается справедливым
все сказанное ранее . Рассмотрим
составляющую е1 . Ранее было
показано ,что :
е1 =∞
, если W(p) – статическая
передаточная функция ;
е1=const≠0
, если W(p) имеет астатизм
первого порядка;
е1=0 ,
если W(p) имеет астатизм
второго и выше порядков .
Таким образом
, необходимо рассмотреть только случай
, когда передаточная функция W(p)
имеет астатизм 1-ог порядка . В этом
случае
и при этом
W*(0)=1.
Тогда
(85)
Из ( ) видно
, что величина составляющей е1
установившейся ошибки пропорциональна
скорости изменения задающего воздействия
и обратного пропорциональна коэффициенту
передачи разомкнутой системы по скорости
К.
Ошибка при
движении с постоянным ускорением.
В этом режиме
f(t)=dt2
, d – ускорение входного
сигнала . Возмущающее воздействие g(t)
предполагается постоянным и тогда
составляющая е2 та же , что и в
первых случаях.
Рассмотрим
составляющую е1 . очевидно , что ,
если :
W(p) – статическая
передаточная функция или передаточная
функция или передаточная функция с
астатизмом 1-ог порядка – е1=∞ ;
W(p)
– передаточная функция с астатизмом
2-ог порядка , то е1=const≠0;
W(p)
имеет астатизм 3-ог и выше порядков
, то е1=0.
Поэтому
остается рассмотреть только случай
астатизма 2-го порядка.
При этом имеем
и
Ошибка при
гармоническом задающем воздействии.
Этот режим движения
рассматривается часто, т.к. он позволяет
достаточно полно оценить динамические
свойства САУ. Задающее воздействие
имеет вид
f(t)=A sin wt .
Возмущающее
воздействие рассматривать не будем
(если оно постоянное , то все сказанное
выше относительно составляющей е2
полностью переноситься на этот случай
.
Рассмотрим
составляющую ошибки , определяемую
наличием задающего воздействия . Имеем
В линейной
системе при гармоническом входном
сигнале ошибка изменяется по гармоническому
закону , т.е.
Точность САУ
может быть оценена по амплитуде ошибки
Ае ; определяемой выражением
Обычно Ае
много меньше амплитуды задающего
воздействия А , т.е.
— большая величина. Тогда
и
(86)
Зависимостью
( ) определяем амплитуду сигнала ошибки
при гармоническом входном сигнале и
оно же позволяет решить обратную задачу
, т.е. сформировать требование к ЛАФЧХ
разомкнутой системы , при выполнении
которых амплитуда Ае не превосходит
заданной величины ∆m. Имеем
из (86)
(87)
откуда
и
Значения (w,
20lg)
определяет точку на плоскости ЛАЧХ
разомкнутой системы . Для выполнения
условия (87) ЛАЧХ системы должна проходить
выше этой точки (см. рис.82).
Р
ис.82.
Подборка по базе: Урок-лекция по теме «Представление об автоматических и автоматиз, КР_Системы управления робототехническими средствами.docx, 1 Практическое домашнее задание Тема 1 Основные подсистемы и эл, Анализ и меры по совершенствованию управления конечными финансов, Основы правового регулирования управления персоналом к.р..docx, Антюшина Екатерина Александровна К.Р. В-7 Теория и методика муз, Тема2 Теория личностных черт лидера.pptx, Отчет ПМ.01 Организация документационного обеспечения управления, Практическа работа экономическая теория Вирченко.docx, Курсовая работа экономическая теория.docx
Астатическая САУ первого порядка
ПФ разомкнутой САУ определяется из (5.10) при
a
0 0
=
:
( )
(
)
(
)
W S
K
S
S
S
S
S
V
m
m
n
n
=
+ +
+
+ +
+
−
−
β
β
γ
γ
1 1
1 1
1 1
,
(5.13) где
K
b
a
V
=
0 1
;
γ
k
k
a
a
=
+
1
Для упрощения анализа можно принять
( )
W S
K
S
S
V
→
=
0
Позиционная ошибка
ε
S
V
S
S
K
S
g
S
=
+
=
=
1 1
0 0
0
(5.14)
В астатических системах позиционная (статическая) ошибка равна нулю.
Скоростная ошибка
ε
V
V
S
V
V
S
K
S
S
V
K
=
+
=
=
2 0
1 1
(5.15)
Для астатической САУ первого порядка скоростная ошибка представляет собой постоянную величину. Коэффициент
K
V
, имеющий размерность
1
c
, называют
добротностью системы по скорости.
Ошибка по ускорению
ε
a
v
S
a
S
K
S
S
=
+
= ∞
=
3 0
1 1
(5.16)
Астатическая САУ второго порядка
ПФ разомкнутой САУ определяется из (5.10) при
a
0 0
=
a
1 0
=
:
( )
(
)
(
)
W S
K
S
S
S
S
S
a
m
m
n
n
=
+ +
+
+ +
+
−
−
β
β
µ
µ
1 2
2 2
1 1
1
, где
K
b
a
a
=
0 2
;
µ
K
K
a
a
=
+
1 2
121
В случае астатической САУ второго порядка позиционная и скоростная ошибки равны нулю.
Ошибка по ускорению
ε
a
a
S
a
a
S
K
S
S
a
K
=
+
=
=
3 2
0 1
1
(5.17)
Коэффициент
K
a
, имеющий размерность
1 2
c
, называют добротностью сис-
темы по ускорению.
Из вышеизложенного следует два важных вывода: чем больше коэффициент передачи в статической или астатической системах, тем меньше величина установившейся ошибки по управлению; в астатических системах (содержащих интегрирующие звенья) позиционная (ста- тическая) ошибка по управлению равна нулю.
Следует отметить, что не всякая система астатическая по “управлению” будет астатическая по отношению к возмущающему воздействию. Для решения этой зада- чи необходимо вычислить ошибку от возмущающего воздействия.
Общая методика вычисления установившейся ошибки от некоторого воздейст- вия z(t), приложенного в произвольном месте структурной схемы, может быть пред- ставлена в виде:
В многоконтурных САУ для вычисления ПФ
( )
Ф
S
z
ε
целесообразно пользовать- ся формулой Мезона.
122
Пример. Для САУ (рис.5.2) определить ошибку
ε
f
при
( )
W S
K
1 1
=
,
( )
W S
K
S
2 2
=
,
( )
f t
f
=
0
. Изображение возмущающего воздействия
( )
{ }
L f t
f
S
=
0
; передаточная функция
( )
Ф
S
K
S
K K
S
K
S
K K
f
ε
=
+
=
+
2 1
2 2
1 2 1
Установившаяся ошибка
ε
f
S
S
f
S
K
S
K K
f
K
=
+
=
=
0 2
1 2 0
0 1
Таким образом, в данном случае , несмотря на наличие интегрирующего звена,
САУ является статической по возмущающему воздействию. Можно показать, что по управлению система будет астатической.
5.2.1.
Установившаяся ошибка при произвольном воздействии (коэффициен-
ты ошибок)
В общем случае изображение ошибки
( )
ε
t
воспроизведения задающего воздей- ствия g(t)
( )
( ) ( )
ε
ε
g S
g
Ф
S G S
=
,
( )
( )
Ф
S
W S
g
ε
=
+
1 1
(5.18)
Передаточную функцию
( )
Ф
S
g
ε
представим в виде ряда
( )
Ф
S
C
C S
C S
C S
g
n
n
ε
=
+
+
+ +
0 1
2 2
(5.19)
Коэффициенты этого ряда
C
i
называются коэффициентами ошибок и опреде- ляются с помощью выражений:
( )
[
]
C
Ф
S
g
S
0 0
=
=
ε
,
( )
C
dФ
S
dS
g
S
1 0
=
=
ε
,
( )
C
n
d Ф
S
dS
n
n
g
n
S
=
=
1 0
!
ε
Но
( )
Ф
S
g
ε
является отношением многочленов при
( )
( )
( )
( )
Ф
S
N S
N S
KM S
g
ε
=
+
Очевидно, что произведя деление многочлена числителя на многочлен знамена- теля по известному алгебраическому правилу, мы получим выражение типа (5.19) , а значит, и значение всех коэффициентов ошибок.
После этого, подставив в выражение (5.18) выражение (5.19) и переходя к ори- гиналам , получим:
( )
( )
( )
ε
ус
C g t
C
dg t
dt
C
d g t
dt
=
+
+
+ +
0 1
2 2
2
(5.20)
Пример. Для САУ с астатизмом первого порядка (рис.5.3) необходимо вычис- лить ошибку при задающем воздействии g(t), имеющем вид
( )
g t
g
V t
at
=
+
+
0 0
2 2
123
Вычислим W(S):
( ) (
)(
)
W S
K
S T S
T S
=
+
+
1 2
1 1
где
K
K K
=
1 2
Вычислим ПФ ошибки по управлению:
( )
( )
(
)
(
)
Ф
S
W S
T T S
T
T S
S
T T S
T
T S
S
K
g
ε
=
+
=
+
+
+
+
+
+ +
1 1
1 2 3
1 2
2 1 2 3
1 2
2
Разделим числитель на знаменатель:
Дальше делить нет смысла , так как g(t) не имеет производных выше второго порядка. Таким образом,
( )
Ф
S
K
S
K
T
T
K
S
s
ε
=
+
+
−
+
1 1
1 1
2 2
Отсюда, сравнивая с ( 5.19 ), получим:
C
0 0
=
,
C
K
1 1
=
,
C
T
T
K
K
2 1
2 2
1
=
+
−
Вычислим производные g(t):
dg
dt
V
at
=
+
0
,
d g
dt
a
2 2
=
В соответствии с (5.20) получим:
( )
( )
(
)
ε
t
C g t
C
dg
dt
C
d g
dt
K
V
at
T
T
K
K
a
=
+
+
=
+
+
+
−
=
0 1
2 2
2 0
1 2
2 1
1
(
)
=
+ +
+
−
1 0
1 2
K
V
at
a T
T
a
K
Из этого примера также видно , что с увеличением добротности системы К ус- тановившаяся ошибка уменьшается , но с течением времени бесконечно увеличива- ется из-за недостаточно большого при заданном g(t) порядке астатизма.
5.2.2.
Точность при гармоническом воздействии
Установившиеся ошибки при гармоническом воздействии определяются ЧХ замкнутой системы
( )
Ф
j
g
ε
ω
и
Φ
ε
ω
f
j
(
)
. Что касается основных частотных характе- ристик
( )
( )
A
Ф j
З
ω
ω
=
,
( )
( )
ϕ ω
ω
З
Ф j
=
arg
, построенных по главной передаточной
Рис. 5.3
_
(
)
(
)
S
T
T S
T T S
S
K
S
T
T
K
S
+
+
+
+
+
+
+
1 2
2 1 2 3
2 1
2 3
1 1
(
)
K
S
T
T S
T T S
+ +
+
+
1 2
2 1 2 3
1 1
1 1
2 2
K
S
K
T
T
K
S
+
+
−
_
T
T
K
S
T T
T T
K
S
T
T
K
S
K
T
T
K
S
1 2
2 1 2 1 2 2
1 2
2 1
2 3
1 1
1 1
1
+
−
+
−
+
−
+
+
−
+
124 функции
( )
Ф j
ω
замкнутой системы, то они включают в себя всю информацию об ус- тановившемся слежении за синусоидальным задающим воздействием
( )
g t
t
=
sin
ω
Поэтому установившаяся ошибка воспроизведения амплитуды g(t) определится за- штрихованными частями ординат. Ошибка в амплитуде при
ω =
0
представляет со- бой статическую ошибку системы (рис.5.4).
ФЧХ
( )
ϕ ω
З
(рис.5.4,в) представляет установившуюся ошибку, выражающуюся в сдвиге фазы на выходе
( )
( )
(
)
x
A
t
З
З
=
+
ω
ω ϕ ω
sin по отношению ко входному воздей- ствию.
АЧХ
( )
A
З
ω
для астатических (рис.5.4.а) и статических (рис.5.4.б) систем обыч- но имеет падающий вид при увеличении частоты
ω
, причем
( )
A
З
ω →
0
при
ω → ∞
. В результате получается ограниченный диапазон частот
ω
n
, в котором ошибка вос- произведения амплитуды
( )
∆
A
A
З
З
= −
1
ω
не превышает допустимого значения. Этот диапазон частот
0
< <
ω ω
n
определяет полосу пропускания системы.
Полоса пропускания является важным показателем точности системы. Она ха- рактеризует возможности системы при воспроизведении быстро меняющихся сигна- лов, то есть инерцию системы.
Ошибка в установившемся состоянии, при изменении управляющего воздейст- вия по гармоническому закону
( )
( )
g t
t
g
=
sin
ω
, равна
( )
( )
(
)
g
t
t
g
g
max max sin
=
+
ε
ω
ϕ ω
(5.21)
то есть является также гармонической функцией.
Величина ошибки в этом случае обычно оценивается по амплитудному значе- нию
( )
( )
ε
ω
ω
ε
max max max
=
=
+
Ф
j
g
g
W j
g
g
g
1
(5.22) при
( )
W j
g
ω
>>
1
;
( ) ( )
ε
ω
ω
max max max
≈
≈
g
W j
g
A
g
g
(5.23) где
( )
A
g
ω
значение АЧХ разомкнутой системы при
ω ω
=
g
. Для астатической системы
Рис.5.4
125
( )
( )
( )
W S
K M S
S N S
=
ν
ν
1
, при
ω →
0
( )
( )
W j
K
j
ω
ω
ν
ν
≈
(рис.5.5)
Поэтому максимальная ошибка
( )
ε
ω
ω
ν
ν
max max max
=
=
g
W j
g
K
g
И при гармоническом воздействии ошибка в первом приближении обратно пропорциональна добротности системы К.
Часто при проектировании и испытании САУ пользуются эквивалентным сину- соидальным задающим сигналом и в том случае, когда требования к системе заданы по максимальной скорости V и ускорению а входного воздействия.
Рассмотрим определение амплитуды
g
m
и частоты
ω
g
эквивалентного гармо- нического сигнала. Если
g
g
t
m
g
=
sin
ω
, то скорость изменения
dg
dt
g
t
m
g
g
=
ω
ω
cos
, a ускорение
d g
dt
g
t
m
g
g
2 2
= −
ω
ω
sin
. Следовательно, максимальное значение скорости и ускорения гармонического сигнала имеют вид
&
max
g
g
m
g
=
ω
,
&&
max
g
g
m
g
=
ω
2
Приравнивая эти величины соответственно V и а ,получим после несложных преобразований:
ω
g
g
g
a
V
=
=
&&
&
max max
,
( )
g
g
g
V
a
m
=
=
&
&&
max max
2 2
. Эти значения
g
m
и
ω
g
принимают за расчетные рабочие значения амплитуды и частоты для данной системы.
5.3.
Требования к показателям качества переходного процесса
Кроме устойчивости и точности система должна удовлетворять требованиям к виду переходного процесса (время затухания, колебательность и т.п.).
Для сравнения различных переходных процессов ( ПП) в инженерной практике используются следующие показатели качества, определяющие поведение системы в переходном режиме: время регулирования Tр, перерегулирование
σ
, число колеба- ний n. Применяются и другие показатели качества.
Временем регулирования Tрназывается время ПП, по истечении которого от- клонение
ε
становится меньше и остается впредь меньше допустимого значения
∆
( рис.5.6 ).
Время регулирования характеризует быстродействие системы:
Рис.5.5
126
( )
( )
( )
( )
ε
T
x
x T
x
p
p
=
∞ −
∞
⋅
≤ ≈
100%
5%
∆
(5.25)
Перерегулированием
σ
называют относительное максимальное отклонение вы- ходной величины от установившегося значения:
( )
( )
σ =
− ∞
∞
⋅
x
x
x
m
100%
(5.26)
По числу колебаний ПП за время T
p
ПП делится на колебательные (больше двух выбросов) , малоколебательные (один выброс) , монотонные (
dx
dt
>
0
при
0
≤
t
≤
T
p
).
Быстродействие системы также характеризуется скоростью нарастания пере- ходного процесса за время t
σ
изменения
( )
x t
от 10 до 90% от установившегося зна- чения. Для систем с единичной обратной связью время t
σ
обратно пропорционально частоте среза
ω
c
:
(
)
t
c
σ
ω
≈
0 3 0 45 1
,
,
K
Построение ПП — достаточно трудоемкая работа, и во многих практических слу- чаях удобно использовать косвенные оценки качества, не требующие построения графика ПП. Существуют три основных вида приближенных оценок качества пере- ходного процесса:
1) частотные;
2) интегральные;
3) корневые.
Рис.5.6
127
5.4.
Частотные оценки качества
5.4.1.
Связь между переходной характеристикой h(t) и частотными характери-
стиками замкнутой САУ
АФХ замкнутой САУ полностью определяет ее динамические свойства. Поэто- му между видом вещественной
( )
P
ω
и мнимой
( )
Q
ω
частями АФХ замкнутой САУ и видом кривой переходного процесса
( )
h t
существует определенная аналитическая зависимость, устанавливаемая на основании интегральных преобразований Фурье.
Рассмотрим вначале предельные значения переходного процесса
( )
h t
при еди- ничном скачке задающего воздействия
( ) ( )
g t
t
=
1
В изображениях по Лапласу
( )
( ) ( )
h S
Ф S g S
=
,
( )
g S
S
=
1
,
(5.27) где
( )
Ф S
— главная ПФ замкнутой системы.
На основании теорем о предельных значениях можно записать для начального значения
( )
( )
h t
h
=
0
( )
( )
( ) ( )
( )
h
S h S
S Ф S g S
Ф S
S
S
S
0
=
=
=
→∞
→∞
→∞
lim lim lim
Заменяя
S
j
= ω
и учитывая
( ) ( )
( )
Ф j
P
jQ
ω
ω
ω
=
+
, получим
( )
( )
( )
[
]
( )
h
P
jQ
P
0
=
+
=
→∞
→∞
lim lim
ω
ω
ω
ω
ω
,
(5.28)
так как МЧХ
( )
Q
ω
при
ω = ∞
равна нулю для различных систем.
Таким образом, начальное значение
( )
h t
равно конечному значению ВЧХ
( )
P
ω
.
Для конечного значения
( ) ( )
h t
h
t
→∞
= ∞
( )
( )
( ) ( )
( )
h
S h S
S Ф S g S
Ф S
S
S
S
∞ =
=
=
→
→
→
lim lim lim
0 0
0
, или при замене
S
j
= ω
( )
( )
( )
[
]
( )
h
P
jQ
P
∞ =
+
=
→
→
lim lim
ω
ω
ω
ω
ω
0 0
,
(5.29) так как
( )
Q
ω =
0
при
ω =
0
для систем любого порядка астатизма.
Таким образом, конечное значение
( )
h t
равно начальному значению
( )
P
ω
.
Для определения общей взаимосвязи ПП
( )
h t
с ВЧХ
( )
P
ω
и МЧХ
( )
Q
ω
запишем выражение интеграла Фурье (обратное преобразование):
( )
( )
( )
h t
h j
e
d
Ф j
j
e
d
j t
j t
=
=
−∞
∞
−∞
∞
∫
∫
1 2
1 2
π
ω
ω
π
ω
ω
ω
ω
ω
(5.30)
Вычтем из (5.30) установившееся значение
( ) ( )
h
P
∞ =
0
:
( ) ( )
( ) ( )
h t
P
Ф j
P
j
e
d
j t
−
=
−
−∞
∞
∫
0 1
2 0
π
ω
ω
ω
ω
(5.31)
128
Здесь учтено, что изображение
( )
{ }
( )
L P
P
S
0 0
=
, а обратное преобразование Фу- рье
( )
P
j
0
ω
равно
( )
P 0
:
( )
( )
P
P
j
e
d
j t
0 1
2 0
=
−∞
∞
∫
π
ω
ω
ω
Используя формулу Эйлера
e
t
j
t
j t
ω
ω
ω
=
+
cos sin и отбрасывая мнимую часть
(5.31) , так как
( )
h t
-вещественная функция, получим:
( ) ( )
( )
( )
( )
[
]
h t
P
P
t
Q
t
P
t d
−
=
+
−
−∞
∞
∫
0 1
2 1
0
π
ω
ω
ω
ω
ω
ω ω
sin cos sin
(5.32)
Подынтегральное выражение представляет собой четную функцию. Поэтому интегрирование в пределах
(
)
−∞ ∞
,
можно заменить на
( )
0,
∞
и удвоить результат.
Заметим, что
( )
( )
1 0
0 2
0
π
ω
ω
ω
P
t
d
P
sin
∞
∫
=
, поскольку —
2 1
0
π
ω
ω
ω
sin t
d
=
∞
∫
— табличный интеграл.
В результате получим:
( )
( )
( )
( )
h t
P
P
t
d
Q
t
d
=
+
+
∞
∞
∫
∫
0 2
1 1
0 0
π
ω
ω
ω
ω
π
ω
ω
ω
ω
sin cos
(5.33)
Поскольку даны нулевые начальные условия, причем нулевые значения функ- ции распространяются на t<0, т.е. h(t)=0 при t<0 , и учитывая, что при t=-t
( )
( )
cos cos
;
sin sin
ω
ω
ω
ω
t
t
t
t
=
−
= −
−
то для t=-tпо аналогии с (5.33) запишем:
( )
( )
( )
0 0
2 1
1 0
0
=
−
+
∞
∞
∫
∫
P
P
t
d
Q
t
d
π
ω
ω
ω
ω
π
ω
ω
ω
ω
sin cos
(5.34)
Складывая и вычитая (5.33) и (5.34) приходим к формулам
( ) ( )
( )
h t
P
Q
t
d
=
+
∞
∫
0 2
0
π
ω
ω
ω
ω
cos
,
(5.35)
или
( )
( )
h t
P
td
=
∞
∫
2 0
π
ω
ω
ω ω
sin
(5.36)
Формулы (5.35) и (5.36) равноценны, однако на практике наибольшее примене- ние получило выражение (5.36).
Приведем здесь также частотный способ определения импульсно-переходной
(весовой) функции.
Как известно,
( )
K t
dh
dt
h
=
, поэтому, дифференцируя (5.36), находим
( )
( )
K
t
P
td
h
=
∞
∫
2 0
π
ω
ω ω
cos
.
Исследование точности замкнутых систем автоматического управления в установившихся режимах
Страницы работы
Содержание работы
5 ЛАБОРАТОРНАЯ РАБОТА №5. ИССЛЕДОВАНИЕ ТОЧНОСТИ ЗАМКНУТЫХ
САУ В УСТАНОВИВШИХСЯ РЕЖИМАХ
5.1 Цель работы
Исследовать
влияние структуры звеньев САУ и типа внешнего воздействия на величину ошибки в
установившемся режиме.
5.2 Краткие
теоретические сведения
Назначение
автоматической системы управления – изменение выходной величины Х(t) в соответствии
с изменением задающего воздействия Хз(t) при любых
изменениях задающего и возмущающего воздействий. Точность системы в
установившемся режиме зависит как от вида воздействия создающего ошибку, так и
от структуры и параметров САУ, т.е. от ее математического описания Фε(s). Качество
регулирования системы в установившемся режиме характеризуется значениями
коэффициентов ошибок.
Точность САУ при
гармоническом воздействии оценивают по значению —
модуля КФЧХ замкнутой системы по ошибке относительно соответствующего внешнего
воздействия, равного отношению амплитуды сигнала ошибки ΔХm(ω) к амплитуде
внешнего воздействия А1(ω) вызвавшего ошибку
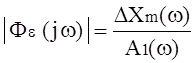
Согласно принципа суперпозиции, ошибка системы
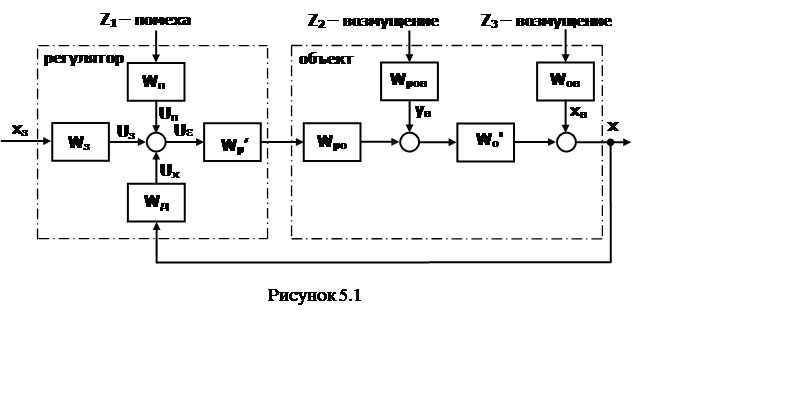
складывается из нескольких составляющих. Так, например, для системы,
представленной на рис. 5.1, ошибка состоит из четырех составляющих
ε = εз + εв + εп + εх ,
где εз – составляющая,
обусловленная неточным воспроизведением системой задания Хз на
выходе объекта;
εв, εп, εх – составляющие,
обусловленные неполной компенсацией регулятором возмущений Yв, Хв
и помехи Хп на управляемую величину Х. Причем каждая составляющая
пропорциональна величине воздействия, создавшего ее.
5.3
Домашняя подготовка
5.3.1 Определить
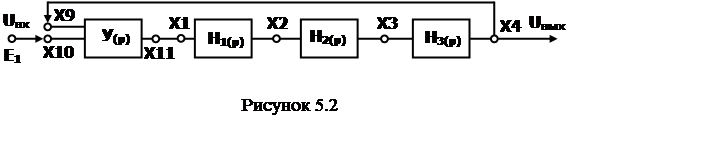
коэффициенты динамической ошибки для замкнутой системы с П, ПД, ПИ,
ПИД-регуляторами, представленной на рис. 5.2, при коэффициентах передачи регулятора
Кр = 1 и Кр = 2. Результаты занести в таблицу 5.1. Параметры объекта управления Н1(р), Н2(р),
Н3(р) и регуляторов Н6(р), Н7(р), Н8(р),
Н9(р) взять из таблиц 1.1 и 1.2 (см. лаб. работу № 1). Расчеты привести
в отчете.
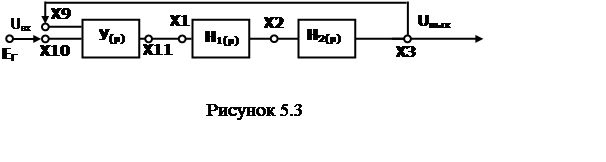
5.3.2 Определить
динамическую ошибку по заданию для замкнутой системы с П и ПД-регулятором,
представленной на рис. 5.3, при коэффициенте передачи регулятора Кр =
2 и частотах входного сигнала 50, 100 и 150 Гц. Результаты занести в табл. 5.2.
Параметры объекта управления и регулятора взять из табл. 1.1 и 1.2 (см. лаб.
работу №1). Расчеты привести в отчете.
 |
|||
 |
5.4
Методические указания к выполнению работы
5.4.1
Подготовить стенд к работе. Установить переключатели: работы – «4, 5, 6»; «S2» и «S5» – в нажатое
положение; «S1»– в отжатое
положение. Вольтметр установить в режим измерения постоянного напряжения.
5.4.2 Исследовать точность замкнутой САУ в
установившемся режиме при постоянном сигнале на входе (статическая точность),
коэффициент усиления регулятора – минимальный, близкий к единице.
5.4.2.1
Регулятор в режиме П (кнопки «S2», «S5» – нажаты, «S1»- отжата).
Установить ручку «Uвх» в положение минимального
усиления (крайнее правое). Подать на вход регулятора X9 сигнал от
источника Е1 = 4В. Измерить вольтметром сигнал на выходе регулятора,
гнездо Х11. Вычислить значение коэффициента усиления регулятора Кр и
результат занести в табл. 5.1. Пересчитать значение сигнала задания по формуле Uз = 0,22Е1 и
занести в табл. 5.1. При исследовании всех типов регуляторов сигнал задания
один и тот же.
5.4.2.2 Собрать схему замкнутой САУ согласно
рисунка 5.2.
5.4.2.3
Исследовать САУ с П-регулятором (кнопки «S2», «S5» – нажаты, «S1»- отжата).
Измерить
вольтметром сигнал на выходе системы, гнездо Х4, результат занести в табл. 5.1.
5.4.2.4 Исследовать
САУ с ПД-регулятором (кнопки «S2», «S1», «S5» – нажаты).
Измерить вольтметром сигнал на выходе системы, гнездо Х4, результат занести в
табл. 5.1.
5.4.2.5
Исследовать САУ с ПИ-регулятором (кнопка «S5» – нажата, «S2», «S1»- отжаты).
Измерить вольтметром сигнал на выходе системы, гнездо Х4, результат занести в
табл. 5.1.
5.4.2.6
Исследовать САУ с ПИД-регулятором (кнопки «S1», «S5» – нажаты, «S2»- отжата).
Измерить вольтметром сигнал на выходе системы, гнездо Х4, результат занести в
табл. 5.1.
5.4.2.7 Разобрать
схему.
5.4.3
Исследовать точность замкнутой САУ в установившемся режиме при подаче на вход
постоянного сигнала (статическая точность) при коэффициенте усиления регулятора
Кр = 2.
5.4.3.1
Регулятор в режиме П (кнопки «S2», «S5» – нажаты, «S1»- отжата).
Подать на вход регулятора X9 сигнал от источника Е1 =
4В. Вращая ручку «Uвх» добиться значения
сигнала на выходе регулятора (гнездо Х11) равного минус 8В. Значение сигнала
задания пересчитать по формуле Uз = 0,22Е1 и
занести в табл. 5.1.
5.4.3.2 Повторить пункты 5.4.2.2, 5.4.2.3, 5.4.2.4,
5.4.2.5, 5.4.2.6, 5.4.2.7.
Таблица 5.1
|
Тип регулятора |
Кр = 1 |
Кр = 2 |
||||||||||
|
Е1,В |
Uз,В |
Uвых,В |
Δ,В |
δ |
Со |
Е1,В |
Uз,В |
Uвых,В |
Δ,В |
δ |
Со |
|
|
П |
||||||||||||
|
ПД |
||||||||||||
|
ПИ |
||||||||||||
|
ПИД |
5.4.4
Исследовать точность замкнутой САУ в установившемся режиме при гармоническом
входном сигнале при коэффициенте усиления регулятора KР = 2.
5.4.5 Установить
коэффициент передачи регулятора Kр = 2. Установить
параметры сигнала на выходе генератора ЕГ : f = 50 Гц, Uвх = 2,5 B, уровень и
частоту сигнала контролировать с помощью вольтметра и функционального
измерителя ИФ(см.лаб.работу №1). Полученные данные занести в таблицу 5.2.
Таблица 5.2
|
Тип регулятора |
Входной сигнал |
Выходной сигнал |
Ошибка Δ х m |
||||||
|
f, |
UВХ, В |
UЗ, В |
f, |
UВЫХ, В |
α, град |
φ = (180˚-α), град. |
расчет |
экспер. |
|
|
П |
|||||||||
|
ПД |
|||||||||
|
П |
|||||||||
|
ПД |
|||||||||
|
П |
|||||||||
|
ПД |
5.4.6 Собрать
схему согласно рис. 5.3. Подать на вход регулятора, гнездо Х10, сигнал от
источника ЕГ, сигнал задания пересчитать по формуле UЗ = 0,22 Uвх и занести в таблицу 5.2.
5.4.7 Исследовать САУ с П- регулятором (кнопки «S2», «S5» – нажаты, «S1»- отжата).
5.4.7.1
Измерить частоту (с помощью осциллографа) и уровень сигнала(с помощью
вольтметра) на выходе системы, гнездо Х3, результат занести в таблицу 5.2.
5.4.7.2 Измерить сдвиг фаз между выходным и входным
сигналами. Для этого соединить гнездо Х3 с гнездом «вых.» функционального
измерителя, вольтметр постоянного напряжения подключить к гнезду φ и получить
значение угла α (см.лаб.работу №1). Результат занести в таблицу 5.2.
5.4.8
Исследовать САУ с ПД-регулятором (кнопки «S1», «S2», «S5» – нажаты).
5.4.8.1 Повторить пункты 5.4.7.1 и 5.4.7.2.
5.4.9 Установить
параметры сигнала на выходе генератора ЕГ :
f = 100 Гц, Uвх = 2,5 B. Подать сигнал
на вход регулятора, гнездо Х10. Сигнал задания пересчитать, данные занести в
таблицу 5.2.
5.4.9.1
Повторить пункты 5.4.7, 5.4.8.
5.4.10
Установить параметры сигнала на выходе генератора ЕГ :
f = 150 Гц, Uвх = 2,5 B. Подать сигнал
на вход регулятора, гнездо Х10. Сигнал задания пересчитать, данные занести в
таблицу 5.2.
5.4.10.1
Повторить пункты 5.4.7, 5.4.8.
5.5
Обработка результатов
5.5.1 По
результатам эксперимента, табл.5.1, рассчитать абсолютную Δ= —
и
относительную δ = Δ/Uз погрешности.
Сравнить их со значениями Со.
5.5.2 По
результатам эксперимента, табл. 5.2 определить значение ошибки ΔХm = Uεm по выражению Uε = Uз – Uвых . Для упрощения
расчета значения Uз и Uвых целесообразно
представить в комплексной форме Uз = Uз еjtЗ ; Uвых = Uвых еjtВЫХ . Результаты расчетов занести в
таблицу.
5.5.3 Построить
временные диаграммы входного и выходного сигналов, а также сигнала ошибки (для
одного из случаев, приведенных в табл. 5.2, по указанию преподавателя).
Похожие материалы
- Исследование частотных характеристик линейных звеньев
- Команды с собственным входным языком (BUILD, MACRO, State и др.). Правила ввода команд и параметров
- Методика снятия временных и частотных характеристик линейных динамических систем. Типовые воздействия
Информация о работе
Тип:
Методические указания и пособия
Лекция 17. Расчет установившейся ошибки в системах управления.
Структурные признаки астатизма
Установившейся (статической) ошибкой называют
постоянное значение сигнала ошибки x(t)=g(t)-y(t),
которое она приобретает по окончании переходного процесса: , рисунок 116.
Очевидно, установившаяся ошибка зависит от законов
изменения и численных характеристик входных сигналов системы. Поэтому при ее
определении принято рассматривать так называемые типовые входные сигналы,
законы изменения которых составляют степенной ряд относительно времени.
Например, для задающего воздействия:
,
,

далее.
При наличии нескольких воздействий на линейную систему
для определения xуст используется
принцип суперпозиции – реакция линейной системы на совокупность входных
сигналов совпадает с алгебраической суммой ее реакций на каждый из сигналов в
отдельности:
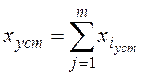
каждое слагаемое, или составляющая сигнала ошибки, определяется
для i-го входного сигнала при условии, что остальные
тождественно равны нулю. Такой подход полностью соответствует определению
передаточной функции и позволяет выполнять расчет установившейся ошибки на
основе структурной схемы системы.
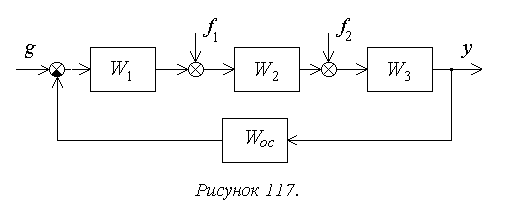
Рассмотрим порядок расчета установившейся ошибки на
следующем достаточно общем примере (рисунок 117).
В соответствии с принципом суперпозиции установившаяся
ошибка будет определяться здесь в виде суммы трех составляющих .
Изображение по Лапласу ошибки от задающего воздействия
получают через передаточную функцию замкнутой системы по ошибке при известном изображении задающего
воздействия G(s):
, где
F(s) – основная передаточная функция замкнутой системы.
Для структурной схемы на рисунке 117
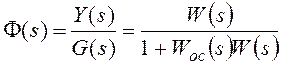
— передаточная функция
разомкнутой системы, или прямой цепи системы, для рассматриваемого примера.
Непосредственно для расчета
установившегося значения ошибки от задающего воздействия используют теорему о
конечном значении для преобразования Лапласа:
В результате:
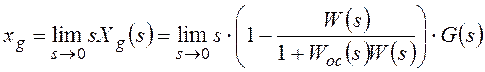
Изображение по Лапласу ошибки от возмущающего
воздействия получают через передаточную функцию замкнутой системы по ошибке от
возмущения при известном изображении возмущающего
воздействия F(s):
, где
Ff(s) –передаточная функция замкнутой системы по
возмущающему воздействию,
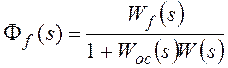
Wf(s)
– передаточная функция разомкнутой системы по возмущению (передаточная функция
участка прямой цепи системы от точки приложения возмущающего воздействия до
выхода системы).
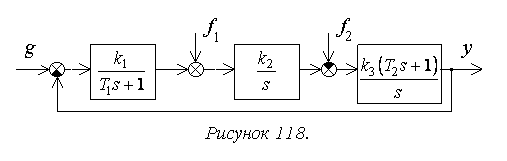
Для структурной схемы на рисунке 8 необходимо
учитывать два возмущающих воздействия, приложенные в различные точки системы.
Для f1:
,
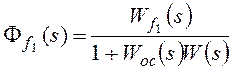
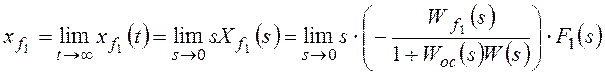
Для f2:
,
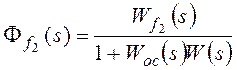
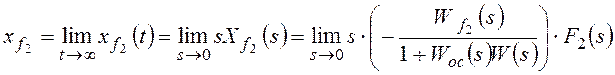
Расчет упрощается для
системы с единичной отрицательной обратной связью (рисунок 118):
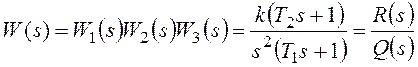
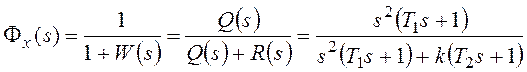
разомкнутой системы.
Найдем установившуюся ошибку
для некоторых типовых вариантов задающего воздействия.
При получим:
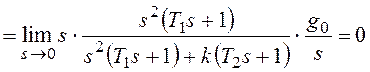
При получим:
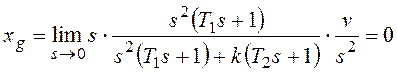
При 
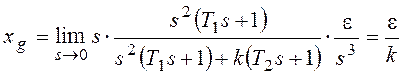
Если установившаяся ошибка
тождественно равна нулю при каком-либо типовом варианте входного сигнала,
независимо от его численных характеристик, систему называют астатической по
рассматриваемому входному сигналу.
Количество типовых вариантов
входного сигнала – членов степенного ряда, при которых установившаяся ошибка
тождественно равна нулю, определяет порядок астатизма.
Рассматриваемая система
обладает свойством астатизма второго порядка по задающему воздействию.
Рассмотрим установившуюся
ошибку от возмущения f1:
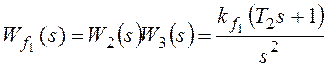
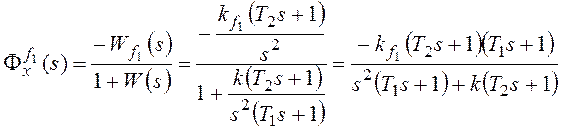
–
коэффициент передачи разомкнутой системы по возмущению f1.
При получим:
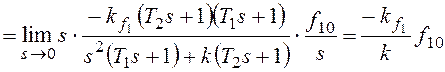
При получим:
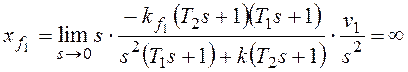
При 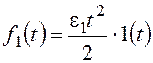
тот же результат.
Отметим, что по возмущению f1 рассматриваемая система
не является астатической. Кроме того, она не в состоянии отработать два последних
варианта входного сигнала.
Рассмотрим установившуюся
ошибку от возмущения f2:
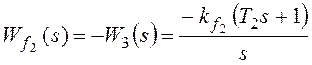
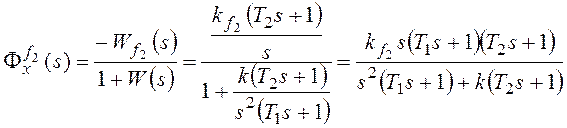
–
коэффициент передачи разомкнутой системы по возмущению f2.
При получим:
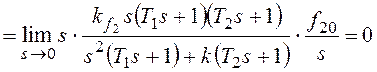
При получим:
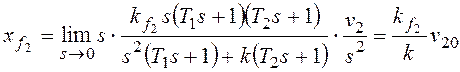
При 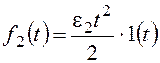
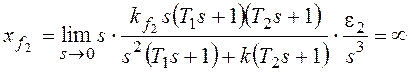
По возмущению f2 рассматриваемая система имеет
астатизм первого порядка. Она не в состоянии отработать возмущающее
воздействие, изменяющееся во времени с постоянным ускорением.
Подведем некоторые итоги:
1. Наличие и глубина
свойства астатизма зависят от точки приложения входного сигнала.
2. Постоянные времени
звеньев системы не влияют на ее точность.
3. Увеличение значения
коэффициента передачи разомкнутой системы приводит к снижению величины
установившейся ошибки.
Для систем с единичной
отрицательной обратной связью существуют достаточно простые структурные
признаки астатизма.
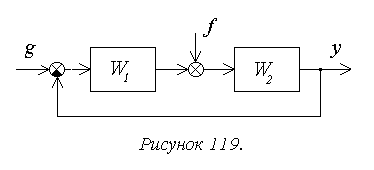
Рассмотрим структуру,
показанную на рисунке 119.
В общем случае передаточная
функция разомкнутой системы может быть представлена в следующей форме:
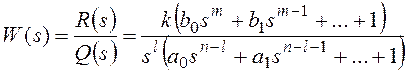
Тогда получим:
и для общего вида задающего воздействия 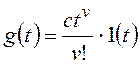
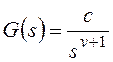
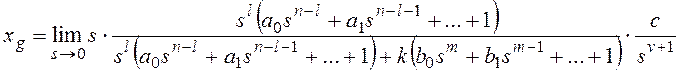
Результат нахождения этого
предела зависит от соотношения показателей степени:
— при l>v установившаяся
ошибка равна нулю независимо от остальных параметров, то есть имеет место
астатизм;
— при l=v получаем
константу;
— при l<v установившаяся
ошибка стремится к бесконечности, то есть система не в состоянии отработать
входной сигнал.
Учитывая, что минимальное
значение v нулевое,
получаем условие астатизма по задающему воздействию: l>0.
Таким образом, структурный
признак астатизма по задающему воздействию в системе с единичной отрицательной
обратной связью состоит в наличии нулевых корней в знаменателе передаточной
функции разомкнутой системы, или интегрирующих звеньев в прямой цепи системы.
Нетрудно также убедиться,
что положительное значение l совпадает
с порядком астатизма.
Для получения признака
астатизма по возмущающему воздействию представим передаточные функции на
рисунке 10 в форме:
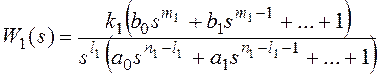
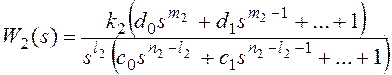
k1k2=k, m1+m2=m,
n1+n2=n,
причем и
.
Тогда получим:
и для общего вида возмущающего воздействия 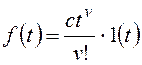
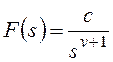
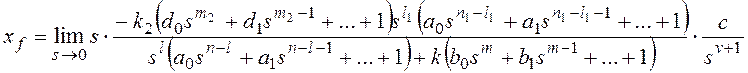
Все вышеприведенные выводы
можно повторить для показателя степени l1.
Таким образом, структурный
признак астатизма по возмущающему воздействию в системе с единичной
отрицательной обратной связью состоит в наличии нулевых корней в знаменателе
передаточной функции участка системы до точки приложения воздействия, или
интегрирующих звеньев на том же участке.
1. Точность систем автоматического управления
ТОЧНОСТЬ СИСТЕМ АВТОМАТИЧЕСКОГО
УПРАВЛЕНИЯ
1) Понятие точности. Постоянные ошибки
2) Установившиеся ошибки при произвольном
входном сигнале
3) Установившиеся ошибки при гармоническом
воздействии
2. 1)Понятие точности. Постоянные ошибки
Основным назначением системы является как
можно более точное воспроизведение управляющего
сигнала.
Точность системы можно оценивать величиной
разности управляющего сигнала v(t) и выхода y(t),
т. е. величиной ошибки
e(t)=v(t)-y(t)
Чем меньше величина e(t) пo модулю в каждый
данный момент времени, тем система с большей
точностью
(меньшей
ошибкой)
воспроизводит
управляющий сигнал.
На практике интересуются не полной ошибкой
системы e(t), а так называемой установившейся
ошибкой e (t )
y
3.
Структурная схема стандартной САУ имеет вид
f
v
e
W1(s)
y
W2(s)
Изображение ошибки имеет вид
E ( s ) e ( s )V ( s ) f ( s ) F ( s )
f ( s)
W2 ( s)
1 W ( s)
e (s)
1
1 W (s)
(1)
W (s) W1 (s)W2 (s)
Ошибка системы определяется суммой двух составляющих:
ошибкой системы от управляющего воздействия и ошибкой системы
от возмущающего воздействия.
4.
При определенных типах воздействий и определенной структуре
системы установившаяся ошибка в системе будет постоянной и может
быть вычислена на основании правил операционного исчисления по
выражению
e y lim e(t ) lim sE(s) lim s e (s)V (s)
t
s 0
(2)
s 0
Входные воздействия:
v (t ) v 01[t ]
v0
V (s)
s
v (t ) v1t
v1
V ( s) 2
s
v (t ) v 2t
2
2v 2
V ( s) 3
s
v (t ) v 0 v1t … v t , v i const
V ( s)
v 0 v1
!v
2 … 1
s s
s
5.
Пусть передаточная функция разомкнутой системы имеет вид
W ( s)
Если
0
v (t ) v 01[t ]
KN ( s )
,
s L0 ( s )
V (s)
0, 1…
v0
s
При подставлении в (2) имеем
v0
e
1 W (0)
0
y
e 0y — статическая ошибка системы
K p lim W ( s )
s 0
— коэффициент ошибки по положению
(3)
6.
Если
1
v (t ) v 01[t ]
v0
s
v1
V ( s) 2
s
v(t ) v1t
e1y
V (s)
e 0y 0
e1y
v1
KV
— ошибка системы по скорости
KV lim sW ( s) — коэффициент ошибки по скорости
s 0
(4)
7.
Если
2
v (t ) v 01[t ]
v(t ) v1t
v (t ) v 2t
ey2
2
V (s)
v0
s
v1
V ( s) 2
s
2v 2
V ( s) 3
s
e 0y 0
e 0
1
y
ey2
(5)
2v 2
Ka
— ошибка системы по ускорению.
K a lim s 2W ( s) — коэффициент ошибки по ускорению
s 0
Из приведенных выражений следует, что ошибки в системе
уменьшаются с ростом порядка астатизма системы и увеличением
общего коэффициента усиления К.
8.
Переходные процессы в различных системах при отработке скачка
по положению и скорости:
1 – для статической системы,
2 – для системы с астатизмом первого порядка,
3 – для системы с астатизмом второго порядка.
y(t),
v(t)
v0
1
v0
v1t
K 1
v1
3
0
2
K
t
9.
Рассмотрим влияние порядка астатизма на точность отработки
задающего воздействия
10.
11.
Пример: Пусть имеем структурную схему системы в виде
f (t ) f 01[t ]
v (t ) v 01[t ]
f
v
e
K1
T1s 1
K2
s
y
Рассмотрим влияние параметров системы на величину
установившейся ошибки, обусловленную действием как входного
сигнала так и сигнала возмущения.
12.
Изображение сигнала ошибки имеет вид
E ( s)
s T1s 1
s T1s 1 K1 K 2
V ( s)
K 2 T1s 1
s T1s 1 K1 K 2
F ( s)
Подставляя в это выражение
V ( s) v0 s
установившаяся ошибка будет равна
F (s) f0 s
e y f0 K1
Таким образом, установившаяся ошибка от управляющего воздействия
равна нулю (система астатическая по отношению к управляющему сигналу), а
ошибка от возмущающего воздействия постоянна (система статическая по
отношению к возмущению). Для уменьшения этой ошибки следует
увеличивать коэффициент усиления K1 первого звена; величина K2 не влияет
на ошибку.
13.
Пусть имеем систему в виде
f (t ) f 01[t ]
v (t ) v 01[t ]
f
v
e
K1
s
K2
T1 s 1
y
Изображение сигнала ошибки имеет вид
E ( s)
s T1s 1
s T1s 1 K1 K 2
V ( s)
Установившаяся ошибка будет равна
K2s
s T1s 1 K1 K 2
F ( s)
ey 0
Система обладает астатизмом первого порядка по отношению к обоим
внешним воздействиям.
14. 2) Установившиеся ошибки при произвольном входном сигнале
Рассмотрим входное воздействие в виде
Установившаяся ошибка будет определяться по формуле
(6)
(7)
Коэффициенты ci носят название коэффициентов ошибок и
характеризуют, с каким весом функция v(t) и ее производные входят в
общее выражение для установившейся ошибки.
15.
Если
В статической системе ν=0
Для системы с астатизмом первого порядка ν=1
Аналогично можно показать, что для астатической системы с астатизмом ν-го
порядка
(8)
16.
На практике используется
коэффициентов ошибок
Разложим передаточную функцию
следующий
e (s)
способ
нахождения
в ряд Маклорена при s = 0
(9)
Так как
есть отношение полиномов,
то, деля полином числителя на полином знаменателя, получим ряд
(10)
Приравнивая коэффициенты при одинаковых степенях s в (9), (10),
получим
(11)
17.
Величина коэффициентов ошибок в конечном итоге определяет
величину ошибки в системе.
Из изложенного следует, что величины ci будут тем меньше, чем
выше
порядок
астатизма
системы
и
чем
больше
величина
коэффициента усиления К разомкнутой системы.
Пример: Пусть передаточная функция разомкнутой системы имеет
вид
K
W (s)
s Ts 1
Найти первые три коэффициента ошибок.
Передаточная функция замкнутой системы по ошибке будет равна
18.
Деля полином числителя на полином знаменателя, получим
Определим установившуюся ошибку в системе при воздействии
19.
Пример: Пусть передаточная функция разомкнутой системы имеет вид
Найти первые четыре коэффициента ошибок.
Передаточная функция замкнутой системы по ошибке будет равна
Примечание. Причем, если какой-либо коэффициент полинома
числителя равен нулю, то в выражении полинома на месте этого
коэффициента необходимо писать число «ноль».
20.
Деля полином числителя на полином знаменателя, получим
Находим
C 0;
0
C1 0;
21. 3) Установившиеся ошибки при гармоническом воздействии
Главная передаточная функция замкнутой системы имеет вид
Входной сигнал задан в виде
Выходной сигнал в установившемся режиме определяется по выражению
(12)
где
22.
Аналогично, зная передаточную функцию по ошибке, можно найти закон
изменения ошибки в установившемся режиме при гармоническом входном
сигнале
(13)
где
Выражения (12), (13) позволяют оценить ошибки воспроизведения
гармонического сигнала в установившемся режиме.
Из этих выражений следует, что, кроме ошибки воспроизведения
амплитуды входного гармонического сигнала, существуют и постоянные
фазовые
ошибки,
которые
определяются
видом
фазочастотных
характеристик замкнутой системы.
Обычно при анализе точности систем управления их не рассматривают,
ограничиваясь лишь анализом ошибок воспроизведения амплитуды.
23.
Из (12), (13) можно получить ошибки воспроизведения амплитуды
гармонического сигнала на заданной частоте, равные
(14)
(15)
Типичный вид АЧХ замкнутой системы для случая астатической системы
A3 ( ) имеет вид
A3 ( )
1
A3 max
0
p
cp
n
24.
Под полосой пропускания системы понимают диапазон частот 0 n
при котором выполняется условие
(16)
Полоса пропускания является важной характеристикой системы. С одной
стороны, чем шире полоса пропускания, тем с меньшими ошибками система
воспроизводит управляющие сигналы.
Однако, с увеличение полосы пропускания система становится
чувствительной к влиянию высокочастотных помех.
Для статической системы
Для астатической системы
25.
Пример:
Дана структурная схема двигателя постоянного тока с управлением
по цепи якоря и тахометрической обратной связью.
Определить значение К, при котором установившаяся ошибка при
отработке линейного входного сигнала не будет превышать 0.1 (при условии,
что D(s)=0)
26.
Передаточная функция разомкнутой системы будет иметь вид
Передаточная функция замкнутой системы по ошибке
27.
Установившаяся ошибка
Входной сигнал имеет вид
Найдем значение К при котором установившаяся не будет превышать 0.1
28.
Установившаяся ошибка
e=0.1
v(t)
y(t)
29.
При К=1, получить выражение для ошибки и изобразить график ее
изменения при действии линейного возмущения d(t)=t, на интервале от 0 до 5
сек.
Входной сигнал имеет вид
v(t ) t
1
V (s) 2
s
Найдем значение К при котором установившаяся не будет превышать 0.1