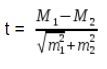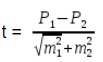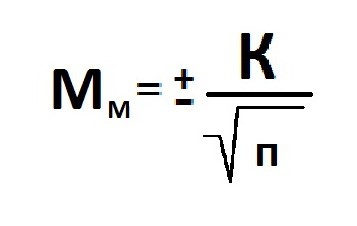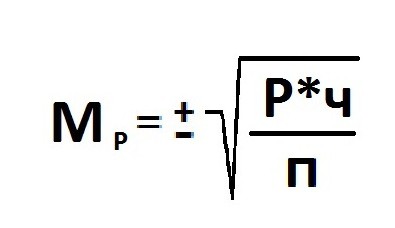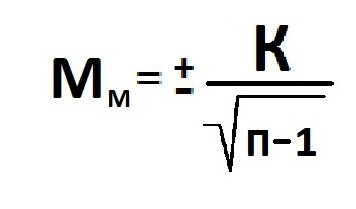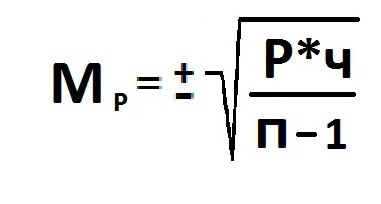В
статистике выделяют два основных метода
исследования — сплошной и выборочный.
При проведении выборочного исследования
обязательным является соблюдение
следующих требований: репрезентативность
выборочной совокупности и достаточное
число единиц наблюдений. При выборе
единиц наблюдения возможны ошибки
смещения,
т.е. такие события, появление которых
не может быть точно предсказуемым. Эти
ошибки являются объективными и
закономерными. При определении степени
точности выборочного исследования
оценивается величина ошибки, которая
может произойти в процессе выборки
— случайная
ошибка репрезентативности (m)
— является
фактической разностью между средними
или относительными величинами, полученными
при проведении выборочного исследования
и аналогичными величинами, которые были
бы получены при проведении исследования
на генеральной совокупности.
Оценка
достоверности результатов исследования
предусматривает определение:
1.
ошибки репрезентативности
2.
доверительных границ средних (или
относительных) величин в генеральной
совокупности
3.
достоверности разности средних (или
относительных) величин (по критерию t)
Расчет
ошибки репрезентативности
(mм)
средней арифметической величины
(М):
,
где σ
— среднее квадратическое отклонение; n
— численность выборки (>30).
Расчет
ошибки репрезентативности (mР)
относительной величины (Р):
,
где Р — соответствующая относительная
величина (рассчитанная, например, в %);
q
=100 — Ρ%
— величина, обратная Р; n
— численность выборки (n>30)
В
клинических и экспериментальных работах
довольно часто приходится использовать
малую
выборку, когда
число наблюдений меньше или равно 30.
При малой выборке для расчета ошибок
репрезентативности, как средних, так
и относительных величин,
число
наблюдений уменьшается на единицу,
т.е.
;
.
Величина
ошибки репрезентативности зависит от
объема выборки: чем больше число
наблюдений, тем меньше ошибка. Для оценки
достоверности выборочного показателя
принят следующий подход: показатель
(или средняя величина) должен в 3 раза
превышать свою ошибку, в этом случае он
считается достоверным.
83. Определение доверительных границ средних и относительных величин.
Знание
величины ошибки недостаточно для того,
чтобы быть уверенным в результатах
выборочного исследования, так как
конкретная ошибка выборочного
исследования может быть значительно
больше (или меньше) величины средней
ошибки репрезентативности. Для
определения точности, с которой
исследователь желает получить результат,
в статистике используется такое понятие,
как вероятность безошибочного
прогноза, которая является характеристикой
надежности результатов выборочных
медико-биологических статистических
исследований. Обычно, при проведении
медико-биологических статистических
исследований используют вероятность
безошибочного прогноза 95% или 99%. В
наиболее ответственных случаях, когда
необходимо сделать особенно важные
выводы в теоретическом или практическом
отношении, используют вероятность
безошибочного прогноза 99,7%
Определенной
степени вероятности безошибочного
прогноза соответствует определенная
величина предельной
ошибки случайной выборки (Δ
— дельта),
которая определяется по формуле:
Δ=t
* m
, где t
— доверительный коэффициент, который
при большой выборке при вероятности
безошибочного прогноза 95% равен 2,6;
при вероятности безошибочного
прогноза 99% — 3,0; при вероятности
безошибочного прогноза 99,7% — 3,3, а при
малой выборке определяется по специальной
таблице значений t
Стьюдента.
Используя
предельную ошибку выборки (Δ),
можно определить доверительные
границы,
в которых с определенной вероятностью
безошибочного прогноза заключено
действительное значение статистической
величины,
характеризующей
всю генеральную совокупность (средней
или относительной).
Для
определения доверительных границ
используются следующие формулы:
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
В
статистике выделяют два основных метода
исследования — сплошной и выборочный.
При проведении выборочного исследования
обязательным является соблюдение
следующих требований: репрезентативность
выборочной совокупности и достаточное
число единиц наблюдений. При выборе
единиц наблюдения возможны ошибки
смещения,
т.е. такие события, появление которых
не может быть точно предсказуемым. Эти
ошибки являются объективными и
закономерными. При определении степени
точности выборочного исследования
оценивается величина ошибки, которая
может произойти в процессе выборки
— случайная
ошибка репрезентативности (m)
— является
фактической разностью между средними
или относительными величинами, полученными
при проведении выборочного исследования
и аналогичными величинами, которые были
бы получены при проведении исследования
на генеральной совокупности.
Оценка
достоверности результатов исследования
предусматривает определение:
1.
ошибки репрезентативности
2.
доверительных границ средних (или
относительных) величин в генеральной
совокупности
3.
достоверности разности средних (или
относительных) величин (по критерию t)
Расчет
ошибки репрезентативности
(mм)
средней арифметической величины
(М):
,
где σ
— среднее квадратическое отклонение; n
— численность выборки (>30).
Расчет
ошибки репрезентативности (mР)
относительной величины (Р):
,
где Р — соответствующая относительная
величина (рассчитанная, например, в %);
q
=100 — Ρ%
— величина, обратная Р; n
— численность выборки (n>30)
В
клинических и экспериментальных работах
довольно часто приходится использовать
малую
выборку, когда
число наблюдений меньше или равно 30.
При малой выборке для расчета ошибок
репрезентативности, как средних, так
и относительных величин,
число
наблюдений уменьшается на единицу,
т.е.
;
.
Величина
ошибки репрезентативности зависит от
объема выборки: чем больше число
наблюдений, тем меньше ошибка. Для оценки
достоверности выборочного показателя
принят следующий подход: показатель
(или средняя величина) должен в 3 раза
превышать свою ошибку, в этом случае он
считается достоверным.
83. Определение доверительных границ средних и относительных величин.
Знание
величины ошибки недостаточно для того,
чтобы быть уверенным в результатах
выборочного исследования, так как
конкретная ошибка выборочного
исследования может быть значительно
больше (или меньше) величины средней
ошибки репрезентативности. Для
определения точности, с которой
исследователь желает получить результат,
в статистике используется такое понятие,
как вероятность безошибочного
прогноза, которая является характеристикой
надежности результатов выборочных
медико-биологических статистических
исследований. Обычно, при проведении
медико-биологических статистических
исследований используют вероятность
безошибочного прогноза 95% или 99%. В
наиболее ответственных случаях, когда
необходимо сделать особенно важные
выводы в теоретическом или практическом
отношении, используют вероятность
безошибочного прогноза 99,7%
Определенной
степени вероятности безошибочного
прогноза соответствует определенная
величина предельной
ошибки случайной выборки (Δ
— дельта),
которая определяется по формуле:
Δ=t
* m
, где t
— доверительный коэффициент, который
при большой выборке при вероятности
безошибочного прогноза 95% равен 2,6;
при вероятности безошибочного
прогноза 99% — 3,0; при вероятности
безошибочного прогноза 99,7% — 3,3, а при
малой выборке определяется по специальной
таблице значений t
Стьюдента.
Используя
предельную ошибку выборки (Δ),
можно определить доверительные
границы,
в которых с определенной вероятностью
безошибочного прогноза заключено
действительное значение статистической
величины,
характеризующей
всю генеральную совокупность (средней
или относительной).
Для
определения доверительных границ
используются следующие формулы:
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
ДЕПАРТАМЕНТ ОБРАЗОВАНИЯ И НАУКИ ГОРОДА МОСКВЫ
Государственное бюджетное профессиональное образовательное учреждение города Москвы
«ЮРИДИЧЕСКИЙ КОЛЛЕДЖ»
(ГБПОУ Юридический колледж)
ПЛАН-КОНСПЕКТ учебного занятия
по ОП.11 Статистика
учебной дисциплине/междисциплинарному курсу
для обучающихся 2 курса
специальность 40.02.01 Право и организация социального обеспечения
(набор 2016 г.)
(углубленная подготовка)
дата проведения занятия по расписанию
Тема 3.1. Выборочное наблюдение
Занятие 15. ПЗ №8 Определение ошибки репрезентативности.
Определение объема выборочной совокупности
Цель занятия: отработать практические навыки по определению доверительных пределов и исчислению ошибок выборки
Задачи занятия:
Обучающая: Обеспечить усвоение обучающимися материала о понятиях: ошибки репрезентативности, выборка, выборочная совокупность;
Воспитательная: воспитывать навыки самостоятельной работы, чувство ответственности за порученный участок работы, дисциплину умственного труда, уверенность в своих силах, стремление к достижению результата;
Развивающая: создавать условия для развития самостоятельности мышления, способности высказывания собственной точки зрения, систематизировать необходимую информацию, анализировать, сравнивать и обобщать информацию, развивать монологическую речь.
Основная литература:
Глава 11. Выборочное наблюдение. (211-220) Статистика: учебник / И.В. Гладун. – 2-е издание, стер. – М.: КНОРУС, 2014. – 232 с. – СПО
Дополнительная литература:
Савюк Л.К. Правовая статистика: Учебник. — М.: Юрист, 2016
Интернет-ресурсы:
- Информационно-издательский центр «Статистика России» http://www.statbook.ru
- Электронный фонд правовой и технической документации http://docs.cntd.ru
- Информационно правовой портал http://www.garant.ru/
Междисциплинарные связи: Право социальное обеспечение
Внутридисциплинарные связи: Тема 2.1. Сводка и группировка статистических данных
1. Актуализация знаний по ранее пройденному материалу учебного курса
(ответить на вопросы (тестовые задания) и провести самооценку усвоенного материала)
Таблица 1.
|
Вопрос (тестовое задание) |
Ответ |
|
|
|
|
|
|
|
|
|
2. Изучаемые вопросы занятия
|
1. Определение ошибки репрезентативности. |
|
2. Определение объема выборочной совокупности. |
Вопрос 1. Определение ошибки репрезентативности
В статистике выделяют два основных метода исследования – сплошной и выборочный. При проведении выборочного исследования обязательным является соблюдение следующих требований: репрезентативность выборочной совокупности и достаточное число единиц наблюдений. При выборе единиц наблюдения возможны Ошибки смещения, т. е. такие события, появление которых не может быть точно предсказуемым. Эти ошибки являются объективными и закономерными. При определении степени точности выборочного исследования оценивается величина ошибки, которая может произойти в процессе выборки – Случайная ошибка репрезентативности (M) – Является фактической разностью между средними или относительными величинами, полученными при проведении выборочного исследования и аналогичными величинами, которые были бы получены при проведении исследования на генеральной совокупности.
Оценка достоверности результатов исследования предусматривает определение:
1. ошибки репрезентативности
2. доверительных границ средних (или относительных) величин в генеральной совокупности
3. достоверности разности средних (или относительных) величин (по критерию t)
Расчет ошибки репрезентативности (mм) средней арифметической величины (М):

Расчет ошибки репрезентативности (mР) относительной величины (Р):

Q =100 – Ρ% – величина, обратная Р; n – численность выборки (n>30)
В клинических и экспериментальных работах довольно часто приходится использовать Малую выборку, Когда число наблюдений меньше или равно 30. При малой выборке для расчета ошибок репрезентативности, как средних, так и относительных величин, Число наблюдений уменьшается на единицу, т. е.


Величина ошибки репрезентативности зависит от объема выборки: чем больше число наблюдений, тем меньше ошибка. Для оценки достоверности выборочного показателя принят следующий подход: показатель (или средняя величина) должен в 3 раза превышать свою ошибку, в этом случае он считается достоверным.
Знание величины ошибки недостаточно для того, чтобы быть уверенным в результатах выборочного исследования, так как конкретная ошибка выборочного исследования может быть значительно больше (или меньше) величины средней ошибки репрезентативности. Для определения точности, с которой исследователь желает получить результат, в статистике используется такое понятие, как вероятность безошибочного прогноза, которая является характеристикой надежности результатов выборочных медико-биологических статистических исследований. Обычно, при проведении медико-биологических статистических исследований используют вероятность безошибочного прогноза 95% или 99%. В наиболее ответственных случаях, когда необходимо сделать особенно важные выводы в теоретическом или практическом отношении, используют вероятность безошибочного прогноза 99,7%
Определенной степени вероятности безошибочного прогноза соответствует определенная величина Предельной ошибки случайной выборки (Δ – дельта), которая определяется по формуле:
Δ=t * m, где t – доверительный коэффициент, который при большой выборке при вероятности безошибочного прогноза 95% равен 2,6; при вероятности безошибочного прогноза 99% – 3,0; при вероятности безошибочного прогноза 99,7% – 3,3, а при малой выборке определяется по специальной таблице значений t Стьюдента.
Используя предельную ошибку выборки (Δ), можно определить Доверительные границы, в которых с определенной вероятностью безошибочного прогноза заключено действительное значение статистической величины, Характеризующей всю генеральную совокупность (средней или относительной).
Для определения доверительных границ используются следующие формулы:
- для средних величин:

Мвыб – средняя величина, Полученная при проведении исследования на выборочной совокупности; t – доверительный коэффициент, значение которого определяется степенью вероятности безошибочного прогноза, с которой исследователь желает получить результат; mM – ошибка репрезентативности средней величины.
2) для относительных величин:

Доверительные границы показывают, в каких пределах может колебаться размер выборочного показателя в зависимости от причин случайного характера.
При малом числе наблюдений (n<30), для вычисления доверительных границ значение коэффициента t находят по специальной таблице Стьюдента. Значения t расположены в таблице на пересечении с избранной вероятностью безошибочного прогноза и строки, Указывающей на имеющееся число степеней свободы (n), Которое равно n-1.
на определение ошибок репрезентативности (m) и доверительных границ средней величины генеральной совокупности (Мген) при числе наблюдений больше 30
Условие задачи: при изучении комбинированного воздействия шума и низкочастотной вибрации на организм человека было установлено, что средняя частота пульса у 36 обследованных водителей сельскохозяйственных машин через 1 ч работы составила 80 ударов в 1 минуту; σ = ± 6 ударов в минуту.
Задание: определить ошибку репрезентативности (mM) и доверительные границы средней величины генеральной совокупности (Мген).
Решение.
- Вычисление средней ошибки средней арифметической (ошибки репрезентативности) (m): m = σ / √n = 6 / √36 = ±1 удар в минуту
- Вычисление доверительных границ средней величины генеральной совокупности (Мген). Для этого необходимо:
- а) задать степень вероятности безошибочного прогноза (Р = 95 %);
- б) определить величину критерия t. При заданной степени вероятности (Р=95%) и числе наблюдений меньше 30 величина критерия t, определяемого по таблице, равна 2 (t = 2). Тогда Мген = Мвыб ± tm = 80 ± 2×1 = 80 ± 2 удара в минуту.
Вывод. Установлено с вероятностью безошибочного прогноза Р = 95%, что средняя частота пульса в генеральной совокупности, т.е. у всех водителей сельскохозяйственных машин, через 1 ч работы в аналогичных условиях будет находиться в пределах от 78 до 82 ударов в минуту, т.е. средняя частота пульса менее 78 и более 82 ударов в минуту возможна не более, чем у 5% случаев генеральной совокупности.
на определение ошибок репрезентативности (m) и доверительных границ относительного показателя генеральной совокупности (Рген)
Условие задачи: при медицинском осмотре 164 детей 3 летнего возраста, проживающих в одном из районов городе Н., в 18% случаев обнаружено нарушение осанки функционального характера.
Задание: определить ошибку репрезентативности (mp) и доверительные границы относительного показателя генеральной совокупности (Рген).
Решение.
- Вычисление ошибки репрезентативности относительного показателя: m = √P x q / n = √18 x (100 — 18) / 164 = ± 3%
- Вычисление доверительных границ средней величины генеральной совокупности (Рген) производится следующим образом:
- необходимо задать степень вероятности безошибочного прогноза (Р=95%);
- при заданной степени вероятности и числе наблюдений больше 30, величина критерия t равна 2 (t = 2). Тогда Рген = Рвыб± tm = 18% ± 2 х 3 = 18% ± 6%.
Вывод. Установлено с вероятностью безошибочного прогноза Р=95%, что частота нарушения осанки функционального характера у детей 3 летнего возраста, проживающих в городе Н., будет находиться в пределах от 12 до 24% случаев.
на оценку достоверности разности средних величин
Условие задачи: при изучении комбинированного воздействия шума и низкочастотной вибрации на организм человека было установлено, что средняя частота пульса у водителей сельскохозяйственных машин через 1 ч после начала работы составила 80 ударов в минуту; m = ± 1 удар в мин. Средняя частота пульса у этой же группы водителей до начала работы равнялась 75 ударам в минуту; m = ± 1 удар в минуту.
Задание: оценить достоверность различий средних значений пульса у водителей сельскохозяйственных машин до и после 1 ч работы.
Решение.
Вывод. Значение критерия t = 3,5 соответствует вероятности безошибочного прогноза Р > 99,7%, следовательно можно утверждать, что различия в средних значениях пульса у водителей сельскохозяйственных машин до и после 1 ч работы не случайно, а достоверно, существенно, т.е. обусловлено влиянием воздействия шума и низкочастотной вибрации.
на оценку достоверности разности относительных показателей
Условие задачи: при медицинском осмотре детей 3 летнего возраста в 18% (m = ± 3%) случаях обнаружено нарушение осанки функционального характера. Частота аналогичных нарушений осанки при медосмотре детей 4-летнего возраста составила 24% (m = ± 2,64%).
Задание: оценить достоверность различий в частоте нарушения осанки у детей 2 возрастных групп.
Решение.
Вывод. Значение критерия t=1,5 соответствует вероятности безошибочного прогноза Р<95%. Следовательно, различие в частоте нарушений осанки среди детей, сравниваемых возрастных групп случайно, недостоверно, несущественно, т.е. не обусловлено влиянием возраста детей.
|
Источники информации по 1 вопросу |
Автор и наименование |
Страницы (форма доступа для Интернет-ресурсов) |
|
Основная литература |
Глава 11. Выборочное наблюдение. Статистика: учебник / И.В. Гладун. – 2-е издание, стер. – М.: КНОРУС, 2014. – 232 с. – СПО |
стр. 211-220 |
|
Интернет ресурсы |
|
http://www.statbook.ru |
|
http://docs.cntd.ru |
|
|
http://www.garant.ru/ |
Контрольное задание по Вопросу 1
- Записать в тетрадь конспект (1-2 стр.)
Вопрос 2. Определение объема выборочной совокупности
Социологические исследования редко бывают сплошными, как, например, перепись населения. Обычно сплошное исследование проводится при небольшой генеральной совокупности.
Чаще всего исследования носят выборочный характер, при котором наиболее важным основанием является возможность распространения полученных результатов и выводов на всю генеральную совокупность. В таком случае сплошное исследование нецелесообразно. Обеспечение этой нецелесообразности — вопрос о репрезентативности выборки, т.е. достаточной количественной и качественной представительности генеральной совокупности в выборке.
Условиями соблюдения репрезентативности выборки являются:
1) равная возможность каждого члена генеральной совокупности попасть в выборку;
2) отбор необходимо проводить независимо от изучаемого признака (иначе в выборку могут попасть, например, только спортсмены);
3) отбор по возможности должен производиться из однородных совокупностей;
4) величина выборки должна быть достаточно большой.
Далее возникает вопрос: как определить достаточный объем выборки? Для этого необходимо иметь характеристики генеральной совокупности по важнейшим (с точки зрения исследования) признакам. К ним, например, можно отнести сведения о количестве желающих заниматься физической культурой и спортом, о числе занимающихся и т.д. Но, как правило, такие характеристики (или многие из них) не известны. Пилотажные исследования как раз и направлены на их выявление.
Приведем пример определения объема выборочной совокупности. В ходе подготовки к проведению конкретно-социологического исследования на основании теоретических посылок были выделены характеристики и признаки, подлежащие изучению. Например, желание заниматься физической культурой, спортом, величина потребности, участие в видах деятельности и др.
На основании результатов изучения этих признаков в пробном исследовании (30 и более респондентов) определяется объем выборки.
Предположим, что в пробном исследовании опрошено 147 студентов 4-х курсов в четырех вузах Республики Беларусь.
Для желания заниматься физической культурой получены следующие распределения:
1.«Нет, не хочу» — 5 человек;
2.«Скорее не хочу, чем хочу» — 3 человека;
3.«Безразлично» — 11 человек;
4.«Скорее хочу, чем не хочу» — 34 человека;
5.«Да, хочу» — 72 человека.
Для расчета объема выборки используются формулы:
t — 1,96 — распределение Стьюдента для вероятности 0,95 или 95% (т.е., если требуемая вероятность соответствия характеристик выборки и характеристик генеральной совокупности 95%, всегда = 1,96. Их соответствие на 95% — общепринятое требование в социологических исследованиях.
Для нашего распределения:
При условии, что выборка в пробном исследовании представляла бы собой модель генеральной совокупности, величина выборочной совокупности для изучения желания заниматься физической культурой должна быть не меньше 147 человек. Тогда с вероятностью 95% можно утверждать, что генеральное среднее лежит в пределах 4,39+0,155.
Поскольку модель выборки в пробном исследовании во вузам не представляет собой модели генеральной совокупности (опрос был в четырех вузах из 30), то увеличиваем полученное n (30/4) в 7,5 раза. Тогда необходимый объем выборки — 1102 респондента.
Качественная представительность полученной выборки оценивается сравнением существенных характеристик (либо связанных с существенными) генеральной совокупности и выборки. Для студенчества, например, такими характеристиками являются: соотношение по полу, охват учебными занятиями по физическому воспитанию, соотношение форм занятий и др.
Когда информация о признаках элементов генеральной совокупности отсутствует, исключается возможность определения объема выборочной совокупности при помощи формул. В этом случае можно опереться на многолетний опыт социологов — практиков, свидетельствующий о том, что для пробных опросов достаточна выборка объемом 100-250 человек. При массовых опросах, если величина генеральной совокупности 5000 человек, достаточный объем выборочной совокупности — не менее 500 человек, если же величина генеральной совокупности 5000 человек и более, то — 10% ее состава (но не более 2000-2500 человек). Это характеризует достаточно достоверные результаты исследования.
ПРИМЕР 1
При проверке импортирования груза на таможне методом случайной выборки было обработано 200 изделий. В результате был установлен средний вес изделия 30г., при СКО=4г с вероятностью 0,997. Определите пределы в которых находится средний вес изделий генеральной совокупности.
Решение.
В данном примере – случайный повторный отбор.
n=200


p=0,997, тогда t=3
Формула средней ошибки для случайного повторного отбора:


Определяем величину средней ошибки.
Ответ: пределы в которых находится средний вес изделий:
ПРИМЕР 2
В городе проживает 250тыс. семей. Для определения среднего числа детей в семье была организована 2%-я бесповторная выборка семей. По ее результатам было получено следующее распространение семей по числу детей:
P=0,954. Найти пределы в которых будет находится среднее число детей в генеральной совокупности.
|
Число детей в семье, xi |
0 |
1 |
2 |
3 |
4 |
5 |
|
Кол-во детей в семье |
1000 |
2000 |
1200 |
400 |
200 |
200 |
Решение
2%-я выборка означает: n=250000*0,02= 5000 семей было исследовано.
Т.к. выборка бесповторная, используем следующую формулу для определения средней величины ошибки:
Найдем среднее число детей в выборочной совокупности:

Определим дисперсию

Т.к p = 0,954, то t = 2


Вывод: из-за слишком малой величины ошибки, среднее число детей в генеральной совокупности можно принять за 1,5 ребенка.
|
Источники информации по 2 вопросу |
Автор и наименование |
Страницы (форма доступа для Интернет-ресурсов) |
|
Основная литература |
Глава 11. Выборочное наблюдение. Статистика: учебник / И.В. Гладун. – 3-е издание, стер. – М.: КНОРУС, 2019. – 232 с. – СПО |
стр. 211-220 |
|
Интернет ресурсы |
|
http://www.statbook.ru |
|
http://docs.cntd.ru |
|
|
http://www.garant.ru/ |
Контрольное задание по Вопросу 2
- Записать в тетрадь конспект (1-2 стр.)
3. Подведение итогов учебного занятия
(ответить на вопросы (тестовые задания) и провести самооценку усвоенного материала)
Таблица 2.
|
Наименование изученного вопроса учебного занятия |
Контрольное задание по изученному вопросу |
Ответ |
|
Определение ошибки репрезентативности. |
ЗАДАНИЕ 1 Условие задачи: при медицинском осмотре 126 детей 6 летнего возраста, проживающих в одном из районов городе А., в 12% случаев обнаружено нарушение осанки функционального характера. Задание: определить ошибку репрезентативности (mp) и доверительные границы относительного показателя генеральной совокупности (Рген). |
|
|
Определение ошибки репрезентативности. |
ЗАДАНИЕ 2. Условие задачи: при медицинском осмотре детей 6 летнего возраста в 15% (m = ± 3%) случаях обнаружено нарушение осанки функционального характера. Частота аналогичных нарушений осанки при медосмотре детей 7-летнего возраста составила 24% (m = ± 2,64%). Задание: оценить достоверность различий в частоте нарушения осанки у детей 2 возрастных групп. |
|
|
Определение объема выборочной совокупности |
ЗАДАНИЕ 3. В городе проживает 300 тыс. семей. Для определения среднего числа детей в семье была организована 2%-я бесповторная выборка семей. По ее результатам было получено следующее распространение семей по числу детей: P=0,954. Найти пределы в которых будет находится среднее число детей в генеральной совокупности |
|
|
Определение объема выборочной совокупности |
Сформулируйте понятие генеральной совокупности |
|
|
Определение объема выборочной совокупности |
Перечислите способы отбора единиц для выборочного наблюдения |
- Домашнее задание на следующее занятие
- Выучить основные понятия. Глава 11. Выборочное наблюдение. Статистика: учебник / И.В. Гладун. – 2-е издание, стер. – М.: КНОРУС, 2014. – 232 с. – СПО (стр. 211-220)
- Выполнить задание 11.1. в тетради (стр. 224) учебник / И.В. Гладун. – 2-е издание, стер. – М.: КНОРУС, 2014. – 232 с. – СПО
Преподаватель Ю.В. Древаль
|
СОГЛАСОВАНО Протокол заседания ЦК дисциплин профессионального цикла специальности «Право и организация социального обеспечения» ГБПОУ Юридический колледж от ____________ 2017 г. № ___ |
ДЕПАРТАМЕНТ ОБРАЗОВАНИЯ И НАУКИ ГОРОДА МОСКВЫ
Государственное бюджетное профессиональное образовательное учреждение города Москвы
«ЮРИДИЧЕСКИЙ КОЛЛЕДЖ»
(ГБПОУ Юридический колледж)
ПЛАН-КОНСПЕКТ учебного занятия
по ОП.11 Статистика
учебной дисциплине/междисциплинарному курсу
для обучающихся 2 курса
специальность 40.02.01 Право и организация социального обеспечения
(набор 2016 г.)
(углубленная подготовка)
дата проведения занятия по расписанию
Тема 3.1. Выборочное наблюдение
Занятие 15. ПЗ №8 Определение ошибки репрезентативности.
Определение объема выборочной совокупности
Цель занятия: отработать практические навыки по определению доверительных пределов и исчислению ошибок выборки
Задачи занятия:
Обучающая: Обеспечить усвоение обучающимися материала о понятиях: ошибки репрезентативности, выборка, выборочная совокупность;
Воспитательная: воспитывать навыки самостоятельной работы, чувство ответственности за порученный участок работы, дисциплину умственного труда, уверенность в своих силах, стремление к достижению результата;
Развивающая: создавать условия для развития самостоятельности мышления, способности высказывания собственной точки зрения, систематизировать необходимую информацию, анализировать, сравнивать и обобщать информацию, развивать монологическую речь.
Основная литература:
Глава 11. Выборочное наблюдение. (211-220) Статистика: учебник / И.В. Гладун. – 2-е издание, стер. – М.: КНОРУС, 2014. – 232 с. – СПО
Дополнительная литература:
Савюк Л.К. Правовая статистика: Учебник. — М.: Юрист, 2016
Интернет-ресурсы:
- Информационно-издательский центр «Статистика России» http://www.statbook.ru
- Электронный фонд правовой и технической документации http://docs.cntd.ru
- Информационно правовой портал http://www.garant.ru/
Междисциплинарные связи: Право социальное обеспечение
Внутридисциплинарные связи: Тема 2.1. Сводка и группировка статистических данных
1. Актуализация знаний по ранее пройденному материалу учебного курса
(ответить на вопросы (тестовые задания) и провести самооценку усвоенного материала)
Таблица 1.
|
Вопрос (тестовое задание) |
Ответ |
|
|
|
|
|
|
|
|
|
2. Изучаемые вопросы занятия
|
1. Определение ошибки репрезентативности. |
|
2. Определение объема выборочной совокупности. |
Вопрос 1. Определение ошибки репрезентативности
В статистике выделяют два основных метода исследования – сплошной и выборочный. При проведении выборочного исследования обязательным является соблюдение следующих требований: репрезентативность выборочной совокупности и достаточное число единиц наблюдений. При выборе единиц наблюдения возможны Ошибки смещения, т. е. такие события, появление которых не может быть точно предсказуемым. Эти ошибки являются объективными и закономерными. При определении степени точности выборочного исследования оценивается величина ошибки, которая может произойти в процессе выборки – Случайная ошибка репрезентативности (M) – Является фактической разностью между средними или относительными величинами, полученными при проведении выборочного исследования и аналогичными величинами, которые были бы получены при проведении исследования на генеральной совокупности.
Оценка достоверности результатов исследования предусматривает определение:
1. ошибки репрезентативности
2. доверительных границ средних (или относительных) величин в генеральной совокупности
3. достоверности разности средних (или относительных) величин (по критерию t)
Расчет ошибки репрезентативности (mм) средней арифметической величины (М):

Расчет ошибки репрезентативности (mР) относительной величины (Р):

Q =100 – Ρ% – величина, обратная Р; n – численность выборки (n>30)
В клинических и экспериментальных работах довольно часто приходится использовать Малую выборку, Когда число наблюдений меньше или равно 30. При малой выборке для расчета ошибок репрезентативности, как средних, так и относительных величин, Число наблюдений уменьшается на единицу, т. е.


Величина ошибки репрезентативности зависит от объема выборки: чем больше число наблюдений, тем меньше ошибка. Для оценки достоверности выборочного показателя принят следующий подход: показатель (или средняя величина) должен в 3 раза превышать свою ошибку, в этом случае он считается достоверным.
Знание величины ошибки недостаточно для того, чтобы быть уверенным в результатах выборочного исследования, так как конкретная ошибка выборочного исследования может быть значительно больше (или меньше) величины средней ошибки репрезентативности. Для определения точности, с которой исследователь желает получить результат, в статистике используется такое понятие, как вероятность безошибочного прогноза, которая является характеристикой надежности результатов выборочных медико-биологических статистических исследований. Обычно, при проведении медико-биологических статистических исследований используют вероятность безошибочного прогноза 95% или 99%. В наиболее ответственных случаях, когда необходимо сделать особенно важные выводы в теоретическом или практическом отношении, используют вероятность безошибочного прогноза 99,7%
Определенной степени вероятности безошибочного прогноза соответствует определенная величина Предельной ошибки случайной выборки (Δ – дельта), которая определяется по формуле:
Δ=t * m, где t – доверительный коэффициент, который при большой выборке при вероятности безошибочного прогноза 95% равен 2,6; при вероятности безошибочного прогноза 99% – 3,0; при вероятности безошибочного прогноза 99,7% – 3,3, а при малой выборке определяется по специальной таблице значений t Стьюдента.
Используя предельную ошибку выборки (Δ), можно определить Доверительные границы, в которых с определенной вероятностью безошибочного прогноза заключено действительное значение статистической величины, Характеризующей всю генеральную совокупность (средней или относительной).
Для определения доверительных границ используются следующие формулы:
- для средних величин:

Мвыб – средняя величина, Полученная при проведении исследования на выборочной совокупности; t – доверительный коэффициент, значение которого определяется степенью вероятности безошибочного прогноза, с которой исследователь желает получить результат; mM – ошибка репрезентативности средней величины.
2) для относительных величин:

Доверительные границы показывают, в каких пределах может колебаться размер выборочного показателя в зависимости от причин случайного характера.
При малом числе наблюдений (n<30), для вычисления доверительных границ значение коэффициента t находят по специальной таблице Стьюдента. Значения t расположены в таблице на пересечении с избранной вероятностью безошибочного прогноза и строки, Указывающей на имеющееся число степеней свободы (n), Которое равно n-1.
на определение ошибок репрезентативности (m) и доверительных границ средней величины генеральной совокупности (Мген) при числе наблюдений больше 30
Условие задачи: при изучении комбинированного воздействия шума и низкочастотной вибрации на организм человека было установлено, что средняя частота пульса у 36 обследованных водителей сельскохозяйственных машин через 1 ч работы составила 80 ударов в 1 минуту; σ = ± 6 ударов в минуту.
Задание: определить ошибку репрезентативности (mM) и доверительные границы средней величины генеральной совокупности (Мген).
Решение.
- Вычисление средней ошибки средней арифметической (ошибки репрезентативности) (m): m = σ / √n = 6 / √36 = ±1 удар в минуту
- Вычисление доверительных границ средней величины генеральной совокупности (Мген). Для этого необходимо:
- а) задать степень вероятности безошибочного прогноза (Р = 95 %);
- б) определить величину критерия t. При заданной степени вероятности (Р=95%) и числе наблюдений меньше 30 величина критерия t, определяемого по таблице, равна 2 (t = 2). Тогда Мген = Мвыб ± tm = 80 ± 2×1 = 80 ± 2 удара в минуту.
Вывод. Установлено с вероятностью безошибочного прогноза Р = 95%, что средняя частота пульса в генеральной совокупности, т.е. у всех водителей сельскохозяйственных машин, через 1 ч работы в аналогичных условиях будет находиться в пределах от 78 до 82 ударов в минуту, т.е. средняя частота пульса менее 78 и более 82 ударов в минуту возможна не более, чем у 5% случаев генеральной совокупности.
на определение ошибок репрезентативности (m) и доверительных границ относительного показателя генеральной совокупности (Рген)
Условие задачи: при медицинском осмотре 164 детей 3 летнего возраста, проживающих в одном из районов городе Н., в 18% случаев обнаружено нарушение осанки функционального характера.
Задание: определить ошибку репрезентативности (mp) и доверительные границы относительного показателя генеральной совокупности (Рген).
Решение.
- Вычисление ошибки репрезентативности относительного показателя: m = √P x q / n = √18 x (100 — 18) / 164 = ± 3%
- Вычисление доверительных границ средней величины генеральной совокупности (Рген) производится следующим образом:
- необходимо задать степень вероятности безошибочного прогноза (Р=95%);
- при заданной степени вероятности и числе наблюдений больше 30, величина критерия t равна 2 (t = 2). Тогда Рген = Рвыб± tm = 18% ± 2 х 3 = 18% ± 6%.
Вывод. Установлено с вероятностью безошибочного прогноза Р=95%, что частота нарушения осанки функционального характера у детей 3 летнего возраста, проживающих в городе Н., будет находиться в пределах от 12 до 24% случаев.
на оценку достоверности разности средних величин
Условие задачи: при изучении комбинированного воздействия шума и низкочастотной вибрации на организм человека было установлено, что средняя частота пульса у водителей сельскохозяйственных машин через 1 ч после начала работы составила 80 ударов в минуту; m = ± 1 удар в мин. Средняя частота пульса у этой же группы водителей до начала работы равнялась 75 ударам в минуту; m = ± 1 удар в минуту.
Задание: оценить достоверность различий средних значений пульса у водителей сельскохозяйственных машин до и после 1 ч работы.
Решение.
Вывод. Значение критерия t = 3,5 соответствует вероятности безошибочного прогноза Р > 99,7%, следовательно можно утверждать, что различия в средних значениях пульса у водителей сельскохозяйственных машин до и после 1 ч работы не случайно, а достоверно, существенно, т.е. обусловлено влиянием воздействия шума и низкочастотной вибрации.
на оценку достоверности разности относительных показателей
Условие задачи: при медицинском осмотре детей 3 летнего возраста в 18% (m = ± 3%) случаях обнаружено нарушение осанки функционального характера. Частота аналогичных нарушений осанки при медосмотре детей 4-летнего возраста составила 24% (m = ± 2,64%).
Задание: оценить достоверность различий в частоте нарушения осанки у детей 2 возрастных групп.
Решение.
Вывод. Значение критерия t=1,5 соответствует вероятности безошибочного прогноза Р<95%. Следовательно, различие в частоте нарушений осанки среди детей, сравниваемых возрастных групп случайно, недостоверно, несущественно, т.е. не обусловлено влиянием возраста детей.
|
Источники информации по 1 вопросу |
Автор и наименование |
Страницы (форма доступа для Интернет-ресурсов) |
|
Основная литература |
Глава 11. Выборочное наблюдение. Статистика: учебник / И.В. Гладун. – 2-е издание, стер. – М.: КНОРУС, 2014. – 232 с. – СПО |
стр. 211-220 |
|
Интернет ресурсы |
|
http://www.statbook.ru |
|
http://docs.cntd.ru |
|
|
http://www.garant.ru/ |
Контрольное задание по Вопросу 1
- Записать в тетрадь конспект (1-2 стр.)
Вопрос 2. Определение объема выборочной совокупности
Социологические исследования редко бывают сплошными, как, например, перепись населения. Обычно сплошное исследование проводится при небольшой генеральной совокупности.
Чаще всего исследования носят выборочный характер, при котором наиболее важным основанием является возможность распространения полученных результатов и выводов на всю генеральную совокупность. В таком случае сплошное исследование нецелесообразно. Обеспечение этой нецелесообразности — вопрос о репрезентативности выборки, т.е. достаточной количественной и качественной представительности генеральной совокупности в выборке.
Условиями соблюдения репрезентативности выборки являются:
1) равная возможность каждого члена генеральной совокупности попасть в выборку;
2) отбор необходимо проводить независимо от изучаемого признака (иначе в выборку могут попасть, например, только спортсмены);
3) отбор по возможности должен производиться из однородных совокупностей;
4) величина выборки должна быть достаточно большой.
Далее возникает вопрос: как определить достаточный объем выборки? Для этого необходимо иметь характеристики генеральной совокупности по важнейшим (с точки зрения исследования) признакам. К ним, например, можно отнести сведения о количестве желающих заниматься физической культурой и спортом, о числе занимающихся и т.д. Но, как правило, такие характеристики (или многие из них) не известны. Пилотажные исследования как раз и направлены на их выявление.
Приведем пример определения объема выборочной совокупности. В ходе подготовки к проведению конкретно-социологического исследования на основании теоретических посылок были выделены характеристики и признаки, подлежащие изучению. Например, желание заниматься физической культурой, спортом, величина потребности, участие в видах деятельности и др.
На основании результатов изучения этих признаков в пробном исследовании (30 и более респондентов) определяется объем выборки.
Предположим, что в пробном исследовании опрошено 147 студентов 4-х курсов в четырех вузах Республики Беларусь.
Для желания заниматься физической культурой получены следующие распределения:
1.«Нет, не хочу» — 5 человек;
2.«Скорее не хочу, чем хочу» — 3 человека;
3.«Безразлично» — 11 человек;
4.«Скорее хочу, чем не хочу» — 34 человека;
5.«Да, хочу» — 72 человека.
Для расчета объема выборки используются формулы:
t — 1,96 — распределение Стьюдента для вероятности 0,95 или 95% (т.е., если требуемая вероятность соответствия характеристик выборки и характеристик генеральной совокупности 95%, всегда = 1,96. Их соответствие на 95% — общепринятое требование в социологических исследованиях.
Для нашего распределения:
При условии, что выборка в пробном исследовании представляла бы собой модель генеральной совокупности, величина выборочной совокупности для изучения желания заниматься физической культурой должна быть не меньше 147 человек. Тогда с вероятностью 95% можно утверждать, что генеральное среднее лежит в пределах 4,39+0,155.
Поскольку модель выборки в пробном исследовании во вузам не представляет собой модели генеральной совокупности (опрос был в четырех вузах из 30), то увеличиваем полученное n (30/4) в 7,5 раза. Тогда необходимый объем выборки — 1102 респондента.
Качественная представительность полученной выборки оценивается сравнением существенных характеристик (либо связанных с существенными) генеральной совокупности и выборки. Для студенчества, например, такими характеристиками являются: соотношение по полу, охват учебными занятиями по физическому воспитанию, соотношение форм занятий и др.
Когда информация о признаках элементов генеральной совокупности отсутствует, исключается возможность определения объема выборочной совокупности при помощи формул. В этом случае можно опереться на многолетний опыт социологов — практиков, свидетельствующий о том, что для пробных опросов достаточна выборка объемом 100-250 человек. При массовых опросах, если величина генеральной совокупности 5000 человек, достаточный объем выборочной совокупности — не менее 500 человек, если же величина генеральной совокупности 5000 человек и более, то — 10% ее состава (но не более 2000-2500 человек). Это характеризует достаточно достоверные результаты исследования.
ПРИМЕР 1
При проверке импортирования груза на таможне методом случайной выборки было обработано 200 изделий. В результате был установлен средний вес изделия 30г., при СКО=4г с вероятностью 0,997. Определите пределы в которых находится средний вес изделий генеральной совокупности.
Решение.
В данном примере – случайный повторный отбор.
n=200


p=0,997, тогда t=3
Формула средней ошибки для случайного повторного отбора:


Определяем величину средней ошибки.
Ответ: пределы в которых находится средний вес изделий:
ПРИМЕР 2
В городе проживает 250тыс. семей. Для определения среднего числа детей в семье была организована 2%-я бесповторная выборка семей. По ее результатам было получено следующее распространение семей по числу детей:
P=0,954. Найти пределы в которых будет находится среднее число детей в генеральной совокупности.
|
Число детей в семье, xi |
0 |
1 |
2 |
3 |
4 |
5 |
|
Кол-во детей в семье |
1000 |
2000 |
1200 |
400 |
200 |
200 |
Решение
2%-я выборка означает: n=250000*0,02= 5000 семей было исследовано.
Т.к. выборка бесповторная, используем следующую формулу для определения средней величины ошибки:
Найдем среднее число детей в выборочной совокупности:

Определим дисперсию

Т.к p = 0,954, то t = 2


Вывод: из-за слишком малой величины ошибки, среднее число детей в генеральной совокупности можно принять за 1,5 ребенка.
|
Источники информации по 2 вопросу |
Автор и наименование |
Страницы (форма доступа для Интернет-ресурсов) |
|
Основная литература |
Глава 11. Выборочное наблюдение. Статистика: учебник / И.В. Гладун. – 3-е издание, стер. – М.: КНОРУС, 2019. – 232 с. – СПО |
стр. 211-220 |
|
Интернет ресурсы |
|
http://www.statbook.ru |
|
http://docs.cntd.ru |
|
|
http://www.garant.ru/ |
Контрольное задание по Вопросу 2
- Записать в тетрадь конспект (1-2 стр.)
3. Подведение итогов учебного занятия
(ответить на вопросы (тестовые задания) и провести самооценку усвоенного материала)
Таблица 2.
|
Наименование изученного вопроса учебного занятия |
Контрольное задание по изученному вопросу |
Ответ |
|
Определение ошибки репрезентативности. |
ЗАДАНИЕ 1 Условие задачи: при медицинском осмотре 126 детей 6 летнего возраста, проживающих в одном из районов городе А., в 12% случаев обнаружено нарушение осанки функционального характера. Задание: определить ошибку репрезентативности (mp) и доверительные границы относительного показателя генеральной совокупности (Рген). |
|
|
Определение ошибки репрезентативности. |
ЗАДАНИЕ 2. Условие задачи: при медицинском осмотре детей 6 летнего возраста в 15% (m = ± 3%) случаях обнаружено нарушение осанки функционального характера. Частота аналогичных нарушений осанки при медосмотре детей 7-летнего возраста составила 24% (m = ± 2,64%). Задание: оценить достоверность различий в частоте нарушения осанки у детей 2 возрастных групп. |
|
|
Определение объема выборочной совокупности |
ЗАДАНИЕ 3. В городе проживает 300 тыс. семей. Для определения среднего числа детей в семье была организована 2%-я бесповторная выборка семей. По ее результатам было получено следующее распространение семей по числу детей: P=0,954. Найти пределы в которых будет находится среднее число детей в генеральной совокупности |
|
|
Определение объема выборочной совокупности |
Сформулируйте понятие генеральной совокупности |
|
|
Определение объема выборочной совокупности |
Перечислите способы отбора единиц для выборочного наблюдения |
- Домашнее задание на следующее занятие
- Выучить основные понятия. Глава 11. Выборочное наблюдение. Статистика: учебник / И.В. Гладун. – 2-е издание, стер. – М.: КНОРУС, 2014. – 232 с. – СПО (стр. 211-220)
- Выполнить задание 11.1. в тетради (стр. 224) учебник / И.В. Гладун. – 2-е издание, стер. – М.: КНОРУС, 2014. – 232 с. – СПО
Преподаватель Ю.В. Древаль
|
СОГЛАСОВАНО Протокол заседания ЦК дисциплин профессионального цикла специальности «Право и организация социального обеспечения» ГБПОУ Юридический колледж от ____________ 2017 г. № ___ |
Весь смысл выборочной совокупности в том, чтоб по ней можно было судить о генеральной совокупности, для этого выборка должна быть репрезентативной. Репрезентативность достигается в том числе достаточным количеством наблюдений (n).
Параметры распределения
Важнейшие параметры распределения случайной величины Х являются — математическое ожидание µ (Мген) и дисперсия σ2.
- Математическое ожидание (Х) — среднее значение случайной величины при стремлении количества выборок к бесконечности.
- Среднеквадратичное отклонение (σ2) — показатель рассеивания значений случайной величины относительно ей математического ожидания.
Распределения бывают непрерывными и дискретными. Наиболее известно из непрерывних распределений — нормальное.
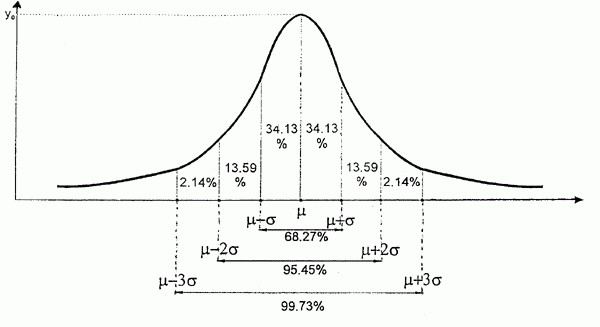
Характеристики нормального распределения
- Совпадение средней арифметической (М), медианы (Ме) и моды (Мо).
- Чем больше величина отклоняется от среднего значения, тем меньше частота его встречаемости.
Пример нормального распределения
Первичные величины, характеризующие распределение
- Средняя арифметическая (М)
- Среднее квадратичное отклонение (σ2)
- Коэффициент вариации
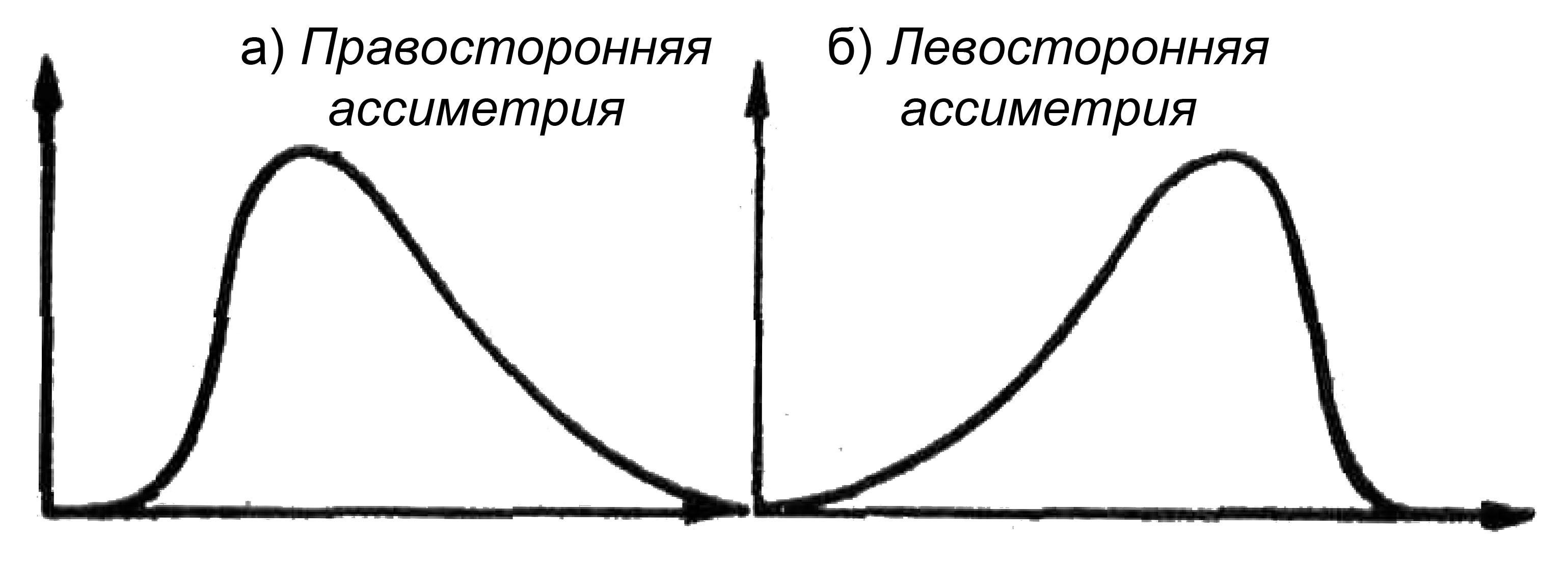
- Коэффициент асимметрии — показатель отклонения распределения в левую и правую сторону по оси абсцесс. Если больше влево — левосторонняя или отрицательная. Если вправо — правосторонняя положительная.
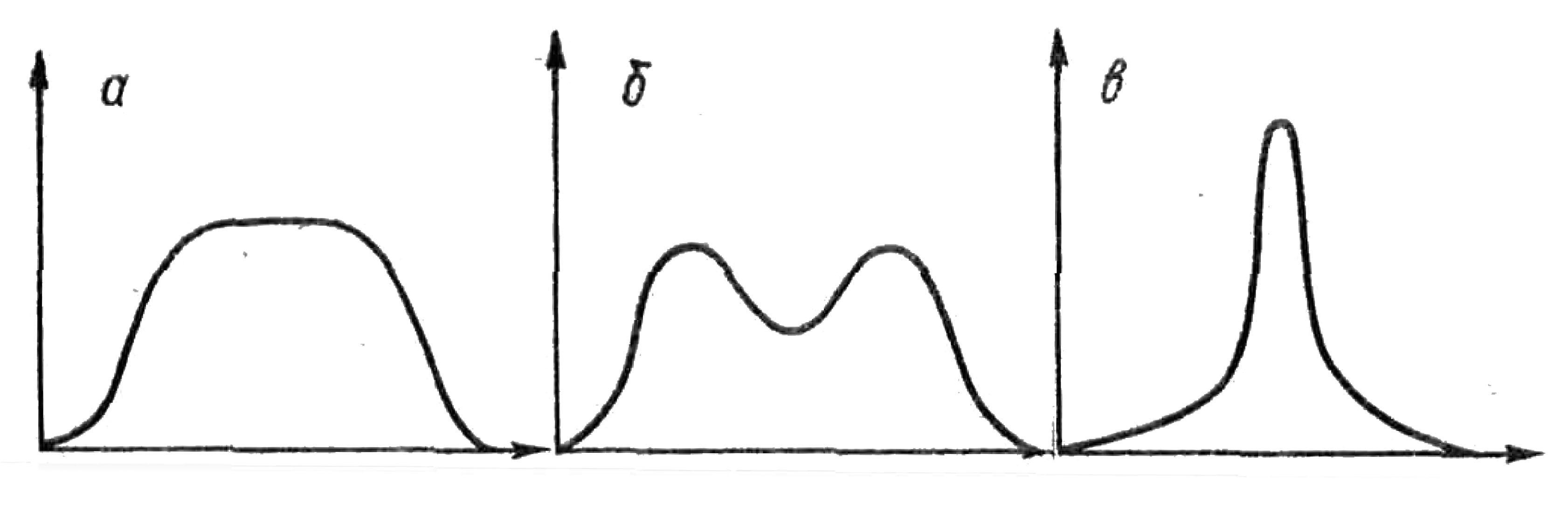
- Эксцесс — мера сглаженности. Если близко к 0, то форма распределения близка к нормальному виду. Если > 0 — то форма остроконечная. Если < 0 — форма плосковершинная. Норма эксцесса от -1 до +1.
Вид графика в зависимости от значения коэффициента асимметрии
Вид графика в зависимости от эксцесса
а,б — отрицательные эксцессы
в — положительный
Значение нормального распределения
Если нормальное распределение, для обработки используют параметрические методы математической статистики для расчёта достоверности различий между выборками:
- Критерий Стьюдента (t)
- Критерий Фишера (F)
- Коэффициент корреляции Пирсона (r)
Если кривая распределения отлична от нормальной, используют методы непараметрической статистики, расчёт достоверности разности по
- Критерию Манна-Уитни (U)
- Коэффициенту ранговой корреляции Спирмена (p)
Альтернативное (дихотомическое) распределение
Параметр математического ожидания выражает относительную величину (долю) единиц совокупности, не которые обладают изученным признаком (Р). Доля совокупности, не обладающая признаком, обозначается q.
Как правило, q = 10 - P.
Дисперсия в таком случае: Рв = nx/nв
Ошибки репрезентативности
- Ошибка выборочного наблюдения (mвн) — разность между значением параметра в генеральной совокупности и его выборочным значением.
Для среднего значения mвн = | Мген - Мв |; для доли: mвн = | Рген - Рв |.
- Средняя ошибка (m) — величина, выражающая среднее квадратичное отклонение выборочной средней от математического ожидания:
m = √(σ2/n) - Соотношение дисперсий между выборочной и генеральной совокупностями:
σ2=σ2в × n/(n-1)
При достаточно больших выборках (n) можно считать, что σ2=σ2в
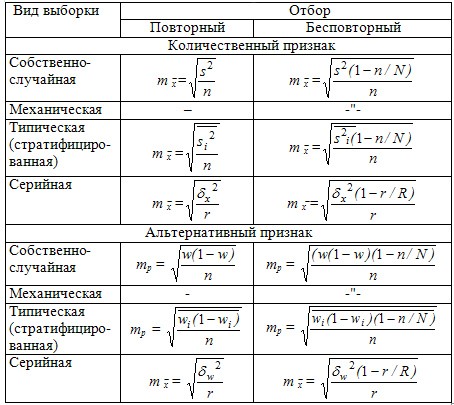
Расчёт средней ошибки (m) для разных видов выборок
На практике чаще используются следующие формулы
- Расчёт ошибки репрезентативности средней арифметической (mM):
mM=σ/√n - Расчёт ошибки репрезентативности относительной величины (mp):
mp=√(P*q / n)
где P — относительная величина (проценты, промилле и т.д.)
q — доля единиц совокупности с альтернативным признаком (1-Р или 100-Р или 1000-Р) в зависимости от основания, на которое рассчитан коэффициент
n — численность выборки
- Если в испытании объём выборки менее 30, то n уменьшается на 1:
(n-1)
Вероятность безошибочного прогноза
В медицинских исследований достаточная вероятность — 95-99%. В некоторых случаях должный прогноз — 99,7%.
Определённой вероятности безошибочного прогноза соответствует величина предельной ошибки случайной выборки (Δ).
Δ = t × m
где t — доверительный коэффициент (критерий Стьюдента)
m — средняя ошибка выборки
Вероятность прогноза (р) при значении критерия Стьюдента (t)
| t | p |
|---|---|
| < 1.96 | < 0.95 |
| 2 | 0.954 |
| 2.5 | 0.988 |
| 3 | 0.997 |
| 3.5 | 0.999 |
- Предельная ошибка выборки:
Δ = t × √( σ2 ÷ n) - Необходимая численность выборки:
n = t2 × σ2 ÷ Δ2
Для определения достоверности различий между двумя показателями или средними величинами при малом числе наблюдений (n ≤ 30, в каждой группе) критерий достоверности оценивается по таблице значений t-критерия Стьюдента по числу степеней свободы/ При этом число степеней свободы определяется, как n´= n1 + n2 - 2.
| Число степеней свободы, n´ | Значение t-критерия Стьюдента при p=0.05 |
|---|---|
| 1 | 12.706 |
| 2 | 4.303 |
| 3 | 3.182 |
| 4 | 2.776 |
| 5 | 2.571 |
| 6 | 2.447 |
| 7 | 2.365 |
| 8 | 2.306 |
| 9 | 2.262 |
| 10 | 2.228 |
| 11 | 2.201 |
| 12 | 2.179 |
| 13 | 2.160 |
| 14 | 2.145 |
| 15 | 2.131 |
| 16 | 2.120 |
| 17 | 2.110 |
| 18 | 2.101 |
| 19 | 2.093 |
| 20 | 2.086 |
| 21 | 2.080 |
| 22 | 2.074 |
| 23 | 2.069 |
| 24 | 2.064 |
| 25 | 2.060 |
| 26 | 2.056 |
| 27 | 2.052 |
| 28 | 2.048 |
| 29 | 2.045 |
| 30 | 2.042 |
| 31 | 2.040 |
| 32 | 2.037 |
| 33 | 2.035 |
| 34 | 2.032 |
| 35 | 2.030 |
| 36 | 2.028 |
| 37 | 2.026 |
| 38 | 2.024 |
| 40-41 | 2.021 |
| 42-43 | 2.018 |
| 44-45 | 2.015 |
| 46-47 | 2.013 |
| 48-49 | 2.011 |
| 50-51 | 2.009 |
| 52-53 | 2.007 |
| 54-55 | 2.005 |
| 56-57 | 2.003 |
| 58-59 | 2.002 |
| 60-61 | 2.000 |
| 62-63 | 1.999 |
| 64-65 | 1.998 |
| 66-67 | 1.997 |
| 68-69 | 1.995 |
| 70-71 | 1.994 |
| 72-73 | 1.993 |
| 74-75 | 1.993 |
| 76-77 | 1.992 |
| 78-79 | 1.991 |
| 80-89 | 1.990 |
| 90-99 | 1.987 |
| 100-119 | 1.984 |
| 120-139 | 1.980 |
| 140-159 | 1.977 |
| 160-179 | 1.975 |
| 180-199 | 1.973 |
| 200 | 1.972 |
| ∞ | 1.960 |
Оценка достоверности разности величин
Для средних величин:
Для относительных величин:
где М1 и М2, Р1 и Р2 — статистические величины, полученные при проведении выборочных исследований;
m1 и m2; — их ошибки репрезентативности; t — коэффициент достоверности.
Понятие репрезентативности часто встречается в статистических отчетностях и при подготовке выступлений и докладов. Пожалуй, без нее трудно представить себе какой-либо из видов подачи информации на обозрение.
Репрезентативность — что это?
Репрезентативность отражает, насколько выбранные объекты или части соответствуют содержанию и смыслу совокупности данных, из которой они были выбраны.
Другие определения
Понятие репрезентативности можно раскрывать в разных контекстах. Но по своему смыслу репрезентативность – это соответствие черт и свойств выбранных единиц из общей совокупности, которые точно отражают характеристики всей генеральной базы данных в целом.
Также репрезентативность информации определяют как способность выборочных данных представить параметры и свойства совокупности, важные с точки зрения проводимого исследования.
Репрезентативная выборка
Принцип формирования выборки заключается в избрании наиболее важных и точно отображающих свойства общей совокупности данных. Для этого используются различные методы, которые позволяют получать точные результаты и общее представление о генеральной совокупности, используя только выборочные материалы, описывающие качества всех данных.
Таким образом, нет необходимости изучать весь материал, а достаточно рассмотреть выборочную репрезентативность. Что это? Это выборка отдельных данных для того, чтобы иметь понятие об общей массе информации.
Их в зависимости от способа различают как вероятностные и невероятностные. Вероятностная – это выборка, которая производится путем вычисления наиболее важных и интересных данных, являющихся в дальнейшем представителями генеральной совокупности. Это обдуманный выбор или случайная выборка, тем не менее, обоснованная своим содержанием.
Невероятностная – это одна из разновидностей случайной выборки, составляющаяся по принципу обычной лотереи. В таком случае не учитывается мнение того, кто составляет такую выборку. Используется лишь слепой жребий.
Вероятностная выборка
Вероятностные выборки также могут подразделяться на несколько видов:
- Одна из самых простых и понятных принципов – это нерепрезентативная выборка. К примеру, такой способ часто используется при проведении социальных опросов. При этом участники опроса не выбираются из толпы по каким-либо определенным признакам, и получение информации производится у первых 50 людей, принявших участие в нём.
- Преднамеренные выборки отличаются тем, что имеют ряд требований и условий при отборе, однако все же полагаются на случайное совпадение, не преследуя своей целью достижение хорошей статистики.
- Выборка на основании квот – это еще одна из вариаций невероятностной выборки, которая часто используется для исследования больших совокупностей данных. Для нее используется множество условий и норм. Подбираются объекты, которые должны им соответствовать. То есть на примере социального опроса можно предположить, что опрошены будут 100 человек, но только мнение некоторого числа людей, которые будут соответствовать установленным требованиям, будут учтены при составлении статистического отчета.
Вероятностные выборки
Для вероятностных выборок исчисляется ряд параметров, которым объекты в выборке будут соответствовать, и среди них разными способами могут избираться именно те факты и данные, которые будут представлены как репрезентативность данных выборки. Такими способами вычисления нужных данных могут быть:
- Простая случайная выборка. Заключается в том, что среди выбранного сегмента совершенно случайным методом лотереи выбирается необходимое количество данных, которые будут являться репрезентативной выборкой.
- Систематическая и случайная выборка дает возможность составить систему вычисления необходимых данных на основе случайно выбранного сегмента. Таким образом, если первое случайное число, которое указывает на порядковый номер данных, выбранных из общей совокупности, будет 5, то последующими данными, которые будут выбраны, могут стать, например, 15, 25, 35 и так далее. Этот пример наглядно объясняет, что даже случайный выбор может основываться на систематических вычислениях необходимых исходных данных.
Выборка потребителей
Осмысленная выборка – это способ, который заключается в рассмотрении каждого отдельного сегмента, и на основании его оценки составляется совокупность, отражающая характеристики и свойства общей базы данных. Таким образом набирается большее количество данных, соответствующих требованиям репрезентативной выборки. Можно легко отобрать некоторое количество вариантов, которые не войдут в общее число, не потеряв при этом качество отобранных данных, представляющих общую совокупность. Таким способом определяется репрезентативность результатов исследования.
Размер выборки
Не последний вопрос, который необходимо решить, – это размер выборки для репрезентативного представления генеральной совокупности. Размер выборки не всегда зависит от количества исходников в генеральной совокупности. Однако репрезентативность выборочной совокупности напрямую зависит от того, на сколько сегментов должен быть в итоге разделён результат. Чем больше таких сегментов, тем больше данных попадает в результативную выборку. Если результаты требуют общего обозначения и не требуют конкретики, тогда, соответственно, выборка становится меньше, поскольку, не вдаваясь в детали, информация излагается более поверхностно, а значит, ее прочтение будет общим.
Понятие ошибки репрезентативности
Ошибка репрезентативности – это конкретные расхождения между характеристиками генеральной совокупности и выборочных данных. При проведении любого выборочного исследования невозможно получить абсолютно точные данные, как при полном исследовании генеральных совокупностей и выборки, представленной лишь частью сведений и параметров, тогда как более детальное изучение возможно только при исследовании всей совокупности. Таким образом, неизбежны некоторые погрешности и ошибки.
Виды ошибок
Различают некоторые ошибки, которые возникают при составлении репрезентативной выборки:
- Систематические.
- Случайные.
- Преднамеренные.
- Непреднамеренные.
- Стандартные.
- Предельные.
Основанием для появления случайных ошибок может быть несплошной характер исследования общей совокупности. Обычно случайная ошибка репрезентативности имеет незначительный размер и характер.
Систематические ошибки между тем возникают при нарушении правил отбора данных из общей совокупности.
Средняя ошибка – это разница между усредненными значениями выборки и основной совокупностью. Она не зависит от количества единиц в выборке. Она обратно пропорциональна объему выборки. Тогда чем больше объем, тем меньше значение средней ошибки.
Предельная ошибка – это наибольшая возможная разница между усредненными значениями сделанной выборки и общей совокупностью. Такая ошибка охарактеризовывается как максимум вероятных ошибок при заданных условиях их появления.
Преднамеренные и непреднамеренные ошибки репрезентативности
Ошибки смещения данных бывают преднамеренными и непреднамеренными.
Тогда причинами появления преднамеренных ошибок является подход к подбору данных по методу определения тенденций. Непреднамеренные ошибки возникают еще на стадии подготовки выборочного наблюдения, формирования репрезентативной выборки. Для недопущения подобных ошибок необходимо создать хорошую основу для выборки, составляющей списки единиц отбора. Она должна полностью соответствовать целям проведения выборки, быть достоверной, охватывающей все аспекты исследования.
Валидность, надежность, репрезентативность. Расчет ошибок
Расчет ошибки репрезентативности (Мм) средней арифметической величины (М).
Среднее квадратическое отклонение: численность выборки (>30).
Ошибка репрезентативности (Мр) и относительная величина (Р): численность выборки (n>30).
В том случае, когда приходится изучать совокупность, где количество выборки мало и составляет меньше 30 единиц, тогда число наблюдений станет меньше на одну единицу.
Величина ошибки прямо порциональна объему выборки. Репрезентативность информации и вычисление степени возможности составления точного прогноза отражает определенная величина предельной ошибки.
Репрезентативные системы
Не только в процессе оценки подачи информации используется репрезентативная выборка, но и сам человек, получающий информацию, использует репрезентативные системы. Таким образом, мозг обрабатывает некоторое количество информации, создавая репрезентативную выборку из всего потока информации, чтобы качественно и быстро оценить подаваемые данные и понять суть вопроса. Ответить на вопрос: «Репрезентативность — что это?» — в масштабах человеческого сознания довольно просто. Для этого мозг использует все подвластные органы чувств, в зависимости от того, какую именно информацию необходимо вычленить из общего потока. Таким образом, различают:
- Визуальную репрезентативную систему, где задействуются органы зрительного восприятия глаза. Люди, часто использующие подобную систему, называются визуалами. С помощью этой системы человек обрабатывает информацию, поступающую в виде изображений.
- Аудиальная репрезентативная система. Главный орган, который используется – это слух. Информация, подаваемая в виде звуковых файлов или речи, обрабатываются именно этой системой. Люди, лучше воспринимающие информацию на слух, называются аудиалами.
- Кинестетическая репрезентативная система представляет собой обработку потока информации, путем восприятия его с помощью обонятельных и осязательных каналов.
- Дигитальная репрезентативная система используется вместе с другими как средство получения информации извне. Это субъективно-логическое восприятие и осмысление полученных данных.
Итак, репрезентативность — что это? Простая выборка из множества или неотъемлемая процедура при обработке информации? Однозначно можно сказать, что репрезентативность во многом определяет наше восприятие потоков данных, помогая вычленить из него наиболее веские и значимые.
Пример об ошибке репрезентативности
Лекция 4.1 Выборочный метод
К настоящему времени Вы заработали баллов: 0 из 0 возможных.
ГЕНЕРАЛЬНАЯ И ВЫБОРОЧНАЯ СОВОКУПНОСТЬ
Генеральная совокупность — вся подлежащая изучению совокупность объектов (наблюдений).
Генеральная совокупность носит гипотетический характер. Она представляет собой совокупность всех мыслимых наблюдений, которые могли бы быть произведены при данных условиях. Даже если бы у нас была возможность провести сплошное исследование всей совокупности признака, все равно в нее не попали бы объекты, которое по какой то причине отсутствуют на текущий момент, но должны были существовать при данных условиях.
Та часть объектов, которая отобрана для непосредственного изучения, называется выборочной совокупностьюили выборкой
Сущность выборочного метода
Сущность выборочного метода состоит в том, чтобы по некоторой части генеральной совокупности выносить суждение о её свойствах в целом
Чтобы по данным выборки иметь возможность судить о генеральной совокупности, она должна быть репрезентативной(представительной).
Репрезентативная выборка сохраняет и повторяет структуру генеральной совокупности.
Если две выборки взяты из одной генеральной совокупности, то разница в получаемых оценках (например, средних) будет носить случайный характер, как следствие ошибки репрезентативности
Ошибка репрезентативности возникает по причине того, что мы исследуем не всю совокупность, а только её части (выборки). Мы получаем случайную комбинацию элементов из генеральной совокупности.
Для того, чтобы минимизировать различия однородных (взятых из одной генеральной совокупности) выборок необходимо правильным образом их формировать.
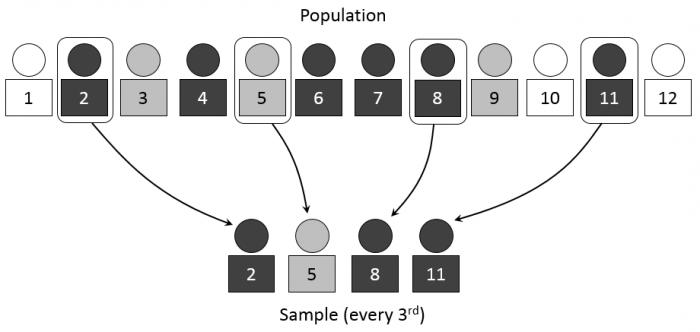
Наилучшим способом формирования репрезентативной выборки является случайный отбор элементов из генеральной совокупности без расчленения на части или группы (случайная выборка).
Пример об ошибке репрезентативности
Рассмотрим следующий пример.
Исследователь задался вопросом: «существуют ли различия в эмпатических способностях между психологами и педагогами?». Для того чтобы это прояснить он набрал две группы испытуемых в соответствии с их профессиональной деятельностью и предложил им заполнить опросник на эмпатические способности. Далее, он рассчитал среднее значение в каждой группе.
В группе психологов среднее составило 23,4 балла, а в группе педагогов 21,1. Таким образом, разница в средних между группами составила2,3 балла (23,4 — 21,1 = 2,3).
Если бы представители этих профессий не отличались по изучаемому признаку, тогда разница в средних равнялась бы нулю.
Однако, можно ли считать эту разницу в 2,3 балла достаточной, чтобы судить о реальных различиях между группами? Может сложится так, что психологи и педагоги по эмпатии в реальности не отличаются (выборки однородны), а разница в 2,3 балла, полученная исследователем носит случайный характер, как ошибка репрезентативности.
Таким образом, мы можем сформулировать две гипотезы:
Гипотезы являются альтернативами по отношению к друг другу. Принятие одной из них как верной влечет за собой исключение «истинности» другой.
СТАТИСТИЧЕСКАЯ ГИПОТЕЗА
Статистическая гипотеза – это любое предположение о виде или параметрах неизвестного закона распределения (закона распределения генеральной совокупности)
В статистике принято формулировать пару гипотез. Первая гипотеза называется нулевой, а вторая – альтернативной.
| Нулевая гипотеза Н | Альтернативная гипотеза Н1 |
| 1. 1. Является проверяемой 2. Обычно гипотеза об отсутствии явления (например, различий или зависимости) | Является логическим отрицанием нулевой |
| Поскольку нулевая гипотеза является проверяемой, то её можно отвергать и принимать | Альтернативную гипотезу принимают как следствие отрицания нулевой гипотезы |
пример:
· Н (нулевая): Женщины не отличаются от мужчин по среднему уровню развития эмпатических способностей (средние значения равны)
· Н1 (альтернативная): Средний уровень эмпатических способностей выше у женщин по сравнению с мужчинами
пример:
· Н (нулевая): Линейная корреляция между самооценкой и тревожностью равна 0
· Н1 (альтернативная): Самооценка отрицательно связана с тревожностью (линейная корреляция меньше нуля / чем выше самооценка, тем ниже тревожность и наоборот)
Вопрос:Какая из двух формулировок соответствует нулевой гипотезе Н?
· А) между психологами и педагогами нет различий по среднему уровню выраженности эмпатии
· Б) между психологами и педагогами есть различия по среднему уровню выраженности эмпатии
Статистический критерий
Правило, по которому нулевая гипотеза отвергается или принимается, называется статистическим критерием.
Статистика – это специально составленная выборочная характеристика (распределение), у которой есть критическое значение такое, что если верна нулевая гипотеза, то вероятность (α) того, что случайная величина превысит это критическое значение, мала (Кремер Н.Ш., 2004).
Критическое значение делит распределение «нулевой гипотезы» на две области: область допустимых значений и область критических значений
Таким образом, критические значения позволяют исследователю либо принять, либо отвергнуть нулевую гипотезу.
В математической статистике можно подбирать критические значение для разных альфа-уровней (уровней значимости). Чаще всего:
1. Критическое значение, которое выделяет критическую область с вероятностью α
Источник
Ошибки статистического наблюдения и основные приёмы их устранения



Всякое статистическое наблюдение должно быть полным и достоверным. Однако по ряду причин степень точности данных может быть различной.
Все ошибки наблюдения подразделяются на два вида:
Ошибки регистрации возникают вследствие неправильного установления фактов в процессе наблюдения или неправильной их записи.
Ошибки регистрации могут возникать как при сплошном наблюдении, так и при несплошном и имеют следующие виды:
Случайные ошибки – это ошибки, которые возникают в результате небрежной описки или невнимательного отношения регистратора при заполнении формуляра (ошибки в подсчёте).
Систематические ошибки – это ошибки, которые искажают сведения по каждой отдельной единице наблюдения в одном и том же направлении.
Систематические ошибки делятся на:
Преднамеренные ошибки (сознательные, тенденциозные ошибки), возникающие в результате сознательного искажения статистической информации. К ним относятся: приписки, неправильные сведения об объёме выпущенной продукции, об остатках сырья и материалов и т. д.
Непреднамеренные ошибки – это ошибки, которые возникают в результате случайных причин, т.е. неумышленно (неисправность измерительных приборов, невнимательность регистратора и т.д.).
Ошибки репрезентативности свойственны несплошному наблюдению. Они возникают в результате выборочного наблюдения, когда отобранная часть единиц совокупности недостаточно полно отражает состав всей изучаемой совокупности.
Ошибки репрезентативности (так же, как и ошибки регистрации) могут быть случайными и систематическими.
Случайные ошибки оцениваются с помощью математических методов.
Систематические ошибки – это отклонения, которые возникают в результате случайного отбора единиц изучаемой совокупности. Их размеры не поддаются количественной оценке.
Для выявления и устранения допущенных при регистрации ошибок применяются следующие методы:
а) внешний контроль;
б) логический контроль;
в) счётный контроль.
При внешнем контроле проверяется: правильность оформления документов; наличие всех необходимых записей, которые предусмотрены инструкцией и т.д.
Логический контроль заключается в проверке ответов на вопросы программы наблюдения путём сопоставления полученных данных с другими источниками.
Сущность счётного (арифметического) контроля заключается в счётной проверке всех итоговых показателей, которые содержатся в отчётности или формуляре исследования. Задачей такого контроля является исправление итогов и отдельных числовых показателей.
В ряде случаев, при счётном контроле данных статистического наблюдения применяется метод балансовой увязки показателей (наличие на начало отчётного периода плюс поступления минус расход должно быть равно наличию на конец отчётного периода). Такой метод применяют: при проверках поголовья скота, при учёте поступления и расхода сырья и материалов и т.д.
Указанные методы проверки достоверности статистического наблюдения позволяют сократить до минимального значения допуск ошибок.
Источник
Репрезентативность — что это за процесс? Ошибка репрезентативности
Понятие репрезентативности часто встречается в статистических отчетностях и при подготовке выступлений и докладов. Пожалуй, без нее трудно представить себе какой-либо из видов подачи информации на обозрение.
Репрезентативность — что это?
Репрезентативность отражает, насколько выбранные объекты или части соответствуют содержанию и смыслу совокупности данных, из которой они были выбраны.
Другие определения
Понятие репрезентативности можно раскрывать в разных контекстах. Но по своему смыслу репрезентативность – это соответствие черт и свойств выбранных единиц из общей совокупности, которые точно отражают характеристики всей генеральной базы данных в целом.
Также репрезентативность информации определяют как способность выборочных данных представить параметры и свойства совокупности, важные с точки зрения проводимого исследования.
Репрезентативная выборка
Принцип формирования выборки заключается в избрании наиболее важных и точно отображающих свойства общей совокупности данных. Для этого используются различные методы, которые позволяют получать точные результаты и общее представление о генеральной совокупности, используя только выборочные материалы, описывающие качества всех данных.
Таким образом, нет необходимости изучать весь материал, а достаточно рассмотреть выборочную репрезентативность. Что это? Это выборка отдельных данных для того, чтобы иметь понятие об общей массе информации.
Их в зависимости от способа различают как вероятностные и невероятностные. Вероятностная – это выборка, которая производится путем вычисления наиболее важных и интересных данных, являющихся в дальнейшем представителями генеральной совокупности. Это обдуманный выбор или случайная выборка, тем не менее, обоснованная своим содержанием.
Невероятностная – это одна из разновидностей случайной выборки, составляющаяся по принципу обычной лотереи. В таком случае не учитывается мнение того, кто составляет такую выборку. Используется лишь слепой жребий.
Вероятностная выборка
Вероятностные выборки также могут подразделяться на несколько видов:
- Одна из самых простых и понятных принципов – это нерепрезентативная выборка. К примеру, такой способ часто используется при проведении социальных опросов. При этом участники опроса не выбираются из толпы по каким-либо определенным признакам, и получение информации производится у первых 50 людей, принявших участие в нём.
- Преднамеренные выборки отличаются тем, что имеют ряд требований и условий при отборе, однако все же полагаются на случайное совпадение, не преследуя своей целью достижение хорошей статистики.
- Выборка на основании квот – это еще одна из вариаций невероятностной выборки, которая часто используется для исследования больших совокупностей данных. Для нее используется множество условий и норм. Подбираются объекты, которые должны им соответствовать. То есть на примере социального опроса можно предположить, что опрошены будут 100 человек, но только мнение некоторого числа людей, которые будут соответствовать установленным требованиям, будут учтены при составлении статистического отчета.
Вероятностные выборки
Для вероятностных выборок исчисляется ряд параметров, которым объекты в выборке будут соответствовать, и среди них разными способами могут избираться именно те факты и данные, которые будут представлены как репрезентативность данных выборки. Такими способами вычисления нужных данных могут быть:
- Простая случайная выборка. Заключается в том, что среди выбранного сегмента совершенно случайным методом лотереи выбирается необходимое количество данных, которые будут являться репрезентативной выборкой.
- Систематическая и случайная выборка дает возможность составить систему вычисления необходимых данных на основе случайно выбранного сегмента. Таким образом, если первое случайное число, которое указывает на порядковый номер данных, выбранных из общей совокупности, будет 5, то последующими данными, которые будут выбраны, могут стать, например, 15, 25, 35 и так далее. Этот пример наглядно объясняет, что даже случайный выбор может основываться на систематических вычислениях необходимых исходных данных.
Выборка потребителей
Осмысленная выборка – это способ, который заключается в рассмотрении каждого отдельного сегмента, и на основании его оценки составляется совокупность, отражающая характеристики и свойства общей базы данных. Таким образом набирается большее количество данных, соответствующих требованиям репрезентативной выборки. Можно легко отобрать некоторое количество вариантов, которые не войдут в общее число, не потеряв при этом качество отобранных данных, представляющих общую совокупность. Таким способом определяется репрезентативность результатов исследования.
Размер выборки
Не последний вопрос, который необходимо решить, – это размер выборки для репрезентативного представления генеральной совокупности. Размер выборки не всегда зависит от количества исходников в генеральной совокупности. Однако репрезентативность выборочной совокупности напрямую зависит от того, на сколько сегментов должен быть в итоге разделён результат. Чем больше таких сегментов, тем больше данных попадает в результативную выборку. Если результаты требуют общего обозначения и не требуют конкретики, тогда, соответственно, выборка становится меньше, поскольку, не вдаваясь в детали, информация излагается более поверхностно, а значит, ее прочтение будет общим.
Понятие ошибки репрезентативности
Ошибка репрезентативности – это конкретные расхождения между характеристиками генеральной совокупности и выборочных данных. При проведении любого выборочного исследования невозможно получить абсолютно точные данные, как при полном исследовании генеральных совокупностей и выборки, представленной лишь частью сведений и параметров, тогда как более детальное изучение возможно только при исследовании всей совокупности. Таким образом, неизбежны некоторые погрешности и ошибки.
Виды ошибок
Различают некоторые ошибки, которые возникают при составлении репрезентативной выборки:
- Систематические.
- Случайные.
- Преднамеренные.
- Непреднамеренные.
- Стандартные.
- Предельные.
Основанием для появления случайных ошибок может быть несплошной характер исследования общей совокупности. Обычно случайная ошибка репрезентативности имеет незначительный размер и характер.
Систематические ошибки между тем возникают при нарушении правил отбора данных из общей совокупности.
Средняя ошибка – это разница между усредненными значениями выборки и основной совокупностью. Она не зависит от количества единиц в выборке. Она обратно пропорциональна объему выборки. Тогда чем больше объем, тем меньше значение средней ошибки.
Предельная ошибка – это наибольшая возможная разница между усредненными значениями сделанной выборки и общей совокупностью. Такая ошибка охарактеризовывается как максимум вероятных ошибок при заданных условиях их появления.
Преднамеренные и непреднамеренные ошибки репрезентативности
Ошибки смещения данных бывают преднамеренными и непреднамеренными.
Тогда причинами появления преднамеренных ошибок является подход к подбору данных по методу определения тенденций. Непреднамеренные ошибки возникают еще на стадии подготовки выборочного наблюдения, формирования репрезентативной выборки. Для недопущения подобных ошибок необходимо создать хорошую основу для выборки, составляющей списки единиц отбора. Она должна полностью соответствовать целям проведения выборки, быть достоверной, охватывающей все аспекты исследования.
Валидность, надежность, репрезентативность. Расчет ошибок
Расчет ошибки репрезентативности (Мм) средней арифметической величины (М).
Среднее квадратическое отклонение: численность выборки (>30).
Ошибка репрезентативности (Мр) и относительная величина (Р): численность выборки (n>30).
В том случае, когда приходится изучать совокупность, где количество выборки мало и составляет меньше 30 единиц, тогда число наблюдений станет меньше на одну единицу.
Величина ошибки прямо порциональна объему выборки. Репрезентативность информации и вычисление степени возможности составления точного прогноза отражает определенная величина предельной ошибки.
Репрезентативные системы
Не только в процессе оценки подачи информации используется репрезентативная выборка, но и сам человек, получающий информацию, использует репрезентативные системы. Таким образом, мозг обрабатывает некоторое количество информации, создавая репрезентативную выборку из всего потока информации, чтобы качественно и быстро оценить подаваемые данные и понять суть вопроса. Ответить на вопрос: «Репрезентативность — что это?» — в масштабах человеческого сознания довольно просто. Для этого мозг использует все подвластные органы чувств, в зависимости от того, какую именно информацию необходимо вычленить из общего потока. Таким образом, различают:
- Визуальную репрезентативную систему, где задействуются органы зрительного восприятия глаза. Люди, часто использующие подобную систему, называются визуалами. С помощью этой системы человек обрабатывает информацию, поступающую в виде изображений.
- Аудиальная репрезентативная система. Главный орган, который используется – это слух. Информация, подаваемая в виде звуковых файлов или речи, обрабатываются именно этой системой. Люди, лучше воспринимающие информацию на слух, называются аудиалами.
- Кинестетическая репрезентативная система представляет собой обработку потока информации, путем восприятия его с помощью обонятельных и осязательных каналов.
- Дигитальная репрезентативная система используется вместе с другими как средство получения информации извне. Это субъективно-логическое восприятие и осмысление полученных данных.
Итак, репрезентативность — что это? Простая выборка из множества или неотъемлемая процедура при обработке информации? Однозначно можно сказать, что репрезентативность во многом определяет наше восприятие потоков данных, помогая вычленить из него наиболее веские и значимые.
Источник