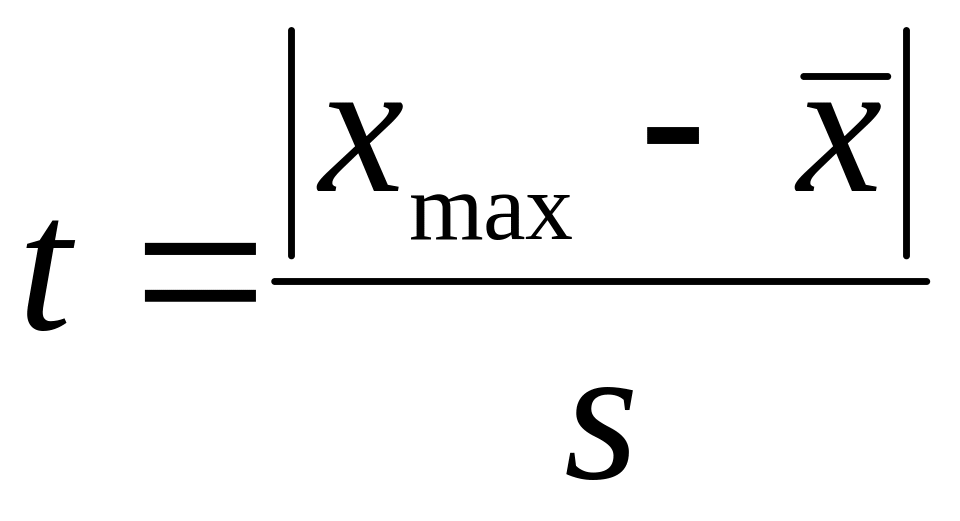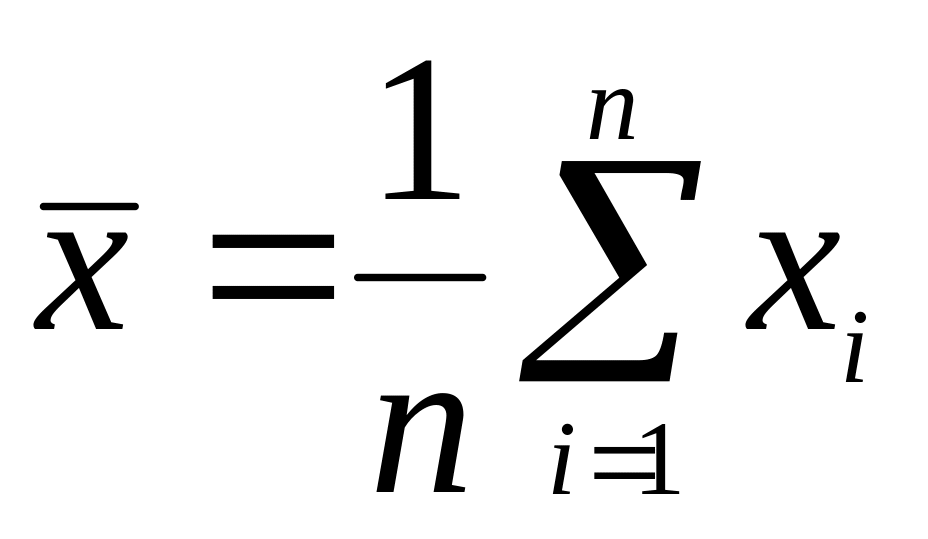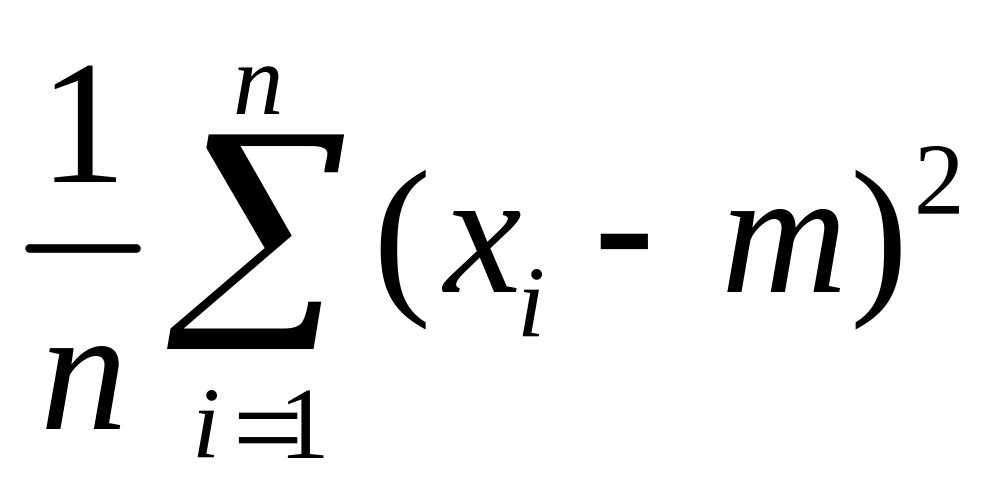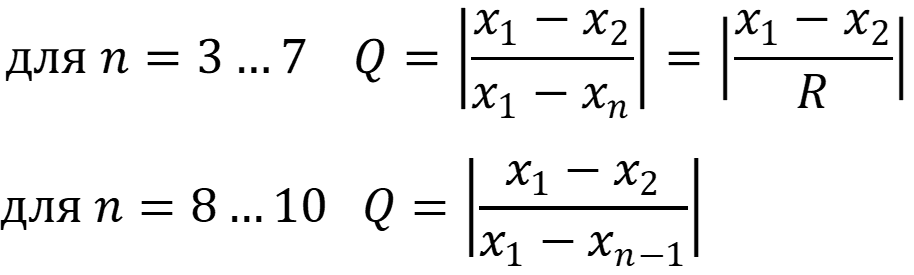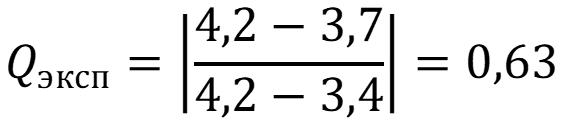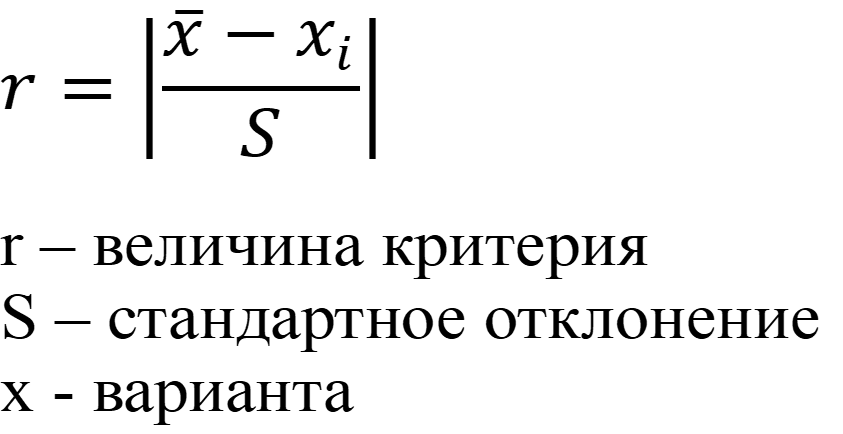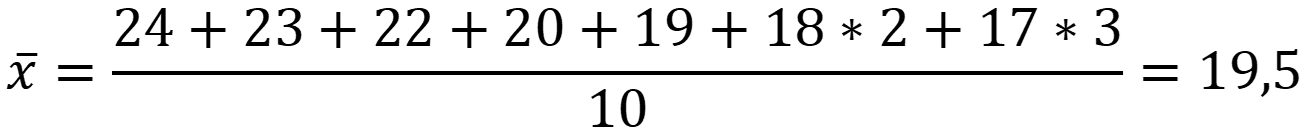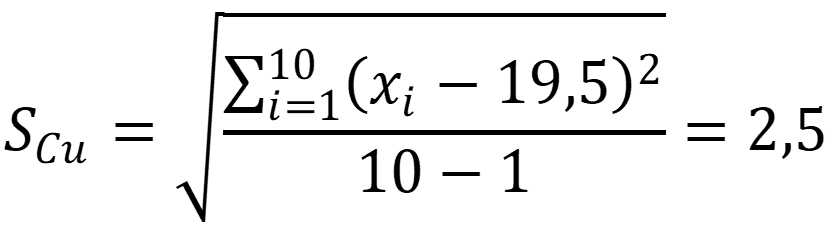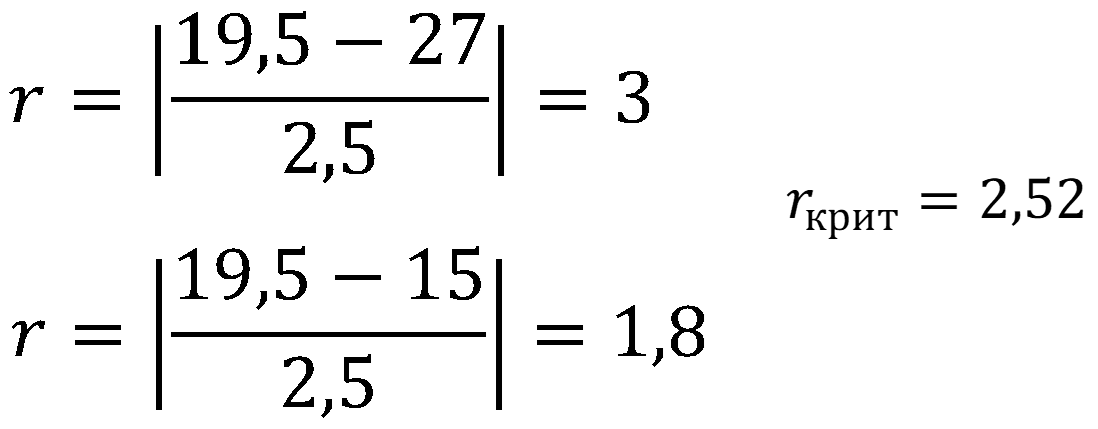1. Измеряли общее периферическое сопротивление сосудов (нормированное) у женщин с рабочим давлением 140/90. Исключите значения, содержащие грубую погрешность
Метод исключения грубых промахов по Q-критерию
Метод заключается в расчете величины Q:
Q = (x1 — x2) / R,
где x1 – возможный промах измерений
x2 – результат измерения, ближайший по значению к х1
R – размах варьирования, т.е. разность между наибольшим и наименьшим значениями.
Если Q < Qтаб – результат остается
Если Q > Qтаб – результат отбрасывается
Значения Q-критерия (при доверительной вероятности 0,9; n — число выполненных измерений):
n| Qтаб
3| 0.94
4| 0.76
5| 0.64
6| 0.56
7| 0.51
8| 0.47
9| 0.44
10 | 0.41
—————————————————————————————————————————
Рассмотрим пример:
Есть значения, равные 0,376; 0,398; 0,371; 0,366; 0,372 и 0,379. Определим содержит ли эта серия грубые ошибки (промахи)?
Располагаем полученные результаты в порядке возрастания:
0,366 0,371 0,372 0,376 0,379 0,398
Выявление кандидата в промахи:
0,371 – 0,366 = 0,005
0,398 – 0,379 = 0,019
таким образом первый кандидат в промахи – значение 0,398
Расчет Q-критерия:
Q = (0,398 — 0,379) / (0,398 — 0,366) = 0,59
Qтаб (P = 0,90, n = 6) равно 0,56.
Видим, что Q > Qтаб, значение 0,398 — является грубой ошибкой измерения (промахом), его следует исключить
Проверяем оставшуюся серию значений:
0,371 – 0,366 = 0,005
0,379 – 0,376 = 0,003
следующий кандидат в промахи – 0,366
Расчет Q-критерия:
Q = (0,371 — 0,366) / ((0,398 — 0,366) = 0,38
Qтаб (р = 0,90, n = 5) равно 0,64. Получаем Q < Qтаб (0,38 < 0,64), значение 0,366 не является грубой ошибкой (промахом).
Надеюсь эта информация будет вам полезна.
Грубая
ошибка измерения – это результат
измерения, не соответствующий закону
распределения СВ.
В
процессе измерений предполагаемая
статистическая обстановка может
нарушиться, поэтому среди реализаций
x1,…,xn
могут появиться ошибочные значения,
которые не соответствуют закону
распределения СВ. Обычно в качестве
грубых ошибок подразумевают xmin
и
xmax.
Для
исключения грубых ошибок используют,
в частности, приближенный (логический)
и точный счетный метод.
По
приближенному методу грубые ошибки
измерения исключаются по признаку
наибольшего отличия проверяемого
результата измерения от других результатов
измерений.
В
соответствии с приближенным методом
для выявления грубых ошибок вычисляется
расстояние l=x(n—1)—x(2).
Затем сравнивается расстояние между
последним (максимальным) элементом и
предпоследним x(n—1)
с
вычисленным расстоянием l:
если
(x(n)
—
x(n—1))
<
l,
то x(n)
–
не является грубой ошибкой,
если
(x(n)
—
x(n—1))
l,
то x(n)
–
грубая ошибка, которая исключается из
выборки.
Аналогично
проводится проверка на грубую ошибку
первого (минимального) элемента
вариационного ряда:
если
(x(2)
—
x(1))
<
l,
то x(1)
–
не является грубой ошибкой,
если
(x(2)
—
x(1))
l,
то x(1)
–
грубая ошибка, которая исключается из
выборки.
При
определении грубых ошибок точным счетным
методом вводится случайная величина
– статистика проверки статистической
гипотезы о том, что реализация Xmax
является грубой ошибкой. Здесь
– среднее значение независимых случайных
величин:
,
S
–
точечная оценка стандартного отклонения:
.
Реализация
статистики T
имеет
вид:
,
где
,
.
Для
проверки гипотезы о грубой ошибке
задается α – уровень значимости,
определяющий вероятность практически
невозможного события
P(t
ta)=
α,
состоящего
в том, что t
– реализация статистики превысит
критическое значение ta
.
Значение
величины ta
определяется по таблице приложения 10
по объему выборки n
и
уровню значимости α. Например, для
объема выборки
n
=
50 и уровня значимости α
=
0,05, значение ta=2,987.
Затем
вычисляются значения величин x*min
=
—
sta
и
x*max
=
+
sta.
Если xmin
x*min
,
или xmax
x*max
то
xmin
и
xmax
не являются грубыми ошибками. В
противоположном случае они являются
грубыми ошибками и исключаются из
выборки.
2.1.4. Построение статистических оценок математического ожидания и дисперсии
Статистические
оценки математического ожидания и
дисперсии разделяют на точечные и
интервальные (доверительные).
Построение точечных оценок
Математическим
ожиданием
M[X]
дискретной случайной величины X
называется сумма произведений всех
возможных значений случайной величины
на вероятности
этих значений:
M[X]
=
Дисперсией
случайной
величины называется математическое
ожидание квадрата соответствующей
центрированной случайной величины:
D[X]
= M[(X—
M[X])
]
=
p
.
Статистической
оценкой а*
неизвестного параметра а
теоретического распределения называют
функцию от случайной выборки g(X1,
X2,
…, Xn).
Точечной
оценкой неизвестного параметра а
называют статистическую оценку,
реализация которой определяется одним
числом a*=
g(x1,
x2,
…, xn),
где x1,
x2,
…, xn
–
выборка измерений, т.е. результаты n
измерений случайной величины Х.
Реализация
точечной оценки математического ожидания
СВ определяется по формуле:
,
где
объем выборки
.
В
том случае, когда математическое ожидание
известно, реализация точечной оценки
дисперсии СВ определяется по формуле:
=
.
Если
математическое ожидание
неизвестно, то в качестве математического
ожидания определяется его оценка
.
В
этом случае, реализация точечной оценки
дисперсии СВ определяется по формуле:
=
.
Выборочная
дисперсия характеризует рассеяние
наблюдаемых значений выборки около
среднего значения
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Грубая
погрешность, промах —
погрешность результата отдельного измерения, входящего в ряд измерений, которая
для данных условий резко отличается от остальных результатов этого
ряда.
Вопрос
о том, содержит ли результат наблюдений промах, решается общими методами
проверки статистических гипотез. Проверяемая гипотеза состоит в утверждении, что
результат
наблюдения X, не содержит грубой
погрешности,
т.е. является одним из значений измеряемой величины. Пользуясь определенными
статистическими критериями, пытаются опровергнуть выдвинутую гипотезу. Если это
удается, то результат наблюдений рассматривают как содержащий грубую погрешность
и его исключают.
Одним
из критериев для проверки на грубые промахи является Q – тест.
Для
проверки на наличие грубых промахов проводят упорядочивание по величине вариант
с последующей проверкой крайних членов выборки. Формулы для вычислений:
Найденное
значение Q для данной варианты X сравнивается с табличным значением Qтабл. для заданной
степени вероятности. При отсутствии данных Р = 0,95.
Если
Q > Qтабл., то X можно считать грубым промахом. Если Q ≤
Qтабл., то результат не отбрасывают.
Задача
№1:
При
определении фосфора в листьях спектрофотометрическим методом были получены
следующие результаты (мкг/кг): 3,4; 3,7; 3,5; 3,6; 4,2; 3,5. Проверить данные на
наличие грубых промахов.
Решение:
Расположим
варианты выборки в порядке убывания величины: 4,2; 3,7; 3,6; 3,5; 3,5; 3,4.
Сомнительной по величине вариантой является 4,2. Проверим по Q –
тесту:
Qтабл. при Р = 0,95 равно 0,56
Ответ:
Qэксп
> Qтабл. – варианта 4,2 является грубым промахом.
Вариантом
для более объёмных выборок является критерий Романовского (10 < n <
20)
Найденное
значение r для данной варианты X сравнивается с табличным значением rтабл. для заданной
степени вероятности.
При
отсутствии данных Р = 0,95.
Если
r > rтабл., то можно считать грубым промахом. Если r ≤
rтабл., то результат не отбрасывают.
Задача
№2:
При
определении меди в почвах методом ААС были получены следующие результаты
(мг/кг): 17; 18; 20; 17; 23; 25; 27; 19; 15; 17; 18; 22. Проверить данные на
наличие грубых промахов.
Решение:
Расположим
варианты выборки в порядке убывания величины: 27; 24; 23; 22; 20; 19; 18; 18;
17; 17; 17; 15.
Сомнительными
по величине вариантами являются 27 и 15.
Рассчитаем
среднее арифметическое для вариант без учёта подозрительных:
Рассчитаем
стандартное отклонение для выборки:
Рассчитаем
экспериментальное значение r для каждой сомнительной варианты:
Ответ:
варианта 27 является грубой погрешностью так как экспериментальное значение
критерия больше критического.
Видео
можно посмотреть тут.
4.2.1. Определение и исключение грубых погрешностей (промахов)
В литературе приведены различные методы оценки и исключения грубых погрешностей. Рассмотрим два наиболее простых для практического использования метода.
Исключение грубых промахов по Q-критерию
При малых выборках с числом измерений п < 10 определение грубых погрешностей лучше оценивать при помощи размаха варьирования по Q-критерию. Для этого составляют отношение:
Q = |х1 – х2|R, (4.11)
|
где х1 – |
подозрительно выделяющийся результат определения (измерения); |
|
х2 – |
результат единичного определения, ближайший по значению к х1; |
|
R – |
размах варьирования, R = хmax –хmin разница между наибольшим и наименьшим значением. |
При малой выборке (n < 10) размах варьирования служит также одной из характеристик рассеяния результатов измерений.
Таблица 4.1
Значения – Q критерия в зависимости от пi и 
|
пi |
Доверительная вероятность |
||
|
0,90 |
0,95 |
0,99 |
|
|
3 |
0,89 |
0,94 |
0,99 |
|
4 |
0,68 |
0,77 |
0,89 |
|
5 |
0,56 |
0,64 |
0,76 |
|
6 |
0,48 |
0,56 |
0,70 |
|
7 |
0,43 |
0,51 |
0,64 |
|
8 |
0,40 |
0,48 |
0,58 |
Вычисленное значение Q сопоставляют с табличным значением Q (

Исключение грубых погрешностей методом вычисления максимального относительного отклонения. Статистический критерий обнаружения грубых погрешностей основан на предположении, что выборка взята из генеральной совокупности, распределенной нормально. Это позволяет использовать распределение наибольшего по абсолютному значению нормированного отклонения:
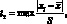
где tт – теоретическое значение квантиля распределения статистики.
Для уровней значимости р = >>0,10; 0,05; 0,01 или доверительной вероятности 1 – р = 0,90; 0,95; 0,99 и п ? 25 значения tт приведены в табл. 4.2. Уровень значимости р = (1 – Р) – максимальная вероятность того, что погрешность превзойдет некое предельное (критическое) значение ±?xkj, т.е. такое значение, что появление этой погрешности можно рассматривать как следствие значимой (неслучайной) причины. На практике обычно используют уровень значимости р = 0,05 (результат получается с 95 %-й доверительной вероятностью).
Для того, чтобы в группе из п наблюдений х1 х2, …, хп отбросить результат хmax (или хmin), надо:
а) вычислить дробь 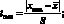
б) по табл. 4.2 найти теоретическое значение tт в зависимости от п и выбранного уровня значимости р;
в) сравнить рассчитанное по п. «а» значение tmax с tт. Если tmax > tт, то результат tmax следует отбросить как промах.
Таблица 4.2
Значения квантилей распределения максимального отклонения, 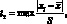
|
n |
Уровни значимости p |
n |
Уровни значимости p |
||||||
|
0,1 |
0,05 |
0,025 |
0,01 |
0,1 |
0,05 |
0,025 |
0,01 |
||
|
3 |
1,41 |
1,41 |
1,41 |
1,41 |
15 |
2,33 |
2,49 |
2,64 |
2,80 |
|
4 |
1,65 |
1,69 |
1,71 |
1,72 |
16 |
2,35 |
2,52 |
2,67 |
2,84 |
|
5 |
1,79 |
1,87 |
1,92 |
1,96 |
17 |
2,38 |
2,55 |
2,70 |
2,87 |
|
6 |
1,89 |
2,00 |
2,07 |
2,13 |
18 |
2,40 |
2,58 |
2,73 |
2,90 |
|
7 |
1,97 |
2,09 |
2,18 |
2,27 |
19 |
2,43 |
2,60 |
2,75 |
2,93 |
|
8 |
2,04 |
2,17 |
2,27 |
2,37 |
20 |
2,45 |
2,62 |
2,78 |
2,96 |
|
9 |
2,10 |
2,24 |
2,35 |
2,46 |
21 |
2,47 |
2,64 |
2,80 |
2;98 |
|
10 |
2,15 |
2,29 |
2,41 |
2,54 |
22 |
2,49 |
2,66 |
2,82 |
3,01 |
|
11 |
2,19 |
2,34 |
2,47 |
2,61 |
23 |
2,50 |
2,68 |
2,84 |
3,03 |
|
12 |
2,23 |
2,39 |
2,52 |
2,66 |
24 |
2,52 |
2,70 |
2,86 |
3,05 |
|
13 |
2,26 |
2,43 |
2,56 |
2,71 |
25 |
2,54 |
2,72 |
2,88 |
3,07 |
|
14 |
2,30 |
2,46 |
2,60 |
2,76 |
Процедуру исключения промахов можно повторить и для следующего по абсолютному значению максимального относительного отклонения, но предварительно необходимо пересчитать 
Предлагаем вашему вниманию журналы, издающиеся в издательстве «Академия Естествознания»
(Высокий импакт-фактор РИНЦ, тематика журналов охватывает все научные направления)