Загрузить PDF
Загрузить PDF
Абсолютная ошибка – это разность между измеренным значением и фактическим значением.[1]
Эта ошибка характеризует точность измерений. Если вам известны фактическое и измеренное значения, можно с легкостью вычислить абсолютную ошибку. Но иногда фактическое значение не дано, поэтому в качестве абсолютной ошибки пользуются максимально возможной ошибкой.[2]
Если даны фактическое значение и относительная ошибка, можно вычислить абсолютную ошибку.
-
1
Запишите формулу для вычисления абсолютной ошибки. Формула:
, где
– абсолютная ошибка (разность между измеренным и фактическим значениями),
– измеренное значение,
– фактическое значение.[3]
-
2
Подставьте в формулу фактическое значение. Фактическое значение должно быть дано; в противном случае используйте принятое опорное значение. Фактическое значение подставьте вместо
.
- Например, нужно измерить длину футбольного поля. Фактическая длина (принятая опорная длина) футбольного поля равна 105 м (именно такое значение рекомендуется FIFA). Таким образом, фактическое значение равно 105 м:
.
- Например, нужно измерить длину футбольного поля. Фактическая длина (принятая опорная длина) футбольного поля равна 105 м (именно такое значение рекомендуется FIFA). Таким образом, фактическое значение равно 105 м:
-
3
Подставьте в формулу измеренное значение. Оно будет дано; в противном случае измерьте величину (длину или ширину и так далее). Измеренное значение подставьте вместо
.
- Например, вы измерили длину футбольного поля и получили значение 104 м. Таким образом, измеренное значение равно 104 м:
.
- Например, вы измерили длину футбольного поля и получили значение 104 м. Таким образом, измеренное значение равно 104 м:
-
4
Вычтите фактическое значение из измеренного значения. Так как абсолютная ошибка всегда положительна, возьмите абсолютное значение этой разницы, то есть не учитывайте знак «минус».[4]
Так вы вычислите абсолютную ошибку.- В нашем примере:
, то есть абсолютная ошибка измерения равна 1 м.
Реклама
- В нашем примере:
-
1
Запишите формулу для вычисления относительной ошибки. Формула:
, где
– относительная ошибка (отношение абсолютной ошибки к фактическому значению),
– измеренное значение,
– фактическое значение.[5]
-
2
Подставьте в формулу относительную ошибку. Скорее всего, она будет дана в виде десятичной дроби. Относительную ошибку подставьте вместо
.
- Например, если относительная ошибка равна 0,02, формула запишется так:
.
- Например, если относительная ошибка равна 0,02, формула запишется так:
-
3
Подставьте в формулу фактическое значение. Оно будет дано. Фактическое значение подставьте вместо
.
- Например, если фактическое значение равно 105 м, формула запишется так:
.
- Например, если фактическое значение равно 105 м, формула запишется так:
-
4
Умножьте обе стороны уравнения на фактическое значение. Так вы избавитесь от дроби.
-
5
Прибавьте фактическое значение к каждой стороне уравнения. Так вы найдете
, то есть измеренное значение.
-
6
Вычтите фактическое значение из измеренного значения. Так как абсолютная ошибка всегда положительна, возьмите абсолютное значение этой разницы, то есть не учитывайте знак «минус».[6]
Так вы вычислите абсолютную ошибку.- Например, если измеренное значение равно 107,1 м, а фактическое значение равно 105 м, вычисления запишутся так:
. Таким образом, абсолютная ошибка равна 2,1 м.
Реклама
- Например, если измеренное значение равно 107,1 м, а фактическое значение равно 105 м, вычисления запишутся так:
-
1
Определите единицу измерения. То есть выясните, было ли значение измерено с точностью до сантиметра, метра и так далее. Возможно, эта информация будет дана (например, «длина поля измерена с точностью до метра»). Чтобы определить единицу измерения, посмотрите на то, как округлено данное значение.[7]
- Например, если измеренная длина поля равна 106 м, значение было округлено до метров. Таким образом, единица измерения равна 1 м.
-
2
-
3
Используйте максимально возможную ошибку в качестве абсолютной ошибки.[9]
Так как абсолютная ошибка всегда положительна, возьмите абсолютное значение этой разницы, то есть не учитывайте знак «минус».[10]
Так вы вычислите абсолютную ошибку.- Например, если измеренная длина поля равна
м, то есть абсолютная ошибка равна 0,5 м.
Реклама
- Например, если измеренная длина поля равна
Советы
- Если фактическое значение не указано, найдите принятое опорное или теоретическое значение.
Реклама
Об этой статье
Эту страницу просматривали 26 271 раз.
Была ли эта статья полезной?
Вычисление погрешностей измерений
Выполнение лабораторных работ связано с измерением физических величин, т. е. определением значений величин опытным путём с помощью измерительных приборов (средств измерения), и обработкой результатов измерений.
Различают прямые и косвенные измерения. При этом результат любого измерения является приблизительным, т. е. содержит погрешность измерения. Точность измерения физической величины характеризуют абсолютная и относительная погрешности.
Прямое измерение — определение значения физической величины непосредственно с помощью измерительного прибора.
Абсолютную погрешность прямых измерений определяют суммой абсолютной инструментальной погрешности и абсолютной погрешности отсчёта Δx = Δиx + Δоx при условии, что случайная погрешность и погрешность вычисления или отсутствуют, или незначительны и ими можно пренебречь.
Абсолютная инструментальная погрешность Δиx связана с классом точности прибора. Абсолютные инструментальные погрешности некоторых средств измерений представлены в таблице 1.
| Средства измерений | Диапазон измерений | Абсолютная инструментальная погрешность |
| Линейки: металлические деревянные пластмассовые |
150, 300, 500 мм 400, 500, 750 мм 200, 250, 300 мм |
0,1 мм 0,5 мм 1 мм |
| Лента измерительная | 150 см | 0,5 см |
| Мензурки 2-го класса | 100, 200, 250 см3 | 5 см3 |
| Амперметр школьный | 2 А | 0,05 А |
| Миллиамперметр | от 0 до Imax | 4 % максимального предела измерений Imax |
| Вольтметр школьный | 6 В | 0,15 В |
| Термометр лабораторный | 100 °С | 1 °С |
| Барометр-анероид | 720–780 мм рт. ст. | 3 мм рт. ст. |
| Штангенциркули с ценой деления 0,1; 0,05 мм | 155, 250, 350 мм | 0,1; 0,05 мм в соответствии с ценой деления нониуса |
| Микрометры с ценой деления 0,01 мм | 0–25, 25–50, 50–75 мм | 0,004 мм |
Абсолютная погрешность отсчёта Δоx связана с дискретностью шкалы прибора. Если величину измеряют с точностью до целого деления шкалы прибора, то погрешность отсчёта принимают равной цене деления. Если при измерении значение величины округляют до половины деления шкалы, то погрешность отсчёта принимают равной половине цены деления.
Абсолютная погрешность определяет значение интервала, в котором лежит истинное значение измеренной величины:
Относительную погрешность прямого измерения определяют отношением абсолютной погрешности к значению измеряемой величины:
Относительная погрешность характеризует точность измерения: чем она меньше, тем точность измерения выше.
Косвенное измерение — определение значения физической величины с использованием формулы, связывающей её с другими величинами, измеренными непосредственно с помощью приборов.
Одним из методов определения погрешности косвенных измерений является метод границ погрешностей. Формулы для вычисления абсолютных и относительных погрешностей косвенных измерений методом границ погрешностей представлены в таблице 2.
| Вид функции y | Абсолютная погрешность Δy | Относительная погрешность |
| x1 + x2 | Δx1 + Δx2 | |
| x1 − x2 | Δx1 + Δx2 | |
| Cx | CΔx | |
| x1x2 | |x1| Δx2 + |x2| Δx1 | |
| xn | |n||x|n−1Δx | |
| lnx | ||
| sinx | |cosx| Δx | |
| cosx | |sinx| Δx | |tgx| Δx |
| tgx |
Абсолютную погрешность табличных величин и фундаментальных физических постоянных определяют как половину единицы последнего разряда значения величины.
Загрузить PDF
Загрузить PDF
Абсолютная ошибка – это разность между измеренным значением и фактическим значением.[1]
Эта ошибка характеризует точность измерений. Если вам известны фактическое и измеренное значения, можно с легкостью вычислить абсолютную ошибку. Но иногда фактическое значение не дано, поэтому в качестве абсолютной ошибки пользуются максимально возможной ошибкой.[2]
Если даны фактическое значение и относительная ошибка, можно вычислить абсолютную ошибку.
-
1
Запишите формулу для вычисления абсолютной ошибки. Формула:
, где
– абсолютная ошибка (разность между измеренным и фактическим значениями),
– измеренное значение,
– фактическое значение.[3]
-
2
Подставьте в формулу фактическое значение. Фактическое значение должно быть дано; в противном случае используйте принятое опорное значение. Фактическое значение подставьте вместо
.
- Например, нужно измерить длину футбольного поля. Фактическая длина (принятая опорная длина) футбольного поля равна 105 м (именно такое значение рекомендуется FIFA). Таким образом, фактическое значение равно 105 м:
.
- Например, нужно измерить длину футбольного поля. Фактическая длина (принятая опорная длина) футбольного поля равна 105 м (именно такое значение рекомендуется FIFA). Таким образом, фактическое значение равно 105 м:
-
3
Подставьте в формулу измеренное значение. Оно будет дано; в противном случае измерьте величину (длину или ширину и так далее). Измеренное значение подставьте вместо
.
- Например, вы измерили длину футбольного поля и получили значение 104 м. Таким образом, измеренное значение равно 104 м:
.
- Например, вы измерили длину футбольного поля и получили значение 104 м. Таким образом, измеренное значение равно 104 м:
-
4
Вычтите фактическое значение из измеренного значения. Так как абсолютная ошибка всегда положительна, возьмите абсолютное значение этой разницы, то есть не учитывайте знак «минус».[4]
Так вы вычислите абсолютную ошибку.- В нашем примере:
, то есть абсолютная ошибка измерения равна 1 м.
Реклама
- В нашем примере:
-
1
Запишите формулу для вычисления относительной ошибки. Формула:
, где
– относительная ошибка (отношение абсолютной ошибки к фактическому значению),
– измеренное значение,
– фактическое значение.[5]
-
2
Подставьте в формулу относительную ошибку. Скорее всего, она будет дана в виде десятичной дроби. Относительную ошибку подставьте вместо
.
- Например, если относительная ошибка равна 0,02, формула запишется так:
.
- Например, если относительная ошибка равна 0,02, формула запишется так:
-
3
Подставьте в формулу фактическое значение. Оно будет дано. Фактическое значение подставьте вместо
.
- Например, если фактическое значение равно 105 м, формула запишется так:
.
- Например, если фактическое значение равно 105 м, формула запишется так:
-
4
Умножьте обе стороны уравнения на фактическое значение. Так вы избавитесь от дроби.
-
5
Прибавьте фактическое значение к каждой стороне уравнения. Так вы найдете
, то есть измеренное значение.
-
6
Вычтите фактическое значение из измеренного значения. Так как абсолютная ошибка всегда положительна, возьмите абсолютное значение этой разницы, то есть не учитывайте знак «минус».[6]
Так вы вычислите абсолютную ошибку.- Например, если измеренное значение равно 107,1 м, а фактическое значение равно 105 м, вычисления запишутся так:
. Таким образом, абсолютная ошибка равна 2,1 м.
Реклама
- Например, если измеренное значение равно 107,1 м, а фактическое значение равно 105 м, вычисления запишутся так:
-
1
Определите единицу измерения. То есть выясните, было ли значение измерено с точностью до сантиметра, метра и так далее. Возможно, эта информация будет дана (например, «длина поля измерена с точностью до метра»). Чтобы определить единицу измерения, посмотрите на то, как округлено данное значение.[7]
- Например, если измеренная длина поля равна 106 м, значение было округлено до метров. Таким образом, единица измерения равна 1 м.
-
2
-
3
Используйте максимально возможную ошибку в качестве абсолютной ошибки.[9]
Так как абсолютная ошибка всегда положительна, возьмите абсолютное значение этой разницы, то есть не учитывайте знак «минус».[10]
Так вы вычислите абсолютную ошибку.- Например, если измеренная длина поля равна
м, то есть абсолютная ошибка равна 0,5 м.
Реклама
- Например, если измеренная длина поля равна
Советы
- Если фактическое значение не указано, найдите принятое опорное или теоретическое значение.
Реклама
Об этой статье
Эту страницу просматривали 24 549 раз.
Была ли эта статья полезной?
Погрешности измерений, представление результатов эксперимента
- Шкала измерительного прибора
- Цена деления
- Виды измерений
- Погрешность измерений, абсолютная и относительная погрешность
- Абсолютная погрешность серии измерений
- Представление результатов эксперимента
- Задачи
п.1. Шкала измерительного прибора
Шкала – это показывающая часть измерительного прибора, состоящая из упорядоченного ряда отметок со связанной с ними нумерацией. Шкала может располагаться по окружности, дуге или прямой линии.
Примеры шкал различных приборов:
п.2. Цена деления
Цена деления измерительного прибора равна числу единиц измеряемой величины между двумя ближайшими делениями шкалы. Как правило, цена деления указана на маркировке прибора.
Алгоритм определения цены деления
Шаг 1. Найти два ближайшие пронумерованные крупные деления шкалы. Пусть первое значение равно a, второе равно b, b > a.
Шаг 2. Посчитать количество мелких делений шкалы между ними. Пусть это количество равно n.
Шаг 3. Разделить разницу значений крупных делений шкалы на количество отрезков, которые образуются мелкими делениями: $$ triangle=frac{b-a}{n+1} $$ Найденное значение (triangle) и есть цена деления данного прибора.
Пример определения цены деления:
 |
Определим цену деления основной шкалы секундомера. Два ближайших пронумерованных деления на основной шкале:a = 5 c b = 10 cМежду ними находится 4 средних деления, а между каждыми средними делениями еще 4 мелких. Итого: 4+4·5=24 деления. Цена деления: begin{gather*} triangle=frac{b-a}{n+1}\ triangle=frac{10-5}{24+1}=frac15=0,2 c end{gather*} |
п.3. Виды измерений
Вид измерений
Определение
Пример
Прямое измерение
Физическую величину измеряют с помощью прибора
Измерение длины бруска линейкой
Косвенное измерение
Физическую величину рассчитывают по формуле, куда подставляют значения величин, полученных с помощью прямых измерений
Определение площади столешницы при измеренной длине и ширине
п.4. Погрешность измерений, абсолютная и относительная погрешность
Погрешность измерений – это отклонение измеренного значения величины от её истинного значения.
Составляющие погрешности измерений
Причины
Инструментальная погрешность
Определяется погрешностью инструментов и приборов, используемых для измерений (принципом действия, точностью шкалы и т.п.)
Погрешность метода
Определяется несовершенством методов и допущениями в методике.
Погрешность теории (модели)
Определяется теоретическими упрощениями, степенью соответствия теоретической модели и реальности.
Погрешность оператора
Определяется субъективным фактором, ошибками экспериментатора.
Инструментальная погрешность измерений принимается равной половине цены деления прибора: $$ d=frac{triangle}{2} $$
Если величина (a_0) — это истинное значение, а (triangle a) — погрешность измерения, результат измерений физической величины записывают в виде (a=a_0pmtriangle a).
Абсолютная погрешность измерения – это модуль разности между измеренным и истинным значением измеряемой величины: $$ triangle a=|a-a_0| $$
Отношение абсолютной погрешности измерения к истинному значению, выраженное в процентах, называют относительной погрешностью измерения: $$ delta=frac{triangle a}{a_0}cdot 100text{%} $$
Относительная погрешность является мерой точности измерения: чем меньше относительная погрешность, тем измерение точнее. По абсолютной погрешности о точности измерения судить нельзя.
На практике абсолютную и относительную погрешности округляют до двух значащих цифр с избытком, т.е. всегда в сторону увеличения.
Значащие цифры – это все верные цифры числа, кроме нулей слева. Результаты измерений записывают только значащими цифрами.
Примеры значащих цифр:
0,403 – три значащих цифры, величина определена с точностью до тысячных.
40,3 – три значащих цифры, величина определена с точностью до десятых.
40,300 – пять значащих цифр, величина определена с точностью до тысячных.
В простейших измерениях инструментальная погрешность прибора является основной.
В таких случаях физическую величину измеряют один раз, полученное значение берут в качестве истинного, а абсолютную погрешность считают равной инструментальной погрешности прибора.
Примеры измерений с абсолютной погрешностью равной инструментальной:
- определение длины с помощью линейки или мерной ленты;
- определение объема с помощью мензурки.
Пример получения результатов прямых измерений с помощью линейки:
 |
Измерим длину бруска линейкой, у которой пронумерованы сантиметры и есть только одно деление между пронумерованными делениями. Цена деления такой линейки: begin{gather*} triangle=frac{b-a}{n+1}= frac{1 text{см}}{1+1}=0,5 text{см} end{gather*} Инструментальная погрешность: begin{gather*} d=frac{triangle}{2}=frac{0,5}{2}=0,25 text{см} end{gather*} Истинное значение: (L_0=4 text{см}) Результат измерений: $$ L=L_0pm d=(4,00pm 0,25) text{см} $$ Относительная погрешность: $$ delta=frac{0,25}{4,00}cdot 100text{%}=6,25text{%}approx 6,3text{%} $$ |
 |
Теперь возьмем линейку с n=9 мелкими делениями между пронумерованными делениями. Цена деления такой линейки: begin{gather*} triangle=frac{b-a}{n+1}= frac{1 text{см}}{9+1}=0,1 text{см} end{gather*} Инструментальная погрешность: begin{gather*} d=frac{triangle}{2}=frac{0,1}{2}=0,05 text{см} end{gather*} Истинное значение: (L_0=4,15 text{см}) Результат измерений: $$ L=L_0pm d=(4,15pm 0,05) text{см} $$ Относительная погрешность: $$ delta=frac{0,05}{4,15}cdot 100text{%}approx 1,2text{%} $$ |
Второе измерение точнее, т.к. его относительная погрешность меньше.
п.5. Абсолютная погрешность серии измерений
Измерение длины с помощью линейки (или объема с помощью мензурки) являются теми редкими случаями, когда для определения истинного значения достаточно одного измерения, а абсолютная погрешность сразу берется равной инструментальной погрешности, т.е. половине цены деления линейки (или мензурки).
Гораздо чаще погрешность метода или погрешность оператора оказываются заметно больше инструментальной погрешности. В таких случаях значение измеренной физической величины каждый раз немного меняется, и для оценки истинного значения и абсолютной погрешности нужна серия измерений и вычисление средних значений.
Алгоритм определения истинного значения и абсолютной погрешности в серии измерений
Шаг 1. Проводим серию из (N) измерений, в каждом из которых получаем значение величины (x_1,x_2,…,x_N)
Шаг 2. Истинное значение величины принимаем равным среднему арифметическому всех измерений: $$ x_0=x_{cp}=frac{x_1+x_2+…+x_N}{N} $$ Шаг 3. Находим абсолютные отклонения от истинного значения для каждого измерения: $$ triangle_1=|x_0-x_1|, triangle_2=|x_0-x_2|, …, triangle_N=|x_0-x_N| $$ Шаг 4. Находим среднее арифметическое всех абсолютных отклонений: $$ triangle_{cp}=frac{triangle_1+triangle_2+…+triangle_N}{N} $$ Шаг 5. Сравниваем полученную величину (triangle_{cp}) c инструментальной погрешностью прибора d (половина цены деления). Большую из этих двух величин принимаем за абсолютную погрешность: $$ triangle x=maxleft{triangle_{cp}; dright} $$ Шаг 6. Записываем результат серии измерений: (x=x_0pmtriangle x).
Пример расчета истинного значения и погрешности для серии прямых измерений:
Пусть при измерении массы шарика с помощью рычажных весов мы получили в трех опытах следующие значения: 99,8 г; 101,2 г; 100,3 г.
Инструментальная погрешность весов d = 0,05 г.
Найдем истинное значение массы и абсолютную погрешность.
Составим расчетную таблицу:
| № опыта | 1 | 2 | 3 | Сумма |
| Масса, г | 99,8 | 101,2 | 100,3 | 301,3 |
| Абсолютное отклонение, г | 0,6 | 0,8 | 0,1 | 1,5 |
Сначала находим среднее значение всех измерений: begin{gather*} m_0=frac{99,8+101,2+100,3}{3}=frac{301,3}{3}approx 100,4 text{г} end{gather*} Это среднее значение принимаем за истинное значение массы.
Затем считаем абсолютное отклонение каждого опыта как модуль разности (m_0) и измерения. begin{gather*} triangle_1=|100,4-99,8|=0,6\ triangle_2=|100,4-101,2|=0,8\ triangle_3=|100,4-100,3|=0,1 end{gather*} Находим среднее абсолютное отклонение: begin{gather*} triangle_{cp}=frac{0,6+0,8+0,1}{3}=frac{1,5}{3}=0,5 text{(г)} end{gather*} Мы видим, что полученное значение (triangle_{cp}) больше инструментальной погрешности d.
Поэтому абсолютная погрешность измерения массы: begin{gather*} triangle m=maxleft{triangle_{cp}; dright}=maxleft{0,5; 0,05right} text{(г)} end{gather*} Записываем результат: begin{gather*} m=m_0pmtriangle m\ m=(100,4pm 0,5) text{(г)} end{gather*} Относительная погрешность (с двумя значащими цифрами): begin{gather*} delta_m=frac{0,5}{100,4}cdot 100text{%}approx 0,050text{%} end{gather*}
п.6. Представление результатов эксперимента
Результат измерения представляется в виде $$ a=a_0pmtriangle a $$ где (a_0) – истинное значение, (triangle a) – абсолютная погрешность измерения.
Как найти результат прямого измерения, мы рассмотрели выше.
Результат косвенного измерения зависит от действий, которые производятся при подстановке в формулу величин, полученных с помощью прямых измерений.
Погрешность суммы и разности
Если (a=a_0+triangle a) и (b=b_0+triangle b) – результаты двух прямых измерений, то
- абсолютная погрешность их суммы равна сумме абсолютных погрешностей
$$ triangle (a+b)=triangle a+triangle b $$
- абсолютная погрешность их разности также равна сумме абсолютных погрешностей
$$ triangle (a-b)=triangle a+triangle b $$
Погрешность произведения и частного
Если (a=a_0+triangle a) и (b=b_0+triangle b) – результаты двух прямых измерений, с относительными погрешностями (delta_a=frac{triangle a}{a_0}cdot 100text{%}) и (delta_b=frac{triangle b}{b_0}cdot 100text{%}) соответственно, то:
- относительная погрешность их произведения равна сумме относительных погрешностей
$$ delta_{acdot b}=delta_a+delta_b $$
- относительная погрешность их частного также равна сумме относительных погрешностей
$$ delta_{a/b}=delta_a+delta_b $$
Погрешность степени
Если (a=a_0+triangle a) результат прямого измерения, с относительной погрешностью (delta_a=frac{triangle a}{a_0}cdot 100text{%}), то:
- относительная погрешность квадрата (a^2) равна удвоенной относительной погрешности
$$ delta_{a^2}=2delta_a $$
- относительная погрешность куба (a^3) равна утроенной относительной погрешности
$$ delta_{a^3}=3delta_a $$
- относительная погрешность произвольной натуральной степени (a^n) равна
$$ delta_{a^n}=ndelta_a $$
Вывод этих формул достаточно сложен, но если интересно, его можно найти в Главе 7 справочника по алгебре для 8 класса.
п.7. Задачи
Задача 1. Определите цену деления и объем налитой жидкости для каждой из мензурок. В каком случае измерение наиболее точно; наименее точно?
Составим таблицу для расчета цены деления:
| № мензурки | a, мл | b, мл | n | (triangle=frac{b-a}{n+1}), мл |
| 1 | 20 | 40 | 4 | (frac{40-20}{4+1}=4) |
| 2 | 100 | 200 | 4 | (frac{200-100}{4+1}=20) |
| 3 | 15 | 30 | 4 | (frac{30-15}{4+1}=3) |
| 4 | 200 | 400 | 4 | (frac{400-200}{4+1}=40) |
Инструментальная точность мензурки равна половине цены деления.
Принимаем инструментальную точность за абсолютную погрешность и измеренное значение объема за истинное.
Составим таблицу для расчета относительной погрешности (оставляем две значащих цифры и округляем с избытком):
| № мензурки | Объем (V_0), мл | Абсолютная погрешность (triangle V=frac{triangle}{2}), мл |
Относительная погрешность (delta_V=frac{triangle V}{V_0}cdot 100text{%}) |
| 1 | 68 | 2 | 3,0% |
| 2 | 280 | 10 | 3,6% |
| 3 | 27 | 1,5 | 5,6% |
| 4 | 480 | 20 | 4,2% |
Наиболее точное измерение в 1-й мензурке, наименее точное – в 3-й мензурке.
Ответ:
Цена деления 4; 20; 3; 40 мл
Объем 68; 280; 27; 480 мл
Самое точное – 1-я мензурка; самое неточное – 3-я мензурка
Задача 2. В двух научных работах указаны два значения измерений одной и той же величины: $$ x_1=(4,0pm 0,1) text{м}, x_2=(4,0pm 0,03) text{м} $$ Какое из этих измерений точней и почему?
Мерой точности является относительная погрешность измерений. Получаем: begin{gather*} delta_1=frac{0,1}{4,0}cdot 100text{%}=2,5text{%}\ delta_2=frac{0,03}{4,0}cdot 100text{%}=0,75text{%} end{gather*} Относительная погрешность второго измерения меньше. Значит, второе измерение точней.
Ответ: (delta_2lt delta_1), второе измерение точней.
Задача 3. Две машины движутся навстречу друг другу со скоростями 54 км/ч и 72 км/ч.
Цена деления спидометра первой машины 10 км/ч, второй машины – 1 км/ч.
Найдите скорость их сближения, абсолютную и относительную погрешность этой величины.
Абсолютная погрешность скорости каждой машины равна инструментальной, т.е. половине деления спидометра: $$ triangle v_1=frac{10}{2}=5 (text{км/ч}), triangle v_2=frac{1}{2}=0,5 (text{км/ч}) $$ Показания каждого из спидометров: $$ v_1=(54pm 5) text{км/ч}, v_2=(72pm 0,5) text{км/ч} $$ Скорость сближения равна сумме скоростей: $$ v_0=v_{10}+v_{20}, v_0=54+72=125 text{км/ч} $$ Для суммы абсолютная погрешность равна сумме абсолютных погрешностей слагаемых. $$ triangle v=triangle v_1+triangle v_2, triangle v=5+0,5=5,5 text{км/ч} $$ Скорость сближения с учетом погрешности равна: $$ v=(126,0pm 5,5) text{км/ч} $$ Относительная погрешность: $$ delta_v=frac{5,5}{126,0}cdot 100text{%}approx 4,4text{%} $$ Ответ: (v=(126,0pm 5,5) text{км/ч}, delta_vapprox 4,4text{%})
Задача 4. Измеренная длина столешницы равна 90,2 см, ширина 60,1 см. Измерения проводились с помощью линейки с ценой деления 0,1 см. Найдите площадь столешницы, абсолютную и относительную погрешность этой величины.
Инструментальная погрешность линейки (d=frac{0,1}{2}=0,05 text{см})
Результаты прямых измерений длины и ширины: $$ a=(90,20pm 0,05) text{см}, b=(60,10pm 0,05) text{см} $$ Относительные погрешности (не забываем про правила округления): begin{gather*} delta_1=frac{0,05}{90,20}cdot 100text{%}approx 0,0554text{%}approx uparrow 0,056text{%}\ delta_2=frac{0,05}{60,10}cdot 100text{%}approx 0,0832text{%}approx uparrow 0,084text{%} end{gather*} Площадь столешницы: $$ S=ab, S=90,2cdot 60,1 = 5421,01 text{см}^2 $$ Для произведения относительная погрешность равна сумме относительных погрешностей слагаемых: $$ delta_S=delta_a+delta_b=0,056text{%}+0,084text{%}=0,140text{%}=0,14text{%} $$ Абсолютная погрешность: begin{gather*} triangle S=Scdot delta_S=5421,01cdot 0,0014=7,59approx 7,6 text{см}^2\ S=(5421,0pm 7,6) text{см}^2 end{gather*} Ответ: (S=(5421,0pm 7,6) text{см}^2, delta_Sapprox 0,14text{%})
Абсолютная и относительная погрешности (ошибки).
Пусть некоторая
величина x
измерена n
раз. В результате получен ряд значений
этой величины: x1,
x2,
x3,
…, xn
Величиной, наиболее
близкой к действительному значению,
является среднее арифметическое этих
результатов:
Отсюда следует,
что каждое физическое измерение должно
быть повторено несколько раз.
Разность между
средним значением
измеряемой
величины и значением отдельного измерения
называется абсолютной
погрешностью отдельного измерения:
(13)
Абсолютная
погрешность может быть как положительной,
так и отрицательной и измеряется в тех
же единицах, что и измеряемая величина.
Средняя абсолютная
ошибка результата — это среднее
арифметическое значений абсолютных
погрешностей отдельных измерений,
взятых по абсолютной величине (модулю):
(14)
Отношения
называются относительными погрешностями
(ошибками) отдельных измерений.
Отношение средней
абсолютной погрешности результата
к среднему арифметическому значению
измеряемой величины называют относительной
ошибкой результата и выражают в процентах:
Относительная
ошибка характеризует точность измерения.
Законы распределения случайных величин.
Результат измерения
физической величины зависит от многих
факторов, влияние которых заранее учесть
невозможно. Поэтому значения, полученные
в результате прямых измерений какого
— либо параметра, являются случайными,
обычно не совпадающие между собой.
Следовательно, случайные
величины —
это такие величины, которые в зависимости
от обстоятельств могут принимать те
или иные значения. Если случайная
величина принимает только определенные
числовые значения, то она называется
дискретной.
Например,
количество заболеваний в данном регионе
за год, оценка, полученная студентом на
экзамене, энергия электрона в атоме и
т.д.
Непрерывная
случайная величина принимает любые
значения в данном интервале.
Например: температура
тела человека, мгновенные скорости
теплового движения молекул, содержание
кислорода в воздухе и т.д.
Под событием
понимается всякий результат или исход
испытания. В теории вероятностей
рассматриваются события, которые при
выполнение некоторых условий могут
произойти, а могут не произойти. Такие
события называются
случайными.
Например, событие, состоящее в появлении
цифры 1 при выполнении условия — бросания
игральной кости, может произойти, а
может не произойти.
Если событие
неизбежно происходит в результате
каждого испытания, то оно называется
достоверным.
Событие называется невозможным,
если оно вообще не происходит ни при
каких условиях.
Два события,
одновременное появление которых
невозможно, называются несовместными.
Пусть случайное
событие А в серии из n
независимых испытаний произошло m
раз, тогда отношение:
называется
относительной частотой события А. Для
каждой относительной частоты выполняется
неравенство:
При небольшом
числе опытов относительная частота
событий в значительной мере имеет
случайный характер и может заметно
изменяться от одной группы опытов к
другой. Однако при увеличении числа
опытов частота событий все более теряет
свой случайный характер и приближается
к некоторому постоянному положительному
числу, которое является количественной
мерой возможности реализации случайного
события А. Предел, к которому стремится
относительная частота событий при
неограниченном увеличении числа
испытаний, называется статистической
вероятностью события:
Например, при
многократном бросании монеты частота
выпадения герба будет лишь незначительно
отличаться от ½. Для достоверного события
вероятность Р(А) равна единице. Если
Р=0, то событие невозможно.
Математическим
ожиданием
дискретной случайной величины называется
сумма произведений всех ее возможных
значений хi
на вероятность этих значений рi:
Статистическим
аналогом математического ожидания
является среднее арифметическое значений
:
,
где mi
— число дискретных случайных величин,
имеющих значение хi.
Для непрерывной
случайной величины математическим
ожиданием служит интеграл:
,
где р(х) — плотность
вероятности.
Отдельные значения
случайной величины группируются около
математического ожидания. Отклонение
случайной величины от ее математического
ожидания (среднего значения) характеризуется
дисперсией,
которая для дискретной случайной
величины определяется формулой:
(15)
(16)
Дисперсия имеет
размерность случайной величины. Для
того, чтобы оценивать рассеяние
(отклонение) случайной величины в
единицах той же размерности, введено
понятие среднего
квадратичного отклонения
σ(Х), которое
равно корню квадратному из дисперсии:
(17)
Вместо среднего
квадратичного отклонения иногда
используется термин «стандартное
отклонение».
Всякое отношение,
устанавливающее связь между всеми
возможными значениями случайной величины
и соответствующими им вероятностями,
называется законом
распределения случайной величины.
Формы задания закона распределения
могут быть разными:
а) ряд распределения
(для дискретных величин);
б) функция
распределения;
в) кривая распределения
(для непрерывных величин).
Существует
относительно много законов распределения
случайных величин.
Нормальный
закон распределения случайных
величин (закон
Гаусса).
Случайная величина
распределена по
нормальному закону, если ее плотность
вероятности f(x)
определяется формулой:
(18),
где <x>
— математическое ожидание (среднее
значение) случайной величины <x>
= M
(X);
—
среднее квадратичное отклонение;
—
основание натурального логарифма
(неперово число);
f
(x)
– плотность вероятности (функция
распределения вероятностей).
Многие случайные
величины (в том числе все случайные
погрешности) подчиняются нормальному
закону распределения (закону Гаусса).
Для этого распределения наиболее
вероятным значением
измеряемой
величины
является
её среднее
арифметическое
значение.
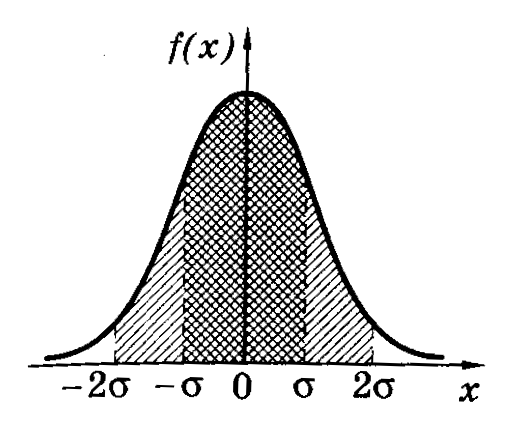
График нормального
закона распределения изображен на
рисунке (колоколообразная кривая).
Кривая симметрична
относительно прямой х=<x>=α,
следовательно, отклонения случайной
величины вправо и влево от <x>=α
равновероятны. При х=<x>±
кривая асимптотически приближается к
оси абсцисс. Если х=<x>,
то функция распределения вероятностей
f(x)
максимальна и принимает вид:
(19)
Таким образом,
максимальное значение функции fmax(x)
зависит от величины среднего квадратичного
отклонения. На рисунке изображены 3
кривые распределения. Для кривых 1 и 2
<x>
= α = 0 соответствующие значения среднего
квадратичного отклонения различны, при
этом 2>1.
(При увеличении
кривая распределения становится более
пологой, а при уменьшении
– вытягивается вверх). Для кривой 3 <x>
= α ≠ 0 и 3
= 2.
Закон
распределения
молекул в газах по скоростям называется
распределением
Максвелла.
Функция плотности вероятности попадания
скоростей молекул в определенный
интервал
теоретически была определена в 1860 году
английским физиком Максвеллом
. На рисунке
распределение Максвелла представлено
графически. Распределение движется
вправо или влево в зависимости от
температуры газа (на рисунке Т1
< Т2).
Закон распределения Максвелла определяется
формулой:
(20),
где mо
– масса молекулы, k
– постоянная Больцмана, Т – абсолютная
температура газа,
—
скорость молекулы.
Распределение
концентрации молекул газа в атмосфере
Земли (т.е.
в силовом поле) в зависимости от высоты
было дано австрийским физиком Больцманом
и называется
распределением
Больцмана:
(21)
Где n(h)
– концентрация молекул газа на высоте
h,
n0
– концентрация у поверхности Земли, g
– ускорение свободного падения, m
– масса молекулы.
Распределение
Больцмана.
Совокупность всех
значений случайной величины называется
простым
статистическим рядом.
Так как простой статистический ряд
оказывается большим, то его преобразуют
в вариационный
статистический
ряд или интервальный
статистический ряд. По интервальному
статистическому ряду для оценки вида
функции распределения вероятностей по
экспериментальным данным строят
гистограмму
– столбчатую
диаграмму. (Гистограмма – от греческих
слов “histos”–
столб и “gramma”–
запись).
n
-
h
Гистограмма
распределения Больцмана.
Для построения
гистограммы интервал, содержащий
полученные значения случайной величины
делят на несколько интервалов xi
одинаковой ширины. Для каждого интервала
подсчитывают число mi
значений случайной величины, попавших
в этот интервал. После этого вычисляют
плотность частоты случайной величины
для каждого интервала xi
и среднее значение случайной величины
<xi
> в каждом интервале.
Затем по оси абсцисс
откладывают интервалы xi,
являющиеся основаниями прямоугольников,
высота которых равна
(или
высотой
– плотностью относительной частоты
).
Расчетами показано,
что вероятность попадания нормально
распределенной случайной величины в
интервале значений от <x>–
до <x>+
в среднем равна 68%. В границах вдвое
более широких (<x>–2;
<x>+2)
размещается в среднем 95% всех значений
измерений, а в интервале (<x>–3;<x>+3)
– уже 99,7%. Таким образом, вероятность
того, что отклонение значений нормально
распределенной случайной величины
превысит 3
(
– среднее квадратичное отклонение)
чрезвычайно мала (~0,003). Такое событие
можно считать практически невозможным.
Поэтому границы <x>–3
и <x>+3
принимаются за границы практически
возможных значений нормально распределенной
случайной величины («правило трех
сигм»).
Если число измерений
(объем выборки) невелико (n<30),
дисперсия вычисляется по формуле:
(22)
Уточненное среднее
квадратичное отклонение отдельного
измерения вычисляется по формуле:
(23)
Напомним, что для
эмпирического распределения по выборке
аналогом математического ожидания
является среднее арифметическое значение
<x>
измеряемой величины.
Чтобы дать
представление о точности и надежности
оценки измеряемой величины, используют
понятия доверительного интервала и
доверительной вероятности.
Доверительным
интервалом
называется интервал (<x>–x,
<x>+x),
в который по определению попадает с
заданной вероятностью действительное
(истинное) значение измеряемой величины.
Доверительный интервал характеризует
точность полученного результата: чем
уже доверительный интервал, тем меньше
погрешность.
Доверительной
вероятностью
(надежностью)
результата серии измерений называется
вероятность того, что истинное значение
измеряемой величины попадает в данный
доверительный интервал (<x>±x).
Чем больше величина доверительного
интервала, т.е. чем больше x,
тем с большей надежностью величина <x>
попадает в этот интервал. Надежность
выбирается самим исследователем
самостоятельно, например, =0,95;
0,98. В медицинских и биологических
исследованиях, как правило, доверительную
вероятность (надежность) принимают
равной 0,95.
Если величина х
подчиняется нормальному закону
распределения Гаусса, а <x>
и <>
оцениваются по выборке (числу измерений)
и если объем выборки невелик (n<30),
то интервал (<x>
– t,n<>,
<x>
+ t,n<>)
будет доверительным интервалом для
известного параметра х с доверительной
вероятностью .
Коэффициент t,n
называется коэффициентом
Стьюдента
(этот коэффициент был предложен в 1908 г.
английским математиком и химиком В.С.
Госсетом, публиковавшим свои работы
под псевдонимом «Стьюдент» – студент).
Значении коэффициента
Стьюдента t,n
зависит от доверительной вероятности
и числа измерений n
(объема выборки). Некоторые значения
коэффициента Стьюдента приведены в
таблице 1.
Таблица 1
|
n |
|
||||||
|
0,6 |
0,7 |
0,8 |
0,9 |
0,95 |
0,98 |
0,99 |
|
|
2 |
1,38 |
2,0 |
3,1 |
6,3 |
12,7 |
31,8 |
63,7 |
|
3 |
1,06 |
1,3 |
1,9 |
2,9 |
4,3 |
7,0 |
9,9 |
|
4 |
0,98 |
1,3 |
1,6 |
2,4 |
3,2 |
4,5 |
5,8 |
|
5 |
0,94 |
1,2 |
1,5 |
2,1 |
2,8 |
3,7 |
4,6 |
|
6 |
0,92 |
1,2 |
1,5 |
2,0 |
2,6 |
3,4 |
4,0 |
|
7 |
0,90 |
1,1 |
1,4 |
1,9 |
2,4 |
3,1 |
3,7 |
|
8 |
0,90 |
1,1 |
1,4 |
1,9 |
2,4 |
3,0 |
3,5 |
|
9 |
0,90 |
1,1 |
1,4 |
1,9 |
2,3 |
2,9 |
3,4 |
|
10 |
0,88 |
1,1 |
1,4 |
1,9 |
2,3 |
2,8 |
3,3 |
В таблице 1 в верхней
строке заданы значения доверительной
вероятности
от 0,6 до 0,99, в левом столбце – значение
n.
Коэффициент Стьюдента следует искать
на пересечении соответствующих строки
и столбца.
Окончательный
результат измерений записывается в
виде:
(25)
Где
– полуширина доверительного интервала.
Результат серии
измерений оценивается относительной
погрешностью:
(26)
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание:
При измерении разных физических величин мы получаем их числовые значения с определенной точностью. Например, при определении размеров листа бумаги (длины, ширины) мы можем указать их с точностью до миллиметра; размеры стола – с точностью до сантиметра, размеры дома, стадиона – с точностью до метра.
Нет необходимости указывать размеры стола с точностью до миллиметра, а размеры стадиона с точностью до сантиметра или миллиметра. Мы сами в каждой ситуации, опыте и эксперименте определяем, с какой точностью нам нужны данные физические величины. Однако очень важно оценивать, насколько точно мы определяем физическую величину, какую ошибку (погрешность) в ее измерении допускаем.
При измерении мы не можем определить истинное значение измеряемой величины, а только пределы, в которых она находится.
Пример:
Измерим ширину стола рулеткой с сантиметровыми и миллиметровыми делениями на ней (рис. 5.1). Значение наименьшего деления шкалы называют ценой деления и обозначают буквой С. Видно, что цена деления рулетки С = 1 мм (или 0,1 см).
Совместим нулевое деление рулетки с краем стола и посмотрим, с каким значением
шкалы линейки совпадает второй край стола (рис. 5.1). Видно, что ширина стола составляет чуть больше 70 см и 6 мм, или 706 мм. Но результат наших измерений мы запишем с точностью до 1 мм, то есть L = 706 мм.
Абсолютная погрешность измерения ∆ (ДЕЛЬТА)
Из рис. 5.1 видно, что мы допускаем определенную погрешность и определить ее «на глаз» достаточно трудно. Эта погрешность составляет не более половины цены деления шкалы рулетки. Эту погрешность называют погрешностью измерения и помечают ∆L («дельта эль»). В данном эксперименте ее можно записать
Сам результат измерения принято записывать таким образом: ширина стола L = (706,0 ± 0,5) мм, читают: 706 плюс-минус 0,5 мм. Эти 0,5 мм в нашем примере называют абсолютной погрешностью. Значения измеряемой величины (706,0 мм) и абсолютной погрешности (0,5 мм) должны иметь одинаковое количество цифр после запятой, то есть нельзя записывать 706 мм ± 0,5 мм.
Такая запись результата измерения означает, что истинное значение измеряемой величины находится между 705,5 мм и 706,5 мм, то есть 705,5 мм ≤ L ≤ 706,5 мм.
Относительная погрешность измерения ε (ЭПСИЛОН)
Иногда важно знать, какую часть составляет наша погрешность от значения
измеряемой величины. Для этого разделим 0,5 мм на 706 мм. В результате получим: 

Относительная погрешность измерения свидетельствует о качестве измерения. Если длина какогото предмета равна 5 мм, а точность измерения – плюс-минус 0,5 мм, то относительная погрешность будет составлять уже 10%.
Стандартная запись результата измерений и выводы
Таким образом, абсолютная погрешность в примере 5.1. составляет ∆L = 0,5 мм, а результат измерений следует записать в стандартном виде: L = (706,0 
На точность измерения влияет много факторов, в частности:
- При совмещении края стола с делением шкалы рулетки мы неминуемо допускаем погрешность, поскольку делаем это «на глаз» — смотреть можно под разными углами.
- Не вполне ровно установили рулетку.
- Наша рулетка является копией эталона и может несколько отличаться от оригинала.
Все это необходимо учитывать при проведении измерений.
Итоги:
- Измерения в физике всегда неточны, и надо знать пределы погрешности измерений, чтобы понимать, насколько можно доверять результатам.
- Абсолютную погрешность измерения можно определить как половину цены деления шкалы измерительного прибора.
- Относительная погрешность есть частное от деления абсолютной погрешности на значение измеряемой величины:
и указывает на качество измерения. Ее можно выразить в процентах.
Измерительные приборы
Устройства, с помощью которых измеряют физические величины, называют измерительными приборами.
Простейший и хорошо известный вам измерительный прибор — линейка с делениями. На ее примере вы видите, что у измерительного прибора есть шкала, на которой нанесены деления, причем возле некоторых делений написано соответствующее значение физической величины. Так, значения длины в сантиметрах нанесены на линейке возле каждого десятого деления (рис. 3.11). Значения же, соответствующие «промежуточным» делениям шкалы, можно найти с помощью простого подсчета.
Разность значений физической величины, которые соответствуютближайшим делениям шкалы, называют ценой деления прибора. Ёе находят так: берут ближайшие деления, возле которых написаны значения величины, и делят разность этих значений на количество промежутков между делениями, расположенными между ними.
Например, ближайшие сантиметровые деления на линейке разделены на десять промежутков. Значит, цена деления линейки равна 0,1 см = 1 мм.
Как определяют единицы длины и времени
В старину мерами длины служили большей частью размеры человеческого тела и его частей. Дело в том, что собственное тело очень удобно как «измерительный прибор», так как оно всегда «рядом». И вдобавок «человек есть мера всех вещей»: мы считаем предмет большим или малым, сравнивая его с собой.
Так, длину куска ткани измеряли «локтями», а мелкие предметы — «дюймами» (это слово происходит от голландского слова, которое означает «большой палец»).
Однако человеческое тело в качестве измерительного прибора имеет существенный недостаток: размеры тела и его частей у разных людей заметно отличаются. Поэтому ученые решили определить единицу длины однозначно и точно. Международным соглашением было принято, что один метр равен пути, который проходит свет в вакууме за 1/299792458 с. А секунду определяют с помощью атомных часов, которые сегодня являются самыми точными.
Можно ли расстояние измерять годами
Именно так и измеряют очень большие расстояния — например, расстояния между звездами! Но при этом речь идет не о годах как промежутках времени, а о «световых годах». А один световой год — это расстояние, которое проходит свет за один земной год. По нашим земным меркам это очень большое расстояние — чтобы убедиться в этом, попробуйте выразить его в километрах! А теперь вообразите себе, что расстояние от Солнца до ближайшей к нему звезды составляет больше четырех световых лет! И по астрономическим масштабам это совсем небольшое расстояние: ведь с помощью современных телескопов астрономы тщательно изучают звезды, расстояние до которых составляет много тысяч световых лет!
Что надо знать об измерительных приборах
Приступая к измерениям, необходимо, прежде всего, подобрать приборы. Что надо знать об измерительных приборах?
Минимальное (нижний предел) и максимальное (верхний предел) значения шкалы прибора — это пределы измерения. Чаще всего предел измерения один, но может быть и два. Например, линейка имеет один предел — верхний. У линейки на рисунке 32 он равен 25 см. У термометра на рисунке 33 два предела: верхний предел измерения температуры равен +50 °С; нижний -40 °С.
На рисунке 34 изображены три линейки с одинаковыми верхними пределами (25 см). По эти линейки измеряют длину с различной точностью. Наиболее точные результаты измерений дает линейка 7, наименее точные — линейка 3. Что же такое точность измерений и от чего она зависит? Для ответа на эти вопросы рассмотрим сначала понятие цена деления шкалы прибора.
Цена деления — это значение наименьшего деления шкалы прибора.
Как определить цену деления шкалы? Для этого необходимо:
- выбрать на шкале линейки два соседних значения, например 3 см и 4 см;
- подсчитать число делений (не штрихов!) между этими значениями; например, на линейке 1 (см. рис. 34) число делений между значениями 3 см и 4 см равно 10;
- вычесть из большего значения меньшее (4 см — 3 см = 1 см) и результат разделить на число делений.
Полученное значение и будет ценой деления шкалы прибора. Обозначим ее буквой С.
Точно так же можно определить и цену деления шкалы мензурок 1 и 2 (рис. 35). Цена деления шкалы мензурки 1:
Цена деления шкалы мензурки 2:
А какими линейкой и мензуркой можно измерить точнее?
Измерим один и тот же объем мензуркой 1 и мензуркой 2. Но показаниям шкал в мензурке 1 объем воды V = 35 мл; в мензурке 2 — V = 37 мл.
Понятно, что точнее измерен объем воды мензуркой 2, цена деления которой меньше 


Итак, любым прибором, имеющим шкалу, измерить физическую величину можно с точностью, не превышающей цены деления шкалы.
Линейкой 1 (см. рис. 34) можно измерить длину с точностью до 1 мм. Точность измерения длины линейками 2 и 3 определите самостоятельно.
Главные выводы:
- Верхний и нижний пределы измерения — это максимальное и минимальное значения шкалы прибора.
- Цена деления шкалы равна значению наименьшего деления шкалы.
- Чем меньше цена деления шкалы, тем точнее будут проведены измерения данным прибором.
Для любознательных:
В истории науки есть немало случаев, когда повышение точности измерений давало толчок к новым открытиям. Более точные измерения плотности азота, выделенного из воздуха, позволили в 1894 г. открыть новый инертный газ — аргон. Повышение точности измерений плотности воды привело к открытию в 1932 г. одной из разновидностей тяжелых атомов водорода — дейтерия. Позже дейтерий вошел в состав ядерного горючего. Оценить расстояния до звезд и создать их точные каталоги ученые смогли благодаря повышению точности при измерении положения ярких звезд на небе.
- Заказать решение задач по физике
Пример решения задачи
Для измерения величины угла используют транспортир. Определите: 1) цену деления каждой шкалы транспортира, изображенного на рисунке 38; 2) значение угла BАС, используя каждую шкалу; укажите точность измерения угла ВАС в каждом случае.
Решение:
1) Цена деления нижней шкалы:
Цена деления средней шкалы:
Цена деления верхней шкалы:
2) Определенный но нижней шкале с точностью до 10° 

- Определение площади и объема
- Связь физики с другими науками
- Макромир, мегамир и микромир в физике
- Пространство и время
- Как зарождалась физика
- Единая физическая картина мира
- Физика и научно-технический прогресс
- Физические величины и их единицы измерения
Вычисление погрешностей измерений
Выполнение лабораторных работ связано с измерением физических величин, т. е. определением значений величин опытным путём с помощью измерительных приборов (средств измерения), и обработкой результатов измерений.
Различают прямые и косвенные измерения. При этом результат любого измерения является приблизительным, т. е. содержит погрешность измерения. Точность измерения физической величины характеризуют абсолютная и относительная погрешности.
Прямое измерение — определение значения физической величины непосредственно с помощью измерительного прибора.
Абсолютную погрешность прямых измерений определяют суммой абсолютной инструментальной погрешности и абсолютной погрешности отсчёта Δx = Δиx + Δоx при условии, что случайная погрешность и погрешность вычисления или отсутствуют, или незначительны и ими можно пренебречь.
Абсолютная инструментальная погрешность Δиx связана с классом точности прибора. Абсолютные инструментальные погрешности некоторых средств измерений представлены в таблице 1.
Таблица 1
| Средства измерений | Диапазон измерений | Абсолютная инструментальная погрешность |
| Линейки: металлические деревянные пластмассовые |
150, 300, 500 мм 400, 500, 750 мм 200, 250, 300 мм |
0,1 мм 0,5 мм 1 мм |
| Лента измерительная | 150 см | 0,5 см |
| Мензурки 2-го класса | 100, 200, 250 см3 | 5 см3 |
| Амперметр школьный | 2 А | 0,05 А |
| Миллиамперметр | от 0 до Imax | 4 % максимального предела измерений Imax |
| Вольтметр школьный | 6 В | 0,15 В |
| Термометр лабораторный | 100 °С | 1 °С |
| Барометр-анероид | 720–780 мм рт. ст. | 3 мм рт. ст. |
| Штангенциркули с ценой деления 0,1; 0,05 мм | 155, 250, 350 мм | 0,1; 0,05 мм в соответствии с ценой деления нониуса |
| Микрометры с ценой деления 0,01 мм | 0–25, 25–50, 50–75 мм | 0,004 мм |
Абсолютная погрешность отсчёта Δоx связана с дискретностью шкалы прибора. Если величину измеряют с точностью до целого деления шкалы прибора, то погрешность отсчёта принимают равной цене деления. Если при измерении значение величины округляют до половины деления шкалы, то погрешность отсчёта принимают равной половине цены деления.
Абсолютная погрешность определяет значение интервала, в котором лежит истинное значение измеренной величины:
Относительную погрешность прямого измерения определяют отношением абсолютной погрешности к значению измеряемой величины:
Относительная погрешность характеризует точность измерения: чем она меньше, тем точность измерения выше.
Косвенное измерение — определение значения физической величины с использованием формулы, связывающей её с другими величинами, измеренными непосредственно с помощью приборов.
Одним из методов определения погрешности косвенных измерений является метод границ погрешностей. Формулы для вычисления абсолютных и относительных погрешностей косвенных измерений методом границ погрешностей представлены в таблице 2.
Таблица 2
| Вид функции y | Абсолютная погрешность Δy | Относительная погрешность |
| x1 + x2 | Δx1 + Δx2 | |
| x1 − x2 | Δx1 + Δx2 | |
| Cx | CΔx | |
| x1x2 | |x1| Δx2 + |x2| Δx1 | |
| xn | |n||x|n−1Δx | |
| lnx | ||
| sinx | |cosx| Δx | |
| cosx | |sinx| Δx | |tgx| Δx |
| tgx |
Абсолютную погрешность табличных величин и фундаментальных физических постоянных определяют как половину единицы последнего разряда значения величины.
Статья обновлена 10.07.2022
Что такое погрешность измерения
Любой расчет состоит из истинного и вычисляемого значения. При этом всегда должны учитываться значения ошибки или погрешности. Погрешность — это расхождение между истинным значением и вычисляемым. В маркетинге выделяют следующие виды погрешностей.
- Математическая погрешность. Она описывается алгебраической формулой и бывает абсолютной, относительной и приведенной. Абсолютная погрешность измерения — это разница между вычисляемым и истинным значением. Относительная погрешность вычисляется в процентном соотношении истинного значения и полученного. Вычисление погрешности приведенной схоже с относительной, указывается она также в процентах, но дает разницу между нормирующей шкалой и полученными данными, то есть между эталонными и полученными значениями.
- Оценочная погрешность. В маркетинге она бывает случайной и систематической. Случайная погрешность возникает из-за любых факторов, которые случайным образом влияют на измерение переменной в выборке. Систематическая погрешность вызывается факторами, которые систематически влияют на измерение переменной в выборке.
Математическая погрешность: формула для каждого типа
Если определение погрешности можно провести точным путем, она считается математической. Зачем нужно вычисление этого значения в маркетинге?
Погрешности возникают настолько часто, что популярной практикой в исследованиях является включение значения погрешности в окончательные результаты. Для этого используются формулы. Математическая погрешность — это значение, которое отражает разницу между выборкой и фактическим результатом. Если при расчетах учитывалась погрешность, в тексте исследования указывается что-то вроде: «Абсолютная погрешность для этих данных составляет 3,25%». Погрешность можно вычислить с любыми цифрами: количество человек, участвующих в опросе, погрешность суммы, затраченной на маркетинговый бюджет, и так далее.
Формулы погрешностей вычисляются следующим образом.
Абсолютная погрешность измерений: формула
Формула дает разницу между измеренным и реальным значением.
Относительная погрешность: формула
Формула использует значение абсолютной погрешности и вычисляется в процентах по отношению к фактическому значению.
Приведенная погрешность: формула
Формула также использует значение абсолютной погрешности. В чем измеряется приведенная погрешность? Тоже в процентах, но в качестве «эталона» используется не реальное значение, а единица измерения любой нормирующей шкалы. Например, для обычной линейки это значение равно 1 мм.
Классификация оценочной погрешности
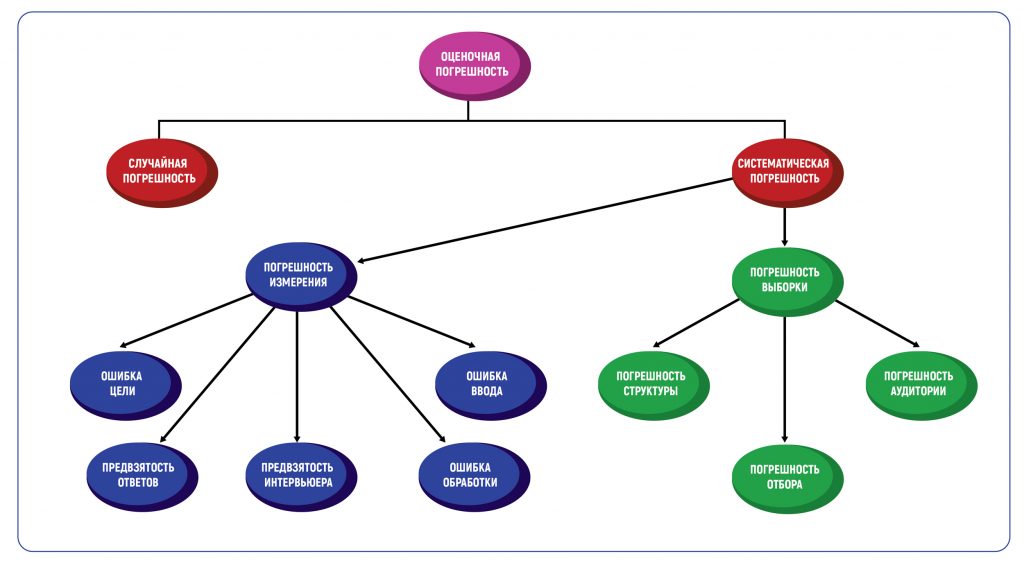
Определение погрешности в оценках — это всегда методическая погрешность, то есть допустимое значение ошибки, основанное на методах проведения исследования. Погрешность метода вызывает два типа погрешностей — случайные и систематические. Таблица погрешностей в графической форме покажет все возможные типы.
Что такое случайная погрешность
Случайная погрешность бывает статической и динамической. Динамическая погрешность возникает, когда мы имеем дело с меняющимися значениями — например, количество человек в выборке при маркетинговом исследовании. Статическая погрешность описывает ошибки при вычислении неизменных величин — вроде количества вопросов в вопроснике. Все они относятся к случайным погрешностям.
Типичный пример возникновения случайной погрешности — настроение участников маркетингового опроса. Как известно, эмоциональный настрой человека всегда влияет на его производительность. В ходе тестирования одни люди могут быть в хорошем расположении духа, а другие — в «миноре». Если настроение влияет на их ответы по заданному критерию выборки, это может искусственно завышать или занижать наблюдаемые оценки. Например, в случае с истинным значением 1 случайная погрешность может дать как -0,8, так и +0,5 к этому числу. Очень часто это случается при оценке времени ответа, например.
Случайная погрешность добавляет изменчивости данным, но не оказывает постоянного влияния на всю выборку. Вместо этого она произвольно изменяет измеряемые значения в диапазоне. В маркетинговой практике считается, что все случайные погрешности в распределении перекрывают друг друга и практически не влияют на конечный результат. Поэтому случайная погрешность считается «шумом» и в расчет не принимается. Эту погрешность нельзя устранить совсем, но можно уменьшить, просто увеличив размер выборки.
Что такое систематическая погрешность
Систематическая погрешность существует в результатах исследования, если эти результаты показывают устойчивую тенденцию к отклонению от истинных значений. Иными словами, если полученные цифры постоянно выше или ниже расчетных, речь идет о том, что в данных имеется систематическая погрешность.
В маркетинговых исследованиях есть два основных типа систематической погрешности: погрешность выборки и погрешность измерения.
Погрешность выборки
Погрешность выборки возникает, когда выборка, используемая в исследовании, не репрезентативна для всей совокупности данных. Типы такой погрешности включают погрешность структуры, погрешность аудитории и погрешность отбора.
Погрешность структуры
Погрешность структуры возникает из-за использования неполной или неточной основы для выборки. Распространенным источником такой погрешности в рамках маркетинговых исследований является проведение какого-либо опроса по телефону на основе существующего телефонного справочника или базы данных абонентов. Многие данные там указаны неполно или неточно — например, если люди недавно переехали или изменили свой номер телефона. Также такие данные часто указывают неполную или неверную демографию.
Если в качестве основы для исследования взят телефонный справочник, оно подвержено погрешности структуры, так как не учитывает всех возможных респондентов.
Погрешность аудитории
Погрешность аудитории возникает, если исследователь не знает, как определить аудиторию для исследования. Пример — оценка результатов исследования, проведенного среди клиентов крупного банка. Доля ответов на анкету составила чуть менее 1%. Анализ профессий всех опрошенных показал, что процент пенсионеров среди них в 20 раз выше, чем в целом по городу. Если эта группа значительно различается по интересующим переменным, то результаты будут неверными из-за погрешности аудитории.
Погрешность отбора
Даже если маркетологи правильно определили структуру и аудиторию, они не застрахованы от погрешности отбора. Она возникает, когда процедуры отбора являются неполными, неправильными или не соблюдаются должным образом. Например, интервьюеры при полевом исследовании могут избегать людей, которые живут в муниципальных домах. Потому что, по их мнению, жители вряд ли согласятся пройти такой опрос. Если жители муниципальных домов отличаются от тех, кто проживает в домах бизнес-класса, в результаты опроса будет внесена погрешность отбора.
Как минимизировать погрешность выборки
- Знайте свою аудиторию.
Знайте, кто покупает ваш продукт, использует его, работает с вами и так далее. Имея базовую социально-экономическую информацию, можно составить стабильную выборку целевой аудитории. Маркетинговые исследования часто касаются одной конкретной группы населения — например, пользователей Facebook или молодых мам. - Разделите аудиторию на группы.
Вместо случайной выборки разбейте аудиторию на группы в соответствии с их численностью в общей совокупности данных. Например, если люди с определенной демографией составляют 35% населения, убедитесь, что 35% респондентов исследования отвечают этому условию. - Увеличьте размер выборки.
Больший размер выборки приводит к более точному результату.
Погрешность измерения
Погрешность измерения представляет собой серьезную угрозу точности исследования. Она возникает, когда существует разница между искомой информацией — то есть истинным значением, и информацией, фактически полученной в процессе измерения. К таким погрешностям приводят различные недостатки процесса исследования. Погрешность измерения, в основном, вызывается человеческим фактором — например, формулировкой вопросника, ошибками ввода данных и необъективными выводами.
К погрешностям измерения приводят следующие виды ошибок.
Ошибка цели
Ошибка цели возникает, когда существует несоответствие между информацией, фактически необходимой для решения проблемы, и данными , которые собирает исследование. Например, компания Kellogg впустую потратила миллионы на разработку завтраков для снижения уровня холестерина. Реальный вопрос, который нужно было бы задать в исследовании, заключался в том, купят ли люди овсяные хлопья для решения своей проблемы. Ответ «Нет» обошелся бы компании дешевле.
Предвзятость ответов
Некоторые люди склонны отвечать на конкретный вопрос определенным образом. Тогда возникает предвзятость ответа. Предвзятость ответа может быть результатом умышленной фальсификации или неосознанного искажения фактов.
Умышленная фальсификация происходит, когда респонденты целенаправленно дают неверные ответы на вопросы. Есть много причин, по которым люди могут сознательно искажать информацию. Например, они хотят скрыть или хотят казаться лучше, чем есть на самом деле.
Бессознательное искажение информации происходит, когда респондент пытается быть правдивым, но дает неточный ответ. Этот тип предвзятости может возникать из-за формата вопроса, его содержания или по другим причинам.
Предвзятость интервьюера
Интервьюер оказывает влияние на респондента — сознательно или бессознательно. Одежда, возраст, пол, выражение лица, язык тела или тон голоса могут повлиять на ответы некоторых или всех респондентов.
Ошибка обработки
Примеры включают наводящие вопросы или элементы дизайна анкеты, которые затрудняют запись ответов или приводят к ошибкам в них.
Ошибка ввода
Это ошибки, возникающие при вводе информации. Например, документ может быть отсканирован неправильно, и его данные по ошибке перенесутся неверно. Или люди, заполняющие опросы на смартфоне или ноутбуке, могут нажимать не те клавиши.
Виды проводимых маркетинговых исследований различны, поэтому универсальных рецептов не существует. Мы дадим несколько общих советов, используемых для минимизации систематических погрешностей разного типа.
Как минимизировать погрешность измерения
- Предварительно протестируйте.
Погрешностей обработки и предвзятости можно избежать, если проводить предварительные тесты вопросника до начала основных интервью. - Проводите выборку случайным образом.
Чтобы устранить предвзятость, при выборке респондентов можно включать каждого четвертого человека из общего списка. - Тренируйте команду интервьюеров и наблюдателей.
Отбор и обучение тех, кто проводит исследования, должен быть тщательным. Особое внимание нужно уделять соблюдению инструкций в ходе каждого исследования. - Всегда выполняйте проверку сделанных записей.
Чтобы исключить ошибки ввода, все данные, вводимые для компьютерного анализа, должны быть перепроверены как минимум дважды.
Мир без ошибок не может существовать. Но понимание факторов, влияющих на маркетинговые исследования и измеряемые погрешности, имеет важное значение для сбора качественных данных.
Физические величины и погрешности их измерений — Задачей физического эксперимента является определение числового значения измеряемых физических величин с заданной точностью. Сразу оговоримся, что при выборе измерительного оборудования часто нужно также знать диапазон измерения и какое именно значение интересует: например, среднеквадратическое значение (СКЗ) измеряемой величины в определённом интервале времени, или требуется измерять среднеквадратическое отклонение (СКО) (для измерения переменной составляющей величины), или требуется измерять мгновенное (пиковое) значение.
- При измерении переменных физических величин (например, напряжение переменного тока) требуется знать динамические характеристики измеряемой физической величины: диапазон частот или максимальную скорость изменения физической величины,
- Эти данные, необходимые при выборе измерительного оборудования, зависят от физического смысла задачи измерения в конкретном физическом эксперименте,
Итак, повторимся: задачей физического эксперимента является определение числового значения измеряемых физических величин с заданной точностью. Эта задача решается с помощью прямых или косвенных измерений, При прямом измерении осуществляется количественное сравнение физической величины с соответствующим эталоном при помощи измерительных приборов.
- Отсчет по шкале прибора указывает непосредственно измеряемое значение.
- Например, термометр дает значения измеряемой температуры, а вольтметр – значение напряжения.
- При косвенных измерениях интересующая нас физическая величина находится при помощи математических операций над непосредственно измеренными физическими величинами (непосредственно измеряя напряжение U на резисторе и ток I через него, вычисляем значение сопротивления R = U / I ).
Точность прямых измерений некоторой величины X оценивается величиной погрешности или ошибки, измерений относительно действительного значения физической величины X Д, Действительное значение величины X Д (согласно РМГ 29-99 ) – это значение физической величины, полученное экспериментальным путем и настолько близкое к истинному значению, что в поставленной измерительной задаче может быть использовано вместо него.
- Различают абсолютную (∆ X) и относительную (δ) погрешности измерений.
- Абсолютная погрешность измерения – это п огрешность средства измерений, выраженная в единицах измеряемой физической величины, характеризующая абсолютное отклонение измеряемой величины от действительного значения физической величины: ∆X = X – X Д,
Относительная погрешность измерения – это п огрешность измерения, выраженная отношением абсолютной погрешности измерения к действительному значению измеряемой величины. Обычно относительную погрешность выражают в процентах: δ = (∆X / Xд) * 100%, При оценке точности косвенных измерений некоторой величины X 1, функционально связанной с физическими величинами X 2, X 3,, X 1 = F (X 2, X 3, ), учитывают погрешности прямых измерений каждой из величин X 2, X 3, и характер функциональной зависимости F (),
Как вычислить погрешность измерений?
Измерение физических величин основано на том, что физика исследует объективные закономерности, которые происходят в природе. Найти значение физической величины — умножить конкретное число на единицу измерения данной величины, которая стандартизирована ( эталоны ).
расположение наблюдателя относительно измерительного прибора: если на линейку смотреть сбоку, погрешность измерений произойдёт по причине неточного определения полученного значения;деформация измерительного прибора: металлические и пластиковые линейки могут изогнуться, сантиметровая лента растягивается со временем;несоответствие шкалы прибора эталонным значениям: при множественном копировании эталонов может произойти ошибка, которая будет множиться;физический износ шкалы измерений, что приводит к невозможности распознавания значений.
Рассмотрим на примере измерения длины бруска линейкой с сантиметровой шкалой. Рис. (1). Линейка и брусок Внимательно рассмотрим шкалу. Расстояние между двумя соседними метками составляет (1) см. Если этой линейкой измерять брусок, который изображён на рисунке, то правый конец бруска будет находиться между (9) и (10) метками.
У нас есть два варианта определения длины этого бруска. (1). Если мы заявим, что длина бруска — (9) сантиметров, то недостаток длины от истинной составит более половины сантиметра ((0,5) см (= 5) мм). (2). Если мы заявим, что длина бруска — (10) сантиметров, то избыток длины от истинной составит менее половины сантиметра ((0,5) см (= 5) мм).
Погрешность измерений — это отклонение полученного значения измерения от истинного. Погрешность измерительного прибора равна цене деления прибора. Для первой линейки цена деления составляет (1) сантиметр. Значит, погрешность этой линейки (1) см. Если нам необходимо произвести более точные измерения, то следует поменять линейку на другую, например, с миллиметровыми делениями. Рис. (2). Деревянная линейка Если же необходимы ещё более точные измерения, то нужно найти прибор с меньшей ценой деления, например, штангенциркуль. Существуют штангенциркули с ценой деления (0,1) мм и (0,05) мм, Рис. (3). Штангенциркуль На процесс измерения влияют следующие факторы: масштаб шкалы прибора, который определяет значения делений и расстояние между ними; уровень экспериментальных умений. Считается, что погрешность прибора превосходит по величине погрешность метода вычисления, поэтому за абсолютную погрешность принимают погрешность прибора.
В чем измеряется погрешность?
Погрешность средств измерения и результатов измерения. Погрешности средств измерений – отклонения метрологических свойств или параметров средств измерений от номинальных, влияющие на погрешности результатов измерений (создающие так называемые инструментальные ошибки измерений).
- Погрешность результата измерения – отклонение результата измерения от действительного (истинного) значения измеряемой величины.
- Инструментальные и методические погрешности.
- Методическая погрешность обусловлена несовершенством метода измерений или упрощениями, допущенными при измерениях.
- Так, она возникает из-за использования приближенных формул при расчете результата или неправильной методики измерений.
Выбор ошибочной методики возможен из-за несоответствия (неадекватности) измеряемой физической величины и ее модели. Причиной методической погрешности может быть не учитываемое взаимное влияние объекта измерений и измерительных приборов или недостаточная точность такого учета.
Например, методическая погрешность возникает при измерениях падения напряжения на участке цепи с помощью вольтметра, так как из-за шунтирующего действия вольтметра измеряемое напряжение уменьшается. Механизм взаимного влияния может быть изучен, а погрешности рассчитаны и учтены. Инструментальная погрешность обусловлена несовершенством применяемых средств измерений.
Причинами ее возникновения являются неточности, допущенные при изготовлении и регулировке приборов, изменение параметров элементов конструкции и схемы вследствие старения. В высокочувствительных приборах могут сильно проявляться их внутренние шумы. Статическая и динамическая погрешности.
Статическая погрешность измерений – погрешность результата измерений, свойственная условиям статического измерения, то есть при измерении постоянных величин после завершения переходных процессов в элементах приборов и преобразователей. Статическая погрешность средства измерений возникает при измерении с его помощью постоянной величины. Если в паспорте на средства измерений указывают предельные погрешности измерений, определенные в статических условиях, то они не могут характеризовать точность его работы в динамических условиях. Динамическая погрешность измерений – погрешность результата измерений, свойственная условиям динамического измерения. Динамическая погрешность появляется при измерении переменных величин и обусловлена инерционными свойствами средств измерений. Динамической погрешностью средства измерений является разность между погрешностью средсва измерений в динамических условиях и его статической погрешностью, соответствующей значению величины в данный момент времени. При разработке или проектировании средства измерений следует учитывать, что увеличение погрешности измерений и запаздывание появления выходного сигнала связаны с изменением условий.
Статические и динамические погрешности относятся к погрешностям результата измерений. В большей части приборов статическая и динамическая погрешности оказываются связаны между собой, поскольку соотношение между этими видами погрешностей зависит от характеристик прибора и характерного времени изменения величины.
Как найти абсолютную погрешность измерительного прибора?
Абсолютную погрешность прямых измерений определяют суммой абсолютной инструментальной погрешности и абсолютной погрешности отсчёта Δx = Δ и x + Δ о x при условии, что случайная погрешность и погрешность вычисления или отсутствуют, или незначительны и ими можно пренебречь.
Что такое погрешность метода измерений?
По источнику возникновения — Инструментальная погрешность Эта погрешность определяется несовершенством прибора, возникающим, например, из-за неточной калибровки, Методическая погрешность Методической называют погрешность, обусловленную несовершенством метода измерений.
Что такое погрешность измерительного прибора?
Определение — Проводя измерение параметров рынка, маркетолог получает результаты в виде таблиц, графиков и пр. Эти данные он предоставляет заказчику. Но в отчетах не все специалисты указывают важную величину — погрешность, о которой клиент не подозревает.
Как определить погрешность деления?
Как определить погрешность и объем жидкости — Погрешность равна половине цены деления мензурки. В нашем случае погрешность составляет 2,5 мл. Чтобы определить объем, берем ближайшее число от верхней границы жидкости (на рисунке — это значение 40 мл) и прибавляем количество штрихов (на рисунке — 2 штриха) по 5 мл: V = 40 + 2 × 5 = 50 мл.
Как рассчитывается приведенная погрешность?
Программа КИП и А Дмитрий Бебякин, инженер — метролог, ИЛИМ Позволю себе вначале небольшое отступление. Такие понятия как погрешность, класс точности довольно подробно описываются в нормативной документации ГОСТ 8.009-84 «Нормируемые метрологические характеристики средств измерений», ГОСТ 8.401-80 «Классы точности средств измерений.
- Общие требования» и им подобных.
- Но открывая эти документы сразу возникает чувство тоски Настолько сухо и непонятно простому начинающему «киповцу», объяснены эти понятия.
- Давайте же пока откинем такие вычурные и непонятные нам определения, как « среднее квадратическое отклонение случайной составляющей погрешности » или « нормализованная автокорреляционная функция » или « характеристика случайной составляющей погрешности от гистерезиса — вариация Н выходного сигнала (показания) средства измерений » и т.п.
Попробуем разобраться, а затем свести в одну небольшую, но понятную табличку, что же такое «погрешность» и какая она бывает. Погрешности измерений – отклонения результатов измерения от истинного значения измеряемой величины. Погрешности неизбежны, выявить истинное значение невозможно.
- Абсолютная погрешность: Δ = X д — X изм, выражается в единицах измеряемой величины, например в килограммах (кг), при измерении массы. где X д – действительное значение измеряемой величины, принимаются обычно показания эталона, образцового средства измерений; X изм – измеренное значение.
- Относительная погрешность: δ = (Δ ⁄ X д ) · 100, выражается в % от действительного значения измеренной величины.
- Приведённая погрешность: γ = (Δ ⁄ X н ) · 100, выражается в % от нормирующего значения. где X н – нормирующее значение, выраженное в тех же единицах, что и Δ, обычно принимается диапазон измерения СИ (шкала).
По характеру проявления:
- систематические (могут быть исключены из результатов);
- случайные;
- грубые или промахи (как правило не включаются в результаты измерений).
В зависимости от эксплуатации приборов:
- основная – это погрешность средства измерения при нормальных условиях; (ГОСТ 8.395-80)
- дополнительная погрешность – это составляющая погрешности средства измерения, дополнительно возникающая из-за отклонения какой-либо из влияющих величин от нормативного значения или выход за пределы нормальной области значений. Например: измерение избыточного давления в рабочих условиях цеха, при температуре окружающего воздуха 40 ºС, относительной влажности воздуха 18% и атмосферном давлении 735 мм рт. ст., что не соответствует номинальным значениям влияющих величин при проведении поверки.
| Наимено вание погреш ности | Формула | Форма выражения, записи | Обозначение класса точности | |||||||||||||||
| В докумен тации | На сред стве изме рений | |||||||||||||||||
| Абсолют ная | Δ = X д — X изм | Δ = ±50 мг Примеры: Номинальная масса гири 1 кг ±50 мг Диапазон измерения весов среднего III класса точности от 20 г до 15 кг ±10 г | Класс точности: М 1 Класс точности: средний III Примечание: на многие виды измерений есть свои НД по выражению погрешностей, здесь для примера взято для гирь и весов. | М 1 | ||||||||||||||
| Относи тельная | δ = (Δ ⁄ X д ) · 100 | δ = ±0,5 Пример: Измеренное значение изб.
Как вычислить абсолютную погрешность формула?Поиск: Абсолютная погрешность Δ измерений, выражаемая в единицах измеряемой величины, представляется разностью между измеренным и истинным (действительным) значениями измеряемой величины: Δ = х изм — х и (х д ). Чему равна абсолютная погрешность?При измерении каких-либо величин важным понятием является понятие о погрешности. Это связано с тем, что абсолютно точно измерить какую либо величину невозможно. Поэтому вводят понятие погрешности. Есть очень много видов погрешности, связанных с человеческим фактором или процессом измерения. Для чего нужна погрешность измерений?Каждое физическое измерение в исследованиях и промышленности сопровождается определенной погрешностью. Даже незначительные колебания в условиях окружающей среды могут влиять на измерение и вызывать отклонения, которые делают результат измерения ненадежным. Для получения правильных результатов измерений необходимо учитывать связанную с результатами погрешность. Погрешность измерений указывает на недостающую информацию о настоящем значении измеряемой величины. Она определяется параметром, выраженным в процентах и относящимся к результату измерения, который обозначает отклонение значений, которое обоснованно можно присвоить измеряемой величине на основе имеющейся информации. Другими словами, это диапазон, в пределах которого с определенной вероятностью находится истинное значение измеряемой величины. Как найти абсолютную погрешность пример?Абсолютная погрешность — Абсолютной погрешностью числа называют разницу между этим числом и его точным значением. Рассмотрим пример : в школе учится 374 ученика. Если округлить это число до 400, то абсолютная погрешность измерения равна 400-374=26. Для подсчета абсолютной погрешности необходимо из большего числа вычитать меньшее.
На практике абсолютной погрешности недостаточно для точной оценки измерения. Редко когда можно точно знать значение измеряемой величины, чтобы рассчитать абсолютную погрешность. Измеряя книгу в 20 см длиной и допустив погрешность в 1 см, можно считать измерение с большой ошибкой.
Границу абсолютной погрешности называют предельной абсолютной погрешностью. Как определить цену деления и погрешность?Найти две соседних отметки шкалы, возле которых написаны величины, соответствующие этим отметкам шкалы; найти разность этих величин; сосчитать количество промежутков между величинами отметок шкалы; полученную разность величин разделить на количество промежутков. Что такое максимальная погрешность измерений?Предельная погрешность измерения в ряду измерений – максимальная погрешность измерения (плюс, минус), допускаемая для данной измерительной задачи. Как рассчитывается приведенная погрешность?Программа КИП и А Дмитрий Бебякин, инженер — метролог, ИЛИМ Позволю себе вначале небольшое отступление. Такие понятия как погрешность, класс точности довольно подробно описываются в нормативной документации ГОСТ 8.009-84 «Нормируемые метрологические характеристики средств измерений», ГОСТ 8.401-80 «Классы точности средств измерений. Общие требования» и им подобных. Но открывая эти документы сразу возникает чувство тоски Настолько сухо и непонятно простому начинающему «киповцу», объяснены эти понятия. Давайте же пока откинем такие вычурные и непонятные нам определения, как « среднее квадратическое отклонение случайной составляющей погрешности » или « нормализованная автокорреляционная функция » или « характеристика случайной составляющей погрешности от гистерезиса — вариация Н выходного сигнала (показания) средства измерений » и т.п. Попробуем разобраться, а затем свести в одну небольшую, но понятную табличку, что же такое «погрешность» и какая она бывает. Погрешности измерений – отклонения результатов измерения от истинного значения измеряемой величины. Погрешности неизбежны, выявить истинное значение невозможно.
По характеру проявления:
В зависимости от эксплуатации приборов:
|
,
где
— абсолютное значение разности между
величинойхi,
полученной вi– том измерении и
средним значением <х>. Абсолютная
погрешность опыта характеризует таким
образом качество проведённых измерений,
т. е. указывает, на сколько истинное
значение измеряемой величины может
отличаться от значения, измеренного в
опыте.
3. Для оценки точности, с которой
определена измеряемая величина,
используется понятие относительной
погрешности:
.
Таким образом, относительная погрешность
показывает, какая часть абсолютной
погрешности приходится на каждую единицу
измеряемой величины.
Пример. При измерении толщиныh
стеклянной пластинки с помощью
микрометра было сделано четыре измерения,
результаты которых занесены в табл. 1:
Таблица 1.
Результаты измерений толщины стеклянной
пластинки
-
№ измерения
h,
мм<
h>, ммΔ
hi, ммΔ
h, ммεh,
%1
3,82
3,84
— 0,02
0,03
0,8
2
3,85
+ 0,01
3
3,89
+ 0,05
4
3,80
— 0,04
-
По данным таблицы рассчитываем среднее
значение толщины:
-
Определяем абсолютную погрешность
опыта (серии измерений):
-
Определяем относительную погрешность:
При косвенных измеренияхискомую
величину вычисляют по результатам
прямого измерения других величин,
связанных с искомой определённой
функциональной зависимостьюy = f
(x1,х2,…,хn).
Абсолютная и относительная погрешности
некоторых простейших функций приведены
в табл.2.
Таблица 2
Погрешности при косвенных измерениях
в простейших случаях
-
Вид функции
Абсолютная
погрешность ΔyОтносительная
погрешность
εy1
2
3
x1
+ x2Δ
x1
+ Δ x21
2
3
x1
— x2Δ
x1
+ Δ x2x1
x2x1
Δ x2
+ x2
Δ x1εx1
+ εx2x1
/ x2εx1
+ εx2xn
nxn-1
Δ xnεx
ex
ex
Δ xΔx
Когда функция y = f (x1,х2,…,хn)удобна для логарифмирования, то вначале
лучше рассчитать относительную
погрешность εyфункции (в %) и затем её абсолютную
погрешность
.
Пример. Ускорение свободного паденияgопределяется по результатам
измерений периодов колебанийТ1иТ2двух математических
маятников с длинамиl1иl2соответственно (l1>l2)
по формуле
,
где a= l1—l2.
Логарифмирование даёт lng=ln(4π2)
+lna–ln.
После дифференцирования lngс заменамиdaна ΔaиdТ на ΔТполучим:
(предполагается, что погрешности
независимых измерений Δa,ΔТ1и ΔТ2усиливают
друг друга, и поэтому их влияние
учитывается в формуле со знаком плюс).
Затем найдём абсолютную погрешность
,
где.
Окончательный результат вычислений
– среднее арифметическое измеряемой
величины записывают в виде числа из
нескольких разрядов. Цифры в этом числе
делятся на значащие и незначащие. К
значащим цифрам относятся все верные
и сомнительные цифры. К незначащим
относятся: а) нули в начале числа,
определяющие разряды десятичных дробей
в числах меньших единицы; б) нули в конце
числа, заменившие цифры после округления;
в) неверные цифры, если они не были
отброшены.
Для определения значащих цифр в
результате измерения необходимо
вычислить абсолютную погрешность опыта,
числовое значение которой тоже может
содержать несколько разрядов. Но
абсолютная погрешность показывает, в
каком разряде полученного результата
содержится неточность. Поэтому её
числовое значение всегда округляется
до одной значащей цифры, кроме того, в
случае когда эта цифра представляет
единицу – в этом случае округление
производится до цифры первого младшего
разряда. Тогда сохранение цифр меньших
разрядов в среднем арифметическом
измеряемой величины теряет смысл.
Пример. В нескольких опытах по
результатам измерений периода колебаний
математического маятника было проведено
с различной погрешностью определение
ускорения свободного падения:
неправильная запись результата
правильная запись результата
g= (10,1835±0,433) м/с2g=
(10,2±0,4) м/с2
g= (9,8167±0,053) м/с2g=
(9,82±0,05) м/с2
g= (9,9423±0,132) м/с2g=
(9,94 ±0,13) м/с2
g= (10,8261±2,026) м/с2g=
(11±2) м/с2
При записи измеренного значения х
последней, таким образом, должна
указываться цифра того десятичного
разряда, который был использован при
указании погрешности. Это правило должно
соблюдаться и в тех случаях, когда
некоторые из цифр являются нулями.
Пусть, например, при вычислении gв
предыдущем опыте было получено значение
9,88 м/с2(точно), а погрешность
составила ± 0,004 м/с2, то окончательный
результат следует представить в таком
виде:
g= 9,880± 0,004 м/с2.
При записи окончательного результата
измерения наряду с основными единицами
СИ и производными от них допускаются к
применению кратные единицы (например,
см, МПа, мВ и т.д.) в тех случаях, когда
это упрощает запись. Полученные в ходе
эксперимента результаты часто изображают
в виде графика.
При построении графика чаще всего
пользуются прямоугольной системой
координат, причем значения аргумента
откладывают по горизонтальной оси, а
значения функции по вертикальной оси.
Начало координат не обязательно должно
совпадать с нулевыми значениями функции
и аргумента. При выборе масштаба величин,
откладываемых на осях координат, исходят
из того, чтобы получить примерно равные
отрезки, которые соответствуют
установленным в опыте интервалам
численных значений функции и аргумента.
Например, по результатам измерения
показателя преломления п водного
раствора глюкозы был построен графикп= п(с), гдес — концентрация
глюкозы (рис.1). На рис.1а график удовлетворяет
необходимым требованиям. На рис. 1б
из-за неудачного выбора масштаба и
начала отсчета дляпзависимостьп(с)почти незаметна, и такой график
бесполезен для практического применения.
Рис. 1
Использование гpафических методов
облегчается в тех случаях, когда гpафик
представляет собой прямую линию. С целью
«спрямления» гpафика исследуемой
зависимости, имеющей сложный характер,
целесообразно использовать нелинейные
шкалы, например, логарифмическую,
квадратичную и т.д. или откладывать не
сами величины аргумента и функции, а их
логарифмы, степени, обратные значения.
Например, в работе «Исследование
теплового излучения чёрного тела» с
целью экспериментальной проверки закона
Стефана – Больцмана
Rэ=σТ4,
где Rэ–
энергетическая светимость тела, аТ– его абсолютная температура, по оси
абсцисс откладывают Т, а по оси ординат
—.
Выбрав рациональные масштаб и размеры
гpафика, на координатные оси наносят
деления через 10-20 мм и обозначают их.
Затем наносят экспериментальные точки,
с которыми совмещают прямоугольные
крестики, размеры которых вдоль осей
координат ОхиОуравны удвоенным
погрешностям соответственно 2Δхи
2Δув выбранном масштабе. По отмеченным
точкам проводят линию так, чтобы она
прошла как можно ближе к экспериментальным
точкам, и чтобы равное количество их
оказалось по обе стороны от этой линии.
Для построения графиков, как правило,
используют масштабно-координатную
(миллиметровую) бумагу.
Если в лабораторной работе по графику
определяется какая-либо константа,
например, как угловой коэффициент
экспериментальной прямой y = x0+kx,
то в этом случае тангенс угла α наклона
прямой к оси абсцисс может быть определён
только с учётом соответствующих масштабов
и единиц измерения.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Как определять погрешности измерений
Измерение – нахождение значения физической величины
опытным путем с помощью средств измерений.
Прямое
измерение
– определение значения физической
величины непосредственно средствами измерения.
Косвенное
измерение
– определение значения физической
величины по формуле, связывающей ее с другими физическими величинами, определяемыми
прямыми измерениями.
А, В, С, … — физические величины.
Апр. – приближенное значение физической величины.
А – абсолютная погрешность измерения физической
величины.
— относительная погрешность измерения
физической величины.
иА
– абсолютная
инструментальная погрешность, определяемая конструкцией прибора.
оА – абсолютная погрешность отсчета, она равна в
большинстве случаев
половине цены деления; при
измерении времени – цене деления секундомера или часов.
Абсолютную погрешность измерения
обычно округляют до одной значащей цифры:
Численное значение результата
измерений округляют так, чтобы его последняя цифра оказалась в том же разряде,
что и цифра погрешности:
Результат
измерения записывается так:
%
Определение погрешности методом среднего арифметического
При многократных
измерениях величины погрешность можно оценить следующим образом:
1.
Определить среднее
значение величины А:

измерениях).
2.Определить отклонение каждого значения от среднего:
3.Определить среднее значение отклонения,
его и принимают за абсолютную погрешность:
4.Определить
относительную погрешность и выразить ее в процентах:
|
|
|
|
|
|
|
1 |
|
|
||
|
2 |
|
|
||
|
3 |
|
|
Многократные измерения
предпочтительнее, так как при их проведении возможна компенсация случайных
факторов, влияющих на результат. Обычно многократные измерения проводят, слегка
изменяя условия опыта, но предполагая, что значение величины А не изменяются
Определение
погрешности косвенных измерений
При косвенных измерениях значение
физической величины находится путем расчетов по формуле.
Относительную погрешность
определяют так, как показано в таблице:
|
Формула величины |
Формула |
|
1. |
|
|
2. 3. |
|
|
4. |
|
Абсолютную погрешность определяют
по формуле:
( выражается десятичной дробью)
Пример: пусть измеряется сопротивление проводника. 
Результаты прямых измерений:
Тогда 


,
;
,
,
.
Графическое
представление результатов эксперимента
Правила построения
графиков
выберите соответствующую бумагу;
выберите масштаб по осям координат;
напишите обозначения измеряемых физических величин;
нанесите на график данные;
нанесите на график доверительные интервалы;
проведите кривую через нанесенные точки;
составьте заголовок графика.
Для построения графиков выпускают
специальную бумагу-миллиметровку.
При выборе масштабов по осям
координат следует руководствоваться следующими правилами:
— значение независимой переменной
откладывают вдоль оси абсцисс, функции – вдоль оси ординат;
— цена наименьшего деления масштабной
сетки должна быть сравнимой с величиной погрешности измерения;
— точка пересечения оси абсцисс и оси
ординат не обязательно должна иметь координаты (0,0).
При построении графиков следует
иметь в виду, что по результатам опытов мы получаем не точку, а прямоугольник
со сторонами и
.

В
|
|
|||||
|
|
|||||
0
А
При выполнении простых лабораторных
работ достаточно обвести экспериментальную точку кружком или пометить
крестиком, не указывая доверительных интервалов.
Этот кружок или крестик будут
обозначать, что данная точка получена с каким-то приближением и истинное
значение измеряемой величины лежит где-то в ее окрестности.
Правила
приближенных вычислений
1. Основное
правило округления.
Если первая
отброшенная цифра равна 5 или больше, то последнюю из сохраняемых цифр
увеличивают на единицу; если первая отброшенная цифра меньше 5, то последнюю из
сохраняемых цифр оставляют без изменения, например:
2. При сложении и
вычитании приближенных чисел
в полученном результате сохраняют столько десятичных знаков, сколько их в числе
с наименьшим количеством десятичных знаков, например:
3. При умножении
и делении приближенных чисел
в полученном результате нужно сохранить столько значащих цифр, сколько их имеет
приближенное число с наименьшим количеством значащих цифр, например:
4. При возведении
в квадрат приближенного числа
нужно в результате сохранять столько значащих цифр, сколько их имеет возводимое
в степень число, например:
5. При извлечении
квадратного корня в результате
нужно сохранять столько значащих цифр, сколько их имеет подкоренное число,
например:
6. При вычислении
промежуточных результатов в
них следует сохранять на одну цифру больше, чем требуют правила 2-5. Причем при
подсчете значащих цифр запасные цифры не учитываются. В окончательном
результате запасная цифра отбрасывается по основному правилу округления.
7. При нахождении
углов или тригонометрических функций значение соответствующего угла записывают с точностью до градуса, если
значение тригонометрической функции имеет две значащие цифры; если угол задан с
точностью до градусов, то в значении тригонометрической функции сохраняют две
значащие цифры, например: