Прямое распространение ошибки нейронная сеть - Решение и исправление самых разных ошибок на TopOshibok.ru

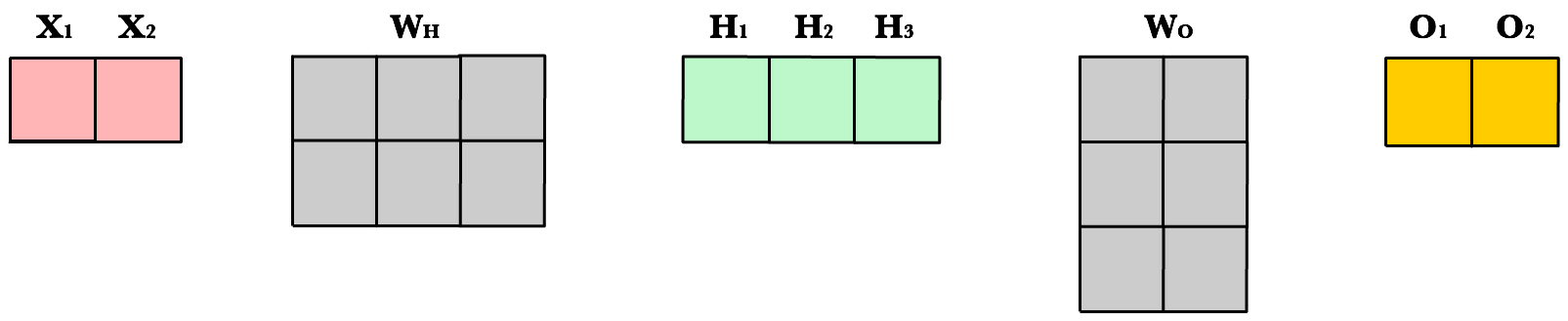
Подробно рассматриваем обратное распространение ошибки для простой нейронной сети. Численный пример

Уровень сложности
Средний

Время на прочтение
6 мин

Количество просмотров 5.4K

В данной статье мы рассмотрим прямое распространение сигнала и обратное распространение ошибки в полносвязной нейронной сети прямого распространения. В результате получим весь набор формул, необходимых для программной реализации нейронной сети. В завершении статьи рассмотрим численный пример.

«Полносвязная» (fully connected) — означает, что каждый нейрон предыдущего слоя соединён с каждым нейроном следующего слоя. «Прямого распространения» (feedforward) — означает, что сигнал проходит через нейронную сеть в одном направлении от входного к выходному слою.

Полносвязная нейронная сеть прямого распространения («перцептрон») — это простейший и наиболее типичный пример искусственной нейронной сети.

Содержание

Нейронная сеть как функция
Дизайн нейронной сети
Прямое распространение сигнала
Обратное распространение ошибки и обновление

4.1. Вычисление новых весов матрицы W^3

4.2. Вычисление новых смещений вектора b^3

4.3. Вычисление новых весов матрицы W^2

4.4. Вычисление новых смещений вектора b^2
Численный пример
Обобщение для произвольного числа слоёв

Нейронная сеть как функция

Искусственная нейронная сеть является математической функцией, а точнее — композицией (суперпозицией) функций.

Было доказано (George Cybenko, 1989), что полносвязная нейронная сеть прямого распространения с хотя бы одним скрытым слоем и достаточным количеством нейронов потенциально может аппроксимировать любую непрерывную функцию, т.е. по своей сути она — универсальный аппроксиматор.

«Свойства универсальной аппроксимации встречаются в математике чаще, чем можно было бы ожидать. Например, теорема Вейерштрасса — Стоуна доказывает, что любая непрерывная функция на замкнутом интервале может быть приближена многочленной функцией. Если ослабить наши критерии далее, можно использовать ряды Тейлора и ряды Фурье, предлагающие некоторые возможности универсальной аппроксимации (в пределах их областей схождения). Тот факт, что универсальная сходимость — довольно обычное явление в математике, дает частичное обоснование эмпирического наблюдения, что существует много малых вариантов полносвязных сетей, которые, судя по всему, дают свойство универсальной аппроксимации».

— Рамсундар Б., Заде Р.Б. TensorFlow для глубокого обучения. Спб., 2019. С. 101.

Запишем нейронную сеть, которую мы будем рассматривать в данной статье, в виде функции:

$\mathbf{a}^3=\mathbf{a}^3(\mathbf{x}^3),\\\mathbf{x}^3=\mathbf{W}^3\times\mathbf{a}^2(\mathbf{x}^2)+\mathbf{b}^3,\\\mathbf{x}^2=\mathbf{W}^2\times\mathbf{x}^1+\mathbf{b}^2,$

где $\mathbf{x}^1$ — вектор входных значений — первый слой, $\mathbf{x}^2$ — второй, скрытый и $\mathbf{x}^3$ — третий слои нейронной сети, $\mathbf{b}^2$ , $\mathbf{b}^3$ — векторы смещений и $\mathbf{W}^2$ , $\mathbf{W}^3$ — матрицы весов второго и третьего слоёв соответственно, $\mathbf{a}^2$ — вектор-функция активации второго слоя, $\mathbf{a}^3$ — вектор-функция активации третьего, последнего слоя и, соответственно, вектор выходных значений нейронной сети.

Мы будем использовать принятую в литературе по нейронам сетям запись ${\mathbf{W}}\times{\mathbf{x}}$ , где $\mathbf{x}$ — вектор-столбец (в литературе по математике под вектором стандартно (по умолчанию) понимается вектор-столбец). Произведение матриц ${\mathbf{A}}\times{\mathbf{B}}$ определено, если число столбцов $\mathbf{A}$ равно числу строк $\mathbf{B}$ . Таким образом число столбцов матрицы $\mathbf{W}_{ij}$ равно числу строк векторов $\mathbf{x}$ и $\mathbf{a}$ .

Для комфортного чтения статьи необходимо обладать некоторым знанием линейной алгебры (обязательный минимум — операции над матрицами), производной сложной функции и частных производных.

Дизайн нейронной сети

Нейронная сеть имеет три слоя с тремя нейронами в каждом из них. Нелинейное изменение проходящего через сеть сигнала обеспечивает функция активации сигмоид (sigmoid) на скрытом и выходном слоях:

$f(x)=\frac{1}{1+e^{-x}}.$

Поскольку на практике большинство реальных данных имеют нелинейный характер, используются нелинейные функции активации, позволяющие извлекать нелинейные зависимости в данных.

Архитектура нейронной сети

Перепишем уравнение рассматриваемой сети для заданных параметров:

$\mathbf{a}^3=\mathbf{f}(\mathbf{x}^3)=\mathbf{f}\left(\left[\begin{matrix}w_{11}^3&w_{12}^3&w_{13}^3\\w_{21}^3&w_{22}^3&w_{23}^3\\w_{31}^3&w_{32}^3&w_{33}^3\\\end{matrix}\right]\times\mathbf{a}^2+\left[\begin{matrix}b_1^3\\b_2^3\\b_3^3\\\end{matrix}\right]\right),$ $\mathbf{a}^2=\mathbf{f}(\mathbf{x}^2)=\mathbf{f}\left(\left[\begin{matrix}w_{11}^2&w_{12}^2&w_{13}^2\\w_{21}^2&w_{22}^2&w_{23}^2\\w_{31}^2&w_{32}^2&w_{33}^2\\\end{matrix}\right]\times\left[\begin{matrix}x_1^1\\x_2^1\\x_3^1\\\end{matrix}\right]+\left[\begin{matrix}b_1^2\\b_2^2\\b_3^2\\\end{matrix}\right]\right).$

Функция активации поэлементно применяется к каждому элементу соответствующего вектора $\mathbf{x}$ .

Прямое распространение сигнала

Запишем уравнения для прямого прохождения сигнала через нейронную сеть:

$a_1^2=\ f(x_1^2)\ =\ f(w_{11}^2x_1^1+w_{12}^2x_2^1+w_{13}^2x_3^1+b_1^2),\\a_2^2=\ f(x_2^2)\ =f(w_{21}^2x_1^1+w_{22}^2x_2^1+w_{23}^2x_3^1+b_2^2),\\a_3^2=\ \ f(x_3^2)\ =f(w_{31}^2x_1^1+w_{32}^2x_2^1+w_{33}^2x_3^1+b_3^2);\\a_1^3=\ f(x_1^3)\ =\ f(w_{11}^3a_1^2+w_{12}^3a_2^2+w_{13}^3a_3^2+b_1^3),\\a_2^3=\ f(x_2^3)\ =f(w_{21}^3a_1^2+w_{22}^3a_2^2+w_{23}^3a_3^2+b_2^3),\\a_3^3=\ \ f(x_3^3)\ =f(w_{31}^3a_1^2+w_{32}^3a_2^2+w_{33}^3a_3^2+b_3^3);$

и функцию стоимости (cost function)

$Cost=\frac{1}{n}\sum_{i=1}^{n}{\left(y_i-a_i^3\right)^2{\rightarrow}min},$

где — номер соответствующего целевого (вектора $\mathbf{y}$ ) и выходного значений, — число выходных значений.

Таким образом, функция стоимости для нашей нейронной сети в развёрнутом виде:

$C=\frac{1}{3}(\left(y_1-a_1^3\right)^2+\left(y_2-a_2^3\right)^2+\left(y_3-a_3^3\right)^2).$

Функция стоимости показывает нам насколько сильно отличаются текущие значения нейронной сети от целевых.

Обратное распространение ошибки и обновление

В сущности, для реализации алгоритма обратного распространения ошибки используется довольно простая идея.

Градиент (в общем случае) — вектор, определяющий направление наискорейшего роста функции нескольких переменных. Вычитая из текущих значений весов и смещений соответствующие значения частных производных как элементов градиента функции стоимости $\nabla{C}$ , мы будем приближаться к одному из ближайших (относительно начальной точки) минимумов функции стоимости и, таким образом, уменьшать величину ошибки. Согласно необходимому условию экстремума, в точках экстремума функции многих переменных её градиент равен нулю, $\nabla{C}=0$ .

Этот подход называется алгоритмом градиентного спуска. Иногда может возникать путаница или отождествление этих двух алгоритмов, поскольку они тесно взаимосвязаны и один используется для реализации другого.

Несмотря на простоту и эффективность, алгоритм градиентного спуска в общем случае имеет свои ограничения, например, седловая точка, локальный минимум, перетренировка (overtraining) (попадание в глобальный минимум).

Найдём частные производные по всем элементам матрицы $\mathbf{W}^3$ :

$\frac{\partial C}{\partial\mathbf{W}^3}=\frac{1}{3}\sum_{i=1}^{3}\frac{\partial\left(y_i-a_i^3\right)^2}{\partial\mathbf{W}^3},\\\frac{\partial C}{\partial\mathbf{W}^3}=\frac{2}{3}\sum_{i=1}^{3}{\left(y_i-a_i^3\right)\frac{\partial\left(y_i-a_i^3\right)}{\partial\mathbf{W}^3}},\\\frac{\partial C}{\partial\mathbf{W}^3}=\frac{2}{3}\sum_{i=1}^{3}\left(y_i-a_i^3\right)\left(\frac{\partial y_i}{\partial\mathbf{W}^3}-\frac{\partial a_i^3}{\partial\mathbf{W}^3}\right),$

поскольку — константа, то $\frac{\partial y_i}{\partial\mathbf{W}^3}=0$ ,

$\frac{\partial C}{\partial\mathbf{W}^3}=-\frac{2}{3}\sum_{i=1}^{3}{\left(y_i-a_i^3\right)\frac{\partial a_i^3}{\partial\mathbf{W}^3}},\\\frac{\partial C}{\partial\mathbf{W}^3}=-\frac{2}{3}\sum_{i=1}^{3}{\left(y_i-a_i^3\right)\frac{\partial a_i^3}{\partial x_i^3}}\frac{\partial x_i^3}{\partial\mathbf{W}^3}.$

Преобразуем функцию активации сигмоид и найдём её производную:

$\frac{\partial C}{\partial\mathbf{W}^3}=-\frac{2}{3}\sum_{i=1}^{3}{\left(y_i-a_i^3\right)\frac{e^{x_i^3}}{\left(1+e^{x_i^3}\right)^2}}\frac{\partial x_i^3}{\partial\mathbf{W}^3}.$

В производной по матрице мы находим производную по каждому из её элементов.

Раскроем сумму для переменной $w_{11}^3$ матрицы $\mathbf{W}^3$ :

$\scriptsize\frac{\partial C}{\partial w_{11}^3}=-\frac{2}{3}(\left(y_1-a_1^3\right)\frac{e^{x_1^3}}{\left(1+e^{x_1^3}\right)^2}\frac{\partial x_1^3}{\partial w_{11}^3}+\left(y_2-a_2^3\right)\frac{e^{x_2^3}}{\left(1+e^{x_2^3}\right)^2}\frac{\partial x_2^3}{\partial w_{11}^3}+\left(y_3-a_3^3\right)\frac{e^{x_3^3}}{\left(1+e^{x_3^3}\right)^2}\frac{\partial x_3^3}{\partial w_{11}^3}).$

Найдём частную производную по переменной $w_{11}^3$ . Поскольку

$x_1^3=w_{11}^3a_1^2+w_{12}^3a_2^2+w_{13}^3a_3^2+b_1^3,\\x_2^3=w_{21}^3a_1^2+w_{22}^3a_2^2+w_{23}^3a_3^2+b_2^3,\\x_3^3=w_{31}^3a_1^2+w_{32}^3a_2^2+w_{33}^3a_3^2+b_3^3,$ $тогда \frac{\partial C}{\partial w_{11}^3}=-\frac{2}{3}(\left(y_1-a_1^3\right)\frac{e^{x_1^3}}{\left(1+e^{x_1^3}\right)^2}a_1^2+0+0).$

Преобразуем сигмоид и получим окончательную форму выражения для $\frac{\partial C}{\partial w_{11}^3}$ :

$\frac{\partial C}{\partial w_{11}^3}=-\frac{2}{3}\left(y_1-a_1^3\right)\frac{e^{x_1^3}}{\left(1+e^{x_1^3}\right)}{\left(1-\frac{e^{x_1^3}}{1+e^{x_1^3}}\right)}a_1^2\\или \frac{\partial C}{\partial w_{11}^3}=-\frac{2}{3}\left(y_1-a_1^3\right)a_1^3\left(x_1^3\right)\left(1-a_1^3\left(x_1^3\right)\right)a_1^2.$

Обратное распространение ошибки является частным случаем автоматического дифференцирования, для реализации которого нам и необходимо привести все вычислительные выражения к определённому виду.

Таким же образом для переменных $w_{12}^3$ и $w_{13}^3$ получим:

$\frac{\partial C}{\partial w_{12}^3}=-\frac{2}{3}\left(y_1-a_1^3\right)a_1^3\left(x_1^3\right)\left(1-a_1^3\left(x_1^3\right)\right)a_2^2,\\\frac{\partial C}{\partial w_{13}^3}=-\frac{2}{3}\left(y_1-a_1^3\right)a_1^3\left(x_1^3\right)\left(1-a_1^3\left(x_1^3\right)\right)a_3^2.$

Найдём новые значения (обновлённые веса) для переменных $w_{11}^3$ , $w_{12}^3$ и $w_{13}^3$ :

$^*w_{11}^3=\ w_{11}^3-\eta(-\frac{2}{3}\left(y_1-a_1^3\right)a_1^3\left(x_1^3\right)\left(1-a_1^3\left(x_1^3\right)\right)a_1^2),\\^*w_{12}^3=\ w_{12}^3-\eta(-\frac{2}{3}\left(y_1-a_1^3\right)a_1^3\left(x_1^3\right)\left(1-a_1^3\left(x_1^3\right)\right)a_2^2),\\^*w_{13}^3=\ w_{13}^3-\eta(-\frac{2}{3}\left(y_1-a_1^3\right)a_1^3\left(x_1^3\right)\left(1-a_1^3\left(x_1^3\right)\right)a_3^2),$

где $\eta$ (и́та) — буква греческого алфавита, обычно используемая для обозначения скорости обучения (learning rate), её значение должно быть установлено на промежутке от 0 до 1; * — новое значение переменной.

Найдём остальные частные производные для матрицы $\mathbf{W}^3$ . Раскроем сумму для $w_{21}^3$ :

$\scriptsize\frac{\partial C}{\partial w_{21}^3}=-\frac{2}{3}(\left(y_1-a_1^3\right)\frac{e^{x_1^3}}{\left(1+e^{x_1^3}\right)^2}\frac{\partial x_1^3}{\partial w_{21}^3}+\left(y_2-a_2^3\right)\frac{e^{x_2^3}}{\left(1+e^{x_2^3}\right)^2}\frac{\partial x_2^3}{\partial w_{21}^3}+\left(y_3-a_3^3\right)\frac{e^{x_3^3}}{\left(1+e^{x_3^3}\right)^2}\frac{\partial x_3^3}{\partial w_{21}^3}).$

Найдём частную производную по переменной $w_{21}^3$ :

$\frac{\partial C}{\partial w_{21}^3}=-\frac{2}{3}(0+\left(y_2-a_2^3\right)\frac{e^{x_2^3}}{\left(1+e^{x_2^3}\right)^2}a_1^2+0).$

Преобразуем сигмоид и получим окончательную форму выражения для $\frac{\partial C}{\partial w_{21}^3}$ :

$\frac{\partial C}{\partial w_{21}^3}=-\frac{2}{3}\left(y_2-a_2^3\right)\frac{e^{x_2^3}}{\left(1+e^{x_2^3}\right)}{\left(1-\frac{e^{x_2^3}}{1+e^{x_2^3}}\right)a_1^2}\\или \frac{\partial C}{\partial w_{21}^3}=-\frac{2}{3}\left(y_2-a_2^3\right)a_2^3\left(x_2^3\right)\left(1-a_2^3\left(x_2^3\right)\right)a_1^2.$

Таким же образом для переменных $w_{22}^3$ и $w_{23}^3$ получим:

$\frac{\partial C}{\partial w_{22}^3}=-\frac{2}{3}\left(y_2-a_2^3\right)a_2^3\left(x_2^3\right)\left(1-a_2^3\left(x_2^3\right)\right)a_2^2,\\\frac{\partial C}{\partial w_{23}^3}=-\frac{2}{3}\left(y_2-a_2^3\right)a_2^3\left(x_2^3\right)\left(1-a_2^3\left(x_2^3\right)\right)a_3^2.$

Найдём новые значения (обновлённые веса) для переменных $w_{21}^3$ , $w_{22}^3$ и $w_{23}^3$ :

$^*w_{21}^3=\ w_{21}^3-\eta(-\frac{2}{3}\left(y_2-a_2^3\right)a_2^3\left(x_2^3\right)\left(1-a_2^3\left(x_2^3\right)\right)a_1^2),\\^*w_{22}^3=\ w_{22}^3-\eta(-\frac{2}{3}\left(y_2-a_2^3\right)a_2^3\left(x_2^3\right)\left(1-a_2^3\left(x_2^3\right)\right)a_2^2),\\^*w_{23}^3=\ w_{23}^3-\eta(-\frac{2}{3}\left(y_2-a_2^3\right)a_2^3\left(x_2^3\right)\left(1-a_2^3\left(x_2^3\right)\right)a_3^2).$

Раскроем сумму для $w_{31}^3$ :

$\scriptsize\frac{\partial C}{\partial w_{31}^3}=-\frac{2}{3}(\left(y_1-a_1^3\right)\frac{e^{x_1^3}}{\left(1+e^{x_1^3}\right)^2}\frac{\partial x_1^3}{\partial w_{31}^3}+\left(y_2-a_2^3\right)\frac{e^{x_2^3}}{\left(1+e^{x_2^3}\right)^2}\frac{\partial x_2^3}{\partial w_{31}^3}+\left(y_3-a_3^3\right)\frac{e^{x_3^3}}{\left(1+e^{x_3^3}\right)^2}\frac{\partial x_3^3}{\partial w_{31}^3}).$

Найдём частную производную по переменной $w_{31}^3$ :

$\frac{\partial C}{\partial w_{31}^3}=-\frac{2}{3}(0+0+\left(y_3-a_3^3\right)\frac{e^{x_3^3}}{\left(1+e^{x_3^3}\right)^2}a_1^2).$

Преобразуем сигмоид и получим окончательную форму выражения для $\frac{\partial C}{\partial w_{31}^3}$ :

$\frac{\partial C}{\partial w_{31}^3}=-\frac{2}{3}\left(y_3-a_3^3\right)\frac{e^{x_3^3}}{\left(1+e^{x_3^3}\right)}{\left(1-\frac{e^{x_3^3}}{1+e^{x_3^3}}\right)a_1^2}\\или \frac{\partial C}{\partial w_{31}^3}=-\frac{2}{3}\left(y_3-a_3^3\right)a_3^3\left(x_3^3\right)\left(1-a_3^3\left(x_3^3\right)\right)a_1^2.$

Таким же образом для переменных $w_{32}^3$ и $w_{33}^3$ получим:

$\frac{\partial C}{\partial w_{32}^3}=-\frac{2}{3}\left(y_3-a_3^3\right)a_3^3\left(x_3^3\right)\left(1-a_3^3\left(x_3^3\right)\right)a_2^2,\\\frac{\partial C}{\partial w_{33}^3}=-\frac{2}{3}\left(y_3-a_3^3\right)a_3^3\left(x_3^3\right)\left(1-a_3^3\left(x_3^3\right)\right)a_3^2.$

Найдём новые значения (обновлённые веса) для переменных $w_{31}^3$ , $w_{32}^3$ и $w_{33}^3$ :

$^*w_{31}^3=\ w_{31}^3-\eta(-\frac{2}{3}\left(y_3-a_3^3\right)a_3^3\left(x_3^3\right)\left(1-a_3^3\left(x_3^3\right)\right)a_1^2),\\^*w_{32}^3=\ w_{32}^3-\eta(-\frac{2}{3}\left(y_3-a_3^3\right)a_3^3\left(x_3^3\right)\left(1-a_3^3\left(x_3^3\right)\right)a_2^2),\\^*w_{33}^3=\ w_{33}^3-\eta(-\frac{2}{3}\left(y_3-a_3^3\right)a_3^3\left(x_3^3\right)\left(1-a_3^3\left(x_3^3\right)\right)a_3^2).$

Теперь найдём частные производные по всем элементам вектора $\mathbf{b}^3$ :

$\frac{\partial C}{\partial\mathbf{b}^3}=-\frac{2}{3}\sum_{i=1}^{3}{\left(y_i-a_i^3\right)\frac{e^{x_i^3}}{\left(1+e^{x_i^3}\right)^2}}\frac{\partial x_i^3}{\partial\mathbf{b}^3}.$

Найдём частную производную по :

$\scriptsize\frac{\partial C}{\partial b_1^3}=-\frac{2}{3}(\left(y_1-a_1^3\right)\frac{e^{x_1^3}}{\left(1+e^{x_1^3}\right)^2}\frac{\partial x_1^3}{\partial b_1^3}+\left(y_2-a_2^3\right)\frac{e^{x_2^3}}{\left(1+e^{x_2^3}\right)^2}\frac{\partial x_2^3}{\partial b_1^3}+\left(y_3-a_3^3\right)\frac{e^{x_3^3}}{\left(1+e^{x_3^3}\right)^2}\frac{\partial x_3^3}{\partial b_1^3}),$ $\frac{\partial C}{\partial b_1^3}=-\frac{2}{3}(\left(y_1-a_1^3\right)\frac{e^{x_1^3}}{\left(1+e^{x_1^3}\right)^2}1+0+0).$

Преобразуем сигмоид и получим окончательную форму выражения для $\frac{\partial C}{\partial b_1^3}$ :

$\frac{\partial C}{\partial b_1^3}=-\frac{2}{3}\left(y_1-a_1^3\right)\frac{e^{x_1^3}}{\left(1+e^{x_1^3}\right)}\left(1-\frac{e^{x_1^3}}{1+e^{x_1^3}}\right)\\или \frac{\partial C}{\partial b_1^3}=-\frac{2}{3}\left(y_1-a_1^3\right)a_1^3\left(x_1^3\right)\left(1-a_1^3\left(x_1^3\right)\right).$

Найдём новое значение для смещения :

$^*b_1^3=\ b_1^3-\eta(-\frac{2}{3}\left(y_1-a_1^3\right)a_1^3\left(x_1^3\right)\left(1-a_1^3\left(x_1^3\right)\right)).$

Вычислим частные производные по и :

$\scriptsize\frac{\partial C}{\partial b_2^3}=-\frac{2}{3}(\left(y_1-a_1^3\right)\frac{e^{x_1^3}}{\left(1+e^{x_1^3}\right)^2}\frac{\partial x_1^3}{\partial b_2^3}+\left(y_2-a_2^3\right)\frac{e^{x_2^3}}{\left(1+e^{x_2^3}\right)^2}\frac{\partial x_2^3}{\partial b_2^3}+\left(y_3-a_3^3\right)\frac{e^{x_3^3}}{\left(1+e^{x_3^3}\right)^2}\frac{\partial x_3^3}{\partial b_2^3}),$ $\frac{\partial C}{\partial b_2^3}=-\frac{2}{3}(0+\left(y_2-a_2^3\right)\frac{e^{x_2^3}}{\left(1+e^{x_2^3}\right)^2}\frac{\partial x_2^3}{\partial b_2^2}+0),\\\frac{\partial C}{\partial b_2^3}=-\frac{2}{3}\left(y_2-a_2^3\right)a_2^3\left(x_2^3\right)\left(1-a_2^3\left(x_2^3\right)\right).$ $\scriptsize\frac{\partial C}{\partial b_3^3}=-\frac{2}{3}(\left(y_1-a_1^3\right)\frac{e^{x_1^3}}{\left(1+e^{x_1^3}\right)^2}\frac{\partial x_1^3}{\partial b_3^3}+\left(y_2-a_2^3\right)\frac{e^{x_2^3}}{\left(1+e^{x_2^3}\right)^2}\frac{\partial x_2^3}{\partial b_3^3}+\left(y_3-a_3^3\right)\frac{e^{x_3^3}}{\left(1+e^{x_3^3}\right)^2}\frac{\partial x_3^3}{\partial b_3^3}),$ $\frac{\partial C}{\partial b_3^3}=-\frac{2}{3}(0+0+\left(y_3-a_3^3\right)\frac{e^{x_3^3}}{\left(1+e^{x_3^3}\right)^2}\frac{\partial x_3^3}{\partial b_3^2}),\\\frac{\partial C}{\partial b_3^3}=-\frac{2}{3}\left(y_3-a_3^3\right)a_3^3\left(x_3^3\right)\left(1-a_3^3\left(x_3^3\right)\right).$

Найдём новые значения для и:

$^*b_2^3=\ b_2^3-\eta(-\frac{2}{3}\left(y_2-a_2^3\right)a_2^3\left(x_2^3\right)\left(1-a_2^3\left(x_2^3\right)\right)),\\^*b_3^3=\ b_3^3-\eta(-\frac{2}{3}\left(y_3-a_3^3\right)a_3^3\left(x_3^3\right)\left(1-a_3^3\left(x_3^3\right)\right)).$

Найдём частные производные по всем элементам матрицы $\mathbf{W}^2$ . Раскроем сумму для переменной $w_{11}^2$ матрицы $\mathbf{W}^2$ . Поскольку

$x_1^3=w_{11}^3a_1^2+w_{12}^3a_2^2+w_{13}^3a_3^2+b_1^3,\\x_2^3=w_{21}^3a_1^2+w_{22}^3a_2^2+w_{23}^3a_3^2+b_2^3,\\x_3^3=w_{31}^3a_1^2+w_{32}^3a_2^2+w_{33}^3a_3^2+b_3^3,$

в свою очередь,

тогда сумма для переменной $w_{11}^2$ матрицы $\mathbf{W}^2$ :

$\frac{\partial C}{\partial w_{11}^2}=-\frac{2}{3}\sum_{i=1}^{3}{\left(y_i-a_i^3\right)\frac{e^{x_i^3}}{\left(1+e^{x_i^3}\right)^2}}\frac{\partial x_i^3}{\partial a_1^2}\frac{\partial a_1^2}{\partial x_1^2}\frac{\partial x_1^2}{\partial w_{11}^2},$ $\scriptsize{\begin{gather}\frac{\partial C}{\partial w_{11}^2}=-\frac{2}{3}(\left(y_1-a_1^3\right)\frac{e^{x_1^3}}{\left(1+e^{x_1^3}\right)^2}\frac{\partial x_1^3}{\partial a_1^2}\frac{\partial a_1^2}{\partial x_1^2}\frac{\partial x_1^2}{\partial w_{11}^2}+\left(y_2-a_2^3\right)\frac{e^{x_2^3}}{\left(1+e^{x_2^3}\right)^2}\frac{\partial x_2^3}{\partial a_1^2}\frac{\partial a_1^2}{\partial x_1^2}\frac{\partial x_1^2}{\partial w_{11}^2}\\+\left(y_3-a_3^3\right)\frac{e^{x_3^3}}{\left(1+e^{x_3^3}\right)^2}\frac{\partial x_3^3}{\partial a_1^2}\frac{\partial a_1^2}{\partial x_1^2}\frac{\partial x_1^2}{\partial w_{11}^2}),\\\frac{\partial C}{\partial w_{11}^2}=-\frac{2}{3}(\left(y_1-a_1^3\right)\frac{e^{x_1^3}}{\left(1+e^{x_1^3}\right)^2}w_{11}^3\frac{e^{x_1^2}}{\left(1+e^{x_1^2}\right)}\left(1-\frac{e^{x_1^2}}{1+e^{x_1^2}}\right)x_1^1\\+\left(y_2-a_2^3\right)\frac{e^{x_2^3}}{\left(1+e^{x_2^3}\right)^2}w_{21}^3\frac{e^{x_1^2}}{\left(1+e^{x_1^2}\right)}\left(1-\frac{e^{x_1^2}}{1+e^{x_1^2}}\right)x_1^1\\+\left(y_3-a_3^3\right)\frac{e^{x_3^3}}{\left(1+e^{x_3^3}\right)^2}w_{31}^3\frac{e^{x_1^2}}{\left(1+e^{x_1^2}\right)}\left(1-\frac{e^{x_1^2}}{1+e^{x_1^2}}\right)x_1^1),\\\frac{\partial C}{\partial w_{11}^2}=-\frac{2}{3}(\left(y_1-a_1^3\right)a_1^3\left(x_1^3\right)\left(1-a_1^3\left(x_1^3\right)\right)w_{11}^3a_1^2\left(x_1^2\right)\left(1-a_1^2\left(x_1^2\right)\right)x_1^1\\+\left(y_2-a_2^3\right)a_2^3\left(x_2^3\right)\left(1-a_2^3\left(x_2^3\right)\right)w_{21}^3a_1^2\left(x_1^2\right)\left(1-a_1^2\left(x_1^2\right)\right)x_1^1\\+\left(y_3-a_3^3\right)a_3^3\left(x_3^3\right)\left(1-a_3^3\left(x_3^3\right)\right)w_{31}^3a_1^2\left(x_1^2\right)\left(1-a_1^2\left(x_1^2\right)\right)x_1^1).\end{gather}}$

Найдём новое значение (обновлённый вес) для переменной $w_{11}^2$ :

$^*w_{11}^2=\ w_{11}^2-\eta\frac{\partial C}{\partial w_{11}^2}.$

Найдём остальные частные производные и их новые значения для матрицы $\mathbf{W}^2$ .

$\scriptsize{\begin{gather}\frac{\partial C}{\partial w_{12}^2}=-\frac{2}{3}(\left(y_1-a_1^3\right)a_1^3\left(x_1^3\right)\left(1-a_1^3\left(x_1^3\right)\right)w_{11}^3a_1^2\left(x_1^2\right)\left(1-a_1^2\left(x_1^2\right)\right)x_2^1\\+\left(y_2-a_2^3\right)a_2^3\left(x_2^3\right)\left(1-a_2^3\left(x_2^3\right)\right)w_{21}^3a_1^2\left(x_1^2\right)\left(1-a_1^2\left(x_1^2\right)\right)x_2^1\\+\left(y_3-a_3^3\right)a_3^3\left(x_3^3\right)\left(1-a_3^3\left(x_3^3\right)\right)w_{31}^3a_1^2\left(x_1^2\right)\left(1-a_1^2\left(x_1^2\right)\right)x_2^1).\end{gather}}$ $\scriptsize{\begin{gather}\frac{\partial C}{\partial w_{13}^2}=-\frac{2}{3}(\left(y_1-a_1^3\right)a_1^3\left(x_1^3\right)\left(1-a_1^3\left(x_1^3\right)\right)w_{11}^3a_1^2\left(x_1^2\right)\left(1-a_1^2\left(x_1^2\right)\right)x_3^1\\+\left(y_2-a_2^3\right)a_2^3\left(x_2^3\right)\left(1-a_2^3\left(x_2^3\right)\right)w_{21}^3a_1^2\left(x_1^2\right)\left(1-a_1^2\left(x_1^2\right)\right)x_3^1\\+\left(y_3-a_3^3\right)a_3^3\left(x_3^3\right)\left(1-a_3^3\left(x_3^3\right)\right)w_{31}^3a_1^2\left(x_1^2\right)\left(1-a_1^2\left(x_1^2\right)\right)x_3^1).\end{gather}}$ $^*w_{12}^2=\ w_{12}^2-\eta\frac{\partial C}{\partial w_{12}^2}, ^*w_{13}^2=\ w_{13}^2-\eta\frac{\partial C}{\partial w_{13}^2}.$ $\scriptsize{\begin{gather}\frac{\partial C}{\partial w_{21}^2}=-\frac{2}{3}(\left(y_1-a_1^3\right)a_1^3\left(x_1^3\right)\left(1-a_1^3\left(x_1^3\right)\right)w_{12}^3a_2^2\left(x_2^2\right)\left(1-a_2^2\left(x_2^2\right)\right)x_1^1\\+\left(y_2-a_2^3\right)a_2^3\left(x_2^3\right)\left(1-a_2^3\left(x_2^3\right)\right)w_{22}^3a_2^2\left(x_2^2\right)\left(1-a_2^2\left(x_2^2\right)\right)x_1^1\\+\left(y_3-a_3^3\right)a_3^3\left(x_3^3\right)\left(1-a_3^3\left(x_3^3\right)\right)w_{32}^3a_2^2\left(x_2^2\right)\left(1-a_2^2\left(x_2^2\right)\right)x_1^1).\end{gather}}$ $\scriptsize{\begin{gather} \frac{\partial C}{\partial w_{22}^2}=-\frac{2}{3}(\left(y_1-a_1^3\right)a_1^3\left(x_1^3\right)\left(1-a_1^3\left(x_1^3\right)\right)w_{12}^3a_2^2\left(x_2^2\right)\left(1-a_2^2\left(x_2^2\right)\right)x_2^1\\+\left(y_2-a_2^3\right)a_2^3\left(x_2^3\right)\left(1-a_2^3\left(x_2^3\right)\right)w_{22}^3a_2^2\left(x_2^2\right)\left(1-a_2^2\left(x_2^2\right)\right)x_2^1\\+\left(y_3-a_3^3\right)a_3^3\left(x_3^3\right)\left(1-a_3^3\left(x_3^3\right)\right)w_{32}^3a_2^2\left(x_2^2\right)\left(1-a_2^2\left(x_2^2\right)\right)x_2^1).\end{gather}}$ $\scriptsize{\begin{gather}\frac{\partial C}{\partial w_{23}^2}=-\frac{2}{3}(\left(y_1-a_1^3\right)a_1^3\left(x_1^3\right)\left(1-a_1^3\left(x_1^3\right)\right)w_{12}^3a_2^2\left(x_2^2\right)\left(1-a_2^2\left(x_2^2\right)\right)x_3^1\\+\left(y_2-a_2^3\right)a_2^3\left(x_2^3\right)\left(1-a_2^3\left(x_2^3\right)\right)w_{22}^3a_2^2\left(x_2^2\right)\left(1-a_2^2\left(x_2^2\right)\right)x_3^1\\+\left(y_3-a_3^3\right)a_3^3\left(x_3^3\right)\left(1-a_3^3\left(x_3^3\right)\right)w_{32}^3a_2^2\left(x_2^2\right)\left(1-a_2^2\left(x_2^2\right)\right)x_3^1).\end{gather}}$ $^*w_{21}^2=\ w_{21}^2-\eta\frac{\partial C}{\partial w_{21}^2}, ^*w_{22}^2=\ w_{22}^2-\eta\frac{\partial C}{\partial w_{22}^2},\\^*w_{23}^2=\ w_{23}^2-\eta\frac{\partial C}{\partial w_{23}^2}.$ $\scriptsize{\begin{gather}\frac{\partial C}{\partial w_{31}^2}=-\frac{2}{3}(\left(y_1-a_1^3\right)a_1^3\left(x_1^3\right)\left(1-a_1^3\left(x_1^3\right)\right)w_{13}^3a_3^2\left(x_3^2\right)\left(1-a_3^2\left(x_3^2\right)\right)x_1^1\\+\left(y_2-a_2^3\right)a_2^3\left(x_2^3\right)\left(1-a_2^3\left(x_2^3\right)\right)w_{23}^3a_3^2\left(x_3^2\right)\left(1-a_3^2\left(x_3^2\right)\right)x_1^1\\+\left(y_3-a_3^3\right)a_3^3\left(x_3^3\right)\left(1-a_3^3\left(x_3^3\right)\right)w_{33}^3a_3^2\left(x_3^2\right)\left(1-a_3^2\left(x_3^2\right)\right)x_1^1).\end{gather}}$ $\scriptsize{\begin{gather}\frac{\partial C}{\partial w_{32}^2}=-\frac{2}{3}(\left(y_1-a_1^3\right)a_1^3\left(x_1^3\right)\left(1-a_1^3\left(x_1^3\right)\right)w_{13}^3a_3^2\left(x_3^2\right)\left(1-a_3^2\left(x_3^2\right)\right)x_2^1\\+\left(y_2-a_2^3\right)a_2^3\left(x_2^3\right)\left(1-a_2^3\left(x_2^3\right)\right)w_{23}^3a_3^2\left(x_3^2\right)\left(1-a_3^2\left(x_3^2\right)\right)x_2^1\\+\left(y_3-a_3^3\right)a_3^3\left(x_3^3\right)\left(1-a_3^3\left(x_3^3\right)\right)w_{33}^3a_3^2\left(x_3^2\right)\left(1-a_3^2\left(x_3^2\right)\right)x_2^1).\end{gather}}$ $\scriptsize{\begin{gather}\frac{\partial C}{\partial w_{33}^2}=-\frac{2}{3}(\left(y_1-a_1^3\right)a_1^3\left(x_1^3\right)\left(1-a_1^3\left(x_1^3\right)\right)w_{13}^3a_3^2\left(x_3^2\right)\left(1-a_3^2\left(x_3^2\right)\right)x_3^1\\+\left(y_2-a_2^3\right)a_2^3\left(x_2^3\right)\left(1-a_2^3\left(x_2^3\right)\right)w_{23}^3a_3^2\left(x_3^2\right)\left(1-a_3^2\left(x_3^2\right)\right)x_3^1\\+\left(y_3-a_3^3\right)a_3^3\left(x_3^3\right)\left(1-a_3^3\left(x_3^3\right)\right)w_{33}^3a_3^2\left(x_3^2\right)\left(1-a_3^2\left(x_3^2\right)\right)x_3^1).\end{gather}}$ $^*w_{31}^2=\ w_{31}^2-\eta\frac{\partial C}{\partial w_{31}^2}, ^*w_{32}^2=\ w_{32}^2-\eta\frac{\partial C}{\partial w_{32}^2},\\^*w_{33}^2=\ w_{33}^2-\eta\frac{\partial C}{\partial w_{33}^2}.$

Теперь найдём частные производные по всем элементам вектора $\mathbf{b}^2$ . Раскроем сумму для переменной :

$\frac{\partial C}{\partial b_1^2}=-\frac{2}{3}\sum_{i=1}^{3}{\left(y_i-a_i^3\right)\frac{e^{x_i^3}}{\left(1+e^{x_i^3}\right)^2}}\frac{\partial x_i^3}{\partial a_1^2}\frac{\partial a_1^2}{\partial x_1^2}\frac{\partial x_1^2}{\partial b_1^2},$ $\scriptsize{\begin{gather}\frac{\partial C}{\partial b_1^2}=-\frac{2}{3}(\left(y_1-a_1^3\right)\frac{e^{x_1^3}}{\left(1+e^{x_1^3}\right)^2}\frac{\partial x_1^3}{\partial a_1^2}\frac{\partial a_1^2}{\partial x_1^2}\frac{\partial x_1^2}{\partial b_1^2}+\left(y_2-a_2^3\right)\frac{e^{x_2^3}}{\left(1+e^{x_2^3}\right)^2}\frac{\partial x_2^3}{\partial a_1^2}\frac{\partial a_1^2}{\partial x_1^2}\frac{\partial x_1^2}{\partial b_1^2}\\+\left(y_3-a_3^3\right)\frac{e^{x_3^3}}{\left(1+e^{x_3^3}\right)^2}\frac{\partial x_3^3}{\partial a_1^2}\frac{\partial a_1^2}{\partial x_1^2}\frac{\partial x_1^2}{\partial b_1^2}),\\\frac{\partial C}{\partial b_1^2}=-\frac{2}{3}(\left(y_1-a_1^3\right)\frac{e^{x_1^3}}{\left(1+e^{x_1^3}\right)^2}w_{11}^3\frac{e^{x_1^2}}{\left(1+e^{x_1^2}\right)}\left(1-\frac{e^{x_1^2}}{1+e^{x_1^2}}\right)\\+\left(y_2-a_2^3\right)\frac{e^{x_2^3}}{\left(1+e^{x_2^3}\right)^2}w_{21}^3\frac{e^{x_1^2}}{\left(1+e^{x_1^2}\right)}\left(1-\frac{e^{x_1^2}}{1+e^{x_1^2}}\right)\\+\left(y_3-a_3^3\right)\frac{e^{x_3^3}}{\left(1+e^{x_3^3}\right)^2}w_{31}^3\frac{e^{x_1^2}}{\left(1+e^{x_1^2}\right)}\left(1-\frac{e^{x_1^2}}{1+e^{x_1^2}}\right)),\\\frac{\partial C}{\partial b_1^2}=-\frac{2}{3}(\left(y_1-a_1^3\right)a_1^3\left(x_1^3\right)\left(1-a_1^3\left(x_1^3\right)\right)w_{11}^3a_1^2\left(x_1^2\right)\left(1-a_1^2\left(x_1^2\right)\right)\\+\left(y_2-a_2^3\right)a_2^3\left(x_2^3\right)\left(1-a_2^3\left(x_2^3\right)\right)w_{21}^3a_1^2\left(x_1^2\right)\left(1-a_1^2\left(x_1^2\right)\right)\\+\left(y_3-a_3^3\right)a_3^3\left(x_3^3\right)\left(1-a_3^3\left(x_3^3\right)\right)w_{31}^3a_1^2\left(x_1^2\right)\left(1-a_1^2\left(x_1^2\right)\right)).\end{gather}}$

Найдём новое значение для :

$^*b_1^2=\ b_1^2-\eta\frac{\partial C}{\partial b_1^2}.$

Найдём остальные частные производные для вектора $\mathbf{b}^2$ :

$\scriptsize{\begin{gather}\frac{\partial C}{\partial b_2^2}=-\frac{2}{3}(\left(y_1-a_1^3\right)a_1^3\left(x_1^3\right)\left(1-a_1^3\left(x_1^3\right)\right)w_{12}^3a_2^2\left(x_2^2\right)\left(1-a_2^2\left(x_2^2\right)\right)\\+\left(y_2-a_2^3\right)a_2^3\left(x_2^3\right)\left(1-a_2^3\left(x_2^3\right)\right)w_{22}^3a_2^2\left(x_2^2\right)\left(1-a_2^2\left(x_2^2\right)\right)\\+\left(y_3-a_3^3\right)a_3^3\left(x_3^3\right)\left(1-a_3^3\left(x_3^3\right)\right)w_{32}^3a_2^2\left(x_2^2\right)\left(1-a_2^2\left(x_2^2\right)\right)).\end{gather}}$ $\scriptsize{\begin{gather}\frac{\partial C}{\partial b_3^2}=-\frac{2}{3}(\left(y_1-a_1^3\right)a_1^3\left(x_1^3\right)\left(1-a_1^3\left(x_1^3\right)\right)w_{13}^3a_3^2\left(x_3^2\right)\left(1-a_3^2\left(x_3^2\right)\right)\\+\left(y_2-a_2^3\right)a_2^3\left(x_2^3\right)\left(1-a_2^3\left(x_2^3\right)\right)w_{23}^3a_3^2\left(x_3^2\right)\left(1-a_3^2\left(x_3^2\right)\right)\\+\left(y_3-a_3^3\right)a_3^3\left(x_3^3\right)\left(1-a_3^3\left(x_3^3\right)\right)w_{33}^3a_3^2\left(x_3^2\right)\left(1-a_3^2\left(x_3^2\right)\right)).\end{gather}}$

Найдём новые значения для переменных и :

$^*b_2^2=\ b_2^2-\eta\frac{\partial C}{\partial b_2^2}, ^*b_3^2=\ b_3^2-\eta\frac{\partial C}{\partial b_3^2}.$

Численный пример

Задача обучения нейронной сети состоит в аппроксимации некоторой неизвестной функции, которая отображает $\mathbf{x}^1$ в $\mathbf{y}$ .

Другими словами, существует некоторая неизвестная нам функция $\mathbf{y}=\mathbf{f}(\mathbf{x}^1)$ , которая для набора значений независимых переменных выдаёт результат, соответствующий набору значений зависимых переменных . Задача нейронной сети в результате обучения «заменить», приблизить, т.е. аппроксимировать неизвестную функцию $\mathbf{y}=\mathbf{f}(\mathbf{x}^1)$ . В случае успешного решения задачи, значения нашей нейронной сети на выходном слое $\mathbf{a}^3$ будут приблизительно равны значениям вектора $\mathbf{y}$ аппроксимируемой функции.

Выберем случайным образом следующие начальные значения для нашей нейронной сети:

$\mathbf{W}^2=\left[\begin{matrix}0.88&0.39&0.9\\0.37&0.14&0.41\\0.96&0.5&0.6\\\end{matrix}\right],\mathbf{W}^3=\left[\begin{matrix}0.29&0.57&0.36\\0.73&0.53&0.68\\0.01&0.02&0.58\\\end{matrix}\right],\\\mathbf{b}^2=\left[\begin{matrix}0.23\\0.89\\0.08\\\end{matrix}\right], \mathbf{b}^3=\left[\begin{matrix}0.78\\0.83\\0.8\\\end{matrix}\right].$

А также входные и целевые значения: $\mathbf{x}^1=\left[\begin{matrix}0.03\\0.72\\0.49\\\end{matrix}\right], \mathbf{y}=\left[\begin{matrix}0.93\\0.74\\0.17\\\end{matrix}\right].$

После первого прямого прохождения сигнала значения скрытого и выходного слоёв:

$\mathbf{a}^2=\left[\begin{matrix}0.726750911\\0.769022513\\0.681961335\\\end{matrix}\right], \mathbf{a}^3=\left[\begin{matrix}0.842189045\\0.903072871\\0.771744079\\\end{matrix}\right].$

Для скорости обучения установим значение $\eta=0.01$ .

Вычислим для первой эпохи (epoch) обучения нейронной сети обновлённые значения весов $w_{11}^3$ и $w_{11}^2$ :

$\scriptsize{\begin{gather}^*w_{11}^3=0.29+0.01\cdot \frac{2}{3}\cdot (0.93-0.842189045)\cdot 0.842189045\cdot (1-0.842189045)\cdot 0.726750911=0.290056544,\\^*w_{11}^2=0.88+0.01\cdot \frac{2}{3}\cdot (\left(0.93-0.842189045\right)\cdot 0.842189045\cdot \left(1-0.842189045\right)\cdot 0.29\cdot 0.726750911\cdot\\ \left(1-0.726750911\right)\cdot 0.03+\left(0.74-0.903072871\right)\cdot \:0.903072871\cdot \left(1-0.903072871\right)\cdot \:0.73\cdot \:0.769022513\cdot\\ \left(1-0.769022513\right)\cdot \:0.03+\left(0.17-0.771744079\right)\cdot \:0.771744079\cdot \left(1-0.771744079\right)\cdot \:0.01\cdot \:0.681961335\cdot\\ \left(1-0.681961335\right)\cdot \:0.03)=0.879999678.\end{gather}}$

Новые значения других весов и смещений находятся аналогичным образом, в соответствии с полученными ранее формулами.

После 10 000 эпох обучения матрицы весов и выходной слой имеют следующие значения:

$\mathbf{W}^2=\left[\begin{matrix}0.881449843&0.424796239&0.923680774\\0.372218081&0.193233937&0.446228651\\0.957567842&0.441628217&0.560274759\\\end{matrix}\right],\\\mathbf{W}^3=\left[\begin{matrix}0.480573892&0.772236752&0.529654336\\0.394700365&0.174298746&0.381672097\\-0.771753134&-0.808346904&-0.127425218\\\end{matrix}\right],\\\mathbf{a}^3=\left[\begin{matrix}0.913047169\\0.741592957\\0.173072228\\\end{matrix}\right].$

Обобщение для произвольного числа слоёв

Мы рассмотрели частный случай алгоритма обратного распространения ошибки для нейронной сети с одним скрытым слоем. Запишем формулы для реализации нейронной сети с произвольным числом скрытых слоёв.

$\delta_i^L=\left(y_i-a_i^L\right)a_i^L\left(x_i^L\right)\left(1-a_i^L\left(x_i^L\right)\right),\\\delta_i^l=\sum_{k=1}^{n}{\delta_k^{l+1}w_{ki}^{l+1}\frac{\partial a_i^l}{\partial x_i^l}},\\\frac{\partial C}{\partial w_{ij}^l}=\frac{1}{n}\delta_i^l\frac{\partial x_i^l}{\partial w_{ij}^l},\\\frac{\partial C}{\partial b_i^l}=\delta_i^l,$

где — номер выходного слоя, — индекс строки матрицы весов, — число выходных значений.

$\delta$ — обобщённое дельта-правило (delta rule).

Надеемся, что статья будет интересной и полезной для всех, кто приступает к изучению глубинного обучения и нейронных сетей!

Источник

Прямое распространение¶

Простая сеть
- Прямой проход по шагам
- Код
Более сложная сеть
- Архитектура
- Инициализация весов
- Bias Terms
- Working with Matrices
- Dynamic Resizing
- Refactoring Our Code
- Final Result

Простая сеть¶

Прямое распространение — это процесс с помощью которого сеть делает предсказание (prediction). Также это основной режим работы обученной нейронной сети. Входные данные «распространяются» через каждый слой сети и выходной слой выдает финальный результат — предсказание. Для простой учебной нейронной сети один проход данных можно выразить математически как:

\[Prediction = A(\;A(\;X W_h\;)W_o\;)\]

Где $A$ это функция активации, например ReLU, $X$ это входные данные, $W_h$ и $W_o$ это веса слоев.

Прямой проход по шагам¶

Вычислить значения входов скрытого слоя умножениием $X$ на веса скрытого слоя $W_h$ и получить $Z_h$.
Применить функцию активации к $Z_h$ и передать результат $H$ в выходной слой.
Вычислить значения входов выходного слоя умножением значения $H$ на веса выходного слоя $W_o$ и получить $Z_o$
Применить функцию активации к $Z_o$. Результатом будет предсказание сети.

Код¶

Давайте напишем метод feed_forward() для распространения входных данных через нейронную сеть с 1-м скрытым слоем. Выход этого метода будет представлять собой предсказание модели.

def relu(z):
    return max(0,z)

def feed_forward(x, Wh, Wo):
    # Hidden layer
    Zh = x * Wh
    H = relu(Zh)

    # Output layer
    Zo = H * Wo
    output = relu(Zo)
    return output

x это вход сети, Zo и Zh это «взвешенный» вход слоев, a Wo и Wh это веса слоев.

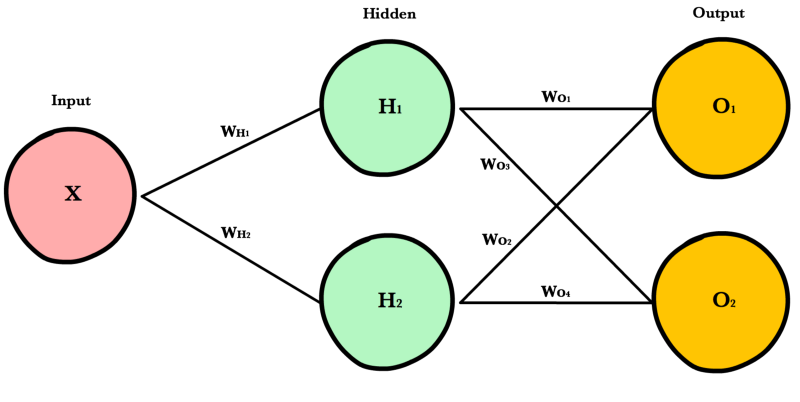
Более сложная сеть¶

Простая сеть очень помогает в учебном процессе, но реальные сети намного больше и сложнее устроены. Современные нейронные сети имеют гораздо больше скрытых слоев, больше нейронов в каждом слое, больше входных переменных. Рассмотрим более крупную (но всё ещё простую) нейронную сеть, которая позволит нам показать универсальный подход, основанный на матричном умножении, используемом в больших, «промышленных» нейронных сетях.

Архитектура¶

Для произвольного изменения количества входов или выходов сети, мы должны сделать наш код более гибким с помощью добавления новых параметров в __init_ метод: inputLayerSize, hiddenLayerSize,outputLayerSize. Мы будем продолжать ограничивать себя в количестве скрытых слоев, но сейчас это не так важно, потому что мы можем менять ширину (количество нейронов) имеющихся слоев.

INPUT_LAYER_SIZE = 1
HIDDEN_LAYER_SIZE = 2
OUTPUT_LAYER_SIZE = 2

Инициализация весов¶

Unlike last time where Wh and Wo were scalar numbers, our new weight variables will be numpy arrays. Each array will hold all the weights for its own layer — one weight for each synapse. Below we initialize each array with the numpy’s np.random.randn(rows, cols) method, which returns a matrix of random numbers drawn from a normal distribution with mean 0 and variance 1.

def init_weights():
    Wh = np.random.randn(INPUT_LAYER_SIZE, HIDDEN_LAYER_SIZE) * \
                np.sqrt(2.0/INPUT_LAYER_SIZE)
    Wo = np.random.randn(HIDDEN_LAYER_SIZE, OUTPUT_LAYER_SIZE) * \
                np.sqrt(2.0/HIDDEN_LAYER_SIZE)

Here’s an example calling random.randn():

arr = np.random.randn(1, 2)

print(arr)
>> [[-0.36094661 -1.30447338]]

print(arr.shape)
>> (1,2)

As you’ll soon see, there are strict requirements on the dimensions of these weight matrices. The number of rows must equal the number of neurons in the previous layer. The number of columns must match the number of neurons in the next layer.

A good explanation of random weight initalization can be found in the Stanford CS231 course notes [1] chapter on neural networks.

Bias Terms¶

Смещение (Bias) terms allow us to shift our neuron’s activation outputs left and right. This helps us model datasets that do not necessarily pass through the origin.

Using the numpy method np.full() below, we create two 1-dimensional bias arrays filled with the default value 0.2. The first argument to np.full is a tuple of array dimensions. The second is the default value for cells in the array.

def init_bias():
    Bh = np.full((1, HIDDEN_LAYER_SIZE), 0.1)
    Bo = np.full((1, OUTPUT_LAYER_SIZE), 0.1)
    return Bh, Bo

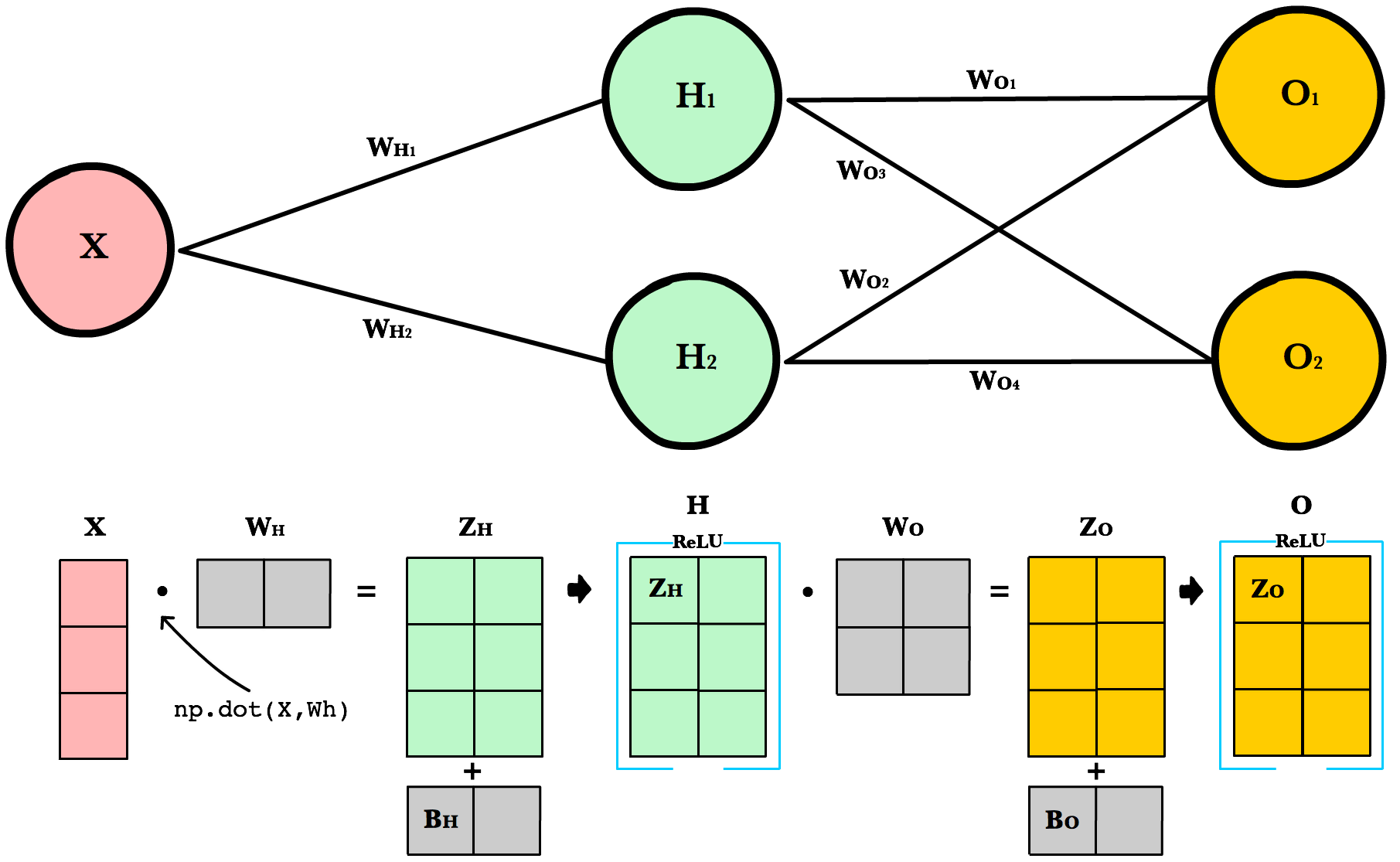
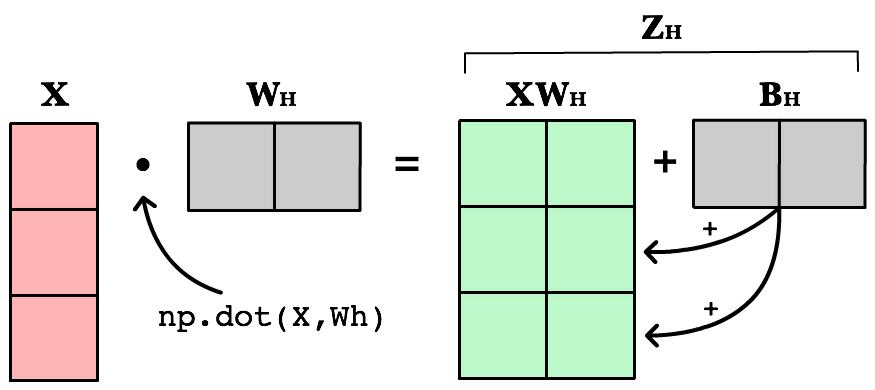
Working with Matrices¶

To take advantage of fast linear algebra techniques and GPUs, we need to store our inputs, weights, and biases in matrices. Here is our neural network diagram again with its underlying matrix representation.

What’s happening here? To better understand, let’s walk through each of the matrices in the diagram with an emphasis on their dimensions and why the dimensions are what they are. The matrix dimensions above flow naturally from the architecture of our network and the number of samples in our training set.

Matrix dimensions

Var	Name	Dimensions	Explanation
`X`	Input	(3, 1)	Includes 3 rows of training data, and each row has 1 attribute (height, price, etc.)
`Wh`	Hidden weights	(1, 2)	These dimensions are based on number of rows equals the number of attributes for the observations in our training set. The number columns equals the number of neurons in the hidden layer. The dimensions of the weights matrix between two layers is determined by the sizes of the two layers it connects. There is one weight for every input-to-neuron connection between the layers.
`Bh`	Hidden bias	(1, 2)	Each neuron in the hidden layer has is own bias constant. This bias matrix is added to the weighted input matrix before the hidden layer applies ReLU.
`Zh`	Hidden weighted input	(1, 2)	Computed by taking the dot product of X and Wh. The dimensions (1,2) are required by the rules of matrix multiplication. Zh takes the rows of in the inputs matrix and the columns of weights matrix. We then add the hidden layer bias matrix Bh.
`H`	Hidden activations	(3, 2)	Computed by applying the Relu function to Zh. The dimensions are (3,2) — the number of rows matches the number of training samples and the number of columns equals the number of neurons. Each column holds all the activations for a specific neuron.
`Wo`	Output weights	(2, 2)	The number of rows matches the number of hidden layer neurons and the number of columns equals the number of output layer neurons. There is one weight for every hidden-neuron-to-output-neuron connection between the layers.
`Bo`	Output bias	(1, 2)	There is one column for every neuron in the output layer.
`Zo`	Output weighted input	(3, 2)	Computed by taking the dot product of H and Wo and then adding the output layer bias Bo. The dimensions are (3,2) representing the rows of in the hidden layer matrix and the columns of output layer weights matrix.
`O`	Output activations	(3, 2)	Each row represents a prediction for a single observation in our training set. Each column is a unique attribute we want to predict. Examples of two-column output predictions could be a company’s sales and units sold, or a person’s height and weight.

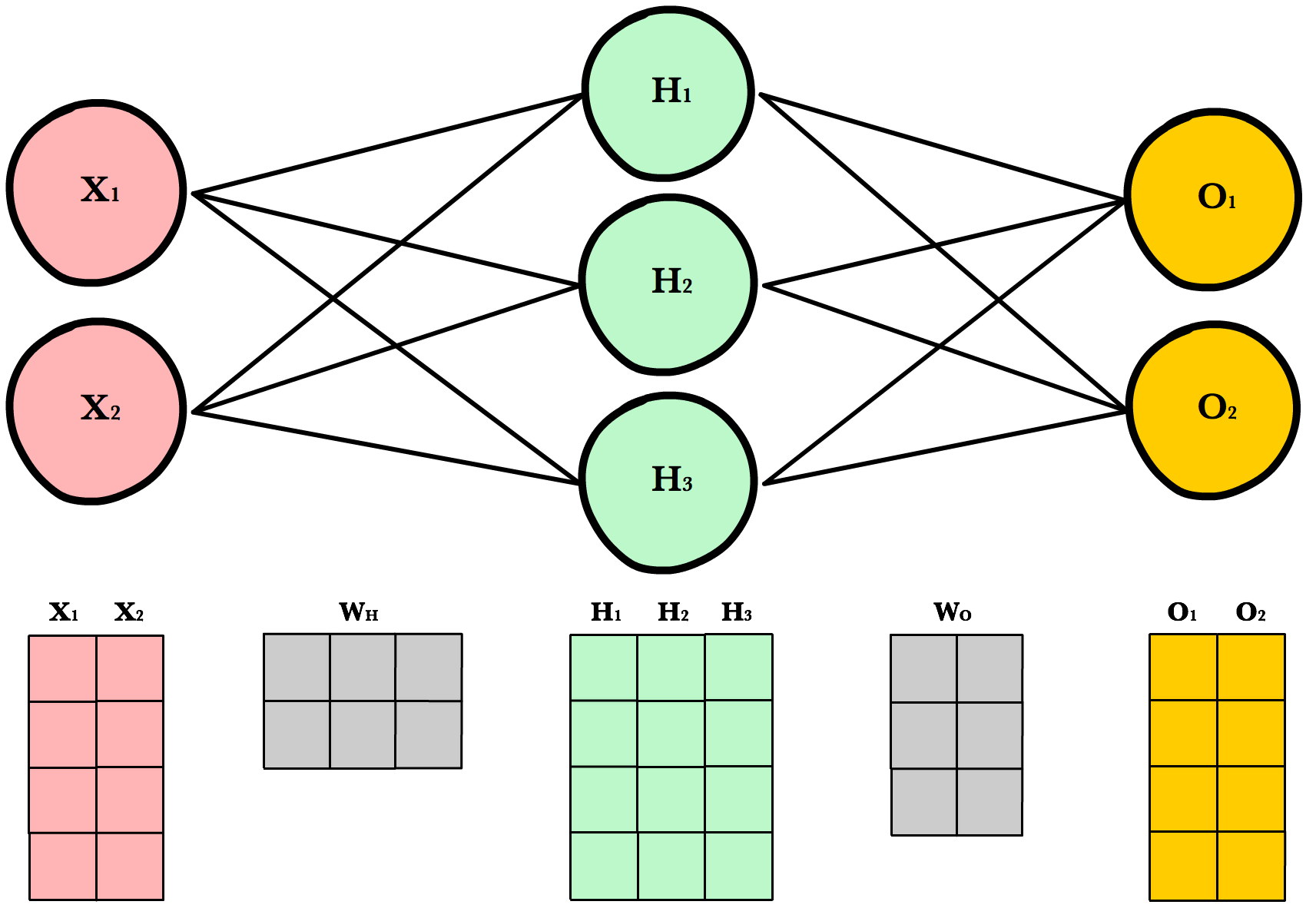
Dynamic Resizing¶

Before we continue I want to point out how the matrix dimensions change with changes to the network architecture or size of the training set. For example, let’s build a network with 2 input neurons, 3 hidden neurons, 2 output neurons, and 4 observations in our training set.

Now let’s use same number of layers and neurons but reduce the number of observations in our dataset to 1 instance:

As you can see, the number of columns in all matrices remains the same. The only thing that changes is the number of rows the layer matrices, which fluctuate with the size of the training set. The dimensions of the weight matrices remain unchanged. This shows us we can use the same network, the same lines of code, to process any number of observations.

Refactoring Our Code¶

Here is our new feed forward code which accepts matrices instead of scalar inputs.

def feed_forward(X):
    '''
    X    - input matrix
    Zh   - hidden layer weighted input
    Zo   - output layer weighted input
    H    - hidden layer activation
    y    - output layer
    yHat - output layer predictions
    '''

    # Hidden layer
    Zh = np.dot(X, Wh) + Bh
    H = relu(Zh)

    # Output layer
    Zo = np.dot(H, Wo) + Bo
    yHat = relu(Zo)
    return yHat

Weighted input

The first change is to update our weighted input calculation to handle matrices. Using dot product, we multiply the input matrix by the weights connecting them to the neurons in the next layer. Next we add the bias vector using matrix addition.

The first column in Bh is added to all the rows in the first column of resulting dot product of X and Wh. The second value in Bh is added to all the elements in the second column. The result is a new matrix, Zh which has a column for every neuron in the hidden layer and a row for every observation in our dataset. Given all the layers in our network are fully-connected, there is one weight for every neuron-to-neuron connection between the layers.

The same process is repeated for the output layer, except the input is now the hidden layer activation H and the weights Wo.

ReLU activation

The second change is to refactor ReLU to use elementwise multiplication on matrices. It’s only a small change, but its necessary if we want to work with matrices. np.maximum() is actually extensible and can handle both scalar and array inputs.

def relu(Z):
    return np.maximum(0, Z)

In the hidden layer activation step, we apply the ReLU activation function np.maximum(0,Z) to every cell in the new matrix. The result is a matrix where all negative values have been replaced by 0. The same process is repeated for the output layer, except the input is Zo.

Final Result¶

Putting it all together we have the following code for forward propagation with matrices.

INPUT_LAYER_SIZE = 1
HIDDEN_LAYER_SIZE = 2
OUTPUT_LAYER_SIZE = 2

def init_weights():
    Wh = np.random.randn(INPUT_LAYER_SIZE, HIDDEN_LAYER_SIZE) * \
                np.sqrt(2.0/INPUT_LAYER_SIZE)
    Wo = np.random.randn(HIDDEN_LAYER_SIZE, OUTPUT_LAYER_SIZE) * \
                np.sqrt(2.0/HIDDEN_LAYER_SIZE)


def init_bias():
    Bh = np.full((1, HIDDEN_LAYER_SIZE), 0.1)
    Bo = np.full((1, OUTPUT_LAYER_SIZE), 0.1)
    return Bh, Bo

def relu(Z):
    return np.maximum(0, Z)

def relu_prime(Z):
    '''
    Z - weighted input matrix

    Returns gradient of Z where all
    negative values are set to 0 and
    all positive values set to 1
    '''
    Z[Z < 0] = 0
    Z[Z > 0] = 1
    return Z

def cost(yHat, y):
    cost = np.sum((yHat - y)**2) / 2.0
    return cost

def cost_prime(yHat, y):
    return yHat - y

def feed_forward(X):
    '''
    X    - input matrix
    Zh   - hidden layer weighted input
    Zo   - output layer weighted input
    H    - hidden layer activation
    y    - output layer
    yHat - output layer predictions
    '''

    # Hidden layer
    Zh = np.dot(X, Wh) + Bh
    H = relu(Zh)

    # Output layer
    Zo = np.dot(H, Wo) + Bo
    yHat = relu(Zo)

References

[1]	http://cs231n.github.io/neural-networks-2/#init

Источник

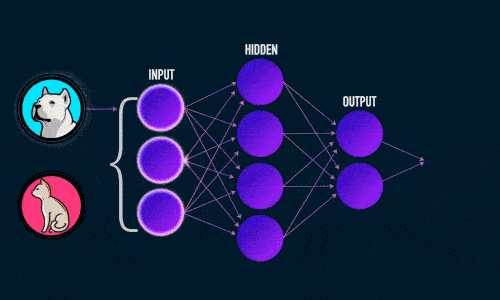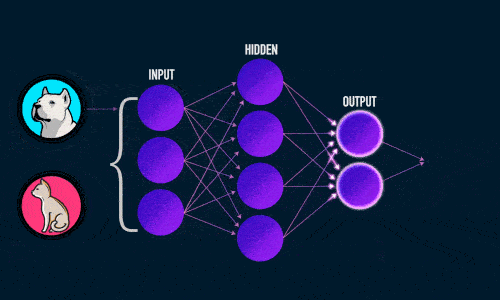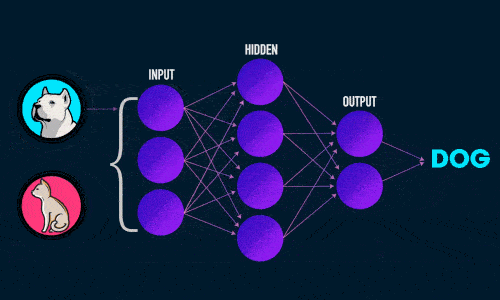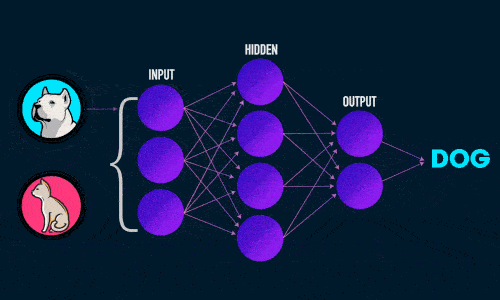
Нейронная сеть — попытка с помощью математических моделей воспроизвести работу человеческого мозга для создания машин, обладающих искусственным интеллектом.

Нейросеть обычно обучается с учителем. Это означает наличие обучающего набора данных (датасета), который содержит примеры с правильными результатами решений: ответами на вопросы, метками, сегментами, классами. Нейронная сеть пытается воспроизвести результат самостоятельно на новом наборе данных.

Неразмеченные наборы также используют для обучения нейронных сетей, но мы не будем здесь это рассматривать.

Например, если вы хотите создать нейросеть для оценки эмоциональную тональности текста, датасетом будет список предложений с соответствующими каждому эмоциональными оценками. Тональность текста определяют признаки (слова, фразы, структура предложения), которые придают негативную или позитивную окраску. Веса признаков в итоговой оценке тональности текста (позитивный, негативный, нейтральный) зависят от математической функции, которая вычисляется во время обучения нейронной сети.

Раньше люди генерировали признаки вручную. Чем больше признаков и точнее подобраны веса, тем точнее ответ. Нейронная сеть автоматизировала этот процесс.

Из чего состоит нейронная сеть

Искусственная нейронная сеть состоит из трех компонентов:

- Входной слой;
- Скрытые (вычислительные) слои;
- Выходной слой.

Обучение нейросети происходит в два этапа:

Прямое распространение ошибки;
Обратное распространение ошибки.

Во время прямого распространения ошибки делается предсказание ответа. При обратном распространении ошибка между фактическим ответом и предсказанным минимизируется.

Визуализация работы нейронной сети для классификации изображений:

Обучение: прямое распространение ошибки

Прямое распространение

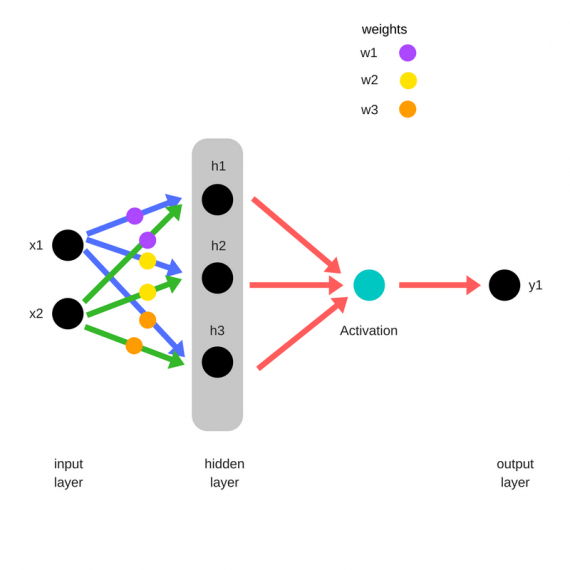
Зададим начальные веса случайным образом:

Умножим входные данные на веса для формирования скрытого слоя:

h1 = (x1 * w1) + (x2 * w1)
h2 = (x1 * w2) + (x2 * w2)
h3 = (x1 * w3) + (x2 * w3)

Выходные данные из скрытого слоя передается через нелинейную функцию (функцию активации), для получения выхода сети:

y_ = fn(h1 , h2, h3)

Обратное распространение

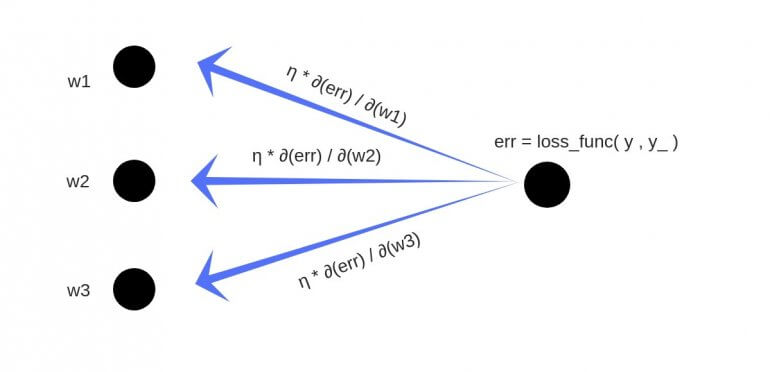
Суммарная ошибка (total_error) вычисляется как разность между ожидаемым значением «y» (из обучающего набора) и полученным значением «y_» (посчитанное на этапе прямого распространения ошибки), проходящих через функцию потерь (cost function).
Частная производная ошибки вычисляется по каждому весу (эти частные дифференциалы отражают вклад каждого веса в общую ошибку (total_loss)).
Затем эти дифференциалы умножаются на число, называемое скорость обучения или learning rate (η).

Полученный результат затем вычитается из соответствующих весов.

В результате получатся следующие обновленные веса:

w1 = w1 — (η * ∂(err) / ∂(w1))
w2 = w2 — (η * ∂(err) / ∂(w2))
w3 = w3 — (η * ∂(err) / ∂(w3))

То, что мы предполагаем и инициализируем веса случайным образом, и они будут давать точные ответы, звучит не вполне обоснованно, тем не менее, работает хорошо.

Популярный мем о том, как Карлсон стал Data Science разработчиком

bias Если вы знакомы с рядами Тейлора, обратное распространение ошибки имеет такой же конечный результат. Только вместо бесконечного ряда мы пытаемся оптимизировать только его первый член.

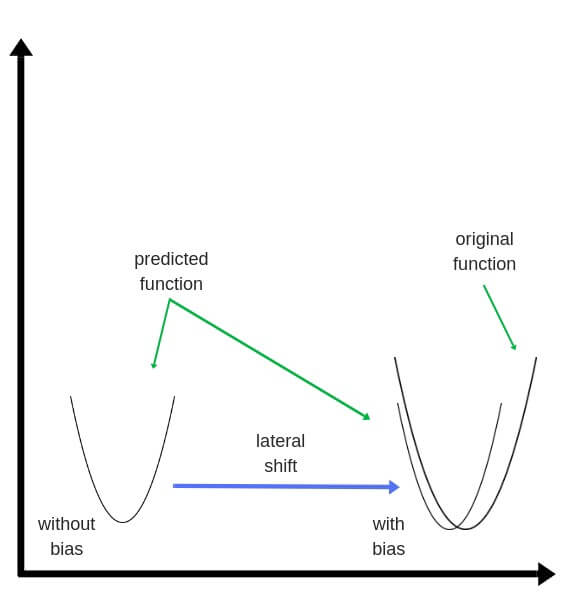
Смещения – это веса, добавленные к скрытым слоям. Они тоже случайным образом инициализируются и обновляются так же, как скрытый слой. Роль скрытого слоя заключается в том, чтобы определить форму базовой функции в данных, в то время как роль смещения – сдвинуть найденную функцию в сторону так, чтобы она частично совпала с исходной функцией.

Частные производные

Частные производные можно вычислить, поэтому известно, какой был вклад в ошибку по каждому весу. Необходимость производных очевидна. Представьте нейронную сеть, пытающуюся найти оптимальную скорость беспилотного автомобиля. Eсли машина обнаружит, что она едет быстрее или медленнее требуемой скорости, нейронная сеть будет менять скорость, ускоряя или замедляя автомобиль. Что при этом ускоряется/замедляется? Производные скорости.

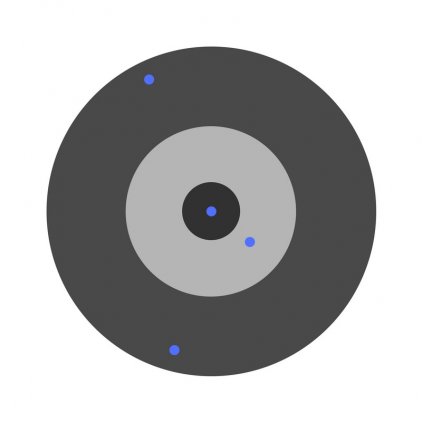
Разберем необходимость частных производных на примере.

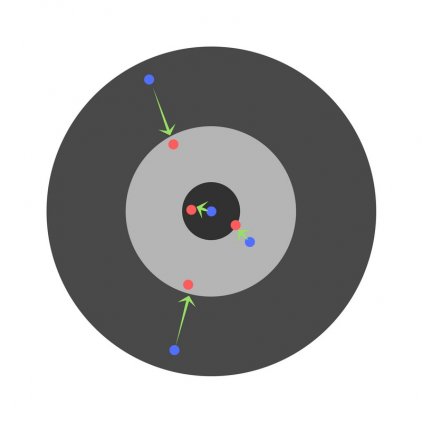
Предположим, детей попросили бросить дротик в мишень, целясь в центр. Вот результаты:

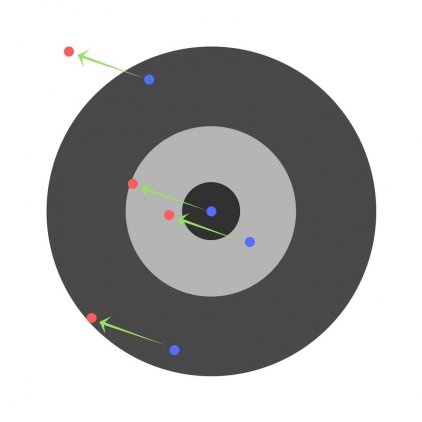
Теперь, если мы найдем общую ошибку и просто вычтем ее из всех весов, мы обобщим ошибки, допущенные каждым. Итак, скажем, ребенок попал слишком низко, но мы просим всех детей стремиться попадать в цель, тогда это приведет к следующей картине:

Ошибка нескольких детей может уменьшиться, но общая ошибка все еще увеличивается.

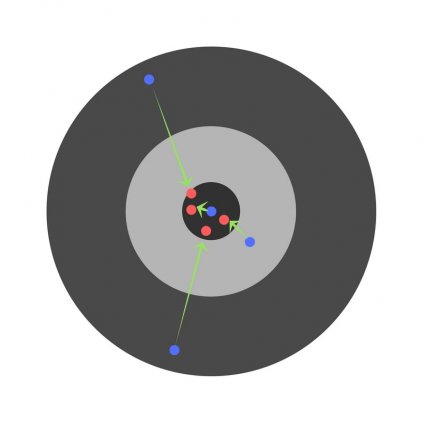
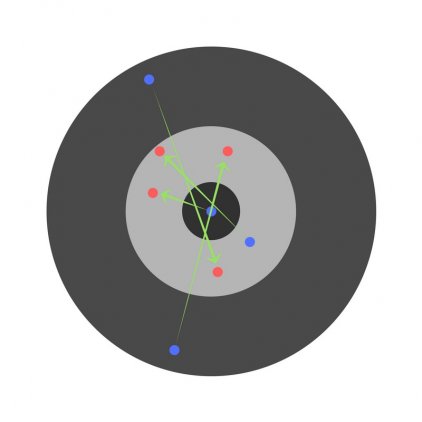
Найдя частные производные, мы узнаем ошибки, соответствующие каждому весу в отдельности. Если выборочно исправить веса, можно получить следующее:

Гиперпараметры нейронной сети

Нейронная сеть используется для автоматизации отбора признаков, но некоторые параметры настраиваются вручную.

Скорость обучения (learning rate) нейросети

Скорость обучения является очень важным гиперпараметром. Если скорость обучения слишком мала, то даже после обучения нейронной сети в течение длительного времени она будет далека от оптимальных результатов. Результаты будут выглядеть примерно так:

С другой стороны, если скорость обучения слишком высока, то сеть очень быстро выдаст ответы. Получится следующее:

Функция активации (activation function) нейронной сети

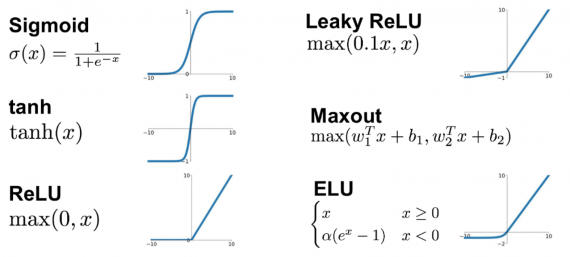
Функция активации — это один из самых мощных инструментов, который влияет на силу, приписываемую нейронным сетям. Отчасти, она определяет, какие нейроны будут активированы, другими словами и какая информация будет передаваться последующим слоям.

Без функций активации глубокие сети теряют значительную часть своей способности к обучению. Нелинейность этих функций отвечает за повышение степени свободы, что позволяет обобщать проблемы высокой размерности в более низких измерениях. Ниже приведены примеры распространенных функций активации:

Функция потери (loss function)

Функция потерь находится в центре нейронной сети. Она используется для расчета ошибки между реальными и полученными ответами. Наша глобальная цель — минимизировать эту ошибку. Таким образом, функция потерь эффективно приближает обучение нейронной сети к этой цели.

Функция потерь измеряет «насколько хороша» нейронная сеть в отношении данной обучающей выборки и ожидаемых ответов. Она также может зависеть от таких переменных, как веса и смещения.

Функция потерь одномерна и не является вектором, поскольку она оценивает, насколько хорошо нейронная сеть работает в целом.

Некоторые известные функции потерь:

Квадратичная (среднеквадратичное отклонение);
Кросс-энтропия;
Экспоненциальная (AdaBoost);
Расстояние Кульбака-Лейблера или прирост информации.

Cреднеквадратичное отклонение – самая простая функция потерь и наиболее часто используемая. Она задается следующим образом:

Функция потерь в нейронной сети должна удовлетворять двум условиям:

Функция потерь должна быть записана как среднее;
Функция потерь не должна зависеть от каких-либо активационных значений нейронной сети, кроме значений, выдаваемых на выходе.

Глубокая нейронная сеть

Глубокое обучение (deep learning) – это класс алгоритмов машинного обучения, которые учатся глубже (более абстрактно) понимать данные. Популярные алгоритмы нейронных сетей глубокого обучения представлены на схеме ниже.

Популярные алгоритмы нейронных сетей (http://www.asimovinstitute.org/neural-network-zoo)

Более формально в deep learning:

Используется каскад (пайплайн, как последовательно передаваемый поток) из множества обрабатывающих слоев (нелинейных) для извлечения и преобразования признаков;
Основывается на изучении признаков (представлении информации) в данных без обучения с учителем. Функции более высокого уровня (которые находятся в последних слоях) получаются из функций нижнего уровня (которые находятся в слоях начальных слоях);
Изучает многоуровневые представления, которые соответствуют разным уровням абстракции; уровни образуют иерархию представления.

Пример простой нейронной сети

Рассмотрим однослойную нейронную сеть:

Здесь, обучается первый слой (зеленые нейроны), он просто передается на выход.

В то время как в случае двухслойной нейронной сети, независимо от того, как обучается зеленый скрытый слой, он затем передается на синий скрытый слой, где продолжает обучаться:

Следовательно, чем больше число скрытых слоев, тем больше возможности обучения сети.

Не следует путать с широкой нейронной сетью.

В этом случае большое число нейронов в одном слое не приводит к глубокому пониманию данных. Но это приводит к изучению большего числа признаков.

Пример:

Изучая английскую грамматику, требуется знать огромное число понятий. В этом случае однослойная широкая нейронная сеть работает намного лучше, чем глубокая нейронная сеть, которая значительно меньше.

Но

В случае изучения преобразования Фурье, ученик (нейронная сеть) должен быть глубоким, потому что не так много понятий, которые нужно знать, но каждое из них достаточно сложное и требует глубокого понимания.

Главное — баланс

Очень заманчиво использовать глубокие и широкие нейронные сети для каждой задачи. Но это может быть плохой идеей, потому что:

Обе требуют значительно большего количества данных для обучения, чтобы достичь минимальной желаемой точности;
Обе имеют экспоненциальную сложность;
Слишком глубокая нейронная сеть попытается сломать фундаментальные представления, но при этом она будет делать ошибочные предположения и пытаться найти псевдо-зависимости, которые не существуют;
Слишком широкая нейронная сеть будет пытаться найти больше признаков, чем есть. Таким образом, подобно предыдущей, она начнет делать неправильные предположения о данных.

Проклятье размерности нейросети

Проклятие размерности относится к различным явлениям, возникающим при анализе и организации данных в многомерных пространствах (часто с сотнями или тысячами измерений), и не встречается в ситуациях с низкой размерностью.

Грамматика английского языка имеет огромное количество аттрибутов, влияющих на нее. В машинном обучении мы должны представить их признаками в виде массива/матрицы конечной и существенно меньшей длины (чем количество существующих признаков). Для этого сети обобщают эти признаки. Это порождает две проблемы:

Из-за неправильных предположений появляется смещение. Высокое смещение может привести к тому, что алгоритм пропустит существенную взаимосвязь между признаками и целевыми переменными. Это явление называют недообучение.
От небольших отклонений в обучающем множестве из-за недостаточного изучения признаков увеличивается дисперсия. Высокая дисперсия ведет к переобучению, ошибки воспринимаются в качестве надежной информации.

Компромисс

На ранней стадии обучения смещение велико, потому что выход из сети далек от желаемого. А дисперсия очень мала, поскольку данные имеет пока малое влияние.

В конце обучения смещение невелико, потому что сеть выявила основную функцию в данных. Однако, если обучение слишком продолжительное, сеть также изучит шум, характерный для этого набора данных. Это приводит к большому разбросу результатов при тестировании на разных множествах, поскольку шум меняется от одного набора данных к другому.

Действительно,

алгоритмы с большим смещением обычно в основе более простых моделей, которые не склонны к переобучению, но могут недообучиться и не выявить важные закономерности или свойства признаков. Модели с маленьким смещением и большой дисперсией обычно более сложны с точки зрения их структуры, что позволяет им более точно представлять обучающий набор. Однако они могут отображать много шума из обучающего набора, что делает их прогнозы менее точными, несмотря на их дополнительную сложность.

Как правило, невозможно иметь маленькое смещение и маленькую дисперсию одновременно.

Есть множество инструментов, с помощью которых можно легко создать сложные модели машинного обучения, переобучение занимает центральное место. Поскольку смещение появляется, когда сеть не получает достаточно информации. Но чем больше примеров, тем больше появляется вариантов зависимостей и изменчивостей в этих корреляциях.

Источник

Говорим о нейронных сетях: легкая подача сложной информации так, что поймет даже ребенок. Изучаем базис и углубляемся в тему с нуля.

Источник изображения

Машинное обучение, data science, нейронные сети – эти сферы не только крайне интересные, но и довольно сложные. Остановимся на нейронных сетях: объясним, что это такое, и расскажем об основных понятиях. Нет времени читать и готовы сразу перейти к практике? Обратите внимание на курс Deep Learning и нейронные сети.

Нейрон – базовая единица нейронной сети. У каждого нейрона есть определённое количество входов, куда поступают сигналы, которые суммируются с учётом значимости (веса) каждого входа. Далее сигналы поступают на входы других нейронов. Вес каждого такого «узла» может быть как положительным, так и отрицательным. Например, если у нейрона есть четыре входа, то у него есть и четыре весовых значения, которые можно регулировать независимо друг от друга.

Искусственная нейронная сеть имитирует работу естественной нейронной сети – человеческого мозга – и используется для создания машин с искусственным интеллектом. Как правило, для обучения ИИ нужен «учитель» – набор информации с определёнными параметрами, значениями и показателями.

Соединения связывают нейроны между собой. Значение веса напрямую связано с соединением, а цель обучения – обновить вес каждого соединения, чтобы в дальнейшем не допускать ошибок.

Источник изображения

Смещение – это дополнительный вход для нейрона, который всегда равен 1 и, следовательно, имеет собственный вес соединения. Это гарантирует, что даже когда все входы будут равны нулю, нейрон будет активен.

Функция активации используется для того, чтобы ввести нелинейность в нейронную сеть. Она определяет выходное значение нейрона, которое будет зависеть от суммарного значения входов и порогового значения.

Также эта функция определяет, какие нейроны нужно активировать, и, следовательно, какая информация будет передана следующему слою. Благодаря функции активации глубокие сети могут обучаться.

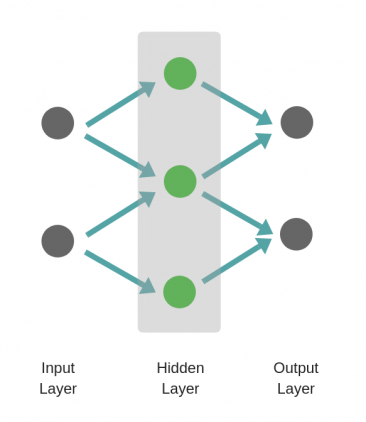
Входной слой – это первый слой в нейронной сети, который принимает входящие сигналы и передает их на последующие уровни.

Скрытый (вычислительный) слой применяет различные преобразования ко входным данным. Все нейроны в скрытом слое связаны с каждым нейроном в следующем слое.

Выходной слой – последний слой в сети, который получает данные от последнего скрытого слоя. С его помощью мы сможем получить нужное количество значений в желаемом диапазоне.

Вес представляет силу связи между нейронами. Например, если вес соединения узлов 1 и 3 больше, чем узлов 2 и 3, это значит, что нейрон 1 оказывает на нейрон 3 большее влияние. Нулевой вес означает, что изменения входа не повлияют на выход. Отрицательный вес показывает, что увеличение входа уменьшит выход. Вес определяет влияние ввода на вывод.

Прямое распространение – это процесс передачи входных значений в нейронную сеть и получения выходных данных, которые называются прогнозируемым значением. Когда входные значения передаются в первый слой нейронной сети, процесс проходит без каких-либо операций. Второй уровень сети принимает значения первого уровня, а после операций по умножению и активации передает значения далее. Тот же процесс происходит на более глубоких слоях.

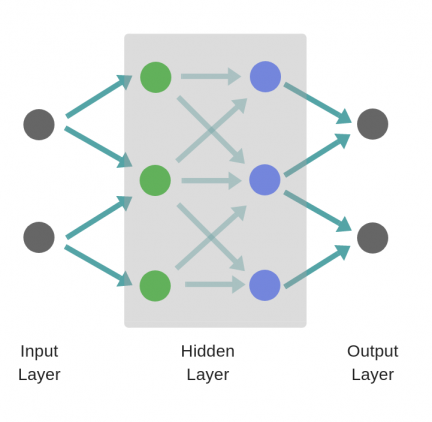
Обратное распространение ошибки. После прямого распространения мы получаем значение, которое называется прогнозируемым. Чтобы вычислить ошибку, мы сравниваем прогнозируемое значение с фактическим с помощью функции потери. Затем мы можем вычислить производную от значения ошибки по каждому весу в нейронной сети.

В методе обратного распространения ошибки используются правила дифференциального исчисления. Градиенты (производные значений ошибок) вычисляются по значениям веса последнего слоя нейронной сети (сигналы ошибки распространяются в направлении, обратном прямому распространению сигналов) и используются для вычисления градиентов слоев.

Этот процесс повторяется до тех пор, пока не будут вычислены градиенты каждого веса в нейронной сети. Затем значение градиента вычитают из значения веса, чтобы уменьшить значение ошибки. Ээто позволяет добиться минимальных потерь.

Скорость обучения – это характеристика, которая используется во время обучения нейронных сетей. Она определяет, как быстро будет обновлено значение веса в процессе обратного распространения. Скорость обучения должна быть высокой, но не слишком, иначе алгоритм будет расходиться. При слишком маленькой скорости обучения алгоритм будет сходиться очень долго и застревать в локальных минимумах.

Источник изображения

Конвергенция – это явление, когда в процессе итерации выходной сигнал становится все ближе к определенному значению. Чтобы не возникло переобучения (проблем работы с новыми данными из-за высокой скорости), используют регуляризацию – понижение сложности модели с сохранением параметров. При этом учитываются потеря и вектор веса (вектор изученных параметров в данном алгоритме).

Нормализация данных – процесс изменения масштаба одного или нескольких параметров в диапазоне от 0 до 1. Этот метод стоит использовать в том случае, если вы не знаете, как распределены ваши данные. Также с его помощью можно ускорить обучение.

Стоит упомянуть и о таком термине, как полностью связанные слои. Это значит, что активность всех узлов в одном слое переходит на каждый узел в следующем. В таком случае слои будут полностью связанными.

С помощью функции потери вы можете вычислить ошибку в конкретной части обучения. Это среднее значение функции для обучения:

‘mse’ – для квадратичной ошибки;
‘binary_crossentropy’ – для двоичной логарифмической;
‘categorical_crossentropy’ – для мультиклассовой логарифмической.

Для обновления весов в модели используются оптимизаторы:

SGD (Stochastic Gradient Descent) для оптимизации импульса.
RMSprop – адаптивная оптимизация скорости обучения по методу Джеффа Хинтона.
Adam – адаптивная оценка моментов, которая также использует адаптивную скорость обучения.

Для измерения производительности нейронной сети используются метрики производительности. Точность, потеря, точность проверки, оценка — это лишь некоторые показатели.

Batch size – количество обучающих примеров за одну итерацию. Чем больше batch size, тем больше места будет необходимо.

Количество эпох показывает, сколько раз модель подвергается воздействию обучения. Эпоха – один проход вперёд или назад для всех примеров обучения.

Так что же такое искусственная нейронная сеть? Это система нейронов, которые взаимодействуют между собой. Каждый нейрон принимает сигналы или же отправляет их другим процессорам (нейронам). Объединённые в одну большую сеть, нейроны, обучаясь, могут выполнять сложные задачи.

Углубиться в сферу искусственного интеллекта и наработать практические навыки по программированию глубоких нейронных сетей вы можете на специализированном курсе Deep Learning и нейронные сети, где познакомитесь с основными библиотеками для Deep Learning, такими как TensorFlow, Keras и другими.

Источник

Все курсы > Вводный курс > Занятие 21

В завершающей лекции вводного курса ML мы изучим основы нейронных сетей (neural network), более сложных алгоритмов машинного обучения.

Алгоритмы нейронных сетей принято относить к области глубокого обучения (deep learning). Все изученные нами ранее алгоритмы относятся к так называемому традиционному машинному обучению (traditional machine learning).

Прежде чем перейти к этому занятию, настоятельно рекомендую пройти предыдущие уроки вводного курса.

Смысл, структура и принцип работы

Смысл алгоритма нейронной сети такой же, как и у классических алгоритмов. Мы также имеем набор данных и цель, которой хотим добиться, обучив наш алгоритм (например, предсказать число или отнести объект к определенному классу).

Отличие нейросети от других алгоритмов заключается в ее структуре.

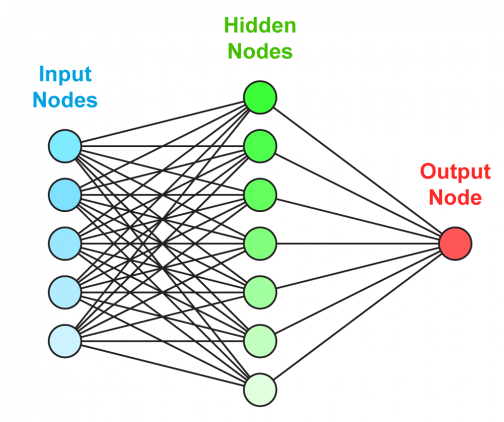
Как мы видим, нейронная сеть состоит из нейронов, сгруппированных в слои (layers), у нее есть входной слой (input layer), один или несколько скрытых слоев (hidden layers) и выходной слой (output layer). Каждый нейрон связан с нейронами предыдущего слоя через определенные веса.

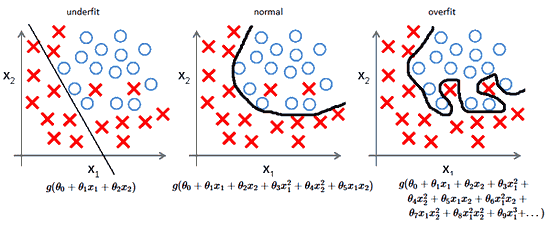
Количество слоев и нейронов не ограничено. Эта особенность позволяет нейронной сети моделировать очень сложные закономерности, с которыми бы не справились, например, линейные модели.

Функционирует нейросеть следующим образом.

На первом этапе данные подаются в нейроны входного слоя (x и y) и умножаются на соответствующие веса (w₁, w₂, w₃, w₄). Полученные произведения складываются. К результату прибавляется смещение (bias, в данном случае b₁ и b₂).

$$ w_{1}\cdot x + w_{3}\cdot y + b_{1} $$

$$ w_{2}\cdot x + w_{4}\cdot y + b_{2} $$

Получившаяся сумма подаётся в функцию активации (activation function) для ограничения диапазона и стабилизации результата. Этот результат записывается в нейроны скрытого слоя (h₁ и h₂).

$$ h_{1} = actfun(w_{1}\cdot x + w_{3}\cdot y + b_{1}) $$

$$ h_{2} = actfun(w_{2}\cdot x + w_{4}\cdot y + b_{2}) $$

На втором этапе процесс повторяется для нейронов скрытого слоя (h₁ и h₂), весов (w₅ и w₆) и смещения (b₃) до получения конечного результата (r).

$$ r = actfun(w_{5}\cdot h_{1} + w_{6}\cdot h_{2} + b_{3}) $$

Описанная выше нейронная сеть называется персептроном (perceptron). Эта модель стремится повторить восприятие информации человеческим мозгом и учитывает три этапа такого процесса:

Восприятие информации через сенсоры (входной слой)
Создание ассоциаций (скрытый слой)
Реакцию (выходной слой)

Основы нейронных сетей на простом примере

Приведем пример очень простой нейронной сети, которая на входе получает рост и вес человека, а на выходе предсказывает пол. Скрытый слой в данном случае мы использовать не будем.

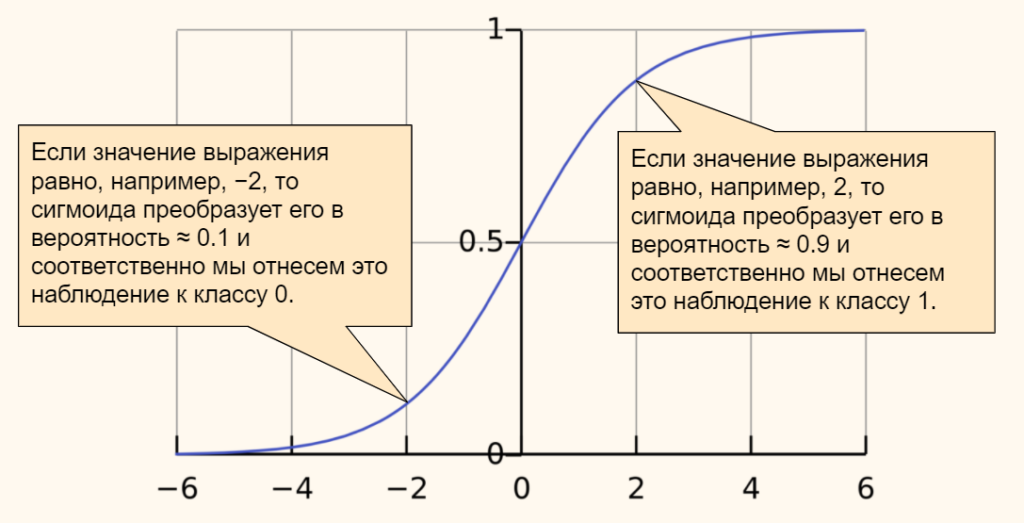
В качестве функции активации мы возьмём сигмоиду. Ее часто используют в задачах бинарной (состоящей из двух классов) классификации. Приведем формулу.

$$ f(x) = \frac{\mathrm{1} }{\mathrm{1} + e^{-x}} $$

График сигмоиды выглядит следующим образом.

Эта функция преобразует любые значения в диапазон (или вероятность) от 0 до 1. В случае задачи классификации, если результат (вероятность) близок к нулю, мы отнесем наблюдение к одному классу, если к единице, то к другому. Граница двух классов пройдет на уровне 0,5.

Общее уравнение нейросети выглядит следующим образом.

$$ r = sigmoid(w_{1}\cdot weight + w_{2}\cdot height + bias) $$

Теперь предположим, что у нас есть следующие данные и параметры нейросети.

Откроем ноутбук к этому занятию⧉

# даны вес и рост трех человек

# единицей мы обозначим мужской пол, а нулем — женский.

data = {

‘Иван’: [84, 180, 1],

‘Мария’: [57, 165, 0],

‘Анна’: [62, 170, 0]

}

# и даны следующие веса и смещение

w1, w2, b = 0.3, 0.1, —39

Пропустим первое наблюдение через нашу нейросеть. Следуя описанному выше процессу, вначале умножим данные на соответствующие веса и прибавим смещение.

r = w1 * data[‘Иван’][0] + w2 * data[‘Иван’][1] + b

Теперь к полученному результату (r) применим сигмоиду.

np.round(1 / (1 + np.exp(—r)), 3)

Результат близок к единице, значит пол мужской. Модель сделала верный прогноз. Повторим эти вычисления для каждого из наблюдений.

# пройдемся по ключам и значениям нашего словаря с помощью метода .items()

for k, v in data.items():

# вначале умножим каждую строчку данных на веса и прибавим смещение

r1 = w1 * v[0] + w2 * v[1] + b

# затем применим сигмоиду

r2 = 1 / (1 + np.exp(—r1))

# если результат больше 0,5, модель предскажет мужской пол

if r2 > 0.5:

print(k, np.round(r2, 3), ‘male’)

# в противном случае, женский

else:

print(k, np.round(r2, 3), ‘female’)

Иван 0.985 male

Мария 0.004 female

Анна 0.032 female

Как мы видим, модель отработала верно.

Обучение нейронной сети

В примере выше был описан первый этап работы нейронной сети, называемый прямым распространением (forward propagation).

И кажется, что этого достаточно. Модель справилась с поставленной задачей. Однако, обратите внимание, веса были подобраны заранее и никаких дополнительных действий от нас не потребовалось.

В реальности начальные веса выбираются случайно и отклонение истинного результата от расчетного (т.е. ошибка) довольно велико.

Как и с обычными алгоритмами ML, для построения модели, нам нужно подобрать идеальные веса или заняться оптимизацией. Применительно к нейронным сетям этот процесс называется обратным распространением (back propagation).

В данном случае мы как бы двигаемся в обратную сторону и, уже зная результат (и уровень ошибки), с учётом имеющихся данных рассчитываем, как нам нужно изменить веса и смещения, чтобы уровень ошибки снизился.

Для того чтобы математически описать процесс оптимизации, нам не хватает знаний математического анализа (calculus) и, если говорить более точно, понятия производной (derivative).

Затем, уже с новыми весами, мы снова повторяем весь процесс forward propagation слева направо и снова рассчитываем ошибку. После этого мы вновь меняем веса в ходе back propagation.

Эти итерации повторяются до тех пор, пока ошибка не станет минимальной, а веса не будут подобраны идеально.

Создание нейросети в библиотеке Keras

Теперь давайте попрактикуемся в создании и обучении нейронной сети с помощью библиотеки Keras. В первую очередь установим необходимые модули и библиотеки.

# установим библиотеку tensorflow (через нее мы будем пользоваться keras) и модуль mnist

!pip install tensorflow mnist

И импортируем их.

# импортируем рукописные цифры

import mnist

# и библиотеку keras

from tensorflow import keras

1. Подготовка данных

Как вы вероятно уже поняли, сегодня мы снова будем использовать уже знакомый нам набор написанных от руки цифр MNIST (только на этот раз воспользуемся не библиотекой sklearn, а возьмем отдельный модуль).

В модуле MNIST содержатся чёрно-белые изображения цифр от 0 до 9 размером 28 х 28 пикселей. Каждый пиксель может принимать значения от 0 (черный) до 255 (белый).

Данные в этом модуле уже разбиты на тестовую и обучающую выборки. Посмотрим на обучающий набор данных.

# сохраним обучающую выборку и соответсвующую целевую переменную

X_train = mnist.train_images()

y_train = mnist.train_labels()

# посмотрим на размерность

print(X_train.shape)

print(y_train.shape)

Как мы видим, обучающая выборка содержит 60000 изображений и столько же значений целевой переменной. Теперь посмотрим на тестовые данные.

# сделаем то же самое с тестовыми данными

X_test = mnist.test_images()

y_test = mnist.test_labels()

# и также посмотрим на размерность

print(X_test.shape)

print(y_test.shape)

Таких изображений и целевых значений 10000.

Посмотрим на сами изображения.

# создадим пространство для четырех картинок в один ряд

fig, axes = plt.subplots(1, 4, figsize = (10, 3))

# в цикле for создадим кортеж из трех объектов: id изображения (всего их будет 4), самого изображения и

# того, что на нем представлено (целевой переменной)

for ax, image, label in zip(axes, X_train, y_train):

# на каждой итерации заполним соответствующее пространство картинкой

ax.imshow(image, cmap = ‘gray’)

# и укажем какой цифре соответствует изображение с помощью f форматирования

ax.set_title(f‘Target: {label}’)

Нейросети любят, когда диапазон входных значений ограничен (нормализован). В частности, мы можем преобразовать диапазон [0, 255] в диапазон от [–1, 1]. Сделать это можно по следующей формуле.

$$ x’ = 2 \frac {x-min(x)}{max(x)-min(x)}-1 $$

Применим эту формулу к нашим данным.

# функция np.min() возвращает минимальное значение,

# np.ptp() — разницу между максимальным и минимальным значениями (от англ. peak to peak)

X_train = 2. * (X_train — np.min(X_train)) / np.ptp(X_train) — 1

X_test = 2. * (X_test — np.min(X_test)) / np.ptp(X_test) — 1

Посмотрим на новый диапазон.

# снова воспользуемся функцией np.ptp()

np.ptp(X_train)

Теперь нам необходимо «вытянуть» изображения и превратить массивы, содержащие три измерения, в двумерные матрицы. Мы уже делали это на занятии по компьютерному зрению.

Применим этот метод к нашим данным.

# «вытянем» (flatten) наши изображения, с помощью метода reshape

# у нас будет 784 столбца (28 х 28), количество строк Питон посчитает сам (-1)

X_train = X_train.reshape((—1, 784))

X_test = X_test.reshape((—1, 784))

# посмотрим на результат

print(X_train.shape)

print(X_test.shape)

Посмотрим на получившиеся значения пикселей.

# выведем первое изображение [0], пиксели с 200 по 209

X_train[0][200:210]

array([—1. , —1. , —1. , —0.61568627, 0.86666667,

0.98431373, 0.98431373, 0.98431373, 0.98431373, 0.98431373])

Наши данные готовы. Теперь нужно задать конфигурацию модели.

2. Конфигурация нейронной сети

Существует множество различных архитектур нейронных сетей. Пока что мы познакомились с персептроном или в более общем смысле нейросетями прямого распространения (Feed Forward Neural Network, FFNN), в которых данные (сигнал) поступают строго от входного слоя к выходному.

Такую же сеть мы и будем использовать для решения поставленной задачи. В частности, на входе мы будем одновременно подавать 784 значения, которые затем будут проходить через два скрытых слоя по 64 нейрона каждый и поступать в выходной слой из 10 нейронов (по одному для каждой из цифр или классов).

В первую очередь воспользуемся классом Sequential библиотеки Keras, который укажет, что мы задаём последовательно связанные между собой слои.

# импортируем класс Sequential

from tensorflow.keras.models import Sequential

# и создадим объект этого класса

model = Sequential()

Далее нам нужно прописать сами слои и связи между нейронами.

Тип слоя Dense, который мы будем использовать, получает данные со всех нейронов предыдущего слоя. Функцией активации для скрытых слоев будет уже известная нам сигмоида.

# импортируем класс Dense

from tensorflow.keras.layers import Dense

# и создадим первый скрытый слой (с указанием функции активации и размера входного слоя)

model.add(Dense(64, activation = ‘sigmoid’, input_shape = (784,)))

# затем второй скрытый слой

model.add(Dense(64, activation = ‘sigmoid’))

# и наконец выходной слой

model.add(Dense(10, activation = ‘softmax’))

Выходной слой будет состоять из 10 нейронов, по одному для каждого из классов (цифры от 0 до 9). В качестве функции активации будет использована новая для нас функция softmax (softmax function).

Если сигмоида подходит для бинарной классификации, то softmax применяется для задач многоклассовой классификации. Приведем формулу.

$$ \text{softmax}(\vec{z})_{i} = \frac{e^{z_i}}{\sum_{j=1}^K e^{z_i}} $$

Функция softmax на входе принимает вектор действительных чисел (z), применяет к каждому из элементов z_i экспоненциальную функцию и нормализует результат через деление на сумму экспоненциальных значений каждого из элементов.

На выходе получается вероятностное распределение любого количества классов (K), причем каждое значение находится в диапазоне от 0 до 1, а сумма всех значений равна единице. Приведем пример для трех классов.

Очевидно, вероятность того, что это кошка, выше. Теперь, когда мы задали архитектуру сети, необходимо заняться ее настройками.

Работа над ошибками. Внимательный читатель безусловно обратил внимание, что вероятности на картинке не соответствуют приведенным в векторе значениям. Если подставить эти числа в формулу softmax вероятности будут иными.

z = ([1, 2, 0.5])

np.exp(z) / sum(np.exp(z))

array([0.2312239 , 0.62853172, 0.14024438])

Впрочем, алгоритм по-прежнему уверен, что речь идет о кошке.

3. Настройки

Настроек будет три:

тип функции потерь (loss function) определяет, как мы будем считать отклонение прогнозного значения от истинного
способ или алгоритм оптимизации этой функции (optimizer) поможет снизить потерю или ошибку и подобрать правильные веса в процессе back propagation
метрика (metric) покажет, насколько точна наша модель

Функция потерь

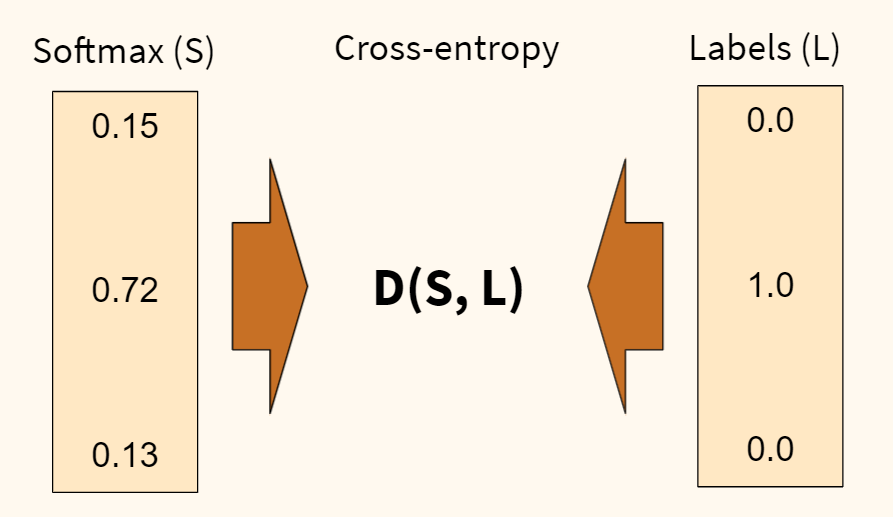
В первую очередь, определимся с функцией потерь. Раньше, например, в задаче регрессии, мы использовали среднеквадратическую ошибку (MSE). Для задач классификации мы будем использовать функцию потерь, называемую перекрестной или кросс-энтропией (cross-entropy). Продолжим пример с собакой, кошкой и попугаем.

Функция перекрестной энтропии (D) показывает степень отличия прогнозного вероятностного распределения (которое мы получили на выходе функции softmax (S)) от истинного (наша целевая переменная (L)). Чем больше отличие, тем выше ошибка.

Также обратите внимание, наша целевая переменная закодирована, вместо слова «кошка» напротив соответсвующего класса стоит единица, а напротив остальных классов — нули. Такая запись называется унитарным кодом, хотя чаще используется анлийский термин one-hot encoding.

Когда мы будем обучать наш алгоритм, мы также применим эту кодировку к нашим данным. Например, если в целевой переменной содержится цифра пять, то ее запись в one-hot encoding будет следующей.

В дополнение замечу, что функция кросс-энтропии, в которой применяется one-hot encoding, называется категориальной кросс-энтропией (categorical cross-entropy).

Отлично! С тем как мы будем измерять уровень ошибки (качество обучения) нашей модели, мы определились. Теперь нужно понять, как мы эту ошибку будем минимизировать. Для этого существует несколько алгоритмов оптимизации.

Алгоритм оптимизации

Классическим алгоритмом является, так называемый, метод стохастического градиентного спуска (Stochastic Gradient Descent или SGD).

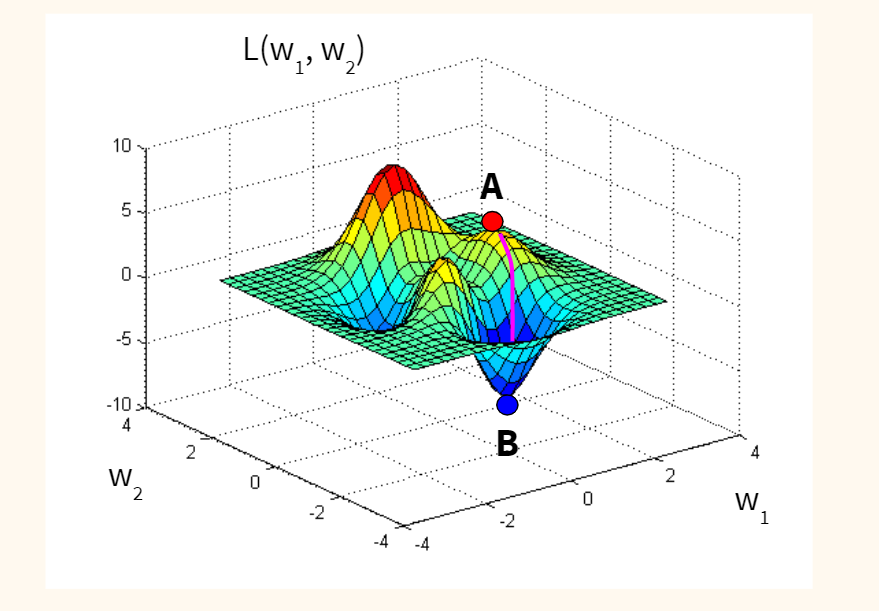
Если предположить для простоты, что наша функция потерь оптимизирует один вес исходной модели, и мы находимся изначально в точке А (с неидеальным случайным весом), то наша задача — оказаться в точке B, где ошибка (L) минимальна, а вес (w) оптимален.

Спускаться мы будем вдоль градиента, то есть по кратчайшему пути. Идею градиента проще увидеть на функции с двумя весами. Такая функция имеет уже три измерения (две независимых переменных, w₁ и w₂, и одну зависимую, L) и графически похожа на «холмистую местность», по которой мы будем спускаться по наиболее оптимальному маршруту.

Стохастичность (или случайность) этого алгоритма заключается в том, что мы берем не всю выборку для обновления весов модели, а лишь одно или несколько случайных наблюдений. Такой подход сильно сокращает время оптимизации.

Метрика

Остается определиться с метрикой качества. Здесь мы просто возьмём знакомую нам метрику accuracy, которая посчитает долю правильно сделанных прогнозов.

Посмотрим на используемый код.

model.compile(

loss = ‘categorical_crossentropy’,

optimizer = ‘sgd’,

metrics = [‘accuracy’]

)

4. Обучение модели

Теперь давайте соберём все описанные выше элементы и посмотрим на работу модели в динамике. Повторим ещё раз изученные выше шаги.

Значения пикселей каждого изображения поступают в 784 нейрона входного слоя
Далее они проходят через скрытые слои, где они умножаются на веса, складываются, смещаются и поступают в соответствующую функцию активации
На выходе из функции softmax мы получаем вероятности для каждой из цифр
После этого результат сравнивается с целевой переменной с помощью функции перекрестной энтропии (функции потерь); делается расчет ошибки
На следующем шаге алгоритм оптимизации стремится уменьшить ошибку и соответствующим образом изменяет веса
После этого процесс повторяется, но уже с новыми весами.

Давайте выполним все эти операции в библиотеке Keras.

# вначале импортируем функцию to_categorical, чтобы сделать one-hot encoding

from tensorflow.keras.utils import to_categorical

# обучаем модель

model.fit(

X_train, # указываем обучающую выборку

to_categorical(y_train), # делаем one-hot encoding целевой переменной

epochs = 10 # по сути, эпоха показывает сколько раз алгоритм пройдется по всем данным

)

Epoch 1/10

1875/1875 [==============================] — 4s 2ms/step — loss: 2.0324 — accuracy: 0.4785

Epoch 2/10

1875/1875 [==============================] — 3s 2ms/step — loss: 1.2322 — accuracy: 0.7494

Epoch 3/10

1875/1875 [==============================] — 3s 2ms/step — loss: 0.7617 — accuracy: 0.8326

Epoch 4/10

1875/1875 [==============================] — 3s 2ms/step — loss: 0.5651 — accuracy: 0.8663

Epoch 5/10

1875/1875 [==============================] — 3s 2ms/step — loss: 0.4681 — accuracy: 0.8827

Epoch 6/10

1875/1875 [==============================] — 3s 2ms/step — loss: 0.4121 — accuracy: 0.8923

Epoch 7/10

1875/1875 [==============================] — 3s 2ms/step — loss: 0.3751 — accuracy: 0.8995

Epoch 8/10

1875/1875 [==============================] — 3s 2ms/step — loss: 0.3487 — accuracy: 0.9045

Epoch 9/10

1875/1875 [==============================] — 3s 2ms/step — loss: 0.3285 — accuracy: 0.9090

Epoch 10/10

1875/1875 [==============================] — 3s 2ms/step — loss: 0.3118 — accuracy: 0.9129

<keras.callbacks.History at 0x7f36c3f09490>

На обучающей выборке мы добились неплохого результата, 91.29%.

5. Оценка качества модели

На этом шаге нам нужно оценить качество модели на тестовых данных.

# для оценки модели воспользуемся методом .evaluate()

model.evaluate(

X_test, # который применим к тестовым данным

to_categorical(y_test) # не забыв закодировать целевую переменную через one-hot encoding

)

313/313 [==============================] — 1s 1ms/step — loss: 0.2972 — accuracy: 0.9173

[0.29716429114341736, 0.9172999858856201]

Результат «на тесте» оказался даже чуть выше, 91,73%.

6. Прогноз

Теперь давайте в качестве упражнения сделаем прогноз.

# передадим модели последние 10 изображений тестовой выборки

pred = model.predict(X_test[—10:])

# посмотрим на результат для первого изображения из десяти

pred[0]

array([1.0952151e-04, 2.4856537e-04, 1.5749732e-03, 7.4032680e-03,

6.2553445e-05, 8.7646207e-05, 9.4199123e-07, 9.7065586e-01,

5.3100550e-04, 1.9325638e-02], dtype=float32)

Работа над ошибками. На видео я говорю про первые десять изображений. Разумеется, это неверно. Срез [-10:] выводит последние десять изображений.

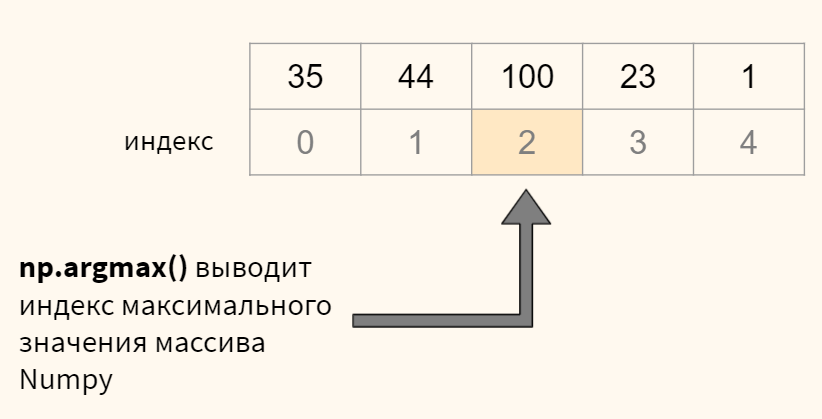
В переменной pred содержится массив numpy с десятью вероятностями для каждого из десяти наблюдений. Нам нужно выбрать максимальную вероятность для каждого изображения и определить ее индекс (индекс и будет искомой цифрой). Все это можно сделать с помощью функции np.argmax(). Посмотрим на примере.

Теперь применим к нашим данным.

# для кажого изображения (то есть строки, axis = 1)

# выведем индекс (максимальное значение), это и будет той цифрой, которую мы прогнозируем

print(np.argmax(pred, axis = 1))

# остается сравнить с целевой переменной

print(y_test[—10:])

[7 8 9 0 1 2 3 4 5 6]

Для первых десяти цифр модель сделала верный прогноз.

7. Пример улучшения алгоритма

Существует множество параметров модели, которые можно настроить. В качестве примера попробуем заменить алгоритм стохастического градиентного спуска на считающийся более эффективным алгоритм adam (суть этого алгоритма выходит за рамки сегодняшней лекции).

Посмотрим на результат на обучающей и тестовой выборке.

# снова укажем настройки модели

model.compile(

loss = ‘categorical_crossentropy’,

optimizer = ‘adam’, # однако заменим алгоритм оптимизации

metrics = [‘accuracy’]

)

# обучаем модель методом .fit()

model.fit(

X_train, # указываем обучающую выборку

to_categorical(y_train), # делаем one-hot encoding целевой переменной

epochs = 10 # прописываем количество эпох

)

Epoch 1/10

1875/1875 [==============================] — 4s 2ms/step — loss: 0.2572 — accuracy: 0.9252

Epoch 2/10

1875/1875 [==============================] — 4s 2ms/step — loss: 0.1738 — accuracy: 0.9497

Epoch 3/10

1875/1875 [==============================] — 4s 2ms/step — loss: 0.1392 — accuracy: 0.9588

Epoch 4/10

1875/1875 [==============================] — 4s 2ms/step — loss: 0.1196 — accuracy: 0.9647

Epoch 5/10

1875/1875 [==============================] — 4s 2ms/step — loss: 0.1062 — accuracy: 0.9685

Epoch 6/10

1875/1875 [==============================] — 4s 2ms/step — loss: 0.0960 — accuracy: 0.9708

Epoch 7/10

1875/1875 [==============================] — 4s 2ms/step — loss: 0.0883 — accuracy: 0.9732

Epoch 8/10

1875/1875 [==============================] — 4s 2ms/step — loss: 0.0826 — accuracy: 0.9747

Epoch 9/10

1875/1875 [==============================] — 4s 2ms/step — loss: 0.0766 — accuracy: 0.9766

Epoch 10/10

1875/1875 [==============================] — 4s 2ms/step — loss: 0.0699 — accuracy: 0.9780

<keras.callbacks.History at 0x7f36c3d74590>

# и оцениваем результат «на тесте»

model.evaluate(

X_test,

to_categorical(y_test)

)

313/313 [==============================] — 1s 1ms/step — loss: 0.1160 — accuracy: 0.9647

[0.11602973937988281, 0.9646999835968018]

Как вы видите, с помощью одного изменения мы повысили долю правильных прогнозов до 96,47%.

Более подходящие для работы с изображениями сверточные нейронные сети (convolutional neural network, CNN) достигают свыше 99% точности на этом наборе данных, как это видно в примере⧉ на официальном сайте библиотеки Keras.

Подведем итог

На сегодняшнем занятии изучили основы нейронных сетей. В частности, мы узнали, что такое нейронная сеть, какова ее структура и алгоритм функционирования. Многие шаги, например, оценка уровня ошибки через функцию кросс-энтропии или оптимизация методом стохастического градиентного спуска, разумеется, требуют отдельного занятия. Эти уроки еще впереди.

При этом, я надеюсь, у вас сложилось целостное представление о том, что значит создать и обучить нейросеть, и какие шаги для этого требуются.

Вопросы для закрепления

Перечислите типы слоев нейронной сети

Посмотреть правильный ответ

Ответ: обычно используется входной слой, один или несколько скрытых слоев и выходной слой.

Из каких двух этапов состоит обучение нейронной сети?

Посмотреть правильный ответ

Ответ: вначале (1) при forward propagation мы пропускаем данные от входного слоя к выходному, затем, рассчитав уровень ошибки, (2) начинается обратный процесс back propagation, при котором, мы улучшаем веса исходной модели.

Для чего используются сигмоида и функция softmax в выходном слое нейронной сети в задачах классификации?

Посмотреть правильный ответ

Ответ: сигмоида используется, когда нужно предсказать один из двух классов, если классов больше двух, применяется softmax.

Ответы на вопросы

Вопрос. Что означает число 1875 в результате работы модели?

Ответ. Я планировал рассказать об этом на курсе по оптимизации, но попробую дать общие определения уже сейчас. Как я уже сказал, при оптимизации методом градиентного спуска мы можем использовать (1) все данные, (2) часть данных или (3) одно наблюдение для каждого обновления весов. Это регулируется параметром batch_size (размер партии).

в первом случае, количество наблюдений (batch, партия) равно размеру датасета, веса не обновляются пока мы не пройдемся по всем наблюдениям, это простой градиентный спуск
во втором случае, мы берем часть наблюдений (mini-batch, мини-партия), и когда обработаем их, то обновляем веса; после этого мы обрабатываем следующую партию
и наконец мы можем взять только одно наблюдение и сразу после его анализа обновить веса, это классический стохастический градиентный спуск (stochastic gradient descent), параметр batch_size = 1

В чем преимущество каждого из методов? Если мы берем всю партию и по результатам ее обработки обновляем веса, то двигаемся к минимуму функции потерь наиболее плавно. Минус в том, что на расчет требуется время и вычислительные мощности.

Если берем только одно наблюдение, то считаем все быстро, но расчет минимума функции потерь менее точен.

В библиотеке Keras (и нашей нейросети) по умолчанию используется второй подход и размер партии равный 32 наблюдениям (
batch_size = 32). С учетом того, что в обучающей выборке 60000 наблюдений, разделив 60000 на 32 мы получим 1875 итераций или обновлений весов в рамках одной эпохи. Отсюда и число 1875.

Повторим, алгоритм обрабатывает 32 наблюдения, обновляет веса и после этого переходит к следующей партии (batch) из 32-х наблюдений. Обработав таким образом 60000 изображений, алгоритм заканчивает первую эпоху и начинает вторую. Размер партии и количество эпох регулируется параметрами batch_size и epochs соответственно.

Источник