Поскольку требования к полосе пропускания увеличиваются, а допуск на ошибки и задержку уменьшаются, разработчики систем передачи данных искали новые способы расширения доступной полосы пропускания и повышения качества передачи. Одно из решений на самом деле не ново, но оказалось весьма полезным. Это называется прямым исправлением ошибок (FEC), в течение многих лет этот метод использовался для обеспечения эффективной высококачественной передачи данных по шумным каналам. Сегодня с увеличением пропускной способности передачи данных и увеличением расстояния, давайте узнаем больше о методике FEC в оптических сетях.
Что такое FEC?
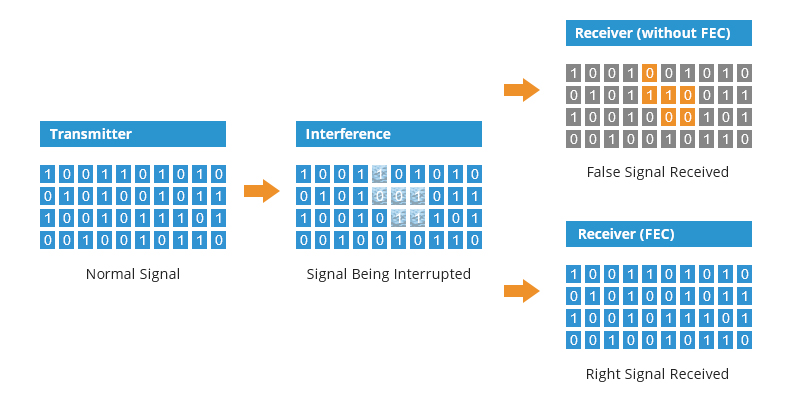
Прямая коррекция ошибок (FEC) — это метод цифровой обработки сигналов, используемый для повышения надежности данных. Это делается путем введения избыточных данных, называемых кодом с исправлением ошибок, перед передачей или хранением данных. FEC предоставляет приемнику возможность исправления ошибок без обратного канала для запроса повторной передачи данных. Как мы знаем, иногда оптические сигналы могут ухудшаться из-за некоторых факторов во время передачи, что может привести к неправильной оценке на стороне приемника, возможно, принятию сигнала «1» за сигнал «0» или сигнала «0» за сигнал «1». Если количество ошибок при передаче находится в пределах корректирующей способности (прерывистые ошибки), канальный декодер обнаружит и исправит ложные “0” или “1” для улучшения качества сигнала.
Рисунок 1. Принцип работы FEC
Развитие прямого исправления ошибок в оптической связи можно разделить на три поколения. FEC первого поколения представляет собой первое, которое будет успешно использоваться в подводных системах и наземных системах. По мере развития систем WDM в коммерческих системах был установлен более мощный FEC второго поколения. Появление FEC третьего поколения открыло новые перспективы для следующего поколения систем оптической связи.
Каковы типы и особенности FEC?
Типы
В настоящее время практические технологии FEC для SDH (синхронная цифровая иерархия) и DWDM (плотное мультиплексирование с разделением по длине волны) в основном следующие:
In-band FEC. In-band FEC поддерживается стандартом ITU-T G.707. Контролируемые символы кода FEC загружаются с использованием части служебных байтов в кадре SDH. Усиление кодирования невелико (3-4 дБ).Внеполосный FEC. Внеполосный FEC поддерживается стандартом ITU-T G.975/709.
Out-of-band FEC обладает большой избыточностью кодирования, возможностью исправления ошибок, высокой гибкостью и высоким коэффициентом усиления кодирования (5-6 дБ).
Enhanced FEC (EFEC). Enhanced FEC в основном используется в системах оптической связи, где требования к задержке не являются строгими, а требования по усилению кодирования особенно высоки. Хотя процесс кодирования и декодирования EFEC является более сложным и менее применимым в настоящее время, благодаря его преимуществам в производительности, он превратится в практическую технологию и станет основным направлением следующего поколения out-of-band FEC.
Характеристики
FEC уменьшает количество ошибок передачи, расширяет рабочий диапазон и снижает требования к питанию для систем связи. FEC также увеличивает эффективную пропускную способность системы, даже с дополнительными контрольными битами, добавленными к битам данных, устраняя необходимость повторной передачи данных, искаженных случайным шумом.
FEC самостоятельно повышает достоверность данных на приемнике. В рамках системного контекста FEC становится технологией, которую разработчик системы может использовать несколькими способами. Наиболее очевидным преимуществом использования FEC является использование систем с ограниченной мощностью. Однако посредством использования сигнализации более высокого порядка ограничения полосы пропускания также могут быть устранены. Во многих беспроводных системах допустимая мощность передатчика ограничена. Эти ограничения могут быть вызваны соблюдением стандарта или практическими соображениями. FEC позволяет передавать с гораздо более высокими скоростями передачи данных, если доступна дополнительная полоса пропускания.
Применение FEC в 100G сетях
В контексте оптоволоконных сетей FEC используется для определения оптического SNR (OSNR) — одного из ключевых параметров, определяющих, как далеко может пройти длина волны, прежде чем она нуждается в регенерации. FEC особенно важен при скоростях высокоскоростной передачи данных, где требуются усовершенствованные схемы модуляции, чтобы минимизировать дисперсию и соответствие сигнала с частотной сеткой. Без включения FEC транспорт 100G был бы ограничен чрезвычайно короткими расстояниями. Для реализации передачи на большие расстояния (> 2500 км) усиление системы должно быть дополнительно улучшено примерно на 2 дБ. Переход FEC с жесткого решения на мягкое решение восполняет этот пробел в производительности.
Поскольку стремление к все более высоким скоростям передачи продолжается, схемы прямого исправления ошибок (SD-FEC) становятся все более популярными. Хотя для этого может потребоваться около 20% байтов — почти в три раза больше, чем в исходной схеме кодирования RS — выгоды, которые они получают в контексте высокоскоростных сетей, значительны. Например, FEC, который приводит к усилению от 1 до 2 дБ в сети 100G, означает увеличение охвата на 20-40%.
Замечания для FEC в сетях 100G
Что следует учитывать при настройке FEC в 100G сетях? Предлагается обратить внимание на следующие советы.
Метод реализации
Некоторые специальные модули имеют свои собственные функции FEC, такие как FS 100G CFP конвертеры интерфейсов. В то время как 100G QSFP28 оптический модуль в основном полагается на конфигурацию функции FEC на устройстве для реализации исправления ошибок, таких как 100G коммутаторы.
Поддерживает ли коммутатор FEC
Конфигурирование FEC на 100G коммутаторах может быть достигнуто только в том случае, если коммутатор поддерживает его, и не все коммутаторы поддерживают это. В то время как все 100G коммутаторы поддерживают FEC, предоставляемые FS.
| Тип коммутатора | Тип порта | Поддержка FEC или нет |
| S5850-48S2Q4C | 48*10Gb, 2*40Gb, 4*100Gb | Да (для оба 40Gb и 100Gb порты) |
| S8050-20Q4C | 20*40Gb, 4*100Gb | Да (для оба 40Gb и 100Gb порты) |
| N8500-48B6C | 40*25Gb, 6*100Gb | Да (для оба 25Gb и 100Gb порты) |
| N8500-32C | 32*100Gb | Да |
Таблица 1. Технические характеристики FS 100G коммутаторов
Внимание: для FS 100G коммутаторов функция FEC включена по умолчанию. Если требуется включить его после выключения, можно настроить команду FEC.
Включить ли FEC на QSFP28 100G модулях
Функция FEC — это не просто преимущество, процесс исправления кода ошибки неизбежно приведет к некоторой задержке пакета данных. Поэтому не все QSFP28 100G модули нуждаются в этом. Согласно стандартному протоколу IEEE не рекомендуется включать FEC при использовании QSFP28-LR4-100G модулей, за исключением того, что рекомендуется включать его. Поскольку технология QSFP28 100G модулей варьируется от компании к компании, поэтому ситуация не совсем одинакова. В следующей таблице объясняется, рекомендуется ли включать FEC при использовании FS 100G QSFP28 модулей.
| Тип модуля | Описание | с FEC |
| QSFP28-SR4-100G | 850nm 100m MTP/MPO Модуль для SMF | Нет |
| QSFP28-LR4-100G | 1310nm 10km Модуль для SMF | Нет |
| QSFP28-PIR4-100G | 1310nm 500m Модуль для SMF | Нет |
| QSFP28-IR4-100G | 1310nm 2km Модуль для SMF | Да |
| QSFP28-EIR4-100G | 1310nm 10km Модуль для SMF | Да |
| QSFP28-ER4-100G | 1310nm 40km Модуль для SMF | Да |
Таблица 2. Технические характеристики FS 100G QSFP28 модулей
Согласованность функций FEC на обоих концах канала
Функция FEC порта является частью автосогласования. Когда автоматическое согласование порта включено, функция FEC определяется согласованием на обоих концах канала. Если функция FEC включена на одном конце, другой конец должен также включить ее, в противном случае порт не работает.
Стекирование & FEC
Настройка команды FEC не поддерживается, если порт уже настроен как физически стековый порт.Наоборот, порты, которые были настроены с помощью команд FEC, не поддерживают настройку в качестве физического стекового члена.
Заключение
FEC стал критически важной в волоконно-оптической связи, так как магистральные сети увеличиваются в скорости до 40 и 100G, особенно в условиях плохой связи оптического сигнала с шумом. Такие среды становятся более распространенными в высокоскоростных средах, поскольку в сетях используется больше оптических усилителей. Со всеми этими событиями, FEC будет продолжать играть роль в будущих сетях. Для обеспечения нормальной работы сети рекомендуется обратить особое внимание на функцию FEC на оптических модулях, которая поможет вам повысить производительность при передаче данных.
В этой статье вы найдете краткое описание технологии прямой коррекции ошибок, принципы её работы и методы применения. Помимо этого, в статье более рассмотрена работа кода Хэмминга, являющегося одним из основных примеров реализации данной технологии.
Прямая коррекция ошибок (FEC) это метод, который использовался в течении нескольких лет в подводных оптоволоконных системах, проложенных по морскому дну. Этот метод позволяет с почти идеальной точностью передать данные, даже если передача осуществляется по каналу с большим количеством шумов. В настоящее время используется несколько алгоритмов FEC, таких как код Хэмминга, кода Рида-Соломона и код БЧХ.
В качестве примера, рассмотрим работу вашего мобильного телефона в условиях слабого сигнала сотовой сети. Допустим, вы хотели сказать человеку на другом конце линии некую последовательность чисел. Есть несколько методов, которые можно использовать для повышения точности. Предположим, что список чисел, которые вы хотите передать, это 7, 3, 8, 10, 12 и 21. Одним из способов может быть повтор списка чисел два раза. Запишите каждый список и сравните их, если они совпадают, передача данных, вероятно, корректна. Основным недостатком такого метода является то, что, поскольку данные передаются дважды, пропускная способность системы делится пополам и, если списки не совпадают, у вас не будет ни малейшего представления, который из них верный. Используя этот метод, для того, чтобы убедиться в хорошем качестве передачи и исправить некоторые ошибки, вам придется отправить данные три раза и проверить, что два из трех списков полностью совпадают. Второй способ будет выглядеть примерно так: в первую очередь, вы будете отправлять количество чисел, которые необходимо принять, затем саму последовательно, и в конце последует передача числа, являющегося суммой последовательности. Передаваемое сообщение при этом примет следующий вид: 6, 7, 3, 8, 10, 12, 21, и 67. Человек, принимающий сообщение, будет смотреть на первое число, чтобы затем убедится, что будет получено правильное количество чисел в сообщении, а затем проверит, что число в конце последовательности, действительно является суммой переданных чисел. Этот метод требует отправки значительно меньшего количества дополнительных данных. Если любое полученное число неверно или пропущено, то число контрольной суммы в конце передачи не будет соответствовать сумме, передаваемых чисел. Показанные выше методы представляют собой примеры кода обнаружения ошибок. Они позволяют определить, была ли передача точной, но не позволяют исправлять ошибки.
Примечание: Термин «Forward» в аббревиатуре FEC означает, что исправление ошибок осуществляется путем передачи некоторой информации вместе с передачей данных.
Код исправления ошибок считаются более сложными, в сравнении с кодом обнаружения ошибок и используются почти в каждом современном коммуникационном приложении. Также, коды исправления ошибок нашли широкое применение в CD и DVD проигрывателях. Для того, чтобы привести пример кода исправления ошибок, нужно ввести и объяснить два термина: двоичность и чётность. В предыдущих примерах кода обнаружения ошибок, мы использовали такие числа, как 7, 3, 8, и т.д. Это базовые числа системы исчисления, знакомой нам в повседневной жизни. Двоичные числа в основе имеют два числа, которые могут иметь только два возможных значения – 0 или 1. Бинарная система используется почти во всех коммуникационных и компьютерных системах. Второе определение, которое необходимо разобрать, называется четность. Чётность — термин, который используется в двоичных системах связи, чтобы указать, является ли число единиц в передаче четным или же нет. Если число единиц является четным, то чётность совпадает и наоборот.
Код Хэмминга
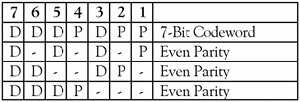
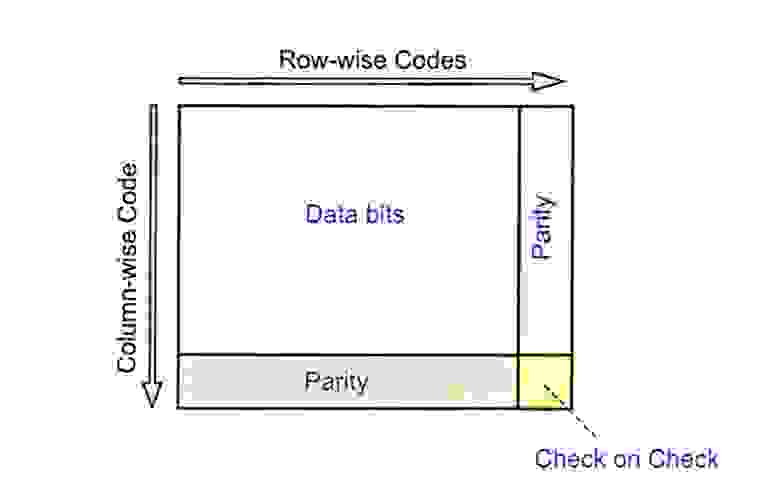
Рассмотрим сообщение, имеющее четыре бита данных (D), которое должно быть передано в 7-битной кодировке с добавлением трёх битов данных для поиска и устранения ошибок. Этот код будет называться (7, 4). Это означает, что общая длина кода составляет семь битов, но только четыре из них на самом деле данные. Три добавленных бита — это три бита проверки на четность (Р), где чётность каждого вычисляется в разных группах битов сообщения, как показано на рисунке 1.
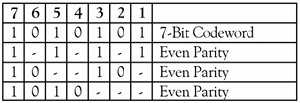
Например, сообщение 1011 будут направлено, как 1010101, как показано на рисунке 2.
Можно заметить, что в случае возникновения ошибки в любом из семи битов, эта ошибка оказывает влияние на различные комбинации трех битов четности в зависимости от битовой позиции.
Например, предположим, что вышеупомянутое сообщение 1010101 передаётся и возникает один бит ошибки, так что получено кодовое слово 1110101:
Передача Приём
Сообщение Сообщение
1 0 1 0 1 0 1 ————> 1 1 1 0 1 0 1
Эта ошибка может быть исправлена путем определения, какой из трех битов четности пострадал, как показано на рисунке ниже:
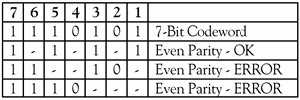
Характер ошибок четности битов указывает, какой бит в кодовом слове с ошибкой, таким образом, он может быть исправлен.
Основные функции кода Хэмминга можно резюмировать:
- Обнаружение 2-битовых ошибок (при условии отсутствия ошибок корректировка не выполняется)
- Коррекция единичных ошибочных битов
- 3 проверочных бита добавляется к 4-битовому сообщению
Способность корректировать одиночные ошибочные биты приводит к снижению себестоимости передачи, которая получается меньше, чем в случае отправки сообщения дважды целиком. (Напомним, что, просто отправив сообщение дважды коррекция ошибок не выполняется.) К тому же, при увеличении размера кодового слова, дополнительная нагрузка исправления ошибочных битов уменьшается. Например, одним из возможных вариантов кода Хэмминга для передачи по морским подводным оптоволоконным системам является код (18880, 18865). Это означает, что кодовое слово 18880 в действительности содержит 18,865 бит данных и 15 бит коррекции ошибок. Более надежные методы прямой коррекции ошибок (FEC) могут содержать гораздо больше битов коррекции ошибок, так что несколько ошибочных битов могут быть обнаружены и исправлены в каждом кодовом слове.
Существует метод прямой коррекции ошибок (FEC), аналогичный коду Хемминга. Как правило, в системах с оптической несущей ОС-192, накладывается около 7% дополнительной нагрузки на систему за счёт процесса коррекции ошибок (FEC). Допустим, базовая скорость передачи данных 10 Гбит/с, с учётом дополнительной нагрузки будет увеличена до 10,7 Гбит/с. Таким образом, с каждой 1000 бит передаваемых данных, отправляется ещё 70 бит коррекции ошибок, чтобы позволить провести проверку целостности полученных данных и исправить ошибки, которые могут возникнуть при передаче по оптическому каналу связи. На рисунке 4 показано влияние прямой коррекции (FEC) на системный коэффициент ошибочных битов (BER). Этот коэффициент является показателем числа ошибок в битах, деленное на общее число переданных битов в исследуемом временном интервале. BER 10-3 означает, что один из каждых 1000 бит будет передан некорректно. Синий график наглядно отображает количество передаваемых данных, если система не имеет FEC. Входной коэффициент BER (input BER) – это показатель ошибок, возникающих в канале передачи. Пока в системе отсутствует FEC, любые ошибки, которые происходят во время передачи появляются на выходе системы. Фиолетовый график показывает, что может произойти, если в системе используется FEC. В отсутствии FEC в системе входной коэффициент BER 10-6 даст аналогичное значение выходного BER 10-6, а в случае использования данной технологии происходит значительное улучшение выходной величины BER 10-14 (output BER).
Таким образом, интеграция прямой коррекции ошибок в систему позволяет разработчику увеличивать расстояние и скорости передачи данных значительнее, чем при использовании любой другой технологии, а также увеличит срок службы системы.
«Interleaver» redirects here. For the fiber-optic device, see optical interleaver.
In computing, telecommunication, information theory, and coding theory, forward error correction (FEC) or channel coding[1][2][3] is a technique used for controlling errors in data transmission over unreliable or noisy communication channels.
The central idea is that the sender encodes the message in a redundant way, most often by using an error correction code or error correcting code (ECC).[4][5] The redundancy allows the receiver not only to detect errors that may occur anywhere in the message, but often to correct a limited number of errors. Therefore a reverse channel to request re-transmission may not be needed. The cost is a fixed, higher forward channel bandwidth.
The American mathematician Richard Hamming pioneered this field in the 1940s and invented the first error-correcting code in 1950: the Hamming (7,4) code.[5]
FEC can be applied in situations where re-transmissions are costly or impossible, such as one-way communication links or when transmitting to multiple receivers in multicast.
Long-latency connections also benefit; in the case of a satellite orbiting Uranus, retransmission due to errors can create a delay of five hours. FEC is widely used in modems and in cellular networks, as well.
FEC processing in a receiver may be applied to a digital bit stream or in the demodulation of a digitally modulated carrier. For the latter, FEC is an integral part of the initial analog-to-digital conversion in the receiver. The Viterbi decoder implements a soft-decision algorithm to demodulate digital data from an analog signal corrupted by noise. Many FEC decoders can also generate a bit-error rate (BER) signal which can be used as feedback to fine-tune the analog receiving electronics.
FEC information is added to mass storage (magnetic, optical and solid state/flash based) devices to enable recovery of corrupted data, and is used as ECC computer memory on systems that require special provisions for reliability.
The maximum proportion of errors or missing bits that can be corrected is determined by the design of the ECC, so different forward error correcting codes are suitable for different conditions. In general, a stronger code induces more redundancy that needs to be transmitted using the available bandwidth, which reduces the effective bit-rate while improving the received effective signal-to-noise ratio. The noisy-channel coding theorem of Claude Shannon can be used to compute the maximum achievable communication bandwidth for a given maximum acceptable error probability. This establishes bounds on the theoretical maximum information transfer rate of a channel with some given base noise level. However, the proof is not constructive, and hence gives no insight of how to build a capacity achieving code. After years of research, some advanced FEC systems like polar code[3] come very close to the theoretical maximum given by the Shannon channel capacity under the hypothesis of an infinite length frame.
Method
Edit
ECC is accomplished by adding redundancy to the transmitted information using an algorithm. A redundant bit may be a complicated function of many original information bits. The original information may or may not appear literally in the encoded output; codes that include the unmodified input in the output are systematic, while those that do not are non-systematic.
A simplistic example of ECC is to transmit each data bit 3 times, which is known as a (3,1) repetition code. Through a noisy channel, a receiver might see 8 versions of the output, see table below.
| Triplet received | Interpreted as |
|---|---|
| 000 | 0 (error-free) |
| 001 | 0 |
| 010 | 0 |
| 100 | 0 |
| 111 | 1 (error-free) |
| 110 | 1 |
| 101 | 1 |
| 011 | 1 |
This allows an error in any one of the three samples to be corrected by «majority vote», or «democratic voting». The correcting ability of this ECC is:
- Up to 1 bit of triplet in error, or
- up to 2 bits of triplet omitted (cases not shown in table).
Though simple to implement and widely used, this triple modular redundancy is a relatively inefficient ECC. Better ECC codes typically examine the last several tens or even the last several hundreds of previously received bits to determine how to decode the current small handful of bits (typically in groups of 2 to 8 bits).
Averaging noise to reduce errors
Edit
ECC could be said to work by «averaging noise»; since each data bit affects many transmitted symbols, the corruption of some symbols by noise usually allows the original user data to be extracted from the other, uncorrupted received symbols that also depend on the same user data.
- Because of this «risk-pooling» effect, digital communication systems that use ECC tend to work well above a certain minimum signal-to-noise ratio and not at all below it.
- This all-or-nothing tendency – the cliff effect – becomes more pronounced as stronger codes are used that more closely approach the theoretical Shannon limit.
- Interleaving ECC coded data can reduce the all or nothing properties of transmitted ECC codes when the channel errors tend to occur in bursts. However, this method has limits; it is best used on narrowband data.
Most telecommunication systems use a fixed channel code designed to tolerate the expected worst-case bit error rate, and then fail to work at all if the bit error rate is ever worse.
However, some systems adapt to the given channel error conditions: some instances of hybrid automatic repeat-request use a fixed ECC method as long as the ECC can handle the error rate, then switch to ARQ when the error rate gets too high;
adaptive modulation and coding uses a variety of ECC rates, adding more error-correction bits per packet when there are higher error rates in the channel, or taking them out when they are not needed.
Types of ECC
Edit
The two main categories of ECC codes are block codes and convolutional codes.
- Block codes work on fixed-size blocks (packets) of bits or symbols of predetermined size. Practical block codes can generally be hard-decoded in polynomial time to their block length.
- Convolutional codes work on bit or symbol streams of arbitrary length. They are most often soft decoded with the Viterbi algorithm, though other algorithms are sometimes used. Viterbi decoding allows asymptotically optimal decoding efficiency with increasing constraint length of the convolutional code, but at the expense of exponentially increasing complexity. A convolutional code that is terminated is also a ‘block code’ in that it encodes a block of input data, but the block size of a convolutional code is generally arbitrary, while block codes have a fixed size dictated by their algebraic characteristics. Types of termination for convolutional codes include «tail-biting» and «bit-flushing».
There are many types of block codes; Reed–Solomon coding is noteworthy for its widespread use in compact discs, DVDs, and hard disk drives. Other examples of classical block codes include Golay, BCH, Multidimensional parity, and Hamming codes.
Hamming ECC is commonly used to correct NAND flash memory errors.[6]
This provides single-bit error correction and 2-bit error detection.
Hamming codes are only suitable for more reliable single-level cell (SLC) NAND.
Denser multi-level cell (MLC) NAND may use multi-bit correcting ECC such as BCH or Reed–Solomon.[7][8] NOR Flash typically does not use any error correction.[7]
Classical block codes are usually decoded using hard-decision algorithms,[9] which means that for every input and output signal a hard decision is made whether it corresponds to a one or a zero bit. In contrast, convolutional codes are typically decoded using soft-decision algorithms like the Viterbi, MAP or BCJR algorithms, which process (discretized) analog signals, and which allow for much higher error-correction performance than hard-decision decoding.
Nearly all classical block codes apply the algebraic properties of finite fields. Hence classical block codes are often referred to as algebraic codes.
In contrast to classical block codes that often specify an error-detecting or error-correcting ability, many modern block codes such as LDPC codes lack such guarantees. Instead, modern codes are evaluated in terms of their bit error rates.
Most forward error correction codes correct only bit-flips, but not bit-insertions or bit-deletions.
In this setting, the Hamming distance is the appropriate way to measure the bit error rate.
A few forward error correction codes are designed to correct bit-insertions and bit-deletions, such as Marker Codes and Watermark Codes.
The Levenshtein distance is a more appropriate way to measure the bit error rate when using such codes.
[10]
Code-rate and the tradeoff between reliability and data rate
Edit
The fundamental principle of ECC is to add redundant bits in order to help the decoder to find out the true message that was encoded by the transmitter. The code-rate of a given ECC system is defined as the ratio between the number of information bits and the total number of bits (i.e., information plus redundancy bits) in a given communication package. The code-rate is hence a real number. A low code-rate close to zero implies a strong code that uses many redundant bits to achieve a good performance, while a large code-rate close to 1 implies a weak code.
The redundant bits that protect the information have to be transferred using the same communication resources that they are trying to protect. This causes a fundamental tradeoff between reliability and data rate.[11] In one extreme, a strong code (with low code-rate) can induce an important increase in the receiver SNR (signal-to-noise-ratio) decreasing the bit error rate, at the cost of reducing the effective data rate. On the other extreme, not using any ECC (i.e., a code-rate equal to 1) uses the full channel for information transfer purposes, at the cost of leaving the bits without any additional protection.
One interesting question is the following: how efficient in terms of information transfer can an ECC be that has a negligible decoding error rate? This question was answered by Claude Shannon with his second theorem, which says that the channel capacity is the maximum bit rate achievable by any ECC whose error rate tends to zero:[12] His proof relies on Gaussian random coding, which is not suitable to real-world applications. The upper bound given by Shannon’s work inspired a long journey in designing ECCs that can come close to the ultimate performance boundary. Various codes today can attain almost the Shannon limit. However, capacity achieving ECCs are usually extremely complex to implement.
The most popular ECCs have a trade-off between performance and computational complexity. Usually, their parameters give a range of possible code rates, which can be optimized depending on the scenario. Usually, this optimization is done in order to achieve a low decoding error probability while minimizing the impact to the data rate. Another criterion for optimizing the code rate is to balance low error rate and retransmissions number in order to the energy cost of the communication.[13]
Concatenated ECC codes for improved performance
Edit
Classical (algebraic) block codes and convolutional codes are frequently combined in concatenated coding schemes in which a short constraint-length Viterbi-decoded convolutional code does most of the work and a block code (usually Reed–Solomon) with larger symbol size and block length «mops up» any errors made by the convolutional decoder. Single pass decoding with this family of error correction codes can yield very low error rates, but for long range transmission conditions (like deep space) iterative decoding is recommended.
Concatenated codes have been standard practice in satellite and deep space communications since Voyager 2 first used the technique in its 1986 encounter with Uranus. The Galileo craft used iterative concatenated codes to compensate for the very high error rate conditions caused by having a failed antenna.
Low-density parity-check (LDPC)
Edit
Low-density parity-check (LDPC) codes are a class of highly efficient linear block
codes made from many single parity check (SPC) codes. They can provide performance very close to the channel capacity (the theoretical maximum) using an iterated soft-decision decoding approach, at linear time complexity in terms of their block length. Practical implementations rely heavily on decoding the constituent SPC codes in parallel.
LDPC codes were first introduced by Robert G. Gallager in his PhD thesis in 1960,
but due to the computational effort in implementing encoder and decoder and the introduction of Reed–Solomon codes,
they were mostly ignored until the 1990s.
LDPC codes are now used in many recent high-speed communication standards, such as DVB-S2 (Digital Video Broadcasting – Satellite – Second Generation), WiMAX (IEEE 802.16e standard for microwave communications), High-Speed Wireless LAN (IEEE 802.11n),[14] 10GBase-T Ethernet (802.3an) and G.hn/G.9960 (ITU-T Standard for networking over power lines, phone lines and coaxial cable). Other LDPC codes are standardized for wireless communication standards within 3GPP MBMS (see fountain codes).
Turbo codes
Edit
Turbo coding is an iterated soft-decoding scheme that combines two or more relatively simple convolutional codes and an interleaver to produce a block code that can perform to within a fraction of a decibel of the Shannon limit. Predating LDPC codes in terms of practical application, they now provide similar performance.
One of the earliest commercial applications of turbo coding was the CDMA2000 1x (TIA IS-2000) digital cellular technology developed by Qualcomm and sold by Verizon Wireless, Sprint, and other carriers. It is also used for the evolution of CDMA2000 1x specifically for Internet access, 1xEV-DO (TIA IS-856). Like 1x, EV-DO was developed by Qualcomm, and is sold by Verizon Wireless, Sprint, and other carriers (Verizon’s marketing name for 1xEV-DO is Broadband Access, Sprint’s consumer and business marketing names for 1xEV-DO are Power Vision and Mobile Broadband, respectively).
Local decoding and testing of codes
Edit
Sometimes it is only necessary to decode single bits of the message, or to check whether a given signal is a codeword, and do so without looking at the entire signal. This can make sense in a streaming setting, where codewords are too large to be classically decoded fast enough and where only a few bits of the message are of interest for now. Also such codes have become an important tool in computational complexity theory, e.g., for the design of probabilistically checkable proofs.
Locally decodable codes are error-correcting codes for which single bits of the message can be probabilistically recovered by only looking at a small (say constant) number of positions of a codeword, even after the codeword has been corrupted at some constant fraction of positions. Locally testable codes are error-correcting codes for which it can be checked probabilistically whether a signal is close to a codeword by only looking at a small number of positions of the signal.
Interleaving
Edit
«Interleaver» redirects here. For the fiber-optic device, see optical interleaver.
Interleaving is frequently used in digital communication and storage systems to improve the performance of forward error correcting codes. Many communication channels are not memoryless: errors typically occur in bursts rather than independently. If the number of errors within a code word exceeds the error-correcting code’s capability, it fails to recover the original code word. Interleaving alleviates this problem by shuffling source symbols across several code words, thereby creating a more uniform distribution of errors.[15] Therefore, interleaving is widely used for burst error-correction.
The analysis of modern iterated codes, like turbo codes and LDPC codes, typically assumes an independent distribution of errors.[16] Systems using LDPC codes therefore typically employ additional interleaving across the symbols within a code word.[17]
For turbo codes, an interleaver is an integral component and its proper design is crucial for good performance.[15][18] The iterative decoding algorithm works best when there are not short cycles in the factor graph that represents the decoder; the interleaver is chosen to avoid short cycles.
Interleaver designs include:
- rectangular (or uniform) interleavers (similar to the method using skip factors described above)
- convolutional interleavers
- random interleavers (where the interleaver is a known random permutation)
- S-random interleaver (where the interleaver is a known random permutation with the constraint that no input symbols within distance S appear within a distance of S in the output).[19]
- a contention-free quadratic permutation polynomial (QPP).[20] An example of use is in the 3GPP Long Term Evolution mobile telecommunication standard.[21]
In multi-carrier communication systems, interleaving across carriers may be employed to provide frequency diversity, e.g., to mitigate frequency-selective fading or narrowband interference.[22]
Example
Edit
Transmission without interleaving:
Error-free message: aaaabbbbccccddddeeeeffffgggg Transmission with a burst error: aaaabbbbccc____deeeeffffgggg
Here, each group of the same letter represents a 4-bit one-bit error-correcting codeword. The codeword cccc is altered in one bit and can be corrected, but the codeword dddd is altered in three bits, so either it cannot be decoded at all or it might be decoded incorrectly.
With interleaving:
Error-free code words: aaaabbbbccccddddeeeeffffgggg Interleaved: abcdefgabcdefgabcdefgabcdefg Transmission with a burst error: abcdefgabcd____bcdefgabcdefg Received code words after deinterleaving: aa_abbbbccccdddde_eef_ffg_gg
In each of the codewords «aaaa», «eeee», «ffff», and «gggg», only one bit is altered, so one-bit error-correcting code will decode everything correctly.
Transmission without interleaving:
Original transmitted sentence: ThisIsAnExampleOfInterleaving Received sentence with a burst error: ThisIs______pleOfInterleaving
The term «AnExample» ends up mostly unintelligible and difficult to correct.
With interleaving:
Transmitted sentence: ThisIsAnExampleOfInterleaving... Error-free transmission: TIEpfeaghsxlIrv.iAaenli.snmOten. Received sentence with a burst error: TIEpfe______Irv.iAaenli.snmOten. Received sentence after deinterleaving: T_isI_AnE_amp_eOfInterle_vin_...
No word is completely lost and the missing letters can be recovered with minimal guesswork.
Disadvantages of interleaving
Edit
Use of interleaving techniques increases total delay. This is because the entire interleaved block must be received before the packets can be decoded.[23] Also interleavers hide the structure of errors; without an interleaver, more advanced decoding algorithms can take advantage of the error structure and achieve more reliable communication than a simpler decoder combined with an interleaver[citation needed]. An example of such an algorithm is based on neural network[24] structures.
Software for error-correcting codes
Edit
Simulating the behaviour of error-correcting codes (ECCs) in software is a common practice to design, validate and improve ECCs. The upcoming wireless 5G standard raises a new range of applications for the software ECCs: the Cloud Radio Access Networks (C-RAN) in a Software-defined radio (SDR) context. The idea is to directly use software ECCs in the communications. For instance in the 5G, the software ECCs could be located in the cloud and the antennas connected to this computing resources: improving this way the flexibility of the communication network and eventually increasing the energy efficiency of the system.
In this context, there are various available Open-source software listed below (non exhaustive).
- AFF3CT(A Fast Forward Error Correction Toolbox): a full communication chain in C++ (many supported codes like Turbo, LDPC, Polar codes, etc.), very fast and specialized on channel coding (can be used as a program for simulations or as a library for the SDR).
- IT++: a C++ library of classes and functions for linear algebra, numerical optimization, signal processing, communications, and statistics.
- OpenAir: implementation (in C) of the 3GPP specifications concerning the Evolved Packet Core Networks.
List of error-correcting codes
Edit
| Distance | Code |
|---|---|
| 2 (single-error detecting) | Parity |
| 3 (single-error correcting) | Triple modular redundancy |
| 3 (single-error correcting) | perfect Hamming such as Hamming(7,4) |
| 4 (SECDED) | Extended Hamming |
| 5 (double-error correcting) | |
| 6 (double-error correct-/triple error detect) | Nordstrom-Robinson code |
| 7 (three-error correcting) | perfect binary Golay code |
| 8 (TECFED) | extended binary Golay code |
- AN codes
- Algebraic geometry code
- BCH code, which can be designed to correct any arbitrary number of errors per code block.
- Barker code used for radar, telemetry, ultra sound, Wifi, DSSS mobile phone networks, GPS etc.
- Berger code
- Constant-weight code
- Convolutional code
- Expander codes
- Group codes
- Golay codes, of which the Binary Golay code is of practical interest
- Goppa code, used in the McEliece cryptosystem
- Hadamard code
- Hagelbarger code
- Hamming code
- Latin square based code for non-white noise (prevalent for example in broadband over powerlines)
- Lexicographic code
- Linear Network Coding, a type of erasure correcting code across networks instead of point-to-point links
- Long code
- Low-density parity-check code, also known as Gallager code, as the archetype for sparse graph codes
- LT code, which is a near-optimal rateless erasure correcting code (Fountain code)
- m of n codes
- Nordstrom-Robinson code, used in Geometry and Group Theory[25]
- Online code, a near-optimal rateless erasure correcting code
- Polar code (coding theory)
- Raptor code, a near-optimal rateless erasure correcting code
- Reed–Solomon error correction
- Reed–Muller code
- Repeat-accumulate code
- Repetition codes, such as Triple modular redundancy
- Spinal code, a rateless, nonlinear code based on pseudo-random hash functions[26]
- Tornado code, a near-optimal erasure correcting code, and the precursor to Fountain codes
- Turbo code
- Walsh–Hadamard code
- Cyclic redundancy checks (CRCs) can correct 1-bit errors for messages at most bits long for optimal generator polynomials of degree , see Mathematics of cyclic redundancy checks#Bitfilters
See also
Edit
- Code rate
- Erasure codes
- Soft-decision decoder
- Burst error-correcting code
- Error detection and correction
- Error-correcting codes with feedback
- Linear code
- Quantum error correction
References
Edit
- ^ Charles Wang; Dean Sklar; Diana Johnson (Winter 2001–2002). «Forward Error-Correction Coding». Crosslink. The Aerospace Corporation. 3 (1). Archived from the original on 14 March 2012. Retrieved 5 March 2006.
- ^ Charles Wang; Dean Sklar; Diana Johnson (Winter 2001–2002). «Forward Error-Correction Coding». Crosslink. The Aerospace Corporation. 3 (1). Archived from the original on 14 March 2012. Retrieved 5 March 2006.
How Forward Error-Correcting Codes Work]
- ^ a b Maunder, Robert (2016). «Overview of Channel Coding».
- ^ Glover, Neal; Dudley, Trent (1990). Practical Error Correction Design For Engineers (Revision 1.1, 2nd ed.). CO, USA: Cirrus Logic. ISBN 0-927239-00-0.
- ^ a b Hamming, Richard Wesley (April 1950). «Error Detecting and Error Correcting Codes». Bell System Technical Journal. USA: AT&T. 29 (2): 147–160. doi:10.1002/j.1538-7305.1950.tb00463.x. S2CID 61141773.
- ^ «Hamming codes for NAND flash memory devices» Archived 21 August 2016 at the Wayback Machine. EE Times-Asia. Apparently based on «Micron Technical Note TN-29-08: Hamming Codes for NAND Flash Memory Devices». 2005. Both say: «The Hamming algorithm is an industry-accepted method for error detection and correction in many SLC NAND flash-based applications.»
- ^ a b «What Types of ECC Should Be Used on Flash Memory?» (Application note). Spansion. 2011.
Both Reed–Solomon algorithm and BCH algorithm are common ECC choices for MLC NAND flash. … Hamming based block codes are the most commonly used ECC for SLC…. both Reed–Solomon and BCH are able to handle multiple errors and are widely used on MLC flash.
- ^ Jim Cooke (August 2007). «The Inconvenient Truths of NAND Flash Memory» (PDF). p. 28.
For SLC, a code with a correction threshold of 1 is sufficient. t=4 required … for MLC.
- ^ Baldi, M.; Chiaraluce, F. (2008). «A Simple Scheme for Belief Propagation Decoding of BCH and RS Codes in Multimedia Transmissions». International Journal of Digital Multimedia Broadcasting. 2008: 1–12. doi:10.1155/2008/957846.
- ^ Shah, Gaurav; Molina, Andres; Blaze, Matt (2006). «Keyboards and covert channels». USENIX. Retrieved 20 December 2018.
- ^ Tse, David; Viswanath, Pramod (2005), Fundamentals of Wireless Communication, Cambridge University Press, UK
- ^ Shannon, C. E. (1948). «A mathematical theory of communication» (PDF). Bell System Technical Journal. 27 (3–4): 379–423 & 623–656. doi:10.1002/j.1538-7305.1948.tb01338.x. hdl:11858/00-001M-0000-002C-4314-2.
- ^ Rosas, F.; Brante, G.; Souza, R. D.; Oberli, C. (2014). «Optimizing the code rate for achieving energy-efficient wireless communications». Proceedings of the IEEE Wireless Communications and Networking Conference (WCNC). pp. 775–780. doi:10.1109/WCNC.2014.6952166. ISBN 978-1-4799-3083-8.
- ^ IEEE Standard, section 20.3.11.6 «802.11n-2009» Archived 3 February 2013 at the Wayback Machine, IEEE, 29 October 2009, accessed 21 March 2011.
- ^ a b Vucetic, B.; Yuan, J. (2000). Turbo codes: principles and applications. Springer Verlag. ISBN 978-0-7923-7868-6.
- ^ Luby, Michael; Mitzenmacher, M.; Shokrollahi, A.; Spielman, D.; Stemann, V. (1997). «Practical Loss-Resilient Codes». Proc. 29th Annual Association for Computing Machinery (ACM) Symposium on Theory of Computation.
- ^ «Digital Video Broadcast (DVB); Second generation framing structure, channel coding and modulation systems for Broadcasting, Interactive Services, News Gathering and other satellite broadband applications (DVB-S2)». En 302 307. ETSI (V1.2.1). April 2009.
- ^ Andrews, K. S.; Divsalar, D.; Dolinar, S.; Hamkins, J.; Jones, C. R.; Pollara, F. (November 2007). «The Development of Turbo and LDPC Codes for Deep-Space Applications». Proceedings of the IEEE. 95 (11): 2142–2156. doi:10.1109/JPROC.2007.905132. S2CID 9289140.
- ^ Dolinar, S.; Divsalar, D. (15 August 1995). «Weight Distributions for Turbo Codes Using Random and Nonrandom Permutations». TDA Progress Report. 122: 42–122. Bibcode:1995TDAPR.122…56D. CiteSeerX 10.1.1.105.6640.
- ^ Takeshita, Oscar (2006). «Permutation Polynomial Interleavers: An Algebraic-Geometric Perspective». IEEE Transactions on Information Theory. 53 (6): 2116–2132. arXiv:cs/0601048. Bibcode:2006cs……..1048T. doi:10.1109/TIT.2007.896870. S2CID 660.
- ^ 3GPP TS 36.212, version 8.8.0, page 14
- ^ «Digital Video Broadcast (DVB); Frame structure, channel coding and modulation for a second generation digital terrestrial television broadcasting system (DVB-T2)». En 302 755. ETSI (V1.1.1). September 2009.
- ^ Techie (3 June 2010). «Explaining Interleaving». W3 Techie Blog. Retrieved 3 June 2010.
- ^ Krastanov, Stefan; Jiang, Liang (8 September 2017). «Deep Neural Network Probabilistic Decoder for Stabilizer Codes». Scientific Reports. 7 (1): 11003. arXiv:1705.09334. Bibcode:2017NatSR…711003K. doi:10.1038/s41598-017-11266-1. PMC 5591216. PMID 28887480.
- ^ Nordstrom, A.W.; Robinson, J.P. (1967), «An optimum nonlinear code», Information and Control, 11 (5–6): 613–616, doi:10.1016/S0019-9958(67)90835-2
- ^ Perry, Jonathan; Balakrishnan, Hari; Shah, Devavrat (2011). «Rateless Spinal Codes». Proceedings of the 10th ACM Workshop on Hot Topics in Networks. pp. 1–6. doi:10.1145/2070562.2070568. hdl:1721.1/79676. ISBN 9781450310598.
Further reading
Edit
- MacWilliams, Florence Jessiem; Sloane, Neil James Alexander (2007) [1977]. Written at AT&T Shannon Labs, Florham Park, New Jersey, USA. The Theory of Error-Correcting Codes. North-Holland Mathematical Library. Vol. 16 (digital print of 12th impression, 1st ed.). Amsterdam / London / New York / Tokyo: North-Holland / Elsevier BV. ISBN 978-0-444-85193-2. LCCN 76-41296. (xxii+762+6 pages)
- Clark, Jr., George C.; Cain, J. Bibb (1981). Error-Correction Coding for Digital Communications. New York, USA: Plenum Press. ISBN 0-306-40615-2.
- Arazi, Benjamin (1987). Swetman, Herb (ed.). A Commonsense Approach to the Theory of Error Correcting Codes. MIT Press Series in Computer Systems. Vol. 10 (1 ed.). Cambridge, Massachusetts, USA / London, UK: Massachusetts Institute of Technology. ISBN 0-262-01098-4. LCCN 87-21889. (x+2+208+4 pages)
- Wicker, Stephen B. (1995). Error Control Systems for Digital Communication and Storage. Englewood Cliffs, New Jersey, USA: Prentice-Hall. ISBN 0-13-200809-2.
- Wilson, Stephen G. (1996). Digital Modulation and Coding. Englewood Cliffs, New Jersey, USA: Prentice-Hall. ISBN 0-13-210071-1.
- «Error Correction Code in Single Level Cell NAND Flash memories» 2007-02-16
- «Error Correction Code in NAND Flash memories» 2004-11-29
- Observations on Errors, Corrections, & Trust of Dependent Systems, by James Hamilton, 2012-02-26
- Sphere Packings, Lattices and Groups, By J. H. Conway, Neil James Alexander Sloane, Springer Science & Business Media, 2013-03-09 – Mathematics – 682 pages.
External links
Edit
- Morelos-Zaragoza, Robert (2004). «The Correcting Codes (ECC) Page». Retrieved 5 March 2006.
- lpdec: library for LP decoding and related things (Python)
Время на прочтение
4 мин
Количество просмотров 21K
Одним из основных ограничений при проектировании протяженных оптических транспортных сетей является соотношение сигнал-шум (OSNR). WDM-сети должны функционировать в допустимых пределах OSNR, чтобы обеспечить корректную работу систем.
Пороговое значение OSNR является одним из ключевых параметров, определяющих как далеко могут передаваться сигналы без необходимости в 3R-регенерации.
Для формирования каналов передачи данных со скоростью выше 10 Гбит используются сложные механизмы модуляции оптических сигналов для достижения аналогичной дальности передачи каналов связи 1-10 Гбит. Данные форматы модуляции необходимы для минимизации последствий таких оптических явлений, как хроматическая и поляризационная модовая дисперсии, а также для формирования оптического сигнала, соответствующего стандартам ITU 100/50-GHz, который используется в современных DWDM-системах. Недостатком высокоскоростных каналов передачи данных является тот факт, что они требуют существенно более высокого соотношения OSNR, чем обычные системы передачи (1-10 Гбит).
В системах 100 Гбит минимальное значение OSNR должно быть на 10 дБ выше, чем для сигналов в системах 10 Гбит. Без определенной коррекции или компенсации OSNR ограничивает 100G передачу данных до очень коротких расстояний, на данный момент максимальная дальность передачи составляет 40 км по стандартному одномодовому оптоволокну. Однако благодаря современным методам коррекции ошибок ( Forward Error Correction — FEC), особенно алгоритму Soft decision FEC, возможно расширение передачи высокоскоростных сигналов на протяженные расстояния.
Forward Error Correction (FEC) является техникой кодирования/декодирования сигнала с возможностью обнаружения ошибок и коррекцией информации методом упреждения. Таким образом, приемное оборудование может выявлять и исправлять ошибки, возникающие в канале передачи. FEC резко снижает количество битовых ошибок (BER), что позволяет увеличить расстояние передачи сигнала без регенерации.
Существует несколько FEC-алгоритмов кодирования, которые различаются по сложности и производительности. Одним из наиболее распространенных кодов первого поколения FEC является код «Рида-Соломона» (255, 239). Данный код добавляет немного — 7% проверочных байтов и около 6 дБ дополнительного запаса OSNR, но для высокоскоростных оптических сетей увеличение на 6 дБ является улучшенным показателем производительности, увеличивая расстояние между регенераторами примерно в четыре раза.
Некоторые производители предлагают в дополнение к коду «Рида-Соломона» более сложные схемы кодирования второго поколения FEC, например, превентивный параметр для оптических интерфейсов 10G и 40G. Данные алгоритмы, называемые «ультра» FEC или «усиленный» FEC (EFEC), также используют не более 7% объема передаваемого кадра, но в них заложены более сложные алгоритмы кодирования/декодирования, которые и обеспечивают бОльший выигрыш по OSNR — от 2 до 3 дБ, нежели код «Рида-Соломона».
Наряду с разработками первого поколения — «Рида-Соломона FEC» и второго поколения — «EFEC», которые позволили существенно улучшить производительность для 10G- и 40G-сигналов, было разработано более производительное FEC-решение третьего поколения, обеспечивающее увеличенную дальность и оптимальную производительность для высокоскоростных каналов передачи данных 100G.
FEC-решение третьего поколения основано на еще более мощных алгоритмах кодирования/декодирования и итеративного кодирования. В hard decision FEC —блок декодирования определяет «твердое» решение на основе входящего сигнала и иницилизирует один бит информации как «1» или «0» путем сравнения с пороговым значением. Значения выше установленного порога определяются «1», а значения ниже определяются как «0». В декодере используются дополнительные биты для обеспечения более детальной и точной индикации входящего сигнала. Иными словами, декодер не только определяет на основе порогового значения — является ли входящий сигнал «1» или «0», но и обеспечивает фактор надежности «принятия решения». Коэффициент надежности определяется индикатором, показывающим насколько сигнал выше или ниже порогового значения.
Использование коэффициента надежности или «вероятности» битов вместе с более сложными алгоритмами FEC-кодирования третьего поколения позволяет декодеру SD-FEC обеспечить дополнительное повышение OSNR на 1-2 дБ. В то время как увеличение OSNR на 1-2 дБ не звучит внушительно, оно может интерпретироваться как возможное увеличение расстояния на 20-40%, что является существенным показателем для 100G.
Одним из недостатков soft decision FEC является тот факт, что для него требуется ~20 % объема передаваемого кадра, а это более чем в два раза больше, чем занимаемый объем FEC первого и второго поколения.
С увеличением скорости в канале передачи данных с 10G до 100G, требование к OSNR увеличилось на 10 дБ. Без определенного вида компенсации или коррекции протяженность трасс с канальной скоростью 100G будет весьма ограниченной и неэкономичной.
Алгоритмы FEC первого и второго поколения были использованы на 10G и 40G для снижения BER и увеличения расстояния. SD-FEC является алгоритмом кодирования третьего поколения, обеспечивая передачу данных для оптических сетей 100G на бо́льшие расстояния и с бо́льшим ретрансляционным участком.
4.3. Метод коррекции ошибок FEC (Forward Error Correction)
Транспортировка данных подвержена влиянию шумов и наводок, которые вносят искажения. Если вероятность повреждения данных мала, достаточно зарегистрировать сам факт искажения и повторить передачу поврежденного фрагмента.
Когда вероятность искажения велика, например, в каналах коммуникаций с геостационарными спутниками, используются методы коррекции ошибок. Одним из таких методов является FEC (Forward Error Correction, иногда называемое канальным кодированием ) [4.1]. Технология FEC в последнее время достаточно широко используется в беспроводных локальных сетях (WLAN). Существуют две основные разновидности FEC: блочное кодирование и кодирование по методу свертки.
Блочное кодирование работает с блоками (пакетами) бит или символов фиксированного размера. Метод свертки работает с потоками бит или символов произвольной протяженности. Коды свертки при желании могут быть преобразованы в блочные коды.
Существует большое число блочных кодов, одним из наиболее важных является алгоритм Рида-Соломона, который используется при работе с CD, DVD и жесткими дисками ЭВМ. Блочные коды и коды свертки могут использоваться и совместно.
Для FEC -кодирования иногда используется метод сверки, который впервые был применен в 1955 году. Главной особенностью этого метода является сильная зависимость кодирования от предыдущих информационных битов и высокие требования к объему памяти. FEC -код обычно просматривает при декодировании 2-8 бит десятки или даже сотни бит, полученных ранее.
В 1967 году Эндрю Витерби (Andrew Viterbi) разработал технику декодирования, которая стала стандартной для кодов свертки. Эта методика требовала меньше памяти. Метод свертки более эффективен, когда ошибки распределены случайным образом, а не группируются в кластеры. Работа же с кластерами ошибок более эффективна при использовании алгебраического кодирования.
Одной из широко применяемых разновидностей коррекции ошибок является турбо-кодирование, разработанное американской аэрокосмической корпорацией. В этой схеме комбинируется два или более относительно простых кодов свертки. В FEC, так же как и в других методах коррекции ошибок (коды Хэмминга, алгоритм Рида-Соломона и др.), блоки данных из k бит снабжаются кодами четности, которые пересылаются вместе с данными и обеспечивают не только детектирование, но и исправление ошибок. Каждый дополнительный (избыточный) бит является сложной функцией многих исходных информационных бит. Исходная информация может содержаться в выходном передаваемом коде, тогда такой код называется систематическим, а может и не содержаться.
В результате через канал передается n -битовое кодовое слово ( n>k ). Конкретная реализация алгоритма FEC характеризуется комбинацией ( n, k ). Применение FEC в Интернете регламентируется документом RFC3452. Коды FEC могут исключить необходимость обратной связи при потере или искажении доставленных данных (запросы повторной передачи). Особенно привлекательна технология FEC при работе с мультикастинг-потоками, где ретрансмиссия не предусматривается (см. RFC-3453).
В 1974 году Йозеф Оденвальдер (Joseph odenwalder) объединил возможности алгебраического кодирования и метода свертки. Хорошего результата можно добиться, введя специальную операцию псевдослучайного перемешивания бит (interleaver).
В 1993 году группой Клода Берроу (Claude Berrou) был разработан турбо-код. В кодеке, реализующем этот алгоритм, содержатся кодировщики как минимум двух компонент (реализующие алгебраический метод или свертку). Кодирование осуществляется для блоков данных. Здесь также используется псевдослучайное перемешивание бит перед передачей. Это приводит к тому, что кластеры ошибок, внесенных при транспортировке, оказываются разнесенными случайным образом в пределах блока данных.
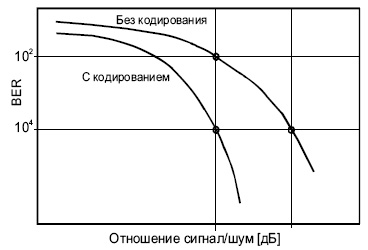
На
рис.
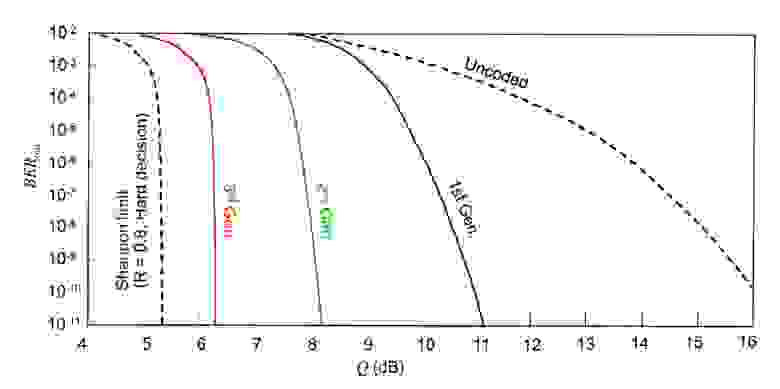
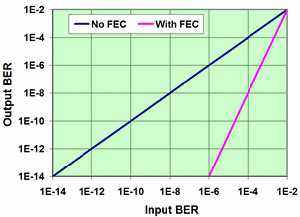
4.8 проводится сравнение вариантов BER (Bit Error Rate) при обычной транспортировке данных через канал и при передаче тех же данных с использованием коррекции ошибок FEC для разных значений отношения сигнал-шум ( S/N ). Из этих данных видно, что при отношении S/N= 8 дБ применение FEC позволяет понизить BER примерно в 100 раз. При этом достигается результат, близкий (в пределах одного децибела) к теоретическому пределу Шеннона.
За последние пять лет были разработаны программы, которые позволяют оптимизировать структуры турбо-кодов. Улучшение BER для турбокодов имеет асимптотический предел, и дальнейшее увеличение S/N уже не дает никакого выигрыша. Но схемы, позволяющие смягчить влияние этого насыщения, продолжают разрабатываться.
Рис.
4.8.
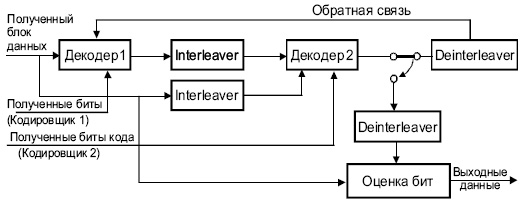
Турбо-кодек должен иметь столько же компонентных декодеров, сколько имеется кодировщиков на стороне передатчика. Декодеры соединяются последовательно.
Рис.
4.9.
Турбо-декодер
Техника FEC находит все большее применение в телекоммуникациях, например, при передачи мультимедиа [2].
Следует помнить, что, как в случае FEC , так и в других известных методах коррекции ошибок ( BCH , Golay, Hamming и др.) скорректированный код является верным лишь с определенной конечной вероятностью.