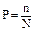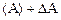Причины возникновения случайных ошибок

Поскольку
выборка охватывает , как правило,
весьма незначительную часть генеральной
совокупности, то следует предполагать,
что будут иметь место различия между
оценкой и характеристикой генеральной
совокупности, которую эта оценка
отображает. Эти различия получили
название ошибок отображения или ошибок
репрезентативности. Ошибки
репрезентативности подразделяются
на два типа : систематические и случайные.

Систематические
ошибки —
это постоянное завышение или занижение
значения оценки по сравнению с
характеристикой генеральной совокупности
. Причиной появления систематической
ошибки является несоблюдение принципа
равновероятности попадания каждой
единицы генеральной совокупности в
выборку , то есть выборка формируется
из преимущественно «худших» ( или «
лучших») представителей генеральной
совокупности. Соблюдение принципа
равновозможности попадания каждой
единицы в выборку позволяет полностью
исключить этот тип ошибок .

Случайные
ошибки –
это меняющиеся
от выборки к выборке по знаку и величине
различия между оценкой и оцениваемой
характеристикой генеральной совокупности
. Причина возникновения случайных
ошибок- игра случая при формировании
выборки, составляющей лишь часть
генеральной совокупности. Этот тип
ошибок органически присущ выборочному
методу. Исключить их полностью нельзя,
задача состоит в том , чтобы предсказать
их возможную величину и свести их к
минимуму. Порядок связанных в связи
с этим действий вытекает из рассмотрения
трех видов случайных ошибок : конкретной
, средней и предельной.

2.2 Конкретная, средняя и предельная ошибки выборки

2.2.1
Конкретная
ошибка – это ошибка одной проведенной
выборки. Если средняя по этой выборке
(
) является оценкой для генеральной
средней (0
) и, если
предположить, что эта генеральная
средняя нам известна , то разница
=—0
и будет
конкретной ошибкой этой выборки. Если
из этой генеральной совокупности
выборку повторим многократно, то каждый
раз получим новую величину конкретной
ошибки :
…,
и так далее.
Относительно этих конкретных ошибок
можно сказать следующее: некоторые из
них будут совпадать между собой по
величине и знаку, то есть имеет место
распределение ошибок, часть из них
будет равна 0, наблюдается совпадение
оценки и параметра генеральной
совокупности;

2.2.2
Средняя ошибка
– это средняя квадратическая из всех
возможных по воле случая конкретных
ошибок оценки :
,
где— величина меняющихся конкретных
ошибок;частота
( вероятность ) встречаемости той или
иной конкретной ошибки. Средняя
ошибка выборки показывает насколько
в среднем можно ошибиться , если на
основе оценки делается суждение о
параметре генеральной совокупности.
Приведенная формула раскрывает
содержание средней ошибки, но она не
может быть использована для практических
расчетов, хотя бы потому, что предполагает
знание параметра генеральной совокупности
, что само по себе исключает необходимость
выборки.

Практические
расчеты средней ошибки оценки
основываются на той предпосылке, что
она ( средняя ошибка ) по сути является
средним квадратическим отклонением
всех возможных значений оценки. Эта
предпосылка позволяет получить алгоритмы
расчета средней ошибки, опирающиеся
на данные одной единственной выборки.
В частности средняя ошибка выборочной
средней может быть установлена на
основе следующих рассуждений. Имеется
выборка (
,…) состоящая изединиц. По выборке в качестве оценки
генеральной средней определена
выборочная средняя. Каждое значение(,…) , стоящее под знаком суммы, следует
рассматривать как независимую случайную
величину, поскольку при бесконечном
повторении выборки первая, вторая и
т.д. единицы могут принимать любые
значения из присутствующих в генеральной
совокупности. СледовательноПоскольку , как известно, дисперсия
суммы независимых случайных величин
равна сумме дисперсий , то.
Отсюда следует, что средняя ошибка для
выборочной средней будет равнаяи находится она в обратной зависимости
от численности выборки ( через корень
квадратный из нее ) и в прямой от среднего
квадратического отклонения признака
в генеральной совокупности. Это логично,
поскольку выборочная средняя является
состоятельной оценкой для генеральной
средней и по мере увеличения численности
выборки приближается по своему значению
к оцениваемому параметру генеральной
совокупности. Прямая зависимость
средней ошибки от колеблемости признака
обусловлена тем, что чем больше
изменчивость признака в генеральной
совокупности, тем сложнее на основе
выборки построить адекватную модель
генеральной совокупности. На практике
среднее квадратическое отклонение
признака по генеральной совокупности
заменяется его оценкой по выборке, и
тогда формула для расчета средней
ошибки выборочной средней приобретает
вид:,
при этом учитывая смещенность
выборочной дисперсии,
выборочное среднее квадратическое
отклонение рассчитывается по формуле=. Так как символомn
обозначена численность выборки. ,то
в знаменателе при расчете среднего
квадратического отклонения должна
использоваться не численность выборки
( n
), а так называемое число степеней
свободы (n-1).
Под числом степеней свободы понимается
число единиц в совокупности, которые
могут свободно варьировать ( изменяться
), если по совокупности определена
какая-либо характеристика. В нашем
случае , поскольку по выборке определена
ее средняя, свободно варьировать могут

единицы.

В
таблице 2.2 приведены формулы для
расчета средних ошибок различных
выборочных оценок . Как видно из этой
таблицы, величина средней ошибки по
всем оценкам находится в обратной связи
с численностью выборки и в прямой с
колеблемостью. Это можно сказать и
относительно средней ошибки выборочной
доли ( частости ). Под корнем стоит
дисперсия альтернативного признака,
установленная по выборке (
)

Приведенные
в таблице 2.2 формулы относятся к так
называемому случайному , повторному
отбору единиц в выборку. При других
способах отбора , о которых речь пойдет
ниже, формулы будут несколько
видоизменяться.

Таблица
2.2

Формулы для
расчета средних ошибок выборочных
оценок

2.2.3
Предельная ошибка выборки
Знание оценки и ее средней ошибки в
ряде случаев совершенно недостаточно
. Например , при использовании гормонов
при кормлении животных знать только
средний размер неразложившихся их
вредных остатков и среднюю ошибку,
значит подвергать потребителей продукции
серьезной опасности. Здесь настоятельно
напрашивается необходимость определения
максимальной ( предельной
ошибки ).
При использовании выборочного метода
предельная ошибка устанавливается не
в виде конкретной величины , а виде
равных границ

(
интервалов) в ту и другую сторону от
значения оценки.

Определение
границ предельной ошибки основывается
на особенностях распределения конкретных
ошибок . Для так называемых больших
выборок, численность которых более 30
единиц (
)
, конкретные ошибки распределяются в
соответствии с нормальным законом
распределения; при малых выборках () конкретные ошибки распределяются
в соответствии с законом распределения
Госсета

(
Стьюдента ). Применительно к конкретным
ошибкам выборочной средней функция
нормального распределения имеет
вид:
,
где— плотность вероятности появления тех
или иных значений,
при условии, что,
гдевыборочные средние;—
генеральная средняя,— средняя ошибка для выборочной
средней. Поскольку средняя ошибка
()
является величиной постоянной, то в
соответствии с нормальным законом
распределяются конкретные ошибки,
выраженные в долях средней ошибки, или
так называемых нормированных отклонениях
.

Взяв
интеграл функции нормального
распределения, можно установить
вероятность того , что ошибка будет
заключена в некотором интервале
изменения t
и вероятность того, что ошибка выйдет
за пределы этого интервала ( обратное
событие ). Например , вероятность того,
что ошибка не превысит половину средней
ошибки ( в ту и другую сторону от
генеральной средней ) составляет
0,3829, что ошибка будет заключена в
пределах одной средней ошибки — 0,6827,
2-х средних ошибок -0,9545 и так далее.

Взаимосвязь
между уровнем вероятности и интервалом
изменения t
( а в конечном счете интервалом
изменения ошибки ) позволяет подойти
к определению интервала ( или границ )
предельной ошибки, увязав его величину
с вероятностью осуществления..
Вероятность осуществления -это
вероятность того, что ошибка будет
находится в некотором интервале.
Вероятность осуществления будет
«доверительной» в том случае, если
противоположное событие ( ошибка будет
находится вне интервала ) имеет такую
вероятность появления, которой можно
пренебречь. Поэтому доверительный
уровень вероятности устанавливают,
как правило, не ниже 0,90 (вероятность
противоположного события равна 0,10 ).
Чем больше негативных последствий
имеет появление ошибок вне установленного
интервала, тем выше должен быть
доверительный уровень вероятности (
0,95; 0,99 ; 0,999 и так далее ).

Выбрав
доверительный уровень вероятности
по таблице интеграла вероятности
нормального распределения, следует
найти соответствующее значение t,
а затем используя выражение
=определить интервал предельной ошибки.
Смысл полученной величины в следующем
– с принятым доверительным уровнем
вероятности предельная ошибка выборочной
средней не превысит величину.

Для
установления границ предельной ошибки
на основе больших выборок для других
оценок ( дисперсии, среднего квадратического
отклонения, доли и так далее ) используется
выше рассмотренный подход, с учетом
того, что для определения средней
ошибки для каждой оценки используется
свой алгоритм.

Что
касается малых выборок () то, как уже говорилось, распределение
ошибок оценок соответствует в этом
случае распределениюt
— Стьюдента. Особенность этого
распределения состоит в том, что в
качестве параметра в нем , наряду с
ошибкой, присутствует численность
выборки ,вернее не численность выборки,
а число степеней свободы
При увеличении численности выборки
распределениеt-Стьюдента
приближается к нормальному, а при
эти распределения практически совпадают.
Сопоставляя значения величиныt-Стьюдента
и t
— нормального распределения при одной
и той же доверительной вероятности
можно сказать , что величина t-Стьюдента
всегда больше t
— нормального распределения, причем,
различия возрастают с уменьшением
численности выборки и с повышением
доверительного уровня вероятности.
Следовательно, при использовании малых
выборок имеют место по сравнению с
выборками большими , более широкие
границы предельной ошибки, причем , эти
границы расширяются с уменьшением
численности выборки и повышением
доверительного уровня вероятности.

Вопросы для
повторения

6-1.Какова
природа конкретной, средней и предельной
ошибок ?

6-2.Как
соблюсти принцип равновероятности
каждой единицы попасть в выборку при
выборочном устном опросе студентов ?

6-3 Каков источник
систематической ошибки ?

6-4.Какова
вероятность появления ошибки в 2.5 раза
превышающей среднюю?

6-5.Какие
различия в знаках ( + , — ) имеют
систематические и случайные ошибки?

6-6.Каковы основные
пути уменьшения средней и предельной
ошибки ?

6-7.При какой
выборочной доле имеет место ее наибольшая
ошибка ?

6-8.При какой доле
признака имеет место ее наименьшая
ошибка 7

6-9.При
каких выборках ( больших или малых )
при прочих равных условиях имеет место
большая предельная ошибка ?

Резюме по
модульной единице 2

Использование
выборочного метода неизбежно сопряжено
с появлением ошибок. Случайный характер
этих ошибок, нормальный или t
— Стьюдента закон их распределения
позволяет определить их средний и
предельный размер и видеть пути их
снижения

Модульная
единица 3 Типовые задачи решаемые на
основе выборочного метода

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Причины возникновения погрешностей.

Введение.

Измерение физических величин и получение их числовых значений являются непосредственной задачей большинства физических экспериментов. При измерениях значение физической величины выражается в виде числа, которое указывает, во сколько раз измеренная величина больше (или меньше) другой величины, например, времени, пути, скорости и т. д. Физика устанавливает связь между такими величинами и выражает ее в виде формул, которые показывают, как числовые значения одних величин могут быть найдены по числовым значениям других.

Получение надежных числовых значений не является простой задачей из-за погрешностей, неизбежно возникающих при измерениях. Мы рассмотрим эти погрешности, а также методы, применяемые при обработке результатов измерений. Владение этими методами нужно для того, чтобы научиться получать из совокупности измерений наиболее близкие к истине результаты, вовремя заметить несоответствия и ошибки, разумно организовать сами измерения и правильно оценить точности полученных значений.

Измерения подразделяются на прямые и косвенные. В зависимости от вида измерений существуют различные методы оценки их точности. В свою очередь погрешности, допускаемые в процессе эксперимента, разделяются на систематические, случайные и грубые ошибки (промахи).

Прямые измерения производятся с помощью приборов, которые измеряют непосредственно саму исследуемую величину. Так, массу тела можно найти с помощью весов, длину измерить линейкой, а время – секундомером.

К косвенным относятся измерения таких физических величин, для нахождения которых необходимо использовать связь в виде формулы с другими, непосредственно измеряемыми величинами, например, нахождение объема тела по его линейным размерам, нахождение плотности тела по измеренным массе и объему, расчет сопротивления проводника по показаниям вольтметра и амперметра.

Причины возникновения погрешностей.

Из-за действия множества искажающих факторов результат каждого отдельного измерения физической величины не совпадает с ее истинным значением. Разность между результатом измерения и истинным значением измеряемой величины называется погрешностью измерений (ошибкой измерений).

Различают три типа погрешностей измерений: грубые ошибки (промахи), систематические и случайные погрешности. Грубые ошибки, или промахи, обычно бывают связаны с неисправностью измерительной аппаратуры, либо с ошибкой экспериментатора в отсчете или записи показаний приборов, либо с резким изменением условий измерений. Результаты измерений, соответствующих грубым ошибкам, нужно отбрасывать и взамен проводить новые измерения.

Методические погрешности обусловлены неадекватностью принимаемых моделей реальным объектам. Например, при измерении геометрических параметров вала или трубы их моделируют цилиндром. Диаметр цилиндра должен быть одинаков во всех сечениях и всех направлениях, образующие также должны иметь одинаковую длину. Однако в силу внутренних особенностей материала и несовершенства используемых технологий изготовления это правило обычно нарушено.

Другая причина – несовершенство методов измерений. Если расстояние между двумя точками порядка 100 м измеряется посредством многократного наложения метровой линейки, то в результате измеряется длина некоторой ломаной линии.

Погрешность может быть обусловлена также упрощением зависимостей, положенных в основу измерений. Например, ускорение свободного падения g можно определить, если измерить время t, в течение которого некоторое тело в свободном падении пройдет определенное расстояние h . При этом пользуются соотношением

,

которое справедливо, если на тело действует только сила тяжести. Реально на тело действует также сила сопротивления, которая в данном случае не учитывается.

Инструментальные (приборные) погрешности обусловлены особенностями принципов и методов измерений, используемых в приборах, а также их схемным, конструктивным и технологическим несовершенством. Одна из причин такой погрешности – погрешность калибровки, возникающая в процессе перехода от эталона к реальному средству измерения. Приборные погрешности определяются при испытании средства измерения и указываются в технической документации. Уменьшение инструментальной погрешности достигается применением более совершенных и точных приборов. Однако полностью устранить приборную погрешность невозможно.

Систематические погрешности сохраняют свою величину и знак во время эксперимента. Они могут быть связаны с ошибками приборов (неправильная шкала, неравномерно растягивающаяся пружина, неравномерный шаг микрометрического винта, неравные плечи весов) и с самой постановкой опыта, например, при взвешивании тела малой плотности без учета выталкивающей архимедовой силы, которая систематически занижает вес тела. Систематические погрешности опыта могут быть изучены и учтены путем внесения поправок в результаты измерений. Если систематическая погрешность опыта слишком велика, то обычно оказывается проще использовать новые, более точные приборы, чем исследовать погрешности старых.

Оценку систематических погрешностей экспериментатор проводит, анализируя особенности методики, паспортную точность прибора и проводя контрольные опыты. В учебном практикуме учет систематических ошибок ограничивается, как правило, лишь случаем инструментальных погрешностей.

Систематические погрешности стрелочных электроизмерительных приборов (амперметров, вольтметров, потенциометров и т. п.) определяется их классом точности, который выражает абсолютную погрешность прибора в процентах от максимального значения включенной шкалы. Пусть на шкале вольтметра с диапазоном показаний от 0 до 10 В в кружке стоит цифра 1. Эта цифра показывает, что класс точности вольтметра равен 1 и предел его допустимой погрешности равен 1% от максимального значения включенной шкалы, т. е. равен 0,1 В. Общая формула для расчета максимальной абсолютной погрешности имеет вид:

,

где K – класс точности прибора, A_макс – верхний предел измерений прибора (либо данного его диапазона).

Кроме того, надо иметь в виду, что наносить деления на шкале принято с таким интервалом, чтобы величина абсолютной погрешности прибора не превышала половины цены деления шкалы.

Класс точности стрелочных электроизмерительных приборов (как и полцены деления шкалы) определяет максимальную (предельную) абсолютную погрешность, величина которой не меняется вдоль всей шкалы. Относительная же погрешность при этом резко меняется, поэтому приборы обеспечивают лучшую точность при отклонении стрелки почти на всю шкалу. Отсюда следует рекомендация: выбирать прибор так, чтобы стрелка прибора при измерениях находилась во второй половине шкалы. Относительную погрешность прибора можно рассчитать по формуле:

.

В последнее время широко используются цифровые универсальные приборы, в том числе и электроизмерительные, отличающиеся высокой точностью и многоцелевым назначением. В отличие от стрелочных приборов систематические погрешности цифровых электроизмерительных приборов оцениваются по формулам, приводимым в инструкциях по эксплуатации.

Если класс точности прибора не указан и в паспорте прибора нет данных относительно его инструментальной погрешности, то обычно считают, что эта погрешность равна половине цены наименьшего деления шкалы прибора. В случае прибора, стрелка которого перемещается не равномерно, а «скачками» (например, у ручного секундомера), приборную погрешность считают равной цене деления шкалы.

Случайные погрешности измерений меняют величину и знак от опыта к опыту. Многократно повторяя одни и те же измерения, можно заметить, что довольно часто их результаты не в точности равны друг другу, а «пляшут» вокруг некоторого среднего значения.

Случайные погрешности могут быть связаны, например, с сухим трением (из-за которого стрелка прибора вместо того, чтобы останавливаться в правильном положении, «застревает» вблизи него), с люфтом в механических приспособлениях, с тряской, которую в городских условиях трудно исключить, с несовершенством объекта измерений (например, при измерении диаметра проволоки, которая из-за случайных причин, возникающих при изготовлении, имеет не вполне круглое сечение) или с особенностями самой измеряемой величины. Примером в последнем случае может быть число космических частиц, регистрируемых счетчиком за 1 минуту. Повторяя измерения, найдем, что в разных опытах получаются разные числа, хотя и не слишком отличающиеся друг от друга, колеблющиеся около некоторого среднего значения.

Случайные погрешности эксперимента исследуются путем сравнения результатов, полученных при нескольких измерениях, проведенных в одинаковых условиях. Если при двух-трех измерениях, проведенных в одинаковых условиях, результаты совпали, то на этом следует остановиться. Если они расходятся, нужно попытаться понять причину расхождения и устранить ее. Если устранить причину не удается, следует произвести 10-12 измерений и, записав все результаты, обработать их в соответствии с полученной закономерностью разброса величин.

Случайные погрешности устранить нельзя, но благодаря тому, что они подчиняются вероятностным закономерностям, всегда можно указать пределы, внутри которых с заданной вероятностью заключается истинное значение измеряемой величины.

Задача определения случайных погрешностей была решена созданием теории, хорошо согласующейся с экспериментом. В основе этой теории лежит закон нормального распределения, включающий следующие закономерности:

1. При большом числе измерений ошибки одинаковой величины, но разного знака, встречаются одинаково часто.

2. Частота появления ошибок уменьшается с ростом величины ошибки. Иначе говоря, большие ошибки наблюдаются реже, чем малые.

3. Ошибки измерений могут принимать непрерывный ряд значений.

Случайные погрешности изучают, опираясь на изложенные закономерности, и для понимания такого подхода требуется ввести понятие вероятности.

Статистическая вероятность события определяется отношением числа n случаев его проявления к общему числу N всех возможных равновероятных случаев:

Надежностью результата измеренияфизической величины А называется вероятность Р того, что истинное значение А действительно лежит в интервале от до

Абсолютной погрешностью измерений называют разность между найденным на опыте и истинным значением физической величины. Обозначая абсолютную погрешность измерения величины А символом , получим

.

Кроме абсолютной погрешности часто бывает важно знать относительную погрешность измерений, которая равна отношению абсолютной погрешности к значению измеряемой величины:

.

Качество измерений обычно определяется именно относительной, а не абсолютной погрешностью. Одна и та же погрешность в 1 мм при измерении длины комнаты не играет роли, при измерении стола может быть существенна, а при определении диаметра болта совершенно недопустима.

За наиболее достоверное значение непосредственно измеряемой величины А принимают среднее арифметическое <A> из всех n результатов ее измерений А₁, А₂, …, А_i, …, А_n:

.

Окончательный результат измерения величины А представляют в форме

.

При числе измерений n 5 с надежностью Р 2/3 можно принять, что абсолютная погрешность равна стандартной (среднеквадратичной) погрешности

.

Если необходимо повысить надежность результата, то значение следует соответственно увеличить, положив

,

где t – положительный коэффициент, задаваемый распределением Стьюдента. Значения коэффициентов Стьюдента рассчитаны и приведены в таблицах.



• 2023

Время и Стекло Так выпала Карта HD VKlipe Net

Оглавление:

• Ключевые вынос
• Случайный пример ошибки и причины
• Пример и причины систематической ошибки
• Ключевые выводы: случайная ошибка против систематической ошибки
• источники

Независимо от того, насколько вы осторожны, всегда есть ошибка в измерении. Ошибка не является «ошибкой» — это часть процесса измерения. В науке ошибка измерения называется экспериментальной ошибкой или наблюдательной ошибкой.

Существует два широких класса ошибок наблюдений: случайная ошибка а также систематическая ошибка, Случайная ошибка изменяется непредсказуемо от одного измерения к другому, в то время как систематическая ошибка имеет одинаковое значение или пропорцию для каждого измерения.

Ключевые вынос

• Случайная ошибка приводит к тому, что одно измерение немного отличается от следующего. Это происходит из-за непредсказуемых изменений во время эксперимента.
• Систематическая ошибка всегда влияет на результаты измерений в одинаковом или одинаковом соотношении, при условии, что показания проводятся каждый раз одинаково. Это предсказуемо.
• Случайные ошибки не могут быть устранены из эксперимента, но большинство систематических ошибок могут быть уменьшены.

Случайный пример ошибки и причины

Если вы делаете несколько измерений, значения группируются вокруг истинного значения. Таким образом, случайная ошибка в первую очередь влияет на точность. Как правило, случайная ошибка влияет на последнюю значащую цифру измерения.

Основными причинами случайной ошибки являются ограничения инструментов, факторы окружающей среды и небольшие изменения в процедуре. Например:

• При взвешивании на весах вы позиционируете себя немного по-разному каждый раз.
• При измерении объема в колбе вы можете каждый раз читать значение под другим углом.
• Измерение массы образца на аналитических весах может привести к различным значениям, когда воздушные потоки влияют на весы или когда вода входит в образец и покидает его.
• Измерение вашего роста зависит от незначительных изменений осанки.
• Измерение скорости ветра зависит от высоты и времени измерения. Многократные чтения должны быть взяты и усреднены, потому что порывы и изменения в направлении влияют на значение.
• Показания должны оцениваться, когда они находятся между отметками на шкале или когда учитывается толщина измерительной отметки.

Поскольку случайная ошибка всегда возникает и не может быть предсказана, важно взять несколько точек данных и усреднить их, чтобы получить представление о величине отклонения и оценить истинное значение.

Пример и причины систематической ошибки

Систематическая ошибка предсказуема и либо постоянна, либо пропорциональна измерению. Систематические ошибки в первую очередь влияют на точность измерения.

Типичные причины систематической ошибки включают в себя ошибку наблюдений, несовершенную калибровку прибора и помехи окружающей среды. Например:

• Если забыть о тарировании или обнулении баланса, получаются измерения массы, которые всегда «выключаются» на одну и ту же величину. Ошибка, вызванная не установкой прибора на ноль до его использования, называется ошибка смещения.
• Не считывание мениска на уровне глаз для измерения объема всегда приводит к неточным показаниям. Значение будет постоянно низким или высоким, в зависимости от того, взяты ли показания сверху или ниже отметки.
• Измерение длины с помощью металлической линейки даст другой результат при холодной температуре, чем при высокой температуре, из-за теплового расширения материала.
• Неправильно откалиброванный термометр может дать точные показания в определенном температурном диапазоне, но стать неточным при более высоких или более низких температурах.
• Измеренное расстояние отличается при использовании новой измерительной ленты от старой натянутой ленты. Пропорциональные ошибки этого типа называются ошибки масштабного коэффициента.
• дрейф происходит, когда последовательные чтения становятся последовательно ниже или выше со временем. Электронное оборудование имеет тенденцию быть склонным к дрейфу. Многие другие инструменты подвержены (как правило, положительному) дрейфу, поскольку устройство нагревается.

Как только его причина установлена, систематическая ошибка может быть уменьшена до некоторой степени. Систематическая ошибка может быть сведена к минимуму путем регулярной калибровки оборудования, использования контрольных элементов в экспериментах, прогрева приборов до снятия показаний и сравнения значений со стандартами.

В то время как случайные ошибки могут быть минимизированы путем увеличения размера выборки и усреднения данных, сложнее компенсировать систематическую ошибку. Лучший способ избежать систематической ошибки — это знать ограничения инструментов и иметь опыт их правильного использования.

Ключевые выводы: случайная ошибка против систематической ошибки

• Двумя основными типами ошибок измерения являются случайная ошибка и систематическая ошибка.
• Случайная ошибка приводит к тому, что одно измерение немного отличается от следующего. Это происходит из-за непредсказуемых изменений во время эксперимента.
• Систематическая ошибка всегда влияет на результаты измерений в одинаковом или одинаковом соотношении, при условии, что показания проводятся каждый раз одинаково. Это предсказуемо.
• Случайные ошибки не могут быть устранены из эксперимента, но большинство систематических ошибок могут быть уменьшены.

источники

• Блэнд, Дж. Мартин и Дуглас Г. Альтман (1996). «Статистические заметки: ошибка измерения». BMJ 313.7059: 744.
• Cochran, W.G. (1968). «Ошибки измерения в статистике». Technometrics, Taylor & Francis, Ltd. от имени Американской статистической ассоциации и Американского общества качества. 10: 637–666. DOI: 10,2307 / 1267450
• Додж Ю. (2003). Оксфордский словарь статистических терминов, ОУП. ISBN 0-19-920613-9.
• Тейлор, Дж. Р. (1999). Введение в анализ ошибок: изучение неопределенностей в физических измерениях, Университетская Наука Книги. п. 94. ISBN 0-935702-75-X.