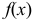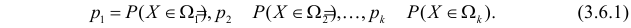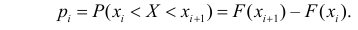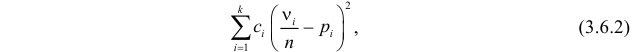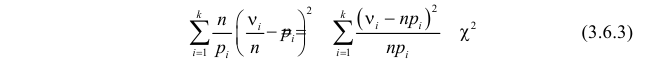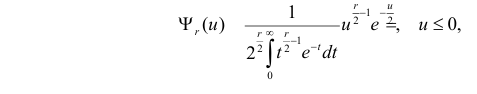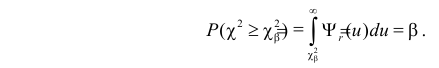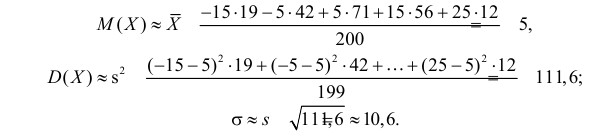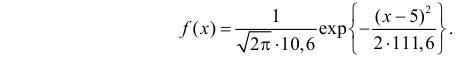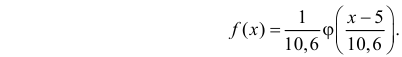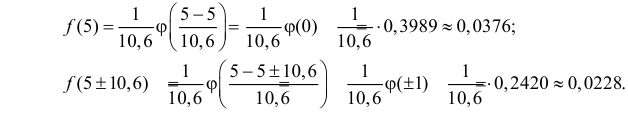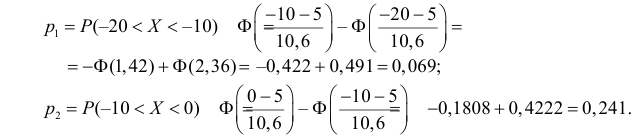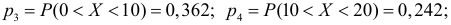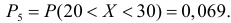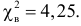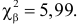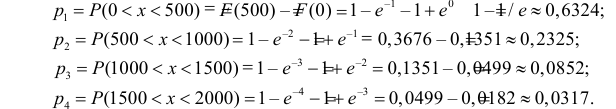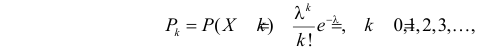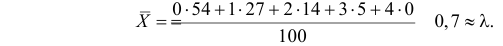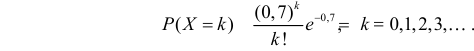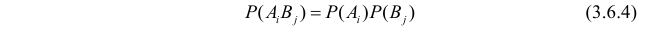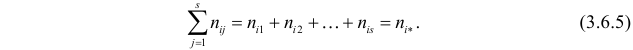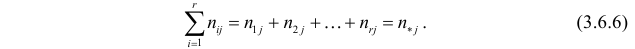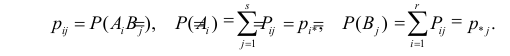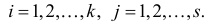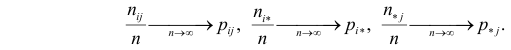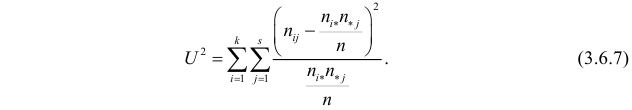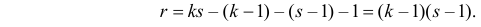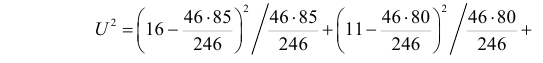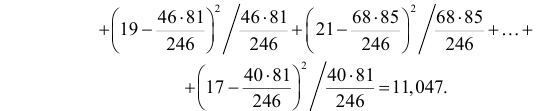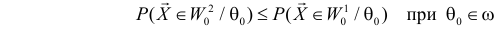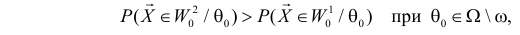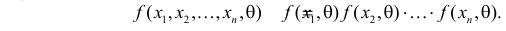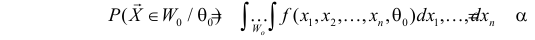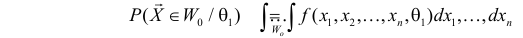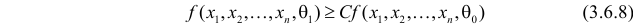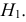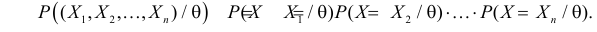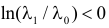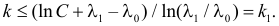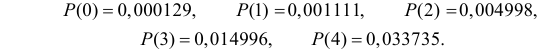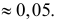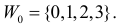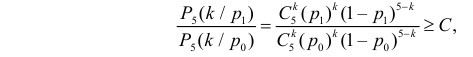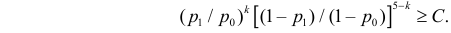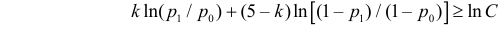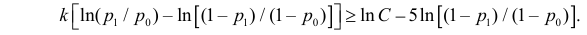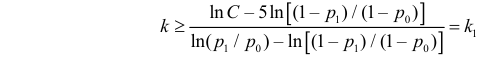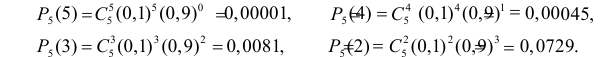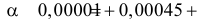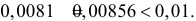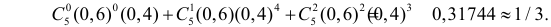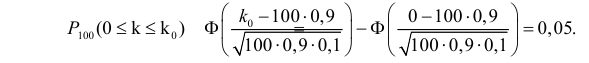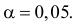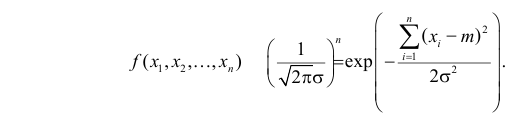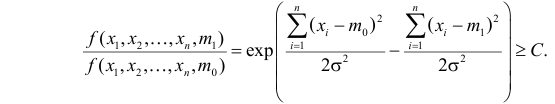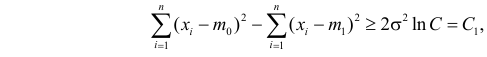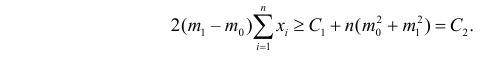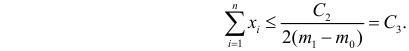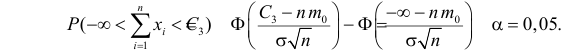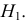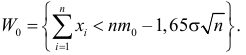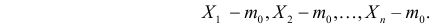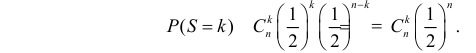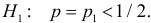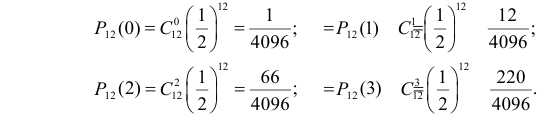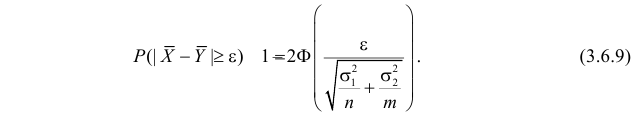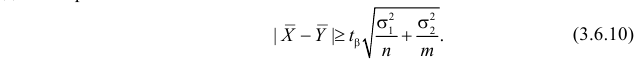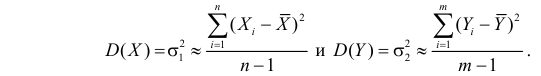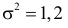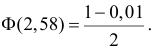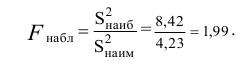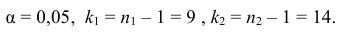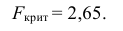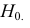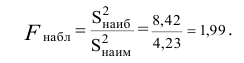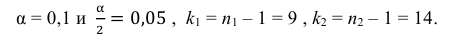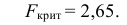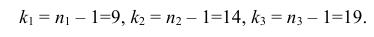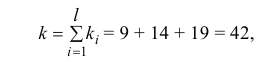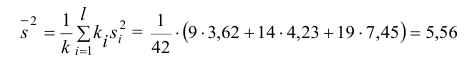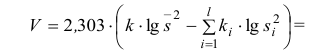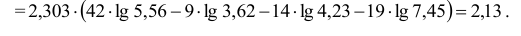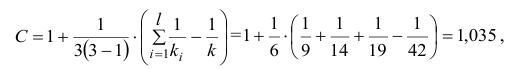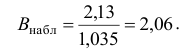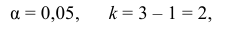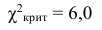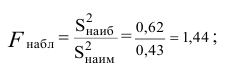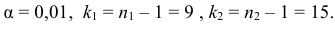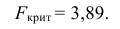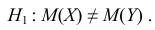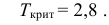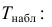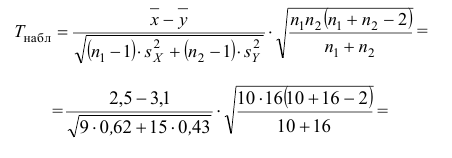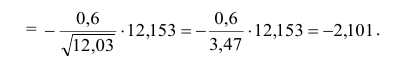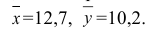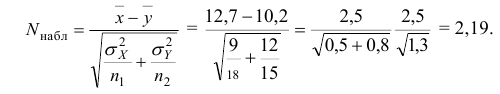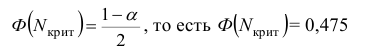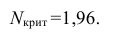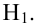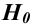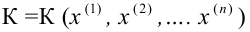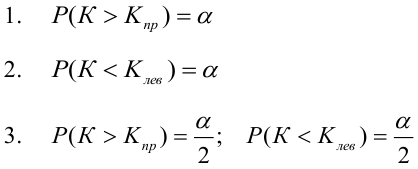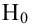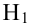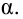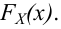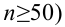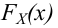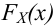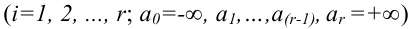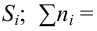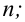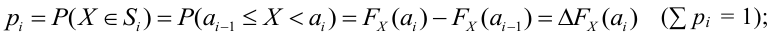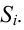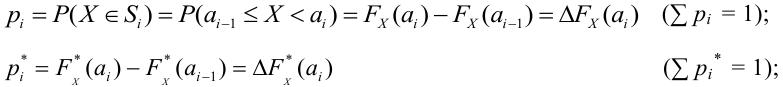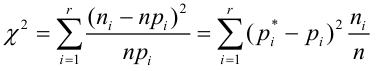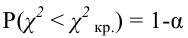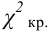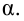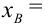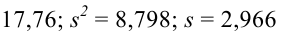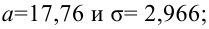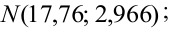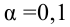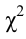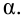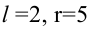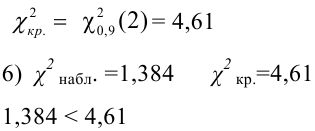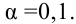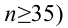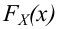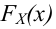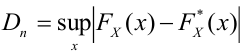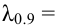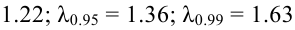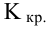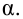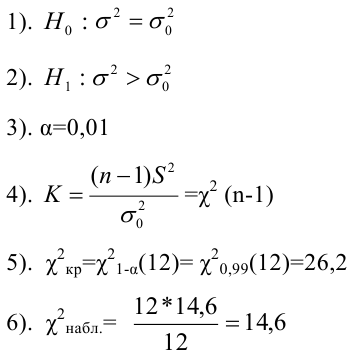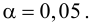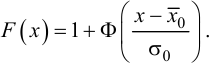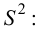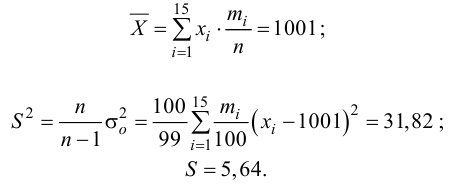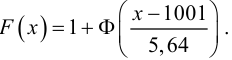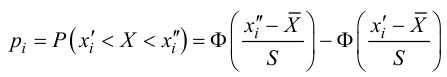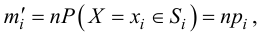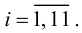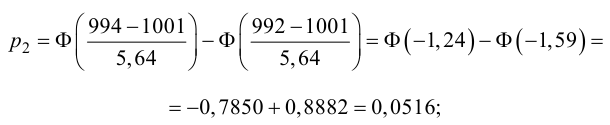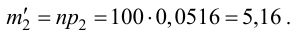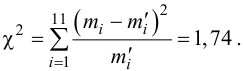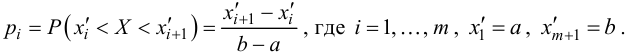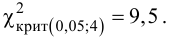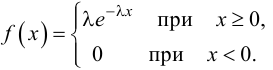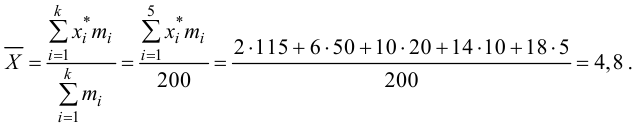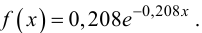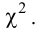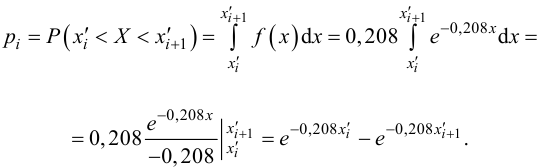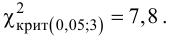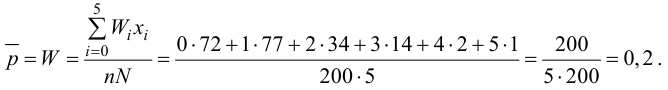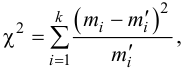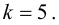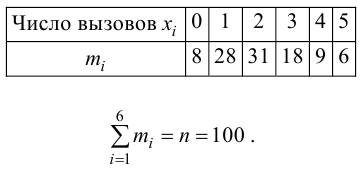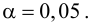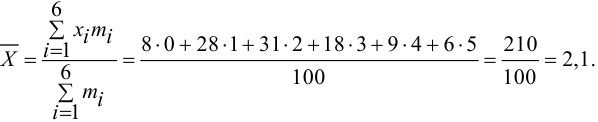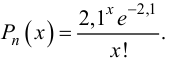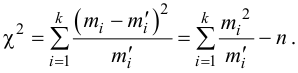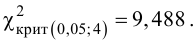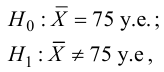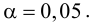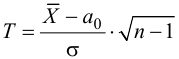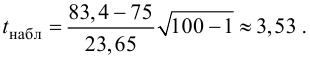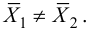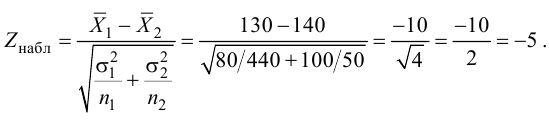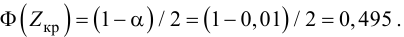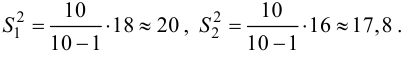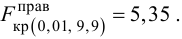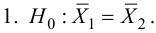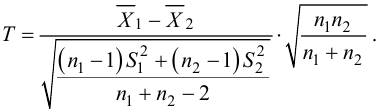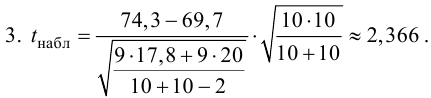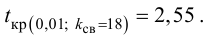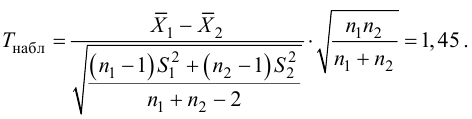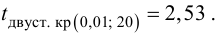План:
1. Статистические гипотезы. Основные понятия.
2. Гипотезы о законе распределения.
3. Гипотезы о числовом значении генерального
среднего и дисперсии.
1.
Статистические гипотезы. Основные понятия.
Статистическая гипотеза— это утверждение о виде неизвестного
распределения или параметрах известного распределения. Статистические гипотезы
проверяются по результатам выборки статистическими методами в ходе эксперимента
(эмпирическим путем) с помощью статистических критериев.
В тех случаях, когда
известен закон, но неизвестны значения его параметров (дисперсия или
математическое ожидание) в конкретной ситуации, статистическую гипотезу
называют параметрической.
Например, предположение
об ожидаемом среднем доходе по акциям или разбросе дохода являются
параметрическими гипотезами.
Когда закон
распределения генеральной совокупности не известен, но есть основания
предположить, каков его конкретный вид, выдвигаемые гипотезы о виде его
распределения называются непараметрическими.
Например, можно
выдвинуть гипотезу, что число дневных продаж в магазине или доход населения
подчинены нормальному закону распределения.
По содержанию статистические гипотезы можно классифицировать:
1.
Гипотезы о типе вероятностного закона
распределения случайной величины, характеризующего явление или процесс.
2.
Гипотезы об однородности двух или более
обрабатываемых выборок. Изучаемое свойство исследуется с помощью двух или более генеральных
совокупностей. Гипотеза в этом случае может заключаться в следующем: исследуемые
выборочные характеристики различаются между собой статистически значимо или
нет.
3.
Гипотезы о свойствах числовых значений
параметров исследуемой генеральной совокупности. Больше ли значения параметров
некоторого заданного номинала или меньше и т.д.
4.
Гипотезы о вероятностной зависимости двух
или более признаков, характеризующих различные свойства рассматриваемого
явления или процесса. При этом определяется характер этой зависимости.
Гипотезы бывают простые (содержащие одно предположение) и сложные (содержащие несколько предположений).
Выдвинутую гипотезу называют основной или нулевой и обозначают H0
. Противоречащую ей гипотезу называют альтернативной или конкурирующей и обозначают
H1.
Под статистическим
критерием понимают однозначно определенное правило, устанавливающее
условие, при котором проверяемая гипотеза отвергается либо не отвергается.
Пример:
Увеличение числа заболевших некоторым
заболеванием дает возможность выдвинуть гипотезу о наличии эпидемии. Для сравнения
доли заболевших в обычных и экстремальных условиях используются статистические
данные, на основании которых делается вывод о том, является ли данное массовое
заболевание эпидемией. Предполагается, что существует некоторый критерий-
уровень доли заболевших, критический для этого заболевания, который
устанавливается по ранее имевшимся случаям.
Различают три вида критериев:
1.
Параметрические критерии—
критерии значимости, которые служат для проверки гипотез о параметрах
распределения генеральной совокупности при известном виде распределения.
2.
Критерии согласия—
позволяют проверить гипотезы о соответствии распределений генеральной
совокупности известной теоретической модели.
3.
Непараметрические критерии—
используются в гипотезах, когда не требуется знаний о конкретном виде
распределения.
Проверка
параметрических гипотез проводится на основе критериев значимости., а
непараметрических- критериев согласия.
Задача проверки
статистических гипотез сводится к исследованию генеральной совокупности по
выборке. Множество возможных значений элементов выборки может быть разделено на
два непересекающихся подмножества- критическую область и область принятия
гипотезы.
Областью принятия гипотезы или областью допустимых значений Iдоп
называют совокупность значений критерия,
при которых эту гипотезу принимают.
Критической областью
Iкр называют множество значений критерия, при
котором гипотезу отвергают.
Наблюдаемые значения критерия (статистика)
Kнабл
называют такое значение критерия, которое
находится по данным выборки.
Границы критической области, отделяющие ее от
области принятия гипотезы, называют критическими точками и обозначают
Kкр.
Для определения
критической области задается уровень значимости
—
некая малая вероятность попадания критерия в критическую область.
Уровень значимости— вероятность принятия
конкурирующей гипотезы, тогда как справедлива основная.
С помощью уровня
значимости определяются границы критической области.
Основной принцип проверки статистических гипотез
состоит в следующем: если наблюдаемое значение статистики критерия попадает (не
попадает) в критическую область, то гипотеза H0
отвергается (принимается), а гипотеза H1
принимается (отвергается) в качестве одного из
возможных решений с формулировкой «гипотеза
H0 противоречит (не противоречит) выборочным
данным на уровне значимости
».
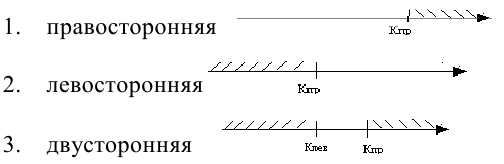
В зависимости от
содержания альтернативной гипотезы осуществляется выбор критической области:
левосторонней, правосторонней, двусторонней. Если смысл исследования заключается
в доказательстве конкретного изменения наблюдаемого параметра (его уменьшения
или увеличения), то говорят об односторонней критической области. Если смысл
исследования- выявить различия в изучаемых параметрах, но характер их
отклонения от контрольных (или теоретических) не известен, то говорят о
двусторонней критической области.
Однако, принятие той
или иной гипотезы не дает оснований утверждать, что она верна. Результат
проверки статистической гипотезы лишь устанавливают на определенном уровне
значимости ее соответствие (несоответствие) результатам эксперимента.
При проверке
статистических гипотез возможны следующие ошибки:
1.
Отвергнута правильная
H0, а принята неправильная гипотеза
H1 — ошибка
первого рода.
2. Отвергнута правильная альтернативная
гипотеза
H1 и
принята неправильная нулевая гипотеза H0
—
ошибка второго рода.
Заметим, что уровень значимости —
есть вероятность ошибки первого рода. Ошибка первого рода называется
-риском. Обычно они задаются
некоторыми конкретными значениями: 0,05; 0,01; 0,005; 0,001. Ошибки второго
рода называются -риском, а вероятность ее
допустить обозначается
(вероятность того, что принята гипотеза
H0
, когда на самом деле справедлива
альтернативная гипотеза H1
.
Можно доказать, что с
уменьшением ошибок первого рода одновременно увеличиваются ошибки второго рода
и наоборот. Поэтому, на практике пытаются подбирать значения параметров
и
опытным путем в целях минимизации суммарного
эффекта от возможных ошибок. При принятии управленческих решений для
одновременного уменьшения ошибок первого и второго рода самым действенным
средством является увеличение объема выборки, что согласуется с законом больших
чисел.
На бытовом уровне
ошибки второго рода могут иметь более трагические последствия, чем ошибки
первого рода.
2. Гипотеза о законе распределения. Критерий согласия Пирсона (
X2
-критерий).
Критериями согласия называют критерии, в
которых гипотеза определяет закон распределения либо полностью, либо с
точностью до небольшого числа параметров.
Причины расхождения
результатов эксперимента и теоретических характеристик могут быть вызваны малым
объемом выборки, неудачным способом группировки наблюдений, ошибками в
выборе гипотезы о виде распределения
генеральной совокупности и др.
Рассмотрим
универсальный критерий согласия Пирсона. Проверка гипотезы о том, что
эмпирическая частота мало отличается от соответствующей теоретической частоты,
осуществляется с помощью величины X2
—
меры расхождения между ними.
Для произвольной
выборки, когда распределение непрерывно или число различных вариант велико, все
пространство наблюдаемых вариант делят на конечное число непересекающихся
областей, в каждой из которых подсчитывают наблюдаемую частоту и теоретическую
вероятность.
Для применения критерия
согласия Пирсона необходимо:
1. Вычислить значение статистики по формуле:
, где
pi –вероятность
принятия значения
xi, ni.
— эмпирическая частота для
соответствующего
xi. n— объем выборки. s— число вариант выборки.
2.
По
соответствующей таблице распределения Пирсона найти критическое значение , где k = s –
r
– 1 – число степеней свободы, s—
число различных вариант или интервалов группировки, r— число неизвестных параметров
предполагаемого теоретического распределения,
— выбранный уровень значимости. Это
значит, что строится правосторонний интервал.
3.
Если
,
то основная гипотеза отвергается, в противном случае- принимается, т.е. чем
больше отклонение, тем меньше согласованы теоретическое и эмпирическое
распределение. Поэтому принято использовать только правостороннюю критическую
область.
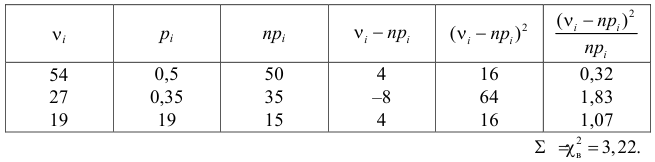
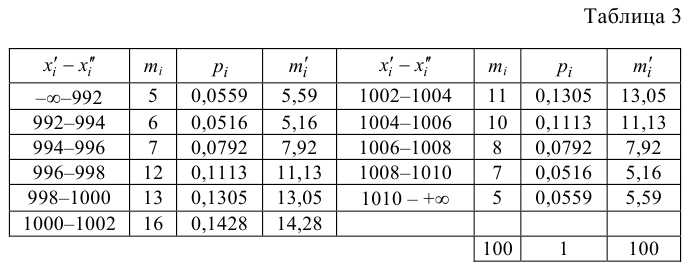
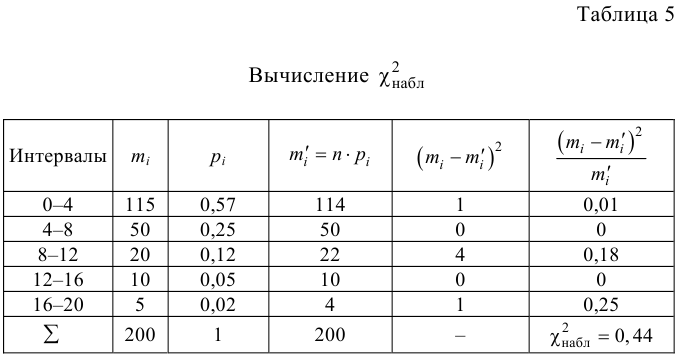
Расчетная таблица имеет вид:
|
Интервалы |
Середины |
Эмпирические |
Вероятности pi |
Теоретические |
|
|
Пример:
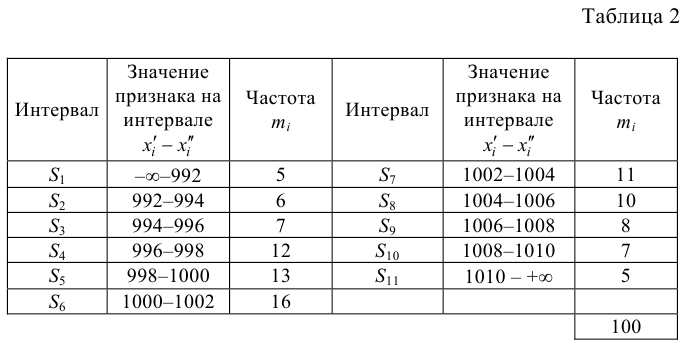
По таблице
эмпирического распределения изменения в процентах темпа роста акций проверьте
гипотезу о нормальном распределении выборки.
|
Интервалы |
(-2; |
(-1; |
(0; |
(1; |
Итого |
|
ni |
7 |
14 |
18 |
11 |
50 |
|
pi |
0,157 |
0,341 |
0,341 |
0,157 |
1 |
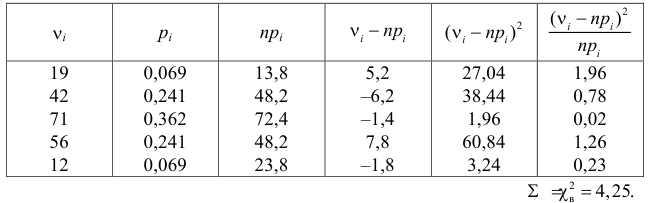
Решение:
Гипотезу о нормальном
распределении проверим по критерию Пирсона.
|
Интервалы |
Эмпирические |
Вероятности pi |
Теоретические |
|
|
|
(-2; |
7 |
0,157 |
7,85 |
0,7225 |
0,092 |
|
(-1; |
14 |
0,341 |
17,05 |
9,3025 |
0,546 |
|
(0; |
18 |
0,341 |
17,05 |
0,9025 |
0,053 |
|
(1; |
11 |
0,157 |
7,85 |
9,925 |
1,264 |
|
Итого |
|
По таблице найдем
при
=0,05
и k = s – r – 1 = 4 – 2 – 1 = 1. s = 4 – число
интервалов. r
= 2- число параметров теоретического (нормального) распределения.
Имеем . Т.к. 1,955 < 3,841, то
, т.е. гипотеза о нормальном
распределении подтверждается.
3. Гипотезы о числовом значении генерального
среднего и дисперсии.
Установление двусторонней критической
области на уровне значимости
для
проверки гипотезы соответствует отысканию соответствующего доверительного
интервала с надежностью
.
Рассмотрим условия применения некоторых
статистических гипотез.
|
Тип гипотезы H0 |
Границы критической области на уровне значимости |
Статистика наблюдений |
|
О числовом значении |
|
|
|
О числовом значении |
Распределение |
|
|
О числовом значении |
Распределение Пирсона |
|
Пример:
Результаты исследований в течение 35 лет
показали, что среднее изменение доходности векселей равно 5,5 %. Полагая, что
изменение доходности подчиняется нормальному закону распределения с
среднеквадратическим отклонением равным 2 %, на уровне значимости
, решите: можно ли принять 6 % в качестве нормативного процента
(математического ожидания) изменения доходности.
Решение:
По условию задачи
нулевая гипотеза
. Так как
, то в качестве альтернативной гипотезы
возьмем гипотезу:
, которой соответствует левосторонняя
критическая область с интервалом.
Найдем границы
критической области:
По таблице значений
функции Ф(х) найдем
, т.е. левосторонняя критическая область
лежит в интервале.
Найдем статистику
наблюдений:
.
Имеем:, нет основания отвергать нулевую
гипотезу. Значит, в качестве нормативного процента можно принять 6 %.
Пример:
Точность работы
программы проверяют по дисперсии контролируемого количества символов в коде,
которая не должна превышать 0,1. По выборке из 15 сообщений вычислена
исправленная оценка дисперсии 0,22. При
уровне значимости 0,05 проверьте, обеспечивает ли программа необходимую
точность.
Решение:
Имеем: n = 15, s2 = 0,22
, ,
.
Сформулируем гипотезу о
числовом значении дисперсии:
H0 — программа обеспечивает необходимую точность
;
H1 —
программа не обеспечивает необходимую точность
.
Определим статистику: .
Найдем границы
критической области:
.
Поскольку 30,8 >
23,7;
, принимаем гипотезу H1, т.к.
H0 противоречит опытным данным. Вывод: программа
не обеспечивает необходимую точность.
Финансовые аналитики часто сталкиваются с конкурирующими идеями о том, как работают финансовые рынки. Некоторые из этих идей развиваются через личные исследования или опыт работы с рынками; другие появляются благодаря взаимодействию с коллегами; и многие другие появляются в результате публикаций в профессиональной литературе по финансам и инвестициям.
Но как может аналитик определить насколько истинны или ложны те или иные идеи?
Когда мы можем свести идею или предположение к определенному утверждению о значении величины, такому как среднее значение совокупности, идея становится статистически проверяемым утверждением или гипотезой.
Аналитик может захотеть исследовать такие вопросы, как:
- Отличается ли средняя доходность данного взаимного фонда от средней эталонной доходности?
- Изменится ли волатильность доходности акции, после того как эта акция будет добавлена в рыночный индекс акций?
- Влияет ли разница между ценами продажи и покупки акции, связанная с числом дилеров, на рынок этой акции?
- Поддерживают ли данные национального рынка облигаций прогноз, полученный на основе экономической теории о временной структуре процентных ставок (связь между доходностью и сроком погашения)?
Для решения этих вопросов, мы используем концепцию и методы проверки статистических гипотез.
Проверка статистических гипотез (англ. ‘hypothesis testing’) является частью статистического вывода, и представляет собой процесс принятия суждений о более крупной группе (совокупности) на основе небольшой фактически наблюдаемой группе (выборке).
Концепции и методы проверки гипотез обеспечивают объективные средства для оценки того, подтверждают ли имеющиеся доказательства гипотезу. После статистической проверки гипотезы мы должны иметь четкое представление о вероятности того, верна ли гипотеза или нет.
Проверка статистических гипотез была мощным инструментом в научном развитии инвестиций. Как написал Роберт Л. Кан (Robert L. Kahn) из Института социальных исследований (Анн-Арбор, штат Мичиган):
«Мельница науки перемалывает только тогда, когда гипотезы и данные находятся в непрерывном и тесном контакте».
Основные акценты этого чтения сосредоточены на основах проверки гипотез и проверке гипотез, касающихся среднего значения и дисперсии, — двух величин, весьма часто использующихся в инвестициях.
Сначала мы приведем обзор процедуры проверки гипотез. Затем обратимся проверке гипотез о среднем, гипотез о разнице между средними и среднем значении разности. В следующем разделе этого чтения, мы рассмотрим проверку гипотез о дисперсии и различиях между дисперсиями, а также проверку гипотез о значении коэффицента корреляции.
В завершение мы рассмотрим непараметрические методы статистического вывода.
Проверка гипотезы, как мы уже упоминали, является частью области статистики, известной как статистический вывод. Традиционно область статистического вывода имеет два направления: статистическая оценка и проверка гипотез.
Статистическая оценка отвечает вопрос:
«Чему равно значение этого параметра (например, среднего значения по совокупности)?»
Ответ на этот вопрос дается в виде доверительного интервала, построенного вокруг точечной оценки. В случае со средним значением, мы строим доверительный интервал для среднего значения совокупности вокруг выборочного среднего, полученного в результате точечной оценки.
Например, предположим, что выборочное среднее равно 50 и 95-процентный доверительный интервал для среднего населения составляет (50 pm 10) (доверительный интервал составляет от 40 до 60). Если доверительный интервал правильно построен, то есть 95-процентная вероятность того, что интервал от 40 до 60 содержит среднее значение совокупности.
Мы обсуждали построение и интерпретацию доверительных интервалов в чтении о выборочном методе и статистической оценке.
Вторая ветвь статистического вывода, проверка гипотез, имеет несколько иную направленность.
Проверка статистических гипотез отвечает на вопрос:
«Равно ли значение параметра (например, среднего значения по совокупности) 45 (или другому конкретному значению)?»
Утверждение «среднее совокупности равно 45» является гипотезой. Статистическая гипотеза (англ. ‘hypothesis’) определяется как утверждение об одной или нескольких совокупностях.
Этот раздел посвящен концепции проверки гипотез. Процесс проверки гипотезы является частью строгого подхода к получению знаний, известного как научный метод (англ. ‘scientific method’).
Научный метод начинается с наблюдений и формулировки теории организации и объяснения наблюдений. Мы судим о правильности теории по ее способности давать точные прогнозы — например, предсказывать результаты новых наблюдений.
Чтобы быть проверяемой, теория должна быть способна делать предсказания, ошибочность которых можно показать.
Если прогнозы верны, мы продолжаем поддерживать теорию, как возможно правильное объяснение наших наблюдений. Когда в результатах наблюдений важна оценка риска, как в области финансов, мы можем попытаться сделать объективное, основанное на вероятности, суждение о том, поддерживают ли новые данные прогноз.
Проверка статистических гипотез играет ключевую роль, когда важна оценка риска.
В своей ежедневной работе финансовый аналитик может сталкиваться с вопросами, на которые он может дать ответы различного качества.
Когда аналитик правильно формулирует проверяемую гипотезу, проверяет ее и составляет отчет о проверке гипотезы, он следует нормам научного метода.
Конечно, логика аналитика, экономическое обоснование, источники информации, и, возможно, другие факторы также оказывают определенное влияние на качество ответа на заданный вопрос.
См. работу Freeley и Steinberg (2008) для обсуждения влияния критического мышления на мотивированное принятие решений.
Мы начнем изучение проверки гипотез со следующего списка из семи шагов.
Этапы проверки статистических гипотез.
Этапы проверки гипотезы заключаются в следующем:
- Формулировка гипотезы.
- Определение соответствующей тестовой статистики (статистики критерия) и ее распределения вероятностей.
- Определение уровня значимости.
- Формулировка правила принятия решения.
- Сбор данных и расчет тестовой статистики.
- Принятие статистического решения.
- Принятие экономического или инвестиционного решения.
Этот список этапов основан на списке из работы Daniel и Terrell (1995).
Мы расскажем о каждом из этих этапов, используя в качестве иллюстрации проверку гипотезы о премии за риск для американских акций. Описанный процесс представляет собой традиционный подход к проверке гипотез.
В завершении мы рассмотрим часто используемую альтернативу этих шагов — подход, основанный на p-значении.
1 этап. Формулировка гипотезы.
Первым шагом в проверке гипотезы является формулировка гипотезы. Мы всегда формулируем две гипотезы: нулевую гипотезу (или нуль), обозначаемую как (H_0), и альтернативную гипотезу, обозначаемую как (H_a).
Определение нулевой гипотезы.
Нулевая гипотеза — это гипотеза, которую нужно проверить. Например, мы могли бы предположить, что среднее по совокупности премии за риск для американских акций меньше или равно нулю.
Нулевая гипотеза (нуль, англ. ‘null hypothesis’) — это утверждение, которое считается истинным, если только используемая для проверки гипотезы выборка не дает убедительные доказательства того, что нулевая гипотеза неверна. Когда такие доказательства присутствуют, мы переходим к альтернативной гипотезе.
Определение альтернативной гипотезы.
Альтернативная гипотеза (альтернатива или конкурирующая гипотеза, англ. ‘alternative hypothesis’) — это гипотеза, которая принимается, когда нулевая гипотеза отвергается. Наша альтернативная гипотеза заключается в том, что среднее по совокупности премии за риск для американских акций больше нуля.
Предположим, что наш вопрос касается значения параметра совокупности (theta), по отношению к одному возможному значению параметра, (theta_0) (они читаются, соответственно, как «тета» и «тета ноль»).
Греческие буквы, такие как (sigma), зарезервированы для параметров совокупности. Римские курсивные буквы, например, (s), используются для выборочных статистик.
Примерами параметра совокупности являются среднее по совокупности (mu) и дисперсия совокупности (sigma^2). Мы можем сформулировать три различные пары нулевых и альтернативных гипотез и обозначить их согласно утверждению альтернативной гипотезы.
Формулировки гипотез.
Мы можем сформулировать нулевые и альтернативные гипотезы тремя различными способами:
- 1-я формулировка: (H_0: theta = theta_0) (нулевая гипотеза) и (H_a: theta neq theta_0) (альтернативная гипотеза «не равно»).
- 2-я формулировка: (H_0: theta leq theta_0) (нулевая гипотеза) и (H_a: theta > theta_0) (альтернативная гипотеза «больше чем»).
- 3-я формулировка: (H_0: theta geq theta_0) (нулевая гипотеза) и (H_a: theta < theta_0) (альтернативная гипотеза «меньше, чем»).
В нашем примере с американскими акциями, (theta = mu_{RP} ), что представляет собой среднее по совокупности премии за риск для американских акций. Кроме того, (theta_0 = 0 ), и мы используем вторую из указанных выше трех пар гипотез.
1-я формулировка представляет собой двустороннюю проверку гипотезы (англ. ‘ two-sided hypothesis test’ или ‘two-tailed hypothesis test’): Мы отвергаем нуль в пользу альтернативы, если данные свидетельствуют о том, что параметр совокупности либо меньше, либо больше, чем (theta_0 ).
В отличие от этого, 2-я и 3-я формулировки являются односторонней проверкой гипотезы (англ. ‘one-sided hypothesis test’ или ‘one-tailed hypothesis test’).
В формулировках 2 и 3 мы отвергаем нуль только тогда, когда данные свидетельствуют о том, что параметр совокупности соответственно, либо больше, либо меньше, чем (theta_0 ). Альтернативная гипотеза имеет только одну сторону.
Обратите внимание, что в каждом из описанных выше случаев, мы формулируем нулевые и альтернативные гипотезы так, что они учитывают все возможные значения параметра. В формулировке 1, например, параметр или равен гипотетическому значению (theta_0 ) (по нулевой гипотезе) или не равен гипотетическому значению (theta_0 ) (по альтернативной гипотезе).
Эти два утверждения логически исчерпывают все возможные значения параметра.
Несмотря на то, что формулировать гипотезы можно различными способами, мы всегда проводим проверку нулевой гипотезы в точке равенства, (theta = theta_0 ). Если нуль это (H_0: theta = theta_0), (H_0: theta leq theta_0) или (H_0: theta geq theta_0), мы на самом деле проверяем (theta = theta_0 ). Логика проста.
Предположим, что гипотетическое значение параметра равно 5.
Рассмотрим нулевую гипотезу (H_0: theta leq 5), с альтернативной гипотезой «больше чем» (H_a: theta > 5) .
Если у нас есть достаточно доказательств, чтобы отклонить (H_a: theta = 5) в пользу (H_a: theta > 5), то у нас, безусловно, также есть достаточные доказательства, чтобы отвергнуть гипотезу о том, что параметр (theta) равен некоторому меньшему значению, например, 4.5 или 4.
Напомним, что расчет для проверки нулевой гипотезы является одинаковым для всех трех формулировок. Различия в трех формулировках мы увидим в ближайшее время, — они заключаются в определении того, следует ли отклонить нулевую гипотезу.
Как мы выбираем нулевые и альтернативные гипотезы?
Вероятно, наиболее распространенными являются альтернативные гипотезы «не равно». Мы отвергаем нуль, поскольку данные свидетельствуют о том, что параметр больше или меньше, чем (theta_0).
Иногда, однако, у нас могут быть условия, имеющие вид «ожидаем», «подозреваем» или «надеемся на то, что», которые означают, что мы хотим найти благоприятные доказательства.
Часть этого обсуждения выбора гипотез взята из работы Bowerman, O’Connell и Murphree (2016).
В этом случае, мы можем сформулировать альтернативную гипотезу, как утверждение о том, что это условие является истинным. При этом нулевой гипотезой будет утверждение о том, что это условие не истинно. Если данные подтверждают отклонение нуля и принятие альтернативы, то мы статистически подтвердили наши ожидания того, что было истиной.
Например, экономическая теория предполагает, что инвесторы требуют положительную премию за риск по акциям (премия за риск определяется как ожидаемая доходность акций за вычетом безрисковой ставки).
Следуя принципу с формулировки альтернативы в виде условия «надеемся на то, что», сформулируем следующие гипотезы:
- (H_0:) Среднее по совокупности премии за риск для американских акций меньше или равно 0.
- (H_a:) Среднее по совокупности премии за риск для американских акций положительно.
Обратите внимание, что альтернативные гипотезы «больше чем» и «меньше чем» отражают убеждения исследователя сильнее, чем альтернативная гипотеза «не равно».
Для того, чтобы подчеркнуть свое нейтральное отношение к гипотезам, исследователь может иногда выбрать альтернативную гипотезу «не равно», когда выбор односторонней альтернативной гипотезы также разумен.
2 этап. Определение тестовой статистики и ее распределения вероятностей.
Второй этап проверки гипотез заключается в определении соответствующей тестовой статистики и ее распределения вероятностей.
Определение тестовой статистики.
Тестовая статистика, тест-статистика или статистика критерия (т.е. статистика, лежащая в основе критерия, англ. ‘test statistic’) является величиной, рассчитанной на основе выборки, значение которой является основанием для принятия решения о том, следует ли отклонить нулевую гипотезу.
Средоточием нашего статистического решения является значение тестовой статистики. Очень часто (во всех случаях, которые мы рассмотрим в этом чтении) тестовая статистика имеет следующий вид:
( Large stBf{Тестовая}{статистика} = { stRm{Выборочная}{статистика} — stRm{Значение параметра}{совокупности при $H_0$} over text{Стандартная ошибка выборочной статистики}} ) (Формула 1)
Для нашей премии за риск, например, интересующий параметр совокупности — это средняя по совокупности премия за риск (mu_{RP}). Мы обозначаем гипотетическое значение среднего по совокупности населения для (H_0) как (mu_0). Переформулировав гипотезу с использованием символов, мы проверяем нуль (H_0: mu_{RP} leq mu_0 ) и альтернативу (H_a: mu_{RP} > mu_0 ).
Однако, поскольку в соответствии с нулем мы проверяем условие ( mu_0 = 0), то мы пишем (H_0: mu_{RP} leq 0 ) и (H_a: mu_{RP} > 0 ).
Выборочное среднее обеспечивает оценку среднего по совокупности. Таким образом, мы можем использовать выборочное среднее премии за риск ( overline X_{RP}), рассчитанное на основе исторических данных, в качестве выборочной статистики в Формуле 1.
Стандартное отклонение выборочной статистики, известное как «стандартная ошибка» статистики, является знаменателем в Формуле 1.
В этом примере выборочной статистикой является выборочное среднее. Для выборочного среднего ( overline X ), рассчитанного по выборке, отобранной из совокупности со стандартным отклонением ( sigma ), стандартная ошибка определяется по одной из двух формул:
(large dst
sigma_{overline X} = {sigma over sqrt n} ) (Формула 2)
если нам известно стандартное отклонение совокупности (sigma), или
(large dst
s_{overline X} = {s over sqrt n} ) (Формула 3)
когда мы не знаем стандартное отклонение совокупности и нам необходимо использовать стандартное отклонение выборки (s) оценки стандартной ошибки.
В этом примере, поскольку мы не знаем стандартное отклонение совокупности, порождающей доходность, мы используем Формулу 3.
Таким образом, тестовая статистика определяется по формуле:
( large dst
{overline X_{RP} — mu_0 over s_{overline X}} = {overline X_{RP} — 0 over s big / sqrt n } )
Заменяя (mu_0) на 0, мы используем тот уже отмеченный факт, что мы тестируем любую нулевую гипотезу в точке равенства, а также тот факт, что здесь (mu_0 = 0).
Итак, мы определили тестовую статистику, чтобы проверить нулевую гипотезу.
Какому распределению вероятностей она соответствует?
В этом чтении мы будет использовать четыре распределения вероятности для тестовых статистик:
- t-распределение Стьюдента (для t-теста);
- Стандартное нормальное или z-распределение (для z-теста);
- Распределение хи-квадрат (( chi^2 )) (для хи-квадрат теста); а также
- F-распределение (для F-теста).
Мы обсудим детали этих вариантов позже, но предположим, что мы можем провести z-тест, основанный на центральной предельной теореме, потому что наша выборка американских акций имеет много наблюдений.
Центральная предельная теорема говорит о том, что выборочное распределение выборочного среднего будет приблизительно нормальным со средним (mu) и дисперсией (sigma^2 / n), когда выборка имеет большой размер.
Выборка, которую мы будем использовать для этого примера, содержит 118 наблюдений.
В итоге, тестовая статистика для проверки гипотезы о средней премии за риск равна ( overline X_{RP} big / s_{overline X}).
Мы можем выполнить z-тест, поскольку мы можем правдоподобно предположить, что тестовая статистика следует стандартному нормальному распределению.
3 этап. Определение уровня значимости.
Третьим этапом проверки гипотез является определение уровня значимости. Когда тестовая статистика рассчитана, возможны два действия:
- Мы отвергаем нулевую гипотезу или
- Мы не отвергаем нулевую гипотезу.
Выбор действия основан на сравнении вычисленной тестовой статистики с заданным возможным значением или значениями. Значения, которые мы выбираем, основаны на выбранном уровне значимости. Уровень значимости отражает то, какие основанные на выборке доказательства нам необходимы, чтобы отвергнуть нуль.
По аналогии с судом, необходимая доказательная база может меняться в зависимости от характера гипотез и серьезности последствий совершения ошибки.
Возможны четыре результата при проверке нулевой гипотезы:
- Мы отвергаем ложную нулевую гипотезу. Это правильное решение.
- Мы отвергаем истинную нулевую гипотезу. Это называется ошибкой I рода (англ. ‘Type I error’).
- Мы не отвергаем ложную нулевую гипотезу. Это называется ошибкой II рода (англ. ‘Type II error’).
- Мы не отвергаем истинную нулевую гипотезу. Это правильное решение.
Проиллюстрируем эти результаты в Таблице 1.
Таблица 1. Ошибки I и II рода при проверке гипотез.
|
Решение |
Ситуация |
|
|---|---|---|
|
(H_0) Истина |
(H_0) Ложь |
|
|
(H_0) не отвергается |
Правильное решение |
Ошибка II рода |
|
(H_0) отвергается (принимается (H_a)) |
Ошибка I рода |
Правильное решение |
Когда мы принимаем решение при проверке гипотезы, мы рискуем допустить ошибку I или II рода. Это взаимоисключающие ошибки:
- Если мы ошибочно отвергаем нуль, мы можем допустить только ошибку I рода.
- Если мы ошибочно не отвергаем нуль, мы можем допустить только ошибку II рода.
Вероятность ошибки I рода при проверке гипотезы обозначается греческой буквой альфа: (alpha). Эта вероятность также известна как уровень значимости проверки (англ. ‘level of significance’).
Например, уровень значимости 0.05 для проверки означает, что есть 5-процентная вероятность отклонения истинной нулевой гипотезы.
Вероятность ошибки II рода обозначается греческой буквой бета: (beta).
Управление вероятностью ошибок двух типов предполагает компромисс. При прочих равных, если мы уменьшаем вероятность ошибки I рода, задав меньший уровень значимости (скажем, 0.01, а не 0.05), мы увеличиваем вероятность совершить ошибку II рода, потому что мы отвергаем нуль реже, в том числе, когда он является ложным.
Единственным способом уменьшить вероятность ошибок обоих типов одновременно является увеличение размера выборки (n).
Количественный компромисс между двумя типами ошибок на практике, как правило, невозможен, потому что вероятность ошибки II рода очень трудно определить количественно.
Рассмотрим пример с парой гипотез: (H_0: theta leq 5) и (H_a: theta > 5).
Поскольку каждое истинное значение (theta) больше 5 делает нулевую гипотезу ложной, каждое значение (theta) больше 5 имеет различную (beta) (вероятность ошибки II рода).
В отличие от этого, нам достаточно только констатировать вероятность ошибки I рода при (theta = 5). Таким образом, как правило, мы указываем только вероятность ошибки I рода, когда выполняем проверку гипотезы.
В то время как уровень значимости проверки является вероятностью ошибочно отвергнуть нулевую гипотезу, то мощностью критерия или мощностью проверки (англ. ‘power of a test’) является вероятность правильного отклонения нулевой гипотезы — то есть вероятность отвергнуть нуль, если он ложный.
Мощность критерия, на самом деле, равна 1 минус вероятность ошибки II рода.
Когда при проведении проверки имеется более одной статистики критерия, мы должны предпочесть самую мощную из них, при прочих равных условиях.
Тем не менее, у нас не всегда есть информация об относительной мощности критерия для конкурирующих статистик критерия.
В итоге, стандартный подход к проверке гипотез включает только определение уровня значимости (вероятности ошибки I рода). Наиболее целесообразно устанавливать этот уровень значимости до расчета тестовой статистики (статистики критерия). Если мы указываем его после вычисления тестовой статистики, на нас может повлиять результат расчета, что умаляет объективность проверки.
Мы можем использовать три наиболее распространенных уровня значимости для проведения проверки гипотезы: 0.10, 0.05 и 0.01.
Если мы можем отклонить нулевую гипотезу на уровне значимости 0.10, то у нас есть доказательства того, что нулевая гипотеза неверна.
Если мы можем отклонить нулевую гипотезу на уровне значимости 0.05, то у нас есть убедительные доказательства того, что нулевая гипотеза неверна.
И если мы можем отклонить нулевую гипотезу на уровне значимости 0.01, то у нас есть очень убедительные доказательства того, что нулевая гипотеза неверна.
Для нашего примера с премией за риск, мы установим уровень значимости 0.05.
4 этап. Формулировка правила принятия решения.
Четвертый этап проверки гипотезы заключается в формулировке правила принятия решения (англ. ‘decision rule’).
Общий принцип формулируется просто.
Когда мы проверяем нулевую гипотезу, если мы находим, что рассчитанное значение статистики критерия (тестовой статистики) является экстремальным или более экстремальным, чем заданное значение или значения, определенные установленным уровнем значимости (alpha), то мы отвергаем нулевую гипотезу. Мы говорим, что результат является статистически значимым (англ. ‘statistically significant’).
В противном случае, мы не отвергаем нулевую гипотезу, и говорим, что результат не является статистически значимым. Значение или значения, с которым мы сравниваем вычисленную статистику критерия, чтобы принять наше решение, являются точками отклонения (критическими значениями) для проверки гипотезы.
Термин «точка отклонения» (англ. ‘rejection point’) является описательным синонимом для более традиционного термина «критическое значение» (англ. ‘critical value’).
Определение критического значения для статистики критерия.
Критическое значение или точка отклонения (англ. ‘critical value’) для тестовой статистики (статистики критерия) представляет собой значение, с которой сравнивается вычисленная тестовая статистика, чтобы решить, следует ли отклонять или не отклонять нулевую гипотезу.
Для односторонней проверки, мы указываем критическое значение, используя символ для тестовой статистики с индексом (alpha), обозначающим заданную вероятность ошибки I рода, например, (z_alpha).
Для двусторонней проверки, мы указываем критическое значение (z_{alpha/2}).
Для того, чтобы проиллюстрировать применение критических значений, предположим, что мы используем z-тест и выбрали уровень значимости 0.05.
Для проверки пары гипотез (H_0: theta = theta_0) и (H_a: theta neq theta_0), существуют два критических значения, — одно отрицательное и одно положительное.
Для двухсторонней проверки при уровне значимости 0.05, суммарная вероятность ошибки I рода должна быть равна 0.05. Таким образом, 0.05 / 2 = 0.025 вероятности должно быть в каждом хвосте распределения тестовой статистики при нулевой гипотезе.
Следовательно, двумя критическими значениями будут (z_{0.025} = 1.96) и (-z_{0.025} = -1.96). Пусть (z) является вычисленным значением тестовой статистики. Мы отвергаем нуль, если находим, что (z < -1.96) или (z > 1.96). И мы не отвергаем нуль, если (-1.96 leq z leq 1.96).
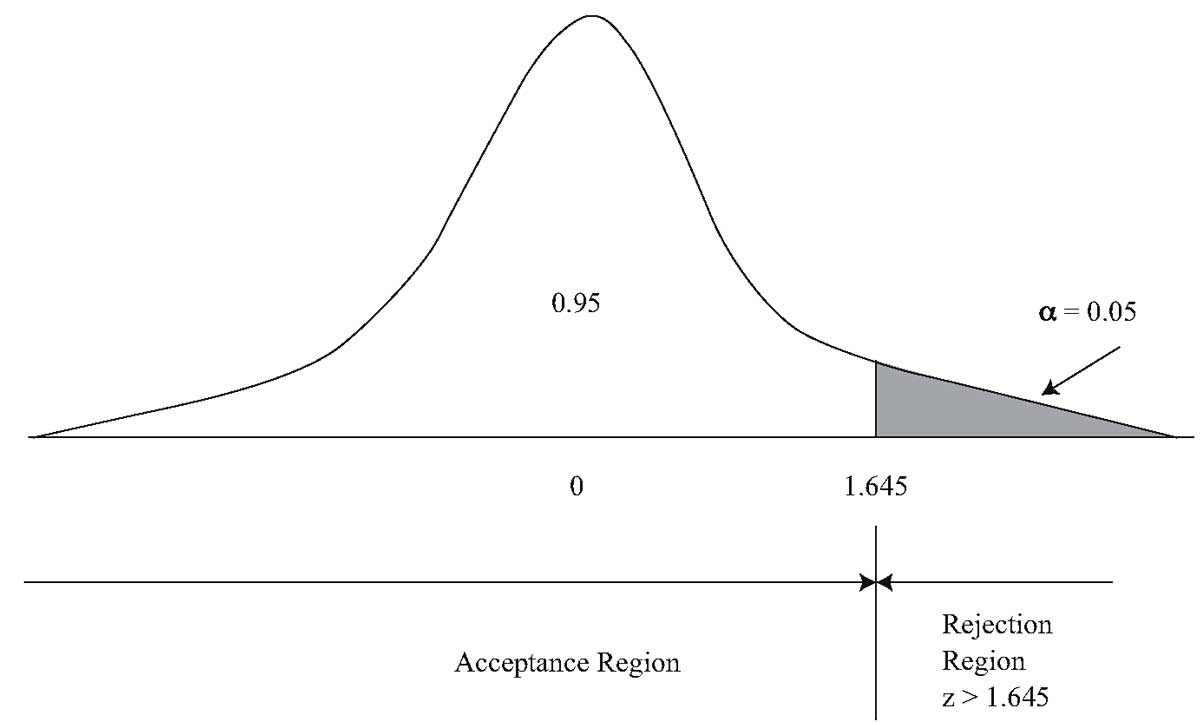
Для проверки пары гипотез (H_0: theta leq theta_0) и (H_a: theta > theta_0) при уровне значимости 0.05, критическим значением будет (z_{0.05} = 1.645). Мы отвергаем нулевую гипотезу, если (z > 1.645). Значение стандартного нормального распределения таково, что 5% результатов лежат правее точки (z_{0.05} = 1.645).
Для проверки пары гипотез (H_0: theta geq theta_0) и (H_a: theta < theta_0), критическим значением будет (-z_{0.05} = -1.645). Мы отвергаем нулевую гипотезу, если (z < -1.645).
График 2 иллюстрирует проверку (H_0: mu = mu_0) и (H_a: mu neq mu_0) при уровне значимости 0.05 с использованием z-теста.
Термин «область принятия гипотезы» (англ. ‘acceptance region’) является традиционным названием для множества значений тестовой статистики, при которых мы не отвергаем нулевую гипотезу.
Традиционное название, однако, неточное. Мы должны избегать использования таких фраз, как «принять нулевую гипотезу», потому что такое утверждение подразумевает неоправданно большую степень убежденности в нуле, когда мы не отвергаем его.
Аналогия с некоторыми судами (например, в Соединенных Штатах) заключается в том, что если присяжные не выносят вердикт о виновности (альтернативная гипотеза), наиболее точным будет сказать, что жюри не удалось отклонить нулевую гипотезу о невиновности обвиняемого (что следует из принципа презумпции невиновности).
По обеим сторонам от области принятия решения находятся области отклонения или критические области (англ. ‘rejection region’ или ‘critical region’).
Если нулевая гипотеза заключается в том, что ( mu = mu_0 ) истинно, тестовая статистика имеет 2.5-процентный шанс попадания в левую критическую область и 2.5-процентный шанс попадания в правую критическую область.
Любое вычисленное значение тестовой статистики, которое попадает в любую из этих двух областей, заставляет нас отвергнуть нулевую гипотезу при уровне значимости 0.05. Критические значения 1.96 и -1.96 рассматриваются как разделительные линии между областями принятия и отклонения гипотезы.
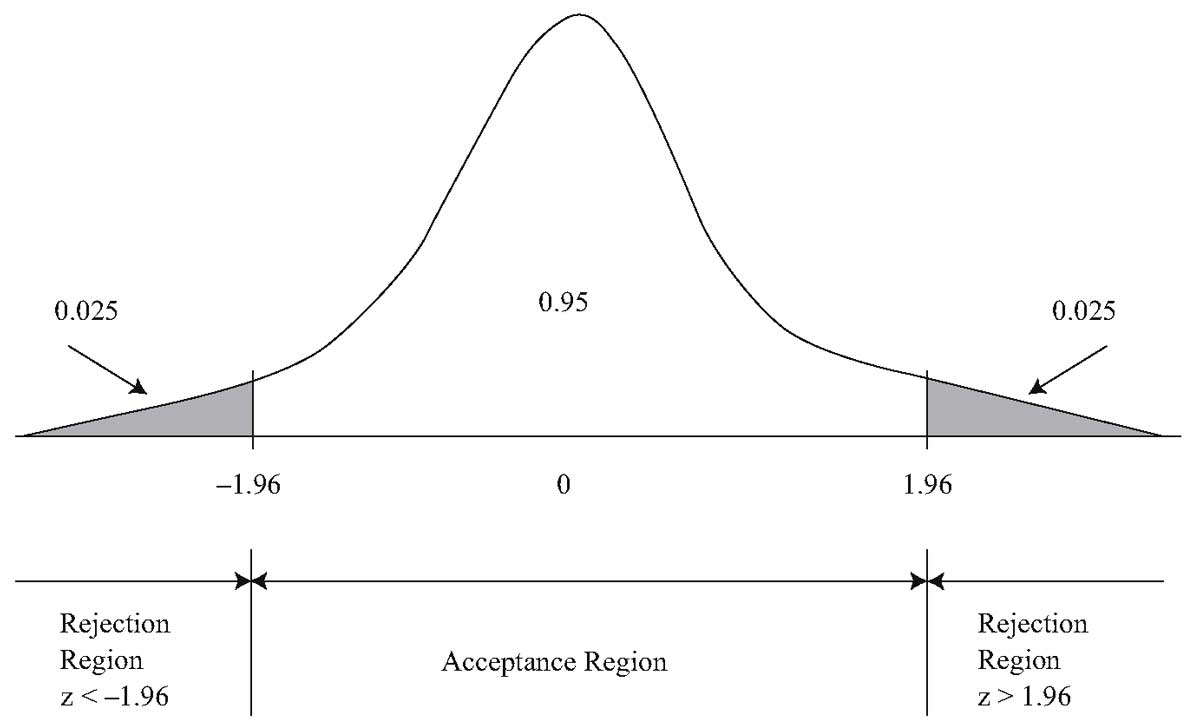
График 2 дает хорошую возможность подчеркнуть взаимосвязь между доверительными интервалами и проверкой гипотез. 95-процентный доверительный интервал для среднего по совокупности (mu), основанного на выборочном среднем (overline X), задается диапазоном от (overline X — 1.96s_{overline X}) до (overline X + 1.96s_{overline X}), где (s_{overline X}) является стандартной ошибкой выборочного среднего (Формула 3).
Так же, как и при проверке гипотезы, мы можем использовать этот доверительный интервал, основанный на стандартном нормальном распределении, когда у нас есть большая выборка.
Альтернативная проверка гипотезы и доверительный интервал используют t-распределение. Мы рассмотрим эти концепции в следующем разделе.
Теперь рассмотрим одно из условий для отклонения нулевой гипотезы:
( dst {overline X — mu_0 over s_{overline X}} > 1.96)
Здесь (mu_0) является гипотетическим значением среднего по совокупности. Условие гласит, что отклонение гипотезы является оправданным, если тестовая статистика превышает 1.96.
Умножив обе стороны неравенства на (s_{overline X}), мы получим ( overline X — mu_0 > 1.96 s_{overline X}), или после преобразования, ( overline X — 1.96 s_{overline X} > mu_0), что можем также записать в виде ( mu_0 < overline X — 1.96 s_{overline X}).
Это выражение означает, что если гипотетическое среднее по совокупности (mu_0), меньше нижнего предела 95-процентного доверительного интервала, основанного на выборочном среднем, мы должны отвергнуть нулевую гипотезу при уровне значимости 5% (тестовая статистика попадает в критическую область справа).
Теперь мы можем взять другое условие для отклонения нулевой гипотезы:
( dst {overline X — mu_0 over s_{overline X}} < -1.96)
и, используя алгебру, как и ранее, мы преобразуем его к виду:
( dst mu_0 > overline X — 1.96 s_{overline X})
Если гипотетическое среднее по совокупности больше, чем верхний предел 95-процентного доверительного интервала, мы отвергаем нулевую гипотезу при уровне значимости 5% (тестовая статистика попадает в критическую область слева).
Таким образом, уровень значимости в двусторонней проверке гипотезы можно интерпретировать точно так же, как доверительный интервал (1 — alpha).
Таким образом, когда гипотетическое значение параметра совокупности для нулевой гипотезы находится вне соответствующего доверительного интервала, то нулевая гипотеза отвергается. Мы могли бы использовать доверительные интервалы для проверки гипотез, но на практике финансовые аналитики, как правило, этого не делают.
Вычисление тестовой статистики (одно число, по сравнению с двумя числами для обычного доверительного интервала) более эффективно. Также, на практике аналитики редко сталкиваются с односторонними доверительными интервалами.
Кроме того, только вычислив тестовую статистику, мы можем получить p-значение, полезный показатель значимости результатов (мы обсудим p-значение далее).
Вернемся к нашей проверке премии за риск.
Мы сформулировали гипотезы (H_0: mu_{RP} leq 0) и (H_a: mu_{RP} > 0). Мы определили тестовую статистику как ( overline X_{RP} / s_{overline X}) и определили, что она следует стандартному нормальному распределению.
Таким образом, мы выполняем односторонний z-тест.
Мы определили уровень значимости 0.05. Для этого одностороннего z-теста, критическая точка при уровне значимости 0.05 составляет 1.645. Мы отвергаем нуль, если вычисленная z-статистика больше, чем 1.645.
График 3 иллюстрирует эту проверку.
5 этап. Сбор данных и расчет тестовой статистики.
Пятый шаг в проверке гипотез заключается в сборе данные и расчете тестовой статистики. Качество наших выводов зависит не только от уместности статистической модели, но и от качества данных, которые мы используем при проведении проверки.
В первую очередь мы должны проверить данные на наличие ошибок измерений. Нам также необходимо учесть другие проблемы, в том числе систематическую ошибку выборки и систематическую ошибку временного периода.
Систематическая ошибка выборки — это смещение выборки, связанное с систематическим исключением некоторых элементов совокупности в соответствии с определенным признаком.
Одним из типов систематической ошибки выборки является систематическая ошибка выжившего. Например, если мы определим нашу выборку, как облигации взаимных фондов США, которые продолжают деятельность в настоящее время, и мы сделаем выборку доходности только по этим фондам, мы будем систематически исключать фонда, которые не выжили (прекратили деятельность) к настоящему моменту.
Прекратившие деятельность фонды, скорее всего, в среднем хуже оставшихся фондов. В результате, эффективность фондов, рассчитанная на основе этой выборки, может быть смещена вверх.
Систематическая ошибка временного периода связана с вероятностью того, что когда мы используем выборку из временных рядов, наш статистический вывод может быть чувствительным к начальным и конечным датам периода выборки.
В нашей гипотезе о премии за риск мы имеем дело с американскими акциями. Согласно Dimson, Marsh и Staunton (2018) за период с 1900 по 2017 год включительно (118 ежегодных наблюдений), среднеарифметическая премия за риск для американских акций по отношению к доходности облигаций (overline X_{RP}) составила 7.5% в год.
Выборочное стандартное отклонение годовой премии за риск составило 19.5%. Используя Формулу 3, найдем стандартную ошибку выборочного среднего:
( dst s_{overline X} = s big / sqrt n = 19.5% / sqrt {118} ) = 1.795%.
Тестовая статистика равна:
( dst z = overline X_{RP} big / s_{overline X}) = 7.5%/1.795% = 4.18.
6 этап. Принятие статистического решения.
Шестой этап проверки гипотезы означает принятие статистического решения.
В нашем примере, поскольку тестовая статистика (z = 4.18) больше критического значения 1.645, мы отвергаем нулевую гипотезу в пользу альтернативной гипотезы о том, что премия за риск для американских акций является положительной.
Первые шесть шагов являются статистическими шагами. Наше итоговое решение принимается с использованием статистического решения.
7 этап. Принятие экономического или инвестиционного решения.
Седьмой и заключительный шаг в проверке гипотез заключается в принятии экономического или инвестиционного решения. Экономическое или инвестиционное решение принимает во внимание не только статистические решения, но и все соответствующие экономические вопросы.
На шестом этапе, мы нашли убедительные статистические доказательства того, что премия за риск для американских акций является положительной. Величина расчетной премии за риск, 7.5% в год, является также очень значимой экономически.
Исходя из этих соображений, инвестор может принять решение инвестировать часть средств в американские акции. Ряд нестатистических соображений, таких как толерантность инвестора к риску и его финансовое положение, может также повлиять на процесс принятия решений.
Предшествующее обсуждение поднимает проблему, которая часто возникает на этом этапе принятия решений. Мы часто находим, что небольшие различия между переменной величиной и ее гипотетическим значением являются статистически значимыми, но не значимыми экономически.
Например, мы можем проверить инвестиционную стратегию и отклонить нулевую гипотезу о том, что средняя доходность стратегии равна нулю на основе большой выборки.
Формула 1 показывает, что чем меньше стандартная ошибка выборочной статистики (делитель в формуле), тем больше значение тестовой статистики и тем больше шанс на то, что нулевая гипотеза будет отклонена, при прочих равных условиях. Стандартная ошибка уменьшается по мере увеличения размера выборки (n), так что при очень больших выборках, мы можем отклонить нулевую гипотезу.
Мы можем обнаружить, что, хотя стратегия обеспечивает статистически значимую положительную среднюю доходность, результаты не являются экономически значимыми, если учесть транзакционные издержки, налоги и риски.
Даже если мы приходим к выводу, что результаты стратегии являются экономически значимыми, мы должны изучить логику того, почему стратегия могла бы работать в будущем, прежде чем реализовывать ее фактически. Такие соображения нельзя включить в проверку гипотезы.
Перед тем как завершить тему процесса проверки гипотез, мы должны обсудить важный альтернативный подход, называемый подходом проверке гипотез с. Аналитики и исследователи часто включают в отчеты о проверке гипотез p-значение (также называемое предельным уровнем значимости, англ. ‘marginal significance level’).
Определение p-значения.
P-значение (p-уровень значимости или p-критерий, англ. ‘p-value’) является наименьшим уровнем значимости, при котором может быть отвергнута нулевая гипотеза.
Для значения тестовой статистики 4.18 в проверке гипотезы о премии за риск, с помощью функции электронной таблицы для стандартного нормального распределения, мы вычисляем р-значение 0.000015. Мы можем отклонить нулевую гипотезу на этом уровне значимости.
Чем меньше р-значение, тем сильнее доказательства против нулевой гипотезы и в пользу альтернативной гипотезы. P-значение для двухсторонней проверки того, что параметр равен нулю, часто генерируется автоматически с помощью статистических и эконометрических программ.
Мы можем использовать электронные таблицы для расчета p-значения. В Microsoft Excel, например, мы можем использовать функции TTEST, NORMSDIST, CHIDIST и FDIST для расчета р-значений для f-тестов, z-тестов, хи-квадрат тестов, и F-тестов, соответственно.
Мы можем использовать р-значение в рамках процедуры проверки гипотез, представленной выше, в качестве альтернативы критическим значениям.
Если р-значение меньше нашего заданного уровня значимости, мы отвергаем нулевую гипотезу. В противном случае, мы не отвергаем нулевую гипотезу.
Используя p-значение таким образом, мы приходим к такому же выводу, что и при использовании критических значений. Например, поскольку 0.000015 меньше 0.05, мы отвергаем нулевую гипотезу в проверке гипотезы о премии за риск.
P-значение, тем не менее, обеспечивает более точную информацию о силе доказательств, чем подход с использованием критических значений. P-значение 0.000015 указывает на то, что нулевая гипотеза отвергается на гораздо меньшем уровне значимости, чем 0.05.
Если один исследователь рассматривает вопрос, используя уровень значимости 0.05, а другой исследователь использует уровень значимости 0.01, читатель может столкнуться с проблемой, сравнивая полученные результаты.
Эта проблема породила подход к представлению результатов проверки гипотез, при котором указываются p-значения и не указывается спецификация уровня значимости (этап 3). Интерпретация статистических результатов остается на усмотрение пользователя исследования. Этот подход к представлению результатов иногда называют подходом к проверке гипотез с использованием р-значения.
Davidson и MacKinnon (1993) оспорили достоинство этого подхода:
«Подход с использование p-значения по не обязательно заставит нас принять решение о нулевой гипотезе. Если мы получим p-значение равное, скажем, 0.000001, мы почти наверняка захотим отклонить нуль.
Но если мы получим p-значение равное, скажем, 0.04, или даже 0.004, мы не обязаны отклонять его. Мы можем просто отбросить результат прочь, как информацию, которая ставит под сомнение нулевую гипотезу, но сама по себе не убедительна.
Мы считаем, что это несколько агностическое отношение к статистическим проверкам, в которых p-значения рассматриваются просто как части информации, которую мы можем использовать, но можем и не использовать». (Стр. 80)
Содержание:
Проверка статистических гипотез:
Статистической гипотезой называется гипотеза, которая относится к виду функции распределения, к параметрам функции распределения, к числовым характеристикам случайной величины и т.д., и которую можно проверить на основе опытных данных. Например, предположение о том, что отклонение истинного размера детали от расчетного имеет нормальный закон распределения, является статистической гипотезой. Предположение о наличии жизни на Марсе статистической гипотезой не является, так как оно не выражает какого-либо утверждения о законе распределения или иных характеристиках случайной величины.
Пример статистической гипотезы
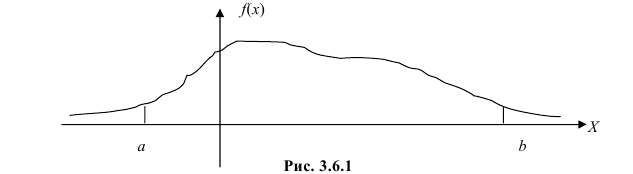
Рассмотрим упрощенный пример. Пусть выдвинута гипотеза о том, что плотность вероятности
Есть возможность произвести только одно наблюдение. В этом случае выборочным пространством служит числовая ось. Из рис. 3.6.1 видно, что значения случайной величины из отрезка 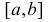
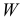
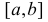
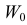
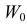
В случае выборки объема 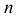
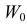
Статистическим критерием называют правило, указывающее, когда статистическую гипотезу следует принять, а когда отвергнуть. Построение статистического критерия сводится к выбору в выборочном пространстве критической области 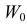
Даже при верной гипотезе наблюдения могут сложиться неблагоприятно, в итоге выборка может попасть в критическую область и гипотеза будет отвергнута. Вероятность такого исхода 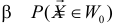
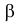
Статистический критерий в описанном виде может быть сложным, и трудно будет установить, принадлежит ли выборка критической области или нет. Поэтому предпочитают на выборочном пространстве задать некоторую функцию, которая каждой выборке ставит в соответствие определенное число. Значения функции, которые соответствуют критической области, естественно считать критическими значениями. Проверка гипотезы тогда сводится к вычислению по выборке значения этой функции и проверке, является ли оно критическим. Есть функции, не зависящие от вида проверяемой гипотезы. Одна из таких функций дает знаменитый критерий «хи-квадрат».
Критерий согласия «хи-квадрат»
Пусть выдвинута гипотеза о законе распределения случайной величины X. Требуется проверить, насколько эта гипотеза правдоподобна. Для этого разобьем множество возможных значений случайной величины на 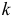
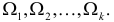
Например, если выдвинута гипотеза, что случайная величина X имеет функцию распределения 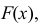
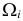
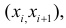
Нужно проверить, согласуется ли наша гипотеза с опытными данными.
Идея проверки гипотезы состоит в сравнении теоретических вероятностей разрядов (3.6.1) с фактически наблюдаемыми частотами попадания в эти разряды. Для этого производится 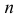
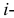

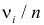
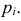
где 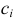
Если же гипотеза ложная, то при больших 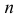
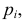
Английский статистик К. Пирсон (1900 г.) показал, что при выборе коэффициентов 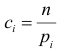
имеет распределение, которое не зависит от выдвинутой гипотезы и определяется функцией плотности вероятности
где 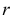
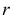


При данной гипотезе и фиксированном числе наблюдений величина 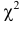
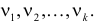



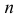
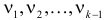
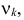


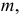

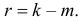


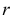
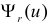
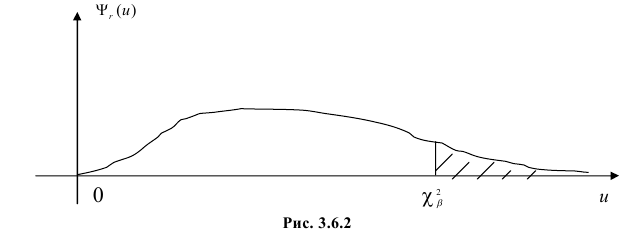
Составлены специальные таблицы (см. прил., табл. П4), в которых для любого 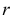

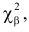
На рис. 3.6.2 заштрихованная площадь равна 
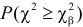
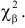
Предположим, что гипотеза верна. Выберем вероятность 

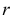
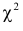
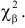
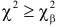
Итак, построена критическая область: 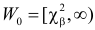

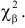
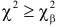
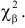
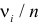
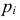
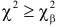
Если же окажется, что 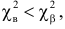
Замечание 1. Хотя и маловероятно, чтобы 
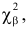


Замечание 2. Каждый разряд вносит в величину 
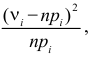
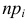
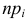
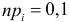

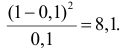
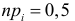
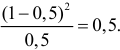
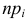
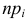
Пример №1
Были исследованы 200 изготовленных деталей на отклонение истинного размера от расчетного. Сгруппированные данные исследований приведены в виде статистического ряда:
Требуется по данному статистическому ряду построить гистограмму. По виду гистограммы выдвинуть гипотезу о типе закона распределения отклонений. Подобрать параметры закона распределения (равные их оценкам на основе опытных данных). Построить на том же графике функцию плотности вероятности, соответствующую выдвинутой гипотезе. С помощью критерия согласия проверить согласуется ли выдвинутая гипотеза с опытными данными. Уровень значимости взять, например, равным 0,05.
Решение. Для того чтобы получить представление о виде закона распределения изучаемой величины, построим гистограмму. Для этого над каждым интервалом построим прямоугольник, площадь которого численно равна частоте попадания в интервал (рис. 3.6.3).
По виду гистограммы можно выдвинуть предположение о том, что исследуемая случайная величина имеет нормальный закон распределения. Параметры нормального закона (математическое ожидание и дисперсию) оценим на основе опытных данных, считая в качестве представителя каждого интервала его середину:
Итак, выдвинем гипотезу, что исследуемая случайная величина имеет нормальный закон распределения 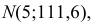
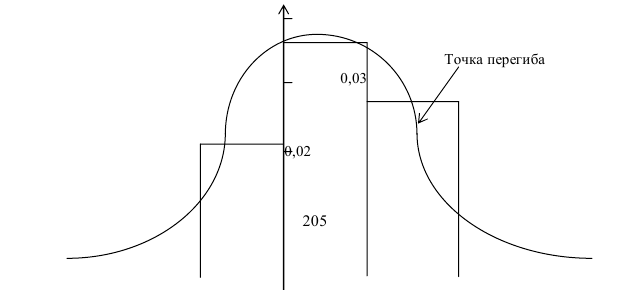
График 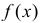
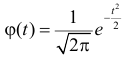
Например, точка максимума и точки перегиба имеют ординаты соответственно
График функции 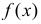
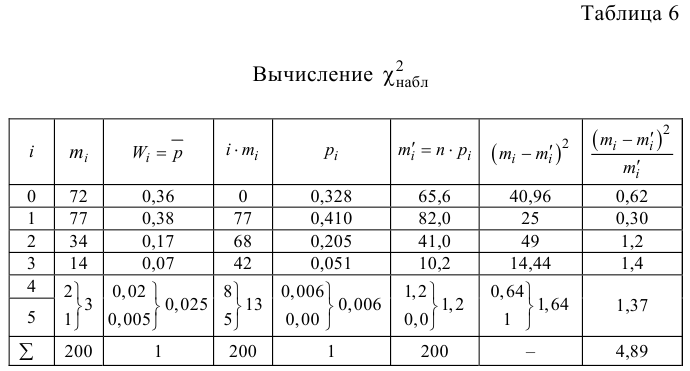
Вычислим меру расхождения между выдвинутой гипотезой и опытными данными, т.е. величину 
Аналогично:
Вычисление 
Итак, мера расхождения между гипотезой и опытными данными равна
Построим критическую область для уровня значимости 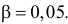


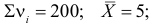
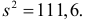
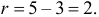

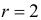

Критическая область для проверки гипотезы имеет вид 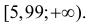
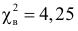
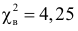
Ответ. Гипотеза опытным данным не противоречит.
Пример №2
В виде статистического ряда приведены сгруппированные данные о времени безотказной работы 400 приборов.
Согласуются ли эти данные с предположением, что время безотказной работы прибора имеет функцию распределения 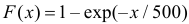
Решение. Вычислим вероятности, приходящиеся в соответствии с гипотезой на интервалы:
Вычислим 
Число степеней свободы равно трем, так как на четыре величины 
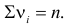
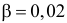
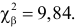
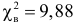
Ответ. Гипотеза опытным данным противоречит.
Пример №3
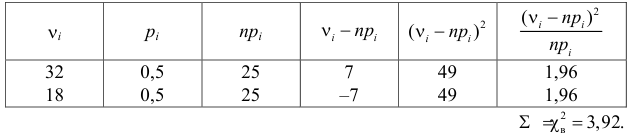
Монету подбросили 50 раз. Герб выпал 32 раза. С помощью критерия «хи-квадрат» проверить, согласуются ли эти результаты с предположением, что подбрасывали симметричную монету.
Решение. Выдвинем гипотезу, что монета была симметричной. Это означает, что вероятность выпадения герба при каждом броске равна 1/2. В описанном опыте герб выпал 32 раза и 18 раз выпала цифра. Вычисляем
Число степеней свободы для 
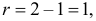

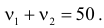
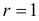
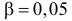
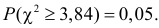
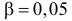

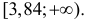
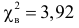
Ответ. Предположение о симметричности монеты не согласуется с опытными данными.
Пример №4
Для каждого из 100 телевизоров регистрировалось число выходов из строя в течение гарантийного срока. Результаты представлены в виде статистического ряда:
Согласуются ли эти данные с предположением о том, что число выходов из строя имеет пуассоновский закон распределения?
Решение. Если случайная величина Х – число выходов из строя телевизора, имеет пуассоновский закон распределения, то
где параметр 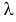
Оценим параметр из опытных данных. В законе распределения Пуассона параметр 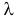
Итак, выдвигаем гипотезу, что изучаемая случайная величина имеет закон распределения
Для проверки выдвинутой гипотезы зададим уровень значимости, например, равный 0,02. Последние три разряда, содержащие мало наблюдений, можно объединить. В итоге имеем три разряда и число степеней свободы равно 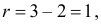

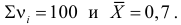
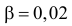
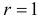
Вычислим теперь 
Вычисление 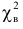
Вычисленное значение в критическую область не входит. Вывод: гипотеза о пуассоновском законе распределения изучаемой случайной величины опытным данным не противоречит.
Ответ. Гипотеза не противоречит опытным данным.
Пример №5
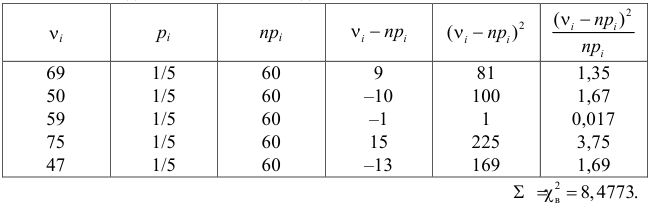
В течение пяти рабочих дней недели на контактный телефон фирмы поступило соответственно 69, 50, 59, 75, 47 звонков. Можно ли считать при уровне значимости 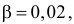
Решение. Сначала построим критическую область. Общее количество звонков равно 300. Число степеней свободы равно 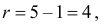
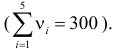
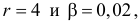
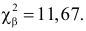
Выдвинем гипотезу, что интенсивность звонков не зависит от дня недели, т.е. с вероятностью 1/5 каждый вызов может поступить в любой рабочий день недели.
В предположении, что гипотеза верна, вычислим значение 
Сумма элементов последнего столбца дает 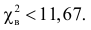
Ответ. Гипотеза опытным данным не противоречит.
Проверка гипотезы о независимости двух случайных величин
Постановка задачи. Можно ли по результатам наблюдений двух случайных величин сделать вывод об их зависимости или независимости. В приложениях эта задача имеет следующую постановку. Пусть каждый элемент генеральной совокупности обладает двумя признаками A и B, признак A имеет градации (или уровни) 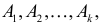
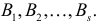
Естественно считать, что A и B независимы, если при выборе любого элемента генеральной совокупности независимы события «признак A принимает значение 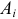
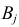
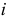
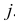
для всех 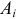
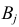
Пусть у взятых наугад 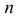
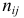
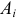
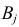
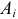
Аналогично, число наблюдений признака 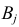
Обычно результаты наблюдений оформляют в виде таблицы, которую называют таблицей сопряженности признаков.
Таблица сопряженности признаков:
Введем обозначения для вероятностей. Положим
Необходимо проверить гипотезу 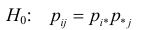
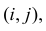
Если наблюдений много (хотя бы несколько десятков), то по теореме Бернулли
Критерий основан на сравнении наблюдаемых чисел появления комбинаций признаков с числами появлений, которые должны были бы быть, если бы признаки были независимы и не подвергались различным случайностям.
Поскольку вероятность наступления двух независимых событий равна произведению вероятностей этих событий, то за оценку вероятности совместного появления событий 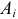
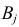
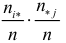
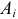
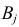
Эту величину можно назвать теоретическим числом появлений пары 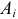
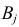
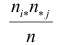
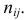
Если гипотеза 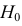
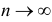
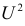
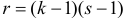
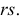
Определяя 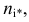
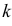
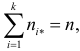
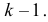
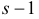
В таблице распределения 
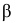
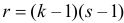
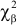
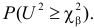
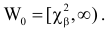
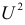
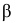
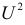
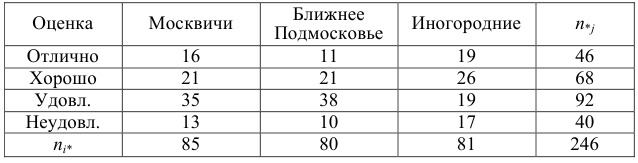
Пример №6
Данные о сдаче экзамена 246 студентами сгруппированы в зависимости от места окончания студентом средней школы.
Можно ли по этим данным заключить, что успеваемость студентов практически не зависит от места получения ими среднего образования? (Уровень значимости взять, например, равным 0,05.)
Решение. Предположим, что успеваемость студентов не зависит от места получения среднего образования (это гипотеза, которую предстоит проверить). Число степеней свободы равно 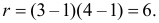
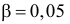
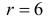
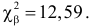
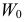
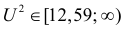
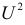
Вычисленное значение 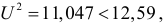
Ответ. Предположение о независимости успеваемости студентов от места получения ими среднего образования не противоречит опытным данным.
Проверка параметрических гипотез
Критерий для проверки гипотезы формируют за счет отнесения к критической области выборок, которые при данной гипотезе наименее вероятны. Но может оказаться, что одинаково маловероятных выборок при данной гипотезе больше, чем это необходимо для формирования критерия данного уровня значимости. Тогда трудно решить какие именно выборки следует включать в критическую область. Этих трудностей можно избежать, если вместе с проверяемой гипотезой рассматривать и альтернативные гипотезы.
Пусть случайная величина Х имеет функцию распределения 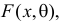
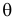
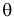
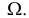
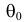
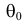
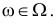
Определение. Параметрической статистической гипотезой 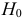
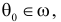
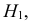
Гипотезу 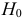
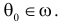
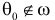
Гипотеза, однозначно определяющая вероятностное распределение, называется простой. В противном случае гипотезу называют сложной. Например, гипотеза о симметричности и однородности игрального кубика проста, так как однозначно определяет вероятности всех исходов при подбрасывании кубика. Гипотеза о том, что ошибка измерений имеет нормальный закон распределения, является сложной, так как при разных значениях параметров получаются разные нормальные законы распределения.
Простая параметрическая гипотеза против простой альтернативы может быть описана указанием одной точки 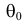
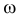
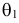
Параметрическую гипотезу проверяют по обычной схеме. Производят 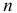
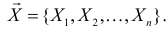
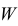
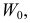
При любом критерии проверки статистической гипотезы по результатам наблюдений возможны ошибки двух типов: ошибка первого рода возникает при отклонении гипотезы 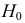
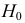
Обозначим через 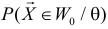
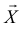
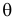
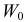
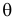
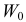
Заметим, что 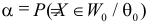
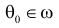
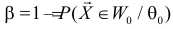
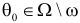
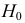
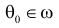
Разным критериям для проверки гипотезы 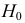
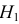
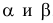
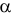
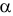
Учет ошибок первого и второго рода позволяет сравнивать между собой критерии. Пусть 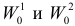
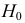
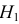
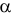
и
то критерий 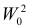
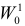
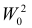
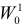
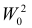
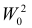
Пусть необходимо проверить гипотезу 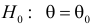
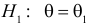
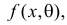
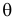
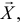
Согласно сформулированным требованиям относительно ошибок первого и второго рода, критическую область следует выбрать так, чтобы при заданном 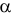
и при этом вероятность
была наибольшей.
Такую задачу впервые решили в начале тридцатых годов прошлого века Ю. Нейман и Э. Пирсон, и полученный ими результат носит их имя. Для формулировки этого результата понадобится понятие взаимной абсолютной непрерывности функций, которое состоит в том, что в каждой точке функции или обе равны нулю, или обе нулю не равны.
Лемма Неймана–Пирсона
Если 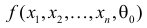
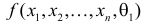
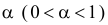
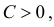
образуют критическую область 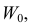
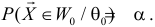
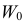
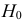
Замечание. Для дискретных величин в неравенстве (3.6.8) роль 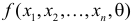
Пример №7
Известно, что при тщательном перемешивании теста изюмины распределяются в нем примерно по закону Пуассона, т.е. вероятность наличия в булочке 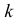
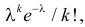
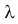
Построить критерий для проверки гипотезы о том, что 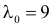
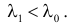
Решение. Для проверки гипотезы 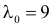
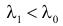
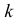
где С – некоторая постоянная.
Тогда 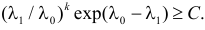
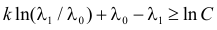
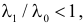
Итак, в критическую область следует включить значения 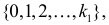
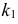
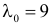
Отсюда следует, что если включить в критическую область значения для числа изюмин 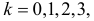
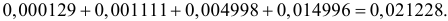
Заметим, что при добавлении в критическую область значения 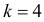
Ответ.
Пример №8
Изготовитель утверждает, что в данной большой партии изделий только 10% изделий низкого сорта. Было отобрано наугад пять изделий и среди них оказалось три изделия низкого сорта. С помощью леммы Неймана–Пирсона построить критерий и проверить гипотезу о том, что процент изделий низкого сорта действительно равен 10 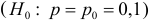
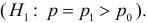
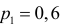
Решение. Согласно проверяемой гипотезе 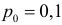
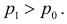
где С – некоторая постоянная.
После сокращения на 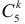
Прологарифмируем обе части неравенства
или
Так как 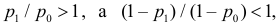
Значит, в критическую область следует включить те из значений 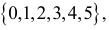
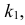
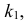
Если к критической области отнести значения 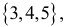
В условиях задачи оказалось, что среди пяти проверенных три изделия бракованных. Значение 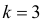
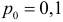
Вероятностью ошибки второго рода называется вероятность принять ложную гипотезу. Гипотеза 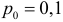
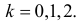
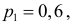
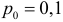
Вероятность ошибки второго рода велика потому, что критерий построен на скудном статистическом материале (всего пять наблюдений!).
Ответ. При уровне значимости 0,01 нулевую гипотезу отвергаем.
Пример №9
Количество первосортных изделий в крупной партии не должно быть менее 90%. Для проверки выбрали наугад 100 изделий. Среди них оказалось только 87 изделий первого сорта. Можно ли считать при вероятности ошибки первого рода, равной 0,05, что в данной партии менее 90 % первосортных изделий?
Решение. Построим критическую область для проверки гипотезы 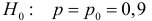
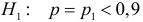
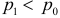
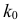
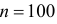
Откуда, с учетом нечетности функции Лапласа, имеем 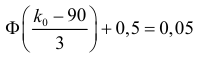
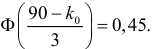
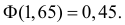
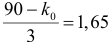
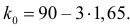
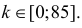
Ответ. Наличие в выборке менее 90% первосортных изделий можно объяснить случайностями выборки.
Пример №10
Случайная величина Х имеет нормальный закон распределения 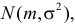
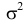
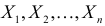
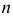
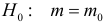
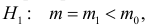
Решение. Так как наблюдения независимы, то 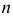
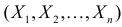
Поэтому по лемме Неймана–Пирсона к критической области должны быть отнесены те выборки, для которых
После логарифмирования неравенства получаем
откуда
Так как по условию 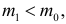
Итак, в критическую область следует включать выборки, для которых 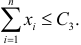
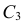
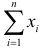
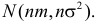
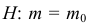
Отсюда 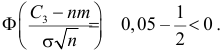
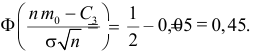
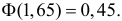
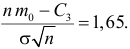
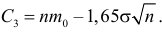
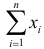
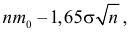
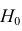
Ответ.
Проверка гипотезы о значении медианы
Пусть Х непрерывная случайная величина, а m – значение ее медианы, т.е. 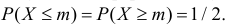
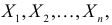
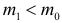
Предположим, что значение m действительно равно m0 (т.е. верна нулевая гипотеза 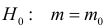
Если гипотеза верна, то 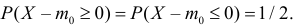
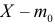
Величину S можно представить в виде 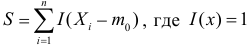
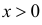
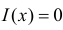
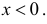
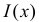
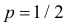
Очевидно, что при медиане равной 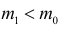
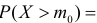
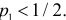
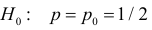
Согласно лемме Неймана–Пирсона для любого 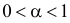
образуют критическую область наиболее мощного критерия. Так же как и в примере 3.19 легко показать, что в критическую область следует относить в первую очередь самые маленькие значения k. Остается только найти наибольшее k, для которого 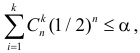
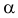
Пример №11
По результатам независимых наблюдений случайной величины 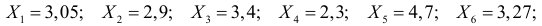
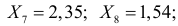
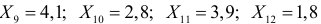
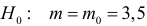
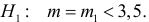
Решение. Ошибка первого рода совершается, когда отвергается верная гипотеза. Предположим, что нулевая гипотеза верна и медиана m действительно равна 3,5. Только в трех наблюдениях результаты превосходят 3,5. Как было показано выше, при альтернативе 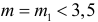
Откуда 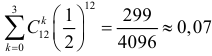
Ответ.
Проверка гипотезы о равенстве математических ожиданий
Пусть над случайной величиной X проделано n независимых наблюдений, в которых получены результаты 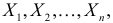
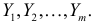
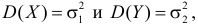
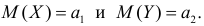
Предположим, что гипотеза верна. Так как серии опытов достаточно велики, то для средних арифметических имеем приближенные равенства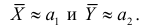
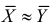
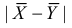
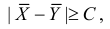
Свяжем эту постоянную C с уровнем значимости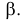
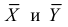
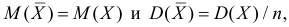
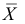
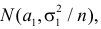
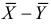
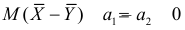
Запишем для нормального закона распределения 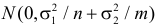
или
По заданному 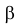
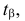
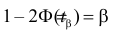
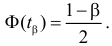
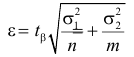
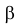
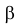
Замечание 1. Если дисперсии неизвестны, то большое число наблюдений в каждой серии позволяет достаточно точно оценить дисперсии по этим же опытным данным:
Пример №12
Среднее арифметическое результатов 25 независимых измерений некоторой постоянной величины равно 90,1. В другой серии из 20 независимых измерений получено среднее арифметическое, равное 89,5. Дисперсия ошибок измерения в обоих случаях одинакова и равна 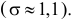
Решение. Выдвигаем гипотезу, что в каждой из серий измерялась одна и та же постоянная величина. Зададимся, например, уровнем значимости 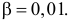
Тогда критическая область для проверки гипотезы определяется неравенством 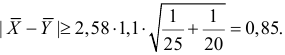
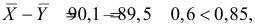
Ответ. Предположение о равенстве математических ожиданий не противоречит опытным данным.
Пример №13
По двум независимым выборкам объемов 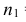
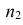
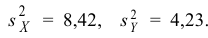
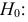
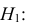
Решение. 1) По данным выборки вычисляем
2) По табл. П 2.7 (см. приложение 2), учитывая значения
находим число:
3) Сравниваем: так как 1,99 < 2,65, т.е. 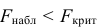
Ответ: гипотеза 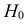
Пример №14
По двум независимым выборкам объемов 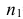
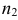
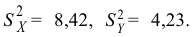
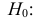
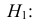
Решение. 1) По данным выборки вычисляем
2) По табл. П 2.7 (см. приложение 1), учитывая значения
находим число:
3) Сравниваем: так как 1,99 < 2,65, т.е. 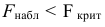
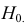
Ответ: гипотеза H0 : D(X)=D(Y) принимается.
Пример №15
По трем независимым выборкам объемов 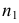
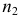
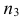
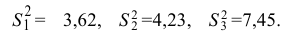
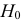
Решение. 1) По данным выборок вычисляем:
2) По табл. П 2.5 (см. приложение 2), учитывая значения
находим число
3) Сравниваем: так как 2,06 < 6,0 , т.е. 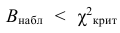
Ответ: гипотезу 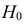
Пример №16
По двум независимым выборкам объемов 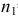
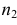
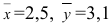
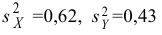
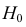
M(X) = M(Y) при конкурирующей гипотезе 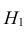
Решение 1) Так как 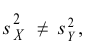
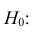
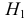
а) По данным выборки вычисляем
б) По табл. П 2.7 (см. приложение 2), учитывая значения
находим число:
в) Сравниваем: так как 1,44 < 3,89, т.е. 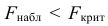
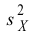
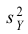
2) Проверим гипотезу 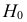
а) Найдем по табл. П 2.6 (см. приложение 2) значение 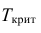
б) Найдем число
в) Сравнить числа 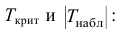
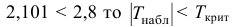
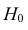
Ответ: гипотеза 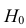
Пример №17
По двум независимым выборкам объемов 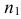
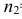
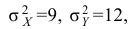
При уровне значимости α = 0,05 проверить гипотезу 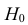
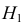
Решение. Воспользуемся замечанием 6. 1) Вычислим:
2) Находим 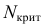
используя табл. П 2.2 (см. приложение 2).
Следовательно,
3) Сравниваем: так как 2,19 > 1,96, т.е. 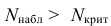
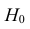
Значит, различие генеральных математических ожиданий значительное.
Ответ: гипотеза 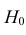
Определение статистической гипотезы
Определение: Статистической гипотезой называется гипотеза о виде неизвестного распределения или о параметрах известного распределения. Выдвинутую гипотезу называется основной (нулевой) и обозначается 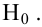
Гипотеза называется простой, если она содержит только одно предположение. Сложная гипотеза состоит из простых.
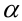
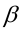
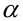
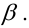
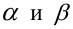
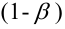
Статистический критерий проверки основной гипотезы Н0
Статистический критерий проверки основной гипотезы
Определение. Для проверки основной гипотезы 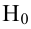
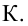
Определение. Областью принятия гипотезы 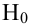
Выбор одного из этих случаев определяется видом конкурирующей гипотезы.
Основные шаги при проверке статистических гипотез:
1) выдвигаем
2) выдвигаем
3) задаем 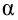
4) строим статистический критерий
5) строим критическую область
6) считаем наблюдаемое значение критерия и сравниваем с критическими точками
7) если наблюдаемое значение попадает в область принятия гипотезы, то нет причины отвергать 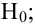
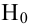
Проверка гипотезы о виде распределения случайной величины. Критерий согласия Пирсона
Пусть 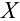
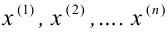
1) 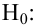
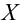
2) 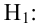
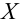
3) задаем 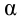
4) строим статистический критерий
Разобьем область, которой принадлежат результаты измерений, на 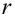
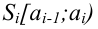
Пусть
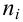
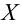
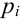
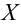
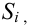
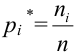
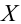
Тогда
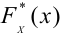
За меру отклонения истинной функции распределения 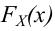
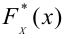
Теорема Пирсона:
Какова бы ни была 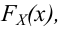
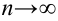
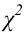
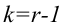
Замечание. Если в процессе проверки гипотезы приходится производить оценку параметров распределения, то количество степеней свободы 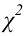
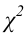
5) строим критическую область
Критическая область — правосторонняя
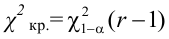
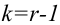
6) считаем наблюдаемое значение критерия 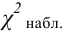
7) Вывод: если 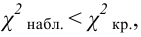
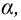
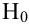
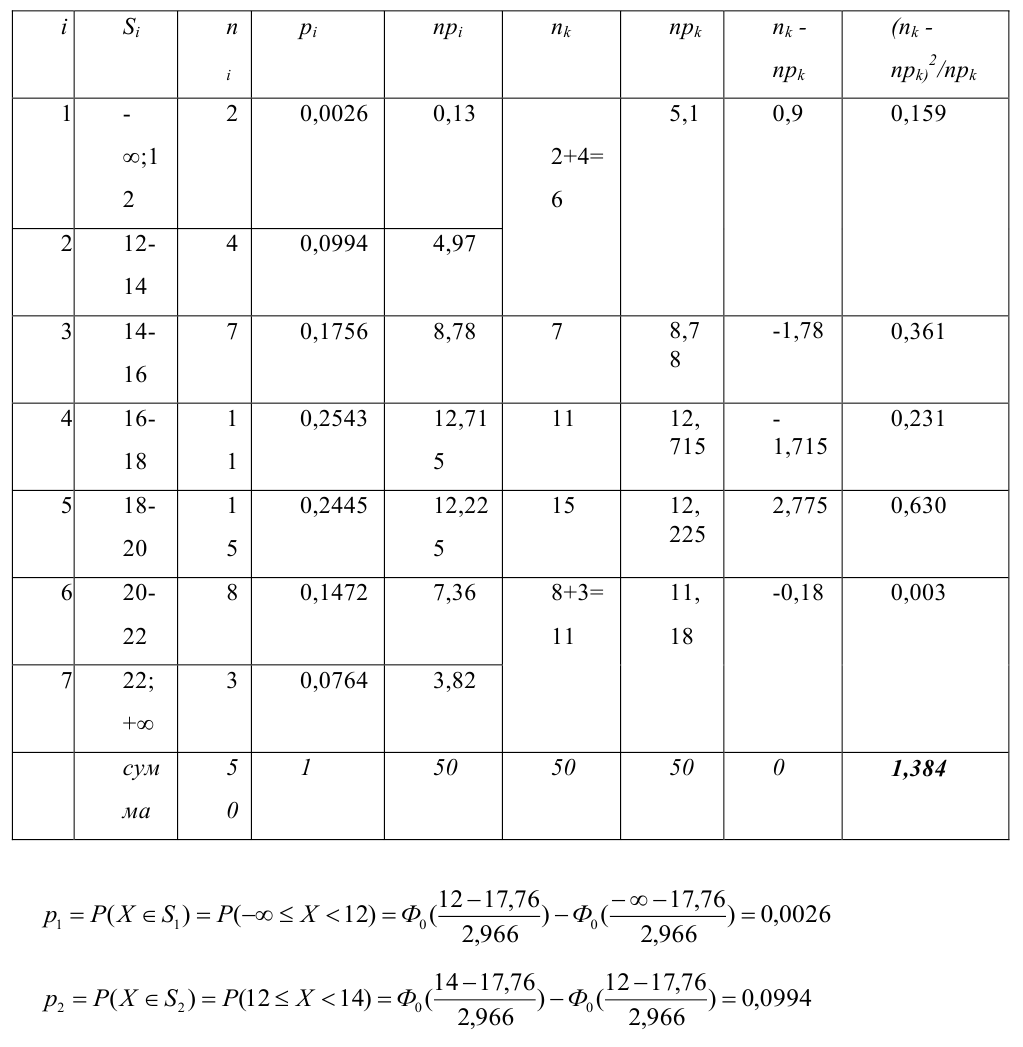
Пример №18
По выборке объема 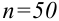
В качестве параметров нормального распределения выберем их точечные оценки:
1) 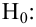
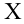
2) 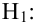
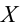
3)
4) строим статистический критерий
Замечание: если для какого-либо интервала не выполняется условие 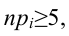
1,384 — наблюдаемое значение статистического критерия
5) строим критическую область
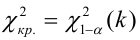
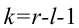
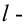
7) Вывод: нет оснований отвергнуть нулевую гипотезу на уровне значимости
Критерий Колмогорова — Смирнова
в классическом виде является более мощным, чем критерий Пирсона; используется для проверки гипотезы о соответствии эмпирического любому теоретическому непрерывному распределению 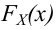
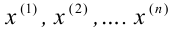
1) 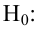
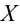
2) 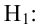
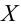
3) 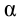
4) строим статистический критерий
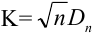
5) строим критическую область
Критическая область — правосторонняя; критические значения 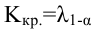
6) сравниваем наблюдаемое значение критерия 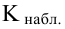
7) Вывод: если 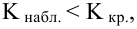
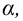
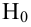
Проверка гипотез о параметрах известного распределения генеральной совокупности
Проверка гипотез о параметрах нормально распределенной генеральной совокупности

Пример №19
На завод поступила партия станков. По результатам исследования 13 станков найдена исправленная выборочная дисперсия размера изготовления станками деталей 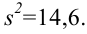
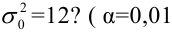
Решение:
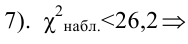
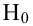
Проверка гипотез о параметре 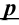
(сравнение относительной частоты с гипотетической вероятностью 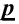
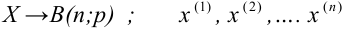
В электронных таблицах Excel для проверки гипотез о параметрах нормально распределенных генеральных совокупностей по результатам экспериментов есть специальные тесты, упрощающие процедуру вычислений.
Двухвыборочный 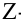
Двухвыборочный 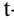
Парный двухвыборочный 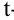
Двухвыборочный 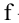
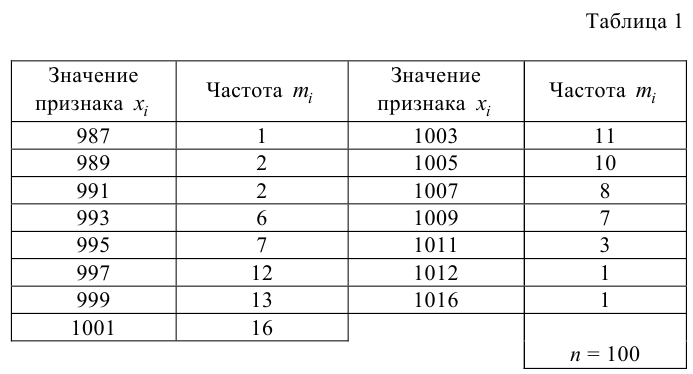
Пример №20
На предприятии провели выборочный опрос работающих об их средней заработной плате за предыдущий год. Данные опроса представлены в табл. 1.
С помощью критерия Пирсона проверить гипотезу о том, что средняя заработная плата по всему предприятию распределена по нормальному закону с уровнем значимости
Решение. Найдем функцию распределения признака 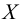
Для этого предварительно вычислим среднюю выборочную и исправленную статическую дисперсию
За функцию распределения признака 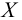
Выполним разбиение области значений случайной величины 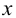
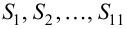
Для расчета теоретического ряда частот необходимо предварительно вычислить значения вероятностей 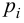
и применить формулу для вычисления теоретических частот:
где —
Например.
Значение функции 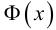
Значения 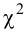
Так как два параметра распределения признака в генеральной совокупности находились на основании выборки, то функцию 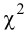
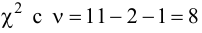
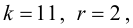
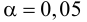
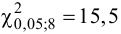
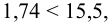
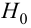
Следует отметить, что на практике все шире начинают применять критерии согласия не столько для проверки согласия экспериментальных данных с некоторой гипотетической функцией, сколько для подбора наилучшей функции распределения, хотя выбор подходящего закона должен основываться прежде всего на понимании механизма изучаемого явления.
Пример №21
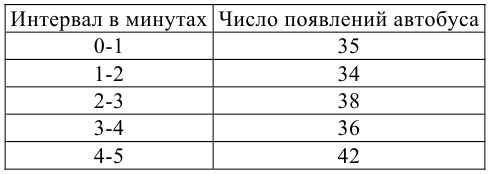
Наблюдалось следующее распределение по минутам числа появлений на остановке автобуса, имеющего пятиминутный интервал движения.
Проверить гипотезу о равномерном законе распределения.
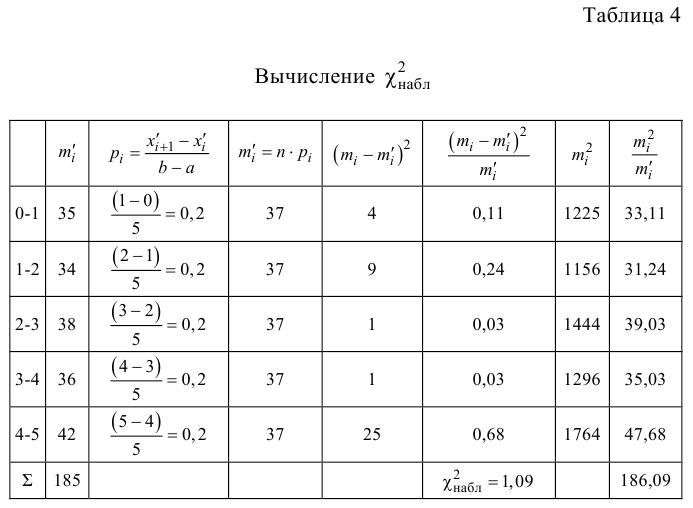
Решение. 1. Вычисляем по данному вариационному ряду вероятности 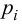
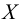
2. Для проверки гипотезы о том, что число появлений автобуса на остановке есть случайная величина, распределенная по равномерному закону, вычисляем критерии 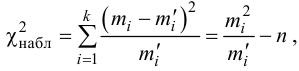
Контроль: 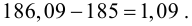
3. Определяем 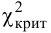
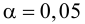
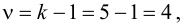
4.Так как 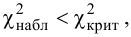
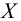
Пример №22
Рассмотрим вариационный ряд.
1. Если построить гистограмму частостей, то ее вид будет напоминать экспоненциальную кривую. Поэтому произведем «выравнивание» статистических данных по показательному закону. Запишем его дифференциальную функцию:
Для нахождения точечной оценки параметра 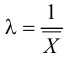
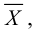
Тогда 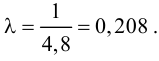
2. Для проверки соответствия эмпирических данных с предполагаемым показательным законом распределения применим критерий согласия
3. Вычислим вероятности попадания случайной величины 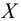
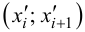
Для нахождения 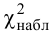
4. Найдем в таблице критических точек 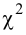
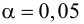
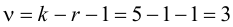
5. Так как 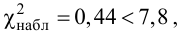
Пример №23
Из продукции цеха случайно отобрано 200 выборок по 5 деталей. Регистрировалось число бракованных деталей. В итоге получен вариационный ряд:
Требуется, используя критерий Пирсона при уровне значимости 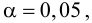
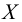
1. Найдем частость 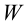
По формуле Бернулли 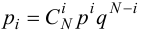
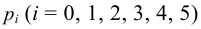
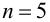
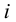
2. Для проверки нулевой гипотезы выдвигаем критерий
где 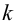
3. Вычисляем 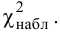
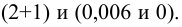
4. Находим 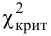
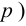
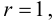
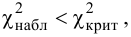
Пример №24
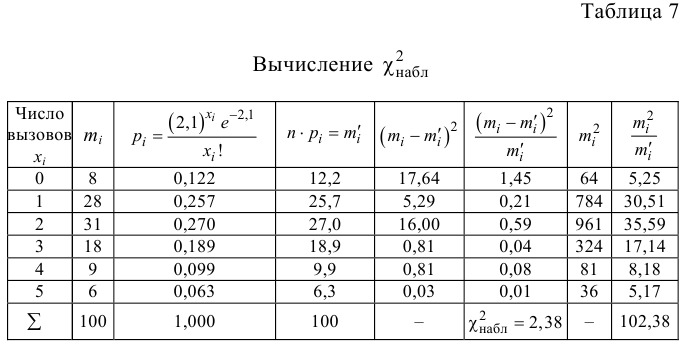
Проведено наблюдение за числом вызовов телефонной станции. С этой целью в течение 100 случайно выбранных 5-секундных интервалов времени регистрировалось число вызовов. Получен следующий вариационный ряд:
Проверить, используя критерий 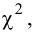
Вероятность ровно 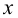
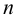
1. Найдем точечную оценку параметра 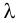
Таким образом, функция вероятностей предполагаемого закона Пуассона имеет вид
2.Применим критерии
3. Находим 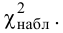
Контроль: 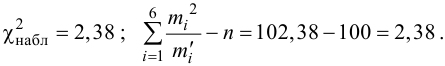
4. По таблице П5 по заданному уровню значимости и числу степеней свободы 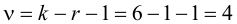
5. Так как 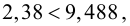
Итак, мы рассмотрели критерий 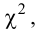
Пример №25
Менеджер кредитного отдела нефтяной компании выясняет, является ли среднемесячный баланс владельцев кредитных карточек, равным 75 у.е. Аудитор случайным образом отобрал 100 счетов и нашел, что среднемесячный баланс владельцев составил 83,4 у.е. с выборочным стандартным отклонением, равным 23,65 у.е. Определить на 5%-м уровне значимости, может ли этот аудитор утверждать, что средний баланс отличен от 75 у.е.
Решение. 1. Исходя из условия задачи, сформулируем гипотезы:
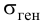
2. Для проверки гипотезы 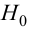
с двусторонней критической областью.
3. Вычислим
5. Так как 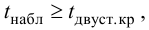
Пример №26
По двум независимым выборкам, объемы которых 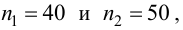
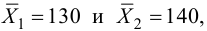
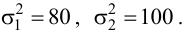
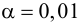
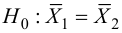
Решение. Найдем наблюдаемое значение критерия:
По условию конкурирующая гипотеза имеет вид 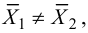
Найдем правую критическую точку из равенства
По таблице П2, часть 1, функции Лапласа находим 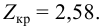
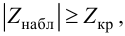
Пример №27
Менеджер предприятия решил выяснить, существует ли разница в производительности труда рабочих дневной и вечерней смены. Случайно организованная выборка 10 рабочих дневной смены показала, что средний выпуск продукции составил 74,3 ед./ч, а выборочная дисперсия оказалась равной 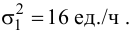
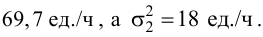
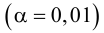
Решение. Так как выборочные дисперсии различны, проверим предварительно нулевую гипотезу 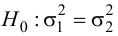
Найдем отношение большей исправленной дисперсии к меньшей: 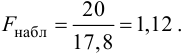
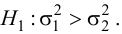
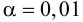
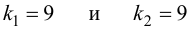
Так как 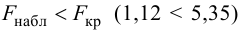
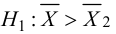
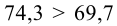
2. В качестве критерия проверки нулевой гипотезы примем случайную величину
4. Находим 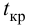
Так как 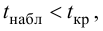
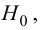
не существует разницы в производительности труда рабочих дневной и вечерней смены, а имеющие место различия случайны, незначимы.
Пример №28
Из двух партий изделий, изготовленных на двух одинаково настроенных станках, извлечены малые выборки, объемы которых 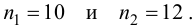
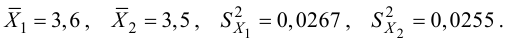
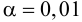
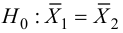
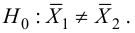
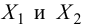
Решение. Рассматриваемый в этом параграфе критерий предполагает, что генеральные дисперсии одинаковы, но исправленные дисперсии различны, поэтому вначале нужно сравнить дисперсии, используя критерий Фишера-Сиедекора. Сделаем это, приняв в качестве альтернативной гипотезы 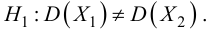
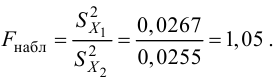
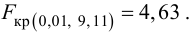
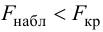
Сравним средние, для чего вычислим наблюдаемое значение критерия Стьюдента:
По условию, альтернативная гипотеза имеет вид 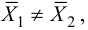
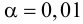
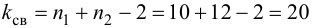
Так как 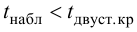
Таким образом, средние размеры изделий существенно не различаются.
- Регрессионный анализ
- Корреляционный анализ
- Статистические решающие функции
- Случайные процессы
- Доверительный интервал для вероятности события
- Проверка гипотезы о равенстве вероятностей
- Доверительный интервал для математического ожидания
- Доверительный интервал для дисперсии
Процедура проверки нулевой гипотезы в
общем случае включает следующие этапы:
1. задается допустимая вероятность
ошибки первого рода (Ркр=0,05)или 5 %
2. выбирается статистика критерия (Т)
3. ищется область допустимых значений
Ткрит.-опред по статис. таблицу
4. по исходным данным вычисляется
значение статистики Т эмп.
5. если Т эмп(статистика критерия)
принадлежит области принятия нулевой
гипотезы( Тэмп<Ткрит), то нулевая
гипотеза принимается. Т О делается
заключение, что исходные данные не
противоречат нулевой гипотезе), а в
противном случае нулевая гипотеза
отвергается и принимается альтернативная
гипотеза. Это основной принцип проверки
всех статистических гипотез.
В современных статистических пакетах
используются не стандартные уровни, а
уровни значимости, подсчитываемые в
процессе работы с соответствующим
статистическим методом.
При проверке статистических гипотез с
помощью статистических пакетов, программа
выводит на экран вычисленное значение
уровня значимости Р и подсказку о
возможности принятия или неприятия
нулевой гипотезы.
Рассчитанный и показанный уровень на
экране необходимо сравнить с допустимой
вероятностью ошибки первого рода. Чем
меньше вычисл. значение тем более
исходные данные противоречат нулевой
гипотезе.
(если вычисленное значение Р превосходит
выбранный уровень Ркр,
то принимается нулевая гипотеза, а в
противном случае — альтернативная
гипотеза).
Число степеней свободы(К) – число
свободно варьируемых наблюдений после
опред интересующего параметра.(из книги
-число опытов, по которым рассчитан
данный параметр, минус количество
одинаковых значений, найденных по этим
опытам независимо друг от друга.)
Мощность критерия (Ф) – вероятность
отклонения неверной нулевой гипотезы,
т.е. вероятность попадания критерия в
критическую область (вероятность
правильного решения).
Чем больше Ф, тем вероятность ошибки
2-го рода меньше, т.е Ф хар-ет его способность
избежать ошибки 2 рода.
=ошибка первого рода- можно отвергнуть
нулевую гипотезу, когда она на самом
деле верна.
=ошибка второго рода -можно принять
нулевую гипотезу, когда она на самом
деле не верна.
Если Р больше 0,1-принимается Но
Р ≤0,1 – сомнения в истинности Но,неопред-ть.
Р ≤0,05 – значимость,отклон. Но
Р≤0,01 – высокая значимость, отклонение
Но.
18.Уровень значимости, репрезентативность. Примеры.
Уровень значимости – это вероятность
ошибки первого рода при принятии решения
(вероятность ошибочного отклонения
нулевой гипотезы).
Альтернативные гипотезы принимаются
тогда и только тогда, когда опровергается
нулевая гипотеза. Это бывает в случаях,
когда различия, скажем, в средних
арифметических экспериментальной и
контрольной групп настолько значимы
(статистически достоверны), что риск
ошибки отвергнуть нулевую гипотезу и
принять альтернативную не превышает
одного из трех принятых уровней значимости
статистического вывода:
=первый уровень — 5% (р=5%); где допускается
риск ошибки в выводе в пяти случаях из
ста теоретически возможных таких же
экспериментов при строго случайном
отборе испытуемых для каждого эксперимента;
=второй уровень — 1%, т. е. соответственно
допускается риск ошибиться только в
одном случае из ста;
=третий уровень — 0,1%, т. е. допускается
риск ошибиться только в одном случае
из тысячи.
Последний уровень значимости предъявляет
очень высокие требования к обоснованию
достоверности результатов эксперимента
и потому редко используется. В
педагогических исследованиях, не
нуждающихся в очень высоком уровне
достоверности, представляется разумным
принять 5% уровень значимости.
При проверке статистических гипотез
возможны ошибки (ошибочные суждения)
двух видов:
=ошибка первого рода- можно отвергнуть
нулевую гипотезу, когда она на самом
деле верна.
=ошибка второго рода -можно принять
нулевую гипотезу, когда она на самом
деле не верна.
Ошибка, состоящая в принятии нулевой
гипотезы, когда она ложна, качественно
отличается от ошибки, состоящей в
отвержении гипотезы, когда она истинна.
Эта разница очень существенна вследствие
того, что различна значимость этих
ошибок.
Пример 1. В результате, прежде чем
выпускать в продажу вновь произведенную
партию лекарства, ее подвергают
исследованию на токсичность биологическими
методами. Малые дозы лекарства вводятся
некоторому количеству подопытных
животных, например, мышей, и результат
регистрируют. Если лекарство токсично,
то все или почти все животные гибнут. В
противном случае норма выживших велика.
Исследование лекарства может привести
к одному из возможных способов действия:
выпустить партию в продажу (а1), вернуть
партию поставщику для доработки или,
может быть, для уничтожения (а2).
Сначала рассмотрим случай, когда
применяется действие а1, в то время когда
предпочтительнее а2. Лекарство опасно
для пациента, в то время как оно признано
безопасным. Ошибка этого вида может
вызвать смерть пациентов, употребляющих
этот препарат. Это ошибка первого рода,
так как нам важнее ее избежать.
Однако случайное отвержение совершенно
безопасного лекарства, очевидно, менее
нежелательно, чем, пусть даже изредка
происходящие гибели пациентов. Отвержение
нетоксичной партии лекарства – ошибка
второго рода.
На всяк случай.
Если Р больше 0,1-принимается Но
Р ≤0,1 – сомнения в истинности Но,неопред-ть.
Р ≤0,05 – значимость,отклон. Но
Р≤0,01 – высокая значимость, отклонение
Но.
Одной из основных задач статистического
анализа является получение по имеющейся
выборке достоверных сведений о
интересующих исследователя характеристиках
генеральной совокупности. Поэтому
важным требованием к выборке является
ее репрезентативность, то есть правильная
представимость в ней пропорций генеральной
совокупности.
Репрезентативность выборки- свойство
выборки представлять изучаемые явления
достаточно полно с точки зрения
изменчивости генерал совокупности.
Достижению репрезентативности может
способствовать такая организация
эксперимента, при которой элементы
выборки извлекаются из генеральной
совокупности случайным образом.В силу
закона больших чисел можно утверждать,
что выборка будет репрезентативной,
если ее осуществить случайно: каждый
объект выборки отобран случайно из
генеральной совокупности, если все
объекты имеют одинаковую вероятность
попасть в выборку.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
2.1.1. Основные понятия о статистической гипотезе
Полученные
в экспериментах выборочные данные
всегда ограничены и носят в значительной
степени случайный характер. Именно
поэтому для анализа таких данных и
используется математическая статистика,
позволяющая обобщать закономерности,
полученные на выборке, и распространять
их на всю генеральную совокупность.
Однако,
в связи с действием случайных причин,
оценка параметров генеральной
совокупности, сделанная на основании
экспериментальных (выборочных) данных,
всегда будет сопровождаться погрешностью,
и поэтому подобного рода оценка должна
рассматриваться как предположительное,
а не как окончательное утверждение.
Подобные предположения о свойствах и
параметрах генеральной совокупности
носят название статистических гипотез.
Сущность
проверки статистической гипотезы
заключается в том, чтобы установить,
согласуются ли экспериментальные
данные и выдвинутая гипотеза, допустимо
ли отнести расхождение между гипотезой
и результатом статистического анализа
экспериментальных данных за счет
случайных причин?
Рассмотрим
простой пример. Подбросим монету 10 раз.
Если монета не имеет дефектов формы,
то количество выпадений герба и цифры
должно быть примерно одинаковым. Таким
образом, возможны гипотезы:
—
монета правильная и частота выпадений
герба и цифры примерно одинакова,
—
монета деформирована и чаще выпадает
герб,
—
монета деформирована и чаще выпадает
цифра.
Но
нам надо выразить понятия «правильная»
или «деформированная» монета в
математических параметрах. В качестве
параметра выбираем вероятность Р
выпадения герба. Тогда приведенные выше
гипотезы можно записать (в порядке
упоминания) так:
—
Р = ½,
—
Р > ½,
—
Р < ½.
При
проведении эксперимента надо ответить
на вопрос, какая же из приведенных
гипотез верна?
При
проверке статистических гипотез
используется два понятия: нулевая
гипотеза (ее обозначают Н0) и альтернативная
гипотеза (обозначение Н1). Как правило,
принято считать, что нулевая гипотеза
Н0 – это гипотеза о сходстве, а
альтернативная Н1 – гипотеза о различии.
Таким образом, принятие нулевой гипотезы
свидетельствует об отсутствии различий,
а альтернативной – о наличии различий.
Для
нашего примера в качестве нулевой
(будем называть ее основной) гипотезы
Н0 принимаем – монета правильная, а
качестве альтернативной гипотезы Н1 –
монета деформированная. Альтернативных
гипотез может быть несколько. В нашем
случае их две (больше и меньше ½).
2.1.2. Ошибки при проверке статистических гипотез
Обозначим
через N множество всевозможных
результатов наблюдений (выборок) m.
Выделим в N область n , исходя из следующих
соображений: если гипотеза Н0 верна,
то наступление события m ∈
n маловероятно. Это записывается так:
Р
{ m ∈
n/Но} = α ,
где
α – малое число, близкое к нулю.
Иными
словами, вероятность Р события m ∈
n при условии, что верна гипотеза Н0,
равна α. Если это событие все же произошло,
то гипотеза Н0 отвергается. При этом
сохраняется небольшая вероятность
(учитывая, что α мало, но не равно нулю),
что гипотеза Н0 отвергается, хотя она
верна. Такая ошибка называется ошибкой
первого рода. Ее вероятность равна α.
Возможна
и ошибка второго рода β, которая состоит
в том, что гипотеза Н0 принимается, хотя
она неверна, а верна альтернативная
гипотеза Н1.
Р
{m ∈
n/Н1} = β.
Разберем
порядок проверки статистических гипотез
на примере. Допустим, что проводится
приемочный контроль партии продукции.
Известно, что в партии могут содержаться
дефектные изделия. Поставщик полагает,
что доля дефектных изделий составляет
не более 3%, а заказчик считает, что
качество изготовления изделий низкое
и доля дефектных изделий значительна
и составляет 20%. Между поставщиком и
заказчиком достигнута следующая
договоренность: партия продукции
принимается, если в выборке из 10 изделий
будет обнаружено не более одного
дефектного изделия.
Требуется
в процессе решения примера сформулировать:
—
нулевую (основную) и альтернативную
гипотезы,
—
определить критическую область и
область принятия нулевой гипотезы,
—
определить, в чем состоят ошибки первого
и второго рода, и найти их вероятность.
Если
смотреть на ситуацию с точки зрения
заказчика (потребителя), учитывая, что
заказчик всегда прав, то нулевой гипотезой
Н0 следует принять гипотезу, что
продукция содержит 20% брака. Альтернативная
гипотеза Н1 соответствует версии
поставщика – 3% брака.
Поскольку
отбирается 10 изделий, то множество
возможных результатов (наличие дефектного
изделия) составит N = (0,1,2,3…10), так как в
выборке может оказаться и 0, и 10 дефектных
изделий. По условиям поставок, принятым
и заказчиком, и поставщиком, гипотеза
заказчика Н0 считается:
− отвергнутой,
если число дефектов находится в области
n = {0,1};
− принятой,
если число дефектов находится в области
n = {2,3,4…10}.
Область
результатов выборки, при попадании в
которую принятая гипотеза отвергается,
называется критической. В нашем
случае это – область n = {0,1}.
Напомним,
что ошибка первого рода возникает тогда,
когда гипотеза Н0 отвергается, хотя
она верна. Для нашего примера это
означает, что партия изделий принимается
(закупается), хотя в ней 20% дефектных
изделий. Ошибка второго рода для
нашего примера возникает тогда, когда
нулевая гипотеза принимается (т.е.
партия бракуется), в то время как верна
альтернативная гипотеза (дефектных
изделий всего 3%). Найдем вероятность
этих ошибок.
Сначала
заметим, что число дефектных изделий m
является биномиальной, случайной
величиной. Если допустить, что гипотеза
Н0 верна то в выборке N=10 этому
соответствует 2 случая: m =0 и m = 1. Тогда
биномиальная величина имеет вид Bi
(10;2). Найдем вероятность каждого из двух
событий:
Р(m
= 0) = (0,8)10
=
0,107,
Р(m
= 1) = 10·(0,8)9·0,2
= 0,268.
Тогда
ошибка первого рода α будет равна сумме
этих вероятностей:
α
= Р (m ≤ 1) = Р (m=0/Н0) + Р (m =1/Н0) = 0,375.
Если
верна гипотеза Н1, то вероятность
выбрать дефектное изделие составляет
по условию примера 0,03 (3%). Ошибка
второго рода произойдет, если из 10
изделий в выборке окажутся дефектных
2 и более. В этом случае биномиальная
величина имеет вид Bi (10;0,03). Тогда для
событий m ≤ 1 вероятность составит:
Р(m=0)
= (0,97)10
=
0,737,
Р(m=1)
= 10·(0,97)9·0,03
= 0,228.
Таким
образом, вероятность альтернативных
событий (m > 1) составит величину ошибки
второго рода β:
β
= Р(m>1/Н1) = 1 – Р(m ≤ 1/Н1) = 1 – Р(m =0/Н1) –
Р(m=1/Н1) = =1 – 0,737 – 0,228 = 0,035.
Из
сравнения ошибок α и β можно заключить,
что оговоренная процедура по приему
партии выгодна скорее поставщику, чем
потребителю (заказчику).
Соседние файлы в папке УК работы
- #
- #
- #
11.08.201936.84 Кб25ЛР 6 УК1.xlsx
- #
11.08.201919.67 Кб23ЛР 6 УК2.xlsx
- #
11.08.201941.03 Кб24лр7.xlsx
- #
11.08.201977.53 Кб25лр8.xlsx
План:
1. Статистические гипотезы. Основные понятия.
2. Гипотезы о законе распределения.
3. Гипотезы о числовом значении генерального
среднего и дисперсии.
1.
Статистические гипотезы. Основные понятия.
Статистическая гипотеза— это утверждение о виде неизвестного
распределения или параметрах известного распределения. Статистические гипотезы
проверяются по результатам выборки статистическими методами в ходе эксперимента
(эмпирическим путем) с помощью статистических критериев.
В тех случаях, когда
известен закон, но неизвестны значения его параметров (дисперсия или
математическое ожидание) в конкретной ситуации, статистическую гипотезу
называют параметрической.
Например, предположение
об ожидаемом среднем доходе по акциям или разбросе дохода являются
параметрическими гипотезами.
Когда закон
распределения генеральной совокупности не известен, но есть основания
предположить, каков его конкретный вид, выдвигаемые гипотезы о виде его
распределения называются непараметрическими.
Например, можно
выдвинуть гипотезу, что число дневных продаж в магазине или доход населения
подчинены нормальному закону распределения.
По содержанию статистические гипотезы можно классифицировать:
1.
Гипотезы о типе вероятностного закона
распределения случайной величины, характеризующего явление или процесс.
2.
Гипотезы об однородности двух или более
обрабатываемых выборок. Изучаемое свойство исследуется с помощью двух или более генеральных
совокупностей. Гипотеза в этом случае может заключаться в следующем: исследуемые
выборочные характеристики различаются между собой статистически значимо или
нет.
3.
Гипотезы о свойствах числовых значений
параметров исследуемой генеральной совокупности. Больше ли значения параметров
некоторого заданного номинала или меньше и т.д.
4.
Гипотезы о вероятностной зависимости двух
или более признаков, характеризующих различные свойства рассматриваемого
явления или процесса. При этом определяется характер этой зависимости.
Гипотезы бывают простые (содержащие одно предположение) и сложные (содержащие несколько предположений).
Выдвинутую гипотезу называют основной или нулевой и обозначают H0
. Противоречащую ей гипотезу называют альтернативной или конкурирующей и обозначают
H1.
Под статистическим
критерием понимают однозначно определенное правило, устанавливающее
условие, при котором проверяемая гипотеза отвергается либо не отвергается.
Пример:
Увеличение числа заболевших некоторым
заболеванием дает возможность выдвинуть гипотезу о наличии эпидемии. Для сравнения
доли заболевших в обычных и экстремальных условиях используются статистические
данные, на основании которых делается вывод о том, является ли данное массовое
заболевание эпидемией. Предполагается, что существует некоторый критерий-
уровень доли заболевших, критический для этого заболевания, который
устанавливается по ранее имевшимся случаям.
Различают три вида критериев:
1.
Параметрические критерии—
критерии значимости, которые служат для проверки гипотез о параметрах
распределения генеральной совокупности при известном виде распределения.
2.
Критерии согласия—
позволяют проверить гипотезы о соответствии распределений генеральной
совокупности известной теоретической модели.
3.
Непараметрические критерии—
используются в гипотезах, когда не требуется знаний о конкретном виде
распределения.
Проверка
параметрических гипотез проводится на основе критериев значимости., а
непараметрических- критериев согласия.
Задача проверки
статистических гипотез сводится к исследованию генеральной совокупности по
выборке. Множество возможных значений элементов выборки может быть разделено на
два непересекающихся подмножества- критическую область и область принятия
гипотезы.
Областью принятия гипотезы или областью допустимых значений Iдоп
называют совокупность значений критерия,
при которых эту гипотезу принимают.
Критической областью
Iкр называют множество значений критерия, при
котором гипотезу отвергают.
Наблюдаемые значения критерия (статистика)
Kнабл
называют такое значение критерия, которое
находится по данным выборки.
Границы критической области, отделяющие ее от
области принятия гипотезы, называют критическими точками и обозначают
Kкр.
Для определения
критической области задается уровень значимости
—
некая малая вероятность попадания критерия в критическую область.
Уровень значимости— вероятность принятия
конкурирующей гипотезы, тогда как справедлива основная.
С помощью уровня
значимости определяются границы критической области.
Основной принцип проверки статистических гипотез
состоит в следующем: если наблюдаемое значение статистики критерия попадает (не
попадает) в критическую область, то гипотеза H0
отвергается (принимается), а гипотеза H1
принимается (отвергается) в качестве одного из
возможных решений с формулировкой «гипотеза
H0 противоречит (не противоречит) выборочным
данным на уровне значимости
».
В зависимости от
содержания альтернативной гипотезы осуществляется выбор критической области:
левосторонней, правосторонней, двусторонней. Если смысл исследования заключается
в доказательстве конкретного изменения наблюдаемого параметра (его уменьшения
или увеличения), то говорят об односторонней критической области. Если смысл
исследования- выявить различия в изучаемых параметрах, но характер их
отклонения от контрольных (или теоретических) не известен, то говорят о
двусторонней критической области.
Однако, принятие той
или иной гипотезы не дает оснований утверждать, что она верна. Результат
проверки статистической гипотезы лишь устанавливают на определенном уровне
значимости ее соответствие (несоответствие) результатам эксперимента.
При проверке
статистических гипотез возможны следующие ошибки:
1.
Отвергнута правильная
H0, а принята неправильная гипотеза
H1 — ошибка
первого рода.
2. Отвергнута правильная альтернативная
гипотеза
H1 и
принята неправильная нулевая гипотеза H0
—
ошибка второго рода.
Заметим, что уровень значимости —
есть вероятность ошибки первого рода. Ошибка первого рода называется
-риском. Обычно они задаются
некоторыми конкретными значениями: 0,05; 0,01; 0,005; 0,001. Ошибки второго
рода называются -риском, а вероятность ее
допустить обозначается
(вероятность того, что принята гипотеза
H0
, когда на самом деле справедлива
альтернативная гипотеза H1
.
Можно доказать, что с
уменьшением ошибок первого рода одновременно увеличиваются ошибки второго рода
и наоборот. Поэтому, на практике пытаются подбирать значения параметров
и
опытным путем в целях минимизации суммарного
эффекта от возможных ошибок. При принятии управленческих решений для
одновременного уменьшения ошибок первого и второго рода самым действенным
средством является увеличение объема выборки, что согласуется с законом больших
чисел.
На бытовом уровне
ошибки второго рода могут иметь более трагические последствия, чем ошибки
первого рода.
2. Гипотеза о законе распределения. Критерий согласия Пирсона (
X2
-критерий).
Критериями согласия называют критерии, в
которых гипотеза определяет закон распределения либо полностью, либо с
точностью до небольшого числа параметров.
Причины расхождения
результатов эксперимента и теоретических характеристик могут быть вызваны малым
объемом выборки, неудачным способом группировки наблюдений, ошибками в
выборе гипотезы о виде распределения
генеральной совокупности и др.
Рассмотрим
универсальный критерий согласия Пирсона. Проверка гипотезы о том, что
эмпирическая частота мало отличается от соответствующей теоретической частоты,
осуществляется с помощью величины X2
—
меры расхождения между ними.
Для произвольной
выборки, когда распределение непрерывно или число различных вариант велико, все
пространство наблюдаемых вариант делят на конечное число непересекающихся
областей, в каждой из которых подсчитывают наблюдаемую частоту и теоретическую
вероятность.
Для применения критерия
согласия Пирсона необходимо:
1. Вычислить значение статистики по формуле:
, где
pi –вероятность
принятия значения
xi, ni.
— эмпирическая частота для
соответствующего
xi. n— объем выборки. s— число вариант выборки.
2.
По
соответствующей таблице распределения Пирсона найти критическое значение , где k = s –
r
– 1 – число степеней свободы, s—
число различных вариант или интервалов группировки, r— число неизвестных параметров
предполагаемого теоретического распределения,
— выбранный уровень значимости. Это
значит, что строится правосторонний интервал.
3.
Если
,
то основная гипотеза отвергается, в противном случае- принимается, т.е. чем
больше отклонение, тем меньше согласованы теоретическое и эмпирическое
распределение. Поэтому принято использовать только правостороннюю критическую
область.
Расчетная таблица имеет вид:
|
Интервалы |
Середины |
Эмпирические |
Вероятности pi |
Теоретические |
|
|
Пример:
По таблице
эмпирического распределения изменения в процентах темпа роста акций проверьте
гипотезу о нормальном распределении выборки.
|
Интервалы |
(-2; |
(-1; |
(0; |
(1; |
Итого |
|
ni |
7 |
14 |
18 |
11 |
50 |
|
pi |
0,157 |
0,341 |
0,341 |
0,157 |
1 |
Решение:
Гипотезу о нормальном
распределении проверим по критерию Пирсона.
|
Интервалы |
Эмпирические |
Вероятности pi |
Теоретические |
|
|
|
(-2; |
7 |
0,157 |
7,85 |
0,7225 |
0,092 |
|
(-1; |
14 |
0,341 |
17,05 |
9,3025 |
0,546 |
|
(0; |
18 |
0,341 |
17,05 |
0,9025 |
0,053 |
|
(1; |
11 |
0,157 |
7,85 |
9,925 |
1,264 |
|
Итого |
|
По таблице найдем
при
=0,05
и k = s – r – 1 = 4 – 2 – 1 = 1. s = 4 – число
интервалов. r
= 2- число параметров теоретического (нормального) распределения.
Имеем . Т.к. 1,955 < 3,841, то
, т.е. гипотеза о нормальном
распределении подтверждается.
3. Гипотезы о числовом значении генерального
среднего и дисперсии.
Установление двусторонней критической
области на уровне значимости
для
проверки гипотезы соответствует отысканию соответствующего доверительного
интервала с надежностью
.
Рассмотрим условия применения некоторых
статистических гипотез.
|
Тип гипотезы H0 |
Границы критической области на уровне значимости |
Статистика наблюдений |
|
О числовом значении |
|
|
|
О числовом значении |
Распределение |
|
|
О числовом значении |
Распределение Пирсона |
|
Пример:
Результаты исследований в течение 35 лет
показали, что среднее изменение доходности векселей равно 5,5 %. Полагая, что
изменение доходности подчиняется нормальному закону распределения с
среднеквадратическим отклонением равным 2 %, на уровне значимости
, решите: можно ли принять 6 % в качестве нормативного процента
(математического ожидания) изменения доходности.
Решение:
По условию задачи
нулевая гипотеза
. Так как
, то в качестве альтернативной гипотезы
возьмем гипотезу:
, которой соответствует левосторонняя
критическая область с интервалом.
Найдем границы
критической области:
По таблице значений
функции Ф(х) найдем
, т.е. левосторонняя критическая область
лежит в интервале.
Найдем статистику
наблюдений:
.
Имеем:, нет основания отвергать нулевую
гипотезу. Значит, в качестве нормативного процента можно принять 6 %.
Пример:
Точность работы
программы проверяют по дисперсии контролируемого количества символов в коде,
которая не должна превышать 0,1. По выборке из 15 сообщений вычислена
исправленная оценка дисперсии 0,22. При
уровне значимости 0,05 проверьте, обеспечивает ли программа необходимую
точность.
Решение:
Имеем: n = 15, s2 = 0,22
, ,
.
Сформулируем гипотезу о
числовом значении дисперсии:
H0 — программа обеспечивает необходимую точность
;
H1 —
программа не обеспечивает необходимую точность
.
Определим статистику: .
Найдем границы
критической области:
.
Поскольку 30,8 >
23,7;
, принимаем гипотезу H1, т.к.
H0 противоречит опытным данным. Вывод: программа
не обеспечивает необходимую точность.
Все, что вам нужно знать о проверке гипотез — часть I
Перевод
Ссылка на автора
Статистика — это все о данных, но одни данные не интересны. Это интерпретация данных, которые нас интересуют …
Область Data Science развивается как никогда раньше. Многие компании в настоящее время ищут профессионалов, которые могут просеять свои данные о добыче золота и помочь им эффективно принимать быстрые бизнес-решения. Это также дает возможность многим работающим профессионалам переключить свою карьеру на область Data Science.
Имея этот ИИ, Data Science окружает многих студентов колледжей и хочет продолжить свою карьеру в области Data Science. И эта шумиха вокруг Data Science правильно провозглашена Томасом Х. Давенпортом и Д.Дж. Патил в одной из статей Harvard Business Review,
«Data Scientist: самая сексуальная работа XXI века»
В современном мире аналитики модели машинного обучения в строительстве стали сравнительно простыми (благодаря более надежным и гибким инструментам и алгоритмам), но фундаментальные концепции по-прежнему сбивают с толку. Одним из таких понятий является проверка гипотез.
В этом посте я пытаюсь прояснить основные понятия проверки гипотез с помощью иллюстраций.
Что такое проверка гипотез? Чего мы пытаемся достичь? Зачем нам нужно проверять гипотезы? Мы должны знать ответы на все эти вопросы, прежде чем мы продолжим.
Статистика это все о данных. Данные сами по себе не интересны. Это интерпретация данных, которые нас интересуют. ИспользованиеПроверка гипотезымы пытаемся интерпретировать или делать выводы о населении, используя выборочные данные.Проверка гипотезоценивает два взаимоисключающих утверждения о совокупности, чтобы определить, какое утверждение лучше всего подтверждается данными выборки. Всякий раз, когда мы хотим заявить о распределении данных или о том, отличается ли один набор результатов от другого набора результатов в прикладном машинном обучении, мы должны полагаться на статистические проверки гипотез.
Есть два возможных результата: если результат подтверждает гипотезу, то вы произвели измерение. Если результат противоречит гипотезе, то вы сделали открытие — Энрико Ферми
Давайте посмотрим на терминологию, которую мы должны знать вПроверка гипотезы
1. Параметр и статистика:
параметрявляется кратким описанием фиксированной характеристики или показателя целевой группы населения. Параметр обозначает истинное значение, которое будет получено при проведении переписи, а не выборки.
Пример:Среднее (μ), дисперсия (σ²), стандартное отклонение (σ), пропорция (π)
Население: Население — это совокупность объектов, которые мы хотим изучить / протестировать. Коллекция объектов может быть города, студенты, фабрики и т. Д. Это зависит от изучения под рукой.
В реальном мире сложно получить полную информацию о населении. Следовательно, мы выбираем выборку из этой совокупности и получаем те же статистические показатели, упомянутые выше. И эти меры называются выборочной статистикой. Другими словами,
статистикаявляется кратким описанием характеристики или меры выборки. Выборочная статистика используется в качестве оценки параметра совокупности.
Пример:Среднее значение выборки (x̄), дисперсия выборки (S²), стандартное отклонение выборки (S), пропорция выборки (п)
2. Распределение выборки:
Распределение выборки — это распределение вероятностей статистики, полученной с помощью большого числа выборок, взятых из определенной совокупности.
Пример:Предположим, что простая выборка из пяти больниц должна быть взята из населения 20 больниц. Возможны следующие варианты: (20, 19, 18, 17, 16) или (1,2,4,7,8) или любая из 15 504 (с использованием комбинаций 20C)) различных образцов размера 5.
В целом среднее значение распределения выборки будет приблизительно эквивалентно среднему значению для населения, т.е. E (x̄) = μ
Чтобы узнать больше о распределении выборки, пожалуйста, проверьте это ниже видео:
3. Стандартная ошибка (SE):
Стандартная ошибка (SE) очень похожа на стандартное отклонение. Оба являются мерами распространения. Чем выше число, тем больше разбросаны ваши данные. Проще говоря, два термина по сути равны, но есть одно важное отличие. Пока стандартная ошибка используетстатистика(пример данных) использование стандартного отклоненияпараметры(данные о населении)
Стандартная ошибка говорит вам, насколько далеко ваша выборочная статистика (например, среднее значение выборки) отклоняется от фактического среднего значения населения. Чем больше размер вашей выборки, тем меньше SE. Другими словами, чем больше размер выборки, тем ближе среднее значение выборки к среднему значению популяции.
Чтобы узнать больше о стандартной ошибке (SE), пожалуйста, смотрите видео ниже
Теперь давайте рассмотрим следующий пример, чтобы лучше понять остальные концепции.
4. (а) Нулевая гипотеза (H₀):
Заявление, в котором не ожидается никакой разницы или эффекта. Если нулевая гипотеза не отклонена, никакие изменения не будут внесены.
Слово «ноль» в данном контексте означает, что общепринятый факт, что исследователи аннулируют. Это не означает, что само утверждение является нулевым! (Возможно, этот термин следует называть «недействительной гипотезой», поскольку это может вызвать меньше путаницы)
4. (б). Альтернативная гипотеза (H₁):
Утверждение, что ожидается некоторое различие или эффект. Принятие альтернативной гипотезы приведет к изменению мнений или действий. Это противоположность нулевой гипотезы.
Чтобы узнать больше о нулевых и альтернативных гипотезах, пожалуйста, посмотрите это видео ниже
5. (а). Односторонний тест:
Односторонний тест — это тест статистической гипотезы, в котором критическая область распределения является односторонней, так что она либо превышает определенное значение, либо меньше, но не одновременно. Если тестируемый образец попадает в одностороннюю критическую область, альтернативная гипотеза будет принята вместо нулевой гипотезы.
Односторонний тест также известен как направленная гипотеза или направленный тест.
Критический регион:Критическая область — это область значений, которая соответствует отклонению нулевой гипотезы на некотором выбранном уровне вероятности.
5. (б). Двусторонний тест:
Двухсторонний тест — это метод, в котором критическая область распределения является двусторонней, и он проверяет, является ли выборка больше или меньше определенного диапазона значений. Если тестируемый образец попадает в одну из критических областей, альтернативная гипотеза принимается вместо нулевой гипотезы.
По соглашению, двусторонние тесты используются для определения значимости на уровне 5%, то есть каждая сторона распределения сокращается на 2,5%.
6. Тестовая статистика:
тестовая статистикаизмеряет, насколько близко образец пришел к нулевой гипотезе. Его наблюдаемое значение изменяется случайным образом от одной случайной выборки к другой выборке. Тестовая статистика содержит информацию о данных, которые имеют значение для принятия решения о том, следует ли отклонить нулевую гипотезу или нет.
Различные тесты гипотез используют разные статистические тесты, основанные на вероятностной модели, принятой в нулевой гипотезе. Общие тесты и их тестовая статистика включают в себя:
В общем, выборочные данные должны предоставить достаточные доказательства, чтобы отвергнуть нулевую гипотезу и сделать вывод, что эффект существует в популяции. В идеале, проверка гипотезы не позволяет отклонить нулевую гипотезу, когда эффект отсутствует в популяции, и отвергает нулевую гипотезу, когда эффект существует.
К настоящему времени мы понимаем, что вся проверка гипотез работает на основе имеющегося образца. Мы можем прийти к другому выводу, если образец будет изменен. Есть два типа ошибок, которые относятся к неверным выводам о нулевой гипотезе.
7. (а). Ошибка типа I:
Тип-IОшибка возникает, когда результаты выборки приводят к отклонению нулевой гипотезы, когда она на самом деле верна.Тип-Iошибки эквивалентны ложным срабатываниям.
Тип-Iошибки можно контролировать. Значение альфа, которое связано суровень значимостичто мы выбрали, имеет прямое отношение кТип-Iошибки.
7. (б). Ошибка типа II:
Тип-IIошибка возникает, когда на основании результатов выборки нулевая гипотеза не отклоняется, если она фактически ложна.Тип-IIошибки эквивалентны ложным негативам.
Уровень значимости (α):
Вероятность сделатьТип-Iошибка, и это обозначаетсяальфа (α), Альфа это максимальная вероятность того, что у нас естьТип-Iошибка. Для уровня достоверности 95% значение альфа составляет 0,05. Это означает, что существует 5% вероятность того, что мы отвергнем истинную нулевую гипотезу.
P-значение:
р-значениеиспользуется во всей статистике, от t-тестов до простого регрессионного анализа до моделей на основе дерева, почти во всех моделях машинного обучения. Мы все используемP-значениеопределить статистическую значимость в тесте гипотезы. Несмотря на то чтоР-значениескользкая концепция, которую люди часто неправильно интерпретируют.
P-значениеоцените, насколько хорошо выборочные данные подтверждают аргумент защитника дьявола о том, что нулевая гипотеза верна. Он измеряет, насколько совместимы ваши данные с нулевой гипотезой. Насколько вероятен эффект, наблюдаемый в ваших данных выборки, если нулевая гипотеза верна?
Другими словами, если нулевая гипотеза верна,Р-значениевероятность получения результата как экстремального или более экстремального, чем результат выборки, только по случайной случайности
Высокие значения P:Ваши данные, скорее всего, с истинным нулем
Низкие значения P:Ваши данные вряд ли с истинным нулем
Пример: Предположим, что вы проверяете следующую гипотезу на уровне значимости (α) 5%, и вы получаете значение p как 3%, и ваша выборочная статистикаИксзнак равно25
H₀: μ = 20
H₁: μ> 20
Интерпретация р-значения выглядит следующим образом:
Мы видели выше, чтоαтакже известен как совершениеТип-Iошибка. Когда мы говорим, αзнак равно5%, мы можем отклонить нашу нулевую гипотезу 5 из 100 раз, даже если это правда. Теперь, когда нашиР-значение3%, что меньшеα(мы определенно ниже порога совершенияТип-Iошибка),означает получение выборочной статистики как можно более экстремальной (x̄>знак равно25) учитывая, что H₀ истинно, очень меньше. Другими словами, мы не можем получить нашу выборочную статистику, если предположим, что H₀ истинно. Следовательно, мы отвергаем H₀ и принимаем H₁. Предположим, вы получаетеР-значениекак 6%, т. е. вероятность получения выборочной статистики как можно более экстремальной, тем выше, учитывая, что нулевая гипотеза верна. Таким образом, мы не можем отказаться от H₀, по сравнению сαмы не можем рисковатьТип-Iошибка больше, чем согласованный уровень значимости. Следовательно, мы не можем отвергнуть нулевую гипотезу и отвергнуть альтернативную гипотезу.
Теперь, когда мы поняли основную терминологию вПроверка гипотезы,Теперь давайте рассмотрим этапы проверки гипотез и приведем пример с примером.
Например, крупный универмаг рассматривает возможность введения услуги интернет-магазина. Новая услуга будет введена, если более 40 процентов интернет-пользователей совершают покупки через Интернет.
Шаг 1: сформулируйте гипотезы:
Подходящий способ сформулировать гипотезы:
H₀: π ≤ 0,40
H₁: π> 0,40
Если нулевая гипотеза H₀ отклонена, то будет принята альтернативная гипотеза H₁ и введена новая услуга интернет-покупок. С другой стороны, если мы не сможем отклонить H₀, то новая услуга не должна быть введена, пока не будут получены дополнительные доказательства. Этот тест нулевой гипотезы являетсяодин хвостТест, потому что альтернативная гипотеза выражается направленно: доля интернет-пользователей, которые используют Интернет для покупок, превышает 0,40.
Шаг 2: Выберите подходящий тест:
Чтобы проверить нулевую гипотезу, необходимо выбрать соответствующий статистический метод. Для этого примераZстатистика, которая соответствует стандартному нормальному распределению, будет уместной.
z = (p-π) / σₚ, где σₚ = sqrt (π (1-π) / n)
Шаг 3: Выберите уровень значимости, α:
Мы поняли чтоУровень значимостиотносится кТип-Iошибка. В нашем примере ошибка Типа I произошла бы, если бы мы пришли к выводу, основываясь на выборочных данных, что доля клиентов, предпочитающих новый тарифный план, была больше 0,40, тогда как на самом деле она была меньше или равна 0,40.
Ошибка типа II возникла бы, если бы мы пришли к выводу, основываясь на выборочных данных, что доля клиентов, предпочитающих новый тарифный план, была меньше или равна 0,40, тогда как фактически она была больше 0,40.
Необходимо сбалансировать два типа ошибок. В качестве компромисса α часто устанавливается на 0,05; иногда это 0,01; другие значения α редки. Мы рассмотрим 0,05 для нашего примера.
Шаг 4: Соберите данные и рассчитайте статистику теста:
Размер выборки определяется после учета требуемого значения α и других качественных соображений, таких как бюджетные ограничения для сбора данных выборки. Для нашего примера, скажем, 30 пользователей были опрошены, а 17 указали, что они использовали Интернет для покупок.
Таким образом, значение пропорции выборки составляетр = 17/30 = 0,567.
Значениеσₚ = SQRT ((0,40) (0,60) / 30) = 0,089.
Тестовая статистикаZможно рассчитать как
г = (р-π) / σₚ = (0.567-0.40) /0.089=1.88
Шаг 5: Определите вероятность (или критическое значение):
Используя стандартные нормальные таблицы из приведенного выше, вероятность полученияZзначение 1,88 составляет 0,96995, т.е.Р (z≤1.88) = 0,96995,Но мы хотели вычислить вероятность справа отz (потому что мы заинтересованы в получении значения вероятности, которое попадает в область отклонения или критическую область),то есть1-0.96995знак равно0,03005, Эта вероятность прямо сопоставима с(поскольку α совершает ошибку Типа I, а рассчитанное нами значение вероятности также попадает в критическую область)
Если вы хотите понять, как искать значения вероятностей для данных z-оценок, посмотрите видео ниже:
В качестве альтернативы, критическое значениег,который даст область справа от критического значения 0,05, находится между 1,64(при 1,64 вероятность составляет 0,94950)и 1,65(при 1,65 вероятность равна 0 95053)и равен 1,645(вероятность равна 0,95, то есть слева от нормального распределения, что означает, что справа она равна 0,05),
Обратите внимание, что при определении критического значения статистики теста, область в хвосте за критическим значением либоα или α / 2.этоαдля одностороннего теста иα / 2для двустороннего теста. Наш пример — односторонний тест.
Если вы хотите понять, как искать критическое значениеα,Пожалуйста, посмотрите видео ниже:
Шаг 6 и 7: сравните вероятность (или критическое значение) и примите решение:
Вероятность, связанная с вычисленным или наблюдаемым значением статистики теста, составляет 0,03005. Это вероятность полученияР-значение0,567 (доля образца =п)когда π = 0,40. Это меньше уровня значимости 0,05. Следовательно, нулевая гипотеза отвергается.
В качестве альтернативы рассчитывается значение тестовой статистикиг = 1,88лежит в области отклонения, за пределами значения 1,645. Снова, тот же самый вывод отклонить нулевую гипотезу сделан.
Обратите внимание, что два способа проверки нулевой гипотезы эквивалентны, но математически противоположны в направлении сравнения. Если вероятность, связанная с вычисленным или наблюдаемым значением тестовой статистики (TSCAL), равнаменьше, чемНа уровне значимости (α) нулевая гипотеза отвергается. Однако, если абсолютное значение рассчитанного значения статистики тестабольше чемабсолютное значение критического значения тестовой статистики (TSCR), нулевая гипотеза отклоняется. Причина этого смещения знака состоит в том, что чем больше абсолютное значение TSCAL, тем меньше вероятность получения более экстремального значения тестовой статистики при нулевой гипотезе.
если вероятность TSCAL <уровень значимости (α), то отклонить H₀.
Но, если | TSCAL | > | TSCR |, затем отклонить H₀
Шаг 8: Вывод:
В нашем примере мы заключаем, что есть свидетельства того, что доля интернет-пользователей, совершающих покупки через Интернет, значительно превышает 0,40. Следовательно, рекомендация для универмага будет заключаться в том, чтобы ввести новый сервис интернет-магазинов.
Этот пример относится к одному образцу теста пропорций. Тем не менее, существует несколько типов тестов, которые зависят от знаний о населении и рассматриваемой проблемы.
Например, у нас есть t-тест, Z-тест. Тест хи-квадрат, тест Манна-Уитни, тест Вилкоксона и т. Д.
На этом я хотел бы завершить часть I «Все, что вам нужно знать о проверке гипотез». Я буду обсуждать параметрические и непараметрические тесты и какой тест использовать в каком сценарии в части II. До тех порСчастливого обучения…
Спасибо за чтение!
Пожалуйста, поделитесь своим мнением в разделе комментариев ниже.
Ссылки:
- Маркетинговые исследования — прикладная ориентация Naresh K Malhotra и Satyabhushan Dash
- https://www.cliffsnotes.com/study-guides/statistics/sampling/populations-samples-parameters-and-statistics
- https://www.statisticshowto.datasciencecentral.com
- https://www.khanacademy.org
- https://blog.minitab.com
Ошибки I и II рода при проверке гипотез, мощность
Общий обзор
Принятие неправильного решения
Мощность и связанные факторы
Проверка множественных гипотез
Общий обзор
Большинство проверяемых гипотез сравнивают между собой группы объектов, которые испытывают влияние различных факторов.
Например, можно сравнить эффективность двух видов лечения, чтобы сократить 5-летнюю смертность от рака молочной железы. Для данного исхода (например, смерть) сравнение, представляющее интерес (например, различные показатели смертности через 5 лет), называют эффектом или, если уместно, эффектом лечения.
Нулевую гипотезу выражают как отсутствие эффекта (например 5-летняя смертность от рака молочной железы одинаковая в двух группах, получающих разное лечение); двусторонняя альтернативная гипотеза будет означать, что различие эффектов не равно нулю.
Критериальная проверка гипотезы дает возможность определить, достаточно ли аргументов, чтобы отвергнуть нулевую гипотезу. Можно принять только одно из двух решений:
- отвергнуть нулевую гипотезу и принять альтернативную гипотезу
- остаться в рамках нулевой гипотезы
Важно: В литературе достаточно часто встречается понятие «принять нулевую гипотезу». Хотелось бы внести ясность, что со статистической точки зрения принять нулевую гипотезу невозможно, т.к. нулевая гипотеза представляет собой достаточно строгое утверждение (например, средние значения в сравниваемых группах равны ).
Поэтому фразу о принятии нулевой гипотезы следует понимать как то, что мы просто остаемся в рамках гипотезы.
Принятие неправильного решения
Возможно неправильное решение, когда отвергают/не отвергают нулевую гипотезу, потому что есть только выборочная информация.
| Верная гипотеза | |||
|---|---|---|---|
| H0 | H1 | ||
| Результат
применения критерия |
H0 | H0 верно принята | H0 неверно принята
(Ошибка второго рода) |
| H1 | H0 неверно отвергнута
(Ошибка первого рода) |
H0 верно отвергнута |
Ошибка 1-го рода: нулевую гипотезу отвергают, когда она истинна, и делают вывод, что имеется эффект, когда в действительности его нет. Максимальный шанс (вероятность) допустить ошибку 1-го рода обозначается α (альфа). Это уровень значимости критерия; нулевую гипотезу отвергают, если наше значение p ниже уровня значимости, т. е., если p < α.
Следует принять решение относительно значения а прежде, чем будут собраны данные; обычно назначают условное значение 0,05, хотя можно выбрать более ограничивающее значение, например 0,01.
Шанс допустить ошибку 1-го рода никогда не превысит выбранного уровня значимости, скажем α = 0,05, так как нулевую гипотезу отвергают только тогда, когда p< 0,05. Если обнаружено, что p > 0,05, то нулевую гипотезу не отвергнут и, следовательно, не допустят ошибки 1-го рода.
Ошибка 2-го рода: не отвергают нулевую гипотезу, когда она ложна, и делают вывод, что нет эффекта, тогда как в действительности он существует. Шанс возникновения ошибки 2-го рода обозначается β (бета); а величина (1-β) называется мощностью критерия.
Следовательно, мощность — это вероятность отклонения нулевой гипотезы, когда она ложна, т.е. это шанс (обычно выраженный в процентах) обнаружить реальный эффект лечения в выборке данного объема как статистически значимый.
В идеале хотелось бы, чтобы мощность критерия составляла 100%; однако это невозможно, так как всегда остается шанс, хотя и незначительный, допустить ошибку 2-го рода.
К счастью, известно, какие факторы влияют на мощность и, таким образом, можно контролировать мощность критерия, рассматривая их.
Мощность и связанные факторы
Планируя исследование, необходимо знать мощность предложенного критерия. Очевидно, можно начинать исследование, если есть «хороший» шанс обнаружить уместный эффект, если таковой существует (под «хорошим» мы подразумеваем, что мощность должна быть по крайней мере 70-80%).
Этически безответственно начинать исследование, у которого, скажем, только 40% вероятности обнаружить реальный эффект лечения; это бесполезная трата времени и денежных средств.
Ряд факторов имеют прямое отношение к мощности критерия.
Объем выборки: мощность критерия увеличивается по мере увеличения объема выборки. Это означает, что у большей выборки больше возможностей, чем у незначительной, обнаружить важный эффект, если он существует.
Когда объем выборки небольшой, у критерия может быть недостаточно мощности, чтобы обнаружить отдельный эффект. Эти методы также можно использовать для оценки мощности критерия для точно установленного объема выборки.
Вариабельность наблюдений: мощность увеличивается по мере того, как вариабельность наблюдений уменьшается.
Интересующий исследователя эффект: мощность критерия больше для более высоких эффектов. Критерий проверки гипотез имеет больше шансов обнаружить значительный реальный эффект, чем незначительный.
Уровень значимости: мощность будет больше, если уровень значимости выше (это эквивалентно увеличению допущения ошибки 1-го рода, α, а допущение ошибки 2-го рода, β, уменьшается).
Таким образом, вероятнее всего, исследователь обнаружит реальный эффект, если на стадии планирования решит, что будет рассматривать значение р как значимое, если оно скорее будет меньше 0,05, чем меньше 0,01.
Обратите внимание, что проверка ДИ для интересующего эффекта указывает на то, была ли мощность адекватной. Большой доверительный интервал следует из небольшой выборки и/или набора данных с существенной вариабельностью и указывает на недостаточную мощность.
Проверка множественных гипотез
Часто нужно выполнить критериальную проверку значимости множественных гипотез на наборе данных с многими переменными или существует более двух видов лечения.
Ошибка 1-го рода драматически увеличивается по мере увеличения числа сравнений, что приводит к ложным выводам относительно гипотез. Следовательно, следует проверить только небольшое число гипотез, выбранных для достижения первоначальной цели исследования и точно установленных априорно.
Можно использовать какую-нибудь форму апостериорного уточнения значения р, принимая во внимание число выполненных проверок гипотез.
Например, при подходе Бонферрони (его часто считают довольно консервативным) умножают каждое значение р на число выполненных проверок; тогда любые решения относительно значимости будут основываться на этом уточненном значении р.
Связанные определения:
p-уровень
Альтернативная гипотеза, альтернатива
Альфа-уровень
Бета-уровень
Гипотеза
Двусторонний критерий
Критерий для проверки гипотезы
Критическая область проверки гипотезы
Мощность
Мощность исследования
Мощность статистического критерия
Нулевая гипотеза
Односторонний критерий
Ошибка I рода
Ошибка II рода
Статистика критерия
Эквивалентные статистические критерии
В начало
Содержание портала