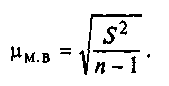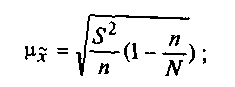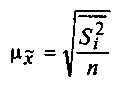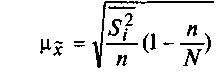При прочих равных условиях минимальную ошибку дает - TopOshibok.ru - решение и исправление самых разных ошибок

1. Статистика

2. Тема: Выборочное наблюдение

1.
2.
3.
4.
5.
Выборка в системе методов несплошного
статистического наблюдения
Основные этапы выборочного наблюдения
Методы и способы, обеспечивающие
репрезентативность выборки
Основные виды статистических показателей
генеральной совокупности, оцениваемые по
данным выборочного наблюдения
Определение объема выборочной совокупности

3. 1. Выборка в системе методов несплошного статистического наблюдения

Статистическое наблюдение – это научно организованный
учет фактов о явлениях общественной жизни и сбор полученных на
основе такого учета массовых первичных данных. Является первым
этапом любого статистического исследования.
По степени охвата единиц совокупности различают следующие виды
статистических наблюдений:
сплошные — учёт всех единиц изучаемой совокупности
несплошные — учёт части единиц совокупности.

4.

Несплошное наблюдение может быть организовано как:
наблюдение основного массива
выборочное наблюдение
монографическое наблюдение.
Выбор вида и метода статистического наблюдения определяется:
• материальными и трудовыми ресурсами, имеющимися в наличии у
организаторов наблюдения;
• составом решаемых статистических задач;
• объемом статистической совокупности;
• необходимой точностью получаемых результатов.

5.

Из перечня несплошных наблюдений статистика отдает
предпочтение выборочным обследованиям, поскольку существует
теория, описывающая поведение выборок.
Ведущий принцип, лежащий в основе процедуры формирования
выборки, – это принцип случайности или рандомизации (от англ. random
– случайный).
«Выборочное исследование … обогащает рабочий инвентарь
статистика орудием, облегчающим работу в ходе наблюдения, не
поступаясь при этом научной объективностью результата».
«Теоретические основания выборочного метода» (1924)
БОУЛИ (BOWLEY) Артур
1869-1957
Англия

6.

В современной статистической практике при проведении
статистических наблюдений используют сочетание сплошного и
выборочного методов, получившее название комбинированного
метода статистического наблюдения. Он реализуется в двух формах:
чередование во времени (например: в один год – сплошное, в другой
выборочное)
одновременное использование (например: часть совокупности (или
ее свойств) наблюдается на сплошной основе, а другая часть – на
выборочной).

7. «О развитии малого и среднего предпринимательства в Российской Федерации» Федеральный Закон РФ от 24. 07.2007 № 209-ФЗ

1.
2.
3.
Статья 5. Федеральные статистические наблюдения
за деятельностью субъектов малого и среднего предпринимательства
Федеральные статистические наблюдения за деятельностью субъектов
малого предпринимательства в Российской Федерации осуществляются
путем
проведения
сплошных
статистических
наблюдений
за
деятельностью субъектов малого и среднего предпринимательства и
выборочных статистических наблюдений за деятельностью отдельных
субъектов малого и среднего предпринимательства на основе
представительной (репрезентативной) выборки.
Сплошные статистические наблюдения за деятельностью субъектов
малого и среднего предпринимательства проводятся один раз в пять лет.
Выборочные
статистические
наблюдения
проводятся
путем
ежемесячных и (или) ежеквартальных обследований деятельности
малых предприятий (за исключением микропредприятий) и средних
предприятий. Выборочные статистические наблюдения проводятся путем
ежегодных обследований деятельности микропредприятий. Порядок
проведения выборочных статистических наблюдений определяется
Правительством Российской Федерации.

8. 2. Основные этапы выборочного наблюдения

1
Определение генеральной
совокупности и единиц
наблюдения
2
Создание основы выборки
3
Формирование выборочной
совокупности через отбор
элементов основы
4
Распространение собранных
по выборке данных на
генеральную совокупность

9.

Генеральная совокупность — множество реально или гипотетически
существующих объектов или явлений, из которых тем или иным
способом формируется совокупность выборочная (население страны,
домашние хозяйства региона, предприятия отрасли и т.п.).
Теоретически генеральная совокупность может быть как конечной,
так и бесконечной. Однако для органов государственной статистики
практический интерес представляет конечная генеральная
совокупность. Конечная совокупность имеет место, например, при
обследовании семейных бюджетов, когда выборка берется из
совокупности домохозяйств, фактически имеющихся в стране, а затем
осуществляются наблюдения за доходами и расходами в отобранных
домохозяйствах. Конечная совокупность также имеет место при
экономических обследованиях организаций — резидентов рынка страны.

10.

Государственное статистическое наблюдение базируется на
создании и поддержании в актуальном состоянии статистических
основ – перечней (списков) единиц реальных совокупностей с
набором признаков, соответствующих целям статистических
исследований.
Информационными источниками для основы выборки являются:
1. Статистический регистр Федеральной службы государственной
статистики (Статрегистр Росстата).
2. База данных государственной бухгалтерской отчетности организаций
(БД БОО).

11. Примеры

ПРИМЕРЫ

12. Основы выборки при проведении выборочных статистических наблюдений за сельскохозяйственным производством в крестьянских

(фермерских) хозяйствах
Основа выборки для получения информации по растениеводству:
Совокупность 1 – список крестьянских (фермерских) хозяйств региона,
имеющих посевы зерновых и зернобобовых культур, ранжированный по
возрастанию показателя «Посевная площадь зерновых и зернобобовых
культур».
Совокупность 2 – список крестьянских (фермерских) хозяйств региона,
имеющих посевы сахарной свеклы, ранжированный по возрастанию
показателя «Посевная площадь сахарной свеклы».
Основа выборки для получения информации по животноводству:
Совокупность 1 – список крестьянских (фермерских) хозяйств региона,
имеющих поголовье крупного рогатого скота, ранжированный по
возрастанию показателя «Численность крупного рогатого скота».
Совокупность 2 – список крестьянских (фермерских) хозяйств региона,
имеющих поголовье свиней, ранжированный по возрастанию показателя
«Численность свиней».

13. Основа выборки при проведении выборочного статистического наблюдения за перевозочной деятельностью предпринимателей (физических

лиц) – владельцев грузовых автомобилей
Цель – оценка сводных статистических показателей об объемах грузовых
перевозок, осуществляемых предпринимателями в регионе в течение
отчетного периода.
Объектом исследования является совокупность физических лиц владельцев грузовых автомобилей, имеющих лицензии на занятие
коммерческой перевозочной деятельностью по состоянию на 1 января
текущего года, а единицами наблюдения — конкретные предприниматели.
Основа выборки — пофамильный список предпринимателей в алфавитном
порядке. Каждому предпринимателю присваивается номер от 1 до N (N общее число предпринимателей в регионе).
Основа выборки формируется территориальными органами
государственной статистики на базе регистра лицензиатов, составляемого
территориальными отделениями Российской транспортной инспекции (РТИ).
Из регистра отбираются лицензиаты, являющиеся индивидуальными
предпринимателями (физическими лицами) и получившие лицензии на
право осуществления грузовых перевозок на коммерческой основе
независимо от вида сообщения.

14.

Федеральный Закон Российской Федерации от 20.08.2004 г. N 113-ФЗ
«О ПРИСЯЖНЫХ ЗАСЕДАТЕЛЯХ ФЕДЕРАЛЬНЫХ СУДОВ ОБЩЕЙ ЮРИСДИКЦИИ В
РОССИЙСКОЙ ФЕДЕРАЦИИ»
Статья 5. Порядок и сроки составления списков кандидатов в присяжные
заседатели
3. Списки кандидатов в присяжные заседатели составляются исполнительнораспорядительными органами муниципальных образований отдельно по каждому
муниципальному образованию субъекта Российской Федерации на основе
персональных данных об избирателях, входящих в информационные ресурсы
Государственной автоматизированной системы Российской Федерации «Выборы»,
путем случайной выборки установленного числа граждан. При этом из числа
отобранных граждан исключаются лица, которые не могут быть присяжными
заседателями в соответствии с частью 2 статьи 3 настоящего Федерального закона
(признанные судом недееспособными или ограниченные судом в дееспособности).

15. 3. Методы и способы, обеспечивающие репрезентативность выборки

Формирование выборки осуществляется различными методами
и способами.
Различают два метода отбора:
повторный
бесповторный.
Используют следующие способы отбора:
• собственно-случайный (простая случайная выборка)
• механический (систематический)
• расслоенный (типический)
• серийный (гнездовой).

16. Собственно-случайный отбор

Собственно-случайным отбором называется способ, при котором извлечение
единиц из совокупности для обследования осуществляется методом
жеребьевки или с использованием таблиц или генератора случайных чисел без
деления этой совокупности на какие-либо классы или группы.
ПРИМЕР (условный): Сформируйте собственно-случайную бесповторную
выборку объемом 3 единицы из следующей совокупности образовательных
учреждений высшего профессионального образования города Новосибирска:
НГАЭиУ, НГТУ, НГУ, СГГА, СибГУТИ, НГАСУ, СГУПС. Используйте следующую
последовательность случайных цифр: 87097253671352349.
Шаг 1: (нумеруем единицы совокупности)
НГУЭиУ – 1; НГТУ – 2; НГУ – 3; СГГА – 4; СибГУТИ – 5; НГАСУ – 6; СГУПС – 7.
Шаг 2: (отбираем случайные цифры)
7; 2; 5.
Шаг 3 (формируем выборку)
СГУПС; НГТУ; СибГУТИ

17. Механический (систематический) отбор

Это способ отбора, при котором выборочная совокупность
формируется на основе отбора единиц через определенный интервал,
определяемый как N/n.
В теории статистики систематический отбор считается более
эффективным, чем простая случайная выборка. Также его легче
осуществлять при работе вручную. Однако это обстоятельство
потеряло свою актуальность в связи с широким распространением
персональных компьютеров.

18. Расслоенный (типический) отбор

Расслоенный случайный отбор — это отбор, предусматривающий разделение
генеральной совокупности на слои, и проведение простого случайного отбора в
каждом из них.
n
N
N1
n1
N2
n2
.
.
.
.
.
.
Nm
nm
N N1 N 2 N m
n n1 n2 nm

19.

Число единиц, отбираемых из каждого слоя, определяется одним из
следующих методов:
непропорциональным
пропорциональным
оптимальным
n
ni
m
Ni
ni n
N
N i i
ni n
Ni i
ni n
N i Wi 1 Wi
N
i
Wi 1 Wi

20. Пример

ПРИМЕР

21. Для оценивания среднего значения признака из генеральной совокупности объемом 10000 ед. планируется провести расслоенную

выборку объемом 2000 ед.
Ni i
Ni i
Ni i
4
1000,0
0,029
2000
6
4898,98
0,144
3
3000
10
9486,83
0,278
4
1500
20
6708,20
0,197
5
3000
16
12000,00
0,352
Итого
10000
…
34094,01
1,000
Номер
слоя
Численность
единиц
Дисперсия
признака
1
500
2
Определите варианты расслоенной выборки.

22. Варианты расслоенной выборки, единиц

Метод формирования
Номер
слоя
Численность
1
непропорциональный
пропорциональный
оптимальный
500
400
100
58
2
2000
400
400
288
3
3000
400
600
556
4
1500
400
300
394
5
3000
400
600
704
Итого
10000
2000
2000
2000

23. Серийный (гнездовой) отбор

Серийный (гнездовой) отбор – способ формирования выборки, при котором
единица отбора состоит из группы или гнезда более мелких единиц, называемых
элементами.
Гнездовая выборочная единица – группа элементов, которая в процессе
извлечения выборки рассматривается как одна единица.
Применение гнездового отбора в статистической практике обусловлено
двумя основными причинами:
1. Для обследования может не существовать основы выборки (списка
элементов совокупности), а ее составление или невозможно, или
обошлось бы дорого.
2. Экономические соображения могут диктовать выбор более крупных
единиц отбора.

24. 4. Основные виды статистических показателей генеральной совокупности, оцениваемые по данным выборочного наблюдения

В практике выборочного наблюдения статистический показатель
имеет более узкий смысл, чем в статистике вообще.
Как правило, определяют и оценивают четыре их вида:
суммарное значение признака в совокупности
среднее значение признака в совокупности
доля единиц наблюдения, обладающих изучаемым
значением признака
число единиц наблюдения, обладающих изучаемым
значением признака
Каждый из этих показателей может быть выражен алгебраически.

25. Основные виды статистических показателей генеральной совокупности и их оценка

Совокупность
Оцениваемый показатель
генеральная
выборочная
n
N
Суммарное значение признака
X x
i 1
Среднее значение признака
Доля единиц наблюдения,
обладающих изучаемым
значением признака
Число единиц наблюдения,
обладающих изучаемым
значением признака
1
X
N
x x
i
i 1
N
x
i 1
A
P
N
A N P
i
i
n
1
x~ xi
n i 1
a
W
n
a n W

26. Основные виды статистических показателей генеральной совокупности и их оценка

Оценкой называют
характеристику
Интервальная
оценка приближенную
— характеристика
генерального
неизвестного
генеральной
совокупности,
Основные
виды
статистических
показателей
Точечная
оценка
-параметра
приближенная
характеристика
параметра
с помощью
интервала,
относительно
которого с
полученную
по данным
выборочного
генеральной
совокупности
инаблюдения.
их оценка
неизвестного
параметра
генеральной
определенной
вероятностью
можносовокупности
утверждать,
что внутри
с него
помощью
одного
числа.
находится
неизвестный
параметр генеральной
совокупности.
Совокупность
Оцениваемый показатель
генеральная
выборочная
X x
i 1
Среднее значение признака
Доля единиц наблюдения,
обладающих изучаемым
значением признака
Число единиц наблюдения,
обладающих изучаемым
значением признака
1
X
N
~
x
x
X
N
x
i
i
i 1
N
x
i 1
A
P
N
A N P
точечная
n
N
Суммарное значение признака
Оценка
i
n
1
x~ xi
n i 1
a
W
n
интервальная
N ~x ~x
X ~x
~x ~
x
P W
W W
a n W A N W N W W

27.

Интервальная оценка предполагает расчет границ доверительного
интервала:
Предельная
Верхняя (нижняя)
Точечная оценка
ошибка точечной
граница
параметра
=
+ оценки параметра
доверительного
генеральной
генеральной
интервала
совокупности
совокупности
Параметр
генеральной
совокупности
Нижняя граница
доверительного интервала
Верхняя граница
доверительного интервала
Числовая ось

28.

Ошибка выборки – расхождение между значением характеристики,
полученной в ходе конкретного исхода выборочного наблюдения, и
параметром генеральной совокупности.
Различают ошибки:
среднюю;
предельную (максимальную).
∆
Величина предельной (максимальной) ошибки зависит от размера
средней ошибки.

29. Формулы расчета предельных ошибок выборки

Оцениваемый показатель
Суммарное значение признака
Среднее значение признака
Доля единиц наблюдения,
обладающих изучаемым
значением признака
Число единиц наблюдения,
обладающих изучаемым
значением признака
Размер предельной ошибки
абсолютный
относительный
N t ~x N ~x
N t ~x
~x
100
100
~
~
Nx
x
~x t ~x
~x
~x 100
W
100
W
W t W
N t W N W
N t W
100 W 100
NW
W

30. Формулы расчета средних ошибок выборки

Метод отбора
Способ
отбора
повторный
для
выборочной
средней
бесповторный
для
выборочной
доли
для
выборочной
средней
для
выборочной
доли
W (1 W )
n
2
n
(1 )
n
N
W (1 W )
n
(1 )
n
N
2
n
W (1 W )
n
2
n
(1 )
n
N
W (1 W )
n
(1 )
n
N
x2
r
r
Собственнослучайный
(механический)
Расслоенный
(пропорциональный)
Серийный
2
n
2
W
x2
r
(1 )
r
R
W2
r
(1 )
r
R

31.

Теоретической основой расчета предельной ошибки выборочной
средней является известная центральная предельная теорема, общие
достаточные условия которой были обоснованы П.Л.Чебышевым и
А.М. Ляпуновым:
P ~
x X t F(t)
F(t)
1
2
t
e
t2
2
dt
t
Значения этой функции при различных величинах t табулированы.
Наиболее часто используемые уровни вероятностей и соответствующие
им значения t:
t
P
Чебышев
Пафнутий Львович
(1821-1894)
1,00
0,683
1,96
0,950
2,00
0,954
3,00
0,997
Ляпунов
Александр Михайлович
(1857-1918)

32. Способ расчета границ и форма записи доверительного интервала (при оценивании генеральной средней)

~
X x ~x
~
x ~x X ~
x ~x
P~
x ~x X ~
x ~x
X ~
x ~ %
x
F(t)

33. Примеры

ПРИМЕРЫ

34.

ПОКАЗАТЕЛИ ТОЧНОСТИ СТАТИСТИЧЕСКОГО ОЦЕНИВАНИЯ
стоимости основных продуктов питания, потребленных в домашних хозяйствах
России в 2008 году
Значение
показателя,
в среднем на
потребителя,
в месяц, руб.
Коэффициент
вариации
оценки, %
Стандартное
отклонение,
руб.
Интервальная
оценка (Р=0,95)
Хлеб и хлебные продукты
415,8
1,2
5,0
406,0 — 425,6
Картофель
87,7
2,0
1,8
84,2 — 91,2
Овощи и бахчевые
294,2
1,6
4,7
285,0 — 303,4
Фрукты и ягоды
259,2
2,1
5,4
248,6 — 269,8
Мясо и мясные продукты
816,9
2,3
18,8
780,1 — 853,7
Молоко и молочные продукты
396,7
1,8
7,1
382,8 — 410,6
Яйца
58,2
1,4
0,8
56,6 — 59,8
Рыба и рыбные продукты
167,9
2,3
3,9
160,3 — 175,5
158,6
1,7
2,7
153,3 — 163,9
59,2
1,3
0,8
57,6 — 60,8
Сахар и кондитерские
изделия
Масло растительное и другие
жиры
ИСТОЧНИК: Потребление продуктов питания в домашних хозяйствах в 2008 году (по итогам выборочного
обследования бюджетов домашних хозяйств):Стат. бюллетень / Росстат, 2009.

35.

ПОКАЗАТЕЛИ ТОЧНОСТИ СТАТИСТИЧЕСКОГО ОЦЕНИВАНИЯ ПО ИСТОЧНИКАМ
ПОСТУПЛЕНИЯ И ПОТРЕБЛЕНИЯ ОСНОВНЫХ ПРОДУКТОВ ПИТАНИЯ
в домохозяйствах РОССИИ
в 2009 году
в городской местности
в сельской местности
Значение
показателя
в среднем на
потребителя,
в год, кг
Коэффициент
вариации
оценки,
%
Стандартное
отклонение
Интервальная оценка
(Р=0,95)
Хлеб и хлебные продукты
куплено
81,5
1,7
1,4
78,8 — 84,2
натуральные поступления
0,5
9,7
0,05
потреблено
91,1
1,4
35,9
натуральные поступления
потреблено
Значение
показателя
в среднем на
потребителя,
в год, кг
Коэффициент
вариации
оценки, %
Стандартное
отклонение
Интервальная оценка
(Р=0,95)
120,4
5,8
7,0
106,7 — 134,1
0,4 — 0,6
2,4
19,3
0,5
1,4 — 3,4
1,3
88,6 — 93,6
121,4
2,6
3,2
115,1 — 127,7
4,4
1,6
32,8 — 39,0
15,6
19,2
3,0
9,7 — 21,5
23,2
8,9
2,1
19,1 — 27,3
66,9
6,5
4,3
58,5 — 75,3
62,2
2,0
1,2
59,8 — 64,6
80,4
3,2
2,6
75,3 — 85,5
69,0
3,9
2,7
63,7 — 74,3
42,2
9,4
4,0
34,4 — 50,0
натуральные поступления
24,0
7,0
1,7
20,7 — 27,3
56,7
5,6
3,2
50,4 — 63,0
потреблено
94,8
2,2
2,1
90,7 — 98,9
94,5
3,9
3,7
87,2 — 101,8
Картофель
куплено
Овощи и бахчевые
куплено
ИСТОЧНИК: Потребление продуктов питания в домашних хозяйствах в 2009 году (по итогам выборочного обследования
бюджетов домашних хозяйств):Стат. бюллетень / Росстат, 2010.

36. Задача

Владелец автостоянки опасается обмана со стороны своих
служащих (охраны). В течение года (365 дней) им проведено 40
проверок. По данным проверок среднее число автомобилей,
оставляемых на ночь на охрану, составило 400 единиц, а среднее
квадратическое отклонение их числа – 10 автомобилей.
Считая отбор собственно-случайным, с вероятностью 0,954
определите границы доверительного интервала, в котором следовало
бы ожидать истинное среднее число автомобилей, оставляемых на
ночь на охрану.
Обоснованы ли опасения владельца автостоянки, если по
отчетности охранников за отчетный год среднее число автомобилей,
оставляемых на ночь на охрану, составило 390 автомобилей?

37.

~x t ~x 2
10
40
1
3 avto
365
40
Границы доверительного интервала для среднего значения:
P 397 X 403 0,954
P 400 3 X 400 3 0,954
Можно утверждать, что служащие автостоянки скрывали от учета
в течение года ежедневно не менее 7 автомобилей, оставляемых ее
клиентами на ночь на охрану.
Границы доверительного интервала для суммарного значения признака:
N t ~x 365 3 1095 avto
P 365 400 1095 X 365 400 1095 0,954
P 144905 X 147095 0,954
SU 365 390 144905 142350 144905 2555 avto

38. Задача

Для определения доли и числа домохозяйств, предоставляющих услуги по
временному проживанию лиц, прибывающих в курортную зону региона на
отдых и лечение, была проведена 1%-ная простая случайная выборка.
В результате обследования выявлено, что из 2700 домохозяйств региона,
попавших в выборку, 26,8 % из них являлись квартиросдатчиками.
С вероятностью 0,954 определите доверительные интервалы, в которых
можно ожидать долю и число домохозяйств, предоставляющих услуги по
временному размещению лиц, прибывающих в регион на отдых и лечение.
Оцените, какой удельный вес в общей численности домохозяйств
региона, сдающих жилье туристам и отдыхающим, составляют домохозяйства,
легально работающие в этом сегменте рынка, если известно, что число
официально зарегистрированных индивидуальных предпринимателей,
предоставляющих такие услуги, составляет 8500.

39.

Дано: n 2700
W 0,268
n
0,01
N
Aналоговые органы = 8500
0,268 (1 0,268) (1 0,01)
W t W 2
0,017
2700
P(0, 268 0,017 p 0, 268 0,017) 0,954
P(0, 251 p 0, 285) 0,954
P(0, 251 270000 A 0, 285 270000) 0,954
P(67700 A 73440) 0,954
Максимальная доля
индивидуальных
предпринимателей,
легально работающих
в этом сегменте рынка
8500
100 12,6%
67700

40. 5. Определение объема выборочной совокупности

Определение объема выборки является неотъемлемым этапом при
проектировании выборочного наблюдения.
Теоретическую возможность определения такого объема дает
формула предельной ошибки выборки, адаптированная к различным
методам и способам отбора, а также оцениваемым статистическим
показателям.
Простейшим примером вывода формулы расчета объема выборки
при простом случайном повторном отборе для оценивания среднего
значения выступает уравнение вида:
~x t
2
n
t2 2
n 2
~x

41. Формулы расчета объема выборочной совокупности при различных способах и видах отбора

Вид отбора
Способ
отбора
повторный
Для
выборочной
средней
Собственнослучайный
t
2x
Расслоенный
(пропорциональный)
t
2x
Серийный
2
2
2
2
t 2 ~x2
2~x
бесповторный
Для
выборочно
й доли
Для выборочной
средней
Для выборочной
доли
t 2 w(1 w)
2w
t 2 2 N
N 2x t 2 2
t 2 w(1 w) N
N 2w t 2 w(1 w)
t 2 w(1 w)
2w
t N
t 2 w2
2w
2
2
N t
2
x
2
2
t 2 x 2 R
R t
2
x
2
t 2 w(1 w)N
N 2w t 2 w(1 w)
t 2 w2 R
2
R t w
2
w
2
2

42.

Для определения объема выборки необходимо располагать
информацией двух видов:
требуемой точностью оценивания статистического показателя;
предварительными сведениями об исследуемой совокупности.
Представление о величине вариации признака получают:
• из проведенных ранее или пробных обследованиях;
• по правилу «трех сигм», в соответствии с которым R 6 * ,
R
откуда
;
6
• если известно, хотя бы приблизительно значение средней
величины признака , то V 0,33 0,33 X .
X
• при отсутствии приблизительных данных о величине дисперсии
альтернативного признака, исходя из его максимального значения,
равного 0,25.

43. Тесты для текущего контроля знаний

Отклонение выборочных характеристик от соответствующих
характеристик генеральной совокупности, возникающее вследствие
нарушения принципа случайности отбора, называется: а) случайной
ошибкой регистрации; б) систематической ошибкой репрезентативности;
в) ошибкой исчисления; г) случайной ошибкой репрезентативности.
При определении объема выборки организаторы наблюдения должны
располагать: а) информацией о составе персонала, привлекаемого к
проведению обследования; б) характеристиками требуемой точности
оценивания статистического показателя; в) информацией о сумме средств,
выделяемых на проведение обследования; г) предварительными сведениями
об исследуемой совокупности.
При прочих равных условиях минимальную ошибку обеспечивает
способ отбора: а) собственно-случайный; б) механический; в) расслоенный;
г) серийный.

44.

Как изменится средняя ошибка собственно-случайной повторной
выборки, если объем выборочной совокупности уменьшить в 2
раза: а) возрастет в 2 раза; б) уменьшится в 2 раза; в) возрастет в
1,41 раза; г) возрастет на 29,3%; д) предсказать нельзя.
По данным выборочного обследования 700 контейнеров из 10000,
хранящихся на складе, обнаружено, что 2,6% контейнеров не готовы к
отгрузке. Были бы Вы удивлены, узнав, что в действительности
3,0% из всех контейнеров, хранящихся на складе, не готовы к
отгрузке?
а) да; б) нет; в) предугадать нельзя.
Имеется выборка из 200 пенсионеров поселка. Среднее значение
возраста этой выборки пенсионеров составляет 68,8 лет, а
стандартное отклонение – 10,2 года. Ваш друг утверждает, что
выборочное среднее отличается от среднего возраста всех
пенсионеров поселка на 10,2 года. Прав ли он?
а) безусловно прав; б) абсолютно неправ; в) прав при выполнении
определенных условий надежности оценивания данного показателя;
г) предсказать нельзя.

Источник

Числостепенейсвободы– количествовариант, могущихприниматьзначения, функционально не связанные друг с другом. Для ряда распределения Ч.С.С. определяется как разность между числом групп и числом параметров теоретического распределения. Для таблиц сопряженности Ч.С.С – количество клеток таблицы, частоты в которых могут принимать произвольные значения при заданных значениях маргинальных частот (итогов по строкам и столбцам).

Шкала измерения – система, принятая для оценки или измерения статистических величин. Применяются в статистике четыре вида Ш.И. Номинальная шкала разбивает совокупность на непересекающиесяклассы, причеммеждуединицамисовокупности, принадлежащимиодномуклассу задается отношение эквивалентности, в то же время между единицами, принадлежащими разным классам, устанавливается отношение неравенства без предпочтений (пол, национальность и т.п.). Порядковая шкала, помимо разбиения на классы, устанавливает отношение предпочтения между классами (больше, меньше) эта шкала расставляет классы на ступеньки различной величины (тарифный разряд, воинское звание и проч.). Интервальная шкала помимо всего прочего дает возможностьоценитьвеличинуотклоненияоднойединицысовокупностиотдругой. Частнымслучаем интервальной шкалы является шкала отношений или пропорциональная шкала – это интервальная шкала, в которой есть условный ноль.

Экономически активное население – часть населения в возрасте, установленном для измеренияэкономическойактивностинаселения(от15 до72 лет), обеспечивающаяврассматриваемый период предложение рабочей силы для производства товаров и услуг. В численность экономически активного населения включаются лица, занятые экономической деятельностью, и безработные.

Экономическая конъюнктура – это один из видов общего понятия конъюнктуры. Экономическая конъюнктура представляет собой точку на кривой экономического цикла, а оценка конъюнктуры сводится к поиску этой точки. Это конкретная экономическая ситуация, сложившаяся на рынке на данный момент или за ограниченный отрезок времени под воздействием комплекса условийифакторов.

Экономически неактивное население – лица в возрасте, установленном для измерения экономическойактивностинаселения, которыенесчитаютсязанятымиэкономическойдеятельностью или безработными.

Экономическая территория – территория, административно управляемая правительством данной страны, в пределах которой лица, товары и деньги могут свободно перемещаться.

Экономические операции – элементарные экономические акты, осуществляемые экономическими агентами в процессе экономической деятельности; это движение объектов экономической деятельности от одного субъекта к другому.

Экономические риски – это риски, обусловленные неблагоприятными изменениями в экономикепредприятияиливэкономикестраны.

Экстраполяция – метод прогнозирования, в основе которого лежит продолжение тенденций прошлого в будущее.

Эмиссия наличных денег – выпуск денег в обращение, при котором увеличивается их масса.

171

МАТЕРИАЛЫ ТЕСТОВОЙ СИСТЕМЫ

Раздел 1. ТЕОРИЯ СТАТИСТИКИ

Тема1. ПРЕДМЕТИМЕТОДСТАТИСТИКИ

1.Какие из перечисленных признаков измеряются с помощью порядковой шкалы:

а) пол; б) заработная плата;

в) воинское звание; г) температура воздуха.

2.Назовите исторически первые научные направления статистики:

а) демография; б) политическая арифметика;

в) теория статистики; г) государствоведение;

д) экономическая статистика.

3. Какой из перечисленных показателей является статистическим:

а) численность населения страны; б) число«пи»;

в) количество деревьев в Новосибирской области; г) индекс Доу-Джонса.

Тема2. СТАТИСТИЧЕСКОЕНАБЛЮДЕНИЕ

1.Какой способ наблюдения применялся при проведении последних переписей населения в

СССР и России:

а) анкетный; б) экспертныхоценок;

в) корреспондентский; г) экспедиционный.

2.Вследствие каких причин возникают ошибки представительности (репрезентативности):

а) приписок; б) различийструктургенеральнойивыборочнойсовокупностей;

в) женского кокетства.

3.Укажите организационную форму и вид по степени охвата единиц совокупности переписи населения России 2002 г.:

а) отчетность; б) специальноорганизованноенаблюдение; в) сплошное;

г) основного массива.

Тема3. СТАТИСТИЧЕСКАЯСВОДКАИГРУППИРОВКА

1.Специализация признаков относится к методологическим вопросам проведения:

а) факторнойгруппировки; б) типологическойгруппировки; в) структурнойгруппировки.

2.Число групп не меньше трех – это одно из основных условий корректного проведения:

а) типологическойгруппировки; б) классификации; в) структурнойгруппировки;

г) аналитическойгруппировки.

3.К статистическим таблицам относятся:

а) столбиковые диаграммы; б) подлежащее; в) макет;

172

г) сказуемое; д) экспликация.

Тема4. СТАТИСТИЧЕСКИЕВЕЛИЧИНЫ

1.Общий коэффициент рождаемости – это относительная величина:

а) динамики; б) координации; в) сравнения;

г) интенсивности.

2.Индекс Доу-Джонса рассчитывается по формуле:

а) средней арифметической; б) средней гармонической; в) средней геометрической; г) моды.

3.Какая из перечисленных средних может быть применена для оценки типического уровня номинального признака:

а) арифметическая; б) гармоническая; в) мода; г) медиана.

4.Если все варианты разделить на два, как изменится средняя арифметическая:

а) не изменится; б) уменьшится в два раза;

в) увеличится на два; г) увеличится в два раза.

Тема5. СТАТИСТИЧЕСКИЙАНАЛИЗВАРИАЦИИ

1.Количественно однородной принято считать совокупность, значение коэффициента вариации в которой:

а) равно 0; б) не превышает 30%;

в) не превышает 100%.

2.Некоторые из приведенных утверждений неверны, какие:

а) дисперсия всегда неотрицательна:

б) среднее квадратическое отклонение всегда меньше по величине дисперсии; в) размахвариациипозволяетоценитьотносительныеграницыизмененияпризнака; г) дисперсия равна 1000 руб.; д) способ моментов предполагает равные интервалы.

3.Межгрупповая дисперсия равна 10, групповые дисперсии 6, 12, 12 соответственно, определите общую дисперсию при условии равенства численности групп:

а) 10; б) 100; в) 20; г) 130.

4.Принято считать, что распределение населения по доходам соответствует:

а) нормальному распределению; б) логарифмически нормальному распределению; в) распределению Пуассона.

Тема6. ВЫБОРОЧНОЕНАБЛЮДЕНИЕ

1. При прочих равных условиях минимальную ошибку дает:

а) механический способ отбора; б) типический отбор; в) собственно-случайный отбор;

г) серийный способ отбора.

173

2.Основное преимущество выборочного наблюдения перед другими видами несплошного заключается в том, что оно:

а) дает более точные результаты; б) требует меньших трудовых и материальных затрат;

в) дает возможность заранее оценить величину случайной ошибки.

3.Чтобы уменьшить предельную ошибку выборки, рассчитанную в условиях собственнослучайного отбора, можно:

а) уменьшить объем выборочной совокупности; б) увеличить объем выборочной совокупности; в) снизить вероятность надежности выводов; г) провести типический отбор; д) провести серийный отбор.

Тема7. СТАТИСТИЧЕСКОЕИЗУЧЕНИЕВЗАИМОСВЯЗИ

1.По таблице сопряженности 2х2 получен коэффициент сопряженности Пирсона, равный 0,85, каким образом можно интерпретировать результат:

а) связь сильная; б) связь средняя;

в) ошибка в вычислениях.

2.Из перечисленных мер тесноты связи отметьте непараметрические:

а) линейныйкоэффициенткорреляции; б) коэффициентсопряженностиЧупрова; в) коэффициентассоциации; г) корреляционноеотношение;

д) симметризованныйкоэффициентнормированнойинформации.

3.По линейному уравнению регрессии вычислены следующие показатели. Какой показатель вычислен неверно:

а) линейныйкоэффициенткорреляции– 0,6; б) индекс корреляции – 0,7; в) коэффициентдетерминации– 0,49;

г) коэффициентрегрессии– 0,25.

4.Остаточная дисперсия равна 0,16, факторная – 0,04. Определите коэффициент детерминации:

а) 0,8; б) 0,2; в) 0,75; г) 0,5.

Тема8. СТАТИСТИЧЕСКОЕИЗУЧЕНИЕДИНАМИКИ

1.Какой метод прогнозирования основан на продолжении в будущее тенденций прошлого:

а) экспертныхоценок; б) сценарий; в) экстраполяция.

2.Какие из перечисленных приемов решают задачу определения тренда:

а) метод Кокса и Стюарта; б) метод наименьших квадратов; в) скользящая средняя;

г) аналитическоевыравнивание; д) интерполяция.

3.Абсолютное содержание одного процента прироста составляет 10, определите предыдущий уровень ряда динамики:

а) 100; б) 1000; в) 1010.

4.Какие из этих утверждений неверны:

а) темп роста всегда больше, чем темп прироста; б) метод наименьших квадратов всегда точнее метода избранных точек; в) базисный прирост равен сумме цепных.

174

Тема 9. ИНДЕКСЫ

1.Индекс структурных сдвигов равен 0,95, индекс переменного состава – 1,14. Определите индекс постоянного состава:

а) 2,09; б) 1,2; в) 0,19; г) 1,083.

2.Имеются следующие данные о реализации товаров:

Товар	Индекс товарооборота	Индекс цен	Индекс физического объема

Молоко		1,00	1.2
Мясо	0,88		1,1
По двум товарам		0,90	1,15

Определите общий индекс товарооборота:

а) 0,92; б) 0,8; в) 0,86; г) 0,968; д) 1,035.

Раздел 2. МАКРОЭКОНОМИЧЕСКАЯ СТАТИСТИКА

Тема10. ОСНОВЫМАКРОЭКОНОМИЧЕСКОЙСТАТИСТИКИ

1.Макроэкономическая статистика призвана обеспечить комплексную характеристику состояния и развития:

а) экономикистраны; б) экономикипредприятия; в) экономикиотрасли.

2.Классификатор – это:

а) знак; б) систематизированный перечень объектов;

в) система показателей.

3.Виды экономической деятельности в РФ изучаются с помощью:

а) ТН ВЭД; б) ОКВЭД; в) ОКАТО; г) ОКОГУ; д) ОКФС.

4.Для макроэкономических расчетов страны с рыночной экономикой используют:

а) Платежный баланс; б) Баланс народного хозяйства;

в) Систему национальных счетов.

5.Расширенная концепция производства предполагает:

а) деятельность только в сфере материального производства; б) деятельность только в непроизводственной сфере; в) любую экономическую деятельность, приносящую доход; г) теневуюэкономику.

6.Экономическая территория не включает в свой состав:

а) воздушное пространство; б) территориальныеанклавымеждународныхорганизаций; в) территориальные воды.

7.Сколько секторов используется в СНС для анализа внутренней экономики:

а) 5; б) 6; в) 1.

175

Тема11. ОСНОВНЫЕМАКРОЭКОНОМИЧЕСКИЕПОКАЗАТЕЛИ

ИИХВЗАИМОСВЯЗЬ

1.Сколько основных счетов разрабатывается для экономики в целом:

а) 7; б) 6; в) 9.

2.Валовой внутренний продукт – это:

а) стоимостьтоваровиуслуг, произведенныхрезидентамиинерезидентамизаотчетныйпериод; б) стоимость конечных товаров и услуг, произведенных резидентами и нерезидентами за

отчетныйпериод; в) стоимость конечных товаров и услуг, произведенных резидентами за отчетный период.

3.Валовая добавленная стоимость – это разность между валовым выпуском и:

а) промежуточным потреблением; б) валовым внутренним продуктом; в) потреблением основного капитала.

4.Налоги на производство включают налоги на:

а) доходы предприятий; б) продукты; в) наследство.

Тема12. ЭКОНОМИЧЕСКИЕАКТИВЫИНАПРАВЛЕНИЯ ИХСТАТИСТИЧЕСКОГОИЗУЧЕНИЯ

1.Из перечисленных экономических активов выделите произведенные нематериальные активы:

а) основные фонды; б) ценности; в) земля;

г) природныересурсы; д) патенты, лицензии;

е) средства программного обеспечения; ж) уникальные произведения искусства.

2.Совокупность произведенных активов, которые многократно участвуют в процессе производства, и срок службы которых превышает один год, – это:

а) запасы материальных оборотных средств; б) основные фонды (средства).

3.Из перечисленных экономических активов выделите произведенные материальные активы:

а) расходы на разведку полезных ископаемых; б) здания; в) машины и оборудование;

г) сырье и материалы; д) хозяйственныйинвентарь.

4.Материальные непроизводственные активы – это:

а) драгоценные металлы и камни; б) полезные ископаемые; в) водные ресурсы;

г) антикварные и ювелирные изделия; д) земля.

5.Из перечисленных экономических активов выделите нематериальные непроизводственные активы:

а) авторские права; б) патенты; в) «гудвилл»; г) земля;

д) богатства недр.

6.Из перечисленных экономических элементов выделите финансовые активы:

а) природные активы; б) монетарное золото и СПЗ;

в) ценные бумаги (кроме акций); г) акцииипрочиевидыакционерногокапитала.

176

7.Какие элементы относятся к запасам материальных оборотных средств:

а) сырье и материалы; б) топливо;

в) драгоценные металлы и камни; г) незавершенное производство; д) предметы антиквариата.

8.Нефинансовые производственные активы включают:

а) природные ресурсы; б) основные фонды; в) авторские права;

г) запасы материальных оборотных средств.

9.Национальное богатство – это:

а) моментный показатель; б) интервальный показатель.

10.Для оценки физического объема национального богатства используют:

а) текущие цены; б) сопоставимые (постоянные) цены.

11.Выделите составляющие активной части основных фондов (средств):

а) здания; б) сооружения;

в) машины и оборудование; г) транспортные средства.

Тема13. СТАТИСТИКАФИНАНСОВЫХРЕСУРСОВ

ИФИНАНСОВОГОРЫНКА

1.Выделение расходов на образование, культуру, искусство и пр. отражается в классификации расходов государственного бюджета:

а) по экономическим элементам; б) поведомственной принадлежности; в) поназначению.

2.Выпуск государственных краткосрочных обязательств относится к:

а) внешним источникам финансирования государственного бюджета; б) внутренним источникам финансирования государственного бюджета.

3.Объем продаж на фондовом рынке характеризует:

а) ликвидностьфинансовогорынка; б) емкость финансового рынка; в) оцененностьфинансовогорынка.

4.Отношение оборота по выдаче ссуд к средним остаткам кредиторской задолженности – это показатель:

а) оборачиваемости кредитов; б) кредитоотдачи;

в) продолжительности оборачиваемости ссуд.

5.Показатель монетизации экономики – это отношение:

а) денежной массы к валовому внутреннему продукту; б) денежной базы к валовому внутреннему продукту; в) денежной массы к денежной базе.

Тема14. СТАТИСТИКАЧИСЛЕННОСТИ, СОСТАВА

ИЗАНЯТОСТИНАСЕЛЕНИЯ

1.Население, по различным причинам оказавшееся на территории на критический момент переписи (обследования), вне зависимости от того, проживает ли оно здесь постоянно или временно, относится к:

а) наличному населению; б) постоянномунаселению;

в) постояннопроживающемунаселению; г) временно отсутствующему населению.

177

2.Относительные показатели рождаемости, смертности, естественного прироста определяются как относительные величины:

а) структуры; б) координации; в) интенсивности; г) сравнения.

3.Неработающие студенты высших учебных заведений относятся к категории:

а) экономически активное население; б) экономическинеактивное население; в) занятое население; г) безработные.

4.По статусу в занятости руководителя семейного фермерского хозяйства можно отнести к группе:

а) наемных работников; б) работодателей;

в) работающихнаиндивидуальнойоснове; г) неоплачиваемых работников семейного предприятия;

д) лиц, самостоятельно обеспечивающих себя работой.

5.Лицо, находящиеся в отпуске с сохранением содержания по инициативе администрации, относится к категории:

а) экономически активное население; б) экономическинеактивное население; в) занятое; г) безработные.

6.В регионе с общей численностью населения 320,0 тыс. чел. из общей численности экономически активного населения занято 256,0 тыс. чел., а безработных 24,0 тыс. чел. Уровень безработицы составляет:

а) 0,075; б) 0,085; в) 0,093.

Тема15. СТАТИСТИКАУРОВНЯЖИЗНИНАСЕЛЕНИЯ

1.Сколько подгрупп показателей включает система показателей уровня жизни населения:

а) 5; б) 6; в) 7.

2.Номинальные доходы населения в базисном периоде составили 6000 у.е.д., а в отчетном – 6120 у.е.д., численность населения в отчетном периоде, по сравнению с базисным, увеличилась на 0,5%. Среднедушевые доходы населения:

а) увеличились на 1,5%; б) сократились на 1,5%; в) сократились на 0,8%.

3.Располагаемые доходы населения в отчетном периоде, по сравнению с базисным, увеличились на 5%, численность населения – на 0,2%, а цены на товары и услуги – на 3,5%. Реальные доходы населения:

а) увеличились на 0,3%; б) сократились на 1,7%; в) сократились на 1,9%.

4.Номинальные доходы населения в отчетном периоде, по сравнению с базисным, увеличились на 14%, а доля налогов и платежей – с 8% до 10%. Располагаемые доходы:

а) сократились на 0,5%; б) сократились на 2,8%; в) увеличились на 11,5%.

5.Максимальный среднедушевой доход 10% самого бедного населения составляет 1840 руб., а минимальный доход 10% самого богатого населения – 12800 руб. Какой показатель, рассчитанный на основе приведенных данных, характеризует дифференциацию доходов:

а) коэффициентдифференциации– 6,9; б) коэффициентфондов– 7,0;

в) коэффициентконцентрацииДжини– 0,144.

178

6. Показатель уровня бедности – это:

а) доля населения, имеющего среднедушевые доходы ниже прожиточного минимума; б) соотношение прожиточных минимумов в отчетном и базисном периодах;

в) относительная«нехватка» доходаунаселения, имеющегодоходынижепрожиточногоминимума.

Тема16. СТАТИСТИЧЕСКИЕМЕТОДЫИССЛЕДОВАНИЯЭКОНОМИЧЕСКОЙ КОНЪЮНКТУРЫИДЕЛОВОЙАКТИВНОСТИ

1.Обследование деловой активности основано:

а) наэкспертных оценках; б) наиспользовании документов; в) насплошном наблюдении.

2.В одной из стран мира экспорт составил 100 млрд USD, импорт – 50, ВВП – 100. Чему равен коэффициент покрытия:

а) 50%; б) 200%; в) 100%.

Раздел 3. МИКРОЭКОНОМИЧЕСКАЯ СТАТИСТИКА

Тема17. ПРЕДПРИЯТИЕКАКХОЗЯЙСТВУЮЩИЙСУБЪЕКТ

ИОБЪЕКТИЗУЧЕНИЯСТАТИСТИКИ

1.Территориально-обособленное подразделение – это:

а) часть местной единицы, осуществляющая определенный вид деятельности; б) часть предприятия, расположенная на одном месте с пространственной точки зрения,

выполняющая экономическую деятельность на этом месте или с этого места; в) наименьшая комбинация правовых единиц, которая представляет собой организационную

единицу.

2. Предприятия по размерам классифицируются как:

а) крупные и малые; б) средние и малые;

в) крупные, средние и малые.

Тема18. СТАТИСТИКАПРОИЗВОДСТВАПРОДУКЦИИ

1. Продукция предприятия – это:

а) результат его финансовой деятельности; б) результат его производственной деятельности;

в) запасы материальных ресурсов (сырья, материалов, топлива и т.д.); г) средства производства на предприятии.

2.Продукция предприятия имеет форму:

а) продукта (товара); б) услуги;

в) незавершенного производства; г) полуфабриката; д) запасов материалов на складе.

3.Система стоимостных показателей объема продукции включает:

а) товарнуюиотгруженнуюпродукцию; б) услуги промышленного характера инезавершенное производство; в) готовые изделия и полуфабрикаты; г) прибыль; д) себестоимость продукции.

4.Товарная продукция (выпуск товаров и услуг) – это:

а) стоимость всех готовых изделий и полуфабрикатов, изготовленных в отчетном периоде; б) объемпродукциипроизведеннойдляреализациинасторону; в) объем продукции отгруженной (переданной) в отчетном периоде потребителям;

г) объем продукции, на которую предъявлены покупателем расчетные документы.

179

5. В объем товарной продукции (выпуск товаров и услуг) включают:

а) стоимость готовых изделий и продуктов, выработанных за отчетный период для реализации на сторону;

б) объем готовых изделий и полуфабрикатов, который используется на собственные промыш- ленно-производственныенужды;

в) изделия, предназначенные зачислению в состав основных средств.

6. Объем продукции по коммерческой деятельности включает:

а) суммувознагражденийподоговорампоручения, комиссионныхиагентскихвознаграждений; б) сумму, поступающую по оплате возмездных услуг по оценке имущества; в) деятельность в области рекламы, аудита, маркетинговых исследований;

г) посредническую деятельность при купле-продаже товаров, ценных бумаг, валюты.

7.Для изучения динамики объема произведенной продукции исчисляют индексы:

а) стоимостивсейпроизведеннойпродукциивдействующихценах; б) стоимости всей произведенной продукции в сопоставимых (базисных) ценах (индекс физи-

ческого объема); в) цен.

8.Стоимость продукции увеличилась на 15%, а цены – в 1,25 раза, как изменился физический объем продукции:

а) увеличился на 13,75%; б) увеличился на 12%; в) увеличился на 0,6 %; г) уменьшился на 8,0%.

Тема19. СТАТИСТИКАРЕСУРСОВПРЕДПРИЯТИЯ

1.В списочную численность персонала включаются:

а) работники, занимающие штатные должности; б) совместители;

в) работники, работавшие по договорам гражданско-правового характера.

2.Выделите элементы, входящие в состав основных производственных средств промышленного предприятия:

а) зданияи сооруженияпроизводственного назначения; б) транспортные средства; в) запасы материальных оборотных средств.

3.Первоначальная стоимость основных производственных фондов – это стоимость объекта:

а) в момент приобретения (создания); б) в момент переоценки основных средств.

4.Выделите составляющие активной части основных средств промышленного предприятия:

а) производственные здания; б) машины и оборудование; в) транспортные средства.

5.Полная восстановительная стоимость основных средств – это:

а) остаточная стоимость + капитальный ремонт; б) стоимость основных средств в современных условиях их воспроизводства.

6.Эффективность использования основных производственных средств изучается с помощью следующих показателей:

а) фондоемкости; б) производительности труда;

в) фондовооруженноститруда; г) материалоемкости; д) фондоотдачи.

7.Динамика фондоотдачи основных производственных средств зависит от двух факторов:

а) от фондоемкости; б) от структуры основных производственных средств;

в) от использования активной части основных средств

8.Какие элементы относятся к запасам материальных оборотных средств:

а) производственные здания; б) готовая продукция на складе; в) сырье и материалы; г) предметы антиквариата.

180

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

При
выборочном наблюдении должна быть
обеспечена случайность
отбора
единиц. Каждая единица должна иметь
равную с другими возможность быть
отобранной. Именно на этом основывается
собственно-случайная выборка.

К
собственно-случайной
выборке
относится
отбор единиц из всей генеральной
совокупности (без предварительного
расчленения ее на какие-либо группы)
посредством жеребьевки (преимущественно)
или какого-либо иного подобного способа,
например, с помощью таблицы случайных
чисел. Случайный
отбор — это
отбор не беспорядочный. Принцип
случайности предполагает, что на
включение или исключение объекта из
выборки не может повлиять какой-либо
фактор, кроме случая. Примером
собственно-случайного
отбора
могут служить тиражи выигрышей: из
общего количества выпущенных билетов
наугад отбирается определенная часть
номеров, на которые приходятся выигрыши.
Причем всем номерам обеспечивается
равная возможность попадания в выборку.
При этом количество отобранных в
выборочную совокупность единиц обычно
определяется исходя из принятой доли
выборки.

Доля,
выборки
есть
отношение числа единиц выборочной
совокупности к числу единиц генеральной
совокупности:

Так,
при 5%-ной выборке из партии деталей в
1000 ед. объем выборки п
составляет
50 ед., а при 10%-ной выборке -100 ед. и т.д.
При правильной научной организации
выборки ошибки репрезентативности
можно свести к минимальном значениям,
в результате — выборочное наблюдение
становится достаточно точным.

Собственно-случайный
отбор «в чистом виде» применяется в
практике выборочного наблюдения редко,
но он является исходным среди всех
других видов отбора, в нем заключаются
и реализуются основные принципы
выборочного наблюдения.

Рассмотрим некоторые
вопросы теории выборочного метода и
формулы ошибок для простой случайной
выборки.

Применяя
выборочный метод в статистике, обычно
используют два основных вида обобщающих
показателей: среднюю
величину количественного признака
и
относительную
величину альтернативного признака
(долю
или удельный вес единиц в статистической
совокупности, которые отличаются от
всех других единиц этой совокупности
только наличием изучаемого признака).

Выборочная
доля
(w),
или
частость, определяется отношением числа
единиц, обладающих изучаемым признаком
т,
к
общему числу единиц выборочной
совокупности п:

w
= т/п.

Например,
если из 100 деталей выборки (и = 100), 95
деталей оказались стандартными (т
=95),
то выборочная доля

w
=
95 / 100 = 0,95 .

Для
характеристики надежности выборочных
показателей различают среднюю
и
предельную
ошибки выборки.

Ошибка
выборки

или,
иначе говоря, ошибка репрезентативности
представляет собой разность соответствующих
выборочных и генеральных характеристик:

• для
средней количественного признака

(1)

• для
доли (альтернативного признака)

(2)

Ошибка выборки
свойственна только выборочным
наблюдениям. Чем больше значение
этой ошибки, тем в большей степени
выборочные показатели отличаются от
соответствующих генеральных
показателей.

Выборочная
средняя и выборочная доля по своей сути
являются случайными
величинами, которые
могут принимать различные значения
в зависимости от того, какие единицы
совокупности попали в выборку.
Следовательно, ошибки выборки также
являются случайными величинами и могут
принимать различные значения. Поэтому
определяют среднюю из возможных
ошибок — среднюю ошибку выборки.

От
чего зависит средняя
ошибка выборки! При
соблюдении принципа случайного отбора
средняя ошибка выборки определяется,
прежде всего объемом
выборки: чем
больше численность при прочих равных
условиях, тем меньше величина средней
ошибки выборки. Охватывая выборочным
обследованием все большее количество
единиц генеральной совокупности, всё
более точно характеризуем всю генеральную
совокупность.

Средняя
ошибка выборки также зависит от степени
варьирования изучаемого
признака. Степень варьирования, как
известно, характеризуется дисперсией

или
w(1
—w)
—
для альтернативного признака. Чем меньше
вариация признака, а следовательно, и
дисперсия, тем меньше средняя ошибка
выборки, и наоборот. При нулевой
дисперсии (признак не варьирует)
средняя ошибка выборки равна нулю, т.
е. любая единица генеральной
совокупности будет совершенно точно
характеризовать всю совокупность
по этому признаку.

Зависимость
средней ошибки выборки от ее объема и
степени варьирования признака
отражена в формулах, с помощью которых
можно рассчитать среднюю ошибку выборки
в условиях выборочного наблюдения,
когда генеральные характеристики (х,р)
неизвестны,
и следовательно, не представляется
возможным нахождение реальной ошибки
выборки непосредственно по формулам
(1), (2).

При
случайном повторном отборе средние
ошибки теоретически рассчитывают по
следующим формулам:

• для
средней количественного признака

(3)

• для
доли (альтернативного признака)

(4)

Поскольку
практически дисперсия признака в
генеральной совокупности

точно неизвестна, на практике пользуются

значением
дисперсии S²
, рассчитанным
для выборочной совокупности на
основании закона больших чисел, согласно
которому выборочная совокупность
при достаточно большом объеме выборки
достаточно точно воспроизводит
характеристики генеральной
совокупности.

Таким
образом, расчетные формулы средней
ошибки выборки
при
случайном повторном отборе будут
следующие:

• для
средней количественного признака

(5)

• для
доли (альтернативного признака)

(6)

Однако
дисперсия выборочной совокупности не
равна дисперсии генеральной
совокупности, и следовательно, средние
ошибки выборки, рассчитанные по формулам
(5) и (6), будут приближенными. Но в
теории вероятностей доказано, что
генеральная дисперсия выражается через
выборочную следующим соотношением:

(7)

Так
как п
/
(n
-1)
при достаточно больших п
— величина,
близкая к единице, то можно принять, что

=S²,
а следовательно,
в практических расчетах средних ошибок
выборки можно использовать формулы
(5) и (6). И только в случаях малой выборки
(когда объем выборки не превышает 30)
необходимо учитывать коэффициент
п/(п-1)
и
исчислять среднюю
ошибку малой выборки по
формуле:

(8)

При
случайном бесповторном отборе
в
приведенные выше формулы расчета средних
ошибок выборки необходимо подкоренное
выражение умножить на 1-(п/N),
поскольку
в процессе бесповторной выборки
сокращается численность единиц
генеральной совокупности. Следовательно,
для бесповторной выборки расчетные
формулы средней
ошибки выборки
примут
такой вид:

• для
средней количественного признака

(9)

• для
доли (альтернативного признака)

(10)

Так
как п
всегда
меньше N,
то
дополнительный множитель 1 — (n
/ N)
всегда
будет меньше единицы. Отсюда следует,
что средняя ошибка при бесповторном
отборе всегда будет меньше, чем при
повторном. В то же время при сравнительно
небольшом проценте выборки этот множитель
близок к единице (например, при 5%-ной
выборке он равен 0,95; при 2%-ной — 0,98 и
т.д.). Поэтому иногда на практике пользуются
для определения средней ошибки выборки
формулами (5) и (6) без указанного множителя,
хотя выборку и организуют как бесповторную.
Это имеет место в тех случаях, когда
число единиц генеральной совокупности
N
неизвестно
или безгранично, или когда п
очень
мало по сравнению с N,
и
по существу, введение дополнительного
множителя, близкого по значению к
единице, практически не повлияет на
значение средней ошибки выборки.

Механическая
выборка
состоит
в том, что отбор единиц в выборочную
совокупность из генеральной, разбитой
по нейтральному признаку на равные
интервалы (группы), производится
таким образом, что из каждой такой группы
в выборку отбирается лишь одна единица.
Чтобы избежать систематической
ошибки, отбираться должна единица,
которая находится в середине каждой
группы.

При организации
механического отбора единицы совокупности
предварительно располагают (обычно в
списке) в определенном порядке
(например, по алфавиту, местоположению,
в порядке возрастания или убывания
значений какого-либо показателя, не
связанного с изучаемым свойством, и
т.д.), после чего отбирают заданное число
единиц механически, через определенный
итервал. При этом размер интервала в
генеральной совокупности равен обратному
значению доли выборки. Так, при 2%-ной
выборке отбирается и проверяется каждая
50-я единица (1 : 0,02), при 5 %-ной выборке —
каждая 20-я единица (1 : 0,05), например,
сходящая со станка деталь.

При
достаточно большой совокупности
механический отбор по точности результатов
близок к собственно-случайному. Поэтому
для определения средней ошибки
механической выборки используют формулы
собственно-случайной бесповторной
выборки (9), (10).

Для
отбора единиц из неоднородной совокупности
применяется, так называемая типическая
выборка, которая
используется в тех случаях, когда все
единицы генеральной совокупности можно
разбить на несколько качественно
однородных, однотипных групп по признакам,
влияющим на изучаемые показатели.

При обследовании
предприятий такими группами могут быть,
например, отрасль и подотрасль, формы
собственности. Затем из каждой типической
группы собственно-случайной или
механической выборкой производится
индивидуальный отбор единиц в выборочную
совокупность.

Типическая выборка
обычно применяется при изучении сложных
статистических совокупностей. Например,
при выборочном обследовании семейных
бюджетов рабочих и служащих в отдельных
отраслях экономики, производительности
труда рабочих предприятия, представленных
отдельными группами по квалификации.

Типическая выборка
дает более точные результаты по сравнению
с другими способами отбора единиц в
выборочную совокупность. Типизация
генеральной совокупности обеспечивает
репрезентативность такой выборки,
представительство в ней каждой
типологической группы, что позволяет
исключить влияние межгрупповой дисперсии
на среднюю ошибку выборки,

При
определении средней
ошибки типической выборки в
качестве показателя вариации выступает
средняя
из внутригрупповых дисперсий.

Среднюю
ошибку выборки находят
по формулам:

• для
средней количественного признака

(повторный отбор);
(11)

(бесповторный
отбор);
(12)

• для
доли (альтернативного признака)

(повторный отбор);
(13)

(бесповторный
отбор), (14)

где

— средняя
из внутригрупповых дисперсий по
выборочной совокупности;

—
средняя из внутригрупповых дисперсий
доли (альтернативного

признака) по
выборочной совокупности.

Серийная
выборка
предполагает
случайный отбор из генеральной
совокупности не отдельных единиц, а их
равновеликих групп (гнезд, серий) с тем,
чтобы в таких группах подвергать
наблюдению все без исключения единицы.

Применение серийной
выборки обусловлено тем, что многие
товары для их транспортировки, хранения
и продажи упаковываются в пачки, ящики
и т.п. Поэтому при контроле качества
упакованного товара рациональнее
проверить несколько упаковок (серий),
чем из всех упаковок отбирать необходимое
количество товара.

Поскольку внутри
групп (серий) обследуются все без
исключения единицы, средняя ошибка
выборки (при отборе равновеликих серий)
зависит только от межгрупповой
(межсерийной) дисперсии.

Среднюю
ошибку выборки для средней количественного
признака
при
серийном отборе находят по формулам:

(повторный отбор);
(15)

(бесповторный
отбор),
(16)

где
r
—
число отобранных серий; R
— общее
число серий.

Межгрупповую
дисперсию серийной выборки вычисляют
следующим образом:

где

—
средняя i-й
серии;

— общая
средняя по всей выборочной совокупности.

Средняя
ошибка выборки для доли (альтернативного
признака)
при
серийном отборе:

(повторный отбор);
(17)

(бесповторный
отбор).
(18)

Межгрупповую
(межсерийную)
дисперсию
доли серийной выборки определяют
по формуле:

(19)

где
w_i
— доля
признака в i-и
серии;

— общая
доля признака во всей выборочной
совокупности.

В
практике статистических обследований
помимо рассмотренных ранее способов
отбора применяется их комбинация
(комбинированный
отбор).

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

1. Статистика

2. Тема: Выборочное наблюдение

3. 1. Выборка в системе методов несплошного статистического наблюдения

4.

5.

6. 7. «О развитии малого и среднего предпринимательства в Российской Федерации» Федеральный Закон РФ от 24. 07.2007 № 209-ФЗ

8. 2. Основные этапы выборочного наблюдения

9.

10. 11. Примеры

ПРИМЕРЫ

12. Основы выборки при проведении выборочных статистических наблюдений за сельскохозяйственным производством в крестьянских

13. Основа выборки при проведении выборочного статистического наблюдения за перевозочной деятельностью предпринимателей (физических

14. 15. 3. Методы и способы, обеспечивающие репрезентативность выборки

16. Собственно-случайный отбор

17. Механический (систематический) отбор

18. Расслоенный (типический) отбор

19. 20. Пример

ПРИМЕР

21. Для оценивания среднего значения признака из генеральной совокупности объемом 10000 ед. планируется провести расслоенную

22. Варианты расслоенной выборки, единиц

23. Серийный (гнездовой) отбор

24. 4. Основные виды статистических показателей генеральной совокупности, оцениваемые по данным выборочного наблюдения

25. Основные виды статистических показателей генеральной совокупности и их оценка

26. Основные виды статистических показателей генеральной совокупности и их оценка

27.

28. 29. Формулы расчета предельных ошибок выборки

30. Формулы расчета средних ошибок выборки

31. 32. Способ расчета границ и форма записи доверительного интервала (при оценивании генеральной средней)

~
X x ~x
~
x ~x X ~
x ~x
P~
x ~x X ~
x ~x
X ~
x ~ %
x
F(t)

33. Примеры

ПРИМЕРЫ

34.

35. 36. Задача

37. 38. Задача

39. 40. 5. Определение объема выборочной совокупности

41. Формулы расчета объема выборочной совокупности при различных способах и видах отбора

42. 43. Тесты для текущего контроля знаний

44.

Источник

Группа предметов	Экономические
Предмет	Статистика
Тема/вариант работы	Контрольная по статистике, вариант 6 (НГУЭиУ)
Кол-во источников:	4
Кол-во страниц:	11 (шрифт 12)
Тип работы:	Контрольная работа, 2015 г. (учебное заведение — НГУЭиУ, вариант 6)
Цена работы	350 руб

Содержание

1. Практическая часть

1.1. Ситуационная (практическая) задача № 1.

1. Используя фрагмент Статрегистра Приложения 2 в качестве генеральной совокупности, построить многофазную бесповторную выборку:

— 1 фаза –35%-ная собственно-случайная выборка;

— 2 фаза –25%-ная механическая выборка.

2. По каждой выборке дать точечную и с вероятностью 0,954 интервальную оценку следующих генеральных параметров:

1) среднесписочная численность работников;

2) доля предприятий с численностью 25 и более человек.

1.2. Ответ на задачу №1.

1.3. Ситуационная (практическая) задача № 2.

В городе проживает 500000 семей. С помощью механической выборки предполагается определить долю семей с числом детей 3 и более. Какова должна быть численность выборки, чтобы с вероятностью 0,954 ошибка выборки доли не превышала 0,03, если на основе предыдущих обследований известно, что дисперсия равна 0,21.

1.4. Ответ на задачу №2.

2. Тестовая часть

1. Та совокупность, из которой производится отбор единиц для изучения, называется:

2. Собственно-случайный отбор выборочной совокупности применяется когда:

3.Статистическим наблюдением, при котором изучению подвергается часть единиц совокупности, отобранная в определенном порядке, называется:

4. Видом отбора из генеральной совокупности, дающим минимальную ошибку выборки при прочих равных условиях, является:

5.Формулой расчета ошибки типической выборки предполагается применение:

6. Способом формирования выборочной совокупности, предполагающим предварительное разбиение генеральной совокупности на группы, количество которых равно численности выборки, и отбор одной единицы из каждой группы, является:

7. Шаг механического отбора равен, если объем генеральной совокупности – 3000, а объем выборки – 100 единиц:

8. Предельная ошибка выборки равна, если средняя ошибка составляет 4 года, а вероятность, с которой будут гарантированы оценки генеральных параметров – 0,954:

9.Предельная ошибка выборки уменьшится в 2 раза, а объем повторной выборки:

10. Коэффициент доверительной вероятности, с которой гарантируются результаты выборочного наблюдения, уменьшится в 2 раза, а объем повторной выборки:

Список использованной литературы

Источник

Лекции по статистике – Способы отбора и виды выборки

Виды и способы отбора

Под способом отбора понимают порядок отбора единиц из генеральной совокупности. Различают два способа отбора: повторный и бесповторный. При повторном отборе каждая отобранная в случайном порядке единица после ее обследования возвращается в генеральную совокупность и при последующем отборе может снова попасть в выборку. Этот способ отбора построен по схеме «возвращенного шара»: вероятность попасть в выборку для каждой единицы генеральной совокупности не меняется независимо от числа отбираемых единиц. При бесповторном отборе каждая единица, отобранная в случайном порядке, после ее обследования в генеральную совокупность не возвращается. Этот способ отбора построен по схеме «невозвращенного шара»: вероятность попасть в выборку для каждой единицы генеральной совокупности увеличивается по мере производства отбора.

В зависимости от методики формирования выборочной совокупности различают следующие основные виды выборки:

собственно случайную;

механическую;

типическую (стратифицированную, районированную);

серийную (гнездовую);

комбинированную;

многоступенчатую;

многофазную;

взаимопроникающую.

Случайная выборка формируется в строгом соответствии с научными принципами и правилами случайного отбора. Для получения собственно случайной выборки генеральная совокупность строго подразделяется на единицы отбора, и затем в случайном повторном или бесповторном порядке отбирается достаточное число единиц.

В том случае, когда собственно случайная выборка организуется как повторная, расчет стандартной ошибки производится в соответствии с формулой. При бесповторном способе отбора формула для расчета стандартной ошибки будет:

где 1 – n / N – доля единиц генеральной совокупности, не попавших в выборку. Так как эта доля всегда меньше единицы, то ошибка при бесповторном отборе при прочих равных условиях всегда меньше, чем при повторном. Бесповторный отбор организовать легче, чем повторный, и он применяется намного чаще. Однако величину стандартной ошибки при бесповторном отборе можно определять по более простой формуле. Такая замена возможна, если доля единиц генеральной совокупности, не попавших в выборку, большая и, следовательно, величина близка к единице.

Формировать выборку в строгом соответствии с правилами случайного отбора практически очень сложно, а иногда невозможно, так как при использовании таблиц случайных чисел необходимо пронумеровать все единицы генеральной совокупности. Довольно часто генеральная совокупность такая большая, что провести подобную предварительную работу чрезвычайно сложно и нецелесообразно, поэтому на практике применяют другие виды выборок, каждая из которых не является строго случайной. Однако организуются они так, чтобы было обеспечено максимальное приближение к условиям случайного отбора.

При чисто механической выборке вся генеральная совокупность единиц должна быть прежде всего представлена в виде списка единиц отбора, составленного в каком-то нейтральном по отношению к изучаемому признаку порядке, например по алфавиту. Затем список единиц отбора разбивается на столько равных частей, сколько необходимо отобрать единиц. Далее по заранее установленному правилу, не связанному с вариацией исследуемого признака, из каждой части списка отбирается одна единица. Этот вид выборки не всегда может обеспечить случайный характер отбора, и полученная выборка может оказаться смещенной. Объясняется это тем, что, во-первых, упорядочение единиц генеральной совокупности может иметь элемент неслучайного характера. Во-вторых, отбор из каждой части генеральной совокупности при неправильном установлении начала отсчета может также привести к ошибке смещения. Однако практически легче организовать механическую выборку, чем собственно случайную, и при проведении выборочных обследований чаще всего пользуются этим видом выборки. Стандартную ошибку при механической выборке определяют по формуле собственно случайной бесповторной выборки.

Типическая (районированная, стратифицированная) выборка преследует две цели:

• обеспечить представительство в выборке соответствующих типических групп генеральной совокупности по интересующим исследователя признакам;

• увеличить точность результатов выборочного обследования.

При типической выборке до начала ее формирования генеральная совокупность единиц разбивается на типические группы. При этом очень важным моментом является правильный выбор группировочного признака. Выделенные типические группы могут содержать одинаковое или различное число единиц отбора. В первом случае выборочная совокупность формируется с одинаковой долей отбора из каждой группы, во втором – с долей, пропорциональной ее доле в генеральной совокупности. Если выборка формируется с равной долей отбора, по существу она равносильна ряду собственно случайных выборок из меньших генеральных совокупностей, каждая из которых и есть типическая группа. Отбор из каждой группы осуществляется в случайном (повторном или бесповторном) либо механическом порядке. При типической выборке, как с равной, так и неравной долей отбора, удается устранить влияние межгрупповой вариации изучаемого признака на точность ее результатов, так как обеспечивается обязательное представительство в выборочной совокупности каждой из типических групп. Стандартная ошибка выборки будет зависеть не от величины общей дисперсии, а от величины средней из групповых дисперсий. Поскольку средняя из групповых дисперсий всегда меньше общей дисперсии, постольку при прочих равных условиях стандартная ошибка типической выборки будет меньше стандартной ошибки собственно случайной выборки.

При определении стандартных ошибок типической выборки применяются следующие формулы:

• при повторном способе отбора

• при бесповторном способе отбора:

– средняя из групповых дисперсий в выборочной совокупности.

Серийная (гнездовая) выборка – это такой вид формирования выборочной совокупности, когда в случайном порядке отбираются не единицы, подлежащие обследованию, а группы единиц (серии, гнезда). Внутри отобранных серий (гнезд) обследованию подвергаются все единицы. Серийную выборку практически организовать и провести легче, чем отбор отдельных единиц. Однако при этом виде выборки, во-первых, не обеспечивается представительство каждой из серий и, во-вторых, не устраняется влияние межсерийной вариации изучаемого признака на результаты обследования. В том случае, когда эта вариация значительна, она приведет к увеличению случайной ошибки репрезентативности. При выборе вида выборки исследователю необходимо учитывать это обстоятельство.

В практике те или иные способы и виды выборок применяются в зависимости от цели и задач выборочных обследований, а также возможностей их организации и проведения. Чаще всего применяется комбинирование способов отбора и видов выборки. Такие выборки получили название комбинированные. Комбинирование возможно в разных сочетаниях: механической и серийной выборки, типической и механической, серийной и собственно случайной и т. д. К комбинированной выборке прибегают для обеспечения наибольшей репрезентативности с наименьшими трудовыми и денежными затратами на организацию и проведение обследования.

При комбинированной выборке величина стандартной ошибки выборки состоит из ошибок на каждой ее ступени и может быть определена как корень квадратный из суммы квадратов ошибок соответствующих выборок.

Особенность многоступенчатой выборки состоит в том, что выборочная совокупность формируется постепенно, по ступеням отбора. На первой ступени с помощью заранее определенного способа и вида отбора отбираются единицы первой ступени. На второй ступени из каждой единицы первой ступени, попавшей в выборку, отбираются единицы второй ступени и т. д. Число ступеней может быть и больше двух. На последней ступени формируется выборочная совокупность, единицы которой подлежат обследованию. Так, например, для выборочного обследования бюджетов домашних хозяйств на первой ступени отбираются территориальные субъекты страны, на второй – районы в отобранных регионах, на третьей – в каждом муниципальном образовании отбираются предприятия или организации и, наконец, на четвертой ступени – в отобранных предприятиях отбираются семьи.

Таким образом, выборочная совокупность формируется на последней ступени. Многоступенчатая выборка более гибкая, чем другие виды, хотя в общем она дает менее точные результаты, чем выборка того же объема, но сформированная в одну ступень. Однако при этом она имеет одно важное преимущество, которое заключается в том, что основу выборки при многоступенчатом отборе нужно строить на каждой из ступеней только для тех единиц, которые попали в выборку, а это очень важно, так как нередко готовой основы выборки нет.

Сущность многофазной выборки состоит в том, что на основе первоначально сформированной выборочной совокупности образуют подвыборку, из этой подвыборки – следующую подвыборку и т. д. Первоначальная выборочная совокупность представляет собой первую фазу, подвыборка из нее – вторую и т. д. Многофазную выборку целесообразно применять в случаях, если:

для изучения различных признаков требуется неодинаковый объем выборки;

колебание изучаемых признаков неодинакова и требуемая точность различна;

в отношении всех единиц первоначальной выборочной совокупности (первая фаза) необходимо собрать менее подробные сведения, а в отношении единиц каждой последующей фазы – более подробные.

Одним из несомненных достоинств многофазной выборки является то обстоятельство, что сведениями, полученными на первой фазе, можно пользоваться как дополнительной информацией на последующих фазах, информацией второй фазы – как дополнительной информацией на следующих фазах и т. д. Такое использование сведений повышает точность результатов выборочного обследования.

При организации многофазной выборки можно применять сочетание различных способов и видов отбора (типическую выборку с механической и т. д.). Многофазный отбор можно сочетать с многоступенчатым. На каждой ступени выборка может быть многофазной.

Стандартная ошибка при многофазной выборке рассчитывается на каждой фазе в отдельности в соответствии с формулами того способа отбора и вида выборки, при помощи которых формировалась ее выборочная совокупность.

Взаимопроникающие выборки – это две или более независимые выборки из одной и той же генеральной совокупности, образованные одним и тем же способом и видом. К взаимопроникающим выборкам целесообразно прибегать, если необходимо за короткий срок получить предварительные итоги выборочных обследований. Взаимопроникающие выборки эффективны для оценки результатов обследования. Если в независимых выборках результаты одинаковы, то это свидетельствует о надежности данных выборочного обследования. Взаимопроникающие выборки иногда можно применять для проверки работы различных исследователей, поручив каждому из них провести обследование разных выборок.

Стандартная ошибка при взаимопроникающих выборках определяется по той же формуле, что и типическая пропорциональная выборка. Взаимопроникающие выборки по сравнению с другими видами требуют больших трудовых затрат и денежных расходов, поэтому исследователь должен учитывать это обстоятельство при проектировании выборочного обследования.

Конспект лекций

Источник