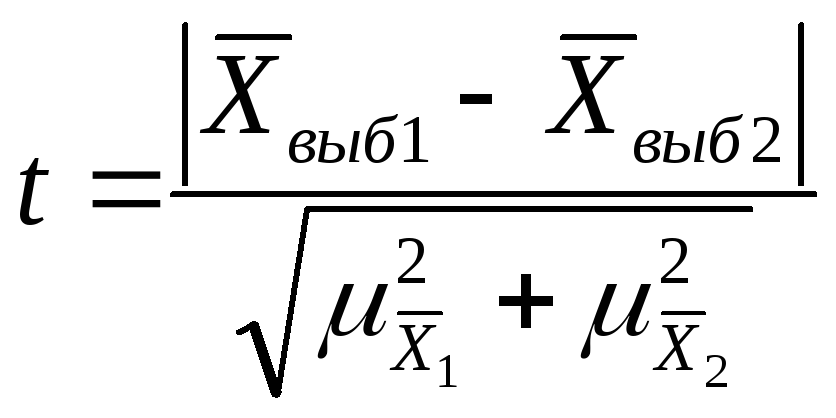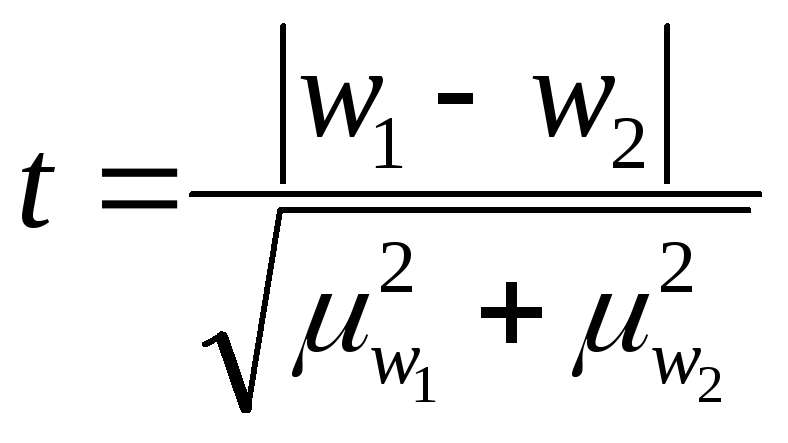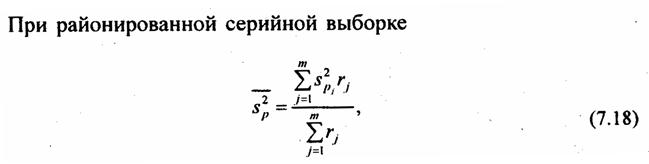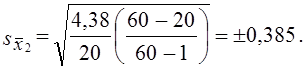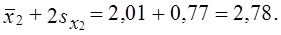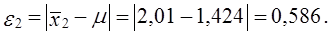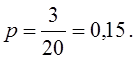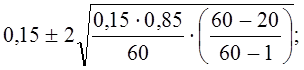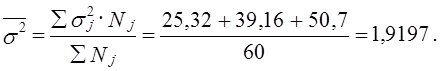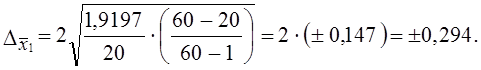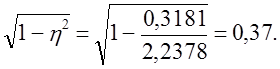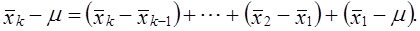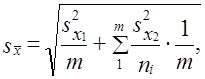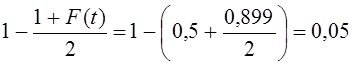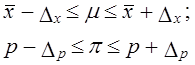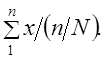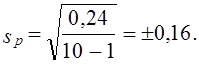Средняя и предельная ошибки выборки
Средняя ошибка выборкивсегда
присутствует в выборочных исследованиях
и появляется вследствие того, что
обследуются не все единицы статистической
совокупности, а лишь ее часть.
Средняя ошибка выборки превращается в
предельную ошибкуΔ
при умножении ее на коэффициент
доверияt, который задается
предварительно, исходя из требуемой
точности наблюдения. Предельная ошибка
позволяет судить об «истинном» размере
параметра в генеральной совокупности
с определенной степенью вероятности
|
|
При типическом и серийном
отборе, при расчете ошибки выборки
вместо общей дисперсии (σ2)
следует использовать
среднюю из внутригрупповых дисперсий
и межгрупповую дисперсию,
где—
частная дисперсия i группы,объем i группы
Формулы предельной ошибки случайной
выборки при определении средней
Для повторного отбора
|
|
где |
Для бесповторного отбора
|
|
Формулы предельной ошибки случайной
выборки при определении доли
Для повторного отбора
|
|
где |
Для бесповторного отбора
|
|
где |
Формулы численности случайной
выборки при определении средней величины
|
Для повторного |
Для |
|
|
|
Формулы численности случайной выборки при определении доли изучаемого признака
|
Для повторного |
Для |
|
|
|
Предельная разница между генеральной
и выборочной средней соответствует
величине предельной ошибки
|
для средней |
для доли: |
|
|
|
Значения вероятности и соответственно
tнаходятся по таблицам
распределения:
-
Лапласа
-
Стьюдента (в случае малой выборки)
Формулы случайной выборки подходят и
для механической выборки.
При необходимости округления, при
случайной выборке – округление в большую
сторону, при механической – в меньшую.
Малая выборка
Если численность выборочной совокупности
не более 30 единиц, то средняя ошибка
малой выборки при определении средней
величины рассчитывается по формуле:
|
при определении доли |
|
|
|
|
Для расчета ошибки малой выборки
применяется уточненная формула дисперсии
|
|
где n-1 — |
Типы задач выборочного наблюдения
-
определение ошибки выборки,
-
определение численности выборочной
совокупности n
, -
определение вероятности того, что
выборочная средняя (или доля) отклонится
от генеральной не более, чем на заданную
величину t=Δ/μ, -
оценка случайности расхождений
показателей выборочных наблюдений, -
перенос выборочных характеристик на
генеральную совокупность.
Проверка гипотез о средней и доле
Оценка случайности расхождений
показателей выборочных наблюдений
|
|
|
-
Если при n>30 коэффициент t<3, то делается
вывод о случайности расхождений. -
Если n≤ 30 , то полученное
значение t сравнивают с табличным,
определяемым по таблице распределения
Стьюдента -
Если
,
расхождение считается существенным. -
Если
,
расхождение считается случайным.
Методы переноса выборочных данных на
генеральную совокупность
-
метод взвешивания;
-
метод перевзвешивания;
-
метод заполнения случайным подбором
в классах замещения.
Повторный и бесповторный отбор.
Ошибка выборки
Краткая теория
На основании выборочных данных дается оценка статистических
показателей по всей (генеральной) совокупности. Подобное возможно, если выборка
основывается на принципах случайности отбора и репрезентативности
(представительности) выборочных данных. Каждая единица генеральной совокупности
должна иметь равную возможность (вероятность) попасть в выборку.
При формировании выборочной совокупности используются следующие
способы отбора: а) собственно-случайный отбор; б) механическая выборка; в)
типический (районированный) отбор; г) многоступенчатая (комбинированная)
выборка; д) моментно-выборочное наблюдение.
Выборка может осуществляться по схеме повторного и бесповторного
отбора.
В первом случае единицы совокупности, попавшие в выборку, снова
возвращаются в генеральную, а во втором случае – единицы совокупности, попавшие
в выборку, в генеральную совокупность уже не возвращаются.
Выборка может осуществляться отдельными единицами или сериями
(гнездами).
Собственно-случайная выборка
Отбор в этом случае производится либо по жребию, либо по таблицам
случайных чисел.
На основании приемов классической выборки решаются следующие
задачи:
а) определяются границы среднего значения показателя по генеральной
совокупности;
б) определяются границы доли признака по генеральной совокупности.
Предельная ошибка средней при собственно-случайном отборе
исчисляется по формулам:
а) при повторном отборе:
б) при бесповторном отборе:
где
– численность выборочной совокупности;
– численность генеральной совокупности;
– дисперсия признака;
– критерий кратности ошибки: при
;
при
;
при
.
Значения
определяются
по таблице функции Лапласа.
Границы (пределы) среднего значения признака по генеральной
совокупности определяются следующим неравенством:
где
– среднее значение признака по выборочной
совокупности.
Предельная ошибка доли при собственно-случайном отборе определяется
по формулам:
а) при повторном отборе:
при бесповторном отборе:
где
– доля единиц совокупности с заданным
значением признака в обзей численности выборки,
– дисперсия доли признака.
Границы (пределы) доли признака по всей (генеральной) совокупности
определяются неравенством:
где
– доля признака по генеральной совокупности.
Типическая (районированная) выборка
Особенность этого вида
выборки заключается в том, что предварительно генеральная совокупность по
признаку типизации разбивается на частные группы (типы, районы), а затем в
пределах этих групп производится выборка.
Предельная ошибка средней
при типическом бесповторном отборе определяется по формуле:
где
– средняя из внутригрупповых дисперсий
по каждой типичной группе.
При пропорциональном отборе из групп генеральной совокупности
средняя из внутригрупповых дисперсий определяется по формуле:
где
– численности единиц совокупности групп по выборке.
Границы (пределы) средней по генеральной совокупности на основании
данных типической выборки определяются по тому же неравенству, что при
собственно-случайной выборке. Только предварительно необходимо вычислить общую
выборочную среднюю
из частных выборочных средних
.
Для случая пропорционального отбора это определяется по формуле:
При непропорциональном отборе средняя из внутригрупповых дисперсий вычисляется по
формуле:
где
– численность единиц групп по генеральной
совокупности.
Общая выборочная средняя в этом случае определяется по формуле:
Предельная ошибка доли
признака при типическом бесповторном отборе определяется формулой:
Средняя дисперсия доли
признака из групповых дисперсий доли
при
типической пропорциональной выборке вычисляется по формуле:
Средняя доля признака по
выборке из показателей групповых долей рассчитывается формуле:
Средняя дисперсия доли при
непропорциональном типическом отборе определяется следующим образом:
а средняя доля признака:
Формулы ошибок выборки при типическом повторном отборе будут те же,
то и для случая бесповторного отбора. Отличие заключается только в том, что в
них будет отсутствовать по корнем сомножитель
.
Серийная выборка
Серийная ошибка выборки
может применяться в двух вариантах:
а) объем серий различный
б) все серии имеют
одинаковое число единиц (равновеликие серии).
Наиболее распространенной
в практике статистических исследований является серийная выборка с
равновеликими сериями. Генеральная совокупность делится на одинаковые по объему
группы-серии
и
производится отбор не единиц совокупности, а серий
. Группы (серии) для обследования отбирают в
случайном порядке или путем механической выборки как повторным, так и
бесповторными способами. Внутри каждой отобранной серии осуществляется сплошное
наблюдение. Предельные ошибки выборки
при
серийном отборе исчисляются по формулам:
а) при повторном отборе
б) при бесповторном отборе
где
– число
серий в генеральной совокупности;
– число
отобранных серий;
– межсерийная дисперсия, исчисляемая для случая равновеликих
серий по формуле:
где
–
среднее значение признака в каждой из отобранных серий;
– межсерийная
средняя, исчисляемая для случая равновеликих серий по формуле:
Определение численности выборочной совокупности
При проектировании
выборочного наблюдения важно наряду с организационными вопросами решить одну из
основных постановочных задач: какова должна быть необходимая численность
выборки с тем, чтобы с заданной степенью точности (вероятности) заранее
установленная ошибка выборки не была бы превзойдена.
Примеры решения задач
Задача 1
На основании результатов проведенного на заводе 5%
выборочного наблюдения (отбор случайный, бесповторный) получен следующий ряд
распределения рабочих по заработной плате:
| Группы рабочих по размеру заработной платы, тыс.р. | до 200 | 200-240 | 240-280 | 280-320 | 320 и выше | Итого |
| Число рабочих | 33 | 35 | 47 | 45 | 40 | 200 |
На основании приведенных данных определите:
1) с вероятностью 0,954 (t=2) возможные пределы, в которых
ожидается средняя заработная плата рабочего в целом по заводу (по генеральной
совокупности);
2) с вероятностью 0,997 (t=3) предельную ошибку и границы доли
рабочих с заработной платой от 320 тыс.руб. и выше.
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Вычислим среднюю з/п: Для этого просуммируем произведения середин
интервалов и соответствующих частот, и полученную сумму разделим на сумму
частот.
2) Выборочная дисперсия:
Найдем доверительный интервал для средней. Предельная ошибка выборочной
средней считается по формуле:
где
—
аргумент функции Лапласа.
Искомые возможные пределы, в которых ожидается средняя заработная плата
рабочего в целом по заводу:
Найдем доверительный интервал для выборочной доли. Предельная ошибка
выборочной доли считается по формуле:
Доля рабочих с з/п от 320 тыс.р.:
Искомые границы доли рабочих с заработной платой от 320 тыс.руб. и выше:
Задача 2
В
городе 23560 семей. В порядке механической выборки предполагается определить
количество семей в городе с числом детей трое и более. Какова должна быть
численность выборки, чтобы с вероятностью 0,954 ошибка выборки не превышала
0,02 человека. На основе предыдущих обследований известно, что дисперсия равна
0,3.
Решение
Численность
выборки можно найти по формуле:
В нашем случае:
Вывод к задаче
Таким образом численность
выборки должна составить 2661 чел.
Задача 3
С
целью определения средней месячной заработной платы персонала фирмы было
проведено 25%-ное выборочное обследование с отбором
единиц пропорционально численности типических групп. Для отбора сотрудников
внутри каждого филиала использовался механический отбор. Результаты
обследования представлены в следующей таблице:
| Номер филиала |
Средняя месячная заработная плата, руб. |
Среднее квадратическое отклонение, руб. |
Число сотрудников, чел. |
| 1 | 870 | 40 | 30 |
| 2 | 1040 | 160 | 80 |
| 3 | 1260 | 190 | 140 |
| 4 | 1530 | 215 | 190 |
С
вероятностью 0,954 определите пределы средней месячной заработной платы всех
сотрудников гостиниц.
Решение
Предельная
ошибка выборочной средней:
Средняя
из внутригрупповых дисперсий:
Получаем:
Средняя
месячная заработная плата по всей совокупности филиалов:
Искомые
пределы средней месячной заработной платы:
Вывод к задаче
Таким
образом с вероятностью 0,954 средняя месячная заработная плата всех сотрудников
гостиниц находится в пределах от 1294,3 руб. до 1325,7 руб.
11.2. Оценка результатов выборочного наблюдения
11.2.1. Средняя и предельная ошибки выборки. Построение доверительных границ для средней и доли
Средняя ошибка выборки показывает, насколько отклоняется в среднем параметр выборочной совокупности от соответствующего параметра генеральной. Если рассчитать среднюю из ошибок всех возможных выборок определенного вида заданного объема (n), извлеченных из одной и той же генеральной совокупности, то получим их обобщающую характеристику — среднюю ошибку выборки (
В теории выборочного наблюдения выведены формулы для определения 
Например, если применяется повторная собственно случайная выборка, то 


При бесповторном собственно случайном отборе в формулы вносится поправка (1 — n/N):


Вероятность получения именно такой величины ошибки всегда равна 0,683. На практике же предпочитают получать данные с большей вероятностью, но это приводит к возрастанию величины ошибки выборки.
Предельная ошибка выборки (

Если ошибку выборки увеличить в два раза (t = 2), то получим гораздо большую вероятность того, что она не превысит определенного предела (в нашем случае — двойной средней ошибки) — 0,954. Если взять t = 3, то доверительная вероятность составит 0,997 — практически достоверность.
Уровень предельной ошибки выборки зависит от следующих факторов:
- степени вариации единиц генеральной совокупности;
- объема выборки;
- выбранных схем отбора (бесповторный отбор дает меньшую величину ошибки);
- уровня доверительной вероятности.
Если объем выборки больше 30, то значение t определяется по таблице нормального распределения, если меньше — по таблице распределения Стьюдента.
Приведем некоторые значения коэффициента доверия из таблицы нормального распределения.
| Значение доверительной вероятности P | 0,683 | 0,954 | 0,997 |
|---|---|---|---|
| Значение коэффициента доверия t | 1,0 | 2,0 | 3,0 |
Доверительный интервал для среднего значения признака и для доли в генеральной совокупности устанавливается следующим образом:
Итак, определение границ генеральной средней и доли состоит из следующих этапов:
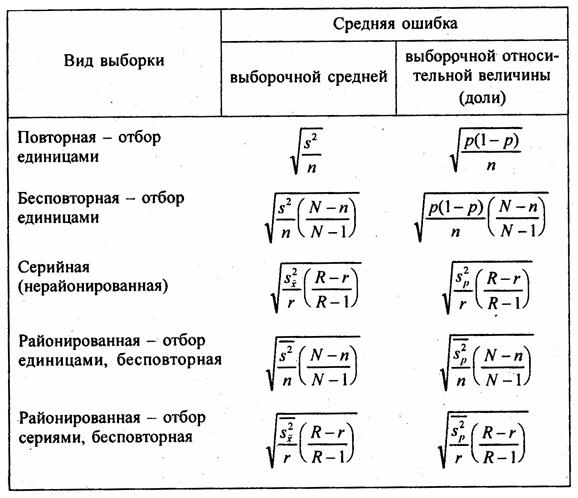
Ошибки выборки при различных видах отбора
- Собственно случайная и механическая выборка. Средняя ошибка собственно случайной и механической выборки находятся по формулам, представленным в табл. 11.3.
 |
|
где |
Пример 11.2. Для изучения уровня фондоотдачи было проведено выборочное обследование 90 предприятий из 225 методом случайной повторной выборки, в результате которого получены данные, представленные в таблице.
| Уровень фондоотдачи, руб. | До 1,4 | 1,4-1,6 | 1,6-1,8 | 1,8-2,0 | 2,0-2,2 | 2,2 и выше | Итого |
|---|---|---|---|---|---|---|---|
| Количество предприятий | 13 | 15 | 17 | 15 | 16 | 14 | 90 |
В рассматриваемом примере имеем 40%-ную выборку (90 : 225 = 0,4, или 40%). Определим ее предельную ошибку и границы для среднего значения признака в генеральной совокупности по шагам алгоритма:
- По результатам выборочного обследования рассчитаем среднее значение и дисперсию в выборочной совокупности:
| Результаты наблюдения | Расчетные значения | |||
|---|---|---|---|---|
| уровень фондоотдачи, руб., xi | количество предприятий, fi | середина интервала, xi\xb4 | xi\xb4fi | xi\xb42fi |
| До 1,4 | 13 | 1,3 | 16,9 | 21,97 |
| 1,4-1,6 | 15 | 1,5 | 22,5 | 33,75 |
| 1,6-1,8 | 17 | 1,7 | 28,9 | 49,13 |
| 1,8-2,0 | 15 | 1,9 | 28,5 | 54,15 |
| 2,0-2,2 | 16 | 2,1 | 33,6 | 70,56 |
| 2,2 и выше | 14 | 2,3 | 32,2 | 74,06 |
| Итого | 90 | — | 162,6 | 303,62 |
Выборочная средняя
Выборочная дисперсия изучаемого признака
- Определяем среднюю ошибку повторной случайной выборки
- Зададим вероятность, на уровне которой будем говорить о величине предельной ошибки выборки. Чаще всего она принимается равной 0,999; 0,997; 0,954.
Для наших данных определим предельную ошибку выборки, например, с вероятностью 0,954. По таблице значений вероятности функции нормального распределения (см. выдержку из нее, приведенную в Приложении 1) находим величину коэффициента доверия t, соответствующего вероятности 0,954. При вероятности 0,954 коэффициент t равен 2.
- Предельная ошибка выборки с вероятностью 0,954 равна
- Найдем доверительные границы для среднего значения уровня фондоотдачи в генеральной совокупности
Таким образом, в 954 случаях из 1000 среднее значение фондоотдачи будет не выше 1,88 руб. и не ниже 1,74 руб.
Выше была использована повторная схема случайного отбора. Посмотрим, изменятся ли результаты обследования, если предположить, что отбор осуществлялся по схеме бесповторного отбора. В этом случае расчет средней ошибки проводится по формуле
Тогда при вероятности равной 0,954 величина предельной ошибки выборки составит:
Доверительные границы для среднего значения признака при бесповторном случайном отборе будут иметь следующие значения:
Сравнив результаты двух схем отбора, можно сделать вывод о том, что применение бесповторной случайной выборки дает более точные результаты по сравнению с применением повторного отбора при одной и той же доверительной вероятности. При этом, чем больше объем выборки, тем существеннее сужаются границы значений средней при переходе от одной схемы отбора к другой.
По данным примера определим, в каких границах находится доля предприятий с уровнем фондоотдачи, не превышающим значения 2,0 руб., в генеральной совокупности:
- рассчитаем выборочную долю.
Количество предприятий в выборке с уровнем фондоотдачи, не превышающим значения 2,0 руб., составляет 60 единиц. Тогда
m = 60, n = 90, w = m/n = 60 : 90 = 0,667;
- рассчитаем дисперсию доли в выборочной совокупности

- средняя ошибка выборки при использовании повторной схемы отбора составит
Если предположить, что была использована бесповторная схема отбора, то средняя ошибка выборки с учетом поправки на конечность совокупности составит
- зададим доверительную вероятность и определим предельную ошибку выборки.
При значении вероятности Р = 0,997 по таблице нормального распределения получаем значение для коэффициента доверия t = 3 (см. выдержку из нее, приведенную в Приложении 1):
- установим границы для генеральной доли с вероятностью 0,997:
Таким образом, с вероятностью 0,997 можно утверждать, что в генеральной совокупности доля предприятий с уровнем фондоотдачи, не превышающим значения 2,0 руб., не меньше, чем 54,7%, и не больше 78,7%.
- Типическая выборка. При типической выборке генеральная совокупность объектов разбита на k групп, тогда
N1 + N2 + … + Ni + … + Nk = N.
Объем извлекаемых из каждой типической группы единиц зависит от принятого способа отбора; их общее количество образует необходимый объем выборки
n1 + n2 + … + ni + … + nk = n.
Существуют следующие два способа организации отбора внутри типической группы: пропорциональной объему типических групп и пропорциональной степени колеблемости значений признака у единиц наблюдения в группах. Рассмотрим первый из них, как наиболее часто используемый.
Отбор, пропорциональный объему типических групп, предполагает, что в каждой из них будет отобрано следующее число единиц совокупности:
n = ni · Ni/N
где ni — количество извлекаемых единиц для выборки из i-й типической группы;
n — общий объем выборки;
Ni — количество единиц генеральной совокупности, составивших i-ю типическую группу;
N — общее количество единиц генеральной совокупности.
Отбор единиц внутри групп происходит в виде случайной или механической выборки.
Формулы для оценивания средней ошибки выборки для среднего и доли представлены в табл. 11.6.

|
Здесь 
Пример 11.3. В одном из московских вузов проведено выборочное обследование студентов с целью определения показателя средней посещаемости вузовской библиотеки одним студентом за семестр. Для этого была использована 5%-ная бесповторная типическая выборка, типические группы которой соответствуют номеру курса. При отборе, пропорциональном объему типических групп, получены следующие данные:
| Номер курса | Всего студентов, чел., Ni | Обследовано в результате выборочного наблюдения, чел., ni | Среднее число посещений библиотеки одним студентом за семестр, xi | Внутригрупповая выборочная дисперсия, 
|
|---|---|---|---|---|
| 1 | 650 | 33 | 11 | 6 |
| 2 | 610 | 31 | 8 | 15 |
| 3 | 580 | 29 | 5 | 18 |
| 4 | 360 | 18 | 6 | 24 |
| 5 | 350 | 17 | 10 | 12 |
| Итого | 2 550 | 128 | 8 | — |
Число студентов, которое необходимо обследовать на каждом курсе, рассчитаем следующим образом:
- общий объем выборочной совокупности:
n = 2550/130*5 =128 (чел.);
- количество единиц, отобранных из каждой типической группы:
аналогично для других групп:
n2 = 31 (чел.);
n3 = 29 (чел.);
n4 = 18 (чел.);
n5 = 17 (чел.).
Проведем необходимые расчеты.
- Выборочная средняя, исходя из значений средних типических групп, составит:
- Средняя из внутригрупповых дисперсий
- Средняя ошибка выборки:
С вероятностью 0,954 находим предельную ошибку выборки:
- Доверительные границы для среднего значения признака в генеральной совокупности:
Таким образом, с вероятностью 0,954 можно утверждать, что один студент за семестр посещает вузовскую библиотеку в среднем от семи до девяти раз.
- Малая выборка. В связи с небольшим объемом выборочной совокупности те формулы для определения ошибок выборки, которые использовались нами ранее при «больших» выборках, становятся неподходящими и требуют корректировки.
Среднюю ошибку малой выборки определяют по формуле
Предельная ошибка малой выборки:
Распределение значений выборочных средних всегда имеет нормальный закон распределения (или приближается к нему) при п > 100, независимо от характера распределения генеральной совокупности. Однако в случае малых выборок действует иной закон распределения — распределение Стьюдента. В этом случае коэффициент доверия находится по таблице t-распределения Стьюдента в зависимости от величины доверительной вероятности Р и объема выборки п. В Приложении 1 приводится фрагмент таблицы t-распределения Стьюдента, представленной в виде зависимости доверительной вероятности от объема выборки и коэффициента доверия t.
Пример 11.4. Предположим, что выборочное обследование восьми студентов академии показало, что на подготовку к контрольной работе по статистике они затратили следующее количество часов: 8,5; 8,0; 7,8; 9,0; 7,2; 6,2; 8,4; 6,6.
Оценим выборочные средние затраты времени и построим доверительный интервал для среднего значения признака в генеральной совокупности, приняв доверительную вероятность равной 0,95.
- Среднее значение признака в выборке равно
- Значение среднего квадратического отклонения составляет
- Средняя ошибка выборки:
- Значение коэффициента доверия t = 2,365 для п = 8 и Р = 0,95 .
- Предельная ошибка выборки:
- Доверительный интервал для среднего значения признака в генеральной совокупности:
То есть с вероятностью 0,95 можно утверждать, что затраты времени студента на подготовку к контрольной работе находятся в пределах от 6,9 до 8,5 ч.
11.2.2. Определение численности выборочной совокупности
Перед непосредственным проведением выборочного наблюдения всегда решается вопрос, сколько единиц исследуемой совокупности необходимо отобрать для обследования. Формулы для определения численности выборки выводят из формул предельных ошибок выборки в соответствии со следующими исходными положениями (табл. 11.7):
- вид предполагаемой выборки;
- способ отбора (повторный или бесповторный);
- выбор оцениваемого параметра (среднего значения признака или доли).
Кроме того, следует заранее определиться со значением доверительной вероятности, устраивающей потребителя информации, и с размером допустимой предельной ошибки выборки.
 |
Примечание: при использовании приведенных в таблице формул рекомендуется получаемую численность выборки округлять в большую сторону для обеспечения некоторого запаса в точности.
Пример 11.5. Рассчитаем, сколько из 507 промышленных предприятий следует проверить налоговой инспекции, чтобы с вероятностью 0,997 определить долю предприятий с нарушениями в уплате налогов. По данным прошлого аналогичного обследования величина среднего квадратического отклонения составила 0,15; размер ошибки выборки предполагается получить не выше, чем 0,05.
При использовании повторного случайного отбора следует проверить
При бесповторном случайном отборе потребуется проверить
Как видим, использование бесповторного отбора позволяет проводить обследование гораздо меньшего числа объектов.
Пример 11.6. Планируется провести обследование заработной платы на предприятиях отрасли методом случайного бесповторного отбора. Какова должна быть численность выборочной совокупности, если на момент обследования в отрасли число занятых составляло 100 000 чел.? Предельная ошибка выборки не должна превышать 100 руб. с вероятностью 0,954. По результатам предыдущих обследований заработной платы в отрасли известно, что среднее квадратическое отклонение составляет 500 руб.
Следовательно, для решения поставленной задачи необходимо включить в выборку не менее 100 человек.
11.2. Оценка результатов выборочного наблюдения
11.2.1. Средняя и предельная ошибки выборки. Построение доверительных границ для средней и доли
Средняя ошибка выборки показывает, насколько отклоняется в среднем параметр выборочной совокупности от соответствующего параметра генеральной. Если рассчитать среднюю из ошибок всех возможных выборок определенного вида заданного объема (n), извлеченных из одной и той же генеральной совокупности, то получим их обобщающую характеристику — среднюю ошибку выборки (
В теории выборочного наблюдения выведены формулы для определения 
Например, если применяется повторная собственно случайная выборка, то 


При бесповторном собственно случайном отборе в формулы вносится поправка (1 — n/N):


Вероятность получения именно такой величины ошибки всегда равна 0,683. На практике же предпочитают получать данные с большей вероятностью, но это приводит к возрастанию величины ошибки выборки.
Предельная ошибка выборки (

Если ошибку выборки увеличить в два раза (t = 2), то получим гораздо большую вероятность того, что она не превысит определенного предела (в нашем случае — двойной средней ошибки) — 0,954. Если взять t = 3, то доверительная вероятность составит 0,997 — практически достоверность.
Уровень предельной ошибки выборки зависит от следующих факторов:
- степени вариации единиц генеральной совокупности;
- объема выборки;
- выбранных схем отбора (бесповторный отбор дает меньшую величину ошибки);
- уровня доверительной вероятности.
Если объем выборки больше 30, то значение t определяется по таблице нормального распределения, если меньше — по таблице распределения Стьюдента.
Приведем некоторые значения коэффициента доверия из таблицы нормального распределения.
Таблица
11.2.
| Значение доверительной вероятности P | 0,683 | 0,954 | 0,997 |
|---|---|---|---|
| Значение коэффициента доверия t | 1,0 | 2,0 | 3,0 |
Доверительный интервал для среднего значения признака и для доли в генеральной совокупности устанавливается следующим образом:
Итак, определение границ генеральной средней и доли состоит из следующих этапов:
Ошибки выборки при различных видах отбора
- Собственно случайная и механическая выборка. Средняя ошибка собственно случайной и механической выборки находятся по формулам, представленным в табл. 11.3.
Таблица
11.3.
Формулы для расчета средней ошибки собственно случайной и механической выборки (
 |
|
где |
Пример 11.2. Для изучения уровня фондоотдачи было проведено выборочное обследование 90 предприятий из 225 методом случайной повторной выборки, в результате которого получены данные, представленные в таблице.
Таблица
11.4.
| Уровень фондоотдачи, руб. | До 1,4 | 1,4-1,6 | 1,6-1,8 | 1,8-2,0 | 2,0-2,2 | 2,2 и выше | Итого |
|---|---|---|---|---|---|---|---|
| Количество предприятий | 13 | 15 | 17 | 15 | 16 | 14 | 90 |
В рассматриваемом примере имеем 40%-ную выборку (90 : 225 = 0,4, или 40%). Определим ее предельную ошибку и границы для среднего значения признака в генеральной совокупности по шагам алгоритма:
- По результатам выборочного обследования рассчитаем среднее значение и дисперсию в выборочной совокупности:
Таблица
11.5.
| Результаты наблюдения | Расчетные значения | |||
|---|---|---|---|---|
| уровень фондоотдачи, руб., xi | количество предприятий, fi | середина интервала, xixb4 | xixb4fi | xixb42fi |
| До 1,4 | 13 | 1,3 | 16,9 | 21,97 |
| 1,4-1,6 | 15 | 1,5 | 22,5 | 33,75 |
| 1,6-1,8 | 17 | 1,7 | 28,9 | 49,13 |
| 1,8-2,0 | 15 | 1,9 | 28,5 | 54,15 |
| 2,0-2,2 | 16 | 2,1 | 33,6 | 70,56 |
| 2,2 и выше | 14 | 2,3 | 32,2 | 74,06 |
| Итого | 90 | — | 162,6 | 303,62 |
Выборочная средняя
Выборочная дисперсия изучаемого признака
- Определяем среднюю ошибку повторной случайной выборки
- Зададим вероятность, на уровне которой будем говорить о величине предельной ошибки выборки. Чаще всего она принимается равной 0,999; 0,997; 0,954.
Для наших данных определим предельную ошибку выборки, например, с вероятностью 0,954. По таблице значений вероятности функции нормального распределения (см. выдержку из нее, приведенную в Приложении 1) находим величину коэффициента доверия t, соответствующего вероятности 0,954. При вероятности 0,954 коэффициент t равен 2.
- Предельная ошибка выборки с вероятностью 0,954 равна
- Найдем доверительные границы для среднего значения уровня фондоотдачи в генеральной совокупности
Таким образом, в 954 случаях из 1000 среднее значение фондоотдачи будет не выше 1,88 руб. и не ниже 1,74 руб.
Выше была использована повторная схема случайного отбора. Посмотрим, изменятся ли результаты обследования, если предположить, что отбор осуществлялся по схеме бесповторного отбора. В этом случае расчет средней ошибки проводится по формуле
Тогда при вероятности равной 0,954 величина предельной ошибки выборки составит:
Доверительные границы для среднего значения признака при бесповторном случайном отборе будут иметь следующие значения:
Сравнив результаты двух схем отбора, можно сделать вывод о том, что применение бесповторной случайной выборки дает более точные результаты по сравнению с применением повторного отбора при одной и той же доверительной вероятности. При этом, чем больше объем выборки, тем существеннее сужаются границы значений средней при переходе от одной схемы отбора к другой.
По данным примера определим, в каких границах находится доля предприятий с уровнем фондоотдачи, не превышающим значения 2,0 руб., в генеральной совокупности:
- рассчитаем выборочную долю.
Количество предприятий в выборке с уровнем фондоотдачи, не превышающим значения 2,0 руб., составляет 60 единиц. Тогда
m = 60, n = 90, w = m/n = 60 : 90 = 0,667;
- рассчитаем дисперсию доли в выборочной совокупности

- средняя ошибка выборки при использовании повторной схемы отбора составит
Если предположить, что была использована бесповторная схема отбора, то средняя ошибка выборки с учетом поправки на конечность совокупности составит
- зададим доверительную вероятность и определим предельную ошибку выборки.
При значении вероятности Р = 0,997 по таблице нормального распределения получаем значение для коэффициента доверия t = 3 (см. выдержку из нее, приведенную в Приложении 1):
- установим границы для генеральной доли с вероятностью 0,997:
Таким образом, с вероятностью 0,997 можно утверждать, что в генеральной совокупности доля предприятий с уровнем фондоотдачи, не превышающим значения 2,0 руб., не меньше, чем 54,7%, и не больше 78,7%.
- Типическая выборка. При типической выборке генеральная совокупность объектов разбита на k групп, тогда
N1 + N2 + … + Ni + … + Nk = N.
Объем извлекаемых из каждой типической группы единиц зависит от принятого способа отбора; их общее количество образует необходимый объем выборки
n1 + n2 + … + ni + … + nk = n.
Существуют следующие два способа организации отбора внутри типической группы: пропорциональной объему типических групп и пропорциональной степени колеблемости значений признака у единиц наблюдения в группах. Рассмотрим первый из них, как наиболее часто используемый.
Отбор, пропорциональный объему типических групп, предполагает, что в каждой из них будет отобрано следующее число единиц совокупности:
n = ni · Ni/N
где ni — количество извлекаемых единиц для выборки из i-й типической группы;
n — общий объем выборки;
Ni — количество единиц генеральной совокупности, составивших i-ю типическую группу;
N — общее количество единиц генеральной совокупности.
Отбор единиц внутри групп происходит в виде случайной или механической выборки.
Формулы для оценивания средней ошибки выборки для среднего и доли представлены в табл. 11.6.
Таблица
11.6.
Формулы для расчета средней ошибки выборки (

Здесь 
Пример 11.3. В одном из московских вузов проведено выборочное обследование студентов с целью определения показателя средней посещаемости вузовской библиотеки одним студентом за семестр. Для этого была использована 5%-ная бесповторная типическая выборка, типические группы которой соответствуют номеру курса. При отборе, пропорциональном объему типических групп, получены следующие данные:
Таблица
11.7.
| Номер курса | Всего студентов, чел., Ni | Обследовано в результате выборочного наблюдения, чел., ni | Среднее число посещений библиотеки одним студентом за семестр, xi | Внутригрупповая выборочная дисперсия,  |
|---|---|---|---|---|
| 1 | 650 | 33 | 11 | 6 |
| 2 | 610 | 31 | 8 | 15 |
| 3 | 580 | 29 | 5 | 18 |
| 4 | 360 | 18 | 6 | 24 |
| 5 | 350 | 17 | 10 | 12 |
| Итого | 2 550 | 128 | 8 | — |
Число студентов, которое необходимо обследовать на каждом курсе, рассчитаем следующим образом:
- общий объем выборочной совокупности:
n = 2550/130*5 =128 (чел.);
- количество единиц, отобранных из каждой типической группы:
аналогично для других групп:
n2 = 31 (чел.);
n3 = 29 (чел.);
n4 = 18 (чел.);
n5 = 17 (чел.).
Проведем необходимые расчеты.
- Выборочная средняя, исходя из значений средних типических групп, составит:
- Средняя из внутригрупповых дисперсий
- Средняя ошибка выборки:
С вероятностью 0,954 находим предельную ошибку выборки:
- Доверительные границы для среднего значения признака в генеральной совокупности:
Таким образом, с вероятностью 0,954 можно утверждать, что один студент за семестр посещает вузовскую библиотеку в среднем от семи до девяти раз.
- Малая выборка. В связи с небольшим объемом выборочной совокупности те формулы для определения ошибок выборки, которые использовались нами ранее при «больших» выборках, становятся неподходящими и требуют корректировки.
Среднюю ошибку малой выборки определяют по формуле
Предельная ошибка малой выборки:
Распределение значений выборочных средних всегда имеет нормальный закон распределения (или приближается к нему) при п > 100, независимо от характера распределения генеральной совокупности. Однако в случае малых выборок действует иной закон распределения — распределение Стьюдента. В этом случае коэффициент доверия находится по таблице t-распределения Стьюдента в зависимости от величины доверительной вероятности Р и объема выборки п. В Приложении 1 приводится фрагмент таблицы t-распределения Стьюдента, представленной в виде зависимости доверительной вероятности от объема выборки и коэффициента доверия t.
Пример 11.4. Предположим, что выборочное обследование восьми студентов академии показало, что на подготовку к контрольной работе по статистике они затратили следующее количество часов: 8,5; 8,0; 7,8; 9,0; 7,2; 6,2; 8,4; 6,6.
Оценим выборочные средние затраты времени и построим доверительный интервал для среднего значения признака в генеральной совокупности, приняв доверительную вероятность равной 0,95.
- Среднее значение признака в выборке равно
- Значение среднего квадратического отклонения составляет
- Средняя ошибка выборки:
- Значение коэффициента доверия t = 2,365 для п = 8 и Р = 0,95 .
- Предельная ошибка выборки:
- Доверительный интервал для среднего значения признака в генеральной совокупности:
То есть с вероятностью 0,95 можно утверждать, что затраты времени студента на подготовку к контрольной работе находятся в пределах от 6,9 до 8,5 ч.
11.2.2. Определение численности выборочной совокупности
Перед непосредственным проведением выборочного наблюдения всегда решается вопрос, сколько единиц исследуемой совокупности необходимо отобрать для обследования. Формулы для определения численности выборки выводят из формул предельных ошибок выборки в соответствии со следующими исходными положениями (табл. 11.7):
- вид предполагаемой выборки;
- способ отбора (повторный или бесповторный);
- выбор оцениваемого параметра (среднего значения признака или доли).
Кроме того, следует заранее определиться со значением доверительной вероятности, устраивающей потребителя информации, и с размером допустимой предельной ошибки выборки.
Таблица
11.8.
Формулы для определения численности выборочной совокупности

Примечание: при использовании приведенных в таблице формул рекомендуется получаемую численность выборки округлять в большую сторону для обеспечения некоторого запаса в точности.
Пример 11.5. Рассчитаем, сколько из 507 промышленных предприятий следует проверить налоговой инспекции, чтобы с вероятностью 0,997 определить долю предприятий с нарушениями в уплате налогов. По данным прошлого аналогичного обследования величина среднего квадратического отклонения составила 0,15; размер ошибки выборки предполагается получить не выше, чем 0,05.
При использовании повторного случайного отбора следует проверить
При бесповторном случайном отборе потребуется проверить
Как видим, использование бесповторного отбора позволяет проводить обследование гораздо меньшего числа объектов.
Пример 11.6. Планируется провести обследование заработной платы на предприятиях отрасли методом случайного бесповторного отбора. Какова должна быть численность выборочной совокупности, если на момент обследования в отрасли число занятых составляло 100 000 чел.? Предельная ошибка выборки не должна превышать 100 руб. с вероятностью 0,954. По результатам предыдущих обследований заработной платы в отрасли известно, что среднее квадратическое отклонение составляет 500 руб.
Следовательно, для решения поставленной задачи необходимо включить в выборку не менее 100 человек.
Калькулятор для расчета достаточного объема выборки
Калькулятор ошибки выборки для доли признака
Калькулятор ошибки выборки для среднего значения
Калькулятор значимости различий долей
Калькулятор значимости различий средних
1. Формула (даже две)
Бытует заблуждение, что чем больше объем генеральной совокупности, тем больше должен быть объем выборки маркетингового исследования. Это отчасти так, когда объем выборки сопоставим с размером генеральной совокупности. Например, при опросах организаций (B2B).
Если речь идет об исследовании жителей городов, то не важно, Москва это или Рязань – оптимальный объем выборки будет одинаков в обоих городах. Этот принцип следует из закона больших чисел и применим, только если выборка простая случайная.
На рис.1. пример выборки 15000 человек (!) при опросе в муниципальном районе. Возможно, от численности населения взяли 10%?
Размер выборки никогда не рассчитывается как процент от генеральной совокупности!
Рис.1. Размер выборки 15000 человек, как реальный пример некомпетентности (или хуже).
В таких случаях для расчета объема выборки используется следующая формула:

где
n – объем выборки,
Z – коэффициент, зависящий от выбранного исследователем доверительного уровня,
p – доля респондентов с наличием исследуемого признака,
q = 1 – p – доля респондентов, у которых исследуемый признак отсутствует,
∆ – предельная ошибка выборки.
Доверительный уровень – это вероятность того, что реальная доля лежит в границах полученного доверительного интервала: выборочная доля (p) ± ошибка выборки (Δ). Доверительный уровень устанавливает сам исследователь в соответствии со своими требованиями к надежности полученных результатов. Чаще всего применяются доверительные уровни, равные 0,95 или 0,99. В маркетинговых исследованиях, как правило, выбирается доверительный уровень, равный 0,95. При этом уровне коэффициент Z равен 1,96.
Значения p и q чаще всего неизвестны до проведения исследования и принимаются за 0,5. При этом значении размер ошибки выборки максимален.
Допустимая предельная ошибка выборки выбирается исследователем в зависимости от целей исследования. Считается, что для принятия бизнес-решений ошибка выборки должна быть не больше 4%. Этому значению соответствует объем выборки 500-600 респондентов. Для важных стратегических решений целесообразно минимизировать ошибку выборки.
Рассмотрим кривую зависимости ошибки выборки от ее объема (Рис.2).

Рис.2. Зависимость ошибки выборки от ее объема при 95% доверительном уровне
Как видно из диаграммы, с ростом объема выборки значение ошибки уменьшается все медленнее. Так, при объеме выборки 1500 человек предельная ошибка выборки составит ±2,5%, а при объеме 2000 человек – ±2,2%. То есть, при определенном объеме выборки дальнейшее его увеличение не дает значительного выигрыша в ее точности.
ШПАРГАЛКА (скопируйте ссылку или текст)
Подходы к решению проблемы:
Случай 1. Генеральная совокупность значительно больше выборки:

Случай 2. Генеральная совокупность сопоставима с объемом выборки: (см. раздел исследований B2B)

где
n – объем выборки,
N – объем генеральной совокупности,
Z – коэффициент, зависящий от выбранного исследователем доверительного уровня,
p – доля респондентов с наличием исследуемого признака,
q = 1 – p – доля респондентов, у которых исследуемый признак отсутствует, (значения p и q обычно принимаются за 0,5, поскольку точно неизвестны до проведения исследования)
∆ – предельная ошибка выборки.
Например,
рассчитаем ошибку выборки объемом 1000 человек при 95% доверительном уровне, если генеральная совокупность значительно больше объема выборки:
Ошибка выборки = 1,96 * КОРЕНЬ(0,5*0,5/1000) = 0,031 = ±3,1%
При расчете объема выборки следует также учитывать стоимость проведения исследования. Например, при цене за 1 анкету 200 рублей стоимость опроса 1000 человек составит 200 000 рублей, а опрос 1500 человек будет стоить 300 000 рублей. Увеличение затрат в полтора раза сократит ошибку выборки всего на 0,6%, что обычно неоправданно экономически.
2. Причины «раздувать» выборку
Анализ полученных данных обычно включает в себя и анализ подвыборок, объемы которых меньше основной выборки. Поэтому ошибка для выводов по подвыборкам больше, чем ошибка по выборке в целом. Если планируется анализ подгрупп / сегментов, объем выборки должен быть увеличен (в разумных пределах).
Рис.3 демонстрирует данную ситуацию. Если для исследования авиапассажиров используется выборка численностью 500 человек, то для выводов по выборке в целом ошибка составляет 4,4%, что вполне приемлемо для принятия бизнес-решений. Но при делении выборки на подгруппы в зависимости от цели поездки, выводы по каждой подгруппе уже недостаточно точны. Если мы захотим узнать какие-либо количественные характеристики группы пассажиров, совершающих бизнес-поездку и покупавших билет самостоятельно, ошибка полученных показателей будет достаточно велика. Даже увеличение выборки до 2000 человек не обеспечит приемлемой точности выводов по этой подвыборке.

Рис.3. Проектирование объема выборки с учетом необходимости анализа подвыборок
Другой пример – анализ подгрупп потребителей услуг торгово-развлекательного центра (Рис.4).

Рис.4. Потенциальный спрос на услуги торгово-развлекательного центра
При объеме выборки в 1000 человек выводы по каждой отдельной услуге (например, социально-демографический профиль, частота пользования, средний чек и др.) будут недостаточно точными для использования в бизнес планировании. Особенно это касается наименее популярных услуг (Таблица 1).
Таблица 1. Ошибка по подвыборкам потенциальных потребителей услуг торгово-развлекательного центра при выборке 1000 чел.

Чтобы ошибка в самой малочисленной подвыборке «Ночной клуб» составила меньше 5%, объем выборки исследования должен составлять около 4000 человек. Но это будет означать 4-кратное удорожание проекта. В таких случаях возможно компромиссное решение:
- увеличение выборки до 1800 человек, что даст достаточную точность для 6 самых популярных видов услуг (от кинотеатра до парка аттракционов);
- добор 200-300 пользователей менее популярных услуг с опросом по укороченной анкете (см. Таблицу 2).
Таблица 2. Разница в ошибке выборки по подвыборкам при разных объемах выборки.

При обсуждении с исследовательским агентством точности результатов планируемого исследования рекомендуется принимать во внимание бюджет, требования к точности результатов в целом по выборке и в разрезе подгрупп. Если бюджет не позволяет получить информацию с приемлемой ошибкой, лучше пока отложить проект (или поторговаться).
КАЛЬКУЛЯТОРЫ ДЛЯ РАСЧЕТА СТАТИСТИЧЕСКИХ ПОКАЗАТЕЛЕЙ И ОПРЕДЕЛЕНИЯ ЗНАЧИМОСТИ РАЗЛИЧИЙ:
КАЛЬКУЛЯТОР ДЛЯ РАСЧЕТА
ДОСТАТОЧНОГО ОБЪЁМА ВЫБОРКИ
Доверительный уровень:
Ошибка выборки (?):
%
Объём генеральной совокупности (N):
(можно пропустить, если больше 100 000)
РЕЗУЛЬТАТ
Один из важных вопросов, на которые нужно ответить при планировании исследования, — это оптимальный объем выборки. Слишком маленькая выборка не сможет обеспечить приемлемую точность результатов опроса, а слишком большая приведет к лишним расходам.
Онлайн-калькулятор объема выборки поможет рассчитать оптимальный размер выборки, исходя из максимально приемлемого для исследователя размера ошибки выборки.
Все дальнейшие формулы и расчеты относятся только к простой случайной выборке!
Формулы для других типов выборки отличаются.
Объем выборки рассчитывается по следующим формулам
1) если объем выборки значительно меньше генеральной совокупности:

2) если объем выборки сопоставим с объемом генеральной совокупности:

В приведенных формулах:
Z – коэффициент, зависящий от выбранного исследователем доверительного уровня. Доверительный уровень (или доверительная вероятность) – это вероятность того, что реальное значение измеряемого показателя (по всей генеральной совокупности) находится в пределах доверительного интервала, полученного в исследовании. Доверительный уровень выбирает сам исследователь, исходя из требований к надежности результатов исследования. В маркетинговых исследованиях обычно применяется 95%-й доверительный уровень. Ему соответствует значение Z = 1,96.
N – объем генеральной совокупности. Генеральная совокупность – это все люди, которые изучаются в исследовании (например, все покупатели соков и нектаров, постоянно проживающие в Москве и Московской области). Если генеральная совокупность значительно больше объема выборки (в сотни и более раз), ее размером можно пренебречь (формула 1).
p – доля респондентов с наличием исследуемого признака. Например, если 20% опрошенных заинтересованы в новом продукте, то p = 0,2.
q = 1 — p – доля респондентов, у которых исследуемый признак отсутствует. Значения p и q обычно принимаются за 0,5, поскольку точно неизвестны до проведения исследования. При этом значении размер ошибки выборки максимален. В данном калькуляторе значения p и q по умолчанию равны 0,5.
Δ– предельная ошибка выборки (для доли признака), приемлемая для исследователя. Считается, что для принятия бизнес-решений ошибка выборки не должна превышать 4%.
n – объем выборки. Объем выборки – это количество людей, которые опрашиваются в исследовании.
ПРИМЕР РАСЧЕТА ОБЪЕМА ВЫБОРКИ:
Допустим, мы хотим рассчитать объем выборки, предельная ошибка которой составит 4%. Мы принимаем доверительный уровень, равный 95%. Генеральная совокупность значительно больше выборки. Тогда объем выборки составит:
n = 1,96 * 1,96 * 0,5 * 0,5 / (0,04 * 0,04) = 600,25 ≈ 600 человек
Таким образом, если мы хотим получить результаты с предельной ошибкой 4%, нам нужно опросить 600 человек.
КАЛЬКУЛЯТОР ОШИБКИ ВЫБОРКИ ДЛЯ ДОЛИ ПРИЗНАКА
Доверительный уровень:
Объём выборки (n):
Объём генеральной совокупности (N):
(можно пропустить, если больше 100 000)
Доля признака (p):
%
РЕЗУЛЬТАТ
Зная объем выборки исследования, можно рассчитать значение ошибки выборки (или, другими словами, погрешность выборки).
Если бы в ходе исследования мы могли опросить абсолютно всех интересующих нас людей, мы могли бы быть на 100% уверены в полученном результате. Но ввиду экономической нецелесообразности сплошного опроса применяют выборочный подход, когда опрашивается только часть генеральной совокупности. Выборочный метод не гарантирует 100%-й точности измерения, но, тем не менее, вероятность ошибки может быть сведена к приемлемому минимуму.
Все дальнейшие формулы и расчеты относятся только к простой случайной выборке! Формулы для других типов выборки отличаются.
Ошибка выборки для доли признака рассчитывается по следующим формулам.
1) если объем выборки значительно меньше генеральной совокупности:
(в данной формуле не используется показатель объема генеральной совокупности N)
2) если объем выборки сопоставим с объемом генеральной совокупности:

В приведенных формулах:
Z – коэффициент, зависящий от выбранного исследователем доверительного уровня. Доверительный уровень (или доверительная вероятность) – это вероятность того, что реальное значение измеряемого показателя (по всей генеральной совокупности) находится в пределах доверительного интервала, полученного в исследовании. Доверительный уровень выбирает сам исследователь, исходя из требований к надежности результатов исследования. В маркетинговых исследованиях обычно применяется 95%-й доверительный уровень. Ему соответствует значение Z = 1,96.
N – объем генеральной совокупности. Генеральная совокупность – это все люди, которые изучаются в исследовании (например, все покупатели шоколада, постоянно проживающие в Москве). Если генеральная совокупность значительно больше объема выборки (в сотни и более раз), ее размером можно пренебречь (формула 1).
n – объем выборки. Объем выборки – это количество людей, которые опрашиваются в исследовании. Существует заблуждение, что чем больше объем генеральной совокупности, тем больше должен быть и объем выборки маркетингового исследования. Это отчасти так, когда объем выборки сопоставим с объемом генеральной совокупности. Например, при опросах организаций (B2B). Если же речь идет об исследовании жителей городов, то не важно, Москва это или Рязань – оптимальный объем выборки будет одинаков в обоих городах. Этот принцип следует из закона больших чисел и применим, только если выборка простая случайная. ВАЖНО: если предполагается сравнивать какие-то группы внутри города, например, жителей разных районов, то выборку следует рассчитывать для каждой такой группы.
p – доля респондентов с наличием исследуемого признака. Например, если 20% опрошенных заинтересованы в новом продукте, то p = 0,2.
q = 1 — p – доля респондентов, у которых исследуемый признак отсутствует. Значения p и q обычно принимаются за 0,5, поскольку точно неизвестны до проведения исследования. При этом значении размер ошибки выборки максимален.
Δ– предельная ошибка выборки.
Таким образом, зная объем выборки исследования, мы можем заранее оценить показатель ее ошибки.
А получив значение p, мы можем рассчитать доверительный интервал для доли признака: (p — ∆; p + ∆)
ПРИМЕР РАСЧЕТА ОШИБКИ ВЫБОРКИ ДЛЯ ДОЛИ ПРИЗНАКА:
Например, в ходе исследования были опрошены 1000 человек (n=1000). 20% из них заинтересовались новым продуктом (p=0,2). Рассчитаем показатель ошибки выборки по формуле 1 (выберем доверительный уровень, равный 95%):
∆ = 1,96 * КОРЕНЬ (0,2*0,8/1000) = 0,0248 = ±2,48%
Рассчитаем доверительный интервал:
(p — ∆; p + ∆) = (20% — 2,48%; 20% + 2,48%) = (17,52%; 22,48%)
Таким образом, с вероятностью 95% мы можем быть уверены, что реальная доля заинтересованных в новом продукте (среди всей генеральной совокупности) находится в пределах полученного диапазона (17,52%; 22,48%).
Если бы мы выбрали доверительный уровень, равный 99%, то для тех же значений p и n ошибка выборки была бы больше, а доверительный интервал – шире. Это логично, поскольку, если мы хотим быть более уверены в том, что наш доверительный интервал «накроет» реальное значение признака, то интервал должен быть более широким.
КАЛЬКУЛЯТОР ОШИБКИ ВЫБОРКИ ДЛЯ СРЕДНЕГО ЗНАЧЕНИЯ
Доверительный уровень:
Объём выборки (n):
Объём генеральной совокупности (N):
(можно пропустить, если больше 100 000)
Среднее значение (x̄):
Стандартное отклонение (s):
РЕЗУЛЬТАТ
Зная объем выборки исследования, можно рассчитать значение ошибки выборки (или, другими словами, погрешность выборки).
Если бы в ходе исследования мы могли опросить абсолютно всех интересующих нас людей, мы могли бы быть на 100% уверены в полученном результате. Но ввиду экономической нецелесообразности сплошного опроса применяют выборочный подход, когда опрашивается только часть генеральной совокупности. Выборочный метод не гарантирует 100%-й точности измерения, но, тем не менее, вероятность ошибки может быть сведена к приемлемому минимуму.
Все дальнейшие формулы и расчеты относятся только к простой случайной выборке! Формулы для других типов выборки отличаются.
Ошибка выборки для среднего значения рассчитывается по следующим формулам.
1) если объем выборки значительно меньше генеральной совокупности:

(в данной формуле не используется показатель объема генеральной совокупности N)
2) если объем выборки сопоставим с объемом генеральной совокупности:

В приведенных формулах:
Z – коэффициент, зависящий от выбранного исследователем доверительного уровня. Доверительный уровень (или доверительная вероятность) – это вероятность того, что реальное значение измеряемого показателя (по всей генеральной совокупности) находится в пределах доверительного интервала, полученного в исследовании. Доверительный уровень выбирает сам исследователь, исходя из требований к надежности результатов исследования. В маркетинговых исследованиях обычно применяется 95%-й доверительный уровень. Ему соответствует значение Z = 1,96
N – объем генеральной совокупности. Генеральная совокупность – это все люди, которые изучаются в исследовании (например, все покупатели мороженого, постоянно проживающие в Москве). Если генеральная совокупность значительно больше объема выборки (в сотни и более раз), ее размером можно пренебречь (формула 1).
n – объем выборки. Объем выборки – это количество людей, которые опрашиваются в исследовании. Существует заблуждение, что чем больше объем генеральной совокупности, тем больше должен быть и объем выборки маркетингового исследования. Это отчасти так, когда объем выборки сопоставим с объемом генеральной совокупности. Например, при опросах организаций (B2B). Если же речь идет об исследовании жителей городов, то не важно, Москва это или Рязань – оптимальный объем выборки будет одинаков в обоих городах. Этот принцип следует из закона больших чисел и применим, только если выборка простая случайная. ВАЖНО: если предполагается сравнивать какие-то группы внутри города, например, жителей разных районов, то выборку следует рассчитывать для каждой такой группы.
s — выборочное стандартное отклонение измеряемого показателя. В идеале на месте этого аргумента должно быть стандартное отклонение показателя в генеральной совокупности (σ), но так как обычно оно неизвестно, используется выборочное стандартное отклонение, рассчитываемое по следующей формуле:
где, x ̅ – среднее арифметическое показателя, xi– значение i-го показателя, n – объем выборки
Δ– предельная ошибка выборки.
Зная среднее значение показателя x ̅ и ошибку ∆, мы можем рассчитать доверительный интервал для среднего значения:(x ̅ — ∆; x ̅ + ∆)
ПРИМЕР РАСЧЕТА ОШИБКИ ВЫБОРКИ ДЛЯ СРЕДНЕГО ЗНАЧЕНИЯ:
Например, в ходе исследования были опрошены 1000 человек (n=1000). Каждого из них попросили указать их примерную среднюю сумму покупки (средний чек) в известной сети магазинов. Среднее арифметическое всех ответов составило 500 руб. (x ̅=500), а стандартное отклонение составило 120 руб. (s=120). Рассчитаем показатель ошибки выборки по формуле 1 (выберем доверительный уровень, равный 95%):
∆ = 1,96 * 120 / КОРЕНЬ (1000) = 7,44
Рассчитаем доверительный интервал:
(x ̅ — ∆; x ̅ + ∆) = (500 – 7,44; 500 + 7,44) = (492,56; 507,44)
Таким образом, с вероятностью 95% мы можем быть уверены, что значение среднего чека по всей генеральной совокупности находится в границах полученного диапазона: от 492,56 руб. до 507,44 руб.
КАЛЬКУЛЯТОР ЗНАЧИМОСТИ РАЗЛИЧИЙ ДОЛЕЙ
Доверительный уровень:
| Измерение 1 | Измерение 2 | |
| Доля признака (p): | % | % |
| Объём выборки (n): |
РЕЗУЛЬТАТ
Если в прошлогоднем исследовании вашу марку вспомнили 10% респондентов, а в исследовании текущего года – 15%, не спешите открывать шампанское, пока не воспользуетесь нашим онлайн-калькулятором для оценки статистической значимости различий.
Сравнивая два разных значения, полученные на двух независимых выборках, исследователь должен убедиться, что различия статистически значимы, прежде чем делать выводы.
Как известно, выборочные исследования не обеспечивают 100%-й точности измерения (для этого пришлось бы опрашивать всю целевую аудиторию поголовно, что слишком дорого). Тем не менее, благодаря методам математической статистики, мы можем оценить точность результатов любого количественного исследования и учесть ее в выводах.
В приведенном здесь калькуляторе используется двухвыборочный z-тест для долей. Для его применения должны соблюдаться следующие условия:
- Обе выборки – простые случайные
- Выборки независимы (между значениями двух выборок нет закономерной связи)
- Генеральные совокупности значительно больше выборок
- Произведения n*p и n*(1-p), где n=размер выборки а p=доля признака, – не меньше 5.
В калькуляторе используются следующие вводные данные:
Доверительный уровень (или доверительная вероятность) – это вероятность того, что реальное значение измеряемого показателя (по всей генеральной совокупности) находится в пределах доверительного интервала, полученного в исследовании. Доверительный уровень выбирает сам исследователь, исходя из требований к надежности результатов исследования. В маркетинговых исследованиях обычно применяется 95%-й доверительный уровень.
Доля признака (p) – доля респондентов с наличием исследуемого признака. Например, если 20% опрошенных заинтересованы в новом продукте, то p = 0,2.
Объем выборки (n) – это количество людей, которые опрашиваются в исследовании.
Результат расчетов – вывод о статистической значимости или незначимости различий двух измерений.
КАЛЬКУЛЯТОР ЗНАЧИМОСТИ РАЗЛИЧИЙ СРЕДНИХ
Доверительный уровень:
| Измерение 1 | Измерение 2 | |
| Среднее значение (x̄): | ||
| Стандартное отклонение (s): | ||
| Объём выборки (n): |
РЕЗУЛЬТАТ
Допустим, выборочный опрос посетителей двух разных ТРЦ показал, что средний чек в одном из них равен 1000 рублей, а в другом – 1200 рублей. Следует ли отсюда вывод, что суммы среднего чека в двух этих ТРЦ действительно отличаются?
Сравнивая два разных значения, полученные на двух независимых выборках, исследователь должен убедиться, что различия статистически значимы, прежде чем делать выводы.
Как известно, выборочные исследования не обеспечивают 100%-й точности измерения (для этого пришлось бы опрашивать всю целевую аудиторию поголовно, что слишком дорого). Тем не менее, благодаря методам математической статистики, мы можем оценить точность результатов любого количественного исследования и учесть ее в выводах.
В приведенном здесь калькуляторе используется двухвыборочный z-тест для средних значений. Для его применения должны соблюдаться следующие условия:
- Обе выборки – простые случайные
- Выборки независимы (между значениями двух выборок нет закономерной связи)
- Генеральные совокупности значительно больше выборок
- Распределения значений в выборках близки к нормальному распределению.
В калькуляторе используются следующие вводные данные:
Доверительный уровень (или доверительная вероятность) – это вероятность того, что реальное значение измеряемого показателя (по всей генеральной совокупности) находится в пределах доверительного интервала, полученного в исследовании. Доверительный уровень выбирает сам исследователь, исходя из требований к надежности результатов исследования. В маркетинговых исследованиях обычно применяется 95%-й доверительный уровень.
Среднее значение ( ̅x) – среднее арифметическое показателя.
Стандартное отклонение (s) – выборочное стандартное отклонение измеряемого показателя. В идеале на месте этого аргумента должно быть стандартное отклонение показателя в генеральной совокупности (σ), но так как обычно оно неизвестно, используется выборочное стандартное отклонение, рассчитываемое по следующей формуле:
где, x ̅ – среднее арифметическое показателя, xi– значение i-го показателя, n – объем выборки
Объем выборки (n) – это количество людей, которые опрашиваются в исследовании.
Результат расчетов – вывод о статистической значимости или незначимости различий двух измерений.
Вы можете подписаться на уведомления о новых материалах СканМаркет
7.4. Влияние вида выборки на величину ошибки выборки
Как указывалось в п. 7.2, при проведении выборочного наблюдения используются различные способы формирования выборочной совокупности: случайный отбор — повторный или бесповторный, механический, серийный, типический. Вид выборки влияет на величину ошибки выборки. При бесповторном отборе формула средней ошибки выборки дополняется множителем
который корректирует величину ошибки выборки и в связи с изменением состава совокупности и вероятности попадания единиц в выборку. В серийной выборке дисперсия определяется как колеблемость между сериями:
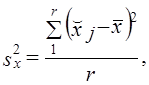
где x̌j — среднее значение признака х в у-й серии;
х̅ — среднее значение в целом по выборке;
r — число отобранных серий.
Формула (7.14) предполагает равенство серий по числу единиц, если это условие не выполняется, то в числитель выражения (7.14) вводится вес — число единиц в j-й серии, fj; тогда в знаменателе указывается не r, а 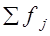
При типическом отборе (стратифицированная или районированная выборка) дисперсия рассчитывается как средняя из внутрирайонных дисперсий:
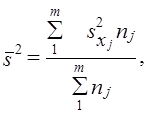
где s2ji — выборочная дисперсия признака х в j-м районе;
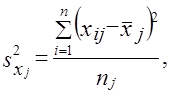
где пj — объем выборки в j-м районе;
т — число районов.
Очевидно, что по правилу сложения дисперсий величина s2 меньше, чем величина общей дисперсии.
Величина ошибки районированной выборки меньше величины ошибки простой (нерайонированной выборки).
Часто используется сочетание районированного отбора с отбором сериями. Такой вид выборки обеспечивает преимущества в организации выборки и уменьшение ошибки выборки. Дисперсия такой выборки представляет среднюю из межсерийных дисперсий для каждого j-го района:
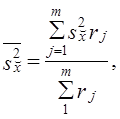
где s2x̌j — межсерийная дисперсия в j-м районе;
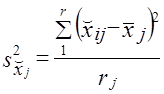
х̌ij — средняя в i-й серии j-го района;
х̅j — средняя ву-м районе;
r— число серий, отобранных в j-м районе;
т — число районов.
Табл. 7.2 содержит формулы средней ошибки выборки для выборочной средней и выборочной относительной величины для разных видов выборки. В приведенных формулах требуют пояснения выражения дисперсий выборочной относительной величины.
При нерайонированной серийной выборке
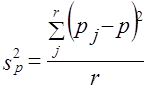
где рj — доля единиц определенной категории в у-й серии;
р — доля единиц этой категории в выборке.
Таблица 7.2
Формулы средней ошибки выборочной средней и выборочной относительной величины
Рассмотрим на примере влияние вида выборки на величину ошибки выборки. Исходные данные представлены в табл. 7.3.
Таблица 7.3
Показатели 60 предприятий легкой промышленности Санкт-Петербурга (по данным статистической отчетности за I полугодие 1995 г.)
|
№ пп |
Форма Собственнос-ти |
Оборачиваемость запасов, х1 |
Коэффициент покрытия, х2 |
№ пп |
Форма собственности |
Оборачиваемость запасов, х1 |
Коэффициент покрытия, х2 |
|
1 |
государственная |
5,65 |
0,22 |
31 |
Частная |
1,23 |
1,18 |
|
2 |
« |
2,86 |
0,35 |
32 |
« |
0,82 |
1,59 |
|
3 |
« |
1,61 |
1,06 |
33 |
« |
2,83 |
0,74 |
|
4 |
« |
3,99 |
1,01 |
34 |
« |
1,83 |
1,52 |
|
5 |
« |
2,17 |
8,88 |
35 |
« |
2,26 |
2,43 |
|
6 |
« |
1,52 |
1,06 |
36 |
« |
2,33 |
3,28 |
|
7 |
« |
0,40 |
0,99 |
37 |
« |
2,35 |
1,13 |
|
8 |
« |
2,18 |
1,07 |
38 |
« |
1,68 |
0,89 |
|
9 |
« |
1,36 |
4,62 |
39 |
« |
2,00 |
1,67 |
|
10 |
« |
3,69 |
1,40 |
40 |
« |
2,64 |
1,48 |
|
11 |
частная |
0,45 |
1,34 |
41 |
« |
2,75 |
1,51 |
|
12 |
« |
1,0 |
1,16 |
42 |
« |
3,29 |
5,96 |
|
13 |
« |
2,05 |
2,00 |
43 |
« |
1,6 |
1,38 |
|
14 |
« |
2,36 |
1,43 |
44 |
« |
1,90 |
2,39 |
|
15 |
« |
4,90 |
1,76 |
45 |
« |
3,27 |
3,62 |
|
16 |
« |
3,12 |
1,26 |
46 |
« |
3,49 |
0,46 |
|
17 |
« |
1,36 |
1,89 |
47 |
« |
2,92 |
1,26 |
|
18 |
« |
1,56 |
12,36 |
48 |
смешання |
3,22 |
0,78 |
|
19 |
« |
4,84 |
1,23 |
49 |
« |
2,61 |
1,67 |
|
20 |
« |
1,23 |
3,26 |
50 |
« |
5,17 |
0,95 |
|
21 |
« |
0,81 |
2,22 |
51 |
« |
8,63 |
0,96 |
|
22 |
« |
0,7 |
1,16 |
52 |
« |
1,06 |
2,51 |
|
23 |
« |
0,87 |
1,21 |
53 |
« |
2,13 |
3,49 |
|
24 |
« |
0,20 |
1,45 |
54 |
« |
2,03 |
1,22 |
|
25 |
« |
1,71 |
4,04 |
55 |
« |
1,82 |
2,92 |
|
26 |
« |
1,83 |
2,07 |
56 |
« |
3,12 |
1,54 |
|
27 |
« |
1,32 |
0,69 |
57 |
« |
0,77 |
0,97 |
|
28 |
« |
1,95 |
1,97 |
58 |
« |
4,15 |
0,93 |
|
29 |
« |
1,46 |
1,31 |
59 |
« |
3,62 |
1,34 |
|
30 |
« |
2,96 |
5,32 |
60 |
« |
3,89 |
3,51 |
Предприятия легкой промышленности примем за генеральную совокупность. Ее характеристики:
численность N = 60;
генеральные средние: μ1 = 2,40 число оборотов;
μ2 = 1,424;
генеральные дисперсии: σ21 = 2,24;
σ22 = 4,38;
средние квадратические σ1 = 1,49 оборотов;
отклонения: σ2 = 2,09.
Остановимся на смысле характеристик предприятий: оборачиваемость запасов рассчитывается делением продолжительности периода (полгода) на среднюю продолжительность одного периода оборота запасов. Очевидно, чем скорее оборачиваются запасы, тем выше их отдача. Коэффициент покрытия рассчитывается как отношение суммы всех источников покрытия запасов к стоимости запасов. Если значение этого показателя меньше единицы, то текущее финансовое состояние предприятия рассматривается как неустойчивое. В нашем примере вариация этого признака примерно в 2 раза превосходит вариацию предприятий по уровню оборачиваемости запасов: ν2 = 147%, ν1 = 62%.
Произведем 30%-ную выборку. Объем выборки составит п = 20 предприятий. При формировании выборки методом механического отбора каждое третье предприятие попадет в выборку. Отбор начинаем с полушага отбора, т. е. первым предприятием, попавшим в выборку, является второе по списку. Средние по выборке равны:
оборачиваемость запасов x̅1 =2,16 оборотов, коэффициент покрытия x̅2=2,01.
Средняя ошибка выборочной средней оборачиваемости запасов
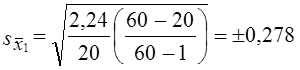
Средняя ошибка выборочного среднего коэффициента покрытия
С вероятностью 0,954 можно утверждать, что средняя оборачиваемость запасов на предприятиях легкой промышленности не ниже
x̅1 — 2sx1 = 2,16 — 0,55 = 1,61 оборотов и не выше x̅1+2sx1 = 2,16 + 0,55 = 2,71 оборотов.
Действительно генеральная средняя (μ1 = 2,40) попадает в этот интервал.
Фактическая ошибка репрезентативности
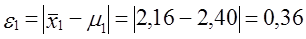
Эта величина меньше предельной ошибки выборки, гарантированной с принятой доверительной вероятностью, 0,36 < 0,55. Следовательно, выборка репрезентативна по этому признаку.
Вычислим предельную ошибку выборки коэффициента покрытия и определим доверительный интервал для этой характеристики. Его нижняя граница с той же вероятностью
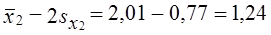
верхняя граница:
Генеральная средняя (μ2 = 1,424) так же попадает в доверительный интервал.
Фактическая ошибка репрезентативности составляет:
Эта величина меньше предельной ошибки выборки (0,77), что дает основание считать выборку репрезентативной и по этому признаку.
В генеральной совокупности доля единиц с неустойчивым финансовым положением (х2 < 1) составила 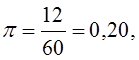
Доверительный интервал для оценки доли таких предприятий в генеральной совокупности составляет с вероятностью 0,954:
0,15 ± 0,076,
т. е. таких предприятий должно быть не меньше 7,4% и не больше 22,6%. Фактически их оказалось 20% от общего числа предприятии, т. е. выборка дает репрезентативный результат и по этому показателю.
Выполненная выборка формировалась как простая бесповторная механическая. Однако, наверняка статистик будет стремиться учесть структуру генеральной совокупности, поэтому более естественной была бы выборка, учитывающая выделение предприятий разных форм собственности. Тогда выборка должна быть районированной.
Рассмотрим пример. Генеральная совокупность состоит из 11 государственных предприятий, 36 частных, 13 смешанных. В выборке эти пропорции соблюдаются следующим образом: отобраны по 4 предприятия государственных и смешанных и 12 — частных:
|
Предприятия |
Генеральные характеристики |
Выборочные характеристики |
||
|
средние |
доли |
средние |
доли |
|
|
Государственные |
μ1 = 2.35 |
π1 = 0,27 |
х̅1 = 1,92 |
Р1 = 0,25 |
|
Частные |
μ1 =2,11 |
π2 = 0,11 |
х̅1 = 1,79 |
Р2=0,08 |
|
Смешанные |
μ1 =3,25 |
π3 = 0,38 |
х̅1 =3,51 |
Рз — 0,25 |
Средняя из внутрирайонных дисперсий, рассчитанных по каждой группе предприятий в генеральной совокупности:
Эта величина меньше общей дисперсии без учета районирования (σ2 = 2,24). Следовательно, и величина ошибки выборки при районированном отборе будет меньше:
Итак, с вероятностью 0,954 генеральная средняя оборачиваемости запасов находится в интервале 2,16 ± 0,294; 1,866 £ μ £ 2,454.
Чтобы понять, насколько целесообразно в том или ином случае применение районированного отбора, можно воспользоваться корреляционным отношением ц. Согласно правилу сложения дисперсий средняя из внутригрупповых дисперсий может быть представлена как
где h2 — квадрат корреляционного отношения, равный б2:s2.
Следовательно, применение районированной (типической) выборки изменяет предельную ошибку на 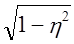
Сопоставим полученный результат с изменением предельной ошибки выборки: 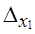
∆x (при районировании) = 0,294, т. е. ошибка уменьшилась примерно вполовину.
Корреляционное отношение используется и при корректировке величины
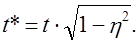
Тогда при вероятности 0,954 и t = 2; t*=2 — Ö0̅,8̅6̅ = 1,85, т. е. вместо t = 2 достаточно взять t = 1,85.
Многие выборки формируются как многоступенчатые. Ошибка многоступенчатой выборки может быть представлена как
Она складывается из ошибок отдельных ступеней. Поэтому практически используется не больше 2-3 ступеней отбора.
Средняя ошибка выборки при двухступенчатом отборе рассчитывается по формуле
где sx1 2 — дисперсия признака х по совокупности «крупных» единиц;
sx22 — дисперсия признака х в каждой из отобранных «крупных» единиц;
пi — число отобранных единиц наблюдения в <-й «крупной» единице;
т — число отобранных «крупных» единиц.
Таким образом, применение многоступенчатой выборки улучшает организацию выборки, но увеличивает ее ошибку.
Кроме рассмотренных, применяется многофазовая выборка, когда одни сведения собираются на основе изучения всех единиц выборки, а другие — только на основании изучения некоторых из этих единиц, отобранных так, что они составляют подвыборки из единиц первоначальной выборки.
При периодическом повторении выборочных обследований с целью изучения динамики явлений применяются либо независимые выборки — через определенные промежутки времени отбор каждый раз производится независимо от предыдущих выборок; либо фиксированные выборки — в этом случае повторные обследования проводятся по одной и той же выборке. В связи с тем, что в фиксированной выборке могут происходить изменения (прежде всего за счет выбытия единиц) практикуют периодическую адаптацию фиксированной выборки происходящим изменениям. Чаще для целей изучения динамики используется промежуточный вариант — ротационная выборка (частичное замещение). При этом нужно следовать определенному плану замещения, например, каждый раз замещать четверть выборки, тогда каждая первоначальная единица останется в выборке в четырех следующих друг за другом обследованиях.
Названные виды выборок ориентированы на отбор конкретных материальных явлений. Кроме них следует назвать как особый вид выборки метод моментных наблюдений.Сущность метода моментных наблюдений состоит в периодической фиксации состояний .наблюдаемых единиц в отобранные моменты времени. Расчет объема такой выборки дает количество моментов. Этот вид выборочного наблюдения применяется при изучении использования производственного оборудования, либо рабочего времени (см. п. 7.13).
7.5. Задачи, решаемые при применении выборочного метода
При применении выборочного наблюдения возникают три основные задачи:
• определение объема выборки, необходимого для получения требуемой точности результатов с заданной вероятностью;
• определение возможного предела ошибки репрезентативности, гарантированного с заданной вероятностью, и сравнение его с величиной допустимой погрешности.
• определение вероятности того, что Ошибка выборки не превысит допустимой погрешности.
Все эти задачи решаются на основе теоремы Чебышева, согласно которой Р {[ х — μ | < e } ³ 1 — h, когда п — достаточно большое число; e и h — сколь угодно малые положительные числа. Это соотношение, как было показано в п. 7.3, может быть выражено через формулу предельной ошибки выборки ∆x = tsx или ∆p = ts. Решение указанных задач зависит от того, какие величины в формуле предельной ошибки заданы, а какие нужно найти.
Объем выборки рассчитывается на стадии проектирования выборочного обследования. Так как
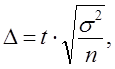
то

где ∆ — допустимая погрешность,, которая задается исследователем исходя из требуемой точности результатов проектируемой выборки;
t — табличная величина, соответствующая заданной доверительной вероятности F(t), с которой будут гарантированы оценки генеральной совокупности по данным выборочного обследования;
σ2 — генеральная дисперсия.
Последняя величина, как правило, неизвестна. Используются какие-либо ее оценки: результаты прошлых обследований той же совокупности, если ее структура и условия развития достаточно стабильны, или же зная примерную величину средней, находят дисперсию из соотношения 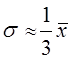
если известны xmax и хmin, то можно определить среднее квадратическое отклонение в соответствии с правилом «трех сигм»
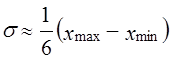
так как в нормальном распределении в размахе вариации «укладывается» 6σ(±3σ). Если распределение заведомо асимметричное, то
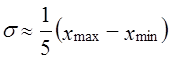
Для относительной величины принимают максимальную величину дисперсии σ2max = 0,5∙0,5 = 0,25.
При расчете п не следует гнаться за большими значениями t и малыми значениями ∆, так как это приведет к увеличению объема выборки, а следовательно, к увеличению затрат средств, труда и времени, вовсе не являющемуся необходимым.
Формула (7.20) не учитывает бесповторности отбора и дает максимальную величину выборки, которую можно скорректировать «на бесповторность». Так как
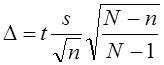
то на основе (7.20) получаем выражение скорректированного объема выборки (п):
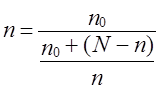
где
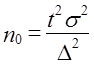
При больших размерах генеральной совокупности скорректированный Объем выборки незначительно отличается от n0.
Например, для изучения структуры и стоимости покупок в универмаге из 10 000 покупателей следует отобрать определенное число человек, которое бы обеспечивало с вероятностью 0,95 определение средней стоимости покупок с точностью не менее 2 тыс. руб. Дисперсию примем по прошлому обследованию равной 625.
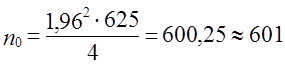
тогда скорректированная численность
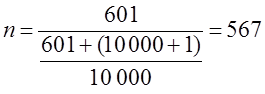
При проектировании районированной выборки рассчитанный объем выборки распределяют пропорционально численности районов (пропорциональный отбор):
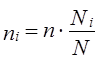
где пi — объем выборки для i-го района;
Ni — объем i-го района в генеральной совокупности;
п — общий объем выборки;
N — общий объем генеральной совокупности.
При различиях в однородности выделенных районов лучшие результаты дает распределение запланированного объема выборки между районами не только с учетом их объема, но и с учетом дисперсии признака (оптимальный отбор). В этом случае объем выборки в i-м районе определяется как
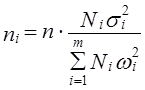
где σ2i — дисперсия признака х в i-м районе.
При любом виде проектируемой выборки расчет объема выборки начинают по формуле повторного отбора (7.20). Если в результате расчета п доля отбора превысит 5%, проводят второй вариант расчета по формуле бесповторного отбора, либо по формуле (7.21), либо как
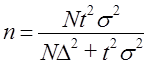
Если доля отбора меньше 5%, к формуле бесповторного отбора не переходят, так как это не скажется существенно на величине п.
Выборка должна быть такой, чтобы выборочные показатели по всем основным характеристикам были репрезентативны. Поэтому численность выборки рассчитывают многократно исходя из допустимых ошибок разных показателей, значения которых в генеральной совокупности известны.
Например, при выборочном учете детей школьного возраста требуется определить число семей, которые надо обследовать. При этом надо учесть: а) число детей в возрасте 6-7 лет, б) число детей в возрасте 6-15 лет; в) число детей в возрасте 16-17 лет;
г) среднедушевой доход (например, для решения вопроса о строительстве базы отдыха).
Так как репрезентируемые признаки могут иметь разную размерность, то допустимая погрешность для каждого их них задается в виде относительной величины (∆ : х̅) (например, планируется, что в определении среднего размера семьи ошибка должна быть не больше 2%, в определении дохода — не больше 3% и т.д.). В этом случае вместо дисперсии в формуле (7.20) берется квадрат коэффициента вариации.
Вычислив значение п, на основе каждой из характеристик получаем разные объемы выборки: 1200; 300; 700; 100. Обследовать необходимо 1200 семей, т.е. из рассчитанных численностей берется максимальная. При резких различиях необходимых объемов выборки для разных вопросов программы проводится многофазный отбор. В рассмотренном примере среднедушевой доход достаточно учитывать в одной из каждых 12 семей, попавших в выборку.
Многофазный отбор, как правило, довольно сложно организовать, может быть нарушен принцип случайности отбора. Поэтому для обеспечения репрезентативности оказывается выгоднее затратить больше средств на учет большего числа единиц совокупности. Многофазный отбор целесообразно применять, если соотношение между рассчитанными объемами выборки по крайней мере 1:6.
Поскольку расчет необходимой численности выборки основан не на точных, а на предположительных данных о колеблемости в совокупности, следует соблюдать следующие рекомендации: абсолютную величину п округлять только вверх; долю отбора округлять только вниз, т.е. из предосторожности планировать несколько больший объем выборки, чем показывают расчеты.
Объем многоступенчатой выборки рекомендуется увеличить не менее чем на 10% от рассчитанной численности, поскольку, как было показано в предыдущем параграфе, многоступенчатость отбора увеличивает ошибку выборки.
После проведения выборки рассчитывают возможные ошибки . выборочных показателей (ошибки репрезентативности), которые используются для оценки результатов выборки и для получения характеристик генеральной совокупности.
Пример. На электроламповом заводе взято для проверки 100 ламп. Средняя продолжительность их горения оказалась 1420 ч со средним квадратическим отклонением 61,03 ч. Поскольку приемщика продукции интересует качество всей партии (50 тыс. электроламп), оценивают точность полученной средней. Средняя возможная ошибка вычисленной выборочной средней
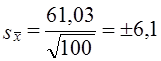
С вероятностью 0,954 предел возможной ошибки
∆х = 2∙6,1 = ± 12,2 ч.
С вероятностью 0,954 можно утверждать, что средняя продолжительность горения 1 электролампы во всей партии будет находиться в пределах от 1408 до 1432 ч; 46 электроламп из 1000 могут иметь срок горения, выходящий за эти пределы.
Приемщика продукции интересуют отклонения от вычисленных пределов только в сторону сокращения продолжительности горения. Меньше чем 1408 ч могут гореть 23 лампы из 1000. На основании этого приемщик продукции решает вопрос о годности всей партии электроламп.
Решение вопроса может быть уточнено: определим, у какой доли ламп срок службы окажется меньше установленного лимита. Для потребителя продукции таким лимитом являются 1410 ч, продукция с меньшим сроком горения неприемлема.
При контрольной проверке 100 ламп 100 ламп горели менее 1410 ч, их удельный вес р = 0,1, или 10%. Средняя возможная ошибка этой доли
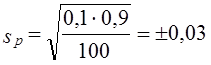
С вероятностью 0,954 предел ошибки доли Д^ = 2 • 0,03 = ± 0,06, или ±6%. Следовательно, во всей партии можно ожидать от 4 до 16% некачественных электроламп.
Чаще всего делают заключение об удовлетворительности выборки, сопоставляя получившиеся пределы ошибок выборочных показателей с величинами допустимых погрешностей. Может получиться, что предел ошибки, рассчитанный с заданной вероятностью, окажется выше допустимого размера погрешности. В этих случаях определяют вероятность того, что ошибка выборки не превзойдет допускаемую погрешность. Решение этой задачи и заключается в отыскании Fft) на основе формулы предела ошибки выборки:
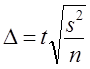
где ∆ — допустимый размер погрешности оцениваемого показателя;
s2 — дисперсия показателя, рассчитанная по данным выборочного наблюдения;
п — объем проведенной выборки.
Продолжим пример с оценкой качества электроламп. Если при приемке партии электроламп ставится условие, что минимальный срок горения электроламп 1410 ч, то, учитывая среднюю продолжительность горения по выборке (х= 1420 ч), допустимая погрешность равна 10 ч: 1410 — 1420 = — 10 ч.
Как было установлено выше, с вероятностью 0,954 предел возможной ошибки выборочной средней составил 12,2 ч, что превосходит допустимую погрешность. Является ли это основанием для браковки всей партии? Для ответа на этот вопрос определяют вероятность риска при приемке продукции:
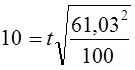
Соответствующая доверительная вероятность 0,899 (см. приложение, табл. 1). Вероятность того, что средний срок горения лампы меньше 1410 ч, равна:
Следовательно, из 100 ламп 5 могут гореть менее 1410 ч — риск появления некачественной продукции достаточно высок.
Аналогично можно определить вероятность того, что предел ошибки доли не превысит допускаемую погрешность доли.
Оценки надежности выборочных показателей, как показано на примере, позволяют принять обоснованные решения в отношении генеральной совокупности.
7.6. Распространение данных выборочного наблюдения на генеральную совокупность
Конечной целью выборочного наблюдения является характеристика генеральной совокупности на основе данных, полученных по выборке. При этом исходят из того, что все средние и относительные показатели, полученные по выборке, являются несмещенными и эффективными характеристиками генеральной совокупности.
Выборочные средние и относительные величины распространяются на генеральную совокупность обязательно с учетом предела их возможной ошибки. Приводится выборочный показатель со справкой о пределах ошибки с указанием доверительной вероятности: x̅ ± ∆x, p ± ∆p. Или же указывают границы значений генеральной характеристики с определенной вероятностью F(t):
Последняя форма записи является основной.
Иногда требуется указать только один (верхний или нижний) предел характеристики генеральной совокупности. При испытании качества продукции часто нас не интересуют положительные ошибки выборки (качество фактически выше, чем получилось по выборке), беспокоит нижний предел, как в примере, рассмотренном в предыдущем параграфе. В некоторых случаях, напротив, интерес вызывают верхние границы оцениваемых показателей, например при анализе расхода материалов. Так что при характеристике генеральной совокупности всегда указывают неблагоприятный предел.
На основе выборки могут быть получены и значения объемных показателей, т. е. подсчетов для генеральной совокупности. Такой расчет осуществляется двумя способами: путем прямого расчета и способом коэффициентов. Прямой расчет заключается в том, что выборочная средняя или доля умножается на объем генеральной совокупности:
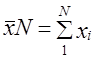
Так как средняя величина имеет ошибку репрезентативности ± А д то можно считать, что итоговый подсчет в генеральной совокупности находится в пределах
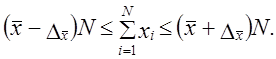
Итоговый подсчет по генеральной совокупности можно получить на основе итогового подсчета по выборке, разделив его на долю отбора единиц совокупности
Прежде чем проводить расчет объемных показателей для генеральной совокупности, нужно убедиться, что структура выборки соответствует структуре генеральной совокупности. При наличии значительных смещений в структуре выборки в долях отдельных групп (0,03 и выше) следует применить метод перевзвешивания, г. в. рассчитывать генеральную среднюю на основе выборочных средних по группам и удельного веса этих групп в генеральной совокупности:
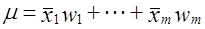
где wi = NiN.
При способе коэффициентов также используются не только выборочные данные, но и сведения о генеральной совокупности.
Этот способ основан на связи признаков друг с другом. Например, в результате выборочного обследования семей города получены размер среднедушевого дохода (х̅), средний доход семьи (у̅) и среднее число человек в семье (z̅). Так что x̅ = y̅ / z̅.
Зная численность населения города, требуется рассчитать общую величину денежного дохода населения. Очевидно, это можно сделать, умножив душевой доход на общее число жителей в городе: x̅N. Общий доход можно получить, суммируя доход отдельных семей; численность населения можно получить, суммируя данные о числе членов семей. Тогда
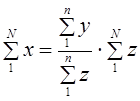
Средний душевой расход 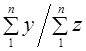
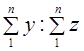
Следовательно,
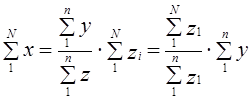
Последний сомножитель не что иное, как обратная величина доли отбора, рассчитанной по значениям признака z.
Итак, итоговый подсчет по генеральной совокупности может быть получен делением соответствующего итогового подсчета по выборке на долю отбора. При прямом расчете берется доля отбора единиц совокупности, при способе коэффициентов — доля отбора по значению какого-либо признака.
Эффективность способа коэффициентов по сравнению с методом прямого расчета зависит от того, насколько тесно связаны между собой признаки, лежащие в основе расчета коэффициента, т.е. признак, по которому подсчитывается итог, и признак, по которому определяется доля отбора. Эффект проявляется, если коэффициент корреляции между ними больше 0,8.
Способ коэффициентов используется для корректировки данных сплошного наблюдения. Например, перепись скота дала сведения, что поголовье свиней в районе составляет 10 000, в том числе в тех хозяйствах, которые потом были охвачены контрольным обходом, сплошное наблюдение показало число свиней 1100. Контрольный обход дал уточненную цифру: не 1100, а 1107 свиней. Тогда поправочный коэффициент
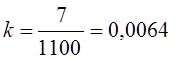
Отсюда скорректированная численность поголовья свиней во всем районе
N =N¢+∆N; ∆N = kN¢ = ∙10 000 = 64.
N = 10 000 + 64 = 10 064 голов.
Таблицы интеграла вероятностей используются для выборок большого объема из бесконечно большой генеральной совокупности. Но уже при п < \ 00 получается несоответствие между табличными данными и вероятностью предела; при п < 100 погрешность становится значительной. Несоответствие вызывается главным образом характером распределения единиц генеральной совокупности. При большом объеме выборки особенность распределения в генеральной совокупности не имеет значения, так как распределение отклонений выборочного показателя от генеральной характеристики при большой выборке всегда оказывается нормальным.
В выборках небольшого объема п £ 30 характер распределения генеральной совокупности сказывается на распределении ошибок выборки. Поэтому для расчета ошибки выборки при небольшом объеме наблюдения (уже менее 100 единиц) отбор должен проводиться из совокупности, имеющей нормальное распределение.
Теория малых выборок разработана английским статистиком В. Госсетом (писавшим под псевдонимом Стьюдент) в начале XX в. В 1908 г. им построено специальное распределение, которое позволяет и при малых выборках соотносить t и доверительную вероятность F(t). При п > 100 таблицы распределения Стьюдента дают те же результаты, что и таблицы интеграла вероятностей Лапласа, при 30 £ п £ 100 различия незначительны. Поэтому практически к малым выборкам относят выборки объемом менее 30 единиц (безусловно, большой считается выборка с объемом более 100 единиц).
Использование малых выборок в ряде случаев обусловлено характером обследуемой совокупности. Так, в селекционной работе «чистого» опыта легче добиться на небольшом числе делянок. Производственный и экономический эксперимент, связанный с экономическими затратами, также проводится на небольшом числе испытаний.
Как уже отмечалось, в случае малой выборки только для нормально распределенной генеральной совокупности могут быть рассчитаны и доверительные вероятности, и доверительные пределы генеральной средней.
Плотность вероятностей распределения Стьюдента описывается функцией
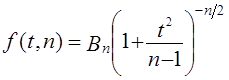
где t — текущая переменная;
п — объем выборки;
В — величина, зависящая лишь от п.
Распределение Стьюдента имеет только один параметр: d.f. —число степеней свободы (иногда обозначается k).
Это распределение, как и нормальное, симметрично относительно точки t = 0, но оно более пологое. При увеличении объема выборки, а следовательно, и числа степеней свободы распределение Стьюдента быстро приближается к нормальному. Число степеней свободы равно числу тех индивидуальных значений признаков, которыми нужно располагать для определения искомой характеристики.
Так, для расчета дисперсии должна быть известна средняя величина. Поэтому при расчете дисперсии d.f. = п — 1
Таблицы распределения Стьюдента публикуются в двух вариантах:
1) аналогично таблицам интеграла вероятностей приводятся значения t и соответствующие вероятности F(t) при разном числе степеней свободы;
2) значения t приводятся для наиболее употребимых доверительных вероятностей 0,90; 0,95 и 0,99 или для 1 — 0,9 = 0,1, 1 — 0,95 = = 0,05 и 1 — 0,99 == 0,01 при разном числе степеней свободы. Такого рода таблица приведена в приложении (табл. 2), а также значение t-критерия Стьюдента при уровне значимости 0,10; 0,05; 0,01.
При малых выборках расчет средней возможной ошибки основан на выборочных дисперсиях, поэтому
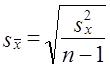
Приведенная формула используется для определения предела возможной ошибки выборочного показателя:
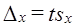
Порядок расчетов тот же, что и при больших выборках.
Пример. Для изучения интенсивности труда было организовано наблюдение за 10 отобранными рабочими. Доля работавших все время оказалась равной 0,40, дисперсия 0,4∙0,6 = 0,24. По табл. 2 приложения находим для F(t) = 0,95 и d.f. = n — 1 = 9, t = 2,26. Рассчитаем среднюю ошибку выборки доли работавших все время:
Тогда предельная ошибка выборки ∆p = 2,26∙0,16 = ± 0,36. Таким образом, с вероятностью 0,95 доля рабочих, работавших без простоев, в данном цехе предприятия находится в пределах
39,64% £ π £ 40,36%
или
39,6% £ π £ 40,4%.
Если бы мы использовали для расчета доверительных границ генерального параметра таблицу интеграла вероятностей, то t было бы равно 1,96 и ∆p — ± 0,31, т. е. доверительный интервал был бы несколько уже.
Малые выборки широко используются для решения задач, связанных с испытанием статистических гипотез, особенно гипотез о средних величинах.