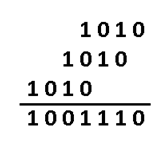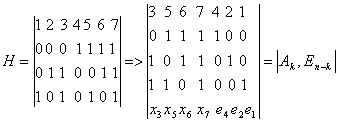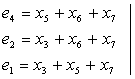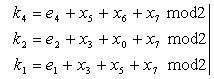При передаче информации
всегда существует некоторая вероятность
искажения кода. Поэтому необходимо
выявлять эти ситуации и исправлять
их. Наиболее простая задача — обнаружение
одиночной ошибки. При этом предполагается,
что наличие более одной ошибки в
сообщении маловероятно.
Для обнаружения одиночной
ошибки вводят дополнительный разряд,
в который заносят 0 или 1, чтобы число
единиц было четным или нечетным
(последнее предпочтительнее, т.к. в
этом случае отсутствует нулевой символ).
Например:
контроль по четности
— 10010010 1, 00000000 0;
контроль по
нечетности — 10010010 0, 00000000 1.
По сути дела, такая проверка
соответствует логической операции XOR
(см. выше). Т.е., например: 1011 XOR
1100 = 0111.
При приеме контрольный разряд
проверяется и при нарушении четности
(нечетности) байт бракуется. При
определении контрольного разряда
используют сложение по модулю «2».
При передаче блоков информации
можно формировать дополнительную строку
и заносить туда контрольную сумму
блока (или ее дополнение до кода FF — этот
метод называют проверкой контрольной
суммы). Контрольная сумма выделена
жирным шрифтом:
-
Исходное
сообщениеПолученное
сообщение01000110
1F
01000110
1F
01001001
1I
01000001
0A
01001100
1L
01001100
1L
01000101
1E
01000101
1E
00000110
000001110
1
Рис.4. Получение контрольной суммы
Если контрольные суммы не
совпадают при передаче и приеме файла,
то он бракуется. При определении
контрольной суммы выполняют сложение
каждого столбца по модулю «2». Проверка
по контрольным суммам (а не по каждому
байту) производится для экономии
машинных ресурсов, ведь гораздо проще
и быстрее сравнить одну пару байтов,
чем, например, 4 пары.
Код называется кодом с
исправлением ошибок, если всегда из
неправильного кодового набора можно
получить правильный. Главное для
исправления ошибок является то, что
необходимо иметь возможность обнаруживать
и выделять местоположение ошибочных
разрядов. Если местоположение ошибки
определено, то ее исправление производится
путем замены ошибочного разряда на его
инверсию. Код, в котором возможно
обнаружить и исправить ошибки, называют
помехозащищенным
или корректирующим.
Одним из первых корректирующих
кодов, для которого одиночная ошибка
не только обнаруживается, но и
исправляется, является код Хэмминга.
Рассмотрим основные принципы его
построения.
Пусть сообщение имеет m
информативных разрядов и k контрольных
разрядов p1p2…pk для проверки на четность.
Присвоим десятичное значение позиции
каждого из (m+k) разрядов кодового набора,
начиная со значения 1 для старшего
разряда и заканчивая значением (m+k) для
младшего. Контрольные разряды
размещаются в позициях:
N=1,2, …,2^(k-1).
(2)
Проведем проверку на четность
в k подгруппах кодового набора. Результат
каждой проверки на четность записывается
как 1 или 0 в зависимости от того, обнаружена
ошибка или нет. По результатам этих
проверок строится двоичное число ck…с1,
равное номеру ошибочного разряда (при
значении ноль ошибка отсутствует).
Код Хэмминга содержит
информативную часть из m разрядов и
контрольную из k разрядов. Получить код
Хэмминга — это сформировать контрольные
разряды и расставить их в нужные позиции.
Минимальное
кодовое расстояние (число несовпадающих
разрядов) для кода Хэмминга = 3, т.е. в
любых двух кодовых наборах одинаковой
длины не может быть меньше трех
несовпадающих разрядов (см. рис.5).
Чтобы
в код из k разрядов можно было записать
значение для (m+k) позиций, должно
выполняться условие
2^k>=m+k+1.
(3)
Так,
например, если m=4, то k=3, а кодовый набор
будет иметь семь разрядов (номера
контрольных разрядов 1,2,4
по формуле (2)); при m=8 k=4, а номера
контрольных разрядов: 1,2,4,8; при m=16
k=5,
номера контрольных разрядов: 1,2,4,8,16 и
т.д.
Опишем, например, способ
построения кода Хэмминга при m=4 и k=3.
На рис.5 приведен перечень
кодовых обозначений позиций (c3c2c1) и их
номера в десятичной системе счисления
(N). Исходя из этого перечня, необходимо
проверять на четность те номера битов,
в позиции которых стоят 1
(смотри столбцы), т.е. ненулевые позиции:
В частности, в столбце с3 —
номера (4,5,6,7); в столбце c2 — (2,3,6,7); и в
столбце c1 — (1,3,5,7). Обратите внимание, что
в позициях 1,2,4 стоят контрольные разряды
р1,р2,р3 (см. формулу (2)), они выделены
зеленым. Непосредственно сама информация
закодирована только в позициях 3,5,6,7,
что соответствует значимым разрядам
m1,m2,m3,m4,
(выделены желтым).
с3
c2 c1 N
0 0 0 0
(ошибка отсутствует)
0 0 1
1 р1
0 1 0
2 р2
0 1 1
3 m1
1 0 0
4 р3
1 0 1
5 m2
1 1 0
6 m3
1 1 1
7 m4
Рис.5. Номера позиций
с3 — (4,5,6,7); c2 — (2,3,6,7); c1 — (1,3,5,7).
Как уже указывалось, исправление
заключается в замене ошибочного разряда
на его инверсию.
Если m=6, то с учетом (3) k=4:
p1=(1,3,5,7,9); p2=(2,3,6,7,10); p3=(4,5,6,7); p4=(8,9,10).
Опишем, например, способ построения
кода Хэмминга при m=4 и k=3.
Дано исходное сообщение: 0 1 0 1
1). пронумеруем номера столбцов от 1 до
7, а ниже – значимые (m) и
контрольные разряды (р)
2). Запишем исходное сообщение в позиции
значимых разрядов. Это будет строка с1.
3). Ниже выписываем в столбик номера
позиций с ненулевыми битами в строке
с1 и сразу переводим их в двоичную форму.
Под чертой записываем контрольную сумму
1,
вычисленную с помощью операцииXOR.
4). В строке с2 повторим исходное сообщение,
а в контрольные позиции (1,2,4)
вставим биты из полученной контрольной
суммы по следующему принципу:
последний (правый) бит вставляем в поз.
1;
предпоследний бит – в поз. 2;
второй бит – в поз. 4. Полученная строка
будет являться кодом Хэмминга.
5). Сделаем проверку полученного кода и
убедимся, что ошибки нет. Для этого снова
выписываем все номера позиций с ненулевыми
битами в строке с2 и находим контрольную
сумму
2.
6). В строке с3 повторим строку с2, но
искусственно введем в один из значимых
разрядов (например, в m3 –
шестая позиция) ошибочный бит «1» вместо
«0».
7). Снова выписываем номера ненулевых
элементов из строки с3 и находим
контрольную сумму
3. Переводим полученную контрольную
сумму в десятичный вид и получаем, что
ошибочна 6-я позиция, поэтому для
исправления в ней нужно сделать инверсию.
1 2 3
4 5 6 7
p1 p2 m1 p3 m2
m3 m4
передаваемое (исходное) сообщение
с1 0 1 0 1

сообщение (код Хэмминга) с201001 0 1
полученное сообщение
с3 0 1 0 0 1 11
по строке с1: 5=0101
7=0111
1=0010
Проверка правильности кода Хэмминга
(по строке с2):
2=0010
5=0101
7=0111
2=0000 – значит ошибки в коде Хэмминга
нет
Проверяем полученное сообщение (строка
с3):
2=0010
5=0101
6=0110
7=0111
3=01102=610
Заметим, что существуют коды,
которые обнаруживают и исправляют и
более одной ошибки.
Код
Хэмминга относится к классу линейных
кодов и представляет собой систематический
код – код, в котором информационные и
контрольные биты расположены на строго
определенных местах в кодовой комбинации.
Код
Хэмминга, как и любой (n,
k)-
код, содержит к
информационных и m
= n-k
избыточных (проверочных) бит.
Избыточная
часть кода строится т. о. чтобы можно
было при декодировании не только
установить наличие ошибки но, и указать
номер позиции в которой произошла ошибка
, а значит и исправить ее, инвертировав
значение соответствующего бита.
Существуют
различные методы реализации кода
Хэмминга и кодов которые являются
модификацией кода Хэмминга. Рассмотрим
алгоритм построения кода для исправления
одиночной ошибки.
1.
По заданному количеству информационных
символов — k,
либо информационных комбинаций N
= 2k
, используя соотношения:
n
= k+m, 2n
(n+1)2k
и
2m
n+1 (14)
m
= [log2
{(k+1)+
[log2(k+1)]}]
вычисляют
основные параметры кода n
и m.
2.
Определяем рабочие и контрольные позиции
кодовой комбинации. Номера контрольных
позиций определяются по закону 2i,
где
i=1,
2, 3,… т.е. они равны 1, 2, 4, 8, 16,… а остальные
позиции являются рабочими.
3.
Определяем значения контрольных разрядов
(0 или 1 ) при помощи многократных проверок
кодовой комбинации на четность. Количество
проверок равно m
= n-k.
В каждую проверку включается один
контро-льный и определенные проверочные
биты. Если результат проверки дает
четное число, то контрольному биту
присваивается значение -0, в противном
случае — 1. Номера информационных бит,
включаемых в каждую проверку, определяются
по двоичному коду натуральных n
–чисел
разрядностью – m
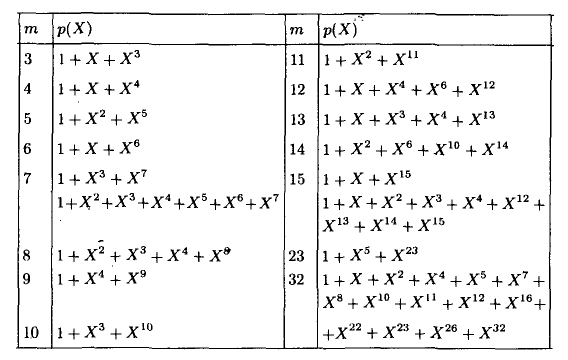
(табл.
1, для m
= 4)
или при помощи проверочной матрицы
H(mn),
столбцы которой представляют запись в
двоичной системе всех целых чисел от 1
до 2k
–1
перечисленных в возрастающем порядке.
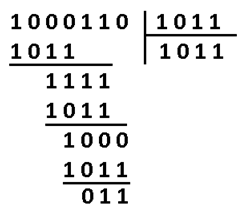
Для
m = 3
проверочная матрица имеет вид

(15 )
Количество
разрядов m
— определяет количество проверок.
В
первую проверку включают коэффициенты,
содержащие 1 в младшем (первом) разряде,
т. е. b1,
b3,
b5
и т. д.
Во
вторую проверку включают коэффициенты,
содержащие 1 во втором разряде, т. е. b2,
b3,
b6
и т. д.
В
третью проверку — коэффициенты которые
содержат 1 в третьем разряде и т. д.
Таблица
1
|
Десятичные
(номера
кодовой |
Двоичные |
||
|
3 |
2 |
1 |
|
|
1 2 3 4 5 6 7 |
0 0 0 1 1 1 1 |
0 1 1 0 0 1 1 |
1 0 1 0 1 0 1 |
Для
обнаружения и исправления ошибки
составляются аналогичные проверки на
четность контрольных сумм, результатом
которых является двоичное (n-k)
-разрядное число, называемое синдромом
и указывающим на положение ошибки, т.
е. номер ошибочной позиции, который
определяется по двоичной записи числа,
либо по проверочной матрице.
Для
исправления ошибки необходимо
проинвертировать бит в ошибочной
позиции. Для исправления одиночной
ошибки и обнаружения двойной используют
дополнительную проверку на четность.
Если при исправлении ошибки контроль
на четность фиксирует ошибку, то значит
в кодовой комбинации две ошибки.
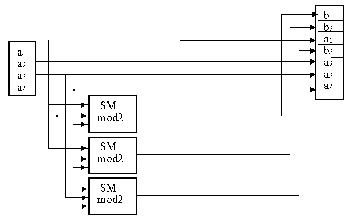
Схема
кодера и декодера для кода Хэмминга
приведена на рис. 1.
Пример
1.
Построить код Хемминга для передачи
сообщений в виде последовательности
десятичных цифр, представленных в виде
4 –х разрярных двоичных слов. Показать
процесс кодирования, декодирования и
исправления одиночной ошибки на примере
информационного слова 0101.
Решение:
1.
По заданной длине информационного слова
(k
= 4),
определим количество контрольных
разрядов m,
используя соотношение:
m
= [log2
{(k+1)+
[log2(k+1)]}]=[log2
{(4+1)+
[log2(4+1)]}]=3,
при
этом n
= k+m = 7,
т. е. получили (7, 4) -код.
2.
Определяем номера рабочих и контрольных
позиции кодовой комбинации. Номера
контрольных позиций выбираем по закону
2i
.
Для
рассматриваемой задачи (при n
= 7)
номера контрольных позиций равны 1, 2,
4. При этом кодовая комбинация имеет
вид:
b1
b2
b3
b4
b5
b6
b7
к1
к2
0
к3
1
0 1
3.
Определяем значения контрольных разрядов
(0 или 1), используя проверочную матрицу
(5).
Первая
проверка:
k1
b3
b5
b7
= k1011
будет четной при k1
=
0.
Вторая
проверка:
k2
b3
b6
b7
= k2001
будет четной при k2
=
1.
Третья
проверка:
k3
b5
b6
b7
= k3101
будет четной при k3
=
0.
1
2 3 4 5 6 7
Передаваемая
кодовая комбинация: 0 1 0 0 1 0 1
Допустим
принято: 0 1 1 0 1 0 1
Для
обнаружения и исправления ошибки
составим аналогичные про-верки на
четность контрольных сумм, в соответствии
с проверочной матрицей результатом
которых является двоичное (n-k)
-разрядное число, называемое синдромом
и указывающим на положение ошибки, т.
е, номер ошибочной позиции.
1)
k1
b3
b5
b7
= 0111 = 1.
2)
k2
b3
b6
b7
= 1101 = 1.
-
k3
b5
b6
b7
= 0101 = 0.
Сравнивая
синдром ошибки со столбцами проверочной
матрицы, определяем номер ошибочного
бита. Синдрому 011 соответствует третий
столбец, т. е. ошибка в третьем разряде
кодовой комбинации. Символ в 3 -й позиции
необходимо изменить на обратный.
Пример
2.
Построить код Хэмминга для передачи
кодовой комбинации 1 1 0 1 1 0 1 1. Показать
процесс обнаружения и исправления
ошибки в соответствующем разряде кодовой
комбинации.
Решение:
Рассмотрим
алгоритм построения кода для исправления
одиночной ошибки.
1.
По заданной длине информационного слова
(k
= 8)
, используя соотношения вычислим основные
параметры кода n
и m.
m
= [log2
{(k+1)+
[log2(k+1)]}]=[log2
{(9+1)+
[log2(9+1)]}]=4,
при
этом n
= k+m = 12,
т. е. получили (12, 8)-код.
2.
Определяем номера рабочих и контрольных
позиции кодовой комбинации. Номера
контрольных позиций выбираем по закону
2i
.
Для
рассматриваемой задачи (при n
= 12)
номера контрольных позиций равны 1, 4,
8.
При
этом кодовая комбинация имеет вид:
b1
b2
b3
b4
b5
b6
b7
b8
b9
b10
b11
b12
к1
к2
1
к3
1
0 1 к4
1
0 1 1
3.
Определяем значения контрольных разрядов
(0 или 1) путем много-кратных проверок
кодовой комбинации на четность. Количество
проверок равно m
= n-k.
В каждую проверку включается один
контрольный и определенные проверочные
биты.
Номера
информационных бит, включаемых в каждую
проверку определяется по двоичному
коду натуральных n-чисел
разрядностью — m.
0001
b1
Количество разрядов m — определяет
количество прове-
0010
b2
верок.
0011
b3
1) к1
b3
b5
b7
b9
а11
=
к111111
=>
0100
b4
четная
при к1=1
0101
b5
2)
к2
b3
b6
b7
b10
b11=
к210101
=>
0110
b6
четная при к2=1
0111
b7
3)
к3
b5
b6
b7
b12
=
к31011=>
1000
b8
четная
при к3=1
1001
b9
4) к4
b9
b10
b11
b12
=
к11011
=>
1010
b10
четная
при к4=1
1011
b11
1100
b12
Передаваемая
кодовая комбинация: 1 2 3 4 5 6 7 8 9 10 11 12
1
1 1 1 1 0 1 1 1 0 1 1
Допустим,
принято: 1 1 1 1 0 0 1 1 1 0 1 1
Для
обнаружения и исправления ошибки
составим аналогичные про-верки на
четность контрольных сумм, результатом
которых является двоичное (n-k)
-разрядное число, называемое синдромом
и указывающим на положение ошибки, т.
е. номер ошибочной позиции.
1)
к1
b3
b5
b7
b9
b11
=
110111 =1
2)
к2
b3
b6
b7
b10
b11
=
110101 =0
3)
к3
b5
b6
b7
b12
=
10011 =1
4)
к4
b9
b10
b11
b12
=
11011 =0
Обнаружена
ошибка в разряде кодовой комбинации с
номером 0101, т. е. в 5 -м разряде. Для
исправления ошибки необходимо
проинвертировать 5 -й разряд в кодовой
комбинации.
Рис.
1. Схема кодера —а
и декодера –б
для простого (7, 4) кода Хэмминга
Рассмотрим
применение кода Хэмминга. В ЭВМ код
Хэмминга чаще всего используется для
обнаружения и исправления ошибок в ОП,
памяти с обнаружением и исправлением
ошибок ECC Memory (Error Checking and Correcting). Код
Хэмминга используется как при параллельной,
так и при последовательной записи. В
ЭВМ значительная часть интенсивности
потока ошибок приходится на ОП. Причинами
постоянных неисправностей являются
отказы ИС, а случайных изменение
содержимого ОП за счет флуктуации
питающего напряжения, кратковременных
помех и излучений. Неисправность может
быть в одном бите, линии выборки разряда,
слова либо всей ИС. Сбой может возникнуть
при формировании кода (параллельного),
адреса или данных, поэтому защищать
необходимо и то и др. Обычно дешифратор
адреса встроен в м/схему и недоступен
для потребителя. Наиболее часто ошибки
дают ячейки памяти ЗУ, поэтому главным
образом защищают записываемые и
считываемые данные.
Наибольшее
применение в ЗУ нашли коды Хэмминга с
dmin=4,
исправляющие одиночные ошибки и
обнаруживающие двойные.
Проверочные
символы записываются либо в основное,
либо специальное ЗУ. Для каждого
записываемого информационного слова
(а не байта, как при контроле по паритету)
по определенным правилам вычисляется
функция свертки, результат которой
разрядностью в несколько бит также
записывается в память. Для 16 -ти разрядного
информационного слова используется 6
дополнительных бит (32- 7 бит, 64 –8 бит).
При считывании информации схема контроля,
используя избыточные биты, позволяет
обнаружить ошибки различной кратности
или исправить одиночную ошибку. Возможны
различные варианты поведения системы:
-
автоматическое
исправление ошибки без уведомления
системы;
—
исправление однократной ошибки и
уведомление системы только о многократных
ошибках;
—
не исправление ошибки, а только уведомление
системы об ошибках;
Модуль
памяти со встроенной схемой исправления
ошибок –EOS 72/64 (ECC on Simm). Аналог микросхема
к 555 вж 1
-это 16 разрядная схема с обнаружением
и исправлением ошибок (ОИО) по коду
Хэмминга (22, 16), использование которой
позволяет исправить однократные ошибки
и обнаружить все двух кратные ошибки в
ЗУ.
Избыточные
(контрольные) разряды позволяют обнаружить
и исправить ошибки в ЗУ в процессе записи
и хранения информации.
В
составе ВЖ-1 используются 16 информационных
и 6 контрольных разрядов. (DB — информационное
слово, CB — контрольное слово).
При
записи осуществляется формирование
кода, состоящего из 16 информационных и
6 контрольных разрядов, представляющих
результат суммирование по модулю 2
восьми информационных разрядов в
соответствии с кодом Хэмминга.
Сформированные контрольные разряды
вместе с информационными поступают на
схему и записываются в ЗУ.
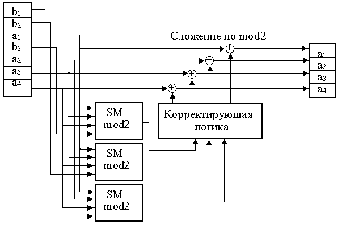
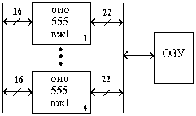
(22,16)
4
схе(72,64)
Рис.2.
Схема контроля
При
считывании шестнадцатиразрядное слово
декодируется, восстанавливаясь вместе
с 6 разрядным словом контрольным,
поступают на схему сравнения и контроля.
Если достигнуто равенство всех контрольных
разрядов и двоичных слов, то ошибки нет.
Любая
однократная ошибка в 16 разрядном слове
данных изменяет 3 байта в 6 разрядном
контрольном слове. Обнаруженный ошибочный
бит инвертируется.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание
Раздел разработан в 2010 г. при поддержке компании RAIDIX
Для понимания материалов настоящего раздела крайне желательно ознакомиться с разделом КОДИРОВАНИЕ
.
Код Хэмминга
Будем рассматривать двоичные коды, т.е. упорядоченные наборы (строки) $ (x_1,dots,x_{n}) $ из $ n_{} $ чисел $ {x_1,dots,x_n}subset {0,1} $. Множество таких наборов, рассматриваемое вместе с операцией умножения на константы $ 0_{} $ или $ 1_{} $ и операцией поразрядного сложения по модулю $ 2_{} $:
$$ (x_1,dots,x_n)oplus (y_1,dots,y_n)=(x_1oplus y_1 ,dots,x_noplus y_n ) =
$$
$$ = (x_1+y_1 pmod{2},dots,x_n+y_n pmod{2}) $$
образует линейное пространство, которое мы будем обозначать $ mathbb V^n $, а собственно составляющие его наборы будем называть векторами; причем, для определенности, именно векторами-строками. Это пространство состоит из конечного числа векторов: $ operatorname{Card} (mathbb V^n)=2^n $.
Расстояние Хэмминга
Расстоянием Хэмминга между двумя векторами $ B=(b_1,dots,b_n) $ и $ C=(c_1,dots,c_n) $ из $ mathbb V^n $ называется число разрядов, в которых эти слова отличаются друг от друга; будем обозначать его $ rho(B,C) $.
?
Доказать, что
$ rho(B,C)= displaystyle sum_{j=1}^n left[ (1-b_j)c_j+ (1-c_j)b_j right] $ .
Весом Хэмминга вектора $ B=(b_1,dots,b_n) $ называется число его отличных от нуля координат, будем обозначать его $ w(B) $. Таким образом1)
$$ w(B)= b_1+dots+b_n, qquad rho(B,C)=|b_1-c_1|+dots+ |b_n-c_n|=w(B-C) . $$
Расстояние Хэмминга является метрикой в пространстве $ mathbb V^n $, т.е. для любых векторов $ {X_1,X_2,X_3} subset mathbb V^n $ выполняются свойства
1.
$ rho(X_1,X_2) ge 0 $, и $ rho(X_1,X_2) = 0 $ тогда и только тогда, когда $ X_1=X_2 $;
2.
$ rho(X_1,X_2) = rho(X_2,X_1) $;
3.
$ rho(X_1,X_3)le rho(X_1,X_2)+ rho(X_2,X_3) $ («неравенство треугольника»).
Пусть теперь во множестве $ mathbb V^n $ выбирается произвольное подмножество $ mathbb U $, содержащее $ s_{} $ векторов: $ mathbb U={ U_1,dots,U_s } $. Будем считать эти векторы кодовыми словами, т.е. на вход канала связи будем подавать исключительно только эти векторы; само множество $ mathbb U $ будем называть кодом. По прохождении канала связи эти векторы могут зашумляться ошибками. Каждый полученный на выходе вектор будем декодировать в ближайшее (в смысле расстояния Хэмминга) кодовое слово множества $ mathbb U $. Таким образом, «хорошим» кодом — в смысле исправления максимального числа ошибок — может считаться код $ mathbb U $, для которого кодовые слова далеко отстоят друг от друга. С другой стороны, количество кодовых слов $ s_{} $ должно быть достаточно велико, чтобы делать использование кода осмысленным; во всяком случае, будем всегда считать $ s>1 $.
Минимальное расстояние между различными кодовыми словами кода $ mathbb U $, т.е.
$$ d=min_{{j,k}subset {1,dots,s } atop jne k} rho (U_j,U_k) $$
называется кодовым расстоянием кода $ mathbb U $; будем иногда также писать $ d(mathbb U) $.
Т
Теорема. Код $ mathbb U $ с кодовым расстоянием $ d_{} $
a) способен обнаружить от $ 1_{} $ до $ d-1 $ (но не более) ошибок;
б) способен исправить от $ 1_{} $ до $ leftlfloor displaystyle frac{d-1}{2} rightrfloor $ (но не более) ошибок. Здесь $ lfloor rfloor $ — целая часть числа.
Доказательство. Если $ U_1 $ — переданное кодовое слово, а $ V_{} $ — полученный на выходе с канала вектор с $ tau_{} $ ошибками, то $ rho(U_1,V)=tau $. Мы не сможем обнаружить ошибку если $ V_{1} $ совпадет с каким-то другим кодовым словом $ U_2 $, т.е. при условии $ rho(U_2,V)=0 $. Оценим
$ rho(U_2,V) $ при условии, что $ tau le d-1 $. По неравенству треугольника
3
получаем
$$ rho(U_2,V) ge rho(U_1,U_2)-rho(U_1,V) ge d-tau ge 1>0 . $$
Для доказательства части б) предположим, что $ 2,tau le d-1 $. Тогда те же рассуждения приведут к заключению
$$ rho(U_2,V) ge d-tau ge (2,tau+1)-t > tau = rho(U_1,V) , $$
т.е. вектор $ V_{} $ ближе к $ U_1 $, чем к любому другому кодовому слову.
♦
П
Пример. Код Адамара строится на основании матрицы Адамара — квадратной матрицы, элементами которой являются только числа $ {+1,-1} $; при этом ее строки (как, впрочем, и столбцы) попарно ортогональны. Так, матрица Адамара порядка $ 8_{} $ —
$$
H=left(
begin{array}{rrrrrrrr}
1 & 1 & 1 & 1 & 1 & 1 & 1 & 1
-1 & 1 &-1 & 1 & -1 & 1 &-1 & 1
1 & 1 & -1 & -1 & 1 & 1 & -1 & -1
-1 & 1 & 1 & -1 & -1 & 1 & 1 & -1
1 & 1 & 1 & 1 & -1 & -1 & -1 & -1
-1 & 1 &-1 & 1 & 1 & -1 &1 & -1
1 & 1 & -1 & -1 & -1 & -1 & 1 & 1
-1 & 1 & 1 & -1 & 1 & -1 & -1 & 1
end{array}
right) .
$$
Код строится следующим образом. Берутся строки матрицы $ H_{} $ и умножаются на $ +1 $ и на $ -1 $; в каждой строке множества
$$ H^{[1]},H^{[2]},dots,H^{[8]},-H^{[1]},-H^{[2]},dots,-H^{[8]} $$
производится замена $ +1 to 0, -1 to 1 $. Получаются $ 16 $ векторов
$$
(00000000), (10101010), (00110011), (10011001), (00001111), (10100101), (00111100),
(10010110),
$$
$$
(11111111), (01010101), (11001100), (01100110), (11110000), (01011010), (11000011),
(01101001),
$$
которые обозначим $ U_1,dots,U_8,U_{-1},dots,U_{-8} $.
Поскольку строки $ pm H^{[j]} $ и $ pm H^{[k]} $ ортогональны при $ jne k_{} $ и состоят только из чисел $ pm 1 $, то ровно в половине своих элементов они должны совпадать, а в половине — быть противоположными. Соответствующие им векторы $ U_{} $ будут совпадать в половине своих компонент и различаться в оставшихся. Таким образом
$$ rho( U_{pm j}, U_{pm k}) = 4 quad npu quad jne k, rho( U_{j}, U_{-j}) = 8 , $$
и кодовое расстояние равно $ 4_{} $. В соответствии с теоремой, этот код способен обнаружить до трех ошибок, но исправить только одну. Так, к примеру, если при передаче по каналу связи слова $ U_8=(00111100) $ возникает только одна ошибка и на выходе получаем $ V_8= (00111101) $, то $ rho(U_8,V_8)=1 $, в то время как $ rho(U_j,V_8)ge 3 $ для других кодовых слов. Если же количество ошибок возрастет до двух —
$ tilde V_8= (00111111) $, — то $ rho(U_8,tilde V_8)=2 $, но при этом также $ rho(U_9,tilde V_8)=2 $. Ошибка обнаружена, но однозначное декодирование невозможно.
♦
Т
Теорема. Если существует матрица Адамара порядка $ n_{}>2 $, то
а) $ n_{} $ кратно $ 4_{} $, и
б) существует код $ mathbb U subset mathbb V^n $, состоящий из $ 2,n $ кодовых слов, для которого кодовое расстояние $ d=n/2 $.
Проблема построения кодов Адамара заключается в том, что существование матриц Адамара произвольного порядка $ n_{} $ кратного $ 4_{} $ составляет содержание не доказанной2) гипотезы Адамара. Хотя для многих частных случаев $ n_{} $ (например, для $ n=2^m, m in mathbb N $, см.
☞
ЗДЕСЬ ) матрицы Адамара построены.
Т
Теорема. Если код $ mathbb U subset mathbb V^n $ может исправлять самое большее $ m_{} $ ошибок, то количество $ s_{} $ его слов должно удовлетворять следующему неравенству
$$ s le frac{2^n}{C_n^0+C_n^1+dots+C_n^m} , $$
где $ C_n^{j} $ означает биномиальный коэффициент.
Число в правой части неравенства называется верхней границей Хэмминга для числа кодовых слов.
Доказательство. Для простоты предположим, что одно из кодовых слов кода $ mathbb U $ совпадает с нулевым вектором: $ U_1=mathbb O_{1times n} $. Все векторы пространства $ mathbb V_n $, отстоящие от $ U_1 $ на расстояние $ 1_{} $ заключаются во множестве
$$ (100dots 0), (010 dots 0), dots, (000 dots 1) ; $$
их как раз $ n=C_n^1 $ штук. Векторы из $ mathbb V^n $, отстоящие от $ mathbb O_{} $ на расстояние $ 2_{} $ получаются в ходе расстановки двух цифр $ 1_{} $ в произвольных местах нулевого вектора. Нахождение количества способов такой расстановки относится к задачам комбинаторики, и решение этой задачи можно найти
☞
ЗДЕСЬ. Оно равно как раз $ C_n^{2}=n(n-1)/2 $. Аналогичная задача расстановки $ j_{} $ единиц в $ n_{} $-векторе имеет решением число $ C_n^j $.
Таким образом общее количество векторов, отстоящих от $ mathbb O_{} $ на расстояние $ le m_{} $
равно $ C_n^1+dots+C_n^m $.
Вместе в самим $ mathbb O_{} $-вектором получаем как раз число из знаменателя границы Хэмминга.
Предыдущие рассуждения будут справедливы и для любого другого кодового слова из $ mathbb U $ — каждое из них можно «окружить $ m_{} $-окрестностью» и каждая из этих окрестностей будет содержать
$$ 1+C_n^1+dots+C_n^m $$
векторов из $ mathbb V^n $. По предположению теоремы, эти окрестности не должны пересекаться. Но тогда общее количество векторов $ mathbb V^n $, попавших в эти окрестности (для всех $ s_{} $ кодовых слов) не должно превышать количества векторов в $ mathbb V^n $, т.е. $ 2^{n} $.
♦
?
Доказать, что если $ n_{} $ — нечетно, а $ m=lfloor n/2 rfloor=(n-1)/2 $ то верхняя граница Хэмминга равна в точности $ 2_{} $.
П
Пример. Для $ n=10 $ имеем
| $ m_{} $ | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| $ sle $ | 93 | 18 | 5 | 2 | 1 |
Чем больше ошибок хотим скорректировать (при фиксированном числе $ n_{} $ разрядов кодовых слов) — тем меньше множество кодовых слов.
Коды, для которых верхняя граница Хэмминга достигается, называются совершенными.
Линейные коды
Идея, лежащая в основе этих кодов достаточно проста: это — обобщение понятия контрольной суммы. Если вектор $ (x_1,dots,x_k) in mathbb V^k $ содержит информационные биты, которые требуется передать, то для контроля целостности при передаче их по каналу присоединим к этому вектору еще один «служебный» бит с вычисленным значением
$$ x_{k+1}=x_1+dots+x_k pmod{2} . $$
Очевидно, $ x_{k+1}=1 $ если среди информационных битов содержится нечетное число единиц, и $ x_{k+1}=0 $ в противном случае. Поэтому этот бит называют битом четности. Кодовым словом становится вектор
$$ X=(x_1,dots,x_k,x_{k+1}) in mathbb V^{k+1} . $$
По прохождении его по каналу, для полученного вектора $ Y=(y_1,dots,y_k,y_{k+1}) $ производится проверка условия
$$ y_{k+1} = y_1+dots+y_k pmod{2} . $$
Если оно не выполнено, то при передаче произошла ошибка. Если же сравнение оказывается справедливым, то это еще не значит, что ошибки при передаче нет — поскольку комбинация из двух (или любого четного числа) ошибок не изменит бита четности.
Для более вероятного обнаружения ошибки вычислим несколько контрольных сумм — выбирая различные разряды информационного вектора $ (x_1,dots,x_k) $:
$$
begin{array}{lclcll}
x_{k+1}&=&x_{i_1}+&dots&+x_{i_s} pmod{2},
x_{k+2}&=&x_{j_1}+&dots&+x_{j_t} pmod{2},
vdots & & vdots
x_n &=&x_{ell_1}+& dots & +x_{ell_w} pmod{2}.
end{array}
$$
Полученные биты присоединим к информационному блоку. Кодовым словом будет вектор
$$ X=(x_1,dots,x_k,x_{k+1},dots,x_n) in mathbb V^n , $$
который и поступает в канал связи. По прохождении его по каналу, для соответствующих разрядов полученного вектора $ Y_{} $ проверяется выполнимость контрольных сравнений. Если все они выполняются, то ошибка передачи считается невыявленной.
На первый взгляд кажется, что при увеличении количества контрольных сумм увеличивается и вероятность обнаружения ошибки передачи. Однако с увеличением количества разрядов кодового слова увеличивается и вероятность появления этой ошибки.
П
Пример. Если вероятность ошибочной передачи одного бита по каналу равна $ P_1=0.1 $, то вероятность появления хотя бы одной ошибки при передаче $ k_{} $ битов равна $ P_k= 1-(0.9)^k $, т.е.
| $ k $ | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| $ P_k $ | 0.1 | 0.19 | 0.271 | 0.344 | 0.410 | 0.469 | 0.522 | 0.570 | 0.613 | 0.651 |
♦
Обычно, количество проверочных соотношений берется меньшим (и даже много меньшим) количества информационных битов3). Осталось только понять как составлять эти проверочные соотношения так, чтобы они смогли реагировать на ошибки передачи по каналу связи.
Сначала формализуем предложенную выше идею. В пространстве $ mathbb V^n $ выделим некоторое подпространство $ mathbb V^n_{[k]} $, состоящее из векторов
$$ (x_1,dots,x_k,x_{k+1},dots,x_n) , $$
первые $ k_{} $ компонентов которых считаются произвольными, а оставшиеся $ n-k_{} $ полностью определяются первыми посредством заданных линейных соотношений:
$$ begin{array}{lclcll}
x_{k+1}&=&h_{k+1,1}x_1+&dots&+h_{k+1,k}x_k pmod{2}
vdots & & vdots
x_n &=&h_{n1}x_1+& dots & +h_{nk}x_k pmod{2}
end{array} qquad npu qquad {h_{jell}} subset {0,1} .
$$
Кодовые слова выбираются именно из подпространства $ mathbb V^n_{[k]} $, их количество равно $ operatorname{Card} (mathbb V^n_{[k]} )=2^k $. При этом начальная часть каждого кодового слова, т.е. вектор $ (x_1,dots,x_k) $, заключает информацию, которую нужно передать — эти разряды называются информационными. Остальные разряды кодового слова, т.е. биты вектора $ (x_{k+1},dots,x_n) $, которые вычисляются с помощью выписанных линейных соотношений, являются служебными — они называются проверочными и предназначены для контроля целостности передачи информационных разрядов по каналу связи (и/или коррекции ошибок). Код такого типа называется линейным (n,k)-кодом.
В дальнейшем будем экономить на обозначениях: знак операции $ +_{} $ будет означать суммирование по модулю $ 2_{} $.
П
Пример. Пусть $ n=5, k=3 $. Пусть проверочные биты связаны с информационными соотношениями
$$ x_4=x_1 + x_2, x_5=x_1 + x_3 . $$
Тогда $ mathbb V^5_{[3]} $ состоит из векторов
$$ (00000), (10011), (01010), (00101), (11001), (10110), (01111), (11100) . $$
♦
Для описания пространства $ mathbb V^n_{[k]} $ привлечем аппарат теории матриц. С одной стороны, в этом подпространстве можно выбрать базис — систему из $ k_{} $ линейно независимых векторов: обозначим их $ {X_1,dots,X_k} $. Матрица, составленная из этих векторов-строк,
$$
mathbf G=left( begin{array}{c} X_1 vdots X_k end{array} right)_{ktimes n}
$$
называется порождающей матрицей кода. Так, в только что приведенном примере в качестве порождающей матрицы может быть выбрана
$$
mathbf G=
left( begin{array}{ccccc}
1 & 0 & 0 & 1 & 1
0 & 1 & 0 & 1 & 0
0 & 0 & 1 & 0 &1
end{array}
right) qquad mbox{ или } qquad
mathbf G=
left( begin{array}{ccccc}
1 & 0 & 0 & 1 & 1
1 & 1 & 0 & 0 & 1
1 & 1 & 1 & 0 & 0
end{array}
right) .
$$
Любая строка $ X_{} $ кода может быть получена как линейная комбинация строк порождающей матрицы:
$$ X=alpha_1 X_1+alpha_2X_2+dots+alpha_k X_k quad npu quad {alpha_1,dots,alpha_k} subset {0,1} . $$
Можно переписать это равенство с использованием операции матричного умножения:
$$ X=(alpha_1,dots,alpha_k) mathbf G . $$
Так, продолжая рассмотрение предыдущего примера:
$$
(x_1,x_2,x_3,x_4,x_5)=(x_1,x_2,x_3)
left( begin{array}{ccccc}
1 & 0 & 0 & 1 & 1
0 & 1 & 0 & 1 & 0
0 & 0 & 1 & 0 &1
end{array}
right)=
$$
$$
=(x_1+x_2,x_2+x_3,x_3)
left( begin{array}{ccccc}
1 & 0 & 0 & 1 & 1
1 & 1 & 0 & 0 & 1
1 & 1 & 1 & 0 & 0
end{array}
right) pmod{2} .
$$
С другой стороны, для описания $ mathbb V^n_{[k]} $ имеются проверочные соотношения. Объединяя их в систему линейных уравнений, перепишем их с использованием матричного формализма:
$$
(x_1,dots,x_k,x_{k+1},dots,x_n) cdot
left(begin{array}{cccc}
h_{k+1,1} & h_{k+2,1} & dots &h_{n1}
h_{k+1,2} & h_{k+2,2} & dots & h_{n2}
vdots & & & vdots
h_{k+1,k} & h_{k+2,k} & dots & h_{nk}
-1 & 0 & dots & 0
0 & -1 & dots & 0
vdots & & ddots & vdots
0 & 0 & dots & -1
end{array}
right)= (0,0,dots,0)_{1times (n-k)}
$$
или, в альтернативном виде, с использованием транспонирования4):
$$
underbrace{left(begin{array}{llclcccc}
h_{k+1,1} & h_{k+1,2} & dots &h_{k+1,k} & 1 & 0 & dots & 0
h_{k+2,1} & h_{k+2,2} & dots & h_{k+2,k}& 0 & 1 & dots & 0
vdots & & & vdots & dots & & ddots & vdots
h_{n1} & h_{n2} & dots & h_{nk} & 0 & 0 & dots & 1
end{array}
right)}_{mathbf H}left( begin{array}{c} x_1 x_2 vdots x_n end{array} right)
=left( begin{array}{c} 0 0 vdots 0 end{array} right)_{(n-k)times 1}
$$
Матрица $ mathbf H_{} $ порядка $ (n-k)times n $ называется проверочной матрицей кода5). Хотя вторая форма записи (когда вектор-столбец неизвестных стоит справа от матрицы) более привычна для линейной алгебры, в теории кодирования чаще используется именно первая — с вектором-строкой $ X_{} $ слева от матрицы:
$$ Xcdot mathbf H^{top} = mathbb O_{1times k} . $$
Для приведенного выше примера проверочные соотношения переписываются в виде
$$ x_1 + x_2 +x_4=0, x_1 + x_3 + x_5=0 $$
и, следовательно, проверочная матрица:
$$ mathbf H=
left( begin{array}{ccccc}
1 & 1 & 0 & 1 & 0
1 & 0 & 1 & 0 & 1
end{array}
right) .
$$
Т
Теорема 1. Имеет место матричное равенство
$$ mathbf G cdot mathbf H^{top} = mathbb O_{ktimes (n-k)} .$$
Доказательство. Каждая строка матрицы $ mathbf G $ — это кодовое слово $ X_{j} $ , которое, по предположению, должно удовлетворять проверочным соотношениям $ X_j cdot mathbf H^{top} = mathbb O_{1times k} $. Равенство из теоремы — это объединение всех таких соотношений в матричной форме. Фактически, порождающая матрица $ mathbf G $ состоит из строк, составляющих фундаментальную систему решений системы уравнений $ X mathbf H^{top}= mathbb O $.
♦
=>
Если проверочная матрица имеет вид $ mathbf H=left[ P^{top} mid E_{n-k} right] $,
где $ E_{n-k} $ — единичная матрица порядка $ n — k_{} $, $ P_{} $ — некоторая матрица порядка $ k times (n-k) $, а $ mid_{} $ означает операцию конкатенации, то порождающая матрица может быть выбрана в виде $ mathbf G = left[ E_k mid P right] $.
Доказательство следует из предыдущей теоремы, правила умножения блочных матриц —
$$ mathbf G cdot mathbf H^{top} = E_k cdot P + P cdot E_{n-k} = 2P equiv mathbb O_{ktimes (n-k)} pmod{2} , $$
и того факта, что строки матрицы $ mathbf G $ линейно независимы. Последнее обстоятельство обеспечивается структурой этой матрицы: первые $ k_{} $ ее столбцов являются столбцами единичной матрицы. Любая комбинация
$$ alpha_1 mathbf G^{[1]}+dots+alpha_k mathbf G^{[k]} $$
строк матрицы дает строку $ (alpha_1,dots,alpha_k,dots ) $ и для обращения ее в нулевую необходимо, чтобы $ alpha_1=0,dots,alpha_k=0 $.
♦
Видим, что по структуре матрицы $ mathbf G $ и $ mathbf H $ очень похожи друг на друга. Задав одну из них, однозначно определяем другую. В одном из следующих пунктов, мы воспользуемся этим обстоятельством — для целей исправления ошибок оказывается выгоднее сначала задавать $ mathbf H $.
Т
Теорема 2. Кодовое расстояние линейного подпространства $ mathbb V^{n}_{[k]} $ равно минимальному весу его ненулевых кодовых слов:
$$ d( mathbb V^{n}_{[k]})= min_{ U in mathbb V^{n}_{[k]} atop U ne mathbb O } w(U) . $$
Доказательство. Линейное подпространство замкнуто относительно операции сложения (вычитания) векторов. Поэтому если $ {U_1,U_2}subset mathbb V^{n}_{[k]} $, то и $ U_1-U_2 in mathbb V^{n}_{[k]} $, а также $ mathbb O in V^{n}_{[k]} $. Тогда
$$ rho(U_1,U_2)=rho(U_1-U_2, mathbb O)= w(U_1-U_2) . $$
♦
Кодовое расстояние дает третью характеристику линейного кода — теперь он описывается набором чисел $ (n,k,d) $.
Т
Теорема 3. Пусть $ d_{} $ означает кодовое расстояние кода $ mathbb V^{n}_{[k]} $ с проверочной матрицей $ mathbf H $. Тогда любое подмножество из $ ell_{} $ столбцов этой матрицы будет линейно независимо при $ ell < d $. Обратно, если любое подмножество из $ ell_{} $ столбцов матрицы $ mathbf H $ линейно независимо, то $ d > ell $.
Доказательство. Если $ d_{} $ — кодовое расстояние, то, в соответствии с теоремой 2, ни одно ненулевое кодовое слово $ Xin mathbb V^{n}_{[k]} $ не должно иметь вес, меньший $ d_{} $. Если предположить,
что столбцы $ {mathbf H_{[i_1]},dots,mathbf H_{[i_{ell}]}} $ линейно зависимы при $ ell< d $, то
существуют числа $ x_{i_1},dots,x_{i_{ell}} $ не все равные нулю, такие что
$$ x_{i_1}mathbf H_{[i_1]}+dots+x_{i_{ell}} H_{[i_{ell}]} = mathbb O . $$
Придавая всем остальным переменным $ {x_1,dots,x_n} setminus { x_{i_1},dots,x_{i_{ell}} } $ нулевые значения, получаем вектор $ X_{} in mathbb V^n $, удовлетворяющий равенству
$$ x_1 mathbf H_{[1]}+dots + x_n mathbf H_{[n]} = mathbb O , $$
и вес этого вектора $ le ell< d $. Но тогда этот вектор принадлежит и $ mathbb V^{n}_{[k]} $ поскольку $ mathbf H X^{top} = mathbb O $.
Это противоречит предположению о весе кодовых слов. Следовательно любые $ ell_{} $ столбцов матрицы $ mathbf H $ линейно независимы если $ ell < d $.
Обратно, пусть любые $ ell_{} $ столбцов матрицы $ mathbf H $ линейно независимы, но существует кодовое слово $ X_{}=(x_1,dots,x_n) ne mathbb O $ веса $ le ell $. Пусть, для определенности, $ x_{ell+1}=0,dots, x_{n}=0 $. Тогда
$$ x_1 mathbf H_{[1]}+dots + x_{ell} mathbf H_{[ell]}= mathbb O $$
при хотя бы одном из чисел $ {x_j}_{j=1}^{ell} $ равном $ 1_{} $. Но это означает, что столбцы
$ mathbf H_{[1]},dots, mathbf H_{[ell]} $ линейно зависимы, что противоречит предположению.
♦
Испровление ашибок
До сих пор мы не накладывали ни каких дополнительных ограничений ни на порождающую ни на проверочную матрицы кода: любая из них могла быть выбрана почти произвольной.
Теперь обратимся собственно к задаче обнаружения (а также возможной коррекции) ошибок при передаче кодового слова по зашумленному каналу связи.
Если $ Xin mathbb V^{n}_{[k]} $ — кодовое слово, а $ Yin mathbb V^n $ — вектор, получившийся по прохождении этого слова по каналу, то $ Y-X $ называется вектором ошибок. Понятно, что при $ w(Y-X)=0 $ ошибки при передаче нет.
Предположим, что $ w(Y-X)=1 $, т.е. что при передаче произошла ошибка ровно в одном разряде кодового слова $ X_{} $. Попробуем ее обнаружить исходя из предположения, что кодовое слово выбиралось во множестве $ mathbb V^{n}_{[k]} $ линейного $ (n,k) $-кода, определенного в предыдущем пункте при какой-то проверочной матрице $ mathbf H $. Если для полученного вектора $ Y_{} $ выполняются все проверочные условия:
$$ Y cdot mathbf H^{top} = mathbb O_{1times k} , $$
(или, что то же $ Y in mathbb V^{n}_{[k]} $), то ошибка передачи считается не выявленной.
Для произвольного вектора $ Y in mathbb V^{n} $ вектор-строка
$$ S=Y cdot mathbf H^{top} in mathbb V^{k} $$
называется синдромом вектора Y. C точки зрения линейной алгебры его можно интерпретировать как показатель отхода вектора $ Y_{} $ от гиперплоскости, заданной системой однородных уравнений $ Xcdot mathbf H^{top}=mathbb O $.
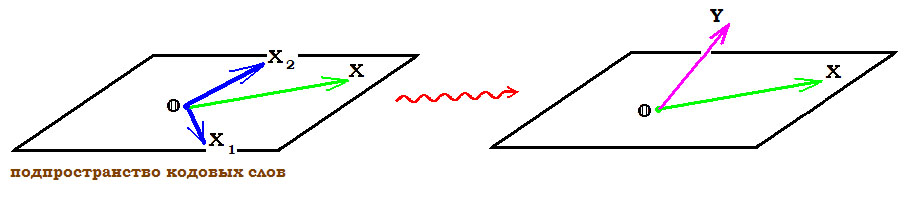
Если синдром $ S_{} $ ненулевой: $ Y cdot mathbf H^{top} ne mathbb O_{1times k} $,
то полученный вектор $ Y_{} $ не принадлежит множеству $ mathbb V^{n}_{[k]} $ допустимых кодовых слов. Факт ошибки подтвержден. Изначально мы предположили, что произошла только одна ошибка, т.е.
$$ Y-X= {mathfrak e}_j = big(underbrace{0,dots,0,1}_{j},0,dots,0big) $$
при некотором $ jin {1,dots n} $. Тогда
$$ S= Y cdot mathbf H^{top} = (X+{mathfrak e}_j) cdot mathbf H^{top}=Xcdot mathbf H^{top}+
{mathfrak e}_j cdot mathbf H^{top}=
$$
$$
=mathbb O_{1times k} + mathbf H_{[j]}^{top} = mathbf H_{[j]}^{top}
$$
при $ mathbf H_{[j]} $ означающем $ j_{} $-й столбец проверочной матрицы $ mathbf H $. Таким образом получили соответствие
$$ {}_{} mathbf{HOMEP} mbox{ поврежденного бита} mathbf{=HOMEP} mbox{ столбца проверочной матрицы.} $$
И, следовательно, мы получили возможность обнаружить место повреждения — по факту совпадения синдрома со столбцом проверочной матрицы. К сожалению, реальность оказывается более сложной…
П
Пример. В примере предыдущего пункта проверочная матрица была выбрана в виде
$$ mathbf H=
left( begin{array}{ccccc}
1 & 1 & 0 & 1 & 0
1 & 0 & 1 & 0 & 1
end{array}
right) .
$$
Если при передаче кодового слова $ (10011) $ произошла ошибка в первом бите, т.е. $ Y=(00011) $, то синдром
$$ S=Y cdot mathbf H^{top} = (11) $$
однозначно укажет на номер столбца матрицы $ mathbf H $. Если же ошибка произошла в четвертом бите, т.е. $ Y=(10001) $, то
$$ S=(10) , $$
но таких6) столбцов в матрице $ mathbf H $ два!
♦
Вывод. Для однозначного обнаружения места ошибки7) достаточно, чтобы все столбцы матрицы $ mathbf H $ были различными.
Столбцами этой матрицы являются транспонированные строки пространства $ mathbb V^{n-k} $.
Построение кода
Итак, исходя из соображений, завершающих предыдущий пункт, будем строить код, исправляющий одну ошибку, беря за стартовую точку именно матрицу $ mathbf H $. Выбираем ее произвольного порядка $ Mtimes N $ при $ {M,N} in mathbb N, M<N $ и вида
$$ mathbf H_{Mtimes N} = left[ tilde P mid E_M right] , $$
где матрица $ E_M $ — единичная порядка $ M_{} $, а матрица $ tilde P $ имеет порядок $ Mtimes (N-M) $, и столбцы ее должны быть различными, ненулевыми и отличаться от столбцов матрицы $ E_M $. По этой проверочной матрице — в соответствии со следствием к теореме $ 1 $ из
☞
ПУНКТА — строим порождающую матрицу:
$$ mathbf G_{(N-M)times N} = left[ E_{N-M} mid tilde P^{top} right] . $$
Строки матрицы $ mathbf G $ могут быть взяты в качестве базисных векторов подпространства кодовых слов.
П
Пример. Пусть $ M=2 $. Здесь имеем единственный вариант:
$$ mathbf H_{2times 3} = left( begin{array}{c|cc} 1 & 1 & 0 1 & 0 & 1 end{array} right) , $$
поскольку в $ mathbb V^2 $ имеется лишь одна ненулевая строка, отличная от $ (10) $ и $ (01) $. Таким образом $ N=3 $ и
$$ mathbf G_{1times 3}=( 1, 1, 1 ) . $$
Следовательно, подпространство кодовых слов в $ mathbb V^3 $ является одномерным, и имеем всего два возможных кодовых слова: $ (000) $ и $ (111) $.
Пусть $ M=3 $. В $ mathbb V^3 $ имеется уже большой выбор строк, отличных от $ (100), (010), (001) $. Так, можно взять
$$
mathbf H_{3times 4} = left( begin{array}{c|ccc} 1 & 1 & 0 & 0 1 & 0 & 1 & 0 1 & 0 & 0 & 1 end{array} right) quad mbox{ или } quad
mathbf H_{3times 5} = left( begin{array}{cc|ccc} 1 & 0 & 1 & 0 & 0 1 & 1 & 0 & 1 & 0 0 & 1 & 0 & 0 & 1 end{array} right)
$$
$$
mbox{ или } quad
mathbf H_{3times 6} =
left( begin{array}{ccc|ccc} 1 & 0 & 1 & 1 & 0 & 0 1 & 1 & 0 & 0 & 1 & 0 0 & 1 & 1 & 0 & 0 & 1 end{array} right) quad mbox{ или } quad
mathbf H_{3times 7} =
left( begin{array}{cccc|ccc} 1 & 1 & 0 & 1 & 1 & 0 & 0 1 & 1 & 1 & 0 & 0 & 1 & 0 1 & 0 & 1 & 1 & 0 & 0 & 1 end{array} right) .
$$
Соответственно,
$$ mathbf G= (1, 1, 1, 1) quad quad mbox{ или } quad
mathbf G=
left( begin{array}{cc|ccc} 1 & 0 & 1 & 1 & 0 0 & 1 & 0 & 1 & 1 end{array} right)
quad
$$
$$
mbox{ или } quad
mathbf G=
left( begin{array}{ccc|ccc} 1 & 0 & 0 & 1 & 1 & 0 0 & 1 & 0 & 0 & 1 & 1 0 & 0 & 1 & 1 & 0 & 1 end{array} right)
quad quad mbox{ или } quad
mathbf G=
left( begin{array}{cccc|ccc} 1 & 0 & 0 & 0 & 1 & 1 & 1 0 & 1 & 0 & 0 & 1 & 1 & 0 0 & 0 & 1 & 0 & 0 & 1 & 1 0 & 0 & 0 & 1 & 1 & 0 & 1
end{array} right) .
$$
Кодовых векторов в соответствующих кодах будет $ 2^1,2^2,2^3,2^4 $. Любой из них способен исправить одну ошибку, полученную в ходе передачи.
♦
Если поставить задачу максимизации числа кодовых слов, то матрицу $ mathbf H $ следует выбирать самой широкой, т.е. делать $ N_{} $ максимально возможным. При фиксированном $ M_{} $ это достигается при выборе $ N=2^M-1 $. Тогда соответствующий линейный $ (n,k) $-код имеет значения параметров $ n=2^M-1,k=2^M-M-1 $, и именно он обычно и выбирается в качестве кода Хэмминга.
Найдем величину его кодового расстояния $ d_{} $. В соответствии с теоремой $ 3 $ из
☞
ПУНКТА, $ d>ell $, если любое подмножество из $ ell_{} $ столбцов матрицы $ mathbf H $ линейно независимо. Поскольку столбцы проверочной матрицы кода Хэмминга все различны, то любая пара из них линейно независима (свойство
3
☞
ЗДЕСЬ ). Следовательно, $ d>2 $. По теореме из
☞
ПУНКТА, получаем —
Если при передаче произошла ровно одна ошибка, то код Хэмминга способен ее исправить; если при передаче произошло ровно две ошибки, то код Хэмминга достоверно устанавливает лишь факт наличия ошибки.
Если попробовать исправить заглавие предыдущего пункта, исходя только из информации о структуре набора составляющих текст букв, то этой информации оказывается недостаточно: набор букв в правильном тексте будет таким же
П
Пример. Для проверочной матрицы $ (7,4) $-кода Хэмминга
$$
mathbf H_{3times 7} =
left( begin{array}{ccccccc} 1 & 1 & 0 & 1 & 1 & 0 & 0 1 & 1 & 1 & 0 & 0 & 1 & 0 1 & 0 & 1 & 1 & 0 & 0 & 1 end{array} right)
$$
вектор $ X=(0011110) $ является кодовым. Если при передаче произошла лишь одна ошибка и на выходе канала получили вектор $ Y=(1011110) $, то синдром этого вектора $ S=Y mathbf H^{top}=(111) $. Поскольку $ S^{top} $ совпадает с первым столбцом матрицы $ mathbf H $, то заключаем, что ошибка произошла в первом разряде. Тут же исправляем его на противоположный: $ X=Y+mathfrak e_1 $.
Если при передаче произошло две ошибки и на выходе канала получили вектор $ tilde Y=(1011010) $, то синдром этого вектора $ S=tilde Y mathbf H^{top}=(011) $. Поскольку синдром ненулевой, то факт наличия ошибки подтвержден. Однако корректно исправить ее — по аналогии с предыдущим — не удается. $ S^{top} $ совпадает с третьим столбцом матрицы $ mathbf H $, но в третьем разряде полученного вектора ошибки нет.
Наконец, если при передаче произошли три ошибки и на выходе канала получили вектор $ widehat Y=(1011011) $, то синдром этого вектора $ S=widehat Y mathbf H^{top}=(010) $. Наличие ошибки подтверждено, исправление невозможно. Если же — при передаче того же вектора $ X=(0011110) $ — получаем вектор
$ widehat Y_1=(1111111) $ (также с тремя ошибками), то его синдром оказывается нулевым: $ widehat Y_1 mathbf H^{top}=(000) $ и ошибка не обнаруживается.
♦
Проблема сравнения синдрома полученного вектора $ Y_{} $ со столбцами проверочной матрицы $ mathbf H $ с целью определения места ошибки — не такая тривиальная, особенно для больших $ n_{} $. Для упрощения этой процедуры воспользуемся следующим простым соображением. Размещение проверочных разрядов в конце кодового слова обусловлено лишь соображениями удобства изложения учебного материала. С точки зрения практической реализации, $ n-k $ проверочных разрядов можно разместить в любых местах кодового слова $ X_{} $ и даже «вразбивку», т.е. не подряд. Перестановке разрядов в кодовом слове будет соответствовать перестановка столбцов в матрице $ mathbf H $, при этом само множество столбцов остается неизменным — это транспонированные строки пространства $ mathbb V^{n-k} $ (ненулевые и различные). Рассмотрим $ (n,k) $-код Хэмминга при $ n=2^M-1,k=2^M-M-1, M ge 2 $. Тогда каждую ненулевую строку пространства $ mathbb V^{n-k}= mathbb V^M $ можно интерпретировать как двоичное представление числа из множества
$ {1,2,3,dots,2^M-1} $. Пусть
$$ j=underline{{mathfrak b}_1{mathfrak b}_2 dots {mathfrak b}_{M-1} {mathfrak b}_{M}}=
{mathfrak b}_1 times 2^{M-1}+{mathfrak b}_2 times 2^{M-2}+dots+{mathfrak b}_{M-1} times 2+ {mathfrak b}_{M} quad npu quad { {mathfrak b}_j}_{j=1}^Msubset {0,1} quad — $$
— двоичное представление числа $ j_{} $. Переупорядочим столбцы проверочной матрицы $ mathbf H $ так, чтобы
$$ mathbf H_{[j]}=left[ {mathfrak b}_1{mathfrak b}_2 dots {mathfrak b}_{M-1} {mathfrak b}_{M}right]^{top} , $$
т.е. чтобы $ j_{} $-й столбец содержал двоичное представление числа $ j_{} $. При таком упорядочении,
синдром произвольного вектора $ Y_{} $, отличающегося от кодового слова $ X_{} $ в единственном разряде, является двоичным представлением номера этого разряда:
$$ {bf mbox{СИНДРОМ }} (Y)=mathbf{HOMEP} (mbox{ошибочный разряд}) . $$
Осталось теперь выяснить какие разряды кодового слова содержат проверочные биты.
П
Пример. Для $ (7,4) $-кода Хэмминга матрицу $ mathbf H $, построенную в предыдущем примере, переупорядочим по столбцам; будем рассматривать ее в виде
$$
begin{array}{c}
left( begin{array}{ccccccc}
0 & 0 & 0 & 1 & 1 & 1 & 1
0 & 1 & 1 & 0 & 0 & 1 & 1
1 & 0 & 1 & 0 & 1 & 0 & 1
end{array} right)
begin{array}{ccccccc}
uparrow & uparrow & uparrow & uparrow & uparrow & uparrow & uparrow
scriptstyle 1 & scriptstyle 2 & scriptstyle 3 & scriptstyle 4 & scriptstyle 5 & scriptstyle 6 & scriptstyle 7
end{array}
end{array}
$$
Распишем проверочные соотношения $ Xmathbf H^{top}=mathbb O $ покомпонентно:
$$
left{
begin{array}{ccccccc}
& & & x_4&+x_5&+x_6&+x_7=0
&x_2&+x_3& & & +x_6&+x_7=0
x_1& & +x_3& & +x_5 & & +x_7=0
end{array} right. quad iff
$$
$$
iff quad
left{
begin{array}{ccccccc}
x_1& & +x_3& & +x_5 & & +x_7=0
&x_2&+x_3& & & +x_6&+x_7=0
& & & x_4&+x_5&+x_6&+x_7=0
end{array} right.
$$
Переписанные в последнем виде, эти уравнения представляют конечный пункт прямого хода метода Гаусса решения системы линейных уравнений, а именно — трапециевидную форму этой системы. Если бы мы поставили задачу поиска общего решения этой (однородной) системы и нахождения фундаментальной системы решений, то в качестве зависимых переменных однозначно бы выбрали $ x_1, x_2, x_4 $. Выпишем это общее решение :
$$
x_1=x_3+x_5+x_7, x_2=x_3+x_6+x_7, x_4=x_5+x_6+x_7 .
$$
Это и есть проверочные соотношения, а проверочными разрядами кодового вектора являются $ 1_{} $-й, $ 2_{} $-й и $ 4_{} $-й.
Проверим правильность этих рассуждений. Придадим оставшимся разрядам произвольные значения, например:
$ x_3=1,x_5=1,x_6=0,x_7=1 $. Тогда $ x_1=1, x_2=0,x_4=0 $ и кодовый вектор $ X=(1010101) $. Пусть на выходе из канала он превратился в $ Y=(1000101) $. Синдром этого вектора $ Ymathbf H^{top}=(011) $ — это двоичное представление числа $ 3_{} $. И ведь действительно: ошибка — в третьем разряде!
♦
Алгоритм построения (n,k)-кода Хэмминга
для $ n=2^M-1,k=2^M-M-1, M ge 2 $.
1.
Строится матрица $ mathbf H $ порядка $ M times (2^M-1) $ из столбцов, представляющих двоичные представления чисел $ {1,2,3,dots,2^M-1} $ (младшие разряды — внизу).
2.
Проверочные разряды имеют номера, равные степеням двойки: $ 1,2,2^2,dots,2^{M-1} $.
3.
Проверочные соотношения получаются из матричного представления $ Xmathbf H^{top}=mathbb O $ выражением проверочных разрядов через информационные.
Можно немного улучшить код Хэмминга, увеличив кодовое расстояние до $ 4_{} $.
?
Является ли $ 8_{} $-мибитный код Адамара из примера
☞
ПУНКТА линейным кодом?
.
Источники
[1]. Питерсон У., Уэлдон Э. Коды, исправляющие ошибки. М.Мир. 1976.
[2]. Марков А.А. Введение в теорию кодирования. М.Наука. 1982
| Binary Hamming codes | |
|---|---|

The Hamming(7,4) code (with r = 3) |
|
| Named after | Richard W. Hamming |
| Classification | |
| Type | Linear block code |
| Block length | 2r − 1 where r ≥ 2 |
| Message length | 2r − r − 1 |
| Rate | 1 − r/(2r − 1) |
| Distance | 3 |
| Alphabet size | 2 |
| Notation | [2r − 1, 2r − r − 1, 3]2-code |
| Properties | |
| perfect code | |
|
In computer science and telecommunication, Hamming codes are a family of linear error-correcting codes. Hamming codes can detect one-bit and two-bit errors, or correct one-bit errors without detection of uncorrected errors. By contrast, the simple parity code cannot correct errors, and can detect only an odd number of bits in error. Hamming codes are perfect codes, that is, they achieve the highest possible rate for codes with their block length and minimum distance of three.[1]
Richard W. Hamming invented Hamming codes in 1950 as a way of automatically correcting errors introduced by punched card readers. In his original paper, Hamming elaborated his general idea, but specifically focused on the Hamming(7,4) code which adds three parity bits to four bits of data.[2]
In mathematical terms, Hamming codes are a class of binary linear code. For each integer r ≥ 2 there is a code-word with block length n = 2r − 1 and message length k = 2r − r − 1. Hence the rate of Hamming codes is R = k / n = 1 − r / (2r − 1), which is the highest possible for codes with minimum distance of three (i.e., the minimal number of bit changes needed to go from any code word to any other code word is three) and block length 2r − 1. The parity-check matrix of a Hamming code is constructed by listing all columns of length r that are non-zero, which means that the dual code of the Hamming code is the shortened Hadamard code. The parity-check matrix has the property that any two columns are pairwise linearly independent.
Due to the limited redundancy that Hamming codes add to the data, they can only detect and correct errors when the error rate is low. This is the case in computer memory (usually RAM), where bit errors are extremely rare and Hamming codes are widely used, and a RAM with this correction system is a ECC RAM (ECC memory). In this context, an extended Hamming code having one extra parity bit is often used. Extended Hamming codes achieve a Hamming distance of four, which allows the decoder to distinguish between when at most one one-bit error occurs and when any two-bit errors occur. In this sense, extended Hamming codes are single-error correcting and double-error detecting, abbreviated as SECDED.
History[edit]
Richard Hamming, the inventor of Hamming codes, worked at Bell Labs in the late 1940s on the Bell Model V computer, an electromechanical relay-based machine with cycle times in seconds. Input was fed in on punched paper tape, seven-eighths of an inch wide, which had up to six holes per row. During weekdays, when errors in the relays were detected, the machine would stop and flash lights so that the operators could correct the problem. During after-hours periods and on weekends, when there were no operators, the machine simply moved on to the next job.
Hamming worked on weekends, and grew increasingly frustrated with having to restart his programs from scratch due to detected errors. In a taped interview, Hamming said, «And so I said, ‘Damn it, if the machine can detect an error, why can’t it locate the position of the error and correct it?’».[3] Over the next few years, he worked on the problem of error-correction, developing an increasingly powerful array of algorithms. In 1950, he published what is now known as Hamming code, which remains in use today in applications such as ECC memory.
Codes predating Hamming[edit]
A number of simple error-detecting codes were used before Hamming codes, but none were as effective as Hamming codes in the same overhead of space.
Parity[edit]
Parity adds a single bit that indicates whether the number of ones (bit-positions with values of one) in the preceding data was even or odd. If an odd number of bits is changed in transmission, the message will change parity and the error can be detected at this point; however, the bit that changed may have been the parity bit itself. The most common convention is that a parity value of one indicates that there is an odd number of ones in the data, and a parity value of zero indicates that there is an even number of ones. If the number of bits changed is even, the check bit will be valid and the error will not be detected.
Moreover, parity does not indicate which bit contained the error, even when it can detect it. The data must be discarded entirely and re-transmitted from scratch. On a noisy transmission medium, a successful transmission could take a long time or may never occur. However, while the quality of parity checking is poor, since it uses only a single bit, this method results in the least overhead.
Two-out-of-five code[edit]
A two-out-of-five code is an encoding scheme which uses five bits consisting of exactly three 0s and two 1s. This provides ten possible combinations, enough to represent the digits 0–9. This scheme can detect all single bit-errors, all odd numbered bit-errors and some even numbered bit-errors (for example the flipping of both 1-bits). However it still cannot correct any of these errors.
Repetition[edit]
Another code in use at the time repeated every data bit multiple times in order to ensure that it was sent correctly. For instance, if the data bit to be sent is a 1, an n = 3 repetition code will send 111. If the three bits received are not identical, an error occurred during transmission. If the channel is clean enough, most of the time only one bit will change in each triple. Therefore, 001, 010, and 100 each correspond to a 0 bit, while 110, 101, and 011 correspond to a 1 bit, with the greater quantity of digits that are the same (‘0’ or a ‘1’) indicating what the data bit should be. A code with this ability to reconstruct the original message in the presence of errors is known as an error-correcting code. This triple repetition code is a Hamming code with m = 2, since there are two parity bits, and 22 − 2 − 1 = 1 data bit.
Such codes cannot correctly repair all errors, however. In our example, if the channel flips two bits and the receiver gets 001, the system will detect the error, but conclude that the original bit is 0, which is incorrect. If we increase the size of the bit string to four, we can detect all two-bit errors but cannot correct them (the quantity of parity bits is even); at five bits, we can both detect and correct all two-bit errors, but not all three-bit errors.
Moreover, increasing the size of the parity bit string is inefficient, reducing throughput by three times in our original case, and the efficiency drops drastically as we increase the number of times each bit is duplicated in order to detect and correct more errors.
Description[edit]
If more error-correcting bits are included with a message, and if those bits can be arranged such that different incorrect bits produce different error results, then bad bits could be identified. In a seven-bit message, there are seven possible single bit errors, so three error control bits could potentially specify not only that an error occurred but also which bit caused the error.
Hamming studied the existing coding schemes, including two-of-five, and generalized their concepts. To start with, he developed a nomenclature to describe the system, including the number of data bits and error-correction bits in a block. For instance, parity includes a single bit for any data word, so assuming ASCII words with seven bits, Hamming described this as an (8,7) code, with eight bits in total, of which seven are data. The repetition example would be (3,1), following the same logic. The code rate is the second number divided by the first, for our repetition example, 1/3.
Hamming also noticed the problems with flipping two or more bits, and described this as the «distance» (it is now called the Hamming distance, after him). Parity has a distance of 2, so one bit flip can be detected but not corrected, and any two bit flips will be invisible. The (3,1) repetition has a distance of 3, as three bits need to be flipped in the same triple to obtain another code word with no visible errors. It can correct one-bit errors or it can detect — but not correct — two-bit errors. A (4,1) repetition (each bit is repeated four times) has a distance of 4, so flipping three bits can be detected, but not corrected. When three bits flip in the same group there can be situations where attempting to correct will produce the wrong code word. In general, a code with distance k can detect but not correct k − 1 errors.
Hamming was interested in two problems at once: increasing the distance as much as possible, while at the same time increasing the code rate as much as possible. During the 1940s he developed several encoding schemes that were dramatic improvements on existing codes. The key to all of his systems was to have the parity bits overlap, such that they managed to check each other as well as the data.
General algorithm[edit]
The following general algorithm generates a single-error correcting (SEC) code for any number of bits. The main idea is to choose the error-correcting bits such that the index-XOR (the XOR of all the bit positions containing a 1) is 0. We use positions 1, 10, 100, etc. (in binary) as the error-correcting bits, which guarantees it is possible to set the error-correcting bits so that the index-XOR of the whole message is 0. If the receiver receives a string with index-XOR 0, they can conclude there were no corruptions, and otherwise, the index-XOR indicates the index of the corrupted bit.
An algorithm can be deduced from the following description:
- Number the bits starting from 1: bit 1, 2, 3, 4, 5, 6, 7, etc.
- Write the bit numbers in binary: 1, 10, 11, 100, 101, 110, 111, etc.
- All bit positions that are powers of two (have a single 1 bit in the binary form of their position) are parity bits: 1, 2, 4, 8, etc. (1, 10, 100, 1000)
- All other bit positions, with two or more 1 bits in the binary form of their position, are data bits.
- Each data bit is included in a unique set of 2 or more parity bits, as determined by the binary form of its bit position.
- Parity bit 1 covers all bit positions which have the least significant bit set: bit 1 (the parity bit itself), 3, 5, 7, 9, etc.
- Parity bit 2 covers all bit positions which have the second least significant bit set: bits 2-3, 6-7, 10-11, etc.
- Parity bit 4 covers all bit positions which have the third least significant bit set: bits 4–7, 12–15, 20–23, etc.
- Parity bit 8 covers all bit positions which have the fourth least significant bit set: bits 8–15, 24–31, 40–47, etc.
- In general each parity bit covers all bits where the bitwise AND of the parity position and the bit position is non-zero.
If a byte of data to be encoded is 10011010, then the data word (using _ to represent the parity bits) would be __1_001_1010, and the code word is 011100101010.
The choice of the parity, even or odd, is irrelevant but the same choice must be used for both encoding and decoding.
This general rule can be shown visually:
-
Bit position 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 … Encoded data bits p1 p2 d1 p4 d2 d3 d4 p8 d5 d6 d7 d8 d9 d10 d11 p16 d12 d13 d14 d15 Parity
bit
coveragep1 p2 p4 p8 p16
Shown are only 20 encoded bits (5 parity, 15 data) but the pattern continues indefinitely. The key thing about Hamming Codes that can be seen from visual inspection is that any given bit is included in a unique set of parity bits. To check for errors, check all of the parity bits. The pattern of errors, called the error syndrome, identifies the bit in error. If all parity bits are correct, there is no error. Otherwise, the sum of the positions of the erroneous parity bits identifies the erroneous bit. For example, if the parity bits in positions 1, 2 and 8 indicate an error, then bit 1+2+8=11 is in error. If only one parity bit indicates an error, the parity bit itself is in error.
With m parity bits, bits from 1 up to 

| Parity bits | Total bits | Data bits | Name | Rate |
|---|---|---|---|---|
| 2 | 3 | 1 | Hamming(3,1) (Triple repetition code) |
1/3 ≈ 0.333 |
| 3 | 7 | 4 | Hamming(7,4) | 4/7 ≈ 0.571 |
| 4 | 15 | 11 | Hamming(15,11) | 11/15 ≈ 0.733 |
| 5 | 31 | 26 | Hamming(31,26) | 26/31 ≈ 0.839 |
| 6 | 63 | 57 | Hamming(63,57) | 57/63 ≈ 0.905 |
| 7 | 127 | 120 | Hamming(127,120) | 120/127 ≈ 0.945 |
| 8 | 255 | 247 | Hamming(255,247) | 247/255 ≈ 0.969 |
| … | ||||
| m |  |
 |
Hamming |

|
Hamming codes with additional parity (SECDED)[edit]
Hamming codes have a minimum distance of 3, which means that the decoder can detect and correct a single error, but it cannot distinguish a double bit error of some codeword from a single bit error of a different codeword. Thus, some double-bit errors will be incorrectly decoded as if they were single bit errors and therefore go undetected, unless no correction is attempted.
To remedy this shortcoming, Hamming codes can be extended by an extra parity bit. This way, it is possible to increase the minimum distance of the Hamming code to 4, which allows the decoder to distinguish between single bit errors and two-bit errors. Thus the decoder can detect and correct a single error and at the same time detect (but not correct) a double error.
If the decoder does not attempt to correct errors, it can reliably detect triple bit errors. If the decoder does correct errors, some triple errors will be mistaken for single errors and «corrected» to the wrong value. Error correction is therefore a trade-off between certainty (the ability to reliably detect triple bit errors) and resiliency (the ability to keep functioning in the face of single bit errors).
This extended Hamming code was popular in computer memory systems, starting with IBM 7030 Stretch in 1961,[4] where it is known as SECDED (or SEC-DED, abbreviated from single error correction, double error detection).[5] Server computers in 21st century, while typically keeping the SECDED level of protection, no longer use the Hamming’s method, relying instead on the designs with longer codewords (128 to 256 bits of data) and modified balanced parity-check trees.[4] The (72,64) Hamming code is still popular in some hardware designs, including Xilinx FPGA families.[4]
[7,4] Hamming code[edit]
Graphical depiction of the four data bits and three parity bits and which parity bits apply to which data bits
In 1950, Hamming introduced the [7,4] Hamming code. It encodes four data bits into seven bits by adding three parity bits. It can detect and correct single-bit errors. With the addition of an overall parity bit, it can also detect (but not correct) double-bit errors.
Construction of G and H[edit]
The matrix

and 
This is the construction of G and H in standard (or systematic) form. Regardless of form, G and H for linear block codes must satisfy

Since [7, 4, 3] = [n, k, d] = [2m − 1, 2m − 1 − m, 3]. The parity-check matrix H of a Hamming code is constructed by listing all columns of length m that are pair-wise independent.
Thus H is a matrix whose left side is all of the nonzero n-tuples where order of the n-tuples in the columns of matrix does not matter. The right hand side is just the (n − k)-identity matrix.
So G can be obtained from H by taking the transpose of the left hand side of H with the identity k-identity matrix on the left hand side of G.
The code generator matrix 


and

Finally, these matrices can be mutated into equivalent non-systematic codes by the following operations:[6]
- Column permutations (swapping columns)
- Elementary row operations (replacing a row with a linear combination of rows)
Encoding[edit]
- Example
From the above matrix we have 2k = 24 = 16 codewords.
Let 
![{displaystyle {vec {a}}=[a_{1},a_{2},a_{3},a_{4}],quad a_{i}in {0,1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/898ddf319567d4af0acecf5c7fd450f5f466e28b)



For example, let ![{displaystyle {vec {a}}=[1,0,1,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e838e2ec81e9fe6223596b61f747b195d3d338fb)


[7,4] Hamming code with an additional parity bit[edit]
The same [7,4] example from above with an extra parity bit. This diagram is not meant to correspond to the matrix H for this example.
The [7,4] Hamming code can easily be extended to an [8,4] code by adding an extra parity bit on top of the (7,4) encoded word (see Hamming(7,4)).
This can be summed up with the revised matrices:
and
Note that H is not in standard form. To obtain G, elementary row operations can be used to obtain an equivalent matrix to H in systematic form:
For example, the first row in this matrix is the sum of the second and third rows of H in non-systematic form. Using the systematic construction for Hamming codes from above, the matrix A is apparent and the systematic form of G is written as
The non-systematic form of G can be row reduced (using elementary row operations) to match this matrix.
The addition of the fourth row effectively computes the sum of all the codeword bits (data and parity) as the fourth parity bit.
For example, 1011 is encoded (using the non-systematic form of G at the start of this section) into 01100110 where blue digits are data; red digits are parity bits from the [7,4] Hamming code; and the green digit is the parity bit added by the [8,4] code.
The green digit makes the parity of the [7,4] codewords even.
Finally, it can be shown that the minimum distance has increased from 3, in the [7,4] code, to 4 in the [8,4] code. Therefore, the code can be defined as [8,4] Hamming code.
To decode the [8,4] Hamming code, first check the parity bit. If the parity bit indicates an error, single error correction (the [7,4] Hamming code) will indicate the error location, with «no error» indicating the parity bit. If the parity bit is correct, then single error correction will indicate the (bitwise) exclusive-or of two error locations. If the locations are equal («no error») then a double bit error either has not occurred, or has cancelled itself out. Otherwise, a double bit error has occurred.
See also[edit]
- Coding theory
- Golay code
- Reed–Muller code
- Reed–Solomon error correction
- Turbo code
- Low-density parity-check code
- Hamming bound
- Hamming distance
Notes[edit]
- ^ See Lemma 12 of
- ^ Hamming (1950), pp. 153–154.
- ^ Thompson, Thomas M. (1983), From Error-Correcting Codes through Sphere Packings to Simple Groups, The Carus Mathematical Monographs (#21), Mathematical Association of America, pp. 16–17, ISBN 0-88385-023-0
- ^ a b c Kythe & Kythe 2017, p. 115.
- ^ Kythe & Kythe 2017, p. 95.
- ^ a b Moon T. Error correction coding: Mathematical Methods and
Algorithms. John Wiley and Sons, 2005.(Cap. 3) ISBN 978-0-471-64800-0
References[edit]
- Hamming, Richard Wesley (1950). «Error detecting and error correcting codes» (PDF). Bell System Technical Journal. 29 (2): 147–160. doi:10.1002/j.1538-7305.1950.tb00463.x. S2CID 61141773. Archived (PDF) from the original on 2022-10-09.
- Moon, Todd K. (2005). Error Correction Coding. New Jersey: John Wiley & Sons. ISBN 978-0-471-64800-0.
- MacKay, David J.C. (September 2003). Information Theory, Inference and Learning Algorithms. Cambridge: Cambridge University Press. ISBN 0-521-64298-1.
- D.K. Bhattacharryya, S. Nandi. «An efficient class of SEC-DED-AUED codes». 1997 International Symposium on Parallel Architectures, Algorithms and Networks (ISPAN ’97). pp. 410–415. doi:10.1109/ISPAN.1997.645128.
- «Mathematical Challenge April 2013 Error-correcting codes» (PDF). swissQuant Group Leadership Team. April 2013. Archived (PDF) from the original on 2017-09-12.
- Kythe, Dave K.; Kythe, Prem K. (28 July 2017). «Extended Hamming Codes». Algebraic and Stochastic Coding Theory. CRC Press. pp. 95–116. ISBN 978-1-351-83245-8.
External links[edit]
- Visual Explanation of Hamming Codes
- CGI script for calculating Hamming distances (from R. Tervo, UNB, Canada)
- Tool for calculating Hamming code
| Binary Hamming codes | |
|---|---|

The Hamming(7,4) code (with r = 3) |
|
| Named after | Richard W. Hamming |
| Classification | |
| Type | Linear block code |
| Block length | 2r − 1 where r ≥ 2 |
| Message length | 2r − r − 1 |
| Rate | 1 − r/(2r − 1) |
| Distance | 3 |
| Alphabet size | 2 |
| Notation | [2r − 1, 2r − r − 1, 3]2-code |
| Properties | |
| perfect code | |
|
In computer science and telecommunication, Hamming codes are a family of linear error-correcting codes. Hamming codes can detect one-bit and two-bit errors, or correct one-bit errors without detection of uncorrected errors. By contrast, the simple parity code cannot correct errors, and can detect only an odd number of bits in error. Hamming codes are perfect codes, that is, they achieve the highest possible rate for codes with their block length and minimum distance of three.[1]
Richard W. Hamming invented Hamming codes in 1950 as a way of automatically correcting errors introduced by punched card readers. In his original paper, Hamming elaborated his general idea, but specifically focused on the Hamming(7,4) code which adds three parity bits to four bits of data.[2]
In mathematical terms, Hamming codes are a class of binary linear code. For each integer r ≥ 2 there is a code-word with block length n = 2r − 1 and message length k = 2r − r − 1. Hence the rate of Hamming codes is R = k / n = 1 − r / (2r − 1), which is the highest possible for codes with minimum distance of three (i.e., the minimal number of bit changes needed to go from any code word to any other code word is three) and block length 2r − 1. The parity-check matrix of a Hamming code is constructed by listing all columns of length r that are non-zero, which means that the dual code of the Hamming code is the shortened Hadamard code. The parity-check matrix has the property that any two columns are pairwise linearly independent.
Due to the limited redundancy that Hamming codes add to the data, they can only detect and correct errors when the error rate is low. This is the case in computer memory (usually RAM), where bit errors are extremely rare and Hamming codes are widely used, and a RAM with this correction system is a ECC RAM (ECC memory). In this context, an extended Hamming code having one extra parity bit is often used. Extended Hamming codes achieve a Hamming distance of four, which allows the decoder to distinguish between when at most one one-bit error occurs and when any two-bit errors occur. In this sense, extended Hamming codes are single-error correcting and double-error detecting, abbreviated as SECDED.
History[edit]
Richard Hamming, the inventor of Hamming codes, worked at Bell Labs in the late 1940s on the Bell Model V computer, an electromechanical relay-based machine with cycle times in seconds. Input was fed in on punched paper tape, seven-eighths of an inch wide, which had up to six holes per row. During weekdays, when errors in the relays were detected, the machine would stop and flash lights so that the operators could correct the problem. During after-hours periods and on weekends, when there were no operators, the machine simply moved on to the next job.
Hamming worked on weekends, and grew increasingly frustrated with having to restart his programs from scratch due to detected errors. In a taped interview, Hamming said, «And so I said, ‘Damn it, if the machine can detect an error, why can’t it locate the position of the error and correct it?’».[3] Over the next few years, he worked on the problem of error-correction, developing an increasingly powerful array of algorithms. In 1950, he published what is now known as Hamming code, which remains in use today in applications such as ECC memory.
Codes predating Hamming[edit]
A number of simple error-detecting codes were used before Hamming codes, but none were as effective as Hamming codes in the same overhead of space.
Parity[edit]
Parity adds a single bit that indicates whether the number of ones (bit-positions with values of one) in the preceding data was even or odd. If an odd number of bits is changed in transmission, the message will change parity and the error can be detected at this point; however, the bit that changed may have been the parity bit itself. The most common convention is that a parity value of one indicates that there is an odd number of ones in the data, and a parity value of zero indicates that there is an even number of ones. If the number of bits changed is even, the check bit will be valid and the error will not be detected.
Moreover, parity does not indicate which bit contained the error, even when it can detect it. The data must be discarded entirely and re-transmitted from scratch. On a noisy transmission medium, a successful transmission could take a long time or may never occur. However, while the quality of parity checking is poor, since it uses only a single bit, this method results in the least overhead.
Two-out-of-five code[edit]
A two-out-of-five code is an encoding scheme which uses five bits consisting of exactly three 0s and two 1s. This provides ten possible combinations, enough to represent the digits 0–9. This scheme can detect all single bit-errors, all odd numbered bit-errors and some even numbered bit-errors (for example the flipping of both 1-bits). However it still cannot correct any of these errors.
Repetition[edit]
Another code in use at the time repeated every data bit multiple times in order to ensure that it was sent correctly. For instance, if the data bit to be sent is a 1, an n = 3 repetition code will send 111. If the three bits received are not identical, an error occurred during transmission. If the channel is clean enough, most of the time only one bit will change in each triple. Therefore, 001, 010, and 100 each correspond to a 0 bit, while 110, 101, and 011 correspond to a 1 bit, with the greater quantity of digits that are the same (‘0’ or a ‘1’) indicating what the data bit should be. A code with this ability to reconstruct the original message in the presence of errors is known as an error-correcting code. This triple repetition code is a Hamming code with m = 2, since there are two parity bits, and 22 − 2 − 1 = 1 data bit.
Such codes cannot correctly repair all errors, however. In our example, if the channel flips two bits and the receiver gets 001, the system will detect the error, but conclude that the original bit is 0, which is incorrect. If we increase the size of the bit string to four, we can detect all two-bit errors but cannot correct them (the quantity of parity bits is even); at five bits, we can both detect and correct all two-bit errors, but not all three-bit errors.
Moreover, increasing the size of the parity bit string is inefficient, reducing throughput by three times in our original case, and the efficiency drops drastically as we increase the number of times each bit is duplicated in order to detect and correct more errors.
Description[edit]
If more error-correcting bits are included with a message, and if those bits can be arranged such that different incorrect bits produce different error results, then bad bits could be identified. In a seven-bit message, there are seven possible single bit errors, so three error control bits could potentially specify not only that an error occurred but also which bit caused the error.
Hamming studied the existing coding schemes, including two-of-five, and generalized their concepts. To start with, he developed a nomenclature to describe the system, including the number of data bits and error-correction bits in a block. For instance, parity includes a single bit for any data word, so assuming ASCII words with seven bits, Hamming described this as an (8,7) code, with eight bits in total, of which seven are data. The repetition example would be (3,1), following the same logic. The code rate is the second number divided by the first, for our repetition example, 1/3.
Hamming also noticed the problems with flipping two or more bits, and described this as the «distance» (it is now called the Hamming distance, after him). Parity has a distance of 2, so one bit flip can be detected but not corrected, and any two bit flips will be invisible. The (3,1) repetition has a distance of 3, as three bits need to be flipped in the same triple to obtain another code word with no visible errors. It can correct one-bit errors or it can detect — but not correct — two-bit errors. A (4,1) repetition (each bit is repeated four times) has a distance of 4, so flipping three bits can be detected, but not corrected. When three bits flip in the same group there can be situations where attempting to correct will produce the wrong code word. In general, a code with distance k can detect but not correct k − 1 errors.
Hamming was interested in two problems at once: increasing the distance as much as possible, while at the same time increasing the code rate as much as possible. During the 1940s he developed several encoding schemes that were dramatic improvements on existing codes. The key to all of his systems was to have the parity bits overlap, such that they managed to check each other as well as the data.
General algorithm[edit]
The following general algorithm generates a single-error correcting (SEC) code for any number of bits. The main idea is to choose the error-correcting bits such that the index-XOR (the XOR of all the bit positions containing a 1) is 0. We use positions 1, 10, 100, etc. (in binary) as the error-correcting bits, which guarantees it is possible to set the error-correcting bits so that the index-XOR of the whole message is 0. If the receiver receives a string with index-XOR 0, they can conclude there were no corruptions, and otherwise, the index-XOR indicates the index of the corrupted bit.
An algorithm can be deduced from the following description:
- Number the bits starting from 1: bit 1, 2, 3, 4, 5, 6, 7, etc.
- Write the bit numbers in binary: 1, 10, 11, 100, 101, 110, 111, etc.
- All bit positions that are powers of two (have a single 1 bit in the binary form of their position) are parity bits: 1, 2, 4, 8, etc. (1, 10, 100, 1000)
- All other bit positions, with two or more 1 bits in the binary form of their position, are data bits.
- Each data bit is included in a unique set of 2 or more parity bits, as determined by the binary form of its bit position.
- Parity bit 1 covers all bit positions which have the least significant bit set: bit 1 (the parity bit itself), 3, 5, 7, 9, etc.
- Parity bit 2 covers all bit positions which have the second least significant bit set: bits 2-3, 6-7, 10-11, etc.
- Parity bit 4 covers all bit positions which have the third least significant bit set: bits 4–7, 12–15, 20–23, etc.
- Parity bit 8 covers all bit positions which have the fourth least significant bit set: bits 8–15, 24–31, 40–47, etc.
- In general each parity bit covers all bits where the bitwise AND of the parity position and the bit position is non-zero.
If a byte of data to be encoded is 10011010, then the data word (using _ to represent the parity bits) would be __1_001_1010, and the code word is 011100101010.
The choice of the parity, even or odd, is irrelevant but the same choice must be used for both encoding and decoding.
This general rule can be shown visually:
-
Bit position 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 … Encoded data bits p1 p2 d1 p4 d2 d3 d4 p8 d5 d6 d7 d8 d9 d10 d11 p16 d12 d13 d14 d15 Parity
bit
coveragep1 p2 p4 p8 p16
Shown are only 20 encoded bits (5 parity, 15 data) but the pattern continues indefinitely. The key thing about Hamming Codes that can be seen from visual inspection is that any given bit is included in a unique set of parity bits. To check for errors, check all of the parity bits. The pattern of errors, called the error syndrome, identifies the bit in error. If all parity bits are correct, there is no error. Otherwise, the sum of the positions of the erroneous parity bits identifies the erroneous bit. For example, if the parity bits in positions 1, 2 and 8 indicate an error, then bit 1+2+8=11 is in error. If only one parity bit indicates an error, the parity bit itself is in error.
With m parity bits, bits from 1 up to 

| Parity bits | Total bits | Data bits | Name | Rate |
|---|---|---|---|---|
| 2 | 3 | 1 | Hamming(3,1) (Triple repetition code) |
1/3 ≈ 0.333 |
| 3 | 7 | 4 | Hamming(7,4) | 4/7 ≈ 0.571 |
| 4 | 15 | 11 | Hamming(15,11) | 11/15 ≈ 0.733 |
| 5 | 31 | 26 | Hamming(31,26) | 26/31 ≈ 0.839 |
| 6 | 63 | 57 | Hamming(63,57) | 57/63 ≈ 0.905 |
| 7 | 127 | 120 | Hamming(127,120) | 120/127 ≈ 0.945 |
| 8 | 255 | 247 | Hamming(255,247) | 247/255 ≈ 0.969 |
| … | ||||
| m |  |
 |
Hamming |

|
Hamming codes with additional parity (SECDED)[edit]
Hamming codes have a minimum distance of 3, which means that the decoder can detect and correct a single error, but it cannot distinguish a double bit error of some codeword from a single bit error of a different codeword. Thus, some double-bit errors will be incorrectly decoded as if they were single bit errors and therefore go undetected, unless no correction is attempted.
To remedy this shortcoming, Hamming codes can be extended by an extra parity bit. This way, it is possible to increase the minimum distance of the Hamming code to 4, which allows the decoder to distinguish between single bit errors and two-bit errors. Thus the decoder can detect and correct a single error and at the same time detect (but not correct) a double error.
If the decoder does not attempt to correct errors, it can reliably detect triple bit errors. If the decoder does correct errors, some triple errors will be mistaken for single errors and «corrected» to the wrong value. Error correction is therefore a trade-off between certainty (the ability to reliably detect triple bit errors) and resiliency (the ability to keep functioning in the face of single bit errors).
This extended Hamming code was popular in computer memory systems, starting with IBM 7030 Stretch in 1961,[4] where it is known as SECDED (or SEC-DED, abbreviated from single error correction, double error detection).[5] Server computers in 21st century, while typically keeping the SECDED level of protection, no longer use the Hamming’s method, relying instead on the designs with longer codewords (128 to 256 bits of data) and modified balanced parity-check trees.[4] The (72,64) Hamming code is still popular in some hardware designs, including Xilinx FPGA families.[4]
[7,4] Hamming code[edit]
Graphical depiction of the four data bits and three parity bits and which parity bits apply to which data bits
In 1950, Hamming introduced the [7,4] Hamming code. It encodes four data bits into seven bits by adding three parity bits. It can detect and correct single-bit errors. With the addition of an overall parity bit, it can also detect (but not correct) double-bit errors.
Construction of G and H[edit]
The matrix

and 
This is the construction of G and H in standard (or systematic) form. Regardless of form, G and H for linear block codes must satisfy

Since [7, 4, 3] = [n, k, d] = [2m − 1, 2m − 1 − m, 3]. The parity-check matrix H of a Hamming code is constructed by listing all columns of length m that are pair-wise independent.
Thus H is a matrix whose left side is all of the nonzero n-tuples where order of the n-tuples in the columns of matrix does not matter. The right hand side is just the (n − k)-identity matrix.
So G can be obtained from H by taking the transpose of the left hand side of H with the identity k-identity matrix on the left hand side of G.
The code generator matrix 


and

Finally, these matrices can be mutated into equivalent non-systematic codes by the following operations:[6]
- Column permutations (swapping columns)
- Elementary row operations (replacing a row with a linear combination of rows)
Encoding[edit]
- Example
From the above matrix we have 2k = 24 = 16 codewords.
Let 
![{displaystyle {vec {a}}=[a_{1},a_{2},a_{3},a_{4}],quad a_{i}in {0,1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/898ddf319567d4af0acecf5c7fd450f5f466e28b)



For example, let ![{displaystyle {vec {a}}=[1,0,1,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e838e2ec81e9fe6223596b61f747b195d3d338fb)


[7,4] Hamming code with an additional parity bit[edit]
The same [7,4] example from above with an extra parity bit. This diagram is not meant to correspond to the matrix H for this example.
The [7,4] Hamming code can easily be extended to an [8,4] code by adding an extra parity bit on top of the (7,4) encoded word (see Hamming(7,4)).
This can be summed up with the revised matrices:
and
Note that H is not in standard form. To obtain G, elementary row operations can be used to obtain an equivalent matrix to H in systematic form:
For example, the first row in this matrix is the sum of the second and third rows of H in non-systematic form. Using the systematic construction for Hamming codes from above, the matrix A is apparent and the systematic form of G is written as
The non-systematic form of G can be row reduced (using elementary row operations) to match this matrix.
The addition of the fourth row effectively computes the sum of all the codeword bits (data and parity) as the fourth parity bit.
For example, 1011 is encoded (using the non-systematic form of G at the start of this section) into 01100110 where blue digits are data; red digits are parity bits from the [7,4] Hamming code; and the green digit is the parity bit added by the [8,4] code.
The green digit makes the parity of the [7,4] codewords even.
Finally, it can be shown that the minimum distance has increased from 3, in the [7,4] code, to 4 in the [8,4] code. Therefore, the code can be defined as [8,4] Hamming code.
To decode the [8,4] Hamming code, first check the parity bit. If the parity bit indicates an error, single error correction (the [7,4] Hamming code) will indicate the error location, with «no error» indicating the parity bit. If the parity bit is correct, then single error correction will indicate the (bitwise) exclusive-or of two error locations. If the locations are equal («no error») then a double bit error either has not occurred, or has cancelled itself out. Otherwise, a double bit error has occurred.
See also[edit]
- Coding theory
- Golay code
- Reed–Muller code
- Reed–Solomon error correction
- Turbo code
- Low-density parity-check code
- Hamming bound
- Hamming distance
Notes[edit]
- ^ See Lemma 12 of
- ^ Hamming (1950), pp. 153–154.
- ^ Thompson, Thomas M. (1983), From Error-Correcting Codes through Sphere Packings to Simple Groups, The Carus Mathematical Monographs (#21), Mathematical Association of America, pp. 16–17, ISBN 0-88385-023-0
- ^ a b c Kythe & Kythe 2017, p. 115.
- ^ Kythe & Kythe 2017, p. 95.
- ^ a b Moon T. Error correction coding: Mathematical Methods and
Algorithms. John Wiley and Sons, 2005.(Cap. 3) ISBN 978-0-471-64800-0
References[edit]
- Hamming, Richard Wesley (1950). «Error detecting and error correcting codes» (PDF). Bell System Technical Journal. 29 (2): 147–160. doi:10.1002/j.1538-7305.1950.tb00463.x. S2CID 61141773. Archived (PDF) from the original on 2022-10-09.
- Moon, Todd K. (2005). Error Correction Coding. New Jersey: John Wiley & Sons. ISBN 978-0-471-64800-0.
- MacKay, David J.C. (September 2003). Information Theory, Inference and Learning Algorithms. Cambridge: Cambridge University Press. ISBN 0-521-64298-1.
- D.K. Bhattacharryya, S. Nandi. «An efficient class of SEC-DED-AUED codes». 1997 International Symposium on Parallel Architectures, Algorithms and Networks (ISPAN ’97). pp. 410–415. doi:10.1109/ISPAN.1997.645128.
- «Mathematical Challenge April 2013 Error-correcting codes» (PDF). swissQuant Group Leadership Team. April 2013. Archived (PDF) from the original on 2017-09-12.
- Kythe, Dave K.; Kythe, Prem K. (28 July 2017). «Extended Hamming Codes». Algebraic and Stochastic Coding Theory. CRC Press. pp. 95–116. ISBN 978-1-351-83245-8.
External links[edit]
- Visual Explanation of Hamming Codes
- CGI script for calculating Hamming distances (from R. Tervo, UNB, Canada)
- Tool for calculating Hamming code
Код
Хэмминга относится к классу линейных
кодов и представляет собой систематический
код – код, в котором информационные и
контрольные биты расположены на строго
определенных местах в кодовой комбинации.
Код
Хэмминга, как и любой (n,
k)-
код, содержит к
информационных и m
= n-k
избыточных (проверочных) бит.
Избыточная
часть кода строится т. о. чтобы можно
было при декодировании не только
установить наличие ошибки но, и указать
номер позиции в которой произошла ошибка
, а значит и исправить ее, инвертировав
значение соответствующего бита.
Существуют
различные методы реализации кода
Хэмминга и кодов которые являются
модификацией кода Хэмминга. Рассмотрим
алгоритм построения кода для исправления
одиночной ошибки.
1.
По заданному количеству информационных
символов — k,
либо информационных комбинаций N
= 2k
, используя соотношения:
n
= k+m, 2n
(n+1)2k
и
2m
n+1 (14)
m
= [log2
{(k+1)+
[log2(k+1)]}]
вычисляют
основные параметры кода n
и m.
2.
Определяем рабочие и контрольные позиции
кодовой комбинации. Номера контрольных
позиций определяются по закону 2i,
где
i=1,
2, 3,… т.е. они равны 1, 2, 4, 8, 16,… а остальные
позиции являются рабочими.
3.
Определяем значения контрольных разрядов
(0 или 1 ) при помощи многократных проверок
кодовой комбинации на четность. Количество
проверок равно m
= n-k.
В каждую проверку включается один
контро-льный и определенные проверочные
биты. Если результат проверки дает
четное число, то контрольному биту
присваивается значение -0, в противном
случае — 1. Номера информационных бит,
включаемых в каждую проверку, определяются
по двоичному коду натуральных n
–чисел
разрядностью – m
(табл.
1, для m
= 4)
или при помощи проверочной матрицы
H(mn),
столбцы которой представляют запись в
двоичной системе всех целых чисел от 1
до 2k
–1
перечисленных в возрастающем порядке.
Для
m = 3
проверочная матрица имеет вид

(15 )
Количество
разрядов m
— определяет количество проверок.
В
первую проверку включают коэффициенты,
содержащие 1 в младшем (первом) разряде,
т. е. b1,
b3,
b5
и т. д.
Во
вторую проверку включают коэффициенты,
содержащие 1 во втором разряде, т. е. b2,
b3,
b6
и т. д.
В
третью проверку — коэффициенты которые
содержат 1 в третьем разряде и т. д.
Таблица
1
|
Десятичные
(номера
кодовой |
Двоичные |
||
|
3 |
2 |
1 |
|
|
1 2 3 4 5 6 7 |
0 0 0 1 1 1 1 |
0 1 1 0 0 1 1 |
1 0 1 0 1 0 1 |
Для
обнаружения и исправления ошибки
составляются аналогичные проверки на
четность контрольных сумм, результатом
которых является двоичное (n-k)
-разрядное число, называемое синдромом
и указывающим на положение ошибки, т.
е. номер ошибочной позиции, который
определяется по двоичной записи числа,
либо по проверочной матрице.
Для
исправления ошибки необходимо
проинвертировать бит в ошибочной
позиции. Для исправления одиночной
ошибки и обнаружения двойной используют
дополнительную проверку на четность.
Если при исправлении ошибки контроль
на четность фиксирует ошибку, то значит
в кодовой комбинации две ошибки.
Схема
кодера и декодера для кода Хэмминга
приведена на рис. 1.
Пример
1.
Построить код Хемминга для передачи
сообщений в виде последовательности
десятичных цифр, представленных в виде
4 –х разрярных двоичных слов. Показать
процесс кодирования, декодирования и
исправления одиночной ошибки на примере
информационного слова 0101.
Решение:
1.
По заданной длине информационного слова
(k
= 4),
определим количество контрольных
разрядов m,
используя соотношение:
m
= [log2
{(k+1)+
[log2(k+1)]}]=[log2
{(4+1)+
[log2(4+1)]}]=3,
при
этом n
= k+m = 7,
т. е. получили (7, 4) -код.
2.
Определяем номера рабочих и контрольных
позиции кодовой комбинации. Номера
контрольных позиций выбираем по закону
2i
.
Для
рассматриваемой задачи (при n
= 7)
номера контрольных позиций равны 1, 2,
4. При этом кодовая комбинация имеет
вид:
b1
b2
b3
b4
b5
b6
b7
к1
к2
0
к3
1
0 1
3.
Определяем значения контрольных разрядов
(0 или 1), используя проверочную матрицу
(5).
Первая
проверка:
k1
b3
b5
b7
= k1011
будет четной при k1
=
0.
Вторая
проверка:
k2
b3
b6
b7
= k2001
будет четной при k2
=
1.
Третья
проверка:
k3
b5
b6
b7
= k3101
будет четной при k3
=
0.
1
2 3 4 5 6 7
Передаваемая
кодовая комбинация: 0 1 0 0 1 0 1
Допустим
принято: 0 1 1 0 1 0 1
Для
обнаружения и исправления ошибки
составим аналогичные про-верки на
четность контрольных сумм, в соответствии
с проверочной матрицей результатом
которых является двоичное (n-k)
-разрядное число, называемое синдромом
и указывающим на положение ошибки, т.
е, номер ошибочной позиции.
1)
k1
b3
b5
b7
= 0111 = 1.
2)
k2
b3
b6
b7
= 1101 = 1.
-
k3
b5
b6
b7
= 0101 = 0.
Сравнивая
синдром ошибки со столбцами проверочной
матрицы, определяем номер ошибочного
бита. Синдрому 011 соответствует третий
столбец, т. е. ошибка в третьем разряде
кодовой комбинации. Символ в 3 -й позиции
необходимо изменить на обратный.
Пример
2.
Построить код Хэмминга для передачи
кодовой комбинации 1 1 0 1 1 0 1 1. Показать
процесс обнаружения и исправления
ошибки в соответствующем разряде кодовой
комбинации.
Решение:
Рассмотрим
алгоритм построения кода для исправления
одиночной ошибки.
1.
По заданной длине информационного слова
(k
= 8)
, используя соотношения вычислим основные
параметры кода n
и m.
m
= [log2
{(k+1)+
[log2(k+1)]}]=[log2
{(9+1)+
[log2(9+1)]}]=4,
при
этом n
= k+m = 12,
т. е. получили (12, 8)-код.
2.
Определяем номера рабочих и контрольных
позиции кодовой комбинации. Номера
контрольных позиций выбираем по закону
2i
.
Для
рассматриваемой задачи (при n
= 12)
номера контрольных позиций равны 1, 4,
8.
При
этом кодовая комбинация имеет вид:
b1
b2
b3
b4
b5
b6
b7
b8
b9
b10
b11
b12
к1
к2
1
к3
1
0 1 к4
1
0 1 1
3.
Определяем значения контрольных разрядов
(0 или 1) путем много-кратных проверок
кодовой комбинации на четность. Количество
проверок равно m
= n-k.
В каждую проверку включается один
контрольный и определенные проверочные
биты.
Номера
информационных бит, включаемых в каждую
проверку определяется по двоичному
коду натуральных n-чисел
разрядностью — m.
0001
b1
Количество разрядов m — определяет
количество прове-
0010
b2
верок.
0011
b3
1) к1
b3
b5
b7
b9
а11
=
к111111
=>
0100
b4
четная
при к1=1
0101
b5
2)
к2
b3
b6
b7
b10
b11=
к210101
=>
0110
b6
четная при к2=1
0111
b7
3)
к3
b5
b6
b7
b12
=
к31011=>
1000
b8
четная
при к3=1
1001
b9
4) к4
b9
b10
b11
b12
=
к11011
=>
1010
b10
четная
при к4=1
1011
b11
1100
b12
Передаваемая
кодовая комбинация: 1 2 3 4 5 6 7 8 9 10 11 12
1
1 1 1 1 0 1 1 1 0 1 1
Допустим,
принято: 1 1 1 1 0 0 1 1 1 0 1 1
Для
обнаружения и исправления ошибки
составим аналогичные про-верки на
четность контрольных сумм, результатом
которых является двоичное (n-k)
-разрядное число, называемое синдромом
и указывающим на положение ошибки, т.
е. номер ошибочной позиции.
1)
к1
b3
b5
b7
b9
b11
=
110111 =1
2)
к2
b3
b6
b7
b10
b11
=
110101 =0
3)
к3
b5
b6
b7
b12
=
10011 =1
4)
к4
b9
b10
b11
b12
=
11011 =0
Обнаружена
ошибка в разряде кодовой комбинации с
номером 0101, т. е. в 5 -м разряде. Для
исправления ошибки необходимо
проинвертировать 5 -й разряд в кодовой
комбинации.
Рис.
1. Схема кодера —а
и декодера –б
для простого (7, 4) кода Хэмминга
Рассмотрим
применение кода Хэмминга. В ЭВМ код
Хэмминга чаще всего используется для
обнаружения и исправления ошибок в ОП,
памяти с обнаружением и исправлением
ошибок ECC Memory (Error Checking and Correcting). Код
Хэмминга используется как при параллельной,
так и при последовательной записи. В
ЭВМ значительная часть интенсивности
потока ошибок приходится на ОП. Причинами
постоянных неисправностей являются
отказы ИС, а случайных изменение
содержимого ОП за счет флуктуации
питающего напряжения, кратковременных
помех и излучений. Неисправность может
быть в одном бите, линии выборки разряда,
слова либо всей ИС. Сбой может возникнуть
при формировании кода (параллельного),
адреса или данных, поэтому защищать
необходимо и то и др. Обычно дешифратор
адреса встроен в м/схему и недоступен
для потребителя. Наиболее часто ошибки
дают ячейки памяти ЗУ, поэтому главным
образом защищают записываемые и
считываемые данные.
Наибольшее
применение в ЗУ нашли коды Хэмминга с
dmin=4,
исправляющие одиночные ошибки и
обнаруживающие двойные.
Проверочные
символы записываются либо в основное,
либо специальное ЗУ. Для каждого
записываемого информационного слова
(а не байта, как при контроле по паритету)
по определенным правилам вычисляется
функция свертки, результат которой
разрядностью в несколько бит также
записывается в память. Для 16 -ти разрядного
информационного слова используется 6
дополнительных бит (32- 7 бит, 64 –8 бит).
При считывании информации схема контроля,
используя избыточные биты, позволяет
обнаружить ошибки различной кратности
или исправить одиночную ошибку. Возможны
различные варианты поведения системы:
-
автоматическое
исправление ошибки без уведомления
системы;
—
исправление однократной ошибки и
уведомление системы только о многократных
ошибках;
—
не исправление ошибки, а только уведомление
системы об ошибках;
Модуль
памяти со встроенной схемой исправления
ошибок –EOS 72/64 (ECC on Simm). Аналог микросхема
к 555 вж 1
-это 16 разрядная схема с обнаружением
и исправлением ошибок (ОИО) по коду
Хэмминга (22, 16), использование которой
позволяет исправить однократные ошибки
и обнаружить все двух кратные ошибки в
ЗУ.
Избыточные
(контрольные) разряды позволяют обнаружить
и исправить ошибки в ЗУ в процессе записи
и хранения информации.
В
составе ВЖ-1 используются 16 информационных
и 6 контрольных разрядов. (DB — информационное
слово, CB — контрольное слово).
При
записи осуществляется формирование
кода, состоящего из 16 информационных и
6 контрольных разрядов, представляющих
результат суммирование по модулю 2
восьми информационных разрядов в
соответствии с кодом Хэмминга.
Сформированные контрольные разряды
вместе с информационными поступают на
схему и записываются в ЗУ.
(22,16)

4
схе(72,64)
Рис.2.
Схема контроля
При
считывании шестнадцатиразрядное слово
декодируется, восстанавливаясь вместе
с 6 разрядным словом контрольным,
поступают на схему сравнения и контроля.
Если достигнуто равенство всех контрольных
разрядов и двоичных слов, то ошибки нет.
Любая
однократная ошибка в 16 разрядном слове
данных изменяет 3 байта в 6 разрядном
контрольном слове. Обнаруженный ошибочный
бит инвертируется.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
§ Для чего нужен код Хэмминга
Иногда случается, что Алиса, передавая Бобу сообщение, совершает фатальную, роковую ошибку и случайно ошибается в одной букве. Боб же, принимая от Алисы послание, читает его и даже не догадывается, что где-то появилась ошибка. Как же тогда быть в этом случае?
Для этого и придуманы коды проверок сообщений, одним из которых является код Хэмминга. Что он умеет?
- Обнаруживать ошибку в переданном сообщении
- Исправлять ошибку, если она была совершена один раз на все сообщение
Код Хэмминга — все лишь один из кодов, которые занимаются поиском и коррекцией ошибок, это один из самых первых, базовых кодов. Теперь же я рассмотрю принцип работы этого кода. Но сначала надо рассказать про биты четности.
§ Бит четности
Продолжая тему Алисы и Боба, (которые являются большими специалистами и экспериментаторами в области связи), допустим, что Алиса, передавая сообщение Бобу, сказала, что количество единиц в этом сообщении, а она передает его в двоичном коде, либо четно, либо не четно.
Например, Алиса хочет передать Бобу сообщение 001101. Подсчитав количество единиц, Алиса приходит к выводу, что это количество — нечетно, и потому добавляет к сообщению также контрольный бит, равный 1. Если бы количество единиц было бы четным, то контрольный бит равнялся бы 0.
Итоговое сообщение получилось 001101 и 1 — бит четности, контрольный бит, контрольная сумма, разные названия есть у него. В один момент, передавая по зашумленному каналу связи, приемник Боба получил следующее сообщение: 101101 и 1. Боб не знает о содержании исходного сообщения, но начинает считать количество единиц и приходит к выводу, что количество единиц — четно, и контрольный бит, вообще-то, должен равняться 0, а он равняется 1.
Исходя из этого, Боб делает вывод, что в сообщении где-то допущена ошибка, но он не знает, где именно. Несмотря на это, этого может даже быть вполне достаточно, чтобы сообщить Алисе, чтобы она выслала сообщение заново.
Проверка бита четности является самым простым, но не всегда надежным способом установить, что где-то есть ошибка. Дело в том, что если изменились 2 бита, то количество нечетных или четных останется тем же, а само сообщение уже не будет правильным. Потому контрольную сумму обычно считают другим методом, например, используя CRC32, где изменение любого количества бит будет менять контрольную сумму на совершенно другое число.
§ Определение четности
Подсчет бита четности ведут через так называемый XOR-элементов, или элемент «Исключающее ИЛИ». Этот элемент находится в основе сумматоров. Его таблица истинности такова, что если A == B, то он выдает 0, иначе 1.
Как известно, нам нужно подсчитать именно четность. Как определяется четность? Для этого обычно делят на 2 и смотрят остаток. Если остаток 1, то число не является четным, и наоборот, если 0, то число — четное. С точки зрения бинарной логики, тут все гораздо проще, четность находится в младшем бите итоговой суммы.
Например, сложим число 1+1 в двоичном коде, получаем 10. Младший бит результата — 0, результат четный. На самом деле, мы можем вообще избавиться от всех битов результата, кроме младшего, оставив только его, и тогда все получается элементарно. Чтобы вычислить результат суммы, необходимо применить A xor B = C, где C будет битом четности.
Сосчитаем четность у числа 10111.
- Берем первые биты, складываем 1+0=10, отбрасываем старшие биты, остается 0
- Складываем полученный результат с третьим битом: 0+1=1
- Опять, результат с четвертым: 1+1=10 (старший бит удаляем)
- И наконец, с пятым: 0+1=1
Итого, на выходе получилось 1, и это значит, что количество единиц не является четным. В общем виде, это записывается так: R = A xor B xor C xor D xor E. Пока что это все, что надо знать про контрольный бит.
§ Определение позиции ошибки
С битом четности мы разобрались, и как находить наличие ошибки в сообщении — тоже, но теперь остался вопрос, а как же теперь найти место, где ошибка произошла? В действительности, это оказалось настолько элементарно, что я удивился, почему раньше это не мог понять (сегодня 2023г, а в родился в 1987).
Для того, чтобы объяснить, я выберу сообщение длиной ровно 8 бит — 1 байт, только сразу оговорюсь, что количество бит в сообщении может быть как угодно большим, этот код работает с любым количеством бит.
Чтобы указать номер бита, в котором находится ошибка, нам потребуется ровно 3 бита. То есть, например, если ошибка в бите 5, то в двоичном коде этот номер был бы записан как 101. Если ошибка в бите 7, то тогда номер бита будет равен 111. То что я говорю сейчас об этом, имеет смысл. Если мы ищем номер бита, в котором произошла ошибка, то нам же и потребуется число, которое может эти номера вместить.
Сделаем одну хитрость. В отличии от контрольного бита, сосчитаем не все подряд биты, а через один бит. Сейчас приведу пример:
1234567 -- номера битов исходного сообщения x x x x -- биты, для которых считаем четность
Казалось бы, нелогично. Зачем считать не всё? А вот как раз в этом и кроется смысл.
Представим, что при передаче сообщения был изменен бит 2. Контрольная сумма останется той же, ничего не изменится в ней, поскольку мы ее просто не считали. Здесь ничего пока что сделать нельзя, сообщение проверить не можем.
Но, что если бит был изменен в 1 или 3, или 5? Тогда контрольная сумма меняется и мы это увидим потому, что контрольная сумма будет уже другой. Что это значит? А то, что мы уже твердо знаем, что да, где-то либо в 1, 3, 5 или 7 бите была допущена ошибка. Иными словами, таким образом, сужается круг поиска с 8 битов до 4.
Как видно, одного бита недостаточно для того, чтобы установить, где произошла ошибка. Для этого введем в игру еще один контрольный бит, который будет считать не через 1 бит, а через 2 бита:
1234567 -- номера битов x x x x -- контрольная сумма r0 xx xx -- контрольная сумма r1
Появляется вспомогательный бит контрольной суммы, который будет уточнять положение ошибочного бита. Сейчас я поясню, как это происходит.
Допустим, что ошибка произошла в бите 1. Видно, что контрольная сумма r1 уже будет не совпадать, и следовательно, у нас ошибка либо в бите 1, либо в бите 5 — всего лишь 2 варианта. Это произошло потому, что был введен уточняющий бит контрольной суммы, которая сужает круг поиска уже с 4 до 2 возможных вариантов.
Получается, что код Хэмминга это своего рода бинарный поиск! Да, теперь у нас 2 варианта, но этого недостаточно, чтобы четко установить, где именно произошла ошибка. И значит, придется добавить еще 1 контрольный бит для этого.
1234567 -- номера битов x x x x -- контрольная сумма r0 xx xx -- контрольная сумма r1 xxxx -- контрольная сумма r2
Вот теперь можно точно и с уверенностью сказать, где именно будет допущена ошибка, основываясь на контрольных битах r0,r1,r2. Давайте проверим.
- Ошибка совершена в бите 5. Это значит, что бит r0 и r2 будут не совпадать, поскольку бит r0 контролирует биты 1,3,5,7, а бит r2 — биты 4,5,6,7. Единственный вариант, где не совпадает r0 и r2, это будет бит 5 и никакой другой
- Допускается ошибка в бите 3. Не совпадет контрольная сумма у r0 и r1 — они изменятся из-за этого.
И тут появляется интересная деталь. Из-за того, что мы особым образом суммируем биты у r0, r1 и r2, допуская ошибку в этих битах, в них будет появляться номер бита с ошибкой!
Это выглядит как какая-то магия, но на самом деле, никакой магии тут нет. Ведь допуская ошибку в 1,3,5 или 7 бите, меняется r0 — младший бит номера ошибки, или допуская ошибку в 2,3,6,7 — меняется второй бит результата, а биты номер 4,5,6,7 содержат третий бит номера ошибки.
§ Код Хэмминга
Пожалуй, сейчас мы подобрались к самой сложной части, это непосредственно к тому, как записываются коды Хэмминга. Дело в том, что в коде, помимо самих битов сообщения, передаются и контрольные биты, при этом, эти же контрольные биты тоже могут быть ошибочные, так что их самих тоже можно восстанавливать. Но как это сделать?
Итак, для 8 битного сообщения ранее определили, что необходимо 3 контрольных бита, чтобы указать номер ошибки. Но, помимо самого сообщения, также надо еще и 3 бита передать. Это значит, что будут переданы как минимум 8+3 бита.
Контрольные биты располагаются, согласно коду Хэмминга в позициях, равных степеней двойки, а именно, бит r0 будет находиться в 1-й позиции, бит r1 — во 2-й, бит r2 — в 4, r3 — в 8 и так далее.
| Сообщение | r0 | r1 | 0 | r2 | 1 | 2 | 3 | r3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Бит № | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| Бит #0 | x | x | x | x | x | x | ||||||
| Бит #1 | x | x | x | x | x | x | ||||||
| Бит #2 | x | x | x | x | x | |||||||
| Бит #3 | x | x | x | x | x |
Рис 1. Код для 8 бит
По этой таблице очень легко понять, что, к примеру, совершенная ошибка в 3-м и 2-м бите дают число 1100, что в десятичном виде даст 12. Как видим, для того чтобы закодировать 8 бит, потребуется 4 бита контроля. Для 16 бит уже потребуется дополнительные 5 бит:
| Сообщение | r0 | r1 | 0 | r2 | 1 | 2 | 3 | r3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | r4 | 11 | 12 | 13 | 14 | 15 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Бит № | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| Бит #0 | x | x | x | x | x | x | x | x | x | x | x | ||||||||||
| Бит #1 | x | x | x | x | x | x | x | x | x | x | |||||||||||
| Бит #2 | x | x | x | x | x | x | x | x | x | x | |||||||||||
| Бит #3 | x | x | x | x | x | x | x | x | |||||||||||||
| Бит #4 | x | x | x | x | x | x |
Рис 2. Код для 16 бит
Почему был выбран такой порядок установки контрольных бит? Не знаю, на самом деле, они могут быть расположены в любом порядке, это не повлияет ни на что, но видимо это сделано из-за определенного удобства. Если взглянуть на иллюстрации кода Хэмминга, то видно, что каждый контрольный бит открывает собственный новый бит так называемого «синдрома» номер 0,1,2 и т.д. Так что порядок расположения контрольных битов в сообщении был выбран по причине его наглядности.
§ Кодирование, декодирование
А теперь, с учетом того, что в сообщении появились новые биты, как теперь кодировать их? Элементарно. Их просто не надо учитывать при кодировании, то есть, они просто будут 0. Все остальные биты, конечно же, будут учитываться. Возьмем, к примеру, сообщение 10010110 и попробуем закодировать его через код Хэмминга.
| Сообщение | r0 | r1 | 0 | r2 | 1 | 2 | 3 | r3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Бит № | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| Данные | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 1 |
| Бит #0 | 0 | 0 | 1 | 0 | 1 | 0 | ||||||
| Бит #1 | 0 | 0 | 1 | 0 | 0 | 0 | ||||||
| Бит #2 | 0 | 1 | 1 | 0 | 1 | |||||||
| Бит #3 | 0 | 1 | 0 | 0 | 1 |
Рис 3. Код сообщения
Сначала впишем в позиции, где должны быть биты сообщения, нужные биты.
- Это значит, что в позицию номер 3 (там где написано «Бит №») пойдет бит 0, потом в позицию 5 пойдет бит 1, далее в 6 — бит 1, в 7 — бит 0. В позициях 9,10,11 и 12 будут оставшиеся 4 бита
1001. - В позициях 1,2,4,8 будут нули
Обращаю внимание на то, что здесь бит 0 сообщения будет младшим битом, а 7 — старшим, так что запись в данном случае как «наоборот», от младшего к старшему. То, в каком порядке передаются биты, не повлияет на результаты.
Теперь, считаем четность для всех контрольных битов.
-
r0 = 0 xor 0 xor 1 xor 0 xor 1 xor 0 = 0 -
r1 = 0 xor 0 xor 1 xor 0 xor 0 xor 0 = 1 -
r2 = 0 xor 1 xor 1 xor 0 xor 1 = 1 -
r3 = 0 xor 1 xor 0 xor 0 xor 1 = 0
Соответственно, теперь эти биты вписываются в то сообщение, которое собираемся отправить, и отправляется. Но считается без них, что очень важно! Получается, что итоговое сообщение будет вот таким: 0 1 0 1 1 1 0 0 1 0 0 1.
Почему так важно не считать биты r0,r1 и т.д. при кодировании? Все просто, это потому что нам необходимо знать изменения именно в исходном сообщений, а также для того, чтобы проверить, не изменился ли сам контрольный бит.
Представим, что при передаче сообщения от Алисы к Бобу изменился контрольный бит r1, который находится в позиции 2. Боб, принимая сообщения, высчитывает контрольные биты заново, сверяя их с теми, которые пришли от Алисы. У Алисы контрольный бит r1 был равен 1, а у Боба он стал равным 0. Боб видит эту ошибку и, поскольку все остальные контрольные биты в порядке, видит, что номер полученного бита по итогу указывает на то, что изменился r1. Но Боб, конечно, и сам догадался.
Еще одна причина, по которой контрольные биты располагаются в сообщении подобным образом в том, что когда регистрируется одиночный бит ошибки, то он всегда указывает на то, что изменился именно контрольный бит, а не бит в самом сообщении. Это, опять-таки, очень удобно получается и наглядно.
Делая вывод, могу сказать следующее. Код Хэмминга быстрый и достаточно хороший, но и он обладает некоторыми недостатками. Для того, чтобы код работал, необходимо передавать избыточные данные. Для 8 битного числа количество избыточных данных составляет аж 4 бита, что в 1.5 раза самого сообщения, так что короткие сообщения передавать накладно. Для 16 бит количество избыточных бит составляет только 5 бит, но и это 30%.
Второй недостаток в том, что при двойной ошибке исправить бит будет уже нельзя, лишь только зафиксировать факт самой ошибки. Также факт того, что это именно двойная ошибка, остается неизвестен.
Код Хэмминга удобно применять там, где количество ошибок единично и они появляются редко, например, в ECC-памяти или еще где-нибудь, к примеру, для регистрации и исправления битов, которые могут измениться в результате космических лучей.
15 янв, 2023
© 2007-2023 Отличная ручка болела
МИНОБРНАУКИ РОССИИ
Федеральное государственное бюджетное образовательное учреждение
высшего образования
«Омский государственный педагогический университет»
(ФГБОУ ВО «ОмГПУ»)
Факультет математики, информатики, физики и технологии
Кафедра прикладной информатики и математики
Курсовая работа
Код Хемминга
Направление: педагогическое образование
Профиль: Информатика и Технология
Дисциплина: Теоретические основы информатики
Выполнила: студентка
32 группы
Коробейникова
Ольга Витальевна
______________________________(подпись)
Научный руководитель:
Курганова
Наталья Александровна
к.п.н., доцент
Оценка _______________
«__» _______________ 20___г.
(подпись)
Омск, 20___
Оглавление
Введение
Глава 1. Теоретические основы изучения помехоустойчивого кодирования
1.1. Виды помехоустойчивого кодирования
1.2. Характеристика кода Хемминга при помехоустойчивом кодировании
1.3. Алгоритмы использования кода Хемминга для нахождения ошибок
Глава 2. Практические основы кода Хемминга
2.1. Примеры использования кода Хемминга для нахождения одной ошибки
2.2. Примеры использования кода Хемминга для нахождения двоичной ошибки
ЗАКЛЮЧЕНИЕ
Список литературы
Введение
На сегодняшний день в мире передается огромное количество информации, хотя системы передачи данных отвечают всем требованиям. Они не являются столь совершенными. При передаче данных могут возникать помехи. Помехоустойчивость – способность системы осуществлять прием информации в условиях наличия помех в линии связи и искажений во внутри аппаратных трактах. Помехоустойчивость обеспечивает надежность и достоверность передаваемой информации (данных).Управление правильностью передачи информации выполняется с помощью помехоустойчивого кодирования. Есть коды, обнаруживающие ошибки, и корректирующие коды, которые еще и исправляют ошибки. Помехозащищенность достигается с помощью введения избыточности, дополнительных битов. В симплексных каналах связи устраняют ошибки с помощью корректирующих кодов. В дуплексных–достаточно применения кодов, обнаруживающих ошибки. [1]
История развития помехоустойчивого кодирования началась еще с 1946г., а именно, после публикации монографии американского ученого К. Шеннона «Работы по теории информации и кибернетике».В этой работе он не показал как построить эти коды, а доказал их существование. Важно отметить, что результаты работы К. Шеннона опирались на работы советских ученых, таких как: А. Я. Хинчин, Р.Р. Варшамов и др. На сегодняшний день проблема передачи данных является особо актуальной,т.к. сбой при передаче может вызвать не только искажение сообщения в целом, но и полную потерю информации. Для этого и существуют помехоустойчивые коды, способные предотвратить потерю и искажение информации. В настоящее время существует ряд разновидностей помехоустойчивых кодов, обеспечивающих высокую достоверность при малой величине избыточности и простоте технической реализации кодирующих и декодирующих устройств. Принципиально коды могут быть использованы как для обнаружения, так и для исправления ошибок. Однако удобства построения кодирующих и декодирующих устройств определили преимущественное применение лишь некоторых из них, в частности корректирующего кода Хемминга.
Цель данной курсовой работы: Ознакомление с помехоустойчивым кодированием и изучение кода Хемминга.
Задачи:
1) Ознакомиться с видами помехоустойчивого кодирования;
2) Ознакомиться с кодом Хемминга, как с одним из видов помехоустойчивого кодирования;
3) Изучить алгоритм построения кода Хемминга.
Объект исследования: помехоустойчивое кодирование.
Предмет исследования: код Хемминга.
Данная курсовая работа состоит из титульного листа, оглавления,введения, двух глав (теоретической и практической), заключения и списка литературы.
Глава 1. Теоретические основы изучения помехоустойчивого кодирования
1.1. Виды помехоустойчивого кодирования
В мире существует немало различных помех и искажений, это могут быть как звуковые искажения, так и на графике. Мы рассмотрим, что понимается под помехой в кодировании информации. Под помехой понимается любое воздействие, накладывающееся на полезный сигнал изатрудняющее его прием. Ниже приведена классификация помех и их источников.
Рис. 1.Помехи и их источники
Внешние источники помех вызывают в основном импульсные помехи, а внутренние –флуктуационные. Помехи, накладываясь на видеосигнал, приводят к двум типам искажений: краевыеи дробления. Краевые искажения связаны со смещением переднего или заднего фронта импульса.Дробление связано с дроблением единого видеосигнала на некоторое количество более коротких сигналов [2].
Приведем классификацию помехоустойчивых кодов.
1) Обнаруживающие ошибки:
блоковые:
А) Разделимые:
- с проверкой на четность;
- корреляционные;
- Хэмминга;
- БЧХ;
Б) Неразделимые:
- с постоянным весом;
- Грея.
2) Корректирующие коды:
Непрерывные:
А) С пороговым декодированием;
Б) По макс. правдоподобия;
В) С последовательным декодированием.
Теперь рассмотрим более подробно каждый вид кодирования.
Код с проверкой на четность.
Проверка четности – очень простой метод для обнаружения ошибок в передаваемом пакете данных. С помощью данного кода мы не можем восстановить данные, но можем обнаружить только лишь одиночную ошибку.
В каждом пакет данных есть один бит четности, или, так называемый, паритетный бит. Этот бит устанавливается во время записи (или отправки) данных, и затем рассчитывается и сравнивается во время чтения (получения) данных. Он равен сумме по модулю 2 всех бит данных в пакете. То есть число единиц в пакете всегда будет четно. Изменение этого бита (например с 0 на 1) сообщает о возникшей ошибке.
Пример:
Начальные данные: 1111
Данные после кодирования: 11110 (1 + 1 + 1 + 1 = 0 (mod 2))
Принятые данные: 10110 (изменился второй бит)
Как мы видим, количество единиц в принятом пакете нечетно, следовательно, при передаче произошла ошибка [3].
Корреляционные коды (код с удвоением).
Элементы данного кода заменяются двумя символами, единица «1» преобразуется в 10, а ноль «0» в 01.
Вместо комбинации 1010011 передается 10011001011010. Ошибка обнаруживается в том случае, если в парных элементах будут одинаковые символы 00 или 11 (вместо 01 и 10) [2].
Код с постоянным весом.
Одним из простейших блочных неразделимых кодов является код с постоянным весом. Примером такого кода может служить семибитный телеграфный код МТК–3, в котором каждая разрешенная кодовая комбинация содержит три единицы и четыре нуля (рис.2). Весом кодовой комбинации называют число содержащихся в ней единиц. В рассматриваемом коде вес кодовых комбинаций равен трем.
Число разрешенных кодовых комбинаций в кодах с постоянным весом определяется как количество сочетаний изnсимволов поgи равно
(1)
Где n–длина кодовой комбинации, аg – вес разрешенной кодовой комбинации. Для кода МТК-3 число разрешенных кодовых комбинаций равно. Таким образом, из общего числа комбинаций
только 35 используются для передачи сообщений[4].
Рис.2. Примеры разрешенных и запрещенных комбинаций кода МТК-3
Инверсный код.
К исходной комбинации добавляется такая же комбинация по длине. В линию посылается удвоенное число символов. Если в исходной комбинации четное число единиц, то добавляемая комбинация повторяет исходную комбинацию, если нечетное, то добавляемая комбинация является инверсной по отношению к исходной.
|
k |
r |
n |
|
11011 |
11011 |
1101111011 |
|
11100 |
00011 |
1110000011 |
Прием инверсного кода осуществляется в два этапа. На первом этапе суммируются единицы в первой основной группе символов. Если число единиц четное, то контрольные символы принимаются без изменения, если нечетное, то контрольные символы инвертируются. На втором этапе контрольные символы суммируются с информационными символами по модулю два. Нулевая сумма говорит об отсутствии ошибок. При ненулевой сумме, принятая комбинация бракуется. Покажем суммирование для принятых комбинаций без ошибок (1,3) и с ошибками (2,4).
|
1) |
11011 11011 |
|
00000 |
|
|
2) |
11111 00100 |
|
11011 |
Обнаруживающие способности данного кода достаточно велики. Данный код обнаруживает практически любые ошибки, кроме редких ошибок смещения, которые одновременно происходят как среди информационных символов, так и среди соответствующих контрольных. Например, при k=5, n=10 и . Коэффициент обнаружения будет составлять
[2].
Код Грея.
По сравнению с простым кодом, код Грея позволяет уменьшить ошибки неоднозначности считывания, а также ошибки из-за помех в канале. Обычно этот код применяется для аналогово-цифрового преобразования непрерывных сообщений.
Недостатком кода Грея является его невесомость, т.е. вес единицы не определяется номером разряда. Информацию в таком виде трудно обрабатывать на ЭВМ. Декодирование кода также связано с большими затратами. Поэтому перед вводом в ЭВМ (или перед декодированием) код Грея преобразуется в простой двоичный код, который удобен для ЭВМ и легко декодируется.
Для перевода простого двоичного кода в код Грея нужно:
- под двоичным числом записать такое же число со сдвигом вправо на один разряд (при этом младший разряд сдвигаемого числа теряется);
- произвести поразрядное сложение двух чисел по модулю 2 (четности). [5].
Таким образом, мы рассмотрели виды помехоустойчивого кодирования и увидели, что их существует не так уж и мало. Каждый код по своему уникален и полезен для кодирования информации. Теперь мы ознакомимся с кодом Хемминга подробнее.
1.2.Характеристика кода Хэмминга при помехоустойчивом кодировании
В середине 40-х годов Ричард Хемминг работал в знаменитых Лабораториях Белла на счётной машине Bell Model V. Это была электромеханическая машина, использующая релейные блоки,скорость которых была очень низка: один оборот за несколько секунд. Данные вводились в машине с помощью перфокарт, и поэтому в процессе чтения часто происходили ошибки. В рабочие дни использовались специальные коды, чтобы обнаруживать и исправлять найденные ошибки, при этом оператор узнавал об ошибке по свечению лампочек, исправлял и запускал машину. В выходные дни, когда не было операторов, при возникновении ошибки машина автоматически выходила из программы и запускала другую.
Р. Хемминг часто работал в выходные дни, и все больше и больше раздражался, потому что часто был должен перегружать свою программу из-за ненадежности перфокарт. На протяжении нескольких лет он проводил много времени над построением эффективных алгоритмов исправления ошибок. В 1950 году он опубликовал способ, который на сегодняшний день мы знаем как код Хемминга.[6.].
Код Хемминга, как и любой (n,k) код, содержит k информационных и избыточных символов. Избыточная часть кода строится таким образом, чтобы при декодировании можно было бы установить не только факт наличия ошибок в принятой – комбинации, но и указать номер позиции, в которой произошла ошибка. Это достигается за счет многократной проверки принятой комбинации на четность. Каждой проверкой должны охватываться часть информационных символов и один из избыточных символов. При каждой проверке получают двоичный контрольный символ. Если результат проверки дает четное число, то контрольному символу присваивается значение 0, если нечетное число– 1. В результате всех проверок получается p-разрядное двоичное число, указывающее номер искаженного символа. Для исправления ошибки достаточно лишь изменить значение данного символа на обратное. [7]
К ним обычно относятся коды с минимальным кодовым расстояниемисправляющие все одиночные ошибки, и коды с расстоянием
исправляющие все одиночные и обнаруживающие все двойные ошибки. Длина кода Хэмминга:
(2)
(r – количество проверочных разрядов).
Характерной особенностью проверочной матрицы кода с является то, что ее столбцы представляют собой любые различные ненулевые комбинации длиной r.Например, при r=4 иn=5 для кода (15,11), проверочная матрица может иметь следующий вид (рис.3)
Рис.3. Проверочная матрица
Перестановкой столбцов, содержащих одну единицу, данную матрицу можно привести к виду(рис.4)
Рис. 4.Измененная матрица
Использование такого кода позволяет исправить любую одиночную ошибку или обнаружить произвольную ошибку кратности два.Если информационные и проверочные разряды кода нумеровать слева направо, то в соответствии с матрицей получаем систему проверочных уравнений, с помощью которых вычисляем проверочные разряды(рис.5):
Рис.5. Система проверочных уравнений
где —
-проверочные разряды;
—
-информационные разряды
Двоичный код Хэмминга с кодовым расстоянием получается путем добавления к коду Хэмминга с
одного проверочного разряда, представляющего собой результат суммирования по модулю два всех разрядов кодового слоя. Длина кода при этом
разрядов, из которых
являются проверочными.
Операция кодирования может выполняться в два этапа. На первом этапе определяется кодовая комбинация с использованием матрицы H, соответствующей коду с на втором — добавляется один проверочный разряд, в котором записывается результат суммирования по модулю два всех разрядов кодового слова, полученного на первом этапе. Операция декодирования также состоит из двух этапов. На первом вычисляется синдром, соответствующий коду на втором — проверяется последнее проверочное соотношение.[8]
Таким образом, ознакомившись с характеристикой кода Хемминга, важно сказать, что состоит код из двух частей и предполагает надежную работу нахождения ошибок и корректировки сообщений.
1.3.Алгоритмы использования кода Хэмминга для нахождения ошибок
Код Хэмминга представляет собой блочный код, который позволяет выявить и исправить ошибочно переданный бит в пределах переданного блока. Код Хэмминга состоит из двух частей. Первая часть кодирует исходное сообщение, вставляя в него в определённых местах контрольные биты (вычисленные особым образом). Вторая часть получает входящее сообщение и заново вычисляет контрольные биты (по тому же алгоритму, что и первая часть). Если все вновь вычисленные контрольные биты совпадают с полученными, то сообщение получено без ошибок. В противном случае, выводится сообщение об ошибке и при возможности ошибка исправляется.
Рассмотрим алгоритм построения кода для исправления одиночной ошибки.
1.По заданному количеству информационных символов – k, либо информационных комбинаций , используя соотношения:
,
(3)
и (4)
(5)
Вычисляют основные параметры кода m и n.
2.Определяем рабочие и контрольные позиции кодовой комбинации. Номера контрольных позиций определяются по закону , где i= 1,2,3,…т.е. они равны 1,2,4,8,16,…а остальные позиции являются рабочими.
3. Определяем значения контрольных разрядов (0 или 1) при помощи многократных проверок кодовой комбинации на четность. Количество проверок равно . В каждую проверку включается один контрольный и определенные проверочные биты. Если результат проверки дает четное число, то контрольному биту присваивается значение – 0, в противном случае – 1. Номера информационных бит, включаемых в каждую проверку, определяются по двоичному коду натуральных n -чисел разрядностью – m (табл. 2, для m = 4) или при помощи проверочной матрицы H(mn), столбцы которой представляют запись в двоичной системе всех целых чисел от 1 до
перечисленных в возрастающем порядке.
Количество разрядов m – определяет количество проверок.
В первую проверку включают коэффициенты, содержащие 1 в младшем (первом) разряде, т.е. b1,b3, b5 и т.д.
Во вторую проверку включают коэффициенты, содержащие 1 во втором разряде, т.е. b2, b3, b6 и т.д.
В третью проверку –коэффициенты которые содержат 1 в третьем разряде и т.д.
Таблица 2
|
Десятичные числа (номера разрядов кодовой комбинации) |
Двоичные числа и их разряды |
|
|
3 |
21 |
|
|
1 |
0 |
01 |
|
2 |
0 |
10 |
|
3 |
0 |
11 |
|
4 |
1 |
00 |
|
5 |
1 |
01 |
|
6 |
1 |
10 |
|
7 |
1 |
11 |
Для обнаружения и исправления ошибки составляются аналогичные проверки на четность контрольных сумм, результатом которых является двоичное (n-k) – разрядное число, называемое синдромом и указывающим на положение ошибки, т.е. номер ошибочной позиции, который определяется по двоичной записи числа, либо по проверочной матрице.
Для исправления ошибки необходимо проинвертировать бит в ошибочной позиции. Для исправления одиночной ошибки и обнаружения двойной используют дополнительную проверку на четность. Если при исправлении ошибки контроль на четность фиксирует ошибку, то значит в кодовой комбинации две ошибки.[9]
Вывод к главе 1: Таким образом, мы узнали, что такое помехоустойчивость, помехоустойчивое кодирование, ознакомились с видами помехоустойчивого кодирования. Затем рассмотрели код Хемминга, изучили алгоритм построения кода Хемминга. При построении кода важно знать, что код Хемминга ищет и исправляет одиночную ошибку, но двойную ошибку. В итоге, изучив теоретическую часть, мы выяснили, какие существуют виды помехоустойчивого кодирования. Ознакомились подробнее с кодом Хемминга, изучили его алгоритм кодирования.
Глава 2. Практические основы кода Хемминга
2.1. Примеры использования кода Хемминга для нахождения одной ошибки
Существует множество различных примеров для нахождения ошибок при помощи кода Хемминга.
Пример 1. Пользуясь кодом Хэмминга найти ошибку в сообщении.
1) 1111 1011 0010 1100 1101 1100 110
РЕШЕНИЕ. Сообщение состоит из 27 символов, из них 22 информационные, а 5 – контрольные. Это разряды b1 = 1, b2 = 1, b4 = 1, b8 = 1, b16=0. Вычислим число J для обнаружения ошибки: Введем для удобства следующие множества:
V1 = 1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25, 27… – все числа у которых первый разрядравен 1
V2 = 2, 3, 6, 7, 10, 11, 14, 15, 18, 19, 22, 23, 26, 27… – все числа, у которых второй разрядравен 1
V3 = 4, 5, 6, 7, 12, 13, 14, 15, 20, 21, 22, 23 … – все числа, у которых третий разряд равен1
V4 = 8, 9, 10, 11, 12, 13, 14, 15, 24, 25, 26, 27 … – все числа, у которых четвертый разрядравен 1,
V5 = 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27 … – все числа, у которых пятый разрядравен 1.
Разряды числа J определяются следующим образом:
j1 = b1 +b3+b5+b7+b9+b11+b13+b15+b17+b19+b21+b23+b25+b27 = 1
j2=b2+b3+b6+b7+b10+b11+b14+b15+b18+b19+b22+b23+b26+b27= 0
j3 = b4+b5+b6+b7 +b12+b13+ b14+ b15+ b20 +b21+b22+b23 = 0
j4 =b9+b10+b11+b12+b13+b14+b15+b24+b25+b26+b27 = 0,
j5 = b16+ b17+b18+b19+b20+b21+b22+b23+b24+b25+b26+b27 = 1
то есть число J= =
.
Таким образом, ошибка произошла в семнадцатом разряде переданного числа.[10]. В этом примере мы рассмотрели, как можно обнаружить одиночную ошибку. Далее мы проанализируем пример, как можно найти и исправить эту ошибку.
Пример 2.
Построить код Хемминга для передачи сообщений в виде последовательности десятичных цифр, представленных в виде 4 –х разрядных двоичных слов. Показать процесс кодирования, декодирования и исправления одиночной ошибки на примере информационного слова 0101.
Решение:
1. По заданной длине информационного слова (k = 4 ), определим количество контрольных разрядов m, используя соотношение:
,
при этом т. е. получили (7, 4) -код.
2. Определяем номера рабочих и контрольных позиции кодовой комбинации. Номера контрольных позиций выбираем по закону .
Для рассматриваемой задачи (при n = 7 ) номера контрольных позиций равны 1, 2, 4. При этом кодовая комбинация имеет вид:
b1 b2 b3 b4 b5 b6 b7
k1 k2 0 k2 1 0 1
3. Определяем значения контрольных разрядов (0 или 1), используя проверочную матрицу (рис.3).
Первая проверка:
k1b3 b5 b7 = k1 011 будет четной при k1 = 0.
Вторая проверка:
k2 b3 b6 b7 = k2 001 будет четной при k2 = 1.
Третья проверка:
k3 b5 b6 b7 = k3 101 будет четной при k3 = 0.
1 2 3 4 5 6 7
Передаваемая кодовая комбинация: 0100101
Допустим принято: 0110101
Для обнаружения и исправления ошибки составим аналогичные проверки на четность контрольных сумм, в соответствии с проверочной матрицей результатом которых является двоичное ( ) – разрядное число, называемое синдромом и указывающим на положение ошибки, т. е, номер ошибочной позиции.
1) k1= b3 b5 b7 = 0111 = 1.
2)k2=b3 b6 b7 = 1101 = 1.
3) k3 =b5 b6 b7 = 0101 =0.
Сравнивая синдром ошибки со столбцами проверочной матрицы, определяем номер ошибочного бита. Синдрому 011 соответствует третий столбец, т. е. ошибка в третьем разряде кодовой комбинации. Символ в третьей позиции необходимо изменить на обратный.
Рассмотрев данные задачи, мы выяснили насколько точно код Хемминга может найти и исправить одиночные ошибки.
2.2. Примеры использования кода Хемминга для нахождения двоичной ошибки
Для обнаружения двойной ошибки следует только добавить еще один проверочный разряд.
Пример 1:
Принята кодовая комбинация С = 101000001001, произошло
искажение 2-го и 5-го разрядов. Обнаружить ошибки.
Решение.
Значения проверок равны:
k1= b1 b3 b5 b7 b9 b11 = 110010= 1
k2= b2 b3 b6 b7 b10 b11= 010000=1
k3=b4 b5 b6 b7 b12= 00001=1
k4= b8 b9 b10 b11 b12= 01001=0
Тогда контрольное число (синдром) ошибкиравен 0111.
Таким образом, при наличии двукратной ошибки декодирование дает
номер разряда с ошибкой в позиции 7, в то время как ошибки произошли
во 2-м и 5-м разрядах. В этом случае составляется расширенный код
Хэмминга, путем добавления одного проверочного символа.
Пример 2 :
Передана кодовая комбинация «01001011», закодированная кодом Хемминга с d = 4. Показать процесс выявления ошибки.
Решение:
Принята комбинация «01001111»:
а) проверка на общую четность указывает на наличие ошибки (число единиц четное);
б) частные проверки производятся так же, как это было в других примерах.
При составлении проверочных сумм последние единицы кодовых комбинаций (дополнительные контрольные символы) не учитываются.
2. Принята комбинация «01101111»:
а) проверка на общую четность показывает, что ошибка не фиксируется;
б) частные проверки (последний символ отбрасывается)
Первая проверка 0 1 1 1 = 1
Вторая проверка 1 1 1 1 = 0
Третья проверка 0 1 1 1 = 1
Таким образом, частные проверки фиксируют наличие ошибки. Она, якобы, имела место на пятой позиции. Но так как при этом первая проверка на общую четность ошибки не зафиксировала, то значит, имела место двойная ошибка. Исправить двойную ошибку такой код не может [14].
Вывод к главе 2: Таким образом, мы показали, как работает код Хемминга на практике. Мы видим, что при одиночной ошибке ее можно исправить, но для этого нам нужно знать, сколько потребуется контрольных разрядов, а двойную ошибку можно лишь обнаружить.
ЗАКЛЮЧЕНИЕ
Высокие требования к достоверности передачи, обработки и хранения информации диктуют необходимость такого кодированияинформации, при котором обеспечивалось бы возможность обнаружения и исправления ошибок. Широкому применению результатов теории помехоустойчивогокодирования в современных системах связи, обработки и хранения информацииследует считать отсутствие достаточно простых решений сложных теоретических достижений теории помехоустойчивого кодирования.В данной работе исследовано помехоустойчивое кодирование, в частности код Хемминга.
Список литературы
- Вернер М. Основы кодирования[Текст].– М.: Техносфера, 2004. – 288 с.
- Помехоустойчивое кодирование [Электронный ресурс]. – Режим доступа:https://clck.ru/9cWsc,свободный. Дата обращения: 27.11.2015.
- Помехоустойчивое кодирование [Электронный ресурс]. – Режим доступа:http://habrahabr.ru/post/111336/, свободный. Дата обращения: 05.12.2015.
- Файловый архив для студентов. Лекция: основные понятия кодирования в ЦСПИ [Электронный ресурс]. – Режим доступа: http://www.studfiles.ru/preview/4087325/,свободный. Дата обращения: 27.11.2015.
- Лекция «Простейшие коды» [Электронный ресурс]. – Режим доступа: http://davaiknam.ru/text/lekciya-3-kodirovanie-informacii-prostejshie-kodi, свободный. Дата обращения: 27.11.2015.
- Академик [Электронный ресурс] – Режим доступа: http://dic.academic.ru/dic.nsf/ruwiki/177544, свободный. Дата обращения: 27.11.2015
- Кузьмин И.В.Основы теории информации и кодирования [Текст]. – Киев,1986. – 237 с.
- Научная библиотека. Код Хемминга [Электронный ресурс]. – Режим доступа: http://info.sernam.ru/book_codb.php?id=28, свободный. Дата обращения: 05.12.2015
- Статья корректирующие коды [Электронный ресурс]. – Режим доступа: http://referatwork.ru/refs/source/ref-11094.html#Текст работы, свободный. Дата обращения: 05.12.2015
- МатБюро- решение задач по высшей математике [Электронный ресурс]. – Режим доступа: http://www.matburo.ru/Examples/Files/Hem2.pdf, свободный. Дата обращения: 06.12.2015.
- Блейхут Р. Теория и практика кодов, контролирующих ошибки. [Текст]. – Москва, 1986г. –576 с.
- Морелос-Сарагоса Р. Искусство помехоустойчивого кодирования – методы, алгоритмы, применение. [Текст]. – Москва, 2005г.–320 с.
- Р.Хемминг Теория кодирования и теория информации. / Перевод с английского С.Гальфанда. // [Текст]. – Москва, 1983г. – 176 с.
- Портал студентов «Седьмой бит» [Электронный ресурс]. – Режим доступа: http://www.itmo.ru/work/253/page4, открытый. Дата обращения: 20.12.2015.
Привет, сегодня поговорим про линейные коды общие методы построения, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое
линейные коды общие методы построения , настоятельно рекомендую прочитать все из категории Теория информации и кодирования.
Тема 5. Регулярные методы построения двоичных помехоустойчивых кодов.
Лекция 7.
7.1 Линейные коды. Общие методы построения.
Рассмотрим класс помехоустойчивых алгебраических кодов, называемых линейными или часто линейными групповыми.
Определение: Линейными называют блоковые коды, дополнительные разряды которых образуются путем линейных операций над информационными разрядами.
Здесь используется понятие линейная операция. В теории кодирования в качестве линейной операции сложения используется сложение по модулю 2 (+).
7.2 Определение числа добавочных разрядов r.
Для определения числа добавочных разрядов можно воспользоваться уже нам известной формулой границы Хэмминга:
<![if !vml]>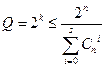
Если s=l, то есть строится код, исправляющий максимум однократные ошибки, то :
<![if !vml]>
откуда получаем
2r≥r+k
С учетом последней формулы ищется наименьшее r при котором удовлетворяется это неравенство.
Пример: n=7, тогда путем простого перебора легко найти, что r=3. И соответствующий код имеет вид n(7,4).
7.3 Построение образующей(порождающей) матрицы |OM|.
Линейные коды обладают следующим свойством:
— из всего множества 2k разрешенных кодовых слов, образующих линейную группу, можно выделить подмножества из k слов, обладающих свойством линейной независимости.
Линейная независимость означает, что никакое из слов, входящих в подмножество линейно-независимых кодовых слов, нельзя получить путем суммирования (с помощью линейного выражения) любых других слов, входящих в это подмножество.
В то же время любое из разрешенных кодовых слов можно получить путем суммирования определенных линейно-независимых слов.
Таким образом, построение кодовых комбинаций линейного кода связано с линейными операциями. Для выполнения таких операций удобно пользоваться хорошо разработанным аппаратом матричных вычислений.
Для образования n -разрядных кодовых слов из k- разрядных кодируемых слов (кодирования) используют матрицу, которая называется образующей(порождающей).
Образующая матрица получается путем записи в столбец k линейно-независимых слов.
Обозначим кодируемую информационную последовательность X и будем записывать ее в виде матрицы-строки ||X|| размерностью 1*k, например:
||X||=||11001||, где k=5.
Один из способов построения образующей (порождающей) матрицы следующий: Она строится из единичной матрицы ||I||размерностью k*k и приписанной к ней справа матрицы добавочных (избыточных) разрядов ||МДР|| размерности k*r.
<![if !vml]>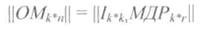
где при k=4
<![if !vml]>
Такая структура ОМ обеспечивает получение систематического кода.
Порядок построения матрицы МДР будет рассмотрен ниже.
7.4 Порядок кодирования.
Кодовое слово КС получается путем умножения матрицы информационной последовательности ||Х|| на образующую матрицу ||ОМ||:
<![if !vml]>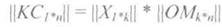
Умножение выполняется по правилам матричного умножения: (ТАК натек)
<![if !vml]>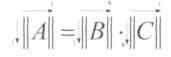
Надо только помнить, что сложение здесь ведется по модулю 2.
Пример:
допустим, образующая матрица
1000 110
0100 111
||ОМ||= 0010 011
0001 101
и вектор-строка информационной последовательности
<![if !vml]>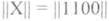
Так как множимая матрица имеет всего одну строку, умножение упрощается . Об этом говорит сайт https://intellect.icu . В этом случае следует поставить в соответствие строкам образующей(порождающей) матрицы ||ОМ|| разряды матрицы информационной последовательности ||X|| и сложить те строки образующей(порождающей) матрицы, которые соответствуют единичным разрядам матрицы ||Х||.
<![if !vml]>
Заметим, что ||KC|| = ||X, ДР||,
где ||X||- информационная последовательность (т.к. умножается на единичную матрицу ||I||),
а ||ДР|| — добавочные разряды, зависящие от матрицы добавочных разрядов ||МДР||:
|| ДР ||= || Х || * || МДР||
7.5 Порядок декодирования.
В результате передачи кодового слова через канал оно может быть искажено помехой. Это приведет к тому, что принятое кодовое слово ||ПКС|| может не совпасть с исходным ||КС||.
Искажение можно описать с помощью следующей формулы:
|| ПКС || = ||КС || + ||ВО ||,
где ||ВО|| — вектор ошибки — матрица-строка размерностью 1*n, с 1 в тех позициях, в которых произошли искажения.
Декодирование основано на нахождении так называемого опознавателя или синдрома ошибки -матрицы-строки ||ОП|| длиной r разрядов (r— количество добавочных или избыточных разрядов в кодовом слове).
Опознаватель используется для нахождения предполагаемого вектора ошибки.
Опознаватель находят по следующей формуле:
||ОП|| = ||ПКС||* ||ТПМ||,
где ||ПКС||- принятое и, возможно, искаженное кодовое слово;
||ТПМ||,- транспонированная проверочная матрица, которая получается из матрицы добавочных разрядов ||МДР|| путем приписывания к ней снизу единичной матрицы:
<![if !vml]>
Пример ||ТПМ||:
<![if !vml]>
Поскольку ||ПКС|| = ||КС|| + ||BO||, последнюю формулу можно записать в виде:
||ОП|| = ||КС|| * ||ТПМ||+||ВО|| * ||ТПМ||.
Рассмотрим первое слагаемое.
||КC|| — матрица-строка, причем первые k разрядов — информационные.
Докажем теперь, что произведение кодового слова ||КС|| на ||ТПМ|| приводит к получению нулевой матрицы ||0||.
Поскольку ||КС|| — матрица-строка, возможен упрощенный порядок умножения матриц, рассмотренных выше.
<![if !vml]>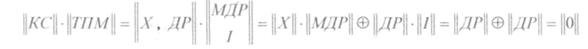
Следовательно, первое слагаемое в
||ОП|| = ||КС|| * ||ТПМ|| + ||ВО|| * ||ТПМ||
всегда равно нулю и опознаватель полностью зависит от вектора ошибки ||ВО||.
Если теперь подобрать такую проверочную матрицу ТПМ, а значит и МДР, чтобы разным векторам ошибки соответствовали разные опознаватели ОП, то по этим опознавателям можно будет находить вектор ошибки ВО, а значит и исправлять эти ошибки.
Соответствие опознавателей векторам ошибки находится заранее путем перемножения векторов исправляемых ошибок на ТПМ;
<![if !vml]>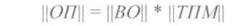
Таким образом, способность кода исправлять ошибки целиком определяется ||МДР||. Для построения МДР для кодов, исправляющих однократные ошибки нужно в каждой строке МДР иметь не менее 2-х единиц. При этом также необходимо иметь хотя бы одно различие между двумя любыми строчками МДР.
Полученный нами код неудобен тем, что опознаватель, хотя и связан однозначно с номером искаженного разряда, как число не равен ему. Для поиска искаженного разряда нужно использовать дополнительную таблицу соответствия между опознавателем и этим номером. Коды, в которых опознаватель как число определяет позицию искаженного разряда, были найдены и получили название кодов Хэмминга.
Построение МДР для случая исправления многократных ошибок значительно усложняется. Разными авторами были найдены различные алгоритмы построения ||МДР || для этого случая, а соответствующие коды называются именами их авторов.
7.6 Систематические коды. Код Хэмминга.
Систематические коды представляют собой такие коды, в которых информационные и корректирующие разряды расположены по строго определенной системе и всегда занимают строго определенные места в кодовых комбинациях .
Систематические коды являются равномерными, т. е. все комбинации кода с заданными корректирующими способностями имеют одинаковую длину. Систематические коды могут строиться, как линейные на основе производящей матрицы, как это уже было рассмотрено.
Обычно производящая матрица строится при помощи двух матриц:
Единичной, ранг которой определяется числом информационных разрядов, и добавочной, число столбцов которой определяется числом контрольных разрядов кода. Каждая строка добавочной матрицы должна содержать не менее d0 -1 единиц, а сумма по модулю для любых строк не менее d0-2 единиц (где d0—минимальное кодовое расстояние).
Производящая матрица позволяет находить все остальные кодовые комбинации.
Код Хэмминга является типичным примером систематического кода. Однако при его построении к матрицам обычно не прибегают. Он настолько хорошо изучен, что уже выработался четкий алгоритм его построения :
Код Хэмминга представляет собой один из важнейших классов линейных кодов, нашедших широкое применение на практике и имеющих простой и удобный для технической реализации алгоритм обнаружения и исправления ошибок.
Соотношения между n, r, k для кода Хэмминга представлены в таблице. Зная основные параметры корректирующего кода, определяют, какие позиции сигналов будут рабочими, а какие — контрольными. Практика показала, что номера контрольных символов удобно выбирать по закону
2i, где i = 0, 1, 2, 3, … — натуральный ряд чисел.
Номера контрольных символов в этом случае равны 1, 2, 4, 16, 32… Затем определяют значения контрольных коэффициентов (0 или 1), руководствуясь следующим правилом:
сумма единиц на проверочных позициях должна быть четной. Если эта сумма четна -значение контрольного коэффициента нуль, в противном случае — единица.
Соотношения между количеством информационных и контрольных символов в коде Хэмминга
Табл.7.1
<![if !vml]>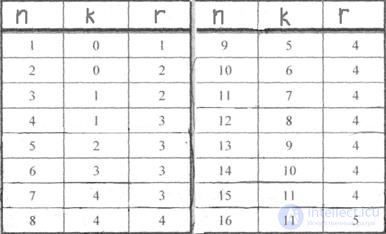
Проверочные позиции выбирают следующим образом. Составляют табличку для ряда натуральных чисел в двоичном коде. Число ее строк n=r+k. Первой строке соответствует проверочный коэффициент a1, второй а2 и т. д.:
<![if !vml]>
Затем выявляют проверочные позиции, выписывая коэффициенты по следующему принципу:
в первую проверку входят коэффициенты, которые содержат единицу в младшем разряде (a1, а3, a5, a7, a9, a11 и т. д.);
во вторую — во втором разряде (а2, а3, а5, а7, а9, a11 и т. д.);
в третью — в третьем разряде и т. д.
Номера проверочных коэффициентов соответствуют номерам проверочных позиций, что позволяет составить общую таблицу проверок.
Номера проверочных позиций кода Хэмминга
Табл.7.2
<![if !vml]>
Построение кода Хэмминга
Пример: Построить макет кода Хемминга и определить значения корректирующих разрядов для кодовой комбинации k=4, X=0101.
Табл.7.3
<![if !vml]>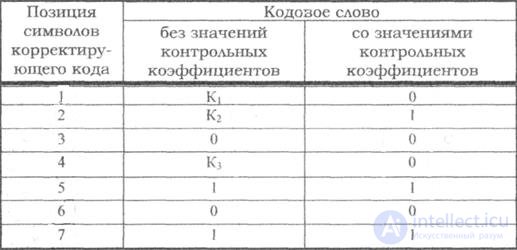
Решение:
Согласно таблице минимальное число контрольных символов r=3, при этом n = 7. Контрольный коэффициенты будут расположены на позициях 1, 2, 4. Составим макет корректирующего кода и запишем его во вторую колонку таблицы. Пользуясь таблицей для номеров проверочных коэффициентов, определим значения коэффициентов К1 К2 и К3.
Первая проверка: сумма П1+П3+П5+П7 должна быть четной, а сумма К1+0+1+1 будет четной при К =0.
Вторая проверка: сумма П2+П3+П6+П7 должна быть четной, а сумма К2+0+0+1 будет четной при К2=1.
Третья проверка: сумма П4+П5+П6+П7 должна быть четной, а сумма К3+1+0+1 будет четной при К3=0.
Окончательное значение искомой комбинации корректирующего кода записываем в третью колонку таблицы макета кода.
7.7 Обнаружение и исправление ошибок в коде Хэмминга.
Пример . Предположим, в канале связи под действием помех произошло искажение и вместо 0100101 было принято 01001(1)1.
Решение: Для обнаружения ошибки производят уже знакомые нам проверки на четность.
Первая проверка: сумма П1+П3+П5+П7 = 0+0+1+1 четна. В младший разряд номера ошибочной позиции запишем 0.
Вторая проверка: сумма П2+П3+П6+П7 = 1+0+1+1 нечетна. Во второй разряд номера ошибочной позиции запишем 1
Третья проверка: сумма П4+П5+П6+П7 = 0+1+1+1 нечетна. В третий разряд номера ошибочной позиции запишем 1. Номер ошибочной позиции 110= 6. Следовательно, символ шестой позиции следует изменить на обратный, и получим правильную кодовую комбинацию.
Код, исправляющий одиночную и обнаруживающий двойную ошибки
Табл.7.4
<![if !vml]>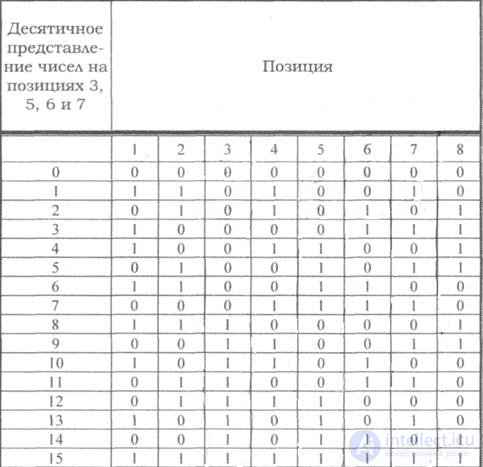
Если по изложенным выше правилам строить корректирующий код с обнаружением и исправлением одиночной ошибки для равномерного двоичного кода, то первые 16 кодовых комбинаций будут иметь вид, показанный в таблице. Такой код может быть использован для построения кода с исправлением одиночной ошибки и обнаружением двойной.
Для этого, кроме указанных выше проверок по контрольным позициям, следует провести еще одну проверку на четность для всей строки в целом. Чтобы осуществить такую проверку, следует к каждой строке кода добавить контрольные символы, записанные в дополнительной колонке (таблица, колонка 8). Тогда в случае одной ошибки проверки по позициям укажут номер ошибочной позиции, а проверка на четность — на наличие ошибки. Если проверки позиций укажут на наличие ошибки, а проверка на четность не фиксирует ее, значит в кодовой комбинации две ошибки.
7.8 Контрольные вопросы.
1. Общий метод построения линейного кода.
2. Требования к образующей матрице.
3. Что такое проверочная матрица ТПМ?
4. В чем преимущество метода кодирования Хемминга?
5. Сколько ошибок может исправить код Хемминга
Я хотел бы услышать твое мнение про линейные коды общие методы построения Надеюсь, что теперь ты понял что такое линейные коды общие методы построения
и для чего все это нужно, а если не понял, или есть замечания,
то нестесняся пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории
Теория информации и кодирования
Ответы на вопросы для самопроверки пишите в комментариях,
мы проверим, или же задавайте свой вопрос по данной теме.
Время на прочтение
6 мин
Количество просмотров 62K
Код Хэмминга – не цель этой статьи. Я лишь хочу на его примере познакомить вас с самими принципами кодирования. Но здесь не будет строгих определений, математических формулировок и т.д. Эта просто неплохой трамплин для понимания более сложных блочных кодов.
Самый, пожалуй, известный код Хэмминга (7,4). Что значат эти цифры? Вторая – число бит информационного слова — то, что мы хотим передать в целости и сохранности. А первое – размер кодового слова: информация удобренная избыточностью. Кстати термины «информационное слово» и «кодовое слово», употребляются во всех 7-ми книгах по теории помехоустойчивого кодирования, которые мне довелось бегло пролистать.
Такой код исправляет 1 ошибку. И не важно где она возникла. Избыточность несёт в себе 3 бита информации, этого достаточно, чтобы указать на одно из 7 положений ошибки или показать, что её нет. То есть ровно 8 вариантов ответов мы ждём. А 8 = 2^3, вот как всё совпало.
Чтобы получить кодовое слово, нужно информационное слово представить в виде полинома и умножить его на порождающий полином g(x). Любое число, переведя в двоичный вид, можно представить в виде полинома. Это может показаться странным и у не подготовленного читателя сразу встаёт только один вопрос «да зачем же так усложнять?». Уверяю вас, он отпадёт сам собой, когда мы получим первые результаты.
К примеру информационное слово 1010, значение каждого его разряда это коэффициент в полиноме:
Во многих книгах пишут наоборот x+x^3. Не поддавайтесь на провокацию, это вносит только путаницу, ведь в записи числа 2-ичного, 16-ричного, младшие разряды идут справа, и сдвиги мы делаем влево/вправо ориентируясь на это. А теперь давайте умножим этот полином на порождающий полином. Порождающий полином специально для Хэмминга (7,4), встречайте: g(x)=x^3+x+1. Откуда он взялся? Ну пока считайте что он дан человечеству свыше, богами (объясню позже).
Если нужно складывать коэффициенты, то делаем по модулю 2: операция сложения заменяется на логическое исключающее или (XOR), то есть x^4+x^4=0. И в конечном итоге результат перемножения как видите из 4х членов. В двоичном виде это 1001110. Итак, получили кодовое слово, которое будем передавать на сторону по зашумлённому каналу. Замете, что перемножив информационное слово (1010) на порождающий полином (1011) как обычные числа – получим другой результат 1101110. Этого нам не надо, требуется именно «полиномиальное» перемножение. Программная реализация такого умножения очень простая. Нам потребуется 2 операции XOR и 2 сдвига влево (1й из которых на один разряд, второй на два, в соответствии с g(x)=1011):
Давайте теперь специально внесём ошибку в полученное кодовое слово. Например в 3-й разряд. Получиться повреждённое слово: 1000110.
Как расшифровать сообщение и исправить ошибку? Разумеется надо «полиномиально» разделить кодовое слово на g(x). Тут я уже не буду писать иксы. Помните что вычитание по модулю 2 — это то же самое что сложение, что в свою очередь, тоже самое что исключающее или. Поехали:
В программной реализации опять же ничего сверх сложного. Делитель (1011) сдвигаем влево до самого конца на 3 разряда. И начинаем удалять (не без помощи XOR) самые левые единицы в делимом (100110), на его младшие разряды даже не смотрим. Делимое поэтапно уменьшается 100110 -> 0011110 -> 0001000 -> 0000011, когда в 4м и левее разрядах не остаётся единиц, мы останавливаемся.
Нацело разделить не получилось, значит у нас есть ошибка (ну конечно же). Результат деления в таком случае нам без надобности. Остаток от деления является синдром, его размер равен размеру избыточности, поэтому мы дописали там ноль. В данном случае содержание синдрома нам никак не помогает найти местоположение повреждения. А жаль. Но если мы возьмём любое другое информационное слово, к примеру 1100. Точно так же перемножим его на g(x), получим 1110100, внесём ошибку в тот же самый разряд 1111100. Разделим на g(x) и получим в остатке тот же самый синдром 011. И я гарантирую вам, что к такому синдрому мы придём в обще для всех кодовых слов с ошибкой в 3-м разряде. Вывод напрашивается сам собой: можно составить таблицу синдромов для всех 7 ошибок, делая каждую из них специально и считая синдром.
В результате собираем список синдромов, и то на какую болезнь он указывает:
Теперь у нас всё есть. Нашли синдром, исправили ошибку, ещё раз поделили в данном случае 1001110 на 1011 и получили в частном наше долгожданное информационное слово 1010. В остатке после исправления уже будет 000. Таблица синдромов имеет право на жизнь в случае маленьких кодов. Но для кодов, исправляющих несколько ошибок – там список синдромов разрастается как чума. Поэтому рассмотрим метод «вылавливания ошибок» не имея на руках таблицы.
Внимательный читатель заметит, что первые 3 синдрома вполне однозначно указывают на положение ошибки. Это касается только тех синдромов, где одна единица. Кол-во единиц в синдроме называют его «весом». Опять вернёмся к злосчастной ошибке в 3м разряде. Там, как вы помните был синдром 011, его вес 2, нам не повезло. Сделаем финт ушами — циклический сдвиг кодового слова вправо. Остаток от деления 0100011 / 1011 будет равен 100, это «хороший синдром», указывает что ошибка во втором разряде. Но поскольку мы сделали один сдвиг, значит и ошибка сдвинулась на 1. Вот собственно и вся хитрость. Даже в случае жуткого невезения, когда ошибка в 6м разряде, вы, обливаясь потом, после 3 мучительных делений, но всё таки находите ошибку – это победа, лишь потому, что вы не использовали таблицу синдромов.
А как насчёт других кодов Хэмминга? Я бы сказал кодов Хэмминга бесконечное множество: (7,4), (15,11), (31,26),… (2^m-1, 2^m-1-m). Размер избыточности – m. Все они исправляют 1 ошибку, с ростом информационного слова растёт избыточность. Помехоустойчивость слабеет, но в случае слабых помех код весьма экономный. Ну ладно, а как мне найти порождающую функцию например для (15,11)? Резонный вопрос. Есть теорема, гласящая: порождающий многочлен циклического кода g(x) делит (x^n+1) без остатка. Где n – нашем случае размер кодового слова. Кроме того порождающий полином должен быть простым (делиться только на 1 и на самого себя без остатка), а его степень равна размеру избыточности. Можно показать, что для Хэмминга (7,4):
Этот код имеет целых 2 порождающих полинома. Не будет ошибкой использовать любой из них. Для остальных «хэммингов» используйте вот эту таблицу примитивных полиномов:
Соответственно для (15,11) порождающий многочлен g(x)=x^4+x+1. Ну а теперь переходим к десерту – к матрицам. С этого обычно начинают, но мы этим закончим. Для начала преобразую g(x) в матрицу, на которую можно умножить информационное слово, получив кодовое слово. Если g = 1011, то:
Называют её «порождающей матрицей». Дадим обозначение информационному слову d = 1010, а кодовое обозначим k, тогда:
Это довольно изящная формулировка. По быстродействию ещё быстрее, чем перемножение полиномов. Там нужно было делать сдвиги, а тут уже всё сдвинуто. Вектор d указывает нам: какие строки брать в расчёт. Самая нижняя строка матрицы – нулевая, строки нумеруются снизу вверх. Да, да, всё потому что младшие разряды располагаются справа и от этого никуда не деться. Так как d=1010, то я беру 1ю и 3ю строки, произвожу над ними операцию XOR и вуаля. Но это ещё не всё, приготовьтесь удивляться, существует ещё проверочная матрица H. Теперь перемножением вектора на матрицу мы можем получить синдром и никаких делений полиномов делать не надо.
Посмотрите на проверочную матрицу и на список синдромов, который получили выше. Это ответ на вопрос откуда берётся эта матрица. Здесь я как обычно подпортил кодовое слово в 3м разряде, и получил тот самый синдром. Поскольку сама матрица – это и есть список синдромов, то мы тут же находим положение ошибки. Но в кодах, исправляющие несколько ошибок, такой метод не прокатит. Придётся вылавливать ошибки по методу, описанному выше.
Чтобы лучше понять саму природу исправления ошибок, сгенерируем в обще все 16 кодовых слов, ведь информационное слово состоит всего из 4х бит:
Посмотрите внимательно на кодовые слова, все они, отличаются друг от друга хотя бы на 3 бита. К примеру возьмёте слово 1011000, измените в нём любой бит, скажем первый, получиться 1011010. Вы не найдёте более на него похожего слова, чем 1011000. Как видите для формирования кодового слова не обязательно производить вычисления, достаточно иметь эту таблицу в памяти, если она мала. Показанное различие в 3 бита — называется минимальное «хэммингово расстояние», оно является характеристикой блокового кода, по нему судят сколько ошибок можно исправить, а именно (d-1)/2. В более общем виде код Хэмминга можно записать так (7,4,3). Отмечу только, что Хэммингово расстояние не является разностью между размерами кодового и информационного слов. Код Голея (23,12,7) исправляет 3 ошибки. Код (48, 36, 5) использовался в сотовой связи с временным разделением каналов (стандарт IS-54). Для кодов Рида-Соломона применима та же запись, но это уже недвоичные коды.
Список используемой литературы:
1. М. Вернер. Основы кодирования (Мир программирования) — 2004
2. Р. Морелос-Сарагоса. Искусство помехоустойчивого кодирования (Мир связи) — 2006
3. Р. Блейхут. Теория и практика кодов, контролирующих ошибки — 1986
Код Хэмминга
Код
Хэмминга, являющийся групповым (n,k)
кодом, с минимальным расстоянием d=3
позволяет обнаруживать и исправлять
однократные ошибки. Для построения кода
Хэмминга используется матрица H.
, где
Ak—
транспонированная подматрица, En—k
—
единичная подматрица порядка n—k.
Если
Х — исходная последовательность, то
произведение Х·Н=0. Пусть E—
вектор ошибок. Тогда
(Х+Е)·Н = Х·Н+Е·Н = 0+Е·Н=E·H
— синдром или корректор, который позволяет
обнаружить и исправить ошибки. Контрольные
символы
e1
,e2
,…,er
образуются из информационных символов,
путем линейной комбинации
, где
аj={0,1}
—
коэффициенты, взятые из подматрицы A
матрицы H.
Рассмотрим
Построение кода Хэмминга для k=4
символам. Число контрольных символов r=n—k
можно определить по неравенству Хэмминга
для
однократной ошибки. Но так, как нам известно,
только исходное число символов k,
то проще вычислить по эмпирической формуле
,
(5.2)
где [.] —
означает округление до большего ближайшего
целого значения. Вычислим для k=4
. Получим код (n,k)=(7,4);
n=7;
k=4;
r=n—k=3;
d=3.
Построим матрицу H.
Контрольные
символы ej
определим
по формуле
. Например,
.
Для простоты оставляем только
слагаемые с единичными коэффициентами. В
результате получим систему линейных
уравнений, с помощью которых вычисляются
контрольные разряды. Каждый контрольный
разряд является как бы дополнением для
определенных информационных разрядов для
проверки на четность.
При
декодировании вычисляем корректор K=k4k2k1
Если
корректор равен нулю, следовательно, ошибок
нет. Если корректор не равен нулю, то
местоположение вектор—столбца
матрицы H,
совпадающего с вычисленным корректором,
указывает место ошибки. При передаче может
возникнуть
двойная и более ошибка. Корректор также
не будет равен нулю. В этом случае
произойдет исправление
случайного символа и нами будет принят
неверный код. Для исключения такого
автоматического исправления вводится еще
один символ
для
проверки всей комбинации на четность.
Кодовое расстояние d=4.
Тогда матрица H
будет иметь вид
Пример
5.4. Дана 1101 —
исходная комбинация (k=4).
Закодировать ее в коде Хэмминга.
По
формуле (5.2) находим число контрольных
символов r=3.
Берем регистр из 7 ячеек памяти. Размещаем
исходную комбинацию в ячейках 3,5,6,7.
1
2 3 4 5 6 7
*
* 1 * 1 0 1
Находим
контрольные символы
е4
= 5 + 6 + 7 = 1 + 0 + 1 = 0
е2
= 3 + 6 + 7 = 1 + 0 + 1 = 0
е1
= 3 + 5 + 7 = 1 + 1 + 1 = 1
Закодированная
комбинация будет иметь вид
1
2 3 4 5 6 7
1
0 1 0 1 0 1
Допустим,
что при передаче возникла ошибка, и мы
приняли неверную комбинацию
1
2 3 4 5 6 7
1
0 1 0 1 1 1
Проверяем ее
к
4 = 4 + 5 + 6 + 7 = 0 + 1 + 1 + 1 = 1
к2
= 2 + 3 + 6 + 7 = 0 + 1 + 1 + 1 = 1
к1
= 1 + 3 + 5 + 7 = 1 + 1 + 1 + 1 + 0
K=
— в шестом
разряде ошибка.
Если
бы нам понадобилось построить код и для
проверки двойных ошибок, необходимо было бы
ввести еще один дополнительный нулевой
разряд.
Получим
следующий код
0
1 2 3 4 5 6 7
0
1 0 1 0 1 0 1
При
передаче и возникновении ошибки код будет
иметь вид
0
1 2 3 4 5 6 7
0
1 0 1 0 1 1 1
Проверка
в этом случае показала бы, что корректор K=110,
а проверка всей комбинации на четность E0
= 0+1+0+1+0+1+1+1=1. Это указывает на одиночную
ошибку. Допускается автоматическое
исправление ошибки.
Существует
следующий алгоритм декодирования кода
Хэмминга с d=4
| Корректор — K |
Значение E0 |
Вывод |
| K=0 |
E0=0 |
Ошибок |
| K#0 |
E0#0 |
Произошла |
| K#0 |
E0=0 |
Произошла
|
| K=0 |
E0#0 |
Произошла |
Код
(7,4) является минимально возможным кодом с
достаточно большой избыточностью.
Эффективность кода (k/n)
растет с увеличением длины кода
| Длина кода — n |
7 | 15 | 31 | 63 |
| Число информационных разрядов — k |
4 | 11 | 26 | 57 |
| Число контрольных разрядов — r |
3 | 4 | 5 | 6 |
| Эффективность кода k/n |
0,57 | 0,73 | 0,84 | 0,9 |
| Обноружение ошибок | ||||
| Исправление ошибок | ||||
| Коррекция ошибок | ||||
| Назад | ||||
Методы обнаружения ошибок
В обычном равномерном непомехоустойчивом коде число разрядов n в кодовых
комбинациях определяется числом сообщений и основанием кода.
Коды, у которых все кодовые комбинации разрешены, называются простыми или
равнодоступными и являются полностью безызбыточными. Безызбыточные коды обладают
большой «чувствительностью» к помехам. Внесение избыточности при использовании
помехоустойчивых кодов связано с увеличением n – числа разрядов кодовой комбинации. Таким
образом, все множество

подмножество разрешенных комбинаций, обладающих определенными признаками, и
подмножество запрещенных комбинаций, этими признаками не обладающих.
Помехоустойчивый код отличается от обычного кода тем, что в канал передаются не все
кодовые комбинации N, которые можно сформировать из имеющегося числа разрядов n, а только
их часть Nk , которая составляет подмножество разрешенных комбинаций. Если при приеме
выясняется, что кодовая комбинация принадлежит к запрещенным, то это свидетельствует о
наличии ошибок в комбинации, т.е. таким образом решается задача обнаружения ошибок. При
этом принятая комбинация не декодируется (не принимается решение о переданном
сообщении). В связи с этим помехоустойчивые коды называют корректирующими кодами.
Корректирующие свойства избыточных кодов зависят от правила их построения, определяющего
структуру кода, и параметров кода (длительности символов, числа разрядов, избыточности и т. п.).
Первые работы по корректирующим кодам принадлежат Хеммингу, который ввел понятие
минимального кодового расстояния dmin и предложил код, позволяющий однозначно указать ту
позицию в кодовой комбинации, где произошла ошибка. К информационным элементам k в коде
Хемминга добавляется m проверочных элементов для автоматического определения
местоположения ошибочного символа. Таким образом, общая длина кодовой комбинации
составляет: n = k + m.
Метричное представление n,k-кодов
В настоящее время наибольшее внимание с точки зрения технических приложений
уделяется двоичным блочным корректирующим кодам. При использовании блочных кодов
цифровая информация передается в виде отдельных кодовых комбинаций (блоков) равной
длины. Кодирование и декодирование каждого блока осуществляется независимо друг от друга.
Почти все блочные коды относятся к разделимым кодам, кодовые комбинации которых
состоят из двух частей: информационной и проверочной. При общем числе n символов в блоке
число информационных символов равно k, а число проверочных символов:
К основным характеристикам корректирующих кодов относятся:
|
— число разрешенных и запрещенных кодовых комбинаций; |
Для блочных двоичных кодов, с числом символов в блоках, равным n, общее число
возможных кодовых комбинаций определяется значением
Число разрешенных кодовых комбинаций при наличии k информационных разрядов в
первичном коде:
Очевидно, что число запрещенных комбинаций:
а с учетом отношение будет
где m – число избыточных (проверочных) разрядов в блочном коде.
Избыточностью корректирующего кода называют величину
откуда следует:
Эта величина показывает, какую часть общего числа символов кодовой комбинации
составляют информационные символы. В теории кодирования величину Bk называют
относительной скоростью кода. Если производительность источника информации равна H
символов в секунду, то скорость передачи после кодирования этой информации будет
поскольку в закодированной последовательности из каждых n символов только k символов
являются информационными.
Если число ошибок, которые нужно обнаружить или исправить, значительно, то необходимо
иметь код с большим числом проверочных символов. Чтобы при этом скорость передачи
оставалась достаточно высокой, необходимо в каждом кодовом блоке одновременно
увеличивать как общее число символов, так и число информационных символов.
При этом длительность кодовых блоков будет существенно возрастать, что приведет к
задержке информации при передаче и приеме. Чем сложнее кодирование, тем длительнее
временная задержка информации.
Минимальное кодовое расстояние – dmin. Для того чтобы можно было обнаружить и
исправлять ошибки, разрешенная комбинация должна как можно больше отличаться от
запрещенной. Если ошибки в канале связи действуют независимо, то вероятность преобразования
одной кодовой комбинации в другую будет тем меньше, чем большим числом символов они
различаются.
Если интерпретировать кодовые комбинации как точки в пространстве, то отличие
выражается в близости этих точек, т. е. в расстоянии между ними.
Количество разрядов (символов), которыми отличаются две кодовые комбинации, можно
принять за кодовое расстояние между ними. Для определения этого расстояния нужно сложить
две кодовые комбинации «по модулю 2» и подсчитать число единиц в полученной сумме.
Например, две кодовые комбинации xi = 01011 и xj = 10010 имеют расстояние d(xi,xj) , равное 3,
так как:
Здесь под операцией ⊕ понимается сложение «по модулю 2».
Заметим, что кодовое расстояние d(xi,x0) между комбинацией xi и нулевой x0 = 00…0
называют весом W комбинации xi, т.е. вес xi равен числу «1» в ней.
Расстояние между различными комбинациями некоторого конкретного кода могут
существенно отличаться. Так, в частности, в безызбыточном первичном натуральном коде n = k это
расстояние для различных комбинаций может изменяться от единицы до величины n, равной
разрядности кода. Особую важность для характеристики корректирующих свойств кода имеет
минимальное кодовое расстояние dmin, определяемое при попарном сравнении всех кодовых
комбинаций, которое называют расстоянием Хемминга.
В безызбыточном коде все комбинации являются разрешенными и его минимальное
кодовое расстояние равно единице – dmin=1. Поэтому достаточно исказиться одному символу,
чтобы вместо переданной комбинации была принята другая разрешенная комбинация. Чтобы код
обладал корректирующими свойствами, необходимо ввести в него некоторую избыточность,
которая обеспечивала бы минимальное расстояние между любыми двумя разрешенными
комбинациями не менее двух – dmin ≥ 2..
Минимальное кодовое расстояние является важнейшей характеристикой помехоустойчивых
кодов, указывающей на гарантируемое число обнаруживаемых или исправляемых заданным
кодом ошибок.
Число обнаруживаемых или исправляемых ошибок
При применении двоичных кодов учитывают только дискретные искажения, при которых
единица переходит в нуль («1» → «0») или нуль переходит в единицу («0» → «1»). Переход «1» →
«0» или «0» → «1» только в одном элементе кодовой комбинации называют единичной ошибкой
(единичным искажением). В общем случае под кратностью ошибки подразумевают число
позиций кодовой комбинации, на которых под действием помехи одни символы оказались
замененными на другие. Возможны двукратные (g = 2) и многократные (g > 2) искажения
элементов в кодовой комбинации в пределах 0 ≤ g ≤ n.
Минимальное кодовое расстояние является основным параметром, характеризующим
корректирующие способности данного кода. Если код используется только для обнаружения
ошибок кратностью g0, то необходимо и достаточно, чтобы минимальное кодовое расстояние
было равно dmin ≥ g0 + 1.
В этом случае никакая комбинация из go ошибок не может перевести одну разрешенную
кодовую комбинацию в другую разрешенную. Таким образом, условие обнаружения всех ошибок
кратностью g0 можно записать
Чтобы можно было исправить все ошибки кратностью gu и менее, необходимо иметь
минимальное расстояние, удовлетворяющее условию dmin ≥ 2gu
В этом случае любая кодовая комбинация с числом ошибок gu отличается от каждой
разрешенной комбинации не менее чем в gu+1 позициях. Если условие не выполнено,
возможен случай, когда ошибки кратности g исказят переданную комбинацию так, что она станет
ближе к одной из разрешенных комбинаций, чем к переданной или даже перейдет в другую
разрешенную комбинацию. В соответствии с этим, условие исправления всех ошибок кратностью
не более gи можно записать:
Из и
следует, что если код исправляет все ошибки кратностью gu, то число
ошибок, которые он может обнаружить, равно go = 2gu. Следует отметить, что эти соотношения
устанавливают лишь гарантированное минимальное число обнаруживаемых или
исправляемых ошибок при заданном dmin и не ограничивают возможность обнаружения ошибок
большей кратности. Например, простейший код с проверкой на четность с dmin = 2 позволяет
обнаруживать не только одиночные ошибки, но и любое нечетное число ошибок в пределах go < n.
Корректирующие возможности кодов
Вопрос о минимально необходимой избыточности, при которой код обладает нужными
корректирующими свойствами, является одним из важнейших в теории кодирования. Этот вопрос
до сих пор не получил полного решения. В настоящее время получен лишь ряд верхних и нижних
оценок (границ), которые устанавливают связь между максимально возможным минимальным
расстоянием корректирующего кода и его избыточностью.
Коды Хэмминга
Построение кодов Хемминга базируется на принципе проверки на четность веса W (числа
единичных символов «1») в информационной группе кодового блока.
Поясним идею проверки на четность на примере простейшего корректирующего кода,
который так и называется кодом с проверкой на четность или кодом с проверкой по паритету
(равенству).
В таком коде к кодовым комбинациям безызбыточного первичного двоичного k-разрядного
кода добавляется один дополнительный разряд (символ проверки на четность, называемый
проверочным, или контрольным). Если число символов «1» исходной кодовой комбинации
четное, то в дополнительном разряде формируют контрольный символ «0», а если число
символов «1» нечетное, то в дополнительном разряде формируют символ «1». В результате
общее число символов «1» в любой передаваемой кодовой комбинации всегда будет четным.
Таким образом, правило формирования проверочного символа сводится к следующему:
где i – соответствующий информационный символ («0» или «1»); k – общее их число а, под
операцией ⊕ здесь и далее понимается сложение «по модулю 2». Очевидно, что добавление
дополнительного разряда увеличивает общее число возможных комбинаций вдвое по сравнению
с числом комбинаций исходного первичного кода, а условие четности разделяет все комбинации
на разрешенные и неразрешенные. Код с проверкой на четность позволяет обнаруживать
одиночную ошибку при приеме кодовой комбинации, так как такая ошибка нарушает условие
четности, переводя разрешенную комбинацию в запрещенную.
Критерием правильности принятой комбинации является равенство нулю результата S
суммирования «по модулю 2» всех n символов кода, включая проверочный символ m1. При
наличии одиночной ошибки S принимает значение 1:
— ошибок нет,
— однократная ошибка
Этот код является (k+1,k)-кодом, или (n,n–1)-кодом. Минимальное расстояние кода равно
двум (dmin = 2), и, следовательно, никакие ошибки не могут быть исправлены. Простой код с
проверкой на четность может использоваться только для обнаружения (но не исправления)
однократных ошибок.
Увеличивая число дополнительных проверочных разрядов, и формируя по определенным
правилам проверочные символы m, равные «0» или «1», можно усилить корректирующие
свойства кода так, чтобы он позволял не только обнаруживать, но и исправлять ошибки. На этом и
основано построение кодов Хемминга.
Коды Хемминга позволяют исправлять одиночную ошибку, с помощью непосредственного
описания. Для каждого числа проверочных символов m =3, 4, 5… существует классический код
Хемминга с маркировкой
т.е. (7,4), (15,11) (31,26) …
При других значениях числа информационных символов k получаются так называемые
усеченные (укороченные) коды Хемминга. Так для кода имеющего 5 информационных символов,
потребуется использование корректирующего кода (9,5), являющегося усеченным от
классического кода Хемминга (15,11), так как число символов в этом коде уменьшается
(укорачивается) на 6.
Для примера рассмотрим классический код Хемминга (7,4), который можно сформировать и
описать с помощью кодера, представленного на рис. 1 В простейшем варианте при заданных
четырех информационных символах: i1, i2, i3, i4 (k = 4), будем полагать, что они сгруппированы в
начале кодового слова, хотя это и не обязательно. Дополним эти информационные символы
тремя проверочными символами (m = 3), задавая их следующими равенствами проверки на
четность, которые определяются соответствующими алгоритмами, где знак ⊕ означает
сложение «по модулю 2»: r1 = i1 ⊕ i2 ⊕ i3, r2 = i2 ⊕ i3 ⊕ i4, r3 = i1 ⊕ i2 ⊕ i4.
В соответствии с этим алгоритмом определения значений проверочных символов mi, в табл.
1 выписаны все возможные 16 кодовых слов (7,4)-кода Хемминга.
Таблица 1 Кодовые слова (7,4)-кода Хэмминга
|
k=4 |
m=4 |
|
i1 i2 i3 i4 |
r1 r2 r3 |
|
0 0 0 0 |
0 0 0 |
|
0 0 0 1 |
0 1 1 |
|
0 0 1 0 |
1 1 0 |
|
0 0 1 1 |
1 0 1 |
|
0 1 0 0 |
1 1 1 |
|
0 1 0 1 |
1 0 0 |
|
0 1 1 0 |
0 0 1 |
|
0 1 1 1 |
0 1 0 |
|
1 0 0 0 |
1 0 1 |
|
1 0 0 1 |
1 0 0 |
|
1 0 1 0 |
0 1 1 |
|
1 0 1 1 |
0 0 0 |
|
1 1 0 0 |
0 1 0 |
|
1 1 0 1 |
0 0 1 |
|
1 1 1 0 |
1 0 0 |
|
1 1 1 1 |
1 1 1 |
На рис.1 приведена блок-схема кодера – устройства автоматически кодирующего
информационные разряды в кодовые комбинации в соответствии с табл.1

Рис. 1 Кодер для (7,4)-кода Хемминга
На рис. 1.4 приведена схема декодера для (7,4) – кода Хемминга, на вход которого
поступает кодовое слово
. Апостроф означает, что любой символ слова может
быть искажен помехой в телекоммуникационном канале.
В декодере в режиме исправления ошибок строится последовательность:
Трехсимвольная последовательность (s1, s2, s3) называется синдромом. Термин «синдром»
используется и в медицине, где он обозначает сочетание признаков, характерных для
определенного заболевания. В данном случае синдром S = (s1, s2, s3) представляет собой
сочетание результатов проверки на четность соответствующих символов кодовой группы и
характеризует определенную конфигурацию ошибок (шумовой вектор).
Число возможных синдромов определяется выражением:
При числе проверочных символов m =3 имеется восемь возможных синдромов (23 = 
Нулевой синдром (000) указывает на то, что ошибки при приеме отсутствуют или не обнаружены.
Всякому ненулевому синдрому соответствует определенная конфигурация ошибок, которая и
исправляется. Классические коды Хемминга имеют число синдромов, точно равное их
необходимому числу (что позволяет исправить все однократные ошибки в любом информативном
и проверочном символах) и включают один нулевой синдром. Такие коды называются
плотноупакованными.
Усеченные коды являются неплотноупакованными, так как число синдромов у них
превышает необходимое. Так, в коде (9,5) при четырех проверочных символах число синдромов
будет равно 24 =16, в то время как необходимо всего 10. Лишние 6 синдромов свидетельствуют о
неполной упаковке кода (9,5).

Рис. 2 Декодер для (7, 4)-кода Хемминга
Для рассматриваемого кода (7,4) в табл. 2 представлены ненулевые синдромы и
соответствующие конфигурации ошибок.
Таблица 2 Синдромы (7, 4)-кода Хемминга
|
Синдром |
001 |
010 |
011 |
100 |
101 |
110 |
111 |
|
Конфигурация ошибок |
0000001 |
0000010 |
0000100 |
0001000 |
0010000 |
0100000 |
1000000 |
|
Ошибка в символе |
m1 |
m2 |
i4 |
m1 |
i1 |
i3 |
i2 |
Таким образом, (7,4)-код позволяет исправить все одиночные ошибки. Простая проверка
показывает, что каждая из ошибок имеет свой единственный синдром. При этом возможно
создание такого цифрового корректора ошибок (дешифратора синдрома), который по
соответствующему синдрому исправляет соответствующий символ в принятой кодовой группе.
После внесения исправления проверочные символы ri можно на выход декодера (рис. 2) не
выводить. Две или более ошибок превышают возможности корректирующего кода Хемминга, и
декодер будет ошибаться. Это означает, что он будет вносить неправильные исправления и
выдавать искаженные информационные символы.
Идея построения подобного корректирующего кода, естественно, не меняется при
перестановке позиций символов в кодовых словах. Все такие варианты также называются (7,4)-
кодами Хемминга.
Циклические коды
Своим названием эти коды обязаны такому факту, что для них часть комбинаций, либо все
комбинации могут быть получены путем циклическою сдвига одной или нескольких базовых
комбинаций кода.
Построение такого кода основывается на использовании неприводимых многочленов в поле
двоичных чисел. Такие многочлены не могут быть представлены в виде произведения
многочленов низших степеней подобно тому, как простые числа не могут быть представлены
произведением других чисел. Они делятся без остатка только на себя или на единицу.
Для определения неприводимых многочленов раскладывают на простые множители бином
хn -1. Так, для n = 7 это разложение имеет вид:
(x7)=(x-1)(x3+x2)(x3+x-1)
Каждый из полученных множителей разложения может применяться для построения
корректирующего кода.
Неприводимый полином g(x) называют задающим, образующим или порождающим
для корректирующего кода. Длина n (число разрядов) создаваемого кода произвольна.
Кодовая последовательность (комбинация) корректирующего кода состоит из к информационных
разрядов и n — к контрольных (проверочных) разрядов. Степень порождающего полинома
r = n — к равна количеству неинформационных контрольных разрядов.
Если из сделанного выше разложения (при n = 7) взять полипом (х — 1), для которого
r=1, то k=n-r=7-1=6. Соответствующий этому полиному код используется для контроля
на чет/нечет (обнаружение ошибок). Для него минимальное кодовое расстояние D0 = 2
(одна единица от D0 — для исходного двоичного кода, вторая единица — за счет контрольного разряда).
Если же взять полином (x3+x2+1) из указанного разложения, то степень полинома
r=3, а k=n-r=7-3=4.
Контрольным разрядам в комбинации для некоторого кода могут быть четко определено место (номера разрядов).
Тогда код называют систематическим или разделимым. В противном случае код является неразделимым.
Способы построения циклических кодов по заданному полиному.
1) На основе порождающей (задающей) матрицы G, которая имеет n столбцов, k строк, то есть параметры которой
связаны с параметрами комбинаций кода. Порождающую матрицу строят, взяв в качестве ее строк порождающий
полином g(x) и (k — 1) его циклических сдвигов:

Пример; Определить порождающую матрицу, если известно, что n=7, k=4, задающий полином g(x)=x3+х+1.
Решение: Кодовая комбинация, соответствующая задающему полиному g(x)=x3+х+1, имеет вид 1011.
Тогда порождающая матрица G7,4 для кода при n=7, к=4 с учетом того, что k-1=3, имеет вид:

Порождающая матрица содержит k разрешенных кодовых комбинаций. Остальные комбинации кода,
количество которых (2k — k) можно определить суммированием по модулю 2 всевозможных сочетаний
строк матрицы Gn,k. Для матрицы, полученной в приведенном выше примере, суммирование по модулю 2
четырех строк 1-2, 1-3, 1-4, 2-3, 2-4, 3-4 дает следующие кодовые комбинации циклического кода:
001110101001111010011011101010011101110100
Другие комбинации искомого корректирующего кода могут быть получены сложением трех комбинаций, например,
из сочетания строк 1-3-4, что дает комбинацию 1111111, а также сложением четырех строк 1-2-3-4, что
дает комбинацию 1101001 и т.д.
Ряд комбинаций искомого кода может быть получено путем дальнейшего циклического сдвига комбинаций
порождающей матрицы, например, 0110001, 1100010, 1000101. Всего для образования искомого циклического
кода требуется 2k=24=16 комбинаций.
2) Умножение исходных двоичных кодовых комбинаций на задающий полином.
Исходными комбинациями являются все k-разрядные двоичные комбинации. Так, например, для исходной
комбинации 1111 (при k = 4) умножение ее на задающий полином g(x)=x3+х+1=1011 дает 1101001.
Полученные на основе двух рассмотренных способов циклические коды не являются разделимыми.
3) Деление на задающий полином.
Для получения разделимого (систематического) циклического кода необходимо разделить многочлен
xn-k*h(x), где h(x) — исходная двоичная комбинация, на задающий полином g(x) и прибавить полученный
остаток от деления к многочлену xn-k*h(x).
Заметим, что умножение исходной комбинации h(x) на xn-k эквивалентно сдвигу h(x) на (n-к) разрядов влево.
Пример: Требуется определить комбинации циклического разделимого кода, заданного полиномом g(x)=x3+х+1=1011 и
имеющего общее число разрядов 7, число информационных разрядов 4, число контрольных разрядов (n-k)=3.
Решение: Пусть исходная комбинация h(x)=1100. Умножение ее на xn-k=x3=1000 дает
x3*(x3+x2)=1100000, то есть эквивалентно
сдвигу исходной комбинации на 3 разряда влево. Деление комбинации 1100000 на комбинацию 1011, эквивалентно задающему полиному, дает:

Полученный остаток от деления, содержащий xn-k=3 разряда, прибавляем к полиному, в результате чего получаем искомую комбинацию
разделимого циклического кода: 1100010. В ней 4 старших разряда (слева) соответствуют исходной двоичной комбинации, а три младших
разряда являются контрольными.
Следует сделать ряд указаний относительно процедуры деления:
1) При делении задающий полином совмещается старшим разрядом со старшим «единичными разрядом делимого.
2) Вместо вычитания по модулю 2 выполняется эквивалентная ему процедура сложения по модулю 2.
3) Деление продолжается до тех пор, пока степень очередного остатка не будет меньше степени делителя (задающего полинома). При достижении
этого полученный остаток соответствует искомому содержанию контрольных разрядов для данной искомой двоичной комбинации.
Для проверки правильности выполнения процедуры определения комбинации циклического кода необходимо разделить полученную комб1шацию на задающий полином с
учетом сделанных выше замечаний. Получение нулевого остатка от такого деления свидетельствует о правильности определения комбинации.
Логический код 4В/5В
Логический код 4В/5В заменяет исходные символы длиной в 4 бита на символы длиной в 5 бит. Так как результирующие символы содержат избыточные биты, то
общее количество битовых комбинаций в них больше, чем в исходных. Таким образом, пяти-битовая схема дает 32 (25) двухразрядных буквенно-цифровых символа,
имеющих значение в десятичном коде от 00 до 31. В то время как исходные данные могут содержать только четыре бита или 16 (24) символов.
Поэтому в результирующем коде можно подобрать 16 таких комбинаций, которые не содержат большого количества нулей, а остальные считать запрещенными кодами
(code violation). В этом случае длинные последовательности нулей прерываются, и код становится самосинхронизирующимся для любых передаваемых данных.
Исчезает также постоянная составляющая, а значит, еще более сужается спектр сигнала. Но этот метод снижает полезную пропускную способность линии,
так как избыточные единицы пользовательской информации не несут, и только «занимают эфирное время». Избыточные коды позволяют приемнику распознавать
искаженные биты. Если приемник принимает запрещенный код, значит, на линии произошло искажение сигнала.
Итак, рассмотрим работу логического кода 4В/5В. Преобразованный сигнал имеет 16 значений для передачи информации и 16 избыточных значений. В декодере
приемника пять битов расшифровываются как информационные и служебные сигналы.
Для служебных сигналов отведены девять символов, семь символов — исключены.
Исключены комбинации, имеющие более трех нулей (01 — 00001, 02 — 00010, 03 — 00011, 08 — 01000, 16 — 10000). Такие сигналы интерпретируются символом
V и командой приемника VIOLATION — сбой. Команда означает наличие ошибки из-за высокого уровня помех или сбоя передатчика. Единственная
комбинация из пяти нулей (00 — 00000) относится к служебным сигналам, означает символ Q и имеет статус QUIET — отсутствие сигнала в линии.
Такое кодирование данных решает две задачи — синхронизации и улучшения помехоустойчивости. Синхронизация происходит за счет исключения
последовательности более трех нулей, а высокая помехоустойчивость достигается приемником данных на пяти-битовом интервале.
Цена за эти достоинства при таком способе кодирования данных — снижение скорости передачи полезной информации.
К примеру, В результате добавления одного избыточного бита на четыре информационных, эффективность использования полосы
частот в протоколах с кодом MLT-3 и кодированием данных 4B/5B уменьшается соответственно на 25%.
Схема кодирования 4В/5В представлена в таблице.
|
Двоичный код 4В |
Результирующий код 5В |
|
0 0 0 0 |
1 1 1 1 0 |
|
0 0 0 1 |
0 1 0 0 1 |
|
0 0 1 0 |
1 0 1 0 0 |
|
0 0 1 1 |
1 0 1 0 1 |
|
0 1 0 0 |
0 1 0 1 0 |
|
0 1 0 1 |
0 1 0 1 1 |
|
0 1 1 0 |
0 1 1 1 0 |
|
0 1 1 1 |
0 1 1 1 1 |
|
1 0 0 0 |
1 0 0 1 0 |
|
1 0 0 1 |
1 0 0 1 1 |
|
1 0 1 0 |
1 0 1 1 0 |
|
1 0 1 1 |
1 0 1 1 1 |
|
1 1 0 0 |
1 1 0 1 0 |
|
1 1 0 1 |
1 1 0 1 1 |
|
1 1 1 0 |
1 1 1 0 0 |
|
1 1 1 1 |
1 1 1 0 1 |
Итак, соответственно этой таблице формируется код 4В/5В, затем передается по линии с помощью физического кодирования по
одному из методов потенциального кодирования, чувствительному только к длинным последовательностям нулей — например, в помощью
цифрового кода NRZI.
Символы кода 4В/5В длиной 5 бит гарантируют, что при любом их сочетании на линии не могут встретиться более трех нулей подряд.
Буква ^ В в названии кода означает, что элементарный сигнал имеет 2 состояния — от английского binary — двоичный. Имеются
также коды и с тремя состояниями сигнала, например, в коде 8В/6Т для кодирования 8 бит исходной информации используется
код из 6 сигналов, каждый из которых имеет три состояния. Избыточность кода 8В/6Т выше, чем кода 4В/5В, так как на 256
исходных кодов приходится 36=729 результирующих символов.
Как мы говорили, логическое кодирование происходит до физического, следовательно, его осуществляют оборудование канального
уровня сети: сетевые адаптеры и интерфейсные блоки коммутаторов и маршрутизаторов. Поскольку, как вы сами убедились,
использование таблицы перекодировки является очень простой операцией, поэтому метод логического кодирования избыточными
кодами не усложняет функциональные требования к этому оборудованию.
Единственное требование — для обеспечения заданной пропускной способности линии передатчик, использующий избыточный код,
должен работать с повышенной тактовой частотой. Так, для передачи кодов 4В/5В со скоростью 100 Мб/с передатчик должен
работать с тактовой частотой 125 МГц. При этом спектр сигнала на линии расширяется по сравнению со случаем, когда по
линии передается чистый, не избыточный код. Тем не менее, спектр избыточного потенциального кода оказывается уже
спектра манчестерского кода, что оправдывает дополнительный этап логического кодирования, а также работу приемника
и передатчика на повышенной тактовой частоте.
В основном для локальных сетей проще, надежней, качественней, быстрей — использовать логическое кодирование данных
с помощью избыточных кодов, которое устранит длительные последовательности нулей и обеспечит синхронизацию
сигнала, потом на физическом уровне использовать для передачи быстрый цифровой код NRZI, нежели без предварительного
логического кодирования использовать для передачи данных медленный, но самосинхронизирующийся манчестерский код.
Например, для передачи данных по линии с пропускной способностью 100М бит/с и полосой пропускания 100 МГц,
кодом NRZI необходимы частоты 25 — 50 МГц, это без кодирования 4В/5В. А если применить для NRZI еще и
кодирование 4В/5В, то теперь полоса частот расширится от 31,25 до 62,5 МГц. Но тем не менее, этот диапазон
еще «влазит» в полосу пропускания линии. А для манчестерского кода без применения всякого дополнительного
кодирования необходимы частоты от 50 до 100 МГц, и это частоты основного сигнала, но они уже не будут пропускаться
линией на 100 МГц.
Скрэмблирование
Другой метод логического кодирования основан на предварительном «перемешивании» исходной информации таким
образом, чтобы вероятность появления единиц и нулей на линии становилась близкой.
Устройства, или блоки, выполняющие такую операцию, называются скрэмблерами (scramble — свалка, беспорядочная сборка) .
При скремблировании данные перемешиваються по определенному алгоритму и приемник, получив двоичные данные, передает
их на дескрэмблер, который восстанавливает исходную последовательность бит.
Избыточные биты при этом по линии не передаются.
Суть скремблирования заключается просто в побитном изменении проходящего через систему потока данных. Практически
единственной операцией, используемой в скремблерах является XOR — «побитное исключающее ИЛИ», или еще говорят —
сложение по модулю 2. При сложении двух единиц исключающим ИЛИ отбрасывается старшая единица и результат записывается — 0.
Метод скрэмблирования очень прост. Сначала придумывают скрэмблер. Другими словами придумывают по какому соотношению
перемешивать биты в исходной последовательности с помощью «исключающего ИЛИ». Затем согласно этому соотношению из текущей
последовательности бит выбираются значения определенных разрядов и складываются по XOR между собой. При этом все разряды
сдвигаются на 1 бит, а только что полученное значение («0» или «1») помещается в освободившийся самый младший разряд.
Значение, находившееся в самом старшем разряде до сдвига, добавляется в кодирующую последовательность, становясь очередным
ее битом. Затем эта последовательность выдается в линию, где с помощью методов физического кодирования передается к
узлу-получателю, на входе которого эта последовательность дескрэмблируется на основе обратного отношения.
Например, скрэмблер может реализовывать следующее соотношение:
где Bi — двоичная цифра результирующего кода, полученная на i-м такте работы скрэмблера, Ai — двоичная цифра исходного
кода, поступающая на i-м такте на вход скрэмблера, Bi-3 и Bi-5 — двоичные цифры результирующего кода, полученные на
предыдущих тактах работы скрэмблера, соответственно на 3 и на 5 тактов ранее текущего такта, ⊕ — операция исключающего
ИЛИ (сложение по модулю 2).
Теперь давайте, определим закодированную последовательность, например, для такой исходной последовательности 110110000001.
Скрэмблер, определенный выше даст следующий результирующий код:
B1=А1=1 (первые три цифры результирующего кода будут совпадать с исходным, так как еще нет нужных предыдущих цифр)

Таким образом, на выходе скрэмблера появится последовательность 110001101111. В которой нет последовательности из шести нулей, п
рисутствовавшей в исходном коде.
После получения результирующей последовательности приемник передает ее дескрэмблеру, который восстанавливает исходную
последовательность на основании обратного соотношения.
Существуют другие различные алгоритмы скрэмблирования, они отличаются количеством слагаемых, дающих цифру
результирующего кода, и сдвигом между слагаемыми.
Главная проблема кодирования на основе скремблеров — синхронизация передающего (кодирующего) и принимающего
(декодирующего) устройств. При пропуске или ошибочном вставлении хотя бы одного бита вся передаваемая информация
необратимо теряется. Поэтому, в системах кодирования на основе скремблеров очень большое внимание уделяется методам синхронизации.
На практике для этих целей обычно применяется комбинация двух методов:
а) добавление в поток информации синхронизирующих битов, заранее известных приемной стороне, что позволяет ей при ненахождении
такого бита активно начать поиск синхронизации с отправителем,
б) использование высокоточных генераторов временных импульсов, что позволяет в моменты потери синхронизации производить
декодирование принимаемых битов информации «по памяти» без синхронизации.
Существуют и более простые методы борьбы с последовательностями единиц, также относимые к классу скрэмблирования.
Для улучшения кода ^ Bipolar AMI используются два метода, основанные на искусственном искажении последовательности нулей запрещенными символами.

Рис. 3 Коды B8ZS и HDB3
На этом рисунке показано использование метода ^ B8ZS (Bipolar with 8-Zeros Substitution) и метода HDB3 (High-Density Bipolar 3-Zeros) для корректировки
кода AMI. Исходный код состоит из двух длинных последовательностей нулей (8- в первом случае и 5 во втором).
Код B8ZS исправляет только последовательности, состоящие из 8 нулей. Для этого он после первых трех нулей вместо оставшихся пяти нулей вставляет пять
цифр: V-1*-0-V-1*. V здесь обозначает сигнал единицы, запрещенной для данного такта полярности, то есть сигнал, не изменяющий полярность предыдущей
единицы, 1* — сигнал единицы корректной полярности, а знак звездочки отмечает тот факт, что в исходном коде в этом такте была не единица, а ноль. В
результате на 8 тактах приемник наблюдает 2 искажения — очень маловероятно, что это случилось из-за шума на линии или других сбоев передачи. Поэтому
приемник считает такие нарушения кодировкой 8 последовательных нулей и после приема заменяет их на исходные 8 нулей.
Код B8ZS построен так, что его постоянная составляющая равна нулю при любых последовательностях двоичных цифр.
Код HDB3 исправляет любые 4 подряд идущих нуля в исходной последовательности. Правила формирования кода HDB3 более сложные, чем кода B8ZS.
Каждые четыре нуля заменяются четырьмя сигналами, в которых имеется один сигнал V. Для подавления постоянной составляющей полярность сигнала
V чередуется при последовательных заменах.
Кроме того, для замены используются два образца четырехтактовых кодов. Если перед заменой исходный код содержал нечетное число единиц, то
используется последовательность 000V, а если число единиц было четным — последовательность 1*00V.
Таким образом, применение логическое кодирование совместно с потенциальным кодированием дает следующие преимущества:
Улучшенные потенциальные коды обладают достаточно узкой полосой пропускания для любых последовательностей единиц и нулей,
которые встречаются в передаваемых данных. В результате коды, полученные из потенциального путем логического кодирования,
обладают более узким спектром, чем манчестерский, даже при повышенной тактовой частоте.
Линейные блочные коды
При передаче информации по каналам связи возможны ошибки вследствие помех и искажений сигналов. Для обнаружения и
исправления возникающих ошибок используются помехоустойчивые коды. Упрощенная схема системы передачи информации
при помехоустойчивом кодировании показана на рис. 4
Кодер служит для преобразования поступающей от источника сообщений последовательности из k информационных
символов в последовательность из n cимволов кодовых комбинаций (или кодовых слов). Совокупность кодовых слов образует код.
Множество символов, из которых составляется кодовое слово, называется алфавитом кода, а число различных символов в
алфавите – основанием кода. В дальнейшем вследствие их простоты и наибольшего распространения рассматриваются главным
образом двоичные коды, алфавит которых содержит два символа: 0 и 1.

Рис. 4 Система передачи дискретных сообщений
Правило, по которому информационной последовательности сопоставляется кодовое слово, называется правилом кодирования.
Если при кодировании каждый раз формируется блок А из k информационных символов, превращаемый затем в n-символьную
кодовую комбинацию S, то код называется блочным. При другом способе кодирования информационная последовательность на
блоки не разбивается, и код называется непрерывным.
С математической точки зрения кодер осуществляет отображение множества из 2k элементов (двоичных информационных
последовательностей) в множество, состоящее из 2n элементов (двоичных последовательностей длины n). Для практики
интересны такие отображения, в результате которых получаются коды, обладающие способностью исправлять часть ошибок
и допускающие простую техническую реализацию кодирующих и декодирующих устройств.
Дискретный канал связи – это совокупность технических средств вместе со средой распространения радиосигналов, включенных
между кодером и декодером для передачи сигналов, принимающих конечное число разных видов. Для описания реальных каналов
предложено много математических моделей, с разной степенью детализации отражающих реальные процессы. Ограничимся рассмотрением
простейшей модели двоичного канала, входные и выходные сигналы которого могут принимать значения 0 и 1.
Наиболее распространено предположение о действии в канале аддитивной помехи. Пусть S=(s1,s2,…,sn)
и Y=(y1,y2,…,yn) соответственно входная и выходная последовательности двоичных символов.
Помехой или вектором ошибки называется последовательность из n символов E=(e1,e2,…,en), которую
надо поразрядно сложить с переданной последовательностью, чтобы получить принятую:
Y=S+E
Таким образом, компонента вектора ошибки ei=0 указывает на то, что 2-й символ принят правильно (yi=si),
а компонента ei=1 указывает на ошибку при приеме (yi≠si).Поэтому важной характеристикой вектора ошибки
является число q ненулевых компонентов, которое называется весом или кратностью ошибки. Кратность ошибки – дискретная случайная величина,
принимающая целочисленные значения от 0 до n.
Классификация двоичных каналов ведется по виду распределения случайного вектора E. Основные результаты теории кодирования получены в
предположении, что вероятность ошибки в одном символе не зависит ни от его номера в последовательности, ни от его значения. Такой
канал называется стационарным и симметричным. В этом канале передаваемые символы искажаются с одинаковой вероятностью
P, т.е. P(ei=1)=P, i=1,2,…,n.
Для симметричного стационарного канала распределение вероятностей векторов ошибки кратности q является биноминальным:
P(Ei)=Pq(1-P)n-q
которая показывает, что при P<0,5 вероятность β2=αj является убывающей функцией q,
т.е. в симметричном стационарном канале более вероятны ошибки меньшей кратности. Этот важный факт используется при построении
помехоустойчивых кодов, т.к. позволяет обосновать тактику обнаружения и исправления в первую очередь ошибок малой кратности.
Конечно, для других моделей канала такая тактика может и не быть оптимальной.
Декодирующее устройство (декодер) предназначено оценить по принятой последовательности Y=(y1,y2,…,yn)
значения информационных символов A‘=(a‘1,a‘2,…,a‘k,).
Из-за действия помех возможны неправильные решения. Процедура декодирования включает решение двух задач: оценивание переданного кодового
слова и формирование оценок информационных символов.
Вторая задача решается относительно просто. При наиболее часто используемых систематических кодах, кодовые слова которых содержат информационные
символы на известных позициях, все сводится к простому их стробированию. Очевидно также, что расположение информационных символов внутри кодового
слова не имеет существенного значения. Удобно считать, что они занимают первые k позиций кодового слова.
Наибольшую трудность представляет первая задача декодирования. При равновероятных информационных последовательностях ее оптимальное решение
дает метод максимального правдоподобия. Функция правдоподобия как вероятность получения данного вектора Y при передаче кодовых слов
Si, i=1,2,…,2k на основании Y=S+E определяется вероятностями появления векторов ошибок:
P(Y/Si)=P(Ei)=Pqi(1-P)n-qi
где qi – вес вектора Ei=Y+Si
Очевидно, вероятность P(Y/Si) максимальна при минимальном qi. На основании принципа максимального правдоподобия оценкой S‘ является кодовое слово,
искажение которого для превращения его в принятое слово Y имеет минимальный вес, т. е. в симметричном канале является наиболее вероятным (НВ):
S‘=Y+EHB
Если несколько векторов ошибок Ei имеют равные минимальные веса, то наивероятнейшая ошибка EHB определяется случайным выбором среди них.
В качестве расстояния между двумя кодовыми комбинациями принимают так называемое расстояние Хэмминга, которое численно равно количеству символов, в которых одна
комбинация отлична от другой, т.е. весу (числу ненулевых компонентов) разностного вектора. Расстояние Хэмминга между принятой последовательностью Y и всеми
возможными кодовыми словами 5, есть функция весов векторов ошибок Ei:

Поэтому декодирование по минимуму расстояния, когда в качестве оценки берется слово, ближайшее к принятой
последовательности, является декодированием по максимуму правдоподобия.
Таким образом, оптимальная процедура декодирования для симметричного канала может быть описана следующей последовательностью операций. По принятому
вектору Y определяется вектор ошибки с минимальным весом EHB, который затем вычитается (в двоичном канале — складывается по модулю 2) из Y:
Y→EHB→S‘=Y+EHB
Наиболее трудоемкой операцией в этой схеме является определение наи-вероятнейшего вектора ошибки, сложность которой
существенно возрастает при увеличении длины кодовых комбинаций. Правила кодирования, которые нацелены на упрощение
процедур декодирования, предполагают придание всем кодовым словам технически легко проверяемых признаков.
Широко распространены линейные коды, называемые так потому, что их кодовые слова образуют линейное
подпространство над конечным полем. Для двоичных кодов естественно использовать поле характеристики p=2.
Принадлежность принятой комбинации Y известному подпространству является тем признаком, по которому
выносится решение об отсутствии ошибок (EHB=0).
Так как по данному коду все пространство последовательностей длины n разбивается на смежные классы,
то для каждого смежного класса можно заранее определить вектор ошибки минимального веса,
называемый лидером смежного класса. Тогда задача декодера состоит в определении номера смежного класса,
которому принадлежит Y, и формировании лидера этого класса.