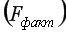Вопросы:
-
Истинное и
выборочное уравнения регрессии. -
Метод наименьших
квадратов. -
Геометрическая
интерпретация метода наименьших
квадратов. -
Экономическая
интерпретация коэффициентов парной
линейной регрессии. -
Основные предпосылки
регрессионного анализа. Теорема
Гаусса-Маркова. -
Расчет стандартных
ошибок коэффициентов регрессии. -
Проверка значимости
коэффициентов регрессии. -
Построение
доверительных интервалов для параметров
теоретической регрессии. -
Проверка общего
качества уровня регрессии. Коэффициент
детерминации. -
Проверка значимости
коэффициента детерминации. -
Оценка тесноты
связи между переменными. Коэффициент
корреляции. -
Проверка значимости
коэффициента корреляции. -
Прогнозирование.
1.
Пусть исследуется
статистическая зависимость экономического
показателя У (объясняемая зависимая
переменная) от экономического показателя
Х (фактора, объясняющей или независимой
переменной). Предположим, что зависимость
носит линейный характер, тогда ее можно
описать уравнением.
У=+
Х+Е
(1),
где Х – неслучайная
величина, У и Е – случайные величины.
Случайная величина
Е отражает воздействие на зависимую
переменную У неучтенных и случайных
факторов и называется ошибкой регрессии.
Уравнение (1) называют истинным
(теоретическим) уравнением
регрессии или линейной регрессионной
моделью. На основе реальных статистических
данных об экономических показателях
Х и У (выборке данных из генеральной
совокупности) оцениваются параметры
регрессии α и β и строится выборочное
уравнение регрессии
,
(2)
а, в,
— коэффициенты регрессии. Уравнение (2)
называют еще эмпирическим уравнением
регрессии.
Одним из методов
нахождения коэффициентов регрессии а
и в
является метод
наименьших квадратов (МНК).
2.
Пусть из генеральной
совокупности выбраны данные об
экономических показателях У: ( у,
у,
…, у)
и Х: ( х,
х,…,
х)
.
Если в (2) подставить наблюдаемое
(выборочное значение хi,
то получим расчетное значение
зависимой переменной у:
(3)
Разность между
фактическими и расчетными значениями
зависимой переменной обозначим ei
и назовем
остатком, т.е.:
(4)
Суть МНК заключается
в следующем: коэффициенты а
и в
должны быть такими, чтобы сумма квадратов
остатков была минимальна
(5)
в (5) уi
и xi
– известные величины, а а
и в
– неизвестные.
Запишем необходимые
условия экстремума функции S
относительно а и в:

Система (6) является
системой двух уравнений относительно
двух неизвестных а
и в.
Она легко преобразовывается в систему
(7):

Разделим оба
уравнения системы на n:

3.
начертим оси
координат Х ,У и изобразим в первой
четверти точки (хi,уi)
Полученное
изображение называется диаграммой
рассеяния или полем корреляции.
Проведем линию
регрессии
Согласно МНК, а
и в должны
быть такими, чтобы построенная линия
была ближайшей к точкам поля корреляции
по их совокупности.
Сумма квадратов
расстояний от точек поля корреляции до
линии регрессии должна быть минимальной.
Пример1: исследуется
зависимость прибыли предприятия от
затрат на приобретение нового оборудования
и техники. Собранны статистические
данные по пяти однотипным предприятиям.
Данные в млн. ден.ед. представлены в
таблице 1.
Таблица
1
|
№ предприятия |
Затраты |
Прибыль, |
|
1 2 3 4 5 |
2 6 10 14 18 |
1 2 4 11 12 |
Построить уравнение
регрессии.
Данные таблицы
представим графически, т.е. построим
поле корреляции:
Из полученной
диаграммы рассеяния видно, что зависимость
статистическая и ее можно представить
линейной регрессией
.
Для оценки коэффициентов регрессииа
и в воспользуемся
формулами (8), для этого построим рабочую
таблицу 2.
Таблица2
е нового оборудования
и техники. в была минимальна00000000
|
№ предприятия |
|
|
|
|
|
|
1 2 3 4 5 |
2 6 10 14 18 |
1 2 4 11 12 |
4 36 100 196 324 |
2 12 40 154 216 |
1 4 16 121 144 |
|
Итого: |
50 |
30 |
660 |
424 |
286 |
|
Среднее |
10 |
6 |
132 |
84,8 |
57,2 |
|
|
|
|
|
|
Подставим результаты,
полученные в таблице 2 в формулы (8):
испр.
Таким образом,
уравнение регрессии, описывающее
зависимость прибыли предприятия от
затрат на новое оборудование и технику
имеет вид:
Выбрав с помощью
диаграммы рассеяния для описания
зависимости линейную регрессию мы
выполнили этап спецификации (подбора
функции), а рассчитав коэффициенты а
и в,
т.е. оценив параметры теоретической
регрессии, мы выполнили этап параметризации.
4.
Коэффициент парной
линейной регрессии в
показывает, как в среднем изменяется
зависимый экономический показатель у
с изменением независимого фактора х на
единицу. Так в примере 1 коэффициент
в=0,775
показывает, что при увеличении расходов
на приобретение нового оборудования и
техники на 1 ден.ед. прибыль предприятия
в среднем увеличится на 0,775 ден. ед.
Коэффициент а
парной
линейной регрессии экономического
смысла не имеет.
5.
Для того, чтобы
оценки параметров теоретической
регрессии, полученные на основе МНК
были лучшими по сравнению с оценками,
найденными с помощью других методов,
должны выполнятся определенные условия,
которые называются основными
предпосылками регрессионного анализа.
Для того, чтобы их
сформулировать, вспомним что теоретическая
регрессия описывается уравнением
,
или для i-го
наблюдения
Предпосылки:
1. Математическое
ожидание случайного члена ε в любом
наблюдении должно быть равно 0:
2. Дисперсия
случайного члена ε должна быть постоянной
для всех наблюдений:
3. Случайные члены
должны быть статистически независимы
друг от друга:
4. Объясняющая
переменная хi
– неслучайная величина
Теорема Гаусса-Маркова:
Если выполняются
предпосылки 1-4 регрессионного анализа,
то оценки параметров теоретической
регрессии а и в есть наилучшие линейные
оценки, обладающие следующими свойствами:
1. Они являются
несмещенными:
2. Они являются
эффективными, т.е. имеют наименьшую
дисперсию в классе всех несмещенных
оценок.

3. Они являются
состоятельными, т.е.
Это значит, что
при достаточно большом объеме выборки
n,
оценки а и в близки к истинным параметрам
линейной регрессионной модели α и β.
6.
Для расчета
дисперсий D(a)
и D(в)
коэффициентов регрессии а
и в
в формулах (9) использовалась дисперсия
σ2
случайного члена ε. Эта дисперсия
неизвестна, но ее можно оценить, используя
выборочные данные. Можно доказать, что
несмещенной оценкой дисперсии σ2
является величина S2,
где:
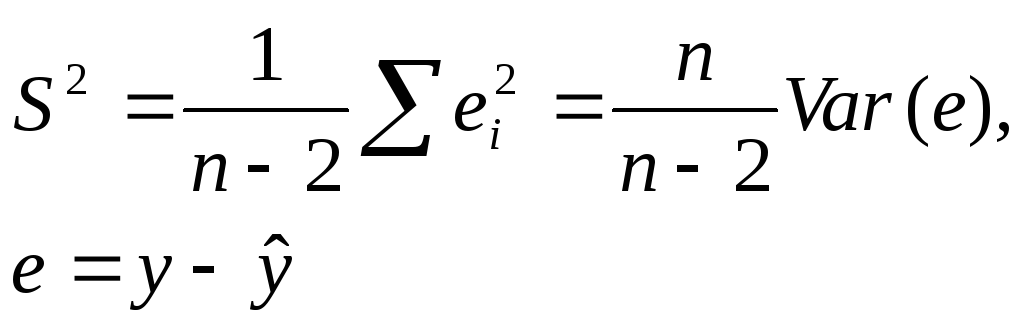
Величина S
называется стандартной ошибкой регрессии.
Она служит мерой разброса зависимой
переменной около линии регрессии.
Запишем в формулах (9) дисперсию σ2
ее оценкой S2:

и
называют
оценками дисперсии коэффициентов
регрессии, а величинаSa
и Sв
– стандартными ошибками коэффициентов
регрессии. Они
используются для построения доверительных
интервалов, которым принадлежат параметры
истинной регрессии и для проверки
значимости коэффициентов регрессии.
Вернемся в Примеру
1 и рассчитаем стандартные ошибки
коэффициентов регрессии:
7.
Коэффициента
регрессии получены на основании
выборочных данных, отобранных случайным
образом. Следовательно, коэффициенты
регрессии а и в являются случайными
числами и их значение может быть лишь
случайно оказались отличными от нуля.
Поэтому проводят проверку значимости
коэффициентов регрессии, т.е. проверку
того, значимо ли они отличны от нуля.
Для этого используют процедуру проверку
гипотез. Проверим значимость коэффициента
в.
Для этого:
1. Сформулируем
гипотезу Н0:
.
Она состоит в том,
что истинный коэффициент β=0,
2. В качестве
критерия проверки гипотезы принимают
случайную величину t:
. (12)
Эта случайная
величина имеет распределение Стьюдента
с ν = n-2
степенями свободы. Подставим в формулу
(12) оцененное по выборке значение
коэффициента в и его стандартную ошибку
Sв,
получим наблюдаемое или расчетное
значение t-критерия
tрасч.
3. Выбирают уровень
значимости проверки гипотезы. Как
правило α= 0,05 или α=0,01, т.е. пятипроцентный
или однопроцентный уровень значимости.
4. По таблице
распределения Стьюдента для выборочного
уровня значимости α/2 и ν = n-2
находят t
кр.
(критическое).
5. Если | tрасч.|
> t
кр.,
то гипотеза Н0
о равенстве параметра β=0 отвергается,
параметр β существенно отличен от нуля,
коэффициент в
значим, а переменная х оказывает
существенное влияние на зависимую у
(Н0
считается неверной с вероятностью 1- α)
6. Если | tрасч.|
< t
кр.,
гипотеза Н0
принимается, коэффициент в
незначим и переменная х не оказывает
существенного влияния на зависимую
переменную у.
Замечание: аналогично
проверяется значимость коэффициента
а
в уравнении регрессии, однако проверка
значимости коэффициента в
имеет гораздо большее значение в
регрессионном анализе.
Вернемся в примеру
1 и проверим значимость коэффициента
в.
Зависимость прибыли предприятия от
расходов на новое оборудование и технику
описывается регрессией:
(1,65) (0,143).
-
Формулируем
гипотезу Н0,
состоящую в том, что истинный коэффициент
β=0,
.
-
Определим tрасч.
.
-
Выбираем уровень
значимости проверки гипотезы
α= 0,05.
-
По таблице
распределения Стьюдента для α/2=0,025 и
числа степеней свободы
ν = 5-2=3
определим t
кр.
= 3,182.
5. | tрасч.|=5,4
> t
кр.=3,182,
поэтому гипотеза Н0
не верна с вероятностью
1-α= 1-0,05 = 0,95, параметр
β существенно отличен от нуля, коэффициент
в
значим и затраты на новое оборудование
и технику оказывают существенное влияние
на прибыль предприятия.
8.
Вспомним, что
линейная регрессионная модель (истинная
или теоретическая регрессия) имеет вид:
(13)
На основании
выборки строится выборочное уравнение
регрессии:
Также на основании
выборки рассчитывается стандартные
ошибки регрессии Sa
и Sв.
Можно доказать,
что с вероятностью 1-α (α – выбранный
уровень значимости) значения параметра
β лежат внутри интервала:
(14)
и с вероятностью
1-α (α – выбранный уровень значимости)
значение параметра α истинной регрессии
лежит внутри интервала:
(15)
Вернемся к Примеру
1 и построим доверительный интервал
для параметра β в регрессионной модели,
описывающей зависимость прибыли
предприятия от затрат на новое
оборудование и технику. Выберем уровень
значимости α= 0,05. т.к. в данном примере
ν = 5-2=3 , то t
кр.
= 3,182, в
= 0,775,
Тогда с вероятностью
1-α= 1-0,05 = 0,95 параметр β истинной регрессии
попадает в интервал
или 0,32<b<1,23
с вероятностью 95%.
9.
Выборочное уравнение
регрессии имеет вид:
тогда
Рассчитаем
выборочную дисперсию (вариацию) Var(y):
.
Из основных
предпосылок регрессионного анализа
следует, что
,
следовательно
т.е. дисперсия
зависимой переменной у (Var(y))
распадается на 2 части:
—
часть, объясняемая уравнением регрессии,
и часть
—
необъяснимая часть, зависящая от неученых
и случайных факторов.
Коэффициентом
детерминации называют отношение R2:
, (16)
которое характеризует
долю вариации зависимой переменной,
объясненную уравнением регрессии. Из
(16) следует что R2
меняется от 0 до 1:
,
чем ближе R2
к единице, тем меньше
,
т.е. доля вариации зависимой переменной,
объясняемая случайными и неучеными
факторами, тем лучше качество уравнения
регрессии. Если=0,
тоR2=1,
имеем функциональную зависимость. Чем
ближе R2
к 0, тем больше,
т.е. больше доля вариации, объясненная
случайными и неучеными факторами, тем
хуже качество регрессии. Т.к.

Вернемся к примеру
1, можно посчитать, что:
Коэффициент
детерминации близок к 1, качество
регрессии хорошее.
Можно утверждать,
что вариация (изменчивость) прибыли
предприятия на 90,7% объясняется затратами
на новое оборудование и технику и на
9,3% — прочими неучтенными и случайными
факторами.
10.
Т.к. R2
оценивается на основании выборочных
данных, то его отличие от 0 может оказаться
случайным. Поэтому проводят проверку
его значимости:
1. Формулируется
гипотеза Н0:
R2=0,
состоящая в том, что истинный коэффициент
детерминации равен 0.
2. В качестве
критерия проверки гипотезы применяют
случайную величину F:
. (18)
Величина F
имеет распределение Фишера с двумя
степенями свободы ν1=1,
ν2=n-2.
-
Выберем уровень
значимости проверки гипотезы значимости:
.
-
На основании α,
ν1, ν2
в таблице
распределения Фишера выбираем Fкр.
(критическое) -
Сравниваем Fрасч
и Fкр..
если Fрасч
> Fкр.,
то с вероятностью 1-α гипотезу Н0
считаем неверной, т.е. истинный коэффициент
детерминации существенно отличен от
нуля, уравнение регрессии значимо и
переменные, включенные в уравнение
регрессии достаточно объясняют поведение
зависимой переменной. Если Fрасч
< Fкр.,
то принимаемая гипотеза Н0,
уравнение регрессии считается незначимым.
Проверим значимость
коэффициента детерминации в примере
1:
-
Формулируем
гипотезу Н0:
R2=0. -
Находим Fрасч..
В (18) подставим значение коэффициента
детерминации, оцененное по выборке:
.
3.Выбираем уровень
значимости α=0,005.
4. В таблице
распределения Фишера на основании
α=0,05 и для степеней свободы ν1=1,
ν2
=5-2=3 найдем
Fкр.
.
-
Fрасч
=29,2> Fкр.=10,13,
поэтому Н0
не верна в вероятностью 1-0,05=0,95, коэффициент
детерминации значим, значимо построенное
в Примере 1 уравнение регрессии.
11.
Уравнение регрессии
всегда дополняется показателем тесноты
связи между переменными. При использовании
линейной регрессии в качестве такого
показателя выступает линейный коэффициент
корреляции:
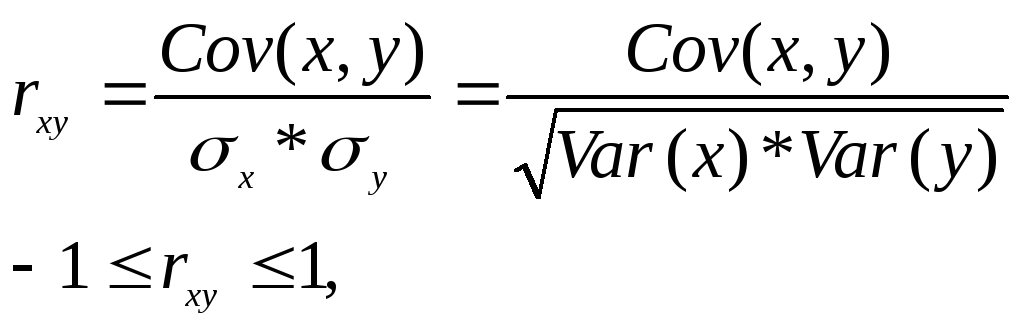
rxy
– безразмерная величина, показывает
степень линейной зависимости между
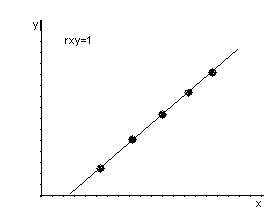
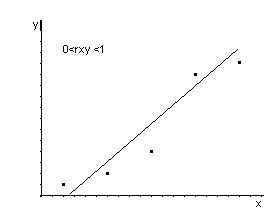
переменными. Чем ближе rxy
к ±1, тем сильнее линейная зависимость.
Чем ближе rxy
к 0, тем линейная зависимость слабее.
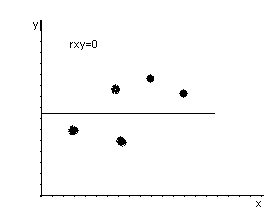
Если rxy
= ±1, то имеет место функциональная
линейная зависимость. Если rxy
= 0, то линейная зависимость отсутствует.
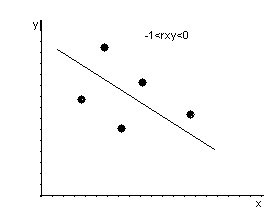
Если rxy
>0, то связь между переменными
положительная, если rxy
<0 – отрицательная.
Рассчитаем
коэффициент корреляции в примере 1:
rxy
>0 и близок к 1 следовательно линейная
зависимость между прибылью предприятия
и затратами на новое оборудование –
положительная и тесная.
12.
Осуществляется
аналогично проверки значимости
коэффициентов регрессии и детерминации,
используется t-статистика:
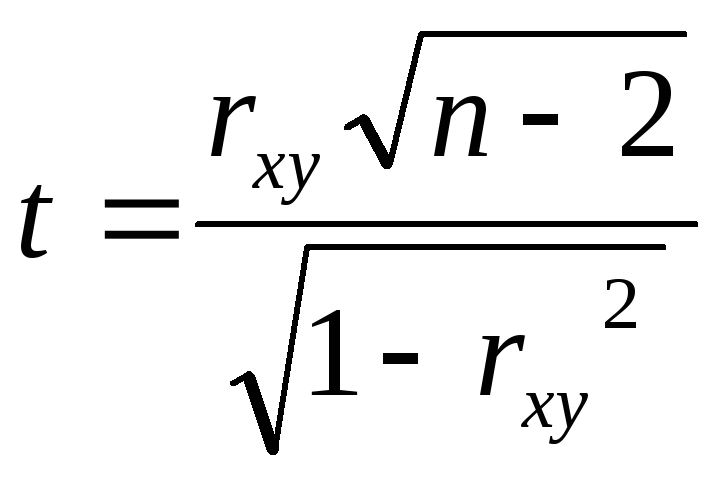
Проведем проверку
значимости коэффициента корреляции в
примере 1:
-
Формулируем
гипотезу, состоящую в том, что истинный
коэффициент корреляции равен нулю:
.
-
Подставим значение
коэффициента корреляции, вычисленное
по выборке в (20):
-
Выбираем уровень
значимости α=0,05. -
Для α/2=0,025 и для
ν=n-2=3
в таблице распределения Стьюдента
находим tкр.:
Следовательно,
истинный коэффициент корреляции
существенно отличен от 0, линейная
зависимость между прибылью предприятия
и затратами на новое оборудование и
технику действительно тесная..
Замечание 1:
В парном линейном
регрессионном анализе проверка значимости
коэффициента в, коэффициента корреляции
и коэффициента детерминации являются
эквивалентными.
Замечание 2:
Легко показать,
что коэффициент детерминации равен
квадрату коэффициента корреляции,
,
13.
Прогнозирование
на основе эконометрических моделей
является одной из основных задач
эконометрики.
Под прогнозированием
в эконометрике понимают построение
оценки зависимой переменной для таких
значений независимых переменных, которых
нет в исходных наблюдениях.
Различают точечное
прогнозирование и интервальное.
.
Точечный прогноз
это число, значение зависимой переменной,
вычисляемое для заданных значений
независимых переменных.
Интервальный
прогноз это интервал, в котором с заданным
уровнем значимости ( с заданной
вероятностью) находится истинное
значение зависимой переменной для
заданных значений независимых переменных.
Рассмотрим парную
линейную регрессионную модель
и соответствующее выборочное уравнение
регрессии.
Обозначим через ур
истинное значение переменной у для
заданного значения независимой переменной
хр,
т.е.
.
Точечным прогнозом
для ур
является
,
т.е. чтобы получить точечный прогноз
нужно в построенное уравнение регрессии
подставить заданное значение независимой
переменной.
Ошибкой
предсказания
()
называют разность между прогнозным и
истинным значениями независимой
переменной.
Можно доказать,
что дисперсия ошибки предсказания
. (21)
Из (21) следует, что
чем ближе заданное значение независимой
переменной
к
тем
меньше дисперсия прогноза и чем больше
объем выборкиn,
тем меньше дисперсия прогноза.
Заменив в (21)
дисперсию
на
ее оценку,
извлечем, квадратный корень и получим
стандартную ошибку предсказания.
(22)
Выберем уровень
значимости α и по таблице распределения
Стьюдента найдем tкр.
Тогда с вероятностью 1- α истинное
значение переменной ур
будет находится внутри интервала:
(23)
Очевидно, что чем
ближе
к
и чем большеn,
тем уже доверительный интервал (тем
точнее прогноз). Это надо учитывать,
выбирая прогнозные значения для
независимой переменной.
Вернемся в Примеру
1 и найдем точечный и интервальный
прогнозы для прибыли предприятия для
затрат на новое оборудование и технику
в размере 20 млн. денежных единиц.
Вывод:
с вероятностью 0,95 истинное значение
прибыли попадет в полученный интервал.
Вопросы:
-
Истинное и
выборочное уравнения регрессии. -
Метод наименьших
квадратов. -
Геометрическая
интерпретация метода наименьших
квадратов. -
Экономическая
интерпретация коэффициентов парной
линейной регрессии. -
Основные предпосылки
регрессионного анализа. Теорема
Гаусса-Маркова. -
Расчет стандартных
ошибок коэффициентов регрессии. -
Проверка значимости
коэффициентов регрессии. -
Построение
доверительных интервалов для параметров
теоретической регрессии. -
Проверка общего
качества уровня регрессии. Коэффициент
детерминации. -
Проверка значимости
коэффициента детерминации. -
Оценка тесноты
связи между переменными. Коэффициент
корреляции. -
Проверка значимости
коэффициента корреляции. -
Прогнозирование.
1.
Пусть исследуется
статистическая зависимость экономического
показателя У (объясняемая зависимая
переменная) от экономического показателя
Х (фактора, объясняющей или независимой
переменной). Предположим, что зависимость
носит линейный характер, тогда ее можно
описать уравнением.
У=+
Х+Е
(1),
где Х – неслучайная
величина, У и Е – случайные величины.
Случайная величина
Е отражает воздействие на зависимую
переменную У неучтенных и случайных
факторов и называется ошибкой регрессии.
Уравнение (1) называют истинным
(теоретическим) уравнением
регрессии или линейной регрессионной
моделью. На основе реальных статистических
данных об экономических показателях
Х и У (выборке данных из генеральной
совокупности) оцениваются параметры
регрессии α и β и строится выборочное
уравнение регрессии
,
(2)
а, в,
— коэффициенты регрессии. Уравнение (2)
называют еще эмпирическим уравнением
регрессии.
Одним из методов
нахождения коэффициентов регрессии а
и в
является метод
наименьших квадратов (МНК).
2.
Пусть из генеральной
совокупности выбраны данные об
экономических показателях У: ( у,
у,
…, у)
и Х: ( х,
х,…,
х)
.
Если в (2) подставить наблюдаемое
(выборочное значение хi,
то получим расчетное значение
зависимой переменной у:
(3)
Разность между
фактическими и расчетными значениями
зависимой переменной обозначим ei
и назовем
остатком, т.е.:
(4)
Суть МНК заключается
в следующем: коэффициенты а
и в
должны быть такими, чтобы сумма квадратов
остатков была минимальна
(5)
в (5) уi
и xi
– известные величины, а а
и в
– неизвестные.
Запишем необходимые
условия экстремума функции S
относительно а и в:

Система (6) является
системой двух уравнений относительно
двух неизвестных а
и в.
Она легко преобразовывается в систему
(7):

Разделим оба
уравнения системы на n:

3.
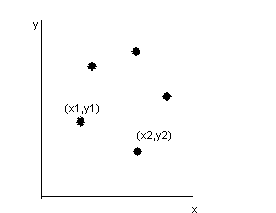
начертим оси
координат Х ,У и изобразим в первой
четверти точки (хi,уi)
Полученное
изображение называется диаграммой
рассеяния или полем корреляции.
Проведем линию
регрессии
Согласно МНК, а
и в должны
быть такими, чтобы построенная линия
была ближайшей к точкам поля корреляции
по их совокупности.
Сумма квадратов
расстояний от точек поля корреляции до
линии регрессии должна быть минимальной.
Пример1: исследуется
зависимость прибыли предприятия от
затрат на приобретение нового оборудования
и техники. Собранны статистические
данные по пяти однотипным предприятиям.
Данные в млн. ден.ед. представлены в
таблице 1.
Таблица
1
|
№ предприятия |
Затраты |
Прибыль, |
|
1 2 3 4 5 |
2 6 10 14 18 |
1 2 4 11 12 |
Построить уравнение
регрессии.
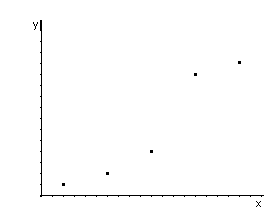
Данные таблицы
представим графически, т.е. построим
поле корреляции:
Из полученной
диаграммы рассеяния видно, что зависимость
статистическая и ее можно представить
линейной регрессией
.
Для оценки коэффициентов регрессииа
и в воспользуемся
формулами (8), для этого построим рабочую
таблицу 2.
Таблица2
е нового оборудования
и техники. в была минимальна00000000
|
№ предприятия |
|
|
|
|
|
|
1 2 3 4 5 |
2 6 10 14 18 |
1 2 4 11 12 |
4 36 100 196 324 |
2 12 40 154 216 |
1 4 16 121 144 |
|
Итого: |
50 |
30 |
660 |
424 |
286 |
|
Среднее |
10 |
6 |
132 |
84,8 |
57,2 |
|
|
|
|
|
|
Подставим результаты,
полученные в таблице 2 в формулы (8):
испр.
Таким образом,
уравнение регрессии, описывающее
зависимость прибыли предприятия от
затрат на новое оборудование и технику
имеет вид:
Выбрав с помощью
диаграммы рассеяния для описания
зависимости линейную регрессию мы
выполнили этап спецификации (подбора
функции), а рассчитав коэффициенты а
и в,
т.е. оценив параметры теоретической
регрессии, мы выполнили этап параметризации.
4.
Коэффициент парной
линейной регрессии в
показывает, как в среднем изменяется
зависимый экономический показатель у
с изменением независимого фактора х на
единицу. Так в примере 1 коэффициент
в=0,775
показывает, что при увеличении расходов
на приобретение нового оборудования и
техники на 1 ден.ед. прибыль предприятия
в среднем увеличится на 0,775 ден. ед.
Коэффициент а
парной
линейной регрессии экономического
смысла не имеет.
5.
Для того, чтобы
оценки параметров теоретической
регрессии, полученные на основе МНК
были лучшими по сравнению с оценками,
найденными с помощью других методов,
должны выполнятся определенные условия,
которые называются основными
предпосылками регрессионного анализа.
Для того, чтобы их
сформулировать, вспомним что теоретическая
регрессия описывается уравнением
,
или для i-го
наблюдения
Предпосылки:
1. Математическое
ожидание случайного члена ε в любом
наблюдении должно быть равно 0:
2. Дисперсия
случайного члена ε должна быть постоянной
для всех наблюдений:
3. Случайные члены
должны быть статистически независимы
друг от друга:
4. Объясняющая
переменная хi
– неслучайная величина
Теорема Гаусса-Маркова:
Если выполняются
предпосылки 1-4 регрессионного анализа,
то оценки параметров теоретической
регрессии а и в есть наилучшие линейные
оценки, обладающие следующими свойствами:
1. Они являются
несмещенными:
2. Они являются
эффективными, т.е. имеют наименьшую
дисперсию в классе всех несмещенных
оценок.

3. Они являются
состоятельными, т.е.
Это значит, что
при достаточно большом объеме выборки
n,
оценки а и в близки к истинным параметрам
линейной регрессионной модели α и β.
6.
Для расчета
дисперсий D(a)
и D(в)
коэффициентов регрессии а
и в
в формулах (9) использовалась дисперсия
σ2
случайного члена ε. Эта дисперсия
неизвестна, но ее можно оценить, используя
выборочные данные. Можно доказать, что
несмещенной оценкой дисперсии σ2
является величина S2,
где:
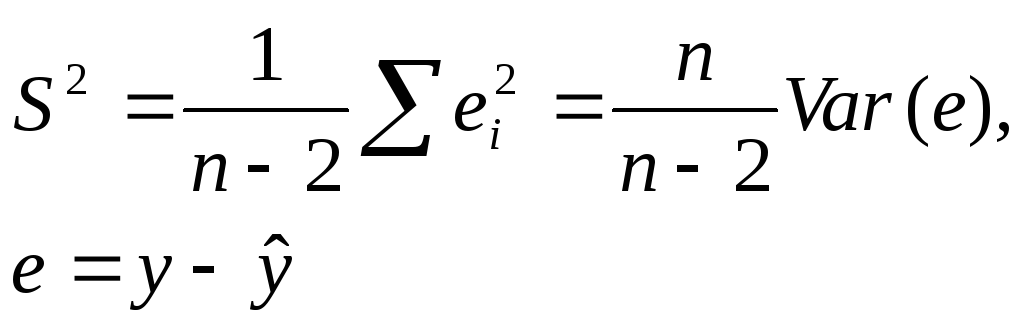
Величина S
называется стандартной ошибкой регрессии.
Она служит мерой разброса зависимой
переменной около линии регрессии.
Запишем в формулах (9) дисперсию σ2
ее оценкой S2:

и
называют
оценками дисперсии коэффициентов
регрессии, а величинаSa
и Sв
– стандартными ошибками коэффициентов
регрессии. Они
используются для построения доверительных
интервалов, которым принадлежат параметры
истинной регрессии и для проверки
значимости коэффициентов регрессии.
Вернемся в Примеру
1 и рассчитаем стандартные ошибки
коэффициентов регрессии:
7.
Коэффициента
регрессии получены на основании
выборочных данных, отобранных случайным
образом. Следовательно, коэффициенты
регрессии а и в являются случайными
числами и их значение может быть лишь
случайно оказались отличными от нуля.
Поэтому проводят проверку значимости
коэффициентов регрессии, т.е. проверку
того, значимо ли они отличны от нуля.
Для этого используют процедуру проверку
гипотез. Проверим значимость коэффициента
в.
Для этого:
1. Сформулируем
гипотезу Н0:
.
Она состоит в том,
что истинный коэффициент β=0,
2. В качестве
критерия проверки гипотезы принимают
случайную величину t:
. (12)
Эта случайная
величина имеет распределение Стьюдента
с ν = n-2
степенями свободы. Подставим в формулу
(12) оцененное по выборке значение
коэффициента в и его стандартную ошибку
Sв,
получим наблюдаемое или расчетное
значение t-критерия
tрасч.
3. Выбирают уровень
значимости проверки гипотезы. Как
правило α= 0,05 или α=0,01, т.е. пятипроцентный
или однопроцентный уровень значимости.
4. По таблице
распределения Стьюдента для выборочного
уровня значимости α/2 и ν = n-2
находят t
кр.
(критическое).
5. Если | tрасч.|
> t
кр.,
то гипотеза Н0
о равенстве параметра β=0 отвергается,
параметр β существенно отличен от нуля,
коэффициент в
значим, а переменная х оказывает
существенное влияние на зависимую у
(Н0
считается неверной с вероятностью 1- α)
6. Если | tрасч.|
< t
кр.,
гипотеза Н0
принимается, коэффициент в
незначим и переменная х не оказывает
существенного влияния на зависимую
переменную у.
Замечание: аналогично
проверяется значимость коэффициента
а
в уравнении регрессии, однако проверка
значимости коэффициента в
имеет гораздо большее значение в
регрессионном анализе.
Вернемся в примеру
1 и проверим значимость коэффициента
в.
Зависимость прибыли предприятия от
расходов на новое оборудование и технику
описывается регрессией:
(1,65) (0,143).
-
Формулируем
гипотезу Н0,
состоящую в том, что истинный коэффициент
β=0,
.
-
Определим tрасч.
.
-
Выбираем уровень
значимости проверки гипотезы
α= 0,05.
-
По таблице
распределения Стьюдента для α/2=0,025 и
числа степеней свободы
ν = 5-2=3
определим t
кр.
= 3,182.
5. | tрасч.|=5,4
> t
кр.=3,182,
поэтому гипотеза Н0
не верна с вероятностью
1-α= 1-0,05 = 0,95, параметр
β существенно отличен от нуля, коэффициент
в
значим и затраты на новое оборудование
и технику оказывают существенное влияние
на прибыль предприятия.
8.
Вспомним, что
линейная регрессионная модель (истинная
или теоретическая регрессия) имеет вид:
(13)
На основании
выборки строится выборочное уравнение
регрессии:
Также на основании
выборки рассчитывается стандартные
ошибки регрессии Sa
и Sв.
Можно доказать,
что с вероятностью 1-α (α – выбранный
уровень значимости) значения параметра
β лежат внутри интервала:
(14)
и с вероятностью
1-α (α – выбранный уровень значимости)
значение параметра α истинной регрессии
лежит внутри интервала:
(15)
Вернемся к Примеру
1 и построим доверительный интервал
для параметра β в регрессионной модели,
описывающей зависимость прибыли
предприятия от затрат на новое
оборудование и технику. Выберем уровень
значимости α= 0,05. т.к. в данном примере
ν = 5-2=3 , то t
кр.
= 3,182, в
= 0,775,
Тогда с вероятностью
1-α= 1-0,05 = 0,95 параметр β истинной регрессии
попадает в интервал
или 0,32<b<1,23
с вероятностью 95%.
9.
Выборочное уравнение
регрессии имеет вид:
тогда
Рассчитаем
выборочную дисперсию (вариацию) Var(y):
.
Из основных
предпосылок регрессионного анализа
следует, что
,
следовательно
т.е. дисперсия
зависимой переменной у (Var(y))
распадается на 2 части:
—
часть, объясняемая уравнением регрессии,
и часть
—
необъяснимая часть, зависящая от неученых
и случайных факторов.
Коэффициентом
детерминации называют отношение R2:
, (16)
которое характеризует
долю вариации зависимой переменной,
объясненную уравнением регрессии. Из
(16) следует что R2
меняется от 0 до 1:
,
чем ближе R2
к единице, тем меньше
,
т.е. доля вариации зависимой переменной,
объясняемая случайными и неучеными
факторами, тем лучше качество уравнения
регрессии. Если=0,
тоR2=1,
имеем функциональную зависимость. Чем
ближе R2
к 0, тем больше,
т.е. больше доля вариации, объясненная
случайными и неучеными факторами, тем
хуже качество регрессии. Т.к.

Вернемся к примеру
1, можно посчитать, что:
Коэффициент
детерминации близок к 1, качество
регрессии хорошее.
Можно утверждать,
что вариация (изменчивость) прибыли
предприятия на 90,7% объясняется затратами
на новое оборудование и технику и на
9,3% — прочими неучтенными и случайными
факторами.
10.
Т.к. R2
оценивается на основании выборочных
данных, то его отличие от 0 может оказаться
случайным. Поэтому проводят проверку
его значимости:
1. Формулируется
гипотеза Н0:
R2=0,
состоящая в том, что истинный коэффициент
детерминации равен 0.
2. В качестве
критерия проверки гипотезы применяют
случайную величину F:
. (18)
Величина F
имеет распределение Фишера с двумя
степенями свободы ν1=1,
ν2=n-2.
-
Выберем уровень
значимости проверки гипотезы значимости:
.
-
На основании α,
ν1, ν2
в таблице
распределения Фишера выбираем Fкр.
(критическое) -
Сравниваем Fрасч
и Fкр..
если Fрасч
> Fкр.,
то с вероятностью 1-α гипотезу Н0
считаем неверной, т.е. истинный коэффициент
детерминации существенно отличен от
нуля, уравнение регрессии значимо и
переменные, включенные в уравнение
регрессии достаточно объясняют поведение
зависимой переменной. Если Fрасч
< Fкр.,
то принимаемая гипотеза Н0,
уравнение регрессии считается незначимым.
Проверим значимость
коэффициента детерминации в примере
1:
-
Формулируем
гипотезу Н0:
R2=0. -
Находим Fрасч..
В (18) подставим значение коэффициента
детерминации, оцененное по выборке:
.
3.Выбираем уровень
значимости α=0,005.
4. В таблице
распределения Фишера на основании
α=0,05 и для степеней свободы ν1=1,
ν2
=5-2=3 найдем
Fкр.
.
-
Fрасч
=29,2> Fкр.=10,13,
поэтому Н0
не верна в вероятностью 1-0,05=0,95, коэффициент
детерминации значим, значимо построенное
в Примере 1 уравнение регрессии.
11.
Уравнение регрессии
всегда дополняется показателем тесноты
связи между переменными. При использовании
линейной регрессии в качестве такого
показателя выступает линейный коэффициент
корреляции:
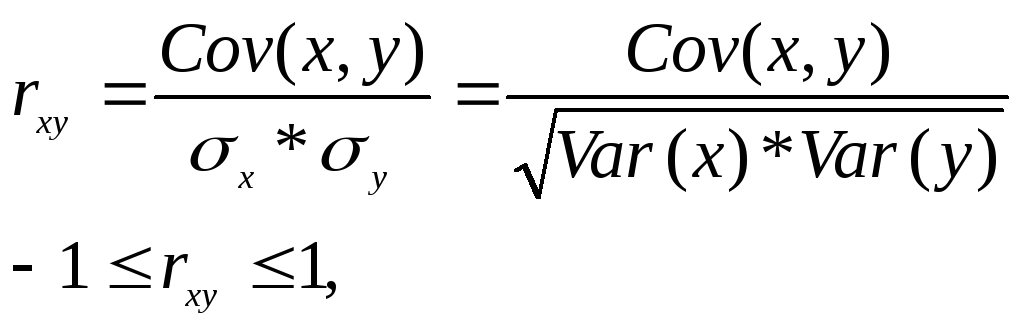
rxy
– безразмерная величина, показывает
степень линейной зависимости между
переменными. Чем ближе rxy
к ±1, тем сильнее линейная зависимость.
Чем ближе rxy
к 0, тем линейная зависимость слабее.
Если rxy
= ±1, то имеет место функциональная
линейная зависимость. Если rxy
= 0, то линейная зависимость отсутствует.
Если rxy
>0, то связь между переменными
положительная, если rxy
<0 – отрицательная.
Рассчитаем
коэффициент корреляции в примере 1:
rxy
>0 и близок к 1 следовательно линейная
зависимость между прибылью предприятия
и затратами на новое оборудование –
положительная и тесная.
12.
Осуществляется
аналогично проверки значимости
коэффициентов регрессии и детерминации,
используется t-статистика:
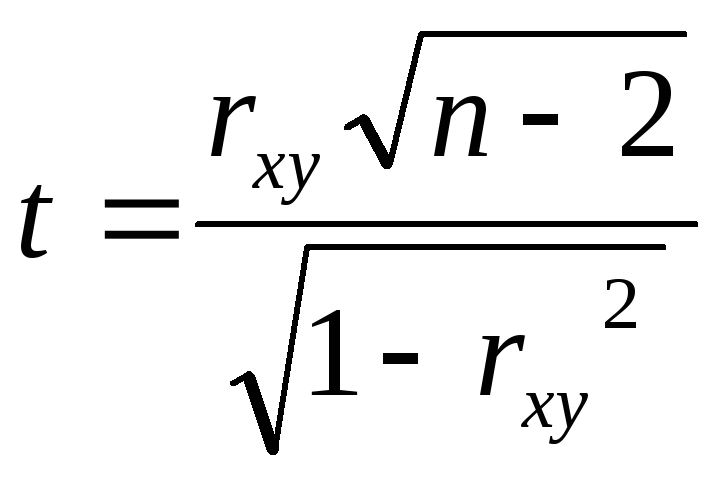
Проведем проверку
значимости коэффициента корреляции в
примере 1:
-
Формулируем
гипотезу, состоящую в том, что истинный
коэффициент корреляции равен нулю:
.
-
Подставим значение
коэффициента корреляции, вычисленное
по выборке в (20):
-
Выбираем уровень
значимости α=0,05. -
Для α/2=0,025 и для
ν=n-2=3
в таблице распределения Стьюдента
находим tкр.:
Следовательно,
истинный коэффициент корреляции
существенно отличен от 0, линейная
зависимость между прибылью предприятия
и затратами на новое оборудование и
технику действительно тесная..
Замечание 1:
В парном линейном
регрессионном анализе проверка значимости
коэффициента в, коэффициента корреляции
и коэффициента детерминации являются
эквивалентными.
Замечание 2:
Легко показать,
что коэффициент детерминации равен
квадрату коэффициента корреляции,
,
13.
Прогнозирование
на основе эконометрических моделей
является одной из основных задач
эконометрики.
Под прогнозированием
в эконометрике понимают построение
оценки зависимой переменной для таких
значений независимых переменных, которых
нет в исходных наблюдениях.
Различают точечное
прогнозирование и интервальное.
.
Точечный прогноз
это число, значение зависимой переменной,
вычисляемое для заданных значений
независимых переменных.
Интервальный
прогноз это интервал, в котором с заданным
уровнем значимости ( с заданной
вероятностью) находится истинное
значение зависимой переменной для
заданных значений независимых переменных.
Рассмотрим парную
линейную регрессионную модель
и соответствующее выборочное уравнение
регрессии.
Обозначим через ур
истинное значение переменной у для
заданного значения независимой переменной
хр,
т.е.
.
Точечным прогнозом
для ур
является
,
т.е. чтобы получить точечный прогноз
нужно в построенное уравнение регрессии
подставить заданное значение независимой
переменной.
Ошибкой
предсказания
()
называют разность между прогнозным и
истинным значениями независимой
переменной.
Можно доказать,
что дисперсия ошибки предсказания
. (21)
Из (21) следует, что
чем ближе заданное значение независимой
переменной
к
тем
меньше дисперсия прогноза и чем больше
объем выборкиn,
тем меньше дисперсия прогноза.
Заменив в (21)
дисперсию
на
ее оценку,
извлечем, квадратный корень и получим
стандартную ошибку предсказания.
(22)
Выберем уровень
значимости α и по таблице распределения
Стьюдента найдем tкр.
Тогда с вероятностью 1- α истинное
значение переменной ур
будет находится внутри интервала:
(23)
Очевидно, что чем
ближе
к
и чем большеn,
тем уже доверительный интервал (тем
точнее прогноз). Это надо учитывать,
выбирая прогнозные значения для
независимой переменной.
Вернемся в Примеру
1 и найдем точечный и интервальный
прогнозы для прибыли предприятия для
затрат на новое оборудование и технику
в размере 20 млн. денежных единиц.
Вывод:
с вероятностью 0,95 истинное значение
прибыли попадет в полученный интервал.
Пример 9.1. По 15 сельскохозяйственным предприятиям (табл. 9.1) известны: 

1) определить зависимость 
2) построить корреляционные поля и график уравнения линейной регрессии
3) сделать вывод о качестве модели и рассчитать прогнозное значение 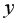
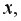
Таблица 9.1
|
i |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
|
x |
2,97 |
1,65 |
9,02 |
4,95 |
3,63 |
6,38 |
3,3 |
7,81 |
1,32 |
11,44 |
5,39 |
5,72 |
12,65 |
10,34 |
7,15 |
|
y |
121 |
77 |
341 |
132 |
82,5 |
187 |
110 |
198 |
33 |
484 |
209 |
165 |
429 |
341 |
253 |
Решение:
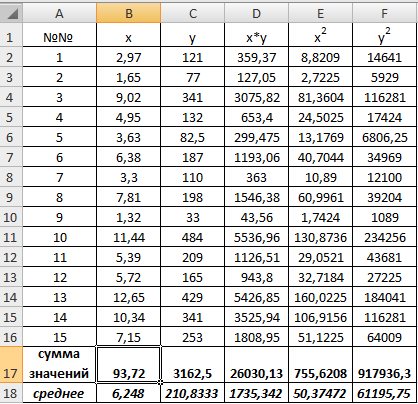
1) В Excel составим вспомогательную таблицу 9.2.
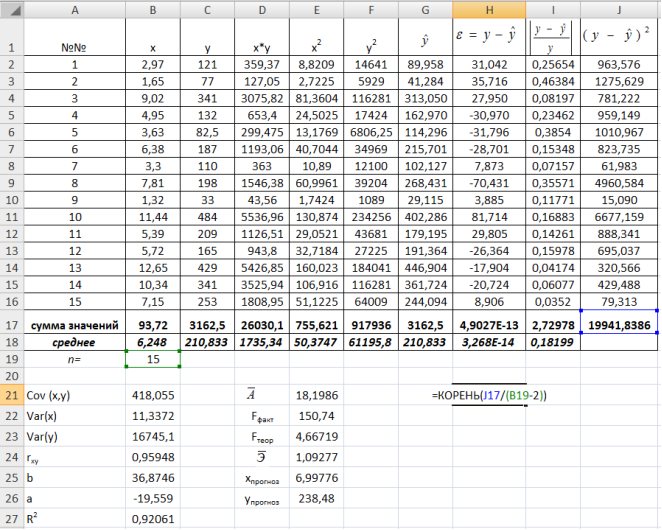
Таблица 9.2
Рис. 9.1. Таблица для расчета промежуточных значений
Вычислим количество измерений 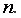
С помощью функции ∑ (Автосумма) на панели инструментов Стандартная найдем сумму всех 
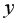
Рис. 9.2. Расчет суммы значений и средних
Для вычисления средних значений используем встроенную функцию MS Excel СРЗНАЧ(), в скобках указывается диапазон значений для определения средней. Таким образом, средний объем выращенной продукции по 15 хозяйствамсоставляет 210,833 тыс.ден. ед., а средние количество техники – 6,248ед/га.
Для заполнения столбцов D, E, Fвведем формулувычисления произведения: в ячейку D2 поместим =B2*C2, затем на клавиатуре нажмем ENTER. Щелкнем левой кнопкой мыши по ячейке D2и, ухватив за правый нижний угол этой ячейки (черный плюсик), потянем вниз до ячейки D16. Произойдет автоматическое заполнение диапазона D3 – D16.
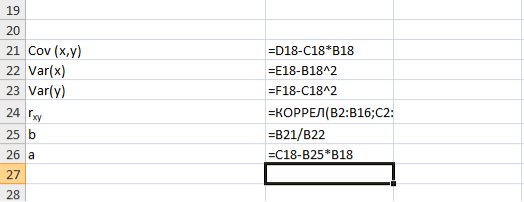
Для вычисления выборочной ковариациимежду 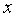
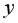
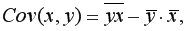
Рис. 9.3. Вычисление
Выборочную дисперсиюдля 
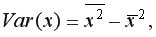
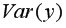
Рис. 9.4. Вычисление Var(x) и Var (y)
Далее используя стандартную функцию MS Excel «КОРРЕЛ» вычисляем значение линейного коэффициента корреляции для нашей задачи функция будет иметь вид «=КОРРЕЛ(B2:B16;C2:C16)», а значение rxy=0,96. Полученное значение коэффициента корреляции указывает на прямую и сильную связь наличия техники и объемов выращенной продукции.
Находим выборочный коэффициент линейной регрессии 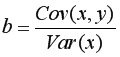
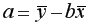
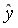
Коэффициент 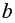
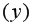
Рис. 9.5. Расчет параметров уравнения регрессии.
Таким образом, уравнение регрессии будет иметь вид: 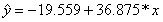
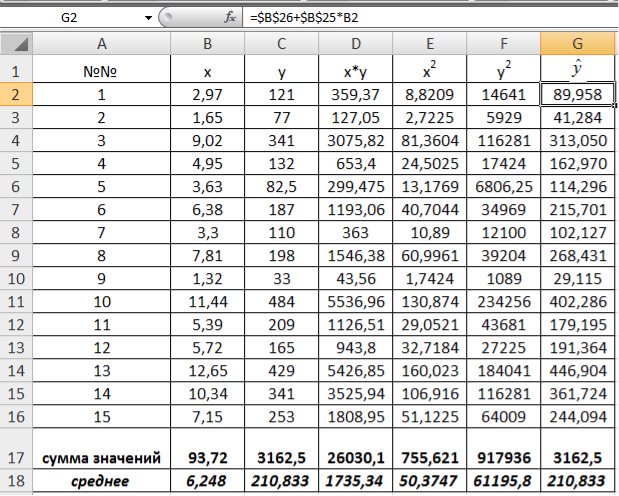
Подставляем в полученное уравнение фактические значения x (количество техники) находим теоретические значения объемов выращенной продукции (рис. 9.6).
Рис. 9.6. Расчет теоретических значений объемов выращенной продукции
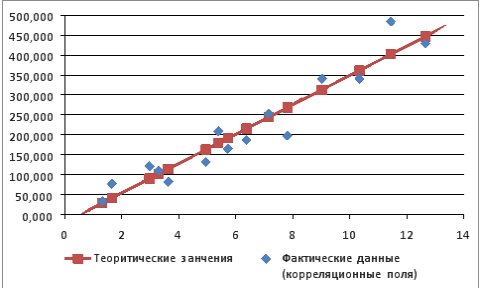
Используя Мастер диаграмм строим корреляционные поля (выделяя столбцы со значениями 


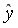
Рис. 9.7. График зависимости объема выращенной продукции от количества техники
Для оценки качества построенной модели регрессии вычислим:
• коэффициент детерминации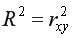
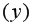
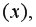
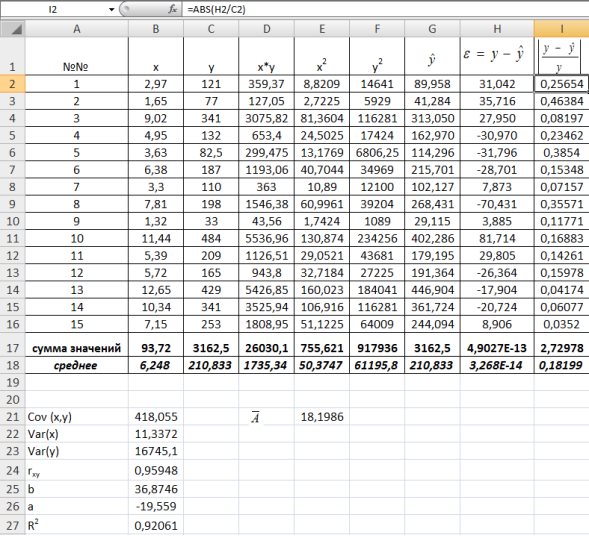
• среднюю ошибку аппроксимации. Для этого в столбце H вычислим разность фактического и теоретического значений 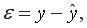
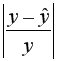
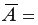
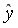
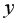
С помощью 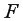
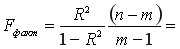
На уровне значимости 0,05 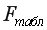
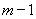
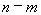
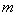
Так как 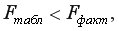
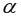
Рис. 9.8. Определение коэффициента детерминации и средней ошибки апроксимации
Рис. 9.9. Диалоговое окно функции FРАСПОБР
Далее определяем средний коэффициент эластичности по формуле. 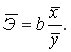
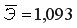
Рассчитаем прогнозное значение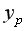
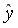
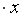
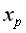
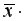
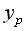
Найдем остаточную дисперсию, для этого вычислим сумму квадратов разности фактического и теоретического значений. 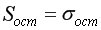
Рис. 9.10. Определение остаточной дисперсии
Средняя стандартная ошибка прогноза:
На уровне значимости 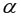
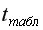
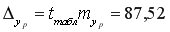
Доверительный интервал прогноза:
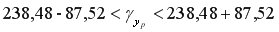
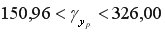
Выполненный прогноз затрат на выпуск продукции оказался надежным (1-0,05=0,95), но неточным, так как диапазон верхней и нижней границ доверительного интервала составляет 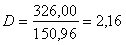
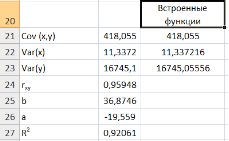
Необходимо отменить, что в MS Excel встроены статистические функции позволяющие значительно снизить количество промежуточных вычислений, например (рис. 9.11.):
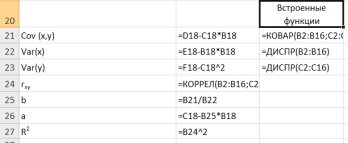
Для вычисления выборочных средних используем функцию СРЗНАЧ(число1:числоN) из категории Статистические.
Выборочная ковариация между 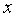
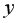
Выборочные дисперсииопределяются статистической функцией ДИСПР(число1:числоN).
Рис.9.11. Вычисление показателей встроенными функциями MSExcel
Параметры линейной регрессии 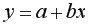
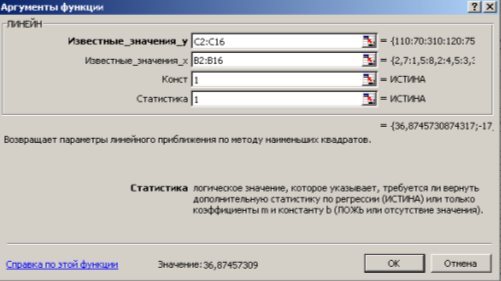
1 способ) С помощью встроенной функции ЛИНЕЙН. Порядок действий следующий:
1. Выделить область пустых ячеек 5×2 (5 строк, 2 столбца) для вывода результатов регрессионной статистики или область 1×2 – для получения только коэффициентов регрессии.
2. С помощью Мастера функций 
Рис. 9.12. Диалоговое окно ввода аргументов функции ЛИНЕЙН
Известные_значения_y – диапазон, содержащий данные результативного признака Y;
Известные_значения_x – диапазон, содержащий данные объясняющего признака X;
Конст – логическое значение (1 или 0), которое указывает на наличие или отсутствие свободного члена в уравнении; ставим 1;
Статистика – логическое значение (1 или 0), которое указывает, выводить дополнительную информацию по регрессионному анализу или нет; ставим 1.
3. В левой верхней ячейке выделенной области появится первое число таблицы. Для раскрытия всей таблицы нужно нажать на клавишу <F2>, а затем – на комбинацию клавиш <CTRL>+ <SHIFT>+ <ENTER>.
Дополнительная регрессионная статистика будет выведена в виде (табл. 9.3):
Таблица 9.3
|
Значение коэффициента |
Значение коэффициента |
|
Среднеквадратическое |
Среднеквадратическое |
|
Коэффициент |
Среднеквадратическое |
|
|
Число степеней свободы |
|
Регрессионная сумма квадратов |
Остаточная сумма квадратов |
В результате применения функции ЛИНЕЙН получим:
|
36,87457 |
-19,55899932 |
|
3,003392 |
21,316623 |
|
0,920606 |
39,16615351 |
|
150,7405 |
13 |
|
231234 |
19941,83855 |
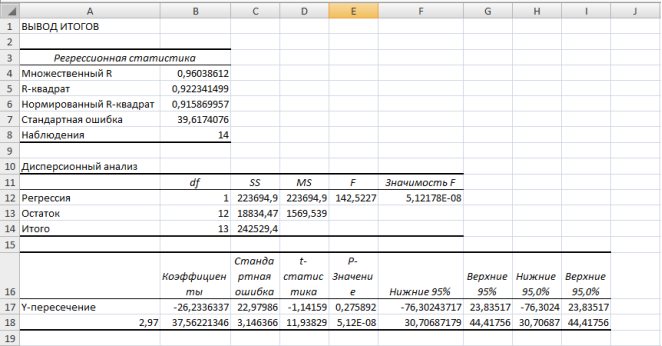
(2 способ) С помощью инструмента анализа данных Регрессия можно получить результаты регрессионной статистики, дисперсионного анализа, доверительные интервалы, остатки, графики подбора линий регрессии, графики остатков и нормальной вероятности. Порядок действий следующий:
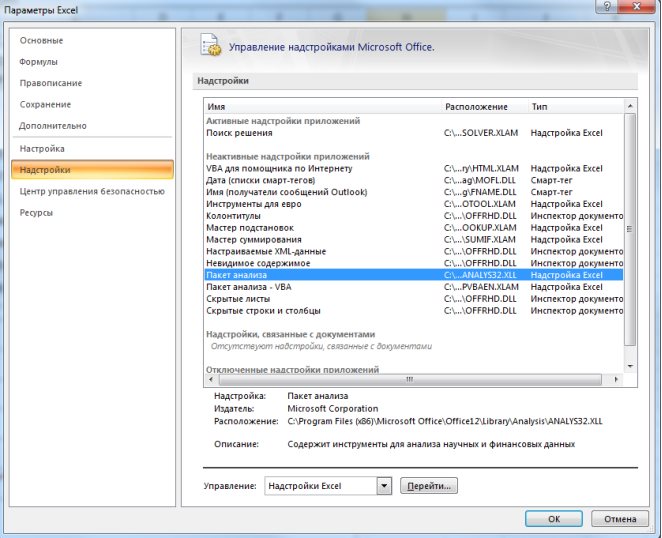
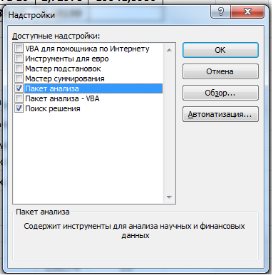
1. Необходимо проверить доступ к Пакету анализа. Для этого в главном меню (через кнопку Microsoft Office получить доступ к параметрам MS Excel) в диалоговом окне «Параметры MSExcel» выбрать команду «Надстройки» и справа выбрать надстройку Пакета анализа далее нажать кнопку «Перейти» (рис. 9.13). В открывшемся диалоговом окне поставить галочку напротив «Пакет анализа» и нажать «ОК» (рис. 9.14).
На вкладке «Данные» в группе «Анализ» появится доступ к установленной надстройке. (рис. 9.15).
Рис. 9.13. Включение надстроек в MSExcel
Рис. 9.14. Диалоговое окно «Надстройки»
Рис. 9.15. Надстройка «Анализ данных» на ленте MSExcel 2007.
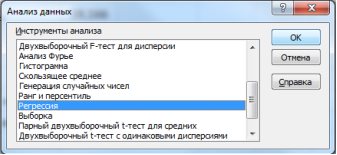
2. Выбрать на «Данные» в группе «Анализ» выбираем команду Анализ данных в открывшемся диалоговом окне выбрать инструмент анализа «Регрессия» и нажать «ОК» (рис. 9.16):
Рис. 9.16. Диалоговое окно «Анализ данных»
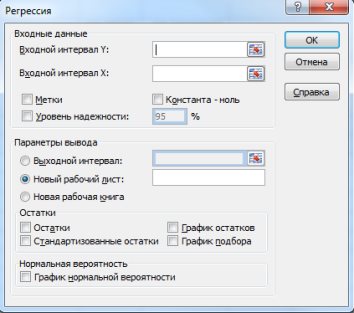
В появившемся диалоговом окне (рис. 9.17) заполнить поля:
Входной интервалY – диапазон, содержащий данные результативного признака Y;
Входной интервалX– диапазон, содержащий данные объясняющего признака X;
Метки – флажок, который указывает, содержит ли первая строка названия столбцов или нет;
Константа-ноль – флажок, указывающий на наличие или отсутствие свободного члена в уравнении;
Выходной интервал – достаточно указать левую верхнюю ячейку будущего диапазона;
Новый рабочий лист – можно задать произвольное имя нового листа, на который будут выведены результаты.
Рис. 9.17. Диалоговое окно «Регрессия»
Для получения информации об остатках, графиков остатков, подбора и нормальной вероятности нужно установить соответствующие флажки в диалоговом окне.
Рис. 9.18. Результаты применения инструмента Регрессия
В MSExcel линия тренда может быть добавлена в диаграмму с областями гистограммы или в график. Для этого:
1. Необходимо выделить область построения диаграммы и в ленте выбрать «Макет» и в группе анализ выбрать команду «Линия тренда» (рис. 9.19.). В выпадающем пункте меню выбрать «Дополнительные параметры линии тренда».
Рис. 1.19. Лента
2. В появившемся диалоговом окне выбрать фактические значения, затем откроется диалоговое окно «Формат линии тренда» (рис. 9.20.) в котором выбирается вид линии тренда и устанавливаются соответствующие параметры.
Рис. 9.20. Диалоговое окно «Формат линии тренда»
Для полиноминального тренда необходимо задать степень аппроксимирующего полинома, для линейной фильтрации – количество точек усреднения.
Выбираем Линейная для построения уравнения линейной регрессии.
В качестве дополнительной информации можно показать уравнение на диаграмме и поместить на диаграмму величину (рис.9.21).
Рис. 9.21. Линейный тренд
Нелинейные модели регрессии иллюстрируются при вычислении параметров уравнения 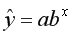
Рассмотрим простейшую модель парной регрессии – Линейную Регрессию. Линейная регрессия находит широкое применение в эконометрике ввиду четкой экономической интерпретации ее параметров.
Линейная регрессия сводится к нахождению уравнения вида
или
. (1.1)
Уравнение вида позволяет по заданным значениям фактора X находить теоретические значения результирующего показателя, подставляя в него фактические значения фактора X.
Построение линейной регрессии сводится к оценке ее параметров – A и B. Классический подход к оцениванию параметров линейной регрессии основан на методе наименьших квадратов (МНК). МНК позволяет получить такие оценки параметров A и B, при которых сумма квадратов отклонений фактических значений результирующего показателя Y от теоретических минимальна:
. (1.2)
Т. е. из всего множества линий линия регрессии на графике выбирается так, чтобы сумма квадратов расстояний по вертикали между точками и этой линией была бы минимальной (рис. 1.2):
Рис. 1.2. Линия регрессии с минимальной дисперсией остатков.
Как известно из курса математического анализа, чтобы найти минимум функции (1.2), надо вычислить частные производные по каждому из параметров A и B и приравнять их к нулю. Обозначая через
, получим:

После несложных преобразований, получим следующую систему линейных уравнений для оценки параметров A и B:

Решая систему уравнений (1.4), найдем искомые оценки параметров A и B. Можно воспользоваться готовыми формулами, которые следуют непосредственно из решения системы (1.4):

, (1.5)
Где – ковариация признаков X и Y,
– дисперсия признака X и
,
,
,
.
Ковариация – числовая характеристика совместного распределения двух случайных величин, равная математическому ожиданию произведения отклонений этих случайных величин от их математических ожиданий. Дисперсия – характеристика случайной величины, определяемая как математическое ожидание квадрата отклонения случайной величины от ее математического ожидания. Математическое Ожидание – сумма произведений значений случайной величины на соответствующие вероятности (см. Приложение 1).
Параметр B называется Коэффициентом Регрессии. Его величина показывает среднее изменение результата с изменением фактора на одну единицу.
Возможность четкой экономической интерпретации коэффициента регрессии сделала линейное уравнение регрессии достаточно распространенным в эконометрических исследованиях.
Формально A – значение Y при . Если фактор X не может иметь нулевого значения, то тогда трактовка свободного члена A не имеет смысла, т. е. параметр A может не иметь экономического содержания.
Уравнение регрессии всегда дополняется показателем тесноты связи. При использовании линейной регрессии в качестве такого показателя выступает линейный коэффициент корреляции , который можно рассчитать по следующим формулам:
. (1.6)
Линейный коэффициент корреляции находится в пределах: . Чем ближе абсолютное значение
к единице, тем сильнее линейная связь между факторами (при
имеем строгую функциональную зависимость). Однако близость абсолютной величины линейного коэффициента корреляции к нулю еще не означает отсутствия связи между признаками. При другой (нелинейной) спецификации модели связь между признаками может оказаться достаточно тесной.
Для оценки качества подбора линейной функции рассчитывается квадрат линейного коэффициента корреляции , называемый Коэффициентом Детерминации. Коэффициент детерминации характеризует долю дисперсии результирующего показателя Y, объясняемую регрессией, в общей дисперсии результирующего показателя:
, (1.7)
Где ,
.
Соответственно величина характеризует долю дисперсии Y, вызванную влиянием остальных, не учтенных в модели, факторов.
После того как найдено уравнение линейной регрессии, проводится оценка значимости как уравнения в целом, так и отдельных его параметров.
Проверить значимость уравнения регрессии – означает установить, соответствует ли математическая модель, выражающая зависимость между переменными, экспериментальным данным и достаточно ли включенных в уравнение объясняющих переменных (одной или нескольких) для описания зависимой переменной.
Чтобы иметь общее суждение о качестве модели из относительных отклонений по каждому наблюдению, определяют Среднюю Ошибку Аппроксимации:

Средняя ошибка аппроксимации не должна превышать 8–10%.
Оценка Значимости Уравнения Регрессии В целом Производится На Основе F—Критерия Фишера, которому предшествует дисперсионный анализ. В математической статистике дисперсионный анализ рассматривается как самостоятельный инструмент статистического анализа. В эконометрике он применяется как вспомогательное средство для изучения качества регрессионной модели.
Согласно основной идее дисперсионного анализа, общая сумма квадратов отклонений переменной Y от среднего значения раскладывается на две части – «объясненную» и «необъясненную»:
,
Где – общая сумма квадратов отклонений;
– сумма квадратов отклонений, объясненная регрессией (или факторная сумма квадратов отклонений);
– остаточная сумма квадратов отклонений, характеризующая влияние неучтенных в модели факторов.
Схема дисперсионного анализа имеет вид, представленный в таблице 1.1 (N – число наблюдений, M – число параметров при переменной X).
Таблица 1.1
|
Компоненты дисперсии |
Сумма квадратов |
Число степеней свободы |
Дисперсия на одну степень свободы |
|
Общая |
|
|
|
|
Факторная |
|
M |
|
|
Остаточная |
|
|
|
Определение дисперсии на одну степень свободы приводит дисперсии к сравнимому виду. Сопоставляя факторную и остаточную дисперсии в расчете на одну степень свободы, получим величину F-критерия Фишера:
. (1.9)
Фактическое значение F-критерия Фишера (1.9) сравнивается с табличным значением при уровне значимости
и степенях свободы
и
. При этом, если фактическое значение F-критерия больше табличного, то признается статистическая значимость уравнения в целом.
Для парной линейной регрессии , поэтому

Величина F-критерия связана с коэффициентом детерминации , и ее можно рассчитать по следующей формуле:

В парной линейной регрессии оценивается значимость не только уравнения в целом, Но и отдельных его параметров. С этой целью по каждому из параметров определяется его стандартная ошибка: и
.
Стандартная ошибка коэффициента регрессии определяется по формуле:

Где 
Величина стандартной ошибки совместно с T-распределением Стьюдента при степенях свободы применяется для проверки существенности коэффициента регрессии и для расчета его доверительного интервала.
Для оценки существенности коэффициента регрессии его величина сравнивается с его стандартной ошибкой, т. е. определяется фактическое значение T-критерия Стьюдента: которое затем сравнивается с табличным значением при определенном уровне значимости
и числе степеней свободы
. Доверительный интервал для коэффициента регрессии определяется как
. Поскольку знак коэффициента регрессии указывает на рост результативного показателя Y при увеличении фактора X (
), уменьшение результативного показателя при увеличении признака-фактора (
) или его независимость от независимой переменной (
) (см. рис. 1.3), то границы доверительного интервала для коэффициента регрессии не должны содержать противоречивых результатов, например,
. Такого рода запись указывает, что истинное значение коэффициента регрессии одновременно содержит положительные и отрицательные величины и даже ноль, чего не может быть.
Рис. 1.3. Наклон линии регрессии в зависимости от значения параметра .
Стандартная ошибка параметра A определяется по формуле:

Процедура оценивания существенности данного параметра не отличается от рассмотренной выше для коэффициента регрессии. Вычисляется T-критерий: , его величина сравнивается с табличным значением при
степенях свободы.
Значимость линейного коэффициента корреляции проверяется на основе величины ошибки коэффициента корреляции :
. (1.14)
Фактическое значение T-критерия Стьюдента определяется как .
Существует связь между T-критерием Стьюдента и F-критерием Фишера:
. (1.15)
В прогнозных расчетах по уравнению регрессии определяется предсказываемое значение как точечный прогноз
при
, т. е. путем подстановки в уравнение регрессии
прогнозного значения X. Точечный прогноз дополняется расчетом доверительного интервала прогнозного значения
:
,
Где , а
– средняя ошибка точечного прогноза:

Пример. По данным проведенного опроса восьми групп семей известны данные связи расходов населения на продукты питания с уровнем доходов семьи.
Таблица 1.2
|
Расходы на продукты питания, Y, тыс. руб. |
0,9 |
1,2 |
1,8 |
2,2 |
2,6 |
2,9 |
3,3 |
3,8 |
|
Доходы семьи, X, тыс. руб. |
1,2 |
3,1 |
5,3 |
7,4 |
9,6 |
11,8 |
14,5 |
18,7 |
Предположим, что связь между доходами семьи и расходами на продукты питания линейная. Для подтверждения нашего предположения построим поле корреляции (Рис. 1.4).
По графику видно, что точки выстраиваются в некоторую прямую линию.
Для удобства дальнейших вычислений составим таблицу (см. табл. 1.3).
Рассчитаем параметры линейного уравнения парной регрессии . Для этого воспользуемся формулами (1.5):
Рис. 1.4.
;
.
Получили уравнение: . Т. е. с увеличением дохода семьи на 1000 руб. расходы на питание увеличиваются на 169 руб.
Рассчитаем показатель тесноты связи – линейный коэффициент корреляции :
.
Близость коэффициента корреляции к 1 указывает на тесную линейную связь между признаками.
Коэффициент детерминации (примерно тот же результат получим, если воспользуемся формулой (1.7)) показывает, что уравнением регрессии объясняется 98,2% дисперсии результативного признака, а на долю прочих факторов приходится лишь 1,8%.
Оценим качество уравнения регрессии в целом с помощью F-критерия Фишера. Сосчитаем фактическое значение F-критерия:

Табличное значение (,
,
):
(см. Приложение 2). Так как
, то признается статистическая значимость уравнения в целом.
Для оценки статистической значимости коэффициентов регрессии и корреляции рассчитаем T-критерий Стьюдента и доверительные интервалы каждого из показателей. Рассчитаем случайные ошибки параметров линейной регрессии и коэффициента корреляции 

Таблица 1.3
|
X |
Y |
|
|
|
|
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
1 |
1,2 |
0,9 |
1,08 |
1,44 |
0,81 |
1,027 |
–0,127 |
0,016 |
14,060 |
|
2 |
3,1 |
1,2 |
3,72 |
9,61 |
1,44 |
1,348 |
–0,148 |
0,022 |
12,328 |
|
3 |
5,3 |
1,8 |
9,54 |
28,09 |
3,24 |
1,720 |
0,080 |
0,006 |
4,440 |
|
4 |
7,4 |
2,2 |
16,28 |
54,76 |
4,84 |
2,075 |
0,125 |
0,016 |
5,668 |
|
5 |
9,6 |
2,6 |
24,96 |
92,16 |
6,76 |
2,447 |
0,153 |
0,023 |
5,867 |
|
6 |
11,8 |
2,9 |
34,22 |
139,24 |
8,41 |
2,820 |
0,080 |
0,006 |
2,773 |
|
7 |
14,5 |
3,3 |
47,85 |
210,25 |
10,89 |
3,276 |
0,024 |
0,001 |
0,718 |
|
8 |
18,7 |
3,8 |
71,06 |
349,69 |
14,44 |
3,987 |
–0,187 |
0,035 |
4,915 |
|
Сумма |
71,6 |
18,7 |
208,71 |
885,24 |
50,83 |
18,700 |
0,000 |
0,125 |
50,769 |
|
Среднее Значение |
8,95 |
2,34 |
26,09 |
110,66 |
6,35 |
2,34 |
– |
0,016 |
6,35 |
|
|
5,53 |
0,943 |
– |
– |
– |
– |
– |
– |
– |
|
|
30,55 |
0,890 |
– |
– |
– |
– |
– |
– |
– |

.
Фактические значения T-статистик: ,
,
. Табличное значение T-критерия Стьюдента при
и числе степеней свободы
есть
(см. Приложение 2). Так как
,
и
, то признается статистическая значимость параметров регрессии и показателя тесноты связи.
Рассчитаем доверительные интервалы для параметров регрессии A и B: и
. Получим, что
и
.
Средняя ошибка аппроксимации (находим с помощью столбца 10 таблицы 1.3; 
говорит о хорошем качестве уравнения регрессии, т. е. свидетельствует о хорошем подборе модели к исходным данным.
И, наконец, найдем прогнозное значение результативного фактора при значении признака-фактора, составляющем 110% от среднего уровня
, т. е. найдем расходы на питание, если доходы семьи составят 9,845 тыс. руб.
(тыс. руб.)
Таким образом, если доходы семьи составят 9,845 тыс. руб., то расходы на питание будут 2,490 тыс. руб.
Найдем доверительный интервал прогноза. Ошибка прогноза

А доверительный интервал ():
.
Т. е. прогноз является статистически надежным.
Теперь на одном графике изобразим исходные данные и линию регрессии:
Рис. 1.5.
| < Предыдущая | Следующая > |
|---|
Пример 9.1. По 15 сельскохозяйственным предприятиям (табл. 9.1) известны: 

1) определить зависимость 
2) построить корреляционные поля и график уравнения линейной регрессии
3) сделать вывод о качестве модели и рассчитать прогнозное значение 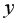
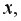
Таблица 9.1
|
i |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
|
x |
2,97 |
1,65 |
9,02 |
4,95 |
3,63 |
6,38 |
3,3 |
7,81 |
1,32 |
11,44 |
5,39 |
5,72 |
12,65 |
10,34 |
7,15 |
|
y |
121 |
77 |
341 |
132 |
82,5 |
187 |
110 |
198 |
33 |
484 |
209 |
165 |
429 |
341 |
253 |
Решение:
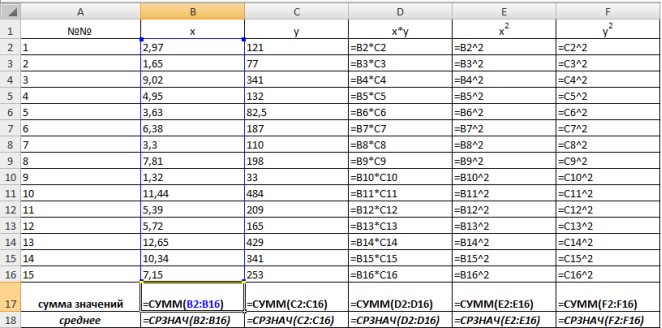
1) В Excel составим вспомогательную таблицу 9.2.
Таблица 9.2
Рис. 9.1. Таблица для расчета промежуточных значений
Вычислим количество измерений 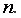
С помощью функции ∑ (Автосумма) на панели инструментов Стандартная найдем сумму всех 
Рис. 9.2. Расчет суммы значений и средних
Для вычисления средних значений используем встроенную функцию MS Excel СРЗНАЧ(), в скобках указывается диапазон значений для определения средней. Таким образом, средний объем выращенной продукции по 15 хозяйствамсоставляет 210,833 тыс.ден. ед., а средние количество техники – 6,248ед/га.
Для заполнения столбцов D, E, Fвведем формулувычисления произведения: в ячейку D2 поместим =B2*C2, затем на клавиатуре нажмем ENTER. Щелкнем левой кнопкой мыши по ячейке D2и, ухватив за правый нижний угол этой ячейки (черный плюсик), потянем вниз до ячейки D16. Произойдет автоматическое заполнение диапазона D3 – D16.
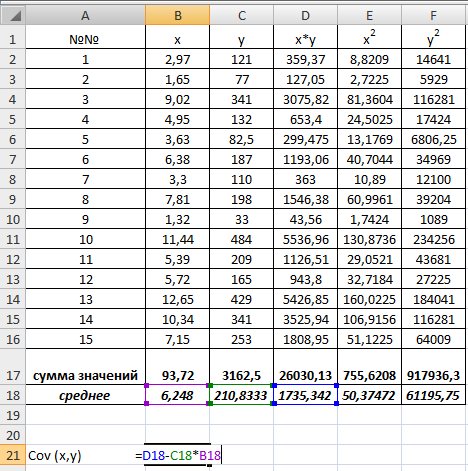
Для вычисления выборочной ковариациимежду 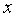
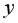
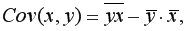
Рис. 9.3. Вычисление
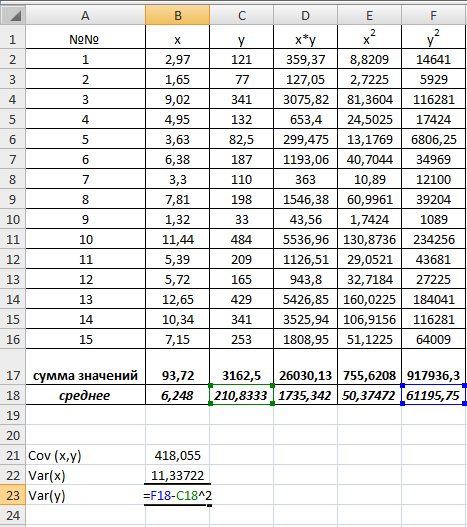
Выборочную дисперсиюдля 
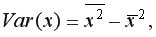
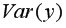
Рис. 9.4. Вычисление Var(x) и Var (y)
Далее используя стандартную функцию MS Excel «КОРРЕЛ» вычисляем значение линейного коэффициента корреляции для нашей задачи функция будет иметь вид «=КОРРЕЛ(B2:B16;C2:C16)», а значение rxy=0,96. Полученное значение коэффициента корреляции указывает на прямую и сильную связь наличия техники и объемов выращенной продукции.
Находим выборочный коэффициент линейной регрессии 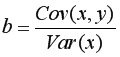
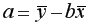
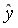
Коэффициент 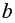
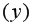
Рис. 9.5. Расчет параметров уравнения регрессии.
Таким образом, уравнение регрессии будет иметь вид: 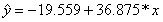
Подставляем в полученное уравнение фактические значения x (количество техники) находим теоретические значения объемов выращенной продукции (рис. 9.6).
Рис. 9.6. Расчет теоретических значений объемов выращенной продукции
Используя Мастер диаграмм строим корреляционные поля (выделяя столбцы со значениями 


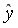
Рис. 9.7. График зависимости объема выращенной продукции от количества техники
Для оценки качества построенной модели регрессии вычислим:
• коэффициент детерминации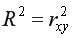
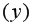
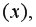
• среднюю ошибку аппроксимации. Для этого в столбце H вычислим разность фактического и теоретического значений 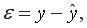
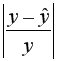
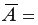
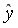
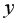
С помощью 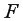
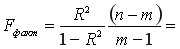
На уровне значимости 0,05 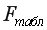
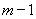
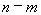
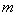
Так как 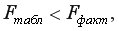
Рис. 9.8. Определение коэффициента детерминации и средней ошибки апроксимации
Рис. 9.9. Диалоговое окно функции FРАСПОБР
Далее определяем средний коэффициент эластичности по формуле. 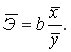
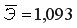
Рассчитаем прогнозное значение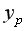
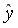
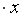
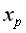
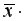
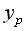
Найдем остаточную дисперсию, для этого вычислим сумму квадратов разности фактического и теоретического значений. 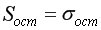
Рис. 9.10. Определение остаточной дисперсии
Средняя стандартная ошибка прогноза:
На уровне значимости 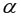
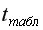
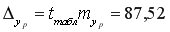
Доверительный интервал прогноза:
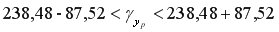
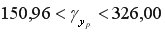
Выполненный прогноз затрат на выпуск продукции оказался надежным (1-0,05=0,95), но неточным, так как диапазон верхней и нижней границ доверительного интервала составляет 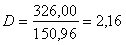
Необходимо отменить, что в MS Excel встроены статистические функции позволяющие значительно снизить количество промежуточных вычислений, например (рис. 9.11.):
Для вычисления выборочных средних используем функцию СРЗНАЧ(число1:числоN) из категории Статистические.
Выборочная ковариация между 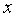
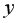
Выборочные дисперсииопределяются статистической функцией ДИСПР(число1:числоN).
Рис.9.11. Вычисление показателей встроенными функциями MSExcel
Параметры линейной регрессии 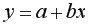
1 способ) С помощью встроенной функции ЛИНЕЙН. Порядок действий следующий:
1. Выделить область пустых ячеек 5×2 (5 строк, 2 столбца) для вывода результатов регрессионной статистики или область 1×2 – для получения только коэффициентов регрессии.
2. С помощью Мастера функций 
Рис. 9.12. Диалоговое окно ввода аргументов функции ЛИНЕЙН
Известные_значения_y – диапазон, содержащий данные результативного признака Y;
Известные_значения_x – диапазон, содержащий данные объясняющего признака X;
Конст – логическое значение (1 или 0), которое указывает на наличие или отсутствие свободного члена в уравнении; ставим 1;
Статистика – логическое значение (1 или 0), которое указывает, выводить дополнительную информацию по регрессионному анализу или нет; ставим 1.
3. В левой верхней ячейке выделенной области появится первое число таблицы. Для раскрытия всей таблицы нужно нажать на клавишу <F2>, а затем – на комбинацию клавиш <CTRL>+ <SHIFT>+ <ENTER>.
Дополнительная регрессионная статистика будет выведена в виде (табл. 9.3):
Таблица 9.3
|
Значение коэффициента |
Значение коэффициента |
|
Среднеквадратическое |
Среднеквадратическое |
|
Коэффициент |
Среднеквадратическое |
|
|
Число степеней свободы |
|
Регрессионная сумма квадратов |
Остаточная сумма квадратов |
В результате применения функции ЛИНЕЙН получим:
|
36,87457 |
-19,55899932 |
|
3,003392 |
21,316623 |
|
0,920606 |
39,16615351 |
|
150,7405 |
13 |
|
231234 |
19941,83855 |
(2 способ) С помощью инструмента анализа данных Регрессия можно получить результаты регрессионной статистики, дисперсионного анализа, доверительные интервалы, остатки, графики подбора линий регрессии, графики остатков и нормальной вероятности. Порядок действий следующий:
1. Необходимо проверить доступ к Пакету анализа. Для этого в главном меню (через кнопку Microsoft Office получить доступ к параметрам MS Excel) в диалоговом окне «Параметры MSExcel» выбрать команду «Надстройки» и справа выбрать надстройку Пакета анализа далее нажать кнопку «Перейти» (рис. 9.13). В открывшемся диалоговом окне поставить галочку напротив «Пакет анализа» и нажать «ОК» (рис. 9.14).
На вкладке «Данные» в группе «Анализ» появится доступ к установленной надстройке. (рис. 9.15).
Рис. 9.13. Включение надстроек в MSExcel
Рис. 9.14. Диалоговое окно «Надстройки»
Рис. 9.15. Надстройка «Анализ данных» на ленте MSExcel 2007.
2. Выбрать на «Данные» в группе «Анализ» выбираем команду Анализ данных в открывшемся диалоговом окне выбрать инструмент анализа «Регрессия» и нажать «ОК» (рис. 9.16):
Рис. 9.16. Диалоговое окно «Анализ данных»
В появившемся диалоговом окне (рис. 9.17) заполнить поля:
Входной интервалY – диапазон, содержащий данные результативного признака Y;
Входной интервалX– диапазон, содержащий данные объясняющего признака X;
Метки – флажок, который указывает, содержит ли первая строка названия столбцов или нет;
Константа-ноль – флажок, указывающий на наличие или отсутствие свободного члена в уравнении;
Выходной интервал – достаточно указать левую верхнюю ячейку будущего диапазона;
Новый рабочий лист – можно задать произвольное имя нового листа, на который будут выведены результаты.
Рис. 9.17. Диалоговое окно «Регрессия»
Для получения информации об остатках, графиков остатков, подбора и нормальной вероятности нужно установить соответствующие флажки в диалоговом окне.
Рис. 9.18. Результаты применения инструмента Регрессия
В MSExcel линия тренда может быть добавлена в диаграмму с областями гистограммы или в график. Для этого:
1. Необходимо выделить область построения диаграммы и в ленте выбрать «Макет» и в группе анализ выбрать команду «Линия тренда» (рис. 9.19.). В выпадающем пункте меню выбрать «Дополнительные параметры линии тренда».
Рис. 1.19. Лента
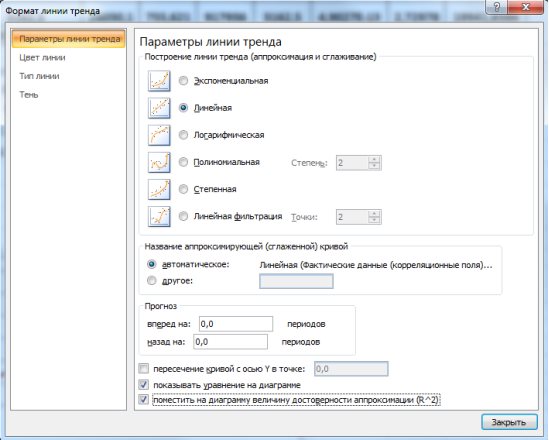
2. В появившемся диалоговом окне выбрать фактические значения, затем откроется диалоговое окно «Формат линии тренда» (рис. 9.20.) в котором выбирается вид линии тренда и устанавливаются соответствующие параметры.
Рис. 9.20. Диалоговое окно «Формат линии тренда»
Для полиноминального тренда необходимо задать степень аппроксимирующего полинома, для линейной фильтрации – количество точек усреднения.
Выбираем Линейная для построения уравнения линейной регрессии.
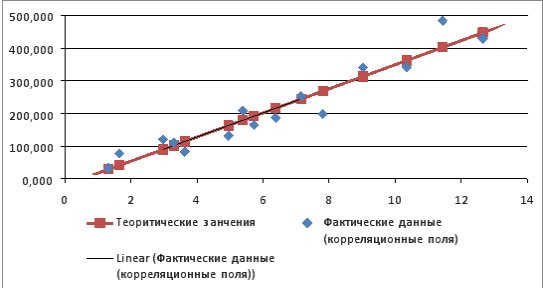
В качестве дополнительной информации можно показать уравнение на диаграмме и поместить на диаграмму величину (рис.9.21).
Рис. 9.21. Линейный тренд
Нелинейные модели регрессии иллюстрируются при вычислении параметров уравнения 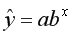


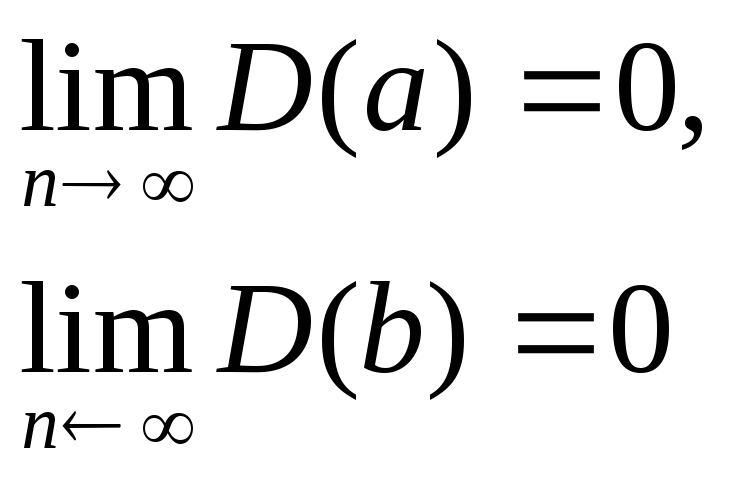
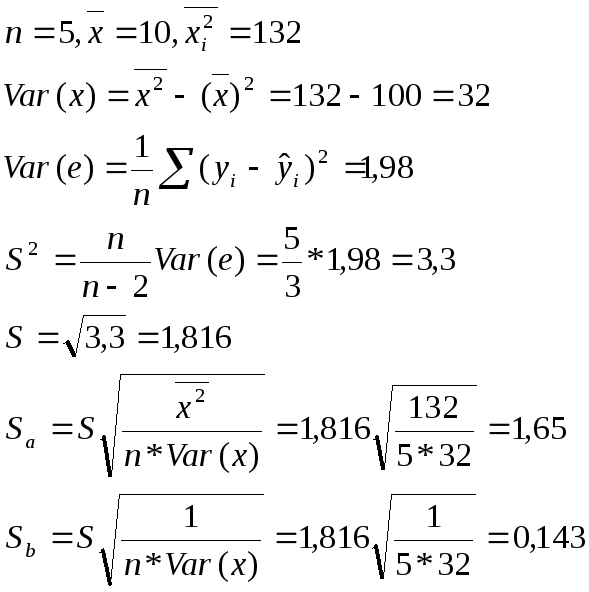




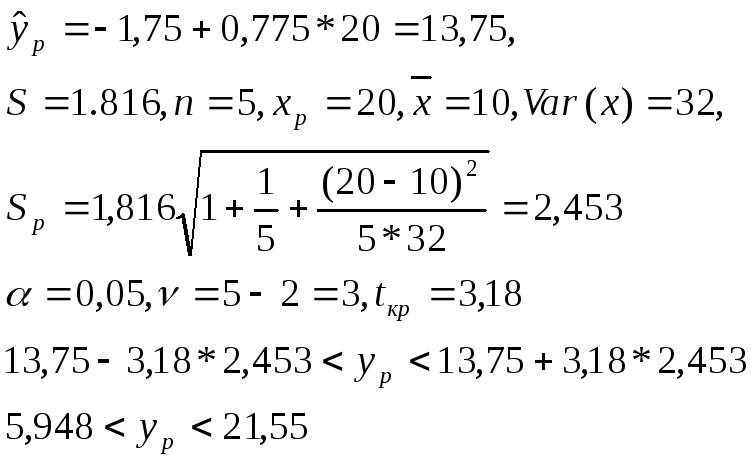
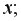
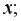
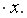
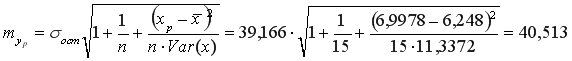
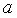
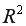
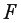 -статистика
-статистика