Основные ошибки статистического анализа

Опираясь на статистику легко лгать,
но без статистики очень трудно выяснить истину.

В любом научном исследовании главное — это полученные результаты. Однако, для того чтобы из них можно было сделать выводы, требуется статистическая обработка полученных данных.

Для тех, кто хорошо разбирается в математике, статистика не вызывает серьезных затруднений. Тем не менее разнообразные исследования показывают, что значительная доля научных публикаций содержит те или иные статистические ошибки. Об ошибках при переводе научных работ читайте в статье.

В. Джонсон из Техасского университета считает, что плохая статистика является одной из главных причин недостаточной воспроизводимости результатов в психологических исследованиях.

В этой статье мы расскажем о часто встречающихся ошибках статистического анализа и о том, как их избежать. С полезными сервисами для авторов можно ознакомиться здесь.

1. Сколько вешать в граммах?

Любой ученый дорожит полученными результатами. Каждая цифра представляется нам достаточно значимой, чтобы представить ее в том виде, в котором она была получена. Получили вес 60,245 кг — так и запишем. Часто кажется, что, округляя данные, мы обесцениваем собственный труд.

Однако, с точки зрения читателя излишняя точность скорее мешает. Цифры с длинными хвостами трудно воспринимать и оценивать. Если их можно округлить без ущерба для точности выводов, нужно это сделать. Например, ни для каких целей нет смысла указывать вес взрослого человека с точностью до грамма.

Учитывайте при округлении точность приборов. Если весы дают погрешность более 100 граммов, указывать десятые доли килограмма не стоит.

При округлении процентов в научных статьях рекомендуется использовать следующие правила: если выборка больше 1 000, результат округляется до сотых; от 100 до 1 000 – до десятых; от 20 до 100 – до целых значений процентов. Для выборки менее 20, лучше дать абсолютные значения. В маленьких группах проценты скорее запутывают читателя и часто выглядят курьезно: в результате лечения 33, 333% животных выздоровели; 33, 333% погибли; третья мышь убежала.

Количество знаков после запятой должно быть одинаковым во всей статье. Если все результаты округляются до сотых, а какой-то из них имеет вид целого числа, то его нужно записать так же, как все остальные цифры, например 24,00.

2. Разбивка непрерывных данных на группы.

Такие данные, как рост, вес или возраст часто делят на категории. Разбивка упрощает статистический анализ, но в любом случае необходимо обосновать принципы, по которым это сделано.

Деление на категории может приводить к некорректным выводам. Например, если выборку разделили на пациентов с нормальной массой тела, дефицитом и избытком массы, то различия между людьми с весом 80 и 150 килограммов могут быть больше, чем между людьми с весом 70 и 80 килограммов, хотя в первом случае они входят в одну группу (с избытком массы), а во втором — в разные.

3. Среднее и сигмальное отклонение, медиана и доверительный интервал.

Представление в статье только средних групповых значений без учета индивидуальных различий может приводить к неверным выводам. Пресловутая средняя температура по больнице не дает представления не только обо всех пациентах, но даже о большинстве из них.

Средняя величина и среднее квадратическое отклонение или сигмальное отклонение δ (standard deviation — sd) описывают вариабельность выборки.

Среднее квадратическое отклонение применяется только в случае нормального распределения данных, то есть когда 68% показателей находятся в пределах ±1δ, 95% в пределах ±2δ, и 99% в пределах ±3δ.

При асимметричном распределении данных среднее квадратическое отклонение не дает правильного представления о выборке. В этом случае используется медиана median и межквартильный диапазон interquartile range (IQR) (как правило, от 25 до 75 центиля).

Точечные данные характеризуют такие показатели, как стандартная ошибка среднего и доверительный интервал.

Стандартная ошибка среднего standard error of the mean (m) показывает отличие фактических данных от значений, полученных на модели. Она позволяет оценить точность модели.

Доверительный интервал confidence interval (CI) демонстрирует, насколько выборка отражает свойства генеральной совокупности. В медицинских исследованиях обычно указывают 95% доверительный интервал.

Средняя величина, указанная без доверительного интервала, не дает полного и правильного представления о полученном эффекте. Например, если среднее снижение артериального давления 20 мм. рт. ст., эффект может показаться клинически значимым. Однако при 95% доверительном интервале от 5 до 30 мм. рт. ст. целесообразность применяемой схемы лечения уже представляется сомнительной, так как снижение показателя на 5 мм. рт. ст. клинически несущественно. Окончательный вывод о целесообразности изучаемой схемы лечения из этих результатов сделать нельзя.

Важно: в медицинских исследованиях результаты, подчиняющиеся нормальному распределению, встречаются довольно редко. Кроме того, средняя величина и среднее квадратическое отклонение плохо работают на малых выборках.

4. p-критерий.

Критерий р недостаточно информативен в медицинских и биологических исследованиях.

Дело в том, что статистическая значимость не равна клиническому значению и целесообразности использования тех или иных выводов на практике. Решение о рациональности использования препарата не может опираться только на статистическую значимость полученного клинического эффекта. Например, статистически значимое снижение артериального давления на 10 мм. рт. ст. клинически можно расценивать как отсутствие эффекта.

р-критерий не может равняться нулю. Это значило бы, что между группами есть действительно достоверное различие. Однако, такое различие невозможно установить методами статистики. Обычно эта ошибка связана с тем, что программы для статистической обработки данных приводят очень малые значения как р=0,00000. На самом деле это означает p<0,000001, что и должно быть указано в статье.

р-критерий не применяется к генеральной совокупности. Он показывает, что имеющиеся различия не являются случайностью и такой же результат может быть получен на другой выборке. В случае генеральной совокупности этот показатель не имеет смысла, так как речь о случайности различий не идет.

Если в исследовании участвует несколько групп, определение нескольких p-критериев повышает вероятность принять случайное совпадение фактов за причинно-следственную связь. Существует несколько методов решения проблемы множественных сравнений, их использование должно быть обосновано и описано.

В рандомизированных клинических исследованиях р-критерий указывать необязательно, так как исходные различия между группами всегда имеют место в силу случайности выбора.

5. Адекватность модели.

Регрессионные модели не работают, если зависимость между переменными не имеет линейного характера.

Чтобы подтвердить или опровергнуть линейный характер связи между величинами, нужно изучить остатки residuals, то есть отклонение реальных данных от линии регрессии, построенной на основании модели.

Регрессионная модель хорошо объясняет реальное положение дел, если остатки:

• независимы
• подчиняются нормальному распределению
• имеют нулевое среднее
• в их величинах нет тренда

Дисперсия остатков variance of the residuals показывает те изменения полученных данных, которые не объясняются моделью. Чем меньше дисперсия, тем лучше работает модель.

6. Понятие нормы.

Отсутствие четкого понимания, что следует принять за норму является серьезным недостатком клинических исследований.

Для определения нормы существует несколько подходов:

• результат говорит о наличии или отсутствии заболевания
• является показанием к назначению лечения
• указывает на риск развития болезни
• встречается у здоровых лиц
• укладывается в определенный диапазон значений

Далеко не во всех случаях норма клинически значима. Например, несовпадение индивидуальных сроков прорезывания зубов с нормальными, как правило, ни о чем не говорит.

Причины, по которым тот или иной показатель принят за норму, должны быть обоснованы.

7. Учет сомнительных и неопределенных результатов.

В медицинских и клинических исследованиях не всегда ясно, как учитываются сомнительные результаты при определении чувствительности и специфичности тестов. При наличии значительного процента сомнительных результатов практическая значимость выводов снижается.

Результат нельзя однозначно оценить как отрицательный или положительный если:

• получены пограничные значения показателя;
• интенсивность окрашивания препарата недостаточная;
• ответы на вопросы психологических тестов неоднозначные;
• нарушены стандарты при проведении исследования.

Если в статистический анализ включены не все результаты и не все участники исследования, возникают вопросы:

• Данные пропустили по ошибке или сознательно исключили из анализа, поскольку они противоречат первоначальной гипотезе и выводам?
• Не приведет ли исключение некоторых данных к тому, что результаты не будут воспроизводиться на другой выборке или при повторном исследовании?
• Если данные не были представлены полностью, то можно ли доверять другим фактам, содержащимся в статье?

Все это не украшает автора и снижает ценность его работы в глазах читателя и редактора журнала. Поэтому в статье нужно указать наличие и количество сомнительных и неопределенных результатов; пояснить, включались ли они в статистический анализ и как были интерпретированы.

8. Понятие объекта исследования.

Неверное определение объекта исследования может приводить к ошибкам и неточностям.

В клинических исследованиях объектом принято считать пациента. Когда в работе о методах лечения переломов единицей учета является не пациент, а сломанная кость, возникает вопрос, сколько больных участвовали в исследовании. Тем более непонятно, что означает 50% эффективность.

Если объектом исследования является язвенная болезнь, то размер выборки будет соответствовать количеству выявленных случаев заболевания, а не количеству обследованных пациентов.

В работах, основанных на заключениях специалистов, может быть необходимым исследовать выборку специалистов, а не общий массив заключений.

9. Статистическая значимость полученных результатов.

Статистическая значимость Statistical significance не равна клиническому значению.

При сравнении больших выборок статистически значимыми могут оказаться различия, не имеющие никакой реальной важности. Например, при среднем сроке службы приборов 5 лет различия на 1-2 недели клинического значения не имеют.

Наоборот, в малых выборках статистически незначимые различия могут быть важными клинически. Например, если в группе из нескольких больных в терминальном состоянии выжил хотя бы один, это безусловно клинически значимо.

10. Влияние факторов риска.

Истинное влияние фактора риска показывает относительный риск relative risk (RR) — отношение риска наступления исхода у подвергавшихся воздействию фактора к риску в контрольной группе. Этот показатель можно рассчитать, если группы набираются по принципу наличия и отсутствия фактора риска.

Если же группы набираются по принципу наличия или отсутствия исхода, то влияние можно оценить только приблизительно, используя показатель отношения шансов odds ratio (OR), описывающий силу связи между факторами.

Заключение

Главный вывод из сказанного: методы статистического анализа должны соответствовать характеру данных. Выбор тех или иных методов анализа нужно обосновать. Во избежание ошибок учтите:

• Характер распределения данных. Нормальное и асимметричное распределение требует разных подходов к анализу.
• Для анализа независимых выборок и парных данных (относящихся к одному и тому же участнику исследования) используются разные методы.
• Характер связи между переменными. Линейный характер связи позволяет использовать регрессионные модели. Чтобы подтвердить или опровергнуть линейную зависимость, нужно проанализировать остатки.
• В медицинских исследованиях клиническая значимость имеет приоритет над статистической.
• Норма должна быть клинически значимой; а выбор значения, принимаемого за норму, нужно обосновать.
• При наличии сомнительных или неопределенных результатов следует объяснить, как они учитываются в статистическом анализе.
• Объектом исследования следует считать человека или животное, а не болезнь и не клинический случай, так как два и более клинических случая могут иметь отношение к одному пациенту.

Статистические показатели в любом случае можно улучшить увеличением числа участников. По мнению В. Джонсона, принимая эталонное значение р-критерия в медицинских и биологических исследованиях на уровне <0.0005, можно существенно повысить качество статистики.

Часто ошибки статистического анализа вытекают из того, что эксперимент или исследование было изначально неправильно спланировано. В сомнительных случаях стоит обратиться к специалистам по статистике, однако делать это нужно на этапе подготовки, а не тогда, когда все работы уже завершены и возник вопрос, что же теперь делать с этими цифрами.

Современные программы для статистической обработки данных сильно облегчают вычисления, однако они не решают проблему выбора адекватных методов анализа и соответствия их характеру полученных данных. Поэтому залог успеха — тщательная подготовка исследования. Убедитесь, что материалы и методы, статистический анализ результатов и выводы соответствуют цели исследования.

а) Виды ошибок

В процессе исследования явлений может
возникать отклонение исчисленных
показателей от их действительной
величины, то есть могут возникать ошибки
статистического наблюдения.

По источникам происхождения ошибки
наблюдения можно подразделить на
следующие:

1. преднамеренные;

2. непреднамеренные,
   которые в свою очередь делятся на:

• случайные;

• систематические;

• репрезентативности
  (представительности).

Преднамеренные(сознательные, злостные) получаются в
результате того, что сознательно
сообщаются неправильные данные. Например,
сокрытие фирмами прибыли от налогообложения,
искажение сведений об объеме выпускаемой
продукции, приписки и т. д.

Законом
предусматривается применение экономических
и административных мер к предприятиям
и лицам за злостные ошибки (иногда и
уголовная ответственность).

Непреднамеренные
случайныеошибки чаще связаны с
невнимательностью регистратора,
небрежностью в заполнении документов,
неточностью измерительных приборов,
ошибками в ответах опрашиваемых.

Непреднамеренные
систематическиеошибки возникают
при округлении признака в большую или
меньшую сторону, при использовании ЭВМ.

Ошибки
репрезентативности(представительности)
свойственны несплошному наблюдению,
они возникают вследствие неправильного
выбора единиц для обследования, нарушен
принцип случайного отбора, и выборочная
совокупность не полно характеризует
генеральную.

Б) Способы предотвращения ошибок статистического наблюдения

Чтобы
предупредить возникновение ошибок или
уменьшить их размеры необходимо:

• обеспечивать
  правильный подбор и подготовку кадров;

• вести широкую
  разъяснительную работу, применять меры
  взыскания за искажение фактов;

• проводить
  систематический контроль.

Контроль может
быть: счетным и логическим.

Счетный контроль
заключается в проверке точности
арифметических расчетов.

Логический
контроль проводится путем сопоставления
полученных данных с известными признаками,
логическое осмысление, сопоставление
с данными за прошлый период.

Например, о
заработной плате работников предприятия
можно судить по отчету, по труду и по
отчету о себестоимости продукции.
Сведения о заработной плате должны быть
одинаковыми, сопоставимыми (приведите
примеры).

__________________________________________________________________________________

__________________________________________________________________________________

__________________________________________________________________________________

__________________________________________________________________________________

__________________________________________________________________________________

__________________________________________________________________________________

__________________________________________________________________________________

__________________________________________________________________________________

__________________________________________________________________________________

__________________________________________________________________________________

__________________________________________________________________________________

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Ошибки, встроенные в систему: их роль в статистике

В прошлой статье я указал, как распространена проблема неправильного использования t-критерия в научных публикациях (и это возможно сделать только благодаря их открытости, а какой трэш творится при его использовании во всяких курсовых, отчетах, обучающих задачах и т.д. — неизвестно). Чтобы обсудить это, я рассказал об основах дисперсионного анализа и задаваемом самим исследователем уровне значимости α. Но для полного понимания всей картины статистического анализа необходимо подчеркнуть ряд важных вещей. И самая основная из них — понятие ошибки.

Ошибка и некорректное применение: в чем разница?

В любой физической системе содержится какая-либо ошибка, неточность. В самой разнообразной форме: так называемый допуск — отличие в размерах разных однотипных изделий; нелинейная характеристика — когда прибор или метод измеряют что-то по строго известному закону в определенных пределах, а дальше становятся неприменимыми; дискретность — когда мы чисто технически не можем обеспечить плавность выходной характеристики.

И в то же время существует чисто человеческая ошибка — некорректное использование устройств, приборов, математических законов. Между ошибкой, присущей системе, и ошибкой применения этой системы есть принципиальная разница. Важно различать и не путать между собой эти два понятия, называемые одним и тем же словом «ошибка». Я в данной статье предпочитаю использовать слово «ошибка» для обозначения свойства системы, а «некорректное применение» — для ошибочного ее использования.

То есть, ошибка линейки равна допуску оборудования, наносящего штрихи на ее полотно. А ошибкой в смысле некорректного применения было бы использовать ее при измерении деталей наручных часов. Ошибка безмена написана на нем и составляет что-то около 50 граммов, а неправильным использованием безмена было бы взвешивание на нем мешка в 25 кг, который растягивает пружину из области закона Гука в область пластических деформаций. Ошибка атомно-силового микроскопа происходит из его дискретности — нельзя «пощупать» его зондом предметы мельче, чем диаметром в один атом. Но способов неправильно использовать его или неправильно интерпретировать данные существует множество. И так далее.

Так, а что же за ошибка имеет место в статистических методах? А этой ошибкой как раз и является пресловутый уровень значимости α.

Ошибки первого и второго рода

Ошибкой в математическом аппарате статистики является сама ее Байесовская вероятностная сущность. В прошлой статье я уже упоминал, на чем стоят статистические методы: определение уровня значимости α как наибольшей допустимой вероятности неправомерно отвергнуть нулевую гипотезу, и самостоятельное задание исследователем этой величины перед исследователем.
Вы уже видите эту условность? На самом деле, в критериальных методах нету привычной математической строгости. Математика здесь оперирует вероятностными характеристиками.
И тут наступает еще один момент, где возможна неправильная трактовка одного слова в разном контексте. Необходимо различать само понятие вероятности и фактическую реализацию события, выражающуюся в распределении вероятности. Например, перед началом любого нашего эксперимента мы не знаем, какую именно величину мы получим в результате. Есть два возможных исхода: загадав некоторое значение результата, мы либо действительно его получим, либо не получим. Логично, что вероятность и того, и другого события равна 1/2. Но показанная в предыдущей статье Гауссова кривая показывает распределение вероятности того, что мы правильно угадаем совпадение.

Наглядно можно проиллюстрировать это примером. Пусть мы 600 раз бросаем два игральных кубика — обычный и шулерский. Получим следующие результаты:

До эксперимента для обоих кубиков выпадение любой грани будет равновероятно — 1/6. Однако после эксперимента проявляется сущность шулерского кубика, и мы можем сказать, что плотность вероятности выпадения на нем шестерки — 90%.

Другой пример, который знают химики, физики и все, кто интересуется квантовыми эффектами — атомные орбитали. Теоретически электрон может быть «размазан» в пространстве и находиться практически где угодно. Но на практике есть области, где он будет находиться в 90 и более процентах случаев. Эти области пространства, образованные поверхностью с плотностью вероятности нахождения там электрона 90%, и есть классические атомные орбитали, в виде сфер, гантелей и т.д.

Так вот, самостоятельно задавая уровень значимости, мы заведомо соглашаемся на описанную в его названии ошибку. Из-за этого ни один результат нельзя считать «стопроцентно достоверным» — всегда наши статистические выводы будут содержать некоторую вероятность сбоя.

Ошибка, формулируемая определением уровня значимости α, называется ошибкой первого рода. Ее можно определить, как «ложная тревога», или, более корректно, ложноположительный результат. В самом деле, что означают слова «ошибочно отвергнуть нулевую гипотезу»? Это значит, по ошибке принять наблюдаемые данные за значимые различия двух групп. Поставить ложный диагноз о наличии болезни, поспешить явить миру новое открытие, которого на самом деле нет — вот примеры ошибок первого рода.

Но ведь тогда должны быть и ложноотрицательные результаты? Совершенно верно, и они называются ошибками второго рода. Примеры — не поставленный вовремя диагноз или же разочарование в результате исследования, хотя на самом деле в нем есть важные данные. Ошибки второго рода обозначаются буквой, как ни странно, β. Но само это понятие не так важно для статистики, как число 1-β. Число 1-β называется мощностью критерия, и как нетрудно догадаться, оно характеризует способность критерия не упустить значимое событие.
Однако содержание в статистических методах ошибок первого и второго рода не является только лишь их ограничением. Само понятие этих ошибок может использоваться непосредственным образом в статистическом анализе. Как?

ROC-анализ

ROC-анализ (от receiver operating characteristic, рабочая характеристика приёмника) — это метод количественного определения применимости некоторого признака к бинарной классификации объектов. Говоря проще, мы можем придумать некоторый способ, как отличить больных людей от здоровых, кошек от собак, черное от белого, а затем проверить правомерность такого способа. Давайте снова обратимся к примеру.

Пусть вы — подающий надежды криминалист, и разрабатываете новый способ скрытно и однозначно определять, является ли человек преступником. Вы придумали количественный признак: оценивать преступные наклонности людей по частоте прослушивания ими Михаила Круга. Но будет ли давать адекватные результаты ваш признак? Давайте разбираться.
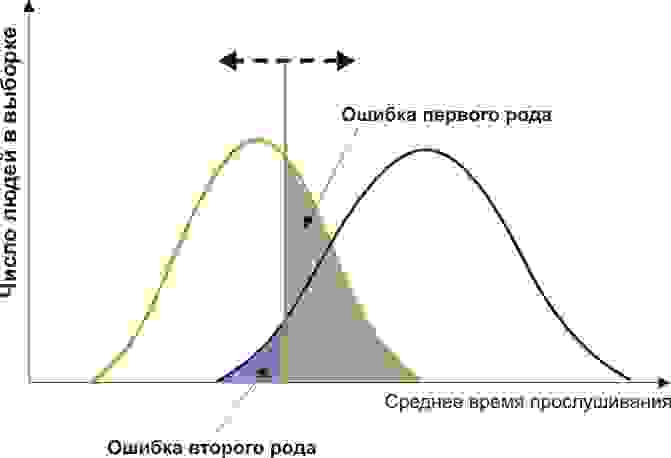
Вам понадобится две группы людей для валидации вашего критерия: обычные граждане и преступники. Положим, действительно, среднегодовое время прослушивания ими Михаила Круга различается (см. рисунок):

Здесь мы видим, что по количественному признаку времени прослушивания наши выборки пересекаются. Кто-то слушает Круга спонтанно по радио, не совершая преступлений, а кто-то нарушает закон, слушая другую музыку или даже будучи глухим. Какие у нас есть граничные условия? ROC-анализ вводит понятия селективности (чувствительности) и специфичности. Чувствительность определяется как способность выявлять все-все интересующие нас точки (в данном примере — преступников), а специфичность — не захватывать ничего ложноположительного (не ставить под подозрение простых обывателей). Мы можем задать некоторую критическую количественную черту, отделяющую одних от других (оранжевая), в пределах от максимальной чувствительности (зеленая) до максимальной специфичности (красная).
Посмотрим на следующую схему:

Смещая значение нашего признака, мы меняем соотношения ложноположительного и ложноотрицательного результатов (площади под кривыми). Точно так же мы можем дать определения Чувствительность = Полож. рез-т/(Полож. рез-т + ложноотриц. рез-т) и Специфичность = Отриц. рез-т/(Отриц. рез-т + ложноположит. рез-т).

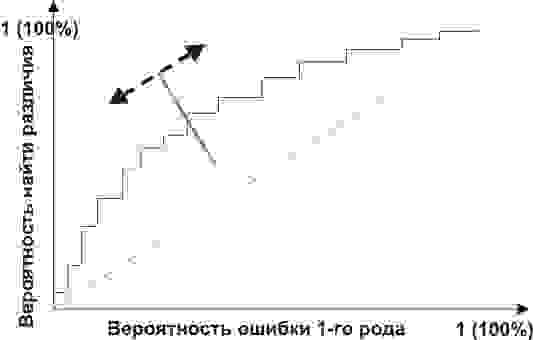
Но главное, мы можем оценить соотношение положительных результатов к ложноположительным на всем отрезке значений нашего количественного признака, что и есть наша искомая ROC-кривая (см. рисунок):

А как нам понять из этого графика, насколько хорош наш признак? Очень просто, посчитать площадь под кривой (AUC, area under curve). Пунктирная линия (0,0; 1,1) означает полное совпадение двух выборок и совершенно бессмысленный критерий (площадь под кривой равна 0,5 от всего квадрата). А вот выпуклость ROC кривой как раз и говорит о совершенстве критерия. Если же нам удастся найти такой критерий, что выборки вообще не будут пересекаться, то площадь под кривой займет весь график. В целом же признак считается хорошим, позволяющим надежно отделить одну выборку от другой, если AUC > 0,75-0,8.

С помощью такого анализа вы можете решать самые разные задачи. Решив, что слишком много домохозяек оказались под подозрением из-за Михаила Круга, а кроме того упущены опасные рецидивисты, слушающие Ноггано, вы можете отвергнуть этот критерий и разработать другой.

Возникнув, как способ обработки радиосигналов и идентификации «свой-чужой» после атаки на Перл-Харбор (отсюда и пошло такое странное название про характеристику приемника), ROC-анализ нашел широкое применение в биомедицинской статистике для анализа, валидации, создания и характеристики панелей биомаркеров и т.д. Он гибок в использовании, если оно основано на грамотной логике. Например, вы можете разработать показания для медицинской диспансеризации пенсионеров-сердечников, применив высокоспецифичный критерий, повысив эффективность выявления болезней сердца и не перегружая врачей лишними пациентами. А во время опасной эпидемии ранее неизвестного вируса вы наоборот, можете придумать высокоселективный критерий, чтобы от вакцинации в прямом смысле не ускользнул ни один чих.

С ошибками обоих родов и их наглядностью в описании валидируемых критериев мы познакомились. Теперь же, двигаясь от этих логических основ, можно разрушить ряд ложных стереотипных описаний результатов. Некоторые неправильные формулировки захватывают наши умы, часто путаясь своими схожими словами и понятиями, а также из-за очень малого внимания, уделяемого неверной интерпретации. Об этом, пожалуй, нужно будет написать отдельно.