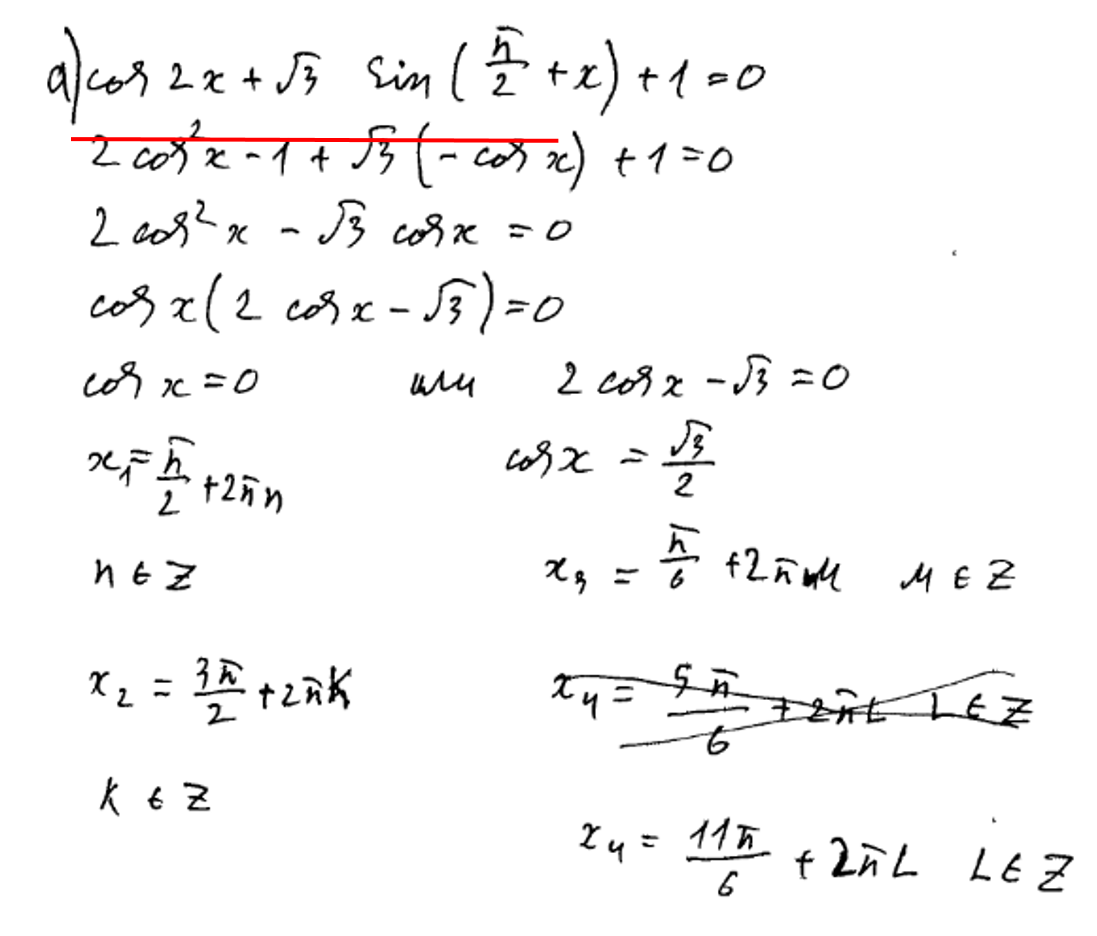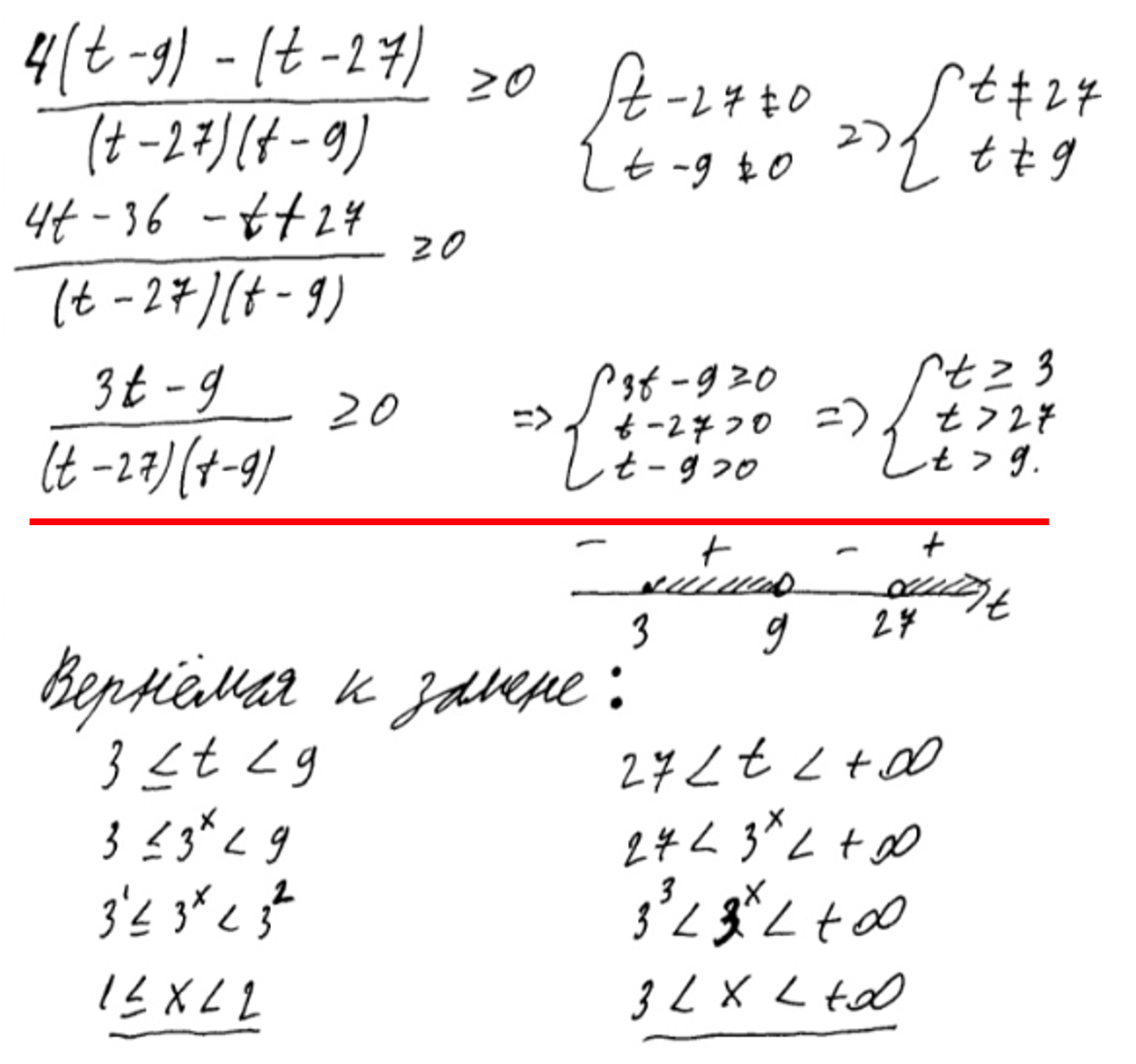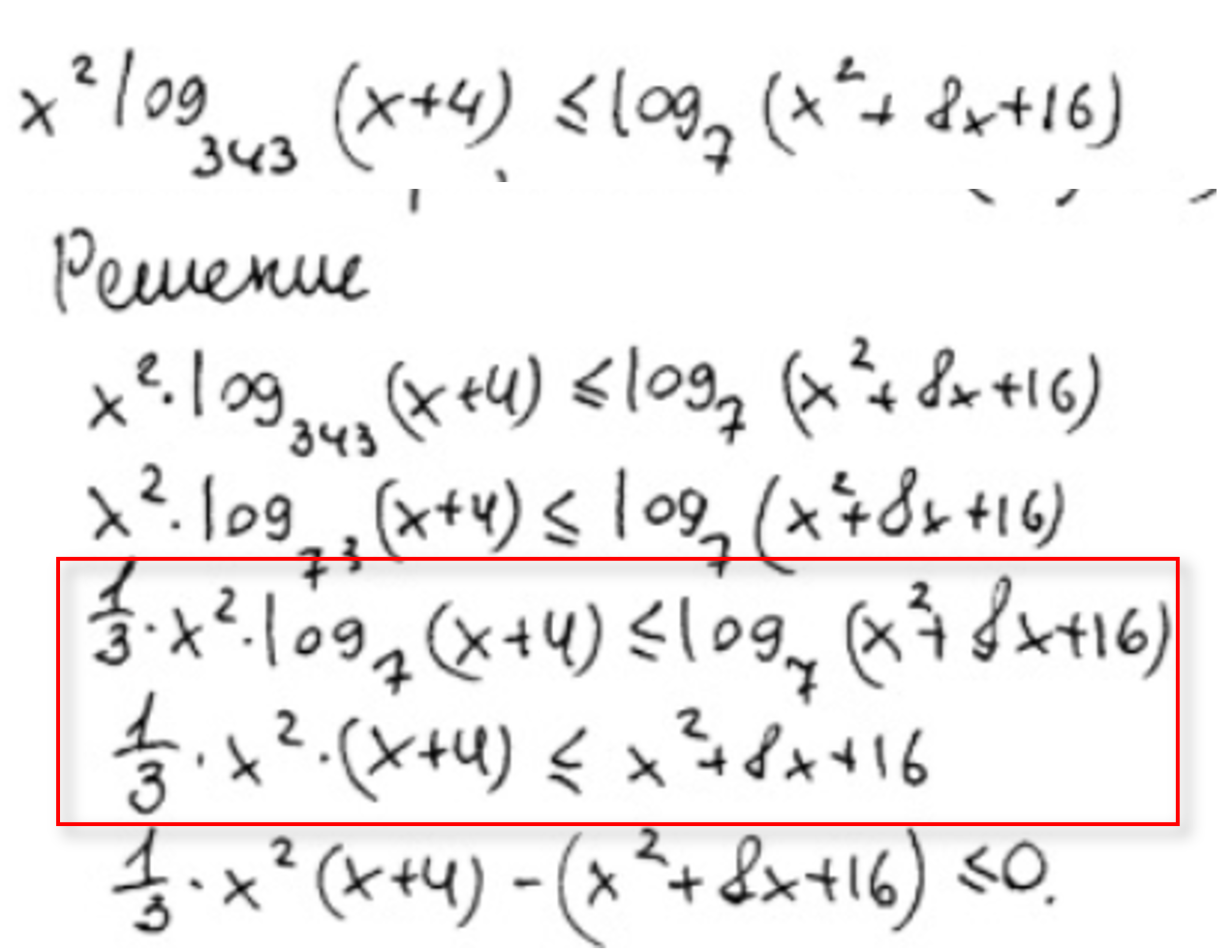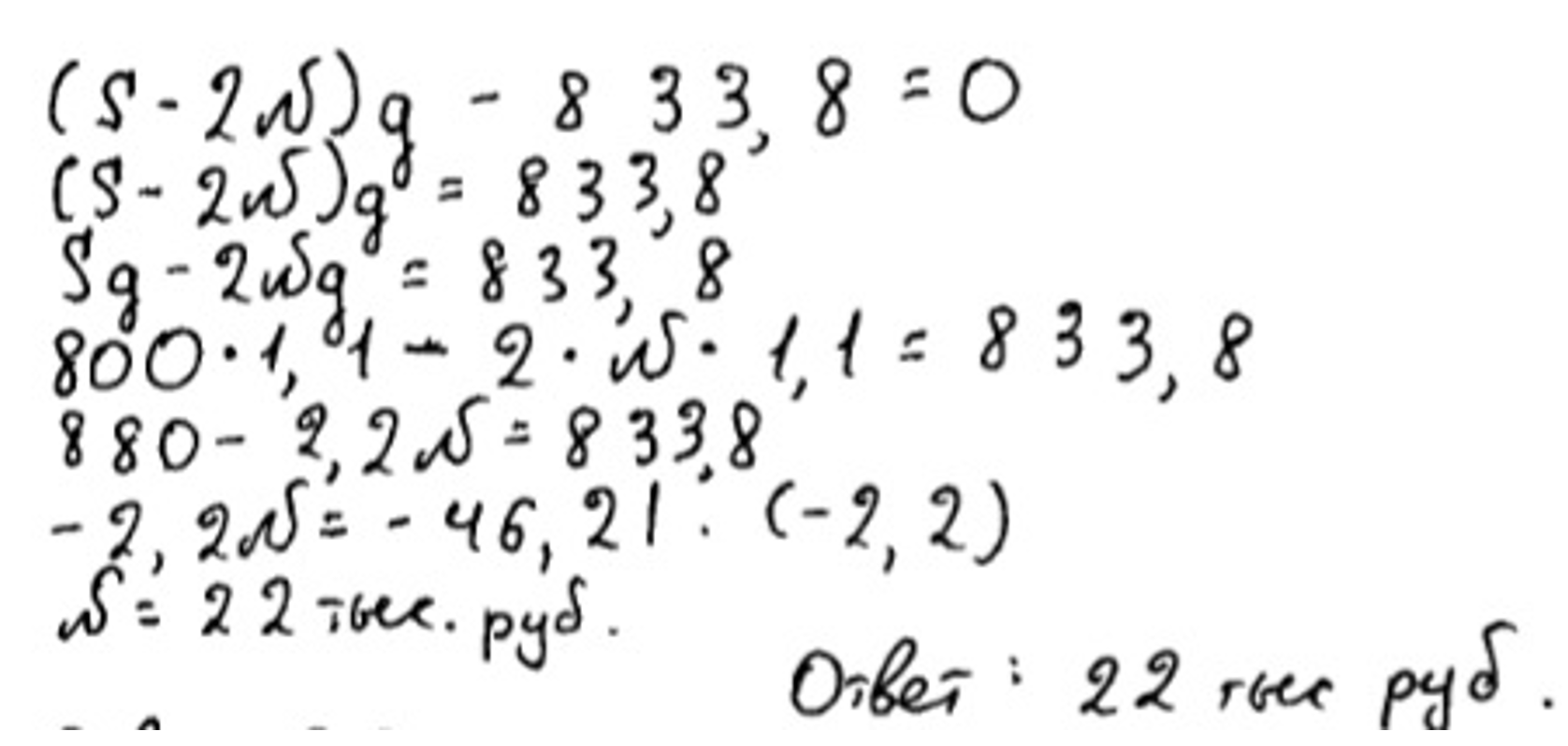Основные ошибки егэ математика профиль

Чтобы успешно сдать экзамен, подготовку нужно начинать заранее. И если вы не можете самостоятельно определить свои слабые места и проблемы, рекомендуем начать с разбора типичных ошибок ЕГЭ и ОГЭ по математике.

Здесь мы приведем анализ типичных ошибок {{year}} и дадим советы, как их не допустить при сдаче ОГЭ/ЕГЭ по математике. Следите за нашим телеграм-каналом – там мы будем разбирать и другие дисциплины, чтобы помочь вам в поступлении.

Базовый уровень математики

Ошибки в задачах на проценты

Чаще всего их допускают, так как не разбираются в сути процента.

Возьмем пример задачи, когда нужно сначала снизить цену на 25%, а потом повысить ее на 25%. Самая частая ошибка – полагать, что эти проценты будут равны одной и той же сумме. На самом же деле база их зачисления будет совершенно разной.

В этом примере 6% участников допустили вариант, что новую цену нужно понизить на 25%. На самом же деле новая цена – это 125% от старой. И вопрос в этой задаче – узнать, сколько будет 100% от старой цены.

Совет: повторить основы расчета процентов, повторить взаимосвязи величин, подумать над способом решения таких задач.

Невнимательное прочтение условия задания

Волнение и психологическое напряжение приводят к тому, что участники часто неправильно понимают условие задания. В итоге – снижение итогового балла по невнимательности, а не по незнанию.

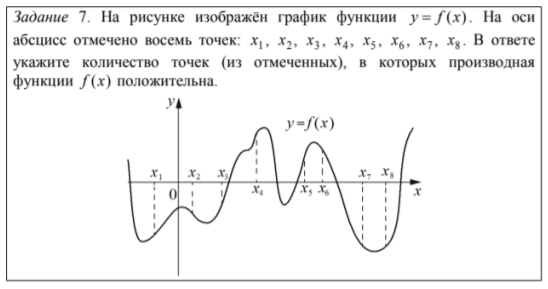
Например:

В 24% участников упомянули те точки, где значение функции (а не производной) положительное. Еще 2% указали номера точек, где производная принимает положительное значение.

Совет: вдумчиво, медленно и несколько раз читайте задание.

Непонимание текста задачи (на повышенном уровне и в практико-ориентированных заданиях)

Учащиеся могут не только неправильно понять, но и вовсе не понять условия. Иногда это происходит из-за незнания величин, единиц их измерения или плохой работы с формулами. Многие просто пропускают эту часть тестирования.

Вот пример задачи:

Её выполнило только 57% участников тестирования. 8% вообще не дали ответа, 6% дали ответ «чем ближе, тем лучше», 4% – «лампочку необходимо поместить в середину разрешенного интервала», еще 4,5% приняли фокус за основной параметр.

Совет: изучайте задания прошлых лет, просите учителя практиковать как можно более разные задачи.

Ошибки в вычислениях

Школьная привычка использовать даже в самых легких примерах калькулятор приводит к плачевному результату на экзамене. Если учащийся не научиться быстро считать в уме или хотя бы на бумаге, во время тестирования он может ошибиться даже в самых простых заданиях. 

Особенно сложно участникам тестирования даются дроби, отрицательные числа, элементарные преобразования выражений и другие проблемы, копившиеся еще с 5 класса.

Совет: если в чем-то не разбираетесь, обязательно отработайте эту тему до автоматизма перед экзаменом, потому что она обязательно попадется.

Ошибки теоретического характера

Это касается фактов по геометрии и алгебре, незнание которых приводит к снижению процента выполнения заданий и базового, и профильного уровней.

Например:

В этой задаче около 8% участников вообще не ответили на поставленное условие, 38% дали ответ с ошибками относительно боковой поверхности конуса, а 12% совершили ошибки в расчёте объёма.

Статистика показывает, что в таких заданиях ошибок гораздо больше, чем в гораздо более сложных профильных заданиях. 

Совет: потренируйтесь перед тестированием. Если ответы не сходятся с ключами, обратитесь за помощью к стороннему специалисту (репетитору или сервису студенческой помощи), чтобы они указали, где вы ошибаетесь.

Ошибки в алгоритмах и методах решения

Этот тип ошибок встречается во всех заданиях.

Например:

Около 15% участников получили нулевые баллы из-за проблем с невнимательным чтением неравенства, непониманием алгоритма решения совокупностей и систем логарифмических неравенств.

Хватает ошибок и в решении дробнорациональных неравенств, когда ученики забывают про знаменатель.

Совет: всегда проверяйте решение. Научитесь правильно находить последовательность в решении алгоритмов.

Ошибки в чтении и построении чертежа

Такое случается, когда ученик не понимает взаимосвязь элементов геометрических конструкций, а также не обладает основными пространственными представлениями. 

Например:

Около 10% участников экзамена сделали ошибки в вычислении углов по их записи, просто перепутав буквы или не понимая, где расположены вершины всех углов. Еще 5% решили, что угол ACD прямой. А 3% увидели в угле ABD равносторонний треугольник. 

Совет: тренируйтесь находить взаимосвязь элементов геометрических конструкций.

Неумение обосновывать и доказывать

14 и 16 задания по стереометрии и планиметрии отличаются повышенным уровнем сложности и требуют развернутого ответа. В каждом по 2 пункта: в первом нужно доказать, во втором – произвести вычисления. 

Самые распространенные ошибки касаются первого пункта, так как у участников выявились проблемы с умением доказывать.

Есть проблемы и в оформлении доказательств. Например:

Основная трудность в отсутствии понимания логики построения доказательства.

Совет: тренируйтесь в доказательной базе, повышайте математическую культуру, учитесь обосновывать выбранные методы и способы их решения.

Ошибки в заданиях по тригонометрии

Из-за невнимательности и неаккуратности, а также отсутствия знаний по большому количеству теоретических фактов и способности их применять на практике, участники совершают частые ошибки в решении тригонометрических заданий.

Например:

Только 34% участников выполнили его. Самые частые ошибки (около 12%) связаны в первую очередь с нахождением тригонометрического знака – чаще всего потеря знака «минус». Еще 22% ждут «красивого» ответа, равного 1 или 2.

Ошибки математического моделирования

В 11 и 17 заданиях проверяют способность учащихся к построению и исследованию простейших математических моделей. 

В текстовых задачах основную роль играет сюжетная часть – она имеет практическую ориентацию. И часто из-за непонимания взаимосвязи величин в этих заданиях допускают ошибки.

Например, в задачах на движение примерно 10% не понимают принципы движения по реке – они умножают собственную скорость на время движения.

Совет: тренируйте текстовые задачи, внимательно читайте условие задачи. 

Профильный уровень

Здесь приведем краткий список трудностей и ошибок участников ЕГЭ по математике:

1. Задание 2 – учащиеся не понимают разницу в сравнении отрицательных чисел и их моделей.
2. Задание 6 – не понимают геометрический рисунок (относятся к нему как к чертежу, где соблюдены все размеры).
3. Задание 7 – отвечают наугад в решениях производных и попытках увидеть ее на чертеже.
4. Задание 8 – ошибаются в наглядном решении. 
5. Задание 9 – неправильно применяют свойства степеней, ошибаются в решении логарифмов из-за отсутствия практики.
6. Задание 12 – ошибаются в задачах с нулями производной.

Как правильно читать задание, чтобы не совершать ошибок по невнимательности

Есть несколько рекомендаций, чтобы избежать ошибок из-за невнимательного прочтения задания. Это и будет алгоритмом решения задачи:

• прочтите условие;
• выпишите данные величины, сделайте рисунок в геометрическом задании;
• установите и запишите отношения и взаимосвязи между известными данными;
• выпишите что найти, ответ на какой вопрос нужно дать;
• определите тип задания;
• сформулируйте содержание и последовательность действий.

Это будет ваш своеобразный чек-лист, который обязательно нужно соблюдать при решении любой задачи, чтобы не допустить обидных ошибок. 

Данные условия важно именно выписывать, а не иметь в виду. Фиксация их в уме чаще всего приводит к записи неправильного ответа.

И еще момент: не приступайте к решению задачи сразу же после ее прочтения. Психологи утверждают, что важно выдержать паузу между стимулом и реакцией – именно при этом условии удастся добиться оптимальных результатов:

• сориентироваться в условии,
• обдумать и спланировать ее решение,
• понять уровень ее сложности и решить, откладывать ли ее решение напоследок. 

Кроме сложности задачи оцените, сколько баллов она принесет и насколько она утомительна. Важно оставить энергию для решения других заданий при сдаче единого государственного экзамена.

Начинайте с самой простой задачи, постепенно продвигаясь к самой сложной. На экзамене важно количество решенных заданий, а не их сложность.

Знание типичных ошибок ЕГЭ и ОГЭ по математике даст вам полную картину того, к каким заданиями нужно готовиться с большим усилием. А чтобы не отвлекаться на другие учебные дела, не забывайте: рядом есть сервис студенческой помощи, который подставит плечо в трудную минуту.

И снова здравствуйте, уважаемые одиннадцатиклассники! Полагаю, что Вы хорошо отдохнули и готовы к работе для достижения своих высоких целей.

В этом году июнь месяц выдался очень продуктивным. Моя работа не закончилась 6 июня, когда мои ученики написали ЕГЭ по физике. После публикации результатов ЕГЭ (сначала по математике, а потом и по физике) стало поступать множество сообщений от учеников, даже тех, с кем я не занималась, с просьбой помочь разобраться, за что сняли баллы. А в некоторых случаях даже была необходима помощь с составлением апелляции. Бесценный опыт, если честно…..Только вот от этого опыта седых волос становится больше. И желание сжечь критерии не отпускает меня.

Сразу замечу, что апелляция возможна только по заданиям второй части. По первой части апелляция производится только тогда, когда компьютер неверно считал знак, записанный Вами в бланке ответов.

Уважаемые одиннадцатиклассники, вы должны понимать, что недостаточно просто получить верный ответ, недостаточно записать решение в стиле «я художник, я так вижу». Ваше решение будут оценивать по вполне определенным критериям. И даже абсолютно верный ответ не гарантирует полный балл за выполненное задание.

Анализ ошибок мы начнем с разбора сканов работ по профильной математике. Эти сканы я собирала не один год. К сожалению, в математике, просто за идею решения, за набор формул, не дадут ни одного балла. А снимают баллы за наличие вычислительных ошибок, недостаточную обоснованность, наличие лишних записей. Не указали необходимые признаки, свойства, теоремы – все, полный балл Вам не дадут.

Основной упор будет сделан на задачи 12, 14, 15 (уравнения, неравенства, задачи с экономическим содержанием). Это так называемый джентельменский набор, который старается выполнить большая часть выпускников. Погнали…

Для удобства статья представлена в двух форматах. Текст и видео. Вот ролик:

Уравнения

Основные ошибки:

1) неправильное использование формул приведения.

При преобразовании допущена ошибка. Минуса перед косинусом быть не должно. Задание оценивается в 0 баллов.

2) незнание свойств четных и нечетных функций.  Также ребята забывают, что косинус функция честная, а вот синус, тангенс и котангенс нечетные.

Классическая ошибка! – нечетная функция, следовательно знак минус выносится вперед, а не пропадает. Если бы функция была четная, то мы смело могли бы убрать знак минус.  Задание оценивается в 0 баллов.

3) неправильное или некорректное использование тригонометрических формул.

Пару лет назад мне написал ученик, которому на экзамене досталось уравнение вида  .

Скан он мне не отправил, но в процессе обсуждений выяснилось, что в первой скобке для он использовал не формулу синуса суммы, а формулы приведения. Чего делать категорически нельзя! Как Вы понимаете, задание оценили в 0 баллов.

4) Самое банальное. Неверное решение простейших тригонометрических уравнений.

При решении простейшего тригонометрического уравнения допущена ошибка. Третий и четвертый корень записаны неверно. Задание оценивается в 0 баллов.

Неравенства

С неравенствами у ребят дела идут посложнее, чем с уравнениями. Тут ваша фантазия разыгрывается по полной. Какие только ошибки не встречались(( Постараюсь выделить основные.

1)Пожалуй, самая распространенная ошибка – ошибка в расстановке знаков на координатной прямой. В идеале, если выпускник умеет определять – перед ним корень четного или нечетного порядка, меняется знак или дублируется.

Нули найдены верно. Но при расстановке знаков на координатной прямой допущена ошибка. Мы видим, что единица – нуль числителя второго порядка, следовательно знак сохраняется, и в крайнем левом интервале должен быть плюс. Эта ошибка уже позволяет эксперту поставить за данное задание 0 баллов.

2)Отбрасывание знаменателя и, как следствие, потеря части корней. В примере, приведенном ниже, выпускник отбросил знаменатель и находил нули только числителя.

Это привело к тому, что на координатной прямой не хватает нулей двух скобок: .

Такая грубая ошибка на экзамене не прощается.

Оценка эксперта – 0 баллов.

3) Неравносильный переход от неравенства к системе неравенств.

Я думаю, эта ошибка даже не нуждается в комментариях. Даже несмотря на то, что ученик верно нашел нули, верно расставил знаки на координатной прямой, это задание оценили в 0 баллов. Если бы системы с тремя неравенствами не было, ученик имел бы возможность взять полный балл.

4) Ошибки при использовании свойств логарифмов.

Стоит заметить, что для снятия логарифмов в правой и левой части, необходимо, чтобы перед логарифмом не было никаких цифр или букв. Выпускник снял логарифмы, хотя по задумке нужно было в правой части свернуть в полный квадрат подлогарифмическое выражение и вынести общий множитель. Как Вы понимаете, эксперт оценил это задание в 0 баллов.

Из моего текста у Вас, возможно, сложилось впечатление, что эксперты по всем поводам снимают сразу два балла. К счастью, это не так. Один балл Вам могут поставить, если Вы допустили ошибку в скобке (вместо круглой написали квадратную или наоборот) или допустили вычислительную ошибку, но при этом присутствует верная последовательность всех шагов решения.

Экономические задачи

В решении задач с экономическим содержанием ребятам в первую очередь нужно определить, какая форма кредитования  – с дифференцированными платежами, аннуитентными или иная форма кредитования.

Могу выделить несколько основных ошибок.

1)Неверное построение математической модели, связанное с неверным определением формы кредитования.

Для лучшего понимания начну с условия задачи.

В июле 2026 года будет взят кредит на три года в размере 800 тыс рублей. Условия возврата таковы:

– каждый январь долг возрастает на 10 процентов по сравнению с концом прошлого года

– размер платежей в 2027 и 2028 годах одинаковый

– к июлю 2029 года долг выплачивается полностью.

Также известно, что в 2029 году платеж составит 833,8 тыс рублей. Сколько рублей будет составлять платеж в 2027 году?

Согласно записям таблицы, ученик решил, что перед ним дифференцированная форма кредитования и остаток уменьшается у него равномерно, ровно на N рублей каждый год. Но это совсем не так. Из условия задачи, мы видим, что выплаты одинаковые первые два года. Но при этом остаток не будет уменьшаться равномерно. Правильная запись остатка во второй строчке должна выглядеть так: .

Основываясь на критериях оценивания данного задания, математическая модель построена неверно, задание оценивается в 0 баллов.

Идем дальше. Наверняка Вы встречали задачи вида:

15 января 2020 года был выдан кредит на сумму 900 тыс. рублей на 31 месяц. Условия возврата таковы:

– 1 -го числа каждого месяца долг увеличивается на 2  по сравнению с концом предыдущего месяца.

– со 2 по 14 число необходимо выплатить часть долга;

– 15 -го числа каждого месяца с 1-го по 30-й долг должен быть на одну и ту же величину меньше долго на 15 число предыдущего месяца;

– 15 июля 2027 года долг составит 300 тыс рублей.

– 15 августа 2027 года долг должен быть выплачен полностью.

Найдите общую сумму выплат после полного погашения кредита.

В этой таблице полностью неправильно записаны столбцы с остатками и выплатами. Согласно условию задачи, первые 30 месяцев долг уменьшается равномерно, на меньше чем, прошлом месяце. Но не забываем, что первоначальный долг – это S, а не Sk рублей. То есть остаток в первые 30 месяцев должен выглядеть так: . Как Вы понимаете, и выплаты будет принимать совсем другой вид, так как они получаются путем вычитания из долга после начисления процентов самого остатка. Для примера запишем первую выплату: .

С учетом полностью неправильно построенной математической модели, задание оценивается в 0 баллов.

2)Ошибки при применении формул арифметической прогрессии и расчета общей суммы выплат.

Год назад ребятам на экзамене попалась задача, где в процессе кредитования менялась процентная ставка. Приведу пример:

25 августа 2020 года был дан кредит на 12 лет в размере 300 тыс рублей.

–  25 января с 2021 по 2026 года долг возрастает на 10 процентов;

–  25 января с 2027 по 2032 года долг возрастает на 15 процентов;

– с февраля по июль необходимо выплатить часть долга;

– в августе каждого года долг должен быть на одну и туже величину меньше по сравнению с августом прошлого года;

– к августу 2032 года кредит должен быть полностью погашен.

Найдите общую сумму выплат после полного погашения кредита.

Я уверена, что для многих ребят покажется очевидным, что нельзя складывать первую и последнюю (двенадцатую) выплату. Но я все же поясню.

Действительно, это задача на дифференцированные платежи. И можно заметить, что выплаты подчиняются арифметической прогрессии. Но так как у вас меняется процентная ставка, у Вас меняется и так называемый коэффициент или разность арифметической прогрессии. Поэтому правильно будет сначала просуммировать по формуле арифметической прогрессии первые шесть выплат, потом вторые шесть и полученные выражения сложить. Таким образом Вы получите верный ответ.

В каком же случае Вы можете получить 1 балл – если Вы верно построили математическую модель, но допустили вычислительную ошибку при получении численного значения.

PS: в подавляющем большинстве работ, которые поступали на проверку, ребята просили пояснить, почему за параметр (17 задание) и за задание на числа и их свойства так сильно срезали баллы. В большинстве случаев ребята получали по одному баллу за параметр, а в задаче на числа им засчитывали только пункт а), который также дает только один балл. Ребята, эти задачи считаются олимпиадными, не зря за их полное выполнение дается целых 4 балла. Критерии оценивания данных номеров очень жесткие. Должно быть и максимальное подробное объяснение, и разбор всех случаев и вариантов. В 17 задании это и правильно построенный график (если это необходимо), и рассчитаные все точки, и правильно раскрытый  модуль, и расписанные все значения параметра и т.д и т.д.

В погоне за «легкими «баллами ребята даже не трогают планиметрию и стереометрию. А они, напомню, оцениваются в три балла каждый. Даже если Вы испытываете трудности в геометрии, пункт а (доказательство) не пропускайте мимо, как правило он значительно легче пункта б), где нужно найти численное значение той или иной величины. Но по одному первичному баллу за каждый номер Вы спокойно можете получить.

На этом мой краткий обзор подошел к концу. Я желаю удачи и сил  всем одиннадцатиклассникам в этом году. Не бойтесь ЕГЭ, настраивайтесь на работу, идите к своей цели. У Вас все получится!

Все, что не убивает, делает нас сильнее!

P.S.: Вот моя группа ВКонтакте, где я выкладываю подобные тексты, ролики и полезности для ЕГЭ по физике и математике: https://vk.com/public185877660 Подписывайтесь!

Знаешь ли ты, что 90% ошибок на экзамене происходит из-за обычной невнимательности?

Знаешь ли, что составители вариантов ЕГЭ специально делают такие задачи, где очень легко допустить ошибку?

А знаешь ли ты, ЧТО это за задачи? Самые коварные. Гадкие. Криповые. Хитроумные ловушки для твоего разума.

Прочитай этот текст до конца. Ты узнаешь своих врагов в лицо!

Мы выловили их среди тысяч задач в Банке заданий ФИПИ, чтобы показать тебе!

И составили Топ-10 – в соответствии с тем, какой процент старшеклассников делает в них ошибки.

Ты узнаешь, как с ними справиться.

Ты сможешь!

Об Анне Малковой

ЕГЭ-Студия 15 лет готовит на высокие баллы

Средний балл на ЕГЭ 2023

Математика 83 баллов

Русский язык 88 баллов

Обществознание 86 баллов

Немного цифр

Позвоните мне

Все поля обязательны для заполнения

Нажимая на кнопку, вы даете согласие на обработку своих персональных данных

В этой статье собрали распространённые ошибки, которые допускают выпускники при сдаче ЕГЭ по профильной математике.

Причины ошибок в ЕГЭ по профильной математике 

Мы попросили наставников онлайн-школы Вебиума проанализировать работы школьников по профильной математике, чтобы выделить самые частые причины, из-за которых теряются баллы на ЕГЭ. 

Среди таких ошибок:

• отсутствие ограничений;
• неправильное составление формул приведения;
• непонимание тригонометрии;
• оформление;
• невнимательность.

Шпаргалка: Полезные материалы для подготовки к ЕГЭ по профильной математике

Отсутствие ограничений

Эту ошибку ребята допускают как и в первой, так и во второй части. Ограничения необходимо прописывать в ходе решения задачи, иначе большая вероятность, что вы забудете это сделать.

Как избежать ошибку: выучить, что корни, логарифмы, тангенсы, котангенсы вызывают ОДЗ (область допустимых значений).

Лайфхаки для первой части ЕГЭ по математике

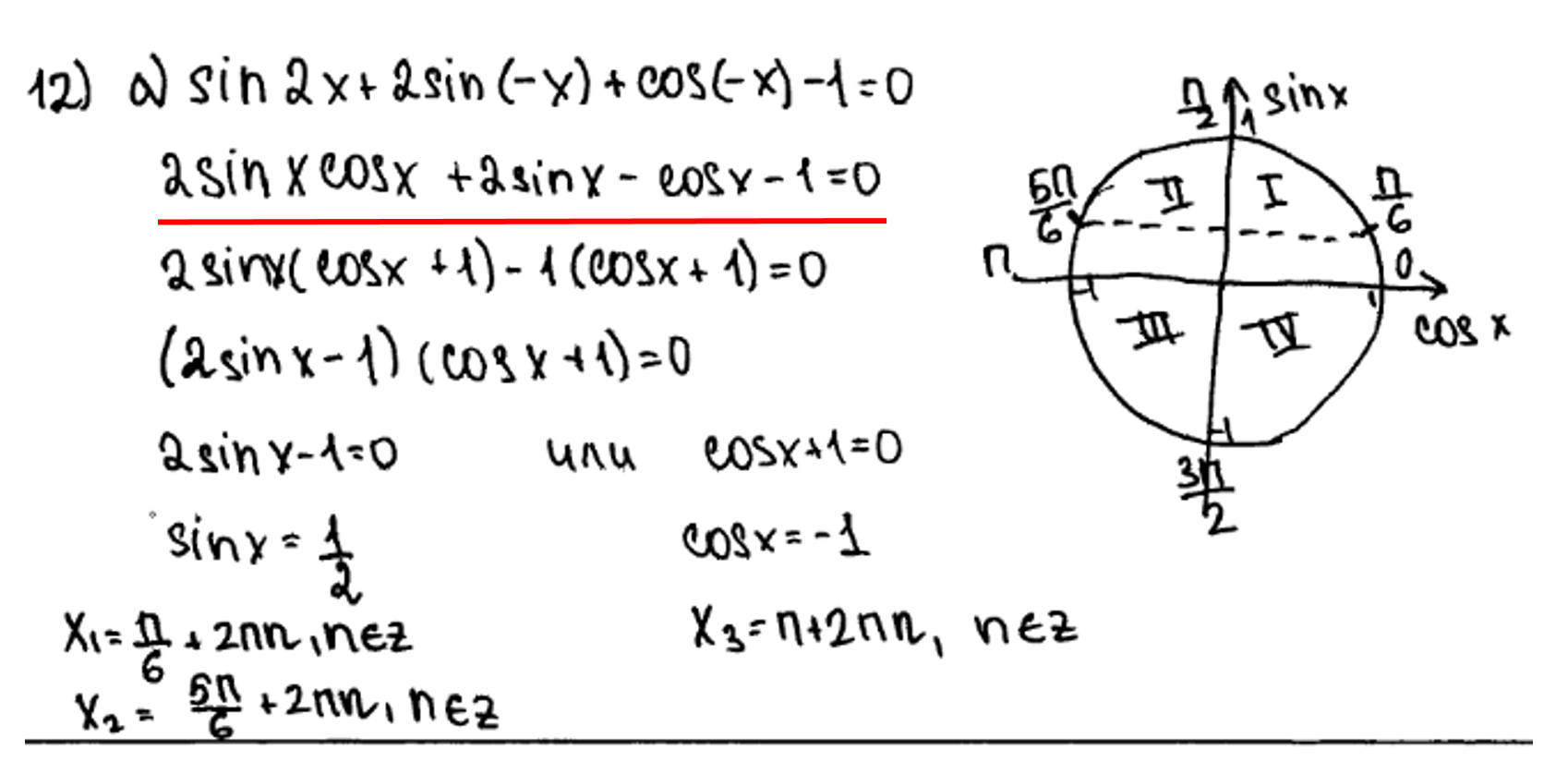
Неправильное составление формул приведения

Самая распространённая ошибки в формуле — sin(3pi/2 + A) = -cosA. Знак у косинуса смотрится по синусу, а не наоборот. 

Как избежать ошибку: выучить формулы приведения. Как их запомнить, рассказываем в видео.

Непонимание тригонометрии

В школах курсу тригонометрии уделяют мало времени, поэтому ребята не умеют работать с окружностью и не понимают её в целом. Все знаки преобразования обычно выбирают на окружности без определения четвертей и чётности — а это неправильно. 

Лучшие ресурсы и пособия для подготовки к ЕГЭ по профильной математике

Как избежать ошибку: научиться самостоятельно чертить тригонометрическую окружность, запомни все оси (тангенс, котангенс) и углы, чтобы не путаться со знаками и аргументами. 

Шпаргалка: Основные формулы тригонометрии

Оформление

Чаще всего на ЕГЭ по профильной математике снижают баллы за оформление задания.

Роман Махмутов, наставник по профильной математике в команде Вебиума, рассказал, как избежать эту ошибку: «Если говорить про недочёты в оформлении, то для большинства важно дойти до правильного ответа, поэтому не все реагируют на мои комментарии по этому поводу. Чтобы это исправить, могу дать несколько советов: 

• Чаще обсуждайте решения заданий с наставником;
• Не только смотреть на правильность/неправильность ответа, но и на советы по оформлению, так как это тоже играет очень важную роль.

Я часто сталкивался со студентами, у которых такая логика мышления: «Самое главное — получить правильный ответ, а красиво оформлять на экзамене буду». Если вы не хотите потерять баллы на экзамене, научитесь учитывать все критерии оценивания работы как можно раньше».

Техники запоминания чисел

Невнимательность 

Наставники команды Вебиума отмечают, что школьники часто невнимательно читают условие задачи. Из-за этого ход решения сразу становится неверным: приходится переделывать задание полностью.

Чтобы сдать ЕГЭ по профильной математике на высокий балл, нужно ознакомиться с темами, которые попадутся на экзамене. А также познакомиться со всеми изменениями в демоверсии — демонстрационном варианте ЕГЭ, по которому составляются реальные варианты экзамена.  

Частые ошибки в ЕГЭ по профильной математике

Научиться решать все виды уравнений — рациональные, показательные, логарифмические, тригонометрические, смешанные —  можно на курсе «Задание 12 — уравнения». Также курс можно взять с проверкой задач от наставника.

Не ошибаться — это навык, который можно проработать путём многочисленной практики. Рассмотренные нами ошибки в большей степени зависят от внимательности и ответственного подхода к заданию. Рекомендуем несколько раз проверять домашнюю работу перед сдачей и выписывать, в каких заданиях были допущены ошибки, чтобы их проанализировать.