Линейная регрессия
Перевод
Ссылка на автора
Введение
Недавно я написал об оценке максимального правдоподобия в своей продолжающейся серии статей об основах машинного обучения:
Оценка максимального правдоподобия
Основы машинного обучения (часть 2)
towardsdatascience.com
В этом посте мы узнали, что значит «моделировать» данные, а затем, как использовать MLE, чтобы найти параметры нашей модели. В этом посте мы собираемся погрузиться в линейную регрессию, одну из наиболее важных моделей в статистике, и научимся формировать ее с точки зрения MLE. Решение представляет собой прекрасный математический пример, который, как и большинство моделей MLE, богат интуицией. Я предполагаю, что вы получили представление о словаре, который я рассмотрел в других сериях (плотности вероятностей, условные вероятности, функция вероятности, данные iid и т. Д.). Если вы видите здесь что-то, что вас не устраивает, проверьте Вероятность а также MLE сообщения из этой серии для ясности.
Модель
Мы используем линейную регрессию, когда наши данные имеют линейную связь между независимыми переменными (нашими функциями) и зависимой переменной (нашей целью). В посте MLE мы увидели некоторые данные, которые тоже выглядели примерно так:
Мы заметили, что между x и y существует линейная зависимость, но она не идеальна. Мы думаем об этих недостатках как о результате некоторой ошибки или шумового процесса. Представьте, что проведете линию прямо через облако точек. Ошибка для каждой точки — это расстояние от точки до нашей линии. Мы хотели бы явно включить эти ошибки в нашу модель. Один из способов сделать это — предположить, что ошибки распределены из гауссовского распределения со средним значением 0 и некоторой неизвестной дисперсией σ². Gaussian кажется хорошим выбором, потому что наши ошибки выглядят симметричными относительно линии, и маленькие ошибки более вероятны, чем большие. Мы пишем нашу линейную модель с гауссовым шумом так:
Термин ошибки взят из нашего гауссовского алгоритма, а затем вычисленный нами у вычисляется путем добавления ошибки к выходным данным линейного уравнения. Эта модель имеет три параметра: наклон и пересечение нашей линии и дисперсию распределения шума. Наша главная цель — найти наилучшие параметры для наклона и пересечения нашей линии.
Функция правдоподобия
Чтобы применить максимальное правдоподобие, нам сначала нужно вывести функцию правдоподобия. Во-первых, давайте перепишем нашу модель сверху как единое условное распределение, заданное x:
Это эквивалентно проталкиванию нашего x через уравнение линии, а затем добавлению шума от среднего гауссова 0.
Теперь мы можем записать условное распределение y для заданного x в терминах этого гауссиана. Это просто уравнение функции плотности вероятности распределения Гаусса с нашим линейным уравнением вместо среднего значения:
Точка с запятой в условном распределении действует как запятая, но это полезное обозначение для отделения наших наблюдаемых данных от параметров.
Каждая точка является независимой и одинаково распределенной (iid), поэтому мы можем записать функцию правдоподобия относительно всех наших наблюдаемых точек как произведение каждой отдельной плотности вероятности. Поскольку σ² одинаково для каждой точки данных, мы можем вычленить термин гауссианы, который не включает x или y из произведения:
Log-правдоподобие:
Следующий шаг в MLE — найти параметры, которые максимизируют эту функцию. Чтобы упростить наше уравнение, давайте возьмем журнал нашей вероятности. Напомним, что максимизация логарифмической вероятности такая же, как максимизация вероятности, поскольку логарифм является монотонным. Натуральный логарифм вычитается по экспоненте, превращает произведения в суммы бревен и делится на вычитание бревен; так что наша логарифмическая вероятность выглядит намного проще:
Сумма квадратов ошибок:
Чтобы еще кое-что прояснить, давайте запишем вывод нашей строки как одно значение:
Теперь наша логарифмическая вероятность может быть записана как:
Чтобы убрать отрицательные знаки, давайте вспомним, что максимизация числа — это то же самое, что минимизация отрицания числа. Поэтому вместо того, чтобы максимизировать вероятность, давайте минимизируем отрицательную логарифмическую вероятность:
Наша конечная цель — найти параметры нашей линии. Чтобы минимизировать отрицательное логарифмическое правдоподобие по отношению к линейным параметрам (θs), мы можем представить, что наш дисперсионный член является фиксированной константой.
Удаление любых констант, которые не включают наши θs, не изменит решение Поэтому мы можем выбросить любые постоянные термины и изящно написать то, что мы пытаемся минимизировать, как:
Оценка максимального правдоподобия для нашей линейной модели — это линия, которая минимизирует сумму квадратов ошибок! Это прекрасный результат, и вы увидите, что минимизация квадратичных ошибок повсеместно встречается в машинном обучении и статистике.
Решение для параметров
Мы пришли к выводу, что оценки максимального правдоподобия для нашего наклона и перехвата можно найти путем минимизации суммы квадратов ошибок. Давайте расширим нашу цель минимизации и используемякак наш индекс над нашимNТочки данных:
Квадрат в формуле SSE делает его квадратичным с одним минимумом. Минимум можно найти, взяв производную по каждому из параметров, установив ее равной 0 и решив для параметров по очереди.
Перехват:
Давайте начнем с решения для перехвата. Взятие частной производной по отношению к перехвату и проработка дает нам:
Горизонтальные полосы над переменными показывают среднее значение этих переменных. Мы использовали тот факт, что сумма значений переменных равна среднему значению этих значений, умноженному на количество значений, которые у нас есть. Установка производной равной 0 и решение для перехвата дает нам:
Это довольно аккуратный результат. Это уравнение линии со средствами х и у вместо этих переменных. Перехват по-прежнему зависит от наклона, поэтому нам нужно найти его дальше.
Склон:
Мы начнем с частной производной SSE относительно нашего наклона. Мы включаем наше решение для перехвата и используем алгебру, чтобы изолировать термин наклона:
Установка этого значения равным 0 и решение для наклона дает нам:
Хотя технически мы закончили, мы можем использовать некоторую причудливую алгебру, чтобы переписать это, не используяN:
Собираем все вместе:
Мы можем использовать эти производные уравнения, чтобы написать простую функцию в python для решения параметров для любой линии, заданной как минимум двумя точками:
def find_line(xs, ys):
"""Calculates the slope and intercept"""# number of points
n = len(xs) # calculate means
x_bar = sum(xs)/n
y_bar = sum(ys)/n# calculate slope
num = 0
denom = 0
for i in range(n):
num += (xs[i]-x_bar)*(ys[i]-y_bar)
denom += (xs[i]-x_bar)**2
slope = num/denom# calculate intercept
intercept = y_bar - slope*x_barreturn slope, intercept
Используя этот код, мы можем поместить строку в наши исходные данные (см. Ниже). Это максимальная оценка правдоподобия для наших данных. Линия минимизирует сумму квадратов ошибок, поэтому этот метод линейной регрессии часто называют обычными наименьшими квадратами.
Последние мысли
Я хотел написать этот пост главным образом для того, чтобы подчеркнуть связь между минимизацией суммы квадратов ошибок и подходом оценки максимального правдоподобия к линейной регрессии. Большинство людей сначала учатся решать линейную регрессию путем минимизации квадратичной ошибки, но, как правило, не понимают, что это происходит из вероятностной модели с запечатленными в допущениях (например, гауссовых распределенных ошибок).
Существует более элегантное решение для нахождения параметров этой модели, но для этого требуется линейная алгебра. Я планирую вернуться к линейной регрессии после того, как расскажу о линейной алгебре в своей серии основ, и покажу, как ее можно использовать для подбора более сложных кривых, таких как полиномы и экспоненты.
Увидимся в следующий раз!
Task 1. Primary data analysis with Pandas
We will use this dataset SOCR.
The dataset contains 25,000 records of human heights and weights. These data were obtained in 1993 by a Growth Survey of 25,000 children from birth to 18 years of age recruited from Maternal and Child Health Centres (MCHC) and schools.
[1]. Если у Вас не установлена библиотека Seaborn — выполните в терминале команду conda install seaborn. (Seaborn не входит в сборку Anaconda, но эта библиотека предоставляет удобную высокоуровневую функциональность для визуализации данных).
import numpy as np import pandas as pd import seaborn as sns import matplotlib.pyplot as plt %matplotlib inline
Считаем данные по росту и весу (weights_heights.csv, приложенный в задании) в объект Pandas DataFrame:
data = pd.read_csv('weights_heights.csv', index_col='Index')
Построим гистограмму распределения роста подростков из выборки data. Используем метод plot для DataFrame data c аргументами y=’Height’ (это тот признак, распределение которого мы строим)
data.plot(y='Height', kind='hist', color='red', title='Height (inch.) distribution')
<matplotlib.axes._subplots.AxesSubplot at 0x11917e9e8>
Аргументы:
- y=’Height’ — тот признак, распределение которого мы строим
- kind=’hist’ — означает, что строится гистограмма
- color=’red’ — цвет
[2]. Посмотрите на первые 5 записей с помощью метода head Pandas DataFrame. Нарисуйте гистограмму распределения веса с помощью метода plot Pandas DataFrame. Сделайте гистограмму зеленой, подпишите картинку.
# Ваш код здесь data.head(5)
| Height | Weight | |
|---|---|---|
| Index | ||
| 1 | 65.78331 | 112.9925 |
| 2 | 71.51521 | 136.4873 |
| 3 | 69.39874 | 153.0269 |
| 4 | 68.21660 | 142.3354 |
| 5 | 67.78781 | 144.2971 |
data.plot(y='Weight', kind='hist', color='green', title='Weight (f.) distribution')
<matplotlib.axes._subplots.AxesSubplot at 0x11b57def0>
Один из эффективных методов первичного анализа данных — отображение попарных зависимостей признаков. Создается $m \times m$ графиков (m — число признаков), где по диагонали рисуются гистограммы распределения признаков, а вне диагонали — scatter plots зависимости двух признаков. Это можно делать с помощью метода $scatter_matrix$ Pandas Data Frame или pairplot библиотеки Seaborn.
Чтобы проиллюстрировать этот метод, интересней добавить третий признак. Создадим признак Индекс массы тела (BMI). Для этого воспользуемся удобной связкой метода apply Pandas DataFrame и lambda-функций Python.
def make_bmi(height_inch, weight_pound): METER_TO_INCH, KILO_TO_POUND = 39.37, 2.20462 return (weight_pound / KILO_TO_POUND) / \ (height_inch / METER_TO_INCH) ** 2
data['BMI'] = data.apply(lambda row: make_bmi(row['Height'], row['Weight']), axis=1)
[3]. Постройте картинку, на которой будут отображены попарные зависимости признаков , ‘Height’, ‘Weight’ и ‘BMI’ друг от друга. Используйте метод pairplot библиотеки Seaborn.
<seaborn.axisgrid.PairGrid at 0x11c089d30>
Часто при первичном анализе данных надо исследовать зависимость какого-то количественного признака от категориального (скажем, зарплаты от пола сотрудника). В этом помогут «ящики с усами» — boxplots библиотеки Seaborn. Box plot — это компактный способ показать статистики вещественного признака (среднее и квартили) по разным значениям категориального признака. Также помогает отслеживать «выбросы» — наблюдения, в которых значение данного вещественного признака сильно отличается от других.
[4]. Создайте в DataFrame data новый признак weight_category, который будет иметь 3 значения: 1 – если вес меньше 120 фунтов. (~ 54 кг.), 3 — если вес больше или равен 150 фунтов (~68 кг.), 2 – в остальных случаях. Постройте «ящик с усами» (boxplot), демонстрирующий зависимость роста от весовой категории. Используйте метод boxplot библиотеки Seaborn и метод apply Pandas DataFrame.
# Ваш код здесь def weight_category(weight): pass # Ваш код здесь if weight<120: return 1 elif weight >=150: return 3 else: return 2 data['weight_cat'] = data['Weight'].apply(weight_category) #sns.boxplot(data=data, x="weight_cat", y="Height").set(xlabel = u"Весовая категория", ylabel = u"Рост") sns.boxplot(data=data, x='weight_cat' , y= 'Height')
[<matplotlib.text.Text at 0x11cf319b0>, <matplotlib.text.Text at 0x11cd5f5c0>]
[5]. Постройте scatter plot зависимости роста от веса, используя метод plot для Pandas DataFrame с аргументом kind=’scatter’. Подпишите картинку.
# Ваш код здесь data.plot(y='Height',x='Weight', kind='scatter', color='blue', title='Height (Weight) depending')
<matplotlib.axes._subplots.AxesSubplot at 0x11cf01b70>
Task 2. Minimizing the squared error
В простейшей постановке задача прогноза значения вещественного признака по прочим признакам (задача восстановления регрессии) решается минимизацией квадратичной функции ошибки.
[6]. Напишите функцию, которая по двум параметрам $w_0$ и $w_1$ вычисляет квадратичную ошибку приближения зависимости роста $y$ от веса $x$ прямой линией $y = w_0 + w_1 * x$:
$$error(w_0, w_1) = \sum_{i=1}^n {(y_i — (w_0 + w_1 * x_i))}^2 $$
Здесь $n$ – число наблюдений в наборе данных, $y_i$ и $x_i$ – рост и вес $i$-ого человека в наборе данных.
Итак, мы решаем задачу: как через облако точек, соответсвующих наблюдениям в нашем наборе данных, в пространстве признаков «Рост» и «Вес» провести прямую линию так, чтобы минимизировать функционал из п. 6. Для начала давайте отобразим хоть какие-то прямые и убедимся, что они плохо передают зависимость роста от веса.
[7]. Проведите на графике из п. 5 Задания 1 две прямые, соответствующие значениям параметров ($w_0, w_1) = (60, 0.05)$ и ($w_0, w_1) = (50, 0.16)$. Используйте метод plot из matplotlib.pyplot, а также метод linspace библиотеки NumPy. Подпишите оси и график.
def error(w0, w1): s=0. x=data['Weight'] y=data['Height'] for i in range(1,len(data.index)): s+=(y[i]-w0-w1*x[i])**2 return s
x=np.array(data['Weight']) w0,w1=60,0.05 y1 = [w0+t*w1 for t in x] w0,w1=50,0.16 y2 = [w0+t*w1 for t in x] data.plot(y='Height',x='Weight', kind='scatter', color='blue', title='Height (Weight) depending') plt.plot(x, y1, color="red", label="line1") plt.plot(x, y2, color="green", label="line2") plt.grid(True) plt.legend(loc='upper left')
<matplotlib.legend.Legend at 0x11dec42b0>
Минимизация квадратичной функции ошибки — относительная простая задача, поскольку функция выпуклая. Для такой задачи существует много методов оптимизации. Посмотрим, как функция ошибки зависит от одного параметра (наклон прямой), если второй параметр (свободный член) зафиксировать.
[8]. Постройте график зависимости функции ошибки, посчитанной в п. 6, от параметра $w_1$ при $w_0$ = 50. Подпишите оси и график.
# Ваш код здесь w0=50. w = np.arange(-0.5, 0.8, 0.1) err = [error(w0,w1) for w1 in w] plt.title('Error') plt.xlabel('w1 ') plt.ylabel('error(50,w1)') plt.plot(w, err, color="red", label="function of error") plt.legend()
<matplotlib.legend.Legend at 0x11d71b940>
Теперь методом оптимизации найдем «оптимальный» наклон прямой, приближающей зависимость роста от веса, при фиксированном коэффициенте $w_0 = 50$.
[9]. С помощью метода minimize_scalar из scipy.optimize найдите минимум функции, определенной в п. 6, для значений параметра $w_1$ в диапазоне [-5,5]. Проведите на графике из п. 5 Задания 1 прямую, соответствующую значениям параметров ($w_0$, $w_1$) = (50, $w_1_opt$), где $w_1_opt$ – найденное в п. 8 оптимальное значение параметра $w_1$.
import scipy from scipy.optimize import minimize_scalar def error50(w1): return error(50,w1) min=minimize_scalar(error50, bounds=(-5,5), method='bounded') w1_opt=min.x min.x, min.fun
(0.14109165115062905, 79510.632440047964)
x=np.array(data['Weight']) w0,w1=50,w1_opt y = [w0+t*w1 for t in x] #xx = np.linspace(np.min(data['Weight']),np.max(data['Weight']),data.count) data.plot(y='Height',x='Weight', kind='scatter', color='blue', title='Height (Weight) depending') plt.plot(x, y, color="red", label="lineOptimum") plt.grid(True) plt.legend(loc='upper left')
<matplotlib.legend.Legend at 0x11de4aa20>
from mpl_toolkits.mplot3d import Axes3D
Создаем объекты типа matplotlib.figure.Figure (рисунок) и matplotlib.axes._subplots.Axes3DSubplot (ось).
[10]. Постройте 3D-график зависимости функции ошибки, посчитанной в п.6 от параметров $w_0$ и $w_1$. Подпишите ось $x$ меткой «Intercept», ось $y$ – меткой «Slope», a ось $z$ – меткой «Error».
fig = plt.figure() ax = fig.gca(projection='3d') # get current axis w0 = np.arange(-5, 5, 0.25) w1 = np.arange(-5, 5, 0.25) W0, W1 = np.meshgrid(w0, w1) E = error(W0,W1) # используем метод *plot_surface* объекта # типа Axes3DSubplot. Также подписываем оси. surf = ax.plot_surface(W0, W1, E) ax.set_xlabel('Intercept') ax.set_ylabel('Slope') ax.set_zlabel('Error') plt.show()
[11]. С помощью метода minimize из scipy.optimize найдите минимум функции, определенной в п. 6, для значений параметра $w_0$ в диапазоне [-100,100] и $w_1$ — в диапазоне [-5, 5]. Начальная точка – ($w_0$, $w_1$) = (0, 0). Используйте метод оптимизации L-BFGS-B (аргумент method метода minimize). Проведите на графике из п. 5 Задания 1 прямую, соответствующую найденным оптимальным значениям параметров $w_0$ и $w_1$. Подпишите оси и график.
def error1(w): s=0. x=data['Weight'] y=data['Height'] for i in range(1,len(data.index)): s+=(y[i]-w[0]-w[1]*x[i])**2 return s import scipy.optimize as optimize min = optimize.minimize(error1, np.array([0,0]), method = 'L-BFGS-B', bounds=((-100,100),(-5, 5))) min.x, min.fun
(array([ 57.57161437, 0.08200743]), 67544.152054243299)
# Ваш код здесь x=np.array(data['Weight']) w0,w1=min.x y = [w0+t*w1 for t in x] data.plot(y='Height',x='Weight', kind='scatter', color='blue', title='Height (Weight) depending') plt.plot(x, y, color="red", label="lineOptimum") plt.grid(True) plt.legend(loc='upper left')
<matplotlib.legend.Legend at 0x11da26a20>
Основы линейной регрессии
Время на прочтение
13 мин
Количество просмотров 116K
Здравствуй, Хабр!
Цель этой статьи — рассказать о линейной регрессии, а именно собрать и показать формулировки и интерпретации задачи регрессии с точки зрения математического анализа, статистики, линейной алгебры и теории вероятностей. Хотя в учебниках эта тема изложена строго и исчерпывающе, ещё одна научно-популярная статья не помешает.
! Осторожно, трафик! В статье присутствует заметное число изображений для иллюстраций, часть в формате gif.
Содержание
- Введение
- Метод наименьших квадратов
- Математический анализ
- Статистика
- Теория вероятностей
- Мультилинейная регрессия
- Линейная алгебра
- Произвольный базис
- Заключительные замечания
- Проблема выбора размерности
- Численные методы
- Реклама и заключение
Введение
Есть три сходных между собой понятия, три сестры: интерполяция, аппроксимация и регрессия.
У них общая цель: из семейства функций выбрать ту, которая обладает определенным свойством.
Интерполяция — способ выбрать из семейства функций ту, которая проходит через заданные точки. Часто функцию затем используют для вычисления в промежуточных точках. Например, мы вручную задаем цвет нескольким точкам и хотим чтобы цвета остальных точек образовали плавные переходы между заданными. Или задаем ключевые кадры анимации и хотим плавные переходы между ними. Классические примеры: интерполяция полиномами Лагранжа, сплайн-интерполяция, многомерная интерполяция (билинейная, трилинейная, методом ближайшего соседа и т.д). Есть также родственное понятие экстраполяции — предсказание поведения функции вне интервала. Например, предсказание курса доллара на основании предыдущих колебаний — экстраполяция.


В этой статье мы рассмотрим линейную регрессию. Это означает, что семейство функций, из которых мы выбираем, представляет собой линейную комбинацию наперед заданных базисных функций
Цель регрессии — найти коэффициенты этой линейной комбинации, и тем самым определить регрессионную функцию (которую также называют моделью). Отмечу, что линейную регрессию называют линейной именно из-за линейной комбинации базисных функций — это не связано с самыми базисными функциями (они могут быть линейными или нет).
Регрессия с нами уже давно: впервые метод опубликовал Лежандр в 1805 году, хотя Гаусс пришел к нему раньше и успешно использовал для предсказания орбиты «кометы» (на самом деле карликовой планеты) Цереры. Существует множество вариантов и обобщений линейной регрессии: LAD, метод наименьших квадратов, Ridge регрессия, Lasso регрессия, ElasticNet и многие другие.
Метод наименьших квадратов
Начнём с простейшего двумерного случая. Пусть нам даны точки на плоскости и мы ищем такую аффинную функцию

.
Как видно из иллюстрации, расстояние от точки до прямой можно понимать по-разному, например геометрически — это длина перпендикуляра. Однако в контексте нашей задачи нам нужно функциональное расстояние, а не геометрическое. Нас интересует разница между экспериментальным значением и предсказанием модели для каждого поэтому измерять нужно вдоль оси
.
Первое, что приходит в голову, в качестве функции потерь попробовать выражение, зависящее от абсолютных значений разниц . Простейший вариант — сумма модулей отклонений
приводит к Least Absolute Distance (LAD) регрессии.
Впрочем, более популярная функция потерь — сумма квадратов отклонений регрессанта от модели. В англоязычной литературе она носит название Sum of Squared Errors (SSE)
Метод наименьших квадратов (по англ. OLS) — линейная регрессия c в качестве функции потерь.
Такой выбор прежде всего удобен: производная квадратичной функции — линейная функция, а линейные уравнения легко решаются. Впрочем, далее я укажу и другие соображения в пользу .
Математический анализ
Простейший способ найти — вычислить частные производные по
и
, приравнять их нулю и решить систему линейных уравнений
Значения параметров, минимизирующие функцию потерь, удовлетворяют уравнениям
которые легко решить
Мы получили громоздкие и неструктурированные выражения. Сейчас мы их облагородим и вдохнем в них смысл.
Статистика
Полученные формулы можно компактно записать с помощью статистических эстиматоров: среднего , вариации
(стандартного отклонения), ковариации
и корреляции
Перепишем как
где это нескорректированное (смещенное) стандартное выборочное отклонение, а
— ковариация. Теперь вспомним, что коэффициент корреляции (коэффициент корреляции Пирсона)
и запишем
Теперь мы можем оценить все изящество дескриптивной статистики, записав уравнение регрессионной прямой так
Во-первых, это уравнение сразу указывает на два свойства регрессионной прямой:
Во-вторых, теперь становится понятно, почему метод регрессии называется именно так. В единицах стандартного отклонения отклоняется от своего среднего значения меньше чем
, потому что
. Это называется регрессией(от лат. regressus — «возвращение») по отношению к среднему. Это явление было описано сэром Фрэнсисом Гальтоном в конце XIX века в его статье «Регрессия к посредственности при наследовании роста». В статье показано, что черты (такие как рост), сильно отклоняющиеся от средних, редко передаются по наследству. Характеристики потомства как бы стремятся к среднему — на детях гениев природа отдыхает.
Возведя коэффициент корреляции в квадрат, получим коэффициент детерминации . Квадрат этой статистической меры показывает насколько хорошо регрессионная модель описывает данные.
, равный
, означает что функция идеально ложится на все точки — данные идеально скоррелированны. Можно доказать, что
показывает какая доля вариативности в данных объясняется лучшей из линейных моделей. Чтобы понять, что это значит, введем определения
— вариация исходных данных (вариация точек
).
— вариация остатков, то есть вариация отклонений от регрессионной модели — от
нужно отнять предсказание модели и найти вариацию.
— вариация регрессии, то есть вариация предсказаний регрессионной модели в точках
(обратите внимание, что среднее предсказаний модели совпадает с
).
Дело в том, что вариация исходных данных разлагается в сумму двух других вариаций: вариации случайного шума (остатков) и вариации, которая объясняется моделью (регрессии)
или
Как видим, стандартные отклонения образуют прямоугольный треугольник.
Мы стремимся избавиться от вариативности, связанной с шумом и оставить лишь вариативность, которая объясняется моделью, — хотим отделить зерна от плевел. О том, насколько это удалось лучшей из линейных моделей, свидетельствует , равный единице минус доля вариации ошибок в суммарной вариации
или доле объясненной вариации (доля вариации регрессии в полной вариации)
равен косинусу угла в прямоугольном треугольнике
. Кстати, иногда вводят долю необъясненной вариации
и она равна квадрату синуса в этом треугольнике. Если коэффициент детерминации мал, возможно мы выбрали неудачные базисные функции, линейная регрессия неприменима вовсе и т.п.
Теория вероятностей
Ранее мы пришли к функции потерь из соображений удобства, но к ней же можно прийти с помощью теории вероятностей и метода максимального правдоподобия (ММП). Напомню вкратце его суть. Предположим, у нас есть
независимых одинаково распределенных случайных величин (в нашем случае — результатов измерений). Мы знаем вид функции распределения (напр. нормальное распределение), но хотим определить параметры, которые в нее входят (например
и
). Для этого нужно вычислить вероятность получить
датапоинтов в предположении постоянных, но пока неизвестных параметров. Благодаря независимости измерений, мы получим произведение вероятностей реализации каждого измерения. Если мыслить полученную величину как функцию параметров (функция правдоподобия) и найти её максимум, мы получим оценку параметров. Зачастую вместо функции правдоподобия используют ее логарифм — дифференцировать его проще, а результат — тот же.
Вернемся к задаче простой регрессии. Допустим, что значения нам известны точно, а в измерении
присутствует случайный шум (свойство слабой экзогенности). Более того, положим, что все отклонения от прямой (свойство линейности) вызваны шумом с постоянным распределением (постоянство распределения). Тогда
где — нормально распределенная случайная величина
Исходя из предположений выше, запишем функцию правдоподобия
и ее логарифм
Таким образом, максимум правдоподобия достигается при минимуме
что дает основание принять ее в качестве функции потерь. Кстати, если
мы получим функцию потерь LAD регрессии
которую мы упоминали ранее.
Подход, который мы использовали в этом разделе — один из возможных. Можно прийти к такому же результату, используя более общие свойства. В частности, свойство постоянства распределения можно ослабить, заменив на свойства независимости, постоянства вариации (гомоскедастичность) и отсутствия мультиколлинеарности. Также вместо ММП эстимации можно воспользоваться другими методами, например линейной MMSE эстимацией.
Мультилинейная регрессия
До сих пор мы рассматривали задачу регрессии для одного скалярного признака , однако обычно регрессор — это
-мерный вектор
. Другими словами, для каждого измерения мы регистрируем
фич, объединяя их в вектор. В этом случае логично принять модель с
независимыми базисными функциями векторного аргумента —
степеней свободы соответствуют
фичам и еще одна — регрессанту
. Простейший выбор — линейные базисные функции
. При
получим уже знакомый нам базис
.
Итак, мы хотим найти такой вектор (набор коэффициентов) , что
Знак «» означает, что мы ищем решение, которое минимизирует сумму квадратов ошибок
Последнее уравнение можно переписать более удобным образом. Для этого расположим в строках матрицы (матрицы информации)
Тогда столбцы матрицы отвечают измерениям
-ой фичи. Здесь важно не запутаться:
— количество измерений,
— количество признаков (фич), которые мы регистрируем. Систему можно записать как
Квадрат нормы разности векторов в правой и левой частях уравнения образует функцию потерь
которую мы намерены минимизировать
Продифференцируем финальное выражение по (если забыли как это делается — загляните в Matrix cookbook)
приравняем производную к и получим т.н. нормальные уравнения
Если столбцы матрицы информации линейно независимы (нет идеально скоррелированных фич), то матрица
имеет обратную (доказательство можно посмотреть, например, в видео академии Хана). Тогда можно записать
где
псевдообратная к . Понятие псевдообратной матрицы введено в 1903 году Фредгольмом, она сыграла важную роль в работах Мура и Пенроуза.
Напомню, что обратить и найти
можно только если столбцы
линейно независимы. Впрочем, если столбцы
близки к линейной зависимости, вычисление
уже становится численно нестабильным. Степень линейной зависимости признаков в
или, как говорят, мультиколлинеарности матрицы
, можно измерить числом обусловленности — отношением максимального собственного значения к минимальному. Чем оно больше, тем ближе
к вырожденной и неустойчивее вычисление псевдообратной.
Линейная алгебра
К решению задачи мультилинейной регрессии можно прийти довольно естественно и с помощью линейной алгебры и геометрии, ведь даже то, что в функции потерь фигурирует норма вектора ошибок уже намекает, что у задачи есть геометрическая сторона. Мы видели, что попытка найти линейную модель, описывающую экспериментальные точки, приводит к уравнению
Если количество переменных равно количеству неизвестных и уравнения линейно независимы, то система имеет единственное решение. Однако, если число измерений превосходит число признаков, то есть уравнений больше чем неизвестных — система становится несовместной, переопределенной. В этом случае лучшее, что мы можем сделать — выбрать вектор , образ которого
ближе остальных к
. Напомню, что множество образов или колоночное пространство
— это линейная комбинация вектор-столбцов матрицы
—
-мерное линейное подпространство (мы считаем фичи линейно независимыми), линейная оболочка вектор-столбцов
. Итак, если
принадлежит
, то мы можем найти решение, если нет — будем искать, так сказать, лучшее из нерешений.
Если в дополнение к векторам мы рассмотрим все вектора им перпендикулярные, то получим еще одно подпространство и сможем любой вектор из
разложить на две компоненты, каждая из которых живет в своем подпространстве. Второе, перпендикулярное пространство, можно характеризовать следующим образом (нам это понадобится в дальнейшем). Пускай
, тогда
равен нулю в том и только в том случае, если перпендикулярен всем
, а значит и целому
. Таким образом, мы нашли два перпендикулярных линейных подпространства, линейные комбинации векторов из которых полностью, без дыр, «покрывают» все
. Иногда это обозначают c помощью символа ортогональной прямой суммы
где . В каждое из подпространств можно попасть с помощью соответствующего оператора проекции, но об этом ниже.
Теперь представим в виде разложения
Если мы ищем решение , то естественно потребовать, чтобы
была минимальна, ведь это длина вектора-остатка. Учитывая перпендикулярность подпространств и теорему Пифагора
но поскольку, выбрав подходящий , я могу получить любой вектор колоночного пространства, то задача сводится к
а останется в качестве неустранимой ошибки. Любой другой выбор
сделает ошибку только больше.
Если теперь вспомнить, что , то легко видеть
что очень удобно, так как у нас нет, а вот
— есть. Вспомним из предыдущего параграфа, что
имеет обратную при условии линейной независимости признаков и запишем решение
где уже знакомая нам псевдообратная матрица. Если нам интересна проекция
, то можно записать
где — оператор проекции на колоночное пространство.
Выясним геометрический смысл коэффициента детерминации.
Заметьте, что фиолетовый вектор пропорционален первому столбцу матрицы информации
, который состоит из одних единиц согласно нашему выбору базисных функций. В RGB треугольнике
Так как этот треугольник прямоугольный, то по теореме Пифагора
Это геометрическая интерпретация уже известного нам факта, что
Мы знаем, что
а значит
Красиво, не правда ли?
Произвольный базис
Как мы знаем, регрессия выполняется на базисных функциях и её результатом есть модель
но до сих пор мы использовали простейшие , которые просто ретранслировали изначальные признаки без изменений, ну разве что дополняли их постоянной фичей
. Как можно было заметить, на самом деле ни вид
, ни их количество ничем не ограничены — главное, чтобы функции в базисе были линейно независимы. Обычно, выбор делается исходя из предположений о природе процесса, который мы моделируем. Если у нас есть основания полагать, что точки
ложатся на параболу, а не на прямую, то стоит выбрать базис
. Количество базисных функций может быть как меньшим, так и большим, чем количество изначальных фич.
Если мы определились с базисом, то дальше действуем следующим образом. Мы формируем матрицу информации
записываем функцию потерь
и находим её минимум, например с помощью псевдообратной матрицы
или другим методом.
Заключительные замечания
Проблема выбора размерности
На практике часто приходится самостоятельно строить модель явления, то есть определяться сколько и каких нужно взять базисных функций. Первый порыв «набрать побольше» может сыграть злую шутку: модель окажется слишком чувствительной к шумам в данных (переобучение). С другой стороны, если излишне ограничить модель, она будет слишком грубой (недообучение).
Есть два способа выйти из ситуации. Первый: последовательно наращивать количество базисных функций, проверять качество регрессии и вовремя остановиться. Или же второй: выбрать функцию потерь, которая определит число степеней свободы автоматически. В качестве критерия успешности регрессии можно использовать коэффициент детерминации, о котором уже упоминалось выше, однако, проблема в том, что монотонно растет с ростом размерности базиса. Поэтому вводят скорректированный коэффициент
где — размер выборки,
— количество независимых переменных. Следя за
, мы можем вовремя остановиться и перестать добавлять дополнительные степени свободы.
Вторая группа подходов — регуляризации, самые известные из которых Ridge(/гребневая/Тихоновская регуляризация), Lasso(
регуляризация) и Elastic Net(Ridge+Lasso). Главная идея этих методов: модифицировать функцию потерь дополнительными слагаемыми, которые не позволят вектору коэффициентов
неограниченно расти и тем самым воспрепятствуют переобучению
где и
— параметры, которые регулируют «силу» регуляризации. Это обширная тема с красивой геометрией, которая заслуживает отдельного рассмотрения. Упомяну кстати, что для случая двух переменных при помощи вероятностной интерпретации можно получить Ridge и Lasso регрессии, удачно выбрав априорное распределения для коэффициента
Численные методы
Скажу пару слов, как минимизировать функцию потерь на практике. SSE — это обычная квадратичная функция, которая параметризируется входными данными, так что принципиально ее можно минимизировать методом скорейшего спуска или другими методами оптимизации. Разумеется, лучшие результаты показывают алгоритмы, которые учитывают вид функции SSE, например метод стохастического градиентного спуска. Реализация Lasso регрессии в scikit-learn использует метод координатного спуска.
Также можно решить нормальные уравнения с помощью численных методов линейной алгебры. Эффективный метод, который используется в scikit-learn для МНК — нахождение псевдообратной матрицы с помощью сингулярного разложения. Поля этой статьи слишком узки, чтобы касаться этой темы, за подробностями советую обратиться к курсу лекций К.В.Воронцова.
Реклама и заключение
Эта статья — сокращенный пересказ одной из глав курса по классическому машинному обучению в Киевском академическом университете (преемник Киевского отделения Московского физико-технического института, КО МФТИ). Автор статьи помогал в создании этого курса. Технически курс выполнен на платформе Google Colab, что позволяет совмещать формулы, форматированные LaTeX, исполняемый код Python и интерактивные демонстрации на Python+JavaScript, так что студенты могут работать с материалами курса и запускать код с любого компьютера, на котором есть браузер. На главной странице собраны ссылки на конспекты, «рабочие тетради» для практик и дополнительные ресурсы. В основу курса положены следующие принципы:
- все материалы должны быть доступны студентам с первой пары;
- лекция нужны для понимания, а не для конспектирования (конспекты уже готовы, нет смысла их писать, если не хочется);
- конспект — больше чем лекция (материала в конспектах больше, чем было озвучено на лекции, фактически конспекты представляют собой полноценный учебник);
- наглядность и интерактивность (иллюстрации, фото, демки, гифки, код, видео с youtube).
Если хотите посмотреть на результат — загляните на страничку курса на GitHub.
Надеюсь вам было интересно, спасибо за внимание.
Мы начнем с самых простых и понятных моделей машинного обучения: линейных. В этой главе мы разберёмся, что это такое, почему они работают и в каких случаях их стоит использовать. Так как это первый класс моделей, с которым вы столкнётесь, мы постараемся подробно проговорить все важные моменты. Заодно объясним, как работает машинное обучение, на сравнительно простых примерах.
Почему модели линейные?
Представьте, что у вас есть множество объектов $mathbb{X}$, а вы хотели бы каждому объекту сопоставить какое-то значение. К примеру, у вас есть набор операций по банковской карте, а вы бы хотели, понять, какие из этих операций сделали мошенники. Если вы разделите все операции на два класса и нулём обозначите законные действия, а единицей мошеннические, то у вас получится простейшая задача классификации. Представьте другую ситуацию: у вас есть данные геологоразведки, по которым вы хотели бы оценить перспективы разных месторождений. В данном случае по набору геологических данных ваша модель будет, к примеру, оценивать потенциальную годовую доходность шахты. Это пример задачи регрессии. Числа, которым мы хотим сопоставить объекты из нашего множества иногда называют таргетами (от английского target).
Таким образом, задачи классификации и регрессии можно сформулировать как поиск отображения из множества объектов $mathbb{X}$ в множество возможных таргетов.
Математически задачи можно описать так:
- классификация: $mathbb{X} to {0,1,ldots,K}$, где $0, ldots, K$ – номера классов,
- регрессия: $mathbb{X} to mathbb{R}$.
Очевидно, что просто сопоставить какие-то объекты каким-то числам — дело довольно бессмысленное. Мы же хотим быстро обнаруживать мошенников или принимать решение, где строить шахту. Значит нам нужен какой-то критерий качества. Мы бы хотели найти такое отображение, которое лучше всего приближает истинное соответствие между объектами и таргетами. Что значит «лучше всего» – вопрос сложный. Мы к нему будем много раз возвращаться. Однако, есть более простой вопрос: среди каких отображений мы будем искать самое лучшее? Возможных отображений может быть много, но мы можем упростить себе задачу и договориться, что хотим искать решение только в каком-то заранее заданном параметризированном семействе функций. Вся эта глава будет посвящена самому простому такому семейству — линейным функциям вида
$$
y = w_1 x_1 + ldots + w_D x_D + w_0,
$$
где $y$ – целевая переменная (таргет), $(x_1, ldots, x_D)$ – вектор, соответствующий объекту выборки (вектор признаков), а $w_1, ldots, w_D, w_0$ – параметры модели. Признаки ещё называют фичами (от английского features). Вектор $w = (w_1,ldots,w_D)$ часто называют вектором весов, так как на предсказание модели можно смотреть как на взвешенную сумму признаков объекта, а число $w_0$ – свободным коэффициентом, или сдвигом (bias). Более компактно линейную модель можно записать в виде
$$y = langle x, wrangle + w_0$$
Теперь, когда мы выбрали семейство функций, в котором будем искать решение, задача стала существенно проще. Мы теперь ищем не какое-то абстрактное отображение, а конкретный вектор $(w_0,w_1,ldots,w_D)inmathbb{R}^{D+1}$.
Замечание. Чтобы применять линейную модель, нужно, чтобы каждый объект уже был представлен вектором численных признаков $x_1,ldots,x_D$. Конечно, просто текст или граф в линейную модель не положить, придётся сначала придумать для него численные фичи. Модель называют линейной, если она является линейной по этим численным признакам.
Разберёмся, как будет работать такая модель в случае, если $D = 1$. То есть у наших объектов есть ровно один численный признак, по которому они отличаются. Теперь наша линейная модель будет выглядеть совсем просто: $y = w_1 x_1 + w_0$. Для задачи регрессии мы теперь пытаемся приблизить значение игрек какой-то линейной функцией от переменной икс. А что будет значить линейность для задачи классификации? Давайте вспомним про пример с поиском мошеннических транзакций по картам. Допустим, нам известна ровно одна численная переменная — объём транзакции. Для бинарной классификации транзакций на законные и потенциально мошеннические мы будем искать так называемое разделяющее правило: там, где значение функции положительно, мы будем предсказывать один класс, где отрицательно – другой. В нашем примере простейшим правилом будет какое-то пороговое значение объёма транзакций, после которого есть смысл пометить транзакцию как подозрительную.
В случае более высоких размерностей вместо прямой будет гиперплоскость с аналогичным смыслом.
Вопрос на подумать. Если вы посмотрите содержание учебника, то не найдёте в нём ни «полиномиальных» моделей, ни каких-нибудь «логарифмических», хотя, казалось бы, зависимости бывают довольно сложными. Почему так?
Ответ (не открывайте сразу; сначала подумайте сами!)Линейные зависимости не так просты, как кажется. Пусть мы решаем задачу регрессии. Если мы подозреваем, что целевая переменная $y$ не выражается через $x_1, x_2$ как линейная функция, а зависит ещё от логарифма $x_1$ и ещё как-нибудь от того, разные ли знаки у признаков, то мы можем ввести дополнительные слагаемые в нашу линейную зависимость, просто объявим эти слагаемые новыми переменными и добавив перед ними соответствующие регрессионные коэффициенты
$$y approx w_1 x_1 + w_2 x_2 + w_3log{x_1} + w_4text{sgn}(x_1x_2) + w_0,$$
и в итоге из двумерной нелинейной задачи мы получили четырёхмерную линейную регрессию.
Вопрос на подумать. А как быть, если одна из фичей является категориальной, то есть принимает значения из (обычно конечного числа) значений, не являющихся числами? Например, это может быть время года, уровень образования, марка машины и так далее. Как правило, с такими значениями невозможно производить арифметические операции или же результаты их применения не имеют смысла.
Ответ (не открывайте сразу; сначала подумайте сами!)В линейную модель можно подать только численные признаки, так что категориальную фичу придётся как-то закодировать. Рассмотрим для примера вот такой датасет
Здесь два категориальных признака – pet_type и color. Первый принимает четыре различных значения, второй – пять.
Самый простой способ – использовать one-hot кодирование (one-hot encoding). Пусть исходный признак мог принимать $M$ значений $c_1,ldots, c_M$. Давайте заменим категориальный признак на $M$ признаков, которые принимают значения $0$ и $1$: $i$-й будет отвечать на вопрос «принимает ли признак значение $c_i$?». Иными словами, вместо ячейки со значением $c_i$ у объекта появляется строка нулей и единиц, в которой единица стоит только на $i$-м месте.
В нашем примере получится вот такая табличка:
Можно было бы на этом остановиться, но добавленные признаки обладают одним неприятным свойством: в каждом из них ровно одна единица, так что сумма соответствующих столбцов равна столбцу из единиц. А это уже плохо. Представьте, что у нас есть линейная модель
$$y sim w_1x_1 + ldots + w_{D-1}x_{d-1} + w_{c_1}x_{c_1} + ldots + w_{c_M}x_{c_M} + w_0$$
Преобразуем немного правую часть:
$$ysim w_1x_1 + ldots + w_{D-1}x_{d-1} + underbrace{(w_{c_1} — w_{c_M})}_{=:w’_{c_1}}x_{c_1} + ldots + underbrace{(w_{c_{M-1}} — w_{c_M})}_{=:w’_{C_{M-1}}}x_{c_{M-1}} + w_{c_M}underbrace{(x_{c_1} + ldots + x_{c_M})}_{=1} + w_0 = $$
$$ = w_1x_1 + ldots + w_{D-1}x_{d-1} + w’_{c_1}x_{c_1} + ldots + w’_{c_{M-1}}x_{c_{M-1}} + underbrace{(w_{c_M} + w_0)}_{=w’_{0}}$$
Как видим, от одного из новых признаков можно избавиться, не меняя модель. Больше того, это стоит сделать, потому что наличие «лишних» признаков ведёт к переобучению или вовсе ломает модель – подробнее об этом мы поговорим в разделе про регуляризацию. Поэтому при использовании one-hot-encoding обычно выкидывают признак, соответствующий одному из значений. Например, в нашем примере итоговая матрица объекты-признаки будет иметь вид:
Конечно, one-hot кодирование – это самый наивный способ работы с категориальными признаками, и для более сложных фичей или фичей с большим количеством значений оно плохо подходит. С рядом более продвинутых техник вы познакомитесь в разделе про обучение представлений.
Помимо простоты, у линейных моделей есть несколько других достоинств. К примеру, мы можем достаточно легко судить, как влияют на результат те или иные признаки. Скажем, если вес $w_i$ положителен, то с ростом $i$-го признака таргет в случае регрессии будет увеличиваться, а в случае классификации наш выбор будет сдвигаться в пользу одного из классов. Значение весов тоже имеет прозрачную интерпретацию: чем вес $w_i$ больше, тем «важнее» $i$-й признак для итогового предсказания. То есть, если вы построили линейную модель, вы неплохо можете объяснить заказчику те или иные её результаты. Это качество моделей называют интерпретируемостью. Оно особенно ценится в индустриальных задачах, цена ошибки в которых высока. Если от работы вашей модели может зависеть жизнь человека, то очень важно понимать, как модель принимает те или иные решения и какими принципами руководствуется. При этом не все методы машинного обучения хорошо интерпретируемы, к примеру, поведение искусственных нейронных сетей или градиентного бустинга интерпретировать довольно сложно.
В то же время слепо доверять весам линейных моделей тоже не стоит по целому ряду причин:
- Линейные модели всё-таки довольно узкий класс функций, они неплохо работают для небольших датасетов и простых задач. Однако, если вы решаете линейной моделью более сложную задачу, то вам, скорее всего, придётся выдумывать дополнительные признаки, являющиеся сложными функциями от исходных. Поиск таких дополнительных признаков называется feature engineering, технически он устроен примерно так, как мы описали в вопросе про «полиномиальные модели». Вот только поиском таких искусственных фичей можно сильно увлечься, так что осмысленность интерпретации будет сильно зависеть от здравого смысла эксперта, строившего модель.
- Если между признаками есть приближённая линейная зависимость, коэффициенты в линейной модели могут совершенно потерять физический смысл (об этой проблеме и о том, как с ней бороться, мы поговорим дальше, когда будем обсуждать регуляризацию).
- Особенно осторожно стоит верить в утверждения вида «этот коэффициент маленький, значит, этот признак не важен». Во-первых, всё зависит от масштаба признака: вдруг коэффициент мал, чтобы скомпенсировать его. Во-вторых, зависимость действительно может быть слабой, но кто знает, в какой ситуации она окажется важна. Такие решения принимаются на основе данных, например, путём проверки статистического критерия (об этом мы коротко упомянем в разделе про вероятностные модели).
- Конкретные значения весов могут меняться в зависимости от обучающей выборки, хотя с ростом её размера они будут потихоньку сходиться к весам «наилучшей» линейной модели, которую можно было бы построить по всем-всем-всем данным на свете.
Обсудив немного общие свойства линейных моделей, перейдём к тому, как их всё-таки обучать. Сначала разберёмся с регрессией, а затем настанет черёд классификации.
Линейная регрессия и метод наименьших квадратов (МНК)
Мы начнём с использования линейных моделей для решения задачи регрессии. Простейшим примером постановки задачи линейной регрессии является метод наименьших квадратов (Ordinary least squares).
Пусть у нас задан датасет $(X, y)$, где $y=(y_i)_{i=1}^N in mathbb{R}^N$ – вектор значений целевой переменной, а $X=(x_i)_{i = 1}^N in mathbb{R}^{N times D}, x_i in mathbb{R}^D$ – матрица объекты-признаки, в которой $i$-я строка – это вектор признаков $i$-го объекта выборки. Мы хотим моделировать зависимость $y_i$ от $x_i$ как линейную функцию со свободным членом. Общий вид такой функции из $mathbb{R}^D$ в $mathbb{R}$ выглядит следующим образом:
$$color{#348FEA}{f_w(x_i) = langle w, x_i rangle + w_0}$$
Свободный член $w_0$ часто опускают, потому что такого же результата можно добиться, добавив ко всем $x_i$ признак, тождественно равный единице; тогда роль свободного члена будет играть соответствующий ему вес:
$$begin{pmatrix}x_{i1} & ldots & x_{iD} end{pmatrix}cdotbegin{pmatrix}w_1\ vdots \ w_Dend{pmatrix} + w_0 =
begin{pmatrix}1 & x_{i1} & ldots & x_{iD} end{pmatrix}cdotbegin{pmatrix}w_0 \ w_1\ vdots \ w_D end{pmatrix}$$
Поскольку это сильно упрощает запись, в дальнейшем мы будем считать, что это уже сделано и зависимость имеет вид просто $f_w(x_i) = langle w, x_i rangle$.
Сведение к задаче оптимизации
Мы хотим, чтобы на нашем датасете (то есть на парах $(x_i, y_i)$ из обучающей выборки) функция $f_w$ как можно лучше приближала нашу зависимость.
Для того, чтобы чётко сформулировать задачу, нам осталось только одно: на математическом языке выразить желание «приблизить $f_w(x)$ к $y$». Говоря простым языком, мы должны научиться измерять качество модели и минимизировать её ошибку, как-то меняя обучаемые параметры. В нашем примере обучаемые параметры — это веса $w$. Функция, оценивающая то, как часто модель ошибается, традиционно называется функцией потерь, функционалом качества или просто лоссом (loss function). Важно, чтобы её было легко оптимизировать: скажем, гладкая функция потерь – это хорошо, а кусочно постоянная – просто ужасно.
Функции потерь бывают разными. От их выбора зависит то, насколько задачу в дальнейшем легко решать, и то, в каком смысле у нас получится приблизить предсказание модели к целевым значениям. Интуитивно понятно, что для нашей текущей задачи нам нужно взять вектор $y$ и вектор предсказаний модели и как-то сравнить, насколько они похожи. Так как эти вектора «живут» в одном векторном пространстве, расстояние между ними вполне может быть функцией потерь. Более того, положительная непрерывная функция от этого расстояния тоже подойдёт в качестве функции потерь. При этом способов задать расстояние между векторами тоже довольно много. От всего этого разнообразия глаза разбегаются, но мы обязательно поговорим про это позже. Сейчас давайте в качестве лосса возьмём квадрат $L^2$-нормы вектора разницы предсказаний модели и $y$. Во-первых, как мы увидим дальше, так задачу будет нетрудно решить, а во-вторых, у этого лосса есть ещё несколько дополнительных свойств:
-
$L^2$-норма разницы – это евклидово расстояние $|y — f_w(x)|_2$ между вектором таргетов и вектором ответов модели, то есть мы их приближаем в смысле самого простого и понятного «расстояния».
-
Как мы увидим в разделе про вероятностные модели, с точки зрения статистики это соответствует гипотезе о том, что наши данные состоят из линейного «сигнала» и нормально распределенного «шума».
Так вот, наша функция потерь выглядит так:
$$L(f, X, y) = |y — f(X)|_2^2 = $$
$$= |y — Xw|_2^2 = sum_{i=1}^N(y_i — langle x_i, w rangle)^2$$
Такой функционал ошибки не очень хорош для сравнения поведения моделей на выборках разного размера. Представьте, что вы хотите понять, насколько качество модели на тестовой выборке из $2500$ объектов хуже, чем на обучающей из $5000$ объектов. Вы измерили $L^2$-норму ошибки и получили в одном случае $300$, а в другом $500$. Эти числа не очень интерпретируемы. Гораздо лучше посмотреть на среднеквадратичное отклонение
$$L(f, X, y) = frac1Nsum_{i=1}^N(y_i — langle x_i, w rangle)^2$$
По этой метрике на тестовой выборке получаем $0,12$, а на обучающей $0,1$.
Функция потерь $frac1Nsum_{i=1}^N(y_i — langle x_i, w rangle)^2$ называется Mean Squared Error, MSE или среднеквадратическим отклонением. Разница с $L^2$-нормой чисто косметическая, на алгоритм решения задачи она не влияет:
$$color{#348FEA}{text{MSE}(f, X, y) = frac{1}{N}|y — X w|_2^2}$$
В самом широком смысле, функции работают с объектами множеств: берут какой-то входящий объект из одного множества и выдают на выходе соответствующий ему объект из другого. Если мы имеем дело с отображением, которое на вход принимает функции, а на выходе выдаёт число, то такое отображение называют функционалом. Если вы посмотрите на нашу функцию потерь, то увидите, что это именно функционал. Для каждой конкретной линейной функции, которую задают веса $w_i$, мы получаем число, которое оценивает, насколько точно эта функция приближает наши значения $y$. Чем меньше это число, тем точнее наше решение, значит для того, чтобы найти лучшую модель, этот функционал нам надо минимизировать по $w$:
$$color{#348FEA}{|y — Xw|_2^2 longrightarrow min_w}$$
Эту задачу можно решать разными способами. В этой главе мы сначала решим эту задачу аналитически, а потом приближенно. Сравнение двух этих решений позволит нам проиллюстрировать преимущества того подхода, которому посвящена эта книга. На наш взгляд, это самый простой способ «на пальцах» показать суть машинного обучения.
МНК: точный аналитический метод
Точку минимума можно найти разными способами. Если вам интересно аналитическое решение, вы можете найти его в главе про матричные дифференцирования (раздел «Примеры вычисления производных сложных функций»). Здесь же мы воспользуемся геометрическим подходом.
Пусть $x^{(1)},ldots,x^{(D)}$ – столбцы матрицы $X$, то есть столбцы признаков. Тогда
$$Xw = w_1x^{(1)}+ldots+w_Dx^{(D)},$$
и задачу регрессии можно сформулировать следующим образом: найти линейную комбинацию столбцов $x^{(1)},ldots,x^{(D)}$, которая наилучшим способом приближает столбец $y$ по евклидовой норме – то есть найти проекцию вектора $y$ на подпространство, образованное векторами $x^{(1)},ldots,x^{(D)}$.
Разложим $y = y_{parallel} + y_{perp}$, где $y_{parallel} = Xw$ – та самая проекция, а $y_{perp}$ – ортогональная составляющая, то есть $y_{perp} = y — Xwperp x^{(1)},ldots,x^{(D)}$. Как это можно выразить в матричном виде? Оказывается, очень просто:
$$X^T(y — Xw) = 0$$
В самом деле, каждый элемент столбца $X^T(y — Xw)$ – это скалярное произведение строки $X^T$ (=столбца $X$ = одного из $x^{(i)}$) на $y — Xw$. Из уравнения $X^T(y — Xw) = 0$ уже очень легко выразить $w$:
$$w = (X^TX)^{-1}X^Ty$$
Вопрос на подумать Для вычисления $w_{ast}$ нам приходится обращать (квадратную) матрицу $X^TX$, что возможно, только если она невырожденна. Что это значит с точки зрения анализа данных? Почему мы верим, что это выполняется во всех разумных ситуациях?
Ответ (не открывайте сразу; сначала подумайте сами!)Как известно из линейной алгебры, для вещественной матрицы $X$ ранги матриц $X$ и $X^TX$ совпадают. Матрица $X^TX$ невырожденна тогда и только тогда, когда её ранг равен числу её столбцов, что равно числу столбцов матрицы $X$. Иными словами, формула регрессии поломается, только если столбцы матрицы $X$ линейно зависимы. Столбцы матрицы $X$ – это признаки. А если наши признаки линейно зависимы, то, наверное, что-то идёт не так и мы должны выкинуть часть из них, чтобы остались только линейно независимые.
Другое дело, что зачастую признаки могут быть приближённо линейно зависимы, особенно если их много. Тогда матрица $X^TX$ будет близка к вырожденной, и это, как мы дальше увидим, будет вести к разным, в том числе вычислительным проблемам.
Вычислительная сложность аналитического решения — $O(N^2D + D^3)$, где $N$ — длина выборки, $D$ — число признаков у одного объекта. Слагаемое $N^2D$ отвечает за сложность перемножения матриц $X^T$ и $X$, а слагаемое $D^3$ — за сложность обращения их произведения. Перемножать матрицы $(X^TX)^{-1}$ и $X^T$ не стоит. Гораздо лучше сначала умножить $y$ на $X^T$, а затем полученный вектор на $(X^TX)^{-1}$: так будет быстрее и, кроме того, не нужно будет хранить матрицу $(X^TX)^{-1}X^T$.
Вычисление можно ускорить, используя продвинутые алгоритмы перемножения матриц или итерационные методы поиска обратной матрицы.
Проблемы «точного» решения
Заметим, что для получения ответа нам нужно обратить матрицу $X^TX$. Это создает множество проблем:
- Основная проблема в обращении матрицы — это то, что вычислительно обращать большие матрицы дело сложное, а мы бы хотели работать с датасетами, в которых у нас могут быть миллионы точек,
- Матрица $X^TX$, хотя почти всегда обратима в разумных задачах машинного обучения, зачастую плохо обусловлена. Особенно если признаков много, между ними может появляться приближённая линейная зависимость, которую мы можем упустить на этапе формулировки задачи. В подобных случаях погрешность нахождения $w$ будет зависеть от квадрата числа обусловленности матрицы $X$, что очень плохо. Это делает полученное таким образом решение численно неустойчивым: малые возмущения $y$ могут приводить к катастрофическим изменениям $w$.
Пара слов про число обусловленности.Пожертвовав математической строгостью, мы можем считать, что число обусловленности матрицы $X$ – это корень из отношения наибольшего и наименьшего из собственных чисел матрицы $X^TX$. Грубо говоря, оно показывает, насколько разного масштаба бывают собственные значения $X^TX$. Если рассмотреть $L^2$-норму ошибки предсказания, как функцию от $w$, то её линии уровня будут эллипсоидами, форма которых определяется квадратичной формой с матрицей $X^TX$ (проверьте это!). Таким образом, число обусловленности говорит о том, насколько вытянутыми являются эти эллипсоиды.ПодробнееДанные проблемы не являются поводом выбросить решение на помойку. Существует как минимум два способа улучшить его численные свойства, однако если вы не знаете про сингулярное разложение, то лучше вернитесь сюда, когда узнаете.
-
Построим $QR$-разложение матрицы $X$. Напомним, что это разложение, в котором матрица $Q$ ортогональна по столбцам (то есть её столбцы ортогональны и имеют длину 1; в частности, $Q^TQ=E$), а $R$ квадратная и верхнетреугольная. Подставив его в формулу, получим
$$w = ((QR)^TQR)^{-1}(QR)^T y = (R^Tunderbrace{Q^TQ}_{=E}R)^{-1}R^TQ^Ty = R^{-1}R^{-T}R^TQ^Ty = R^{-1}Q^Ty$$
Отметим, что написать $(R^TR)^{-1} = R^{-1}R^{-T}$ мы имеем право благодаря тому, что $R$ квадратная. Полученная формула намного проще, обращение верхнетреугольной матрицы (=решение системы с верхнетреугольной левой частью) производится быстро и хорошо, погрешность вычисления $w$ будет зависеть просто от числа обусловленности матрицы $X$, а поскольку нахождение $QR$-разложения является достаточно стабильной операцией, мы получаем решение с более хорошими, чем у исходной формулы, численными свойствами.
-
Также можно использовать псевдообратную матрицу, построенную с помощью сингулярного разложения, о котором подробно написано в разделе про матричные разложения. А именно, пусть
$$A = Uunderbrace{mathrm{diag}(sigma_1,ldots,sigma_r)}_{=Sigma}V^T$$
– это усечённое сингулярное разложение, где $r$ – это ранг $A$. В таком случае диагональная матрица посередине является квадратной, $U$ и $V$ ортогональны по столбцам: $U^TU = E$, $V^TV = E$. Тогда
$$w = (VSigma underbrace{U^TU}_{=E}Sigma V^T)^{-1}VSigma U^Ty$$
Заметим, что $VSigma^{-2}V^Tcdot VSigma^2V^T = E = VSigma^2V^Tcdot VSigma^{-2}V^T$, так что $(VSigma^2 V^T)^{-1} = VSigma^{-2}V^T$, откуда
$$w = VSigma^{-2}underbrace{V^TV}_{=E}Sigma U^Ty = VSigma^{-1}Uy$$
Хорошие численные свойства сингулярного разложения позволяют утверждать, что и это решение ведёт себя довольно неплохо.
Тем не менее, вычисление всё равно остаётся довольно долгим и будет по-прежнему страдать (хоть и не так сильно) в случае плохой обусловленности матрицы $X$.
Полностью вылечить проблемы мы не сможем, но никто и не обязывает нас останавливаться на «точном» решении (которое всё равно никогда не будет вполне точным). Поэтому ниже мы познакомим вас с совершенно другим методом.
МНК: приближенный численный метод
Минимизируемый функционал является гладким и выпуклым, а это значит, что можно эффективно искать точку его минимума с помощью итеративных градиентных методов. Более подробно вы можете прочитать о них в разделе про методы оптимизации, а здесь мы лишь коротко расскажем об одном самом базовом подходе.
Как известно, градиент функции в точке направлен в сторону её наискорейшего роста, а антиградиент (противоположный градиенту вектор) в сторону наискорейшего убывания. То есть имея какое-то приближение оптимального значения параметра $w$, мы можем его улучшить, посчитав градиент функции потерь в точке и немного сдвинув вектор весов в направлении антиградиента:
$$w_j mapsto w_j — alpha frac{d}{d{w_j}} L(f_w, X, y) $$
где $alpha$ – это параметр алгоритма («темп обучения»), который контролирует величину шага в направлении антиградиента. Описанный алгоритм называется градиентным спуском.
Посмотрим, как будет выглядеть градиентный спуск для функции потерь $L(f_w, X, y) = frac1Nvertvert Xw — yvertvert^2$. Градиент квадрата евклидовой нормы мы уже считали; соответственно,
$$
nabla_wL = frac2{N} X^T (Xw — y)
$$
Следовательно, стартовав из какого-то начального приближения, мы можем итеративно уменьшать значение функции, пока не сойдёмся (по крайней мере в теории) к минимуму (вообще говоря, локальному, но в данном случае глобальному).
Алгоритм градиентного спуска
w = random_normal() # можно пробовать и другие виды инициализации
repeat S times: # другой вариант: while abs(err) > tolerance
f = X.dot(w) # посчитать предсказание
err = f - y # посчитать ошибку
grad = 2 * X.T.dot(err) / N # посчитать градиент
w -= alpha * grad # обновить веса
С теоретическими результатами о скорости и гарантиях сходимости градиентного спуска вы можете познакомиться в главе про методы оптимизации. Мы позволим себе лишь несколько общих замечаний:
- Поскольку задача выпуклая, выбор начальной точки влияет на скорость сходимости, но не настолько сильно, чтобы на практике нельзя было стартовать всегда из нуля или из любой другой приятной вам точки;
- Число обусловленности матрицы $X$ существенно влияет на скорость сходимости градиентного спуска: чем более вытянуты эллипсоиды уровня функции потерь, тем хуже;
- Темп обучения $alpha$ тоже сильно влияет на поведение градиентного спуска; вообще говоря, он является гиперпараметром алгоритма, и его, возможно, придётся подбирать отдельно. Другими гиперпараметрами являются максимальное число итераций $S$ и/или порог tolerance.
Иллюстрация.Рассмотрим три задачи регрессии, для которых матрица $X$ имеет соответственно маленькое, среднее и большое числа обусловленности. Будем строить для них модели вида $y=w_1x_1 + w_2x_2$. Раскрасим плоскость $(w_1, w_2)$ в соответствии со значениями $|X_{text{train}}w — y_{text{train}}|^2$. Тёмная область содержит минимум этой функции – оптимальное значение $w_{ast}$. Также запустим из из двух точек градиентный спуск с разными значениями темпа обучения $alpha$ и посмотрим, что получится:
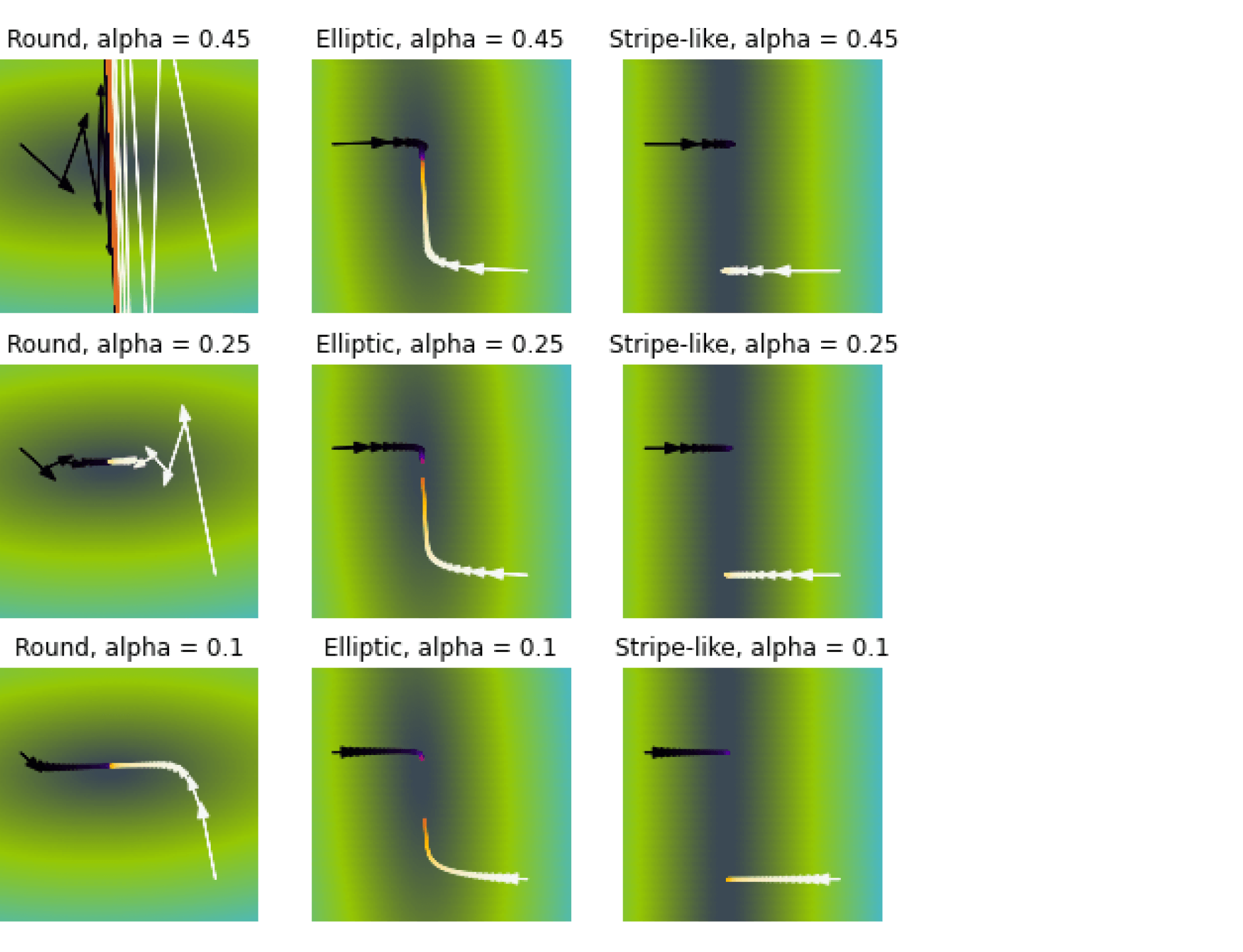
Итог: при неудачном выборе $alpha$ алгоритм не сходится или идёт вразнос, а для плохо обусловленной задачи он сходится абы куда.
Вычислительная сложность градиентного спуска – $O(NDS)$, где, как и выше, $N$ – длина выборки, $D$ – число признаков у одного объекта. Сравните с оценкой $O(N^2D + D^3)$ для «наивного» вычисления аналитического решения.
Сложность по памяти – $O(ND)$ на хранение выборки. В памяти мы держим и выборку, и градиент, но в большинстве реалистичных сценариев доминирует выборка.
Стохастический градиентный спуск
На каждом шаге градиентного спуска нам требуется выполнить потенциально дорогую операцию вычисления градиента по всей выборке (сложность $O(ND)$). Возникает идея заменить градиент его оценкой на подвыборке (в английской литературе такую подвыборку обычно именуют batch или mini-batch; в русской разговорной терминологии тоже часто встречается слово батч или мини-батч).
А именно, если функция потерь имеет вид суммы по отдельным парам объект-таргет
$$L(w, X, y) = frac1Nsum_{i=1}^NL(w, x_i, y_i),$$
а градиент, соответственно, записывается в виде
$$nabla_wL(w, X, y) = frac1Nsum_{i=1}^Nnabla_wL(w, x_i, y_i),$$
то предлагается брать оценку
$$nabla_wL(w, X, y) approx frac1Bsum_{t=1}^Bnabla_wL(w, x_{i_t}, y_{i_t})$$
для некоторого подмножества этих пар $(x_{i_t}, y_{i_t})_{t=1}^B$. Обратите внимание на множители $frac1N$ и $frac1B$ перед суммами. Почему они нужны? Полный градиент $nabla_wL(w, X, y)$ можно воспринимать как среднее градиентов по всем объектам, то есть как оценку матожидания $mathbb{E}nabla_wL(w, x, y)$; тогда, конечно, оценка матожидания по меньшей подвыборке тоже будет иметь вид среднего градиентов по объектам этой подвыборки.
Как делить выборку на батчи? Ясно, что можно было бы случайным образом сэмплировать их из полного датасета, но даже если использовать быстрый алгоритм вроде резервуарного сэмплирования, сложность этой операции не самая оптимальная. Поэтому используют линейный проход по выборке (которую перед этим лучше всё-таки случайным образом перемешать). Давайте введём ещё один параметр нашего алгоритма: размер батча, который мы обозначим $B$. Теперь на $B$ очередных примерах вычислим градиент и обновим веса модели. При этом вместо количества шагов алгоритма обычно задают количество эпох $E$. Это ещё один гиперпараметр. Одна эпоха – это один полный проход нашего сэмплера по выборке. Заметим, что если выборка очень большая, а модель компактная, то даже первый проход бывает можно не заканчивать.
Алгоритм:
w = normal(0, 1)
repeat E times:
for i = B, i <= n, i += B
X_batch = X[i-B : i]
y_batch = y[i-B : i]
f = X_batch.dot(w) # посчитать предсказание
err = f - y_batch # посчитать ошибку
grad = 2 * X_batch.T.dot(err) / B # посчитать градиент
w -= alpha * grad
Сложность по времени – $O(NDE)$. На первый взгляд, она такая же, как и у обычного градиентного спуска, но заметим, что мы сделали в $N / B$ раз больше шагов, то есть веса модели претерпели намного больше обновлений.
Сложность по памяти можно довести до $O(BD)$: ведь теперь всю выборку не надо держать в памяти, а достаточно загружать лишь текущий батч (а остальная выборка может лежать на диске, что удобно, так как в реальности задачи, в которых выборка целиком не влезает в оперативную память, встречаются сплошь и рядом). Заметим, впрочем, что при этом лучше бы $B$ взять побольше: ведь чтение с диска – намного более затратная по времени операция, чем чтение из оперативной памяти.
В целом, разницу между алгоритмами можно представлять как-то так:
Шаги стохастического градиентного спуска заметно более шумные, но считать их получается значительно быстрее. В итоге они тоже сходятся к оптимальному значению из-за того, что матожидание оценки градиента на батче равно самому градиенту. По крайней мере, сходимость можно получить при хорошо подобранных коэффициентах темпа обучения в случае выпуклого функционала качества. Подробнее мы об этом поговорим в главе про оптимизацию. Для сложных моделей и лоссов стохастический градиентный спуск может сходиться плохо или застревать в локальных минимумах, поэтому придумано множество его улучшений. О некоторых из них также рассказано в главе про оптимизацию.
Существует определённая терминологическая путаница, иногда стохастическим градиентным спуском называют версию алгоритма, в которой размер батча равен единице (то есть максимально шумная и быстрая версия алгоритма), а версии с бОльшим размером батча называют batch gradient descent. В книгах, которые, возможно, старше вас, такая процедура иногда ещё называется incremental gradient descent. Это не очень принципиально, но вы будьте готовы, если что.
Вопрос на подумать. Вообще говоря, если объём данных не слишком велик и позволяет это сделать, объекты лучше случайным образом перемешивать перед тем, как подавать их в алгоритм стохастического градиентного спуска. Как вам кажется, почему?
Также можно использовать различные стратегии отбора объектов. Например, чаще брать объекты, на которых ошибка больше. Какие ещё стратегии вы могли бы придумать?
Ответ (не открывайте сразу; сначала подумайте сами!)Легко представить себе ситуацию, в которой объекты как-нибудь неудачно упорядочены, скажем, по возрастанию таргета. Тогда модель будет попеременно то запоминать, что все таргеты маленькие, то – что все таргеты большие. Это может и не повлиять на качество итоговой модели, но может привести и к довольно печальным последствиям. И вообще, чем более разнообразные батчи модель увидит в процессе обучения, тем лучше.
Стратегий можно придумать много. Например, не брать объекты, на которых ошибка слишком большая (возможно, это выбросы – зачем на них учиться), или вообще не брать те, на которых ошибка достаточно мала (они «ничему не учат»). Рекомендуем, впрочем, прибегать к этим эвристикам, только если вы понимаете, зачем они вам нужны и почему есть надежда, что они помогут.
Неградиентные методы
После прочтения этой главы у вас может сложиться ощущение, что приближённые способы решения ML задач и градиентные методы – это одно и тоже, но вы будете правы в этом только на 98%. В принципе, существуют и другие способы численно решать эти задачи, но в общем случае они работают гораздо хуже, чем градиентный спуск, и не обладают таким хорошим теоретическим обоснованием. Мы не будем рассказывать про них подробно, но можете на досуге почитать, скажем, про Stepwise regression, Orthogonal matching pursuit или LARS. У LARS, кстати, есть довольно интересное свойство: он может эффективно работать на выборках, в которых число признаков больше числа примеров. С алгоритмом LARS вы можете познакомиться в главе про оптимизацию.
Регуляризация
Всегда ли решение задачи регрессии единственно? Вообще говоря, нет. Так, если в выборке два признака будут линейно зависимы (и следовательно, ранг матрицы будет меньше $D$), то гарантировано найдётся такой вектор весов $nu$ что $langlenu, x_irangle = 0 forall x_i$. В этом случае, если какой-то $w$ является решением оптимизационной задачи, то и $w + alpha nu $ тоже является решением для любого $alpha$. То есть решение не только не обязано быть уникальным, так ещё может быть сколь угодно большим по модулю. Это создаёт вычислительные трудности. Малые погрешности признаков сильно возрастают при предсказании ответа, а в градиентном спуске накапливается погрешность из-за операций со слишком большими числами.
Конечно, в жизни редко бывает так, что признаки строго линейно зависимы, а вот быть приближённо линейно зависимыми они вполне могут быть. Такая ситуация называется мультиколлинеарностью. В этом случае у нас, всё равно, возникают проблемы, близкие к описанным выше. Дело в том, что $Xnusim 0$ для вектора $nu$, состоящего из коэффициентов приближённой линейной зависимости, и, соответственно, $X^TXnuapprox 0$, то есть матрица $X^TX$ снова будет близка к вырожденной. Как и любая симметричная матрица, она диагонализуется в некотором ортонормированном базисе, и некоторые из собственных значений $lambda_i$ близки к нулю. Если вектор $X^Ty$ в выражении $(X^TX)^{-1}X^Ty$ будет близким к соответствующему собственному вектору, то он будет умножаться на $1 /{lambda_i}$, что опять же приведёт к появлению у $w$ очень больших по модулю компонент (при этом $w$ ещё и будет вычислен с большой погрешностью из-за деления на маленькое число). И, конечно же, все ошибки и весь шум, которые имелись в матрице $X$, при вычислении $ysim Xw$ будут умножаться на эти большие и неточные числа и возрастать во много-много раз, что приведёт к проблемам, от которых нас не спасёт никакое сингулярное разложение.
Важно ещё отметить, что в случае, когда несколько признаков линейно зависимы, веса $w_i$ при них теряют физический смысл. Может даже оказаться, что вес признака, с ростом которого таргет, казалось бы, должен увеличиваться, станет отрицательным. Это делает модель не только неточной, но и принципиально не интерпретируемой. Вообще, неадекватность знаков или величины весов – хорошее указание на мультиколлинеарность.
Для того, чтобы справиться с этой проблемой, задачу обычно регуляризуют, то есть добавляют к ней дополнительное ограничение на вектор весов. Это ограничение можно, как и исходный лосс, задавать по-разному, но, как правило, ничего сложнее, чем $L^1$- и $L^2$-нормы, не требуется.
Вместо исходной задачи теперь предлагается решить такую:
$$color{#348FEA}{min_w L(f, X, y) = min_w(|X w — y|_2^2 + lambda |w|^k_k )}$$
$lambda$ – это очередной параметр, а $|w|^k_k $ – это один из двух вариантов:
$$color{#348FEA}{|w|^2_2 = w^2_1 + ldots + w^2_D}$$
или
$$color{#348FEA}{|w|_1^1 = vert w_1 vert + ldots + vert w_D vert}$$
Добавка $lambda|w|^k_k$ называется регуляризационным членом или регуляризатором, а число $lambda$ – коэффициентом регуляризации.
Коэффициент $lambda$ является гиперпараметром модели и достаточно сильно влияет на качество итогового решения. Его подбирают по логарифмической шкале (скажем, от 1e-2 до 1e+2), используя для сравнения моделей с разными значениями $lambda$ дополнительную валидационную выборку. При этом качество модели с подобранным коэффициентом регуляризации уже проверяют на тестовой выборке, чтобы исключить переобучение. Более подробно о том, как нужно подбирать гиперпараметры, вы можете почитать в соответствующей главе.
Отдельно надо договориться о том, что вес $w_0$, соответствующий отступу от начала координат (то есть признаку из всех единичек), мы регуляризовать не будем, потому что это не имеет смысла: если даже все значения $y$ равномерно велики, это не должно портить качество обучения. Обычно это не отображают в формулах, но если придираться к деталям, то стоило бы написать сумму по всем весам, кроме $w_0$:
$$|w|^2_2 = sum_{color{red}{j=1}}^{D}w_j^2,$$
$$|w|_1 = sum_{color{red}{j=1}}^{D} vert w_j vert$$
В случае $L^2$-регуляризации решение задачи изменяется не очень сильно. Например, продифференцировав новый лосс по $w$, легко получить, что «точное» решение имеет вид:
$$w = (X^TX + lambda I)^{-1}X^Ty$$
Отметим, что за этой формулой стоит и понятная численная интуиция: раз матрица $X^TX$ близка к вырожденной, то обращать её сродни самоубийству. Мы лучше слегка исказим её добавкой $lambda I$, которая увеличит все собственные значения на $lambda$, отодвинув их от нуля. Да, аналитическое решение перестаёт быть «точным», но за счёт снижения численных проблем мы получим более качественное решение, чем при использовании «точной» формулы.
В свою очередь, градиент функции потерь
$$L(f_w, X, y) = |Xw — y|^2 + lambda|w|^2$$
по весам теперь выглядит так:
$$
nabla_wL(f_w, X, y) = 2X^T(Xw — y) + 2lambda w
$$
Подставив этот градиент в алгоритм стохастического градиентного спуска, мы получаем обновлённую версию приближенного алгоритма, отличающуюся от старой только наличием дополнительного слагаемого.
Вопрос на подумать. Рассмотрим стохастический градиентный спуск для $L^2$-регуляризованной линейной регрессии с батчами размера $1$. Выберите правильный вариант шага SGD:
(а) $w_imapsto w_i — 2alpha(langle w, x_jrangle — y_j)x_{ji} — frac{2alphalambda}N w_i,quad i=1,ldots,D$;
(б) $w_imapsto w_i — 2alpha(langle w, x_jrangle — y_j)x_{ji} — 2alphalambda w_i,quad i=1,ldots,D$;
(в) $w_imapsto w_i — 2alpha(langle w, x_jrangle — y_j)x_{ji} — 2lambda N w_i,quad i=1,ldots D$.
Ответ (не открывайте сразу; сначала подумайте сами!)Не регуляризованная функция потерь имеет вид $mathcal{L}(X, y, w) = frac1Nsum_{i=1}^Nmathcal{L}(x_i, y_i, w)$, и её можно воспринимать, как оценку по выборке $(x_i, y_i)_{i=1}^N$ идеальной функции потерь
$$mathcal{L}(w) = mathbb{E}_{x, y}mathcal{L}(x, y, w)$$
Регуляризационный член не зависит от выборки и добавляется отдельно:
$$mathcal{L}_{text{reg}}(w) = mathbb{E}_{x, y}mathcal{L}(x, y, w) + lambda|w|^2$$
Соответственно, идеальный градиент регуляризованной функции потерь имеет вид
$$nabla_wmathcal{L}_{text{reg}}(w) = mathbb{E}_{x, y}nabla_wmathcal{L}(x, y, w) + 2lambda w,$$
Градиент по батчу – это тоже оценка градиента идеальной функции потерь, только не на выборке $(X, y)$, а на батче $(x_{t_i}, y_{t_i})_{i=1}^B$ размера $B$. Он будет выглядеть так:
$$nabla_wmathcal{L}_{text{reg}}(w) = frac1Bsum_{i=1}^Bnabla_wmathcal{L}(x_{t_i}, y_{t_i}, w) + 2lambda w.$$
Как видите, коэффициентов, связанных с числом объектов в батче или в исходной выборке, во втором слагаемом нет. Так что верным является второй вариант. Кстати, обратите внимание, что в третьем ещё и нет коэффициента $alpha$ перед производной регуляризационного слагаемого, это тоже ошибка.
Вопрос на подумать. Распишите процедуру стохастического градиентного спуска для $L^1$-регуляризованной линейной регрессии. Как вам кажется, почему никого не волнует, что функция потерь, строго говоря, не дифференцируема?
Ответ (не открывайте сразу; сначала подумайте сами!)Распишем для случая батча размера 1:
$$w_imapsto w_i — alpha(langle w, x_jrangle — y_j)x_{ji} — frac{lambda}alpha text{sign}(w_i),quad i=1,ldots,D$$
Функция потерь не дифференцируема лишь в одной точке. Так как в машинном обучении чаще всего мы имеем дело с данными вероятностного характера, это не влечёт каких-то особых проблем. Дело в том, что попадание прямо в ноль очень маловероятно из-за численных погрешностей в данных, так что мы можем просто доопределить производную в одной точке, а если даже пару раз попадём в неё за время обучения, это не приведёт к каким-то значительным изменениям результатов.
Отметим, что $L^1$- и $L^2$-регуляризацию можно определять для любой функции потерь $L(w, X, y)$ (и не только в задаче регрессии, а и, например, в задаче классификации тоже). Новая функция потерь будет соответственно равна
$$widetilde{L}(w, X, y) = L(w, X, y) + lambda|w|_1$$
или
$$widetilde{L}(w, X, y) = L(w, X, y) + lambda|w|_2^2$$
Разреживание весов в $L^1$-регуляризации
$L^2$-регуляризация работает прекрасно и используется в большинстве случаев, но есть одна полезная особенность $L^1$-регуляризации: её применение приводит к тому, что у признаков, которые не оказывают большого влияния на ответ, вес в результате оптимизации получается равным $0$. Это позволяет удобным образом удалять признаки, слабо влияющие на таргет. Кроме того, это даёт возможность автоматически избавляться от признаков, которые участвуют в соотношениях приближённой линейной зависимости, соответственно, спасает от проблем, связанных с мультиколлинеарностью, о которых мы писали выше.
Не очень строгим, но довольно интуитивным образом это можно объяснить так:
- В точке оптимума линии уровня регуляризационного члена касаются линий уровня основного лосса, потому что, во-первых, и те, и другие выпуклые, а во-вторых, если они пересекаются трансверсально, то существует более оптимальная точка:
- Линии уровня $L^1$-нормы – это $N$-мерные октаэдры. Точки их касания с линиями уровня лосса, скорее всего, лежат на грани размерности, меньшей $N-1$, то есть как раз в области, где часть координат равна нулю:
Заметим, что данное построение говорит о том, как выглядит оптимальное решение задачи, но ничего не говорит о способе, которым это решение можно найти. На самом деле, найти такой оптимум непросто: у $L^1$ меры довольно плохая производная. Однако, способы есть. Можете на досуге прочитать, например, вот эту статью о том, как работало предсказание CTR в google в 2012 году. Там этой теме посвящается довольно много места. Кроме того, рекомендуем посмотреть про проксимальные методы в разделе этой книги про оптимизацию в ML.
Заметим также, что вообще-то оптимизация любой нормы $L_x, 0 < x leq 1$, приведёт к появлению разреженных векторов весов, просто если c $L^1$ ещё хоть как-то можно работать, то с остальными всё будет ещё сложнее.
Другие лоссы
Стохастический градиентный спуск можно очевидным образом обобщить для решения задачи линейной регрессии с любой другой функцией потерь, не только квадратичной: ведь всё, что нам нужно от неё, – это чтобы у функции потерь был градиент. На практике это делают редко, но тем не менее рассмотрим ещё пару вариантов.
MAE
Mean absolute error, абсолютная ошибка, появляется при замене $L^2$ нормы в MSE на $L^1$:
$$color{#348FEA}{MAE(y, widehat{y}) = frac1Nsum_{i=1}^N vert y_i — widehat{y}_ivert}$$
Можно заметить, что в MAE по сравнению с MSE существенно меньший вклад в ошибку будут вносить примеры, сильно удалённые от ответов модели. Дело тут в том, что в MAE мы считаем модуль расстояния, а не квадрат, соответственно, вклад больших ошибок в MSE получается существенно больше. Такая функция потерь уместна в случаях, когда вы пытаетесь обучить регрессию на данных с большим количеством выбросов в таргете.
Иначе на эту разницу можно посмотреть так: MSE приближает матожидание условного распределения $y mid x$, а MAE – медиану.
MAPE
Mean absolute percentage error, относительная ошибка.
$$MAPE(y, widehat{y}) = frac1Nsum_{i=1}^N left|frac{widehat{y}_i-y_i}{y_i}right|$$
Часто используется в задачах прогнозирования (например, погоды, загруженности дорог, кассовых сборов фильмов, цен), когда ответы могут быть различными по порядку величины, и при этом мы бы хотели верно угадать порядок, то есть мы не хотим штрафовать модель за предсказание 2000 вместо 1000 в разы сильней, чем за предсказание 2 вместо 1.
Вопрос на подумать. Кроме описанных выше в задаче линейной регрессии можно использовать и другие функции потерь, например, Huber loss:
$$mathcal{L}(f, X, y) = sum_{i=1}^Nh_{delta}(y_i — langle w_i, xrangle),mbox{ где }h_{delta}(z) = begin{cases}
frac12z^2, |z|leqslantdelta,\
delta(|z| — frac12delta), |z| > delta
end{cases}$$
Число $delta$ является гиперпараметром. Сложная формула при $vert zvert > delta$ нужна, чтобы функция $h_{delta}(z)$ была непрерывной. Попробуйте объяснить, зачем может быть нужна такая функция потерь.
Ответ (не открывайте сразу; сначала подумайте сами!)Часто требования формулируют в духе «функция потерь должна слабее штрафовать то-то и сильней штрафовать вот это». Например, $L^2$-регуляризованный лосс штрафует за большие по модулю веса. В данном случае можно заметить, что при небольших значениях ошибки берётся просто MSE, а при больших мы начинаем штрафовать нашу модель менее сурово. Например, это может быть полезно для того, чтобы выбросы не так сильно влияли на результат обучения.
Линейная классификация
Теперь давайте поговорим про задачу классификации. Для начала будем говорить про бинарную классификацию на два класса. Обобщить эту задачу до задачи классификации на $K$ классов не составит большого труда. Пусть теперь наши таргеты $y$ кодируют принадлежность к положительному или отрицательному классу, то есть принадлежность множеству ${-1,1}$ (в этой главе договоримся именно так обозначать классы, хотя в жизни вам будут нередко встречаться и метки ${0,1}$), а $x$ – по-прежнему векторы из $mathbb{R}^D$. Мы хотим обучить линейную модель так, чтобы плоскость, которую она задаёт, как можно лучше отделяла объекты одного класса от другого.
В идеальной ситуации найдётся плоскость, которая разделит классы: положительный окажется с одной стороны от неё, а отрицательный с другой. Выборка, для которой это возможно, называется линейно разделимой. Увы, в реальной жизни такое встречается крайне редко.
Как обучить линейную модель классификации, нам ещё предстоит понять, но уже ясно, что итоговое предсказание можно будет вычислить по формуле
$$y = text{sign} langle w, x_irangle$$
Почему бы не решать, как задачу регрессии?Мы можем попробовать предсказывать числа $-1$ и $1$, минимизируя для этого, например, MSE с последующим взятием знака, но ничего хорошего не получится. Во-первых, регрессия почти не штрафует за ошибки на объектах, которые лежат близко к *разделяющей плоскости*, но не с той стороны. Во вторых, ошибкой будет считаться предсказание, например, $5$ вместо $1$, хотя нам-то на самом деле не важно, какой у числа модуль, лишь бы знак был правильным. Если визуализировать такое решение, то проблемы тоже вполне заметны:
Нам нужна прямая, которая разделяет эти точки, а не проходит через них!
Сконструируем теперь функционал ошибки так, чтобы он вышеперечисленными проблемами не обладал. Мы хотим минимизировать число ошибок классификатора, то есть
$$sum_i mathbb{I}[y_i neq sign langle w, x_irangle]longrightarrow min_w$$
Домножим обе части на $$y_i$$ и немного упростим
$$sum_i mathbb{I}[y_i langle w, x_irangle < 0]longrightarrow min_w$$
Величина $M = y_i langle w, x_irangle$ называется отступом (margin) классификатора. Такая фунция потерь называется misclassification loss. Легко видеть, что
-
отступ положителен, когда $sign(y_i) = sign(langle w, x_irangle)$, то есть класс угадан верно; при этом чем больше отступ, тем больше расстояние от $x_i$ до разделяющей гиперплоскости, то есть «уверенность классификатора»;
-
отступ отрицателен, когда $sign(y_i) ne sign(langle w, x_irangle)$, то есть класс угадан неверно; при этом чем больше по модулю отступ, тем более сокрушительно ошибается классификатор.
От каждого из отступов мы вычисляем функцию
$$F(M) = mathbb{I}[M < 0] = begin{cases}1, M < 0,\ 0, Mgeqslant 0end{cases}$$
Она кусочно-постоянная, и из-за этого всю сумму невозможно оптимизировать градиентными методами: ведь её производная равна нулю во всех точках, где она существует. Но мы можем мажорировать её какой-нибудь более гладкой функцией, и тогда задачу можно будет решить. Функции можно использовать разные, у них свои достоинства и недостатки, давайте рассмотрим несколько примеров:
Вопрос на подумать. Допустим, мы как-то обучили классификатор, и подавляющее большинство отступов оказались отрицательными. Правда ли нас постигла катастрофа?
Ответ (не открывайте сразу; сначала подумайте сами!)Наверное, мы что-то сделали не так, но ситуацию можно локально выправить, если предсказывать классы, противоположные тем, которые выдаёт наша модель.
Вопрос на подумать. Предположим, что у нас есть два классификатора с примерно одинаковыми и достаточно приемлемыми значениями интересующей нас метрики. При этом одна почти всегда выдаёт предсказания с большими по модулю отступами, а вторая – с относительно маленькими. Верно ли, что первая модель лучше, чем вторая?
Ответ (не открывайте сразу; сначала подумайте сами!)На первый взгляд кажется, что первая модель действительно лучше: ведь она предсказывает «увереннее», но на самом деле всё не так однозначно: во многих случаях модель, которая умеет «честно признать, что не очень уверена в ответе», может быть предпочтительней модели, которая врёт с той же непотопляемой уверенностью, что и говорит правду. В некоторых случаях лучше может оказаться модель, которая, по сути, просто отказывается от классификации на каких-то объектах.
Ошибка перцептрона
Реализуем простейшую идею: давайте считать отступы только на неправильно классифицированных объектах и учитывать их не бинарно, а линейно, пропорционально их размеру. Получается такая функция:
$$F(M) = max(0, -M)$$
Давайте запишем такой лосс с $L^2$-регуляризацией:
$$L(w, x, y) = lambdavertvert wvertvert^2_2 + sum_i max(0, -y_i langle w, x_irangle)$$
Найдём градиент:
$$
nabla_w L(w, x, y) = 2 lambda w + sum_i
begin{cases}
0, & y_i langle w, x_i rangle > 0 \
— y_i x_i, & y_i langle w, x_i rangle leq 0
end{cases}
$$
Имея аналитическую формулу для градиента, мы теперь можем так же, как и раньше, применить стохастический градиентный спуск, и задача будет решена.
Данная функция потерь впервые была предложена для перцептрона Розенблатта, первой вычислительной модели нейросети, которая в итоге привела к появлению глубокого обучения.
Она решает задачу линейной классификации, но у неё есть одна особенность: её решение не единственно и сильно зависит от начальных параметров. Например, все изображённые ниже классификаторы имеют одинаковый нулевой лосс:
Hinge loss, SVM
Для таких случаев, как на картинке выше, возникает логичное желание не только найти разделяющую прямую, но и постараться провести её на одинаковом удалении от обоих классов, то есть максимизировать минимальный отступ:
Это можно сделать, слегка поменяв функцию ошибки, а именно положив её равной:
$$F(M) = max(0, 1-M)$$
$$L(w, x, y) = lambda||w||^2_2 + sum_i max(0, 1-y_i langle w, x_irangle)$$
$$
nabla_w L(w, x, y) = 2 lambda w + sum_i
begin{cases}
0, & 1 — y_i langle w, x_i rangle leq 0 \
— y_i x_i, & 1 — y_i langle w, x_i rangle > 0
end{cases}
$$
Почему же добавленная единичка приводит к желаемому результату?
Интуитивно это можно объяснить так: объекты, которые проклассифицированы правильно, но не очень «уверенно» (то есть $0 leq y_i langle w, x_irangle < 1$), продолжают вносить свой вклад в градиент и пытаются «отодвинуть» от себя разделяющую плоскость как можно дальше.
К данному выводу можно прийти и чуть более строго; для этого надо совершенно по-другому взглянуть на выражение, которое мы минимизируем. Поможет вот эта картинка:
Если мы максимизируем минимальный отступ, то надо максимизировать $frac{2}{|w|_2}$, то есть ширину полосы при условии того, что большинство объектов лежат с правильной стороны, что эквивалентно решению нашей исходной задачи:
$$lambda|w|^2_2 + sum_i max(0, 1-y_i langle w, x_irangle) longrightarrowminlimits_{w}$$
Отметим, что первое слагаемое у нас обратно пропорционально ширине полосы, но мы и максимизацию заменили на минимизацию, так что тут всё в порядке. Второе слагаемое – это штраф за то, что некоторые объекты неправильно расположены относительно разделительной полосы. В конце концов, никто нам не обещал, что классы наши линейно разделимы и можно провести оптимальную плоскость вообще без ошибок.
Итоговое положение плоскости задаётся всего несколькими обучающими примерами. Это ближайшие к плоскости правильно классифицированные объекты, которые называют опорными векторами или support vectors. Весь метод, соответственно, зовётся методом опорных векторов, или support vector machine, или сокращённо SVM. Начиная с шестидесятых годов это был сильнейший из известных методов машинного обучения. В девяностые его сменили методы, основанные на деревьях решений, которые, в свою очередь, недавно передали «пальму первенства» нейросетям.
Почему же SVM был столь популярен? Из-за небольшого количества параметров и доказуемой оптимальности. Сейчас для нас нормально выбирать специальный алгоритм под задачу и подбирать оптимальные гиперпараметры для этого алгоритма перебором, а когда-то трава была зеленее, а компьютеры медленнее, и такой роскоши у людей не было. Поэтому им нужны были модели, которые гарантированно неплохо работали бы в любой ситуации. Такой моделью и был SVM.
Другие замечательные свойства SVM: существование уникального решения и доказуемо минимальная склонность к переобучению среди всех популярных классов линейных классификаторов. Кроме того, несложная модификация алгоритма, ядровый SVM, позволяет проводить нелинейные разделяющие поверхности.
Строгий вывод постановки задачи SVM можно прочитать тут или в лекции К.В. Воронцова.
Логистическая регрессия
В этом параграфе мы будем обозначать классы нулём и единицей.
Ещё один интересный метод появляется из желания посмотреть на классификацию как на задачу предсказания вероятностей. Хороший пример – предсказание кликов в интернете (например, в рекламе и поиске). Наличие клика в обучающем логе не означает, что, если повторить полностью условия эксперимента, пользователь обязательно кликнет по объекту опять. Скорее у объектов есть какая-то «кликабельность», то есть истинная вероятность клика по данному объекту. Клик на каждом обучающем примере является реализацией этой случайной величины, и мы считаем, что в пределе в каждой точке отношение положительных и отрицательных примеров должно сходиться к этой вероятности.
Проблема состоит в том, что вероятность, по определению, величина от 0 до 1, а простого способа обучить линейную модель так, чтобы это ограничение соблюдалось, нет. Из этой ситуации можно выйти так: научить линейную модель правильно предсказывать какой-то объект, связанный с вероятностью, но с диапазоном значений $(-infty,infty)$, и преобразовать ответы модели в вероятность. Таким объектом является logit или log odds – логарифм отношения вероятности положительного события к отрицательному $logleft(frac{p}{1-p}right)$.
Если ответом нашей модели является $logleft(frac{p}{1-p}right)$, то искомую вероятность посчитать не трудно:
$$langle w, x_irangle = logleft(frac{p}{1-p}right)$$
$$e^{langle w, x_irangle} = frac{p}{1-p}$$
$$p=frac{1}{1 + e^{-langle w, x_irangle}}$$
Функция в правой части называется сигмоидой и обозначается
$$color{#348FEA}{sigma(z) = frac1{1 + e^{-z}}}$$
Таким образом, $p = sigma(langle w, x_irangle)$
Как теперь научиться оптимизировать $w$ так, чтобы модель как можно лучше предсказывала логиты? Нужно применить метод максимума правдоподобия для распределения Бернулли. Это самое простое распределение, которое возникает, к примеру, при бросках монетки, которая орлом выпадает с вероятностью $p$. У нас только событием будет не орёл, а то, что пользователь кликнул на объект с такой вероятностью. Если хотите больше подробностей, почитайте про распределение Бернулли в теоретическом минимуме.
Правдоподобие позволяет понять, насколько вероятно получить данные значения таргета $y$ при данных $X$ и весах $w$. Оно имеет вид
$$ p(ymid X, w) =prod_i p(y_imid x_i, w) $$
и для распределения Бернулли его можно выписать следующим образом:
$$ p(ymid X, w) =prod_i p_i^{y_i} (1-p_i)^{1-y_i} $$
где $p_i$ – это вероятность, посчитанная из ответов модели. Оптимизировать произведение неудобно, хочется иметь дело с суммой, так что мы перейдём к логарифмическому правдоподобию и подставим формулу для вероятности, которую мы получили выше:
$$ ell(w, X, y) = sum_i big( y_i log(p_i) + (1-y_i)log(1-p_i) big) =$$
$$ =sum_i big( y_i log(sigma(langle w, x_i rangle)) + (1-y_i)log(1 — sigma(langle w, x_i rangle)) big) $$
Если заметить, что
$$
sigma(-z) = frac{1}{1 + e^z} = frac{e^{-z}}{e^{-z} + 1} = 1 — sigma(z),
$$
то выражение можно переписать проще:
$$
ell(w, X, y)=sum_i big( y_i log(sigma(langle w, x_i rangle)) + (1 — y_i) log(sigma(-langle w, x_i rangle)) big)
$$
Нас интересует $w$, для которого правдоподобие максимально. Чтобы получить функцию потерь, которую мы будем минимизировать, умножим его на минус один:
$$color{#348FEA}{L(w, X, y) = -sum_i big( y_i log(sigma(langle w, x_i rangle)) + (1 — y_i) log(sigma(-langle w, x_i rangle)) big)}$$
В отличие от линейной регрессии, для логистической нет явной формулы решения. Деваться некуда, будем использовать градиентный спуск. К счастью, градиент устроен очень просто:
$$
nabla_w L(y, X, w) = -sum_i x_i big( y_i — sigma(langle w, x_i rangle)) big)
$$
Вывод формулы градиентаНам окажется полезным ещё одно свойство сигмоиды:
$$
frac{d log sigma(z)}{d z} = left( log left( frac{1}{1 + e^{-z}} right) right)’ = frac{e^{-z}}{1 + e^{-z}} = sigma(-z)
$$ $$
frac{d log sigma(-z)}{d z} = -sigma(z)
$$
Отсюда:
$$
nabla_w log sigma(langle w, x_i rangle) = sigma(-langle w, x_i rangle) x_i
$$ $$
nabla_w log sigma(-langle w, x_i rangle) = -sigma(langle w, x_i rangle) x_i
$$
и градиент оказывается равным
$$
nabla_w L(y, X, w) = -sum_i big( y_i x_i sigma(-langle w, x_i rangle) — (1 — y_i) x_i sigma(langle w, x_i rangle)) big) =
$$ $$
= -sum_i big( y_i x_i (1 — sigma(langle w, x_i rangle)) — (1 — y_i) x_i sigma(langle w, x_i rangle)) big) =
$$ $$
= -sum_i big( y_i x_i — y_i x_i sigma(langle w, x_i rangle) — x_i sigma(langle w, x_i rangle) + y_i x_i sigma(langle w, x_i rangle)) big) =
$$ $$
= -sum_i big( y_i x_i — x_i sigma(langle w, x_i rangle)) big)
$$
Предсказание модели будет вычисляться, как мы договаривались, следующим образом:
$$p=sigma(langle w, x_irangle)$$
Это вероятность положительного класса, а как от неё перейти к предсказанию самого класса? В других методах нам достаточно было посчитать знак предсказания, но теперь все наши предсказания положительные и находятся в диапазоне от 0 до 1. Что же делать? Интуитивным и не совсем (и даже совсем не) правильным является ответ «взять порог 0.5». Более корректным будет подобрать этот порог отдельно, для уже построенной регрессии минимизируя нужную вам метрику на отложенной тестовой выборке. Например, сделать так, чтобы доля положительных и отрицательных классов примерно совпадала с реальной.
Отдельно заметим, что метод называется логистической регрессией, а не логистической классификацией именно потому, что предсказываем мы не классы, а вещественные числа – логиты.
Вопрос на подумать. Проверьте, что, если метки классов – это $pm1$, а не $0$ и $1$, то функцию потерь для логистической регрессии можно записать в более компактном виде:
$$mathcal{L}(w, X, y) = sum_{i=1}^Nlog(1 + e^{-y_ilangle w, x_irangle})$$
Вопрос на подумать. Правда ли разделяющая поверхность модели логистической регрессии является гиперплоскостью?
Ответ (не открывайте сразу; сначала подумайте сами!)Разделяющая поверхность отделяет множество точек, которым мы присваиваем класс $0$ (или $-1$), и множество точек, которым мы присваиваем класс $1$. Представляется логичным провести отсечку по какому-либо значению предсказанной вероятности. Однако, выбор этого значения — дело не очевидное. Как мы увидим в главе про калибровку классификаторов, это может быть не настоящая вероятность. Допустим, мы решили провести границу по значению $frac12$. Тогда разделяющая поверхность как раз задаётся равенством $p = frac12$, что равносильно $langle w, xrangle = 0$. А это гиперплоскость.
Вопрос на подумать. Допустим, что матрица объекты-признаки $X$ имеет полный ранг по столбцам (то есть все её столбцы линейно независимы). Верно ли, что решение задачи восстановления логистической регрессии единственно?
Ответ (не открывайте сразу; сначала подумайте сами!)В этот раз хорошего геометрического доказательства, как было для линейной регрессии, пожалуй, нет; нам придётся честно посчитать вторую производную и доказать, что она является положительно определённой. Сделаем это для случая, когда метки классов – это $pm1$. Формулы так получатся немного попроще. Напомним, что в этом случае
$$L(w, X, y) = -sum_{i=1}^Nlog(1 + e^{-y_ilangle w, x_irangle})$$
Следовательно,
$$frac{partial}{partial w_{j}}L(w, X, y) = sum_{i=1}^Nfrac{y_ix_{ij}e^{-y_ilangle w, x_irangle}}{1 + e^{-y_ilangle w, x_irangle}} = sum_{i=1}^Ny_ix_{ij}left(1 — frac1{1 + e^{-y_ilangle w, x_irangle}}right)$$
$$frac{partial^2L}{partial w_jpartial w_k}(w, X, y) = sum_{i=1}^Ny^2_ix_{ij}x_{ik}frac{e^{-y_ilangle w, x_irangle}}{(1 + e^{-y_ilangle w, x_irangle})^2} =$$
$$ = sum_{i=1}^Ny^2_ix_{ij}x_{ik}sigma(y_ilangle w, x_irangle)(1 — sigma(y_ilangle w, x_irangle))$$
Теперь заметим, что $y_i^2 = 1$ и что, если обозначить через $D$ диагональную матрицу с элементами $sigma(y_ilangle w, x_irangle)(1 — sigma(y_ilangle w, x_irangle))$ на диагонали, матрицу вторых производных можно представить в виде:
$$nabla^2L = left(frac{partial^2mathcal{L}}{partial w_jpartial w_k}right) = X^TDX$$
Так как $0 < sigma(y_ilangle w, x_irangle) < 1$, у матрицы $D$ на диагонали стоят положительные числа, из которых можно извлечь квадратные корни, представив $D$ в виде $D = D^{1/2}D^{1/2}$. В свою очередь, матрица $X$ имеет полный ранг по столбцам. Стало быть, для любого вектора приращения $une 0$ имеем
$$u^TX^TDXu = u^TX^T(D^{1/2})^TD^{1/2}Xu = vert D^{1/2}Xu vert^2 > 0$$
Таким образом, функция $L$ выпукла вниз как функция от $w$, и, соответственно, точка её экстремума непременно будет точкой минимума.
А теперь – почему это не совсем правда. Дело в том, что, говоря «точка её экстремума непременно будет точкой минимума», мы уже подразумеваем существование этой самой точки экстремума. Только вот существует этот экстремум не всегда. Можно показать, что для линейно разделимой выборки функция потерь логистической регрессии не ограничена снизу, и, соответственно, никакого экстремума нет. Доказательство мы оставляем читателю.
Вопрос на подумать. На картинке ниже представлены результаты работы на одном и том же датасете трёх моделей логистической регрессии с разными коэффициентами $L^2$-регуляризации:
Наверху показаны предсказанные вероятности положительного класса, внизу – вид разделяющей поверхности.
Как вам кажется, какие картинки соответствуют самому большому коэффициенту регуляризации, а какие – самому маленькому? Почему?
Ответ (не открывайте сразу; сначала подумайте сами!)Коэффициент регуляризации максимален у левой модели. На это нас могут натолкнуть два соображения. Во-первых, разделяющая прямая проведена достаточно странно, то есть можно заподозрить, что регуляризационный член в лосс-функции перевесил функцию потерь исходной задачи. Во-вторых, модель предсказывает довольно близкие к $frac12$ вероятности – это значит, что значения $langle w, xrangle$ близки к нулю, то есть сам вектор $w$ близок к нулевому. Это также свидетельствует о том, что регуляризационный член играет слишком важную роль при оптимизации.
Наименьший коэффициент регуляризации у правой модели. Её предсказания достаточно «уверенные» (цвета на верхнем графике сочные, то есть вероятности быстро приближаются к $0$ или $1$). Это может свидетельствовать о том, что числа $langle w, xrangle$ достаточно велики по модулю, то есть $vertvert w vertvert$ достаточно велик.
Многоклассовая классификация
В этом разделе мы будем следовать изложению из лекций Евгения Соколова.
Пусть каждый объект нашей выборки относится к одному из $K$ классов: $mathbb{Y} = {1, ldots, K}$. Чтобы предсказывать эти классы с помощью линейных моделей, нам придётся свести задачу многоклассовой классификации к набору бинарных, которые мы уже хорошо умеем решать. Мы разберём два самых популярных способа это сделать – one-vs-all и all-vs-all, а проиллюстрировать их нам поможет вот такой игрушечный датасет
Один против всех (one-versus-all)
Обучим $K$ линейных классификаторов $b_1(x), ldots, b_K(x)$, выдающих оценки принадлежности классам $1, ldots, K$ соответственно. В случае с линейными моделями эти классификаторы будут иметь вид
$$b_k(x) = text{sgn}left(langle w_k, x rangle + w_{0k}right)$$
Классификатор с номером $k$ будем обучать по выборке $left(x_i, 2mathbb{I}[y_i = k] — 1right)_{i = 1}^{N}$; иными словами, мы учим классификатор отличать $k$-й класс от всех остальных.
Логично, чтобы итоговый классификатор выдавал класс, соответствующий самому уверенному из бинарных алгоритмов. Уверенность можно в каком-то смысле измерить с помощью значений линейных функций:
$$a(x) = text{argmax}_k left(langle w_k, x rangle + w_{0k}right) $$
Давайте посмотрим, что даст этот подход применительно к нашему датасету. Обучим три линейных модели, отличающих один класс от остальных:
Теперь сравним значения линейных функций
и для каждой точки выберем тот класс, которому соответствует большее значение, то есть самый «уверенный» классификатор:
Хочется сказать, что самый маленький класс «обидели».
Проблема данного подхода заключается в том, что каждый из классификаторов $b_1(x), dots, b_K(x)$ обучается на своей выборке, и значения линейных функций $langle w_k, x rangle + w_{0k}$ или, проще говоря, «выходы» классификаторов могут иметь разные масштабы. Из-за этого сравнивать их будет неправильно. Нормировать вектора весов, чтобы они выдавали ответы в одной и той же шкале, не всегда может быть разумным решением: так, в случае с SVM веса перестанут являться решением задачи, поскольку нормировка изменит норму весов.
Все против всех (all-versus-all)
Обучим $C_K^2$ классификаторов $a_{ij}(x)$, $i, j = 1, dots, K$, $i neq j$. Например, в случае с линейными моделями эти модели будут иметь вид
$$b_{ij}(x) = text{sgn}left( langle w_{ij}, x rangle + w_{0,ij} right)$$
Классификатор $a_{ij}(x)$ будем настраивать по подвыборке $X_{ij} subset X$, содержащей только объекты классов $i$ и $j$. Соответственно, классификатор $a_{ij}(x)$ будет выдавать для любого объекта либо класс $i$, либо класс $j$. Проиллюстрируем это для нашей выборки:
Чтобы классифицировать новый объект, подадим его на вход каждого из построенных бинарных классификаторов. Каждый из них проголосует за своей класс; в качестве ответа выберем тот класс, за который наберется больше всего голосов:
$$a(x) = text{argmax}_ksum_{i = 1}^{K} sum_{j neq i}mathbb{I}[a_{ij}(x) = k]$$
Для нашего датасета получается следующая картинка:
Обратите внимание на серый треугольник на стыке областей. Это точки, для которых голоса разделились (в данном случае каждый классификатор выдал какой-то свой класс, то есть у каждого класса было по одному голосу). Для этих точек нет явного способа выдать обоснованное предсказание.
Многоклассовая логистическая регрессия
Некоторые методы бинарной классификации можно напрямую обобщить на случай многих классов. Выясним, как это можно проделать с логистической регрессией.
В логистической регрессии для двух классов мы строили линейную модель
$$b(x) = langle w, x rangle + w_0,$$
а затем переводили её прогноз в вероятность с помощью сигмоидной функции $sigma(z) = frac{1}{1 + exp(-z)}$. Допустим, что мы теперь решаем многоклассовую задачу и построили $K$ линейных моделей
$$b_k(x) = langle w_k, x rangle + w_{0k},$$
каждая из которых даёт оценку принадлежности объекта одному из классов. Как преобразовать вектор оценок $(b_1(x), ldots, b_K(x))$ в вероятности? Для этого можно воспользоваться оператором $text{softmax}(z_1, ldots, z_K)$, который производит «нормировку» вектора:
$$text{softmax}(z_1, ldots, z_K) = left(frac{exp(z_1)}{sum_{k = 1}^{K} exp(z_k)},
dots, frac{exp(z_K)}{sum_{k = 1}^{K} exp(z_k)}right).$$
В этом случае вероятность $k$-го класса будет выражаться как
$$P(y = k vert x, w) = frac{
exp{(langle w_k, x rangle + w_{0k})}}{ sum_{j = 1}^{K} exp{(langle w_j, x rangle + w_{0j})}}.$$
Обучать эти веса предлагается с помощью метода максимального правдоподобия: так же, как и в случае с двухклассовой логистической регрессией:
$$sum_{i = 1}^{N} log P(y = y_i vert x_i, w) to max_{w_1, dots, w_K}$$
Масштабируемость линейных моделей
Мы уже обсуждали, что SGD позволяет обучению хорошо масштабироваться по числу объектов, так как мы можем не загружать их целиком в оперативную память. А что делать, если признаков очень много, или мы не знаем заранее, сколько их будет? Такое может быть актуально, например, в следующих ситуациях:
- Классификация текстов: мы можем представить текст в формате «мешка слов», то есть неупорядоченного набора слов, встретившихся в данном тексте, и обучить на нём, например, определение тональности отзыва в интернете. Наличие каждого слова из языка в тексте у нас будет кодироваться отдельной фичой. Тогда размерность каждого элемента обучающей выборки будет порядка нескольких сотен тысяч.
- В задаче предсказания кликов по рекламе можно получить выборку любой размерности, например, так: в качестве фичи закодируем индикатор того, что пользователь X побывал на веб-странице Y. Суммарная размерность тогда будет порядка $10^9 cdot 10^7 = 10^{16}$. Кроме того, всё время появляются новые пользователи и веб-страницы, так что на этапе применения нас ждут сюрпризы.
Есть несколько хаков, которые позволяют бороться с такими проблемами:
- Несмотря на то, что полная размерность объекта в выборке огромна, количество ненулевых элементов в нём невелико. Значит, можно использовать разреженное кодирование, то есть вместо плотного вектора хранить словарь, в котором будут перечислены индексы и значения ненулевых элементов вектора.
- Даже хранить все веса не обязательно! Можно хранить их в хэш-таблице и вычислять индекс по формуле
hash(feature) % tablesize. Хэш может вычисляться прямо от слова или id пользователя. Таким образом, несколько фичей будут иметь общий вес, который тем не менее обучится оптимальным образом. Такой подход называется hashing trick. Ясно, что сжатие вектора весов приводит к потерям в качестве, но, как правило, ценой совсем небольших потерь можно сжать этот вектор на много порядков.
Примером открытой библиотеки, в которой реализованы эти возможности, является vowpal wabbit.
Parameter server
Если при решении задачи ставки столь высоки, что мы не можем разменивать качество на сжатие вектора весов, а признаков всё-таки очень много, то задачу можно решать распределённо, храня все признаки в шардированной хеш-таблице
Кружки здесь означают отдельные сервера. Жёлтые загружают данные, а серые хранят части модели. Для обучения жёлтый кружок запрашивает у серого нужные ему для предсказания веса, считает градиент и отправляет его обратно, где тот потом применяется. Схема обладает бесконечной масштабируемостью, но задач, где это оправдано, не очень много.
Подытожим
На линейную модель можно смотреть как на однослойную нейросеть, поэтому многие методы, которые были изначально разработаны для них, сейчас переиспользуются в задачах глубокого обучения, а базовые подходы к регрессии, классификации и оптимизации вообще выглядят абсолютно так же. Так что несмотря на то, что в целом линейные модели на сегодня применяются редко, то, из чего они состоят и как строятся, знать очень и очень полезно.
Надеемся также, что главным итогом прочтения этой главы для вас будет осознание того, что решение любой ML-задачи состоит из выбора функции потерь, параметризованного класса моделей и способа оптимизации. В следующих главах мы познакомимся с другими моделями и оптимизаторами, но эти базовые принципы не изменятся.
В статистике , обычный метод наименьших квадратов ( МНК ) представляет собой тип линейной наименьших квадратов метода оценки неизвестных параметров в линейной регрессии модели. OLS выбирает параметры линейной функции набора объясняющих переменных по принципу наименьших квадратов : минимизируя сумму квадратов различий между наблюдаемой зависимой переменной (значения наблюдаемой переменной) в данном наборе данных и предсказанными линейной функцией независимой переменной .
Геометрически это рассматривается как сумма квадратов расстояний, параллельных оси зависимой переменной, между каждой точкой данных в наборе и соответствующей точкой на поверхности регрессии — чем меньше различия, тем лучше модель соответствует данным. . Результирующая оценка может быть выражена простой формулой, особенно в случае простой линейной регрессии , в которой в правой части уравнения регрессии есть единственный регрессор .
МНК — оценка является последовательным , когда регрессоры экзогенные , и по- Гаусс-Марков теоремы — оптимальным в классе линейных несмещенных оценок , когда ошибки являются гомоскедастичными и последовательно коррелированны . В этих условиях метод OLS обеспечивает несмещенную оценку с минимальной дисперсией, когда ошибки имеют конечную дисперсию . При дополнительном предположении, что ошибки имеют нормальное распределение , OLS является оценкой максимального правдоподобия .
Линейная модель
Закон Окуня в макроэкономике гласит, что в экономике рост ВВП должен линейно зависеть от изменений уровня безработицы. Здесь для построения линии регрессии, описывающей этот закон, используется обычный метод наименьших квадратов.
Предположим, что данные состоят из наблюдений . Каждое наблюдение включает в себя скалярный ответ и вектор — столбец из параметров (регрессор), то есть . В модели линейной регрессии переменная отклика является линейной функцией регрессоров:

или в векторной форме,
где , как было введено ранее, — вектор-столбец -го наблюдения всех независимых переменных; — вектор неизвестных параметров; а скаляр представляет ненаблюдаемые случайные величины ( ошибки ) -го наблюдения. учитывает влияние на ответы источников, отличных от поясняющих . Эта модель также может быть записана в матричных обозначениях как
где и — векторы переменных отклика и ошибок наблюдений, а — матрица регрессоров, также иногда называемая матрицей плана , строка которой является и содержит -е наблюдение по всем независимым переменным.
Как правило, постоянный член всегда входит в набор регрессоров , например, принимая для всех . Коэффициент , соответствующий этому регрессора называется перехватывают .
Регрессоры не обязательно должны быть независимыми: между регрессорами может быть любое желаемое отношение (при условии, что оно не является линейным). Например, мы можем подозревать, что ответ линейно зависит как от значения, так и от его квадрата; в этом случае мы должны включить один регрессор, значение которого является просто квадратом другого регрессора. В этом случае модель будет квадратичной во втором регрессоре, но, тем не менее, по-прежнему считается линейной моделью, потому что модель по- прежнему линейна по параметрам ( ).
Матричная / векторная формулировка
Рассмотрим переопределенную систему
из линейных уравнений в неизвестных коэффициентов , с . (Примечание: для линейной модели, как указано выше, не все элементы содержат информацию о точках данных. Первый столбец заполнен единицами . Только другие столбцы содержат фактические данные. Таким образом, здесь количество регрессоров равно количеству регрессоров плюс один. ) Это можно записать в матричной форме как

куда
Такая система , как правило , не имеет точного решения, поэтому цель вместо того, чтобы найти коэффициенты , которые соответствуют уравнениям «лучшие», в смысле решения квадратичной минимизации проблемы

где целевая функция определяется выражением
Обоснование выбора этого критерия приведено в разделе «Свойства» ниже. Эта задача минимизации имеет единственное решение, при условии , что столбцы матрицы являются линейно независимыми , данным решением нормальных уравнений
Матрица известна как матрица Грама, а матрица известна как матрица регрессии моментов и регрессоров. Наконец, — вектор коэффициентов гиперплоскости наименьших квадратов , выраженный как
или
Предварительный расчет
Предположим, что b — значение «кандидата» для вектора параметров β . Величина y i — x i T b , называемая остатком для i -го наблюдения, измеряет расстояние по вертикали между точкой данных ( x i , y i ) и гиперплоскостью y = x T b , и, таким образом, оценивает степень отклонения. соответствие между фактическими данными и моделью. Сумма квадратов остатков ( SSR ) (также называется сумма ошибки квадратов ( ESS ) или остаточной суммы квадратов ( RSS )) является мерой общей модели , пригодной:
где Т обозначает матрицу транспонирование , а строки X , обозначая значения всех независимых переменных , связанных с конкретным значением зависимой переменной, являются Х я = х я Т . Значение b, которое минимизирует эту сумму, называется оценкой МНК для β . Функция S ( b ) квадратична по b с положительно определенным гессианом , и поэтому эта функция обладает единственным глобальным минимумом в точке , который может быть задан явной формулой: [доказательство]
Продукт Н = Х Т Х является матрицей Грама и обратное, Q = N -1 , является кофактором матрицы из р , тесно связано с его ковариационной матрицей , C р . Матрица ( X T X ) –1 X T = Q X T называется псевдообратной матрицей Мура – Пенроуза для X. Эта формулировка подчеркивает, что оценка может быть проведена тогда и только тогда, когда нет идеальной мультиколлинеарности между независимые переменные (которые заставили бы матрицу грамма не иметь инверсии).
После того, как мы оценили β , подогнанные значения (или предсказанные значения ) из регрессии будут
где Р = Х ( Х Т Х ) -1 Х Т является матрица проекции на пространство V , натянутого на столбцы X . Эту матрицу P также иногда называют матрицей шляпы, потому что она «накладывает шляпу» на переменную y . Другая матрица, тесно связанная с P, — это аннигиляторная матрица M = I n — P ; это матрица проекции на пространство , ортогональное V . Обе матрицы P и M являются симметричными и идемпотентная ( что означает , что Р 2 = Р и М 2 = М ), и относятся к данным матрицы X с помощью тождеств PX = Х и МХ = 0 . Матрица M создает остатки из регрессии:
Используя эти остатки, мы можем оценить значение σ 2, используя приведенную статистику хи-квадрат :
Знаменатель n — p — это статистические степени свободы . Первая величина s 2 является оценкой OLS для σ 2 , а вторая — оценкой MLE для σ 2 . Эти две оценки очень похожи в больших выборках; первый оценщик всегда несмещен , а второй оценщик смещен, но имеет меньшую среднеквадратичную ошибку . На практике s 2 используется чаще, так как это более удобно для проверки гипотез. Квадратный корень из s 2 называется стандартной ошибкой регрессии , стандартной ошибкой регрессии или стандартной ошибкой уравнения .
Обычно для оценки благость-о-приступе регрессии методом наименьших квадратов, сравнивая , сколько начальное изменение в образце может быть уменьшено регресс на X . Коэффициент детерминации R 2 определена как отношение «объяснено» дисперсии к «общему» дисперсии зависимой переменной у , в тех случаях , когда сумма квадратов регрессии равна сумме квадратов остатков:
где ТСС является общая сумма квадратов для зависимой переменной, и является п × п матрица из них. ( представляет собой центрирующую матрицу, которая эквивалентна регрессии по константе; она просто вычитает среднее значение из переменной.) Для того, чтобы R 2 был значимым, матрица X данных в регрессорах должна содержать вектор-столбец из единиц для представления константа, коэффициент которой является отрезком регрессии. В этом случае R 2 всегда будет числом от 0 до 1, а значения, близкие к 1, указывают на хорошую степень соответствия.
Дисперсия предсказания независимой переменной как функции зависимой переменной приведена в статье Полиномиальные наименьшие квадраты .
Модель простой линейной регрессии
Если матрица данных X содержит только две переменные, константу и скалярный регрессор x i , то это называется «моделью простой регрессии». Этот случай часто рассматривается в классах статистики для начинающих, поскольку он предоставляет гораздо более простые формулы, подходящие даже для ручного расчета. Параметры обычно обозначаются как ( α , β ) :
Оценки наименьших квадратов в этом случае даются простыми формулами
Альтернативные производные
В предыдущем разделе оценка методом наименьших квадратов была получена как значение, которое минимизирует сумму квадратов остатков модели. Однако можно получить такую же оценку и из других подходов. Во всех случаях формула для оценки OLS остается той же: ^ β = ( X T X ) −1 X T y ; единственная разница в том, как мы интерпретируем этот результат.
Проекция
МНК-оценку можно рассматривать как проекцию на линейное пространство, охватываемое регрессорами. (Здесь каждый из и относится к столбцу матрицы данных.)
Для математиков OLS — это приближенное решение переопределенной системы линейных уравнений Xβ ≈ y , где β — неизвестное. Предполагая, что система не может быть решена точно (количество уравнений n намного больше, чем количество неизвестных p ), мы ищем решение, которое могло бы обеспечить наименьшее расхождение между правой и левой частями. Другими словами, мы ищем решение, удовлетворяющее
где || · || является стандартом L 2 норма в п — мерном евклидовом пространстве R п . Прогнозируемая величина Xβ — это просто некоторая линейная комбинация векторов регрессоров. Таким образом, остаточный вектор у — хр будет иметь наименьшую длину , когда у является прогнозируемое ортогонально на линейное подпространство , натянутое на столбцы X . МНК — оценка в этом случае можно интерпретировать как коэффициенты вектора разложения по ^ у = Py вдоль основе X .
Другими словами, уравнения градиента в минимуме можно записать как:
Геометрическая интерпретация этих уравнений является то , что вектор невязок, ортогональна к колонке пространства в X , так как скалярное произведение равно нулю для любого конформного вектора, об . Это означает, что это самый короткий из всех возможных векторов , то есть дисперсия остатков минимально возможна. Это показано справа.
Вводя матрицу K в предположении, что матрица невырожденная и K T X = 0 (см. Ортогональные проекции ), остаточный вектор должен удовлетворять следующему уравнению:
![[X K]](https://wikimedia.org/api/rest_v1/media/math/render/svg/b0c7583e31f8e4111806d1612b81b39d3f76af01)
Таким образом, уравнение и решение линейных наименьших квадратов описываются следующим образом:
Другой способ взглянуть на это — рассматривать линию регрессии как средневзвешенное значение линий, проходящих через комбинацию любых двух точек в наборе данных. Хотя этот способ вычисления более затратен с точки зрения вычислений, он обеспечивает лучшую интуицию на OLS.
Максимальная вероятность
Оценщик OLS идентичен оценщику максимального правдоподобия (MLE) в предположении нормальности для членов ошибки. [доказательство] Это предположение о нормальности имеет историческое значение, поскольку оно легло в основу ранних работ Юла и Пирсона по линейному регрессионному анализу . Из свойств MLE мы можем сделать вывод, что оценка OLS асимптотически эффективна (в смысле достижения границы Крамера – Рао для дисперсии), если выполняется предположение нормальности.
Обобщенный метод моментов
В iid случае оценщик МНК можно также рассматривать как ОММ оценщик, возникающий из моментных условий
Эти моментные условия утверждают, что регрессоры не должны коррелировать с ошибками. Поскольку x i является p -вектором, количество моментов равно размерности вектора параметров β , и, таким образом, система точно идентифицируется. Это так называемый классический случай GMM, когда оценка не зависит от выбора весовой матрицы.
Отметим, что исходное предположение строгой экзогенности E [ ε i | x i ] = 0 подразумевает гораздо более богатый набор моментных условий, чем указано выше. В частности, из этого предположения следует, что для любой вектор-функции ƒ будет выполнено моментное условие E [ ƒ ( x i ) · ε i ] = 0 . Однако с помощью теоремы Гаусса – Маркова можно показать, что оптимальный выбор функции ƒ состоит в том, чтобы взять ƒ ( x ) = x , что приводит к уравнению моментов, опубликованному выше.
Характеристики
Предположения
Существует несколько различных структур, в которых можно применить модель линейной регрессии , чтобы применить метод OLS. Каждый из этих параметров дает одинаковые формулы и одинаковые результаты. Единственная разница заключается в интерпретации и допущениях, которые должны быть наложены, чтобы метод давал значимые результаты. Выбор применяемой структуры зависит главным образом от природы имеющихся данных и от задачи вывода, которую необходимо выполнить.
Одна из линий разницы в интерпретации заключается в том, следует ли рассматривать регрессоры как случайные величины или как предопределенные константы. В первом случае ( случайный план ) регрессоры x i являются случайными и отбираются вместе с y i из некоторой совокупности , как в наблюдательном исследовании . Такой подход позволяет более естественно изучить асимптотические свойства оценок. В другой интерпретации ( фиксированный план ) регрессоры X рассматриваются как известные константы, установленные планом , а y выбирается условно на основе значений X, как в эксперименте . Для практических целей это различие часто несущественно, так как оценка и вывод осуществляется в то время кондиционирования на X . Все результаты, изложенные в этой статье, находятся в рамках случайного проектирования.
Классическая модель линейной регрессии
Классическая модель фокусируется на оценке и выводе «конечной выборки», что означает, что количество наблюдений n фиксировано. Это контрастирует с другими подходами, которые изучают асимптотическое поведение OLS и в которых количество наблюдений может расти до бесконечности.
- Правильная спецификация . Линейная функциональная форма должна совпадать с формой фактического процесса генерации данных.
-
Строгая экзогенность . Ошибки в регрессии должны иметь условное среднее значение ноль:
- Непосредственным следствием предположения об экзогенности является то, что ошибки имеют нулевое среднее значение: E [ ε ] = 0 , и что регрессоры не коррелируют с ошибками: E [ X T ε ] = 0 .
- Предположение экзогенности имеет решающее значение для теории OLS. Если это так, то переменные регрессора называются экзогенными . В противном случае те регрессоры, которые коррелируют с ошибкой, называются эндогенными , и тогда оценки OLS становятся недействительными. В таком случае для вывода можно использовать метод инструментальных переменных .
-
Нет линейной зависимости . Все регрессоры в X должны быть линейно независимыми . Математически это означает, что матрица X почти наверняка должна иметь полный ранг столбца :
- Обычно также предполагается, что регрессоры имеют конечные моменты, по крайней мере, до второго момента. Тогда матрица Q xx = E [ X T X / n ] конечна и положительно полуопределена.
- Когда это предположение нарушается, регрессоры называют линейно зависимыми или полностью мультиколлинеарными . В таком случае значение коэффициента регрессии β невозможно узнать, хотя предсказание значений y все еще возможно для новых значений регрессоров, которые лежат в том же линейно зависимом подпространстве.
-
Сферические ошибки :
- где I n — единичная матрица в размерности n , а σ 2 — параметр, определяющий дисперсию каждого наблюдения. Этот параметр σ 2 считается мешающим параметром в модели, хотя обычно он также оценивается. Если это предположение нарушается, то оценки OLS по-прежнему действительны, но уже неэффективны.
- Это предположение принято разделять на две части:
- Гомоскедастичность : E [ ε i 2 | X ] = σ 2 , что означает, что член ошибки имеет одинаковую дисперсию σ 2 в каждом наблюдении. Когда это требование нарушается, это называется гетероскедастичностью , в этом случае более эффективной оценкой будет взвешенный метод наименьших квадратов . Если ошибки имеют бесконечную дисперсию, тогда оценки OLS также будут иметь бесконечную дисперсию (хотя по закону больших чисел они, тем не менее, будут стремиться к истинным значениям, пока ошибки имеют нулевое среднее). В этом случаерекомендуются надежные методы оценки .
- Нет автокорреляции : ошибки между наблюдениями не коррелированы : E [ ε i ε j | X ] = 0 для i ≠ j . Это предположение может быть нарушено в контексте данных временных рядов , панельных данных , кластерных выборок, иерархических данных, данных повторных измерений, продольных данных и других данных с зависимостями. В таких случаях обобщенный метод наименьших квадратов является лучшей альтернативой, чем МНК. Еще одно выражение автокорреляции — это серийная корреляция .
-
Нормальность . Иногда дополнительно предполагается, что ошибки имеют нормальное распределение, обусловленное регрессорами:
- Это предположение не требуется для достоверности метода OLS, хотя некоторые дополнительные свойства конечной выборки могут быть установлены в том случае, если это произойдет (особенно в области проверки гипотез). Также, когда ошибки являются нормальными, оценщик OLS эквивалентен оценщику максимального правдоподобия (MLE), и, следовательно, он асимптотически эффективен в классе всех обычных оценщиков . Важно отметить, что предположение о нормальности применимо только к ошибочным членам; Вопреки распространенному заблуждению, не требуется, чтобы переменная ответа (зависимая) имела нормальное распределение.
Независимые и идентично распределенные (iid)
В некоторых приложениях, особенно с данными поперечного сечения , накладывается дополнительное предположение — что все наблюдения независимы и одинаково распределены. Это означает, что все наблюдения берутся из случайной выборки, что упрощает все перечисленные ранее допущения и упрощает их интерпретацию. Также эта структура позволяет сформулировать асимптотические результаты (размер выборки n → ∞ ), которые понимаются как теоретическая возможность получения новых независимых наблюдений из процесса генерации данных . Список предположений в этом случае:
- iid наблюдений : ( x i , y i ) не зависит от, и имеет то же распределение, что и, ( x j , y j ) для всех i ≠ j ;
- нет идеальной мультиколлинеарности : Q xx = E [ x i x i T ] — положительно определенная матрица ;
- экзогенность : E [ ε i | x i ] = 0;
- гомоскедастичность : Var [ ε i | х i ] = σ 2 .
Модель временного ряда
- Случайный процесс { х я , у я } является стационарным и эргодическая ; если { x i , y i } нестационарен, результаты OLS часто бывают ложными, если только { x i , y i } не совмещает .
- Регрессоры предопределены : E [ x i ε i ] = 0 для всех i = 1, …, n ;
- Р × р матрица Q хх = Е [ х я х я Т ] имеет полный ранг, и , следовательно , положительно определена ;
- { x i ε i } — разностная последовательность мартингалов с конечной матрицей вторых моментов Q xxε ² = E [ ε i 2 x i x i T ] .
Свойства конечного образца
Прежде всего, под строгой Экзогенностью предположению МНКА оценки и S 2 являются беспристрастными , а это означает , что их ожидаемые значения совпадают с истинными значениями параметров: [доказательством]
Если строгая экзогенность не соблюдается (как в случае со многими моделями временных рядов , где экзогенность предполагается только в отношении прошлых шоков, но не будущих), то эти оценки будут смещены в конечных выборках.
Матрица ковариационной (или просто ковариационная матрица ) из равна
В частности, стандартная ошибка каждого коэффициента равна квадратному корню из j-го диагонального элемента этой матрицы. Оценка этой стандартной ошибки получается заменой неизвестной величины σ 2 ее оценкой s 2 . Таким образом,
Также легко показать, что оценка не коррелирует с остатками модели:
Теорема Гаусса – Маркова утверждает, что в предположении сферических ошибок (то есть ошибки должны быть некоррелированными и гомоскедастическими ) оценка эффективна в классе линейных несмещенных оценок. Это называется лучшей линейной несмещенной оценкой (СИНИЙ). Эффективность следует понимать так, как если бы мы должны были найти какую-то другую оценку, которая была бы линейной по y и несмещенной, тогда
в том смысле, что это неотрицательно определенная матрица . Эта теорема устанавливает оптимальность только в классе линейных несмещенных оценок, что весьма ограничительно. В зависимости от распределения членов ошибки ε другие, нелинейные оценки могут дать лучшие результаты, чем OLS.
Предполагая нормальность
Все перечисленные до сих пор свойства действительны независимо от основного распределения условий ошибки. Однако, если вы готовы предположить, что выполняется предположение нормальности (то есть, что ε ~ N (0, σ 2 I n ) ), тогда можно указать дополнительные свойства оценок МНК.
Оценщик имеет нормальное распределение со средним значением и дисперсией, как указано выше:
где Q — матрица сомножителей . Эта оценка достигает границы Крамера – Рао для модели и, таким образом, является оптимальной в классе всех несмещенных оценок. Обратите внимание, что в отличие от теоремы Гаусса – Маркова , этот результат устанавливает оптимальность как линейных, так и нелинейных оценок, но только в случае нормально распределенных членов ошибки.
Оценщик s 2 будет пропорционален распределению хи-квадрат :
Дисперсия этой оценки равна 2 σ 4 / ( п - р ) , который не достигает Крамера-Рао из 2 сг 4 / п . Однако было показано, что не существует несмещенных оценок σ 2 с дисперсией меньше, чем у оценки s 2 . Если мы готовы допустить предвзятые оценки и рассмотреть класс оценок, которые пропорциональны сумме квадратов остатков (SSR) модели, то лучшей (в смысле среднеквадратичной ошибки ) оценкой в этом классе будет ~ σ 2 = SSR / ( n - p + 2) , что даже превосходит границу Крамера – Рао в случае, когда имеется только один регрессор ( p = 1 ).
Кроме того, оценщики и s 2 являются независимыми , факт , который приходит в полезно при построении t- и F-тесты для регрессии.
Влиятельные наблюдения
Как упоминалось ранее, оценка линейна по y , что означает, что она представляет собой линейную комбинацию зависимых переменных y i . Веса в этой линейной комбинации являются функциями регрессоров X и обычно не равны. Наблюдения с большим весом называются влиятельными, потому что они оказывают более выраженное влияние на значение оценки.
Чтобы проанализировать, какие наблюдения имеют влияние, мы удаляем конкретное j-е наблюдение и рассматриваем, насколько предполагаемые количества изменятся (аналогично методу складного ножа ). Можно показать, что изменение МНК-оценки для β будет равно
где h j = x j T ( X T X ) −1 x j — j-й диагональный элемент матрицы P , а x j — вектор регрессоров, соответствующих j- му наблюдению. Точно так же изменение прогнозируемого значения для j -го наблюдения в результате исключения этого наблюдения из набора данных будет равно
Из свойств матрицы шляпы 0 ≤ h j ≤ 1 , и они в сумме дают p , так что в среднем h j ≈ p / n . Эти величины h j называются рычагами , а наблюдения с высокими h j называются точками рычагов . Обычно наблюдения с большим кредитным плечом должны быть изучены более тщательно, на случай, если они ошибочны, выбросы или иным образом нетипичны для остальной части набора данных.
Разделенная регрессия
Иногда переменные и соответствующие параметры в регрессии можно логически разделить на две группы, так что регрессия принимает вид
где X 1 и X 2 имеют размерности n × p 1 , n × p 2 и β 1 , β 2 — векторы p 1 × 1 и p 2 × 1, причем p 1 + p 2 = p .
Теорема Фриша – Во – Ловелла утверждает, что в этой регрессии остатки и оценка МНК будут численно идентичны остаткам и оценке МНК для β 2 в следующей регрессии:
где M 1 — матрица аннигилятора для регрессоров X 1 .
Теорема может быть использована для получения ряда теоретических результатов. Например, наличие регрессии с константой и другим регрессором эквивалентно вычитанию средних значений из зависимой переменной и регрессора и последующему запуску регрессии для переменных, не имеющих значения, но без постоянного члена.
Ограниченная оценка
Предположим, известно, что коэффициенты регрессии удовлетворяют системе линейных уравнений
где Q — это матрица полного ранга размера p × q , а c — вектор известных констант размером q × 1, где q <p . В этом случае оценка по методу наименьших квадратов эквивалентно минимизации суммы квадратов остатков модели при условии ограничения А . Оценка методом наименьших квадратов с ограничениями (CLS) может быть задана явной формулой:
Это выражение для оценки с ограничениями действительно до тех пор, пока матрица X T X обратима. С самого начала этой статьи предполагалось, что эта матрица имеет полный ранг, и было отмечено, что, когда условие ранга не выполняется, β не будет идентифицироваться. Однако может случиться так, что добавление ограничения A сделает β идентифицируемым, и в этом случае нужно будет найти формулу для оценки. Оценщик равен
где R — матрица размера p × ( p — q ) такая, что матрица [ QR ] неособая, и R T Q = 0 . Такую матрицу всегда можно найти, хотя в целом она не уникальна. Вторая формула совпадает с первой в случае обратимости
X T X.
Свойства большого образца
Оценщики наименьших квадратов представляют собой точечные оценки параметров модели линейной регрессии β . Однако обычно мы также хотим знать, насколько близки эти оценки к истинным значениям параметров. Другими словами, мы хотим построить интервальные оценки .
Поскольку мы не делали никаких предположений о распределении члена ошибки ε i , невозможно вывести распределение оценок и . Тем не менее, мы можем применить центральную предельную теорему для вывода их асимптотических свойств, когда размер выборки n стремится к бесконечности. Хотя размер выборки обязательно конечен, принято считать, что n «достаточно велико», так что истинное распределение оценки OLS близко к его асимптотическому пределу.
Можно показать , что в модельных предположениях, оценка наименьших квадратов для р является последовательным (т.е. сходится по вероятности к р ) и асимптотически нормальна: [доказательство]
куда 
Интервалы
Используя это асимптотическое распределение, приближенные двусторонние доверительные интервалы для j -го компонента вектора могут быть построены как
-
на уровне достоверности 1 — α ,
где q обозначает функцию квантиля стандартного нормального распределения, а [·] jj — j-й диагональный элемент матрицы.
Точно так же оценка наименьших квадратов для σ 2 также согласована и асимптотически нормальна (при условии, что существует четвертый момент ε i ) с предельным распределением
Эти асимптотические распределения можно использовать для прогнозирования, проверки гипотез, построения других оценок и т. Д. В качестве примера рассмотрим проблему прогнозирования. Предположим, есть некоторая точка в области распределения регрессоров, и кто-то хочет знать, какой была бы переменная ответа в этой точке. Средний ответ является количество , в то время как предсказывал реакция является . Очевидно, что прогнозируемый ответ является случайной величиной, его распределение может быть получено из следующего :
что позволяет построить доверительные интервалы для построения среднего отклика :
-
на уровне достоверности 1 — α .
Проверка гипотезы
Особенно широко используются две проверки гипотез. Во-первых, кто-то хочет знать, лучше ли оценочное уравнение регрессии, чем простое предсказание, что все значения переменной ответа равны ее выборочному среднему (в противном случае, говорят, что оно не имеет объяснительной силы). Нулевая гипотеза не имеет объяснительного значения расчетной регрессии тестировалась с помощью F-тест . Если вычисленное F-значение оказывается достаточно большим, чтобы превышать его критическое значение для предварительно выбранного уровня значимости, нулевая гипотеза отклоняется и принимается альтернативная гипотеза о том , что регрессия обладает объяснительной силой. В противном случае принимается нулевая гипотеза об отсутствии объяснительной силы.
Во-вторых, для каждой представляющей интерес объясняющей переменной нужно знать, существенно ли отличается ее оценочный коэффициент от нуля, то есть действительно ли эта конкретная независимая переменная имеет объяснительную силу при прогнозировании переменной отклика. Здесь нулевая гипотеза состоит в том, что истинный коэффициент равен нулю. Эта гипотеза проверяется путем вычисления t-статистики коэффициента как отношения оценки коэффициента к его стандартной ошибке . Если t-статистика больше заданного значения, нулевая гипотеза отклоняется, и выясняется, что переменная имеет объяснительную силу, а ее коэффициент значительно отличается от нуля. В противном случае принимается нулевая гипотеза о нулевом значении истинного коэффициента.
Кроме того, тест Чоу используется для проверки того, имеют ли две подвыборки одинаковые основные истинные значения коэффициентов. Сумма квадратов остатков регрессий для каждого из подмножеств и для комбинированного набора данных сравнивается путем вычисления F-статистики; если это превышает критическое значение, нулевая гипотеза об отсутствии разницы между двумя подмножествами отклоняется; в противном случае принимается.
Пример с реальными данными
Следующий набор данных дает средние показатели роста и веса для американских женщин в возрасте 30–39 лет (источник: The World Almanac and Book of Facts, 1975 ).
-
Высота (м) 1,47 1,50 1,52 1,55 1,57 1,60 1,63 1,65 1,68 1,70 1,73 1,75 1,78 1,80 1,83 Вес (кг) 52,21 53,12 54,48 55,84 57,20 58,57 59,93 61,29 63,11 64,47 66,28 68,10 69,92 72,19 74,46
Когда моделируется только одна зависимая переменная, диаграмма рассеяния предложит форму и силу связи между зависимой переменной и регрессорами. Он также может выявить выбросы, гетероскедастичность и другие аспекты данных, которые могут усложнить интерпретацию подобранной регрессионной модели. Диаграмма рассеяния предполагает, что связь сильная и может быть аппроксимирована квадратичной функцией. OLS может обрабатывать нелинейные отношения, вводя регрессор HEIGHT 2 . Затем регрессионная модель становится множественной линейной моделью:
Результаты наиболее популярных статистических пакетов будут выглядеть примерно так:
-
Метод Наименьших квадратов Зависимая переменная МАССА Наблюдения 15
Параметр Ценить Стандартная ошибка t-статистика p-значение
128,8128 16.3083 7,8986 0,0000 –143,1620 19,8332 –7,2183 0,0000 61,9603 6,0084 10,3122 0,0000
R 2 0,9989 SE регрессии 0,2516 Скорректированный R 2 0,9987 Сумма кв. 692,61 Логарифмическая вероятность 1.0890 Остаточная кв. 0,7595 Стат. Дурбина – Ватсона. 2,1013 Общая сумма кв. 693,37 Критерий Акаике 0,2548 F-статистика 5471,2 Критерий Шварца 0,3964 p-значение (F-stat) 0,0000
В этой таблице:
- В столбце « Значение» приведены оценки параметров β j по методу наименьших квадратов.
- Std ошибка колонка показывает стандартные ошибки каждого коэффициента оценки:
- В т-статистические и р-значение колонки тестируют ли какой — либо из коэффициентов может быть равна нулю. Т -статистики рассчитывается просто как . Если ошибки ε подчиняются нормальному распределению, t следует распределению Стьюдента-t. В более слабых условиях t асимптотически нормально. Большие значения t указывают на то, что нулевая гипотеза может быть отклонена и соответствующий коэффициент не равен нулю. Второй столбец, p -значение , выражает результаты проверки гипотезы в виде уровня значимости . Обычно p-значения меньше 0,05 принимаются как свидетельство того, что коэффициент совокупности отличен от нуля.
- R-квадрат — это коэффициент детерминации, указывающий на соответствие регрессии. Эта статистика будет равна единице, если соответствие идеально, и нулю, если регрессоры X вообще не обладают объяснительной силой. Это смещенная оценка R-квадрата популяции , и она никогда не уменьшится при добавлении дополнительных регрессоров, даже если они не имеют отношения к делу.
-
Скорректированный R-квадрат — это слегка измененная версия , предназначенная для наказания за избыточное количество регрессоров, которые не увеличивают объяснительную силу регрессии. Эта статистика всегда меньше , может уменьшаться при добавлении новых регрессоров и даже быть отрицательной для плохо подходящих моделей:
- Логарифмическое правдоподобие рассчитывается в предположении, что ошибки подчиняются нормальному распределению. Несмотря на то, что это предположение не очень разумно, эта статистика все же может найти свое применение при проведении тестов LR.
- Статистика Дарбина-Ватсона проверяет, есть ли какие-либо доказательства серийной корреляции между остатками. Как показывает опыт, значение меньше 2 свидетельствует о положительной корреляции.
- Для выбора модели используются информационный критерий Акаике и критерий Шварца . Обычно при сравнении двух альтернативных моделей меньшие значения одного из этих критериев указывают на лучшую модель.
- Стандартная ошибка регрессии — это оценка σ , стандартная ошибка члена ошибки.
- Общая сумма квадратов , модельная сумма квадратов и остаточная сумма квадратов говорят нам, какая часть начальных вариаций в выборке была объяснена регрессией.
- F-статистика пытается проверить гипотезу о том, что все коэффициенты (кроме точки пересечения) равны нулю. Эта статистика имеет распределение F ( p – 1 , n – p ) при нулевой гипотезе и предположении нормальности, а ее значение p указывает вероятность того, что гипотеза действительно верна. Обратите внимание, что если ошибки не являются нормальными, эта статистика становится недействительной, и следует использовать другие тесты, такие как тест Вальда или тест LR .
Обычный анализ методом наименьших квадратов часто включает использование диагностических графиков, предназначенных для обнаружения отклонений данных от предполагаемой формы модели. Вот некоторые из распространенных диагностических графиков:
- Остатки против независимых переменных в модели. Нелинейная связь между этими переменными предполагает, что линейность функции условного среднего может не соблюдаться. Различные уровни изменчивости остатков для разных уровней объясняющих переменных предполагают возможную гетероскедастичность.
- Остатки против объясняющих переменных, которых нет в модели. Любая связь остатков с этими переменными предполагает рассмотрение этих переменных для включения в модель.
- Остаточные против подобранных значений, .
- Остатки против предыдущего остатка. Этот график может выявить серийные корреляции в остатках.
Важным моментом при выполнении статистического вывода с использованием регрессионных моделей является выборка данных. В этом примере это средние данные, а не измерения по отдельным женщинам. Подгонка модели очень хорошая, но это не означает, что вес отдельной женщины можно предсказать с высокой точностью только на основе ее роста.
Чувствительность к округлению
Этот пример также демонстрирует, что коэффициенты, определяемые этими вычислениями, чувствительны к тому, как подготовлены данные. Первоначально высота была округлена до ближайшего дюйма, а затем была преобразована и округлена до ближайшего сантиметра. Поскольку коэффициент преобразования составляет от одного дюйма до 2,54 см, это не точное преобразование. Исходные дюймы можно восстановить с помощью функции Round (x / 0,0254), а затем преобразовать в метрическую систему без округления. Если это будет сделано, результаты станут:
| Const | Рост | Высота 2 | |
|---|---|---|---|
| Преобразовано в метрическую систему с округлением. | 128,8128 | -143,162 | 61,96033 |
| Преобразуется в метрическую систему без округления. | 119,0205 | -131,5076 | 58,5046 |
Невязки к квадратичной аппроксимации для правильно и неправильно преобразованных данных.
Использование любого из этих уравнений для прогнозирования веса женщины ростом 5 футов 6 дюймов (1,6764 м) дает аналогичные значения: 62,94 кг с округлением по сравнению с 62,98 кг без округления. Таким образом, кажущиеся незначительными отклонения в данных реально влияют на коэффициенты. но небольшое влияние на результаты уравнения.
Хотя это может выглядеть безобидным в середине диапазона данных, оно может стать значимым в крайних случаях или в случае, когда подобранная модель используется для проецирования за пределы диапазона данных ( экстраполяция ).
Это подчеркивает общую ошибку: этот пример представляет собой злоупотребление OLS, которое по своей сути требует, чтобы ошибки в независимой переменной (в данном случае высоте) были равны нулю или, по крайней мере, незначительны. Первоначальное округление до ближайшего дюйма плюс любые фактические ошибки измерения составляют конечную погрешность, которой нельзя пренебречь. В результате подобранные параметры не являются лучшими оценками, как предполагалось. Хотя это и не является полностью ложным, ошибка в оценке будет зависеть от относительного размера ошибок x и y .
Другой пример с менее реальными данными
Постановка задачи
Мы можем использовать механизм наименьших квадратов, чтобы выяснить уравнение орбиты двух тел в полярных координатах. Обычно используется уравнение: где — радиус расстояния от объекта до одного из тел. В уравнении параметры и используются для определения траектории орбиты. Мы измерили следующие данные.
 (в градусах) (в градусах)
|
43 год | 45 | 52 | 93 | 108 | 116 |
|---|---|---|---|---|---|---|

|
4,7126 | 4,5542 | 4,0419 | 2,2187 | 1,8910 | 1,7599 |
Нам нужно найти приближение по методу наименьших квадратов и для приведенных данных.
Решение
Сначала нам нужно представить e и p в линейной форме. Итак, мы собираемся переписать уравнение как . Теперь мы можем использовать эту форму для представления наших данных наблюдений как:


При решении получаем 
так и
Смотрите также
- Байесовский метод наименьших квадратов
- Регрессия Фамы – Макбета
- Нелинейный метод наименьших квадратов
- Численные методы линейных наименьших квадратов
- Идентификация нелинейной системы
использованная литература
дальнейшее чтение
- Догерти, Кристофер (2002). Введение в эконометрику (2-е изд.). Нью-Йорк: Издательство Оксфордского университета. С. 48–113. ISBN 0-19-877643-8.
- Гуджарати, Дамодар Н .; Портер, Дон С. (2009). Основы эконометики (Пятое изд.). Бостон: Макгроу-Хилл Ирвин. С. 55–96. ISBN 978-0-07-337577-9.
- Хейдж, христианский; Бур, Пол; Franses, Philip H .; Клок, Теун; ван Дейк, Герман К. (2004). Эконометрические методы с приложениями в бизнесе и экономике (1-е изд.). Оксфорд: Издательство Оксфордского университета. С. 76–115. ISBN 978-0-19-926801-6.
- Хилл, Р. Картер; Гриффитс, Уильям Э .; Лим, Гуай С. (2008). Принципы эконометрики (3-е изд.). Хобокен, Нью-Джерси: Джон Уайли и сыновья. С. 8–47. ISBN 978-0-471-72360-8.
- Вулдридж, Джеффри (2008). «Модель простой регрессии» . Вводная эконометрика: современный подход (4-е изд.). Мейсон, Огайо: Обучение Cengage. С. 22–67. ISBN 978-0-324-58162-1.
Предложите, как улучшить StudyLib
(Для жалоб на нарушения авторских прав, используйте
другую форму
)
Ваш е-мэйл
Заполните, если хотите получить ответ
Оцените наш проект
1
2
3
4
5
оглавление
Линейная регрессия
Метод абсолютного значения (учитывается только значение p, то есть расстояние от оси y, значение q не рассматривается)
Квадратная техника
Градиентный спуск
Средняя абсолютная ошибка
Средняя квадратичная ошибка
Минимизировать функцию ошибок
Среднеквадратичная ошибка и полная квадратная ошибка
Небольшой пакетный градиентный спуск
Метод пакетного градиентного спуска и метод стохастического градиентного спуска
Небольшой пакетный градиентный спуск
Ошибка абсолютного значения VS квадратная ошибка
Линейная регрессия в scikit-learn
Упражнение по линейной регрессии
Высокая размерность
Множественная линейная регрессия
Решите математические уравнения на аренду (продолжение следует …)
Соображения линейной регрессии
Лучше всего для линейных данных
Уязвим к выбросам
Полиномиальная регрессия (нелинейные данные)
Регуляризация
Как настроить эти зеленые параметры?
Сравнение L1 и L2
Регрессия нейронной сети
Попробуйте нейронную сеть
Основное различие между классификацией и регрессией: классификация предсказывает состояние; регрессия предсказывает значение.
Линейная регрессия
Соблюдайте данные и проведите наиболее подходящую прямую линию.
Метод абсолютного значения (учитывается только значение p, то есть расстояние от оси y, значение q не рассматривается)
Определенная точка: M (p, q), прямая:, Чтобы приблизить линию к точке M, измените
,получить
, Но после этого преобразования прямая выходит за точку M. Чтобы двигаться меньшими шагами, вводится скорость обучения: скорость обучения:
,
Для точки M над линией выполните указанное выше преобразование, а под линией выполните следующее преобразование:
Знак «плюс» с правой стороны оси y по-прежнему является знаком «плюс» с левой стороны, поэтому он называется методом абсолютного значения.
Квадратная техника
Этот метод не имеет значения, находится ли точка выше или ниже линии, также учитывается значение q. Преобразованное уравнение:
Градиентный спуск
Чтобы уменьшить погрешность, используйте метод градиентного спуска. При достижении самой нижней точки на рисунке это становится лучшим решением линейной задачи.
Средняя абсолютная ошибка
Функция ошибки: ошибка среднего абсолютного значения, среднеквадратичная ошибка.
Средняя квадратичная ошибка
Минимизировать функцию ошибок
Чтобы минимизировать среднюю абсолютную ошибку, используется метод градиентного спуска, который в точности совпадает с методом абсолютного значения. Чтобы минимизировать квадратную ошибку, метод градиентного спуска точно такой же, как и метод квадрата.
Среднеквадратичная ошибка и полная квадратная ошибка
Небольшой пакетный градиентный спуск
Метод пакетного градиентного спуска и метод стохастического градиентного спуска
Небольшой пакетный градиентный спуск
На практике в большинстве случаев два вышеуказанных метода не используются. Если ваши данные очень большие, скорость расчета обоих методов будет очень низкой.Лучший способ линейной регрессии — разбить данные на множество небольших пакетов. Каждый пакет имеет примерно одинаковое количество точек данных, и затем каждый пакет используется для обновления веса.Этот метод называется градиентным спуском малых пакетов.
Ошибка абсолютного значения VS квадратная ошибка
Три ошибки абсолютного значения на приведенном выше рисунке равны. Но прямая линия B имеет наименьшую квадратную ошибку, а среднеквадратическая ошибка фактически является квадратичной функцией.
Линейная регрессия в scikit-learn
>>>from sklearn.linear_model import LinearRegression
>>> # Модель линейной регрессии с использованием LinearRegression из scikit-learn
>>>model = LinearRegression()
>>> # fit () Подгоняем модель под данные
>>>model.fit(x_values, y_values)
>>> # Функция прогнозирования () для прогнозов
>>>print(model.predict([ [127], [248] ]))
[[ 438.94308857, 127.14839521]]Упражнение по линейной регрессии
Вам необходимо выполнить следующие действия:
1. Загрузить данные
- Данные в файле
bmi_and_life_expectancy.csvв. - Используйте панд
read_csvЗагрузите данные во фрейм данных (не забудьте импортировать панд!) - Назначьте фрейм данных переменной
bmi_life_data。
2. Постройте модель линейной регрессии.
- Используйте scikit-learn
LinearRegressionСоздайте регрессионную модель и назначьте ееbmi_life_model。 - Подгоните модель к данным.
3. Используйте модель, чтобы делать прогнозы.
- Используйте значение ИМТ 21,07931, чтобы делать прогнозы и присваивать результат переменной.
laos_life_exp。
# TODO: Add import statements
import pandas as pd
from sklearn.linear_model import LinearRegression
# Assign the dataframe to this variable.
# TODO: Load the data
bmi_life_data = pd.read_csv('bmi_and_life_expectancy.csv')
# Make and fit the linear regression model
#TODO: Fit the model and Assign it to bmi_life_model
bmi_life_model = LinearRegression()
x_values = bmi_life_data[['BMI']]
y_values = bmi_life_data[['Life expectancy']]
bmi_life_model.fit(x_values, y_values)
# Make a prediction using the model
# TODO: Predict life expectancy for a BMI value of 21.07931
laos_life_exp = bmi_life_model.predict([[21.07931]])
Высокая размерность
Для определения весов от W1 до Wn этот алгоритм в точности совпадает с алгоритмом, содержащим две переменные.Вы можете использовать метод абсолютных значений или метод квадратов, или вычислить среднее абсолютное значение или квадратную ошибку.
Множественная линейная регрессия
Если вы используете n переменных-предикторов, модель может быть представлена следующим уравнением:
Если модель имеет несколько переменных-предикторов, ее трудно представить графически, но, к счастью, все остальные аспекты линейной регрессии остаются неизменными. Мы по-прежнему можем соответствовать модели и делать прогнозы таким же образом.
Решите математические уравнения на аренду (продолжение следует …)
Соображения линейной регрессии
Линейная регрессия подразумевает ряд предпосылок и предположений, которые подходят не для всех ситуаций, поэтому следует обратить внимание на следующие два вопроса.
Лучше всего для линейных данных
Линейная регрессия создаст линейную модель на основе данных обучения. Если обучающие данные содержат нелинейные отношения, вам необходимо выбрать: настроить данные (для преобразования данных), увеличить количество функций или переключиться на другие модели.
Уязвим к выбросам
Цель линейной регрессии — найти «наиболее подходящую» прямую для данных обучения. Если в наборе данных есть выбросы, которые не соответствуют общему закону, окончательный результат будет иметь большое отклонение.
Однако добавление некоторых выбросов, не соответствующих закону, значительно изменит результаты прогнозирования модели.
В большинстве случаев модель должна соответствовать большей части данных, поэтому остерегайтесь выбросов!
Полиномиальная регрессия (нелинейные данные)
Для решения 4 весов требуется только среднее или абсолютное значение квадрата ошибки, получается вывод 4 переменных, и для изменения 4 весов для минимизации ошибки используется метод градиентного спуска. Этот алгоритм называется полиномиальной регрессией.
Регуляризация
Регуляризация — это эффективный метод улучшения модели и гарантии того, что она не переоснащается. Эту концепцию можно использовать для регрессии и классификации. Используйте проблемы классификации для объяснения регуляризации.
Используйте коэффициенты зеленого, чтобы преобразовать их в часть ошибки.
L1 регуляризация:
В сложных моделях возникают большие ошибки. Регуляризация L1 связана с абсолютной величиной.
L2 регуляризация:
Больше штрафов за сложные модели.
Как настроить эти зеленые параметры?
параметр,
Умножьте этот зеленый параметр и получите следующее: если есть большой
, Еще больше штрафуйте сложность, выбирайте более простые модели. Если есть небольшой
, Накажет за сложность на меньшую сумму и воспользуется более сложными моделями.
Сравнение L1 и L2
1. Фактическая эффективность вычисления L1 невысока. Хотя это выглядит проще, получить абсолютное значение (дифференцирование) сложно, квадрат L2 — хорошая производная, и его легче вычислить.
2. Когда только данные являются разреженными, регуляризация L1 будет быстрее, чем регуляризация L2. Например (есть 1000 операций с данными, но актуальны только 10, которые содержат много 0, L1 будет лучше.) L1 подходит для разреженного вывода, L2 подходит для не разреженного вывода.
3. Если несколько столбцов содержат 0, лучше регуляризация L1. Но если данные равномерно распределены в каждом столбце, регуляризация L2 лучше.
В-четвертых, самым большим преимуществом регуляризации L1 является возможность выбора функций. Если имеется 1000 столбцов данных, но только 10 столбцов данных являются релевантными, а остальные представляют собой помехи, L1 может это заметить и преобразовать нерелевантные данные в 0. L2 не может этого сделать. L2 будет обрабатывать все столбцы одинаково, и В качестве результата дайте нам сумму всех данных.
Регрессия нейронной сети
Другой способ решения нелинейных данных: кусочно-линейная функция.
Использование нейронных сетей не для классификации, а для регрессии, нужно удалить только последнюю функцию активации.
Попробуйте нейронную сеть
Джей Аламмар создал эту волшебную «игровую площадку» нейронной сети, где вы можете увидеть великолепные эффекты визуализации и использовать параметры для решения задач линейной регрессии, а затем попробовать регрессию нейронной сети.https://jalammar.github.io/visual-interactive-guide-basics-neural-networks/






























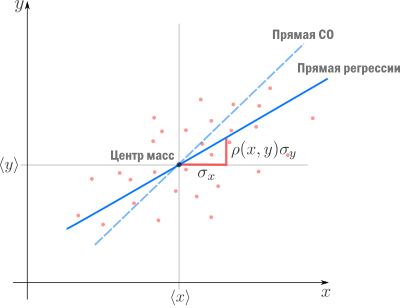


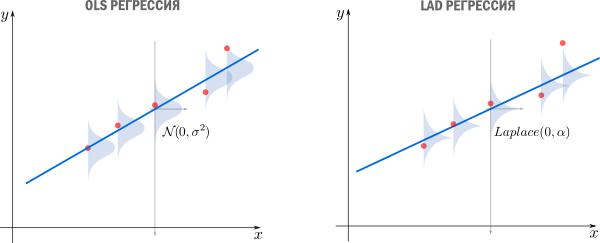


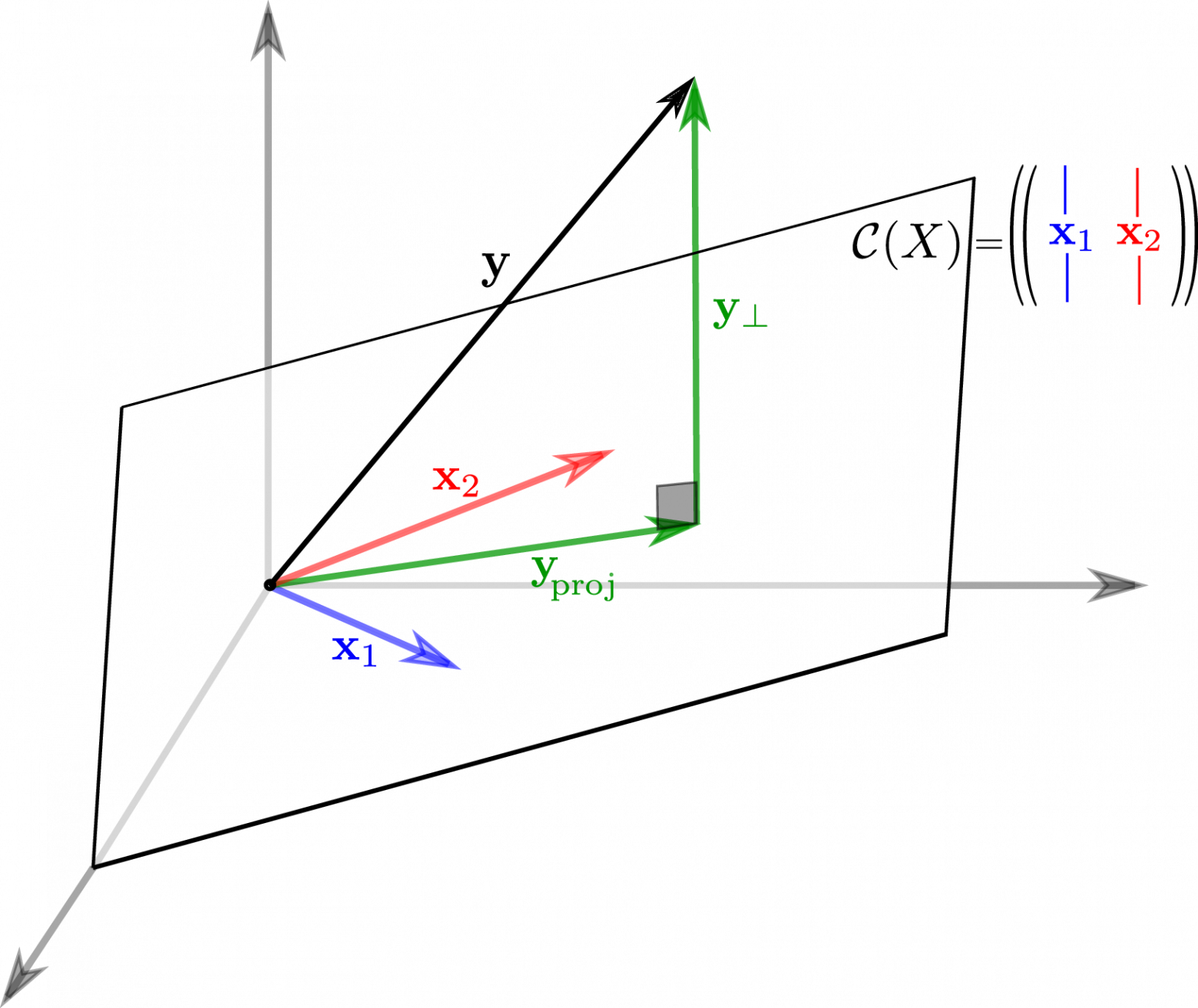



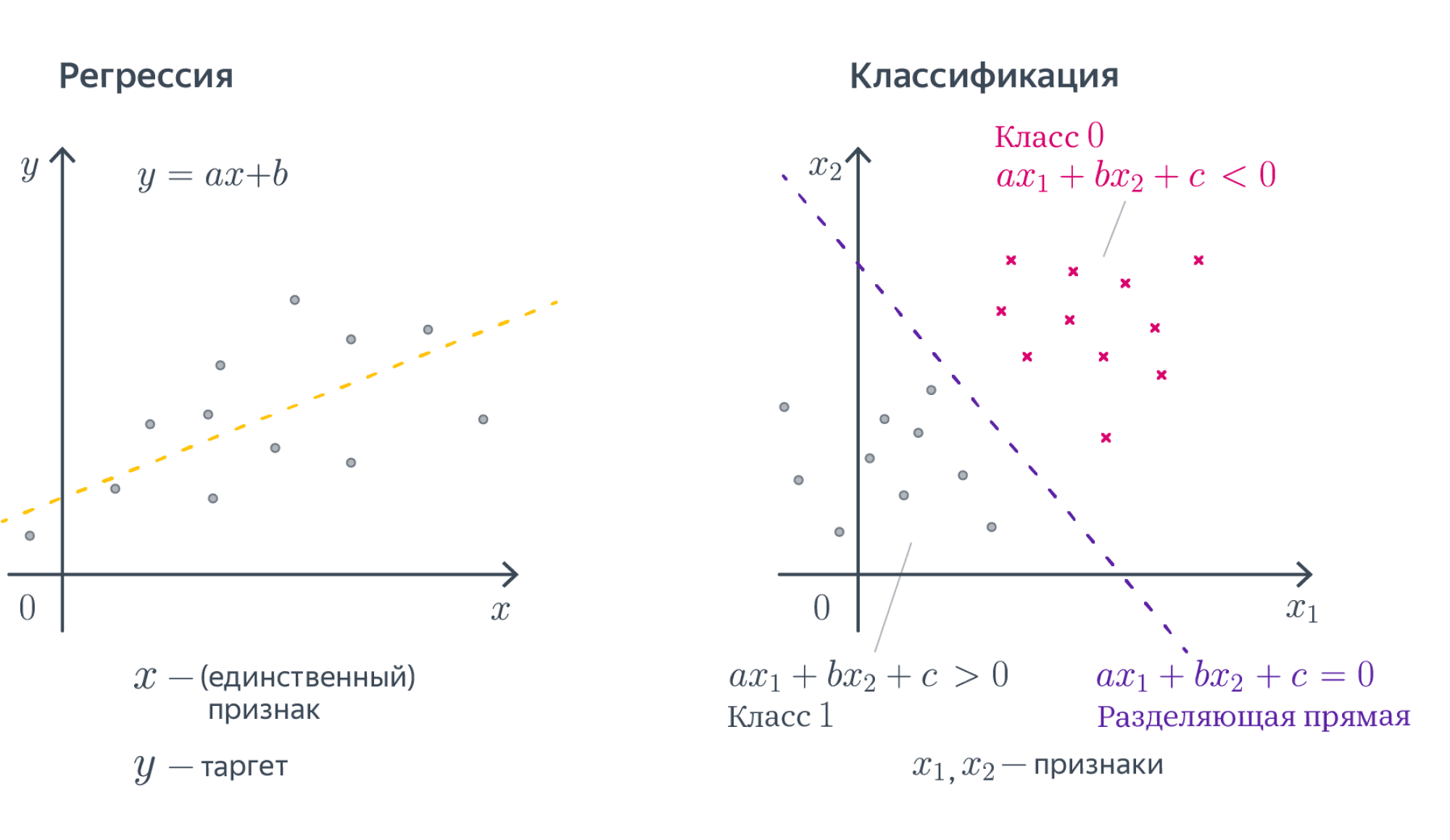

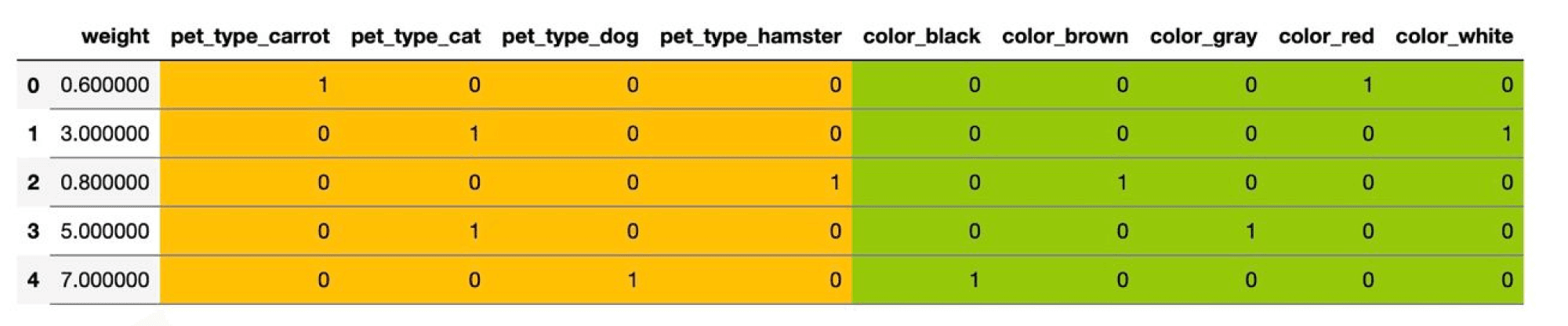

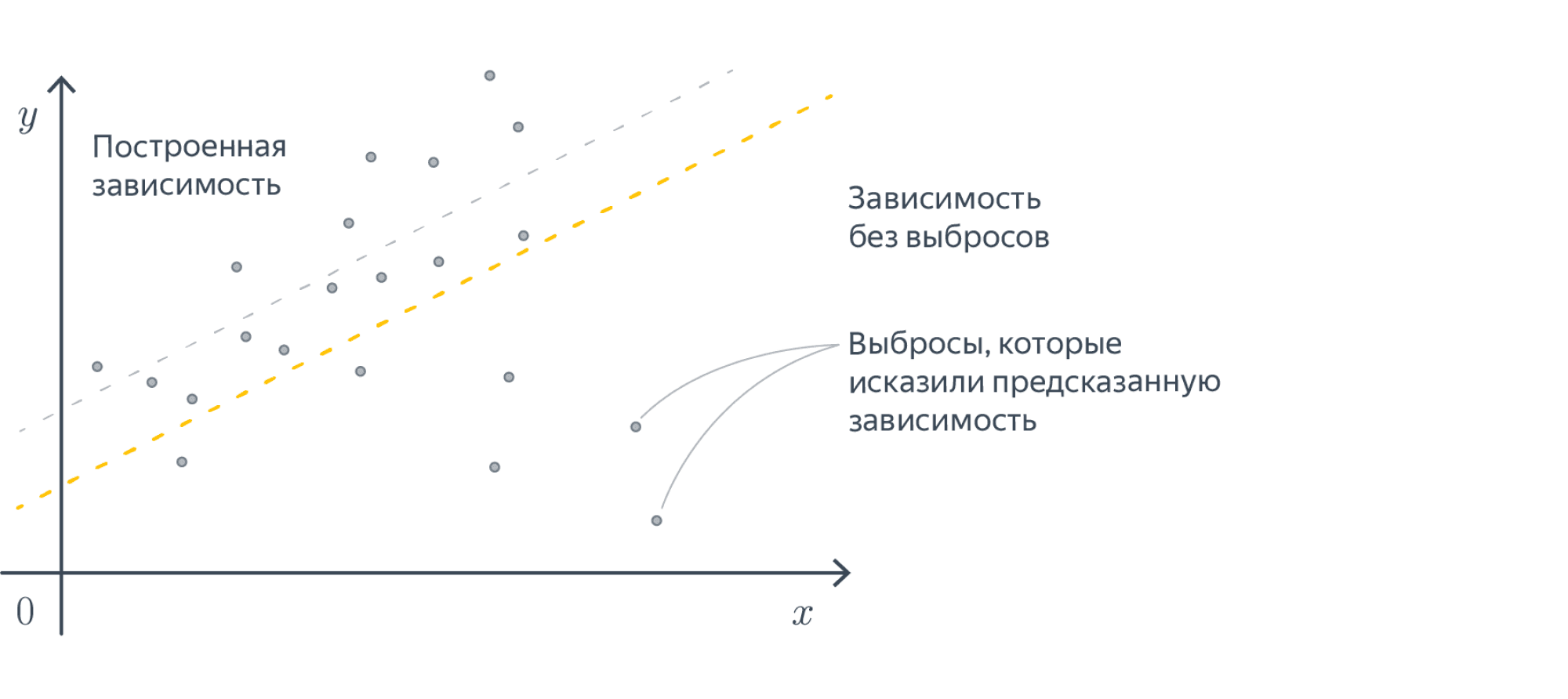
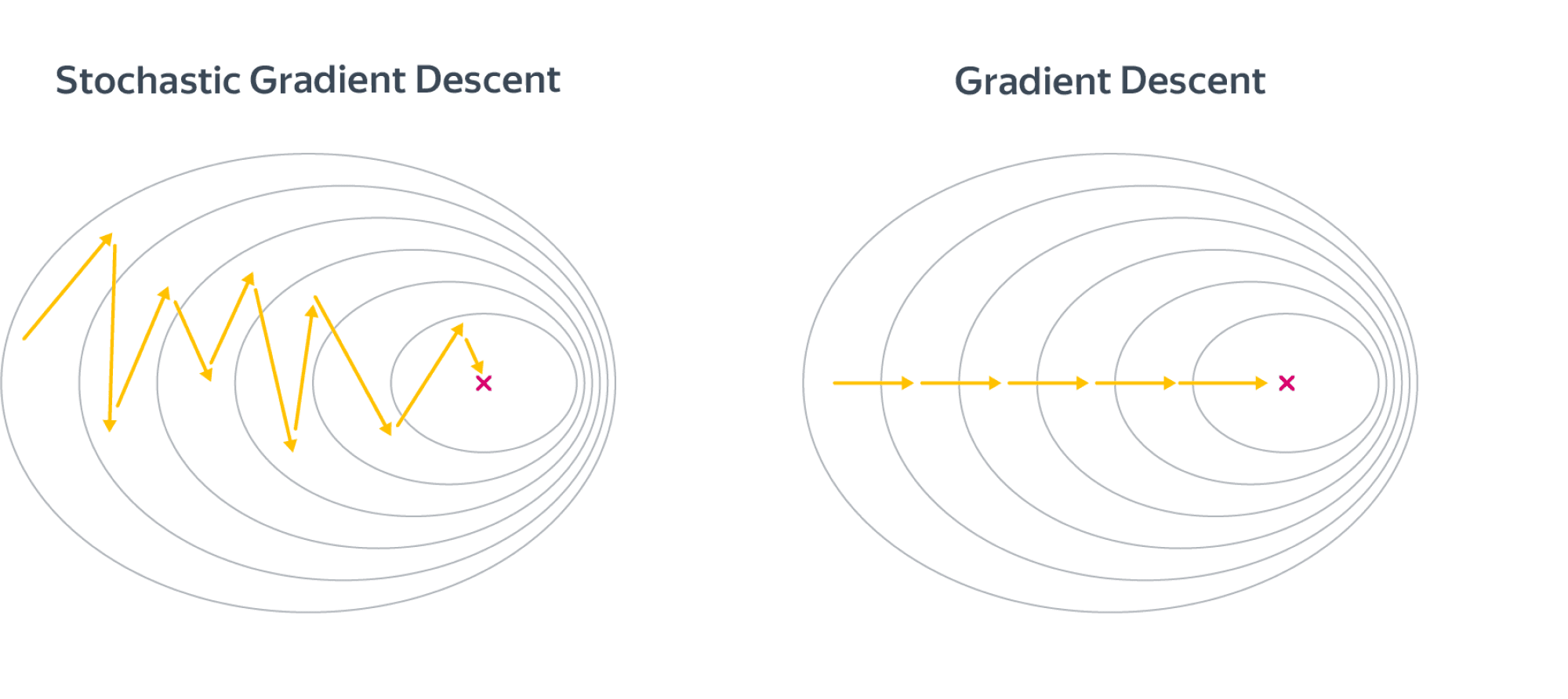
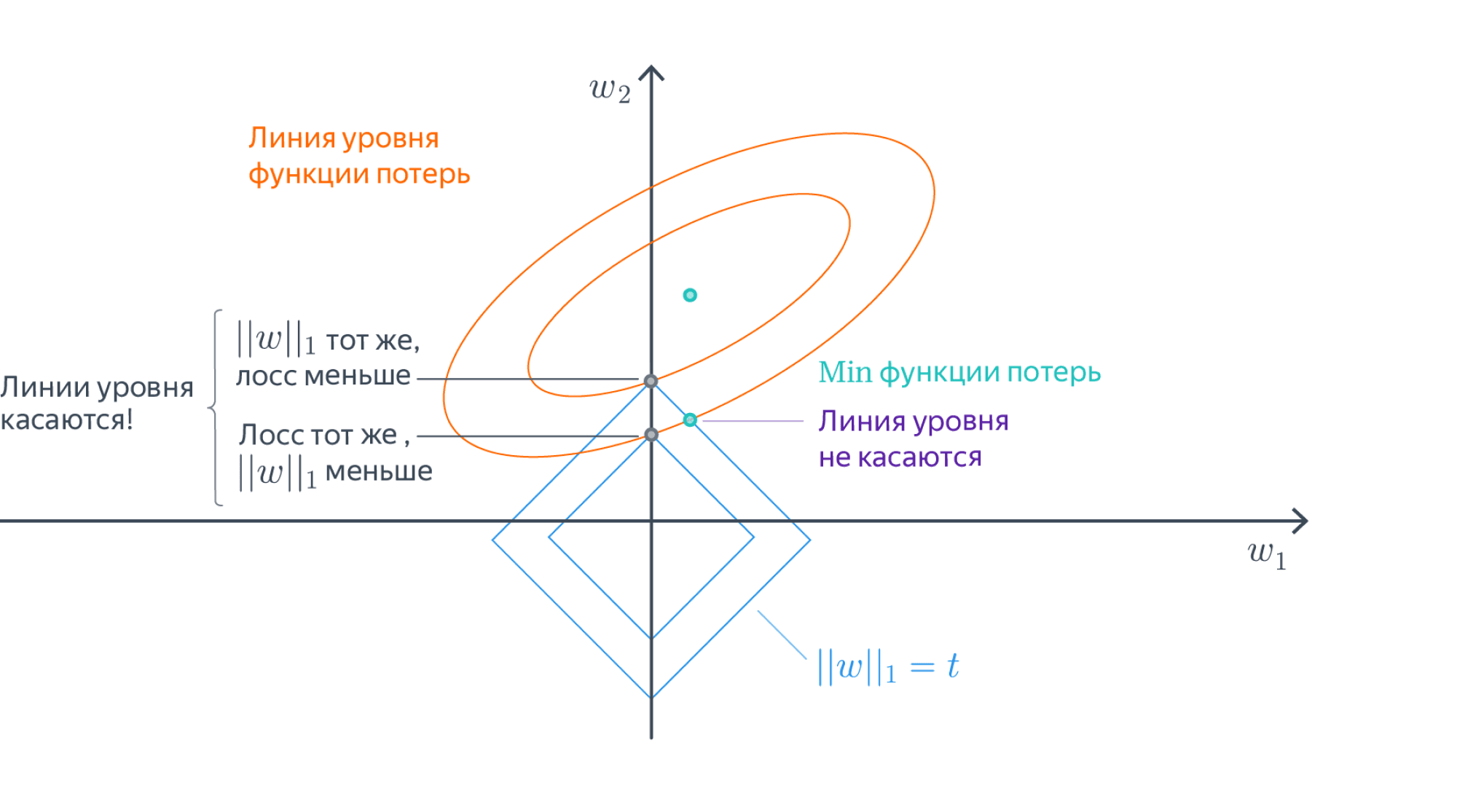
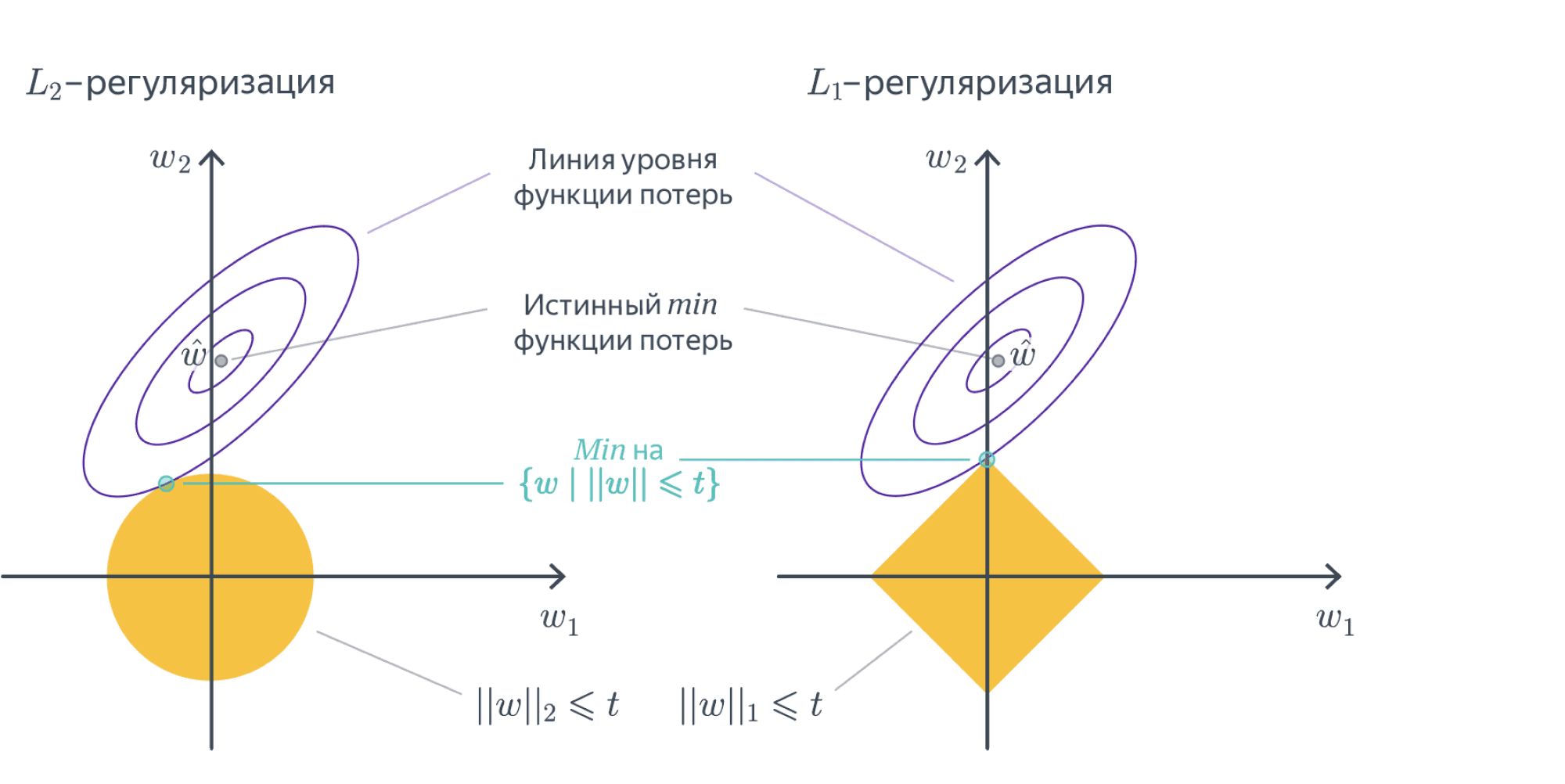
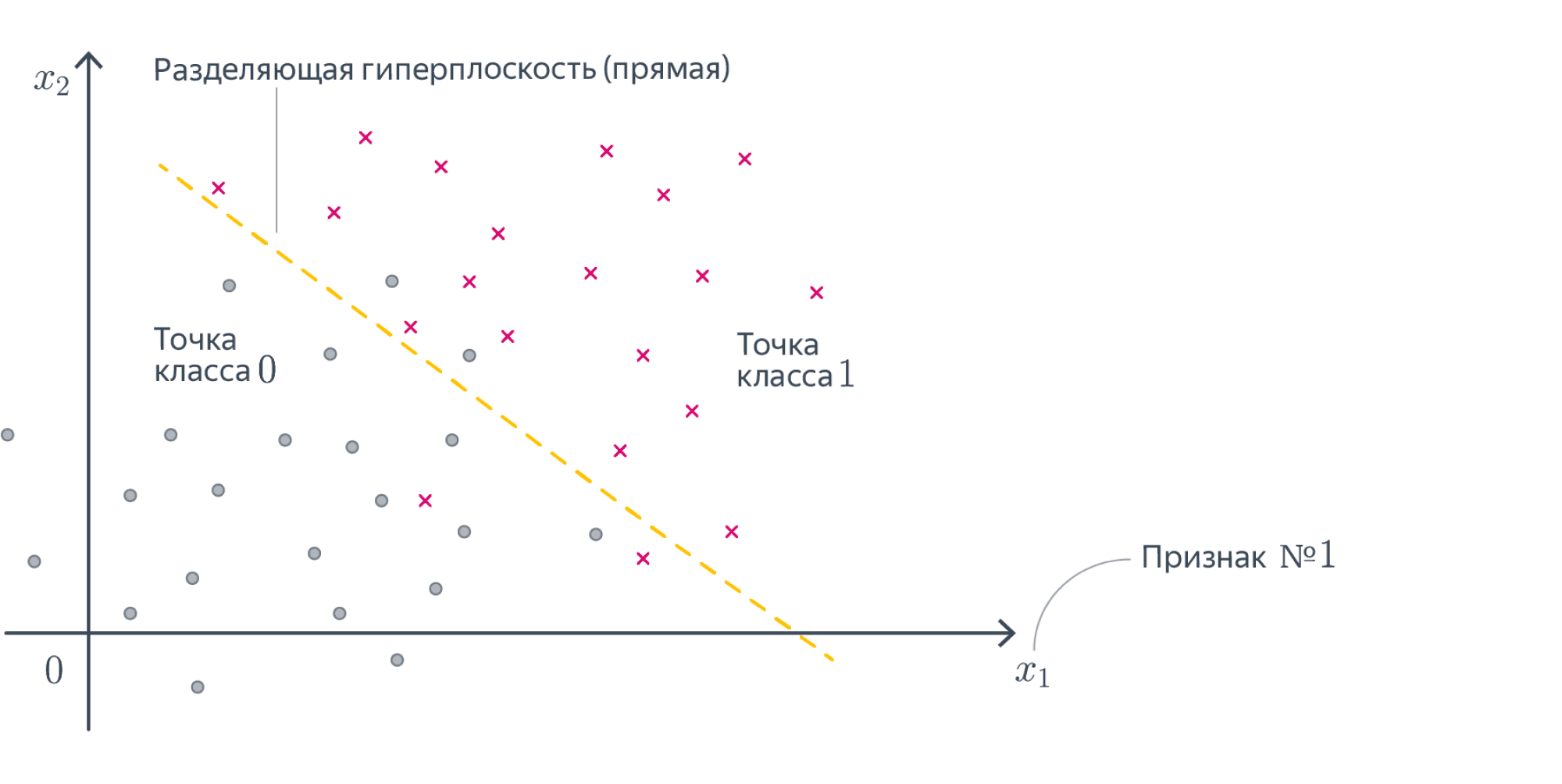
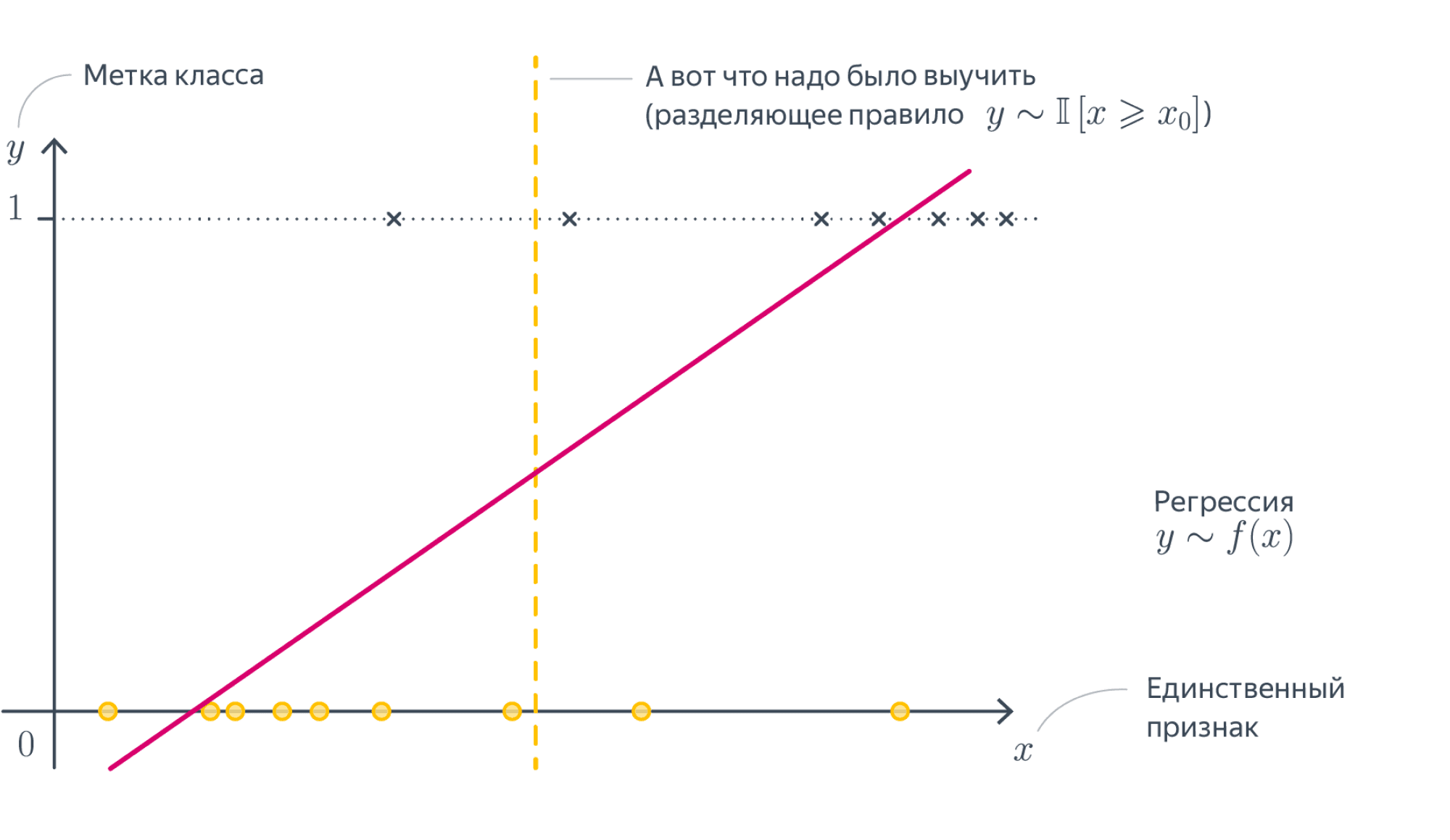
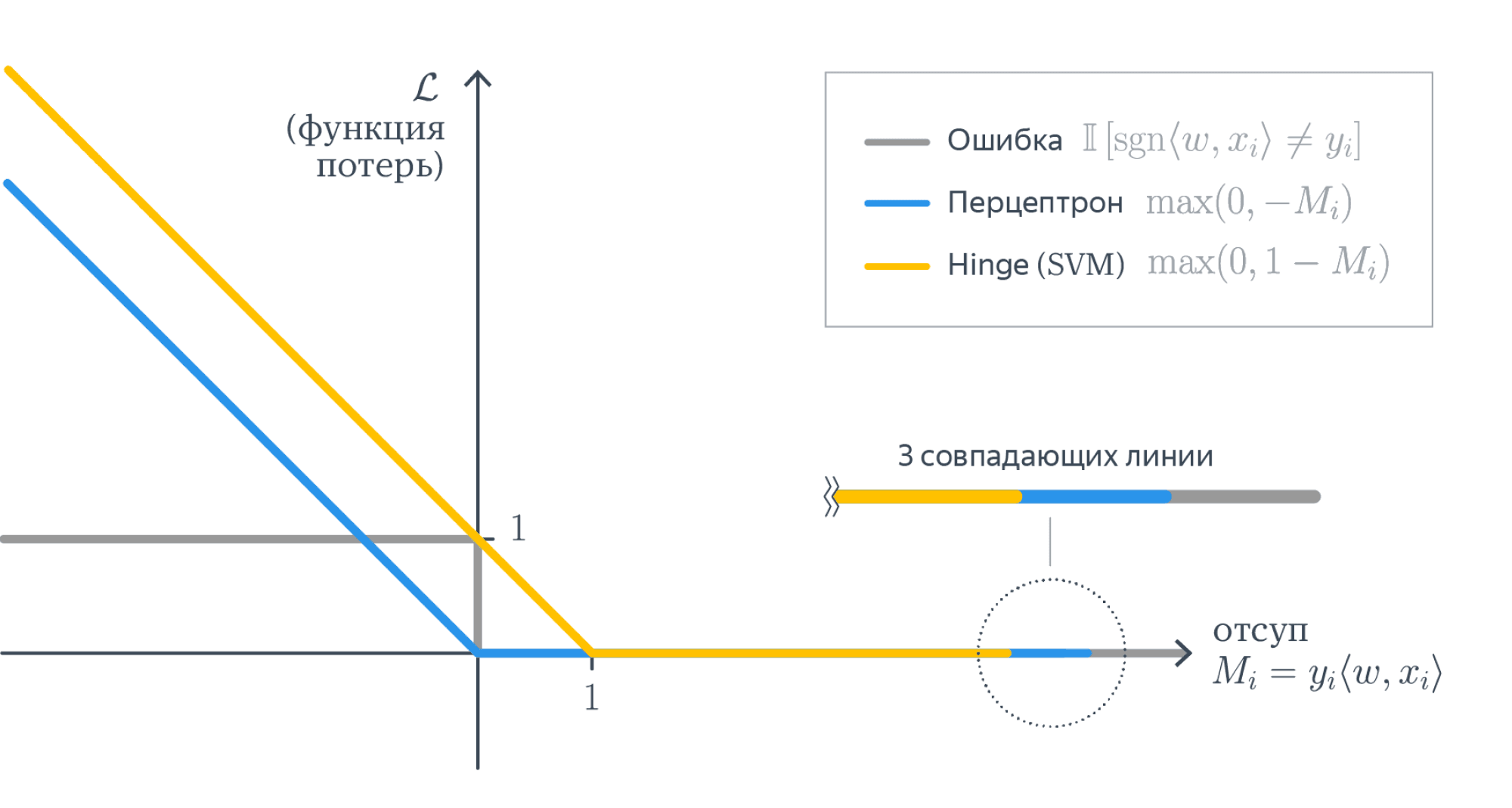
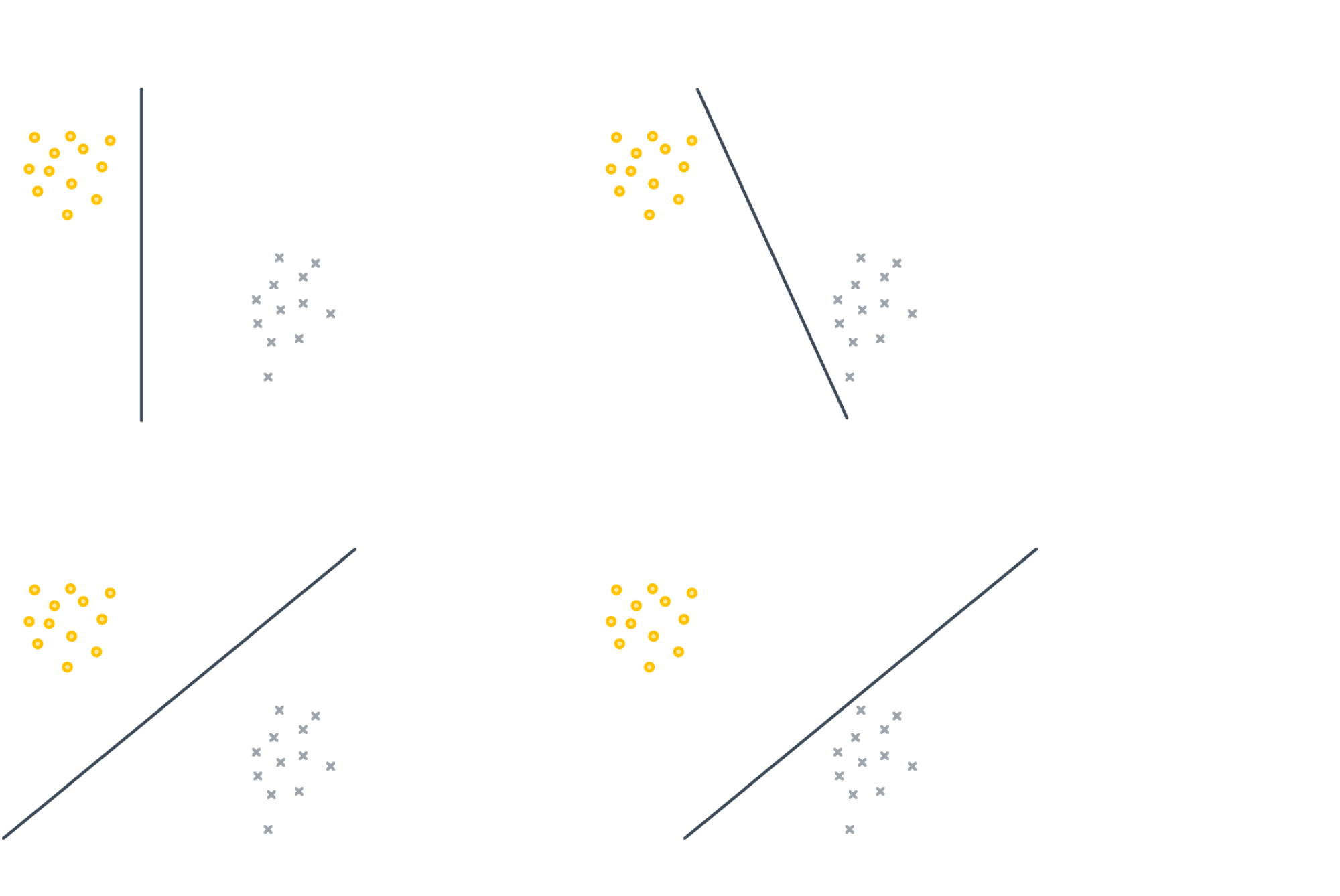

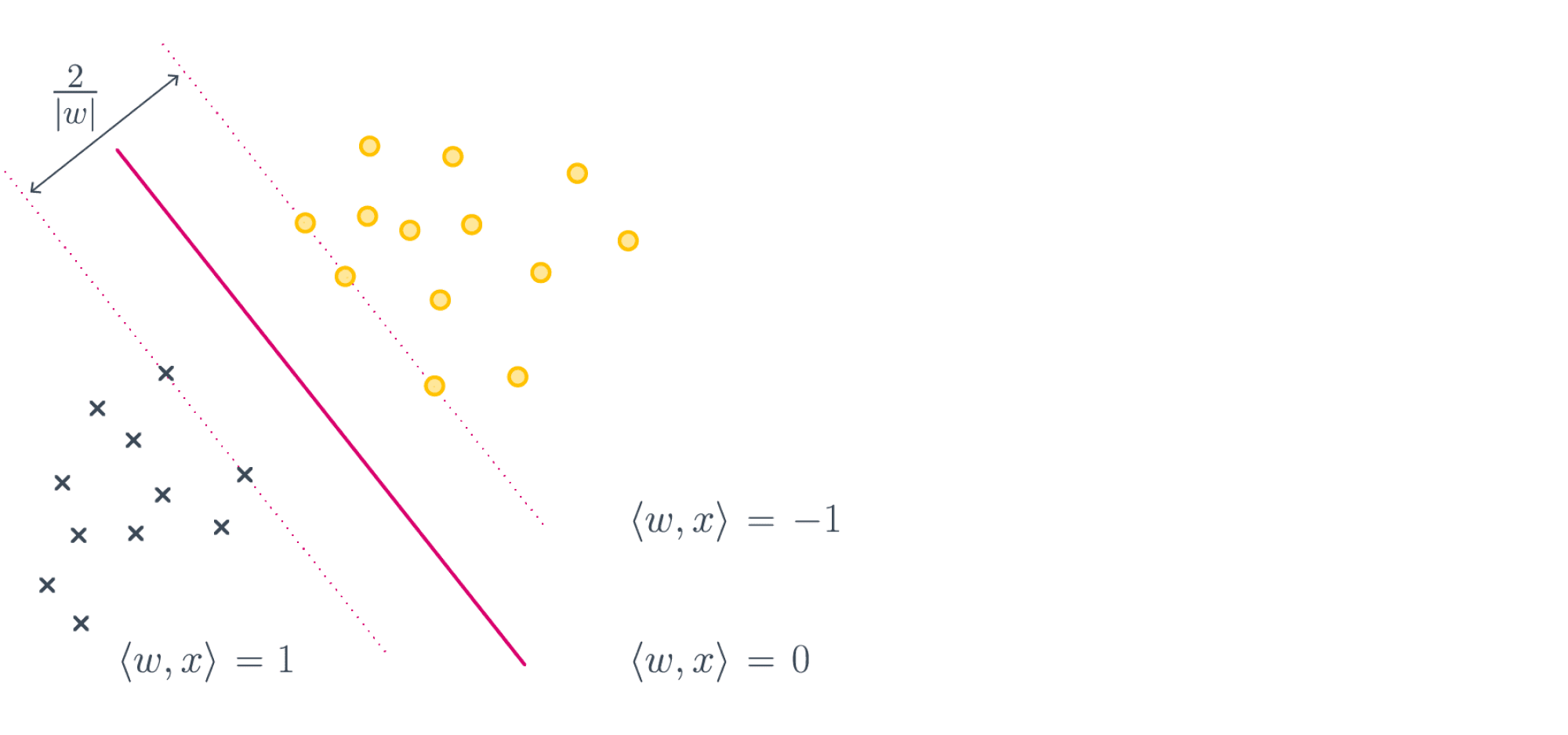
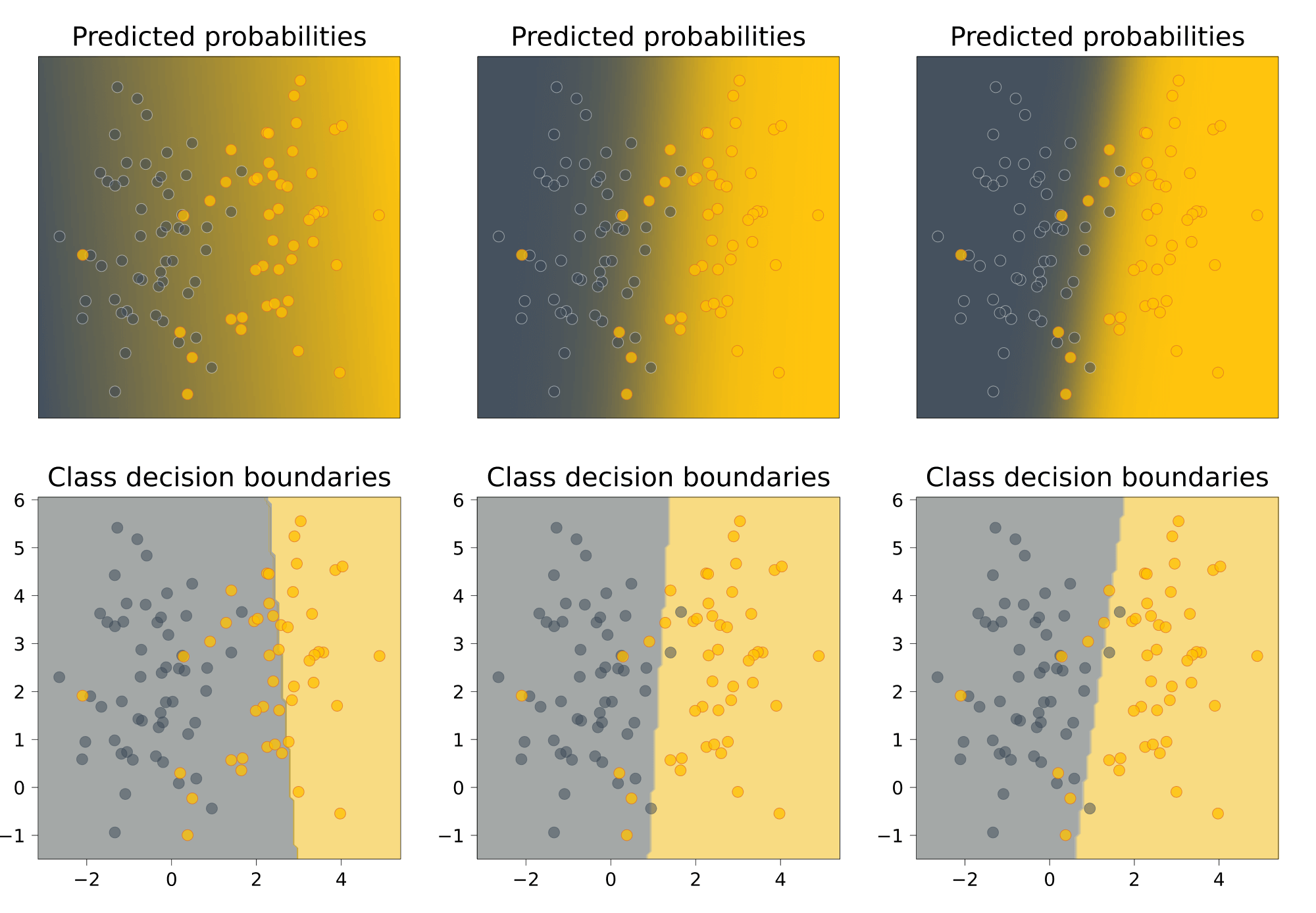


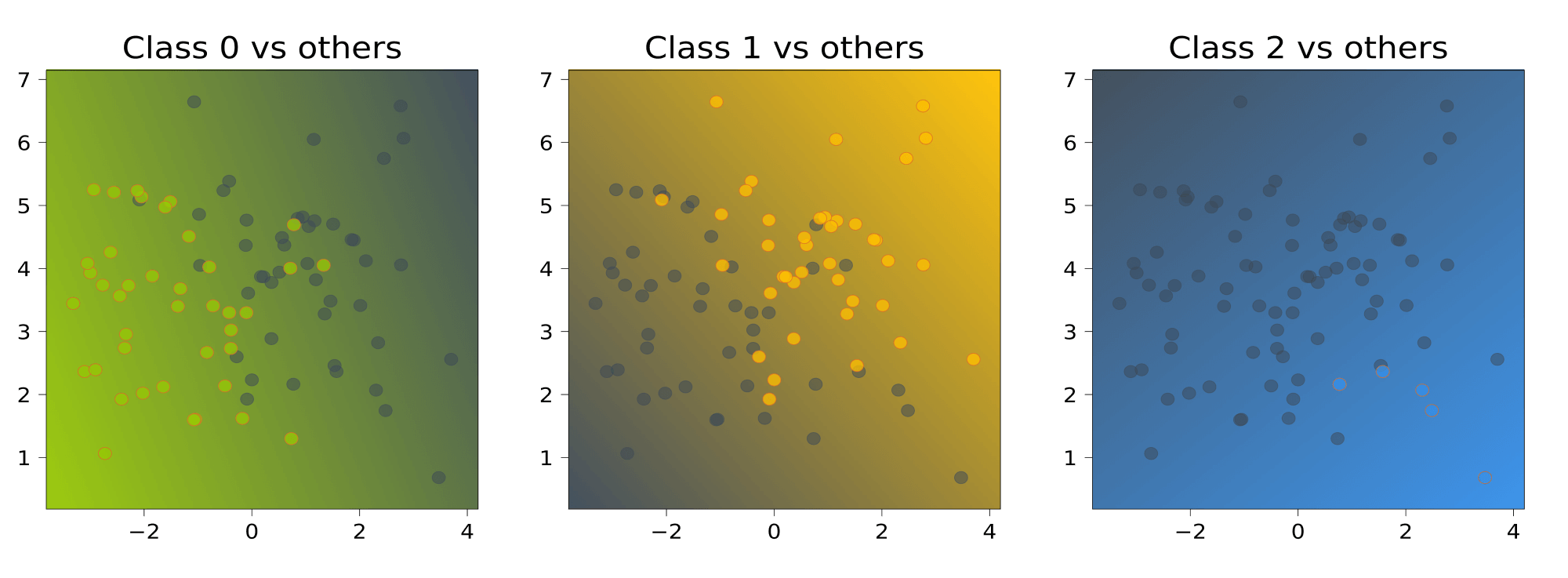

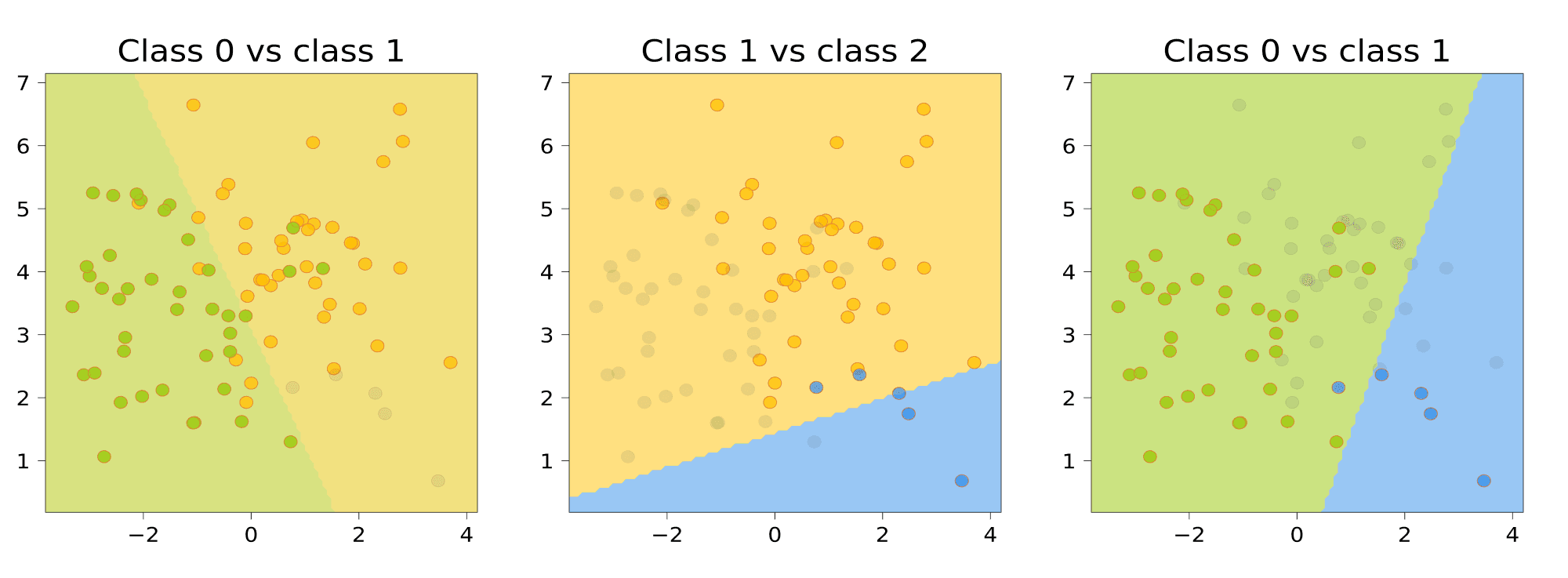

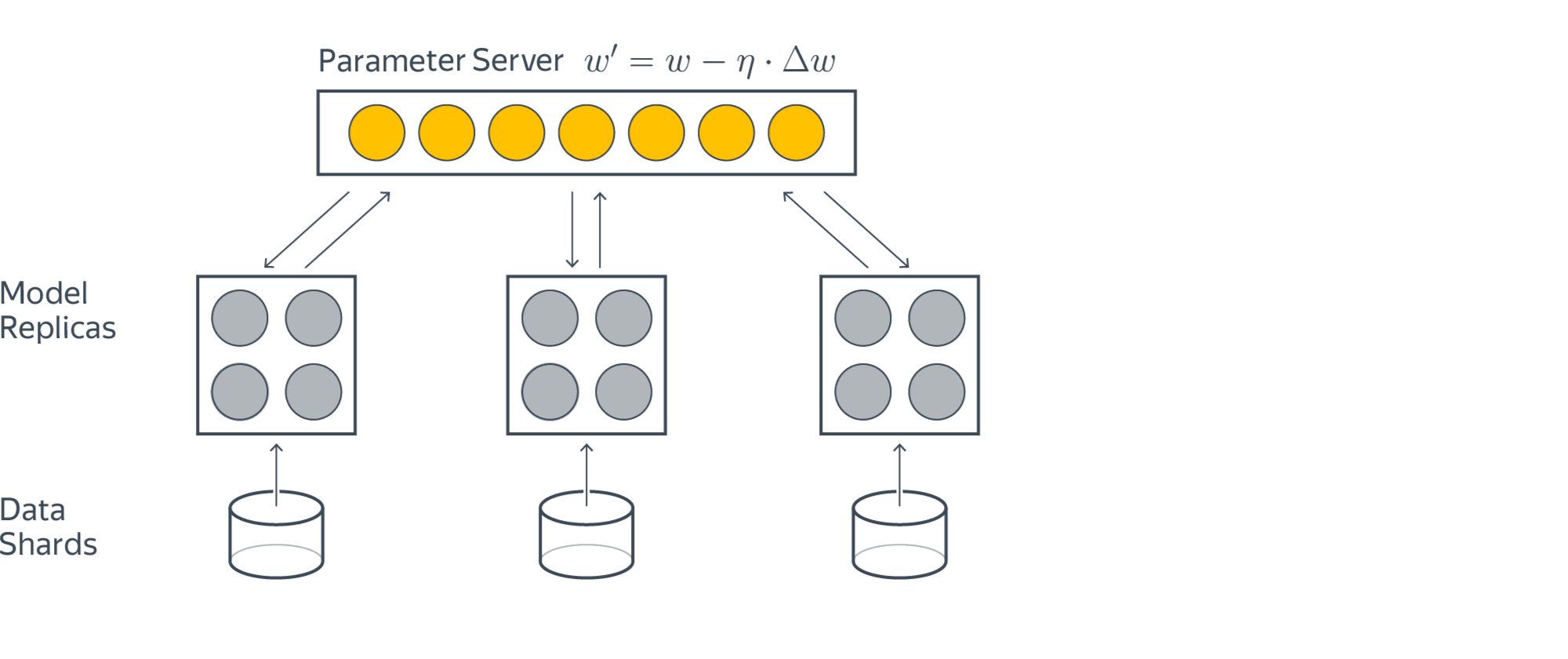






![{ displaystyle mathbf {x} _ {i} = left [x_ {i1}, x_ {i2}, dots, x_ {ip} right] ^ { mathsf {T}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/daad19b2eabb379c5fce21e00f9e77f64b7a2808)





















































![mathrm {E} { big [} , x_ {i} (y_ {i} -x_ {i} ^ {T} beta) , { big]} = 0.](https://wikimedia.org/api/rest_v1/media/math/render/svg/cb1a1f1cb2be7e80f44761892bf788fe2b2af548)
![{ Displaystyle OperatorName {E} [, varepsilon mid X ,] = 0.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dcdfa07f07180573874658708bc2a889d5416199)
![Pr ! { Big [} , operatorname {rank} (X) = p , { big]} = 1.](https://wikimedia.org/api/rest_v1/media/math/render/svg/6a11be3b89ce51c6441155fddbe512a991132fbf)
![operatorname {Var} [, varepsilon mid X ,] = sigma ^ {2} I_ {n},](https://wikimedia.org/api/rest_v1/media/math/render/svg/0df70427bd7e0b69175caf9150b2d465dd152474)

![operatorname {E} [, { hat { beta}} mid X ,] = beta, quad operatorname {E} [, s ^ {2} mid X ,] = sigma ^ {2}.](https://wikimedia.org/api/rest_v1/media/math/render/svg/67bc2fd0f90c46da207712893fdcea01e729026c)
![{ displaystyle operatorname {Var} [, { hat { beta}} mid X ,] = sigma ^ {2} (X ^ {T} X) ^ {- 1} = sigma ^ { 2} Q.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4f96b58e87986e32ad2375a1db34fb64a7a16e2f)


![operatorname {Cov} [, { hat { beta}}, { hat { varepsilon}} mid X ,] = 0.](https://wikimedia.org/api/rest_v1/media/math/render/svg/664c1a5e37957a1aa2ae381b9bcb07350c2c816c)

![operatorname {Var} [, { tilde { beta}} mid X ,] - operatorname {Var} [, { hat { beta}} mid X ,] geq 0](https://wikimedia.org/api/rest_v1/media/math/render/svg/53796c9205889cc4d675b9749a58eb97fcd998f1)













![{ displaystyle beta _ {j} in { bigg [} { hat { beta}} _ {j} pm q_ {1 - { frac { alpha} {2}}} ^ {{{ mathcal {N}} (0,1)} ! { sqrt {{ hat { sigma}} ^ {2} left [Q_ {xx} ^ {- 1} right] _ {jj}} } { bigg]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cf79688aac9f662ff39253fbfb0d234246d370e5)
![{ displaystyle ({ hat { sigma}} ^ {2} - sigma ^ {2}) { xrightarrow {d}} { mathcal {N}} left (0, ; operatorname { E} left [ varepsilon _ {i} ^ {4} right] - sigma ^ {4} right).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7c909dea2a4f0bf40e253680b953d1bfbb66298f)





![{ displaystyle y_ {0} in left [ x_ {0} ^ { mathrm {T}} { hat { beta}} pm q_ {1 - { frac { alpha} {2}} } ^ {{ mathcal {N}} (0,1)} ! { sqrt {{ hat { sigma}} ^ {2} x_ {0} ^ { mathrm {T}} Q_ {xx} ^ {- 1} x_ {0}}} right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cf86d7a311c97d35fb6e039c3cd74bc9f3e752bf)


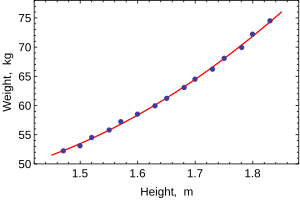


![{ displaystyle { hat { sigma}} _ {j} = left ({ hat { sigma}} ^ {2} left [Q_ {xx} ^ {- 1} right] _ {jj} right) ^ { frac {1} {2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5087e66171bf3ef9ad3ac75decdd715274919669)
















































