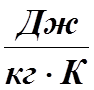Погрешность
результата измерения имеет много
составляю-щих, каждая из которых
обусловлена различными факторами и
источниками. Типичный подход к анализу
и оцениванию погреш-ностей состоит в
выделении этих составляющих, их изучении
по отдельности и суммировании по принятым
правилам. Определив количественные
параметры всех составляющих погрешности
и зная способы их суммирования, можно
правильно оценить погрешность результата
измерений и при возможности скорректировать
его с помощью введения поправок.
Ниже
приводятся некоторые источникипоявления погре-ностей измерений:
-
неполное соответствие
объекта измерений принятой его модели; -
неполное знание
измеряемой величины; -
неполное знание
влияния условий окружающей среды на
измерение; -
несовершенное
измерение параметров окружающей среды; -
конечная разрешающая
способность прибора или порог его
чувствительности; -
неточность передачи
значения единицы величины от эталонов
к рабочим средствам измерений; -
неточные знания
констант и других параметров, используемых
в алгоритме обработки результатов
измерения; -
аппроксимации и
предположения, реализуемые в методе
измерений; -
субъективная
погрешность оператора при проведении
измерений; -
изменения в
повторных наблюдениях измеряемой
величины при очевидно одинаковых
условиях и другие.
Группируя
перечисленные выше и другие причины
появления погрешностей измерений, их
можно разделить на погрешности метода
измерений,средств измерений
(инструмен-та) и оператора,проводящего измерения. Несовершенство
каждо-го этого компонента измерения
вносит вклад в погрешность измерения.
Поэтому в общем виде погрешность можно
выразить следующей формулой:
где
М
– методическая погрешность (погрешность
метода); И
— инструментальная погрешность
(погрешность средств измерений); Л
— личная (субъективная) погрешность.
Основные причины
возникновения инструментальной
погрешности приведены в разделе о
средствах измерений.
Методическая
погрешность
возникает из-за недостатков используемого
метода измерений. Чаще всего это является
следстви-ем различных допущений при
использовании эмпирических зави-симостей
между измеряемыми величинами или
конструктив-ных упрощений в приборах,
используемых в данном методе измерений.
Субъективная
погрешность
связана с такими индивидуальными
особенностями операторов, как
внимательность, сосредоточенность,
быстрота реакции, степень профессиональной
подготовленности. Такие погрешности
чаще встречаются при большой доле
ручного труда при проведении измерений
и почти отсутствуют при использовании
автоматизированных средств измерений.
4.4 Классификация погрешностей измерений
Представленная
выше классификация погрешностей
измерений связана с причинами
их
возникновения. Кроме этого существуют
и другие признаки, по которым
классифицируются погрешности.
По
характеру
проявления
(свойствам погрешностей) они разделяются
на систематические и случайные, по
способам
выражения
на абсолютные и относительные.
Абсолютная
погрешность
выражается в единицах измеряемой
величины, а относительная
погрешность
представляет собой отношение абсолютной
погрешности к измеренному (действительному)
значению величины и ее численное значение
выражается либо в процентах, либо в
долях единицы.
Опыт
проведения измерений показывает, что
при многократ-ных измерениях одной и
той же неизменной физической величины
при постоянных условиях погрешность
измерений можно представить в виде двух
слагаемых, которые по-разному проявляются
от измерения к измерению. Существуют
факторы, постоянно или закономерно
изменяющиеся в процессе проведения
измерений и влияющие на результат
измерений и его погрешность. Погрешности,
вызываемые такими факторами, называются
систематическими.
Систематическая
погрешность
– составляющая погреш-ности измерения,
остающаяся постоянной или закономерно
изменяющаяся при повторных измерениях
одной и той же величины. В зависимости
от характера изменения систематические
погрешности подразделяются на постоянные,
прогрессирующие, периодические,
изменяющиеся по сложному закону.
Близость
к нулю систематической погрешности
отражает правильность
измерений.
Систематические
погрешности обычно оцениваются либо
путем теоретического анализа
условий измерения,
основываясь на известных свойствах
средств измерений, либо использованием
более точных
средств
измерений.
Как правило, систематические погрешности
стараются исключить с помощью поправок.
Поправка
представляет собой значение величины,
вводимое в неисправленный результата
измерения с целью исключения систематической
погрешности. Знак поправки противоположен
знаку величины. На возникновение
погрешностей влияют также и факторы,
нерегулярно появляющиеся и неожиданно
исчезающие. Причем интенсивность их
тоже не остается постоянной. Результаты
измерения в таких условиях имеют
различия, которые индивидуально
непредсказуемы, а присущие им закономерности
проявляются лишь при значительном числе
измерений. Погрешности, появляющиеся
в результате действия таких факторов,
называются случайными
погрешностями.
Случайная
погрешность
– составляющая погрешности измерения,
изменяющаяся случайным образом (по
знаку и значению) при повторных измерениях
одной и той же величины, проведенных с
одинаковой тщательностью.
Незначительность
случайных погрешностей говорит о хорошей
сходимости
измерений,
то есть о близости друг к другу результатов
измерений, выполненных повторно одними
и теми же средствами, одним и тем же
методом, в одинаковых условиях и с
одинаковой тщательностью.
Обнаруживаются
случайные погрешности путем повторных
измерений
одной и той же величины в одних и тех же
условиях. Они не могут быть исключены
опытным путем, но могут быть оценены
при обработке результатов наблюдений.
Деление погрешностей измерений на
случайные и систематические очень
важно, т.к. учет и оценка этих составляющих
погрешности требует разных подходов.
Факторы,
вызывающие погрешности, как правило,
можно свести к общему уровню, когда
влияние их на формирование погрешности
является более или менее одинаковым.
Однако некоторые факторы могут проявляться
неожиданно сильно, например, резкое
падение напряжения в сети. В таком случае
могут возникать погрешности, существенно
превышающие погрешности, оправданные
условиями измерений, свойствами средств
измерений и метода измерений, квалификацией
оператора. Такие погрешности называются
грубыми,
или промахами.
Грубая
погрешность (промах)
– погрешность результата отдельного
измерения, входящего в ряд измерений,
которая для данных условий резко
отличается от остальных значений
погрешности. Грубые погрешности
необходимо всегда исключать из
рассмотрения, если известно, что они
являются результатом очевидных промахов
при проведении измерений. Если же причины
появления резко выделяющихся наблюдений
установить нельзя, то для решения вопроса
об их исключении используют статистические
методы. Существует несколько критериев,
которые позволяют выявить грубые
погрешности. Некоторые из них рассмотрены
ниже в разделе об обработке результатов
измерений.
1. Понятие о погрешности измерения
Всякий процесс измерения независимо от условий, в которых его проводят, сопряжен с погрешностями, которые искажают представление о действительном значении измеряемой величины.
Погрешностью называют отличие между объективно существующим истинным значением физической величины и найденным в результате измерения действительным значением физической величины.
Истинное значение физической величины идеальным образом отражает соответствующее свойство объекта. Практически получено быть не может.
Действительное значение физической величины находится как результат измерения и приближается к истинному значению настолько, что для данной цели может применяться вместо него.
Источниками появления погрешностей при измерениях могут служить различные факторы, основными из которых являются: несовершенство конструкции средств измерений или принципиальной схемы метода измерения; неточность изготовления средств измерений; несоблюдение внешних условий при измерениях; субъективные погрешности и др.
Относительная
ошибка определения теплоемкости
вычисляется по формуле
. (23.6)
Погрешность
определения
зависит от точности поддержания
адиабатических условий и линейности
температурного хода системы и составляет
около
1
10-4
К. Таким образом, ошибка в измерении
теплоемкости из-за неопределенности
хода в зависимости от
составляет:
При
= 1 градус
/
=1
10-2 %
При
= 1 10-2
градуса
/
=1
%.
Эта
ошибка может существенно возрастать
при большом времени установления
термодинамического равновесия образца,
что довольно часто наблюдается при
исследовании фазовых переходов первого
рода.
Ошибка
в определении количества тепла
,
подведенного к образцу, слагается из
ошибок измерений напряжений
и
потенциометром, ошибки измерения времени
нагрева секундомером и класса точности
используемого эталонного сопротивления.
Все это приводит к небольшой величине
0,1 %.
Таким
образом, при
= 1 К максимально возможная расчетная
погрешность определения теплоемкости
составляет
%.
23.4. Калориметрический сосуд
Калориметрический
сосуд представляет собой не только
контейнер для образца, но также является
вполне определенной частью аппаратуры,
в которой подведенное тепло и
соответствующее изменение температуры
тщательно измеряются. Простейший
калориметрический сосуд — вакуумный
контейнер, снабженный подходящими
термометром и нагревателем, а также
имеющий устройство для введения образца
внутрь и аппаратуру для подачи
теплообменного газа, облегчающего
установление теплового равновесия.
Общие
требования к такому калориметрическому
сосуду обычно сводятся к следующему.
Этот сосуд должен быть достаточно
прочным, чтобы выдержать перепад
давлений, равный, по крайней мере, 1 атм.;
не должен химически реагировать с
образцом; должен иметь хорошую
теплопроводность и хороший тепловой
контакт системы нагреватель — термометр
— калориметрический сосуд — образец.
Желательно,
что бы теплоемкость калориметра была
мала по сравнению с теплоемкостью
образца. Кроме того необходимо обеспечить
удобство заполнения калориметра
образцом.
Для
измерений теплоемкости порошкообразных
материалов целесообразно также
использовать внутренние хорошо проводящие
тепло перегородки для улучшения
выравнивания температуры внутри образца.
23.5. Измерения в режиме непрерывного нагрева
В
методе непрерывного нагрева, энергия
к нагревателю образца подается постоянно.
В этом методе производная от температуры
по времени определяется для тех моментов
времени, при которых измеряется подводимая
мощность, теплоемкость
рассчитывается из соотношения:
(23.7)
В
идеальном случае метод постоянного
(непрерывного) нагрева требует мгновенного
распределения тепла по калориметрическому
сосуду и его содержимому. Подвод энергии
делают достаточно малым, чтобы отклонение
температуры в любой части калориметрической
системы от наблюдаемой усредненной
температуры было незначительным.
Наиболее
часто этот метод используется для
квазистатического термографирования
в области фазового перехода. При этом
скорости нагрева или охлаждения
выбираются малыми
град/сек.
В
режиме непрерывного нагрева предварительно
устанавливается нулевая разность
температур между фурнитурой с образцом
и адиабатической оболочкой. В этом
случае джоулево тепло, выделяемое на
нагревателе, определяет рост температуры
в соответствии с формулой. Для снятия
термограмм в режиме охлаждения
осуществляется снижение до необходимого
уровня температуры адиабатической
оболочки относительно температуры
образца путем подачи напряжения
на вход системы регулирования
адиабатических условий. Так как скорость
изменения температуры образца зависит
от его теплоемкости, то для области
фазового перехода первого и второго
рода вид зависимости
будет разным. В точке фазового перехода
второго рода теплоемкость изменяется
скачком, соответственно в зависимости
будет излом. В случае фазового перехода
первого рода теплоемкость принимает
аномально большие значения, связанные
со скрытой теплотой перехода. Поэтому
температура исследуемого образца при
нагреве (охлаждении) не будет меняться
до тех пор, пока не завершится поглощение
(выделение) скрытой теплоты. Это приводит
к тому, что при температуре фазового
перехода на термограмме будет наблюдаться
горизонтальный участок.
Из
термограммы в режиме нагрева скрытая
теплота
вычисляется как
,
где
— мощность нагрева,
— время поглощения, определяемое
продолжительностью горизонтального
участка. Чувствительность метода
термограмм высока и позволяет
регистрировать тепловые эффекты 0,5 10-4
— 10-3 Дж.
Кроме
величины скрытой теплоты и точного
значения температуры перехода метод
термограмм позволяет получить величину
температурного гистерезиса путем
сравнения термограммы в режиме нагрева
и охлаждения. Поскольку термометр
вынесен на адиабатическую оболочку,
при определении температуры перехода
в режиме охлаждения необходимо учитывать
разность температур между образцом и
оболочкой.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
8
Контрольные задания
1. В чем заключается метод электрического нагрева для определения
теплоемкости твердых тел ?
2. Выведите формулу для экспериментального определения теплоемкости.
3. Почему во время эксперимента нагревание пустого калориметра и
калориметра с образцом необходимо производить при одной и той же
мощности нагревателя?
4. Чем ограничена максимально допустимая температура нагревания
калориметра?
5. Основные источники ошибок данного метода измерений .
8
Контрольные задания
1. В чем заключается метод электрического нагрева для определения
теплоемкости твердых тел?
2. Выведите формулу для экспериментального определения теплоемкости.
3. Почему во время эксперимента нагревание пустого калориметра и
калориметра с образцом необходимо производить при одной и той же
мощности нагревателя?
4. Чем ограничена максимально допустимая температура нагревания
калориметра?
5. Основные источники ошибок данного метода измерений.
ЛАБОРАТОРНАЯ РАБОТА № 14
ОПРЕДЕЛЕНИЕ УДЕЛЬНОЙ ТЕПЛОЕМКОСТИ ТВЕРДЫХ ТЕЛ МЕТОДОМ
НАГРЕВАНИЯ.
Цель
работы: определение удельной
теплоемкости твердого тела и проверка закона Дюлонга и Пти.
Принадлежности: установка, исследуемые тела, секундомер, термопара,
гальванометр типа М.
ТЕОРЕТИЧЕСКОЕ
ОБОСНОВАНИЕ.
Удельной теплоемкостью вещества называется физическая величина,
численно равная количеству теплоты , которое надо сообщить, чтобы нагреть 1кг вещества на
1К.
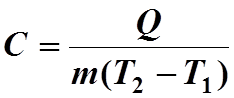
Эта формула справедлива в том случае, если
теплоемкость изменяется незначительно с изменением температуры. С учетом
зависимости теплоемкости от температуры, формула для С запишется
в виде:
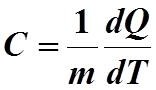
Формула (2) дает действительную теплоемкость
для каждой данной температуре, а формула (1) — среднюю теплоемкость в
интервале температур от Т1 до Т2.
У большинства тел с повышением температуры
теплоемкость увеличивается. Количество теплоты, необходимое для нагревания тела
от температуры Т1 до Т2 будет
равно:
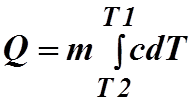
Теплоемкость тела можно найти, если известно
количество тепла , подведенного к телу, и
изменение температуры :
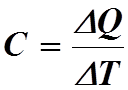
В данной работе температуру исследуемого образца
измеряют термопарой — спай двух разнородных металлов. Тепло подводится за счет
электрического нагревателя и определяется формулой:
(5)
Вследствие теплопроводности стенок калориметра часть
энергии рассеивается в окружающей среде, поэтому оставшееся в калориметре количество
тепла будет:
(6)
где l — коэффициент теплопроводности стенок калориметра,
T- температура тела,
Tк
— комнатная температура,
Dt – время
нагревания.
Тогда, используя (4)
получим, что:
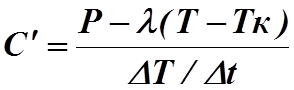
(7)
Теплоемкость калориметр С0
определятся отдельно. Если не давать теплу заметных перегревов и производить
все измерения при комнатных температурах, то утечка тепла будет небольшой.
Однако при небольших нагревах возникает большая погрешность в измерении DT=T-Tк. Чтобы исключить эту трудность, измерения необходимо
производить следующим образом. Для широкого интервала температур определяют
скорость нагревания тела DT/Dt. Затем по полученным данным строят график зависимости 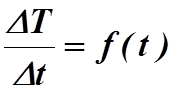
Экстраполируя график на температуру T=Tк ,
определяют скорость нагревания при комнатной температуре .
Подставив полученные значения в формулу (7) и учтя, что при Т=Тк
,l(T-Tк)=0 имеем:
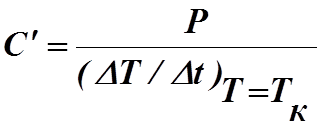
Описание
установки
2.ОПИСАНИЕ УСТАНОВКИ.
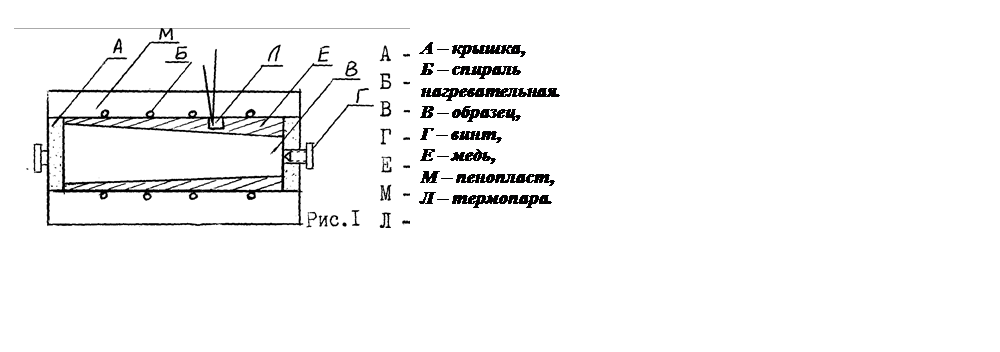
Рис. 14.1
Установка (рис.14.1)
состоит из калориметра с пенопластовой изоляцией. Внутренние стенки калориметра
выполнены из материала с высокой теплопроводностью. Для обеспечения надежного
теплового контакта исследуемые образцы и стенки калориметра выполнены в форме
усеченных конусов и плотно прилегают друг к другу. В теплоизолированную стенку
калориметра вмонтированы электронагреватель и термопара. Для выталкивания
образца служат плоскогубцы.
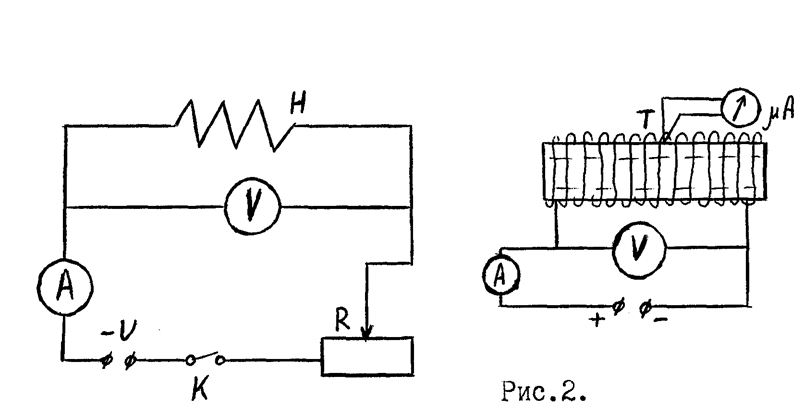
Cхема включения нагревателя Н
изображена на рис.14.2.
Рис. 14.2 Схема подключения нагревателя Н.
ПОДГОТОВКА
И ПРОВЕДЕНИЕ ИЗМЕРЕНИЙ.
1.
Подготовить калориметр к работе.
Установить термопару в гнездо калориметра до упора.
2.
Замкнуть ключ (рис14.2) и
установить ток в 3-4 А. Выключить нагреватель.
3.
Установить предел
измерения на деление либо 5mVи
нуль гальванометра.
4.
Замкнуть цепь нагревателя,
одновременно включить секундомер. Через каждые 2мин. записывать
показания гальванометра в течении 20мин.
5.
Определить мощность
нагревателя по показаниям амперметра и вольтметра P=IU.
6.
Построить график
зависимости температуры от времени T=f(t), используя
градуировочный график термопары n=f(T).
7.
На основе зависимости T=f(t),
постороить график зависимости скорости нагревания калориметра от температуры 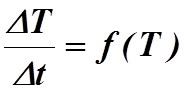
разделить на 10-12 одинаковых отрезков и для каждого из них определить тангенс
угла наклона 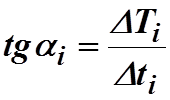
посторить график
,
где T=Tср. для
данного интервала температур.
Произведя
экстраполяцию этого графика на Тк найти значение
8.
Подставить значение
скорости нагрева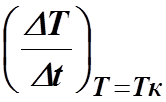
теплоемкость калориметра С0.
9.
Охладить калориметр,
поместить в него исследуемое тело, предварительно взвесив его, найти
теплоемкость по описанной методике (п.4-8). Теплоемкость
исследуемого образца равна CT=-C0.
Полученные результаты занести в таблицу № 14.1 .
10.
Удельную теплоемкость
найти по формуле: 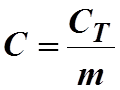
образца.
11.
Рассчитать молярную
теплоемкость по формуле 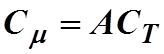
атомная масса вещества (для одноатомных веществ и молярная масса совпадают), СТ
– удельная теплоемкость тела.
12.
Определите основные
источники погрешности данного метода измерения.
ЭКСТРАПОЛЯЦИЯ
— приближенное определение значений функции f (x) в точках х,
лежащих вне отрезка [а,
в], по ее значениям f1…fi , в
точках хi
, принадлежащих отрезку [а, в].
Таблица № 14.1
|
I, A |
U В |
t, мин |
n, дел |
T, 0С |
0С/c |
Tср 0C |
Tк 0C |
|
с, |
с/, |
|
|
|
|||||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
Калориметр |
0 2 4 … 20 |
||||||||||
|
Калориметр + исследуемое тело |
0 2 4 … 20 |
КОНТРОЛЬНЫЕ ВОПРОСЫ.
1. Что называется теплоемкостью? В каких единицах
она измеряется?
2. Классическая и квантовая теория теплоемкости.
3. В чем состоит закон Дюлонга и Пти?
- « первая
- 3
- 4
- 5


Функция «чтения» служит для ознакомления с работой. Разметка, таблицы и картинки документа могут отображаться неверно или не в полном объёме!
коэффициента , определить теплоемкость образца по формуле , где – ток, идущий через нагреватель; – напряжение на нагревателе; – масса образца.Вычислить молярную теплоемкость вещества по формуле , где μ-молярная масса образца (табл. величина).Оценить погрешность измерений.
Для оценки относительной погрешности данной формулы необходимо произвести следующие действия:
,
где — относительная погрешность амперметра,
— относительная погрешность вольтметра,
— относительная погрешность формулы, использовавшейся для вычисления массы.
,
где -абсолютная погрешность амперметра ( написана на приборе)
– показание амперметра
,
где — абсолютная погрешность вольтметра ( написана на приборе)
– показание вольтметра Контрольные вопросы.
Как с помощью метода электрического нагрева определить теплоемкость твердых тел?Выведите формулу для экспериментального определения теплоемкости методом нагрева.Почему во время эксперимента нагревание пустого калориметра и калориметра с образцом необходимо производить при одной и той же мощности нагревателя?Чем ограничена максимально допустимая температура нагревания калориметра?Основные источники ошибок данного метода измерений.
Литература:
Б. Н. Юдаев «Техническая термодинамика. Теплопередача : учебник для неэнергетич. спец. втузов» — М.: Высш. шк., 1988.-479 с. А. А. Детлаф «Курс физики. Учебное пособие для втузов» — М.: Высш. шк.,
1989 – 608с.
- « первая
- 3
- 4
- 5
Интересная статья: Быстрое написание курсовой работы

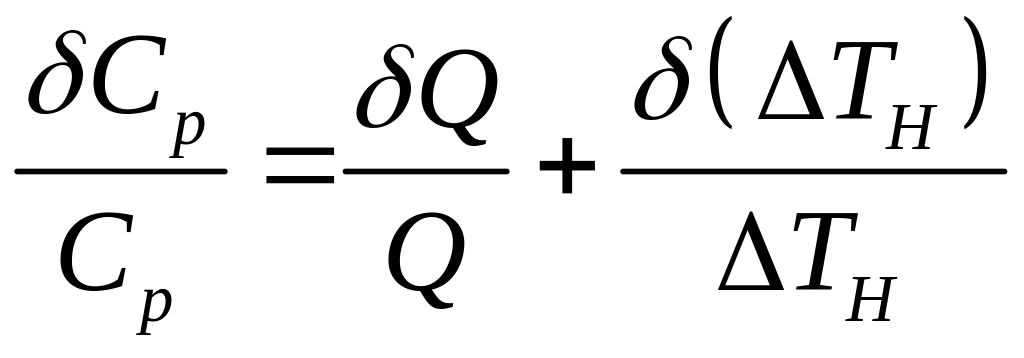

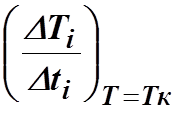 0С/c
0С/c