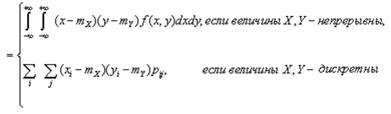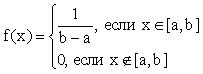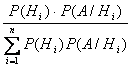Вопрос посетителя
Верны ли определения?
А) Односторонняя критическая область — критическая область, определяемая неравенством K > kкр, где К — значение критерия, kкр — критическая точка и kкр — положительное число.
В) Двусторонняя критическая область — критическая область, определяемая неравенствами K < k1, K > k2, где К — значение критерия, k1, k2 — критические точки и k2 > k1.
Подберите правильный ответ.
(*ответ*) А — нет, В — да
А — да, В — да
А — да, В — нет
А — нет, В — нет
Верны ли определения?
А) Ошибку первого рода совершают, отвергнув гипотезу, когда она истинна.
В) Ошибку второго рода совершают, приняв ложную гипотезу.
Подберите правильный ответ.
(*ответ*) А — да, В — да
А — да, В — нет
А — нет, В — да
А — нет, В — нет
Верны ли определения?
А) Принцип практической уверенности состоит в следующем: если наблюдаемое значение критерия принадлежит критической области — гипотезу отвергают, если наблюдаемое значение критерия принадлежит области принятия гипотезы — гипотезу принимают.
В) Гипотезы об однородности выборок — гипотезы о том, что рассматриваемые выборки извлечены из одной и той же генеральной совокупности.
Подберите правильный ответ
(*ответ*) А — нет, В — да
А — да, В — да
А — да, В — нет
А — нет, В — нет
Верны ли определения?
А) Сложная статистическая гипотеза — гипотеза, допускающая бесконечное множество значений параметров распределения.
В) Простая статистическая гипотеза — гипотеза, допускающая бесконечное множество значений параметров распределения.
Подберите правильный ответ.
(*ответ*) А — да, В — нет
А — да, В — да
А — нет, В — да
А — нет, В — нет
Верны ли определения?
А) Статистическая гипотеза — соотношение, устанавливающее соответствие между возможными значениями случайной величины и их вероятностями.
В) Конкурирующая (альтернативная) гипотеза — гипотеза, противоречащая нулевой статистической гипотезе.
Подберите правильный ответ
(*ответ*) А — нет, В — да
А — да, В — да
А — да, В — нет
А — нет, В — нет
Верны ли определения?
А) Статистический критерий — значение критерия, вычисленное по выборкам.
В) Уровень значимости критерия — вероятность допустить ошибку первого рода.
Подберите правильный ответ
(*ответ*) А — нет, В — да
А — да, В — да
А — да, В — нет
А — нет, В — нет
Верны ли определения?
А) Число степеней свободы — количество значений в итоговом вычислении статистики, способных варьироваться.
В) Вид критической области зависит от нулевой гипотезы и не зависит от альтернативной.
Подберите правильный ответ
(*ответ*) А — да, В — нет
А — да, В — да
А — нет, В — да
А — нет, В — нет
Верны ли определения?
А) Область допустимых значений — совокупность значений критерия, при которых нулевая гипотеза принимается.
В) Отыскивая двустороннюю критическую область при уровне значимости , тем самым находят и соответствующий доверительный интервал с надежностью .
Подберите правильный ответ
(*ответ*) А — нет, В — да
А — да, В — да
А — да, В — нет
А — нет, В — нет
Ответ эксперта
Верны ли определения?
А) Односторонняя критическая область — критическая область, определяемая неравенством K > kкр, где К — значение критерия, kкр — критическая точка и kкр — положительное число.
В) Двусторонняя критическая область — критическая область, определяемая неравенствами K < k1, K > k2, где К — значение критерия, k1, k2 — критические точки и k2 > k1.
Подберите правильный ответ.
(*ответ*) А — нет, В — да
А — да, В — да
А — да, В — нет
А — нет, В — нет
Верны ли определения?
А) Ошибку первого рода совершают, отвергнув гипотезу, когда она истинна.
В) Ошибку второго рода совершают, приняв ложную гипотезу.
Подберите правильный ответ.
(*ответ*) А — да, В — да
А — да, В — нет
А — нет, В — да
А — нет, В — нет
Верны ли определения?
А) Принцип практической уверенности состоит в следующем: если наблюдаемое значение критерия принадлежит критической области — гипотезу отвергают, если наблюдаемое значение критерия принадлежит области принятия гипотезы — гипотезу принимают.
В) Гипотезы об однородности выборок — гипотезы о том, что рассматриваемые выборки извлечены из одной и той же генеральной совокупности.
Подберите правильный ответ
(*ответ*) А — нет, В — да
А — да, В — да
А — да, В — нет
А — нет, В — нет
Верны ли определения?
А) Сложная статистическая гипотеза — гипотеза, допускающая бесконечное множество значений параметров распределения.
В) Простая статистическая гипотеза — гипотеза, допускающая бесконечное множество значений параметров распределения.
Подберите правильный ответ.
(*ответ*) А — да, В — нет
А — да, В — да
А — нет, В — да
А — нет, В — нет
Верны ли определения?
А) Статистическая гипотеза — соотношение, устанавливающее соответствие между возможными значениями случайной величины и их вероятностями.
В) Конкурирующая (альтернативная) гипотеза — гипотеза, противоречащая нулевой статистической гипотезе.
Подберите правильный ответ
(*ответ*) А — нет, В — да
А — да, В — да
А — да, В — нет
А — нет, В — нет
Верны ли определения?
А) Статистический критерий — значение критерия, вычисленное по выборкам.
В) Уровень значимости критерия — вероятность допустить ошибку первого рода.
Подберите правильный ответ
(*ответ*) А — нет, В — да
А — да, В — да
А — да, В — нет
А — нет, В — нет
Верны ли определения?
А) Число степеней свободы — количество значений в итоговом вычислении статистики, способных варьироваться.
В) Вид критической области зависит от нулевой гипотезы и не зависит от альтернативной.
Подберите правильный ответ
(*ответ*) А — да, В — нет
А — да, В — да
А — нет, В — да
А — нет, В — нет
Верны ли определения?
А) Область допустимых значений — совокупность значений критерия, при которых нулевая гипотеза принимается.
В) Отыскивая двустороннюю критическую область при уровне значимости , тем самым находят и соответствующий доверительный интервал с надежностью .
Подберите правильный ответ
(*ответ*) А — нет, В — да
А — да, В — да
А — да, В — нет
А — нет, В — нет
 |
 |
Детали файла
| Имя файла: | 5419.02.01;МТ.02;1 |
| Размер: | 118 Kb |
| Дата публикации: | 2015-03-09 04:46:16 |
| Описание: | |
| Математическая статистика (магистр, курс 1) — Модульный тест
Список вопросов теста (скачайте файл для отображения ответов): Верны ли определения? |
|
| Для скачивания этого файла Вы должны ввести код указаный на картинке справа в поле под этой картинкой —> |  |
| ВНИМАНИЕ: | |
| Нажимая на кнопку «Скачать бесплатно» Вы подтверждаете свое полное и безоговорочное согласие с «Правилами сервиса» | |
| Ошибка: | |
| Введенный Вами код не соответствует указанному на картинке! Сгенерирован новый код. Попробуйте снова. Не скачивается нивкакую? |
|
Ошибки первого и второго рода. Понятие о статистических критериях
Проверить статистическую гипотезу – значит проверить, согласуются ли данные, полученные из выборки с этой гипотезой. При этом проверяемая гипотеза может подтвердиться, а может и не подтвердиться. Проверка статистических гипотез сопряжена с возможностью допустить ошибку.
Ошибка первого рода состоит в том, что будет отвергнута верная гипотеза.
Ошибка второго рода состоит в том, что будет принята ложная гипотеза.
Вероятность совершения ошибки первого рода обозначается 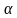
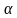
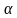
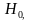
Вероятность не отклонить ложную гипотезу обозначается 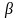
При проверке нулевой гипотезы могут возникнуть следующие ситуации (табл.):
|
|
верная |
ложная |
|
отклоняется |
Ошибка второго рода |
Решение верное |
|
не отклоняется |
Решение верное |
Ошибка второго рода |
Проверка любой статистической гипотезы осуществляется с помощью статистического критерия.
Статистический критерий – это случайная величина [статистика], которая используется с целью проверки нулевой гипотезы.
В дальнейшем статистический критерий непараметрических гипотез будем обозначать, как правило, буквой
Статистические критерии носят название соответственно распределению: 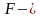
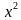
Наблюдаемое значение статистического критерия – это значение критерия, которое рассчитано по выборке с определенным законом распределения.
Множество всех возможных значений выбранного статистического критерия разделяется на два непересекающихся подмножества. Первое из этих подмножеств включает в себя значения критерия, при которых нулевая гипотеза отвергается, а второе – те значения критерия, при которых нулевая гипотеза принимается.
Критическая область – это множество возможных значений статистического критерия, при которых нулевая гипотеза отвергается.
Область принятия гипотезы [область допустимых значений] – это множество возможных значений статистического критерия, при которых нулевая гипотеза принимается.
В том случае, если наблюдаемое значение статистического критерия (рассчитанное по выборочной совокупности) принадлежит критической области, нулевую гипотезу отвергают. Если же наблюдаемое значение статистического критерия принадлежит области принятия гипотезы, то нулевая гипотеза принимается.
Критические точки [квантили] – это точки, которые разграничивают критическую область и область принятия гипотезы.
Выделяют одностороннюю и двустороннюю критические области. Дадим определения данных критических областей на примере условного статистического критерия 
Правосторонняя критическая область определяется неравенством 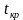
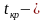
Левосторонняя критическая область определяется неравенством 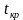
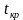
Двусторонняя критическая область определяется неравенствами 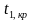
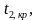
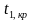
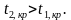
Теория вероятностей и математическая статистика (СПО, курс 1)
Установите соответствие между профессиональными терминами и их определениями:
Основной принцип проверки статистических гипотез
ее совершают, отвергнув гипотезу, когда она истинна
вероятность того, что нулевая гипотеза будет отвергнута, когда она неверна (верна конкурирующая гипотеза)
ее совершают, приняв ложную гипотезу
если наблюдаемое значение критерия принадлежит критической области — гипотезу отвергают, если наблюдаемое значение критерия принадлежит области принятия гипотезы — гипотезу принимают
Теория вероятностей и математическая статистика (СПО, курс 1)
Установите соответствие между профессиональными терминами и их определениями:
появление одного из них исключает появление другого: АÇВ = Æ
событие, которое обязательно произойдёт в результате эксперимента, Р(Е) = 1
событие, состоящее из точек пространства элементарных событий, не принадлежащих А: + А = Е;
×А = Æ
событие, которое в данном опыте произойти не может, Р(а) = 0
Теория вероятностей и математическая статистика (СПО, курс 1)
Вероятность того, что в серии из n независимых испытаний событие А наступит ровно k раз (безразлично в какой последовательности) находят по формуле _________, если n является достаточно небольшим значением: Pn(k) = Сnkpkqn-k, где Сnk = n! / k!(n-k)! – число сочетаний из n по k, р – вероятность события А, q – вероятность противоположного события a.
Теория вероятностей и математическая статистика (СПО, курс 1)
Установите соответствие между профессиональными терминами и их определениями:
Правосторонняя критическая область
критическая область, определяемая неравенством К < kкр , где К – значение критерия, kкр – критическая точка и kкр – отрицательное число
Двусторонняя критическая область
правосторонняя или левосторонняя критическая область
Односторонняя критическая область
критическая область, определяемая неравенствами К < k1, К > k2, где К – значение критерия, k1, k2 – критические точки и k2 > k1
Левосторонняя критическая область
критическая область, определяемая неравенством К > kкр , где К – значение критерия, kкр – критическая точка и kкр – положительное число
Теория вероятностей и математическая статистика (СПО, курс 1)
Установите соответствие между профессиональными терминами и их определениями:
Корреляционная зависимость (корреляция)
зависимость, при которой изменение одной случайной величины влечет изменение распределения другой
признаки, изменяющиеся под действием других связанных с ними признаков
признаки, обуславливающие изменения результативных признаков
Статистическая (стохастическая) зависимость
функциональная зависимость между значениями одной случайной величины и условным математическим ожиданием другой случайной величины
Теория вероятностей и математическая статистика (СПО, курс 1)
Установите соответствие между профессиональными терминами и их определениями:
Эмпирическая функция распределения
распределение дискретной случайной величины, принимающей значения х1, х2,… xn с вероятностями, равными рi = 1/п
функция распределения F (х) генеральной совокупности
Теоретическая функция распределения
вероятностное пространство, элементами которого являются наблюдения (х1), (х2), (xn) и все элементы которого равновероятны: (Р(хi) = 1/п)
функция F* (х), определяющая для каждого значения nх относительную частоту события X < х
Теория вероятностей и математическая статистика (СПО, курс 1)
Установите соответствие между профессиональными терминами и их определениями:
Коэффициент корреляции случайных величин и
Ковариация случайных величин и
Центральный момент порядка случайного вектора
математическое ожидание произведения центрированных величин: =
Момент порядка случайного вектора
Теория вероятностей и математическая статистика (СПО, курс 1)
Установите соответствие между профессиональными терминами и их определениями:
Показательное (экспоненциальное) распределение
распределение вероятностей, определяемое формулой Бернулли: . k = 0,1,2,… n
плотность распределения случайной величины на интервале [a,b] постоянна и равна
Равномерное распределение
Р(Х = к) = 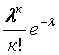
Биномиальное распределение
плотность распределения случайной величины имеет вид: 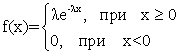
Теория вероятностей и математическая статистика (СПО, курс 1)
Установите соответствие между профессиональными терминами и их определениями:
если Н1, Н2, … , Нn — полная группа событий, то Р(Hi /A) =
Формула условной вероятности
Р(А) = , где Р(А/Нi) – условные вероятности события А, если известно, что событие Нi произошло
Формула полной вероятности
Р(В/А) = , при Р(В) > 0
Pn(k) = Сnkpkqn-k, где Сnk = n! / k!(n-k)! – число сочетаний из n по k, р – вероятность события А, q – вероятность противоположного события a
Теория вероятностей и математическая статистика (СПО, курс 1)
Установите соответствие между профессиональными терминами и их определениями:
Нормальное распределение n(a,s)
Р(êХ – mx ê³ a ) £ , где Х – случайная величина, имеющая конечные математическое ожидание mX и дисперсию DX, а > 0
Нормированное и центрированное нормальное распределение
плотность распределения случайной величины имеет вид: 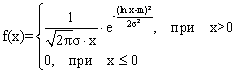
Логарифмически нормальное распределение
плотность распределения случайной величины имеет вид: f(x) =
плотность распределения случайной величины имеет вид: 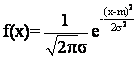
Теория вероятностей и математическая статистика (СПО, курс 1)
Установите соответствие между профессиональными терминами и их определениями:
Вероятность пересечения двух событий А и В
если пересечение Hi Ç Hj = Æ для i ¹ j , i,j = 1,2,…, n, и сумма вероятностей Р(Н1) + Р(Н2) + …+ Р(Нn ) = 1
система S подмножеств, для которой выполнены условия: а) система S содержит достоверное и невозможное события; б) если системе S принадлежат события А и В, то ей принадлежат также события А×В, А + В, А\В
наступление одного события не изменяет вероятность наступления другого: Р(АВ) = Р(А)×Р(В), Р(А/В) = Р(А), Р(В/А) = Р(В)
Полная группа событий Н1, Н2, … , Нn
если Р(А) > 0 и Р(В) > 0, то Р(АВ) = Р(В), Р(А/В) = Р(А)×Р(В/А)