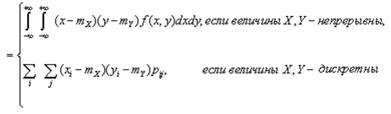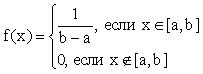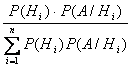Список вопросов теста (скачайте файл для отображения ответов):
10 % всех мужчин и 5 % женщин дальтоники. Число мужчин и женщин одинаково. Вероятность того, что наугад выбранное лицо оказалось дальтоником равна:
DX = 3, тогда D(2x + 5) равна:
X и Y – независимы DX = 2, DY = 3, тогда D(2x – 4y) равно:
X и Y – независимы. DX = 2, DY = 3, тогда D(4x – 2y) равно:
X и Y – независимые случайные величины DX = 4; DY = 3, тогда D(2x + 3y) = _______ (наберите число).
МХ = 2, МY = 3, тогда М(3х – 2y) равно _________ (наберите число).
МХ = 2, тогда М(3х – 4) равно:
В таблице распределения случайной величины С =
(наберите десятичную дробь).
В таблице распределения случайной величины С =
(Наберите десятичную дробь).
В таблице статистического распределения, построенного по выборке, на одно число попала клякса .
Это число
Верны ли определения?
A) Величина уровня доверия влияет на величину доверительного интервала: чем больше уровень доверия, тем уже интервал.
B) Доверительным интервалом с уровнем доверия – интервал, накрывающий значение оцениваемого параметра с вероятностью
Подберите правильный ответ
Верны ли определения?
A) Величина уровня доверия влияет на величину доверительного интервала: чем больше уровень доверия, тем шире интервал.
B) Доверительный интервал с уровнем доверия – интервал, накрывающий значение оцениваемого параметра с вероятностью .
Подберите правильный ответ
Верны ли определения?
A) геометрический смысл определенного интеграла —
площадь криволинейной трапеции, ограниченной непрерывной кривой y = f(x), где на [a, b], численно равна определенному интегралу .
B) Постоянный множитель можно выносить за знак интеграла
Подберите правильный ответ
Верны ли определения?
A) Двусторонний доверительный интервал с уровнем доверия для математического ожидания a нормального распределения для случая, когда среднеквадратическое отклонение распределения неизвестно:
B) Односторонний доверительный интервал с уровнем доверия для математического ожидания a нормального распределения для случая, когда среднеквадратическое отклонение распределения неизвестно:
Подберите правильный ответ
Верны ли определения?
A) Дисперсионный анализ – статистический метод, предназначенный для оценки влияния различных факторов на результат эксперимента
B) Статистическая зависимость – такая зависимость между случайными величинами Х и Y, при которой изменение одной величины влечет изменение распределения другой
Подберите правильный ответ
Верны ли определения?
A) Дисперсия суммы двух случайных величин = .
B) Если случайные величины и независимы, то дисперсия их разности = .
Подберите правильный ответ
Верны ли определения?
A) Для построения доверительного интервала для дисперсии надо пользоваться таблицами распределения Пирсона ()
B) Для того, чтобы по выборке объема n построить доверительный интервал для математического ожидания нормального распределения, дисперсия которого неизвестна, нужны таблицы распределения Стьюдента
Подберите правильный ответ
Верны ли определения?
A) Для того, чтобы по выборке объема n построить доверительный интервал для математического ожидания нормального распределения, дисперсия которого известна, нужны таблицы распределения Стьюдента
B) Для построения доверительного интервала для дисперсии надо пользоваться таблицами нормального распределения.
Подберите правильный ответ
Верны ли определения?
A) Для того, чтобы построить доверительный интервал математического ожидания по выборке, когда дисперсия известна, необходимо определить выборочное среднее и выборочное среднеквадратическое s
B) Для того, чтобы по выборке объема n построить доверительный интервал для математического ожидания нормального распределения, дисперсия которого неизвестна, нужны таблицы распределения Стьюдента
Подберите правильный ответ
Верны ли определения?
A) Для того, чтобы построить доверительный интервал математического ожидания по выборке, когда дисперсия неизвестна, необходимо определить выборочное среднее и выборочное среднеквадратическое s
B) Для построения доверительного интервала для дисперсии надо пользоваться таблицами нормального распределения
Подберите правильный ответ
Верны ли определения?
A) Если случайные величины независимы, то коэффициент корреляции равен нулю.
B) Если коэффициент корреляции равен нулю, то случайные величины независимы.
Подберите правильный ответ
Верны ли определения?
A) Критическая область – область, при попадании в которую значения статистики критерия, сосчитанной по выборке, основная гипотеза отвергается
B) Критические значения — точки, разделяющие критическую область и область допустимых значений
Подберите правильный ответ
Верны ли определения?
A) Линейная регрессия имеет место, если функция регрессии – линейная функция, т.е. ее можно представить в виде уравнения y = f(x) = ax + b
B) Функция регрессии Х на Y — условное математическое ожидание M(Y/Х = x) как функция от х: M(Y/Х = x) = f(x)
Подберите правильный ответ
Верны ли определения?
A) Мощностью критерия называется вероятность (1–) не допустить ошибку 2-го рода, т.е. отвергнуть гипотезу Н0, когда она верна
B) Уровень значимости – вероятность a попадания в критическую область в случае, если основная гипотеза истинна
Подберите правильный ответ
Верны ли определения?
A) Мощностью критерия называется вероятность (1–) не допустить ошибку 2-го рода, т.е. отвергнуть гипотезу Н0, когда она неверна
B) Ошибка первого рода – ошибка a, которую совершают, отвергнув основную гипотезу, когда она истинна
Подберите правильный ответ
Верны ли определения?
A) Несобственный интеграл от непрерывной функции на всей прямой определяется равенством:,
B) Для вычисления определенного интеграла применяется формула Ньютона-Лейбница:, где F(x) – одна из первообразных f(x)
Подберите правильный ответ
Верны ли определения?
A) Определенный интеграл Римана от функции f(x) на отрезке [a,b] — предел интегральных сумм при условии , обозначаемый .
B) Аддитивность определенного интеграла – свойство, состоящее в том, что = + для любого .
Подберите правильный ответ
Верны ли определения?
A) Ошибка первого рода – ошибка a, которую совершают, отвергнув основную гипотезу, когда она истинна
B) Ошибка второго рода – ошибка b, которую совершают, приняв основную гипотезу, когда она ложна
Подберите правильный ответ
Верны ли определения?
A) Ошибка первого рода – ошибка b, которую совершают, приняв основную гипотезу, когда она ложна
B) Ошибка второго рода – ошибка a, которую совершают, отвергнув основную гипотезу, когда она истинна
Подберите правильный ответ
Верны ли определения?
A) При проверке гипотезы о виде распределения, когда параметры его неизвестны, применяется критерий χ2 с заменой неизвестных параметров на эмпирические значения и уменьшается число степеней свободы
B) При проверке гипотез о численном значении дисперсии (s = s0) при неизвестном среднем а используется статистика , имеющая распределение χ2n-1
Подберите правильный ответ
Верны ли определения?
A) При проверке с помощью критерия χ2 гипотезы о равномерном распределении R(a,b), когда концы интервала a и b неизвестны, а число интервалов группировки равно m, статистика χ2 имеет распределение χ2 с числом степеней свободы m – 3
B) При проверке с помощью критерия χ2 гипотезы о равномерном распределении R(a,b), когда концы интервала a и b известны, а число интервалов группировки равно m, статистика χ2 имеет распределение χ2 с числом степеней свободы m – 2
Подберите правильный ответ
Верны ли определения?
A) Распределение вероятностей, которое имеет случайная величина , где и – независимые случайные величины, распределенные по с n1 и n2 степенями свободы, называется распределением Фишера-Снедекора, оно определяется двумя параметрами – n1 и n2
B) Статистика F, использующаяся в процедуре проверки равенства дисперсий двух генеральных совокупностей, имеет распределение Стьюдента
Подберите правильный ответ
Верны ли определения?
A) Регрессионная модель — модель, в которой один из двух признаков изучаемой двумерной величины, например x, выступает в качестве независимой компоненты (чаще всего это время), т.е. переменная x вообще не случайна, а случайна только переменная y
B) Функция регрессии Y на Х — условное математическое ожидание M(Y/Х = x) как функция от х: M(Y/Х = x) = f(x)
Подберите правильный ответ
Верны ли определения?
A) Случайные величины, имеющие нулевой коэффициент, называют некоррелированными.
B) Некоррелированные случайные величины не зависимы.
Подберите правильный ответ
Верны ли определения?
A) Случайным вектором или n-мерной случайной величиной называют упорядоченный набор из n случайных величин
B) Непрерывный случайный вектор – это
случайный вектор, компоненты которого непрерывные случайные величины
Подберите правильный ответ
Верны ли определения?
A) Статистика F, использующаяся в процедуре проверки равенства дисперсий двух генеральных совокупностей, имеет распределение Фишера-Снедекора
B) Для проверки гипотезы о виде распределения применяется статистика , имеющая распределение χ2 , число степеней которого равно m – 2 (число заменяемых параметров равно 2)
Подберите правильный ответ
Верны ли определения?
A) Статистика, с помощью которой по эмпирическому значению коэффициента корреляции r и числу испытаний n проверяется значимость коэффициента корреляции, вычисляется по формуле
B) Статистика, с помощью которой по эмпирическому значению коэффициента корреляции r и числу испытаний n проверяется значимость коэффициента корреляции, имеет распределение Фишера-Снедекора
Подберите правильный ответ
Верны ли определения?
A) Статистическая зависимость — такая зависимость между случайными величинами Х и Y, при которой изменение одной величины не влечет изменение распределения другой
B) Корреляционная статистическая зависимость — такая зависимость, в которой при изменении одной величины изменяется среднее значение (математическое ожидание) другой
Подберите правильный ответ
Верны ли определения?
A) Точность интервальной оценки определяется доверительной вероятностью
B) Надежность интервальной оценки определяется центром доверительного интервала
Подберите правильный ответ
Верны ли определения?
A) Уровень значимости – вероятность a попадания в критическую область в случае, если основная гипотеза истинна
B) Критическая область – область, при попадании в которую значения статистики критерия, сосчитанной по выборке, основная гипотеза принимается
Подберите правильный ответ
Верны ли определения?
A) Условная функция распределения случайной величины при условии равна
B) Случайные величины и называют независимыми, если функция распределения вектора равна
Подберите правильный ответ
Верны ли определения?
A). Величина коэффициента корреляции заключена в пределах
B) Для независимых случайных величин ковариация равна нулю.
Подберите правильный ответ
Верны ли определения?
A). вероятность попадания случайной величины на заданный интервал выражается через плотность распределения
.
B) интервал практически возможных значений нормально распределенной случайной величины равен (, где m, – параметры нормального распределения.
Подберите правильный ответ
Верны ли определения?
A). Математическое ожидание случайной величины, имеющей показательное распределение с параметром :
B) Математическое ожидание случайной величины, имеющей равномерное распределение на отрезке [a, b]: MX=
Подберите правильный ответ
Верны ли определения?
A). Плотность распределения и функция распределения двумерной случайной величины связаны соотношением
B) Закон распределения дискретного случайного вектора – это совокупность всех возможных значений данного вектора и вероятностей , равных
Подберите правильный ответ
Верны ли определения?
A). Плотность распределения случайной величины, равномерно распределенной на [a,b], имеет вид:
.
B) Непрерывная случайная величина Х имеет нормальное распределение с параметрами m и , если ее плотность распределения имеет вид
.
Подберите правильный ответ
Верны ли определения?
A). Случайная величина Х распределена равномерно на отрезке (a, b), если ее плотность постоянна и равна
.
B) Непрерывная случайная величина Х, принимающая неотрицательные значения, имеет показательное (экспоненциальное) распределение с параметром , если плотность распределения имеет вид
.
Подберите правильный ответ
Верны ли определения?
A). Функция распределения случайной величины, равномерно распределенной на [a,b], имеет вид:
.
B) Непрерывная случайная величина Х, принимающая неотрицательные значения, имеет показательное (экспоненциальное) распределение с параметром , если функция распределения имеет вид:
.
Подберите правильный ответ
Верны ли определения?
А) Геометрический смысл дифференциала функции – дифференциал функции y = f(x) в точке x0 равен приращению ординаты касательной при x ® x0.
B) График дифференцируемой функции называется выпуклым в интервале (a,b), если он расположен ниже любой своей касательной в этом интервале.
Подберите правильный ответ
Верны ли определения?
А) Дифференциал функции y = f(x) в точке x0 – произведение производной функции f¢(x0) на приращение аргумента Dx.
B) Если функция y = f(x) возрастает на интервале (a,b), то f¢(x) > 0 на этом интервале.
Подберите правильный ответ
Верны ли определения?
А) Для проверки гипотезы о виде распределения применяется статистика , имеющая распределение χ2 , число степеней которого равно m – r – 1, где m – число слагаемых, а r – число параметров распределения, замененных на эмпирические значения
В) При проверке гипотезы об однородности m выборок при m>2 в качестве теоретических частот используются эмпирические частоты, полученные при объединении всех выборок
Подберите правильный ответ
Верны ли определения?
А) Достаточный признак существования экстремума функции y = f(x): f¢¢(x) = 0.
B) Точка максимума функции y = f(x) – точка x0, для которой существует такая окрестность точки x0, что для всех x ¹ x0, принадлежащих этой окрестности, выполняется неравенство f(x0) > f(x).
Подберите правильный ответ
Верны ли определения?
А) Достаточный признак существования экстремума функции y = f(x): f¢¢(x) = 0.
B) Точка максимума функции y = f(x) – точка x0, для которой существует такая окрестность точки x0, что для всех x ¹ x0, принадлежащих этой окрестности, выполняется неравенство f(x0) > f(x).
Подберите правильный ответ
Верны ли определения?
А) Если и – две переменные величины, причем , , то есть.
B) Переменная величина является бесконечно малой (б.м.), если , т.е. для , начиная с некоторого момента в изменении выполняется неравенство .
Подберите правильный ответ
Верны ли определения?
А) Если функция y = f(x) убывает на интервале (a,b), то f¢(x) > 0 на этом интервале
B) График дифференцируемой функции называется вогнутым в интервале (a,b), если он расположен ниже любой своей касательно в этом интервале.
Подберите правильный ответ
Верны ли определения?
А) Задана числовая последовательность, если каждому натуральному числу по некоторому закону поставлено в соответствие определенное действительное число .
B) С помощью логических символов определение предела последовательности выражается .
Подберите правильный ответ
Верны ли определения?
А) Надежность интервальной оценки определяется доверительной вероятностью
B) Точность интервальной оценки определяется длиной доверительного интервала
Подберите правильный ответ
Верны ли определения?
А) Неопределенный интеграл функции y = f(x) – совокупность всех первообразных: òf(x)dx = F(x) + C.
B) Первообразная функция от данной функции f(x) – функция F(x), производная которой равна f(x).
Верны ли определения?
А) Постоянный множитель можно выносить за знак интеграла.
B) Формула интегрирования по частям .
Верны ли определения?
А) Свойство определенного интеграла: .
B) Несобственный интеграл сходится, если существует конечный предел .
Верны ли определения?
А) Точка M0(x0,y0), лежащая на графике и отделяющая выпуклую часть графика от вогнутой, называется точкой перегиба функции y = f(x).
B) Если вторая производная функции y = f(x) равна нулю в точке x0 , то x0 – точка перегиба.
Подберите правильный ответ
Верны ли определения?
А) Функцией называется отображение числового множества X в числовое множество Y.
B) Областью определения функции называют множество Y.
Подберите правильный ответ
Верны ли определения?
А) Функцией распределения двумерной случайной величины называют функцию двух переменных , равную
В) Плотность распределения и функция распределения двумерной случайной величины связаны соотношением
Подберите правильный ответ
Верны ли утверждения?
A) Дана выборка объема n: х1, х2, х3, …, хn. Выборочное среднее находится по формуле:
B) Дана выборка объема n: х1, х2, х3, …, хn. Выборочная дисперсия находится по формуле:
Верны ли утверждения?
А) Вариационным рядом для выборки объема n = 7: 3, 5, -2, 1, 0, 4, 3 является ряд –2, 0, 1, 3, 3, 4, 5
В) Вариационным рядом для выборки объема n = 9: -2, 0, 3, 3, 4, 5, 9, 11, 12 является ряд – 0, -2, 3, 3, 4, 5, 9, 11, 12
Подберите правильный ответ
Верны ли утверждения?
А) Вариационным рядом для выборки объема n = 8: 3, 2, -2, 1, 0, 2, 4, 3 является ряд 0, 1, -2, 2, 3, 4
В) Вариационным рядом для выборки объема n = 9: -2, 0, 3, 3, 4, 5, 9, 4, 12 является ряд -2, 0, 3, 3, 4, 4, 5, 9, 12
Подберите правильный ответ
Верны ли утверждения?
А) Дан вариационный ряд выборки объема n = 10: -2, 0, 3, 3, 4, 5, 9, 9, 11, 12, выборочная медиана для этого ряда – d равна 4.
В) Дан вариационный ряд выборки объема n = 8: –2, 0, 1, 3, 4, 4, 5, 8, выборочная медиана для этого ряда – d равна 3.
Подберите правильный ответ
Верны ли утверждения?
А) Дан вариационный ряд выборки объема n = 9: -2, 0, 3, 3, 4, 5, 9, 11, 12, выборочная медиана для этого ряда – d равна 4.
В) Дан вариационный ряд выборки объема n = 7: –2, 0, 1, 3, 3, 4, 5, выборочная медиана для этого ряда – d равна 3.
Подберите правильный ответ
Верны ли утверждения?
А) Дана выборка объема n: х1, х2, …, хn. Если каждый элемент выборки увеличить в 5 раз, то выборочное среднее возрастет в 25 раз.
В) Дана выборка объема n: х1, х2, …, хn. Если каждый элемент выборки увеличить на 10 , то выборочное среднее возрастет на 10.
Подберите правильный ответ
Верны ли утверждения?
А) Дана выборка объема n: х1, х2, …, хn. Если каждый элемент выборки увеличить в 9 раз, то выборочное среднее возрастет в 9 раз.
В) Дана выборка объема n: х1, х2, …, хn. Если каждый элемент выборки увеличить на 5 , то выборочное среднее возрастет на 25.
Подберите правильный ответ
Верны ли утверждения?
А) Дана выборка объема n: х1, х2, …, хn. Если каждый элемент выборки уменьшить в 3 раза, то выборочное среднее уменьшится в 3 раза.
В) Дана выборка объема n: х1, х2, …, хn. Если каждый элемент выборки увеличить в 3 раза, то выборочная дисперсия S2 возрастет в 9 раз.
Подберите правильный ответ
Верны ли утверждения?
А) Дана выборка объема n: х1, х2, …, хn. Если каждый элемент выборки уменьшить на 10, то выборочное среднее не изменится.
В) Дана выборка объема n: х1, х2, …, хn. Если каждый элемент выборки увеличить на 10, то выборочная дисперсия S2 не изменится.
Подберите правильный ответ
Верны ли утверждения?
А) Для того чтобы в 5 раз сузить доверительный интервал, построенный для математического ожидания, число наблюдений надо увеличить в 25 раз.
В) Для того чтобы в вдвое расширить доверительный интервал, построенный для математического ожидания, число наблюдений надо уменьшить в 4 раза.
Верны ли утверждения?
А) Для того чтобы вдвое сузить доверительный интервал, построенный для математического ожидания, число наблюдений надо увеличить в 4 раза
В) Для того чтобы вдвое расширить доверительный интервал, построенный для математического ожидания, число наблюдений надо увеличить в 2 раза.
Верны ли утверждения?
А) Для того чтобы вдвое сузить доверительный интервал, построенный для математического ожидания, число наблюдений надо уменьшить вдвое.
В) Для того чтобы втрое расширить доверительный интервал, построенный для математического ожидания, число наблюдений надо уменьшить в 9 раз.
Верны ли утверждения?
А) Размах вариационного ряда для выборки объема n = 7: 5, 2, -3, 1, 0, 2, 4, 3 равен 5.
В) Размах вариационного ряда для выборки объема n = 9: 0,-2,-3, 3, 4, 5, 9, 4, 12 равен 12.
Подберите правильный ответ
Верны ли утверждения?
А) Размах вариационного ряда для выборки объема n = 8: 3, 2, -2, 1, 0, 2, 4, 3 равен 6.
В) Размах вариационного ряда для выборки объема n = 9: 0,-2, 3, 3, 4, 5, 9, 4, 12 равен 14.
Подберите правильный ответ
Верными являются высказывания:
А) Вероятность попадания непрерывной случайной величины в интервал (a, b), выражается через функцию распределения следующей формулой P (a < X < b) = F(b) – F(a)
В) Плотность распределения непрерывной случайной величины является
неотрицательной
Верными являются высказывания:
А) Вероятность попадания случайной величины в интервал (a, b) выражена через плотность распределения следующей формулой P (a < X < b) = f(b) – f(a)
В) Функция распределения случайной величины F(x) выражается через ее плотность распределения f(x) следующим образом F(x) =(x)dx
Верными являются высказывания:
А) Вероятность суммы двух случайных событий вычисляется по формуле Р(А+В) = Р(А) + Р(В)
В) Условную вероятность события А при условии, что произошло событие В можно вычислить по формуле: Р(А)=
Верными являются высказывания:
А) Два события будут несовместными, если Р(АВ) = 0
В) Два события будут совместными, если Р(АВ) = 1
Верными являются высказывания:
А) Если события А и В несовместны, то для них справедливо равенство Р(А + В) = Р(А) + Р(В)
В) Два события А и В называются независимыми, если Р(АВ) = Р(А) Р(В)
Верными являются высказывания:
А) Математическое ожидание дискретной случайной величины равно
В) Математическое ожидание суммы случайной величины Х и постоянной С равно M (X + C) = MX
Верными являются высказывания:
А) Нормальное распределение имеет вид
В) Распределение Пуассона имеет вид
Верными являются высказывания:
А) Случайной величиной называется переменная величина,
которая определяется совокупностью возможных значений
В) Пределы функции распределения F(x) на плюс и минус бесконечности равны соответственно F = 1, F =
Верными являются высказывания:
А) Среднеквадратическое отклонение дискретной случайной величины вычисляется по формуле
В) Среднеквадратическое отклонение непрерывной случайной величины вычисляется по формуле
Верными являются высказывания:
А) Среднеквадратическое отклонение дискретной случайной величины вычисляется по формуле
В) Среднеквадратическое отклонение непрерывной случайной величины вычисляется по формуле
Верными являются высказывания:
А) Формула Бейеса имеет вид
В) Если события А, В, С независимы, то Р(А + В + С) = Р(А) Р(В) Р(С)
Верными являются высказывания:
А) Формула Бейеса имеет вид
В) Если события А, В, С независимы, то Р(А + В + С) = Р(А) Р(В) Р(С)
Верными являются высказывания:
А) Формула полной вероятности имеет вид
В) Формула Бейеса имеет вид
Верными являются высказывания:
А) Функция распределения случайной величины F(x) выражается через ее плотность распределения f(x) следующим образом F(x) = (x)dx
В) Вероятность попадания случайной величины в интервал (a, b) выражена через плотность распределения следующей формулой
P (a < X < b) = (x) dx
Верными являются высказывания:
А) Функция распределения случайной величины не убывает
В) Функция распределения дискретной случайной величины разрывная, ступенчатая
Вероятность выиграть в рулетку равна 1/38. Игрок делает 190 ставок.
Вероятность того, что он выиграет не менее 5 раз можно установить, используя таблицу
Дан вариационный ряд выборки объема n = 5: -2, -1, 0, 1, 3.
Поставьте в соответствие:
Дан вариационный ряд выборки объема n = 5: -2, -1, 0, 1, 3.
Поставьте в соответствие:
Дан вариационный ряд выборки объема n = 5: -2, 0, 1, 5, 6.
Поставьте в соответствие:
Дан вариационный ряд выборки объема n = 5: -2, 0, 1, 5, 6.
Поставьте в соответствие:
Дан вариационный ряд выборки объема n = 5: 1, 2, 5, 6, 7.
Поставьте в соответствие:
Данные о прибыли, полученной в течение месяца, за последние 5 месяцев оказались следующими:
С помощью метода наименьших квадратов по этим точкам строится прямая. Эта прямая для прибыли в мае даст значение (для получения этого значения строить прямую не надо) (наберите число)
Дано статистическое распределение выборки объема n=50
Эмпирическая функция распределения для этого ряда имеет вид
Дано статистическое распределение выборки с числом вариант m:
Верны ли утверждения?
A) Выборочное среднее находится по формуле:
B) Выборочная дисперсия находится по формуле:
Из генеральной совокупности извлечена выборка объема n=70, полигон частот которой имеет вид
Тогда число вариант xi = 1 в выборке равно_____ наберите число
Из генеральной совокупности извлечена выборка объема n = 49, полигон частот которой имеет вид:
Тогда число вариант в выборке равно______ наберите число
Из генеральной совокупности извлечена выборка, данные по ней сведены в таблицу
Оценка генеральной средней
По выборке построена гистограмма
медиана равна: (наберите число).
По выборке построена гистограмма:
Медина равна: (наберите число).
По выборке построена гистограмма:
По виду гистограммы можно предполагать, что генеральная совокупность, из которой произведена выборка, имеет распределение:
По выборке построена гистограмма
Медиана равна (наберите число).
По таблице распределения случайной величины
Вероятности равны:
По таблице распределения случайной величины вероятности
равны:
Пределы функции распределения F(x) на плюс и минус бесконечности равны соответственно
При проверке гипотезы о том, что генеральное распределение – равномерное на отрезке [0,1], по выборке объема 100 построили такую таблицу частот:
Можно ли утверждать, что гипотеза о виде распределения по критерию χ2 проходит? Чему равно значение статистики, по которой оценивается мера расхождения?
При проверке гипотезы о том, что генеральное распределение – равномерное на отрезке [0,1], по выборке объема 100 построили такую таблицу частот:
Можно ли утверждать, что гипотеза о виде распределения по критерию Колмогорова проходит на уровне значимости 0,05? Чему равно значение статистики, по которой оценивается мера расхождения?
Результаты наблюдений над системой (x, y) 2-х величин записаны в таблицу
N
X
Y
1
2
3
4
4
8
6
2
–2
–4
–3
–1
Коэффициент корреляции равен: (наберите число)
Результаты наблюдений над системой (x, y) двух величин записаны в таблицу
N
X
Y
1
2
3
4
3
2
4
1
9
6
12
3
Коэффициент корреляции равен: (наберите число)
Эмпирический коэффициент корреляции между весом и ростом для выборки равен:
(наберите число )
Эмпирический коэффициент корреляции между весом и ростом для выборки равен:
=
равен:
равен (наберите целое число)
равен (наберите целое число)
равен
равен (наберите число)
равен
равен (наберите число)
равен (наберите число)
и – две б.м. высшего порядка в сравнении с , если
равен
равен (наберите число)
равен (наберите число)
равен (наберите число)
, тогда
. Тогда
. Тогда производная равна
равен
равен
равен (набрать число)
равен (набрать число):
равен (набрать число)
равен (набрать число)
равен:
равен ________ (набрать число):
равен ________ (набрать число):
равен ________ (набрать число)
, – две б.м. при . Тогда
X и Y – независимы. DX = 2, DY = 1. Дисперсия D(2X-3Y) равна
X и Y – независимы. DX = 2, DY = 1. Дисперсия D(2X-4Y) равна (наберите число)
X и Y – независимы. DX = 2, DY =3. Дисперсия D(4X+5Y) равна (наберите число)
Бросается 5 монет. Вероятность, что герб выпадет более трех раз равна
Брошено 10 игральных костей. Предполагается, что все комбинации выпавших очков равновероятны. Укажите соответствие между событием и значением его вероятности:
Брошены две игральные кости. Вероятность того, что произведение выпавших очков равно 4, равно _______ (набрать число в виде десятичной дроби с тремя значащими цифрами)
Брошены две игральные кости. Вероятность того, что сумма выпавших очков меньше 4, равно _____ (набрать число в виде десятичной дроби с тремя значащими цифрами)
Брошены две монеты. Вероятность того, что выпадет и герб и решка, равна _____ (наберите десятичную дробь с точностью до одного знака)
В группе 30 студентов, из которых отлично учится 5 человек, хорошо – 18, удовлетворительно – 5 и слабо – 2. Преподаватель вызывает студента. Вероятность того, что вызванный студент или отличник или «хорошист», равна
В жилом доме 4000 ламп. Вероятность выключения лампы в вечернее время равна 0.5. Вероятность включения одновременно 2500 ламп можно вычислить, используя:
В итоге четырех измерений некоторой физической величины одним прибором получены следующие результаты: 8, 9, 11, 12. Выборочная средняя результатов измерений, выборочная и исправленная дисперсии ошибок прибора равны соответственно
В магазин поступает товар с трех фабрик. Вероятности доставки товара в срок равны соответственно 0.6; 0.7; 0.5. Все партии не будут доставлены в срок с вероятностью:
В магазин поступает товар с трех фабрик. Вероятности доставки товара в срок равны соответственно 0.8; 0.7; 0.5. Хотя бы одна партия не будет доставлена в срок с вероятностью:
В таблице статистического распределения, построенного по выборке, одна цифра написана неразборчиво Эта цифра равна (наберите число).
В точке с абсциссой х = 0 точку перегиба имеют функции
В точке с абсциссой х = 0 точку экстремума имеют функции
В урне 3 белых и 7 черных шаров наугад вынимают два шара. Вероятность того, что оба шара черные, равна _______ (набрать число в виде десятичной дроби с тремя значащими цифрами)
В урне из 50 билетов 10 выигрышные. Вероятность того, что два вынутых билета выигрышные равна:
Вероятность выигрыша по облигации займа равна 0.4. Вероятность того, что некто, приобретая 4 облигации, выиграет хотя бы по одной из них равна:
Вероятность достоверного события равна (наберите число)
Вероятность невозможного события равна (наберите число)
Вероятность попадания непрерывной случайной величины в интервал (a, b), выражается через функцию распределения следующей формулой
Вероятность попадания случайной величины в интервал (a, b) выражена через плотность распределения следующей формулой
Вероятность появления успеха в каждом испытании равна 0,3. Тогда вероятность наступления 75 успехов при 200 испытаниях может быть определена с помощью
Вероятность того, что в столбике из 150 наугад отобранных монет число монет, расположенных «гербом» вверх, будет от 50 до 75, может быть определена с помощью теоремы
Вероятность того, что дни рождения у двух случайно выбранных человек людей придутся на январь равна:
Вероятность того, что дом может сгореть в течение года равна 0.01. Застраховано 400 домов. При вычислении вероятности того, что сгорит не более 5 домов можно воспользоваться:
Вероятность успешной сдачи экзамена по трем предметам у данного студента соответственно равны 0.5, 0.7, 0.8. Вероятность успешной сдачи всех экзаменов равна _______ (наберите десятичную дробь с двумя значащими цифрами)
Вертикальной асимптотой графика функции является прямая
Вертикальной асимптотой графика функции является прямая
Всхожесть семян некоторого растения равна 0,8. Тогда вероятность того, что из 1000 посаженных семян число проросших будет заключено между 750 и 850, можно определить с помощью
Вся площадь между графиком плотности распределения f(x) и осью ОХ равна ________ (наберите число).
Гипотезы об однородности выборок – это гипотезы о том, что рассматриваемые выборки извлечены из
Дан вариационный ряд выборки n = 7: –5, –4, 0, 1, 2, 3, 3. Для этого ряда:
Дан вариационный ряд выборки n = 8: -3, -2, 0, 0, 2, 3, 4, 4. Для этого ряда:
Дан вариационный ряд выборки n = 8: -5, -4,-1, 0, 2, 2, 3, 3. Для этого ряда:
Дан вариационный ряд выборки n = 8: –3, –1, 0, 2, 4, 6, 7, 8. Медиана этого ряда d = ______ (наберите число).
Дан вариационный ряд выборки n = 8: –6, –2, 0, 3, 5, 7, 8, 9. Для этого ряда:
Дан вариационный ряд выборки объема n = 7: –3, –1, 0, 2, 4, 6, 7. Медиана этого ряда d = _____ (наберите число).
Дан вариационный ряд выборки объема n = 10: -2, 0, 3, 3, 4, 5, 9, 11, 12, 15. Выборочная медиана для этого ряда – d равна
Дан вариационный ряд выборки объема n = 9: -2, 0, 3, 3, 4, 5, 9, 11, 12. Выборочная медиана для этого ряда – d равна
Дана выборка n = 5: -3, -1, 0, 1, 3. Выборочная дисперсия равна S2 = _____ (наберите число)
Дана выборка n = 5: -3, -1, 0, 1, 3. Выборочная дисперсия равна S2 = _____ (наберите число)
Дана выборка объема n = 10: –1, –1, 2, 2, 2, 3, 3, 5, 5, 5. Статистическое распределение этой выборки имеет вид:
Дана выборка объема n = 5: -4,-2,0,2,4. Выборочная дисперсия S2 = ______(Наберите число)
Дана выборка объема n = 5: -5,-3,0,3,5. Выборочная дисперсия S2 = ______(Наберите число)
Дана выборка объема n = 6: -4,-2,-1,0, 1, 2, 4. Выборочная дисперсия S2 = ______(Наберите число)
Дана выборка объема n = 7: -5,-3,-1,0,1,3,5. Выборочная дисперсия S2 = ______(Наберите число)
Дана выборка объема n = 5: -2,-1,0, 3, 5. Выборочное среднее и выборочная дисперсия S2 равны
Дана выборка объема n = 5: -3, -2, 0, 2, 3. Выборочное среднее и выборочная дисперсия S2 равны
Дана выборка объема n = 5: 2, 3, 5, 7, 8. Выборочное среднее = ______(наберите число)
Дана выборка объема n = 5: 2, 3, 5, 7, 8. Выборочное среднее и выборочная дисперсия S2 равны
Дана выборка объема n = 7: 3, 5, -2, 1, 0, 4, 3. Вариационный ряд для этой выборки и размах вариационного ряда
Дана выборка объема n: х1, х2, х3, …, хn. Ее выборочное среднее равно . Выборочная дисперсия находится по формуле (выберите две правильных)
Дискретный случайный вектор – это
Дисперсия случайной величины определяется по формуле
Дисперсия суммы двух случайных величин равна
Дифференциал функции в точке с абсциссой равен
Дифференциал функции равен
Дифференциал функции в точке с абсциссой равен (наберите число)
Дифференциал функции равен
Для выборки объема n = 8 рассчитали выборочную дисперсию S2 = 7. Исправленная дисперсия равна _____ (наберите число)
Для выборки объема n = 8 рассчитали выборочную дисперсию S2 = 7. Исправленная дисперсия равна _____ (наберите число)
Для вычисления наибольших и наименьших значений функции на отрезке [ a,b] требуется:
Для зависимых случайных величин соотношение при
Для нахождения интервалов монотонности требуется:
Для независимых величин X и Y верными являются формулы:
Для обработки наблюдений методом наименьших квадратов построена прямая. Верным является из график
Для определения точек перегиба функции требуется:
Для оценки тесноты связи между признаками (Х,Y) в числовой форме вычисляют безразмерную характеристику, выражающую тесноту связи между признаками в числовой форме. Это
Для плотности распределения непрерывной двумерной случайной величины справедлива нормировка : , равная: (наберите число)
Для построения доверительного интервала для дисперсии надо пользоваться таблицами
Для построения доверительного интервала для дисперсии надо пользоваться таблицами
Для проверки гипотезы Н0 , состоящей в том, что s21 = s22, на уровне значимости a используется статистика F, вычисляются
Для проверки гипотезы о виде распределения вероятностей по критерию Колмогорова в качестве меры расхождения между теоретическим и эмпирическим распределениями используется статистика l, имеющая распределение Колмогорова. Она вычисляется по формуле
Для проверки гипотезы о виде распределения применяется статистика , имеющая распределение χ2 , число степеней которого равно
Для проверки гипотезы о равенстве 2-х генеральных средних надо пользоваться таблицами
Для событий А и В в некотором эксперименте известно Р(А) = 0,5; Р(В) = 0,6; . События A и B являются ____________ (набрать слово)
Для событий Н1, Н2, А в некотором случайном эксперименте известно: Н1Н2 = 0; Р(Н1) = 0.3; Р(Н2) = 0.7; Р(А/Н1) = 0.4; Р(А/Н2) = 0.6. Вероятность Р(А) равна ______ (наберите десятичную дробь с двумя значащими цифрами)
Для событий Н1, Н2, А в некотором случайном эксперименте известно: Н1Н2 = 0; Р(Н1) = 0.3; Р(Н2) = 0.7; Р(А/Н1) = 0.4; Р(А/Н2) = 0.6. Вероятность Р(А) равна
Для сравнения 2-х генеральных средних совокупностей X и Y из них извлекли выборки объема n и m соответственно. Для проверки гипотезы о том, что mх = my, надо вычислить статистику
Для того чтобы вдвое сузить доверительный интервал, построенный для математического ожидания, число наблюдений надо увеличить
Для того чтобы построить 95 %-ый доверительный интервал для математического ожидания m случайной величины, распределенной нормально с известной дисперсией s2 по выборке объема n, вычисляется и используется формула
Для того чтобы сузить доверительный интервал, построенный для математического ожидания, в два раза, число наблюдений надо увеличить в ____ раза (набрать число)
Для того, чтобы по выборке объема n построить доверительный интервал для математического ожидания нормального распределения, дисперсия которого неизвестна, нужны таблицы
Для того, чтобы построить 95%-ый доверительный интервал для математического ожидания m случайной величины, распределенной нормально с известной дисперсией s2, по выборке объема n вычисляется и используется следующая формула:
Для того, чтобы построить доверительный интервал математического ожидания по выборке, когда дисперсия неизвестна, необходимо определить (выберите два параметра):
Для того, чтобы сузить доверительный интервал, построенный для математического ожидания, в четыре раза, число наблюдений надо увеличить в ____ раз (набрать число).
Для упрощения счета из всех значений выборки вычли 1280. При этом эмпирическая дисперсия
Для уровня значимости a = 0,05 критическое значение распределения Колмогорова равно = (наберите число с двумя знаками после запятой)
Для функции точка М (1, 0) является точкой
Для функции точка М (1, 0) является точкой
Доверительный интервал для математического ожидания m случайной величины, распределенной нормально с известной дисперсией s2, считается по следующей формуле:
Если выборка группируется для проверки гипотезы о виде распределения по критерию χ2 и если в какие-то интервалы группировки попало слишком мало наблюдений, необходимо
Если выборка группируется для проверки гипотезы о виде распределения по критерию χ2, на интервалы группировки накладывается строгое ограничение: необходимо, чтобы
Если основная гипотеза имеет вид , то конкурирующей гипотезой может являться (выберите две)…
Если основная гипотеза имеет вид , то конкурирующей может быть гипотеза (выберите две)
Если основная гипотеза имеет вид , то конкурирующей может быть гипотеза (выберите две)
Если основная гипотеза имеет вид , то конкурирующей может быть гипотеза (выберите две)
Если основная гипотеза имеет вид , то конкурирующей может быть гипотеза (выберите две)
Если основная гипотеза имеет вид , то конкурирующей может быть гипотеза (выберите две)
Если основная гипотеза имеет вид , то конкурирующей может быть гипотеза
Если основная гипотеза имеет вид , то конкурирующей может быть гипотеза (выберите две)
Если основная гипотеза имеет вид , то конкурирующей может быть гипотеза (выберите две)
Если случайные величины и связаны линейной зависимостью (где , – любое), то коэффициент корреляции равен (наберите число)
Если случайные величины и связаны линейной зависимостью , то коэффициент корреляции равен
Если средствами дисперсионного анализа показано, что гипотеза о совпадении средних при разных уровнях фактора не противоречит данным опыта, в качестве оценки общего среднего можно взять
Завод в среднем дает 25 % продукции высшего сорта и 70 % – первого сорта. Вероятность того, что наудачу взятое изделие не будет высшего или первого сорта, равна
Законом распределения является таблица:
Законом распределения является таблица:
Значение кумуляты, построенной по таблице, в точке 162, и медианы равны
Значение кумуляты, построенной по таблице, в точке 170, и медианы равны
Значение функции распределения двумерной случайной величины при равенстве аргументов равно (наберите число)
Изделия изготавливаются независимо друг от друга. В среднем 1 % изделий оказывается бракованным. Вероятность того, что из двух взятых наугад изделий окажутся неисправными оба, составляет
Имеется m выборок объема n из m нормальных законов с одинаковыми дисперсиями s2 и математическими ожиданиями а1,а2,…,аm. Задача проверки нулевой гипотезы Н0 о совпадении m математических ожиданий – Н0: а1 = а2 = …аm решается методами
Интеграл равен (набрать число)
Интервалы между автобусами 10 минут. Вероятность того, что пассажиру, появившемуся на остановке в случайный момент времени, не придется ждать более 8 и не менее3 минут равна ______ (наберите десятичную дробь с точностью до одного знака)
Интервалы между автобусами 10 минут. Вероятность того, что пассажиру, появившемуся на остановке в случайный момент времени, придется ждать автобуса не более 4-х минут равна ______ (наберите десятичную дробь с точностью до одного знака)
Корректура книги объемом в 500 страниц имеет 500 ошибок. Число опечаток на одной странице – случайная величина, распределенная по закону Пуассона. Вероятность того, что на случайно выбранной странице окажется 2 опечатки, равна
Коэффициент корреляции может принимать значения
Математическое ожидание и дисперсия случайной величины, имеющей плотность распределения , равны MX= , DX= (набрать два числа через запятую)
Математическое ожидание и дисперсия случайной величины, имеющей плотность распределения равны МХ = ____, DX = _____ (набрать два целых числа, через запятую без пробелов).
Математическое ожидание и среднеквадратическое отклонение случайной величины, имеющей плотность распределения равны: МХ = ____, = _____ (набрать два целых числа, через запятую без пробелов).
Медиана выборки равна (наберите число).
Методом дисперсионного анализа можно проверить гипотезу о
Наблюдения проводятся над системой (X : Y) двух случайных величин. Выборка состоит из пар чисел: (х1: y1), (х2: y2), …, (хn : yn). Найдены , S для хi и , S для yi (). Тогда выборочный коэффициент корреляции rxy находится по формуле
Непрерывный случайный вектор – это
Неравенство Чебышева:
Несмещенная оценка для дисперсии вычисляется по эмпирической дисперсии S2 по формуле
Область определения функции
Общий вид первообразных для функции имеет вид:
Общий вид первообразных для функции имеет вид:
Плотность распределения и функция распределения двумерной случайной величины связаны соотношением
По выборке 1, 0, 4, 3, 1, 2, 3, 2, 0, 4 построен полигон:
По выборке объема n = 100 вычислены выборочное среднее – 54 и выборочная дисперсия – 16. 95 %-ый доверительный интервал для генерального среднего равен
По выборке объема n = 9 вычислили выборочное среднее 15 и исправленную несмещенную дисперсию 9. 95 %-ый доверительный интервал для математического ожидания m (t8,0.95 = 2,3) равен
По выборке объема n надо построить доверительный интервал для математического ожидания нормального распределения, дисперсия которого известна. Для этого необходимо воспользоваться
По выборке построены прямые регрессии: y = 4x + 4 и x = 0,04y + 2. Коэффициент корреляции равен
По теореме Муавра-Лапласа вероятность неравенства при больших вычисляется следующим образом:
Показательными функциями являются
Поставьте в соответствие точечную оценку математического ожидания нормального распределения и его возможную интервальную оценку:
Поставьте в соответствие точечную оценку математического ожидания нормального распределения и его возможную интервальную оценку:
При больших соотношение
При проведении расчетов для двух выборок получили два коэффициента корреляции. Ошибки допущено не было. Значения r1 и r2 составили
При проведении расчетов для дисперсионной модели от выборочных значений xij перешли к более удобным для расчета значениям yij = 100xij – 30. Расчеты дали эмпирическое среднее по всем данным = 3. Гипотеза о влиянии фактора на среднее значение не подтвердилась. В качестве оценки для генерального среднего можно взять значение
При проведении расчетов для дисперсионной модели от выборочных значений xij перешли к более удобным для расчета значениям yij = xij – 20. Расчеты дали эмпирическое среднее по всем данным = 4. Гипотеза о влиянии фактора на среднее значение не подтвердилась. В качестве оценки для генерального среднего можно взять значение (наберите число)
При проверке гипотезы об однородности m выборок при m>2 в качестве теоретических частот используются
Производится выборка объема n = 100 из генеральной совокупности, имеющей распределение N(20, 4). По выборке строится выборочное среднее . Эта случайная величина имеет распределение N(20;___) наберите число
Производная функции :
Производная функции равна:
Производная функции равна
Производная функции равна
Производная функции равна
Производная функции равна
Производная функции равна
Производная функции равна
Производная функции равна
Производная функции равна
Производной f¢ (x0) называют
Производные функции равны
Производные функции равны
Производные функции равны
Производные функции равны
Производные функции равны
Производство дает 1,5 % брака. Тогда вероятность того, что из взятых на исследование 1000 изделий выбраковано будет не больше 15, может быть определена с помощью теоремы
Пусть , где одинаково распределены и , . Утверждение
Расположите статистические выборки в порядке возрастания размаха.
Расположите статистические выборки в порядке возрастания размаха.
Расположите статистические выборки в порядке возрастания размаха.
Самое маленькое значение в выборке 0, самое большое 8, медиана 2. По этой выборке построена гистограмма:
Случайная величина Х принимает значения –2, 1, 3, –4, 7 с равными вероятностями, тогда МХ = _____ (наберите число).
Случайная величина U, характеризующая степень расхождения теоретического и эмпирического закона распределения при проверке с помощью критерия χ2 нулевой гипотезы Н0 о том, что исследуемая случайная величина имеет определенный закон распределения, вычисляется по формуле
Случайная величина X принимает значения 2, -2, 0, -5, 8 с равными вероятностями. Математическое ожидание MX, равно (наберите десятичную дробь)
Случайная величина имеет плотность распределения Тогда параметр равен: (наберите десятичную дробь)
Случайная величина имеет показательное распределение с математическим ожиданием, равным 7. Плотность вероятности такой величины равна
Случайная величина имеет показательное распределение с плотностью Тогда функция распределения равна
Случайная величина распределена по нормальному закону, ее математическое ожидание равно 1, а дисперсия – 25. Тогда ее функция распределения имеет вид
Случайная величина Х имеет биномиальное распределение с параметрами тогда ее числовые характеристики таковы:
Случайная величина Х имеет биномиальное распределение с параметрами тогда ее числовые характеристики таковы:
Случайная величина Х имеет биномиальное распределение с параметрами Ее числовые характеристики таковы:
Случайная величина Х имеет показательное распределение с параметром . Тогда ее функция распределения равна
Случайная величина Х имеет распределение Пуассона с параметром. Ее числовые характеристики равны MX = , DX = (набрать два числа через запятую)
Случайная величина Х имеет распределение Пуассона с параметром. Ее числовые характеристики равны MX = , DX= (набрать два числа через запятую)
Случайная величина Х равномерно распределена на , тогда ее математическое ожидание и дисперсия соответственно равны
Случайная величина Х равномерно распределена на . Тогда вероятность попасть в интервал будет равна (наберите десятичную дробь)
Случайная величина Х равномерно распределена на . Тогда вероятность попасть в интервал будет равна: (наберите десятичную дробь)
Случайная величина Х распределена по биномиальному закону с параметрами Ее числовые характеристики равны
Случайная величина Х распределена по биномиальному закону с параметрами Ее числовые характеристики равны
Случайная величина Х распределена по нормальному закону. Известно, что математическое ожидание и среднеквадратическое отклонение этой случайной величины соответственно равны 30 и 10. Плотность распределения Х имеет вид
Случайная величина Х распределена равномерно на отрезке (a, b), тогда математическое ожидание и дисперсия равны
Случайная величина Х распределена равномерно, ее плотность равна Тогда параметр равен: (наберите число)
Случайная величина, распределенная по нормальному закону, имеет математическое ожидание, равное 5, и среднеквадратическое отклонение, равное 15. Тогда ее функция распределения имеет вид
Случайным вектором или n-мерной случайной величиной называют
Среднеквадратическое отклонение дискретной случайной величины вычисляется по формуле
Станок-автомат производит изделия трех сортов. Первого сорта – 60 %, второго – 20 %. Вероятность того, что наудачу взятое изделие будет или второго, или третьего сорта, равна
Статистика , использующаяся в процедуре проверки гипотезы о виде распределения, имеет распределение
Статистика F, использующаяся в процедуре проверки равенства дисперсий двух генеральных совокупностей, имеет распределение
Стационарными точками функции являются точки с абсциссами (набрать числа в порядке возрастания через запятую в порядке возрастания)
Стационарными точками функции являются точки с абсциссами
Степенными функциями являются
Страхуется 1500 машин. Вероятность попадания машины в аварию 0.15. При вычислении вероятности того, что число аварий не превысит 300, можно воспользоваться:
Студент сдает два экзамена. Первый с вероятностью 0.8; второй – 0.7. Вероятность сдачи хотя бы одного экзамена можно вычислить следующим образом:
Студент сдает два экзамена. Первый с вероятностью 0.9; второй – 0.6. Вероятность сдачи хотя бы одного экзамена можно вычислить следующим образом:
Сумма вероятностей , составляющих закон распределения двумерного дискретного случайного вектора, равна
Сумма квадратов отклонений S от точек (1,1), (1,3) (3,2), (3,4) до прямой y=x/2+1,5 равна (наберите число)
Тангенс угла наклона касательной к графику функции в точке с абсциссой равен (наберите число)
Тангенс угла наклона касательной к графику функции в точке с абсциссой равен (наберите число)
Тангенс угла наклона касательной к графику функции в точке с абсциссой равен (наберите число)
Тангенс угла наклона касательной к графику функции в точке с абсциссой равен (наберите число)
Термины «некоррелированные» и «независимые» случайные величины эквивалентны для случая
Точечная оценка математического ожидания нормального распределения равна 11. Тогда его интервальная оценка может иметь вид
Точечная оценка математического ожидания нормального распределения равна 12. Тогда его интервальная оценка может иметь вид…
Точечная оценка математического ожидания нормального распределения равна 13. Тогда его интервальная оценка может иметь вид…
Точка для функции является точкой
Точка с абсциссой для функции является точкой перегиба (наберите число)
Точкой перегиба функции является точка с абсциссой (набрать число)
Точкой перегиба функции является точка с абсциссой (наберите целое число)
Точкой перегиба функции является точка с абсциссой (набрать число)
Точкой перегиба функции является точка с абсциссой (наберите число)
Укажите соответствие между двумя частями определений
Укажите соответствие между двумя частями определений
Укажите соответствие между условием и заключением
Укажите соответствие между характером изменения функции f(x) на интервале (а, b) и величиной ее производной
Уравнение регрессии Y на Х, выраженное через коэффициент корреляции r, имеет вид
Установите соотношение между значением показателей степени и значением предела дроби
Утверждение
Формула для коэффициента корреляции имеет вид
Функцией распределения двумерной случайной величины называют функцию двух переменных , равную
Функции дифференцируемы в точке x. Установите соответствия между левыми и правыми частями правил дифференцирования
Функция F(x) называется первообразной для функции f(x), если для всех х
Функция y = f(x) на интервале (а, b) является выпуклой вверх, следовательно
Функция y = f(x) на интервале (а, b) является выпуклой вниз, следовательно
Функция имеет минимум в точке с координатами (набрать через запятую координаты точки)
Функция имеет максимуму в точке с координатами (набрать через запятую координаты точки):
Функция имеет минимум в точке с координатами (набрать через запятую координаты точки)
Функция распределения случайной величины F(x) выражается через ее плотность распределения f(x) следующим образом
Элементарными являются функции
Вопрос посетителя
Верны ли определения?
А) Односторонняя критическая область — критическая область, определяемая неравенством K > kкр, где К — значение критерия, kкр — критическая точка и kкр — положительное число.
В) Двусторонняя критическая область — критическая область, определяемая неравенствами K < k1, K > k2, где К — значение критерия, k1, k2 — критические точки и k2 > k1.
Подберите правильный ответ.
(*ответ*) А — нет, В — да
А — да, В — да
А — да, В — нет
А — нет, В — нет
Верны ли определения?
А) Ошибку первого рода совершают, отвергнув гипотезу, когда она истинна.
В) Ошибку второго рода совершают, приняв ложную гипотезу.
Подберите правильный ответ.
(*ответ*) А — да, В — да
А — да, В — нет
А — нет, В — да
А — нет, В — нет
Верны ли определения?
А) Принцип практической уверенности состоит в следующем: если наблюдаемое значение критерия принадлежит критической области — гипотезу отвергают, если наблюдаемое значение критерия принадлежит области принятия гипотезы — гипотезу принимают.
В) Гипотезы об однородности выборок — гипотезы о том, что рассматриваемые выборки извлечены из одной и той же генеральной совокупности.
Подберите правильный ответ
(*ответ*) А — нет, В — да
А — да, В — да
А — да, В — нет
А — нет, В — нет
Верны ли определения?
А) Сложная статистическая гипотеза — гипотеза, допускающая бесконечное множество значений параметров распределения.
В) Простая статистическая гипотеза — гипотеза, допускающая бесконечное множество значений параметров распределения.
Подберите правильный ответ.
(*ответ*) А — да, В — нет
А — да, В — да
А — нет, В — да
А — нет, В — нет
Верны ли определения?
А) Статистическая гипотеза — соотношение, устанавливающее соответствие между возможными значениями случайной величины и их вероятностями.
В) Конкурирующая (альтернативная) гипотеза — гипотеза, противоречащая нулевой статистической гипотезе.
Подберите правильный ответ
(*ответ*) А — нет, В — да
А — да, В — да
А — да, В — нет
А — нет, В — нет
Верны ли определения?
А) Статистический критерий — значение критерия, вычисленное по выборкам.
В) Уровень значимости критерия — вероятность допустить ошибку первого рода.
Подберите правильный ответ
(*ответ*) А — нет, В — да
А — да, В — да
А — да, В — нет
А — нет, В — нет
Верны ли определения?
А) Число степеней свободы — количество значений в итоговом вычислении статистики, способных варьироваться.
В) Вид критической области зависит от нулевой гипотезы и не зависит от альтернативной.
Подберите правильный ответ
(*ответ*) А — да, В — нет
А — да, В — да
А — нет, В — да
А — нет, В — нет
Верны ли определения?
А) Область допустимых значений — совокупность значений критерия, при которых нулевая гипотеза принимается.
В) Отыскивая двустороннюю критическую область при уровне значимости , тем самым находят и соответствующий доверительный интервал с надежностью .
Подберите правильный ответ
(*ответ*) А — нет, В — да
А — да, В — да
А — да, В — нет
А — нет, В — нет
Ответ эксперта
Верны ли определения?
А) Односторонняя критическая область — критическая область, определяемая неравенством K > kкр, где К — значение критерия, kкр — критическая точка и kкр — положительное число.
В) Двусторонняя критическая область — критическая область, определяемая неравенствами K < k1, K > k2, где К — значение критерия, k1, k2 — критические точки и k2 > k1.
Подберите правильный ответ.
(*ответ*) А — нет, В — да
А — да, В — да
А — да, В — нет
А — нет, В — нет
Верны ли определения?
А) Ошибку первого рода совершают, отвергнув гипотезу, когда она истинна.
В) Ошибку второго рода совершают, приняв ложную гипотезу.
Подберите правильный ответ.
(*ответ*) А — да, В — да
А — да, В — нет
А — нет, В — да
А — нет, В — нет
Верны ли определения?
А) Принцип практической уверенности состоит в следующем: если наблюдаемое значение критерия принадлежит критической области — гипотезу отвергают, если наблюдаемое значение критерия принадлежит области принятия гипотезы — гипотезу принимают.
В) Гипотезы об однородности выборок — гипотезы о том, что рассматриваемые выборки извлечены из одной и той же генеральной совокупности.
Подберите правильный ответ
(*ответ*) А — нет, В — да
А — да, В — да
А — да, В — нет
А — нет, В — нет
Верны ли определения?
А) Сложная статистическая гипотеза — гипотеза, допускающая бесконечное множество значений параметров распределения.
В) Простая статистическая гипотеза — гипотеза, допускающая бесконечное множество значений параметров распределения.
Подберите правильный ответ.
(*ответ*) А — да, В — нет
А — да, В — да
А — нет, В — да
А — нет, В — нет
Верны ли определения?
А) Статистическая гипотеза — соотношение, устанавливающее соответствие между возможными значениями случайной величины и их вероятностями.
В) Конкурирующая (альтернативная) гипотеза — гипотеза, противоречащая нулевой статистической гипотезе.
Подберите правильный ответ
(*ответ*) А — нет, В — да
А — да, В — да
А — да, В — нет
А — нет, В — нет
Верны ли определения?
А) Статистический критерий — значение критерия, вычисленное по выборкам.
В) Уровень значимости критерия — вероятность допустить ошибку первого рода.
Подберите правильный ответ
(*ответ*) А — нет, В — да
А — да, В — да
А — да, В — нет
А — нет, В — нет
Верны ли определения?
А) Число степеней свободы — количество значений в итоговом вычислении статистики, способных варьироваться.
В) Вид критической области зависит от нулевой гипотезы и не зависит от альтернативной.
Подберите правильный ответ
(*ответ*) А — да, В — нет
А — да, В — да
А — нет, В — да
А — нет, В — нет
Верны ли определения?
А) Область допустимых значений — совокупность значений критерия, при которых нулевая гипотеза принимается.
В) Отыскивая двустороннюю критическую область при уровне значимости , тем самым находят и соответствующий доверительный интервал с надежностью .
Подберите правильный ответ
(*ответ*) А — нет, В — да
А — да, В — да
А — да, В — нет
А — нет, В — нет
Теория вероятностей и математическая статистика (СПО, курс 1)
Установите соответствие между профессиональными терминами и их определениями:
Основной принцип проверки статистических гипотез
ее совершают, отвергнув гипотезу, когда она истинна
вероятность того, что нулевая гипотеза будет отвергнута, когда она неверна (верна конкурирующая гипотеза)
ее совершают, приняв ложную гипотезу
если наблюдаемое значение критерия принадлежит критической области — гипотезу отвергают, если наблюдаемое значение критерия принадлежит области принятия гипотезы — гипотезу принимают
Теория вероятностей и математическая статистика (СПО, курс 1)
Установите соответствие между профессиональными терминами и их определениями:
появление одного из них исключает появление другого: АÇВ = Æ
событие, которое обязательно произойдёт в результате эксперимента, Р(Е) = 1
событие, состоящее из точек пространства элементарных событий, не принадлежащих А: + А = Е;
×А = Æ
событие, которое в данном опыте произойти не может, Р(а) = 0
Теория вероятностей и математическая статистика (СПО, курс 1)
Вероятность того, что в серии из n независимых испытаний событие А наступит ровно k раз (безразлично в какой последовательности) находят по формуле _________, если n является достаточно небольшим значением: Pn(k) = Сnkpkqn-k, где Сnk = n! / k!(n-k)! – число сочетаний из n по k, р – вероятность события А, q – вероятность противоположного события a.
Теория вероятностей и математическая статистика (СПО, курс 1)
Установите соответствие между профессиональными терминами и их определениями:
Правосторонняя критическая область
критическая область, определяемая неравенством К < kкр , где К – значение критерия, kкр – критическая точка и kкр – отрицательное число
Двусторонняя критическая область
правосторонняя или левосторонняя критическая область
Односторонняя критическая область
критическая область, определяемая неравенствами К < k1, К > k2, где К – значение критерия, k1, k2 – критические точки и k2 > k1
Левосторонняя критическая область
критическая область, определяемая неравенством К > kкр , где К – значение критерия, kкр – критическая точка и kкр – положительное число
Теория вероятностей и математическая статистика (СПО, курс 1)
Установите соответствие между профессиональными терминами и их определениями:
Корреляционная зависимость (корреляция)
зависимость, при которой изменение одной случайной величины влечет изменение распределения другой
признаки, изменяющиеся под действием других связанных с ними признаков
признаки, обуславливающие изменения результативных признаков
Статистическая (стохастическая) зависимость
функциональная зависимость между значениями одной случайной величины и условным математическим ожиданием другой случайной величины
Теория вероятностей и математическая статистика (СПО, курс 1)
Установите соответствие между профессиональными терминами и их определениями:
Эмпирическая функция распределения
распределение дискретной случайной величины, принимающей значения х1, х2,… xn с вероятностями, равными рi = 1/п
функция распределения F (х) генеральной совокупности
Теоретическая функция распределения
вероятностное пространство, элементами которого являются наблюдения (х1), (х2), (xn) и все элементы которого равновероятны: (Р(хi) = 1/п)
функция F* (х), определяющая для каждого значения nх относительную частоту события X < х
Теория вероятностей и математическая статистика (СПО, курс 1)
Установите соответствие между профессиональными терминами и их определениями:
Коэффициент корреляции случайных величин и
Ковариация случайных величин и
Центральный момент порядка случайного вектора
математическое ожидание произведения центрированных величин: =
Момент порядка случайного вектора
Теория вероятностей и математическая статистика (СПО, курс 1)
Установите соответствие между профессиональными терминами и их определениями:
Показательное (экспоненциальное) распределение
распределение вероятностей, определяемое формулой Бернулли: . k = 0,1,2,… n
плотность распределения случайной величины на интервале [a,b] постоянна и равна
Равномерное распределение
Р(Х = к) = 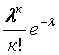
Биномиальное распределение
плотность распределения случайной величины имеет вид: 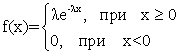
Теория вероятностей и математическая статистика (СПО, курс 1)
Установите соответствие между профессиональными терминами и их определениями:
если Н1, Н2, … , Нn — полная группа событий, то Р(Hi /A) =
Формула условной вероятности
Р(А) = , где Р(А/Нi) – условные вероятности события А, если известно, что событие Нi произошло
Формула полной вероятности
Р(В/А) = , при Р(В) > 0
Pn(k) = Сnkpkqn-k, где Сnk = n! / k!(n-k)! – число сочетаний из n по k, р – вероятность события А, q – вероятность противоположного события a
Теория вероятностей и математическая статистика (СПО, курс 1)
Установите соответствие между профессиональными терминами и их определениями:
Нормальное распределение n(a,s)
Р(êХ – mx ê³ a ) £ , где Х – случайная величина, имеющая конечные математическое ожидание mX и дисперсию DX, а > 0
Нормированное и центрированное нормальное распределение
плотность распределения случайной величины имеет вид: 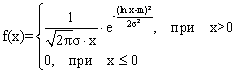
Логарифмически нормальное распределение
плотность распределения случайной величины имеет вид: f(x) =
плотность распределения случайной величины имеет вид: 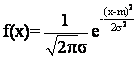
Теория вероятностей и математическая статистика (СПО, курс 1)
Установите соответствие между профессиональными терминами и их определениями:
Вероятность пересечения двух событий А и В
если пересечение Hi Ç Hj = Æ для i ¹ j , i,j = 1,2,…, n, и сумма вероятностей Р(Н1) + Р(Н2) + …+ Р(Нn ) = 1
система S подмножеств, для которой выполнены условия: а) система S содержит достоверное и невозможное события; б) если системе S принадлежат события А и В, то ей принадлежат также события А×В, А + В, А\В
наступление одного события не изменяет вероятность наступления другого: Р(АВ) = Р(А)×Р(В), Р(А/В) = Р(А), Р(В/А) = Р(В)
Полная группа событий Н1, Н2, … , Нn
если Р(А) > 0 и Р(В) > 0, то Р(АВ) = Р(В), Р(А/В) = Р(А)×Р(В/А)
 |
 |
Детали файла
| Имя файла: | 5419.02.01;МТ.02;1 |
| Размер: | 118 Kb |
| Дата публикации: | 2015-03-09 04:46:16 |
| Описание: | |
| Математическая статистика (магистр, курс 1) — Модульный тест
Список вопросов теста (скачайте файл для отображения ответов): Верны ли определения? |
|
| Для скачивания этого файла Вы должны ввести код указаный на картинке справа в поле под этой картинкой —> |  |
| ВНИМАНИЕ: | |
| Нажимая на кнопку «Скачать бесплатно» Вы подтверждаете свое полное и безоговорочное согласие с «Правилами сервиса» | |
| Ошибка: | |
| Введенный Вами код не соответствует указанному на картинке! Сгенерирован новый код. Попробуйте снова. Не скачивается нивкакую? |
|
Ошибки первого и второго рода
Выдвинутая гипотеза
может быть правильной или неправильной,
поэтому возникает необходимость её
проверки. Поскольку проверку производят
статистическими методами, её называют
статистической. В итоге статистической
проверки гипотезы в двух случаях может
быть принято неправильное решение, т.
е. могут быть допущены ошибки двух родов.
Ошибка первого
рода состоит в том, что будет отвергнута
правильная гипотеза.
Ошибка второго
рода состоит в том, что будет принята
неправильная гипотеза.
Подчеркнём, что
последствия этих ошибок могут оказаться
весьма различными. Например, если
отвергнуто правильное решение «продолжать
строительство жилого дома», то эта
ошибка первого рода повлечёт материальный
ущерб: если же принято неправильное
решение «продолжать строительство»,
несмотря на опасность обвала стройки,
то эта ошибка второго рода может повлечь
гибель людей. Можно привести примеры,
когда ошибка первого рода влечёт более
тяжёлые последствия, чем ошибка второго
рода.
Замечание 1.
Правильное решение может быть принято
также в двух случаях:
-
гипотеза принимается,
причём и в действительности она
правильная; -
гипотеза отвергается,
причём и в действительности она неверна.
Замечание 2.
Вероятность совершить ошибку первого
рода принято обозначать через
;
её называют уровнем значимости. Наиболее
часто уровень значимости принимают
равным 0,05 или 0,01. Если, например, принят
уровень значимости, равный 0,05, то это
означает, что в пяти случаях из ста
имеется риск допустить ошибку первого
рода (отвергнуть правильную гипотезу).
Статистический
критерий проверки нулевой гипотезы.
Наблюдаемое значение критерия
Для проверки
нулевой гипотезы используют специально
подобранную случайную величину, точное
или приближённое распределение которой
известно. Обозначим эту величину в целях
общности через
.
Статистическим
критерием
(или просто критерием) называют случайную
величину
,
которая служит для проверки нулевой
гипотезы.
Например, если
проверяют гипотезу о равенстве дисперсий
двух нормальных генеральных совокупностей,
то в качестве критерия
принимают отношение исправленных
выборочных дисперсий:
Эта величина
случайная, потому что в различных опытах
дисперсии принимают различные, наперёд
неизвестные значения, и распределена
по закону Фишера – Снедекора.
Для проверки
гипотезы по данным выборок вычисляют
частные значения входящих в критерий
величин и таким образом получают частное
(наблюдаемое) значение критерия.
Наблюдаемым
значением
называют значение критерия, вычисленное
по выборкам. Например, если по двум
выборкам найдены исправленные выборочные
дисперсиии
,
то наблюдаемое значение критерия
Критическая
область. Область принятия гипотезы.
Критические точки
После выбора
определённого критерия множество всех
его возможных значений разбивают на
два непересекающихся подмножества:
одно из них содержит значения критерия,
при которых нулевая гипотеза отвергается,
а другая – при которых она принимается.
Критической
областью называют совокупность значений
критерия, при которых нулевую гипотезу
отвергают.
Областью принятия
гипотезы (областью допустимых значений)
называют совокупность значений критерия,
при которых гипотезу принимают.
Основной принцип
проверки статистических гипотез можно
сформулировать так: если наблюдаемое
значение критерия принадлежит критической
области – гипотезу отвергают, если
наблюдаемое значение критерия принадлежит
области принятия гипотезы – гипотезу
принимают.
Поскольку критерий
— одномерная случайная величина, все её
возможные значения принадлежат некоторому
интервалу. Поэтому критическая область
и область принятия гипотезы также
являются интервалами и, следовательно,
существуют точки, которые их разделяют.
Критическими
точками (границами)
называют точки, отделяющие критическую
область от области принятия гипотезы.
Различают
одностороннюю (правостороннюю или
левостороннюю) и двустороннюю критические
области.
Правосторонней
называют критическую область, определяемую
неравенством
>
,
где— положительное число.
Левосторонней
называют критическую область, определяемую
неравенством
<
,
где— отрицательное число.
Односторонней
называют правостороннюю или левостороннюю
критическую область.
Двусторонней
называют критическую область, определяемую
неравенствами
где
.
В частности, если
критические точки симметричны относительно
нуля, двусторонняя критическая область
определяется неравенствами ( в
предположении, что
>0):
,
или равносильным неравенством
.
Отыскание
правосторонней критической области
Как найти критическую
область? Обоснованный ответ на этот
вопрос требует привлечения довольно
сложной теории. Ограничимся её элементами.
Для определённости начнём с нахождения
правосторонней критической области,
которая определяется неравенством
>
,
где>0.
Видим, что для отыскания правосторонней
критической области достаточно найти
критическую точку. Следовательно,
возникает новый вопрос: как её найти?
Для её нахождения
задаются достаточной малой вероятностью
– уровнем значимости
.
Затем ищут критическую точку,
исходя из требования, чтобы при условии
справедливости нулевой гипотезы
вероятность того, критерийпримет значение, большее
,
была равна принятому уровню значимости:
Р(>
)=
.
Для каждого критерия
имеются соответствующие таблицы, по
которым и находят критическую точку,
удовлетворяющую этому требованию.
Замечание 1.
Когда
критическая точка уже найдена, вычисляют
по данным выборок наблюдаемое значение
критерия и, если окажется, что
>
,
то нулевую гипотезу отвергают; если же<
,
то нет оснований, чтобы отвергнуть
нулевую гипотезу.
Пояснение. Почему
правосторонняя критическая область
была определена, исходя из требования,
чтобы при справедливости нулевой
гипотезы выполнялось соотношение
Р(>
)=
?
(*)
Поскольку вероятность
события
>
мала (
— малая вероятность), такое событие при
справедливости нулевой гипотезы, в силу
принципа практической невозможности
маловероятных событий, в единичном
испытании не должно наступить. Если всё
же оно произошло, т.е. наблюдаемое
значение критерия оказалось больше,
то это можно объяснить тем, что нулевая
гипотеза ложна и, следовательно, должна
быть отвергнута. Таким образом, требование
(*) определяет такие значения критерия,
при которых нулевая гипотеза отвергается,
а они и составляют правостороннюю
критическую область.
Замечание 2.
Наблюдаемое значение критерия может
оказаться большим
не потому, что нулевая гипотеза ложна,
а по другим причинам (малый объём выборки,
недостатки методики эксперимента и
др.). В этом случае, отвергнув правильную
нулевую гипотезу, совершают ошибку
первого рода. Вероятность этой ошибки
равна уровню значимости.
Итак, пользуясь требованием (*), мы с
вероятностьюрискуем совершить ошибку первого рода.
Замечание 3. Пусть
нулевая гипотеза принята; ошибочно
думать, что тем самым она доказана.
Действительно, известно, что один пример,
подтверждающий справедливость некоторого
общего утверждения, ещё не доказывает
его. Поэтому более правильно говорить,
«данные наблюдений согласуются с нулевой
гипотезой и, следовательно, не дают
оснований её отвергнуть».
На практике для
большей уверенности принятия гипотезы
её проверяют другими способами или
повторяют эксперимент, увеличив объём
выборки.
Отвергают гипотезу
более категорично, чем принимают.
Действительно, известно, что достаточно
привести один пример, противоречащий
некоторому общему утверждению, чтобы
это утверждение отвергнуть. Если
оказалось, что наблюдаемое значение
критерия принадлежит критической
области, то этот факт и служит примером,
противоречащим нулевой гипотезе, что
позволяет её отклонить.
Отыскание
левосторонней и двусторонней критических
областей***
Отыскание
левосторонней и двусторонней критических
областей сводится (так же, как и для
правосторонней) к нахождению соответствующих
критических точек. Левосторонняя
критическая область определяется
неравенством
<
(
<0).
Критическую точку находят, исходя из
требования, чтобы при справедливости
нулевой гипотезы вероятность того, что
критерий примет значение, меньшее,
была равна принятому уровню значимости:
Р(<
)=
.
Двусторонняя
критическая область определяется
неравенствами
Критические
точки находят, исходя из требования,
чтобы при справедливости нулевой
гипотезы сумма вероятностей того, что
критерий примет значение, меньшееили большее
,
была равна принятому уровню значимости:
.
(*)
Ясно, что критические
точки могут быть выбраны бесчисленным
множеством способов. Если же распределение
критерия симметрично относительно нуля
и имеются основания (например, для
увеличения мощности) выбрать симметричные
относительно нуля точки (-
)и
(
>0),
то
Учитывая (*), получим
.
Это соотношение
и служит для отыскания критических
точек двусторонней критической области.
Критические точки находят по соответствующим
таблицам.
Дополнительные
сведения о выборе критической области.
Мощность критерия
Мы строили
критическую область, исходя из требования,
чтобы вероятность попадания в неё
критерия была равна
при условии, что нулевая гипотеза
справедлива. Оказывается целесообразным
ввести в рассмотрение вероятность
попадания критерия в критическую область
при условии, что нулевая гипотеза неверна
и, следовательно, справедлива конкурирующая.
Мощностью критерия
называют вероятность попадания критерия
в критическую область при условии, что
справедлива конкурирующая гипотеза.
Другими словами, мощность критерия есть
вероятность того, что нулевая гипотеза
будет отвергнута, если верна конкурирующая
гипотеза.
Пусть для проверки
гипотезы принят определённый уровень
значимости и выборка имеет фиксированный
объём. Остаётся произвол в выборе
критической области. Покажем, что её
целесообразно построить так, чтобы
мощность критерия была максимальной.
Предварительно убедимся, что если
вероятность ошибки второго рода (принять
неправильную гипотезу) равна
,
то мощность равна 1-.
Действительно, если— вероятность ошибки второго рода, т.е.
события «принята нулевая гипотеза,
причём справедливо конкурирующая», то
мощность критерия равна 1 —.
Пусть мощность 1
—
возрастает; следовательно, уменьшается
вероятностьсовершить ошибку второго рода. Таким
образом, чем мощность больше, тем
вероятность ошибки второго рода меньше.
Итак, если уровень
значимости уже выбран, то критическую
область следует строить так, чтобы
мощность критерия была максимальной.
Выполнение этого требования должно
обеспечить минимальную ошибку второго
рода, что, конечно, желательно.
Замечание 1.
Поскольку вероятность события «ошибка
второго рода допущена» равна
,
то вероятность противоположного события
«ошибка второго рода не допущена» равна
1 —,
т.е. мощности критерия. Отсюда следует,
что мощность критерия есть вероятность
того, что не будет допущена ошибка
второго рода.
Замечание 2. Ясно,
что чем меньше вероятности ошибок
первого и второго рода, тем критическая
область «лучше». Однако при заданном
объёме выборки уменьшить одновременно
и
невозможно; если уменьшить
,
тобудет возрастать. Например, если принять
=0,
то будут приниматься все гипотезы, в
том числе и неправильные, т.е. возрастает
вероятностьошибки второго рода.
Как же выбрать
наиболее целесообразно? Ответ на этот
вопрос зависит от «тяжести последствий»
ошибок для каждой конкретной задачи.
Например, если ошибка первого рода
повлечёт большие потери, а второго рода
– малые, то следует принять возможно
меньшее.
Если
уже выбрано, то, пользуясь теоремой Ю.
Неймана и Э.Пирсона, можно построить
критическую область, для которойбудет минимальным и, следовательно,
мощность критерия максимальной.
Замечание 3.
Единственный способ одновременного
уменьшения вероятностей ошибок первого
и второго рода состоит в увеличении
объёма выборок.
Соседние файлы в папке Лекции 2 семестр
- #
- #
- #
- #