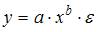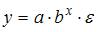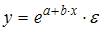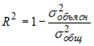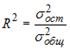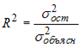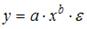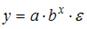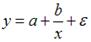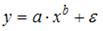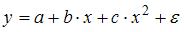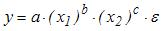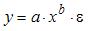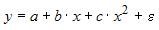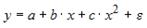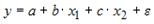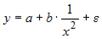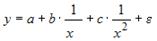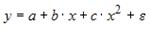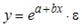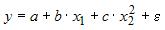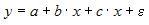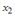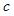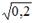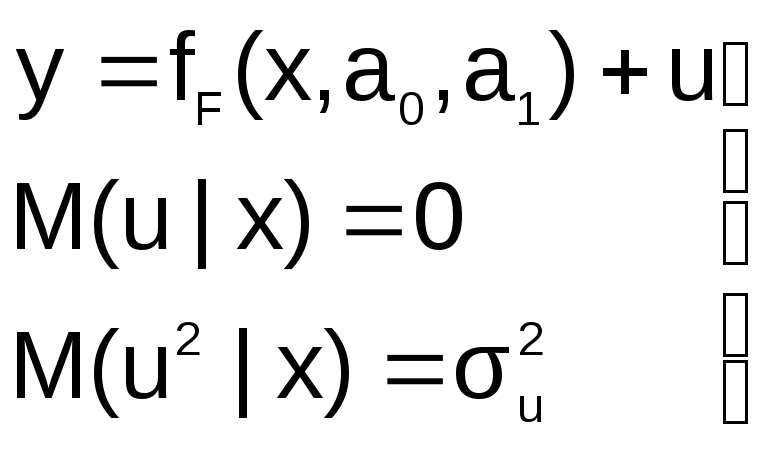Ошибки спецификации эконометрической модели имеют место вследствие …
Спецификацией модели называется отбор факторов, включаемых в модель, и выбор математической функции для 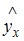
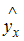
Эконометрика : учеб. / И.И. Елисеева и [др.]; под ред. И.И. Елисеевой. – 2-е изд., перераб. и доп. – М. : Финансы и статистика, 2005. – С. 45.
Прикладная статистика. Основы эконометрики: Учебник для вузов: В 2 т. 2-е изд., испр. – Т. 2: Айвазян С.А. Основы эконометрики. – М.: ЮНИТИ-ДАНА, 2001. – С. 20–30 .
ответ тест i-exam
Тема 2: Отбор факторов, включаемых в модель множественной регрессии
Тема 1: Спецификация эконометрической модели
1. Ошибки спецификации эконометрической модели имеют место вследствие …
неправильного выбора математической функции или недоучета в уравнении регрессии какого-то существенного фактора
недостоверности или недостаточности исходной информации
неоднородности данных в исходной статистической совокупности
недостаточного количества данных
Решение:
Спецификацией модели называется отбор факторов, включаемых в модель, и выбор математической функции для 

2. Для регрессионной модели вида 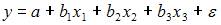
Решение:
Считается, на каждый оцениваемый коэффициент регрессии необходимо не менее 5–7 объектов статистических наблюдений. Так как представленная модель содержит 3 независимые переменные, то на каждый из параметров регрессии при независимой переменной необходимо по 5–7 наблюдений, то есть в совокупности не менее 15–21 наблюдения. Берем нижнюю границу интервала, тогда правильный вариант ответа – «15».
3. Нелинейным по объясняющим переменным, но линейным по параметрам уравнением регрессии является …
Решение:
Из приведенных функций только в функции 
4. В модели вида 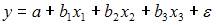
Решение:
Эконометрическая модель уравнения регрессии может быть представлена линейным уравнением множественной регрессии в виде выражения 

5. При идентификации модели множественной регрессии 
Решение:
При оценке модели множественной регрессии 
Тема 2: Отбор факторов, включаемых в модель множественной регрессии
1. В модели множественной регрессии 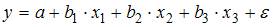






Решение:
Для оценки мультиколлинеарности факторов может использоваться определитель матрицы парных коэффициентов корреляции между факторами. Если факторы не коррелированы между собой, то матрица парных коэффициентов корреляции между факторами была бы единичной. Поскольку все недиагональные элементы 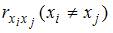

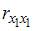
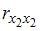
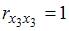
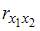
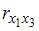
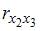
Если между факторами существует полная линейная зависимость и все коэффициенты парной корреляции равны единице, то определитель такой матрицы равен нулю.
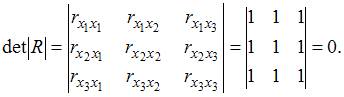
Чем ближе к нулю определитель матрицы межфакторной корреляции, тем сильнее мультиколлинеарность факторов и ненадежнее результаты множественной регрессии. И, наоборот, чем ближе к единице определитель матрицы межфакторной корреляции, тем меньше мультиколлинеарность факторов.
2. При моделировании линейного уравнения множественной регрессии вида 
Решение:
Эконометрическая модель уравнения регрессии может быть представлена линейным уравнением множественной регрессии в виде выражения 

V7: Система линейных одновременных уравнений
S: При выполнении предпосылок метода наименьших квадратов (МНК) оценки параметров регрессионной модели, рассчитанные с помощью МНК, обладают свойствами
-: состоятельности, смещенности и эффективности
+: состоятельности, несмещенности и эффективности
-: состоятельности, смещенности и неэффективности
-: несостоятельности, смещенности и эффективности
S: Для регрессионной модели вида 
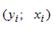
S: Для обнаружения автокорреляции в остатках используется
+: статистика Дарбина – Уотсона
-: критерий Гольдфельда – Квандта
S: Величина 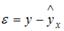
S: Строится эконометрическая модель линейного уравнения множественной регрессии вида
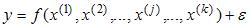

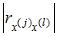
S: Для учета влияния на исследуемую (зависимую) переменную признаков качественного характера используются фиктивные переменные, при этом фиктивной переменной может присваиваться значение
S: В эконометрической модели линейного уравнения регрессии
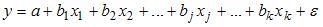
S: Система эконометрических уравнений включает совокупность _________ переменных.
S: Несмещенность оценок параметров регрессии означает, что …
-: дисперсия остатков минимальная
-: точность оценок выборки увеличивается с увеличением объема выборки
+: математическое ожидание остатков равно нулю
-: дисперсия остатков не зависит от величины
S: Дана автокорреляционная функция временного ряда
Верным будет утверждение, что ряд …
-: содержит только тенденцию, и не содержит сезонной компоненты
-: не имеет ни тенденции, ни сезонной компоненты, имеет только случайную компоненту
+: имеет выраженную сезонную компоненту с лагом 4
-: имеет выраженную сезонную компоненту с лагом 6
S: Если параметр эконометрической модели является статистически значимым, то его значение признается …
+: равным коэффициенту парной корреляции
S: Для регрессионной модели вида 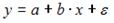
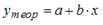

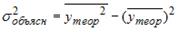

-:
+:
-:
-:
S: Построена эконометрическая модель для зависимости прибыли от реализации единицы продукции (руб., у) от величины оборотных средств предприятия (тыс. р., х1): 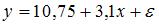
S: Нелинейным по объясняющим переменным, но линейным по параметрам уравнением регрессии является …
-:
-:
-:
+:
S: Примерами фиктивных переменных в эконометрической модели зависимости стоимости 1 м2 жилья не являются …
-: принадлежность тому или иному региону
-: категория жилья: первичное (новое) жилье / вторичное (неновое) жилье
+: площадь жилья (м2)
S: Среди предложенных нелинейных зависимостей нелинейной существенно (внутренне нелинейной) является …
+:
-:
-:
-:
S: При линеаризации нелинейных регрессионных моделей как один из видов преобразований используется логарифмирование уравнения. Указанным способом не может быть линеаризовано уравнение …
-:
-:
-:
+:
S: По результатам проведения исследования торговых точек было построено уравнение нелинейной регрессии 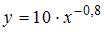
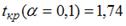
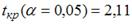
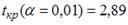
-: при уровне значимости 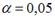
-: при уровне значимости 
-: эластичность спроса по цене составляет –0,8
+: при уровне значимости 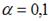
S: По типу функциональной зависимости между переменными эконометрической модели различают _____ уравнения регрессии.
-: стохастические и вероятностные
-: линейные и парные
-: множественные и парные
+: линейные и нелинейные
S: Дана таблица исходных данных для построения эконометрической регрессионной модели:
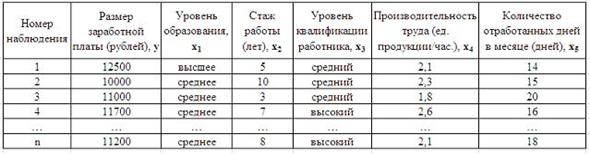
Фиктивными переменными не являются …
-: уровень квалификации работника
S: При моделировании уравнения множественной регрессии проверку тесноты связи между независимыми переменными (объясняющими переменными, регрессорами, факторами) модели осуществляют на основе …
-: коэффициента множественной корреляции
-: показателей существенности параметров модели
+: матрицы парных коэффициентов линейной корреляции
-: системы нормальных уравнений МНК
S: Для регрессионной модели зависимости среднедушевого денежного дохода населения (руб., у) от объема валового регионального продукта (тыс. р., х1) и уровня безработицы в субъекте (%, х2) получено уравнение 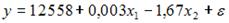
-: увеличится на 1,67
-: изменится на (-1,67)
-: изменится на 0,003
+: уменьшится на (-1,67)
S: В модели вида 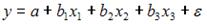
S: В модели множественной регрессии 
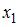
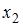
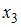
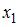
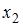
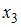
S: В уравнении линейной множественной регрессии: 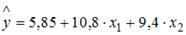
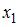
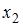
-: на 1 тыс. руб. … уменьшится на 10,8 тыс. руб.
-: на 1% … увеличится на 10,8%
-: на 1 тыс. руб. … увеличится на 10,8%
+: на 1 тыс. руб. … увеличится на 10,8 тыс. руб.
S: Переменная х является нелинейной в уравнении
-:
-:
+:
-:
S: Уравнением нелинейной регрессии, отражающей полиномиальную зависимость y от x, является
-:
-:
+:
-:
S: При линеаризации нелинейных регрессионных моделей как один из видов преобразований используется способ приведения уравнения к обратному виду, то есть к переменной 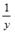
-:
-:
-:
+:
S: Для регрессионной модели парной регрессии рассчитано значение коэффициента детерминации 
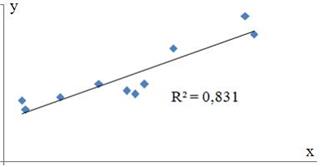
На дисперсию зависимой переменной, объясненную построенным уравнением приходится ________ общей дисперсии зависимой переменной.
S: Пусть 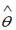




S: Степенной модельюне является регрессионная модель …
-:
+:
-:
-:
S: Нелинейным уравнением множественной регрессии является …
+:
-:
-:
-:
S: Система эконометрических уравнений может состоять из _____ уравнения (-ий) регрессии.
+: бесконечно большого количества
S: В эконометрической модели линейного уравнения регрессии 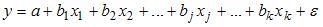
+:
S: Для эконометрической модели линейного уравнения множественной регрессии вида 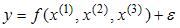
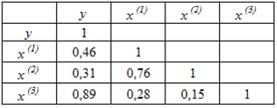
Коллинеарными (тесносвязанными) независимыми (объясняющими) переменными являются …
S: Регрессионная модель вида 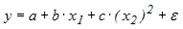
-: переменной
+: переменной
-: параметра
-: переменной
S: Известно, что доля остаточной дисперсии зависимой переменной в ее общей дисперсии равна 0,2. Тогда значение коэффициента детерминации составляет
-:
-:
S: Обобщенный метод наименьших квадратов применяется для оценки параметров линейных регрессионных моделей с __________ остатками.
-: гомоскедастичными и некоррелированными
+: автокоррелированными и/или гетероскедастичными
S: Метод наименьших квадратов (МНК) может применяться для оценки параметров исходной регрессионной модели в _________ форме.
S: Автокорреляцией уровней ряда называется корреляционная зависимость между …
-: факторами, формирующими уровень ряда
-: уровнями двух рядов
+: последовательными уровнями ряда
-: компонентами, образующими уровни ряда
S: Самым коротким интервалом изменения коэффициента корреляции для уравнения парной линейной регрессии 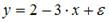
S: Левая часть системы эконометрических уравнений представлена совокупностью _________ переменных.
S: При расчете скорректированного коэффициента множественной детерминации пользуются формулой 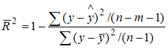
+: n – число наблюдений; m – число факторов, включенных в модель множественной регрессии
-: n – число параметров при независимых переменных; m – число наблюдений
-: n – число параметров при независимых переменных; m – число факторов, включенных в модель множественной регрессии
-: m – число наблюдений; n – число факторов, включенных в модель множественной регрессии
S: Для эконометрической модели вида 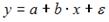


S: Ошибкой спецификации эконометрической модели уравнения регрессии является …
+: использование парной регрессии вместо множественной
-: расчет показателей качества модели
-: учет случайных факторов
-: оценка параметров при помощи МНК
S: В модели множественной регрессии 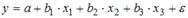
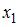
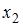
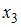
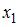
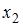
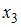
S: Совокупность значений экономического показателя за несколько последовательных моментов (периодов) времени называется …
S: Автокорреляционной функцией временного ряда называется последовательность коэффициентов автокорреляции …
-: между трендовой, сезонной и случайной компонентами
+: первого, второго, третьего и последующих порядков
-: факторов, формирующих уровень ряда
-: между несколькими временными рядами
S: Уровень временного ряда (yt) формируется под воздействием различных факторов – компонент: Т (тенденция), S (циклические и/или сезонные колебания), Е (случайные факторы). Мультипликативную модель временного ряда формируют следующие значения компонент уровня временного ряда …
-: yt = 7; T = 6,5; S = 0; E = 0,5
-: yt = 7; T = -3,5; S = -2; E = -1
+: yt = 7; T = 3,5; S = 2; E = 1
-: yt = 7; T = 3,5; S = -2; E = 1
источники:
http://poisk-ru.ru/s16310t6.html
http://lektsia.com/2×1276.html
Ошибкой спецификации эконометрической модели уравнения регрессии является …
- учет случайных факторов
- оценка параметров при помощи МНК
- использование парной регрессии вместо множественной
- расчет показателей качества модели
Тип вопроса: Вопрос с одним правильными вариантом
Ответ на этот вопрос уже получили: 376 раз(а)
Помогли ответы? Ставь лайк 👍
Вопрос задал(а): Анонимный пользователь, 09 Январь 2017 в 20:42
На вопрос ответил(а): Астафьева Любовь, 09 Январь 2017 в 20:42
Возможные ошибки спецификации модели:
1. Неправильный выбор вида уравнения
регрессии
2. В уравнение регрессии включена лишняя
(незначимая) переменная
3. В уравнении регрессии пропущена
значимая переменная
-
Неправильный выбор вида функции в
уравнении
Пусть на первом этапе была сделана
спецификация модели в виде:
в
которой функция fF(x,a0,a1)
выбрана не верно. Предположим, что
yT=fT(x,a0,a1)+v
– правильный вид функции регрессии.
Тогда справедливо выражение:
И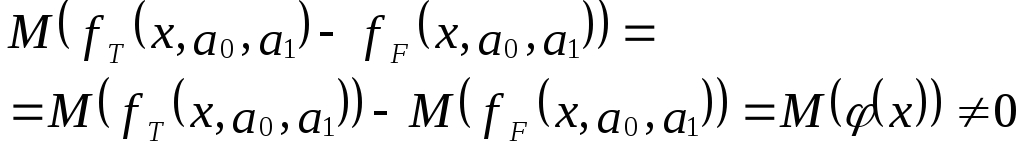
выражения следует:
Иными словами, математические ожидания
эндогенной переменной, полученные с
помощью функций fT
и fF
не совпадают, т.е. первая предпосылка
теоремы Гаусса-Маркова M(ulx)=0
не выполняется
Следовательно, в результате оценивания
такой модели параметры а0 и а1
будут смещенными
Симптомы наличия ошибки спецификации
первого типа:
1. Несоответствие диаграммы рассеяния,
построенной по имеющейся выборке виду
функции, принятой в спецификации
2. В динамических моделях длительно
сохраняется знак значений оценок
случайных возмущений у смежных (по
номеру t ) уравнений
наблюдений
Именно этот симптом и улавливается
статистикой DW Дарбина–Уотсона!
В силу данного обстоятельства тесту
Дарбина–Уотсона в эконометрике придается
большое значение.
Способ устранения: выбор другой формы
спецификации модели. Например, нелинейная
вместо линейной и т.д.
2. В уравнение регрессии включена
лишняя переменная
П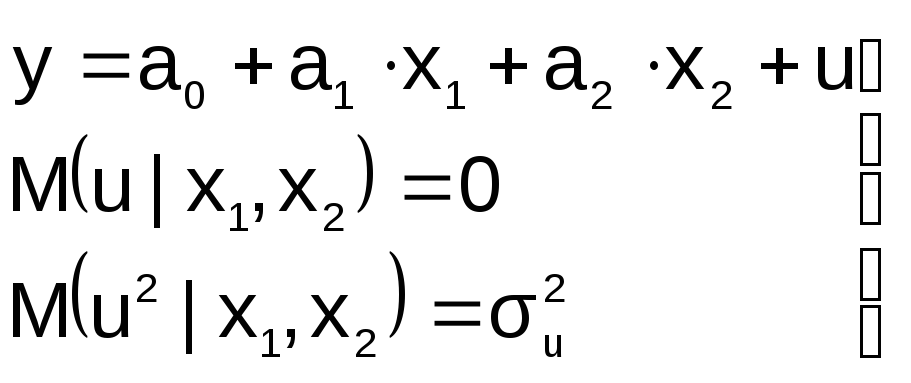
на этапе спецификации в модель включена
«лишняя» переменная, например, X2
«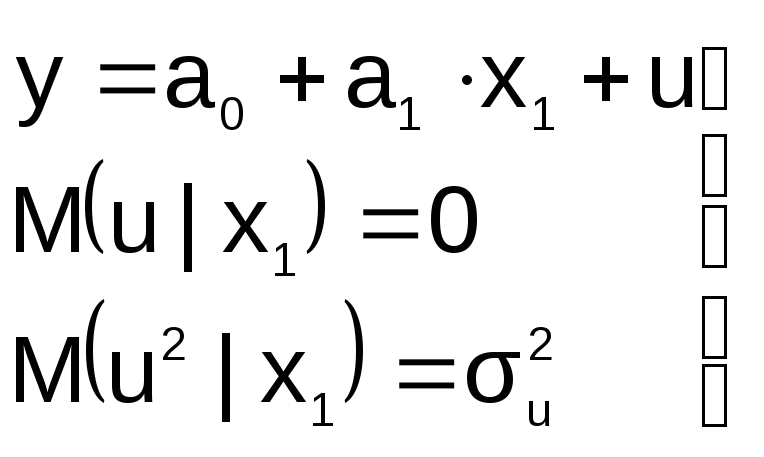
спецификация должна иметь вид:
Последствия:
1.
Оценки параметров а0, а1, а2
останутся несмещенными, но потеряют
свою эффективность (точность)
2. Увеличивается ошибка прогноза по
модели
как за счет ошибок оценок коэффициентов
и σu,
так и за счет последнего слагаемого.
Это особенно опасно при больших абсолютных
значениях регрессора
Диагностика:
В моделях множественной регрессии
необходимо для каждого коэффициента
уравнения проверять статистическую
гипотезу H0: ai=0.
Вспомним, что для этого достаточно
оценить дробь Стьюдента и сравнить ее
значение с критическим значением
распределения Стьюдента, которое
вычисляется по значению доверительной
вероятности и значению степени свободы
n2 = n – (k+1)
3.
В модели не достает важной переменной
Последствия такие же, как и в первом
случае: получаем смещенные оценки
параметров модели
Для устранения необходимо вернуться к
изучению особенностей поведения
экономического объекта, выявить опущенные
переменные и дополнить ими модель
29. Фиктивные переменные и особенности их использования в моделях.
На практике приходится учитывать в
моделях факторы, носящие качественный
характер, значения которых в наблюдениях
не возможно измерить с помощью числовой
шкалы.
Примеры.
Моделирование влияния пола специалистов
на уровень зарплаты.
Моделирование доходов граждан от типа
учебного заведения, в котором он получил
образование (государственное, частное,
специализированное,…)
Модель инфляции с учетом различных
видов регулирования со стороны государства
Возможны два подхода к решению задачи:
— построить несколько моделей отдельно
для каждого значения (градации)
качественной переменной
— учесть влияние качественного фактора
в одной модели
Второй способ представляется более
прогрессивным, т.к в этом случае появляется
возможность оценить статистическую
значимость влияния данного фактора на
поведение эндогенной переменной на
фоне других факторов, внесенных в
спецификацию модели
Пример. Изучается зависимость
расходов на образование «С» в «обычных»
и «специализированных» школах в
зависимости от числа учащихся N
Предположим:
-
Зависимость затрат на обучение от
количества учащихся N в
обоих типах школ одинакова
2. Разница в затратах объясняется
необходимостью приобретения
специализированного оборудования для
обучения специальным дисциплинам
Тогда если строить различные модели
для каждого типа школ, то спецификацию
моделей можно записать в виде:
Yo
= a0 +
a1N +u
Ys
= b0 +
a1N +
v
О
модели можно объединить, если ввести
переменную d, область
определения которой два целых числа :
0 и 1. При этом:
Спецификация такой модели имеет вид:
Y = a0
+ a1N
+ δd + u
Тогда при d=0 получим Yo
= a0 + a1N
+ u
при d=1 получим Ys
= (a0+δ)
+a1N +
v
d – фиктивная переменная
сдвига
Фиктивные переменные часто применяются
при построении динамических моделей,
когда с определенного момента времени
начинает действовать какой-либо
качественный фактор
Пусть некоторый качественный фактор
имеет несколько градаций (более 2-х)
Введение в модель фиктивных переменных
с несколькими градациями рассмотрим
на примере шанхайских школ, где имеются
4 категории школ: общеобразовательные,
технические, ПТУ и специализированные
Казалось достаточно ввести фиктивную
переменную сдвига d, придав
ей четыре различных значения и проблема
будет решена
Такой подход мало эффективен, т.к не
удается оценить статистическую значимость
влияния каждой градации на значения
эндогенной переменной
В этом случае имеет смысл ввести отдельную
переменную для каждой градации фактора
Н
Однако, если взять спецификацию модели
в виде:
Y=a0
+ a1d1+a2d2+a3d3+a4d4+a5N+u
при этом всегда верно тождество
d1+d2+d3+d4=1
Это означает, что матрица Х коэффициентов
системы уравнений наблюдений будет
коллинеарной т.к в ней присутствует
столбец из 1, и как следствие отсутствует
возможность применения МНК для оценки
параметров модели.
Предлагается в спецификацию ввести
(к-1) фиктивную переменную (к- кол-во
градаций), сделав одну из градаций
базовой, относительно которой изучать
влияние остальных градаций. Проблемы
мультиколинеарности в этом случае не
возникает
Для учета возможного изменения наклона
графика модели при изменении градации
качественного фактора предлагается
ввести в спецификацию модели еще одно
слагаемое вида «d умноженное
на x»
Вернемся к примеру изучения зависимости
расходов на образование в различных
школах. Для простоты ограничимся лишь
двумя градациями фактора «тип школы»:
d=0 – обычная школа;
d=1 – профессиональная
школа
Спецификацию модели следует записать
в виде:
Y = a0
+ a1N
+ a2*d
+ a3dN
+U
50
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
4.
Использование
предварительной информации о значениях некоторых параметров. Иногда значения некоторых неизвестных параметров
модели могут быть определены по пробным выборочным наблюдениям, тогда
мультиколлинеарность может быть устранена путем установления значений параметра
у одной коррелирующих переменных. Ограниченность метода – в сложности получения
предварительных значений параметров с высокой точностью.
5.
Преобразование переменных. Для устранения мультиколлинеарности можно
преобразовать переменные, например, путем линеаризации или получения
относительных показателей, а также перехода от номинальных к реальным
показателям (особенно в макроэкономических исследованиях).
При построении модели множественной регрессии с точки
зрения обеспечения ее высокого качества возникают следующие вопросы:
1.
Каковы признаки качественной
модели?
2.
Какие ошибки спецификации могут
быть?
3.
Каковы последствия ошибок
спецификации?
4.
Какие существуют методы
обнаружения и устранения ошибок спецификации?
Рассмотрим основные признаки качественной модели
множественной регрессии:
1.
Простота. Из двух моделей примерно одинаковых статистических
свойств более качественной является та, которая содержит меньше переменных, или
же более простая по аналитической форме.
2.
Однозначность. Метод вычисления коэффициентов должен быть одинаков
для любых наборов данных.
3.
Максимальное соответствие. Этот признак говорит о том, что основным критерием
качества модели является коэффициент детерминации, отражающий объясненную
моделью вариацию зависимой переменной. Для практического использования выбирают
модель, для которой расчетное значение F-критерия для
коэффициента детерминации б четыре раза больше табличного.
4.
Согласованность с теорией. Получаемые значения коэффициентов должны быть
интерпретируемы с точки зрения экономических явлений и процессов. К примеру,
если строится линейная регрессионная модель спроса на товар, то соответствующий
коэффициент при цене товара должен быть отрицательным.
5.
Хорошие прогнозные качества.
Обязательным условием построения
качественной модели является возможность ее использования для прогнозирования.
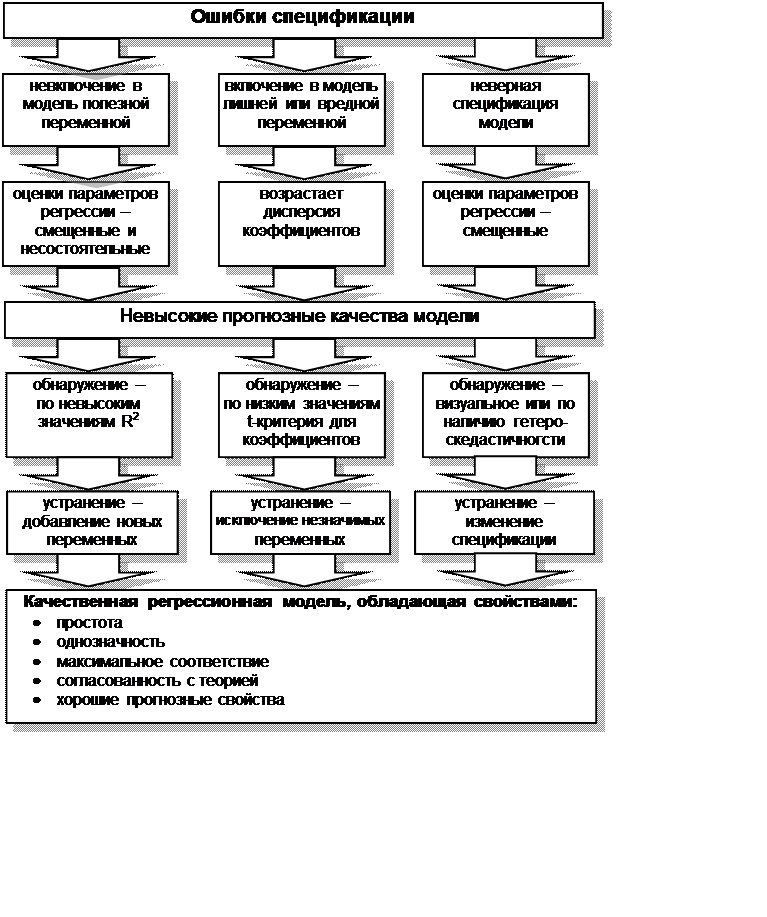
Одной из основных ошибок, допускаемых при построении
регрессионной модели, является ошибка спецификации (рис. 4.3).
Под ошибкой спецификации понимается неправильный выбор функциональной формы
модели или набора объясняющих переменных.
Различают следующие виды ошибок спецификации:
1.
Невключение в модель полезной
(значимой) переменной.
2.
Добавление в модель лишней
(незначимой) переменной
3.
Выбор неправильной функциональной
формы модели
Последствия ошибки первого вида (невключение в
модель значимой переменной) заключаются в том, что полученные по МНК оценки
параметров являются смещенными и несостоятельными, а значение коэффициента
детерминации значительно снижаются.
При добавлении в модель лишней переменной
(ошибка второго вида) ухудшаются статистические свойства оценок
коэффициентов, возрастают их дисперсии, что ухудшает прогнозные качества модели
и затрудняет содержательную интерпретацию параметров, однако по сравнению с
другими ошибками ее последствия менее серьезны.
Если же осуществлен неверный выбор
функциональной формы модели, то есть допущена ошибка третьего вида, то
получаемые оценки будут смещенными, качество модели в целом и отдельных
коэффициентов будет невысоким. Это может существенно сказаться на прогнозных
качествах модели.
Ошибки спецификации первого вида можно обнаружить только
по невысокому качеству модели, низким значениям R2.
Обнаружение ошибок спецификации второго вида, если лишней
является только одна переменная, осуществляется на основе расчета t — статистики для коэффициентов. При лишней переменной коэффициент
будет статистически незначим.
Рис. 4.3 Ошибки спецификации и свойства качественной
регрессионной модели
1. Если у Вас есть аккаунт в WhatsApp, жмите на кнопку и читайте инструкцию:
2. Если у Вас есть аккаунт в Viber, Вы можете написать нам, нажмите на кнопку и следуйте инструкции:
3. Если Вы пользуетесь месенджером от Telegram, можете писать нам с него, нажмите на кнопку и ознакомьтесь с инструкцией:
Как написать нам через Telegram?
1. Если у Вас Telegram установлен на компьютере, для связи НАЖМИТЕ и подтвердите запуск приложения.

2. Если у Вас Telegram в мобильном телефоне:
4. Если Вы зарегистрированны в соц.сети ВКонтакте, нажмите на кнопку и пишите нам со своего аккаунта:
5. Если Вы зарегистрированны в соц.сети Facebook, нажмите на кнопку и пишите нам со своего аккаунта: