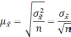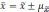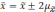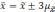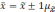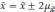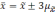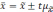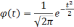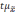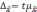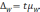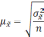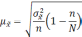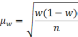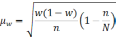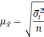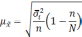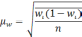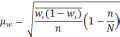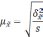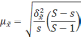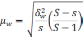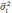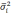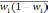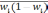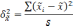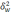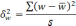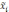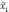Ошибка
репрезентативности
— расхождение между выборочной
характеристикой и характеристикой
генеральной совокупности.
Ошибки
репрезентативности
-
Систематические
— возникают в результате нарушения
научных принципов отбора единиц
совокупности (преднамеренные и
непреднамеренные). -
Случайные
возникают в результате несплошного
характера наблюдения (средняя и
предельная ошибки выбора).
Случайные
ошибки могут быть доведены до незначительных
размеров, а главное, их размеры и пределы
можно определить с достаточной точностью
на основании закона больших чисел.
Средняя
ошибка выборки
— такое расхождение между средними
выборочной и генеральной совокупностями,
которое не превышает ±.
В
математической статистике доказывается,
что значения средней ошибки выборки
определяются по формулам:
Формула
для определения величины средней ошибки
выборки для количественного признака:
Формула
для определения величины средней ошибки
выборки для альтернативного признака:
Полученное
значение средней ошибки необходимо для
установления возможного значения 
Которое определяется по формуле:
Но
такое суждение можно гарантировать не
с абсолютной
достоверностью, а лишь с определенной
степенью
вероятности.
В
математической статистике доказывается,
что пределы значений характеристик
генеральной совокупности отличаются
от характеристик выборочной совокупности
лишь с вероятностью, которая определена
числом 0,683.
Это
означает, что в 683 случаях из 1000 генеральная
средняя будет находиться в установленных
пределах, т.е. отклонение ГС от ВС не
превысит однократной средней ошибки
выборки. В остальных 317 случаях они могут
выйти за эти пределы. Вероятность можно
повысить, если расширить пределы
отклонений. Так, при удвоенном значении

вероятность достигает 0,954 (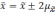
Если утроить значение то вероятность
увеличится до 0,997 (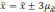
|
Возможное |
Вероятность |
|
|
0,683 |
|
|
0,954 |
|
|
0,997 |
Если
обозначить значение увеличения
за
t,
то можно записать в общем виде:
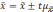
Множитель
t
называется коэффициентом
доверия.
Известный русский математик А.М.Ляпунов
дал выражение конкретных значений
множителя t
для различных степеней вероятности в
виде функции:
На
практике пользуются готовыми таблицами
этой функции.
|
t |
0 |
0,1 |
0,5 |
1 |
1,5 |
2 |
2,5 |
2,6 |
3 |
4 |
|
(t) |
0,1 |
0,0797 |
0,3829 |
0,6827 |
0,8664 |
0,9545 |
0,9876 |
0,9907 |
0,9973 |
0,99994 |
Из
вышесказанного следует, что лишь с
определенной степенью вероятности
можно утверждать, что показатели
генеральной совокупности и их отклонения
не превысят величину 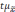
Полученную величину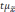
ошибкой выборки.
Предельная
ошибка выборки
—
максимально
возможное расхождение выборочной и
генеральной средних,
т.е.
максимум ошибки при заданной вероятности
ее появления.
Предельная
ошибка выборки для количественного
признака:
Предельная
ошибка выборки для альтернативного
признака:
В
связи с тем, что существуют различные
методы, виды и способы отбора единиц из
генеральной совокупности формулы для
расчета средней ошибки выборки также
будут различаться:
|
Способ |
Оцениваемый |
Повторный |
Бесповторный |
|
Собственно случайный механический |
Средняя |
|
|
|
Доля |
|
|
|
|
Типический |
Средняя |
|
|
|
Доля |
|
|
|
|
Серийный |
Средняя |
|
|
|
Доля |
|
|
— средняя из групповых дисперсий;
wi
— доля
единиц совокупности, обладающих изучаемым
признаком в i-й
типической
группе;
— средняя из групповых дисперсий для
доли. В табл. 6.6 представлены формулы
для исчисления средней ошибки выборки
при типическом отборе;
S
– общее число серий;
s
– число отобранных серий;
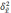
межгрупповая дисперсия средних,
определяемая по формуле:
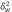
межгрупповая дисперсия доли, определяемая
по формуле:
— средняя
i-й
серии;
—
средняя по всей выборочной совокупности;
w
— доля признака i-й
серии;
— общая доля признака во всей выборочной
совокупности.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Ошибка
репрезентативности
— расхождение между выборочной
характеристикой и характеристикой
генеральной совокупности.
Ошибки
репрезентативности
-
Систематические
— возникают в результате нарушения
научных принципов отбора единиц
совокупности (преднамеренные и
непреднамеренные). -
Случайные
возникают в результате несплошного
характера наблюдения (средняя и
предельная ошибки выбора).
Случайные
ошибки могут быть доведены до незначительных
размеров, а главное, их размеры и пределы
можно определить с достаточной точностью
на основании закона больших чисел.
Средняя
ошибка выборки
— такое расхождение между средними
выборочной и генеральной совокупностями,
которое не превышает ±.
В
математической статистике доказывается,
что значения средней ошибки выборки
определяются по формулам:
Формула
для определения величины средней ошибки
выборки для количественного признака:
Формула
для определения величины средней ошибки
выборки для альтернативного признака:
Полученное
значение средней ошибки необходимо для
установления возможного значения 
Которое определяется по формуле:
Но
такое суждение можно гарантировать не
с абсолютной
достоверностью, а лишь с определенной
степенью
вероятности.
В
математической статистике доказывается,
что пределы значений характеристик
генеральной совокупности отличаются
от характеристик выборочной совокупности
лишь с вероятностью, которая определена
числом 0,683.
Это
означает, что в 683 случаях из 1000 генеральная
средняя будет находиться в установленных
пределах, т.е. отклонение ГС от ВС не
превысит однократной средней ошибки
выборки. В остальных 317 случаях они могут
выйти за эти пределы. Вероятность можно
повысить, если расширить пределы
отклонений. Так, при удвоенном значении

вероятность достигает 0,954 (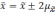
Если утроить значение то вероятность
увеличится до 0,997 (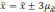
|
Возможное |
Вероятность |
|
|
0,683 |
|
|
0,954 |
|
|
0,997 |
Если
обозначить значение увеличения
за
t,
то можно записать в общем виде:
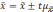
Множитель
t
называется коэффициентом
доверия.
Известный русский математик А.М.Ляпунов
дал выражение конкретных значений
множителя t
для различных степеней вероятности в
виде функции:
На
практике пользуются готовыми таблицами
этой функции.
|
t |
0 |
0,1 |
0,5 |
1 |
1,5 |
2 |
2,5 |
2,6 |
3 |
4 |
|
(t) |
0,1 |
0,0797 |
0,3829 |
0,6827 |
0,8664 |
0,9545 |
0,9876 |
0,9907 |
0,9973 |
0,99994 |
Из
вышесказанного следует, что лишь с
определенной степенью вероятности
можно утверждать, что показатели
генеральной совокупности и их отклонения
не превысят величину 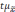
Полученную величину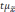
ошибкой выборки.
Предельная
ошибка выборки
—
максимально
возможное расхождение выборочной и
генеральной средних,
т.е.
максимум ошибки при заданной вероятности
ее появления.
Предельная
ошибка выборки для количественного
признака:
Предельная
ошибка выборки для альтернативного
признака:
В
связи с тем, что существуют различные
методы, виды и способы отбора единиц из
генеральной совокупности формулы для
расчета средней ошибки выборки также
будут различаться:
|
Способ |
Оцениваемый |
Повторный |
Бесповторный |
|
Собственно случайный механический |
Средняя |
|
|
|
Доля |
|
|
|
|
Типический |
Средняя |
|
|
|
Доля |
|
|
|
|
Серийный |
Средняя |
|
|
|
Доля |
|
|
— средняя из групповых дисперсий;
wi
— доля
единиц совокупности, обладающих изучаемым
признаком в i-й
типической
группе;
— средняя из групповых дисперсий для
доли. В табл. 6.6 представлены формулы
для исчисления средней ошибки выборки
при типическом отборе;
S
– общее число серий;
s
– число отобранных серий;
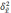
межгрупповая дисперсия средних,
определяемая по формуле:
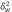
межгрупповая дисперсия доли, определяемая
по формуле:
— средняя
i-й
серии;
—
средняя по всей выборочной совокупности;
w
— доля признака i-й
серии;
— общая доля признака во всей выборочной
совокупности.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Ошибки репрезентативности
- Ошибки репрезентативности
- возможные пределы отклонений выборочной доли и выборочной средней от доли и средней в генеральной совокупности. По своей природе такие ошибки могут быть систематическими и случайными. В социологической и статистической литературе систематические ошибки часто называются также ошибками смещения. Ошибки такого рода имеют в основном одну и ту же постоянную величину или измеряются по определенному закону, имеющему функциональный характер. Систематическими ошибками называются ошибки, являющиеся следствием действия (в одних и тех же условиях) определенной причины или небольшого числа причин, которые искажают полученную информацию в определенном направлении, причем эти причины поддаются изучению. Систематические О. р. наиболее опасны, так как их источником являются неправильные принципы проведения процедуры исследования, способы формирования выборочной совокупности, методы сбора и расчета полученной информации.
К основным причинам появления систематических ошибок репрезентативности относят: 1) преднамеренное или непреднамеренное отступление от принципов случайного отбора при формировании выборочной совокупности; 2) замена единиц наблюдения другими единицами, которые не попали в выборочную совокупность; 3) неполный охват опросом единиц выборочной совокупности; 4) практическая невозможность абсолютно точно реализовать первоначальный план выборки вследствие отказов респондентов от участия в опросе, естественной смертности и подвижности населения, ошибочно написанных адресов, изменений адресов респондентов и пр. Случайными являются такие О. р., которые при повторных измерениях принимают различные взаимонезависимые положительные или отрицательные значения. О случайных ошибках речь может идти только тогда, когда помимо основных у нас имеются еще и дополнительно проведенные измерения. Случайные О. р. предстают в форме случайных величин или функций, то есть пределов, в которых находится результат. Их с некоторой вероятностью можно предвидеть. Т. е. величину случайной ошибки можно априори измерить.
Социологический справочник. — К.: Политиздат Украины.
.
1990.
Полезное
Смотреть что такое «Ошибки репрезентативности» в других словарях:
-
Ошибки — вид неадекватности знания объекту познания. О. являются неотъемлемой частью любого исследования так как их невозможно исключить полностью. Их просто необходимо учитывать как неоспоримый факт того, что получение определенного количества искомой… … Социологический справочник
-
ВЫБОРКИ ОШИБКИ СЛУЧАЙНЫЕ — англ. sample error, random; нем. Stichprobenfehler, zufalliger. Статист, погрешности, представляющие собой отклонения характеристик выборочного распределения от генеральной совокупности (ошибка репрезентативности). Antinazi. Энциклопедия… … Энциклопедия социологии
-
ВЫБОРКИ ОШИБКИ СЛУЧАЙНЫЕ — англ. sample error, random; нем. Stichprobenfehler, zufalliger. Статист, погрешности, представляющие собой отклонения характеристик выборочного распределения от генеральной совокупности (ошибка репрезентативности) … Толковый словарь по социологии
-
Контролирование репрезентативности — сравнение средних генеральной и выборочной совокупностей, на основе этого определение ошибки выборки и ее уменьшение … Социология: словарь
-
Многоступенчатая выборка — характеризуется тем, что на всех ступенях осуществляется отбор объектов репрезентации, а наблюдение единиц производится на последней ступени. Необходимость многоступенчатого отбора вызвана, как правило, огсутствием информации по всей генеральной… … Социологический справочник
-
ОБЪЕМ ВЫБОРКИ — число элементов, включенных в выборочную совокупность; зависит от вероятности заключения о достоверности выводов, от величины предельной ошибки репрезентативности, от вероятности появлений события и определяется: 1) задачами исследования; 2)… … Современный образовательный процесс: основные понятия и термины
-
Статистическое наблюдение — Начальной стадией статистического исследования является статистическое наблюдение научно организованный сбор ссведений об изучаемых социально экономических процессах или явлений. Полученные данные являются исходным материалом для последующих… … Википедия
-
Отбор случайный единиц совокупности — это такой отбор социологической информации, при котором каждая единица генеральной совокупности имеет равную вероятность попадания в выборочную совокупность. Существует несколько видов О. с.: а) вероятностный отбор при котором, во первых, каждая… … Социологический справочник
-
Коэффициент корреляции — (Correlation coefficient) Коэффициент корреляции это статистический показатель зависимости двух случайных величин Определение коэффициента корреляции, виды коэффициентов корреляции, свойства коэффициента корреляции, вычисление и применение… … Энциклопедия инвестора
-
ИЗМЕРЕНИЕ НАДЕЖНОСТИ СОЦИОЛОГИЧЕСКОЙ ИНФОРМАЦИИ — один из этапов, необходимых для обеспечения требуемого качества социологич. исследования. Надежность является наиболее общей характеристикой качества эмпирич. данных, полученных в социологич. исследовании. Под надежной понимают информацию, в к… … Российская социологическая энциклопедия
Концепция репрезентативности часто встречается в статистических отчетах и при подготовке выступлений и отчетов. Пожалуй, без него сложно представить какое-либо представление информации для ознакомления.
Содержание
- 1 Репрезентативность — что это?
- 2 Другие определения
- 3 Репрезентативная выборка
- 4 Вероятностная выборка
- 5 Вероятностные выборки
- 6 Выборка потребителей
- 7 Размер выборки
- 8 Понятие ошибки репрезентативности
- 9 Виды ошибок
- 10 Преднамеренные и непреднамеренные ошибки репрезентативности
- 11 Валидность, надежность, репрезентативность. Расчет ошибок
- 12 Репрезентативные системы
Репрезентативность — что это?
Репрезентативность отражает степень, в которой выбранные объекты или части соответствуют содержанию и значению набора данных, из которого они были выбраны.
Другие определения
Репрезентативность можно понимать в разных контекстах. Но по своему смыслу репрезентативность — это соответствие характеристик и свойств выбранных единиц генеральной совокупности, которые точно отражают характеристики всей генеральной базы данных в целом.
Кроме того, репрезентативность информации определяется как способность данных выборки представлять параметры и свойства совокупности, которые важны с точки зрения проводимых исследований.
Репрезентативная выборка
Принцип выборки заключается в выборе наиболее важных свойств, которые точно отражают общую совокупность данных. Для этого используются различные методы, позволяющие получить точные результаты и общее представление о генеральной совокупности, используя только выборочные материалы, описывающие качество всех данных.
Таким образом, нет необходимости изучать весь материал, но достаточно учесть выборочную репрезентативность. Что это? Это набор отдельных данных, чтобы получить представление об общей массе информации.
В зависимости от метода они делятся на вероятностные и маловероятные. Вероятностный — это выборка, которая создается путем вычисления наиболее важных и интересных данных, которые в будущем будут репрезентативными для генеральной совокупности. Это осознанный выбор или случайная выборка, однако оправданная своим содержанием.
Маловероятно — это одна из разновидностей случайной выборки, составленной по принципу обычной лотереи. В этом случае мнение лица, взявшего такую пробу, не принимается во внимание. Используется только слепая жребий.
Вероятностная выборка
Вероятностные выборки также можно разделить на несколько типов:
- Один из самых простых и понятных принципов — нерепрезентативная выборка. Например, этот метод часто используется при проведении социальных опросов. При этом участники опроса не выбираются из общей массы по каким-либо конкретным критериям, а информация берется от первых 50 человек, принявших участие.
- Выборка вероятностей — это еще одна разновидность выборки невероятности, которая часто используется для исследования больших наборов данных. Для этого используется множество условий и правил. Выбираются объекты, которые должны им соответствовать. То есть на примере социального опроса можно предположить, что будет опрошено 100 человек, но при составлении статистического отчета будет учитываться только мнение определенного количества людей, которые будут соответствовать установленным требованиям.
- Преднамеренные выборки отличаются тем, что они имеют ряд требований и условий для отбора, но все же полагаются на совпадения, не преследуя цели получения хорошей статистики.
Вероятностные выборки
Для вероятностных выборок рассчитывается ряд параметров, которым будут соответствовать объекты в выборке, и среди них различными способами могут быть выбраны именно те факты и данные, которые будут представлены как репрезентативность данных выборки. Эти методы расчета требуемых данных могут быть:
- Простая случайная выборка. Он заключается в том, что среди выделенного сегмента методом полностью случайной лотереи выбирается необходимый объем данных, который будет репрезентативной выборкой.
- Систематическая и случайная выборка позволяет составить систему расчета необходимых данных на основе случайно выбранного сегмента. Итак, если первое случайное число, указывающее порядковый номер данных, выбранных из общей совокупности, равно 5, следующими данными для выбора могут быть, например, 15, 25, 35 и так далее. Этот пример ясно объясняет, что даже случайный выбор может быть основан на систематических вычислениях требуемых входных данных.
Выборка потребителей
Осмысленная выборка — это способ взглянуть на каждый отдельный сегмент, и на основе его оценки составляется генеральная совокупность, отражающая характеристики и свойства всей базы данных. Таким образом, собирается больше данных, отвечающих требованиям репрезентативной выборки. Легко выбрать набор параметров, которые не будут включены в общее количество, без потери качества выбранных данных, представляющих генеральную совокупность. Таким образом определяется репрезентативность результатов исследования.
Размер выборки
Не последняя проблема, которую необходимо решить, — это размер выборки для репрезентативной репрезентативности населения. Размер выборки не всегда зависит от количества источников в генеральной совокупности. Однако репрезентативность выборки напрямую зависит от того, на сколько сегментов в конечном итоге следует разделить результат. Чем больше таких сегментов, тем больше данных включается в итоговую выборку. Если результаты требуют общих обозначений и не требуют конкретики, то в результате выборка становится меньше, поскольку, не вдаваясь в детали, информация представлена более поверхностно, а значит, ее прочтение будет общим.
Понятие ошибки репрезентативности
Репрезентативная систематическая ошибка — это конкретное несоответствие между характеристиками населения и данными выборки. При проведении выборочного исследования невозможно получить абсолютно точные данные, как при полном изучении генеральных популяций и выборки, представленной только частью информации и параметров, в то время как более детальное изучение возможно только при изучении всей совокупности численность населения. Поэтому некоторые ошибки и ошибки неизбежны.
Виды ошибок
При составлении репрезентативной выборки возникают некоторые ошибки:
- Случайный.
- Стандарт.
- Не намеренно.
- Систематический.
- Предел.
- Умышленное.
Причиной появления случайных ошибок может быть прерывистый характер исследования генеральной совокупности. Обычно ошибка случайной репрезентативности незначительна по величине и характеру.
Между тем систематические ошибки возникают, когда нарушаются правила отбора данных из генеральной совокупности.
Средняя ошибка — это разница между средним значением выборки и основной совокупностью. Это не зависит от количества единиц в выборке. Он обратно пропорционален размеру выборки. Таким образом, чем больше объем, тем меньше среднее значение ошибки.
Предельная ошибка — это наибольшая возможная разница между средним значением выполненной выборки и всей генеральной совокупностью. Эта ошибка характеризуется как максимум возможных ошибок в данных условиях их возникновения.
Преднамеренные и непреднамеренные ошибки репрезентативности
Ошибки искажения данных могут быть преднамеренными или непреднамеренными.
Итак, причины появления преднамеренных ошибок — это подход к отбору данных с использованием метода выявления трендов. Непреднамеренные ошибки возникают и на этапе подготовки выборочного наблюдения, формирования репрезентативной выборки. Чтобы избежать таких ошибок, необходимо создать хорошую основу выборки для списков единиц выборки. Он должен полностью соответствовать целям выборки, быть надежным и охватывать все аспекты исследования.
Валидность, надежность, репрезентативность. Расчет ошибок
Расчет ошибки репрезентативности (Mm) среднего арифметического (M).
Стандартное отклонение: размер выборки (> 30).
Репрезентативная ошибка (Мр) и относительная величина (Р): размер выборки (n> 30).
В случае, если необходимо изучить совокупность, где размер выборки невелик и менее 30 единиц, количество наблюдений уменьшится на одну единицу.
Величина ошибки прямо пропорциональна размеру выборки. Репрезентативность информации и расчет степени возможности составления точного прогноза отражает определенное значение предельной погрешности.
Репрезентативные системы
В процессе оценки представления информации используется не только репрезентативная выборка, но и лицо, получающее информацию, также использует репрезентативные системы. Таким образом, мозг обрабатывает определенный объем информации, создавая репрезентативную выборку всего потока информации, чтобы качественно и быстро оценить предоставленные данные и понять суть проблемы. Ответьте на вопрос: «Представление — что это?» — В масштабе человеческого сознания это довольно просто. Для этого мозг использует все подчиненные органы чувств, в зависимости от типа информации, которую необходимо изолировать от общего потока. Поэтому проводится различие между:
- Система визуального представления, в которой задействованы органы зрительного восприятия глаза. Людей, которые часто используют эту систему, называют визуалами. С помощью этой системы человек обрабатывает информацию, поступающую в виде изображений.
- Система кинестетической репрезентации — это обработка потока информации путем ее восприятия через обонятельные и тактильные каналы.
- Система слухового представления. Основной используемый орган — слух. Информация, предоставленная в виде аудио- или голосового файла, обрабатывается именно этой системой. Людей, которые лучше всего воспринимают информацию на слух, называют аудиалами.
- Система цифрового представления используется вместе с другими как средство получения информации извне. Это субъективно-логическое восприятие и понимание полученных данных.
Так что же такое репрезентативность? Простая выборка из набора или целостная процедура обработки информации? Мы можем однозначно сказать, что репрезентативность во многом определяет наше восприятие потоков данных, помогая выделить самые тяжелые и наиболее важные из них.
Как мы уже знаем, репрезентативность — свойство выборочной совокупности представлять характеристику генеральной. Если совпадения нет, говорят об ошибке репрезентативности — мере отклонения статистической структуры выборки от структуры соответствующей генеральной совокупности. Предположим, что средний ежемесячный семейный доход пенсионеров в генеральной совокупности составляет 2 тыс. руб., а в выборочной — 6 тыс. руб. Это означает, что социолог опрашивал только зажиточную часть пенсионеров, а в его исследование вкралась ошибка репрезентативности. Иными словами, ошибкой репрезентативности называется расхождение между двумя совокупностями — генеральной, на которую направлен теоретический интерес социолога и представление о свойствах которой он хочет получить в конечном итоге, и выборочной, на которую направлен практический интерес социолога, которая выступает одновременно как объект обследования и средство получения информации о генеральной совокупности.
Наряду с термином «ошибка репрезентативности» в отечественной литературе можно встретить другой — «ошибка выборки». Иногда они употребляются как синонимы, а иногда «ошибка выборки» используется вместо «ошибки репрезентативности» как количественно более точное понятие.
Ошибка выборки — отклонение средних характеристик выборочной совокупности от средних характеристик генеральной совокупности.
На практике ошибка выборки определяется путем сравнения известных характеристик генеральной совокупности с выборочными средними. В социологии при обследованиях взрослого населения чаще всего используют данные переписей населения, текущего статистического учета, результаты предшествующих опросов. В качестве контрольных параметров обычно применяются социально-демографические признаки. Сравнение средних генеральной и выборочной совокупностей, на основе этого определение ошибки выборки и ее уменьшение называется контролированием репрезентативности. Поскольку сравнение своих и чужих данных можно сделать по завершении исследования, такой способ контроля называется апостериорным, т.е. осуществляемым после опыта.
В опросах Института Дж. Гэллапа репрезентативность контролируется по имеющимся в национальных переписях данным о распределении населения по полу, возрасту, образованию, доходу, профессии, расовой принадлежности, месту проживания, величине населенного пункта. Всероссийский центр изучения общественного мнения (ВЦИОМ) использует для подобных целей такие показатели, как пол, возраст, образование, тип поселения, семейное положение, сфера занятости, должностной статус респондента, которые заимствуются в Государственном комитете по статистике РФ. В том и другом случае генеральная совокупность известна. Ошибку выборки невозможно установить, если неизвестны значения переменной в выборочной и генеральной совокупностях.
Специалисты ВЦИОМ обеспечивают при анализе данных тщательный ремонт выборки, чтобы минимизировать отклонения, возникшие на этапе полевых работ. Особенно сильные смещения наблюдаются по параметрам пола и возраста. Объясняется это тем, что женщины и люди с высшим образованием больше времени проводят дома и легче идут на контакт с интервьюером, т.е. являются легко достижимой группой по сравнению с мужчинами и людьми «необразованными»35.
Ошибка выборки обусловливается двумя факторами: методом формирования выборки и размером выборки.
Ошибки выборки подразделяются на два типа — случайные и систематические. Случайная ошибка — это вероятность того, что выборочная средняя выйдет (или не выйдет) за пределы заданного интервала. К случайным ошибкам относят статистические погрешности, присущие самому выборочному методу. Они уменьшаются при возрастании объема выборочной совокупности.
Второй тип ошибок выборки — систематические ошибки. Если социолог решил узнать мнение всех жителей города о проводимой местными органами власти социальной политике, а опросил только тех, у кого есть телефон, то возникает предумышленное смещение выборки в пользу зажиточных слоев, т.е. систематическая ошибка.
Таким образом, систематические ошибки — результат деятельности самого исследователя. Они наиболее опасны, поскольку приводят к довольно значительным смещениям результатов исследования. Систематические ошибки считаются страшнее случайных еще и потому, что они не поддаются контролю и измерению.
Они возникают, когда, например:
- выборка не соответствует задачам исследования (социолог решил изучить только работающих пенсионеров, а опросил всех подряд);
- налицо незнание характера генеральной совокупности (социолог думал, что 70% всех пенсионеров не работает, а оказалось, что не работает только 10%);
- отбираются только «выигрышные» элементы генеральной совокупности (например, только обеспеченные пенсионеры).
Внимание! В отличие от случайных ошибок систематические ошибки при возрастании объема выборки не уменьшаются.
Обобщив все случаи, когда происходят систематические ошибки, методисты составили их реестр. Они полагают, что источником неконтролируемых перекосов в распределении выборочных наблюдений могут быть следующие факторы:
- нарушены методические и методологические правила проведения социологического исследования;
- выбраны неадекватные способы формирования выборочной совокупности, методы сбора и расчета данных;
- произошла замена требуемых единиц наблюдения другими, более доступными;
- отмечен неполный охват выборочной совокупности (недополучение анкет, неполное их заполнение, труднодоступность единиц наблюдения).
Намеренные ошибки социолог допускает редко. Чаще ошибки возникают из-за того, что социологу плохо известна структура генеральной совокупности: распределение людей по возрасту, профессии, доходам и т.д.
Систематические ошибки легче предупредить (по сравнению со случайными), но их очень трудно устранить. Предупреждать систематические ошибки, точно предвидя их источники, лучше всего заранее — в самом начале исследования.
Вот некоторые способы избежать ошибок выборки:
- каждая единица генеральной совокупности должна иметь равную вероятность попасть в выборку;
- отбор желательно производить из однородных совокупностей;
- надо знать характеристики генеральной совокупности;
- при составлении выборочной совокупности надо учитывать случайные и систематические ошибки.
Если выборочная совокупность (или просто выборка) составлена правильно, то социолог получает надежные результаты, харастеризующие всю генеральную совокупность. Если она составлена неправильно, то ошибка, возникшая на этапе составления выборки, на каждом следующем этапе проведения социологического исследования приумножается и достигает в конечном счете такой величины, которая перевешивает ценность проведенного исследования. Говорят, что от такого исследования больше вреда, нежели пользы.
Подобные ошибки могут произойти только с выборочной совокупностыо. Чтобы избежать или уменьшить вероятность ошибки, самый простой способ — увеличивать размеры выборки (в идеале до объема генеральной: когда обе совокупности совпадут, ошибка выборки вообще исчезнет). Экономически такой метод невозможен. Остается другой путь — совершенствовать математические методы составления выборки. Они то и применяются на практике. Таков первый канал проникновения в социологию математики. Второй канал — математическая обработка данных.
Особенно важной проблема ошибок становится в маркетинговых исследованиях, где используются не очень большие выборки. Обычно они составляют несколько сотен, реже — тысячу респондентов. Здесь исходным пунктом расчета выборки выступает вопрос об определении размеров выборочной совокупности. Численность выборочной совокупности зависит от двух факторов:
- стоимости сбора информации,
- стремления к определенной степени статистической достоверности результатов, которую надеется получить исследователь.
Конечно, даже не искушенные в статистике и социологии люди интуитивно понимают, что чем больше размеры выборки, т.е. чем ближе они к размерам генеральной совокупности в целом, тем более надежны и достоверны полученные данные. Однако выше мы уже говорили о практической невозможности сплошных опросов в тех случаях, когда они проводятся на объектах, численность которых превышает десятки, сотни тысяч и даже миллионы. Понятно, что стоимость сбора информации (включающая оплату тиражирования инструментария, труда анкетеров, полевых менеджеров и операторов по компьютерному вводу) зависит от той суммы, которую готов выделить заказчик, и слабо зависит от исследователей. Что же касается второго фактора, то мы остановимся на нем чуть подробнее.
Итак, чем больше величина выборки, тем меньше возможная ошибка. Хотя необходимо отметить, что при желании увеличить точность вдвое вам придется увеличить выборку не в два, а в четыре раза. Например, чтобы сделать в два раза более точной оценку данных, полученных путем опроса 400 человек, вам потребуется опросить не 800, а 1600 человек. Впрочем, вряд ли маркетинговое исследование испытывает нужду в стопроцентной точности. Если пивовару необходимо узнать, какая часть потребителей пива предпочитает именно его марку, а не сорт его конкурента, — 60% или 40%, то на его планы никак не повлияет разница между 57%, 60 или 63%.
Ошибка выборки может зависеть не только от ее величины, но и от степени различий между отдельными единицами внутри генеральной совокупности, которую мы исследуем. Например, если нам нужно узнать, какое количество пива потребляется, то мы обнаружим, что внутри нашей генеральной совокупности нормы потребления у различных людей существенно различаются (гетерогенная генеральная совокупность). В другом случае мы будем изучать потребление хлеба и установим, что у разных людей оно различается гораздо менее существенно {гомогенная генеральная совокупность). Чем больше различия (или гетерогенность) внутри генеральной совокупности, тем больше величина возможной ошибки выборки. Указанная закономерность лишь подтверждает то, что нам подсказывает простой здравый смысл. Таким образом, как справедливо утверждает В. Ядов, «численность (объем) выборки зависит от уровня однородности или разнородности изучаемых объектов. Чем более они однородны, тем меньшая численность может обеспечить статистически достоверные выводы».
Определение объема выборки зависит также от уровня доверительного интервала допустимой статистической ошибки. Здесь имеются в виду так называемые случайные ошибки, которые связаны с природой любых статистических погрешностей. В.И. Паниотто приводит следующие расчеты репрезентативной выборки с допущением 5%-ной ошибки:
Это означает,что если вы, опросив, предположим, 400 человек в районном городе, где численность взрослого платежеспособного населения составляет 100 тыс. человек, выявили, что 33% опрошенных покупателей предпочитают продукцию местного мясокомбината, то с 95%-ной вероятностью можете утверждать, что постоянными покупателями этой продукции являются 33+5% (т.е. от 28 до 38%) жителей этого города.
Можно также воспользоваться расчетами института Гэллапа для оценки соотношения размеров выборки и ошибки выборки.
2.4. Точность статистического наблюдения
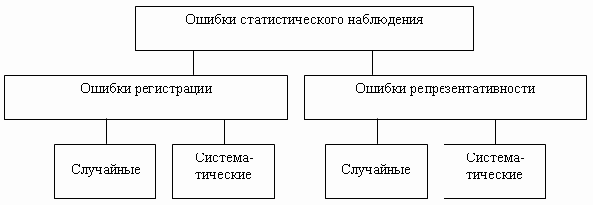
Под точностью статистического наблюдения понимают степень соответствия значения наблюдаемого показателя, вычисленного по материалам обследования, его действительной величине. Расхождение, или разница, между ними называется ошибкой статистического наблюдения.
Различают две группы ошибок:
- ошибки регистрации;
- ошибки репрезентативности.
Ошибки регистрации присущи любому статистическому наблюдению, как сплошному, так и несплошному. Они делятся на случайные ошибки регистрации и систематические ошибки регистрации.
Случайными ошибками регистрации называют ошибки, возникающие вследствие действия случайных факторов. К ним можно отнести различного рода непреднамеренные описки: например, вместо возраста человека «15 лет» указано «5 лет», у Ивановой Марии Петровны в графе пол отмечен «Мужской» и т. п. Такие ошибки легко выявляются методом логического анализа, например, если человеку 8 лет, но имеется высшее образование, а в графе «Семейное положение» указано «Состоит в браке», то, естественно, следует исправить возраст. Если объем исследуемой совокупности велик или велика доля отбора при выборочном наблюдении, случайные ошибки регистрации имеют тенденцию взаимопогашаться вследствие действия закона больших чисел, поскольку ошибки, как правило, разнонаправлены и искажают статистический показатель как в большую, так и в меньшую сторону. При небольшом объеме наблюдения требуется тщательная выверка его результатов — логический анализ данных.
Систематические ошибки регистрации чаще всего имеют однонаправленные искажения: они либо увеличивают, либо уменьшают статистический показатель, и, что характерно, подобная ситуация повторяется от обследования к обследованию. Так, по результатам переписей (практически всех!) число замужних женщин превышает число женатых мужчин — мужчинам приятнее ощущать себя неженатыми, а для женщины как бы «стыдно» быть не замужем. Другой пример, когда человек округляет свой возраст — вместо 32 лет говорит 30, вместо 79-80 и т. п. (это явление широко известно и даже получило свое название — «аккумуляция возрастов»). Систематические ошибки регистрации могут возникать и из-за неточностей измерительных приборов, если сбор информации проводят путем непосредственного наблюдения.
Ошибки репрезентативности присущи только несплошному обследованию. Они также делятся на случайные и систематические ошибки.
Случайные ошибки репрезентативности возникают из-за того, что обследованию подвергается не вся совокупность в целом, а только ее часть, и, следовательно, при несплошном наблюдении они присутствуют всегда. В теории статистики разработаны специальные методы для оценки величин таких ошибок, на их основе для наблюдаемых показателей строят доверительные интервалы, т.д. эти ошибки вычисляются и находятся как бы «под контролем».
Хуже обстоит дело, если наряду со случайными ошибками имеются и ошибки систематические.
Систематические ошибки репрезентативности возникают, если при несплошном наблюдении кардинально нарушаются технологии отбора единиц из генеральной совокупности объектов, но чаще — если в ходе обследования не удается получить информацию обо всех отобранных для наблюдения единицах, например, вследствие отказа отвечать на вопросы анкеты, или если человека не удалось застать дома и т. п.
Ошибки статистического наблюдения для наглядности можно изобразить в виде схемы (рис. 2.1).
Рис.
2.1.
Виды ошибок статистического наблюдения
Для повышения точности наблюдения необходимо:
- правильно разработать формуляр статистического наблюдения: вопросы должны быть четкими, однозначными, не допускающими двойного толкования;
- иметь хорошо обученный персонал для проведения обследования;
- строго придерживаться выбранной технологии обследования (если проводится несплошное наблюдение) и помнить, что если не удается опросить какую-то конкретную единицу, отобранную для наблюдения, замена ее на другую единицу может привести к возникновению систематической ошибки репрезентативности;
- провести логический анализ данных, основанный на логических взаимосвязях показателей, после сбора всей совокупности анкет или формуляров;
- целесообразно провести и арифметический контроль данных, т.д. заново пересчитать расчетные величины, если какие-либо показатели получаются в результате определенных арифметических действий;
- предпринять определенные меры по восстановлению данных при наличии незаполненных анкет или формуляров либо при получении результатов обследования сделать поправку на неответы респондентов.
Лекция 2. Ошибка репрезентативности и доверительный интервал для
генерального параметра
Выборочные характеристики, представляющие собой числа (точки на
шкале) называют точечными оценками (существуют также и интервальные
оценки). Оценки должны удовлетворять следующим требованиям: быть
состоятельными, эффективными, несмещенными. Только при удовлетворении
этих требований оценки хорошо представляют соответствующие параметры.
В математической статистике введено понятие статистической ошибки
или ошибки репрезентативности; она связана с точностью, с которой
выборочная оценка представляет, репрезентирует свой параметр.
Когда ошибка оценивания генерального параметра стремится к нулю при
возрастании объема выборки, т.е. значение оценки стремится к значению
параметра, то такая оценка называется состоятельной. Оценка называется
эффективной,
если
она
имеет
наименьшую
дисперсию
выборочного
распределения по сравнению с другими аналогичными оценками.
К примеру,
из трех показателей, описывающих положение центра
нормального распределения (средняя, медиана, мода), наиболее эффективной
является средняя арифметическая, наименее эффективной — мода.
Оценка
ожидание)
называется
ее
несмещенной,
выборочного
если
распределения
среднее
совпадает
(математическое
со
значением
генерального параметра. Выборочная средняя является несмещенной оценкой
генеральной средней, а тогда как выборочная дисперсия представляет собой
смещенную оценку.
Например, чтобы получить несмещенную оценку, надо при вычислении
выборочной дисперсии использовать формулу, где в знаменателе (N — 1):
D=S2=
1
2
( Xi X )
N 1
Для понимания смысла этих требований нужно рассмотреть понятие
выборочного распределения оценок какого-либо параметра.
Рассмотрим
условный
пример
для
такого
понятия,
как
арифметическое среднее: пусть ГС представляет собой 5 результатов
выполнения некоторого психологического теста: 8 16 20 24 32:
=
8 16 20 24 32
= 20
5
Таким образом, 20 — это значение генерального параметра.
Заменим изучение генеральной совокупности изучением выборок объемом
n = 4. Рассмотрим все возможные варианты таких выборок:
1) 8
16 20 24
= 17
2) 16 20 24 32
= 23
3) 8
16 24 32
= 20
4) 8
16 20 32
= 19
Из нашего примера видно, что из 5 оценок средних лишь одна совпала
с параметром. Заранее мы не можем знать, как составить (отобрать) выборку,
чтобы оценка параметра по ней была близка к параметру.
Однако очевидно, что чем больше объем выборки, тем меньше вероятность
того, что , определяемое по выборке, будет значительно отличаться от
генерального среднего (крайние случаи n=N-1 и n=2 ,т.е. N>>n) .
Когда
генеральная совокупность велика и, соответственно, число
возможных выборок велико, то совокупность выборочных оценок средних для
каждой
из
этих
концентрирующееся
выборок
вокруг
«концентрация» (дисперсия)
Дисперсия
образует
генерального
тем
выше,
нормальное
среднего,
чем
больше
распределение,
причем
эта
объемы выборок.
распределения средних имеет особое название, она именуется
ошибкой репрезентативности.
Выше речь шла о распределении выборочных средних.
Это же
рассуждение можно повторить для оценок дисперсии, моды, коэффициентов
корреляции и т.д.
В теории математической статистики доказано, что нормального
распределения при достаточном объеме выборки (на практике n 30),
стандартное отклонение среднего арифметического равно:
Sx =
S
N
; где
S — стандартное отклонение
N — объем выборки.
Эту величину называют также статистической ошибкой или ошибкой
репрезентативности, т.е. это средняя ошибка, которая допускается, когда
рассматривается как генеральный параметр.
Для других параметров ошиб ки репрезентативности таковы:
Ошибка репрезентативности дисперсии:
Ss2=S2/ 2N
Ошибка репрезентативности стандартного отклонения
Ss=S/ 2N
Ошибка репрезентативности показателя асимметрии:
Sa= 6 / N
Ошибка репрезентативности показателя эксцесса:
Se= 24 / N
Теперь перейдем к понятию доверительного интервала, которое применяется
для любого параметра. Мы рассмотрим его для генеральной средней. По
известным выборочным характеристикам можно построить интервал, в котором
с той или иной степенью вероятности находится генеральное среднее. Понятие
доверительного интервала связано с понятием доверительной вероятности.
Согласно этому принципу, маловероятные события считаются практически
невозможными,
а
события,
вероятность
которых
близка
к
единице,
принимаются за почти достоверные. Обычно в психологии в качестве
доверительных используют вероятности р = 0,95 и р = 0,99. Это означает, что
при оценивании генерального параметра по известной выборочной оценке риск
ошибиться в первом случае — один раз на 20 испытаний, во втором случае 1 раз
на 100 испытаний.
С доверительной вероятностью связано понятие уровня значимости
= 1- р
Геометрически — это площадь под нормальной кривой выборочного
распределения, выходящая за пределы той его части, которая соответствует
Р%, поскольку в сумме они соответствуют всей площади под кривой. Иначе
говоря,
означает площадь двух хвостов под кривой нормального
распределения. При при р = 0,95 и = 0, 05 на каждый «хвост» приходится
по 2,5 % площади.
Вероятность того, что будет находиться в пределах
доверительного интервала x — t SX + t SX,
описывается
особой функцией, которая сведена в таблице (обычно это таблица 1 в
приложении учебников по математической статистике)
для р= 0,95
t=1,96
для р=0,99
t = 2,58
для p=0, 999 t =3,29
График нормальной кривой
Выбор того или иного уровня доверительной вероятности зависит от
исследователя, от его оценки ответственности за ошибочность выводов
относительно генерального параметра .
Пример: При измерении объема памяти у 100 испытуемых
получено среднее значение числа запоминаемых сигналов
было
= 9 и
стандартное отклонение S = 3. 27. Построить доверительный
интервал для генеральной средней .
Вычисления проводятся по формуле:
x — t SX + t SX
9 — 1,96
3271
.
327
.
92+1,96
100
100
или 9+ 0.196 3,27 9 + 1..96 3,27 или 8. 36 9.64.
Таким образом, с вероятностью р = 0.95 генеральный параметр
находится в интервале 8.36 — 9.64.
95%