Обучение нейронных сетей
Перед использованием нейронной сети ее необходимо обучить.
Процесс обучения нейронной сети заключается в подстройке ее внутренних параметров под конкретную задачу.
Алгоритм работы нейронной сети является итеративным, его шаги называют эпохами или циклами.
Эпоха — одна итерация в процессе обучения, включающая предъявление всех примеров из обучающего множества и, возможно, проверку качества обучения на контрольном множестве.
Процесс обучения осуществляется на обучающей выборке.
Обучающая выборка включает входные значения и соответствующие им выходные значения набора данных. В ходе обучения нейронная сеть находит некие зависимости выходных полей от входных.
Таким образом, перед нами ставится вопрос — какие входные поля (признаки) нам необходимо использовать. Первоначально выбор осуществляется эвристически, далее количество входов может быть изменено.
Сложность может вызвать вопрос о количестве наблюдений в наборе данных. И хотя существуют некие правила, описывающие связь между необходимым количеством наблюдений и размером сети, их верность не доказана.
Количество необходимых наблюдений зависит от сложности решаемой задачи. При увеличении количества признаков количество наблюдений возрастает нелинейно, эта проблема носит название «проклятие размерности». При недостаточном количестве данных рекомендуется использовать линейную модель.
Аналитик должен определить количество слоев в сети и количество нейронов в каждом слое.
Далее необходимо назначить такие значения весов и смещений, которые смогут минимизировать ошибку решения. Веса и смещения автоматически настраиваются таким образом, чтобы минимизировать разность между желаемым и полученным на выходе сигналами, которая называется ошибка обучения.
Ошибка обучения для построенной нейронной сети вычисляется путем сравнения выходных и целевых (желаемых) значений. Из полученных разностей формируется функция ошибок.
Функция ошибок — это целевая функция, требующая минимизации в процессе управляемого обучения нейронной сети.
С помощью функции ошибок можно оценить качество работы нейронной сети во время обучения. Например, часто используется сумма квадратов ошибок.
От качества обучения нейронной сети зависит ее способность решать поставленные перед ней задачи.
Переобучение нейронной сети
При обучении нейронных сетей часто возникает серьезная трудность, называемая проблемой переобучения (overfitting).
Переобучение, или чрезмерно близкая подгонка — излишне точное соответствие нейронной сети конкретному набору обучающих примеров, при котором сеть теряет способность к обобщению.
Переобучение возникает в случае слишком долгого обучения, недостаточного числа обучающих примеров или переусложненной структуры нейронной сети.
Переобучение связано с тем, что выбор обучающего (тренировочного) множества является случайным. С первых шагов обучения происходит уменьшение ошибки. На последующих шагах с целью уменьшения ошибки (целевой функции) параметры подстраиваются под особенности обучающего множества. Однако при этом происходит «подстройка» не под общие закономерности ряда, а под особенности его части — обучающего подмножества. При этом точность прогноза уменьшается.
Один из вариантов борьбы с переобучением сети — деление обучающей выборки на два множества (обучающее и тестовое).
На обучающем множестве происходит обучение нейронной сети. На тестовом множестве осуществляется проверка построенной модели. Эти множества не должны пересекаться.
С каждым шагом параметры модели изменяются, однако постоянное уменьшение значения целевой функции происходит именно на обучающем множестве. При разбиении множества на два мы можем наблюдать изменение ошибки прогноза на тестовом множестве параллельно с наблюдениями над обучающим множеством. Какое-то количество шагов ошибки прогноза уменьшается на обоих множествах. Однако на определенном шаге ошибка на тестовом множестве начинает возрастать, при этом ошибка на обучающем множестве продолжает уменьшаться. Этот момент считается концом реального или настоящего обучения, с него и начинается переобучение.
Описанный процесс проиллюстрирован на рис. 11.2.
Рис.
11.2.
Процесс обучений сети. Явление переобучения
На первом шаге ошибки прогноза для обучающего и тестового множества одинаковы. На последующих шагах значения обеих ошибок уменьшаются, однако с семидесятого шага ошибка на тестовом множестве начинает возрастать, т.е. начинается процесс переобучения сети.
Прогноз на тестовом множестве является проверкой работоспособности построенной модели. Ошибка на тестовом множестве может являться ошибкой прогноза, если тестовое множество максимально приближено к текущему моменту.
Обучение нейронных сетей
Перед использованием нейронной сети ее необходимо обучить.
Процесс обучения нейронной сети заключается в подстройке ее внутренних параметров под конкретную задачу.
Алгоритм работы нейронной сети является итеративным, его шаги называют эпохами или циклами.
Эпоха — одна итерация в процессе обучения, включающая предъявление всех примеров из обучающего множества и, возможно, проверку качества обучения на контрольном множестве.
Процесс обучения осуществляется на обучающей выборке.
Обучающая выборка включает входные значения и соответствующие им выходные значения набора данных. В ходе обучения нейронная сеть находит некие зависимости выходных полей от входных.
Таким образом, перед нами ставится вопрос — какие входные поля (признаки) нам необходимо использовать. Первоначально выбор осуществляется эвристически, далее количество входов может быть изменено.
Сложность может вызвать вопрос о количестве наблюдений в наборе данных. И хотя существуют некие правила, описывающие связь между необходимым количеством наблюдений и размером сети, их верность не доказана.
Количество необходимых наблюдений зависит от сложности решаемой задачи. При увеличении количества признаков количество наблюдений возрастает нелинейно, эта проблема носит название «проклятие размерности». При недостаточном количестве данных рекомендуется использовать линейную модель.
Аналитик должен определить количество слоев в сети и количество нейронов в каждом слое.
Далее необходимо назначить такие значения весов и смещений, которые смогут минимизировать ошибку решения. Веса и смещения автоматически настраиваются таким образом, чтобы минимизировать разность между желаемым и полученным на выходе сигналами, которая называется ошибка обучения.
Ошибка обучения для построенной нейронной сети вычисляется путем сравнения выходных и целевых (желаемых) значений. Из полученных разностей формируется функция ошибок.
Функция ошибок — это целевая функция, требующая минимизации в процессе управляемого обучения нейронной сети.
С помощью функции ошибок можно оценить качество работы нейронной сети во время обучения. Например, часто используется сумма квадратов ошибок.
От качества обучения нейронной сети зависит ее способность решать поставленные перед ней задачи.
Переобучение нейронной сети
При обучении нейронных сетей часто возникает серьезная трудность, называемая проблемой переобучения (overfitting).
Переобучение, или чрезмерно близкая подгонка — излишне точное соответствие нейронной сети конкретному набору обучающих примеров, при котором сеть теряет способность к обобщению.
Переобучение возникает в случае слишком долгого обучения, недостаточного числа обучающих примеров или переусложненной структуры нейронной сети.
Переобучение связано с тем, что выбор обучающего (тренировочного) множества является случайным. С первых шагов обучения происходит уменьшение ошибки. На последующих шагах с целью уменьшения ошибки (целевой функции) параметры подстраиваются под особенности обучающего множества. Однако при этом происходит «подстройка» не под общие закономерности ряда, а под особенности его части — обучающего подмножества. При этом точность прогноза уменьшается.
Один из вариантов борьбы с переобучением сети — деление обучающей выборки на два множества (обучающее и тестовое).
На обучающем множестве происходит обучение нейронной сети. На тестовом множестве осуществляется проверка построенной модели. Эти множества не должны пересекаться.
С каждым шагом параметры модели изменяются, однако постоянное уменьшение значения целевой функции происходит именно на обучающем множестве. При разбиении множества на два мы можем наблюдать изменение ошибки прогноза на тестовом множестве параллельно с наблюдениями над обучающим множеством. Какое-то количество шагов ошибки прогноза уменьшается на обоих множествах. Однако на определенном шаге ошибка на тестовом множестве начинает возрастать, при этом ошибка на обучающем множестве продолжает уменьшаться. Этот момент считается концом реального или настоящего обучения, с него и начинается переобучение.
Описанный процесс проиллюстрирован на рис. 11.2.
Рис.
11.2.
Процесс обучений сети. Явление переобучения
На первом шаге ошибки прогноза для обучающего и тестового множества одинаковы. На последующих шагах значения обеих ошибок уменьшаются, однако с семидесятого шага ошибка на тестовом множестве начинает возрастать, т.е. начинается процесс переобучения сети.
Прогноз на тестовом множестве является проверкой работоспособности построенной модели. Ошибка на тестовом множестве может являться ошибкой прогноза, если тестовое множество максимально приближено к текущему моменту.
Нейронные сети считаются универсальными моделями в машинном обучении, поскольку позволяют решать широкий класс задач. Однако, при их использовании могут возникать различные проблемы.
Содержание
- 1 Взрывающийся и затухающий градиент
- 1.1 Определение
- 1.2 Причины
- 1.3 Способы определения
- 1.3.1 Взрывающийся градиент
- 1.3.2 Затухающий градиент
- 1.4 Способы устранения
- 1.4.1 Использование другой функции активации
- 1.4.1.1 Tanh
- 1.4.1.2 ReLU
- 1.4.1.3 Softplus
- 1.4.2 Изменение модели
- 1.4.3 Использование Residual blocks
- 1.4.4 Регуляризация весов
- 1.4.5 Обрезание градиента
- 1.4.1 Использование другой функции активации
- 2 См. также
- 3 Примечания
- 4 Источники
Взрывающийся и затухающий градиент
Определение
Напомним, что градиентом в нейронных сетях называется вектор частных производных функции потерь по весам нейронной сети. Таким образом, он указывает на направление наибольшего роста этой функции для всех весов по совокупности. Градиент считается в процессе тренировки нейронной сети и используется в оптимизаторе весов для улучшения качества модели.
В процессе обратного распространения ошибки при прохождении через слои нейронной сети в элементах градиента могут накапливаться большие значения, что будет приводить к сильным изменениям весов. Это в свою очередь может сделать нестабильным алгоритм обучения нейронной сети. В таком случае элементы градиента могут переполнить тип данных, в котором они хранятся. Такое явление называется взрывающимся градиентом (англ. exploding gradient).
Существует аналогичная обратная проблема, когда в процессе обучения при обратном распространении ошибки через слои нейронной сети градиент становится все меньше. Это приводит к тому, что веса при обновлении изменяются на слишком малые значения, и обучение проходит неэффективно или останавливается, то есть алгоритм обучения не сходится. Это явление называется затухающим градиентом (англ. vanishing gradient).
Таким образом, увеличение числа слоев нейронной сети с одной стороны увеличивает ее способности к обучению и расширяет ее возможности, но с другой стороны может порождать данную проблему. Поэтому для решения сложных задач с помощью нейронных сетей необходимо уметь определять и устранять ее.
Причины
Рисунок 1. График сигмоиды и ее производной[1]
Такая проблема может возникнуть при использовании нейронных сетях классической функцией активации (англ. activation function) сигмоиды (англ. sigmoid):
$sigma(x) = frac{1}{1 + e^{-x}}.$
Эта функция часто используется, поскольку множество ее возможных значений — отрезок $[0, 1]$ — совпадает с возможными значениями вероятностной меры, что делает более удобным ее предсказание. Также график сигмоиды соответствует многим естественным процессам, показывающим рост с малых значений, который ускоряется с течением времени, и достигающим своего предела[2] (например, рост популяции).
Пусть сеть состоит из подряд идущих нейронов с функцией активации $sigma(x)$; функция потерть (англ. loss function) $L(y) = MSE(y, hat{y}) = (y — hat{y})^2$ (англ. MSE — Mean Square Error); $u_d$ — значение, поступающее на вход нейрону на слое $d$; $w_d$ — вес нейрона на слое $d$; $y$ — выход из последнего слоя. Оценим частные производные по весам такой нейронной сети на каждом слое. Оценка для производной сигмоиды видна из рисунка 1.
$frac{partial(L(y))}{partial(w_d)} = frac{partial(L(y))}{partial(y)} cdot frac{partial(y)}{partial(w_d)} = 2 (y — hat{y}) cdot sigma'(w_d u_d) u_d leq 2 (y — hat{y}) cdot frac{1}{4} u_d$
$frac{partial(L(y))}{partial(w_{d — 1})} = frac{partial(L(y))}{partial(w_d)} cdot frac{partial(w_d)}{partial(w_{d — 1})} leq 2 (y — hat{y}) cdot (frac{1}{4})^2 u_d u_{d-1}$
$ldots$
Откуда видно, что оценка элементов градиента растет экспоненциально при рассмотрении частных производных по весам слоев в направлении входа в нейронную сеть (уменьшения номера слоя). Это в свою очередь может приводить либо к экспоненциальному росту градиента от слоя к слою, когда входные значения нейронов — числа, по модулю большие $1$, либо к затуханию, когда эти значения — числа, по модулю меньшие $1$.
Однако, входные значения скрытых слоев есть выходные значения функций активаций предшествующих им слоев. В частности, сигмоида насыщается (англ. saturates) при стремлении аргумента к $+infty$ или $-infty$, то есть имеет там конечный предел. Это приводит к тому, что более отдаленные слои обучаются медленнее, так как увеличение или уменьшение аргумента насыщенной функции вносит малые изменения, и градиент становится все меньше. Это и есть проблема затухающего градиента.
Способы определения
Взрывающийся градиент
Возникновение проблемы взрывающегося градиента можно определить по следующим признакам:
- Модель плохо обучается на данных, что отражается в высоком значении функции потерь.
- Модель нестабильна, что отражается в значительных скачках значения функции потерь.
- Значение функции потерь принимает значение
NaN.
Более непрозрачные признаки, которые могут подтвердить возникновение проблемы:
- Веса модели растут экспоненциально.
- Веса модели принимают значение
NaN.
Затухающий градиент
Признаки проблемы затухающего градиента:
- Точность модели растет медленно, при этом возможно раннее срабатывание критерия останова, так как алгоритм может решить, что дальнейшее обучение не будет оказывать существенного влияния.
- Градиент ближе к концу показывает более сильные изменения, в то время как градиент ближе к началу почти не показывает никакие изменения.
- Веса модели уменьшаются экспоненциально во время обучения.
- Веса модели стремятся к $0$ во время обучения.
Способы устранения
Использование другой функции активации
Рисунок 2. Графики функций активации: sigmoid, tanh, ReLU, softplus
Как уже упоминалось выше, подверженность нейронной сети проблемам взрывающегося или затухающего градиента во многом зависит от свойств используемых функций активации. Поэтому правильный их подбор важен для предотвращения описываемых проблем.
Tanh
$tanh(x) = frac{e^x — e^{-x}}{e^x + e^{-x}}$
Функция аналогична сигмоиде, но множество возможных значений: $[-1, 1]$. Градиенты при этом сосредоточены около $0$,. Однако, эта функция также насыщается в обоих направлениях, поэтому также может приводить к проблеме затухающего градиента.
ReLU
$h(x) = max(0, x)$
Функция проста для вычисления и имеет производную, равную либо $1$, либо $0$. Также есть мнение, что именно эта функция используется в биологических нейронных сетях. При этом функция не насыщается на любых положительных значениях, что делает градиент более чувствительным к отдаленным слоям.
Недостатком функции является отсутствие производной в нуле, что можно устранить доопределением производной в нуле слева или справа. Также эту проблему устраняет использование гладкой аппроксимации, Softplus.
Существуют модификации ReLU:
- Noisy ReLU: $h(x) = max(0, x + varepsilon), varepsilon sim N(0, sigma(x))$.
- Parametric ReLU: $h(x) = begin{cases} x & x > 0 \ beta x & text{otherwise} end{cases}$.
- Leaky ReLU: Paramtetric ReLU со значением $beta = 0.01$.
Softplus
$h(x) = ln(1 + e^x)$
Гладкий, везде дифференцируемый аналог функции ReLU, следовательно, наследует все ее преимущества. Однако, эта функция более сложна для вычисления. Эмпирически было выявлено, что по качеству не превосходит ReLU.
Графики всех функций активации приведены на рисунок 2.
Изменение модели
Для решения проблемы может оказаться достаточным сокращение числа слоев. Это связано с тем, что частные производные по весам растут экспоненциально в зависимости от глубины слоя.
В рекуррентных нейронных сетях можно воспользоваться техникой обрезания обратного распространения ошибки по времени, которая заключается в обновлении весов с определенной периодичностью.
Использование Residual blocks
Рисунок 3. Устройство residual block[3]
В данной конструкции вывод нейрона подается как следующему нейрону, так и нейрону на расстоянии 2-3 слоев впереди, который суммирует его с выходом предшествующего нейрона, а функция активации в нем — ReLU (см. рисунок 3). Такая связка называется shortcut. Это позволяет при обратном распространении ошибки значениям градиента в слоях быть более чувствительным к градиенту в слоях, с которыми связаны с помощью shortcut, то есть расположенными несколько дальше следующего слоя.
Регуляризация весов
Регуляризация заключается в том, что слишком большие значения весов будут увеличивать функцию потерь. Таким образом, в процессе обучения нейронная сеть помимо оптимизации ответа будет также минимизировать веса, не позволяя им становиться слишком большими.
Обрезание градиента
Образание заключается в ограничении нормы градиента. То есть если норма градиента превышает заранее выбранную величину $T$, то следует масштабировать его так, чтобы его норма равнялась этой величине:
$nabla_{clipped} = begin{cases} nabla & || nabla || leq T \ frac{T}{|| nabla ||} cdot nabla & text{otherwise} end{cases}.$
См. также
- Нейронные сети, перцептрон
- Обратное распространение ошибки
- Регуляризация
- Глубокое обучение
- Сверточные нейронные сети
Примечания
- ↑ towardsdatascience.com — Derivative of the sigmoid function
- ↑ wikipedia.org — Sigmoid function, Applications
- ↑ wikipedia.org — Residual neural network
Источники
- Курс Machine Learning, ИТМО, 2020;
- towardsdatascience.com — The vanishing exploding gradient problem in deep neural networks;
- machinelearningmastery.com — Exploding gradients in neural networks.
На хабре было множество публикаций по данной теме, но все они говорят о разных вещах. Решил собрать всё в одну кучку и рассказать людям.
Это первая статья серии введения в нейронные сети, «Нейронные сети для начинающих». Здесь и далее мы постараемся разобраться с таким понятием — как нейронные сети, что они вообще из себя представляют и как с ними «подружиться», на практике решая простые задачи.
О чём будем говорить:
- Нейронные сети. Что это такое и какие они бывают?
- Виды нейронных сетей и конструкция нейронных сетей.
- Где они применяются?
- Перцептрон.
- Классификация. Что это такое и почему это важно?
- Функции активации (ФА).
- Зачем они нужны?
- Виды ФА.
- Как обучить нейронную сеть?
- Цели и задачи обучения.
- Обучение с учителем и без.
- Понятие ошибки.
- Задача минимизации ошибки.
- Градиентный спуск.
- Как вычислить градиент?
- Пресловутые «Ирисы Фишера».
- Постановка задачи.
- Softmax()+ Relu()
- Ура! Пишем код (Наконец-то).
Что такое нейронные сети?
Нейро́нная сеть — математическая модель, а также её программное или аппаратное воплощение, построенная по принципу организации и функционирования биологических нейронных сетей — сетей нервных клеток живого организма (в частности, мозга).
▍ Виды нейронных сетей:
Есть десятки видов нейросетей, которые отличаются архитектурой, особенностями функционирования и сферами применения. При этом чаще других встречаются сети трёх видов.
Нейронные сети прямого распространения (Feed forward neural networks, FFNN). Прямолинейный вид нейросетей, при котором соседние узлы слоя не связаны, а передача информации осуществляется напрямую от входного слоя к выходному. FFNN имеют малую функциональность, поэтому часто используются в комбинации с сетями других видов.
Свёрточные нейронные сети (Convolutional neural network, CNN). Состоят из слоёв пяти типов:
- входного,
- свёртывающего,
- объединяющего,
- подключённого,
- выходного.
Каждый слой выполняет определённую задачу: например, обобщает или соединяет данные.
Свёрточные нейросети применяются для классификации изображений, распознавания объектов, прогнозирования, обработки естественного языка и других задач.
Рекуррентные нейронные сети (Recurrent neural network, RNN). Используют направленную последовательность связи между узлами. В RNN результат вычислений на каждом этапе используется в качестве исходных данных для следующего. Благодаря этому, рекуррентные нейронные сети могут обрабатывать серии событий во времени или последовательности для получения результата вычислений.
RNN применяют для языкового моделирования и генерации текстов, машинного перевода, распознавания речи и других задач.
▍ Типы задач, которые решают нейронные сети
Выделяют несколько базовых типов задач, для решения которых могут использоваться нейросети.
- Классификация. Для распознавания лиц, эмоций, типов объектов: например, квадратов, кругов, треугольников. Также для распознавания образов, то есть выбора конкретного объекта из предложенного множества: например, выбор квадрата среди треугольников.
- Регрессия. Для определения возраста по фотографии, составления прогноза биржевых курсов, оценки стоимости имущества и других задач, требующих получения в результате обработки конкретного числа.
- Прогнозирования временных рядов. Для составления долгосрочных прогнозов на основе динамического временного ряда значений. Например, нейросети применяются для предсказания цен, физических явлений, объёма потребления и других показателей. По сути, даже работу автопилота Tesla можно отнести к процессу прогнозирования временных рядов.
- Кластеризация. Для изучения и сортировки большого объёма неразмеченных данных в условиях, когда неизвестно количество классов на выходе, то есть для объединения данных по признакам. Например, кластеризация применяется для выявления классов картинок и сегментации клиентов.
- Генерация. Для автоматизированного создания контента или его трансформации. Генерация с помощью нейросетей применяется для создания уникальных текстов, аудиофайлов, видео, раскрашивания чёрно-белых фильмов и даже изменения окружающей среды на фото.
Как выглядит простая нейронная сеть?
Выяснив, как же она выглядит, мы перед тем, как разобрать её строение: что, зачем и почему — разберёмся, где же они применяются и что с помощью них можно сделать. Вот примерный список областей, где решение такого рода задач имеет практическое значение уже сейчас:
- Экономика и бизнес.
- Медицина и здравоохранение.
- Авионика.
- Связь.
- Интернет.
- Автоматизация производства.
- Политологические и социологические исследования.
- Безопасность, охранные системы.
- Ввод и обработка информации.
- Геологоразведка.
- Компьютерные и настольные игры.
- И т.д.
Теперь разберём подробнее самую простую модель искусственного нейрона — перцептрон:
Согласно общему определению перцептро́н или персептрон — математическая или компьютерная модель восприятия информации мозгом, предложенная Фрэнком Розенблаттом в 1958 году и впервые реализованная в виде электронной машины «Марк-1» в 1960 году. Перцептрон стал одной из первых моделей нейросетей, а «Марк-1» — первым в мире нейрокомпьютером.
Вы уже могли видеть подобные иллюстрации на просторах интернета:
Но что же это всё означает?
Давайте по порядку:
Х1, Х2, Х3, …, Хn — входные классы, данные, которые мы подаём на вход нашей сети. Т.е. здесь у нас идут те данные, которые пришли к нам от клиента или же от нашего сервиса, который каким-то образом собирает/парсит данные , далее эти данные умножаются на случайные веса (стандартное обозначение W1, …, Wn) и суммируются с так называемым нейроном смещения или bias нейрон в «Сумматоре» (из названия следует, что данные, Хn * Wn , суммируются друг с другом). Далее результат Σ(Хn * Wn + b) подаётся в функцию активации, о которой поговорим далее.
Данные метаморфозы проиллюстрированы на следующем слайде:
▍ Задача классификации
Проговорив в общих чертах строение «базовой нейронной сети», плавно перейдём к рассмотрению задачи классификации — основной задачи нейронных сетей.
Итак, из определения следует, что классификация — это задача, при которой по некоторому объекту — исходные данные, нужно предсказать, к какому
классу объектов он принадлежит.
Примитивно эту задачу можно проиллюстрировать следующим образом:
Мы с вами, с лёгкостью можем понять, что ответ будет следующий:
Но а что на это скажет компьютер?
Для него это лишь набор пикселей/байтов, который ему ни о чём не говорит. По-простому — это 0 и 1. Подробнее про это, можете почитать здесь.
Для того, чтобы компьютер понял, что происходит внутри предложенных ему данных, мы должны «объяснить» ему всё и дать какой-то алгоритм, т.е. написать программу.
▍ Функции активации — ФА
Но это будет не просто программа, помимо базового кода, нам необходимо ввести так называемую математическую модель или же функцию активации, что же это такое?
Функция активации определяет выходное значение нейрона в зависимости от результата взвешенной суммы входов и порогового значения. Пример: 𝒚=𝒇(𝒕).
Давайте рассмотрим некоторые распространённые ФА:
Первое, что приходит в голову, это вопрос о том, что считать границей активации для активационной функции. Если значение Y больше некоторого порогового значения, считаем нейрон активированным. В противном случае говорим, что нейрон неактивен. Такая схема должна сработать, но сначала давайте её формализуем.
Функция А = активирована, если Y > граница, иначе нет.
Другой способ: A = 1, если Y > граница, иначе А = 0.
Функция, которую мы только что создали, называется ступенчатой.
Функция принимает значение 1 (активирована), когда Y > 0 (граница), и значение 0 (не активирована) в противном случае.
Пользуясь определением, становится понятно, что ReLu возвращает значение х, если х положительно, и 0 в противном случае.
ReLu нелинейна по своей природе, а комбинация ReLu также нелинейна! (На самом деле, такая функция является хорошим аппроксиматором, так как любая функция может быть аппроксимирована комбинацией ReLu). Это означает, что мы можем стэкать слои. Область допустимых значений ReLu — [ 0,inf ].
ReLu менее требовательно к вычислительным ресурсам, так как производит более простые математические операции. Поэтому имеет смысл использовать ReLu при создании глубоких нейронных сетей.
Сигмоида выглядит гладкой и подобна ступенчатой функции. Рассмотрим её преимущества.
Во-первых, сигмоида — нелинейна по своей природе, а комбинация таких функций производит тоже нелинейную функцию.
Ещё одно достоинство такой функции — она не бинарна, что делает активацию аналоговой, в отличие от ступенчатой функции. Для сигмоиды также характерен гладкий градиент.
Если вы заметили, в диапазоне значений X от -2 до 2 значения Y меняется очень быстро. Это означает, что любое малое изменение значения X в этой области влечёт существенное изменение значения Y. Такое поведение функции указывает на то, что Y имеет тенденцию прижиматься к одному из краёв кривой.
Сигмоида действительно выглядит подходящей функцией для задач классификации. Она стремится привести значения к одной из сторон кривой (например, к верхнему при х=2 и нижнему при х=-2). Такое поведение позволяет находить чёткие границы при предсказании.
Другое преимущество сигмоиды над линейной функцией заключается в следующем. В первом случае имеем фиксированный диапазон значений функции — [0,1], тогда как линейная функция изменяется в пределах (-inf, inf). Такое свойство сигмоиды очень полезно, так как не приводит к ошибкам в случае больших значений активации.
Сегодня сигмоида является одной из самых частых активационных функций в нейросетях.
Как же обучить нейронную сеть?
Теперь перейдём к другим немаловажным терминам.
Что нам понадобится:
- Данные для обучения
- Функция потерь
- Понятие «градиентного спуска»
Цель обучения нейронной сети — найти такие параметры сети, при которых нейронная сеть будет ошибаться наименьшее количество раз.
Ошибка нейронной сети — отличие между предсказанным значением и правильным.
Самая простая функция потерь — Евклидово Расстояние или функция MSE:
yi – правильный результат.
zi – предсказанный результат.
Задача минимизации ошибки:
Используем метод оптимизации:
𝒂𝒓𝒈𝒎𝒊𝒏(𝒕) — функция, возвращающая элемент вектора, где достигается минимум.
𝒂𝒓𝒈𝒎𝒂𝒙(𝒕) — функция, возвращающая элемент вектора, где достигается максимум.
Градиентный спуск — метод нахождения локального минимума или максимума функции при помощи движения вдоль градиента.
Для вычисления градиентного спуска нам надо посчитать частные производные функции ошибки, по всем обучаемым параметрам нашей модели.
Пресловутые «Ирисы Фишера»
Теперь немного уйдём от голой теории и сделаем простую программу, решив базовую задачу классификации. Это базовая задача для специалистов, начинающих свой путь в нейронных сетях, своеобразный «Hello world!», для этого направления.
Здесь хотелось бы сделать небольшое отступление и рассказать подробнее про саму задачу «Ирисов Фишера» зачем и почему она здесь.
Ирисы Фишера — это набор данных для задачи классификации, на примере которого, Рональд Фишер в 1936 году продемонстрировал работу разработанного им метода дискриминантного анализа. Иногда его также называют ирисами Андерсона, так как данные были собраны американским ботаником Эдгаром Андерсоном. Этот набор данных стал уже классическим, и часто используется в литературе для иллюстрации работы различных статистических алгоритмов.
Вот так распределяются данные в датасете:
Ирисы Фишера состоят из данных о 150 экземплярах ириса, по 50 экземпляров из трёх видов:
- Ирис щетинистый (Iris setosa).
- Ирис виргинский (Iris virginica).
- Ирис разноцветный (Iris versicolor).
Для каждого экземпляра измерялись четыре характеристики (в сантиметрах):
- Длина чашелистника (sepal length).
- Ширина чашелистника (sepal width).
- Длина лепестка (petal length).
- Ширина лепестка (petal width).
Конструкция нейронной сети:
На входе у нас есть 4 класса(характеристики) — Х, также нам понадобится всего один внутренний слой — Н, в нём будет 10 нейронов (выбирается методом подбора), далее на выходе мы имеем 3 класса, которые зависят от характеристики цветов — Z. Получается вот такая конструкция сети:
Далее распишем математическое обоснование для нашей задачи:
Ура-а-а-а! Наконец-то код!
Нам потребуется:
- Язык программирования Python.
- Базовая библиотека языка Python, для работы с линейными данными, NumPy.
- Базовая библиотека языка Python, для «рандомизации» значений, random.
Для начала нам необходимо импортировать библиотеки numpy и random:
import numpy as np
import random as rdТеперь пропишем некоторые гиперпараметры:
INPUT_DIM = 4 #кол-во входных нейронов
OUT_PUT = 3 #кол-во выходных нейронов
H_DIM = 10 #кол-во нейронов в скрытом слое
Теперь зададим входной вектор и его веса (вначале рандомим данные, для получения реальной картины весов):
x = np.random.randn(INPUT_DIM)
w1 = np.random.randn(INPUT_DIM, H_DIM)
b1 = np.random.randn(H_DIM)
w2 = np.random.randn(H_DIM, OUT_DIM)
b2 = np.random.randn(OUT_DIM)
Расписываем вложенный слой — наше математическое обоснование:
t1 = x @ w1 + b1
h1 = relu(t1)Точно также сделаем и для остальных.
Теперь обернём наш код в функцию:
def predict(x):
t1 = x @ W1 + b1
h1 = relu(t1)
t2 = h1 @ W2 + b2
z = softmax(t2)
print('z =', z)
return z
Оформим функцию relu():
def relu(t):
print('relu:', np.maximum(t, 0))
return np.maximum(t, 0)
Теперь добавим softmax():
def softmax(t):
out = np.exp(t)
print('softmax:', out / np.sum(out))
return out / np.sum(out)
Добавим вызов функции predict(), также class_names — имена выходных классов и вывод результатов предсказания:
probs = predict(x)
pred_class = np.argmax(probs)
class_names = ['Setosa', 'Versicolor', 'Virginica']
print('Predicted:', class_names[pred_class])
Наш код здесь нарандомит значения входных коэффициентов и весов, поэтому и результат будет случайный. Для тех, кто хочет весь код сразу:
import numpy as np
import random as rd
INPUT_DIM = 4
OUT_DIM = 3
H_DIM = 10
x = []
for i in range(4):
x.append(float(input()))
print(x)
# Рандомно вводим значения гиперпараметров:
x = np.random.randn(INPUT_DIM)
w1 = np.random.randn(INPUT_DIM, H_DIM)
b1 = np.random.randn(H_DIM)
w2 = np.random.randn(H_DIM, OUT_DIM)
b2 = np.random.randn(OUT_DIM)
def relu(t):
print('relu:1', np.maximum(t, 0))
return np.maximum(t, 0)
def softmax(t):
out = np.exp(t)
print('softmax:', out / np.sum(out))
return out / np.sum(out)
def predict(x):
t1 = x @ w1 + b1
h1 = relu(t1)
t2 = h1 @ w2 + b2
z = softmax(t2)
print('z =1', z)
return z
tl = x @ w1 + b1
hl = relu(tl)
probs = predict(x)
pred_class = np.argmax(probs)
class_names = ['Setosa', 'Versicolor', 'Virginica']
print('Predicted:', class_names[pred_class])Вот теперь добавим полученные после обучения веса и входные данные:
w1 = np.array([[ 0.33462099, 0.10068401, 0.20557238, -0.19043767, 0.40249301, -0.00925352, 0.00628916, 0.74784975, 0.25069956, -0.09290041 ], [ 0.41689589, 0.93211640, -0.32300143, -0.13845456, 0.58598293, -0.29140373, -0.28473491, 0.48021000, -0.32318306, -0.34146461 ], [-0.21927019, -0.76135162, -0.11721704, 0.92123373, 0.19501658, 0.00904006, 1.03040632, -0.66867859, -0.01571104, -0.08372566 ], [-0.67791724, 0.07044558, -0.40981071, 0.62098450, -0.33009159, -0.47352435, 0.09687051, -0.68724299, 0.43823402, -0.26574543 ]])
b1 = np.array([-0.34133575, -0.24401602, -0.06262318, -0.30410971, -0.37097632, 0.02670964, -0.51851308, 0.54665141, 0.20777536, -0.29905165 ])
w2 = np.array([[ 0.41186367, 0.15406952, -0.47391773 ], [ 0.79701137, -0.64672799, -0.06339983 ], [-0.20137522, -0.07088810, 0.00212071 ], [-0.58743081, -0.17363843, 0.93769169 ], [ 0.33262125, 0.18999841, -0.14977653 ], [ 0.04450406, 0.26168097, 0.10104333 ], [-0.74384144, 0.33092591, 0.65464737 ], [ 0.45764631, 0.48877246, -1.16928700 ], [-0.16020630, -0.12369116, 0.14171301 ], [ 0.26099978, 0.12834471, 0.20866959 ]])
b2 = np.array([-0.16286677, 0.06680119, -0.03563594 ])
Опять же для любителей всего кода в одном месте:
import numpy as np
import random as rd
INPUT_DIM = 4
OUT_DIM = 3
H_DIM = 10
x = []
# Входные тестовые данные вводятся в следующем формате: "7.9 3.1 7.5 1.8"
# Длина чашелистника: 7.9
# Ширина чашелистника: 3.1
# Длина лепестка: 7.5
# Ширина лепестка: 1.8
for i in range(4):
x.append(float(input()))
print(x)
w1 = np.array([[ 0.33462099, 0.10068401, 0.20557238, -0.19043767, 0.40249301, -0.00925352, 0.00628916, 0.74784975, 0.25069956, -0.09290041 ], [ 0.41689589, 0.93211640, -0.32300143, -0.13845456, 0.58598293, -0.29140373, -0.28473491, 0.48021000, -0.32318306, -0.34146461 ], [-0.21927019, -0.76135162, -0.11721704, 0.92123373, 0.19501658, 0.00904006, 1.03040632, -0.66867859, -0.01571104, -0.08372566 ], [-0.67791724, 0.07044558, -0.40981071, 0.62098450, -0.33009159, -0.47352435, 0.09687051, -0.68724299, 0.43823402, -0.26574543 ]])
b1 = np.array([-0.34133575, -0.24401602, -0.06262318, -0.30410971, -0.37097632, 0.02670964, -0.51851308, 0.54665141, 0.20777536, -0.29905165 ])
w2 = np.array([[ 0.41186367, 0.15406952, -0.47391773 ], [ 0.79701137, -0.64672799, -0.06339983 ], [-0.20137522, -0.07088810, 0.00212071 ], [-0.58743081, -0.17363843, 0.93769169 ], [ 0.33262125, 0.18999841, -0.14977653 ], [ 0.04450406, 0.26168097, 0.10104333 ], [-0.74384144, 0.33092591, 0.65464737 ], [ 0.45764631, 0.48877246, -1.16928700 ], [-0.16020630, -0.12369116, 0.14171301 ], [ 0.26099978, 0.12834471, 0.20866959 ]])
b2 = np.array([-0.16286677, 0.06680119, -0.03563594 ])
# x = np.random.randn(INPUT_DIM)
# w1 = np.random.randn(INPUT_DIM, H_DIM)
# b1 = np.random.randn(H_DIM)
# w2 = np.random.randn(H_DIM, OUT_DIM)
# b2 = np.random.randn(OUT_DIM)
def relu(t):
print('relu:1', np.maximum(t, 0))
return np.maximum(t, 0)
def softmax(t):
out = np.exp(t)
print('softmax:', out / np.sum(out))
return out / np.sum(out)
def predict(x):
t1 = x @ w1 + b1
h1 = relu(t1)
t2 = h1 @ w2 + b2
z = softmax(t2)
print('z =1', z)
return z
tl = x @ w1 + b1
hl = relu(tl)
probs = predict(x)
pred_class = np.argmax(probs)
class_names = ['Setosa', 'Versicolor', 'Virginica']
print('Predicted:', class_names[pred_class])И в итоге мы получим нужное нам предсказание
Полноценный код можно также посмотреть в моём github-репозитории по ссылке.
Ну что же, мы с вами написали свой «Hello world» с нейронными сетями! Эта задача показывает одно из самых популярных направлений в DataSciense — направление классификации данных. Этим мы приоткрыли дверь в большой и быстроразвивающийся мир человекоподобных технологий. Дальше больше!
А какие примеры классификации и интересные задачи из направления DataSciense вы знаете? Пишите свой вариант в комментариях!
Введение в нейронные сети. Общая постановка задачи. Персептрон. Функции активации нейронов.
Общая постановка задачи
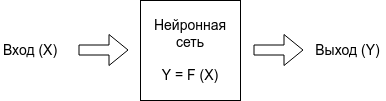
В общем случае задача программирования нейронной сети — это разработать такую нейронную сеть, которая по входу X, будет выдавать правильные ответы Y.
Входом в нейронную сеть могут быть:
- сырые данные, например, звук или фотография.
- либо уже заранее обработанные данные алгоритмом, которые по входу X выдаст признаки (feauture), которые будут передаваться нейронной сети. Данные признаки могут быть определены другой нейронной сетью.
- и т.п.
Выходом могут являться:
- Ответ да или нет.
- Номер категории, к которой принадлежат входные данные.
- Картинка, изображение, звук.
- и т.п.
Задача программиста:
- определить что будет считаться входом в нейронную сеть, а что выходом.
- в каком формате будет принимать нейронная сеть данные.
- структурировать и привести в единую форму входные и выходные данные.
- определить признаки данных, которые могут быть дополнительно поданы на вход в нейронную сеть.
- определить количество слоев нейронной сети.
- определить дополнительные алгоритмы в архитектуре нейронной сети, как отдельные слои.
- создать и разметить DataSet, на котором будет проходить обучение нейронная сеть.
- создать правильную архитектуру нейронной сети.
- обучить нейронную сеть и проверить ее на контрольной выборке.
- внедрить полученную нейронную сеть.
Размеченный DataSet ((D)) — это набор данных и известных ответов к ним. По этому датасету обучаются нейронные сети. При этом датасет делится на две части. Обучающий и контрольный. По обучающему датасету нейронная сеть учится, а по контрольному тестируется. Важно, чтобы данные контрольного датасета не попадали в обучающий, иначе нейронная сеть просто заучит правильные ответы.
Правильным результатом считается, когда нейронная сеть наименьше всего ошибается на обоих дата сетах. Берутся ответы нейронной сети и сравниваются с правильными. Чем меньше ошибка, тем лучше работает нейронная сеть.
Функцией ошибки ((Q)) называется разница между правильными ответами и ответами, которая выдает нейронная сеть на обучающем и контрольном датасете.
Обучение по размеченному датасету называется обучением с учителем. Есть также другие варианты обучения. Например, без учителя. В данном случае правильные ответы отсуствуют и нейронная сеть должна найти их сама. Эта задача хорошо подходит, например, для нахождения общих признаков на большом количестве данных.
Математикой обучения занимаются алгоритмы популярных библиотек TensorFlow, Keros.
Ахитектурой нейронной сети ((F)) — называется цепочка, последовательность слоев этой сети.
Архитектура нейронных сетей может быть разной формы и длины, состоять из нескольких последовательных или паралельных слоев или других цепочек.
Слой — это набор персептронов или определенный алгоритм, который преобразует, по некоторому принципу, входные сигналы p в выходные p’.
Создание архитектуры нейронной сети напоминает конструктор лего, где программист опытным путем подбирает правильный порядок слоев в архитектуре нейронной сети, чтобы она на выходе выдавала правильный результат и значение функии ошибки стремилось к нулю (Q(F, D) to 0)

Каждый слой выполняет определенную функцию. Слои могут отличаться друг от друга.
Примеры слоев:
- простой слой персептронов.
- сверточный слой.
- слой конвертации изображения из двухмерной картинки в одномерный вектор.
- нахождение максимума или минимума.
- фильтрация значения по критерию
- измененя яркости или контрастности.
- удаления или добавление шума.
- Max Pooling и Average Pooling.
- и т.п.
Архитектура нейронной сети может быть иерархической.
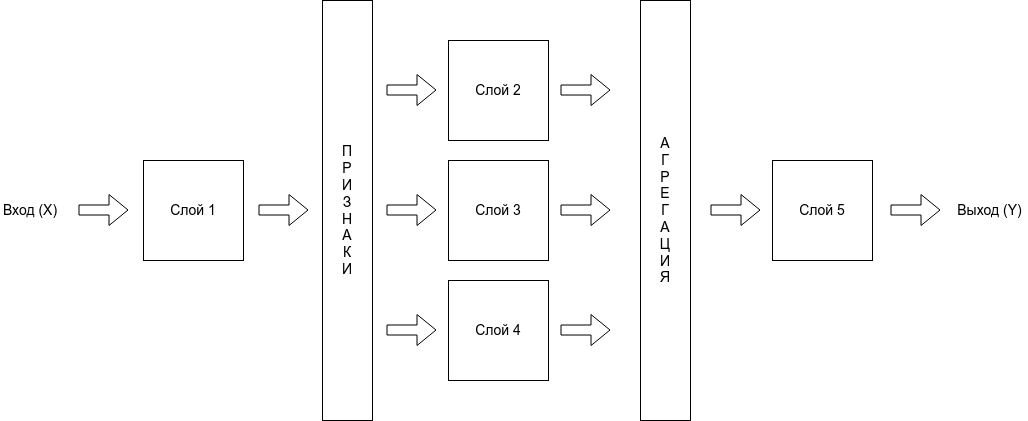
Математическое описание задачи обучения с учителем
Дано:
(X) — это входные тестовые данные. Вектор вида ((x_1, x_2, x_3, … , x_n))
(Y) — выходные тестовые данные. Вектор вида ((y_1, y_2, y_3, … , y_k))
(D) — это обучающая выборка, множество кортежей вида ((X_i,Y_i)), множество входных значений и ответов к ним (выходных значений), где для каждого (X_i) известно (Y_i).
(n) — длинна вектора (X)
(k) — длинна вектора (Y)
(m) — размер выборки, количество кортежей в множестве (D)
Требуется:
Найти функцию (F), которая (Y approx F(X))
Обозначим функцию потерь как:
(L(F,X_i)=|Y_i — F(X_i)|)
Эта функция означает, насколько ошибается функция (F) на конкретном примере ((X_i,Y_i)).
Функция (Q), будет называться функцией ошибки (F) на множестве (D) и определена как сумма всех значений функции (L)
(Q (F) = frac{ sum_{i=1}^{m} L(F,X_i) } {m})
Функция (F) и ее веса будут найдена при условии (Q(F) to 0)
Есть разные варианты формул ошибки:
Абсолютная ошибка:
(Q (F) = frac{ sum_{i=1}^{m} |Y_i — F(X_i)| } {m})
В Tenzorflow loss=’mean_absolute_error’
Среднеквадратическая ошибка:
(Q (F) = frac{ sqrt {sum_{i=1}^{m} (Y_i — F(X_i))^2} } {m})
В Tenzorflow loss=’mean_squared_error’
Математическая модель нейрона
Нейрон — это атом нейронной сети. У каждого нейрона есть несколько входов и один выход.
Ниже представлена математическая модель одного нейрона.
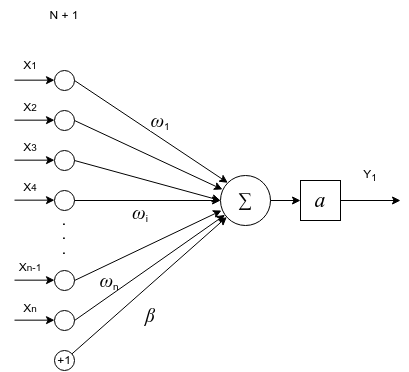
Основная задача нейрона проводить сигнал или гасить его в зависимости от входных значений.
Выходной сигнал нейрона считается как сумма входных значений, умноженная на их веса плюс базис, обработанная функцией активации.
(y = a(sum_{i=1}^{n} omega_i * x_i + beta))
(a(v)) — функция активации нейрона. Функция активации нейрона нужна, чтобы определить при каких входных значениях должен активироваться (включаться) нейрон, т.е. проводить сигнал. А при каких нет. Нейрон включается, если достигается нужный уровень сигнала, после этого нейрон передает сигнал дальше. Поэтому функция и называется функцией активации.
(omega_i) — вес нейронной связи. Задает какой входящий сигнал и с какой силой должен учитываться, а какой нет.
(beta) — смещение bias. Это пороговое значение, которое смещает аргумент активационной функции, потому что активация (включение) нейрона может происходит не в точке 0, а в какой-то другой точке. А т.к. функция активации работает в точке ноль, то аргумент нужно сместить по оси x на смещение bias.
Ниже отображена функция активациции со смещением bias. На графике видно, что нейрон будет включаться после аргумента функции больше 2, а не больше 0. Смещение bias в данном случае равно +2.
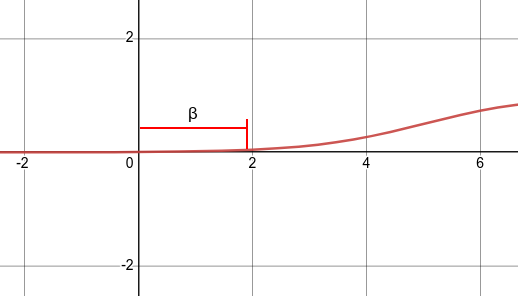
Смещение bias также является входом в нейронную сеть, для которого подбирается свой вес. Этот вес и является смещением. Обычно вес смещения является нулевым весом (omega_0), при входном сигнале равным 1. Получается само смещение вычисляется по формуле (beta = omega_0 *1)
Тогда формула активации нейрона примет вид:
(y = a(omega_0 + sum_{i=1}^{n} omega_i * x_i))
Это удобно, потому что в данном случае формула принимает одинаковый вид, и для обучения нейрона требуется подобрать кортеж весов ((omega_0, omega_1, omega_2, omega_3, … , omega_n))
Функция ошибки и активации являются важными параметрами архитектуры нейронной сети.
Однослойный персептрон
Архитектура нейронной сети состоит из последовательности слоев, которые соединены между собой.
Нейронная сеть состоящая только из входных и выходных слоев называется однослойным персептроном и обозначается упрощенно:
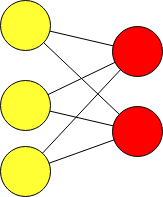
Данная нейронная сеть очень простая. Однослойный персептрон называют более простым термином полносвязный слой. В библиотеке Tensorflow полносвязный слой создается через класс Dense.
Многослойный персептрон
Данный вид нейронной сети имеет следующие названия:
- нейронная сеть с прямой связью
- Feed Forward neural network
- полносвязная сеть
- классификатор
Полносвязная сеть используется очень часто, и хорошо решают задачи на классификацию, например:
- Распознать какая цифра по ее изображению.
- Отличить кошку от собаки.
- Определить какой цветок, по его параметрам (цвет, форма цветка, длинна и т.д.)
- и т.п.
Во сверточных нейронных сетях, полносвязная сеть используется как классификатор на выходе. Сверточная сеть выделяет признаки по картинке и передает ее в полносвязную. А полносвязная уже квалифицирует и выдает ответ.
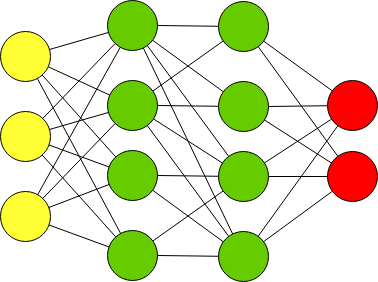
Многослойный персептрон (полносвязная сеть) — это последовательность полносвязных слоев однослойных персептронов. Основным отличием многослойного персептрона от одногослойного — в наличии одного или более скрытого слоя. Входные и выходные значения соединяются через скрытый слой, а не напрямую, как в однослойном персептроне.
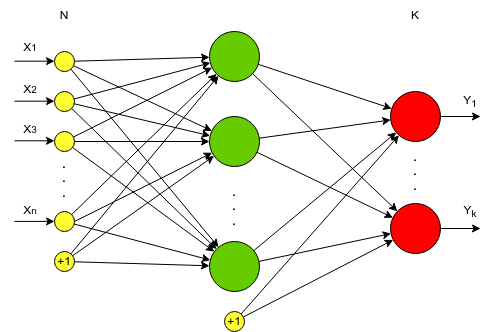
Желтым обозначены входной слой X.
Красным — выходной слой нейронов Y.
Зеленый — это скрытый слой нейронов.
Каждый выход нейрона вычисляется по формуле:
(p’_j = a(omega_0 + sum_{i=1}^{n} omega_i * p_i)), где p — это входные значения, а p’ — это выходные значения нейрона.
В данной нейронной сети 3 слоя. Входной, скрытый и выходной слой. Данную нейронную сеть часто обозначают упрощенно:
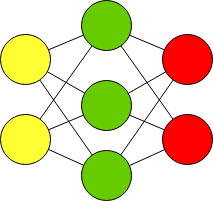
Feed Forward neural network
Текстовая нотация Feed Forward:
ff = [
"Input",
"Dense",
"Output"
];Многослойный персептрон с более чем одним скрытым слоем называют Deep Feed Forward.
Текстовая нотация Deep Feed Forward:
dff = [
"Input",
"Dense",
"Dense",
"Output"
];
Функции активации нейрона
Пороговая функция активации
(sign(x) = begin{cases} -1 & ,x < 0 \ 0 & ,x = 0 \ 1 &, x > 0 end{cases})
Сигмоида sigm
(sigm(x) = frac{1}{1+e^{-x}})
relu
(relu(x) = max(0,x) = begin{cases} 0 , x leq 0 \ x , x > 0 end{cases})
leaky relu
(lerelu(x) = begin{cases} 0.01x & ,x leq 0 \ x &, x > 0 end{cases})
Материалы
- Обучение многослойного персептрона операции XOR
- Материалы для самостоятельного изучения нейронных сетей
- Базы датасетов для обучения нейронных сетей
- AIML-4-1 Персептроны
- AIML-4-2 Метод обратного распространения ошибки
- Формулы обратного распространения
- Архитектуры нейронных сетей
- Сервис чтобы строить графики
- Ускорение обучения, начальные веса, стандартизация, подготовка выборки
- Переобучение — что это и как этого избежать, критерии останова обучения
- Функции активации, критерии качества работы НС
- Функции активации. Краткий обзор применений CNN и RNN.
- Playground Tensorflow
Библиографическое описание:
Кураева, Е. С. Проблемы обучения нейронных сетей / Е. С. Кураева. — Текст : непосредственный // Молодой ученый. — 2020. — № 14 (304). — С. 72-74. — URL: https://moluch.ru/archive/304/68605/ (дата обращения: 30.01.2023).
В данной статье рассматриваются проблемы, которые могут возникнуть при работе с нейронными сетями, а также способы их устранения.
Ключевые слова: нейронные сети, обучение, подготовка начальных значений весовых коэффициентов, планирование выходных значений.
Нейронные сети не всегда работают так, как запланировано. Необходимо спланировать тренировочные данные и начальные значения весов, а также спланировать выходные значения. Факторы, которые влияют на незапланированную работу нейронной сети и будут рассмотрены в данной работе.
Распространенной проблемой является насыщение сети. Она возникает, если присутствуют большие значения сигналов, часто спровоцированные большими начальными весовыми коэффициентами. Таким образом сигналы попадут в область близких к нулю градиенту функции активации. Что в свою очередь влияет на способность к обучению, а именно на подбор лучших коэффициентов.
- Входные значения
Если использовать в качестве функции активации — сигмоиду, то при слишком больших значениях входных данных, прямая будет выглядеть, как прямая. Поэтому рекомендуется задавать небольшие значения. Однако слишком маленькие значения также будут плохо сказываться на обучение, так как точность компьютерных вычислений снижается. Поэтому советуется выбирать значения входных данных от 0.0 до 1.0. При этом можно ввести смещение равное 0.01. [2, c. 124].
На рисунке 1 видно, что при увеличении входных данных, способность нейронной сети к обучению снижается, так как сигмоида почти выпрямляется.
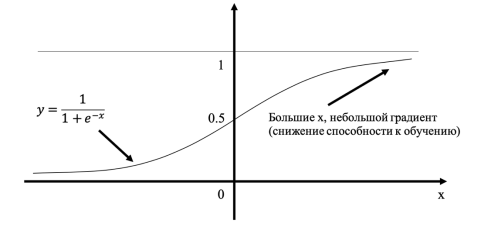
Рис. 1. Подготовка входных данных
- Выходные значения
Выходные значения следует подбирать, в зависимости от выбранной функции активации. Если она не способна обеспечивать значения свыше 1.0, но выходные значения мы хотим получить больше 1.0, то весовые коэффициенты будут увеличиваться, чтобы подстроиться под ситуацию. Но ничего не выйдет, выходные значения все равно не будут больше максимального значения функции активации. Поэтому выходные значения следует масштабировать в пределах от 0.0 до 1.0. Так как граничные значения не достигаются, то советуется выбирать значения от 0.01 до 0.99. На рис. 2 продемонстрировано данное правило.
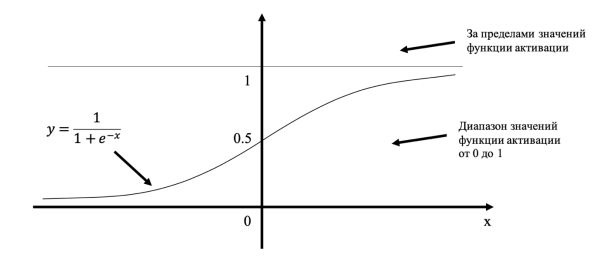
Рис. 2. Ограничение по выходных значениям
- Случайные начальные значения весовых коэффициентов
Самый простой вариант в выборе начальных значений весовых коэффициентов — выбирать их из диапазона от -1.0 до +1.0.
Но существуют подходы, которые позволяют определить коэффициенты в зависимости от конфигурации сети. Цель заключается в том, чтобы если на узел сети поступает множество сигналов и их поведение известно, то весовые коэффициенты не должны нарушать их состояние. То есть веса не должна нарушать тщательную подготовку входных и выходных значений, описанный в пунктах 1 и 2.
Если грубо описать правило, то оно звучит так: «Весовые коэффициенты инициализируются числами, случайно выбираемыми из диапазона, которые определяются обратной величиной квадратного корня из количества связей, ведущих к узлу» [2, с. 126].
На рис. 3 иллюстрируются подходы для выбора начальных весов.
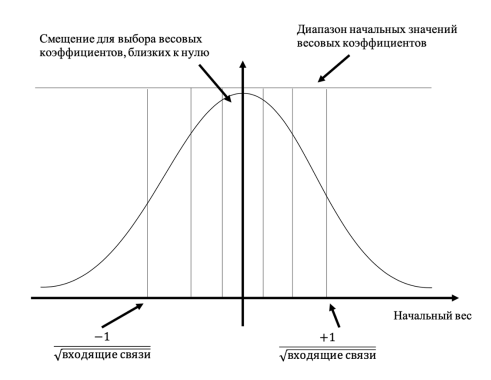
Рис. 3. Подходы к выбору весовых коэффициентов
Советуется не задавать одинаковые веса. Таким образом бы в узлы пришли бы одинаковые сигналы и выходные значения получились бы одинаковыми. И после обновления весов, их значения все равно будут равными.
Также нельзя задавать нулевые значения для весовых коэффициентов, так как входные значения в этом случае «теряют свою силу».
Вывод
Чтобы нейронные сети работали удовлетворительно, необходимо входные и выходные данные, а также начальные значения весовых коэффициентов задавать в зависимости от структуры нейронной сети. Также преградой для наилучшего обучения сети являются нулевые значения сигналов и весов. А значения весовых коэффициентов должны отличаться друг от друга.
Входные и выходные значения должна быть масштабированными.
Литература:
1. Хайкин С. Нейронные сети. — М.: Вильямс, 2006.
2. Рашид Т. Создает нейронную сеть. — М.: Диалектика, 2019.
Основные термины (генерируются автоматически): выходной, коэффициент, нейронная сеть, данные.
нейронные сети, обучение, подготовка начальных значений весовых коэффициентов, планирование выходных значений
Похожие статьи
Использование искусственных нейронных сетей для…
нейронная сеть, обратное распространение ошибки, сеть, коэффициент корреляции, прямой проход, левый желудочек, корреляционный анализ, диастолическая дисфункция, гиперболический тангенс… Исследование и сравнительный анализ работы нейронных сетей…
Нейросетевые технологии и их применение при прогнозировании…
Технически обучение заключается в нахождении коэффициентов связей между нейронами. В процессе обучения нейронная сеть способна выявлять сложные зависимости между входными данными и выходными, а также выполнять обобщение.
нейронная сеть, сеть, эта, нейрон, данные, архитектура…
Ключевые слова: сеть, нейронная сеть, искусственный интеллект, язык программирования, протон, python, сигмоида, входной слой, скрытый слой, выходной слой, функция активации, jupiter notebook. Структура нейронной сети пришла в мир программирования из биологии.
Исследование и сравнительный анализ работы нейронных сетей…
Каждая нейронная сеть, подключенная к группе, генерирует случайные весовые коэффициенты, затем каждая сеть обучается отдельно на
Для объединения выходных данных группы нейронных сетей используется усредненную простую группировку.
Анализ и классификация погрешностей обучения…
Нейронная сеть, решающая задачу прогнозирования фронта пика, состоит из входного и выходного слоев с одним нейроном и 4-х слоёв по 50 нейронов в. Анализ и классификация погрешностей обучения информационно-измерительных систем на базе нейронных сетей.
Исследование возможностей использования нейронных сетей
В данной статье рассматриваются теоретические основы нейронных сетей, исследование их видов и описание их математической модели. Целью данной статьи является исследование возможностей использования нейронных сетей.
Модель математической нейронной сети | Статья в журнале…
Выходные данные передаем дальше.
Тренировочный сет— это последовательность данных, которыми оперирует нейронная сеть. В нашем случае исключающего или (xor) у нас всего 4 разных исхода то есть у нас будет 4 тренировочных сета: 0xor0=0, 0xor1=1, 1xor0=1…
нейронная сеть, сеть, эта, нейрон, данные, архитектура…
Ключевые слова: нейронная сеть, интеллектуальные технологии, анализ
Нейронная сеть — это система, состоящая из многих простых вычислительных элементов, или нейронов
Для построения нейросетевой модели использовано 6 входных факторов ( ), 1 выходное значение…
нейронная сеть, сеть, эта, нейрон, данные, архитектура…
После загруженных данных, нейронная сеть начинает свое обучение с помощью выбранного алгоритма управляемого обучения.
нейронная сеть, слой, карт признаков, изображение, результат работы сети, машинное обучение, выходной слой, математическая модель, буква…
Похожие статьи
Использование искусственных нейронных сетей для…
нейронная сеть, обратное распространение ошибки, сеть, коэффициент корреляции, прямой проход, левый желудочек, корреляционный анализ, диастолическая дисфункция, гиперболический тангенс… Исследование и сравнительный анализ работы нейронных сетей…
Нейросетевые технологии и их применение при прогнозировании…
Технически обучение заключается в нахождении коэффициентов связей между нейронами. В процессе обучения нейронная сеть способна выявлять сложные зависимости между входными данными и выходными, а также выполнять обобщение.
нейронная сеть, сеть, эта, нейрон, данные, архитектура…
Ключевые слова: сеть, нейронная сеть, искусственный интеллект, язык программирования, протон, python, сигмоида, входной слой, скрытый слой, выходной слой, функция активации, jupiter notebook. Структура нейронной сети пришла в мир программирования из биологии.
Исследование и сравнительный анализ работы нейронных сетей…
Каждая нейронная сеть, подключенная к группе, генерирует случайные весовые коэффициенты, затем каждая сеть обучается отдельно на
Для объединения выходных данных группы нейронных сетей используется усредненную простую группировку.
Анализ и классификация погрешностей обучения…
Нейронная сеть, решающая задачу прогнозирования фронта пика, состоит из входного и выходного слоев с одним нейроном и 4-х слоёв по 50 нейронов в. Анализ и классификация погрешностей обучения информационно-измерительных систем на базе нейронных сетей.
Исследование возможностей использования нейронных сетей
В данной статье рассматриваются теоретические основы нейронных сетей, исследование их видов и описание их математической модели. Целью данной статьи является исследование возможностей использования нейронных сетей.
Модель математической нейронной сети | Статья в журнале…
Выходные данные передаем дальше.
Тренировочный сет— это последовательность данных, которыми оперирует нейронная сеть. В нашем случае исключающего или (xor) у нас всего 4 разных исхода то есть у нас будет 4 тренировочных сета: 0xor0=0, 0xor1=1, 1xor0=1…
нейронная сеть, сеть, эта, нейрон, данные, архитектура…
Ключевые слова: нейронная сеть, интеллектуальные технологии, анализ
Нейронная сеть — это система, состоящая из многих простых вычислительных элементов, или нейронов
Для построения нейросетевой модели использовано 6 входных факторов ( ), 1 выходное значение…
нейронная сеть, сеть, эта, нейрон, данные, архитектура…
После загруженных данных, нейронная сеть начинает свое обучение с помощью выбранного алгоритма управляемого обучения.
нейронная сеть, слой, карт признаков, изображение, результат работы сети, машинное обучение, выходной слой, математическая модель, буква…
-
Обучение нейронных сетей
Способность
к обучению является фундаментальным
свойством мозга. В контексте ИНС процесс
обучения может рассматриваться как
настройка архитектуры сети и весов
связей для эффективного выполнения
специальной задачи. Обычно нейронная
сеть должна настроить веса связей по
имеющейся обучающей выборке.
Функционирование сети улучшается по
мере итеративной настройки весовых
коэффициентов. Свойство сети обучаться
на примерах делает их более привлекательными
по сравнению с системами, которые следуют
определенной системе правил
функционирования, сформулированной
экспертами.
Для
конструирования процесса обучения,
прежде всего, необходимо иметь модель
внешней среды, в которой функционирует
нейронная сеть — знать доступную для
сети информацию. Эта модель определяет
парадигму обучения.
Существуют
три парадигмы обучения: «с учителем»,
«без учителя» (самообучение) и
смешанная. В первом случае нейронная
сеть располагает правильными ответами
(выходами сети) на каждый входной пример.
Веса настраиваются так, чтобы сеть
производила ответы как можно более
близкие к известным правильным ответам.
Усиленный вариант обучения с учителем
предполагает, что известна только
критическая оценка правильности выхода
нейронной сети, но не сами правильные
значения выхода. Обучение без учителя
не требует знания правильных ответов
на каждый пример обучающей выборки. В
этом случае раскрывается внутренняя
структура данных или корреляции между
образцами в системе данных, что позволяет
распределить образцы по категориям.
При смешанном обучении часть весов
определяется посредством обучения с
учителем, в то время как остальная
получается с помощью самообучения.
Теория
обучения рассматривает три фундаментальных
свойства, связанных с обучением по
примерам: емкость, сложность образцов
и вычислительная сложность. Известны
4 основных типа правил обучения: коррекция
по ошибке, машина Больцмана, правило
Хебба и обучение методом соревнования.
Правило
коррекции по ошибке.
При обучении с учителем для каждого
входного примера задан желаемый выход
d. Реальный выход сети y может не совпадать
с желаемым. Принцип коррекции по ошибке
при обучении состоит в использовании
сигнала (d-y) для модификации весов,
обеспечивающей постепенное уменьшение
ошибки. Обучение имеет место только в
случае, когда перцептрон ошибается.
Известны различные модификации этого
алгоритма обучения.
Обучение
Больцмана.
Представляет собой стохастическое
правило обучения, которое следует из
информационных теоретических и
термодинамических принципов. Целью
обучения Больцмана является такая
настройка весовых коэффициентов, при
которой состояния видимых нейронов
удовлетворяют желаемому распределению
вероятностей. Обучение Больцмана может
рассматриваться как специальный случай
коррекции по ошибке, в котором под
ошибкой понимается расхождение корреляций
состояний в двух режимах .
Правило
Хебба. Самым
старым обучающим правилом является
постулат обучения Хебба. Хебб опирался
на следующие нейрофизиологические
наблюдения: если нейроны с обеих сторон
синапса активизируются одновременно
и регулярно, то сила синаптической связи
возрастает. Важной особенностью этого
правила является то, что изменение
синаптического веса зависит только от
активности нейронов, которые связаны
данным синапсом. Это существенно упрощает
цепи обучения в реализации VLSI.
Обучение
методом соревнования.
В отличие от обучения Хебба, в котором
множество выходных нейронов могут
возбуждаться одновременно, при
соревновательном обучении выходные
нейроны соревнуются между собой за
активизацию. Это явление известно как
правило «победитель берет все».
Подобное обучение имеет место в
биологических нейронных сетях. Обучение
посредством соревнования позволяет
кластеризовать входные данные: подобные
примеры группируются сетью в соответствии
с корреляциями и представляются одним
элементом.
При
обучении модифицируются только веса
«победившего» нейрона. Эффект этого
правила достигается за счет такого
изменения сохраненного в сети образца
(вектора весов связей победившего
нейрона), при котором он становится чуть
ближе ко входному примеру.
Любая
нейронная сеть, прежде всего, должна
быть обучена. Процесс обучения заключается
в подстройке внутренних параметров
нейросети под конкретную задачу.
При
обучении «классической» многослойной
нейросети на вход подаются данные или
индикаторы, а выход нейросети сравнивается
с эталонным значением (с так называемым
«учителем»). Разность этих значений
называется ошибкой нейронной сети,
которая и минимизируется в процессе
обучения. Таким образом, обычные нейронные
сети выявляют закономерности между
входными данными и прогнозируемой
величиной. Если такие закономерности
есть, то нейросеть их выделит, и прогноз
будет успешным.
Технология
обучения с учителем НС предполагает
наличие двух однотипных множеств:
-
множество
учебных примеров — используется для
«настройки» НС; -
множество
контрольных примеров — используется
для оценки качества работы НС.
Элементами
этих двух множеств есть пары (X, YI),
где
-
X
— входной вектор для обучаемой НС; -
YI
— верный (желаемый) выходной вектор
для X.
Так
же необходимо определить функцию ошибки
E. Обычно это средняя квадратичная ошибка
(mean squared error — MSE)
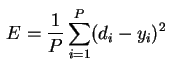
где
-
P
— количество обработанных НС примеров; -
yi
— реальный выход НС; -
di
— желаемый (идеальный) выход НС.
Процедура
обучения НС сводится к процедуре
коррекции весов связей HC. Целью процедуры
коррекции весов есть минимизация функции
ошибки E.
Общая
схема обучения с учителем выглядит так:
1.
Перед началом обучения весовые
коэффициенты НС устанавливаются
некоторым образом, на пример — случайно.
2.
На первом этапе на вход НС в определенном
порядке подаются учебные примеры. На
каждой итерации вычисляется ошибка для
учебного примера EL(ошибка
обучения) и по определенному алгоритму
производится коррекция весов НС. Целью
процедуры коррекции весов есть минимизация
ошибки EL.
3.
На втором этапе обучения производится
проверка правильности работы НС. На
вход НС в определенном порядке подаются
контрольные примеры. На каждой итерации
вычисляется ошибка для контрольного
примера EG
(ошибка обобщения). Если результат
неудовлетворительный то, производится
модификация множества учебных примеров1
и повторение цикла обучения НС.
В
случае однослойной сети алгоритм
обучения с учителем прост. Желаемые
выходные значения нейронов единственного
слоя заведомо известны, и подстройка
весов синаптических связей идет в
направлении, минимизирующем ошибку на
выходе сети.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Оглавление:
- Что такое искусственные нейронные сети?
- Виды обучения нейронных сетей
- Многослойные нейронные сети и их базовые понятия
- Разбираемся на примере
- Заключение
Что такое искусственные нейронные сети?
Данная статья предназначена для ознакомления читателя с искусственными нейронными сетями (далее ANN – Artificial Neural Network) и базовыми понятиями многослойных нейронных сетей.
Основным элементом ANN является нейрон. Его основной задачей является перемножение предыдущих значений нейронов или входных значений с соответствующими им весовыми коэффициентами связей между соответствующими нейронами, после активации вычисленного значения.
Основными задачами ANN является классификация, принятие решения, анализ данных, прогнозирование, оптимизация.
Искусственные нейронные сети категорируются по топологии (полносвязные, многослойные, слабосвязные), способу обучения (с учителем, без учителя, с подкреплением), модели нейронной сети (прямого распространения, рекррентные нейронные сети, сверточные нейронные сети, радиально-базисные функции), а также по типу связей (полносвязные, многослойные, слабосвязные). Такой значительно большой тип категорирования связан с разнообразием задач, которые ставятся перед ANN. Примеры, приведенные в скобках являются одними из самых распространенных типов категорирования, на самом деле их значительно больше.
Виды обучения нейронных сетей
Обучение с учителем
Данный тип обучения является самым простым, за счет того, что нет необходимости в написании алгоритмов самообучения. Для обучения с учителем требуется размеченный и структурированный набор данных для обучения. Под словом «размеченный» подразумевается процесс обозначения верного ответа на конкретный набор входных данных, который мы ожидаем от нейронной сети как результат работы. За счет таких данных нейронная сеть будет ориентироваться на разметку и корректировать процесс обучения за счет определения совершенных ошибок, которые будут определяться из данных разметки и ее предсказанных данных.
Обучение без учителя
Под обучением без учителя подразумевается процесс обучения нейронной сети без какого-либо контроля с нашей стороны. Весь процесс будет протекать за счет нахождения нейронной сетью корреляции в данных, извлечения полезных признаков и их анализа.
Существуют несколько способов обучения без учителя: обнаружение аномалий, ассоциации, автоэнкодеры и кластеризация.
На основе алгоритмов, описанных выше, в процессе обучения будет определяться значение ошибки, допущенной на каждом шаге обучения, за счет чего будет происходить корректировка обучения, следовательно, нейронная сеть обучится. За счет наличия алгоритмов, процесс написания которых занимает много времени и сильно усложняет моделирование нейронной сети, данный тип обучения считается самым сложным.
Обучение с подкреплением
Обучение с подкреплением или частичным вмешательством учителя можно считать золотой серединой в обучении нейронных сетей. Данный тип обучения представляет собой обучение без учителя с периодической его корректировкой. Корректировка обучения происходит тогда, когда нейронная сеть допускает ошибки при обучении.
Многослойные нейронные сети и их базовые понятия
Каждая ANN имеет входной, выходной и скрытые слои. Количество скрытых слоев и их сложность (количество искусственных нейронов) зачастую играют важную роль в процессе обучения, обеспечивая хорошее обучение модели нейронной сети.
Многослойными ANN называются нейронные сети, у которых количество скрытых слоев более одного. Пример многослойной нейронной сети:
Входной, выходной и скрытые слои, нормализация и зачем все это нужно?
Входной слой дает возможность «скормить» данные, на которых требуется производить обучение. Выходной, в свою очередь, выдает результат работы нейронной сети. Вся суть заключается в скрытых слоях. Повторюсь, количество скрытых слоев и их сложность определяют качество обучения. Объясню на простом примере. Я, при написании модели нейронной сети, которая классифицирует рукописные цифры, смоделировал нейронную сеть из двух скрытых слоев по 30 нейронов в каждом. На вход подавал изображение 28х28 пикселей, но предварительно проведя нормализацию (объясню чуть ниже) входных значений и приведение изображения к виду 784х1, путем расставления всех столбцов в один. Т.е. входными значениями являлись 0 и 1, а если быть точнее — значения из данного диапазона. Так вот эти 0 и 1 оказались на входном слое, т.е. каждый нейрон входного слоя представлял из себя пиксель исходного изображения. Далее следовал скрытый слой, состоящий из 30 нейронов. Так вот, эти 30 нейронов представляют собой 30 участков исходного изображения, а каждый участок в свою очередь содержит какие-либо признаки, характеризующие изображение как определенную цифру. Т.е. чем больше нейронов в скрытых слоях, тем точнее будет представление и градуировка исходного изображения. Будет «плодиться» больше характеристик, по которым нейронная сеть будет классифицировать изображение должным образом.
Вернусь к такому понятию, как нормализация. Она необходима для приведения входных значений к значениям из диапазона 0 и 1. Смысл заключается в том, что нейронная сеть должна явно или с долей вероятности классифицировать изображение, или дать какое-то предсказание. Раз предсказание представляет собой вероятность, то и входные значения должны быть в диапазоне от 0 до 1. Поэтому нормализация, к примеру, значений пикселей изображения, происходит путем деления на 255, т.к. значения пикселей находятся в диапазоне от 0 до 255 и максимальным значением является значение 255.
Весовые коэффициенты
Каждая связь между искусственными нейронами обладает весовым коэффициентом, который постоянно изменяется в процессе обучения и является величиной, которая увеличивает или уменьшает предсказанную вероятность. К примеру, при уменьшении веса связи между 1 и 2 нейроном и увеличении веса между 1 и 3 получим, что, используя сигмоидальную функцию активации, значение на ее выходе в 1-ом случае будет стремиться к 0, а во втором к 1. Т.е. весовые коэффициенты являются своего рода возбудителями искусственных нейронов к прогнозированию.
Функция активация, виды и особенности
Функция активации является нормализующим звеном на каждом слое нейронной сети. Она представляет из себя функцию, которая приводит входное значение к значению от 0 до 1. Одной из самых распространенных функция активации является сигмоидальная функция активации:
Значение ‘х’ является значением, которое обрабатывается функцией активации. Оно включает в себя алгебраическую сумму произведений значений нейронов на предыдущем слое на соответствующие им связи с тем нейроном, на котором мы производим расчет функции активации, а также нейрон смещения.
Пример вычисления функции активации приведен на рис. 5
Распространенные виды функций активации:
- Активация пороговой функции; функция активирована, если x, не активирована, если х<0
- Гиперболическая касательная функция ошибки; функция нелинейна, ее значения находятся в диапазоне (-1;1)
- ReLu и LeakyReLu; функция ReLu равна при х, при x, а при х<0 равна 0. Отличием LeakyReLu от ReLu является наличие коэффициента, определяющего значение функции при х<0 как ах
Функция ошибки, виды
Функция ошибки необходима для определения ошибки прогнозирования, допускаемой нейронной сетью на каждом этапе обучения и корректировкой процесса обучения, за счет корректировки весовых значений связей между искусственными нейронами.
Примеры функций ошибок:
- Кросс-энтропия
- Квадратичная (среднеквадратичное отклонение)
- Расстояние Кульбака — Лейблера
- Экспоненциальная
Самая простая и часто используемая функция ошибок (функция потерь) – среднеквадратичное отклонение.
Она вычисляется как половина от алгебраической суммы квадрата разности, прогнозируемого нейронной сетью значения и реальным значением – разметкой данных.
Backpropagation или обратное распространение ошибки
Для корректировки весов на каждом слое нейронной сети необходима метрика для определения ошибки каждого веса, с этой целью был разработан алгоритм обратного распространения ошибки. Он работает следующим образом:
- Вычисляется прогнозируемое нейронной сетью значение на выходе ANN
- Производится расчет функции ошибки, к примеру, среднеквадратичной
- Корректируются веса связей нейронов на последнем слое на основе вычисленной ошибки на выходе
- Происходит расчет ошибки на предпоследнем слое нейронной сети на основании скорректированных весов связей на последнем слое и ошибки на выходе ANN
- Процесс повторяется до первого слоя нейронной сети
Пример работы алгоритма обратного распространения ошибки:
Bias или нейрон смещения
Значение смещения позволяет сместить функцию активации влево или вправо, что может иметь решающее значение для успешного обучения, а также позволяет быть более гибким при выборе решения или прогнозировании.
При наличии нейрона смещения, его значение тоже поступает на вход функции активации, складываясь с алгебраической суммой произведений нейронов и их весовых коэффициентов.
Пример работы нейрона смещения:
Разбираемся на примере
В данном примере напишем классификатор рукописных цифр на языке программирования С++. Обучающую выборку найдем на официальном сайте MNIST.
В первую очередь импортируем модули:
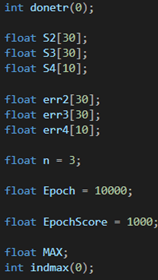
Определим обучающую выборку ‘dataset’, и загрузим в нее размеченные изображения MNIST.
Создадим входной слой равный 784 нейронам, так как наши изображения равны 28х28 пикселей и мы разложим их в цепочку пикселей 784х1, чтобы подать на вход нейронной сети; два скрытых слоя размера 30 нейронов каждый (размеры скрытых слоев подбирались случайно); выходной слой размером 10 нейронов, так как наша нейросеть будет классифицировать числа в диапазоне 0-9, где первый нейрон будет отвечать за классификацию числа 0, второй за число 1 и так далее до 9.
Необходимо сразу инициализировать наши значения слоев, к примеру 0.
Создадим матрицы весов между входным и 1-м скрытым слоями, 1-м скрытым и 2-м скрытым слоями, 2-м скрытым и выходным слоями, и инициализируем матрицы случайными значениями, как показано на рисунке. На примере значения весов находятся в диапазоне [-1;1].
Также необходимо создать массивы, которые будут содержать в себе значения алгебраической суммы произведения весов на соответствующие нейроны, как было описано выше в статье, после чего эти значения будут подаваться в функцию активации.
Ниже были созданы массивы ошибок на каждом слое. Для сохранения результатов ошибок на каждом нейроне, были инициализированы количество эпох и скорость обучения (определяет скорость перемещения по функции в поисках минимума во время обучения; необходимо быть осторожным с этим значением, так как если оно будет слишком мало, то, есть вероятность остаться в локальном минимуме, не найдя настоящий минимум функции или наоборот, при слишком большом значении, есть вероятность перескочить главный минимум функции.)
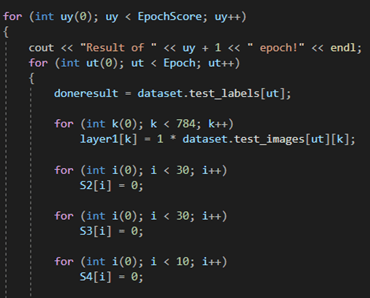
На данном этапе начинается процесс обучения нашей нейронной сети. Внешний цикл определяет количество эпох обучения, а внутренний количество итераций обучения в каждой эпохе.
На рисунке ниже инициализируются значения из обучающей выборки MNIST и занесения их на входной слой нейронной сети, а после происходит инициализация S-величин, о которых было сказано выше, нулями
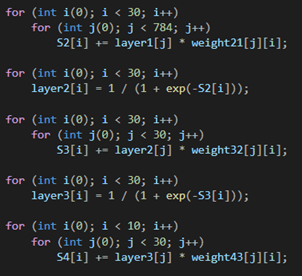
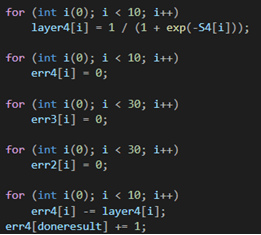
Ниже происходит подсчет алгебраической суммы значений произведений веса на соответствующий нейрон, а после прохождение их через функцию активации, где в роли функции активации выступает сигмоидальная функция.
Подсчитав значения на каждом слое, происходит инициализация массивов ошибок, путем заполнения их 0, а также определение ошибок на выходном слое, путем вычитания полученных значений из 1, и последующим умножением на произведение значений нейронов прошедших через функцию активации на выходном слое на разницу между 1 и этими же значениями.
Далее необходимо определить ошибки на каждом слое нейронной сети методом обратного распространения ошибки. К примеру, чтобы найти ошибку на первом нейроне предыдущего слоя от выходного слоя, необходимо найти алгебраическую сумму произведения ошибок нейронов на выходном слое на соответствующие им веса связей с первым нейроном предыдущего слоя и перемножить на произведение значения нейронов на предпоследнем слое на разницу 1 и этих же значений. Таким образом необходимо найти допущенные ошибки нейронной сетью на каждом слое.
После определения ошибок, допущенных нейронной сетью на каждом нейроне, приступаем к корректировке весовых коэффициентов связей между каждым нейроном. Алгоритм корректировки представлен ниже.
Скорректировав веса, определяем максимальное полученное значение на выходном слое, тем самым определим ответ нейронной сети после прохождения через нее изображения.
Заключение
В этой статье мы разобрались с базовыми понятиями искусственных нейронных сетей, а именно с такими как: входной, выходной, скрытые слои и их предназначение, весовыми коэффициентами связи между искусственными нейронами, функцией активации и ее предназначением, методами определения ошибки на каждом искусственном, с понятием нейрона смещения и функциями ошибки. В следующей статье мы перейдем к изучению нового класса нейронных сетей, таких как сверточные нейронные сети (CNN).
Желаю всем успехов в изучении!
Нейронные сети считаются универсальными моделями в машинном обучении, поскольку позволяют решать широкий класс задач. Однако, при их использовании могут возникать различные проблемы.
Содержание
- 1 Взрывающийся и затухающий градиент
- 1.1 Определение
- 1.2 Причины
- 1.3 Способы определения
- 1.3.1 Взрывающийся градиент
- 1.3.2 Затухающий градиент
- 1.4 Способы устранения
- 1.4.1 Использование другой функции активации
- 1.4.1.1 Tanh
- 1.4.1.2 ReLU
- 1.4.1.3 Softplus
- 1.4.2 Изменение модели
- 1.4.3 Использование Residual blocks
- 1.4.4 Регуляризация весов
- 1.4.5 Обрезание градиента
- 1.4.1 Использование другой функции активации
- 2 См. также
- 3 Примечания
- 4 Источники
Взрывающийся и затухающий градиент
Определение
Напомним, что градиентом в нейронных сетях называется вектор частных производных функции потерь по весам нейронной сети. Таким образом, он указывает на направление наибольшего роста этой функции для всех весов по совокупности. Градиент считается в процессе тренировки нейронной сети и используется в оптимизаторе весов для улучшения качества модели.
В процессе обратного распространения ошибки при прохождении через слои нейронной сети в элементах градиента могут накапливаться большие значения, что будет приводить к сильным изменениям весов. Это в свою очередь может сделать нестабильным алгоритм обучения нейронной сети. В таком случае элементы градиента могут переполнить тип данных, в котором они хранятся. Такое явление называется взрывающимся градиентом (англ. exploding gradient).
Существует аналогичная обратная проблема, когда в процессе обучения при обратном распространении ошибки через слои нейронной сети градиент становится все меньше. Это приводит к тому, что веса при обновлении изменяются на слишком малые значения, и обучение проходит неэффективно или останавливается, то есть алгоритм обучения не сходится. Это явление называется затухающим градиентом (англ. vanishing gradient).
Таким образом, увеличение числа слоев нейронной сети с одной стороны увеличивает ее способности к обучению и расширяет ее возможности, но с другой стороны может порождать данную проблему. Поэтому для решения сложных задач с помощью нейронных сетей необходимо уметь определять и устранять ее.
Причины
Рисунок 1. График сигмоиды и ее производной[1]
Такая проблема может возникнуть при использовании нейронных сетях классической функцией активации (англ. activation function) сигмоиды (англ. sigmoid):
$\sigma(x) = \frac{1}{1 + e^{-x}}.$
Эта функция часто используется, поскольку множество ее возможных значений — отрезок $[0, 1]$ — совпадает с возможными значениями вероятностной меры, что делает более удобным ее предсказание. Также график сигмоиды соответствует многим естественным процессам, показывающим рост с малых значений, который ускоряется с течением времени, и достигающим своего предела[2] (например, рост популяции).
Пусть сеть состоит из подряд идущих нейронов с функцией активации $\sigma(x)$; функция потерть (англ. loss function) $L(y) = MSE(y, \hat{y}) = (y — \hat{y})^2$ (англ. MSE — Mean Square Error); $u_d$ — значение, поступающее на вход нейрону на слое $d$; $w_d$ — вес нейрона на слое $d$; $y$ — выход из последнего слоя. Оценим частные производные по весам такой нейронной сети на каждом слое. Оценка для производной сигмоиды видна из рисунка 1.
$\frac{\partial(L(y))}{\partial(w_d)} = \frac{\partial(L(y))}{\partial(y)} \cdot \frac{\partial(y)}{\partial(w_d)} = 2 (y — \hat{y}) \cdot \sigma'(w_d u_d) u_d \leq 2 (y — \hat{y}) \cdot \frac{1}{4} u_d$
$\frac{\partial(L(y))}{\partial(w_{d — 1})} = \frac{\partial(L(y))}{\partial(w_d)} \cdot \frac{\partial(w_d)}{\partial(w_{d — 1})} \leq 2 (y — \hat{y}) \cdot (\frac{1}{4})^2 u_d u_{d-1}$
$\ldots$
Откуда видно, что оценка элементов градиента растет экспоненциально при рассмотрении частных производных по весам слоев в направлении входа в нейронную сеть (уменьшения номера слоя). Это в свою очередь может приводить либо к экспоненциальному росту градиента от слоя к слою, когда входные значения нейронов — числа, по модулю большие $1$, либо к затуханию, когда эти значения — числа, по модулю меньшие $1$.
Однако, входные значения скрытых слоев есть выходные значения функций активаций предшествующих им слоев. В частности, сигмоида насыщается (англ. saturates) при стремлении аргумента к $+\infty$ или $-\infty$, то есть имеет там конечный предел. Это приводит к тому, что более отдаленные слои обучаются медленнее, так как увеличение или уменьшение аргумента насыщенной функции вносит малые изменения, и градиент становится все меньше. Это и есть проблема затухающего градиента.
Способы определения
Взрывающийся градиент
Возникновение проблемы взрывающегося градиента можно определить по следующим признакам:
- Модель плохо обучается на данных, что отражается в высоком значении функции потерь.
- Модель нестабильна, что отражается в значительных скачках значения функции потерь.
- Значение функции потерь принимает значение
NaN.
Более непрозрачные признаки, которые могут подтвердить возникновение проблемы:
- Веса модели растут экспоненциально.
- Веса модели принимают значение
NaN.
Затухающий градиент
Признаки проблемы затухающего градиента:
- Точность модели растет медленно, при этом возможно раннее срабатывание критерия останова, так как алгоритм может решить, что дальнейшее обучение не будет оказывать существенного влияния.
- Градиент ближе к концу показывает более сильные изменения, в то время как градиент ближе к началу почти не показывает никакие изменения.
- Веса модели уменьшаются экспоненциально во время обучения.
- Веса модели стремятся к $0$ во время обучения.
Способы устранения
Использование другой функции активации
Рисунок 2. Графики функций активации: sigmoid, tanh, ReLU, softplus
Как уже упоминалось выше, подверженность нейронной сети проблемам взрывающегося или затухающего градиента во многом зависит от свойств используемых функций активации. Поэтому правильный их подбор важен для предотвращения описываемых проблем.
Tanh
$\tanh(x) = \frac{e^x — e^{-x}}{e^x + e^{-x}}$
Функция аналогична сигмоиде, но множество возможных значений: $[-1, 1]$. Градиенты при этом сосредоточены около $0$,. Однако, эта функция также насыщается в обоих направлениях, поэтому также может приводить к проблеме затухающего градиента.
ReLU
$h(x) = \max(0, x)$
Функция проста для вычисления и имеет производную, равную либо $1$, либо $0$. Также есть мнение, что именно эта функция используется в биологических нейронных сетях. При этом функция не насыщается на любых положительных значениях, что делает градиент более чувствительным к отдаленным слоям.
Недостатком функции является отсутствие производной в нуле, что можно устранить доопределением производной в нуле слева или справа. Также эту проблему устраняет использование гладкой аппроксимации, Softplus.
Существуют модификации ReLU:
- Noisy ReLU: $h(x) = \max(0, x + \varepsilon), \varepsilon \sim N(0, \sigma(x))$.
- Parametric ReLU: $h(x) = \begin{cases} x & x > 0 \\ \beta x & \text{otherwise} \end{cases}$.
- Leaky ReLU: Paramtetric ReLU со значением $\beta = 0.01$.
Softplus
$h(x) = \ln(1 + e^x)$
Гладкий, везде дифференцируемый аналог функции ReLU, следовательно, наследует все ее преимущества. Однако, эта функция более сложна для вычисления. Эмпирически было выявлено, что по качеству не превосходит ReLU.
Графики всех функций активации приведены на рисунок 2.
Изменение модели
Для решения проблемы может оказаться достаточным сокращение числа слоев. Это связано с тем, что частные производные по весам растут экспоненциально в зависимости от глубины слоя.
В рекуррентных нейронных сетях можно воспользоваться техникой обрезания обратного распространения ошибки по времени, которая заключается в обновлении весов с определенной периодичностью.
Использование Residual blocks
Рисунок 3. Устройство residual block[3]
В данной конструкции вывод нейрона подается как следующему нейрону, так и нейрону на расстоянии 2-3 слоев впереди, который суммирует его с выходом предшествующего нейрона, а функция активации в нем — ReLU (см. рисунок 3). Такая связка называется shortcut. Это позволяет при обратном распространении ошибки значениям градиента в слоях быть более чувствительным к градиенту в слоях, с которыми связаны с помощью shortcut, то есть расположенными несколько дальше следующего слоя.
Регуляризация весов
Регуляризация заключается в том, что слишком большие значения весов будут увеличивать функцию потерь. Таким образом, в процессе обучения нейронная сеть помимо оптимизации ответа будет также минимизировать веса, не позволяя им становиться слишком большими.
Обрезание градиента
Образание заключается в ограничении нормы градиента. То есть если норма градиента превышает заранее выбранную величину $T$, то следует масштабировать его так, чтобы его норма равнялась этой величине:
$\nabla_{clipped} = \begin{cases} \nabla & || \nabla || \leq T \\ \frac{T}{|| \nabla ||} \cdot \nabla & \text{otherwise} \end{cases}.$
См. также
- Нейронные сети, перцептрон
- Обратное распространение ошибки
- Регуляризация
- Глубокое обучение
- Сверточные нейронные сети
Примечания
- ↑ towardsdatascience.com — Derivative of the sigmoid function
- ↑ wikipedia.org — Sigmoid function, Applications
- ↑ wikipedia.org — Residual neural network
Источники
- Курс Machine Learning, ИТМО, 2020;
- towardsdatascience.com — The vanishing exploding gradient problem in deep neural networks;
- machinelearningmastery.com — Exploding gradients in neural networks.
-
Обучение нейронных сетей
Способность
к обучению является фундаментальным
свойством мозга. В контексте ИНС процесс
обучения может рассматриваться как
настройка архитектуры сети и весов
связей для эффективного выполнения
специальной задачи. Обычно нейронная
сеть должна настроить веса связей по
имеющейся обучающей выборке.
Функционирование сети улучшается по
мере итеративной настройки весовых
коэффициентов. Свойство сети обучаться
на примерах делает их более привлекательными
по сравнению с системами, которые следуют
определенной системе правил
функционирования, сформулированной
экспертами.
Для
конструирования процесса обучения,
прежде всего, необходимо иметь модель
внешней среды, в которой функционирует
нейронная сеть — знать доступную для
сети информацию. Эта модель определяет
парадигму обучения.
Существуют
три парадигмы обучения: «с учителем»,
«без учителя» (самообучение) и
смешанная. В первом случае нейронная
сеть располагает правильными ответами
(выходами сети) на каждый входной пример.
Веса настраиваются так, чтобы сеть
производила ответы как можно более
близкие к известным правильным ответам.
Усиленный вариант обучения с учителем
предполагает, что известна только
критическая оценка правильности выхода
нейронной сети, но не сами правильные
значения выхода. Обучение без учителя
не требует знания правильных ответов
на каждый пример обучающей выборки. В
этом случае раскрывается внутренняя
структура данных или корреляции между
образцами в системе данных, что позволяет
распределить образцы по категориям.
При смешанном обучении часть весов
определяется посредством обучения с
учителем, в то время как остальная
получается с помощью самообучения.
Теория
обучения рассматривает три фундаментальных
свойства, связанных с обучением по
примерам: емкость, сложность образцов
и вычислительная сложность. Известны
4 основных типа правил обучения: коррекция
по ошибке, машина Больцмана, правило
Хебба и обучение методом соревнования.
Правило
коррекции по ошибке.
При обучении с учителем для каждого
входного примера задан желаемый выход
d. Реальный выход сети y может не совпадать
с желаемым. Принцип коррекции по ошибке
при обучении состоит в использовании
сигнала (d-y) для модификации весов,
обеспечивающей постепенное уменьшение
ошибки. Обучение имеет место только в
случае, когда перцептрон ошибается.
Известны различные модификации этого
алгоритма обучения.
Обучение
Больцмана.
Представляет собой стохастическое
правило обучения, которое следует из
информационных теоретических и
термодинамических принципов. Целью
обучения Больцмана является такая
настройка весовых коэффициентов, при
которой состояния видимых нейронов
удовлетворяют желаемому распределению
вероятностей. Обучение Больцмана может
рассматриваться как специальный случай
коррекции по ошибке, в котором под
ошибкой понимается расхождение корреляций
состояний в двух режимах .
Правило
Хебба. Самым
старым обучающим правилом является
постулат обучения Хебба. Хебб опирался
на следующие нейрофизиологические
наблюдения: если нейроны с обеих сторон
синапса активизируются одновременно
и регулярно, то сила синаптической связи
возрастает. Важной особенностью этого
правила является то, что изменение
синаптического веса зависит только от
активности нейронов, которые связаны
данным синапсом. Это существенно упрощает
цепи обучения в реализации VLSI.
Обучение
методом соревнования.
В отличие от обучения Хебба, в котором
множество выходных нейронов могут
возбуждаться одновременно, при
соревновательном обучении выходные
нейроны соревнуются между собой за
активизацию. Это явление известно как
правило «победитель берет все».
Подобное обучение имеет место в
биологических нейронных сетях. Обучение
посредством соревнования позволяет
кластеризовать входные данные: подобные
примеры группируются сетью в соответствии
с корреляциями и представляются одним
элементом.
При
обучении модифицируются только веса
«победившего» нейрона. Эффект этого
правила достигается за счет такого
изменения сохраненного в сети образца
(вектора весов связей победившего
нейрона), при котором он становится чуть
ближе ко входному примеру.
Любая
нейронная сеть, прежде всего, должна
быть обучена. Процесс обучения заключается
в подстройке внутренних параметров
нейросети под конкретную задачу.
При
обучении «классической» многослойной
нейросети на вход подаются данные или
индикаторы, а выход нейросети сравнивается
с эталонным значением (с так называемым
«учителем»). Разность этих значений
называется ошибкой нейронной сети,
которая и минимизируется в процессе
обучения. Таким образом, обычные нейронные
сети выявляют закономерности между
входными данными и прогнозируемой
величиной. Если такие закономерности
есть, то нейросеть их выделит, и прогноз
будет успешным.
Технология
обучения с учителем НС предполагает
наличие двух однотипных множеств:
-
множество
учебных примеров — используется для
«настройки» НС; -
множество
контрольных примеров — используется
для оценки качества работы НС.
Элементами
этих двух множеств есть пары (X, YI),
где
-
X
— входной вектор для обучаемой НС; -
YI
— верный (желаемый) выходной вектор
для X.
Так
же необходимо определить функцию ошибки
E. Обычно это средняя квадратичная ошибка
(mean squared error — MSE)
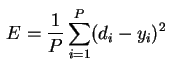
где
-
P
— количество обработанных НС примеров; -
yi
— реальный выход НС; -
di
— желаемый (идеальный) выход НС.
Процедура
обучения НС сводится к процедуре
коррекции весов связей HC. Целью процедуры
коррекции весов есть минимизация функции
ошибки E.
Общая
схема обучения с учителем выглядит так:
1.
Перед началом обучения весовые
коэффициенты НС устанавливаются
некоторым образом, на пример — случайно.
2.
На первом этапе на вход НС в определенном
порядке подаются учебные примеры. На
каждой итерации вычисляется ошибка для
учебного примера EL(ошибка
обучения) и по определенному алгоритму
производится коррекция весов НС. Целью
процедуры коррекции весов есть минимизация
ошибки EL.
3.
На втором этапе обучения производится
проверка правильности работы НС. На
вход НС в определенном порядке подаются
контрольные примеры. На каждой итерации
вычисляется ошибка для контрольного
примера EG
(ошибка обобщения). Если результат
неудовлетворительный то, производится
модификация множества учебных примеров1
и повторение цикла обучения НС.
В
случае однослойной сети алгоритм
обучения с учителем прост. Желаемые
выходные значения нейронов единственного
слоя заведомо известны, и подстройка
весов синаптических связей идет в
направлении, минимизирующем ошибку на
выходе сети.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Рад снова всех приветствовать, и сегодня продолжим планомерно двигаться в выбранном направлении. Речь, конечно, о масштабном разборе искусственных нейронных сетей для решения широкого спектра задач. Продолжим ровно с того момента, на котором остановились в предыдущей части, и это означает, что героем данного поста будет ключевой процесс — обучение нейронных сетей.
- Градиентный спуск
- Функция ошибки
- Метод обратного распространения ошибки
- Пример расчета
Тема эта крайне важна, поскольку именно процесс обучения позволяет сети начать выполнять задачу, для которой она, собственно, и предназначена. То есть нейронная сеть функционирует не по какому-либо жестко заданному на этапе проектирования алгоритму, она совершенствуется в процессе анализа имеющихся данных. Этот процесс и называется обучением нейронной сети. Математически суть процесса обучения заключается в корректировке значений весов синапсов (связей между имеющимися нейронами). Изначально значения весов задаются случайно, затем производится обучение, результатом которого будут новые значения синаптических весов. Это все мы максимально подробно разберем как раз в этой статье.
На своем сайте я всегда придерживаюсь концепции, при которой теоретические выкладки по максимуму сопровождаются практическими примерами для максимальной наглядности. Так мы поступим и сейчас 👍
Итак, суть заключается в следующем. Пусть у нас есть простейшая нейронная сеть, которую мы хотим обучить (продолжаем рассматривать сети прямого распространения):

То есть на входы нейронов I1 и I2 мы подаем какие-либо числа, а на выходе сети получаем соответственно новое значение. При этом нам необходима некая выборка данных, включающая в себя значения входов и соответствующее им, правильное, значение на выходе:
| \bold{I_1} | \bold{I_2} | \bold{O_{net}} |
|---|---|---|
| x_{11} | x_{12} | y_{1} |
| x_{21} | x_{22} | y_{2} |
| x_{31} | x_{32} | y_{3} |
| … | … | … |
| x_{N1} | x_{N2} | y_{N} |
Допустим, сеть выполняет суммирование значений на входе, тогда данный набор данных может быть таким:
| \bold{I_1} | \bold{I_2} | \bold{O_{net}} |
|---|---|---|
| 1 | 4 | 5 |
| 2 | 7 | 9 |
| 3 | 5 | 8 |
| … | … | … |
| 1000 | 1500 | 2500 |
Эти значения и используются для обучения сети. Как именно — рассмотрим чуть ниже, пока сконцентрируемся на идее процесса в целом. Для того, чтобы иметь возможность тестировать работу сети в процессе обучения, исходную выборку данных делят на две части — обучающую и тестовую. Пусть имеется 1000 образцов, тогда можно 900 использовать для обучения, а оставшиеся 100 — для тестирования. Эти величины взяты исключительно ради наглядности и демонстрации логики выполнения операций, на практике все зависит от задачи, размер обучающей выборки может спокойно достигать и сотен тысяч образцов.
Итак, итог имеем следующий — обучающая выборка прогоняется через сеть, в результате чего происходит настройка значений синаптических весов. Один полный проход по всей выборке называется эпохой. И опять же, обучение нейронной сети — это процесс, требующий многократных экспериментов, анализа результатов и творческого подхода. Все перечисленные параметры (размер выборки, количество эпох обучения) могут иметь абсолютно разные значения для разных задач и сетей. Четкого правила тут просто нет, в этом и кроется дополнительный шарм и изящность )
Возвращаемся к разбору, и в результате прохода обучающей выборки через сеть мы получаем сеть с новыми значениями весов синапсов.
Далее мы через эту, уже обученную в той или иной степени, сеть прогоняем тестовую выборку, которая не участвовала в обучении. При этом сеть выдает нам выходные значения для каждого образца, которые мы сравниваем с теми верными значениями, которые имеем.
Анализируем нашу гипотетическую выборку:

Таким образом, для тестирования подаем на вход сети значения x_{(M+1)1}, x_{(M+1)2} и проверяем, чему равен выход, ожидаем очевидно значение y_{(M+1)}. Аналогично поступаем и для оставшихся тестовых образцов. После чего мы можем сделать вывод, успешно или нет работает сеть. Например, сеть дает правильный ответ для 90% тестовых данных, дальше уже встает вопрос — устраивает ли нас данная точность или процесс обучения необходимо повторить, либо провести заново, изменив какие-либо параметры сети.
В этом и заключается суть обучения нейронных сетей, теперь перейдем к деталям и конкретным действиям, которые необходимо осуществить для выполнения данного процесса. Двигаться снова будем поэтапно, чтобы сформировать максимально четкую и полную картину. Поэтому начнем с понятия градиентного спуска, который используется при обучении по методу обратного распространения ошибки. Обо всем этом далее…
Обучение нейронных сетей. Градиентный спуск.
Рассмотрев идею процесса обучения в целом, на данном этапе мы можем однозначно сформулировать текущую цель — необходимо определить математический алгоритм, который позволит рассчитать значения весовых коэффициентов таким образом, чтобы ошибка сети была минимальна. То есть грубо говоря нам необходима конкретная формула для вычисления:
Здесь \Delta w_{ij} — величина, на которую необходимо изменить вес синапса, связывающего нейроны i и j нашей сети. Соответственно, зная это, необходимо на каждом этапе обучения производить корректировку весов связей между всеми элементами нейронной сети. Задача ясна, переходим к делу.
Пусть функция ошибки от веса имеет следующий вид:
Для удобства рассмотрим зависимость функции ошибки от одного конкретного веса:

В начальный момент мы находимся в некоторой точке кривой, а для минимизации ошибки попасть мы хотим в точку глобального минимума функции:
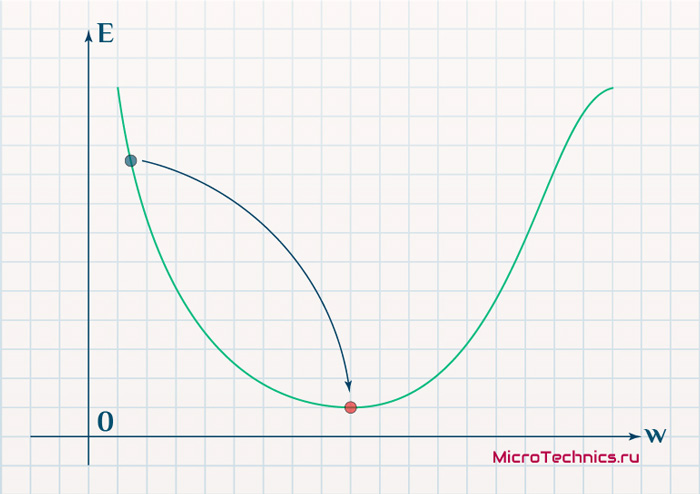
Нанесем на график вектора градиентов в разных точках. Длина векторов численно равна скорости роста функции в данной точке, что в свою очередь соответствует значению производной функции по данной точке. Исходя из этого, делаем вывод, что длина вектора градиента определяется крутизной функции в данной точке:
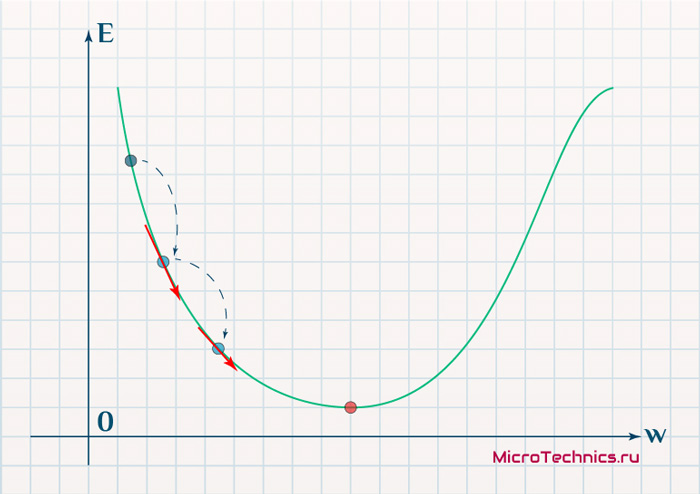
Вывод прост — величина градиента будет уменьшаться по мере приближения к минимуму функции. Это важный вывод, к которому мы еще вернемся. А тем временем разберемся с направлением вектора, для чего рассмотрим еще несколько возможных точек:
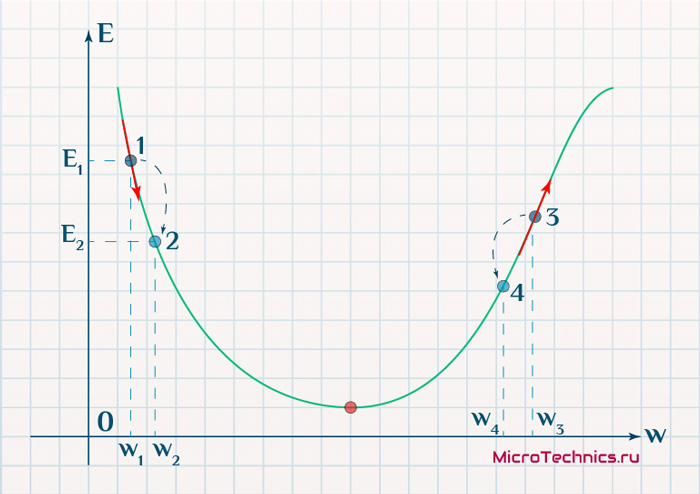
Находясь в точке 1, целью является перейти в точку 2, поскольку в ней значение ошибки меньше (E_2 < E_1), а глобальная задача по-прежнему заключается в ее минимизации. Для этого необходимо изменить величину w на некое значение \Delta w (\Delta w = w_2 — w_1 > 0). При всем при этом в точке 1 градиент отрицательный. Фиксируем данные факты и переходим к точке 3, предположим, что мы находимся именно в ней.
Тогда для уменьшения ошибки наш путь лежит в точку 4, а необходимое изменение значения: \Delta w = w_4 — w_3 < 0. Градиент же в точке 3 положителен. Этот факт также фиксируем.
А теперь соберем воедино эту информацию в виде следующей иллюстрации:
| Переход | \bold{\Delta w} | Знак \bold{\Delta w} | Градиент |
|---|---|---|---|
| 1 \rArr 2 | w_2 — w_1 | + | — |
| 3 \rArr 4 | w_4 — w_3 | — | + |
Вывод напрашивается сам собой — величина, на которую необходимо изменить значение w, в любой точке противоположна по знаку градиенту. И, таким образом, представим эту самую величину в виде:
\Delta w = -\alpha \cdot \frac{dE}{dw}
Имеем в наличии:
- \Delta w — величина, на которую необходимо изменить значение w.
- \frac{dE}{dw} — градиент в этой точке.
- \alpha — скорость обучения.
Собственно, логика метода градиентного спуска и заключается в данном математическом выражении, а именно в том, что для минимизации ошибки необходимо изменять w в направлении противоположном градиенту. В контексте нейронных сетей имеем искомый закон для корректировки весов синаптических связей (для синапса между нейронами i и j):
\Delta w_{ij} = -\alpha \cdot \frac{dE}{dw_{ij}}
Более того, вспомним о важном свойстве, которое мы отдельно пометили. И заключается оно в том, что величина градиента будет уменьшаться по мере приближения к минимуму функции. Что это нам дает? А то, что в том случае, если наша текущая дислокация далека от места назначения, то величина, корректирующая вес связи, будет больше. А это обеспечит скорейшее приближение к цели. При приближении к целевому пункту, величина \frac{dE}{dw_{ij}} будет уменьшаться, что поможет нам точнее попасть в нужную точку, а кроме того, не позволит нам ее проскочить. Визуализируем вышеописанное:
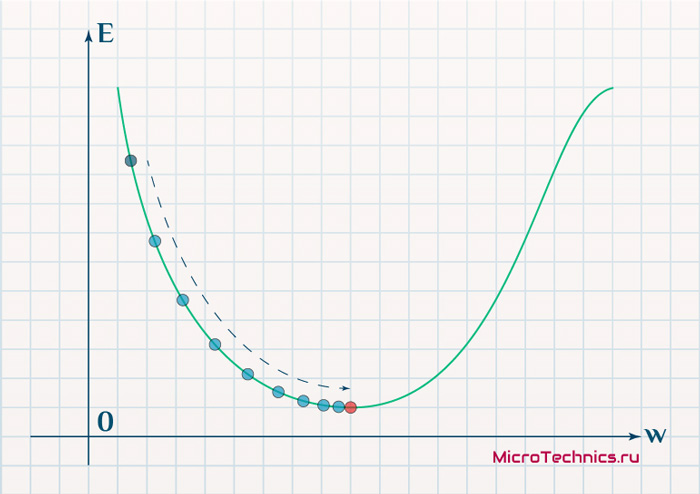
Скорость же обучения несет в себе следующий смысл. Она определяет величину каждого шага при поиске минимума ошибки. Слишком большое значение приводит к тому, что точка может «перепрыгнуть» через нужное значение и оказаться по другую сторону от цели:
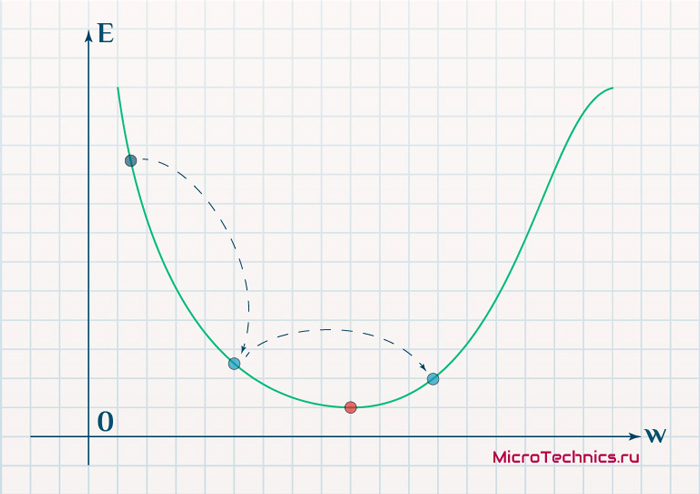
Если же величина будет мала, то это приведет к тому, что спуск будет осуществляться очень медленно, что также является нежелательным эффектом. Поэтому скорость обучения, как и многие другие параметры нейронной сети, является очень важной величиной, для которой нет единственно верного значения. Все снова зависит от конкретного случая и оптимальная величина определяется исключительно исходя из текущих условий.
И даже на этом еще не все, здесь присутствует один важный нюанс, который в большинстве статей опускается, либо вовсе не упоминается. Реальная зависимость может иметь совсем другой вид:
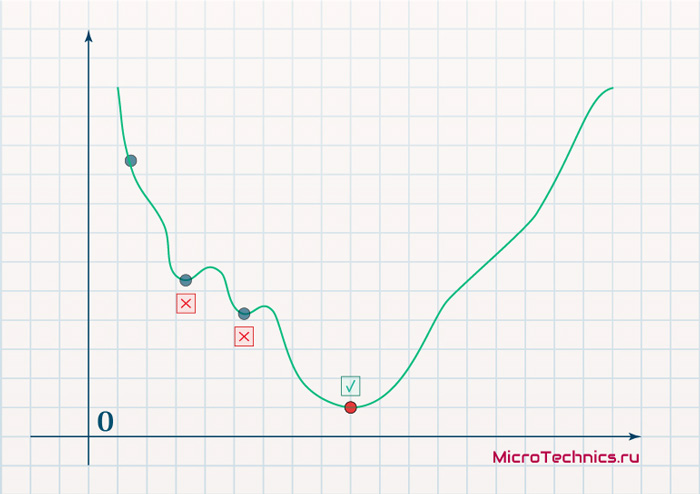
Из чего вытекает потенциальная возможность попадания в локальный минимум, вместо глобального, что является большой проблемой. Для предотвращения данного эффекта вводится понятие момента обучения и формула принимает следующий вид:
\Delta w_{ij} = -\alpha \cdot \frac{dE}{dw_{ij}} + \gamma \cdot \Delta w_{ij}^{t - 1}
То есть добавляется второе слагаемое, которое представляет из себя произведение момента на величину корректировки веса на предыдущем шаге.
Итого, резюмируем продвижение к цели:
- Нашей задачей было найти закон, по которому необходимо изменять величину весов связей между нейронами.
- Наш результат — \Delta w_{ij} = -\alpha \cdot \frac{dE}{dw_{ij}} + \gamma \cdot \Delta w_{ij}^{t — 1} — именно то, что и требовалось 👍
И опять же, полученный результат логичным образом перенаправляет нас на следующий этап, ставя вопросы — что из себя представляет функция ошибки, и как определить ее градиент.
Обучение нейронных сетей. Функция ошибки.
Начнем с того, что определимся с тем, что у нас в наличии, для этого вернемся к конкретной нейронной сети. Пусть вид ее таков:
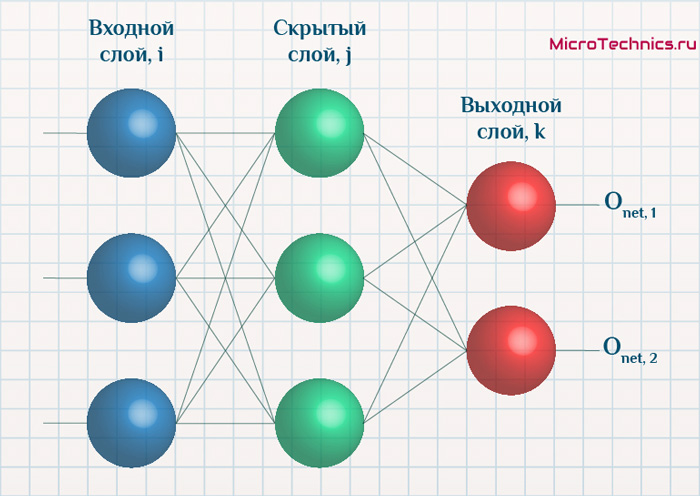
Интересует нас, в первую очередь, часть, относящаяся к нейронам выходного слоя. Подав на вход определенные значения, получаем значения на выходе сети: O_{net, 1} и O_{net, 2}. Кроме того, поскольку мы ведем речь о процессе обучения нейронной сети, то нам известны целевые значения: O_{correct, 1} и O_{correct, 2}. И именно этот набор данных на этом этапе является для нас исходным:
- Известно: O_{net, 1}, O_{net, 2}, O_{correct, 1} и O_{correct, 2}.
- Необходимо определить величины \Delta w_{ij} для корректировки весов, для этого нужно вычислить градиенты (\frac{dE}{dw_{ij}}) для каждого из синапсов.
Полдела сделано — задача четко сформулирована, начинаем деятельность по поиску решения.
В плане того, как определять ошибку, первым и самым очевидным вариантом кажется простая алгебраическая разность. Для каждого из выходных нейронов:
E_k = O_{correct, k} - O_{net, k}
Дополним пример числовыми значениями:
| Нейрон | \bold{O_{net}} | \bold{O_{correct}} | \bold{E} |
|---|---|---|---|
| 1 | 0.9 | 0.5 | -0.4 |
| 2 | 0.2 | 0.6 | 0.4 |
Недостатком данного варианта является то, что в том случае, если мы попытаемся просуммировать ошибки нейронов, то получим:
E_{sum} = e_1 + e_2 = -0.4 + 0.4 = 0
Что не соответствует действительности (нулевая ошибка, говорит об идеальной работе нейронной сети, по факту оба нейрона дали неверный результат). Так что вариант с разностью откидываем за несостоятельностью.
Вторым, традиционно упоминаемым, методом вычисления ошибки является использование модуля разности:
E_k = | O_{correct, k} - O_{net, k} |
Тут в действие вступает уже проблема иного рода:
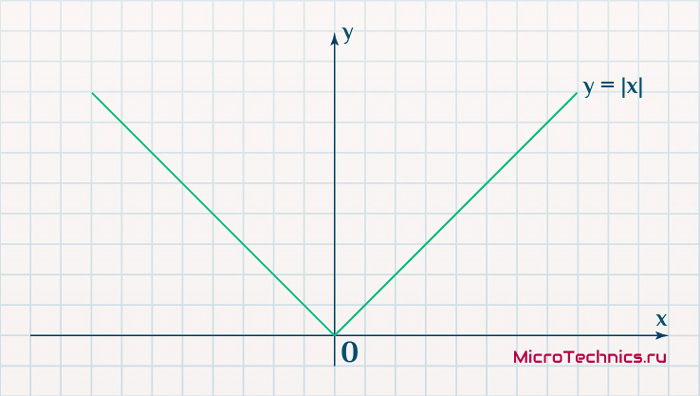
Функция, бесспорно, симпатична, но при приближении к минимуму ее градиент является постоянной величиной, скачкообразно меняясь при переходе через точку минимума. Это нас также не устраивает, поскольку, как мы обсуждали, концепция заключалась в том числе в том, чтобы по мере приближения к минимуму значение градиента уменьшалось.
В итоге хороший результат дает зависимость (для выходного нейрона под номером k):
E_k = (O_{correct, k} - O_{net, k})^2
Функция по многим своим свойствам идеально удовлетворяет нуждам обучения нейронной сети, так что выбор сделан, остановимся на ней. Хотя, как и во многих аспектах, качающихся нейронных сетей, данное решение не является единственно и неоспоримо верным. В каких-то случаях лучше себя могут проявить другие зависимости, возможно, что какой-то вариант даст большую точность, но неоправданно высокие затраты производительности при обучении. В общем, непаханное поле для экспериментов и исследований, это и привлекательно.
Краткий вывод промежуточного шага, на который мы вышли:
- Имеющееся: \frac{dE}{dw_{jk}} = \frac{d}{d w_{jk}}(O_{correct, k} — O_{net, k})^2.
- Искомое по-прежнему: \Delta w_{jk}.
Несложные диффернциально-математические изыскания выводят на следующий результат:
\frac{dE}{d w_{jk}} = -(O_{correct, k} - O_{net, k}) \cdot f{\Large{\prime}}(\sum_{j}w_{jk}O_j) \cdot O_j
Здесь эти самые изыскания я все-таки решил не вставлять, дабы не перегружать статью, которая и так выходит объемной. Но в случае необходимости и интереса, отпишите в комментарии, я добавлю вычисления и закину их под спойлер, как вариант.
Освежим в памяти структуру сети:
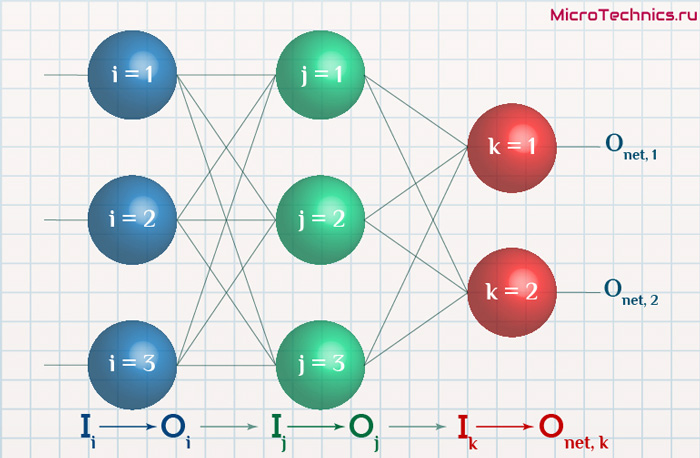
Формулу можно упростить, сгруппировав отдельные ее части:
- (O_{correct, k} — O_{net, k}) \cdot f{\Large{\prime}}(\sum_{j}w_{jk}O_j) — ошибка нейрона k.
- O_j — тут все понятно, выходной сигнал нейрона j.
f{\Large{\prime}}(\sum_{j}w_{jk}O_j) — значение производной функции активации. Причем, обратите внимание, что \sum_{j}w_{jk}O_j — это не что иное, как сигнал на входе нейрона k (I_{k}). Тогда для расчета ошибки выходного нейрона: \delta_k = (O_{correct, k} — O_{net, k}) \cdot f{\Large{\prime}}(I_k).
Итог: \frac{dE}{d w_{jk}} = -\delta_k \cdot O_j.
Одной из причин популярности сигмоидальной функции активности является то, что ее производная очень просто выражается через саму функцию:
f{'}(x) = f(x)\medspace (1\medspace-\medspace f(x))
Данные алгебраические вычисления справедливы для корректировки весов между скрытым и выходным слоем, поскольку для расчета ошибки мы используем просто разность между целевым и полученным результатом, умноженную на производную.
Для других слоев будут незначительные изменения, касающиеся исключительно первого множителя в формуле:
\frac{dE}{d w_{ij}} = -\delta_j \cdot O_i
Который примет следующий вид:
\delta_j = (\sum_{k}{}{\delta_k\medspace w_{jk}}) \cdot f{\Large{\prime}}(I_j)
То есть ошибка для элемента слоя j получается путем взвешенного суммирования ошибок, «приходящих» к нему от нейронов следующего слоя и умножения на производную функции активации. В результате:
\frac{dE}{d w_{ij}} = -(\sum_{k}{}{\delta_k\medspace w_{jk}}) \cdot f{\Large{\prime}}(I_j) \cdot O_i
Снова подводим промежуточный итог, чтобы иметь максимально полную и структурированную картину происходящего. Вот результаты, полученные нами на двух этапах, которые мы успешно миновали:
- Ошибка:
- выходной слой: \delta_k = (O_{correct, k} — O_{net, k}) \cdot f{\Large{\prime}}(I_k)
- скрытые слои: \delta_j = (\sum_{k}{}{\delta_k\medspace w_{jk}}) \cdot f{\Large{\prime}}(I_j)
- Градиент: \frac{dE}{d w_{ij}} = -\delta_j \cdot O_i
- Корректировка весовых коэффициентов: \Delta w_{ij} = -\alpha \cdot \frac{dE}{dw_{ij}} + \gamma \cdot \Delta w_{ij}^{t — 1}
Преобразуем последнюю формулу:
\Delta w_{ij} = \alpha \cdot \delta_j \cdot O_i + \gamma \cdot \Delta w_{ij}^{t - 1}
Из этого мы делаем вывод, что на данный момент у нас есть все, что необходимо для того, чтобы произвести обучение нейронной сети. И героем следующего подраздела будет алгоритм обратного распространения ошибки.
Метод обратного распространения ошибки.
Данный метод является одним из наиболее распространенных и популярных, чем и продиктован его выбор для анализа и разбора. Алгоритм обратного распространения ошибки относится к методам обучение с учителем, что на деле означает необходимость наличия целевых значений в обучающих сетах.
Суть же метода подразумевает наличие двух этапов:
- Прямой проход — входные сигналы двигаются в прямом направлении, в результате чего мы получаем выходной сигнал, из которого в дальнейшем рассчитываем значение ошибки.
- Обратный проход — обратное распространение ошибки — величина ошибки двигается в обратном направлении, в результате происходит корректировка весовых коэффициентов связей сети.
Начальные значения весов (перед обучением) задаются случайными, есть ряд методик для выбора этих значений, я опишу в отдельном материале максимально подробно. Пока вот можно полистать — ссылка.
Вернемся к конкретному примеру для явной демонстрации этих принципов:
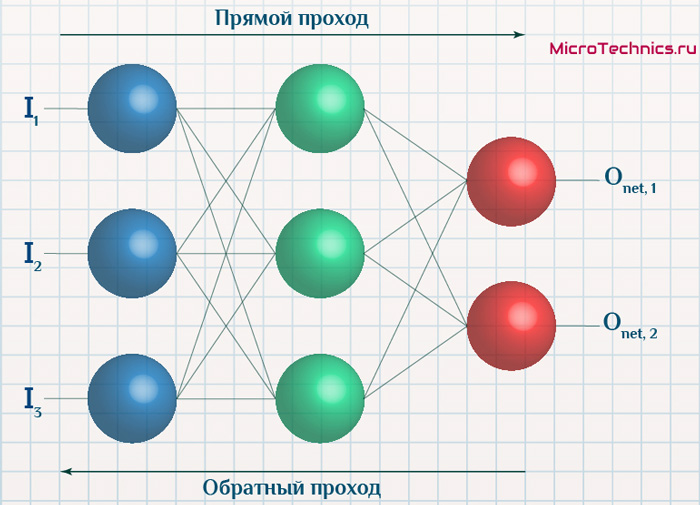
Итак, имеется нейронная сеть, также имеется набор данных обучающей выборки. Как уже обсудили в начале статьи — обучающая выборка представляет из себя набор образцов (сетов), каждый из которых состоит из значений входных сигналов и соответствующих им «правильных» значений выходных величин.
Процесс обучения нейронной сети для алгоритма обратного распространения ошибки будет таким:
- Прямой проход. Подаем на вход значения I_1, I_2, I_3 из обучающей выборки. В результате работы сети получаем выходные значения O_{net, 1}, O_{net, 2}. Этому целиком и полностью был посвящен предыдущий манускрипт.
- Рассчитываем величины ошибок для всех слоев:
- для выходного: \delta_k = (O_{correct, k} — O_{net, k}) \cdot f{\Large{\prime}}(I_k)
- для скрытых: \delta_j = (\sum_{k}{}{\delta_k\medspace w_{jk}}) \cdot f{\Large{\prime}}(I_j)
- Далее используем полученные значения для расчета \Delta w_{ij} = \alpha \cdot \delta_j \cdot O_i + \gamma \cdot \Delta w_{ij}^{t — 1}
- И финишируем, рассчитывая новые значения весов: w_{ij \medspace new} = w_{ij} + \Delta w_{ij}
- На этом один цикл обучения закончен, данные шаги 1 — 4 повторяются для других образцов из обучающей выборки.
Обратный проход завершен, а вместе с ним и одна итерация процесса обучения нейронной сети по данному методу. Собственно, обучение в целом заключается в многократном повторении этих шагов для разных образцов из обучающей выборки. Логику мы полностью разобрали, при повторном проведении операций она остается в точности такой же.
Таким образом, максимально подробно концентрируясь именно на сути и логике процессов, мы в деталях разобрали метод обратного распространения ошибки. Поэтому переходим к завершающей части статьи, в которой разберем практический пример, произведя полностью все вычисления для конкретных числовых величин. Все в рамках продвигаемой мной концепции, что любая теоретическая информация на порядок лучше может быть осознана при применении ее на практике.
Пример расчетов для метода обратного распространения ошибки.
Возьмем нейронную сеть и зададим начальные значения весов:
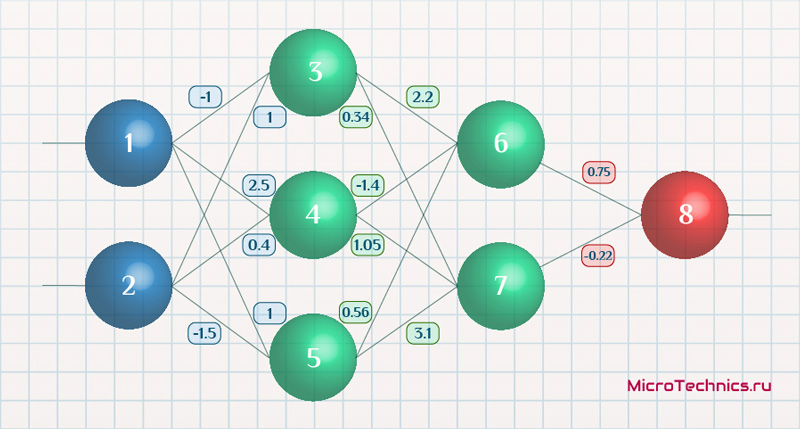
Здесь я задал значения не в соответствии с существующими на сегодняшний день методами, а просто случайным образом для наглядности примера.
В качестве функции активации используем сигмоиду:
f(x) = \frac{1}{1 + e^{-x}}
И ее производная:
f{\Large{\prime}}(x) = f(x)\medspace (1\medspace-\medspace f(x))
Берем один образец из обучающей выборки, пусть будут такие значения:
- Входные: I_1 = 0.6, I_1 = 0.7.
- Выходное: O_{correct} = 0.9.
Скорость обучения \alpha пусть будет равна 0.3, момент — \gamma = 0.1. Все готово, теперь проведем полный цикл для метода обратного распространения ошибки, то есть прямой проход и обратный.
Прямой проход.
Начинаем с выходных значений нейронов 1 и 2, поскольку они являются входными, то:
O_1 = I_1 = 0.6 \\ O_2 = I_2 = 0.7
Значения на входе нейронов 3, 4 и 5:
I_3 = O_1 \cdot w_{13} + O_2 \cdot w_{23} = 0.6 \cdot (-1\medspace) + 0.7 \cdot 1 = 0.1 \\
I_4 = 0.6 \cdot 2.5 + 0.7 \cdot 0.4 = 1.78 \\
I_5 = 0.6 \cdot 1 + 0.7 \cdot (-1.5\medspace) = -0.45
На выходе этих же нейронов первого скрытого слоя:
O_3 = f(I3\medspace) = 0.52 \\ O_4 = 0.86\\ O_5 = 0.39
Продолжаем аналогично для следующего скрытого слоя:
I_6 = O_3 \cdot w_{36} + O_4 \cdot w_{46} + O_5 \cdot w_{56} = 0.52 \cdot 2.2 + 0.86 \cdot (-1.4\medspace) + 0.39 \cdot 0.56 = 0.158 \\
I_7 = 0.52 \cdot 0.34 + 0.86 \cdot 1.05 + 0.39 \cdot 3.1 = 2.288 \\
O_6 = f(I_6) = 0.54 \\
O_7 = 0.908
Добрались до выходного нейрона:
I_8 = O_6 \cdot w_{68} + O_7 \cdot w_{78} = 0.54 \cdot 0.75 + 0.908 \cdot (-0.22\medspace) = 0.205 \\
O_8 = O_{net} = f(I_8) = 0.551
Получили значение на выходе сети, кроме того, у нас есть целевое значение O_{correct} = 0.9. То есть все, что необходимо для обратного прохода, имеется.
Обратный проход.
Как мы и обсуждали, первым этапом будет вычисление ошибок всех нейронов, действуем:
\delta_8 = (O_{correct} - O_{net}) \cdot f{\Large{\prime}}(I_8) = (O_{correct} - O_{net}) \cdot f(I_8) \cdot (1-f(I_8)) = (0.9 - 0.551\medspace) \cdot 0.551 \cdot (1-0.551\medspace) = 0.0863 \\
\delta_7 = (\sum_{k}{}{\delta_k\medspace w_{jk}}) \cdot f{\Large{\prime}}(I_7) = (\delta_8 \cdot w_{78}) \cdot f{\Large{\prime}}(I_7) = 0.0863 \cdot (-0.22\medspace) \cdot 0.908 \cdot (1 - 0.908\medspace) = -0.0016 \\
\delta_6 = 0.086 \cdot 0.75 \cdot 0.54 \cdot (1 - 0.54\medspace) = 0.016 \\
\delta_5 = (\sum_{k}{}{\delta_k\medspace w_{jk}}) \cdot f{\Large{\prime}}(I_5) = (\delta_7 \cdot w_{57} + \delta_6 \cdot w_{56}) \cdot f{\Large{\prime}}(I_7) = (-0.0016 \cdot 3.1 + 0.016 \cdot 0.56) \cdot 0.39 \cdot (1 - 0.39\medspace) = 0.001 \\
\delta_4 = (-0.0016 \cdot 1.05 + 0.016 \cdot (-1.4)) \cdot 0.86 \cdot (1 - 0.86\medspace) = -0.003 \\
\delta_3 = (-0.0016 \cdot 0.34 + 0.016 \cdot 2.2) \cdot 0.52 \cdot (1 - 0.52\medspace) = -0.0087
С расчетом ошибок закончили, следующий этап — расчет корректировочных величин для весов всех связей. Для этого мы вывели формулу:
\Delta w_{ij} = \alpha \cdot \delta_j \cdot O_i + \gamma \cdot \Delta w_{ij}^{t - 1}
Как вы помните, \Delta w_{ij}^{t — 1} — это величина поправки для данного веса на предыдущей итерации. Но поскольку у нас это первый проход, то данное значение будет нулевым, соответственно, в данном случае второе слагаемое отпадает. Но забывать о нем нельзя. Продолжаем калькулировать:
\Delta w_{78} = \alpha \cdot \delta_8 \cdot O_7 = 0.3 \cdot 0.0863 \cdot 0.908 = 0.0235 \\
\Delta w_{68} = 0.3 \cdot 0.0863 \cdot 0.54= 0.014 \\
\Delta w_{57} = \alpha \cdot \delta_7 \cdot O_5 = 0.3 \cdot (−0.0016\medspace) \cdot 0.39= -0.00019 \\
\Delta w_{47} = 0.3 \cdot (−0.0016\medspace) \cdot 0.86= -0.0004 \\
\Delta w_{37} = 0.3 \cdot (−0.0016\medspace) \cdot 0.52= -0.00025 \\
\Delta w_{56} = \alpha \cdot \delta_6 \cdot O_5 = 0.3 \cdot 0.016 \cdot 0.39= 0.0019 \\
\Delta w_{46} = 0.3 \cdot 0.016 \cdot 0.86= 0.0041 \\
\Delta w_{36} = 0.3 \cdot 0.016 \cdot 0.52= 0.0025 \\
\Delta w_{25} = \alpha \cdot \delta_5 \cdot O_2 = 0.3 \cdot 0.001 \cdot 0.7= 0.00021 \\
\Delta w_{15} = 0.3 \cdot 0.001 \cdot 0.6= 0.00018 \\
\Delta w_{24} = \alpha \cdot \delta_4 \cdot O_2 = 0.3 \cdot (-0.003\medspace) \cdot 0.7= -0.00063 \\
\Delta w_{14} = 0.3 \cdot (-0.003\medspace) \cdot 0.6= -0.00054 \\
\Delta w_{23} = \alpha \cdot \delta_3 \cdot O_2 = 0.3 \cdot (−0.0087\medspace) \cdot 0.7= -0.00183 \\
\Delta w_{13} = 0.3 \cdot (−0.0087\medspace) \cdot 0.6= -0.00157
И самый что ни на есть заключительный этап — непосредственно изменение значений весовых коэффициентов:
w_{78 \medspace new} = w_{78} + \Delta w_{78} = -0.22 + 0.0235 = -0.1965 \\
w_{68 \medspace new} = 0.75+ 0.014 = 0.764 \\
w_{57 \medspace new} = 3.1 + (−0.00019\medspace) = 3.0998\\
w_{47 \medspace new} = 1.05 + (−0.0004\medspace) = 1.0496\\
w_{37 \medspace new} = 0.34 + (−0.00025\medspace) = 0.3398\\
w_{56 \medspace new} = 0.56 + 0.0019 = 0.5619 \\
w_{46 \medspace new} = -1.4 + 0.0041 = -1.3959 \\
w_{36 \medspace new} = 2.2 + 0.0025 = 2.2025 \\
w_{25 \medspace new} = -1.5 + 0.00021 = -1.4998 \\
w_{15 \medspace new} = 1 + 0.00018 = 1.00018 \\
w_{24 \medspace new} = 0.4 + (−0.00063\medspace) = 0.39937 \\
w_{14 \medspace new} = 2.5 + (−0.00054\medspace) = 2.49946 \\
w_{23 \medspace new} = 1 + (−0.00183\medspace) = 0.99817 \\
w_{13 \medspace new} = -1 + (−0.00157\medspace) = -1.00157\\
И на этом данную масштабную статью завершаем, конечно же, не завершая на этом деятельность по использованию нейронных сетей. Так что всем спасибо за прочтение, любые вопросы пишите в комментариях и на форуме, ну и обязательно следите за обновлениями и новыми материалами, до встречи!

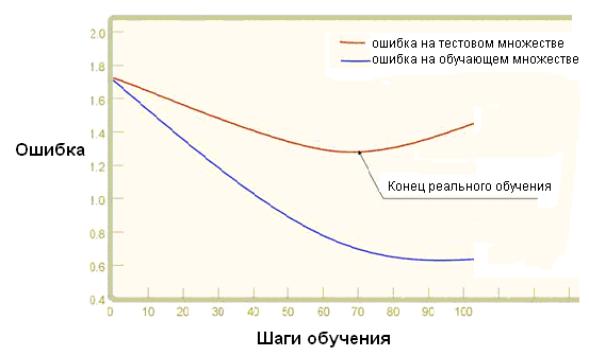

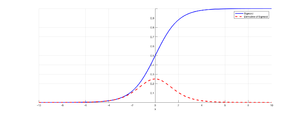
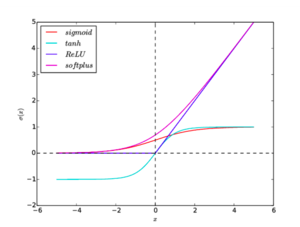
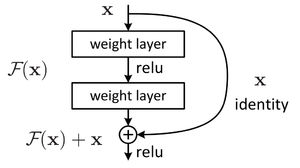
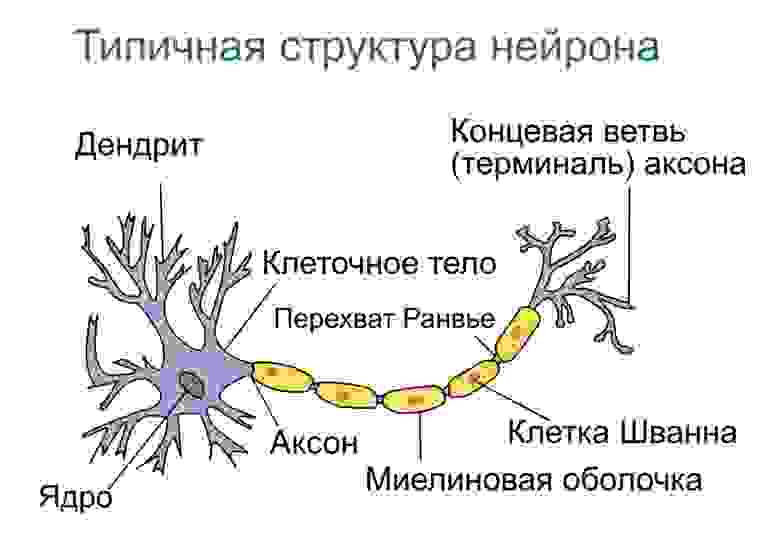



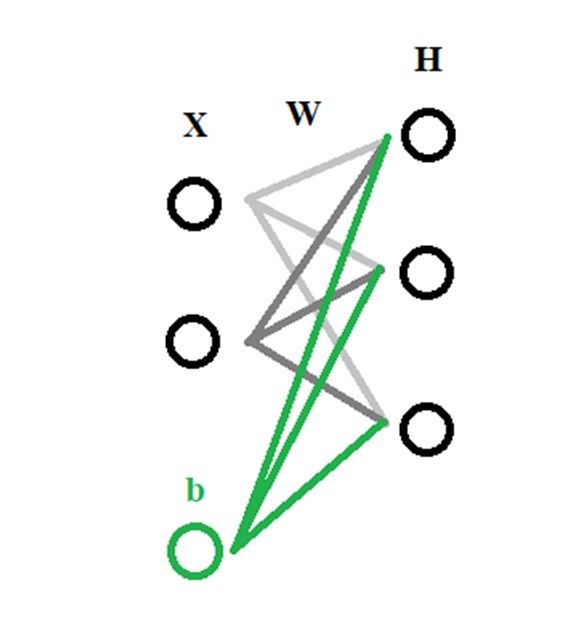






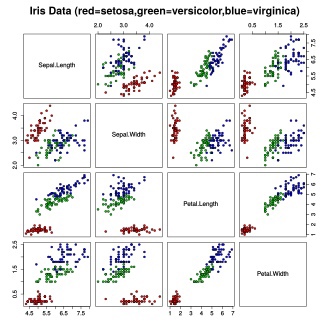

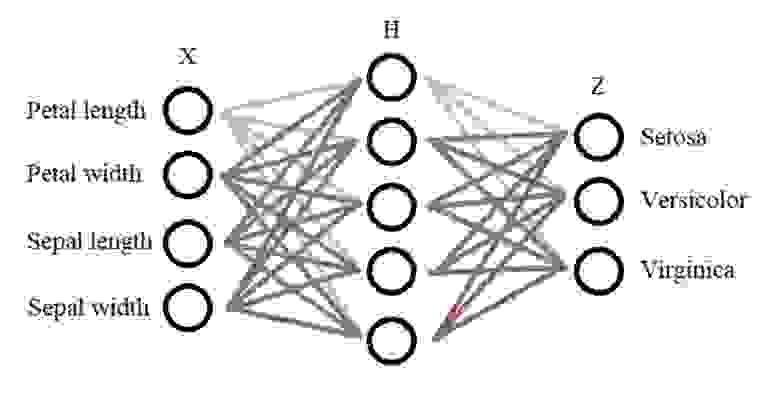
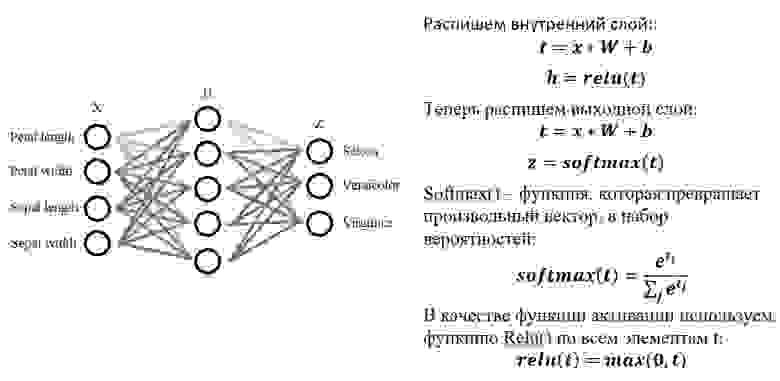
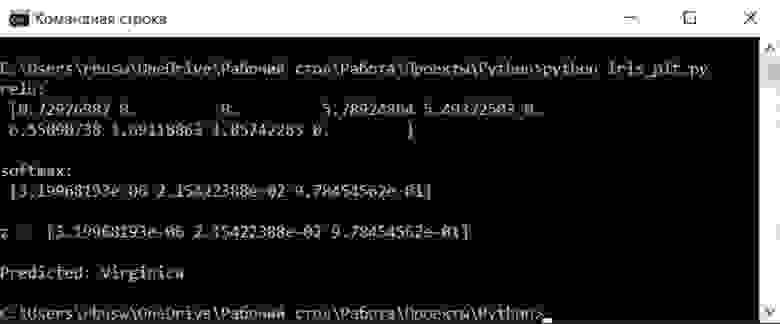

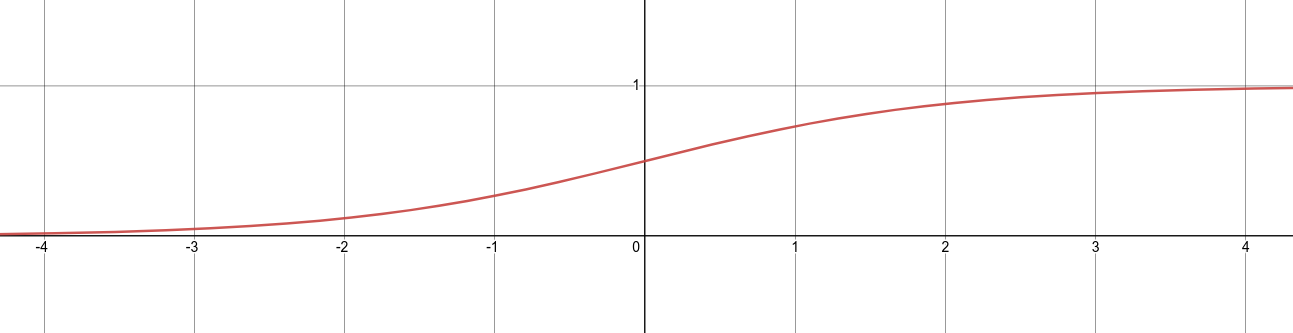
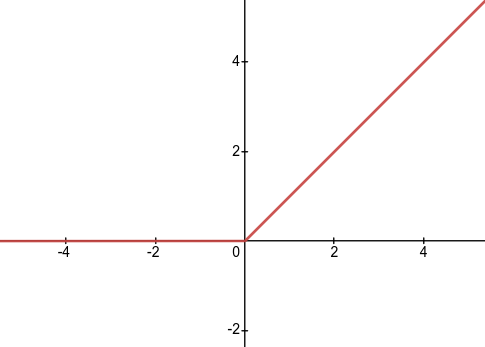

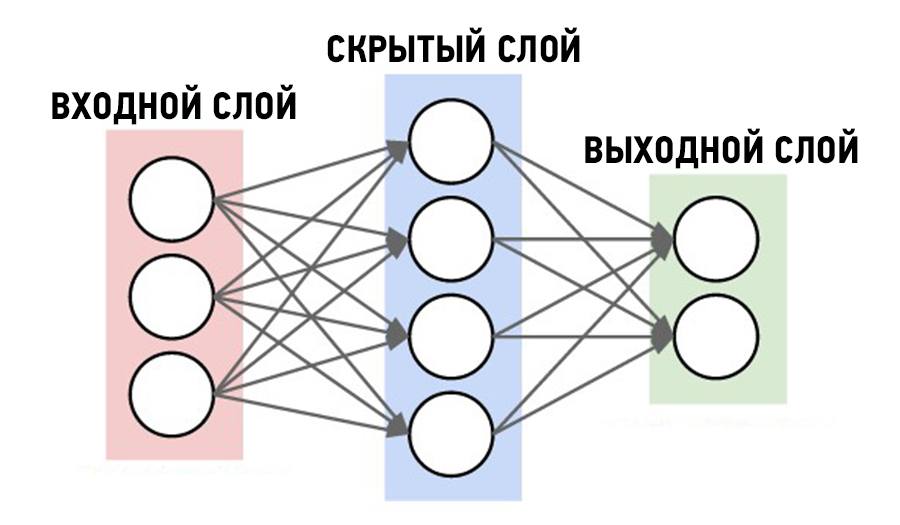
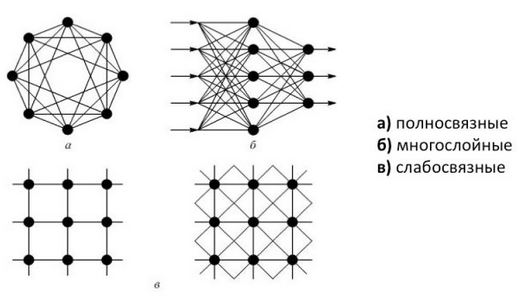
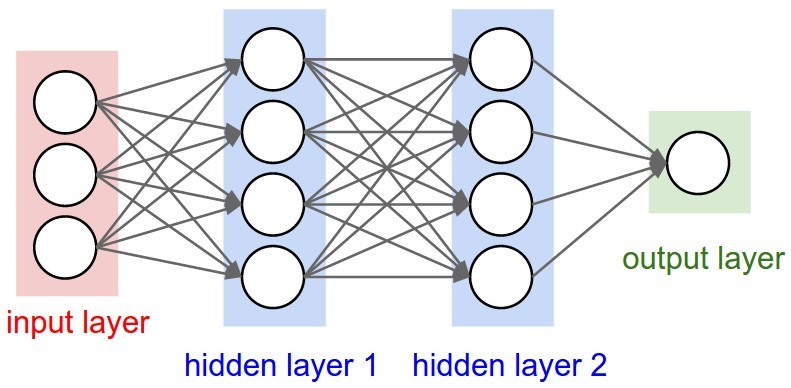
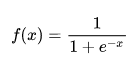
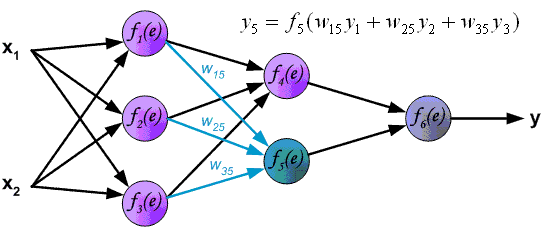
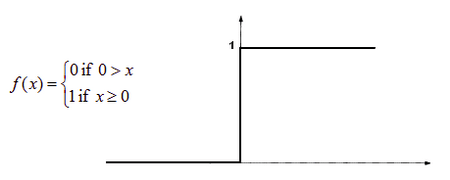
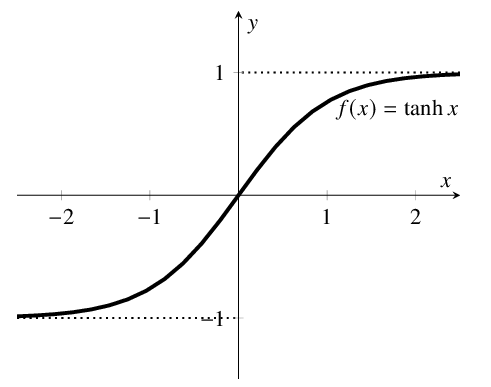
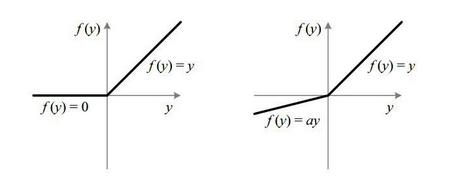
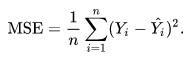
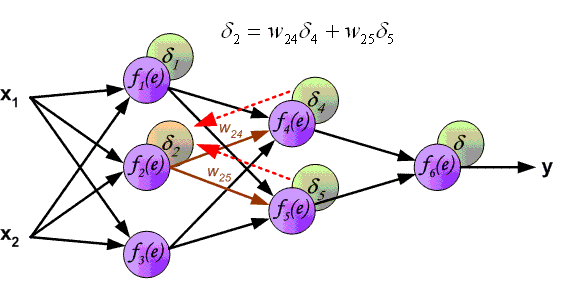
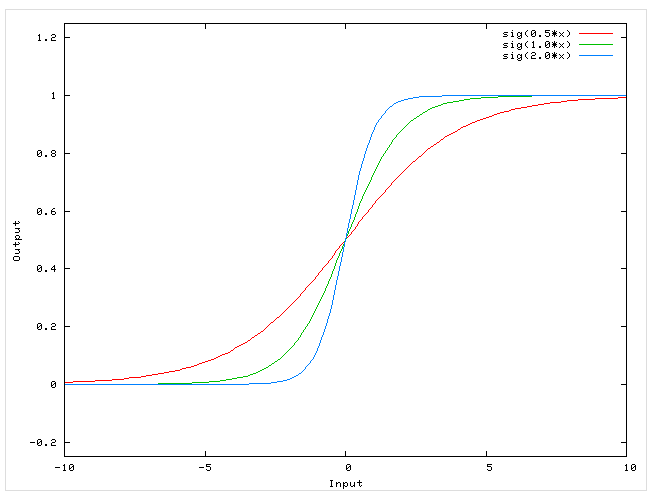
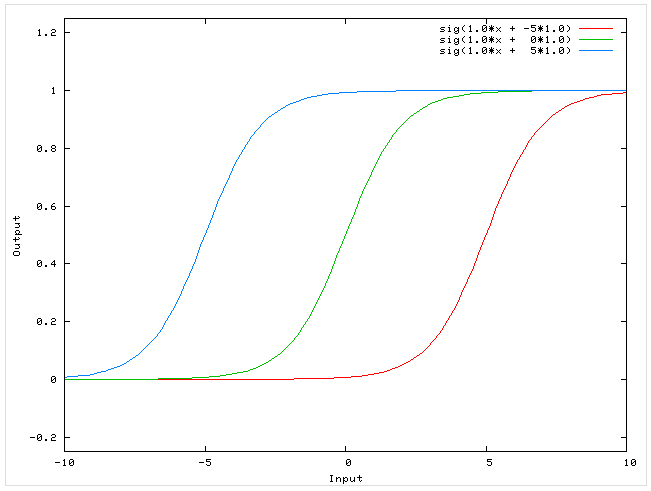


![Пример весов в диапазоне [-1;1]](https://codeby.school/images/immersion_in_ml_part1/16.png)