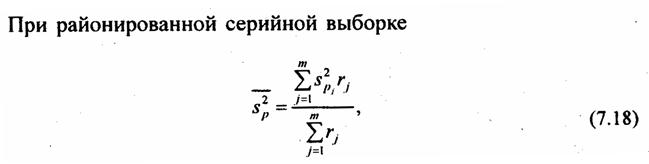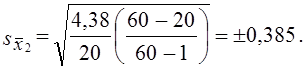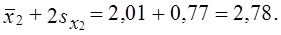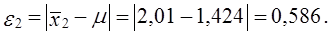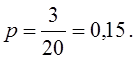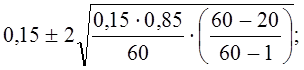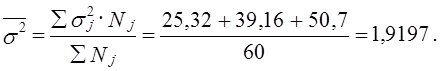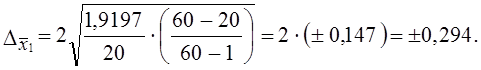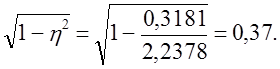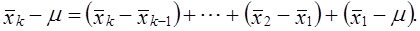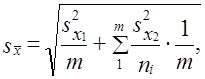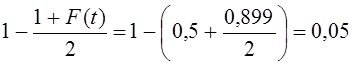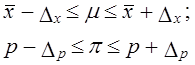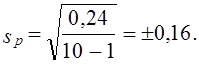Ошибки выборочного наблюдения полнота выборки

Между
признаками выборочной совокупности и
признаками генеральной совокупности,
как правило, существует некоторое
расхождение, которое называется ошибкой
статистического наблюдения. При массовом
наблюдении ошибки неизбежны, но возникают
они в результате действия различных
причин. Величина возможной ошибки
выборочного признака происходит из-за
ошибок регистрации и ошибок
репрезентативности. Ошибки регистрации,
или технические ошибки, связаны с
недостаточной квалификацией наблюдателей,
неточностью подсчетов, несовершенством
приборов и т. п.

Под
ошибкой
репрезентативности
(представительства) понимают расхождение
между выборочной характеристикой и
предполагаемой характеристикой
генеральной совокупности. Ошибки
репрезентативности бывают случайными
и систематическими. Систематические
ошибки связаны с нарушением установленных
правил отбора. Случайные
ошибки объясняются недостаточно
равномерным представлением в выборочной
совокупности различных категорий
единиц генеральной совокупности.

В
результате первой причины выборка
легко может оказаться смещенной, так
как при отборе каждой единицы допускается
ошибка, всегда направленная в одну и
ту же сторону. Эта ошибка получила
название ошибки
смещения.
Ее размер может превышать величину
случайной ошибки. Особенность ошибки
смещения состоит в том, что, являясь
постоянной частью ошибки репрезентативности,
она увеличивается с увеличением объема
выборки. Случайная же ошибка с увеличением
объема выборки уменьшается. Кроме того,
величину случайной ошибки можно
определить, тогда как размер ошибки
смещения практически определить очень
сложно, а иногда и невозможно, поэтому
важно знать причины, вызывающие ошибку
смещения, и предусмотреть мероприятия
по ее устранению.

Ошибки
смещения бывают преднамеренные и
непреднамеренные. Причиной возникновения
преднамеренной
ошибки
является тенденциозный подход к выбору
единиц из генеральной совокупности.
Чтобы не допустить появление такой
ошибки, необходимо соблюдать принцип
случайности отбора единиц.

Непреднамеренные
ошибки
могут возникать на стадии подготовки
выборочного наблюдения, формирования
выборочной совокупности и анализа ее
данных. Чтобы не допустить появление
таких ошибок, необходима хорошая основа
выборки, т. е. та генеральная
совокупность, из которой предполагается
производить отбор, например список
единиц отбора. Основа выборки должна
быть достоверной, полной и соответствовать
цели исследования, а единицы отбора и
их характеристики должны соответствовать
действительному их состоянию на момент
подготовки выборочного наблюдения.
Нередки случаи, когда в отношении
некоторых единиц, попавших в выборку,
трудно собрать сведения из-за их
отсутствия на момент наблюдения,
нежелания дать сведения и т. п. В
таких случаях эти единицы приходится
заменять другими. Необходимо следить,
чтобы замена осуществлялась равноценными
единицами.

Случайная
ошибка
выборки возникает в результате случайных
различий между единицами, попавшими в
выборку, и единицами генеральной
совокупности, т. е. она связана со
случайным отбором. Теоретическим
обоснованием появления случайных
ошибок выборки является теория
вероятностей и ее предельные теоремы.

Сущность
предельных
теорем
состоит в том, что в массовых явлениях
совокупное влияние различных случайных
причин на формирование закономерностей
и обобщающих характеристик будет сколь
угодно малой величиной или практически
не зависит от случая. Так как случайная
ошибка выборки возникает в результате
случайных различий между единицами
выборочной и генеральной совокупностей,
то при достаточно большом объеме выборки
она будет сколь угодно мала.

Предельные
теоремы теории вероятностей позволяют
определять размер случайных ошибок
выборки. Различают среднюю (стандартную)
и предельную ошибку выборки. Под средней
(стандартной) ошибкой
выборки понимают такое расхождение
между средней выборочной и генеральной
совокупностями (~ —), которое не превышает
±.
Предельной
ошибкой
выборки принято считать максимально
возможное расхождение (~ —), т. е.
максимум ошибки при заданной вероятности
ее появления.

В
математической теории выборочного
метода сравниваются средние характеристики
признаков выборочной и генеральной
совокупностей и доказывается, что с
увеличением объема выборки вероятность
появления больших ошибок и пределы
максимально возможной ошибки уменьшаются.
Чем больше обследуется единиц, тем
меньше будет величина расхождений
выборочных и генеральных характеристик.
На основании теоремы, доказанной П.Л.
Чебышевым, величину стандартной ошибки
простой случайной выборки при достаточно
большом объеме выборки (n)
можно определить по формуле

– стандартная
ошибка.

Из
этой формулы средней (стандартной)
ошибки простой случайной выборки видно,
что величина зависит от изменчивости
признака в генеральной совокупности
(чем больше вариация признака, тем
больше ошибка выборки) и от объема
выборки n
(чем больше обследуется единиц, тем
меньше будет величина расхождений
выборочных и генеральных характеристик).

Академик
A.M. Ляпунов доказал, что вероятность
появления случайной ошибки выборки
при достаточно большом ее объеме
подчиняется закону нормального
распределения. Эта вероятность
определяется по формуле

В
математической статистике употребляют
коэффициент доверия t, значения функции
F(t)
табулированы при разных его значениях,
при этом получают соответствующие
уровни доверительной вероятности
(табл. 6.1).

Таблица
6.1

Коэффициент
доверия t и соответствующие уровни
доверительной вероятности

Коэффициент
доверия позволяет вычислить предельную
ошибку выборки,

т. е.
предельная ошибка выборки равна
t-кратному числу средних ошибок выборки.

Таким
образом, величина предельной ошибки
выборки может быть установлена с
определенной вероятностью. Как видно
из последней графы табл. 6.1, вероятность
появления ошибки равной или большей
утроенной средней ошибки выборки,
т. е. 

крайне
мала и равна 0,003(1–0,997). Такие маловероятные
события считаются практически
невозможными, а потому величину

можно
принять за предел возможной ошибки
выборки.

Выборочное
наблюдение дает возможность определить
среднюю арифметическую выборочной
совокупности и величину предельной
ошибки этой средней, которая показывает
(с определенной вероятностью), насколько
выборочная величина может отличаться
от генеральной средней в большую или
меньшую сторону. Тогда величина
генеральной средней будет представлена
интервальной оценкой, для которой
нижняя граница будет равна

Интервал,
в который с данной степенью вероятности
будет заключена неизвестная величина
оцениваемого параметра, называют
доверительным,
а вероятность Р
– доверительной вероятностью.
Чаще всего доверительную вероятность
принимают равной 0,95 или 0,99, тогда
коэффициент доверия t
равен соответственно 1,96 и 2,58. Это
означает, что доверительный интервал
с заданной вероятностью заключает в
себе генеральную среднюю.

Наряду
с абсолютной величиной предельной
ошибки выборки рассчитывается и
относительная
ошибка
выборки, которая определяется как
процентное отношение предельной ошибки
выборки к соответствующей характеристике
выборочной совокупности:

Чем
больше величина предельной ошибки
выборки, тем больше величина доверительного
интервала и тем, следовательно, ниже
точность оценки. Средняя (стандартная)
ошибка выборки зависит от объема выборки
и степени вариации признака в генеральной
совокупности.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #

  12.04.2015613.89 Кб24pr.doc

• #
• #
• #
• #

1.1. Ошибки
выборочного наблюдения

Средняя
ошибка выборки показывает, как генеральная средняя отклоняется в среднем от выборочной средней в ту или другую сторону. Формула
расчета средней ошибки выборки определяется видом исследуемого признака единиц
совокупности (количественный или альтернативный) и
способом отбора (бесповторный или повторный).

·        
Если отбор повторный, а признак количественный
средняя ошибка выборки определяется по формуле

 , где — дисперсия признака в выборочной совокупности

n- число единиц
в выборке

·        
Если отбор бесповторный, а признак
количественный

, где N—
число единиц в генеральной совокупности

·        
Если отбор повторный, а признак альтернативный

, где w-выборочная
доля

·        
Если отбор бесповторный, а признак
альтернативный

Предельная ошибка выборки— показывающая с определенной степенью вероятности
отклонения средней от выборочной средней.

Предельная ошибка выборки

 , где параметр t зависит
от вероятности

Некоторые значения параметра t приведены
в таблице:

Вероятность, p	0.95	0.954	0.9876	0.9907	0.9973	0.9999
Параметр t	1.96	2.0	2.5	2.6	3.0	4.0

·        
Если отбор повторный, а признак количественный
средняя ошибка выборки определяется по формуле

 , где — дисперсия признака в выборочной совокупности

n- число единиц
в выборке

·        
Если отбор бесповторный, а признак
количественный

, где N—
число единиц в генеральной совокупности

·        
Если отбор повторный, а признак альтернативный

, где w-выборочная
доля

·        
Если отбор бесповторный, а признак
альтернативный

Доверительный интервал для генеральной средней

 

 Доверительный интервал для
генеральной доли

Пример расчета  доверительного
интервала:

При выборочном обследовании 5% продукции по методу случайного
бесповторного отбора получены данные о содержании сахара в образцах:

Сахарность, %	Число проб ,ед.
16-17 17-18 18-19 19-20 20-21	10 158 154  50  28
ИТОГО:                            400

На основании этих данных вычислите:

1. Средний процент сахаристости.

2. Дисперсию и среднее квадратическое
отклонение.

3. С вероятностью 0.954 возможные пределы среднего значения
саха­ристости продукции для всей партии.

4. С вероятностью 0.997 возможный процент продукции высшего
сорта по всей партии, если известно, что из 400 проб, попавших в вы­борку , 80
ед. отнесены к продукции высшего сорта.

Решение.

1.
Средний процент сахаристости найдем по формуле средней взвешенной

, где x_i–
середина i-го интервала

=18,32 %

2.
Дисперсия

=336,49

D(X)=336.49–
18.32²=0.8676

Среднее квадратическое отклонение

=0,93%

5. Предельная ошибка  для
среднего процента сахаристости

для вероятности 0,954 параметр t=2.0

 

Доверительный интервал для среднего значения процента
сахаристости

С вероятностью 0,954 можно утверждать, что в генеральной
совокупности средний процент сахаристости лежит в пределах от 18,23% до 18,41%.

5. Доля продукции высшего сорта в выборочной совокупности

Предельная ошибка  для
доли продукции высшего сорта

для вероятности 0,997 параметр t=3.0

Доверительный интервал для доли продукции высшего сорта

С вероятностью 0,997 можно утверждать, что в генеральной
совокупности доля продукции высшего сорта лежит в пределах от 14,0% до 26,0%.

Тема 8. Выборочный метод

8.1. Сущность выборочного наблюдения, причины и практика его применения

Выборочное обследование – наиболее распространенный вид несплошного наблюдения в практике отечественной и зарубежной статистики. Сущность этого вида наблюдения состоит в том, что характеристика всей совокупности единиц дается по некоторой их части, отобранной научно обоснованным методом. В основе отбора единиц в выборку лежит принцип случайности, который обеспечивает равную возможность попадания в отобранную часть любой из единиц всей генеральной совокупности. Именно принцип случайности, заложенный в основу выборочного метода, и обеспечивает объективность результатов наблюдения, позволяет установить границы возможных ошибок и получить достоверные данные для характеристики всей совокупности.

Если отбор единиц произведен строго случайно, выборочная совокупность будет представительной или репрезентативной.

Выборочное наблюдение является наиболее совершенным и научно обоснованным методом несплошного наблюдения. При выборочном методе численность и доля единиц, которая будет обследоваться, известна до начала наблюдения, этим оно отличается от анкетного. В отличие от способа основного массива и монографического описания при проведении выборки неизвестно какие единицы совокупности будут подвергнуты обследованию. Выборочный метод, таким образом, в отличие от названных, исключает тенденциозность отбора и в большей степени обеспечивает представительство всех видов, групп, составляющих изучаемую совокупность.

Выборочный метод широко применяется в социально-экономических исследованиях, т.к. обладает рядом достоинств. Во-первых, он дает большую экономию средств и требует меньше времени для проведения наблюдения. То есть, выборочное наблюдение более экономичное, а результаты его носят более оперативный характер, чем при сплошном наблюдении. Во-вторых, при выборочном наблюдении при значительном сокращении объема работы обследование можно провести по более широкой программе, т.е. изучить явление более глубоко и детально. В-третьих, поскольку объем работы сокращается, то при выборке допускается меньше ошибок регистрации, и часто получают более точные результаты, чем при сплошном наблюдении.

Выборочный метод иногда является единственно возможным методом изучения явления, т.к. применение сплошного обследования может привести к физическому уничтожению всех единиц наблюдения. Например, при контроле качества некоторых видов продукции в промышленности, проверке семян на всхожесть в сельском хозяйстве и т.д.

Применение выборочного метода вызывается необходимостью контроля данных сплошного наблюдения. Например, контрольные проверки размеров посевных площадей и численности скота в личных хозяйствах населения.

Использование этого метода является целесообразным при изучении расходов населения, времени работы оборудования, рабочего времени и т.д.

Часто выборочный метод применяется в сочетании со сплошным наблюдением, например, при переписях населения.

8.2. Ошибки репрезентативности и теоретические основы их определения

В статистике принято называть совокупность отобранных единиц выборочной совокупностью (n), а совокупность единиц, из которых производится отбор – генеральной совокупностью (N). Генеральная и выборочная совокупности характеризуются такими показателями как средний размер признака, дисперсия, доля.

Рекомендуемые материалы

Задача выборочного наблюдения – дать верное представление о показателях всей генеральной совокупности на основе данных их некоторой части, попавшей в выборку.

Естественно, что когда изучают не всю, а только часть совокупности, результаты расчетов показателей выборочной и генеральной совокупности не совпадают. Эти отклонения выборочной средней и выборочной доли от доли и средней в генеральной совокупности называются ошибками выборки, или ошибками репрезентативности. Ошибки репрезентативности – это специфические ошибки, присущие только выборке и появляются они вследствие расхождения структуры выборочной и генеральной совокупности.

Как уже отмечалось, при выборочном наблюдении имеют место и ошибки регистрации, но они незначительны.

Основной организационный принцип выборочного наблюдения состоит в том, чтобы не допустить тенденциозного подбора выборочной совокупности, т.е. обеспечить строгое соблюдение принципа случайности отбора единиц в выборку. На результаты выборочного наблюдения можно полагаться именно благодаря тому, что отбор носит случайный характер. Это и позволяет максимально сократить возможные пределы отклонений выборочных результатов от показателей, вычисленных по всей генеральной совокупности.

Обобщенное действие механизма случайности в математике представляет закон больших чисел. Теория выборочного метода, основывается на доказательствах теорем русских математиков П.Л. Чебышева и А.М. Ляпунова. Из сущности закона больших чисел вытекает:

1) хотя каждая выборочная средняя и доля являются случайной величиной, однако средняя арифметическая из всех выборочных средних равняется генеральной средней;

2) каждый из возможных результатов выборочного наблюдения имеет свою вероятность появления, которая зависит от доли индивидуальных значений в генеральной совокупности. Чем больше доля индивидуальных показателей в генеральной совокупности, тем выше вероятность этих значений попасть в выборку;

3) каждая выборочная средняя отличается от генеральной средней. Разница между выборочной и генеральной средними представляет собой ошибку репрезентативности (выборки). Последняя измеряется средним квадратом отклонений всех возможных значений выборочных средних от генеральной средней, т.е. дисперсией.

В математической статистике доказывается, что между дисперсией выборочных средних и генеральной дисперсией существует определенное соотношение.

Дисперсия выборочных средних равна отношению генеральной дисперсии к численности выборочной совокупности.

Корень квадратный из этого отношения представляет собой стандартную (среднюю) ошибку репрезентативности (выборки):

.

Эта величина средней ошибки играет огромную роль в теории выборочного метода. Знание ее позволяет определять размер конкретных выборок и сказать какая выборка будет лучше еще до самой работы по выборочному обследованию.

Если выборочное обследование проводится с целью определения доли единиц, обладающих изучаемым признаком, то используются те же формулы расчетов, но в этом случае средняя и дисперсия заменяются аналогичными показателями альтернативного признака. Отсюда средняя ошибка выборки равна:

,

где  – доля единиц , обладающих данным признаком в выборочной совокупности.

Из приведенной формулы видно, что величина средней ошибки выборки зависит от вариации признака в генеральной совокупности, которая характеризуется дисперсией, и объема выборочной совокупности. Чем сильнее колеблется изучаемый признак у единиц генеральной совокупности, тем больше дисперсия, а отсюда и больше ошибка выборки, и, наоборот, чем больше объем выборочной совокупности, тем меньше ошибка выборки.

При организации выборки величина колеблемости признака в генеральной совокупности (N) неизвестна. В математической статистике доказано, что соотношение между дисперсиями генеральной и выборочной совокупностей выражается формулой:

.

Поскольку величина  при достаточно большой численности выборки близка к 1, то приближенно считают, что выборочная дисперсия равна генеральной дисперсии, т.е. , и в формуле средней ошибки выборки генеральная дисперсия заменяется выборочной.

4) при достаточно большом объеме выборки распределение средних вокруг генеральной средней подчинено закону нормального распределения. Это означает, что отклонение от генеральной средней расположено в ту или другую сторону симметрично. Если взять одно среднее квадратическое отклонение в ту или другую сторону, то тем самым будет принято во внимание 68,3% всех выборочных средних, т.е. выборочная средняя не отклонится в ту или другую сторону на одну сигму. Если взять два средних квадратических отклонения, то во внимание будет принято 95,4% всех выборочных средних, если взять три средних квадратических отклонения – 99,7% средних. Зная среднюю ошибку выборки и вероятности с какой уверенностью хотят гарантировать результаты выборочного наблюдения можно установить пределы ошибок.

,

где  – предельная ошибка выборки;

     – коэффициент доверия.

Коэффициент доверия выражает число средних ошибок, которые нужно взять, чтобы получить заданную вероятность. Так при вероятности 0,683 , при вероятности 0,954 , при вероятности 0,997 .

При выборочном наблюдении утверждения носят ориентировочный характер и выборочные показатели выражаются в интервале от и до.

Границы этих интервалов называются доверительными пределами. Нижний доверительный предел равен выборочной средней (доли) минус ошибка выборки.

8.3. Способы отбора и виды выборочного наблюдения

Репрезентативность выборки зависит не только от объема выборочной совокупности, но и от того как она образована, от характера отбора.

В генеральной совокупности могут отбираться отдельные единицы совокупности или же их группы.

В зависимости от того что является единицей отбора, последний делится на два вида: индивидуальный и групповой.

При индивидуальном отборе единицей отбора является непосредственно единица наблюдения. Например, проверка качества продукции непосредственно на рабочем месте. Контролер проверяет не каждую изготовленную деталь, а отбирает часть деталей из всей партии, которые подвергает проверке.

Групповой отбор заключается в том, что для наблюдения отбираются не только единицы совокупности, а их группы или серии. Примером могут служить контрольные проверки веса продукции, если она реализуется в упаковке (чай, макаронные изделия, сахар-рафинад и т.д.). Для контроля отбираются ящики, в отобранных ящиках взвешивается каждая пачка.

В некоторых случаях групповой отбор производится в сочетании с индивидуальным. Такой отбор называется комбинированным и связан со ступенчатостью. Здесь выборочная совокупность формируется не сразу, а проходит несколько стадий, ступеней, поэтому он еще называется многоступенчатым. Наиболее простым его случаем является двухступенчатый отбор, когда на первой ступени отбираются группы, на второй – отдельные единицы из отобранных групп.

Например, для контроля за соблюдением весовых стандартов пачек чая, сахара сначала отбираются ящики, в которых упакованы пачки, а из этих ящиков отбираются отдельные пачки.

Средняя ошибка выборки при двухступенчатом отборе исчисляется по формуле:

где  – число отобранных групп

     – среднегрупповая дисперсия из отобранных единиц

     – межгрупповая дисперсия.

Иногда сплошное наблюдение проводится в комбинации с выборочным. Например, переписи населения. Все население обследуется по основной программе, а 25% его обследуется по расширенной программе. Сплошное наблюдение может комбинироваться и с несколькими выборочными обследованиями, различающимися детализацией программ и числом обследуемых единиц.

Точность результатов и размеры ошибок выборочного наблюдения во многом зависят и от способа отбора единиц выборочной совокупности.

В зависимости от цели изучения и характера исходных данных, для обеспечения наибольшей репрезентативности выборки применяются следующие виды и способы отбора единиц совокупности для наблюдения:

а) собственно-случайная выборка,

б) механическая,

в) типическая (районированная),

г) серийно-гнездовая.

Собственно-случайная выборка.

При собственно-случайной выборке из генеральной совокупности отбираются для наблюдения отдельные единицы в случайном порядке. Для этого используются таблицы случайных чисел или жеребьевка.

Собственно-случайная выборка может проводиться по способу повторного и бесповторного отбора.

При повторном отборе отобранная единица после регистрации ее данных возвращается в генеральную совокупность и таким образом может попасть в выборку вторично и даже несколько раз. При бесповторном отборе каждая единица участвует в выборке только один раз.

Случайный отбор дает хорошие результаты в условиях, когда между единицами исследуемой совокупности нет резких различий.

При проведении собственно-случайной выборки нужно иметь исчерпывающий перечень всех единиц генеральной совокупности. Может оказаться, что пока организуется жеребьевка, единицы совокупности снова возникнут или ликвидируются. А при изучении качества продукции в течение дня вообще не имеется исчерпывающего перечня единиц. Неудобство этого способа отбора еще состоит и в том, что для жеребьевки на каждую единицу генеральной совокупности изготавливаются карточки (фишки) для жеребьевки.

Среднюю ошибку выборки для средней определяют в зависимости от способа отбора по разным формулам.

При повторном отборе:

.

При бесповторном отборе:

.

Аналогично вычисляют среднюю ошибку выборки для доли признака.

При повторном отборе:

.

При бесповторном отборе:

.

Бесповторный отбор обеспечивает большую репрезентативность выборки, чем повторный.

Собственно-случайная выборка применяется при контроле качества продукции, качества уборочных работ в сельском хозяйстве, при изучении оплаты пассажирами проезда в общественном транспорте и т.д.

Механическая выборка.

Механическая выборка представляет собой последовательный отбор единиц через равные интервалы в порядке определенного расположения их в генеральной совокупности или каком-нибудь перечне. Интервалы отбора определяются в соответствие с долей выборочной совокупности. Если, например, десятипроцентная выборка, то отбирается каждая десятая единица, если пятипроцентная – каждая двадцатая единица и т.д.

Расположение единиц генеральной совокупности в списке может быть двояким – упорядоченным или неупорядоченным относительно изучаемого признака. Так, списки рабочих могут быть составлены в алфавитном порядке по первым буквам фамилий; поскольку первые буквы фамилий рабочих не связаны с выполнением норм выработки, такое расположение является неупорядоченным относительно изучаемого признака. Если рабочих в списки записать по возрастанию или убыванию процента выполнения норм, расположение будет упорядоченным. Способ расположения единиц генеральной совокупности влияет на порядок их отбора в выборочную совокупность. В случае неупорядоченного расположения единиц из первых десяти рабочих можно взять любого (первого, второго, десятого) и затем последовательно брать одного через 10 человек. Если расположение упорядоченное, в выборочную совокупность следует отбирать рабочих, стоящих посредине каждого десятка; в противном случае может образоваться систематическая ошибка выборки. В самом деле, если рабочие в списках расположены по нисходящему проценту выполнения норм, то первые номера в каждом десятке будут всегда лучше по изучаемому признаку, а последние номера – худшими. Следовательно, отобрав в выборку первые номера, статистик завысит выборочный показатель выполнения норм, отобрав последние номера – занизит. Поэтому следует брать из каждого десятка пятые или шестые номера.

Механический отбор из упорядоченной (ранжированной) совокупности иногда называют систематическим отбором.

Механический отбор можно применять и не прибегая к спискам, а используя тот естественный порядок, в котором фактически расположены единицы генеральной совокупности, если только этот порядок не приведет к тенденциозным ошибкам.

Механическая выборка всегда бывает бесповторной и ошибки определяются по формулам собственно-случайной выборки.

Применяется механическая выборка при контроле за результатами сплошного наблюдения, при изучении потерь рабочего времени и т.д.

Например, из общего числа пенсионных вкладов банка была проведена 5%-ная механическая выборка. Результаты выборки следующие:

Таблица 8.1

Определить: 1) с вероятностью 0,683 пределы среднего размера пенсионного вклада во всей генеральной совокупности; 2) с вероятностью 0,954 пределы доли вкладов, размер которых превышает 80 тыс. р.

Решение:

1. Предельная ошибка выборки на средний размер пенсионного вклада при механической выборке определяется по формуле:

.

Вероятности 0,683 соответствует коэффициент доверия (t), равный 1.

Вычислим среднюю и дисперсию по выборочной совокупности.

;  .

Вывод: с вероятностью 0,683 можно утверждать, что средний размер пенсионного вклада у всех вкладчиков банка будет находиться в пределах:

;

2. Предельная ошибка доли:

.

При вероятности 0,954  t=2.

W – доля вкладов, размер которых превышает 80 тыс. р.

.

.

Вывод: с вероятностью 0,954 можно утверждать, что доля вкладов, размер которых составляет 80 тыс. р. и выше во всей генеральной совокупности будет находиться в следующих доверительных пределах:

;

Типическая выборка.

Типический (районированный) отбор применяют в том случае, если изучаемая совокупность неоднородна.

При этом отборе генеральная совокупность предварительно расчленяется на типы (районы) из которых отбираются единицы либо посредством жеребьевки, либо механическим способом.

Типы (районы) могут быть образованы искусственно или использованы те, которые сложились естественно.

Количество единиц, отбираемых из каждого типа (района), как правило, берется пропорционально численности типов в генеральной совокупности. Однако в принципе наиболее точный результат дает типический отбор, учитывающий вариацию признака в отдельных частях (типах, районах) генеральной совокупности. Для достижения этого численность частей выборочной совокупности, имеющих большую вариацию, несколько увеличивается.

Случайная ошибка при типическом отборе меньше, чем при собственно-случайном и механическом отборах, так как типический отбор дает более репрезентативную выборку, лучше обеспечивает возможность сохранить в выборке то соотношение между типами (районами), которое имеется в генеральной совокупности.

Предельная ошибка при пропорциональной типической выборке исчисляется по нижеследующим формулам.

При повторном отборе:

,

.

При бесповторном отборе:

,

.

Пропорциональная типическая выборка широко применяется в социологических, бюджетных обследованиях, при изучении урожайности по типам хозяйств.

Например, для исчисления среднего размера депозита в банке была проведена 2% – типическая выборка. Распределение депозитов по срокам хранения и их статистические характеристики в выборке представлены в табл. 8.2.

Таблица 8.2

Вычислим средний размер депозита:

С вероятностью 0,954 установить предельную ошибку выборки на средний размер депозита.

Вычислим среднюю групповую дисперсию:

Средняя ошибка выборки составит:

Предельная ошибка выборки при вероятности 0,954 составит:

Таким образом, средний размер депозита в генеральной совокупности будет находиться в пределах от 58,26 до 60,74 тыс. р.

Серийная (гнездовая) выборка.

Весьма часто в практике выборочного наблюдения применяется гнездовой или серийный отбор. При гнездовой или серийной выборке отбор производится не единицами, а целыми гнездами, сериями единиц совокупности, в пределах которых обследуются все единицы полностью. Например, 200 рабочих из 2000 можно отобрать целыми бригадами; отбор бригад может быть осуществлен посредством жеребьевки или механически. В отобранных бригадах общей численностью 200 человек должны быть обследованы все рабочие сплошь.

Серии (гнезда) состоят из единиц, связанных между собой или территориально, или организационно, или, наконец, во времени. Отбор серий может производится в порядке повторного и бесповторного отбора. Серии могут быть равновеликими и неравновеликими. На практике чаще применяется серийный отбор с равными сериями.

Серийный отбор значительно проще в организационном отношении и дешевле других способов. Однако получающаяся в процессе этого отбора ошибки выборки в подавляющем большинстве случаев больше, чем при любом другом способе отбора.

Средняя ошибка выборки при отборе равновеликими сериями будет выражаться формулами:

при повторном отборе:        ;

при бесповторном отборе: ,

где  – число отобранных серий;

   – общее число серий в генеральной совокупности.

Приведем пример. Выборочное наблюдение урожайности зерновых культур по области проводилось при помощи отбора районов. По каждому отобранному району находилась средняя урожайность, которая оказалась следующей: I район – 14 ц с 1 га, II район – 15 ц с 1 га, III район – 14,5 ц с 1 га, IV район – 15,5 ц с 1 га, V район – 16 ц с 1 га. С вероятностью 0,997 оценить урожайность зерновых во всей области. В области 25 районов.

Найдем сначала общую среднюю:

затем межгрупповую дисперсию:

Средняя ошибка серийного бесповторного отбора:

Найдем предельную ошибку выборки:

Следовательно, с вероятностью 0,997 можно ожидать, что средняя урожайность зерновых в этой области заключается в пределах:

8.5. Определение необходимой численности выборки

Ошибки выборочного наблюдения и доверительные пределы генеральной средней (генеральной доли) определяются после того, как получены данные, характеризующие каждую единицу выборочной совокупности. А поэтому при проведении выборки первоначально необходимо определить сколько единиц или какая часть генеральной совокупности должна быть подвергнута наблюдению. Это важный момент в проведении выборочного наблюдения. Важность его в том, что излишняя численность выборочной совокупности вызывает необоснованное завышение затрат времени, труда, материальных и денежных средств, а недостаточная – дает результаты с большей погрешностью. Объем выборки должен быть оптимальным.

Факторами, определяющими численность выборки, являются:

1. Показатели вариации данного признака. Здесь обнаруживается прямая зависимость, т.е. чем больше показатель вариации, тем больше объем выборки.

2. Размер вероятности. Зависимость также прямая. Чем выше вероятность, тем выше коэффициент доверия, а, следовательно, и численность выборки. Величина вероятности зависит от того какое явление изучается. Естественно, что при контроле качества продовольственной продукции величина вероятности выше, чем непродовольственной продукции.

3. Размер возможной допустимой ошибки (). Зависимость обратная. Чем меньше размер допустимой ошибки, тем больше должна быть необходимая численность выборки.

4. Способ отбора единиц для обследования. При прочих равных условиях для бесповторной выборки требуется меньшая численность выборки, чем при повторном отборе.

Основной трудностью, возникающей при установлении необходимой численности выборки, является определение среднеквадратического отклонения, которое характеризует вариацию признака. Значение этого показателя отсутствует как для генеральной, так и выборочной совокупности, поскольку задача определения необходимой численности выборки возникает тогда, когда еще выборка не проведена. Поэтому на практике используют несколько методов приближенного расчета среднеквадратического отклонения. Рассмотрим некоторые из них.

1. Вместо среднеквадратического отклонения данного отчетного периода берут значение данного показателя в базисном периоде. Этот прием применяется в тех случаях, когда мы в отчетном периоде, по сравнению с базисным, не ожидаем резкого изменения в исследуемых признаках.

2. Расчет среднеквадратического отклонения может быть основан на той связи, которая существует между показателями средней арифметической и коэффициентом вариации. Практика показывает, что во всех более или менее однородных совокупностях коэффициент вариации колеблется в пределах от 25-35%. Иначе говоря, коэффициент вариации обычно приблизительно равен  среднеарифметической величины. А, следовательно, и показатель вариации при расчете необходимой численности выборки будет равен  среднеарифметической величины соответствующего признака.

3. Следующий прием опирается на величину размаха вариации. Разность между максимальным и минимальным значениями признака равна приблизительно шести средним квадратическим отклонениям. Разделив размах колебаний на шесть, мы получим приближенное значение среднего квадратического отклонения. Этот прием можно использовать, т.к. максимальное и минимальное значение изучаемого признака известны до проведения наблюдения.

При установлении колеблемости доли, как и средней, в первую очередь надо попытаться найти ориентировочные данные о величине W. Если таких данных нет, то берется максимальная величина произведения W на (1-W). Эта величина равна 0,25.

Необходимую численность выборочной совокупности определяют на основе алгебраического преобразования формулы предельной ошибки выборки для разных видов и способов отбора.

Для собственно-случайной повторной выборки:

.

Чтобы найти численность выборки, нужно освободиться от радикала. Это достигается возведением левой и правой частей уравнения в квадрат.

,

отсюда численность выборки: .

Объем выборочной совокупности прямо пропорционален квадрату коэффициента доверия и дисперсии и обратно пропорционален квадрату предельной ошибки выборки.

При бесповторном собственно-случайном и механическом отборе численность выборки будет равна:

.

Для доли признака численность выборки будет определяться по формулам:

 – при повторном отборе,

 – при бесповторном отборе.

Аналогичным преобразованием предельной ошибки определяется численность выборочной совокупности при типической и серийной выборке.

Допустим, что для установления средней дневной выработки рабочих предприятия проводится собственно-случайная бесповторная выборка. Сколько рабочих должно быть обследовано, чтобы получить результат с точностью 0,3 р. с вероятностью 0,954. Общая численность рабочих завода 5000 человек. По данным прошлогоднего обследования среднее квадратическое отклонение выработки составляет 1,6 р.

.

Следовательно, должно быть обследовано 112 рабочих, чтобы выполнить поставленные перед наблюдением требования.

8.6. Способы распространения данных выборочного наблюдения

Конечной целью выборочного наблюдения является характеристика генеральной совокупности на основе данных, полученных по выборочной совокупности. Существуют два способа распространения данных выборочного наблюдения на генеральную совокупность – способ прямого пересчета и способ поправочных коэффициентов.

Способ прямого перерасчета заключается в том, что выборочная средняя или доля умножаются на численность генеральной совокупности и получается соответствующий объемный показатель. Так, в статистике сельского хозяйства выход шерсти от овец, находящихся в личном пользовании, определяется путем умножения полученных по выборке данных о среднем настриге шерсти с одной овцы на всю численность овец, находящихся в личной собственности. Например, согласно выборке, в области годовой настриг шерсти с одной овцы составляет 3 кг (с ошибкой выборки  г), среднегодовая численность овец в хозяйствах – 30 тыс голов. Исходя из этого годовой выход шерсти в хозяйствах определяется как произведение настрига с одной овцы на все поголовье овец:  кг, или 900 ц; с учетом ошибки выборки  – от 885 до 915 ц.

Второй пример. в 3%-ной выборке численностью 150 светильников 6 светильников оказались бракованными (ошибка выборки 1 светильник). По количеству брака, имеющемуся в выборочной совокупности (4%), можно подсчитать, сколько брака будет во всей партии светильников, составляющей 5 000 шт. Брак составит:

 светильников.

Вместе с этой лекцией читают «22 Сатурн».

Данный способ применяется тогда, когда известна численность единиц в генеральной совокупности.

Способ поправочных коэффициентом используется при проведении контрольных выборочных наблюдений для проверки и уточнения данных сплошного наблюдения. Он заключается в том, что по одним и тем же объектам сопоставляют данные сплошного и контрольного выборочного наблюдения. В результате такого сопоставления исчисляют поправочные коэффициенты, которые применяют для внесения поправок в данные сплошных наблюдений. Поправочные коэффициенты исчисляют, например, на основе данных контрольных выборочных обследований скота, находящегося в личной собственности населения сельской местности, при контроле за качеством деталей непосредственно на рабочем месте и т.д.

Например, по данным сплошного наблюдения численность крупного рогатого скота в личном подсобном хозяйстве граждан составляет 1 0000 голов.

Для контрольной проверки отобрано 1 000 семей, в хозяйствах которых сплошным наблюдением определена численность поголовья скота 1000 голов. В результате контрольного обхода в этих хозяйствах установлена численность крупного рогатого скота 1 050 голов.

Отсюда поправочный коэффициент составляет 1 050:1 000=1,05.

Общее поголовье скота в личном подсобном хозяйстве граждан равно  голов.

7.4. Влияние вида выборки на величину ошибки выборки

Как указывалось в п. 7.2, при проведении выборочного наблюдения используются различные способы формирования выборочной совокупности: случайный отбор — повторный или бесповторный, механический, серийный, типический. Вид выборки влияет на величину ошибки выборки. При бесповторном отборе формула средней ошибки выборки дополняется множителем

который корректирует величину ошибки выборки и в связи с изменением состава совокупности и вероятности попадания единиц в выборку. В серийной выборке дисперсия определяется как колеблемость между сериями:

 (7.14)

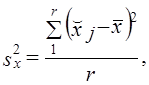
где x̌_j — среднее значение признака х в у-й серии;

х̅ — среднее значение в целом по выборке;

r — число отобранных серий.

Формула (7.14) предполагает равенство серий по числу единиц, если это условие не выполняется, то в числитель выражения (7.14) вводится вес — число единиц в j-й серии, f_j; тогда в  знаменателе указывается не r, а 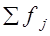. Межсерийная дисперсия представляет часть общей дисперсии признака х, и потому ее использование направлено на уменьшение ошибки выборки. Однако значение г намного меньше п, так как число отобранных гнезд намного меньше числа единиц наблюдения. Этот фактор увеличивает ошибку выборки. Его действие более значительно, нежели понижающее влияние межсерийной дисперсии — в результате ошибка серийной выборки в среднем больше ошибки выборки при отборе единицами.

При типическом отборе (стратифицированная или районированная выборка) дисперсия рассчитывается как средняя из внутрирайонных дисперсий:

                                                        (7.15′)

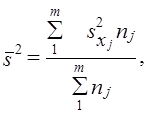
где     s²_ji — выборочная дисперсия признака х в j-м районе;

                                                              

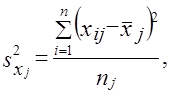
где     п_j — объем выборки в j-м районе;

т — число районов.

Очевидно, что по правилу сложения дисперсий величина s² меньше, чем величина общей дисперсии.

Величина ошибки районированной выборки меньше величины ошибки простой (нерайонированной выборки).

Часто используется сочетание районированного отбора с отбором сериями. Такой вид выборки обеспечивает преимущества в организации выборки и уменьшение ошибки выборки. Дисперсия такой выборки представляет среднюю из межсерийных дисперсий для каждого j-го района:

                                                            (7.16)

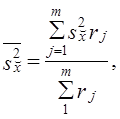
где s²_x̌j — межсерийная дисперсия в j-м районе;

 ,

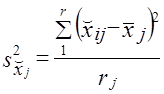
х̌_ij — средняя в i-й серии  j-го района;

х̅_j — средняя ву-м районе;

r— число серий, отобранных в j-м районе;

т — число районов.

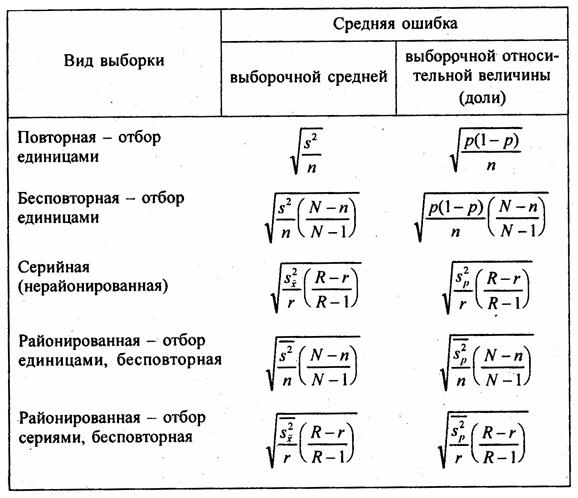
Табл. 7.2 содержит формулы средней ошибки выборки для выборочной средней и выборочной относительной величины для разных видов выборки. В приведенных формулах требуют пояснения выражения дисперсий выборочной относительной величины.

При нерайонированной серийной выборке

,

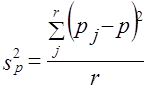
где     р_j — доля единиц определенной категории в у-й серии;

р — доля единиц этой категории в выборке.

Таблица 7.2

Формулы средней ошибки выборочной средней и выборочной относительной величины

 

Рассмотрим на примере влияние вида выборки на величину ошибки выборки. Исходные данные представлены в табл. 7.3.

Таблица 7.3

Показатели 60 предприятий легкой промышленности Санкт-Петербурга (по данным статистической отчетности за I полугодие 1995 г.)

№ пп	Форма Собственнос-ти	Оборачиваемость запасов, х1	Коэффициент покрытия, х2	№ пп	Форма собственности	Оборачиваемость запасов, х1	Коэффициент покрытия, х2
1	государственная	5,65	0,22	31	Частная	1,23	1,18
2	«	2,86	0,35	32	«	0,82	1,59
3	«	1,61	1,06	33	«	2,83	0,74
4	«	3,99	1,01	34	«	1,83	1,52
5	«	2,17	8,88	35	«	2,26	2,43
6	«	1,52	1,06	36	«	2,33	3,28
7	«	0,40	0,99	37	«	2,35	1,13
8	«	2,18	1,07	38	«	1,68	0,89
9	«	1,36	4,62	39	«	2,00	1,67
10	«	3,69	1,40	40	«	2,64	1,48
11	частная	0,45	1,34	41	«	2,75	1,51
12	«	1,0	1,16	42	«	3,29	5,96
13	«	2,05	2,00	43	«	1,6	1,38
14	«	2,36	1,43	44	«	1,90	2,39
15	«	4,90	1,76	45	«	3,27	3,62
16	«	3,12	1,26	46	«	3,49	0,46
17	«	1,36	1,89	47	«	2,92	1,26
18	«	1,56	12,36	48	смешання	3,22	0,78
19	«	4,84	1,23	49	«	2,61	1,67
20	«	1,23	3,26	50	«	5,17	0,95
21	«	0,81	2,22	51	«	8,63	0,96
22	«	0,7	1,16	52	«	1,06	2,51
23	«	0,87	1,21	53	«	2,13	3,49
24	«	0,20	1,45	54	«	2,03	1,22
25	«	1,71	4,04	55	«	1,82	2,92
26	«	1,83	2,07	56	«	3,12	1,54
27	«	1,32	0,69	57	«	0,77	0,97
28	«	1,95	1,97	58	«	4,15	0,93
29	«	1,46	1,31	59	«	3,62	1,34
30	«	2,96	5,32	60	«	3,89	3,51

Предприятия легкой промышленности примем за генеральную совокупность. Ее характеристики:

численность N = 60;

генеральные средние: μ₁ = 2,40 число оборотов;

       μ₂ = 1,424;

генеральные дисперсии: σ²₁ = 2,24;

                                          σ²₂ = 4,38;

средние квадратические σ₁ = 1,49 оборотов;

отклонения:                      σ₂ = 2,09.

Остановимся на смысле характеристик предприятий: оборачиваемость запасов рассчитывается делением продолжительности периода (полгода) на среднюю продолжительность одного периода оборота запасов. Очевидно, чем скорее оборачиваются запасы, тем выше их отдача. Коэффициент покрытия рассчитывается как отношение суммы всех источников покрытия запасов к стоимости запасов. Если значение этого показателя меньше единицы, то текущее финансовое состояние предприятия рассматривается как неустойчивое. В нашем примере вариация этого признака примерно в 2 раза превосходит вариацию предприятий по уровню оборачиваемости запасов: ν₂ = 147%, ν₁ = 62%.

Произведем 30%-ную выборку. Объем выборки составит п = 20 предприятий. При формировании выборки методом механического отбора каждое третье предприятие попадет в выборку. Отбор начинаем с полушага отбора, т. е. первым предприятием, попавшим в выборку, является второе по списку. Средние по выборке равны:

оборачиваемость запасов x̅₁ =2,16 оборотов, коэффициент покрытия x̅₂=2,01.

Средняя ошибка выборочной средней оборачиваемости запасов

   оборотов.

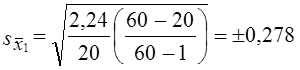
Средняя ошибка выборочного среднего коэффициента покрытия

 

С вероятностью 0,954 можно утверждать, что средняя оборачиваемость запасов на предприятиях легкой промышленности не ниже

x̅₁ — 2s_x1 = 2,16 — 0,55 = 1,61 оборотов и не выше x̅₁+2s_x1 = 2,16 +  0,55 = 2,71 оборотов.

Действительно генеральная средняя (μ₁ = 2,40) попадает в этот интервал.

Фактическая ошибка репрезентативности

  оборотов.

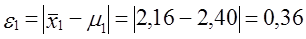
Эта величина меньше предельной ошибки выборки, гарантированной с принятой доверительной вероятностью, 0,36 < 0,55. Следовательно, выборка репрезентативна по этому признаку.

Вычислим предельную ошибку выборки коэффициента покрытия и определим доверительный интервал для этой характеристики. Его нижняя граница с той же вероятностью

;

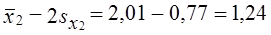
верхняя граница:

 

Генеральная средняя (μ₂ = 1,424) так же попадает в доверительный интервал.

Фактическая ошибка репрезентативности составляет:

Эта величина меньше предельной ошибки выборки (0,77), что дает основание считать выборку репрезентативной и по этому признаку.

В генеральной совокупности доля единиц с неустойчивым финансовым положением (х₂ < 1) составила 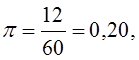  в выборке  

Доверительный интервал для оценки доли таких предприятий в генеральной совокупности составляет с вероятностью 0,954:

 

0,15 ± 0,076,

т. е. таких предприятий должно быть не меньше 7,4% и не больше 22,6%. Фактически их оказалось 20% от общего числа предприятии, т. е. выборка дает репрезентативный результат и по этому показателю.

Выполненная выборка формировалась как простая бесповторная механическая. Однако, наверняка статистик будет стремиться учесть структуру генеральной совокупности, поэтому  более естественной была бы выборка, учитывающая выделение предприятий разных форм собственности. Тогда выборка должна быть районированной.

Рассмотрим пример. Генеральная совокупность состоит из 11 государственных предприятий, 36 частных, 13 смешанных. В выборке эти пропорции соблюдаются следующим образом: отобраны по 4 предприятия государственных и смешанных и 12 — частных:

Предприятия	Генеральные характеристики	Выборочные характеристики
средние	доли	средние	доли
Государственные	μ1 = 2.35	π1 = 0,27	х̅1 = 1,92	Р1 = 0,25
Частные	μ1 =2,11	π2 = 0,11	х̅1  = 1,79	Р2=0,08
Смешанные	μ1 =3,25	π3 = 0,38	х̅1  =3,51	Рз — 0,25

Средняя из внутрирайонных дисперсий, рассчитанных по каждой группе предприятий в генеральной совокупности:

Эта величина меньше общей дисперсии без учета районирования (σ² = 2,24). Следовательно, и величина ошибки выборки при районированном отборе будет меньше:

 

Итак, с вероятностью 0,954 генеральная средняя оборачиваемости запасов находится в интервале 2,16 ± 0,294; 1,866 £ μ £ 2,454.

Чтобы понять, насколько целесообразно в том или ином случае применение районированного отбора, можно воспользоваться корреляционным отношением ц. Согласно правилу сложения дисперсий средняя из внутригрупповых дисперсий может быть представлена как

где h² — квадрат корреляционного отношения, равный б²:s².

Следовательно, применение районированной (типической) выборки изменяет предельную ошибку на 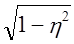 . В нашем примере для первой переменной (оборачиваемость) имеем:

          

Сопоставим полученный результат с изменением предельной ошибки выборки: 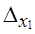 (без учета районирования) =0,55;

∆_x (при районировании) = 0,294, т. е. ошибка уменьшилась примерно вполовину.

Корреляционное отношение используется и при корректировке величины

                                                  (7.18′)

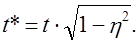
Тогда при вероятности 0,954 и t = 2; t*=2 — Ö0̅,8̅6̅ = 1,85, т. е. вместо t = 2 достаточно взять t = 1,85.

Многие выборки формируются как многоступенчатые. Ошибка многоступенчатой выборки может быть представлена как

Она складывается из ошибок отдельных ступеней. Поэтому практически используется не больше 2-3 ступеней отбора.

Средняя ошибка выборки при двухступенчатом отборе рассчитывается по формуле

где s_x1 ² — дисперсия признака х по совокупности «крупных» единиц;

s_x2² — дисперсия признака х в каждой из отобранных «крупных» единиц;

п_i — число отобранных единиц наблюдения в <-й «крупной» единице;

т — число отобранных «крупных» единиц.

Таким образом, применение многоступенчатой выборки улучшает организацию выборки, но увеличивает ее ошибку.

Кроме рассмотренных, применяется многофазовая выборка, когда одни сведения собираются на основе изучения всех единиц выборки, а другие — только на основании изучения некоторых из этих единиц, отобранных так, что они составляют подвыборки из единиц первоначальной выборки.

При периодическом повторении выборочных обследований с целью изучения динамики явлений применяются либо независимые выборки — через определенные промежутки времени отбор каждый раз производится независимо от предыдущих выборок; либо фиксированные выборки — в этом случае повторные обследования проводятся по одной и той же выборке. В связи с тем, что в фиксированной выборке могут происходить изменения (прежде всего за счет выбытия единиц) практикуют периодическую адаптацию фиксированной выборки происходящим изменениям. Чаще для целей изучения динамики используется промежуточный вариант — ротационная выборка (частичное замещение). При этом нужно следовать определенному плану замещения, например, каждый раз замещать четверть выборки, тогда каждая первоначальная единица останется в выборке в четырех следующих друг за другом обследованиях.

Названные виды выборок ориентированы на отбор конкретных материальных явлений. Кроме них следует назвать как особый вид выборки метод моментных наблюдений.Сущность метода моментных наблюдений состоит в периодической фиксации состояний .наблюдаемых единиц в отобранные моменты времени. Расчет объема такой выборки дает количество моментов. Этот вид выборочного наблюдения применяется при изучении использования производственного оборудования, либо рабочего времени (см. п. 7.13).

7.5. Задачи, решаемые при применении выборочного метода

При применении выборочного наблюдения возникают три основные задачи:

• определение объема выборки, необходимого для получения требуемой точности результатов с заданной вероятностью;

• определение возможного предела ошибки репрезентативности, гарантированного с заданной вероятностью, и сравнение его с величиной допустимой погрешности.

• определение вероятности того, что Ошибка выборки не превысит допустимой погрешности.

Все эти задачи решаются на основе теоремы Чебышева, согласно которой Р {[ х — μ | < e } ³ 1 — h, когда п — достаточно большое число; e и h — сколь угодно малые положительные числа. Это соотношение, как было показано в п. 7.3, может быть выражено через формулу предельной ошибки выборки ∆_x = ts_x или ∆_p = ts. Решение указанных задач зависит от того, какие величины в формуле предельной ошибки заданы, а какие нужно найти.

Объем выборки рассчитывается на стадии проектирования выборочного обследования. Так как

                                                      

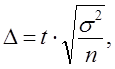
то

 ,                                                                (7.20)

где   ∆ — допустимая погрешность,, которая задается исследователем исходя из требуемой точности результатов проектируемой выборки;

t — табличная величина, соответствующая заданной доверительной вероятности F(t), с которой будут гарантированы оценки генеральной совокупности по данным выборочного обследования;

σ² — генеральная дисперсия.

Последняя величина, как правило, неизвестна. Используются какие-либо ее оценки: результаты прошлых обследований той же совокупности, если ее структура и условия развития достаточно стабильны, или же зная примерную величину средней, находят дисперсию из соотношения  ;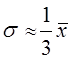

если известны x_max и х_min, то можно определить среднее квадратическое отклонение в соответствии с правилом «трех сигм»

   ,

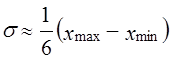
так как в нормальном распределении в размахе вариации «укладывается» 6σ(±3σ). Если распределение заведомо асимметричное, то

 .

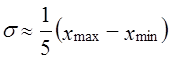
Для относительной величины принимают максимальную величину дисперсии σ²_max = 0,5∙0,5 = 0,25.

При расчете п не следует гнаться за большими значениями t и малыми значениями ∆, так как это приведет к увеличению объема выборки, а следовательно, к увеличению затрат средств, труда и времени, вовсе не являющемуся необходимым.

Формула (7.20) не учитывает бесповторности отбора и дает максимальную величину выборки, которую можно скорректировать «на бесповторность». Так как

  ,

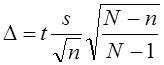
то на основе (7.20) получаем выражение скорректированного объема выборки (п):

  ,                                         (7.21)

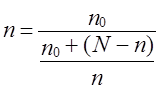
где

 .

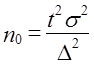
При больших размерах генеральной совокупности скорректированный Объем выборки незначительно отличается от n₀.

Например, для изучения структуры и стоимости покупок в универмаге из 10 000 покупателей следует отобрать определенное число человек, которое бы обеспечивало с вероятностью 0,95 определение средней стоимости покупок с точностью не менее 2 тыс. руб. Дисперсию примем по прошлому обследованию равной 625.

   человек;

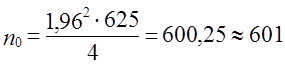
тогда скорректированная численность

   человек (≈ 570 человек).

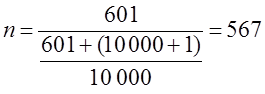
При проектировании районированной выборки рассчитанный объем выборки распределяют пропорционально численности районов (пропорциональный отбор):

  ,                                                              (7.22)

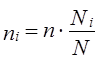
где  п_i — объем выборки для i-го района;

N_i — объем i-го района в генеральной совокупности;

п — общий объем выборки;

N — общий объем генеральной совокупности.

При различиях в однородности выделенных районов лучшие результаты дает распределение запланированного объема выборки между районами не только с учетом их объема, но и с учетом дисперсии признака (оптимальный отбор). В этом случае объем выборки в i-м районе определяется как

 ,                                                      (7.23)

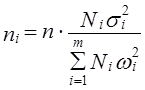
где σ²_i — дисперсия признака х в i-м районе.

При любом виде проектируемой выборки расчет объема выборки начинают по формуле повторного отбора (7.20). Если в результате расчета п доля отбора превысит 5%, проводят второй вариант расчета по формуле бесповторного отбора, либо по формуле (7.21), либо как

 .

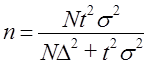
Если доля отбора меньше 5%, к формуле бесповторного отбора не переходят, так как это не скажется существенно на величине п.

Выборка должна быть такой, чтобы выборочные показатели по всем основным характеристикам были репрезентативны. Поэтому численность выборки рассчитывают многократно исходя из допустимых ошибок разных показателей, значения которых в генеральной совокупности известны.

Например, при выборочном учете детей школьного возраста требуется определить число семей, которые надо обследовать. При этом надо учесть: а) число детей в возрасте 6-7 лет, б) число детей в возрасте 6-15 лет; в) число детей в возрасте 16-17 лет;

г) среднедушевой доход (например, для решения вопроса о строительстве базы отдыха).

Так как репрезентируемые признаки могут иметь разную размерность, то допустимая погрешность для каждого их них задается в виде относительной величины (∆ : х̅) (например, планируется, что в определении среднего размера семьи ошибка должна быть не больше 2%, в определении дохода — не больше 3% и т.д.). В этом случае вместо дисперсии в формуле (7.20) берется квадрат коэффициента вариации.

Вычислив значение п, на основе каждой из характеристик получаем разные объемы выборки: 1200; 300; 700; 100. Обследовать необходимо 1200 семей, т.е. из рассчитанных численностей берется максимальная. При резких различиях необходимых объемов выборки для разных вопросов программы проводится многофазный отбор. В рассмотренном примере среднедушевой доход достаточно учитывать в одной из каждых 12 семей, попавших в выборку.

Многофазный отбор, как правило, довольно сложно организовать, может быть нарушен принцип случайности отбора. Поэтому для обеспечения репрезентативности оказывается выгоднее затратить больше средств на учет большего числа единиц совокупности. Многофазный отбор целесообразно применять, если соотношение между рассчитанными объемами выборки по крайней мере 1:6.

Поскольку расчет необходимой численности выборки основан не на точных, а на предположительных данных о колеблемости в совокупности, следует соблюдать следующие рекомендации: абсолютную величину п округлять только вверх; долю отбора округлять только вниз, т.е. из предосторожности планировать несколько больший объем выборки, чем показывают расчеты.

Объем многоступенчатой выборки рекомендуется увеличить не менее чем на 10% от рассчитанной численности, поскольку, как было показано в предыдущем параграфе, многоступенчатость отбора увеличивает ошибку выборки.

После проведения выборки рассчитывают возможные ошибки . выборочных показателей (ошибки репрезентативности), которые используются для оценки результатов выборки и для получения характеристик генеральной совокупности.

Пример. На электроламповом заводе взято для проверки 100 ламп. Средняя продолжительность их горения оказалась 1420 ч со средним квадратическим отклонением 61,03 ч. Поскольку приемщика продукции интересует качество всей партии (50 тыс. электроламп), оценивают точность полученной средней. Средняя возможная ошибка вычисленной выборочной средней

  ч.

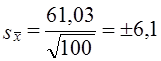
С вероятностью 0,954 предел возможной ошибки

∆_х = 2∙6,1 = ± 12,2 ч.

С вероятностью 0,954 можно утверждать, что средняя продолжительность горения 1 электролампы во всей партии будет находиться в пределах от 1408 до 1432 ч; 46 электроламп из 1000 могут иметь срок горения, выходящий за эти пределы.

Приемщика продукции интересуют отклонения от вычисленных пределов только в сторону сокращения продолжительности горения. Меньше чем 1408 ч могут гореть 23 лампы из 1000. На основании этого приемщик продукции решает вопрос о годности всей партии электроламп.

Решение вопроса может быть уточнено: определим, у какой доли ламп срок службы окажется меньше установленного лимита. Для потребителя продукции таким лимитом являются  1410 ч, продукция с меньшим сроком горения неприемлема.

При контрольной проверке 100 ламп 100 ламп горели менее 1410 ч, их удельный вес р = 0,1, или 10%. Средняя возможная ошибка этой доли

, или ± 3%.

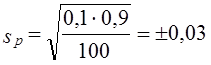
С вероятностью 0,954 предел ошибки доли Д^ = 2 • 0,03 = ± 0,06, или ±6%. Следовательно, во всей партии можно ожидать от 4 до 16% некачественных электроламп.

Чаще всего делают заключение об удовлетворительности выборки, сопоставляя получившиеся пределы ошибок выборочных показателей с величинами допустимых погрешностей. Может получиться, что предел ошибки, рассчитанный с заданной вероятностью, окажется выше допустимого размера погрешности. В этих случаях определяют вероятность того, что ошибка выборки не превзойдет допускаемую погрешность. Решение этой задачи и заключается в отыскании Fft) на основе формулы предела ошибки выборки:

,

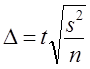
где ∆ — допустимый размер погрешности оцениваемого показателя;

s² — дисперсия показателя, рассчитанная по данным выборочного наблюдения;

п — объем проведенной выборки.

Продолжим пример с оценкой качества электроламп. Если при приемке партии электроламп ставится условие, что минимальный срок горения электроламп 1410 ч, то, учитывая среднюю продолжительность горения по выборке (х= 1420 ч), допустимая погрешность равна 10 ч: 1410 — 1420 = — 10 ч.

Как было установлено выше, с вероятностью 0,954 предел возможной ошибки выборочной средней составил 12,2 ч, что превосходит допустимую погрешность. Является ли это основанием для браковки всей партии? Для ответа на этот вопрос определяют вероятность риска при приемке продукции:

 , отсюда t= 1,64.

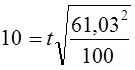
Соответствующая доверительная вероятность 0,899 (см. приложение, табл. 1). Вероятность того, что средний срок горения лампы меньше 1410 ч, равна:

 

Следовательно, из 100 ламп 5 могут гореть менее 1410 ч — риск появления некачественной продукции достаточно высок.

Аналогично можно определить вероятность того, что предел ошибки доли не превысит допускаемую погрешность доли.

Оценки надежности выборочных показателей, как показано на примере, позволяют принять обоснованные решения в отношении генеральной совокупности.

7.6. Распространение данных выборочного наблюдения на генеральную совокупность

Конечной целью выборочного наблюдения является характеристика генеральной совокупности на основе данных, полученных по выборке. При этом исходят из того, что все средние и относительные показатели, полученные по выборке, являются несмещенными и эффективными характеристиками генеральной совокупности.

Выборочные средние и относительные величины распространяются на генеральную совокупность обязательно с учетом предела их возможной ошибки. Приводится выборочный показатель со справкой о пределах ошибки с указанием доверительной вероятности:  x̅ ± ∆_x, p ± ∆_p.  Или же указывают границы значений генеральной характеристики с определенной вероятностью F(t):

 

Последняя форма записи является основной.

Иногда требуется указать только один (верхний или нижний) предел характеристики генеральной совокупности. При испытании качества продукции часто нас не интересуют положительные ошибки выборки (качество фактически выше, чем получилось по выборке), беспокоит нижний предел, как в примере, рассмотренном в предыдущем параграфе. В некоторых случаях, напротив, интерес вызывают верхние границы оцениваемых показателей, например при анализе расхода материалов. Так что при характеристике генеральной совокупности всегда указывают неблагоприятный предел.

На основе выборки могут быть получены и значения объемных показателей, т. е. подсчетов для генеральной совокупности. Такой расчет осуществляется двумя способами: путем прямого расчета и способом коэффициентов. Прямой расчет заключается в том, что выборочная средняя или доля умножается на объем генеральной совокупности:

 .

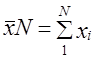
Так как средняя величина имеет ошибку репрезентативности ± А д то можно считать, что итоговый подсчет в генеральной совокупности находится в пределах

                                  (7.24)

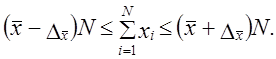
Итоговый подсчет по генеральной совокупности можно получить на основе итогового подсчета по выборке, разделив его на долю отбора единиц совокупности

 

Прежде чем проводить расчет объемных показателей для генеральной совокупности, нужно убедиться, что структура выборки соответствует структуре генеральной совокупности. При наличии значительных смещений в структуре выборки в долях отдельных групп (0,03 и выше) следует применить метод перевзвешивания, г. в. рассчитывать генеральную среднюю на основе выборочных средних по группам и удельного веса этих групп в генеральной совокупности:

  ,

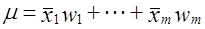
где w_i = N_iN.

При способе коэффициентов также используются не только выборочные данные, но и сведения о генеральной совокупности.

Этот способ основан на связи признаков друг с другом. Например, в результате выборочного обследования семей города получены размер среднедушевого дохода (х̅), средний доход семьи (у̅) и среднее число человек в семье (z̅). Так что x̅ = y̅ / z̅.

Зная численность населения города, требуется рассчитать общую величину денежного дохода населения. Очевидно, это можно сделать, умножив душевой доход на общее число жителей в городе: x̅N. Общий доход можно получить, суммируя доход отдельных семей; численность населения можно получить, суммируя данные о числе членов семей. Тогда

 .

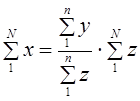
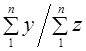
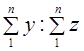
Средний душевой расход  представляет собой коэффициент, подсчитанный по выборке, который связывает две характеристики. Этот коэффициент рассчитывается как отношение двух итоговых подсчетов по выборке:

 .

Следовательно,

 .      

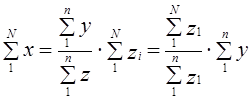
Последний сомножитель не что иное, как обратная величина доли отбора, рассчитанной по значениям признака z.

Итак, итоговый подсчет по генеральной совокупности может быть получен делением соответствующего итогового подсчета по выборке на долю отбора. При прямом расчете берется доля отбора единиц совокупности, при способе коэффициентов — доля отбора по значению какого-либо признака.

Эффективность способа коэффициентов по сравнению с методом прямого расчета зависит от того, насколько тесно связаны между собой признаки, лежащие в основе расчета коэффициента, т.е. признак, по которому подсчитывается итог, и признак, по которому определяется доля отбора. Эффект проявляется, если коэффициент корреляции между ними больше 0,8.

Способ коэффициентов используется для корректировки данных сплошного наблюдения. Например, перепись скота дала сведения, что поголовье свиней в районе составляет 10 000, в том числе в тех хозяйствах, которые потом были охвачены контрольным обходом, сплошное наблюдение показало число свиней 1100. Контрольный обход дал уточненную цифру: не 1100, а 1107 свиней. Тогда поправочный коэффициент

  .

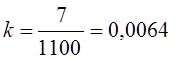
Отсюда скорректированная численность поголовья свиней во всем районе

N =N¢+∆N;  ∆N = kN¢ = ∙10 000 = 64.

N = 10 000 + 64 = 10 064 голов.

Таблицы интеграла вероятностей используются для выборок большого объема из бесконечно большой генеральной совокупности. Но уже при п < \ 00 получается несоответствие между табличными данными и вероятностью предела; при п < 100 погрешность становится значительной. Несоответствие вызывается главным образом характером распределения единиц генеральной совокупности. При большом объеме выборки особенность распределения в генеральной совокупности не имеет значения, так как распределение отклонений выборочного показателя от генеральной характеристики при большой выборке всегда оказывается нормальным.

В выборках небольшого объема п £ 30 характер распределения генеральной совокупности сказывается на распределении ошибок выборки. Поэтому для расчета ошибки выборки при небольшом объеме наблюдения (уже менее 100 единиц) отбор должен проводиться из совокупности, имеющей нормальное распределение.

Теория малых выборок разработана английским статистиком В. Госсетом (писавшим под псевдонимом Стьюдент) в начале XX в. В 1908 г. им построено специальное распределение, которое позволяет и при малых выборках соотносить t и доверительную вероятность F(t). При п > 100 таблицы распределения Стьюдента дают те же результаты, что и таблицы интеграла вероятностей Лапласа, при 30 £ п £ 100 различия незначительны. Поэтому практически к малым выборкам относят выборки объемом менее 30 единиц (безусловно, большой считается выборка с объемом более 100 единиц).

Использование малых выборок в ряде случаев обусловлено характером обследуемой совокупности. Так, в селекционной работе «чистого» опыта легче добиться на небольшом числе  делянок. Производственный и экономический эксперимент, связанный с экономическими затратами, также проводится на небольшом числе испытаний.

Как уже отмечалось, в случае малой выборки только для нормально распределенной генеральной совокупности могут быть рассчитаны и доверительные вероятности, и доверительные пределы генеральной средней.

Плотность вероятностей распределения Стьюдента описывается функцией

,                               (7.25)

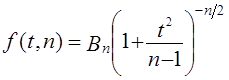
где  t — текущая переменная;

п — объем выборки;

В — величина, зависящая лишь от п.

Распределение Стьюдента имеет только один параметр: d.f. —число степеней свободы (иногда обозначается k).

Это распределение, как и нормальное, симметрично относительно точки t = 0, но оно более пологое. При увеличении объема выборки, а следовательно, и числа степеней свободы распределение Стьюдента быстро приближается к нормальному. Число степеней свободы равно числу тех индивидуальных значений признаков, которыми нужно располагать для определения искомой характеристики.

Так, для расчета дисперсии должна быть известна средняя величина. Поэтому при расчете дисперсии d.f. = п — 1

Таблицы распределения Стьюдента публикуются в двух вариантах:

1) аналогично таблицам интеграла вероятностей приводятся значения t и соответствующие вероятности F(t) при разном числе степеней свободы;

2) значения t приводятся для наиболее употребимых доверительных вероятностей 0,90; 0,95 и 0,99 или для 1 — 0,9 = 0,1, 1 — 0,95 = = 0,05 и 1 — 0,99 == 0,01 при разном числе степеней свободы. Такого рода таблица приведена в приложении (табл. 2), а также значение t-критерия Стьюдента при уровне значимости 0,10; 0,05; 0,01.

При малых выборках расчет средней возможной ошибки основан на выборочных дисперсиях, поэтому

 .

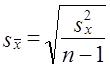
Приведенная формула используется для определения предела возможной ошибки выборочного показателя:

.

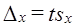
Порядок расчетов тот же, что и при больших выборках.

Пример. Для изучения интенсивности труда было организовано наблюдение за 10 отобранными рабочими. Доля работавших все время оказалась равной 0,40, дисперсия 0,4∙0,6 = 0,24. По табл. 2 приложения находим для F(t) = 0,95 и d.f. = n — 1 = 9, t = 2,26. Рассчитаем среднюю ошибку выборки доли работавших все время:

 

Тогда предельная ошибка выборки ∆_p = 2,26∙0,16 = ± 0,36. Таким образом, с вероятностью 0,95 доля рабочих, работавших без простоев, в данном цехе предприятия находится в пределах

39,64% £ π £ 40,36%

или

39,6% £ π £ 40,4%.

Если бы мы использовали для расчета доверительных границ генерального параметра таблицу интеграла вероятностей, то t было бы равно 1,96 и ∆_p — ± 0,31, т. е. доверительный интервал был бы несколько уже.

Малые выборки широко используются для решения задач, связанных с испытанием статистических гипотез, особенно гипотез о средних величинах.