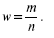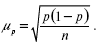Между
признаками выборочной совокупности и
признаками генеральной совокупности,
как правило, существует некоторое
расхождение, которое называется ошибкой
статистического наблюдения. При массовом
наблюдении ошибки неизбежны, но возникают
они в результате действия различных
причин. Величина возможной ошибки
выборочного признака происходит из-за
ошибок регистрации и ошибок
репрезентативности. Ошибки регистрации,
или технические ошибки, связаны с
недостаточной квалификацией наблюдателей,
неточностью подсчетов, несовершенством
приборов и т. п.
Под
ошибкой
репрезентативности
(представительства) понимают расхождение
между выборочной характеристикой и
предполагаемой характеристикой
генеральной совокупности. Ошибки
репрезентативности бывают случайными
и систематическими. Систематические
ошибки связаны с нарушением установленных
правил отбора. Случайные
ошибки объясняются недостаточно
равномерным представлением в выборочной
совокупности различных категорий
единиц генеральной совокупности.
В
результате первой причины выборка
легко может оказаться смещенной, так
как при отборе каждой единицы допускается
ошибка, всегда направленная в одну и
ту же сторону. Эта ошибка получила
название ошибки
смещения.
Ее размер может превышать величину
случайной ошибки. Особенность ошибки
смещения состоит в том, что, являясь
постоянной частью ошибки репрезентативности,
она увеличивается с увеличением объема
выборки. Случайная же ошибка с увеличением
объема выборки уменьшается. Кроме того,
величину случайной ошибки можно
определить, тогда как размер ошибки
смещения практически определить очень
сложно, а иногда и невозможно, поэтому
важно знать причины, вызывающие ошибку
смещения, и предусмотреть мероприятия
по ее устранению.
Ошибки
смещения бывают преднамеренные и
непреднамеренные. Причиной возникновения
преднамеренной
ошибки
является тенденциозный подход к выбору
единиц из генеральной совокупности.
Чтобы не допустить появление такой
ошибки, необходимо соблюдать принцип
случайности отбора единиц.
Непреднамеренные
ошибки
могут возникать на стадии подготовки
выборочного наблюдения, формирования
выборочной совокупности и анализа ее
данных. Чтобы не допустить появление
таких ошибок, необходима хорошая основа
выборки, т. е. та генеральная
совокупность, из которой предполагается
производить отбор, например список
единиц отбора. Основа выборки должна
быть достоверной, полной и соответствовать
цели исследования, а единицы отбора и
их характеристики должны соответствовать
действительному их состоянию на момент
подготовки выборочного наблюдения.
Нередки случаи, когда в отношении
некоторых единиц, попавших в выборку,
трудно собрать сведения из-за их
отсутствия на момент наблюдения,
нежелания дать сведения и т. п. В
таких случаях эти единицы приходится
заменять другими. Необходимо следить,
чтобы замена осуществлялась равноценными
единицами.
Случайная
ошибка
выборки возникает в результате случайных
различий между единицами, попавшими в
выборку, и единицами генеральной
совокупности, т. е. она связана со
случайным отбором. Теоретическим
обоснованием появления случайных
ошибок выборки является теория
вероятностей и ее предельные теоремы.
Сущность
предельных
теорем
состоит в том, что в массовых явлениях
совокупное влияние различных случайных
причин на формирование закономерностей
и обобщающих характеристик будет сколь
угодно малой величиной или практически
не зависит от случая. Так как случайная
ошибка выборки возникает в результате
случайных различий между единицами
выборочной и генеральной совокупностей,
то при достаточно большом объеме выборки
она будет сколь угодно мала.
Предельные
теоремы теории вероятностей позволяют
определять размер случайных ошибок
выборки. Различают среднюю (стандартную)
и предельную ошибку выборки. Под средней
(стандартной) ошибкой
выборки понимают такое расхождение
между средней выборочной и генеральной
совокупностями (~ —), которое не превышает
±.
Предельной
ошибкой
выборки принято считать максимально
возможное расхождение (~ —), т. е.
максимум ошибки при заданной вероятности
ее появления.
В
математической теории выборочного
метода сравниваются средние характеристики
признаков выборочной и генеральной
совокупностей и доказывается, что с
увеличением объема выборки вероятность
появления больших ошибок и пределы
максимально возможной ошибки уменьшаются.
Чем больше обследуется единиц, тем
меньше будет величина расхождений
выборочных и генеральных характеристик.
На основании теоремы, доказанной П.Л.
Чебышевым, величину стандартной ошибки
простой случайной выборки при достаточно
большом объеме выборки (n)
можно определить по формуле
– стандартная
ошибка.
Из
этой формулы средней (стандартной)
ошибки простой случайной выборки видно,
что величина зависит от изменчивости
признака в генеральной совокупности
(чем больше вариация признака, тем
больше ошибка выборки) и от объема
выборки n
(чем больше обследуется единиц, тем
меньше будет величина расхождений
выборочных и генеральных характеристик).
Академик
A.M. Ляпунов доказал, что вероятность
появления случайной ошибки выборки
при достаточно большом ее объеме
подчиняется закону нормального
распределения. Эта вероятность
определяется по формуле
В
математической статистике употребляют
коэффициент доверия t, значения функции
F(t)
табулированы при разных его значениях,
при этом получают соответствующие
уровни доверительной вероятности
(табл. 6.1).
Таблица
6.1
Коэффициент
доверия t и соответствующие уровни
доверительной вероятности
Коэффициент
доверия позволяет вычислить предельную
ошибку выборки,
т. е.
предельная ошибка выборки равна
t-кратному числу средних ошибок выборки.
Таким
образом, величина предельной ошибки
выборки может быть установлена с
определенной вероятностью. Как видно
из последней графы табл. 6.1, вероятность
появления ошибки равной или большей
утроенной средней ошибки выборки,
т. е.
крайне
мала и равна 0,003(1–0,997). Такие маловероятные
события считаются практически
невозможными, а потому величину
можно
принять за предел возможной ошибки
выборки.
Выборочное
наблюдение дает возможность определить
среднюю арифметическую выборочной
совокупности и величину предельной
ошибки этой средней, которая показывает
(с определенной вероятностью), насколько
выборочная величина может отличаться
от генеральной средней в большую или
меньшую сторону. Тогда величина
генеральной средней будет представлена
интервальной оценкой, для которой
нижняя граница будет равна
Интервал,
в который с данной степенью вероятности
будет заключена неизвестная величина
оцениваемого параметра, называют
доверительным,
а вероятность Р
– доверительной вероятностью.
Чаще всего доверительную вероятность
принимают равной 0,95 или 0,99, тогда
коэффициент доверия t
равен соответственно 1,96 и 2,58. Это
означает, что доверительный интервал
с заданной вероятностью заключает в
себе генеральную среднюю.
Наряду
с абсолютной величиной предельной
ошибки выборки рассчитывается и
относительная
ошибка
выборки, которая определяется как
процентное отношение предельной ошибки
выборки к соответствующей характеристике
выборочной совокупности:
Чем
больше величина предельной ошибки
выборки, тем больше величина доверительного
интервала и тем, следовательно, ниже
точность оценки. Средняя (стандартная)
ошибка выборки зависит от объема выборки
и степени вариации признака в генеральной
совокупности.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
12.04.2015613.89 Кб24pr.doc
- #
- #
- #
- #
3. Ошибки выборки
Каждая единица при выборочном наблюдении должна иметь равную с другими возможность быть отобранной – это является основой собственнослучайной выборки.
Собственнослучайная выборка – это отбор единиц из всей генеральной совокупности посредством жеребьевки или другим подобным способом.
Принципом случайности является то, что на включение или исключение объекта из выборки не может повлиять любой фактор, кроме случая.
Доля выборки – это отношение числа единиц выборочной совокупности к числу единиц генеральной совокупности:
Собственнослучайный отбор в чистом виде является исходным среди всех других видов отбора, в нем заключаются и реализуются основные принципы выборочного статистического наблюдения.
Два основных вида обобщающих показателей, которые используют в выборочном методе – это средняя величина количественного признака и относительная величина альтернативного признака.
Выборочная доля (w), или частность, определяется отношением числа единиц, обладающих изучаемым признаком m, к общему числу единиц выборочной совокупности (n):
Для характеристики надежности выборочных показателей различают среднюю и предельную ошибки выборки.
Ошибка выборки, ее еще называют ошибкой репрезентативности, представляет собой разность соответствующих выборочных и генеральных характеристик:
1) для средней количественного признака:
?х =|х – х|;
2) для доли (альтернативного признака):
?w =|х – p|.
Только выборочным наблюдениям присуща ошибка выборки
Выборочная средняя и выборочная доля – это случайные величины, принимающие различные значения в зависимости от единиц изучаемой статистической совокупности, которые попали в выборку. Соответственно ошибки выборки – тоже случайные величины и также могут принимать различные значения. Поэтому определяют среднюю из возможных ошибок – среднюю ошибку выборки.
Средняя ошибка выборки определяется объемом выборки: чем больше численность при прочих равных условиях, тем меньше величина средней ошибки выборки. Охватывая выборочным обследованием все большее количество единиц генеральной совокупности, все более точно характеризуем всю генеральную совокупность.
Средняя ошибка выборки зависит от степени варьирования изучаемого признака, в свою очередь степень варьирования характеризуется дисперсией ?2 или w(l – w) – для альтернативного признака. Чем меньше вариация признака и дисперсия, тем меньше средняя ошибка выборки, и наоборот.
При случайном повторном отборе средние ошибки теоретически рассчитывают по следующим формулам:
1) для средней количественного признака:
где ?2 – средняя величина дисперсии количественного признака.
2) для доли (альтернативного признака):
Так как дисперсия признака в генеральной совокупности ?2 точно неизвестна, на практике пользуются значением дисперсии S2 , рассчитанным для выборочной совокупности на основании закона больших чисел, согласно которому выборочная совокупность при достаточно большом объеме выборки достаточно точно воспроизводит характеристики генеральной совокупности.
Формулы средней ошибки выборки при случайном повторном отборе следующие. Для средней величины количественного признака: генеральная дисперсия выражается через выборную следующим соотношением:
где S2 – значение дисперсии.
Механическая выборка – это отбор единиц в выборочную совокупность из генеральной, которая разбита по нейтральному признаку на равные группы; производится так, что из каждой такой группы в выборку отбирается лишь одна единица.
При механическом отборе единицы изучаемой статистической совокупности предварительно располагают в определенном порядке, после чего отбирают заданное число единиц механически через определенный интервал. При этом размер интервала в генеральной совокупности равен обратному значению доли выборки.
При достаточно большой совокупности механический отбор по точности результатов близок к собственнослучайному Поэтому для определения средней ошибки механической выборки используют формулы собственнослучайной бесповторной выборки.
Для отбора единиц из неоднородной совокупности применяется так называемая типическая выборка, используется, когда все единицы генеральной совокупности можно разбить на несколько качественно однородных, однотипных групп по признакам, от которых зависят изучаемые показатели.
Затем из каждой типической группы собственнослучайной или механической выборкой производится индивидуальный отбор единиц в выборочную совокупность.
Типическая выборка обычно применяется при изучении сложных статистических совокупностей.
Типическая выборка дает более точные результаты. Типизация генеральной совокупности обеспечивает репрезентативность такой выборки, представительство в ней каждой типологической группы, что позволяет исключить влияние межгрупповой дисперсии на среднюю ошибку выборки. Поэтому при определении средней ошибки типической выборки в качестве показателя вариации выступает средняя из внутригрупповых дисперсий.
Серийная выборка предполагает случайный отбор из генеральной совокупности равновеликих групп для того, чтобы в таких группах подвергать наблюдению все без исключения единицы.
Поскольку внутри групп (серий) обследуются все без исключения единицы, средняя ошибка выборки (при отборе равновеликих серий) зависит только от межгрупповой (межсерийной) дисперсии.
Данный текст является ознакомительным фрагментом.
Читайте также
Ошибки резидента
Ошибки резидента
Относиться к ошибкам можно по-разному: можно бояться их совершить и переживать из-за каждой из них, можно радоваться своим ошибкам и кризисам, как указателям на пути к успеху и личным победам. Неизменно в ошибках только одно – за них приходится платить.
Формирование выборки
Формирование выборки
Процедура выборки является неотъемлемым этапом проекта внутреннего аудита. Она подробно описана в различных источниках, посвященных теме аудита. Однако во многом такие описания носят академичный характер. Предлагаю заострить внимание на тех
Ошибки в инвестициях – это ошибки инвесторов
Ошибки в инвестициях – это ошибки инвесторов
Сейчас я больше, чем когда бы то ни было, убежден в том, что все ошибки в инвестициях на самом деле ошибки инвесторов.Инвестиции не совершают ошибок. В отличие от инвесторов.Инвестирование – это выбор. Именно об этой
29. Определение необходимой численности выборки
29. Определение необходимой численности выборки
Одним из научных принципов в теории выбороч–ного метода является обеспечение достаточного чи–сла отобранных единиц.Уменьшение стандартной ошибки выборки всег–да связано с увеличением объема выборки. Расчет
30. Способы отбора и виды выборки. Собственно случайная выборка
30. Способы отбора и виды выборки. Собственно случайная выборка
В теории выборочного метода разработаны раз–личные способы отбора и виды выборки, обеспечи–вающие репрезентативность. Под способом отбора понимают порядок отбора единиц из генеральной со–вокупности.
31. Механическая и типическая выборки
31. Механическая и типическая выборки
При чисто механической выборке вся ге–неральная совокупность единиц должна быть прежде всего представлена в виде списка единиц отбора, со–ставленного в каком-то нейтральном по отношению к изучаемому признаку порядке. Затем список
32. Серийная и комбинированная выборки
32. Серийная и комбинированная выборки
Серийная (гнездовая) выборка – это такой вид формирования выборочной совокупности, когда в случайном порядке отбираются не единицы, подле–жащие обследованию, а группы единиц (серии, гнез–да). Внутри отобранных серий (гнезд)
33. Многоступенчатая, многофазная и взаимопроникающая выборки.
33. Многоступенчатая, многофазная и взаимопроникающая выборки.
Особенность многоступенчатой выборки со–стоит в том, что выборочная совокупность формиру–ется постепенно, по ступеням отбора. На первой ступени с помощью заранее определенного спосо–ба и вида отбора
3. Определение необходимой численности выборки
3. Определение необходимой численности выборки
Одним из научных принципов в теории выборочного метода является обеспечение достаточного числа отобранных единиц. Теоретически необходимость соблюдения этого принципа представлена в доказательствах предельных теорем
4. Способы отбора и виды выборки
4. Способы отбора и виды выборки
В теории выборочного метода разработаны различные способы отбора и виды выборки, обеспечивающие репрезентативность. Под способом отбора понимают порядок отбора единиц из генеральной совокупности. Различают два способа отбора: повторный
36. Ошибки выборки
36. Ошибки выборки
Собственнослучайная выборка – это отбор единиц из всей генеральной совокупности посредством жеребьевки или другим подобным способом. Принципом случайности является то, что на включение или исключение объекта из выборки не может повлиять любой фактор,
Лексические ошибки
Лексические ошибки
1. Неправильное использование слов и терминовОсновная масса ошибок в деловых письмах относится к лексическим. Недостаточная грамотность приводит не только к курьезной бессмыслице, но и абсурду.Отдельные термины и профессиональные жаргонные слова
5 Наши ошибки
5
Наши ошибки
Мы настаиваем: выбранный курс рыночных реформ был верным. И они вовсе не потерпели неудачу, они только еще раз споткнулись. Но ошибки и упущения были. Это и наши ошибки, и ошибки руководства страны, которые мы не сумели предотвратить. Ошибки — во многом
Важность размера выборки
Важность размера выборки
Как я уже говорил, люди склонны уделять слишком много внимания редким случаям возникновения какого-то феномена, несмотря на то что со статистической точки зрения из нескольких случаев невозможно извлечь много информации. Это – основная причина
Репрезентативные выборки
Репрезентативные выборки
Репрезентативность наших тестов для целей предсказания будущего определяется двумя факторами:– Количество рынков: тесты, проводимые на различных рынках, будут, скорее всего, включать рынки с разной степенью волатильности типов
Размер выборки
Размер выборки
Концепция размера выборки проста: для того чтобы делать статистически достоверные заключения, нужно иметь достаточно большую выборку. Чем меньше выборка, тем грубее выводы, которые можно сделать; чем выборка больше, тем выводы качественнее. Нет никакого
ДЕПАРТАМЕНТ ОБРАЗОВАНИЯ И НАУКИ ГОРОДА МОСКВЫ
Государственное бюджетное профессиональное образовательное учреждение города Москвы
«ЮРИДИЧЕСКИЙ КОЛЛЕДЖ»
(ГБПОУ Юридический колледж)
ПЛАН-КОНСПЕКТ учебного занятия
по ОП.11 Статистика
учебной дисциплине/междисциплинарному курсу
для обучающихся 2 курса
специальность 40.02.01 Право и организация социального обеспечения
(набор 2016 г.)
(углубленная подготовка)
дата проведения занятия по расписанию
Тема 3.1. Выборочное наблюдение
Занятие 15. ПЗ №8 Определение ошибки репрезентативности.
Определение объема выборочной совокупности
Цель занятия: отработать практические навыки по определению доверительных пределов и исчислению ошибок выборки
Задачи занятия:
Обучающая: Обеспечить усвоение обучающимися материала о понятиях: ошибки репрезентативности, выборка, выборочная совокупность;
Воспитательная: воспитывать навыки самостоятельной работы, чувство ответственности за порученный участок работы, дисциплину умственного труда, уверенность в своих силах, стремление к достижению результата;
Развивающая: создавать условия для развития самостоятельности мышления, способности высказывания собственной точки зрения, систематизировать необходимую информацию, анализировать, сравнивать и обобщать информацию, развивать монологическую речь.
Основная литература:
Глава 11. Выборочное наблюдение. (211-220) Статистика: учебник / И.В. Гладун. – 2-е издание, стер. – М.: КНОРУС, 2014. – 232 с. – СПО
Дополнительная литература:
Савюк Л.К. Правовая статистика: Учебник. — М.: Юрист, 2016
Интернет-ресурсы:
- Информационно-издательский центр «Статистика России» http://www.statbook.ru
- Электронный фонд правовой и технической документации http://docs.cntd.ru
- Информационно правовой портал http://www.garant.ru/
Междисциплинарные связи: Право социальное обеспечение
Внутридисциплинарные связи: Тема 2.1. Сводка и группировка статистических данных
1. Актуализация знаний по ранее пройденному материалу учебного курса
(ответить на вопросы (тестовые задания) и провести самооценку усвоенного материала)
Таблица 1.
|
Вопрос (тестовое задание) |
Ответ |
|
|
|
|
|
|
|
|
|
2. Изучаемые вопросы занятия
|
1. Определение ошибки репрезентативности. |
|
2. Определение объема выборочной совокупности. |
Вопрос 1. Определение ошибки репрезентативности
В статистике выделяют два основных метода исследования – сплошной и выборочный. При проведении выборочного исследования обязательным является соблюдение следующих требований: репрезентативность выборочной совокупности и достаточное число единиц наблюдений. При выборе единиц наблюдения возможны Ошибки смещения, т. е. такие события, появление которых не может быть точно предсказуемым. Эти ошибки являются объективными и закономерными. При определении степени точности выборочного исследования оценивается величина ошибки, которая может произойти в процессе выборки – Случайная ошибка репрезентативности (M) – Является фактической разностью между средними или относительными величинами, полученными при проведении выборочного исследования и аналогичными величинами, которые были бы получены при проведении исследования на генеральной совокупности.
Оценка достоверности результатов исследования предусматривает определение:
1. ошибки репрезентативности
2. доверительных границ средних (или относительных) величин в генеральной совокупности
3. достоверности разности средних (или относительных) величин (по критерию t)
Расчет ошибки репрезентативности (mм) средней арифметической величины (М):

Расчет ошибки репрезентативности (mР) относительной величины (Р):

Q =100 – Ρ% – величина, обратная Р; n – численность выборки (n>30)
В клинических и экспериментальных работах довольно часто приходится использовать Малую выборку, Когда число наблюдений меньше или равно 30. При малой выборке для расчета ошибок репрезентативности, как средних, так и относительных величин, Число наблюдений уменьшается на единицу, т. е.


Величина ошибки репрезентативности зависит от объема выборки: чем больше число наблюдений, тем меньше ошибка. Для оценки достоверности выборочного показателя принят следующий подход: показатель (или средняя величина) должен в 3 раза превышать свою ошибку, в этом случае он считается достоверным.
Знание величины ошибки недостаточно для того, чтобы быть уверенным в результатах выборочного исследования, так как конкретная ошибка выборочного исследования может быть значительно больше (или меньше) величины средней ошибки репрезентативности. Для определения точности, с которой исследователь желает получить результат, в статистике используется такое понятие, как вероятность безошибочного прогноза, которая является характеристикой надежности результатов выборочных медико-биологических статистических исследований. Обычно, при проведении медико-биологических статистических исследований используют вероятность безошибочного прогноза 95% или 99%. В наиболее ответственных случаях, когда необходимо сделать особенно важные выводы в теоретическом или практическом отношении, используют вероятность безошибочного прогноза 99,7%
Определенной степени вероятности безошибочного прогноза соответствует определенная величина Предельной ошибки случайной выборки (Δ – дельта), которая определяется по формуле:
Δ=t * m, где t – доверительный коэффициент, который при большой выборке при вероятности безошибочного прогноза 95% равен 2,6; при вероятности безошибочного прогноза 99% – 3,0; при вероятности безошибочного прогноза 99,7% – 3,3, а при малой выборке определяется по специальной таблице значений t Стьюдента.
Используя предельную ошибку выборки (Δ), можно определить Доверительные границы, в которых с определенной вероятностью безошибочного прогноза заключено действительное значение статистической величины, Характеризующей всю генеральную совокупность (средней или относительной).
Для определения доверительных границ используются следующие формулы:
- для средних величин:

Мвыб – средняя величина, Полученная при проведении исследования на выборочной совокупности; t – доверительный коэффициент, значение которого определяется степенью вероятности безошибочного прогноза, с которой исследователь желает получить результат; mM – ошибка репрезентативности средней величины.
2) для относительных величин:

Доверительные границы показывают, в каких пределах может колебаться размер выборочного показателя в зависимости от причин случайного характера.
При малом числе наблюдений (n<30), для вычисления доверительных границ значение коэффициента t находят по специальной таблице Стьюдента. Значения t расположены в таблице на пересечении с избранной вероятностью безошибочного прогноза и строки, Указывающей на имеющееся число степеней свободы (n), Которое равно n-1.
на определение ошибок репрезентативности (m) и доверительных границ средней величины генеральной совокупности (Мген) при числе наблюдений больше 30
Условие задачи: при изучении комбинированного воздействия шума и низкочастотной вибрации на организм человека было установлено, что средняя частота пульса у 36 обследованных водителей сельскохозяйственных машин через 1 ч работы составила 80 ударов в 1 минуту; σ = ± 6 ударов в минуту.
Задание: определить ошибку репрезентативности (mM) и доверительные границы средней величины генеральной совокупности (Мген).
Решение.
- Вычисление средней ошибки средней арифметической (ошибки репрезентативности) (m): m = σ / √n = 6 / √36 = ±1 удар в минуту
- Вычисление доверительных границ средней величины генеральной совокупности (Мген). Для этого необходимо:
- а) задать степень вероятности безошибочного прогноза (Р = 95 %);
- б) определить величину критерия t. При заданной степени вероятности (Р=95%) и числе наблюдений меньше 30 величина критерия t, определяемого по таблице, равна 2 (t = 2). Тогда Мген = Мвыб ± tm = 80 ± 2×1 = 80 ± 2 удара в минуту.
Вывод. Установлено с вероятностью безошибочного прогноза Р = 95%, что средняя частота пульса в генеральной совокупности, т.е. у всех водителей сельскохозяйственных машин, через 1 ч работы в аналогичных условиях будет находиться в пределах от 78 до 82 ударов в минуту, т.е. средняя частота пульса менее 78 и более 82 ударов в минуту возможна не более, чем у 5% случаев генеральной совокупности.
на определение ошибок репрезентативности (m) и доверительных границ относительного показателя генеральной совокупности (Рген)
Условие задачи: при медицинском осмотре 164 детей 3 летнего возраста, проживающих в одном из районов городе Н., в 18% случаев обнаружено нарушение осанки функционального характера.
Задание: определить ошибку репрезентативности (mp) и доверительные границы относительного показателя генеральной совокупности (Рген).
Решение.
- Вычисление ошибки репрезентативности относительного показателя: m = √P x q / n = √18 x (100 — 18) / 164 = ± 3%
- Вычисление доверительных границ средней величины генеральной совокупности (Рген) производится следующим образом:
- необходимо задать степень вероятности безошибочного прогноза (Р=95%);
- при заданной степени вероятности и числе наблюдений больше 30, величина критерия t равна 2 (t = 2). Тогда Рген = Рвыб± tm = 18% ± 2 х 3 = 18% ± 6%.
Вывод. Установлено с вероятностью безошибочного прогноза Р=95%, что частота нарушения осанки функционального характера у детей 3 летнего возраста, проживающих в городе Н., будет находиться в пределах от 12 до 24% случаев.
на оценку достоверности разности средних величин
Условие задачи: при изучении комбинированного воздействия шума и низкочастотной вибрации на организм человека было установлено, что средняя частота пульса у водителей сельскохозяйственных машин через 1 ч после начала работы составила 80 ударов в минуту; m = ± 1 удар в мин. Средняя частота пульса у этой же группы водителей до начала работы равнялась 75 ударам в минуту; m = ± 1 удар в минуту.
Задание: оценить достоверность различий средних значений пульса у водителей сельскохозяйственных машин до и после 1 ч работы.
Решение.
Вывод. Значение критерия t = 3,5 соответствует вероятности безошибочного прогноза Р > 99,7%, следовательно можно утверждать, что различия в средних значениях пульса у водителей сельскохозяйственных машин до и после 1 ч работы не случайно, а достоверно, существенно, т.е. обусловлено влиянием воздействия шума и низкочастотной вибрации.
на оценку достоверности разности относительных показателей
Условие задачи: при медицинском осмотре детей 3 летнего возраста в 18% (m = ± 3%) случаях обнаружено нарушение осанки функционального характера. Частота аналогичных нарушений осанки при медосмотре детей 4-летнего возраста составила 24% (m = ± 2,64%).
Задание: оценить достоверность различий в частоте нарушения осанки у детей 2 возрастных групп.
Решение.
Вывод. Значение критерия t=1,5 соответствует вероятности безошибочного прогноза Р<95%. Следовательно, различие в частоте нарушений осанки среди детей, сравниваемых возрастных групп случайно, недостоверно, несущественно, т.е. не обусловлено влиянием возраста детей.
|
Источники информации по 1 вопросу |
Автор и наименование |
Страницы (форма доступа для Интернет-ресурсов) |
|
Основная литература |
Глава 11. Выборочное наблюдение. Статистика: учебник / И.В. Гладун. – 2-е издание, стер. – М.: КНОРУС, 2014. – 232 с. – СПО |
стр. 211-220 |
|
Интернет ресурсы |
|
http://www.statbook.ru |
|
http://docs.cntd.ru |
|
|
http://www.garant.ru/ |
Контрольное задание по Вопросу 1
- Записать в тетрадь конспект (1-2 стр.)
Вопрос 2. Определение объема выборочной совокупности
Социологические исследования редко бывают сплошными, как, например, перепись населения. Обычно сплошное исследование проводится при небольшой генеральной совокупности.
Чаще всего исследования носят выборочный характер, при котором наиболее важным основанием является возможность распространения полученных результатов и выводов на всю генеральную совокупность. В таком случае сплошное исследование нецелесообразно. Обеспечение этой нецелесообразности — вопрос о репрезентативности выборки, т.е. достаточной количественной и качественной представительности генеральной совокупности в выборке.
Условиями соблюдения репрезентативности выборки являются:
1) равная возможность каждого члена генеральной совокупности попасть в выборку;
2) отбор необходимо проводить независимо от изучаемого признака (иначе в выборку могут попасть, например, только спортсмены);
3) отбор по возможности должен производиться из однородных совокупностей;
4) величина выборки должна быть достаточно большой.
Далее возникает вопрос: как определить достаточный объем выборки? Для этого необходимо иметь характеристики генеральной совокупности по важнейшим (с точки зрения исследования) признакам. К ним, например, можно отнести сведения о количестве желающих заниматься физической культурой и спортом, о числе занимающихся и т.д. Но, как правило, такие характеристики (или многие из них) не известны. Пилотажные исследования как раз и направлены на их выявление.
Приведем пример определения объема выборочной совокупности. В ходе подготовки к проведению конкретно-социологического исследования на основании теоретических посылок были выделены характеристики и признаки, подлежащие изучению. Например, желание заниматься физической культурой, спортом, величина потребности, участие в видах деятельности и др.
На основании результатов изучения этих признаков в пробном исследовании (30 и более респондентов) определяется объем выборки.
Предположим, что в пробном исследовании опрошено 147 студентов 4-х курсов в четырех вузах Республики Беларусь.
Для желания заниматься физической культурой получены следующие распределения:
1.«Нет, не хочу» — 5 человек;
2.«Скорее не хочу, чем хочу» — 3 человека;
3.«Безразлично» — 11 человек;
4.«Скорее хочу, чем не хочу» — 34 человека;
5.«Да, хочу» — 72 человека.
Для расчета объема выборки используются формулы:
t — 1,96 — распределение Стьюдента для вероятности 0,95 или 95% (т.е., если требуемая вероятность соответствия характеристик выборки и характеристик генеральной совокупности 95%, всегда = 1,96. Их соответствие на 95% — общепринятое требование в социологических исследованиях.
Для нашего распределения:
При условии, что выборка в пробном исследовании представляла бы собой модель генеральной совокупности, величина выборочной совокупности для изучения желания заниматься физической культурой должна быть не меньше 147 человек. Тогда с вероятностью 95% можно утверждать, что генеральное среднее лежит в пределах 4,39+0,155.
Поскольку модель выборки в пробном исследовании во вузам не представляет собой модели генеральной совокупности (опрос был в четырех вузах из 30), то увеличиваем полученное n (30/4) в 7,5 раза. Тогда необходимый объем выборки — 1102 респондента.
Качественная представительность полученной выборки оценивается сравнением существенных характеристик (либо связанных с существенными) генеральной совокупности и выборки. Для студенчества, например, такими характеристиками являются: соотношение по полу, охват учебными занятиями по физическому воспитанию, соотношение форм занятий и др.
Когда информация о признаках элементов генеральной совокупности отсутствует, исключается возможность определения объема выборочной совокупности при помощи формул. В этом случае можно опереться на многолетний опыт социологов — практиков, свидетельствующий о том, что для пробных опросов достаточна выборка объемом 100-250 человек. При массовых опросах, если величина генеральной совокупности 5000 человек, достаточный объем выборочной совокупности — не менее 500 человек, если же величина генеральной совокупности 5000 человек и более, то — 10% ее состава (но не более 2000-2500 человек). Это характеризует достаточно достоверные результаты исследования.
ПРИМЕР 1
При проверке импортирования груза на таможне методом случайной выборки было обработано 200 изделий. В результате был установлен средний вес изделия 30г., при СКО=4г с вероятностью 0,997. Определите пределы в которых находится средний вес изделий генеральной совокупности.
Решение.
В данном примере – случайный повторный отбор.
n=200


p=0,997, тогда t=3
Формула средней ошибки для случайного повторного отбора:


Определяем величину средней ошибки.
Ответ: пределы в которых находится средний вес изделий:
ПРИМЕР 2
В городе проживает 250тыс. семей. Для определения среднего числа детей в семье была организована 2%-я бесповторная выборка семей. По ее результатам было получено следующее распространение семей по числу детей:
P=0,954. Найти пределы в которых будет находится среднее число детей в генеральной совокупности.
|
Число детей в семье, xi |
0 |
1 |
2 |
3 |
4 |
5 |
|
Кол-во детей в семье |
1000 |
2000 |
1200 |
400 |
200 |
200 |
Решение
2%-я выборка означает: n=250000*0,02= 5000 семей было исследовано.
Т.к. выборка бесповторная, используем следующую формулу для определения средней величины ошибки:
Найдем среднее число детей в выборочной совокупности:

Определим дисперсию

Т.к p = 0,954, то t = 2


Вывод: из-за слишком малой величины ошибки, среднее число детей в генеральной совокупности можно принять за 1,5 ребенка.
|
Источники информации по 2 вопросу |
Автор и наименование |
Страницы (форма доступа для Интернет-ресурсов) |
|
Основная литература |
Глава 11. Выборочное наблюдение. Статистика: учебник / И.В. Гладун. – 3-е издание, стер. – М.: КНОРУС, 2019. – 232 с. – СПО |
стр. 211-220 |
|
Интернет ресурсы |
|
http://www.statbook.ru |
|
http://docs.cntd.ru |
|
|
http://www.garant.ru/ |
Контрольное задание по Вопросу 2
- Записать в тетрадь конспект (1-2 стр.)
3. Подведение итогов учебного занятия
(ответить на вопросы (тестовые задания) и провести самооценку усвоенного материала)
Таблица 2.
|
Наименование изученного вопроса учебного занятия |
Контрольное задание по изученному вопросу |
Ответ |
|
Определение ошибки репрезентативности. |
ЗАДАНИЕ 1 Условие задачи: при медицинском осмотре 126 детей 6 летнего возраста, проживающих в одном из районов городе А., в 12% случаев обнаружено нарушение осанки функционального характера. Задание: определить ошибку репрезентативности (mp) и доверительные границы относительного показателя генеральной совокупности (Рген). |
|
|
Определение ошибки репрезентативности. |
ЗАДАНИЕ 2. Условие задачи: при медицинском осмотре детей 6 летнего возраста в 15% (m = ± 3%) случаях обнаружено нарушение осанки функционального характера. Частота аналогичных нарушений осанки при медосмотре детей 7-летнего возраста составила 24% (m = ± 2,64%). Задание: оценить достоверность различий в частоте нарушения осанки у детей 2 возрастных групп. |
|
|
Определение объема выборочной совокупности |
ЗАДАНИЕ 3. В городе проживает 300 тыс. семей. Для определения среднего числа детей в семье была организована 2%-я бесповторная выборка семей. По ее результатам было получено следующее распространение семей по числу детей: P=0,954. Найти пределы в которых будет находится среднее число детей в генеральной совокупности |
|
|
Определение объема выборочной совокупности |
Сформулируйте понятие генеральной совокупности |
|
|
Определение объема выборочной совокупности |
Перечислите способы отбора единиц для выборочного наблюдения |
- Домашнее задание на следующее занятие
- Выучить основные понятия. Глава 11. Выборочное наблюдение. Статистика: учебник / И.В. Гладун. – 2-е издание, стер. – М.: КНОРУС, 2014. – 232 с. – СПО (стр. 211-220)
- Выполнить задание 11.1. в тетради (стр. 224) учебник / И.В. Гладун. – 2-е издание, стер. – М.: КНОРУС, 2014. – 232 с. – СПО
Преподаватель Ю.В. Древаль
|
СОГЛАСОВАНО Протокол заседания ЦК дисциплин профессионального цикла специальности «Право и организация социального обеспечения» ГБПОУ Юридический колледж от ____________ 2017 г. № ___ |
Тема 8. Выборочный метод
8.1. Сущность выборочного наблюдения, причины и практика его применения
Выборочное обследование – наиболее распространенный вид несплошного наблюдения в практике отечественной и зарубежной статистики. Сущность этого вида наблюдения состоит в том, что характеристика всей совокупности единиц дается по некоторой их части, отобранной научно обоснованным методом. В основе отбора единиц в выборку лежит принцип случайности, который обеспечивает равную возможность попадания в отобранную часть любой из единиц всей генеральной совокупности. Именно принцип случайности, заложенный в основу выборочного метода, и обеспечивает объективность результатов наблюдения, позволяет установить границы возможных ошибок и получить достоверные данные для характеристики всей совокупности.
Если отбор единиц произведен строго случайно, выборочная совокупность будет представительной или репрезентативной.
Выборочное наблюдение является наиболее совершенным и научно обоснованным методом несплошного наблюдения. При выборочном методе численность и доля единиц, которая будет обследоваться, известна до начала наблюдения, этим оно отличается от анкетного. В отличие от способа основного массива и монографического описания при проведении выборки неизвестно какие единицы совокупности будут подвергнуты обследованию. Выборочный метод, таким образом, в отличие от названных, исключает тенденциозность отбора и в большей степени обеспечивает представительство всех видов, групп, составляющих изучаемую совокупность.
Выборочный метод широко применяется в социально-экономических исследованиях, т.к. обладает рядом достоинств. Во-первых, он дает большую экономию средств и требует меньше времени для проведения наблюдения. То есть, выборочное наблюдение более экономичное, а результаты его носят более оперативный характер, чем при сплошном наблюдении. Во-вторых, при выборочном наблюдении при значительном сокращении объема работы обследование можно провести по более широкой программе, т.е. изучить явление более глубоко и детально. В-третьих, поскольку объем работы сокращается, то при выборке допускается меньше ошибок регистрации, и часто получают более точные результаты, чем при сплошном наблюдении.
Выборочный метод иногда является единственно возможным методом изучения явления, т.к. применение сплошного обследования может привести к физическому уничтожению всех единиц наблюдения. Например, при контроле качества некоторых видов продукции в промышленности, проверке семян на всхожесть в сельском хозяйстве и т.д.
Применение выборочного метода вызывается необходимостью контроля данных сплошного наблюдения. Например, контрольные проверки размеров посевных площадей и численности скота в личных хозяйствах населения.
Использование этого метода является целесообразным при изучении расходов населения, времени работы оборудования, рабочего времени и т.д.
Часто выборочный метод применяется в сочетании со сплошным наблюдением, например, при переписях населения.
8.2. Ошибки репрезентативности и теоретические основы их определения
В статистике принято называть совокупность отобранных единиц выборочной совокупностью (n), а совокупность единиц, из которых производится отбор – генеральной совокупностью (N). Генеральная и выборочная совокупности характеризуются такими показателями как средний размер признака, дисперсия, доля.
Рекомендуемые материалы
Задача выборочного наблюдения – дать верное представление о показателях всей генеральной совокупности на основе данных их некоторой части, попавшей в выборку.
Естественно, что когда изучают не всю, а только часть совокупности, результаты расчетов показателей выборочной и генеральной совокупности не совпадают. Эти отклонения выборочной средней и выборочной доли от доли и средней в генеральной совокупности называются ошибками выборки, или ошибками репрезентативности. Ошибки репрезентативности – это специфические ошибки, присущие только выборке и появляются они вследствие расхождения структуры выборочной и генеральной совокупности.
Как уже отмечалось, при выборочном наблюдении имеют место и ошибки регистрации, но они незначительны.
Основной организационный принцип выборочного наблюдения состоит в том, чтобы не допустить тенденциозного подбора выборочной совокупности, т.е. обеспечить строгое соблюдение принципа случайности отбора единиц в выборку. На результаты выборочного наблюдения можно полагаться именно благодаря тому, что отбор носит случайный характер. Это и позволяет максимально сократить возможные пределы отклонений выборочных результатов от показателей, вычисленных по всей генеральной совокупности.
Обобщенное действие механизма случайности в математике представляет закон больших чисел. Теория выборочного метода, основывается на доказательствах теорем русских математиков П.Л. Чебышева и А.М. Ляпунова. Из сущности закона больших чисел вытекает:
1) хотя каждая выборочная средняя и доля являются случайной величиной, однако средняя арифметическая из всех выборочных средних равняется генеральной средней;
2) каждый из возможных результатов выборочного наблюдения имеет свою вероятность появления, которая зависит от доли индивидуальных значений в генеральной совокупности. Чем больше доля индивидуальных показателей в генеральной совокупности, тем выше вероятность этих значений попасть в выборку;
3) каждая выборочная средняя отличается от генеральной средней. Разница между выборочной и генеральной средними представляет собой ошибку репрезентативности (выборки). Последняя измеряется средним квадратом отклонений всех возможных значений выборочных средних от генеральной средней, т.е. дисперсией.
В математической статистике доказывается, что между дисперсией выборочных средних и генеральной дисперсией существует определенное соотношение.
Дисперсия выборочных средних равна отношению генеральной дисперсии к численности выборочной совокупности.
Корень квадратный из этого отношения представляет собой стандартную (среднюю) ошибку репрезентативности (выборки):

Эта величина средней ошибки играет огромную роль в теории выборочного метода. Знание ее позволяет определять размер конкретных выборок и сказать какая выборка будет лучше еще до самой работы по выборочному обследованию.
Если выборочное обследование проводится с целью определения доли единиц, обладающих изучаемым признаком, то используются те же формулы расчетов, но в этом случае средняя и дисперсия заменяются аналогичными показателями альтернативного признака. Отсюда средняя ошибка выборки равна:

где 
Из приведенной формулы видно, что величина средней ошибки выборки зависит от вариации признака в генеральной совокупности, которая характеризуется дисперсией, и объема выборочной совокупности. Чем сильнее колеблется изучаемый признак у единиц генеральной совокупности, тем больше дисперсия, а отсюда и больше ошибка выборки, и, наоборот, чем больше объем выборочной совокупности, тем меньше ошибка выборки.
При организации выборки величина колеблемости признака в генеральной совокупности (N) неизвестна. В математической статистике доказано, что соотношение между дисперсиями генеральной и выборочной совокупностей выражается формулой:

Поскольку величина 

4) при достаточно большом объеме выборки распределение средних вокруг генеральной средней подчинено закону нормального распределения. Это означает, что отклонение от генеральной средней расположено в ту или другую сторону симметрично. Если взять одно среднее квадратическое отклонение в ту или другую сторону, то тем самым будет принято во внимание 68,3% всех выборочных средних, т.е. выборочная средняя не отклонится в ту или другую сторону на одну сигму. Если взять два средних квадратических отклонения, то во внимание будет принято 95,4% всех выборочных средних, если взять три средних квадратических отклонения – 99,7% средних. Зная среднюю ошибку выборки и вероятности с какой уверенностью хотят гарантировать результаты выборочного наблюдения можно установить пределы ошибок.

где 

Коэффициент доверия выражает число средних ошибок, которые нужно взять, чтобы получить заданную вероятность. Так при вероятности 0,683 


При выборочном наблюдении утверждения носят ориентировочный характер и выборочные показатели выражаются в интервале от и до.
Границы этих интервалов называются доверительными пределами. Нижний доверительный предел равен выборочной средней (доли) минус ошибка выборки.
8.3. Способы отбора и виды выборочного наблюдения
Репрезентативность выборки зависит не только от объема выборочной совокупности, но и от того как она образована, от характера отбора.
В генеральной совокупности могут отбираться отдельные единицы совокупности или же их группы.
В зависимости от того что является единицей отбора, последний делится на два вида: индивидуальный и групповой.
При индивидуальном отборе единицей отбора является непосредственно единица наблюдения. Например, проверка качества продукции непосредственно на рабочем месте. Контролер проверяет не каждую изготовленную деталь, а отбирает часть деталей из всей партии, которые подвергает проверке.
Групповой отбор заключается в том, что для наблюдения отбираются не только единицы совокупности, а их группы или серии. Примером могут служить контрольные проверки веса продукции, если она реализуется в упаковке (чай, макаронные изделия, сахар-рафинад и т.д.). Для контроля отбираются ящики, в отобранных ящиках взвешивается каждая пачка.
В некоторых случаях групповой отбор производится в сочетании с индивидуальным. Такой отбор называется комбинированным и связан со ступенчатостью. Здесь выборочная совокупность формируется не сразу, а проходит несколько стадий, ступеней, поэтому он еще называется многоступенчатым. Наиболее простым его случаем является двухступенчатый отбор, когда на первой ступени отбираются группы, на второй – отдельные единицы из отобранных групп.
Например, для контроля за соблюдением весовых стандартов пачек чая, сахара сначала отбираются ящики, в которых упакованы пачки, а из этих ящиков отбираются отдельные пачки.
Средняя ошибка выборки при двухступенчатом отборе исчисляется по формуле:
где 


Иногда сплошное наблюдение проводится в комбинации с выборочным. Например, переписи населения. Все население обследуется по основной программе, а 25% его обследуется по расширенной программе. Сплошное наблюдение может комбинироваться и с несколькими выборочными обследованиями, различающимися детализацией программ и числом обследуемых единиц.
Точность результатов и размеры ошибок выборочного наблюдения во многом зависят и от способа отбора единиц выборочной совокупности.
В зависимости от цели изучения и характера исходных данных, для обеспечения наибольшей репрезентативности выборки применяются следующие виды и способы отбора единиц совокупности для наблюдения:
а) собственно-случайная выборка,
б) механическая,
в) типическая (районированная),
г) серийно-гнездовая.
Собственно-случайная выборка.
При собственно-случайной выборке из генеральной совокупности отбираются для наблюдения отдельные единицы в случайном порядке. Для этого используются таблицы случайных чисел или жеребьевка.
Собственно-случайная выборка может проводиться по способу повторного и бесповторного отбора.
При повторном отборе отобранная единица после регистрации ее данных возвращается в генеральную совокупность и таким образом может попасть в выборку вторично и даже несколько раз. При бесповторном отборе каждая единица участвует в выборке только один раз.
Случайный отбор дает хорошие результаты в условиях, когда между единицами исследуемой совокупности нет резких различий.
При проведении собственно-случайной выборки нужно иметь исчерпывающий перечень всех единиц генеральной совокупности. Может оказаться, что пока организуется жеребьевка, единицы совокупности снова возникнут или ликвидируются. А при изучении качества продукции в течение дня вообще не имеется исчерпывающего перечня единиц. Неудобство этого способа отбора еще состоит и в том, что для жеребьевки на каждую единицу генеральной совокупности изготавливаются карточки (фишки) для жеребьевки.
Среднюю ошибку выборки для средней определяют в зависимости от способа отбора по разным формулам.
При повторном отборе:

При бесповторном отборе:

Аналогично вычисляют среднюю ошибку выборки для доли признака.
При повторном отборе:

При бесповторном отборе:

Бесповторный отбор обеспечивает большую репрезентативность выборки, чем повторный.
Собственно-случайная выборка применяется при контроле качества продукции, качества уборочных работ в сельском хозяйстве, при изучении оплаты пассажирами проезда в общественном транспорте и т.д.
Механическая выборка.
Механическая выборка представляет собой последовательный отбор единиц через равные интервалы в порядке определенного расположения их в генеральной совокупности или каком-нибудь перечне. Интервалы отбора определяются в соответствие с долей выборочной совокупности. Если, например, десятипроцентная выборка, то отбирается каждая десятая единица, если пятипроцентная – каждая двадцатая единица и т.д.
Расположение единиц генеральной совокупности в списке может быть двояким – упорядоченным или неупорядоченным относительно изучаемого признака. Так, списки рабочих могут быть составлены в алфавитном порядке по первым буквам фамилий; поскольку первые буквы фамилий рабочих не связаны с выполнением норм выработки, такое расположение является неупорядоченным относительно изучаемого признака. Если рабочих в списки записать по возрастанию или убыванию процента выполнения норм, расположение будет упорядоченным. Способ расположения единиц генеральной совокупности влияет на порядок их отбора в выборочную совокупность. В случае неупорядоченного расположения единиц из первых десяти рабочих можно взять любого (первого, второго, десятого) и затем последовательно брать одного через 10 человек. Если расположение упорядоченное, в выборочную совокупность следует отбирать рабочих, стоящих посредине каждого десятка; в противном случае может образоваться систематическая ошибка выборки. В самом деле, если рабочие в списках расположены по нисходящему проценту выполнения норм, то первые номера в каждом десятке будут всегда лучше по изучаемому признаку, а последние номера – худшими. Следовательно, отобрав в выборку первые номера, статистик завысит выборочный показатель выполнения норм, отобрав последние номера – занизит. Поэтому следует брать из каждого десятка пятые или шестые номера.
Механический отбор из упорядоченной (ранжированной) совокупности иногда называют систематическим отбором.
Механический отбор можно применять и не прибегая к спискам, а используя тот естественный порядок, в котором фактически расположены единицы генеральной совокупности, если только этот порядок не приведет к тенденциозным ошибкам.
Механическая выборка всегда бывает бесповторной и ошибки определяются по формулам собственно-случайной выборки.
Применяется механическая выборка при контроле за результатами сплошного наблюдения, при изучении потерь рабочего времени и т.д.
Например, из общего числа пенсионных вкладов банка была проведена 5%-ная механическая выборка. Результаты выборки следующие:
Таблица 8.1
|
Размер пенсионного вклада, тыс р. |
Число вкладов |
|
до 20 |
25 |
|
20-40 |
37 |
|
40-60 |
70 |
|
60-80 |
50 |
|
80 и выше |
18 |
|
Итого |
200 |
Определить: 1) с вероятностью 0,683 пределы среднего размера пенсионного вклада во всей генеральной совокупности; 2) с вероятностью 0,954 пределы доли вкладов, размер которых превышает 80 тыс. р.
Решение:
1. Предельная ошибка выборки на средний размер пенсионного вклада при механической выборке определяется по формуле:

Вероятности 0,683 соответствует коэффициент доверия (t), равный 1.
Вычислим среднюю и дисперсию по выборочной совокупности.


Вывод: с вероятностью 0,683 можно утверждать, что средний размер пенсионного вклада у всех вкладчиков банка будет находиться в пределах:

2. Предельная ошибка доли:

При вероятности 0,954 t=2.
W – доля вкладов, размер которых превышает 80 тыс. р.


Вывод: с вероятностью 0,954 можно утверждать, что доля вкладов, размер которых составляет 80 тыс. р. и выше во всей генеральной совокупности будет находиться в следующих доверительных пределах:

Типическая выборка.
Типический (районированный) отбор применяют в том случае, если изучаемая совокупность неоднородна.
При этом отборе генеральная совокупность предварительно расчленяется на типы (районы) из которых отбираются единицы либо посредством жеребьевки, либо механическим способом.
Типы (районы) могут быть образованы искусственно или использованы те, которые сложились естественно.
Количество единиц, отбираемых из каждого типа (района), как правило, берется пропорционально численности типов в генеральной совокупности. Однако в принципе наиболее точный результат дает типический отбор, учитывающий вариацию признака в отдельных частях (типах, районах) генеральной совокупности. Для достижения этого численность частей выборочной совокупности, имеющих большую вариацию, несколько увеличивается.
Случайная ошибка при типическом отборе меньше, чем при собственно-случайном и механическом отборах, так как типический отбор дает более репрезентативную выборку, лучше обеспечивает возможность сохранить в выборке то соотношение между типами (районами), которое имеется в генеральной совокупности.
Предельная ошибка при пропорциональной типической выборке исчисляется по нижеследующим формулам.
При повторном отборе:


При бесповторном отборе:


Пропорциональная типическая выборка широко применяется в социологических, бюджетных обследованиях, при изучении урожайности по типам хозяйств.
Например, для исчисления среднего размера депозита в банке была проведена 2% – типическая выборка. Распределение депозитов по срокам хранения и их статистические характеристики в выборке представлены в табл. 8.2.
Таблица 8.2
|
Срок хранения депозита |
Число депозитов |
Средний размер депозита, тыс. р. |
Дисперсия |
|
3 месяца |
500 |
40 |
340 |
|
6 месяцев |
300 |
65 |
580 |
|
1 год |
200 |
100 |
260 |
Вычислим средний размер депозита:
С вероятностью 0,954 установить предельную ошибку выборки на средний размер депозита.
Вычислим среднюю групповую дисперсию:
Средняя ошибка выборки составит:
Предельная ошибка выборки при вероятности 0,954 составит:
Таким образом, средний размер депозита в генеральной совокупности будет находиться в пределах от 58,26 до 60,74 тыс. р.
Серийная (гнездовая) выборка.
Весьма часто в практике выборочного наблюдения применяется гнездовой или серийный отбор. При гнездовой или серийной выборке отбор производится не единицами, а целыми гнездами, сериями единиц совокупности, в пределах которых обследуются все единицы полностью. Например, 200 рабочих из 2000 можно отобрать целыми бригадами; отбор бригад может быть осуществлен посредством жеребьевки или механически. В отобранных бригадах общей численностью 200 человек должны быть обследованы все рабочие сплошь.
Серии (гнезда) состоят из единиц, связанных между собой или территориально, или организационно, или, наконец, во времени. Отбор серий может производится в порядке повторного и бесповторного отбора. Серии могут быть равновеликими и неравновеликими. На практике чаще применяется серийный отбор с равными сериями.
Серийный отбор значительно проще в организационном отношении и дешевле других способов. Однако получающаяся в процессе этого отбора ошибки выборки в подавляющем большинстве случаев больше, чем при любом другом способе отбора.
Средняя ошибка выборки при отборе равновеликими сериями будет выражаться формулами:
при повторном отборе: 
при бесповторном отборе: 
где 

Приведем пример. Выборочное наблюдение урожайности зерновых культур по области проводилось при помощи отбора районов. По каждому отобранному району находилась средняя урожайность, которая оказалась следующей: I район – 14 ц с 1 га, II район – 15 ц с 1 га, III район – 14,5 ц с 1 га, IV район – 15,5 ц с 1 га, V район – 16 ц с 1 га. С вероятностью 0,997 оценить урожайность зерновых во всей области. В области 25 районов.
Найдем сначала общую среднюю:
затем межгрупповую дисперсию:
Средняя ошибка серийного бесповторного отбора:
Найдем предельную ошибку выборки:
Следовательно, с вероятностью 0,997 можно ожидать, что средняя урожайность зерновых в этой области заключается в пределах:
8.5. Определение необходимой численности выборки
Ошибки выборочного наблюдения и доверительные пределы генеральной средней (генеральной доли) определяются после того, как получены данные, характеризующие каждую единицу выборочной совокупности. А поэтому при проведении выборки первоначально необходимо определить сколько единиц или какая часть генеральной совокупности должна быть подвергнута наблюдению. Это важный момент в проведении выборочного наблюдения. Важность его в том, что излишняя численность выборочной совокупности вызывает необоснованное завышение затрат времени, труда, материальных и денежных средств, а недостаточная – дает результаты с большей погрешностью. Объем выборки должен быть оптимальным.
Факторами, определяющими численность выборки, являются:
1. Показатели вариации данного признака. Здесь обнаруживается прямая зависимость, т.е. чем больше показатель вариации, тем больше объем выборки.
2. Размер вероятности. Зависимость также прямая. Чем выше вероятность, тем выше коэффициент доверия, а, следовательно, и численность выборки. Величина вероятности зависит от того какое явление изучается. Естественно, что при контроле качества продовольственной продукции величина вероятности выше, чем непродовольственной продукции.
3. Размер возможной допустимой ошибки (
4. Способ отбора единиц для обследования. При прочих равных условиях для бесповторной выборки требуется меньшая численность выборки, чем при повторном отборе.
Основной трудностью, возникающей при установлении необходимой численности выборки, является определение среднеквадратического отклонения, которое характеризует вариацию признака. Значение этого показателя отсутствует как для генеральной, так и выборочной совокупности, поскольку задача определения необходимой численности выборки возникает тогда, когда еще выборка не проведена. Поэтому на практике используют несколько методов приближенного расчета среднеквадратического отклонения. Рассмотрим некоторые из них.
1. Вместо среднеквадратического отклонения данного отчетного периода берут значение данного показателя в базисном периоде. Этот прием применяется в тех случаях, когда мы в отчетном периоде, по сравнению с базисным, не ожидаем резкого изменения в исследуемых признаках.
2. Расчет среднеквадратического отклонения может быть основан на той связи, которая существует между показателями средней арифметической и коэффициентом вариации. Практика показывает, что во всех более или менее однородных совокупностях коэффициент вариации колеблется в пределах от 25-35%. Иначе говоря, коэффициент вариации обычно приблизительно равен 

3. Следующий прием опирается на величину размаха вариации. Разность между максимальным и минимальным значениями признака равна приблизительно шести средним квадратическим отклонениям. Разделив размах колебаний на шесть, мы получим приближенное значение среднего квадратического отклонения. Этот прием можно использовать, т.к. максимальное и минимальное значение изучаемого признака известны до проведения наблюдения.
При установлении колеблемости доли, как и средней, в первую очередь надо попытаться найти ориентировочные данные о величине W. Если таких данных нет, то берется максимальная величина произведения W на (1-W). Эта величина равна 0,25.
Необходимую численность выборочной совокупности определяют на основе алгебраического преобразования формулы предельной ошибки выборки для разных видов и способов отбора.
Для собственно-случайной повторной выборки:

Чтобы найти численность выборки, нужно освободиться от радикала. Это достигается возведением левой и правой частей уравнения в квадрат.

отсюда численность выборки: 
Объем выборочной совокупности прямо пропорционален квадрату коэффициента доверия и дисперсии и обратно пропорционален квадрату предельной ошибки выборки.
При бесповторном собственно-случайном и механическом отборе численность выборки будет равна:

Для доли признака численность выборки будет определяться по формулам:


Аналогичным преобразованием предельной ошибки определяется численность выборочной совокупности при типической и серийной выборке.
Допустим, что для установления средней дневной выработки рабочих предприятия проводится собственно-случайная бесповторная выборка. Сколько рабочих должно быть обследовано, чтобы получить результат с точностью 0,3 р. с вероятностью 0,954. Общая численность рабочих завода 5000 человек. По данным прошлогоднего обследования среднее квадратическое отклонение выработки составляет 1,6 р.

Следовательно, должно быть обследовано 112 рабочих, чтобы выполнить поставленные перед наблюдением требования.
8.6. Способы распространения данных выборочного наблюдения
Конечной целью выборочного наблюдения является характеристика генеральной совокупности на основе данных, полученных по выборочной совокупности. Существуют два способа распространения данных выборочного наблюдения на генеральную совокупность – способ прямого пересчета и способ поправочных коэффициентов.
Способ прямого перерасчета заключается в том, что выборочная средняя или доля умножаются на численность генеральной совокупности и получается соответствующий объемный показатель. Так, в статистике сельского хозяйства выход шерсти от овец, находящихся в личном пользовании, определяется путем умножения полученных по выборке данных о среднем настриге шерсти с одной овцы на всю численность овец, находящихся в личной собственности. Например, согласно выборке, в области годовой настриг шерсти с одной овцы составляет 3 кг (с ошибкой выборки 


Второй пример. в 3%-ной выборке численностью 150 светильников 6 светильников оказались бракованными (ошибка выборки 

Вместе с этой лекцией читают «22 Сатурн».
Данный способ применяется тогда, когда известна численность единиц в генеральной совокупности.
Способ поправочных коэффициентом используется при проведении контрольных выборочных наблюдений для проверки и уточнения данных сплошного наблюдения. Он заключается в том, что по одним и тем же объектам сопоставляют данные сплошного и контрольного выборочного наблюдения. В результате такого сопоставления исчисляют поправочные коэффициенты, которые применяют для внесения поправок в данные сплошных наблюдений. Поправочные коэффициенты исчисляют, например, на основе данных контрольных выборочных обследований скота, находящегося в личной собственности населения сельской местности, при контроле за качеством деталей непосредственно на рабочем месте и т.д.
Например, по данным сплошного наблюдения численность крупного рогатого скота в личном подсобном хозяйстве граждан составляет 1 0000 голов.
Для контрольной проверки отобрано 1 000 семей, в хозяйствах которых сплошным наблюдением определена численность поголовья скота 1000 голов. В результате контрольного обхода в этих хозяйствах установлена численность крупного рогатого скота 1 050 голов.
Отсюда поправочный коэффициент составляет 1 050:1 000=1,05.
Общее поголовье скота в личном подсобном хозяйстве граждан равно