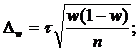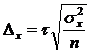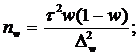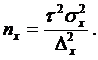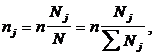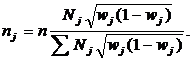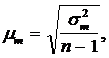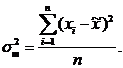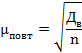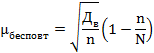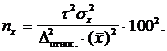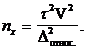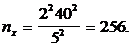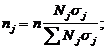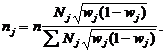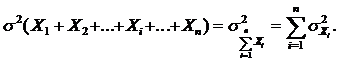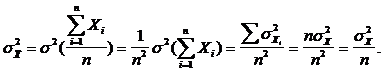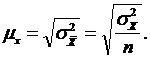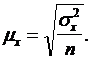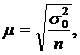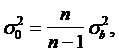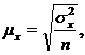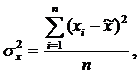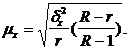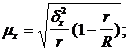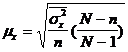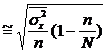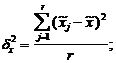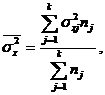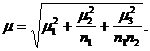Ошибки выборочного наблюдения доклад

Между
признаками выборочной совокупности и
признаками генеральной совокупности,
как правило, существует некоторое
расхождение, которое называется ошибкой
статистического наблюдения. При массовом
наблюдении ошибки неизбежны, но возникают
они в результате действия различных
причин. Величина возможной ошибки
выборочного признака происходит из-за
ошибок регистрации и ошибок
репрезентативности. Ошибки регистрации,
или технические ошибки, связаны с
недостаточной квалификацией наблюдателей,
неточностью подсчетов, несовершенством
приборов и т. п.

Под
ошибкой
репрезентативности
(представительства) понимают расхождение
между выборочной характеристикой и
предполагаемой характеристикой
генеральной совокупности. Ошибки
репрезентативности бывают случайными
и систематическими. Систематические
ошибки связаны с нарушением установленных
правил отбора. Случайные
ошибки объясняются недостаточно
равномерным представлением в выборочной
совокупности различных категорий
единиц генеральной совокупности.

В
результате первой причины выборка
легко может оказаться смещенной, так
как при отборе каждой единицы допускается
ошибка, всегда направленная в одну и
ту же сторону. Эта ошибка получила
название ошибки
смещения.
Ее размер может превышать величину
случайной ошибки. Особенность ошибки
смещения состоит в том, что, являясь
постоянной частью ошибки репрезентативности,
она увеличивается с увеличением объема
выборки. Случайная же ошибка с увеличением
объема выборки уменьшается. Кроме того,
величину случайной ошибки можно
определить, тогда как размер ошибки
смещения практически определить очень
сложно, а иногда и невозможно, поэтому
важно знать причины, вызывающие ошибку
смещения, и предусмотреть мероприятия
по ее устранению.

Ошибки
смещения бывают преднамеренные и
непреднамеренные. Причиной возникновения
преднамеренной
ошибки
является тенденциозный подход к выбору
единиц из генеральной совокупности.
Чтобы не допустить появление такой
ошибки, необходимо соблюдать принцип
случайности отбора единиц.

Непреднамеренные
ошибки
могут возникать на стадии подготовки
выборочного наблюдения, формирования
выборочной совокупности и анализа ее
данных. Чтобы не допустить появление
таких ошибок, необходима хорошая основа
выборки, т. е. та генеральная
совокупность, из которой предполагается
производить отбор, например список
единиц отбора. Основа выборки должна
быть достоверной, полной и соответствовать
цели исследования, а единицы отбора и
их характеристики должны соответствовать
действительному их состоянию на момент
подготовки выборочного наблюдения.
Нередки случаи, когда в отношении
некоторых единиц, попавших в выборку,
трудно собрать сведения из-за их
отсутствия на момент наблюдения,
нежелания дать сведения и т. п. В
таких случаях эти единицы приходится
заменять другими. Необходимо следить,
чтобы замена осуществлялась равноценными
единицами.

Случайная
ошибка
выборки возникает в результате случайных
различий между единицами, попавшими в
выборку, и единицами генеральной
совокупности, т. е. она связана со
случайным отбором. Теоретическим
обоснованием появления случайных
ошибок выборки является теория
вероятностей и ее предельные теоремы.

Сущность
предельных
теорем
состоит в том, что в массовых явлениях
совокупное влияние различных случайных
причин на формирование закономерностей
и обобщающих характеристик будет сколь
угодно малой величиной или практически
не зависит от случая. Так как случайная
ошибка выборки возникает в результате
случайных различий между единицами
выборочной и генеральной совокупностей,
то при достаточно большом объеме выборки
она будет сколь угодно мала.

Предельные
теоремы теории вероятностей позволяют
определять размер случайных ошибок
выборки. Различают среднюю (стандартную)
и предельную ошибку выборки. Под средней
(стандартной) ошибкой
выборки понимают такое расхождение
между средней выборочной и генеральной
совокупностями (~ —), которое не превышает
±.
Предельной
ошибкой
выборки принято считать максимально
возможное расхождение (~ —), т. е.
максимум ошибки при заданной вероятности
ее появления.

В
математической теории выборочного
метода сравниваются средние характеристики
признаков выборочной и генеральной
совокупностей и доказывается, что с
увеличением объема выборки вероятность
появления больших ошибок и пределы
максимально возможной ошибки уменьшаются.
Чем больше обследуется единиц, тем
меньше будет величина расхождений
выборочных и генеральных характеристик.
На основании теоремы, доказанной П.Л.
Чебышевым, величину стандартной ошибки
простой случайной выборки при достаточно
большом объеме выборки (n)
можно определить по формуле

– стандартная
ошибка.

Из
этой формулы средней (стандартной)
ошибки простой случайной выборки видно,
что величина зависит от изменчивости
признака в генеральной совокупности
(чем больше вариация признака, тем
больше ошибка выборки) и от объема
выборки n
(чем больше обследуется единиц, тем
меньше будет величина расхождений
выборочных и генеральных характеристик).

Академик
A.M. Ляпунов доказал, что вероятность
появления случайной ошибки выборки
при достаточно большом ее объеме
подчиняется закону нормального
распределения. Эта вероятность
определяется по формуле

В
математической статистике употребляют
коэффициент доверия t, значения функции
F(t)
табулированы при разных его значениях,
при этом получают соответствующие
уровни доверительной вероятности
(табл. 6.1).

Таблица
6.1

Коэффициент
доверия t и соответствующие уровни
доверительной вероятности

Коэффициент
доверия позволяет вычислить предельную
ошибку выборки,

т. е.
предельная ошибка выборки равна
t-кратному числу средних ошибок выборки.

Таким
образом, величина предельной ошибки
выборки может быть установлена с
определенной вероятностью. Как видно
из последней графы табл. 6.1, вероятность
появления ошибки равной или большей
утроенной средней ошибки выборки,
т. е. 

крайне
мала и равна 0,003(1–0,997). Такие маловероятные
события считаются практически
невозможными, а потому величину

можно
принять за предел возможной ошибки
выборки.

Выборочное
наблюдение дает возможность определить
среднюю арифметическую выборочной
совокупности и величину предельной
ошибки этой средней, которая показывает
(с определенной вероятностью), насколько
выборочная величина может отличаться
от генеральной средней в большую или
меньшую сторону. Тогда величина
генеральной средней будет представлена
интервальной оценкой, для которой
нижняя граница будет равна

Интервал,
в который с данной степенью вероятности
будет заключена неизвестная величина
оцениваемого параметра, называют
доверительным,
а вероятность Р
– доверительной вероятностью.
Чаще всего доверительную вероятность
принимают равной 0,95 или 0,99, тогда
коэффициент доверия t
равен соответственно 1,96 и 2,58. Это
означает, что доверительный интервал
с заданной вероятностью заключает в
себе генеральную среднюю.

Наряду
с абсолютной величиной предельной
ошибки выборки рассчитывается и
относительная
ошибка
выборки, которая определяется как
процентное отношение предельной ошибки
выборки к соответствующей характеристике
выборочной совокупности:

Чем
больше величина предельной ошибки
выборки, тем больше величина доверительного
интервала и тем, следовательно, ниже
точность оценки. Средняя (стандартная)
ошибка выборки зависит от объема выборки
и степени вариации признака в генеральной
совокупности.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

  • #
  • #
  • #
  • #
  • #
  • #
  • #

    12.04.2015613.89 Кб24pr.doc

  • #
  • #
  • #
  • #
Источник

Выборочное наблюдение

Курсовая работа по дисциплине Статистика

Работу выполнила студентка 1 курса вечернего отделения
специальности 0604 группы ЭФ-0603 шифр 060141 Куценко Евгения

Московский государственный университет приборостроения
и информатики

Москва 2007

Введение

Изучение
статистических совокупностей, состоящих из множеств единиц, связано с большими
трудовыми и материальными затратами.

С
давних пор представлялось заманчивым не изучать все единицы совокупности, а
отобрать лишь некоторую часть, по которой можно было бы судить о свойствах всей
совокупности в целом. Попытки такого рода делались еще в ХVII в.

Выборочный
метод обследования, или как его часто называют выборка, применяется прежде
всего в тех случаях, когда сплошное наблюдение вообще невозможно. Обследование
может быть связано с уничтожением или порчей обследуемых единиц. Так, например,
при контроле качества хлебобулочных изделий, консервов и т.д. изделие после
контрольных операций становится непригодным для реализации, что делает сплошной
контроль невозможным.

Невозможно
сплошное обследование и в тех случаях, когда обследуемая совокупность очень
велика, практически безгранична. Например, совокупность участков морского дна
или совокупность колосьев пшеницы на поле.

Во
всех случаях выборочный метод позволяет сберегать значительные количества труда
и средств как на этапе сбора сведений, так и на этапе их обработки и анализа.
Экономия же труда и средств, получаемая при замене сплошного наблюдения выборочным
имеет немаловажное значение.

Все
эти положительные качества привили к широкому применению метода выборочного
наблюдения. В нынешних условиях организации производственной и торговой
деятельности данный метод как способ проверки качества продукции применяется
большинством предприятий и организаций, также ни одно предприятие системы
Потребкооперации не обходится без выборочного метода наблюдения.

1. Понятие выборочного наблюдения

При
сплошном наблюдении – множество всех единиц данной совокупности носит название
генеральной совокупности. Средняя арифметическая какого-либо признака,
вычисленная для всех единиц этой совокупности, носит название генеральной
средней и обозначается символом х.

В
результате обследования можно получить не только средние величины, но и
относительные. Допустим, удельный вес называется генеральной долей.

Приведенным
понятиям генеральной совокупности, генеральной средней, генеральной доли при
выборочном обследовании соответствуют понятия выборочной совокупности,
выборочной средней, выборочной доли.

Выборочная
совокупность – это совокупность единиц, попавших в выборку. Средняя
арифметическая, вычисленная на основе значений какого-либо признака у всех
единиц выборочной совокупности, носит название выборочной средней и
обозначается символом х.

Относительная
величина доли, полученная в результате выборочного наблюдения, носит название
выборочной доли. Если, например, в результате обследования взятых на выборку
200 шт. какого-либо изделия,. 4 оказались негодными, то это означает, что
выборочная доля брака равна 4/200, т.е. = 0,02.

В
зависимости от конкретных условий для выборки единиц применяются различные
приемы отбора:

собственно
случайный отбор — состоит в отборе случайно попавших единиц совокупности;

механический
отбор – когда все единицы наблюдаемой совокупности располагают в определенной
последовательности (по номерам, по алфавиту и т.д.), единицы выбирают через
определенный промежуток;

гнездовой
отбор – производится в том случае, если для изучения берут не отдельные единицы
совокупности, а отдельные группы единиц или гнезда;

типический
отбор – состоит в том, что все единицы совокупности предварительно распределяют
на группы по какому-либо типичному признаку, после чего из каждой типической
группы отбирают единицы для обследования;

комбинированный
отбор – применяют сразу два вида отбора.

В
экономико-статистических исследованиях используют следующие способы отбора
единиц из генеральной совокупности:

индивидуальный
отбор – в выборку отбираются отдельные единицы;

групповой
отбор – в выборку попадаются качественно однородные группы или серии изучаемых
явлений;

комбинированный
отбор – как комбинация индивидуального и группового отбора.

В
статистике различают также одноступенчатый и многоступенчатый способы отбора
единиц в выборочную совокупность.

При
одноступенчатой выборке каждая отобранная единица сразу же подвергается
изучению по заданному признаку. Так обстоит дело при собственно-случайной и
серийной выборке.

При
многоступенчатой выборке производят отбор из генеральной совокупности отдельный
групп, а из групп выбираются отдельные единицы. Так производится типичная
выборка с механическим способом отбора единиц в выборочную совокупность.

Комбинированная
выборка может быть двухступенчатой. При этом генеральная совокупность сначала
разбивается на группы. Затем производят отбор групп, а внутри последних
осуществляется отбор отдельных единиц.

В
зависимости от способа отбора единиц различают:

повторная
выборка. При повторном отборе вероятность попадания каждой отдельной единицы в
выборку остается постоянной, так как после отбора какой-то единицы, она снова
возвращается в совокупность и снова может быть выбранной;

бесповторная
выборка. В этом случае каждая отобранная единица не возвращается обратно, и
вероятность попадания отдельных единиц в выборку все время изменяется (для
оставшихся единиц она возрастает).

2. Ошибки выборочного наблюдения

При
любом наблюдении могут происходить ошибки при регистрации единиц. В зависимости
от объекта, субъекта и способа наблюдения эти ошибки могут возникнуть из-за
сообщения ошибочных сведений объектом, неточной фиксации сообщаемых сведений
субъектом наблюдения, неточного подсчета или измерения фиксируемых признаков
при непосредственном наблюдении.

При
несплошном наблюдении, в частности при выборочном, кроме ошибок регистрации
возможны так называемые ошибки репрезентативности (представительности), которые
возникают в связи с тем, что отобранная для обследования часть совокупности
имеет по изучаемому признаку иную структуру, чем совокупность в целом. При
выборочном обследовании их источником является нарушение принципа случайности
отбора, его тенденциозность. Случайные же ошибки возможны и при совершенно
правильно организованном отборе за счет того, что случайно могут отказаться
отобранными единицы с характеристиками, в среднем отличными от всей
совокупности. Таким образом, ошибка наблюдения (eнв) является при
выборочном наблюдении суммой ошибки регистрации (eрв) и ошибки
репрезентативности (eпв),
а при сплошном наблюдении ошибка наблюдения (eнс) равна ошибке
регистрации (eрс).

3. Определение необходимого объема выборки

При
организации выборочного обследования следует иметь в виду, что размер ошибки
выборки прежде всего зависит от численности выборочной совокупности n. Средняя
ошибка выборки обратно пропорциональна n, т.е. при увеличении, например,
численности выборки в четыре раза ее ошибки уменьшатся вдвое.

 Пример, отбираем из генеральной совокупности
не 5 %, а, например, 20 % готовой продукции. Численность выборки n будет равна
400 шт. Тогда при условии, что sw = 15,4 г, размер ошибки для выборочной средней при
повторном отборе составит:

 15,42

mх = ———
= ±
0,17 г.

 400

Увеличивая
численность выборки, можно довести ее ошибку до сколь угодно малых размеров.
Можно представить, что при доведении n до размеров N ошибка выборки m
становится равной нулю. Но так как при проведении выборочных обследований в
торговле определение характеристик выборки в ряде случаев сопровождается
разрушением обследуемых образцов, то нормы отбора проб в выборку должны быть
минимальными. Это сообразуется с основным преимуществом несплошного наблюдения:
получением необходимой информации с минимальными затратами времени и труда.
Поэтому вопрос об оптимальной численности выборки имеет важное практическое значение.
Повышение процента выборки, как правило, ведет к увеличению объема
исследовательской работы, вызывает дополнительные затраты труда и материальных
средств. Но, с другой стороны, если в выборку взять недостаточное количество
проб (образцов), то результаты исследования могут содержать большие
погрешности. Все это необходимо учитывать при организации выборочного
обследования.

Условные обозначения:

N
– объем генеральной совокупности (число входящих в нее единиц);

n
– объем выборки (число обследованных единиц);

х
– генеральная средняя (среднее значение признака в генеральной совокупности);

х
– выборочная средняя;

s2 –
генеральная дисперсия (дисперсия признака в генеральной совокупности);

s —
среднее квадратическое отклонение в генеральной совокупности;

Заключение

Переход
к рыночной экономике в значительной мере способствует расширению сферы
использования выборочного наблюдения. Проблемы применения конкретных видов
выборочного наблюдения для решения тех или иных теоретических или прикладных
задач решаются с учетом их специфики.

Выборочное
наблюдение широко используется для: 1) статистического оценивания и проверки
гипотез; 2) решения производственных и управленческих задач; 3) отраслевых
социально-экономических исследований; 4) разрешения задач в сфере
предпринимательской деятельности.

Совершенствование
теории и практики выборочного наблюдения, все более широкое применение
различных сочетаний комбинированного, многоступенчатого отбора, современных компьютерных
технологий информационной обработки в значительной мере расширяют области
использования, скорость получения и качество результатов выборочного
наблюдения.

Список литературы

Экономика
и статистика фирм: Учебник/ В.Е. Адамова, С.Д. Ильенкова, Т.П. Сиротина и др.;
Под ред. д-ра э.н. С.Д. Ильенковой. — М.: Финансы и статистика, 2005г

Рунион
Р. Справочник по статистике. Современный подход. — М.: Финансы и статистика,
2002.

Смоляк
С.А., Титаренко Б.П. Устойчивые методы оценивания. -М.:Статистика, 2000

Для
подготовки данной работы были использованы материалы с сайта http://referat.ru

Дата добавления: 30.05.2007

База рефератов на портале KM.RU существует с 1999 года. Она пополнялась не только готовыми рефератами, докладами, курсовыми, но и авторскими публикациями, чтобы учащиеся могли использовать их и цитировать при самостоятельном написании работ.

Это популяризирует авторские исследования и научные изыскания, что и является целью работы истинного ученого или публициста. Таким образом, наша база — электронная библиотека, созданная в помощь студентам и школьникам.

Уважаемые авторы! Если Вы все же возражаете против размещения Вашей публикации или хотите внести коррективы, напишите нам на почту info@corp.km.ru, мы незамедлительно выполним Вашу просьбу или требование.

Источник

Выборочное наблюдение в статистическом исследовании

СОДЕРЖАНИЕ

ВВЕДЕНИЕ

1.
ТЕОРЕТИЧЕСКОЕ ОБОСНОВАНИЕ ВЫБОРКИ И ВЫБОРОЧНОГО НАБЛЮДЕНИЯ

1.1 Понятие
выборочного наблюдения, основные виды

.2
Определение объема выборки

.3 Ошибки
выборочного наблюдения

2.
СТАТИСТИЧЕСКИЙ АНАЛИЗ ВЫБОРОЧНОГО НАБЛЮДЕНИЯ

2.1 Выборочное
исследование в статистическом анализе

.2 Методика
расчета ошибок выборочного наблюдения

.3 Расчет
средних ошибок выборочной доли и выборочной средней

ЗАКЛЮЧЕНИЕ

СПИСОК
ИСПОЛЬЗУЕМЫХ ИСТОЧНИКОВ

ПРИЛОЖЕНИЕ


ВВЕДЕНИЕ

В современном мире многие процессы, с одной стороны, являются достаточно
сложными и изменчивыми, а, с другой стороны, эти процессы можно выразить с
помощью числовых значений.

В экономике, как и в других областях деятельности человека, часто
применение сплошного наблюдения физически невозможно из-за большого массива
данных или экономически нецелесообразно. Поэтому в статистическом анализе
применяется выборочное наблюдение. Физическая невозможность имеет место,
например, при изучении пассажиропотоков, рыночных цен, семейных бюджетов.
Экономическая нецелесообразность имеет место при оценке качества товаров,
связанной с их уничтожением, например, дегустация, испытание кирпичей на
прочность и т.п. Поэтому в статистическом анализе применяется выборочное
наблюдение.

Из этого следует, что тема выбранной курсовой работы является весьма
актуальной.

Целью данной курсовой работы является теоретическое, а также практическое
обоснование выбранной темы.

В связи с поставленной целью можно выделить ряд задач:

.   Раскрытие понятия выборочного наблюдения, ее категории.

2.      Обосновать виды отбора в выборочном наблюдении.

.        Дать определение численности выборки.

.        Показать практическое применение в статистическом анализе
выборочного наблюдения.

Объектом данной курсовой работы является выборочное наблюдение в
статистическом исследовании.

Предмет курсовой работы — это выборка и выборочная совокупность.

По результатам написания данной работы будут сделаны определенные
теоретические и практические выводы.

1. ТЕОРЕТИЧЕСКОЕ
ОБОСНОВАНИЕ ВЫБОРКИ И ВЫБОРОЧНОГО НАБЛЮДЕНИЯ

1.1    Понятие выборочного наблюдения, основные виды

Теория выборочного наблюдения базируется на статистических
закономерностях, которые формируются и обнаруживаются в массовых явлениях и
процессах. Это свойство закономерностей получило название закона больших чисел.
Математической основой закона больших чисел, да и статистической науки в целом,
служит теория вероятностей. Последняя представляет собой раздел математики, в
котором изучаются случайные явления (события), имеющие устойчивую частность, а,
следовательно, и вероятность, что помогает выявлять закономерности при массовом
повторении явлений [2].

Основная задача выборочного метода — определение ошибки выборки, ибо,
если не известен размер ошибки, данные выборки не могут иметь практического
значения.

Под выборочным наблюдением (сокращенно выборка) понимается не сплошное
наблюдение, при котором статистическому обследованию (наблюдению) подвергается
не всё, а отдельные единицы (обычно до 5-10%, реже до 15-20%), отобранные с
соблюдением определенных условий.

Выборочный метод — это наиболее совершенная с научной точки зрения
разновидность несплошного статистического наблюдения на основе статистической
индукции, при котором характеристики всей статистической (генеральной)
совокупностью (N) получаются в результате изучения некоторой ее части (n),
отобранной с соблюдением определенных правил (на основе случайного отбора) и
поэтому являющейся репрезентативной, т.е. репрезентативной и достоверной.

Самый важный признак выборочного наблюдения как вида сплошного наблюдения
— случайный характер выборки, а главная его особенность заключается в том, что
при отборе единиц совокупности для обследования обеспечивается равная
возможность в отобранную часть любой из единиц.

В зависимости от характеристик выборочных совокупностей выборки могут
быть представительными, расслоенными, засоренными и цензурированными.

Представительная выборка — выборка наблюдений из генеральной
совокупности, наиболее полно и адекватно представляющая ее свойства.

Расслоенная выборка — выборка, включающая ряд выборочных совокупностей,
взятых из соответствующих слоев генеральной совокупности. Широко используется
при выборочном обследовании в экономике, демографии и социологии [7].

Засоренная
выборка — выборка наблюдений, содержащая «грубые» ошибки. Основная масса
элементов засоренной выборки является реализацией случайной величины X, закон
распределения которой известен. Такие элементы («типичные») появляются в
совокупности с вероятностью . С
вероятностью  элементы совокупности оказываются реализацией другой
случайной величины Y, закон распределения которой в общем случае неизвестен.
Такие элементы называются “грубыми” ошибками. Обычные оценки, например, средняя
арифметическая выборочная, на засоренной выборке теряют свои оптимальные
свойства (эффективность, несмещенность) с ростом интенсивности засорения.

Цензурированная
выборка — выборка, полученная из вариационного ряда наблюдений путем
отбрасывания некоторого числа экстремальных наблюдений. Если отбрасывание
производится по признаку выхода наблюдений за пределы заданного интервала, то
такой прием называется цензурирование первого типа. В этом случае число
оставшихся наблюдений является случайной величиной. Если отбрасывается
фиксированная доля крайних малых значений и фиксированная доля крайних больших
значений, то это называется цензурированием второго типа уровня. При этом,
число оставшихся в рассмотрении наблюдений является величиной заранее заданной.

Проведение
выборочных исследований статистической информации состоит из следующих этапов:

¾      формулировка цели статистического наблюдения;

¾      обоснование целесообразности выборочного наблюдения;

¾      отграничение генеральной совокупности;

¾      установление системы отбора единиц для наблюдения;

¾      определение числа единиц, подлежащих отбору;

¾      проведение отбора единиц;

¾      проведение наблюдения;

¾      расчет выборочных характеристик и их ошибок;

¾      распространение выборочных данных на генеральную
совокупность.

Выборочное исследование осуществляется с минимальными затратами труда и
средств и в более короткие сроки, чем сплошное наблюдение, что повышает
оперативность статистической информации, уменьшает ошибки регистрации. В
проведении ряда исследований выборочный метод является единственно возможным,
например, при контроле качества продукции, сопровождающимся разрушением
проверяемого изделия [10].

Выборочный метод дает достаточно точные результаты, поэтому он может
применяться для проверки данных сплошного наблюдения. Минимальная численность
обследуемых единиц позволяет провести исследование более тщательно и
квалифицированно. Например, при переписях населения практикуются выборочные
контрольные наблюдения для проверки правильности записей сплошного наблюдения.

В основе теории выборочного наблюдения лежат теоремы законов больших
чисел, которые позволяют решить два взаимосвязанных вопроса выборки: рассчитать
ее объем при заданной точности исследования и определить ошибку при данном
объеме выборки.

При использовании выборочного метода обычно используются два вида обобщающих
показателей: относительную величину альтернативного признака и среднюю величину
количественного признака.

Относительная величина альтернативного признака характеризует долю
(удельный вес) единиц в статистической совокупности, обладающих изучаемым признаком.
В генеральной совокупности эта доля единиц называется генеральной долей (p), а
в выборочной совокупности — выборочной долей (w).

Средняя
величина количественного признака в генеральной совокупности называется
генеральной средней (), а в выборочной совокупности — выборочной средней ().

Процесс
образования выборки называется отбором, который осуществляется в порядке
беспристрастного, случайного отбора единиц из генеральной совокупности.

Основным
условием проведения выборочного наблюдения является предупреждение
возникновения систематических (тенденциозных) ошибок, возникающих вследствие
нарушения принципа равных возможностей попадания в выборку каждой единицы
совокупности. Предупреждение систематических ошибок достигается в результате
применения научно обоснованных способов формирования выборочной совокупности.

Существуют
различные способы отбора: индивидуальный, групповой (серийный),
комбинированный, повторный (возвратный), бесповторный (безвозвратный),
одноступенчатый, многоступенчатый, собственно-случайный, механический,
типический, двухфазный и многофазный отбор [3].

При
индивидуальном отборе в выборку отбираются отдельные единицы совокупности.
Отбор повторяется столько раз, сколько необходимо отобрать единиц.

Групповой
(серийный) отбор заключается в отборе серий (например, отбор изделий для
проверки их целыми партиями). Если обследованию подвергаются все единицы
отобранных серий, отбор называется серийным, а если обследуется только часть
единиц каждой серии, отбираемых в индивидуальным порядке из серии, то —
комбинированным.

Если
в процессе отбора отобранная единица не исключается из совокупности, т.е.
возвращается в совокупность, и может быть повторно отобранной, то такой отбор
называется повторным или возвратным, в противном случае — бесповторным или
безвозвратным. Серийный отбор, как правило, безвозвратный.

При
одноступенчатом отбираются единицы совокупности (или серии) непосредственно для
наблюдения. При многоступенчатом отбираются сначала крупные серии единиц
(первая ступень отбора), наблюдению они не подвергаются. Затем из них
отбираются серии, меньшие по численности единиц (вторая ступень), наблюдению не
подвергаются, и так до тех пор, пока не будут отобраны те единицы совокупности
(серии), которые будут подвергнуты наблюдению.

Собственно-случайный
отбор состоит в отборе единиц (серий) из всей генеральной совокупности в целом
посредством жеребьевки или на основании таблиц случайных чисел.

Жеребьевка
состоит в том, что на каждую единицу отбора составляется карточка, которой
присуждается порядковый номер. После тщательного перемешивания по очереди
извлекаются карточки, пока не будет отобрано требуемое число единиц [8].

Случайными
числами называются ряды чисел, являющихся реализациями последовательности
взаимно независимых и одинаково распределенных случайных величин. Эти
последовательности чисел получаются либо с помощью физических генераторов
(подбрасывание кубиков с нанесенными на их сторонами цифрами; вытягиванием из
урны карточек с написанными на них цифрами, преобразование случайных сигналов и
др. физико-технические процессы), либо с помощью программных генераторов
(аналитическим методом с помощью программ для ЭВМ). Числа, являющиеся
результатами соответствующей вычислительной процедуры, называются
псевдослучайными числами. Последовательность псевдослучайных чисел носит
детерминированный характер, но в определенных границах она удовлетворяет
свойствам равномерного распределения и свойству случайности.

Механический
отбор заключается в том, что составляется список единиц генеральной
совокупности и в зависимости от числа отбираемых единиц (серий) устанавливается
шаг отбора, т.е. через какой интервал следует брать для наблюдения единицы
(серии). Например, в простейшем случае, при 10%-м отборе, отбирается каждая
десятая единица по этому списку, т.е. если первой взята единица за №1, то
следующими отбираются 11-я, 21-я и т.д. В такой последовательности производится
отбор, если единицы совокупности расположены в списке без учета их “рангов”,
т.е. значимости по изучаемым признакам. Начало отбора в этом случае не имеет
значения, его можно начать в приведенном примере от любой единицы из первого
десятка. При расположении единиц совокупности в ранжированном порядке за начало
отбора должна быть принята середина интервала (шага отбора) во избежание
систематической ошибки выборки.

При
типическом отборе генеральная совокупность разбивается на типические группы
единиц по какому-либо признаку (формируются однородные совокупности), а затем
из каждой из них производится механический или собственно-случайный отбор.
Отбор единиц из типов производится тремя методами: пропорционально численности
единиц типических групп, непропорционально численности единиц типических групп
и пропорционально колеблемости признака в группах.

В
целях экономии средств данные по некоторым интересующим исследователя признакам
можно анализировать на основании изучения всех единиц выборочной совокупности,
а по другим признакам — на основании части единиц выборочной совокупности, которые
представляют подвыборку из единиц первоначальной выборки. Этот метод называется
двухфазным отбором. При наличии нескольких подвыборок — метод многофазного
отбора.

Многофазный
отбор по своей структуре отличается от многоступенчатого отбора, так при многофазном
отборе используются на каждой фазе одни и те же отобранные единицы, при
многоступенчатом отборе на разных ступенях применяются единицы отбора разных
порядков. Многофазным отбором чаще всего пользуются в тех случаях, когда
различно число единиц, необходимых для определения отдельных показателей с
заданной точностью. Это связано как с различиями в степени колеблемости
признаков, так и с разной точностью, требуемой для расчетов. Ошибки при
многофазной выборке рассчитываются на каждой фазе отдельно.

Отличие
в методах повторного и бесповторного отбора математически отображают с помощью
поправочного коэффициента на бесповторность (К):

—
численность единиц выборочной совокупности;- численность единиц генеральной
совокупности.

В
математической статистике разработана методика анализа выборочного наблюдения
случайных явлений. Основой такого анализа является предположение о
множественности производимых выборочных наблюдений, и, как следствие,
построение целого ряда распределения вероятностей различных характеристик
полученных выборок. Предполагается осуществление только отдельного выборочного
наблюдения.

Результаты
выборочного наблюдения должны быть корректно перенесены на генеральную
совокупность. При применении выборочного метода всегда происходит погашение
особенностей отдельных единиц генеральной совокупности. Именно поэтому
предполагается несоответствие параметров генеральной совокупности параметрам
выборочной, т.е. наличие больших или меньших ошибок наблюдения. Чтобы исключить
такое несоответствие параметры генеральной совокупности обычно представляют не
с помощью отдельного значения, а в виде границ интервала, в пределах которого
могут происходить колебания параметров.

Применение
выборочного исследования предполагает определение параметров совокупности с
некоторой степенью точности. Причем, точность зависит от меры
репрезентативности выборки относительно генеральной совокупности, т.е. от
качества выборочных данных. Чем хуже представлена в выборке генеральная
совокупность, тем меньше степень точности выводов. Следовательно, тем дальше
должны быть «раздвинуты» пределы интервала, в которых может колебаться параметр
генеральной совокупности.

Еще
одним определителем степени точности выводов служит их последующее применение.
То есть, чем более корректные данные о генеральной совокупности требуется
получить, тем дальше «раздвигаются» пределы интервала. Например, если
исследование проводится в целях обучения студентов методике выборки, то
принимается условная (низкая) степень точности. Тогда как, исследование,
необходимое для государственного управления, предполагает высокую степень
точности.

Как
уже говорилось ранее, основным условием проведения выборочного наблюдения
является предупреждение возникновения систематических (тенденциозных) ошибок,
возникающих вследствие нарушения принципа равных возможностей попадания в
выборку каждой единицы совокупности. Поэтому в следующем разделе речь пойдет об
ошибках, возникающих при статистическом исследовании [4].

1.2    Определение объема выборки

Определение необходимого объема выборки n основывается на формулах
предельных ошибок выборочной доли и выборочной средней. Например, для
повторного отбора предельные ошибки равны:

Отсюда
объемы выборок для расчета выборочной доли nw и выборочной средней nx
следующие:

Аналогичным
образом определяются объемы выборок при различных способах отбора выборочной
совокупности. Для серийного отбора определяется число отобранных серий.

При
серийном или типическом отборе, не пропорциональном объему групп, общее число
отбираемых единиц делится на количество групп. Полученная величина является
объемом выборки из каждой группы.

При
отборе, пропорциональном числу единиц в группе, число наблюдений по каждой
группе определяется по формуле:

где
nj —
объем выборки из j -й группы; — общий объем выборки;

Nj — объем j -й
группы;

N
— объем генеральной совокупности.

При
отборе с учетом вариации признака, приводящем к минимальной ошибке выборки,
процент выборки из каждой типической группы должен быть пропорционален среднему
квадратическому отклонению в этой группе.

Расчет
численности выборки производится по формулам:

для
средней

, для
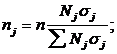
доли

Под
малой выборкой понимается такое выборочное наблюдение, численность единиц
которого не превышает 20-30 и может составлять 5-6. С увеличением численности
выборочной совокупности повышается точность выборочных данных, однако приходится
иногда ограничиваться малым числом наблюдений. Эта необходимость возникает,
например, при проверке качества продукции, связанной с уничтожением проверяемой
единицы продукции. В математической статистике доказывается, что при малых
выборках характеристики выборочной совокупности можно распространять на
генеральную, но расчет средней и предельной ошибок выборки имеет особенности.

Ранее
указывалось, что при большом объеме выборочной совокупности (n > 100)
коэффициент , на который необходимо умножить выборочную дисперсию,
чтобы получить генеральную, не играет большой роли. Но когда выборочная
совокупность небольшая, этот коэффициент необходимо принимать во внимание.
Средняя ошибка малой выборки ()
вычисляется по формуле:

где
 — дисперсия в малой выборке, которая определяется
следующим образом:

Предельная
ошибка имеет вид:

Значение
коэффициента доверия  зависит не только от заданной доверительной
вероятности, но и от численности единиц выборки n. Английский ученый Стьюдент
доказал, что в случаях малой выборки действует особый закон распределения
вероятности.

При
большом числе единиц исследуемой совокупности ошибки и неточности могут
погашаться, однако, если применяется выборочное наблюдение, тогда ошибки могут
существенно повлиять на результаты исследования. В следующем разделе речь
пойдет об ошибках выборочного наблюдения [6].

1.3    Ошибки
выборочного наблюдения

Выборочную совокупность можно сформировать по количественному признаку
статистических величин, а также по альтернативному или атрибутивному. В первом
случае обобщающей характеристикой выборки служит выборочная средняя величина,
обозначаемая , а во втором — выборочная доля величин, обозначаемая w. В генеральной
совокупности соответственно: генеральная средняя  и генеральная доля р.

В ходе наблюдения могут возникнуть следующие ошибки:

1. Ошибки регистрации — ошибочные результаты наблюдения, полученные в
результате недостаточной квалификации исследователя, неточности измерительных
приборов, некорректности подсчетов и т.д.

2.      Ошибки могут быть случайными и систематическими:

¾      систематические ошибки репрезентативности — ошибки, вызванные
нарушением правил выбора единиц совокупности для наблюдения;

¾      ошибки репрезентативности (случайные) — ошибки, отражающие
несовпадение выводов о части явления с выводами о явлении в целом. Такие ошибки
возникают при применении несплошного метода наблюдения, случайные ошибки
репрезентативности — ошибки, отражающие неравномерное распределение единиц в
совокупности, в связи с чем, выборочная совокупность не корректно характеризует
генеральную совокупность.

Разности —  и W — р называются ошибкой выборки, которая делится на
ошибку регистрации и ошибку репрезентативности.

Величина ошибки выборки может быть разной для разных выборок из одной
генеральной совокупности, поэтому в статистике определяется средняя ошибка
повторной и бесповторной выборки по формулам:

Средняя ошибка повторной выборки — повторная;

где Дв — выборочная дисперсия.

При определении величины репрезентативной ошибки предполагается, что
ошибка регистрации равна нулю. Определение ошибки производится по формулам
ошибки выборочной доли и ошибки выборочной средней. Систематическая ошибка
репрезентативности возникает вследствие нарушения правил отбора единиц
генеральной совокупности, в частности принципа беспристрастного,
непреднамеренного отбора. Систематическая ошибка может привести к полной
непригодности результатов наблюдений.

Ошибка
выборочной средней представляет собой расхождение (разность) между выборочной
средней  и генеральной средней ,
возникающее вследствие несплошного выборочного характера наблюдения. Величина
ошибки выборочной средней определяется как предел отклонения от ,
гарантируемый с заданной вероятностью:

где
 — гарантийный коэффициент, зависящий от вероятности , с которой гарантируется невыход разности  за пределы ; — средняя ошибка выборочной средней.

В
математической статистике разработана методика анализа выборочного наблюдения
случайных явлений. Основой такого анализа является предположение о
множественности производимых выборочных наблюдений, и, как следствие,
построение целого ряда распределения вероятностей различных характеристик
полученных выборок. Предполагается осуществление только отдельного выборочного
наблюдения [2].

Результаты
выборочного наблюдения должны быть корректно перенесены на генеральную
совокупность. При применении выборочного метода всегда происходит погашение
особенностей отдельных единиц генеральной совокупности. Именно поэтому
предполагается несоответствие параметров генеральной совокупности параметрам
выборочной, т.е. наличие больших или меньших ошибок наблюдения. Чтобы исключить
такое несоответствие параметры генеральной совокупности обычно представляют не
с помощью отдельного значения, а в виде границ интервала, в пределах которого
могут происходить колебания параметров.

Применение
выборочного исследования предполагает определение параметров совокупности с
некоторой степенью точности. Причем, точность зависит от меры репрезентативности
выборки относительно генеральной совокупности, т.е. от качества выборочных
данных. Чем хуже представлена в выборке генеральная совокупность, тем меньше
степень точности выводов. Следовательно, тем дальше должны быть «раздвинуты»
пределы интервала, в которых может колебаться параметр генеральной
совокупности.

Еще
одним определителем степени точности выводов служит их последующее применение.
То есть, чем более корректные данные о генеральной совокупности требуется
получить, тем дальше «раздвигаются» пределы интервала. Например, если
исследование проводится в целях обучения студентов методике выборки, то
принимается условная (низкая) степень точности. Тогда как, исследование,
необходимое для государственного управления, предполагает высокую степень
точности.

Практическая
часть рассматриваемой курсовой работы будет представлена в следующем разделе
[9].

статистический выборочный средний ошибка

2.
СТАТИСТИЧЕСКИЙ АНАЛИЗ ВЫБОРОЧНОГО НАБЛЮДЕНИЯ

2.1    Выборочное исследование в статистическом анализе

Рассмотрим на практике как проводится статистический анализ выборочного
наблюдения.

Случайные числа могут быть выбраны по таблице случайных чисел
(ПРИЛОЖЕНИЕ), которая содержит 2000 случайных чисел, объединенных для удобства
пользования таблицей в 500 блоков по 4 значения. Например, 5489, 5583, 3156,
0835, 1988, 3912.

Применение комбинаций этих цифр зависит от размера совокупности: если в
генеральной совокупности 1000 единиц, то порядковый номер каждой единицы должен
состоять из двух цифр от 000 до 999. В этом случае первые 8 номеров единиц
выборочной совокупности следующие:

, 955, 833, 156, 083, 519, 883, 912.

При произвольном объеме генеральной совокупности, отличающегося от 100,
1000, 10000 могут использоваться псевдослучайные числа, сформированные на ЭВМ,
или из таблицы случайных чисел формируется последовательность случайных
величин, распределенных в интервале от 0 до 1. Например, в приведенном выше
примере:

,5489; 0,5583; 0,3156; 0,0835; 0,1988; 0,3912 и т.д.

Если генеральная совокупность состоит из 2000 единиц, то в выборочную
совокупность должны войти единицы с номерами:

* 0,5489 = 1097,8 или 1099;

* 0,5583 = 1116,6 или 1117;

* 0,3156 = 631,2 или 631;

* 0,0835 = 167,0 или 167;

* 0,1988 = 397,6 или 398;

* 0,3912 = 782,4 или 782.

Процесс формирования случайных чисел и определения номера отбираемой
единицы продолжается до тех пор, пока не будет получен заданный объем
выборочной совокупности.

Можно предложить другой способ случайного отбора единиц в выборку.
Допустим, что выборка состоит из 75 единиц, а генеральная совокупность — из
780. Из таблицы случайных чисел выбираются, например, следующие: 5489, 5583,
3156, 0835, 1988, 3912.

В выборку могут войти только единицы, порядковые номера которых равны
трехзначным числам меньше 780. Поэтому, используя только три последние цифры
каждого числа, отбирается необходимые 75 номеров: 489, 583, 156 и т.д. Можно
использовать и первые три цифры каждого числа, тогда отобранные номера: 548,
558, 315, 83, 198, 391. Можно разбить случайные четырехзначные случайные числа
на ряд, состоящий из трехзначных чисел:

, 955, 833, 156, 083, 519, 883, 912

и отобрать из них номера, которые меньше 780, а именно: 548, 156, 83,
519.

В целях экономии средств данные по некоторым интересующим исследователя
признакам можно анализировать на основании изучения всех единиц выборочной
совокупности, а по другим признакам — на основании части единиц выборочной
совокупности, которые представляют подвыборку из единиц первоначальной выборки.
Этот метод называется двухфазным отбором. При наличии нескольких подвыборок —
метод многофазного отбора.

Многофазный отбор по своей структуре отличается от многоступенчатого
отбора, так при многофазном отборе используются на каждой фазе одни и те же
отобранные единицы, при многоступенчатом отборе на разных ступенях применяются
единицы отбора разных порядков. Многофазным отбором чаще всего пользуются в тех
случаях, когда различно число единиц, необходимых для определения отдельных
показателей с заданной точностью. Это связано как с различиями в степени
колеблемости признаков, так и с разной точностью, требуемой для расчетов.
Ошибки при многофазной выборке рассчитываются на каждой фазе отдельно [3].

Как уже отмечалось в предыдущей главе определение необходимого объема
выборки n основывается на формулах предельных ошибок выборочной доли и
выборочной средней.

Для серийного отбора определяется число отобранных серий. Формулы расчета
приведены в табл.1.

Таблица 1

Методы отбора выборки

Объем выборки или число
серий для определения

выборочной доли

выборочной средней

Механический и
собственно-случайный повторный отбор

Механический и
собственно-случайный бесповторный отбор

Серийный отбор при
повторном отборе равновеликих серий

Серийный отбор при
бесповторном отборе равновеликих серий

Типический отбор при
повторном случайном отборе внутри групп, пропорциональном объему групп

Типический отбор при
бесповторном случайном отборе внутри групп, пропорциональном объему групп

где nw, nx — объемы выборок соответственно для
определения ошибок выборочной доли и выборочной средней;w, rx —
число отобранных серий соответственно для определения ошибок выборочной доли и
выборочной средней;

 —
предельные ошибки соответственно выборочной доли и выборочной средней.

Вариация
() признака существует объективно, независимо от
исследователя, но к началу выборочного наблюдения она неизвестна. Для
приближенной оценки  используются следующие способы:

1. Дисперсия определяется на основе результатов проведения
«пробного» обследования (обычно небольшого объема). По данным
нескольких пробных обследований выбирается наибольшее значение дисперсии.

2.      Дисперсия принимается из предыдущих исследований.

3.      По
правилу «трех сигм» общий размах вариации Н укладывается в 6 сигм,
среднее квадратическое отклонение принимается равным  Для большей точности размах делится на 5.

.        Если
хотя бы приблизительно известна средняя величина изучаемого признака, то .

.        При
изучении альтернативного признака (изучении доли), если нет даже
приблизительных сведений о доле единиц, обладающих заданным значением этого
признака, принимается максимально возможная величина дисперсии, равная 0,25.

В связи с тем, что генеральная дисперсия оценивается приближенно,
рекомендуется рассчитанный объем выборки округлять в большую сторону.

Часто
на практике задается не величина абсолютной предельной ошибки , а величина относительной погрешности , выраженная в процентах к средней величине

откуда

В
этом случае объем выборки будет:

Если
известен коэффициент вариации , то
объем выборки будет:

Например,
по данным пробного обследования коэффициент вариации составляет 40%. Сколько
необходимо отобрать единиц, чтобы с вероятностью 0,954 предельная относительная
ошибка выборки не превышала 5%?

При

При
серийном или типическом отборе, не пропорциональном объему групп, общее число
отбираемых единиц делится на количество групп. Полученная величина является
объемом выборки из каждой группы.

При
отборе, пропорциональном числу единиц в группе, число наблюдений по каждой
группе определяется по формуле

где
nj —
объем выборки из j -й группы; — общий объем выборки;

Nj — объем j -й
группы;

N
— объем генеральной совокупности.

При
отборе с учетом вариации признака, приводящем к минимальной ошибке выборки,
процент выборки из каждой типической группы должен быть пропорционален среднему
квадратическому отклонению в этой группе. Расчет численности выборки производится
по формулам:

для
средней

для
доли

Таким
образом, планомерность статистического наблюдения заключается в том, что оно
готовится и проводится по разработанному плану, который входит в план всего
статистического анализа выборочного наблюдения и включает вопросы методологии,
организации, техники сбора информации, контроля ее достоверности и оформления
итоговых результатов.

Далее
рассмотрим на практике как определяются в статистическом анализе ошибки
выборочного наблюдения.

2.2    Методика расчета ошибок выборочного наблюдения

Как говорилось ранее, при определении величины репрезентативной ошибки
предполагается, что ошибка регистрации равна нулю. Определение ошибки
производится по формулам ошибки выборочной доли и ошибки выборочной средней.
Систематическая ошибка репрезентативности возникает вследствие нарушения правил
отбора единиц генеральной совокупности, в частности принципа беспристрастного,
непреднамеренного отбора. Систематическая ошибка может привести к полной
непригодности результатов наблюдений.

Рассмотрим на примере, насколько отличаются выборочные и генеральные
показатели по данным об успеваемости студентов (две 10%-е выборки) (табл. 2).

Таблица 2

Данные по выборкам

Оценка

Число студентов, чел

Генеральная совокупность

Первая выборка

Вторая выборка

2 3 4 5

100 300 520 80

9 27 54 10

12 29 52 7

Итого

1000

100

100

Средний балл для генеральной совокупности

по
первой выборке

по
второй выборке

Доля
студентов, получивших оценки «4» и «5»:

по
генеральной совокупности

по
первой выборке

по
второй выборке

Разность
между показателями выборочной и генеральной совокупности является случайной
ошибкой репрезентативности (ошибкой выборки).

Ошибки
репрезентативности:

Как
видно из расчетов, выборочная средняя и выборочная доля являются случайными
величинами, которые могут принимать различные значения в зависимости от того,
какие единицы совокупности попали в выборку.

Ошибка
выборочной средней представляет собой расхождение (разность) между выборочной
средней  и генеральной средней ,
возникающее вследствие несплошного выборочного характера наблюдения. Величина
ошибки выборочной средней определяется как предел отклонения от ,
гарантируемый с заданной вероятностью:

где
 — гарантийный коэффициент, зависящий от вероятности  ,с которой гарантируется невыход разности  за пределы ;  — средняя ошибка выборочной средней.

Значения
гарантийного коэффициента  и соответствующие им вероятности  приведены в таблице 3. Обычно вероятность принимается
равной 0,9545 или 0,9973, а  при этом
равно соответственно 2 и 3.

Таблица 3

Значения
гарантийного коэффициента

1,00 1,10 1,20 1,30 1,40
1,50 1,60 1,70 1,80 1,90 2,00 2,10 2,20 2,30 2,40 2,50 2,60 2,70 2,80 2,90
3,00

0,6827 0,7287 0,7699 0,8064
0,8385 0,8664 0,8904 0,9109 0,9281 0,9426 0,9545 0,9643 0,9722 0,9786 0,9836
0,9876 0,9907 0,9931 0,9949 0,9963 0,9973

Средняя ошибка определяется как среднее квадратическое отклонение средней
величины в генеральной совокупности (средней генеральной)

В
математической статистике доказывается, что величина средней квадратической
стандартной ошибки простой случайной повторной выборки может быть определена по
формуле:

где
— дисперсия признака в генеральной совокупности.

Дисперсия
суммы независимых величин равна сумме дисперсий слагаемых

Если
все величины Xi имеют
одинаковую дисперсию, то:

Тогда
дисперсия средней будет:

Тогда
средняя ошибка при определении средней:

Между
дисперсиями в генеральной и выборочной совокупностях существует следующее
соотношение:

где
— дисперсия признака в выборке.

Если
n достаточно велико, то  близко к единице и дисперсию в генеральной
совокупности можно заменить на дисперсию в выборке.

Тогда
средняя ошибка средней в генеральной совокупности может быть как среднее
квадратическое отклонение средней величины в выборочной совокупности (средней
выборочной)

Средняя
ошибка выборочной средней:

Значения
средней ошибки выборки определяются по формуле:

где
 — дисперсия в генеральной совокупности.

Между
дисперсиями в генеральной и выборочной совокупностях существует следующее
соотношение:

где
— дисперсия в выборке.

Если
n достаточно велико, то  близко к единице и дисперсию в генеральной
совокупности можно заменить на дисперсию в выборке.

При
повторном отборе средняя ошибка определяется следующим образом:

где
 — средняя величина дисперсии количественного признака
, которая рассчитывается по формуле средней
арифметической невзвешенной

или
средней арифметической взвешенной:

где
fi — статистический вес.

В
данном разделе были показаны общие формулы расчета ошибок выборочного
наблюдения в статистическом анализе. Однако, в зависимости от способов отбора
выборочной совокупности, расчет средней ошибки выборочной средней имеет свои
особенности и формулы расчета. Это будет проиллюстрировано в следующем разделе.

2.3    Расчет
средних ошибок выборочной доли и выборочной средней

Формулы расчета средней ошибки выборочной средней для различных, наиболее
часто используемых способов отбора выборочной совокупности приведены в таблице
4.

Таблица 4

Формулы расчета средних ошибок выборочной доли и выборочной средней

Метод отбора выборки

Средняя ошибка

выборочной доли

выборочной средней

Механический или
собственно-случайный повторный отбор

Механический или
собственно-случайный бесповторный отбор

Серийный отбор при
повторном отборе равновеликих серий

Серийный отбор при
бесповторном отборе равновеликих серий

Типический отбор при
повторном случайном отборе внутри групп, пропорциональном объему групп

Типический отбор при
бесповторном случайном отборе внутри групп, пропорциональном объему групп

где N — численность генеральной совокупности;

 —
межсерийная дисперсия выборочной доли;- число отобранных серий;- число серий в
генеральной совокупности;

 —
средняя из групповых дисперсий выборочной доли;

 —
дисперсия признака x в выборке;

 —
межсерийная дисперсия выборочных средних;

 —
средняя из групповых дисперсий выборочной средней.

При
бесповторном оборе с каждой отобранной единицей или серией вероятность отбора
оставшихся единиц или серий повышается, при этом средняя ошибка выборочной
средней уменьшается по сравнению с повторным отбором и имеет следующий вид:

1) для механического или собственно случайного бесповторного отбора:

При
достаточно большом объеме совокупности N можно
воспользоваться формулой:

2) для серийного бесповторного отбора равновеликих серий:

При
достаточно большом числе серий в генеральной совокупности R
можно воспользоваться формулой:

3) для типического отбора с бесповторным случайном отборе внутри групп,
пропорциональном объему групп:

Межсерийная
дисперсия выборочных средних  и
средняя из выборочных дисперсий типических групп  вычисляются
следующим образом:

где
 — среднее значение показателя в j — й
серии;

 —
дисперсия признака x в j — й типической группе;j — число
единиц в j -й типической группе.

Средние
ошибки выборки при типическом методе отбора, пропорциональном объему групп и
колеблемости признака в группе приведены в таблице 5.

Таблица 5

Формулы расчета средних ошибок выборочной средней и выборочной доли при
типическом методе отбора

Метод отбора выборки

Средняя ошибка

выборочной доли

выборочной средней

повторный случайный отбор
внутри групп, непропорциональный объему групп

бесповторный случайный
отбор внутри групп, непропорциональный объему групп

повторный случайный отбор
внутри групп, пропорциональный колеблемости признака в группах

бесповторный случайный
отбор внутри групп, пропорциональный колеблемости признака в группах

где Nj — число
единиц в j -й типической группе;j — число отобранных единиц в j -й типической группе;

 —
выборочная дисперсия признака x в j — й типической группе
(дисперсия признака в выборке из j — й типической группы);

 —
выборочная дисперсия доли в j — й типической группе

(дисперсия
доли в выборке из j — й типической группы);

 —
среднее квадратическое отклонение признака x в выборке из j — й
типической группе.

Средние
ошибки выборки при комбинированной выборке с равновеликими сериями приведены в
табл.6.

Таблица 6

Формулы расчета средних ошибок выборки при комбинированной выборке с
равновеликими сериями

Метод отбора выборки

Средняя ошибка

выборочной доли

выборочной средней

повторный отбор серий

бесповторный отбор серий

где
 — общее число единиц в отобранных сериях ();

n — выбранное
число единиц, подвергающихся обследованию, из

отобранных
серий.

При
многоступенчатом отборе на каждой ступени отбора может быть найдена своя
средняя ошибка. При отборе, например,  крупных
групп из генеральной совокупности средняя ошибка выборки — ; при отборе  мелких
групп из крупных средняя ошибка выборки — ; при
отборе  отдельных единиц совокупности из мелких групп средняя
ошибка выборки — . Если численность групп одинаковая, то средняя
ошибка, как для средней, так и для доли, трехступенчатого отбора может быть
определена по формуле:

Предельная
ошибка выражается следующим образом:

и
зависит от вариации изучаемого признака в генеральной совокупности, объема и
доли выборки, способа отбора единиц из генеральной совокупности и от величины
вероятности, с которой гарантируются результаты выборочного наблюдения.

Из
всего вышесказанного можно сделать следующие выводы:

1. Определение объема выборки зависит от метода отбора, который может
быть механический бесповторный и механический повторный отбор, серийный при
повторном и серийный при бесповторном отборе, типический при повторном
случайном и типический при бесповторном случайном отборе. В зависимости от
принадлежности к тому или иному методу, объем выборки рассчитывается по
определенным формулам.

2.      Планомерность статистического наблюдения заключается в том, что
оно готовится и проводится по разработанному плану, который входит в план всего
статистического анализа выборочного наблюдения и включает вопросы методологии,
организации, техники сбора информации, контроля ее достоверности и оформления
итоговых результатов.

.        Разность между показателями выборочной и генеральной
совокупности называется ошибкой выборки. Ошибки выборки подразделяются на
ошибки регистрации и ошибки репрезентативности. Во 2 и 3 разделе были
представлены формулы расчета ошибок выборочного наблюдения в статистическом
анализе в зависимости от способов отбора выборочной совокупности.

ЗАКЛЮЧЕНИЕ

Выборочное наблюдение относится к разновидности несплошного наблюдения.
Оно охватывает отобранную часть единиц генеральной совокупности. Цель
выборочного наблюдения — по отобранной части единиц дать характеристику всей
совокупности единиц. Чтобы отобранная часть была репрезентативна (т.е.
представляла всю совокупность единиц), выборочное наблюдение должно быть
специально организовано. Следовательно, в отличие от генеральной совокупности,
представляющей всю совокупность исследуемых единиц, выборочная совокупность
представляет ту часть единиц генеральной совокупности, которая является
объектом непосредственного наблюдения.

Данная курсовая работа содержит 2 главы, а именно: теоретические аспекты
выборочного наблюдения и статистический анализ выборочного наблюдения.

Поставленная во введении цель дипломного проекта достигнута и решены
основные задачи.

В результате решения вышеизложенных проблем можно сделать следующие
выводы.

Теоретическое обоснование поставленного вопроса выявило понятие выборочного
наблюдения, его основные виды, определение объема выборки, ошибки выборочного
наблюдения.

Статистический анализ выборочного наблюдения показал следующие основные
моменты:

. Определение объема выборки зависит от метода отбора, который может быть
механический бесповторный и механический повторный отбор, серийный при
повторном и серийный при бесповторном отборе, типический при повторном
случайном и типический при бесповторном случайном отборе. В зависимости от
принадлежности к тому или иному методу, объем выборки рассчитывается по
определенным формулам.

. Планомерность статистического наблюдения заключается в том, что оно
готовится и проводится по разработанному плану, который входит в план всего
статистического анализа выборочного наблюдения и включает вопросы методологии,
организации, техники сбора информации, контроля ее достоверности и оформления
итоговых результатов.

. Разность между показателями выборочной и генеральной совокупности
называется ошибкой выборки. Ошибки выборки подразделяются на ошибки регистрации
и ошибки репрезентативности. Во 2 и 3 разделе были представлены формулы расчета
ошибок выборочного наблюдения в статистическом анализе в зависимости от
способов отбора выборочной совокупности.

И в заключение следует отметить, что практическое применение анализа
статистического наблюдения активно используется во многих областях
жизнедеятельности людей, например, широко применяется в социальной и
экономической статистике, в частности в контроле за коммерческой деятельностью
юридических и физических лиц со стороны финансовых организаций. Это
подтверждает актуальность выбора данной темы курсовой работы.

СПИСОК
ИСПОЛЬЗУЕМЫХ ИСТОЧНИКОВ

1.   Статистика:
учебник: Васильева Э.К., Лялин В.С. Издательство: Юнити Дана, 2012 г. — 398
страниц.

2.      Статистика:
учебное пособие: Эриашвили Н.Д., Воронин В.Ф., Жильцова Ю.В. Издательство:
Юнити-Дана, 2012 г. — 536 страниц.

.        Социально-экономическая
статистика: учебное пособие: Мухина И.А. Издательство: ФЛИНТА, 2011 г. — 116
страниц.

.        Статистика:
учебное пособие: Кузнецова Е.И., Гусаров В.М. Издательство: Юнити-Дана, 2011 г.
— 479 страниц.

.        Общая
теория статистики: Учебное пособие: Балдин К.В., Рукосуев А.В. Издательство:
Дашков и К, 2010 г. — 312 страниц.

.        Общая
теория статистики: учебник: Илышев А.М. Издательство: Юнити-Дана, 2008 г. — 535
страниц.

.        Статистика
предприятий и бизнес-статистика: учебное пособие: Образцова О.И. Издательство:
Издательский дом Высшей школы экономики, 2011 г. — 698 страниц.

.        Статистика:
учебное пособие: Плохотников К.Э., Колков С.В. Издательство: ФЛИНТА, 2012 г. —
286 страниц.

.        Методология
статистического исследования социально-экономических процессов: под ред. В.Г.
Минашкина. Издательство: Юнити-Дана, 2012 г. — 391 страница.

.        Статистика.
Учебник / Под. Ред. Елисеевой И.И., — М.: Высшее образование, 2009. — 252
страницы.

11.   

ПРИЛОЖЕНИЕ

Таблица случайных чисел

5489

5583

3156

0835

1988

3912

0938

7460

0869

4420

3522

0935

7877

5665

7020

9555

7375

7124

7878

5544

7555

7579

2550

2487

9477

0864

2349

1012

8250

2633

5759

3554

5080

9074

7001

6249

3224

6368

9102

2672

6303

6895

3371

3196

7231

2918

7380

0438

7547

2644

7351

5634

5323

2623

7803

8374

2191

0464

0696

9529

7068

7803

8832

5119

6350

0120

5026

3684

5657

0304

3613

1428

1796

8447

0503

5654

3254

7336

9536

19441

5143

4534

2105

0368

7890

2473

4240

8652

9435

1422

9815

5144

7649

8638

6137

8070

5345

4865

2456

5708

5780

1277

6816

1013

2867

9938

3930

3203

5696

1769

1187″

0951

5991

5245

5700

5564

7352

0891

6249

6568;

4184

2179

4554

9083

2254

2435

2965

5154

1209

7069

2916

2972

9885

0275

0144

8034

8122

3213

7666

0230

5524

1341

9860

6565

6981

9842

0171

2284

2707

3008

0146

5291

2354

5694

0377

5336

6460

9585

3415

2358

4920

2826

5238

5402

7937

1993

4332

2327

6875

5230

7978

1947

, 6380

3425

7267

7285

1130

7722

0164

8573

7453

0653

3645

7497

5969

8682

4191

2976

0361

9334

1473

6938

4899

5348

1641

3652

0852

5296

4538

4456

8162

8797

8000

4707

1880

9660

8446

1883

9768

0881

5645

4219

0807

3301

4279

4168

4305

9937

3120

5547

2042

1192

1175

8851

6432

4635

5757

6656

1660

5389

5470

7702

6958

9080

5925

8519

0127

9233

2452

7341

4045

1730

6005

1704

0345

3275

4738

4862

2556

8333

5880

1257

6163

4439

7276

6353

6912

0731

9033

5294

9083

4260

5277

4998

4298

5204

3965,

4028

8936

5148

1762

8713

1189

1090

8989

7273

3213

1935

9321

4820

2023

2589

1740

0424

8924

0005

1969

1636

7237

1227

7965

3855

4765

0703

1678

0841

7543

0308

9732

1289

7690

0480

8098

9629

4819

7219

7241

5128

3853

1921

9292

0426

9573

4903

5916

6576

8368

3270

6641

0033

0867

1656

7016

2533

6345

8227

1904

5138

2537

0505

2127

8255

5276

2233

3956

4118

8199

6380

6340

6295

9795

1112

5761

2575

6837

3336

9322

7403

8345

6323

2615

3410

3365′

1117

2417

3176

2434

5240

5455

8672

8536

2966

5773

5412

8114

0930

4697

6919

4569

1422

5507

7596

0670

3013

1351

3886

3268

9469

2584

2653

1472

5113

5735

1469

9545

9331

5303

9914

6394

0438

4376

3328

8649

8327

0110

4549

7955

5275

2890

2851

2157

0047

7085

1129

0460

6821

8323

2572

8962

7962

2753

3077

8718

7418

8004

1425

3706

8822

1494

3837

4098

0220

1217

4732

0150

1637

1097

1040

7372

8542

4126

9274

2251

0607

4301

8730

7690

6235

3477

0139

0765

8039

9484

2577

7859

1976

0623

1418

6685

6687

1943

4307

0579

8171

8224

8641

7034

3595

3875

6242

5582

5872

3197

4919

2792

5991

4058

9769

1918

6859

9606

0522

4993

0345

8958

1289

8825

6941

7685

6590

1932

6043

3623

1973

4112

1795

8465

2110

8045

3482

0478

0221

6738

7323

5643

4767

0106

2272

9862

Источник

Содержание курса лекций “Статистика”

Выборочное наблюдение как источник статистической информации в изучении социально-экономических явлений и процессов

Тема 10 Выборочное наблюдение

Статистическая методология исследования массовых явлений различает, как известно, два способа наблюдения в зависимости от полноты охвата объекта: сплошное и несплошное. Разновидностью несплошного наблюдения является выборочное, которое в условиях рыночных отношений в России находит все более широкое применение. Переход статистики РФ на международные стандарты системы национального счетоводства требует более широкого применения выборки для получения и анализа показателей СНС не только в промышленности, но и в других секторах экономики.

Под выборочным наблюдением понимается несплошное наблюдение, при котором статистическому обследованию (наблюдению) подвергаются единицы изучаемой совокупности, отобранные случайным способом. Выборочное наблюдение ставит перед собой задачу ‑ по обследуемой части дать характеристику всей совокупности единиц при условии соблюдения всех правил и принципов проведения статистического наблюдения и науч­но организованной работы по отбору единиц.

К выборочному наблюдению статистика прибегает по различным причинам. На современном этапе появилось множество субъектов хозяйствен­ной деятельности, которые характерны для рыночной экономики. Речь идет об акционерных обществах, малых и совместных предприятиях, фермерских хозяйствах и т.д. Сплошное обследование этих статистических совокупностей, состоящих из десятков и сотен тысяч единиц, потребовало бы огромных материальных, финансовых и иных затрат. Использование же выборочного обследования позволяет значительно сэкономить силы и средства, что имеет немаловажное значение.

Наряду с экономией ресурсов одной из причин превращения выборочного наблюдения в важнейший источник статистической информации является возможность значительно ускорить получение необходимых данных. Ведь при обследовании, скажем, 10% единиц совокупности будет затрачено гораздо меньше времени, а результаты могут быть представлены быстрее, и будут более актуальными. Фактор времени важен для статисти­ческого исследования особенно в условиях изменяющейся социально-экономической ситуации.

Реализация выборочного метода базируется на понятиях генеральной и выборочной совокупностей.

Генеральной совокупностью называется вся исходная изучаемая статистическая совокупность, из которой на основе отбора единиц или групп единиц формируется совокупность выборочная. Поэтому генеральную совокупность также называют основой выборки.

Отбор единиц в выборочную совокупность может быть повторным или беспо­вторным.

При повторном отборе попавшая в выборку единица подвергается обследованию, т.е. регистрации значений ее признаков, возвращается в генеральную совокупность и наравне с другими единицами участвует в дальнейшей процедуре отбора. Таким образом, некоторые единицы могут попадать в выборку дважды, трижды или даже большее число раз. И при изучении выборочной совокупности они будут рассматриваться как отдельные независимые наблюдения.

Отметим, что число единиц генеральной совокупности, участвующих в отборе, при таком подходе остается постоянным. Поэтому вероятность попадания в выборку для всех единиц совокупности на протяжении всего процесса отбора также не меняется.

На практике методология повторного отбора обычно используется в тех случаях, когда объем генеральной совокупности не известен и теоретически возможно повторение единиц с уже встречавшимися значениями всех регистрируемых признаков.

Например, при проведении маркетинговых исследований мы не можем сколько-нибудь точно оценить, какое число потребителей предпочитают стиральный порошок конкретной торговой марки, сколько покупателей предпочитают делать покупки именно в данном супермаркете и т.д. Поэтому возможно повторение совершенно идентичных единиц как по причине практически неограниченных объемов совокупности, так и вследствие возможной повторной регистрации. Предположим, при проведении обследования один и тот же покупатель может дважды прийти в магазин и дважды подвергнуться обследованию.

При выборочном контроле качества продукции объем генеральной совокупности также часто не определен, так как процесс производства может осуществляться постоянно, каждый день дополняя генеральную совокупность новыми единицами-изделиями. Поэтому в выборочную совокупность могут попасть два и более изделий с абсолютно одинаковыми характеристиками. Следовательно, и в этом случае при обработке результатов выборки необходимо ориентироваться на методологию, используемую при повторном отборе.

При бесповоротном отборе попавшая в выборку единица подвергается обследова­нию и в дальнейшей процедуре отбора не участвует. Такой отбор целесообразен и практически возможен в тех случаях, когда объем генеральной совокупности четко определен. Получаемые при этом результаты, как правило, являются более точными по сравнению с результатами, основанными на повторной выборке.

Как уже отмечалось выше, выборочное наблюдение всегда связано с определенны­ми ошибками получаемых характеристик. Эти ошибки называются ошибками репрезента­тивности (представительности).

Ошибки репрезентативности обусловлены тем обстоятельством, что выборочная совокупность не может по всем параметрам в точности воспроизвести совокупность генеральную. Получаемые расхождения или ошибки репрезентативности позволяют заключить, в какой степени попавшие в выборку единицы могут представлять всю генеральную совокупность. При этом следует различать систематические и случайные ошибки репре­зентативности.

Систематические ошибки репрезентативности связаны с нарушением принципов формирования выборочной совокупности. Например, вследствие каких-либо причин, связанных с организацией отбора, в выборку попали единицы, характеризующиеся несколько большими или, наоборот, несколько меньшими по сравнению с другими единицами значениями наблюдаемых признаков. В этом случае и рассчитанные выборочные характеристики будут завышенными или заниженными.

Случайные ошибки репрезентативности обусловлены действием случайных факторов, не содержащих каких-либо элементов системности в направлении воздействия на рассчитываемые выборочные характеристики. Но даже при строгом соблюдении всех принципов формирования выборочной совокупности выборочные и генеральные характе­ристики будут несколько различаться. Получаемые случайные ошибки могут быть стати­стически оценены и учтены при распространении результатов выборочного наблюдения на всю генеральную совокупность. Оценка ошибок выборочного наблюдения основана на теоремах теории вероятностей.

При дальнейшем рассмотрении теории и методов выборочного наблюдения используются следующие общепринятые условные обозначения:

    N ‑ объем (число единиц) генеральной совокупности;

    n ‑ объем (число единиц) выборочной совокупности;

генеральная средняя

 ‑ генеральная средняя, т.е. среднее значение изучаемого признака по генераль­ной совокупности (средняя прибыль, средняя величина активов, средняя численность ра­ботников предприятия и т.п.);

выбороноая средняя

‑ выборочная средняя,
т.е. среднее значение изучаемого признака по выборочной совокупности;
 

     М ‑ численность единиц генеральной совокупности, обладающих определенным вариантом или вариантами изучаемого признака (численность городского населения, численность сельского населения, количество бракованных изделий, число нерентабельных предприятий и т.п.);

     р ‑ генеральная доля, т.е. доля единиц, обладающих определенным вариантом или вариантами изучаемого признака, во всей генеральной совокупности (доля городского населения в общей численности населения, доля бракованной продукции в общем выпуске, доля нерентабельных предприятий в общей численности предприятий и т.п.); определяетcя как

     m ‑ численность единиц выборочной совокупности, обладающих определенным вариантом или вариантами изучаемого признака;

     w ‑ выборочная доля, т.е. доля единиц, обладающих определенным вариантом или вариантами изучаемого признака, в выборочной совокупности,

определяется как ;

средняя ошибка выборки

‑ средняя ошибка выборки;

предельная ошибка выборки

‑ предельная ошибка выборки;

‑ коэффициент доверия, определяемый в зависимости от уровня вероятности.

Ошибка выборки или отклонение выборочной средней от средней генеральной находится в прямой зависимости от дисперсии изучаемого признака в генеральной совокуп­ности, и в обратной зависимости ‑ от объема выборки.

Таким образом среднюю ошибку выборки можно представить как

Формула 10.1

(10.1)

При проведении выборочного наблюдения дисперсия изучаемого признака в генеральной совокупности, как правило, не известна. В то же время, между генеральной дисперсией и средней из всех возможных выборочных дисперсий существует следующее соотношение:

Формула 10.2

(10.2)

В связи с тем, что на практике в большинстве случаев из генеральной совокупности в определенный момент времени производится только одна выборка, дисперсия изучаемого признака по этой выборке и используется при расчете ошибки.

Учитывая, что при достаточно большом объеме выборки отношение отношение близко к 1, формула средней ошибки повторной выборки принимает следующий вид:

Формула 10.3

(10.3)

Где  ‑ дисперсия дисперсия изучаемого признака по выборочной совокупности.

При определении возможных границ значений характеристик генеральной сово­купности рассчитывается предельная ошибка выборки, которая зависит от величины ее средней ошибки и уровня вероятности, с которым гарантируется, что генеральная средняя не выйдет за указанные границы.

Согласно теореме А.М. Ляпунова, вероятность той или иной величины предельной ошибки, при достаточно большом объеме выборочной сово­купности, подчиняется нормальному закону распределения и может быть определена на основе интеграла Лапласа.

Значения интеграла Лапласа при различных величинах t табулированы и представ­лены в статистических справочниках.

При обобщении результатов выборочного наблюдения наиболее часто используются следующие уровни вероятности и соответствующие им значения t:

Таблица 10.1 ‑ !!!Некоторые значения t

Вероятность, рi. 0,683 0,866 0,954 0,988 0,997 0,999
Значение t 1,0 1,5 2,0 2,5 3,0 3,5

Например, если при расчете предельной ошибки выборки мы используем значение t=2, то с вероятностью 0,954 можно утверждать, что расхождение между выборочной средней и генеральной средней не превысит двукратной величины средней ошибки вы­борки.

Теоретической основой для определения границ генеральной доли, т.е. доли еди­ниц, обладающих тем или иным вариантом признака, является теорема Вернули. Согласно данной теореме вероятность получения сколь угодно малого расхождения между выборочной долей и генеральной долей при достаточно большом объеме выборки будет стремиться к единице. С учетом того, что вероятность расхождения между выборочной и генеральной долями подчиняется нормальному закону распределения, эта вероятность также определяется по функции F(t) при заданном значении t.

Процесс подготовки и проведения выборочного наблюдения включает ряд после­довательных этапов:

  1. Определение цели обследования.
  2. Установление границ генеральной совокупности.
  3. Составление программы наблюдения и программы разработки данных
  4. Определение вида выборки, процента отбора и метода отбора
  5. Отбор и регистрация наблюдаемых признаков у отобранных единиц.
  6. Насчет выборочных характеристик и их ошибок.
  7. Распространение полученных результатов на генеральную совокупность.

В зависимости от состава и структуры генеральной совокупности выбирается вид выборки или способ отбора.

К наиболее распространенным на практике видам относятся:

  • собственно-случайная (простая случайная) выборка;
  • механическая (систематическая) выборка;
  • типическая (стратифицированная, расслоенная) выборка;
  • серийная (гнездовая) выборка.

Отбор единиц из генеральной совокупности может быть комбинированным, много­ступенчатым и многофазным.

Комбинированный отбор предполагает объединение нескольких видов выборки. Так, например, можно комбинировать типическую и серийную, серийную и собственно-случайную выборки. Ошибка такой выборки определяется ступенчатостью отбора.

Многоступенчатым называется отбор, при котором из генеральной совокупности сначала извлекаются укрупненные группы, потом ‑ более мелкие и так до тех пор, пока не будут отобраны те единицы, которые подвергаются обследованию.

Многофазная выборка, в отличие от многоступенчатой, предполагает сохранение одной и той же единицы отбора на всех этапах его проведения; при этом отобранные на каждой стадии единицы подвергаются обследованию, каждый раз – по более расширенной программе.

Собственно-случайная (простая случайная) выборка заключается в отборе единиц из генеральной совокупности наугад или наудачу без каких-либо элементов системности.

Однако прежде чем производить собственно-случайный отбор, необходимо убедиться, что все без исключения единицы генеральной совокупности имеют абсолютно равные шансы попадания в выборку, в списках или перечне отсутствуют пропуски, игнорирования отдельных единиц и т.п. Следует также установить четкие границы генеральной сово­купности таким образом, чтобы включение или не включение в нее отдельных единиц не вызывало сомнений. Так, например, при обследовании студентов необходимо указать, будут ли приниматься во внимание лица, находящиеся в академическом отпуске, студенты негосударственных вузов, военных училищ и т.п.; при обследовании торговых предприятий важно определиться, включит ли генеральная совокупность торговые павильоны, коммерческие палатки и прочие подобные объекты.

Технически собственно-случайный отбор проводят методом жеребьевки или по таблице случайных чисел.

Расчет ошибок позволяет решить одну из главных проблем организации выборочного наблюдения – оценить репрезентативность (представительность) выборочной совокупности.

Различают среднюю и предельную ошибки выборки. Эти два вида связаны следующим соотношением:

Формула 10.4

(10.4)

Величина средней ошибки выборки рассчитывается дифференциро­ванно в зависимости от способа отбора и процедуры выборки.

Так, при собственно-случайном повторном отборе средняя ошибка определяется по формуле:

Формула 10.5

(10.5)

а при расчете средней ошибки  собственно-случайной бесповторной выборки:

Формула 10.6

(10.6)

Расчет средней и предельной ошибок выборки позволяет определить возможные пределы, в которых будут находиться характеристики генеральной совокупности.

Например, для выборочной средней такие пределы устанавливаются на основе следующих соотношений:

Формула 10.7

(10.7)

где  генеральная средняяи выборочная средняя‑ генеральная и выборочная средняя соответственно;

предельная ошибка выборочной средней‑ предельная ошибка выборочной средней.

Пример.

При проверке веса импортируемого груза на таможне методом случайной повторной выборки было отобрано 200 изделий. В результате был установлен средний вес изделия 30 г. при среднем квадратическом отклонении 4 г. С вероятностью 0,997 определите пределы, в которых находится средний вес изделия в генеральной совокупности.

Решение. Рассчитаем сначала предельную ошибку выборки. Так как при р = 0,997, t = 3, она равна:

Определим пределы генеральной средней:

или

Вывод: Следовательно, с вероятностью 0,997 можно утверждать, что средний вес изделий в генеральной совокупности находится в пределах от 29,16 г. до 30,84 г.

Пример 2.

В городе проживает 250 тыс. семей. Для определения среднего числа детей в семье была организована 2%-ная случайная бесповторная выборка семей. По ее результатам было получено следующее распре­деление семей по числу детей:

Таблица 10.2 ‑ Распределение семей по числу детей в городе N

Число детей в семье 0 1 2 3 4 5
Количество

семей

 1000 2000 1200 400 200 200

С вероятностью 0,954 определите пределы, в которых будет находить­ся среднее число детей в генеральной совокупности.

Решение. В начале на основе имеющегося распределения семей определим выборочные среднюю и дисперсию:

Таблица 10.3 ‑ Вспомогательная таблица для расчета среднего числа детей

Число детей

в семье, х;

 Количество семей,     f

0

1

2

3

4

5

1000

2000

1200

400

200

200

 0

2000

2400

1200

800

1000

 -1,5

-0,5

0,5

1,5

2,5

3,5

 2,25

0,25

0,25

2,25

6,25

12,25

2250

500

300

900

1250

2450
 

Итого

 5000 7400 – – 7650

Вычислим теперь предельную ошибку выборки (с учетом того, что при р = 0,954 t = 2).

Следовательно, пределы генеральной средней:

Таким образом, с вероятностью 0,954 можно утверждать, что среднее число детей в семьях города практически не отличается от 1,5, т.е. в среднем на каждые две семьи приходится три ребенка.

Наряду с определением ошибок выборки и пределов для генеральной средней эти же показатели могут быть определены для доли признака.

В этом случае особенности расчета связаны с определением дисперсии доли, которая вычисляется так:

формула 10.8

(10.8)

где формула 10.8 пояснение ‑ доля единиц, обладающих данным признаком в выборочной совокупности, определяемая как отношение количества соответствующих единиц к объему выборки.

Тогда, например, при собственно-случайном повторном отборе для определения предельной ошибки выборки используется следующая формула:

формула 10.9

(10.9)

Соответственно, при бесповторном отборе:

формула 10.10

(10.10)

Пределы доли признака в генеральной совокупности p выглядят следующим образом:

формула 10.11

(10.11)

Рассмотрим пример.

С целью определения средней фактической продолжитель­ности рабочего дня в государственном учреждении с численностью слу­жащих 480 человек, в январе 2009 г. было проведена 25%-ная случайная бесповторная выборка. По результатам наблюдения оказалось, что у 10% обследованных потери времени достигали более 45 мин. в день. С вероят­ностью 0,683 установите пределы, в которых находится генеральная доля служащих с потерями рабочего времени более 45 мин. в день.

Решение. Определим объем выборочной совокупности:

n= 480 х 0,25 = 120 чел.

Выборочная доля w равна по условию 10%.

Учитывая, что при р = 0,683   t=1, вычислим предельную ошибку выборочной доли:

формула 10.10 решение

Пределы доли признака в генеральной совокупности:

формула 10.11 пример

Таким образом, с вероятностью 0,683 можно утверждать, что доля ра­ботников учреждения с потерями рабочего времени более 45 мин. в день находится в пределах от 7,6% до 12,4%.

Мы рассмотрели определение границ генеральной средней и генеральной доли по результатам уже проведенного выборочного наблюдения, при известном объеме выборки или проценте отбора. На этапе же проектирования выборочного наблюдения именно объ­ем выборочной совокупности и требует определения.

Для определения необходимого объема собственно-случайной повторной выборки применяют следующую формулу:

формула 10.12

(10.12)

Полученный на основе использования данной формулы результат всегда округляется в большую сторону. Например, если мы получили, что необходимый объем выборки составляет 493,1 единицы, то обследовав 493 единицы мы не достигнем требуемой точности. Поэтому, для достижения желаемого результата обследованием должны быть охвачены 494 единицы.

С другой стороны, рассчитанное значение необходимого объема выборки свободно может быть увеличено в большую сторону на несколько единиц. Если мы располагаем необходимыми ресурсами, если по причинам организационного порядка (компактность расположения единиц, фиксированная нагрузка на каждого регистратора и т.п.) мы вполне можем охватить больший объем, то включение в выборочную совокуп­ность 500 или, например, 550 единиц только уменьшит значения полученных случайной и предельной ошибок.

При определении необходимого объема выборки для определения границ генеральной доли задача оценки вариации решается значительно проще. Если дисперсия изучаемого альтернативного признака неизвестна, то можно использовать ее максимальное возможное значение:

формула 10.12 после 1 расчет

Например, предприятию связи с вероятностью 0,954 необходимо определить удельный вес телефонный разговоров продолжительностью менее 1 минуты с предельной ошибкой 2%. Сколько разговоров нужно обследовать в порядке собственно-случайного повторного отбора для решения этой задачи?

Для получения ответа на поставленный вопрос воспользуемся формулой (10.12) и будем ориентироваться на максимальную возможную дисперсию доли телефонных разговоров такой продолжительности. Расчет приводит к следующему результату:

формула 10.12 пример

Таким образом, обследованием должны быть охвачены не менее 2500 разговоров на предмет их продолжительности.

Необходимый объем собственно-случайной бесповторной выборки может быть определен по следующей формуле:

формула 10.13

(10.13)

Укажем на одну особенность формулы (10.13). При проведении вычислений объем генеральной совокупности должен быть выражен только в единицах, а не в тысячах или в миллионах единиц.

Например, подставив в данную формулу общую численность населения региона, выраженную в тысячах человек, мы не получим правильное значение необходимой численности выборки, также выраженное в тысячах человек, как это иногда бывает в других расчетах. Результат вычислений будет неверен.

Механическая выборка может быть применена в тех случаях, когда генеральная совокупность каким-либо образом упорядочена, т.е. имеется определенная последова­тельность в расположении единиц (табельные номера работников, списки избирателей, телефонные номера респондентов, номера домов и квартир и т.п.). Для проведения отбора желательно, чтобы все единицы также имели порядковые номера от 1 до N.

Для проведения механической выборки устанавливается пропорция отбора, которая определяется соотнесением объемов выборочной и генеральной совокупностей.

Так, если из совокупности в 500000 единиц предполагается отобрать 10000 единиц, то пропорция отбора составит

формула 10.13вставка после

Отбор единиц осуществляется в соответствии с установленной пропорцией через равные интервалы.

Например, при пропорции 1:50 (2%-ная выборка) отбирается каждая 50-я единица, при пропорции 1:20 (5%-ная выборка) – каждая 20-я единица и т.д.

Интервал отбора также можно определить как частное от деления 100% на уста­новленный процент отбора.

Так, например  при 2%-ном отборе интервал составит 50 (100%:2%), при 4%-ном отборе ‑ 25 (100%:4%). В тех случаях, когда результат деления получается дробным, сформировать выборку механическим способом при строгом соблюдении процента отбора не представляется возможным.

Например, по этой причине нельзя сформировать 3%-ную или 6%-ную выборки.

Генеральную совокупность при механическом отборе можно ранжировать или упорядочить по величине изучаемого или коррелирующего с ним признака, что позволит повысить репрезентативность выборки. Однако в этом случае возрастает опасность систе­матической ошибки, связанной с занижением значений изучаемого признака (если из каждого интервала регистрируется первое значение) или его завышением (если из каждого интервала регистрируется последнее значение). Поэтому целесообразно из каждого интервала отбирать центральную или одну из двух центральных единиц.

Например, при 5%-ной выборке интервал отбора составит 20 единиц, тогда отбор целесообразно начинать с 10-й или с 11-й единицы. В первом случае в выборку попадут 10, 30, 50, 70 и с таким же интервалом последующие единицы; во втором случае – единицы с номерами 11,31,51,71 и т.д.

При механической выборке также может появиться опасность систематической ошибки, обусловленной случайным совпадением выбранного интервала и циклических закономерностей в расположении единиц генеральной совокупности. Так, при переписи населения 1989 г. в ходе 25%-го выборочного обследования семей имела место опасность попадания в выборку квартир только одного типа (например, только однокомнатных или только трехкомнатных), так как на лестничных площадках многих типовых домов распо­лагаются именно по 4 квартиры. Чтобы избежать систематической ошибки, в каждом новом подъезде счетчик менял начало отбора.

Для определения средней ошибки механической выборки, а также необходимой ее численности, используются соответствующие формулы, применяемые при собственно-случайном бесповторном отборе(10.6 и 10.13). При этом, определив необходимую численность выборки и сопоставив ее с объемом генеральной совокупности, как правило, приходится производить соответствующее округление для получения целочисленного интервала отбора.

Например, в области зарегистрировано 12000 фермерских хозяйств. Определим, сколько из них нужно отобрать в порядке механического отбора для определения средней площади сельхозугодий с ошибкой ± 2 га. (Р=0,997). По результатам ранее проведенного обследования известно, что среднее квадратическое отклонение площади сельхозугодий составляет 8 га. Произведем расчет, воспользовавшись формулой (10.13).

формула 10.13 пример

С учетом полученного необходимого объема выборки (143 фермерских хозяйства) определим интервал отбора: 12000:143=83,9.

Определенный таким способом интервал всегда округляется в меньшую сторону, так как при округлении в большую сторону про­изведенная выборка не достигнет рассчитанного по формуле необходимого объема.

Сле­довательно, в нашем примере, из общего списка фермерских хозяйств необходимо отобрать для обследования каждое 83-е хозяйство. При этом процент отбора составит 1,2% (100% : 83).

Типический отбор целесообразно использовать в тех случаях, когда все единицы генеральной совокупности объединены в несколько крупных типических групп.. Такие группы также называют стартами или слоями, в связи с чем типический отбор также называют стратифицированным или расслоенным. При обследованиях населения в качестве типических групп могут быть выбраны области, районы, социальные, возрастные или об­разовательные группы, при обследовании предприятий – отрасли или подотрасли, формы собственности и т.п.

Рассматривать генеральную совокупность в разрезе нескольких крупных групп единиц имеет смысл только в том случае, если средние значения изучаемых признаков по группам существенно различаются. Например, с большой уверенностью можно предпо­ложить, что доходы населения крупного города будут в среднем выше доходов населения, проживающего в сельской местности; численность работников промышленного предприятия в среднем будет выше численности работников торгового или сельскохозяйственного предприятия; средний возраст студентов будет значительно меньше среднего возраста занятого населения и, тем более, пенсионеров. В то же время, нет никакого смысла при выделении типических групп ориентироваться на признак, не связанный или очень слабо связанный с изучаемым.

Отбор единиц в выборочную совокупность из каждой типической группы осущест­вляется собственно-случайным или механическим способом. Поскольку в выборочную совокупность в той или иной пропорции обязательно попадают представители всех групп, типизация генеральной совокупности позволяет исключить влияние межгрупповой дисперсии на среднюю ошибку выборки. В то же время, в выделенных типических группах обследуются далеко не все единицы, а только включенные в выборку. Следовательно, на величине полученной ошибки будет сказываться различие между единицами внутри этих групп, т.е. внутригрупповая вариация. Поэтому, ошибка типической выборки будет опре­деляться величиной не общей дисперсии, а только ее части – средней из внутригрупповых дисперсий.

При типической выборке, пропорциональной объему типических групп, число еди­ниц, подлежащих отбору из каждой группы, определяется следующим образом:

формула 10.14

 (10.14)

Где Ni – объем i-ой группы. а ni ‑ объем выборки из i-ой группы.

Пример. Предположим, общая численность населения области составляет 1,5 млн. чел., в том числе городское – 900 тыс. чел. и сельское – 600 тыс. чел. Если в ходе выборочного наблюдения планируется обследовать 100 тыс. жителей, то эта численность должна быть поделена пропорционально объему типических групп следующим образом:

формула 10.14пример

Средняя ошибка типической выборки определяется по формулам:

формула 10.15

(10.15)

                                    формула 10.16               (10.16)

где формула 10.16пояснение – средняя из внутригрупповых дисперсий.

При выборке, пропорциональной дифференциации признака, число наблюдений по каждой группе рассчитывается по формуле:

формула 10.17

(10.17)

Где формула 10.17 пояснение‑ среднее отклонение признака в i-ой группе.

Cредняя ошибка такого отбора определяется следующим образом:

формула 10.18

(10.18)

формула 10.19

(10.19)

Отбор, пропорциональный дифференциации признака, дает лучшие результаты, однако на практике его применение затруднено вследствие трудности получения сведений о вариации до проведения выборочного наблюдения.

Таблица 10.4 ‑ Результаты обследования рабочих предприятия

Цех Всего рабочих, человек Обследовано, человек Число дней временной не­трудоспособности за год
средняя дисперсия
I

II

III

 1000

1400

800

 100

140

80

 18

12

15

 49

25

16

Рассмотрим оба варианта типической выборки на условном примере. Предположим, 10% бесповторный типический отбор рабочих предприятия, пропорциональный размерам цехов, проведенный с целью оценки потерь из-за временной нетрудоспособности, привел к следующим результатам (табл. 10.4)

Рассчитаем среднюю из внутригрупповых дисперсий:

пример к табл 10.4

Определим  среднюю  и  предельную  ошибки  выборки  (с  вероятностью 0,954):

Рассчитаем выборочную среднюю:

пример к табл 10.4_3

С вероятностью 0,954 можно сделать вывод, что среднее число дней временной нетрудоспособности одного рабочего в целом по предприятию находится в пределах:

пример к табл 10.4_4

Воспользуемся полученными внутригрупповыми дисперсиями для проведения отбора пропорционального дифференциации признака. Опре­делим необходимый объем выборки по каждому цеху:

пример к табл 10.4_5

пример к табл 10.4_6

С учетом полученных значений рассчитаем среднюю ошибку выборки:

пример к табл 10.4_7

В данном случае средняя, а следовательно, и предельная ошибки будут несколько меньше, что отразится и на границах генеральной средней.

Серийный отбор. Данный способ отбора удобен в тех случаях, когда единицы совокупности объединены в небольшие группы или серии. В качестве таких серий могут рассматриваться упаковки с определенным количеством готовой продукции, партии товара, студенческие группы, бригады и другие объединения. Сущность серийной выборки заключается в собственно-случайном или механическом отборе серий, внутри которых произ­водится сплошное обследование единиц.

Поскольку внутри групп (серий) обследуются все без исключения единицы, средняя ошибка серийной выборки (при отборе равновеликих серий) зависит от величины только межгрупповой (межсерийной) дисперсии и определяется по следующим формулам:

формула 10.20

(10.20)

формула 10.21

(10.21)

Где r ‑ число отобранных серий; R ‑ общее число серий.

Межгрупповую дисперсию вычисляют следующим образом:

 формула 10.22(10.22)

где формула 10.22 пояснение 1 ‑ средняя i-й серии;

формула 10.22 пояснение 2‑ общая средняя по всей выборочной совокупности.

Пример.

В области, состоящей из 20 районов, проводилось выборочное обследование урожайности на основе отбора серий (районов). Выбо­рочные средние по районам составили соответственно 14,5 ц/га; 16 ц/га; 15,5 ц/га; 15 ц/га и 14 ц/га. С вероятностью 0,954 определите пределы урожайности во всей области.

Решение. Рассчитаем общую среднюю:

Межгрупповая (межсерийная) дисперсия равна:

Определим теперь предельную ошибку серийной бесповторной выборки (t = 2 при р = 0,954):

Вывод: Следовательно, урожайность будет с вероятностью 0,954 находиться в пределах:

Определение необходимого объема выборки

При проектировании выборочного наблюдения возникает вопрос о необходимой численности выборки. Эта численность может быть определена на базе допустимой ошибки при выборочном наблюдении, исходя из вероятности, на основе которой можно гарантировать величину устанавливае­мой ошибки, и, наконец, на базе способа отбора.

Формулы необходимого объема выборки для различных способов формирования выборочной совокупности могут быть выведены из соот­ветствующих соотношений, используемых при расчете предельных ошибок выборки. Приведем наиболее часто применяемые на практике выражения необходимого объема выборки:

– собственно-случайная и механическая выборка:

Формула 10.23

(10.23)

Формула 10.24

(10.24)

– типическая выборка:

Формула 10.25

(10.25)

Формула 10.26

(10.26)

 – серийная выборка:

Формула 10.27

(10.27)

Формула 10.28

(10.28)

При этом в зависимости от целей исследования дисперсии и ошибки выборки могут быть рассчитаны для средней величины или доли признака.

Рассмотрим примеры определения необходимого объема выборки при различных способах формирования выборочной совокупности.

Пример.

В 100 туристических агентствах города предполагается провести обследование среднемесячного количества реализованных путевок методом механического отбора. Какова должна быть численность вы­борки, чтобы с вероятностью 0,683 ошибка не превышала 3 путевок, если по данным пробного обследования дисперсия составляет 225.

Решение. Рассчитаем необходимый объем выборки:

29

Пример.

С целью определения доли сотрудников коммерческих банков области в возрасте старше 40 лет предполагается организовать типическую выборку пропорциональную численности сотрудников мужского и женского пола с механическим отбором внутри групп. Общее число сотрудников банков составляет 12 тыс. чел., в том числе 7 тыс. мужчин и 5 тыс. женщин.

На основании предыдущих обследований известно, что средняя из внутригрупповых дисперсий составляет 1600. Определите необходимый объем выборки при вероятности 0,997 и ошибке 5%.

Решение. Рассчитаем общую численность типической выборки:

30

Вычислим теперь объем отдельных типических групп:

31

Вывод: Таким образом, необходимый объем выборочной совокупности сотрудников банков составляет 550 чел., в т.ч. 319 мужчин и 231 женщина.

Пример.

В акционерном обществе 200 бригад рабочих. Планируется проведение выборочного обследования с целью определения удельного ве­са рабочих, имеющих профессиональные заболевания. Известно, что межсерийная дисперсия доли равна 225. С вероятностью 0,954 рассчитайте необходимое количество бригад для обследования рабочих, если ошибка вы­борки не должна превышать 5%.

Решение. Необходимое количество бригад рассчитаем на основе формулы объема серийной бесповторной выборки:

32

Содержание курса лекций “Статистика”

Контрольные задания

Самостоятельно проведите выборочное наблюдение и произведите соответствующие расчеты.

Источник

Понравилась статья? Поделить с друзьями:
  • Ошибки водителей зимой
  • Ошибки выборки случайные и систематические способы устранения ошибок
  • Ошибки времени выполнения программы
  • Ошибки во время публичного выступления
  • Ошибки времени выполнения java