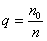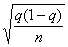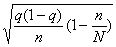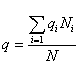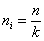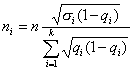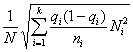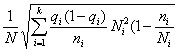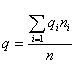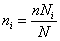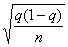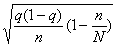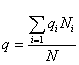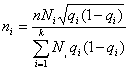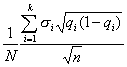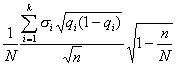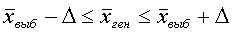From Wikipedia, the free encyclopedia
In statistics, sampling errors are incurred when the statistical characteristics of a population are estimated from a subset, or sample, of that population. It can produce biased results. Since the sample does not include all members of the population, statistics of the sample (often known as estimators), such as means and quartiles, generally differ from the statistics of the entire population (known as parameters). The difference between the sample statistic and population parameter is considered the sampling error.[1] For example, if one measures the height of a thousand individuals from a population of one million, the average height of the thousand is typically not the same as the average height of all one million people in the country.
Since sampling is almost always done to estimate population parameters that are unknown, by definition exact measurement of the sampling errors will not be possible; however they can often be estimated, either by general methods such as bootstrapping, or by specific methods incorporating some assumptions (or guesses) regarding the true population distribution and parameters thereof.
Description[edit]
Sampling Error[edit]
The sampling error is the error caused by observing a sample instead of the whole population.[1] The sampling error is the difference between a sample statistic used to estimate a population parameter and the actual but unknown value of the parameter.[2]
Effective Sampling[edit]
In statistics, a truly random sample means selecting individuals from a population with an equivalent probability; in other words, picking individuals from a group without bias. Failing to do this correctly will result in a sampling bias, which can dramatically increase the sample error in a systematic way. For example, attempting to measure the average height of the entire human population of the Earth, but measuring a sample only from one country, could result in a large over- or under-estimation. In reality, obtaining an unbiased sample can be difficult as many parameters (in this example, country, age, gender, and so on) may strongly bias the estimator and it must be ensured that none of these factors play a part in the selection process.
Even in a perfectly non-biased sample, the sample error will still exist due to the remaining statistical component; consider that measuring only two or three individuals and taking the average would produce a wildly varying result each time. The likely size of the sampling error can generally be reduced by taking a larger sample.[3]
Sample Size Determination[edit]
The cost of increasing a sample size may be prohibitive in reality. Since the sample error can often be estimated beforehand as a function of the sample size, various methods of sample size determination are used to weigh the predicted accuracy of an estimator against the predicted cost of taking a larger sample.
Bootstrapping and Standard Error[edit]
As discussed, a sample statistic, such as an average or percentage, will generally be subject to sample-to-sample variation.[1] By comparing many samples, or splitting a larger sample up into smaller ones (potentially with overlap), the spread of the resulting sample statistics can be used to estimate the standard error on the sample.
In Genetics[edit]
The term «sampling error» has also been used in a related but fundamentally different sense in the field of genetics; for example in the bottleneck effect or founder effect, when natural disasters or migrations dramatically reduce the size of a population, resulting in a smaller population that may or may not fairly represent the original one. This is a source of genetic drift, as certain alleles become more or less common), and has been referred to as «sampling error»,[4] despite not being an «error» in the statistical sense.
See also[edit]
- Margin of error
- Propagation of uncertainty
- Ratio estimator
- Sampling (statistics)
References[edit]
- ^ a b c Sarndal, Swenson, and Wretman (1992), Model Assisted Survey Sampling, Springer-Verlag, ISBN 0-387-40620-4
- ^ Burns, N.; Grove, S. K. (2009). The Practice of Nursing Research: Appraisal, Synthesis, and Generation of Evidence (6th ed.). St. Louis, MO: Saunders Elsevier. ISBN 978-1-4557-0736-2.
- ^ Scheuren, Fritz (2005). «What is a Margin of Error?». What is a Survey? (PDF). Washington, D.C.: American Statistical Association. Archived from the original (PDF) on 2013-03-12. Retrieved 2008-01-08.
- ^ Campbell, Neil A.; Reece, Jane B. (2002). Biology. Benjamin Cummings. pp. 450–451. ISBN 0-536-68045-0.
Расхождения
между величиной какого-либо показателя,
найденного посредством статистического
наблюдения, и действительными его
размерами называются ошибками
наблюдения.В зависимости от
причин возникновения различают ошибки
регистрации и ошибки репрезентативности.
Ошибки
регистрациивозникают в результате
неправильного установления фактов или
ошибочной записи в процессе наблюдения
или опроса. Они бывают случайными или
систематическими. Случайные ошибки
регистрации могут быть допущены как
опрашиваемыми в их ответах, так и
регистраторами. Систематические ошибки
могут быть и преднамеренными, и
непреднамеренными. Преднамеренные –
сознательные, тенденциозные искажения
действительного положения дела.
Непреднамеренные вызываются различными
случайными причинами (небрежность,
невнимательность).
Ошибки
репрезентативности(представительности)
возникают в результате неполного
обследования и в случае, если обследуемая
совокупность недостаточно полно
воспроизводит генеральную совокупность.
Они могут быть случайными и систематическими.
Случайные ошибки репрезентативности
– это отклонения, возникающие при
несплошном наблюдении из-за того, что
совокупность отобранных единиц наблюдения
(выборка) неполно воспроизводит всю
совокупность в целом. Систематические
ошибки репрезентативности – это
отклонения, возникающие вследствие
нарушения принципов случайного отбора
единиц. Ошибки репрезентативности
органически присущи выборочному
наблюдению и возникают в силу того, что
выборочная совокупность не полностью
воспроизводит генеральную. Избежать
ошибок репрезентативности нельзя,
однако, пользуясь методами теории
вероятностей, основанными на использовании
предельных теорем закона больших чисел,
эти ошибки можно свести к минимальным
значениям, границы которых устанавливаются
с достаточно большой точностью.
Ошибки
выборки –разность между
характеристиками выборочной и генеральной
совокупности. Для среднего значения
ошибка будет определяться по формуле
(7.1)
где
Величина
называетсяпредельной ошибкойвыборки.
Предельная
ошибка выборки – величина случайная.
Исследованию закономерностей случайных
ошибок выборки посвящены предельные
теоремы закона больших чисел. Наиболее
полно эти закономерности раскрыты в
теоремах П. Л. Чебышева и А. М. Ляпунова.
Теорему П.
Л. Чебышева применительно к
рассматриваемому методу можно
сформулировать следующим образом: при
достаточно большом числе независимых
наблюдений можно с вероятностью, близкой
к единице (т. е. почти с достоверностью),
утверждать, что отклонение выборочной
средней от генеральной будет сколько
угодно малым. В теореме П. Л. Чебышева
доказано, что величина ошибки не должна
превышать.
В свою очередь величина,
выражающая среднее квадратическое
отклонение выборочной средней от
генеральной средней, зависит от
колеблемости признака в генеральной
совокупностии числа отобранных единицn. Эта
зависимость выражается формулой
,
(7.2)
где
зависит также от способа производства
выборки.
Величину
=
называютсредней ошибкой выборки. В
этом выражении– генеральная дисперсия,n– объем
выборочной совокупности.
Рассмотрим, как
влияет на величину средней ошибки число
отбираемых единиц n. Логически
нетрудно убедиться, что при отборе
большого числа единиц расхождения между
средними будут меньше, т. е. существует
обратная связь между средней ошибкой
выборки и числом отобранных единиц. При
этом здесь образуется не просто обратная
математическая зависимость, а такая
зависимость, которая показывает, что
квадрат расхождения между средними
обратно пропорционален числу отобранных
единиц.
Увеличение
колеблемости признака влечет за собой
увеличение среднего квадратического
отклонения, а следовательно, и ошибки.
Если предположить, что все единицы будут
иметь одинаковую величину признака, то
среднее квадратическое отклонение
станет равно нулю и ошибка выборки
также исчезнет. Тогда нет необходимости
применять выборку. Однако следует иметь
в виду, что величина колеблемости
признака в генеральной совокупности
неизвестна, поскольку неизвестны размеры
единиц в ней. Можно рассчитать лишь
колеблемость признака в выборочной
совокупности. Соотношение между
дисперсиями генеральной и выборочной
совокупности выражается формулой
Поскольку
величина
при достаточно большихnблизка к
единице, можно приближенно считать, что
выборочная дисперсия равна генеральной
дисперсии, т. е.
Следовательно,
средняя ошибка выборки показывает,
какие возможны отклонения характеристик
выборочной совокупности от соответствующих
характеристик генеральной совокупности.
Однако о величине этой ошибки можно
судить с определенной вероятностью. На
величину вероятности указывает множитель
Теорема А.
М. Ляпунова. А. М. Ляпунов доказал,
что распределение выборочных средних
(следовательно, и их отклонений от
генеральной средней) при достаточно
большом числе независимых наблюдений
приближенно нормально при условии, что
генеральная совокупность обладает
конечной средней и ограниченной
дисперсией.
Математически
теорему Ляпуноваможно записать
так:

где
,
(7.4)
где – математическая постоянная;
–предельная ошибка выборки,которая дает возможность выяснить, в
каких пределах находится величина
генеральной средней.
Значения этого
интеграла для различных значений
коэффициента доверия tвычислены и
приводятся в специальных математических
таблицах. В частности, при:
Поскольку tуказывает на вероятность расхождения,
т. е. на вероятность того, на какую
величину генеральная средняя будет
отличаться от выборочной средней, то
это может быть прочитано так: с вероятностью
0,683 можно утверждать, что разность между
выборочной и генеральной средними не
превышает одной величины средней ошибки
выборки. Другими словами, в 68,3 % случаев
ошибка репрезентативности не выйдет
за пределыС вероятностью 0,954 можно утверждать,
что ошибка репрезентативности не
превышает(т. е. в 95 % случаев). С вероятностью
0,997, т. е. довольно близкой к единице,
можно ожидать, что разность между
выборочной и генеральной средней не
превзойдет трехкратной средней ошибки
выборки и т. д.
Логически связь
здесь выглядит довольно ясно: чем больше
пределы, в которых допускается
возможная ошибка, тем с большей
вероятностью судят о ее величине.
Зная выборочную
среднюю величину признака
и предельную ошибку выборки
,
можно определить границы (пределы),
в которых заключена генеральная
средняя
(7.5)
1.
Собственно-случайная выборка–
этот способ ориентирован на выборку
единиц из генеральной совокупности без
всякого расчленения на части или группы.
При этом для соблюдения основного
принципа выборки – равной возможности
всем единицам генеральной совокупности
быть отобранным – используются схема
случайного извлечения единиц путем
жеребьевки (лотереи) или таблицы случайных
чисел. Возможен повторный и бесповторный
отбор единиц
Средняя ошибка
собственно-случайной выборки
представляет собой среднеквадратическое
отклонение возможных значений выборочной
средней от генеральной средней. Средние
ошибки выборки при собственно-случайном
методе отбора представлены в табл. 7.2.
Таблица 7.2
|
Средняя ошибка |
При отборе |
|
|
повторном |
бесповторном |
|
|
Для средней |
|
|
|
Для доли |
|
|
В таблице
использованы следующие обозначения:
– дисперсия выборочной совокупности;
– численность выборки;
– численность генеральной совокупности;
– выборочная доля единиц, обладающих
изучаемым признаком;
– число единиц, обладающих изучаемым
признаком;
– численность выборки.
Для увеличения
точности вместо множителя
следует
брать множитель
,
но при большой численностиNразличие
между этими выражениями практического
значения не имеет.
Предельная
ошибка собственно-случайной выборки
рассчитывается по формуле
,
(7.6)
где t
– коэффициент доверия зависит от
значения вероятности.
Пример.При
обследовании ста образцов изделий,
отобранных из партии в случайном порядке,
20 оказалось нестандартными. С вероятностью
0,954 определите пределы, в которых
находится доля нестандартной продукции
в партии.
Решение.
Вычислим генеральную долю (Р):
.
Доля нестандартной
продукции:

Предельная
ошибка выборочной доли с вероятностью
0,954 рассчитывается по формуле (7.6) с
применением формулы табл. 7.2 для доли:
С вероятностью
0,954 можно утверждать, что доля нестандартной
продукции в партии товара находится в
пределах 12 % ≤ P≤ 28 %.
В практике
проектирования выборочного наблюдения
возникает потребность определения
численности выборки, которая необходима
для обеспечения определенной точности
расчета генеральных средних. Предельная
ошибка выборки и ее вероятность при
этом являются заданными. Из формулы
и формул средних ошибок выборки
устанавливается необходимая численность
выборки. Формулы для определения
численности выборки (n) зависят от
способа отбора. Расчет численности
выборки для собственно-случайной выборки
приведен в табл. 7.3.
Таблица 7.3
|
Предполагаемый |
Формулы |
|
|
для средней |
для доли |
|
|
Повторный |
|
|
|
Бесповторный |
|
|
2.
Механическая выборка– при этом
методе исходят из учета некоторых
особенностей расположения объектов в
генеральной совокупности, их упорядоченности
(по списку, номеру, алфавиту). Механическая
выборка осуществляется путем отбора
отдельных объектов генеральной
совокупности через определенный интервал
(каждый 10-й или 20-й). Интервал рассчитывается
по отношению,
гдеn– численность выборки,N–
численность генеральной совокупности.
Так, если из совокупности в 500 000 единиц
предполагается получить 2 %-ную выборку,
т. е. отобрать 10 000
единиц, то пропорция отбора составитОтбор
единиц осуществляется в соответствии
с установленной пропорцией через равные
интервалы. Если расположение объектов
в генеральной совокупности носит
случайный характер, то механическая
выборка по содержанию аналогична
случайному отбору. При механическом
отборе применяется только бесповторная
выборка [1, 5–10].
Средняя ошибка
и численность выборки при механическом
отборе подсчитывается по формулам
собственно-случайной выборки (см.
табл. 7.2 и 7.3).
3.
Типическая выборка, при котрой
генеральная совокупность делится по
некоторым существенным признакам на
типические группы; отбор единиц
производится из типических групп. При
этом способе отбора генеральная
совокупность расчленяется на однородные
в некотором отношении группы, которые
имеют свои характеристики, и вопрос
сводится к определению объема выборок
из каждой группы. Может бытьравномерная
выборка– при этом способе из каждой
типической группы отбирается одинаковое
число единицТакой подход оправдан лишь при равенстве
численностей исходных типических групп.
При типическом отборе, непропорциональном
объему групп, общее число отбираемых
единиц делится на число типических
групп, полученная величина дает
численность отбора из каждой типической
группы.
Более совершенной
формой отбора является пропорциональная
выборка. Пропорциональной называется
такая схема формирования выборочной
совокупности, когда численность выборок,
взятых из каждой типической группы в
генеральной совокупности, пропорциональна
численностям, дисперсиям (или комбинированно
и численностям, и дисперсиям). Условно
определяем численность выборки в 100
единиц и отбираем единицы из групп:
– пропорционально
численности их генеральной совокупности
(табл. 7.4). В таблице
обозначено:
Ni– численность типической группы;
dj
– доля (Ni/N);
N– численность
генеральной совокупности;
ni– численность выборки из типической
группы вычисляется:
, (7.7)
n – численность выборки из генеральной
совокупности.
Таблица
7.4
-
Группы
Ni
dj
ni
1
300
0,3
30
2
500
0,5
50
3
200
0,2
20
1000
1,0
100
–
пропорционально среднему квадратическому
отклонению(табл. 7.5).
здесь
i– среднее
квадратическое отклонение типических
групп;
ni
– численность выборки из типической
группы вычисляется по формуле
(7.8)
Таблица
7.5
-
Ni
i
ni
300
5
0,25
25
500
7
0,35
35
200
8
0,40
40
1000
20
1,0
100
–
комбинированно (табл. 7.6).
Численность
выборки вычисляется по формуле
. (7.9)
Таблица 7.6
-
i
iNi
300
5
1500
0,23
23
500
7
2100
0,53
53
200
8
1600
0.24
24
1000
20
6600
1,0
100
При проведении
типической выборки непосредственный
отбор из каждой группы проводится
методом случайного отбора.
Средние ошибки
выборки рассчитываются по формулам
табл. 7.7 в зависимости от способа отбора
из типических групп.
Таблица 7.7
|
Способ |
Повторный |
Бесповторный |
||
|
для |
для |
для |
для |
|
|
Непропорциональный |
|
|
|
|
|
Пропорциональный объему групп |
|
|
|
|
|
Пропорциональный |
|
|
|
|
здесь
– средняя из внутригрупповых дисперсий
типических групп;
– доля единиц, обладающих изучаемым
признаком;
– средняя из внутригрупповых дисперсий
для доли;
– среднее квадратическое отклонение
в выборке изi-й типической группы;
– объем выборки из типической группы;
– общий объем выборки;
–
объем типической группы;
– объем генеральной совокупности.
Численность
выборки из каждой типической группы
должна быть пропорциональна среднему
квадратическому отклонению в этой
группе
.Расчет численности
производится по формулам, приведенным
в табл. 7.8.
Таблица 7.8
|
Повторный |
Бесповторный |
|
|
Для определения |
|
|
|
Для определения |
|
|
4. Серийная
выборка– удобена в тех случаях,
когда единицы совокупности объединены
в небольшие группы или серии. При серийной
выборке генеральную совокупность делят
на одинаковые по объему группы – серии.
В выборочную совокупность отбираются
серии. Сущность серийной выборки
заключается в случайном или механическом
отборе серий, внутри которых производится
сплошное обследование единиц. Средняя
ошибка серийной выборки с равновеликими
сериями зависит от величины только
межгрупповой дисперсии. Средние ошибки
сведены в табл. 7.9.
Таблица 7.9
|
Способ |
Формулы |
|
|
для |
для |
|
|
Повторный |
|
|
|
Бесповторный |
|
|
Здесь
R– число серий в генеральной
совокупности;
r – число
отобранных серий;
– межсерийная (межгрупповая) дисперсия
средних;
– межсерийная (межгрупповая) дисперсия
доли.
При серийном
отборе необходимую численность отбираемых
серий определяют так же, как и при
собственно-случайном методе отбора.
Расчет численности
серийной выборки производится по
формулам, приведенным в табл. 7.10.
Таблица 7.10
|
Повторный |
Бесповторный |
|
|
Для |
|
|
|
Для |
|
|
Пример.В
механическом цехе завода в десяти
бригадах работает 100 рабочих. В целях
изучения квалификации рабочих была
произведена 20 %-ная серийная бесповторная
выборка, в которую вошли две бригады.
Получено следующее распределение
обследованных рабочих по разрядам:
|
Рабочие |
Разряды рабочих |
Разряды рабочих |
Рабочие |
Разряды |
Разряды |
|
1 2 3 4 5 |
2 4 5 2 5 |
3 6 1 5 3 |
6 7 8 9 10 |
6 5 8 4 5 |
4 2 1 3 2 |
Необходимо
определить с вероятностью 0,997 пределы,
в которых находится средний разряд
рабочих механического цеха.
Решение.
Определим выборочные средние по
бригадам и общую среднюю как среднюю
взвешенную из групповых средних:
Определим
межсерийную дисперсию по формулам
(5.25):
Рассчитаем
среднюю ошибку выборки по формуле табл.
7.9:
Вычислим
предельную ошибку выборки с вероятностью
0,997:
С вероятностью
0,997 можно утверждать, что средний разряд
рабочих механического цеха находится
в пределах
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
3. Ошибки выборки
Каждая единица при выборочном наблюдении должна иметь равную с другими возможность быть отобранной – это является основой собственнослучайной выборки.
Собственнослучайная выборка – это отбор единиц из всей генеральной совокупности посредством жеребьевки или другим подобным способом.
Принципом случайности является то, что на включение или исключение объекта из выборки не может повлиять любой фактор, кроме случая.
Доля выборки – это отношение числа единиц выборочной совокупности к числу единиц генеральной совокупности:
Собственнослучайный отбор в чистом виде является исходным среди всех других видов отбора, в нем заключаются и реализуются основные принципы выборочного статистического наблюдения.
Два основных вида обобщающих показателей, которые используют в выборочном методе – это средняя величина количественного признака и относительная величина альтернативного признака.
Выборочная доля (w), или частность, определяется отношением числа единиц, обладающих изучаемым признаком m, к общему числу единиц выборочной совокупности (n):
Для характеристики надежности выборочных показателей различают среднюю и предельную ошибки выборки.
Ошибка выборки, ее еще называют ошибкой репрезентативности, представляет собой разность соответствующих выборочных и генеральных характеристик:
1) для средней количественного признака:
?х =|х – х|;
2) для доли (альтернативного признака):
?w =|х – p|.
Только выборочным наблюдениям присуща ошибка выборки
Выборочная средняя и выборочная доля – это случайные величины, принимающие различные значения в зависимости от единиц изучаемой статистической совокупности, которые попали в выборку. Соответственно ошибки выборки – тоже случайные величины и также могут принимать различные значения. Поэтому определяют среднюю из возможных ошибок – среднюю ошибку выборки.
Средняя ошибка выборки определяется объемом выборки: чем больше численность при прочих равных условиях, тем меньше величина средней ошибки выборки. Охватывая выборочным обследованием все большее количество единиц генеральной совокупности, все более точно характеризуем всю генеральную совокупность.
Средняя ошибка выборки зависит от степени варьирования изучаемого признака, в свою очередь степень варьирования характеризуется дисперсией ?2 или w(l – w) – для альтернативного признака. Чем меньше вариация признака и дисперсия, тем меньше средняя ошибка выборки, и наоборот.
При случайном повторном отборе средние ошибки теоретически рассчитывают по следующим формулам:
1) для средней количественного признака:
где ?2 – средняя величина дисперсии количественного признака.
2) для доли (альтернативного признака):
Так как дисперсия признака в генеральной совокупности ?2 точно неизвестна, на практике пользуются значением дисперсии S2 , рассчитанным для выборочной совокупности на основании закона больших чисел, согласно которому выборочная совокупность при достаточно большом объеме выборки достаточно точно воспроизводит характеристики генеральной совокупности.
Формулы средней ошибки выборки при случайном повторном отборе следующие. Для средней величины количественного признака: генеральная дисперсия выражается через выборную следующим соотношением:
где S2 – значение дисперсии.
Механическая выборка – это отбор единиц в выборочную совокупность из генеральной, которая разбита по нейтральному признаку на равные группы; производится так, что из каждой такой группы в выборку отбирается лишь одна единица.
При механическом отборе единицы изучаемой статистической совокупности предварительно располагают в определенном порядке, после чего отбирают заданное число единиц механически через определенный интервал. При этом размер интервала в генеральной совокупности равен обратному значению доли выборки.
При достаточно большой совокупности механический отбор по точности результатов близок к собственнослучайному Поэтому для определения средней ошибки механической выборки используют формулы собственнослучайной бесповторной выборки.
Для отбора единиц из неоднородной совокупности применяется так называемая типическая выборка, используется, когда все единицы генеральной совокупности можно разбить на несколько качественно однородных, однотипных групп по признакам, от которых зависят изучаемые показатели.
Затем из каждой типической группы собственнослучайной или механической выборкой производится индивидуальный отбор единиц в выборочную совокупность.
Типическая выборка обычно применяется при изучении сложных статистических совокупностей.
Типическая выборка дает более точные результаты. Типизация генеральной совокупности обеспечивает репрезентативность такой выборки, представительство в ней каждой типологической группы, что позволяет исключить влияние межгрупповой дисперсии на среднюю ошибку выборки. Поэтому при определении средней ошибки типической выборки в качестве показателя вариации выступает средняя из внутригрупповых дисперсий.
Серийная выборка предполагает случайный отбор из генеральной совокупности равновеликих групп для того, чтобы в таких группах подвергать наблюдению все без исключения единицы.
Поскольку внутри групп (серий) обследуются все без исключения единицы, средняя ошибка выборки (при отборе равновеликих серий) зависит только от межгрупповой (межсерийной) дисперсии.
Данный текст является ознакомительным фрагментом.
Читайте также
Ошибки резидента
Ошибки резидента
Относиться к ошибкам можно по-разному: можно бояться их совершить и переживать из-за каждой из них, можно радоваться своим ошибкам и кризисам, как указателям на пути к успеху и личным победам. Неизменно в ошибках только одно – за них приходится платить.
Формирование выборки
Формирование выборки
Процедура выборки является неотъемлемым этапом проекта внутреннего аудита. Она подробно описана в различных источниках, посвященных теме аудита. Однако во многом такие описания носят академичный характер. Предлагаю заострить внимание на тех
Ошибки в инвестициях – это ошибки инвесторов
Ошибки в инвестициях – это ошибки инвесторов
Сейчас я больше, чем когда бы то ни было, убежден в том, что все ошибки в инвестициях на самом деле ошибки инвесторов.Инвестиции не совершают ошибок. В отличие от инвесторов.Инвестирование – это выбор. Именно об этой
29. Определение необходимой численности выборки
29. Определение необходимой численности выборки
Одним из научных принципов в теории выбороч–ного метода является обеспечение достаточного чи–сла отобранных единиц.Уменьшение стандартной ошибки выборки всег–да связано с увеличением объема выборки. Расчет
30. Способы отбора и виды выборки. Собственно случайная выборка
30. Способы отбора и виды выборки. Собственно случайная выборка
В теории выборочного метода разработаны раз–личные способы отбора и виды выборки, обеспечи–вающие репрезентативность. Под способом отбора понимают порядок отбора единиц из генеральной со–вокупности.
31. Механическая и типическая выборки
31. Механическая и типическая выборки
При чисто механической выборке вся ге–неральная совокупность единиц должна быть прежде всего представлена в виде списка единиц отбора, со–ставленного в каком-то нейтральном по отношению к изучаемому признаку порядке. Затем список
32. Серийная и комбинированная выборки
32. Серийная и комбинированная выборки
Серийная (гнездовая) выборка – это такой вид формирования выборочной совокупности, когда в случайном порядке отбираются не единицы, подле–жащие обследованию, а группы единиц (серии, гнез–да). Внутри отобранных серий (гнезд)
33. Многоступенчатая, многофазная и взаимопроникающая выборки.
33. Многоступенчатая, многофазная и взаимопроникающая выборки.
Особенность многоступенчатой выборки со–стоит в том, что выборочная совокупность формиру–ется постепенно, по ступеням отбора. На первой ступени с помощью заранее определенного спосо–ба и вида отбора
3. Определение необходимой численности выборки
3. Определение необходимой численности выборки
Одним из научных принципов в теории выборочного метода является обеспечение достаточного числа отобранных единиц. Теоретически необходимость соблюдения этого принципа представлена в доказательствах предельных теорем
4. Способы отбора и виды выборки
4. Способы отбора и виды выборки
В теории выборочного метода разработаны различные способы отбора и виды выборки, обеспечивающие репрезентативность. Под способом отбора понимают порядок отбора единиц из генеральной совокупности. Различают два способа отбора: повторный
36. Ошибки выборки
36. Ошибки выборки
Собственнослучайная выборка – это отбор единиц из всей генеральной совокупности посредством жеребьевки или другим подобным способом. Принципом случайности является то, что на включение или исключение объекта из выборки не может повлиять любой фактор,
Лексические ошибки
Лексические ошибки
1. Неправильное использование слов и терминовОсновная масса ошибок в деловых письмах относится к лексическим. Недостаточная грамотность приводит не только к курьезной бессмыслице, но и абсурду.Отдельные термины и профессиональные жаргонные слова
5 Наши ошибки
5
Наши ошибки
Мы настаиваем: выбранный курс рыночных реформ был верным. И они вовсе не потерпели неудачу, они только еще раз споткнулись. Но ошибки и упущения были. Это и наши ошибки, и ошибки руководства страны, которые мы не сумели предотвратить. Ошибки — во многом
Важность размера выборки
Важность размера выборки
Как я уже говорил, люди склонны уделять слишком много внимания редким случаям возникновения какого-то феномена, несмотря на то что со статистической точки зрения из нескольких случаев невозможно извлечь много информации. Это – основная причина
Репрезентативные выборки
Репрезентативные выборки
Репрезентативность наших тестов для целей предсказания будущего определяется двумя факторами:– Количество рынков: тесты, проводимые на различных рынках, будут, скорее всего, включать рынки с разной степенью волатильности типов
Размер выборки
Размер выборки
Концепция размера выборки проста: для того чтобы делать статистически достоверные заключения, нужно иметь достаточно большую выборку. Чем меньше выборка, тем грубее выводы, которые можно сделать; чем выборка больше, тем выводы качественнее. Нет никакого
Общее понятие о выборочном методе. Множество всех единиц совокупности, обладающих определенным признаком и подлежащих изучению, носит в статистике название генеральной совокупности.
На практике по тем или иным причинам не всегда возможно или же нецелесообразно рассматривать всю генеральную совокупность. Тогда ограничиваются изучением лишь некоторой части ее, конечной целью которого является распространение полученных результатов на всю генеральную совокупность, т. е. применяют выборочный метод.
Для этого из генеральной совокупности особым образом отбирается часть элементов, так называемая выборка, и результаты обработки выборочных данных (например, средние арифметические значения) обобщаются на всю совокупность.
Теоретической основой выборочного метода является закон больших чисел. В силу этого закона при ограниченном рассеивании признака в генеральной совокупности и достаточно большой выборке с вероятностью, близкой к полной достоверности, выборочная средняя может быть сколь угодно близка к генеральной средней. Закон этот, включающий в себя группу теорем, доказан строго математически. Таким образом, средняя арифметическая, рассчитанная по выборке, может с достаточным основанием рассматриваться как показатель, характеризующий генеральную совокупность в целом.
Разумеется, не всякая выборка может быть основой для характеристики всей совокупности, к которой она принадлежит. Таким свойством обладают лишь репрезентативные (представительные) выборки, т. е. выборки, которые правильно отражают свойства генеральной совокупности. Существуют способы, позволяющие гарантировать достаточную репрезентативность выборки. Как доказано в ряде теорем математической статистики, таким способом при условии достаточно большой выборки является метод случайного отбора элементов генеральной совокупности, такого отбора, когда каждый элемент генеральной совокупности имеет равный с другими элементами шанс попасть в выборку. Выборки, полученные таким способом, называются случайными выборками. Случайность выборки является, таким образом, существенным условием применения выборочного метода
Области применения выборочного метода в исторических исследованиях. Сфера приложения этого метода в изучении истории обширна. Во-первых, историки могут применять выборочный метод при проведении всякого рода обследований с целью изучения различных явлений и процессов современности. Правда, сейчас такими исследованиями больше занимаются социологи, чем историки, хотя именно историки могут проводить конкретно-социологические обследования, опираясь на исторические данные, и добиваться наибольшего эффекта таких исследований.
Во-вторых, историки нередко имеют дело с сохранившимися данными ранее проведенных собственно выборочных обследований. Такие обследования стали все более широко применяться с конца XIX в. Так, при проведении ряда сплошных обследований и переписей выборочно собирались и собираются сведения по более широкой программе. Многие данные собирались только выборочно. Наиболее интересными среди них для историков являются описания разного рода хозяйственных комплексов (крестьянских хозяйств, промышленных предприятий, колхозов, совхозов и т. д.), а также бюджетные и другого рода обследования различных слоев населения.
В-третьих, в распоряжении историков имеется значительное число разнообразных первичных сплошных массовых данных, полная обработка которых весьма затруднительна даже при применении современной вычислительной техники. При изучении их может быть применен выборочный метод. Такие материалы имеются по всем периодам истории, но особенно много их по истории XIX—XX вв.
Наконец, историкам очень часто приходится иметь дело с частичными данными, так называемыми естественными выборками. При обработке этих данных также может быть применен выборочный метод. Характер естественных выборок бывает различным. Прежде всего они могут представлять собой сохранившийся остаток некогда существовавшей более или менее полной совокупности данных. Так, многие актовые материалы, документы текущего делопроизводства и отчетности представляют остатки в прошлом обширных и систематических массивов данных. Далее, при систематическом сборе тех или иных сведений отдельные показатели могли учитываться лишь частично (именно частично, а не выборочно). Так, при составлении «Экономических примечаний» к Генеральному межеванию второй половины XVIII в., которое охватило большую часть территории страны, ряд показателей (количество населения, площадь земельных угодий и др.) учитывался повсеместно, а некоторые важные данные (о величине барских запашек, размерах оброка) были собраны в силу целого ряда причин лишь частично. Многие сведения вообще собирались только частично. Это прежде всего относится к тем из них, которые не являлись нормативными и сбором которых занимались различные местные органы, научные и общественные организации и отдельные лица.
Итак, области выборочного метода в исторических исследованиях весьма обширны, а задачи, которые следует при этом решать, различны.
Так, при организации выборочного обследования и формировании выборки из имеющихся сплошных данных исследователь располагает определенной свободой маневра для обеспечения репрезентативности выборок. При этом он может опираться на хорошо разработанную в математической статистике теорию, методику и технику получения таких выборок.
При оперировании же данными ранее проведенных выборочных обследований следует проверить, в какой мере они были выполнены в соответствии с требованиями, предъявляемыми к выборочному методу. Для этого надо знать, как было проведено это обследование. Чаще всего это вполне можно сделать.
И совсем иное дело — естественные выборки данных, с которыми очень часто имеет дело историк. Прежде всего необходимо доказать их репрезентативность. Без этого экстраполяция показателей выборок на всю изучаемую совокупность будет необоснованной. Поскольку пока еще нет достаточно надежных методов математической проверки репрезентативности естественных выборок, то решающую роль здесь играет выяснение истории их возникновения и содержательный анализ имеющихся данных.
Виды выборочного изучения. В зависимости от того, как осуществляется отбор элементов совокупности в выборку, различают несколько видов выборочного обследования. Отбор может быть случайным, механическим, типическим и серийным.
Случайным является такой отбор, при котором все элементы генеральной совокупности имеют равную возможность быть отобранными. Другими словами, для каждого элемента генеральной совокупности обеспечена равная вероятность попасть в выборку.
Требование случайности отбора достигается на практике с помощью жребия или таблицы случайных чисел.
При отборе способом жеребьевки все элементы генеральной совокупности предварительно нумеруются и номера их наносятся на карточки. После тщательной перетасовки из пачки любым способом (подряд или в любом другом порядке) выбирается нужное число карточек, соответствующее объему выборки. При этом можно либо откладывать отобранные карточки в сторону (тем самым осуществляется так называемый бесповторный отбор), либо, вытащив карточку, записать ее номер и возвратить в пачку, тем самым давая ей возможность появиться в выборке еще раз (повторный отбор). При повторном отборе всякий раз после возвращения карточки пачка должна быть тщательно перетасована.
Способ жеребьевки применяется в тех случаях, когда число элементов всей изучаемой совокупности невелико. При большом объеме генеральной совокупности осуществление случайного отбора методом жеребьевки становится сложным. Более надежным и менее трудоемким в случае большого объема обрабатываемых данных является метод использования таблицы случайных чисел.
Таблиц случайных чисел существует несколько, одна из них приведена в приложении (табл. 9). Способ отбора с помощью таблицы случайных чисел рассмотрим на примере.
Пример 1. Пусть совокупность состоит из 900 элементов, а намеченный объем выборки равен 20 единицам.
Из таблицы случайных чисел (см. табл. 9 приложения) отбираем числа, не превосходящие 900, до тех пор, пока не наберем нужных 20 чисел. Получаем:
146 867 505 139 653 480 426 765 478 807 47 220 522 221 835 368 275 424 703
Выписанные числа будем считать порядковыми номерами тех элементов генеральной совокупности, которые попали в выборку.
Для очень больших совокупностей отбор с помощью таблицы случайных чисел становится трудно осуществимым, так как сложно перенумеровать всю совокупность. Здесь лучше применить механический отбор.
Механический отбор производится следующим образом. Если формируется 10%-ная выборка, т. е. из каждых десяти элементов должен быть отобран один, то вся совокупность условно разбивается на равные части по 10 элементов. Затем из первой десятки выбирается случайным образом элемент. Например, жеребьевка указала девятый номер. Отбор остальных элементов выборки полностью определяется указанной пропорцией отбора N номером первого отобранного элемента. В рассматриваемом случае выборка будет состоять из элементов 9, 19, 29 и т. д.
Механическим отбором следует пользоваться осторожно, так как существует реальная опасность возникновения так называемых систематических ошибок (см. § 2). Поэтому прежде чем делать механическую выборку, необходимо проанализировать изучаемую совокупность. Если ее элементы расположены случайным образом, то выборка, полученная механическим способом, будет случайной. Однако нередко элементы исходной совокупности бывают частично или даже полностью упорядочены. Весьма нежелательным для механического отбора является порядок элементов, имеющий правильную повторяемость, период которой может совпасть с периодом механической выборки.
Нередко элементы совокупности бывают упорядочены по величине изучаемого признака в убывающем или возрастающем порядке и не имеют периодичности. Механический отбор из такой совокупности приобретает характер направленного отбора, так как отдельные части совокупности оказываются представленными в выборке пропорционально их численности во всей совокупности, т. е. отбор направлен на то, чтобы сделать выборку представительной.
Механический отбор, как никакой другой, широко использовался в русской и советской статистике.
Большую ценность представляют обследования земских статистиков, которые наряду со сплошным подворным обследованием крестьянских хозяйств по сокращенной «похозяйственней карточке» изучали по расширенной программе определенную часть хозяйств, отобранных механическим способом.
Механический отбор использовался советскими статистиками для учета посевных площадей, численности скота, размеров урожая и многого другого накануне сплошной коллективизации, когда в сельском хозяйстве насчитывалось 25 млн. мелких крестьянских хозяйств (так называемый 10%-ный весенний опрос крестьянских хозяйств и 5%-ный осенний опрос).
Другим видом направленного отбора является типический отбор. Следует отличать типический отбор от отбора типичных объектов. Отбор типичных объектов применялся в земской статистике, а также при бюджетных обследованиях. При этом отбор «типичных селений» или «типичных хозяйств» производился по некоторым экономическим признакам, например по размерам землевладения на двор, по роду занятий жителей и т. п. Отбор такого рода не может быть основой для применения выборочного метода, так как здесь не выполнено основное его требование — случайность отбора.
При собственно типическом отборе в выборочном методе совокупность разбивается на группы, однородные в качественном отношении, а затем уже внутри каждой группы производится случайный отбор. Типический отбор организовать сложнее, чем собственно случайный, так как необходимы определенные знания о составе и свойствах генеральной совокупности, но зато он дает более точные результаты.
При серийном отборе вся совокупность разбивается на группы (серии). Затем путем случайного или механического отбора выделяют определенную часть этих серий и производят их сплошную обработку. По сути дела, серийный отбор представляет собой случайный или механический отбор, осуществленный для укрупненных элементов исходной совокупности.
В теоретическом плане серийная выборка является самой несовершенной из рассмотренных. Для обработки материала она, как правило, не используется, но представляет определенные удобства при организации обследования, особенно в изучении сельского хозяйства. Например, ежегодные выборочные обследования крестьянских хозяйств в годы, предшествовавшие коллективизации, проводились способом серийного отбора. Историку полезно знать о серийной выборке, поскольку он может встретиться с результатами таких обследований.
Кроме описанных выше классических способов отбора в практике выборочного метода используются и другие способы. Рассмотрим два из них.
Изучаемая совокупность может иметь многоступенчатую структуру, она может состоять из единиц первой ступени, которые, в свою очередь, состоят из единиц второй ступени, и т. д. Например, губернии включают в себя уезды, уезды можно рассматривать как совокупность волостей, волости состоят из сел, а села — из дворов.
К таким совокупностям можно применять многоступенчатый отбор, т. е. последовательно осуществлять отбор на каждой ступени. Так, из совокупности губерний механическим, типическим или случайным способом можно отобрать уезды (первая ступень), затем одним из указанных способов выбрать волости (вторая ступень), далее провести отбор сел (третья ступень) и, наконец, дворов (четвертая ступень).
Примером двухступенчатого механического отбора может служить давно практикуемый отбор бюджетов рабочих. На первой ступени механически выбираются предприятия, на второй — рабочие, бюджет которых обследуется.
Изменчивость признаков исследуемых объектов может быть различной. Например, обеспеченность крестьянских хозяйств собственной рабочей силой колеблется меньше, чем, скажем, размеры их посевов. В связи с этим меньшая по объему выборка по обеспеченности рабочей силой будет столь же представительной, как и большая по числу элементов выборка данных о размерах посевов. В этом случае из выборки, по которой определяются размеры посевов, можно сделать под выборку, достаточно репрезентативную для определения обеспеченности рабочей силой, осуществив тем самым двухфазный отбор. В общем случае можно добавить и следующие фазы, т. е. из полученной подвыборки сделать еще подвыборку и т. д. Этот же способ отбора применяется в тех случаях, когда цели исследования требуют различной точности при исчислении разных показателей.
Потребность в многофазном отборе возникла при выборочной обработке материалов профессиональной переписи 1918 года. Как показали исследования, для выявления доли рабочих Ярославской губернии, уходящих на полевые работы, требовалась выборка одного объема, тогда как для изучения общей связи рабочих с землей можно было ограничиться выборкой меньшего объема. Разные объемы выборок потребовались и при изучении групп рабочих различных отраслей промышленности Ярославской губернии. Так, предварительные расчеты показали, что для достаточно надежных выводов по группе рабочих полиграфической промышленности требовалась, по крайней мере, 5%-ная выборка, а для исследования рабочих текстильной, пищевой, металлообрабатывающей и машиностроительной промышленности достаточной оказалась 1%-ная выборка (См.: Соколов А. К. Методика выборочной обработки первичных материалов профессиональной переписи 1918 г.— История СССР, 1971, № 4.).
Изложенные выше способы формирования выборок не исчерпывают собой всех типов отбора, применяемых на практике (Наиболее полное описание видов отбора дано в кн.: Пейте Ф. Выборочный метод в переписях и обследованиях. М., 1965.).
Стандартные ошибки выборок
Как уже отмечалось, выборочный метод позволяет результаты выборочной обработки материалов переносить на всю генеральную совокупность. При этом, естественно, имеет место некоторая ошибка, и эффективность выборочного метода заключается в том, что он позволяет оценить эту ошибку.
Ошибки, возникающие при использовании выборочных данных для суждения о всей совокупности, показывают, насколько хорошо характеристики выборки представляют соответствующие характеристики генеральной совокупности, и называются поэтому ошибками представительности (репрезентативности). Различают ошибки представительности двоякого рода: систематические и случайные.
Систематические ошибки возникают в том случае, если не выполнены условия случайности отбора.
Систематическая ошибка может возникнуть и в случае, когда формально отбор произведен случайным образом, но исходная совокупность не является полной и представительной для решения поставленной задачи.
В теории выборочного метода не рассматриваются систематические ошибки, но исследователь должен помнить о возможности их появления и принять меры, обеспечивающие их исключение. С помощью выборочного метода определяются величины ошибок второго рода, т. е. величины случайных ошибок.
Случайные ошибки выборок возникают за счет того, что для анализа всей совокупности используется только часть ее.
Хотя выборочный метод и позволяет обоснованно судить о средней арифметической некоторого количественного признака генеральной совокупности по средней арифметической, исчисленной по выборке, это, однако, не означает, что выборочная средняя совпадает с генеральной средней. Она, как правило, в той или иной степени от нее отличается.
Величина ошибки выборки представляет собой разность между генеральной и выборочной средними. Ошибки выборки различны для каждой конкретной выборки и в принципе могут быть обобщенно охарактеризованы с помощью средней из всех таких отдельных ошибок.
В математической статистике получены формулы, которые позволяют приближенно вычислить среднюю ошибку выборки, основываясь на данных только той выборки, которая имеется в распоряжении исследователя. Вычисление средней ошибки выборки зависит от способа отбора элементов из совокупности в выборку.
Средняя ошибка выборки при собственно случайном повторном методе отбора определяется формулой
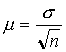
где о — оценка среднего квдаратического отклонения в генеральной совокупности по выборке; n — число элементов в выборке (ее объем) (На практике величину а заменяют на среднее квадратическое отклонение выборки по формуле (4.7), но пользоваться этой формулой можно лишь при достаточно большом объеме выборки(n>30). Методы расчета средней ошибки для малых выборок изложены в § 4 этой главы.).
Как видим, средняя ошибка выборки (ее называют иногда стандартной ошибкой выборки) существенно зависит от среднего квадратического отклонения отдельных значений признака от выборочной средней: чем больше среднее квадратическое отклонение, т. е. чем больше разброс значений признака, тем, при прочих равных условиях, больше средняя ошибка выборки. Объем выборки воздействует на среднюю ошибку выборки в обратном направлении: чем больше численность выборки, тем меньше средняя ошибка выборки, что вполне объяснимо, так как большая выборка лучше представляет всю совокупность.
Средняя ошибка выборки при случайном бесповторном отборе находится по формуле

где N — объем генеральной совокупности.
Формула (5.2) отличается от формулы (5.1) только множителем— 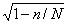
Рассмотрим расчет средней (стандартной) ошибки выборки на конкретных примерах.
Пример 2. Из 2689 уставных грамот Тамбовской губернии необходимо сделать случайную 10%-ную выборку бесповторным способом и определить средние размеры дореформенного и пореформенного наделов на душу и соответствующие им средние ошибки выборки (Занесенные на специальные бланки материалы уставных грамот были любезно предоставлены авторам Б. Г. Литваком. Комплекс этих материалов, включающих данные о размерах дореформенного и пореформенного наделов, о форме эксплуатации, о величине высшего душевого надела и некоторые другие, возник в связи с отменой крепостного права и определял поземельные отношения крестьян и помещиков.).
Формирование выборки осуществим с помощью таблицы случайных чисел (табл. 9 приложения). Воспользуемся следующим способом, позволяющим рациональнее использовать таблицу случайных чисел. Из чисел от 3001 до 6000 будем вычитать 3000, а из чисел от 6001 до 9000 будем вычитать 6000. Из полученных чисел будем, как указывалось, отбирать те, которые не превосходят 2689. Так, первое число таблицы 5489 дает нам 2489, второе — 3522 дает 522 и т. д. В итоге получаем номера единиц совокупности, попавших в выборку.
Для дальнейшей работы полезно полученные числа расположить в возрастающем порядке. Во-первых, это облегчит отбор уставных грамот с соответствующими порядковыми номерами, во-вторых, выявит повторения, от которых нам нужно избавиться, так как выборка делается бесповторным способом. Исключение повторяющихся чисел приводит к тому, что количество отобранных чисел уменьшается. Обращаясь снова к таблице случайных чисел, доводим объем выборки до нужного размера.
Отобрав соответствующие уставные грамоты (их оказалось 264), переходим к расчету средних арифметических и соответствующих им средних ошибок выборки (В этом примере и во всех остальных примерах этой главы, базирующихся на материалах уставных грамот, мы из-за недостатка места не будем давать исходные данные, служащие для расчета выборочных характеристик, и ограничимся приведением результатов проделанных на их основе вычислений.).
Средний дореформенный надел на душу оказался равным 3,16 дес. (суммируем все наделы на душу и делим на число слагаемых — количество грамот):
Средний пореформенный надел на душу равен 2,71 дес. ( 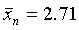
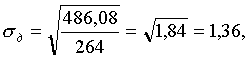
Пользуясь полученными результатами и учитывая, что N =2689, имеем
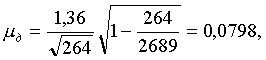
Поставленная задача полностью решена.
Пример 3. Из тех же 2689 уставных грамот Тамбовской губернии необходимо сделать случайную 10%-ную выборку повторным способом, определить средний размер дореформенного надела на душу по выборке и среднюю ошибку выборки
Техника подготовительной работы та же, что и в предыдущем примере, только повторно попавшие в выборку грамоты не исключаются. Результаты расчетов среднего размера дореформенного надела и среднего квадратического отклонения выборки по сформированной указанным способом выборке следующие:
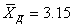
Для расчета средней ошибки выборки воспользуемся формулой (5.1):
Итак, средняя ошибка выборки при повторном способе отбора оказалась большей (0,0846), чем при бесповторном (0,0798). Но разница между ними небольшая, так как отношение n к N невелико.
Средняя ошибка выборки при механическом способе отбора вычисляется по формуле случайной бесповторной выборки (5.2) или в случае, когда множителем 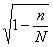
Пример 4. Генеральная совокупность та же, что и в предыдущих примерах Необходимо сделать 10%-ную механическую выборку, вычислить средний надел земли на душу до реформы и определить среднюю ошибку выборки.
Случайным образом отбираем в выборку одну уставную грамоту из первых десяти. По жребию выпало число 10. Следовательно, в выборку попадут грамоты с порядковыми номерами 10, 20, 30 и т. д.
Для этой выборки, включающей 263 элемента, средний размер дореформенного надела на душу (xд) равен 2,97 дес., а среднее квадратическое отклонение выборочных данных ?=1,48. Воспользовавшись формулой (5.2), определяем среднюю ошибку выборки:
Как правило, средняя ошибка выборки при механическом отборе оказывается меньше средней ошибки выборки при собственно случайном отборе.
Средняя ошибка выборки при типическом отборе определяется следующими формулами:
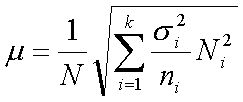
для повторной выборки и
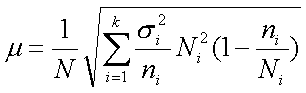
для бесповторной выборки, где N — объем генеральной совокупности; Ni—объем i-й типической группы; ni—объем выборки из i-й типической группы; ?i— среднее квадратическое отклонение i-й типической группы; k — число типических групп.
Средняя арифметическая типической выборки рассчитывается по формуле
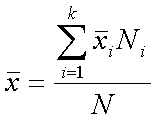
где 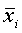
Для того чтобы сделать типическую выборку, нужно прежде всего решить вопрос о том, каковы должны быть объемы выборки по каждой из выделенных типических групп. В зависимости от исследовательских задач и характера изучаемой совокупности, можно воспользоваться одним из следующих приемов.
Самый простой способ определения объема выборки из каждой типической группы, состоит в том, что объем всей намеченной выборки п делят на число типических групп k, т. е.
ni=n/k (5,6)
Второй, наиболее широко применяемый способ заключается в том, что объемы выборок из групп устанавливаются пропорционально объемам соответствующих типических групп, т. е.
В итоге для расчетов получается такая формула:
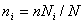
где ni — объем выборки из i-й типической группы; n — общий объем выборки из генеральной совокупности; Ni — объем i-й типической группы; N — объем генеральной совокупности.
Третий способ состоит в том, что число элементов в выборке для каждой типической группы определяется пропорционально средним квадратическим отклонениям соответствующих типических групп (?i), т. е. при определении ni руководствуются следующим соотношением:

Такой прием часто дает ощутимый выигрыш в точности. Сложность его использования состоит в том, что необходимо предварительно знать средние квадратические отклонения признака в типических группах, из которых будет извлекаться выборка. Для этого используются результаты расчетов по аналогичным данным либо делают пробные выборки из каждой группы и их средние квадратические отклонения кладут в основу расчета. Формула для расчета ni будет такой:
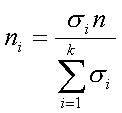
где ?i, — среднее квадратическое отклонение i-й группы; 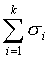
Наконец, четвертый способ образования типической выборки учитывает и размеры типических групп (Ni) и колеблемость признака в этих группах (?i); при формировании выборки исходят из того, что
Формула для расчета ni, четвертым способом такова:
где Ni — объем i-й типической группы; ?i — среднее квадратическое отклонение i-й группы; n—общий объем выборки из генеральной совокупности; k— число типических групп.
Из указанных четырех способов определения численности выборок из типических групп самым простым, но и самым несовершенным является первый. Несложен для расчетов второй способ. Его целесообразно применять в тех случаях, когда типические группы резко отличаются по объему. Если типические группы имеют примерно одинаковый объем, то лучше формировать выборки с учетом рассеивания признака, т. е. третьим способом. Если, наконец, объемы типических групп различны и заметно отличны их средние квадратические отклонения, то наилучшие результаты достигаются при применении четвертого способа.
Рассмотрим теперь на примерах методику вычисления средних арифметических типических выборок и возникающих при этом стандартных ошибок.
Случайный отбор элементов из типических групп может проводиться двумя способами. Если типические группы в исходных данных разделены и каждая имеет собственную нумерацию, то случайный отбор элементов до нужного объема производится из каждой группы отдельно. Если же элементы типических групп расположены в генеральной совокупности вперемешку, как в нашем случае, то отбор осуществляется из всей совокупности, при этом следят, чтобы объемы отдельных групп не были превышены. Случайные числа, соответствующие элементам тех групп, объемы выборок по которым достигнуты, отбрасываются.
Пример 5. Из совокупности уставных грамот Тамбовской губернии сделать 10%-ную типическую выборку с учетом численности групп. Вычислить средний пореформенный надел на душу и среднюю ошибку выборки.
При знакомстве с уставными грамотами обращает на себя внимание тот факт, что надел земли на душу после реформы тяготеет к высшему душевному наделу. Естественно предположить, что типические группы, образованные с учетом размера высшего душевого надела, будут более однородными, чем вся совокупность в целом.
Разобьем всю совокупность на три группы. К первой группе отнесем селения с размером высшего душевого надела, равным 3,00 дес., ко второй — 3,25 дес., к третьей — 3,50 дес. Объемы групп будут равны соответственно 1717, 445 и 525 (Две грамоты мы не учитываем, так как в одной из них указан высший размер душевого надела, равный 2,0 дес., в другой—2,75 дес., в результате чего общий объем совокупности составил N1+N2+N3=2687 грамот.).
Получены следующие результаты расчетов средних характеристик по каждой из трех групп выборки:
для первой группы (высший душевой надел—3,00 дес.)
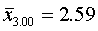
для второй типической группы (высший душевой надел — 3,25 дес.)
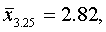
для третьей типической группы (высший душевой надел — 3,50 дес.)
Пользуясь соответствующими формулами табл. 2, имеем окончательно:
Средняя ошибка выборки, полученная таким способом, оказалась несколько меньше средней ошибки выборки, полученной при случайном отборе. В данном случае различие типических групп невелико. При больших различиях групп выигрыш в точности, даваемый типическим отбором, бывает более существенным.
Пример 6. Определить объемы выборок каждой типической группы так, чтобы они оказались пропорциональными средним квадратическим отклонениям соответствующих групп. Совокупность и общий объем выборки те же, что и в предыдущем примере.
Воспользуемся промежуточными результатами примера 5:
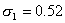
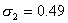
Тогда по формуле (5.8) объемы выборок типических групп будут такими:
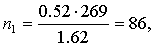
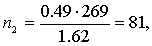
т. е. из первой типической группы (высший размер душевого надела равен 3,00 дес.) следует отобрать 86 грамот, из второй типической группы (высший размер душевого надела — 3,25 дес.) — 81 грамоту, из третьей типической группы (высший размер душевого надела — 3,50 дес.) — 102 грамоты.
Пример 7. Генеральная совокупность и критерий, по которому происходит деление на типические группы, те же, что и в предыдущих двух примерах. Сделать типическую 10%-ную выборку, отбирая количество элементов в типических группах пропорционально численности этих групп и средним квадратическим отклонениям.
Рассчитать средний пореформенный надел на душу и среднюю ошибку выборки.
По формуле (5.9) численность выборок из типических групп будет следующей:
Аналогично рассчитываются n2 и n3: n2=41, n3=60.
Следовательно, из первой типической группы нужно взять 168 грамот, из второй — 41 грамоту, из третьей — 60. Отобрав требуемое количество грамот (техника отбора была изложена выше), переходим к вычислению интересующих нас характеристик.
Результаты расчета средних по группам следующие:
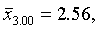
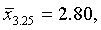
Соответствующие им средние квадратические отклонения равны:
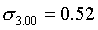
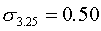
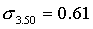
Средний по всей выборке пореформенный надел на душу равен (по формуле (5.5)):
Для расчета средней ошибки выборки воспользуемся соответствующей формулой из сводной табл. 2:
Средняя ошибка выборки получилась меньше, чем при случайном методе отбора, но несколько больше соответствующей характеристики, полученной для типической выборки, образованной пропорционально численности типических групп. Последнее произошло, надо полагать, потому, что типические группы по размеру высшего душевого надела отличаются, в основном, по численности и значительно меньше—по разбросу признака.
Сведем воедино итоги рассмотренных примеров, чтобы еще раз сравнить полученные результаты (см. табл. 1).
В целом приведенные примеры подтверждают установленные в статистике общие положения. Важнейшим для применения выборочного метода в исторических исследованиях является то, что наиболее точные результаты дает типический отбор. Стандартная ошибка средней при этом методе отбора получается меньшей, чем при случайном и механическом отборе (сравним процентные отношения ошибок к средним арифметическим). При этом следует иметь в виду, что размеры наделов крестьян являются признаком, рассеивание которого является небольшим. При большей неоднородности изучаемых совокупностей данных преимущества типического отбора будут еще очевиднее. Что касается собственно случайного и механического отбора, то они в общем дают близкие результаты. Надо лишь всегда проверять, насколько механический отбор является близким к случайному. Принципиальных различий между бесповторным и повторным случайным отбором нет.
Для удобства пользования формулы выборочного метода, применяемые для вычисления выборочных средних арифметических и их стандартных ошибок при разных видах отбора, сведены в табл. 2. В эту таблицу не вошли формулы для расчета средних ошибок выборок при многоступенчатом способе отбора (Эти сведения можно найти в кн.: Йейтс Ф. Выборочный метод в переписях и обследованиях.). Что касается многофазного отбора, то он равносилен взятию выборок различных объемов для разных признаков и ничего нового в вычислительные процедуры не вносит.
Таблица 2. Формулы выборочного метода для средней арифметической при различных видах отбора.
|
Выборочная средняя |
Объем выборки из типических групп |
Средняя ошибка выборки ? |
||
|
при повторном отборе |
при повторном отборе |
|||
|
Собственно случайный отбор и механический отбор (При механическом отборе применяется формула бесповторной выборки, за исключением тех случаев, когда множителем |
|
|
|
|
|
Типический отбор: |
|
|
|
|
|
Эти формулы являются одновременно и общим для всех случаев типического отбора |
||||
|
в) при объемах выборки, пропорциональных объемам типических групп |
|
|
|
|
|
г) при объемах выборки, пропорциональных объемам типических групп и их средним квадратическим отклонениям |
|
|
|
Таблица 3.Формулы выборочного метода для доли признака при различных видах отбора.
|
Выборочная средняя |
Объем выборки из типических групп |
Средняя ошибка выборки ? |
||
|
при повторном отборе |
При повторном отборе |
|||
|
Собственно случайный отбор и механический отбор (При механическом отборе применяется формула бесповторной выборки, за исключением тех случаев, когда множителем |
|
|
|
|
|
Типический отбор: |
|
|
|
|
|
Эти формулы являются одновременно и общим для всех случаев типического отбора |
||||
|
в) при объемах выборки, пропорциональных объемам типических групп |
|
|
|
|
|
г) при объемах выборки, пропорциональных объемам типических групп и их средним квадратическим отклонениям |
|
|
|
|
Средняя ошибка выборки для доли признака. Выборочный метод позволяет оценить не только среднюю арифметическую генеральной совокупности, но и долю некоторого (качественного или количественного) признака во всей совокупности.
Доля признака во всей совокупности (q) вычисляется как отношение числа элементов, обладающих этим признаком (No), к числу элементов всей совокупности (N), т. е. q=Nо/N.
Отметим, что рассмотренная выше теория и методика применения выборочного метода для расчета средней может быть применена и для расчета доли без каких-либо принципиальных изменений.
Сводка всех формул выборочного метода для доли признака дана в табл. 3.
Пример 8. На основе 10%-ной случайной бесповторной выборки из совокупности уставных грамот Тамбовской губернии вычислить доли селений с системой эксплуатации крестьян; а) оброчной, б) барщинной и в) смешанной, а также соответствующие им средние ошибки выборки
Из 264 грамот, составивших 10%-ную случайную бесповторную выборку, грамот, описывающих селения с оброчной, барщинной и смешанной системами эксплуатации, оказалось соответственно 51, 197 и 16 Тогда выборочная доля селений с оброчной системой эксплуатации равна 
Воспользовавшись формулой для собственно случайной бесповторной выборки из табл. 3, рассчитаем средние ошибки выборки для доли:
?б=0,03; ?ом=0,01
Точность и надежность выборочного метода: предельные ошибки. Определение объема выборки
Предельная ошибка выборки и доверительный интервал. Средняя ошибка выборки дает некоторое представление об ошибке репрезентативности, т. е. об ошибке, с которой выборочная средняя представляет действительное значение генеральной средней. Именно она показывает, какова будет ошибка в среднем, если из одной и той же генеральной совокупности сделать много выборок одинакового объема. Однако в каждой конкретной выборке ошибка может существенно отличаться от средней ошибки, т. е. нет гарантии, что ошибка, которая действительно была допущена в конкретном выборочном исследовании,
не превышает средней ошибки.
Поэтому гораздо полезнее было бы знать те границы, в которых «практически наверняка» находится действительная ошибка, допущенная в данной конкретной выборке. Эти границы (пределы) указываются предельной ошибкой выборки (обозначим ее Δ). Предельная ошибка выборки показывает тот предел,
которого практически наверняка не превосходит действительная ошибка. Иначе говоря, предельная ошибка Δ показывает действительно допущенную ошибку с избытком, с превышением (возможно, очень значительным) и тем самым гарантирует, что действительная ошибка не превосходит Δ.
Предельная ошибка Δ вычисляется на основе знания средней ошибки μ по формуле
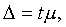
где t — величина, вычисляемая по специальной таблице. Обратим внимание на то, что в определении предельной ошибки постоянно употреблялись слова «практически наверняка». Необходимо пояснить смысл понятия «практическая уверенность».
Установленный предел Δ для ошибки выборки лишь указывает, что если из генеральной совокупности сделать много выборок, то для подавляющего большинства из них ошибка выборки не превысит вычисленного нами предела Δ. При этом, правда, могут быть все-таки и такие выборки, у которых ошибка выборки больше Δ, и не исключено, что конкретная выборка входит в их число. Однако можно точно измерить степень уверенности в том, что ошибка конкретной выборки не превысит Δ. Для этого нужно указать долю выборок, у которых ошибка выборки не превосходит Δ. Обозначим эту долю выборок через Р, где 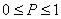
Значением Р фактически измеряется надежность результатов выборочного исследования: для значений Р, достаточно близких к единице, практически исключается возможность того, что генеральная средняя будет отличаться от вычисленной выборочной средней больше чем на Δ. Со своей стороны Δ указывает точность, гарантируемую заданным уровнем надежности Р. Таким образом, предельная ошибка выборки позволяет одновременно и взаимосвязано указать точность и надежность результатов выборочного исследования.
В математической статистике доказано, что распределение выборочных средних при достаточно больших n подчиняется нормальному закону (см. § 3, гл. 4) со средним значением, равным генеральной средней 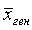
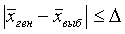
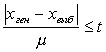
Эта же таблица позволяет решать и обратную задачу: по заданной вероятности Р найти величину предельной ошибки Δ, которая соответствует Р, другими словами, найти точность, соответствующую данному уровню надежности. Какова, например, предельная ошибка, соответствующая надежности 0,9545? По табл. 1 приложения найдем значение t, соответствующее вероятности Ф(t)= 0,9545. Оказывается, t=2. С вероятностью 0,9545 отклонение выборочной средней от генеральной по модулю не превосходит Δ=2μ, т. е. не выше двукратной средней ошибки выборки.
Разумеется, всегда желательно обеспечить большую надежность результатов, поэтому надо стараться выбрать Р возможно ближе к 1. Однако необходимо учитывать, что с возрастанием надежности увеличивается и t, а значит, и предельная ошибка Δ=tμ, т. е. падает точность результатов, что может оказаться по тем или иным соображениям недопустимым. Поэтому на практике приходится довольствоваться некоторым компромиссом между противоречивыми требованиями максимальной надежности и максимальной точности. Если такого компромисса достичь не удается и надежность и точность неудовлетворительны, следует сделать вывод, что объем выборки недостаточен и необходимо произвести новую выборку большего объема или же дополнить старую.
Знание предельной ошибки выборки позволяет указать и пределы для генеральной средней. Действительно, поскольку выборочная средняя 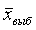
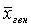
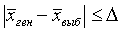
или, иначе,
(5.11)
Таким образом, с помощью вычисления выборочной средней и предельной ошибки выборки можно указать интервал, в котором практически наверняка находится генеральная средняя (так называемый доверительный интервал). При этом всегда указывается надежность Р этого результата (то значение Р, которое использовалось в вычислении Δ).
Пример 9. Вычислить предельные ошибки выборки по результатам примера 2 § 1 и определить пределы для генеральной средней.
Выборочная средняя для дореформенного надела равна 3,16, средняя ошибка выборки—0,0798.
Пусть Р=0,9545. Этому значению Р по табл. 1 приложения соответствует t=2. Пользуясь формулой (5.10), имеем Δ=2*0,0798=0,1596=0,16, т. е. предельная ошибка выборки равна приблизительно 0.16.
Переходим к определению пределов. Чтобы вычислить нижний предел, нужно из выборочной средней вычесть предельную ошибку выборки:
3,16—0,16=3,00.
Верхний предел получаем, прибавив к выборочной средней предельную ошибку:
3,16+0.16=3,32.
Тогда имеем следующие пределы для генеральной средней 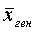
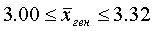
Результаты можно интерпретировать так: с надежностью (вероятностью) 0,95 генеральная средняя будет не меньше 3,00 дес. и не больше 3,32 дес. Или, другими словами, если выборки повторять много раз, то в 95 случаях из 100 получим, что выборочная средняя будет отстоять от генеральной средней не далее, чем на величину вычисленной нами предельной ошибки, равной 0,16 дес.
Возьмем теперь Р= 0,9876=0,99. Тогда t=2,5,.
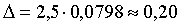
и генеральная средняя заключена в следующих пределах:
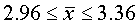
Пределы для генеральной средней расширились, но зато увеличилась степень доверия к результатам: уже примерно в 99 случаях из 100 мы не ошибаемся, указывая эти границы для средней.
Как правило, в исторических исследованиях рассмотренный в примере уровень надежности (Р=0,95; P=0,99) оказывается достаточным.
Порядок вычисления предельной ошибки выборки для доли признака ничем не отличается от вычисления предельной ошибки для средней арифметической.
Определение объема выборки. Вопрос об определении объема выборки является в выборочном методе исходным, ибо всякая выборка имеет заданный объем.
Заметим сразу, что зачастую исследователь лишен возможности решать вопрос об объеме выборки либо в силу ограниченности имеющихся в его распоряжении данных (естественные выборки), либо в силу тех или иных технических причин.
В тех же случаях, когда постановка вопроса об определении объема выборки возможна, его решение производится в следующем порядке.
Прежде всего производится пробная выборка произвольного объема. При этом можно пойти по одному из двух различных путей. Во-первых, можно попытаться сразу угадать нужный объем выборки, основываясь на каких-либо соображениях разумности объема выборки (например, можно попробовать 10%- или 20%-ную выборку). В случае если объем этой выборки окажется недостаточным, можно будет впоследствии дополнить эту выборку до нужного объема.
При втором подходе пробная выборка берется совсем небольшой (как правило, 1% и менее от объема генеральной совокупности). При этом практически следует руководствоваться некоторым компромиссом между требованием достаточной репрезентативности выборки и желанием уменьшить объем предварительных расчетов. На основе этой пробной выборки по приведенной ниже формуле (5.12) определяется необходимый объем окончательной выборки. Далее уже можно делать выборку заданного объема и проводить по ней выборочное исследование.
Анализ пробной выборки начинается с вычисления выборочной средней 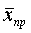
Например, если 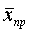
Δ=10*5/100==0,5.
Далее, зададимся уровнем надежности результатов. Выберем, например, Р=0,95.
Заметим, что стремясь к большей точности и надежности результатов, не следует излишествовать в этом направлении, так как может оказаться, что для достижения поставленных требований придется брать выборку объемом во всю совокупность. При этом теряет смысл само применение выборочного метода. Как правило, такие повышенные требования к результатам не оправдываются целями исследования и без ущерба для дела можно остановиться на более умеренных ограничениях. В том же случае, когда высокие требования вытекают из целей исследования и вычисленный объем выборки оказывается порядка объема всей совокупности, следует сделать вывод о том, что в данном случае применение выборочного метода нецелесообразно.
Рассчитав характеристики пробной выборки, переходят к оценке результатов этой выборки. Если используется первый путь исследования (относительно большой пробной выборки), то задав предельную ошибку Δ, следует сравнить ее с предельной ошибкой, вычисленной по пробной выборке Δпр (при одном и том же значении Р). Если окажется, что Δпр<=Δ то пробной выборки вообще достаточно, она может рассматриваться в качестве основной и ее результаты служат результатами всего выборочного исследования. Если же Δпр> Δ, что нередко имеет место при втором пути исследования, то определяют необходимый объем выборки по следующей формуле:
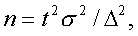
(5.12)
где σ2 — дисперсия признака, вычисленная по пробной выборке; Δ— заданная точность результатов выборочного исследования (заданная предельная ошибка выборки); t — величина, которая находится по табл. 1 приложения исходя из заданной надежности Р результатов выборочного исследования.
Заметим, что если пробная выборка мала (n<30), то для определения t используется табл. 2 приложения. В ней при определении t учитывается также объем пробной выборки (для нахождения табличного значения t берется объем пробной выборки, предварительно уменьшенный на единицу). Кроме того, в том случае и вычисляется так, как указано в § 4 этой главы.
Отметим, что приведенная формула дает общий объем выборки приближенно. Поэтому желательно если есть возможность, еще несколько увеличить объем выборки по сравнению с вычисленным.
Сделав окончательную выборку найденного объема, следует обязательно проверить, совпадает ли ее предельная ошибка с заданной, т. е. удовлетворяются ли заданные требования к точности и надежности результатов. В том редком случае, когда окажется, что действительная предельная ошибка существенно больше заданной (это может произойти из-за нерепрезентативности пробной выборки), придется еще раз повторить процедуру определения объема выборки уже на основе полученных более полных и точных данных.
Приведем также формулу для нахождения необходимого объема выборки при определении доли признака:
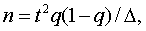
где t и Δ имеют тот же смысл, что и в предыдущей формуле,a q — доля признака в пробной выборке.
Рассмотрим пример, поясняющий основные моменты решения задачи об определении объема выборки.
Пример 10. Воспользовавшись данными по предприятиям европейской России за 1879 г. (См.: Указатель фабрик и заводов европейской России/Сост. П. А. Орлов. Спб., 1881, вып. 1. В «Указателе» содержатся сведения по фабрикам и заводам со стоимостью производимой продукции свыше 2 тыс. руб. (всего около 12000 предприятий).), определить объемы выборок, необходимые для расчетов средней стоимости произведенной продукции в расчете на одного рабочего на предприятиях: а) с паровыми двигателями, б) без паровых двигателей.
Сделаем сначала пробную 1%-ную выборку (случайным бесповторным способом) (Из-за недостатка места выборочные данные не приведены). Отметим, что среди предприятий, попавших в выборку (128 предприятий), 87 составляют предприятия без паровых двигателей и 41 —с паровыми двигателями.
Пользуясь выборочными данными, вычисляем по каждому типу предприятий среднюю стоимость произведенной на одного рабочего продукции 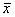
Для предприятий без паровых двигателей получаем соответственно 
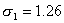
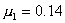
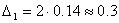
Для предприятий с паровыми двигателями получим 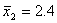
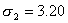
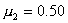
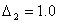
для предприятий без паровых двигателей
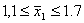
для предприятий с паровыми двигателями
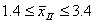
При сопоставлении полученных результатов напрашиваются следующие выводы: средняя стоимость продукции на одного рабочего на предприятиях без паровых двигателей и на предприятиях с паровыми двигателями различна, причем на предприятиях с паровыми двигателями она заметно выше. Однако, строго говоря, такой вывод пока еще неправомерен и может рассматриваться лишь как гипотеза. Дело в том, что доверительные интервалы для генеральных средних по предприятиям без паровых двигателей (1,1; 1,7) и по предприятиям с паровыми двигателями (1,4; 3,4) пересекаются, так что средние генеральные вполне могут совпадать или даже находиться в соотношении, противоположном высказанной гипотезе.
Нетрудно заметить, что указанная неопределенность результатов получается главным образом в силу того, что предельная ошибка выборки по предприятиям с паровыми двигателями Δ2 слишком велика. В самом деле, различие между выборочными средними по двум типам предприятий составляет
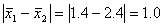
Поэтому, чтобы попытаться подтвердить и обосновать высказанную выше гипотезу, достаточно, чтобы предельные ошибки выборок для обеих групп предприятий (Δ1, Δ2) не превышали половины этой разности, т. е. 0,5, тогда доверительные интервалы не будут пересекаться.
Отметим, что предельная ошибка выборки по предприятиям без паровых двигателей Δ=0.3 вполне удовлетворительна. Чтобы обеспечить предельную ошибку выборки, равную 0,5, для другой группы предприятий, рассчитаем необходимый объем выборки из совокупности предприятий с паровыми двигателями. Выбирая t по табл. 1 приложения, соответствующие значению Р= 0,9545, и пользуясь формулой (5.12), получим
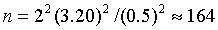
Дополнив теперь выборку из группы предприятий с паровыми двигателями до рассчитанного объема, получим новые значения средней, среднего квадратического отклонения, средней и предельной ошибок выборки:
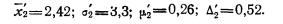
Сравним интервалы для генеральных средних. Для предприятий без паровых двигателей используем результат пробной выборки (которая оказалась для этой группы предприятий и окончательной):
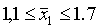
А для предприятий с паровыми двигателями имеем после увеличения объема выборки
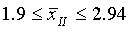
Как видим, теперь доверительные интервалы действительно не пересекаются и высказанная выше гипотеза о том, что средняя стоимость продукции на одного рабочего существенно больше для предприятий с паровыми двигателями, получает убедительное и надежное подтверждение. Другими словами, данные, использованные в примере 10, свидетельствуют о том, что внедрение машин повышало производительность труда.
Интересно отметить, что для достижения нужной точности и надежности результатов из совокупности предприятий с паровыми двигателями нам пришлось сделать примерно в два раза большую выборку, чем из группы предприятий без паровых двигателей. Это объясняется тем, что для предприятий с паровыми двигателями существенно больше разброс изучаемого признака, что вполне естественно для прогрессивной технологии, применяемой на этих предприятиях.
В заключение отметим еще один поучительный факт, с которым мы столкнулись в рассмотренном примере. По предприятиям с паровыми двигателями первоначальный объем выборки составлял 41 единицу, при этом обеспечивалась точность, определяемая предельной ошибкой выборки, равная единице (Δ2=1). Такая точность, как оказалось, была недостаточной, потребовалась в два раза большая точность—Δ2`=0.5. Это привело к тому, что объем новой выборки составил 164 единицы, что в четыре раза больше первоначального.
Следовательно, необходимый объем выборки растет пропорционально квадрату требуемой точности, что следует прямо из формулы (5.12). А так как квадраты чисел при возрастании самих чисел возрастают очень быстро, то повышенные требования к точности могут привести к неумеренному росту объема выборки. Поэтому важно, чтобы требования к точности выборочного исследования всегда диктовались целями и содержанием исследования. В рассмотренном примере такой целью было обоснование содержательной научной гипотезы.
§ 4. Малые выборки
Рассмотренные выше приемы расчета ошибок выборки основаны на доказанном в математике факте нормальности распределения выборочных средних. Однако этот факт имеет место только при достаточно большом объеме выборки n. Если пользоваться изложенными приемами при п меньшем 20, могут возникнуть грубые ошибки.
Выборки, объем которых меньше 20—30 единиц совокупности, будем называть малыми (Четкой границы между большой и малой выборками в общем случае указать невозможно. Выборка, сделанная из совокупности с небольшим разбросом признака, может считаться большой, тогда как выборка такого же объема, произведенная из более разнородной совокупности, окажется малой. Вопрос о том, к какой категории отнести выборку, решается в каждом конкретном случае). Для расчета ошибок таких выборок используется несколько иной математический аппарат.
Средняя ошибка малой выборки вычисляется по формуле
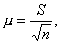
где S — оценка среднего квадратического отклонения в генеральной совокупности по малой выборке. Она равна:
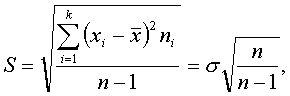
где σ вычисляется по формуле (4.7); n — объем выборки;k — число вариант, т. е. S несколько отличается от оценки среднего квадратического отклонения в генеральной совокупности по большой выборке, см. (5.1).
Пример 11. В табл. 4 приведены данные о размерах оброка в конце XVIII в. (в руб. серебром на муж. душу). Первая выборка состоит из 16 уездов нечерноземной полосы, вторая выборка—из 16 уездов черноземной полосы. Перед нами две «естественные выборки», которые можно рассматривать как случайные, т. е. репрезентативные Требуется рассчитать выборочные средние и средние ошибки выборок.
Вычисляем последовательно средние арифметические, средние квадратические отклонения малых выборок, и, наконец, стандартные ошибки выборок Получаем:
для нечерноземной полосы
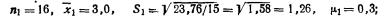
для черноземной полосы
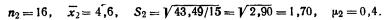
Заметим, что в пределах интересующей нас точности вычислений поправка на малую выборку не изменила величины стандартной ошибки. Заметное различие появляется при вычислении предельной ошибки выборки.
Предельная ошибка малой выборки вычисляется по формуле
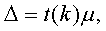
где t рассчитывают исходя из так называемого закона распределения Стьюдента с k степенями свободы (в отличие от больших выборок, где t вычисляется на основе нормального закона распределения).
Связь между t и вероятностью (уровнем надежности) Р в распределении Стьюдента сложнее, чем в нормальном распределении и опосредствуется через объем выборки. При возрастании объема выборки распределение Стьюдента приближается к нормальному, практически с ним совпадая при достаточно больших n.
При вычислении предельной ошибки малой выборки значение t(k) определяется по таблице распределения Стьюдента с k степенями свободы (табл. 2 приложения), с учетом заданного уровня надежности Р и объема выборки (для подстановки в таблицу фактический объем выборки надо предварительно уменьшить на единицу: k=n—1).
Пример 12. Используя данные предыдущего примера, найти предельные ошибки выборки для средних размеров оброка с уровнем надежности P=0,9 и Р=0,95 и определить границы для генеральной средней.
Обращаясь к табл. 2 приложения и учитывая, что при объеме выборки, равном 16, k, используемое для нахождения табличного значения t, равно 16—1=15, а заданный уровень надежности—0,9, находим t (15) =1,75.
Тогда предельная ошибка выборки для среднего размера оброка нечерноземной полосы по формуле (5.16) будет равна
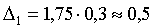
Следовательно, границы генеральной средней таковы:
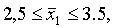
т. е. с вероятностью 0,9 средний размер оброка в нечерноземной полосе не выйдет за указанные границы.
Предельная ошибка второй выборки (для размеров оброка в черноземной полосе) и границы генеральной средней находятся аналогично. Имеем:
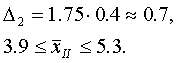
Чтобы получить более достоверные результаты, возьмем большую вероятность (уровень надежности). Пусть Р=0,95, тогда из табл. 2 приложения найдем t (15)=2,13, и для нечерноземной полосы
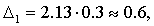
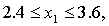
для черноземной полосы
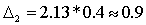
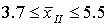
Итак, в конце XVIII в. средний размер оброка в черноземной полосе выше, чем средний размер оброка в нечерноземной полосе. Важно, что границы, в которых заключены средние, не пересекаются. Это свидетельствует о том, что различие размеров оброка в двух районах имело не случайный, а закономерный характер.
Для более строгих выводов о существенности различия между двумя выборочными средними есть специальные методы, изложенные в гл. 9 (§2 — критерии для средних, § 3 — критерии для дисперсий). Так, если имеются две выборочные средние 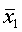
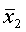
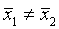
Отметим, что в тех же разделах гл. 9 рассмотрены аналогичные критерии для больших выборок, которые вместо распределения Стьюдента используют нормальное распределение, поскольку при возрастании объема выборки распределение Стьюдента стремится к нормальному.
В заключение скажем несколько слов о больших и малых выборках. Различать большие и малые выборки необходимо, но точной границы между ними установить нельзя. Важно иметь в виду, что к большим выборкам можно применять аппарат теории малых выборок, тогда как обратное приводит к значительным ошибкам. В сомнительных случаях для получения надежных результатов рекомендуется пользоваться аппаратом малых выборок.
В больших выборках средние теснее группируются около генеральной средней, что позволяет получать более точные и надежные результаты, тогда как в малых выборках приходится довольствоваться более широкими границами для средних или меньшей достоверностью результатов. Тем не менее теория малых выборок нашла в практике широкое распространение и применяется даже в тех случаях, когда во власти исследователя сделать выборку большой (См., например: Дружинин Н. К. Выборочный метод и его применение в социально-экономических исследованиях М., 1970, с. 77.).
Историку обычно не приходится выбирать между формированием большой или же малой выборки, поскольку он часто имеет дело с естественными малыми «выборками, число которых он не может изменить, т. е. он стоит перед альтернативой: либо воспользоваться данными малой выборки для анализа исследуемых явлений, либо отказаться от такого анализа. Обработка этих выборок методами математической статистики позволяет в ряде случаев (когда само использование выборочного метода возможно) обоснованно решить вопрос о правомерности или неправомерности тех или иных выводов и заключений на основе имеющихся материалов. И в том и в другом случае исследование приобретает более объективный и глубокий характер, нежели при традиционных методах.
Для того чтобы применить выборочный метод к естественным выборкам, необходимо доказать тем или иным способом случайность образования имеющейся выборки. В проверке случайности выборки ведущая роль принадлежит традиционным методам содержательного источниковедческого анализа. Отсутствие преднамеренности в порядке сбора и хранения тех сведений, след от которых остался в виде естественной выборки, свидетельствует о случайности последней. Математические методы позволяют дополнить этот анализ (см. гл. 9).
И наконец, последнее замечание. В этой главе мы ограничились оценкой средней арифметической генеральной совокупности с помощью характеристик, вычисленных по выборке. Но выборочный метод позволяет решать и более сложные вопросы анализа совокупностей. В частности, по выборке можно судить о наличии или об отсутствии связи между признаками, о форме связи. К процедурам выборочного метода мы будем обращаться при необходимости в соответствующих главах.
Как мы уже знаем, репрезентативность — свойство выборочной совокупности представлять характеристику генеральной. Если совпадения нет, говорят об ошибке репрезентативности — мере отклонения статистической структуры выборки от структуры соответствующей генеральной совокупности. Предположим, что средний ежемесячный семейный доход пенсионеров в генеральной совокупности составляет 2 тыс. руб., а в выборочной — 6 тыс. руб. Это означает, что социолог опрашивал только зажиточную часть пенсионеров, а в его исследование вкралась ошибка репрезентативности. Иными словами, ошибкой репрезентативности называется расхождение между двумя совокупностями — генеральной, на которую направлен теоретический интерес социолога и представление о свойствах которой он хочет получить в конечном итоге, и выборочной, на которую направлен практический интерес социолога, которая выступает одновременно как объект обследования и средство получения информации о генеральной совокупности.
Наряду с термином «ошибка репрезентативности» в отечественной литературе можно встретить другой — «ошибка выборки». Иногда они употребляются как синонимы, а иногда «ошибка выборки» используется вместо «ошибки репрезентативности» как количественно более точное понятие.
Ошибка выборки — отклонение средних характеристик выборочной совокупности от средних характеристик генеральной совокупности.
На практике ошибка выборки определяется путем сравнения известных характеристик генеральной совокупности с выборочными средними. В социологии при обследованиях взрослого населения чаще всего используют данные переписей населения, текущего статистического учета, результаты предшествующих опросов. В качестве контрольных параметров обычно применяются социально-демографические признаки. Сравнение средних генеральной и выборочной совокупностей, на основе этого определение ошибки выборки и ее уменьшение называется контролированием репрезентативности. Поскольку сравнение своих и чужих данных можно сделать по завершении исследования, такой способ контроля называется апостериорным, т.е. осуществляемым после опыта.
В опросах Института Дж. Гэллапа репрезентативность контролируется по имеющимся в национальных переписях данным о распределении населения по полу, возрасту, образованию, доходу, профессии, расовой принадлежности, месту проживания, величине населенного пункта. Всероссийский центр изучения общественного мнения (ВЦИОМ) использует для подобных целей такие показатели, как пол, возраст, образование, тип поселения, семейное положение, сфера занятости, должностной статус респондента, которые заимствуются в Государственном комитете по статистике РФ. В том и другом случае генеральная совокупность известна. Ошибку выборки невозможно установить, если неизвестны значения переменной в выборочной и генеральной совокупностях.
Специалисты ВЦИОМ обеспечивают при анализе данных тщательный ремонт выборки, чтобы минимизировать отклонения, возникшие на этапе полевых работ. Особенно сильные смещения наблюдаются по параметрам пола и возраста. Объясняется это тем, что женщины и люди с высшим образованием больше времени проводят дома и легче идут на контакт с интервьюером, т.е. являются легко достижимой группой по сравнению с мужчинами и людьми «необразованными»35.
Ошибка выборки обусловливается двумя факторами: методом формирования выборки и размером выборки.
Ошибки выборки подразделяются на два типа — случайные и систематические. Случайная ошибка — это вероятность того, что выборочная средняя выйдет (или не выйдет) за пределы заданного интервала. К случайным ошибкам относят статистические погрешности, присущие самому выборочному методу. Они уменьшаются при возрастании объема выборочной совокупности.
Второй тип ошибок выборки — систематические ошибки. Если социолог решил узнать мнение всех жителей города о проводимой местными органами власти социальной политике, а опросил только тех, у кого есть телефон, то возникает предумышленное смещение выборки в пользу зажиточных слоев, т.е. систематическая ошибка.
Таким образом, систематические ошибки — результат деятельности самого исследователя. Они наиболее опасны, поскольку приводят к довольно значительным смещениям результатов исследования. Систематические ошибки считаются страшнее случайных еще и потому, что они не поддаются контролю и измерению.
Они возникают, когда, например:
- выборка не соответствует задачам исследования (социолог решил изучить только работающих пенсионеров, а опросил всех подряд);
- налицо незнание характера генеральной совокупности (социолог думал, что 70% всех пенсионеров не работает, а оказалось, что не работает только 10%);
- отбираются только «выигрышные» элементы генеральной совокупности (например, только обеспеченные пенсионеры).
Внимание! В отличие от случайных ошибок систематические ошибки при возрастании объема выборки не уменьшаются.
Обобщив все случаи, когда происходят систематические ошибки, методисты составили их реестр. Они полагают, что источником неконтролируемых перекосов в распределении выборочных наблюдений могут быть следующие факторы:
- нарушены методические и методологические правила проведения социологического исследования;
- выбраны неадекватные способы формирования выборочной совокупности, методы сбора и расчета данных;
- произошла замена требуемых единиц наблюдения другими, более доступными;
- отмечен неполный охват выборочной совокупности (недополучение анкет, неполное их заполнение, труднодоступность единиц наблюдения).
Намеренные ошибки социолог допускает редко. Чаще ошибки возникают из-за того, что социологу плохо известна структура генеральной совокупности: распределение людей по возрасту, профессии, доходам и т.д.
Систематические ошибки легче предупредить (по сравнению со случайными), но их очень трудно устранить. Предупреждать систематические ошибки, точно предвидя их источники, лучше всего заранее — в самом начале исследования.
Вот некоторые способы избежать ошибок выборки:
- каждая единица генеральной совокупности должна иметь равную вероятность попасть в выборку;
- отбор желательно производить из однородных совокупностей;
- надо знать характеристики генеральной совокупности;
- при составлении выборочной совокупности надо учитывать случайные и систематические ошибки.
Если выборочная совокупность (или просто выборка) составлена правильно, то социолог получает надежные результаты, харастеризующие всю генеральную совокупность. Если она составлена неправильно, то ошибка, возникшая на этапе составления выборки, на каждом следующем этапе проведения социологического исследования приумножается и достигает в конечном счете такой величины, которая перевешивает ценность проведенного исследования. Говорят, что от такого исследования больше вреда, нежели пользы.
Подобные ошибки могут произойти только с выборочной совокупностыо. Чтобы избежать или уменьшить вероятность ошибки, самый простой способ — увеличивать размеры выборки (в идеале до объема генеральной: когда обе совокупности совпадут, ошибка выборки вообще исчезнет). Экономически такой метод невозможен. Остается другой путь — совершенствовать математические методы составления выборки. Они то и применяются на практике. Таков первый канал проникновения в социологию математики. Второй канал — математическая обработка данных.
Особенно важной проблема ошибок становится в маркетинговых исследованиях, где используются не очень большие выборки. Обычно они составляют несколько сотен, реже — тысячу респондентов. Здесь исходным пунктом расчета выборки выступает вопрос об определении размеров выборочной совокупности. Численность выборочной совокупности зависит от двух факторов:
- стоимости сбора информации,
- стремления к определенной степени статистической достоверности результатов, которую надеется получить исследователь.
Конечно, даже не искушенные в статистике и социологии люди интуитивно понимают, что чем больше размеры выборки, т.е. чем ближе они к размерам генеральной совокупности в целом, тем более надежны и достоверны полученные данные. Однако выше мы уже говорили о практической невозможности сплошных опросов в тех случаях, когда они проводятся на объектах, численность которых превышает десятки, сотни тысяч и даже миллионы. Понятно, что стоимость сбора информации (включающая оплату тиражирования инструментария, труда анкетеров, полевых менеджеров и операторов по компьютерному вводу) зависит от той суммы, которую готов выделить заказчик, и слабо зависит от исследователей. Что же касается второго фактора, то мы остановимся на нем чуть подробнее.
Итак, чем больше величина выборки, тем меньше возможная ошибка. Хотя необходимо отметить, что при желании увеличить точность вдвое вам придется увеличить выборку не в два, а в четыре раза. Например, чтобы сделать в два раза более точной оценку данных, полученных путем опроса 400 человек, вам потребуется опросить не 800, а 1600 человек. Впрочем, вряд ли маркетинговое исследование испытывает нужду в стопроцентной точности. Если пивовару необходимо узнать, какая часть потребителей пива предпочитает именно его марку, а не сорт его конкурента, — 60% или 40%, то на его планы никак не повлияет разница между 57%, 60 или 63%.
Ошибка выборки может зависеть не только от ее величины, но и от степени различий между отдельными единицами внутри генеральной совокупности, которую мы исследуем. Например, если нам нужно узнать, какое количество пива потребляется, то мы обнаружим, что внутри нашей генеральной совокупности нормы потребления у различных людей существенно различаются (гетерогенная генеральная совокупность). В другом случае мы будем изучать потребление хлеба и установим, что у разных людей оно различается гораздо менее существенно {гомогенная генеральная совокупность). Чем больше различия (или гетерогенность) внутри генеральной совокупности, тем больше величина возможной ошибки выборки. Указанная закономерность лишь подтверждает то, что нам подсказывает простой здравый смысл. Таким образом, как справедливо утверждает В. Ядов, «численность (объем) выборки зависит от уровня однородности или разнородности изучаемых объектов. Чем более они однородны, тем меньшая численность может обеспечить статистически достоверные выводы».
Определение объема выборки зависит также от уровня доверительного интервала допустимой статистической ошибки. Здесь имеются в виду так называемые случайные ошибки, которые связаны с природой любых статистических погрешностей. В.И. Паниотто приводит следующие расчеты репрезентативной выборки с допущением 5%-ной ошибки:
Это означает,что если вы, опросив, предположим, 400 человек в районном городе, где численность взрослого платежеспособного населения составляет 100 тыс. человек, выявили, что 33% опрошенных покупателей предпочитают продукцию местного мясокомбината, то с 95%-ной вероятностью можете утверждать, что постоянными покупателями этой продукции являются 33+5% (т.е. от 28 до 38%) жителей этого города.
Можно также воспользоваться расчетами института Гэллапа для оценки соотношения размеров выборки и ошибки выборки.













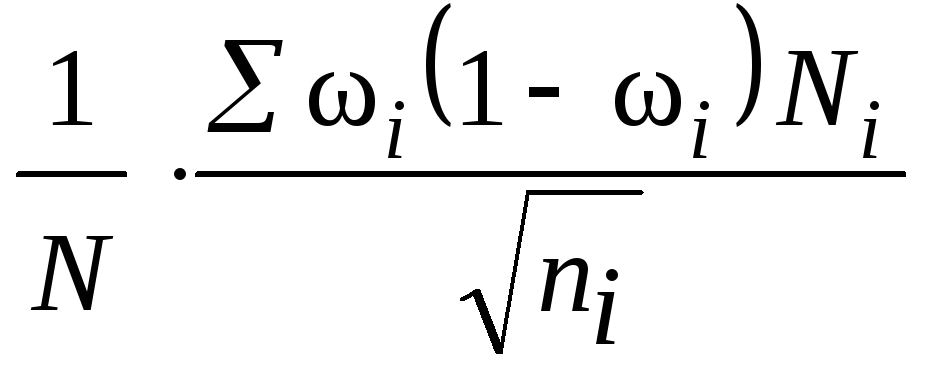


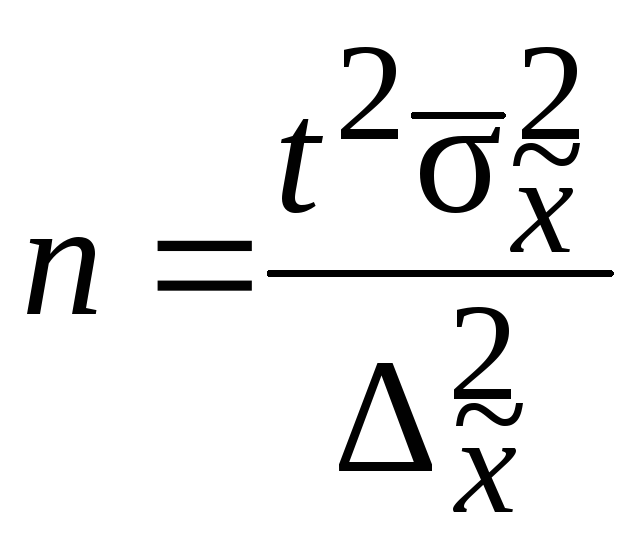

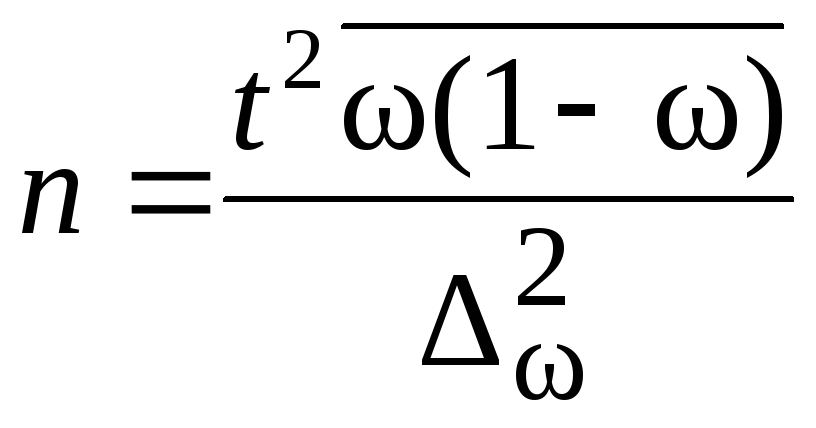



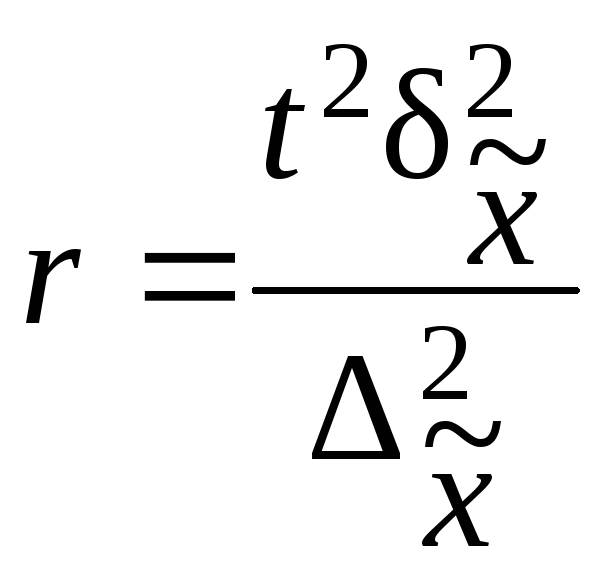

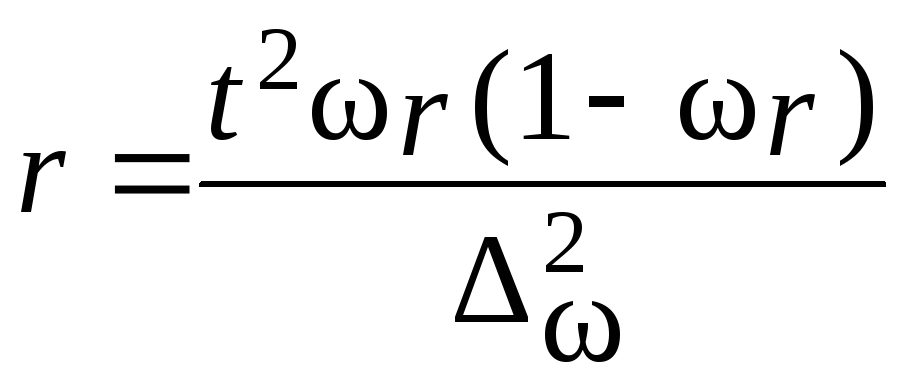



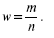

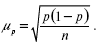

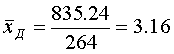
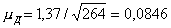
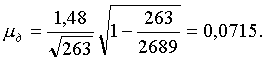
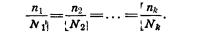
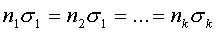
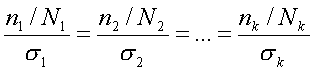
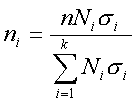
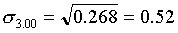
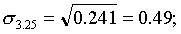
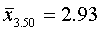
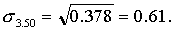
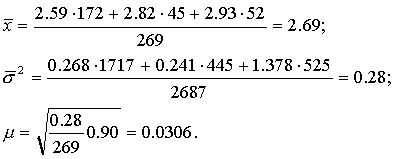
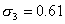
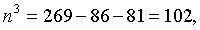
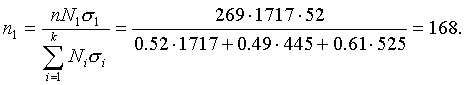
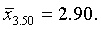
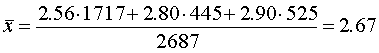
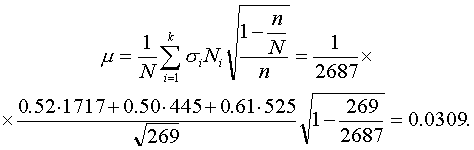
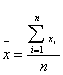
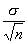
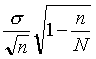
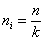
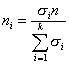
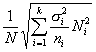
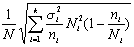
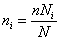
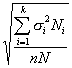
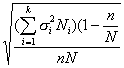
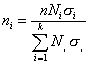
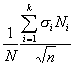
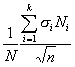
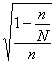
 можно пренебречь.
можно пренебречь.