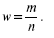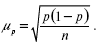Ошибки выборки и их типология

Выборочный метод
в соц. исс. Основные понятия выборочного
метода. Этапы формирования выб. сов-сти.

Соц.
исс. обычно бывают выборочными, поскольку
сплошной охват изучаемой совокупности
требует недопустимо высоких материальных
и временных затрат. Поэтому при
проектировании исс. одна из главных
задач состоит в формировании такой
выборки, которая была бы одновременно
и
репрезентативной,
и экономичной.

Репрезентативность
–
это св-во выборочной сов-ти быть моделью
генеральной сов-ти, т.е. воспроизвести
структуру генер. сов-ти по значимым
признакам.

Генеральная
совокупность
– это сов-ть всех единиц объекта исс.
относит. которых делаются выводы в исс.
Пример: человечество, население страны,
факультет и т.д. Любое выборочное
исследование имеет своей целью получить
достоверные выводы, относящиеся именно
к генеральной совокупности.

Выборочная
сов-ть
— это часть соц. объектов ген. сов-ти,
выступающих в кач-ве непоср. объектов
изучения в соц. исс.

Единицы
отбора
– это элементы ген. сов-ти, отбираемые
на каждой ступени выборки.

Единица
наблюдения
– это элементы сформированной выборочной
сов-ти, подвергающиеся непоср-му изучению
в иссл-ии.

Критериями
для выборки
могут быть: социально-профессиональный
состав, поло-возрастной, имущественный,
национальный состав.

В
целом все методы
делятся на сплошные
и выборочные.
СМ- охват всех без исключения объектов
исс. (перепись населения) Наиболее часто
исп. несплошные методы – монография,
метод основного массива, выборочный
метод. Тип и способ выборки прямо зависит
от целей исс. и его гипотез. Наиболее
строгие требования предъявляются к
выборкам аналитико-экспериментальных
и описательных исс., наименее строгие
– к исс. по разведывательному плану. В
этом случае отбор “единиц наблюдения”
на объекте подчиняется довольно простым
правилам: следует выделять полярные
группы по существу для анализа критериев.
Численность таких несистематичных
выборок строго не определяется. Все
зависит от состояния полученной инф.
Наблюдение или опрос в таком исс.
продолжается до тех пор, пока не
обнаружится, что полученная инф.,
достаточно разнообразна для формулировки
гипотез. Следовательно, состав и объем
выборки заранее не фиксируется, а
устанавливается опытным путем по мере
развития исс. В исс. описательного плана
выборка, напротив, д/б строго
репрезентативной.

Преимущества ВМ:

1. меньшая стоимость,
затраты на получение данных небольшой
части меньше, чем при СИ;

2. короче сроки,
данные можно собрать и обобщить быстрее;

3. шире образ
применения;

4. большая
достоверность.

Гл. особенности
выб. сов-ти закл. в том, что:

1. выборочная сов-ть
непосредственно изучается в исс.;

2. выб. сов-ть
строится из тех элементов, что и ген.
сов-ть, представляя собой ее часть.

Этапы формирования
выборки:

1. Выбор параметров
   в соответствии с целями и задачами исс.
   (пол, возраст, образование, мат. положение
   и т.д.)

2. Устанавливается
   — располагает ли исс-ль или может
   располагать инф. о распределении этих
   характеристик ген. сов-сти.

3. В зав-сти от ответа
   на пункт (2) опред-ся тип выборки на
   последующие ступени отбора.

4. Опред-ся объем
   выборки, взвешивая факторы на увеличение
   объема и его уменьшение.

5. Опред-ся возможность
   районирования выборки на 1-ой ступени
   многоступенчатого отбора.

6. Опред-ся кол-во
   ступеней выборки, объекты отбора на
   каждой ступени (ед-ца отбора), объем и
   тип выборки на каждой ступени с учетом
   общего объема.

7. Оценивается основа
   выборки, ее качество, полнота, отсутствия
   дублирования и т.д.

Пример: отношение
пенсионеров Самары к размеру пенсии.
Ген. сов-ть- 250000 ч-к.

• Размер пенсии

• Если обладаем
  инц-цией о том , сколько ч-к получают
  какцю пенсию, тогда исп-ем квотную
  выборку, если нет , то применяем др.
  выборку.

• Определяем объем
  выб. сов-ти=1000 ч-к

• Определяем
  возможность районир-я

• Применить случайную
  или механическую выборку на 2 ой ступени

• Выбираем ЖЭУ, где
  потом берем список.

Определение
объема выборочной совокупности.

Важнейшей задачей
социолога, предпринимающего исс.,
является определение выборки, то есть
ответ на вопрос, сколько нужно опросить.

Для определения
объема выборки существуют статистические
формулы, которыми мало кто пользуется.
Как правило, объем выборки колеблется
в диапазоне 400-1200 человек. Минимальные
границы обусловлены тем, что, как
утверждает статистика, результаты,
полученные на меньших объемах,
статистически незначимы, т.е. не имеют
права называться закономерностью.
Верхний предел обусловлен тем
обстоятельством, что, как доказала
Элизабет Ноэль в своей книге «Массовые
опросы» после опроса 1000-1200 человек
начинает идти повторяющаяся инф.

Соц-гу н/ж знать,
что в массовом сознании эта идея выборки
плохо входит в голову. Выборочным опросам
не доверяют. Выбор конкретной величины
выборки в рамках этих пределов зависит
от нескольких факторов.

Факторы, работающие
на увеличение объема выборки.

1. Необходимо брать
   как можно больший объем выб. сов. если
   ген. сов. разнородна, т.е. чем разнородней
   сов., тем при прочих равных условиях
   нужно брать больший объем выборки.

2. Дробность
   предполагаемого анализа полученной
   инф.

Отношение к
правительству

V=500
(300 женщин, 200 мужчин)

мнения	мужчин	женщин	Итого
Поддерживают	70	150	220
Не поддерживают	100	50	150
Затрудняются ответить	30	100	130
	200	300	500

Опытным путем
установлено, что, если в клеточке
аналитической таблицы оказывается
меньше 10 человек, то эти цифры статистически
незначимы и значит, что дробный анализ
социолог сделать не может. Чем более
дробным соц-г хочет сделать свой
последующий анализ, т.е. анализировать
не по одному признаку, а по нескольким,
да еще связанным друг с другом, тем при
прочих равных условиях он должен брать
больший объем выборки.

1. Финансовые и
   организационные возможности.

2. Факторы, работающие
   на уменьшение выборки

3. Однородность
   генеральной совокупности

4. Малая дробность

5. Отсутствие
   возможностей.

Ошибки выборки, их классификация.

Репрезентативность
– это свойство выб. сов. воспроизводить
структуру ген. сов. по важным критериям,
признакам. Ошибками выборки называют
отклонение структуры выборки от структуры
соответствующей ген. сов. Существуют
два типа ошибок, которые необходимо
учитывать при использовании выборочного
метода и организации выборок: случайные
(СО) и систематические (СИО).

СО.
Ошибки репрезентативности, или
статистичечкой погрешности, присущие
самому выб. методу. Они, как правило,
задаются исс-ем изначально, в зависимости,
от требуемой надежности результатов
исс. Исс. повышенной надежности допускают
ошибки до 3%, обычной – от 3 до 10%,
ориентировочные – от 20-40%, грубое исс.
выше. Как правило, достаточно точные
исс.: в политике — рейтинг, электоральное
поведение; маркетинговые ислл-я (в
области рынка) — запросы потребителей,
спрос (размеры). Т.е. достаточно точные
исс. проводятся там, где по итогам исс.
принимаются конкретные упр. решения. К
источникам этих ошибок можно отнести
следующие:

1. замена намеченных
по плану выборки единиц наблюдения
другими, более доступными, которые,
однако, оказываются неполноценными с
точки зрения выработанного плана
выборки. Такого рода ошибки могут
происходить при использовании недостаточно
квалифицированных кадров анкетеров и
интервьюеров. Например, опрос намечено
проводить в каждой десятой квартире
жилого массива, номера которых определены
процедурой систематического отбора.
Никого не застав в части выбранных
квартир, интервьюер иногда обращается
в соседнюю квартиру и берет интервью.
В итоге в выборке может оказаться
значительный перевес пенсионеров,
больших семей и могут быть слабо
представлены одинокие лица и малочисленные
семьи. Ошибки этого типа (ошибки
подстановки) м/б предотвращены выборочным
контролем за деятельностью анкетеров
и интервьюеров и качеством собранной
ими инф. Они могут привести к серьезным
смещениям в выборке.

2. неполный охват
выб. сов., т. е. неполучение инф. от части
единиц наблюдения, включенных в выборку
(например, недополучение почтовых анкет,
не полностью заполненные анкеты). Эти
ошибки устанавливаются путем сравнения
реально сформированной выборки с ее
разработанным планом. Ошибки подобного
рода “снимаются” так называемой
процедурой “корректировки” выборки,
т. е. организацией дополнительного сбора
недостающей инф.

Наряду
со случайными возможны ошибки
систематического
характера.
Они зависят от организации выборочного
обследования. Это разнообразные смещения
выборки
в сторону одного из полюсов выборочного
параметра.Смещение выборки – всякое
значительное отклонение выборки от
ген. сов. Источником смещения выступают
возможные ошибки выборки.

СИО.
Неадекватное воспроизведение в выборке
генеральных распределений м/б вызвано
причинами, носящими неслучайный
(вероятностный) характер, такие ошибки
называют СИО. Они приводят к искажению
в выборке характера генерального
распределения: либо к резкому завышению,
либо к резкому занижению значений
характеристик генеральной совокупности.
СИО могут обесценить результаты всего
исс. Эти ошибки характеризуют квалификацию
исс-ля. Основными источниками СИО м/б:

а) неадекватность
сформированной выборки задачам исс.;

б) незнание
характера распределений в ген. сов. и
выбор процедур отбора, которые могут
исказить эти распределения, например,
нарушение необходимой для репрезентативной
выборки пропорциональности в
представительстве различного типа
элементов ген. Сов. (если последняя
статистически неоднородна) вследствие
отсутствия необходимой информации;

в) сознательный
отбор наиболее удобных и “выигрышных”
для решения задач исс. элементов ген.
сов., которые, однако, не представляют
ее в целом (например, отбор только
передовых предприятий, совхозов и т.
п.).

г) ремонт выборки
— это процедура исправления СИО
(довыборка).

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

What Is a Sampling Error?

A sampling error is a statistical error that occurs when an analyst does not select a sample that represents the entire population of data. As a result, the results found in the sample do not represent the results that would be obtained from the entire population.

Sampling is an analysis performed by selecting a number of observations from a larger population. The method of selection can produce both sampling errors and non-sampling errors.

Understanding Sampling Errors

A sampling error is a deviation in the sampled value versus the true population value. Sampling errors occur because the sample is not representative of the population or is biased in some way. Even randomized samples will have some degree of sampling error because a sample is only an approximation of the population from which it is drawn.

Calculating Sampling Error

The sampling error formula is used to calculate the overall sampling error in statistical analysis. The sampling error is calculated by dividing the standard deviation of the population by the square root of the size of the sample and then multiplying the resultant with the Z-score value, which is based on the confidence interval.

Sampling Error

=

Z

×

σ

n

where:

Z

=

Z

 score value based on the

 confidence interval (approx

=

1.96

)

σ

=

Population standard deviation

n

=

Size of the sample

\begin{aligned}&\text{Sampling Error}=Z\times\frac{\sigma}{\sqrt{n}}\\&\textbf{where:}\\&Z=Z\text{ score value based on the}\\&\qquad\ \text{confidence interval (approx}=1.96)\\&\sigma=\text{Population standard deviation}\\&n=\text{Size of the sample}\end{aligned}

​Sampling Error=Z×n​σ​where:Z=Z score value based on the confidence interval (approx=1.96)σ=Population standard deviationn=Size of the sample​

Types of Sampling Errors

There are different categories of sampling errors.

Population-Specific Error

A population-specific error occurs when a researcher doesn’t understand who to survey.

Selection Error

Selection error occurs when the survey is self-selected, or when only those participants who are interested in the survey respond to the questions. Researchers can attempt to overcome selection error by finding ways to encourage participation.

Sample Frame Error

A sample frame error occurs when a sample is selected from the wrong population data.

Non-response Error

A non-response error occurs when a useful response is not obtained from the surveys because researchers were unable to contact potential respondents (or potential respondents refused to respond).

Eliminating Sampling Errors

The prevalence of sampling errors can be reduced by increasing the sample size. As the sample size increases, the sample gets closer to the actual population, which decreases the potential for deviations from the actual population. Consider that the average of a sample of 10 varies more than the average of a sample of 100. Steps can also be taken to ensure that the sample adequately represents the entire population.

Researchers might attempt to reduce sampling errors by replicating their study. This could be accomplished by taking the same measurements repeatedly, using more than one subject or multiple groups, or by undertaking multiple studies.

Random sampling is an additional way to minimize the occurrence of sampling errors. Random sampling establishes a systematic approach to selecting a sample. For example, rather than choosing participants to be interviewed haphazardly, a researcher might choose those whose names appear first, 10th, 20th, 30th, 40th, and so on, on the list.

Examples of Sampling Errors

Assume that XYZ Company provides a subscription-based service that allows consumers to pay a monthly fee to stream videos and other types of programming via an Internet connection.

The firm wants to survey homeowners who watch at least 10 hours of programming via the Internet per week and that pay for an existing video streaming service. XYZ wants to determine what percentage of the population is interested in a lower-priced subscription service. If XYZ does not think carefully about the sampling process, several types of sampling errors may occur.

A population specification error would occur if XYZ Company does not understand the specific types of consumers who should be included in the sample. For example, if XYZ creates a population of people between the ages of 15 and 25 years old, many of those consumers do not make the purchasing decision about a video streaming service because they may not work full-time. On the other hand, if XYZ put together a sample of working adults who make purchase decisions, the consumers in this group may not watch 10 hours of video programming each week.

Selection error also causes distortions in the results of a sample. A common example is a survey that only relies on a small portion of people who immediately respond. If XYZ makes an effort to follow up with consumers who don’t initially respond, the results of the survey may change. Furthermore, if XYZ excludes consumers who don’t respond right away, the sample results may not reflect the preferences of the entire population.

Sampling Error vs. Non-sampling Error

There are different types of errors that can occur when gathering statistical data. Sampling errors are the seemingly random differences between the characteristics of a sample population and those of the general population. Sampling errors arise because sample sizes are inevitably limited. (It is impossible to sample an entire population in a survey or a census.)

Company XYZ will also want to avoid non-sampling errors. Non-sampling errors are errors that result during data collection and cause the data to differ from the true values. Non-sampling errors are caused by human error, such as a mistake made in the survey process.

If one group of consumers only watches five hours of video programming a week and is included in the survey, that decision is a non-sampling error. Asking questions that are biased is another type of error.

The Bottom Line

Sampling error occurs when a sample drawn from a population deviates somewhat from that true population. Large sampling errors can lead to incorrect estimates or inferences made about the population based on statistical analysis of that sample.

In general, sampling errors can be placed into four categories: population-specific error, selection error, sample frame error, or non-response error. A population-specific error occurs when the researcher does not understand who they should survey. A selection error occurs when respondents self-select their participation in the study. (This results in only those that are interested in responding, which skews the results.) A sample frame error occurs when the wrong sub-population is used to select a sample. Finally, a non-response error occurs when potential respondents are not successfully contacted or refuse to respond.

3. Ошибки выборки

Каждая единица при выборочном наблюдении должна иметь равную с другими возможность быть отобранной – это является основой собственнослучайной выборки.

Собственнослучайная выборка – это отбор единиц из всей генеральной совокупности посредством жеребьевки или другим подобным способом.

Принципом случайности является то, что на включение или исключение объекта из выборки не может повлиять любой фактор, кроме случая.

Доля выборки – это отношение числа единиц выборочной совокупности к числу единиц генеральной совокупности:

Собственнослучайный отбор в чистом виде является исходным среди всех других видов отбора, в нем заключаются и реализуются основные принципы выборочного статистического наблюдения.

Два основных вида обобщающих показателей, которые используют в выборочном методе – это средняя величина количественного признака и относительная величина альтернативного признака.

Выборочная доля (w), или частность, определяется отношением числа единиц, обладающих изучаемым признаком m, к общему числу единиц выборочной совокупности (n):

Для характеристики надежности выборочных показателей различают среднюю и предельную ошибки выборки.

Ошибка выборки, ее еще называют ошибкой репрезентативности, представляет собой разность соответствующих выборочных и генеральных характеристик:

1) для средней количественного признака:

?х =|х – х|;

2) для доли (альтернативного признака):

?w =|х – p|.

Только выборочным наблюдениям присуща ошибка выборки

Выборочная средняя и выборочная доля – это случайные величины, принимающие различные значения в зависимости от единиц изучаемой статистической совокупности, которые попали в выборку. Соответственно ошибки выборки – тоже случайные величины и также могут принимать различные значения. Поэтому определяют среднюю из возможных ошибок – среднюю ошибку выборки.

Средняя ошибка выборки определяется объемом выборки: чем больше численность при прочих равных условиях, тем меньше величина средней ошибки выборки. Охватывая выборочным обследованием все большее количество единиц генеральной совокупности, все более точно характеризуем всю генеральную совокупность.

Средняя ошибка выборки зависит от степени варьирования изучаемого признака, в свою очередь степень варьирования характеризуется дисперсией ?² или w(l – w) – для альтернативного признака. Чем меньше вариация признака и дисперсия, тем меньше средняя ошибка выборки, и наоборот.

При случайном повторном отборе средние ошибки теоретически рассчитывают по следующим формулам:

1) для средней количественного признака:

где ?² – средняя величина дисперсии количественного признака.

2) для доли (альтернативного признака):

Так как дисперсия признака в генеральной совокупности ?² точно неизвестна, на практике пользуются значением дисперсии S² , рассчитанным для выборочной совокупности на основании закона больших чисел, согласно которому выборочная совокупность при достаточно большом объеме выборки достаточно точно воспроизводит характеристики генеральной совокупности.

Формулы средней ошибки выборки при случайном повторном отборе следующие. Для средней величины количественного признака: генеральная дисперсия выражается через выборную следующим соотношением:

где S² – значение дисперсии.

Механическая выборка – это отбор единиц в выборочную совокупность из генеральной, которая разбита по нейтральному признаку на равные группы; производится так, что из каждой такой группы в выборку отбирается лишь одна единица.

При механическом отборе единицы изучаемой статистической совокупности предварительно располагают в определенном порядке, после чего отбирают заданное число единиц механически через определенный интервал. При этом размер интервала в генеральной совокупности равен обратному значению доли выборки.

При достаточно большой совокупности механический отбор по точности результатов близок к собственнослучайному Поэтому для определения средней ошибки механической выборки используют формулы собственнослучайной бесповторной выборки.

Для отбора единиц из неоднородной совокупности применяется так называемая типическая выборка, используется, когда все единицы генеральной совокупности можно разбить на несколько качественно однородных, однотипных групп по признакам, от которых зависят изучаемые показатели.

Затем из каждой типической группы собственнослучайной или механической выборкой производится индивидуальный отбор единиц в выборочную совокупность.

Типическая выборка обычно применяется при изучении сложных статистических совокупностей.

Типическая выборка дает более точные результаты. Типизация генеральной совокупности обеспечивает репрезентативность такой выборки, представительство в ней каждой типологической группы, что позволяет исключить влияние межгрупповой дисперсии на среднюю ошибку выборки. Поэтому при определении средней ошибки типической выборки в качестве показателя вариации выступает средняя из внутригрупповых дисперсий.

Серийная выборка предполагает случайный отбор из генеральной совокупности равновеликих групп для того, чтобы в таких группах подвергать наблюдению все без исключения единицы.

Поскольку внутри групп (серий) обследуются все без исключения единицы, средняя ошибка выборки (при отборе равновеликих серий) зависит только от межгрупповой (межсерийной) дисперсии.

Данный текст является ознакомительным фрагментом.