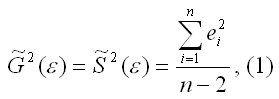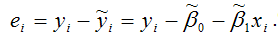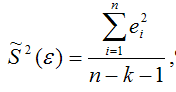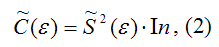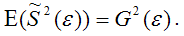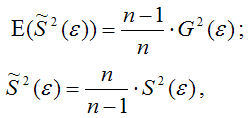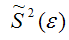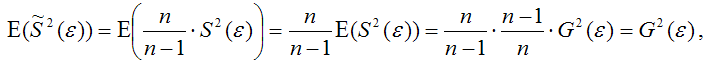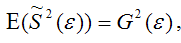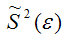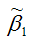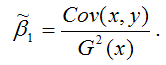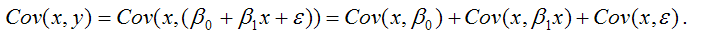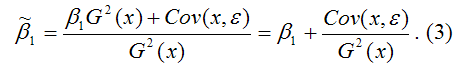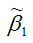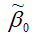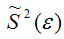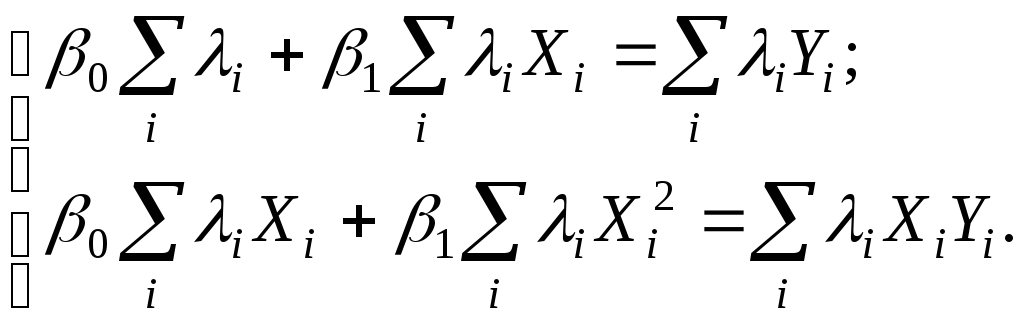15. Оценка дисперсии случайной ошибки модели регрессии
При проведении регрессионного анализа основная трудность заключается в том, что генеральная дисперсия случайной ошибки является неизвестной величиной, что вызывает необходимость в расчёте её несмещённой выборочной оценки.
Несмещённой оценкой дисперсии (или исправленной дисперсией) случайной ошибки линейной модели парной регрессии называется величина, рассчитываемая по формуле:
где n – это объём выборочной совокупности;
еi– остатки регрессионной модели:
Для линейной модели множественной регрессии несмещённая оценка дисперсии случайной ошибки рассчитывается по формуле:
где k – число оцениваемых параметров модели регрессии.
Оценка матрицы ковариаций случайных ошибок Cov(?) будет являться оценочная матрица ковариаций:
где In – единичная матрица.
Оценка дисперсии случайной ошибки модели регрессии распределена по ?2(хи-квадрат) закону распределения с (n-k-1) степенями свободы.
Для доказательства несмещённости оценки дисперсии случайной ошибки модели регрессии необходимо доказать справедливость равенства
Доказательство. Примем без доказательства справедливость следующих равенств:
где G2(?) – генеральная дисперсия случайной ошибки;
S2(?) – выборочная дисперсия случайной ошибки;
– выборочная оценка дисперсии случайной ошибки.
Тогда:
т. е.
что и требовалось доказать.
Следовательно, выборочная оценка дисперсии случайной ошибки
является несмещённой оценкой генеральной дисперсии случайной ошибки модели регрессии G2(?).
При условии извлечения из генеральной совокупности нескольких выборок одинакового объёма n и при одинаковых значениях объясняющих переменных х, наблюдаемые значения зависимой переменной у будут случайным образом колебаться за счёт случайного характера случайной компоненты ?. Отсюда можно сделать вывод, что будут варьироваться и зависеть от значений переменной у значения оценок коэффициентов регрессии и оценка дисперсии случайной ошибки модели регрессии.
Для иллюстрации данного утверждения докажем зависимость значения МНК-оценки
от величины случайной ошибки ?.
МНК-оценка коэффициента ?1 модели регрессии определяется по формуле:
В связи с тем, что переменная у зависит от случайной компоненты ? (yi=?0+?1xi+?i), то ковариация между зависимой переменной у и независимой переменной х может быть представлена следующим образом:
Для дальнейших преобразования используются свойства ковариации:
1) ковариация между переменной х и константой С равна нулю: Cov(x,C)=0, C=const;
2) ковариация переменной х с самой собой равна дисперсии этой переменной: Cov(x,x)=G2(x).
Исходя из указанных свойств ковариации, справедливы следующие равенства:
Cov(x,?0)=0 (?0=const);
Cov(x, ?1x)= ?1*Cov(x,x)= ?1*G2(x).
Следовательно, ковариация между зависимой и независимой переменными Cov(x,y) может быть записана как:
Cov(x,y)= ?1G2(x)+Cov(x,?).
В результате МНК-оценка коэффициента ?1 модели регрессии примет вид:
Таким образом, МНК-оценка
может быть представлена как сумма двух компонент:
1) константы ?1, т. е. истинного значения коэффициента;
2) случайной ошибки Cov(x,?), вызывающей вариацию коэффициента модели регрессии.
Однако на практике подобное разложение МНК-оценки невозможно, потому что истинные значения коэффициентов модели регрессии и значения случайной ошибки являются неизвестными. Теоретически данное разложение можно использовать при изучении статистических свойств МНК-оценок.
Аналогично доказывается, что МНК-оценка
коэффициента модели регрессии и несмещённая оценка дисперсии случайной ошибки
могут быть представлены как сумма постоянной составляющей (константы) и случайной компоненты, зависящей от ошибки модели регрессии ?.
Данный текст является ознакомительным фрагментом.
Читайте также
11. Критерии оценки неизвестных коэффициентов модели регрессии
11. Критерии оценки неизвестных коэффициентов модели регрессии
В ходе регрессионного анализа была подобрана форма связи, которая наилучшим образом отражает зависимость результативной переменной у от факторной переменной х:y=f(x).Необходимо оценить неизвестные
14. Оценка коэффициентов модели парной регрессии с помощью выборочного коэффициента регрессии
14. Оценка коэффициентов модели парной регрессии с помощью выборочного коэффициента регрессии
Помимо метода наименьших квадратов, с помощью которого в большинстве случаев определяются неизвестные параметры модели регрессии, в случае линейной модели парной регрессии
18. Характеристика качества модели регрессии
18. Характеристика качества модели регрессии
Качеством модели регрессии называется адекватность построенной модели исходным (наблюдаемым) данным.Для оценки качества модели регрессии используются специальные показатели.Качество линейной модели парной регрессии
22. Проверка гипотезы о значимости коэффициентов модели парной регрессии
22. Проверка гипотезы о значимости коэффициентов модели парной регрессии
Проверкой статистической гипотезы о значимости отдельных параметров модели называется проверка предположения о том, что данные параметры значимо отличаются от нуля.Необходимость проверки
25. Точечный и интервальный прогнозы для модели парной регрессии
25. Точечный и интервальный прогнозы для модели парной регрессии
Одна из задач эконометрического моделирования заключается в прогнозировании поведения исследуемого явления или процесса в будущем. В большинстве случаев данная задача решается на основе регрессионных
32. Построение частных коэффициентов корреляции для модели множественной регрессии через показатель остаточной дисперсии и коэффициент множественной детерминации
32. Построение частных коэффициентов корреляции для модели множественной регрессии через показатель остаточной дисперсии и коэффициент множественной детерминации
Помимо рекуррентных формул, которые используются для построения частных коэффициентов корреляции для
35. Проверка гипотезы о значимости коэффициентов регрессии и модели множественной регрессии в целом
35. Проверка гипотезы о значимости коэффициентов регрессии и модели множественной регрессии в целом
Проверка значимости коэффициентов регрессии означает проверку основной гипотезы об их значимом отличии от нуля.Основная гипотеза состоит в предположении о незначимости
39. Модели регрессии, нелинейные по факторным переменным
39. Модели регрессии, нелинейные по факторным переменным
При исследовании социально-экономических явлений и процессов далеко не все зависимости можно описать с помощью линейной связи. Поэтому в эконометрическом моделировании широко используется класс нелинейных
40. Модели регрессии, нелинейные по оцениваемым коэффициентам
40. Модели регрессии, нелинейные по оцениваемым коэффициентам
Нелинейными по оцениваемым параметрам моделями регрессииназываются модели, в которых результативная переменная yi нелинейно зависит от коэффициентов модели ?0…?n.К моделям регрессии, нелинейными по
41. Модели регрессии с точками разрыва
41. Модели регрессии с точками разрыва
Определение. Моделями регрессии с точками разрыва называются модели, которые нельзя привести к линейной форме, т. е. внутренне нелинейные модели регрессии.Модели регрессии делятся на два класса:1) кусочно-линейные модели регрессии;2)
44. Методы нелинейного оценивания коэффициентов модели регрессии
44. Методы нелинейного оценивания коэффициентов модели регрессии
Функцией потерь или ошибок называется функционал вида
Также в качестве функции потерь может быть использована сумма модулей отклонений наблюдаемых значений результативного признака у от теоретических
46. Проверка гипотезы о значимости нелинейной модели регрессии. Проверка гипотезы о линейной зависимости между переменными модели регрессии
46. Проверка гипотезы о значимости нелинейной модели регрессии. Проверка гипотезы о линейной зависимости между переменными модели регрессии
На нелинейные модели регрессии, которые являются внутренне линейными, т. е. сводимыми к линейному виду, распространяются все
57. Гетероскедастичность остатков модели регрессии
57. Гетероскедастичность остатков модели регрессии
Случайной ошибкой называется отклонение в линейной модели множественной регрессии:?i=yi–?0–?1x1i–…–?mxmiВ связи с тем, что величина случайной ошибки модели регрессии является неизвестной величиной, рассчитывается
60. Устранение гетероскедастичности остатков модели регрессии
60. Устранение гетероскедастичности остатков модели регрессии
Существует множество методов устранения гетероскедастичности остатков модели регрессии. Рассмотрим некоторые из них.Наиболее простым методом устранения гетероскедастичности остатков модели регрессии
63. Устранение автокорреляции остатков модели регрессии
63. Устранение автокорреляции остатков модели регрессии
В связи с тем, что наличие в модели регрессии автокорреляции между остатками модели может привести к негативным результатам всего процесса оценивания неизвестных коэффициентов модели, автокорреляция остатков
67. Модели регрессии с переменной структурой. Фиктивные переменные
67. Модели регрессии с переменной структурой. Фиктивные переменные
При построении модели регрессии может возникнуть ситуация, когда в неё необходимо включить не только количественные, но и качественные переменные (например, возраст, образование, пол, расовую
Обобщим
КЛММР вида (3.1). Пусть по-прежнему мы
располагаем выборочными наблюдениями
над k
переменными Yi
и
,j=1,…,
k,
i=1,2,…,n
и строим
регрессию:
(4.3)
Откажемся
от предположения КЛММР о некоррелированности
и гомоскедастичности случайной ошибки
(3.3). То есть относительно переменных
модели в уравнении (4.3) примем следующие
основные гипотезы:
E(ui)=0;
(4.4)

X1,
X3,
…, Xk
– неслучайные переменные; (4.6)
Не должно существовать
строгой линейной
зависимости
между переменными X1,
X3,
…, Xk.
(4.7)
Суть
гипотезы (4.5) в том, что все случайные
ошибки ui
имеют непостоянную дисперсию, то есть
не выполняется условие гомоскедастичности
дисперсии – имеет место гетероскедастичность
дисперсии
ошибок. Кроме того, ковариации остатков
могут быть произвольными и отличными
от нуля (вторая строчка соотношения
(4.5)).
Модель
вида (4.3)-(4-7) называется обобщенной
линейной моделью множественной регрессии
(ОЛММР).
Отличие ОЛММР от КЛММР состоит в изменении
предположений о поведении случайной
ошибки (4.5).
К
ОЛММР может быть применен метод наименьших
квадратов, однако (3.6) оказывается
неприменимой к модели (4.3)-(4-7) в силу
потери свойства оптимальности оценок.
Но МНК к ОЛММР может быть применен.
Критерий
минимизации суммы квадратов ошибок МНК
в силу условия (4.5) заменяется на другой
– минимизация обобщенной суммы квадратов
отклонений (с учетом ненулевых ковариаций
случайной ошибки для разных наблюдений
и непостоянной дисперсии ошибки) и
соответственно усложняется вид системы
уравнений для определения оценок
коэффициентов по сравнению с системой
(3.6) для МНК. После решения полученной
системы линейных алгебраических
уравнений получим линейные несмещенные
оценки коэффициентов ОЛММР, которые
будут эффективными. Указанный метод
получения оценок называется обобщенным
методом наименьших квадратов (ОМНК) или
методом Айткена.
Обозначим6:
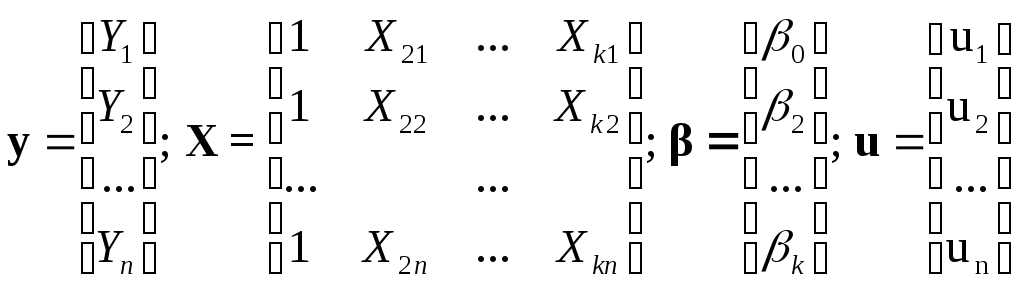
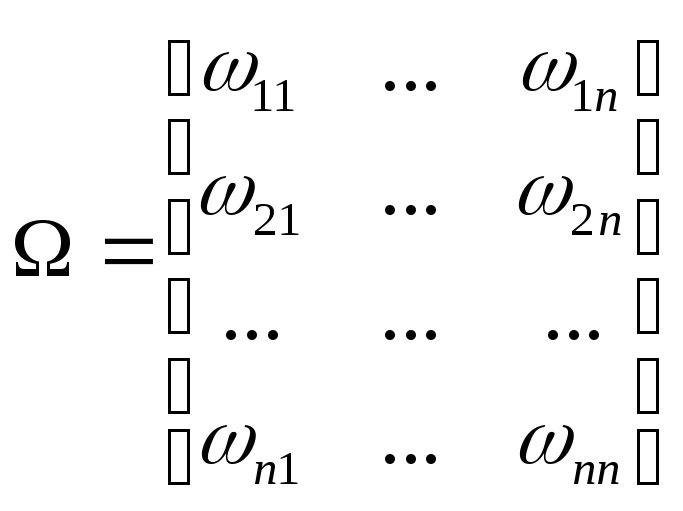
Тогда
модель (4.3)-(4.7) запишется в матричном
виде:
y=X+u,
при
условиях
E(u)=0;
E(uuT)=2;
X
– не из случайных чисел;
rank(X)=k+1<n.
Оценки
МНК получаются по формуле
.
Оценки ОМНК получаются по формуле.
Подчеркнем,
что для применения ОМНК в (4.5) необходимо
знать значения в правой части равенства
(в частности элементы матрицы ),
что на практике случается крайне редко.
Поэтому каким-либо способом оценивают
величины
i,
j=1,…,n.
А затем используют эти оценки в расчетах
коэффициентов модели. Этот подход
составляет суть так называемого
доступного
обобщенного метода наименьших квадратов.
Конкретные способы оценки неизвестных
ковариаций будут рассмотрены ниже.
4.3 Линейная модель множественной регрессии
с
гетероскедастичными остатками
Довольно
часто при построении регрессии
анализируемые объекты неоднородны,
например, при исследовании структуры
потребления домохозяйств естественно
ожидать, что колебания в структуре будут
выше для богатых, чем для бедных
домохозяйств. В этой ситуации предположение
(3.3) о постоянстве
дисперсии случайной
ошибки (имеется в виду возможное поведение
случайного члена до того, как сделана
выборка) оказывается не соответствующим
действительности. В случаях, когда
дисперсия u
одинакова
в каждый момент времени или для каждого
значения X,
существуют определенные ограничения
(в некоторой полосе) для расположения
точек на графике X
и Y,
согласно которым отчетливой тенденции
к увеличению или уменьшению дисперсии
по мере ростаX
не наблюдается.
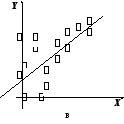
На
рис. 4.1 приводятся примеры изменения
разброса (гетероскедастичности) случайной
ошибки регрессии.
На
рис. 4.1а изображена ситуация, когда
значения дисперсии
растут по мере увеличения значений
регрессораX.
На рис. 4.1б дисперсия ошибки достигает
максимальной величины при средних
значениях X,
уменьшаясь по мере приближения к крайним
значениям. Наконец, на рис. 4.1в дисперсия
ошибки оказывается наибольшей при малых
значениях X,
быстро уменьшается и становится
однородной по мере увеличения независимой
переменной X.
Y
Рис.
4.1. Примеры гетероскедастичности
Гетероскедастичность
дисперсии
случайного члена означает, что
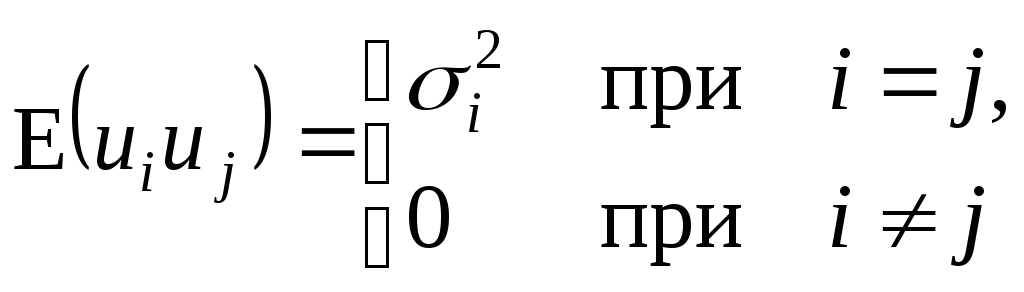
(4.8)
т.е.
нарушается предположение (3.3) в КЛММР,
и мы должны рассматривать ОЛММР с нулевой
ковариацией случайных ошибок (ср. (4.5) и
(4.8)).
Основные
последствия гетероскедастичности
проявляются в получении неэффективных
оценок МНК и занижении стандартных
ошибок коэффициентов регрессии, что
завышает t-статистику
и дает неправильное представление о
точности уравнения регрессии.
Поэтому
для оценивания регрессии с гетероскедастичными
случайными ошибками применяется ОМНК.
Предположим,
что нам известны значения величин
i
=1,…,n.
Тогда уравнение (4.3) разделим на i:
,
и
получим регрессию с постоянной
(гомоскедастичной) дисперсией случайного
члена, действительно
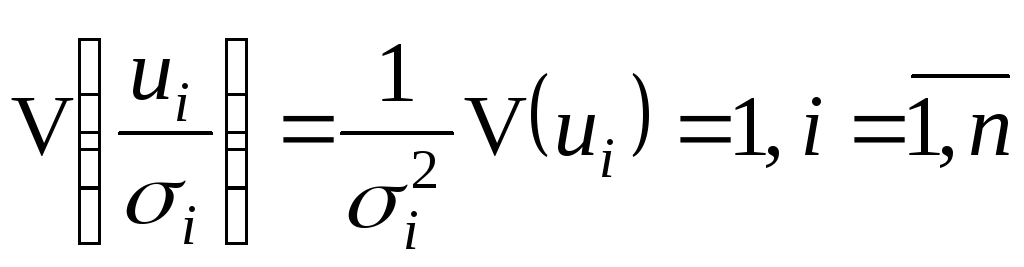
Для
получения оценок неизвестных дисперсий
i
=1,…,n
будем
предполагать, что они пропорциональны
некоторым числам, т.е.
,
где 2
– некоторая константа.
Принимая
различные гипотезы относительно
характера гетероскедастичности, будем
иметь соответствующие значения i.
Если
дисперсия случайного члена пропорциональна
квадрату регрессора X,
так что
,
то
,i
=1,…,n.
Если
дисперсия случайного члена пропорциональна
X,
так что
,
то
,i
=1,…,n.
Например, для случая одной объясняющей
переменной имеем в этом случае систему
уравнений ОМНК вида:
Поскольку значения
i,i=1,…,nявляются фактически весами, которые
устраняют неоднородность дисперсии,
то ОМНК для системы с гетероскедастичностью
часто называютметодом взвешенных
наименьших квадратов.
Существуют также
и другие методы коррекции модели на
гетероскедастичность, в частности
состоятельное оценивание стандартных
ошибок. Известны способы коррекции
стандартных ошибок Уайта и Невье-Веста
[5, с. 144-146].
О проверке выборки
на гомоскедастичность.
Рассмотрим вопрос
тестирования выборки на наличие
гомоскедастичности. Возможности такой
проверки зависят от природы исходных
данных.
Если
имеется обширная выборка, то можно
воспользоваться стандартным критерием
однородности дисперсии Бартлетта.
Расчленяя
выборку на m
независимых групп (каждой из них
соответствует единственное значение
переменной X),
вычислим величины:
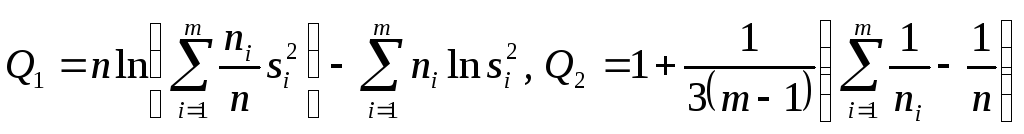
причем
ni=n,
здесь ni
— число наблюдений в i
группе,
— дисперсия ошибки вi
группе. Величина Q1/Q2
будет приближенно удовлетворять
распределению 2
с (m-1)
степенями свободы. Если вычисленное по
выборке значение 2
меньше критического, то гипотеза об
однородности выборочной дисперсии
принимается, в противном случае
отклоняется.
В
случаях малого количества наблюдений
в выборке, когда группировка данных
невозможна, используется тест
Голдфелда и Куандта.
Он предусматривает осуществление
следующих шагов:
1. Упорядочить
наблюдения по убыванию той независимой
переменной, относительно которой есть
подозрение на гетероскедастичность.
2.
Опустить v
наблюдений, оказавшихся в центре (v
должно быть примерно равно четверти
общего количества наблюдений n).
3.
Оценить отдельно обыкновенным методом
наименьших квадратов регрессии на
первых (n—v)/2
наблюдениях и на последних (n—v)/2
наблюдениях при условии, что (n—v)/2
больше числа оцениваемых параметров
k.
4.
Пусть e1
и e2
— суммы квадратов остатков от первой и
второй регрессий соответственно. Тогда
статистика Q=e1/e2
будет удовлетворять F
— распределению с ((n—v-2k)/2;
(n—v-2k)/2)
степенями свободы. При Q
< F
гипотеза об однородности выборочной
дисперсии принимается, в противном
случае (с ростом величины Q)
отклоняется.
Очевидно,
что решающим для этого теста является
выбор величины v.
Слишком большое значение v
уменьшает надежность теста. Экспериментально
авторами теста установлено, что для
одной объясняющей переменной оптимальное
v=8
при n=30
и v=16
при n=60.
Кроме
перечисленных, могут использоваться
тесты на гетероскедастичность Уайта,
Бреуша-Пагана и др.
Пример.
Проверим по критерию Бартлетта данные
из примера 1 раздела 3. Будем иметь табл.
4.1. В табл. 4.1 учтено, что среднее значение
ei
равно 0, а значит,
.
Примем m=2.
Тогда:
Q1=20ln(10/20167,41
+ 10/2059,69)
(10ln(167,41)+10ln(59,69))=2,55;
Q2=1+1/3(1/10+1/10-1/20)=1,05;
Q1/Q2=2,43.
При
одной степени свободы критическое
значение 2
при 5% уровне значимости равно 3,84, а
следовательно, гипотеза об однородности
выборочной дисперсии принимается.
Для
тех же данных применим тест Гольдфельда
и Куандта. В нашем случае число объясняющих
переменных k=2,
количество исходных данных в выборке
n=20.
Упорядочим наблюдения по убыванию
независимой переменной X2
– расстояние перевозки, относительно
которой есть подозрение на
гетероскедастичность. Опустим 4
наблюдения, оказавшихся в центре, т.е.
v=4.
При значении v=4
получим суммы квадратов остатков от
первой и второй регрессий соответственно
e1=1167,38
и e2=31,49.
Статистика Q=e1/e2=1167,38/31,49
= 37,07 удовлетворяет F-распределению
с (6; 6) степенями свободы. F0,05(6,
6) = 4,28, Q
> F
и гипотеза об однородности выборочной
дисперсии должна быть отвергнута.
Поскольку
тесты дают противоположные результаты
(что не редкость в эконометрике), то
лучше согласиться с наихудшим вариантом,
т.е. предположить наличие гетероскедастичности
и предпринять соответствующие
корректирующие меры. В частности,
скорректировать стандартные ошибки по
формуле Невье-Веста. В таблице 4.2
представлены результаты регрессии до
корректировки и после корректировки
на гетероскедастичность. Видно, что на
величине коэффициентов регрессии
корректировка на гетероскедастичность
не отражается, а стандартные ошибки и
значения статистик были пересчитаны.
Таблица
4.1
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Линейная регрессия: моделирование и допущения
Перевод
Ссылка на автора
Регрессионный анализ — это мощный статистический процесс для поиска отношений в наборе данных, при этом основное внимание уделяется отношениям между независимыми переменными (предикторами) и зависимой переменной (результатом). Он может быть использован для построения моделей для вывода или прогнозирования. Среди нескольких методов регрессионного анализа, линейная регрессия устанавливает основу и довольно широко используется для несколько реальных приложений,
В этой статье мы рассмотрим построение модели линейной регрессии для вывода. Набор данных, который мы будем использовать, это данные о страховых сборах, полученные из Kaggle, Этот набор данных состоит из 1338 наблюдений и 7 столбцов: возраст, пол, bmi, дети, курильщик, регион и сборы.
Ключевые вопросы, которые мы будем задавать:
- Существует ли связь между медицинскими расходами и другими переменными в наборе данных?
- Насколько верна модель, которую мы построили?
- Что мы можем сделать, чтобы улучшить модель?
Начнем с импорта основных необходимых библиотек и данных:
library(magrittr)
library(car)
library(broom)
library(ggplot2)fileName <- './input/medicalCost/insurance.csv'insurance <- read.csv(fileName)
summary(insurance)
Некоторые простые наблюдения, которые можно сделать из резюме:
- Возраст участников варьируется от 18 до 64 лет.
- Около 49,48% участников составляют женщины.
- Bmi участников колеблется от 15,96 до 53,13.
- Только 20,48% участников являются курильщиками.
Давайте начнем с построения линейной модели. Вместо простой линейной регрессии, где у вас есть один предиктор и один результат, мы будем использовать множественную линейную регрессию, где у вас есть более одного предиктора и один результат.
Множественная линейная регрессия следует формуле:
Коэффициенты в этом линейном уравнении обозначают величину аддитивного отношения между предиктором и откликом. Проще говоря, если все остальное зафиксировать, изменение единицы в x1 приведет к изменению β1 в результате, и так далее.
Есть ли связь между медицинскими расходами и предикторами?
Наш первый шаг — выяснить, есть ли связь между результатом и предикторами.
Нулевая гипотеза состояла бы в том, что нет никакой связи между какими-либо предикторами и ответом, что можно проверить путем вычисления F статистика, Значение p статистики F можно использовать для определения, можно ли отклонить нулевую гипотезу или нет.
Мы начнем с подбора модели множественной линейной регрессии с использованием всех предикторов:
lm.fit <- lm(formula = charges~., data = insurance)
#Here '.' means we are using all the predictors in the dataset.
summary(lm.fit)
Высокое значение F-статистики с очень низким p-значением (<2,2e-16) подразумевает, что нулевая гипотеза может быть отклонена. Это означает, что существует потенциальная связь между предикторами и результатом.
RSE (Остаточная стандартная ошибка) — это оценка стандартного отклонения неприводимой ошибки (ошибки, которую нельзя уменьшить, даже если мы знали истинную линию регрессии; следовательно, неприводимую). Проще говоря, это среднее отклонение между фактическим результатом и истинной линией регрессии. Большое значение RSE (6062) означает большое отклонение нашей модели от истинной линии регрессии.
R-квадрат (R²) измеряет долю изменчивости в результате, которая может быть объяснена моделью, и является почти всегда между 0 и 1 ; чем выше значение, тем лучше модель способна объяснить изменчивость в результате. Однако увеличение числа предикторов в основном приводит к увеличению значения R² из-за инфляция R-квадрат, Скорректированный R-квадрат регулирует значение R², чтобы избежать этого эффекта. Высокое значение скорректированного R² (0,7494) показывает, что более 74% отклонений в данных объясняется моделью.
Std. Ошибка дает нам среднюю величину, на которую оценочный коэффициент предиктора отличается от фактического коэффициента предиктора. Он может быть использован для вычисления доверительного интервала предполагаемого коэффициента, который мы увидим позже.
т значениепредиктора говорит нам, сколько стандартных отклонений его расчетный коэффициент от 0.Pr (> | t |)для предиктора — это значение p для оцененного коэффициента регрессии, которое аналогично тому, как сказать, какова вероятность увидеть значение t для коэффициента регрессии. Очень низкое значение p (<0,05) для предиктора может быть использовано для того, чтобы сделать вывод, что существует связь между предиктором и результатом.
Наш следующий шаг должен быть валидация регрессионного анализа, Это может означать проверку основополагающих допущений модели, проверку структуры модели с разными предикторами, поиск наблюдений, которые не были достаточно хорошо представлены в модели, и многое другое. Мы рассмотрим некоторые из этих методов и предположений.
Какие переменные имеют сильное отношение к медицинским расходам?
Теперь, когда мы определили, что существует связь между предикторами и результатом, наш следующий шаг будет выяснить, все ли или только некоторые из предикторов связаны с результатом
Если мы посмотрим на p-значения оценочных коэффициентов выше, мы увидим, что не все коэффициенты статистически значимы (<0,05). Это означает, что только часть предикторов связана с результатом.
Мы можем посмотреть на отдельные p-значения для выбора переменных. Это не может быть проблемой, когда количество предикторов (7) довольно мало по сравнению с количеством наблюдений (1338). Однако этот метод не будет работать, когда число предикторов больше числа наблюдений из-за проблема множественного тестирования, Лучший способ выбора предикторов выбор функции / переменной методы, такие как прямой выбор, обратный выбор или смешанный выбор.
Прежде чем перейти к выбору объектов, используя любой из этих методов, давайте попробуем линейную регрессию, используя объекты только со значимыми значениями p.
lm.fit.sel <- lm(charges~age+bmi+children+smoker+region,
data = insurance)
Мы сравним это с смешанный выбор, который является комбинацией прямого и обратного выбора. Это можно сделать в R, используяstepAIC ()функция, которая использует Информационный критерий Акайке (AIC), чтобы выбрать лучшую модель из нескольких моделей.
#selecting direction = "both" for mixed selection
step.lm.fit <- MASS::stepAIC(lm.fit, direction = "both",
trace = FALSE)
Давайте сравним две модели:
step.lm.fit$call
lm.fit.sel$call
Модель, заданная пошаговым отбором, такая же, как модель, которую мы получили, выбрав предикторы со значительными значениями p (работает в этом случае)
Есть ли мультиколлинеарные особенности?
Мультиколлинеарность в множественной регрессии — это явление, при котором два или более предиктора тесно связаны друг с другом, и, следовательно, один предиктор может использоваться для прогнозирования значения другого. Проблема с мультиколлинеарностью состоит в том, что это может затруднить оценку индивидуальных эффектов предикторов на результат.
Мультиколлинеарность может быть обнаружена с использованием дисперсионного фактора инфляции (VIF). VIF любого предиктора — это отношение дисперсии его оценочного коэффициента в полной модели к дисперсии его оценочного коэффициента, когда он подходит для результата только сам по себе (как в простой линейной регрессии). VIF 1 указывает на отсутствие мультиколлинеарности. Обычно значение VIF выше 5 или 10 принимается как показатель мультиколлинеарности. Самый простой способ избавиться от мультиколлинеарности в этом случае — отказаться от предиктора с высоким значением VIF.
vif(step.lm.fit) %>%
knitr::kable()
Ни один из предикторов в нашем случае не имеет высокого значения VIF. Следовательно, нам не нужно беспокоиться о мультиколлинеарности в нашем случае.
Являются ли отношения линейными?
Применяя линейную регрессию, мы предполагаем, что существует линейная связь между предикторами и результатом. Если исходные отношения довольно далеки от линейных, то большинство сделанных нами выводов будет сомнительным.
Нелинейность модели может быть определена с использованием остаточного графика подгоночных значений по отношению к остаточным значениям. остаточный для любого наблюдения — это разница между фактическим результатом и соответствующим результатом в соответствии с моделью. Наличие шаблона на остаточном графике будет означать проблему с линейным допущением модели.
#type = "rstandard" draws a plot for standardized residualsresidualPlot(step.lm.fit, type = "rstandard")
Синяя линия представляет плавный узор между установленными значениями и стандартными невязками. Кривая в нашем случае обозначает небольшую нелинейность в наших данных.
Нелинейность можно дополнительно изучить, посмотрев на Остаточные участки (Графики ЧР).
ceresPlots(step.lm.fit)
Розовая линия (линия остатка) моделируется для связи между предиктором и остатками. Синяя пунктирная линия (линия компонента) предназначена для линии наилучшего соответствия. Значительная разница между двумя линиями для предиктора подразумевает, что предиктор и результат не имеют линейных отношений.
Этот вид несоответствия можно увидеть на графике CR дляиндекс массы тела, Одним из методов исправления этого является введение нелинейного преобразования предикторов модели. Давайте попробуем добавить нелинейное преобразованиеиндекс массы телак модели.
#update() can be used to update an existing model with new requirementsstep.lm.fit.new <- update(step.lm.fit, .~.+I(bmi^1.25)) ceresPlots(step.lm.fit.new)
График CR bmi больше не имеет разницы между остаточной линией и компонентной линией.
Мы можем использовать ANOVA, чтобы проверить, значительно ли новая модель лучше предыдущей. Низкое значение p (<0,05) для новой модели будет означать, что мы можем сделать вывод, что она лучше, чем в предыдущей модели:
anova(step.lm.fit, step.lm.fit.new, test = "F")
Поскольку модель с нелинейным преобразованиеминдекс массы телаимеет достаточно низкое значение p (<0,05), можно сделать вывод, что оно лучше, чем в предыдущей модели, хотя значение p незначительно.
Давайте посмотрим на остаточный сюжет этой новой модели.
residualPlot(step.lm.fit.new, type = "rstandard")
Глядя на остаточный график новой модели, не наблюдается больших изменений в общей структуре стандартных остатков.
Другим методом решения проблемы нелинейности является введение взаимодействие между некоторыми предикторами. Человек, который курит и имеет высокий BMI, может иметь более высокие расходы по сравнению с человеком, который имеет более низкий BMI и является некурящим Давайте обновим модель, чтобы ввести взаимодействие междуиндекс массы телаа такжекурильщики посмотреть, если это имеет значение:
lm.fit1 <- update(step.lm.fit.new, ~ .+bmi*smoker)residualPlot(lm.fit1, type = "rstandard", id=TRUE)
anova(step.lm.fit.new, lm.fit1, test = "F")
Мало того, что отношение становится более линейным с меньшим появлением рисунка на остаточном графике, новая модель значительно лучше, чем предыдущая модель (без взаимодействий), что можно увидеть при значении p (<2.2e-16).
#checking the value of adjusted r-squared of new model summary(lm.fit1)$adj.r.squared
Значение R² модели также увеличилось до более чем 0,84.
Непостоянная дисперсия ошибок
Постоянная дисперсия (гомоскедастичность) ошибок — еще одно предположение о модели линейной регрессии. Термины ошибок могут, например, изменяться со значением переменной отклика в случае непостоянной дисперсии (гетероскедастичности) ошибок. Некоторые из графических методов определения гетероскедастичности — это наличие воронкообразной формы на остаточном графике или наличие кривой на остаточном графике. На приведенном выше графике мы не видим четкой картины.
Статистический способ — это расширение теста Бреуша-Пагана, доступное в R какncvTest ()в пакете машин. Предполагается, что нулевая гипотеза о постоянной дисперсии ошибок отличается от альтернативной гипотезы о том, что дисперсия ошибок изменяется в зависимости от уровня ответа или от линейной комбинации предикторов.
# non-constant error variance test
ncvTest(lm.fit1)
Очень низкое значение p (~ 0,000023) означает, что нулевая гипотеза может быть отклонена. Другими словами, существует высокая вероятность того, что ошибки имеют непостоянную дисперсию.
Одним из методов решения этой проблемы является преобразование переменной результата.
yTransformer <- 0.8
trans.lm.fit <- update(lm.fit1, charges^yTransformer~.)# non-constant error variance test
ncvTest(trans.lm.fit)
residualPlot(trans.lm.fit, type = "rstandard", id=T)
Значение p, равное ~ 0,94, подразумевает, что мы не можем отвергнуть нулевую гипотезу о постоянной дисперсии членов ошибки. Однако наблюдается небольшое увеличение нелинейности модели, что видно на остаточном графике. Это может быть исправлено в дальнейшем, глядя на отношения между отдельными предикторами и результатами.
Соотношение условий ошибок
Важным допущением модели линейной регрессии является то, что члены последовательных ошибок некоррелированы. Стандартные ошибки оцененных коэффициентов регрессии рассчитываются на основе этого предположения. Если последовательные члены ошибки коррелируют, стандартные ошибки оцененных коэффициентов регрессии могут быть намного больше.
Мы можем проверить автокорреляцию ошибок с помощью Тест Дурбина-Ватсона, Нулевая гипотеза состоит в том, что последовательные ошибки не имеют автокорреляции.
set.seed(1)# Test for Autocorrelated Errors
durbinWatsonTest(trans.lm.fit, max.lag = 5, reps=1000)
Значение р ни для одного из 5 лагов не меньше 0,05. Следовательно, мы не можем отвергнуть нулевую гипотезу о том, что последовательные ошибки не коррелированы, заключив, что последовательные ошибки не зависят друг от друга.
Интерпретации
Давайте посмотрим на фактические расходы в сравнении с установленными значениями для окончательной модели и сравним ее с результатами исходной модели. Функция для построения fit_vs_actual, которая будет использоваться перед следующим блоком, Вот:
#fitted values of initial modelfitted_init <- predict(lm.fit, insurance,
interval = "confidence") %>%
tidy()
g1 <- fitted_vs_actual(fitted_init, "Initial Model")#fitted values of final modelfitted_final <- predict(trans.lm.fit, insurance,
interval = "confidence")^(1/yTransformer) %>%
tidy()
g2 <- fitted_vs_actual(fitted_final, "Final Model")#creating the two plots side-by-side
gridExtra::grid.arrange(g1,g2, ncol = 2)
Первоначальная модель способна приблизить фактические расходы ниже 17 000 долларов США, но, поскольку фактические расходы превышают 20 000 долларов США, разрыв между фактическими расходами и установленными значениями продолжает увеличиваться. В соответствии с первоначальной моделью, фактические расходы около 50 000 долларов США устанавливаются примерно на уровне 40 000 долларов США или ниже, и этот разрыв продолжает увеличиваться.
Для сравнения, установленные значения в новой модели намного ближе к фактическим расходам, хотя есть еще много изменений, не объясняемых этой моделью. Это все еще значительное улучшение по сравнению с первоначальной моделью.
Мы можем посмотреть на оценочные коэффициенты предикторов и их доверительные интервалы для интерпретации того, как они определяют модель.
confint(trans.lm.fit) %>%
tidy() %>%
tibble::add_column(coefficients = trans.lm.fit$coefficients,
.after = 2) %>%
knitr::kable()
В приведенной выше таблице X2.5 и X97.5 отмечают нижнюю и верхнюю границы для 95% доверительного интервала коэффициентов регрессии. Они рассчитываются с использованием стандартных ошибок оценочных коэффициентов. В качестве примера длявозрастоценочный коэффициент составляет ~ 33,69, а 95% -ный доверительный интервал находится между ~ 31,56 и ~ 35,83. Это означает, что в соответствии с моделью, сохраняя все остальное фиксированным, увеличение возраста в 1 год приведет к увеличению стоимости обвинений на 33,69 ^ (0,8). (так как мы изменили результат). Тем не менее, это оценка и, следовательно, есть возможность для вариаций. Это изменение объясняется доверительным интервалом, означающим, что примерно в 95% случаев изменение величины зарядов ^ (0,8) будет между 31,56 и 35,83, сохраняя все остальное фиксированным.
Давайте визуализируем эти эффекты, чтобы лучше понять, как предикторы связаны с результатом в соответствии с моделью. Функция для получения эффектов модели на преобразованный результат Вот,
plot_effect('age', 'age') %>%
ggplot(aes(x = age, y = fit)) +
theme_bw() +
geom_line() +
geom_ribbon(aes(ymin = lower, ymax = upper), alpha = 0.5)
Для среднего значения других предикторов страховые сборы увеличиваются с увеличением возраста. Более интересные эффекты можно увидеть для взаимодействия междуиндекс массы телаа такжекурильщик:
plot_effect('bmi*smoker', 'bmi') %>%
ggplot(aes(x = x.bmi, y = fit)) +
facet_wrap(~x.smoker) +
theme_bw() +
geom_line() +
geom_ribbon(aes(ymin = lower, ymax = upper), alpha = 0.5)
Некурящие, независимо от их bmi, имеют в основном низкие страховые взносы для среднего значения других предикторов Курильщики с низким bmi имеют низкие страховые взносы, хотя все еще выше, чем некурящие с любым значением bmi. Более того, по мере того как их bmi увеличивается, страховые сборы курильщиков быстро растут.
Вывод
Модель, которую мы построили, может использоваться для вывода о том, как различные предикторы влияют на результат Это далеко от совершенства. Их по-прежнему наличие нелинейности и непостоянной дисперсии ошибок. Кроме того, выбросы и точки воздействия должны быть проанализированы, чтобы найти лучшую модель. Он не может (и, скорее всего, не даст) аналогичных результатов, когда используется для прогнозирования результата для новых невидимых данных. Чтобы использовать его для прогнозирования, необходимо принять более конкретные меры для обеспечения точности модели, например перекрестную проверку. Это все еще помогает, предоставляя хорошие оценки значимых отношений между предикторами и результатом. Эти оценки могут быть использованы для обобщения данных в более полезной и представительной форме.
Вы можете увидеть оригинальный пост Вот или найди меня на LinkedIn,
источники
- Введение в статистическое обучение, с применением в R. Джеймс Дж., Виттен Д., Хасти Х., Тибширани Р.
- Википедия
- Quick-R
- Статистика Как
- StackExchange
- Переполнение стека
The consequences of heteroscedasticity are:
-
The ordinary least squares (OLS) estimator $\hat{\mathbf{b}} = \left(X’X \right)X’\mathbf{y}$ is still consistent but it is no longer efficient.
-
The estimate $\hat{\mathrm{Var}}\left(\mathbf{b} \right) = \left( X’X\right)^{-1} \hat{\sigma}^2$ where $\hat{\sigma}^2 = \frac{1}{n-k} \mathbf{e’}{\mathbf{e}}$ is not a consistent estimator anymore for the covariance matrix of your estimator $\hat{\mathbf{b}}$. It may be both biased and inconsistent. And in practice, it can substantially underestimate the variance.
Point (1) may not be a major issue; people often use the ordinary OLS estimator anyway. But point (2) must be addressed. What to do?
You need heteroscedasticity-consistent standard errors. The standard approach is to lean on large-sample assumptions, asymptotic results and estimate the variance of $\mathbf{b}$ using:
$$\hat{\mathrm{Var}}\left(\mathbf{b}\right)=\frac{1}{n}\left( \frac{X’X}{n} \right)^{-1} S \left( \frac{X’X}{n} \right)^{-1}$$
where $S$ is estimated as $S = \frac{1}{n-k}\sum_i \left(\mathbf{x}_i e_i\right) \left(\mathbf{x}_i e_i \right)’$.
This gives heteroskedasticity-consistent standard errors. They’re also known as Huber-White standard errors, robust standard errors, «sandwich» estimator, etc… Any basic standard statistics package has an option for robust standard errors. Use it!
Some additional comments (update)
If the heteroskedasticity is large enough, the regular OLS estimate can have big practical problems. While still a consistent estimator, you may have small sample problems where your whole estimate is driven by a few, high variance observations. (This is what @seanv507 is alluding to in comments). The OLS estimator is inefficient in that it’s giving more weight to high variance observations than optimal. The estimate may be extremely noisy.
A problem with trying to fix the inefficiency is that you probably don’t know the covariance matrix for the error terms either, hence using something like GLS can make things even worse if your estimate of the error term covariance matrix is garbage.
Also, the Huber-White standard errors I give above may have big problems in small samples. There is a long literature on this topic. Eg. see Imbens and Kolesar (2016), «Robust Standard Errors in Small Samples: Some Practical Advice.»
Direction for further study:
If this is self-study, the next practical thing to consider are clustered standard errors. These correct for arbitrary correlation within clusters.
Обобщим
КЛММР вида (3.1). Пусть по-прежнему мы
располагаем выборочными наблюдениями
над k
переменными Yi
и
,j=1,…,
k,
i=1,2,…,n
и строим
регрессию:
(4.3)
Откажемся
от предположения КЛММР о некоррелированности
и гомоскедастичности случайной ошибки
(3.3). То есть относительно переменных
модели в уравнении (4.3) примем следующие
основные гипотезы:
E(ui)=0;
(4.4)

X1,
X3,
…, Xk
– неслучайные переменные; (4.6)
Не должно существовать
строгой линейной
зависимости
между переменными X1,
X3,
…, Xk.
(4.7)
Суть
гипотезы (4.5) в том, что все случайные
ошибки ui
имеют непостоянную дисперсию, то есть
не выполняется условие гомоскедастичности
дисперсии – имеет место гетероскедастичность
дисперсии
ошибок. Кроме того, ковариации остатков
могут быть произвольными и отличными
от нуля (вторая строчка соотношения
(4.5)).
Модель
вида (4.3)-(4-7) называется обобщенной
линейной моделью множественной регрессии
(ОЛММР).
Отличие ОЛММР от КЛММР состоит в изменении
предположений о поведении случайной
ошибки (4.5).
К
ОЛММР может быть применен метод наименьших
квадратов, однако (3.6) оказывается
неприменимой к модели (4.3)-(4-7) в силу
потери свойства оптимальности оценок.
Но МНК к ОЛММР может быть применен.
Критерий
минимизации суммы квадратов ошибок МНК
в силу условия (4.5) заменяется на другой
– минимизация обобщенной суммы квадратов
отклонений (с учетом ненулевых ковариаций
случайной ошибки для разных наблюдений
и непостоянной дисперсии ошибки) и
соответственно усложняется вид системы
уравнений для определения оценок
коэффициентов по сравнению с системой
(3.6) для МНК. После решения полученной
системы линейных алгебраических
уравнений получим линейные несмещенные
оценки коэффициентов ОЛММР, которые
будут эффективными. Указанный метод
получения оценок называется обобщенным
методом наименьших квадратов (ОМНК) или
методом Айткена.
Обозначим6:

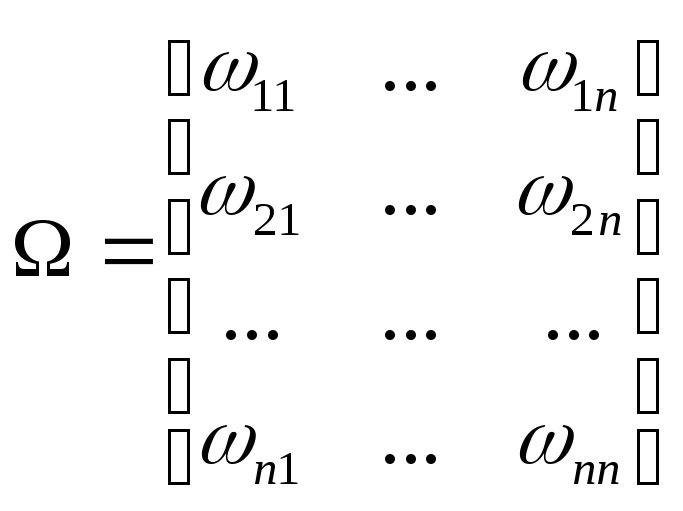
Тогда
модель (4.3)-(4.7) запишется в матричном
виде:
y=X+u,
при
условиях
E(u)=0;
E(uuT)=2;
X
– не из случайных чисел;
rank(X)=k+1<n.
Оценки
МНК получаются по формуле
.
Оценки ОМНК получаются по формуле.
Подчеркнем,
что для применения ОМНК в (4.5) необходимо
знать значения в правой части равенства
(в частности элементы матрицы ),
что на практике случается крайне редко.
Поэтому каким-либо способом оценивают
величины
i,
j=1,…,n.
А затем используют эти оценки в расчетах
коэффициентов модели. Этот подход
составляет суть так называемого
доступного
обобщенного метода наименьших квадратов.
Конкретные способы оценки неизвестных
ковариаций будут рассмотрены ниже.
4.3 Линейная модель множественной регрессии
с
гетероскедастичными остатками
Довольно
часто при построении регрессии
анализируемые объекты неоднородны,
например, при исследовании структуры
потребления домохозяйств естественно
ожидать, что колебания в структуре будут
выше для богатых, чем для бедных
домохозяйств. В этой ситуации предположение
(3.3) о постоянстве
дисперсии случайной
ошибки (имеется в виду возможное поведение
случайного члена до того, как сделана
выборка) оказывается не соответствующим
действительности. В случаях, когда
дисперсия u
одинакова
в каждый момент времени или для каждого
значения X,
существуют определенные ограничения
(в некоторой полосе) для расположения
точек на графике X
и Y,
согласно которым отчетливой тенденции
к увеличению или уменьшению дисперсии
по мере ростаX
не наблюдается.
На
рис. 4.1 приводятся примеры изменения
разброса (гетероскедастичности) случайной
ошибки регрессии.
На
рис. 4.1а изображена ситуация, когда
значения дисперсии
растут по мере увеличения значений
регрессораX.
На рис. 4.1б дисперсия ошибки достигает
максимальной величины при средних
значениях X,
уменьшаясь по мере приближения к крайним
значениям. Наконец, на рис. 4.1в дисперсия
ошибки оказывается наибольшей при малых
значениях X,
быстро уменьшается и становится
однородной по мере увеличения независимой
переменной X.
Y
Рис.
4.1. Примеры гетероскедастичности
Гетероскедастичность
дисперсии
случайного члена означает, что
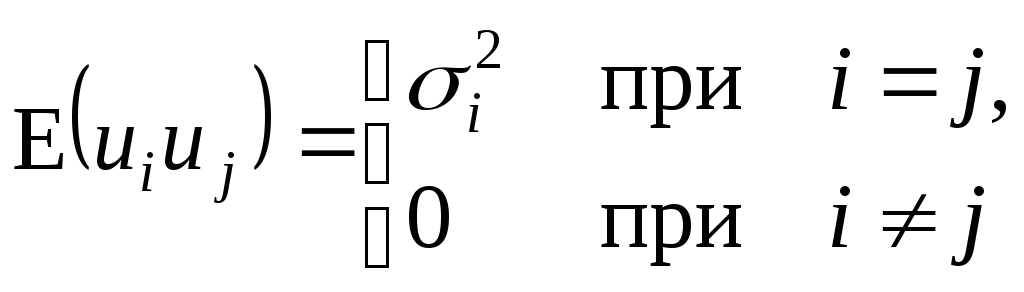
(4.8)
т.е.
нарушается предположение (3.3) в КЛММР,
и мы должны рассматривать ОЛММР с нулевой
ковариацией случайных ошибок (ср. (4.5) и
(4.8)).
Основные
последствия гетероскедастичности
проявляются в получении неэффективных
оценок МНК и занижении стандартных
ошибок коэффициентов регрессии, что
завышает t-статистику
и дает неправильное представление о
точности уравнения регрессии.
Поэтому
для оценивания регрессии с гетероскедастичными
случайными ошибками применяется ОМНК.
Предположим,
что нам известны значения величин
i
=1,…,n.
Тогда уравнение (4.3) разделим на i:
,
и
получим регрессию с постоянной
(гомоскедастичной) дисперсией случайного
члена, действительно
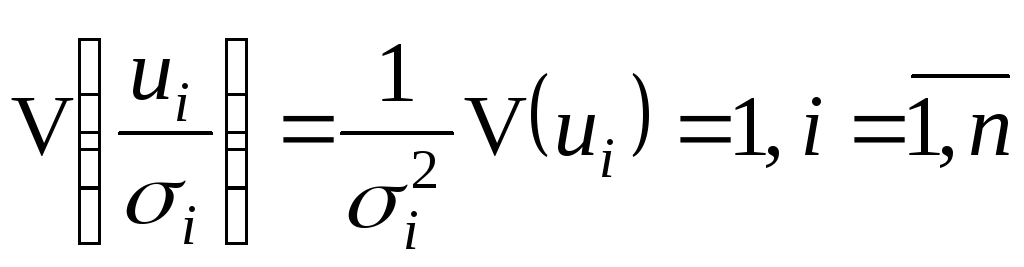
Для
получения оценок неизвестных дисперсий
i
=1,…,n
будем
предполагать, что они пропорциональны
некоторым числам, т.е.
,
где 2
– некоторая константа.
Принимая
различные гипотезы относительно
характера гетероскедастичности, будем
иметь соответствующие значения i.
Если
дисперсия случайного члена пропорциональна
квадрату регрессора X,
так что
,
то
,i
=1,…,n.
Если
дисперсия случайного члена пропорциональна
X,
так что
,
то
,i
=1,…,n.
Например, для случая одной объясняющей
переменной имеем в этом случае систему
уравнений ОМНК вида:
Поскольку значения
i,i=1,…,nявляются фактически весами, которые
устраняют неоднородность дисперсии,
то ОМНК для системы с гетероскедастичностью
часто называютметодом взвешенных
наименьших квадратов.
Существуют также
и другие методы коррекции модели на
гетероскедастичность, в частности
состоятельное оценивание стандартных
ошибок. Известны способы коррекции
стандартных ошибок Уайта и Невье-Веста
[5, с. 144-146].
О проверке выборки
на гомоскедастичность.
Рассмотрим вопрос
тестирования выборки на наличие
гомоскедастичности. Возможности такой
проверки зависят от природы исходных
данных.
Если
имеется обширная выборка, то можно
воспользоваться стандартным критерием
однородности дисперсии Бартлетта.
Расчленяя
выборку на m
независимых групп (каждой из них
соответствует единственное значение
переменной X),
вычислим величины:
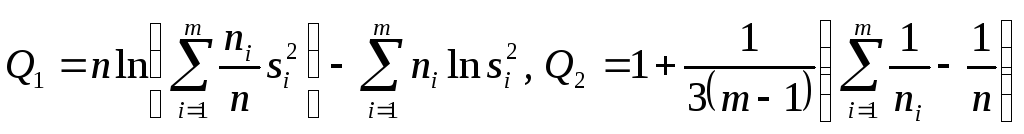
причем
ni=n,
здесь ni
— число наблюдений в i
группе,
— дисперсия ошибки вi
группе. Величина Q1/Q2
будет приближенно удовлетворять
распределению 2
с (m-1)
степенями свободы. Если вычисленное по
выборке значение 2
меньше критического, то гипотеза об
однородности выборочной дисперсии
принимается, в противном случае
отклоняется.
В
случаях малого количества наблюдений
в выборке, когда группировка данных
невозможна, используется тест
Голдфелда и Куандта.
Он предусматривает осуществление
следующих шагов:
1. Упорядочить
наблюдения по убыванию той независимой
переменной, относительно которой есть
подозрение на гетероскедастичность.
2.
Опустить v
наблюдений, оказавшихся в центре (v
должно быть примерно равно четверти
общего количества наблюдений n).
3.
Оценить отдельно обыкновенным методом
наименьших квадратов регрессии на
первых (n—v)/2
наблюдениях и на последних (n—v)/2
наблюдениях при условии, что (n—v)/2
больше числа оцениваемых параметров
k.
4.
Пусть e1
и e2
— суммы квадратов остатков от первой и
второй регрессий соответственно. Тогда
статистика Q=e1/e2
будет удовлетворять F
— распределению с ((n—v-2k)/2;
(n—v-2k)/2)
степенями свободы. При Q
< F
гипотеза об однородности выборочной
дисперсии принимается, в противном
случае (с ростом величины Q)
отклоняется.
Очевидно,
что решающим для этого теста является
выбор величины v.
Слишком большое значение v
уменьшает надежность теста. Экспериментально
авторами теста установлено, что для
одной объясняющей переменной оптимальное
v=8
при n=30
и v=16
при n=60.
Кроме
перечисленных, могут использоваться
тесты на гетероскедастичность Уайта,
Бреуша-Пагана и др.
Пример.
Проверим по критерию Бартлетта данные
из примера 1 раздела 3. Будем иметь табл.
4.1. В табл. 4.1 учтено, что среднее значение
ei
равно 0, а значит,
.
Примем m=2.
Тогда:
Q1=20ln(10/20167,41
+ 10/2059,69)
(10ln(167,41)+10ln(59,69))=2,55;
Q2=1+1/3(1/10+1/10-1/20)=1,05;
Q1/Q2=2,43.
При
одной степени свободы критическое
значение 2
при 5% уровне значимости равно 3,84, а
следовательно, гипотеза об однородности
выборочной дисперсии принимается.
Для
тех же данных применим тест Гольдфельда
и Куандта. В нашем случае число объясняющих
переменных k=2,
количество исходных данных в выборке
n=20.
Упорядочим наблюдения по убыванию
независимой переменной X2
– расстояние перевозки, относительно
которой есть подозрение на
гетероскедастичность. Опустим 4
наблюдения, оказавшихся в центре, т.е.
v=4.
При значении v=4
получим суммы квадратов остатков от
первой и второй регрессий соответственно
e1=1167,38
и e2=31,49.
Статистика Q=e1/e2=1167,38/31,49
= 37,07 удовлетворяет F-распределению
с (6; 6) степенями свободы. F0,05(6,
6) = 4,28, Q
> F
и гипотеза об однородности выборочной
дисперсии должна быть отвергнута.
Поскольку
тесты дают противоположные результаты
(что не редкость в эконометрике), то
лучше согласиться с наихудшим вариантом,
т.е. предположить наличие гетероскедастичности
и предпринять соответствующие
корректирующие меры. В частности,
скорректировать стандартные ошибки по
формуле Невье-Веста. В таблице 4.2
представлены результаты регрессии до
корректировки и после корректировки
на гетероскедастичность. Видно, что на
величине коэффициентов регрессии
корректировка на гетероскедастичность
не отражается, а стандартные ошибки и
значения статистик были пересчитаны.
Таблица
4.1
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
1. Гетероскедастичность случайной составляющей
Гетероскедастичность означает, что ошибки
регрессии имеют непостоянные дисперсии
yi a1 xi1 a2 xi 2
ar 1 xir 1 ar i
i 1, n
D i const
1
2. Примеры моделей с гетероскедастичной случайной составляющей
а)
б)
в)
а) Дисперсия 2 растет по мере увеличения значений
объясняющей переменной X
б) Дисперсия 2 имеет наибольшие значения при средних
значениях X, уменьшаясь по мере приближения к крайним
значениям
в) Дисперсия ошибки наибольшая при малых значениях X,
быстро уменьшается и становится однородной по мере
увеличения X
2
3. ПРИМЕР (зависимость инвестиций от ВРП в 2006г. по российским регионам)
Регион
Белгородская область
VRP
INV
119673,20
48422
Брянская область
61888,30
10973
Владимирская область
76328,10
20292
Воронежская область
70849,40
36265
Ивановская область
47949,80
14652
4. ПРИМЕР (зависимость инвестиций от ВРП в 2006г. по российским регионам)
Коэффи
циенты
Станда
ртная
ошибка
Yпересечение
5164,439
11352,89 0,454901 0,650428
VRP
0,345983 0,070519 4,906268
INV 0,346 VRP 5164
tстатис
тика
PЗначени
е
4,88E-06
5. ПРИМЕР (зависимость инвестиций от ВРП в 2006г. по российским регионам)
600000
500000
INV
400000
300000
y = 0,346x + 5164,4
200000
100000
0
0,00
200000,0 400000,0 600000,0 800000,0 1000000,
0
0
0
0
00
VRP
5
6. ПРИМЕР (зависимость инвестиций от ВРП в 2006г. по российским регионам)
e
Остатки
500000
400000
300000
200000
100000
0
-1000000,00
-200000
-300000
Остатки
200000 400000 600000 800000 100000
,00
,00
,00
,00
0,00
VRP
6
7.
Наиболее распространенный случай истинной
гетероскедастичности: дисперсия растет с
ростом одного из факторов.
8. ПОСЛЕДСТВИЯ ГЕТЕРОСКЕДАСТИЧНОСТИ
1. Обычная МНК оценка несмещенная
состоятельная, но неэффективная.
2. Стандартные ошибки коэффициентов
(вычисленные в предположении.
гомоскедастичности) будут занижены. Это приведет
к завышению t-статистик и даст
неправильное (завышенное) представление о
точности оценок.
8
9. ОБНАРУЖЕНИЕ ГЕТЕРОСКЕДАСТИЧНОСТИ
1.
Визуальный метод.
Диаграмма рассеяния
Y
Y
X
Гомоскедастичность
X
Гетероскедастичность
9
10. ОБНАРУЖЕНИЕ ГЕТЕРОСКЕДАСТИЧНОСТИ
1.
Визуальный метод.
Графики остатков после построения оценок по
методу МНК
e
e
X или Y
Гомоскедастичность
X или Y
Гетероскедастичность
10
11.
ОБНАРУЖЕНИЕ ГЕТЕРОСКЕДАСТИЧНОСТИ
5E5
5,5578E5
4E5
3E5
e
INV
2E5
2,2503E5
1,5894E5
1E5
0
1,0411E5
-1E5
47208
481
-2E5
42728,4
1,6877E5
1,0377E5
-3E5
4,9319E5
2,8986E5
7,8243E5
VRP
42728,4
1,6877E5
1,0377E5
4,9319E5
2,8986E5
7,8243E5
VRP
19
12. ОБНАРУЖЕНИЕ ГЕТЕРОСКЕДАСТИЧНОСТИ
Тесты:
1. Тест ранговой корреляции Спирмена.
2. Тест Глейзера.
3. Тест Голдфелда-Квандта.
4. Тест Уайта.
В специализированных эконометрических пакетах эти тесты есть
12
13. Устранение ГЕТЕРОСКЕДАСТИЧНОСТИ
Использовать обобщенный метод
наименьших квадратов
В этом методе предполагается, что
стандартное отклонение остатков
пропорционально одной из объясняющих
переменных
Например,
INVi a1VRPi a2 i , i 1, n
D i
2
i
i k VRPi , i 1, n
13
14. Устранение гетероскедастичности пример
INVi a1 VRPi a2 i , i 1, n
Делим уравнение на ВРП
INVi
i
1
a1 a2
, i 1, n
VRPi
VRPi VRPi
15. Устранение гетероскедастичности пример
INVi
i
1
a1 a2
, i 1, n
VRPi
VRPi VRPi
Создаем новые переменные
INV
1
,
VRP VRP
Регион
Белгородская область
VRP
INV
INV/VRP
1/VRP
119673,20
48422
0,40
8,36E-06
Брянская область
61888,30
10973
0,18
1,62E-05
Владимирская область
76328,10
20292
0,27
1,31E-05
Воронежская область
70849,40
36265
0,51
1,41E-05
Ивановская область
47949,80
14652
0,31
2,09E-05
Калужская область
83817,40
16268
0,19
1,19E-05
16. Устранение гетероскедастичности пример
INVi
i
1
a1 a2
, i 1, n
VRPi
VRPi VRPi
Коэффициент
ы
Стандартная
ошибка
t-статистика
Y-пересечение
0,491025
0,0864
5,683151
2,13E-07
1/VRP
-11337,2
7354,391
-1,54156
0,127178
INV
1
0,5 11,337
,
VRP
VRP
INV 0,5 VRP 11,337
P-Значение
17. Устранение гетероскедастичности пример
INVi
i
1
a1 a2
, i 1, n
VRPi
VRPi VRPi
Остатки
1,5
1
0,5
e
Остатки
0
-0,5 0
5E-06
0,00001 1,5E-05 0,00002 2,5E-05
-1
1/VRP
18. Гетероскедастичность как результат неправильной спецификации модели (ложная гетероскедастичность).
1) В модель не включен фактор, существенно влияющий на объясняемую
переменную.
Пример. Предполагается, что имеется зависимость импорта M от ВВП
страны (GDP) и отношение отечественных цен к мировым (PR).
M i a1 GDPi a2 PRi a3 i
Исследователь рассчитывает сокращенный вариант модели:
M i a2 PRi a3 i
Остатки в такой модели покажут на гетероскедастичность, так как будут
зависеть от GDP
i a1 GDPi i
19. Гетероскедастичность как результат неправильной спецификации модели (ложная гетероскедастичность).
2) Неправильно выбрана функциональная форма
модели.
Scatterplot (Spreadsheet1 10v*119c)
y = -2554,0902+132,073*x
35000
30000
25000
y
20000
15000
10000
5000
0
-5000
-20
0
20
40
60
x
80
100
120
140
20. Гетероскедастичность как результат неправильной спецификации модели (ложная гетероскедастичность).
2) Неправильно выбрана функциональная форма
модели.
Прологарифмируем данные и построим модель в логарифмах
Scatterplot (Spreadsheet1 10v*119c)
12
10
8
ln(y)
6
4
2
0
-2
-1
0
1
2
ln(x)
3
4
5
15. Оценка дисперсии случайной ошибки модели регрессии
При проведении регрессионного анализа основная трудность заключается в том, что генеральная дисперсия случайной ошибки является неизвестной величиной, что вызывает необходимость в расчёте её несмещённой выборочной оценки.
Несмещённой оценкой дисперсии (или исправленной дисперсией) случайной ошибки линейной модели парной регрессии называется величина, рассчитываемая по формуле:
где n – это объём выборочной совокупности;
еi– остатки регрессионной модели:
Для линейной модели множественной регрессии несмещённая оценка дисперсии случайной ошибки рассчитывается по формуле:
где k – число оцениваемых параметров модели регрессии.
Оценка матрицы ковариаций случайных ошибок Cov(?) будет являться оценочная матрица ковариаций:
где In – единичная матрица.
Оценка дисперсии случайной ошибки модели регрессии распределена по ?2(хи-квадрат) закону распределения с (n-k-1) степенями свободы.
Для доказательства несмещённости оценки дисперсии случайной ошибки модели регрессии необходимо доказать справедливость равенства
Доказательство. Примем без доказательства справедливость следующих равенств:
где G2(?) – генеральная дисперсия случайной ошибки;
S2(?) – выборочная дисперсия случайной ошибки;
– выборочная оценка дисперсии случайной ошибки.
Тогда:
т. е.
что и требовалось доказать.
Следовательно, выборочная оценка дисперсии случайной ошибки
является несмещённой оценкой генеральной дисперсии случайной ошибки модели регрессии G2(?).
При условии извлечения из генеральной совокупности нескольких выборок одинакового объёма n и при одинаковых значениях объясняющих переменных х, наблюдаемые значения зависимой переменной у будут случайным образом колебаться за счёт случайного характера случайной компоненты ?. Отсюда можно сделать вывод, что будут варьироваться и зависеть от значений переменной у значения оценок коэффициентов регрессии и оценка дисперсии случайной ошибки модели регрессии.
Для иллюстрации данного утверждения докажем зависимость значения МНК-оценки
от величины случайной ошибки ?.
МНК-оценка коэффициента ?1 модели регрессии определяется по формуле:
В связи с тем, что переменная у зависит от случайной компоненты ? (yi=?0+?1xi+?i), то ковариация между зависимой переменной у и независимой переменной х может быть представлена следующим образом:
Для дальнейших преобразования используются свойства ковариации:
1) ковариация между переменной х и константой С равна нулю: Cov(x,C)=0, C=const;
2) ковариация переменной х с самой собой равна дисперсии этой переменной: Cov(x,x)=G2(x).
Исходя из указанных свойств ковариации, справедливы следующие равенства:
Cov(x,?0)=0 (?0=const);
Cov(x, ?1x)= ?1*Cov(x,x)= ?1*G2(x).
Следовательно, ковариация между зависимой и независимой переменными Cov(x,y) может быть записана как:
Cov(x,y)= ?1G2(x)+Cov(x,?).
В результате МНК-оценка коэффициента ?1 модели регрессии примет вид:
Таким образом, МНК-оценка
может быть представлена как сумма двух компонент:
1) константы ?1, т. е. истинного значения коэффициента;
2) случайной ошибки Cov(x,?), вызывающей вариацию коэффициента модели регрессии.
Однако на практике подобное разложение МНК-оценки невозможно, потому что истинные значения коэффициентов модели регрессии и значения случайной ошибки являются неизвестными. Теоретически данное разложение можно использовать при изучении статистических свойств МНК-оценок.
Аналогично доказывается, что МНК-оценка
коэффициента модели регрессии и несмещённая оценка дисперсии случайной ошибки
могут быть представлены как сумма постоянной составляющей (константы) и случайной компоненты, зависящей от ошибки модели регрессии ?.
Данный текст является ознакомительным фрагментом.
Читайте также
11. Критерии оценки неизвестных коэффициентов модели регрессии
11. Критерии оценки неизвестных коэффициентов модели регрессии
В ходе регрессионного анализа была подобрана форма связи, которая наилучшим образом отражает зависимость результативной переменной у от факторной переменной х:y=f(x).Необходимо оценить неизвестные
14. Оценка коэффициентов модели парной регрессии с помощью выборочного коэффициента регрессии
14. Оценка коэффициентов модели парной регрессии с помощью выборочного коэффициента регрессии
Помимо метода наименьших квадратов, с помощью которого в большинстве случаев определяются неизвестные параметры модели регрессии, в случае линейной модели парной регрессии
18. Характеристика качества модели регрессии
18. Характеристика качества модели регрессии
Качеством модели регрессии называется адекватность построенной модели исходным (наблюдаемым) данным.Для оценки качества модели регрессии используются специальные показатели.Качество линейной модели парной регрессии
22. Проверка гипотезы о значимости коэффициентов модели парной регрессии
22. Проверка гипотезы о значимости коэффициентов модели парной регрессии
Проверкой статистической гипотезы о значимости отдельных параметров модели называется проверка предположения о том, что данные параметры значимо отличаются от нуля.Необходимость проверки
25. Точечный и интервальный прогнозы для модели парной регрессии
25. Точечный и интервальный прогнозы для модели парной регрессии
Одна из задач эконометрического моделирования заключается в прогнозировании поведения исследуемого явления или процесса в будущем. В большинстве случаев данная задача решается на основе регрессионных
32. Построение частных коэффициентов корреляции для модели множественной регрессии через показатель остаточной дисперсии и коэффициент множественной детерминации
32. Построение частных коэффициентов корреляции для модели множественной регрессии через показатель остаточной дисперсии и коэффициент множественной детерминации
Помимо рекуррентных формул, которые используются для построения частных коэффициентов корреляции для
35. Проверка гипотезы о значимости коэффициентов регрессии и модели множественной регрессии в целом
35. Проверка гипотезы о значимости коэффициентов регрессии и модели множественной регрессии в целом
Проверка значимости коэффициентов регрессии означает проверку основной гипотезы об их значимом отличии от нуля.Основная гипотеза состоит в предположении о незначимости
39. Модели регрессии, нелинейные по факторным переменным
39. Модели регрессии, нелинейные по факторным переменным
При исследовании социально-экономических явлений и процессов далеко не все зависимости можно описать с помощью линейной связи. Поэтому в эконометрическом моделировании широко используется класс нелинейных
40. Модели регрессии, нелинейные по оцениваемым коэффициентам
40. Модели регрессии, нелинейные по оцениваемым коэффициентам
Нелинейными по оцениваемым параметрам моделями регрессииназываются модели, в которых результативная переменная yi нелинейно зависит от коэффициентов модели ?0…?n.К моделям регрессии, нелинейными по
41. Модели регрессии с точками разрыва
41. Модели регрессии с точками разрыва
Определение. Моделями регрессии с точками разрыва называются модели, которые нельзя привести к линейной форме, т. е. внутренне нелинейные модели регрессии.Модели регрессии делятся на два класса:1) кусочно-линейные модели регрессии;2)
44. Методы нелинейного оценивания коэффициентов модели регрессии
44. Методы нелинейного оценивания коэффициентов модели регрессии
Функцией потерь или ошибок называется функционал вида
Также в качестве функции потерь может быть использована сумма модулей отклонений наблюдаемых значений результативного признака у от теоретических
46. Проверка гипотезы о значимости нелинейной модели регрессии. Проверка гипотезы о линейной зависимости между переменными модели регрессии
46. Проверка гипотезы о значимости нелинейной модели регрессии. Проверка гипотезы о линейной зависимости между переменными модели регрессии
На нелинейные модели регрессии, которые являются внутренне линейными, т. е. сводимыми к линейному виду, распространяются все
57. Гетероскедастичность остатков модели регрессии
57. Гетероскедастичность остатков модели регрессии
Случайной ошибкой называется отклонение в линейной модели множественной регрессии:?i=yi–?0–?1x1i–…–?mxmiВ связи с тем, что величина случайной ошибки модели регрессии является неизвестной величиной, рассчитывается
60. Устранение гетероскедастичности остатков модели регрессии
60. Устранение гетероскедастичности остатков модели регрессии
Существует множество методов устранения гетероскедастичности остатков модели регрессии. Рассмотрим некоторые из них.Наиболее простым методом устранения гетероскедастичности остатков модели регрессии
63. Устранение автокорреляции остатков модели регрессии
63. Устранение автокорреляции остатков модели регрессии
В связи с тем, что наличие в модели регрессии автокорреляции между остатками модели может привести к негативным результатам всего процесса оценивания неизвестных коэффициентов модели, автокорреляция остатков
67. Модели регрессии с переменной структурой. Фиктивные переменные
67. Модели регрессии с переменной структурой. Фиктивные переменные
При построении модели регрессии может возникнуть ситуация, когда в неё необходимо включить не только количественные, но и качественные переменные (например, возраст, образование, пол, расовую